You are currently viewing a beta version of our website. If you spot anything unusual, kindly let us know.

Preprint

Article

On Induced Topologies by Ideal, Primal, Filter and Grill

Altmetrics

Downloads

174

Views

Comments

A peer-reviewed article of this preprint also exists.

Milan Matejdes^*

This version is not peer-reviewed

Abstract

In this paper the one-to-one correspondences and equivalences between ideals, primals, filters and grills are introduced. It is shown the local functions and the topological spaces induced by them are the same. From this point of view, the topological properties with respect to one topology can be derived from topological properties valid in the corresponding topology.

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

Many topologies with important applications in mathematics have been defined using some additional mathematical structure. For example, if a topological space

(X, τ)

and an ideal

I

on X are given, a new topology (called an ideal topology) can be obtained by an ideal-associated local function. The ideal topological spaces are extensively studied, see [4,5,7,8,10]. A similar concept was used for a grill [9,13,14,15,16,17], a filter [3,11,12] and a primal [1,2,6].

In general, we can consider four systems, namely an ideal

I

, a primal

P

, a filter

F

and a grill

G

on a topological space

(X, τ)

, see Definition 1. A derivation of a new topology that is finer than the original topology

τ

is as follows: The local function

A_{I}^{*}

A_{P}^{*}

A_{F}^{*}

A_{G}^{*}

, see Definition 1, derived from

I, P, F, G

and

τ

defines the Kuratowski closure operator

c l_{I}

c l_{P}

c l_{F}

c l_{G}

, see Definition 3. In the final step, a new topology on X is defined, denoted by

τ_{I}

τ_{P}

τ_{F}

τ_{G}

, respectively, see Theorem 9. If we look at the achieved results, we can see a striking similarity. In fact, the local functions and topologies generated by this way are equivalent.

The main concept of the article is as follows: Using correspondence between two systems (Theorem 1–6), it is possible to define their equivalence, see Definition 2. Two equivalent systems generate the same topology (Theorem 10), and the results achieved in one topology can be used in a topology determined by an equivalent system. In the last part, we will show the application of this equivalence on examples of compatibility and codense topologies.

Definition 1.

Let X be a nonempty set. A nonempty system

I

P

F

G

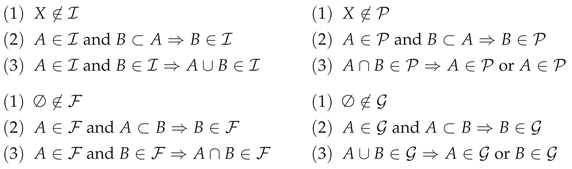
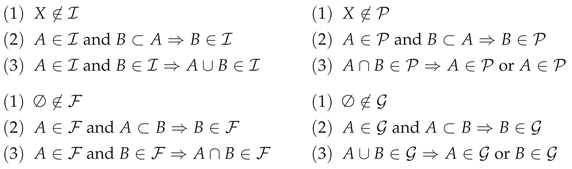
of subsets of X is said be an ideal, a primal, a filter, a grill on X if it satisfies the following conditions Preprints 100694 i001

respectively. Furthermore, if τ is a topology on X, for

A \subset X

we define four local functions

\begin{matrix} A_{I}^{*} = {x \in X : A \cap U \notin I for any U \in τ, x \in U}, \\ A_{P}^{*} = {x \in X : (X ∖ A) \cup (X ∖ U) \in P for any U \in τ, x \in U}, \\ A_{F}^{*} = {x \in X : (X ∖ A) \cup (X ∖ U) \notin F for any U \in τ, x \in U}, \\ A_{G}^{*} = {x \in X : A \cap U \in G for any U \in τ, x \in U} . \end{matrix}

An ideal topological space, a primal topological space, a filter topological space, a grill topological space is a topological space

(X, τ)

with an ideal

I

, a primal

P

, a filter

F

, a grill

G

and it is denoted by

(X, τ, I)

(X, τ, P)

(X, τ, F)

(X, τ, G)

, respectively. Let

I, P, F, G

be a family of all ideals, primals, filters, grills on X, respectively. Put

X = I \cup P \cup F \cup G

. If

Z \in X

, then

(X, τ, Z)

is called a

Z

-topological space.

2. Main Results

In the following two parts we present sixteen operators

H_{Z_{2}}^{Z_{1}}

(Theorem 1–6) between pairs of systems

Z_{1}, Z_{2} \in {I, P, F, G}

and their properties and compositions are studied. Next, the equivalence between

Z_{1}, Z_{2} \in X

is defined (Definotion 2). The equality of local functions and the equality of generated topologies are proved, provided that

Z_{1}

and

Z_{2}

and equivalent.

Define four identity operators

\begin{matrix} H_{I}^{I} : I \to I by H_{I}^{I} (I) = I, & H_{P}^{P} : P \to P by H_{P}^{P} (P) = P, \\ H_{F}^{F} : F \to F by H_{F}^{F} (F) = F, & H_{G}^{G} : G \to G by H_{G}^{G} (G) = G . \end{matrix}

In the next six theorems the proofs of items (1)–(10) are left to the reader. The rest will be proven.

Theorem 1.

Let

I

P

be an ideal, a primal on X, respectively. Define

H_{P}^{I} : I \to P

H_{P}^{I} (I) = {A \subset X : X ∖ A \notin I}

H_{I}^{P} : P \to I

H_{I}^{P} (P) = {A \subset X : X ∖ A \notin P}

Then

H_{P}^{I} (I)

H_{I}^{P} (P)

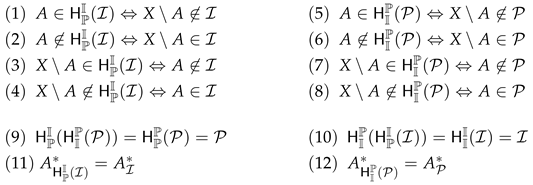
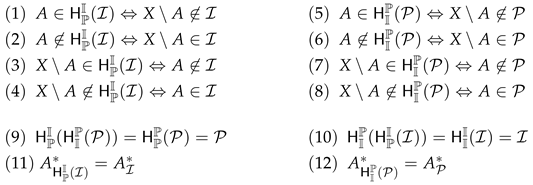
is a primal, an ideal on X, respectively and Preprints 100694 i002

Proof.

We prove

H_{P}^{I} (I)

is a primal. Since

\emptyset \in I

X \notin H_{P}^{I} (I)

Let

A \in H_{P}^{I} (I)

and

B \subset A

. Then

X ∖ A \notin I

. Since

X ∖ A \subset X ∖ B

and

I

is an ideal,

X ∖ B \notin I

, so

B \in H_{P}^{I} (I)

. Let

A \cap B \in H_{P}^{I} (I)

. Then

(X ∖ A) \cup (X ∖ B) = X ∖ A \cap B \notin I

. Since

I

is an ideal,

X ∖ A

X ∖ B

is not from

I

. So

A \in H_{P}^{I} (I)

B \in H_{P}^{I} (I)

. That means

H_{P}^{I} (I)

is a primal.

We prove

H_{I}^{P} (P)

is an ideal. Since

\emptyset \in P

X \notin H_{I}^{P} (P)

Let

A \in H_{I}^{P} (P)

and

B \subset A

. Then

X ∖ A \notin P

. Since

X ∖ A \subset X ∖ B

and

P

is a primal,

X ∖ B \notin P

, so

B \in H_{I}^{P} (P)

. Let

A, B \in H_{I}^{P} (P)

. Then

X ∖ A \notin P

X ∖ B \notin P

and

(X ∖ A) \cap (X ∖ B) = X ∖ A \cup B \notin P

. So

A \cup B \in H_{I}^{P} (P)

. That means

H_{I}^{P} (P)

is an ideal.

(11):

x \in A_{H_{P}^{I} (I)}^{*}

if and only if

(X ∖ A) \cup (X ∖ U) = X ∖ A \cap U \in H_{P}^{I} (I)

for any nbhd U of x if and only if

A \cap U \notin I

if and only if

x \in A_{I}^{*}

(12):

x \in A_{H_{I}^{P} (P)}^{*}

if and only if

A \cap U \notin H_{I}^{P} (P)

for any nbhd U of x if and only if

X ∖ A \cap U = (X ∖ A) \cup (X ∖ U) \in P

if and only if

x \in A_{P}^{*}

. □

Theorem 2.

Let

I

G

be an ideal, a grill on X, respectively. Define

H_{G}^{I} : I \to G

H_{G}^{I} (I) = {A \subset X : A \notin I}

H_{I}^{G} : G \to I

H_{I}^{G} (G) = {A \subset X : A \notin G}

Then

H_{G}^{I} (I)

H_{I}^{G} (G)

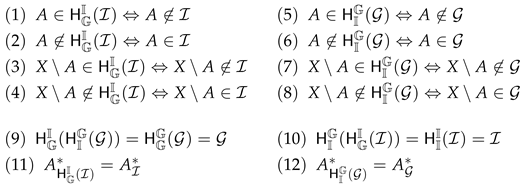
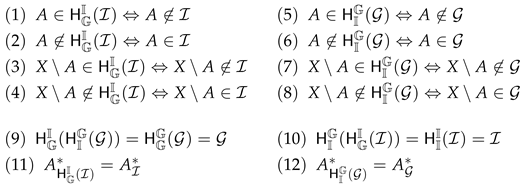
is a grill, an ideal on X, respectively and Preprints 100694 i003

Proof.

We prove

H_{G}^{I} (I)

is a grill. Since

\emptyset \in I

\emptyset \notin H_{G}^{I} (I)

Let

A \in H_{G}^{I} (I)

and

A \subset B

. Then

A \notin I

. Since

I

is an ideal,

B \notin I

, so

B \in H_{G}^{I} (I)

. Let

A \cup B \in H_{G}^{I} (I)

. Then

A \cup B \notin I

. Since

I

is an ideal, A or B is not from

I

. So

A \in H_{G}^{I} (I)

B \in H_{G}^{I} (I)

. That means

H_{G}^{I} (I)

is a grill.

We prove

H_{I}^{G} (G)

is an ideal. Since

X \in G

X \notin H_{I}^{G} (G)

Let

A \in H_{I}^{G} (G)

and

B \subset A

. Then

A \notin G

. Since

G

is a grill,

B \notin G

, so

B \in H_{I}^{G} (G)

. Let

A, B \in H_{I}^{G} (G)

. Then

A, B \notin G

. Since

G

is a grill,

A \cup B \notin G

. So

A \cup B \in H_{I}^{G} (G)

. That means

H_{I}^{G} (G)

is an ideal.

(11):

x \in A_{H_{G}^{I} (I)}^{*}

if and only if

A \cap U \in H_{G}^{I} (I)

for any nbhd U of x if and only if

A \cap U \notin I

if and only if

x \in A_{I}^{*}

(12):

x \in A_{H_{I}^{G} (G)}^{*}

if and only if

A \cap U \notin H_{I}^{G} (G)

for any nbhd U of x if and only if

A \cap U \in G

if and only if

x \in A_{G}^{*}

. □

Theorem 3.

Let

F

G

be a filter, a grill on X, respectively. Define

H_{G}^{F} : F \to G

H_{G}^{F} (F) = {A \subset X : X ∖ A \notin F}

H_{F}^{G} : G \to F

H_{F}^{G} (G) = {A \subset X : X ∖ A \notin G}

Then

H_{G}^{F} (F)

H_{F}^{G} (G)

is a grill, a filter on X, respectively and

\begin{matrix} (1) A \in H_{G}^{F} (F) \Leftrightarrow X ∖ A \notin F & (5) A \in H_{F}^{G} (G) \Leftrightarrow X ∖ A \notin G \\ (2) A \notin H_{G}^{F} (F) \Leftrightarrow X ∖ A \in F & (6) A \notin H_{F}^{G} (G) \Leftrightarrow X ∖ A \in G \\ (3) X ∖ A \in H_{G}^{F} (F) \Leftrightarrow A \notin F & (7) X ∖ A \in H_{F}^{G} (G) \Leftrightarrow A \notin G \\ (4) X ∖ A \notin H_{G}^{F} (F) \Leftrightarrow A \in F & (8) X ∖ A \notin H_{F}^{G} (G) \Leftrightarrow A \in G \\ (9) H_{G}^{F} (H_{F}^{G} (G)) = H_{G}^{G} (G) = G & (10) H_{F}^{G} (H_{G}^{F} (F)) = H_{F}^{F} (F) = F \\ (11) A_{H_{G}^{F} (F)}^{*} = A_{F}^{*} & (12) A_{H_{F}^{G} (G)}^{*} = A_{G}^{*} \end{matrix}

Proof.

We prove

H_{G}^{F} (F)

is a grill. Since

X \in F

\emptyset \notin H_{G}^{F} (F)

Let

A \in H_{G}^{F} (F)

and

A \subset B

. Then

X ∖ A \notin F

. Since

F

is a filter and

X ∖ B \subset X ∖ A

X ∖ B \notin F

, so

B \in H_{G}^{F} (F)

. Let

A \cup B \in H_{G}^{F} (F)

. Then

X ∖ A \cup B = (X ∖ A) \cap (X ∖ B) \notin F

. Since

F

is an filter,

X ∖ A

X ∖ B

is not from

F

. So

A \in H_{G}^{F} (I)

B \in H_{G}^{F} (I)

. That means

H_{G}^{F} (I)

is a grill.

We prove

H_{F}^{G} (G)

is a filter. Since

X \in G

\emptyset \notin H_{F}^{G} (G)

Let

A \in H_{F}^{G} (G)

and

A \subset B

. Then

X ∖ A \notin G

. Since

G

is a grill and

X ∖ B \subset X ∖ A

X ∖ B \notin G

, so

B \in H_{F}^{G} (G)

. Let

A, B \in H_{F}^{G} (G)

. Then

X ∖ A \notin G

X ∖ B \notin G

. Then

(X ∖ A) \cup (X ∖ B) = X ∖ A \cap B \notin G

. So,

A \cap B \in H_{F}^{G} (G)

. That means

H_{F}^{G} (G)

is a filter.

(11):

x \in A_{H_{G}^{F} (F)}^{*}

if and only if

A \cap U \in H_{G}^{F} (F)

for any nbhd U of x if and only if

X ∖ A \cap U \notin F

if and only if

x \in A_{F}^{*}

(12):

x \in A_{H_{F}^{G} (G)}^{*}

if and only if

X ∖ A \cap U \notin H_{F}^{G} (G)

for any nbhd U of x if and only if

A \cap U \in G

if and only if

x \in A_{G}^{*}

. □

Theorem 4.

Let

F

P

be a filter, a primal on X, respectively. Define

H_{P}^{F} : F \to P

H_{P}^{F} (F) = {A \subset X : A \notin F}

H_{F}^{P} : P \to F

H_{F}^{P} (P) = {A \subset X : A \notin P}

Then

H_{P}^{F} (F)

H_{F}^{P} (P)

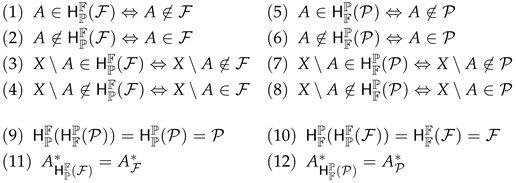
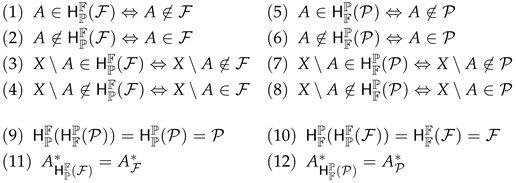
is a primal, a filter on X, respectively and Preprints 100694 i004

Proof.

We prove

H_{P}^{F} (F)

is a primal. Since

X \in F

X \notin H_{P}^{F} (F)

Let

A \in H_{P}^{F} (F)

and

B \subset A

. Then

A \notin F

. Since

F

is a filter,

B \notin F

, so

B \in H_{P}^{F} (F)

. Let

A \cap B \in H_{P}^{F} (F)

. Then

A \cap B \notin F

. Since

F

is a filter, A or B is not from

F

. So

A \in H_{P}^{F} (F)

B \in H_{P}^{F} (F)

. That means

H_{P}^{F} (F)

is a primal.

We prove

H_{F}^{P} (P)

is a filter. Since

\emptyset \in P

\emptyset \notin H_{F}^{P} (P)

Let

A \in H_{F}^{P} (P)

and

A \subset B

. Then

A \notin P

. Since

P

is a primal,

B \notin P

, so

B \in H_{F}^{P} (P)

. Let

A, B \in H_{F}^{P} (P)

. Then

A, B \notin P

. Since

P

is a primal,

A \cap B \notin P

. So

A \cap B \in H_{F}^{P} (P)

. That means

H_{F}^{P} (P)

is a filter.

(11):

x \in A_{H_{P}^{F} (F)}^{*}

if and only if

(X ∖ A) \cup (X ∖ U) = X ∖ A \cap U \in H_{P}^{F} (F)

for any nbhd U of x if and only if

X ∖ A \cap U \notin F

if and only if

x \in A_{F}^{*}

(12):

x \in A_{H_{F}^{P} (P)}^{*}

if and only if

X ∖ A \cap U \notin H_{F}^{P} (P)

for any nbhd U of x if and only if

X ∖ A \cap U = (X ∖ A) \cup (X ∖ U) \in P

if and only if

x \in A_{P}^{*}

. □

Theorem 5.

Let

G

P

be a grill, a primal on X, respectively. Define

H_{P}^{G} : G \to P

F_{P}^{G} (G) = {A \subset X : X ∖ A \in G}

H_{G}^{P} : P \to G

H_{G}^{P} (P) = {A \subset X : X ∖ A \in P}

Then

H_{P}^{G} (G)

H_{G}^{P} (P)

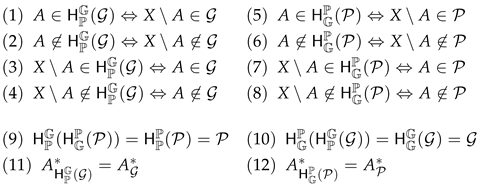
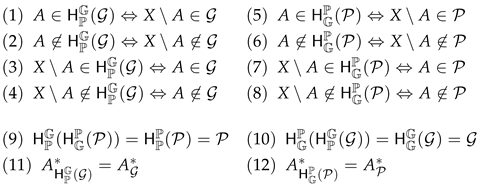
is a primal, a grill on X, respectively and Preprints 100694 i005

Proof.

We prove

H_{P}^{G} (G)

is a primal. Since

\emptyset \notin G

X \notin H_{P}^{G} (G)

Let

A \in H_{P}^{G} (G)

and

B \subset A

. Then

X ∖ A \in G

. Since

G

is a grill and

X ∖ A \subset X ∖ B

X ∖ B \in G

, so

B \in H_{P}^{G} (G)

. Let

A \cap B \in H_{P}^{G} (G)

. Then

X ∖ A \cap B = (X ∖ A) \cup (X ∖ B) \in G

. Since

G

is a grill,

X ∖ A

X ∖ B

is from

G

. So

A \in H_{P}^{G} (G)

B \in H_{P}^{G} (G)

. That means

H_{P}^{G} (G)

is a primal.

We prove

H_{G}^{P} (P)

is a grill. Since

X \notin P

\emptyset \notin H_{G}^{P} (P)

Let

A \in H_{G}^{P} (P)

and

A \subset B

. Then

X ∖ A \in P

. Since

P

is a primal and

X ∖ B \subset X ∖ A

X ∖ B \in P

, so

B \in H_{G}^{P} (P)

. Let

A \cup B \in H_{G}^{P} (P)

. Then

X ∖ A \cup B = (X ∖ A) \cap (X ∖ B) \in P

. Since

P

is a primal,

X ∖ A

X ∖ B

is from

P

. So

A \in H_{G}^{P} (P)

B \in H_{G}^{P} (P)

. That means

H_{G}^{P} (P)

is a grill.

(11):

x \in A_{H_{P}^{G} (G)}^{*}

if and only if

(X ∖ A) \cup (X ∖ U) = X ∖ A \cap U \in H_{P}^{G} (G)

for any nbhd U of x if and only if

A \cap U \in G

if and only if

x \in A_{G}^{*}

(12):

x \in A_{H_{G}^{P} (P)}^{*}

if and only if

A \cap U \in H_{G}^{P} (P)

for any nbhd U of x if and only if

X ∖ A \cap U = (X ∖ A) \cup (X ∖ U) \in P

if and only if

x \in A_{P}^{*}

. □

Theorem 6.

Let

F

I

be a filter, a ideal on X, respectively. Define

H_{I}^{F} : F \to I

H_{I}^{F} (F) = {A \subset X : X ∖ A \in F}

H_{F}^{I} : I \to F

H_{F}^{I} (I) = {A \subset X : X ∖ A \in I}

Then

H_{I}^{F} (F)

H_{F}^{I} (I)

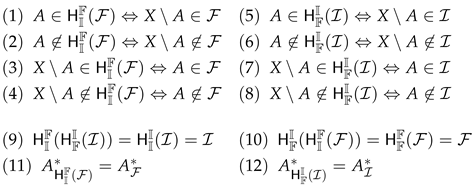
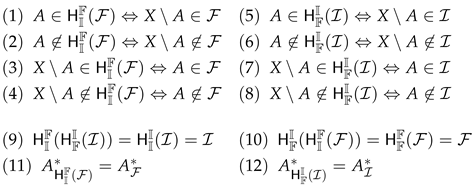
is an ideal, a filter on X, respectively and Preprints 100694 i006

Proof.

We prove

H_{I}^{F} (F)

is an ideal. Since

\emptyset \notin F

X \notin H_{I}^{F} (F)

Let

A \in H_{I}^{F} (F)

and

B \subset A

. Then

X ∖ A \in F

. Since

X ∖ A \subset X ∖ B

and

F

is a filter,

X ∖ B \in F

, so

B \in H_{I}^{F} (F)

. Let

A, B \in H_{I}^{F} (F)

. Then

X ∖ A, X ∖ B \in F

. Since

F

is a filter,

(X ∖ A) \cap (X ∖ B) = X ∖ A \cup B \in F

. So

A \cup B \in H_{I}^{F} (F)

. That means

H_{I}^{F} (F)

is an ideal.

We prove

H_{F}^{I} (I)

is a filter. Since

X \notin I

\emptyset \notin H_{F}^{I} (I)

Let

A \in H_{F}^{I} (I)

and

A \subset B

. Then

X ∖ A \in I

. Since

X ∖ B \subset X ∖ A

and

I

is an ideal,

X ∖ B \in I

, so

B \in H_{F}^{I} (I)

. Let

A, B \in H_{F}^{I} (I)

. Then

X ∖ A, X ∖ B \in I

. Since

I

is an ideal,

(X ∖ A) \cup (X ∖ B) = X ∖ A \cap B \in I

. So

A \cap B \in H_{F}^{I} (I)

. That means

H_{F}^{I} (I)

is a filter.

(11):

x \in A_{H_{I}^{F} (F)}^{*}

if and only if

A \cap U \notin H_{I}^{F} (F)

for any nbhd U of x if and only if

X ∖ A \cap U \notin F

if and only if

x \in A_{F}^{*}

(12):

x \in A_{H_{F}^{I} (I)}^{*}

if and only if

X ∖ A \cap U \notin H_{F}^{I} (I)

for any nbhd U of x if and only if

A \cap U \notin I

if and only if

x \in A_{I}^{*}

. □

Proposition 1.

Let

Z_{1}, Z_{2} \in {I, P, F, G}

. If

Z_{1} \neq Z_{2}

, then each of the twelve operators

H_{Z_{2}}^{Z_{1}}

from Theorem 1-6 is bijective and

{(H_{Z_{2}}^{Z_{1}})}^{- 1} = H_{Z_{1}}^{Z_{2}}

, consequently

H_{Z_{2}}^{Z_{1}}

and

H_{Z_{1}}^{Z_{2}}

are mutually inverse, so

H_{Z_{1}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z_{1}}^{Z_{1}}

Proof.

It follows from Theorem 1-6 items (9) and (10). □

Proposition 2.

H_{F}^{P} \circ H_{P}^{I} = H_{F}^{I}

H_{I}^{G} \circ H_{G}^{F} = H_{I}^{F}

H_{G}^{F} \circ H_{F}^{P} = H_{G}^{P}

H_{P}^{I} \circ H_{I}^{G} = H_{P}^{G}

Proof.

A \in H_{F}^{P} (H_{P}^{I} (I))

H_{I}^{G} (H_{G}^{F} (F)) \Leftrightarrow

A \notin H_{P}^{I} (I)

H_{G}^{F} (F)

⇔

X ∖ A \in I, F \Leftrightarrow A \in H_{F}^{I} (I), H_{I}^{F} (F)

, respectively. So,

H_{F}^{P} \circ H_{P}^{I} = H_{F}^{I}

H_{I}^{G} \circ H_{G}^{F} = H_{I}^{F}

A \in H_{G}^{F} (H_{F}^{P} (P))

H_{P}^{I} (H_{I}^{G} (G)) \Leftrightarrow

X ∖ A \notin H_{F}^{P} (P)

H_{I}^{G} (G) \Leftrightarrow

X ∖ A \in P, G \Leftrightarrow

A \in H_{G}^{P} (P), H_{P}^{G} (G)

, respectively. So,

H_{G}^{F} \circ H_{F}^{P} = H_{G}^{P}

H_{P}^{I} \circ H_{I}^{G} = H_{P}^{G}

. □

Proposition 3.

Let

Z, Z_{1}, Z_{2} \in {I, P, F, G}

. The next conditions are equivalent

(1): $H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}$ (2) $H_{Z_{1}}^{Z} \circ H_{Z}^{Z_{2}} = H_{Z_{1}}^{Z_{2}}$
(3): $H_{Z}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z}^{Z_{1}}$ (4) $H_{Z_{1}}^{Z_{2}} \circ H_{Z_{2}}^{Z} = H_{Z_{1}}^{Z}$
(5): $H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z} = H_{Z_{2}}^{Z}$ (6) $H_{Z}^{Z_{1}} \circ H_{Z_{1}}^{Z_{2}} = H_{Z}^{Z_{2}}$

Proof.

(1) \Leftrightarrow (2)

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

⇔

{(H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}})}^{- 1} = {(H_{Z_{2}}^{Z_{1}})}^{- 1}

⇔

H_{Z_{1}}^{Z} \circ H_{Z}^{Z_{2}} = H_{Z_{1}}^{Z_{2}}

(1) \Leftrightarrow (3)

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

⇔

H_{Z}^{Z_{1}} = {(H_{Z_{2}}^{Z})}^{- 1} \circ H_{Z_{2}}^{Z_{1}} \Leftrightarrow H_{Z}^{Z_{1}} = H_{Z}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}}

(3) \Leftrightarrow (4)

H_{Z}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z}^{Z_{1}}

⇔

{(H_{Z}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}})}^{- 1} = {(H_{Z}^{Z_{1}})}^{- 1}

⇔

H_{Z_{1}}^{Z_{2}} \circ H_{Z_{2}}^{Z} = H_{Z_{1}}^{Z}

(1) \Leftrightarrow (5)

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

⇔

H_{Z_{2}}^{Z} = H_{Z_{2}}^{Z_{1}} \circ {(H_{Z}^{Z_{1}})}^{- 1} \Leftrightarrow H_{Z_{2}}^{Z} = H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z}

(5) \Leftrightarrow (6)

H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z} = H_{Z_{2}}^{Z}

⇔

{(H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z})}^{- 1} = {(H_{Z_{2}}^{Z})}^{- 1}

⇔

H_{Z}^{Z_{1}} \circ H_{Z_{1}}^{Z_{2}} = H_{Z}^{Z_{2}}

□

Proposition 4.

Let

Z, Z_{1}, Z_{2} \in {I, P, F, G}

. Then for 64 possibilities the equation

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

holds.

Proof.

By Proposition 2 and Proposition 3, the equation

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

holds for 24 possibilities (

Z, Z_{1}, Z_{2}

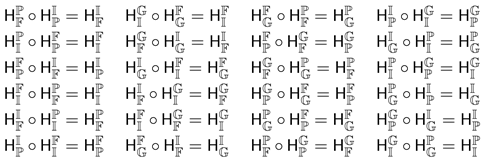
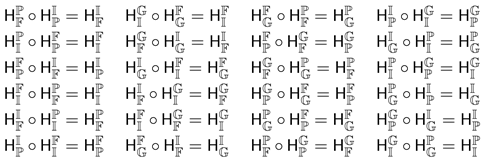
are mutually different): Preprints 100694 i007

Other cases for

Z_{1} \neq Z_{2}

are trivial:

H_{Z_{1}}^{Z_{1}} \circ H_{Z_{1}}^{Z_{2}} = H_{Z_{1}}^{Z_{2}}

(12 possibilities),

H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

(12 possibilities),

H_{Z_{1}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z_{1}}^{Z_{1}}

(12 possibilities),

H_{Z_{1}}^{Z_{1}} \circ H_{Z_{1}}^{Z_{1}} = H_{Z_{1}}^{Z_{1}}

(4 possibilities).

□

For a composition of finitely many operators, the domain (the codomain) of the resulting operator is equal to the domain (codomain) of the first (last) operator and the value of local function is independent on the operators as the following theorem states.

Theorem 7.

Let

Z_{k} \in {I, P, F, G}

k = 1, \dots, n

and

Z \in Z_{1}

. Then

H_{Z_{n}}^{Z_{n - 1}} \circ H_{Z_{n - 1}}^{Z_{n - 2}} \circ \dots \circ H_{Z_{3}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z_{n}}^{Z_{1}}

A_{(H_{Z_{n}}^{Z_{n - 1}} \circ H_{Z_{n - 1}}^{Z_{n - 2}} \circ \dots \circ H_{Z_{3}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}}) (Z)}^{*} = A_{H_{Z_{n}}^{Z_{1}} (Z)}^{*} = A_{Z}^{*}

Consequently,

(1): $A_{I}^{*} = A_{H_{I}^{I} (I)}^{*} = A_{H_{P}^{I} (I)}^{*} = A_{H_{G}^{I} (I)}^{*} = A_{H_{F}^{I} (I)}^{*}$
(2): $A_{P}^{*} = A_{H_{P}^{P} (P)}^{*} = A_{H_{I}^{P} (P)}^{*} = A_{H_{F}^{P} (P)}^{*} = A_{H_{G}^{P} (P)}^{*}$
(3): $A_{F}^{*} = A_{H_{F}^{F} (F)}^{*} = A_{H_{G}^{F} (F)}^{*} = A_{H_{P}^{F} (F)}^{*} = A_{H_{I}^{F} (F)}^{*}$
(4): $A_{G}^{*} = A_{H_{G}^{G} (G)}^{*} = A_{H_{I}^{G} (G)}^{*} = A_{H_{F}^{G} (G)}^{*} = A_{H_{P}^{G} (G)}^{*}$

Proof.

For the first equation we use the mathematical induction. If

n = 3

, it follows from Proposition 4. Suppose the equation holds for

n > 3

. Then

H_{Z_{n + 1}}^{Z_{n}} \circ H_{Z_{n}}^{Z_{n - 1}} \circ H_{Z_{n - 1}}^{Z_{n - 2}} \circ \dots \circ H_{Z_{3}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z_{n + 1}}^{Z_{n}} \circ H_{Z_{n}}^{Z_{1}} = H_{Z_{n + 1}}^{Z_{1}}

, by Proposition 4. The second equation follows from the first one and from Theorem 1–6. □

The set

{H_{Z_{2}}^{Z_{1}} : Z_{1}, Z_{2} \in {I, P, F, G}}

consisting of 16 operators is enclosed under composition. The results can be interpreted by the next diagram.

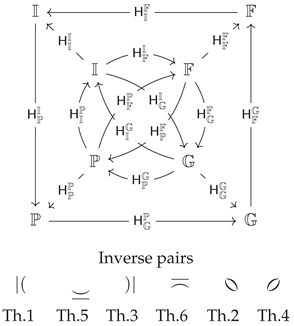
3. Applications

We have defined 16 operators, which can be expressed by one notation

H_{Z_{2}}^{Z_{1}}

where

Z_{1}, Z_{2} \in {I, P, F, G}

. Between the members of

Z_{1}

and the members of

Z_{2}

we can define an equivalence as the next definition states. Note if

Z \in X

, then

Z \in Z

for some

Z \in {I, P, F, G}

Definition 2.

Let

Z_{1}, Z_{2} \in X

Z_{1}

is equivalent to

Z_{2}

H_{Z_{2}}^{Z_{1}} (Z_{1}) = Z_{2}

and

H_{Z_{1}}^{Z_{2}} (Z_{2}) = Z_{1}

where

Z_{1} \in Z_{1}

Z_{2} \in Z_{2}

and

Z_{1}, Z_{2} \in {I, P, F, G}

. This relation is denoted by

Z_{1} \sim Z_{2}

Lemma 1.

For any

Z \in X

Z \sim H_{Z_{2}}^{Z_{1}} (Z)

where

Z \in Z_{1}

and

Z_{1}, Z_{2} \in {I, P, F, G}

. Moreover, ∼ is an equivalence relation.

Proof.

Since

H_{Z_{2}}^{Z_{1}} (Z) = H_{Z_{2}}^{Z_{1}} (Z)

and

Z = H_{Z_{1}}^{Z_{2}} (H_{Z_{2}}^{Z_{1}} (Z))

Z \sim H_{Z_{2}}^{Z_{1}} (Z)

. It is clear ∼ is reflexive and symmetric. Let

Z_{1} \sim Z_{2} \sim Z_{3}

. Then

Z_{2} = H_{Z_{2}}^{Z_{1}} (Z_{1})

and

Z_{3} = H_{Z_{3}}^{Z_{2}} (Z_{2}) = H_{Z_{3}}^{Z_{2}} (H_{Z_{2}}^{Z_{1}} (Z_{1})) = H_{Z_{3}}^{Z_{1}} (Z_{1})

and

Z_{1} = H_{Z_{1}}^{Z_{3}} (Z_{3})

, so

Z_{1} \sim Z_{3}

. □

In the next definition we define a dual operator

A_{Z}^{▹}

(see [5]) to the operator

A_{Z}^{*}

and a closure

c l_{Z} (\cdot)

and an interior

i n t_{Z} (\cdot)

operator.

Definition 3.

Let

Z \in X

. Define the next operators

A_{Z}^{▹} = X ∖ {(X ∖ A)}_{Z}^{*},

c l_{Z} (A) = A \cup A_{Z}^{*},

i n t_{Z} (A) = A \cap A_{Z}^{▹} .

Lemma 2.

Let

Z_{1}, Z_{2} \in X

. If

Z_{1} \sim Z_{2}

, then

A_{Z_{2}}^{*} = A_{Z_{1}}^{*}

A_{Z_{2}}^{▹} = A_{Z_{1}}^{▹}

c l_{Z_{2}} (A) = c l_{Z_{1}} (A)

i n t_{Z_{2}} (A) = i n t_{Z_{1}} (A)

. Consequently, if

I \sim P \sim F \sim G

, then

A_{I}^{*} = A_{P}^{*} = A_{F}^{*} = A_{G}^{*}

Proof.

Suppose

Z_{1} \sim Z_{2}

. Then

H_{Z_{2}}^{Z_{1}} (Z_{1}) = Z_{2}

. By Theorem 7,

A_{Z_{2}}^{*} = A_{H_{Z_{2}}^{Z_{1}} (Z_{1})}^{*} = A_{Z_{1}}^{*}

. Other equalities are obvious. □

Remark 1.

It is well known (see for example [7]) that an ideal topology

τ_{I}

derived from a topology τ on a set X and an ideal

I

on X is defined by a Kuratowski closure operator

c l_{I} (A) = A \cup A_{I}^{*}

and

τ_{I}

is finer then τ. A base for

τ_{I}

is described as

β (τ, I) = {G ∖ A : G \in τ, A \in I}

and

τ_{I} = {A \subset X : c l_{I} (X ∖ A) = X ∖ A}

In the literature we can find many properties of local functions. Designation of operators is different. For example,

A_{P}^{*} = A_{P}^{⋄}

A_{P}^{▹} = Ψ (A)

in [1] or

A_{G}^{*} = Φ_{G} (A)

A_{G}^{▹} = Γ_{G} (A)

in [15]. We will list some of them below regardless of what system

Z \in Z

they apply to.

Theorem 8.

Let

Z \in X

. Then

(1): $\emptyset_{Z}^{*} = \emptyset$ ,
(2): If $A \subset B$ , then $A_{Z}^{*} \subset B_{Z}^{*}$ ,
(3): ${(A \cup B)}_{Z}^{*} = A_{Z}^{*} \cup B_{Z}^{*}$ ,
(4): $A_{Z}^{*} ∖ B_{Z}^{*} = {(A ∖ B)}_{Z}^{*} ∖ B_{Z}^{*}$ ,
(5): ${(A_{Z}^{*})}_{Z}^{*} \subset A_{Z}^{*}$ ,
(6): If $A \subset B$ , then $A_{Z}^{▹} \subset B_{Z}^{▹}$ ,
(7): $A_{Z}^{▹} \subset {(A_{Z}^{▹})}_{Z}^{▹}$ ,
(8): ${(A \cap B)}_{Z}^{▹} = A_{Z}^{▹} \cap B_{Z}^{▹}$ .

Proof.

Let

I : = H_{I}^{Z} (Z)

. Then

A_{I}^{*} = A_{H_{I}^{Z} (Z)}^{*} = A_{Z}^{*}

, by Theorem 7. Since all items hold for

I \in I

(see for example [7]), they hold for

Z \in P \cup F \cup G

. □

Similarly, the next theorem holds for

I \in I

, so it holds for any

Z \in X

Theorem 9.

Let

Z \in X

. A family

τ_{Z} = {A \subset X : c l_{Z} (X ∖ A) = X ∖ A}

is a topology finer then τ and the next conditions are equivalent.

(1): $A \in τ_{Z}$ ,
(2): $i n t_{Z} (A) = A$ ,
(3): $A \subset i n t_{Z} (A)$ ,
(4): $A \subset A_{Z}^{▹} (A)$ ,
(5): $c l_{Z} (X ∖ A) = X ∖ A$ ,
(6): $c l_{Z} (X ∖ A) \subset X ∖ A$ ,
(7): ${(X ∖ A)}_{Z}^{*} \subset X ∖ A$ .

Theorem 10.

Let

Z_{1}, Z_{2} \in X

. If

Z_{1} \sim Z_{2}

, then

τ_{Z_{1}} = τ_{Z_{2}}

. Consequently, if

I \sim P \sim F \sim G

, then

τ_{I} = τ_{P} = τ_{F} = τ_{G}

. A simple base for the open sets of

τ_{I}, τ_{P}, τ_{F}, τ_{G}

is described as follows:

β (τ, I) = {G ∖ A : G \in τ, A \in I}

β (τ, P) = {G \cap A : G \in τ, A \notin P}

β (τ, F) = {G \cap A : G \in τ, A \in F}

β (τ, G) = {G ∖ A : G \in τ, A \notin G}

, respectively.

Proof.

The equality

τ_{Z_{1}} = τ_{Z_{2}}

follows from Lemma 2.

By Remark 1,

β (τ, I) = {G ∖ A : G \in τ, A \in I}

is a base for

τ_{I}

H \in β (τ, I)

if and only if

H = G ∖ A = G \cap (X ∖ A)

where

G \in τ

and

A \in I

if and only if

H = G \cap B

where

G \in τ

and

B : = X ∖ A \notin P

(by Theorem 1 (4)), so

H \in β (τ, P)

if and only if

H = G \cap B

where

G \in τ

and

B \in F

(by Theorem 4 (5)), so

H \in β (τ, F)

if and only if

H = G ∖ A = G ∖ (X ∖ B)

where

G \in τ

and

X ∖ B \notin G

(by Theorem 3 (4)), so

H \in β (τ, G)

. □

Definition 4.

A set A is

I

-small (

P

-small,

F

-small,

G

-small) if

A \in I

(

X ∖ A \notin P

X ∖ A \in F

A \notin G

) and A is locally

I

-small (

P

-small,

F

-small,

G

-small) if for any

a \in A

there is a set

U \in τ

containing a such that

A \cap U

I

-small (

P

-small,

F

-small,

G

-small). Let

Z \in X

Z

is said to be compatible with τ if any locally

Z

-small set is

Z

-small, denoted by

Z \sim τ

Remark 2.

Let

I \sim P \sim F \sim G

. Then

I = H_{I}^{P} (P)

F = H_{F}^{P} (P)

G = H_{G}^{F} (F)

. So,

A \in I \Leftrightarrow X ∖ A \notin P \Leftrightarrow X ∖ A \in F \Leftrightarrow A \notin G

. That means if

Z_{1}, Z_{2} \in X

and

Z_{1} \sim Z_{2}

, a set A is

Z_{1}

-small (locally

Z_{1}

-small) if and only if A is

Z_{2}

-small (locally

Z_{2}

-small) and

Z_{1} \sim τ

if and only if

Z_{2} \sim τ

. Consequently,

(1): If $I \sim τ$ , then $H_{P}^{I} (I) \sim τ, H_{F}^{I} (I) \sim τ, H_{G}^{I} (I) \sim τ$ .
(2): If $P \sim τ$ , then $H_{F}^{P} (P) \sim τ, H_{G}^{P} (P) \sim τ, H_{I}^{P} (P) \sim τ$ .
(3): If $F \sim τ$ , then $H_{G}^{F} (F) \sim τ, H_{I}^{F} (F) \sim τ, H_{P}^{F} (F) \sim τ$ .
(4): If $G \sim τ$ , then $H_{I}^{G} (G) \sim τ, H_{P}^{G} (G) \sim τ, H_{F}^{G} (G) \sim τ$ .

In the theory of ideal topological spaces there are several characterizations of compatibility. For

(X, τ, I)

the most common equivalent conditions are as follows (see for example [5,7]).

Theorem 11.

The next are equivalent

(1): $I \sim τ$ ,
(2): for every $A \subset X$ , if $A \cap A_{I}^{*} = \emptyset$ , then $A \in I$ ,
(3): for every $A \subset X$ , $A ∖ A_{I}^{*} \in I$ ,
(4): for every $A \subset X$ , if $(X ∖ A) \cup {(X ∖ A)}_{I}^{▹} = X$ , then $A \in I$ ,
(5): for every $A \subset X$ , $A_{I}^{▹} ∖ A \in I$ .

Regardless of a concept we work in, a compatibility of

Z_{1}

can be characterized by another equivalent system

Z_{2}

and by operators

{(\cdot)}_{Z_{2}}^{*}

and

{(\cdot)}_{Z_{2}}^{▹}

Theorem 12.

Let

Z_{1}, Z_{2} \in X

. If

Z_{1} \sim Z_{2}

, then the next are equivalent

(1): $Z_{1} \sim τ$ ,
(2): for every $A \subset X$ , if $A \cap A_{Z_{2}}^{*} = \emptyset$ , then A is $Z_{2}$ -small,
(3): for every $A \subset X$ , $A ∖ A_{Z_{2}}^{*}$ is $Z_{2}$ -small,
(4): for every $A \subset X$ , if $(X ∖ A) \cup {(X ∖ A)}_{Z_{2}}^{▹} = X$ , then A is $Z_{2}$ -small,
(5): for every $A \subset X$ , $A_{Z_{2}}^{▹} ∖ A$ is $Z_{2}$ -small.

Proof.

Let

I_{1} : = H_{I}^{Z_{1}} (Z_{1})

where

Z_{1} \in Z_{1} \in {P, F, G}

. Since

I_{1} \sim Z_{1} \sim Z_{2}

Z_{1} \sim τ

if and only if

I_{1} \sim τ

(by Remark 2), A is

I_{1}

-small if and only if A is

Z_{2}

-small (by Remark 2),

A_{I_{1}}^{*} = A_{Z_{1}}^{*} = A_{Z_{2}}^{*}

A_{I_{1}}^{▹} = A_{Z_{1}}^{▹} = A_{Z_{2}}^{▹}

(by Lemma 2). Then the next are equivalent (note

(ii) \Leftrightarrow (2), (iii) \Leftrightarrow (3), (iv) \Leftrightarrow (4), (v) \Leftrightarrow (5)

)

(1): $Z_{1} \sim τ$ ,
(i): $I_{1} \sim τ$ ,
(ii): for every $A \subset X$ , if $A \cap A_{I_{1}}^{*} = \emptyset$ , then A is $I_{1}$ -small,
(iii): for every $A \subset X$ , $A ∖ A_{I_{1}}^{*}$ is $I_{1}$ -small,
(iv): for every $A \subset X$ , if $(X ∖ A) \cup {(X ∖ A)}_{I_{1}}^{▹} = X$ , then A is $I_{1}$ -small,
(v): for every $A \subset X$ , $A_{I_{1}}^{▹} ∖ A$ is $I_{1}$ -small.
(2): for every $A \subset X$ , if $A \cap A_{Z_{2}}^{*} = \emptyset$ , then A is $Z_{2}$ -small,
(3): for every $A \subset X$ , $A ∖ A_{Z_{2}}^{*}$ is $Z_{2}$ -small,
(4): for every $A \subset X$ , if $(X ∖ A) \cup {(X ∖ A)}_{Z_{2}}^{▹} = X$ , then A is $Z_{2}$ -small,
(5): for every $A \subset X$ , $A_{Z_{2}}^{▹} ∖ A$ is $Z_{2}$ -small.

□

Remark 3.

Note, in a primal case (see for example [1]) a compatibility is called "a topology suitable for a primal". More precisely, we prove τ is suitable for a primal

P

if and only if

H_{I}^{P} (P)

is compatible with τ. Proof: τ is suitable for a primal

P

if and only if

X ∖ A \notin P

whenever

A \cap A_{P}^{⋄} = \emptyset

(see [1] Theorem 4.2) if and only if

X ∖ A \notin P

whenever

A \cap A_{P}^{*} = \emptyset

if and only if A is

P

-small whenever

A \cap A_{H_{I}^{P} (P)}^{*} = \emptyset

if and only if A is

H_{I}^{P} (P)

-small whenever

A \cap A_{H_{I}^{P} (P)}^{*} = \emptyset

if and only if

H_{I}^{P} (P)

is compatible with τ.

Definition 5.

A set A is

I

-big (

P

-big,

F

-big,

G

-big) if A is not

I

-small (

P

-small,

F

-small,

G

-small), equivalently

A \notin I

(

X ∖ A \in P

X ∖ A \notin F

A \in G

). Let

Z \in Z

. A topology τ is

Z

-codense, if any nonempty open set is

Z

-big.

Remark 4.

Let

I \sim P \sim F \sim G

. Then

I = H_{I}^{P} (P)

F = H_{F}^{P} (P)

G = H_{G}^{F} (F)

. So,

A \notin I \Leftrightarrow X ∖ A \in P \Leftrightarrow X ∖ A \notin F \Leftrightarrow A \in G

. That means if

Z_{1}, Z_{2} \in X

and

Z_{1} \sim Z_{2}

, a set A is

Z_{1}

-big if and only if A is

Z_{2}

-big and τ is

Z_{1}

-codense if and only if τ is

Z_{2}

-codense.

From the theory of ideal topological spaces we have the next characterization.

Theorem 13.

τ is

I

-codense if and only if

X_{I}^{*} = X

The property of being

Z_{1}

-codense can be characterized by the operators

{(\cdot)}_{Z_{2}}^{*}

and

{(\cdot)}_{Z_{2}}^{▹}

with respect to another equivalent system

Z_{2}

Theorem 14.

Let

Z_{1}, Z_{2} \in X

. If

Z_{1} \sim Z_{2}

, then the next are equivalent

(1): τ is $Z_{1}$ -codense,
(2): $X_{Z_{2}}^{*} = X$ ,
(3): $\emptyset_{Z_{2}}^{▹} = \emptyset$ .

Proof.

Let

I : = H_{I}^{Z_{2}} (Z_{2})

where

Z_{2} \in Z_{2} \in {P, F, G}

. Then

Z_{2} \sim I

. By Remark 4 and Theorem 13,

τ

Z_{1}

-codense if and only if

τ

Z_{2}

-codense if and only if

τ

I

-codense if and only if

X = X_{I}^{*} = X_{H_{I}^{Z_{2}} (Z_{2})}^{*} = X_{Z_{2}}^{*}

(by Theorem 7), so

(1) \Leftrightarrow (2)

. The equivalence

(2) \Leftrightarrow (3)

follows from equation

\emptyset_{Z_{2}}^{▹} = X ∖ X_{Z_{2}}^{*}

. □

4. Conclusions

The main result of the work is based on the unification of approaches to the creation of new topologies derived from ideals, primals, filters and grills. Each approach has its equivalent counterparts in other approaches, and results valid in one approach can be used in others according to the following scheme: Definitions, theorems and proof methods in a space

(X, τ, Z)

Z \in X

, are valid and usable in the other three spaces

(X, τ, H_{Z_{1}}^{Z_{2}} (Z))

where

Z \in Z_{2} \in {I, P, F, G}

and

Z_{1} \in {I, P, F, G}

Z_{1} \neq Z_{2}

. From this point of view, many proofs do not need to be done, and it is enough to do them only once in one space. On the other hand, such diversity, even if equivalent, can be a stimulus for further research and applications.

This article does not contain any studies with human participants or animals performed by the author.

Funding

This research received no external funding.

Data Availability Statement

No data has been used in the manuscript.

Acknowledgments

The article was supported by the Slovak Research and Development Agency, Grant No. APVV-20-0045.

Conflicts of Interest

The author declares that he has no conflict of interest.

References

Al-Omari, A.; Acharjee, S.; Özkoç, M. A new operator of primal topological space. Mathematica 2023, 65, 175–183. [Google Scholar] [CrossRef]
Acharjee, S.; Özkoç, M.; Issaka, F.Y. Primal topological spaces. arXiv 2022, arXiv:2209.12676. [Google Scholar] [CrossRef]
Choquet, G. Sur les notions de filtre et grille. C. R. Acad. Sci. Paris 1947, 224, 171–173. [Google Scholar]
Hamlett, T. R.; Jankovic, D. Ideals in general topology. General Topology and Applications 1988, 115–125. [Google Scholar]
Hamlett, T. R.; Jankovic, D. Ideals in topological spaces and the set operator ψ. Bollettino dell’ Unione Matematica Italiana 1990, 7, 863–874. [Google Scholar]
Al-Saadi, H.; Al-Malki, H. Generalized primal topological spaces. AIMS Math. 2023, 8, 24162–24175. [Google Scholar] [CrossRef]
Jankovic, D.; Hamlett, T. R. New topologies from old via ideals. Am. Math. Mon. 1990, 97, 295–310. [Google Scholar] [CrossRef]
Jankovic, D.; Hamlett, T. R. Compatible extensions of ideals. Bollettino dell’ Unione Matematica Italiana 1992, 6, 453–465. [Google Scholar]
Mandal, D. On separation axioms weaker and stronger than regularity and normality via grill. Jour. Pure Math. 2014, 31, 89–100. [Google Scholar]
Mandal, D.; Mukherjee, M. N. Certain new classes of generalized closed sets and their applications in ideal topological spaces. Filomat 2015, 29, 1113–1120. [Google Scholar] [CrossRef]
Modak, S. Topology on grill-filter space and continuity. Bol. Soc. Paran. Mat. 2013, 2013 31, 219–230. [Google Scholar] [CrossRef]
Modak, S. Grill-filter space. J. Indian Math. Soc. 2013, 80, 313–320. [Google Scholar]
Roy, B.; Mukherjee, M. N. On a typical topology induced by a grill. Soochow J. Math. 2007, 33, 771–786. [Google Scholar]
Roy, B.; Mukherjee, M. N. On a type of compactness via grills. Mat. Ves. 2007, 59, 113–120. [Google Scholar]
Roy, B.; Mukherjee, M. N.; Ghosh, S. K. (2008) On a new operator based on grill and its associated topology. Arab. J. Math. Sci. 2007, 14, 21–32. [Google Scholar]
Roy, B.; Mukherjee, M. N. Concerning topologies induced by principal grills. An. Stiint. Univ. AL. I. Cuza Iasi. Mat.(N. S.) 2009, 55, 285–294. [Google Scholar]
Thron, W. J. Proximity structure and grill. Math. Ann. 1973, 206, 35–62. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Submitted:

06 March 2024

Posted:

07 March 2024

Read the latest preprint version here

Alerts

Abstract

Keywords:

Subject: Computer Science and Mathematics - Mathematics

1. Introduction

Many topologies with important applications in mathematics have been defined using some additional mathematical structure. For example, if a topological space

(X, τ)

and an ideal

I

In general, we can consider four systems, namely an ideal

I

, a primal

P

, a filter

F

and a grill

G

on a topological space

(X, τ)

, see Definition 1. A derivation of a new topology that is finer than the original topology

τ

is as follows: The local function

A_{I}^{*}

A_{P}^{*}

A_{F}^{*}

A_{G}^{*}

, see Definition 1, derived from

I, P, F, G

and

τ

defines the Kuratowski closure operator

c l_{I}

c l_{P}

c l_{F}

c l_{G}

, see Definition 3. In the final step, a new topology on X is defined, denoted by

τ_{I}

τ_{P}

τ_{F}

τ_{G}

, respectively, see Theorem 9. If we look at the achieved results, we can see a striking similarity. In fact, the local functions and topologies generated by this way are equivalent.

Definition 1.

Let X be a nonempty set. A nonempty system

I

P

F

G

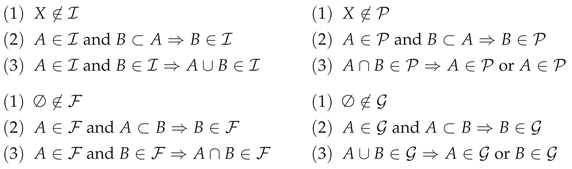
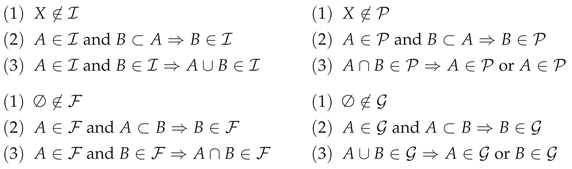
of subsets of X is said be an ideal, a primal, a filter, a grill on X if it satisfies the following conditions Preprints 100694 i001

respectively. Furthermore, if τ is a topology on X, for

A \subset X

we define four local functions

\begin{matrix} A_{I}^{*} = {x \in X : A \cap U \notin I for any U \in τ, x \in U}, \\ A_{P}^{*} = {x \in X : (X ∖ A) \cup (X ∖ U) \in P for any U \in τ, x \in U}, \\ A_{F}^{*} = {x \in X : (X ∖ A) \cup (X ∖ U) \notin F for any U \in τ, x \in U}, \\ A_{G}^{*} = {x \in X : A \cap U \in G for any U \in τ, x \in U} . \end{matrix}

An ideal topological space, a primal topological space, a filter topological space, a grill topological space is a topological space

(X, τ)

with an ideal

I

, a primal

P

, a filter

F

, a grill

G

and it is denoted by

(X, τ, I)

(X, τ, P)

(X, τ, F)

(X, τ, G)

, respectively. Let

I, P, F, G

be a family of all ideals, primals, filters, grills on X, respectively. Put

X = I \cup P \cup F \cup G

. If

Z \in X

, then

(X, τ, Z)

is called a

Z

-topological space.

2. Main Results

In the following two parts we present sixteen operators

H_{Z_{2}}^{Z_{1}}

(Theorem 1–6) between pairs of systems

Z_{1}, Z_{2} \in {I, P, F, G}

and their properties and compositions are studied. Next, the equivalence between

Z_{1}, Z_{2} \in X

is defined (Definotion 2). The equality of local functions and the equality of generated topologies are proved, provided that

Z_{1}

and

Z_{2}

and equivalent.

Define four identity operators

\begin{matrix} H_{I}^{I} : I \to I by H_{I}^{I} (I) = I, & H_{P}^{P} : P \to P by H_{P}^{P} (P) = P, \\ H_{F}^{F} : F \to F by H_{F}^{F} (F) = F, & H_{G}^{G} : G \to G by H_{G}^{G} (G) = G . \end{matrix}

In the next six theorems the proofs of items (1)–(10) are left to the reader. The rest will be proven.

Theorem 1.

Let

I

P

be an ideal, a primal on X, respectively. Define

H_{P}^{I} : I \to P

H_{P}^{I} (I) = {A \subset X : X ∖ A \notin I}

H_{I}^{P} : P \to I

H_{I}^{P} (P) = {A \subset X : X ∖ A \notin P}

Then

H_{P}^{I} (I)

H_{I}^{P} (P)

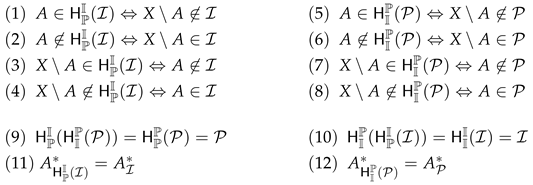
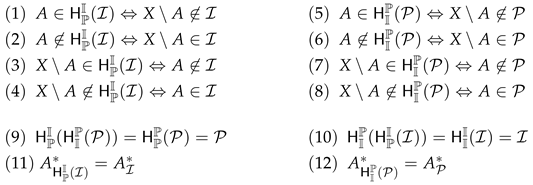
is a primal, an ideal on X, respectively and Preprints 100694 i002

Proof.

We prove

H_{P}^{I} (I)

is a primal. Since

\emptyset \in I

X \notin H_{P}^{I} (I)

Let

A \in H_{P}^{I} (I)

and

B \subset A

. Then

X ∖ A \notin I

. Since

X ∖ A \subset X ∖ B

and

I

is an ideal,

X ∖ B \notin I

, so

B \in H_{P}^{I} (I)

. Let

A \cap B \in H_{P}^{I} (I)

. Then

(X ∖ A) \cup (X ∖ B) = X ∖ A \cap B \notin I

. Since

I

is an ideal,

X ∖ A

X ∖ B

is not from

I

. So

A \in H_{P}^{I} (I)

B \in H_{P}^{I} (I)

. That means

H_{P}^{I} (I)

is a primal.

We prove

H_{I}^{P} (P)

is an ideal. Since

\emptyset \in P

X \notin H_{I}^{P} (P)

Let

A \in H_{I}^{P} (P)

and

B \subset A

. Then

X ∖ A \notin P

. Since

X ∖ A \subset X ∖ B

and

P

is a primal,

X ∖ B \notin P

, so

B \in H_{I}^{P} (P)

. Let

A, B \in H_{I}^{P} (P)

. Then

X ∖ A \notin P

X ∖ B \notin P

and

(X ∖ A) \cap (X ∖ B) = X ∖ A \cup B \notin P

. So

A \cup B \in H_{I}^{P} (P)

. That means

H_{I}^{P} (P)

is an ideal.

(11):

x \in A_{H_{P}^{I} (I)}^{*}

if and only if

(X ∖ A) \cup (X ∖ U) = X ∖ A \cap U \in H_{P}^{I} (I)

for any nbhd U of x if and only if

A \cap U \notin I

if and only if

x \in A_{I}^{*}

(12):

x \in A_{H_{I}^{P} (P)}^{*}

if and only if

A \cap U \notin H_{I}^{P} (P)

for any nbhd U of x if and only if

X ∖ A \cap U = (X ∖ A) \cup (X ∖ U) \in P

if and only if

x \in A_{P}^{*}

. □

Theorem 2.

Let

I

G

be an ideal, a grill on X, respectively. Define

H_{G}^{I} : I \to G

H_{G}^{I} (I) = {A \subset X : A \notin I}

H_{I}^{G} : G \to I

H_{I}^{G} (G) = {A \subset X : A \notin G}

Then

H_{G}^{I} (I)

H_{I}^{G} (G)

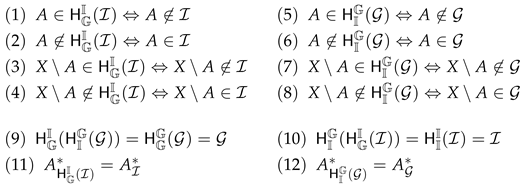
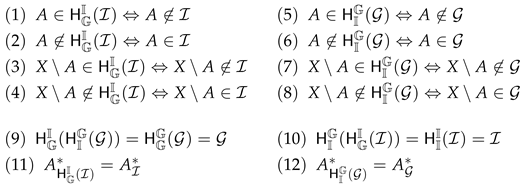
is a grill, an ideal on X, respectively and Preprints 100694 i003

Proof.

We prove

H_{G}^{I} (I)

is a grill. Since

\emptyset \in I

\emptyset \notin H_{G}^{I} (I)

Let

A \in H_{G}^{I} (I)

and

A \subset B

. Then

A \notin I

. Since

I

is an ideal,

B \notin I

, so

B \in H_{G}^{I} (I)

. Let

A \cup B \in H_{G}^{I} (I)

. Then

A \cup B \notin I

. Since

I

is an ideal, A or B is not from

I

. So

A \in H_{G}^{I} (I)

B \in H_{G}^{I} (I)

. That means

H_{G}^{I} (I)

is a grill.

We prove

H_{I}^{G} (G)

is an ideal. Since

X \in G

X \notin H_{I}^{G} (G)

Let

A \in H_{I}^{G} (G)

and

B \subset A

. Then

A \notin G

. Since

G

is a grill,

B \notin G

, so

B \in H_{I}^{G} (G)

. Let

A, B \in H_{I}^{G} (G)

. Then

A, B \notin G

. Since

G

is a grill,

A \cup B \notin G

. So

A \cup B \in H_{I}^{G} (G)

. That means

H_{I}^{G} (G)

is an ideal.

(11):

x \in A_{H_{G}^{I} (I)}^{*}

if and only if

A \cap U \in H_{G}^{I} (I)

for any nbhd U of x if and only if

A \cap U \notin I

if and only if

x \in A_{I}^{*}

(12):

x \in A_{H_{I}^{G} (G)}^{*}

if and only if

A \cap U \notin H_{I}^{G} (G)

for any nbhd U of x if and only if

A \cap U \in G

if and only if

x \in A_{G}^{*}

. □

Theorem 3.

Let

F

G

be a filter, a grill on X, respectively. Define

H_{G}^{F} : F \to G

H_{G}^{F} (F) = {A \subset X : X ∖ A \notin F}

H_{F}^{G} : G \to F

H_{F}^{G} (G) = {A \subset X : X ∖ A \notin G}

Then

H_{G}^{F} (F)

H_{F}^{G} (G)

is a grill, a filter on X, respectively and

\begin{matrix} (1) A \in H_{G}^{F} (F) \Leftrightarrow X ∖ A \notin F & (5) A \in H_{F}^{G} (G) \Leftrightarrow X ∖ A \notin G \\ (2) A \notin H_{G}^{F} (F) \Leftrightarrow X ∖ A \in F & (6) A \notin H_{F}^{G} (G) \Leftrightarrow X ∖ A \in G \\ (3) X ∖ A \in H_{G}^{F} (F) \Leftrightarrow A \notin F & (7) X ∖ A \in H_{F}^{G} (G) \Leftrightarrow A \notin G \\ (4) X ∖ A \notin H_{G}^{F} (F) \Leftrightarrow A \in F & (8) X ∖ A \notin H_{F}^{G} (G) \Leftrightarrow A \in G \\ (9) H_{G}^{F} (H_{F}^{G} (G)) = H_{G}^{G} (G) = G & (10) H_{F}^{G} (H_{G}^{F} (F)) = H_{F}^{F} (F) = F \\ (11) A_{H_{G}^{F} (F)}^{*} = A_{F}^{*} & (12) A_{H_{F}^{G} (G)}^{*} = A_{G}^{*} \end{matrix}

Proof.

We prove

H_{G}^{F} (F)

is a grill. Since

X \in F

\emptyset \notin H_{G}^{F} (F)

Let

A \in H_{G}^{F} (F)

and

A \subset B

. Then

X ∖ A \notin F

. Since

F

is a filter and

X ∖ B \subset X ∖ A

X ∖ B \notin F

, so

B \in H_{G}^{F} (F)

. Let

A \cup B \in H_{G}^{F} (F)

. Then

X ∖ A \cup B = (X ∖ A) \cap (X ∖ B) \notin F

. Since

F

is an filter,

X ∖ A

X ∖ B

is not from

F

. So

A \in H_{G}^{F} (I)

B \in H_{G}^{F} (I)

. That means

H_{G}^{F} (I)

is a grill.

We prove

H_{F}^{G} (G)

is a filter. Since

X \in G

\emptyset \notin H_{F}^{G} (G)

Let

A \in H_{F}^{G} (G)

and

A \subset B

. Then

X ∖ A \notin G

. Since

G

is a grill and

X ∖ B \subset X ∖ A

X ∖ B \notin G

, so

B \in H_{F}^{G} (G)

. Let

A, B \in H_{F}^{G} (G)

. Then

X ∖ A \notin G

X ∖ B \notin G

. Then

(X ∖ A) \cup (X ∖ B) = X ∖ A \cap B \notin G

. So,

A \cap B \in H_{F}^{G} (G)

. That means

H_{F}^{G} (G)

is a filter.

(11):

x \in A_{H_{G}^{F} (F)}^{*}

if and only if

A \cap U \in H_{G}^{F} (F)

for any nbhd U of x if and only if

X ∖ A \cap U \notin F

if and only if

x \in A_{F}^{*}

(12):

x \in A_{H_{F}^{G} (G)}^{*}

if and only if

X ∖ A \cap U \notin H_{F}^{G} (G)

for any nbhd U of x if and only if

A \cap U \in G

if and only if

x \in A_{G}^{*}

. □

Theorem 4.

Let

F

P

be a filter, a primal on X, respectively. Define

H_{P}^{F} : F \to P

H_{P}^{F} (F) = {A \subset X : A \notin F}

H_{F}^{P} : P \to F

H_{F}^{P} (P) = {A \subset X : A \notin P}

Then

H_{P}^{F} (F)

H_{F}^{P} (P)

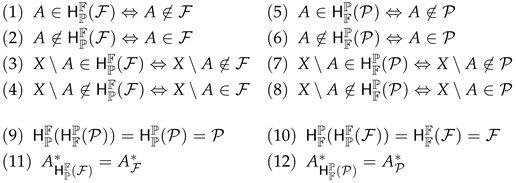
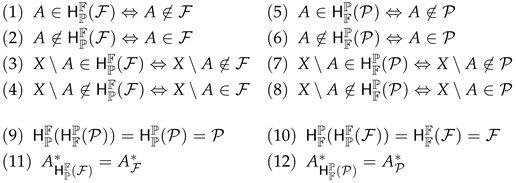
is a primal, a filter on X, respectively and Preprints 100694 i004

Proof.

We prove

H_{P}^{F} (F)

is a primal. Since

X \in F

X \notin H_{P}^{F} (F)

Let

A \in H_{P}^{F} (F)

and

B \subset A

. Then

A \notin F

. Since

F

is a filter,

B \notin F

, so

B \in H_{P}^{F} (F)

. Let

A \cap B \in H_{P}^{F} (F)

. Then

A \cap B \notin F

. Since

F

is a filter, A or B is not from

F

. So

A \in H_{P}^{F} (F)

B \in H_{P}^{F} (F)

. That means

H_{P}^{F} (F)

is a primal.

We prove

H_{F}^{P} (P)

is a filter. Since

\emptyset \in P

\emptyset \notin H_{F}^{P} (P)

Let

A \in H_{F}^{P} (P)

and

A \subset B

. Then

A \notin P

. Since

P

is a primal,

B \notin P

, so

B \in H_{F}^{P} (P)

. Let

A, B \in H_{F}^{P} (P)

. Then

A, B \notin P

. Since

P

is a primal,

A \cap B \notin P

. So

A \cap B \in H_{F}^{P} (P)

. That means

H_{F}^{P} (P)

is a filter.

(11):

x \in A_{H_{P}^{F} (F)}^{*}

if and only if

(X ∖ A) \cup (X ∖ U) = X ∖ A \cap U \in H_{P}^{F} (F)

for any nbhd U of x if and only if

X ∖ A \cap U \notin F

if and only if

x \in A_{F}^{*}

(12):

x \in A_{H_{F}^{P} (P)}^{*}

if and only if

X ∖ A \cap U \notin H_{F}^{P} (P)

for any nbhd U of x if and only if

X ∖ A \cap U = (X ∖ A) \cup (X ∖ U) \in P

if and only if

x \in A_{P}^{*}

. □

Theorem 5.

Let

G

P

be a grill, a primal on X, respectively. Define

H_{P}^{G} : G \to P

F_{P}^{G} (G) = {A \subset X : X ∖ A \in G}

H_{G}^{P} : P \to G

H_{G}^{P} (P) = {A \subset X : X ∖ A \in P}

Then

H_{P}^{G} (G)

H_{G}^{P} (P)

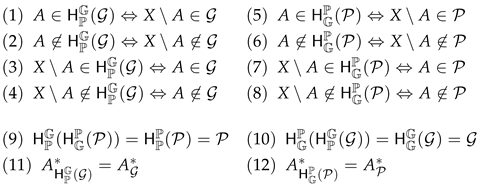
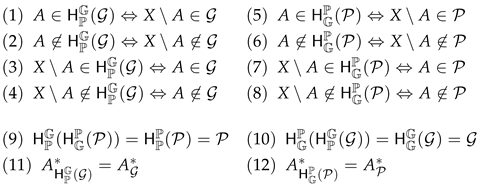
is a primal, a grill on X, respectively and Preprints 100694 i005

Proof.

We prove

H_{P}^{G} (G)

is a primal. Since

\emptyset \notin G

X \notin H_{P}^{G} (G)

Let

A \in H_{P}^{G} (G)

and

B \subset A

. Then

X ∖ A \in G

. Since

G

is a grill and

X ∖ A \subset X ∖ B

X ∖ B \in G

, so

B \in H_{P}^{G} (G)

. Let

A \cap B \in H_{P}^{G} (G)

. Then

X ∖ A \cap B = (X ∖ A) \cup (X ∖ B) \in G

. Since

G

is a grill,

X ∖ A

X ∖ B

is from

G

. So

A \in H_{P}^{G} (G)

B \in H_{P}^{G} (G)

. That means

H_{P}^{G} (G)

is a primal.

We prove

H_{G}^{P} (P)

is a grill. Since

X \notin P

\emptyset \notin H_{G}^{P} (P)

Let

A \in H_{G}^{P} (P)

and

A \subset B

. Then

X ∖ A \in P

. Since

P

is a primal and

X ∖ B \subset X ∖ A

X ∖ B \in P

, so

B \in H_{G}^{P} (P)

. Let

A \cup B \in H_{G}^{P} (P)

. Then

X ∖ A \cup B = (X ∖ A) \cap (X ∖ B) \in P

. Since

P

is a primal,

X ∖ A

X ∖ B

is from

P

. So

A \in H_{G}^{P} (P)

B \in H_{G}^{P} (P)

. That means

H_{G}^{P} (P)

is a grill.

(11):

x \in A_{H_{P}^{G} (G)}^{*}

if and only if

(X ∖ A) \cup (X ∖ U) = X ∖ A \cap U \in H_{P}^{G} (G)

for any nbhd U of x if and only if

A \cap U \in G

if and only if

x \in A_{G}^{*}

(12):

x \in A_{H_{G}^{P} (P)}^{*}

if and only if

A \cap U \in H_{G}^{P} (P)

for any nbhd U of x if and only if

X ∖ A \cap U = (X ∖ A) \cup (X ∖ U) \in P

if and only if

x \in A_{P}^{*}

. □

Theorem 6.

Let

F

I

be a filter, a ideal on X, respectively. Define

H_{I}^{F} : F \to I

H_{I}^{F} (F) = {A \subset X : X ∖ A \in F}

H_{F}^{I} : I \to F

H_{F}^{I} (I) = {A \subset X : X ∖ A \in I}

Then

H_{I}^{F} (F)

H_{F}^{I} (I)

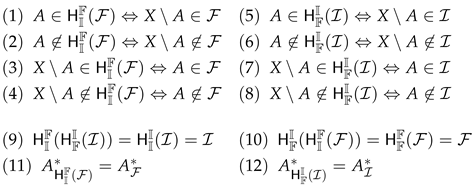
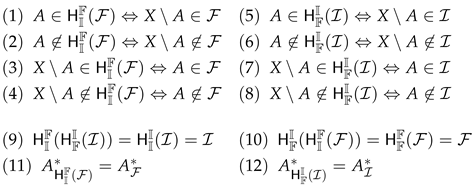
is an ideal, a filter on X, respectively and Preprints 100694 i006

Proof.

We prove

H_{I}^{F} (F)

is an ideal. Since

\emptyset \notin F

X \notin H_{I}^{F} (F)

Let

A \in H_{I}^{F} (F)

and

B \subset A

. Then

X ∖ A \in F

. Since

X ∖ A \subset X ∖ B

and

F

is a filter,

X ∖ B \in F

, so

B \in H_{I}^{F} (F)

. Let

A, B \in H_{I}^{F} (F)

. Then

X ∖ A, X ∖ B \in F

. Since

F

is a filter,

(X ∖ A) \cap (X ∖ B) = X ∖ A \cup B \in F

. So

A \cup B \in H_{I}^{F} (F)

. That means

H_{I}^{F} (F)

is an ideal.

We prove

H_{F}^{I} (I)

is a filter. Since

X \notin I

\emptyset \notin H_{F}^{I} (I)

Let

A \in H_{F}^{I} (I)

and

A \subset B

. Then

X ∖ A \in I

. Since

X ∖ B \subset X ∖ A

and

I

is an ideal,

X ∖ B \in I

, so

B \in H_{F}^{I} (I)

. Let

A, B \in H_{F}^{I} (I)

. Then

X ∖ A, X ∖ B \in I

. Since

I

is an ideal,

(X ∖ A) \cup (X ∖ B) = X ∖ A \cap B \in I

. So

A \cap B \in H_{F}^{I} (I)

. That means

H_{F}^{I} (I)

is a filter.

(11):

x \in A_{H_{I}^{F} (F)}^{*}

if and only if

A \cap U \notin H_{I}^{F} (F)

for any nbhd U of x if and only if

X ∖ A \cap U \notin F

if and only if

x \in A_{F}^{*}

(12):

x \in A_{H_{F}^{I} (I)}^{*}

if and only if

X ∖ A \cap U \notin H_{F}^{I} (I)

for any nbhd U of x if and only if

A \cap U \notin I

if and only if

x \in A_{I}^{*}

. □

Proposition 1.

Let

Z_{1}, Z_{2} \in {I, P, F, G}

. If

Z_{1} \neq Z_{2}

, then each of the twelve operators

H_{Z_{2}}^{Z_{1}}

from Theorem 1-6 is bijective and

{(H_{Z_{2}}^{Z_{1}})}^{- 1} = H_{Z_{1}}^{Z_{2}}

, consequently

H_{Z_{2}}^{Z_{1}}

and

H_{Z_{1}}^{Z_{2}}

are mutually inverse, so

H_{Z_{1}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z_{1}}^{Z_{1}}

Proof.

It follows from Theorem 1-6 items (9) and (10). □

Proposition 2.

H_{F}^{P} \circ H_{P}^{I} = H_{F}^{I}

H_{I}^{G} \circ H_{G}^{F} = H_{I}^{F}

H_{G}^{F} \circ H_{F}^{P} = H_{G}^{P}

H_{P}^{I} \circ H_{I}^{G} = H_{P}^{G}

Proof.

A \in H_{F}^{P} (H_{P}^{I} (I))

H_{I}^{G} (H_{G}^{F} (F)) \Leftrightarrow

A \notin H_{P}^{I} (I)

H_{G}^{F} (F)

⇔

X ∖ A \in I, F \Leftrightarrow A \in H_{F}^{I} (I), H_{I}^{F} (F)

, respectively. So,

H_{F}^{P} \circ H_{P}^{I} = H_{F}^{I}

H_{I}^{G} \circ H_{G}^{F} = H_{I}^{F}

A \in H_{G}^{F} (H_{F}^{P} (P))

H_{P}^{I} (H_{I}^{G} (G)) \Leftrightarrow

X ∖ A \notin H_{F}^{P} (P)

H_{I}^{G} (G) \Leftrightarrow

X ∖ A \in P, G \Leftrightarrow

A \in H_{G}^{P} (P), H_{P}^{G} (G)

, respectively. So,

H_{G}^{F} \circ H_{F}^{P} = H_{G}^{P}

H_{P}^{I} \circ H_{I}^{G} = H_{P}^{G}

. □

Proposition 3.

Let

Z, Z_{1}, Z_{2} \in {I, P, F, G}

. The next conditions are equivalent

(1): $H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}$ (2) $H_{Z_{1}}^{Z} \circ H_{Z}^{Z_{2}} = H_{Z_{1}}^{Z_{2}}$
(3): $H_{Z}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z}^{Z_{1}}$ (4) $H_{Z_{1}}^{Z_{2}} \circ H_{Z_{2}}^{Z} = H_{Z_{1}}^{Z}$
(5): $H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z} = H_{Z_{2}}^{Z}$ (6) $H_{Z}^{Z_{1}} \circ H_{Z_{1}}^{Z_{2}} = H_{Z}^{Z_{2}}$

Proof.

(1) \Leftrightarrow (2)

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

⇔

{(H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}})}^{- 1} = {(H_{Z_{2}}^{Z_{1}})}^{- 1}

⇔

H_{Z_{1}}^{Z} \circ H_{Z}^{Z_{2}} = H_{Z_{1}}^{Z_{2}}

(1) \Leftrightarrow (3)

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

⇔

H_{Z}^{Z_{1}} = {(H_{Z_{2}}^{Z})}^{- 1} \circ H_{Z_{2}}^{Z_{1}} \Leftrightarrow H_{Z}^{Z_{1}} = H_{Z}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}}

(3) \Leftrightarrow (4)

H_{Z}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z}^{Z_{1}}

⇔

{(H_{Z}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}})}^{- 1} = {(H_{Z}^{Z_{1}})}^{- 1}

⇔

H_{Z_{1}}^{Z_{2}} \circ H_{Z_{2}}^{Z} = H_{Z_{1}}^{Z}

(1) \Leftrightarrow (5)

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

⇔

H_{Z_{2}}^{Z} = H_{Z_{2}}^{Z_{1}} \circ {(H_{Z}^{Z_{1}})}^{- 1} \Leftrightarrow H_{Z_{2}}^{Z} = H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z}

(5) \Leftrightarrow (6)

H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z} = H_{Z_{2}}^{Z}

⇔

{(H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z})}^{- 1} = {(H_{Z_{2}}^{Z})}^{- 1}

⇔

H_{Z}^{Z_{1}} \circ H_{Z_{1}}^{Z_{2}} = H_{Z}^{Z_{2}}

□

Proposition 4.

Let

Z, Z_{1}, Z_{2} \in {I, P, F, G}

. Then for 64 possibilities the equation

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

holds.

Proof.

By Proposition 2 and Proposition 3, the equation

H_{Z_{2}}^{Z} \circ H_{Z}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

holds for 24 possibilities (

Z, Z_{1}, Z_{2}

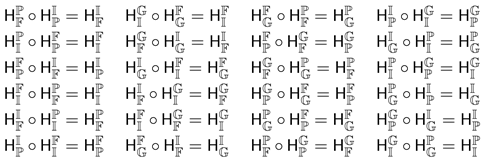
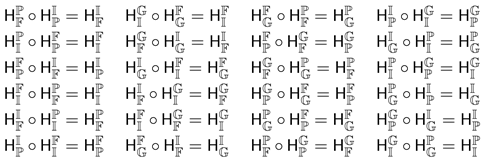
are mutually different): Preprints 100694 i007

Other cases for

Z_{1} \neq Z_{2}

are trivial:

H_{Z_{1}}^{Z_{1}} \circ H_{Z_{1}}^{Z_{2}} = H_{Z_{1}}^{Z_{2}}

(12 possibilities),

H_{Z_{2}}^{Z_{1}} \circ H_{Z_{1}}^{Z_{1}} = H_{Z_{2}}^{Z_{1}}

(12 possibilities),

H_{Z_{1}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z_{1}}^{Z_{1}}

(12 possibilities),

H_{Z_{1}}^{Z_{1}} \circ H_{Z_{1}}^{Z_{1}} = H_{Z_{1}}^{Z_{1}}

(4 possibilities).

□

Theorem 7.

Let

Z_{k} \in {I, P, F, G}

k = 1, \dots, n

and

Z \in Z_{1}

. Then

H_{Z_{n}}^{Z_{n - 1}} \circ H_{Z_{n - 1}}^{Z_{n - 2}} \circ \dots \circ H_{Z_{3}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z_{n}}^{Z_{1}}

A_{(H_{Z_{n}}^{Z_{n - 1}} \circ H_{Z_{n - 1}}^{Z_{n - 2}} \circ \dots \circ H_{Z_{3}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}}) (Z)}^{*} = A_{H_{Z_{n}}^{Z_{1}} (Z)}^{*} = A_{Z}^{*}

Consequently,

(1): $A_{I}^{*} = A_{H_{I}^{I} (I)}^{*} = A_{H_{P}^{I} (I)}^{*} = A_{H_{G}^{I} (I)}^{*} = A_{H_{F}^{I} (I)}^{*}$
(2): $A_{P}^{*} = A_{H_{P}^{P} (P)}^{*} = A_{H_{I}^{P} (P)}^{*} = A_{H_{F}^{P} (P)}^{*} = A_{H_{G}^{P} (P)}^{*}$
(3): $A_{F}^{*} = A_{H_{F}^{F} (F)}^{*} = A_{H_{G}^{F} (F)}^{*} = A_{H_{P}^{F} (F)}^{*} = A_{H_{I}^{F} (F)}^{*}$
(4): $A_{G}^{*} = A_{H_{G}^{G} (G)}^{*} = A_{H_{I}^{G} (G)}^{*} = A_{H_{F}^{G} (G)}^{*} = A_{H_{P}^{G} (G)}^{*}$

Proof.

For the first equation we use the mathematical induction. If

n = 3

, it follows from Proposition 4. Suppose the equation holds for

n > 3

. Then

H_{Z_{n + 1}}^{Z_{n}} \circ H_{Z_{n}}^{Z_{n - 1}} \circ H_{Z_{n - 1}}^{Z_{n - 2}} \circ \dots \circ H_{Z_{3}}^{Z_{2}} \circ H_{Z_{2}}^{Z_{1}} = H_{Z_{n + 1}}^{Z_{n}} \circ H_{Z_{n}}^{Z_{1}} = H_{Z_{n + 1}}^{Z_{1}}

, by Proposition 4. The second equation follows from the first one and from Theorem 1–6. □

The set

{H_{Z_{2}}^{Z_{1}} : Z_{1}, Z_{2} \in {I, P, F, G}}

consisting of 16 operators is enclosed under composition. The results can be interpreted by the next diagram.

3. Applications

We have defined 16 operators, which can be expressed by one notation

H_{Z_{2}}^{Z_{1}}

where

Z_{1}, Z_{2} \in {I, P, F, G}

. Between the members of

Z_{1}

and the members of

Z_{2}

we can define an equivalence as the next definition states. Note if

Z \in X

, then

Z \in Z

for some

Z \in {I, P, F, G}

Definition 2.

Let

Z_{1}, Z_{2} \in X

Z_{1}

is equivalent to

Z_{2}

H_{Z_{2}}^{Z_{1}} (Z_{1}) = Z_{2}

and

H_{Z_{1}}^{Z_{2}} (Z_{2}) = Z_{1}

where

Z_{1} \in Z_{1}

Z_{2} \in Z_{2}

and

Z_{1}, Z_{2} \in {I, P, F, G}

. This relation is denoted by

Z_{1} \sim Z_{2}

Lemma 1.

For any

Z \in X

Z \sim H_{Z_{2}}^{Z_{1}} (Z)

where

Z \in Z_{1}

and

Z_{1}, Z_{2} \in {I, P, F, G}

. Moreover, ∼ is an equivalence relation.

Proof.

Since

H_{Z_{2}}^{Z_{1}} (Z) = H_{Z_{2}}^{Z_{1}} (Z)

and

Z = H_{Z_{1}}^{Z_{2}} (H_{Z_{2}}^{Z_{1}} (Z))

Z \sim H_{Z_{2}}^{Z_{1}} (Z)

. It is clear ∼ is reflexive and symmetric. Let

Z_{1} \sim Z_{2} \sim Z_{3}

. Then

Z_{2} = H_{Z_{2}}^{Z_{1}} (Z_{1})

and

Z_{3} = H_{Z_{3}}^{Z_{2}} (Z_{2}) = H_{Z_{3}}^{Z_{2}} (H_{Z_{2}}^{Z_{1}} (Z_{1})) = H_{Z_{3}}^{Z_{1}} (Z_{1})

and

Z_{1} = H_{Z_{1}}^{Z_{3}} (Z_{3})

, so

Z_{1} \sim Z_{3}

. □

In the next definition we define a dual operator

A_{Z}^{▹}

(see [5]) to the operator

A_{Z}^{*}

and a closure

c l_{Z} (\cdot)

and an interior

i n t_{Z} (\cdot)

operator.

Definition 3.

Let

Z \in X

. Define the next operators

A_{Z}^{▹} = X ∖ {(X ∖ A)}_{Z}^{*},

c l_{Z} (A) = A \cup A_{Z}^{*},

i n t_{Z} (A) = A \cap A_{Z}^{▹} .

Lemma 2.

Let

Z_{1}, Z_{2} \in X

. If

Z_{1} \sim Z_{2}

, then

A_{Z_{2}}^{*} = A_{Z_{1}}^{*}

A_{Z_{2}}^{▹} = A_{Z_{1}}^{▹}

c l_{Z_{2}} (A) = c l_{Z_{1}} (A)

i n t_{Z_{2}} (A) = i n t_{Z_{1}} (A)

. Consequently, if

I \sim P \sim F \sim G

, then

A_{I}^{*} = A_{P}^{*} = A_{F}^{*} = A_{G}^{*}

Proof.

Suppose

Z_{1} \sim Z_{2}

. Then

H_{Z_{2}}^{Z_{1}} (Z_{1}) = Z_{2}

. By Theorem 7,

A_{Z_{2}}^{*} = A_{H_{Z_{2}}^{Z_{1}} (Z_{1})}^{*} = A_{Z_{1}}^{*}

. Other equalities are obvious. □

Remark 1.

It is well known (see for example [7]) that an ideal topology

τ_{I}

derived from a topology τ on a set X and an ideal

I

on X is defined by a Kuratowski closure operator

c l_{I} (A) = A \cup A_{I}^{*}

and

τ_{I}

is finer then τ. A base for

τ_{I}

is described as

β (τ, I) = {G ∖ A : G \in τ, A \in I}

and

τ_{I} = {A \subset X : c l_{I} (X ∖ A) = X ∖ A}

In the literature we can find many properties of local functions. Designation of operators is different. For example,

A_{P}^{*} = A_{P}^{⋄}

A_{P}^{▹} = Ψ (A)

in [1] or

A_{G}^{*} = Φ_{G} (A)

A_{G}^{▹} = Γ_{G} (A)

in [15]. We will list some of them below regardless of what system

Z \in Z

they apply to.

Theorem 8.

Let

Z \in X

. Then

(1): $\emptyset_{Z}^{*} = \emptyset$ ,
(2): If $A \subset B$ , then $A_{Z}^{*} \subset B_{Z}^{*}$ ,
(3): ${(A \cup B)}_{Z}^{*} = A_{Z}^{*} \cup B_{Z}^{*}$ ,
(4): $A_{Z}^{*} ∖ B_{Z}^{*} = {(A ∖ B)}_{Z}^{*} ∖ B_{Z}^{*}$ ,
(5): ${(A_{Z}^{*})}_{Z}^{*} \subset A_{Z}^{*}$ ,
(6): If $A \subset B$ , then $A_{Z}^{▹} \subset B_{Z}^{▹}$ ,
(7): $A_{Z}^{▹} \subset {(A_{Z}^{▹})}_{Z}^{▹}$ ,
(8): ${(A \cap B)}_{Z}^{▹} = A_{Z}^{▹} \cap B_{Z}^{▹}$ .

Proof.

Let

I : = H_{I}^{Z} (Z)

. Then

A_{I}^{*} = A_{H_{I}^{Z} (Z)}^{*} = A_{Z}^{*}

, by Theorem 7. Since all items hold for

I \in I

(see for example [7]), they hold for

Z \in P \cup F \cup G

. □

Similarly, the next theorem holds for

I \in I

, so it holds for any

Z \in X

Theorem 9.

Let

Z \in X

. A family

τ_{Z} = {A \subset X : c l_{Z} (X ∖ A) = X ∖ A}

is a topology finer then τ and the next conditions are equivalent.

(1): $A \in τ_{Z}$ ,
(2): $i n t_{Z} (A) = A$ ,
(3): $A \subset i n t_{Z} (A)$ ,
(4): $A \subset A_{Z}^{▹} (A)$ ,
(5): $c l_{Z} (X ∖ A) = X ∖ A$ ,
(6): $c l_{Z} (X ∖ A) \subset X ∖ A$ ,
(7): ${(X ∖ A)}_{Z}^{*} \subset X ∖ A$ .

Theorem 10.

Let

Z_{1}, Z_{2} \in X

. If

Z_{1} \sim Z_{2}

, then

τ_{Z_{1}} = τ_{Z_{2}}

. Consequently, if

I \sim P \sim F \sim G

, then

τ_{I} = τ_{P} = τ_{F} = τ_{G}

. A simple base for the open sets of

τ_{I}, τ_{P}, τ_{F}, τ_{G}

is described as follows:

β (τ, I) = {G ∖ A : G \in τ, A \in I}

β (τ, P) = {G \cap A : G \in τ, A \notin P}

β (τ, F) = {G \cap A : G \in τ, A \in F}

β (τ, G) = {G ∖ A : G \in τ, A \notin G}

, respectively.

Proof.

The equality

τ_{Z_{1}} = τ_{Z_{2}}

follows from Lemma 2.

By Remark 1,

β (τ, I) = {G ∖ A : G \in τ, A \in I}

is a base for

τ_{I}

H \in β (τ, I)

if and only if

H = G ∖ A = G \cap (X ∖ A)

where

G \in τ

and

A \in I

if and only if

H = G \cap B

where

G \in τ

and

B : = X ∖ A \notin P

(by Theorem 1 (4)), so

H \in β (τ, P)

if and only if

H = G \cap B

where

G \in τ

and

B \in F

(by Theorem 4 (5)), so

H \in β (τ, F)

if and only if

H = G ∖ A = G ∖ (X ∖ B)

where

G \in τ

and

X ∖ B \notin G

(by Theorem 3 (4)), so

H \in β (τ, G)

. □

Definition 4.

A set A is

I

-small (

P

-small,

F

-small,

G

-small) if

A \in I

(

X ∖ A \notin P

X ∖ A \in F

A \notin G

) and A is locally

I

-small (

P

-small,

F

-small,

G

-small) if for any

a \in A

there is a set

U \in τ

containing a such that

A \cap U

I

-small (

P

-small,

F

-small,

G

-small). Let

Z \in X

Z

is said to be compatible with τ if any locally

Z

-small set is

Z

-small, denoted by

Z \sim τ

Remark 2.

Let

I \sim P \sim F \sim G

. Then

I = H_{I}^{P} (P)

F = H_{F}^{P} (P)

G = H_{G}^{F} (F)

. So,

A \in I \Leftrightarrow X ∖ A \notin P \Leftrightarrow X ∖ A \in F \Leftrightarrow A \notin G

. That means if

Z_{1}, Z_{2} \in X

and

Z_{1} \sim Z_{2}

, a set A is

Z_{1}

-small (locally

Z_{1}

-small) if and only if A is

Z_{2}

-small (locally

Z_{2}

-small) and

Z_{1} \sim τ

if and only if

Z_{2} \sim τ

. Consequently,

(1): If $I \sim τ$ , then $H_{P}^{I} (I) \sim τ, H_{F}^{I} (I) \sim τ, H_{G}^{I} (I) \sim τ$ .
(2): If $P \sim τ$ , then $H_{F}^{P} (P) \sim τ, H_{G}^{P} (P) \sim τ, H_{I}^{P} (P) \sim τ$ .
(3): If $F \sim τ$ , then $H_{G}^{F} (F) \sim τ, H_{I}^{F} (F) \sim τ, H_{P}^{F} (F) \sim τ$ .
(4): If $G \sim τ$ , then $H_{I}^{G} (G) \sim τ, H_{P}^{G} (G) \sim τ, H_{F}^{G} (G) \sim τ$ .

In the theory of ideal topological spaces there are several characterizations of compatibility. For

(X, τ, I)

the most common equivalent conditions are as follows (see for example [5,7]).

Theorem 11.

The next are equivalent

(1): $I \sim τ$ ,
(2): for every $A \subset X$ , if $A \cap A_{I}^{*} = \emptyset$ , then $A \in I$ ,
(3): for every $A \subset X$ , $A ∖ A_{I}^{*} \in I$ ,
(4): for every $A \subset X$ , if $(X ∖ A) \cup {(X ∖ A)}_{I}^{▹} = X$ , then $A \in I$ ,
(5): for every $A \subset X$ , $A_{I}^{▹} ∖ A \in I$ .

Regardless of a concept we work in, a compatibility of

Z_{1}

can be characterized by another equivalent system

Z_{2}

and by operators

{(\cdot)}_{Z_{2}}^{*}

and

{(\cdot)}_{Z_{2}}^{▹}

Theorem 12.

Let

Z_{1}, Z_{2} \in X

. If

Z_{1} \sim Z_{2}

, then the next are equivalent

(1): $Z_{1} \sim τ$ ,
(2): for every $A \subset X$ , if $A \cap A_{Z_{2}}^{*} = \emptyset$ , then A is $Z_{2}$ -small,
(3): for every $A \subset X$ , $A ∖ A_{Z_{2}}^{*}$ is $Z_{2}$ -small,
(4): for every $A \subset X$ , if $(X ∖ A) \cup {(X ∖ A)}_{Z_{2}}^{▹} = X$ , then A is $Z_{2}$ -small,
(5): for every $A \subset X$ , $A_{Z_{2}}^{▹} ∖ A$ is $Z_{2}$ -small.

Proof.

Let

I_{1} : = H_{I}^{Z_{1}} (Z_{1})

where

Z_{1} \in Z_{1} \in {P, F, G}

. Since

I_{1} \sim Z_{1} \sim Z_{2}

Z_{1} \sim τ

if and only if

I_{1} \sim τ

(by Remark 2), A is

I_{1}

-small if and only if A is

Z_{2}

-small (by Remark 2),

A_{I_{1}}^{*} = A_{Z_{1}}^{*} = A_{Z_{2}}^{*}

A_{I_{1}}^{▹} = A_{Z_{1}}^{▹} = A_{Z_{2}}^{▹}

(by Lemma 2). Then the next are equivalent (note

(ii) \Leftrightarrow (2), (iii) \Leftrightarrow (3), (iv) \Leftrightarrow (4), (v) \Leftrightarrow (5)

)

(1): $Z_{1} \sim τ$ ,
(i): $I_{1} \sim τ$ ,
(ii): for every $A \subset X$ , if $A \cap A_{I_{1}}^{*} = \emptyset$ , then A is $I_{1}$ -small,
(iii): for every $A \subset X$ , $A ∖ A_{I_{1}}^{*}$ is $I_{1}$ -small,
(iv): for every $A \subset X$ , if $(X ∖ A) \cup {(X ∖ A)}_{I_{1}}^{▹} = X$ , then A is $I_{1}$ -small,
(v): for every $A \subset X$ , $A_{I_{1}}^{▹} ∖ A$ is $I_{1}$ -small.
(2): for every $A \subset X$ , if $A \cap A_{Z_{2}}^{*} = \emptyset$ , then A is $Z_{2}$ -small,
(3): for every $A \subset X$ , $A ∖ A_{Z_{2}}^{*}$ is $Z_{2}$ -small,
(4): for every $A \subset X$ , if $(X ∖ A) \cup {(X ∖ A)}_{Z_{2}}^{▹} = X$ , then A is $Z_{2}$ -small,
(5): for every $A \subset X$ , $A_{Z_{2}}^{▹} ∖ A$ is $Z_{2}$ -small.

□

Remark 3.

Note, in a primal case (see for example [1]) a compatibility is called "a topology suitable for a primal". More precisely, we prove τ is suitable for a primal

P

if and only if

H_{I}^{P} (P)

is compatible with τ. Proof: τ is suitable for a primal

P

if and only if

X ∖ A \notin P

whenever

A \cap A_{P}^{⋄} = \emptyset

(see [1] Theorem 4.2) if and only if

X ∖ A \notin P

whenever

A \cap A_{P}^{*} = \emptyset

if and only if A is

P

-small whenever

A \cap A_{H_{I}^{P} (P)}^{*} = \emptyset

if and only if A is

H_{I}^{P} (P)

-small whenever

A \cap A_{H_{I}^{P} (P)}^{*} = \emptyset

if and only if

H_{I}^{P} (P)

is compatible with τ.

Definition 5.

A set A is

I

-big (

P

-big,

F

-big,

G

-big) if A is not

I

-small (

P

-small,

F

-small,

G

-small), equivalently

A \notin I

(

X ∖ A \in P

X ∖ A \notin F

A \in G

). Let

Z \in Z

. A topology τ is

Z

-codense, if any nonempty open set is

Z

-big.

Remark 4.

Let

I \sim P \sim F \sim G

. Then

I = H_{I}^{P} (P)

F = H_{F}^{P} (P)

G = H_{G}^{F} (F)

. So,

A \notin I \Leftrightarrow X ∖ A \in P \Leftrightarrow X ∖ A \notin F \Leftrightarrow A \in G

. That means if

Z_{1}, Z_{2} \in X

and

Z_{1} \sim Z_{2}

, a set A is

Z_{1}

-big if and only if A is

Z_{2}

-big and τ is

Z_{1}

-codense if and only if τ is

Z_{2}

-codense.

From the theory of ideal topological spaces we have the next characterization.

Theorem 13.

τ is

I

-codense if and only if

X_{I}^{*} = X

The property of being

Z_{1}

-codense can be characterized by the operators

{(\cdot)}_{Z_{2}}^{*}

and

{(\cdot)}_{Z_{2}}^{▹}

with respect to another equivalent system

Z_{2}

Theorem 14.

Let

Z_{1}, Z_{2} \in X

. If

Z_{1} \sim Z_{2}

, then the next are equivalent

(1): τ is $Z_{1}$ -codense,
(2): $X_{Z_{2}}^{*} = X$ ,
(3): $\emptyset_{Z_{2}}^{▹} = \emptyset$ .

Proof.

Let

I : = H_{I}^{Z_{2}} (Z_{2})

where

Z_{2} \in Z_{2} \in {P, F, G}

. Then

Z_{2} \sim I

. By Remark 4 and Theorem 13,

τ

Z_{1}

-codense if and only if

τ

Z_{2}

-codense if and only if

τ

I

-codense if and only if

X = X_{I}^{*} = X_{H_{I}^{Z_{2}} (Z_{2})}^{*} = X_{Z_{2}}^{*}

(by Theorem 7), so

(1) \Leftrightarrow (2)

. The equivalence

(2) \Leftrightarrow (3)

follows from equation

\emptyset_{Z_{2}}^{▹} = X ∖ X_{Z_{2}}^{*}

. □

4. Conclusions

(X, τ, Z)

Z \in X

, are valid and usable in the other three spaces

(X, τ, H_{Z_{1}}^{Z_{2}} (Z))

where

Z \in Z_{2} \in {I, P, F, G}

and

Z_{1} \in {I, P, F, G}

Z_{1} \neq Z_{2}

This article does not contain any studies with human participants or animals performed by the author.

Funding

This research received no external funding.

Data Availability Statement

No data has been used in the manuscript.

Acknowledgments

The article was supported by the Slovak Research and Development Agency, Grant No. APVV-20-0045.

Conflicts of Interest

The author declares that he has no conflict of interest.

References

Al-Omari, A.; Acharjee, S.; Özkoç, M. A new operator of primal topological space. Mathematica 2023, 65, 175–183. [Google Scholar] [CrossRef]
Acharjee, S.; Özkoç, M.; Issaka, F.Y. Primal topological spaces. arXiv 2022, arXiv:2209.12676. [Google Scholar] [CrossRef]
Choquet, G. Sur les notions de filtre et grille. C. R. Acad. Sci. Paris 1947, 224, 171–173. [Google Scholar]
Hamlett, T. R.; Jankovic, D. Ideals in general topology. General Topology and Applications 1988, 115–125. [Google Scholar]
Hamlett, T. R.; Jankovic, D. Ideals in topological spaces and the set operator ψ. Bollettino dell’ Unione Matematica Italiana 1990, 7, 863–874. [Google Scholar]
Al-Saadi, H.; Al-Malki, H. Generalized primal topological spaces. AIMS Math. 2023, 8, 24162–24175. [Google Scholar] [CrossRef]
Jankovic, D.; Hamlett, T. R. New topologies from old via ideals. Am. Math. Mon. 1990, 97, 295–310. [Google Scholar] [CrossRef]
Jankovic, D.; Hamlett, T. R. Compatible extensions of ideals. Bollettino dell’ Unione Matematica Italiana 1992, 6, 453–465. [Google Scholar]
Mandal, D. On separation axioms weaker and stronger than regularity and normality via grill. Jour. Pure Math. 2014, 31, 89–100. [Google Scholar]
Mandal, D.; Mukherjee, M. N. Certain new classes of generalized closed sets and their applications in ideal topological spaces. Filomat 2015, 29, 1113–1120. [Google Scholar] [CrossRef]
Modak, S. Topology on grill-filter space and continuity. Bol. Soc. Paran. Mat. 2013, 2013 31, 219–230. [Google Scholar] [CrossRef]
Modak, S. Grill-filter space. J. Indian Math. Soc. 2013, 80, 313–320. [Google Scholar]
Roy, B.; Mukherjee, M. N. On a typical topology induced by a grill. Soochow J. Math. 2007, 33, 771–786. [Google Scholar]
Roy, B.; Mukherjee, M. N. On a type of compactness via grills. Mat. Ves. 2007, 59, 113–120. [Google Scholar]
Roy, B.; Mukherjee, M. N.; Ghosh, S. K. (2008) On a new operator based on grill and its associated topology. Arab. J. Math. Sci. 2007, 14, 21–32. [Google Scholar]
Roy, B.; Mukherjee, M. N. Concerning topologies induced by principal grills. An. Stiint. Univ. AL. I. Cuza Iasi. Mat.(N. S.) 2009, 55, 285–294. [Google Scholar]
Thron, W. J. Proximity structure and grill. Math. Ann. 1973, 206, 35–62. [Google Scholar] [CrossRef]

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On Induced Topologies by Ideal, Primal, Filter and Grill

Abstract

1. Introduction

2. Main Results

3. Applications

4. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

Abstract

1. Introduction

2. Main Results

3. Applications

4. Conclusions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe