Prerpints.org logo
Preprint
Article

On Rhythmic Figures and Cardiac Auscultation

Altmetrics

Downloads

93

Views

29

Comments

0

This version is not peer-reviewed

Submitted:

05 March 2024

Posted:

07 March 2024

You are already at the latest version

Alerts
Abstract
The present article seeks to study whether there is any relationship between the equation of the rhythmic figures (Lugos Abarca, 2023) and cardiac auscultation using Field's method, which consists of representing cardiac sounds by means of musical notation (Field, 2010). A new meaning is given to the equation, concluding a mathematical equality between the equation of the rhythmic figures and the formula for calculating the RR Interval.
Keywords: 
Subject: Medicine and Pharmacology  -   Cardiac and Cardiovascular Systems

1. Introduction

It is probable that the oldest antecedent in reference to the relationship between rhythmic figures and cardiac auscultation dates back to 1824, when René Laënnec, the inventor of the stethoscope, used musical notation to describe the melodic rhythm of a cardiac disorder called venous hum that he heard in a woman with signs of tuberculosis. This event was the first time that musical notation was used in a cardiac context (Segall, 1962; Chew, 2021).
Some time later, the physicist, flutist and nephrologist Michael Field, proposed the analogy between rhythmic perception and cardiac auscultation, which motivated him to musically represent cardiac sounds and murmurs with the intention of training the hearing of medical students and thus improve the medical diagnosis of cardiac injuries and conditions (Field, 2010). An action that simulates the auditory training of musicians.
On the other hand, in a recent investigation an equation was derived to calculate the number of musical measures μ m a r that a song has, by means of the variables of tempo T , the time signature β and the duration of a song t (Lugos Abarca, 2023). From such an expression another formula was derived to calculate the duration of a rhythmic figure, which we will seek to study its possible relationship with the work done by Field.
Therefore, in this article we will study the relationship between rhythmic figures and cardiac auscultation. To do so, we will consider the following hypothesis valid: musical tempo can be considered as an analog to heart rate given its unit of measurement (Vogel et al., 2004), being that of tempo: beats per minute and heart rate: beats per minute. Accepting such a premise, it becomes correct to assume that a beat is equivalent to a musical pulse, hence, the variable T would represent the beats per minute, while the variable β would be the pulses that the waves would generate before a cardiac impulse, finally, the variable t is the RR interval (Montoya, 2013).

2. Preliminaries

The RR interval is the time elapsed between two successive R waves in the ECG, it is measured from the onset of one R wave to the onset of the next (Hall & Guyton, 2021; Thaler, 2023; Alvarado Serrano, 2001), which is a function of the heart rate Τ (Montoya, 2013; Montoya, 2021). Next, we will introduce two base equations for this research, which calculate the RR interval and the R-wave voltage.
For its deduction we start from the standard calibration of millimeter paper for ECG (Lara Prado, 2016): on the x-axis, one second is recorded along 25 mm of paper, while, on the y-axis; one millimeter in voltage reflects a change of 0.1 mV. With this information, the following equations are formulated to determine the time and voltage in the ECG:
The time in seconds of an RR interval is expressed by:
t = 1 25 n
Where, t is the RR interval, n the number of small squares on the x -axis between the RR interval.
The voltage for any R wave in mV is calculated with:
V = 1 10 N
Where, V is the voltage of an R-wave, N the number of small squares on the y -axis of the R-wave.

3. The Equation of Rhythmic Figures and Musical Notation in Cardiac Auscultation

Rhythmic figures are symbols that allow us to read and write rhythmic patterns within scores (Taylor, 2002; Herrera, 2022). They also indicate the duration of a sound according to the tempo value Τ and the pulse corresponding to the figure β (Lugos Abarca, 2023), which is calculated by means of the following equation:
t = 1 Τ β
When analyzing Equation (3.1) from a non-musical perspective, we realize that such an expression could share certain characteristics with cardiac phenomenology, above all, when concluding theoretically that the variables Τ and β can represent analogously: heart rate and heart pulse respectively (Vogel et al., 2004). All of this is based on the units of measurement of musical parameters.
The representation of Laënnec and Field are contrasting, since Laënnec uses a melodic notation, while Field relies on only representing the heart sounds with the musical rhythm. For the purpose of this article, we will make use of Field’s notation because its representation is approximate and detailed with the use of ornamentation notes, articulations and dynamics.
In relation to Field’s work. Chew manages to make a rhythmic transcription of the following ECG (Chew, 2018):
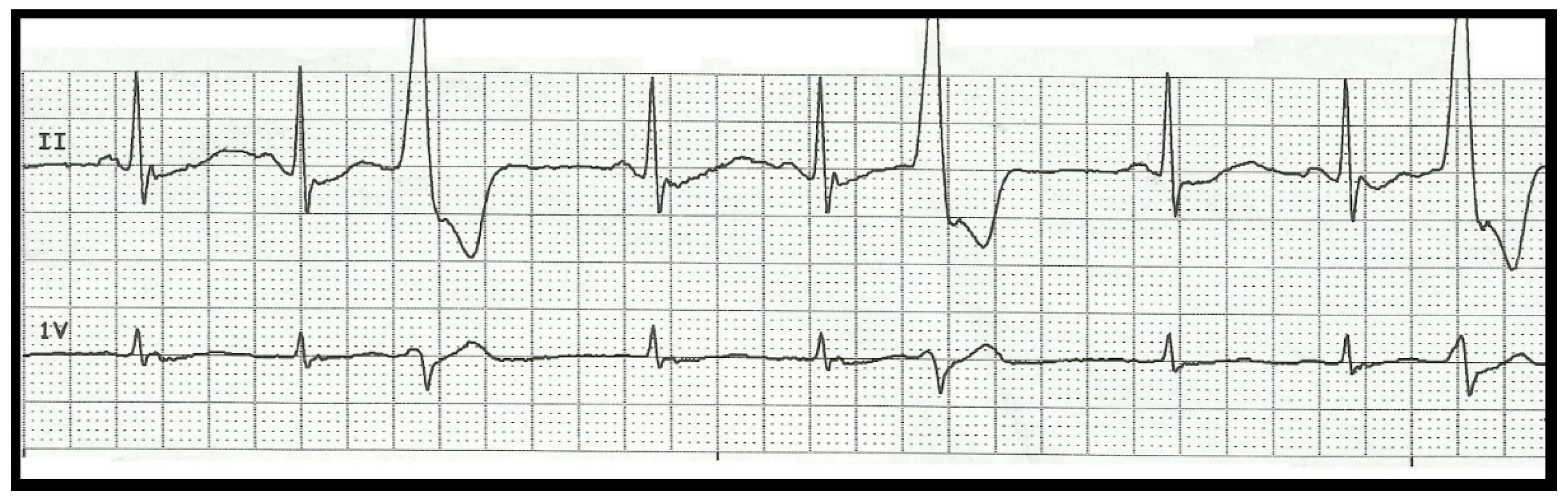
Preprints 100646 g001
Figure 3.1. ECG of trigeminal premature ventricular contractions (2013). From http://floatnurse-mike.blogspot.com/2013/05/ekg-rhythm-strip quiz-123.html.
Figure 3.1. ECG of trigeminal premature ventricular contractions (2013). From http://floatnurse-mike.blogspot.com/2013/05/ekg-rhythm-strip quiz-123.html.
Preprints 100646 g001
Preprints 100646 g002
Figure 3.2. Rhythmic transcription of the ECG in Figure 3.1.
Figure 3.2. Rhythmic transcription of the ECG in Figure 3.1.
Preprints 100646 g002
The transcription is:
This methodology is used by Chew as a creative resource in musical composition (Chew, 2018), Field uses it for clinical purposes. Anyway, both positions give us an argument to consider the following mathematical equality:
1 25 n = 1 Τ β
The term 1 25 n determines the RR interval in seconds, while 1 Τ β in minutes.
Therefore, to satisfy the unit of measure between the two equations; we rewrite the equality as:
1 25 n = 60 Τ β
Where the number 60 works to convert minutes to seconds. Let us return to Equation (3.1) and study it from a cardiac rather than a musical point of view.
t = 60 1 Τ β
As can be seen, the RR interval is inversely proportional to the heart rate Τ and directly proportional to the cardiac pulse β . Here the variable β , now represents the number of R-wave pulses elapsed in the electrocardiogram.
To better understand this concept, let’s assume the following application problem: What will be the RR interval, given three pulses at a heart rate of 100 beats per minute?
From the question the following data are extracted: Τ = 100   l p m ,   β = 3 b , thus, solving 3.4 we obtain as a result:
t = 60 1 Τ β = 60 1 100   l p m 3 b = 1.8   s e g
Let us corroborate such a result with the Formula (2.1). 100 beats per minute corresponds to n = 15 (Rawdy, 2017), i.e., fifteen squares on the x -axis, hence:
t = 1 25 n = 15 25 = 0.6   s e g
Then, we add it three times:
0.6   s e g + 0.6   s e g + 0.6   s e g = 1.8   s e g
Here is another resolution. Consider the following data:
n = 18 , T = 250 3 l ∙ m i n
Solving Equations (2.1) and (3.4) we obtain the same values for time:
1 25 n = 1 25 18 = 0.72   s e g 60 Τ β = 60 250 3 1 = 0.72   s e g
We see that both results coincide, demonstrating the equivalence between both equations and that the result of 3.5 and 3.9 are correct.
Then, we can rewrite 3.4 as follows:
t β = 60 Τ × ∑ 0 β
Such that β ∈ N .
Within a real clinical setting, heart rate is not regular; various pathological and non-pathological factors such as sleep, exercise, emotions, respiration, age, anxiety, stress, certain medications, pollution, etc., cause different kinds of heart rate variations to occur (Aldredge & Welch, 1973; Kanters et al., 1996; Lamberts et al., 2004; Massin et al., 2000; Rajendra Acharya et al., 2006; Cerruto et al., 2017; Riojas-Rodríguez et al., 2006; Nieto-Jimenez et al., 2020). This phenomenon is called: heart rate variation HRV which, are all those temporal variations of heart rate or beat-to-beat interval (Kulinski et al., 2022).
However, for Equation (3.4) to be practical, it must be adapted to HRV. Therefore, considering the heart rate variation forces us to reinterpret the variable Τ since, for our objective, it is convenient to study it as a differential: d Τ .
So, if we consider this modification; the expression 3.10 is rewritten as:
t β = 60 d d Τ ∑ 0 β β
Equation (3.11) is discrete due to the nature of the cardiac pulses (Rodríguez, 2012), however, it is valid to consider it continuous, since it is possible to calculate the time when β = 0.1   b or β = 0.6   b .
t = 60 d β d Τ
In Equation (3.12), what is reflected in the article by Montoya (2013) is satisfactorily fulfilled: for in such research; it was made clear that the variation of the heart rate depends on the RR interval and the other way around, similar to what is understood when interpreting Equation (3.12).

4. Conclusion

In this article, through the methodology designed by Field to express murmurs and heart sounds with musical notation, we were able to give a new meaning to the equation of the rhythmic figures t by associating it with the formula of the RR interval. As a result, Equation (3.12) can be used to calculate the heart rate and the RR interval.
It is believed that the equations presented here provide a sufficient theoretical framework for the purpose of further expanding the opportunities for study and research that rhythmic figures have with respect to the electrocardiogram. Knowing that Equation (3.12) is capable of calculating the RR interval as a function of the heart rate and the cardiac pulses to occur, it could become a clinical tool since such an equation would allow knowing whether a cardiac rhythm will be regular or irregular by means of a mathematical model (Veloza et al., 2019; Cabrera Rojo et al., 1997; Jugo et al., 2008), in order to reduce cardiac morbidity and mortality (Tsuji et al., 1994; Vaishnav et al., 1994).

References

  1. Aldredge, J. L., & Welch, A. J. (1973). Variations of heart rate during sleep as a function of the sleep cycle. Electroencephalography and Clinical Neurophysiology, 35(2), 193-198. [CrossRef]
  2. Alvarado Serrano, C. (2001). Análisis de la variabilidad de intervalos de tiempo del ECG. Universitat Politècnica de Catalunya.
  3. Cabrera Rojo, I., Cabrera Santos, A., & Gallardo Montes de Oca, G. (1997). Variabilidad de la frecuencia cardíaca en el joven normal. Revista Cubana de Investigaciones Biomédicas, 16(2), 98-103.
  4. Cerruto, G., Mainardi, L., Koelsch, S., & Orini, M. (2017, September). The periodic repolarization dynamics index identifies changes in ventricular repolarization oscillations associated with music-induced emotions. In 2017 Computing in Cardiology (CinC) (pp. 1-4). IEEE. [CrossRef]
  5. Chew, E. (2018). Notating disfluencies and temporal deviations in music and arrhythmia. Music & Science, 1, 2059204318795159. [CrossRef]
  6. Chew, E. (2021). On making music with heartbeats. Handbook of Artificial Intelligence for Music: Foundations, Advanced Approaches, and Developments for Creativity, 237-261. [CrossRef]
  7. Chew, E., Taggart, P., & Lambiase, P. (2019, September). Cardiac Response to Live Music Performance: Computing Techniques for Feature Extraction and Analysis. In 2019 Computing in Cardiology (CinC) (pp. Page-1). IEEE. [CrossRef]
  8. Field, M. J. (2010). Music of the heart. The Lancet, 376(9758), 2074. [CrossRef]
  9. Hall, J. E., & Guyton, A. C. (2021). Tratado de fisiología médica, 14.a Edición. España: Elsevier Castellano.
  10. Herrera, E. (2022). Teoria Musical y Armonia Moderna vol. 1. España: Antoni Bosch Editor.
  11. Jugo, D., Medina, R., Rojas, R., Nuñez, T., Arellano, E., & Borrego, A. (2008). Nuevos métodos de análisis de la variabilidad de la frecuencia cardiaca. In IV Latin American Congress on Biomedical Engineering 2007, Bioengineering Solutions for Latin America Health: September 24th–28th, 2007 Margarita Island, Venezuela (pp. 1182-1185). Springer Berlin Heidelberg. 1182. [CrossRef]
  12. Kanters, J. K., Højgaard, M. V., Agner, E., & Holstein-Rathlou, N. H. (1996). Short-and long-term variations in non-linear dynamics of heart rate variability. Cardiovascular research, 31(3), 400-409.
  13. Kulinski, J., Ofori, E. K., Visotcky, A., Smith, A., Sparapani, R., & Fleg, J. L. (2022). Effects of music on the cardiovascular system. Trends in cardiovascular medicine, 32(6), 390-398. [CrossRef]
  14. Lamberts, R. P., Lemmink, K. A., Durandt, J. J., & Lambert, M. I. (2004). Variation in heart rate during submaximal exercise: implications for monitoring training. The Journal of strength & conditioning research, 18(3), 641-645. [CrossRef]
  15. Lara Prado, J. I. (2016). El electrocardiograma: una oportunidad de aprendizaje. Revista de la Facultad de Medicina (México), 59(6), 39-42.
  16. Lugos Abarca, J. A. (2023). Sobre la matemática de los compases musicales y su relación con la geometría. Ricercare, (16), 27–58. [CrossRef]
  17. Massin, M. M., Maeyns, K., Withofs, N., Ravet, F., & Gérard, P. (2000). Circadian rhythm of heart rate and heart rate variability. Archives of disease in childhood, 83(2), 179-182. [CrossRef]
  18. Montoya, J. R. (2021). Detección de picos R en ECGs y su aplicación en serie de tiempos RR. INNOVA UNTREF. Revista Argentina De Ciencia Y Tecnología, 1(2). Recuperado a partir de http://revistas.untref.edu.ar/index.php/innova/article/view/970.
  19. Montoya, J. R. A. (2013). Determinación de intervalos RR a partir de datos crudos del ECG. Revista científica de la Universidad de Mendoza, (1).
  20. Nieto-Jimenez, C., Ruso-Álvarez, J., Pardos-Mainer, E. E., & Orellana, J. N. (2020). La variabilidad de la frecuencia cardiaca en el control del entrenamiento en un corredor de Ironman. Estudio de caso (Heart Rate Varibility in the training monitoring of an Ironman runner. A case study). Retos, 37, 339-343.
  21. Rajendra Acharya, U., Paul Joseph, K., Kannathal, N., Lim, C. M., & Suri, J. S. (2006). Heart rate variability: a review. Medical and biological engineering and computing, 44, 1031-1051.
  22. Rawdy [@DrRawdy]. (2017, May 13). CALCULA TU FRECUENCIA CARDIACA EN EL EKG. Youtube. https://www.youtube.com/watch?v=oApju3HEDl0.
  23. Riojas-Rodríguez, H., Holguin, F., González-Hermosillo, A., & Romieu, I. (2006). Uso de la variabilidad de la frecuencia cardiaca como marcador de los efectos cardiovasculares asociados con la contaminación del aire. Salud pública de México, 48, 348-357.
  24. Rodríguez, J. (2012). Nuevo diagnóstico físico y matemático de la monitoria fetal: predicción de aplicación clínica. MOMENTO, (44), 49-65.
  25. Segall, H. N. (1962). Evolution of graphic symbols for cardiovascular sounds and murmurs. British heart journal, 24(1), 1.
  26. Taylor, E. R. (2002). La teoría musical en la práctica. Music Theory in Practice (ABRSM).
  27. Thaler, M. S. (2023). El libro del ECG (10th ed.). Lippincott Williams and Wilkins.
  28. Tsuji, H., Venditti Jr, F. J., Manders, E. S., Evans, J. C., Larson, M. G., Feldman, C. L., & Levy, D. (1994). Reduced heart rate variability and mortality risk in an elderly cohort. The Framingham Heart Study. Circulation, 90(2), 878-883. [CrossRef]
  29. Vaishnav, S., Stevenson, R., Marchant, B., Lagi, K., Ranjadayalan, K., & Timmis, A. D. (1994). Relation between heart rate variability early after acute myocardial infarction and long-term mortality. The American journal of cardiology, 73(9), 653-657. [CrossRef]
  30. Veloza, L., Jiménez, C., Quiñones, D., Polanía, F., Pachón-Valero, L. C., & Rodríguez-Triviño, C. Y. (2019). Variabilidad de la frecuencia cardíaca como factor predictor de las enfermedades cardiovasculares. Revista Colombiana de Cardiología, 26(4), 205-210. [CrossRef]
  31. Vogel, C. U., Wolpert, C., & Wehling, M. (2004). How to measure heart rate?. European journal of clinical pharmacology, 60, 461-466. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated