Prerpints.org logo
Preprint
Article

Hexa-Propeller Airship for Environmental Surveillance and Monitoring in Amazon Rainforest

Altmetrics

Downloads

81

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

06 March 2024

Posted:

07 March 2024

You are already at the latest version

Alerts
Abstract
This paper proposes a new kind of airship actuator configuration for surveillance and environmental monitoring missions. We present the design and application of a 6-propeller electrical airship (Noamini) with independent tilting propellers, allowing improved and flexible maneuverability. The vehicle has different combinations of differential propulsion and can be used in 2, 4 or 6 motors configuration. We developed a high-fidelity airship simulator for the Noamini airship, which was used to test and validate a control-guidance approach. Incremental Nonlinear Dynamic Inversion (INDI) is used for the velocity/attitude control to follow a high-level L1 guidance reference in a simulated waypoint tracking mission with wind and turbulence. The proposed framework will be soon implemented in the onboard control system of the Noamini, an autonomous airship for environmental monitoring and surveillance applications.
Keywords: 
Subject: Engineering  -   Aerospace Engineering

1. Introduction

Dirigibles, or airships, present a unique operational advantage by combining energy-efficient cruising, a distinctive characteristic of fixed-wings aircraft, with the capability to hover, present in rotary-wings vehicles [1]. Even the best hybrids VTOL aircrafts fail to hover efficiently, due to the energy needed to counteract the gravitational force, which in airships is granted by the buoyancy gas. They are also safer than other platforms under failure or degradation, as they would descend slowly to the ground in such a case. The combination of these features with the notable evolution in aerial robotics in the last 20 years lead to a renewed interest in the use of airships for applications like cargo transportation [2], telecommunications [3] and environmental monitoring [4].
This last theme is the focus of this work, in the context of the national project InSAC1. The project aims to develop a semi-autonomous airship for performing environmental monitoring/surveillance tasks in Amazon rainforest, including cruise flights and ground-hover (i.e., keep a stationary position with respect to a ground target).
Usually, these two flight modes (cruise/hover) encompass two conflicting flight mission objectives: total mission covered area vs. detailed data acquisition. Considering the aircraft autonomy and the amount of time needed to acquire a given unit of data, cruising is associated to minimizing the total mission time per unit of data, allowing to cover a larger area. Hovering flight, instead, seeks to maximize the amount of data acquired in an specific location.
However, in both cases, the robust flight under actual weather conditions is still one of the biggest issues that prevents airships to fully benefit from its maneuverability advantages. In this way, the safe and accurate airship control under strong wind conditions is still an open theme of research investigations, due to the limited lateral actuation available in the vehicle [3,5].
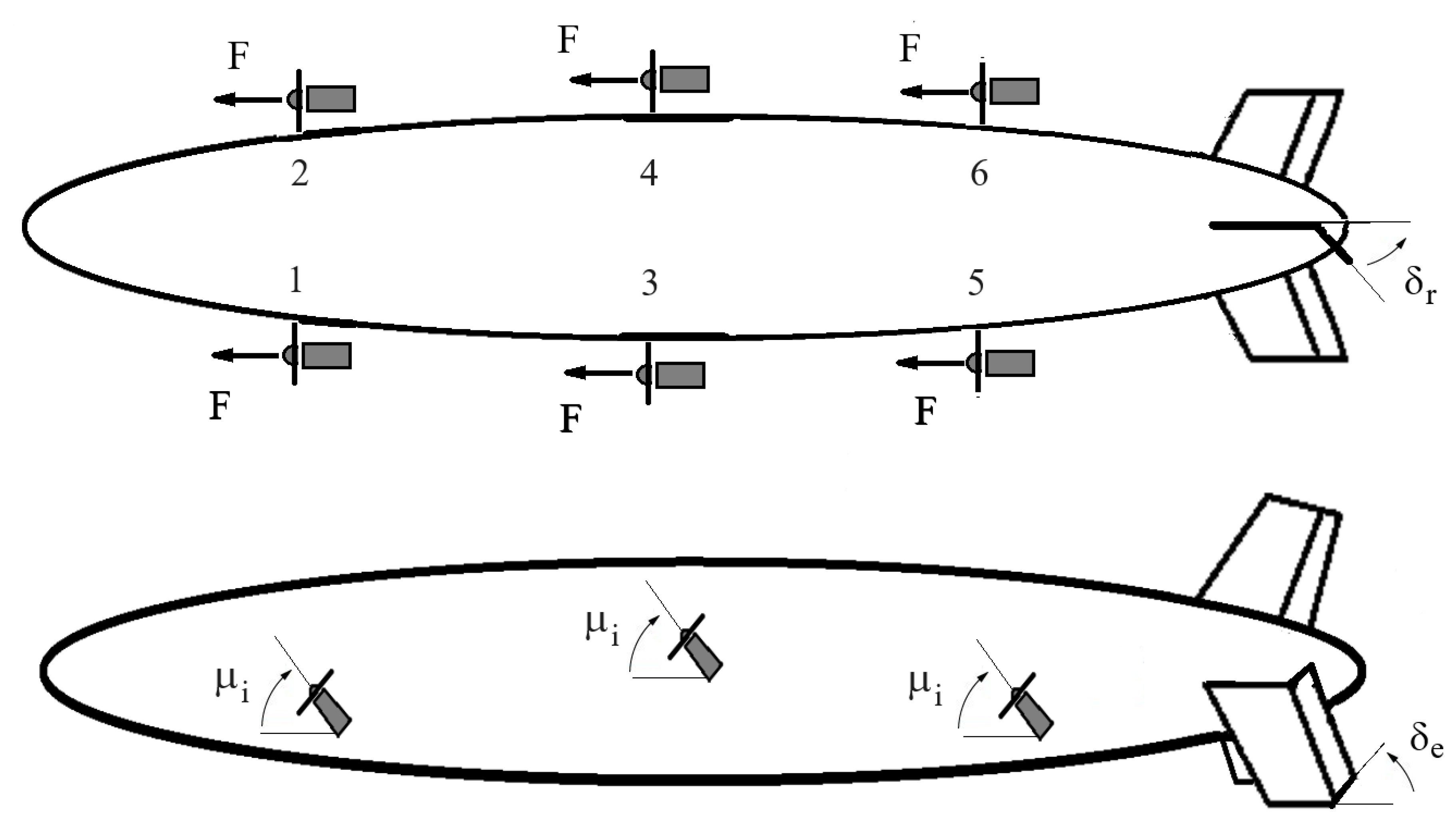
The proposal of an airship design with an increased maneuvering capability is the first contribution of this work. We present here the design and application of a new kind of 6-propeller electrical airship with improved actuation features (Figure 1). The airship prototype, named Noamini, is tailored for a specific class of semi-autonomous airships designed for environmental monitoring, a context where large covered areas and quantity of acquired data are equally important.
The blimp, built in Germany, has an important innovation: an actuation system with six electric motors with independent tilting propellers (up to 360 deg), allowing the craft to take off and land vertically, perform faster yaw/pitch maneuvers and improve its hover controlability in the presence of wind. The vehicle can be used in 2, 4 or 6 motors configuration, depending on the mission to be executed. It also enables the use of differential propulsion in front-rear, left-right or cross configurations, improving the control torque to compensate the wind disturbances at low airspeeds, where the tail efficiency fails.
Further, we developed a high-fidelity airship simulator for the Noamini airship, whose aerodynamic model is adapted from the seminal work of [6], making use of a large wind tunnel database. The airship simulator, in Simulink/Matlab, also includes modeling of sensors/actuators, derivative filters and wind estimators [9,10]. The simulator environment is used to test and validate a control/guidance approach derived for the path tracking task of Noamini airship.
Airship control is known to be a challenge for the control systems designers as they are underactuated vehicles with strong nonlinear underdamped dynamics [11]. Further, many nonlinear control approaches, developed previously, like sliding mode [12], backstepping [13] and dynamic inversion [14], are not sufficiently robust, requiring an accurate knowledge of the vehicle model [15].
In this work, we apply the approach of Incremental Nonlinear Dynamic Inversion (INDI), developed in 2010, which is a natural evolution of the classic Nonlinear Dynamic Inversion (NDI). Aiming to reduce the model dependency of classic controllers, INDI assumes that the change in control is significantly faster than the change in the states, such that the sensor feedback supplies the necessary information about the model for the controller, which is thus considered a "sensor-based" controller [15], instead of a "model-based" one. Due to its robustness properties, INDI control has been successfully applied to a number of different aerial vehicles since then, including an e-VTOL aircraft of NASA Ames [16], a Passenger Aircraft from DLR [17] and conventional drones [18,19,20,21].
For the guidance approach, we implemented the L1 guidance, which is a path-following algorithm that expands the capabilities of conventional autopilots, by adding a virtual target running along the path, with the vehicle’s attitude control effectors following this virtual target [22].
In this way, the second contribution of this paper is the design and test of a control/guidance approach for the waypoint tracking mission of the 6-propeller airship.
The remaining of this paper is organized as follows. Section 2 describes the vehicle application scenario: the surveillance and environmental monitoring of forest segments in the Amazon rainforest region. Section 3 describes the Noamini platform and its subsystems. Section 4 summarizes the vehicle modelling and simulator. Section 5 presents the proposed guidance and control approach for the waypoint tracking problem. Section 6 presents the simulation results for a typical waypoint tracking mission, and Section 7 concludes the paper.

2. Forest Surveillance and Environmental Monitoring

The Amazon biome is immensely rich and of recognized ecological relevance [23]. The Amazon rainforest is dense, flooded by the Amazon river and its tributaries, forming the world’s larger river basin, with a total areal with the same scale of the lagers countries, and it is sparsely occupied by humans. Therefore, the protection of the ecosystem, the conservation and sustainable use of natural resources, and the sustainable development of existing population centers, pose complex challenges that are beyond the capability of any current technology. In this work, the authors are interested in two different missions, the aerial surveillance and environmental monitoring.

2.1. Aerial Surveillance

As aerial surveillance, we are interested on a specific, although crucial, aspect of the Amazon forest conservation: the interaction between urban areas and the surrounding forest. The inevitable anthropogenic pressure promotes deforestation by extending the urban occupation towards the forest. Consider, for instance, the native forest segment where the campus of the Federal University of Amazon is located (Figure 2). This 6.7 M m 2 protected reserve is the third world largest native forest segment in urban area. Despite being protected by both state and federal laws, for decades residents have enlarged their properties towards the forest. Figure 2 presents two examples (among many others) of such occurrences, indicated by red arrows. Furthermore, we can clearly see the value of low altitude data over high altitude images to timely detect these events.
Currently, a significant portion of information available about the forest comes from satellite images provided at intervals of days or even weeks [24]. Even when considering the importance of these data, they are less effective for short-term actions, such as triggering the response to a wildfire before it spreads or dispatching law reinforcement agents to an area where deforestation is occurring. In those contexts, the application of low-altitude aerial monitoring systems brings indisputable advantages by providing multimodal information with high regularity (time between samples), small granularity (order of magnitude of the sampling unit), and low latency (time between acquisition and availability of the sample) [27].
The surveillance mission profile combines flyover with hovering at specific points of interest. The typical zig-zag scan flight for area coverage is not suited here, as the conflicting areas are in the forest border, and fixed wings aircraft would require more than one pass over a suspected location, or off-line inspection of the acquired imagery data, to search for anomalies (irregular deforestation) [24]. On the other hand, one may realize that even considering a urban segment, this reserve is too large for hover-capable rotary-wings aircraft. Only airships can combine cruise flight mode with hover to go through the reserve border and focus on points of interests, whenever necessary [4]. Moreover, the airship has the capability to modulate the hovering altitude according to the situation and, as a bonus, it can zig-zag an area if a scanning is necessary.

2.2. Environmental Monitoring

The environmental monitoring missions concern the gathering of multimodal sensory data. The payload includes images in multiple spectral ranges, lidar, air chemical and physical parameters. Three are the mission objectives identified so far:
  • Analysis of the aerosol layer above the canopy. This layer is of great research importance, as the rain forest is known for having a thick aerosol layer, which droplets captures all sort of suspended particles. Airships are the only aerial vehicle capable to sense the aerosol composition and density. Rotary wings disperse the droplets and the turbulence of fixed-wings reduces the correlation between the acquired data and the actual layer [25];
  • Forest inventory. The native segment is a valid representation of the Amazon forest. Researchers are interested in mapping the specimens of trees, their changes during the year, and even the production forecast for those with economic value. Airships cruise flight capability is of use in this case [26,28];
  • Wildlife monitoring. Forest areas close to human occupation are known to have a severe depletion in wildlife diversity. Moreover, street dogs and cats act as invasive specimens, decimating small animals, such as wild rodents and birds. Once more, airships are a very suited monitoring platform due to its capacity to quietly flyover an area of interest and stay above a point of interest [4].
The payload details are not yet available, but the authors are very confident that Noamini will be able to perform a diverse variety of missions simultaneously.

3. Airship Platform

In order to provide a general idea of this kind of aerial vehicle, including configurations and limitations and mentioning its usual sensors and actuators available, the Noamini prototype is described in this section.
The primary actuators within the Noamini airship (refer to Figure 3) consist of three aerodynamic tail fins in Y-inverted configuration, functioning as rudder, elevator, aileron, and six vectorizable electric thrusters. These thrusters serve the dual purpose of offsetting the aircraft’s excess weight during low-speed operation (e.g. hovering) and enhancing maneuverability across the entire flight profile. The airship is equipped with a ballonet to allow reaching altitudes up to 200m while keeping the envelope pressure.
The vector of control inputs u = [ δ e , δ a , δ r , δ 1 , ⋯ , δ 6 , μ 1 , ⋯ , μ 6 ] T , is composed by the equivalent deflections of elevator, aileron, and rudder ( δ e , δ a , and δ r ), plus the six δ i inputs representing the normalized input voltages of the i-th thruster, and the vectoring angles of the i-th propeller, given by μ i , i = 1 , . . . , 6 .
To reduce the redundancy, while making the controller design more natural, propeller powers are configured for joint use at forward power δ f = ( δ 1 + δ 2 + δ 3 + δ 4 + δ 5 + δ 6 ) / 6 , left/right differential δ l r = ( δ 1 + δ 2 − δ 5 − δ 6 ) / 4 , front/back differential δ f b = ( δ 1 − δ 2 − δ 5 + δ 6 ) / 4 , and cross-differential δ c = ( δ 1 − δ 2 + δ 5 − δ 6 ) / 4 . Similar configurations have been set for vectorizations.

4. Airship Model and Simulator

A good knowledge of the airship model and behavior, together with a truthful simulator, are essential conditions for a successful control design [14]. For this reason, the airship model and respective simulator are presented in this section, with the airship modeling in subsections 4.1 and 4.2, and the simulator description in subsection 4.3.

4.1. Airship Dynamic Model

The airship dynamic model is a mathematical description of the airship motion, representing the relations between the control inputs and the state variables [10], that is:
x ˙ = f ( x , u , d )
where:
  • The state x = [ v T , ω T , p T , Φ T ] ∈ R 12 includes the linear v = [ u , v , w ] ∈ R 3 , and angular ω = [ p , q , r ] ∈ R 3 inertial velocities of the airship expressed in the body-fixed frame, the cartesian position p = [ p N , p E , p D ] ∈ R 3 of its center of volume in the inertial frame, and the attitude of the airship, given by the Euler angles Φ = [ ϕ , θ , ψ ] ∈ R 3 .
  • The input vector u = [ δ e , δ a , δ r , δ 1 , ⋯ , δ 6 , μ 1 , ⋯ , μ 6 ] T ∈ R 15 where δ e , δ a , and δ r was described above.
  • The disturbance vector d ∈ R 6 includes the wind input (wind velocity) expressed in the inertial frame with a constant (deterministic) term and a six components vector modelling the atmospheric turbulence (nonconstant wind). It is represented by linear wind velocity p ˙ W = [ p ˙ N W , p ˙ E W , p ˙ D W ] T and angular wind velocity ω W = [ p W , q W , r W ] T .
We should remark here a set of important assumptions and considerations regarding the development of the airship model [14], as stated below:
  • The airship displaces a very large volume of air and its virtual (added) mass and inertia properties become significant, i.e., the lighter-than-air vehicle behaves as if it had a mass and moments of inertia substantially higher than those indicated by conventional physical methods.
  • Three kinds of masses and inertia matrices must be considered: the mass and inertia ( m ∈ R , J ∈ R 3 × 3 ) of the vehicle itself; the mass and inertia ( m B ∈ R , J B ∈ R 3 × 3 ) of the buoyancy air, corresponding to the air displaced by the total volume of the airship; and the virtual mass and inertia ( M V ∈ R 3 × 3 , J V ∈ R 3 × 3 ) , which may be regarded as the mass of air around the airship and displaced with the relative motion of the airship in the air.
  • The airship mass changes in flight due to ballonet deflation or inflation.
  • The airship is assumed to be a rigid body, and the aeroelastic effects are neglected.
The differential equation describing the airship movement is obtained from the second Newton Law applied for the vehicle inertial velocities given in the local frame. If we represent these linear and angular velocities as V = [ v T , ω T ] T , then, the dynamic equation can be derived as [29]:
M V ˙ = F d + F a + F p + F g + F w
where, M represents the 6 × 6 mass matrix, encompassing both real and virtual inertia elements characteristic of the dynamics of floating air vehicles. The 6 × 1 vectors given by Fd , Fa , Fp , Fg , and Fw correspond, respectively, to the inertial, aerodynamic, propulsive, gravitational/buoyancy, and wind-influenced forces and moments.

4.2. Airship Dynamic Simulator

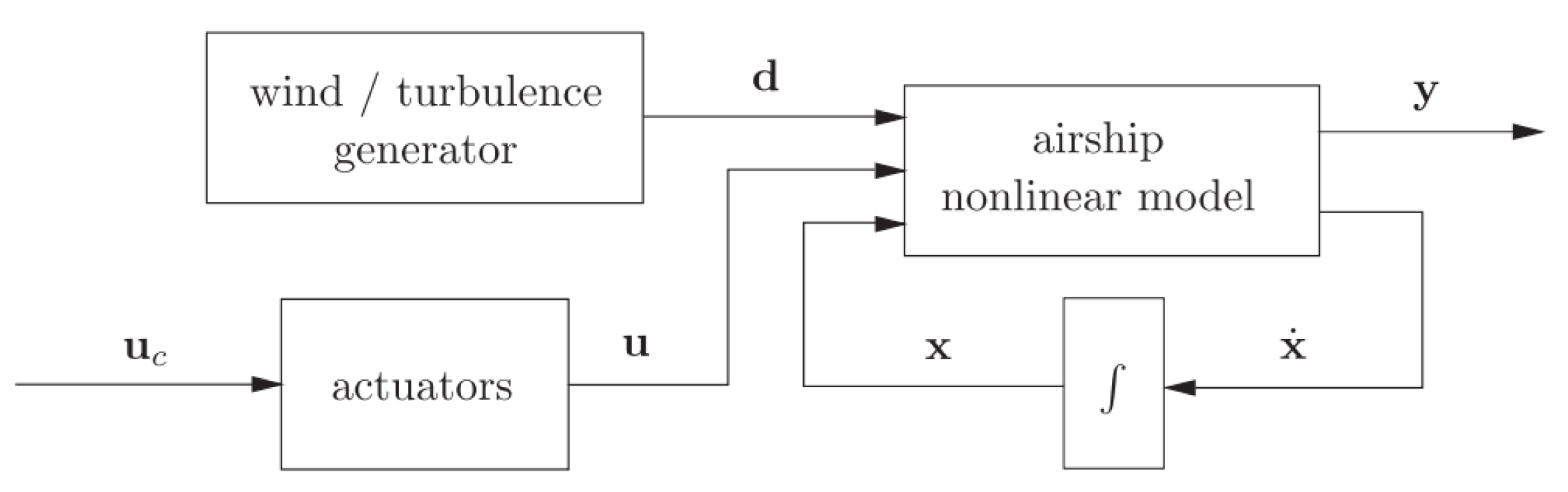
The dynamic model, derived above, encompasses 6 degrees of freedom and serves as the foundation for a MATLAB/Simulink simulator, facilitating the design and validation of the airship control and guidance strategies [10].
The simulator block diagram of the airship open-loop model is represented in Figure 4 below.
The airship nonlinear model, as described by (1), is a function of the state variables x , the actuators input u and the wind disturbances d . These last include both constant wind and atmospheric turbulence as a Dryden model with three white noise inputs [37]. The actuators model includes the propellers and control surfaces dynamics, delays and saturations applied to the actuators command input u c . The output vector y consists of variables of interest to be monitored, and depends on the available sensors. The sensors modeling include errors like noise, bias, saturation and quantification [9]. Also, some variables like attitude are not directly measured, requiring state observers that are included in the simulator, together with a Kalman Filter for the wind estimation [10].
The aerodynamic model considered is based on the seminal work presented in [6,7] and takes advantage of information from a wind tunnel database built to model the Westinghouse YEZ-2A airship. The aerodynamic coefficients available in this database are a function of the aerodynamic incidence angles and the deflections of the tail surfaces. The aerodynamic incidence angles, originally limited to ±30 degrees, were further extended to cope with the whole range of airspeeds and angles of a usual flight, using curve fitting and extrapolation procedure [8].
Additional features of the Noamini airship simulator are:
  • Inclusion of models of the motors and propellers, as well as the discharge model of the batteries (3 packs, each for one pair of motors).
  • Inclusion of a nonlinear-based optimization routine to find the trim conditions and linearized models, which can be computed for different propulsion modes.
  • Finally, the 6 propellers result in a redundant propulsion, and we assume each of them may be controlled both in throttle command and vectoring angle. With this redundancy, it may be possible to choose among active propellers, minimizing a given cost function.

4.3. Linearized Longitudinal/Lateral Dynamics

The airship dynamics is highly nonlinear flight dependent, with very different behavior as the airspeed varies from the hovering flight (HF), or low speed flight, to the cruise or aerodynamic flight (AF) [10,14]. The complexity of the nonlinear model equations justifies the search for a linearized version, which will also be useful for the design of the incremental controller (INDI).
The linearization of the dynamic equations is performed for trimmed conditions around equilibrium, which is commonly a horizontal straight flight, without wind incidence [10,14]. As a consequence of the linearization process, a decoupled vehicle description is also obtained, such that two independent motions may be considered: the motion in the vertical plane, named longitudinal, and the motion in the horizontal plane and rolling, named lateral.
The longitudinal (v) and lateral (h) models are represented by:
x ˙ ˜ v = A v x ˜ v + B v u ˜ v
x ˙ ˜ h = A h x ˜ h + B h u ˜ h
The state vector x ˜ v = [ u ˜ , w ˜ , q ˜ , θ ˜ , h ˜ ] T comprises the small variations on longitudinal velocity, vertical velocity, pitch rate, pitch angle, and altitude. The input u ˜ v = [ δ ˜ e , δ ˜ f , δ ˜ f b , μ ˜ f ] T represent the variations on elevator deflection, total thrust, forward differential thrust, and synchronized vectoring angles respectively.
The state vector x ˜ h = [ β ˜ , p ˜ , r ˜ , ϕ ˜ , ψ ˜ ] T comprises the small variations on sideslip angle, roll rate, yaw rate, roll angle and yaw angle, respectively. The input u h = [ δ ˜ a , δ ˜ r , δ ˜ l r , δ ˜ c , μ ˜ l r ] T includes the variations on aileron and rudder deflections, left/right differential thrust, cross-differential thrust, and left/right differential vectoring, respectively.

5. Control and Guidance Proposal

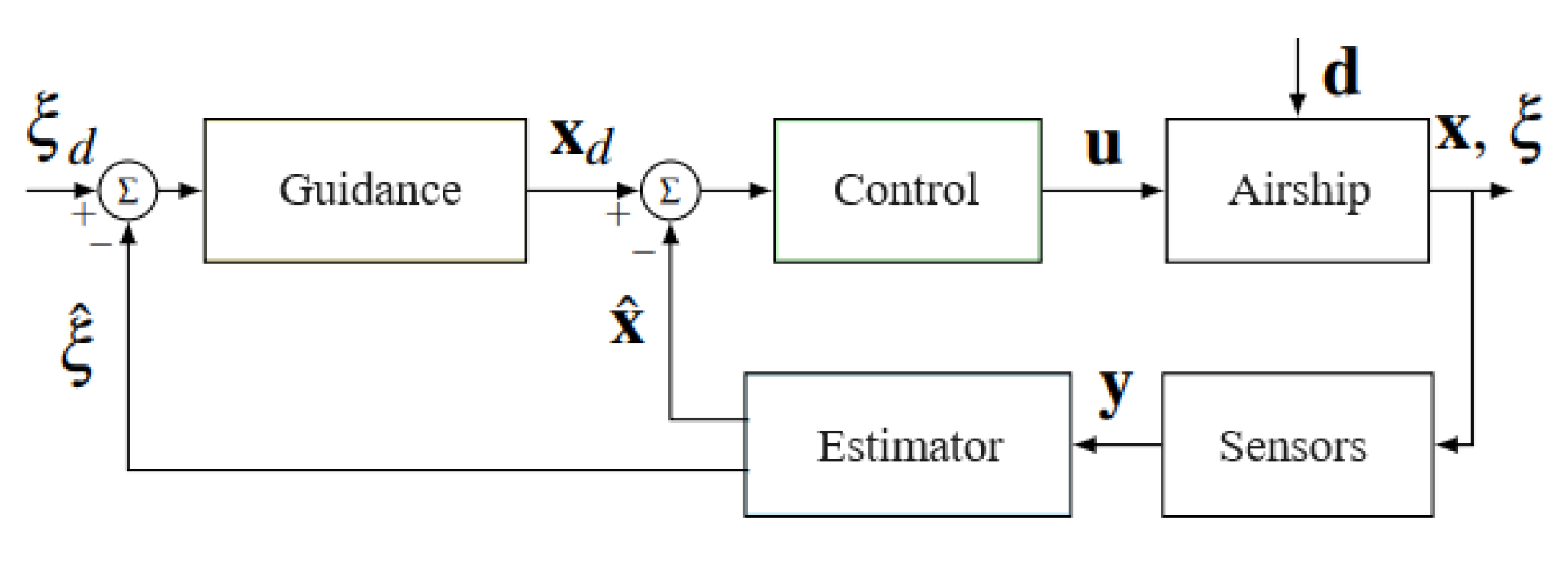
Aiming at the autonomous airship goal, aerial platform positioning and path-tracking should be assured by a control and navigation system, which involves four basic topics: path planning, guidance, control, and data acquisition [5,10].
This separation modularizes the platform allowing to switch the guidance strategy without losing guarantees given by the control loop or estimation loop. Also, the tuning is easier, once the tests can be done with a modular procedure. The path planner is responsible for generating a trajectory for the guidance loop, which aims to minimize the pose (position/orientation) error. Meanwhile, the control level aims to correct velocity and/or acceleration errors. The data acquisition block includes data sensing, filtering, and estimation, which aims to extract the necessary information about the vehicle motion for closing the control and guidance loops [9].
Figure 5 shows a block diagram with the proposed overall navigation architecture, where x is the vector of linear and angular velocities in body frame, ξ is the vector of position in the global frame, u is the control input for the airship, d is the disturbance vector and ξ d is the desired position.
Prior to present the control/guidance approaches it is important to remark the challenges related to the control of this type of hexa-propeller lighter-than-air vehicle.
Firstly, we have to consider the issue of the actuators efficiency, which is heavily dependent on the airship flight region.
In the low airspeed region (HF), the tail surfaces have reduced authority, since the action from the surface deflections is a function of the dynamic pressure and varies with the square of the airspeed. This leaves the airship to be mainly controlled by the propulsion force inputs of the six propellers, which provide longitudinal and vertical forces, pitching and rolling torques [10,14].
As opposed to this, in aerodynamic flight (AF), the tilting angle of the propellers is no longer necessary to compensate the excess of weight, and the maneuvering is mostly accomplished by the tail fins. The surface deflections of the inverted "Y" correspond to the three standard inputs of aileron, elevator and rudder deflections which generate the torque inputs for the roll, pitch and yaw motions.
Another important point is that although presenting 15 control inputs (see the components of vector u ) to control 6 forces (three forces and three torques), the airship still presents numerous limitations for the control design of the full flight envelope, among which we can state:
  • The majority of the actuators indeed act on the longitudinal motion.
  • No actuator is really available to oppose the aerodynamic side force ( F Y ) .
  • Although independent vectoring angles for the six engines are possible, it is safe and practical to consider all of them with the same vectoring angle, except, eventually, for the front-back differential case, in the four down motors configuration.
  • The tail surfaces depend on the airspeed and their authority vanishes in the no-wind case, leaving the airship to be controlled solely by the force inputs.
  • All the actuators have level and rate saturation limits that cannot be avoided.
  • The engines, in particular, have their own dynamics, with response times, that must be taken into account.
All these aspects greatly increase the complexity of the design of the airship control/guidance system, described in the sequel.

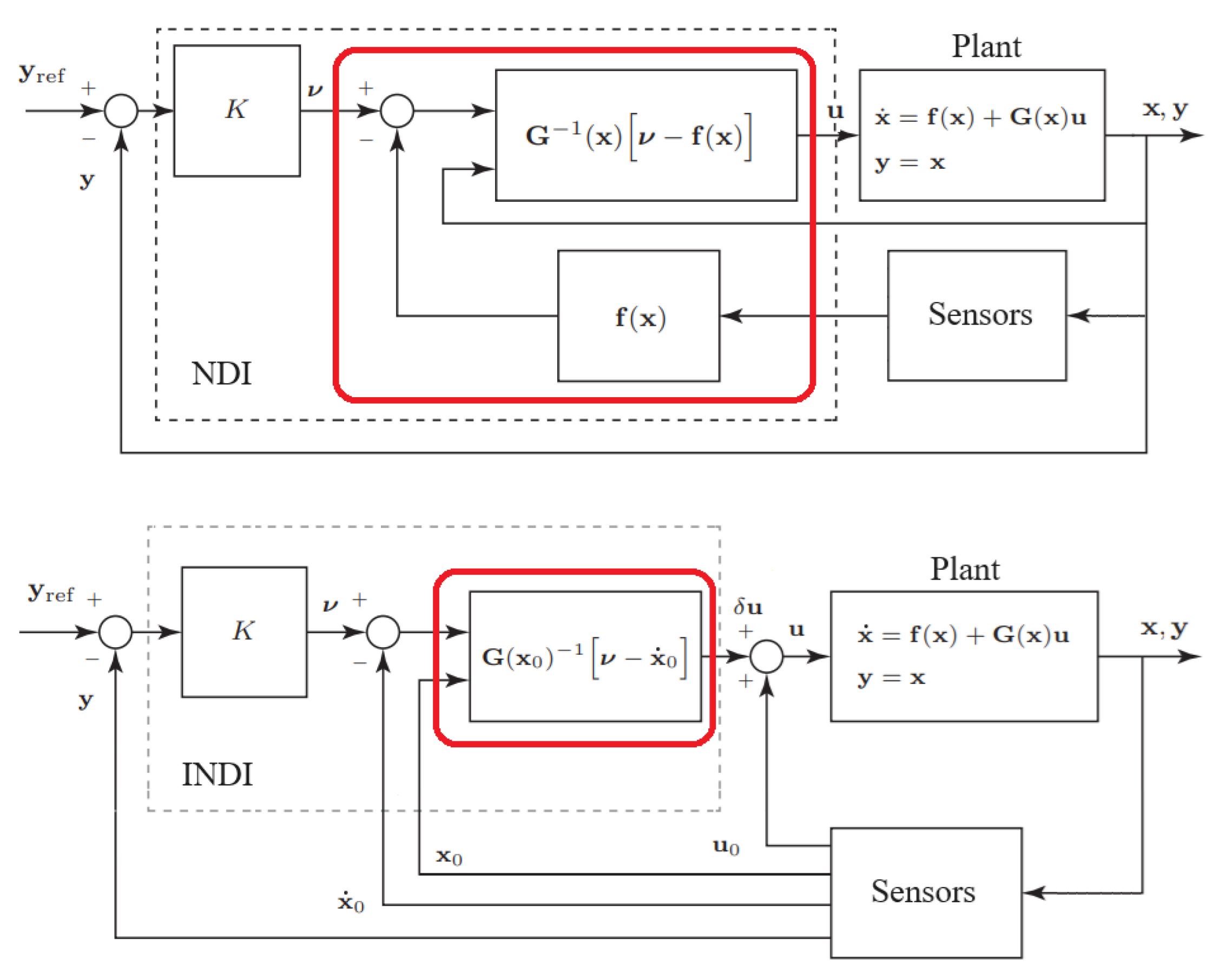
5.1. Incremental Nonlinear Dynamic Inversion Control (INDI)

In the last 20 years, we have investigated different airship control approaches like sliding-modes (SMC) [12], backstepping [13], dynamic inversion, gain schedulling [14], and backstepping-SMC [29]. But none of them is as promising as the Incremental Nonlinear Dynamic Inversion (INDI), that we have been investigating since 2015 [10,30].
INDI was a natural evolution of one of the most known nonlinear control methods - Nonlinear Dynamic Inversion (NDI), or "feedback linearization", which uses nonlinear feedback to cancel out the plant nonlinearities. A serious drawback of NDI-based control law, which motivated the development of INDI, is that accurate modelling of the nonlinear plant dynamics is required for such an explicit cancellation, making it a non-robust approach [15].
In this way, the incremental version of NDI, known as INDI, was proposed in 2010 to solve the robustness problem by reducing the model-dependency through the use of fast sensor measurements [33]. Following INDI principles, the model to be inverted is first written in an incremental form, using Taylor series expansion, and an incremental control input is evaluated at every time step [32]. To reduce the model dependency, INDI assumes that the change in control is significantly faster than the change in the states, which is known as the "time scale separation" [15]. In this way, the sensor feedback supplies the necessary information about the model for INDI, which is thus considered a "sensor-based" controller [15]. Due to its robustness properties, INDI control has been successfully applied to a number of different aerial vehicles since then, including an e-VTOL aircraft of NASA Ames [16], a Passenger Aircraft from DLR [17] and conventional drones [19,20,21].
The general idea of the incremental dynamic inversion is as follows. Consider the nonlinear plant dynamics, assumed to be affine in the input:
x ˙ = f ( x ) + G ( x ) u
where x is the state vector and u is the control input.
Instead of inverting the entire system dynamics like in NDI, INDI linearizes and inverts the system dynamics at the previous state x 0 and previous input u 0 .
In this way, if we apply a Taylor series expansion to the plant equation (5), and if we neglect the higher-order terms, we have:
x ˙ ≈ x ˙ 0 + ∂ f ( x ) ∂ x | x 0 , u 0 ( x − x 0 ) + ∂ G ( x ) u ∂ x | x 0 , u 0 ( x − x 0 ) + ∂ G ( x ) u ∂ u | x 0 , u 0 ( u − u 0 )
Further, if we use sufficiently fast sampling time on the flight control computer, we can assume that the state changes are negligible ( x ≈ x 0 ). This assumption only holds when the actuators are sufficiently fast and have more effect compared to the changes in the state vector [32].
Hence, Eq. (6) can be simplified to:
x ˙ ≈ x ˙ 0 + ∂ G ( x ) u ∂ u | x 0 , u 0 ( u − u 0 ) = x ˙ 0 + G ( x 0 ) ( u − u 0 )
Such that the INDI control law is derived as:
u = u 0 + G − 1 ( x 0 ) ( x ˙ r e f − x ˙ 0 ) ︸ δ u = incremental action
To confirm the correctness of the design, we substitute this control law in the linearized system dynamics, to get:
x ˙ ≈ x ˙ 0 + G ( x 0 ) ( u − u 0 ) x ˙ ≈ x ˙ 0 + G ( x 0 ) [ u 0 + G − 1 ( x 0 ) ( x ˙ r e f − x ˙ 0 ) − u 0 ] x ˙ ≈ x ˙ r e f = ν
where we denoted by ν the desired commanded reference x ˙ r e f . Note that we can impose ν = K ( x d − x 0 ) , with x d as the desired state and K as a gain matrix that stabilizes the closed-loop system (Figure 6).
In the specific scenario of a linearized airship model around an equilibrium condition, the effectiveness matrix G corresponds to the input matrix B of the linearized dynamics, resulting from the airship lateral and longitudinal decoupled models (equations 3 and 4).
Finally, note that for the classical NDI approach, the control law would be:
u = G − 1 ( x ) ( ν − f ( x ) )
As the substitution of this equation in the dynamics of the plant (5) leads to a perfect cancellation of the system nonlinearities, assuming that the controller has perfect knowledge of G ( x ) and f ( x ) .
Both NDI and INDI principles are summarized in Figure 6. Note that NDI controller is much more dependent on the plant model than INDI, while INDI is more sensor-dependent than NDI.

5.2. L1 Guidance Approach for Path Following

Among the different types of missions to be executed by the airship, one important navigation problem is the flight path following of the vehicle through a set of predefined waypoints in latitude/longitude. Given the mission waypoints, the first task consists of defining the path passing through the waypoints. Given that airships typically fly in open-sky scenarios, obstacle avoidance may not be required and the path can be set using straight paths linking the waypoints, or depending on the mission, using a more sophisticated optimal solution such as dubins paths [35,36].
Once the path is defined, a lateral guidance strategy is required to ensure that the airship follows the desired path, being the LOS-based (Line-of-Sight) guidance the standard approach [38,39]. However, the LOS strategy can lead to undesired errors when dealing with discontinuities in the path curvature, which is the case from straight-line paths and dubins paths. An alternative considered in this project is the L1 guidance strategy [40].
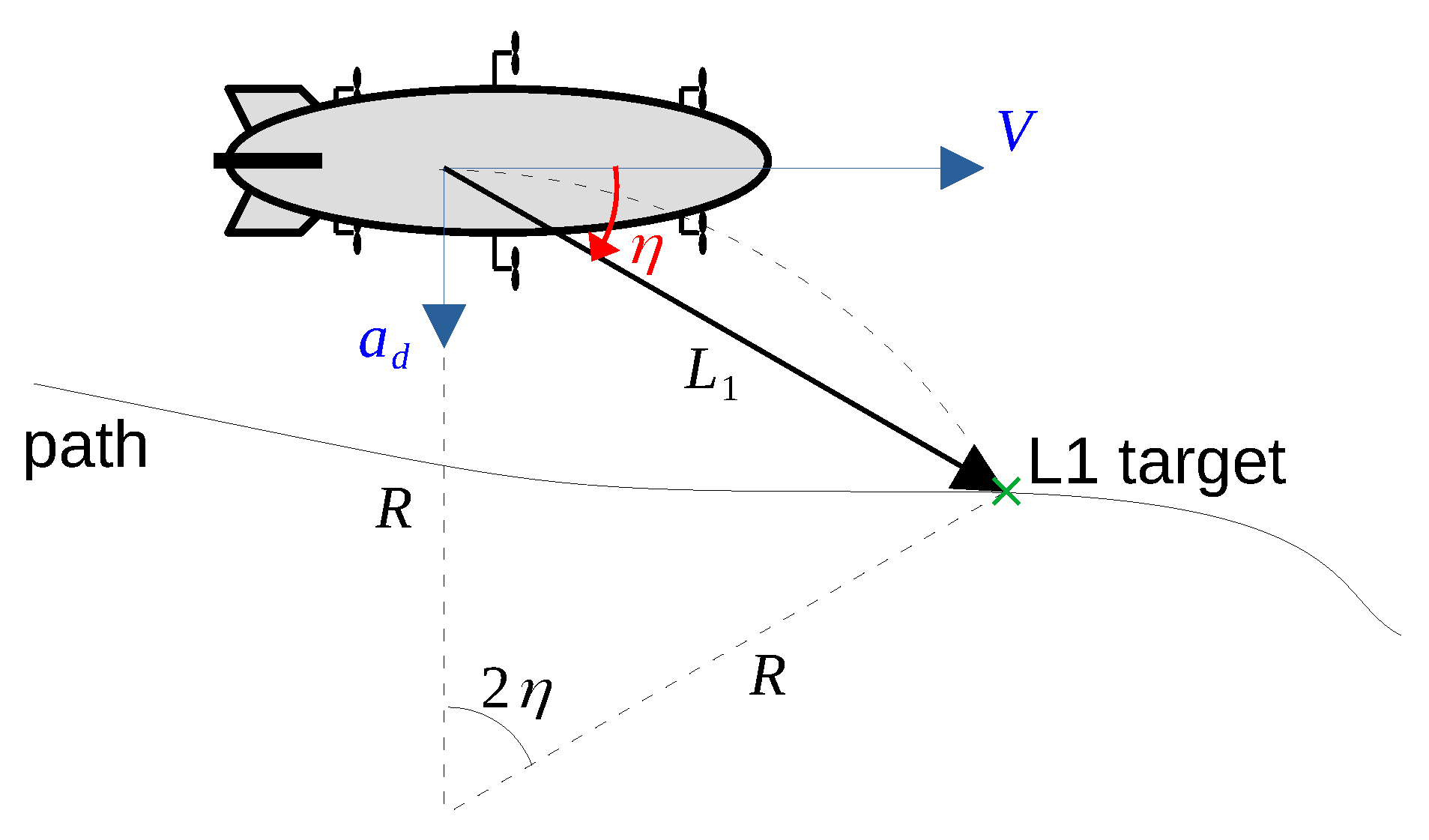
The L1 guidance is a nonlinear path following strategy that defines a circular path towards a target point located at the desired path and within and L 1 distance from the airship, as shown in Figure 7.
The L1 guidance provides the desired centripetal acceleration a d for the airship to perform the circular path to the target point. Considering η as the angle between the airship, and knowing from the geometry shown in Figure 7 that L 1 = 2 R sin η , the desired acceleration is given as:
a d = V r d = V 2 R = 2 V 2 L 1 sin η
Some important properties of the L1 guidance strategy are [40]:
  • The sign of the angle η between the airspeed vector and the target vector defines the sign of the centripetal acceleration and, therefore, defines the direction of the turn
  • The angle η increases when the aircraft is far away from the path, leading to a larger acceleration. When approximating the path, the acceleration decreases, leading to a smooth approximation to the desired path.
From (12), it is clear that the desired acceleration can be directly converted in a desired yaw rate:
r d = 2 V L 1 sin η
The desired yaw rate provided by the L1 guidance strategy can then be used as a reference for the INDI inner loop.

6. Simulation Results

This section presents a simulation experiment for the Noamini waypoint path-tracking problem, when applying the INDI controller at the low level and the L1 algorithm at the high level guidance.
The mission is usually defined by the user for a set of consecutive waypoints i indicated by a table of reference vectors [ N i , E i , D i , ψ i , a s i ] T , where ( N i , E i , D i ) defines the 3-D coordinates of a given waypoint i (with D i as the negative of the altitude), ψ i indicates the heading to the next ( i + 1 ) waypoint (with 0 for a straight flight segment and ψ r rad for an arc of circle), and a s i is the reference airspeed for the segment.
In this simulation, we assumed a +1 kg weighting mass, a reference airspeed of 10 m/s and a reference altitude of 50 m. We tested the 4-motor configuration with a control rate of 100 Hz. We also considered a constant wind (4 m/s) blowing from northeast at 45 deg, added to a continuous Dryden turbulence ( σ = 4 m/s).
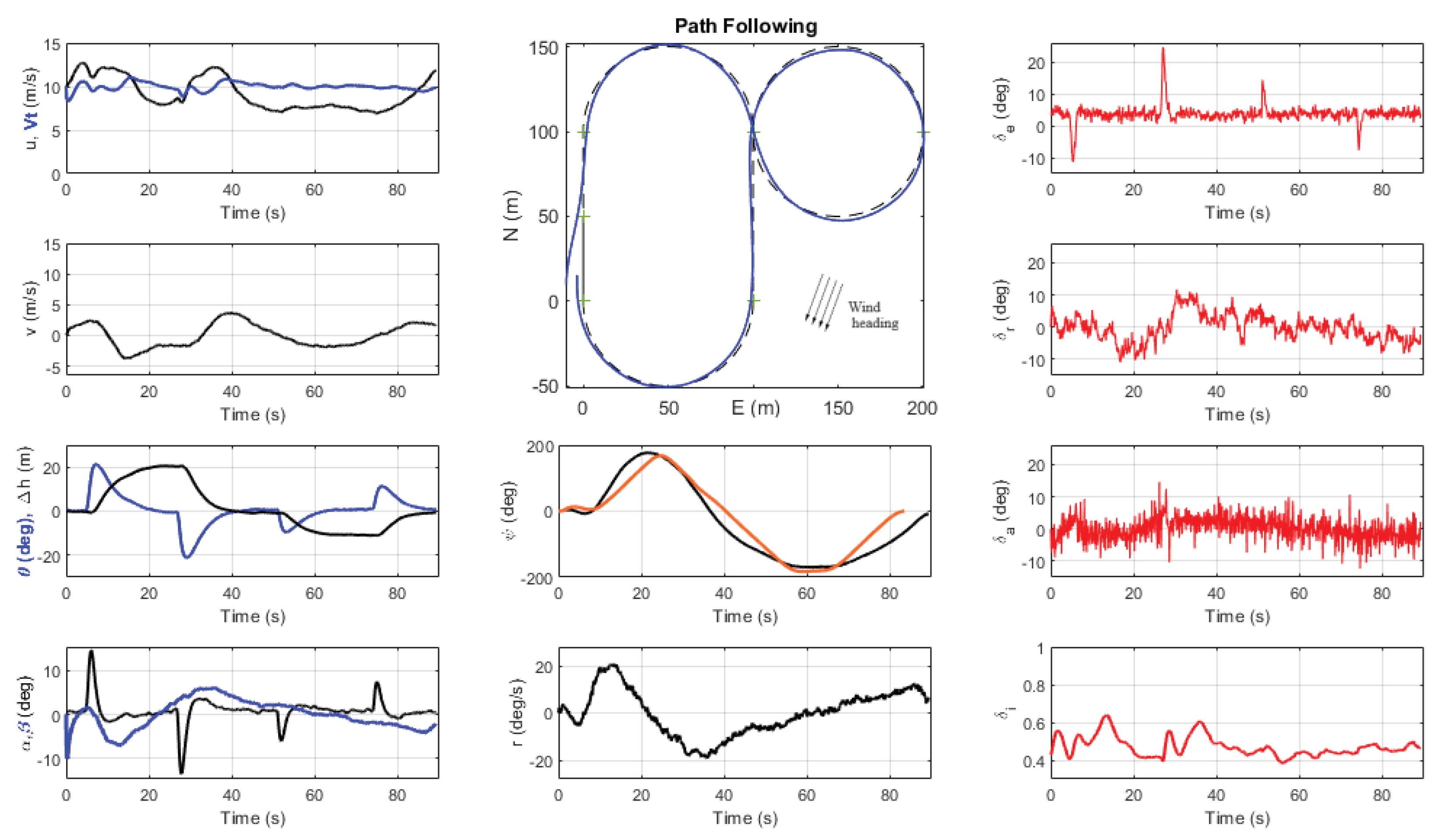
The airship starts at [ N 0 , E 0 , D 0 ] = [ 10 , − 10 , − 50 ] (m), in a position slightly "out of the path" to be followed, which is the classic ¨8¨ configuration, as shown in Figure 8. Note also that the reference altitude of 50 m is subject to up-down changes ( Δ h ) in four different points of the path.
Figure 8 shows the tracking results, along with the main input/output airship signals. The four red signals show the control inputs of elevator ( δ e ), rudder ( δ r ), aileron ( δ a ) and thrust command signal ( δ i , i = 1 , 2 , 5 , 6 ), corresponding to the 2 front and 2 rear propellers. The elevator peaks occur to increase/decrease the pitch angle ( θ ) at the points where an altitude change ( Δ h ) is requested, around the 50 m reference. The airspeed ( V t ) is kept around 10 m/s, while the ground speed (u) varies between 7.5 and 12.5 m/s, as the airship faces the wind in different directions.
The thrust command ( δ i ) stands around 0.4 to 0.5, with two main peaks that occur at the instants where a larger lateral velocity v appears (as well as the sideslip angle β ). The tail deflections of rudder and aileron, although noisy due to the gust presence, act to assure the necessary turning rate for the circular paths. The lateral acceleration command, which comes from the L1 guidance algorithm generates the necessary yaw-rate reference (r) as to obtain a smooth path, with smooth changes in yaw angle ( ψ ), and a minimum error in the path tracking, despite the strong wind and turbulence. In the same plot of the yaw angle ( ψ ) we show, in orange color, the yaw angle for the "no wind" case. It is interesting to note the compensation angle in the "wind case", with the classic "crab moving" of the airship under crosswind to minimize the sideslip angle.

7. Conclusions

This paper proposes a new kind of airship actuator configuration for surveillance and environmental monitoring missions. We present the design and application of a 6-propeller electrical airship with independent tilting propellers (up to 360 degrees), that can be used in 2, 4 or 6 motors configuration, as well as with differential propulsion in front-rear, left-right or cross configurations.
The use of the differential propulsion in 3 pairs of motors distributed around the envelope improves the airship lateral control, as well as the torque generation used to compensate the wind disturbances, and further provides faster yaw/pitch maneuvers, both for hover (or low speeds) as well for the cruise flight.
The proposal of this new airship concept with increased maneuverability is tailored for a specific class of semi-autonomous airships designed for environmental monitoring, a context where both the area coverage as well as the detailed local data acquisition are important.
Finally, we developed a high-fidelity airship simulator for the Noamini airship, which was used to test and validate a control/guidance approach. We designed an Incremental Nonlinear Dynamic Inversion (INDI), for the velocity/attitude control of the airship, which is commanded by a high-level L1 guidance algorithm, which were used for a simulated waypoint tracking mission undeer wind and gust disturbances.

Funding

The authors gratefully acknowledge the agencies Fapespand CNPq for the financial support. From Fapesp INCT-SAC Project (2014/50851-0), co-funded by CNPq (465755/2014-3).

References

  1. Carvalho, José; Rueda, Miguel; Azinheira, José; Moutinho, Alexandra; Bizarro Mirisola, Luiz Gustavo; Paiva, Ely; Nogueira, Lucas; Fonseca, Gustavo; Ramos, Josue; Koyama, Mauro; Bueno, Samuel; Amaral, Christian. (2021). System Architecture of a Robotics Airship. [CrossRef]
  2. Murugaiah, Manikandan and Pant, Rajkumar. (2021). Research and advancements in hybrid airships—A review. Progress in Aerospace Sciences. 127. 100741. [CrossRef]
  3. Yang, Y., Wu, J., and Zheng, W. (2012). Design, modeling and control for a stratospheric telecommunication platform. Acta Astronautica, 80(November–December), 181–189. [CrossRef]
  4. Bueno, S.S.; de Paiva, E. C.; Azinheira, J. R.; Bueno, S. S.; Ramos, J. J. G.; Carvalho, J. R. H. ;Elfes, A.;Rives, P.; Silveira, G. S. Project AURORA – An Autonomous Robotic Airship. In: Work. on Aerial Robotics; 2002 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, Switzerland.
  5. Bestaoui, Y. Lighter than air robots: Guidance and Control of Autonomous Airships. Publisher: Springer. Editor: Kimon Valavanis. ISBN: 978-94-007-2662-8. [CrossRef]
  6. Gomes, S.B.V. An Investigation of the Flight Dynamics of Airships with Application to the YEZ-2A. PhD thesis, Cranfield Institute of Technology, 1990.
  7. Gomes, S.B.V. and J. G. Ramos, "Airship dynamic modeling for autonomous operation." IEEE International Conference on Robotics and Automation, Leuven, Belgium, 1998, pp. 3462-3467 vol.4. [CrossRef]
  8. Azinheira, J.R., de Paiva, E.C., Ramos, J.G., Bueno, S.S., and Bergerman, M. Extended dynamic model for AURORA robotic airship. 14th AIAA Lighter-Than-Air Systems Technology Conference, Akron, Ohio, 2001.
  9. Marton, A.S.; Azinheira, J.R.; Fioravanti, A.R.; De Paiva, E.C.; Carvalho, J.R.H.; Costa, R.R. Filtering and Estimation of State and Wind Disturbances Aiming Airship Control and Guidance. Aerospace 2022, 9, 470. [CrossRef]
  10. Marton, A.S. Control Architecture for the Navigation System of Robotic Airship using Incremental Controllers. PhD thesis, Universidade de Campinas, 2021.
  11. Yang, Y.; Wu, J.; Zheng, W. Positioning Control for an Autonomous Airship. Journal of Aircraft 2016, 53, 1638–1646. [CrossRef]
  12. Paiva E. C., Fabio Benjovengo, Samuel Bueno and Paulo Ferreira. Sliding Mode Control Approaches for an Autonomous Unmanned Airship, AIAA 2009-2869. 18th AIAA Lighter-Than-Air Systems Technology Conference. May 2009. [CrossRef]
  13. Azinheira, J. R., Moutinho, A., and de Paiva, E. C. (2009). A backstepping controller for path-tracking of an underactuated autonomous airship. International Journal of Robust and Nonlinear Control, 19 (March (4)), 418–441. [CrossRef]
  14. Moutinho, A.; Azinheira, J.R.; de Paiva, E.C.; Bueno, S.S. Airship robust path-tracking: A tutorial on airship modelling and gain-scheduling control design. Control Engineering Practice 2016, 50, 22–36. [CrossRef]
  15. Van Kampen, Erik-Jan. “Robust Nonlinear Spacecraft Attitude Control using Incremental Nonlinear Dynamic Inversion” . AIAA Guidance, Navigation, and Control Conference, 2012. [CrossRef]
  16. Thomas Lombaerts, John Kaneshige, Stefan Schuet, Bimal L. Aponso, Kimberlee H. Shish and Gordon Hardy. “Dynamic Inversion based Full Envelope Flight Control for an eVTOL Vehicle using a Unified Framework”. AIAA 2020-1619. AIAA Scitech 2020 Forum. January 2020. [CrossRef]
  17. Fabian Grondman, Gertjan Looye, Richard O. Kuchar, Q Ping Chu and Erik-Jan Van Kampen. “Design and Flight Testing of Incremental Nonlinear Dynamic Inversion-based Control Laws for a Passenger Aircraft”. AIAA 2018-0385. AIAA Guidance, Navigation, and Control Conference, January 2018. [CrossRef]
  18. Xiaodong Zhang, Xiaoli Li, Kang Wang, and Yanjun Lu. “A Survey of Modelling and Identification of Quadrotor Robot”. Hindawi Publishing Corporation. Volume 2014, Article ID 320526. [CrossRef]
  19. E. Tal and S. Karaman, “Accurate Tracking of Aggressive Quadrotor Trajectories Using Incremental Nonlinear Dynamic Inversion and Differential Flatness”. IEEE Transactions on Control Systems Technology, vol. 29, no. 3, pp. 1203-1218, 2021. [CrossRef]
  20. Ewoud J. J. Smeur, Qiping Chu, and Guido C. H. E. de Croon. “Adaptive Incremental Nonlinear Dynamic Inversion for Attitude Control of Micro Air Vehicles” . Journal of Guidance, Control, and Dynamics, 2016, 39:3, 450-461. [CrossRef]
  21. Zexin Wang, Jiang Zhao, Zhihao Cai, Yingxun Wang, Ningjun Liu. “Onboard actuator model-based Incremental Nonlinear Dynamic Inversion for quadrotor attitude control: Method and application.” Chinese Journal of Aeronautics, Volume 34, Issue 11, 2021, Pages 216-227. [CrossRef]
  22. Sanghyuk Park, John Deyst and Jonathan How. "A New Nonlinear Guidance Logic for Trajectory Tracking," AIAA 2004-4900. AIAA Guidance, Navigation, and Control Conference and Exhibit. August 2004. [CrossRef]
  23. Cope, John A. and Andrew Parks. “Frontier Security: The Case of Brazil.” National Defense University Press, Washington, D.C., 2016. [CrossRef]
  24. Beuchle, René; Frédéric, Achard; Bourgoin, Clément; Vancutsem, Christelle; Eva, Hugh and Follador, Marco. “Deforestation and Forest Degradation in the Amazon - Status and trends up to year 2020”. [CrossRef]
  25. Moran-Zuloaga et al. “Long-term study on coarse mode aerosols in the Amazon rain forest with the frequent intrusion of Saharan dust plumes.” Atmos. Chem. Phys., 2018, 18, 10055–10088. [CrossRef]
  26. Pinagé, Felipe; H, Carvalho J.R.H., Queiroz-Neto. (2013). “Visual-Based Natural Landmark Tracking Method to Support UAV Navigation over Rain Forest Areas.” Proceedings of the 2012 Brazilian Symposium on Computing System Engineering, November 2012, pp. 105-110. [CrossRef]
  27. Ribeiro E. et al. “Weightless neural systems for deforestation surveillance and image-based navigation of UAVs in the Amazon forest.” European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning. Bruges (Belgium), 24-26 April 2019, i6doc.com publ., ISBN 978-287-587-065-0. Available from https://www.esann.org/sites/default/files/proceedings/legacy/es2019-153.pdf.
  28. Tejada, G., Gorgens, E.B., Espírito-Santo, F.D.B. et al. “Evaluating spatial coverage of data on the aboveground biomass in undisturbed forests in the Brazilian Amazon”. Carbon Balance Manage 14, 11 (2019). [CrossRef]
  29. Vieira, H.S.; de Paiva, E.C.; Moriguchi, S.K.; Carvalho, J.R.H. Unified Backstepping Sliding Mode Framework for Airship Control Design. IEEE Transactions on Aerospace and Electronic Systems 2020, 56, 3246–3258. [CrossRef]
  30. Azinheira, J.; Moutinho, A.; Carvalho, J. Lateral Control of Airship with Uncertain Dynamics using Incremental Nonlinear Dynamics Inversion. IFAC-PapersOnLine 2015, 48, 69–74. [CrossRef]
  31. Wang, X.; Kampen, E.J.v.; Chu, Q.; Lu, P. Incremental Sliding-Mode Fault-Tolerant Flight Control. Journal of Guidance, Control, and Dynamics 2019, 42, 244–259. [CrossRef]
  32. Xuerui Wang, Erik-Jan van Kampen, Qiping Chu, and Peng Lu. “Stability Analysis for Incremental Nonlinear Dynamic Inversion Control.” Journal of Guidance, Control, and Dynamics 2019 42:5, 1116-1129, https://doi.org/10.1145/3301273. [CrossRef]
  33. Simplicio, P., Pavel, M., van Kampen, E., and Chu, Q., “An Acceleration Measurements-Based Approach for Helicopter Nonlinear Flight Control Using Incremental Nonlinear Dynamic Inversion”. Control Engineering Practice, Vol. 21, No. 8, 2013, pp. 1065–1077. [CrossRef]
  34. R. A. Cordeiro, J. R. Azinheira and A. Moutinho. “Robustness of Incremental Backstepping Flight Controllers: The Boeing 747 Case Study.” IEEE Transactions on Aerospace and Electronic Systems, vol. 57, no. 5, pp. 3492-3505, Oct. 2021. [CrossRef]
  35. Dubins, L.E. “On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents”. American Journal of Mathematics 1957, 79, 497–516. [CrossRef]
  36. Bouvier, B.; Pascal, P.; Piet-Lahanier, H. “Optimal route design for an airship collecting and delivering logs in difficult environmental conditions”. IFAC-PapersOnLine 2022, 55, 255–260. 22nd IFAC Symposium on Automatic Control in Aerospace ACA 2022. [CrossRef]
  37. Donald McLean. (1990). “Automatic flight control systems”. Cambridge: Prentice-Hall International, pp. 130-134.
  38. Atmeh, G.; Subbarao, K. “Guidance, Navigation and Control of Unmanned Airships under Time-Varying Wind for Extended Surveillance”. Aerospace 2016, 3, 8. [CrossRef]
  39. Wang, J.; Meng, X.; Wu, G. “Path following of the autonomous airship with compensation of unknown wind and modeling uncertainties”. Aerospace Science and Technology 2019, 93, 105349. [CrossRef]
  40. Park, S.; Deyst, J.; How, J. “A New Nonlinear Guidance Logic for Trajectory Tracking”. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Providence, Rhode Island, 2004. [CrossRef]
1
https://insac.eesc.usp.br/
Preprints 100761 g001
Figure 1. Noamini airship in the maiden flight in Brasil. Bottom: Y-inverted tail and tilting propeller, which is rotated by a servo in its base.
Figure 1. Noamini airship in the maiden flight in Brasil. Bottom: Y-inverted tail and tilting propeller, which is rotated by a servo in its base.
Preprints 100761 g001
Preprints 100761 g002
Figure 2. Urban forest segment in Manaus under strong deforestation pressure. The red arrows show two example of residents who enlarged their properties toward the forest. This is a scenario where an airship is of great value. Source: Mosaic manually elaborated by the authors using Google maps.
Figure 2. Urban forest segment in Manaus under strong deforestation pressure. The red arrows show two example of residents who enlarged their properties toward the forest. This is a scenario where an airship is of great value. Source: Mosaic manually elaborated by the authors using Google maps.
Preprints 100761 g002
Preprints 100761 g003
Figure 3. Actuators distribution around Noamini airship: top view and lateral view.
Figure 3. Actuators distribution around Noamini airship: top view and lateral view.
Preprints 100761 g003
Preprints 100761 g004
Figure 4. Block diagram of airship simulator in open-loop.
Figure 4. Block diagram of airship simulator in open-loop.
Preprints 100761 g004
Preprints 100761 g005
Figure 5. Proposed Guidance and Control architecture.
Figure 5. Proposed Guidance and Control architecture.
Preprints 100761 g005
Preprints 100761 g006
Figure 6. Principles of Dynamic Inversion (NDI) and Incremental Dynamic Inversion (INDI) control approaches. The model-based components of the controllers are indicated by the red boxes.
Figure 6. Principles of Dynamic Inversion (NDI) and Incremental Dynamic Inversion (INDI) control approaches. The model-based components of the controllers are indicated by the red boxes.
Preprints 100761 g006
Preprints 100761 g007
Figure 7. Principle of the nonlinear L1 guidance strategy.
Figure 7. Principle of the nonlinear L1 guidance strategy.
Preprints 100761 g007
Preprints 100761 g008
Figure 8. Path tracking and relevant signals for a trajectory in "8", with an airspeed V t of 10 m/s. Wind speed of 4 m/s at 45 deg NE, with turbulence of σ =4 m/s. Control input signals shown in red. Airship heading ψ for "no wind" condition shown in orange.
Figure 8. Path tracking and relevant signals for a trajectory in "8", with an airspeed V t of 10 m/s. Wind speed of 4 m/s at 45 deg NE, with turbulence of σ =4 m/s. Control input signals shown in red. Airship heading ψ for "no wind" condition shown in orange.
Preprints 100761 g008
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated