A Computational Procedure for Testing Conditional Independence in Causal Directed Acyclic Graphs

This study introduces a novel computational approach for testing conditional independence (BB CI test) within causal Directed Acyclic Graphs (DAGs), leveraging Bayesian non-parametric bootstrap and machine learning techniques. Our method offers an alternative for validating the assumptions underpinning causal DAGs. Through simulation studies and an industrial case analysis, we demonstrate the test procedure in accurately assessing conditional independence, comparing it with the Generalized Covariance Measure (GCM) test. Our findings suggest that the BB CI test is advantageous in scenarios where existing methods may falter due to violations of model assumptions. This research contributes to the causal inference literature by providing a computational tool for researchers and practitioners to validate causal models.

Keywords:

Subject: Computer Science and Mathematics - Probability and Statistics

1. Introduction

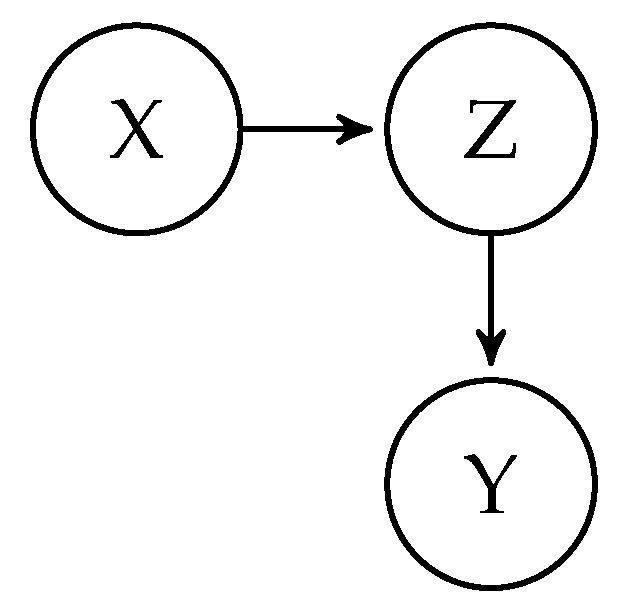
Statistical modeling founded on directed acyclic graphs (DAGs), as introduced by Pearl [1], has gained increasing popularity as a framework to guide researchers in constructing statistical models for causal inference estimation. A (causal) DAG is a graphical model representing the theorized causal structure of the data-generating process, consisting of nodes representing variables connected causally by directed edges (arrows). An example of a simple DAG with three variables (X, Y, and Z) is shown in Figure 1. The edges represent the direction of causal relationships and do not give information on the functional form of the causal effects. For instance, a causal relation could be linear, interact with other variables, or have a non-linear form.

A causal DAG is accompanied by a set of general statistical conditions, as outlined in, for instance, [1] (Section 2.5), which we refer to as the implied marginal and conditional independence assumptions. For example, the DAG in Figure 1 implies that Y and X are conditionally independent given Z. This independence is evident by the causal structure, as there is no direct influence from X on Y, only an effect through Z. Therefore, if we know Z, there is no way for X to influence Y, i.e., they are independent. We denote the conditional independence implied in Figure 1 as

X ⊥ ⊥ Y | Z

, which is equivalent to

Y ⊥ ⊥ X | Z

. If we expand Z to include a set of variables

Z

, conditional independence can be expressed using probability distributions

p (Y | X, Z) = p (Y | Z)

for any values of X, Y, and

Z

and where

p (Z) > 0

Testing the implied conditional independence assumptions in causal DAGs is essential for the accuracy, validity, and applicability of any inferences based on the DAG. Despite this, it is, to our knowledge, uncommon in applied research to conduct such statistical tests, as noted by Ankan (2021) [2]. Testing causal DAGs can identify hidden biases and unknown confounding effects, which can potentially bias any estimated causal effect. The implied conditions allow for local testing as one can identify where in a causal DAG a potential problem may lay, and steps can be taken to ”fix” the problem by adding edges and nodes, see Section 2.5 in Pearl, Glymour, and Jewell’s book ”Causal Inference: A Primer” [1].

1.1. Current Testing Recommendations

Ankan et al. [2] provide a testing protocol for DAGs based on well-known statistical methods. For continuous data, they recommend checking residual correlation with linear regression. They also recommend not relying on p-values alone but also assessing effect sizes. Testing by linear regression assumes approximately Gaussian error terms and a linear and homoscedastic relationship between the dependent and the independent variables. An obvious weakness of testing conditional independence with a parametric regression model is that a correct functional form needs to be specified. Testing by a parametric regression model is potentially misleading if the regression equations are wrongly specified.

Further, if all variables in a conditional independence statement are categorical, the recommendation is to use the conditional

χ^{2}

test, also known as the Cochran-Mantel-Haenszel test. The conditional

χ^{2}

test needs sufficient observations in each conditioned variable category ([3], pp. 231-232). In cases where the conditional independence statements involve a mixture of binary, categorical, and continuous variables, they suggest using statistical models such as logistic regression or forgo testing altogether.

Richard MacElreath presents an approach for testing the conditional independence assumptions implied by DAGs using a linear parametric Bayesian model in his textbook ”Statistical Rethinking” ([4], pp. 130-133). While useful, this method is contingent on the correct specification of the parametric form.

Shah & Peters [5] propose a test statistic termed the Generalized Covariance Measure (GCM). Given a large but well-behaved set of distribution functions

p_{1}

and

p_{2}

, they formulate (from [6]) a generic null hypothesis for conditional independence;

X ⊥ ⊥ Y

given

Z

, if and only if,

\begin{matrix} E [p_{1} (X, Z) p_{2} (Y, Z)] = 0 . \end{matrix}

(1)

Shah & Peters suggest a test statistic for conditional independence with the above null hypothesis, which they called the generalized covariance measure (GCM). The GCM assumes that

Z

can be regressed on X and Y. The residuals from both regressions can be assumed independent across observations and are homoscedastic with zero means. To calculate the GCM test statistic for the condition

X ⊥ ⊥ Y | Z

, the first step is to estimate the regressions,

\begin{matrix} x & = h_{1} (z) + ϵ_{x} \\ y & = h_{2} (z) + ϵ_{y}, \end{matrix}

(2)

to get residuals

{\hat{ϵ}}_{x}

and

{\hat{ϵ}}_{y}

. Then, the normalized covariance between them is calculated,

\begin{matrix} T : = \sqrt{n} \frac{\frac{1}{n} \sum_{i = 1}^{n} ({\hat{ϵ}}_{x} {\hat{ϵ}}_{y})}{\sqrt{(\frac{1}{n} \sum_{i = 1}^{n} {\hat{ϵ}}_{x}^{2}) (\frac{1}{n} \sum_{i = 1}^{n} {\hat{ϵ}}_{y}^{2})}} . \end{matrix}

(3)

The test statistic has an asymptotic standard normal distribution under the null (Equation 1). The GCM test is flexible and robust and can account for different functional forms, data types, and interaction effects (depending on the regression method). The default implementation of GCM in R statistical software uses Extreme Gradient Boosting (XGBoost) [7] to estimate the regressions. Simulation results in [5] show that the method should preferably have a sample size

n > 400

1.2. The Null Hypothesis in Conditional Independence Testing in Causal DAGs

Without theoretical development and test statistic modification, the only valid null hypothesis in any kind of conditional independence testing posits that the conditional independence statement holds. This fundamental premise provides a theoretical challenge inherent to implied conditions in causal DAGs.

In most cases, the default conditional independence null hypothesis is acceptable. However, if we look closer at frequentist null hypothesis testing theory and philosophy, the null hypothesis should not automatically be the hypothesis of conditional independence. According to theory, the null hypothesis of a statistical test should be a statement presumed to be false (see, for instance, [8,9,10]). The implied conditional independence statements from a causal DAG are precisely the opposite; these statements are propositions that are presumed to be true. This is because we assume there is no causal effect between two variables, X and Y, without a direct edge between them in the DAG, i.e., conditional independence. As a result, conducting statistical tests to calculate p-values for these non-existent causal effects is not sound statistical practice. However, a Bayesian testing procedure would circumvent the issue of the null hypothesis by approximating a posterior distribution.

This paper uses machine learning methodology in combination with Bayesian bootstrapping to create an alternative (Bayesian) method for testing conditional independences accompanying causal DAGs. Our article is organized as follows: Section 2 introduces and delineates our proposed testing procedure, followed by a simulation study in Section 3 and a practical illustrative example in Section 4. A general discussion is given in Section 5 and a short conclusion in Section 6.

2. A new Bayesian Non-Parametric Bootstrap Method

This section introduces our new Bayesian non-parametric Bootstrap procedure for testing conditional independence (BB CI test) in causal DAGs.

2.1. The Basic Premise

Conditional independence

p (Y | X, Z) = p (Y | Z)

says that X carries no information about the conditional distribution of Y once

Z

is known. That is, the distribution of Y, conditioned on

Z

, is the same regardless of X. Consider the regression model

Y = f (X, Z)

which tries to predict using both X and

Z

as predictors, X in this case would not contribute to reducing the prediction error of Y. The simpler regression model

Y = g (Z)

with

Z

as the sole predictor should, therefore, capture all available information about Y that is contained in X. Thus, we have the expectation equality for the Mean Squared Error (MSE) of these two models,

\begin{matrix} E [{(Y - f (X, Z))}^{2}] = E [{(Y - g (Z))}^{2}] . \end{matrix}

(4)

The key assumption is that both

f ()

and

g ()

are optimal regression functions that capture the true relationships between the variables. Then, given conditional independence, the MSE of

f (X, Z)

cannot be lower than

g (Z)

for optimal regressors. MSE is used as an example; the equality in Equation 4 should hold for any appropriate performance measure.

This premise leads to a straightforward inference: If

X^{*}

represents a permuted version of X, which by construction does not carry information about Y, and if

f (X, Z)

and

g (X^{*}, Z)

are optimal predictors, we can evaluate a specific conditional independence assumption in a DAG by comparing the predictive performances of these two models. By applying Bayesian (two-tier) bootstrapping, we can estimate a posterior distribution of the difference in model performance between

f ()

and

g ()

. In some bootstrap samples, if the conditional independence condition holds,

g ()

will incidentally score better than

f ()

, but, on average, the difference between

f ()

and

g ()

should be centered on zero. If

f ()

is better than

g ()

, indicating significant prediction power in X even though we condition on

Z

, the difference in MSE will center on some positive number, meaning that the conditional independence does not hold.

2.2. Bayesian Bootstrap

The Bayesian bootstrap (BB), as introduced by Rubin (1981) [11], is a computational method for estimating a posterior distribution of a statistic in scenarios where analytical uncertainty measures are unavailable. In its original form, the BB assigns a different weight to each observation for each bootstrap sample. These weights are drawn from a Dirichlet prior with concentration parameter

α = {α_{1}, . . ., α_{n}}

, where

α_{i} > 0

and n is the number of units in the original sample. Then, one calculates a statistic of interest based on these weights and repeats it many times. However, BB can also be employed as a two-tier bootstrap procedure. In the first step, each observation in the dataset is assigned the weight drawn from the Dirichlet prior. This effectively creates a ”weighted” sample of the original data; then, resample from this weighted sample to create a Bayesian bootstrap sample. In the resulting bootstrap sample, the influence of each observation on the calculated statistic of interest is proportional to its weight, as in the original BB.

The Dirichlet distribution serves as a prior, and by specifying

α

, one can express prior beliefs about the data. For instance, if some observations have less measurement error, these observations can be weighted up by increasing the corresponding

α

’s. The weighting of samples to account for measurement error or other prior beliefs about the data is the main gain of utilizing BB. Additionally, it provides a Bayesian interpretation of the bootstrap distribution.

Dirichlet(

1_{1}, . . . 1_{n}

) corresponds to a flat prior, and the classic bootstrap sample is a ”special case” of the BB with all

α

’s set to infinity. Setting all the

α

’s simultaneously to values less than one means that fewer observations get a large weight such that more of the sample is left out for each bootstrap run.

2.3. The test Procedure

The procedure’s most crucial part is estimating the prediction models

\hat{f} ()

and

\hat{g} ()

as optimal as possible. These models should use the same underlying algorithm and model complexities to avoid differences that are due solely to how these functions are estimated. The first step is to select a suitable supervised machine-learning algorithm and establish a base hyperparameter range using standard cross-validation tuning on the original sample. In this article, we use the XGBoost-algorithm [7], but any other supervised machine learning method may be used. Once the hyperparameters are optimized, we proceed with a standard bootstrap approach. In each bootstrap sample, the data is divided into training and test sets. The models

\hat{f} ()

and

\hat{g} ()

are fitted using the training set, and the predictive performance is calculated on the test set.

To evaluate the conditional independence assumption

Y ⊥ ⊥ X | Z

with i.i.d. data

D \in {y, x, z}

, where

z

is a vector representing one or more variables, we perform the following Bayesian bootstrap procedure, which we call the BB CI test:

Establish a Dirichlet distribution: Set the $α$ values of the Dirichlet distribution.
Initial tuning: Tune the regression model $y = f (x, z)$ using the original data $D$ . This tuning is done through n-fold cross-validation and a grid search over the hyperparameters $Θ$ to determine the best (range) of hyperparameters $Θ^{*}$ .
Generate weights: Generate n sample weights from a prior Dirichlet distribution, which will be used for resampling.
Bootstrap sample: Resample $D$ according to the sample weights, to create the bootstrap sample $B$ .
Train test split: Split $B$ into a training set $B_{train}$ and a test set $B_{test}$ .
Bootstrap-specific tuning: For $f ()$ , perform a grid search over the best set of hyperparameters $Θ^{*}$ determining the best bootstrap-specific set of hyperparameters $Θ^{* *}$ , using $B_{train}$ .
Train $\hat{f} ()$ : Train $\hat{f} ()$ using hyperparameters $Θ^{* *}$ and $B_{train}$ .
Permute: Reorder elements in x to obtain $x^{*}$ in $B_{train}$ .
Train $\hat{g} ()$ : With the same bootstrap-specific hyperparameters as for $f ()$ , train $\hat{g} ()$ using $B_{train}$ .
Predict: Predict $\hat{y}$ using $\hat{f}$ and $\hat{g}$ for the test set $B_{test}$ .
Comparison Calculate performance metrics (e.g., prediction error) of each model, $m_{\hat{f ()}}, m_{\hat{g ()}}$ , and compare these using their difference: $δ_{m} = m_{\hat{f ()}} - m_{\hat{g ()}}$ .

Repeat steps 3 to 11

η

times (e.g., 2000).

In this work, we consider the Root Mean Squared Error of prediction (RMSE) as performance metric if the response is continuous and the accuracy or Kappa score if the outcome is categorical. RMSE is somewhat sensitive to outliers but is a robust performance measure overall. An alternative for continuous responses would be R², but we consider RMSE more suitable since R² is bounded to the unit interval.

Accuracy quantifies the proportion of correct predictions made by the model out of all predictions made. Accuracy is suited when there is a balance between the outcome classes. In cases where the outcome classes are unbalanced, we use the Kappa score given by,

\begin{matrix} Kappa Score = \frac{p_{0} - p_{e}}{1 - p_{e}}, \end{matrix}

(5)

where

p_{0}

is the accuracy, and

p_{e}

is the empirical probability of having a correct prediction by chance. Kappa score adjusts the accuracy by accounting for chance agreement and is more robust when the outcome variable is unbalanced.

After

η

bootstrap runs, one obtains three vectors containing the performance metrics of

f ()

and

g ()

and their differences. These vectors represent estimated posterior distributions of the model performance and the difference in predictive performance. As a rule of thumb, we can reject conditional independence if 0 is outside the 2.5 and 97.2 percentiles of the distribution.

3. Simulation Study

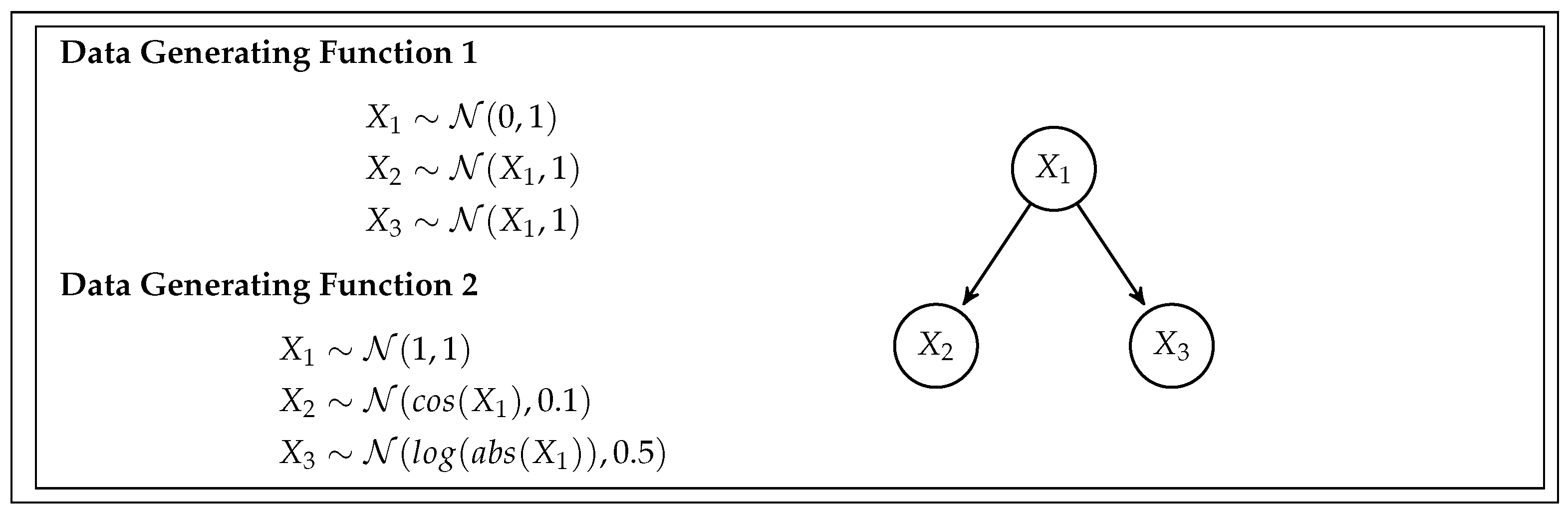
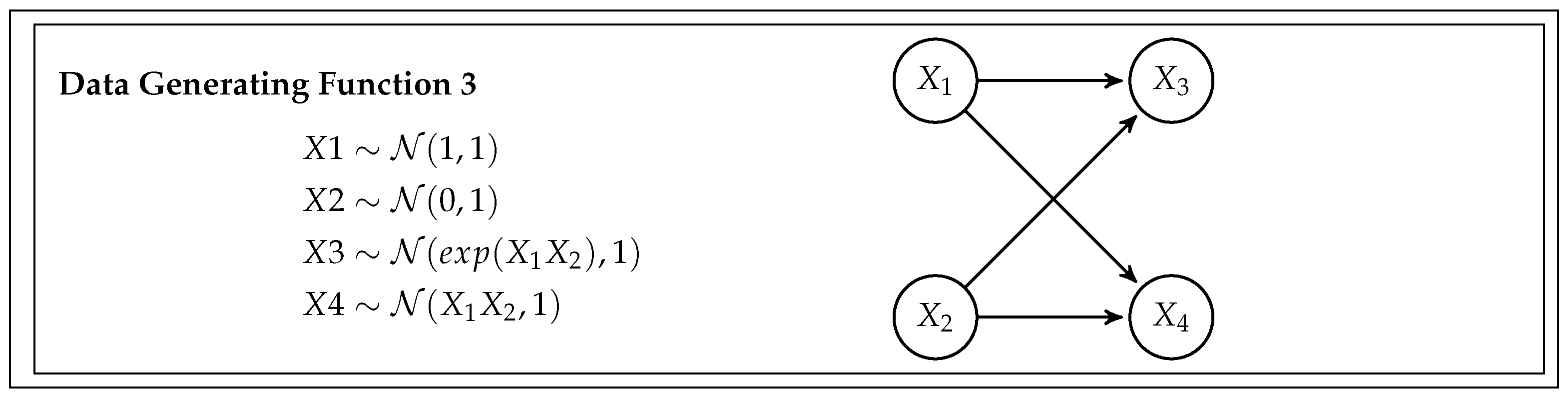
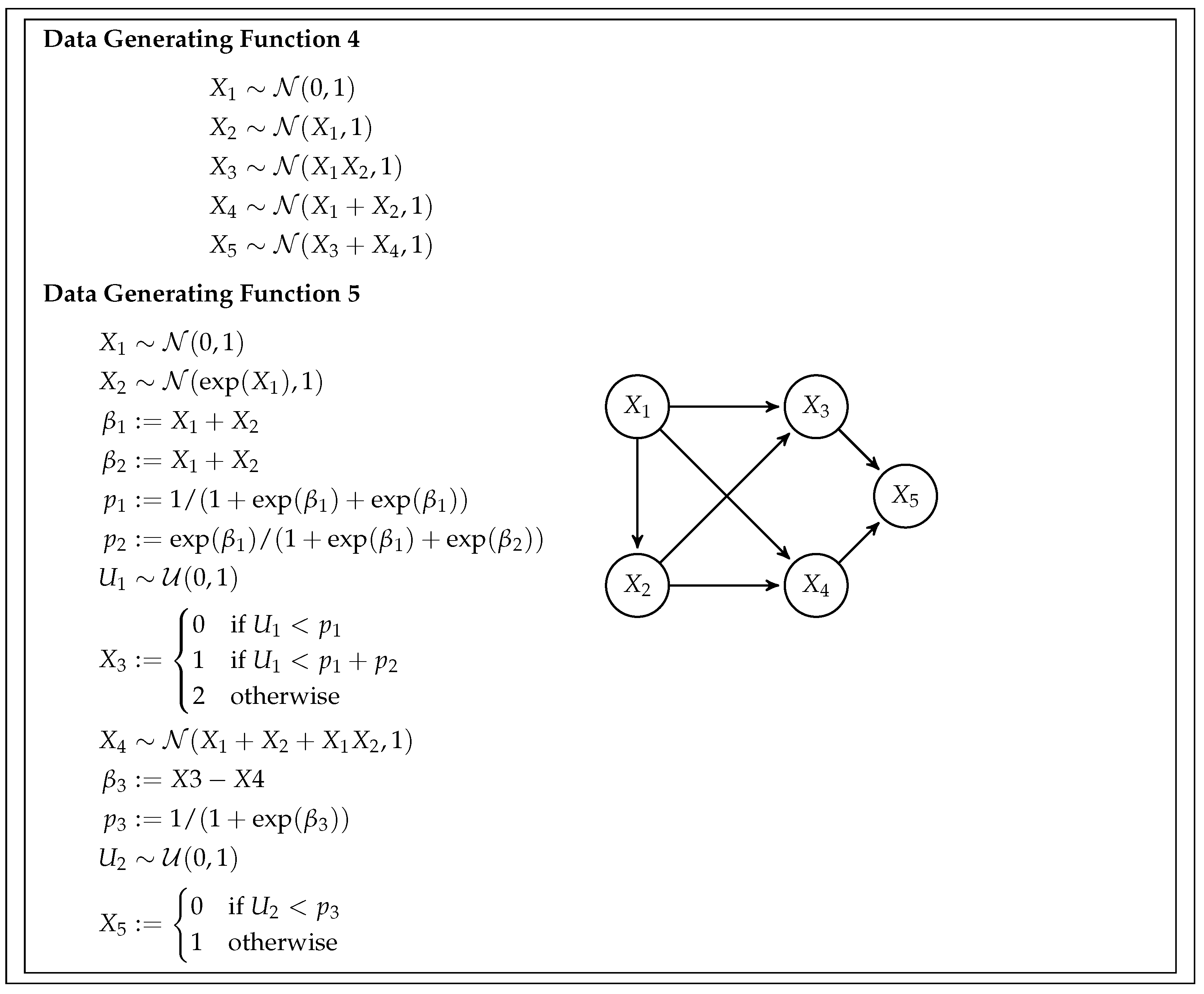
This simulation study is designed to assess the feasibility and efficiency of the BB CI testing procedure and compare it with the existing Generalized Covariance Measure (GCM) test. To do so, we generate data from five different scenarios, or data-generating functions, with increasing complexity. Each scenario also has different data types and relationships between variables. The specifics of the simulation are given by the data generating functions (DGF), and are detailed in Figure 2, Figure 3 and Figure 4.

DGF 1 – Simple Linear Fork: This function simulates data from a straightforward fork-shaped DAG, utilizing a linear model for the relationships.
DGF 2 – Non-Linear Fork: DGF 2 also derives from a fork DAG structure but introduces non-linear functional forms, adding complexity to the data simulation.
DGF 3 – Double Fork with Non-Linearity: DGF 3 evolves from a single fork to a double fork configuration, maintaining non-linear relationships among the variables.
DGF 4 – Mixed Relationship Model: This function is based on a five-variable DAG. It encompasses both linear and non-linear relations, presenting a more intricate scenario.
DGF 5 – Diverse Variable Types: Originating from the same five-variable DAG as DGF 4, DGF 5 incorporates non-linear relationships and incorporates categorical data types. It includes both continuous variables ( $X_{1}$ , $X_{2}$ , $X_{4}$ ) and categorical variables ( $X_{3}$ , $X_{5}$ ).

For each DGF, we generate data sets with five different sample sizes (200, 400, 800, 1600, and 3200 samples), and for each sample size, we generate one hundred distinct datasets. We do not test all the implied conditional independence assumptions, only those listed in Table 1 and Table 2.

3.1. Implementation of the BB CI Test Procedure

The BB CI test and all simulations were implemented using R statistical software [12]. For each test, we construct the posterior distribution from 1000 bootstrap samples. In setting up the XBGoost parameters, we opted for conservative defaults to ensure robustness, especially given that XGBoost models are prone to overfitting when data exhibits simple linear patterns. We set the maximum depth to a default vector of

{1, 2, 3}

and the maximum number of boosting trees to 50. Additionally, we implemented an early stopping parameter of 10, which means that boosting is stopped if the test set predictions are not improved over ten boosting rounds. The early stopping parameter is set in an attempt to limit computation time. When dealing with data from a DAG suspected to follow a linear pattern, it is best to choose conservative hyperparameter settings or employ a linear prediction model to avoid overfitting. For DGF 1, a simple linear model, we retained the conservative value for max depth to default values. For DGF 2, we expanded our parameter tuning to include a grid search for the max depth, ranging from 2 to 4, while keeping the maximum number of boosting rounds at 50, keeping the early stopping criterion. For DGF 3, the max depth values were from 2 to 5, and with simulations DGF 4, the grid search consisted of a max depth range from 3 to 5 in both cases with 50 boosting rounds. In DGF 5, our grid search consisted of default hyperparameter values when the outcomes were categorical (

X_{3}

and

X_{5}

). In the case of DGF 5 with a continuous outcome, we increased the number of boosting rounds to 100 and employed a grid search over max depth parameters 5 and 6 while also increasing early stopping to 30. The learning rate was equal to 0.1 in all cases, and we used the same values of grid search hyperparameters for testing both true and false conditions given the DGF.

In conducting tests with the GCM, we utilize the implementation available in the R-package, as documented in the ’GeneralisedCovarianceMeasure’ library hosted on The Comprehensive R Archive Network (CRAN). For the GCM test, the default configuration employs the XGBoost algorithm to train both regression models. This process involves a grid search with 10-fold cross-validation, with an array of maximum depth values {1, 3, 4, 5, 6} and limiting the boosting rounds to a maximum of 50 without any early stopping.

3.2. Simulation Results

Table 1 presents the outcomes of evaluating valid and invalid implied conditional independence assumptions utilizing the Generalized Covariance Measure (GCM) test. The GCM test has a false positive rate of about 5 % for the proper conditions, which is expected since the significance level is 0.05. The GCM performs well for all simulation scenarios except DGF 3. When examining the DGF 3 (in Figure 3), we observe that

X_{3}

must have a highly skewed distribution, characterized predominantly by a concentration of values around 0, where the exponentiation of

X_{1} X_{2}

leads to a few values far from 0. Therefore, a prediction model predicting

X_{3}

will typically have a few residuals with very large values. Given that in the GCM test statistic expression (see Equation 3), squared residuals are multiplied in the denominator, the poor performance of the GCM test could be that the test statistic is sensitive to individual residuals with high values, which also could be seen as a violation of the homoscedasticity assumption. The sensitivity to outliers can lead to ’artificially’ low values of the test statistics, i.e., failing to reject the null hypothesis.

Table 2 shows the results from the BB CI test procedure. In the lower part of the table, we test the assumptions associated with DGF 5, where we switch the dependent variable between the continuous choice (

X_{1}

and

X_{4}

) and categorical (

X_{3}

and

X_{5}

). Initially, we do not expect that the change from a continuous variable to a categorical outcome variable should impact the results to a large degree. However, this was not the case. We see that when the outcome is binary and unbalanced (condition

X_{5} ⊥ ⊥ X_{1} | X_{3}, X_{4}

and

X_{5} ⊥ ⊥ X_{1} | X_{3}

), using the Kappa score as the evaluation metric is better. This is expected since the Kappa score adjusts for unbalanced classes. In the case where the dependent variable is an evenly distributed categorical outcome (condition

X_{3} ⊥ ⊥ X_{4} | X_{1}, X_{2}

and

X_{3} ⊥ ⊥ X_{4} | X_{1}

), accuracy and Kappa score performed equally well. For the same conditional independence assumptions using a continuous outcome,

X_{1}

instead of

X_{5}

and

X_{4}

instead of

X_{3}

, the results were not as convincing when testing the false conditions (

X_{5} ⊥ ⊥ X_{1} | X_{3}

and

X_{3} ⊥ ⊥ X_{4} | X_{1}

). The poor results with ”low” sample sizes are due to the limited prediction strength of the binary

X_{5}

and categorical

X_{3}

variables on

X_{1}

and

X_{4}

, respectively.

From our simulation study, we observed that the posterior bootstrap distribution consistently included 0 across all simulation scenarios when testing a valid conditional independence assumption. Likewise, we see that the GCM test aligns with the asymptotic qualities. However, it is crucial to note that the BB CI test procedure lacks a formal asymptotic proof of convergence. This absence suggests that the BB CI test might lose accuracy in very large samples, a hypothesis that can only be confirmed through testing with such samples. Initial experimentation with sample sizes between 5000 and 10,000 observations indicates that the BB CI test procedure maintains accuracy up to 10,000 observations. It is recommended that a smaller sub-sample be used for testing purposes in large samples (10,000+) and that the minimum sample size for testing is 800 observations.

4. Industrial Case

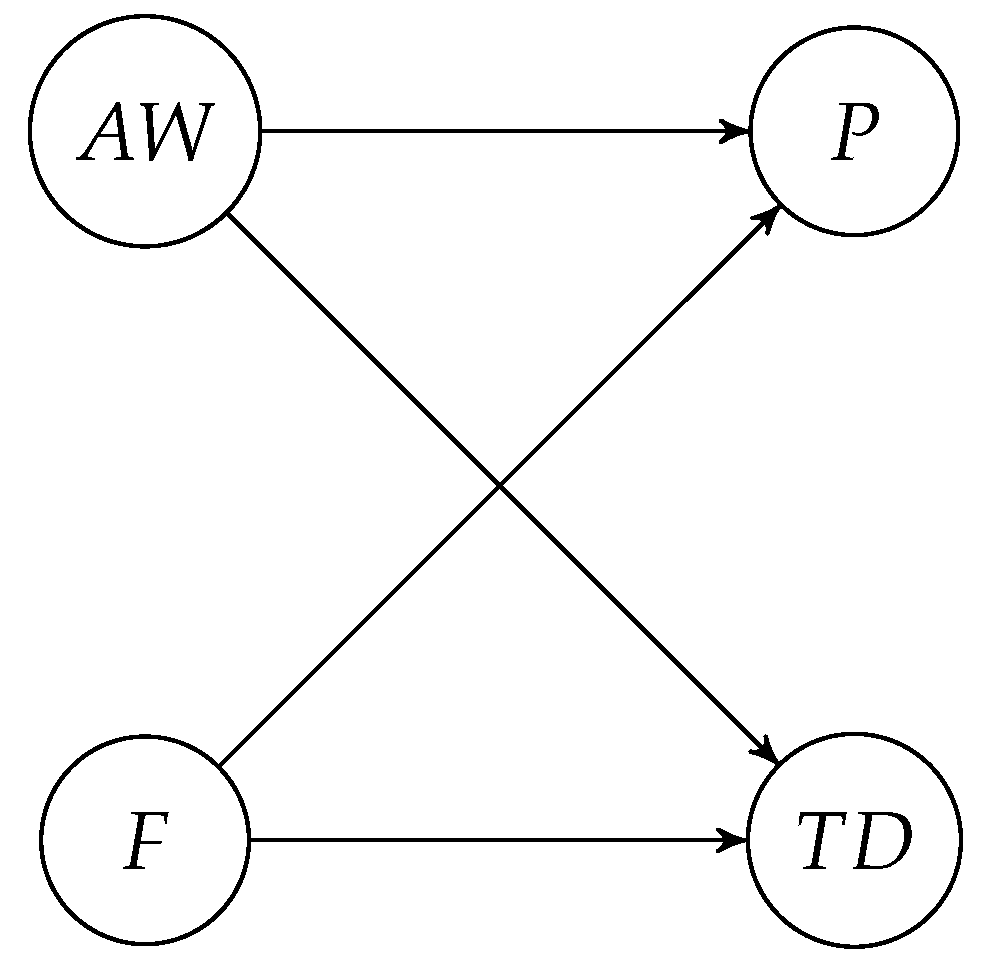
In this study, we analyze data from a biorefining company that processes rest raw materials from poultry using a patented continuous enzymatic hydrolysis process. In this process, the grinded raw material is mixed with water and enzymes before it is heated to a specific temperature. Then, the mixture is passed through a series of long pipes where the enzymatic reaction occurs. The operators have noticed that the temperature drop (TD) along the pipes varies more than expected, and they want to understand why. The central hypothesis is that fat content in the raw material (F) and the addition of water (AW) are the leading causes. These two variables also have causal effects on the pressure in the pipes (P), but the pressure does not cause the temperature drop. Figure 5 shows the causal DAG for this research question.

All variables were measured continuously during 16 production days. The data was pre-processed by removing periods when the process was not running under normal conditions, synchronizing different sensor measurements in time, and down-sampling the time resolution to 10-minute intervals. The resulting data set consists of 516 instances.

If the DAG in Figure 5 is a good representation of the data-generating process, the causal effect of added water on the temperature difference could be estimated by

E [T D | A W = h i g h] - E [T D | A W = l o w]

, i.e., without an adjustment set. The critical assumption we want to test is

P ⊥ ⊥ T D | A W, F

We evaluate

P ⊥ ⊥ T D | A W, F

with our BB procedure, where

f () = f (T D, A W, F)

and

g () = g (T D^{*}, A W, F)

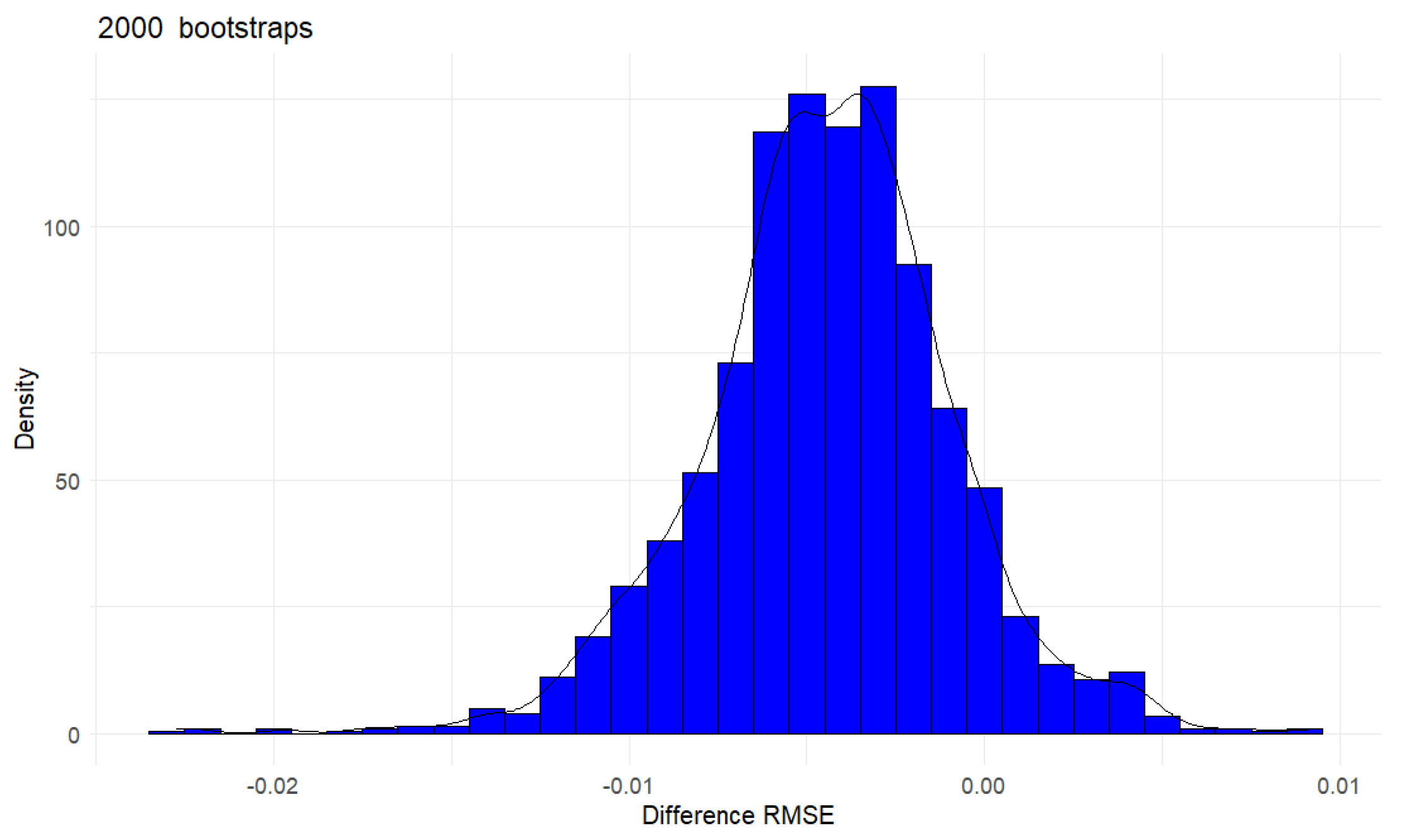
. The first step is to optimize hyperparameters for the XGBoost algorithm by applying 10-fold cross-validation. Then, we apply the BB CI test with 1500 bootstrap replications and with a flat prior. Figure 6 shows the bootstrap distributions of difference in RMSE between

\hat{f}

and

\hat{g}

, the mean: is -0.004 and the 95 % empirical bootstrap credible interval is [-0.011, 0.002]. Therefore, The BB CI test indicates that the conditional independence condition holds, which is also confirmed by the GCM test (p-value

= 0.67

5. Discussion

The theoretical rationale for the BB CI test procedure is that basic frequentist statistical theory recommends against having a presumptively true null hypothesis, which is the case for conditional independence in causal DAGs. The problem of null testing statements assumed to be true may seem like a minor detail. However, in many applied settings with causal inference based on DAGs, the set of implied conditional independence statements can be in the tens, even in the hundreds. Even when adjusting the significance level, accepting lower power, and assuming all conditional independence statements are true, one still has a high risk of rejecting at least one statement; for instance, we cannot assume that each test is independent. The BB CI test offers a Bayesian probabilistic alternative to the problem of testing conditional independence in DAGs, and it can provide a richer and potentially more informative testing approach.

A preliminary step in employing the BB CI test involves assessing the complexity of the causal relationships in the DAG under study. This assessment is not merely procedural but important in selecting an appropriate predictive model for the analysis. In this work, we found that the XGBoost algorithm is a good default choice for modeling

f ()

and

g ()

. XGBoost is a high-performance prediction algorithm for regression and classification, and it can handle different data types, interaction effects, and functional forms. The XGBoost algorithm is fairly easy to tune and fast to train. However, the choice of regression method should not be made automatically. In scenarios where causal links are linear and devoid of complex interactions, simpler predictive models such as lasso or ridge regression are preferable. These models are designed to capture, in essence, linear relationships without introducing unnecessary complexity, unlike more sophisticated ensemble methods like XGBoost, which are likely to create an overcomplicated model, in other words, not optimal for the regression problem. The initial tuning phase serves dual purposes: selecting a suitable predictive algorithm and narrowing the hyperparameter space to mitigate overfitting and computational inefficiency. Effective initial tuning can, therefore, enhance computational efficiency by precluding inapplicable hyperparameters.

Choosing between the BB CI test, the GCM, or any other testing method hinges on assumptions. The BB CI test is a robust and viable alternative when the foundational assumptions of GCM, or other methods may not be fully satisfied, as shown by simulations involving DGF 3. In GCM, the residuals from the two regressions in Equation 2 must either have no relationship (i.e., independence) or a linear (i.e., dependence) relationship. The BB CI test is designed to work as long as one can exhaust the information on the dependent variable from the conditioned variables and avoid overfitting. However, BB CI’s adaptability comes at the cost of requiring a larger dataset—preferably upwards of 1000 observations—to ensure the reliability of the test outcomes, a running knowledge of machine learning tuning, and considerably longer computation time. In the case study test, each bootstrap run took a little less than a second on a normal laptop.

Heterogenity of Conditional Independencies

A potential advantage of using BB CI test is that the shape of the posterior distribution can give insights into whether the conditional independence only holds for a subset of observations, i.e., if it is heterogeneous. If a conditional independence assumption holds for all observations, one expects that the distribution of the difference in RMSE between

\hat{f}

and

\hat{g}

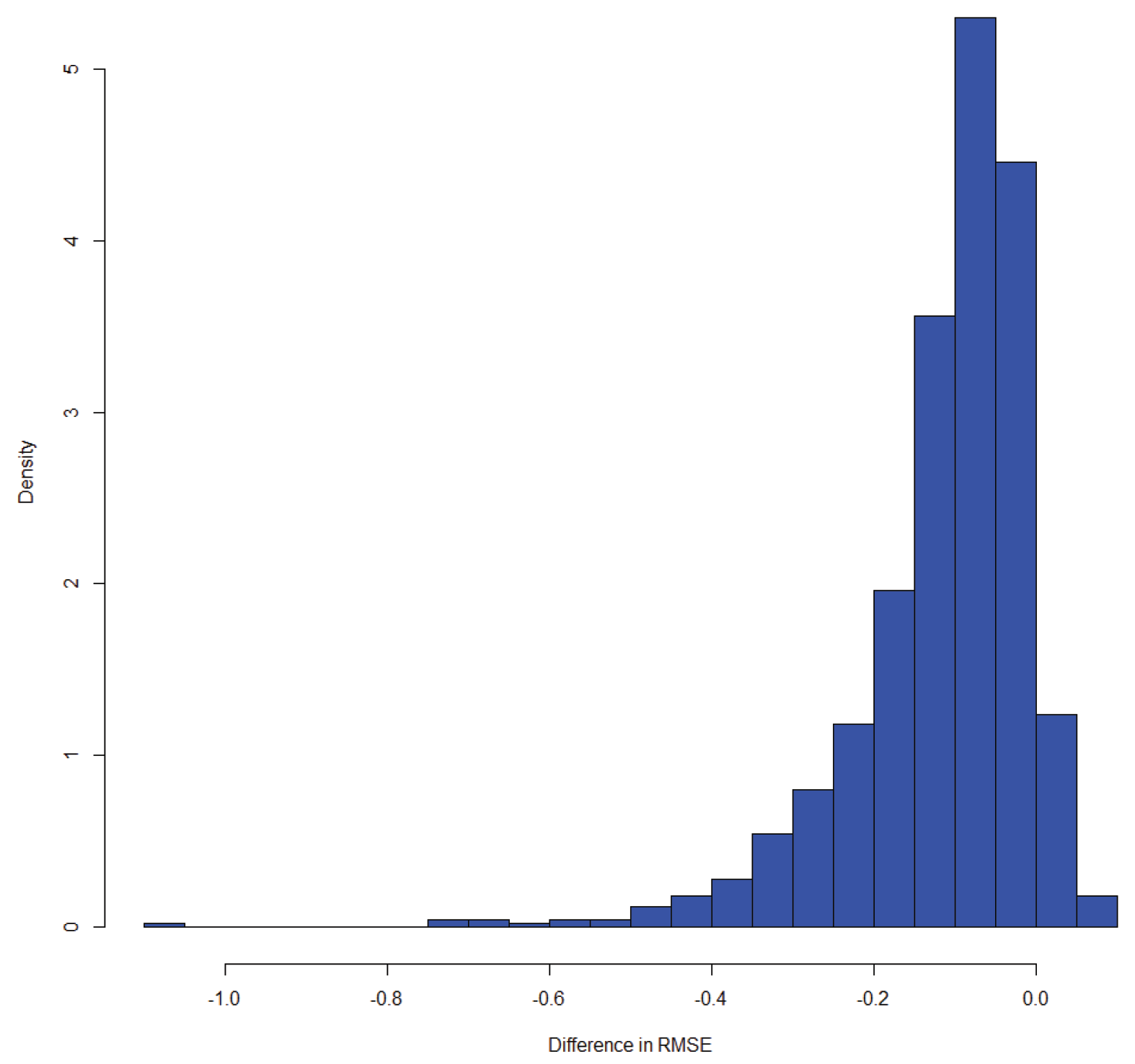
should be approximately symmetrical, as shown in Figure 6. However, a skewed posterior bootstrap distribution can indicate that for a subset of observations, the condition does not hold, or at least the strength of conditional dependence is heterogeneous. In Figure 7, we see the results of testing the independence condition

X_{3} ⊥ ⊥ X_{2} | X_{1}

, which is implied by the DAG

X_{2} \leftarrow X_{1} \to X_{3}

, where the condition does not hold for a subset of the data due to the influence of a fourth (unknown) variable.

One possible way of evaluating heterogeneity in BB CI testing is to apply stratified bootstrapping, i.e., split the dataset into subgroups (strata) and resample from each subgroup independently. This approach holds potential in scenarios where conditional independence exhibits heterogeneity across different population segments. Another option is to consider other machine learning ”metrics”, such as Shapley values. Shapley values are designed to provide insights into the contribution of individual features in a machine-learning model and give information on the importance of features for a specific prediction. Since a conditional independence assumption in a causal DAG must hold for all observations, a methodical study of Shapley values might be used systematically to assess both conditional independence assumptions and the heterogeneity of a conditional independence assumption. More research is needed to evaluate methods for diagnosing heterogeneity from BB CI testing.

6. Conclusion

In this article, we have shown a computational procedure for testing the conditional independence assumptions in causal DAGs by estimating a probability distribution over the difference in predictive performance between two predictive models, which should have equal predictive performance under conditional independence. To create this distribution, we apply Bayesian bootstrapping and machine learning methodology. Therefore, our procedure can handle any types of variables and functional relationships between them, avoiding the problem of testing true null hypotheses.

Our simulation results showed that the BB CI test procedure worked when the underlying conditional independence assumption was true and false. For cases with a false conditional independence assumption, the BB CI test was comparable to the GCM test; however, the method needs more observations. Although we had focused on testing causal DAGs, the BB CI test had the potential to test any conditional independence statement, given sufficient data.

Our principal conclusion was that the BB CI test was accurate, could give insights into the possible violation of the implied conditional independence in causal DAGs, and could be used successfully with or as an alternative to existing methods, such as the GCM.

Author Contributions

Conceptualization, Christian B. H. Thorjussen, Ingrid Måge, Kristian H. Liland and Lars Erik Solberg; methodology, Christian B. H. Thorjussen, Ingrid Måge, Kristian H. Liland and Lars Erik Solberg; software, Christian B. H. Thorjussen and Kristian H. Liland; validation, Christian B. H. Thorjussen; formal analysis, Christian B. H. Thorjussen; data curation, Ingrid Måge and Christian B. H. Thorjussen; writing—original draft preparation, Christian B. H. Thorjussen; writing—review and editing, Christian B. H. Thorjussen, Ingrid Måge, Kristian H. Liland and Lars Erik Solberg; visualization, Christian B. H. Thorjussen; supervision, Ingrid Måge, Kristian H. Liland and Lars Erik Solberg; project administration, Ingrid Måge, Kristian H. Liland; funding acquisition, Ingrid Måge. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by "Stiftelsen for Landbrukets Næringsmiddelforskning" (SLNF), The Research Council of Norway through the projects SFI Digital Food Quality (project number 309259), and by the Norwegian Agricultural Food Research Foundation through the project Precision Food Production (project number 314111).

Data Availability Statement

R simulation functions are available at the Github repository https://github.com/ChristianBHT/BnBCItest_simulations. Industrial data used in the article is confidential.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

Abbreviations

The following abbreviations are used in this manuscript:

DAG	Directed Acyclic Graph
CI	Conditional Independence
BB CI test	Bayesian Bootstrap Conditional Independence test
GCM	Generalized Covariance Measure
MSE	Mean Square Error
RMSE	Root Mean Square Error
BB	Bayesian Bootstrap

References

Pearl, J.; Glymour, M.; Jewell, N.P. Causal Inference in Statistics - A Primer; Wiley, 2016.
Ankan, A.; Wortel, I.M.N.; Textor, J. Testing Graphical Causal Models Using the R Package ”dagitty”. Current Protocols 2021, 1. [Google Scholar] [CrossRef] [PubMed]
Agresti, A. Categorical Data Analysis; John Wiley and Sons, 2002.
McElreath, R. Statistical Rethinking A Bayesian Course with examples in R and Stan; CRC Press, 2020.
Shah, R.D.; Peters, J. The Hardness of Conditional Independence Testing and the Generalised Covariance Measure. Annals of Statistics 2018, 48, 1514–1538. [Google Scholar] [CrossRef]
Daudin, J.J. Partial association measures and an application to qualitative regression. Biometrika 1980, 67, 581–590. [Google Scholar] [CrossRef]
Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM: New York, NY, USA, 2016; KDD’16; pp. 785–794. [Google Scholar] [CrossRef]
Fisher, R. Statistical Methods and Scientific Induction. Journal of the Royal Statistical Society. Series B (Methodological) 1955, 17, 69–78. [Google Scholar] [CrossRef]
Gill, J. The Insignificance of Null Hypothesis Significance Testing. Political Research Quarterly 1999, 52, 647–674. [Google Scholar] [CrossRef]
Gigerenzer, G. Mindless statistics. The Journal of Socio-Economics 2004, 33, 587–606. [Google Scholar] [CrossRef]
Rubin, D.B. The Bayesian Bootstrap. The Annals of Statistics 1981, 9, 130–134. [Google Scholar] [CrossRef]
R Core Team. R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing: Vienna, Austria, 2024.

Figure 1. Example of a causal DAG: First, X happens and causes Z, which again causes Y. The DAG implies the statistical condition

X ⊥ ⊥ Y | Z

, which is testable in the data.

Figure 1. Example of a causal DAG: First, X happens and causes Z, which again causes Y. The DAG implies the statistical condition

X ⊥ ⊥ Y | Z

, which is testable in the data.

Figure 2. Data Generating Functions 1 and 2 and a corresponding graphical representation.

Figure 3. Data Generating Function 3 and a corresponding graphical representation.

Figure 4. Data Generating Functions 4 and 5 and a corresponding graphical representation.

Figure 5. The DAG describing the causal structure in the enzymatic hydrolysis process.

A W

= Added Water, F = Fat Percentage, P = Pressure,

T D

= Temperature Drop.

Figure 5. The DAG describing the causal structure in the enzymatic hydrolysis process.

A W

= Added Water, F = Fat Percentage, P = Pressure,

T D

= Temperature Drop.

Figure 6. BB CI test result: The posterior distribution of RMSE differences between

f ()

and

g ()

from 2000 bootstrap Samples. The distribution centers on a negative number close to zero, and zero is within the 2.5th and 97.5th percentile, indicating that the conditional independence assumption holds .

Figure 6. BB CI test result: The posterior distribution of RMSE differences between

f ()

and

g ()

Figure 7. A skewed posterior distribution can indicate that the conditional independence assumption only holds for a subset of the data.

Table 1. Results from tests using the Generalized Covariance Measure; percentage of simulated tests not rejecting the null hypothesis at significance level 0.05.

			Observations
DGF	C.I. Condition	[T/F]¹	200	400	800	1600	3200
			P-value $> 0.05$
1	$X_{3} ⊥ ⊥ X_{2} \| X_{1}$	[T]	93 %	94 %	94 %	95 %	95 %
1	$X_{3} ⊥ ⊥ X_{2}$	[F]	0 %	0 %	0 %	0 %	0 %
2	$X_{3} ⊥ ⊥ X_{2} \| X_{1}$	[T]	93 %	94 %	94 %	95 %	95 %
2	$X_{3} ⊥ ⊥ X_{2}$	[F]	0 %	0 %	0 %	0 %	0 %
3	$X_{4} ⊥ ⊥ X_{3} \| X_{2}, X_{1}$	[T]	92 %	88 %	87 %	83 %	80 %
3	$X_{4} ⊥ ⊥ X_{3} \| X_{2}$	[F]	49 %	48 %	40 %	37 %	34 %
4	$X_{5} ⊥ ⊥ X_{1} \| X_{3}, X_{4}$	[T]	95 %	95 %	97 %	95 %	94 %
4	$X_{5} ⊥ ⊥ X_{1} \| X_{3}$	[F]	0 %	0 %	0 %	0 %	0 %
4	$X_{3} ⊥ ⊥ X_{4} \| X_{1}, X_{2}$	[T]	88 %	90 %	92 %	92 %	94 %
4	$X_{3} ⊥ ⊥ X_{4} \| X_{1}$	[F]	3 %	0 %	0 %	0 %	0 %
5	$X_{5} ⊥ ⊥ X_{1} \| X_{3}, X_{4}$	[T]	93 %	94 %	96 %	94 %	95 %
5	$X_{5} ⊥ ⊥ X_{1} \| X_{3}$	[F]	0 %	0 %	0 %	0 %	0 %
5	$X_{3} ⊥ ⊥ X_{4} \| X_{1}, X_{2}$	[T]	96 %	96 %	95 %	95 %	95 %
5	$X_{3} ⊥ ⊥ X_{4} \| X_{1}$	[F]	29 %	6 %	0 %	0 %	0 %

Table 2. Results from tests using the BB CI test procedure; percentage of tests where 0 is included in the 2.5 to 97.5 percentile in the posterior distribution of differences between

\hat{f} ()

and

\hat{g} ()

Table 2. Results from tests using the BB CI test procedure; percentage of tests where 0 is included in the 2.5 to 97.5 percentile in the posterior distribution of differences between

\hat{f} ()

and

\hat{g} ()

		Observations
DGF	C.I. Condition	[T/F]¹	Metric	200	400	800	1600	3200
				0 within 2.5th and 97.5th percentile
1	$X_{3} ⊥ ⊥ X_{2} \| X_{1}$	[T]	RMSE	100 %	100 %	100 %	100 %	100 %
1	$X_{3} ⊥ ⊥ X_{2}$	[F]	RMSE	0 %	0 %	0 %	0 %	0 %
2	$X_{3} ⊥ ⊥ X_{2} \| X_{1}$	[T]	RMSE	100 %	100 %	100 %	100 %	100 %
2	$X_{3} ⊥ ⊥ X_{2}$	[F]	RMSE	0 %	0 %	0 %	0 %	0 %
3	$X_{4} ⊥ ⊥ X_{3} \| X_{2}, X_{1}$	[T]	RMSE	100 %	100 %	100 %	100 %	100 %
3	$X_{4} ⊥ ⊥ X_{2} \| X_{2}$	[F]	RMSE	49 %	0 %	0 %	0 %	0 %
4	$X_{5} ⊥ ⊥ X_{1} \| X_{3}, X_{4}$	[T]	RMSE	100 %	100 %	100 %	100 %	100 %
4	$X_{5} ⊥ ⊥ X_{1} \| X_{3}$	[F]	RMSE	86 %	20 %	0 %	0 %	0 %
4	$X_{3} ⊥ ⊥ X_{4} \| X_{1}, X_{2}$	[T]	RMSE	100 %	100 %	100 %	100 %	100 %
4	$X_{3} ⊥ ⊥ X_{4} \| X_{1}$	[F]	RMSE	1 %	0 %	0 %	0 %	0 %
5	$X_{5} ⊥ ⊥ X_{1} \| X_{3}, X_{4}$	[T]	RMSE	100 %	100 %	100 %	100 %	100 %
5	$X_{5} ⊥ ⊥ X_{1} \| X_{3}$	[F]	RMSE	84 %	79 %	18 %	0 %	0 %
5	$X_{3} ⊥ ⊥ X_{4} \| X_{1}, X_{2}$	[T]	RMSE	100 %	100 %	100 %	100 %	100 %
5	$X_{3} ⊥ ⊥ X_{4} \| X_{1}$	[F]	RMSE	100 %	99 %	30 %	0 %	0 %
				Categorical outcome
5	$X_{5} ⊥ ⊥ X_{1} \| X_{3}, X_{4}$	[T]	Acc.	100 %	100 %	100 %	100 %	100 %
5	$X_{5} ⊥ ⊥ X_{1} \| X_{3}, X_{4}$	[T]	Kappa	100 %	100 %	100 %	100 %	100 %
5	$X_{5} ⊥ ⊥ X_{1} \| X_{3}$	[F]	Acc.	61 %	18 %	3 %	0 %	0 %
5	$X_{5} ⊥ ⊥ X_{1} \| X_{3}$	[F]	Kappa	16 %	0 %	0 %	0 %	0 %
5	$X_{3} ⊥ ⊥ X_{4} \| X_{1}, X_{2}$	[T]	Acc.	100 %	100 %	100 %	100 %	100 %
5	$X_{3} ⊥ ⊥ X_{4} \| X_{1}, X_{2}$	[T]	Kappa	100 %	100 %	100 %	100 %	100 %
5	$X_{3} ⊥ ⊥ X_{4} \| X_{1}$	[F]	Acc.	22 %	1 %	0 %	0 %	0 %
5	$X_{3} ⊥ ⊥ X_{4} \| X_{1}$	[F]	Kappa	24 %	1 %	0 %	0 %	0 %

¹ [T/F] indicates if the statement is True or False in the data.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Computational Procedure for Testing Conditional Independence in Causal Directed Acyclic Graphs

Abstract

1. Introduction

1.1. Current Testing Recommendations

1.2. The Null Hypothesis in Conditional Independence Testing in Causal DAGs

2. A new Bayesian Non-Parametric Bootstrap Method

2.1. The Basic Premise

2.2. Bayesian Bootstrap

2.3. The test Procedure

3. Simulation Study

3.1. Implementation of the BB CI Test Procedure

3.2. Simulation Results

4. Industrial Case

5. Discussion

Heterogenity of Conditional Independencies

6. Conclusion

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe