Prerpints.org logo
Preprint
Article

Experimental Study on the Dowel-Bearing Strength of Bambusa Blumeana

Altmetrics

Downloads

166

Views

111

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 March 2024

Posted:

08 March 2024

You are already at the latest version

Alerts
Abstract
This study addresses the critical issue of dowel-bearing strength in Bambusa blumeana, a key sus-tainable construction material crucial for climate change mitigation. Given the lack of bamboo connection standards, the research focuses on determining the dowel-bearing strength of Bambusa blumeana, emphasizing factors such as dowel diameter, node placements, and the physical prop-erties of bamboo. A predictive equation is derived, enhancing the practicality of bamboo in struc-tural design. The results underscore a notable correlation between dowel diameter and character-istic strength, with implications for engineering practices. Node placements significantly affect dowel-bearing capacity, while bamboo's physical attributes, including thickness, culm diameter, and moisture content, exhibit modest correlations with strength. The derived equation aims to assist in structural design, mitigating splitting and bearing failures in bamboo structures. This research establishes a foundation for optimizing the use of Bambusa blumeana in sustainable construction, advancing the understanding of its dowel-bearing strength for improved sustainability and resili-ence in the construction industry. Future research suggestions include exploring bamboo-mortar composites, additional node placements, and employing more comprehensive empirical equations and curve-fitting techniques. The study advocates for further investigations with more diverse and larger bamboo samples to bolster robustness. Additionally, delving into bamboo ductility may offer valuable insights.
Keywords: 
Subject: Engineering  -   Civil Engineering

1. Introduction

Climate change is a significant global challenge resulting in global warming and various ecological, environmental, socio-political, and socio-economic impacts, highlighting the need for immediate mitigation [1]. Around a third of the world’s carbon emissions are from the construction industry [2], wherein it was found that reinforced concrete is identified as having the highest negative impact, emphasizing the importance of early consideration of construction materials and their embodied carbon in reducing overall carbon emissions [3].
In the Philippines, bamboo is one of the most useful materials for domestic and commercial consumption, especially in rural areas as they are called "poor man's timber" [4]. It is considered a material for sustainable development due to its diverse usage. easy availability, renewable aspect, strength, and workability [5,6]. Bamboo is frequently used in roofing material, partition walls, flooring, scaffolding, and reinforcement. Compared to steel, it has a higher tensile strength and elasticity, making it an ideal material for earthquake-prone areas. Additionally, bamboo structures are increasingly getting more complex, as it is used as a composite material for various interior and exterior purposes in buildings like foundations, flyovers, dwellings, multistory buildings, large span structures, and interiors of airports, and recreational buildings, which increases the demand for better standards [5]. With this, there is a need for further research to identify and counter the disadvantages that bamboo has as a construction material.
Bamboo connections have been a major challenge in construction due to their longitudinal fibers, thin walls, hollow nature, and geometric irregularities [7]. Such connections are points of failure of bamboo structures when subjected to extreme loading conditions [8]. In modern bamboo connection designs, using metal to join culms contributed to its reliability and ductility. Dowel-type fasteners have been utilized in bamboo connections in addition to being commonly used in wooden structures. They consist of simple, affordable, and widely accessible materials including screws, dowels, nails, or bolts. These fasteners have major use in practice because of their ability to be used in a variety of applications [9]. The dowels form a mechanical connection that aids in the transfer of loads between the bamboo parts by being inserted into the culm at key points. A prime example of this is bolted connections, although such connections require piercing through the culm making it susceptible to splitting and tensile failure due to its fibrous nature [10]. Other possible modes of failure due to dowel application are brittle splitting [11], bearing failure [12], and a combination of both. Among the different failure modes, splitting failure should be avoided [13]. The application of dowel fasteners, specifically bolted connections, can be seen in Figure 1.
Studies show that bamboo is ductile and a good reinforcing material with an appreciable tensile strength that could be suitable as a substitute for steel in addition to its capacity for compression and bending [15]. However, the embedment properties of bamboo, which is crucial in connections, were not explored. Dowel bearing strength is the property of connection members that imparts resistance to the embedding of a dowel. To provide strength and stability to bamboo structures, the dowel bearing strength needs to be carefully considered [16]. It is critical to consider the bamboo culm’s bearing capacity while employing a dowel-type fastener in bamboo connections. Dowel embedding may result in localized fiber compression and deformation, which may cause failure if the bearing strength is insufficient [17]. In terms of connections, there is a lack of studies in the Philippines for local bamboo species. Bambusa blumeana, locally known as kawayan tinik or spiny bamboo, is the most abundantly available species in the Philippines and the most common raw material used by the rural population for building, making it a preferred material for construction due to its economical nature. Studies in Malaysia and the Philippines have been conducted on the species utilizing the Indian Standard (IS), with results showing that the species, at three to four years old, has a high relative density, compressive strength, and modulus of elasticity during static bending. It exhibits structural quality, making it suitable for use in low-rise construction and further experimental studies on bamboo connections in the Philippines [18].
Consequently, this surge in bamboo's utilization necessitates the establishment of improved standards, particularly in terms of connections, to ensure safe and reliable construction practices. According to [19], the properties of the bamboo culm are enough to estimate the mechanical potential of bamboo in bamboo-based composites. Various studies showed experimental results utilizing different variables, such as bolt diameter [16], the distance of fastener to node [20], moisture content [21], temperature, and more, that would affect the dowel-bearing strength of bamboo, such as a study that exhibited an increase in the ultimate failure stress as end distances of joints increase while the increase of bolt diameter would result in the decrease of the ultimate bearing stress of bamboo under a bolt [22]. While some studies focused on the variability of factors, others would have species-specific studies, just like how wood species for joints also play a crucial role in determining its strength [23]. A review of bamboo connections stated that the same concerns still reside in identifying which joints prove to be more efficient and that the determination of dowel bearing strength is the key to getting the dowel bearing capacity of bolted connections [24]. Different variables such as the flexural strength of the embedded bolt, or the embedding strength of the member ultimately determine the plausibility of using bolted joints as a connector. Although there are more parameters to consider than just the two variables, the new set of parameters that engineered bamboo has to offer makes it equally challenging to make rigidly fixed joints with raw bamboo culms. The application of bamboo in engineering structures has always been on a smaller scale due to the lack of a certain level of integrity when it comes to the connections that bamboo has to offer. While some species have mechanical properties that are on par with wood and are even economically viable as compared to steel, bamboo has yet to standardize an efficient way to create joints that do not rely on frequently used fish mouth joints or beveled joints.
The International Organization for Standardization (ISO) 22157 is the first international standard on bamboo that was prepared by a technical committee on timber structures, in collaboration with the International Network for Bamboo and Rattan. It consists of the standards for Bamboo in terms of determining its physical and mechanical properties including moisture content, shrinkage, compression, bending, shear, and tension [25]. However, it does not tackle bamboo standards regarding connections. The Department of Trade and Industry’s Bureau of Philippine Standards (DTI-BPS) adopted the ISO 22157:2020 standards on bamboo structures as Philippine National Standards (PNS) along with the ISO standards for grading bamboo culms with no mentions regarding the connections of the culms [26].
The main purpose of this experimental research is to determine the dowel-bearing strength of Bambusa blumeana through tests following the Half-hole Testing Setup from the ASTM D5764 Standard Test Method for Evaluating Dowel-Bearing Strength of Wood and Wood-Based Products. Moreover, the combined effects of the variations in the diameter of the dowel and the placement of the nodes are evaluated to highlight the performance of the bamboo connections. The test results would define parameters that may contribute to the outline of test protocols for the future design of these connections considering factors such as the physical properties of the bamboo, the diameters of the round bars as the chosen dowel, and node positions.
As previously stated, in ISO 22157, the specifications for dowel bearing strength test are currently lacking, thus there is a need to establish the specified properties of bamboo to continuously improve on the research done regarding joints of the chosen species. While ISO 22157 is not specifically limited to the dowel bearing strength of bamboo, the mechanical properties that are established on it require a lot of experimental data, thus the significance of the research done. As it currently stands, the development of joints requires much-needed data on the properties of bamboo, this includes the thickness, height, node distance, moisture content, and especially the dowel bearing strength. Finding the right parameters that would output the highest dowel bearing strength would determine the optimal conditions at which to create the joint. Node distance would indicate where to embed a bolt with the highest performance, and the thickness would indicate which members to use given a certain load. Overall, the research on bamboo joints would be significantly improved, given that the results of the research would steer future studies on what parameters affect performance positively and negatively. Additionally, the results of the experiment would help complete the foundation of ISO 22157, ergo contributing to the National Structural Code of the Philippines (NSCP), in establishing the physical and mechanical properties of the specified bamboo species, which would ultimately broaden the possibilities that can be achieved with bamboo structures.

2. Materials and Methods

Given the urgent challenges of climate change and the growing focus on sustainable construction, research on bamboo, specifically its connections, is crucial. This study addresses the lack of standards and aims to contribute to the progress of sustainable architecture and engineering. Bamboo culms, classified under Bambusa blumeana, were tested, and sourced from the Base Bahay Foundation (BBF) and local bamboo farms, along with round bar samples from a local manufacturer. With 12 combinations (see Table 1) and 30 replicate tests per combination, over 360 bamboo samples were used. On-site fabrication produced three round bars mounted on steel plates, as detailed in Table 1
Bamboo samples, sourced from BBF, were assessed for physical properties. Each sample, with a length approximately equal to its diameter, was taken from different culms. Four nodal placements—top, middle, bottom, or none—were considered for each sample. The naming convention included the bamboo species "BB," rod diameter (⅜, ½, ⅝), nodal placement ("T," "M," "B," or "N"), and sample number ("S"). For example, "BB-⅜-T-S1" represented the first bamboo sample with a ⅜ round bar diameter and top nodal placement.
Testing, following ASTM D5764 methods, determined load deformation relationships, maximum load, yield loads, and mode of failure. Three round bars were welded to steel plates, serving as bracing to prevent round bar deformation. The steel plate dimensions were consistent—approximately 100 mm in height and 150-mm in length—for all three plate-mounted round bar diameters. Refer to Figure 2 for the setup details. The hole diameter was determined as the round bar diameter plus one (1) mm.
All bamboo samples used in the study belong to the Bambusa blumeana species. The cut sample length was determined by the average diameter. For round bars, three diameters (⅜", ½", and ⅝") were used, with a constant length measured as the diameter plus two inches (or four (4) rod diameters), approximately 150mm. Nodal placements varied: top, where the node aligns with the pre-drilled hole; middle, where the node is at half the sample length; bottom, where the node is at the very bottom; and none, where no nodes are present along the sample length. Figure 3 illustrates these nodal placements.
This study employed a quantitative method and experimental design to assess the dowel bearing strength of bamboo under various conditions. The collected experimental data were converted into quantitative form and analyzed by the researchers. Despite substantial differences between bamboo and wood, the test methods for wood were deemed applicable to bamboo materials, as demonstrated by previous researchers in the field [13,27,28]. ASTM D5764 was employed to gauge the dowel bearing strength of bamboo, providing data on static load resistance and deformation characteristics. The method involved applying a compressive load through a round bar into a predrilled hole, akin to the approach used on Guadua Angustifolia Kunth [29]. Figures 4 through 2.5 depict the test setup.
Preprints 100787 g005
Figure 5. Half-hole specimen testing setup (adapted from ASTM D5764-97a) [30].
Figure 5. Half-hole specimen testing setup (adapted from ASTM D5764-97a) [30].
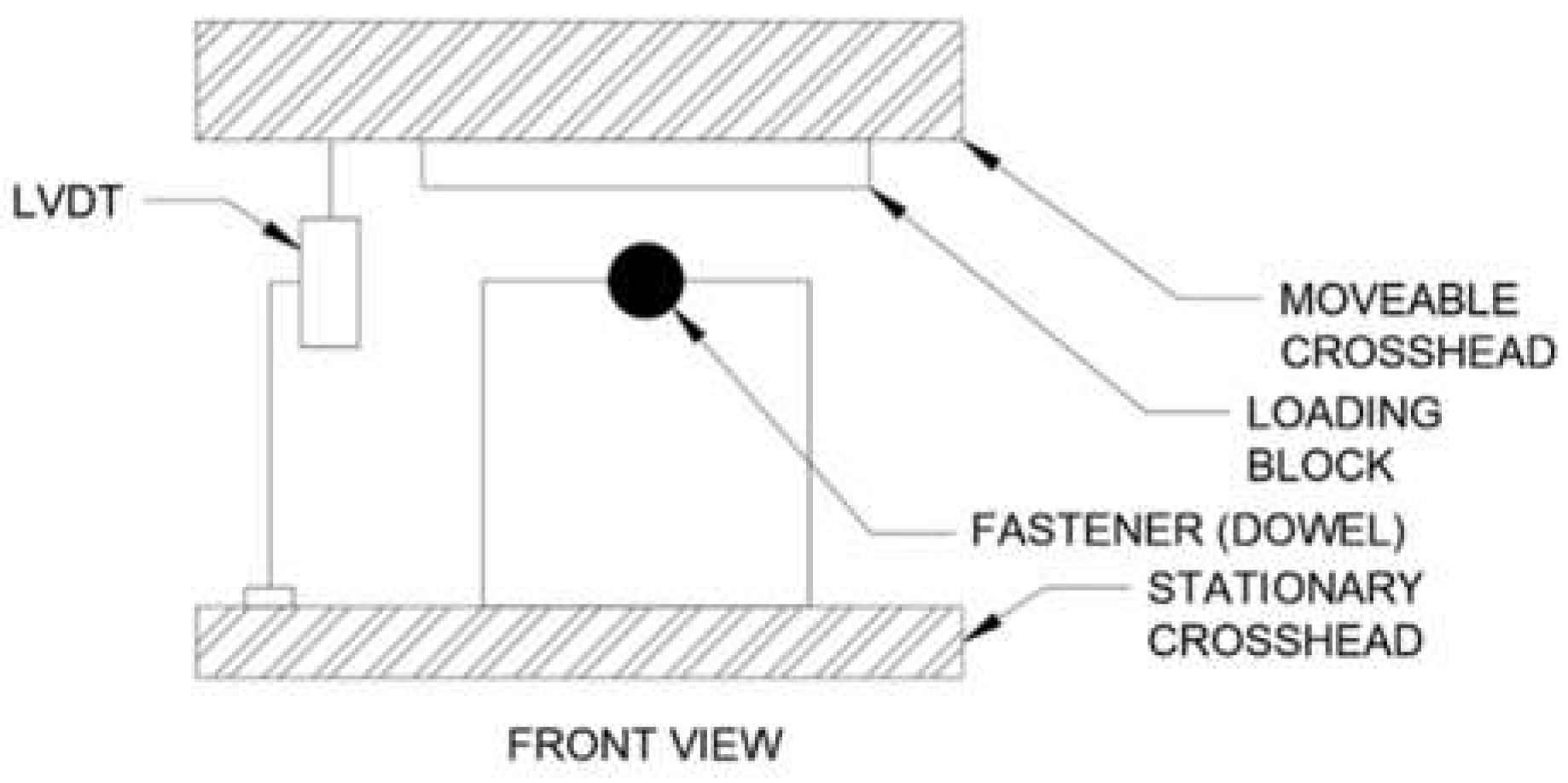
Preprints 100787 g005
Preprints 100787 g006
Figure 6. Actual testing configuration of the study.
Figure 6. Actual testing configuration of the study.
Preprints 100787 g006
After the tests, the analysis focused on the load-deformation relationships, maximum load, yield loads, and mode of failure. A universal testing machine (UTM) was used to test with a compression force and measure deformation. The study maintained a constant rate of movement at 2 mm per minute, adhering to the standard for bamboo testing, which specified a test duration of 3 to 7 minutes [25]. The speed was calibrated using the UTM for consistency across subsequent tests. All results were meticulously recorded and plotted in load-deformation diagrams. Sample acceptance and rejection were determined based on the identified mode of failure for each sample. Considering six major modes of failure in bamboo structural members, the study considered only the following modes as acceptable: longitudinal failure of fibers, splitting under axial compression, and bulging under axial compression [31]. Moreover, samples were rejected if they exhibited cracks before testing or if their moisture content significantly deviated from the standard range of 9%-11% set by the BBF. These selective criteria ensured a rigorous evaluation of sample integrity and adherence to specified standards. The study employed multiple linear regression analysis to develop an equation for predicting the dowel-bearing strength of Bambusa blumeana. For this purpose, the researchers utilized the Data Analysis feature in MS Excel as a tool to facilitate the execution of the multivariate regression analysis.

3. Results

3.1. Raw Force vs. Displacement Graphs

The experimental study involved conducting 12 combinations and performing 30 replicate tests for each combination, resulting in approximately 360 data points. The raw data for the experiment was obtained from force versus displacement graphs exported by the Universal Testing Machine (UTM). The data for each combination are presented in the figures below. While there is some variability among the samples, they exhibit consistent behavior overall.
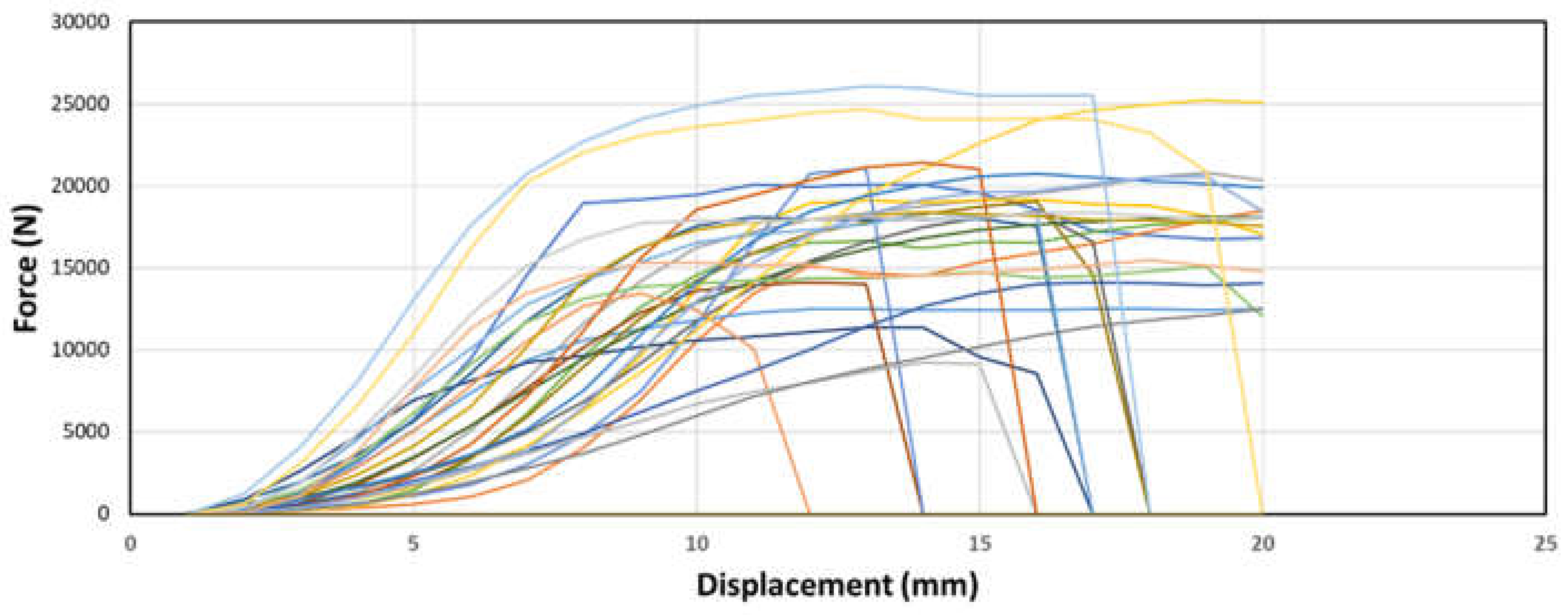
Figures 7 through 8 above depict the behavior of top node samples across the three round bar diameters. It can be observed that the force increases exponentially initially, followed by a linear increase, and eventually reaches a plateau. This behavior resembles a plastic response, indicating deformation before failure. The consistency of this pattern across different diameters suggests a predictable and characteristic behavior of the top node samples during the testing process.
Preprints 100787 g007
Figure 7. Sample force-displacement graphs of samples with top node placement and (a) ⅜” dowel diameter.
Figure 7. Sample force-displacement graphs of samples with top node placement and (a) ⅜” dowel diameter.
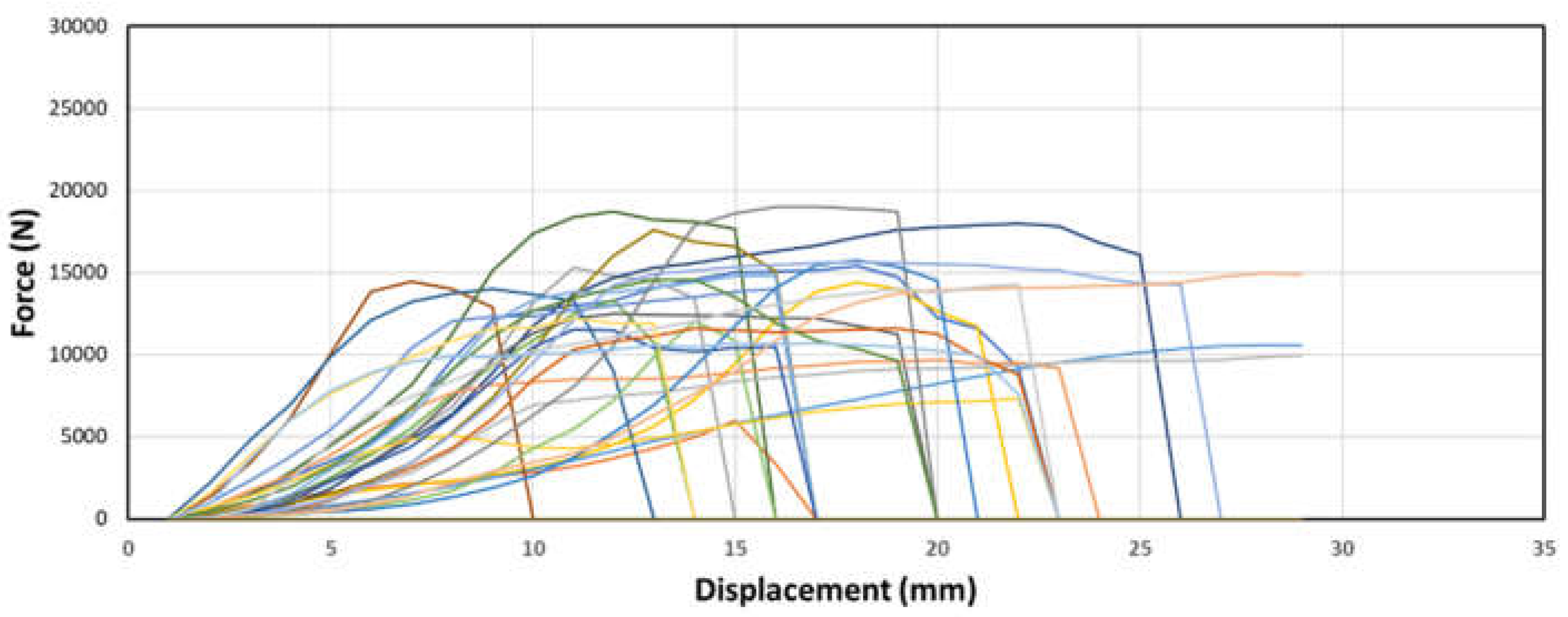
Preprints 100787 g007
Preprints 100787 g008
Figure 8. Sample force-displacement graphs of samples with top node placement and (b) ½” dowel diameter.
Figure 8. Sample force-displacement graphs of samples with top node placement and (b) ½” dowel diameter.
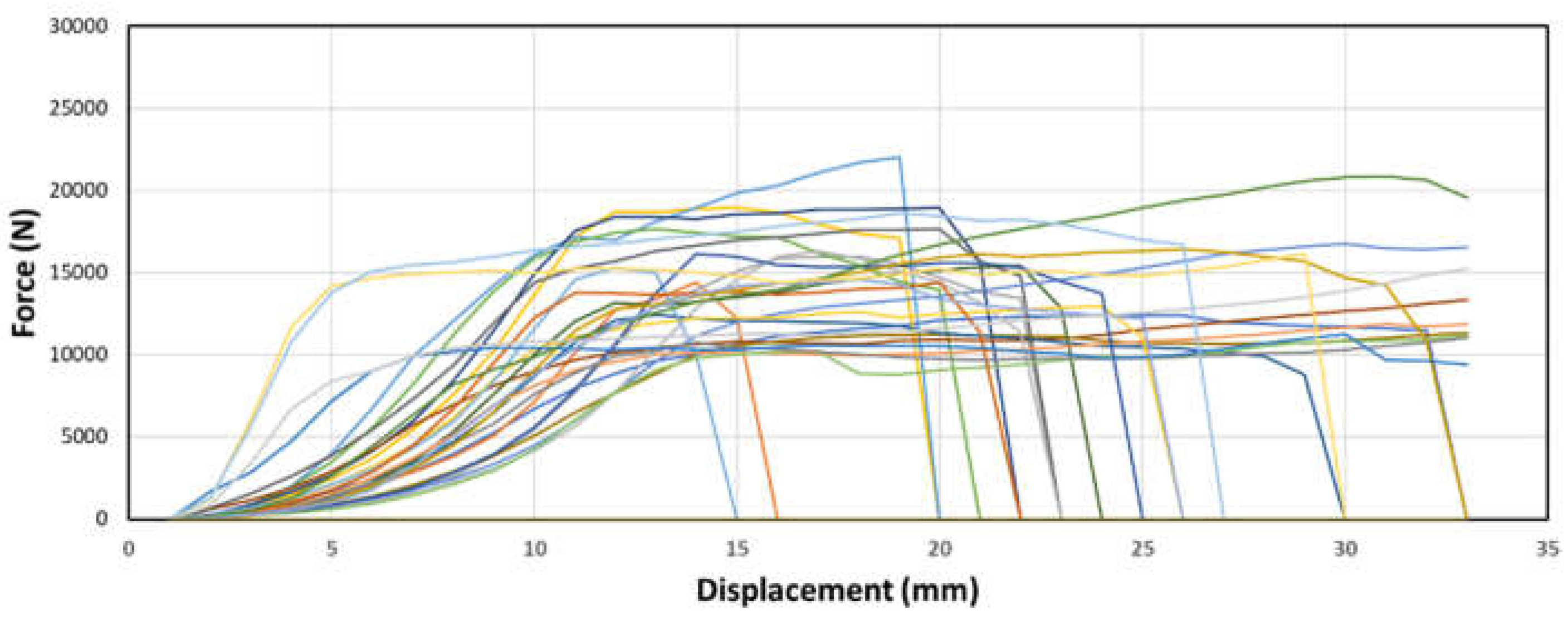
Preprints 100787 g008
Preprints 100787 g009
Figure 9. Sample force-displacement graphs of samples with top node placement and (c) ⅝” dowel diameter.
Figure 9. Sample force-displacement graphs of samples with top node placement and (c) ⅝” dowel diameter.
Preprints 100787 g009
The behavior of the middle node samples, as shown in the figures 10 through 12 above, exhibits a similar trend to that of the top node samples. The force increases exponentially and then linearly before reaching a plateau, displaying a plastic-like behavior. However, in the case of the middle node samples, this plastic behavior is even more pronounced than in the top node samples. Additionally, the strength of the middle node samples is significantly weaker compared to the top node samples. These consistent results highlight the distinct characteristics and lower strength exhibited by the middle node samples during the testing process.
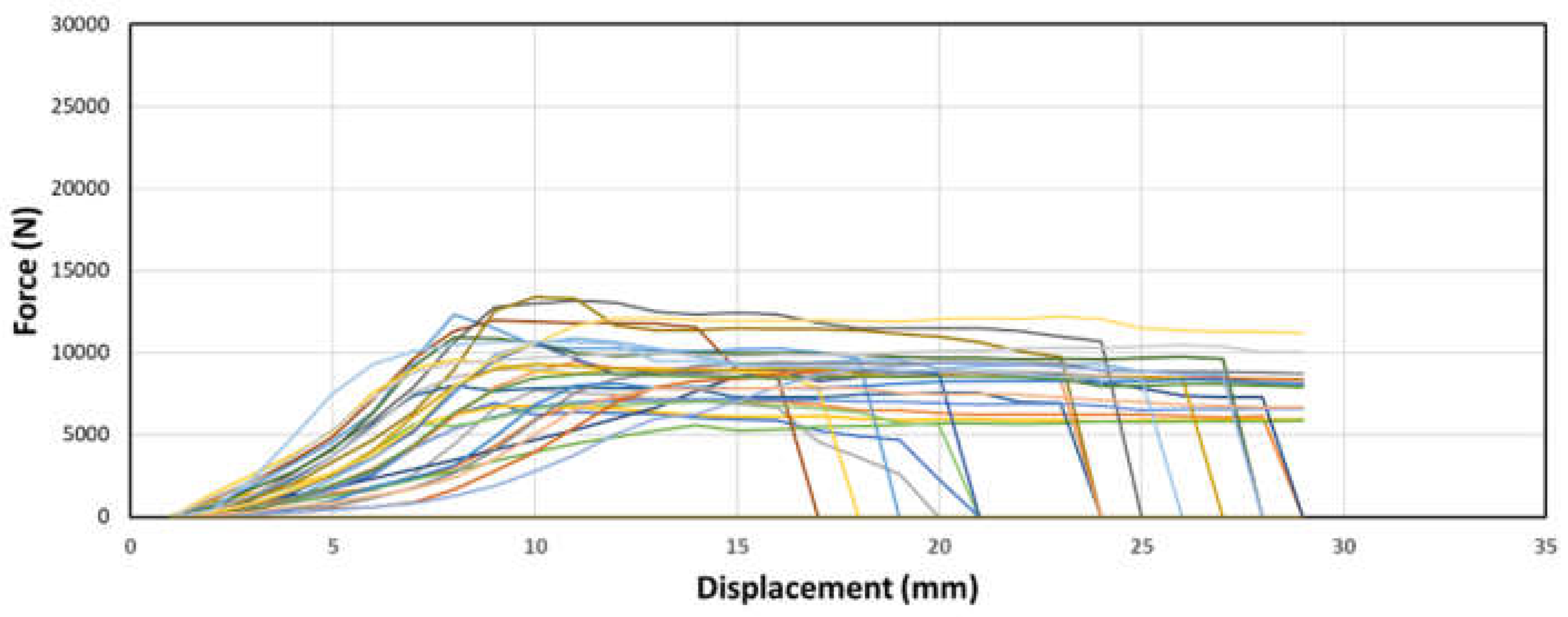
Preprints 100787 g010
Figure 10. Sample force-displacement graphs of samples with middle node placement and (a) ⅜” dowel diameter.
Figure 10. Sample force-displacement graphs of samples with middle node placement and (a) ⅜” dowel diameter.
Preprints 100787 g010
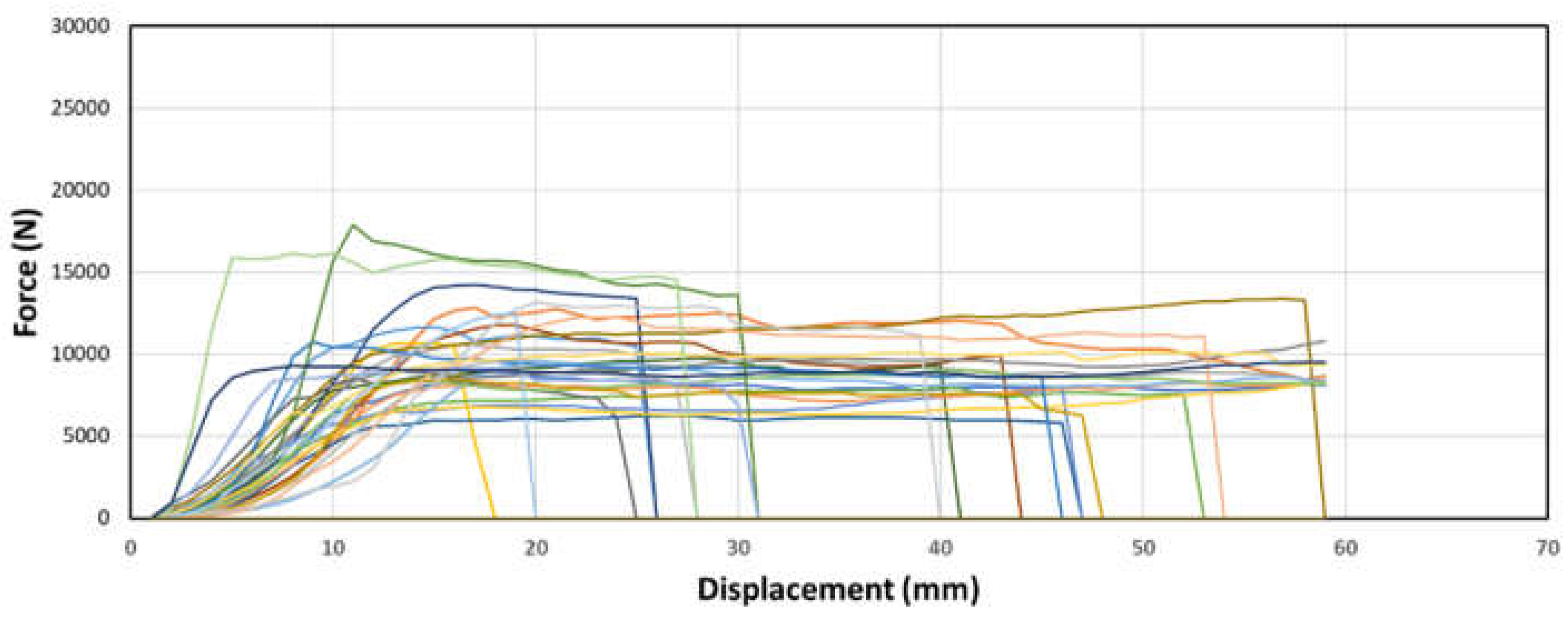
Preprints 100787 g011
Figure 11. Sample force-displacement graphs of samples with middle node placement and (b) ½” dowel diameter.
Figure 11. Sample force-displacement graphs of samples with middle node placement and (b) ½” dowel diameter.
Preprints 100787 g011
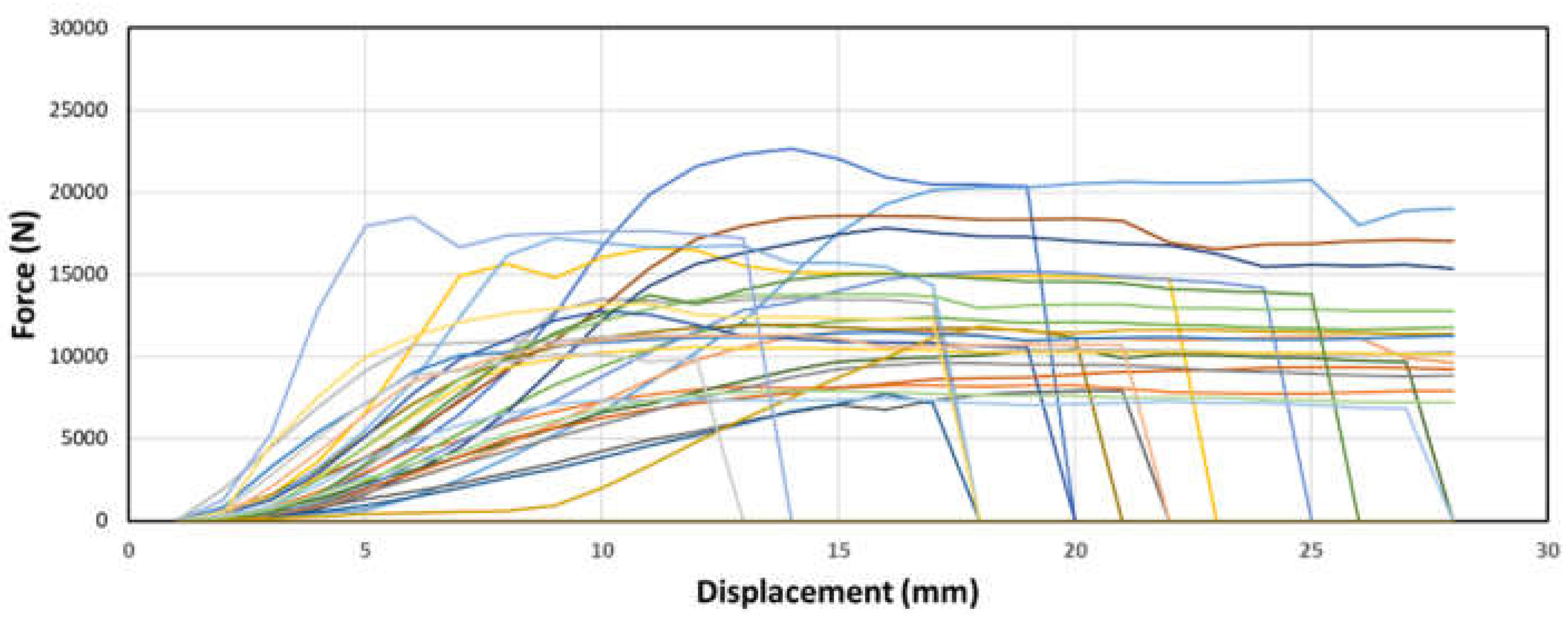
Preprints 100787 g012
Figure 12. Sample force-displacement graphs of samples with middle node placement and (c) ⅝” dowel diameter.
Figure 12. Sample force-displacement graphs of samples with middle node placement and (c) ⅝” dowel diameter.
Preprints 100787 g012
The bottom node samples, as observed in figures 13 through 15 above, exhibit a behavior like the previous samples with an exponential and linear increase in force. However, unlike the previous samples, there is no flat-lining observed in the force-displacement curve. This indicates that the deformation continues without reaching a plateau before failing. Furthermore, the bottom node samples display considerably weaker strength compared to the other samples. These findings highlight the distinct behavior and lower strength of the bottom node samples in comparison to the other samples.
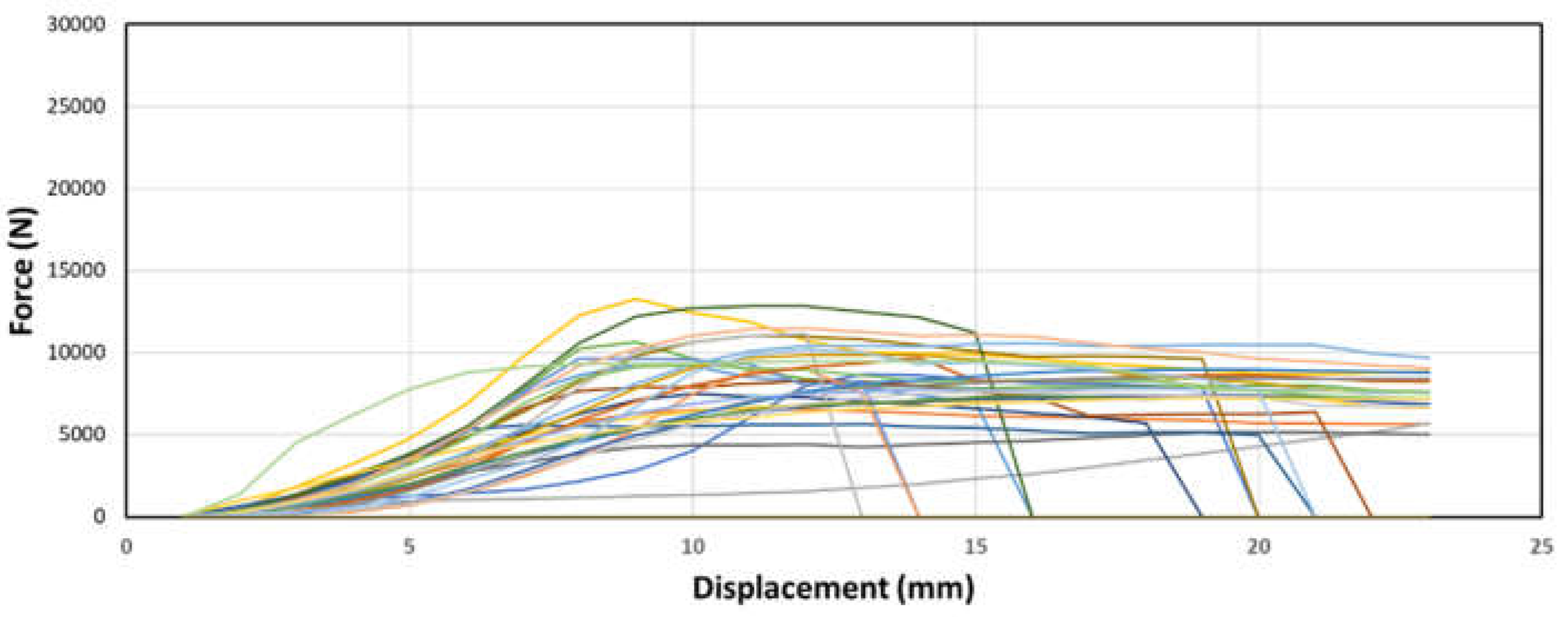
Preprints 100787 g013
Figure 13. Sample force-displacement graphs of samples with bottom node placement and (c) ⅝” dowel diameter.
Figure 13. Sample force-displacement graphs of samples with bottom node placement and (c) ⅝” dowel diameter.
Preprints 100787 g013
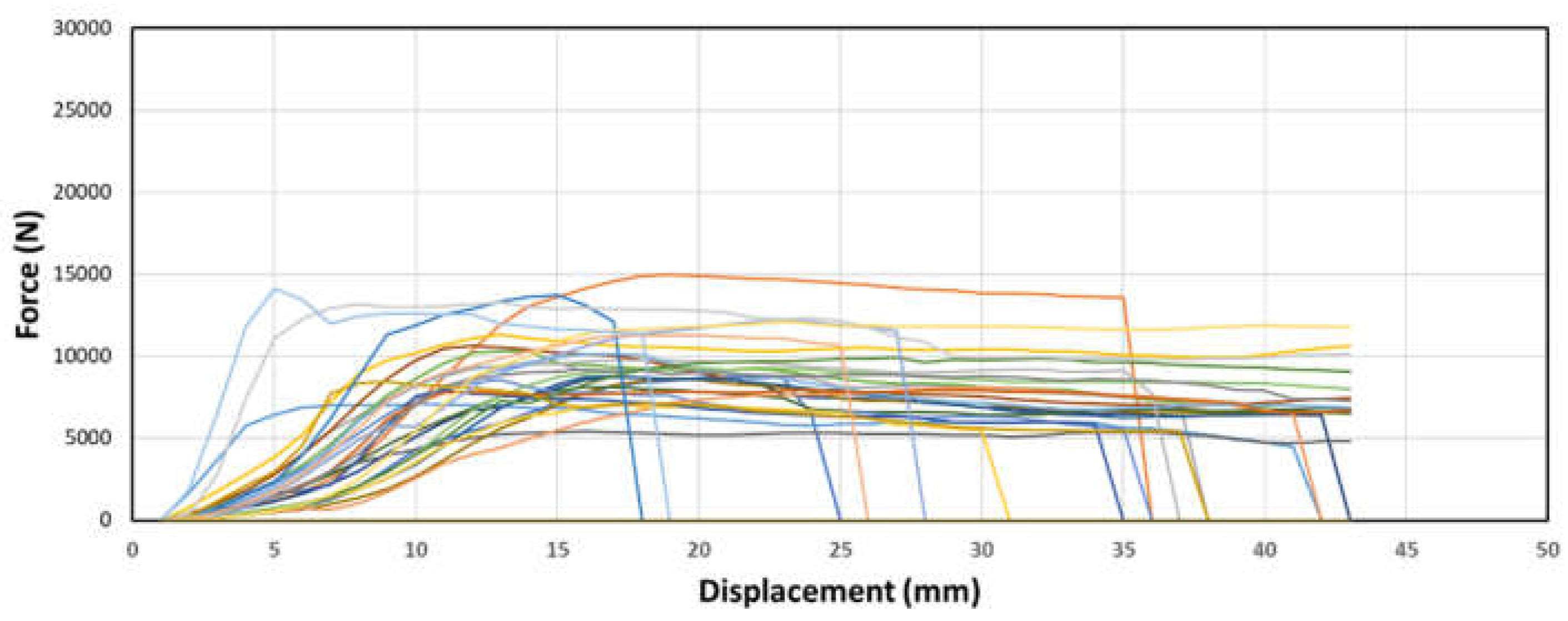
Preprints 100787 g014
Figure 14. Sample force-displacement graphs of samples with bottom node placement and (c) ⅝” dowel diameter.
Figure 14. Sample force-displacement graphs of samples with bottom node placement and (c) ⅝” dowel diameter.
Preprints 100787 g014
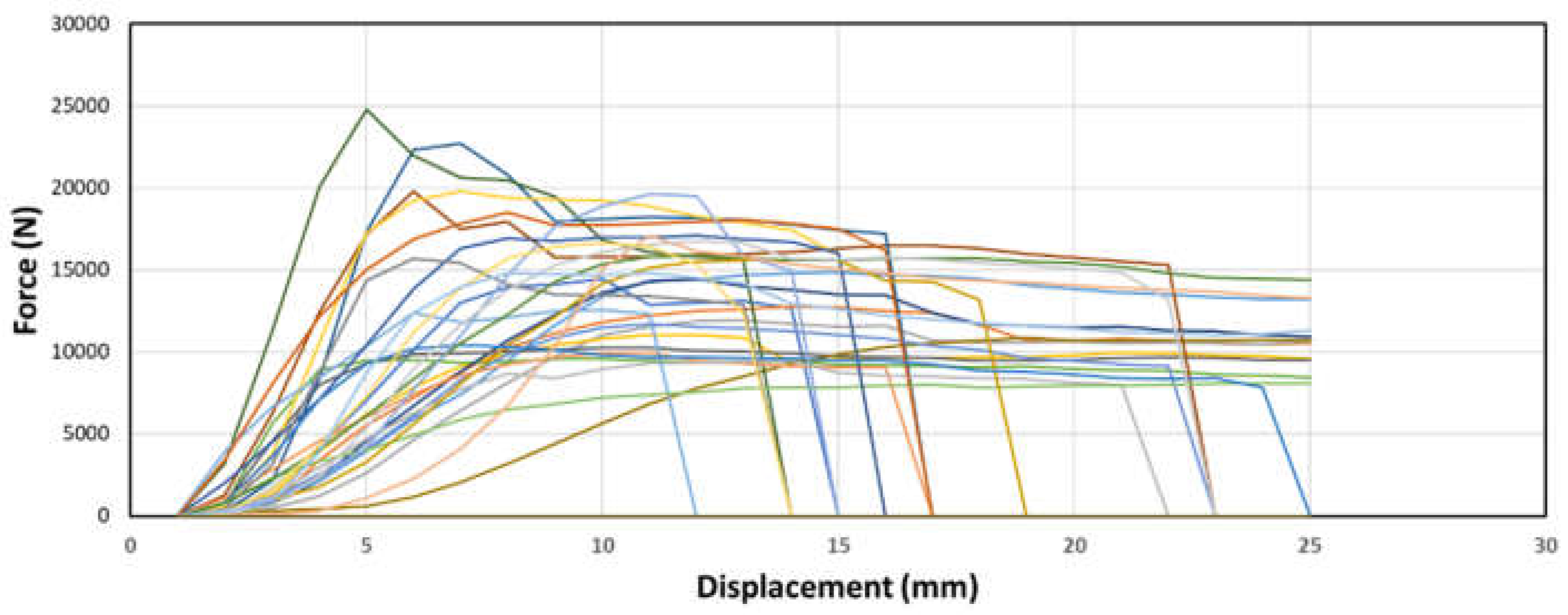
Preprints 100787 g015
Figure 15. Sample force-displacement graphs of samples with bottom node placement and (c) ⅝” dowel diameter.
Figure 15. Sample force-displacement graphs of samples with bottom node placement and (c) ⅝” dowel diameter.
Preprints 100787 g015
The behavior of the samples without node placement, as observed in the 3 figures above, closely resembles that of the bottom node samples. There is minimal or almost no flat-lining observed in the force-displacement curve, indicating continuous deformation without reaching a plateau. Furthermore, these samples exhibit significantly weaker strength compared to the other samples. This consistent behavior and weaker strength suggest that the absence of node placement has a notable impact on the structural performance, resulting in a lack of dowel-bearing capacity and less resistance to deformation.
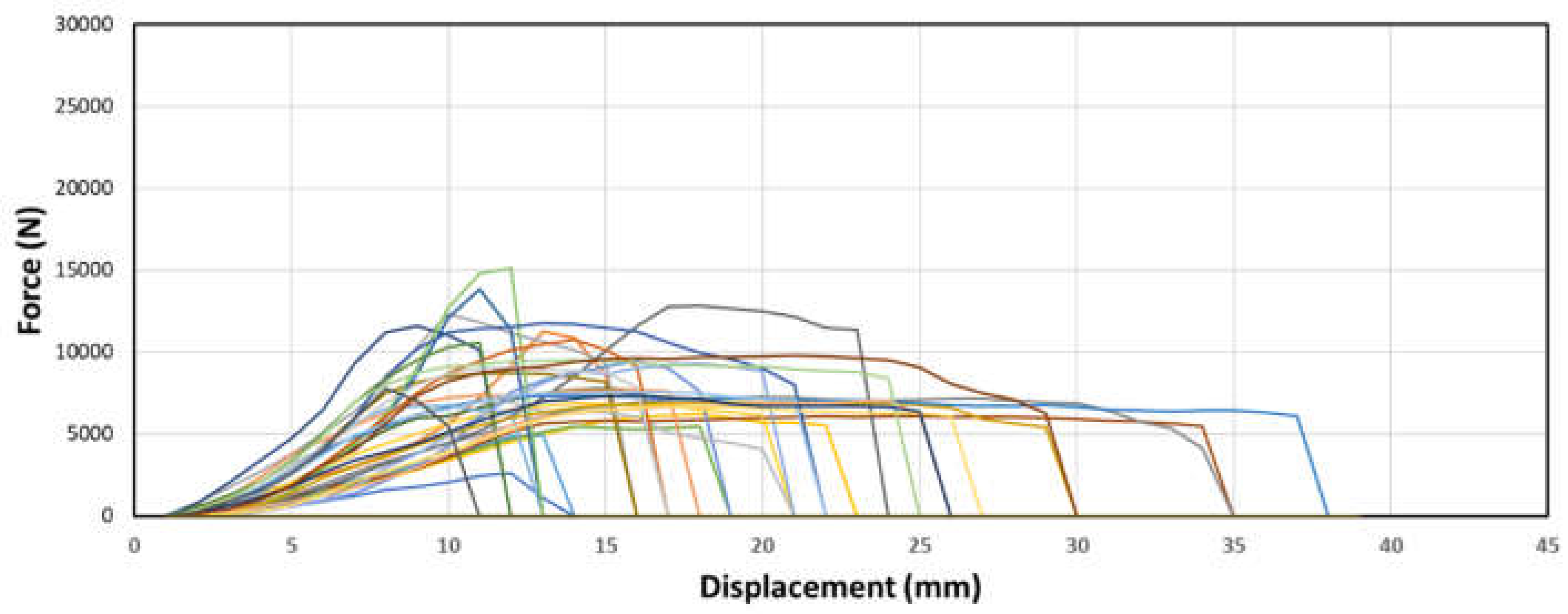
Preprints 100787 g016
Figure 16. Sample force-displacement graphs of samples with no node placement and (c) ⅝” dowel diameter.
Figure 16. Sample force-displacement graphs of samples with no node placement and (c) ⅝” dowel diameter.
Preprints 100787 g016
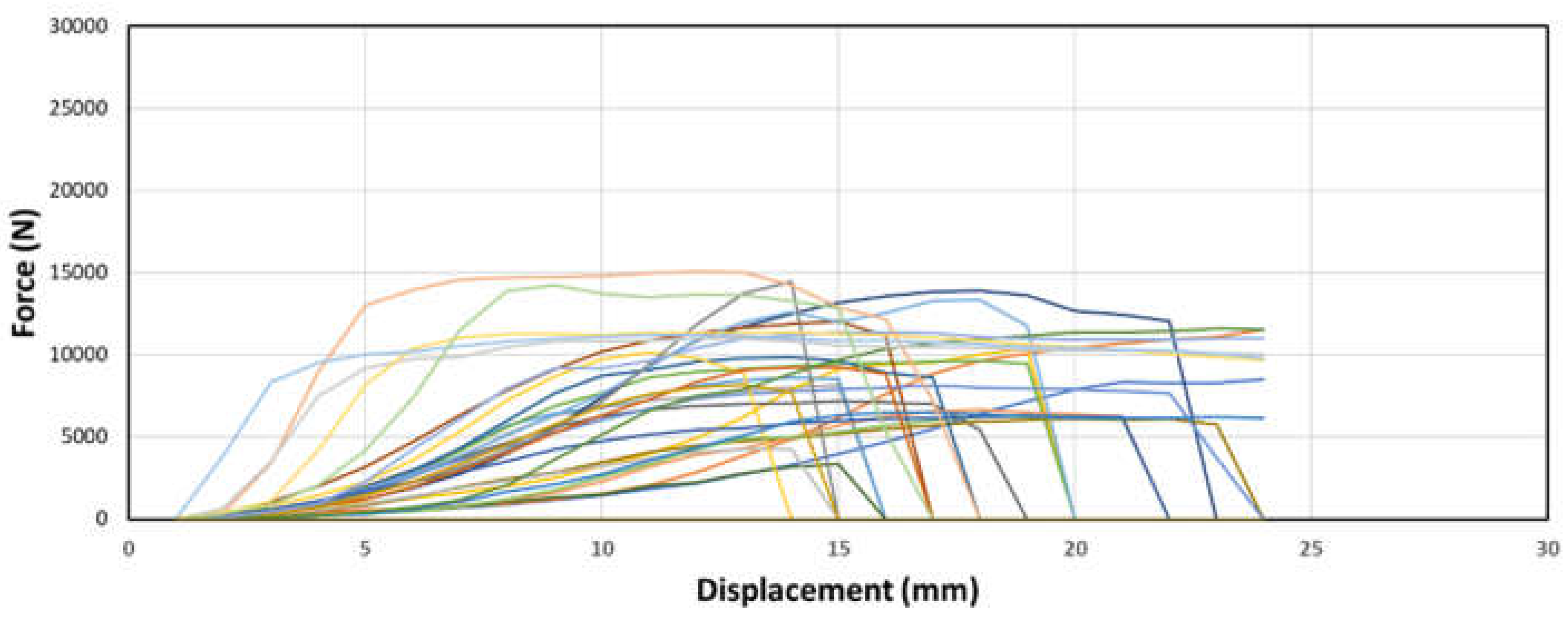
Preprints 100787 g017
Figure 17. Sample force-displacement graphs of samples with no node placement and (c) ⅝” dowel diameter.
Figure 17. Sample force-displacement graphs of samples with no node placement and (c) ⅝” dowel diameter.
Preprints 100787 g017
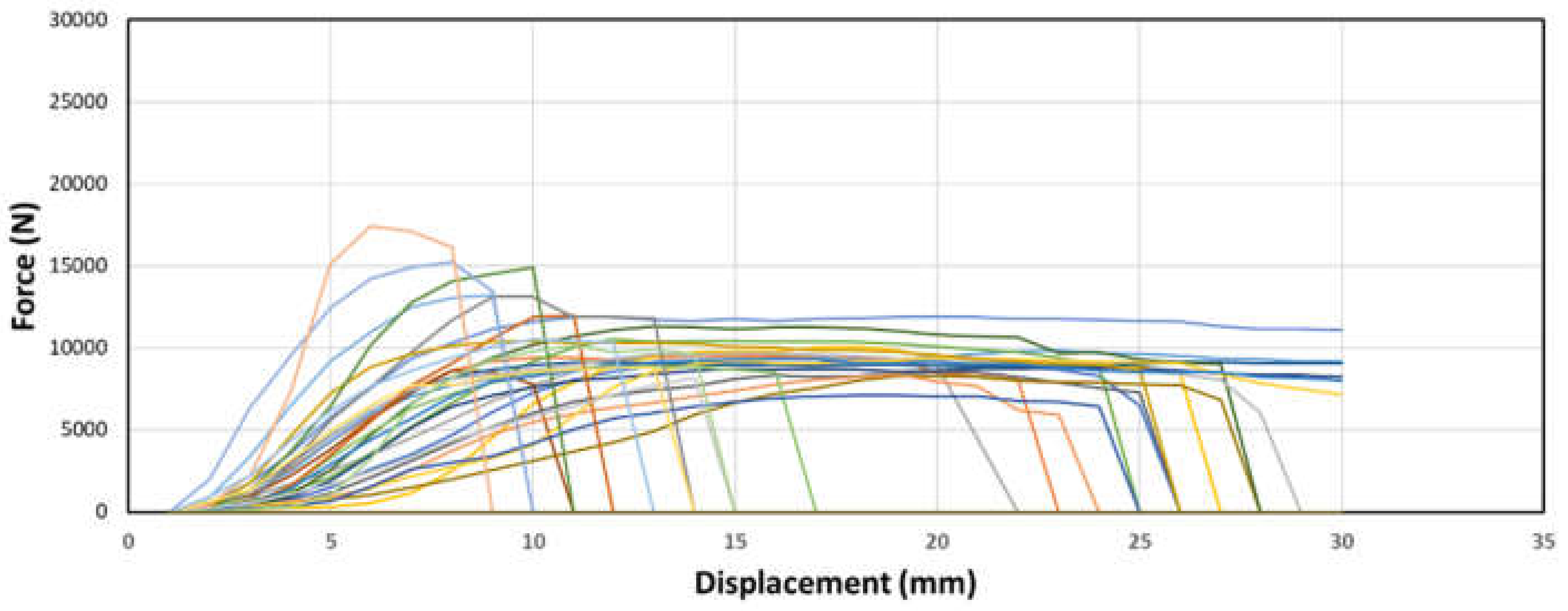
Preprints 100787 g018
Figure 18. Sample force-displacement graphs of samples with no node placement and (c) ⅝” dowel diameter.
Figure 18. Sample force-displacement graphs of samples with no node placement and (c) ⅝” dowel diameter.
Preprints 100787 g018

3.2. Dowel Bearing Strength with Varying Parameters

The peak strength values were determined by identifying the maximum force from the raw force versus displacement graphs. These peak strengths represent the ultimate dowel-bearing strength of the samples. Figure 19 and Figure 20 below illustrate the plotted data, showcasing the variations in strength based on node placements and dowel diameters. Correspondingly, the dowel-bearing strength of the samples from the box-and-whisker plots is tabulated as the maximum, mean, and minimum values shown in the associated table 2
Preprints 100787 g019
Figure 19. Box and whisker plot of the dowel-bearing strength in terms of node placement.
Figure 19. Box and whisker plot of the dowel-bearing strength in terms of node placement.
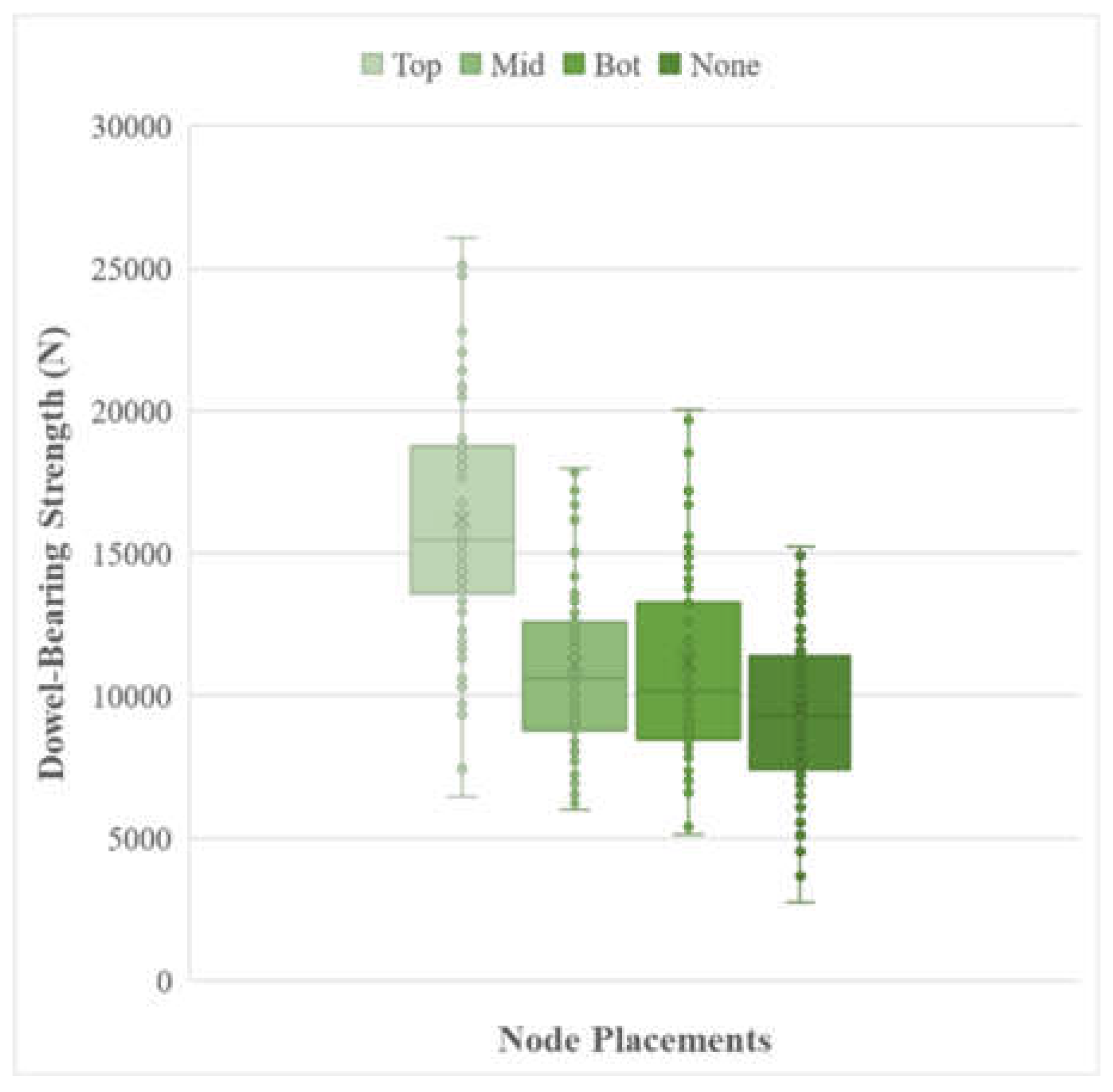
Preprints 100787 g019
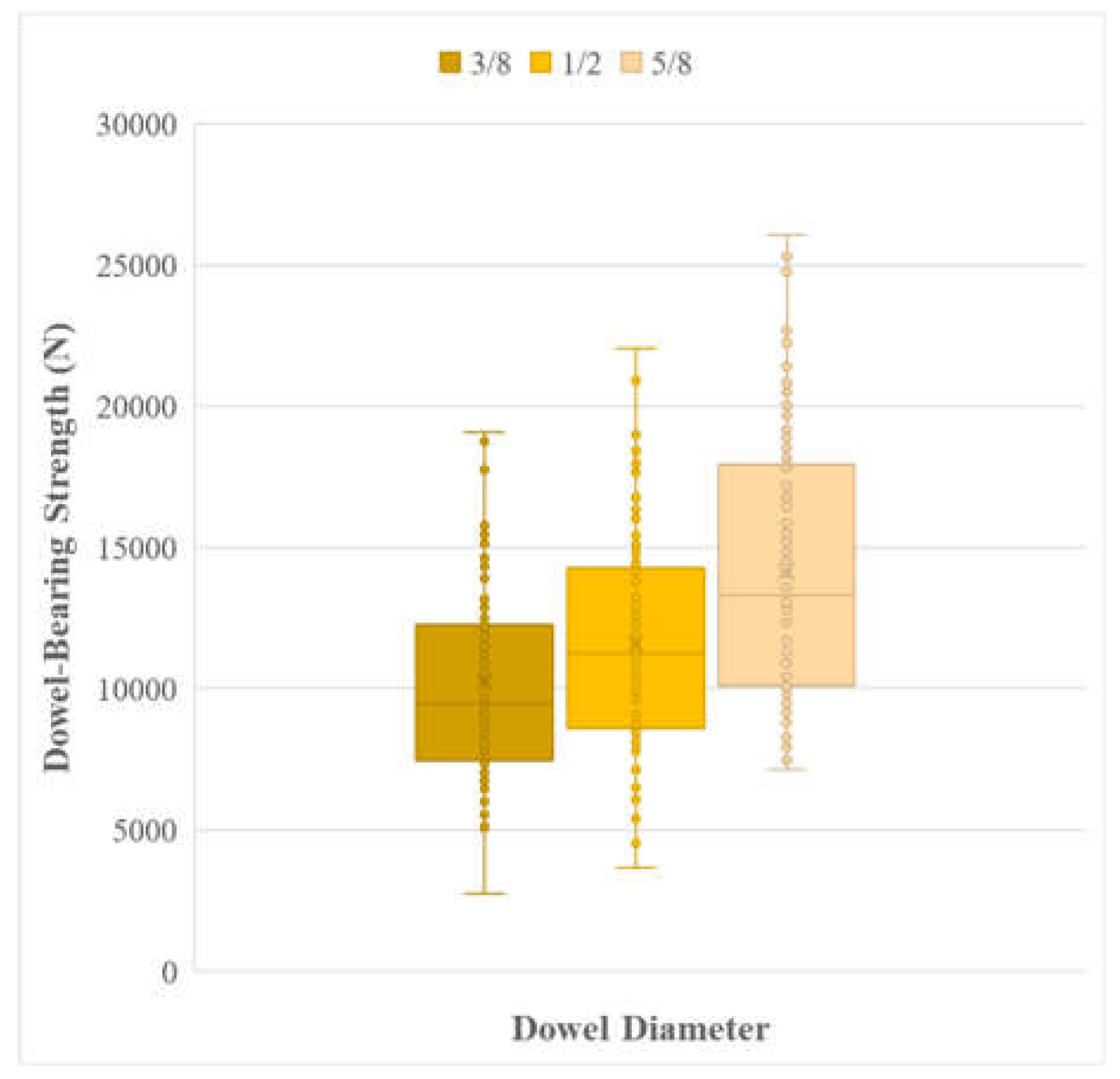
Preprints 100787 g020
Figure 20. Box and whisker plot of the dowel-bearing strength in terms of dowel diameter.
Figure 20. Box and whisker plot of the dowel-bearing strength in terms of dowel diameter.
Preprints 100787 g020
Table 2. Dowel-Bearing Strength from the Box-and-Whisker Plots.
Table 2. Dowel-Bearing Strength from the Box-and-Whisker Plots.
Dowel-Bearing Strength (N)
Maximum Mean Minimum
Node
Placement 		Top 18776.89 15471.15 13594.08
Middle 12563.43 10601.44 8765.35
Bottom 13253.51 10167.93 8477.35
None 11368.06 9301.47 7429.10
Dowel
Diameter 		3/8 12234.81 9484.04 7471.06
1/2 14262.02 11239.78 8616.42
5/8 17909.58 13291.56 10118.16
The first figure indicates that the top node placement consistently exhibits the highest strength among the different placements, and this is further backed by the table where the mean strength is 15471.15N, 31.0%-40.0% stronger than the means of other node placements. On the other hand, there is no significant difference in strength observed among the mid, bottom placements, and no nodes. The mean values shown in the table differ only from 4.1%-12.1%. Additionally, an increase in dowel diameter results in an increase in the ultimate strength that the samples can withstand, with a seemingly linear relationship between the three variables. Looking at the associated table, the lowest strength came from the ⅜” dowel diameter, with a mean of 9484.04N, while the strongest came from the ⅝” dowel diameter, with a mean of 13291.56N. Comparing them side by side, from ⅜” to ½” there is a strength increase of 15.6%, from ½” to ⅝”, on the other hand, there is a strength increase of 15.4%. These findings suggest that the top node placement (31-40% stronger than other node placements) and larger dowel diameters (15.6%-15.4% stronger every ⅛” added to dowel diameter) contribute to higher overall strength in the tested samples.

3.3. Dowel Bearing Strength vs. Thickness

To assess the potential impact of thickness on the strength of the bamboo samples, force and thickness graphs were evaluated, as depicted in the figures 21 through 23 below. These graphs illustrate the relationship between the applied force and the thickness of the samples. By analyzing these figures, the influence of thickness on the strength of the bamboo samples be examined and any correlations or trends identified.
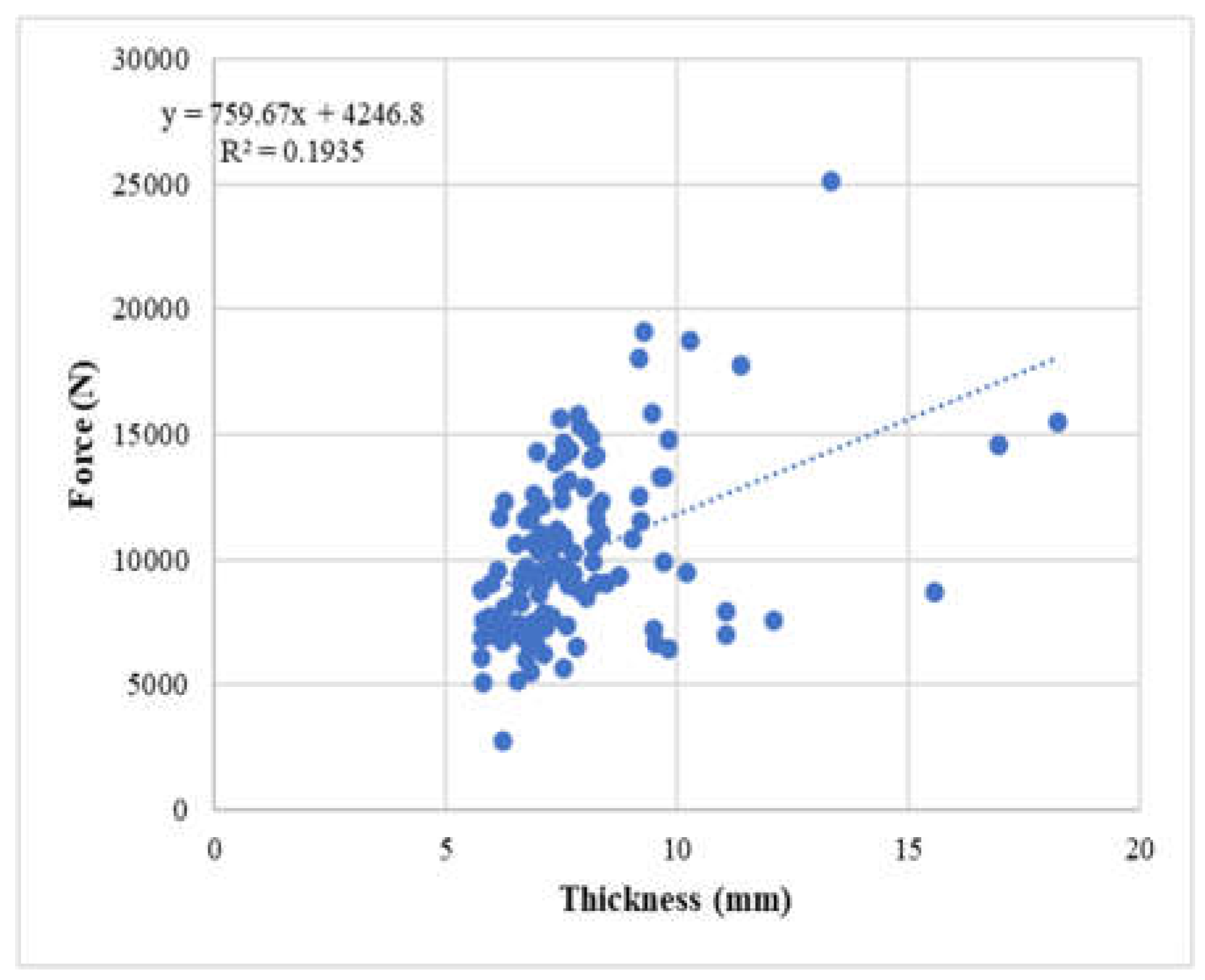
Preprints 100787 g021
Figure 21. Force vs thickness plot of ⅜“ dowel diameter samples.
Figure 21. Force vs thickness plot of ⅜“ dowel diameter samples.
Preprints 100787 g021
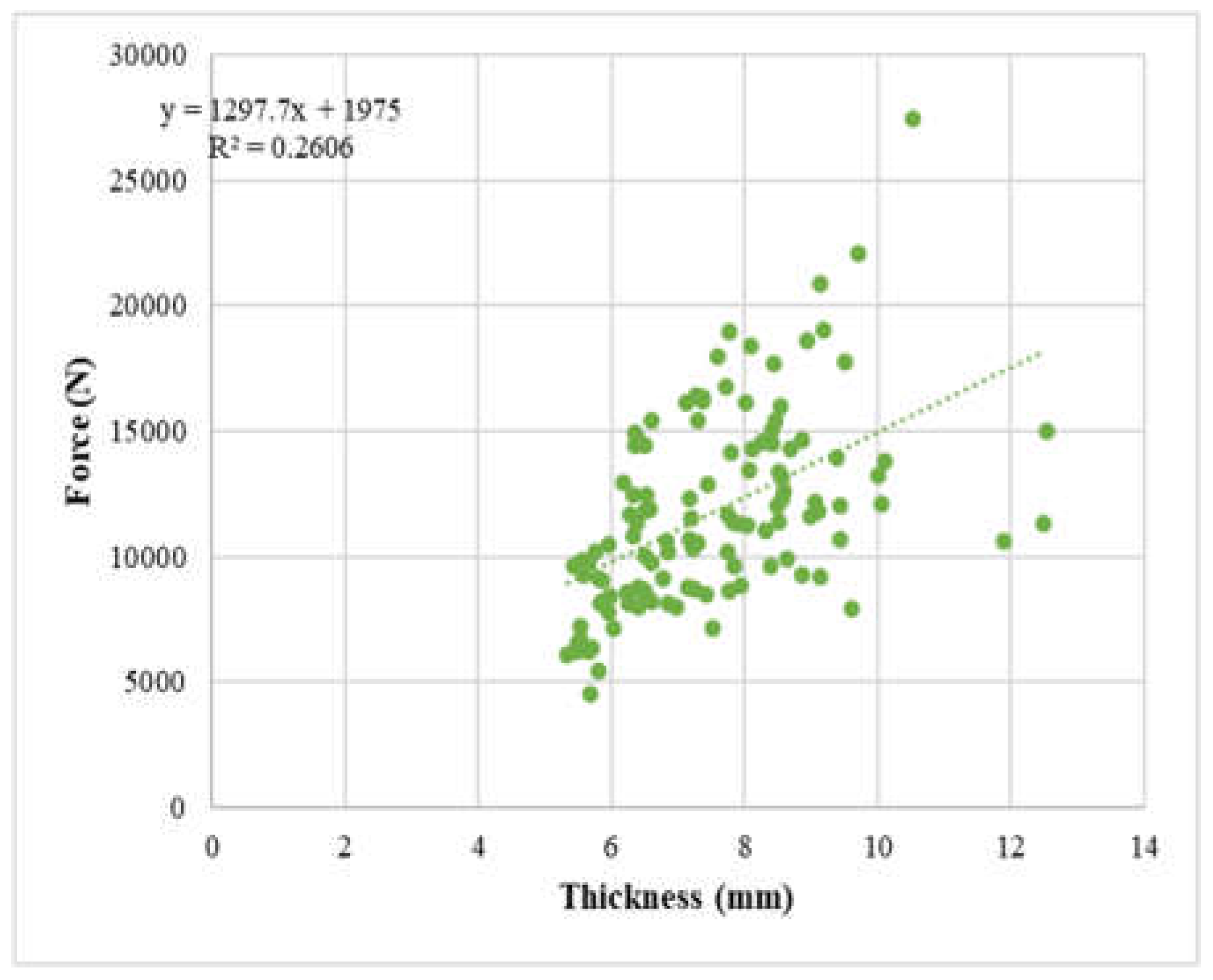
Preprints 100787 g022
Figure 22. Force vs thickness plot of ½“ dowel diameter samples.
Figure 22. Force vs thickness plot of ½“ dowel diameter samples.
Preprints 100787 g022
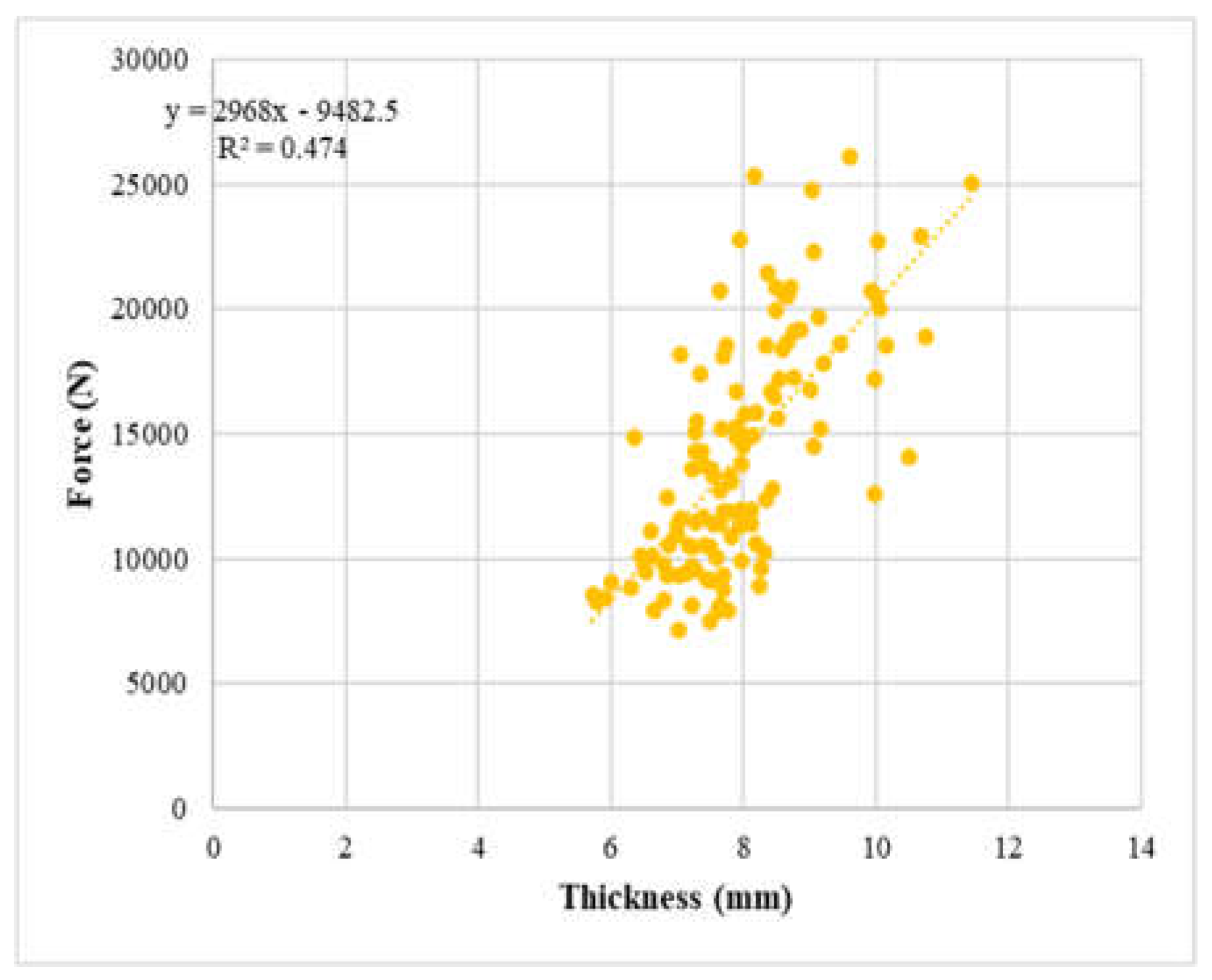
Preprints 100787 g023
Figure 23. Force vs thickness plot of ⅝“ dowel diameter samples.
Figure 23. Force vs thickness plot of ⅝“ dowel diameter samples.
Preprints 100787 g023
The figures above demonstrate that the samples with 3/8", 1/2", and 5/8" diameter round bars exhibit a weak positive correlation between force and thickness. This indicates that there is a tendency for the force applied to increase slightly as the thickness of the samples increases, although the correlation is not very strong. The relationship suggests that thicker bamboo samples may have a slightly higher capacity to withstand greater forces compared to thinner samples, but the extent of this relationship is relatively modest.

3.4. Dowel Bearing Strength vs. Culm Diameter

To assess the potential impact of culm diameter on the strength of the bamboo samples, force versus bamboo diameter graphs were evaluated, as depicted in figures 24 through 26 below. These graphs illustrate the relationship between the applied force and the diameter of the bamboo culms. By analyzing these figures, the influence of the culm diameter on the strength of the bamboo samples can be examined, and any correlations or trends can be identified.
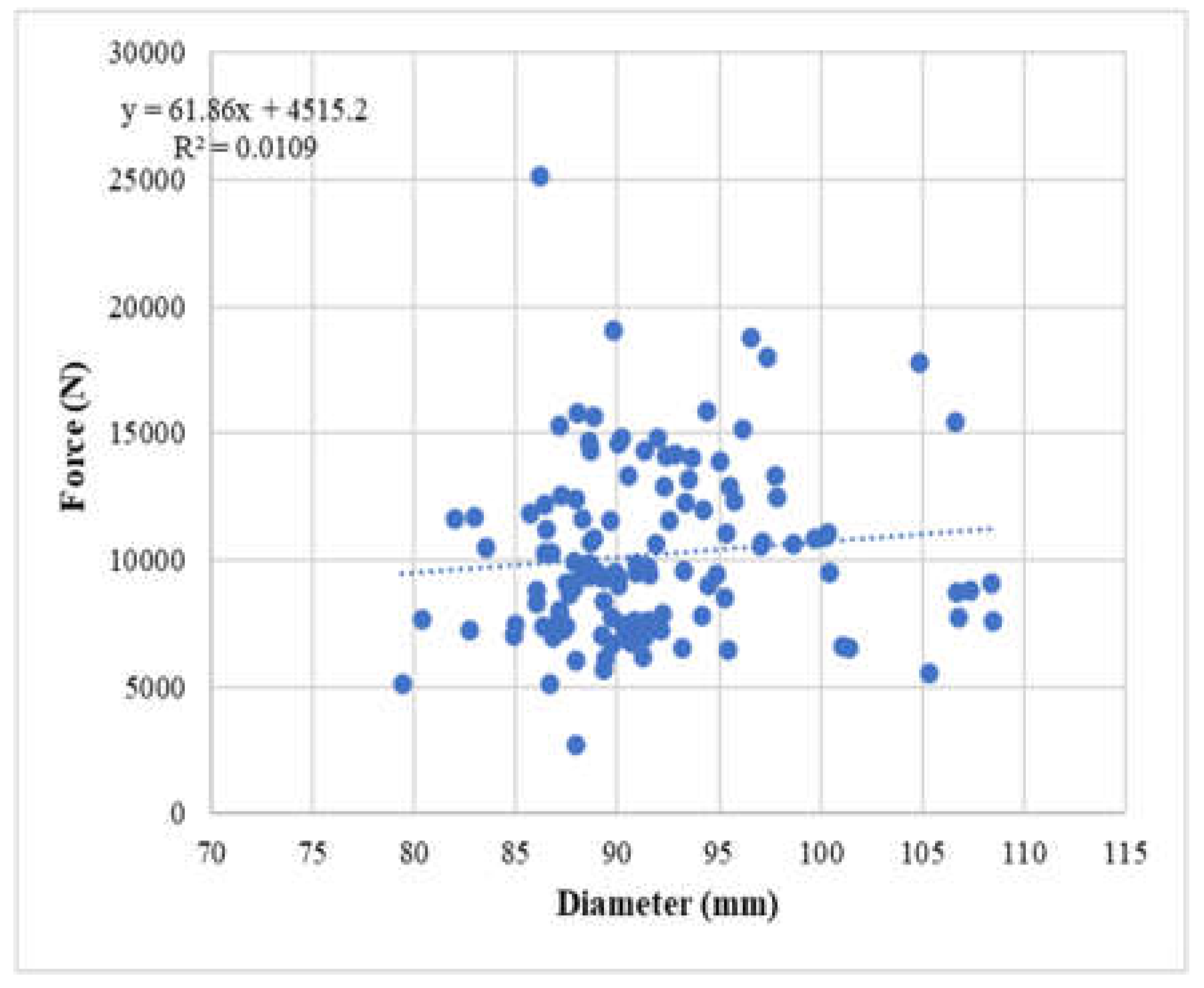
Preprints 100787 g024
Figure 24. Force vs diameter plot of ⅝“ dowel diameter samples.
Figure 24. Force vs diameter plot of ⅝“ dowel diameter samples.
Preprints 100787 g024
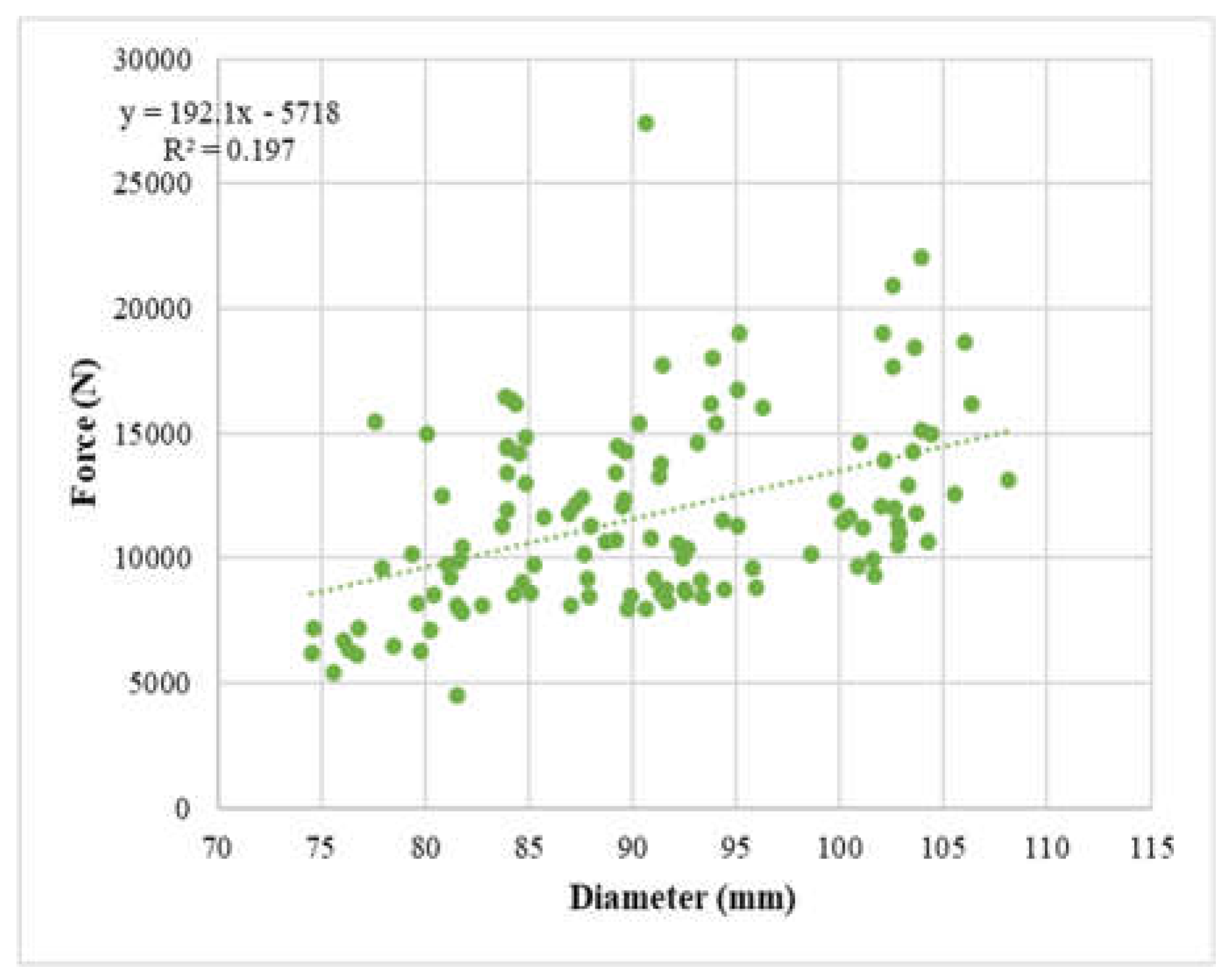
Preprints 100787 g025
Figure 25. Force vs diameter plot of ⅝“ dowel diameter samples.
Figure 25. Force vs diameter plot of ⅝“ dowel diameter samples.
Preprints 100787 g025
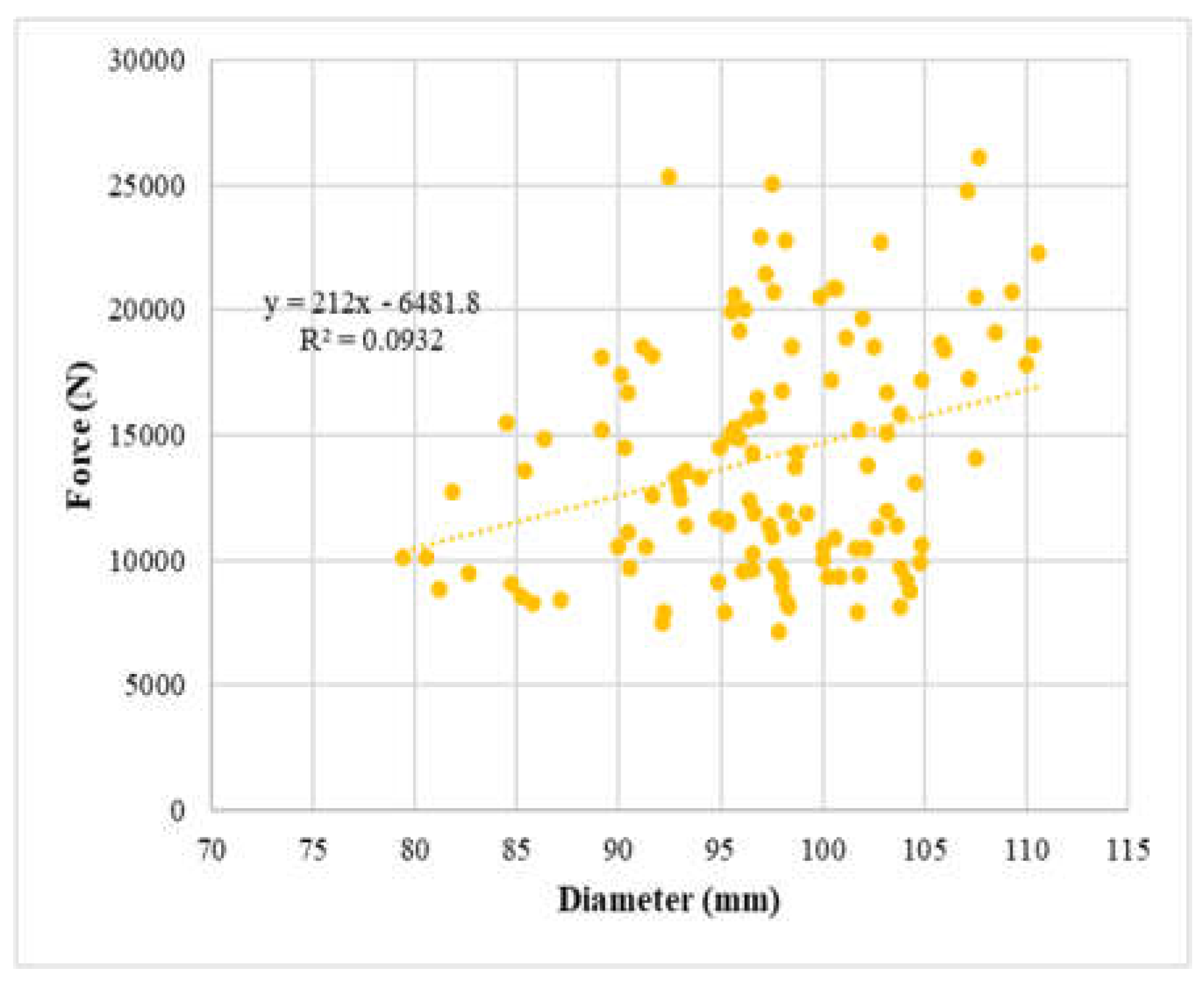
Preprints 100787 g026
Figure 26. Force vs diameter plot of ⅝“ dowel diameter samples.
Figure 26. Force vs diameter plot of ⅝“ dowel diameter samples.
Preprints 100787 g026
The analysis of the force versus bamboo diameter graphs reveals a very weak positive correlation between the diameters of the bamboo culms and the dowel bearing strength of the samples. This suggests that culm diameter may not be a reliable indicator of strength. On the other hand, the results indicate that thickness is a better indicator of dowel bearing strength. The thicker the bamboo sample, the stronger it tends to be. Therefore, the thickness should be considered as a more suitable parameter for assessing the strength of bamboo samples, while the culm diameter may not provide a consistent measure of strength.
The analysis of the dowel bearing strength versus density plots reveals a very weak positive correlation between the strength and density of the bamboo samples. However, it is important to note that the samples exhibit very similar densities, ranging from 600 to 1000 g/mm3. This suggests that density may not be a robust indicator of strength in this context. While there may be some relationship between strength and density, it appears to be minimal and not consistently discernible. Therefore, it is advisable to consider alternative factors or parameters as potential indicators of strength in bamboo samples, as density alone may not provide reliable insights.

3.8. Proposed Equations for the Dowel-Bearing Strength of Bambusa

The formulation of the empirical equation to find the dowel-bearing strength of the bamboo specimen will be attributed to three important variables as found in the observation of the group. The three variables are the dowel diameter, culm thickness, and node placement, all of which are a measure of length and must be modified to fit the multilinear regression analysis. The equation accounts for specimens that only have nodes thus reducing the number of trials used in formulating the equation. It is important to note that in the observed relation of the node distance and dowel bearing strength is of a logarithmic equation, hence the variables will have to be altered to perform linear regression on the following variables. For node distance vs dowel bearing strength, an empirical conversion factor is used to change the output maximum forces into its linear counterpart. It was found that the slope and y-intercept of the equation are as follows:
y = − 0.00172 x + 4.173838 ,
The equation is then used to find a direct conversion of the node distance to the maximum force, accounting that the original relation is logarithmic, now turned linear relation. The derivation is as follows:
N o d e   d i s t a n c e   ( N D )   t o   D o w e l   B e a r i n g   S t r e n g t h   ( D B S ) :   N D = D B S
− 0.00172 ( N D ) + 4.173838 = l n ( D B S ) l n ( 10 )
l n ( 10 ) [ − 0.00172 ( N D ) + 4.173838 ] = l n ( D B S )
e { l n ( 10 ) [ − 0.00172 ( N D ) + 4.173838 ] } = D B S
This conversion, alongside the combination of both culm thickness and dowel diameter into a new variable called contact area, will be the final variables used in the making of the final empirical equation of the dowel bearing strength. Performing multilinear regression analysis on the raw data arranged as stated, the following equation can be made.
103.569 ( A ) + 1.366 e { l n ( 10 ) [ − 0.00172 ( N D ) + 4.173838 ] } − 14644.593 = D B S
where:
A = Contact Area (Culm Thickness * Dowel Diameter) in mm2
ND = Node Distance in mm
DBS = Dowel Bearing Strength in N
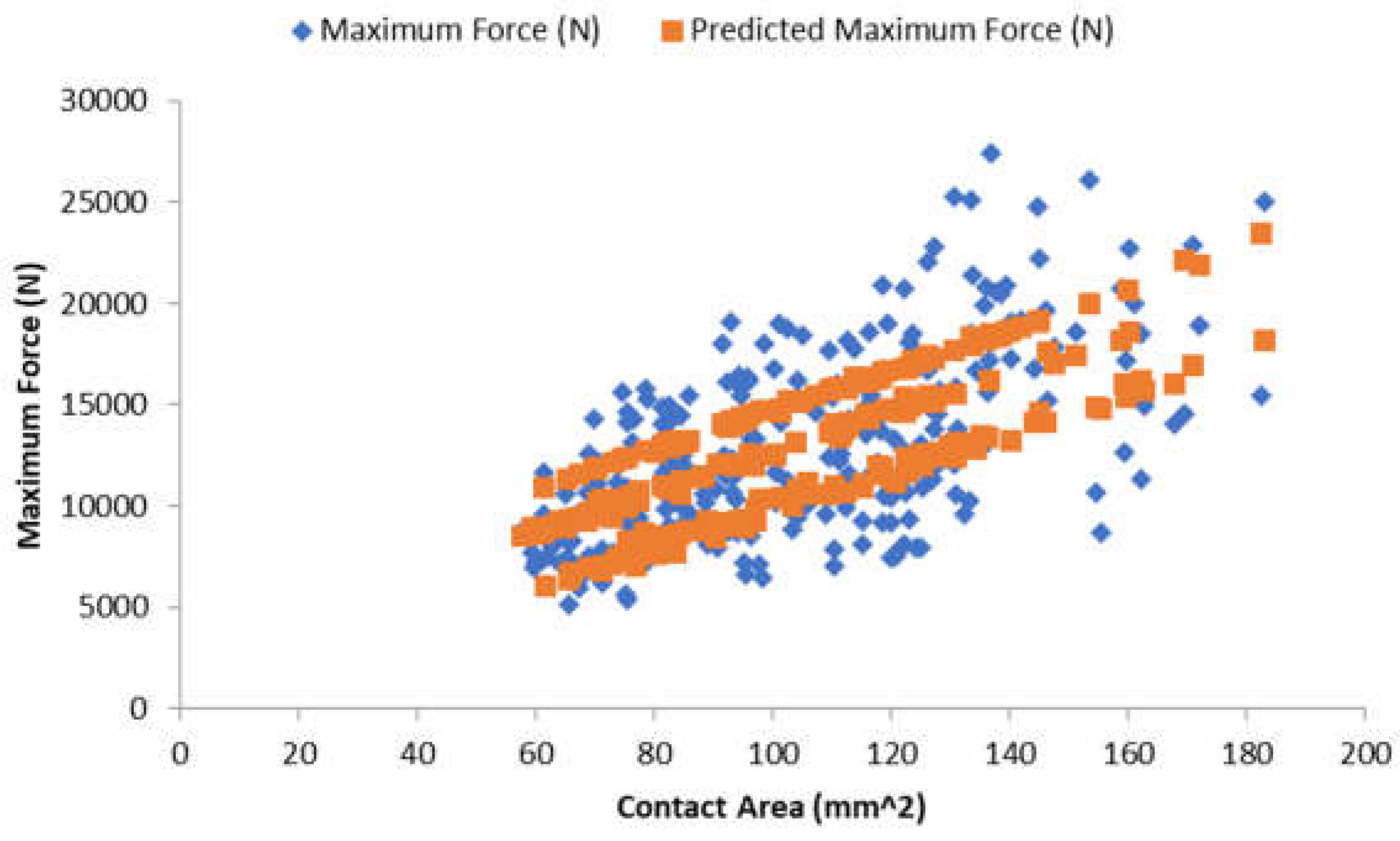
The equation outputs an average percent difference of 5% when compared to the actual output. The R2 of the equation is at 57.17% when compared to the actual output. The following figures show the predicted and actual results obtained from both the equation and lab tests respectively. The line fits and regression models are shown in figures 27 through 28 below.
Preprints 100787 g027
Figure 27. Line Fit Plot for Converted Node Distance.
Figure 27. Line Fit Plot for Converted Node Distance.
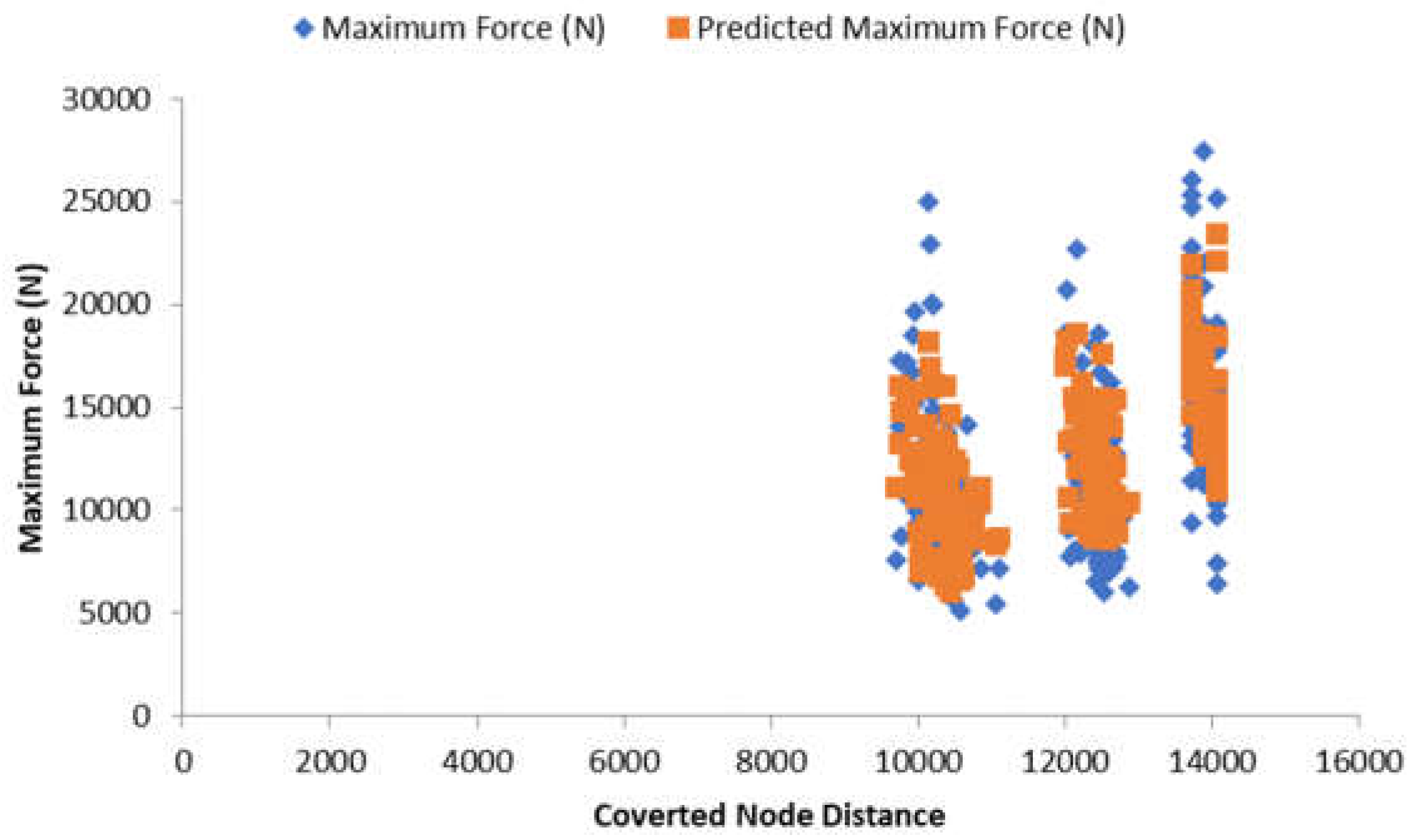
Preprints 100787 g027
Preprints 100787 g028
Figure 28. Line Fit Plot for Contact Area.
Figure 28. Line Fit Plot for Contact Area.
Preprints 100787 g028

4. Discussion

The results determined the correlation of differing physical properties of the bamboo specimens over their dowel bearing strength with the maximum forces output by the UTM machine over every sample. The independent variables are the node placements along the specimen and the dowel diameter, while the dependent variables are the bamboo thickness, diameter, density, and moisture content.
The first set of data resulting from the experiment is the associated maximum forces and their corresponding displacements as seen in Section 3.1. The behavior of the dowel-bearing strength for the top and middle node placements exhibits an exponential to linear increase followed by flat-lining. This flat lining before failing is more pronounced for the middle node placement due to the node being at the middle of the sample with the round bar compressing the node at a later stage in the test. In Table 3.2.1, the magnitudes of the dowel-bearing strength revealed that the top node placements have the highest maximum (18776.89N) and minimum (13594.08N) magnitudes with the node directly accommodating these forces until failure. In comparison to the bottom node placement, there is minimal to almost no flat-lining behavior, as the sample had already failed before the round bar reached the node, like samples with no node placements. Correspondingly, the bamboo samples without node placements have the lowest maximum (11368.06N) and minimum (7429.10N) magnitudes in compression, as there is no node to accommodate these forces.
By comparing the four (4) node placements in mean dowel-bearing strength, the decreasing trend of dowel-bearing strength is from the top, middle, bottom, and none node placements generating 15471.15N, 10601.44N, 10167.93N, and 9301.47N, respectively.
The behavior of the dowel-bearing strength in relation to the dowel diameter indicates a linear relationship with the ⅝’’ dowel diameter generating the highest maximum and minimum dowel-bearing strength of 17909.58N and 10118.16N, respectively. By comparing the three (3) dowel diameters in mean dowel-bearing strength, the increasing trend of dowel-bearing strength is with the use of a ⅜’’, ½’’, to a ⅝’’ dowel diameters generating 9484.04N, 11239,78N, and 13291.56N, respectively. Notably, several samples with varying displacements experience either splitting under axial compression (splitting failure) or longitudinal failure of fibers (bearing failure) shown in Figure 29 below.
The next set of data is the box and whiskers graph which visually represents the maximum forces of each specimen combination as seen in Section 3.2. This is in mind of the varying independent variables to see its correlation with the ultimate dowel bearing strength of each combination.
Across the specimens, there is a general increase in the ultimate bearing strength of the specimens with an incremental increase in dowel diameter. This trend is seen regardless of the associated node placement along the specimen, indicating that the two (2) variables are independent of each other and can be analyzed separately. The exact correlation of the dowel diameter towards the ultimate dowel bearing strength of the specimen is influenced by various factors as per several studies et al [16].
As stated in the study, the correlation of the dowel diameter to ultimate bearing strength is low (R2=0.547) positive correlation, indicating a higher capacity given that there is a higher dowel diameter. This trend is prevalent even in studies like a study which made use of laminated veneer lumber (LVL), showcasing a positive correlation between both variables, exhibiting a higher ultimate strength with an increase in dowel diameter [32].
However, not all studies raised indicate the same positive correlation [16]. The experiments done on laminated Guadua angustifolia bamboo indicate an inverse correlation between the dowel diameter and ultimate dowel bearing strength [33]. The variance and lack of a definite correlation can be attributed to the innate dissimilarity of every specimen.
From a theoretical perspective, the load that would be applied to the bamboo specimen should gradually convert from a point load to a uniform load as the dowel diameter increases, hence a higher dowel bearing strength as the dowel diameter increases. Given that the data follows the theoretical trend, the consistency of the experiment variables can be the cause of the positive correlation in the experiment.
The ultimate dowel-bearing strength of a specimen is not only influenced by the dowel diameter but also by the node placement, as observed in the study by when experimenting with Guadua angustifolia [20]. This can also be seen in Section 3.2 where the individual correlation of the node placement affects the overall strength of the specimen. The general trend that can be observed is that the performance of the specimen from worse to the best is, none, bottom, middle, and top, respectively. This trend can be attributed to the immediate resistance provided by the nodes given that the location of the node is atop the specimen. Meanwhile, specimens with nodes located at the middle of the specimen are more prone to having a bearing failure mode and prolonged plastic zones that can maintain a consistent ultimate strength of equal magnitude with the yield strength of the specimen.
As opposed to specimens where the node is located at the top, while there may be a higher ultimate strength due to the node location, a sudden splitting failure can be expected with the fracture of this specimen. Conversely, specimens with nodes at the bottom or entirely non-existent exhibit the lowest performance relative to the other specimens containing a node. For specimens that have a node at the bottom, its necessity is only at work post-splitting specimen failure, as seen in Section 3.2, where the bottom and none (node) specimens demonstrate almost a similar performance.
In real-world applications, the expected node placement along a jointed member is to ensure the smallest distance between the node and joint [34]. Considering this standard method in bamboo construction projects, the highest strength in the account of the node configuration makes sense to be specimens with a node atop the bamboo.
The correlation of the ultimate dowel bearing strength, thickness of the specimen culm walls, and the diameter of the bamboo specimen are explored in Section 3.3 and Section 3.4. As seen in Section 3.3, the correlation between the thickness of the culm wall plays a minor role in determining the maximum dowel-bearing strength of the specimen. Through the increase of the thickness of the culm wall, a slight increase in the ultimate strength can be observed from the scatterplot. While the data points are not as linear as intended to create an exact correlation between the two properties, it can be inferred that there is only a slight effect on the performance of the specimen through this variable.
As for Section 3.4, here the diameter of each specimen varies based on the natural diameter of the bamboo, the lack of variability in this physical property does not enable a valid correlation from being established. Given as well that the more prominent variables such as the dowel diameter and the node placement significantly affect the ultimate strength of the specimen throughout the experiment, the lack of an individual experiment solely for the thickness and diameter of the specimen does not enable the researchers to make a direct correlation between the thickness and diameter of the specimen with the ultimate strength of the specimen, much like what was shown in other studies [16].
Nevertheless, given the data presented in Section 3.4, it can be slightly expected that an increase in the diameter of the specimen should result in a higher ultimate strength of the bamboo specimen, as minute as it may be.
In the case of the density and moisture content of the specimen, as seen in Sections 3.5 and 3.6, the correlation between the two physical properties is near negligible and may be disregarded as a key indicator of the dowel bearing strength of the specimen. Despite this observation, the slight positive correlation between density and a slight negative correlation of the moisture content may lead to a more definitive study on the precise correlation between these properties and the dowel-bearing strength of bamboo. Given the limited variability of the specimens with these properties, the inconclusive assumption that can be inferred from the data is that a higher dowel bearing strength can be associated with an increase in the bamboo density or a decrease in the bamboo moisture content.
With all these trends and relationships established, an equation for dowel bearing capacity given physical properties of bamboo is derived and proposed by the researchers (reiterated from Equation 6):
103.569 A + 1.366 e { l n 10 − 0.00172 N D + 4.173838 } − 14644.593 = D B S
The equation presented demonstrates the utilization of two key parameters: the contact area (A) in square millimeters (mm²) and the node distance (ND) in millimeters (mm). Through a methodical multiple linear regression analysis, the resulting equations yield an R-squared (R²) value of 0.5717, indicating a moderate level of correlation. The Adjusted R-squared (Adjusted R²) value is computed at 0.5685, suggesting that approximately 56.85% of the observed samples align with the trends predicted by the proposed equation. Additionally, the absolute average percentage difference between the collected samples and the equation is calculated to be 5.04%. This finding instills a reasonable degree of confidence in the reliability of the equation, particularly within the specific sample population under the researcher's purview. Importantly, this equation holds promise as a practical tool for estimating the dowel-bearing strength of Bambusa blumeana under axial forces parallel to its grain. This predictive model bears significance in scenarios where precise dowel placement near a node presents challenges. By employing this established equation, it becomes feasible to estimate Bambusa blumeana's strength at various points along its length, even when located away from nodes. This capacity empowers the facilitation of informed design approaches, enhancing the practicality of applications involving this bamboo species.

5. Conclusions

Bamboo in the construction industry is a promising material given that there is a comprehensive understanding of the factors at play. Based on the experiment results, the following conclusions can be drawn:
  • Considering the investigation into Bambusa blumeana's dowel-bearing strength, with consideration for dowel diameter, a notable pattern emerges augmenting the dowel diameter results in a consistent increase in characteristic strength, ranging from 15.4% to 15.16% for every ⅛” increment. The specific dowel sizes studied further validate this trend. For instance, dowels with a diameter of ⅜” exhibit capacities between 7471.06N to 12234.81N, averaging at 9484.04N. Meanwhile, ½” diameter samples show even greater capacities, spanning 8616.42N to 14262.02N, and a mean of 11239.78N, surpassing the previous diameter by 15.4%. The most compelling outcome surfaces with the ⅝” diameter dowels, showcasing the highest strengths across all samples, an impressive 15.6% higher than the ½” counterparts. These findings elucidate the direct impact of dowel diameter on Bambusa blumeana's bearing strength, furnishing valuable insights for engineering applications.
  • The investigation into the dowel-bearing strength of Bambusa blumeana, considering various node placements, reveals notable findings. The top node placements exhibit the highest dowel-bearing capacity, ranging from 13,591.08N to 18,776.89N, with a mean value of 15,471.15N. These results surpass the capacities observed in other node placements by a significant margin, ranging from 31.0% to 40.0%. Conversely, samples without nodes exhibit the lowest dowel-bearing capacity, ranging from 7,429.10N to 11,368.06N, with a mean value of 9,301.47N. However, it is crucial to highlight that the dowel-bearing strengths of samples with bottom and middle nodes display only a modest increase, approximately 4.1% to 12.1% higher, respectively, than those without nodes.
  • The investigation into the dowel-bearing strength of Bambusa blumeana, considering its physical properties, reveals that thicker samples, larger diameters, higher densities, and lower moisture content are associated with greater strength. Nevertheless, it is noteworthy that these correlations exhibited weak to very weak magnitudes, consistent with the findings of other bamboo studies.
  • A predictive equation for the dowel bearing strength of Bambusa blumeana has been successfully formulated and presented as follows:
    103.569 A + 1.366 e { l n 10 − 0.00172 N D + 4.173838 } − 14644.593 = D B S
    This derived equation holds significant potential for diverse applications in bamboo structure design, particularly when multiple dowels are utilized, and the configurations may not always be ideal. By incorporating this equation into the design process, accurate estimations of capacities can be achieved, enhancing the overall robustness and safety of the structure. The equation offers a practical tool for engineers and designers, enabling them to make informed decisions and optimize the performance of Bambusa blumeana in various construction scenarios.
  • For the failure modes, only two modes of failure can be expected: splitting failure and bearing failure. Splitting failure occurs the most on top and no nodal placements while bearing failure occurs the most on middle and bottom nodal placements.
In the context of dowel connections involving Bambusa blumeana, the preferred configuration entails positioning the dowel above the node (top nodal placement) and utilizing the largest available dowel diameter. Furthermore, it is advisable to select bamboo culms with greater thickness and girth, while ensuring the moisture content remains within acceptable limits. However, it should be noted that such a configuration may result in an abrupt failure mode characterized by axial splitting. Consequently, caution is warranted when employing plain bamboo for applications subjected to significant loads, as its capacity in such scenarios is not deemed favorable.
Additionally, a noteworthy consideration arises from the organic nature of bamboo culms, where no two bamboo culms are identical. Consequently, the ideal configuration may not always be attainable. In such cases, alternative configurations varying in distance from the node and area of contact will benefit from the application of the derived equation to forecast their strength. This adaptability underscores the equation's versatility, offering a valuable tool to anticipate the bearing capacity of diverse bamboo configurations, thereby contributing to more accurate and effective structural design practices.
There are still areas that require further study and evaluation. For the physical and mechanical aspects: (1) explore bamboo-mortar composites utilizing the same methodology employed in this research, focusing specifically on Bambusa blumeana. (2) Investigate other bamboo species abundant in the Philippines. (3) Examine the influence of the length of the node from the hole. (4) Incorporate smaller and larger dowel diameters. (5) Consider a wider range of diameters and thicknesses. (6) Establish empirical equations and curve fitting techniques to determine the dowel-bearing strength of bamboo. (7) Conduct future studies with an even larger sample size and (8) explore ductile properties of middle node placements in bamboo. By addressing these areas for future research, it can enhance the understanding and effectiveness of bamboo as a sustainable construction material.

Author Contributions

Conceptualization, C.D.O.B., J.Y.F., H.A.F.L., S.R.A.Z., L.E.O.G., L.F.L.; methodology, C.D.O.B., J.Y.F., H.A.F.L., S.R.A.Z., C.J.D.C., L.F.L.; validation, L.E.O.G., C.J.D.C.; formal analysis, C.D.O.B., S.R.A.Z., C.J.D.C.; investigation, C.D.O.B., J.Y.F., H.A.F.L., S.R.A.Z.; resources, L.E.O.G., C.J.D.C., L.F.L.; data curation, C.D.O.B., S.R.A.Z., C.J.D.C.; writing— original draft preparation, C.D.O.B., J.Y.F., H.A.F.L., S.R.A.Z.; writing—review and editing, C.D.O.B., J.Y.F., H.A.F.L., S.R.A.Z., L.E.O.G., C.J.D.C.; visualization, C.D.O.B., J.Y.F., H.A.F.L., S.R.A.Z.; supervision, L.E.O.G., L.F.L.; project administration, C.D.O.B., C.J.D.C.; funding acquisition, L.E.O.G., C.J.D.C., L.F.L.. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the privacy policies of the Base Bahay Foundation Inc.

Acknowledgments

We extend our heartfelt appreciation to Don Bosco Technical Institute - Makati (DBTI) for the technical assistance extended in the experiments.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Abbass, K.; Qasim, M. Z.; Song, H. A Review of the Global Climate Change Impacts, Adaptation, and Sustainable Mitigation Measures. Environ. Sci. Pollut. Res. 2022, 29(43), 42539–42559. [Google Scholar] [CrossRef] [PubMed]
  2. Ürge-Vorsatz, D.; Novikova, A. Potentials, and costs of carbon dioxide mitigation in the world’s buildings. Energy Policy. 2008, 36, 642–661. [Google Scholar] [CrossRef]
  3. Ahmed, N.; Abdel-Hamid, M.; Abd El-Razik, M. M.; El-Dash, K. M. Impact of sustainable design in the construction sector on climate change. Ain Shams Eng. J. 2020. [CrossRef]
  4. Lessard, G.; Chouinard, A. Bamboo research in Asia: proceedings of a workshop held in Singapore, 28-30 May 1980. IDRC, Ottawa, ON, CA.
  5. Yadav, M.; Mathur, A. Bamboo as a sustainable material in the construction industry: An overview. Mater. Today: Proc. 2021, 43, 2872–2876. [Google Scholar] [CrossRef]
  6. Manandhar, R.; Kim, J. H; Kim, J. T. Environmental, Social and Economic Sustainability of Bamboo and Bamboo-based Construction Materials in Buildings. J. Asian Archit. Build. Eng. 2019, 18(2), 49–59. [Google Scholar] [CrossRef]
  7. Lao, H. Connections for Bamboo Structures. IOP Conf. Ser.: Earth Environ. Sci. 2021, 783(1), 012028. [CrossRef]
  8. Bautista, B.; Lessandro, G.; Lopez, L. Establishing the Characteristic Shear Strength of a Local Bamboo Species: Bambusa blumeana (Kawayan Tinik). DLSU Res. Congress 2021, De La Salle Univ.. Manila, Philippines. [Google Scholar]
  9. Dias, A. M. P. G.; Kuhlmann, U.; Kudla, K.; Mönch, S.; Dias, A. M. A. Performance of Dowel-Type Fasteners and Notches for Hybrid Timber Structures. Eng. Struct. 2018, 171, 40–46. [Google Scholar] [CrossRef]
  10. Disén, K.; Clouston, P. L. BUILDING WITH BAMBOO: A REVIEW OF CULM CONNECTION TECHNOLOGY. J. Green Build. 2013, 8(4), 83–93. [Google Scholar] [CrossRef]
  11. Paraskeva, T.; Pradhan, N. P.; Stoura, C. D.; Dimitrakopoulos, E. G. Monotonic loading testing and characterization of new multi-full-culm bamboo to steel connections. Constr. Build. Mater. 2019, 201, 473–483. [Google Scholar] [CrossRef]
  12. Wang, F.; Yang, J. Experimental and Numerical Investigations on Load-Carrying Capacity of Dowel-Type Bolted Bamboo Joints. Eng. Struct. 2020, 209, 109952. [Google Scholar] [CrossRef]
  13. Jockwer, R.; Fink, G.; Kohler, J. Assessment of The Failure Behavior and Reliability of Timber Connections With Multiple Dowel–type Fasteners. Eng. Struct. 2018, 172, 76–84. [Google Scholar] [CrossRef]
  14. Mitch, D. R. Splitting Capacity Characterization of Bamboo Culms. Honors College thesis, Univ. of Pittsburgh, Pittsburgh, 2009.
  15. Karthik, S.; Rao, P. R. M.; Awoyera, P. O. Strength properties of bamboo and steel reinforced concrete containing manufactured sand and mineral admixtures. J. King Saud Univ. - Eng. Sci. 2017, 29(4), 400–406. [CrossRef]
  16. Ji, S.; Mou, Q.; Yuan, G.; Ren, H.; Li, X. Dowel–bearing behavior of bamboo scrimber for bolted–type joint. Ind. Crops Prod. 2023, 193, 116178. [Google Scholar] [CrossRef]
  17. Maia, B. B.; Miotto, J. L.; Góes, J. L. N. D. Embedding strength of fully threaded dowel-type fasteners in cross-laminated timber: an experimental study. Matéria (Rio De Janeiro) 2021, 26(3). [CrossRef]
  18. Salzer, C.; Wallbaum, H.; Alipon, M.; Lopez, L. Determining Material Suitability for Low-Rise Housing in the Philippines: Physical and Mechanical Properties of the Bamboo Species Bambusa Blumeana. Bamboo Housing Properties 2018, 13(1), 346–369. [Google Scholar] [CrossRef]
  19. Javadian, A.; Smith, I. F. C.; Saeidi, N.; Hebel, D. E. Mechanical Properties of Bamboo Through Measurement of Culm Physical Properties for Composite Fabrication of Structural Concrete Reinforcement. Front. Mater. 2019, 6, 15. [Google Scholar] [CrossRef]
  20. Correal, J. F.; Echeverry, J. S. Dowel-bearing strength behaviour of Guadua angustifolia Kunth bamboo. Proceedings of 16th NOCMAT Conference, Winnipeg.
  21. Oka, G. M.; Triwiyono, A.; Awaludin, A.; Siswosukarto, S. Experimental and Theoretical Investigation of Bolted Bamboo Joints without Void Filled Material. Appl. Mech. Mater. 2015, 776, 59–65. [Google Scholar] [CrossRef]
  22. Sonar, I. P.; Siddhaye, V. R. Theoretical and experimental investigation on single and double bolted bamboo joint under axial tension. J. Struct. Eng. 2009, 36(3), 164–171. [Google Scholar]
  23. Lefevre, B.; West, R.; O’Reilly, P.; Taylor, D. A new method for joining bamboo culms. Eng. Struct. 2019, 190, 1–8. [Google Scholar] [CrossRef]
  24. Hong, C.; Li, H.; Xiong, Z.; Lorenzo, R.; Corbi, I.; Corbi, O.; Wei, D.; Yuan, C.; Yang, D.; Zhang, H. Review of Connections for Engineered Bamboo Structures. J. Build. Eng. 2020, 30, 101324. [Google Scholar] [CrossRef]
  25. International Standardization Organization (ISO). Bamboo structures — Determination of physical and mechanical properties of bamboo culms — Test methods (ISO 22157:2019). https://www.iso.org/standard/65950.html.
  26. Philippine National Standards (PNS). Bamboo structures – Determination of physical and mechanical properties of bamboo culms – Test methods (PNS ISO 22157:2020). https://www.bps.dti.gov.ph/index.php/component/booklibrary/115/view_bl/191/wood-sawlogs-and-sawn-timber/3328/bamboo-structures-determination-of-physical-and-mechanical-properties-of-bamboo-culms-test-methods.
  27. Archila, H.; Kaminski, S.; Trujillo, D.; Zea Escamilla, E.; Harries, K. A. Bamboo reinforced concrete: a critical review. Mater. Struct. 2018, 51(4). [CrossRef]
  28. Fu, Y. G., Shao, B. S., & Fu, S. C. (2013). Comparative study of mechanical performance of bamboo joints. In Proceedings of 2013 Word Congress on Advances in Structural Engineering and Mechanics, Jeju, Korea.
  29. Mouka, T.; Dimitrakopoulos, E. Prediction of Bamboo Culm Embedment Properties Parallel to Grain via Dimensional Analysis. Constr. Build. Mater. 2022, 347, 128434. [Google Scholar] [CrossRef]
  30. American Society for Testing and Materials (ASTM). Standard Test Method for Evaluating Dowel-Bearing Strength of Wood and Wood-Based Products (ASTM D5764). [CrossRef]
  31. Cabanas, G. Assessing the structural response of a mortar-infilled steel eyebolt bamboo connection under bending and cyclic loads. https://www.researchgate.net/publication/331960255_Assessing_the_structural_response_of_a_mortar_infilled_steel_eyebolt_bamboo_connection_under_bending_and_cyclic_loads.
  32. Schweigler, M.; Bader, T. K. ; Georg Hochreiner, Unger, G; Eberhardsteiner, J. Load-to-grain angle dependence of the embedment behavior of dowel-type fasteners in laminated veneer lumber. Constr. Build. Mater. 2016, 126, 1020–1033. [Google Scholar] [CrossRef]
  33. Correal, J. F.; Ramirez, F.; Gonzalez, S.; Camacho, J. Structural behavior of Glued Laminated Guadua Bamboo as a construction material. ResearchGate; unknown. https://www.researchgate.net/publication/287526530_Structural_behavior_of_Glued_Laminated_Guadua_Bamboo_as_a_construction_material.
  34. Follett, P. R. Bamboo in construction. 2008, 35–44. [CrossRef]
Preprints 100787 g001
Figure 1. Splitting failure due to bolted connections [14].
Figure 1. Splitting failure due to bolted connections [14].
Preprints 100787 g001
Preprints 100787 g002
Figure 2. Dowel (round bar) Setup.
Figure 2. Dowel (round bar) Setup.
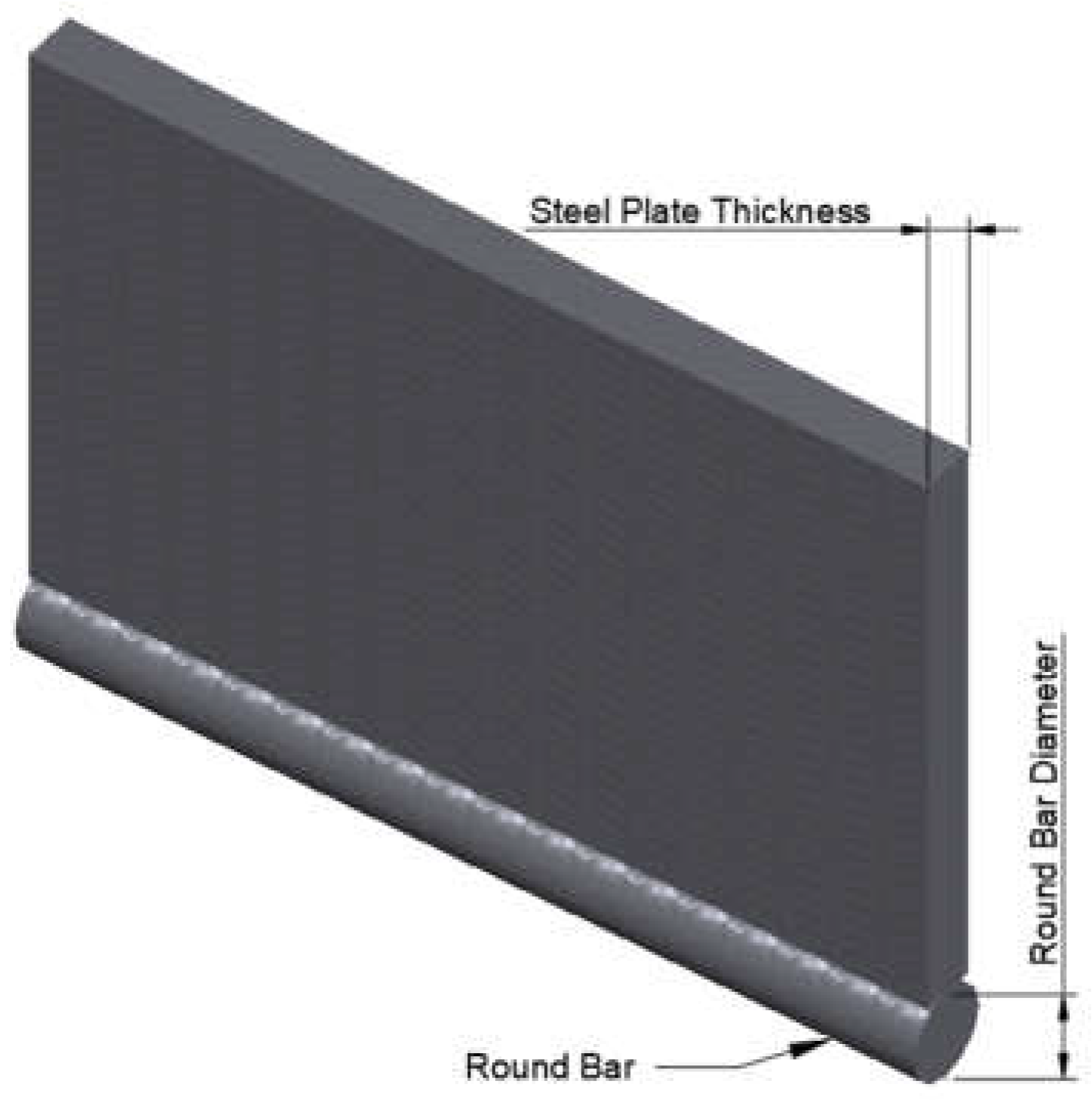
Preprints 100787 g002
Preprints 100787 g003
Figure 3. Node placements from left to right: a) None; b) Bottom; c) Middle; d) Top.
Figure 3. Node placements from left to right: a) None; b) Bottom; c) Middle; d) Top.
Preprints 100787 g003
Preprints 100787 g004
Figure 4. Specimen configuration of the study.
Figure 4. Specimen configuration of the study.
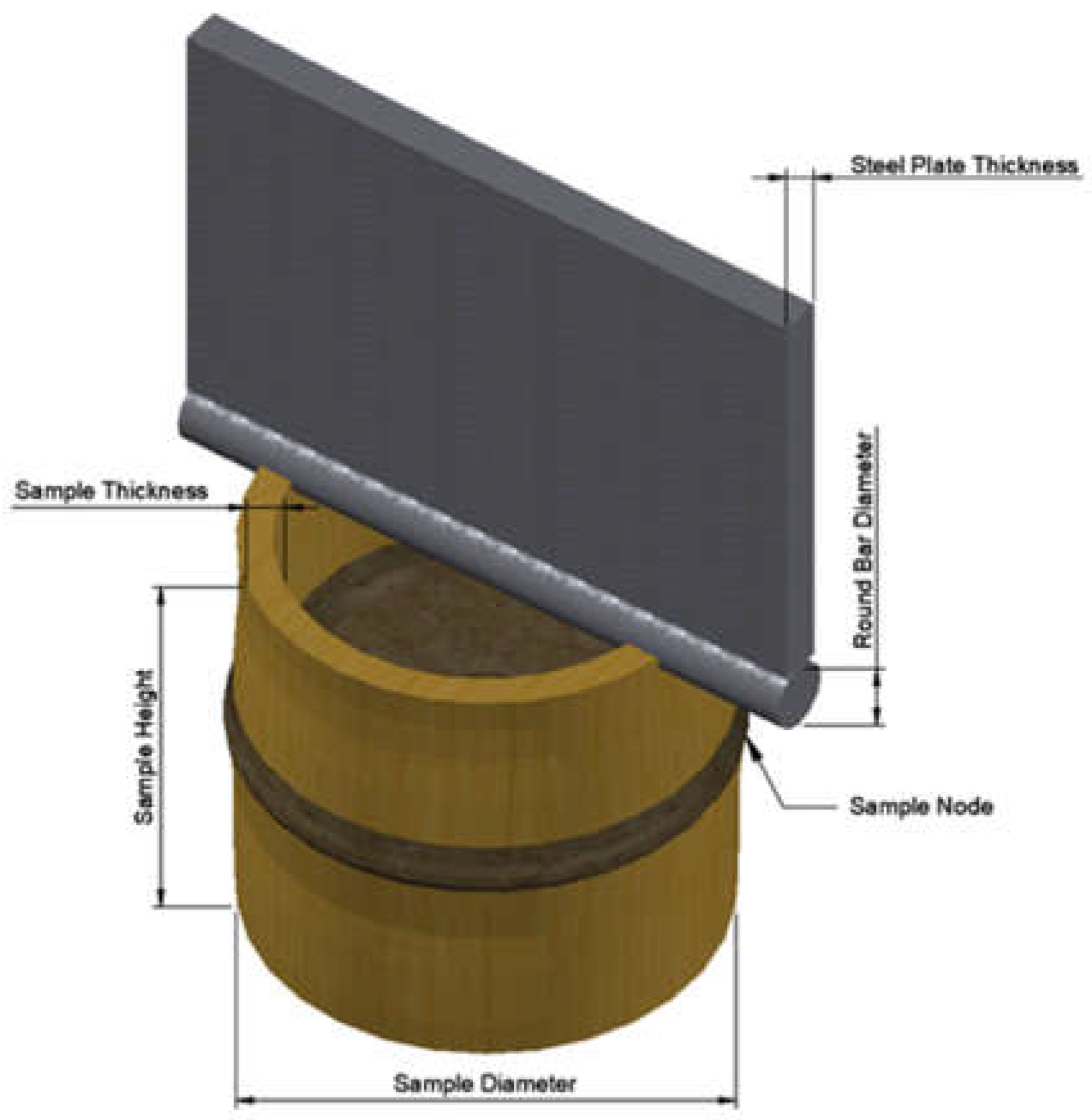
Preprints 100787 g004
Preprints 100787 g029
Figure 29. Failure Modes of Bamboo Samples.
Figure 29. Failure Modes of Bamboo Samples.
Preprints 100787 g029
Table 1. Test combinations of the research.
Table 1. Test combinations of the research.
Factors Steps
Bar Diameter 3/8”
3/8”, ½”, 5/8”
5/8”
Node Placement Top, Middle, Bottom, None
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated