Preprint

Article

Enhancing Urban Resilience with Smart Technologies and Predictive Analytics in Setagaya, Tokyo

Altmetrics

Downloads

106

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

07 March 2024

Posted:

07 March 2024

You are already at the latest version

Alerts

Abstract

This paper addresses challenges and solutions in urban development and infrastructure resilience, particularly in the context of Japan's rapidly urbanizing landscape. It explores the integration of smart city concepts to combat land subsidence and liquefaction, phenomena highlighted by the 2011 Great East Japan Earthquake. Using advanced technologies such as smart sensing and predictive analytics through kriging and ensemble learning, the study aims to improve the accuracy of geotechnical investigations and urban planning. By analyzing data from 433 geotechnical surveys in Setagaya, Tokyo, it develops predictive models to accurately determine the depth of bearing layers critical to urban infrastructure. The results demonstrate the superiority of ensemble learning in predicting the depth of bearing layers, with significant implications for smart city development and the sustainability of urban environments. This interdisciplinary approach not only seeks to mitigate risks associated with geological disturbances, but also promotes sustainable urban growth that prioritizes safety and prosperity. Through advanced technology and comprehensive research, the study underscores the potential of smart cities to address urban complexities and ensure a resilient, sustainable future.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

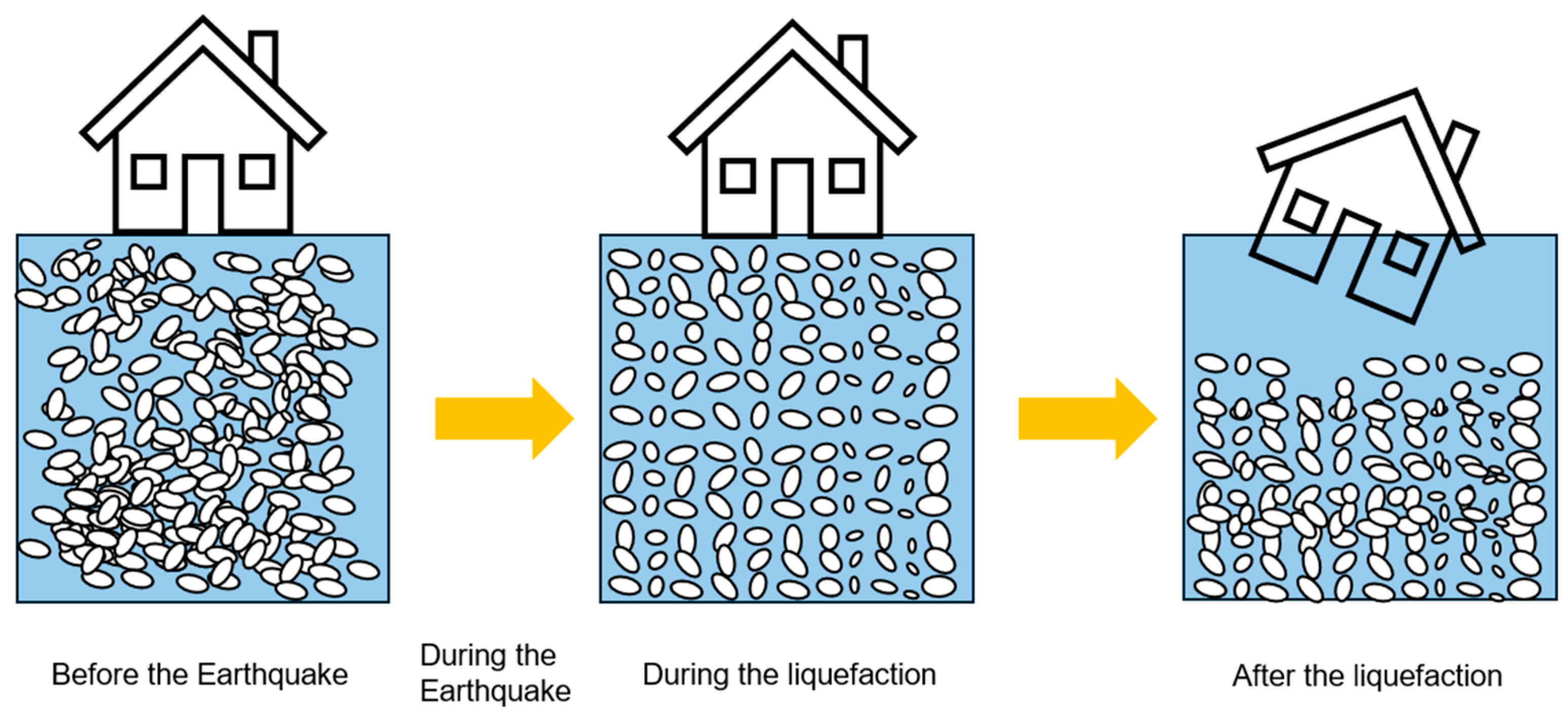
Japan’s urban landscape, characterized by rapid urbanization and cutting-edge technological advances, is at the forefront of addressing complex challenges in the construction and infrastructure sectors. In Japan, the significant structural damage often caused by the settlement or tilting of structures, due to the liquefaction of saturated sandy soils during large earthquakes, has long been a major concern in the field of geotechnical engineering, as shown in Figure 1. This phenomenon, which can have serious consequences, was particularly documented in a seminal study [1,2,3,4]. In particular, the phenomena of land subsidence and liquefaction pose significant obstacles, as highlighted by the devastating effects of the Great East Japan Earthquake on March 11, 2011. This catastrophic event, particularly in areas such as Urayasu City in Chiba Prefecture, brought to light the extensive vulnerability of the built environment to such geological disturbances. The sudden instability of the ground during such events can lead to the catastrophic destruction of buildings and infrastructures, resulting in significant economic losses as well as the tragic loss of human life. This critical issue was further highlighted in [5,6]. These concerns have led to a significant increase in the study and development of activities aimed at improving liquefaction resistance and developing other mitigation methods. This focus was particularly high-lighted by the groundbreaking work of [7,8], which contributed to a better under-standing of these challenges [9].

In response to these pressing issues, the concept of smart cities emerges as a key strategy that combines the resilience of smart buildings, the precision of smart sensing technologies, and the efficiency of smart grids and infrastructures. Smart buildings, using advanced materials and structural designs, can withstand the damaging effects of subsidence and liquefaction, thereby ensuring the integrity and durability of infrastructure assets. In addition, the use of smart sensing technologies is revolutionizing the process of monitoring and assessing geotechnical risks. Seamlessly integrated into the urban fabric, these sensors provide continuous, real-time data on critical factors such as ground movement and moisture levels, which are essential for maintaining soil stability. In addition, the integration of smart grids and infrastructure strengthens the resilience of urban spaces by optimizing the distribution of resources and energy. This harmonious integration ensures the continued operation of essential services in the aftermath of a disaster, facilitating rapid recovery. The collaborative functioning of smart grids, infrastructure, and sensing technologies promotes a proactive approach to disaster management and mitigation, moving from reactive measures to preventive strategies.

Despite continued advances in monitoring and mitigation techniques for liquefaction and subsidence, significant limitations remain. Challenges related to site availability, time, funding, and physical constraints underscore the need for groundbreaking approaches. Traditional empirical methods, while widely used, lack the precision and reliability required for robust risk management. In this light, the fields of geostatistics and machine learning emerge as promising areas for improving predictive accuracy and understanding of geotechnical phenomena. Techniques such as kriging [10,11], a sophisticated interpolation tool, and ensemble learning [12,13], which enhances prediction through algorithmic diversity, are at the forefront of spatial and temporal data analysis.

This study aims to transcend conventional geotechnical investigation techniques by harnessing the dynamic potential of smart technologies. It seeks to refine the prediction of unknown soil points or areas with unprecedented accuracy using existing datasets. By combining kriging and ensemble learning with the innovative application of smart buildings, sensing technologies, and infrastructure, the study proposes a holistic approach to address the problems of subsidence and liquefaction in Japan. In a broader context, the vision of smart cities, underpinned by intelligent infrastructure and data-driven insights, heralds a new era of urban development. This interdisciplinary approach aims not only to mitigate the risks associated with geological disturbances, but also to promote sustainable urban growth that prioritizes the safety and prosperity of its inhabitants. Through the synergy of advanced technology and comprehensive research, we are poised to navigate the complexities of urban development and ensure a resilient, sustainable, and safe future for cities worldwide.

2. Overview of Predictive Analytics for Bearing Layer Depth

In the field of urban development and smart city planning, the intricate interplay between geotechnical engineering and urban infrastructure is of paramount importance. This paper reports on a comprehensive study conducted in Setagaya, Tokyo, focusing on the prediction of the depth of the bearing layer - a critical factor in the foundation and stability of urban structures. By applying sophisticated methods such as kriging and ensemble learning, the study utilizes data from 433 geotechnical surveys and provides insights into optimizing construction processes in the context of smart cities.

The foundation of this study is the use of data from the standard penetration test and the mini-ram sounding test. Introduced in 1951, the standard penetration test has become a staple of soil investigation methods due to its proven applicability to Japanese soil types (excluding special soils). The test was originally designed to determine the relative density of cohesionless soils, but its use has been extended to include the design of foundations by determining the load and the required embedment of piles into the bearing strata. The standard penetration test is performed by the use of the cable percussion drilling rig and its accessories [14], quickly gained popularity for its effectiveness in evaluating soil suitability for buildings, condominiums, and other civil structures. Complementing this, the mini-ram sounding test uses half the impact energy of the automatic ram sounding test, providing an alternative dynamic penetration testing method.

A key aspect of soil mechanics is the calculation of the pressure on the bearing layer, which decreases with depth until it reaches a point where it becomes negligible. This critical depth, beyond which the pressure can be ignored, defines the bearing layer - a key concept in pile foundation design. Soil selection for the bearing layer is stringent, with viscous soils with low compressibility, silty soils, and medium-density or dense sands favored due to their superior bearing properties. The study underscores the importance of selecting the appropriate soil type to ensure the stability and longevity of urban infrastructure, a principle that is increasingly relevant in the context of smart cities, where efficiency and sustainability are paramount.

The methodology of this study involved the construction of a predictive model based on the results of geotechnical surveys at 433 locations within Setagaya, Tokyo. The model identifies layers with an N value of 15 or more that extend more than 2 m as indicating the presence of a bearing layer. Notably, the study introduces “bearing layer depth A” as a standardized measure, adjusting for elevation differences by subtracting elevation from all bearing layer depths. This adjustment allows for more accurate comparison and analysis across sites, thereby increasing the reliability of predictions. Figures and table presented in the paper, such as Figure 2 and Figure 3 and Table 1, detail the statistical analysis and data used to make the predictions for Setagaya, Tokyo. Table 2 details the difference in the target variable used by two methods. These visual aids not only illustrate the methodology and results, but also serve as a valuable reference for future studies and applications in urban planning and smart city development.

In the broader context of smart cities, the implications of this study are many. Using advanced predictive models, urban planners and engineers can more accurately assess the suitability of sites for development and optimize the design and placement of buildings, infrastructure, and public utilities. This proactive approach to urban development aligns with the principles of smart cities, which emphasize the use of technology and data to improve the efficiency, sustainability, and resilience of urban environments. In addition, the study’s focus on the depth of the bearing layer aligns with the growing interest in sustainable building practices. By ensuring that urban structures are built on solid foundations, cities can reduce the risk of structural failure, minimize maintenance costs, and extend the life of buildings and infrastructure. This not only contributes to the economic viability of urban projects, but also supports the environmental and social pillars of sustainability.

The study presented in this paper provides valuable insights into the prediction of bearing layer depth in Setagaya, Tokyo, and demonstrates the potential of kriging and ensemble learning methods in improving urban construction practices. As cities worldwide strive to become smarter and more sustainable, the integration of geotechnical engineering principles with advanced predictive analytics will play a critical role in shaping the urban landscapes of the future.

3. Models Used in Predictive Analysis

In the rapidly evolving landscape of urban development, smart cities have emerged as a beacon of innovation, using technology to improve infrastructure, sustainability, and living conditions. A critical aspect of this transformation lies in the careful design and construction of urban infrastructure, where the stability and safety of buildings depend on the accurate prediction of geotechnical properties, such as the depth of the bearing layer. This study explores the application of advanced predictive analytics, specifically kriging and ensemble learning, to predict the bearing layer depth in Setagaya, Tokyo, using a dataset of 433 data points.

Kriging, a geostatistical method named after South African engineer D.G. Krige, provides a sophisticated approach to spatial interpolation. By incorporating the geographic coordinates of the data points, this method makes it possible to create a spatial model that predicts the depth of the bearing layer at various locations in Setagaya, Tokyo. The essence of kriging lies in its ability to provide not only an estimate, but also a measure of the uncertainty of the estimate, making it invaluable for urban planning in smart cities, where risk assessment is critical. Ordinary kriging is by far the most popular method, partly because it is robust with respect to departures from the underlying assumptions [15].

Ensemble learning, on the other hand, use multiple machine learning algorithms to produce weakly predictive results based on features extracted through a variety of projections on the data and fuse the results with various voting mechanisms to achieve a better performance than that obtained by any constituent algorithm alone [16]. By aggregating predictions from different models, ensemble learning reduces the likelihood of overfitting and increases the robustness of the prediction. In this study, ensemble learning used the same input variables, latitude and longitude, to predict bearing layer depth, illustrating the method’s versatility and power in handling complex urban datasets.

The comparative analysis of the two methods, kriging and ensemble learning, focused on the prediction accuracy against measured values and the mean prediction error at validation points. Such an evaluation is critical in urban planning contexts, where the accuracy of predicting geotechnical properties directly impacts the feasibility, safety, and cost-effectiveness of construction projects.

Smart cities, with their emphasis on data-driven decision making, will benefit significantly from advances in predictive analytics, as demonstrated in this study. In addition, the horizontal analysis between Case 1 (kriging) and Case 2 (ensemble learning) provided insights into the suitability of each method for urban geotechnical prediction, such as Table 3, details introduced the difference between Case 1 and Case 2. This analysis is not only academic, but has practical implications for urban developers, engineers, and policy makers involved in smart city projects. The method that exhibits higher accuracy and lower average error can inform more reliable geotechnical investigation protocols, contributing to safer and more sustainable urban environments.

The implications of this study extend beyond the boundaries of Setagaya, Tokyo or even Tokyo. As cities around the world strive to become smarter by integrating technology into every facet of urban life, the methods validated by this research provide a blueprint for using predictive analytics in urban planning. By accurately predicting the depth of bearing layers, city planners can optimize the location and design of buildings and infrastructure, mitigate risks associated with soil instability, and ensure the long-term resilience of urban developments. This study exemplifies the synergy between geotechnical engineering and smart city concepts and highlights the potential of kriging and ensemble learning to improve urban infrastructure projects. As smart cities continue to evolve, the use of data-driven methodologies will be paramount in addressing the complex challenges of urban development, ensuring that cities become not only smarter, but also safer and more sustainable for future generations.

3.1. Kriging

Smart cities represent the pinnacle of urban planning and development, where technology, data, and efficient resource management converge to create environments that are sustainable, livable, and technologically advanced. At the heart of smart cities is the need for accurate, reliable data about the urban landscape, its resources, and the environment. Geostatistics provides a powerful toolkit for analyzing and predicting variables across space and time, which is essential for the complex task of urban planning and management in smart cities.

Kriging comes from the earth sciences and has been progressively developed since the 1950’s along with the discipline called geostatistics [17]. Using geology data, researchers established geology models primarily based on the statistical method, which produced geostatistics [18,19]. In land resource inventories, kriging and its variants have been widely recognized as primary spatial interpolation techniques from the 1970s. In the 1990s, with the emerging of GIS and remote sensing technologies, soil surveyors became interested to use exhaustively mapped secondary variables to directly map soil variables. The first applications were based on the use of simple linear regression models between terrain attribute maps and soil parameters. In the next phase, the predictors were extended to a set of environmental variables and remote sensing images [20,21]. This evolution reflects a broader trend toward comprehensive, data-driven approaches to urban planning and resource management. By enabling precise mapping of soil variables, terrain attributes, and other environmental factors, kriging facilitates the detailed, accurate modeling of urban spaces that is essential for smart city development.

In this study, ordinary kriging is utilized, which imposes constraints on weighting and can relatively express spatial random fields. The method predicts the bearing layer depth. [22] define a functional random variable as a random variable taking values in a space of functions [23]. In this paper, at a certain point

x

, the estimated value of the target value ŵ(x) is generally the measured value at n points

x_{i}

around it. It is given as the weighted average of

w ̂ (x)

(

i

= 1, 2, ⋯,

n

), that is Eq. (1) [24,25].

w ̂ (x) = \sum_{i = 1}^{n} b_{i} w (x_{i})

(1)

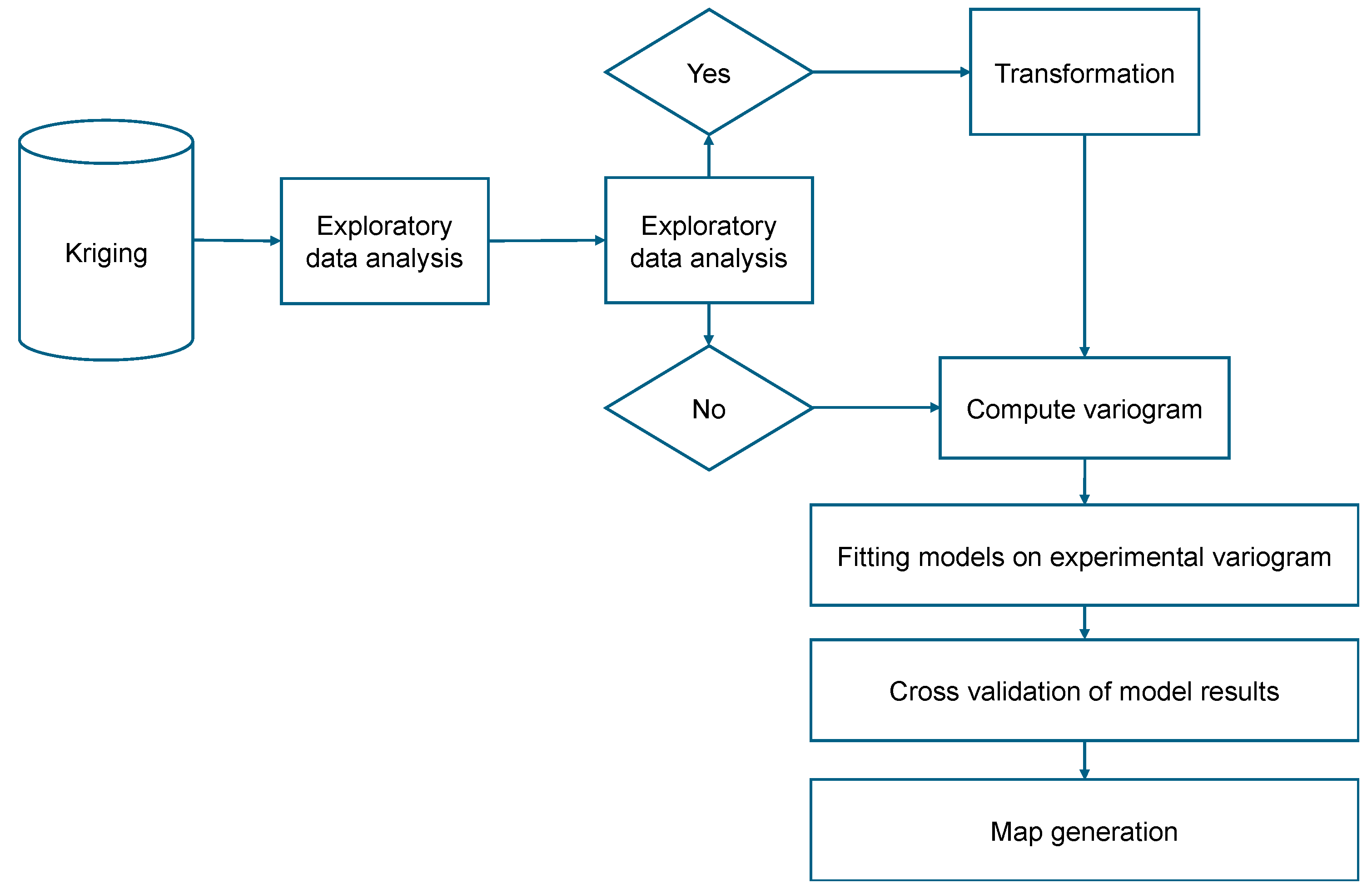
The ordinary kriging used in this study is an example of integrating geostatistical methods with smart city technologies. By imposing constraints on the weighting and expression of spatial random fields, ordinary kriging allows for the accurate prediction of bearing layer depths, a critical factor in urban infrastructure development. The transformation of latitude and longitude data into Transverse Mercator coordinates for kriging prediction exemplifies the methodological precision required for smart city planning. The orthogonal UTM coordinate system, by representing the spherical Earth in a planar view, ensures accurate distance representation, essential for the meticulous design and layout of urban infrastructure [26]. The kriging procedure is depicted in Figure 4.

The application of kriging to the prediction of bearing layer depth illustrates the utility of the method in a smart city context. By converting geographic data to UTM coordinates and incorporating elevation conditions, this study demonstrates how geostatistical predictions can inform urban infrastructure development. The resulting three-dimensional map of the predicted distribution of bearing layer depth provides a fundamental tool for planners and engineers to make informed decisions in the construction of buildings, roads, and other critical infrastructure components.

The impact of accurate geostatistical predictions extends beyond infrastructure development to include environmental management, resource allocation, and emergency response planning. In smart cities, where efficiency and sustainability are paramount, the ability to accurately predict environmental and spatial variables is invaluable. It informs the deployment of resources, the management of environmental challenges, and the planning of future development with an unprecedented level of precision and foresight.

The integration of geostatistics, and kriging in particular, into the fabric of smart cities represents a significant advancement in urban planning and management. By enabling accurate spatial predictions and analysis, these methods provide the data-driven foundation necessary for the efficient, sustainable development of urban environments. As smart cities continue to evolve, the role of geostatistical methods will undoubtedly expand, driving innovation in urban planning, infrastructure development, and environmental management. The case study presented in this analysis, focusing on the prediction of bearing layer depth, exemplifies the practical applications and potential of kriging in the context of smart cities, underscoring its importance in the quest for more livable, technologically advanced urban spaces.

3.2. Ensemble Learning

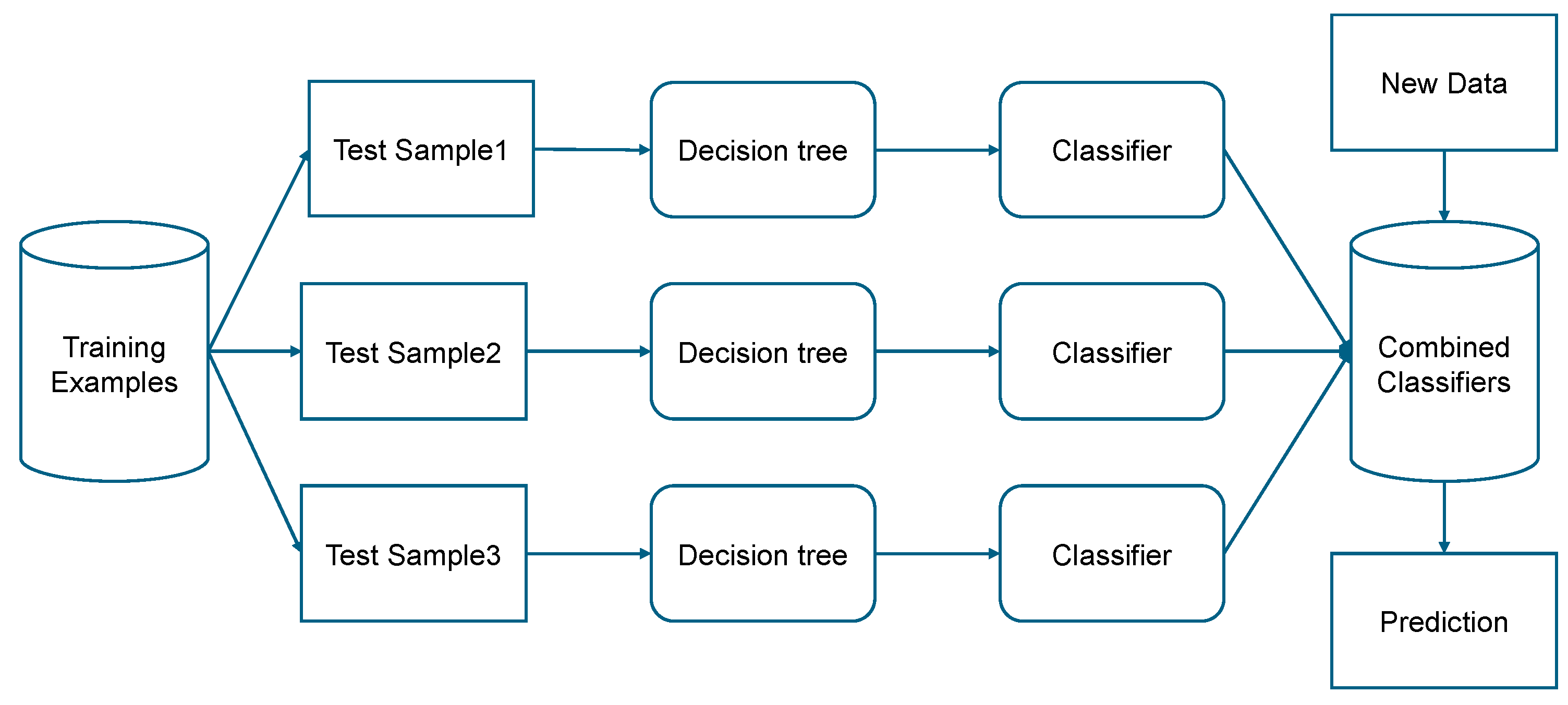
Ensemble learning methods utilize a variety of machine learning algorithms that aim to produce weakly predictive results through a variety of data projections. These results are then aggregated using various voting mechanisms to outperform the performance achievable by each individual algorithm [27]. This strategy can be broadly categorized into three different types. Among them, our study highlights the use of the bagging method due to its effectiveness and simplicity.

The bagging technique, a cornerstone of ensemble learning, involves generating multiple subsets of the original training data set through random sampling. These subsets are then used to train basic models in parallel, and their outputs are integrated to form a comprehensive predictive model [28]. Bagging is characterized by its simple, yet powerful approach of combining multiple basic learners to construct a highly accurate predictive model [29].

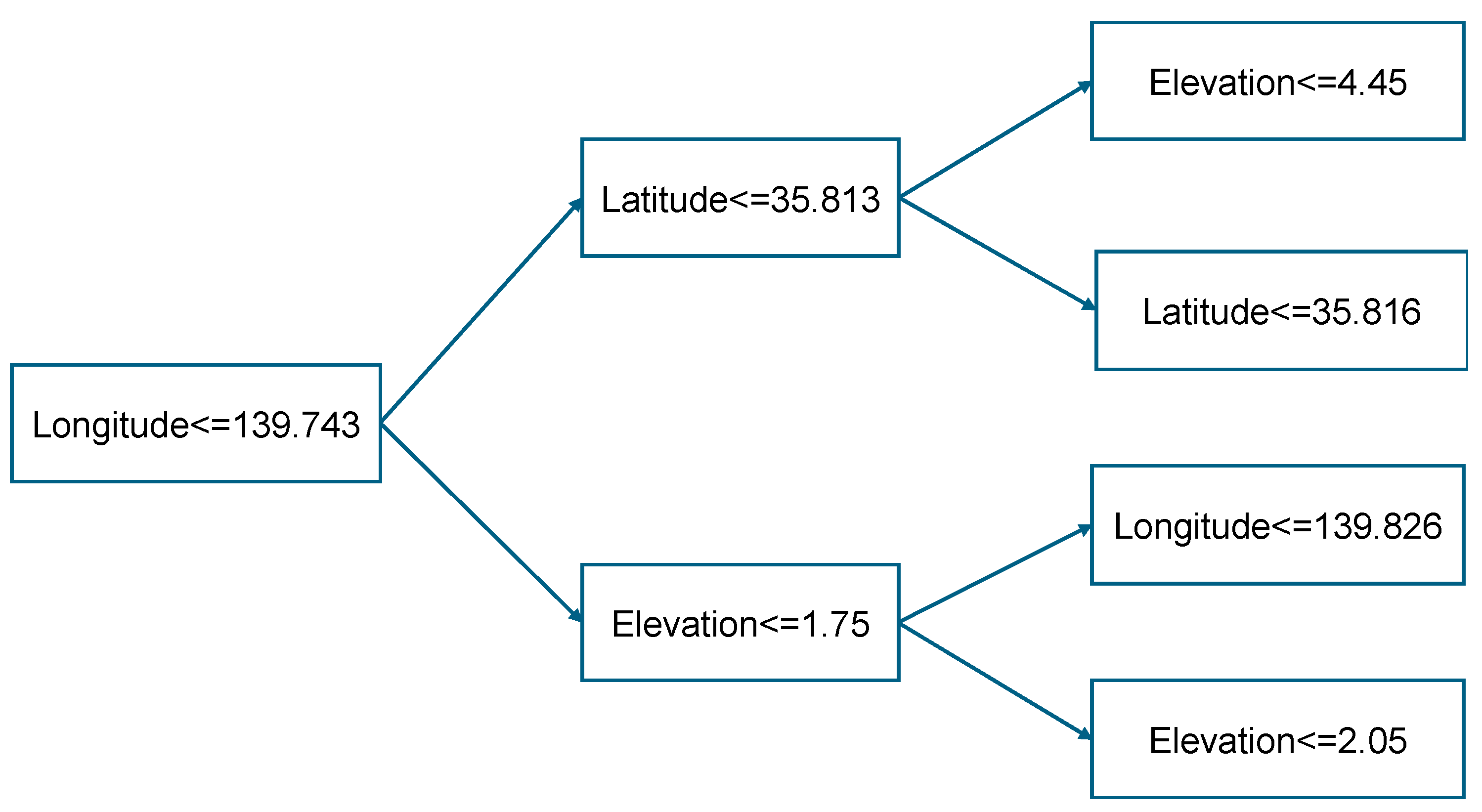
The procedural essence of bagging is illustrated in Figure 5, which shows the use of decision trees for each bagging-derived data segment. In addition, a decision tree diagram is shown in Figure 6, highlighting the structural foundation of the method. Prior to actual model assembly, hyperparameter optimization is meticulously performed, identifying the optimal model configuration that achieves peak accuracy with 91 decision trees. Decision tree is the most commonly used algorithm because of its ease of implementation and easier to understand compared to other classification algorithms [30,31].

Building a predictive forest by bagging involves several key steps. First, “sample data” is generated by randomly selecting from the training dataset, allowing for data reuse across different samples. Next, 91 decision trees are cultivated using the sample data, and their predictions are averaged to derive the final prediction. This averaging process follows Eq. (2).

Y ＝ \frac{１}{N} \sum_{n ＝ １}^{N} X_{n}

(2)

where

Y

is the predicted value of the forest,

X_{n}

is the prediction of an individual decision tree, and

N

is the total number of decision trees.

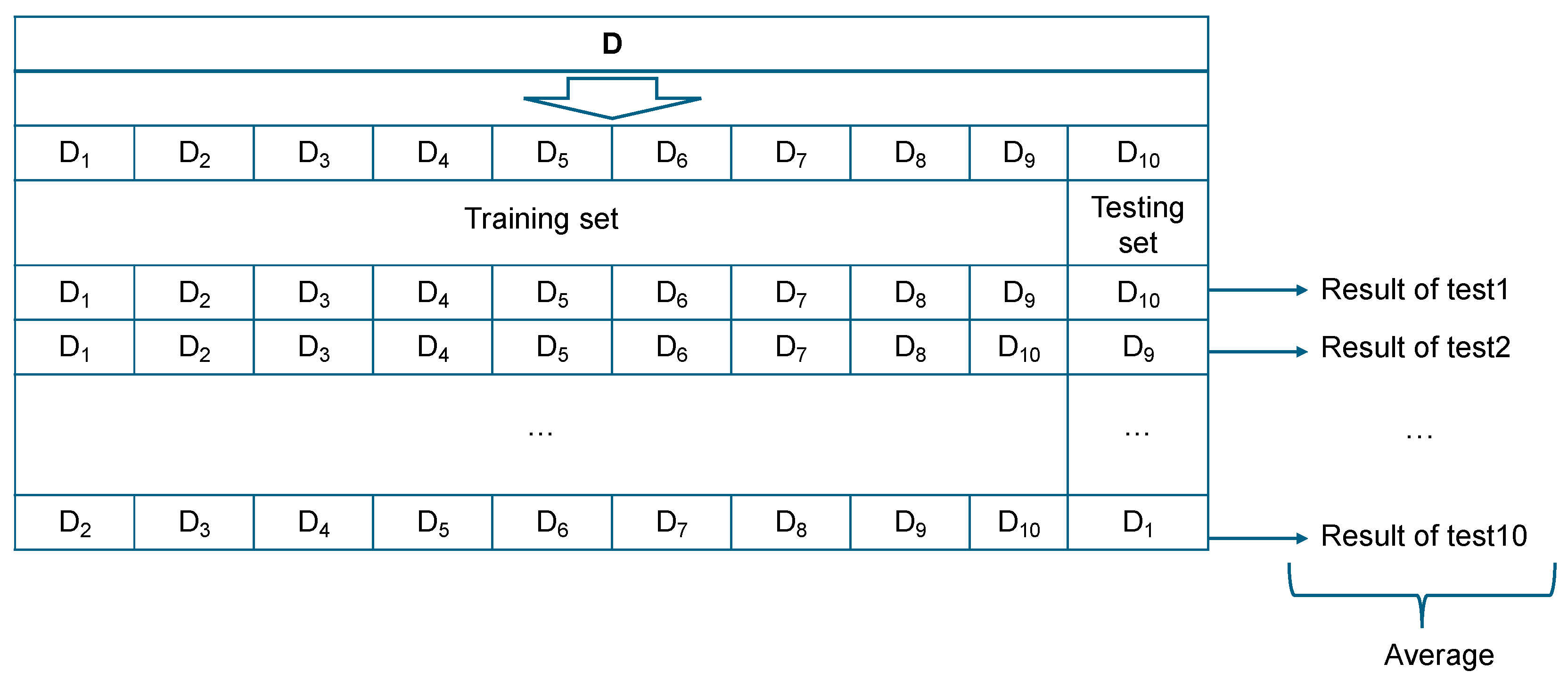
Cross-validation is a data resampling method used to assess the generalization ability of predictive models and to prevent overfitting [32,33]. This study uses k-fold cross validation to examine the performance of model built with certain data test. The k value used in this k-fold cross validation is 10 with the review of 433 data test as testing data and with using 10-fold cross validation so that the prediction will be repeated 10 times [34]. As depicted in Figure 7, testing data are randomly extracted, while the remaining data are divided into training and validation sets.

In smart cities, the implications of using ensemble learning, particularly the bagging technique, are profound. By harnessing the collective intelligence of multiple predictive models, city officials can achieve unprecedented accuracy in predicting and managing citywide systems. Whether optimizing traffic flow, improving energy efficiency, or enhancing public safety, the strategic application of ensemble learning paves the way for smarter, more responsive urban environments. As smart cities continue to evolve, the integration of advanced ensemble learning techniques will play a critical role in shaping their future. By bridging the gap between complex data patterns and actionable insights, ensemble learning is a testament to the transformative power of machine learning in the quest for more livable, efficient, and sustainable urban landscapes.

4. Results and Discussion

In the context of smart city development, the integration of advanced spatial analysis techniques can significantly improve urban planning and management. This study focuses on two case studies in Setagaya, Tokyo, where the kriging method and the bagging algorithm are used to predict the distribution of bearing layers, a critical factor in urban infrastructure development. The accuracy and effectiveness of these methods are crucial for smart city applications, including urban planning, environmental monitoring, and infrastructure management.

4.1. Results of Cases 1 and 2

In the first case study, the kriging method, a geostatistical technique, was used to predict the distribution of bearing layers at 10 locations in Setagaya, Tokyo. Actual measurements at these locations provided a basis for evaluating the accuracy of the predictions, with error values calculated between the predicted and actual values. The results, detailed in Table 4, underscore the accuracy of the method in spatial prediction. Figure 8 illustrates the distribution of bearing layers, providing a visual representation of the predicted values over the area. To understand the relationship between data density and prediction error, we calculated the correlation coefficient (

r

) using Eq. (3).

r ＝ \frac{s_{x y}}{s_{x} \times s_{y}} = \frac{\frac{1}{n} \sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} \times \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}

(3)

Where,

r

is the correlation coefficient between

x

and

y

s_{x y}

is the covariance of

x

and

y

s_{x}

is the standard deviation of

x

s_{y}

is the standard deviation of

y

n

is the total number of data,

x_{i}

and

y_{i}

are the value of

i

th data respectively,

\bar{x}

is the average of

x

, and

\bar{y}

is the average of

y

[35].

Table 4. Average error of prediction of bearing layer depth for ten locations in Case 1.

Prediction location	Error (m)
1	1.5
2	1.8
3	1.3
4	4.9
5	3.2
6	3.3
7	2.2
8	7.1
9	3.5
10	2.6
Average error (m)	3.1

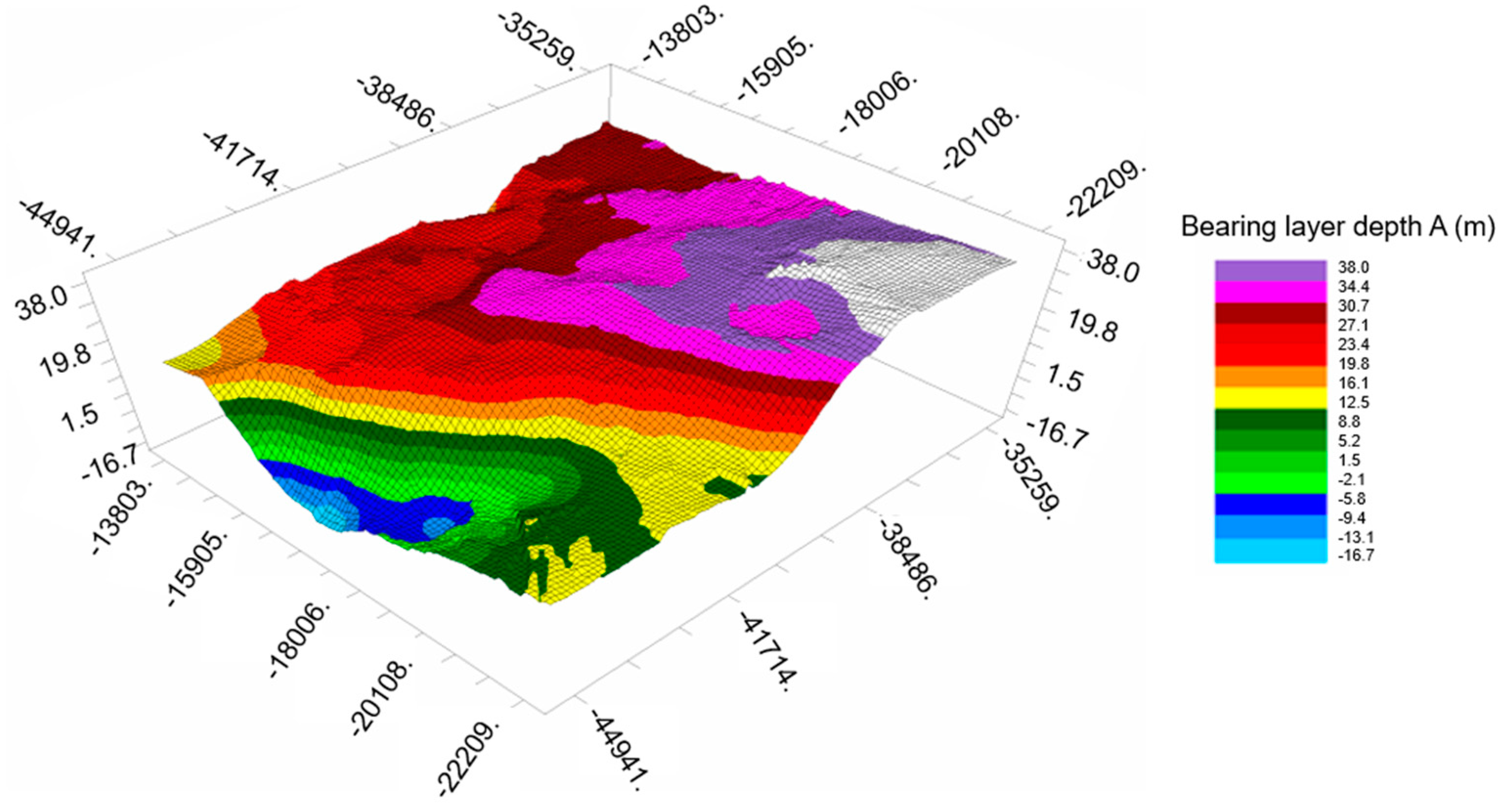
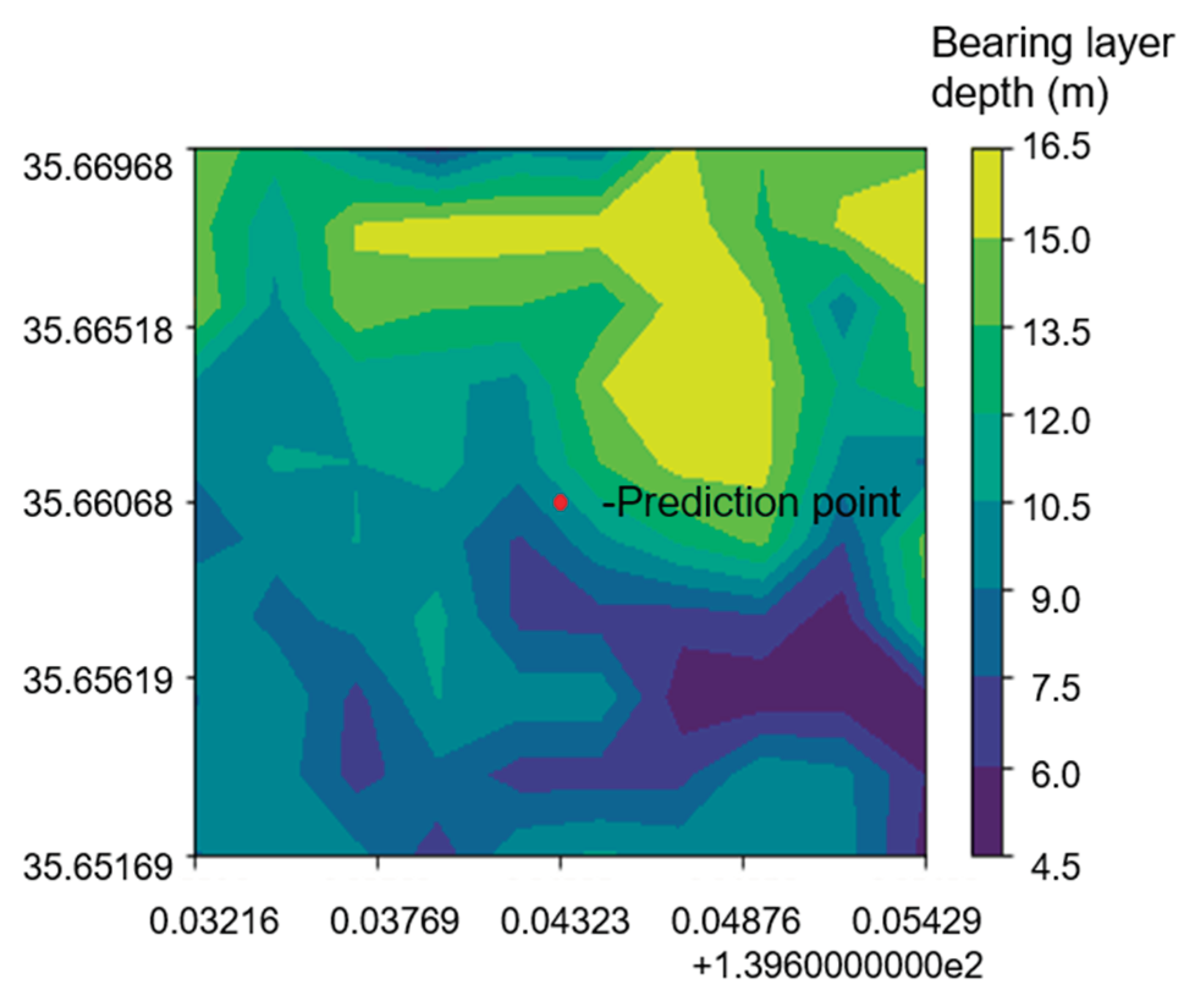
Figure 8. Prediction map of bearing layer depth A by using kriging in Case 1.

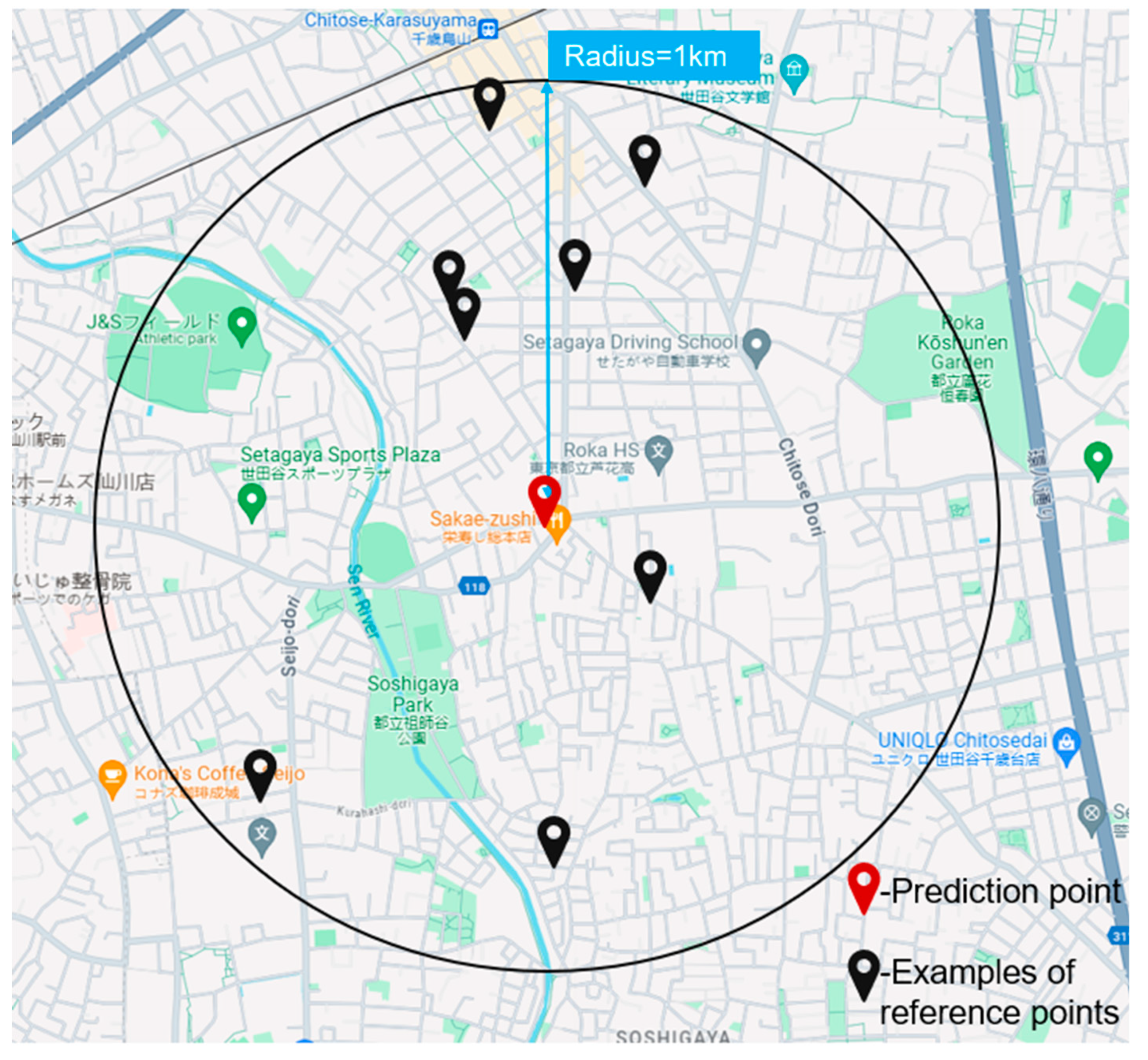
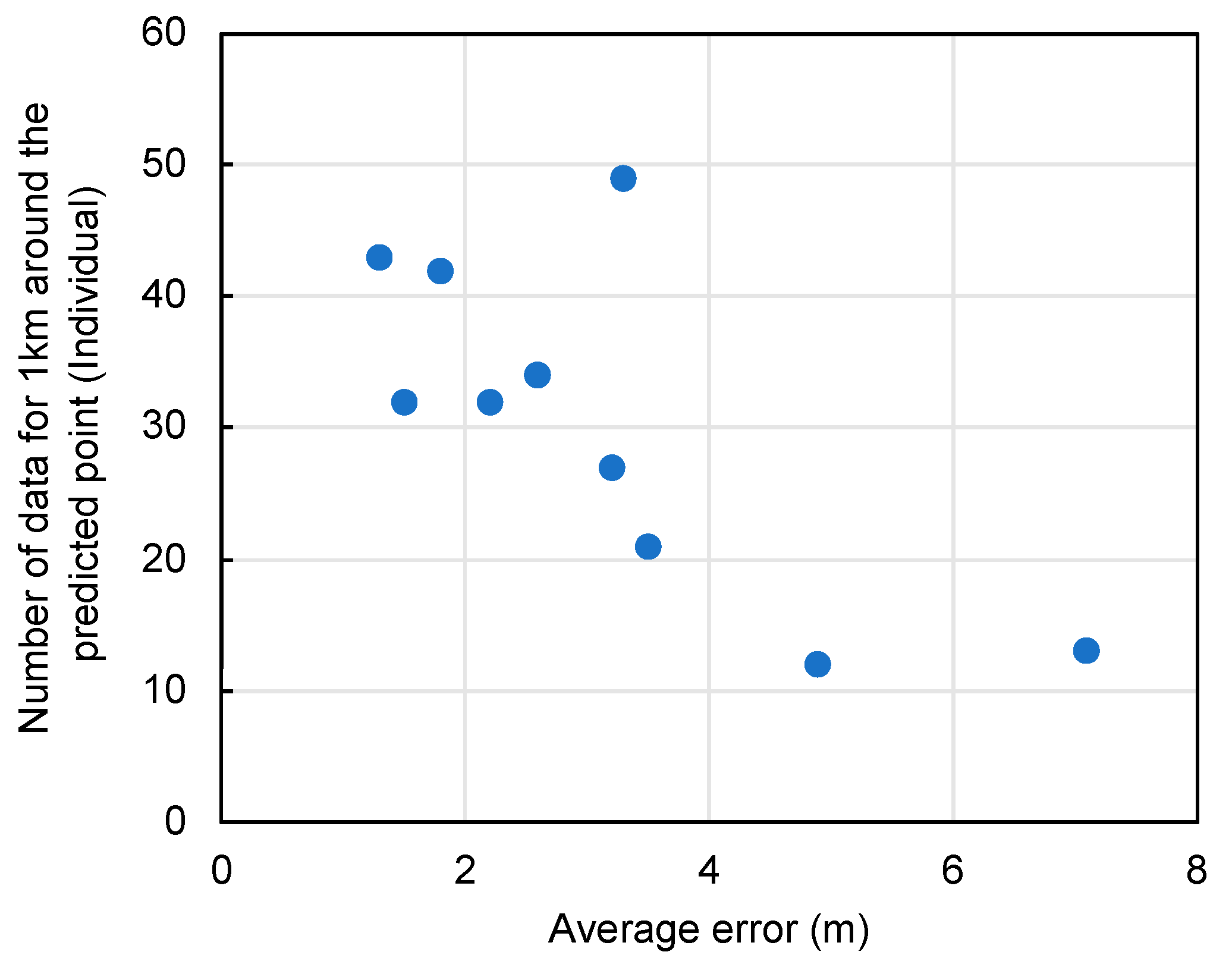
This statistical analysis revealed a correlation coefficient of -0.62, indicating a moderate inverse relationship between data density and error. This finding suggests that areas with denser data points tend to have lower prediction errors, highlighting the importance of data quality and quantity in spatial analysis. The proximity of data points to the prediction location plays a critical role, with more neighboring data points contributing to higher accuracy. Thus, the quantity of data existing within a 1 km radius (as depicted in Table 5) is reassessed. This principle is visualized in Figure 9 and Figure 10, which show the data density around a given point and the correlation between density and error, respectively.

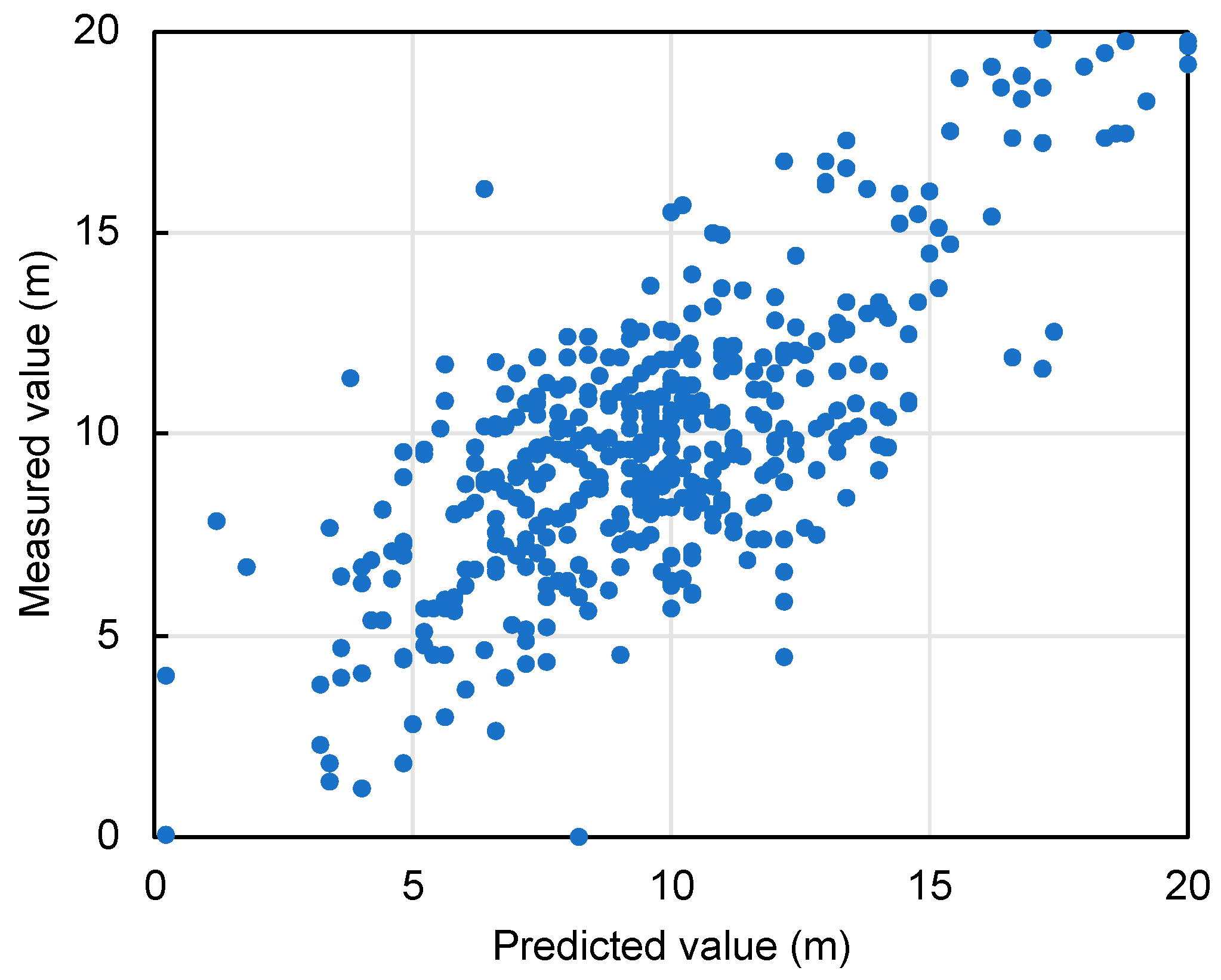
The second case study advances the application of machine learning through the bagging algorithm by incorporating multiple predictors such as latitude, longitude, and elevation along with geotechnical data from 433 locations. This ensemble learning method aims to improve the prediction accuracy of bearing layer depths, a critical component in urban infrastructure planning. The error analysis shown in Table 6 and the prediction accuracy shown in Figure 11 demonstrate the effectiveness of the bagging method. The proximity of the data points to the diagonal in Figure 11 indicates high accuracy, with an average error value of 1.99m, demonstrating the potential of machine learning to improve urban planning processes.

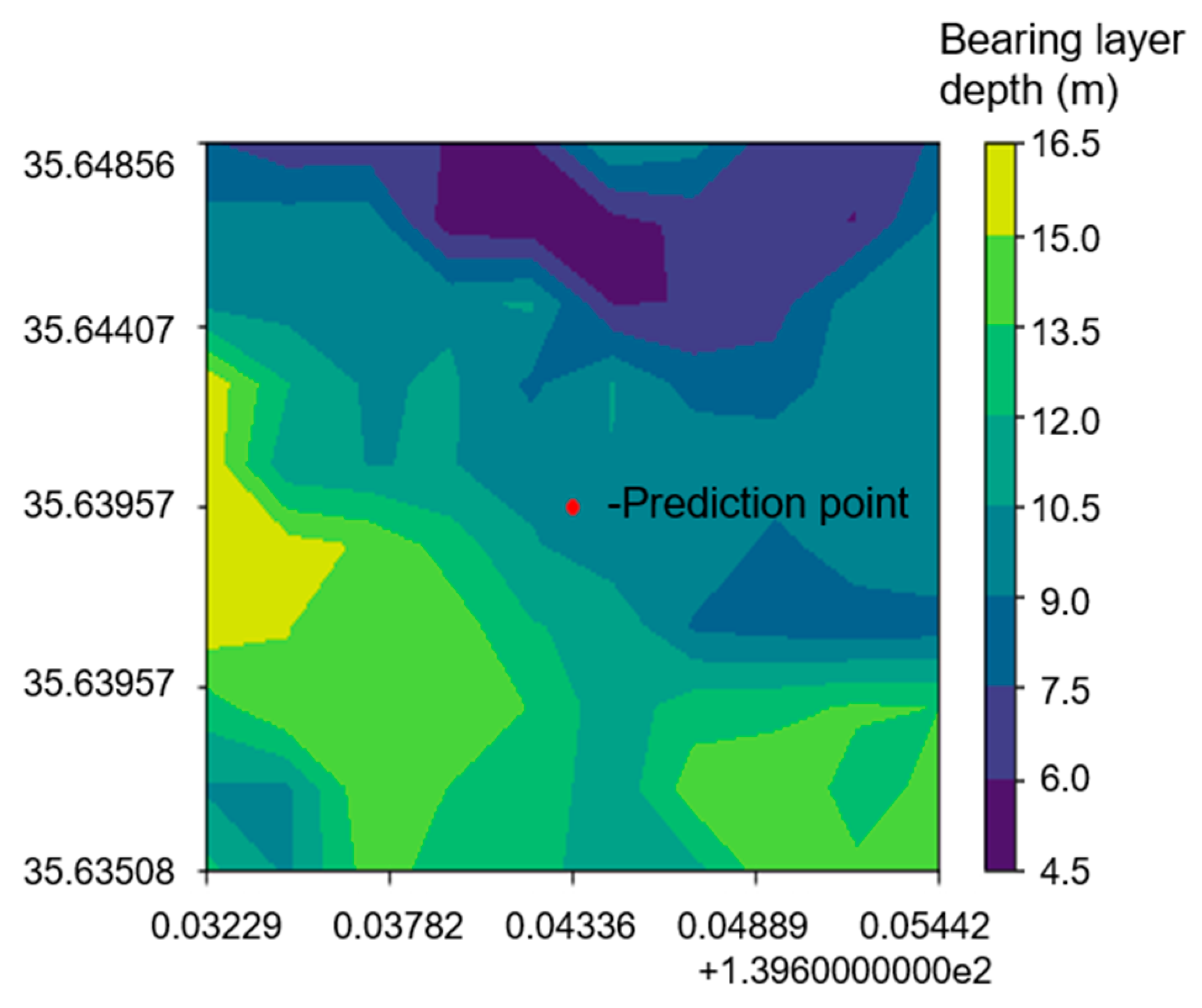
Both case studies contribute to the concept of smart cities by providing methodologies for accurate urban mapping and planning. The ability to accurately predict underground bearing layers is invaluable for infrastructure development, risk management, and environmental protection in urban areas. In addition, these predictive models facilitate the creation of real-time contour maps, as shown in Figure 12 and Figure 13, providing urban planners and engineers with dynamic tools for decision making. The results of both case studies highlight the potential of integrating geostatistical and machine learning methods into the smart city framework. The accuracy of spatial predictions has a direct impact on urban planning, infrastructure development, and environmental management. By leveraging accurate data and advanced analytical techniques, cities can optimize resource allocation, mitigate risks associated with urban development, and improve sustainability.

The inverse relationship between data density and forecast error underscores the importance of comprehensive data collection and management strategies. For smart cities, this means investing in advanced sensors, IoT devices, and data collection platforms to collect high-quality spatial data. Such investments not only improve forecast accuracy, but also enable real-time monitoring and management of urban environments. Looking ahead, the integration of more sophisticated machine learning algorithms and the incorporation of additional variables, such as soil composition, water table levels, and urban density, could further refine predictions. In addition, exploring the potential of real-time data collection and analysis could improve the adaptability and efficiency of urban planning and management in smart cities. Collaboration among government agencies, research institutions, and technology companies is critical to advancing smart city initiatives. By sharing data, expertise, and resources, stakeholders can drive innovation and develop more resilient, sustainable, and livable urban environments.

The application of kriging and bagging algorithms in Setagaya, Tokyo demonstrates the value of advanced spatial analysis in the context of smart cities. These case studies provide insights into the potential of geostatistical and machine learning techniques to improve urban planning, infrastructure development, and environmental management. As cities around the world strive to become smarter and more sustainable, the integration of these technologies will play a critical role in shaping the urban landscapes of the future.

4.2. Comparison of Average Error Values for Kriging and Ensemble Learning

In the context of the advancement of smart cities, the implementation of accurate and efficient predictive modeling techniques is crucial for the development and maintenance of urban infrastructure. As smart cities leverage data and technology to improve the efficiency of services and meet the needs of residents, the accuracy of predictive models such as kriging and ensemble learning, especially bagging, is critical for planning and operational efficiency. This analysis focuses on comparing the average error values for kriging and bagging methods used to predict the depth of the bearing layer in Setagaya, Tokyo, providing insights into their suitability for smart city applications.

For Setagaya, Tokyo, the prediction error using the kriging method is found to be 3.1 m, while the prediction error using bagging is significantly lower at 1.99 m. The prediction results for both the kriging and bagging methods are meticulously documented in Table 7, which shows that the prediction model using bagging outperforms kriging in terms of accuracy. This discrepancy in performance prompts a deeper analysis of the advantages and disadvantages of each method, particularly in the context of their application in smart city planning and development.

The kriging method, although widely used for its interpolation capabilities, has several limitations:

(1): Sensitivity to the number and distribution of data points: The performance of kriging is highly dependent on the availability and spatial arrangement of sampling points. A sparse or uneven distribution can significantly affect the model’s interpolation accuracy.
(2): Error increases with interpolation distance: As the distance over which interpolation is performed increases, the potential for error accumulation increases, potentially limiting the effectiveness of the method over larger areas.
(3): Over-smoothing in the presence of spatial variability: Kriging can over-smooth data and fail to capture subtle but important variations across terrain surfaces, which is critical for accurate urban planning in smart cities.

These limitations highlight the need for a dense, uniformly distributed dataset when using kriging for predictive modeling in urban areas. However, the case of Setagaya, Tokyo illustrates the challenges that arise when the data is sparse and unevenly distributed at the depth of the bearing layer, which leads to compromised prediction accuracy with the kriging method.

Conversely, bagging has several advantages that are well suited to the needs of predictive modeling in smart cities:

(1): Strong resistance to noise: The method’s inherent robustness to noisy data, due to random sampling and optimal feature selection, enhances its reliability in urban data analysis.
(2): Parallel computing capability: Bagging’s design allows for independent training of basic learners, facilitating parallel processing that can significantly speed up the model training process - a critical factor in the fast-paced environment of smart city development.
(3): Applicability to High-Dimensional Data: Without the need for feature selection, bagging’s ability to process high-dimensional data makes it particularly suitable for the complex datasets typical of urban environments.
(4): Insensitivity to missing features: The method’s tolerance for missing data points ensures that predictive models remain effective even when datasets are incomplete, a common occurrence in urban data collection.

Given these advantages, bagging emerges as a more suitable method for predicting bearing layer depth in smart cities, where data complexity, dimensionality, and quality can vary widely. The higher accuracy of bagging in predicting the bearing layer depth in Setagaya, Tokyo underscores its potential to enhance the predictive modeling capabilities of smart cities, ensuring more informed decision-making and efficient urban management.

The comparison between kriging and bagging in the context of predicting bearing layer depth in Setagaya, Tokyo reveals significant differences in performance, with bagging showing superior accuracy. This finding suggests that ensemble learning methods, such as bagging, hold promise for improving the data analysis framework of smart cities. By leveraging these advanced predictive models, smart cities can optimize their infrastructure and services, ultimately improving the quality of life for their residents.

5. Conclusions

Smart cities represent the pinnacle of urban development and innovation, integrating technology into the fabric of urban planning and management to create more efficient, sustainable, and livable communities. At the heart of smart city advancements is the critical role of predictive analytics, which uses data to predict future scenarios and inform decision-making processes. This study explores the development and establishment of a highly accurate prediction method for unknown points or areas in new territory, demonstrating the potential of smart cities to harness data for urban improvement.

The effectiveness of this prediction was validated using two sophisticated methods: kriging and ensemble learning, applied to data derived from ground survey results. The study achieved remarkable results, highlighting the capabilities of these methods in urban context applications, particularly in smart cities. Here’s a detailed look at the results and their implications for smart cities:

(1): The study demonstrated highly accurate predictions of bearing layer depth by learning critical geographic and geological variables such as “latitude”, “longitude”, “elevation”, and “bearing layer depth”. This accuracy is critical for smart cities, where understanding the geotechnical properties of the ground can significantly impact infrastructure development, from building construction to transportation network design.
(2): Kriging analysis revealed a strong correlation between the size of the dataset used to create the prediction map and the accuracy of the predictions. This finding is particularly relevant to smart cities, as it underscores the importance of comprehensive data collection and analysis in improving prediction accuracy, thereby facilitating better urban planning and management.
(3): The study found that when predicting geotechnical survey results using bagging, a technique in ensemble learning, the small variation in the bearing layer depth of the training data significantly affected the accuracy of the predictions. For smart cities, this finding suggests that even small discrepancies in data can affect the results of predictive models, emphasizing the need for accurate data collection and processing.
(4): A comparative analysis between kriging and bagging showed that for the same amount of training data, the prediction model for bearing layer depth was more accurate when bagging was used. This finding provides valuable guidance to smart city planners and developers in selecting the most effective predictive models for their projects to ensure optimal outcomes.

Looking ahead, the study suggests areas for future improvement to further enhance the accuracy of predictions that are critical to the development and management of smart cities:

(1): The study used a Gaussian semi-variogram in kriging, which assumes a gradual increase in predicted values. However, kriging offers several models, including spherical, exponential, and linear. Future research should quantitatively determine which prediction model achieves the highest accuracy by considering these other models. This effort will provide smart cities with a more robust toolkit for predictive analytics, enabling more accurate forecasting and planning.
(2): For ensemble learning, the study suggests considering more influencing factors and identifying the impact each factor has on prediction accuracy. By creating new models that incorporate a broader range of variables, smart cities can further improve predictive accuracy. This approach will allow for more nuanced and comprehensive planning, taking into account various factors that influence urban development and management.

This study not only confirms the effectiveness of using kriging and ensemble learning for high-precision prediction in new areas, but also highlights their potential applications in the context of smart cities. By further refining these predictive models and incorporating a wider range of data and factors, smart cities can achieve unprecedented levels of efficiency, sustainability, and livability. The insights gained from this study pave the way for future research and development in urban planning and management, marking a significant step forward in the quest to realize the full potential of smart cities.

Author Contributions

Conceptualization, S.I.; methodology, S.I.; software, Y.C.; validation, S.I.; formal analysis, Y.C.; investigation, Y.C.; resources, S.I.; data curation, Y.C.; writing—original draft preparation, Y.C.; writing—review and editing, S.I.; visualization, S.I.; supervision, S.I.; project administration, S.I.; funding acquisition, S.I. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author, Shinya Inazumi, upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Kuribayashi, E.; Tatsuoka, F. Brief review of liquefaction during earthquakes in Japan. Soils Found 1975, 4, 81–92. [Google Scholar] [CrossRef] [PubMed]
Huang, Y.; Yu, M. Review of soil liquefaction characteristics during major earthquakes of the twenty-first century. Nat Hazards 2013, 65, 2375–2384. [Google Scholar] [CrossRef]
Hasheminezhad, A.; Bahadori, H. Three dimensional finite difference simulation of liquefaction phenomenon. Int J Geotech Eng 2019, 15, 245–251. [Google Scholar] [CrossRef]
Nakao, K.; Inazumi, S.; Takahashi, T.; Nontananandh, S. Numerical simulation of the liquefaction phenomenon by MPSM-DEM coupled CAES. Sustainability 2022, 14, 7517. [Google Scholar] [CrossRef]
Lo, R.C.; Wang, Y. Lessons learned from recent earthquakes-geoscience and geotechnical perspectives. In Advances in Geotechnical Earthquake Engineering–Soil Liquefaction and Seismic Safety of Dams and Monuments; IntechOpen: Rijeka, Croatia, 2012; pp. 1–42. [Google Scholar] [CrossRef]
Hazout, L.; Zitouni, Z.E.A.; Belkhatir, M.; Schanz, T. Evaluation of static liquefaction characteristics of saturated loose sand through the mean grain size and extreme grain sizes. Geotech Geol Eng 2017, 35, 2079–2105. [Google Scholar] [CrossRef]
Bao, X.; Ye, B.; Ye, G.; Zhang, F. Co-seismic and post-seismic behavior of a wall type breakwater on a natural ground composed of liquefiable layer. Nat Hazards 2016, 83, 1799–1819. [Google Scholar] [CrossRef]
Bao, X.; Jin, Z.; Cui, H.; Chen, X.; Xie, X. Soil liquefaction mitigation in geotechnical engineering: An overview of recently developed methods. Soil Dyn Earthq Eng 2019, 120, 273–291. [Google Scholar] [CrossRef]
Cong, Y.; Motohashi, T.; Nakao, K.; Inazumi, S. Machine learning predictive analysis of liquefaction resistance for sandy soils enhanced by chemical injection, Machine Learning and Knowledge Extraction 2024, 6, 1, 402-419. [CrossRef]
Pokhrel, R.M.; Kuwano, J.; Tachibana, S. A Kriging method of interpolation used to map liquefaction potential over alluvial ground. Eng Geol 2012, 152, 26–37. [Google Scholar] [CrossRef]
Farmer, W.H. Ordinary kriging as a tool to estimate historical daily streamflow records. Hydrol. Earth Syst. Sci 2016, 20, 2721–2735. [Google Scholar] [CrossRef]
Mienye, I.D.; Sun, Y. A survey of ensemble learning: concepts, algorithms, applications, and prospects. IEEE Access 2022, 10, 99129–99149. [Google Scholar] [CrossRef]
Yang, P.; Yang, Y.H.; Zhou, B.B.; Zomaya, A.Y. A review of ensemble methods in bioinformatics. Curr Bioinform 2010, 5, 296–308. [Google Scholar] [CrossRef]
Wazoh, H.N.; Mallo, S.J. Standard penetration test in engineering geological site investigations – A review. The International Journal of Engineering and Science 2014, 3, 40–48. [Google Scholar]
Oliver, M.A.; Webster, R. Geostatistical Prediction: Kriging. In: Basic Steps in Geostatistics: The Variogram and Kriging. SpringerBriefs in Agriculture 2015. [CrossRef]
B. Krawczyk.; L. L. Minku.; J. Gama.; J. Stefanowski,; M. Woźniak. Ensemble learning for data stream analysis: A survey. Information Fusion 2017, 37,132–156.
Ginsbourger, D.; Le Riche, R.; Carraro, L. Kriging is well-suited to parallelize optimization. Computational Intelligence in Expensive Optimization Problems 2010, 2, 131–162. [Google Scholar]
Zhou, C.; He, Y.; Wang, L.; Li, S; Yu, S.; Liu, Y.; Dong, W. A method for enhancing the simulation continuity of the snesim algorithm in 2D using multiple search trees. Energies 2024, 17, 1022. [Google Scholar] [CrossRef]
Eldeiry, A.A.; Garcia, L.A. Ordinary kriging for function-valued spatial data Kriging, Regression Kriging, and cokriging techniques to estimate soil salinity using LANDSAT images. J Irrig Drain Eng 2010, 136, 355–364. [Google Scholar] [CrossRef]
Lark, R.M. Towards soil geostatistics. Spatial Statistics 2012, 1, 92–99. [Google Scholar] [CrossRef]
Lamamra, A.; Neguritsa, D.L.; Mazari, M. Geostatistical modeling by the ordinary kriging in the estimation of mineral resources on the kieselguhr mine, Algeria. IOP Conference Series: Earth and Environmental Science 2019, 362, 1, 012051. [CrossRef]
Oliver, M.; Webster, R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
Giraldo, R.; Delicado, P.; Mateu, J. Ordinary kriging for function-valued spatial data. Environ Ecol Stat 2011, 8, 411–426. [Google Scholar] [CrossRef]
Omuto, C.T.; Vargas, R.R. Re-tooling of regression kriging in R for improved digital mapping of soil properties. Geosci J 2015, 19, 157–165. [Google Scholar] [CrossRef]
Gia Pham, T.; Kappas, M.; Van Huynh, C.; Hoang Khanh Nguyen, L. Application of ordinary kriging and regression kriging method for soil properties mapping in Hilly region of central Vietnam. ISPRS Int. J. Geo-Inf. 2019, 8, 147. [CrossRef]
Buchroithner, M.F.; Pfahlbusch, R. Geodetic grids in authoritative maps – new findings about the origin of the UTM grid. Cartography and Geographic Information Science 2017, 44, 186–200. [Google Scholar] [CrossRef]
Ngo, G.; Beard, R.; Chandra, R. Evolutionary bagging for ensemble learning. Neurocomputing 2022, 510, 1–14. [Google Scholar] [CrossRef]
Dong, X.; Yu, Z.; Cao, W.; Shi, Y.; Ma, Q. A survey on ensemble learning. Front Comput Sci 2020, 14, 241–258. [Google Scholar] [CrossRef]
Liang, G.; Zhu, X.; Zhang, C. An empirical study of Bagging predictors for different learning algorithms. Proceedings of the 25th AAAI Conference on Artificial Intelligence 2011, 25, 1802–1803. [Google Scholar] [CrossRef]
Priyama, A.; Abhijeeta; Guptaa, R.; Ratheeb, A.; Srivastavab, S. Comparative analysis of decision tree classification algorithms. International Journal of Current Engineering and Technology 2013, 3, 2, 334-7.
Prajwala, T.R. A comparative study on decision tree and random forest using R tool. International Journal of Advanced Research in Computer and Communication Engineering 2015, 4, 196–199. [Google Scholar] [CrossRef]
Browne, M.W. Cross-validation methods. J Math Psychol 2000, 44, 108–132. [Google Scholar] [CrossRef] [PubMed]
Bates, S.; Hastie, T.; Tibshirani, R. Cross-validation: what does it estimate and how well does it do it? . Journal of the American Statistical Association 2023, 1–12. [Google Scholar] [CrossRef]
Hanmastiana, I.M.; Warsito, B.; Rahmawati, R.; Yasin, H.; Kartikasari, P. Classification of public opinion on social media twitter concerning the education in Indonesia using the K-nearest neighbors (K-NN) algorithm and K-fold cross validation. STATISTIKA Journal of Theoretical Statistics and Its Applications 2021, 21, 99–106. [Google Scholar] [CrossRef]
Winter, J.C.F.; Gosling, S.D.; Potter, J. Comparing the Pearson and Spearman correlation coefficients across distributions and sample sizes: A tutorial using simulations and empirical data. Psychol Meth 2016, 21, 273–279. [Google Scholar] [CrossRef]

Figure 1. Illustration of liquefaction mechanism and an example of liquefaction disaster.

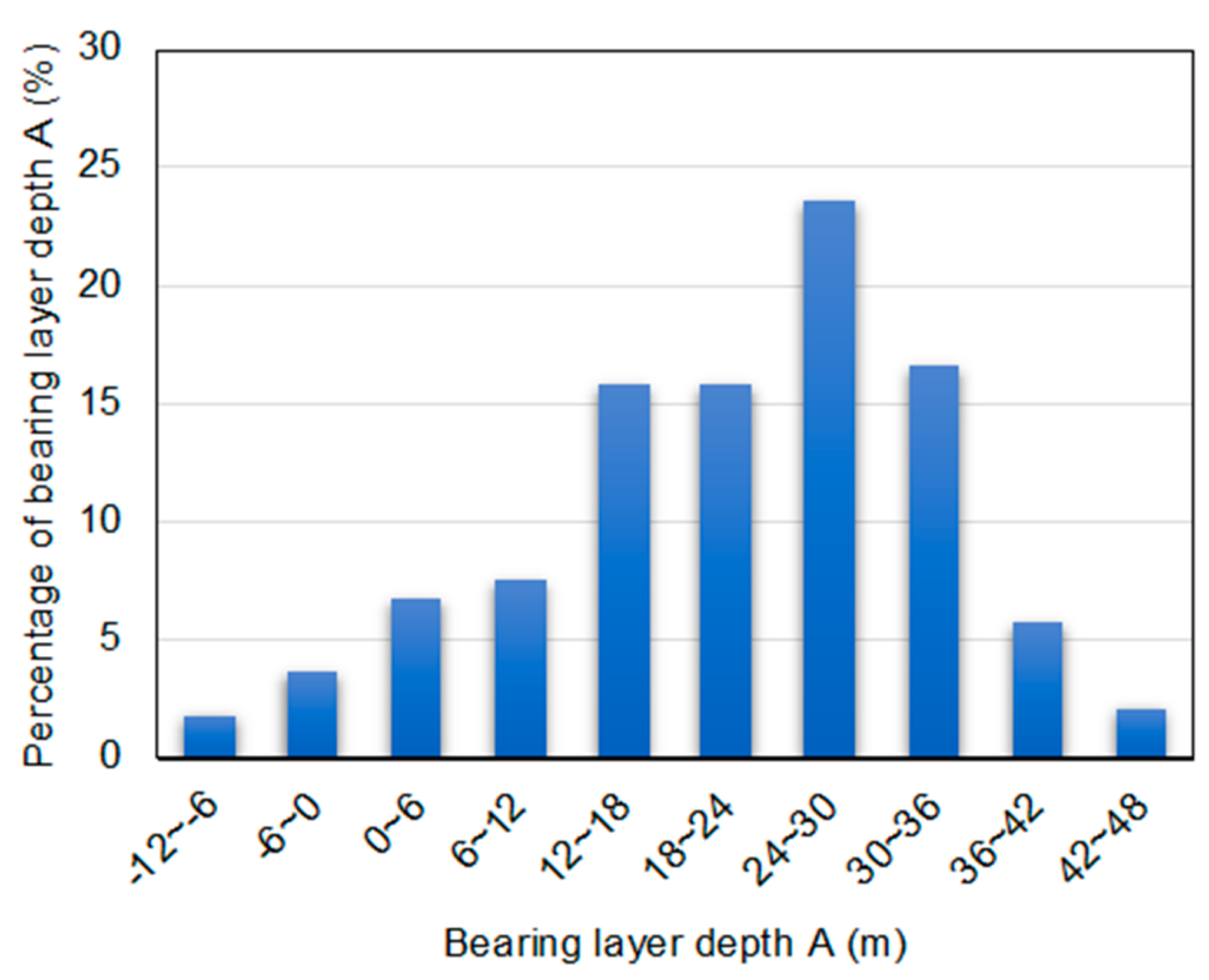
Figure 2. Histogram of bearing layer depth A for Case 1.

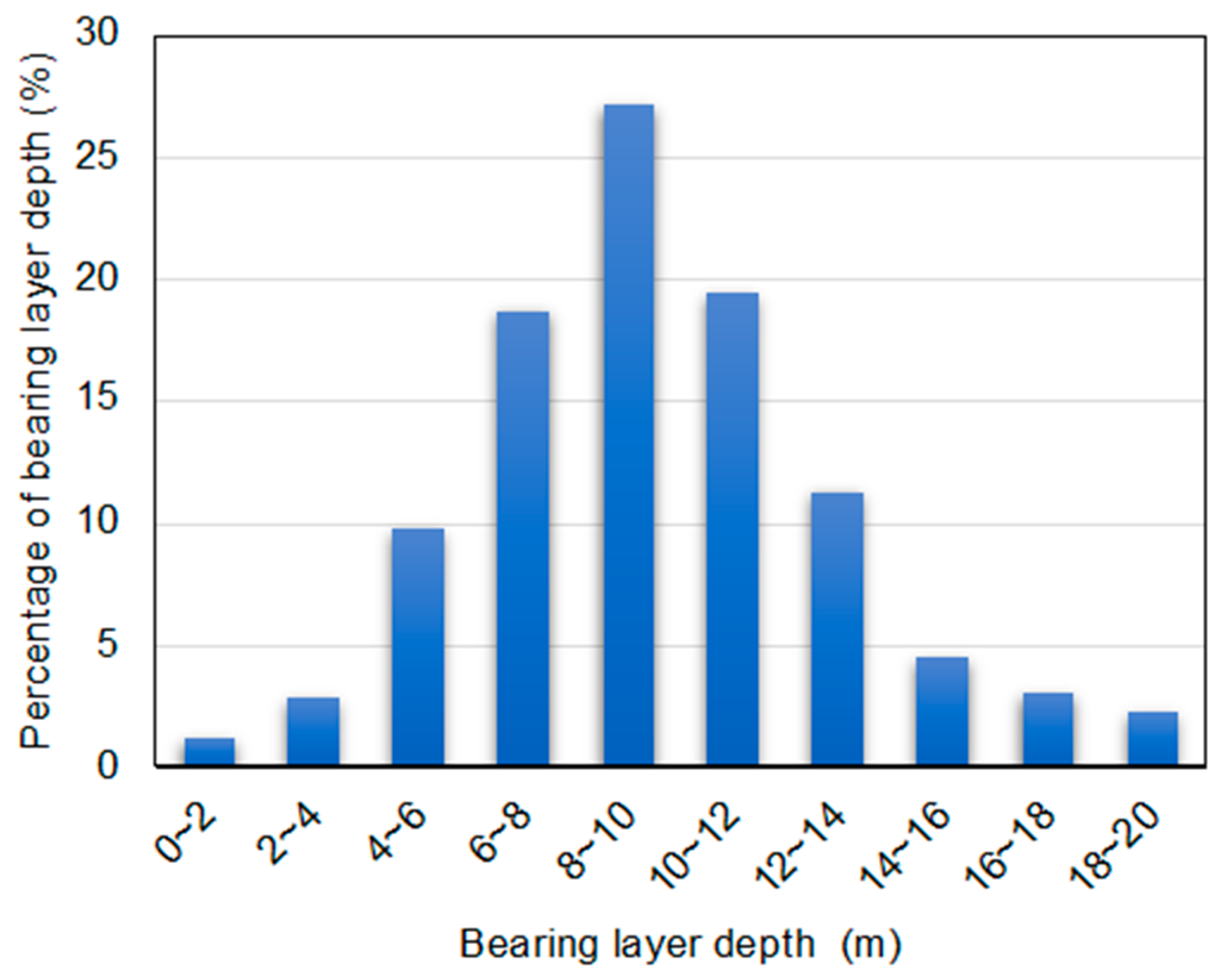
Figure 3. Histogram of bearing layer depth for Case 2.

Figure 4. Process of creating a model by using kriging of Case 1.

Figure 5. Process of creating a model by using bagging of Case 2.

Figure 6. Dendrogram of decision tree of Case 2.

Figure 7. Overview of 10-fold cross-validation process.

Figure 9. Data distribution chart within a 1 km radius with No. 1 as the center.

Figure 10. Relationship between number of data existing within 1 km of center of prediction point and average error.

Figure 11. Prediction results of Case 2 by using bagging.

Figure 12. Contour plot of predicted bearing layer depth within 1 km centered on No. 1.

Figure 13. Contour plot of predicted bearing layer depth within 1 km centered on No. 9.

Table 1. Data conditions used in predicting bearing layer depth for Setagaya, Tokyo.

	Area (km²)	Number of data (pcs)	Data density (pcs/km²)	Standard deviation of data
Setagaya	58.1	433	7.46	9.53

Table 2. Differences in target variable used by two methods.

Case	Target variable	Actual value of target variable
Case1	Bearing layer depth A	Bearing layer depth - Elevation
Case2	Bearing layer depth	Bearing layer depth

Table 3. Explanatory variables and target variable used in two cases.

Case	Explanatory variables	Target variable
Case 1	Bearing layer depth A	Bearing layer depth A
	Latitude
	Longitude
Case 2	Bearing layer depth	Bearing layer depth
	Latitude
	Longitude
	Elevation

Table 5. Comparison of amount of data within 1 km with ten prediction locations as center in Setagaya, Tokyo.

Prediction location	Error (m)	Within 1km surrounding area amount of data (Individual)
1	1.5	32
2	1.8	42
3	1.3	43
4	4.9	12
5	3.2	27
6	3.3	49
7	2.2	32
8	7.1	13
9	3.5	21
10	2.6	34
Average error (m)	3.1

Table 6. Average error of prediction of bearing layer depth for ten locations in Case 2.

Prediction location	Error (m)
1	1.8
2	1.9
3	1.21
4	3.31
5	2.48
6	3.8
7	2.2
8	1.21
9	0.8
10	1.16
Average error (m)	1.99

Table 7. Kriging method and bagging prediction results of bearing layer depth.

	Predictive method	Average error (m)
Setagaya	Kriging	3.1
Setagaya	Bagging	1.99

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer