Prerpints.org logo
Preprint
Article

Very Short-Term Prediction of Ship Motion Using Deep Operator Networks

Altmetrics

Downloads

127

Views

54

Comments

0

This version is not peer-reviewed

Submitted:

08 March 2024

Posted:

08 March 2024

You are already at the latest version

Alerts
Abstract
The intense motion of a ship can greatly impacts the comfort of crew members and the safety of the vessel. Therefore, accurately estimating and predicting ship attitudes has become an important issue. This paper introduces the latest development in functional deep learning model called DeepOnet. It takes wave height as input and ship motion as output, using a cause-to-result prediction approach. The modeling data used in this study is sourced from publicly available experimental data from the Iowa Institute of Hydraulic Research. Firstly, parameters system tuning was conducted for the neural network's hyperparameters to determine the appropriate combination of parameters. Secondly, the DeepOnet model for wave height and multi-degree-of-freedom motion was established, and the influence of increasing time steps on prediction accuracy was examined. Finally, a comparison was made between the DeepOnet model and the classical time series model LSTM. It was found that the DeepOnet model had a 10-fold improvement in accuracy for roll and heave attitudes. Moreover, as the forecast duration increased, the advantage of DeepOnet showed a trend of strengthening. As a functional prediction model, DeepOnet provides a new promising tool for very short-term prediction of ship motion.
Keywords: 
Subject: Engineering  -   Marine Engineering

1. Introduction

When ships sailing at sea, they are influenced by uncertain factors such as wind, waves, and currents, which result in highly complex nonlinear motions in all six degrees of freedom. These motions are interrelated and collectively impact the ship, leading to a constantly irregular motion pattern. Thus, accurate prediction of a ship’s motion and attitude plays a crucial role in improving maritime safety through effective motion compensation. Currently, the very short-term prediction of ship motion and attitude is mainly carried out using data-driven modeling methods.
The data-driven modeling methods include the Kalman filtering method [1,2,3,4], the autoregressive model-based method [5], spectral estimation method [6], support vector machine [7], grey theory [8], and chaotic analysis methods [9]. These methods can forecast the time history curves of very short-term ship movements. In recent years, with the rise of machine learning, an increasing number of scholars have utilized artificial neural networks for the very short-term prediction of ship movements [10,11]. Liu Wanting [12] employed Kalman filtering, radial basis neural networks, and Elman neural networks to forecast ship heaving motions, and the results indicated that the Elman neural network achieved better prediction accuracy. Li et al. [13] used error backpropagation (BP) neural networks to forecast ship roll motions and compared them with autoregressive moving average methods, demonstrating that BP neural networks had superior prediction accuracy. Guodong Wang [14] conducted predictive analysis of actual ship roll and pitch motion data using autoregressive models, traditional recurrent neural network models, and Long Short-Term Memory (LSTM) neural network models. The results showed that the LSTM neural network exhibited better prediction accuracy. Compared to traditional time series forecasting methods, artificial neural networks, due to their arbitrary non-linear approximation and self-learning capabilities, demonstrate significant advantages.
Ni Chenhua et al. [15] applied LSTM to predict wave heights under polar conditions. Y. Zhao et al. [16,17] employed the LSTM neural network method for forecasting abnormal waves, effectively predicting sudden events hidden in ordinary wave sequences with good accuracy and efficiency. Yue Liu et al. [18]designed a deep learning wave prediction (Deep-WP) model based on a “probability” strategy for short-term forecasting of random waves. The Deep-WP model utilizes Long Short-Term Memory (LSTM) units to gather relevant information from the wave height time series. This model demonstrates the capability for real-time prediction of nonlinear random waves. Sun Qian et al. [19]proposed a ship motion attitude mixed prediction model based on LSTM and Gaussian Process Regression (GPR). In handling nonlinear regression problems, the LSTM model can achieve high-precision point predictions, while the lower-precision GPR model can provide interval predictions with probabilistic significance. The accuracy of various neural network models for prediction theory and algorithms is correlated with sea conditions and degrees of freedom. In the application of artificial neural networks for ship motion prediction, most scholars built their modeling on the ship’s own oscillation duration data, and there are few reports on ship motion duration prediction based on wave height duration data. Chongyang Han et al. [20] proposes a ship motion prediction method based on a variable step-variable sampling frequency characteristic LSTM (Long Short-Term Memory) neural network. Ling Liu et al. [21] employed machine learning techniques based on the reservoir computing (RC) model to predict the surge, sway, heave, roll, pitch, and yaw of the KVLCC2 ship in an irregular wave environment. The trained RC model can forecast the 6 degrees of freedom motion, providing predictions for the next 2-5 wave periods with good accuracy.Xianrui Hou et al. [22] used Convolutional Neural Networks (CNN) to predict the roll motion of ships in waves. The research results show that CNN achieves the same prediction accuracy for ship roll motion as LSTM.
Wenhai Yi and Zhiliang Gao et al. [23] improved the prediction accuracy of LSTM models based on wave height data input under sea states 4 and 5, especially with a significant improvement in prediction accuracy under sea state 5, resulting in a reduction of over 40% in root mean square error and maximum absolute error. Models based on wave height input data overall perform better than models based on historical roll data input. Ferrandis et al. [24] used random wave height data as input to predict ship roll, pitch, and heave in extreme sea state. The authors conclude that this functional prediction model would constitute a potentially powerful predictive tool to avoid associated hazards encountered in these situations.
Deep Operator Networks (DeepOnet), known as a functional neural network method, was proposed by the research group of Professor Karniadakis from the Applied Mathematics Department at Brown University in 2021 [25]. To the best of our knowledge, this paper is the first to apply DeepOnet model for predicting ship motion attitude of the extreme short-term.
The rest of the paper is organized as follows. The DeepOnet algorithm and training process, along with the data source. i.e., the experimental data from Iowa Institute of Hydraulic Research of Iowa University are introduced in Section 2. Results and discussion are presented to demonstrate its effectiveness and higher precision compared with the LSTM model in Section 3. Finally, a summary is concluded in Section 4.

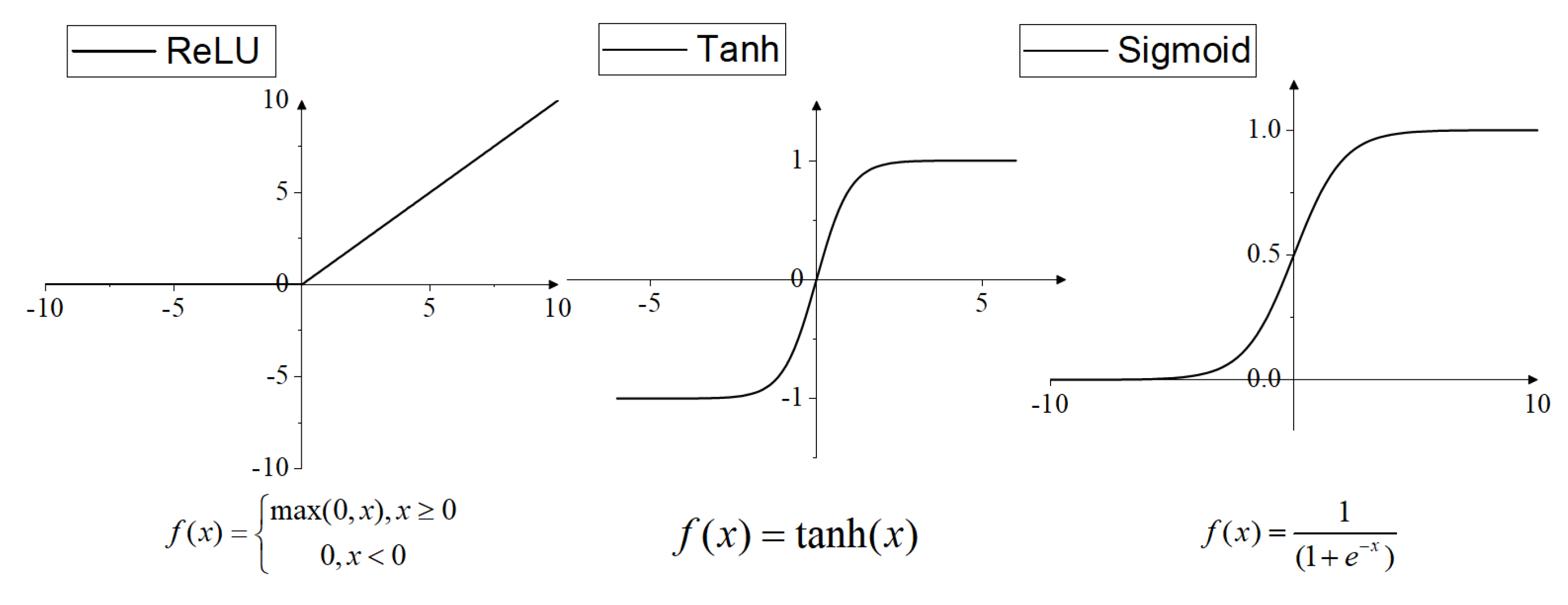
2. DeepOnet Algorithm and Modeling

Principle of Operator Approximation: Assuming that σ is a continuous non-polynomial function, X is a Banach space, K 1 and K 2 are two closed sets with K 1 ∈ X , K 2 ∈ R d , V is a closed set in C K 1 , and G is a nonlinear continuous operator that maps V to C K 2 . For any ε > 0 , there exist positive integers n , p , m ,constants c i k , ξ i k , θ i k , ζ k ∈ R , w k ∈ R d , x j ∈ K 1 , i = 1 , … , n , k = 1 , … , p , j = 1 , … , m such that
G u y − ∑ k = 1 p ∑ i = 1 n c i k σ ∑ j = 1 m ξ i j k u x j + θ i k σ w k · y + ζ k < ε
holds. Wherein:
B r a n c h n e t : ∑ i = 1 n c i k σ ∑ j = 1 m ξ i j k u x j + θ i k
T r u n k n e t : ∑ k = 1 p σ w k · y + ζ k
Formula (1) can be represented by Figure 1. The network takes G as the operator for the input function u, so G(u) becomes the output function. For any y in the domain of the output function G(u), the output G(u)(y) is the true value. Therefore, DeepONet consists of two parts—u and y.
The structure of neural network models consists of input layers, hidden layers, and output layers. Despite having multiple hidden layers, the overall structure can still be considered as a network. The DeepOnet divides the entire hidden layer into two sub-networks—branch net and trunk net. The branch net is used to extract the potential patterns of the input function, while the trunk net is used to extract the potential patterns of the input data. The potential patterns extracted by these two sub-networks are combined through dot product.
G θ u y = ∑ k = 1 p ∑ i = 1 n c i k σ ∑ j = 1 m ξ i j k u x j + θ i k σ w k · y + ζ k = ∑ k = 1 Q b k u x 1 , u x 2 , … , u x m · t k Ф
During the training process, the sample points are discretized as the input function, and their discrete forms, along with the corresponding y in the domain of the output function G(u), are simultaneously input into the network. The network utilizes two distinct sub-networks to independently train their respective parameters. Subsequently, the values output by the sub-networks are compared with the ground truth, and the error is calculated. Finally, the entire set of weights is updated using the backpropagation method, thereby determining the parameters for each network to fit the operator. The training procedure of the DeepOnet model is outlined in Table 1.
The ship motion data in regular waves under head seas are derived from ship model experiments conducted in the Iowa Institute of Hydraulic Research wave basin [26]. The experiments utilized a ship model based on the DTMB5415 prototype, scaled down to 1/46.6 proportions, known as the DTMB5512 ship model. The experimental schematic diagram and ship model parameters are illustrated in Figure 2 and Table 2.
The experiment conducted was a regular wave test, involving four different ship speeds. Each speed maintained a constant wave steepness, and the wave incidence angle (Ak) was kept unchanged by controlling the heading angle. The experiment focused on varying the wave height and wavelength while keeping the same ship speed and wave steepness, aiming to further investigate the ship motion under different combinations of wave lengths and heights. Table 3 presents the experimental conditions corresponding to Froude number of 0.28, a wave incidence angle of 0.025, and the associated ship model parameters.
Taking the first working condition as an example, the experiment recorded the ship’s motion data under four wave conditions, each lasting 20 seconds, with a time interval △ t = 0.0125 s , resulting in a total of 1600 sample data points. The transverse rolling, pitch, and heave motion curves of the ship model in head waves are shown in Figure 3.

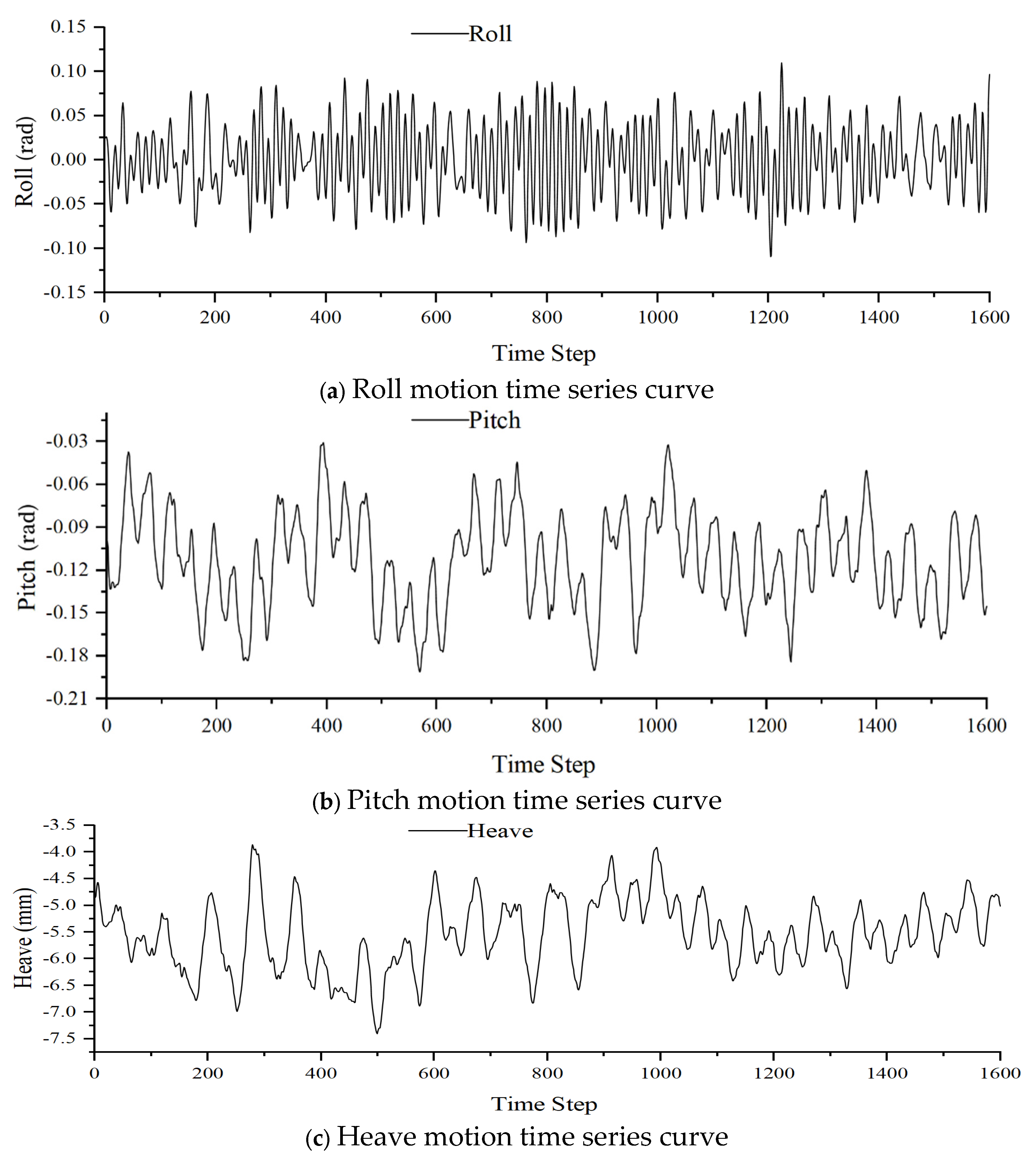
3. Results and Analysis

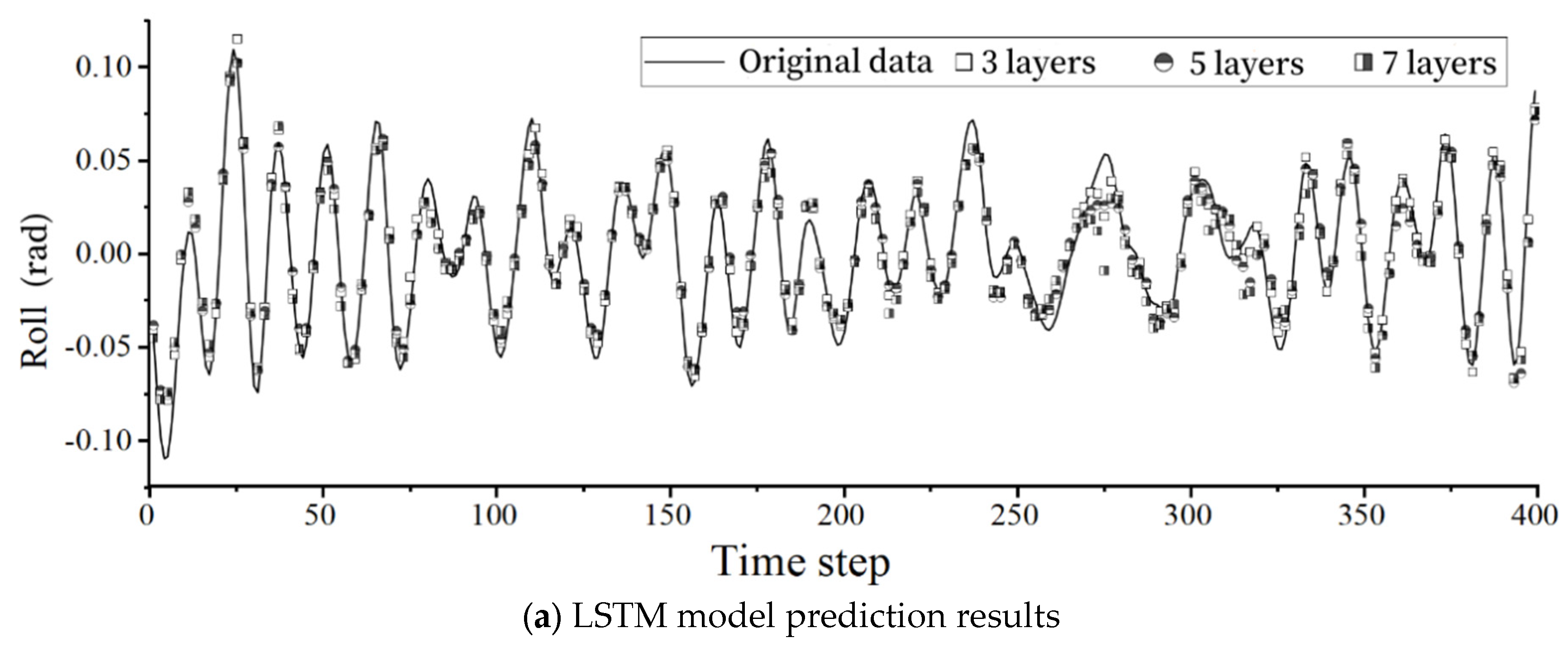
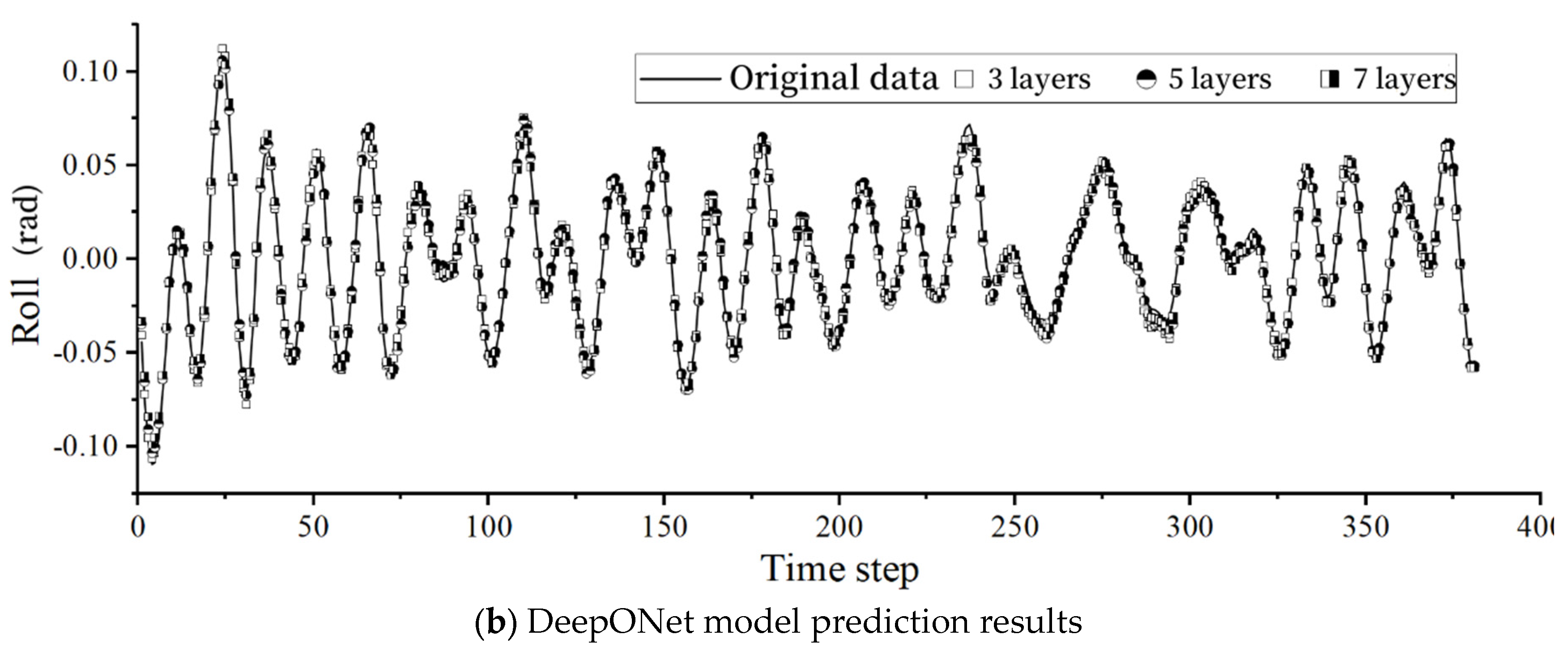
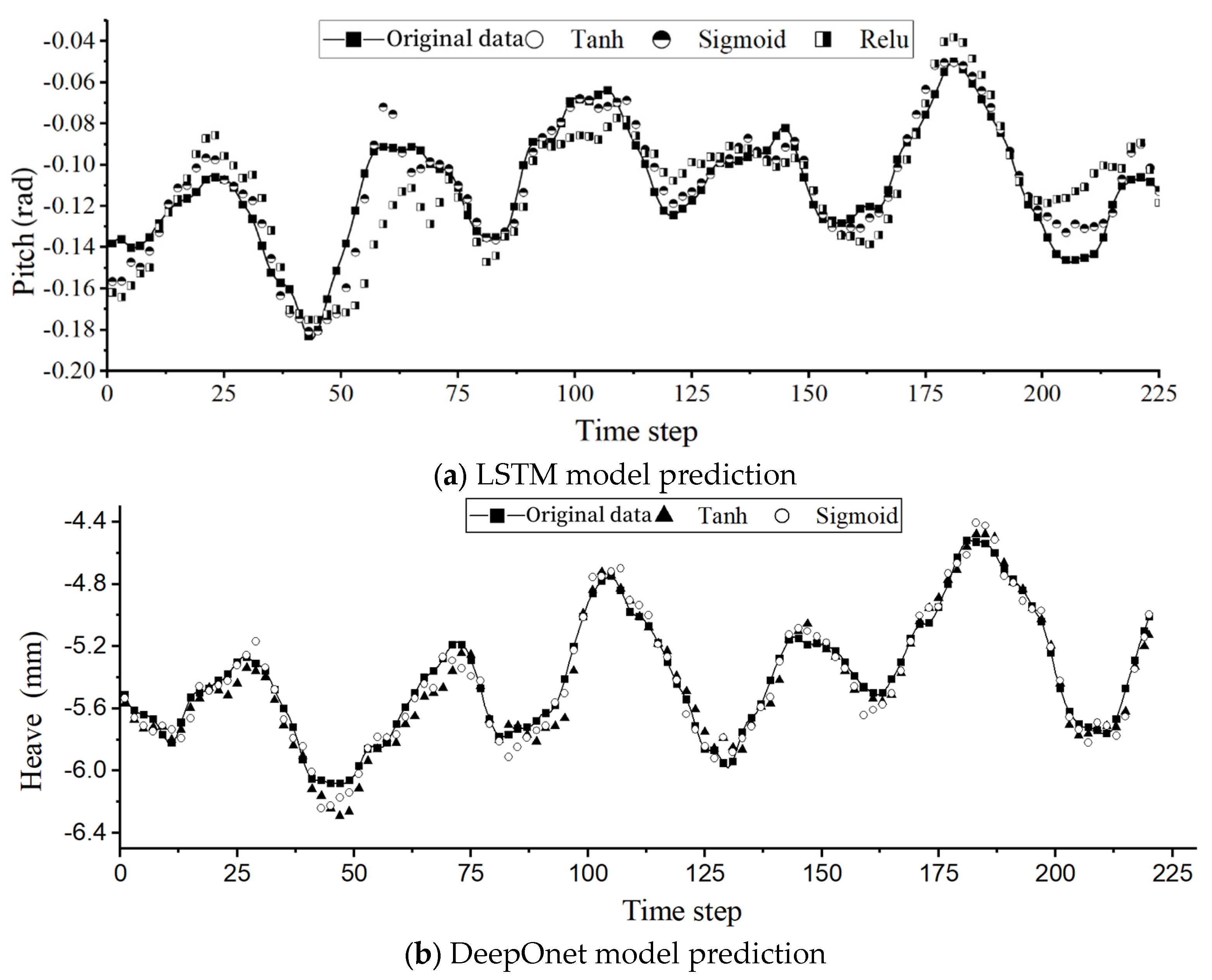
3.1. Hyperparameters Tuning for DeepOnet and LSTM Models

In the modeling process, it is essential to tune the hyperparameters of the network model, which can be categorized into five types: network layers and neuron count, training and testing set partition ratio, activation function selection, loss function, and optimizer function.
In this subsection, the experimental data for roll motion under wave height H of 5.6mm in the ship model experiments were used, comprising 1600 sample points. A 20-second dataset of ship roll motion was employed to discuss the hyperparameters of the DeepOnet and LSTM models. To enhance the persuasiveness of the experimental results, parameters other than the hyperparameters under discussion were set as default: training set ratio of 70%, 5 layers and 80 neurons for both the trunk and branch networks of the DeepOnet model, and 3 layers and 100 neurons for the LSTM model. Other shared parameters between the two models were set to the same values: optimizer as Adam, loss function as MSE, and batch size as 32.
If a neural network does not impose restrictions on the number of layers and neurons, it can approximate any non-linear function. However, stacking too many layers and increasing the number of neurons will consume significant computational resources. If the features of a model are not overly complex, setting too many layers and neurons is not economical. The roll motion predictions were conducted by varying the network layers of DeepOnet and LSTM to 3, 5, and 7, and the neuron count to 80, 100, and 120. The prediction results are presented in Table 4.
Figure 4a,b depict the prediction results of the LSTM model and the DeepOnet model with 80 neurons under different numbers of layers. It is evident that the prediction performance of the two models is nearly identical when the number of layers is the same under the condition of the same number of neurons.
As shown in Table 4, the mean square errors of the testing sets for both models can reach the magnitude of 10-4 or below. Regarding the number of network layers, it can be observed that a higher number of layers does not necessarily result in better predictive capabilities. This is due to the risk of overfitting the function to the training data, leading to a decrease in the model’s generalization ability when faced with new datasets. Regarding the number of neurons, it is observed that, like the network layers, more neurons do not necessarily yield better results, and fewer neurons do not imply worse results. The model exhibits better performance when configured with 5 layers and 100 neurons.
As a data-driven approach, it is evident that the size of the training set will influence the predictive results of both network models. Experiments were conducted using the DeepOnet model and the LSTM model to investigate the impact of the training set percentage on the ship roll prediction. The experiments involved varying the training set size for both the DeepOnet and LSTM models to 60%, 70%, and 80%. The prediction results are presented in Table 5.
To comprehensively analyze the predictive capabilities of the two models under different dataset partitions, the following section will take the dataset with the smallest prediction ratio as the baseline. Specifically, the comparison will be based on the data quantity where the testing set comprises 80% of the total data. The predictive results are presented in Figure 5.
For a more intuitive representation of the impact of different training set sizes on predictive performance, the Mean Square Error (MSE) in Table 5 is converted into Root Mean Square Error (RMSE). It can be observed that as the training set increases, the predictive error decreases. In the results predicted by the DeepOnet model, the forecast error for the 80% training set is reduced by 24.5% compared to the 60% training set. Similarly, in the results predicted by the LSTM model, the forecast error for the 80% training set is reduced by 42.7% compared to the 60% training set. This implies that a larger training set allows the model to learn more features, leading to better predictive performance on the testing set.
The motion of ships in the actual ocean exhibits highly pronounced nonlinearity. Therefore, determining which activation function can endow the network model with more potent nonlinear fitting capabilities is particularly crucial. Commonly used activation functions include the hyperbolic tangent function (tanh), the sigmoid function, and the rectified linear unit (ReLU) function. Their specific schematic diagrams are depicted in Figure 6.
The sigmoid function shown in Figure 6 has an output range of 0 to 1. Consequently, it normalizes the output for each neuron, making it more suitable for models where probability is used as the output. The tanh function, a hyperbolic tangent function, exhibits a similar graph to the sigmoid function but with an output range between [-1, 1]. It provides a smoother and smaller gradient, addressing the slow convergence issue compared to the sigmoid function. The ReLU activation function is a piecewise function. When x is greater than 0, it linearly outputs the value; when x is less than 0, the output is zero. Therefore, this activation function is suitable for certain classification problems. Based on the distinctive characteristics of each activation function, all three are employed in the LSTM and DeepOnet models. Under these activation functions, predictions are made for different ship roll, pitch, and heave motions. The prediction results are summarized in Table 6.
Table 6 presents the test set loss values for different activation functions in the prediction results. The term “Error” indicates that, under the same network structure, changing the activation function to the ReLU function alone renders the entire network unable to learn the feature vectors of roll, pitch, and heave motions. The network fails to train, and even after multiple adjustments to other hyperparameters, it remains ineffective for prediction, producing constant values for all predictions. This issue arises from the inherent structure of the ReLU function, where the derivative is zero for values less than zero, leading to neuron death—certain neurons outputting zero. In contrast, the LSTM network can make predictions because, before prediction, the data undergo normalization, constraining all values to the range [0, 1].
From the comparative results in Figure 7a,b and Table 6, it is evident that there are significant differences in the predictive performance under different activation functions. The tanh activation function consistently exhibits better predictive performance relative to other activation functions across all prediction experiments. In contrast, the performance of the sigmoid activation function varies widely and is highly unstable, especially when dealing with complex data situations such as the heave motion in this experiment. This instability is attributed to the vanishing gradient problem that the sigmoid activation function is prone to during the propagation process in deep networks.
The most used loss functions in regression problems are Mean Squared Error (MSE) and Mean Absolute Error (MAE). The MSE function has a smooth, continuous, and everywhere-differentiable curve, facilitating the gradient descent algorithm. Moreover, as the error decreases, the gradient also decreases, aiding in the rapid convergence of the model. However, when the difference between the true value and the predicted value is greater than 1, the square calculation amplifies the error, making it sensitive to outliers. In comparison to MSE, the advantage of MAE lies in its insensitivity to outliers, stable gradients, and a reduced risk of gradient explosion. Nevertheless, its main drawback is that when the predicted value equals the true value or approaches it infinitely, the function becomes non-differentiable, and gradients are mostly equal, hindering convergence and model training.
MAE and MSE loss functions are utilized to predict roll, pitch, and heave motions for both DeepONet and LSTM. The experimental results are summarized in Table 7.
Figure 8 illustrates that both Mean Squared Error (MSE) and Mean Absolute Error (MAE) exhibit favorable predictive performance, with MSE showing better performance in detail. Simultaneously, observing the prediction results of the two models for heave motion reveals that MSE performs better when facing predictive problems with weak periodic regularity and numerous outliers. The same conclusion can be drawn from Table 7. The reason behind this outcome is that the Mean Absolute Error loss function is more sensitive to outliers, while the Mean Squared Error loss function places greater emphasis on overall smoothness.
Optimizers are algorithms, such as the gradient descent algorithm, used to compute the optimal values of parameters, including network weights and biases, during the training process of neural networks. Essentially, the goal is to find the solution to mathematical optimization problems by seeking the optimal parameter values among all possible combinations, often represented as the extremum in the function’s graph.
This study discusses two optimizers: Adaptive Moment Estimation (Adam) and Stochastic Gradient Descent (SGD). Adam combines first-moment estimation (mean of gradients) and second-moment estimation (uncentered variance of gradients) to calculate the update step size. It possesses advantages such as simplicity, computational efficiency, low memory requirements, insensitivity to gradient scaling transformations, the ability to limit the update step size within a reasonable range (initial learning rate), suitability for large-scale data and parameter scenarios, and applicability to unstable target functions.
On the other hand, SGD, a core optimization algorithm in various scientific and engineering fields, minimizes the mathematical problem of minimizing the objective function. While SGD has low requirements for gradients and fast gradient computation, it tends to fall into local minima. To address this limitation, SGD often needs to be combined with other algorithms to achieve better optimization results. Additionally, in situations with high data noise, the weight update direction may not always be correct.
Adam and SGD are separately applied to predict roll, pitch, and heave motions for DeepONet and LSTM. The experimental results are presented in Table 8.
From Figure 9, it is evident that the predictive performance of the Adam optimizer is significantly superior to that of the SGD optimizer. On average, the predictive performance of the Adam optimizer is 2-3 orders of magnitude higher than that of the SGD optimizer.

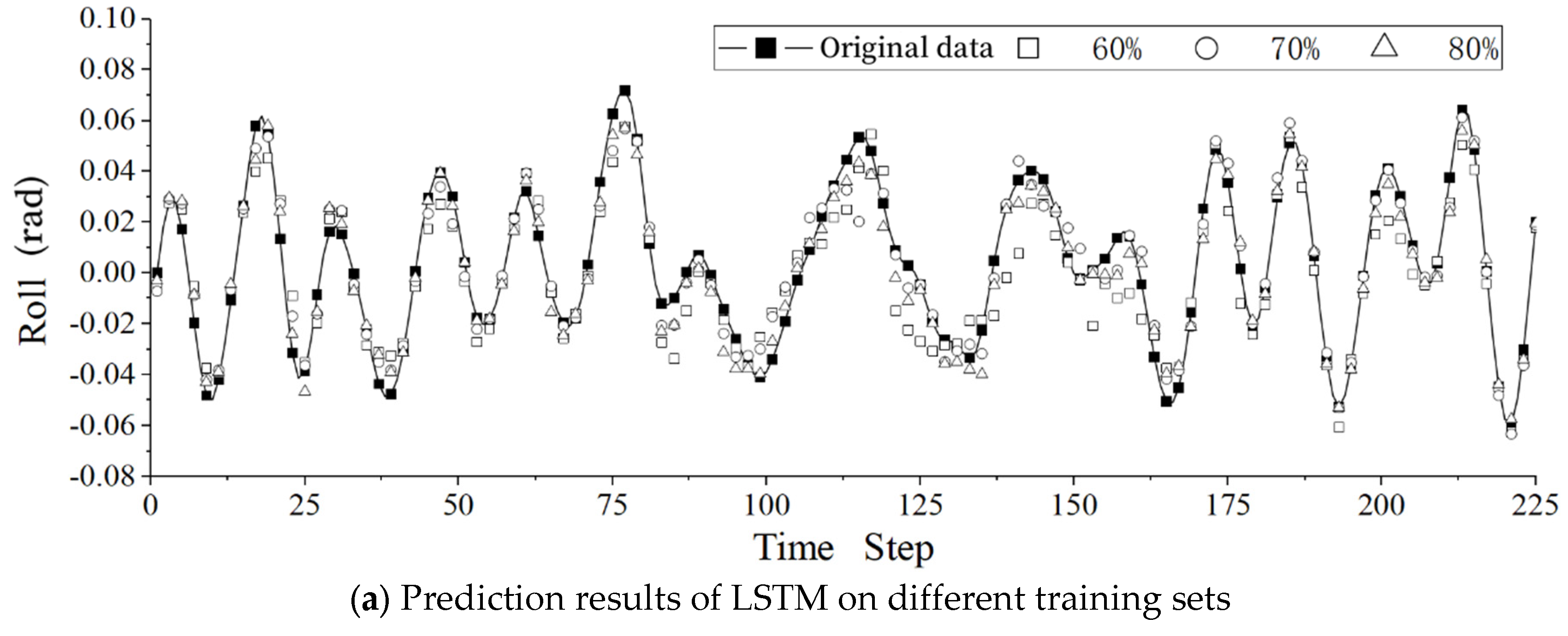
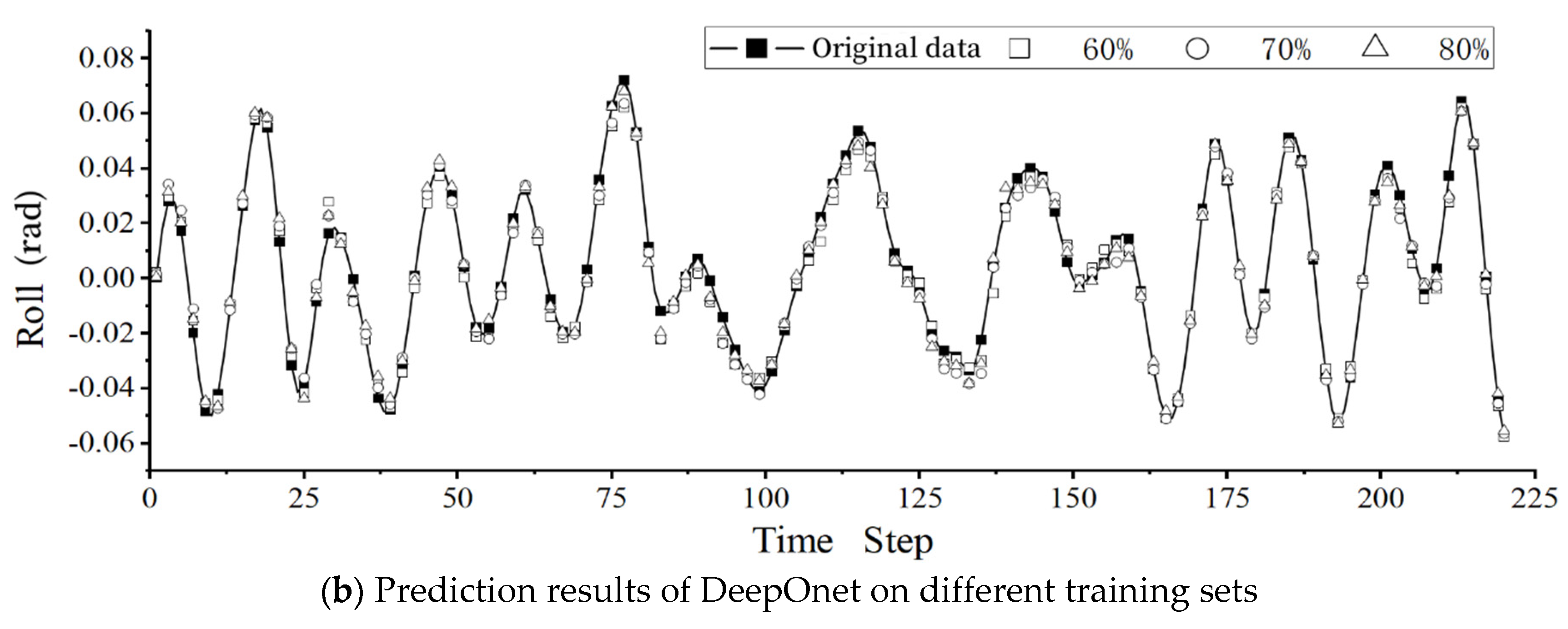
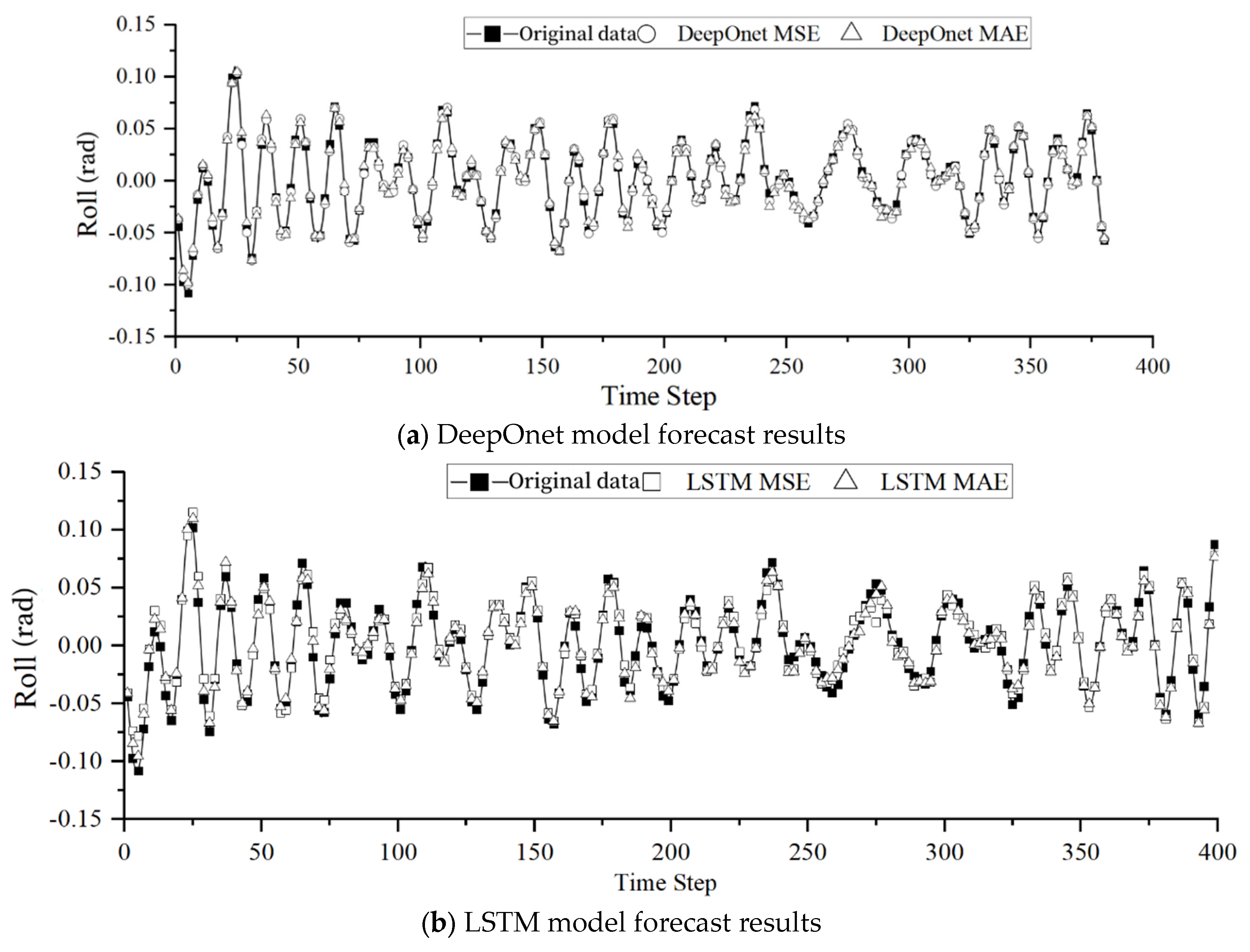
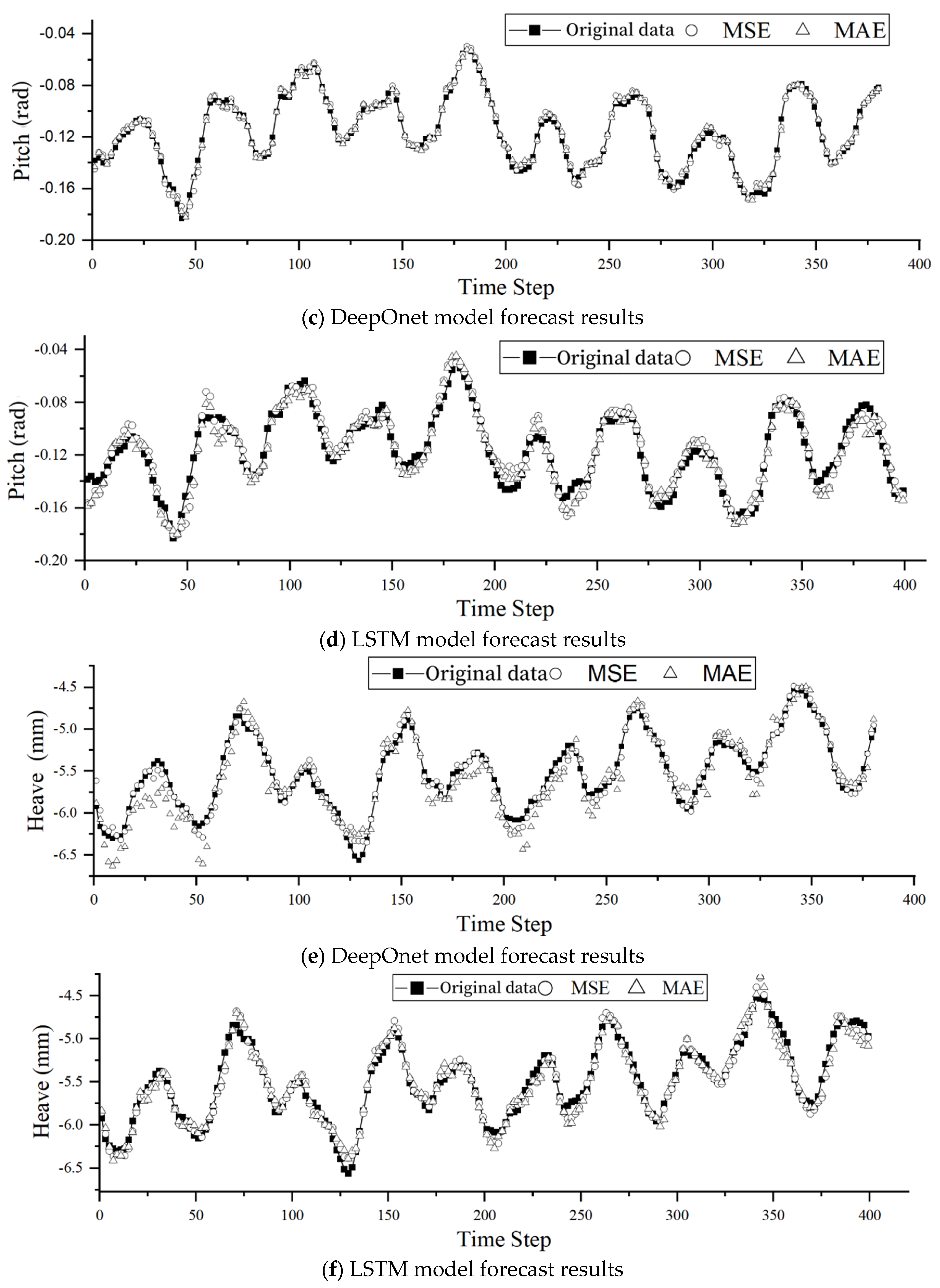
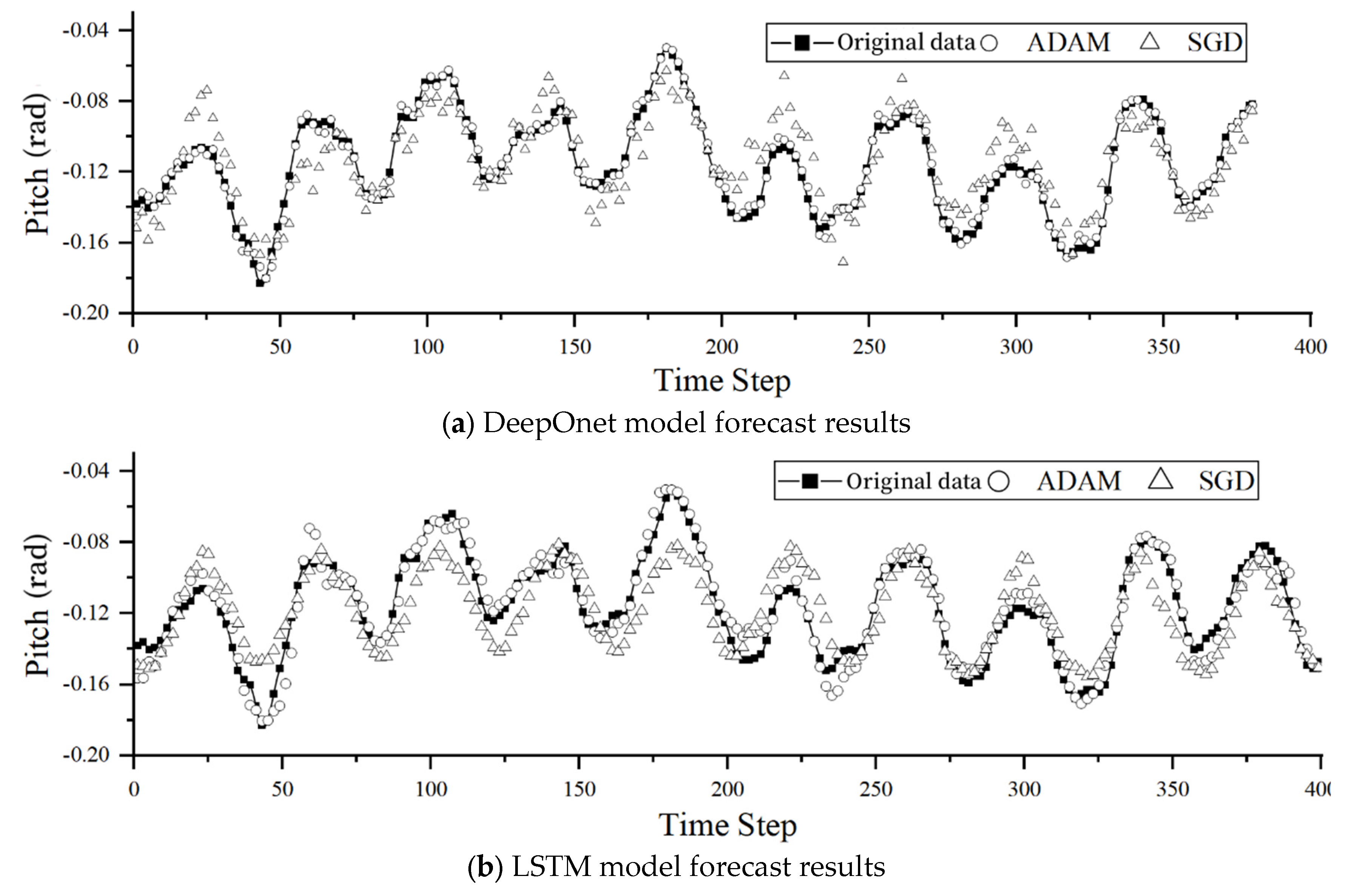
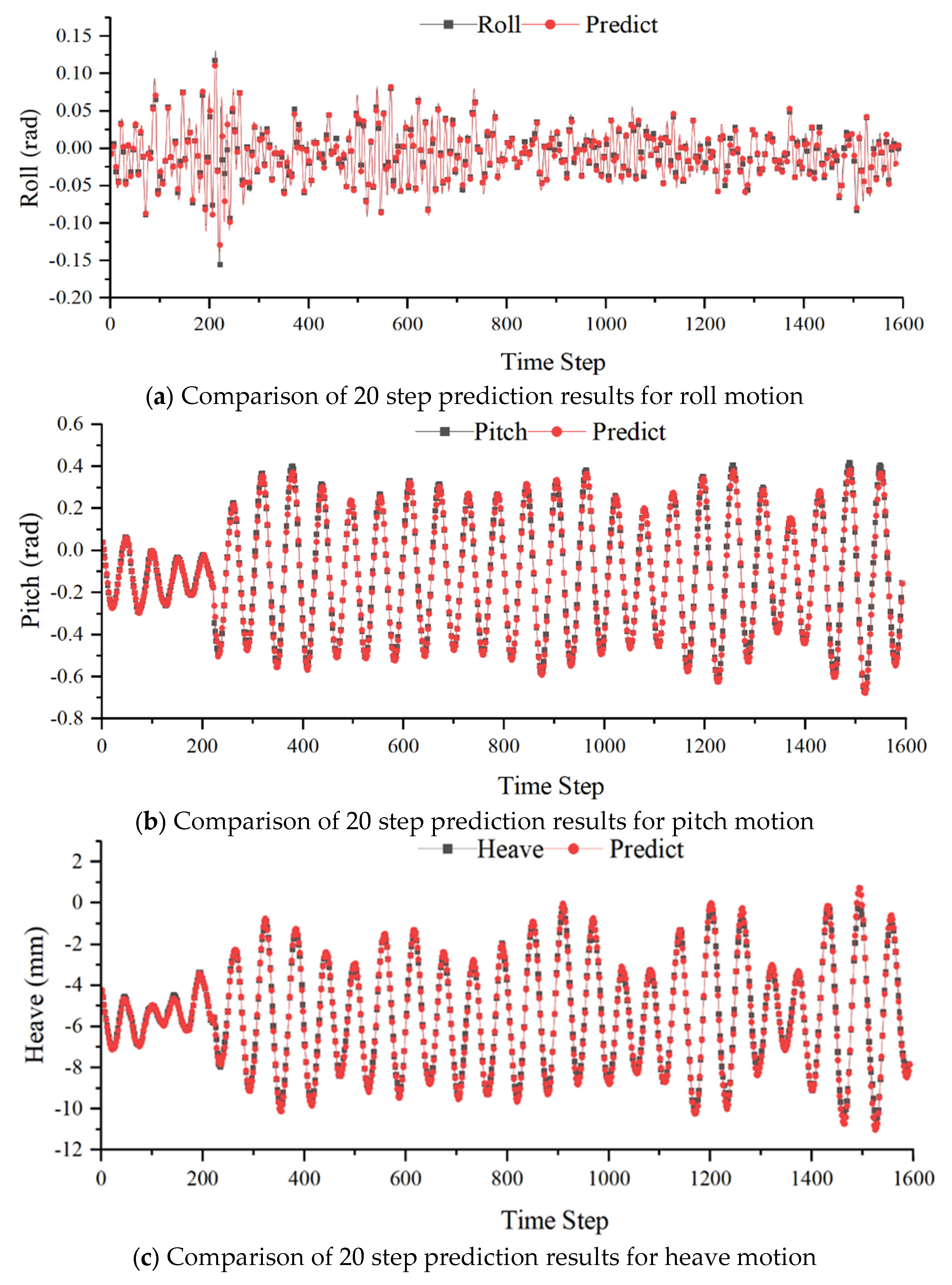
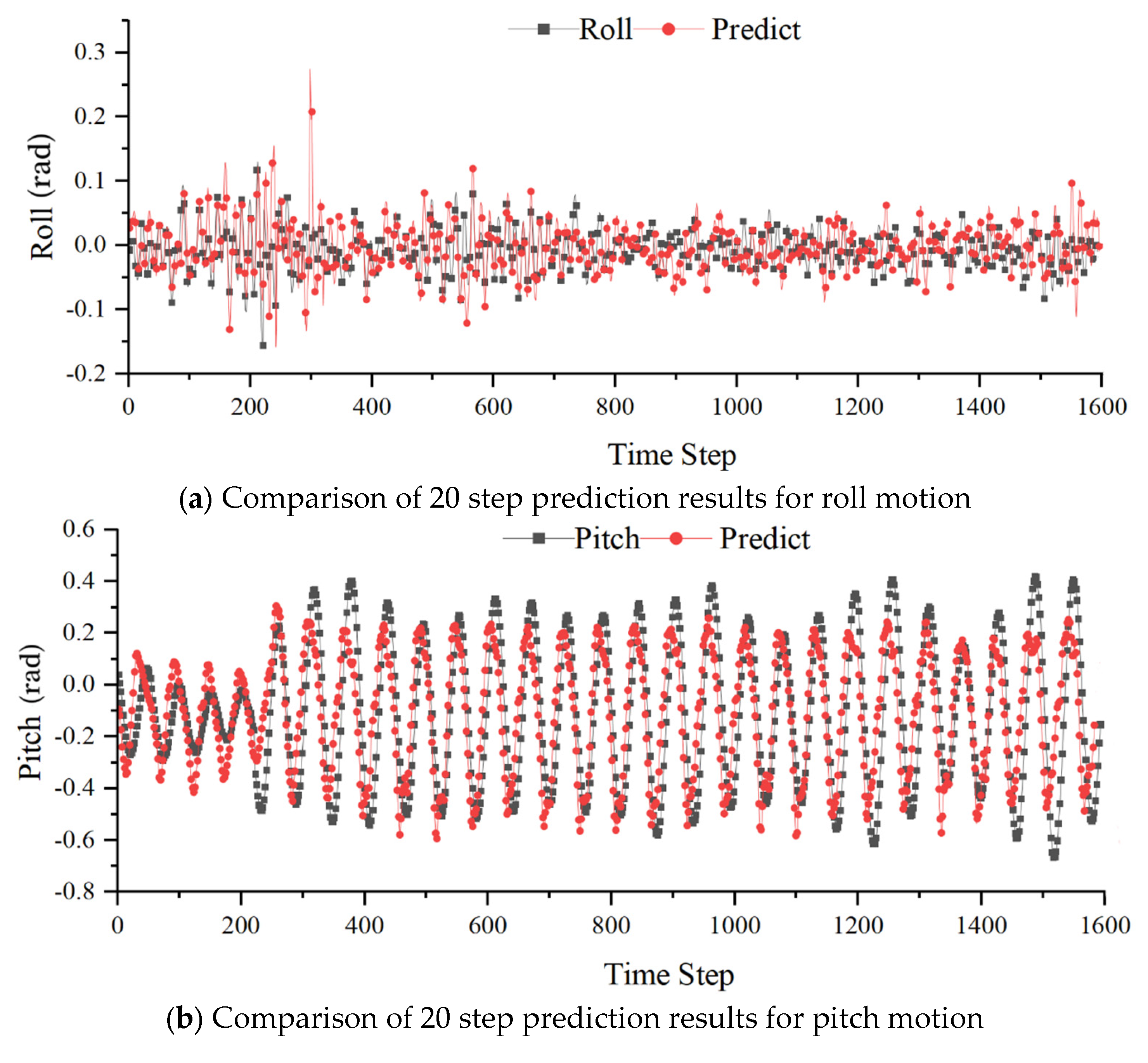
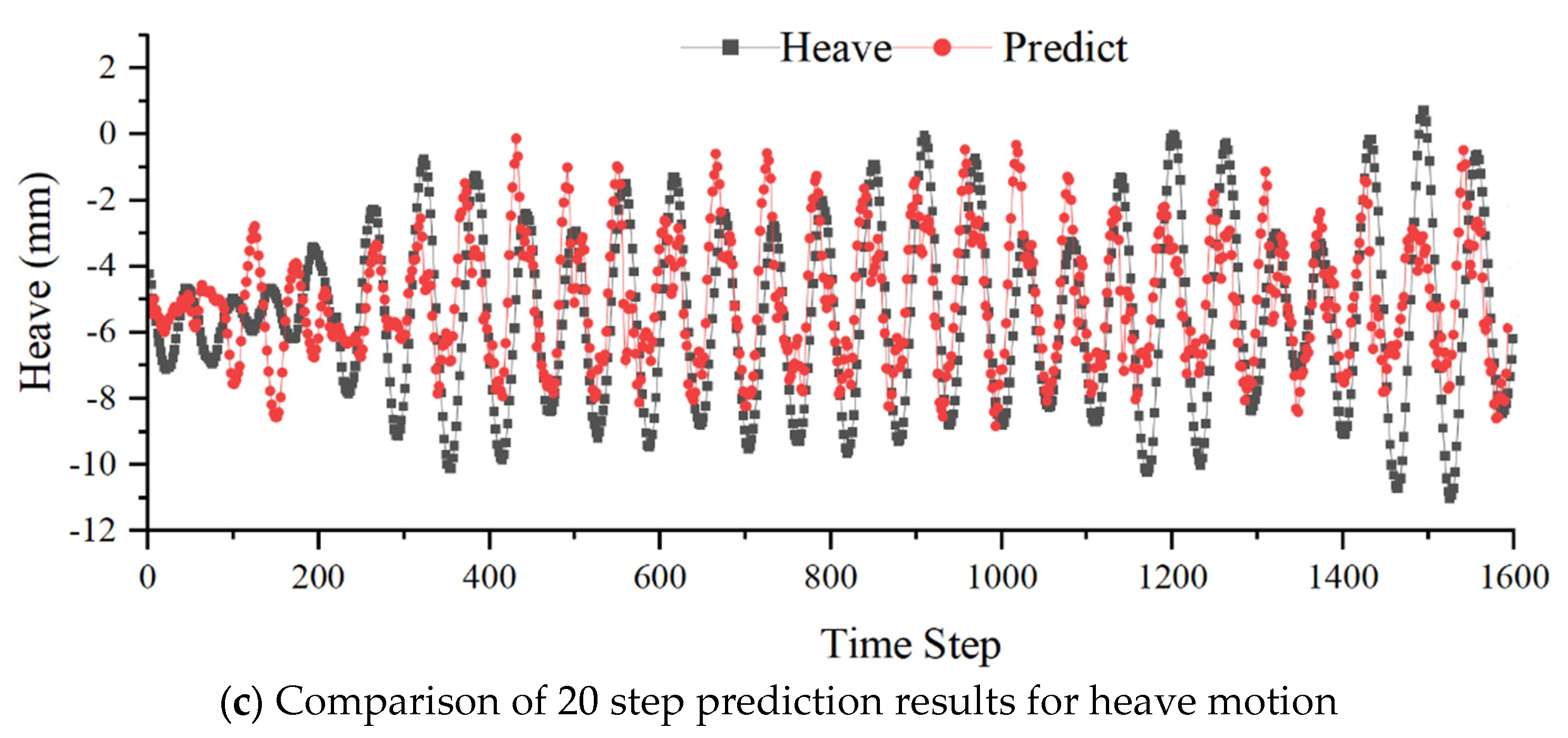
3.2. Multi-Steps Prediction by DeepOnet and LSTM Models

Following the hyperparameter optimization in Section 3.1, the branch sub-network of the DeepOnet network has 7 layers with 100 neurons, and the trunk sub-network also has 7 layers with 100 neurons. The input for the branch sub-network is a history of 80 wave height data points, and for the trunk sub-network, it is a history of 20 degrees of freedom data points. Other network parameters include: activation function as tanh, iteration times as 10,000 steps, optimizer as Adam with a learning rate of 0.001, and loss function as MSE. After normalizing the data, it is input into the DeepOnet network for training and testing set forecasting. The prediction errors are shown in Table 9, and the prediction curves for a prediction step of 20 are depicted in Figure 10.
The results demonstrate that DeepOnet proficiently predicts and fits the three degrees of freedom motion of a ship. The distinctive feature of this neural network lies in the convolution of results separately computed by the branch and trunk networks, facilitating the learning of operator functions between data. As depicted in Figure 10, the entire fitted points closely approximate the original values, underscoring that DeepOnet effectively learns the operator functions between waves and each degree of freedom motion.
Based on the trial calculations of hyperparameters in section 3.1, the dataset is divided into a 70% training set and a 30% test set. The LSTM network parameters are as follows: the network has 5 layers of hidden neurons, each layer containing 100 neurons. The length of the input vector is 80, with the activation function being tanh, the loss function is Mean Squared Error (MSE), the number of iterations is set to 500, the optimizer chosen is Adam, and the learning rate is 0.001. Table 10 shows the relationship between degrees of freedom errors and forecast lead times. Figure 11 compares the forecast results with the true values when the forecast lead time is 20. From the figure, it can be observed that LSTM can achieve multi-step prediction with excellent accuracy.
Figure 11 represents the multi-degree-of-freedom coupled motion prediction with a forecast lead time of 20 steps. As the forecast extends over multiple steps, the prediction performance deteriorates due to the accumulation of errors. Additionally, since the network model simultaneously takes input data from three degrees of freedom, it learns the motion characteristics of all three degrees simultaneously. Consequently, the prediction accuracy for a specific degree of freedom may decrease, but it remains above 85%.
To compare the accuracy of LSTM and DeepOnet under regular waves, we juxtapose Table 9 and Table 10 for comparison, as shown in Table 11. It is evident that the prediction error of the DeepOnet model is significantly lower than that of the LSTM model. In the cases of roll and heave motion, the MSE has decreased by more than 10 times.

4. Conclusion

Based on experimental data of the DTMB5415 model under regular waves, this study successfully establishes a DeepOnet functional prediction model, achieving short-term ship motion prediction from wave height. The performance of the model is compared in detail with the LSTM model, leading to the following conclusions:
1)Similar to grid partitioning and turbulence models in CFD, hyperparameters determine the scale and structure of the neural network, so it is necessary to tune the hyperparameters. In the hyperparameters tuning stage, the DeepOnet model progresses better than the LSTM model.
2)After hyperparameters tuning, DeepOnet and LSTM models are established separately. The results show that in most cases, the DeepOnet model outperforms the LSTM model in terms of accuracy, especially in roll and pitch attitudes, where the accuracy is ten times higher. As the forecast duration increases, the accuracy of DeepOnet remains more stable.
This study is the first to apply the DeepOnet model for very short-term ship motion prediction, and the DeepOnet functional prediction model is more suitable for wave height-motion pattern prediction. In future research, we will consider additional factors such as irregular waves and oblique waves.

Author Contributions

Conceptualization, Yong Zhao and Jinxiu Zhao; Methodology, Yong Zhao, Jinxiu Zhao and Sinan Lu; Software, Sinan Lu; Validation, Jinxiu Zhao and Sinan Lu; Formal analysis, Yong Zhao and Jinxiu Zhao; Investigation, Yong Zhao and Jinxiu Zhao; Resources, Yong Zhao; Data curation, Jinxiu Zhao; Writing – original draft, Jinxiu Zhao; Writing – review & editing, Yong Zhao; Supervision, Yong Zhao; Project administration, Yong Zhao; Funding acquisition, Yong Zhao. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by National Natural Science Foundation of China (No.51679021); Open Fund of Key Laboratory of High Performance Ship Technology (Wuhan University of Technology), Ministry of Education (No.gxnc21112704); Open Fund of National Center for International Research of Subsea Engineering Technology and Equipment (No. 3132023355). The authors wish to appreciate Iowa Institute of Hydraulic Research of Iowa University for their open data used in this paper.

Data Availability Statement

The data and code that support the findings of this study are available from the corresponding author upon reasonable request and they will be uploaded to GitHub in a short time.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Triantafyllou M., Bodson M., Athans M. Real time estimation of ship motions using Kalman filtering techniques. IEEE Journal of Oceanic Engineering1983, 8(1), 9-20 . [CrossRef]
  2. Peng X.Y., Dong H. Y., Zhang B. Echo state network ship motion modeling prediction based on Kalman filter. 2017 IEEE International Conference on Mechatronics and Automation (ICMA)2017,95-100 .
  3. Haiping Fan. Study on the prediction and Estimation of Ship Roll Motion Based on Kalman Filter. Harbin Engineering University 2008, 6-35.[in Chinese] .
  4. Zhonghua Zhang, Mengda Wu. Time-Sequence Method for the Real-Time Filtering and Prediction of the Ship-Swaying Data. Journal of Chinese Inertial Technology 2000, 04, 25-31. [in Chinese] .
  5. Suhermi N., Suhartono, Prastyo D. D., Ali B. Roll motion prediction using a hybrid deep learning and ARIMA model. Procedia Computer Science 2018, 144, 251-258 . [CrossRef]
  6. Likun Li. Directional spectral estimation of ship motion based on parameter method. Ship Science and Technology 2017, 39(1), 10-12. [in Chinese] .
  7. Duan W., Huang L., Han Y. A hybrid AR-EMD-SVR model for the short-term prediction of nonlinear and non-stationary ship motion. Journal of Zhejiang University Science 2015, A16 (7), 562-576 .
  8. Zeng B, Liu S.A self-adaptive intelligence gray prediction model with the optimal fractional order accumulating operator and its application. Mathematical Methods in the Applied Sciences 2017,40(18),7843-7857 . [CrossRef]
  9. Min Gu, Changde Liu, Jinfeng Zhang. Extreme short-term prediction of ship motion based on chaotic theory and RBF neural network. Ship mechanics 2013, 17(10), 1147-1152. [in Chinese] .
  10. Yin J. C., Wang L. D, Wang N.N. Avariable-structure gradient RBF network with its application to predictive ship motion control. Asian Journal of Control 2012,14,716-725 .
  11. Yin J. C., Perakis A.N, Wang N. A real-time ship roll motion prediction using wavelet transform and variable RBF network. Ocean Engineering 2018,160,10-19 .
  12. Wanting Liu. Study on Heave Motion Prediction od Ship. Dalian Maritime University 2016, 7-28. [in Chinese] .
  13. Li X., Lv X., Yu J., Li J. Neural network application on ship motion prediction. Proceedings of 9th International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou 2017, 414-417 .
  14. Guodong Wang. Short-term Prediction and simulation of Ship’s Moyion Based onLSTM. Jiangsu university of science and technology 2017, 8-46. [in Chinese] .
  15. Ni C, Ma X. An integrated long-short term memory algorithm for predicting polar westerlies wave height. Ocean Engineering 2020, 215(1):107715 . [CrossRef]
  16. Y Zhao, Dan Su. Rogue Wave Prediction Based on Four Combined Long Short-Term Memory Neural Network Models, Journal of Shanghai Jiao tong University 2022, 56(04), 516-522. [in Chinese] .
  17. Y Zhao, Dan Su. Rogue wave prediction based on LSTM neural network, Journal of Huazhong University of Science and Technology (Natural Science Edition) 2020, 48(7), 47-51. [in Chinese] .
  18. Yue Liu, Xiantao Zhang, Gang Chen, Qing Dong, Xiaoxian Guo, Xinliang Tian, Wenyue Lu, Tao Peng, Deterministic wave prediction model for irregular long‐crested waves with Recurrent Neural Network, Journal of Ocean Engineering and Science 2022. [CrossRef]
  19. Sun Q, Tang Z, Gao J,et al. Short-term ship motion attitude prediction based on LSTM and GPR. Applied Ocean Research 2022, (118-):118 .
  20. Han C, Hu X. A Prediction Method of Ship Motion Based on LSTM Neural Network with Variable Step-Variable Sampling Frequency Characteristics. Journal of Marine Science and Engineering 2023, 11(5):919 . [CrossRef]
  21. Ling Liu, Yu Yang, Tao Peng, Machine learning prediction of 6-DOF motions of KVLCC2 ship based on RC model, Journal of Ocean Engineering and Science 2022. [CrossRef]
  22. Hou X, Xia S. Short-Term Prediction of Ship Roll Motion in Waves Based on Convolutional Neural Network. Journal of Marine Science and Engineering 2024, 12(1):102 . [CrossRef]
  23. Wenhai Yi, Zhiliang Gao. Very Short-term Prediction of ship Rolling Motion in Random Transverse Waves Based on LSTM Neural Network. Journal of Wuhan University of Technology: Transportation Science and Engineering Edition 2021, 45(6):5. [in Chinese] .
  24. Ferrandis JDG, Triantafyllou MS, Chryssostomidis C, et al. Learning functionals via LSTM neural networks for predicting vessel dynamics in extreme sea states. Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences 2021, 477(2245), 20190897 . [CrossRef]
  25. Lu, L., Jin, P., Pang, G. et al. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature Machine Intelligence 2021, 3, 218–229 . [CrossRef]
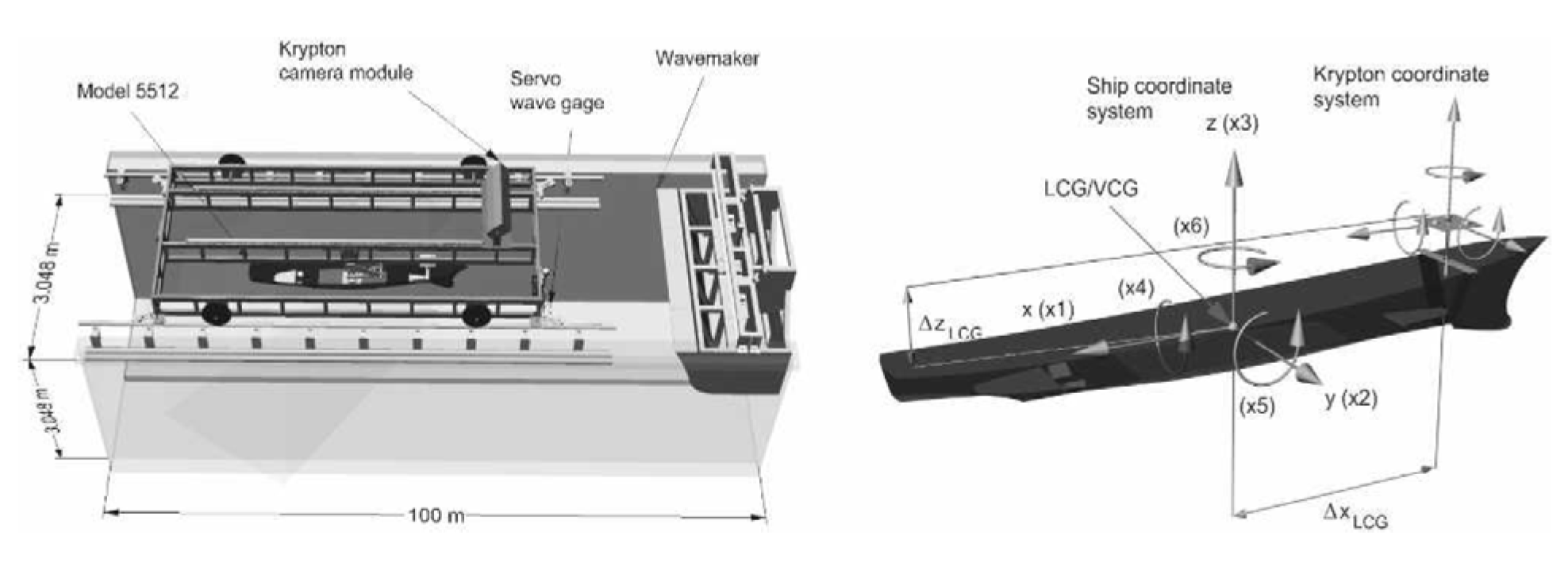
  26. Jr M I, Longo J, Stern F. Pitch and Heave Tests and Uncertainty Assessment for a Surface Combatant in Regular Head Waves. Journal of Ship Research 2008, 52(2), 146-163 .
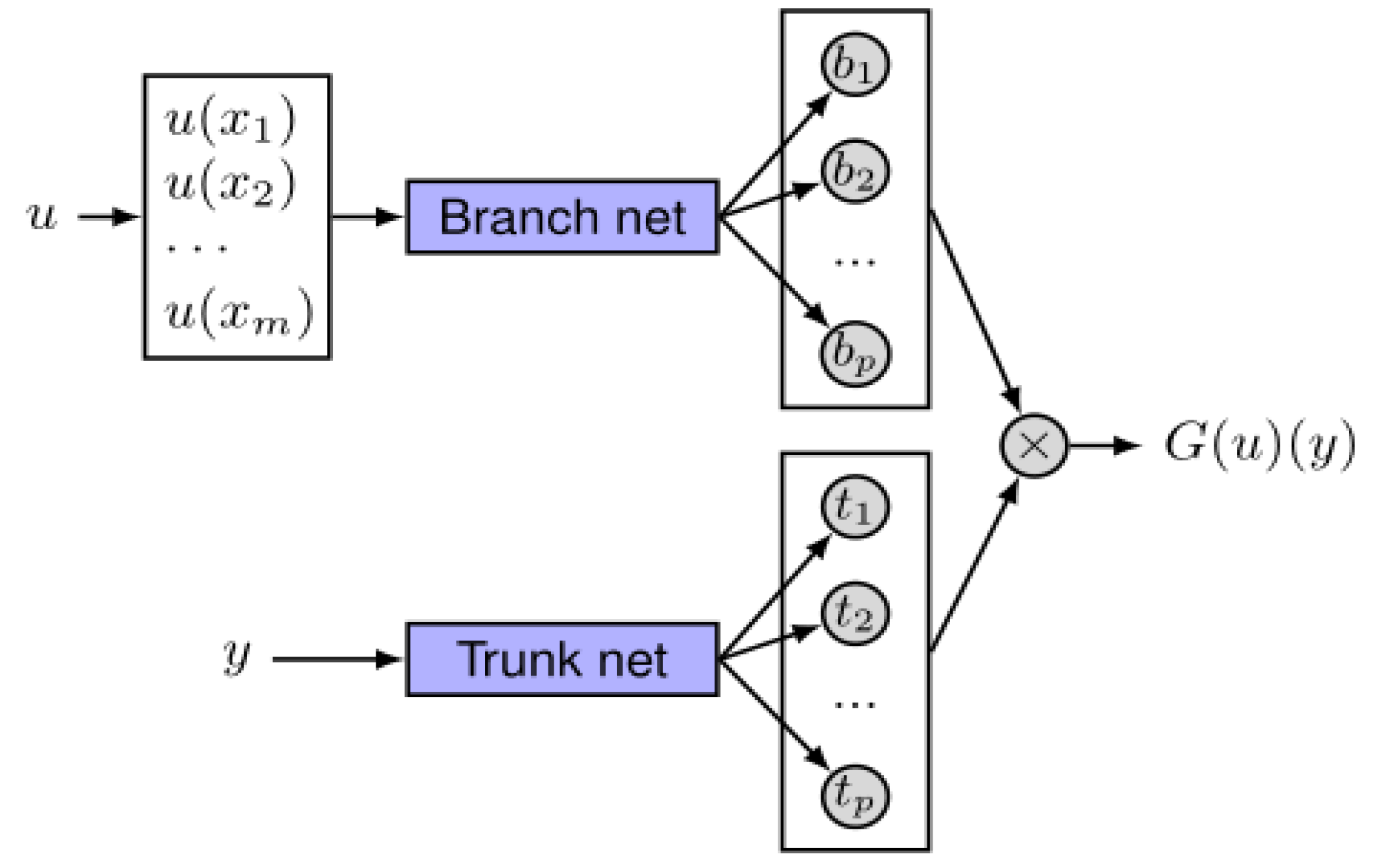
Preprints 100875 g001
Figure 1. DeepOnet Network Structure [25].
Figure 1. DeepOnet Network Structure [25].
Preprints 100875 g001
Preprints 100875 g002
Figure 2. Explanation of the IIHR laboratory’s lifting and pitching experimental setup and reference coordinate system [26].
Figure 2. Explanation of the IIHR laboratory’s lifting and pitching experimental setup and reference coordinate system [26].
Preprints 100875 g002
Preprints 100875 g003
Figure 3. The motion time series curve of the ship model under the first working condition, from top to bottom, is in order of roll, pitch, and heave.
Figure 3. The motion time series curve of the ship model under the first working condition, from top to bottom, is in order of roll, pitch, and heave.
Preprints 100875 g003
Preprints 100875 g004aPreprints 100875 g004b
Figure 4. Comparison of roll motion prediction effects of different network layers and neurons.
Figure 4. Comparison of roll motion prediction effects of different network layers and neurons.
Preprints 100875 g004aPreprints 100875 g004b
Preprints 100875 g005aPreprints 100875 g005b
Figure 5. Prediction results for different training sets.
Figure 5. Prediction results for different training sets.
Preprints 100875 g005aPreprints 100875 g005b
Preprints 100875 g006
Figure 6. Typical activation function image.
Figure 6. Typical activation function image.
Preprints 100875 g006
Preprints 100875 g007
Figure 7. Prediction results of different activation functions on pitch and heave motion.
Figure 7. Prediction results of different activation functions on pitch and heave motion.
Preprints 100875 g007
Preprints 100875 g008aPreprints 100875 g008b
Figure 8. Forecast results of roll, pitch, and heave motion using different loss functions.
Figure 8. Forecast results of roll, pitch, and heave motion using different loss functions.
Preprints 100875 g008aPreprints 100875 g008b
Preprints 100875 g009
Figure 9. Prediction results of pitch motion using different optimizers.
Figure 9. Prediction results of pitch motion using different optimizers.
Preprints 100875 g009
Preprints 100875 g010
Figure 10. Comparison between the 20 step forecast results and the actual values of the DeepOnet model.
Figure 10. Comparison between the 20 step forecast results and the actual values of the DeepOnet model.
Preprints 100875 g010
Preprints 100875 g011aPreprints 100875 g011b
Figure 11. Comparison between the 20 step forecast results and the actual values of the LSTM model.
Figure 11. Comparison between the 20 step forecast results and the actual values of the LSTM model.
Preprints 100875 g011aPreprints 100875 g011b
Table 1. DeepOnet Model Training Process.
Table 1. DeepOnet Model Training Process.
Algorithm process: DeepOnet network
Input:
Window sliding is used to process the training set D1 and the test set D2. Hyperparameters are defined, including the number of layers and neurons in the two sub-networks (branch hidden layer and trunk hidden layer), the number of iterations, activation functions, learning rate, and loss function.
Process:
1: Network initialization: Construct a list for hidden layers and initialize model parameters such as weights and biases.
2: Repeat;
3: For all D1;
4: Calculate the output y_branch based on the current weight parameters and the data passed into the branch network.
5: Calculate the output y_trunk based on the current weight parameters and the data passed into the trunk network.
6: Perform Einstein summation on the y_branch and y_trunk values in matrix form to obtain G(u)(y).
7: Calculate the gradient term of the output layer neurons.
8: Calculate the gradient term of the hidden layer neurons.
9: Calculate and update the connection weights.
10: End for.
11: Until the stopping condition is met.
Output: The network model with the model parameters.
Table 2. Main dimensions of DTMB 5512 ship model.
Table 2. Main dimensions of DTMB 5512 ship model.
Parameter unit ship model 5512 full ship size
Scale ratio -- 46.6 1
Ship length (Lpp) m 3.048 142.04
Beam (B) m 0.405 18.87
Draft(T) m 0.132 6.15
Block coefficient (CB) -- 0.506 0.506
Table 3. Setting of regular wave parameters for given speed and wave inclination angle.
Table 3. Setting of regular wave parameters for given speed and wave inclination angle.
Fr Uc(m/s) H/λ=1/126 AK H(mm)
1 0.28 1.531 1/126 0.025 5.6
2 0.28 1.531 1/126 0.025 7.0
3 0.28 1.531 1/126 0.025 8.2
4 0.28 1.531 1/126 0.025 10.2
Table 4. The MSE results of roll motion prediction based on the number of network layers and neurons.
Table 4. The MSE results of roll motion prediction based on the number of network layers and neurons.
Number of neurons 80 100 120
Number of layers DeepOnet LSTM DeepOnet LSTM DeepOnet LSTM
3 1.526e-5 7.993e-5 9.166e-6 8.803e-5 1.605e-5 1.398e-4
5 1.768e-5 1.049e-4 8.258e-6 1.044e-4 1.605e-5 1.261e-4
7 1.517e-5 1.463e-4 9.660e-6 1.277e-4 6.431e-6 1.280e-4
Table 5. MSE results of roll motion prediction for different training set sizes.
Table 5. MSE results of roll motion prediction for different training set sizes.
Training set percentage DeepOnet LSTM
MSE RMSE MSE RMSE
60% 2.061e-5 4.5398e-3 1.731e-4 1.3157e-2
70% 1.768e-5 4.2048e-3 8.803e-5 9.3820e-2
80% 1.329e-5 3.6456e-3 5.243e-5 7.2410e-3
Table 6. Comparison of MSE prediction results with different activation functions.
Table 6. Comparison of MSE prediction results with different activation functions.
MSE Sigmoid Tanh ReLu
DeepOnet LSTM DeepOnet LSTM DeepOnet LSTM
Roll prediction 8.64e-6 1.15e-4 8.25e-6 7.92e-5 - 4.69e-3
Pitch prediction 7.77e-4 1.19e-4 8.77e-6 6.52e-5 - 2.43e-4
Heave prediction 5.71e-3 1.28e-2 7.93e-3 7.33e-3 - 1.21e-2
Table 7. Forecast MSE and MAE Results for Different Loss Functions.
Table 7. Forecast MSE and MAE Results for Different Loss Functions.
Roll Pitch Heave
DeepOnet LSTM DeepOnet LSTM DeepOnet LSTM
MSE 8.25e-6 7.92e-5 8.77e-6 6.52e-5 7.93e-3 7.331e-3
MAE 3.29e-3 5.76e-3 2.61e-3 6.18e-3 1.44e-1 7.902e-3
Table 8. Comparison of Forecast MSE Results for Different Optimizers.
Table 8. Comparison of Forecast MSE Results for Different Optimizers.
Roll Pitch Heave
DeepOnet LSTM DeepOnet LSTM DeepOnet LSTM
Adam 8.25e-6 7.92e-5 8.77e-6 6.52e-5 7.93e-3 7.33e-3
SGD 1.32e-3 1.44e-3 2.58e-4 3.08e-4 7.29e-1 3.14e-2
Table 9. DeepOnet Multi step Forecast MSE Error Results.
Table 9. DeepOnet Multi step Forecast MSE Error Results.
Prediction step size Roll Pitch Heave
1 3.472e-5 3.830e-4 8.680e-3
5 2.258e-5 1.893e-4 1.845e-2
10 2.083e-5 1.545e-4 1.822e-2
15 2.009e-5 1.459e-4 1.871e-2
20 2.022e-5 1.579e-3 1.889e-2
Table 10. LSTM Multi step Forecast MSE Error Results.
Table 10. LSTM Multi step Forecast MSE Error Results.
Prediction step size Roll Pitch Heave
5 5.395e-4 1.782e-4 1.133e-1
10 6.675e-4 2.185e-4 1.211e-1
15 7.509e-4 3.488e-4 1.501e-1
20 8.490e-4 4.452e-4 2.290e-1
Table 11. The MSE Comparison between DeepOnet and LSTM models.
Table 11. The MSE Comparison between DeepOnet and LSTM models.
Prediction step size DeepOnet Roll LSTM Roll DeepOnet Pitch LSTM Pitch DeepOnet Heave LSTM Heave
5 2.258e-5 5.395e-4 1.893e-4 1.782e-4 1.845e-2 1.133e-1
10 2.083e-5 6.675e-4 1.545e-4 2.185e-4 1.822e-2 1.211e-1
15 2.009e-5 7.509e-4 1.459e-4 3.488e-4 1.871e-2 1.501e-1
20 2.022e-5 8.490e-4 1.579e-3 4.452e-4 1.889e-2 2.290e-1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated