Prerpints.org logo
Preprint
Article

Lactic Acid Production by Lactiplantibacillus plantarum AC 11S – Kinetics, and Modeling

Altmetrics

Downloads

120

Views

43

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 March 2024

Posted:

08 March 2024

You are already at the latest version

Alerts
Abstract
Lactic acid production from lactose by Lactiplantibacillus plantarum AC 11S was studied. The influence of initial substrate concentration was investigated, and optimal pH and temperature were determined. An unstructured mathematical model was developed comprising equations for bacterial growth, substrate consumption, and product formation. The model was solved with different terms for specific growth rates considering substrate and/or product inhibition. The best bacterial growth and lactic acid production were achieved at pH = 6.5 and 30 oC. Production of lactic acid was mainly growth-associated and at substrate concentration over 15 g/L a considerable product inhibition was observed. The parameters of different models were determined and compared. While the modified Gompertz equation gave the best fit for biomass growth, a variant of the logistic equation including a term for product inhibition described in the best way the entire set of equations comprising bacterial growth, substrate consumption, and product formation at different initial substrate concentrations.
Keywords: 
Subject: Biology and Life Sciences  -   Biology and Biotechnology

1. Introduction

Lactic acid bacteria (LAB) are a multitudinous microbial group of microorganisms with diverse beneficial applications in the food and pharmaceutical industry. LAB share the same characteristics of metabolism and physiology, with strain-specific functionality and potential. Their main common feature is the production of lactic acid as an end-product of the fermentation of various carbohydrates. From a taxonomic point of view, they comprise a large variety of Gram-positive, catalase-negative, and anaerobic non-sporulation bacteria belonging to the Lactobacillaceae family, with different G+C Firmicutes groups. They are producers of organic acids, polyols, bacteriocins, exopolysaccharides (EPS), and aromatic compounds, among others [1]. Several LAB species are widely accepted as probiotics, with functional characteristics and beneficial healthy effects based on their metabolic activity.
Lactiplantibacillus plantarum can be found in various ecological niches - in dairy products, fermented vegetables and cereals, meats, fish, silage, wine, gastrointestinal, urogenital and vaginal tracts [2]. It is one of the most exploited LABs for producing various postmetabolites. The L. plantarum is well known for its versatility in substrate utilization [3]. Various L. plantarum strains are capable of utilizing different monosaccharides either hexoses or pentoses [4], as well as different lignocellulosic hydrolysates from rice straw [5], corncobs [6], sugarcane bagasse [7], Opuntia ficus indica waste [8], algal biomass [3] among others. These species are considered the most advantageous among LAB in the production of lactic acid (LA) from lactose and it is also capable of utilizing other nutrients presented in whey [9].
L. plantarum has a larger genome than other LAB species, (size of about 3.3 Mbp and more than 3000 genes) which indicates its strong adaptability, high versatility, enormous diversity in phenotypic properties, metabolic capacity, and industrial applications [10]. According to Zhang et al. [11.] L. plantarum group represents the evolutionary link between heterofermentative and homofermentative LAB. Though L. plantarum is phylogenetically related to heterofermentative lactobacilli, it shares different metabolic features with homofermentative lactobacilli. L. plantarum has been widely used as a model species for ecological, genetic, and metabolic studies in lactobacilli. The major commercial use of L. plantarum is as a starter culture for various food fermentations and in recent years as a probiotic culture [11].
L. plantarum is considered to belong to the group of facultatively heterofermentative lactobacilli. Via the Embden–Meyerhof–Parnas pathway, hexoses are almost completely converted to lactic acid. On the other hand, pentoses are converted to acetic and lactic acids via the 6-phosphogluconate/phosphoketolase pathway by the induction of phosphoketolase [12]. L. plantarum like other LAB possesses specific nutritional requirements and thus, a complex growth media, which must contain peptides, vitamins, nucleic, fatty, and amino acids, besides the carbon source is needed. Another particular characteristic of the process of lactic acid production is the end-product inhibition. Due to the lactic acid accumulation, the fast acidification of the fermentation medium leads to low substrate utilization, low conversion, and low final product concentration.
In the process of a comprehensive investigation of lactic acid production, kinetic studies are an indispensable step. A proper mathematical model is very useful in understanding, describing, evaluating, and predicting the fermentation process. Mathematical models help disclose the relationship between cell growth, substrate consumption, and product formation and can be used for control optimization and scale-up of a fermentation process. Mathematical models have been classified according to different criteria [13]. One of these criteria distinguishes between structured and unstructured mathematical models. Structured models are more accurate and take into account cell functions, structure, and composition. Unstructured models, on the other hand, treat the cells as a black box, a sole component without involving any cells’ physiological characteristics. Although the structured models are more detailed and precise, providing a better understanding of the system, unstructured models are widely used, because of their applicability and simplicity in describing bacterial kinetics. Different models have been used in the modeling of lactic acid production from various substrates. Some of them are summarized in the works of Zacharof & Lovitt [13], Bouguettoucha et al. [14], and Gordeev et al. [15].
The present work aims to investigate Lactiplantibacillus plantarum strain AC 11S, as a promising producer of lactic acid from lactose, to determine the optimum conditions for growth and production, and to compare some kinetics models describing the fermentation dynamics.

2. Materials and Methods

2.1. Strain, Growth Media, and Culture Conditions

Lactiplantibacillus plantarum AC 11S was isolated from a homemade white brined cheese [16]. It was cultured in de Man, Rogosa, and Sharpe broth (MRS Merck, Darmstadt, Germany) and stored at – 20oC in MRS broth, supplemented with glycerol 20% v/v. Before the experiments, the strain was pre-cultured twice in modified MRS broth with lactose. The strain was cultured on growth medium contained: lactose monohydrate - 11 g/L, yeast extract - 5.5 g/L, peptone from casein - 12.5 g/L, sodium acetate - 10 g/L, KH2PO4 - 0.25 g/L, K2HPO4 - 0.25 g/L, MgSO4.7H2O - 0.1 g/L, MnSO4.7H2O - 0.05 g/L, Fe2(SO4)3 - 0.05 g/L. All chemicals were p. a. grade (Fluka). The inoculum (10% v/v) was prepared from overnight culture in MRS broth with lactose monohydrate (11 g/L). All experiments were carried out in flasks (100 m growth medium in 300 mL Erlenmeyer flasks at 30°C with an initial pH of 6.5) using a WiseCube® WIS30 shaking incubator (Witeg Labortechnik GmbH, Germany).

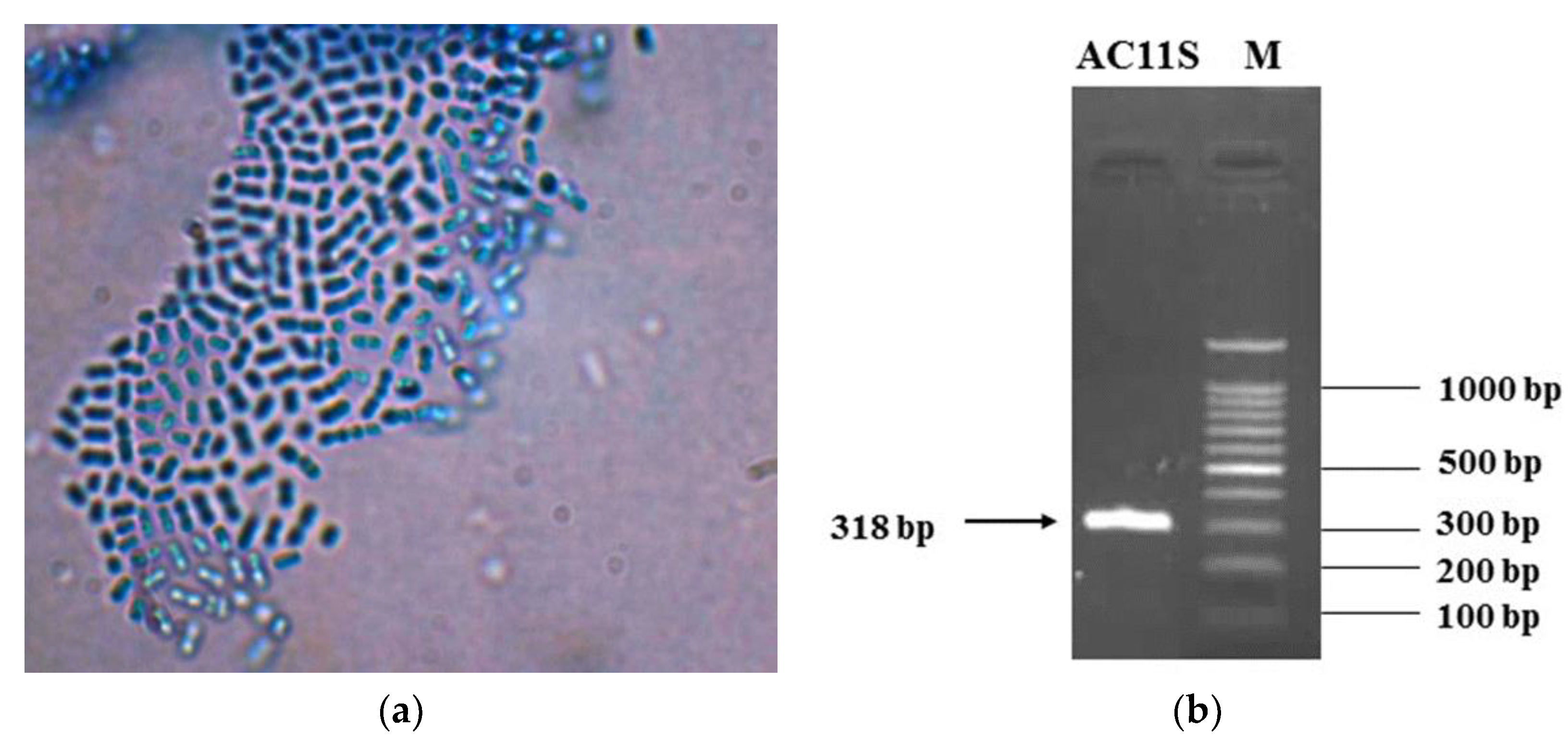
2.2. The LAB Species Identification

The strain AC 11S was identified as Lactiplantibacillus plantarum by classical phenotypic methods Gram staining, oxidase (kit HiMedia, Mumbai, India), catalase tests, and carbohydrate fermentation test with 49 carbon sources (using API 50 CHL, bioMérieux, Marcy l’Etoile, France). The species affiliation was confirmed by Multiplex PCR amplification with primers targeting the recA gene, according to Torriani et al. [17]. The PCR analysis was performed on a PCR thermocycler (BioRad, laboratories, Inc. group), using ready to use PCR mix (IllistraTM PuRe TaqTM Ready To GoTM PCR beads; Amersham Biosciences, Amersham, UK). The target DNAs were isolated from an overnight LAB culture of the strain AC 11S using the Gene Matrix Bacterial and Yeast Genomic DNA Purification Kit (EURx Ltd., Gdańsk, Poland), following the manufacturer’s instructions. The PCR reaction conditions are as previously described [18].

2.3. In Vitro Assessment of Acid Tolerance of L. plantarum AC11S.

In vitro test, in 96-well U-bottomed, polystyrene microtiter plates (Corning, NY, USA) with a final volume of 150 µL, was carried out. The cells from 10 mL overnight culture were harvested by centrifugation (9000x g Hermle, Germany centrifuge) and washed twice with sterile saline. Washed cells re-suspended in 10 mL were adjusted to 6.0 x 108 CFU/mL (2x McFarland). The cells from 5 mL were harvested and re-suspended in 5 mL simulated gastric fluid with low pH - 1.5, NaCl 0.8% w/v, and pepsin 3 mg/mL (Sigma-Aldrich, Saint Louis, MO, USA). The resting 5 mL was used as a control re-suspended in sterile saline pH 6.5. They were incubated for 3 h at 30oC. After treatment, they were washed 2 times, with sterile saline. Following the treated culture, the control was used as inoculum (10% v/v) in modified MRS broth (with lactose 20 g/L) in 96-well microplates. Viability, after treatment was monitored spectrophotometrically (OD 600nm) during 24 h cultivation at 30 oC using Elisa Plate Reader (INNO, Seongnam-si, Korea). The results are presented as a mean of triplicate.

2.4. Analytical Procedures

For biomass determination, optical density (OD) was measured at 620 nm (UV-VIS spectrophotometer Milton Roy 401, Rochester, USA). From OD data, by using a previously prepared calibration curve, the biomass concentration was calculated. An HPLC system composed of a Knauer Smartline-100 pump, a Pekin-Elmer LC-25RI refractometric detector, and data processing software Eurochrome (Knauer) was used for lactic acid measurements. Aminex HPX-87H (Bio-Rad) column was used. A 0.005 M solution of H2SO4 at a flow rate of 0.6 mL/min was used as the mobile phase. For standard solutions preparation pure (98 % mass, Sigma), crystalline L (+)-lactic acid was used. All measurements were made in triplicate.

2.5. Fermentation

All experiments for lactic acid production were carried out in MRS broth with lactose as a carbon source in 300 mL flasks at 30 oC and 6.5 initial pH of the medium (except those for optimum pH and temperature determination).

2.6. Modeling

The main goal in a fermentation process is complete substrate utilization, leading to a maximum product yield. The development of a proper mathematical model and correct determination of model parameters will permit to conduct the fermentation in its optimal conditions. The mathematical model should contain equations describing cell growth, substrate consumption, and product formation and their interrelationship. In an unstructured mathematical model, only the total cell concentration is considered. In general, the bacterial growth rate can be described as follows:
d X d t = μ X − k d X
where X is the cell concentration, g/L; t is time; μ is the specific growth rate, h-1 and kd is the specific cell death rate. In many cases, the cell death was not observed and the second term can be omitted.
The simplest model representing the specific growth rate as a function of substrate concentration is the Monod equation:
μ = μ m a x ( S k S + S )
where μmax is the maximum specific growth rate, h-1; S is the initial substrate concentration, g/L; KS – the substrate saturation constant, g/L. The Monod equation describes the increase of cell concentration with time and considers limiting substrate concentration. It is widely accepted that lactic acid fermentation is limited by substrate and inhibited by the product. Many authors insert different terms in the Monod equation to take inhibition effects into account. Some of them are presented in Table 1.
Other authors have used different sigmoidal models for the description of microbial growth. The most utilized are the logistic equation and the modified Gompertz model:
ln ( X X 0 ) = a [ 1 − e x p ( b − c t ) ]
ln ( X X 0 ) = a exp [ − exp ( b − c t ) ]
These models do not include the consumption of the substrate and describe only the number of cells.
With the aim to give a biological meaning to the parameters a, b, and c Zwietering [26] reparametrized the above equations to:
X ( t ) = X 0 + A 1 + e x p [ 4 μ m a x A ( λ − t ) + 2 ]
X ( t ) = X 0 + A e x p { − e x p [ μ m a x e A ( λ − t ) ] + 1 }
The Luedeking – Piret equation [27] is the most used for the description of lactic acid formation. It takes into account the fact that the rate of product accumulation dP/dt, depends on bacterial growth dX/dt, as well as on the bacterial density X.
d P d t = α d X d t + β X
α and β are coefficients related to growth and non-growth product formation.
The rate of substrate consumption is closely related to the cell’s growth rate and the rate of product formation. This relationship is usually given by the following equation:
d S d t = − 1 Y X / S d X d t − 1 Y P / S d P d t − m s X
where YX/S and YP/S are yield coefficients for biomass on substrate and product on substrate respectively, g/g, while mS is the biomass maintenance energy coefficient, g/g.h. In many cases, the latter was neglected.

3. Results

3.1. Isolation and Identification of Lactiplantibacillus plantarum AC 11S

L. plantarum AC 11S, was isolated from a sample of white brined cheese, homemade on a small farm, in the village of Arda, Rodopa mountain, Bulgaria, near the border with Turkey. The strain is a part of the laboratory collection of the “Stephan Angeloff” Institute of Microbiology, BAS, Bulgaria.
The strain AC 11S was characterized as Gram-positive, catalase, and oxidase-negative rod-shaped cells’ morphology (Figure 1 A), non-motile, non-spore-forming facultative anaerobe. It was initially identified as a mesophilic bacterium presumptive Lactiplantobacillus plantarum by carbohydrate fermentation test with 49 carbon sources (using API 50 CHL, bioMérieux, Marcy l’Etoile, France). The accurate species affiliation was achieved by multiplex PCR (Figure 1 B), according to Torriani et al. [17]. With primers, targeting the rec A gene, a PCR product 318 bp was obtained corresponding to the species L. plantarum. This molecular method was preferred as a discriminative approach for three highly similar species from the group of Lactiplantibacillus as reported by Toriani et al. [17] and Georgieva et al. [18].

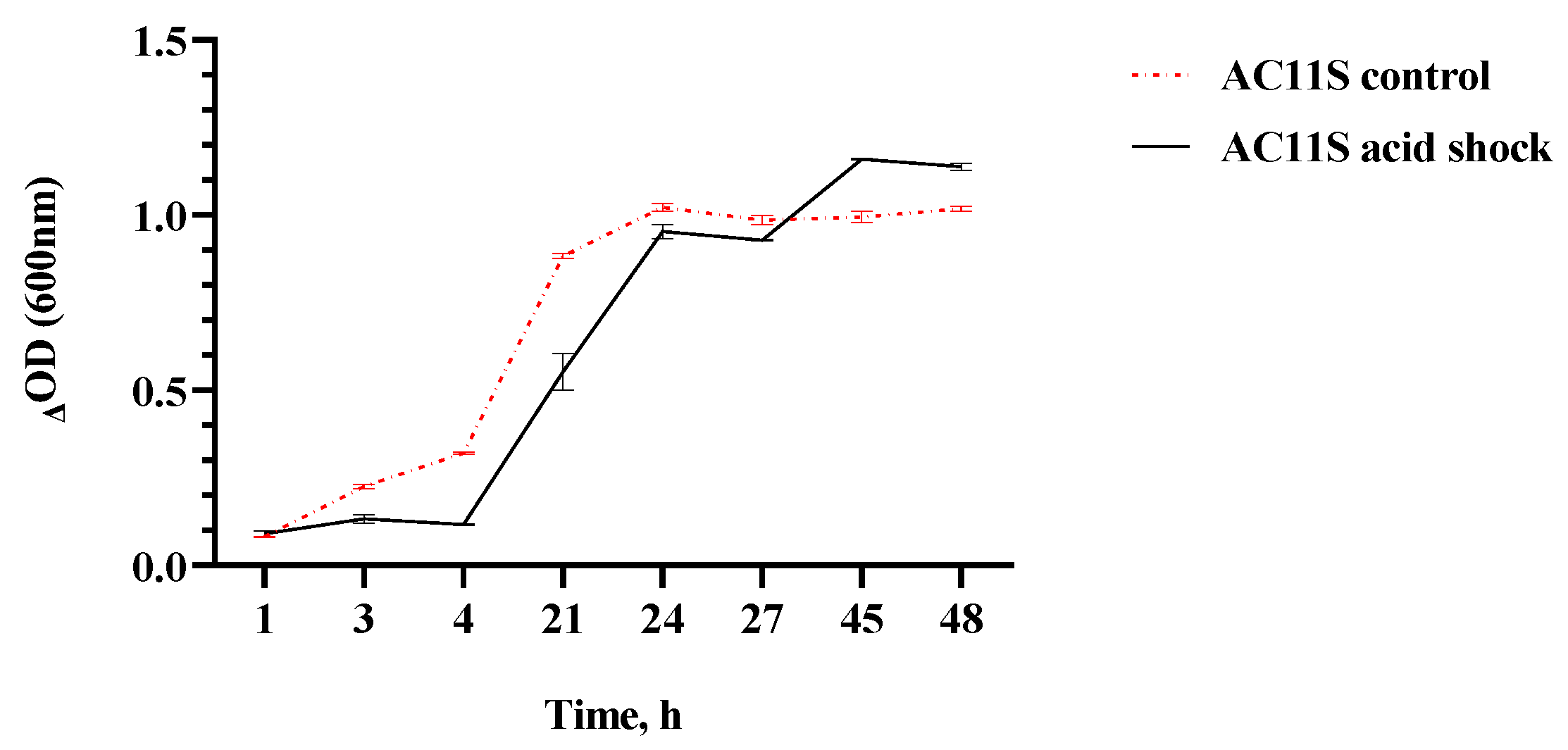
3.2. Viability of L. plantarum AC 11S in an Acidic Environment

L. plantarum is one of the most often employed as a starter LAB species and/or as an adjunct for various biotechnological processes and food production [28]. So, it may be exposed to various stress conditions, such as temperature, and osmotic stress freeze-drying in fermented food [29]. In addition, probiotics must withstand extremely high acidity levels and, a variety of digestive enzymes throughout the entire gastrointestinal tract [30]. The acid stress is a pivotal issue for microbial survival.
L. plantarum AC 11S showed extremely high viability under in vitro passage in simulated stomach juice. After 3-hour exposure to pH 1.5 and pepsin, the growth dynamics is similar to the control. Just a small difference with a longer lag phase may be pointed out (Figure 2). Moreover, the control showed an earlier stationary phase (Figure 2 – red lines)

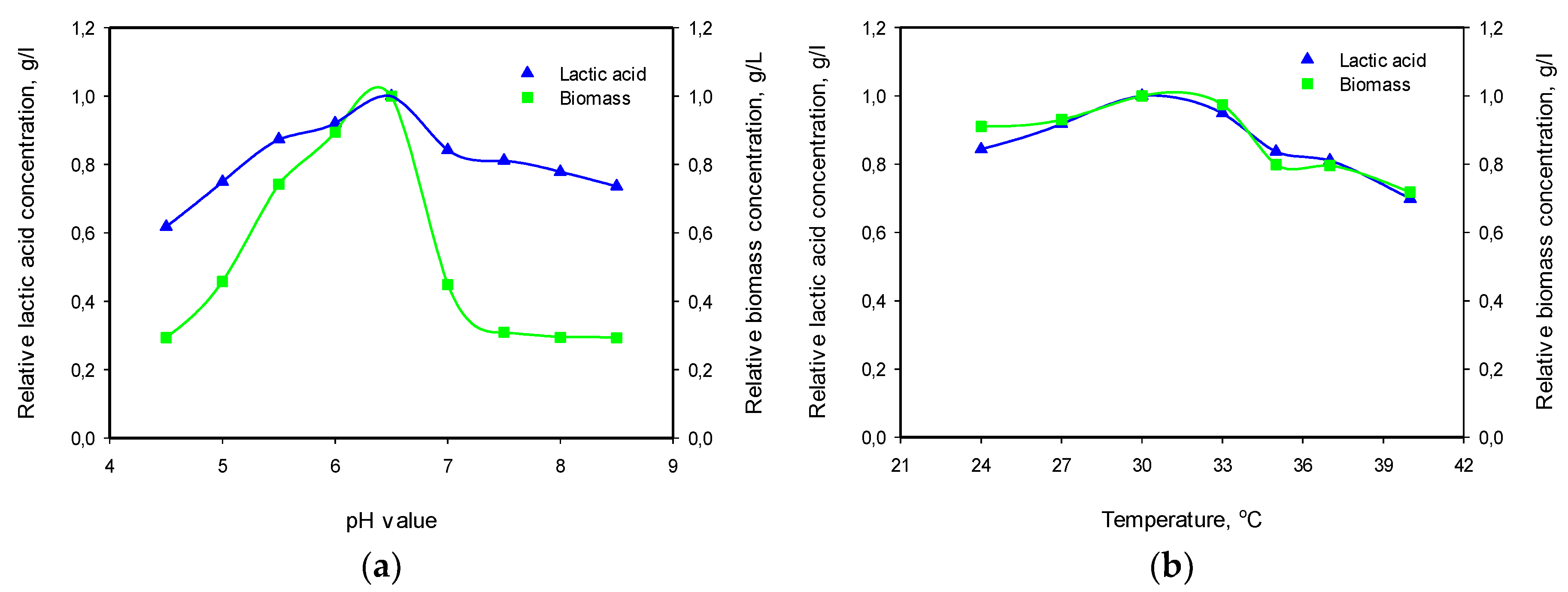
3.3. Influence of pH and Temperature

Fermentation productivity is strongly influenced by the medium pH value and temperature. Although LAB can grow in a broad range of temperatures and pH levels, their growth rate and population density are affected by these factors [12].
With the aim to determine optimum conditions for L. plantarum AC11S two series of experiments were carried out. In the first one, the initial medium pH was varied from 4.5 to 8.5 at 30 oC., and in the second set of experiments, conducted at pH 6.5, the temperature was changed from 24 to 40 oC. 100 mL LA broth was inoculated with 10% seeding culture and fermentation was carried out at appropriate temperature and pH value under anaerobic and static conditions for 24 hours.
The results of these experiments are presented in Figure 3. As can be seen from the figure the optimum conditions for lactic acid production are pH = 6.5 and temperature of 30 oC. The influence of pH is more pronounced, especially on the cell concentration.
L. plantarum is a mesophilic bacterium, capable of growing at temperatures between 10 and 40 oC. In support of our findings, other researchers also cultivated L. plantarum at 30 oC as an optimal temperature [31,32,33,34,35], but there are enough investigations in which the strain was cultivated at 37 oC - see for example [5,6,9].
L. plantarum possesses high acidity tolerance and can grow in pH values between 4 and 7. It is generally accepted that lactic acid production is growth growth-associated process. Anyway, during the fermentation, due to the lactic acid accumulation, the pH value of the broth decreases to about 3.0-3.5 in pH uncontrolled mode [36,37]. Many authors assumed that both dissociated and undissociated forms of the acid could exhibit an inhibition effect on cell growth, as the undissociated form is the stronger inhibitor. It is logical because at low pH (below pKa) the acid is mainly in undissociated form. As pointed out by Peetermans et al. [38] other factors besides pKa, like volatility, and lipophilicity of the acid, as well as medium pH or acid concentration influence the microbial growth inhibition in the presence of weak acids. Mercier et al. [39] investigated lactic acid fermentation with glucose as substrate in the pH range of 5.4 – 7.8. Based on experimental results the authors suggest a pH value between 6.0 and 6.5 as optimal for maximal yields for biomass and lactic acid production. W. Fu and A.P. Mathews [9] studied the lactic acid production from lactose with L. plantarum in the pH range of 4.0-7.0 and found optimal values for cell growth and acid production between 5.0 and 6.0. Yetiman et al. [4] have characterized a new L. plantarum strain isolated from shalgam – a traditional fermented beverage. The authors investigated the cell growth at different pH values (2, 3, 4, 5, and 7) at two temperatures – 30 and 37 oC. Maximum cell density was achieved at pH = 7.0 for both temperatures, but the lag phase was shorter, and the specific growth rate was higher at 37 oC. The same behavior was observed in the presence of different concentrations of bile salts. It is worth mentioning that despite a longer lag phase and lower specific growth rate the final cell densities were higher at 30 oC, especially in the presence of bile salts.

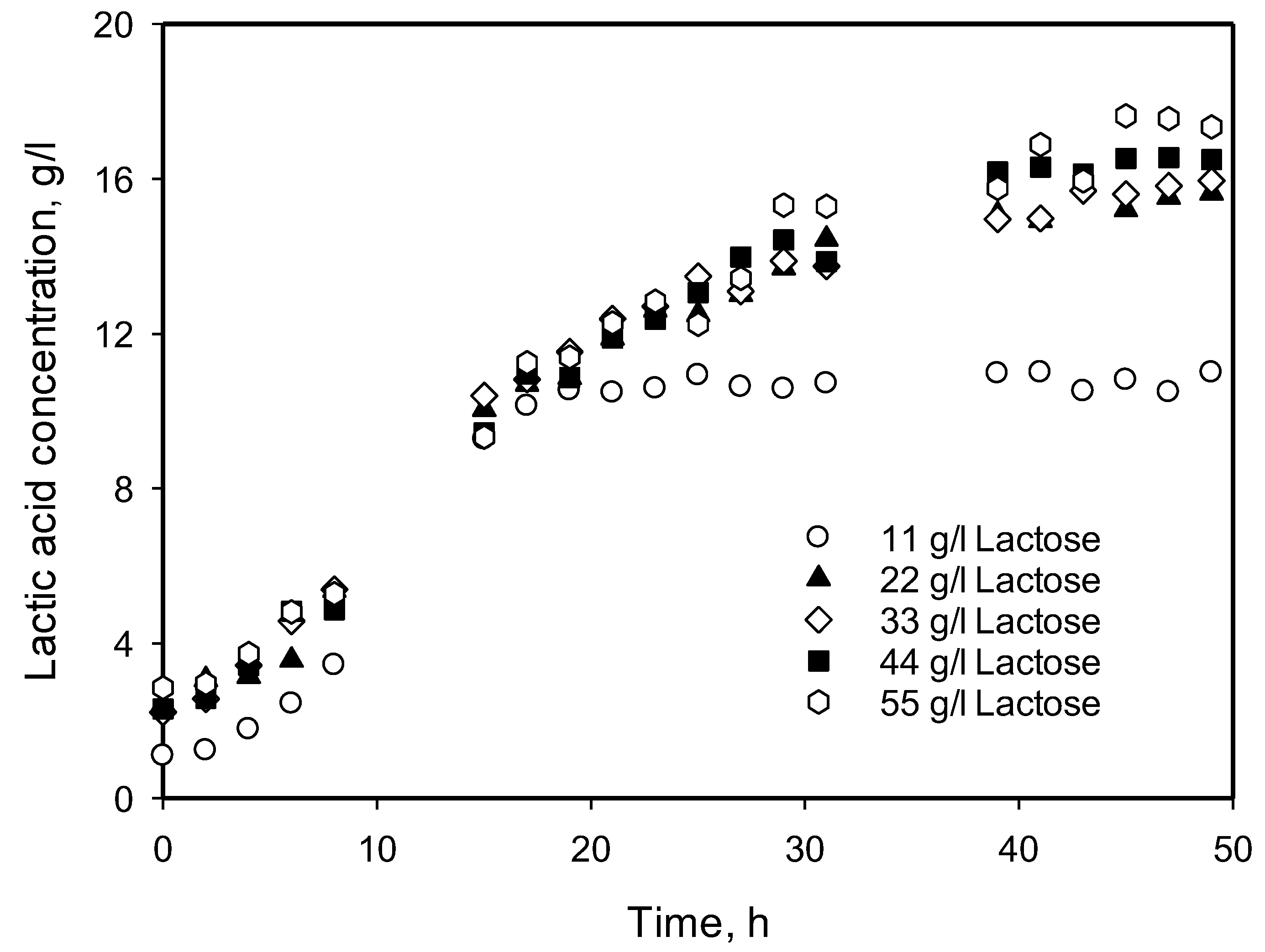
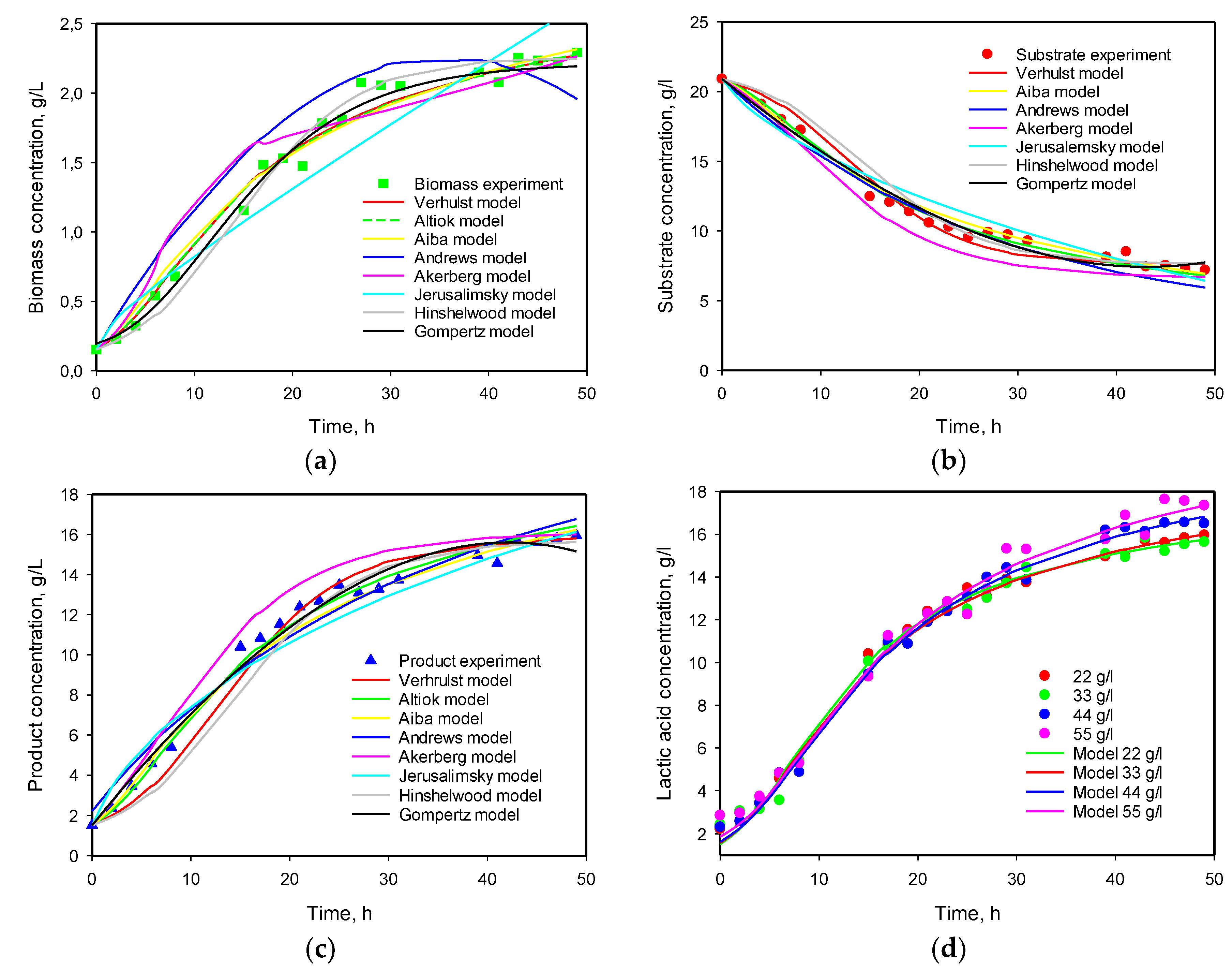
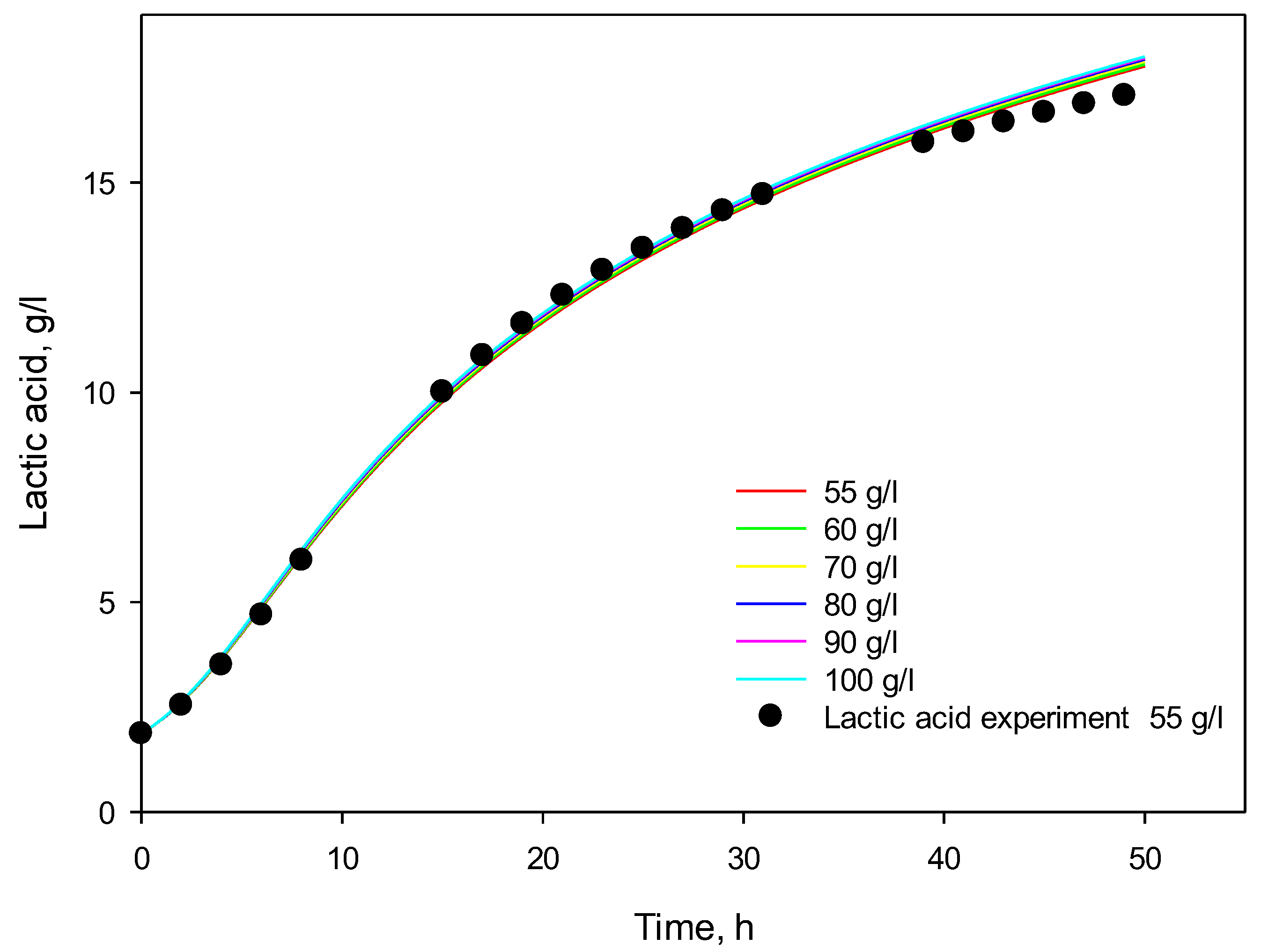
3.4. Influence of Initial Substrate Concentration

In order to elucidate the influence of substrate concentration on cell growth and lactic acid production a set of experiments was carried out at 30 oC and initial pH 6.5 with lactose monohydrate concentrations 11, 22, 33, 44, and 55 g/L without pH control during fermentation. The results obtained are presented in Figure 4. From the figure, it is clearly seen that while at 11 g/L substrate concentration, the conversion is almost complete, and close to the theoretical. The degree of conversion decreased with increasing the substrate concentration, probably due to the inhibition of high substrate concentration and/or product accumulation. It is worth mentioning that during the fermentation period (about 50 h) cell death was not observed.

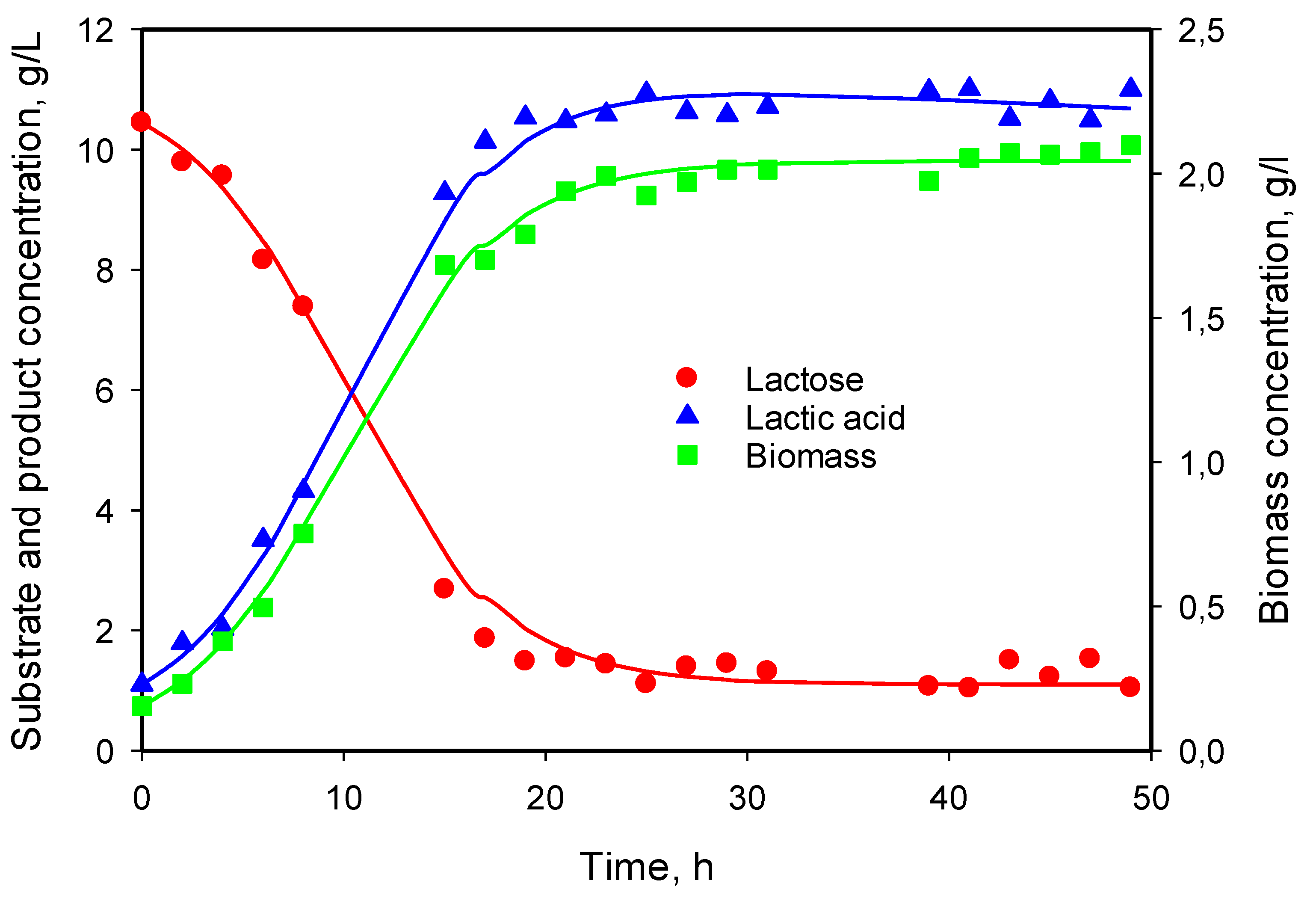
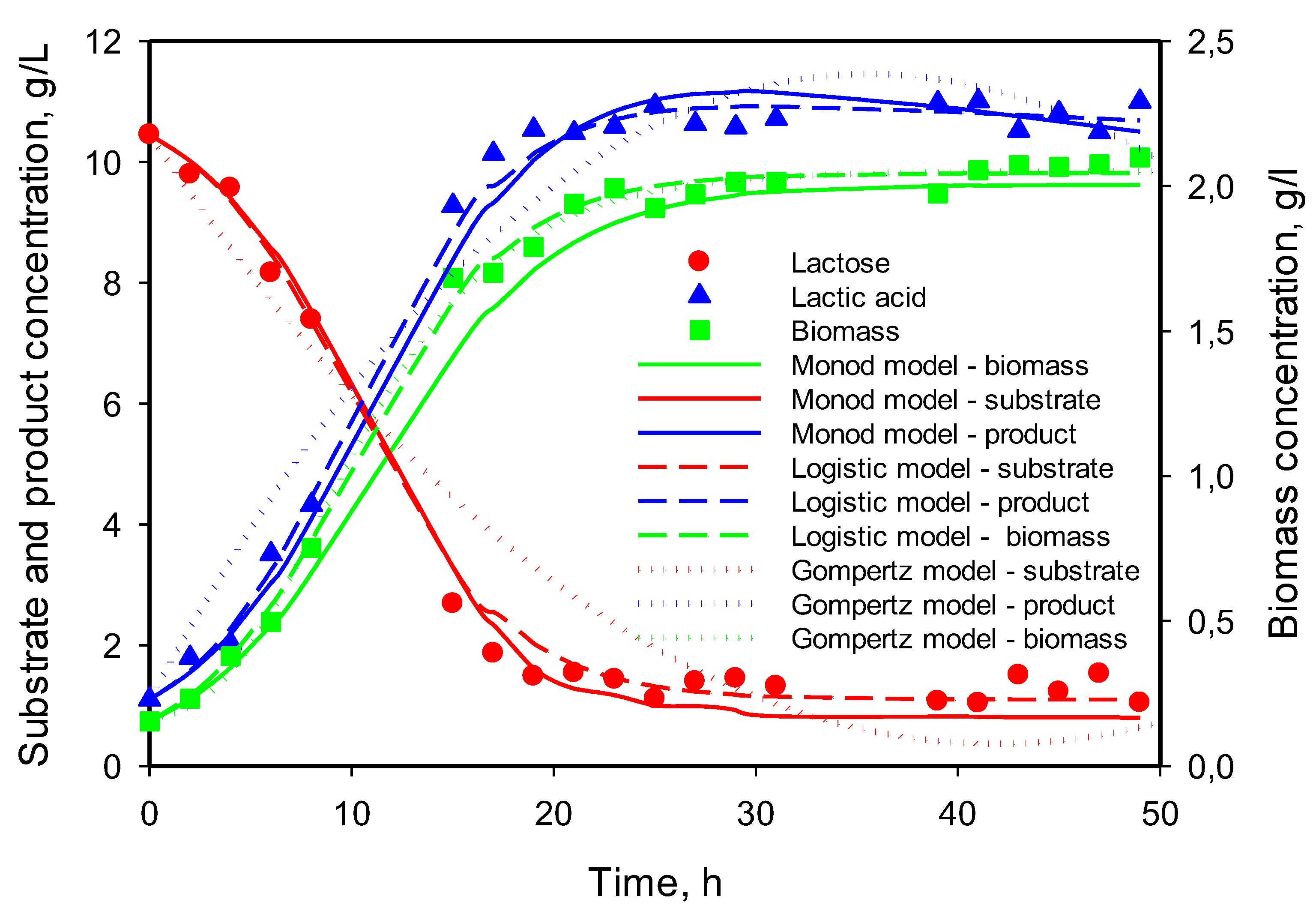
3.5. Modeling of Cell Growth, Substrate Consumption, and Product Accumulation

As can be seen in Figure 5 (growth, substrate, and product for 11 g/L) no cell death was observed during the process. The same hold and for others initial substrate concentrations.
Therefore, in the eq. 1 the second term was omitted as well as the last term in eq. 4 and the set of differential equations describing the process becomes:
d X d t = μ X d S d t = − 1 Y X / S d X d t − 1 Y P / S d P d t   d P d t = α d X d t + β X
with initial conditions t = 0, X = X0, S = S0, P = P0.
With the aim of finding the best expression for specific biomass growth rate, all kinetic models listed in Table 1, as well as the modified logistic and Gompertz equations were used.
An algorithm for simultaneously solving the model equations describing the fermentation process at different initial substrate concentrations was developed.
Using this algorithm, own experimental data were used to identify the model parameters by least square function minimization using MATLAB 2013A software.
For this purpose, the experimental data were processed by minimization procedure of the target function Q, being the sum of the squares of the differences between the measured biomass, substrate, and lactic acid concentrations and the model values:
Q ( μ m a x , k i , X m a x ,   Y X / S ,   α , β , Y P / S ) = 1 N ∑ j = 1 N ( X j − X j e x p ) 2 + 1 N ∑ j = 1 N ( S j − S j e x p ) 2 + 1 N ∑ j = 1 N ( P j − P j e x p ) 2 → m i n
where i is the number of constants in each equation for μ, and j is the number of experimental points.
The attempt to solve the model with the data for all 5 substrate concentrations wasn’t very successful, the discrepancies between model and experimental data were large and the Q function value was too big.
Analyzing the data for product accumulation in Figure 4 it can be concluded that while at 11 g/L substrate concentration, the conversion is almost complete, while increasing the substrate concentration from 22 to 55 g/L leads to strong inhibition of the process and the conversion drops up to about 30%. It was decided to solve the model for 11 g/L separately, using an expression for μ without any additional terms for substrate and product inhibition. Four equations were used – the Monod equation, Verhulst equation, modified logistic, and modified Gompertz equations.
The results are presented in Figure 6 and the values of the model’s parameters are given in Table 2. All four equations described very well the biomass growth as Gompertz and Verhulst’s equations gave the best fit. Solving together the system for biomass growth, substrate consumption, and product formation, however, the results were a little bit different – the best fit was obtained with the Verhulst equation, while the value of the Q function was higher in case of the Gompertz equation and the discrepancies between model and experimental data are high for substrate and product. The obtained values for maximum cell concentration (Xmax and A) are very close, as well as some other model parameters. A very short lag phase was observed and modified Gompertz and logistic models predict - 3-4 h. From the values of the parameters α and β it is evident that the production of lactic acid with L. plantarum AC 11S is related to biomass growth and practically there is no lactic acid production during the stationary phase.
For the rest of the experimental data (from 22 to 55 g/L initial substrate concentration) the mathematical model was solved with all equations that include different types of inhibition in the expressions for specific growth rate μ listed in Table 1. Calculated values of model parameters from simultaneous solution for all 4 initial substrate concentrations are listed in Table 3 and presented in Figure 7.
One can see that the best fit (lowest Q value) was obtained with the model proposed by Altıok [20]. The models of Verhulst [19], and Aiba [21] also very well described the growth and production kinetics.
None of both models including substrate inhibition produce good agreement with experimental data. The same observation was made also by Altıok et al. [20]. Åkerberg et al. [23] also reported that the substrate inhibition was very small compared to the product one.
The values of the yield coefficients YX/S and YP/S are of the same magnitude except those obtained by the Monod-Jerusalimsky model. The ratio between values of the parameters α and β is also high which confirms that product formation is growth-related in this concentration range.
Analyzing the literature data, it is obvious that kinetics constant values are not only strain and substrate specific but also depend on other factors like temperature, pH, media composition, etc. Some of the published data for values of maximal growth rate μ are summarized in Table 4.
Because other authors have solved models separately for each initial substrate concentration, similar calculations were made with the proposed model (eq. 9). Some of the calculated values are presented in Table 5. Experimental values of α were calculated from experimental data for biomass and product according to the equation 11:
α = ( P − P 0 ) ( X − X 0 )
Both mean values are very close to the value predicted by the model solving all data for different substrate concentrations simultaneously.

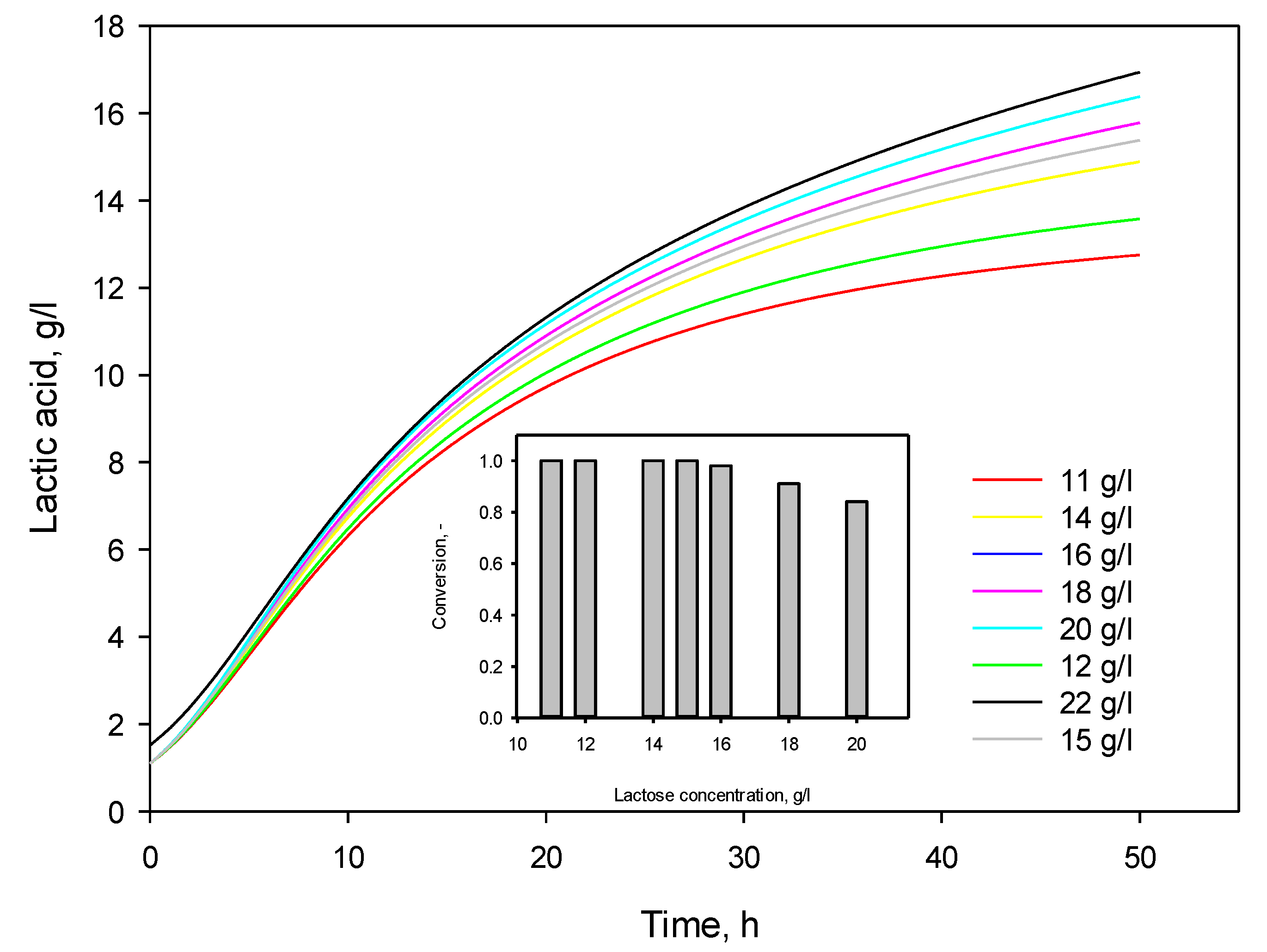
3.6. Model Predictions

One of the advantages of the proper mathematical models of a fermentation process is its ability to predict the system behavior in various conditions. With determined model parameters, some calculations were made in view to predict the starting point of the inhibition and lactic acid production at high substrate concentrations. The model was solved for 6 initial substrate concentrations between 11 and 22 g/L. The model predictions are presented in Figure 8. From the inner picture, one can see that the inhibition starts between 15 and 16 g/L.
The model was also solved for higher initial substrate concentrations – from 60 to 100 g/l and the results are presented in Figure 9. The model predicted a very low increase in product concentration – from 17.07 g/L at 55 g/L to 18.00 at 100 g/L. These values are close to the Pmax value determined according to model 3 (see Table 3).

4. Conclusions

Lactic acid fermentation on lactose by means of Lactiplantibacillus plantarum strain AC 11S was investigated in batch mode without pH control. The optimum pH and temperature were determined to be 6.5 and 30 oC. The strain is extremely acid-resistant and easily recovers from an acid shock. A mathematical model was developed including equations describing biomass growth, substrate consumption, and product formations. When solving the model only for bacterial growth, the modified Gompertz equation gave the best fit for all initial substrate concentrations in the investigated range. Including this equation in the system with equations for substrate depletion and product accumulation, however, didn’t produce a good fit with experimental data. The best fit was achieved with a modified Verhulst equation with an added product inhibition term. The results obtained are a good base for further investigation of the strain capabilities in pH-controlled fermentation at fed-batch and continuous mode.

Author Contributions

For research articles with several authors, a short paragraph specifying their individual contributions must be provided. The following statements should be used “Conceptualization, D.Y. and S.D.; methodology, D.Y. and PP-K; software, P.P.-K. and D.Y.; validation, DY, and S.D., formal analysis, N.A. and P.P.-K.; resources, D.Y. and S.D.; data curation, P.P.-K.; writing—original draft preparation, D.Y. and S.D..; writing—review and editing, S.D. and D.Y. visualization, P.P.-K. and N.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Hatti-Kaul, R.; Chen, L.; Dishisha, T.; El Enshasy, H. Lactic acid bacteria: from starter cultures to producers of chemicals. FEMS Microbiology Letters 2018, 365, fny213. [CrossRef]
  2. Filannin, P.; De Angelis, M.; Di Cagno, R.; Gozzi, G.; Riciputi, Y., Gobbetti, M. How Lactobacillus plantarum shapes its transcriptome in response to contrasting habitats., Environmental Microbiology 2018, 20, 3700-3716. [CrossRef]
  3. Chen, P.-T.; Hong, Z.-S.; Cheng, Ch.-L.; Ng, I-S.; Lo, Y.-Ch.; Nagarajan, D.; Chang, J.-S. Exploring fermentation strategies for enhanced lactic acid production with polyvinyl alcohol-immobilized Lactobacillus plantarum using microalgae as feedstock. Bioresource Technology 2020, 308, 123266. [CrossRef]
  4. Yetiman, A. E.; Keskin, A.; Nur, D. B.; Kotil, S. E.; Ortakci, F.; Dogan, M. Characterization of genomic, physiological, and probiotic features Lactiplantibacillus plantarum DY46 strain isolated from traditional lactic acid fermented shalgam beverage. Food Bioscience 2022, 46, 101499. [CrossRef]
  5. Yadav, N.; Nain, L.; Khare, K. S. One-pot production of lactic acid from rice straw pretreated with ionic liquid. Bioresource Technology 2021, 323, 124563. [CrossRef]
  6. David, A. N.; Sewsynker-Sukai, Y.; Gueguim, Kana, E.B. Co-valorization of corn cobs and dairy wastewater for simultaneous sacharification and lactic acid production: Process optimization and kinetic assessment. Bioresource Technology 2022, 348, 126815. [CrossRef]
  7. Haokok, Ch.; Lunprom, S.; Reungsang, A.; Salakkam, A. Efficient production of lactic acid from cellulose and xylan in sugarcane bagasse by newly isolated Lactiplantibacillus plantarum and Levilactobacillus brevis through simultaneous saccharification and co-fermentation process Heliyon 2023, 9, e17935. [CrossRef]
  8. Derabli, B.; Nancib, A.; Nancib, N.; Aníbal, J.; Raposo, S.; Rodrigues, B.; Boudrant, J. Opuntia ficus indica waste as a cost effective carbon source for lactic acid production by Lactobacillus plantarum. Food Chemistry 2022, 370, 131005. [CrossRef]
  9. Fu, W.; Mathews, A.P. Lactic acid production from lactose by Lactobacillus plantarum: kinetic model and effects of pH, substrate, and oxygen Biochemical Engineering Journal 1999, 3, 163-170. [CrossRef]
  10. Seddik, H. A.; Bendali, F.; Gancel, F.; Fliss, I.; Spano, G.; Drider, D. Lactobacillus plantarum and Its Probiotic and Food Potentialities. Probiotics & Antimicrob. Prot., 2017, 9, 111–122. [CrossRef]
  11. Zheng, J.; Wittouck, S.; Salvetti, E.; Franz, C.M.A.P.; Harris, H.M.B.; Mattarelli, P.; O’Toole, P. W.; Pot, B.; Vandamme, P.; Walter, J.; Watanabe, K.; Wuyts, S.; Felis, G.E.; Gänzle, M.G.; Lebeer, S. A taxonomic note on the genus Lactobacillus: Description of 23 novel genera, emended description of the genus Lactobacillus Beijerinck 1901, and union of Lactobacillaceae and Leuconostocaceae. Int. J. Syst. Evol. Microbiol. 2020, 70, 2782–2858. [CrossRef]
  12. Corsetti, A.; Ciarrocchi, A.; Prete, R. Lactic Acid Bacteria: Lactobacillus spp.: Lactobacillus plantarum. Reference Module in Food Sciences, Elsevier. Amsterdam, 2016. [CrossRef]
  13. Zacharof, M.-P.; Lovitt, R.W. Modelling and Simulation of Cell Growth Dynamics, Substrate Consumption, and Lactic Acid Production Kinetics of Lactococcus lactis. Biotechnology and Bioprocess Engineering 2013, 18, 52-64. [CrossRef]
  14. Bouguettoucha, A.; Balannec, B.; Amrane A. Unstructured Models for Lactic Acid Fermentation—A Review. Food Technol. Biotechnol. 2011, 49, 3–12.
  15. Gordeev, L.S.; Koznov, A.V.; Skichko, A.S.; Gordeeva, Yu. L. Unstructured Mathematical Models of Lactic Acid Biosynthesis Kinetics: A Review. Theoretical Foundations of Chemical Engineering 2017, 51, 175–190. [CrossRef]
  16. Danova, S.; Georgieva, R.; Koleva, P.; Tropcheva, R.; Manasiev, J.; Nikolova, D. Biodiversity and activity of Lactic acid bacteria from traditional Bulgarian milk products. Scientific Works of UFT - Plovdiv 2009, 56, 275-280.
  17. Torriani, S.; Felis, G.E.; Dellaglio, F. Differentiation of Lactobacillus plantarum, L. pentosus, and L. paraplantarum by recA gene sequence analysis and multiplex PCR assay with recA gene-derived primers. Appl. Environ. Microbiol. 2001, 67, 3450–3454. [CrossRef]
  18. Georgieva, R.N.; Iliev, I.N.; Chipeva, V.A.; Dimitonova, S.P.; Samelis, J.; Danova, S.T. Identification and in vitro characterisation of Lactobacillus plantarum strains from artisanal Bulgarian white brined cheeses. J. Basic. Microbiol. 2008, 48, 234–244. [CrossRef]
  19. Verhulst, P.-F. Notice sur la loi que la population suit dans son accroissement. Corr. math. phys. 1838, 10, 113-121. [CrossRef]
  20. Altıok, D.; Tokatlı, F.; Harsa Ş. Kinetic modelling of lactic acid production from whey by Lactobacillus casei (NRRL B-441). J Chem Technol Biotechnol 2006, 81, 1190–1197 (). [CrossRef]
  21. Aiba, S.; Shoda, M.; Nagatani M. Biotechnol. Bioeng. 1968, 10, 845–864.
  22. Andrews, J. F. A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates. Biotechnology and bioengineering, 1968, 10, 707-723. [CrossRef]
  23. Åkerberg, C.; Hofvendahl, K.; Zacchi, G.; Hahn-Hägerdal, B. Modelling the infuence of pH, temperature, glucose and lactic acid concentrations on the kinetics of lactic acid production by Lactococcus lactis ssp. lactis ATCC 19435 in whole-wheat flour. Appl Microbiol Biotechnol 1998, 49, 682-690. [CrossRef]
  24. Ierusalimskiĭ, N.D.; Neronova, N.M. Quantitative relationship between the concentration of metabolic products and the rate of growth of microorganisms. Doklady Akademii nauk SSSR 1965, 161, 1437-1440 (in Russian).
  25. Hinshelwood, C. N. The chemical kinetics of the bacterial cell, 1st ed., Clarendon Press, Oxford, 1946.
  26. Zwietering, M.H.; Jongenburger, I.; Rombouts, F. M.; van ‘t Riet, K. Modeling of the Bacterial Growth Curve. Applied and Environmental Microbiology 1990, 56, 1875-1881. [CrossRef]
  27. Luedeking, R.; Piret, E.L. A Kinetic Study of the Lactic Acid Fermentation. Batch Process at Controlled pH. Journal of Biochemical and Microbiological Technology and Engineering 1959, 1, 393-412.
  28. Brinques, GB.; Ayub, M.A.Z. Effect of microencapsulation on survival of Lactobacillus plantarum in simulated gastrointestinal conditions, refrigeration, and yogurt. J Food Eng 2011, 103,123–128. [CrossRef]
  29. van de Guchte, M.; Serror, P.; Chervaux, C.; Smokvina, T.; Ehrlich, S.D.; Maguin E. Stress responses in lactic acid bacteria. Antonie Van Leeuwenhoek, 2002, 82, 187–216.
  30. Wall, T.; Båth, K.; Britton, R.A.; Jonsson, H.; Versalovic, J.; Roos, S. The early response to acid shock in Lactobacillus reuteri involves the ClpL chaperone and a putative Cell Wall-altering esterase. Appl Environ Microbiol 2007, 73, 3924–3935. [CrossRef]
  31. Barbosa, J.; Albano, H.; Silva, B.; Almeida, M.H.; Nogueira, T.; Teixeira, P.; Caracterization of a Lactiplantibacillus plantarum R23 Isolated from Arugula by Whole-Genome Sequencing and Its Bacteriocin Production Ability. Int. J. Environ. Res. Public Health 2021, 18, 5515 . [CrossRef]
  32. Bomrungnok, W.; Sonomoto, K.; Pinitglang, S.; Wongwicharn, A. Single Step Lactic Acid Production from Cassava Starch by Lactobacillus plantarum SW14 in Conventional Continuous and Continuous with High Cell Density. APCBEE Procedia, 2012, 2, 97 – 103. [CrossRef]
  33. Jang, H.-Y.; Kim, M. J.; Bae, M., Hwang, I.M.; Lee, J.-H. Transcriptional analysis of the molecular mechanism underlying the response of Lactiplantibacillus plantarum to lactic acid stress conditions., Heliyon, 2023, 9, e16520, DOI: 10.1016/j.heliyon.2023.e16520. [CrossRef]
  34. Baltà-Foix, R.; Serrano-Adrover, C.; López-Cano, A.; Gifre-Renom, L.; Sanchez-Chardi, A.; Arís, A.; Garcia-Fruitós, E. Lactiplantibacillus plantarum: a new example of inclusion body producing bacteria, Microbial Cell Factories, 2023, 22, 111. [CrossRef]
  35. Adesokan, I.A.; Odetoyinbo B.B.; Okanlawon, B.M. Optimization of lactic acid production by lactic acid bacteria isolated from some traditional fermented food in Nigeria. Pakistan Journal of Nutrition, 2009, 8, 611 – 615.
  36. Venkatesh, K.V.; Okos, M.R.; Wankat, P.C. Kinetic Model of Growth and Lactic Acid Production from Lactose by Lactobacillus bulgaricus. Process Biochemistry 1993, 28, 231-241. [CrossRef]
  37. Lunelli, B.H.; Melo, D.N.C.; de Morais, E.R.; Victorino, I.R.S.; Vasco de Toledo, E.C.; Maciel, M.R.W.; Filho, R.M. Real-time optimization for lactic acid production from sucrose fermentation by Lactobacillusplantarum. Computer Aided Chemical Engineering, 2011, 29, 1396-1400. [CrossRef]
  38. Peetermans, A.; Foulquié-Moreno, M.R.; Thevelein, J.M. Mechanisms underlying lactic acid tolerance and its influence on lactic acid production in Saccharomyces cerevisiae. Microbial Cell 2021, 8, 111-130. [CrossRef]
  39. Mercier, P.; Yerushalmi, L.; Rouleau, D.; Dochain D. Kinetics of Lactic Acid Fermentation on Glucose and Corn by Lactobacillus amylophilus. J. Chem. Tech. Biotechnol. 1992, 55, 111-121. [CrossRef]
  40. Kostov, G.; Angelov, M.; Denkova, Z.; Dobrev, I.; Goranov, B. Lactic acid production with Lactobacillus casei ssp. rhamnosus NBIMCC 1013: Modeling and optimization of the nutrient medium. Eng. Life Sci. 2011, 11, 517–527. [CrossRef]
  41. Liu, B.; Yang, M.; Qi, B.; Chen, X.; Su, Zh.; Wan, Y. Optimizing l-(+)-lactic acid production by thermophile Lactobacillus plantarum As.1.3 using alternative nitrogen sources with response surface method. Biochemical Engineering Journal 2010, 52, 212–219. [CrossRef]
  42. Tomás, M.S.J.; Ocaña, V.S.; Wiese, B.; Nader-Macías ,M.E. Growth and lactic acid production by vaginal Lactobacillus acidophilus CRL 1259, and inhibition of uropathogenic Escherichia coli. Journal of Medical Microbiology 2003, 52, 1117–1124. [CrossRef]
  43. Amrane, A.; Prigent, Y. Mathematical Model for Lactic Acid Production from Lactose in Batch Culture: Model Development and Simulation. J. Chem. Tech. Biotechnol. 1994, 60, 241-246. [CrossRef]
  44. Colucci Cante, R.; Gallo, M.; Nigro, F.; Passannanti, F.; Budelli, A.; Nigro, R. Mathematical Modeling of Lactobacillus paracasei CBA L74 Growth during Rice Flour Fermentation Performed with and without pH Control. Appl. Sci. 2021, 11, 2921. [CrossRef]
  45. Barragán, P.J.; Sánchez, Ó.J.; Henao-Rojas, J.C. Evaluation of the Growth Kinetics of Lactobacillus Plantarum ATCC 8014 on a Medium Based on Hydrolyzed Bovine Blood Plasma at Laboratory and Bench-Scale Levels and Its Application as a Starter Culture in a Meat Product. Fermentation 2020, 6, 45. [CrossRef]
  46. Palaniraj, R.; Nagarajan, P. Kinetic Studies In Production Of Lactic Acid From Waste Potato Starch Using Lactobacillus casei. Int. J. Chem Tech Res. 2012, 4, 1601-1614,.
  47. Vázquez, J.A.; Murado, M.A. Unstructured mathematical model for biomass, lactic acid and bacteriocin production by lactic acid bacteria in batch fermentation. J Chem Technol Biotechnol 2008, 83, 91–96. [CrossRef]
  48. Trontel, A.; Baršić, V.; Slavica, A.; Šantek, B.; Novak S. Modelling the Effect of Different Substrates and Temperature on the Growth and Lactic Acid Production by Lactobacillus amylovorus DSM 20531T in Batch Process. Food Technol. Biotechnol. 2010, 48, 352–361.
  49. Goranov, B.; Shopska, V.; Denkova, R.; Kostov, G. Kinetics of Batch Fermentation in the Cultivation of a Probiotic Strain Lactobacillus delbrueckii ssp. Bulgaricus B1. Acta Universitatis Cibiniensis Series E: Food Technology 2015, XIX, 61-72. [CrossRef]
  50. Gonçaives, L.M.D.; Xavier, A.M.R.B.; Almeida, J.S.; Carrondo, M.J.T. Concomitant substrate and product inhibition kinetics in lactic acid production. Enzyme Microb. Technol. 1991, 13, 314-319. [CrossRef]
  51. Anuradha, R.; Suresh, A.K.; Venkatesh K.V. Simultaneous saccharification and fermentation of starch to lactic acid. Process Biochemistry 1999, 35, 367-375. [CrossRef]
  52. Balannec, B.; Bouguettoucha, A.; Amrane A. Unstructured model for batch cultures without pH control of Lactobacillus helveticus—Inhibitory effect of the undissociated lactic acid. Biochemical Engineering Journal 2007, 35, 289–294. [CrossRef]
  53. Biazar, J.; Tango, M.; Babolian, E.; Islam, R. Solution of the kinetic modeling of lactic acid fermentation using Adomian decomposition method. Appl. Math. Comput. 2003, 144 433–439. [CrossRef]
  54. Ben Youssef, C.; Goma, G.; Olmos-Dichara, A. Kinetic modelling of Lactobacillus casei ssp. rhamnosus growth and lactic acid production in batch cultures under various medium conditions. Biotechnology Letters 2005, 27, 1785–1789. [CrossRef]
  55. Gupta, S.; Abu-Ghannam, N.; Scannell, A.G.M. Growth and kinetics of Lactobacillus plantarum in the fermentation of edible Irish brown seaweeds. Food and Bioproducts Processing 2011,89, 346–355. [CrossRef]
  56. Sharma, V.; Mishra, H.N. Unstructured kinetic modeling of growth and lactic acid production by Lactobacillus plantarum NCDC 414 during fermentation of vegetable juices. LWT Food Science and Technology 2014, 59, 1123e11. [CrossRef]
Preprints 100825 g001
Figure 1. (a) Cells morphology of the strain AC 11S (1000x dimension light microscopy Boeco, China microscope); (b) Identification of the strain as L. plantarum, with Multiplex PCR using primers targeting recA gen (according to Torriani et al. [17].
Figure 1. (a) Cells morphology of the strain AC 11S (1000x dimension light microscopy Boeco, China microscope); (b) Identification of the strain as L. plantarum, with Multiplex PCR using primers targeting recA gen (according to Torriani et al. [17].
Preprints 100825 g001
Preprints 100825 g002
Figure 2. Growth curve of L. plantarum AC 11S in mMRS broth with lactose (pH 6.5) at 30 oC after an acidic shock in simulated stomach juice.
Figure 2. Growth curve of L. plantarum AC 11S in mMRS broth with lactose (pH 6.5) at 30 oC after an acidic shock in simulated stomach juice.
Preprints 100825 g002
Preprints 100825 g003
Figure 3. (a) Influence of initial pH value on biomass growth and lactic acid production at 30 oC; (b) Influence of temperature on biomass growth and lactic acid production at initial pH 6.5.
Figure 3. (a) Influence of initial pH value on biomass growth and lactic acid production at 30 oC; (b) Influence of temperature on biomass growth and lactic acid production at initial pH 6.5.
Preprints 100825 g003
Preprints 100825 g004
Figure 4. Influence of initial substrate concentration on the lactic acid production at 30 oC and initial pH value 6.5 without pH control.
Figure 4. Influence of initial substrate concentration on the lactic acid production at 30 oC and initial pH value 6.5 without pH control.
Preprints 100825 g004
Preprints 100825 g005
Figure 5. Time course of substrate consumption, biomass growth, and lactic acid production from 11 g/L lactose monohydrate at 30 oC and initial pH value 6.5 without pH control.
Figure 5. Time course of substrate consumption, biomass growth, and lactic acid production from 11 g/L lactose monohydrate at 30 oC and initial pH value 6.5 without pH control.
Preprints 100825 g005
Preprints 100825 g006
Figure 6. Experimental and model results for microbial growth, substrate consumption, and lactic acid production from 11 g/L initial substrate concentration.
Figure 6. Experimental and model results for microbial growth, substrate consumption, and lactic acid production from 11 g/L initial substrate concentration.
Preprints 100825 g006
Preprints 100825 g007
Figure 7. (a) Comparison of various model data for biomass growth – 22 g/l initial substrate concentration; (b) Comparison of various model data for substrate consumption – 22 g/l initial substrate concentration; (c) Comparison of various model data for product formation – 22 g/l initial substrate concentration; (d) Comparison of experimental data and Altıok model predictions for lactic acid production – 22-55 g/l initial substrate concentration.
Figure 7. (a) Comparison of various model data for biomass growth – 22 g/l initial substrate concentration; (b) Comparison of various model data for substrate consumption – 22 g/l initial substrate concentration; (c) Comparison of various model data for product formation – 22 g/l initial substrate concentration; (d) Comparison of experimental data and Altıok model predictions for lactic acid production – 22-55 g/l initial substrate concentration.
Preprints 100825 g007
Preprints 100825 g008
Figure 8. Model predictions for initial substrate concentrations in the range of 11-22 g/L.
Figure 8. Model predictions for initial substrate concentrations in the range of 11-22 g/L.
Preprints 100825 g008
Preprints 100825 g009
Figure 9. Model predictions for initial substrate concentrations in the range of 55-100 g/L.
Figure 9. Model predictions for initial substrate concentrations in the range of 55-100 g/L.
Preprints 100825 g009
Table 1. Modified Monod models describing cell growth.
Table 1. Modified Monod models describing cell growth.
No Model name Equation of biomass specific growth rate Ref.
1 Verhulst μ = μ max ( 1 − X X max ) n if n=1
μ = μ max ( 1 − X X max ) 		[19]
2 Altıok μ = μ max ( 1 − X X max ) n 1 ( 1 − P P max ) n 2 if n1, n2 = 1 μ = μ max ( 1 − X X max ) ( 1 − P P max ) [20]
3 Aiba μ = μ max ( S k S + S ) e − k P P [21]
4 Andrews μ = μ max ( S k S + S + S 2 / k i ) [22]
5 Akerberg μ = μ max ( S k S + S + S 2 / k i ) ( 1 − k P P ) n [23]
6 Monod-Jerusalimsky μ = μ max ( S k S + S ) ( k P k P + P ) [24]
7 Hinshelwood μ = μ max ( S k S + S ) ( 1 − k P P ) [25]
Table 2. Model parameters determined by solving the system 9 for 11 g/L initial substrate concentrations.
Table 2. Model parameters determined by solving the system 9 for 11 g/L initial substrate concentrations.
Model μmax KS Xmax λ A YX/S YP/S α β Q
Monod 0.420 5.511 0.175 4.016 5.965 0.0197 1.019
Verhulst 0.253 2.045 0.202 6.394 5.396 0.0077 0.352
Gompertz 0.048 2.959 1.925 0.205 5.986 6.086 0.0042 3.846
Logistic 0.138 4.0705 1.875 0.229 2.011 4.591 0.0 1.949
Table 3. Model parameters determined by solving the system 9 for 22 - 55 g/L initial substrate concentrations.
Table 3. Model parameters determined by solving the system 9 for 22 - 55 g/L initial substrate concentrations.
Model No μmax KS KP Ki Xmax Pmax n1 n2 YX/S YP/S α β Q
1
 0.179
0.322		 1.754
3.673
2.060		 0.121
0.154		 3.650
3.346		 8.337
7.015		 0.0156
0.0014		 0.991
0.348
2 0.257
0.302
2.268
3.013		 19.389
17.087
2.248
1.767		 0.419
0.151		 3.803
2.951		 7.263
6.948		 0.0069
0.0029		 0.494
0.305
3 0.365 3.464 0.247 0.155 1.855 6.784 0.005 0.463
4 0.168 0.550 0.077 0.144 5.269 6.232 0.0549 4.099
5 0.113 17.306 2.506 6.406 0.011 58.27 29.07 1.2367 4.71
6 0.185 4.293 1.052 0.114 1.231 7.287 0.0231 3.287
7 0.233 4.847 0.064 0.158 3.262 6.524 0.0028 1.348
Table 4. Values of the maximal growth rate determined by other authors.
Table 4. Values of the maximal growth rate determined by other authors.
Microorganism Substrate Growth model μmax (h-1) Reference
L. amylophilus Glucose 20 g/L μ = μ m a x   ( 1 − X ⁄ X m a x ) 0.32 (pH 6.5) [39]
L. casei Lactose 20 g/L μ = μ m a x   ( 1 − X ⁄ X m a x ) 0.511 [40]
L. plantarum Glucose 100 g/L μ = μ m a x   ( 1 − X ⁄ X m a x ) 0.64 [41]
L. lactis Glucose 20 g/L μ = ( μ m a x S ( K P + P ) ) / ( ( K S + S ) P ) 0.66 (pH 6.5) [13]
L. acidophilus Glucose 10 g/L Four parameter Gompertz model 0.35 (pH 6.5, 30 oC)
0.43 (pH 6.5, 37 oC)		 [42]
L. helveticus Whey ultrafiltrate powder μ = μ m a x 1 / ( 1 + c e d t / ( μ m − c ) ) 0.56 [43]
L. paracasei Rice flour μ = μ m a x ( S / ( S + K S X ) )
μ = μ max ( 1 − X / X max )
μ = μ m a x S / ( K S + S ) 		0.993


0.619


0.811		 [44]
L. plantarum Sucrose 20 g/L μ = μ m a x   ( 1 − ( X ⁄ X m a x ) n ) . 0.0545 [45]
L.plantarum Hydrolysed wheat flour μ = μ m a x ( S / ( K S + S + S 2 / K i ) ) ( 1 − K P P ) n 0.403 [23]
L. plantarum Lactose 40 g/L μ = μ m a x S / ( K S + S ) 0.364 (pH 6.0) [9]
L. plantarum Dairy waste water μ = μ m a x   ( 1 − X ⁄ X m a x ) 0.35 [6]
L. casei Waste potato starch μ = μ m a x S / ( K S + S ) 0.115 [46]
L. lactis Glucose μ = μ m a x   ( 1 − X ⁄ X m a x ) 0.687 [47]
L. amylovorus Glucose
Sucrose
Starch		 μ = ( μ m a x S / ( K S + S ) ) ( K I / ( K I + P ) ) 0.58
0.32
0.61		 [48]
L. delbrueckii Glucose 10 g/L Logistic equation 0.031 [49]
L. delbrueckii Glucose μ = μ m a x / ( 1 + S / K I )
μ = μ m a x e − S / K I
μ = μ m a x   ( 1 − S / S m ) n 		0.55


0.59


0.58		 [50]
L. casei Whey lactose μ = μ m a x   ( S / ( K S + S ) ) ( 1 − X ⁄ X m a x ) 0.265 [20]
L. delbrueckii Potato starch μ = μ m a x e − K P P ( K S + S + S 2 / K i ) 0.372(pH 5.5) [51]a
L. helveticus Whey lactose μ = μ m a x   ( 1 − X ⁄ X m a x ) 0.64 [52]
L. helveticus Lactose 50 g/L μ = ( μ m a x S / ( K S + S ) ) e − ( S / K I ) n 1 e − ( P / K P ) n 2 0.25 [53]
L. casei Glucose 50 g/L μ = μ m a x ( K P / ( K P + P ) ) ( S / ( K S + S ) ) ( 1 − P / P c ) 0.45 [54]
L. plantarum Irish brown seaweeds
L. digitata
L. saccharina 		Modified Gompertz equation

0.4
0.29		 [55]
L. plantarum Glucose- 20 g/L
Vegetable juice – 3 g/L RS		 Modified Gompertz equation 0.6

0.45		 [56]
L. plantarum Glucose- 20 g/L
Vegetable juice – 3 g/L RS		 Logistic equation 0.62

0.53		 [56]
Table 5. Experimental and calculated values of α and µmax.
Table 5. Experimental and calculated values of α and µmax.
Initial substrate concentration, g/L α exp α calc µmax, calc
11 5.091 6.850 0.249
22 6.748 6.782 0.334
33 6.959 6.768 0.343
44 6.947 7.197 0.311
55 7.651 7.195 0.309
Mean value 6.679 6.958 0.309
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated