Prerpints.org logo
Preprint
Article

Numerical Modelling of a Female Brain: Effect of the Dura Mater

Altmetrics

Downloads

166

Views

105

Comments

0

Submitted:

08 March 2024

Posted:

08 March 2024

You are already at the latest version

Alerts
Abstract
Traumatic Brain Injury represents a significant public health concern due to its role in traumatic death and disability, often caused by head impacts or rapid accelerations. Despite advancements in Finite Element Head Models, existing models primarily represent adult males, neglecting anatomical and physiological differences between genders and age groups. Additionally, the mechanistic roles of specific intracranial tissues, such as the dura mater, have conventionally been overlooked. To better understand the mechanical behavior of the brain and its injured regions in the context of TBI, including the dura mater, this study proposes the development of a Female Finite Element Head Model. This model, representative of a middle-aged female subject, was developed using medical image-derived geometry and finite element modeling techniques. The validation results demonstrate a similarity between the numerical displacement curves and those obtained experimentally. In the model with dura mater, the numerical results show analogous behavior to the experimental results, despite minimal variations in the amplitude of the curves. These advancements highlight the significance of including the dura mater in biomechanical brain modeling. Incorporating the dura mater in Finite Element Head Models produces more realistic results than models without it. This emphasizes the importance of enhancing biomechanical models to better represent anatomical complexity.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Among the spectrum of injury types, those affecting the brain are particularly predisposed to resulting in either death or long-term disability. Traumatic Brain Injury (TBI), often referred to as the ’silent epidemic,’ is a significant public health concern given its prominent role as a primary contributor to traumatic death and disability [1].
Globally, TBI is estimated to affect 69 million individuals each year [2]. TBI can be penetrating or non-penetrating (blunt). A penetrating TBI occurs when an object pierces the skull, like shrapnel, a bullet or a knife, causing damage to the brain tissue. A non-penetrating TBIs occur when a force hits the head, causing the brain to ricochet or twist inside the skull. These injuries commonly result from vehicle accidents, falls, impacts, explosions, or contact sports [3].
The incidence of TBI may continue to rise over time due to increases in population density, population aging, and the growing use of motor vehicles, motorcycles, and bicycles [4].
This complex injury spans a spectrum from mild TBI (mTBI) to the most severe forms. While severe TBIs often result in devastating brain damage and are typically easily diagnosed, it is crucial to recognize that mTBI may not exhibit objective manifestation on standard clinical magnetic resonance imaging (MRI) scans. However, it still causes significant long-term health risks over the years [5]. Additionally, mTBI constitutes 80–90 percent of all TBI cases, highlighting its substantial prevalence and impact [6].
The complexity of TBI contributed to the proposal of various alternative mechanisms for explaining its development. However, the mechanism by which skull accelerations cause neurological impairment remains incompletely understood. Nevertheless, all hypotheses agree that injury is caused by head acceleration or deceleration, regardless of whether the impact is applied directly or indirectly [7,8].
Another significant aspect to consider is that what is known about TBI comes mostly from preclinical and clinical studies of male subjects. As a result, there are large gaps in the understanding of gender-related differences [3]. Recent trends show increased women’s involvement in sports and active military duty. Additionally, there is growing awareness of the significant number of women who experience TBI due to Intimate Partner Violence (IPV) but do not report it. This suggests that the number of women with TBI is significantly higher than previously believed [9]. Also, the emerging body of recent studies aimed at detecting the effects of biological sex suggests that young women (those in the premenopausal stage) are more likely to die from TBI compared to men of the same age group [9].
Age also plays an important role in TBI research. The impact of TBI varies depending on age group, with different groups facing specific challenges.
In elderly people (>65 years), TBI is often associated with falls due to physical changes resulting from aging, leading to a higher susceptibility to head injuries and elevated mortality rates [10,11]. However, comorbidities and cognitive and functional impairments in this age group complicate the clinical diagnosis of TBI. Children and adolescents are in a critical stage of brain development. TBI in this age group can impact cognitive and emotional development, particularly in children under 4 years old, whose brains are rapidly evolving.
Sports-related TBIs have gained media attention due to their risks to brain health, potentially leading to Chronic Traumatic Encephalopathy (CTE) over time [5].
Computational modeling using biofidelic finite element models is an increasingly promising approach for understanding the mechanopathological mechanisms underlying TBI [12,13,14].
Over recent decades, significant advancements have been made in improving these models’ biofidelity and predictive capacity. The enhancements in model validation scores can be attributed to several factors, including the improved representation of cranial tissue anatomy, better depiction of interactions among intracranial tissues, and the utilization of more representative constitutive models to describe tissue mechanical behavior mathematically.
Despite these improvements, the mechanistic roles of specific intracranial tissues during TBI remain unclear, potentially limiting the ability of finite element models to drive the development of effective safety measures. The meninges, notably the human dura mater, have conventionally been overlooked. There is a limited body of literature exploring their role in the course of a TBI [15]. Due to their relatively rigid mechanical behavior and their proximity to the comparatively soft brain tissue, the meninges have been shown to have a significantly influential role in the mechanopathology of TBI, influencing the concentration of trauma on various brain structures [16].
To better understand the mechanical behaviour of the brain and its injured regions in the context of TBI, including the dura mater, this study proposes the development of a Female Finite Element Head Model (FeFEHM). Currently, there is an already developed FeFEHM representative of an elderly female subject [17]. The goal is to develop the second FeFEHM that will represent the middle-aged life stage.
The developed FeFEHM will be useful for research related to neurodegenerative diseases and replicate case studies of real-life events. With it, it will be possible to imply injury tolerance threshold limits based on the literature. This could be helpful if applied in sports, domestic violence, and other causes that might lead to TBI.

1.1. Objectives

This work aims to develop a detailed female model using medical images from computerized tomography (CT) and MRI of a middle-aged female subject (57 years old) to represent the principal head constituents. The model intends to represent the middle-aged female population, enabling comparisons with existing models based on the male population and a previous FeFEHM representative of the elderly female population. The work is structured as follows:
  • Segmentation of the main head components, including two brain hemispheres (with gray and white matter differentiated), cerebellum and brainstem, corpus callosum, cerebrospinal fluid (CSF), dura mater and skull;
  • Development of subject-specific finite element meshes and material models for all constituent structures of the model.
  • Validation of the FeFEHM using recent experimental data from unembalmed cadaveric subject heads;
  • Conducting a case study of a real scenario resulting in mTBI to assess the future potential of the FeFEHM.

2. Methods

In this section, the development of the FeFEHM is described. It starts with modelling steps necessary to obtain the geometry of the finite element mesh. Next, the model validation process is explained, and finally, the future potential of the model is tested by implementing a case study.

2.1. Segmentation

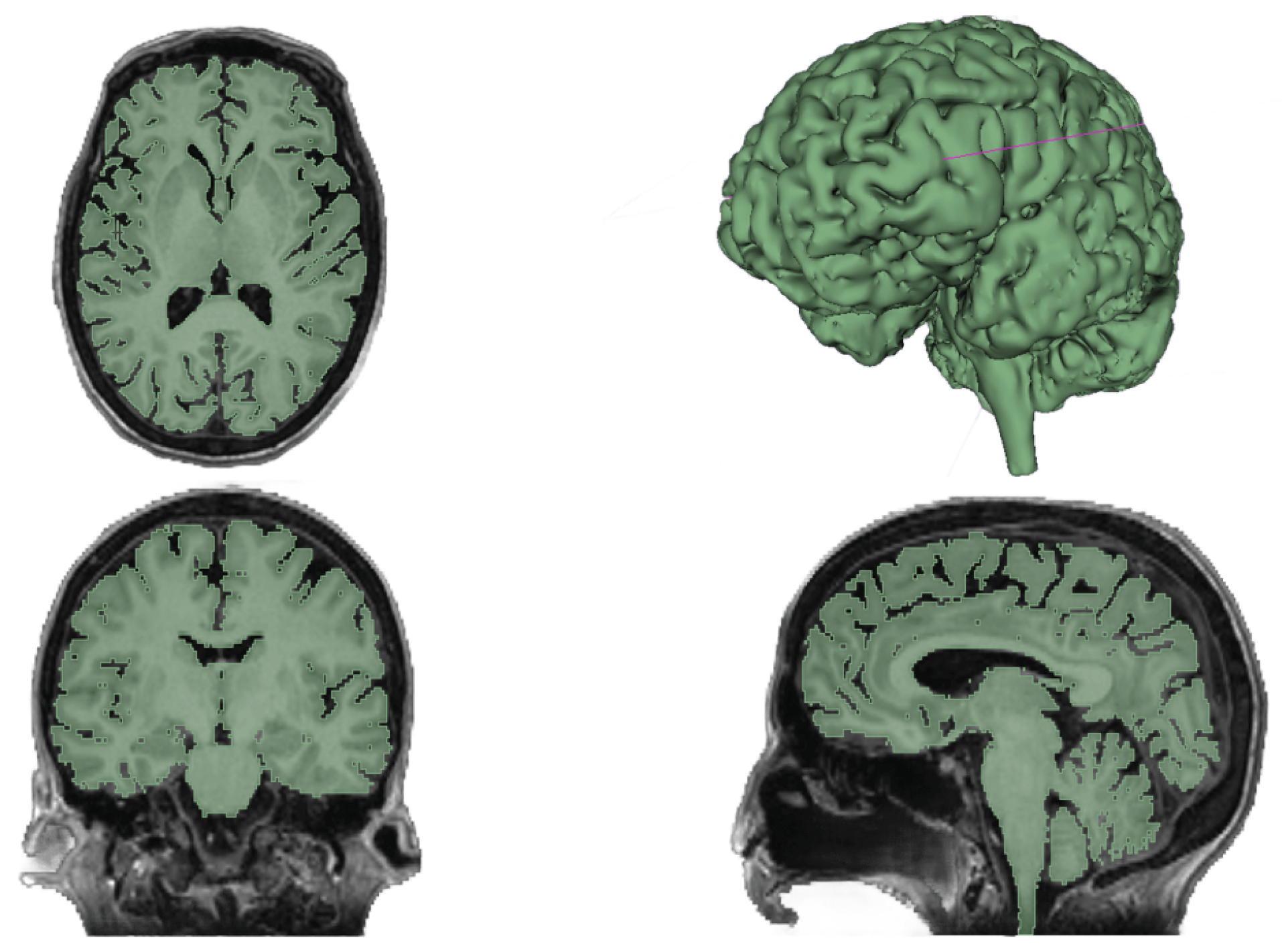
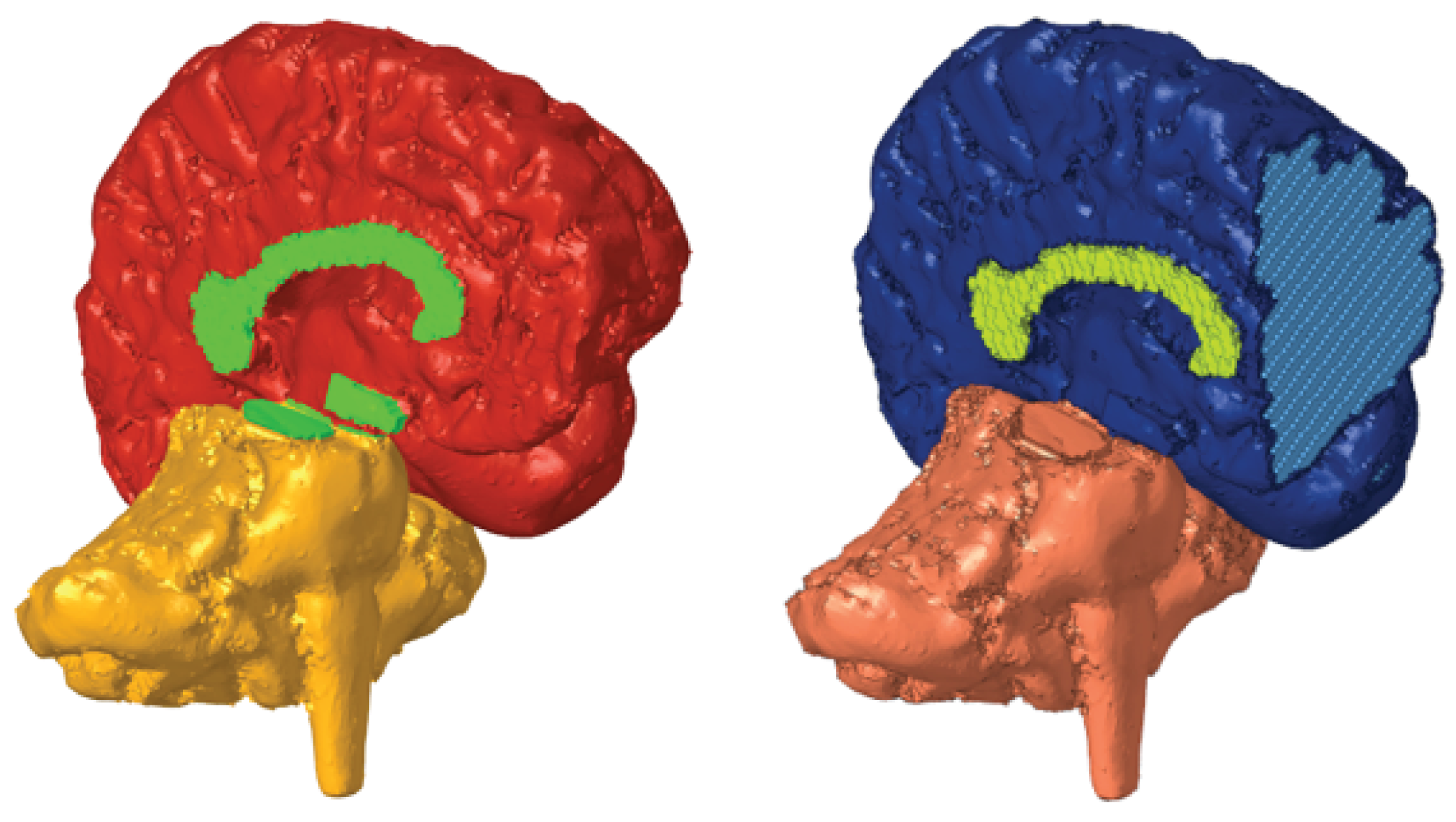
This study used medical images from a middle-aged woman (57 years old) with a healthy brain for the segmentation process. Regarding soft tissues such as the brain, MRI was employed, while CT was chosen for skull segmentation. Both segmentations were conducted using 3D Slicer, a platform for subject-specific image analysis, visualization, and clinical support.
The segmentation involved several processing tools to segment the brain and its different structures accurately. Even though the structure appears to be clearly delineated in the medical images, the brain cannot be precisely represented by a single threshold due to the presence of other irrelevant soft tissues in the head. Therefore, other tools could remove any isolated or irregular voxel groups and perform a phased segmentation by selecting brain tissue and growing it until all brain tissue was covered. The segmentation results from the MRI of the soft tissues are illustrated in Figure 1.
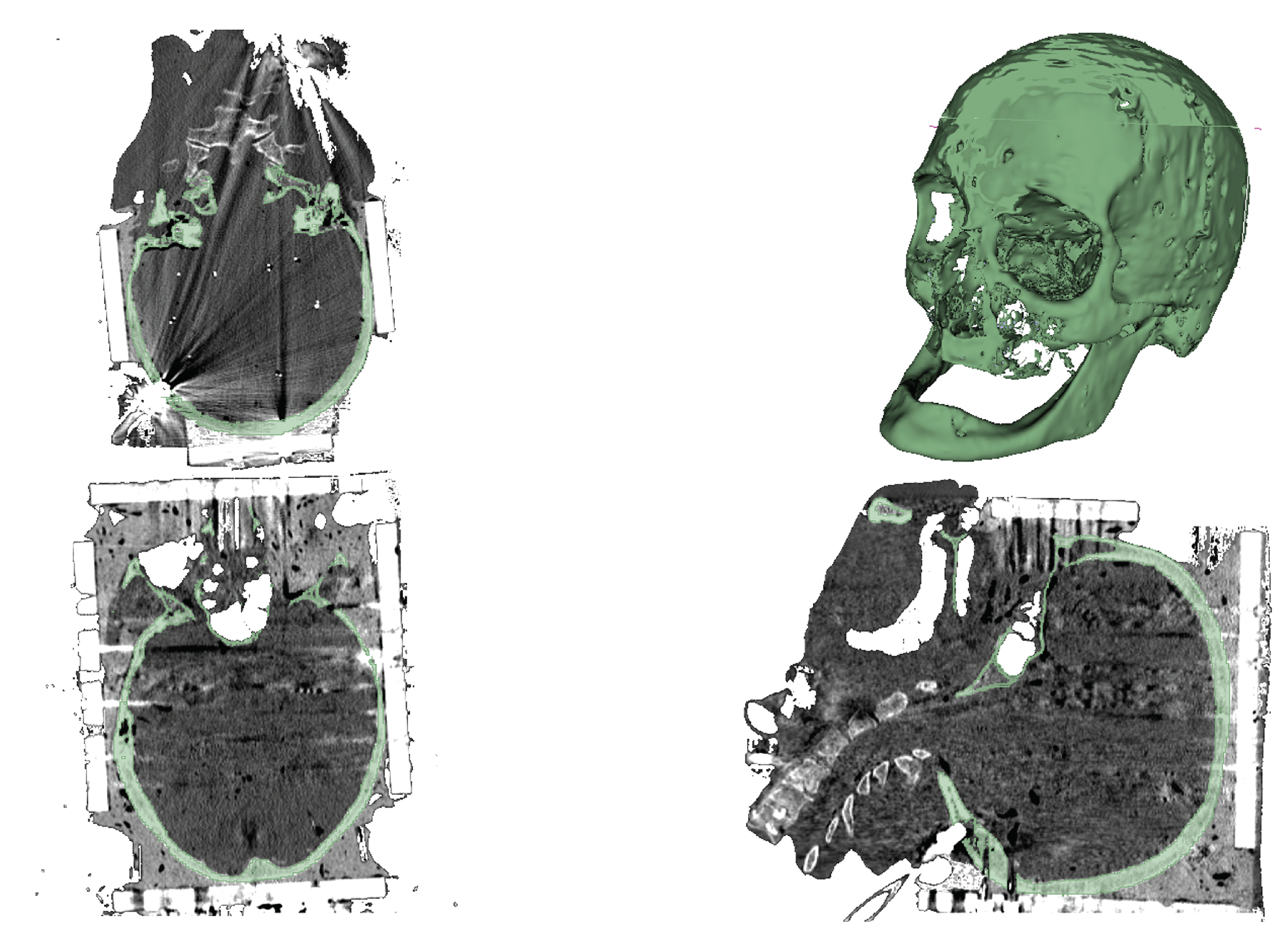
In the skull segmentation, an initial threshold was applied to separate the skull from the rest of the image. However, due to the presence of a metal box on the head during the CT scan, reflections and noise compromised the image quality. To address this issue, the initial threshold included the bones, the metal, and its reflections. The subsequent and final step involved manually removing parts of the image that did not correspond to the skull bones. The results can be seen in Figure 2.

2.2. Surface Geometry Correction

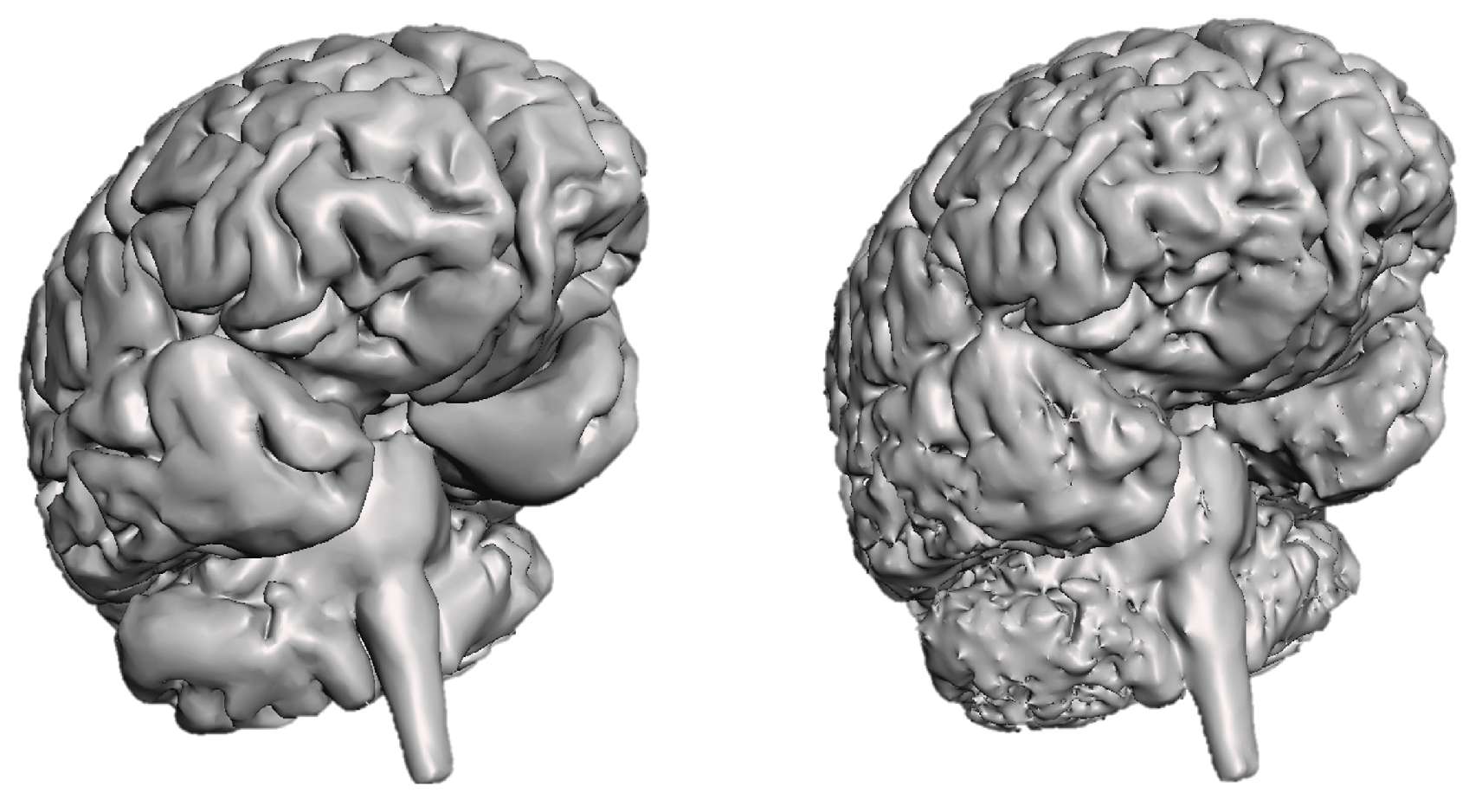
After segmentation, both geometries had imperfections due to software limitations and image quality. Autodesk Meshmixer, along with an anatomical atlas, was used to rectify them. The mesh was reduced to a reasonable number of elements, and hidden defects were automatically detected and corrected.
For the brain geometry, the main concerns included defining sulci, separating hemispheres except for the corpus callosum, and connecting the cerebellum to the brain via the brainstem. These corrections’ results are presented in Figure 3.
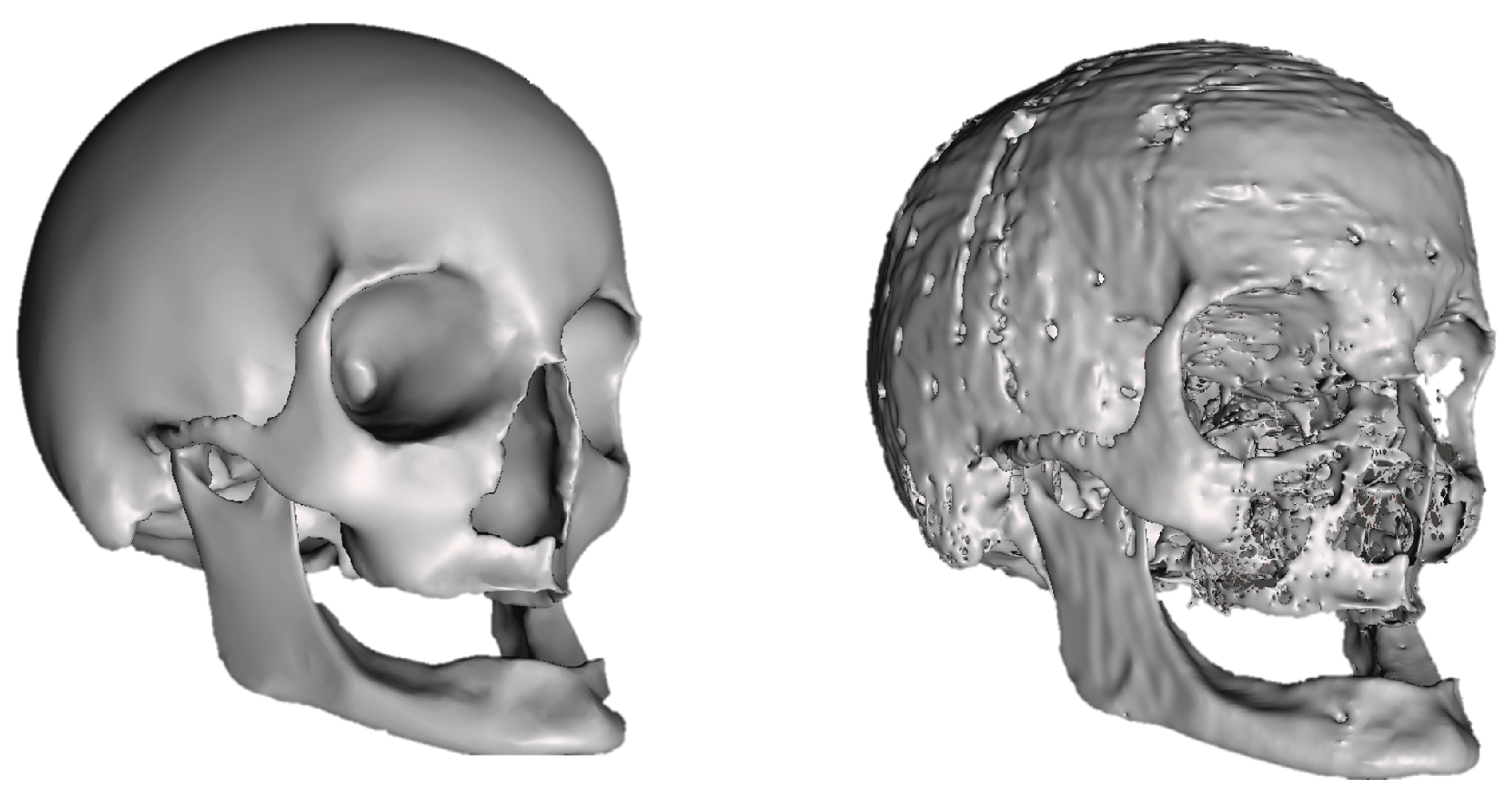
Regarding the skull geometry, key priorities included accurately recreating it from segmentation data and simplifying non-essential structures to expedite simulation time. Additionally, the mandible was connected to the main skull structure for analysis convenience. All skull openings were closed except for the foramen magnum to prevent CSF leaks during simulation. The surface geometry correction of the skull is illustrated in Figure 4.

2.3. Meshing

After obtaining the final brain and skull geometries, the files were exported to Altair® Hypermesh®, a finite element pre-processor. Using a CAD geometry file, this software enables the generation of a mesh and the exportation of a finished ready-to-run solver file. Therefore, for the purpose of this work, this software was used to segment different brain parts and generate and edit the multiple FE meshes of the brain, skull, and CSF.

2.3.1. Brain Tissue Meshing

Recent works on the Finite Element Human Model (FEHM) [17,18,19] utilize hexahedral meshes to define the brain, as quadratic hexahedral elements are more stable and versatile in terms of locking phenomena circumvention and less influenced by mesh refinement compared to tetrahedral meshes [17,18,19].
Due to the brain’s complex geometry, initially attempting a single mesh led to incorrect connections between hemispheres. Therefore, the brain was segmented into different parts for individual meshing. While using smaller elements could provide more precise geometry, it required unavailable computational resources. To address this, the brain geometry was divided by the Corpus Callosum and Hypothalamus to separate the cerebral hemispheres and by the Cerebral Penducles to separate each hemisphere from the Cerebellum and Brainstem.
The next step involved creating new surfaces to close these openings, ensuring a solid mesh. Two parallel surfaces were created for each opening, resulting in eight new surfaces. However, due to some imperfections in the geometry, these new surfaces couldn’t completely close the openings. Therefore, new elements were created to connect the brain surface to the closing surfaces.
After closing all brain parts, meshes were generated for each, with an average element size of 1 mm3 and a minimum Jacobian value of 0.3. Each component underwent evaluation to identify intersections or distorted elements, which were manually corrected or removed. Intersections were assessed using the "penetration" tool, identifying elements intersecting between hexahedra of different or the same component. Meanwhile, distorted elements were identified using the "check elements" tool with the requirement "Jacobian value < 0.3 ". New elements were created (Figure 5) to connect brain parts, with varying thicknesses depending on the region. All elements were reviewed for distortions or intersections.
To distinguish between GM and WM, three layers were selected inward from the outer layer of the cerebral hemispheres, corresponding to GM. This selection was based on previous studies that found an average GM thickness of approximately 2.589 mm [20,21,22]. The selected elements were assigned to GM, while the remaining elements were assigned to WM.
The corpus callosum was assigned to an individual property. Whereas, the cerebellum and brainstem were assigned to the same property, as well as the connecting elements in cerebral peduncles. Meanwhile, the connecting elements in the hypothalamus were assigned the same property as GM, as shown in Figure 5. The creation and assignment of properties were done in preparation for future material modelling.

2.3.2. Skull Meshing

The approach to mesh the skull was similar to the first attempt at the brain. That is, a solid mesh was created with 1 mm3 hexahedra and 0.3 as the minimum Jacobian value considered. After checking for distortions and intersections, a property was assigned to the new meshed elements.

2.3.3. Brain and Skull Assembly

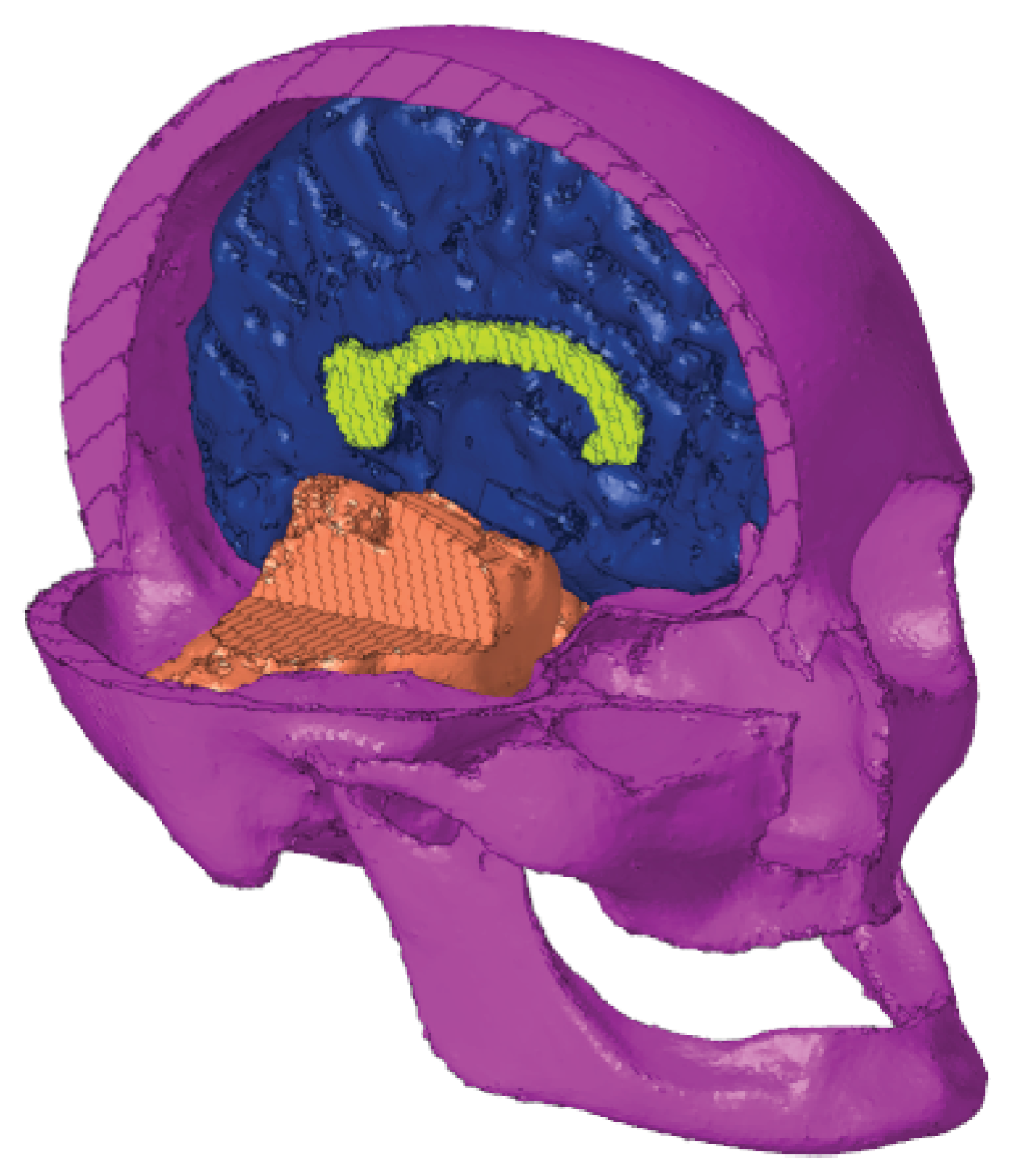
The next step in the meshing process was the assembly of the brain and skull. To do this, the meshed skull was imported to the same file as the meshed brain. Due to the fact that the skull and geometry were obtained in different scanners, their coordinate systems were not aligned. Therefore, there was an iterative process of manual translations and rotations of the skull and checking for intersections until the brain was inside the skull without intersections (Figure 6).

2.3.4. Cerebrospinal Fluid Modelling

The CSF was generated from aligned brain and skull surfaces, filling the subarachnoid spaces around the brain, spinal cord, and cerebral ventricles. CSF acts as a shock absorber, cushion, or buffer, providing basic mechanical and immunological protection to the brain inside the skull.
After creating a component with the brain and skull surfaces, they were converted into triangular elements for compatibility with Meshmixer. In Meshmixer, geometry adjustments were made, including flipping the normals of the elements due to the geometry being inverted, deleting the external surface of the skull and the tip of the spinal cord, and allowing connection between the inner surface of the skull and the spinal cord. Following these adjustments, the CSF geometry was defined and imported back into HyperMesh, where a solid mesh was generated with 1 mm3 hexahedra and 0.3 as the minimum Jacobian value considered. 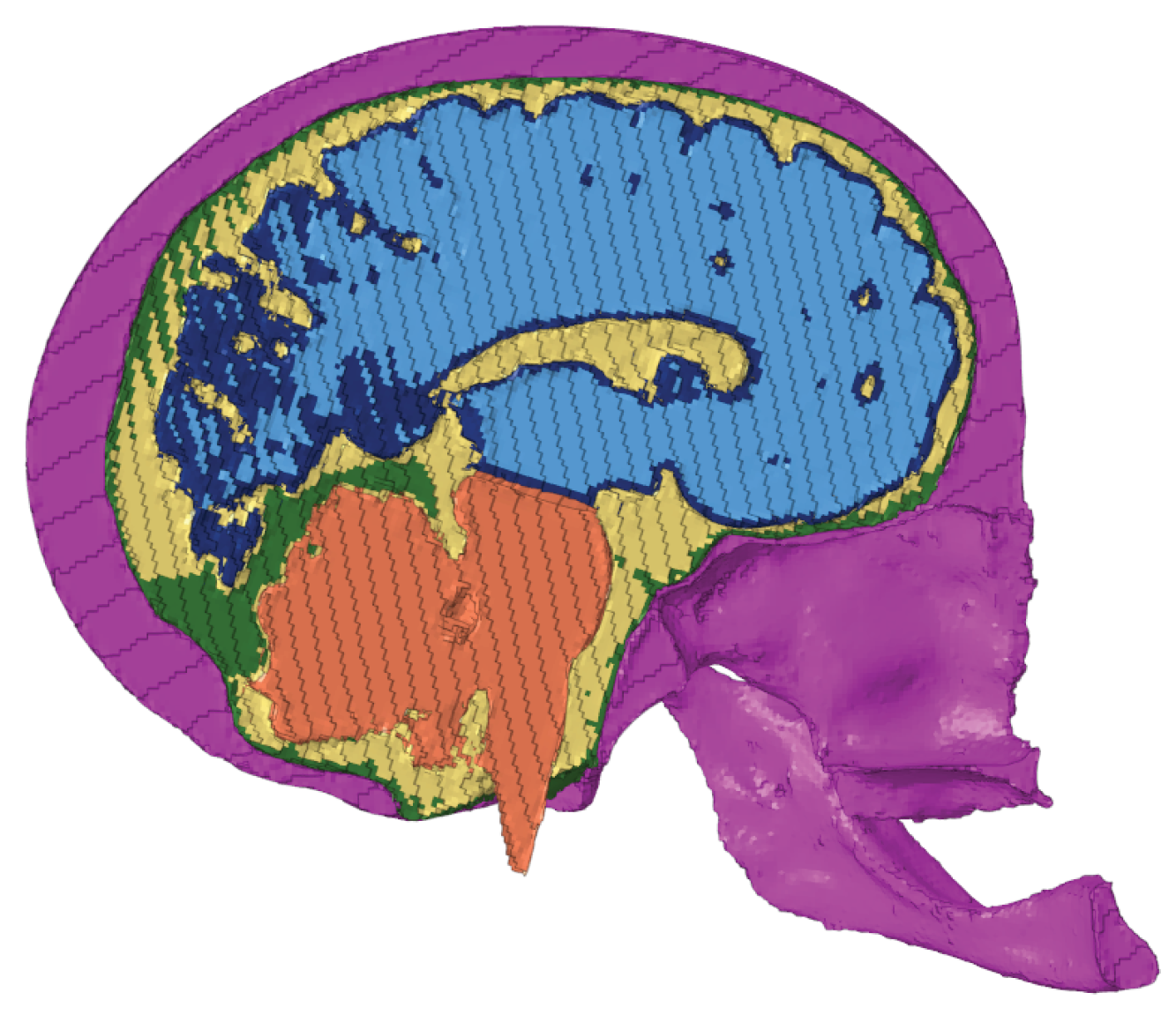The resulting mesh was then evaluated to identify and correct distortions or elements causing interference, and a new property was assigned to the elements representing the CSF (Figure 7). The model was saved and exported to Abaqus (Dassault Systèmes®).

2.3.5. Dura Mater Modelling

In an attempt to achieve a more realistic FEHM, a dura mater was created. Despite the significant role of cranial meninges that provide protection to the brain tissue in head injury mechanics, the understanding of their mechanical behavior and structural composition remains limited [15]. Therefore, it is crucial to include them in this FeFEHM to facilitate their investigation. With these in mind, there was created a duplicated of the model until now and added the meninge.
Obtaining the dura mater was achieved in Hypermesh using the existing CSF. From the latter, the two outer layers of elements were selected and were anatomically corrected to correspond to the dura mater. A new property was created and assigned to these elements.
One thing that was taken into account while correcting the geometry of the dura mater was its thickness. The thickness influences the stress and strain behaviour of the implemented dura mater. According to the literature, the dura mater has a non-uniform thickness across the complete surface of the brain [23]. The region of most interest is around the falx cerebri, therefore its thickness was set to 1 mm, as it is often implemented in FEHM [24,25]. The resulting dura mater is presented in Figure 7.
In this head model, hexahedral elements (C3D8R) are assigned to every property. The numbers of elements and nodes in each property are detailed in Table 1.

2.4. Material Modelling

After uploading the model file in Abaqus, it was time to assign the material parameters to each property. These parameters are summarized in Table 2.
The recent work (2022) by Hasgall et al. [26] was taken into account for the value of density for all properties. The skull was considered rigid due to the brain being the subject of this study.
According to Kegel et al. [25], the majority of FEHM represent dura mater as a linear elastic material model with the Young’s Modulus (E) and Poisson’s Ratio ( ν ) based on Galford and McElhaney tensile tests [27]. Therefore, these parameters were chosen for this work.
Regarding CSF, its material parameters were chosen based on Gilchrist et al. [7] work, where the CSF is described using a Mooney-Rivlin formulation with a strain energy function Ψ MR with the form:
Ψ MR = C 10 ( I ¯ 1 − 3 ) + C 01 ( I ¯ 2 − 3 ) + 1 D 1 ( J e l − 1 ) 2 ,
where C 10 , C 01 and D 1 are temperature-dependent material parameters, J e l is the elastic volume ratio and I ¯ 1 and I ¯ 2 are the first and second deviatoric strain invariants [28]. The initial shear and bulk moduli are defined as μ = 2 ( C 10 + C 01 ) and κ = 2 D 1 , respectively. This approach was employed in recently (2018 and 2023) validated FEHM [29,30].
The work of Menichetti et al. [31] was selected to characterize the remaining properties of the brain. Even though this experimental work was performed in brains older than the one being modeled, it is recent and the most comprehensive study of the mechanical brain properties to date [32].
The mechanical properties of the brain were characterized by micro indentation in several brain regions. The response of the brain tissue to the indentation was described with a quasi-linear viscoelastic framework [33], where a standard relaxation function g ( t ) is used, taking the form
g ( t ) = g ∞ + ∑ i = 1 N g i e ( − t / τ i )
where g i is the i-th relaxation modulus, τ i is the i-th time constant and g ∞ is the long-term relaxation modulus.
The non-linear elasticity is characterized using a neo-Hookean constitutive law that uses a strain energy function Ψ H , with the formulation
Ψ H = C 1 ( I ¯ 1 − 3 ) + 1 D 1 ( J e l − 1 ) 2 ,
where I ¯ 1 = ( J e l ) 2 / 3 ; I 1 = t r ( C ) and J e l = d e t ( F ) , in which F is the deformation gradient tensor and I ¯ 1 is the isochoric part of the first invariant ( I 1 ) of the right Cauchy-Green deformation tensor C . C 1 and D 1 are material-dependent parameters defined as C 1 = μ 0 2 and D 1 = 2 10000 × μ 0 respectively, in accordance with the work of Menichetti et al. [31].

2.4.1. Validation

When a model is created, it needs to be validated to ensure the biofidelity of the results. Validation of a finite element head model involves comparing simulation data with experimental data. A recent study by Alshareef et al. was chosen due to its inclusivity (including both male and female individuals with displacements in all three anatomical planes) and its potential for future FEHM validations [34,35].
The geometry to create the FEHM was obtained from medical images of subject 896 from this study. Coronal rotation was considered due to its impact on the duration of post-traumatic loss of consciousness and the severity of axonal injury in primates [8,36]. Receiver coordinates in the brain were used for comparison with the FEHM.
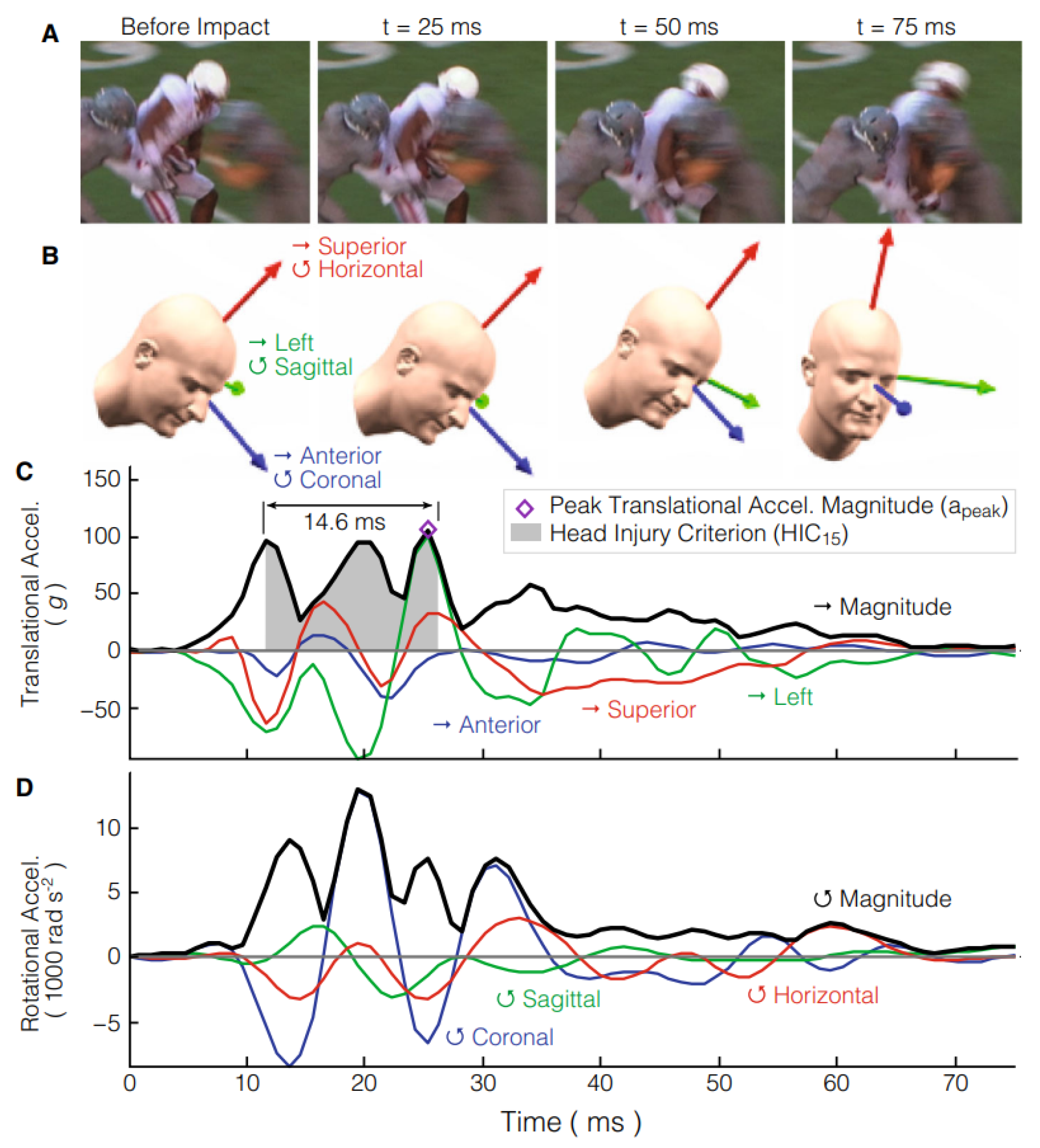
In the experiment, four different accelerations were applied for each anatomical rotation (sagittal, coronal, and axial). For the purpose of this work, the slowest acceleration curve over the longest period of time was selected (20 r a d / s 2 over 60 ms) consistent with the study of mTBI.
The identification of the Anatomical Center of Gravity (CG) is crucial to ensure that rotation is applied through it with the rotation axes oriented orthogonally to the main anatomical planes of the head. This reference point was used as the basis for the local head coordinate system, where all brain deformation and kinematic data were transformed, following the same method as in the experiments by Alshareef et al. [35].
Twenty-four sonomicrometry crystals (receivers) were inserted into the brain, numbered from 9 to 32 according to the channel they were plugged into in the sonomicrometry data acquisition box. The corresponding numbers were used to represent each receiver, allowing for comparison between the results of the experiments and the simulation. The coordinates of each receiver were obtained from Alshareef et al. following the SAE J211 standard [37]. In Abaqus, twenty-four reference points were created, whose coordinates are detailed in Table 3.
The displacements presented in the work by Alshareef et al. [35] are the trilaterated trajectories relative to the initial coordinates of the receivers. Sets were created for the brain matter nodes closest to each receiver’s reference point to record triaxial displacement.
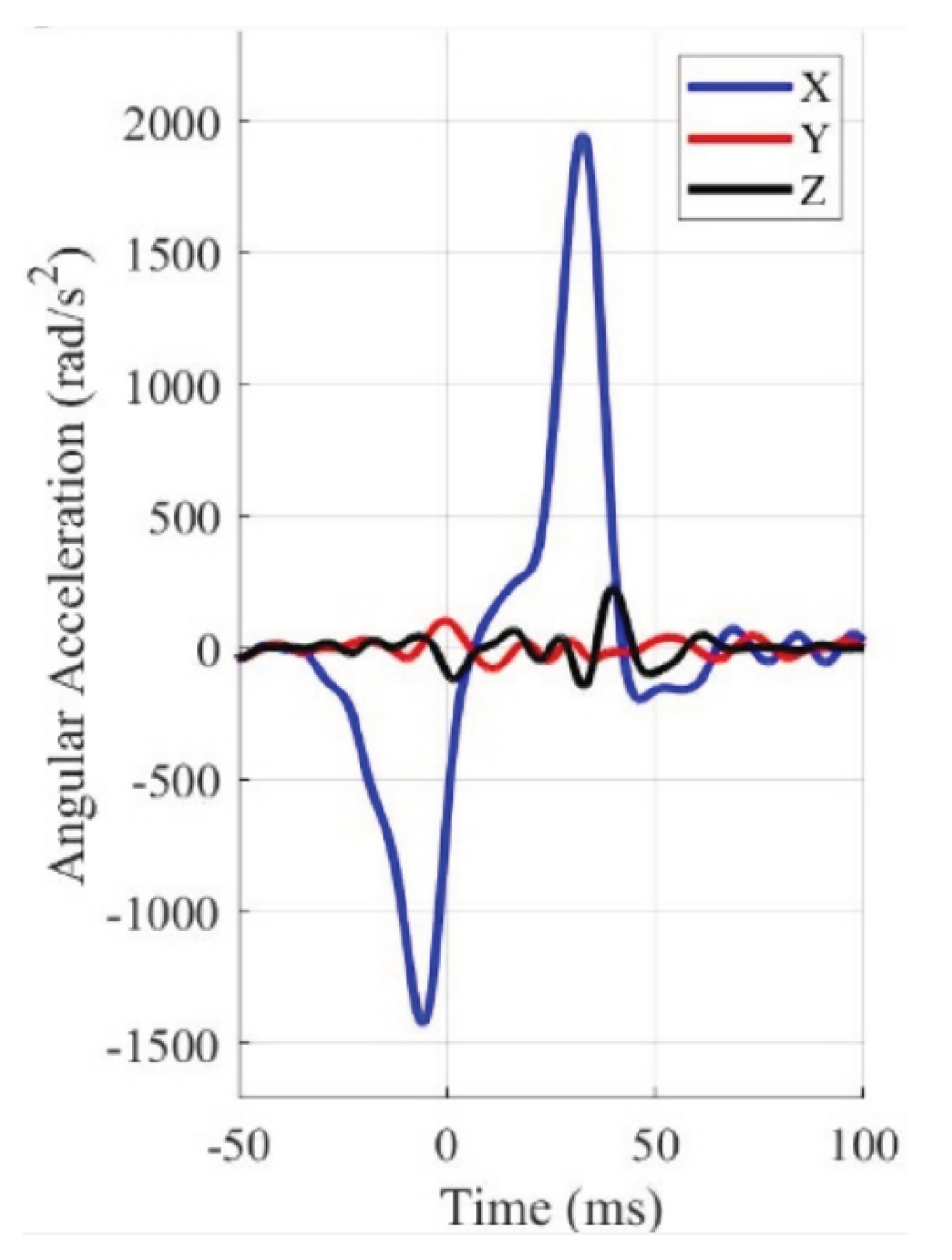
The angular acceleration curve that was chosen for this work (20 r a d / s 2 over 60 ms) is represented in blue in Figure 8. It was extracted with WebPlotDigitizer [38] from Alshareef et al. [35]. In Abaqus, only the curve with positive time stamps was considered, where the first input was manually introduced as 0 ms with 0 r a d / s 2 . These inputs were introduced as an amplitude with the correct unit system.
This experiment is replicated using pure rotation, where the entire head rotates around a single axis. The head rotates "side-to-side" along the x-axis, normal to the coronal plane. Angular accelerations around other axes were considered negligible for validation purposes.
A step was created with a time period corresponding to the last input time value in the angular acceleration curve, in this case, 97 ms. A general contact interaction was established, where contact between parts was considered frictionless in the tangential direction. A total of 50 "field output requests" were created, one for the entire model with a frequency of 1 ms, with output variables including stresses, strains, displacements, reaction forces, contact stresses, and void/material volume fraction in elements. The next 49 "field output requests" also have a frequency of 1 ms, with output variables being translations and rotations (U) for each receiver’s node, receiver’s reference point, and CG.
Two types of constraints were created: "Rigid Body" and "Coupling". A "Rigid Body" connection was defined between the CG and the skull nodes, allowing rotation of the skull around the CG. A "Coupling" constraint was created between each receiver (set of reference points) and the CG. These kinematic ties on all six degrees of freedom ensure that the reference points maintain their relative position to the skull. This resulted in a total of 25 constraints.
Two boundary conditions were established, the first one being the input of the angular acceleration curve on the CG. Although a point cannot rotate mathematically, Abaqus allows for the rotation of reference points, which enables the motion of the skull through the CG (due to the restriction between the CG and the skull). The other boundary condition pins the CG to prevent translations in all three orthogonal directions. It solely serves as a fail-safe.

2.4.2. Case Study

Among the causes that can lead to TBI such as falls or traffic accidents, this study explored dynamics in a sports scenario.
This study is based on Hernandez et al. research [39,40]. The author focused on investigating whether direct measurement of head rotation improves the prediction of mTBI. Six degrees of freedom (6DOF) of translational and rotational head kinematics were measured. These preliminary data were used to evaluate the deviation of existing injury criteria from a perfectly predictive model.
These measurements were achieved using instrumented mouthguards equipped with triaxial accelerometers and gyroscopes, along with a microprocessor to record the kinematic sensor measurements at 1 kHz for 10 ms before and 90 ms after the triggering acceleration. These mouthguards were fixed to the upper dentition for a close approximation of skull motion. High-definition videos of all athletic events were recorded to refine the mouthguard dataset for investigating injury biomechanics. Participants recruited for this study were individuals exposed to repeated head impacts during various athletic conditions.
In the present study, the impact on the head of a collegiate American football player during a regular season game resulting in a mTBI that caused loss of consciousness (LOC) was analyzed. To complement the study, simulations of head impacts were conducted to better understand how head kinematics produce stress and strain in the brain. These simulations utilized a FEHM developed in Sweden at KTH Royal Institute of Technology in Stockholm [41]. This model represents an average adult male head, incorporating components such as the scalp, skull, brain, meninges, CSF and eleven pairs of parasagittal bridging veins, differentiating between WM, GM and the ventricles. The KTH FEHM was validated against displacement data from cadaver head impact experiments performed by Hardy et al. [42,43].
The approach to this case study was similar to the methodology described earlier, except for the receivers and outputs. In this case, there was no displacement of receivers as output to analyze the results. Instead, pressure was considered for the whole head.
While in the validation, only a coronal rotational acceleration was implemented, in this case, there were applied acceleration curves for all 6DOF of the CG. These curves were retrieved from Figure 9. As shown in this figure, the acceleration curves are not in accordance with the coordinate system described in the previous chapter. Therefore, when implementing the boundary conditions of the acceleration curves, special attention was paid to correctly applying the accelerations according to the axes.
In the context of mTBI, the results are more relevant at the peak acceleration magnitude that, in this case, happens around 25 ms. With this in mind, the simulation was terminated shortly after the peak acceleration time to reduce its overall runtime. There were performed three simulations: one with the model developed for this work with dura mater and one without, and the third was with the FeFEHM representative of an elderly subject.

3. Results

3.1. Validation Results

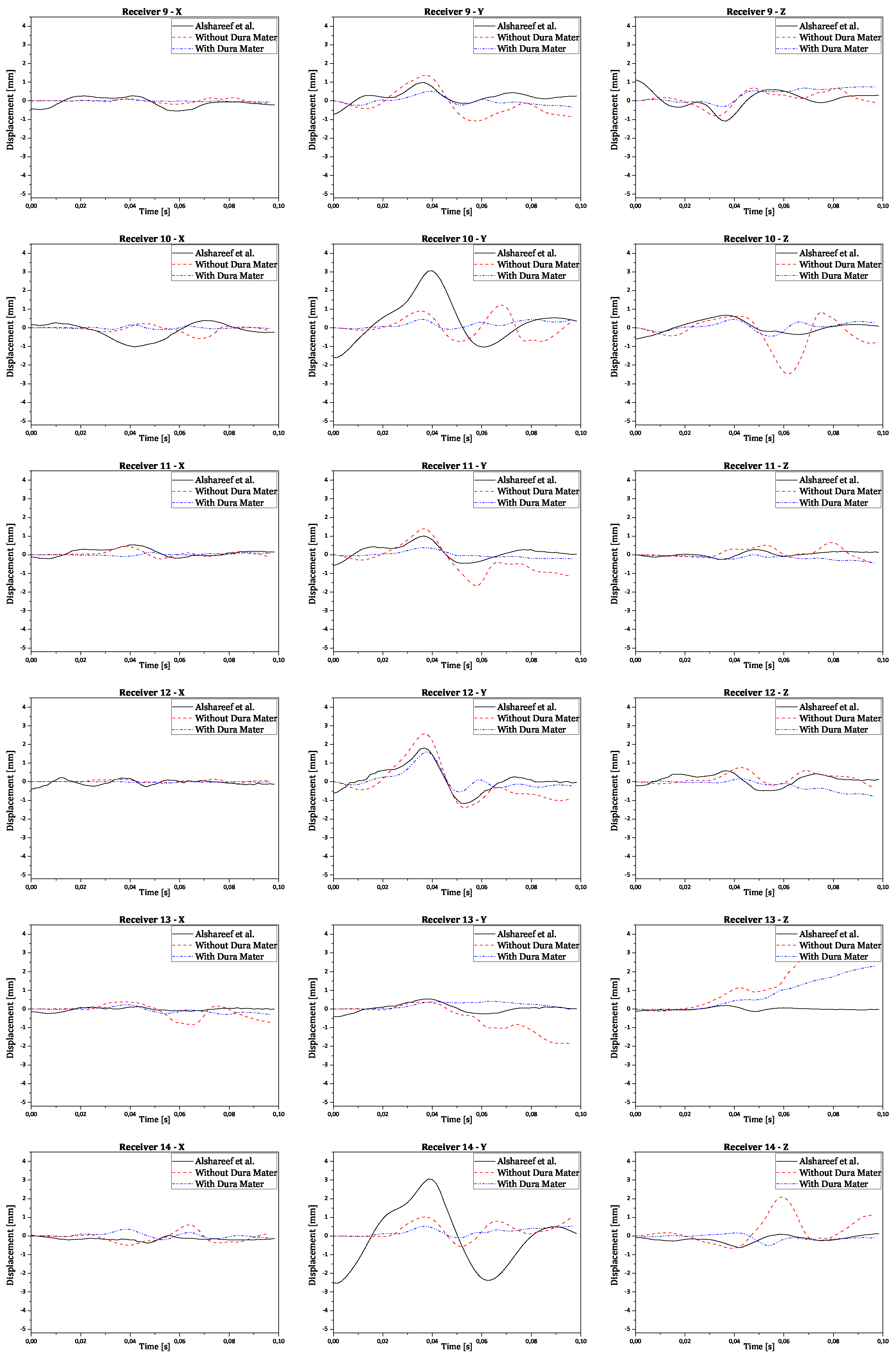
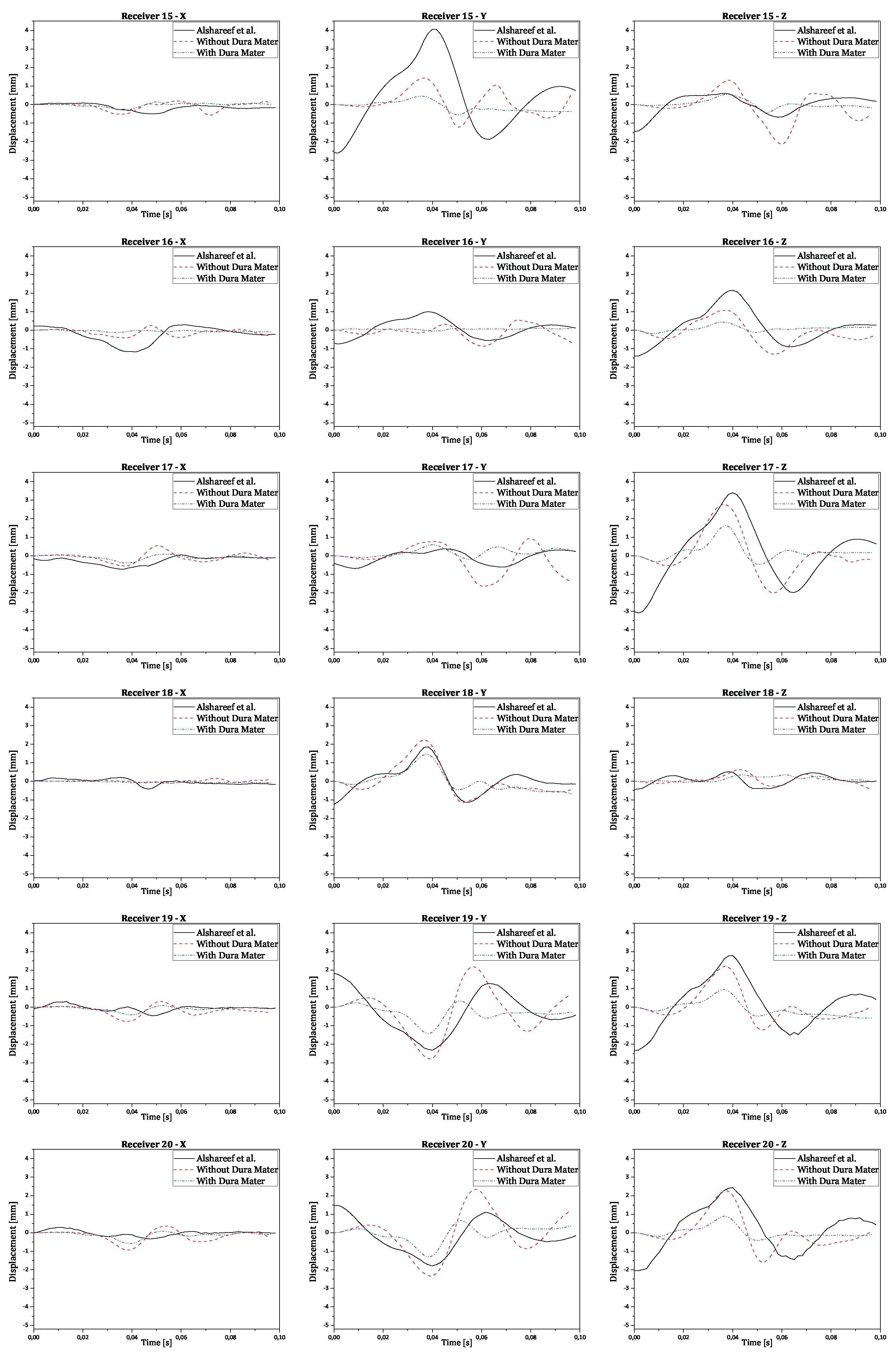
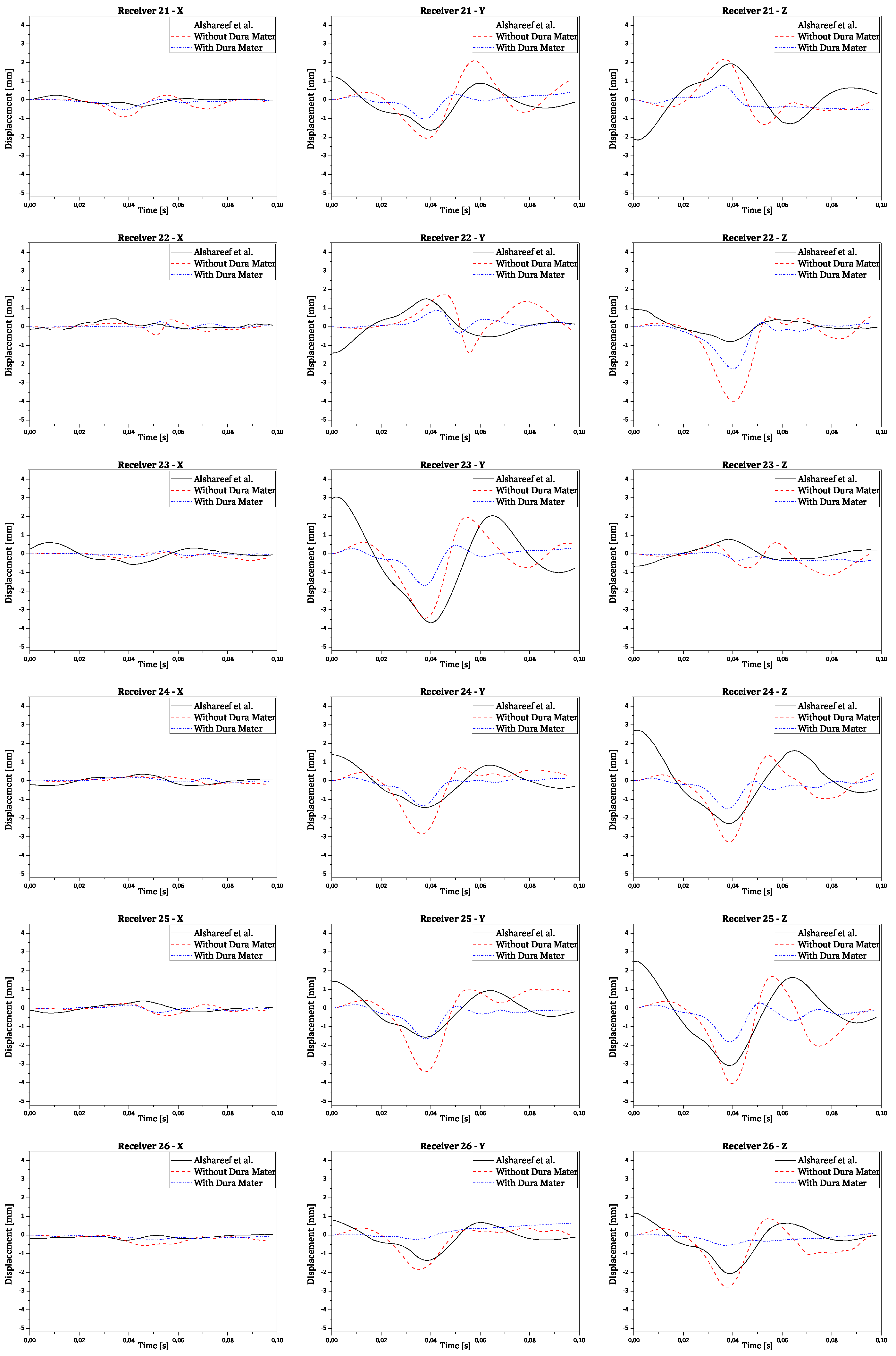
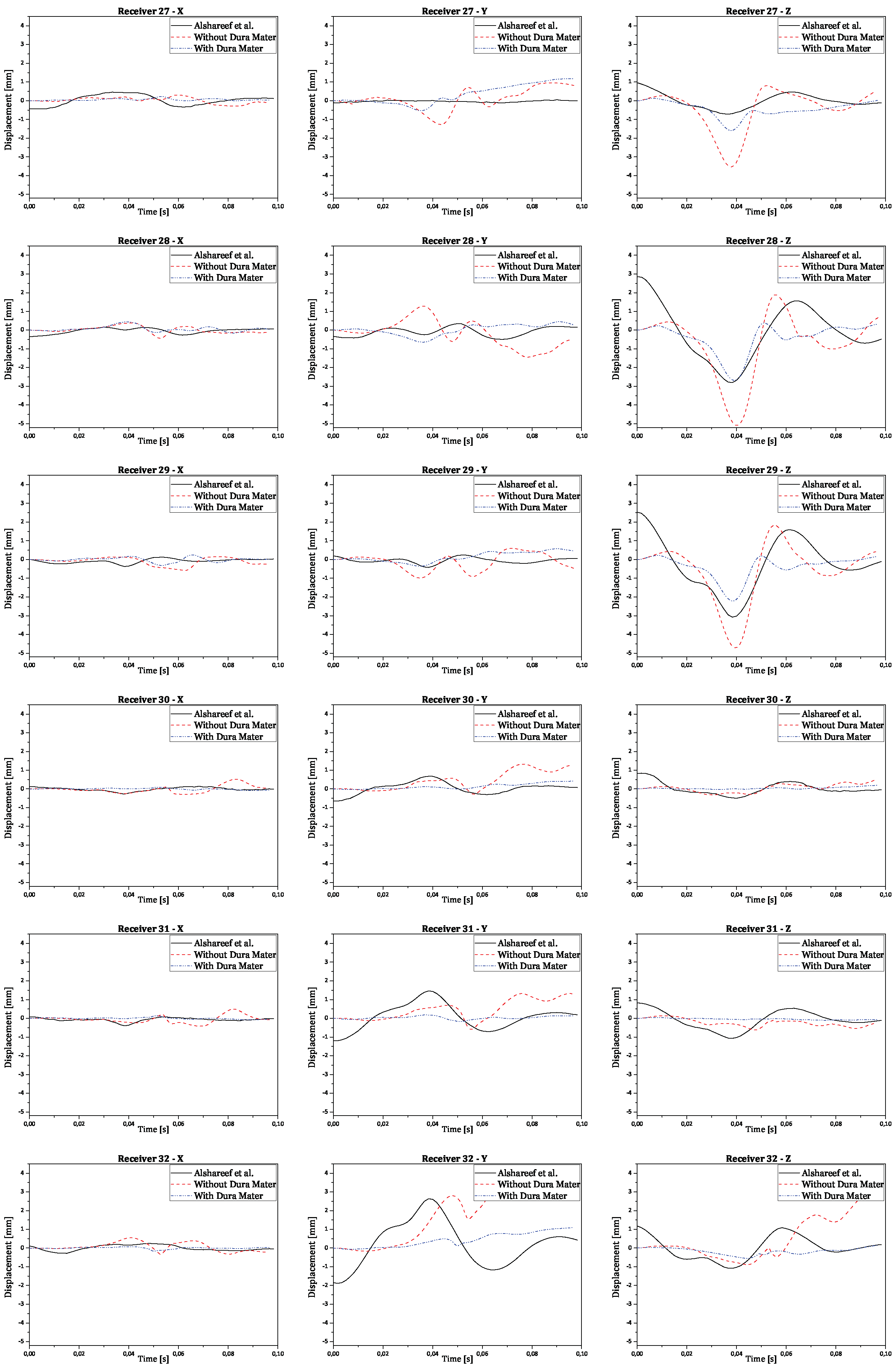
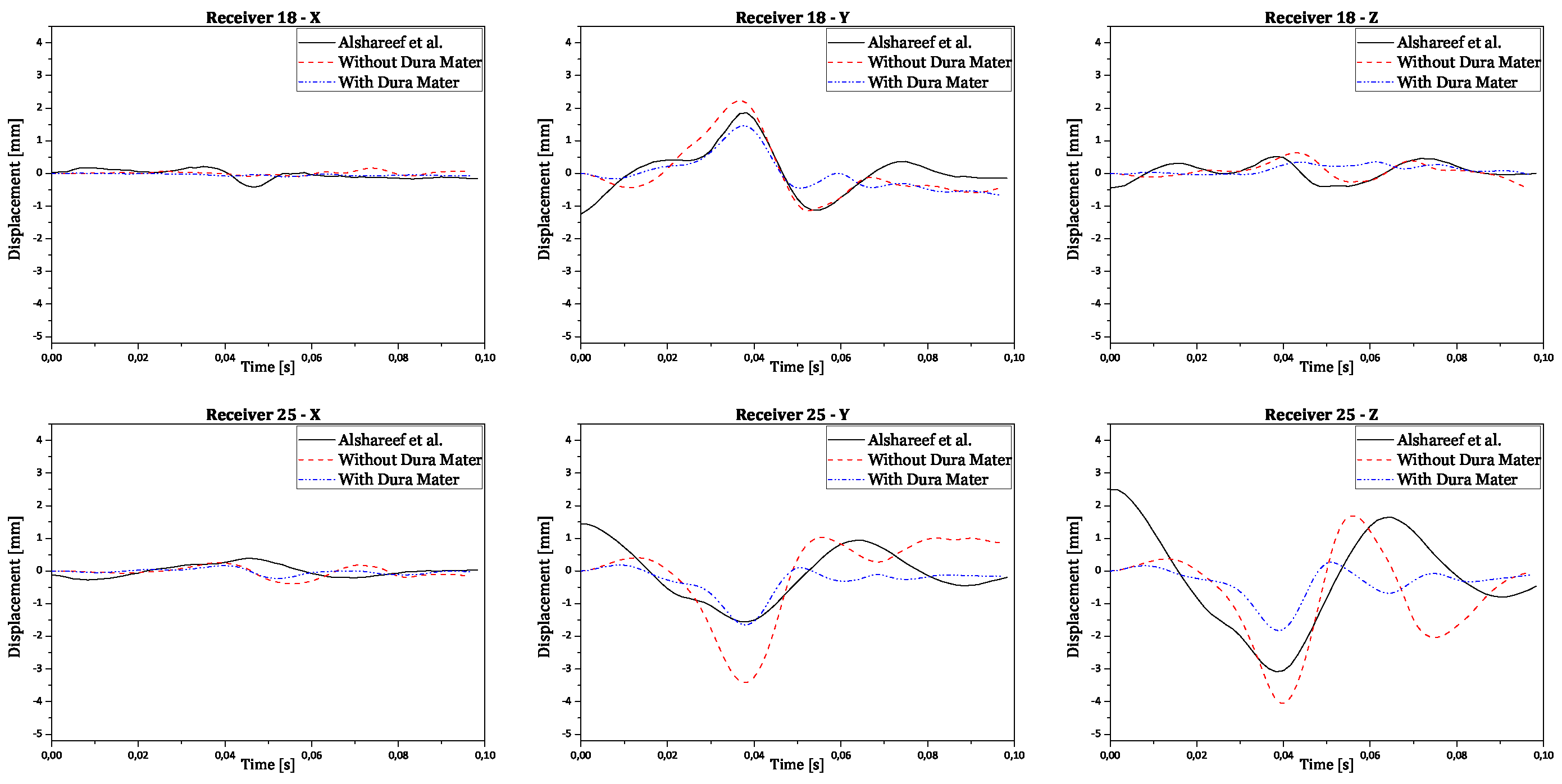
Regarding validation, the displacement results in all three orthogonal axes were obtained by subtracting the reference point coordinates from its node coordinates. This ensures the displacement is relative to the initial brain position, instead of the absolute positioning of the brain nodes in relation to the CG. The final numerical curves obtained were compared to each corresponding experimental and numerical curve. The full results are presented in the Appendix A. In Figure 10 there are shown two examples of trilaterated displacements of receivers 18 and 25.

3.2. Case Study Results

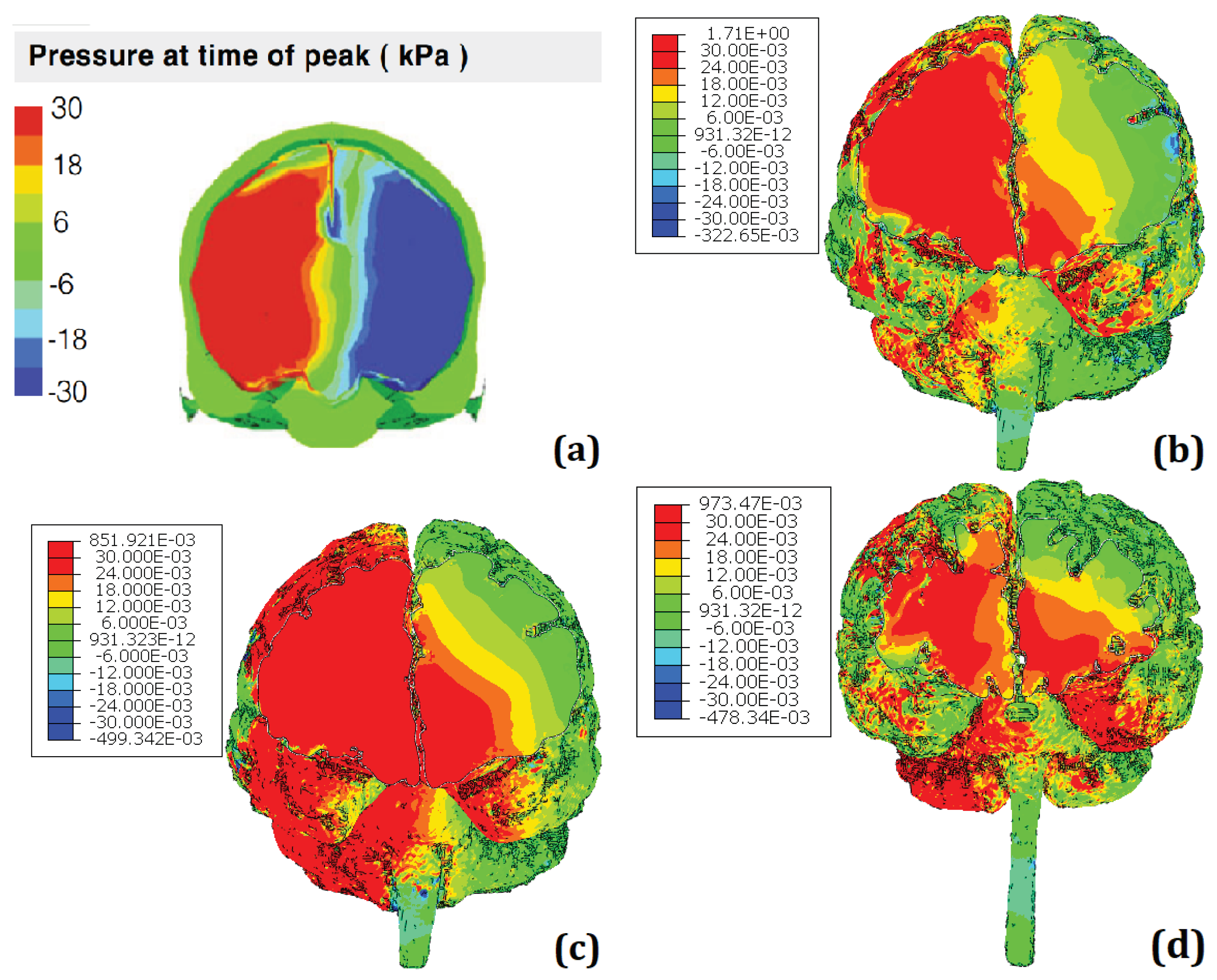
Figure 11 presents the comparison between the results of the simulations regarding the head impact that lead to LOC. It is worth noting that the scale of KTH FEHM (image a) is in kPa and peaks at 30 whereas the scale for the other FeFEHM is in MPa and peaks above 30. Therefore, the colour scale used to represent the intracranial pressure field on the FeFEHM was set to peak (represented by the colour red) starting at 30 kPa. Furthermore, to better visualize the results the skull, CSF, and dura mater were hidden.

4. Discussion

The complexity and severity of TBI represent a significant public health concern, being one of the leading causes of death and disability [1]. Despite the evident effects of moderate to severe TBI, there is less knowledge about the long-term outcomes of mTBI, partly due to the lack of immediate medical treatment seeking and the underestimation of the term ’mild’ [5]. Additionally, most TBI studies focus on males, leaving significant gaps in understanding the effects on females [3]. Age also plays a crucial role, with different age groups facing specific challenges.
Computational modeling using FEHM is a promising approach to understanding the underlying mechanisms of TBI [12,13,14]. However, the specific role of intracranial tissues during TBI remains unclear, which may limit the ability of finite element models to drive the development of effective safety measures. Meninges, especially the human dura mater, have been traditionally overlooked in the literature despite playing an important role in TBI.
This study proposed the development of a Middle-Aged FeFEHM to better understand the mechanical behavior of the brain and its injured regions in the context of TBI, including the dura mater.
In this study, the development of the FeFEHM is described. It begins with modeling steps necessary to obtain the geometry of the finite element mesh and the material modeling for all model structures to ensure accurate representation of their biomechanical properties in analyzing injury mechanisms and biomechanical responses associated with cranial trauma. Next, the model validation process is explained, and finally, the future potential of the model is tested by implementing a case study.
When a model is created, it needs to be validated to ensure the biofidelity of the results. FEHM validation involves comparing simulation data with experimental data. Experimental data from a recent study by Alshareef et al. were used, which included individuals of both sexes and considered displacement in three anatomical planes [34,35]. The geometry to create the FeFEHM was derived from the study’s medical images of a specific individual. Coronal rotation was considered due to its impact on the severity of post-traumatic LOC and axonal injury.
The displacements reported in the study by Alshareef et al. were used as validation data. The study was replicated using specific angular acceleration, with motion restricted to pure rotation around a single axis, the x-axis. The results were recorded for comparison with experimental data. This validation methodology aimed to ensure the accuracy and reliability of the FeFEHM by comparing simulation results with experimental data.
In Figure 10, validation results for receptors 18 and 25 are presented in each graph with three curves for the displacements of each receptor (x, y, and z axes), comparing experimental results with numerical simulation results with and without dura mater.
Upon analyzing the results, it is observed that displacement along the x-axis is much smaller than displacement along the other axes, as expected, due to the nature of rotation, which is purely coronal. Considering the similarity between the curves, it is worth noting that the scale of displacements, compared to those obtained experimentally by Alshareef et al., is indeed similar [35]. In contrast, numerical results without dura mater generally exhibit larger amplitudes than experimental results along the y and z axes. However, in most cases, numerical results with dura mater show smaller amplitudes than experimental results. This difference suggests that the properties of the dura mater used make it excessively rigid compared to reality. Nevertheless, the curves demonstrate analogous behavior, despite minimal variations in amplitude. Some factors that may help explain the differences recorded between the obtained results:
  • Although the brain has been modeled in detail, some important structures were not included in the modeling. Adding the missing components of a human head would allow for more realistic results.
  • Some mechanical properties of certain components were simplified for this study, such as the dura mater with linear elastic behavior and the CSF with a solid mesh with low rigidity. This approach commonly validates FEHM Nahum1, Hardy1, and Hardy2. However, this new and rigorous experiment by Alshareef et al. presents a new challenge in validation, requiring different considerations for successful validation [35].
  • Another aspect to consider is using data from studies on brain mechanical properties in brains of the same age as the one being modeled. In this case, material properties were obtained from a study on brains corresponding to older individuals, which may influence the numerical results.
  • The experimental data from Alshareef et al. were collected repeatedly in each individual, contributing to the reduction of random errors. However, there is potential for systematic errors [35].
  • Finally, the experiments were conducted on cadavers, which only have a partial representation of the behavior of the human brain in living and intact conditions [8].
These considerations emphasize the importance of improving the modeling to more accurately reflect the complexity of the cerebral system and ensure that the numerical results increasingly approximate the experimental data.
A case study of a real scenario of mTBI (in this case, in a sports context) was conducted to explore the dynamics and assess the future potential of FeFEHM. This was based on the Hernandez et al. study, which investigated whether direct measurement of head rotation improves the prediction of mTBI [39,40]. The participants recruited for the study were individuals exposed to repeated head impacts during various athletic conditions.
Thus, the scenario of an impact on the head of a collegiate American football player resulting in mTBI, which caused LOC, was analyzed. Simulations of head impacts were also conducted to understand how head kinematics produce stress and strain in the brain.
The simulations used an FEHM designated as the KTH model in this study [41]. This model represents the average head of an adult male, including structures such as the scalp, skull, brain, meninges, CSF, and parasagittal veins.
Analyzing the results in Figure 11, it can be observed that the results from the different models are very similar. The FeFEHM with results closest to the KTH model (represented in image a) is the model presented in the image (b), corresponding to the model developed for this work with dura mater despite overestimating pressure in some areas.
This similarity can be explained by the presence of the dura mater, known to be a protective membrane; in an impact situation, this membrane plays a crucial role in absorbing and distributing force, helping to cushion the impact and thus reduce the risk of direct brain damage.
The other two FeFEHM (images c, d) lack this structure, whixh justifies the overall pressure overestimation.
There are some important differences between the FeFEHM, especially the one with dura mater, and the KTH model, which are worth noting and may help explain the difference in the results obtained:
  • The KTH model has more structures, such as the scalp, pia and arachnoid mater, veins, and ventricles, compared to the FeFEHM with dura mater in this study. However, the latter has a geometry closer to human anatomy due to the use of real medical images.
  • The models were validated in different experiments. The KTH model was validated considering the experiments by Hardy et al. [42,43]. The other models were validated according to the experiments by Alshareef et al. [34,35].
  • The KTH model was created to represent the head of an average adult male. In contrast, the FeFEHM was created based on medical images of an adult female.
Thus, these results highlight the crucial importance of including the dura mater in the biomechanical modeling of the head and demonstrate the potential of FeFEHM for future analyses of head impacts and acceleration scenarios. They suggest that the accuracy and fidelity of the models are directly influenced by anatomical complexity and material characteristics. The comparison between the different models underscores the urgent need to consider a variety of factors in modeling to obtain more realistic and relevant results for the understanding and prevention of brain injuries. These results provide valuable insights for the ongoing improvement of biomechanical models and the progress of research in safety and health.

5. Conclusion

The creation of a detailed FEHM representative of a middle-aged woman from medical images, including a high level of detail, was successfully achieved. This 3D FeFEHM can predict how induced head acceleration affects brain structures and shows potential for further studies concerning the Corpus Calossum and pituitary system.
The advancements underscore the dura mater’s importance in the biomechanical modeling of the brain and pave the way for a more comprehensive and accurate understanding of TBI and its prevention, especially in underrepresented populations in previous studies. Additionally, the study revealed that FEHMs incorporating the dura mater yield results closer to reality than models that do not consider it.
It is important to emphasize the need to improve biomechanical models to more accurately reflect the human brain’s anatomical complexity and its material characteristics.
Thus, in this area of study, there is a need to consider various factors, including sex, age, and individual anatomy, to obtain more realistic and relevant results. The close attention to detail in these specific areas will make possible future research on post-traumatic incidents that might be sex-specific.

Limitations

This work presents some limitations that might have a certain impact on the results and should be considered.
Starting with the basic definition of an FEHM, which is a discretization of a continuous physical domain into finite elements, the resulting outcomes always have an implicit degree of error. Nevertheless, it is possible to obtain results close to reality, up to a specific threshold, by applying the right boundary conditions and assumptions.
When obtaining the geometry, it suffered some alterations that might make it less reliable. Regarding the skull, some parts had to be reconstructed manually. In addition, during meshing, the brain was divided and joined together again, which might have caused slight changes to its original geometry.
The material properties needed to replicate the experimental test were not provided for the model validation. Therefore, there was a need to look for these properties in the literature. Thus, the material properties on the experimental test are not the same as in the numerical simulation. In addition, the material properties found in the literature were obtained by studies on subjects older than the subject the model was being based on.
It is important to remember that experiments on cadavers are only partially representative of the behavior of an intact, living human brain. Measuring strains at injurious levels on the living human brain is currently impossible. Hence, the direct assessment of the FE model under these conditions cannot be performed [8].
This model is subject-specific, which is advantageous since it is possible to predict with more accuracy the effects of acceleration on the head of the specific subject or of a different subject whose head anthropometry is similar. However, if the subject being studied has a different anthropometry or considerable age difference, their outcomes might be significantly different, which makes the FeFEHM unable to predict it.
Despite all of these factors, the results in this work are satisfactory and highlight the potential of this FeFEHM for future research regarding TBI.
This work tries to decrease the gap in neurodegenerative disorders studies for women using FEHM. However, there are still many variables not yet understood by the scientific community that, hopefully, will be a hot topic of debate in the years to come.

Acknowledgments

University of Aveiro authors acknowledge the support given by the Portuguese Science Foundation under grants PTDC/EME-EME/1239/2021, UIDB/00481/2020 and UIDP/00481/2020; and CENTRO-01-0145-FEDER-022083 - Portugal Regional Operational Programme (Centro2020) under the PORTUGAL 2020 Partnership Agreement, through the European Regional Development Fund.

Appendix A. Validation Results

In this Appendix, it is presented every curve obtained in the validation simulations. In each graph there are three curves for the displacements: experimental results, numerical results with and without dura mater.
Preprints 100877 g0a1
Figure A1. Validation results for receivers from 9 to 14 for each orthogonal axis.
Figure A1. Validation results for receivers from 9 to 14 for each orthogonal axis.
Preprints 100877 g0a1
Preprints 100877 g0a2
Figure A2. Validation results for receivers from 15 to 20 for each orthogonal axis.
Figure A2. Validation results for receivers from 15 to 20 for each orthogonal axis.
Preprints 100877 g0a2
Preprints 100877 g0a3
Figure A3. Validation results for receivers from 21 to 26 for each orthogonal axis.
Figure A3. Validation results for receivers from 21 to 26 for each orthogonal axis.
Preprints 100877 g0a3
Preprints 100877 g0a4
Figure A4. Validation results for receivers from 27 to 32 for each orthogonal axis.
Figure A4. Validation results for receivers from 27 to 32 for each orthogonal axis.
Preprints 100877 g0a4

References

  1. et al, A.I.R.M. Traumatic brain injury: progress and challenges in prevention, clinical care, and research. Annals of Biomedical Engineering 2022, 21, P1004–1060. [CrossRef]
  2. et al, S.M. Outcomes and associated factors of traumatic brain injury among adult patients treated in Amhara regional state comprehensive specialized hospitals. BMC Emergency Medicine 2023, 23. [CrossRef]
  3. Valera, E.M.; Joseph, A.L.C.; Snedaker, K.; Breiding, M.J.; Robertson, C.L.; Colantonio, A.; Levin, H.; Pugh, M.J.; Yurgelun-Todd, D.; Mannix, R.; Bazarian, J.J.; Turtzo, L.C.; Turkstra, L.S.; Begg, L.; Cummings, D.M.; Bellgowan, P.S.F. Understanding Traumatic Brain Injury in Females: A State-of-the-Art Summary and Future Directions. Journal of Head Trauma Rehabilitation 2021, 36, E1–E17. [Google Scholar] [CrossRef]
  4. et al, S.L.J. Global, regional, and national burden of traumatic brain injury and spinal cord injury, 1990-2016: A systematic analysis for the Global Burden of Disease Study 2016. The Lancet Neurology 2019, 18, 56–87. [CrossRef]
  5. Horstemeyer, M.F.; Berthelson, P.R.; Moore, J.; Persons, A.K.; Prabhu2, A.D.R.K. A Mechanical Brain Damage Framework Used to Model Abnormal Brain Tau Protein Accumulations of National Football League Players. Annals of Biomedical Engineering 2019, 47, 1873–1888. [CrossRef]
  6. Skandsen, T.; Nilsen, T.L.; Einarsen, C.; Normann, I.; McDonagh, D.; Haberg, A.K.; Vik, A. Incidence of Mild Traumatic Brain Injury: A Prospective Hospital, Emergency Room and General Practitioner-Based Study. Frontiers in Neurology 2019, 10. [Google Scholar] [CrossRef] [PubMed]
  7. Gilchrist, M.D. Modelling and Accident Reconstruction of Head Impact Injuries. Key Engineering Materials 2003, 245–246, 417–432. [Google Scholar] [CrossRef]
  8. Hernandez, F.; Giordano, C.; Goubran, M.; Parivash, S.; Grant, G.; Zeineh, M.; Camarillo, D. Lateral impacts correlate with falx cerebri displacement and corpus callosum trauma in sports-related concussions. Biomechanics and Modeling in Mechanobiology 2019. [Google Scholar] [CrossRef] [PubMed]
  9. Biegon, A. Considering Biological Sex in Traumatic Brain Injury. Frontiers in Neurology 2021, 12. [Google Scholar] [CrossRef] [PubMed]
  10. James, L.M.; Christova, P.; Lewis, S.M.; Engdahl, B.E.; Georgopoulos, A.; Georgopoulos, A.P. Protective Effect of Human Leukocyte Antigen (HLA) Allele DRB1*13:02 on Age-Related Brain Gray Matter Volume Reduction in Healthy Women. EBioMedicine 2018, 29, 31–37. [Google Scholar] [CrossRef] [PubMed]
  11. Jeon, Y.K.; Jeong, J.; Shin, S.D.; Song, K.J.; Kim, Y.J.; Hong, K.J.; Ro, Y.S.; Park, J.H. The effect of age on in-hospital mortality among elderly people who sustained fall-related traumatic brain injuries at home: A retrospective study of a multicenter emergency department-based injury surveillance database. Injury 2022, 53, 3276–3281. [Google Scholar] [CrossRef] [PubMed]
  12. Xiaogai Li, Z.Z.; Kleiven, S. An anatomically detailed and personalizable head injury model: Significance of brain and white matter tract morphological variability on strain. Biomechanics and Modeling in Mechanobiolog 2021, 20, 403–431. [Google Scholar] [CrossRef]
  13. Budday, S.; Ovaert, T.C.; Holzapfel, G.A.; Steinmann, P.; Kuhl, E. Fifty Shades of Brain: A Review on the Mechanical Testing and Modeling of Brain Tissue. Archives of Computational Methods in Engineering 2019, 27, 1187–1230. [Google Scholar] [CrossRef]
  14. et al, S.J. Use of Brain Biomechanical Models for Monitoring Impact Exposure in Contact Sports. Annals of Biomededical Engineering 2022, 50, 1389–1408. [CrossRef]
  15. et al, D.R.W. Mechanical characterisation of the human dura mater, falx cerebri and superior sagittal sinus. Acta Biomaterialia 2021, 134, 388–400. [CrossRef]
  16. et al, Q.P. Systematic review and meta-analysis of the biomechanical properties of the human dura mater applicable in computational human head models. Biomechanics and Modeling in Mechanobiology 2022, 21, 755–770. [CrossRef]
  17. Carmo, G.P.; Dymek, M.; Ptak, M.; de Sousa, R.J.A.; Fernandes, F.A.O. Development, validation and a case study: The female finite element head model (FeFEHM). Computer Methods and Programs in Biomedicine 2023, 231, 107430. [Google Scholar] [CrossRef] [PubMed]
  18. Trotta, A.; Clark, J.M.; McGoldrick, A.; Gilchrist, M.D.; Annaidh, A.N. Biofidelic finite element modelling of brain trauma: Importance of the scalp in simulating head impact. International Journal of Mechanical Sciences 2020, 173, 105448. [Google Scholar] [CrossRef]
  19. Li, X.; Zhou, Z.; Kleiven, S. An anatomically detailed and personalizable head injury model: Significance of brain and white matter tract morphological variability on strain. Biomechanics and Modeling in Mechanobiology 2021, 20, 403–431. [Google Scholar] [CrossRef]
  20. Winkler, A.M.; Kochunov, P.; Blangero, J.; Almasy, L.; Zilles, K.; Fox, P.T.; Duggirala, R.; Glahn, D.C. Cortical thickness or grey matter volume? The importance of selecting the phenotype for imaging genetics studies. NeuroImage 2010, 53, 1135–1146, Imaging Genetics. [Google Scholar] [CrossRef]
  21. Joy, A.; Nagarajan, R.; Daar, E.S.; Paul, J.; Saucedo, A.; Yadav, S.K.; Guerrero, M.; Haroon, E.; Macey, P.; Thomas, M.A. Alterations of gray and white matter volumes and cortical thickness in treated HIV-positive patients. Magnetic Resonance Imaging 2023, 95, 27–38. [Google Scholar] [CrossRef] [PubMed]
  22. Fischl, B.; Dale, A.M. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Sciences 2000, 97, 11050–11055. [Google Scholar] [CrossRef]
  23. van Noort, R.; Black, M.; Martin, T.; Meanley, S. A study of the uniaxial mechanical properties of human dura mater preserved in glycerol. Biomaterials 1981, 2, 41–45. [Google Scholar] [CrossRef] [PubMed]
  24. Chafi, M.S.; Dirisala, V.; Karami, G.; Ziejewski, M. A finite element method parametric study of the dynamic response of the human brain with different cerebrospinal fluid constitutive properties. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine 2009, 223, 1003–1019. [Google Scholar] [CrossRef]
  25. De Kegel, D.; Vastmans, J.; Fehervary, H.; Depreitere, B.; Vander Sloten, J.; Famaey, N. Biomechanical characterization of human dura mater. Journal of the Mechanical Behavior of Biomedical Materials 2018, 79, 122–134. [Google Scholar] [CrossRef]
  26. P. A. Hasgall, F. Di Gennaro, C. Baumgartner, E. Neufeld, B. Lloyd, M. C. Gosselin, D. Payne, A. Klingenbck, N. Kuster, Itis database for thermal and electromagnetic parameters of biological tissues version 4.1 (2022). [CrossRef]
  27. Galford, J.E.; McElhaney, J.H. A viscoelastic study of scalp, brain, and dura. Journal of Biomechanics 1970, 3, 211–221. [Google Scholar] [CrossRef]
  28. Hibbitt, H.; Karlsson, B.; Sorensen, P. Abaqus analysis user’s manual version 6.10. Dassault Systèmes Simulia Corp.: Providence, RI, USA 2011.
  29. Khanuja, T.; Unni, H.N. Intracranial pressure–based validation and analysis of traumatic brain injury using a new three-dimensional finite element human head model. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine 2020, 234, 3–15. [Google Scholar] [CrossRef]
  30. Fernandes, F.; Alves de Sousa, R.; Ptak, M., Validation of YEAHM; 2018; pp. 41–58. [CrossRef]
  31. Menichetti, A.; MacManus, D.B.; Gilchrist, M.D.; Depreitere, B.; Vander Sloten, J.; Famaey, N. Regional characterization of the dynamic mechanical properties of human brain tissue by microindentation. International Journal of Engineering Science 2020, 155, 103355. [Google Scholar] [CrossRef]
  32. MacManus, D.B.; Ghajari, M. Material properties of human brain tissue suitable for modelling traumatic brain injury. Brain Multiphysics 2022, 3, 100059. [Google Scholar] [CrossRef]
  33. Puso, M.A.; Weiss, J.A. Finite Element Implementation of Anisotropic Quasi-Linear Viscoelasticity Using a Discrete Spectrum Approximation. Journal of Biomechanical Engineering 1998, 120, 62–70. [Google Scholar] [CrossRef]
  34. Alshareef, A.; Giudice, J.S.; Forman, J.; Salzar, R.S.; Panzer, M.B. A novel method for quantifying human in situ whole brain deformation under rotational loading using sonomicrometry. Journal of Neurotrauma 2018, 35, 780–789. [Google Scholar] [CrossRef]
  35. Alshareef, A.; Giudice, J.S.; Forman, J.; Shedd, D.F.; Reynier, K.A.; Wu, T.; Sochor, S.; Sochor, M.R.; Salzar, R.S.; Panzer, M.B. Biomechanics of the Human Brain during Dynamic Rotation of the Head. Journal of Neurotrauma 2020, 37, 1546–1555. [Google Scholar] [CrossRef] [PubMed]
  36. Gennarelli, T.A.; Thibault, L.E.; Tomei, G.; Wiser, R.; Graham, D.; Adams, J. Directional Dependence of Axonal Brain Injury due to Centroidal and Non-Centroidal Acceleration. 31st Stapp Car Crash Conference. SAE International, 1987. [CrossRef]
  37. S. International, Sign convention for vehicle crash testing (1994). Available online: https://ia801401.us.archive.org/33/items/gov.law.sae.j1733.1994/sae.j1733.1994.html.
  38. Rohatgi, A. Webplotdigitizer: Version 4.6, 2022.
  39. Hernandez, F.; Wu, L.C.; Yip, M.C.; Laksari, K.; Hoffman, A.R.; Lopez, J.R.; Grant, G.A.; Kleiven, S.; Camarillo, D.B. Six Degree-of-Freedom Measurements of Human Mild Traumatic Brain Injury. Annals of Biomedical Engineering 2015, 43, 1918–1934. [Google Scholar] [CrossRef] [PubMed]
  40. Hernandez, F.; Wu, L.C.; Yip, M.C.; Laksari, K.; Hoffman, A.R.; Lopez, J.R.; Grant, G.A.; Kleiven, S.; Camarillo, D.B. Erratum to: Six Degree-of-Freedom Measurements of Human Mild Traumatic Brain Injury. Annals of Biomedical Engineering 2016, 44, 828–829. [Google Scholar] [CrossRef]
  41. Kleiven, S. Predictors for traumatic brain injuries evaluated through accident reconstructions. Stapp car crash journal 2007, 51, 81–114. [Google Scholar] [PubMed]
  42. Hardy, W.N.; Foster, C.D.; Mason, M.J.; Yang, K.H.; King, A.I. Investigation of Head Injury Mechanisms Using Neutral Density Technology and High-Speed Biplanar X-ray. STAPP Car Crash Conference. The Stapp Association, 2001. [CrossRef]
  43. Hardy, W.N.; Mason, M.J.; Foster, C.D.; Shah, C.S.; Kopacz, J.M.; Yang, K.H.; King, A.I.; Bishop, J.; Bey, M.; Anderst, W.; Tashman, S. A Study of the Response of the Human Cadaver Head to Impact. 51st Stapp Car Crash Conference. The Stapp Association, 2007. [CrossRef]
Preprints 100877 g001
Figure 1. Segmented brain image from three anatomical views.
Figure 1. Segmented brain image from three anatomical views.
Preprints 100877 g001
Preprints 100877 g002
Figure 2. Segmented skull image from three anatomical views.
Figure 2. Segmented skull image from three anatomical views.
Preprints 100877 g002
Preprints 100877 g003
Figure 3. Comparison between brain segmentation (right) and surface geometry correction (left).
Figure 3. Comparison between brain segmentation (right) and surface geometry correction (left).
Preprints 100877 g003
Preprints 100877 g004
Figure 4. Comparison between skull segmentation (right) and surface geometry correction (left).
Figure 4. Comparison between skull segmentation (right) and surface geometry correction (left).
Preprints 100877 g004
Preprints 100877 g005
Figure 5. On the left side, the connections of the elements (in green) link the meshed brain parts. On the right side, the different brain properties are color-coded as follows: Cerebellum and Brainstem (orange), GM (dark blue), WM (light blue) and Corpus Callosum (light green).
Figure 5. On the left side, the connections of the elements (in green) link the meshed brain parts. On the right side, the different brain properties are color-coded as follows: Cerebellum and Brainstem (orange), GM (dark blue), WM (light blue) and Corpus Callosum (light green).
Preprints 100877 g005
Preprints 100877 g006
Figure 6. Overview of the brain placed inside the skull.
Figure 6. Overview of the brain placed inside the skull.
Preprints 100877 g006
Preprints 100877 g007
Figure 7. CSF (represented in yellow) inside the Dura Mater (green) which is inside the skull (purple), surrounding the brain (light and dark blue and orange).
Figure 7. CSF (represented in yellow) inside the Dura Mater (green) which is inside the skull (purple), surrounding the brain (light and dark blue and orange).
Preprints 100877 g007
Preprints 100877 g008
Figure 8. Angular acceleration curve for specimen 896 coronal tests. Retrieved from Alshareef et al. [35] work.
Figure 8. Angular acceleration curve for specimen 896 coronal tests. Retrieved from Alshareef et al. [35] work.
Preprints 100877 g008
Preprints 100877 g009
Figure 9. Measurement of human mTBI. A collegiate American football player lost consciousness after sustaining a head impact during a regular season game. (A) Broadcast footage at 40 frames s21 is compared with a (B) animation of head position and orientation during the impact calculated by integrating (C) device measurements of translational acceleration and (D) rotational acceleration. Retrieved from Hernandez et. al. [39].
Figure 9. Measurement of human mTBI. A collegiate American football player lost consciousness after sustaining a head impact during a regular season game. (A) Broadcast footage at 40 frames s21 is compared with a (B) animation of head position and orientation during the impact calculated by integrating (C) device measurements of translational acceleration and (D) rotational acceleration. Retrieved from Hernandez et. al. [39].
Preprints 100877 g009
Preprints 100877 g010
Figure 10. Validation results for receivers 18 and 25. In each graph there are three curves for the displacements of each receiver for each axis: experimental results, numerical results with and without dura mater.
Figure 10. Validation results for receivers 18 and 25. In each graph there are three curves for the displacements of each receiver for each axis: experimental results, numerical results with and without dura mater.
Preprints 100877 g010
Preprints 100877 g011
Figure 11. Coronal view cut of the brain with numerical results of pressure for the LOC head impact: a) The KTH FEHM (results in kPa whereas the other FeFEHM results are in MPa); (b) The results of the model developed for this work with dura mater; (c) The results of the model developed for this work without dura mater; (d) The previously model created which is representative of an elderly female subject. Adapted from Hernandez et. al. [40].
Figure 11. Coronal view cut of the brain with numerical results of pressure for the LOC head impact: a) The KTH FEHM (results in kPa whereas the other FeFEHM results are in MPa); (b) The results of the model developed for this work with dura mater; (c) The results of the model developed for this work without dura mater; (d) The previously model created which is representative of an elderly female subject. Adapted from Hernandez et. al. [40].
Preprints 100877 g011
Table 1. Number of elements and nodes assigned to each property.
Table 1. Number of elements and nodes assigned to each property.
Property Number of Elements Number of Nodes
Cerebrum and Brainstem 188,161 205,455
Cerebrospinal Fluid 412,504 568,422
Corpus Callosum 1,937 3,628
Dura Mater 271,423 400,354
Grey Matter 338,360 490,954
Skull 938,137 1,069,402
White Matter 738,560 813,237
Total 2,889,082 3,246,100
Table 2. Material parameters for each property.
Table 2. Material parameters for each property.
Property Formulation Parameters
ρ (kg/m   3 ) μ 0 (kPa) g 1 (-) g 2 (-) τ 1 (s) τ 2 (s)
Cerebrum and Brainstem Visco-hyperelastic 1045 3.40 0.52 0.20 0.018 0.33
Corpus Callossum 1041 4.49 0.57 0.22 0.021 0.30
Grey Matter 1044.5 5.06 0.50 0.20 0.015 0.30
White Matter 1041 7.63 0.57 0.22 0.020 0.31
CSF Hyperelastic 1007 0.9 1 0.9
Dura Mater Linear Elastic 1174 31.5 0.45
Skull Rigid 1908
Table 3. Receiver coordinates in the local head coordinate system in mm. Retrieved from Alshareef et al. [34].
Table 3. Receiver coordinates in the local head coordinate system in mm. Retrieved from Alshareef et al. [34].
Receiver X Y Z Receiver X Y Z
9 -38.129 20.140 30.521 21 -16.652 -29.072 -35.781
10 -12.106 -31.459 9.732 22 -7.700 32.768 7.365
11 -60.935 3.082 19.646 23 -1.163 -14.550 -51.034
12 -45.179 -13.961 36.192 24 14.908 29.688 -40.154
13 44.034 -12.704 1.714 25 -22.937 29.876 -38.122
14 14.327 -16.067 2.164 26 -64.700 32.084 -38.951
15 -25.111 -15.652 7.118 27 31.776 37.789 -19.912
16 28.015 -38.027 -17.072 28 -3.815 37.741 -17.110
17 -12.695 -38.707 -16.657 29 -45.488 36.850 -18.943
18 -47.961 -14.865 37.516 30 37.0142 12.198 0.042
19 -20.544 -31.677 -41.239 31 28.342 12.798 2.824
20 -34.790 -26.436 -33.775 32 -33.865 16.801 3.858
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated