Optimising Ion Conductivity in NdBaInO4 Based Phases

Preprint

Article

Optimising Ion Conductivity in NdBaInO₄ Based Phases

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Manyu Chen^*

Cheng Li

,Kai Zhu,Jieyu Wang,Sida Liu,Weina Kong,Zifa Ban,Chao Shen

Manyu Chen^*

Cheng Li

,Kai Zhu,Jieyu Wang,Sida Liu,Weina Kong,Zifa Ban,Chao Shen

This version is not peer-reviewed

Submitted:

07 March 2024

Posted:

11 March 2024

You are already at the latest version

Alerts

Abstract

Based on the previous work done by Fujii et al., NdBaInO4 compounds present modest oxide-ion conductivities. Therefore, it has been an attractive system of significant interest. In this paper, the Ca element has been attempted to partially substitute for Nd and the total electrical conductivity has been successfully improved due to the generation of oxygen vacancies. The synthesis, crystal structure, density, surface topography and electrical properties of NdBaInO4 and Ca-doped NdBaInO4 have been studied respectively. NdBaInO4, 10% and 20% molar fraction of Ca doped NdBaInO4 were synthesized through solid state reaction and they were calcined at 1000 °C for 14 hours and sintered at 1440 °C,1430 °C and 1420 °C respectively. The crystal structure of them has been obtained from Le Bail refinement of the XRD pattern, giving the result of the monoclinic structure which belongs to P21/c space group. The size of particles processed with different ball milling time and surface topography have been detected by the scanning electron microscope. The total electrical conductivities of Nd1-xCaxBaInO4-x/2 (x = 0, 0.1 and 0.2) were measured in the dry atmosphere by AC impedance spectroscopy and Nd0.9Ca0.1BaInO3.95 exhibited the highest total electrical conductivity and the lowest activation energy. What is more, the total conductivity of Nd0.9Ca0.1BaInO3.95 in the wet atmosphere at moderate temperature is relatively higher than that in the dry atmosphere while this phenomenon was not found in NdBaInO4. Therefore, the excess conductivity suggests that potential proton conduction may exist in wet atmospheres. In addition, Ca-doped NdBaInO4 were chosen for the oxygen isotope exchange which aims to obtain the diffusion coefficient and surface exchange coefficient, and Nd0.9Ca0.1BaInO3.95 shows the highest diffusion coefficient and D* decreases with the increase of the molar fraction of the Ca element.

Keywords:

Subject: Chemistry and Materials Science - Ceramics and Composites

1. Introduction

Solid oxide materials with high oxide-ion conductivity have been widely applied to many technological applications such as oxygen separation membranes and solid oxide fuel cells (SOFCs) [1,2,3,4,5,6], thus they have attracted a great deal of interest. A perovskite-related structure family with monoclinic P2₁/c phase and AA’BO₄ composition which is based on NdBaInO₄ has been reported by Fujii et al. [7]. It is surprising that it is an oxide-ion conductor, but the ionic conductivity is relatively modest. Therefore, many investigations have been carried out on this structure.

The transport properties in ceramic oxides are dominated by type, concentration and mobility of charge carriers in the materials. Therefore, not only the crystal structure but also the defects, point defects in particular, have dramatic effects on the oxide-ion conductivity of the material. There are two types of defects in solid oxides, one is intrinsic defects and another is extrinsic defects. Extrinsic defects are mainly influenced by some external factors such as temperature, oxygen partial pressure and doping elements. Doping effects has benefits of promoting the charge carriers’ concentration, which improve the electrical conductivity apparently. Therefore, it is practicable to chemically modify the composition of NdBaInO₄ to enhance the oxide-ion conductivity, which can be realized by introducing oxygen vacancies into NdBaInO₄ through doping with aliovalent cations.

It has been investigated by Fujii et al. [8] that Sr has been successfully doped at the Nd site and the electrical conductivity was significantly improved due to the increase of the concentration of oxygen vacancies which act as carriers for oxide-ion conduction. In addition, the activation energy has been reduced through doping with Sr.

In this work, a small amount of Ca element has been attempted to partially substitute for Nd, which has the potential to improve the total electrical conductivity and decrease the activation energy by introducing the oxygen vacancies. The crystal structure and lattice parameters of Ca-doped NaBaInO₄ have been characterized by X-ray diffraction and Le Bail refinement. The electrical conductivity of Ca-doped NaBaInO₄ has been measured through AC impedance spectroscopy. The properties of NaBaInO₄ have also been analyzed for comparison. Furthermore, the effects of Ca²⁺ doping on the electrical properties and the mechanism of the ion diffusion have also been studied and discussed in this work.

2. Materials and Methods

2.1. Synthesis

The precursors of NaBaInO₄ and Ca-doped NaBaInO₄ compounds were synthesized by solid-state reactions. For the NaBaInO₄, the constituent component oxides, Nd₂O₃ (Alfa Aesar, 99.9% purity), In₂O₃ (Alfa Aesar, 99.9% purity) and BaCO₃ (Aldrich, 99+% purity) were accurately weighed in 1: 1: 1 cation molar ratios. As for Nd_1-xCa_xBaInO_4-x/2(x=0.1, 0.2), Nd₂O₃, CaCO₃(AnalaR, 99.9% purity), BaCO₃ and In₂O₃ were exactly weighed in 1-x: x: 1: 1 cation molar ratios. Then the starting materials were mixed and finely ground using a ball mill for 3 hours. Then a controlled amount of dried mixed powder (about 1g) was loaded into a polished cylindrical die cavity with 13mm in diameter, and uniaxially prepressed into compacts through a rigid punch at 1.6 tonnes of weight for 2 min. In order to further enhance the density of the green compacts, a Stansted Fluid Power Isostatic Press (Model FPG2560A) was used to press them to 300MPa pressure for 2 min.

The green pellets were first calcined at 1000 °C for 14 hours. Then, for undoped green pellets, they were sintered at 1440 °C while for green pellets which are doped with 0.1 and for 0.2 molar fractions of Ca²⁺, they were sintered at 1430 °C and 1420 °C respectively. The dwelling time for the sintering process was 20 hours. The heating rate was 10 °C min^-1 for calcinations while it was 20 °C min^-1 for sintering progress. The cooling rate was 10 °C min^-1.

2.2. Characterization of the Chemical Composition

The ceramic pellets were analyzed by X-ray diffraction at room temperature to confirm the crystallographic data of the pellets. X-ray diffraction patterns were collected on an instrument called Bruker D2 Phaser Diffractometer which uses Cu-K_α radiation (λ=1.5418 Å). Scans were continuous from 10° to 80° (2θ) with an increment of 0.032° (2θ) and step time of 0.9 s over a period of about 35 min. The analysis of crystallographic data was further performed with the Le Bail refinement by using Fullprof refinement program and WinPLOTR software was used to plot diffraction patterns.

2.3. Scanning Electron Microscopy and Energy Dispersive Spectrometry

In order to determine the optimum ball milling time, the morphologies of the starting ceramic powders which were ball milled with different time were studied by using the instrument which is called JEOL JSM-6010 LA analytical scanning electron microscope (Using 20 kV with the working distance of 15 mm and 19 mm). The sample was coated with gold by plasma sputtering at a sputtering current of 20 mA for 2 min. The instrument used for sputtering is K550 Gold Target.

In addition, in order to analyze the porosity of pellets, the morphologies of the pellets’ surface were characterized by scanning electron microscopy as well. Before characterization, these pellets were gradually ground with silicon carbide paper from 800-grit size to 4000-grit size. Then, all ceramic pellets were coated with gold by sputter coater at a sputtering current of 20mA for 2 min. The accelerating voltage used was 20 kV.

Furthermore, the cationic ratio of NaBaInO₄ and Ca-doped NaBaInO₄ compounds were confirmed by energy dispersive spectrometry (EDS).

2.4. Electrical Conductivity Measurements

The electrical conductivities of NaBaInO₄ and Ca-doped NaBaInO₄ were first measured in the dry air by a 2-probe AC impedance spectroscopy with a Solartron 1260 frequency response analyzer (FRA) which uses platinum mesh to form a contact. The tasks for the impedance measurements were set up by SMaRT (Version 3.2.1) software and the measurements run automatically once projects were created.

These sintered pellets were coated with electrode paste made of platinum and then dealt with curing at 800 °C for 1 hour. The pellets were then annealed at 823 °C for 5 hours before the impedance measurements which were performed in the process of lowering temperature from 760 °C to 270 °C at 50 °C intervals and the frequency range from 10⁷ Hz to 1 Hz. The compressed air which was dried by 98% sulfuric acid was flowing through the pipe to create a dry atmosphere.

What is more, in order to investigate the effects of the humidified atmosphere on oxygen transport, the electrical conductivity measurements were also conducted in the wet atmosphere for NaBaInO₄ and Nd_0.9Ca_0.1BaInO_3.95 pellets separately with using AC impedance spectroscopy. The pellets were also annealed at 823 °C for 5 hours and measured with the same temperature range and frequency range as before. The wet atmosphere was created by making the compressed air flowing through a water bubbler at room temperature, and the humidity was estimated to be 2% (vol).

2.5. Oxygen Isotope Exchange

Two samples composed of Nd_0.9Ca_0.1BaInO_3.95 and Nd_0.8Ca_0.2BaInO_3.90 which have relative density 97% of the calculated density were chosen for the isotope exchange. Because the rough surface will have the diffusion entering from other directions, which affects the diffusion profile significantly, the samples were gradually ground with silicon carbide paper from 800-grit size to 4000-grit size and then polished down to 1 micron by using polishing discs. Then, these well-polished surfaces were coated with a very thin layer of diluted platinum paste and carried out curing at 800 °C for one hour in order to assist the isotope exchange.

After that, both samples were put into a tube and located next to a thermocouple. Before annealing, the tube was evacuated to a pressure of 4 × 10^-7 mbar. Then, ¹⁶O₂ with high purity (99.999%) was pumped into the tube to a pressure of 200 mbar and two samples were both pre-annealed at 850 °C in a furnace under this atmosphere for 40 hours which is 10 times longer than that of ¹⁸O₂ isotope exchange [9]. This pre-annealing process aims to remove the surface damage caused by the polishing [10]. After these two samples were cooled down to room temperature, evacuation was done again as before and 51.4% ¹⁸O₂ was pumped into the tube to the same pressure. Then, the isotope exchange was performed at 850 °C for 4 hours. At the end of the experiment, the ¹⁸O₂ was recycled by liquid nitrogen due to the high cost of ¹⁸O₂.

2.6. Secondary Ion Mass Spectrometry

Both samples were then cut perpendicular to the polished surface by the diamond saw and the cross sections of the samples were polished down to 1 micron with the same steps as before. After preparation, the cross sections of both samples were analyzed by SIMS with line scanning mode. The instrument is equipped with a Bi primary ion beam as well as a Cs secondary ion. The surface of the samples was cleaned by sputtering with 1 keV Cs until the yield of the contamination species has dropped to its minimum and the yield for ¹⁶O stopped changing. Then the elements were detected by TOF mass spectroscopy.

3. Results

3.1. Ball Milling Time Determination

The secondary electron images of these ball milled powders with different time interval are shown in Figure 1. From the SEM micrographs, it is observed that the particle size become smaller and has more uniform distribution when the ball milling time is increased to 3 h. The morphologies varied from irregular-shaped (1h) to long and thick needle-shaped (2h), and short and thin needle-shaped (3h) particles. When the ball milling time increases to 4h, the size of the needle-shaped particles become larger again. With further increasing the ball milling time, the particles started to agglomerate, which have bad effects on the following sintering process, for instance, the porosity of the pellets will be increased. Finally, the size of a part of the particles becomes very large. As a result, 3 h-milled powders are the optimum choice for the next sintering stage.

3.2. Crystal Structure of NaBaInO₄ and Ca-doped NaBaInO₄ via Le Bail Refinement

The X-ray diffraction patterns of NaBaInO₄ and Ca-doped NaBaInO₄ compounds are shown in Figure 2. For NaBaInO₄ compound, the experimental pattern shows no difference with the pattern which was reported by Fujii et al. [7]. Therefore, the sample can be confirmed to be NdBaInO₄ compounds and no secondary phase was detected. In addition, the space group can be identified as P2₁/c and the structure system was confirmed to be monoclinic. Based on the X-ray diffraction data which were detected using Bruker D2 Phaser Diffractometer, Le Bail refinement was carried out for NdBaInO₄, Nd_0.9Ca_0.1BaInO_3.95 and Nd_0.8Ca_0.2BaInO_3.90 so as to explore the structure and crystal lattice parameters’ changes in NdBaInO₄ by 10 mol% and 20 mol% Ca doping. The final Le Bail patterns are shown in Figure 2 and final refined crystallographic parameters are shown in Table 1.

As for Ca-doped NaBaInO₄ compounds, their experimental patterns (peak positions and peak shapes) are in great agreement with Le Bail refinement patterns. Therefore, the refined lattice parameters can be determined accurately and the results are also shown in Table 1. In addition, there is no other peak appearing when compared with the experimental patterns of NaBaInO₄ compounds. As a result, Nd_0.9Ca_0.1BaInO_3.95 and Nd_0.8Ca_0.2BaInO_3.90 can also be identified as monoclinic P2₁/c NaBaInO₄ phase.

3.3. Fractional Change in Crystallographic Data

The variations of crystal lattice parameters between NdBaInO₄, 10 mol% and 20 mol% Ca doped NdBaInO₄ were investigated in this work. The fractional changes in lattice parameters (a-, b- and c-axes, β-angle and unit-cell volume V) compared with NdBaInO₄ are shown in Figure 3. It is observed that apart from c-axes which is slightly increased and β-angle which is stable, other unit-cell parameters and unit-cell volume drop significantly when the molar fraction of Ca-doping is raised to 0.2. The inconsistent trend for c-axes value compared with others can be possible attributed to the big step size set during the X-ray diffraction analysis. A big step size gives rise to a short data collection time and thus insufficient data, which influence the accuracy of Le Bail refinement.

This phenomenon can be interpreted in terms of the effective ionic radii of the Ca²⁺ dopant and other respect such as defects. The effective ionic radius of Nd³⁺ (CN=9) is 1.163 Å which is a little smaller than that of Ca²⁺ (CN=9) which is 1.18 Å. The ionic radii presented in this work are all taken from Shannon [11]. Therefore, it should have had expansion of the unit-cell after doping. However, some defects such as oxygen vacancies will be introduced after doping, which indicates that the distances between the ions will be altered and thus deformation may occur. So there must have some balance between the increasing in ionic radii and introduction of oxygen vacancies. In this system, it is very likely that Ca²⁺ with a bigger radius has interaction with oxygen vacancies and finally results in the reduction of the lattice parameters as well as the unit-cell volume. But the specific interactions have not been studied and investigated in this paper and the further work need to be done to explain this phenomenon.

3.4. Microscope Structure of NaBaInO₄ and Ca-doped NaBaInO₄

The surface topography of an NdBaInO₄ pellet with the relative density of 93.7% of theoretical density was observed by SEM and the images are shown in Figure 4. The pictures with low magnification shows that there are a lot of obvious pores and a majority of them are closed pores and few pores is connected with each other, which demonstrates it is a pellet with high density. From the images taken in high magnification (×2500), the size of some small pores are estimated to be 1-2 microns while the size of some large pores can even achieve to be 5 microns or bigger.

The surface topography of the pellets composed of Nd_0.9Ca_0.1BaInO_3.95 and Nd_0.8Ca_0.2BaInO_3.90 with the relative density of 96.6% and 97.3% of calculated density respectively were also observed by SEM and the images are shown in Figure 5. There are some scratches on the surface due to the rough polishing by the silicon carbide papers. Apart from some obvious pores which are in black color and round shape, some craters with some particles attached on the surface can be seen from the first two images in particular. This unexpected surface topography may result from the incomplete and rough polishing and contaminants produced during polishing.

3.5. Energy Dispersive Spectrometry

In order to deduce the stoichiometric ratio of synthesized materials quantitatively, energy dispersive spectrometry analysis was applied in different surface areas of polished samples. The EDS spectra and quantitative stoichiometric values are shown in Figure 6 and Table 2 respectively. It is observed that apart from Nd, Ba, In, Ca and O signals, Au and C signals were also detected which can be attributed to the Au thin film which were sputtering coated on the surface before detection and some organic contaminants produced during sample preparation. It is noticeable that the cationic ratio of Nd, Ba and In is quite close to 1: 1: 1 for NaBaInO₄ while the oxygen percent obtained from the EDS measurements are not considered very accurate when compared with calculated values. The reason for this is that X-ray from elements lighter than Na cannot pass through the beryllium window which is placed in front of the detector to prevent impurities. Therefore, oxygen counts are generally less than the expected values due to the detection limit.

3.6. Temperature Programme Modification

In this work, the temperature programme of heat treatment has been improved and modified in order to achieve higher densities of pellets. The theoretical density reported by Fujii et al. is 6.92 Mg m^-3 and relative densities obtained in this work are based on it. When the sintering time was reduced from 24 hours to 22 hours at 1400°C sintering temperature, the density was enhanced apparently. In this work, 1450 °C sintering temperature was first tried for NdBaInO₄ and sintering time was reduced to 20 hours. But the pellets were found to be molten and evaporated away at the end of heat treatment. Therefore, the sintering temperature for NdBaInO₄ was increased from 1410 °C to 1440 °C. With increasing the temperature, the relative density was improved apparently from about 92% to more than 96%.

Generally, doping the materials with other elements will reduce the melting point. As a result, sintering temperatures for Nd_0.9Ca_0.1BaInO_3.95 and Nd_0.8Ca_0.2BaInO_3.90 were set to be 1430 °C and 1420 °C respectively. Because there is no theoretical density that can be referenced for Ca-doped NdBaInO₄, the density calculated with refined lattice parameters was used as theoretical density. The results show that the relative density could even achieve to 97% after modifications.

3.7. Electrical Conductivity of NdBaInO₄ and Ca-doped NdBaInO₄ in the Dry Air

The electrical conductivities of NdBaInO₄ were measured in the dry air and the Nyquist plots of its impedance data at low temperature (280 °C) and high temperature (720 °C) are shown in Figure 7 (a) and (b). The AC impedance data of NdBaInO₄ at low temperature was perfectly fitted with two equivalent circuits which are both composed of R-CPE elements. However, there is only one semicircle which is observable in Figure 7 (a), which means the semicircle which corresponds to the bulk component overlaps with the semicircle which corresponds to the grain boundary component. Therefore, the total resistance of NdBaInO₄ at 280 °C can be calculated as the sum of the resistance of the bulk and grain boundary or can be obtained from the right intercept of the semicircle and the resulting value is 9.9 × 10⁵ Ω. However, the resistance of the rig (about 4 Ω) also exists in the system, so it is necessary to get rid of the contribution of the rig resistance to obtain the actual resistance of the sample. It is so small when compared with the total resistance at low temperature, but it has significant contribution to the total resistance when the temperature goes higher.

At high temperature, the bulk response is absent due to the instrumental detection limit, so it is difficult to fit the whole impedance data. For the high frequency response, the shape of the semicircle is no longer observed, hence, only the low frequency response was fitted and the capacitance was estimated to be 4.4 × 10^-10 F. In order to assign the corresponding semicircles to the different regions of the sample, it is multiplied by l/A=0.149 cm^-1 of the pellet, giving the result of 6.56 × 10^-11 F. Therefore, this low frequency response corresponds to the grain boundary component and the total resistance of the sample can be obtained from the right intercepts of the semicircle. The resulting resistance is 3480 Ω after reduced by 4 Ω of the rig resistance.

The electrical conductivities of Nd_0.9Ca_0.1BaInO_3.95 and Nd_0.8Ca_0.2BaInO_3.90 in the dry air were also measured in this p and the Nyquist plots of their impedance data at low temperatures and high temperatures are shown in Figure 7 (c), (d), (e) and (f). As for Nd_0.9Ca_0.1BaInO_3.95 at low temperature (270 °C), from Figure 7 (c) and the enlarged view in it, it is obviously observed that there are three frequency responses existing and the grain boundary region which corresponds to the middle frequency response is significantly overlapped with the sample-electrode interface region. But it’s difficult to use the R-CPE elements to fit them, hence, only the sample-electrode interface region was fitted manually and the total resistance of the sample at low temperature can be estimated to be the left intercept of the sample-electrode interface semicircle on Z^’ axis, giving the result of 39585 Ω. Compared with the impedance spectra at low temperature, it can be deduced that the semicircle in the middle of the high temperature impedance spectra corresponds to the sample-electrode interface component. As can be seen from the Figure 7 (d), a part of the sample-electrode interface semicircle is in the positive imaginary impedance area, as a consequence, the intersection of this semicircle and Z^’ axis can be directly regarded as the total resistance of the pellet at high temperature. Then, after reduced by 4 Ω of the rig resistance, the resulting value of Nd_0.9Ca_0.1BaInO_3.95 was calculated to be 33.4 Ω for the dry atmosphere.

As for Nd_0.8Ca_0.2BaInO_3.90 at low temperature (390 °C) in Figure 7 (e), it can be obviously seen that there are two complete semicircles which correspond two frequency responses. After multiplied by l/A=0.196 cm^-1, the capacitance of the low frequency response was estimated to be 3.45 × 10^-9 F which can be assigned to the grain boundary component. Then, these two semicircles were perfectly fitted with two equivalent circuits which are both composed of R-CPE elements, and the corresponding resistances for the bulk and grain boundary were fitted to be 4469 Ω and 28981 Ω respectively. Therefore, the total electrical resistance of Nd_0.8Ca_0.2BaInO_3.90 at low temperature was calculated to be 33450 Ω. At high temperature (760 °C), the high frequency response is in the positive imaginary impedance area and the total resistance can be directly calculated to be the right intercept of the grain boundary semicircle (low frequency) on Z^’ axis, giving the result of 47.2 Ω. The same methodology was used to fit all of the data set.

The total resistance which was determined by impedance spectroscopy data can be transformed into the total conductivity by Equation (1)

σ = \frac{l}{A R}

(1)

where σ is the total conductivity (S m^-1), l is the thickness of the pellet (m), A is the surface area of the pellet (cm²), and R is the total resistance (Ω).

The total conductivity is expressed by the Arrhenius equation (Equation (2)):

σ = \frac{σ_{0}}{T} e x p (\frac{- E_{a}}{R T})

(2)

where E_a is the activation energy (J mol^-1), R is the gas constant (J K^-1 mol^-1), T is the temperature (K), and σ₀ is a pre-exponential factor.

Therefore, the logarithm of the conductivity against the reciprocal of temperature is commonly plotted to get a linear relationship. The results of NdBaInO₄ and Ca-doped NdBaInO₄ which were measured in the dry air are shown in Figure 8.

From the Arrhenius equation, it is obvious that low activation energy has the benefit of promoting the total electrical conductivity. Therefore, it is important to determine the activation energy and in order to obtain its value, the Arrhenius equation can be rearranged to Equation (3) by taking the natural logarithm:

\ln (σ T) = - \frac{E_{a}}{R T} + l n (σ_{0})

(3)

Then a plot of the ln(σT) against the reciprocal of temperature gives a straight line and the activation energy (E_a) can be calculated from the gradient of the line by multiplying the gas constant R which is 8.314 J K^-1 mol^-1, giving the results of 0.68 eV for NdBaInO₄. It can be seen from Figure 8 that the total electrical conductivity of NdBaInO₄ at 760 °C in the dry atmosphere is about 6.36 × 10^-5 S cm^-1. In addition, the activation energy E_a of Nd_0.9Ca_0.1BaInO_3.95 (0.93 eV) is relatively higher than that of NdBaInO₄ (0.68 eV) when the temperature is below 464 °C. The possible explanation for this phenomenon is that at low temperatures, the dopant aliovalent cations can be seen as the nucleation centers where oxygen vacancies and dopant cations bind together into defect clusters with low mobility. When the temperature is above 464 °C (737 K), those bound vacancies are dissolved and become mobile, which reduces the activation energy E_a to be 0.58 eV which is lower than that of NdBaInO₄, indicating better mobility of the oxygen species in Nd_0.9Ca_0.1BaInO_3.95. What is more, after doping the NdBaInO₄ with 10% molar fraction of Ca²⁺, it can be seen from the Figure 8 that the total electrical conductivity of the sample at 760 °C has been significantly increased by two orders of magnitude (4.91 × 10^-3 S cm^-1) due to the generation of oxygen vacancies.

When the Ca dopant concentration was increased to 20% molar fraction, the activation energy was raised to 1.15 eV which is even bigger than that of the NdBaInO₄, but the total electrical conductivity was improved to a certain extent when compared with the undoped material. Above all, Nd_0.9Ca_0.1BaInO_3.95 exhibited the highest total electrical conductivity and the lowest activation energy among Nd_1-xCa_xBaInO_4-x/2 (x = 0, 0.1 and 0.2).

3.8. The Effects of the Humidified Atmosphere on the Conductivity of NdBaInO₄ and Nd_0.9Ca_0.1BaInO_3.95

The electrical conductivity measurements were also conducted in the wet atmosphere for NdBaInO₄ and Nd_0.9Ca_0.1BaInO_3.95 pellets separately with using AC impedance spectroscopy and the Nyquist plots of the impedance data for Nd_0.9Ca_0.1BaInO_3.95 at low temperature (270°C) and high temperature (760 °C) in the wet atmosphere are shown in Figure 9. As the same with the Nyquist plots of the dry atmosphere, the sample-electrode interface region was fitted manually and the total resistance of the sample at low temperature can be estimated to be the left intercept of the sample-electrode interface semicircle on Z^’ axis, giving the result of 9089.4 Ω. At high temperature, the intersection of the semicircle and Z^’ axis can be directly regarded as the total resistance of the pellet. Then, after reduced by 4 Ω of the rig resistance, the resulting value of Nd_0.9Ca_0.1BaInO_3.95 was calculated to be 31.7 Ω for the wet atmosphere.

As before, the logarithm of the total conductivity against the inverse temperature of undoped and 10% Ca-doped material were also plotted to get linear relationships and the resulting graph is displayed in Figure 10. It can be observed that the total conductivity of Nd_0.9Ca_0.1BaInO_3.95 measured in the wet atmosphere at moderate temperature is relatively higher than that in the dry atmosphere. On the contrary, the total conductivity of the undoped pellet which was performed in the dry atmosphere is lightly higher than that in the wet atmosphere. So this slight deviation at low temperature requires further investigation. Therefore, the excess conductivity of Nd_0.9Ca_0.1BaInO_3.95 in wet atmosphere suggests that potential proton conduction may exist because oxygen vacancies generally make contributions to the proton conduction. What is more, the proton conductivity of the doped material reaches the maximum and the total conductivity tends to be uniform at a certain high temperature (800 °C), which might results from the depleted proton charge carrier at elevated temperature. Similar behavior has been observed in other proton conducting system such as BaCeZr_3-d and Ca doped LaNbO ₄ [12].

3.9. IEDP of Ca-doped NdBaInO₄

The diffusion profile was obtained by TOF-SIMS and one of the profiles for 20% doped sample are shown in Figure 11. These experimental data were fitted appropriately with a MatLab script that utilize the least square fitting to obtain

k^{*}

and D^* parameters. The results of the diffusion coefficients and surface exchange coefficients are listed in Table 3 and the fitting error which was introduced by the measurement should be around 10% percent. The oxygen diffusion coefficients of Nd_0.9Ca_0.1BaInO_3.95 (D*=1.82 × 10^-8 cm²/s, 850 °C) is about two times higher than that of Nd_0.8Ca_0.2BaInO_3.90 (D*=7.95 × 10^-9 cm²/s, 850 °C). When compared with the oxygen diffusion coefficient of the undoped NdBaInO₄ (D*=8.25× 10^-11 cm²/s, 850 °C), the diffusion coefficients of Nd_0.9Ca_0.1BaInO_3.95 was increased significantly by two orders of magnitude. In addition, it is worth noting that Nd_0.9Ca_0.1BaInO_3.95 shows the highest diffusion coefficient and D^* decreases with the increase of the molar fraction of the Ca element, since when the doping concentration exceeds certain value, the ordered-vacancy phase will be formed, which leads to the dramatic drop of the conductivity. As the surface of both samples was coated with a thin layer of Pt, the surface of them cannot be characterized by the obtained surface exchange coefficient.

4. Discussion

Synthesis method used in this work is the solid state reaction and three hours’ ball milling has been determined to be the optimum choice for the next sintering stage. In addition, the temperature programme of heat treatment has been improved and modified in order to achieve higher densities. The sintering temperatures for NdBaInO₄, Nd_0.9Ca_0.1BaInO_3.95 and Nd_0.8Ca_0.2BaInO_3.90 have been increased from 1400 °C to 1440 °C, 1430 °C and 1420 °C respectively and the sintering time has been reduced from 24 hours to 20 hours. With increasing sintering temperatures and reducing the time, the relative densities were improved dramatically from about 92% to more than 96%.

The results of X-ray diffraction analysis indicate that NdBaInO₄ compounds with a single phase of monoclinic P2₁/c has been successfully synthesized and it remains this single phased structure after doped with 0.1 and 0.2 molar fraction of Ca²⁺ into the Nd site. Then, the lattice parameters have been determined by Le Bail refinement of XRD data. The results show that apart from c-axes which is slightly increased and β-angle which is stable, other unit-cell parameters and unit-cell volume drops significantly when the molar fraction of Ca-doping is raised to 0.2. What is more, the stoichiometric ratios of these synthesized materials have been further confirmed by energy dispersive spectrometry. The cationic ratio of Nd, Ba and In is quite close to 1:1:1 for NdBaInO₄ and the detected Ca concentration is quite reasonable for Ca-doped NdBaInO₄.

The total electrical conductivity of NdBaInO₄ at 760 °C in the dry atmosphere is about 6.36 × 10^-5 S cm^-1. However, after doping the NdBaInO₄ with 0.1 molar fraction of Ca²⁺, the total electrical conductivity at 760 °C has been significantly increased by two orders of magnitude (4.91 × 10^-3 S cm^-1) and the activation energy was reduced from 0.68 eV to 0.58 eV when the temperature is above 464 °C (737 K). What is more, after doping 0.1 molar fraction of Ca²⁺, the activation energy was raised to 0.93 eV when the temperature is below 464 °C (737 K), which is possible due to the formation of the defect clusters with low mobility. Although the activation energy of Nd_0.8Ca_0.2BaInO_3.90 (1.15 eV) is even larger than that of undoped material, the total conductivity was also improved. Above all, Nd_0.9Ca_0.1BaInO_3.95 exhibited the highest total electrical conductivity and the lowest activation energy among Nd_1-xCa_xBaInO_4-x/2 (x = 0, 0.1 and 0.2).

In addition, the total conductivity of Nd_0.9Ca_0.1BaInO_3.95 in the wet atmosphere at moderate temperature is relatively higher than that in the dry atmosphere. Therefore, the excess conductivity suggests that potential proton conduction may exist in wet atmospheres. Besides, the proton conductivity reaches the maximum and the total conductivity tends to be uniform at a certain high temperature.

The oxygen diffusion coefficients of Nd_0.9Ca_0.1BaInO_3.95 (D*=1.82 × 10^-8 cm²/s, 850 °C) is about two times higher than that of Nd_0.8Ca_0.2BaInO_3.90 (D*=7.95 × 10^-9 cm²/s, 850 °C) and was increased significantly by two orders of magnitude when compared with the oxygen diffusion coefficient of the undoped NdBaInO₄ (D*=8.25× 10^-11 cm²/s, 850 °C).

5. Future Work

The results of the Le Bail refinement show that there is a reduction in the lattice parameters as well as the unit-cell volume when the molar fraction of Ca-doping is raised to 0.2, but the specific reasons for that have not been studied and investigated in this project and further work need to be done to explain this phenomenon.

Although the activation energy was reduced when the dopant was introduced into the material, the reason of this phenomenon has not been studied in this work. In order to understand it, it is necessary to carry out further work on the oxide-ion diffusion pathways which can be achieved by bond valence based energy (BVE). Besides, whether the Ca-doped materials have pure oxide-ion conduction is not yet known. Therefore, the oxygen partial pressure dependence of the total electrical conductivity and oxide-ion conductivity need to be measured by controlling and monitoring the P(O₂) in the future work.

The potential proton conduction has been found to exist in the wet atmospheres at moderate temperature. It was supposed to be caused by the oxygen vacancies but we do not have evidence yet. Therefore, the mechanism of the proton conduction is required to be further investigated and discussed. In addition, the dependence of the Ca dopant concentration on proton conduction can be further studied to find the relationship between the charge carrier concentration and proton conductivity.

Author Contributions

Software, Manyu Chen.; validation, Manyu Chen and Cheng Li; formal analysis, Manyu Chen and Cheng Li; investigation, Jieyu Wang and Sida Liu; data curation, Weina Kong and Zifa Ban; writing—original draft preparation, Manyu Chen; writing—review and editing, Cheng Li; supervision, Kai Zhu and Chao Shen. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.

Acknowledgments

First of all, We would like to express our appreciation to our supervisor, Stephen J Skinner, for his helpful advice, scientific discussions and patient guidance. His experience in the solid oxide fuel cell field is invaluable. Next we would like to thank some research staff at Imperial College who has been important to our work: Richard Sweeney for his permission to let us use the Bruker D2 Phaser Diffractometer, Mahmoud G Ardakani for helpful guidance during the SEM. We would also like to thank Florent Tonus who guided us with the Stansted Fluid Power Isostatic Press and furnace apparatus and gave a comprehensive teaching on Le Bail refinement. In addition, we would like to thank Zonghao Shen for her friendly help with the isotope exchange, Duke for his assistance with the density measurement.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Goodenough, J.B.; Ruiz-Diaz, J.E.; Zhen, Y.S. Oxide-ion conduction in Ba2In2O5 and Ba3In2MO8 (M= Ce, Hf, or Zr). Solid State Ionics 1990, 44, 21–31. [Google Scholar] [CrossRef]
Ishihara, T.; Matsuda, H.; Takita, Y. Doped LaGaO3 perovskite type oxide as a new oxide ionic conductor. Journal of the American chemical society 1994, 116, 3801–3803. [Google Scholar] [CrossRef]
Goodenough, J.B. Oxide-ion conductors by design. Nature 2000, 404, 821–823. [Google Scholar] [CrossRef] [PubMed]
León-Reina, L. High oxide ion conductivity in Al-doped germanium oxyapatite. Chemistry of materials 2005, 17, 596–600. [Google Scholar] [CrossRef]
Li, M. A family of oxide ion conductors based on the ferroelectric perovskite Na_0.5Bi_0.5TiO₃. Nature materials 2014, 13, 31–35. [Google Scholar] [CrossRef] [PubMed]
Zhang, W. Oxide-ion conduction in the Dion−Jacobson phase CsBi₂Ti₂NbO_10-δ. Nature communications 2020, 11, 1224. [Google Scholar] [CrossRef] [PubMed]
Fujii, K. New Perovskite-Related Structure Family of Oxide-Ion Conducting Materials NdBaInO4. Chemistry of Materials 2014, 26, 2488–2491. [Google Scholar] [CrossRef]
Fujii, K. Improved oxide-ion conductivity of NdBaInO 4 by Sr doping. Journal of Materials Chemistry A 2015, 3, 11985–11990. [Google Scholar] [CrossRef]
De Souza, R.; Chater, R. Oxygen exchange and diffusion measurements: The importance of extracting the correct initial and boundary conditions. Solid State Ionics 2005, 176, 1915–1920. [Google Scholar] [CrossRef]
Kilner, J.; Steele, B.; Ilkov, L. Oxygen self-diffusion studies using negative-ion secondary ion mass spectrometry (SIMS). Solid State Ionics 1984, 12, 89–97. [Google Scholar] [CrossRef]
Shannon, R.t. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallographica Section A: Crystal Physics, Diffraction, Theoretical and General Crystallography 1976, 32, 751–767. [Google Scholar] [CrossRef]
Haugsrud, R.; Norby, T. Proton conduction in rare-earth ortho-niobates and ortho-tantalates. Nature Materials 2006, 5, 193–196. [Google Scholar] [CrossRef]

Figure 1. SEM micrographs of mixed powder (Nd₂O₃, BaCO₃ and In₂O₃) which were ball milled for (a) 1h; (b) 2h; (c) 3h; (d) 4h; (e) 5h; and (f) 6h.

Figure 2. Le Bail refinement for the X-ray diffraction pattern collected at room temperature of (a) NaBaInO₄; (b) Nd_0.9Ca_0.1BaInO_3.95; and (c) Nd_0.8Ca_0.2BaInO_3.90. The experimental data are in red dots, the refined pattern is in black solid line, the difference between the experimental and calculated data is in green solid line, and peak positions are in blue vertical bars.

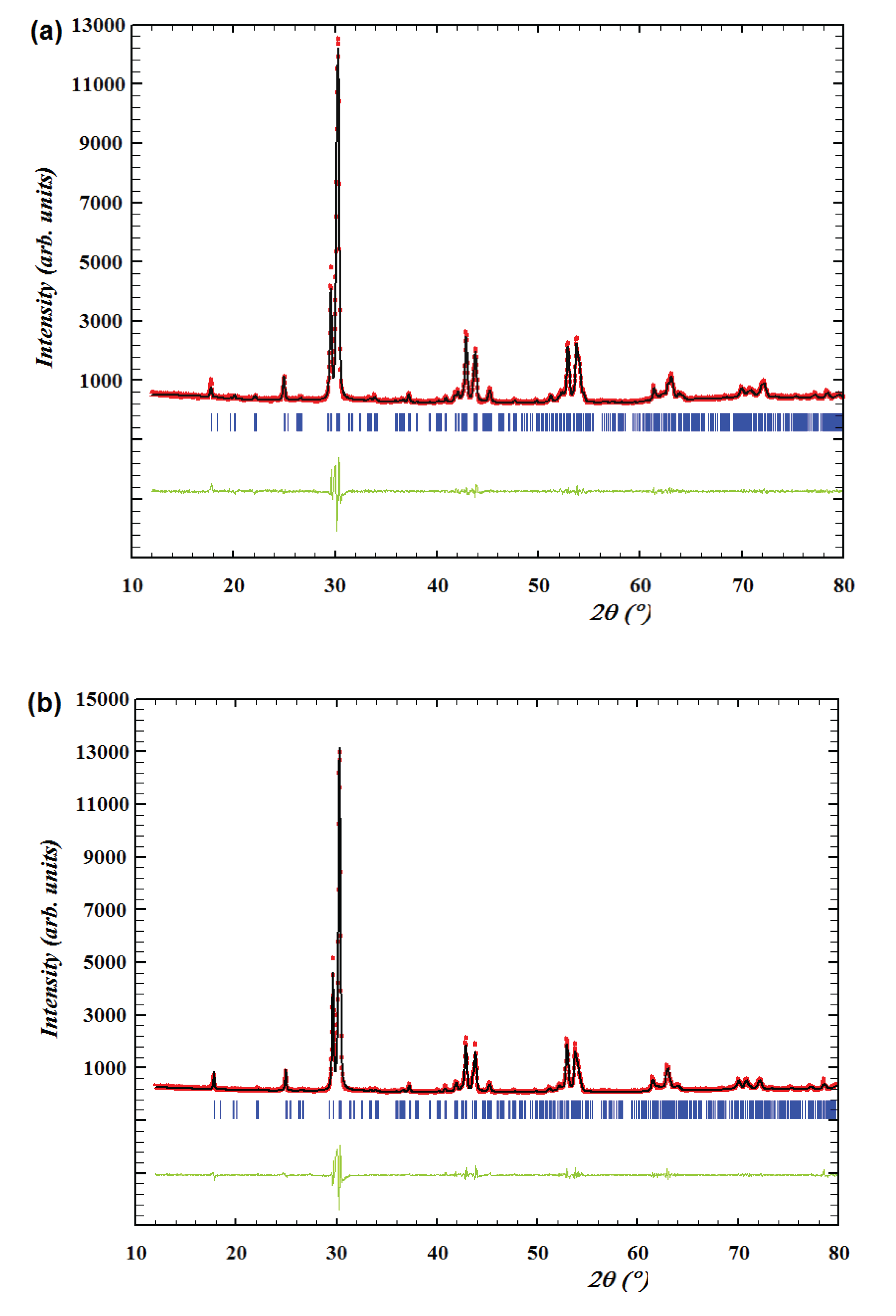
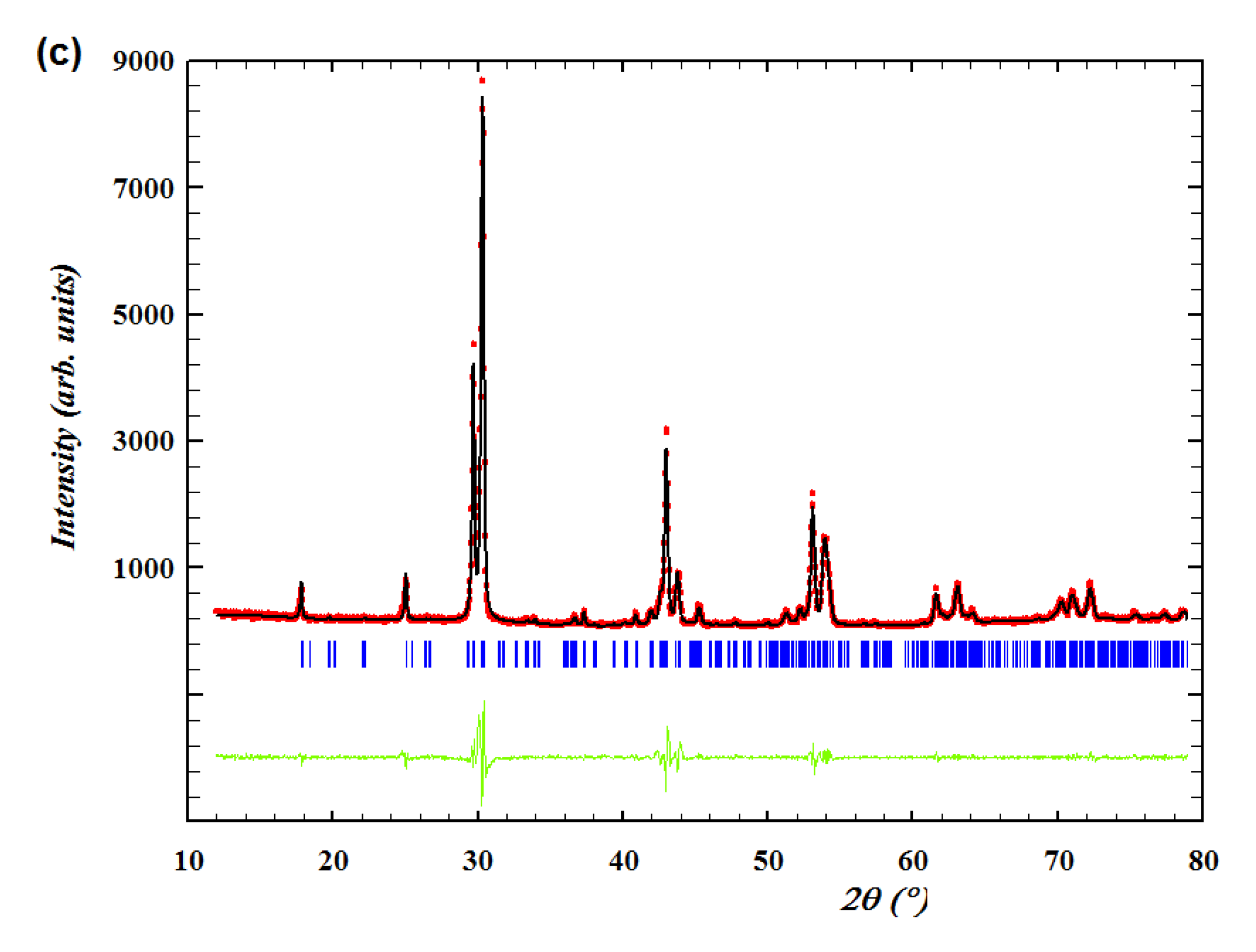
Figure 3. Fractional changes in lattice parameters (a-, b- and c-axes, β-angle and unit-cell volume V) of 10 mol% and 20 mol% Ca doped NdBaInO₄ compared with undoped NdBaInO₄.

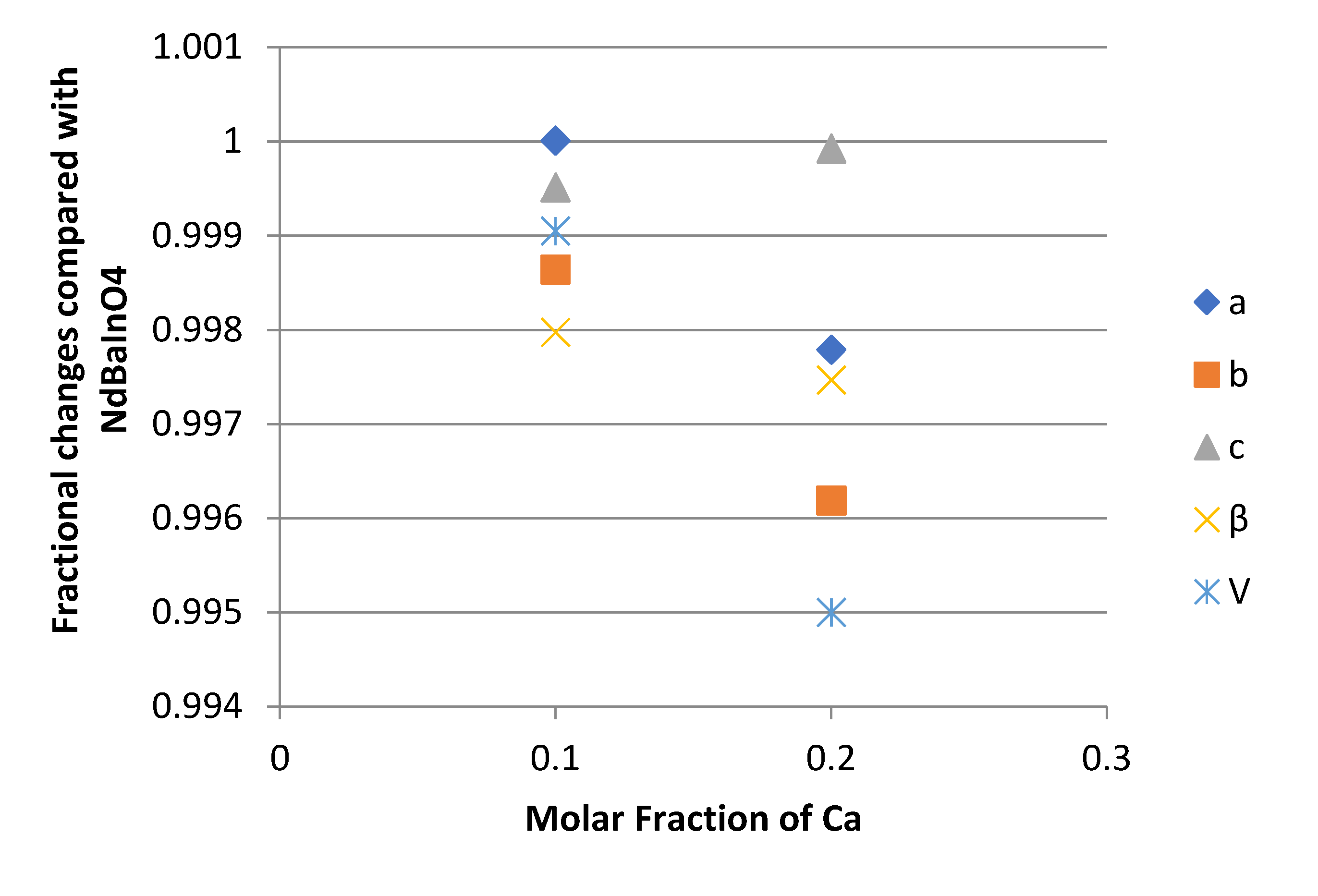
Figure 4. Secondary electron images of the polished surface of NaBaInO₄ pellet with 93% density (a) 500 magnification (b) 2500 magnification.

Figure 5. Secondary electron images of the polished surface of Nd_0.9Ca_0.1BaInO_3.95 pellet with 96.6% relative density with (a) 500 magnification; and (b) 2500 magnification; Nd_0.8Ca_0.2BaInO_3.90 pellet with 97.3% the relative density with (c) 500 magnification; (d) 2000 magnification.

Figure 6. Energy dispersive spectra detected from a polished surface of (a) NaBaInO₄; (b) Nd_0.9Ca_0.1BaInO_3.95; and (c) Nd_0.8Ca_0.2BaInO_3.90.

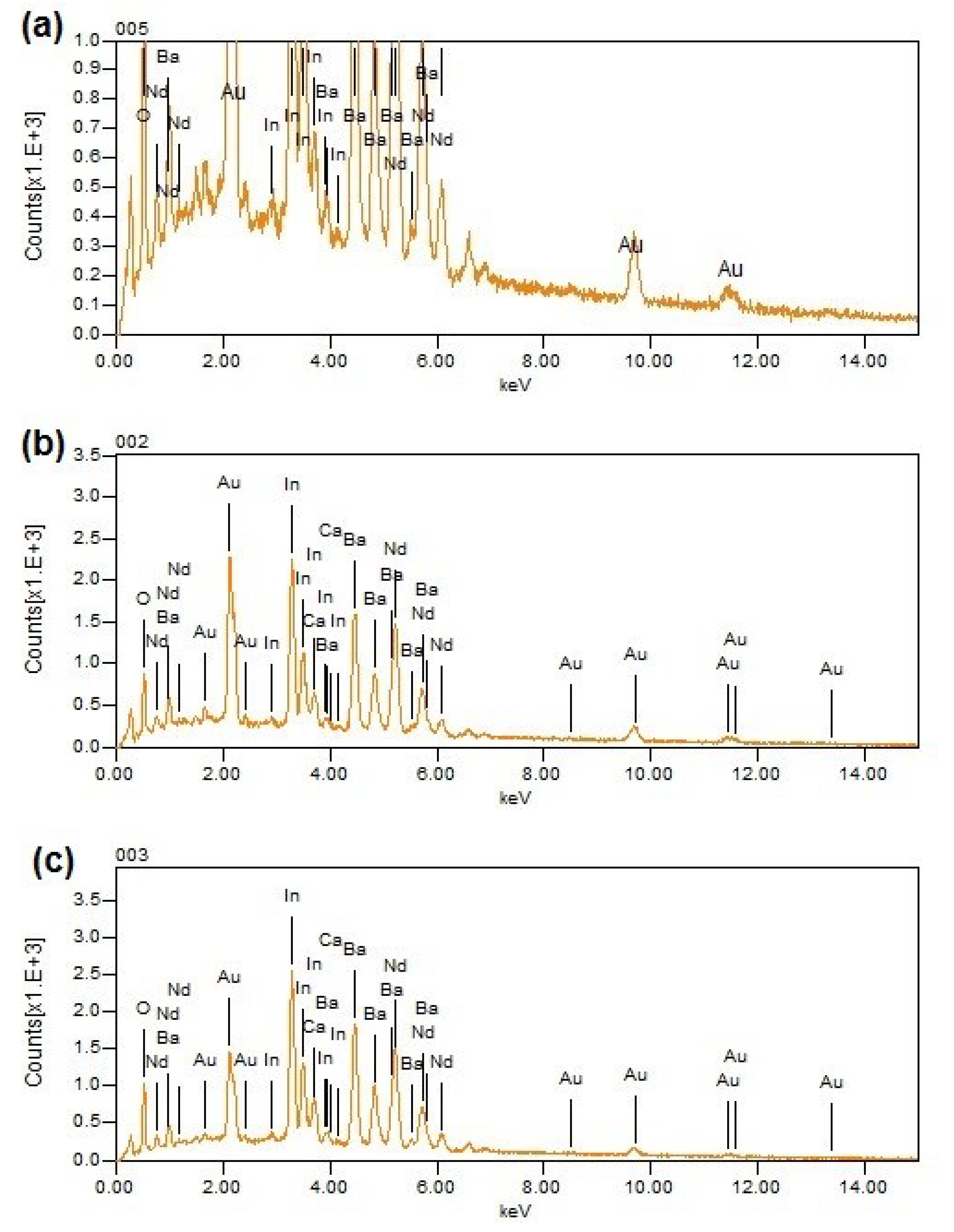
Figure 7. Impedance spectra measured in the dry air at (a) 280 °C and (b) 720 °C for NdBaInO₄; (c) 270 °C and (d) 760 °C for Nd_0.9Ca_0.1BaInO_3.95; (e) 390 °C and (f) 760 °C for Nd_0.8Ca_0.2BaInO_3.90. The experimental data are in red solid lines with blue dots, the fitting curves are in green solid lines. The equivalent circuits used in (a) and (e) to model each physical feature are inserted in the spectra.

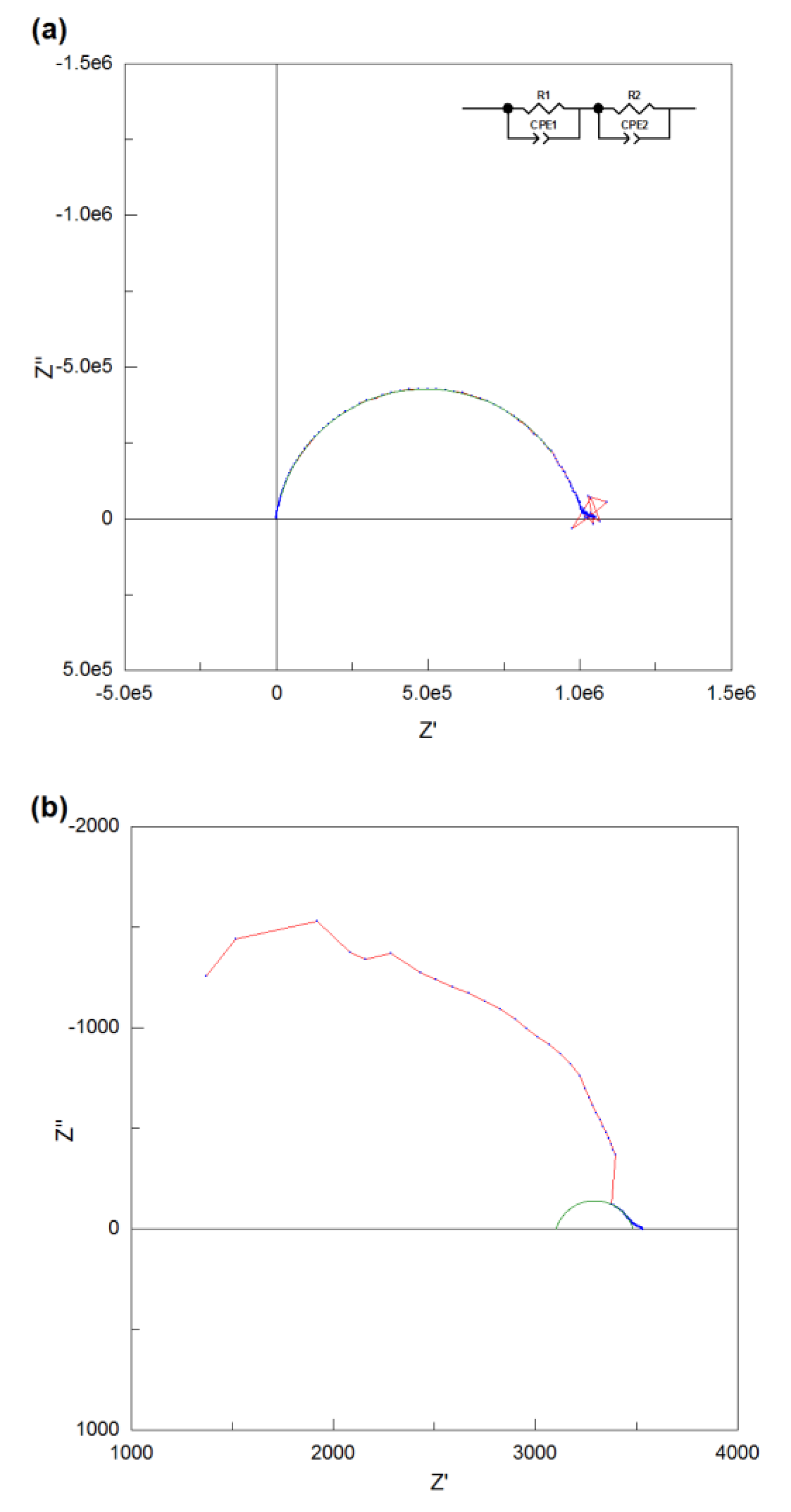
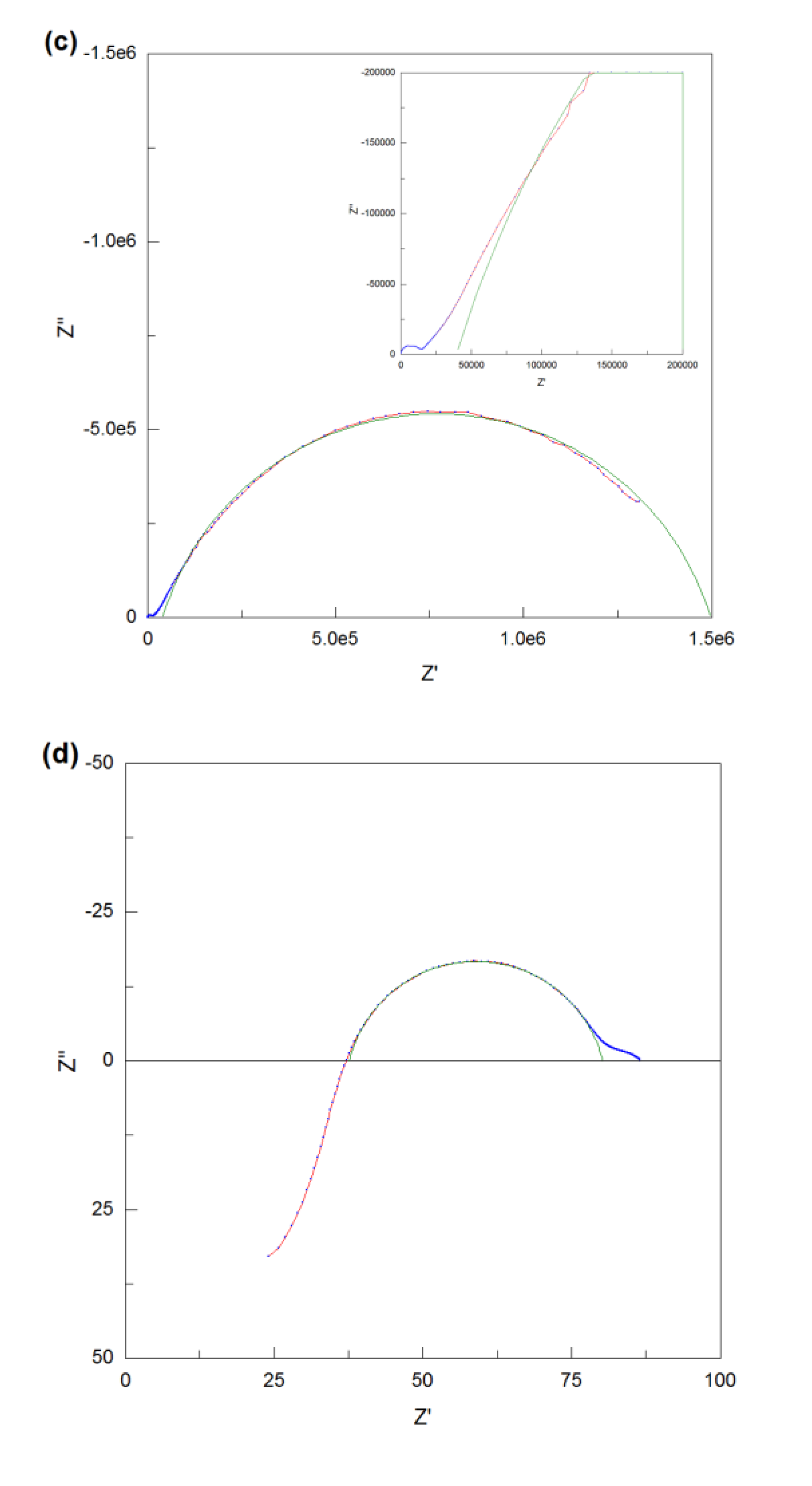
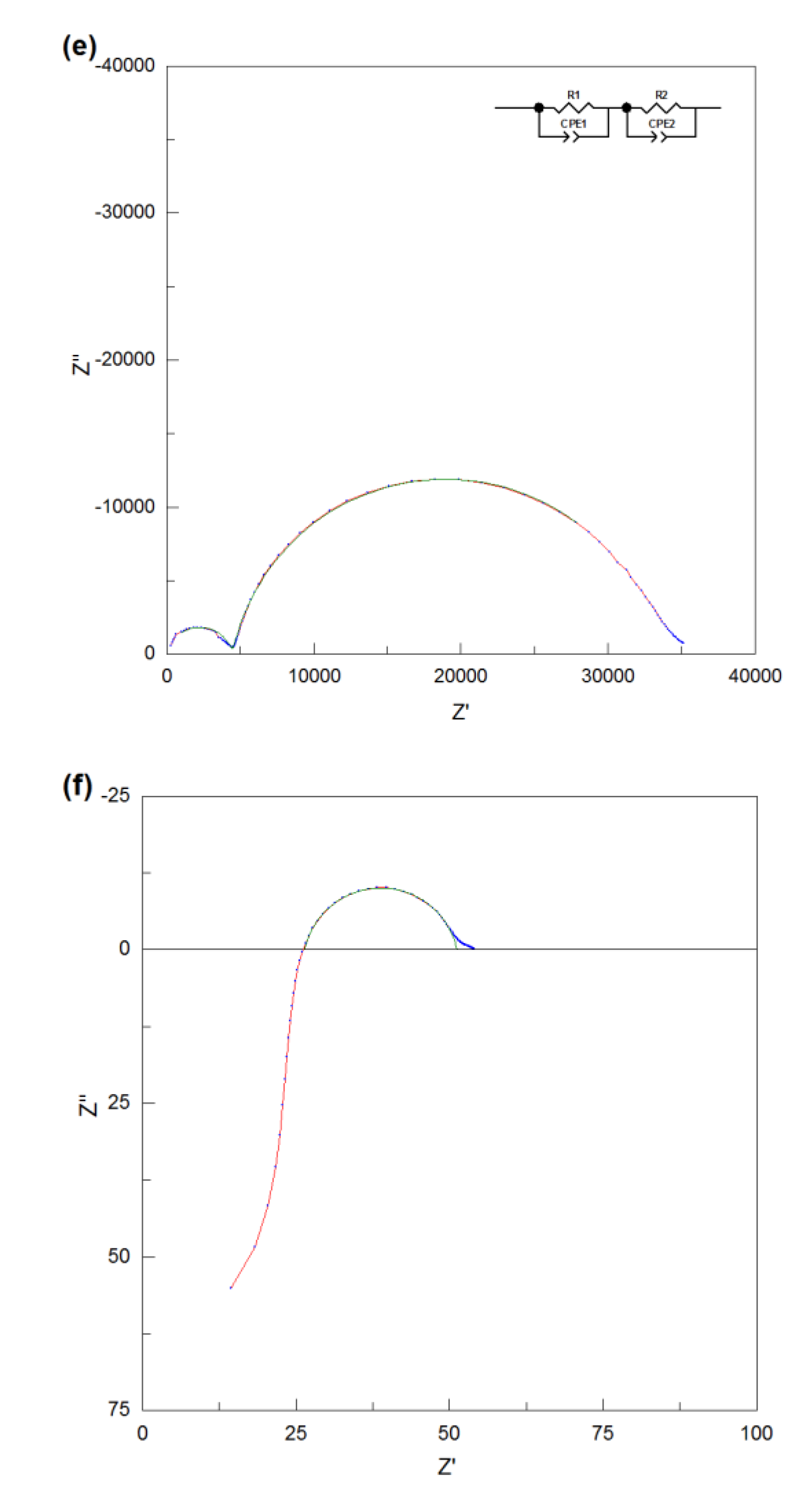
Figure 8. The Arrhenius plot of the total conductivity of NdBaInO₄ and Ca-doped NdBaInO₄ measured in the dry air.

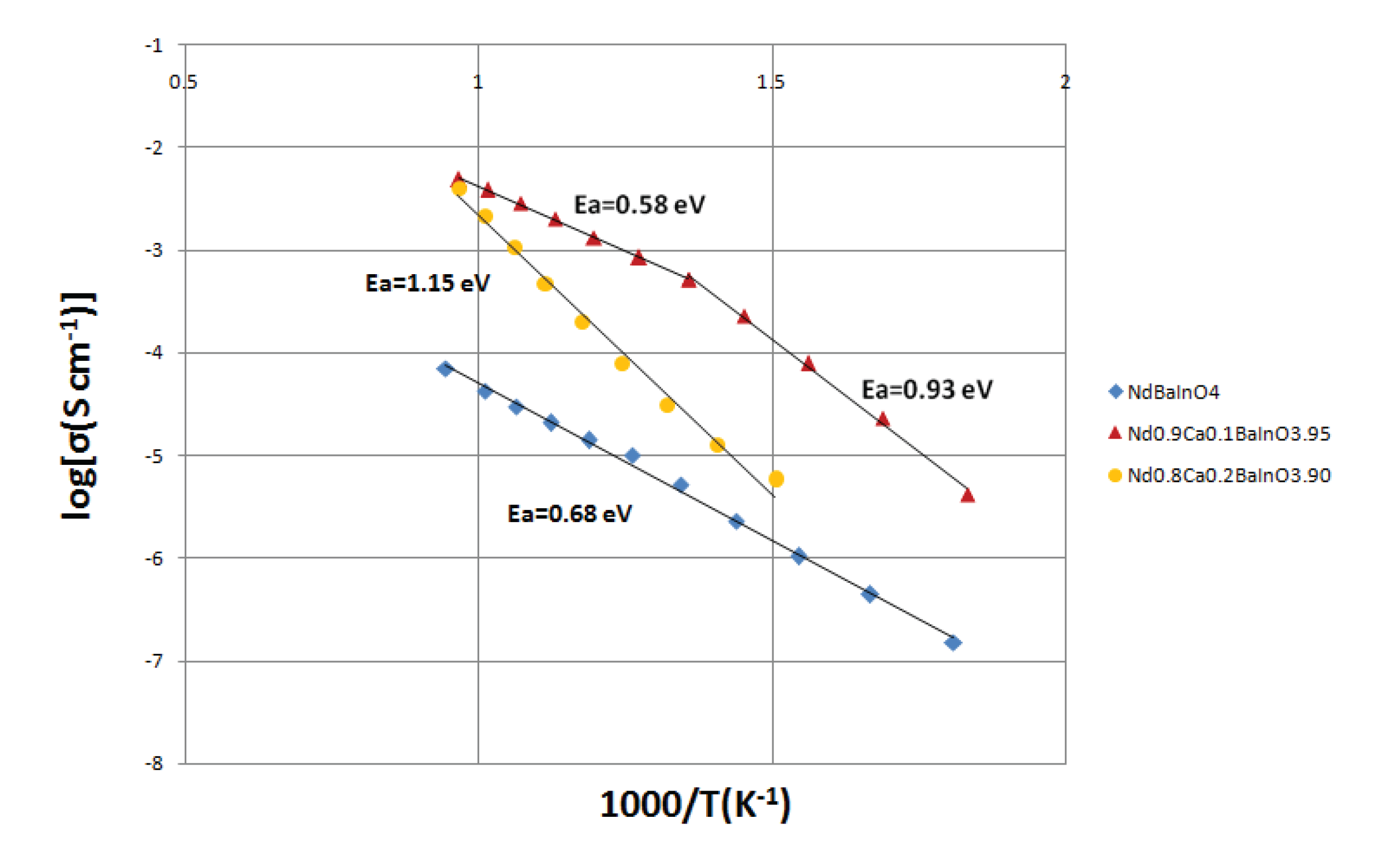
Figure 9. Impedance spectra of Nd_0.9Ca_0.1BaInO_3.95 measured in the wet atmosphere at (a) low temperature (270 °C) and (b) high temperature (760 °C). The experimental data are in red solid lines with blue dots, the fitting curves are in green solid lines.

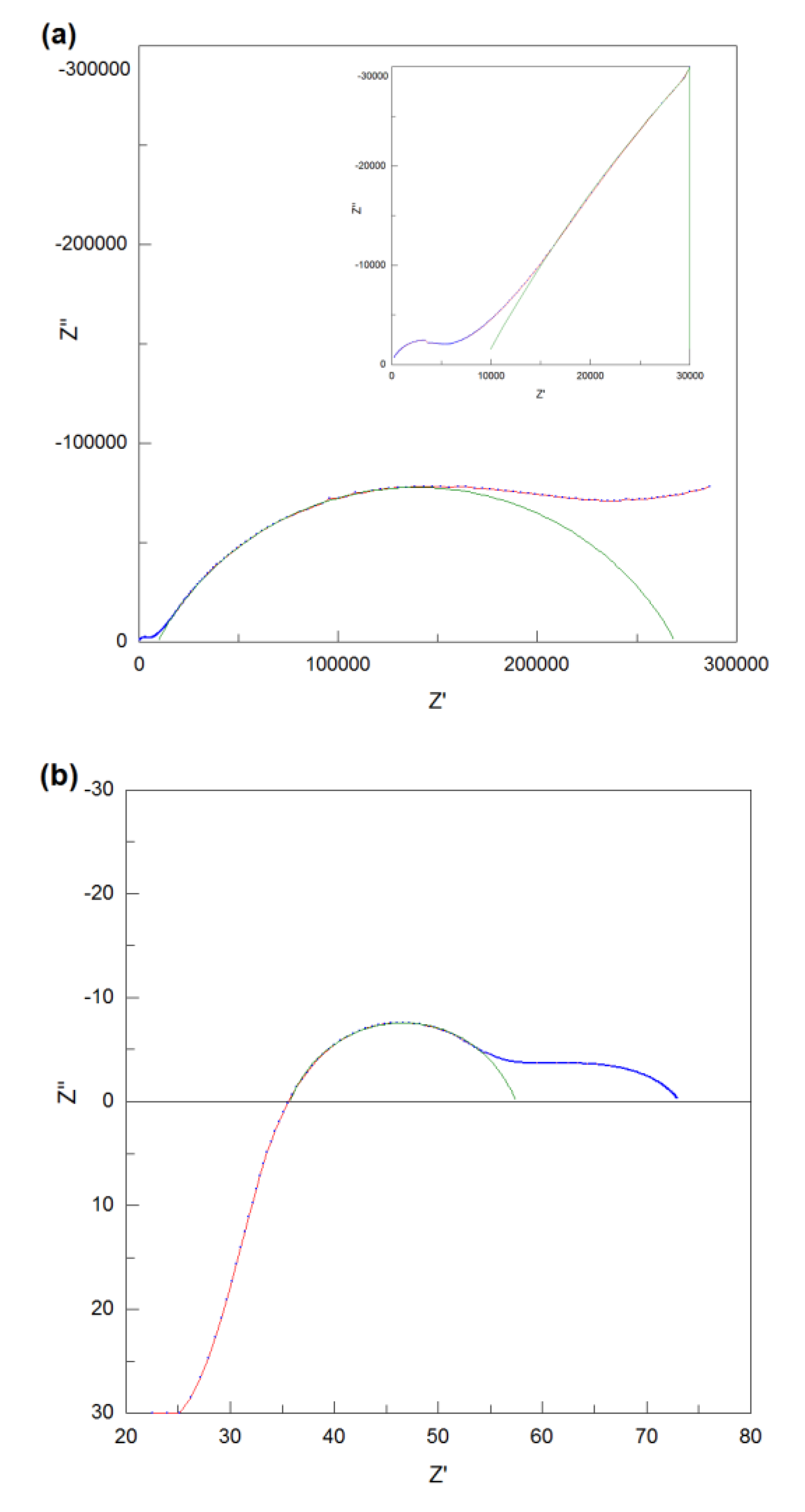
Figure 10. The Arrhenius plot of the total conductivities of NdBaInO₄ and Nd_0.9Ca_0.1BaInO_3.95 measured in the dry atmosphere and wet atmosphere.

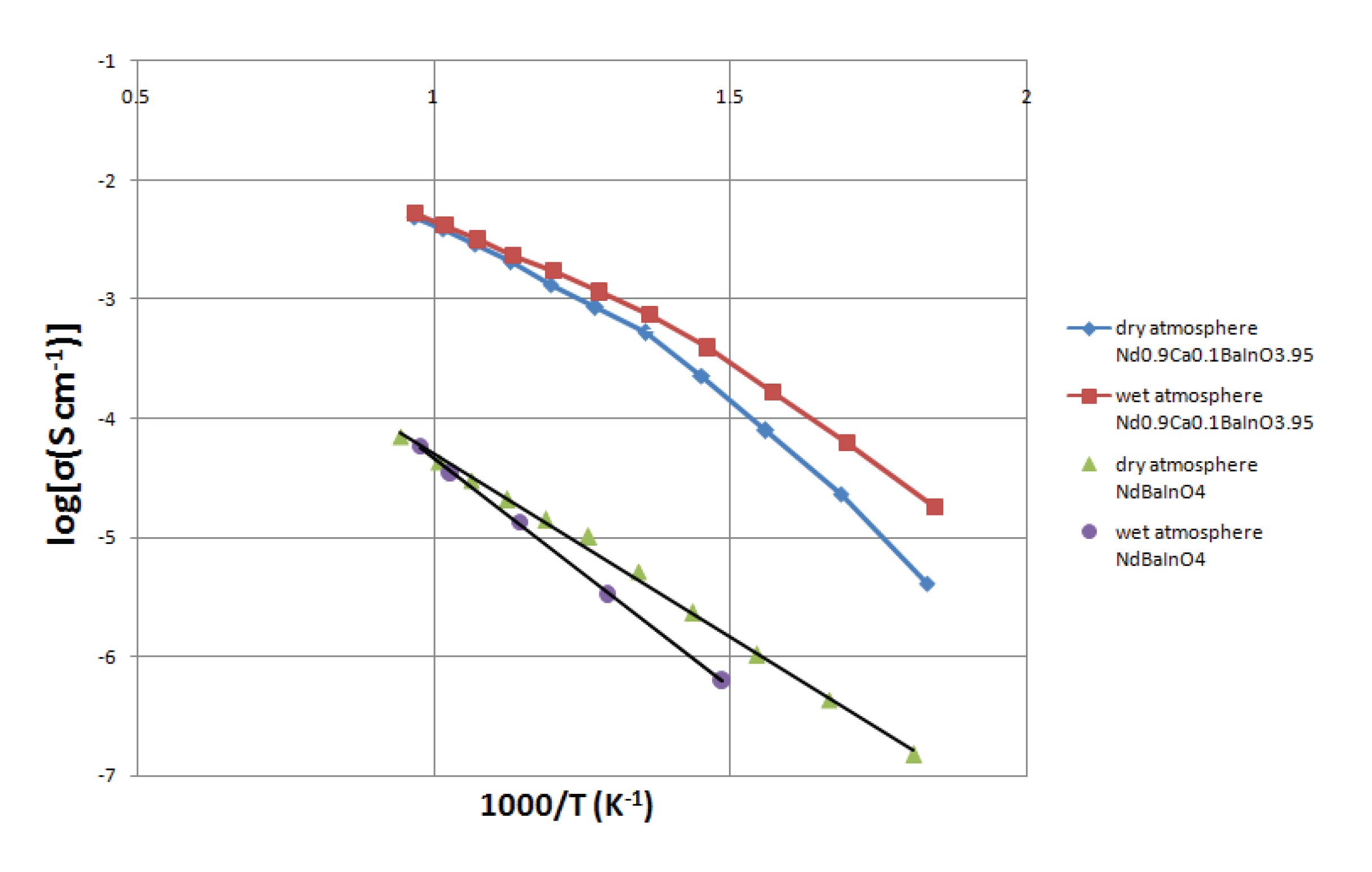
Figure 11. The fitting of the ¹⁸O line scanning diffusion profile for Nd_0.8Ca_0.2BaInO_3.90. Experimental data are in blue dots and the fitting result is in red solid line.

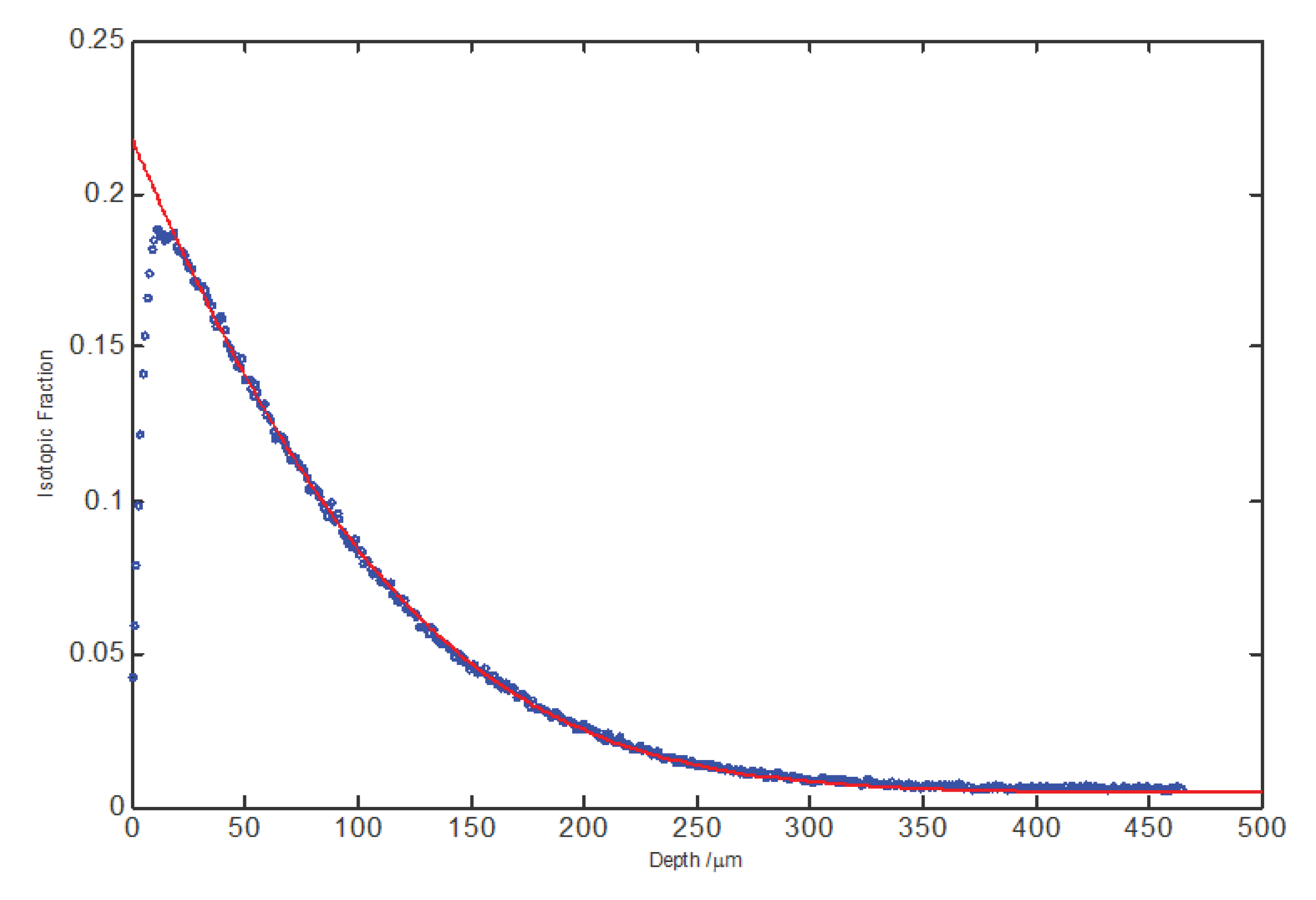
Table 1. Crystallographic data of NdBaInO₄ compared with data on literature, and crystallographic data of Nd_0.9Ca_0.1BaInO_3.95 and Nd_0.8Ca_0.2BaInO_3.90 compared with data of NdBaInO₄ resulted from experiment.

Chemical formula	NdBaInO₄ Ref [7]	NdBaInO₄ Exp.	Nd_0.9Ca_0.1BaInO_3.95	Nd_0.8Ca_0.2BaInO_3.90
Formula weight	460.39	460.39	449.17	437.96
Crystal system	Monoclinic	Monoclinic	Monoclinic	Monoclinic
Space group	P2₁/c	P2₁/c	P2₁/c	P2₁/c
a / Å	9.09538(3)	9.0882(37)	9.0883 (39)	9.0681(41)
b / Å	6.04934(2)	6.0372(18)	6.0290 (18)	6.0142(21)
c / Å	8.25620(2)	8.2633(23)	8.2593 (25)	8.2627 (34)
β/ ˚	103.4041(3)	103.599(254)	103.389 (259)	103.337(381)
Unit-cell volume / Å³	441.89(2)	440.674	440.255	438.470
Calculated density/ Mg m^-3	6.92		6.78	6.63
Measured density/ Mg m^-3		6.68	6.55	6.45
Relative density		96.53%	96.61%	97.29%

Table 2. The atomic ratio of NaBaInO₄ and Ca-doped NaBaInO₄ compounds which were detected by energy dispersive spectrometry (EDS).

	NaBaInO₄	Nd_0.9Ca_0.1BaInO_3.95	Nd_0.8Ca_0.2BaInO_3.90
Elements
O, atom%	58.06	51.45	54.78
In, atom%	14.21	15.81	14.68
Ba, atom%	12.53	16.28	15.34
Nd, atom%	15.20	14.93	12.91
Ca, atom%		1.54	2.29

Table 3. Calculated oxygen diffusion coefficients and surface exchange coefficients of the samples doped with 10% and 20% molar fraction of Ca²⁺

	Nd_0.9Ca_0.1BaInO_3.95	Nd_0.8Ca_0.2BaInO_3.90
D^* (cm²/s)	1.82 × 10^-8	9.30 × 10^-9
D^* (cm²/s)	1.80 × 10^-8	6.60 × 10^-9
Average D^* (cm²/s)	1.81× 10^-8	7.95× 10^-9
$k^{*}$ cm.s^-1	6.60 × 10^-7	7.00 × 10^-7

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer