Multi-Time-Scale Energy Storage Optimization Configuration for Power Balance in Distribution Systems

As the adoption of renewable energy sources grows, ensuring a stable power balance across various time frames has become a central challenge for modern power systems. In line with the "dual carbon" objectives and the seamless integration of renewable energy sources, harnessing the advantages of various energy storage resources and coordinating the operation of long-term and short-term storage have become pivotal directions for future energy storage deployment. To address the complexities arising from the coupling of different time scales in optimizing energy storage capacity, this paper proposes a method for energy storage planning that accounts for power imbalance risks across multiple time scales. Initially, the Seasonal and Trend decomposition using the Loess (STL) decomposition method is utilized to temporally decouple actual operational data. Subsequently, power balance computations are performed based on the obtained data at various time scales to optimize the allocation of different types of energy storage capacities and assess the associated imbalance risks. Finally, the effectiveness of the proposed approach is validated through hourly applications using real-world data from a province in China over recent years.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

With the continuous advancement of electrification, energy has become the primary battleground for mitigating global climate change [1]. Electricity serves as the vanguard in driving the development of a low-carbon society. Promoting the construction of a new type of power system, with wind and solar power as the main components, is a crucial pathway for energy conservation and emission reduction. However, the output of renewable energy sources such as wind and solar power is significantly influenced by weather changes, posing considerable challenges due to their intermittency and volatility [2]. Furthermore, mismatches between renewable energy generation and demand at different scales can also affect electricity supply, leading to power imbalances [3]. This is manifested in various aspects such as fluctuations in electricity prices and power rationing [4]. For instance, since 2021, natural gas prices in Europe have fluctuated dramatically, increasing by over 600%. The average electricity price in major European countries has exceeded €300 per megawatt-hour, reaching historic highs [5]. In September 2021, power rationing was "forced" in the three northeastern provinces of China due to significant supply-demand gaps, impacting the lives of residents and societal production.

To address the challenges facing the construction of new power systems and the seasonal imbalances between renewable energy and demand [2], and to mitigate the drastic fluctuations in electricity prices and occurrences of power rationing, several measures need to be taken. On one hand, it is essential to strategically plan for flexible resources like energy storage, which exhibit temporal and spatial transfer characteristics, while also maintaining the adequate capacity of traditional energy generation [6,7]. On the other hand, ensuring the economic viability of energy storage resource allocation is crucial alongside ensuring the reliability of grid operations [8,9]. Efficient utilization of various types of energy storage resources to address energy imbalances is vital [10,11]. This involves swiftly adjusting and activating energy storage systems during fluctuations in renewable energy output to ensure a stable electricity supply, thereby facilitating energy transition and promoting the development of renewable energy [12,13]. Therefore, it is imperative to strategically plan energy storage resources, leveraging the unique characteristics of different types of storage to tackle the imbalance issues in power systems [14].

Current research by experts and scholars has extensively addressed the issue of seasonal imbalance in electricity supply. Article [15] developed a coordinated optimization model for generation-grid-storage systems, incorporating a comprehensive yearly hourly operational simulation and utilizing compact panoramic time series to expedite model solving. Article [16] proposed an energy storage planning model that considers the seasonal imbalances resulting from the long-term uncertainty of renewable energy generation, yet it did not account for the impacts of short-term electricity fluctuations. However, there is a lack of research specifically addressing the imbalance risks arising from both the long-term and short-term uncertainties in electricity supply. Articles [17,18,19] integrated renewable energy with ammonia production, presenting a planning approach that considers renewable energy uncertainty, ammonia storage, and renewable energy generation. Article [20] combined renewable energy generation with flexible resources like thermal power generation, establishing an optimization model for generating combinations to minimize load loss. Article [21] optimized energy storage in regional energy internet based on user energy demands and future load trends, facilitating multi-energy coordination. Nevertheless, fewer studies have focused on the coordinated integration of multiple renewable energy sources with energy storage and other flexible resources [22].

Addressing the aforementioned shortcomings, this paper proposes an energy storage planning method that considers power imbalance risks across multiple time scales. Based on the collection of actual operational data from a specific province, a decomposition method is employed to temporally decouple the output of renewable energy sources and load profiles, thereby obtaining seasonal and periodic components of both renewable energy output and load variations. Utilizing the obtained decomposition results and considering the characteristics of different types of energy storage, hydrogen storage suitable for long-term storage and electrochemical storage capable of rapid charge and discharge are selected as different types of energy storage technologies in the planning process to meet the energy system’s demands across different time scales. In the process of energy storage planning, the marginal costs of energy storage construction are taken into account to optimize energy storage planning decisions, maximizing resource utilization efficiency and economic benefits. The main contributions of this paper are summarized as follows:

Considering the inclusion of marginal costs in energy storage cost calculations to optimize the relationship between energy storage capacity and storage costs.
Addressing the characteristics of changes in renewable energy and load profiles with economic development and seasonal variations in the new power system, utilizing a hybrid energy storage technology combining hydrogen storage and chemical energy storage to achieve supply-demand balance.
Employing STL decomposition technology to analyze and decompose data at long time scales, enabling the derivation of regional energy storage deployment schemes.

The remaining sections of the article are organized as follows: Chapter 2 provides an overview of the overall methodology and approach adopted in the study. Chapter 3 elaborates on the mathematical model used for energy storage planning. Chapter 4 presents the optimization configuration of energy storage resources for a specific region based on recent operational data of wind power, solar power, and load profiles. This chapter integrates the proposed model to offer an optimized allocation plan for energy storage resources in the region.

2. Structure

2.1. Energy Storage Type Selection

In the selection of energy storage types, this paper adopts hydrogen storage and electrochemical storage as two energy storage technologies [23], which are respectively used to balance the long-term uncertainty and short-term uncertainty in the new energy system [24,25]. On the one hand, hydrogen can be obtained through clean energy power electrolysis technology, the obtained hydrogen is stored in efficient hydrogen storage devices, and then, using fuel cell technology, the stored energy is fed back to the grid. On the other hand, hydrogen has high energy density, relatively low operation and maintenance costs, can be stored for a long time without losing too much energy, and there is no self-discharge phenomenon [26,27]. Therefore, it is suitable for large-scale long-term storage to cope with the seasonal imbalance caused by fluctuations in new energy output or the intermittency of solar and wind power generation, thereby alleviating the long-term uncertainty of the system.

In contrast, electrochemical energy storage technologies such as lithium-ion batteries and sodium-sulfur batteries offer advantages such as rapid response times and high energy densities, enabling the quick release of stored energy over short durations. However, they have limited cycle life, higher safety risks, and are relatively expensive. As a result, they are primarily deployed in scenarios requiring grid peak shaving and frequency regulation, particularly suited to address short-term load fluctuations or unpredictable energy supply variations in the system, thereby mitigating short-term uncertainty.

In conclusion, hydrogen storage and electrochemical energy storage offer distinct solutions for addressing the long-term uncertainty and short-term uncertainty in renewable energy systems, respectively. Together, they can provide support for the balance and stability of energy systems.

2.2. Energy Storage Planning Methodology

The objective of this paper is to utilize the temporal and spatial transfer characteristics of different types of energy storage to mitigate the risk of power imbalance in the new power system, thereby achieving the core goal of clean and low-carbon electricity and promoting the development of green power.

Figure 1 illustrates the flow of energy in the new power system. The primary sources of energy include solar power, wind power, and other types of clean energy. Energy storage predominantly occurs through hydrogen storage and electrochemical energy storage, while energy is consumed across various types of electrical load demand systems.

2.3. STL Decomposition Method

Seasonal-trend decomposition using LOESS (STL) [28] is a robust method for decomposing time series data based on the additive principle [29]. This decomposition method was proposed by R. B. Cleveland, Cleveland, McRae, & Terpenning in 1990. Its distinguishing feature is its ability to obtain stable trends and seasonal components, with strong resistance to short-term anomalies in the data. Due to the strong seasonality and regularity of new energy output such as photovoltaic and wind power, it is possible to decompose the data of new energy output and load data based on historical data. Assuming the net load data is a time series

y (t)

, and assuming it follows an additive model, it can be decomposed as follows:

y (t) = S (t) + T (t) + R (t)

(1)

Where

T (t)

represents the trend value at time t,

S (t)

denotes the seasonal component at time t, and

R (t)

stands for the residual component at time t.

The decomposition mainly consists of two parts: the inner loop and the outer loop. The main function of the inner loop is to perform trend fitting and calculate the periodic components, while the main function of the outer loop is to adjust the weights of robust optimization. The process is illustrated in Table 1, as shown in the decomposition flowchart.

To validate the trend and seasonality of the selected data, the variances of the trend component, seasonal component, and residual component can be calculated respectively. For data with strong trends, the magnitude of variation in the seasonally adjusted data is larger than that of the residual component. Therefore, the strength of the trend can be defined as:

F_{T} = max (0, 1 - \frac{V a r (R (t))}{V a r (T (t) + R (t))})

(2)

Hence, the strength of the trend lies between

0 - 1

and

F_{T}

, where a value closer to 0 indicates that the sequence has almost no trend, and a value closer to 1 indicates a stronger trend intensity in the time series.

Similarly, the strength of seasonality can be defined as:

F_{S} = max (0, 1 - \frac{V a r (R (t))}{V a r (S (t) + R (t))})

(3)

The strength of seasonality lies between

0 - 1

, and

F_{S}

, where a larger

F_{S}

value corresponds to a stronger seasonality intensity.

3. Mathematical Model

The established model is based on the following assumptions:

Only photovoltaic and other new energy devices, as well as flexible resources such as energy storage, participate in the operation balance of the power system.
Considering the insufficiency of renewable energy output to meet the system load demand, the addition of hydrogen energy from alternative sources to compensate for the imbalance in power is being considered.
Only consider hydrogen obtained through clean energy sources and fed back to the grid through fuel cell technology. The model does not consider the demand for hydrogen energy by the hydrogen industry chain.

3.1. Objective Function

The model aims to minimize the total cost and establishes the objective function as shown in the formula (4). The total cost of the power system includes two parts: the investment cost of energy storage construction and the operational cost of the system.

min C = C^{INV} + C^{OPE}

(4)

where C represents the total cost of the grid,

C^{INV}

represents the investment cost of the grid, and

C^{OPE}

represents the operational cost of the grid.

C^{INV} = (C^{INV_che} + C^{INV_hyd}) \times C R F

(5)

C R F = \frac{γ {(1 + γ)}^{n}}{({(1 + γ)}^{n} - 1)}

(6)

C^{INV_che} = c_{mc, che} c a p_{pre, che} + c_{unit, che} N_{unit, che}

(7)

C^{INV_hyd} = c_{mc, hyd} c a p_{pre, hyd} + c_{unit, hyd} N_{unit, hyd}

(8)

N_{unit, che} = ⌈\frac{c a p_{pre, che}}{c a p_{N, che}}⌉

(9)

N_{unit, hyd} = ⌈\frac{c a p_{pre, hyd}}{c a p_{N, hyd}}⌉

(10)

Formulas (5) - (10) demonstrate the investment cost of energy storage and related equations.

C R F

represents the capital recovery factor. In the formula,

γ

represents the annual interest rate of investment cost and n represents the total lifespan of energy storage. Considering the capacity constraints of electrochemical energy storage and hydrogen storage, formulas (7) - (8) incorporate the calculation of marginal costs when calculating the construction cost of energy storage, aiming to optimize the capacity allocation of energy storage. Additionally, discrete variables are transformed into continuous variables to facilitate subsequent optimization calculations.

C^{INV_che}

represents the upfront cost of electrochemical energy storage,

C^{INV_hyd}

represents the upfront cost of hydrogen energy storage,

c_{mc, che}

represents the marginal cost of electrochemical energy storage,

c_{mc, hyd}

represents the marginal cost of hydrogen energy storage,

c a p_{pre, che}

represents the capacity of pre-installed electrochemical energy storage,

c a p_{pre, hyd}

represents the capacity of pre-installed hydrogen energy storage,

c_{unit, che}

represents the cost per unit of electrochemical energy storage,

c_{unit, hyd}

represents the cost per unit of hydrogen energy storage,

N_{unit, che}

represents the number of pre-installed electrochemical energy storage units,

N_{unit, hyd}

represents the number of pre-installed hydrogen energy storage units,

c a p_{N, che}

represents the capacity per unit of electrochemical energy storage, and

c a p_{N, hyd}

represents the capacity per unit of hydrogen.

C^{OPE} = C^{CUT_LOAD} + C^{CUT_NE} + C^{GET_NE} - C^{SUP_LOAD}

(11)

C^{CUT_LOAD} = c_{load, cut} \sum_{d = 1}^{D} \sum_{t = 1}^{T} E_{load, cut}

(12)

C^{CUT_NE} = c_{ne, cut} \sum_{d = 1}^{D} \sum_{t = 1}^{T} E_{ne, cut}

(13)

C^{SUP_LOAD} = c_{load, get} (\sum_{d = 1}^{D} \sum_{t = 1}^{T} c a p_{load} - \sum_{d = 1}^{D} \sum_{t = 1}^{T} c a p_{load, cut} + \sum_{d = 1}^{D} \sum_{t = 1}^{T} c a p_{ne, cut})

(14)

The operational cost of the power system and its specific expressions are shown in equations (11) - (14). The operational cost of the power system consists of four parts: shedding load penalty cost, wind and solar spillage cost, profit from supplying load, and energy storage operation cost. In the equations,

C^{CUT_LOAD}

represents the total cost of shedding the load,

c_{load, cut}

represents the unit cost of shedding the load,

C^{CUT_NE}

represents the total cost of wind and solar spillage,

c_{ne, cut}

represents the unit cost of wind and solar spillage,

C^{SUP_LOAD}

represents the total revenue from the power supply,

c_{l o a d, g e t}

represents the unit revenue from the power supply,

E_{load, cut}

represents the total amount of shed load,

E_{ne, cut}

represents the total amount of wind and solar spillage,

E_{load}

represents the total load, and

E_{ne}

represents the total amount of renewable energy generation.

3.2. Constraint Conditions

The constraints established in this paper include power balance constraints, maximum shedding load constraints, maximum wind and solar spillage constraints, battery operation constraints, etc.

3.2.1. Power Balance Constraint

P_{d, t}^{che, long} + P_{d, t}^{hyd, long} = Δ P_{d, t}^{ne, trend}, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(15)

P_{d, t}^{che, short} + P_{d, t}^{hyd, short} = Δ P_{d, t}^{ne, seasonal} + Δ P_{d, t}^{ne, resid}, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(16)

P_{d, t}^{che} + P_{d, t}^{hyd} - P_{d, t}^{load, cut} ⩾ Δ P_{d, t}^{ne} - P_{d, t}^{ne, cut}, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(17)

In the equations,

P_{d, t}^{che, long}

P_{d, t}^{hyd, long}

represents the charging and discharging power of long-term energy storage,

P_{d, t}^{che, short}

P_{d, t}^{hyd, short}

represents the charging and discharging power of short-term energy storage,

Δ P_{d, t}^{ne, trend}

represents the trend component, and

Δ P_{d, t}^{ne, seasonal}

represents the seasonal component. Formulas (15) - (17) represent the constraints on the power balance of the system, including the balance between long-term energy storage and trend components, the balance between short-term energy storage and seasonal components, and the real-time balance of power during grid operation.

3.2.2. Load Cut Constraint

0 ⩽ P_{d, t}^{load, cut} ⩽ P_{d, t}^{load, cut, max}, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(18)

In the equation,

P_{d, t}^{load, cut}

represents the total amount of load shedding. The formula (18) represents that the maximum shedding load cannot exceed the specified maximum value

P_{d, t}^{load, cut, max}

3.2.3. Wind and Solar Spillage Constraint

0 ⩽ P_{d, t}^{ne, cut} ⩽ P_{d, t}^{ne, cut, max}, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(19)

In the equation,

P_{d, t}^{ne, cut}

represents the total amount of wind and solar spillage. The formula (19) represents that the maximum wind and solar spillage at different times must not exceed the given maximum value

P_{d, t}^{ne, cut, max}

3.2.4. Battery Operation Constraint

E_{d, t + Δ t}^{che} = E_{d, t}^{che} {(1 - η_{loss}^{che})}^{Δ t} + (P_{d, t}^{che, cha} η_{cha}^{che} - P_{d, t}^{che, dis} / η_{dis}^{che}) Δ t, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(20)

E_{d, t + Δ t}^{hyd} = E_{d, t}^{hyd} {(1 - η_{loss}^{hyd})}^{Δ t} + (P_{d, t}^{hyd, cha} η_{cha}^{hyd} - P_{d, t}^{hyd, dis} / η_{dis}^{hyd}) Δ t, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(21)

0 ⩽ P_{d, t}^{che, cha}, P_{d, t}^{che, dis} ⩽ P_{d, t}^{che, max}, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(22)

0 ⩽ P_{d, t}^{hyd, cha}, P_{d, t}^{hyd, dis} ⩽ P_{d, t}^{hyd, max}, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(23)

E_{d, t}^{che, min} ⩽ E_{d, t}^{che} ⩽ E_{d, t}^{che, max}, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(24)

E_{d, t}^{hyd, min} ⩽ E_{d, t}^{hyd} ⩽ E_{d, t}^{hyd, max}, 1 ⩽ d ⩽ D, 1 ⩽ t ⩽ T

(25)

E_{d + 1, 0}^{che} = E_{d, 0}^{che}, 1 ⩽ d ⩽ D

(26)

E_{d + 1, 0}^{hyd} = E_{d, 0}^{hyd}, 1 ⩽ d ⩽ D

(27)

Formulas (20) - (21) calculate the capacity of energy storage at different times, including self-discharge, charging, and discharging of energy storage. Formulas (22) - (23) constrain the maximum charging and discharging rates of energy storage. Formulas (24) - (25) restrict the upper and lower bounds of energy storage charging and discharging. Formulas (26) - (27) ensure that the energy storage capacity remains constant within a day. In these equations,

P_{d, t}^{che, cha}

P_{d, t}^{che, dis}

represents the charging and discharging power of electrochemical energy storage,

Δ P_{d, t}^{ne}

represents the power output of renewable energy,

P_{d, t}^{hyd, cha}

P_{d, t}^{hyd, dis}

represents the charging and discharging power of hydrogen energy storage,

η_{loss}^{che}

η_{loss}^{hyd}

represents the efficiency of energy storage charging and discharging,

P_{d, t}^{load, cut, max}

represents the maximum load shedding amount,

P_{d, t}^{ne, cut, max}

represents the maximum removal amount of renewable energy,

P_{d, t}^{che, max}

P_{d, t}^{hyd, max}

represents the maximum charging and discharging power of energy storage,

E_{d, t}^{che}

E_{d, t}^{hyd}

represents the capacity of energy storage,

E_{d, t}^{che, min}

E_{d, t}^{hyd, min}

represents the minimum capacity allowed for energy storage,

E_{d, t}^{che, max}

E_{d, t}^{hyd, max}

represents the maximum capacity allowed for energy storage, and

E_{d, 0}^{che}

E_{d, 0}^{hyd}

represents the initial capacity of energy storage.

4. Case Study

Based on the photovoltaic, wind power, and load data for a certain region over a year, the above model is applied for validation. Firstly, the obtained data is organized and analyzed to obtain net load data, and a net load curve is plotted. Secondly, the net load data is decomposed using the decomposition method to obtain trend components, seasonal components, and residual components, and the trend strength and seasonality strength are calculated. Then, based on the multi-type energy storage planning model in Section 3, the configuration of hydrogen storage and electrochemical energy storage, as well as the output during each period throughout the year, are obtained. Finally, the effectiveness of the model is validated.

Firstly, based on the operational data of wind power, photovoltaic power, and load for 8760 hours in the region, the net load curve is plotted as shown in Figure 2. From the graph, it can be observed that the load exhibits significant variations throughout the day, characterized by "two peaks and one trough". The "two peaks" occur around 6-9 AM and 6-10 PM, primarily driven by residential, commercial, and industrial electricity consumption. The "trough" occurs around 11 AM-4 PM, mainly due to the substantial generation of wind and solar power. Over the year, the net load shows significant seasonal variations. In winter and spring, the net load is negative, indicating that the generation of renewable energy exceeds electricity consumption. In summer and autumn, the net load is positive, indicating that the generation of renewable energy is lower than electricity consumption.

The trend component, seasonal component, and residual component obtained through STL decomposition are shown in Figure 3 and Figure 4. By using formulas (2)-(3) to calculate the strength of trend and seasonality after decomposition, we obtain

F_{T} = 0.87154

and

F_{S} = 0.96619

, both of which are close to 1. This indicates that the net load data for this location exhibits both trend and seasonality, hence validating the use of the STL decomposition method for calculation.

After obtaining the trend component, seasonal component, and residual component of the net load for 8760 hours, the multi-type energy storage planning model described in Section 3 and the initial value settings in Table 2 are utilized [30]. Hydrogen energy storage is used to balance the long-term imbalance component of the power system, while electrochemical energy storage, with its rapid charging and discharging properties, is utilized to balance the short-term power imbalance of the power system. This process results in the configuration of hydrogen energy storage and electrochemical energy storage, along with the power output throughout the year at different times.

The configured capacity of electrochemical energy storage is 51 MWh, and the configured capacity of hydrogen energy storage is 47 MWh.

As shown in Figure 5, the total shedding load throughout the year is 0, and the total wind and solar spillage throughout the year is 0. Selecting a day from the year, and plotting the net load and energy storage output situation as shown in Figure 8, it can be observed from the graph that the power sources and loads achieve a balance of power throughout the day, with hydrogen energy mainly used to balance long-term power output and electrochemical energy storage used to balance short-term fluctuations in net load. Additionally, the long-term and short-term charging and discharging situations of electrochemical energy storage are shown in Figure 6, and the long-term and short-term charging and discharging situations of hydrogen energy storage are shown in Figure 7. Comparing Figure 4 and Figure 6, it can be observed that the long-term charging and discharging curve of hydrogen energy storage coincides with the long-term imbalance component of power while comparing the Figure 4 and Figure 7, it can be observed that the short-term charging and discharging curve of electrochemical energy storage coincides with the seasonal imbalance component of power, which meets the expected situation. As the existing renewable energy generation capacity cannot meet the requirements of the load operation, additional hydrogen energy is considered to achieve the balance of power quantity in the system. The situation with additional hydrogen energy storage is illustrated in the Figure 9.

5. Conclusions

To address the power imbalance issue resulting from the large-scale integration of renewable energy and load, this paper proposes a multi-timescale energy storage planning method considering the risk of power imbalance. The model takes into account the annual variations in renewable energy and load, captured using decomposition methods, and uses the decomposition results as the basis for planning the capacities of hydrogen storage and electrochemical energy storage. Intending to minimize the total cost, the energy storage planning model considers marginal costs during energy storage construction to optimize cost calculations. To improve energy utilization efficiency and leverage the advantages of different types of energy storage, hydrogen storage, which has no self-discharge phenomenon, is used to address seasonal fluctuations, while electrochemical energy storage with fast charging and discharging rates is employed for short-term energy fluctuations. Case studies using operational data from a province are conducted to demonstrate the effectiveness of the proposed model.

Author Contributions

Conceptualization, Q.L., X.Z.; methodology, Y.Y.; validation, Q.H., G.W., Y.H.; formal analysis, Y.L.; investigation, G.L.; resources, Q.L.; data curation, X.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This work is supported by the Science and Technology Project of China Southern Power Grid Corporation. (Project No.036000KK52220025 (GDKJXM20220329)).

Data Availability Statement

We are unable to publicly share the data supporting the reported results due to legal restrictions. However, upon request, we are willing to provide the data to qualified researchers under appropriate confidentiality agreements.

Acknowledgments

We would like to express our gratitude to all the reviewers for providing valuable feedback.

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:

STL	Seasonal and Trend decomposition using Loess

References

Ge, X.; Hou, H.; Hou, T. Review of key technologies of low-carbon transition on the power supply side. IEEE 5th International Conference on Electronics Technology (ICET). IEEE. 2022, 275-279.
Denholm, P.; Arent,D. J.; Baldwin, S. F.; Bilello, D. E.; Brinkman, T. The challenges of achieving a 100% renewable electricity system in the United States. Joule. 2021, 5, 1331–1352. [Google Scholar] [CrossRef]
Huang, H.; Zhou, M.; Zhang, S.; Zhang, L.; Li, G.; and Sun, T. Exploiting the operational flexibility of wind-integrated hybrid AC/DC power systems. IEEE Transactions Power System. 2021, 36, 818––826. [Google Scholar] [CrossRef]
Lazzeroni, P.; Mariuzzo, I.; Quercio, T. Economic, Energy, and Environmental Analysis of PV with Battery Storage for Italian Households. Electronics. 2021, 10. [Google Scholar] [CrossRef]
Liu, G.Q.; Zeng, Q.; Lei, T. Dynamic risks from climate policy uncertainty: a case study for the natural gas market. Resources. 2022, 79, 103014. [Google Scholar] [CrossRef]
Lajnef, T.; Abid, S.; Ammous, T. Modeling, Control, and Simulation of a Solar Hydrogen/Fuel Cell Hybrid Energy System for Grid-Connected Applications. Advances in Power Electronics. 2023. [Google Scholar] [CrossRef]
Diaz, N. L.; Luna, A. C.; Vasquez, T. Centralized control architecture for coordination of distributed renewable generation and energy storage in islanded AC microgrids. IEEE Transactions on Power Electronics. 2016, 32, 5202–5213. [Google Scholar] [CrossRef]
Georgios, R.; Refaat, R.; Garcia, T. Review on energy storage systems in microgrids. Electronics. 2021, 10. [Google Scholar] [CrossRef]
Zsiborács, H.; Baranyai, N.H.; Vincze, T. Intermittent renewable energy sources: The role of energy storage in the European power system of 2040. Electronics. 2019, 8. [Google Scholar] [CrossRef]
Zhou, H.; Bhattacharya, T.; Tran, T. Composite energy storage system involving battery and ultracapacitor with dynamic energy management in microgrid applications. IEEE Transactions on Power Electronics. 2010, 26, 923–930. [Google Scholar] [CrossRef]
Pedram, M.; Chang, N.; Kim, T. Hybrid electrical energy storage systems. Proceedings of the 16th ACM/IEEE international symposium on Low power electronics and design. 2010; 363–368. [Google Scholar]
Javed, K.; Ashfaq, H.; Ashfaq, T. Design and performance analysis of a stand-alone PV system with hybrid energy storage for rural India. Electronics. 2019, 8. [Google Scholar] [CrossRef]
Adedoja, O. S.; Saleh, U. A.; Alesinloye, T. An energy balance and multicriterial approach for the sizing of a hybrid renewable energy system with hydrogen storage. Electronics and Energy. 2023, 4, 100146. [Google Scholar] [CrossRef]
Koohi-Fayegh, S.; Rosen, T. A review of energy storage types, applications and recent developments. Journal of Energy Storage 2020, 27, 101047. [Google Scholar] [CrossRef]
Zhang, N.; Jiang, H.; Du, T. An Efficient Power System Planning Model Considering Year-Round Hourly Operation Simulation. IEEE Transactions Power System. 2022, 37, 4925–4935. [Google Scholar] [CrossRef]
Jiang, H.; Du, E.; Zhang, T. Renewable Electric Energy System Planning Considering Seasonal Electricity Imbalance Risk. IEEE Transactions Power System. 2023, 38, 5432–5444. [Google Scholar] [CrossRef]
Yu, Z.; Lin, J.; Liu, T. Optimal Sizing of Isolated Renewable Power Systems with Ammonia Synthesis: Model and Solution Approach, ArXiv., 2024.
Yu, Z.; Lin, J.; Liu, T. Optimal Sizing and Pricing of Grid-Connected Renewable Power to Ammonia Systems Considering the Limited Flexibility of Ammonia Synthesis. IEEE Transactions Power System 2024, 39, 3631–3648. [Google Scholar] [CrossRef]
Pham, M. C.; Tran, T. Q.; Bacha, T. Optimal sizing of battery energy storage system for an island microgrid, IECON 2018-44th Annual Conference of the IEEE Industrial Electronics Society. IEEE, 2018; 1899–1903. [Google Scholar]
Yu, Y.; Du, E.; Chen, T. Optimal portfolio of a 100% renewable energy generation base supported by concentrating solar power. Renewable Sustainable Energy Rev. 2022; 170. [Google Scholar]
Yan, P.; Zhao, L.; Xie, T. Optimal control method of regional energy interconnection energy storage considering user demand. ICEMEE 2022. SPIE 2023, 12598, 239–244. [Google Scholar]
Garcia-Torres, F.; Bordons, T. Optimal economical schedule of hydrogen-based microgrids with hybrid storage using model predictive control. IEEE Transactions on Industrial Electronics. 2015, 62, 5195–5207. [Google Scholar] [CrossRef]
Riyaz, A.; Sadhu, P. K.; Iqbal, T. Comprehensive survey of various energy storage technology used in hybrid energy. Electronics 2021, 10, 2037. [Google Scholar] [CrossRef]
Barthélémy, T. Hydrogen storage–Industrial prospectives. International Journal of Hydrogen Energy. 2012, 37, 17364–17372. [Google Scholar] [CrossRef]
Preuster, P.; Alekseev, A.; Wasserscheid, T. Hydrogen storage technologies for future energy systems. Annual Review of Chemical and Biomolecular Engineering. 2017, 8, 445–471. [Google Scholar] [CrossRef]
Vivas, F. J.; Segura, F.; Andújar, T. Multi-objective fuzzy logic-based energy management system for microgrids with battery and hydrogen energy storage system. Electronics 2020, 9, 1074. [Google Scholar] [CrossRef]
Monforti, F. A.; Vivas, F. J.; Segura, T. Hydrogen vs. battery in the long-term operation. A comparative between energy management strategies for hybrid renewable microgrids. Electronics. 2020, 9. [Google Scholar] [CrossRef]
Cleveland, R. B.; Cleveland, W. S.; McRae, T. STL: A seasonal-trend decomposition. J. Off. Stat. 1990, 6, 3–37. [Google Scholar]
Wang, X.; Smith, K. A.; Hyndman, T. Characteristic-based clustering for time series data. Data Mining Knowl. Discov. 2006, 13, 335–364. [Google Scholar] [CrossRef]
Wu, J.; Xing, X.; Liu, T. Energy management strategy for grid-tied microgrids considering the energy storage efficiency. IEEE Transactions on Industrial Electronics. 2018, 65, 9539–9549. [Google Scholar] [CrossRef]

Figure 1. Energy Flow in Distribution Systems.

Figure 2. Net load curve for 8760 hours.

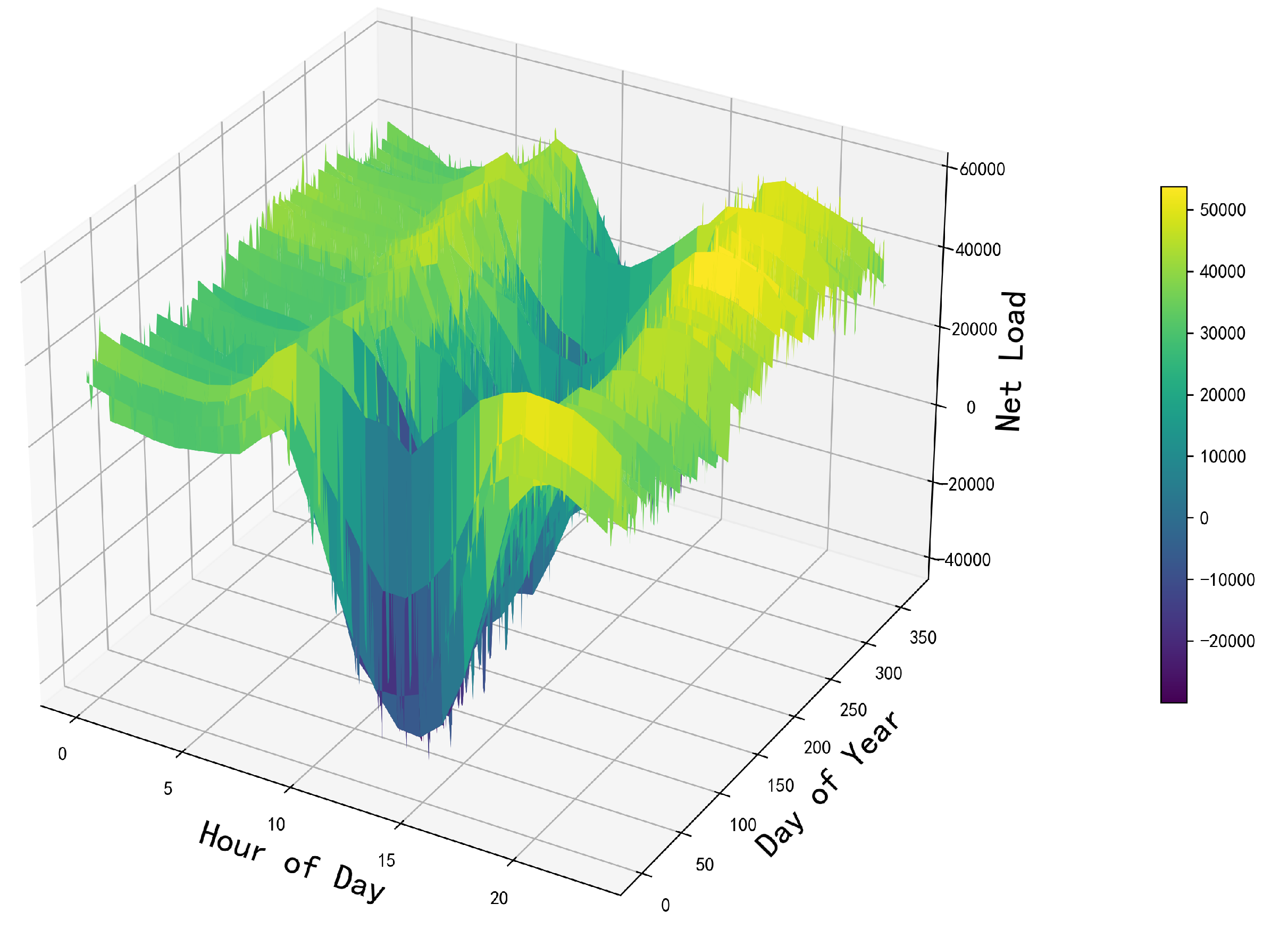
Figure 3. Two-dimensional decomposition plot of the net load.

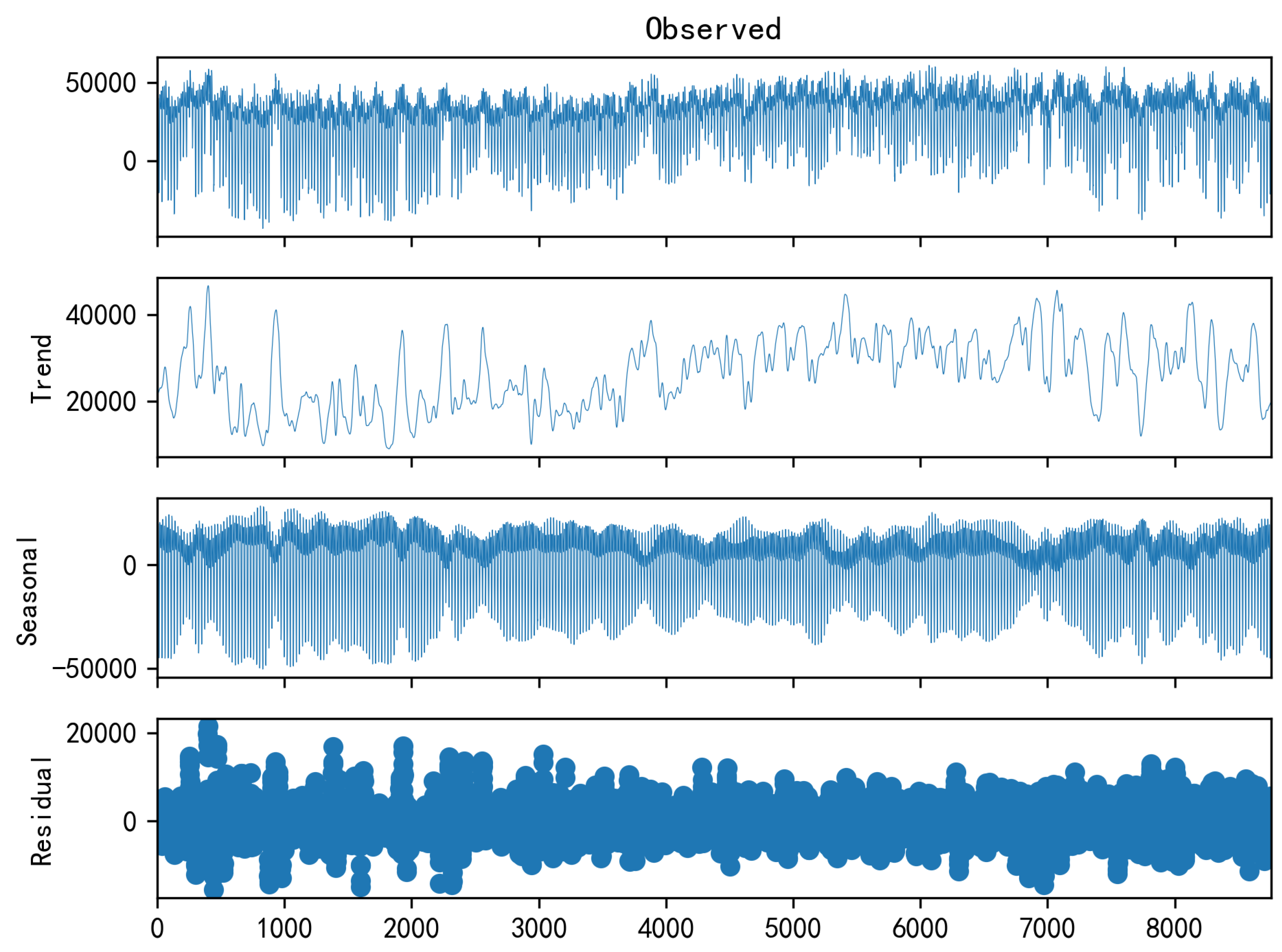
Figure 4. Three-dimensional decomposition plot of the net load.

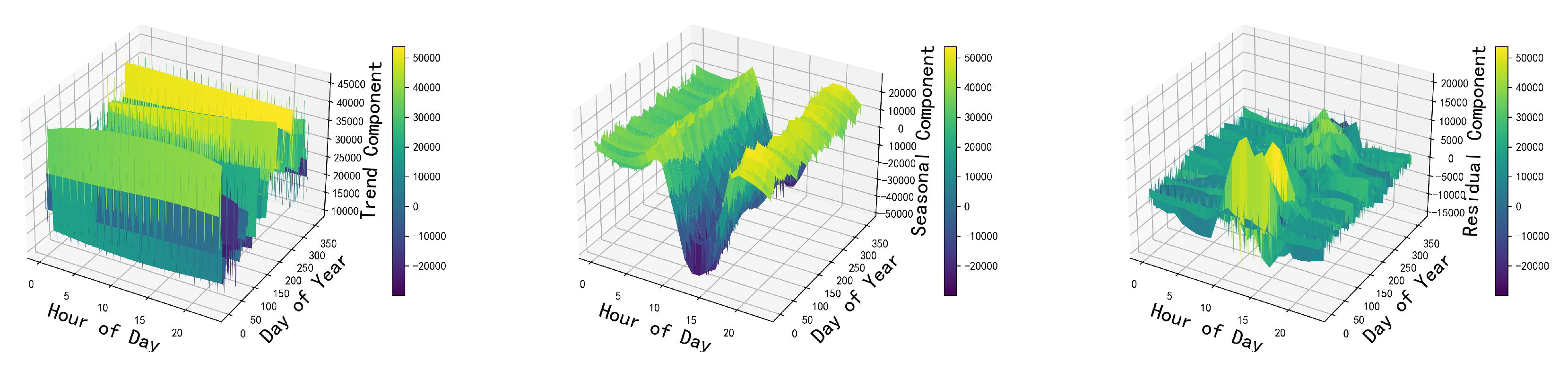
Figure 5. Wind and solar spillage versus load shedding situation.

Figure 6. Hydrogen energy storage power output situation.

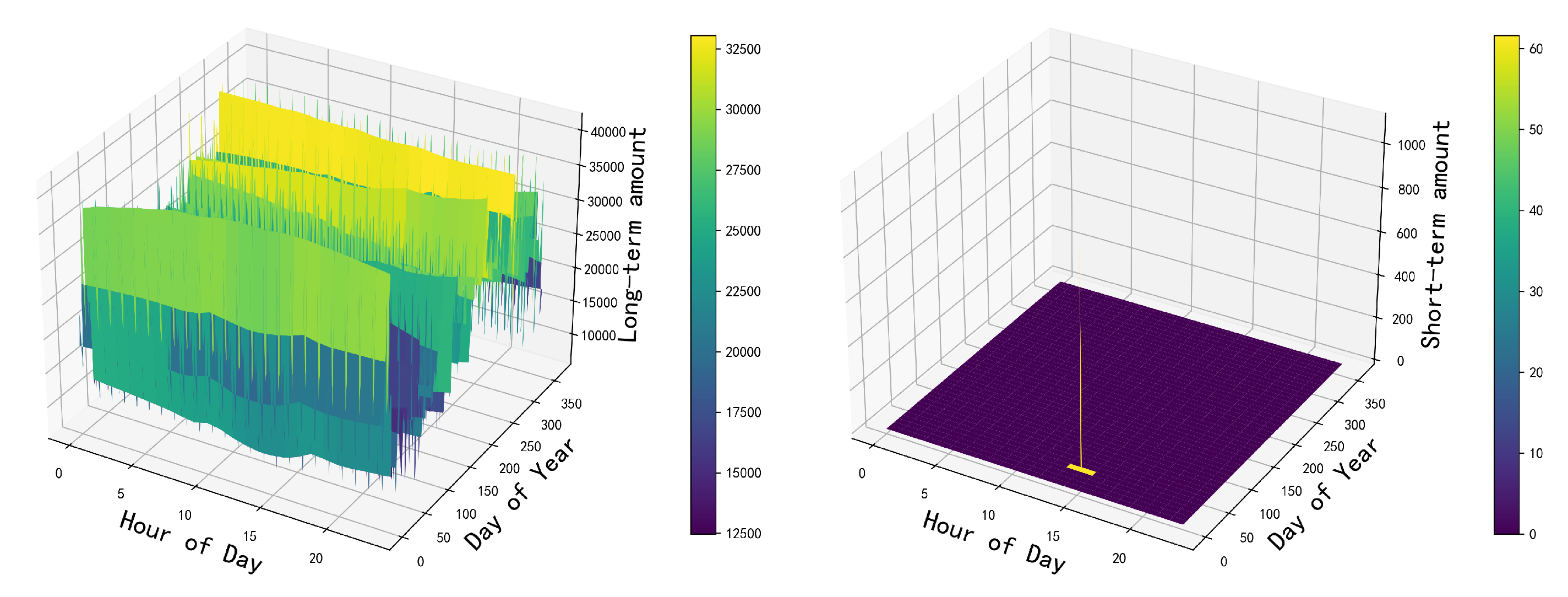
Figure 7. Electrochemical energy storage power output situation.

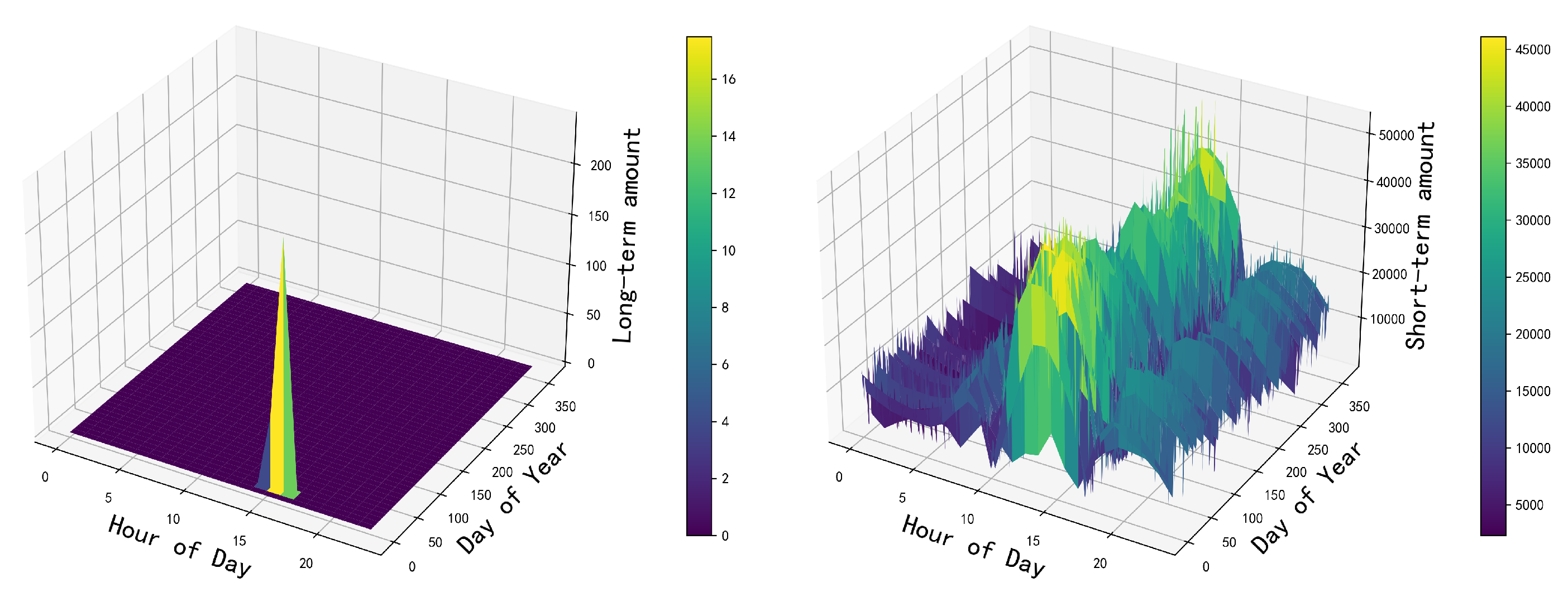
Figure 8. Overall power balance situation in the system.

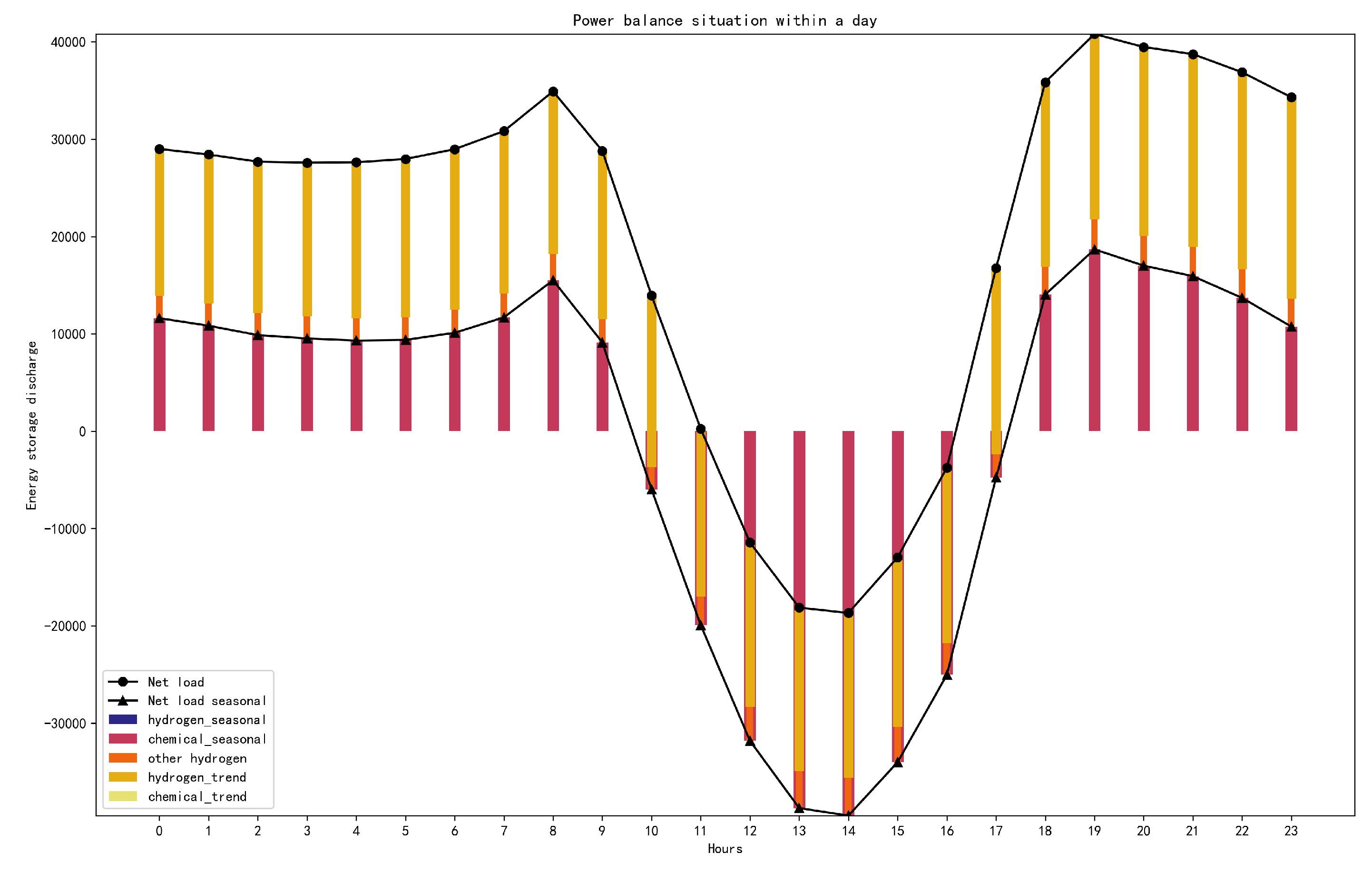
Figure 9. Externally provided hydrogen energy.

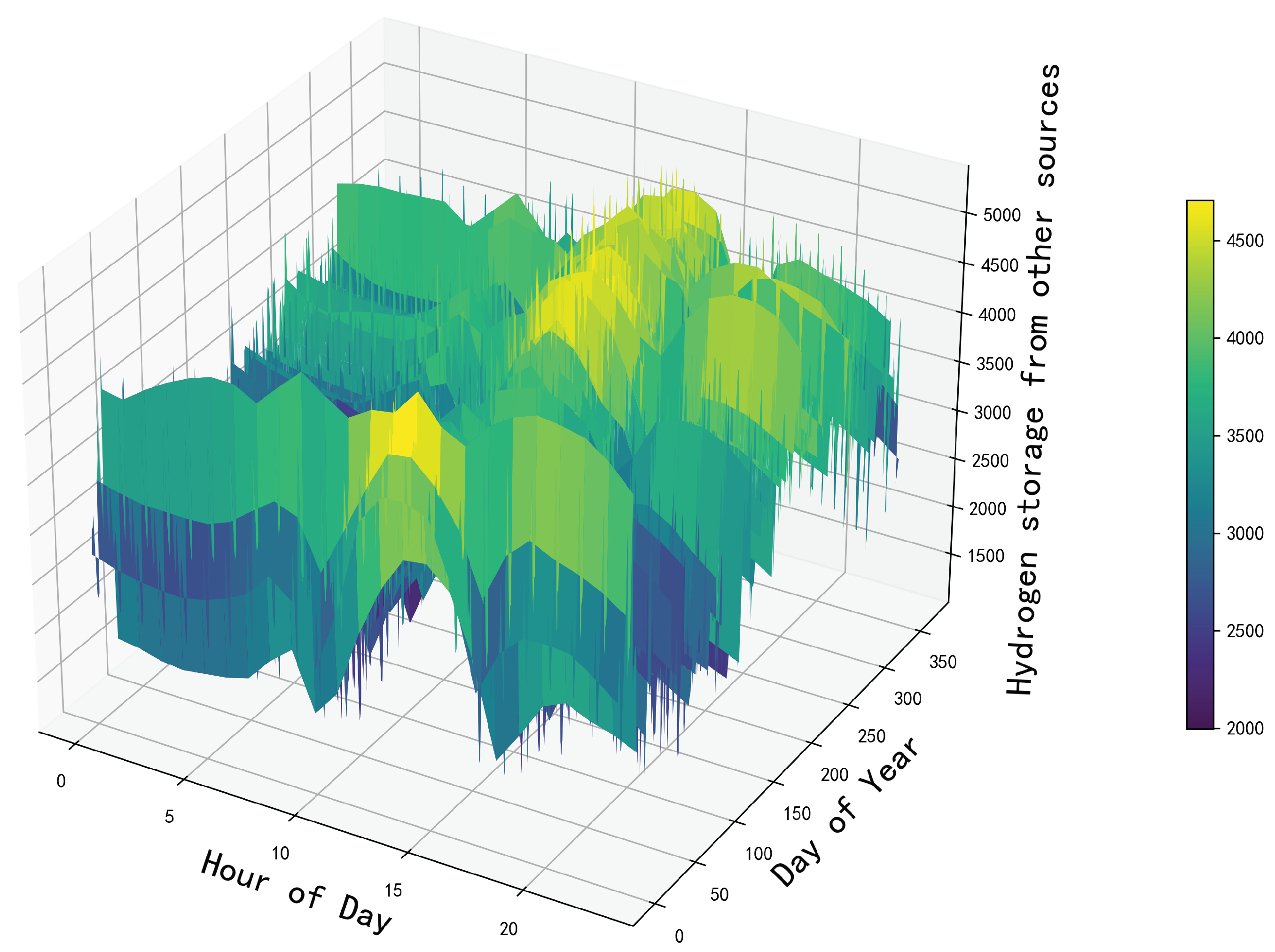
Table 1. STL decomposition process.

Outer Loop
Calculate weights
Inner Loop
Step 1: detrend;
Step 2: smooth periodic subsequence;
Step 3: low-pass filtering of periodic subsequences;
Step 4: remove trend from smoothed periodic subsequences;
Step 5: detrending;
Step 6: trend smoothing;

Table 2. Reference value settings.

Name	Numerical values
The installation cost of electrochemical energy storage	1.66 RMB/kWh
The installation cost of hydrogen energy storage	8 RMB/kWh
The marginal cost of electrochemical energy storage	1 RMB/kWh
The marginal cost of hydrogen energy storage	4 RMB/kWh
The operating cost of electrochemical energy storage	0.5 RMB/kWh
The operating cost of hydrogen energy storage	0.1 RMB/kWh
The cost of wind and solar spillage 5	10 RMB/kWh
The cost of load shedding	15 RMB/kWh
The maximum load shedding amount per unit time	100 kWh/h
The maximum wind and solar spillage amount per unit time	100 kWh/h

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer