Information Data Length Theory of Human Emotions, How, What and Why

Preprint

Article

Information Data Length Theory of Human Emotions, How, What and Why

Altmetrics

Downloads

Views

Comments

Ismail A Mageed^*

This version is not peer-reviewed

This preprints belongs to the Topic

Physical Exercise Impacts on Human Physical and Psychological Health

Submitted:

09 March 2024

Posted:

11 March 2024

You are already at the latest version

Alerts

Abstract

The current paper provides a cutting-edge information data length- theoretic approach to human emotions. This is a revolutionary breakthrough that unifies information data length and the dynamics of emotions. The significant impact of both time and its mean value associate on both the upper and lower bounds of the obtained information data length is observed and noted. The paper concludes with some challenging open problems, combined with concluding remarks and future research pathways.

Keywords:

Subject: Computer Science and Mathematics - Applied Mathematics

1. Introduction

1.1. Modelling Human Emotions

A mathematical model of human emotion processing in group settings [1], focusing on how individuals receive and react to emotions from events was developed. It explains how emotions are modelled using a one-dimensional random walk or Wiener process and represented by fixed probability distributions. The author demonstrates that when individuals form a group, the distribution of emotions can also be represented by a fixed distribution, providing insights into emotional responses and behaviours within social dynamics.

[1,2,3,4,5,6,7] investigated the mathematical modelling of human emotions and decision-making processes within group dynamics. It highlights the application of decision field theory to understand how individuals make decisions and how mathematical models are used in psychology and other fields to study dynamic events and decision-making processes. The research [1] aims to provide insights into human behaviours and emotional responses within social contexts through mathematical analysis and modelling techniques. While mathematical models have been applied in experimental psychology and Bayesian modelling, there seems to be a gap in integrating mathematical methods with the study of human emotions and behaviours. This highlights a potential area for further research and exploration in the field of psychology.

Going through the hypothetical scenario [1] where an event (

X

) triggers an emotion (

x

), which then leads to a reaction denoted as

F (x) .

This relationship is illustrated in Figure 1, showing how events, emotions, and reactions are interconnected. The author [1] suggested that individuals determine whether an event produces positive or negative emotions and adjust their emotional state towards a stable and neutral state (

x = 0

) through a series of reactions and emotional responses, as illustrated by Figure 1(c.f., [1]).

In the context of personal emotion processing [1], individuals determine whether events elicit positive or negative emotions and whether they lead to large or small emotional or behavioural responses. The process involves randomly starting with an emotion value and then adding 1 or -1 to aim for emotional balance at

x = 0

, representing stability and emotionlessness. This one-dimensional random walk model suggests that emotions are processed by continuously adding or subtracting values, with the mean emotion value being 0 and variance increasing with the number of processing iterations.

This explains that the process of emotion processing can be likened to a one-dimensional random walk, where positive and negative emotions are determined with a probability of

1 / 2

and then added together to obtain the total emotion. In this scenario, the mean

μ

(expected value) of the emotion is 0, indicating a balance between positive and negative emotions, while the variance represents the variability or spread of emotions experienced during the process. This perspective provides a mathematical framework to understand how emotions may fluctuate and balance out over time.

This shows how an individual's reactions are determined by events and emotions they experience [1], with reactions being like a dictionary once events and emotions are established. It emphasizes that individuals cannot influence events or the type of emotions they receive, but they can influence their reactions based on the initial emotional value assigned to an event. The relationship between the magnitude of emotions and corresponding reactions is highlighted, where strong positive emotions lead to favourable reactions and strong negative emotions lead to unfavourable reactions.

The text discusses the relationship between a stochastic differential equation and the Fokker-Planck equation in the context of probability density functions and random walk processes. It introduces the concept of a Wiener process, represented by the equation:

𝑥 = 𝛽 W_{t}

(1)

where 𝛽 is a positive real number and

W_{t}

is a standard Brownian motion. The equations derived illustrate how changes in probability density functions over time can be described mathematically in the context of random processes.

Thus, the suggested mathematical model can relate to the change in emotions over time, comparing it to a one-dimensional random walk. It introduces equations that describe how emotions change per unit time and how these changes can be represented using partial differential equations. This highlights the relationship between different mathematical expressions and emphasizes the concept of 𝛽 in the context of the model.

The time-dependent probability distribution of emotions during emotional processing,

p (x, t),

which provides insights into how emotions evolve over time during the processing phase, helping to understand the average distribution of emotions as the process unfolds. Engaging the mathematical vision provided by [1],

p (x, t)

reads as:

p (x, t) = \frac{1}{\sqrt (2 π t)} e^{- (\frac{x^{2}}{2 t})}

(2)

When individuals are grouped together [1], the emotion processing of the group is viewed as the average of the individual emotions. This means that the probability density function (PDF) of the group's emotions,

p_{g r o u p} (x)

reads:

p_{g r o u p} (x) = \frac{1}{\sqrt (2 π)} e^{- (\frac{x^{2}}{2})}

(3)

which describes how emotions are distributed within the group based on statistical principles. This approach simplifies the understanding of how emotions are processed collectively within a group setting, as visualized by Figure 2(c.f., [1]).

[1] highlighted how individuals and groups share a common equation for expressing emotions, emphasizing the role of understanding social indications in preventing bullying and moral harassment. Some strategies for individuals to adapt to their surroundings, manage their reactions, and handle challenging situations effectively were suggested by [1].

1.2. Information Length Theory

Shannon entropy is not the best descriptor [8] of a time series’ statistical variations, which has made using other unique information theoretic notions, including Fisher Information [9,10,11], highly motivating. Differential entropy [12], Kullback-Leibler divergence (KLD) [13], or information length (IL) [14,15,16]. Time-dependent PDFs provide the ability to trace time series evolution and measure variability [8], which is the basis of the IL metric's attractiveness. In conclusion, [17,18,19,20,21,22,23] provide an examination of the interval learning (IL) computation of linear stochastic autonomous processes. This broadens the scope of application, enabling IL to be used for the abruption of event prediction and facilitating application to different engineering contexts.

1.3. IL as a Concept

Mathematically speaking, if

x

serves as a nth- order stochastic variable and

p (x, t)

is a time-dependent PDF of

x

, then the Information Length

L (t)

corresponding to its evolution from the initial time

t_{0} = 0

to the final time

t_{F} = t

reads:

L (t) = \int_{0}^{t} \frac{d t_{1}}{τ (t_{1})} = \int_{0}^{t} \sqrt (ε (t_{1})) d t_{1}

(4)

(t_{1}) = \int_{R^{n}} (\frac{1}{p (x, t_{1})} {[\frac{\partial p (x, t_{1})}{\partial t_{1}}]}^{2}) d x

(5)

provided that

\sqrt (ε (t)

serves as the root-mean- squared fluctuating energy rate.

Having a closer look at (3), it is essential to note that

τ (t)

serves as a dynamic temporal unit which provides the correlation time over which the changes of

p (x, t)

take place [16]. Furthermore,

τ (t)

defines the statistical space’s time unit. Having said that,

\sqrt (ε (t) = \frac{1}{τ (t)}

, quantifies the information velocity [18].

It is preferable to compute the underlying value of the mathematical model of the related physical process to comprehend the meaning of

L

. Taking the Langevin equation-described first-order stochastic process into consideration:

\frac{d x}{d t} = - γ (t) (x - f (t)) + ξ

(6)

x

serves as a random variable,

f

defines a deterministic force,

ξ

represents a short-correlated random force satisfying that:

< ξ (t) ξ (t_{1}) > = 2 D δ (t - t_{1}) a n d < ξ (t) > = 0

(7)

where

D

serves as the amplitude (temperature) of the deterministic force

(s t o c h a s t i c n o s e) ξ

It is to be noted that equation (7) is so popular to be used as a descriptor of the motion of a particle under a harmonic potential in the form:

V (x) = \frac{1}{2} γ {(x - f (t))}^{2}

(8)

Following [23,24], it is found that:

ε (t) = \frac{{(\frac{d β}{d t})}^{2}}{2 β^{2}} + 2 β {(\frac{d y}{d t})}^{2}

(9)

p (x, t) = \sqrt{\frac{β}{π}} e^{- (β (x - y {))}^{2}}, y (t) = < x > = x (0) e^{- G (t)} + F (t)

\frac{1}{2 β (t)} = < (x (t) - y (t))^{2} > = \int_{0}^{t} 2 D e^{- 2 (G (t) - G (t_{1}))} d t_{1},

F (t) = \int_{0}^{t} e^{- (G (t) - G (t_{1}))} γ (t_{1}) f (t_{1}) d t_{1},

(10)

provided that

G (t) = \int_{0}^{t} 2 D γ (t^{'}) d t^{'} .

Considering equation (5), it is clear that

ε (t)

is dependent on the changes in both mean and variance defined by the corresponding dynamics of equation (4), portraying

p (x, t)

three-dimensional space variations, namely

(t, x, p (x, t))

as in Figure 3(c.f., [8]), where the variation of the information velocity,

\sqrt (ε (t)

would occur along the path starting initially from the state probability density function

p (x, t_{0})

to the final state at

p (x, t_{F})

as a descriptor of the speed limit from the statistical deviations of the observables [16].

Essentially, we might not be able to see the temporal statistical fluctuations that are occurring when we use differential entropy [12]. This directly follows from the locality's insufficiency because differential entropy primarily measures the differences between any two given PDFs while ignoring any intermediate states [17]. In an alternative symbolism, it merely alerts us to the distinctions that impact the overall evolution of the underlying system. In contrast, any localised changes that take place over the course of the system are measured by IL

L (t)

, [14,17]. What's more, IL has been hailed as a powerful metric that can bring geometry and stochasticity together, as well as a state-of-the-art method for representing an attractor structure [20,21]. The analogous value of

{l i m}_{t \to \infty} L (t)

would grow linearly from the point of stable equilibrium, based on the location of the mean PDF

p (x, 0)

of the starting state [15,24]. More significantly, using any other information metric results in the loss of this specific trait [17,23].

Preliminary Theorem(PT)

(c.f., [24])

Let f be a function that is defined and differentiable on an open interval (c,d).

If f^{'} (x) > (< 0) for all x \in (c, d), then f is increasing decreasing on (c, d) .

(11)

The road of this current paper reads: A spotlight introduction is presented in section 1. The key findings are established in section 2. Some challenging open problems, conclusion, and future research work are given in section 3.

2. The Upper and Lower Bounds of The Data Information Length of Human Emotions(HEs), ${U B}_{H E s}, {L B}_{H E s}$ ,

This section is concerned with calculating

{U B}_{H E s}, {L B}_{H E s}

2.1. Key Findings

Theorem 1.

TheIL of HEs ,

L_{H E s}

satisfies the following inequality:

t \sqrt (\frac{λ^{- 3}}{8} (λ + 1)) > L_{H E s} (t, λ) > t \sqrt{(\frac{λ^{- 3}}{8} (1 - λ^{\frac{3}{2}}))}, f o r s o m e λ \in (0, t], λ \leq 1

(12)

Proof.

We have

p (x, t) = \frac{1}{\sqrt (2 π t)} e^{- (\frac{x^{2}}{2 t})}

(c.f., (2))

Consequently,

\frac{\partial p (x, t)}{\partial t} = \frac{t^{- \frac{5}{2}} e^{- (\frac{x^{2}}{2 t})}}{2 \sqrt (2 π)} (x^{2} - t)

(13)

\frac{{(\frac{\partial p (x, t)}{\partial t})}^{2}}{p (x, t)} = \frac{t^{- \frac{9}{2}} e^{- (\frac{x^{2}}{2 t})}}{4 \sqrt (2 π)} {(x^{2} - t)}^{2}

(14)

It is well known that:

\int_{0}^{\infty} e^{- u^{2}} d u = \frac{\sqrt π}{2} (c.f., [25])

(15)

Let

I = \int_{0}^{\infty} \frac{{(\frac{\partial p (x, t)}{\partial t})}^{2}}{p (x, t)} d x

. Then,

I = \frac{t^{- \frac{9}{2}}}{4 \sqrt (2 π)} (\int_{0}^{\infty} x^{2} e^{- (\frac{x^{2}}{2 t})} d x + \int_{0}^{\infty} t^{2} e^{- (\frac{x^{2}}{2 t})} d x - 2 t \int_{0}^{\infty} x e^{- (\frac{x^{2}}{2 t})} d x)

(16)

Engaging (15), and communicating lengthy steps of mathematical manipulation, yields

I = \frac{t^{- \frac{7}{2}}}{4 \sqrt (2 π)} ((\sqrt (\frac{π}{2})) t^{\frac{1}{2}} + (\sqrt (\frac{π}{2})) t^{\frac{3}{2}} - 2 t^{2})

(17)

Communicating(16),

I < \frac{t^{- \frac{7}{2}}}{4 \sqrt (2 π)} (\sqrt (\frac{π}{2})) t^{\frac{1}{2}} (t + 1) = \frac{t^{- 3}}{8} (t + 1)

(18)

On another separate note,

I > \frac{t^{- \frac{7}{2}}}{4 \sqrt (2 π)} t^{\frac{1}{2}} ((\sqrt (\frac{π}{2})) t^{\frac{1}{2}} - (\sqrt (\frac{π}{2})) t^{2}) = \frac{t^{- 3}}{8} (1 - t^{\frac{3}{2}})

(19)

Combining (4), (18), and (19), one gets

\int_{0}^{t} \sqrt (\frac{t^{- 3}}{8} (t + 1)) d t > L (t) > \int_{0}^{t} \sqrt (\frac{t^{- 3}}{8} (1 - t^{\frac{3}{2}})) d t

(20)

Following the mean value theorem for definite integrals:

{t \sqrt (\frac{λ^{- 3}}{8} (λ + 1)) > L}_{H E s} (t, λ) > t \sqrt (\frac{λ^{- 3}}{8} (1 - λ^{\frac{3}{2}})) for some λ \in (0, t]

(c.f., (12)

Notably,

λ \leq 1

, would guarantee that

{L B}_{H E s}

t \sqrt (\frac{λ^{- 3}}{8} (1 - λ^{\frac{3}{2}}))

is real, otherwise

{L B}_{H E s}

would be complex valued, which is not acceptable.

Theorem 2.

{L B}_{H E s}, {U B}_{H E s}

(c.f., Theorem 1) satisfy:

(i)

{L B}_{H E s}

is forever decreasing in

λ

(ii)

{U B}_{H E s}

is forever decreasing in

λ .

(iii)

{U B}_{H E s}

is forever increasing in time.

(iv)

{L B}_{H E s}

is forever increasing in time.

Proof.

(i) We have

\frac{\partial {L B}_{H E s}}{\partial λ} = \frac{t (- 3 λ^{- 4} + \frac{3}{2} λ^{- \frac{5}{2}})}{4 \sqrt 2 \sqrt (λ^{- 3} (1 - λ^{\frac{3}{2}}))}

(21)

\frac{\partial {L B}_{H E s}}{\partial λ} < 0

⟺

(- 3 λ^{- 4} + \frac{3}{2} λ^{- \frac{5}{2}}) < 0

, which holds for all

λ \in (0,1)

Communicating (11), and (21), (i) follows.

(ii)

\frac{\partial {U B}_{H E s}}{\partial λ} = - \frac{t (3 λ^{- 4} + 2 λ^{- 3})}{4 \sqrt 2 \sqrt ((λ^{- 3} + λ^{- 2}))}

(22)

Clearly,

\frac{\partial {U B}_{H E s}}{\partial λ} < 0

, which implies (ii)

(iii), and (iv) are straightforward.

Define

{U B}_{H E s} (λ, t) = t \sqrt (\frac{λ^{- 3}}{8} (λ + 1)) and {L B}_{H E s} (λ, t) = t \sqrt (\frac{λ^{- 3}}{8} (1 - λ^{\frac{3}{2}}))

(19)

2.2. Numerical Experiments

Figure 4 depicts the decreasability of

{L B}_{H E s} (λ, 1) = \sqrt (\frac{λ^{- 3}}{8} (1 - λ^{\frac{3}{2}}))

λ

, which validates the analytic findings.

Figure 5 illustrates the decreasability of

{U B}_{H E s} (λ, 1) = \sqrt (\frac{λ^{- 3}}{8} (λ + 1))

λ

, which validates the analytic findings.

The numerical findings match the analytic results as shown by Figure 6.

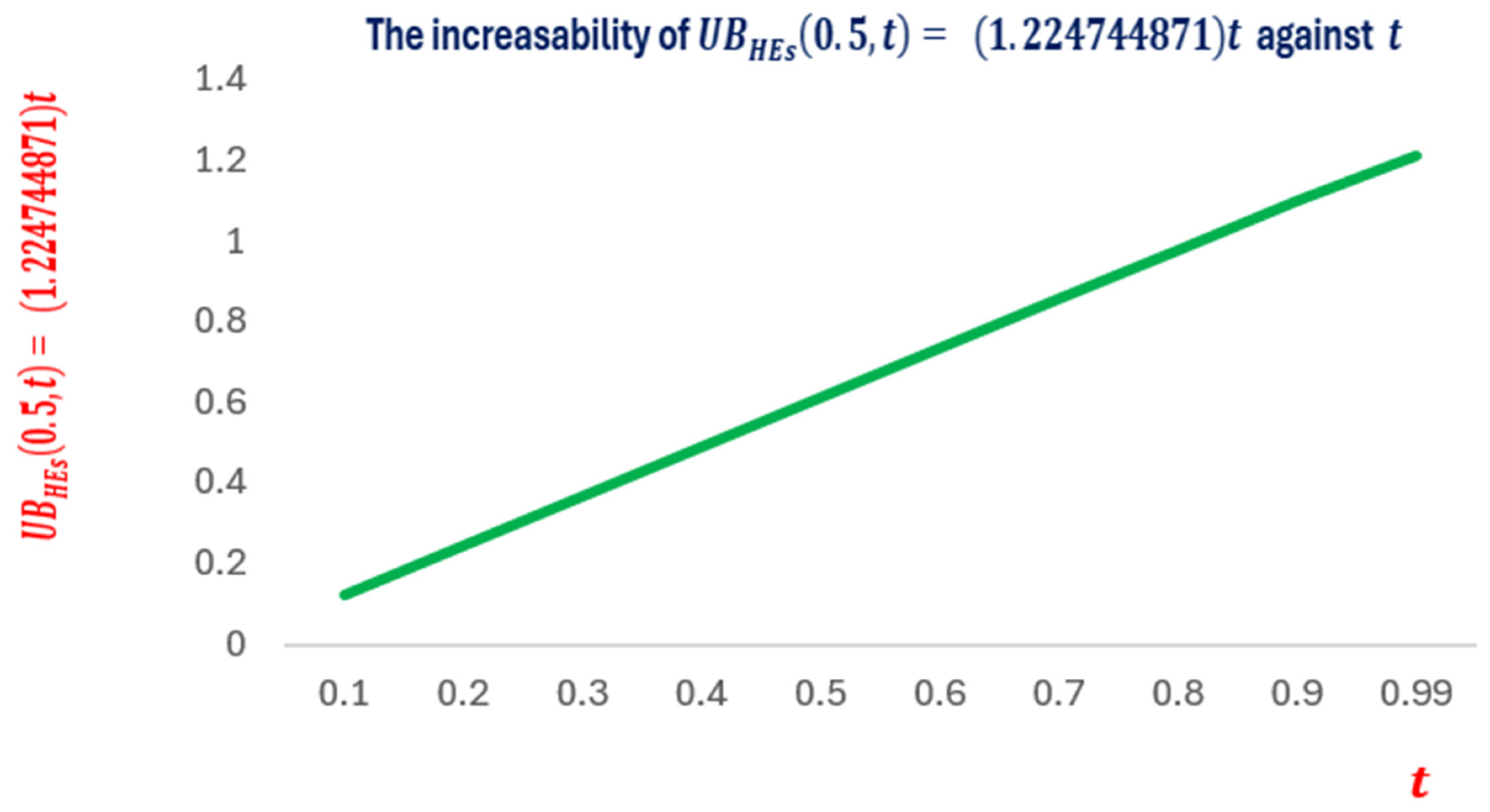
Figure 7 visualizes how

{U B}_{H E s} (0.5, t) = (1.224744871) t

increases as times increases.

3. Concluding Remarks, Open Problems, and Future Research

This paper contributes to the establishment of Information Length Theory of HEs. The novel mathematical derivations are undertaken by finding the integral formula of the information length of HEs. Because of the higher complexity to derive the closed form result of the later integral formula, both the upper and the lower bounds of that integral, namely

{U B}_{H E s}, {L B}_{H E s}

were derived.

Notably,

{U B}_{H E s} (λ, t), {L B}_{H E s} (λ, t)

are both (

λ, t)

-dependent. Moreover, these analytic findings were validated numerically.

Here are some emerging open problems:

Open Problem One

Is it mathematically feasible to unlock the challenging problem of finding the exact analytic form of,

L_{H E s}

(c.f., (18)), rather than obtaining its upper and lower bounds? This problem is still open.

Open Problem Two

Looking at Eqn (18), can we find any other strict upper and lower bounds for

L_{H E s}

Future research pathways include the attempting to solve the proposed open problems and extending the information data length theory to explain other fields of human knowledge, such as engineering, physics and much more.

References

Yabu, T. (2020). Mathematical approach to the psychological aspects of human.psyarxiv.com.
Beck, S. J. (2020). Cognitive Behavior Therapy, Third Edition: Basics and Beyond.The Guilford Press.
Bolger, N., Zee, K. S., Rossignac-Milon, M., & Hassin, R. R. (2019). Causal processes in psychology are heterogeneous.Journal of Experimental Psychology: General, 148(4). [CrossRef]
Burigana, L., & Vicovaro, M. (2020). Algebraic aspects of Bayesian modelling in psychology.Journal of Mathematical Psychology, Vol.94. [CrossRef]
Cox, G. E., & Criss, A. H. (2020). Similarity leads to correlated processing: A dynamic model of encoding and recognition of episodic associations.Psychological Review, 127(5). [CrossRef]
Hancock, T. O. (2019). Travel behaviour modelling at the interface between econometrics and mathematical psychology.PhD thesis, University of Leeds.
Hancock, T. O., Hess, S., & Choudhury, C. F. (2019). Theoretical considerations for a dynamic model for dynamic data: Bridging choice modelling with mathematical 18 psychology.International Choice Modelling Conference 2019.
Chamorro, HR; et al. (2020). “ Information Length Quantification and Forecasting of Power Systems Kinetic Energy.” IEEE Transactions on Power Systems. [CrossRef]
Mageed, I. A., Yin, X., Liu, Y., & Zhang, Q. (2023, August). ℤ_(a,b) of the Stable Five-Dimensional M/G/1 𝑀/𝐺/1 Queue Manifold Formalism's Info-Geometric Structure with Potential Info-Geometric Applications to Human Computer Collaborations and Digital Twins. In 2023 28th International Conference on Automation and Computing (ICAC) (pp. 1-6). IEEE. [CrossRef]
Mageed, I. A., Zhang, Q., Akinci, T. C., Yilmaz, M., & Sidhu, M. S. (2022, October). Towards Abel Prize: The Generalized Brownian Motion Manifold's Fisher Information Matrix With Info-Geometric Applications to Energy Works. In 2022 Global Energy Conference (GEC) (pp. 379-384). IEEE. [CrossRef]
Mageed, I. A., Zhou, Y., Liu, Y., & Zhang, Q. (2023, August). Towards a Revolutionary Info-Geometric Control Theory with Potential Applications of Fokker Planck Kolmogorov (FPK) Equation to System Control, Modelling and Simulation. In 2023 28th International Conference on Automation and Computing (ICAC) (pp. 1-6). IEEE. [CrossRef]
Mageed, I. A., & Kouvatsos, D. D. (2021, February). The Impact of Information Geometry on the Analysis of the Stable M/G/1 Queue Manifold. In ICORES (pp. 153-160).
Van Erven, T. and Harremos, P. (2014). “Rényi divergence and Kullback-Leibler divergence.” IEEE Transactions on Information Theory 60(7), 3797-3820. [CrossRef]
Mageed, I.A. "A Unified Information Data Length (IDL) Theoretic Approach to Information- Theoretic Pathway Model Queueing Theory (QT) with Rényi entropic applications to Fuzzy Logic," 2023 International Conference on Computer and Applications (ICCA), Cairo, Egypt, 2023, pp. 1-6. [CrossRef]
Kim, E. and R. Hollerbach.(2017). “Signature of nonlinear damping in geometric structure of a nonequilibrium process.” Physical Review E vol. 95, no. 2, p. 022137. [CrossRef]
Nicholson, S,B. et al.(2020) “Time–information uncertainty relations in thermodynamics.” Nature Physics16.12: 1211-1215. [CrossRef]
Heseltine, J., and E. Kim.(2019). “Comparing information metrics for a coupled- Ornstein–Uhlenbeck process.” Entropy 21(8):775. [CrossRef]
Kim, E.(2021). “Information geometry and non-equilibrium thermodynamic relations in the over-damped stochastic processes.” Journal of Statistical Mechanics: Theory and Experiment vol. 2021, no. 9, p. 093406. [CrossRef]
Kim, E. and A.-J. Guel-Cortez. (2021). “Causal information rate.” Entropy vol. 23, no. 8, p. 1087. [CrossRef]
Guel-Cortez, A.-J. And E. Kim. (2020). “Information length analysis of linear autonomous stochastic processes.” Entropy 22(11). [CrossRef]
Guel-Cortez, A.-J. and E. Kim. (2021). “Information geometric theory in the prediction of abrupt changes in system dynamics.” Entropy vol. 23, no. 6, p. 694. [CrossRef]
Heseltine, J. and E. Kim.(2016). “Novel mapping in non-equilibrium stochastic processes.”Journal of Physics A: Mathematical and Theoretical vol. 49, no. 17, p. 175002. [CrossRef]
Kim, E.(2016). “Geometric structure and geodesic in a solvable model of non-equilibrium process.” Physical Review E vol. 93, no. 6, p. 062127.Entropy vol. 20, no. 8, p. 550. [CrossRef]
I. A. Mageed and Q. Zhang, “The Rényian-Tsallisian Formalisms of the Stable M/G/1 Queue with Heavy Tails Entropian Threshold Theorems for the Squared Coefficient of Variation,” electronic Journal of Computer Science and Information Technology, vol. 9, no. 1, 2023, p. 7-14.
Sales, L. L., Silva, J. A., Bento, E. P., Souza, H. T., Farias, A. D., & Lavor, O. P. (2018). An alternative method for solving the Gaussian integral. arXiv preprint arXiv:1811.03957. [CrossRef]

Figure 1. The relationship between events, emotions, and reactions in the context of individual emotion processing.

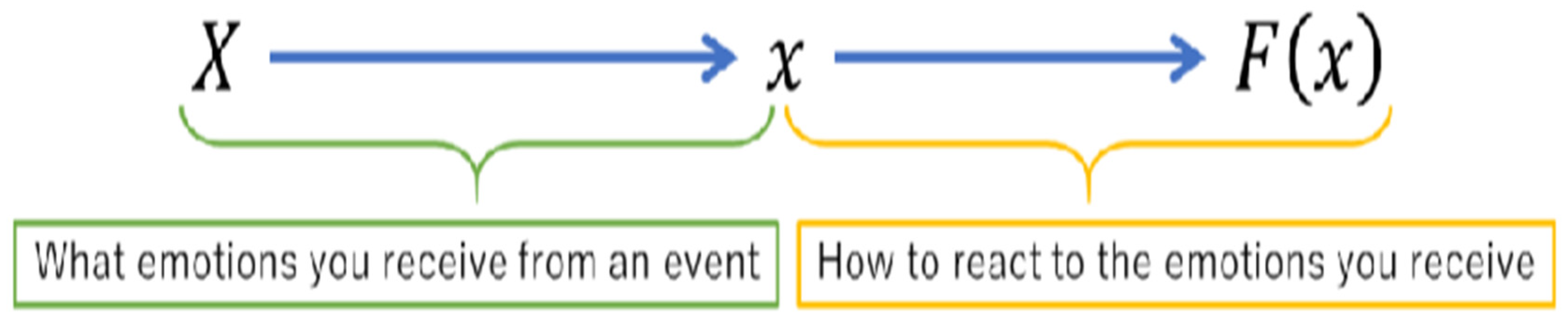
Figure 2. The portrayed PDF allows us to analyse and compare emotional patterns within individuals and groups, highlighting similarities in emotional processing when people are grouped together.

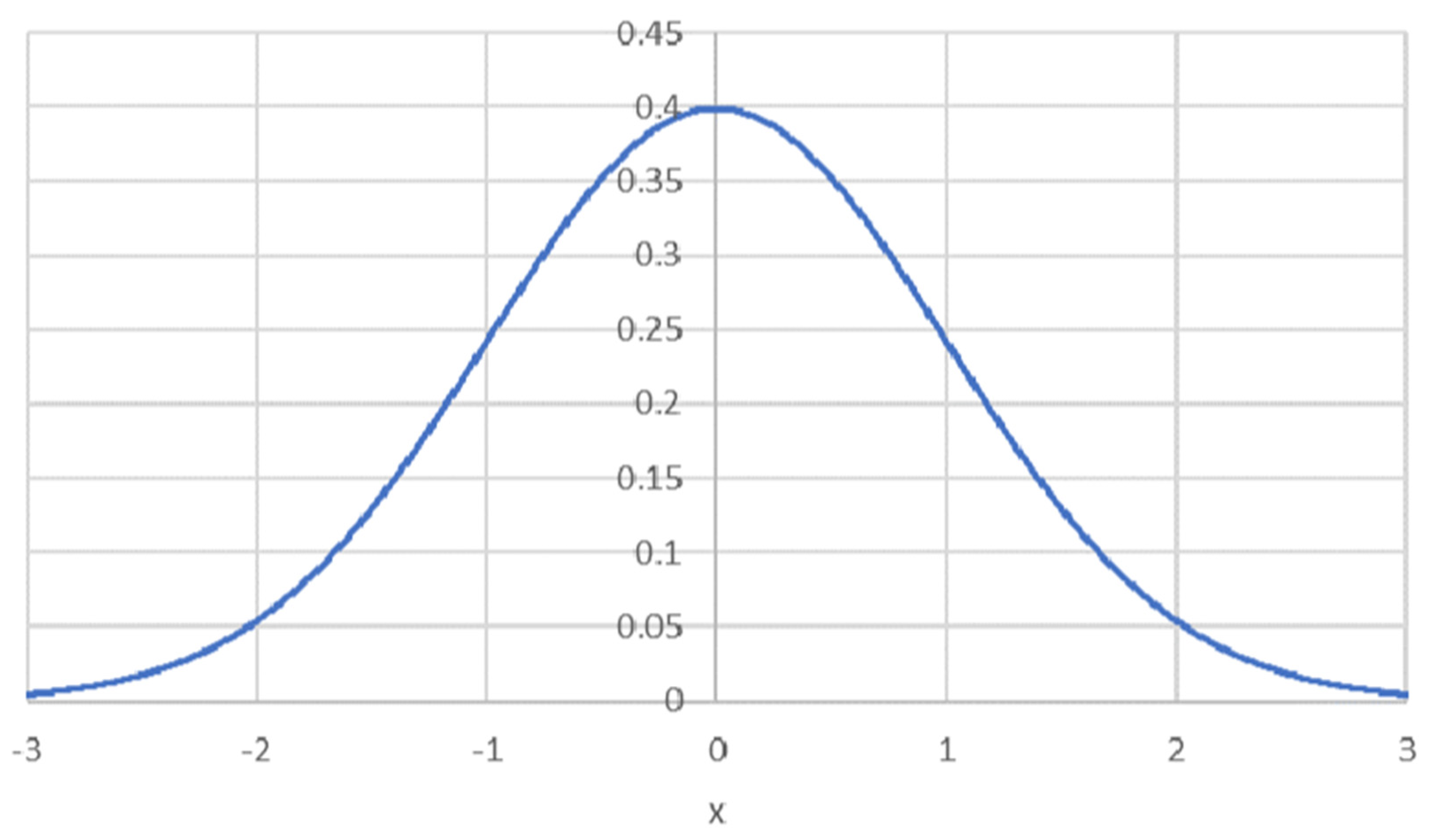
Figure 3.

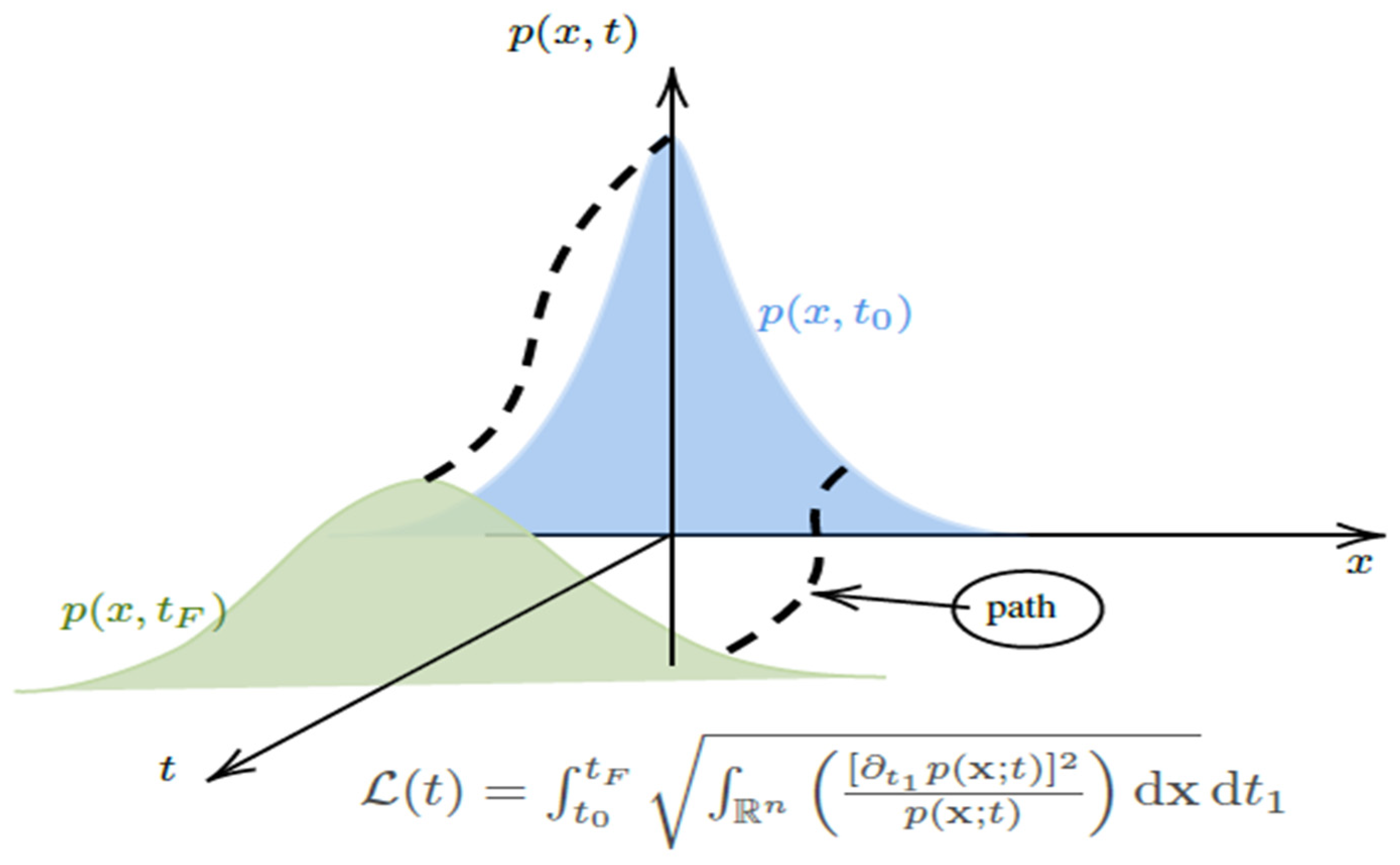
Figure 4.

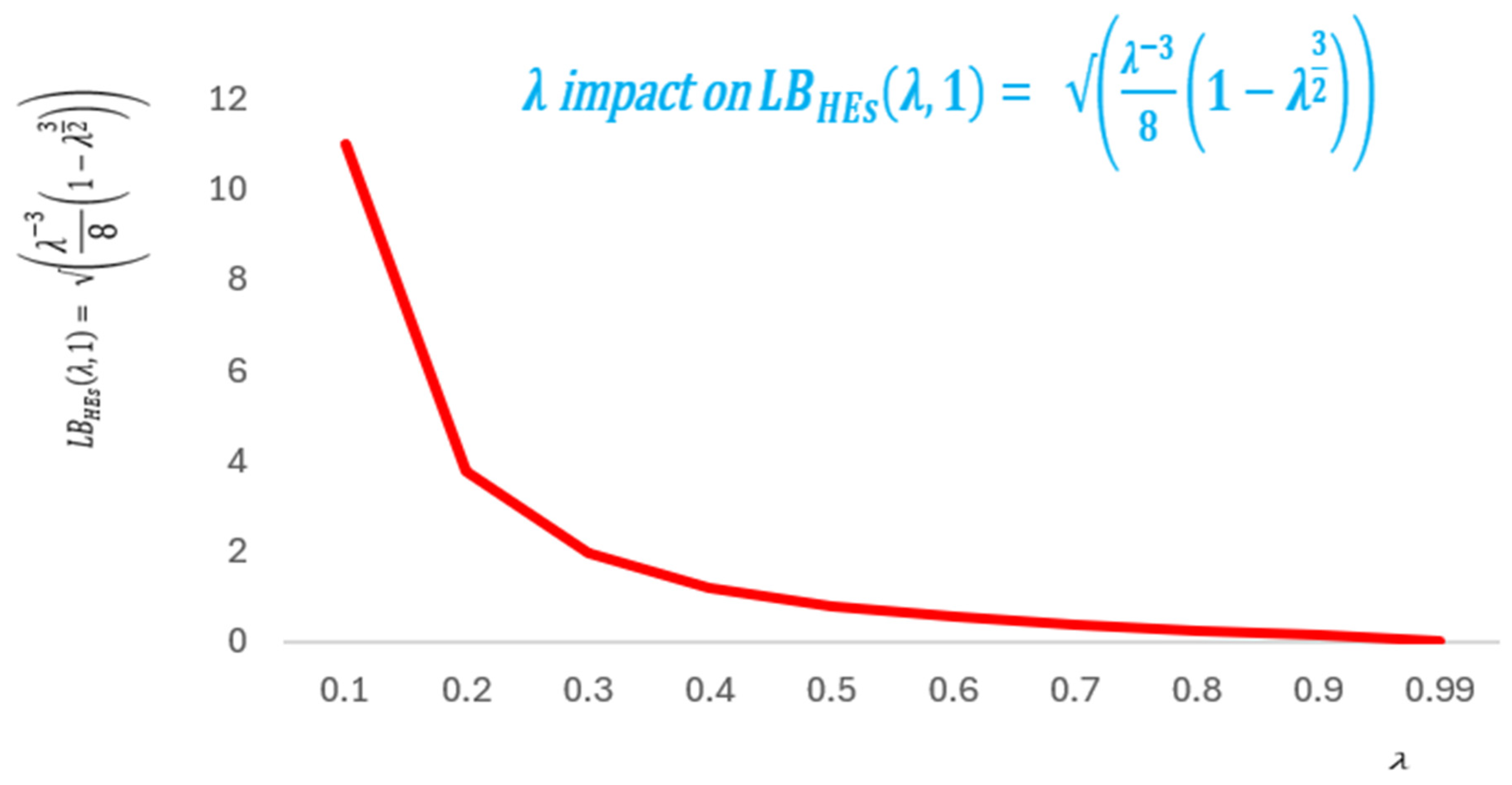
Figure 5.

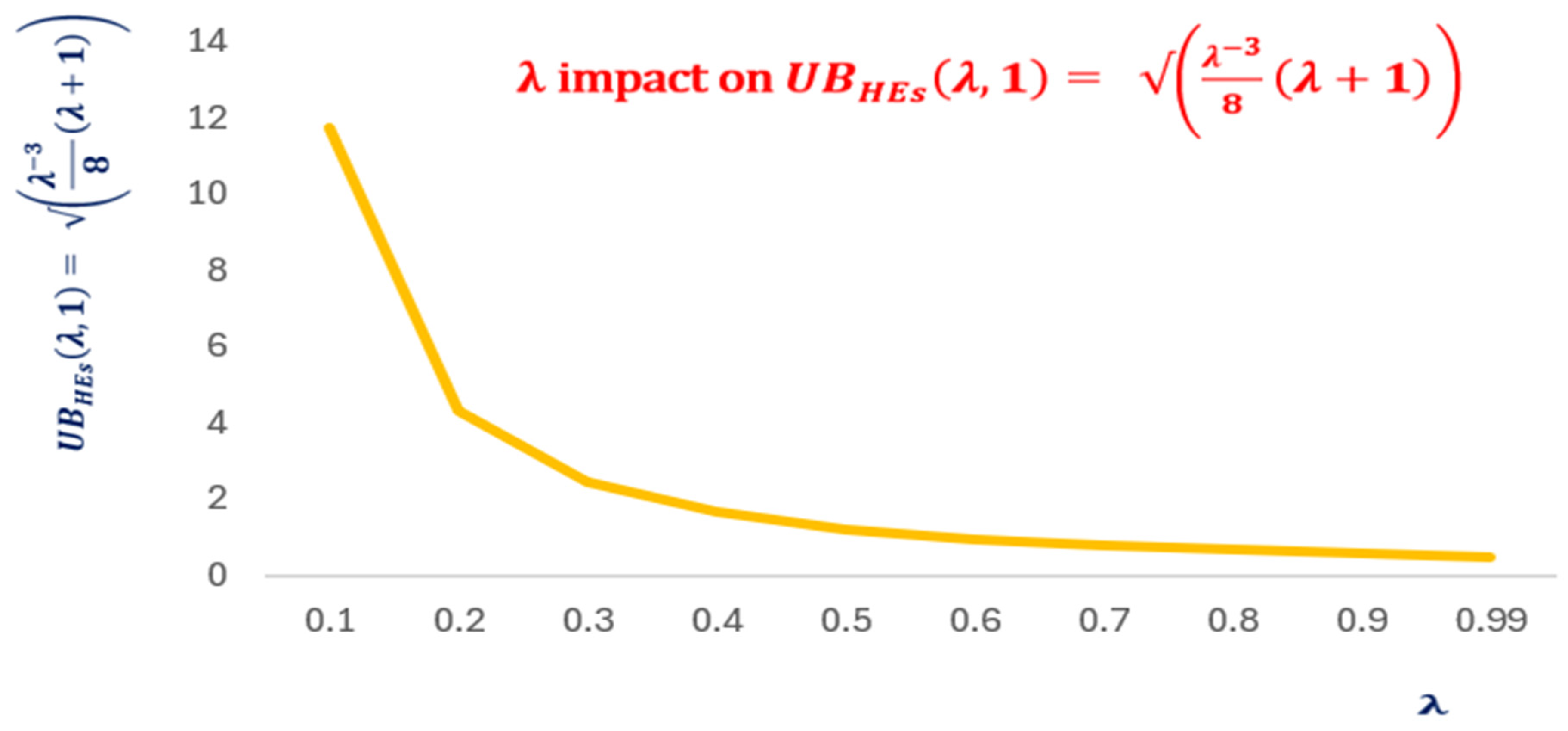
Figure 6.

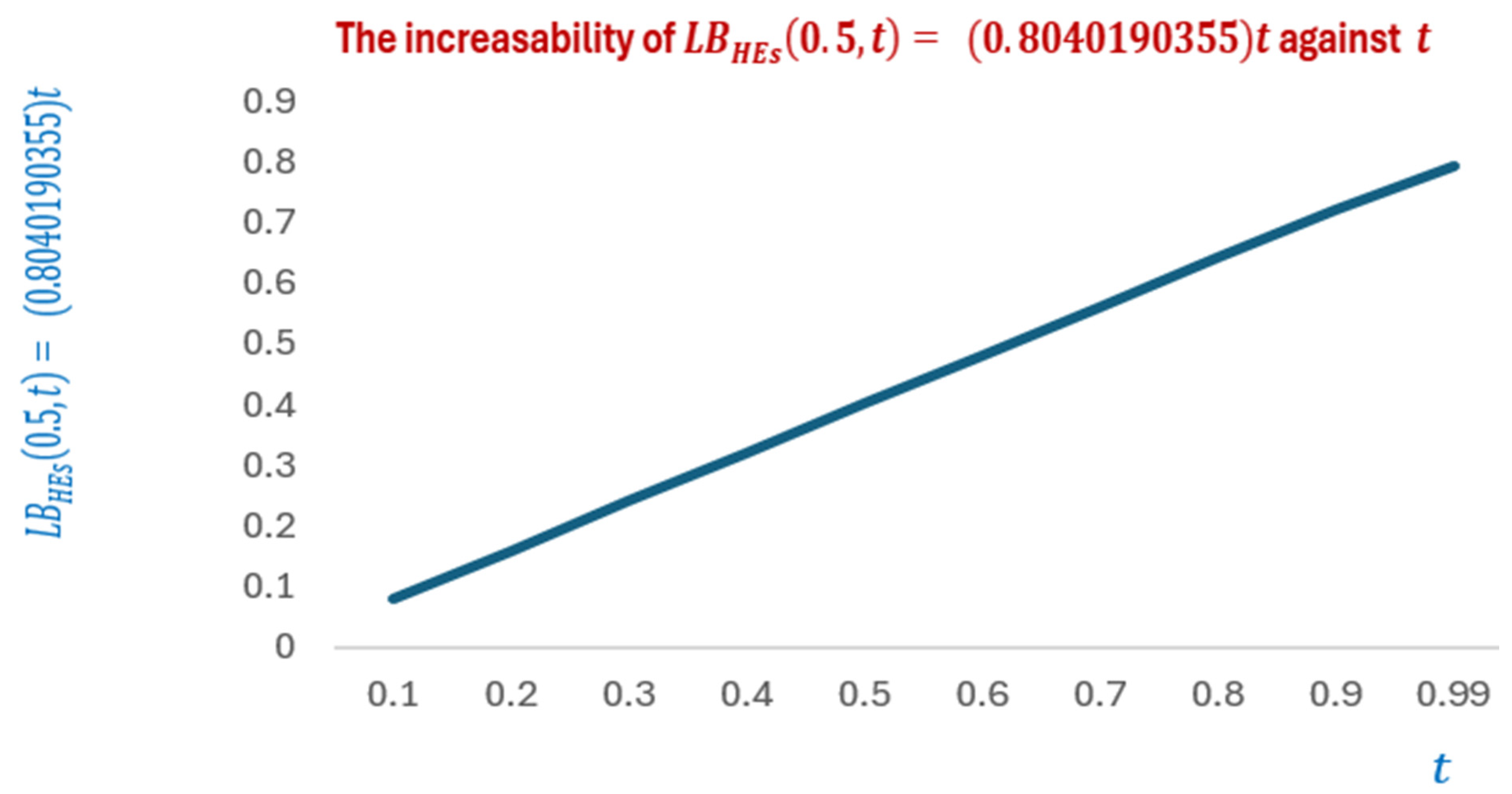
Figure 7.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Information Data Length Theory of Human Emotions, How, What and Why

Abstract

1. Introduction

1.1. Modelling Human Emotions

1.2. Information Length Theory

1.3. IL as a Concept

2. The Upper and Lower Bounds of The Data Information Length of Human Emotions(HEs), U B H E s , L B H E s ,

2.1. Key Findings

2.2. Numerical Experiments

3. Concluding Remarks, Open Problems, and Future Research

References

MDPI Initiatives

Important Links

Subscribe

2. The Upper and Lower Bounds of The Data Information Length of Human Emotions(HEs), ${U B}_{H E s}, {L B}_{H E s}$ ,