Preprint
Article
Corrosion Assessment and Classification in SPCC Steel Using Eddy Current Testing
Altmetrics
Downloads
96
Views
50
Comments
0
A peer-reviewed article of this preprint also exists.
Submitted:
09 March 2024
Posted:
11 March 2024
You are already at the latest version
Alerts
Abstract
it still undergoes corrosion when exposed to corrosive environments. This paper proposes an evaluation method for assessing the corrosion level of SPCC steel specimens using traditional eddy current testing (ECT), along with two different machine learning approaches. The objective is to classify the corroded state of the specimens into two states: a less corroded state (state-1) and a highly corroded state (state-2). Generative and discriminative models were implemented for classification. The generative classifier was based on the Gaussian mixture model (GMM), while the discriminative model was based on the logistic regression model. The models used features based on the absolute maximum of the perturbation magnetic field components at two different frequencies. The performance of the classifiers was evaluated using metrics such as absolute error, accuracy, precision, recall, and F1 score. The results indicate that high classification accuracy can be achieved based on both methods using traditional eddy current testing.
Keywords:
Subject: Engineering - Electrical and Electronic Engineering
1. Introduction
Steel Plate Cold-Rolled Commercial (SPCC) denotes a steel variant that has undergone a cold-rolling process, enhancing its strength and hardness. Predominantly, it is utilized in sectors demanding precise shapes and dimensions, such as automotive manufacturing [1]. Notably, SPCC offers heightened corrosion resistance compared to hot-rolled steels, rendering it a preferred choice for applications exposed to harsh environmental conditions. However, when a material corrodes, it undergoes oxidation and other chemical changes that lead to the loss of material, formation of surface irregularities, and degradation of its mechanical properties [2,3]. These changes can include the loss of structural integrity, reduced tensile strength, and increased susceptibility to fractures.
Over time, the cumulative effects of corrosion can significantly weaken the material, potentially leading to structural failure or diminished performance in various applications. The cost of corrosion has been estimated as losses to the national economy due to corrosion of up to 5% of Gross Domestic Product (GDP) in several countries including Japan, UK, USA [4]. Hence, the detection and classification of corrosion levels play a vital role in ensuring the safety, reliability, and performance of assets and infrastructures.
Over the years several nondestructive testing techniques based on radiography, acoustic emission, and thermography have been widely used for the monitoring of the material’s properties and characterization of corrosion [5,6,7,8]. One way for the detection of corrosion is based on electromagnetic method like eddy current testing [5,8]. Frankowski et al. validated the feasibility of eddy current testing for the detection of both uniform and localized corrosion in reinforcing bars [9], while Yusa et al. [10] successfully applied eddy current testing for the detection of fatigue cracks and pressure corrosion cracks. In addition, Li et al. [11] used pulsed modulation eddy current testing to detect subsurface corrosion.
Investigations pertaining to detection and monitoring of corrosion have paved the way for their characterization. Characterization of the corroded regions is necessary because small pits on the surface of the material pose no big threat to the materials underneath. On the other hand, the presence of deeper pits forces the replacement of the material. One method to characterize the extent of corrosion under coatings in steel samples, performed by Kopf et al. [12]. It was based on binarizing the thermal images obtained from pulsed thermography technique, yielding an absolute error of less than 3% in quantifying the extent of corrosion. Alamin et al. [13] employed pulsed eddy current testing for corrosion detection in mild steel, and based on principal component analysis, classified and characterized the corrosion. Postolache et al. [14] utilized giant magnetoresistance (GMR) magnetic sensors to detect changes in the magnetic field for defect characterization, followed by defect classification using neural networks. Nevertheless, the exploration of classifying corrosion through eddy current testing remains on going. Hence this paper aims to detect corrosion using traditional eddy current testing and characterize the corrosive state of SPCC steel specimens, using a generative model and a discriminative model and classifying them in two states: a less corroded state (state-1) and a highly corroded state (state-2).
The content of this paper is organized as follows. In Section 2, the experimental setup and the experiments carried out to detect the corrosion based on eddy current testing are detailed, with emphasis on measuring the magnetic field components at two different frequencies, and the extraction of features for the subsequent classification models are presented. Section 3 describes supervised generative and discriminative classifiers and classifies some unknown data (test data) in two states; demonstrates the classification results and evaluates the performance of the models based on metrics such as accuracy, precision, recall and F1 scores. In Section 4, some important conclusions about the classification models are discussed.
2. Experiments and Metrology
2.1. SPCC Steel Specimens and Magnetic Sensors
In this work, 49 SPCC steel specimens, each measuring 50 × 100 × 2 mm3 are evaluated. The specimens were artificially corroded with a solution of ferric chloride to obtain different corroded states. Eight of the specimens under investigation depicting the two corroded states are shown in Figure 1.
To measure the magnetic field, a Hall sensor and a Tunneling Magneto Resistance (TMR) sensor are used. Each probe contains an excitation coil and a magnetic sensor, as shown in Figure 2 (a) and (b). The fabricated ECT probe is shown in Figure 2 (c), featuring an excitation coil with 460 turns, internal radius r = 6 mm, external radius R = 12 mm, and the height H = 10 mm.
2.2. Experimental Setup
The experimental setup is illustrated in Figure 3, with the lift-off settled at 1 mm. A sinusoidal voltage generated by the Agilent-33210A waveform generator is injected into the excitation coil after passing through the TS250 waveform amplifier.
The output from the sensor goes through the signal conditioning circuit, which contains two parts: first part is composed of a high pass filter and an instrumentation amplifier to filter the DC bias and amplify the signal; the second part is a digital lock-in amplifier from Zurich Instruments MFLI which is integrated with a high-order low pass filter. Then the PC obtains the signal from an acquisition board integrated within the lock-in amplifier.
2.3. Measurements
Due to the measuring range of the magnetic sensor, the ECT probe with the Hall sensor is used to measure the magnetic field component Bz. Another probe with the TMR sensor is used to measure the magnitude of Bx. The coil is excited at two different frequencies, 2.5 kHz and 5 kHz, and the signals of Bz and Bx are measured. The real part and imaginary part of the signals are analyzed and recorded. Figure 4 shows the differences in the characteristics of Bz and Bx from the same specimen at these two frequencies.
After the measurements, eight features of each specimen are generated to train and test with the generative and discriminative models. The peaks of the real and imaginary parts of the perturbed magnetic field components, Bx and Bz are selected as the features, as listed in Table 1. To have statistical significance in the data for the classification models, to better estimate the model parameters, a technique using interclass averaging of the features is performed so that there are 100 features in each class.
3. Classification Algorithms
There are several supervised machine learning algorithms that can classify unknown data (test data) based on previously defined data (training data). There are two major perspectives in supervised machine learning techniques: a generative model (GM) and a discriminative model (DM) [15]. In its broadest sense, a classifier based on GM models the distribution of features in individual class together with the class prior and then using Bayes' theorem to compute the posterior distribution, whereas a classifier based on DM models the posteriors directly from the learning examples. In this work, we have used two different techniques to classify the corrosive state of steel specimens: Gaussian mixture model (a type of GM) and logistic regression model (a type of DM). To know specific metrics on the model performance, confusion matrix and subsequently other evaluation metrics such as accuracy, precision, recall and F1 scores have been computed for both the cases.
3.1. Gaussian Mixture Model
In the Gaussian mixture models (GMM), the observation sets are needed to compute the empirical mean, , and empirical covariance, , of a given class j. From the mean and the covariance matrix, we can construct the probability density function for each class i.e.,
where represents the feature domain, represents the class, and in our case is the state-1 of corrosion and is the state-2 of corrosion). The parameters () and are the parameters of the Gaussian distribution . The circumflex hat indicates that the parameters are estimated empirically. For brevity and clarity, we show examples of 2-D data (considering only two features) of each state of corrosion in Figure 5.
To validate the model, out of the 100 observations of each class, 80% of them were randomly sampled (without repetition) to estimate the Gaussian parameters for each class. In this case we have assumed the priors (the probability of occurrence of a class ) to be the same for each class as there is no information about the occurrence of the class. The remaining 20% of the data for each class was used to test the model. The test data was assigned to one of the classes based on the Mahalanobis distance between the test point and the Gaussian’s centers. The Mahalanobis norm, for a test point is given by
which is the normed distance between the test point and the center of the Gaussian distribution of the jth class. Assignments to the classes are made by the following rule:
3.2. Logistic Regression Model
A binary classifier is represented as . Let the domain of the observed samples be represented as , where is the total number of observed samples (training set). This follows Bernoulli’s distribution. The samples are independent and identically distributed with , where . The logistic function squashes the outputs between 0 and 1. The logistic function is represented as
where the parameter w is the weight function that determines the slope and the shift of the logistic function. Thus, for a binary class model, the posterior distribution is written as
In this case corresponds to corrosion state-1 and corresponds to corrosion state-2. Now to estimate the w, it is necessary to form the likelihood function from the set of n independent observations. The likelihood function for the Bernoulli’s distribution is given by
As the closed-form solution for the weight estimate cannot be found directly, generally gradient-descent algorithms will be preferred to get its optimal estimate. The main problem with this technique is the time consumption for multiple evaluations. So, alternatively, in this work, we used the logistic regression model, expressed in log scale as . The advantage of this form is the existence of a closed-form solution. However, in this case, the right-hand side is as is either or or . To overcome this, we took the class as either () or (), where . Thus, we were able to successfully apply the least-squares technique to get . For brevity and clarity, in Figure 6, we show examples of 2-D data (considering only two features) of each state of corrosion.
Similar to GMM, to validate the logistic regression model, we randomly split the observations to training dataset (80% data) and testing dataset (20% data). Once the weights are found (training step), the test data is substituted into Eq. (4) yielding
3.3. Classification Results and Discussion
Both the GMM and logistic regression model were evaluated for 10000 times, where in each iteration the train data (80%) and test data (20%) for each class were randomly chosen. Once the test points are introduced, the absolute errors, , were recorded and summed to find the total errors in each iteration of the GMM and the logistic regression model. The total absolute errors with their frequencies are shown in Figure 7.
We saw that, for the case of GMM, there was an expected error of 1.637 miscalculations in a test sample set of 40 (20 for each class). On the other hand, the logistic regression gave an expected error of 0.903 in a test sample set of 40. The absolute errors only provide us the misclassification due to the model, however, do not provide us with the details of those classes that were misclassified. Hence to get the class-specific performance of the models, other metrics based on the confusion matrix were computed for the GMM model and logistic regression model as shown in Figure 8 and Figure 9, respectively.
An important observation on the GMM, to be made here is the false negatives and true positives are 0% and 100% respectively i.e., the model always correctly predicts the highly corroded samples and never misclassifies it as less corroded. On the other hand, for the logistic regression model, the true negatives and false positives are always 100% and 0%, meaning that the model always correctly predicts less corroded samples. To extract further information about the class-specific performance of the models, we used metrics such as accuracy, precision, recall and F1 score, which were all derived from the confusion matrix. Figure 10 depicts these metrics for both the GMM and logistic regression model.
The accuracy of the model dictates the rate of correct classification, and the GMM can correctly classify the corrosive state of the samples 95.9% of the time with an uncertainty of 3.18%, while for the logistic regression model it is 97.69% with an uncertainty of 2.14%. It can be seen that the recall score is 100% for the GMM model whereas, the recall score of the logistic regression model is not as good as the GMM. Giving a misclassification rate of 4.62% with an uncertainty of 4.2%. The recall score dictates the rate of misclassification of highly corroded state-2 samples. For the study presented here, it is important that the recall score is as high as possible, so that potential mis-happenings of the structure can be avoided.
Precision score dictates the rate of misclassification error of less corroded state-1 samples (false positives). It can be seen that the precision score of the model is 100% which means there is never a misclassification of less corroded samples. However, the GMM model does not have a satisfactory performance giving a misclassification rate of 4.62% with an uncertainty of 4.2%. The F1 score, which is basically the geometric mean between the precision and recall is 97.63% for the GMM, while it is 96.19% for the logistic regression model.
It can be noted that the GMM has provided a very good performance in terms of no misclassification errors due to the state-2 samples and hence it is potentially a very good classifier to identify the highly corroded samples. On the other hand, the logistic regression model has also provided a good classification performance in terms of accuracy and precision. The misclassification errors due to the less corroded samples is 0, and hence it is a potentially very good classifier to identify the less corroded samples.
4. Conclusions
Classification of corrosion states of a material is crucial because it enables precise assessment of damage severity and informs tailored maintenance strategies. Hence, in this study, we have investigated the classification of the corrosive states of steel specimens by supervised machine learning algorithms using features from traditional eddy current testing. Two broad methodologies based on generative modelling (Gaussian mixture model) and discriminative modelling (logistic regression model) were investigated for the classification and to compare the models’ performance in distinguishing two states of corrosion, a less corroded state (state-1) and a highly corroded state (state-2), often denoted in the paper as and respectively. The features that were used for the study were the peaks of the perturbations in the magnetic field components, real and imaginary parts of Bx and Bz, at two different frequencies amounting to 8 independent features. Both the models were trained with 80% of randomly selected data and the remaining 20% were used to test the models and determine the absolute error of misclassification. Further statistics on the model performance and class-wise misclassification rate, such as accuracy, precision, recall and F1-scores, were estimated from the confusion matrix. The results have dictated us the following:
- Both the models, GMM and logistic regression model, can classify the corrosive state of the steel samples, using features from the perturbed magnetic flux density components.
- The GMM model had a recall score of 1, indicating that it never misclassified the samples that are highly corroded (state-2). On the other hand, the logistic regression model occasionally misclassified the state-2 samples.
- The logistic regression model had a precision score of 1, indicating that it never mis-classified those samples that are less corroded (state-1), while the GMM model occasionally misclassified them.
- Both the models have a good F1 score indicating the potential application of these models to classify the corrosive state of steels.
Author Contributions
Conceptualization, L.X., P.B. and A.L.R.; methodology, L.X., P.B., A.L.R. F.C.A. and H.G.R.; software, L.X. and P.B.; investigation, L.X. and P.B.; writing—original draft preparation, L.X. and P.B.; writing—review and editing, A.L.R. F.C.A. and H.G.R.; supervision, A.L.R. F.C.A. and H.G.R.; project administration, H.G.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was developed at Instituto de Telecomunicações (IT) and was supported by the Portuguese Science and Technology Foundation (FCT), under project UIDBASE-LX - UIDB/50008/2020. The support from the FCT under a Ph.D. grant 2022.14456.BD is also gratefully acknowledged.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank Professor Noritaka Yusa from Tohoku University for providing us with the test specimens that were used in this study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lin, C.-H.; Lee, J.-R. Characterization of SPCC Steel Stress Behaviour in Brine Water Environment. Int. J. Electrochem. Sci. 2019, 14, 2321–2332. [Google Scholar] [CrossRef]
- Corrosion Mechanisms in Theory and Practice, Corrosion technology, 3rd ed.; Marcus, P. (Ed.) CRC Press: Boca Raton, 2012; ISBN 978-1-4200-9462-6. [Google Scholar]
- Revie, R.W.; Uhlig, H.H. Corrosion and Corrosion Control: An Introduction to Corrosion Science and Engineering; Fourth edition.; Wiley-Interscience, a John Wiley & Sons, Inc., Publication: Hoboken, New Jersey, 2008; ISBN 978-0-470-27725-6. [Google Scholar]
- Biezma, M.V.; San Cristóbal, J.R. Methodology to Study Cost of Corrosion. Corros. Eng. Sci. Technol. 2005, 40, 344–352. [Google Scholar] [CrossRef]
- He, Y.; Tian, G.; Zhang, H.; Alamin, M.; Simm, A.; Jackson, P. Steel Corrosion Characterization Using Pulsed Eddy Current Systems. IEEE Sens. J. 2012, 12, 2113–2120. [Google Scholar] [CrossRef]
- Fregonese, M.; Idrissi, H.; Mazille, H.; Renaud, L.; Cetre, Y. Initiation and Propagation Steps in Pitting Corrosion of Austenitic Stainless Steels: Monitoring by Acoustic Emission. Corros. Sci. 2001, 43, 627–641. [Google Scholar] [CrossRef]
- Edalati, K.; Rastkhah, N.; Kermani, A.; Seiedi, M.; Movafeghi, A. The Use of Radiography for Thickness Measurement and Corrosion Monitoring in Pipes. Int. J. Press. Vessels Pip. 2006, 83, 736–741. [Google Scholar] [CrossRef]
- Ishkov, A.V.; Dmitriev, S.F.; Katasonov, A.O.; Fadeev, D.A.; Malikov, V.N. Inspection of Corrosion Defects of Steel Pipes by Eddy Current Method. J. Phys. Conf. Ser. 2021, 1728, 012006. [Google Scholar] [CrossRef]
- Frankowski, P.K. Corrosion Detection and Measurement Using Eddy Current Method. In Proceedings of the 2018 International Interdisciplinary PhD Workshop (IIPhDW); IEEE: Swinoujście, May, 2018; pp. 398–400. [Google Scholar]
- Yusa, N.; Perrin, S.; Mizuno, K.; Chen, Z.; Miya, K. Eddy Current Inspection of Closed Fatigue and Stress Corrosion Cracks. Meas. Sci. Technol. 2007, 18, 3403–3408. [Google Scholar] [CrossRef]
- Li, Y.; Yan, B.; Li, D.; Jing, H.; Li, Y.; Chen, Z. Pulse-Modulation Eddy Current Inspection of Subsurface Corrosion in Conductive Structures. NDT E Int. 2016, 79, 142–149. [Google Scholar] [CrossRef]
- Kopf, L.; Tighe, R. Thermographic Identification of Hidden Corrosion. In Proceedings of the 2021 36th International Conference on Image and Vision Computing New Zealand (IVCNZ); IEEE: Tauranga, New Zealand, December 9, 2021; pp. 1–6. [Google Scholar]
- Alamin, M.; Tian, G.Y.; Andrews, A.; Jackson, P. Principal Component Analysis of Pulsed Eddy Current Response From Corrosion in Mild Steel. IEEE Sens. J. 2012, 12, 2548–2553. [Google Scholar] [CrossRef]
- Postolache, O.; Ramos, H.G.; Ribeiro, A.L. Detection and Characterization of Defects Using GMR Probes and Artificial Neural Networks. Comput. Stand. Interfaces 2011, 33, 191–200. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information science and statistics; Springer: New York, 2006; ISBN 978-0-387-31073-2. [Google Scholar]
Figure 1.
Samples with: (a) Less corroded state; (b) Highly corroded state.


Figure 2.
ECT probe. (a) Probe schematic with a TMR sensor; (b) Probe schematic with a Hall sensor; (c) Probe and signal conditioning circuits.
Figure 2.
ECT probe. (a) Probe schematic with a TMR sensor; (b) Probe schematic with a Hall sensor; (c) Probe and signal conditioning circuits.
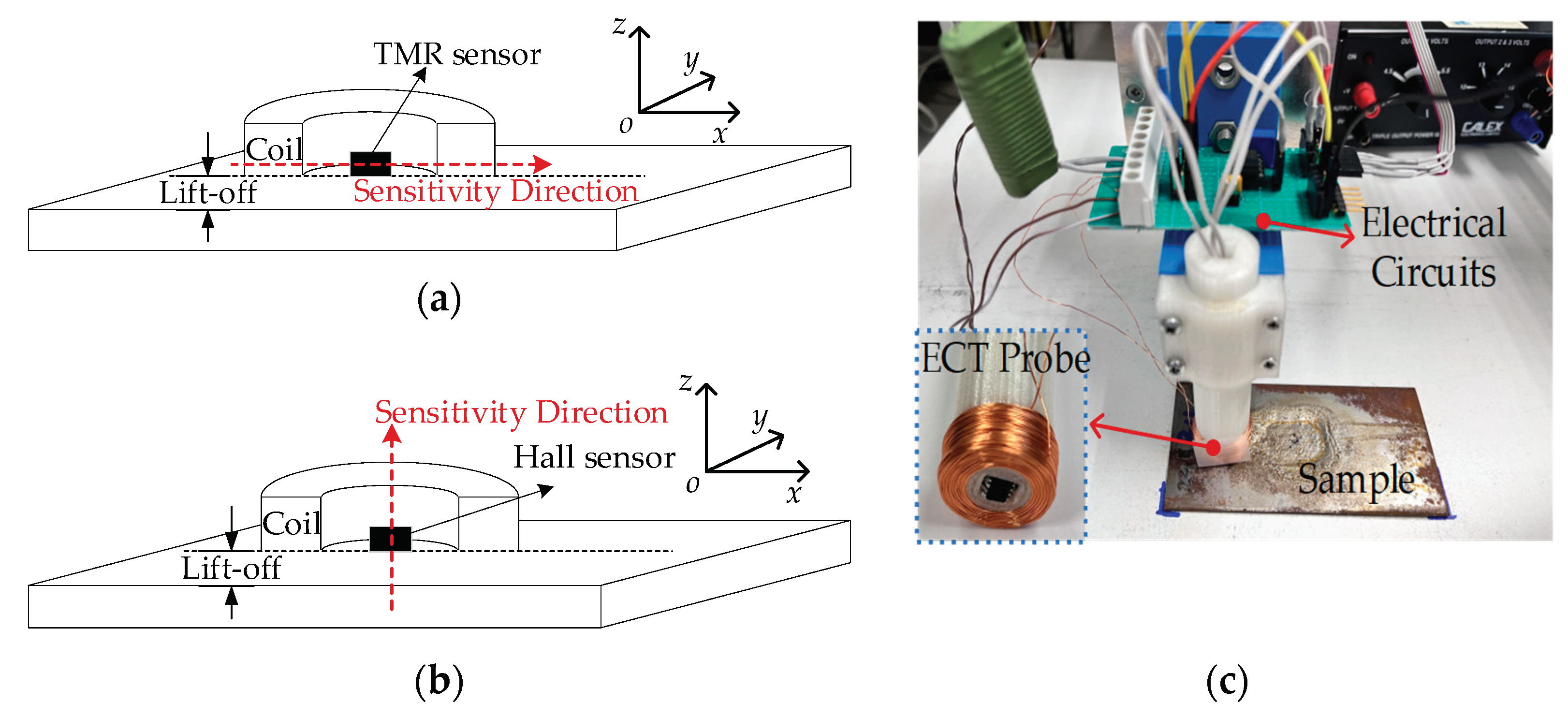
Figure 3.
Experimental setup.
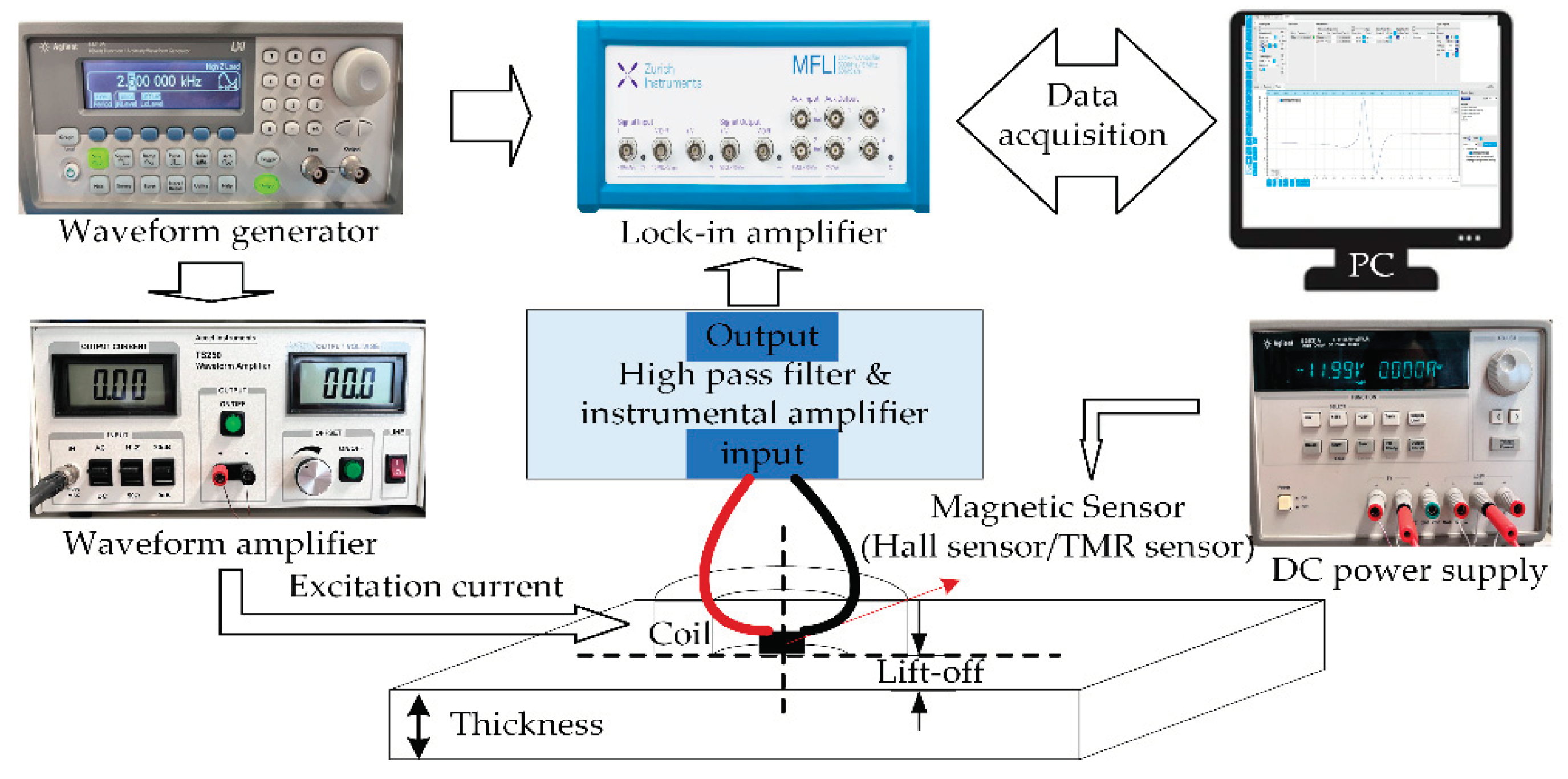
Figure 4.
Signal response of the same corroded sample: (a) Real and Imaginary parts of Bx at 2.5 kHz; (b) Real and Imaginary parts of Bz at 2.5 kHz; (c) Real and Imaginary parts of Bx at 5 kHz; (d) Real and Imaginary parts of Bz at 5 kHz.
Figure 4.
Signal response of the same corroded sample: (a) Real and Imaginary parts of Bx at 2.5 kHz; (b) Real and Imaginary parts of Bz at 2.5 kHz; (c) Real and Imaginary parts of Bx at 5 kHz; (d) Real and Imaginary parts of Bz at 5 kHz.
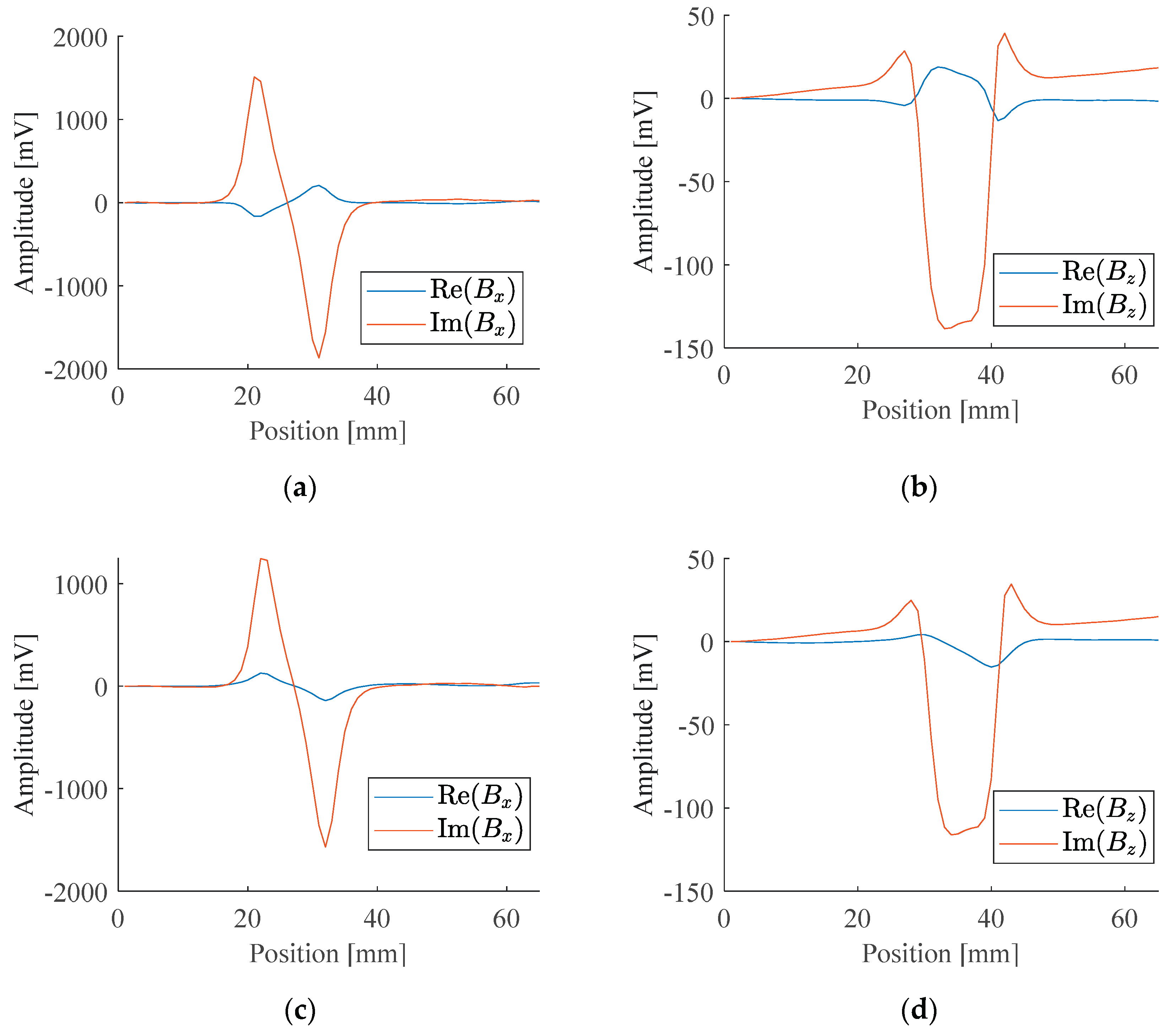
Figure 5.
Maximum perturbation features: (a) Real and Imaginary parts of Bx at 2.5 kHz; (b) Real and Imaginary parts of Bz at 5 kHz.
Figure 5.
Maximum perturbation features: (a) Real and Imaginary parts of Bx at 2.5 kHz; (b) Real and Imaginary parts of Bz at 5 kHz.
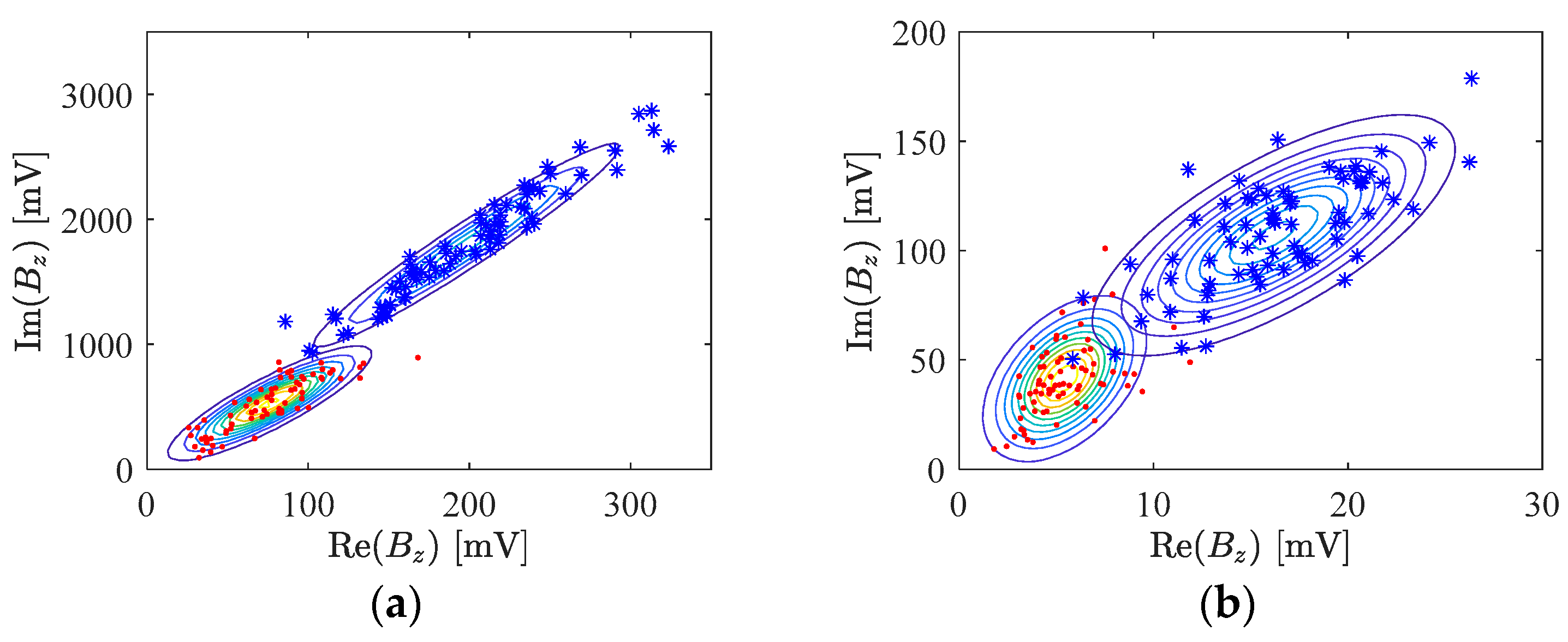
Figure 6.
Logistic regression model: Maximum perturbation features of (a) Real and Imaginary parts of Bx at 2.5 kHz; (b) Real and Imaginary parts of Bz at 5 kHz.
Figure 6.
Logistic regression model: Maximum perturbation features of (a) Real and Imaginary parts of Bx at 2.5 kHz; (b) Real and Imaginary parts of Bz at 5 kHz.
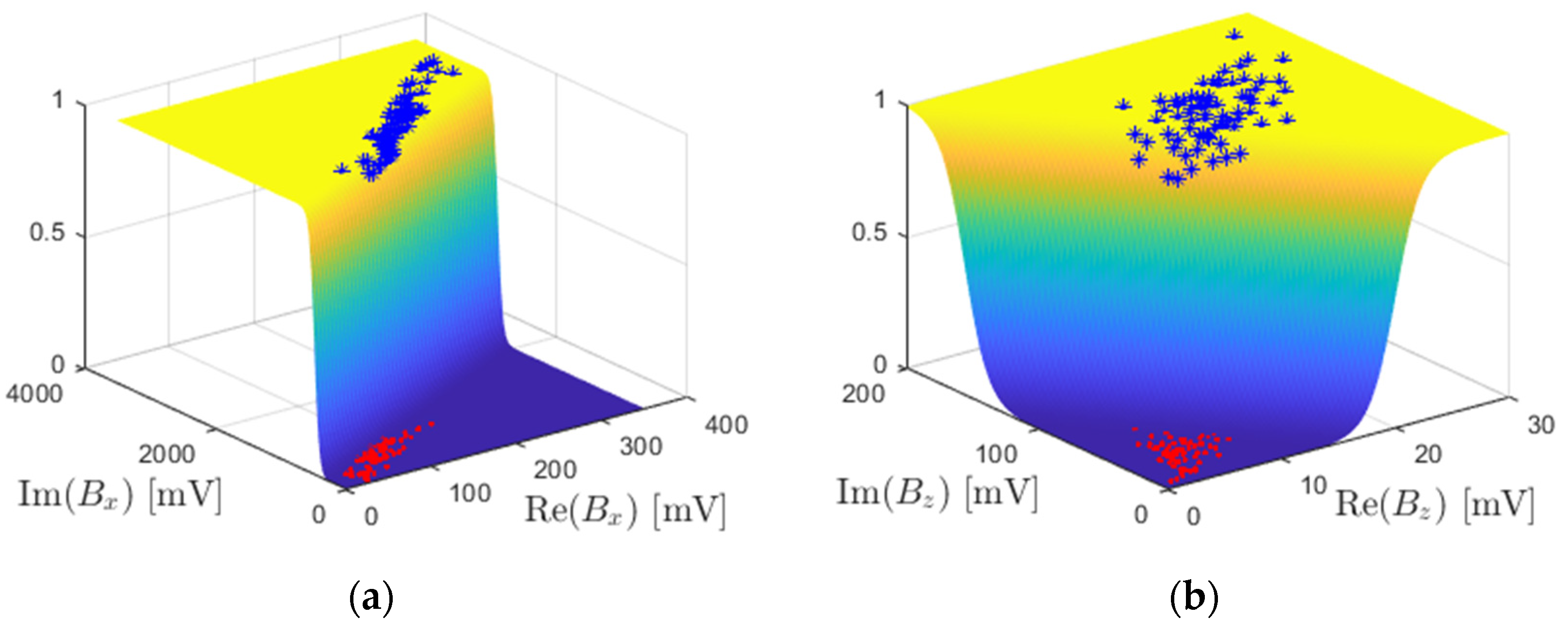
Figure 7.
Classification errors of (a) GMM; (b) logistic regression model.
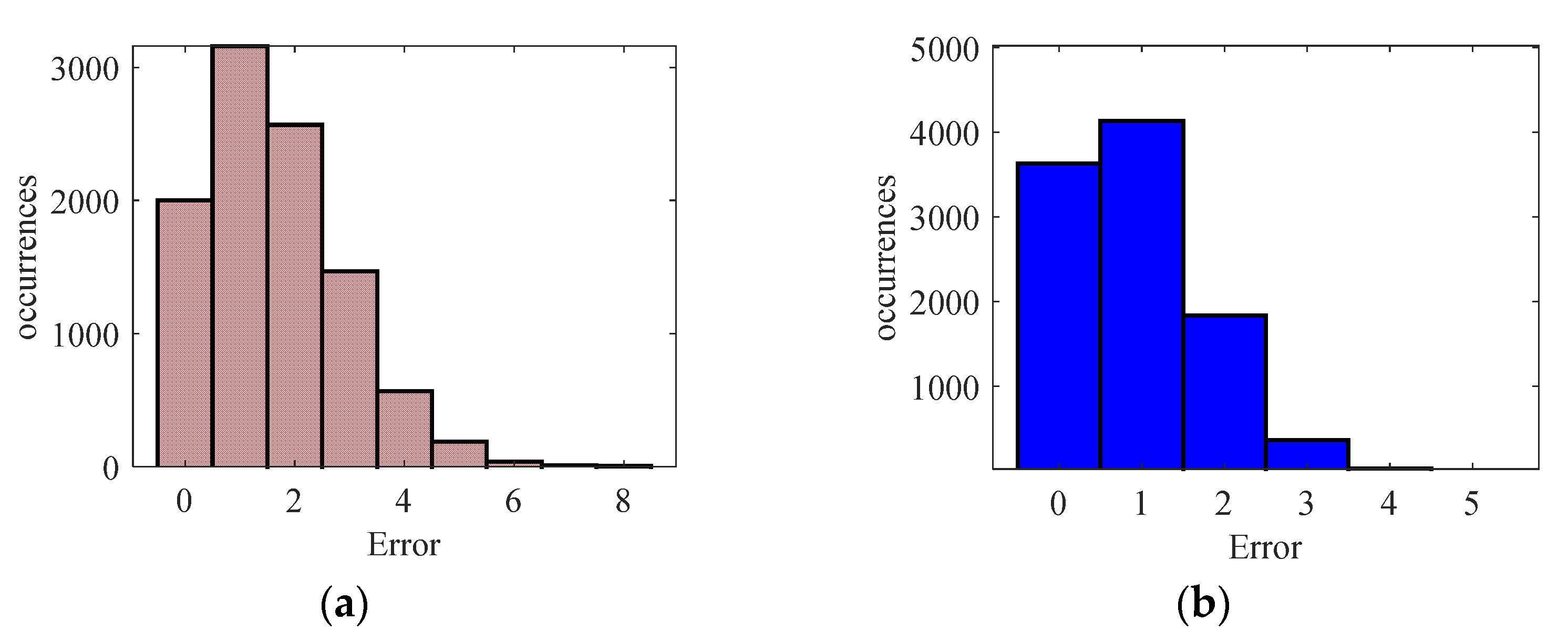
Figure 8.
Confusion matrix depicting the correct classification and misclassification histograms GMM. (a) True Negative; (b) False positive; (c) False negative; (d) True positive.
Figure 8.
Confusion matrix depicting the correct classification and misclassification histograms GMM. (a) True Negative; (b) False positive; (c) False negative; (d) True positive.
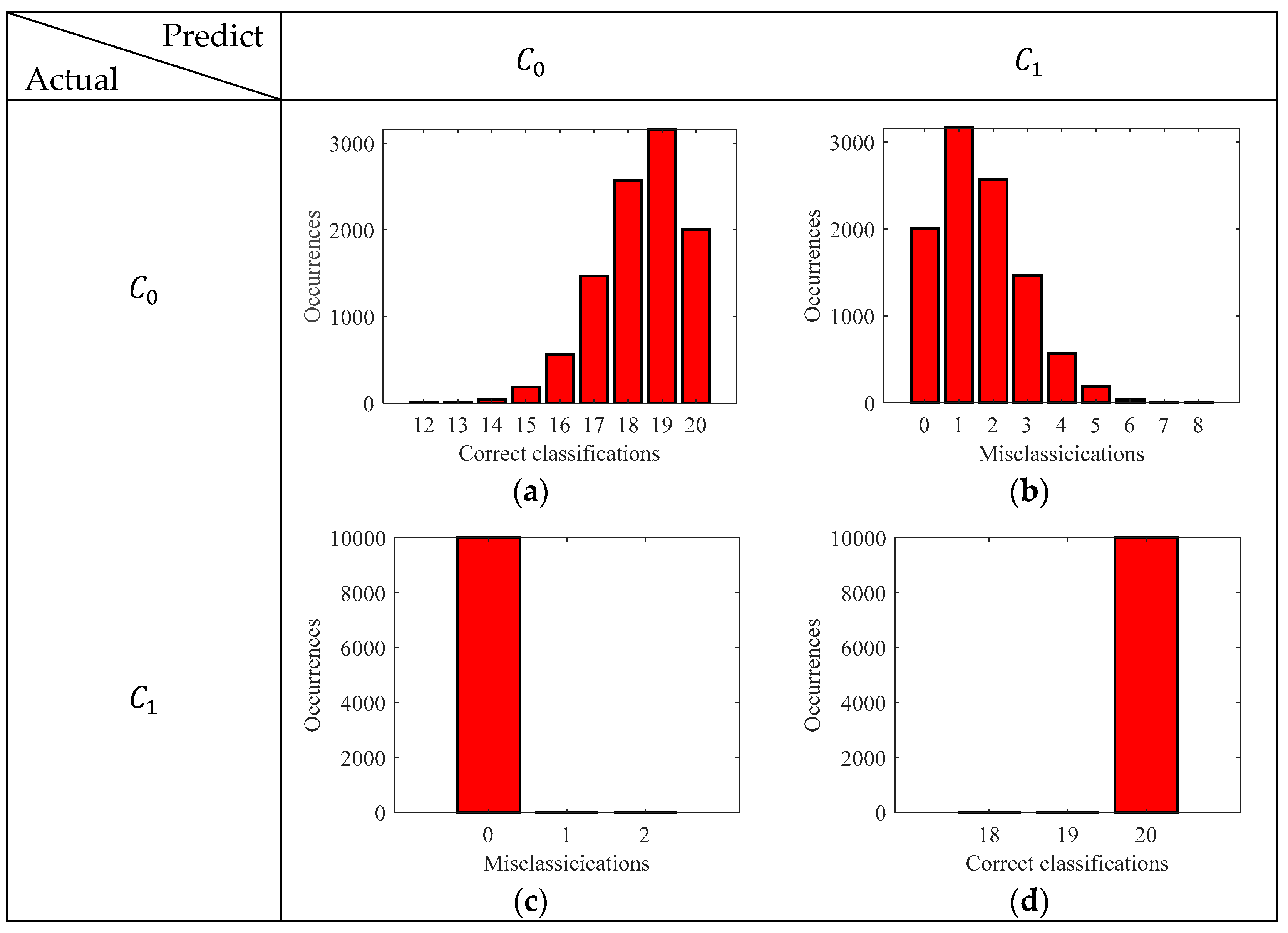
Figure 9.
Confusion matrix depicting the correct classification and misclassification histograms logistic regression model. (a) True Negative; (b) False positive; (c) False negative; (d) True positive.
Figure 9.
Confusion matrix depicting the correct classification and misclassification histograms logistic regression model. (a) True Negative; (b) False positive; (c) False negative; (d) True positive.
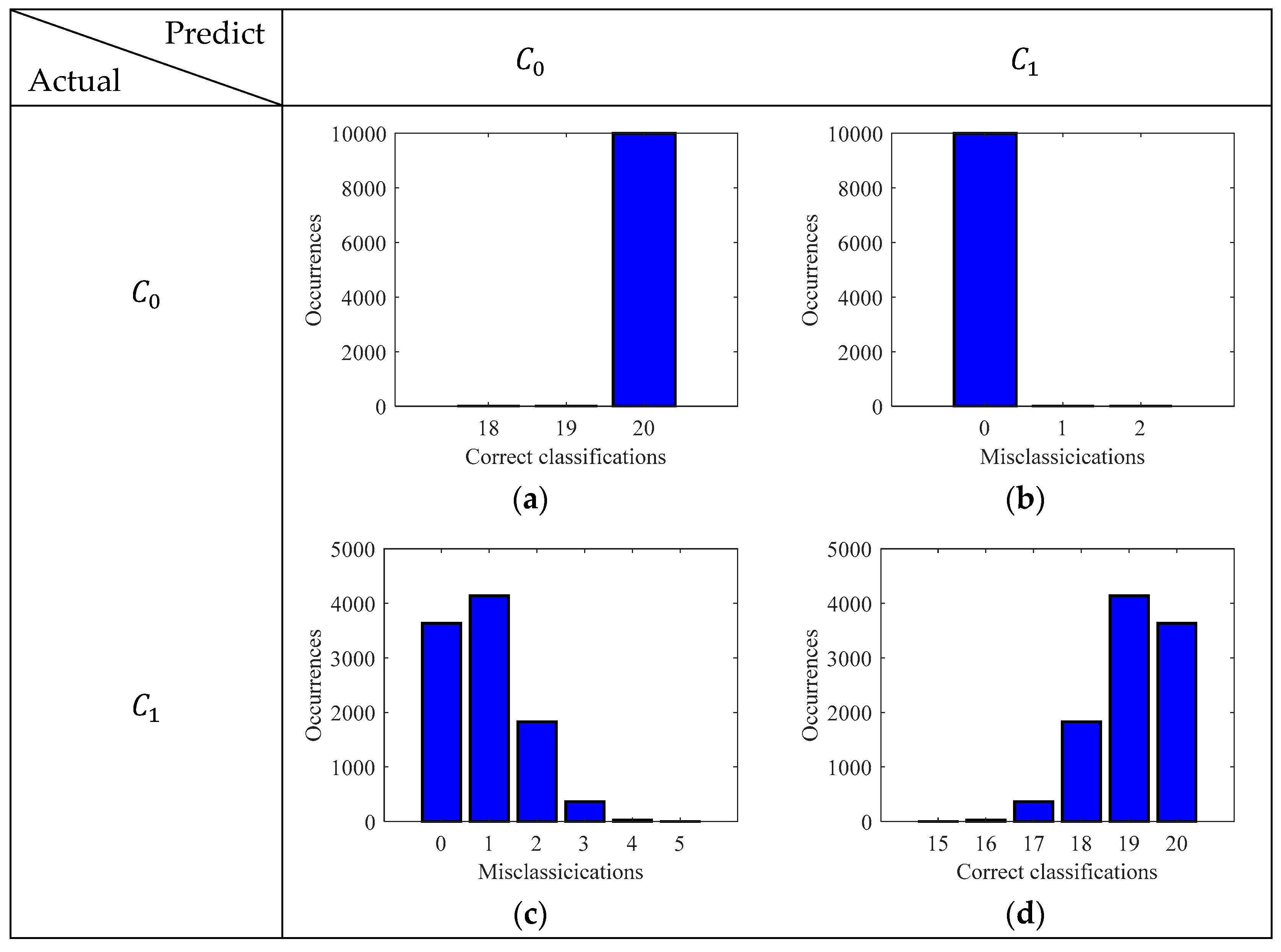
Figure 10.
Class specific performance metrics for the GMM and logistic regression model.
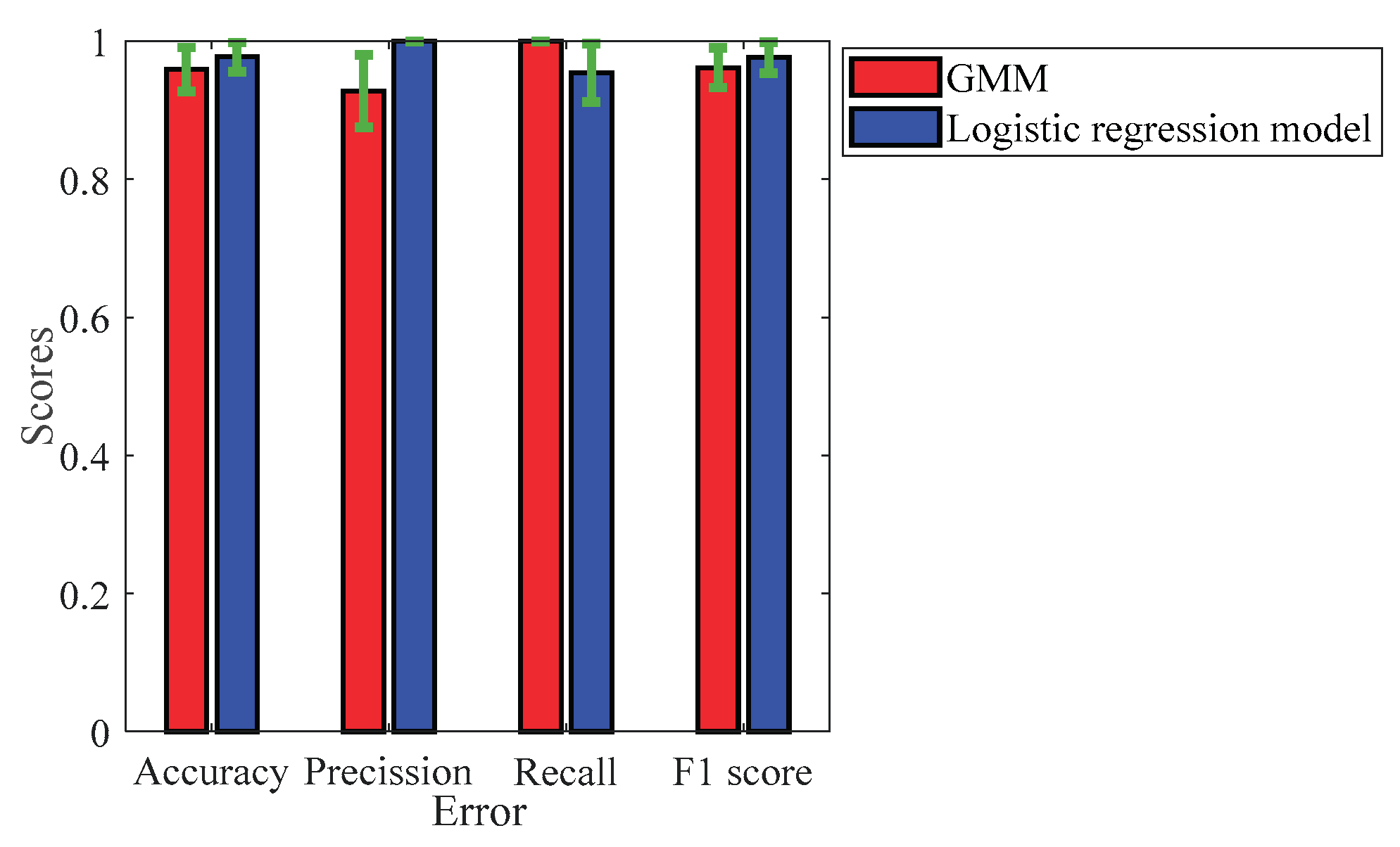
Table 1.
Features used for classification.
| Frequency | 2.5 kHz | 5 kHz |
|---|---|---|
| Features | Re (Bx) | Re (Bx) |
| Im (Bx) | Im (Bx) | |
| Re (Bz) | Re (Bz) | |
| Im (Bz) | Im (Bz) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






