Ab Initio Molecular Dynamics Investigation on the Permeation of Sodium and Chloride Ions through Nanopores in Graphene and Hexagonal Boron Nitride Membranes

Nanoporous membranes promise energy-efficient water desalination. Hexagonal boron nitride (h-BN), like graphene, exhibits outstanding physical and chemical properties, making it a promising candidate for water treatment. We employed Car–Parrinello molecular dynamics simulations to establish accurate modeling of Na+ and Cl- permeation through hydrogen passivated nanopores in graphene and h-BN membranes. In these complex systems the classical potentials cannot properly account for the physics at play. We demonstrate that ion separation works well for the h-BN by imposing a barrier of 0.13 eV and 0.24 eV for Na+ and Cl- permeation respectively, compared to the graphene where the Cl- ion faces a negative barrier of 0.68 eV and is prone toward blockade and Na+ permeation is associated with a slightly negative barrier of 0.03 eV. From the change in the solvation shell, we get the following trend: Na/h-BN > Na/G > Cl/G > Cl/h-BN. We argue that the trend in the permeation barrier changes to Cl-h-BN > Na-h-BN > Na-G > Cl-G due to a combination of several interactions, including the distortion of the water network induced by the ions, the ion-water interaction, and the ion-nanopore interaction. Overall, the desalination performance of h-BN surpasses that of their graphene counterparts.

Keywords:

Subject: Chemistry and Materials Science - Nanotechnology

1. Introduction:

By 2050, more than half of the world’s population will live in water-stressed areas, and another billion may lack sufficient water. According to the recent estimation by the UN, just 200,000 cubic kilometers of 1.4 billion cubic kilometers of water on earth represent accessible freshwater for human consumption, which means that a meagre 0.014% of all water on earth is procurable and fresh. Furthermore, the dissemination of contaminants, due to the extended industrial and agricultural activities, gives rise to aquatic pollution of limited available water, followed by water-borne diseases for the consumers of that water. Seawater desalination, wastewater treatment, and water reclamation are considered as solutions to provide enough fresh water and to meet the increasing demands [1].

Membrane-based distillation and reverse osmosis (RO) are frequently applied techniques for seawater desalination, but are immensely costly and arduous [2,3]. In the RO process, saline water is pressurized through a semi-permeable membrane which permits water passage while hindering salts [4,5]. The first commercially feasible semi-permeable membranes developed in the 1960s were asymmetric cellulose acetates [6]. In the 1980s, robust thin-film composite membranes were established, which are more durable and exhibit higher water permeability [7]. Despite the tremendous improvements in thin-film composite membranes, there are still limitations associated with their applications. These membranes are susceptible to fouling, which reduces their functionality in terms of limited water flow and leads to reduced membrane durability and low selectivity. These problems diminish the efficiency of the membrane and consequently required higher input energy to drive the water through the membrane [8,9]. Even the most efficient reverse osmosis desalination facility consumes about 3-4 kW of energy per hour and releases about 1.4-1.8 kg CO₂ to supply one cubic meter of potable water [4,10]. Thermal-based methods that evaporate feed water take four times higher energy to produce the same amount of water [11]. Therefore, much attention has been focused on developing and implementing efficient membranes to reduce energy consumption.

Nanomaterials have come to aid as an effective solution to many existing challenges [12,13,14]. It is predicted that nanoporous membranes with their atomic thickness may be a suitable alternative to current membranes. In recent years, two-dimensional nanostructures such as graphene, hexagonal boron nitride (h-BN), graphene oxides, transition metal oxide, dichalcogenides and carbides as well as one-dimensional nanostructures such as carbon nanotubes have been investigated with respect to their potential application in the desalination process [15,16,17,18,19,20,21,22,23,24]. 2D desalination nanoporous membranes can be fabricated by either top-down methods, where the nanopores are created in an initially nonporous membrane, or bottom-up approaches, where the pores are grown in an intrinsically porous membrane [25,26,27,28,29,30,31,32,33].

Electrically driven salt permeation through nanopores in various membranes has been investigated due to ionic current utilization in DNA sequencing analysis. The first experimental indication of ionic hydration contribution in salt transport was demonstrated by S. Garaj et al. They found that defects smaller than the monovalent salt hydration shell permit larger ions with lower hydration energy and exhibit a higher conductance compared to smaller ones [34]. T. Jain et al. measured the conductance of isolated graphene nanopore defects. They reported that the nonlinear I-V characteristic corresponds to the hydration shell deficiencies proportional to the nanopore diameter. At higher voltages due to the activation of ion transport, the linear rectified I-V characteristic is observed, which is corresponding to the electrostatic interaction of ions with the charged pore [35]. S. C. O’Hern et al. measured the ionic current through controlled nanopores that were first introduced into a monolayer graphene membrane by ion bombardment and afterward were enlarged by chemical etching. The nanopores that were exposed to 5 minutes of chemical etching exhibited selective transfer of K⁺ while hindering Cl^- due to the presence of negative functional groups caused by chemical etching [36]. Another study reported that the surface and edge charges of graphene and the pore defects lead to a preferential selectivity of potassium over chloride in even large defect pores [37]. The ionic current through a nanopore with 6 Å diameter that was initially created by sulfide vacancy in MoS₂ membrane was studied by J. Feng et al. They measured almost zero ion current at low applied voltages. They suggested that a combination of dehydration and Coulomb blockade are leading to the single ion permeation through the nanopore [38].

The 2D h-BN, reputed as “white graphene,” has been also studied extensively [39,40,41]. The atomic structure of h-BN is identical to the graphene structure in such a way that their lattice mismatch is less than 2%. Compared with graphene, it has a large band gap and features as an electrical insulator. It exhibits good thermal stability and thermal conductivity. Moreover, it is resistant to being oxidized and chemically inert [42,43,44,45]. It has been demonstrated that highly porous h-BN nanosheets, synthesized by thermal treatment, can absorb organic dyes and oil more than 33 times of their weight and repel water, owing to their oxidation resistance. Exceptional thermal stability of h-BN also makes it recyclable. The saturated structures can be exposed to fire and operate with a slight decrease in their sorption efficiency [45].

The permeation of water and ions through nanopores in 2D single atomic layer membranes and the fundamental mechanisms influencing these transports are currently an emerging issue. However, experimental observations on this subject are still sparse. There exist stringent requirements on the fabrication process as well as size-control and distribution of the nanopores.

On the other hand, molecular dynamics simulations have been utilized in several studies to investigate and characterize the structure and dynamics of water molecules and salt ions in the desalination process. Classical molecular dynamics simulations have been extensively applied to probe ion transport and water flow under an applied electric field or pressure-driven mechanism. A variety of functionalized graphene nanopores (-H, -O, -OH, -COOH, -CO, -NH₄, -N, and -F), as well as nitrogen terminated and boron terminated nanopores in h-BN membranes, are considered in those studies [46,47,48,49,50,51,52]. Nanopores in other 2D membranes such as graphene-oxide and MoS₂ are also investigated [53,54]. It has been demonstrated that the pore size, ion hydration shell, steric effect on the surface of the membranes as well as the passivation of nanopore edges play crucial roles in ionic and water permeation [46,47,48,49,50,51,52,53,54]. These simulations are based upon a set of fixed predefined force field parameters that describe the interatomic forces, which do not exclusively include the electronic wave functions and quantum mechanical interactions, and therefore lead to limited accuracy or transferability [55,56].

Quantum molecular dynamics can be utilized to characterize a system consisting of a nanoporous desalination membrane in an aqueous medium and more accurately explains the physics at play. Using Born-Oppenheimer molecular dynamic (BOMD) to study water molecule, Cl^- and Na⁺ transport through (-H) and (-O,-H) functionalized nanopores in the graphene membrane, R. Guerrero-Avilés et al. reported that both nanopores inhibit the salt permeation, while the (-O,-H) functionalized nanopore exhibits higher rate for water molecule transport [57]. Ab initio molecular dynamics was employed by G. Tocci et al. to closely investigate the structural and dynamic properties of water molecules in contact with the pristine graphene and h-BN sheets. They showed that the dynamics of water molecules are completely different, in such a way that water molecules on the boron nitride surface experience a three-fold higher friction as on the graphene surface. The particular electronic structure and charge distribution in h-BN give rise to a more corrugated free energy surface compared to graphene. Therefore, the dynamics of water molecules is accompanied by more friction on the h-BN surface [58]. B. Grosjean et al., by means of ab initio molecular dynamic simulations, showed that the graphene and boron nitride surfaces that are in contact with water and hydroxide ions (alkaline water) get charged through the interaction of the hydroxide ion with the surface. However, the hydroxide ions are weakly physisorbed on the graphene surface and exhibit fast lateral dynamics, while on the h-BN surface, they tend to be adsorbed on the boron sites but can still remain physisorbed and mobile [59].

Considering the clues given in previous studies, graphene and h-BN nanopores show different ion and water permeation behaviors and the underlying aspects of these differences require more in depth analysis. However, to the best of our knowledge, no research has yet been conducted to compare and investigate the involved mechanisms in the sodium and chloride permeation through the hydrogen passivated nanopore in graphene and h-BN membranes at the ab initio level. In this work, we exploit the Car-Parrinello molecular dynamics framework to establish a more accurate understanding of the physics at play during salt ions permeation through hydrogen-passivated nanopores in graphene and h-BN membranes. We demonstrate better separation of monovalent salt ions through hydrogen passivated nanopores in an h-BN membrane. Our results show that an h-BN membrane exhibits a significantly higher efficiency in filtering Na⁺ in comparison to a graphene membrane. On the other hand, while Cl- ions get filtered through h-BN nanopores, they get blocked in graphene nanopores and hinder water permeation.

2. Materials & Methods

The atomic structure of the graphene and h-BN membranes containing a nanopore of 8.5 Å diameter was optimized within the SIESTA implementation of density functional theory [60,61,62]. All edge atoms at the nanopores are passivated by hydrogen atoms. Generalized gradient approximation as parametrized by Perdew, Burke, and Ernzerhof (GGA-PBE) with the DF2 correction due to the dispersion forces are used for the exchange-correlation part of the Hamiltonian [63,64]. The electronic wave functions are expanded over a set of numerical atomic orbitals at the double-zeta plus polarization level (DZP) and the norm-conserving Troullier–Martins pseudopotentials are employed for all atoms [65]. For the real and reciprocal space sampling a mesh cutoff energy of 300 Ry and a 2×2×1 Monkhorst-Pack grid have been employed, respectively.

The simulation box, with orthorhombic symmetry and 19.73 × 21.59 × 10.00 Å dimensions, is then filled with 78 water molecules considering the steric effect and the water density of 1 g/cm³ at ambient temperature. Hereafter, all calculations were carried out using the ab initio Car-Parrinello molecular dynamics framework, CPMD, under periodic boundary conditions [66,67]. The water-membrane equilibration runs were performed in the NVE ensemble, for 20000 steps with time steps equal to 2. a.u. (whole calculation time of circa 1 ps). The trajectories of the last 10000 steps were taken as production runs.

The fictitious electron mass was set to 200 a.u. The Grimme DFT-D2 corrected PBE functional [68] and a plane wave cutoff energy of 70 Ry are employed in all CPMD calculations. For all atoms the Troullier-Martins pseudopotentials [65] are used. After equilibration, to model saline water, sodium and chloride ions were added to the equilibrated simulation box containing 75 water molecules (3 water molecules were omitted and replaced by sodium and chloride) by placing each of the sodium and chloride ions once in the center of the nanopore and once 3.5 Å above the nanopore center. The systems were first equilibrated for 4000 steps in the NVT canonical ensemble using Nose-Hoover thermostat chains [69,70,71] to stabilize the temperature at 300 K followed by 6000 steps simulation in the NVE ensemble, which gives a total of 10000 steps. The course of the fictitious kinetic energy of the electrons and the total (Hamiltonian) energies during the simulations which demonstrate the stability of the calculated trajectories, are presented in the Supplementary Material.

A comparison of the energies for different positioning of ions in graphene and h-BN nanopores provides useful information regarding energy changes in the systems when they permeate through the nanopores. These differences in Kohn-Sham energies for the last 6000 steps are considered as criteria to assess the permeation energies. The trajectories of the last 6000 steps were exploited to investigate the effect of ion hydration and the contribution of the nanopore.

3. Results and Discussion

Atomic structure of membranes and their electron density. The surface of a graphene membrane is made of covalently bonded identical carbon atoms with almost uniformly distributed electron density. At the edge of a graphene nanopore, the hydrogen atoms, which passivate the edge carbon atoms, carry a positive partial charge (Figure 1a), due to the higher electronegativity of carbon compared to hydrogen (carbon and hydrogen have electronegativities equal to 2.55 and 2.20, respectively). However, the bonding in h-BN has polar character, where the negative charges are concentrated around the nitrogen atoms (electronegativity of 3.04) and the boron sites (electronegativity of 2.04) are positively charged. The edge of the h-BN nanopores consists of both nitrogen and boron atoms, which are passivated with hydrogen atoms. As the electronegativity of hydrogen lies in between the electronegativities of the nitrogen and boron atoms, half of the passivating hydrogen atoms (B-H) are negatively charged while the other half (N-H) are positively charged (Figure 1b). Overall, the edge of an h-BN nanopore shows negative charge character in contrast to the positively charged edges of a graphene nanopore. The polarity and charge distribution on the surface of the membrane and the edge of the nanopores has substantial influence on the way they interact with water molecules in an aqueous environment.

Planar average density profile of water molecules in two membranes. After filling the simulation box with water molecules and performing the equilibration run, the radial distribution functions (RDF) of O-O (Figure 2c) and O-H (Figure 2d) bonds in water are calculated. Water molecules form a network of hydrogen bonds in the liquid phase. The oxygen atom of each water molecule forms a hydrogen bond with two hydrogen atoms of other water molecules and each water molecule shares its two hydrogen atoms to the oxygen atoms of other molecules to form hydrogen bonds. These hydrogen bonds are reflected in the first peak of the oxygen-oxygen radial distribution functions and the first peak of the hydrogen-oxygen radial distribution functions. The objective is the assessment of the hydrogen bonds, hence the first peak of gOH(r) which represents the covalent bonding between oxygen and hydrogen atoms in water molecules has been eliminated. Our results show good agreement with previous experimental and theoretical results [72,73].

The planar average densities of the water molecules in the simulation boxes (including graphene and h-BN) are depicted in Figure 2e. The density profiles in the two systems exhibit a similar trend, whereby the density peaks around 3 Å above the membrane surface and decreases in the middle of the box. Similar water density fluctuations on the surface of different membranes are also reported in previous studies [58,74,75,76]. The density peaks for graphene membranes are more pronounced (Figure 2e), due to the repulsive forces between the π electrons on the graphene surface and the electron density of the oxygen atoms in the water molecules. The polar nature of the bonding in the h-BN membrane leads to higher water densities close to the surface. According to Tocci et al., the water molecules on an h-BN surface are aligned so that their dipoles are parallel to the sheet and one of its OH bonds points towards nitrogen atoms [58]. Our results in Figure 2e show that, unlike in the graphene system, water molecules in the h-BN membrane get closer to the surface, which is in good agreement with a recent study [77], where the average distance of water molecules on graphene and h-BN surfaces are reported to be 2.95 Å and 2.92 Å, respectively.

Oxygen radial distribution around the hydrogenated nanopores. To further investigate the structure of water molecules in nanopores, we calculated the distribution of oxygen atoms around the passivating hydrogen atoms at the edge of the nanopores, using RDF data (Figure 3a). The first RDF peak for a graphene nanopore occurs at a significantly farther distance compared to the length of standard hydrogen bonds in equilibrated water (1.8 Å). This reveals the hydrophobic nature of the nanopore edges in graphene membranes. In the h-BN membrane, the first peak is shifted to shorter distances, which indicates that the oxygen atoms are distributed closer to the edge of the hydrogenated h-BN nanopore in comparison to the graphene nanopore. The edge of h-BN nanopore, however, consists of less electronegative boron and more electronegative nitrogen atoms, both passivated by hydrogen atoms. The water molecules exhibit different interactions with these two types of edges as depicted in Figure 3b. The first peak in the RDF plot is related to the distance between oxygen atoms and N-H edge and shows that the water molecules are attracted to the N-H sites. The peak occurs at a distance (ca. 2 Å) close to the hydrogen bond length in equilibrated water. In other words, the N-H terminations with partially positively charged hydrogen atoms get involved in a network of hydrogen bonds with the oxygen atoms in water with partial negative charges. This leads to the hydrophilic character of h-BN nanopores in contrast to the hydrophobic property of graphene nanopores. These results are in line with the recent study [77], where the behavior of water molecules on the h-BN surface is explained on the basis of the interaction between two dipoles, namely the dipoles of water molecules and the dipoles of B-N bonds on the surface.

Arrangement of water molecules in the hydrogenated nanopores. For a more detailed analysis of the structure of water molecules in graphene and h-BN nanopores, we monitored the trajectories of water molecules around the nanopore during the simulation. The trajectories are recorded in a cylindrical volume centered at the nanopores (cross section equal to the nanopores) with a height of 3 Å (-1.5<z<1.5, where z=0 corresponds to the surface of the membrane). The trajectories are projected on the surface of the membranes (X-Y) and depicted in Figure 4a,b. The schematic of the cylinder is also shown in Figure 4c,d. In the graphene nanopore the water molecules form a ring-shaped cluster in the center of the nanopore (Figure 4a). This result clearly illustrates the hydrophobicity of the nanopore edge in graphene and indicates that no hydrogen bond exists between the water molecules and the nanopore edge. The water molecules preserve their hydrogen bonding with each other in the center of the graphene nanopore. On the contrary, the water molecules in the h-BN nanopore form a quadrilateral shape due to the formation of hydrogen bonds between the N-H edges (the red rectangles in Figure 4b) and the water molecules. The water molecules linked to these terminals are also connected to the other water molecules with hydrogen bonds and form a strong network of water molecules with anchoring points at the nanopore edge. Snapshots of these quadrilateral configurations are shown in Figure 4b. The results in Figure 4 corroborate the previous discussion based on RDF data (Figure 3). As we will show, these different structures of water molecules within the graphene and h-BN nanopore edges play an essential role in the permeation of Na⁺ and Cl^- ions through the porous membranes.

Permeation barriers. Considering the different behavior that nanoporous graphene and h-BN membranes exhibit in interaction with water molecules, one may suspect that hydration of restricted species (ions) near the nanopores would be affected by these interactions, and consequently graphene and h-BN nanopores exhibit distinct Na⁺ and Cl^- sieving behavior. To assess the Na⁺ and Cl^- permeation energy profiles through graphene and h-BN nanopores, as explained in the methods section, the changes in the Kohn-Sham energies of the equilibrated systems are calculated once the ion fixed in the center of the nanopores and once fixed concentrically to the nanopore at a distance of 3.5 Å above the nanopore center. Our results (Figure 5) indicate that Na⁺ experiences a slightly negative barrier of 0.03 eV (essentially zero) and Cl^- experiences a negative barrier of 0.68 eV to pass through the hydrogen passivated nanopores in graphene and barriers of +0.13 eV and +0.24 eV to pass through the hydrogen passivated nanopores in h-BN membranes, respectively.

Apart from the nanopore size and the passivating atoms, the permeation of ions is affected by the variation in the ion hydration shell [78]. It is well known that in an aqueous medium, water molecules get polarized in the electric field created by the ion, leading to the formation of hydration shells around the ion.

When investigating the physics at play during Na⁺ or Cl^- permeation through the nanopores, three aspects must be considered:

To what extent do the electrostatically attracted water molecules to anion or cation get dehydrated?
Does the nanopore provide the available space for ion permeation?
How do these surrounded ions or partially surrounded ions interact with the nanopore edges?

Different chemistry of the graphene and h-BN nanopores causes characteristic changes in the hydration shell of ions in each membrane. We will show that a combination of these changes determines in essence the energy barrier experienced by the ions. In the following the first aspect is addressed by investigating ion hydration and by studying the nanopore contribution, the second and third aspects are taken into account.

Na⁺ and Cl^- hydration. We inspect the contribution of hydration/dehydration in the salt ion permeation by means of RDF plots. Figure 6 illustrates the hydration behavior of ions at different positions relative to the nanopores. The first peak in these RDF plots characterizes the solvation shell with hydration radius, the radius where the oxygen or hydrogen atoms orient toward Na⁺ or Cl^- as well as the hydration number, the number of polarized water molecules in each spherical layer around Na⁺/Cl^-. Hydration numbers and radii are tabulated in Table 1.

Water molecules in the graphene system do not interact strongly with the membrane. As a result, they have already structured and oriented themselves in such a way to minimize the entropic effects. Therefore with the introduction of Na⁺ at Z=3.5 Å, the ones adjacent to Na⁺ become polarized in the Na⁺ electric field and get electrostatically bound to it. On the other hand, it seems that the polar-polar interaction between the h-BN membrane and water molecules outweighs the Na⁺-water interaction. The Na⁺ electric field does not exhibit the same ability to polarize its surrounding water molecules in the h-BN system as in the graphene system, which reflects in different hydration numbers for their positioning at 3.5 Å above the nanopore. This finding is in agreement with the recent study, where it has been demonstrated that the different interactions between h-BN or graphene flakes and water molecules affect the Ca²⁺-water interaction, i.e., Ca²⁺ hydration, in these systems [77].

We should note that the hydration number and radius of Na⁺ in the bulk water are equal to 3.5 and 2.18 Å respectively (density of 1 g/cm³) [79]. In our case, the repulsive force between the graphene surface and the water molecules as well as the polar-polar interaction between the h-BN surface and water molecules give rise to higher water densities above the nanopore, which results in the deviation of the hydration radius and number from the values in bulk water.

This difference becomes even more pronounced for Na cation positioning in the center of the nanopore. As mentioned previously the graphene nanopore is hydrophobic, therefore Na⁺-water interaction preponderates over nanopore-water interaction. In stark contrast to this, in the h-BN nanopore, hydrophilic nanopore-water interaction takes precedence over Na⁺-water interaction. In fact, within a span of 3.5 Å from the nanopores, the interplay between water-membrane/nanopore interaction and water-Na cation interaction determines the Na cation hydration number.

Overall, the change in Na cation hydration as it enters the h-BN nanopore is twice the change in the graphene nanopore, the Na⁺ hydration number decreases by approximately 0.74 and 1.49 as it permeates the graphene and h-BN nanopores, respectively.

The first solvation shell of a Cl^- at 3.5 Å above the graphene nanopore, contains 2.66 water molecules. This number increases to 3.11 for the same positioning of the anion in the h-BN system. As the Cl anion permeates the graphene nanopore, it loses 0.43 water molecules from its hydration shell but as it permeates the h-BN nanopore the hydration shell gains 0.13 water molecules. The hydration number and radius of Cl^- in the bulk water are equal to 2.18 and 2.24 Å, respectively (density of 1 g/cm³) [79].

The hydration number of the Cl anion experiences a negligible change as it enters the nanopores in comparison with the Na cation. The cation hydration number in the graphene system exceeds that in the h-BN system, nevertheless, the Cl^- hydration number in the h-BN system is greater than that in the graphene system. According to Tocci et. al. [58], “the most stable structure for a water monomer is on the center of the hexagon with its dipole pointing down toward the sheet. While on BN water preferentially adsorbs in the center of the hexagon with the dipole moment parallel to the membrane with one of the O-H bonds pointing toward the N atom.” Therefore, the distinct way of oxygen-membrane interaction appears in different cation hydration in these two systems and the disparate orientation and arrangement of the water molecules relative to the membranes emerges in different anion hydration. It should be mentioned that a Cl anion has a different configuration of hydration compared to Na cation. Only one hydrogen atom of the water molecule is electrostatically attracted to the Cl anion. Another hydrogen atom gets involved in forming the second solvation shell, while the hydration of Na⁺ is such that only the oxygen atoms point to Na⁺. Different ways of cation/anion hydration in addition to the combination of water-membrane/nanopore interaction result in the difference between Na and Cl hydration numbers for each specific position.

We define this difference as

{∆ n}_{C - a}

{∆ n}_{c - a} = c a t i o n h y d r a t i o n n u m b e r - a n i o n h y d r a t i o n n u m b e r

{∆ n}_{c - a}

is equal to 3.41 and 2.11 for ion positioning 3.5 Å above the graphene and h-BN nanopores. If the ion is positioned in the center of the nanopores,

{∆ n}_{c - a}

is equal to 1.5 and 0.49 for the graphene and h-BN nanopores, respectively.

Our results indicate that Na⁺ permeation through the nanopores is associated with more significant changes in the hydration number than the Cl^-. The trend of the change in the hydration number is like:

N a / h - B N > N a / G > C l / G > C l / h - B N

The first solvation shell for anion in the graphene system contains only very few molecules which do not contribute to the permeation barrier height significantly as they can arrange in a way so that they do not interact strongly with the nanopore, rather the interaction between Cl^- itself and nanopore induces a higher permeation barrier. To study this more closely, the role of the nanopores should be investigated

Nanopore Contribution. It seems there is a complex interaction between the electron density of the rim’s atoms, water molecules, and ions which may induce a steric exclusion or blockade. To study the contribution of the nanopores to the permeation barriers, three parameters of the radial distribution, the number of water molecules within the nanopore, and the planar arrangement of water molecules in the vicinity of the nanopore during the anion and cation permeation through the nanopore have been investigated.

The radial distribution of the oxygen atoms relative to the edge increases with Na cation positioning in the center of the graphene nanopore. The number of water molecules within the nanopore increases by 0.48 with this displacement. The planar arrangement of water molecules (Figure 8a) illustrates that the spatial distribution of the water molecules occupying the nanopore changes significantly as the Na⁺ ion enters the graphene nanopore. One may suspect that the spatial positioning of approximately six water molecules at a distance of 2.25 Å from a Na⁺ ion above the nanopore induces a repulsion between the oxygen atoms and the observation of a negative barrier is due to the reduction of this repulsion as a result of the decrease in the hydration number.

Cl^- anion positioning in the nanopore center, in contrast to Na⁺, affects the radial distribution of the oxygen atoms relative to the rim (Figure 7b) such that the water molecules get distant from the nanopore. The average number of water molecules within the nanopore is reduced by 2.3 molecules as well. The planar arrangement of water molecules (Figure 8b) also indicates a deficit of water molecules within the nanopore. The Cl anion within the graphene nanopore breaks all hydrogen bonds across the nanopore. As a result, the combination of the two factors, Coulombic electrostatic attraction between positively charged edge and anion and better reorganization of the water below and above the nanopore and consequently forming of strong hydrogen bonds, induces a negative barrier.

Figure 7. Distribution of water molecules around the nanopore edges in the presence of the ions above the center, Z=3.5 Å (solid blue curves) and in the center of nanopores, Z=0 Å (solid red curves) for a & b) graphene nanopore and c and d) h-BN nanopore.

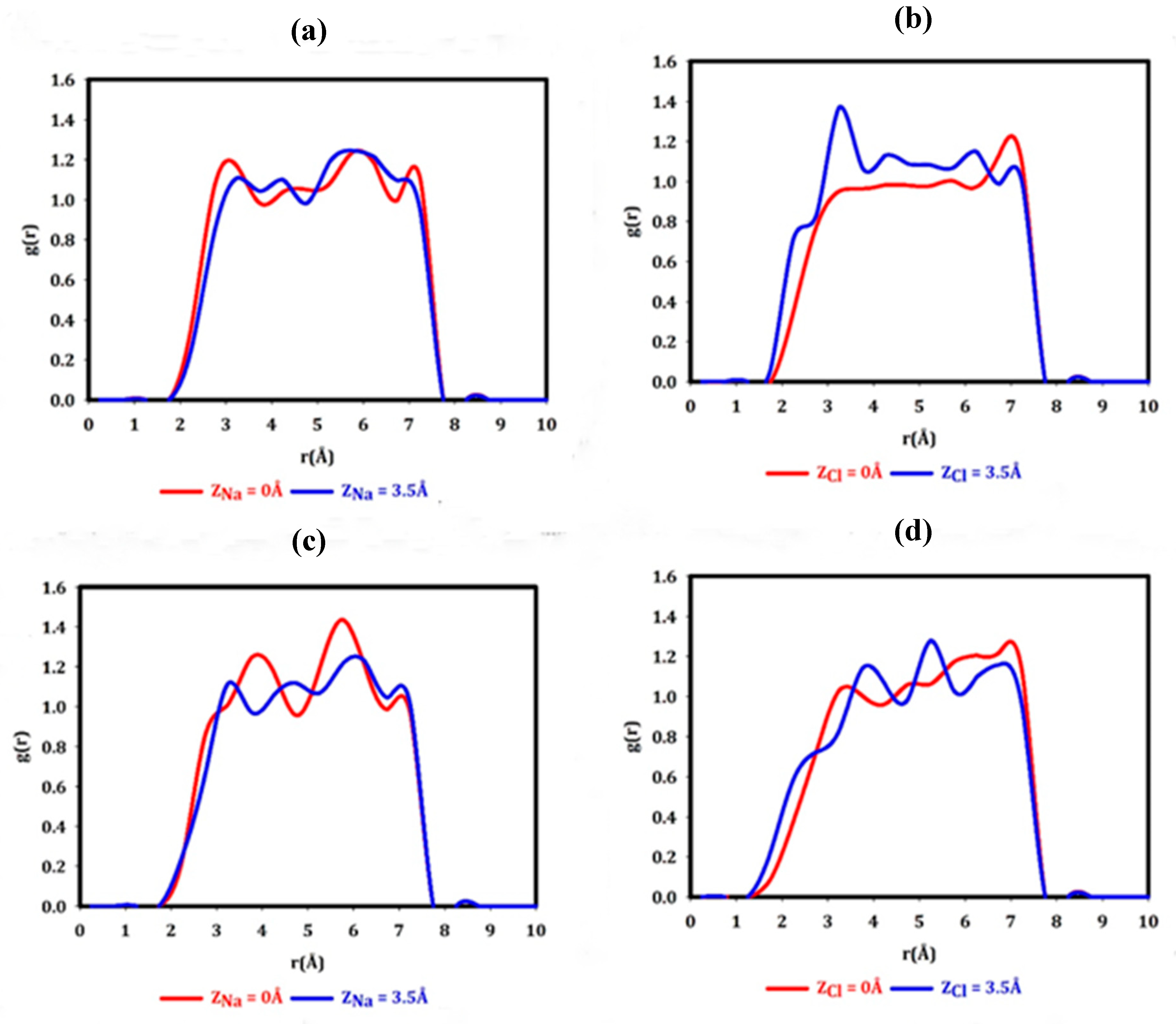
Figure 8. The planar trajectories of water molecules inside graphene (a & b) and h-BN (c & d) nanopores for different ion positions (Z=0 Å & (upper panel of each figure) Z=3.5 Å(lower panel of each figure)) The gray, blue, pink, red, white, purple and green spheres present carbon, nitrogen, boron, oxygen, hydrogen, sodium, and chloride, respectively.

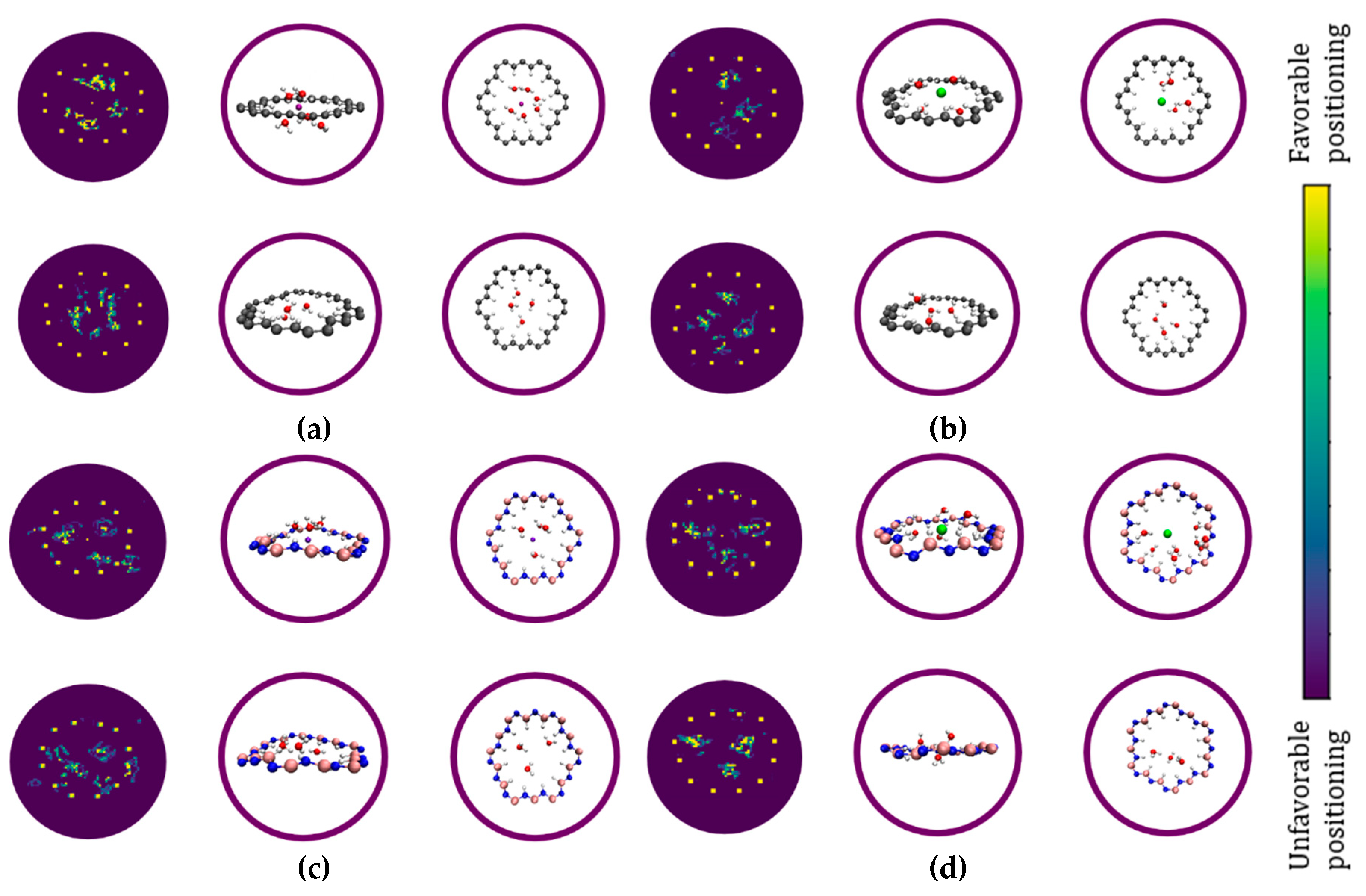
Na cation positioning in the center of the h-BN nanopore induces a slight change in the radial distribution of oxygens (Figure 7c) such that they get closer to the nanopore edge. The average number of water molecules inside the nanopore increases by 0.75. At first glance, it might seem that the attraction between BH terminations of the nanopore and partially dehydrated Na⁺ might induce a negative barrier but these terminals interact with water in such a way that they distort from the nanopore plane, and they don’t affect Na⁺ significantly. Figure 7d indicates that the oxygen atoms move farther from the edge as the Cl^- anion enters the h-BN nanopore center. This change depletes the nanopore from the water molecules and leads to the reduction of average number of water molecules by 1.6. The planar arrangements (Figure 8d) indicate that the remaining water molecules in the pore screen the positively charged NH terminations. The repulsive electrostatic Coulomb interaction between the negatively charged BH terminations and the anion leads to the creation of a potential barrier. Different monovalent cations have different interaction with water molecules which appears in their hydration numbers and radii. Here we show that a combination of ion-water interaction within the nanopore, water-nanopore interaction, and ion-nanopore interaction has a determinant role in Na⁺ and Cl^- transport.

4. Conclusion

Salt ion permeation through graphene and h-BN nanopores of 8.5 Å diameter was investigated employing ab initio Car-Parrinello molecular dynamics. The extracted permeation barriers reveal that the h-BN nanopore exhibits a potential barrier of +0.13 eV and +0.24 eV for Na⁺ and Cl^- permeation, respectively, while the graphene nanopore imposes an essentially zero barrier of -0.03 eV for Na⁺ permeation and a strongly negative barrier of -0.68 eV for Cl^- permeation. We demonstrate that from the change in the solvation shell, we get the following trend: Na/h-BN > Na/G > Cl/G > Cl/h-BN. Due to the complex combination of interactions, this trend changes to Cl/h-BN > Na/h-BN > Na/G > Cl/G for the permeation barrier. Ion separation works well for the h-BN membrane while once the Cl^- anion enters its counterpart, the graphene pore, the anion stays there and blocks it, this blockade makes graphene the less attractive system compared to h-BN. Different interactions of water molecules with graphene and h-BN membranes as well as nanopores impose distinct barriers for Na⁺ and Cl anion.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Author Contributions

Conceptualization, E.N.; Methodology, I.F., E.N., A.K., and Y.D.; Software, I.F.; Validation, I.F., E.N., A.K., and Y.D.; Formal Analysis, I.F., E.N., A.K. and Y.D.; Investigation, I.F., E.N., A.K. and Y.D.; Resources, I.F.; Data Curation, I.F., E.N., A.K. and Y.D.; Writing – Original Draft Preparation, Y.D.; Writing – Review & Editing, I.F., E.N; Visualization, Y.D.; Supervision, I.F., E.N.; Funding Acquisition, DFG and HLRN.”.

Funding

The authors thank the German Research Foundation (DFG) for partial financial support. Part of the calculations were performed at the Höchstleistungsrechner Nord (HLRN) supercomputing system (project nic00061).

Conflicts of Interest

The authors declare no conflict of interest.

References

https://www.unwater.org/water-facts/water-scarcity.
Elimelech, M. and Phillip, W.A., 2011. The future of seawater desalination: energy, technology, and the environment. Science, 333(6043), pp.712-717. [CrossRef]
Shannon, M.A., Bohn, P.W., Elimelech, M., Georgiadis, J.G., Mariñas, B.J. and Mayes, A.M., 2008. Science and technology for water purification in the coming decades. Nature, 452(7185), pp.301-310. [CrossRef]
Fritzmann, C., Löwenberg, J., Wintgens, T. and Melin, T., 2007. State-of-the-art of reverse osmosis desalination. Desalination, 216(1-3), pp.1-76. [CrossRef]
Lee, K.P., Arnot, T.C. and Mattia, D., 2011. A review of reverse osmosis membrane materials for desalination—Development to date and future potential. Journal of Membrane Science, 370(1-2), pp.1-22. [CrossRef]
LOEB, S. and Sourirajan, S., 1962. Sea Water Demineralization by Means of an Osmotic Membrane. Advances in Chemistry, 38, pp.117-132. [CrossRef]
Larson, R.E., Cadotte, J.E. and Petersen, R.J., 1981. The FT-30 seawater reverse osmosis membrane--element test results. Desalination, 38, pp.473-483. [CrossRef]
Greenlee, L.F., Lawler, D.F., Freeman, B.D., Marrot, B. and Moulin, P., 2009. Reverse osmosis desalination: water sources, technology, and today’s challenges. Water research, 43(9), pp.2317-2348. [CrossRef]
Matin, A., Khan, Z., Zaidi, S.M.J. and Boyce, M.C., 2011. Biofouling in reverse osmosis membranes for seawater desalination: phenomena and prevention. Desalination, 281, pp.1-16. [CrossRef]
Raluy, G., Serra, L. and Uche, J., 2006. Life cycle assessment of MSF, MED and RO desalination technologies. Energy, 31(13), pp.2361-2372. [CrossRef]
Von Medeazza, G.M., 2005. “Direct” and socially-induced environmental impacts of desalination. Desalination, 185(1-3), pp.57-70. [CrossRef]
Yankovych, H.B., Abreu-Jaureguí, C., Farrando-Perez, J., Melnyk, I., Václavíková, M. and Silvestre-Albero, J., 2024. Advanced Removal of Dyes with Tuning Carbon/TiO2 Composite Properties. Nanomaterials, 14(3), p.309. [CrossRef]
Maio, A., Pibiri, I., Morreale, M., Mantia, F.P.L. and Scaffaro, R., 2021. An overview of functionalized graphene nanomaterials for advanced applications. Nanomaterials, 11(7), p.1717. [CrossRef]
Kiakojouri, A., Frank, I. and Nadimi, E., 2023. Exploring the dynamics of DNA nucleotides in graphene/h-BN nanopores: insights from ab initio molecular dynamics. Physical Chemistry Chemical Physics, 25(19), pp.13452-13464. [CrossRef]
Ma, X., Janowska, K., Boffa, V., Fabbri, D., Magnacca, G., Calza, P. and Yue, Y., 2019. Surfactant-assisted fabrication of alumina-doped amorphous silica nanofiltration membranes with enhanced water purification performances. Nanomaterials, 9(10), p.1368. [CrossRef]
Rashid, M.H.O. and Ralph, S.F., 2017. Carbon nanotube membranes: synthesis, properties, and future filtration applications. Nanomaterials, 7(5), p.99. [CrossRef]
Sharma, B.B. and Parashar, A., 2020. Mechanical strength of a nanoporous bicrystalline h-BN nanomembrane in a water submerged state. Physical Chemistry Chemical Physics, 22(36), pp.20453-20465. [CrossRef]
Sapkota, B., Liang, W., VahidMohammadi, A., Karnik, R., Noy, A. and Wanunu, M., 2020. High permeability sub-nanometre sieve composite MoS2 membranes. Nature Communications, 11(1), pp.1-9. [CrossRef]
Folaranmi, G., Bechelany, M., Sistat, P., Cretin, M. and Zaviska, F., 2021. Activated carbon blended with reduced graphene oxide nanoflakes for capacitive deionization. Nanomaterials, 11(5), p.1090. [CrossRef]
Zhang, X., Lian, G., Zhang, S., Cui, D. and Wang, Q., 2012. Boron nitride nanocarpets: controllable synthesis and their adsorption performance to organic pollutants. CrystEngComm, 14(14), pp.4670-4676. [CrossRef]
Peng, H., Wang, R., Mei, L., Zhang, Q., Ying, T., Qian, Z., Farimani, A.B., Voiry, D. and Zeng, Z., 2023. Transition metal dichalcogenide-based functional membrane: Synthesis, modification, and water purification applications. Matter, 6(1), pp.59-96. [CrossRef]
Wang, R., Chen, D., Wang, Q., Ying, Y., Gao, W. and Xie, L., 2020. Recent advances in applications of carbon nanotubes for desalination: A review. Nanomaterials, 10(6), p.1203. [CrossRef]
Oliveira, A.R., Correia, A.A. and Rasteiro, M.G., 2021. Heavy metals removal from aqueous solutions by multiwall carbon nanotubes: Effect of MWCNTs dispersion. Nanomaterials, 11(8), p.2082. [CrossRef]
Chae, J., Lim, T., Cheng, H., Hu, J., Kim, S. and Jung, W., 2021. Graphene oxide and carbon nanotubes-based polyvinylidene fluoride membrane for highly increased water treatment. Nanomaterials, 11(10), p.2498. [CrossRef]
Koenig, S.P., Wang, L., Pellegrino, J. and Bunch, J.S., 2012. Selective molecular sieving through porous graphene. Nature Nanotechnology, 7(11), pp.728-732. [CrossRef]
Lehtinen, O., Dumur, E., Kotakoski, J., Krasheninnikov, A.V., Nordlund, K. and Keinonen, J., 2011. Production of defects in hexagonal boron nitride monolayer under ion irradiation. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 269(11), pp.1327-1331. [CrossRef]
Lehtinen, O., Kotakoski, J., Krasheninnikov, A.V. and Keinonen, J., 2011. Cutting and controlled modification of graphene with ion beams. Nanotechnology, 22(17), p.175306. [CrossRef]
Lehtinen, O., Tsai, I.L., Jalil, R., Nair, R.R., Keinonen, J., Kaiser, U. and Grigorieva, I.V., 2014. Non-invasive transmission electron microscopy of vacancy defects in graphene produced by ion irradiation. Nanoscale, 6(12), pp.6569-6576. [CrossRef]
Lucchese, M.M., Stavale, F., Ferreira, E.M., Vilani, C., Moutinho, M.V.D.O., Capaz, R.B., Achete, C.A. and Jorio, A., 2010. Quantifying ion-induced defects and Raman relaxation length in graphene. Carbon, 48(5), pp.1592-1597. [CrossRef]
Russo, C.J. and Golovchenko, J.A., 2012. Atom-by-atom nucleation and growth of graphene nanopores. Proceedings of the National Academy of Sciences, 109(16), pp.5953-5957. [CrossRef]
Rozada, R., Solís-Fernández, P., Paredes, J.I., Martínez-Alonso, A., Ago, H. and Tascón, J.M.D., 2014. Controlled generation of atomic vacancies in chemical vapor deposited graphene by microwave oxygen plasma. Carbon, 79, pp.664-669. [CrossRef]
Xie, G., Yang, R., Chen, P., Zhang, J., Tian, X., Wu, S., Zhao, J., Cheng, M., Yang, W., Wang, D. and He, C., 2014. A general route towards defect and pore engineering in graphene. Small, 10(11), pp.2280-2284. [CrossRef]
Yamada, Y., Murota, K., Fujita, R., Kim, J., Watanabe, A., Nakamura, M., Sato, S., Hata, K., Ercius, P., Ciston, J. and Song, C.Y., 2014. Subnanometer vacancy defects introduced on graphene by oxygen gas. Journal of the American Chemical Society, 136(6), pp.2232-2235. [CrossRef]
Garaj, S., Hubbard, W., Reina, A., Kong, J., Branton, D. and Golovchenko, J.A., 2010. Graphene as a subnanometre trans-electrode membrane. Nature, 467(7312), pp.190-193. [CrossRef]
Jain, T., Rasera, B.C., Guerrero, R.J.S., Boutilier, M.S., O’hern, S.C., Idrobo, J.C. and Karnik, R., 2015. Heterogeneous sub-continuum ionic transport in statistically isolated graphene nanopores. Nature Nanotechnology, 10(12), pp.1053-1057. [CrossRef]
O’Hern, S.C., Boutilier, M.S., Idrobo, J.C., Song, Y., Kong, J., Laoui, T., Atieh, M. and Karnik, R., 2014. Selective ionic transport through tunable subnanometer pores in single-layer graphene membranes. Nano Letters, 14(3), pp.1234-1241. [CrossRef]
Rollings, R.C., Kuan, A.T. and Golovchenko, J.A., 2016. Ion selectivity of graphene nanopores. Nature Communications, 7(1), pp.1-7. [CrossRef]
Feng, J., Liu, K., Graf, M., Dumcenco, D., Kis, A., Di Ventra, M. and Radenovic, A., 2016. Observation of ionic Coulomb blockade in nanopores. Nature Materials, 15(8), pp.850-855. [CrossRef]
Tay, R.Y., Griep, M.H., Mallick, G., Tsang, S.H., Singh, R.S., Tumlin, T., Teo, E.H.T. and Karna, S.P., 2014. Growth of large single-crystalline two-dimensional boron nitride hexagons on electropolished copper. Nano Letters, 14(2), pp.839-846. [CrossRef]
Li, J., Lin, J., Xu, X., Zhang, X., Xue, Y., Mi, J., Mo, Z., Fan, Y., Hu, L., Yang, X. and Zhang, J., 2013. Porous boron nitride with a high surface area: hydrogen storage and water treatment. Nanotechnology, 24(15), p.155603. [CrossRef]
de Souza, F.A., Amorim, R.G., Scopel, W.L. and Scheicher, R.H., 2017. Electrical detection of nucleotides via nanopores in a hybrid graphene/h-BN sheet. Nanoscale, 9(6), pp.2207-2212. [CrossRef]
Ziolkowski, R.W., Balmain, K.G., Pendry, J.B., Wiltshire, M.C.K. and Itoh, T., 2014. Applications M., Shalaev VM, Schurig D., Smith DR, Engheta N., et al. Heteroepitaxial growth of two-dimensional hexagonal boron nitride templated by graphene edges. Science, 343, pp.163-167. [CrossRef]
Chen, Z.G., Zou, J., Liu, G., Li, F., Wang, Y., Wang, L., Yuan, X.L., Sekiguchi, T., Cheng, H.M. and Lu, G.Q., 2008. Novel boron nitride hollow nanoribbons. Acs Nano, 2(10), pp.2183-2191. [CrossRef]
Jin, C., Lin, F., Suenaga, K. and Iijima, S., 2009. Fabrication of a freestanding boron nitride single layer and its defect assignments. Physical Review Letters, 102(19), p.195505. [CrossRef]
Lei, W., Portehault, D., Liu, D., Qin, S. and Chen, Y., 2013. Porous boron nitride nanosheets for effective water cleaning. Nature Communications, 4(1), pp.1-7. [CrossRef]
Prasad, V., Kannam, S.K., Hartkamp, R. and Sathian, S.P., 2018. Water desalination using graphene nanopores: influence of the water models used in simulations. Physical Chemistry Chemical Physics, 20(23), pp.16005-16011. [CrossRef]
Verma, A., Zhang, W. and Van Duin, A.C., 2021. ReaxFF reactive molecular dynamics simulations to study the interfacial dynamics between defective h-BN nanosheets and water nanodroplets. Physical Chemistry Chemical Physics, 23(18), pp.10822-10834. [CrossRef]
Nguyen, C.T. and Beskok, A., 2019. Charged nanoporous graphene membranes for water desalination. Physical Chemistry Chemical Physics, 21(18), pp.9483-9494. [CrossRef]
Sahu, P. and Ali, S.M., 2019. Breakdown of continuum model for water transport and desalination through ultrathin graphene nanopores: insights from molecular dynamics simulations. Physical Chemistry Chemical Physics, 21(38), pp.21389-21406. [CrossRef]
Fu, Y., Su, S., Zhang, N., Wang, Y., Guo, X. and Xue, J., 2020. Dehydration-determined ion selectivity of graphene subnanopores. ACS Applied Materials & Interfaces, 12(21), pp.24281-24288. [CrossRef]
Konatham, D., Yu, J., Ho, T.A. and Striolo, A., 2013. Simulation insights for graphene-based water desalination membranes. Langmuir, 29(38), pp.11884-11897. [CrossRef]
Liu, L., Liu, Y., Qi, Y., Song, M., Jiang, L., Fu, G. and Li, J., 2020. Hexagonal boron nitride with nanoslits as a membrane for water desalination: a molecular dynamics investigation. Separation and Purification Technology, 251, p.117409. [CrossRef]
Rajasekaran, M. and Ayappa, K.G., 2022. Influence of the extent of hydrophobicity on water organization and dynamics on 2D graphene oxide surfaces. Physical Chemistry Chemical Physics, 24(24), pp.14909-14923. [CrossRef]
Abal, J.P. and Barbosa, M.C., 2021. Water mobility in MoS₂ nanopores: effects of the dipole–dipole interaction on the physics of fluid transport. Physical Chemistry Chemical Physics, 23(21), pp.12075-12081. [CrossRef]
Berne, B.J., Ciccotti, G. and Coker, D.F. eds., 1998. Classical and quantum dynamics in condensed phase simulations: Proceedings of the International School of Physics. World Scientific.
Frenkel, D., Smit, B. and Ratner, M.A., 1996. Understanding molecular simulation: from algorithms to applications (Vol. 2). San Diego: Academic press. [CrossRef]
Guerrero-Avilés, R. and Orellana, W., 2017. Energetics and diffusion of liquid water and hydrated ions through nanopores in graphene: ab initio molecular dynamics simulation. Physical Chemistry Chemical Physics, 19(31), pp.20551-20558. [CrossRef]
Tocci, G., Joly, L. and Michaelides, A., 2014. Friction of water on graphene and hexagonal boron nitride from ab initio methods: very different slippage despite very similar interface structures. Nano Letters, 14(12), pp.6872-6877. [CrossRef]
Grosjean, B., Bocquet, M.L. and Vuilleumier, R., 2019. Versatile electrification of two-dimensional nanomaterials in water. Nature Communications, 10(1), pp.1-8. [CrossRef]
Hohenberg, P. and Kohn, W., 1964. Inhomogeneus Electron Gas. Physical Review, 136, pp.864-871. [CrossRef]
Kohn, W. and Sham, L.J., 1965. Self-consistent equations including exchange and correlation effects. Physical Review, 140(4A), p.A1133. [CrossRef]
Soler, J.M., Artacho, E., Gale, J.D., García, A., Junquera, J., Ordejón, P. and Sánchez-Portal, D., 2002. The SIESTA method for ab initio order-N materials simulation. Journal of Physics: Condensed Matter, 14(11), p.2745. [CrossRef]
Perdew, J.P., Burke, K. and Ernzerhof, M., 1996. Generalized gradient approximation made simple. Physical Review Letters, 77(18), p.3865. [CrossRef]
Lee, K., Murray, É.D., Kong, L., Lundqvist, B.I. and Langreth, D.C., 2010. Higher-accuracy van der Waals density functional. Physical Review B, 82(8), p.081101. [CrossRef]
Troullier, N. and Martins, J.L., 1991. Efficient pseudopotentials for plane-wave calculations. Physical Review B, 43(3), p.1993. [CrossRef]
Car, R. and Parrinello, M., 1985. Unified approach for molecular dynamics and density-functional theory. Physical Review Letters, 55(22), p.2471. [CrossRef]
CPMD, Version 4.1, J. Hutter. https://www.cpmd.org/, Copyright IBM Corp. 1990–2015, Copyright MPI für Festkörperforschung, Stuttgart 1997– 2001.
Grimme, S., 2006. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. Journal of Computational Chemistry, 27(15), pp.1787-1799. [CrossRef]
Hoover, W.G., 1985. Canonical dynamics: Equilibrium phase-space distributions. Physical Review A, 31(3), p.1695. [CrossRef]
Nosé, S., 1984. A molecular dynamics method for simulations in the canonical ensemble. Molecular Physics, 52(2), pp.255-268. [CrossRef]
Tuckerman, M.E. and Parrinello, M., 1994. Integrating the Car–Parrinello equations. I. Basic integration techniques. The Journal of Chemical Physics, 101(2), pp.1302-1315. [CrossRef]
Skinner, L.B., Huang, C., Schlesinger, D., Pettersson, L.G., Nilsson, A. and Benmore, C.J., 2013. Benchmark oxygen-oxygen pair-distribution function of ambient water from x-ray diffraction measurements with a wide Q-range. The Journal of Chemical Physics, 138(7), p.074506. [CrossRef]
Soper, A.K. and Benmore, C.J., 2008. Quantum differences between heavy and light water. Physical Review Letters, 101(6), p.065502. [CrossRef]
Lee, C.Y., McCammon, J.A. and Rossky, P.J., 1984. The structure of liquid water at an extended hydrophobic surface. The Journal of Chemical Physics, 80(9), pp.4448-4455. [CrossRef]
Cicero, G., Grossman, J.C., Schwegler, E., Gygi, F. and Galli, G., 2008. Water confined in nanotubes and between graphene sheets: A first principle study. Journal of the American Chemical Society, 130(6), pp.1871-1878. [CrossRef]
Tocci, G. and Michaelides, A., 2014. Solvent-induced proton hopping at a water–oxide interface. The Journal of Physical Chemistry Letters, 5(3), pp.474-480. [CrossRef]
Zuo, K., Zhang, X., Huang, X., Oliveira, E.F., Guo, H., Zhai, T., Wang, W., Alvarez, P.J., Elimelech, M., Ajayan, P.M. and Lou, J., 2022. Ultrahigh resistance of hexagonal boron nitride to mineral scale formation. Nature Communications, 13(1), p.4523. [CrossRef]
Cohen-Tanugi, D. and Grossman, J.C., 2015. Nanoporous graphene as a reverse osmosis membrane: recent insights from theory and simulation. Desalination, 366, pp.59-70. [CrossRef]
Marcus, Y., 1991. Thermodynamics of solvation of ions. Part 5.—Gibbs free energy of hydration at 298.15 K. Journal of the Chemical Society, Faraday Transactions, 87(18), pp.2995-2999. [CrossRef]

Figure 1. Atomic structures of a) graphene and b) h-BN membranes with nanopores and the corresponding electron densities for c) graphene and d) h-BN membranes. The gray, blue, pink, and white spheres in the upper panel depict carbon, nitrogen, boron, and hydrogen atoms, respectively.

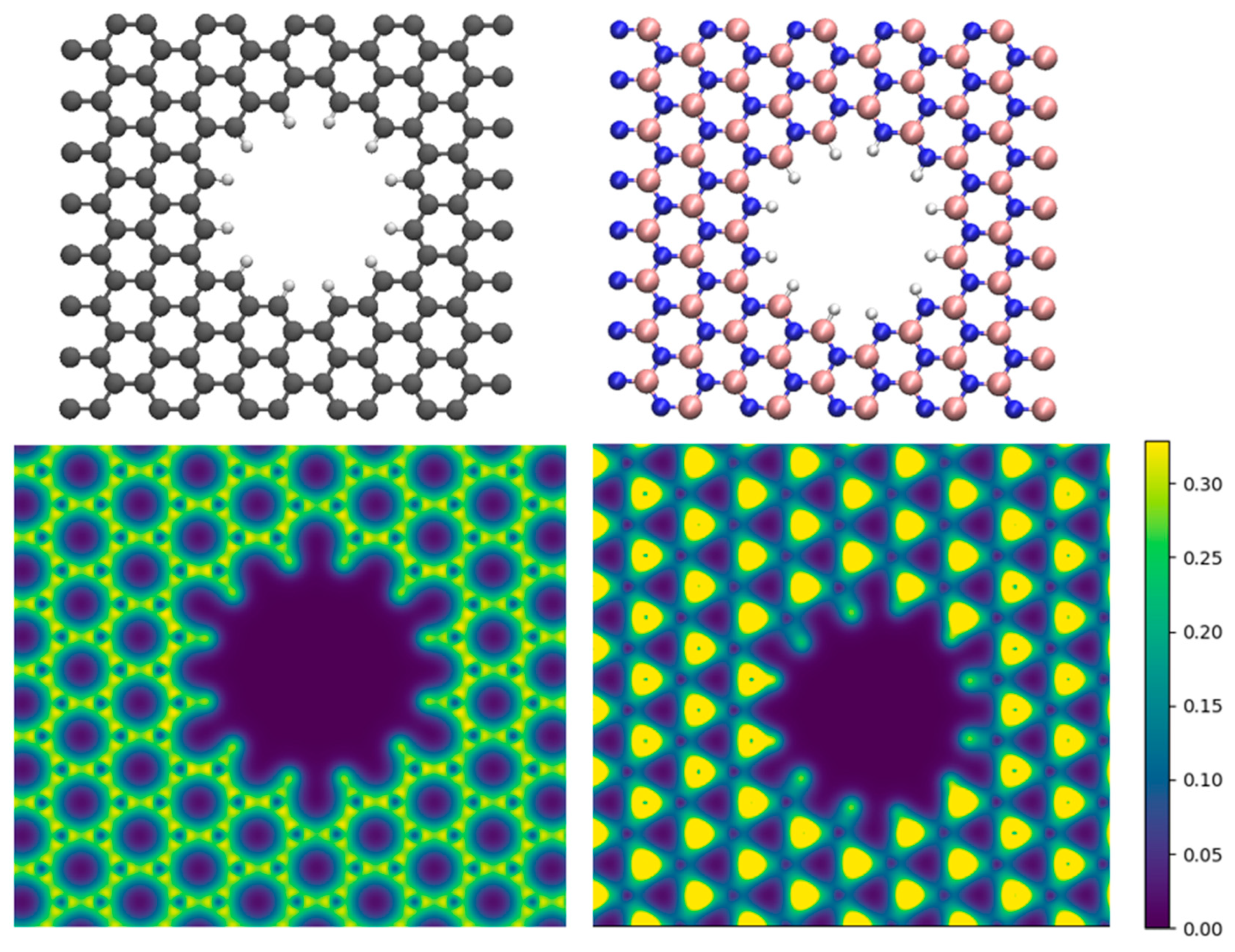
Figure 2. Schematic of simulation boxes filled with water molecules a) graphene and b) h-BN membranes, c) oxygen-oxygen radial distribution function and d) oxygen-hydrogen radial distribution function of equilibrated liquid water. e) planar average density profile of water molecules between graphene (the blue dashed curve) and h-BN membranes (the red solid curve). The gray, blue, pink, red, and white spheres depict carbon, nitrogen, boron, oxygen, and hydrogen atoms, respectively.

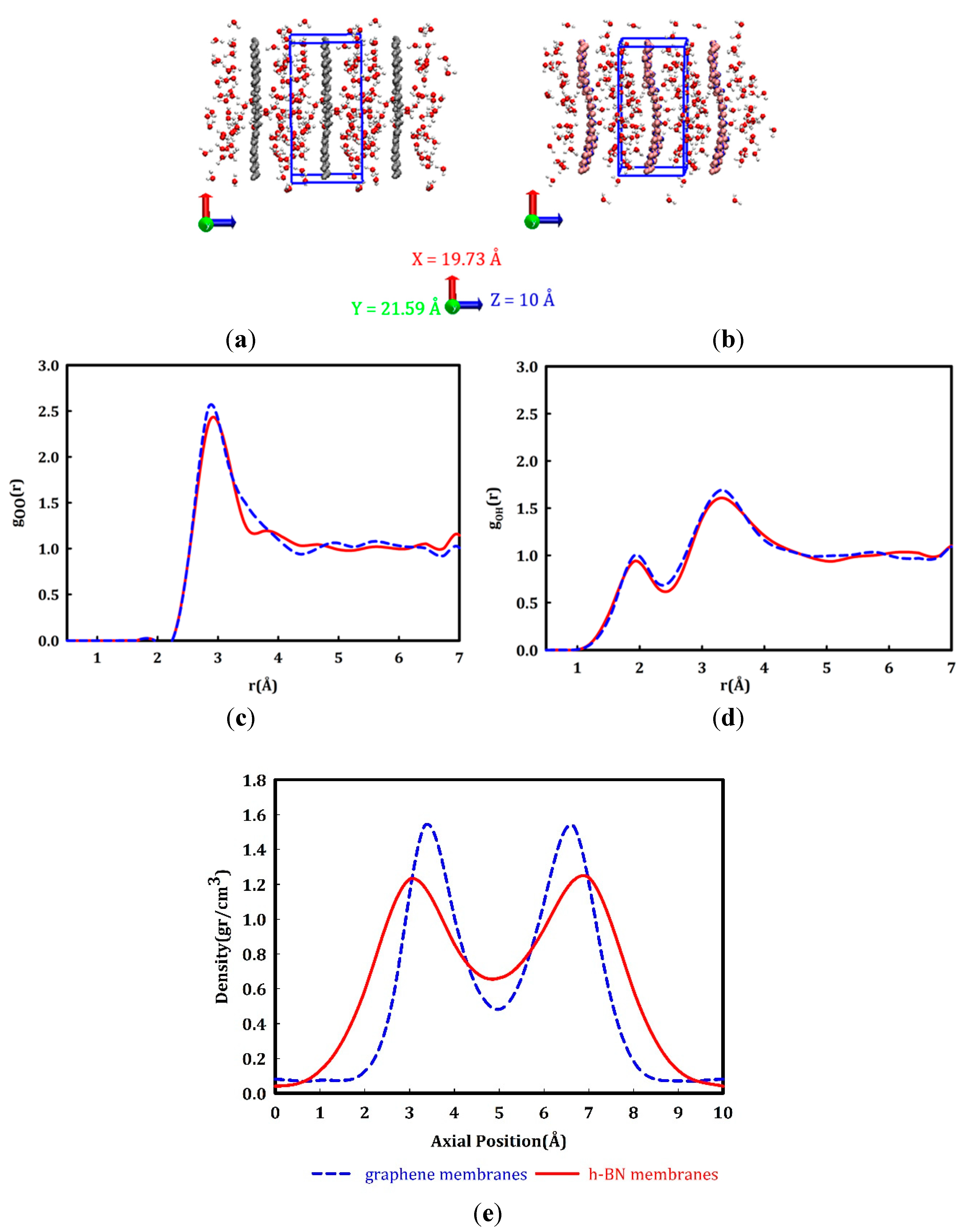
Figure 3. Radial distribution function (RDF) of oxygen atoms of water molecules (within the nanopores) and passivating hydrogen atoms at the edge on nanopores in a) graphene (blue dashed curve) and h-BN nanopore (red solid curve), b) separating the contribution of N-H (cyan solid curve) and B-H (pink dashed curve) edges in the h-BN nanopore.

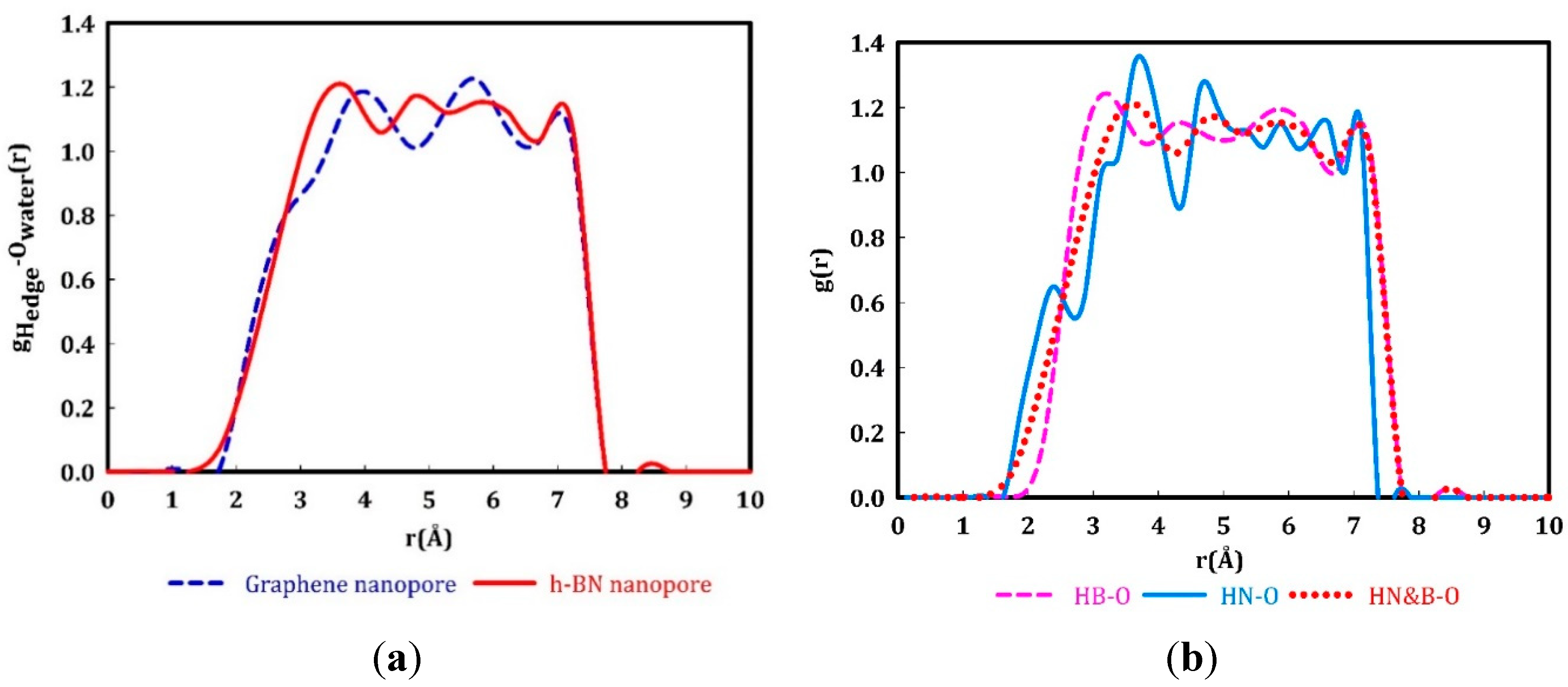
Figure 4. The planar trajectories of water molecules inside a) graphene and b) h-BN nanopores and snapshots of corresponding atomic structures. The yellow squares in A and B correspond to the hydrogen atoms at the edge and the red rectangles correspond to the N-H rims. Hypothetical cylinder for studying water molecules structuring near c) graphene and d) h-BN nanopores. The gray, blue, pink, red and white spheres present carbon, nitrogen, boron, oxygen, and hydrogen atoms, respectively. The blue dashed lines in the upper panel correspond to the hydrogen bonds in N-H...O and the red dashed lines correspond to the hydrogen bonds in O-H...O.

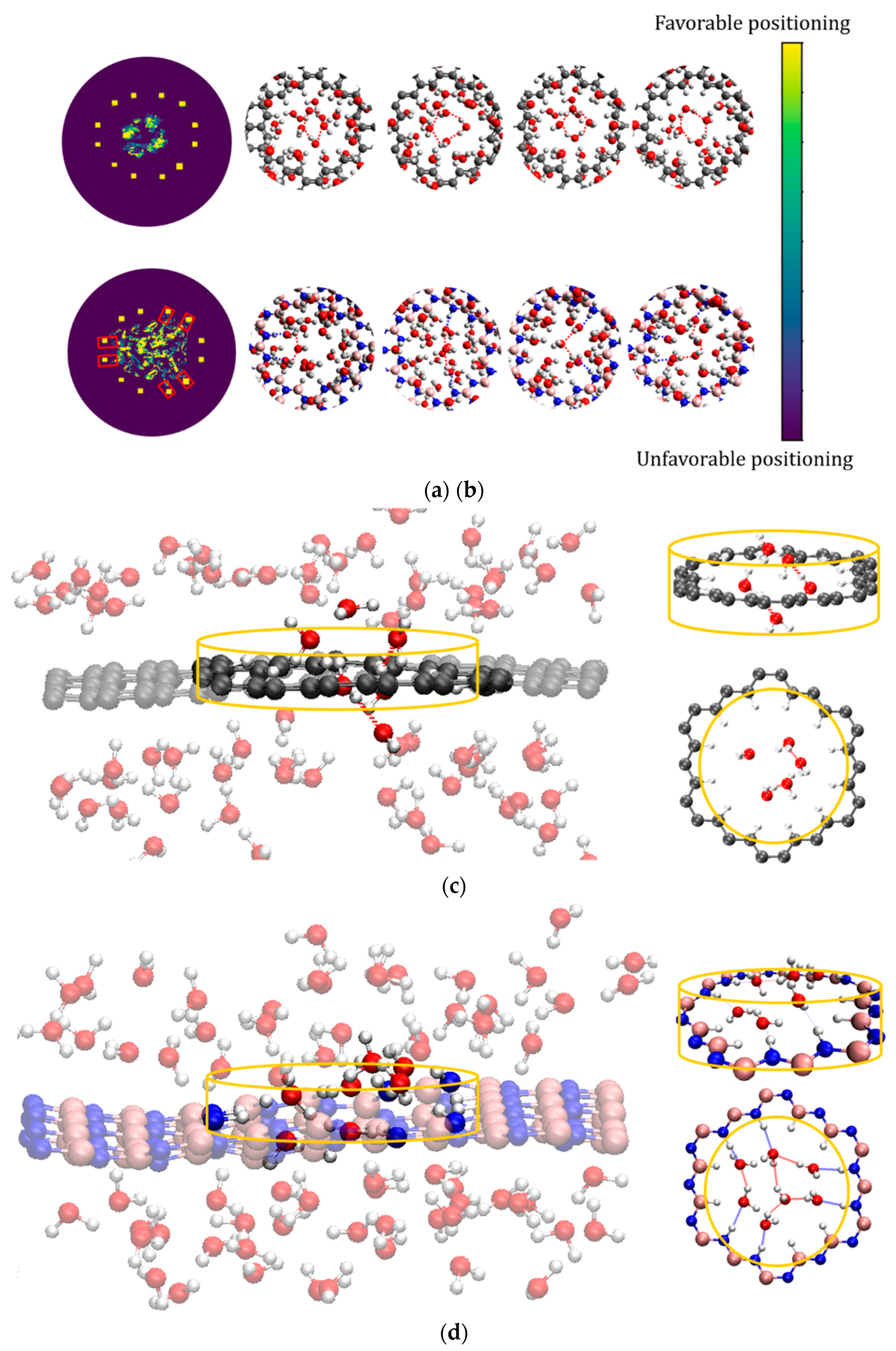
Figure 5. Permeation energy for Na⁺ and Cl^- through the hydrogenated graphene (solid red and blue curves) and the h-BN (dashed red and blue curves) nanopores.

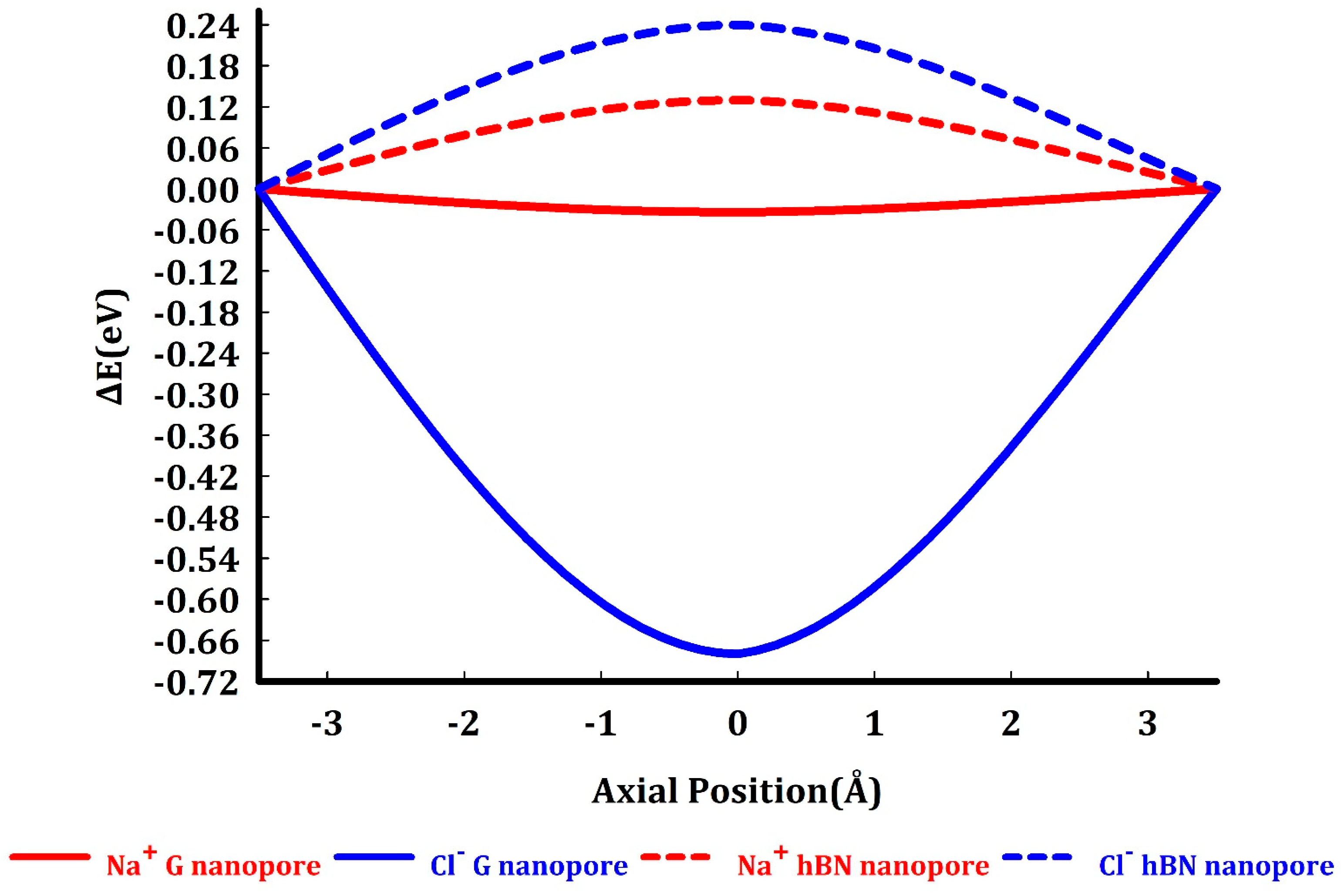
Figure 6. Na+ and Cl- hydration (Na-O and Cl-H radial distribution function) as the ions are positioned above the nanopores, Z=3.5 Å (solid blue curve) and as they are positioned in the nanopore centers, Z=0 Å (solid red curve) for a & b) graphene nanopore, c & d) h-BN nanopore.

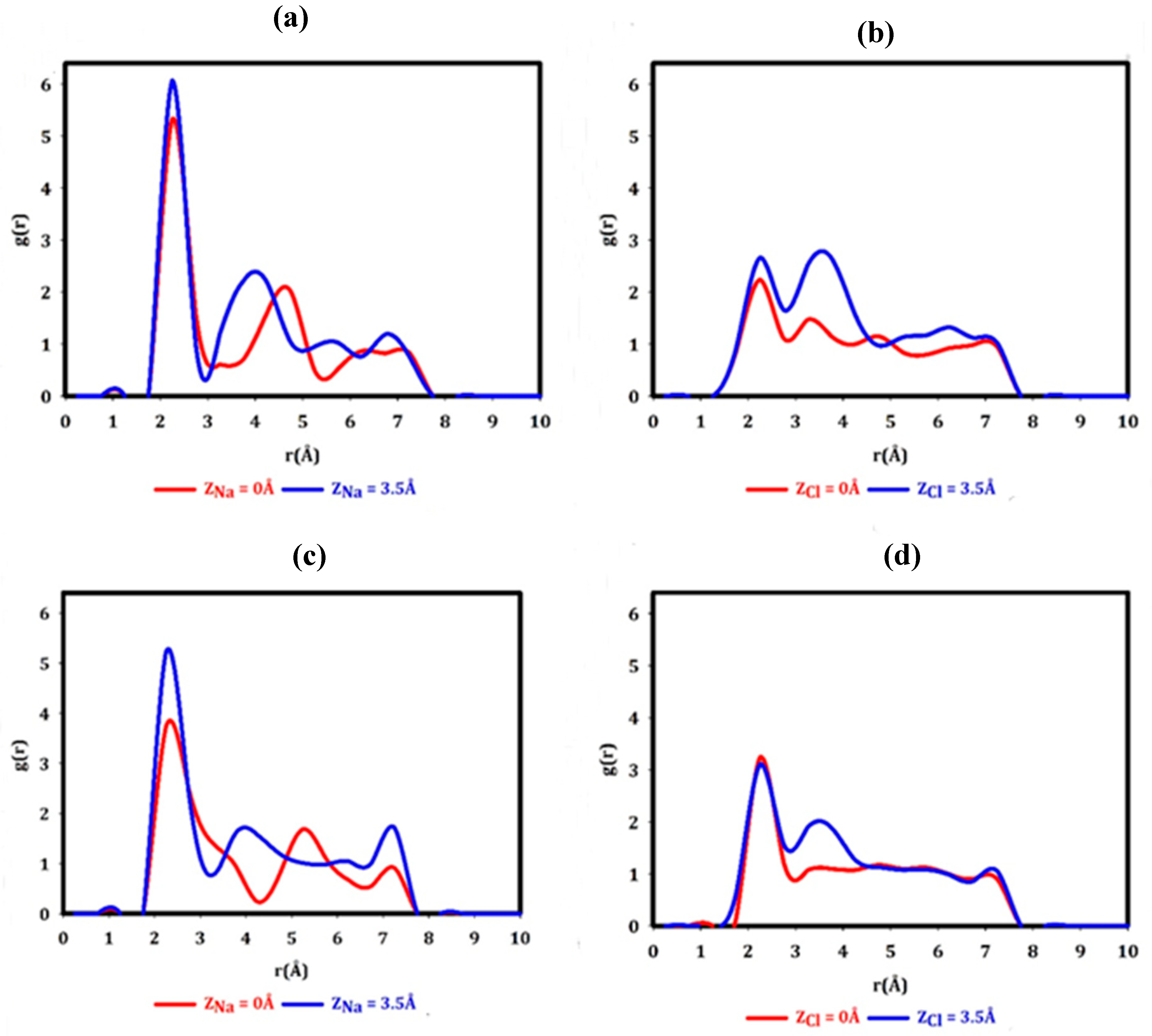
Table 1. Hydration numbers and radii for Na⁺ and Cl^- ions at the center of nanopore (z=0) and at 3.5 Å above the nanopore center.

		Graphene		h-BN
	Ion position (Å)	$n_{h y d r a t i o n}$	$r_{h y d r a t i o n} (Å)$	$n_{h y d r a t i o n}$	$r_{h y d r a t i o n} (Å)$
Na+	Z = 3.5	6.07	2.25	5.22	2.25
Na+	Z = 0	5.33	2.25	3.73	2.25
Cl^-	Z = 3.5	2.66	2.25	3.11	2.25
Cl^-	Z = 0	2.23	2.25	3.24	2.25

Table 2. The average number of H₂O molecules within the cylindrical volume centered on nanopores.

	Ion position (Å)	Graphene nanopore	h-BN nanopore
Na Cation	Z_Na = 0	3.24	2.95
Na Cation	Z_Na = 3.5	2.76	2.25
Cl anion	Z_Cl = 0	1.34	1.71
Cl anion	Z_Cl = 3.5	3.64	3.31

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer