Prerpints.org logo
Preprint
Article

A Mathematical Model of Stochastic Synaptic Noise Dynamics Based Spontaneous Action Potential in Non-neural Cell

Altmetrics

Downloads

113

Views

68

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

08 March 2024

Posted:

11 March 2024

You are already at the latest version

Alerts
Abstract
The main sources of intrinsic noise in excitable cells at the microcircuit and network levels are the stochastic characteristics of ion channel gating and activation of the synaptic conductance. Studies using in vivo, in vitro, and in silico methods to examine the effects of synaptic background activity were not adequately investigated in non-neuronal excitatory cells, where neurotransmitter-based innervation also occurs. We created a mathematical model to replicate the background synaptic noise dynamics in a non-neuronal cell. We utilized the stochastic Ornstein-Uhlenbeck process to represent excitatory synaptic conductance, which was incorporated into a whole-cell model to produce spontaneous and evoked cellular electrical activities. The single-cell model includes many biophysically detailed ion channels represented by a set of ordinary differential equations in Hodgkin-Huxley and Markov formalisms. This paradigm effectively induced irregular spontaneous depolarizations (SDs) and spontaneous action potential (sAP) resembling in vitro-like electrical activity in the cells. The input resistance decreased by multiple factors, and the spontaneous action potential firing rate elevated. The potential to reach the action potential threshold is altered. Background synaptic activity can alter the input/output characteristics of non-neuronal excitatory cells. Suppressing these baseline activities would facilitate the discovery of new pharmaceutical targets for different clinical diseases.
Keywords: 
Subject: Computer Science and Mathematics  -   Applied Mathematics

1. Introduction

Electrically excitable cells generate membrane depolarization and action potential (AP) to initiate various physiological functions and information exchange between cells [1]. Action potential or spike initiation in excitable cells adheres to the all-or-none principle: a characteristic action potential is generated and sent when the cell is adequately stimulated, and no spike is triggered if the potential is below the threshold [2]. 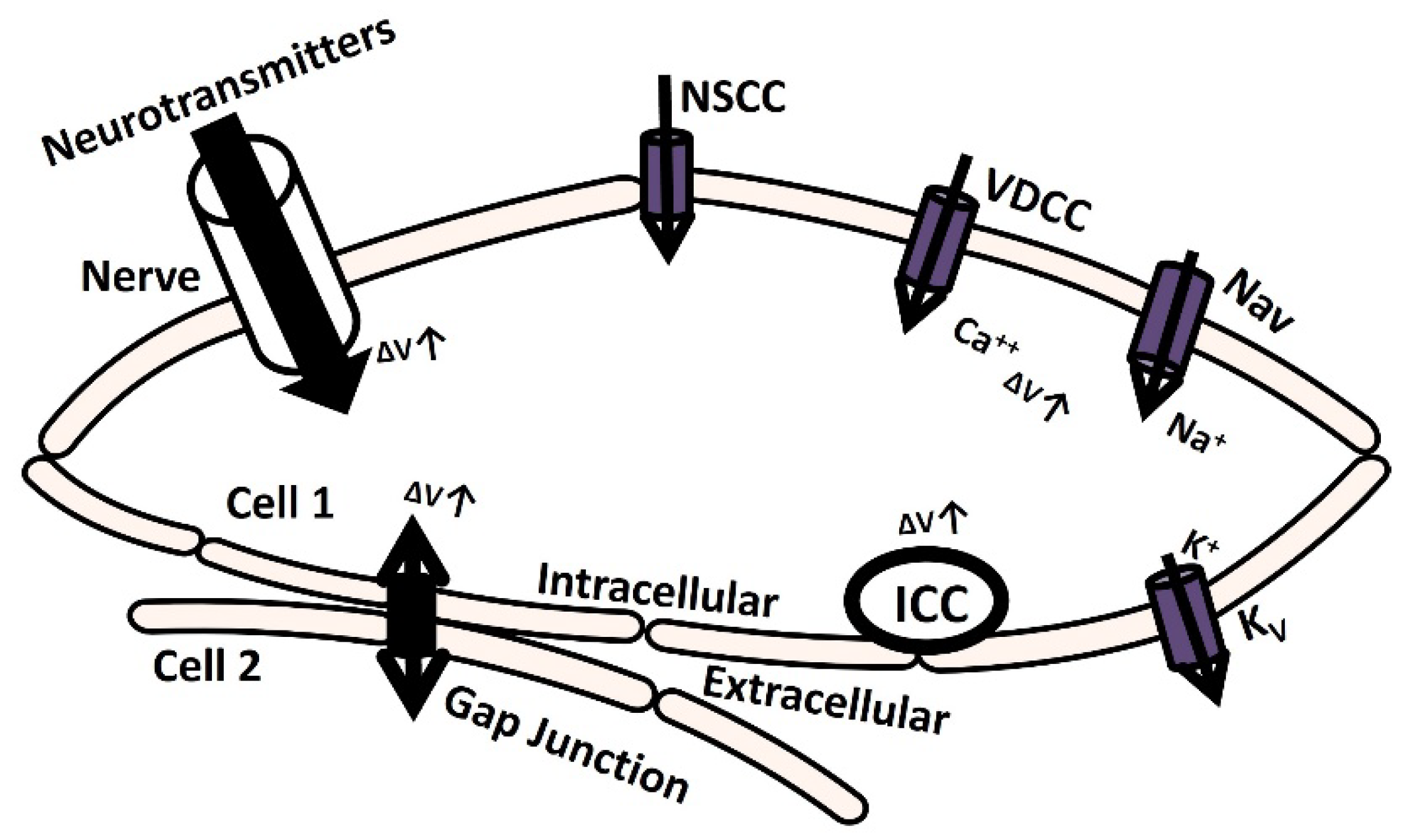Specific ion channels are activated at a particular threshold potential, which is the crucial factor responsible for generating spikes [3]. The membrane is depolarized till the threshold potential by several mechanisms, which are illustrated in Figure 1. The elevation of transient membrane depolarization is denoted by ΔV.
The membrane can depolarize when positive ions accumulate in the intracellular space as a result of the opening of particular ion channels: nonspecific cation channels (NSCC), voltage-dependent calcium channels (VDCC), and voltage-gated sodium channels (Nav) [4]. The voltage-gated potassium channel (Kv) repolarizes the membrane by moving positive ions out of the cell [5,6,7]. Additionally, the transmission of electrical potential from one cell to another (from cell 2 to cell 1) through a gap junction can cause membrane depolarization [8]. Furthermore, certain cells are myogenic, meaning they contain Interstitial Cells of Cajal (ICC) pacemaking cells that can depolarize the membrane through self-activation [9]. In another neurogenic process mechanism, the release of several neurotransmitters with excitatory synaptic conductance can depolarize the membrane either triggered or spontaneously [10].
The nervous system innervates most excitable cells, making this process crucial in various pathophysiological conditions. Neurotransmitter release from the synapse is orchestrated by the nervous system. Electrical activities involving stochastic neurotransmitter release occur as background events in intracellular recordings of excitable cells [11]. The main causes of inherent variability in excitable cells at the microcircuit and network levels are the stochastic characteristics of ion channel gating and synaptic conductance activation [12,13,14,15]. Studies were conducted using in vivo, in vitro, and in silico methods to examine the effects of synaptic background activity on neuronal cells. Nevertheless, this research was not adequately explored in non-neuronal excitatory cells such as cardiac and smooth muscle cells, where neurotransmitter-based innervation also occurs.
The primary physiological function of the urinary bladder, a component of the urinary system, is to facilitate the process of micturition, which involves storing and releasing urine. The parasympathetic innervation pathway is activated by the brain and spinal cord to facilitate the micturition process by causing the contraction of detrusor smooth muscle (DSM) cells. The DSM is highly innervated, linking around 16000 afferent and efferent axons from ganglion neurons across different species [16,17,18]. Research conducted over the past 50 years has established that DSM cells exhibit spontaneous phasic contraction activities through spontaneously evoked depolarizations (SDs) and action potentials (sAPs) [16,18,19,20]. Intracellular recordings from mouse DSM cells also show characteristics of SDs and sAPs [18,21,22,23]. The neurogenic hypothesis suggests that the increase in resting membrane potential (RMP) caused by the spontaneous release of neurotransmitters and the interaction of intrinsic ion channels in the DSM cell membrane are important factors in triggering sAPs and SDs [18,24,25,26,27]. Young et al. 2008 [18] found that ATP, a purinergic neurotransmitter, is released randomly into the DSM cells from the parasympathetic nerve terminals. Varicosities at parasympathetic nerve terminals produce ATP, which then activates P2X receptors on the DSM cell membrane, allowing the entry of cation X+ through the metabotropic process. At times, the increase in X+ leads to enough membrane depolarization to trigger the voltage-dependent calcium channels on the membrane.
Mathematical modeling methods are essential for quantitatively studying complicated biological processes [28]. Modeling intracellular electrophysiological processes creates a virtual physiological system to study the impact of different pharmaceutical targets on excitable cells [29]. Many mathematical models have been used to study the cellular excitability qualities of neuronal cells influenced by synaptic background noise [30]. These models are restricted to non-neuronal cells such as heart cells and smooth muscle cells. The current study seeks to replicate the spontaneous intracellular electrical behaviors in DSM cells by introducing continuous fluctuating conductance in the cell membrane. It is known that excitable cells with dense innervation can exhibit significant synaptic conductances as a result of neurotransmitter leaking [31]. The DSM tissue also fits into this category according to Gabella, G. 1999 [17]. Fellous et al. 2003 [32] presented a new model of background activity to imitate continuous synaptic conductance activities in neocortical neurons. We have modified their model and included specific adjustments to replicate SDs and sAPs in the DSM cell model [33,34,35,36,37].

2. Materials and METHODS

A point-conductance model was built to simulate the neurotransmitter-based background activity in DSM cells. The neurotransmitter current Int in equation 1, was considered as an independent excitatory conductance in the model:
I n t = g e x ( V − E e x )
where gex(t) is the excitatory conductance as a function of time, and Eex is the excitatory neurotransmitter reversal potential.
The excitatory conductance gex(t) in equation 2 is described by a one-variable stochastic process:
d g e x ( t ) d t = − 1 τ e x [ g e x t − g e x 0 ] + D e x λ 1 ( t ) ]
where gex0 is the average conductances, τex is the time constants, Dex is the diffusion coefficients to generate noise, λ1(t) is the Gaussian white noise. The numerical integration procedure to compute the differential equations is adapted from Fellous et al., 2003 [32].
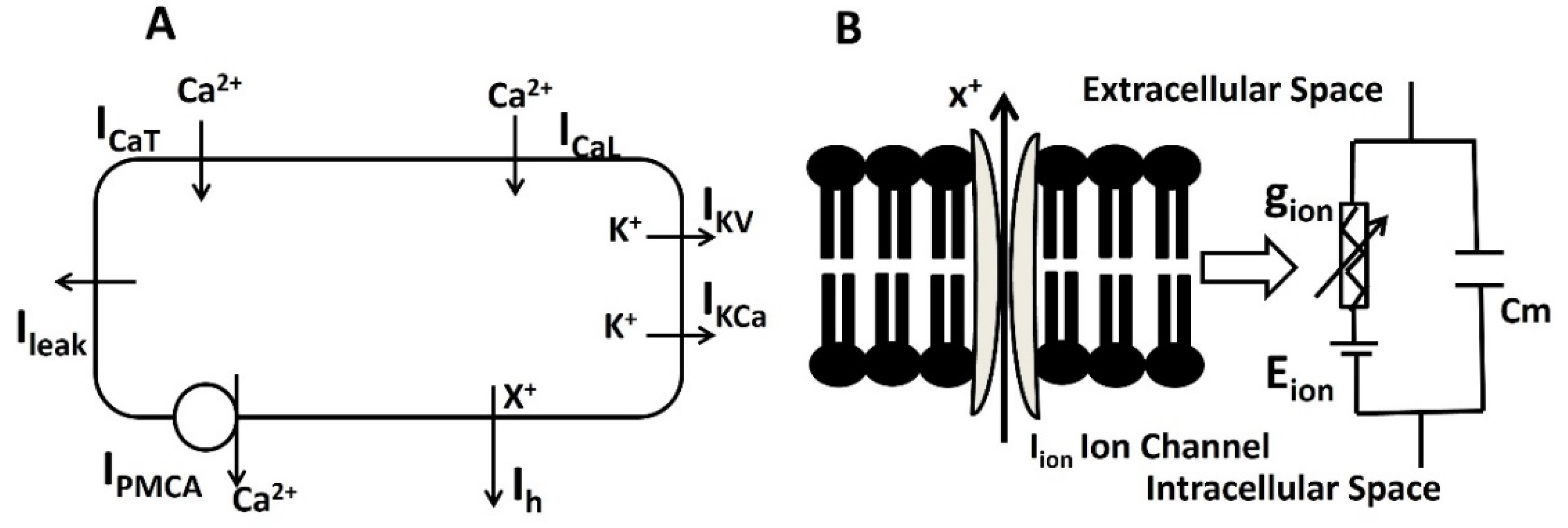
The point-conductance is incorporated into a single DSM cell model based on a single cylindrical compartment [33,34,35,36,37]. All active ion channels are modeled according to the Hodgkin-Huxley formulation [38]. The DSM cell membrane is interpreted as a conductance-based model consisting of multiple variable ion channel conductances and a membrane capacitance Cm. Figure 2. (a) presents the schematic overview of ion channel mechanisms in single DSM cells and (b) shows the schematic overview of the parallel conductance model for ionic current.
Schematic overview of parallel conductance model for ionic current
The length and diameter magnitudes of the single cylindrical compartment are 200 μm and 6μm respectively. In addition to morphological values, the membrane capacitance (Cm), membrane resistance (Rm), and axial resistance values are taken as 1μF/cm2, 138MΩ–cm2, and 181Ω-cm [39] to simulate the passive electrical properties. In the single DSM cell model, PMCA, ICaT, ICaL, IKCa, IKv, ILeak and Ih represent the Ca2+ pump, T-type Ca2+ channel, L-type Ca2+ channel, Ca2+ dependent K+ channel, voltage-dependent K+ channel, leakage channel, and hyperpolarization-activated cation current respectively.
The time-dependence characteristics of membrane potential (Vm) are represented in equation one.
    d V m ( t ) d t = − I i o n   t + I s t i m   t C m
Applying Kirchhoff’s current law after injecting stimulus current Istim, we get the following differential equation describing changes in transmembrane potential Vm:
d V m d t = − 1 C m ( I C a + I K + I h + I l e a k + I s t i m )
All membrane currents except large conductance (BK) Ca2+-dependent activation K+ channel were modeled using the Hodgkin-Huxley formalism:
I = g ¯ [ m ( V m , t , C a 2 + i ) ] x h [ ( V m , t , C a 2 + i ) ] y ( V m − E r e v )
where g ¯ is maximum ionic conductance, Erev is the ion’s reversal potential, the dimensionless gating variable ‘m’ describes the time/voltage/Ca2+-dependent activation, and ‘h’ is the time/voltage/Ca2+-dependent inactivation of the channel conductance. The ‘x’ and ‘y’ are power to the functions.
The variation of each gating variable (m or h) can be expressed by first-order differential equation (6,7)
d m ( V m , t ) d t = m ∞ ( V m ) − m ( V m , t ) τ m
d h ( V m , t ) d t = h ∞ ( V m ) − h ( V m , t ) τ h
where m∞ and h∞ are the steady-state values, τm and τh the time constants, all being functions of voltage and/or intracellular Ca2+ ionic concentrations.
Here the state parameter dependence on vm for ion channels is described by the Boltzman equation
  m ∞ ( V m ,     t ) = 1 1 + e x p ⁡ ( ( V m + V m 1   2 ) / S m )
          h ∞ ( V m ,     t ) = 1 1 + e x p ⁡ ( ( V m + V h 1   2 ) / S h )  
where V1/2 is the half activation potential and S is the slope factor.
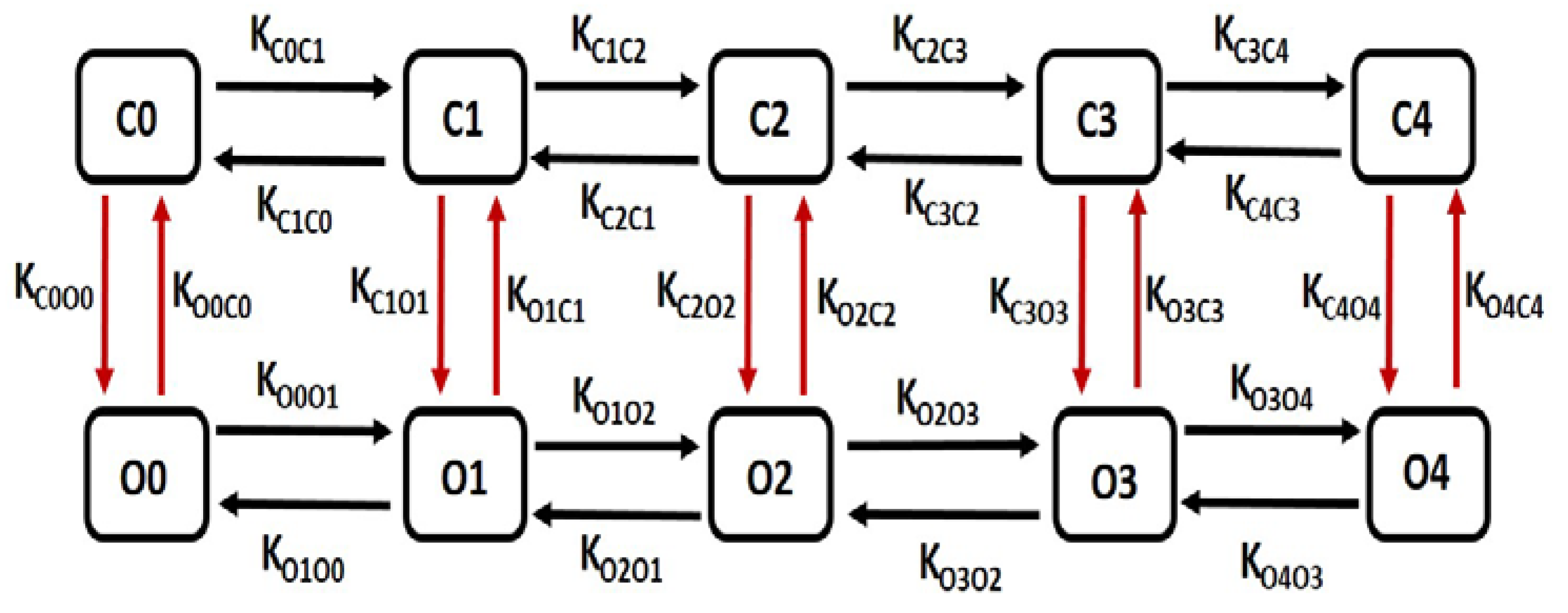
BK channels kinetics have been described by a multiple-state Markov model (MM), in which the channel’s Ca2+-dependence is modelled at a finer grain, thus affording greater accuracy. In this model there are five closed “horizontal” conformation states, namely C0, C1, C2, C3 and C4 and five open-oriented “horizontal” conformation states O0, O1, O2, O3 and O4, each corresponding to the appropriate closed state. The open conformation state O4 permits the flow of K+ ions through the BK channels under the instantaneous electrochemical driving force (EDF). The BK current, IBK is calculated by the following equation
I B K = g B K ¯   ∗ O ∗ ( V − E K )
where g B K ¯   is the maximum conductance and O is summation of O1, O2, O3 and O4.
Common rate equations:
Kon=345,Kcoff=25,Kooff=25,O=O1+O2+O3+O4
Rate equations for voltage dependent transitions:
KC0O0 = 0.02162 ∗ a, KC1O1 = 0.000869 ∗ a, KC2O2 = 0.0000281 ∗ a, KC3O3 = 0.000781 ∗ a, KC4O4 = 0.044324 ∗ a, KO0C0 = 318.1084 ∗ b, KO1C1 = 144. 1736 ∗ b, KO2C2 = 32.6594 ∗ b, KO3C3= 0.095312 ∗b,KO4C4=0.000106∗b∗cai
State equations for calcium dependent transitions:
KC0C1= 4 ∗ Kon ∗ cai, KC1C2= 3∗ Kon ∗ cai, KC2C3= 2 ∗ Kon ∗ cai, KC3C4= Kon ∗ cai
KC4C3= 4 ∗ Kcoff ∗ cai, KC3C2= 3 ∗ Kcoff ∗ cai, KC2C1= 2 ∗ Kcoff ∗ cai, KC1C0= Kcoff ∗ cai
KO0O1= 4 ∗ Kon ∗ cai, KO1O2= 3 ∗ Kon ∗ cai, KO2O3= 2 ∗ Kon ∗ cai, KO3O4= Kon ∗ cai
KO4O3= 4 ∗ Kooff ∗ cai, KO3O2= 3 ∗ Kooff ∗ cai, KO2O1= 2 ∗ Kooff ∗ cai, KO1O0 = Kooff ∗ cai
The Calcium dependent intermediate potassium current in (IIK ) in [33] has been modified with following equations.
I I K = g I K ¯   ∗ l 2 ∗ k ∗ ( V − E K )
l ∞ = 0.37 1 + exp ⁡ l i − v 16
l i = − 180 + ( 38 ∗ e x p c i ∗ 60   ) + ( 86 ∗   e x p − 27 ∗ c i )
τ l = 17 ∗   ( ( 30 1 + exp ⁡ V + 20.52 36 ) )
k ∞ = 0.36 1 + exp ⁡ 67 + v 9
τ k = 55 ∗ ( 1 − 1 ( 1 + exp ⁡ v + 13.9629 45.3782 ) ∗ ( 1 + exp − ( v + 9.49866 ) 3.3945 ⁡ ) )
Action potentials in our DSM cell model were triggered by providing either an external stimulus current (Ist) or a current derived from synaptic input (Isyn). An external stimulus current was applied either as a short rectangular pulse for a single action potential or with longer rectangular pulses for a series of action potentials. The simulations were performed with a fixed time step of 0.04 ms using the Euler Method on a PC equipped with an Intel (R) Core (TM) i7 CPU running at 3.80 GHz with a dual-core processor. The model utilizes the NEURON [40] simulation environment, known for its widespread usage in realistic modelling of excitable cells. The Euler method is a basic numerical approach used to solve ordinary differential equations (ODEs). The method is a first-order approach that involves discretizing the time domain and utilizing the derivative at the present point to approximate the function's value at the next point.

3. Results

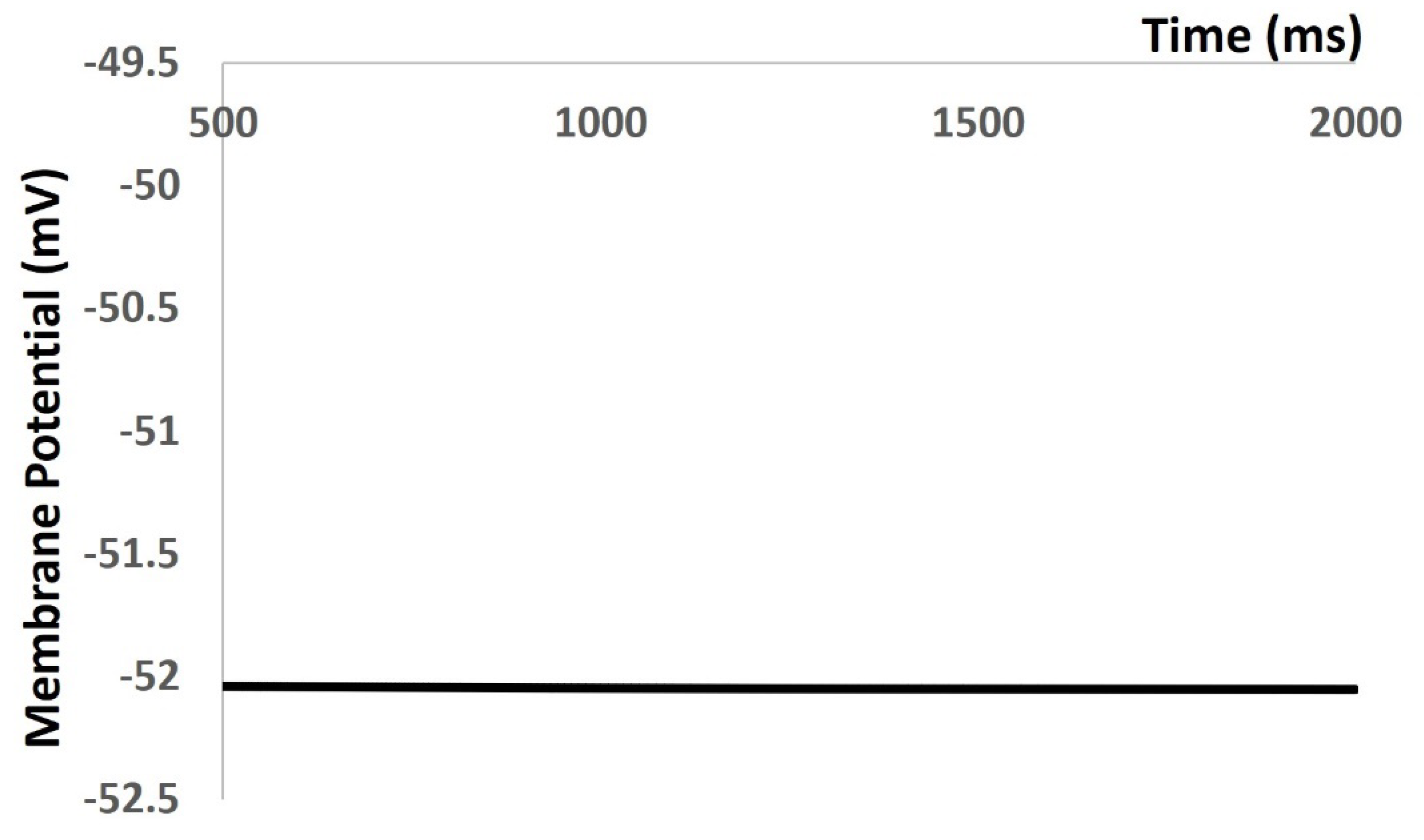
In our simulation part of the result section, , we reproduced all types of electrical activities in the DSM cell with and without noise conductance. We investigated the properties of mebrane excitibility as a result of spontaneous purinergic neurotransmitter release in the DSM cells [Young et al., 2008]. Before we reproduced any AP and mebrane depolarization, we tesated the robustness and fklexibilty of our mathematical model. Aftewr incoorprating all ion channel models, we tried to maintain the physiological value of RMP at ─ 52 mV. Our model is validated its robustness by maintaining the RMP at ─ 52 mV for 1000 ms (Figure 1). However, at 0 ms, the model needs few ms to settle down as the all ion channels are not stable. It creates some fluctuation for few ms. The Figure 3 time scale in X axis is start from 500 ms to cross these fluctuations.
Preprints 100945 g003
Figure 3. Schematic diagram of 10 state marcov model for BK channel.
Figure 3. Schematic diagram of 10 state marcov model for BK channel.
Preprints 100945 g003
Preprints 100945 g004
Figure 4. Model maintains the RMP at – 52 mV.
Figure 4. Model maintains the RMP at – 52 mV.
Preprints 100945 g004
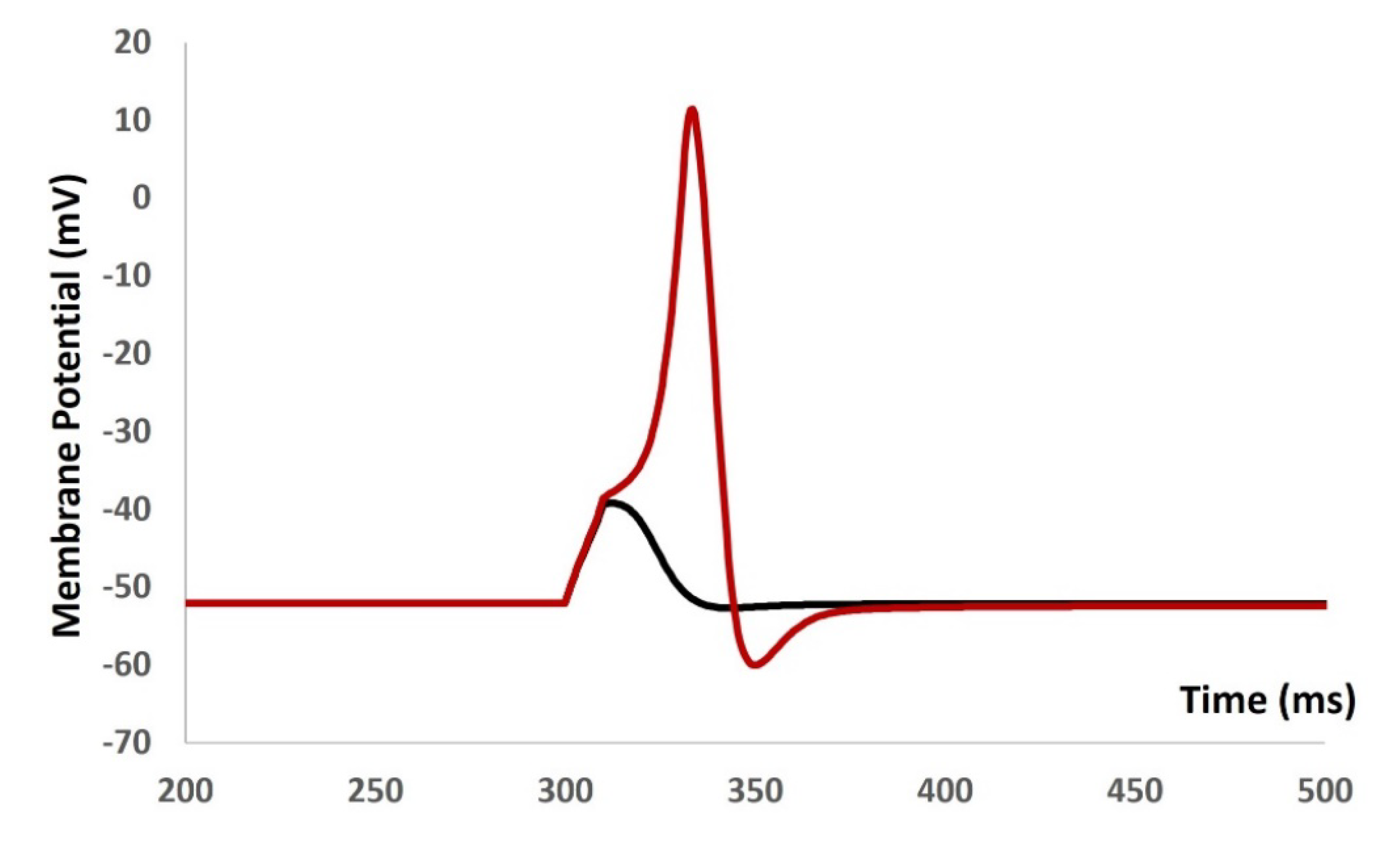
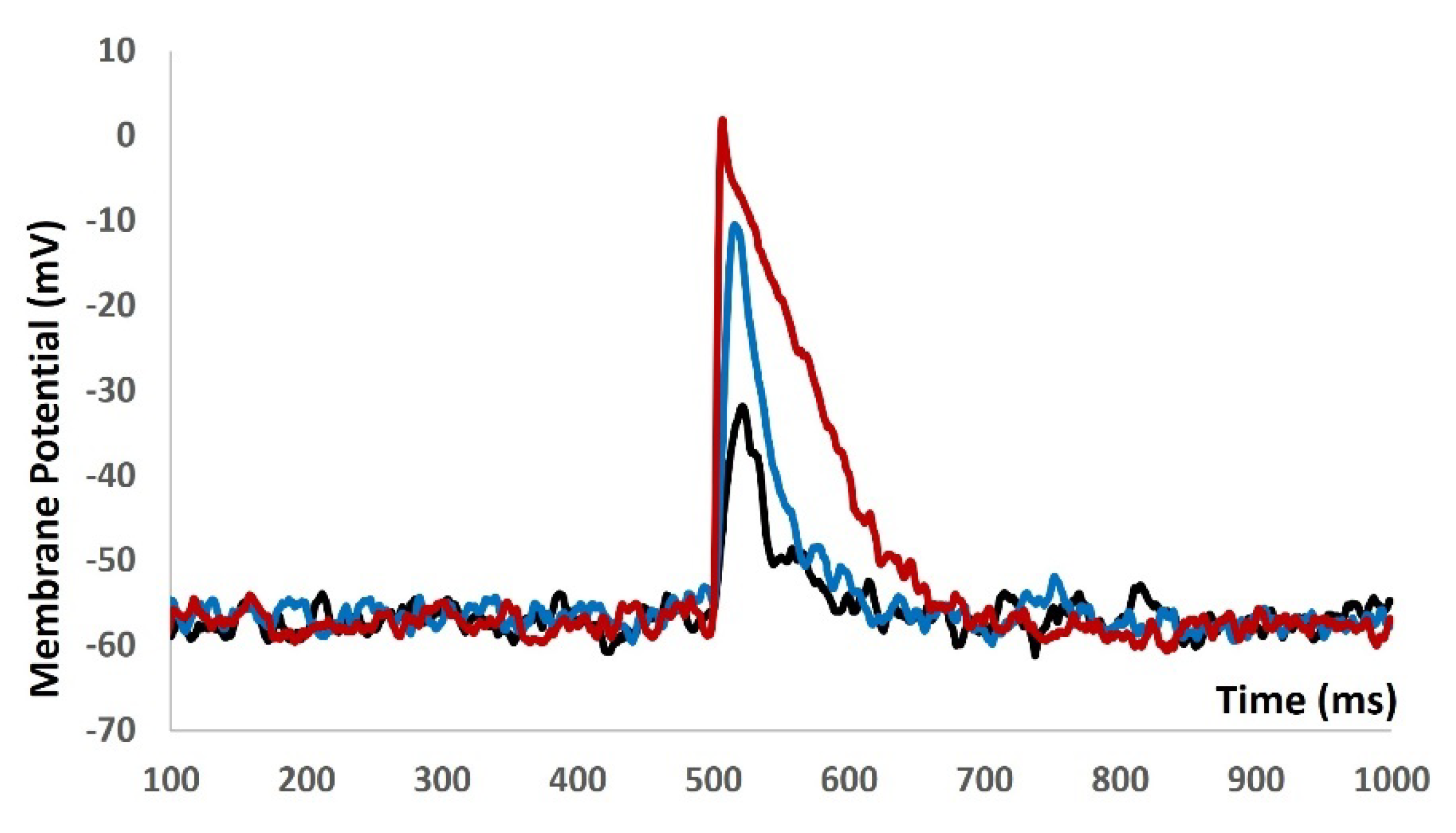
We injected current stimulus of various amplitude for 10 ms duration to investigate the current evoked depolarization, AP, and threshold prediction. Till the stimulus of 0.55 mA, there were no spike and with 0.55 mA, the AP was generated. From the AP (red solid line in Figure 5) and depolarization (black solid line in Figure 5) , the threshold to trigger the AP is predicted at ─ 38.36 mV.
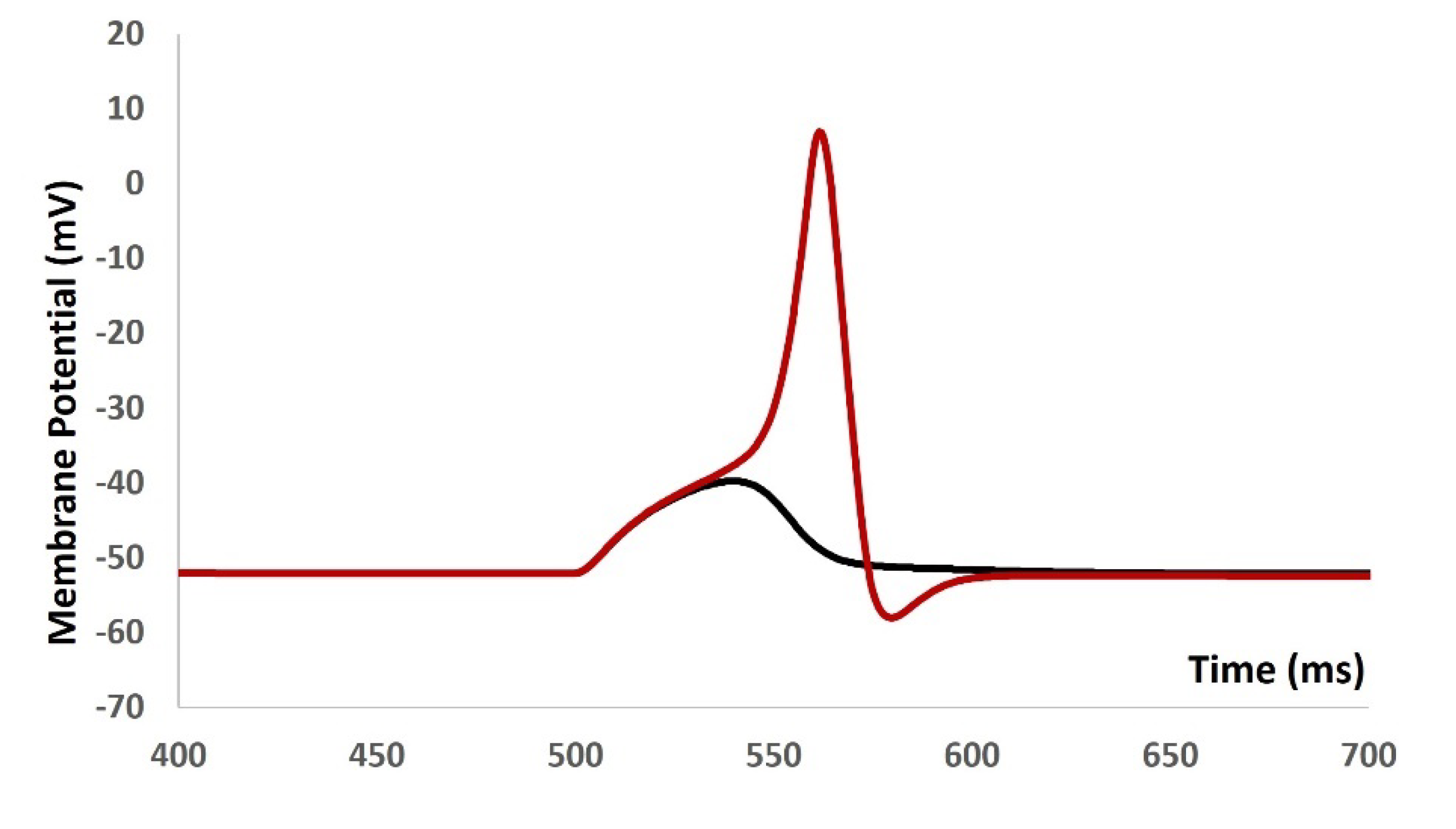
We then introduced synaptic input of various amplitude to investigate the evoked depolarization, AP, and threshold prediction. With the stimulus of 0.0076 µS, there were no spike and with 0.0077 µS, the AP was generated. From the AP (red solid line in Figure 6) and depolarization (black solid line in Figure 6) , the threshold to trigger the AP is predicted at ─ 38.42 mV.
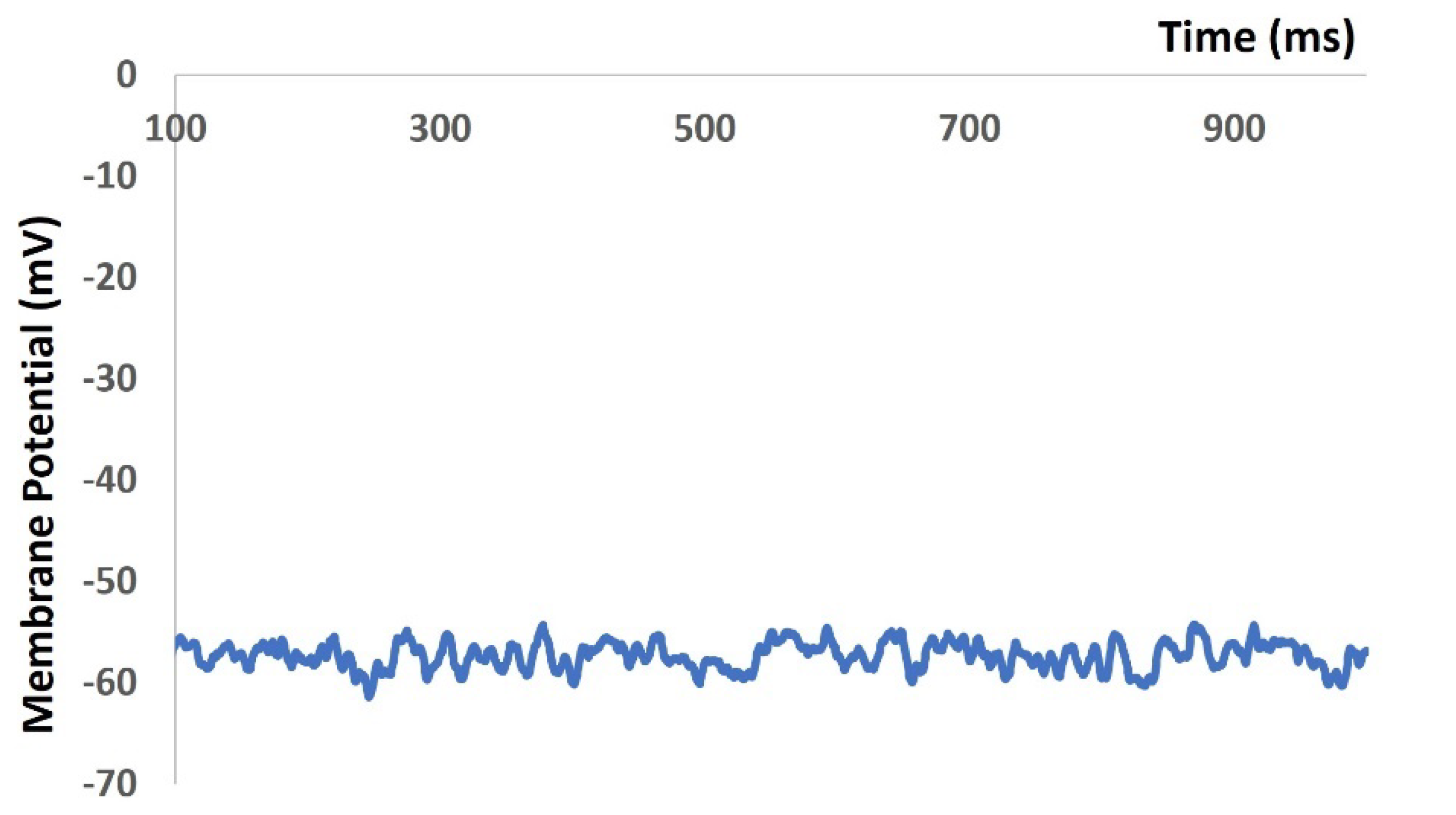
We then repeated our model to generate Figure 4, Figure 5 and Figure 6 with the addition of stochastic synaptic background conductance noise. The value of gex(t) in equation 1 was varied to investigate the fluctation of RMP with the synaptic background conductance noise. Figure 7 shows the membrane potential with value of 0.012 mho. The RMP is flactuated between ─ 51.43 mV and ─ 60.26 mV.
Preprints 100945 g007
Figure 7. Model shows the RMP with synaptic background conductance noise.
Figure 7. Model shows the RMP with synaptic background conductance noise.
Preprints 100945 g007
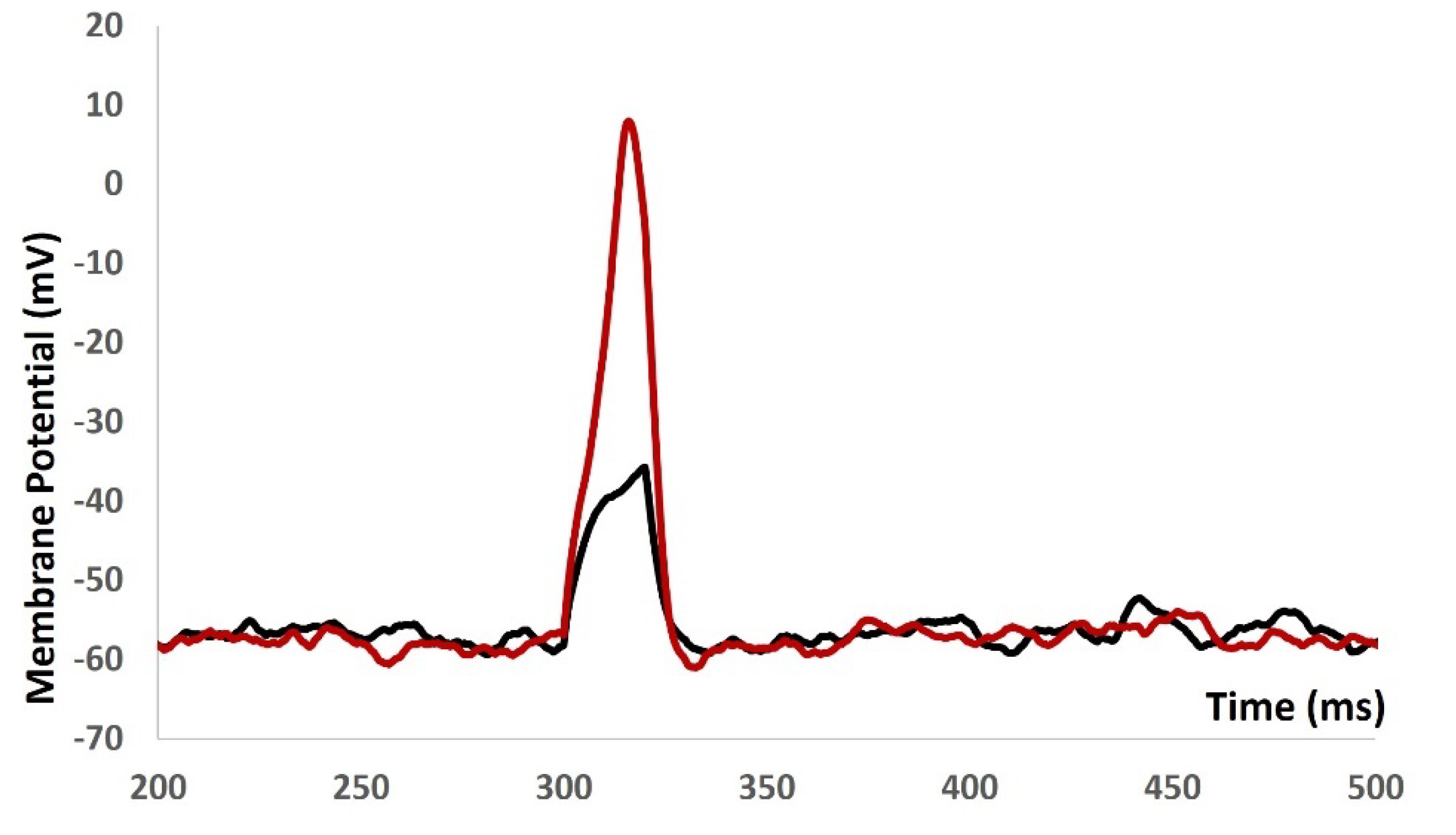
We injected current stimulus of various amplitude for 10 ms duration to investigate the current evoked depolarization, AP, and threshold prediction with stochastic synaptic background conductance noise . Till the stimulus of 1.9 mA, there were no spike and with 2 mA, the AP was generated. From the AP (red solid line in Figure 8) and depolarization (black solid line in Figure 8) , the threshold to trigger the AP is predicted at ─ 34.68 mV.
We then introduced synaptic input of various amplitude to investigate the evoked depolarization, AP, and threshold prediction with stochastic synaptic background conductance noise. Figure 9 shows that with the stimulus of 0.05 µS (black solid line), 0.09 µS (blue solid line), and 0.5 µS (red solid line) there were no spikes. There were no ways to predict the threshold potential due to lack of AP. The input resistance is altered by multiple fold times and model was not generating any AP. The active components of the biophysical system were disabled and system only generated the passive properties.
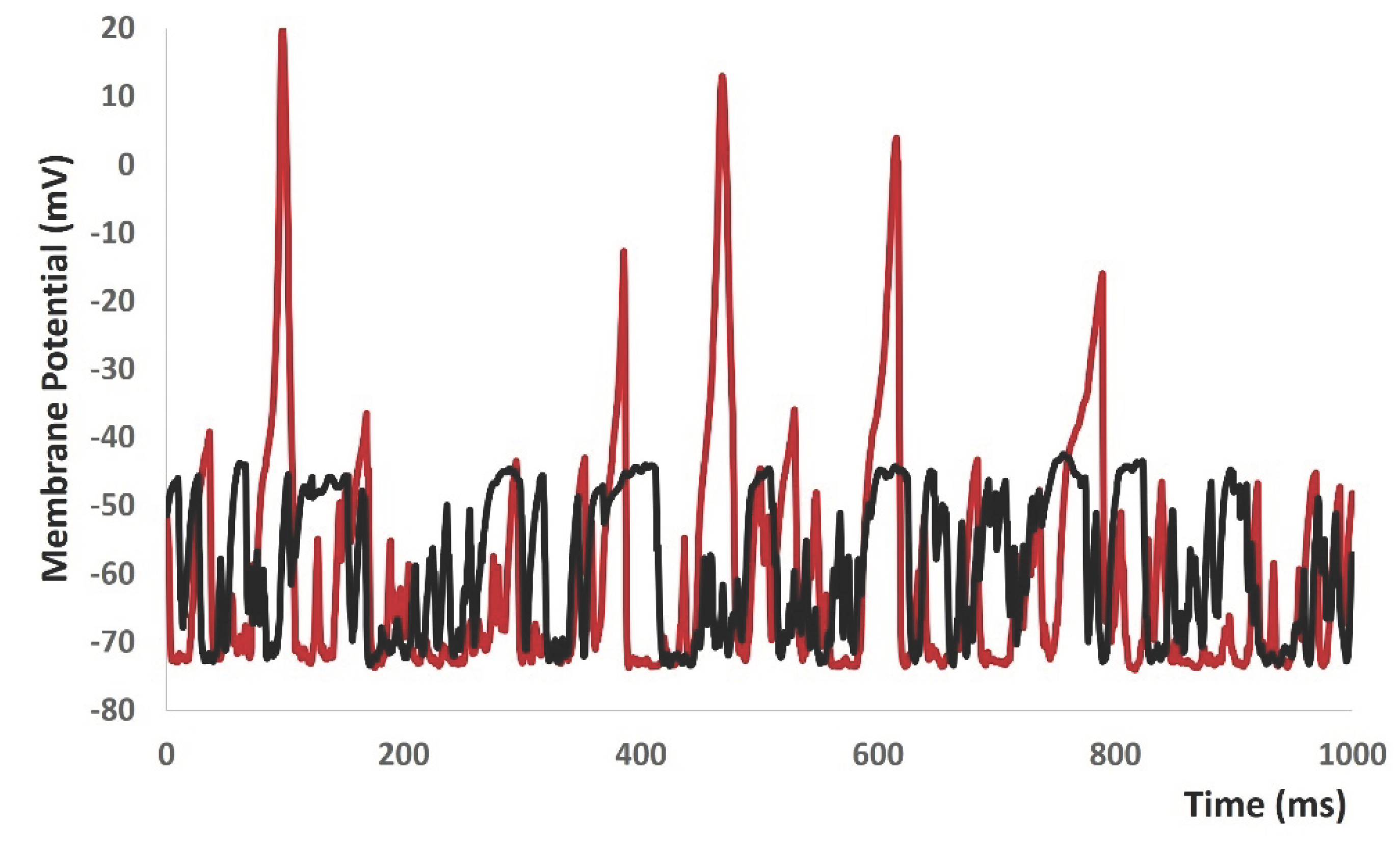
When we increased value of gex(t) in equation 1 to more positive values, the model started to generate spontaneous depolarizations and sponatneous APs (red solid lines in Figure 10) without any current or synaptic stimulus. To investigate the active propereties of all ion channels, we made the conductances of both L- type and T- type calcium channels to zero. As expected, the active part of the mebrane potential was diminished (black solid lines in Figure 10).

4. Discussion

Electrically excitable cells experience membrane depolarization, which leads to the generation of action potentials (APs) that start many physiological processes and aid in intercellular communication. Neurotransmitters are released, both in response to stimuli and spontaneously, causing an increase in excitatory synaptic conductance, which leads to membrane depolarization. The nervous system extensively innervates excitable cells, and these mechanisms are critical in numerous pathological settings. Neurotransmitters are released randomly, causing electrical activity that can be seen as background events in recordings of excitable cells. Studies have explored synaptic background activity utilizing in vivo, in vitro, and in silico methods, however non-neuronal excitatory cells such as cardiac and smooth muscle cells, which also receive neurotransmitter-based innervation, have not been thoroughly researched.
Mathematical modeling approaches are crucial for quantitatively assessing intricate biological systems, allowing for the simulation of intracellular electrophysiological activity. We introduced a mathematical model that includes stochastic synaptic background noise dynamics in a whole-cell DSM cell model. This model replicates the spontaneous depolarization and action potential generation seen in experimental recordings by focusing on the electrophysiological traits of urinary bladder smooth muscle cells. The simulation shows that random depolarization triggers T-type Ca2+ channels first, then L-type Ca2+ channels, resulting in the production of action potentials. Multiple potassium channels are then triggered to restore the resting membrane potential after an action potential. The model also mimics the impacts of T-type and L-type Ca2+ channel blockers and generates membrane voltage variations of around few mV.
This model is a basic prototype used to understand the electrophysiological characteristics of non-neuronal excitatory cells, without utilizing intricate mathematical formulae for detailed analysis. Suppressing these baseline activities would facilitate the discovery of new pharmaceutical targets for different clinical diseases.

Author Contributions

Conceptualization, C.M. and I.S.; methodology, C.M. and I.S.; software, C.M. and I.S.; validation, C.M. and I.S.; formal analysis, C.M. and I.S.; investigation, C.M. and I.S.; resources, C.M. and I.S.; data curation, C.M. and I.S.; writing—original draft preparation, C.M.; writing—review and editing, C.M. and I.S.; visualization, C.M. and I.S.; supervision, I.S.; project administration, C.M. and I.S.; funding acquisition, I.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Data available within the manuscript.

Acknowledgments

The authors would like to thank the reviewers for their fruitful comments and suggestions for improving the manuscript.

Conflicts of Interest

The authors declare no conflicts of interests.

References

  1. Abdul Kadir, L. , Stacey, M., & Barrett-Jolley, R. Emerging roles of the membrane potential: action beyond the action potential. Frontiers in physiology 2018, 1661. [Google Scholar]
  2. Platkiewicz, J. , & Brette, R. A threshold equation for action potential initiation. PLoS computational biology 2010, 6, e1000850. [Google Scholar]
  3. Schneidman, E. , Freedman, B., & Segev, I. Ion channel stochasticity may be critical in determining the reliability and precision of spike timing. Neural computation 1998, 10, 1679–1703. [Google Scholar] [PubMed]
  4. Petkov, G. V. Ion channels. In Pharmacology 2009, pp. 387–427. Academic Press.
  5. Kim, D. M. , & Nimigean, C. M. Voltage-gated potassium channels: a structural examination of selectivity and gating. Cold Spring Harbor perspectives in biology 2016, 8, a029231. [Google Scholar]
  6. Mahapatra, C. , & Manchanda, R. Computational studies on bladder smooth muscle: modeling ion channels and their role in generating electrical activity. Biophysical Journal 2015, 108, 588a. [Google Scholar]
  7. Mahapatra, C. , Brain, K. L., & Manchanda, R. Computational study of Hodgkin-Huxley type calcium-dependent potassium current in urinary bladder over activity. In 2018 IEEE 8th international conference on computational advances in bio and medical sciences (ICCABS) 2018, pp. 1–4. IEEE.
  8. Nielsen, M. S. , Axelsen, L. N., Sorgen, P. L., Verma, V., Delmar, M., & Holstein-Rathlou, N. H. Gap junctions. Comprehensive Physiology 2012, 2. [Google Scholar]
  9. He, P. , Deng, J., Zhong, X., Zhou, Z., Song, B., & Li, L. Identification of a hyperpolarization-activated cyclic nucleotide-gated channel and its subtypes in the urinary bladder of the rat. Urology 2012, 79, 1411-e7. [Google Scholar]
  10. Kavalali, E. T. The mechanisms and functions of spontaneous neurotransmitter release. Nature Reviews Neuroscience 2015, 16, 5–16. [Google Scholar] [CrossRef] [PubMed]
  11. Faisal, A. A. Stochastic simulation of neurons, axons and action potentials. Stochastic methods in neuroscience 2010, 297–343. [Google Scholar]
  12. Yarom, Y. , & Hounsgaard, J. Voltage fluctuations in neurons: signal or noise? Physiological reviews 2011, 91, 917–929. [Google Scholar]
  13. Mahapatra, C., & Manchanda, R. Simulation of In Vitro-Like Electrical Activities in Urinary Bladder Smooth Muscle Cells. Journal of Biomimetics, Biomaterials and Biomedical Engineering 2017, 33, 45–51.
  14. Mahapatra, C. Computational study of inward rectifying ion channel in urinary bladder over activity: student research abstract. In Proceedings of the Symposium on Applied Computing 2017; pp. 31–32.
  15. Mahapatra, C. , & Manchanda, R. MP42-01 quantitative study of inward rectifying ion channel in detrusor instability. The Journal of Urology 2017, 197, e544–e544. [Google Scholar]
  16. Brading, A. F. Spontaneous activity of lower Urinary tract smooth muscles: correlation between ion channels and tissue function. The Journal of physiology 2006, 570, 13–22. [Google Scholar] [CrossRef] [PubMed]
  17. Gabella, G. Structure of the intramural nerves of the rat bladder. Journal of neurocytology 1999, 28, 615–637. [Google Scholar] [CrossRef]
  18. Young, J. S. , Meng, E., Cunnane, T. C., & Brain, K. L. Spontaneous purinergic neurotransmission in the mouse urinary bladder. The Journal of physiology 2008, 586, 5743–5755. [Google Scholar] [PubMed]
  19. Mahapatra, C., & Manchanda, R. Modulating Properties of Hyperpolarization-Activated Cation Current in Urinary Bladder Smooth Muscle Excitability: A Simulation Study. In Recent Findings in Intelligent Computing Techniques: Proceedings of the 5th ICACNI 2017, Volume 1 2019, pp. 61-266. Springer Singapore.
  20. Mahapatra, C. Simulation study of transient receptor potential current in urinary bladder over activity: student research abstract. In Proceedings of the 33rd Annual ACM Symposium on Applied Computing 2018; pp. 74–75.
  21. Heppner, T. J. , Bonev, A. D., & Nelson, M. T.: Elementary purinergic Ca2+ transients evoked by nerve stimulation in rat urinary bladder smooth muscle. The Journal of physiology 2005, 564, 201–212. [Google Scholar] [PubMed]
  22. Brading, A. F. , & Brain, K. L. Ion channel modulators and urinary tract function. Urinary Tract, 2011; 375–393. [Google Scholar]
  23. Meng, En, John S. Young, and Alison F. Brading. Spontaneous activity of mouse detrusor smooth muscle and the effects of the urothelium. Neurourology and urodynamics 2008, 27.1, 79-87.
  24. Mahapatra, C., Brain, K., & Manchanda, R. (2024). Biophysically Realistic Models of Detrusor Ion Channels: role in shaping spike and excitability. In Urinary Bladder Physiology: Computational Insights. Publ Narosa Publishing House.
  25. Mahapatra, C. , & Manchanda, R. Quantitative Studies of Spontaneous Electrical Activities in Detrusor Smooth Muscle Cells towards Understanding Urinary Bladder Overactivities. The FASEB Journal 2020, 34, 1–1. [Google Scholar]
  26. Mahapatra, C. , & Manchanda, R. In Silico Pharmacological Assessment of Mibefradil in Single Detrusor Smooth Muscle Cell towards Understanding Urinary Bladder Overactivity. The FASEB Journal 2020, 34, 1–1. [Google Scholar]
  27. Mahapatra, C. , & Manchanda, R. Quantitative Study of pharmacological regulation of TRPM channel in Urinary Bladder over Activity. The FASEB Journal 2018, 32, 770–772. [Google Scholar]
  28. Mogilner, A. , Wollman, R., & Marshall, W. F. Quantitative modeling in cell biology: what is it good for? Developmental cell 2006, 11, 279–287. [Google Scholar]
  29. Vagos, M. , van Herck, I. G., Sundnes, J., Arevalo, H. J., Edwards, A. G., & Koivumäki, J. T. Computational modeling of electrophysiology and pharmacotherapy of atrial fibrillation: recent advances and future challenges. Frontiers in physiology 2018, 9, 1221. [Google Scholar]
  30. Rinzel, J. , & Huguet, G. Nonlinear dynamics of neuronal excitability, oscillations, and coincidence detection. Communications on Pure and Applied Mathematics 2013, 66, 1464–1494. [Google Scholar]
  31. Mahapatra, C., Manchanda, R., & Brain, K. In silico pharmacological assessment of Nifedipine and Mibefradil in mouse detrusor smooth muscle cells towards detrusor instability. Proceedings for Annual Meeting of The Japanese Pharmacological Society WCP2018 (The 18th World Congress of Basic and Clinical Pharmacology) 2018, pp. OR31–4.
  32. Fellous, J. M. , Rudolph, M., Destexhe, A., & Sejnowski, T. J. Synaptic background noise controls the input/output characteristics of single cells in an in vitro model of in vivo activity. Neuroscience 2003, 122, 811–829. [Google Scholar]
  33. Mahapatra, C. , Brain, K. L., & Manchanda, R. A biophysically constrained computational model of the action potential of mouse urinary bladder smooth muscle. PloS one 2018, 13, e0200712. [Google Scholar]
  34. Mahapatra, C., Brain, K. L., & Manchanda, R. Computational studies on urinary bladder smooth muscle: Modeling ion channels and their role in generating electrical activity. 2015 7th International IEEE/EMBS Conference on Neural Engineering (NER) 2015, pp. 832–835.
  35. Mahapatra, C. A computational model of action potential in the mouse detrusorsmooth muscle cell. 2017 Winter Simulation Conference (WSC) 2017, pp. 4634–4635.
  36. Mahapatra, C. , Brain, K. L., & Manchanda, R. Computational study of ATP gated Potassium ion channel in urinary bladder over activity. 2016 International Conference on Inventive Computation Technologies (ICICT) 2016, Vol. 2, pp. 1–4.
  37. Mahapatra, C. , Dave, V., & Manchanda, R. A Mathematical Modeling of Voltage gated Calcium ion channel based Calcium Transient Response in UrinaryBladder Smooth Muscle Cell. International Journal of Pure and Applied Mathematics 2017, 117, 71–75. [Google Scholar]
  38. Hodgkin, A. L. , & Huxley, A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. The Journal of physiology 1952, 117, 500. [Google Scholar]
  39. Fry, C. H. , et al. "Measurement of intercellular electrical coupling in guinea-pig detrusor smooth muscle." The Journal of urology 1999, 161.2, 660-664.
  40. Hines, M. L. , & Carnevale, N. T. The NEURON simulation environment. Neural computation 1997, 9, 1179–1209. [Google Scholar]
Preprints 100945 g001
Figure 1. Schematic diagram of cellular mechanisms for membrane depolarization.
Figure 1. Schematic diagram of cellular mechanisms for membrane depolarization.
Preprints 100945 g001
Preprints 100945 g002
Figure 2. (a) Schematic overview of ion channel mechanisms in single DSM cells; (b) .
Figure 2. (a) Schematic overview of ion channel mechanisms in single DSM cells; (b) .
Preprints 100945 g002
Preprints 100945 g005
Figure 5. Model shows the AP (red line) and depolarization (black line) with current stimulus.
Figure 5. Model shows the AP (red line) and depolarization (black line) with current stimulus.
Preprints 100945 g005
Preprints 100945 g006
Figure 6. Model shows the AP (red line) and depolarization (black line) with synaptic input stimulus.
Figure 6. Model shows the AP (red line) and depolarization (black line) with synaptic input stimulus.
Preprints 100945 g006
Preprints 100945 g008
Figure 8. Model shows the AP (red line) and depolarization (black line) with current stimulus and synaptic background conductance noise.
Figure 8. Model shows the AP (red line) and depolarization (black line) with current stimulus and synaptic background conductance noise.
Preprints 100945 g008
Preprints 100945 g009
Figure 9. Model shows the eveoked response for synaptic inputs with syaptic background conductance noise.
Figure 9. Model shows the eveoked response for synaptic inputs with syaptic background conductance noise.
Preprints 100945 g009
Preprints 100945 g010
Figure 10. Model shows the spontaneous AP generation with higher noise and application of L and T type Calcium channel blockers.
Figure 10. Model shows the spontaneous AP generation with higher noise and application of L and T type Calcium channel blockers.
Preprints 100945 g010
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated