Preprint
Article
Adaptive Control of Quadrotors in Uncertain Environments
Altmetrics
Downloads
78
Views
22
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
11 March 2024
Posted:
11 March 2024
You are already at the latest version
Alerts
Abstract
The problem addressed in this article consists of the motion control of a quadrotor, comprising model disturbances and uncertainties. In order to tackle model uncertainty, adaptive control based on reinforcement learning is used. The distinctive feature of this article, in comparison with other works on quadrotor control using reinforcement learning is the exploration of the underlying optimal control problem in which a quadratic cost and a linear dynamics allow an algorithm that runs in real time. Instead of identifying a plant model, adaptation is obtained by approximating the performance index given by the Q-function using directional forgetting recursive least squares that rely on a linear regressor build from quadratic functions of input/output data. The adaptive algorithm proposed is tested in simulation in a cascade control structure that drives a quadrotor. Simulations show the improvement in performance that results when the proposed algorithm is turned on.
Keywords:
Subject: Engineering - Control and Systems Engineering
1. Introduction
1.1. Motivation
Unmanned Air Vehicles are currently becoming an important player in areas such as inspection and maintenance, photography, surveillance, mapping, agriculture, military warfare, delivery, and more [1,2]. Fully automated vehicles without human intervention have been receiving increased attention [3], as advanced controller architectures are [1,2] progressing towards full autonomy, an example of which being adaptive controllers that can tackle wind perturbations or uncertainty in the model parameters.
Reinforcement learning (RL) is a technique in which the control action to apply to the manipulated variable of the plant is selected such as to maximize a reward signal [4]. Some RL algorithms can provide adaptation in unique ways, for example, without the need for any model knowledge about the system upon which it acts. This opens a gateway for a new class of adaptive controllers, that can attain some degree of control robustness, even when faced with unmodeled dynamics. The topic of drone control using RL has been the subject of many recent works. In addition to the works reviewed in [2], other references include [5,6,7], as well as [8,9], that address real-time RL.
Although general RL based controllers yield remarkable performances for a wide variety of robotic and aircraft plants [10], the fact that they rely on deep neural networks imply long training periods, with a massive computational load, that may only be executed off-line. Nevertheless, for a class of problems in which the plant dynamics is linear and the cost to optimize is quadratic, the computational cost is greatly reduced, being compatible with on-line adaptive control.
This work has the objective of developing an adaptive controller for a quadrotor based on such a specific RL model-free algorithm, according to the lines presented in [11]. It is stressed that, opposite to the works reported in [2], the algorithm proposed in this article does not rely on off-line training using massive amounts of data but, instead, provides real time adaptation of a vector of state feedback gains, without knowing or estimating the parameters of any plant model. By real time adaptation it is meant that the algorithm is fast enough to be run as the drone operates. This procedure is possible because we restrain the class of problems addressed to be of linear quadratic type, i. e., defined by an underlying plant dynamics to be linear but unknown and a quadratic performance cost to be minimized.
Assuming the underlying plant dynamics to be linear is justified by the type of application envisaged;: the algorithm, developed is embedded in the control part of the quadrotor GNC (guidance, navigation and control) system and has the task of regulating the quadrotor state around a reference trajectory generated by the guidance system. Hence, the controller is required to tackle only incremental dynamics that may be approximated by a linear model.
With respect to other works described in the literature for motion control of quadrotors based on reinforcement learning [2], the approach proposed here has the drawback of not allowing large amplitude maneuvers, in which the nonlinear character of the dynamics dominates. In compensation, the control algorithm proposed provides a model free adaptive controller that operates in real time with little a priori plant knowledge. The definition and use of such a controller for drone motion is the focus of this article.
1.2. Problem Definition, Objectives and Contribution
A common control architecture for quadrotors consists of two controllers interconnected in a cascade structure: an outer control loop, responsible for keeping the quadrotor in a desired position, and an inner control loop, that tracks the quadrotor attitude demanded by the outer controller.
The attitude controller works on the premise that the quadrotor is not performing extreme maneuvers, so that it is valid to assume that the drone dynamics is approximately linear. In order to tackle uncertainty in dynamics, the inner loop, that regulates the attitude, relies on an adaptive controller that embeds a reinforcement learning (RL) algorithm to learn the gains that optimize a quadrati cost.
The outer loop consists of a linear quadratic (LQ) controller with constant gains, designed using a nominal model and is such that it has a time scale that is much slower than the one of the inner loop.
The contribution of this article consists on the design of the above cascade adaptive control architecture and its demonstrations in simulations for a quadrotor model. The main innovative feature is the embedding of a reinforcement learning algorithm in the inner loop to yield a model free adaptive controller. The use of a directional forgetting least-squares estimation algorithm to avoid identifiability problems in the Q-function approximator is also is also a contribution.
The article is organised as follows: section 2 describes the drone model used in the simulations; section 3 presents the control architecture; section 4 explains the class of RL based contriol algorithms used; section 5 peresents simulation results; finally, section 6 draws conclusions.
2. Dynamics Modeling
Although the proposed controller does not rely on a model, the dynamics of the drone considered is described in this section for the purposes of simulation and interpretation of the results presented later-on.
The model dynamics follows the rigid body equations of motion [12]. For this sake, an inertial reference frame attached to the ground and a fixed body frame , attached to the vehicle, are defined as represented in Figure 1.
The rigid body state comprises a position in the inertial frame p, a velocity in the body frame v, an angular velocity in the body frame , and a rotation matrix R that represents the transformation between the body fixed frame and the inertial frame orientations. The full kinematics equations are
where the quadrotor attitude is expressed in Euler angles, a vector with the elements as the angle of rotation about the x axis, as the angle of rotation about the y axis and as the angle of rotation about the z axis. The matrix Q is defined as
The dynamics equations are
where J represents the moment of inertia matrix, that is assumed to be diagonal. The application corresponds to a skew-symmetric matrix. The inputs T and n represent the thrust force and torque respectively.
3. Controlling the Quadrotor
3.1. Controller Structure
The relationship between both sets of equations (1) and (3) allows the development of a cascade control structure that has an inner loop for controlling the attitude of the quadrotor, and an outer loop for controlling the position and that generates as manipulated variable the desired orientation to the inner (attitude) controller. This type of controller is commonly used in UAVs and its block diagram is shown in Figure 2.
The trajectory generator block creates the references , and for the position controller, and the reference for the attitude controller. These signals represent the desired position and its derivatives, and the desired angle, respectively. Besides generating an input thrust T, the position controller also generates a desired upwards orientation , corresponding to the third column of R, that is combined with in the attitude controller to track the desired orientation angles.
3.2. Position Controller
Neglecting the rotational dynamics, it is assumed that the desired orientation , can be forced upon the system. Considering that , the virtual input is defined, and transforms the first line of (3) into
which is now a linear system, that can be controlled with a linear controller.
For the sake of reference trajectory tracking, the error variable is defined as
where represents the reference position. Taking the second derivative of (5) and resorting to the system defined in (4), the error dynamics
is obtained. Selecting to be
introduces linear state feedback, where each state has a proportional gain. There is also a correction term in order to eliminate the second derivative of the error present in the dynamics. Applying the control law transforms (6) into
where the gains and are selected such as to the error e to zero, enabling reference tracking given a desired trajectory , and its derivatives and .
The virtual control input, which is a three-dimensional vector, is translated into the thrust T input and desired orientation (forced upon the system) values. Via equation (7) the thrust T is calculated with
and the desired orientation is obtained through
The thrust input is fed directly into the system, as opposed to , which is passed to the attitude controller so that the orientation errors can also be regulated.
3.3. Attitude Controller
Neglecting the translational dynamics, a desired orientation is fed to the attitude controller, that produces an input torque for the system.
To track the desired orientation value, the desired angle, is combined with to obtain the remaining desired angles and .
Through decomposition of the desired R matrix, the equation
allows the computation of the desired attitude . To track this value, a possible strategy is to linearize the second equations of systems 1 and 3 around the hover condition, a valid approach for smooth trajectories where aggressive maneuvers are not required, resulting in
given that the matrix J is diagonal. The linearized system obtained is also a double integrator. The input n is chosen to account for the angle and angular velocity error, resulting in
The inner loop that comprises the attitude controller must react faster than the outer loop containing the position controller. This time scale separation is forced to ensure that the system quickly corrects angle displacements, that are detrimental to effectively tracking the desired position. To guarantee correctness, the gains of each controller must be chosen such that the inner loop poles contain a real part that is ten times (or more) larger than the real part of the outer loop poles.
3.4. Underlying LQ control
The adaptive RL controller proposed in this article consists of a state feedback in which the gains converge to the ones of a LQ controller. Hereafter, the model and the quadratic cost that define this underlying controller are defined. Assuming that the inputs are piece-wise constant over the sampling period h, the discrete-time equivalent [13] of the double integrator dynamics takes the form , where
where is the diagonal element from the inertial moment matrix J associated with the angle to be controlled, for the rotational dynamics. This value is unitary for the translational dynamics.
Having both and , the discrete controller gains for the control laws in (7) and (13) can be calculated resorting to the LQR algorithm, that aims at minimizing the quadratic cost
A careful choice of the and weight matrices is necessary for a good performance.
The sampling period selected throughout all experiences is , equivalent to a frequency of 100 Hz. The quadrotor state variables are assumed to be fully observable. However, a sensor noise effect is reproduced by adding white noise after the A/D sampling process. A standard deviation of (with zero mean) is used in the simulation.
4. Reinforcement Learning
4.1. Introduction
Reinforcement learning is an area of Machine Learning that aims to learn what is the best action an agent can execute as it interacts with the environment on which it acts upon [4]. From a control perspective, we can think of the environment as the system and the action as the output produced by the controller, which is the agent [14].
In this setting, the action is now the control action and the state is . The control policy determines the value of and it is defined as
consisting of a map from the state space to the control space. Since this map depends only on the current state , it defines a state feedback controller. This definition needs to be coherent with the definition of the reward signal, as detailed further ahead.
Let the system be described by
where A and b are matrices that define the linearized quadrotor dynamics.
4.2. Dynamic Programming and Q-Function
The control policy is to be designed such as to minimize
often called the cost-to-go or return. The discount factor factor, takes values in the interval .
For the reward signals, this article considers the quadratic function
In order to obtain model-free controllers, define the Q-function
The Q-function verifies a Bellman like equation given by
The optimal control policy is then calculated through
In the absence of constraints, the optimal control policy can then be computed by solving
4.3. Approximate Dynamic Programming
To determine the optimal policy at time k, it is necessary to know the optimal policy at time . This minimization process is done backwards in time, and it is only feasible as an off-line planning method, using iterative algorithms. The resulting Dynamic Programming methods are not enough to obtain a controller which can learn in real time. Approximate Dynamic Programming solves this problem and introduces two other concepts that will make the operation forwards in time possible.
The first concept is that of Temporal Difference (TD). Taking advantage of equation (21), it is possible to define a residual error given by
If the Bellman Equation is satisfied, then the error is zero. This error can be seen as the difference between observed and predicted performances as a previously calculated action is applied. The next important tool is the Value Function Approximation (VFA), that approximates the Q-function by a parametric approximator. For linear plants and quadratic costs, it can be shown [11] that the Q-function can be rewritten as
where W is a vector of coefficients and is a vector containing the basis functions with the square terms and cross terms for all elements of and .
Combining the equations (25) and (24), the TD error becomes
that defines a linear regression model with parameters W. Approximating by a linear combination of basis functions, enables the use of estimation techniques to obtain the coefficients which will then define the closest approximation [11]. Equations (21), (22) and (25) allow building an on-line forward-time learning algorithm for state feedback control.
4.4. Q Learning Policy Iteration
In this article, the Policy Iteration adapted for Q Learning is chosen to be applied in the controller.
The Policy Evaluation step, where the VFA coefficients are estimated, requires determining a least squares solution to find the estimate of the parameter vector W in the linear regression model (26). This can be done by resorting to Recursive Least Squares (RLS) or batch least squares. In this article Directional Forgetting RLS is used.
A Gaussian dither noise is added to the observed control input signal , derived from the current policy obtained from (23). The reason behind this procedure is the necessity to ensure a persistency of excitation condition. The absence of this effect can cause the algorithm to completely fail [11].
For estimation purposes, Recursive Least Squares with Directional Exponential Forgetting (RLS-DF) is used [15], where the estimated Q-function gains are updated at every time step k every time step, and the policy is updated after a fixed number of time steps. This approach divides the computational effort of estimation across every time step, whereas a batch least-squares update concentrates all estimation in one run. The Q-Learning algorithm for the versions using RLS-DF is detailed in Algorithm 1.


For a two-dimensional state system, the VFA is defined as (25) with the basis functions given by
which means that the policy improvement step at the update , as defined in Algorithm 1, takes the form
The control action takes the form of a linear state feedback , with a K gain of
where represents the estimate of the ith element of W.
The importance of the use of DF-RLS stems from the fact that, although there are only 2 controller gains, the Q-function is approximated by 6 parameters, a fact that may cause identifiability problems.
5. Simulation Stusdy
In this section, simulations are shown to illustrate the results obtained when applying the above algorithm to control the motion of the quadrotor model described in Section 2. The simulation experiments show that, with the proposed controller, the algorithm is able to track a reference in which there are curved sections followed by segments that are approximately straight. Most important, the simulations illustrate adaptation. In the experiments, there is an initial period in which a constant vector of, a priori chosen, controller gains is used. During this period the algorithm is learning the optimal gains but these ones are not used in feedback. After this initial period, the gains learned by the RL algorithm are used. There are two sets of experiments. In the first set, the initial gains are far from the optimum. In the second set of experiments, the initial set of gains are not optimal, but they are closer to optimum than the gains in the first set. Two relevant results are shown: one is the capacity of the algorithm to improve the performance when the gains obtained by RL are used; furthermore, the dither noise can be reduced when the initial gains are closer to the optimum (that is to say, when more a priori information is available). The evaluation and comparison of the different situations is done using an objective index (the “score”) defined below.
The wind force w is characterized by its x, y, and z components, that determine its direction and magnitude. White noise is applied to a low-pass filter and added to w to produce more realistic deviations from the average magnitude. The average value of the disturbance is assumed to be measurable and is compensated for, but the model is still affected by the white noise effect, that has a standard deviation of . The wind disturbance value for the i component is described as
where represents the generated wind, represents the average value, and represents the filtered white noise. The dynamics of the motor are neglected, being considered much faster than the remaining quadrotor dynamics. The aerodynamic drag effect is also neglected, since most of the quadrotor operations are maintained in a near hover condition.
The model considered has the following parameters:
- Kg
- m
- Kg.m2
- Kg.m2
For simulation purposes, the constant wind disturbance is compensated, assuming that it is possible to measure its average value. The noisy oscillations around the average value still affect the system.
To gain a better insight on how well the controller performs before and after the learning process, a performance metric is defined as
where represents the desired position and p the actual position. The metric calculates the average value of the distance between the moving point in the reference trajectory and the actual position of the quadrotor. The lower this value, the better the controller can track the given reference trajectory.
5. The control algorithm parameters are selected by trial and error in simulations. The main parameters to adjust are the weights in the quadratic cost considered and the dither noise variance, added to the control variable. The dither noise variance must be chosen according to a trade-off between not disturbing optimality (meaning that the variance must be small) and providing enough excitation to identify the parameters of the quadratic function that approximates the Q-function (which requires increasing the dither variance). The weight adjusts the controller bandwidth and must be selected to ensure that the inner loop is much faster than the outer loop.
In order to avoid singularities on the model, the references are such that the attitude angle deviates only by a maximum value with respect to the vertical.
5.1. Experiment 1
The first test attempts to improve on a controller that is tuned with the following weights in relation to the quadratic cost defined above:
- Position controller: = diag(200,1), = 100;
- Attitude controller (except ): = diag(100,1), = 10;
- Attitude controller (): = diag(10,5), = 10;
This calibration affects the attitude control of the angle , where a poor selection of weights is chosen so it can be improved on.
The algorithm has the parameters shown in Table 1.
The learning process (during which a priori chosen controller gains are used) lasts 400 seconds, and the trajectory in the form of a lemniscate has cycles of 20 seconds, meaning that each learning cycle of 10 seconds comprises half a curve. The starting point is (2,0,0) at rest. The lemniscate has been selected as a test reference since it combines approximated straight and curved stretches.
Simulation results for the trajectory tracking improvement are presented in Figure 3. To test the performance of both the initial and learned gains, a single cycle of the lemniscate curve is used.
For a starting point at (2,0,3), that starts right at the beginning of the lemniscate curve, the controller after learning a better set of gains has a score (as defined in equation (31)) of 0.0177, whereas the untuned controller produced a score of 0.1203. These results show a clear improvement in the trajectory tracking performance. The corresponding gain evolution in time is presented in Figure 4.
Despite some oscillations, the convergence is quick. This happens due to the selection of high variance for the dither noise. However, this procedure can be a problem, given that in real life quadrotors have limitations on the actuators that might render such high values impossible. The magnitudes of the input during the learning stage can induce big oscillations in the quadrotor, since the angular velocity and the angle get excited by the effect of the dither noise.
In order to be able to reduce the dither noise power and still obtain satisfactory results, an alternative is to increase the number of steps required for an update. However, this approach slows down the learning process. Another possibility is to increase the values of the covariance matrix of the LS estimator at each update, so that the updates are less influenced by previous updates. This comes at the price of bigger oscillations. The new parameters are shown in Table 2.
With these updates, a new simulation rendered the results in Figure 5 that shows the evolution of the gains with time. Even though the learning process slows down as expected, improvements are still achieved. Figure 6 demonstrates that good trajectory tracking was obtained.
For a starting point at (2,0,3), that coincides with the beginning of the lemniscate curve, the controller performs reference tracking with a score (as defined in equation (31) of 0.0175 after the learning process, whereas the untuned controller produced a score of 0.1204, with the input torque acquiring smaller values as a direct consequence of the reduction of the dither noise.
5.2. Experiment 2
The previous two tests aim to improve the controller gains starting from a non-optimum scenario. The following three tests try to improve on already optimized results. This might pose a better challenge for the algorithm, since there will be no need for big amounts of excitation to learn an improved set of gains.
The starting point for the controller gains corresponds to the following configuration of weights:
- Position controller: = diag(200,1), = 100;
- Attitude controller: = diag(100,1), = 10;
The difference between experiments is the value of the moment of inertia , which is assumed in each experiment to be:
- Third experiment Kg.m2
- Fourth experiment Kg.m2
- Fifth experiment Kg.m2
The real value of is 0.01 Kg.m2. This means that each experience has its attitude controller gains with different values, upon the application of the LQR algorithm.
The algorithm has the same parameters throughout all three experiences, presented in Table 3.
The dither is now significantly reduced, as less excitation is required. The small expected improvements allow for some reduction of the confidence matrix P values, to dampen more some oscillations that might appear.
A closer look at the trajectories reveals that improvements do occur, with the improved gains producing a better tracking performance. The score for the unoptimized version is 0.0202, whereas the version with learned gains scored 0.0175, reflecting a small improvement over the original configuration.
The score for the performance metric before RL is 0.01781, and after applying the algorithm, the score becomes 0.01765. Even if there was an improvement, in this case, it is almost negligible. This can be seen in Figure 10 where both trajectories pratically overlap each other, ending up having the same distance to the reference lemniscate curve.
The score metric for the original set of gains is 0.01811, and after applying the algorithm, the score becomes 0.01765. In this last experience, a small improvement was achieved, even with the real value of being known and used to calculate the controller gains that are used before applying RL. A good tuning of the algorithm allowed for a small performance improvement over a very optimized controller.
6. Conclusions
The development of a reinforcement learning based adaptive controller for a quadrotor, that includes an adapted version of the Q-learning policy iteration algorithm for linear-quadratic problems, was performed. The particular class of RL based controllers considered is such that it allows adaptation in real time.
Adjustments to the baseline algorithm were necessary to make it robust to external perturbations, something achieved through thoughtful choices of the parameters.
Disturbances affecting the system input and output have a big effect on the correct functioning of the algorithm. A careful choice of algorithm parameters and balance between the estimation algorithm parameters is the solution to this problem. However, when big disturbances are present, it is only possible to make the gains converge close to optimality. Increasing the influence of prior estimations allows for a greater degree of robustness, with the drawback of deviating the convergence process to nearby values of the original optimal gains. Nonetheless, that is necessary to prevent harsh oscillations in the learned gains, which are still present in the quadrotor tests, most likely due to the non-linear nature of the rotational dynamics and other unmodelled dynamics, besides the perturbations.
Still, the algorithm produced good results provided that the drone is kept working within the near-linear zone of operation, that is, where safe maneuvers with the quadrotor close to the hovering position are prevalent.
Author Contributions
D. Leitão: research, implementation, writing; R. Cunha: research, methodology, writing; J. M. Lemos: research, methodology, writing
Funding
Part of this work was supported by INESC-ID under project UIDB/50021/2020 and by LARSyS under project UIDB/50009/2020, both financed by Fundação para a Ciência e a Tecnologia (Portugal).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data are not publicly available. The data files are stored in corresponding instruments in personal computers.
Acknowledgments
No acknowledgments.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RL | Reinforcement Learning |
| LQR | Linear Quadratic Regulator |
| VFA | Value Function Approximation |
| TD | Temporal Difference |
| RLS | Recursive Least-Squares |
| MDP | Markov Decision Process |
| ZOH | Zero-Order Hold |
References
- Kangunde, V.; Jamisola, R.S.; Theophilus, E.K. A review on drones controlled in real-time. International journal of dynamics and control 2021, 9, 1832–1846. [Google Scholar] [CrossRef] [PubMed]
- Azar, A.T.; Koubaa, A.; Ali Mohamed, N.; Ibrahim, H.A.; Ibrahim, Z.F.; Kazim, M.; Ammar, A.; Benjdira, B.; Khamis, A.M.; Hameed, I.A.; others. Drone deep reinforcement learning: A review. Electronics 2021, 10, 999. [Google Scholar] [CrossRef]
- Elmokadem, T.; Savkin, A.V. Towards fully autonomous UAVs: A survey. Sensors 2021, 21, 6223. [Google Scholar] [CrossRef] [PubMed]
- Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction; MIT press, 2018.
- Koch, W.; Mancuso, R.; West, R.; Bestavros, A. Reinforcement learning for UAV attitude control. ACM Transactions on Cyber-Physical Systems 2019, 3, 1–21. [Google Scholar] [CrossRef]
- Deshpande, A.M.; Minai, A.A.; Kumar, M. Robust deep reinforcement learning for quadcopter control. IFAC-PapersOnLine 2021, 54, 90–95. [Google Scholar] [CrossRef]
- Deshpande, A.M.; Kumar, R.; Minai, A.A.; Kumar, M. Developmental Reinforcement Learning of Control Policy of a Quadcopter UAV With Thrust Vectoring Rotors. Dynamic Systems and Control Conference, American Society of Mechanical Engineers, 2020, Vol. 2, p. V002T36A011.
- Koh, S.; Zhou, B.; Fang, H.; Yang, P.; Yang, Z.; Yang, Q.; Guan, L.; Ji, Z. Real-time deep reinforcement learning based vehicle navigation. Applied Soft Computing 2020, 96, 106694. [Google Scholar] [CrossRef]
- Ramstedt, S.; Pal, C. Real-Time Reinforcement Learning. Advances in Neural Information Processing Systems. Curran Associates, Inc., 2019, Vol. 32.
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv preprint 2019, arXiv:1509.02971. [Google Scholar]
- Lewis, F.L.; Vrabie, D. Reinforcement learning and adaptive dynamic programming for feedback control. IEEE circuits and systems magazine 2009, 9, 32–50. [Google Scholar] [CrossRef]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics; Advanced textbooks in control and signal processing, Springer London, London, 2009.
- Franklin, G.F.; Powell, J.D.; Workman, M.L.; others. Digital control of dynamic systems; Vol. 3, Addison-wesley Reading, MA, 1998.
- Recht, B. A tour of reinforcement learning: The view from continuous control. Annual Review of Control, Robotics, and Autonomous Systems 2019, 2, 253–279. [Google Scholar] [CrossRef]
- Coelho, J.; Cunha, J.B.; Oliveira, P.d.M. Recursive parameter estimation algorithms. Controlo 2004-Sixth Portuguese Conference on Automatic Control, 2004.
Figure 1.
Quadrotor with inertial reference frame and fixed body frame defined.
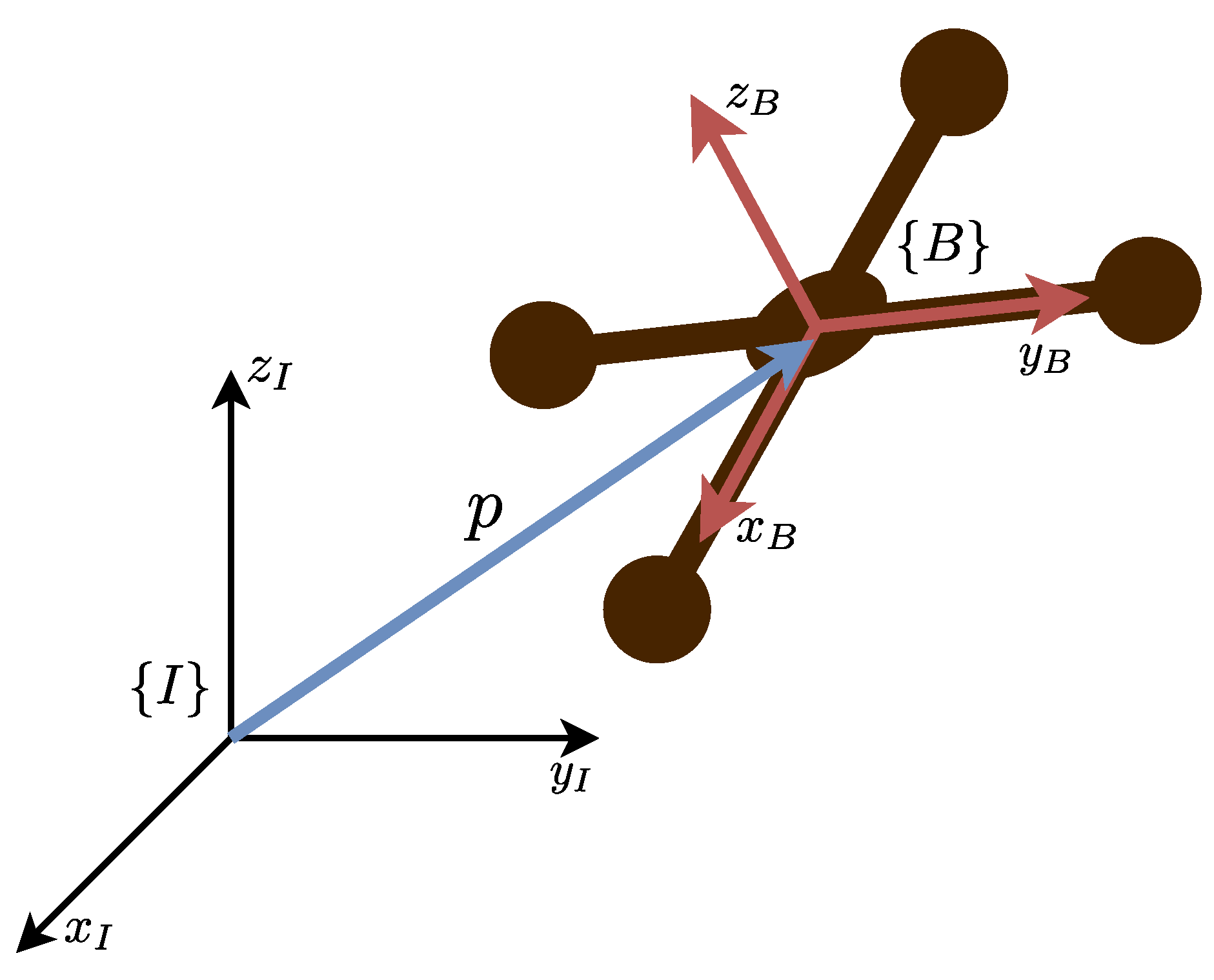
Figure 2.
Cascade controller for the quadrotor motion.
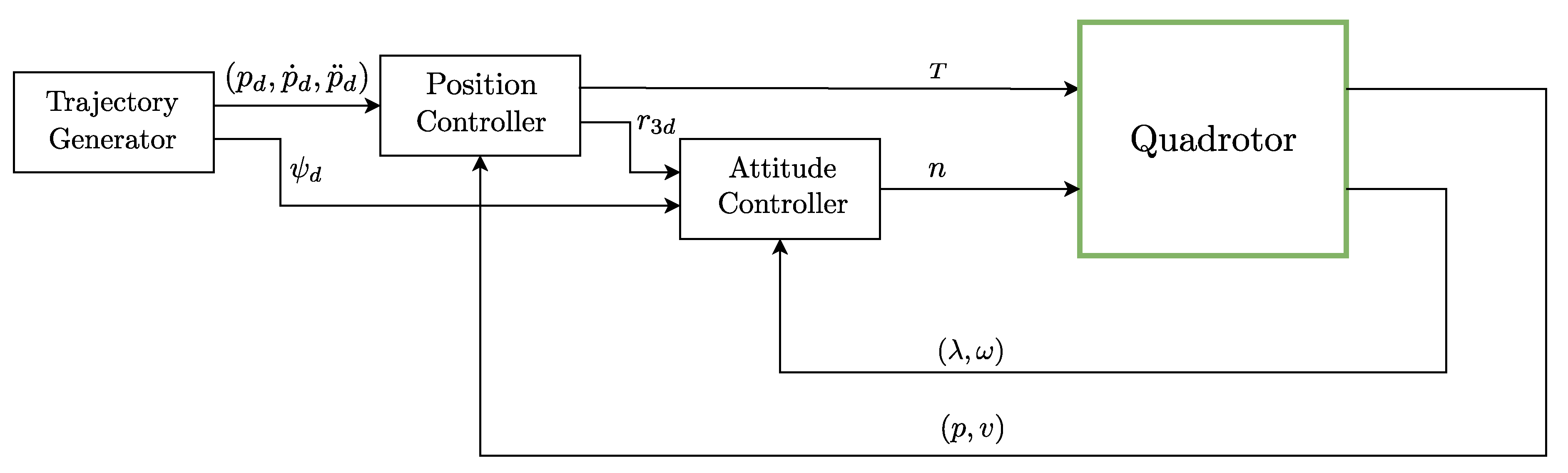
Figure 3.
Trajectory before and after RL; first case.
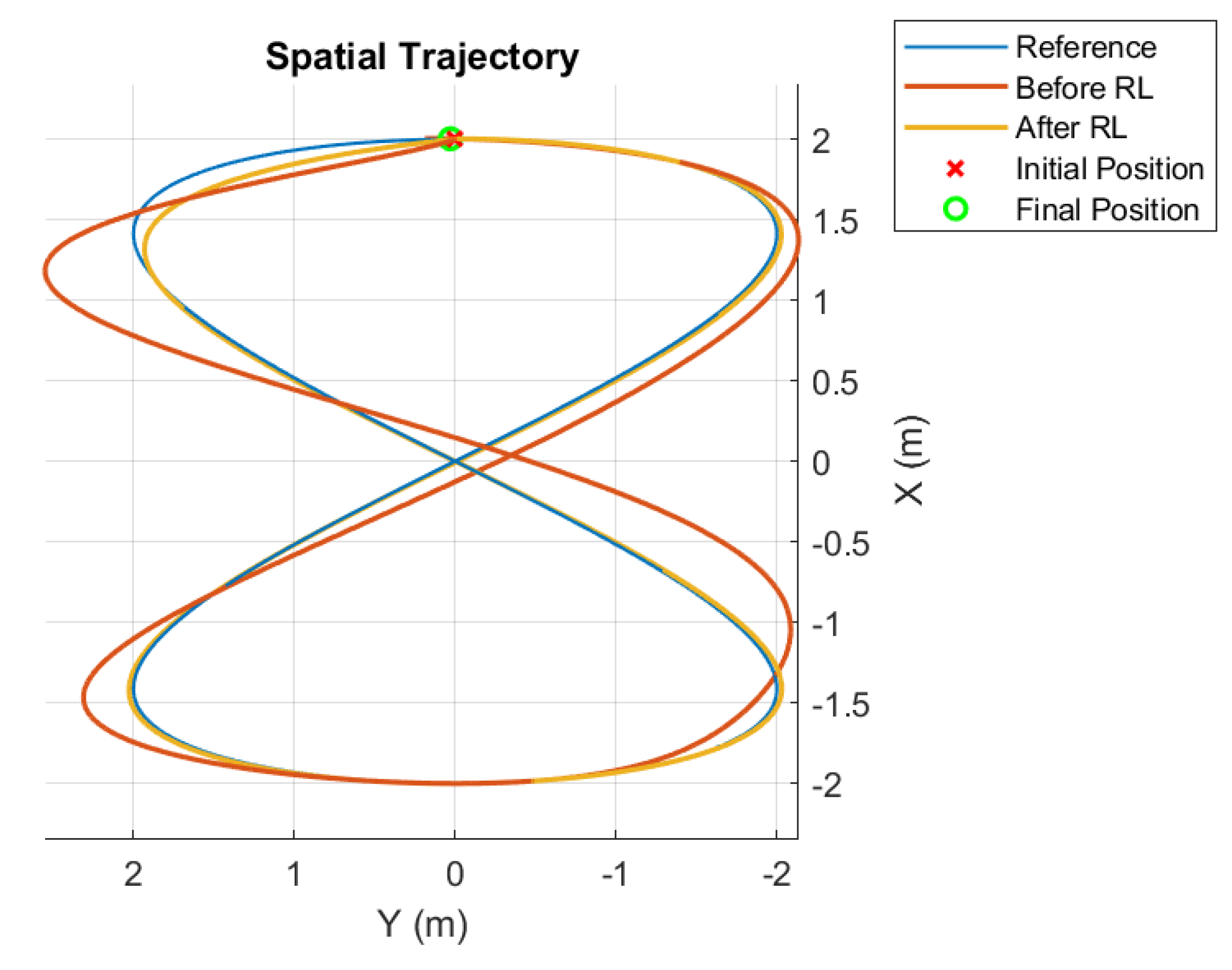
Figure 4.
Evolution of the learned attitude controller gains with time (1st case: dither covariance ); the blue line represents the first gain and the red the second gain.
Figure 4.
Evolution of the learned attitude controller gains with time (1st case: dither covariance ); the blue line represents the first gain and the red the second gain.
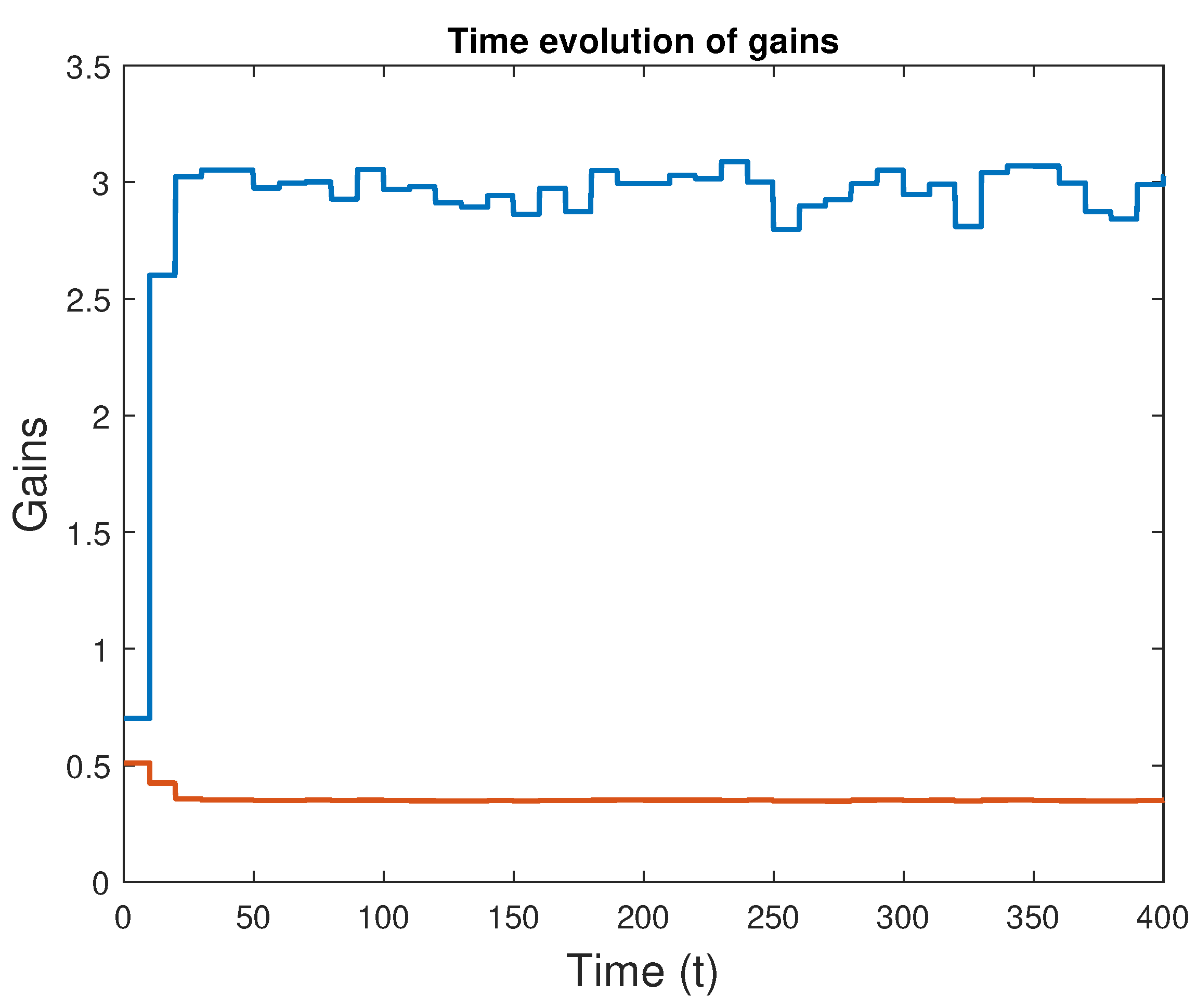
Figure 5.
Evolution of the learned attitude controller gains with time (2nd case: dither covariance ).
Figure 5.
Evolution of the learned attitude controller gains with time (2nd case: dither covariance ).
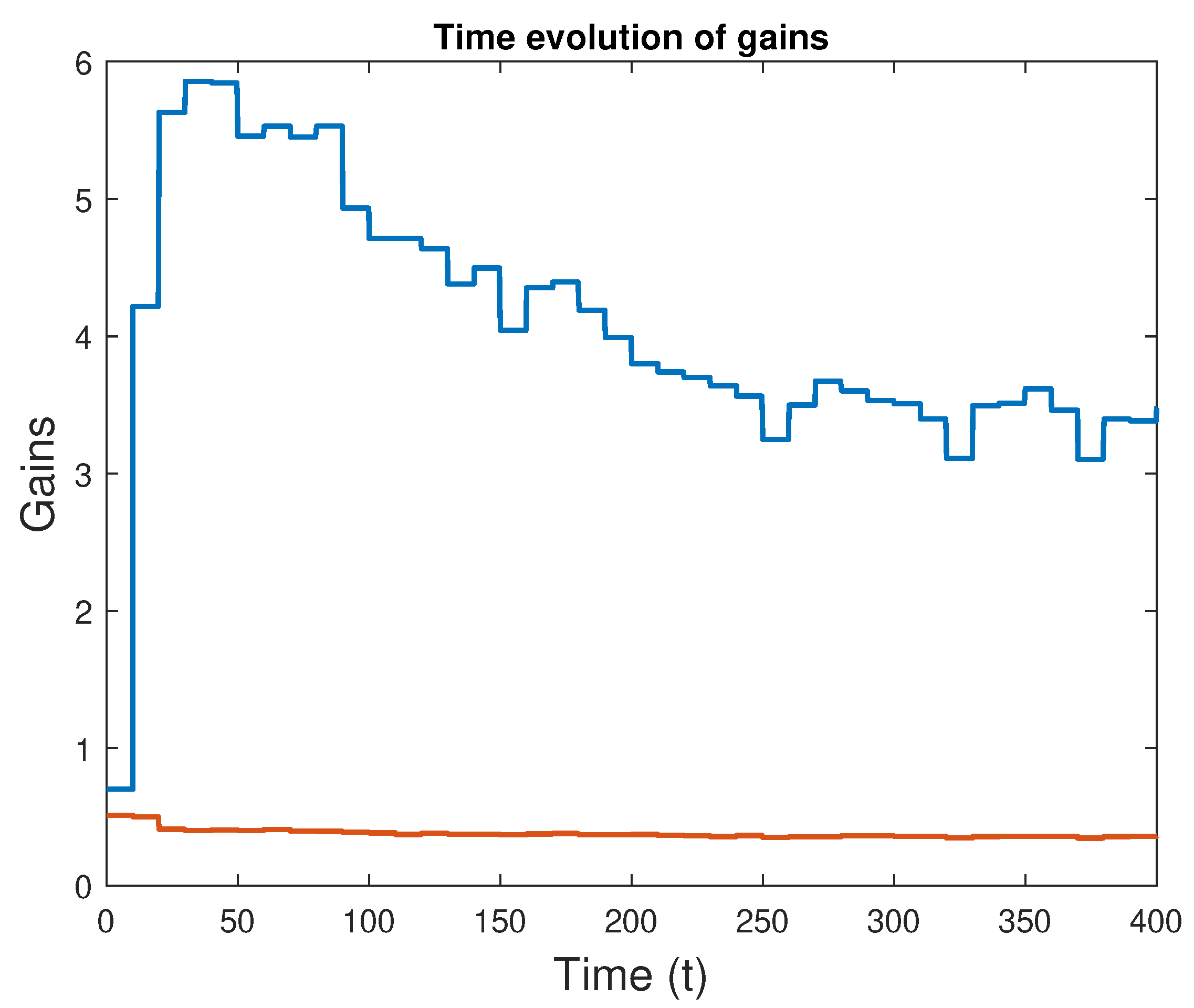
Figure 6.
Trajectory before and after RL; second case.
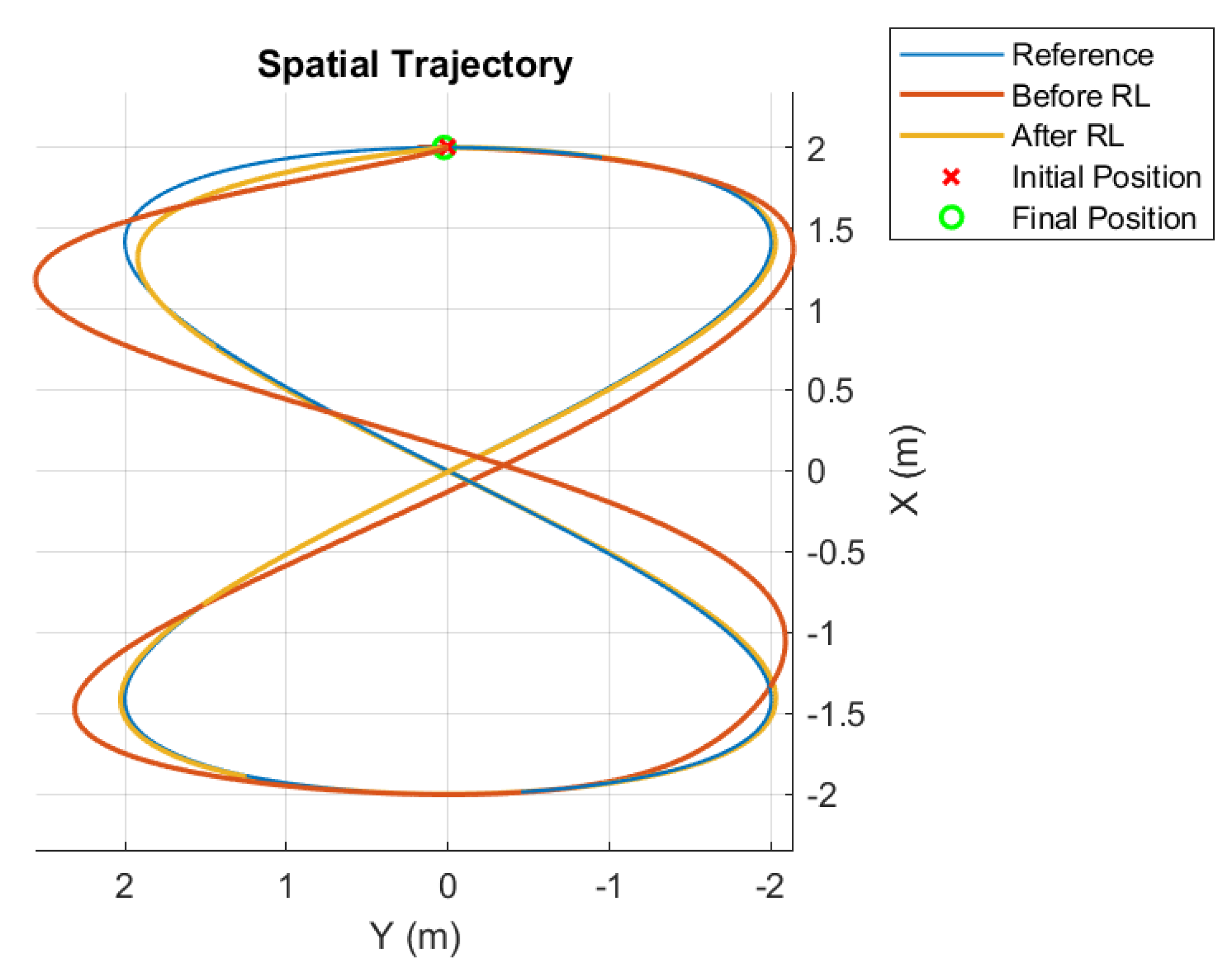
Figure 7.
Evolution of the learned attitude controller gains with time (3rd case: dither covariance ).
Figure 7.
Evolution of the learned attitude controller gains with time (3rd case: dither covariance ).
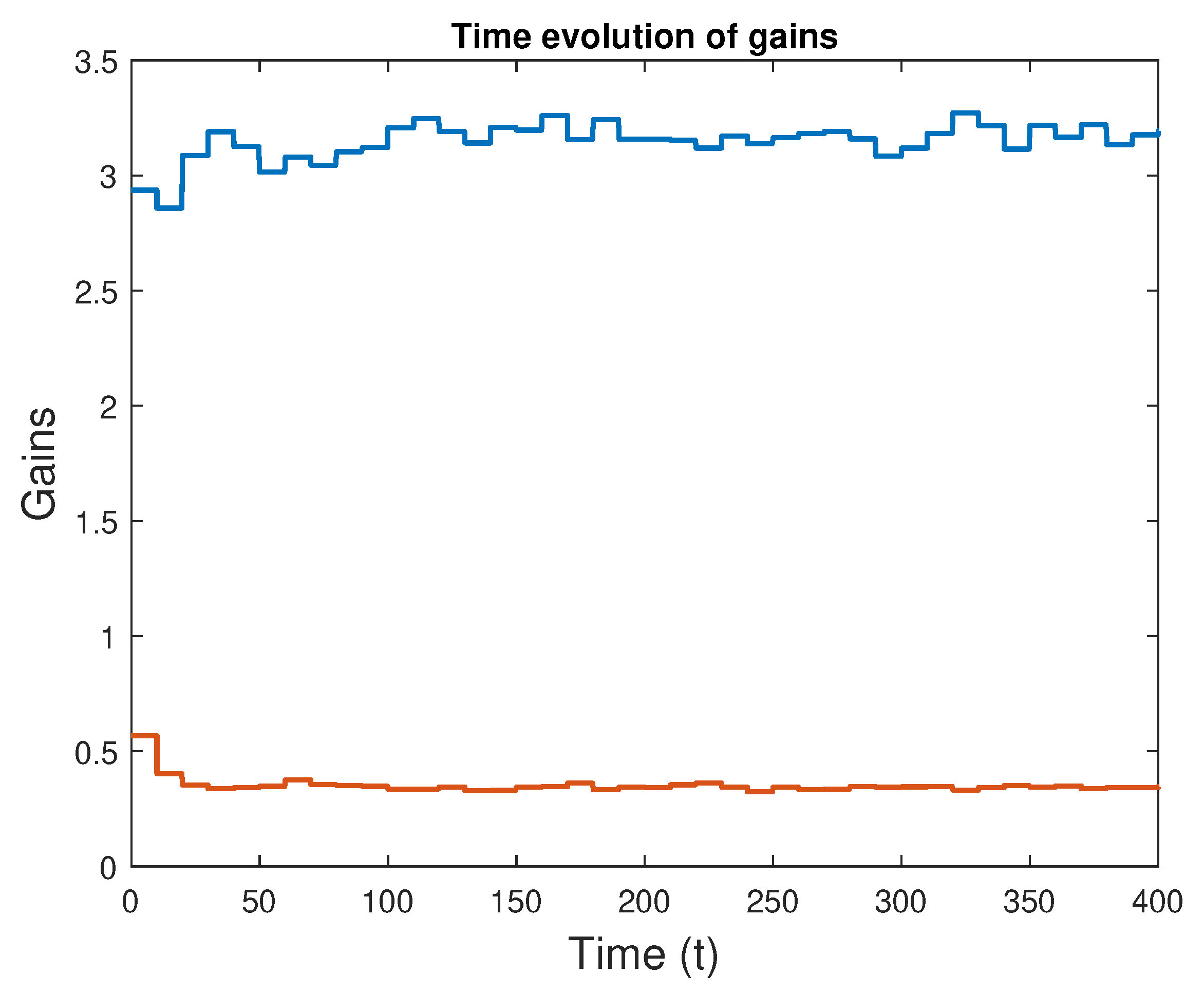
Figure 8.
Detail of the trajectory before and after RL; third case.
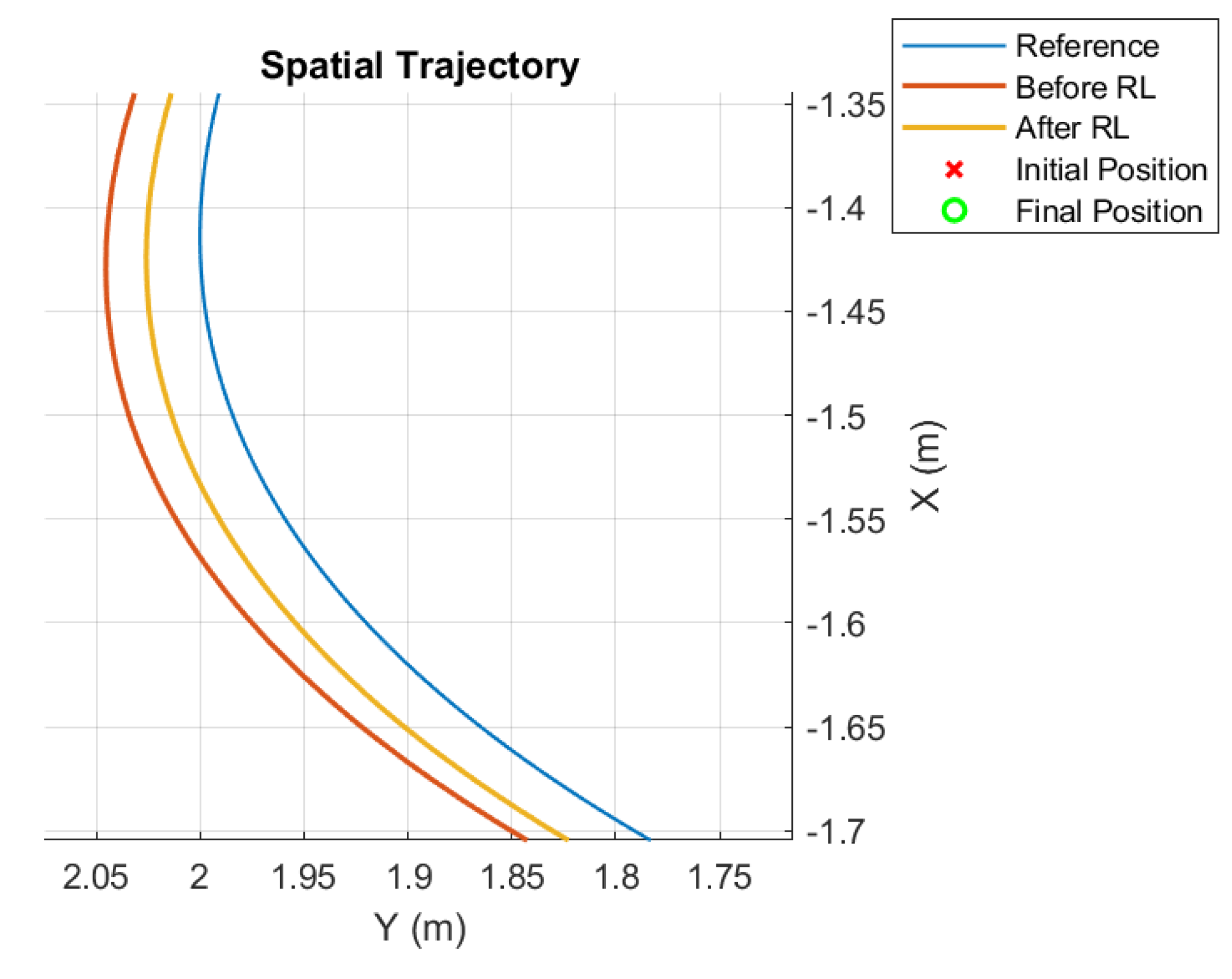
Figure 9.
Evolution of the learned attitude controller gains with time; fourth case.

Figure 10.
Detail of the trajectory before and after RL; fourth case.
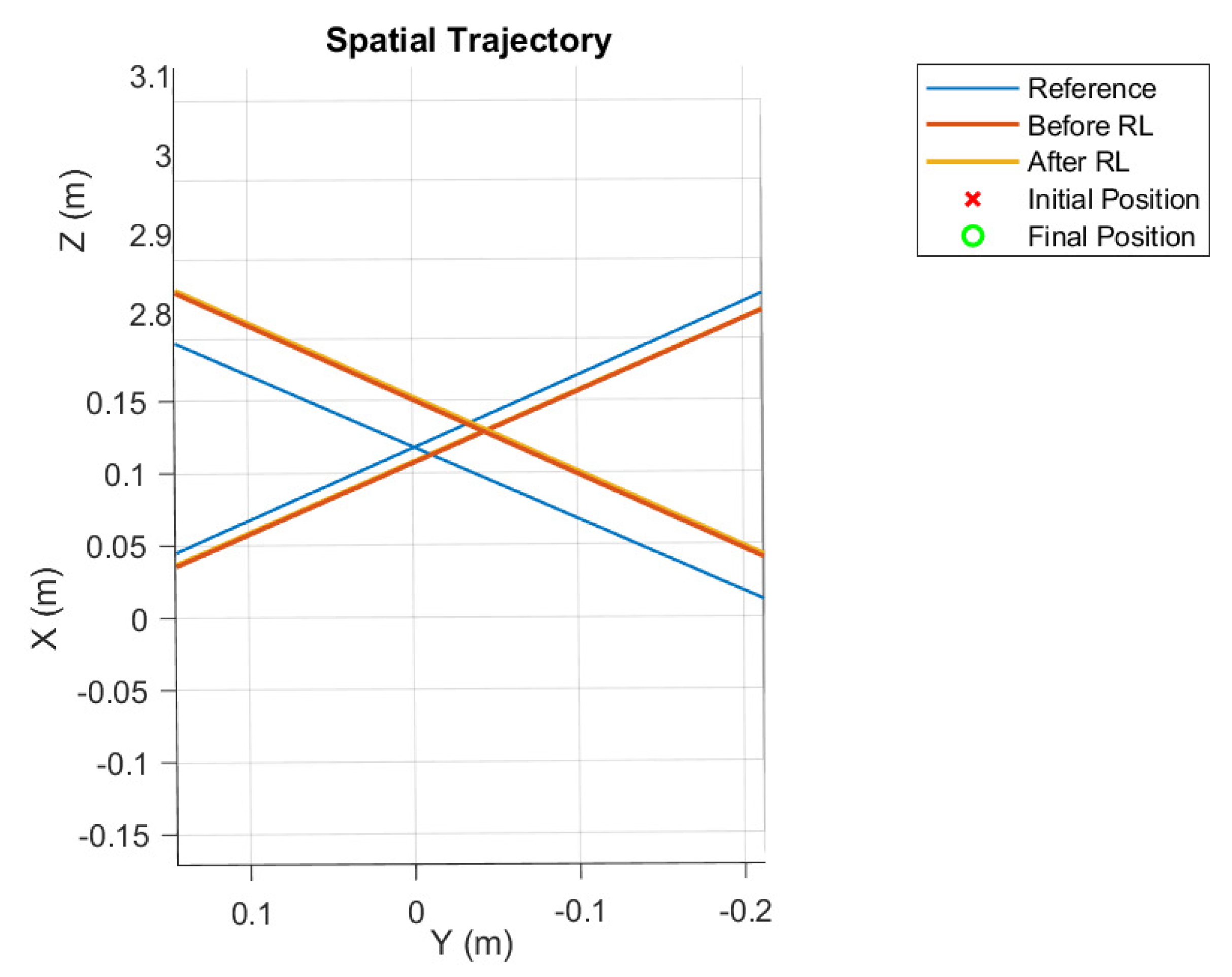
Figure 11.
Evolution of the learned attitude controller gains with time; fifth case.
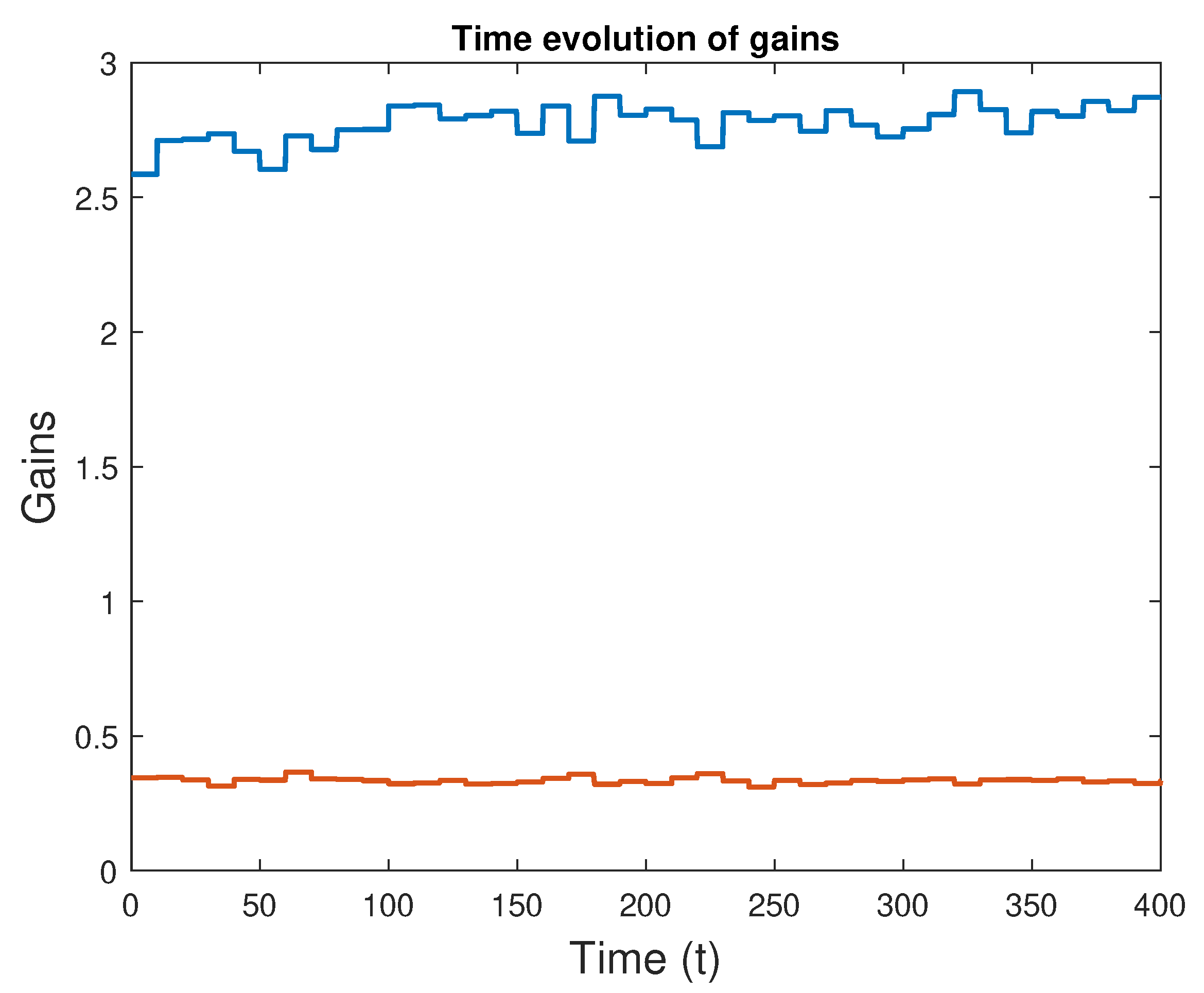
Figure 12.
Detail of the trajectory before and after RL; fourth case.
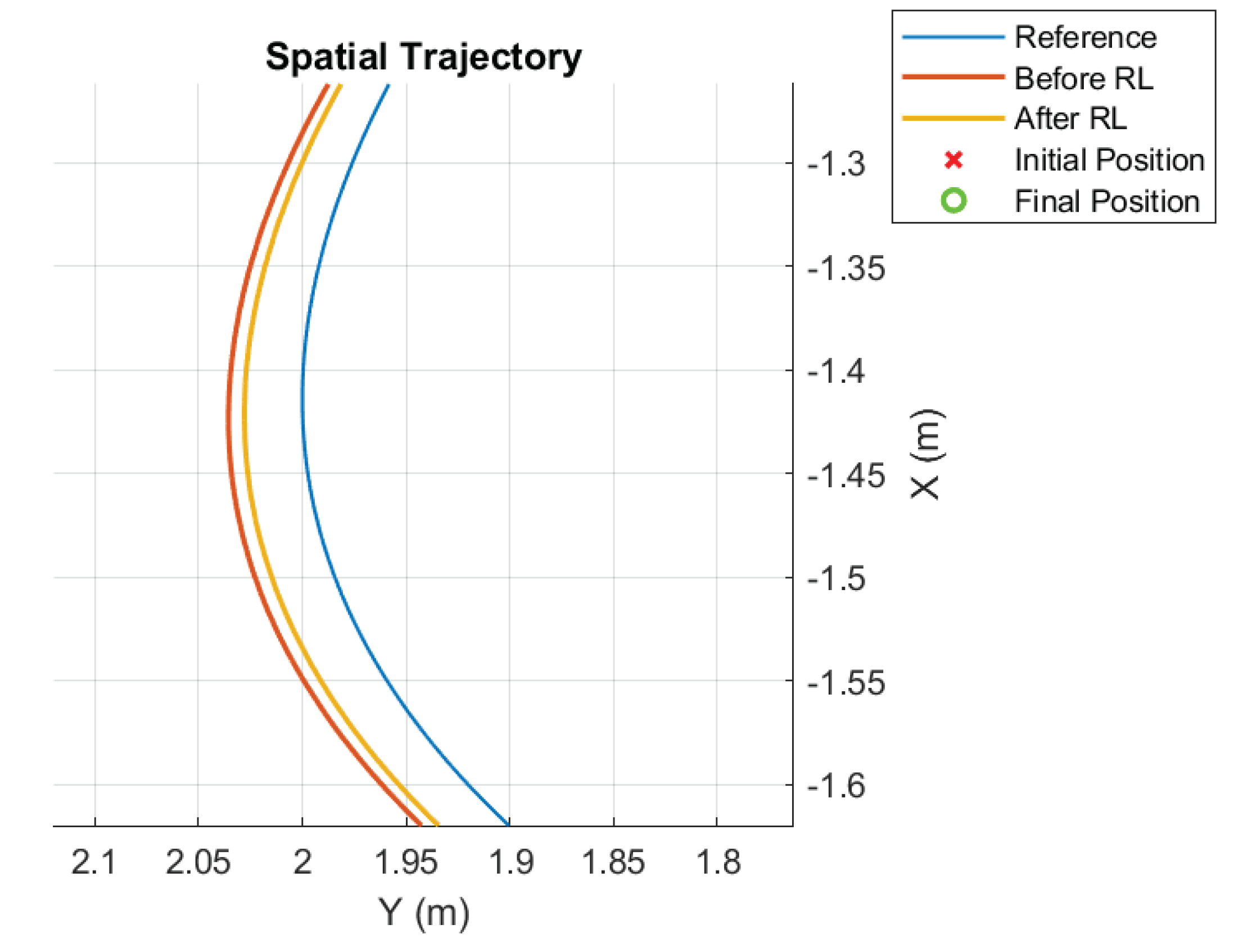
Table 1.
Algorithm parameters for the first test.
| Weight matrices | |
| 0.99 | |
| Update step | 1000 (10 seconds) |
| 0.99 | |
| 0.5 | |
| w | |
Table 2.
Algorithm parameters for the second test.
| Weight matrices | |
| 0.99 | |
| Update step | 1000 (10 seconds) |
| 0.99 | |
| 0.1 | |
| w | |
Table 3.
Algorithm parameters for the third, fourth and fifth tests.
| Weight matrices | |
| 0.99 | |
| Update step | 1000 (10 seconds) |
| 0.99 | |
| 0.05 | |
| w | |
| 500 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






