Preprint
Article
Pin-on-Plate vs. Pin-on-Disk Wear Tests: Theoretical and Numerical Observations on the Initial Transient Phase
Altmetrics
Downloads
120
Views
22
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
09 March 2024
Posted:
11 March 2024
You are already at the latest version
Alerts
Abstract
Pin-on-plate and pin-on-disk wear tests are typically used for assessing the wear behavior of a given material coupling. Such a behavior is frequently described by a wear coefficient k, which is estimated, according to the Archard’s law, as the ratio between the measured wear volume V and the product of the applied normal force F and the sliding distance s, i.e. k=V/(F s). This study demonstrates that such a relationship is correct for pin-on-plate but not for pin-on-disk, particularly for flat-ended pins. Both analytical and finite element models of the two tests were developed, considering three different distances pin-disk axis. As results, wear volumes, pressure and wear depth maps were examined and compared for the same sliding distance. Though this study is focused only on the initial transient part of the wear tests, some interesting aspects arose: i) rotational effect in pin-on-disk tests affects k estimation, especially when the pin is near to the disk axis; ii) a simple analytical function is defined to correct the wear volume estimation for pin-on-disk tests; iii) due to the different sliding distances of contact points in pin-on-disk tests, pressure redistribution occurs with higher values on the inner side (closer to disk axis); the opposite trend is observed in wear depth maps. From a computational point of view, the pin-on-disk problem, only apparently simple, required very small time increments to correctly describe the circular trajectories of points, with high computational costs. Numerical strategies are currently under investigation to extend the study to the steady state phase of both tests.
Keywords:
Subject: Engineering - Mechanical Engineering
1. Introduction
Wear is a phenomenon as complex as it is widespread in everyday life. It can be observed in shoes, teeth, brakes and in many other elements. From an engineering point of view, it is important to consider wear when designing mechanical components and this requires an estimation of their wear resistance. Experimental tests are carried out at this purpose. Since this phenomenon is affected by many factors as materials properties, kinematic and loading conditions and so on, which can hardly be reproduced in laboratory, such tests most frequently apply simplified conditions. The two most common wear tests are performed on Pin-on-Plate (PoP) or Pin-on-Disk (PoD) apparati.
Pin-on-Plate wear tests are used to study reciprocating sliding wear and fretting. In both cases, a pin is loaded against a flat surface in presence of reciprocating motion; depending on the stroke length, sliding and fretting conditions are distinguished, the former having a wide stroke, much longer than the contact width, and the latter a small stroke, typically of the order of magnitude of the contact width. A schematic view of the two wear tests is given in Figure 1(a). These tests are well described in the ASTM-G133 [1] and D4170 [2], respectively.
Pin-on-disk wear tests reproduce continuous sliding contact conditions between a rotating disk and pin located at a given distance from the disk axis, as represented in fig. Figure 1(b). For PoD wear tests, the standard commonly adopted is ASTM-G99 [1].
Both in PoP and PoD tests, two cases can occur: only one body wears out, i.e. the pin or the plate/disk, or both contact surfaces wear. According to the standards, the tests output are the wear volumes of each component measured directly (by means of gravimetric method) or, more often, computed from measurements of the worn scar and initial unworn pin geometry [1,2,3].
These experimental wear volumes are used to compute the wear coefficient k that characterizes the wear rate of the tribo-pair and is useful to compare material couplings, and also to calibrate numerical wear models [4,5,6,7]. The wear coefficient is commonly estimated according to the Archard wear law [8,9], i.e.
stating that the wear volume V is proportional to the normal load F and the sliding distance s. In wear tests, F and s are imposed whilst the worn mass or volume is measured, so that the wear coefficient can be calculated as
In the literature, Eq.(2) is used to estimate k from PoP and PoD wear tests, as reported in very recent experimental studies both on unilateral [4,10,11] and bilateral [5,12,13] wear. However, eq. (2) holds only for a translating body under constant load, and thus while it is correct for PoP wear tests, it provides only an approximation of k for PoD tests where a relative rotation pin-disk occurs. Nevertheless, to the best of author knowledge such equation has never been revised for the case of PoD wear tests.
This study compares PoP and PoD wear tests by means of both analytical and numerical FE models considering the real contact conditions and thus applying the Archard wear law in local instantaneous form. The final aim is to investigate how the rotational effect in PoD tests affects the estimation of k by varying the distance between pin axis and disk axis.
2. Materials and Methods
To compare the PoP and PoD wear tests, firstly Finite Element (FE) models were developed in Ansys®. Then, to clarify and generalize numerical results, the pertinent analytical relationships were formulated and solved in Matlab.
2.1. Test Cases
In the examined test cases, a cylindrical flat pin having radius rp=5 mm was assumed to be in contact with the plane surface of a plate or a disc (Figure 1 and Figure 2). For the PoD test, three conditions were examined differing in the distance Rd between the pin and disk axes, i.e. Rd= 1.25-2.5-5 rp . All the bodies were assumed to be made of structural steel, with Young modulus of 200 GPa and Poisson ratio equal to 0.3. However, only the pin was considered as affected by wear, with a wear coefficient k=1.25 10-7 mm2/N, value taken from the reference [14]. A 21 N normal load was applied to the pin and the same final sliding distance sf corresponding to 1 round of the highest Rd (sf=10 π rp=157.08 mm) was simulated for both PoP and PoD cases.
2.2. Finite Element Models
The FE simulations were performed in Ansys Workbench® 2023, taking advantage of the dedicated tool for wear assessment.
2.2.1. Geometry and Materials
To simplify the analyses, the plate and the disk were treated as rigid bodies, only the pin was considered deformable and affected by wear.
2.2.2. Mesh
The cylinder was meshed with 3D prism (WED6) elements by employing the "Sweep method" while the plate/disc surface with TRI3 (3 nodes linear triangle) 2D elements (Figure 3). The contact surfaces were meshed with CONTA174 and TARGE170 elements (see Sec. 2.2.3)
2.2.3. Contact and Wear Conditions
The contact was assumed as asymmetric as in this case only one body wears out. Moreover, the contact was simulated as frictionless, since the effect of the friction on wear is negligible as demonstrated in [15]. The analysis was solved by means of an Augmented Lagrange algorithm and the nodal-projected normal from contact was adopted as detection method with the cylinder and plate/disk as contact and target body, respectively.
The wear behavior was activated through an APDL command script inserted in the contact section and calling the Ansys tool which applies the Archard’s wear law in the generalized form
where H is the material hardness, k is the wear coefficient, and m and n exponents of pressure and sliding velocity, respectively. In particular, the command TB WEAR with option ARCD was used for applying Eq. (3); TBDATA command was used to set the parameters of Eq.(3) and the TBFIELD command for selecting the time instants during which activate or deactivate wear. Parameters were set as H=m=n=1, so that the traditional form of the Archard wear law was adopted according to Eq.(1).
2.2.4. Boundary Conditions
The vertical load of 21 N was applied to the pin, which could only translate in the vertical direction to keep the contact with the counterpart. The motion was applied to the plate and the disk a translation of s in the first case and a rotation
in the second one. This small displacement was considered to limit the computational time below 4 hours using a processor Intel(R) Xeon(R) Silver 4214R CPU @ 2.40GHz with 64 GB RAM.
2.2.5. Analysis Settings
The time increment was set to 10-4 to 2.5 10-2 s which allowed to discretize the arc length with the chord along the node trajectories with a maximum error of 0.1%, making the computational time affordable.
2.3. Analytical Approach
The analytical description of both tests moves from the local instantaneous form of the Archard’s law that can be rewritten as
relating the wear depth rate at a point P to the pressure p and sliding speed v both varying with time and point. The wear depth at a given instant is simply obtained integrating Eq.(4)
Accordingly, the wear volume is calculated as
In PoP tests, we can neglect the wear produced when reversing the motion and consider that the speed v is uniform and constant, therefore it can be written:
Rather interestingly, the wear volume in PoP tests does not depend pressure distribution, i.e. on the shape of the pin, flat-ended or hemispherical.
On the other hand, when we consider a PoD test, the relative motion of the pin with respect to the disk is a rotation about the disk axis of an angle
. Therefore, the sliding distance of each point P, , is proportional to the radial distance R of P from the disk axis (Figure 4), i.e.
Introducing the angular speed of the disc , assumed constant for simplicity, and substituting , Eq.(5) becomes
Another difference between PoP and PoD models is that in the latter one the wear volume depends on pressure distribution, as Eq.(7) cannot be exploited
In the present study, for a flat ended pin and a low friction, we assumed that in the initial part of the test, pressure remained almost uniform and the contact area constant. Therefore, the main difference between the two tests lies in the sliding distance.
Thus, we can write:
being with s equal to the arc described by the center of the pin.
Equation (11) requires further manipulation of the integral
with
With few passages, being
we obtain
The last term on the right is dimensionless, depends on the geometry of the system and is typically omitted in the literature, for example when using PoD tests for evaluating k. We can consider that as the ratio between PoD and PoP wear volumes, when a uniform pressure distribution is considered. It can be expressed as a function of a dimensionless geometric parameter
Its trend is shown is Figure 5 for , that is a limited range of practical values of . It is preferred to its inverse that should be considered in the field [1,∞). It is worth stressing that when , i.e. , the PoD →PoP.
From Eq. (16), it can be observed that the ratio is maximum when γ =1, and g(1)=32/(9 π) ≅ 1.132, meaning that the PoD produced higher wear volumes than PoP over the same sliding distance when pressure can be considered uniform, as in the initial part of a test, until wear affects the geometry of the contact surface.
The above equations were implemented in a Matlab® script for estimating the wear volumes with a constant pressure approximation and compare it with FE results in a short sliding distance.
3. Results
The FE simulations of the four cases, one PoP and three track radii PoD, were completed and as results the wear volumes and the maps of the contact pressure and wear depth over the contact area were analyzed. They are discussed for increasing values of the parameter γ, considering that represents the PoP test, the PoD cases with decreasing Rd= 5, 2.5 and 1.25 rp respectively.
Figure 6 shows the trends of the wear volumes over the sliding distance, obtained from FE analyses. It can be observed that they are almost linear and that the PoP case has the lowest volume, slightly smaller than PoD γ=0.2−0.4, while the PoD γ=0.8 (smallest radius Rd) has the highest one.
Differences in FE and analytical volumes can be easily appreciated from histograms in Figure 7 (a), where volumes are compared considering the final instant. A good agreement between the two approaches can be observed, with differences below 0.8% with the exception of the case γ=0.8 for which we obtained 2.4% deviation. Figure 7 (b) shows that the error increases with the sliding distance, particularly for the PoD case with γ=0.8, i.e. the lowest track radius. The reason for this highest error can be explained with the approximation of uniform contact pressure at the base of the analytical approach, as cleared below.
The maps of the contact pressure at the same final sliding distance for the four examined cases are reported at the top of Figure 8. The maps of each case are shown both on the same scale (first row) and in its own full scale (second row) to highlight the main characteristics and ease the discussion. For the PoP test, the contact pressure was uniform over the contact area (with p=0.255 MPa), whilst it was not so in the PoD cases, which showed a pressure gradient, being the pressure higher in the region closer to the disk axis (at Rm), and lower far from it (at RM). Additionally, the pressure gradient was more marked for higher values of , that means with the pin closer to the disk axis.
In the case of PoP, the uniform contact pressure combined to uniform sliding velocity/distance over the pin surface, caused a uniform wear depth, as shown at the bottom of Figure 8. Differently, a gradient of the wear depth was predicted in all PoD cases, as opposite to the pressure one, with the minimum values at Rm and the maximum ones at RM. As for the pressure, the gradient of the wear depth increased with values. At the end of the test, the surface was no more planar.
In order to fully understand the contact pressure and wear maps for the PoD tests, it is necessary to consider what happens during the wear tests, and thus their evolution with the sliding distance. For brevity, only the case γ=0.8 is detailed, being the most interesting and peculiar one. The evolution of pressure and wear depth during the simulation are reported in Figure 9 for 4 instants: in addition to the initial/unworn and final conditions, data at 1/3 and 2/3 sf were considered. It can be observed that initially, pressure was uniformly distributed, as in the PoP case. During the test, a redistribution of contact pressure occurred, which can be explained considering the different sliding distance of the pin points: those farther from the disk axis describe a longer trajectory with respect to those nearer to the axis. Consequently, the wear rate is higher on the outer part of the pin surface, which becomes curved, and this causes a pressure reduction. The trend of the maximum and minimum values of the contact pressure and the wear depth (hmax, hmin) with the sliding distance is well depicted in Figure 10. It can be observed that at the final sliding distance, the percentage pressure difference (pmax-pmin) with respect to the initial value p was of 57.6%, while the percentage difference of the wear depth (hmax-hmin) with respect to its average value (hmax + hmin)/2 was of 141%.
This effect for which a higher sliding distance causes a reduction of pressure is expected to reach an equilibrium in a kind of stationary wear evolution that is not caught in the present simulation.
Similar considerations hold for all the PoD cases but in a more limited way, as proven by data in Table 1.
4. Discussion
The wear behavior of a given material couple is typically described by a wear coefficient k that can be estimated from wear volume measurements in PoP and PoD tests, using the Archard wear law k=V/(F s) (Eq.(2)).
The present study provides an analytical proof that Eq.(2) can be correctly applied to the PoP case, i.e. of a translating body under load, but is an approximation for the PoD one. Thus, differences between the two tests are deepened with an analytical and a FE approach, examining wear volume, wear maps and contact pressure in the first part, i.e. the transient phase, of the wear test. We considered four cases: one PoP and three PoD models with the pin placed at three different radii from the disc axis. Introducing a parameter , we distinguished the four cases as FE analyses showed that wear volumes at the end of the test were different, increasing with from 4.09, 4.14, 4.18 to 4.36 10-4 mm3 for the same load and sliding distance. These differences demonstrate that the use of Eq.(2) for PoD tests introduces an error which increases by reducing the distance between the pin and the disk axis (up to 6% for ), whilst tends to zero when the pin is far away from the disk axis, i.e. in conditions similar to the PoP. By means of an analytical approach, assuming a uniform pressure distribution also for PoD cases in the transient phase, a nondimensional function g( was introduced which provides an estimation of the wear volume in PoD vs. PoP for the same load and sliding distance. It can be approximated with a quadratic function
stating that the ratio is higher for higher , i.e. when the pin is closer to the disk axis.
Analytical and FE approaches provided very similar wear volumes with percentage differences lower that 2.4%, higher for the PoD with , i.e. when the pin is placed near to the disk axis. Such differences are caused by the assumption of a uniform contact pressure adopted in the analytical formulation, while plots in Figure 9 clearly show that this is true at the beginning but it is not the case at the end of the test, as confirmed by Table 1. However, in the present case such an assumption affects wear estimation only marginally.
It is worth stressing that the standard ASTM G99 suggests a track radius within the range 12.5-17.5 mm for a pin with , as in the present case, corresponding to 0.286
Actually, the standard suggests a spherical head for the pin so that the contact area is very small (initially) and the case is equivalent to . Until wear causes an important increment of the contact area, for a PoD test with a spherical pin Eq.(2) can be applied. An estimation of the extension of the contact area may be obtained through the simple formulation proposed by these authors in [16,17].
The FE investigation of the evolution of pressure and wear depth clarified the role of the sliding distance on pressure redistribution with time. It was observed that contact pressure, initially uniform, tends to increase close to the disk axis and decrease far from it, while its integral remains the same, corresponding to the external load. Indeed, the pin surface undergoes to higher sliding distances in the outer region, compared to the inner one, and thus higher wear. Similarly wear depth evolves but in an opposite way with respect to pressure gradient. Interestingly, the pin surface is no more planar, although, thanks to elastic deformations, it comes fully into contact with the disk surface under load.
However, as mentioned above, this study is focused on the transient phase of the wear process while a steady phase is expected to be achieved at longer sliding distance. Since very small time increments were necessary to describe the circular trajectories of points, the computational cost of the proposed simulations was rather high. To complete the study with the steady state phase, strategies for accelerating simulations are going to be pursued.
In conclusion, the present study highlights the need to deepen the methodology for k estimation, not described in standard ASTM [1,3]. The rotational effect in PoD tests, which varies with the distance between pin axis and disk axis and even change during the wear process in case of spherical pin tip, should be considered in k estimation. Its neglection could explain in part the high data dispersion of k values reported in experimental studies. The hypothesis of a constant k should be taken with cautions even for metallic materials traditionally used in tribo-couples, and the real contact conditions should be considered in its estimation particularly for plastic materials such as the UHMWPE characterized by cross-shearing [7]. Such aspects are going to be tackled in future studies.
Author Contributions
Conceptualization, F.DP. and L.M.; methodology, F.DP. and L.M.; software, A.DP.; validation, F.DP.; formal analysis, F.DP. and L.M.; data curation, A.DP.; writing—review and editing, F.DP. and L.M.; funding acquisition, F.DP. All authors have read and agreed to the published version of the manuscript.
Funding
National Recovery and Resilience Plan (PNRR), Mission 4, Component 2, Investment 1.4, “National Centre for HPC, BigData and Quantum Computing”, European Union-Next Generation EU.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- G02 Committee ASTM G99 - Test Method for Wear Testing with a Pin-on-Disk Apparatus.
- ASTM D4170-16 Standard Test Method for Fretting Wear Protection by Lubricating Greases.
- ASTM G133 - Standard Test Method for Linearly Reciprocating Ball-on-Flat Sliding Wear.
- Liu, H.; Chen, Y.; Wang, X.; Guo, Y.; Xue, W.; Li, D.; Chen, X.-Q. Correlating Numerical Modelling with Experimental Studies to Quantify the Wear Resistance of High-Carbon Chromium Bearing Steel in Mixed Lubrication. Tribology International 2023, 188, 108819. [Google Scholar] [CrossRef]
- Bastola, A.; McCarron, R.; Shipway, P.; Stewart, D.; Dini, D. Experimental and Numerical Investigations of Sliding Wear Behaviour of an Fe-Based Alloy for PWR Wear Resistance Applications. Wear 2024, 540–541, 205186. [Google Scholar] [CrossRef]
- Mattei, L.; Di Puccio, F. How Accurate Is the Archard Law to Predict Wear of UHMWPE in Hard-on-Soft Hip Implants? A Numerical and Experimental Investigation. Tribology International 2023, 187, 108768. [Google Scholar] [CrossRef]
- Mattei, L.; Di Puccio, F.; Joyce, T.J.; Ciulli, E. Numerical and Experimental Investigations for the Evaluation of the Wear Coefficient of Reverse Total Shoulder Prostheses. Journal of the Mechanical Behavior of Biomedical Materials 2016, 55, 53–66. [Google Scholar] [CrossRef] [PubMed]
- Archard, J.F. Contact and Rubbing of Flat Surfaces. Journal of Applied Physics 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Lancaster, J.K. The Influence of Substrate Hardness on the Formation and Endurance of Molybdenum Disulphide Films. Wear 1967, 10, 103–117. [Google Scholar] [CrossRef]
- Matkovič, S.; Pogačnik, A.; Kalin, M. Wear-Coefficient Analyses for Polymer-Gear Life-Time Predictions: A Critical Appraisal of Methodologies. Wear 2021, 480–481, 203944. [Google Scholar] [CrossRef]
- Borawski, A. Testing Passenger Car Brake Pad Exploitation Time’s Impact on the Values of the Coefficient of Friction and Abrasive Wear Rate Using a Pin-on-Disc Method. Materials 2022, 15, 1991. [Google Scholar] [CrossRef] [PubMed]
- Bastola, A.; Stewart, D.; Dini, D. Three-Dimensional Finite Element Simulation and Experimental Validation of Sliding Wear. Wear 2022, 504–505, 204402. [Google Scholar] [CrossRef]
- Reichelt, M.; Cappella, B. Large Scale Multi-Parameter Analysis of Wear of Self-Mated 100Cr6 Steel – A Study of the Validity of Archard’s Law. Tribology International 2021, 159, 106945. [Google Scholar] [CrossRef]
- Põdra, P.; Andersson, S. Simulating Sliding Wear with Finite Element Method. Tribology International 1999, 32, 71–81. [Google Scholar] [CrossRef]
- Mattei, L.; Di Puccio, F. Frictionless vs. Frictional Contact in Numerical Wear Predictions of Conformal and Non-Conformal Sliding Couplings. Tribol Lett 2022, 70, 115. [Google Scholar] [CrossRef]
- Di Puccio, F.; Mattei, L. Simple Analytical Description of Contact Pressure and Wear Evolution in Non-Conformal Contacts. Tribology International 2023, 178, 108084. [Google Scholar] [CrossRef]
- Di Puccio, F.; Mattei, L. Further Validation of a Simple Mathematical Description of Wear and Contact Pressure Evolution in Sliding Contacts. Lubricants 2023, 11, 230. [Google Scholar] [CrossRef]
Figure 1.
Schemes of Pin-on-Plate (PoP) (a) and Pin-on-Disk (PoD) (b) wear tests.
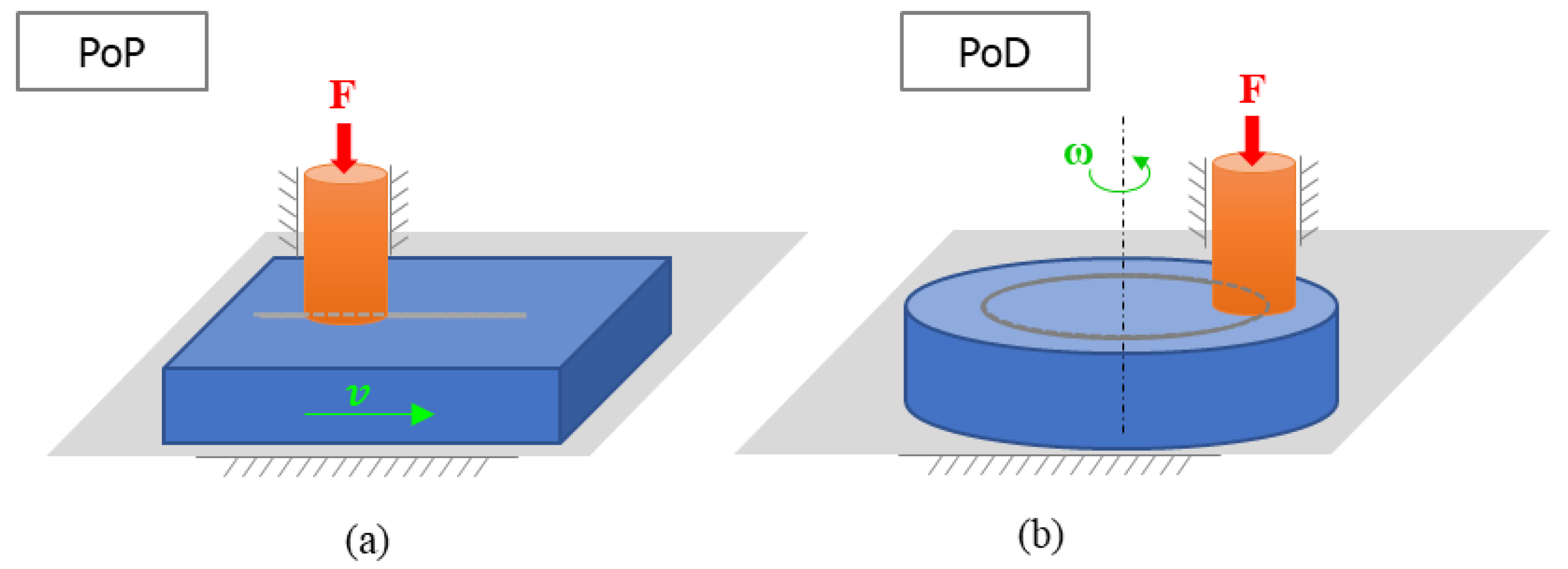
Figure 2.
Schemes of the simulated PoP (a) and PoD (b) wear tests with the boundary conditions adopted in respective FE models.
Figure 2.
Schemes of the simulated PoP (a) and PoD (b) wear tests with the boundary conditions adopted in respective FE models.
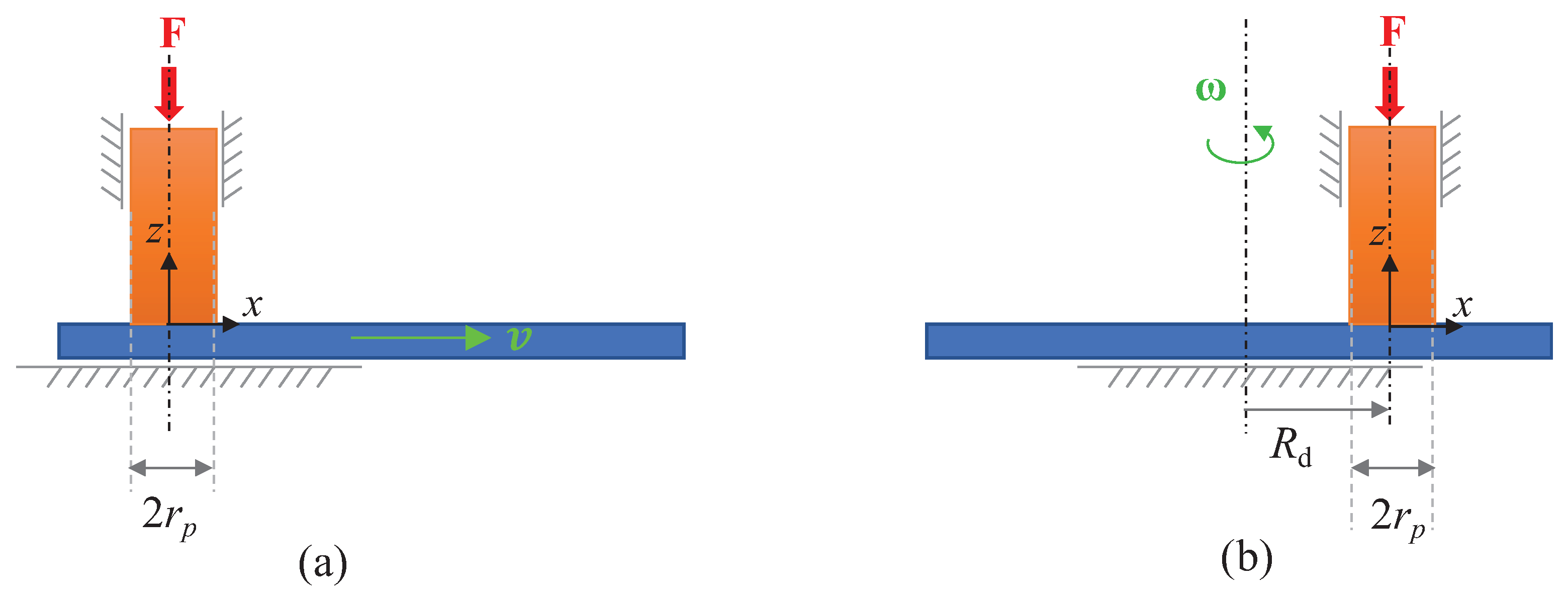
Figure 3.
FE model of PoP (a) PoD (b) wear tests and details on the mesh (c).
Figure 4.
Main geometrical parameters used in Equations (9-15).
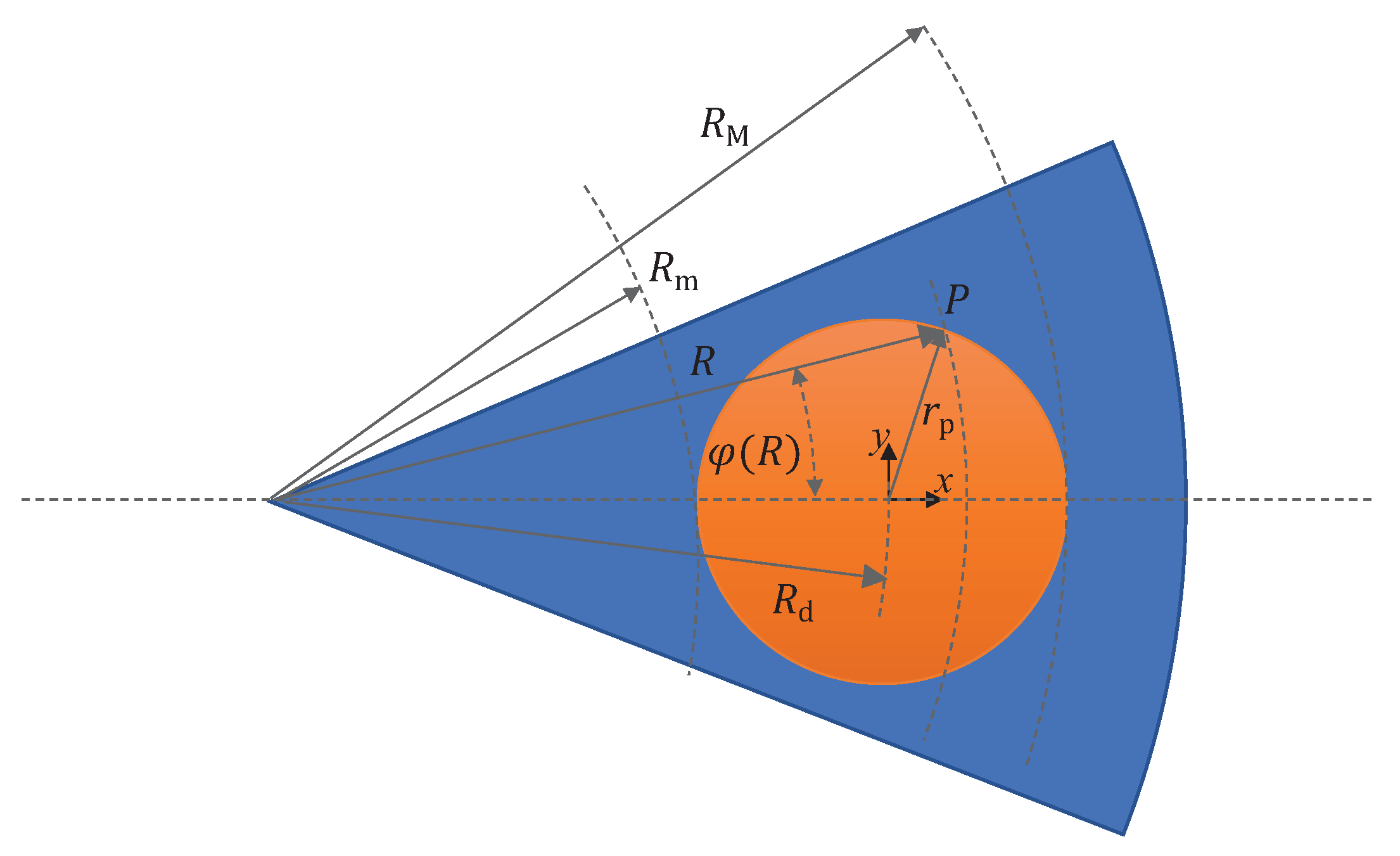
Figure 5.
Trend of the function of Equation (14).
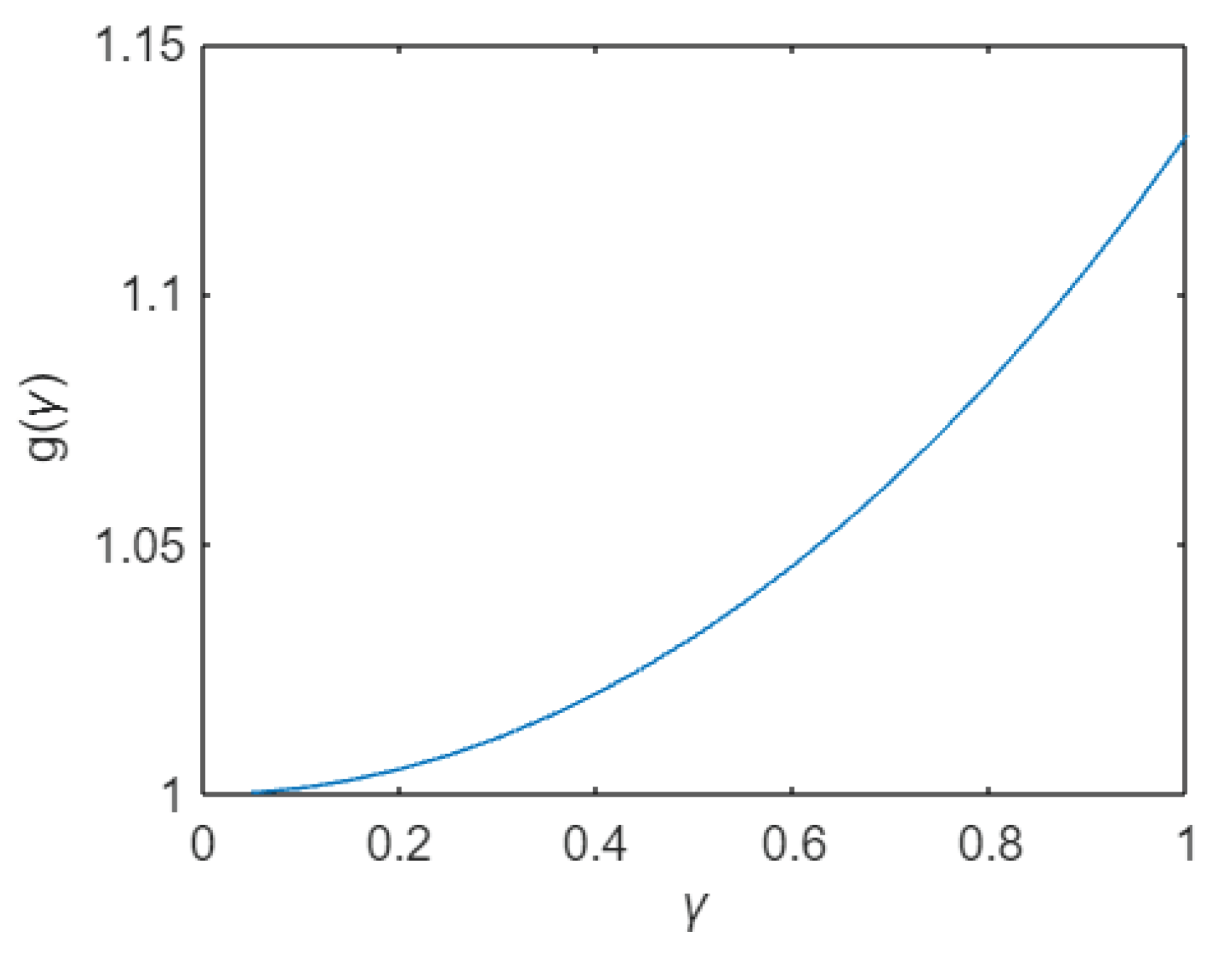
Figure 6.
Wear volumes predicted by the FE vs. sliding distance, sf=157.08 mm.
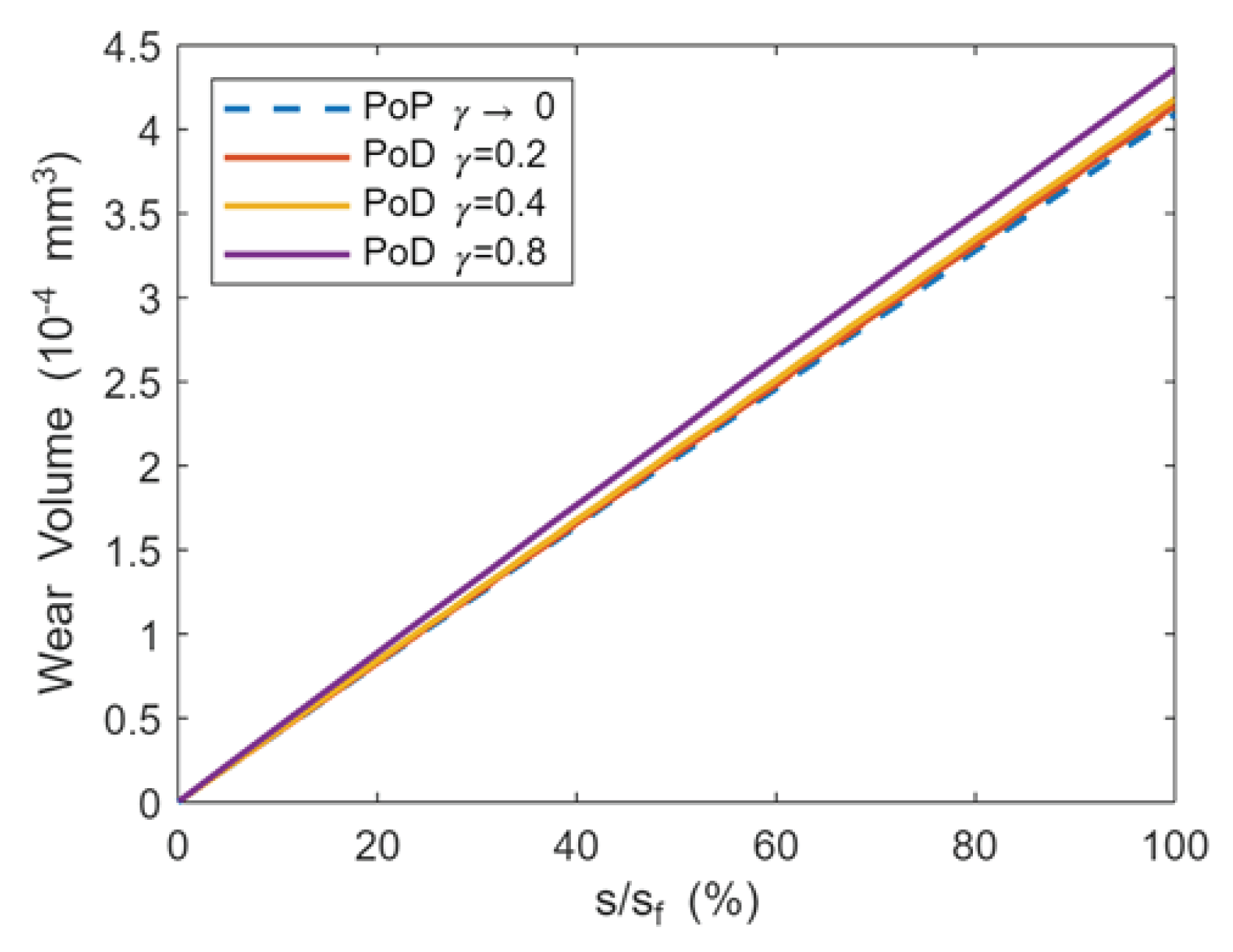
Figure 7.
Comparison of the wear volumes predicted by the FE wear models and analytical formulations: (a) histograms of the final wear volumes, (b) errors in volume estimations between FE and analytical results. Final sliding distance sf=157.08 mm.
Figure 7.
Comparison of the wear volumes predicted by the FE wear models and analytical formulations: (a) histograms of the final wear volumes, (b) errors in volume estimations between FE and analytical results. Final sliding distance sf=157.08 mm.
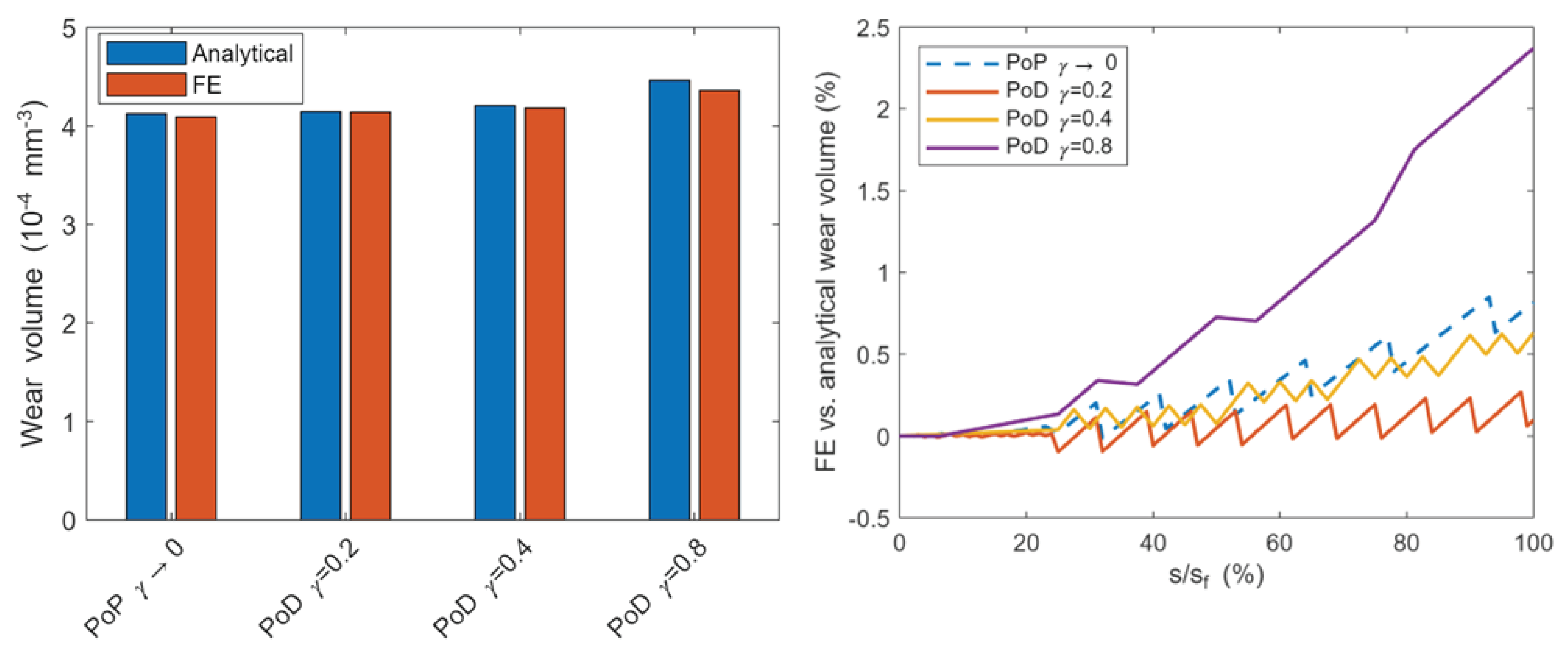
Figure 8.
Maps of the contact pressure and wear depth in the four examined cases at the final sliding distance sf=157.08 mm. For both pressure and wear depth, first row: all the cases are plotted with the same color band; second row: each plot in its color band. ( correspond to decreasing Rd= 5, 2.5 and 1.25 rp, respectively).
Figure 8.
Maps of the contact pressure and wear depth in the four examined cases at the final sliding distance sf=157.08 mm. For both pressure and wear depth, first row: all the cases are plotted with the same color band; second row: each plot in its color band. ( correspond to decreasing Rd= 5, 2.5 and 1.25 rp, respectively).
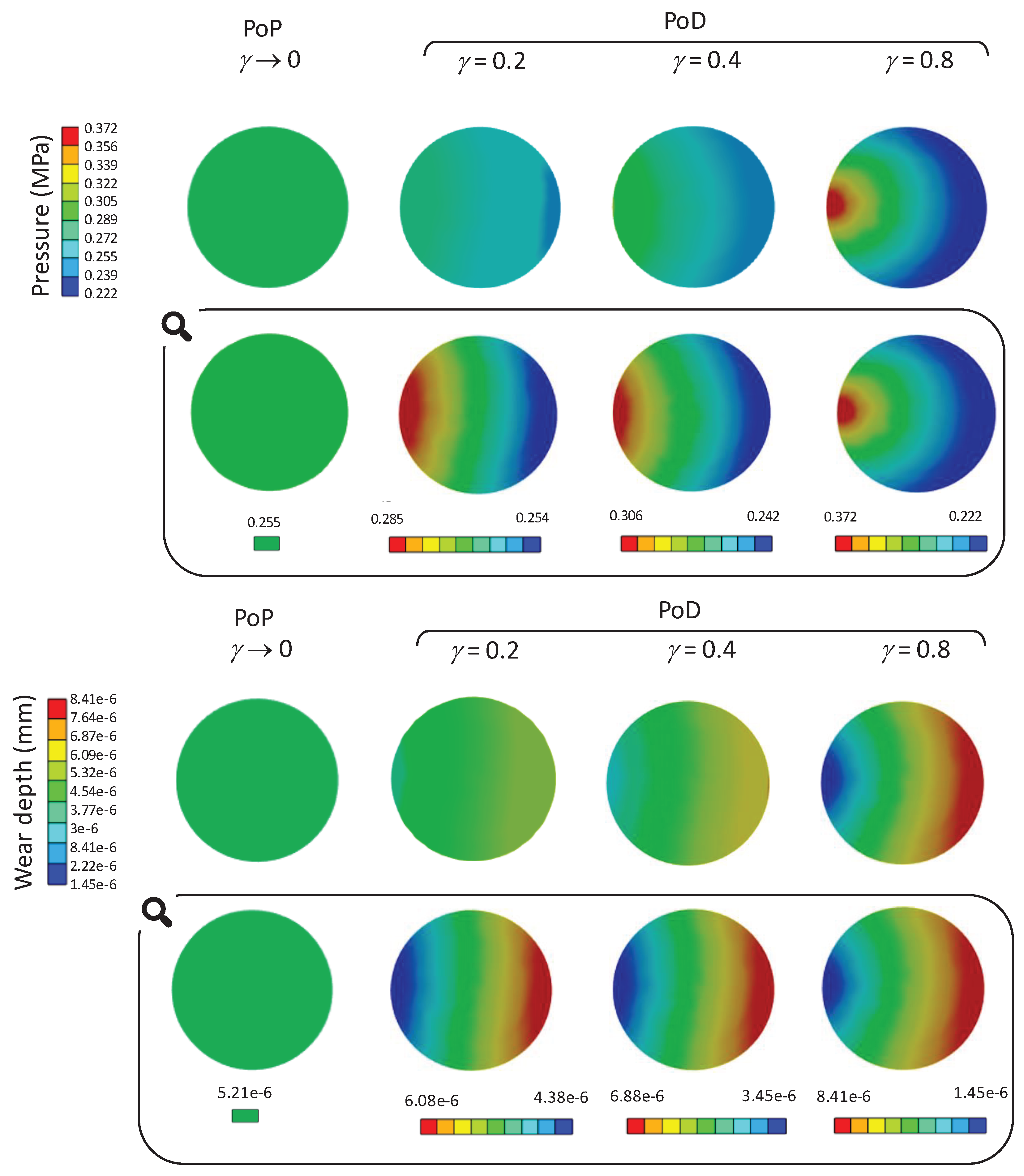
Figure 9.
Evolution of the contact pressure (first row) and the wear depth (second row) over the contact area, with increasing sliding distance, from the left to the right. The final sliding distance sf=157.08 mm corresponds to 100%. (PoD case with =0.8.)
Figure 9.
Evolution of the contact pressure (first row) and the wear depth (second row) over the contact area, with increasing sliding distance, from the left to the right. The final sliding distance sf=157.08 mm corresponds to 100%. (PoD case with =0.8.)
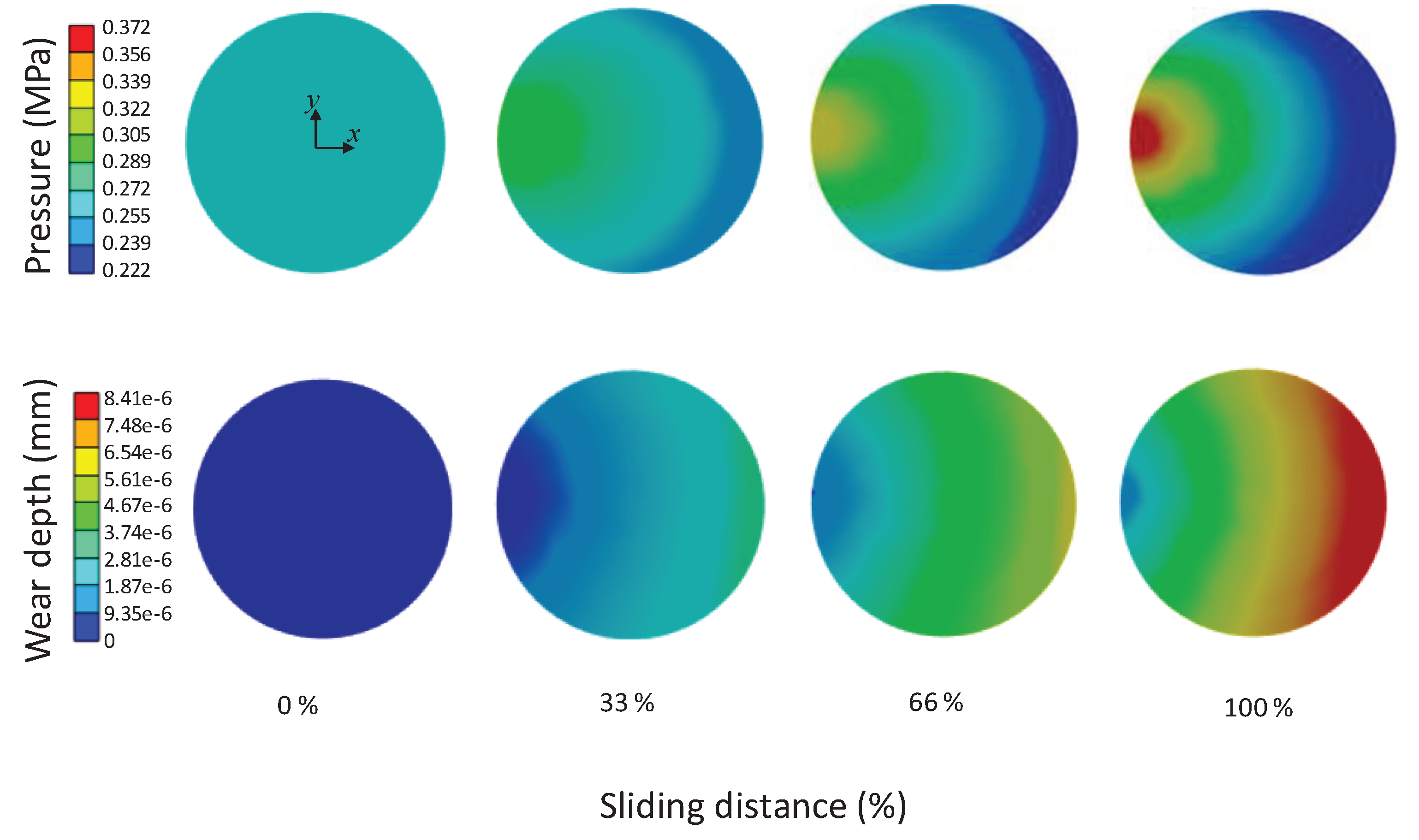
Figure 10.
Evolution of the minimum and maximum wear depth and contact pressure with the sliding distance. Pressure is maximum when the wear depth is minimum and viceversa. (PoD case with =0.8.)
Figure 10.
Evolution of the minimum and maximum wear depth and contact pressure with the sliding distance. Pressure is maximum when the wear depth is minimum and viceversa. (PoD case with =0.8.)
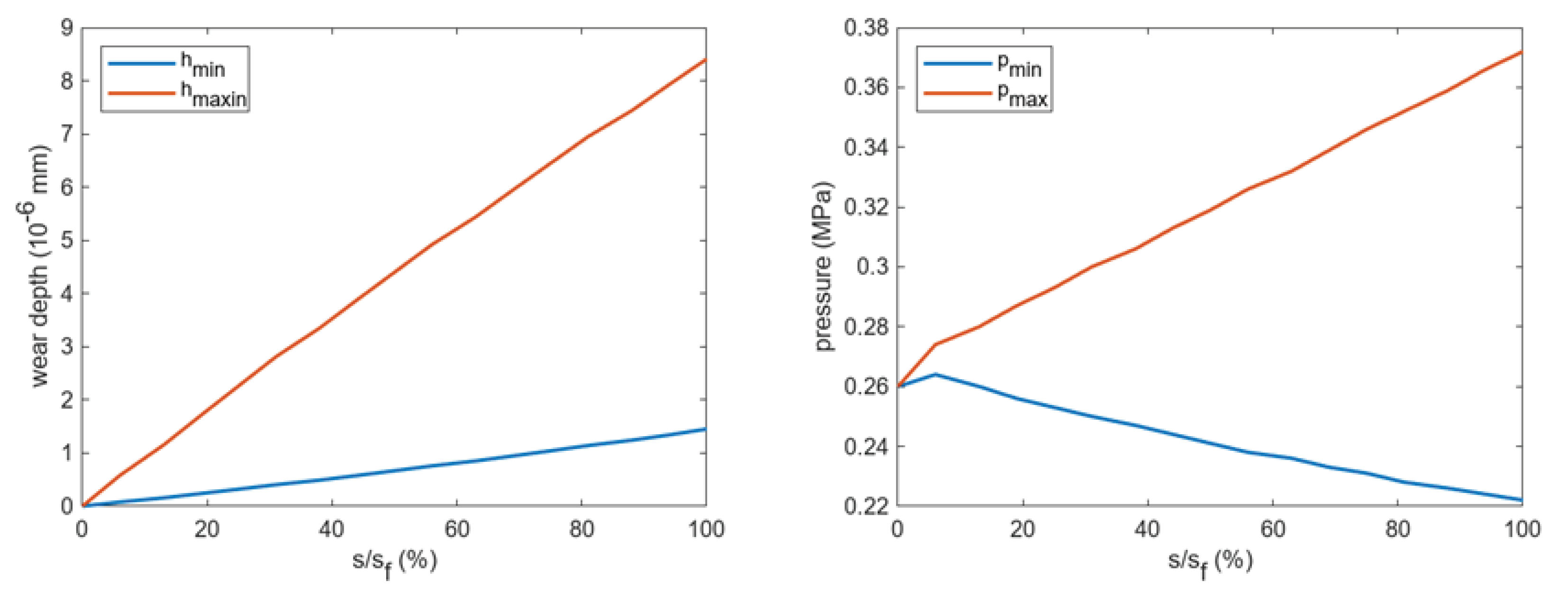
Table 1.
Gradient of pressure and wear depth at the end of the simulation for PoD cases. p is the initial contact pressure.
Table 1.
Gradient of pressure and wear depth at the end of the simulation for PoD cases. p is the initial contact pressure.
| g | 100 | 100 |
| 0.2 | 12.1% | 32.5% |
| 0.4 | 25% | 66.4% |
| 0.8 | 57.6% | 141% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated







