Prerpints.org logo
Preprint
Article

New Goodness-of-Fit Tests for the Kumaraswamy Distribution: A Simulation Study

Altmetrics

Downloads

106

Views

35

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

10 March 2024

Posted:

11 March 2024

You are already at the latest version

Alerts
Abstract
The two-parameter distribution introduced by Kumaraswamy (1980) is a very flexible alternative to the Beta distribution with the same (0,1) support. Originally proposed in the field of hydrology, it has subsequently received a good deal of positive attention in both the theoretical and applied statistics literatures. Interestingly, the problem of testing formally for the appropriateness of the Kumaraswamy distribution appears to have received little or no attention to date. To fill this gap, in this paper we apply the “biased transformation” methodology proposed by Raschke (2009) to several standard goodness-of-fit tests based on the empirical distribution function. A simulation study reveals that these (modified) tests perform well in the context of the Kumaraswamy distribution, in terms of both low size distortion, and respectable power. In particular, the “biased transformation” Anderson-Darling test dominates the other tests that are considered.
Keywords: 
Subject: Computer Science and Mathematics  -   Probability and Statistics

1. Introduction

The two-parameter distribution introduced by Kumaraswamy (1980) is a very flexible alternative to the Beta distribution with the same (0,1) support. Originally proposed for the analysis of hydrological data, it has subsequently received a good deal of attention in both the theoretical and applied statistics literature. For example, Sundar and Subbiah (1989), Seifi et al. (2000), Ponnambalam et al. (2001), Ganji et al. (2006), and Courard-Hauri (2007 provide applications in various fields, and theoretical extensions are implemented by Cordeiro and Castro (2010), Bayer and Pumi (2017), and Cordeiro et al. (2018), among others.
The distribution function for a random variable, X, that follows the Kumaraswamy distribution is
F x = 1 − 1 − x a b         a ,   b > 0   ;   0 < x < 1 ,
which can be inverted to give the quantile function,
Q y ≡ F − 1 y = 1 − ( 1 − y ) 1 / b 1 / a         ;                 0 < y < 1
The corresponding density function is:
f x = a b x a − 1 ( 1 − x a ) b − 1
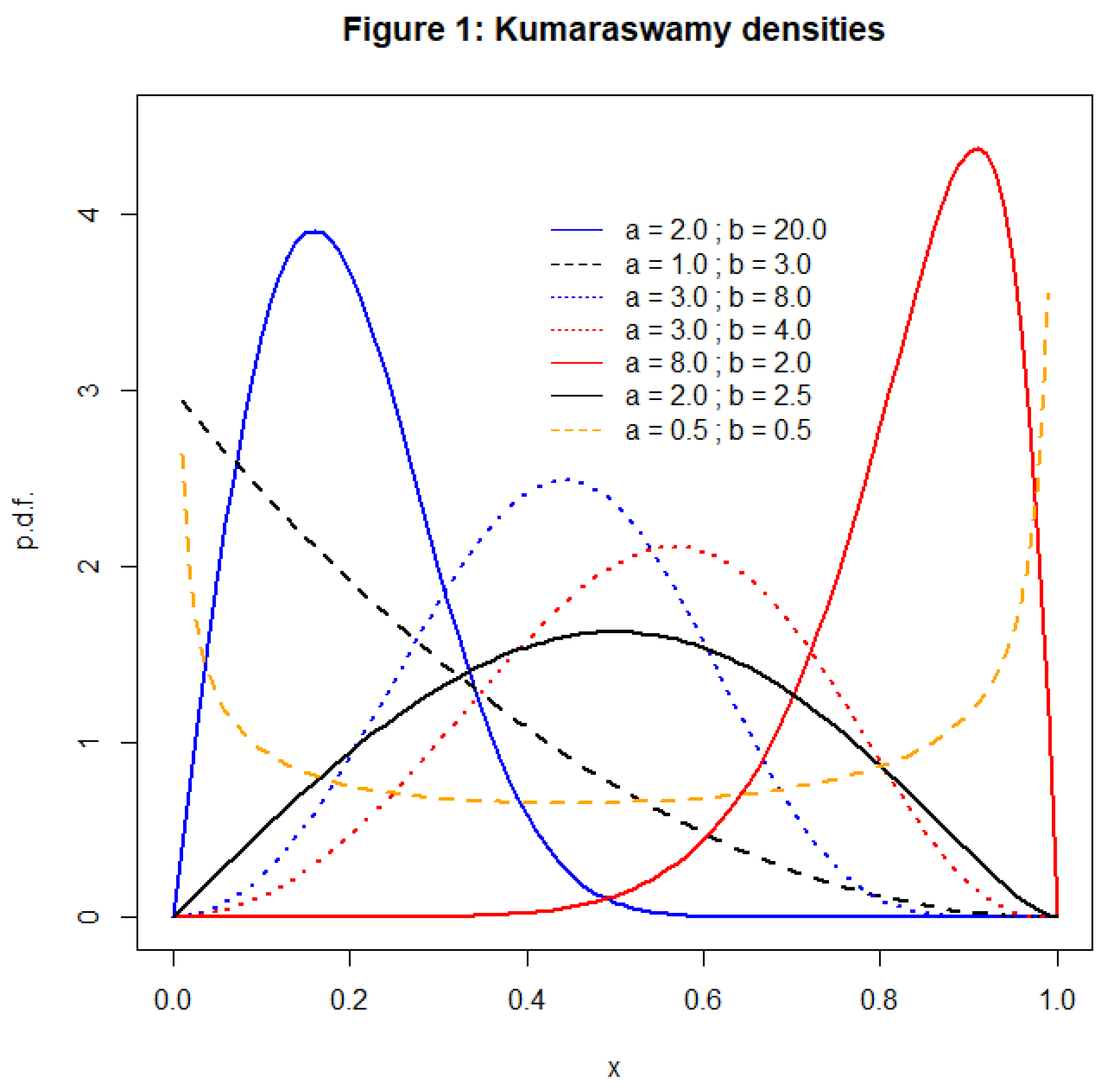
where ‘a’ and ‘b’ are both shape parameters. Some examples of the forms that this density can take are illustrated in Figure 1. In particular, in common with the beta density f x  is unimodal if a > 1  and b > 1 ; uniantimodal if  a < 1  and b < 1; increasing (decreasing) in x if a > 1  and b ≤   1 ( a ≤ 1  and b > 1; and constant if  a = b = 1 . Nadarajah (2008) notes that the Kumaraswamy distribution is in fact a special case of a generalized beta distribution proposed by McDonald (1984).
The r’th central moment of the Kumaraswamy distribution exists if r > − a , and is given by
E X r = b B 1 + r a , b
where B (. , .) is the complete beta function; and from (2), the median of the distribution is
m d = 1 − 0.5 1 b 1 a
See Jones (2009), Garg (2008), and Mitnik (2013) for a detailed discussion of the additional properties of the Kumaraswamy distribution.
These properties, compared with those of the beta distribution, are considered by many to give the Kumaraswamy distribution a competitive edge. For example, compared with the formula for the cumulative distribution function of the beta distribution, the invertible closed-form expression in (1) is seen by some as being advantageous in the context of computer-intensive simulation analysis, and modelling based on quantiles. The latter consideration is of particular interest in the context of regression analysis. Beta regression, based on the closed-form mean of that distribution, is well-established (e.g., Ferrari and Cribari-Neto, 2004), but robust regression based on the median is impractical. In contrast, the median of the Kumaraswamy distribution has the simple form given in (5), and so robust regression based on this distribution is straightforward. See Mitnik and Baek (2013) and Hamedi-Shahraki et al. (2021), for example. 
Interestingly, the problem of testing formally for the appropriateness of the Kumaraswamy distribution appears to have received little or no attention in the literature. Goodness-of-fit tests based on the empirical distribution function (EDF) are obvious candidates, but their properties are unexplored for this distribution. Raschke (2009) observed that such tests were unavailable for the beta distribution, and he proposed a “biased transformation” that he then applied to the test of Anderson and Darling (1952, 1954) to fill this gap. He also used this approach to construct an EDF test for the gamma distribution. Subsequently, Raschke (2011) provided extensive simulation results that favoured the use of the “bias-transformed” Anderson-Darling test over various other tests based on the EDF, such as those of Kuiper (1962), Watson (1961), the Cramér-von Mises test (Cramér,1928; von Mises, 1928) and the Kolmogorov-Smirnov test (Kolmogorov, 1933; Smirnov, 1948).
In this paper we apply Raschke’s methodology to the problem of constructing EDF goodness-of-fit tests for the Kumaraswamy distribution, and we compare the performances of several such standard tests in terms of both size and power. We find that Raschke’s method performs well in this context, with the Kolmogorov-Smirnov and Cramér-von Mises tests exhibiting the least size distortion, and the Anderson-Darling test being a clear choice in terms of power against a wide range of alternatives.
In the next section we introduce the “biased transformation” testing strategy suggested by Raschke and describe the five well-known EDF tests that we consider in this paper. Section 3 provides the results of a simulation experiment that evaluates the sizes and powers of the tests; and an empirical application is included in section 4. Some concluding remarks are presented in section 5.

2. Rasccke’s “Biased Transformation” Testing

In very simple terms, the procedure proposed by Raschke involves the use of a transformation that converts the problem of testing the null hypothesis that the data follow the Kumaraswamy distribution into one of testing the null hypothesis of normality. The latter, of course, is readily performed using standard EDF tests. More specifically, the steps involved are as follows (Raschke, 2011, p.80):
(i)
Assuming that the data, X, follow the Kumaraswamy distribution, estimate the shape parameters, a and b, using maximum likelihood (ML) estimation. See Lemonte (2011, pp. 1972-1973) and Jones (2009, pp.76-77) for details of the ML estimator for this distribution.
(ii)
Generate sample of Y, where Y = Φ − 1 ( F ( X ) ) , where Φ  is the distribution function for the standard Normal distribution, and F ( . )  is given in (1).
(iii)
Obtain the ML estimates of the parameters of the normal distribution for Y.
(iv)
Apply an EDF test for normality to the Y data.
(v)
For a chosen significance level, α, the null hypothesis, reject H 0 :  “X is Kumaraswamy” if H 0 ′ :  “Y is Normal” is rejected.
We consider five standard EDF tests for normality at step (iv), with the n values of the Y data in ascending order. See Stephens (1986) for more details. The first two of these tests are based on the two quantities D + = m a x ( i ) ⁡ [ i / n − F ( Y i ) ] , D − = m a x ( i ) ⁡ [ F Y i − ( i − 1 ) / n ] , and D = m a x ⁡ [ D + , D − ] . The Kolmogorov-Smirnov test statistic is D * = D ( n − 0.01 + 0.85 / n ) ; and Kuiper’s test statistic is V * = V ( n + 0.05 + 0.82 / n ) , where V = ( D + + D − ) . In each case, H 0 ′ is rejected if the test statistic exceeds the appropriate critical value.
Further, defining W 2 = ∑ i = 1 n [ F Y i − ( 2 i − 1 ) / ( 2 n ) ] 2 , the Cramér-von Mises test statistic is given by W 2 * = W 2 ( 1.0 + 0.5 / n ) ) . Similarly, if U 2 = W 2 − n { ∑ i = 1 n [ F Y i ] / n − 0.5 } 2 , the Watson’s test statistic is defined as U 2 * = U 2 ( 1.0 + 0.5 / n ) . Finally, the Anderson-Darling test statistic is defined as A 2 * = A 2 ( 1.0 _ 0.75 / n / + 2.25 / n 2 ) , where A 2 = − n − ∑ i = 1 n 2 i − 1 l n F Y i + ln ⁡ 1 − F Y n + 1 − i / n . Again, for these last three tests, the null hypothesis is rejected if the test statistic exceeds the appropriate critical value. In the next section we consider nominal significance levels of α = 5% and α =10%. The relevant critical values for the five tests are obtained from Table 4.7 of Stephens (1986, p.123), and appear in the last row of Table 1 in the next section.

3. A Simulation Study

Using Raschke’s “biased transformation” each of the five EDF tests for the Kumaraswamy null hypothesis has been evaluated in a simulation experiment, using the R (R Core Team, 2024). In all parts of the Monte Carlo study, 10,000 Monte Carlo replications were used. The ‘univariateML’ package (Moss and Nagler, 2022) was used for obtaining the ML estimates of the Kumaraswamy distribution in step (i), and the ‘GoFKernel’ package (Pavia, 2022) was used to invert the distribution in step (ii), in the last section. Random numbers for the truncated log-normal and triangular distribution were generated using the ‘EnvStats’ package (Millard and Kowarik, 2023); while those for the Kumaraswamy distribution itself were generated using the ‘VGAM’ package (Yee, 2023). The ‘trapezoid’ package (Hetzel, 2022), and the ‘truncnorm’ package (Mersmann et al., 2023) were used to generate random variates from the trapezoidal and truncated normal distributions respectively; and the R base ‘stats’ package was used for the beta variates. Finally, random variates from the truncated gamma distribution were generated using the ‘cascsim’ package (Bear et al., 2022); and those for the truncated Weibull distribution were obtained using the ‘ReIns’ package (Reynkens, 2023). The R code that was used for the simulation experiment is available for downloading from https://github.com/DaveGiles1949/r-code.
In the first part of the experiment we investigate the true “size” of each of the five EDF tests for various sample sizes (n) and a selection of values of the parameters (a and b) of the null distribution. As noted above, the tests are applied using nominal significance levels of both 5% and 10%, and we are concerned here with the extent of any “size distortion” that may arise.
The results obtained with six representative (a, b) pairs, and sample sizes ranging from n = 10 to n = 1,000 are shown in Table 1. The corresponding Kumaraswamy densities appear in Figure 1. The simulated sizes of all of the tests are very close to the nominal significance levels in all cases. This result is very encouraging, and provides initial support for adopting the “biased transformation” EDF testing strategy for the Kumaraswamy distribution.
Of the five tests considered, the Kolmogorov-Smirnov test performs best, in terms if least absolute difference between the nominal and simulated sizes, in 16 of the 36 cases at the 5% nominal level and 10 of the 36 cases at the 10% nominal level in Table 1. In the latter case it is out-performed by the Cramér-von Mises test, which dominates for 14 of the 36 cases that are considered. Further, there is a general tendency for simulated sizes of all of the tests to exceed the nominal significance levels when n ≤ 25 , while the converse is true (in general) when n ≥ 50 . An exception is when both of the distribution’s parameters equal 0.5, do the density is uniantimodal. These size distortions are generally small, but their direction has implications for the results relating to the powers of the tests.
The second part of the Monte Carlo experiment investigates the powers of the five tests against a range of alternative hypotheses. The latter all involve distributions on the (0 , 1) interval, with some distributions truncated accordingly. It should be noted that the simulated powers that are reported are “raw powers”, and are not “size-adjusted”. That is, the various critical values that are used are those reported at the end of Table 1. In practical applications, this is how a researcher would proceed.
The results of this part of the study are reported in Table 2. The same set of samples sizes (n) is used as in Table 1. A wide range of parameter values was considered for each of the alternative distributions, and a representative selection of the results that were obtained are reported here.
One immediate result that emerges is that, with only two exceptions, all of the tests are “unbiased” in all of the settings considered. That is, the power of the test exceeds the nominal significance level. The only exceptions that were encountered are when the alternative distributions is truncated log-normal, with both parameters equal to 0.5, and with a sample size of n = 10. This is a very encouraging result. A test that is “biased” has the unfortunate property that it rejects the null hypothesis less frequently when it is false than when it is true. Moreover, as the various tests are “consistent”, their powers increase as the sample size increases, for any given case.
The results in Table 2 also provide overwhelming support for the Anderson-Darling test in terms power. Interestingly, this result is totally consistent with the conclusion reached by Rashcke (2011) for the same “biased transformation” EDF tests in the context of the beta distribution. This may reflect that fact that the latter distribution and the Kumaraswamy distributions have densities that are capable of following very similar shapes, depending on the values of the associated parameters. Moreover, Stephens (1986) recommends the Anderson-Darling test over other EDF tests in general.
The Anderson-Darling test has the highest power among all five tests, in all cases, except for very small samples when the alternative distribution is Trapezoidal, with parameters m1 = 5/8, m2 = 7/8; n1 = n3 = 2; and for the truncated Weibull alternative with n = 10. Of the other tests under study, the Cramér-von Mises test ranks second in terms of power, followed by Watson’s test and the Kolmogorov-Smirnov test. We find that Kuiper’s test is the least powerful, in general.
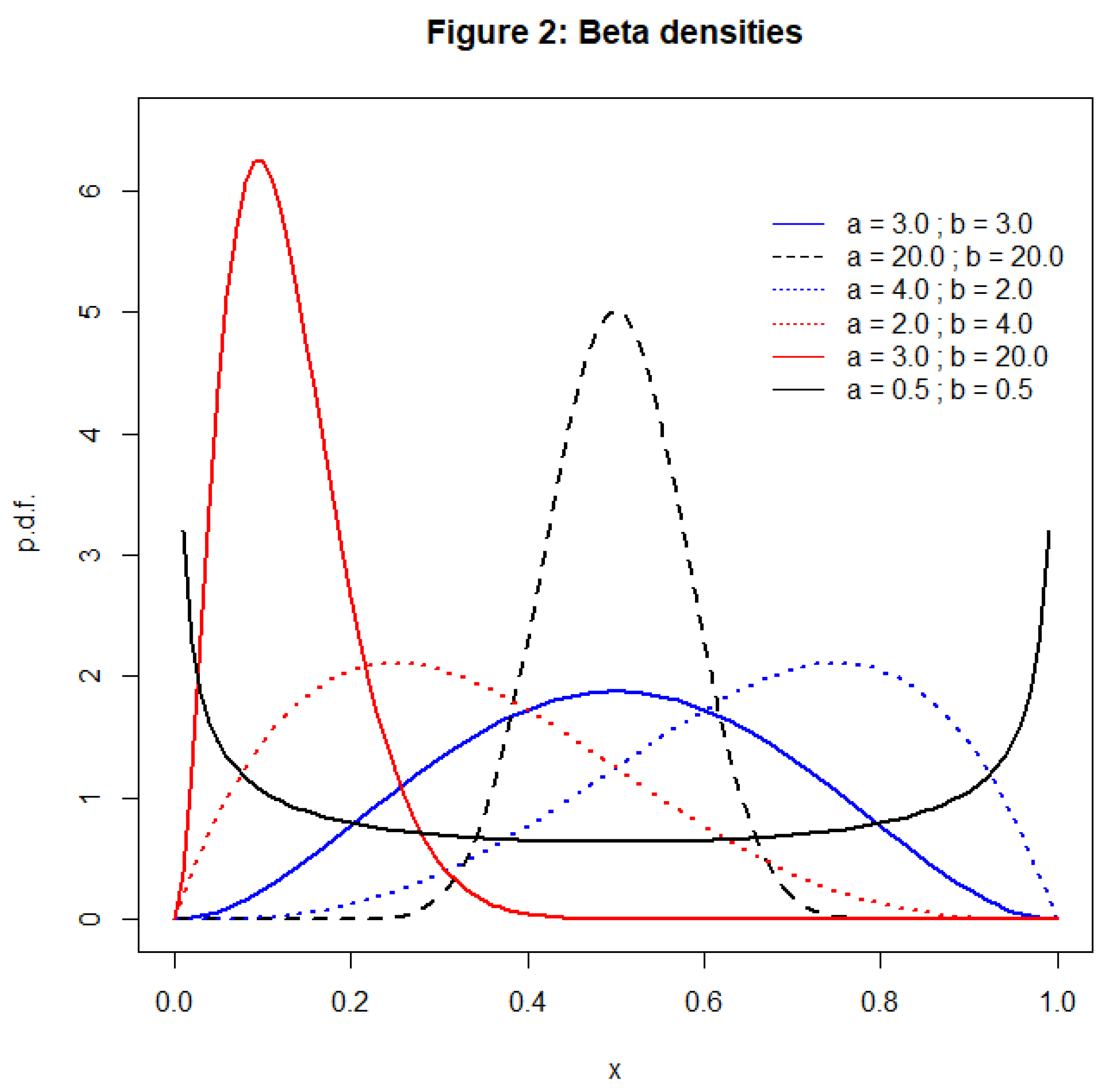
As was noted in section 1, the density for the Kumaraswamy distribution can take shapes very similar to those of the beta density, as the values of the two shape parameters vary in each case. The densities for the alternative beta distributions that are considered in the power analysis are depicted in Figure 2, and may be compared with the Kumaraswamy densities in Figure 1. This similarity suggests that there may be instances where the proposed EDF tests have relatively low power. If the data are generated by a beta distribution whose characteristics can be mimicked extremely closely by a Kumaraswamy distribution with the same, or similar, shape parameters, the tests may fail to reject the latter distribution. An obvious case in point is when the values of both of these shape parameters are 0.5, and the densities of both distributions are uniantimodal, though not identical. As can be seen in Figure 1, the density for the Kumaraswamy distribution is slightly asymmetric in this case, while its beta distribution counterpart is symmetric. The relatively low power of all of the EDF tests, even for n = 1,000, in this case can be seen in Table 2.
In view of these observations, we have considered a wide range of different values for the shape parameters associated with the beta distributions that are considered as alternative hypotheses in the power analysis of the EDF tests. A representative selection of the results appears in Table 2. There, we see that although the various tests have modest power when the data are generated by Beta (2, 4), Beta (4,2), and Beta (3,3) distributions, they perform extremely well against several other beta alternatives.

4. Empirical Applications

To illustrate the effectiveness of the “biased transformation” Anderson-Darling test, we present two applications with actual (economic) data. The R code and associated data files can be downloaded from https://github.com/DaveGiles1949/r-code.
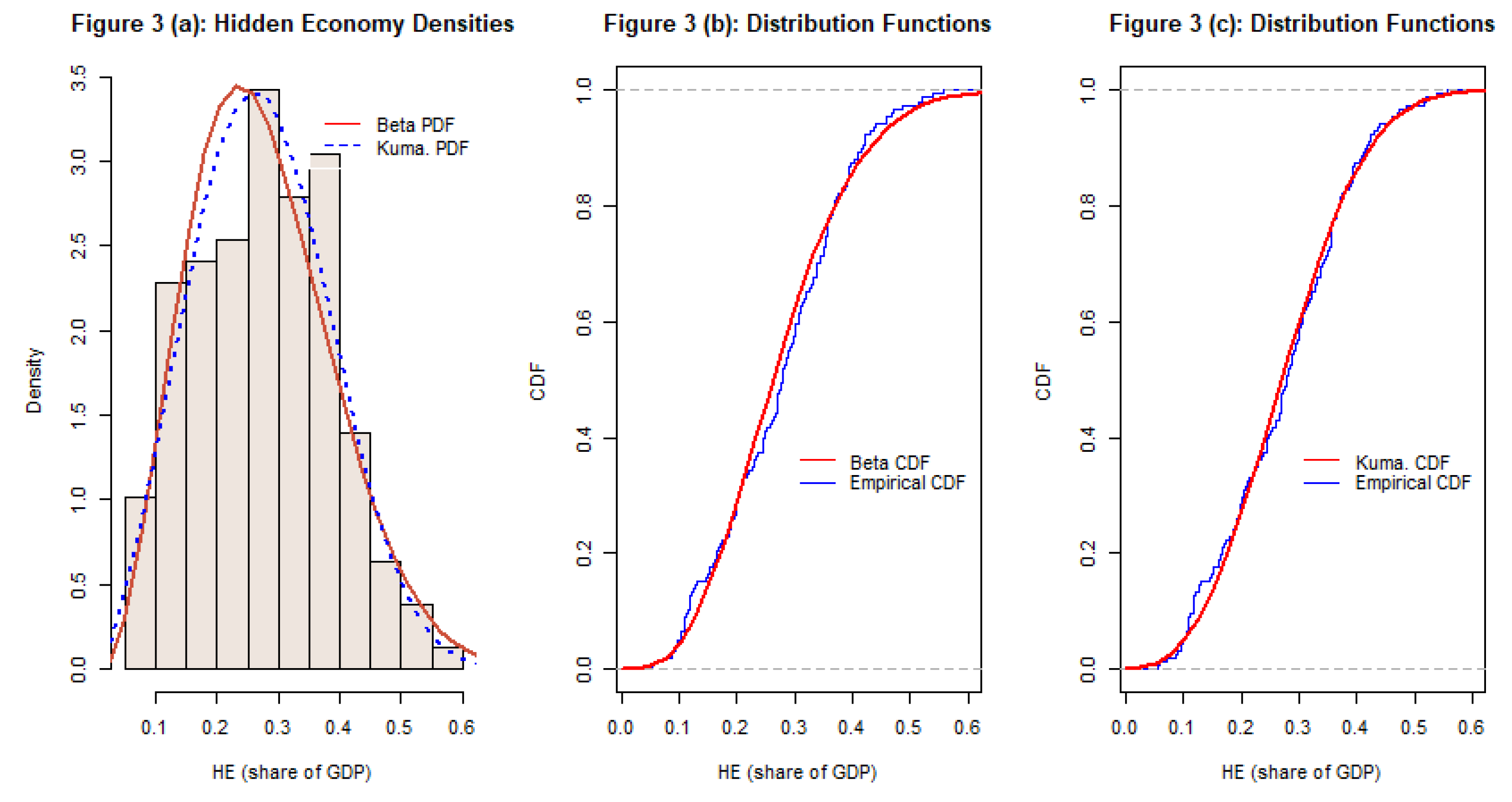
The first application uses data for the size of the so-called “hidden economy”, or “underground economy” for 158 countries in 2017. These data measure the size of the hidden economy (HE) relative to the value of Gross Domestic Product (GDP) in each country, and are reported by Medina and Schneider (2019). These ratios range from 0.0543 for Switzerland, to 0.5578 for Bolivia, with a mean of 0.2741 and a standard deviation of 0.1120.
When a Kumaraswamy distribution is fitted to the data, the estimates of the two shape parameters are 2.6065 and 20.7094. See Figure 3(a) and Figure 3(c). The value for the Anderson-Darling statistic is 0.5344, which is less than the 10% critical value of 0.631, and so we would not reject the hypothesis that the data follow a Kumaraswamy distribution. If a beta distribution is fitted to the data, the estimates of the two shape parameters are 3.8801 and 10.3253. See Figure 3(a) and Figure 3(b). The corresponding Anderson-Darling statistic (using the “biased transformation” and the beta distribution) is 1.0577. This exceeds the 5% critical value of 0.752, leading us to reject the hypothesis that the data follow a beta distribution. These two test results support each other.
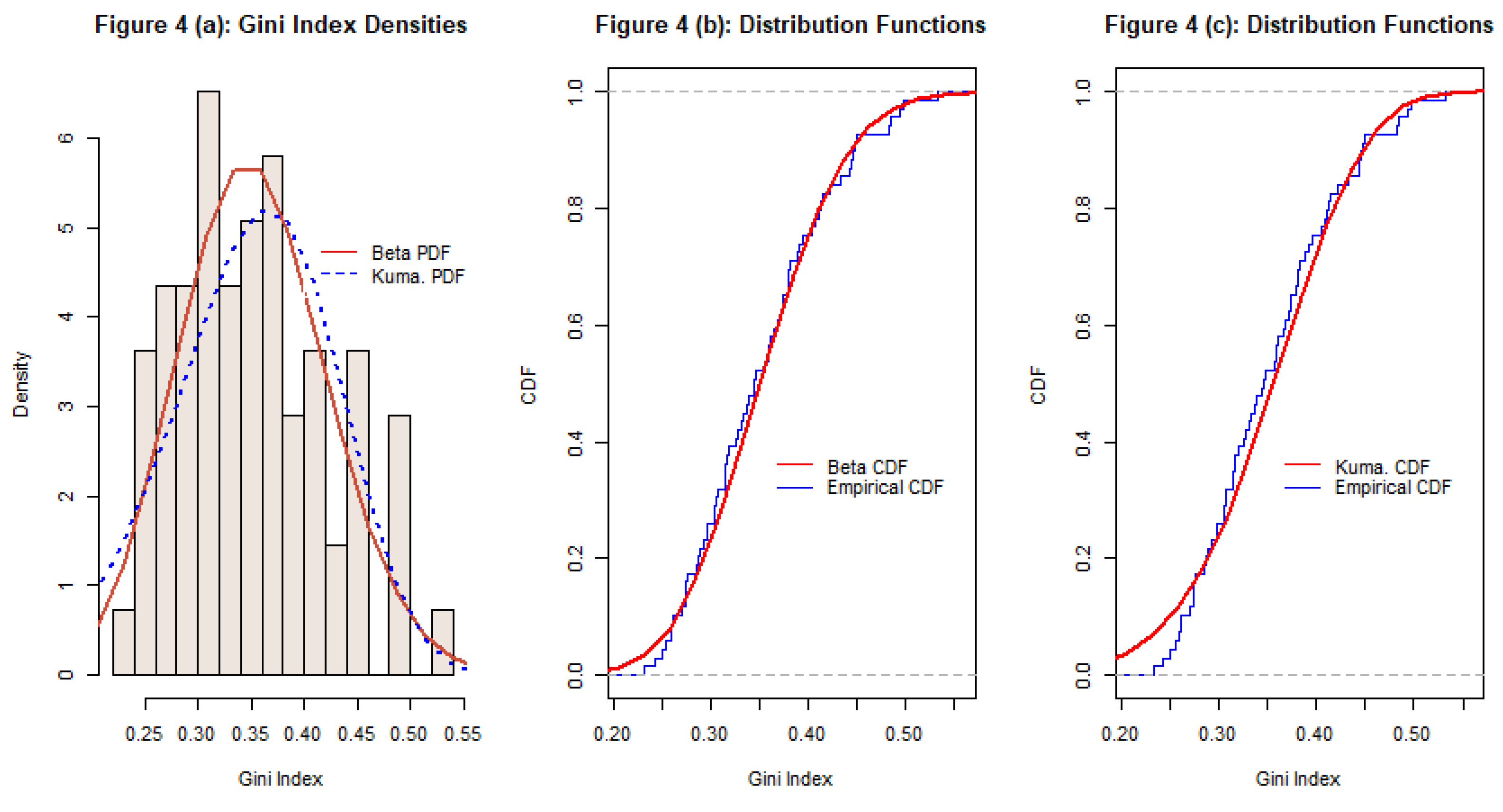
The second application uses a sample data for the Gini indices for income inequality in 69 countries in 2017, as reported by the World Bank (2024). The Gini index ranges in value from 0 (perfect equality) to 1 (perfect inequality). In our sample the smallest value is 0.2320 (for the Slovak Republic) and the largest value is 0.5330 (for Brazil). The sample mean and standard deviation are 0.3522 and 0.0701 respectively. When a Kumaraswamy distribution is fitted to the data the estimates of the two scale parameters are 5.3065 and 165.9645. See Figure 4(a) and Figure 4(c). The Anderson-Darling statistic is 0.8635, which exceeds the 5% critical value, suggesting a rejection of the hypothesis that the data are Kumaraswamy-distributed. Fitting a beta distribution to the data yields estimates of 16.6524 and 30.6073 for the shape parameters. The corresponding Anderson-Darling statistic is 0.3668, suggesting that the hypothesis that the data are beta-distributed cannot be rejected.

5. Conclusions

The Kumuraswamy distribution is an alternative to the beta distribution that has been applied in statistical studies in a wide range of disciplines. Its theoretical properties are well-established, but the literature is lacking a discussion of formal goodness-of-fit tests for this distribution. In this paper we have applied the “biased transformation” methodology suggested by Raaschke (2009) to various standard tests based on the empirical distribution function, and investigated their performance for the Kumaraswamy distribution.
The results of our simulation experiment that focuses on both the size and power of these tests can be summarized as follows. The “biased transformation” EDF goodness-of-fit testing strategy performs well for the Kumaraswamy distribution, against a wide range of possible alternatives, though it needs to treated with caution against certain beta distribution alternatives. In all cases, the Anderson-Darling test emerges clearly as the most powerful test of those considered, and is recommended for practitioners.

Acknowledgments

I am most grateful to Prof. Dr. Friedrich Schneider for supplying the data from Medina and Schneider (2109) in electronic format.

References

  1. Anderson, T. W. and D. A. Darling, 1952. Asymptotic theory of certain “goodness of fit” criteria based on stochastic processes. Annals of Mathematical Statistics, 23,193–212. [CrossRef]
  2. Anderson, T. W. and D. A. Darling, 1954. A test for goodness of fit. Journal of the American Statistical Association, 49,300–310.
  3. Bayer, F. M., D. M. Bayer, and G. Pumi, 2017. Kumaraswamy autoregressive moving average models for double bounded environmental data. Journal of Hydrology,555, 385-396. [CrossRef]
  4. Bear, R., K. Shang, H. You, and B. Fannin, 2022. Package ‘cascsim’. https://cran.r-project.org/web/packages/cascsim/cascsim.pdf.
  5. Cordeiro, G. M. and M. Castro, 2010. A new family of generalized distributions. Journal of Statistical Computation and Simulation, 81, 883–898. [CrossRef]
  6. Cordeiro, G. M., E. C. Machado, D. A. Botter, and M. C. Sandoval, 2018. The Kumaraswamy normal linear regression model with applications. Communications in Statistics – Simulation and Computation, 47, 3062-3082. [CrossRef]
  7. Courard-Hauri, D., 2007. Using Monte Carlo analysis to investigate the relationship between overconsumption and uncertain access to one's personal utility function. Ecological Economics, 64, 152-162. [CrossRef]
  8. Cramér, H., 1928. On the composition of elementary errors. Scandinavian Actuarial Journal, 1928, 13– 74. [CrossRef]
  9. Ferrari, S. and F. Cribari-Neto, 2004. Beta regression for modelling rates and proportions. Journal of Applied Statistics, 31, 799-815. [CrossRef]
  10. Ganji, A., K. Ponnambalam, K., and D. Khalili, 2006. Grain yield reliability analysis with crop water demand uncertainty. Stochastic Environmental Research and Risk Assessment, 20, 259–277. [CrossRef]
  11. Garg, M., 2008. On distribution of order statistics from Kumaraswamy distribution. Kyungpook Mathematical Journal, 48, 411–417. [CrossRef]
  12. Hamedi-Shahraki, S., A. Rasekhi, M. R. Eshraghian, M. S. Yekaninejab, and A. H. Pakpour, 2021. Kumaraswamy regression modelling for bounded outcome score. Pakistan Journal of Statistics and Operation Research, 17, 79-88. [CrossRef]
  13. Hetzel, J. T., 2022. Package ‘trapezoid’. https://cran.r-project.org/web/packages/trapezoid/trapezoid.pdf.
  14. Jones, M. C., 2009. Kumaraswamy’s distribution: A beta-type distribution with some tractability advantages. Statistical Methodology, 6, 70-81. [CrossRef]
  15. Kolmogorov, A., 1933. Sulla determinazione empirica di una legge di distribuzione. Giornale dell’Istituto Italiano degli Attuari, 4, 83–91.
  16. Kuiper, N. H., 1962. Tests concerning random points on a circle. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen A, 63, 38-47.
  17. Mises, R. E. von, 1928. Wahrscheinlichkeit, Statistik und Wahrheit. Julius Springer, Vienna.
  18. Kumaraswamy, P., 1980. A generalized probability density function for double-bounded random processes, Journal of Hydrology, 46, 79–88. [CrossRef]
  19. Lemonte, A. J., 2011. Improved point estimation for the Kumaraswamy distribution. Journal of Statistical Computation and Simulation, 81, 1971-1982. [CrossRef]
  20. Medina, L. and H. Schneider, 2019. Shedding light on the shadow economy: A global database and the interaction with the official one. http://doi.org/10.2139/ssrn.3502028.
  21. Kuiper, N. H., 1962. Tests concerning random points on a circle. Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen A, 63, 38-47. CESifo Working Paper No. 7981.
  22. McDonald, J. B., 1984. Some generalized functions for the size distribution of income. Econometrica, 52, 647–664. [CrossRef]
  23. Mersmann, O., H. Trautmann, D. Steuer, and B. Bornkamp, 2023. Package ‘truncnorm’. https://cran.r-project.org/web/packages/truncnorm/truncnorm.pdf.
  24. Millard, S. P. and A. Kowarik, 2023. Package ‘EnvStats’. https://cran.r-project.org/web/packages/EnvStats/EnvStats.pdf.
  25. Mises, R. E. von, 1928. Wahrscheinlichkeit, Statistik und Wahrheit. Julius Springer, Vienna.
  26. Mitnik, P. A., 2013. New properties of the Kumaraswamy distribution. Communications in Statistics – Theory and Methods, 42, 741-755.
  27. Mitnik, P. A. and S. Baek, 2013. The Kumaraswamy distribution: Median-dispersion re-parameterizations for regression modeling and simulation-based estimation. Statistical Papers, 54, 177-192. [CrossRef]
  28. Moss, J. and T. Nagler, 2022. Package ‘univariateML’. https://cran.r-project.org/web/packages/univariateML/univariateML.pdf.
  29. Nadarajah, S., 2008. On the distribution of Kumaraswamy. Journal of Hydrology, 348, 568–569. [CrossRef]
  30. Ponnambalam, K., A. Seifi, and J. Vlach, 2001. Probabilistic design of systems with general distributions of parameters. International Journal of Circuit Theory and Applications, 29, 527–536. [CrossRef]
  31. Pavia, J. M., 2022. Package ‘GoFKernel’. https://cran.r-project.org/web/packages/GoFKernel/GoFKernel.pdf.
  32. R Core Team, 2024. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. https://www.R-project.org/.
  33. Raschke, M., 2009. Biased transformation and its application in goodness-of-fit tests for the beta and gamma distribution. Communications in Statistics - Simulation and Computation, 38, 1870–1890. [CrossRef]
  34. Raschke, M., 2011. Empirical behaviour of tests for the beta distribution and their application in environmental research. Stochastic Environmental Research and Risk Assessment, 25, 79-89. [CrossRef]
  35. Reykens, T., 2023. Package ‘ReIns’. https://cran.r-project.org/web/packages/ReIns/ReIns.pdf.
  36. Smirnov, N., 1948. Table for estimating the goodness of fit of empirical distributions. Annals of Mathematical Statistics, 19, 279–281. [CrossRef]
  37. Seifi, A., Ponnambalam, K., & Vlach, J. (2000). Maximization of Manufacturing Yield of Systems with Arbitrary Distributions of Component Values. Annals of Operations Research, 99, 373-383. [CrossRef]
  38. Stephens, M. A., 1986. Tests based on EDF statistics. In: D’Augustino, R. B. and M. A. Stephens, eds., Goodness-of-Fit Techniques. Marcel Dekker, New York, 97-194.
  39. Sundar, V., and K. Subbiah, 1989. Application of double bounded probability density-function for analysis of ocean waves. Ocean Engineering, 16, 193–200. [CrossRef]
  40. Watson, G. S., 1961. Goodness-of-fit tests on a circle. I. Biometrika, 48, 109-114. [CrossRef]
  41. World Bank, 2024. World development indicators database. https://databank.worldbank.org/reports.aspx?source=2&series=SI.POV.GINI#.
  42. Yee, T., 2023. Package ‘VGAM’. https://cran.r-project.org/web/packages/VGAM/VGAM.pdf.
Preprints 101015 g001
Figure 1.
Figure 1.
Preprints 101015 g001
Preprints 101015 g002
Figure 2.
Figure 2.
Preprints 101015 g002
Preprints 101015 g003
Figure 3.
Figure 3.
Preprints 101015 g003
Preprints 101015 g004
Figure 4.
Figure 4.
Preprints 101015 g004
Table 1. Simulated sizes of the EDF tests *,**.
Table 1. Simulated sizes of the EDF tests *,**.
Preprints 101015 i001
Preprints 101015 i002
* Crit. = Upper-tail critical values when the normal distribution’s parameters are both estimated. Source: Stephens (1986, p.123), Table 4.7. ** K-S = Kolmogorov and Smirnov; C-M = Cramér and von Mises; A-D = Anderson and Darling.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated