Prerpints.org logo
Preprint
Article

Optimizing Well Placement in Carbon Capture and Storage (CCS): A Bayesian Optimization Framework under Permutation Invariance

Altmetrics

Downloads

116

Views

117

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

11 March 2024

Posted:

12 March 2024

You are already at the latest version

Alerts
Abstract
Carbon Capture and Storage (CCS) stands as a pivotal technological stride toward a sustainable future, with the practice of injecting supercritical CO2 into subsurface formations having already been an established practice for enhanced oil recovery operations. The overarching objective of CCS is to protract the operational viability and sustainability of platforms and oilfields, thereby facilitating a seamless transition towards sustainable practices. This study introduces a comprehensive framework for optimizing well placements in CCS operations, employing a derivative-free method known as Bayesian optimization. The development plan is tailored for scenarios featuring aquifers devoid of flow boundaries, incorporating production wells tasked with controlling pressure buildup and injection wells dedicated to CO2 sequestration. Notably, the wells operate under group control, signifying predefined injection and production targets and constraints that must be adhered to throughout the project’s lifespan. As a result, the objective function remains invariant under specific permutations of the well locations. Our investigation delves into the efficacy of Bayesian optimization under the introduced permutation invariance. The results reveal that it demonstrates critical efficiency in handling the optimization task extremely fast. In essence, this study advocates for the efficacy of Bayesian optimization in the context of optimizing well placements for CCS operations, emphasizing its potential as a preferred methodology for enhancing sustainability in the energy sector.
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

In recent years, the discourse surrounding climate change has intensified, with a growing consensus on the imperative need to transition the global economy towards achieving net-zero greenhouse gas emissions by mid-century. This ambitious goal, essential for averting dangerous anthropogenic interference with the climate system, requires rapid investment increase in near-zero emissions technologies across all sectors [1]. Among these technologies, Carbon Capture and Storage (CCS), also referred as CCUS where “U” stands for utilization show to be a pivotal solution for reducing carbon emissions, addressing climate change, and facilitating the transition to a carbon-neutral future [2,3]. Its significance lies in its potential to address emissions from various sources, including power generate-on plants, hard-to-abate industries (such as cement and refineries) and hydrogen production. CCUS is the only technology capable of guiding industries to absolute net neutrality by capturing and treating emissions.
Once CO2 is captured, it undergoes compression and transport to be permanently stored in geological formations, acting as a "sink" through injection. These geological formations must possess certain key characteristics [4]. Essential conditions for a formation to be considered a suitable carbon storage site include the formation of a pore unit with sufficient capacity to store the intended CO2 volume, pore interconnectivity allowing the injection at the required rate, and the presence of an extensive cap rock or barrier at the top of the formation to retain the injected CO2, prevent unwanted migration, and ensure long-term containment [5]. Saline water-bearing formations (CO2-Saline) and depleted oil and gas fields emerge as the most mature options, proven in several projects worldwide [6,7].
Deploying CCUS technology on a large scale in saline aquifers or hydrocarbon fields necessitates accurate characterization of the storage site and reservoir, involving a complex process from screening to deep geological and geophysical characterization [8]. Numerical simulation and modeling using computational fluid dynamics (CFD), possibly coupled with reactive transport simulations, are employed to address complex subsurface geology, simulating the flow behavior of the injected and the in situ fluids. The goal of such models is to estimate the field sequestration capacity of injected CO2 under different trapping mechanisms such as structural, dissolution, residual and mineral storage during all project phases [9,10].
Reservoir simulation is a crucial tool in the field of petroleum engineering that aids in modeling and predicting fluid flow behavior within subsurface reservoirs. The primary objective is to simulate the complex interactions among various components, such as rock, fluids, and wells. One of the fundamental principles underlying reservoir simulation is Darcy’s law, which describes the flow of fluids through porous media. The Darcy equation relates fluid velocity to the pressure gradient, permeability, and fluid viscosity [11]. The simulator employs numerical methods to solve the mass, momentum, and energy differential equations governing fluid flow in the porous medium. However, various analytical solutions, corroborated by numerical simulations, have been proposed to address related issues such as cap rock uplift [12], plume pressure buildup [13], and the analysis of flow regimes [14] among others.
When combined to mass conservation, the Darcy equation is a second-order partial differential equation (PDE) and can be analytically solved under simplifying assumptions. However, when trying to model realistic subsurface formations, these assumptions do not hold. In this case, the discretization of the equation through linearization is a key step in numerical reservoir simulation. This process involves dividing the reservoir into a grid to represent the spatial distribution of rock properties and fluid flow. Common methods for discretization include finite differences, finite volumes, and finite elements. Finite volumes [15], in particular, are widely used in reservoir simulation due to their simplicity and efficiency. Gridding plays a vital role in the discretization process, involving defining the size and shape of the cells within the reservoir grid. Various types of grids, such as Cartesian, corner-point, and unstructured grids, are used based on the geological complexity of the reservoir. The choice of grid impacts the accuracy and computational efficiency of the simulation.
Petrophysical fluid properties, including rock and fluid properties, are crucial inputs for reservoir simulation, including porosity, permeability, fluid saturations, compressibility, and relative permeability. Accurate characterization of these properties is essential for realistic simulation results. Furthermore, the incorporation of phase behavior models is essential to capture the complex interactions between different phases of hydrocarbons, especially in multi-phase flow simulations.
In the realm of carbon storage, the optimization of well placements plays a pivotal role in enhancing the sequestration potential of the aquifer. The primary objective of CCS projects is to maximize CO2 storage while adhering to constraints and technical policies. In its most commonly employed form, the CCS plan requires that brine producers be closed off once significant CO2 breakthrough occurs whereas the injectors rate is reduced when the bottomhole pressure reaches the safety limit. Consequently, optimal well placement significantly influences the overall success of the sequestration project by delaying the breakthrough time. The objective function maximization in this context is defined as achieving the highest attainable CO2 storage, considering the spatial distribution of the injection and brine withdrawal wells. This multidimensional function has an unknown functional form and its point values are expensive to compute since each one requires a fully implicit simulation to be run. Therefore, it needs to be treated as a black box function.
Well placement decisions cannot rely solely on static properties since geologic variables are mostly non-linearly correlated to production performance. This is demonstrated in Figure 1 where the objective function of oil production in the form of the expected Net Present Value (NPV), is evaluated for the placement of a single oil producer at each cell. In general well placement optimization poses a formidable challenge due to the large number of the decision variables involved, the high non-linearity of the system response, the abundance of local optima and the well placement constraints. Due to the discontinuities and the inherent non smoothness of the objective, research has been mostly focused on derivative-free optimization methods such as Genetic Algorithms [16] and Particle Swarm Optimization [17] combined with various heuristics.
Guyaguler et al. (2002) [18] developed and applied the Hybrid Genetic Algorithm (HGA) [19] to determine optimal location and number of vertical wells while Badru et al. (2003) [20], extended this work to also include horizontal wells. In essence, HGA comprises Genetic Algorithm (GA), the polytope algorithm for selecting the fittest individuals and a kriging proxy to expedite the optimization process. Results showed that after a few simulation runs, the method was able to optimize the production’s NPV compared to the base case. In another work, Emerick et al. in 2009 [21] designed a tool for well placement optimization using a GA with non linear constraints. They applied the GENOCOP III algorithm [22] which utilizes two separate populations where the evolution in one influences the evaluation of the other. The first population, named the "search population", consists of individuals that satisfy the linear constraints, whereas the second, called the "reference population", consists only of those that satisfy both linear and non linear constraints. Using this procedure the research team developed a tool that handled a total of 8 decision variables per well (6 in total that define the heel and toe coordinates of the well, one binary for producer or injector and one defining active or inactive well). Results showed a significant increase in the NPV of the production plan in comparison to the base case proposed plans. Besides the mentioned landmark works, there have been dozens more published on this optimization problem. Islam et al. (2020) [23] provides a detailed review of research done on the well placement optimization problem of oil production, focusing mostly on derivative-free and machine learning regression methods.
Bayesian Optimization (BO) [24] is a global optimization method that has not been sufficiently covered in the well placement problem in either oil production or CCS. In this work, our goal is to apply this method to optimize the carbon sequestration capabilities of a saline aquifer. BO represents a cutting-edge methodology that dynamically balances the exploration of the solution space with the exploitation of promising regions to efficiently discover well placements that can lead to the global optimum configuration. BO relies on constructing a probabilistic surrogate model, often a Gaussian Process (GP), to approximate the underlying objective function, which in this context measures total carbon storage. This surrogate model not only captures the observed data but also quantifies the uncertainty associated with predictions, allowing for the incorporation of prior knowledge and continuous refinement as new information becomes available through successive simulation runs. By iteratively selecting well locations based on the surrogate model’s predictions and subsequently updating the model with the actual reservoir response, BO intelligently adapts its search strategy. This adaptive nature makes it particularly well-suited for navigating the high-dimensional and uncertain parameter space, providing a systematic and data-driven means of identifying optimal well configurations for enhanced carbon sequestration.
The rest of the paper is organized as follows. In Section 2, we delve into a comprehensive explanation of the Bayesian Optimization method. Following that, Section 3 offers a detailed description of the specific problem, elucidating how BO was strategically applied to address the challenges encountered such as non linear constraints and permutation invariance in the input space. Moving forward to Section 4, we present results stemming from various implementations of the BO method, comparing performance of various acquisition functions and inspecting the exploration-exploitation trade-off. Section 5 initiates an expansive discussion of the obtained results. Finally, Section 6 draws insightful conclusions based on the findings and discussions presented throughout the study.
Preprints 101122 g001
Figure 1. NPV evaluation for oil production with a single well [25].
Figure 1. NPV evaluation for oil production with a single well [25].
Preprints 101122 g001

2. Bayesian Optimization

2.1. Gaussian Process (GP) Regression

In order to properly understand BO, the GP framework needs to be explained in detail. The complete treatment of GP can be found in Rasmussen and Williams (2006) [26]. Most of the material in this Section has been inspired from Frazier 2018 [24] and Dou 2015 [27], whereas the articles from Distill ([28] and [29]) provide visual and interactive explanations of the materials discussed here. Furthermore, it is assumed that the reader is already familiar with the concept of Multivariate Gaussian distributions (MVN) [30]. The probability density of a MVN in d dimensions is shown in Equation 1
N ( x | μ , ∑ ) = 1 ( 2 π ) d / 2 ∑ 1 / 2 exp ∑ 1 2 ( x − μ ) T ∑ − 1 ( x − μ )
where μ is the d × 1 mean vector and Σ is the d × d covariance matrix. A GP is the extension of this MVN to the space of functions, defining a probability measure on a function space. This function space acts as the probabilistic surrogate objective function, which will eventually converge to the actual objective function through sampling and utilization of the GP regression algorithm. At first, the probability measure is interpreted as our prior knowledge about the unknown objective function before data is seen. A GP is defined via its mean and covariance just like the MVN, however those now represent functions. Given a finite collection of q points x 1 : q ∈ R d that discretize appropriately the d dimensional input space, the objective function’s values f ( x 1 : q ) are assumed to be drawn by a MVN.
f ( x 1 : q ) ∼ N ( m ( x 1 : q ) , K ( x 1 : q , x 1 : q ) )
Compared to a multivariate normal we have
  • a random function vector f ( · ) instead of a random vector x
  • a mean function vector m ( · ) instead of a mean vector μ
  • a covariance (kernel) function matrix K ( · , · ) instead of a covariance matrix ∑
where K ( · , · ) = { k ( x i , x j ) } and k ( x i , x j ) is the kernel function discussed below.
Equation 2 states that the vector of functions conditional on the inputs x 1 : q and the mean and covariance functions follows a q dimensional MVN distribution. To avoid confusion, it needs to be stated that no assumption has been made on the distribution of the inputs. So far, the prior Gaussian distribution of the objective function has been defined. Function values selected in the prior are commonly referred to in literature as the test data.
In the prior distribution it is common to set the mean function to a constant value of zero. This is a reasonable assumption since no prior knowledge is assumed. If prior knowledge can be assumed to exist, then the mean function can be set to Equation 3
m ( x ) = μ 0 + ∑ i = 1 p β i Ψ i ( x )
where Ψ i are often parametric low-order polynomials which summarize our prior knowledge on the objective function.
When it comes to choosing a kernel function, it is typically needed to select it based on certain properties. First of all, kernel functions need to be positive semi definite. Secondly, it is important that points closer in the input space are more strongly correlated, i.e. if | | x − x ′ | | < | | x − x ′ ′ | | then k ( x , x ′ ) > k ( x , x ′ ′ ) . There are many kernel functions commonly used in BO, however the Matérn kernel [31] will be the main focus, since it is a more general form of kernel functions.
k ( x , x ′ ) = α 0 2 1 − ν Γ ( ν ) ( 2 ν | | x − x ′ | | ) ν K ν ( 2 ν | | x − x ′ | | )
where K ν is the modified Bessel function [32], Γ ( ν ) is the Gamma function and α 0 is a hyperparamter [33]. Certain values of ν in Equation 4 reduce the equation to other popular kernels including
  • Radial basis function (RBF) kernel [34] for ν → inf
  • Absolute exponential kernel for ν = 0.5
  • Once differentiable functions for ν = 1.5
  • Twice differentiable functions for ν = 2.5
So far, the prior distribution of functions has been constructed but, no observed information has been introduced to the model yet. To do so, the objective function’s value has to be measured at some points, which are denoted as y 1 : n . These points, commonly referred to as training data are observed by sampling the black box objective function. By incorporating this information into our model, the posterior distribution can be defined. First of all, the distribution of f ( x 1 : q , y 1 : n ) is now a ( q + n ) dimensional MVN. To acquire the posterior distribution on a certain point of x 1 : q , conditioning and marginalization have to be applied. Using Bayes rule Equation 5 is obtained.
f ( x ) | f ( y 1 : n ) ∼ N ( μ n ( x ) , σ n 2 ( x ) )
where the mean value μ n ( x ) is given from Equation 6 and represents a weighted average between the prior and an estimate based on the training data.
μ n ( x ) = k ( x , y 1 : n ) K ( y 1 : n , y 1 : n ) − 1 f ( y 1 : n ) − μ 0 ( y 1 : n ) + μ 0 ( x )
and the posterior variance σ n 2 ( x ) seen in Equation 7 is equal to the previous covariance, less a term that corresponds to the variance removed by observing the training data.
σ n 2 ( x ) = k ( x , x ) − k ( x , y 1 : n ) K ( y 1 : n , y 1 : n ) − 1 k ( y 1 : n , x )
This regression process updates the surrogate objective function’s values by conditioning on the training data.

2.2. Kernel Functions

Kernel functions are essential in BO since they define the shape of the prior and posterior distributions. For a function to be a valid kernel, it needs to satisfy Mercer’s Theorem [35].
A symmetric function k ( x , y ) defined on X × X , where X is some input space, is a valid kernel function if and only if it satisfies the following conditions:
  • Symmetry:  k ( x , y ) = k ( y , x ) for all x , y ∈ X .
  • Positive semidefiniteness: For any finite set of points x 1 , x 2 , … , x n ∈ X where i , j ∈ { 1 , . . . , n } , the corresponding kernel matrix K ( x i , x j ) is positive semidefinite.
If there exists a mapping function ϕ ( x ) that maps x to a higher-dimensional space such that the inner product in that space is equivalent to the kernel function k ( x , y ) = < ϕ ( x ) , ϕ ( y ) > , then according to Mercer’s theorem, k ( x , y ) is a valid kernel function. Kernel functions have important properties commonly used to modify and non linearly combine existing kernels to obtain new ones better suited for handling specific problems.
  • Linearity: If k 1 ( x , y ) and k 2 ( x , y ) are valid kernel functions, then for any constants a , b ≥ 0 , the linear combination a · k 1 ( x , y ) + b · k 2 ( x , y ) is also a valid kernel function.
  • Product: If k 1 ( x , y ) and k 2 ( x , y ) are valid kernel functions, then their product k ( x , y ) = k 1 ( x , y ) · k 2 ( x , y ) is also a valid kernel function.
  • Exponential: If k ( x , y ) is a valid kernel function, then exp ( k ( x , y ) ) is also a valid kernel function.
  • Function: If k ( x , y ) is a valid kernel, and f : X → R , then g ( x , y ) = f ( x ) k ( x , y ) f ( y ) is also a valid kernel.

2.3. Acquisition Functions

So far, the GP framework under which BO operates has been defined. This of course does not constitute a complete optimization algorithm since an iterative solution update rule is yet to be defined. This is where acquisition functions come into play. The main idea is for BO to utilize the posterior GP to determine a new point of high expected value and make an additional valuable observation on that point. Subsequently, the posterior GP is conditioned against the new information and the procedure is repeated until there is enough confidence that the algorithm has converged to the global optimum.
BO is specifically tailored to problems where data acquisition is considered computationally intractable. Therefore BO’s goal is to find good sequential acquisition policies which converge to the optimum in as few objective function evaluations as possible. These policies inherently include the exploration-exploitation trade off. In BO, exploration is related to looking for the next iteration estimate in areas of the solution space where the variance is high, while exploitation is related to searching areas where the current maximum is located and trying to find even better solutions.
Given a posterior distribution based on n observed function values, the goal is to find the most valuable point x n + 1 for receiving the next objective function calculation. The proposed solution is founded on the concept of the value of information [36]. Let’s assume that a hypothetical new observation at x has an objective function value of y. The value of making this observation is denoted by v ( x , y ; f ( x 1 : n ) ) , By integrating y out of the picture using the point predictive distribution of the posterior GP, we can define the expected value of observing x (Equation 8).
v ( x ; f ( x 1 : n ) ) = E y | x ; f ( x 1 : n ) v ( x , y ; f ( x 1 : n ) )
As a result, the data acquisition policy is defined by solving the optimization problem
x n + 1 = arg max x v ( x ; f ( x 1 : n ) ) i.e. the next trial point should be the one exhibiting maximum expected value. A natural stopping criterion for such a policy is to stop when the maximum expected value of the current iteration is smaller than a threshold v ( x n + 1 ; f ( x 1 : n ) ) < ϵ . There are many choices for the value function but three in particular are the most commonly utilized ones.
  • Probability of improvement (PI): PI (Equation 9) picks the point that is most likely to yield an improvement over the current maximum y ^ n [37].
    v ( x ; f ( x 1 : n ) ) = P I ( x ) = P [ f ( x ) ≥ y ^ n ] = Φ y ^ n − m n ( x ) σ n
    This is considered to be an exploitation oriented policy.
  • Expected improvement (EI): EI (equation 10) involves computing how much improvement we expect, especially over a highly uncertain domain [38]. It picks the point with the highest expectation of difference between predicted function value and current maximum.
    v ( x ; f ( x 1 : n ) ) = E I ( x ) = E max ( 0 , y − y ^ n ) = = σ n ( x ) φ m n ( x ) − y ^ n σ n ( x ) + ( m n ( x ) − y ^ n ) Φ m n ( x ) − y ^ n σ n ( x )
    where φ and Φ are the normal density and cumulative distribution.
  • Upper confidence bound (UCB): UCB (Equation 11) is one of the simplest acquisition functions, with a tunable parameter λ designed to favor either exploration or exploitation
    v ( x ; f ( x 1 : n ) ) = U C B ( x ) = μ ( x ) + λ σ ( x )

3. Problem Description

3.1. The Reservoir System

In this study, the sequestration potential of a deep and highly permeable aquifer (Figure 2) is investigated. The aquifer exhibits an inclined profile, with a pronounced steepness near the crest, expanding horizontally across a wide area and is comprised of four sedimentary layers, each one with varying average permeability value. Furthermore, it maintains a temperature profile consistent with typical thermal gradient expectations at the reservoir depth. The characteristics of the aquifer can be seen in Table 1. Due to its high permeability, the pressure distribution within the aquifer adheres to the pressure gradient, remaining isotropic in the x-y plane. The aquifer is considered to be slightly overpressurized, prompting the simultaneous production of brine during CCS operations to postpone reaching the fracturing pressure. The significance of this approach is underscored by the zero flow conditions at the aquifer’s sides, as dictated by no-flow boundary conditions in the simulation model [39].

3.2. BO Framework

To formulate a BO framework, the objective function, its constraints and the decision variables have to be defined. The target is to maximize the total amount of CO2 sequestered in the aquifer after continuous injection for several decades and concurrent brine production with constant target rates. This is handled by introducing two types of groups, injectors and producers, each group consisting of a number of identical wells.
Constraints are set to the maximum and minimum bottomhole pressure thresholds, as well as to the maximum afforded breakthrough rate of CO2 recycling. High non linearity is introduced to the problem by the effect of the wells location to the objective function and of the dynamic schedule changes occurring when operational constraints are violated. If for example an injector is placed close to a producer, then it is likely that CO2 breakthrough will occur way sooner than otherwise. Subsequently, the producer will be closed off and pressure will build up at a faster rate so that the constraint of maximum bottomhole pressure for the injector will be reached sooner, resulting in reduced sequestration. The depth at which each well is situated plays a huge part in the breakthrough time as well. Since CO2 tends to migrate upwards, CO2 will travel faster to a producer situated near the crest. In contrast, if the producer is situated closer to the reservoir bottom CO2’s breakthrough will be delayed. The theoretical maximum amount of CO2 stored is easily calculated as the target rate of the injectors over the timespan of injection. However, this maximum may be unobtainable due to the constraints already mentioned.
The well placement optimization probelm can be formulated as shown in Equation 12.
maximize x f ( x ) subject to g i ( x ) ≤ 0 , i = 1 , 2 , … , m
where f ( x ) corresponds to the CO2 mass sequestered which can be sampled by simulation runs and g i ( x ) ≤ 0 are the scheduling constraints, where x are the decision variables, which in this case are the coordinates ( x , y ) of each vertical well. Most commercial and research reservoir simulators can embed scheduling constraints to their runs thus ensuring that the simulation will be operationally feasible. This way the scheduling constraints are handled by the simulator and are thus need not be explicitly handled by the optimizer. There are however additional constraints related to the feasibility of the input space discussed in the next subsection. For the optimization process the python package Bayesian Optimization [40] was utilized.

3.3. Decision Variables Constraints

Constraints need to be imposed to the input space to define the feasible region of the objective function. For a CCS system with N wells, the input space consists of 2 N decision variables and the wells location may be written as in Equation 13
x = ( x 1 , y 1 , x 2 , y 2 , … , x N , y N )
The first constraint to be imposed on the input space is that two wells can not take up the same cells on the grid, since the simulator issues a simulation error instantly. As such, the optimizer is instructed to penalty such cases by giving a very negative value for the objective function when the simulator crashes.
The second and much more troublesome to handle constraint is the one regarding the valid position of each well. Since the aquifer’s shape is not a square box, there are coordinate values within the grid enclosing volume that correspond to null (non-existent) grid cell as seen in Figure 3. The recommended solution would be to add a severe penalty term by introducing a large negative objective function value for inputs in the infeasible area. For a reservoir with an active to total cells ratio of 50 % , this ratio corresponds to the probability of a well being placed within the feasible area. If the location of a single well would have been sought, the optimizer would have been able to map the infeasible area quite quickly. However when N wells have to be placed rather than just one, the probability of selecting all of them inside the feasible space is only ( 0.5 ) N . Clearly, the timeframe for the determination of the feasible area increases exponentially with the number of wells selected.
To overcome this challenge, a mapping from this 2D input space to a 1D space is employed while maintaining an one-to-one relationship, using a transformation based on the cell distance from the origin. Subsequently an ascending order sorting operation is applied to the Euclidean norms of each cell to arrange them. The Algorithm 1 of the map can be seen below.
Algorithm 1: Mapping Function f : R 2 → R
Preprints 101122 i001
This mapping is one-to-one (1-1) because each point ( x , y ) ∈ R 2 is uniquely associated with a real number f ( x , y ) ∈ R . Note that this is not a homeomorphism as it does not preserve topological properties such as closeness of points.
This mapping allows for dimensionality reduction from a 2 N dimensional input space to an N dimensional one. Furthermore, all values in the new input space represent the feasible region so no more constraints on the input region need to be handled. The mapped values of each cell are shown in Figure 4.

3.4. Permutation Invariance of the Input Space

As mentioned earlier, the simulator splits wells into two groups, injectors and producers, managing them collectively under group control policies. Targets and constraints are set for each group, with an embedded optimizer in the simulator responsible for adjusting schedule parameters for individual wells within each group. Essentially, a group comprises wells of the same type, distinguished solely by their location on the grid. On the other hand, wells locations serve as input variables in the BO framework, ordered in a vector. Therefore, the simulator handles wells positions as two sets of unordered objects, partitioned on the respective group, while BO treats them as a vector. Consequently for the simulator, the input space is invariant under permutations for wells positions within a group, whereas for BO it is not.
Consider a scenario following the mapping described in Algorithm 1. If variables m and n represent the positions of injectors and producers, respectively, the input space’s invariance implies that a sampled input exerts the same effect on the simulator and therefore on the objective function as well, across m ! · n ! vectors, generated by all of the permutations of the inputs within the same group.
To illustrate this concept, let’s consider a simple case with two wells of the same type placed on a 3 × 3 Cartesian grid (refer to Figure 5). In this scenario, the top-left cell is denoted as [1,1]. Moving right from [1,1] brings us to [1,2], while moving downwards from [1,1] leads to [2,1]. This structure mirrors the conventions of matrix elements, facilitating a straightforward understanding of the grid’s layout. The coordinates for the left sample are x = ( f ( [ 2 , 1 ] ) , f ( [ 3 , 2 ] ) ) , and for the right sample, x = ( f ( [ 3 , 2 ] ) , f ( [ 2 , 1 ] ) ) where f is the mapping defined by Algorithm 1. Despite the differing configurations, the simulator produces identical outputs for both samples since they belong to the same group and the simulator handles them as a set, regardless of their order. Each sample has its counterpart, or "doppelganger." As the number of wells increases, the number of potential configurations grows exponentially since for N wells, each unordered configuration can result from N ! different orderings. This example highlights the fundamental principle of group control and the resultant invariance in the input space, offering insight into the system’s behavior regardless of the specific arrangement of wells.

3.5. Modified Kernel Function

These observations are crucial to better acknowledge the principle idea introduced in this work. Since the black box function of the BO framework (i.e. the simulator) considers the inputs as sets, it would be extremely beneficial for this to be incorporated in the BO framework as well. By sampling an input vector, not only is information obtained about what its objective function value is, but also for all input vectors that are derived from same-group permutations of its elements. For instance in the N dimensional input space, where N = n + m and n, m correspond to the dimensions of the groups, a single sample would give information about n ! · m ! vectors. It is now obvious that incorporating this information in BO would greatly benefit its efficiency.
To incorporate this in the BO, we need to recall that BO builds a surrogate objective function that is mostly influenced by samples and the covariance matrix which is derived from a kernel function. Modifying the kernel function is a clear pathway for improving the efficiency of the BO. The kernel function calculates the covariance between points of the input space and acts as a measure of how similar the surrogate objective function’s values are based on the distance between inputs. The Matérn Kernel utilized in this work is a stationary kernel i.e. invariant to translations where the covariance of two input vectors is only dependent on their relative position k ( x , y ) = k ( | | x − y | | ) . Inputs have high covariance when their distance approaches zero whereas it decreases as they move further apart.
The modified input space generated by the mapping of Algorithm 1 is useful for generating inputs inside the feasible region but the caveat is that it is not homogeneous. Points that are close in the modified input space might be very far apart when translated to the original input space. The lack of preservation of this closeness property in the modified input space can be expressed as follows:
If | | c 1 − c 2 | | ≤ | | c 1 − c 3 | |
it does not necessarily imply that | | f ( c 1 ) − f ( c 2 ) | | ≤ | | f ( c 1 ) − f ( c 3 ) | | .
where c i are cells coordinates and f is the mapping from Algorithm 1. In other words, the mapping function is not an increasing function of the wells distance. It follows that if the kernel function utilizes the distances of the mapped input space directly, there will likely be a discrepancy between the calculated covariance and the actual covariance between inputs when this translates to the original input space.
To overcome this problem, the kernel function was modified so that covariance is calculated based on the inverse mapping of the input space i.e. from the N dimensional input space to the 2 N dimensional one which now represents the actual distance between two cells ( x , y ) = k ( | | f − 1 ( x ) − f − 1 ( y ) | | ) , where f − 1 ( x ) = ( f − 1 ( x 1 ) , f − 1 ( x 2 ) , . . . f − 1 ( x 11 ) ) . By utilizing this technique, the kernel function now considers the actual distance between two cells.
The last issue to be addressed is the permutation invariance. Since each input vector is invariant under m ! · n ! permutations, to calculate the representative covariance between two inputs, the permutation ordering that minimizes the distance of the one input to the other needs to be applied. This is a key modification that transforms BO from considering inputs as vectors to now view them as sets. By permuting, it is now able to minimize the distance between sets rather than vectors.
To solve this, a matrix D is generated with each value d i j representing the distance of the i t h well in x to the j t h well in y and is given by Equation 14
D = d i j = { | | f − 1 ( x i ) − f − 1 ( y j ) | | }
Since, the goal is to find the permutation that minimizes the distance between wells in the two samples, the problem can be expressed as to finding the permutation of rows (or columns) that minimize the trace of Matrix D  Table 2 which has complexity of O ( N ! ) . Since permutation invariance only affects injectors and producers separately, the problem can be reduced to the two counterparts i.e., finding the right ordering of the injectors which has complexity O ( m ! ) and finding the right ordering of the producers with complexity O ( n ! ) . This is a very well known problem in the literature called the assignment problem Algorithm 4 (Appendix A) known as the Hungarian method [41] or Munkres algorithm [42] is commonly utilized to reduce its complexity to the order of O ( N 3 ) , or in our case O ( m 3 ) + O ( n 3 ) , saving valuable computational time. Algorithm 2 describing the full Kernel modification is shown below.
Algorithm 2: Covariance calculation
Preprints 101122 i002
The modified kernel function is represented by a functional form
k ( x , y ) = k ( min m | | f − 1 ( x ) − f − 1 ( P m y ) | | ) , where P m denotes the permutation matrix. This functional form introduces significant non-linearity, making it challenging to establish proof that the resulting modified kernel function satisfies the Mercer conditions outlined in Section 2.2. However, through extensive sampling efforts across thousands of input samples, the resulting covariance matrix always remained positive semi-definite. This observation serves as a compelling indication that this function is indeed a valid kernel.
Importantly, due to the permutation invariance inherent in the function, it can be construed as a kernel function operating between sets rather than individual vectors. Algorithm 3 delineates the primary workflow of the Bayesian Optimization (BO) framework employed in this study.
Algorithm 3: Bayesian Optimization Framework
Preprints 101122 i003

4. Case Study

To properly solve the multi-phase compressible fluid flow problem, reservoir simulation is utilized through OPM’s open source Flow software [43]. The number of injectors selected and producers selected is m = 3 and n = 8 respectively.

4.1. Exploration/Exploitation Trade off

The first phase of testing the BO algorithm involved the utilization of all three candidate acquisition functions introduced in Section 2.3, shown in equations 9-11. Each function will be utilized twice, once with explorative hyperparameters values and once with exploitative ones. In total, 6 BO models were generated, each one trained through 50 iterations, by an equivalent amount of simulation runs conducted for each model to refine the surrogate objective function. Details of the selected schedule are outlined in Table 3.
In the table above, ’M’ denotes 1,000, ’MM’ denotes 10 6 and ’T’ corresponds to 10 12 while ’stb’ and ’scf’ represent units of volume: stock tank barrel and standard cubic feet respectively, measured at surface conditions. The theoretical maximum volume shown in Table 3 has been calculated by multiplying the target injection rate with the duration of the simulation and represents the target value for the optimizer to reach. However, it’s crucial to note that this value may not be feasible without violating the imposed constraints, therefore it may not be achievable under any set of well configurations. Mass wise, the target injection CO2 rates correspond to 2.3 MMtn/yr and the maximum sequestration volume to 90 MMtn.
At first, the performance of all six models was compared in terms of maximum storage value attained by timestep as seen in Figure 6.
The first component of the series names signifies the hyperparameter value selection guiding the model towards either exploration (XPR) or exploitation (XPT), while the second component indicates the acquisition function employed (see Equations 9-11). It is notable that all models approached a storage result close to the theoretical maximum by iteration 15 already. Certain models (XPT EI, XPT PI, XPR PI) were fortunate to nearly achieve their optimum value early on, possibly due to a lucky initial guess. This suggests that the targeted objectives of the schedule were relatively easy to maintain throughout the simulation. In contrast to other exploitative models, XPT UCB attained an optimal value by the third iteration. Both XPT EI and XPT UCB demonstrated their ability to refine their predictions in later iterations. However, XPT PI peaked at the 10th iteration but failed to reach the 1.5 · 10 9 mark, likely because PI inherently leans towards exploitation. In contrast, XPR PI continued to exhibit improvements even after 20 iterations. Notably, both XPR UCB and XPR EI consistently found enhancements throughout the iterations, owing to their explorative nature as well as initially exploring suboptimal regions.
Since the results produced for the max value seem to be heavily reliant on the initial estimation, the distribution of the storage results that each model generated at every iteration was investigated, illustrated in Figure 7 to offer valuable insights into the impact of the strategy on model performance. Notably, exploratory strategies (illustrated in the right hand side plots) demonstrate a higher susceptibility to unfavorable outputs which arises from their emphasis on exploring uncharted territories within the input space. This trend is clearly evidenced by the elongated tail of the distribution estimation line (kde) and the behavior of the 20th percentile line (dashed green) of the distribution, indicating that these strategies occasionally arrive to suboptimal outcomes. Conversely, exploitative strategies, as indicated by the 80th percentile line (dashed blue), tend to sample inputs that enable them to remain in proximity to the maximum value. However, an exception emerges with XPT PI, which appears to have become stuck to a local optima, failing to fully capitalize on potential improvements. This divergence underscores the nuanced interplay between exploitation and exploration strategies and their respective impacts on model behavior and performance.
Finally, to give a measure of the wells location change per iteration, in Figure 8 the L 1 norm between the location in subsequent iterations is depicted as "Vector Distances" defined as the trace of matrix D  Table 2, aiming to offer insights into the level of exploration across the models. However, since distance alone isn’t the optimal metric due to permutation invariance, akin to the modification of the kernel function, the "Set Distances" value between subsequent runs is calculated, utilizing Algorithm 4 on D to yield the minimum distance. This approach offered a more accurate depiction of the exploration dynamics among the models, mitigating the limitations associated with the traditional distance metric.
The median of the ’Vector Distances’ series of exploration strategies is clearly higher than that of exploitation ones, as exploration inherently involves probing a wider range of the input space. However, it’s noteworthy that due to the acquisition function not being directly dependent on the kernel, the Set Distances between the inputs is considerably higher in exploitative strategies. This observation suggests that exploitative strategies ultimately explore the space more efficiently. In essence, while exploration strategies cover more ground in terms of distance, exploitative strategies manage to navigate the space effectively, potentially due to their focused search around promising areas guided by the acquisition function.

4.2. Kernel Comparisons

To further evaluate the performance of the proposed method, a comparison between the modified kernel against the original Matérn kernel and an approach that randomly selects well positions is facilitated. This test is performed on a more strenuous schedule having increased the target injection rate by more than 50% as seen in Table 4. The target injection rate now corresponds to 3.6 MMtn/yr and the maximum sequestration volume to 142 MMtn.
This comparison aims to elucidate the impact of the two modifications made to the kernel described in Section 3 on the final outcome. Specifically, we seek to understand their influence on the end result as well as their ability to expedite the optimization process. The acquisition function utilized is EI with moderate hyperparameter values, striking a balance between exploration and exploitation. By evaluating these aspects, valuable insights can be gained into the efficacy and efficiency of the proposed modified kernel in comparison to both the original kernel and a random selection strategy.
As illustrated in Figure 9, the modified kernel surpasses the two alternatives in terms of maximum CO2 sequestered. Furthermore, it demonstrates consistent improvement, initiating enhancement as early as at the third timestep and continuing to refine its performance a total of four times before the 15th timestep. In contrast, the original kernel demonstrates improvement only twice, and its performance is comparable only to that of the random process. This stark discrepancy underscores the critical importance of effectively managing kernel functions. Failure to comprehend and address the nuances of optimization caveats would have hindered our ability to achieve such promising outcomes.
Notably, the original kernel function’s performance is akin to that of a random process. This outcome is attributable not only to improper distance calculations based on the 1D modified input space in the covariance, but also to the lack of comprehensive information regarding permutation invariance and the need to manage a considerably larger input space as a consequence. Figure 10 further supports this argument by demonstrating that the density distribution of the results of the original kernel and the random optimization are very close, as opposed to the Modified Kernel’s results where the density function is clearly skewed towards the optimal value.

5. Discussion

In this study, the well placement optimization problem has been handled as a Bayesian optimization one. To our knowledge this was the first attempt of applying BO in a CCS setting. Rather than applying BO in a "out of the shelf" straightforward fashion, several key modifications and analyses were employed aiming at enhancing optimization efficiency and effectiveness. Firstly, by utilizing a formation with complex geometry rather than a simple "sugar box", the issue of infeasible areas within the input space emerged and had to be addressed by implementing a transformation technique. This step allowed circumventing infeasible regions that took up the majority of the original input space.
This modification was not tax free as it introduced a severe issue to the kernel. The non homeomorphic nature of the map implied that kernel closeness of points in the new modified input space did not translate to the same closeness on the original, thus violating the need for the kernel function consitency to calculate the covariance properly. To address this, modifications were further introduced to the Matérn kernel, utilizing the inverse mapping to capture real distances between well positions. By recalculating covariances based on actual distances, this adapted kernel accurately represented the spatial relationships crucial for optimal well placement.
A significant advancement in the proposed methodology was the integration of our knowledge of permutation invariance into the kernel function. From a mathematical point of view, this innovation enabled the kernel to operate on sets rather than conventional vectors, effectively considering the minimum distances between well positions under permutations. The resulting kernel showed to be instrumental in improving optimization outcomes, as demonstrated through rigorous experimentation.
Subsequently, comprehensive analyses were conducted using various acquisition functions, including Expected Improvement (EI), Upper Confidence Bound (UCB) and Probability of Improvement (POI). Through comparative graphs, the performance differences among these functions was illustrated, providing valuable insights into their respective strengths and limitations in the context of CCS well placement optimization. One of the primary contributions of this study was the comparative evaluation of the developed modified kernel against its unmodified counterpart and a random function. The obtained findings unequivocally demonstrated the substantial impact of the modified kernel on optimization efficacy.
Clearly, the enhanced kernel exhibited superior performance, highlighting its pivotal role in driving significant improvements in well placement optimization outcomes. It is our strong belief that a solid foundation has been laid for future research endeavors aimed at optimizing the well placement problem with enhanced precision and efficiency. The proposed method is generalizable to other applications of well placement optimization, not necessarily restricted to a BO framework. These modifications can also find applications to more learning algorithms characterized by permutation invariant inputs.
In addition to the comparisons facilitated thus far, it is important to address the optimal placement identified by the algorithms and consider what insights engineers’ intuition could offer. Generally, in a closed system, producers and injectors should be positioned as far apart as possible. For this aquifer, an alternative configuration could involve injecting CO2 at the crest and placing the producers around the periphery, which would potentially enforce the resulting plume to remain relatively stationary and not descend as rapidly. As depicted in Figure 11, the solution derived by the BO algorithm reflects a blend of both engineering perspectives and considerations.
Injectors are strategically positioned as far away as possible from the majority of the producers, situated in the region resembling a fork at the base of the aquifer. Conversely, most producers are sited on the opposing side of the crest that resembles a "hill". CO2 naturally migrates upwards, facilitated by a clear pathway to the crest. It is reasonable to assume that producer P6 was strategically placed along the anticipated path of the plume for pressure maintenance, given the substantial injection rate from day 1. Producer P4 was strategically located to ensure a uniformly distributed plume. Considering the gravitational pressure differential that causes CO2 to migrate towards the crest, the advancement of the resulting plume’s front would be uneven. However, P4 counteracts this by moderating the pressure in its vicinity resulting in an even plume migration by the end of the CCS period, as illustrated in Figure 12.
Finally, the remaining six producers are positioned behind the crest, utilizing the second intuition that is the deceleration of the CO2 plume once it reaches the crest, primarily due to density differences between CO2 and the brine. At this juncture, breakthrough to the producers becomes inevitable, marking the conclusion of the injection period. It is noteworthy that the simulation ran successfully for approximately 40 years, during which the injection rate naturally decelerated due to pressure buildup. However, as depicted in Figure 13, the plume had not yet reached the producers by this point.
Overall, the BO optimization successfully captured, without any explicit guidance and at a very limited number of simulation runs, the two primary insights crucial for injection optimization, which an experienced engineer would typically independently deduce.

6. Conclusions

In this study, the application of a Bayesian optimization framework within the context of a CCS project was investigated. The analysis focused on several key modifications and comparisons to enhance the efficiency and effectiveness of the optimization process. Firstly, the issue of the input space’s infeasible area was addressed by introducing a mapping to a modified input space. This adjustment allowed the algorithm to not be concerned with exploring the infeasible regions by itself a process which would require hundreds of thousands of iterations. Furthermore, a novel kernel modification was proposed aiming at achieving invariance under permutations of the input vectors. This adaptation not only enhanced the robustness of the optimization process but also ensured that the model’s performance remained consistent across different permutations, a crucial consideration in real-world well optimization.
After extensive testing, we successfully optimized the sequestration of CO2 in a saline aquifer. The resulting scenario reflects both intuitive engineering principles and computational efficiency. Our efforts culminated in a comprehensive case study outlining the optimal sequestration of 115 million tonnes of CO2 over a four-decade period. This achievement represents 80% of the theoretically maximum value of 142 million tonnes, signifying exceptional efficiency within a closed system. Typically, breakthrough and pressure buildup pose significant challenges in such processes, often limiting their duration and effectiveness.
In conclusion, this study contributes to the growing body of research in Bayesian optimization and its applications in complex domains such as CCS. By introducing tailored modifications and conducting thorough comparative analyses, we have laid the groundwork for future advancements in optimization methodologies tailored to the intricacies of real-world problems. As we continue to refine and expand upon these techniques, we move closer towards unlocking the full potential of Bayesian optimization in the well placement problem by introducing advanced exotic Bayesian optimization procedures and frameworks.

Author Contributions

Conceptualization, S.F and V.G.; methodology, S.F; software, S.F.; validation, S.F. and V.G.; formal analysis, S.F.; investigation, S.F.; resources, S.F.; data curation, S.F.; writing—original draft preparation, S.F.; writing—review and editing, S.F., I.I. and VG; visualization, S.F.; supervision, V.G. All authors have read and agreed to the published version of the manuscript.,

Funding

This research was supported by the Special Account for Research Funding (E.L.K.E.) of National Technical University of Athens (N.T.U.A.) and by the Hellenic Foundation for Research and Innovation (HFRI) under the 3rd Call for HFRI PhD Fellowships (fellowship number 61/513800 Preprints 101122 i005

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Algorithm 4: Hungarian Method (Munkres Algorithm)
Preprints 101122 i004

References

  1. Jarvis, S.M.; Samsatli, S. Technologies and infrastructures underpinning future CO2 value chains: A comprehensive review and comparative analysis. Renewable and Sustainable Energy Reviews 2018, 85, 46–68. [Google Scholar] [CrossRef]
  2. Gabrielli, P.; Gazzani, M.; Mazzotti, M. The role of carbon capture and utilization, carbon capture and storage, and biomass to enable a net-zero-CO2 emissions chemical industry. Industrial & Engineering Chemistry Research 2020, 59, 7033–7045. [Google Scholar]
  3. Bui, M.; Puxty, G.D.; Gazzani, M.; Soltani, S.M.; Pozo, C. The Role of Carbon Capture and Storage (CCS) Technologies in a Net-Zero Carbon Future 2021.
  4. Rackley, S.; Rackley, S. Introduction to geological storage. Carbon Capture and Storage; Elsevier: Amsterdam, The Netherlands, 2017; pp. 285–304. [Google Scholar]
  5. Tomić, L.; Maričić, V.K.; Danilović, D.; Crnogorac, M. Criteria for CO2 storage in geological formations. Podzemni radovi 2018, 61–74. [Google Scholar] [CrossRef]
  6. Ji, X.; Zhu, C. CO2 storage in deep saline aquifers. In Novel materials for carbon dioxide mitigation technology; Elsevier, 2015; pp. 299–332.
  7. Mohammadian, E.; Jan, B.M.; Azdarpour, A.; Hamidi, H.; Othman, N.H.B.; Dollah, A.; Hussein, S.N.B.C.M.; Sazali, R.A.B. CO 2-EOR/Sequestration: Current Trends and Future Horizons. In Enhanced Oil Recovery Processes-New Technologies; IntechOpen, 2019.
  8. Ismail, I.; Gaganis, V. Carbon Capture, Utilization, and Storage in Saline Aquifers: Subsurface Policies, Development Plans, Well Control Strategies and Optimization Approaches—A Review. Clean Technologies 2023, 5, 609–637. [Google Scholar] [CrossRef]
  9. Pruess, K.; García, J.; Kovscek, T.; Oldenburg, C.; Rutqvist, J.; Steefel, C.; Xu, T. Code intercomparison builds confidence in numerical simulation models for geologic disposal of CO2. Energy 2004, 29, 1431–1444. [Google Scholar] [CrossRef]
  10. Class, H.; Ebigbo, A.; Helmig, R.; Dahle, H.K.; Nordbotten, J.M.; Celia, M.A.; Audigane, P.; Darcis, M.; Ennis-King, J.; Fan, Y.; others. A benchmark study on problems related to CO 2 storage in geologic formations: summary and discussion of the results. Computational geosciences 2009, 13, 409–434. [Google Scholar] [CrossRef]
  11. Whitaker, S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transport in porous media 1986, 1, 3–25. [Google Scholar] [CrossRef]
  12. Gravanis, E.; Sarris, E. A working model for estimating CO2-induced uplift of cap rocks under different flow regimes in CO2 sequestration. Geomechanics for Energy and the Environment 2023, 33, 100433. [Google Scholar] [CrossRef]
  13. Sarris, E.; Gravanis, E. Flow regime analysis of the pressure build-up during CO2 injection in saturated porous rock formations. Energies 2019, 12, 2972. [Google Scholar] [CrossRef]
  14. Ernestos, S.; Elias, G.; Panos, P. Investigation of self-similar interface evolution in carbon dioxide sequestration in saline aquifers. Transport in porous media 2014, 103, 341–359. [Google Scholar] [CrossRef]
  15. Eymard, R.; Gallouët, T.; Herbin, R. Finite volume methods. Handbook of numerical analysis 2000, 7, 713–1018. [Google Scholar]
  16. Mirjalili, S.; Mirjalili, S. Genetic algorithm. Evolutionary Algorithms and Neural Networks: Theory and Applications 2019, pp. 43–55.
  17. Kennedy, J.; Eberhart, R. Particle swarm optimization. Proceedings of ICNN’95-international conference on neural networks. IEEE, 1995, Vol. 4, pp. 1942–1948.
  18. Guyaguler, B.; Horne, R.N.; Rogers, L.; Rosenzweig, J.J. Optimization of well placement in a Gulf of Mexico waterflooding project. SPE Reservoir Evaluation & Engineering 2002, 5, 229–236. [Google Scholar]
  19. El-Mihoub, T.A.; Hopgood, A.A.; Nolle, L.; Battersby, A. Hybrid Genetic Algorithms: A Review. Eng. Lett. 2006, 13, 124–137. [Google Scholar]
  20. Badru, O.; Kabir, C. Well placement optimization in field development. SPE Annual Technical Conference and Exhibition. OnePetro, 2003.
  21. Emerick, A.A.; Silva, E.; Messer, B.; Almeida, L.F.; Szwarcman, D.; Pacheco, M.A.C.; Vellasco, M.M. Well placement optimization using a genetic algorithm with nonlinear constraints. SPE Reservoir Simulation Conference? SPE, 2009, pp. SPE–118808.
  22. Michalewicz, Z.; Nazhiyath, G. Genocop III: A co-evolutionary algorithm for numerical optimization problems with nonlinear constraints. Proceedings of 1995 IEEE International Conference on Evolutionary Computation. IEEE, 1995, Vol. 2, pp. 647–651.
  23. Islam, J.; Vasant, P.M.; Negash, B.M.; Laruccia, M.B.; Myint, M.; Watada, J. A holistic review on artificial intelligence techniques for well placement optimization problem. Advances in engineering software 2020, 141, 102767. [Google Scholar] [CrossRef]
  24. Frazier, P.I. A tutorial on Bayesian optimization. arXiv preprint 2018, arXiv:1807.02811. [Google Scholar]
  25. Onwunalu, J.E.; Durlofsky, L.J. Application of a particle swarm optimization algorithm for determining optimum well location and type. Computational Geosciences 2010, 14, 183–198. [Google Scholar] [CrossRef]
  26. Williams, C.K.; Rasmussen, C.E. Gaussian processes for machine learning; Vol. 2, MIT press Cambridge, MA, 2006.
  27. Dou, Z. Bayesian global optimization approach to the oil well placement problem with quantified uncertainties. PhD thesis, Purdue University, 2015.
  28. Agnihotri, A.; Batra, N. Exploring bayesian optimization. Distill 2020, 5, e26. [Google Scholar] [CrossRef]
  29. Görtler, J.; Kehlbeck, R.; Deussen, O. A visual exploration of gaussian processes. Distill 2019, 4, e17. [Google Scholar] [CrossRef]
  30. Do, C.B. The multivariate Gaussian distribution. Section Notes, Lecture on Machine Learning, CS 2008, 229. [Google Scholar]
  31. Genton, M.G. Classes of kernels for machine learning: a statistics perspective. Journal of machine learning research 2001, 2, 299–312. [Google Scholar]
  32. Olver, F.W.; Maximon, L.C. Bessel functions., 2010.
  33. Artin, E. The gamma function; Courier Dover Publications, 2015.
  34. Buhmann, M.D. Radial basis functions. Acta numerica 2000, 9, 1–38. [Google Scholar] [CrossRef]
  35. Minh, H.Q.; Niyogi, P.; Yao, Y. Mercer’s theorem, feature maps, and smoothing. International Conference on Computational Learning Theory. Springer, 2006, pp. 154–168.
  36. Lawrence, D.B. The economic value of information; Springer Science & Business Media, 2012.
  37. Jones, D.R. A taxonomy of global optimization methods based on response surfaces. Journal of global optimization 2001, 21, 345–383. [Google Scholar] [CrossRef]
  38. Vazquez, E.; Bect, J. Convergence properties of the expected improvement algorithm with fixed mean and covariance functions. Journal of Statistical Planning and inference 2010, 140, 3088–3095. [Google Scholar] [CrossRef]
  39. Peaceman, D.W. Fundamentals of numerical reservoir simulation; Elsevier, 2000.
  40. Nogueira, F. Bayesian Optimization: Open source constrained global optimization tool for Python, 2014–.
  41. Kuhn, H.W. The Hungarian method for the assignment problem. Naval research logistics quarterly 1955, 2, 83–97. [Google Scholar] [CrossRef]
  42. Munkres, J. Algorithms for the assignment and transportation problems. Journal of the society for industrial and applied mathematics 1957, 5, 32–38. [Google Scholar] [CrossRef]
  43. Rasmussen, A.F.; Sandve, T.H.; Bao, K.; Lauser, A.; Hove, J.; Skaflestad, B.; Klöfkorn, R.; Blatt, M.; Rustad, A.B.; Sævareid, O.; others. The open porous media flow reservoir simulator. Computers & Mathematics with Applications 2021, 81, 159–185. [Google Scholar]
Preprints 101122 g002
Figure 2. Aquifer visualization through ResInsight. The z axis is scaled by a factor of 5 for visualization purposes. ResInsight is an open source cross-platform 3D visualization, curve plotting, and post processing tool for reservoir models and simulations.
Figure 2. Aquifer visualization through ResInsight. The z axis is scaled by a factor of 5 for visualization purposes. ResInsight is an open source cross-platform 3D visualization, curve plotting, and post processing tool for reservoir models and simulations.
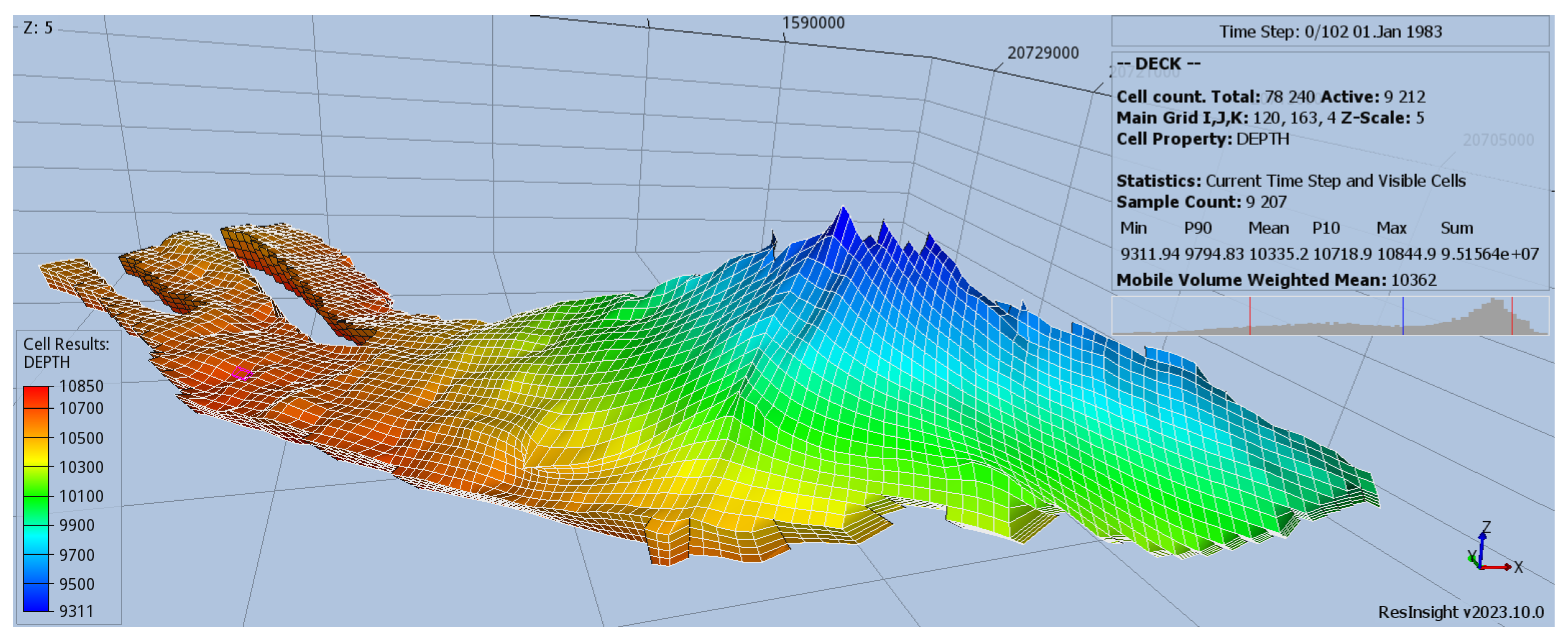
Preprints 101122 g002
Preprints 101122 g003
Figure 3. Feasible region for the wells on the reservoir grid top view.
Figure 3. Feasible region for the wells on the reservoir grid top view.
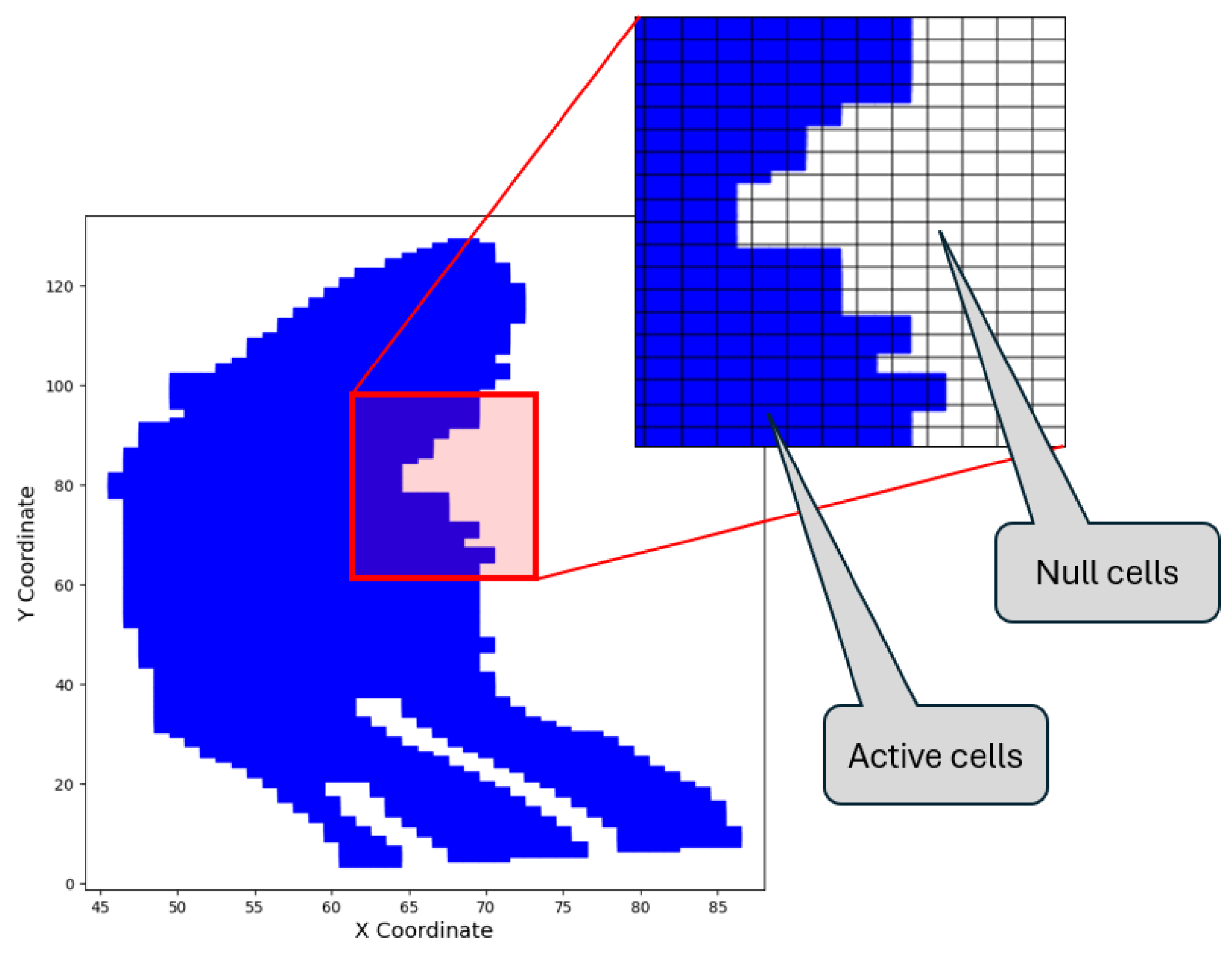
Preprints 101122 g003
Preprints 101122 g004
Figure 4. Mapped value of each cell
Figure 4. Mapped value of each cell
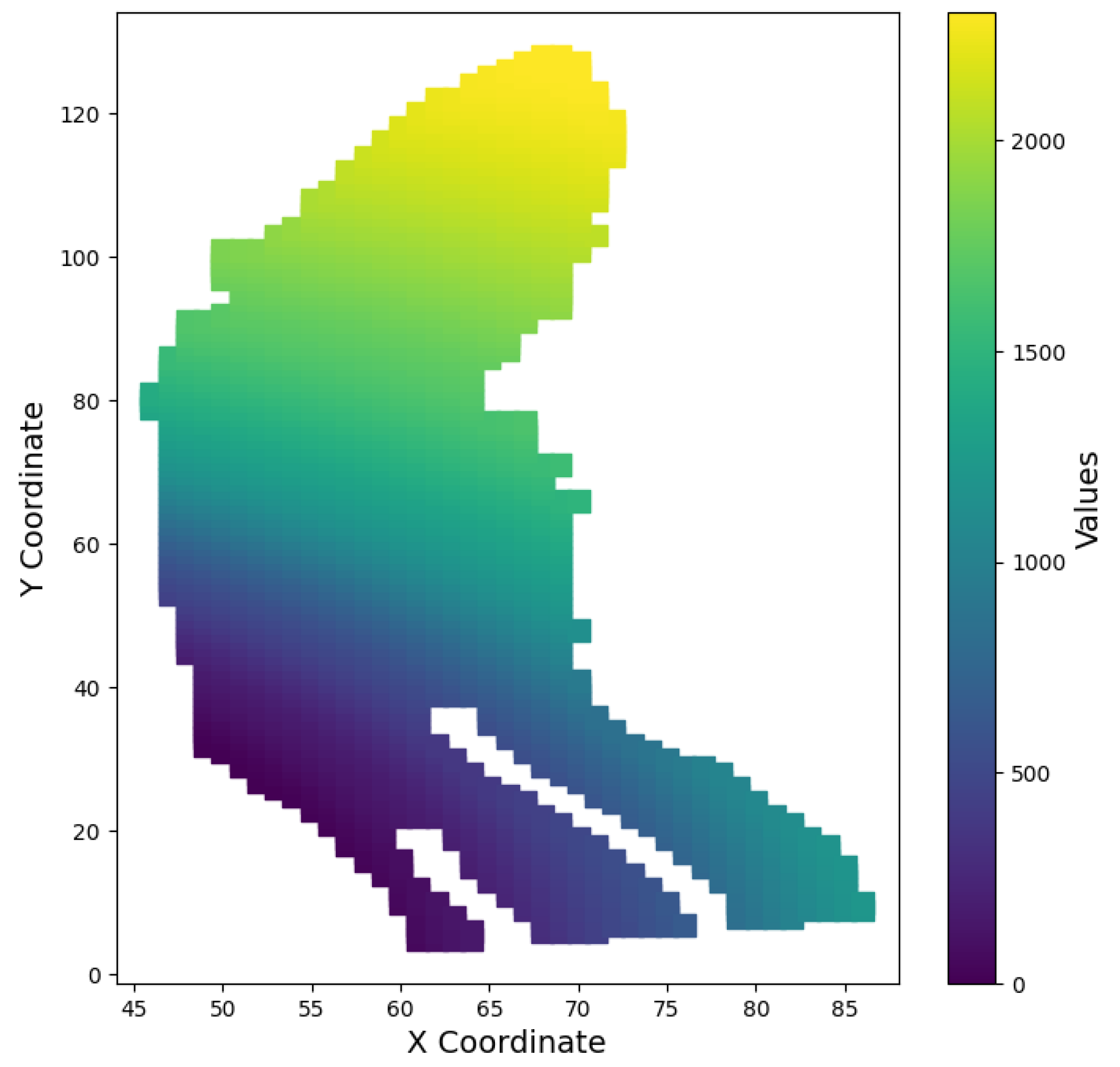
Preprints 101122 g004
Preprints 101122 g005
Figure 5. Both ordered configurations produce the same output
Figure 5. Both ordered configurations produce the same output
Preprints 101122 g005
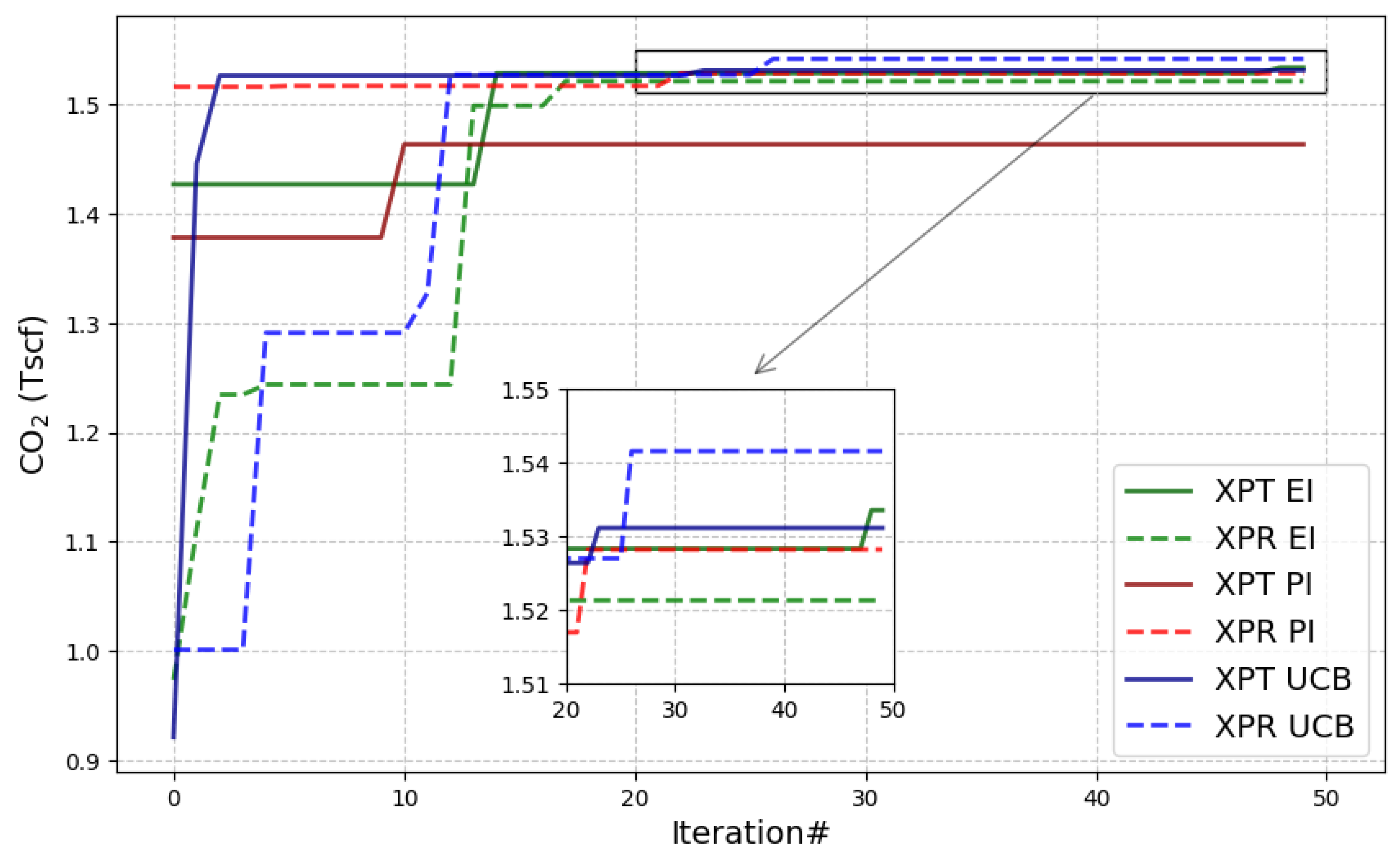
Preprints 101122 g006
Figure 6. Maximum obtained CO2 storage value vs iteration number
Figure 6. Maximum obtained CO2 storage value vs iteration number
Preprints 101122 g006
Preprints 101122 g007
Figure 7. Histogram and probability density estimation of storage values
Figure 7. Histogram and probability density estimation of storage values
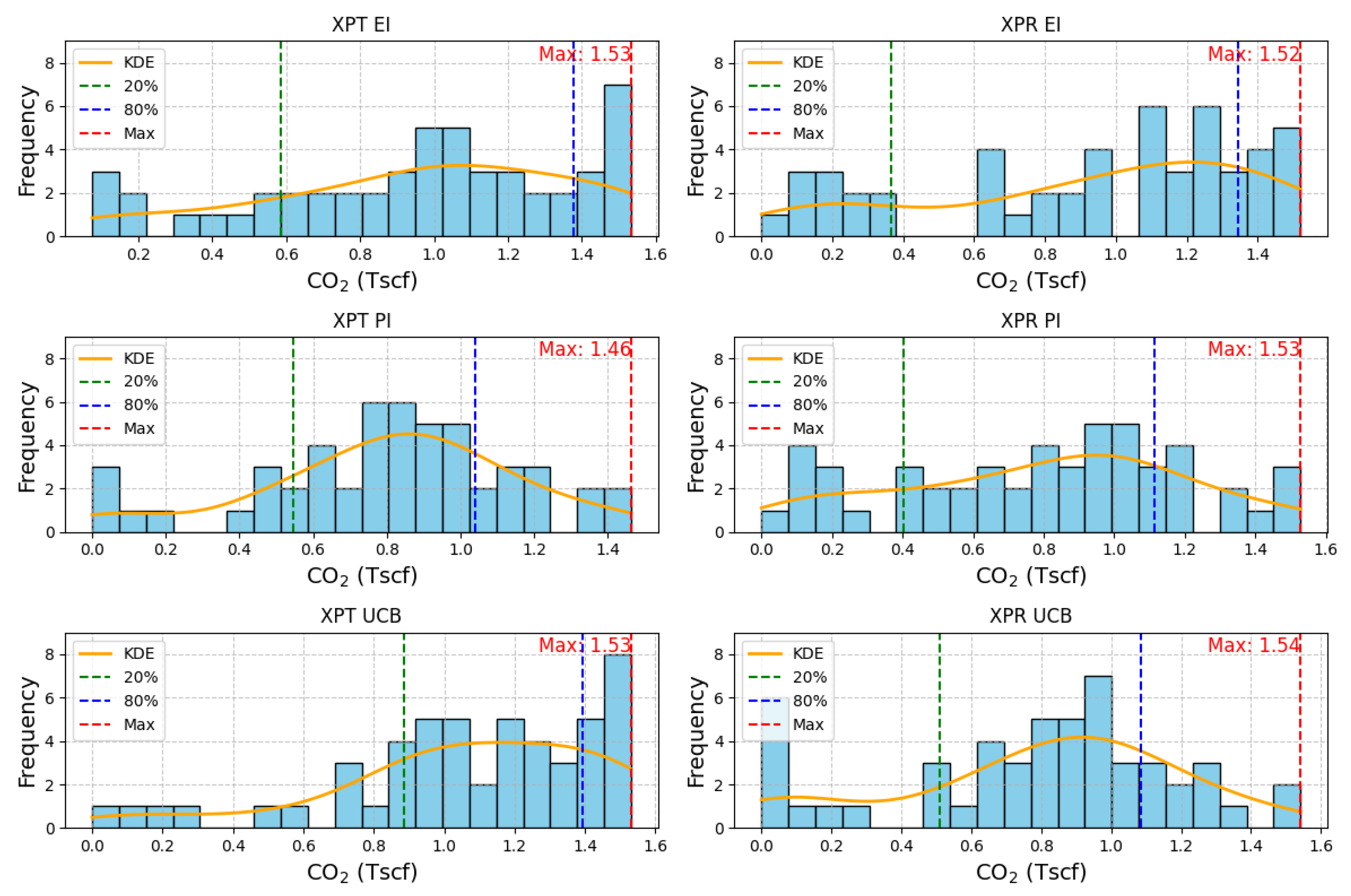
Preprints 101122 g007
Preprints 101122 g008
Figure 8. ’Vector Distances’ and ’Set distances’ between subsequent inputs for all six investigated models.
Figure 8. ’Vector Distances’ and ’Set distances’ between subsequent inputs for all six investigated models.
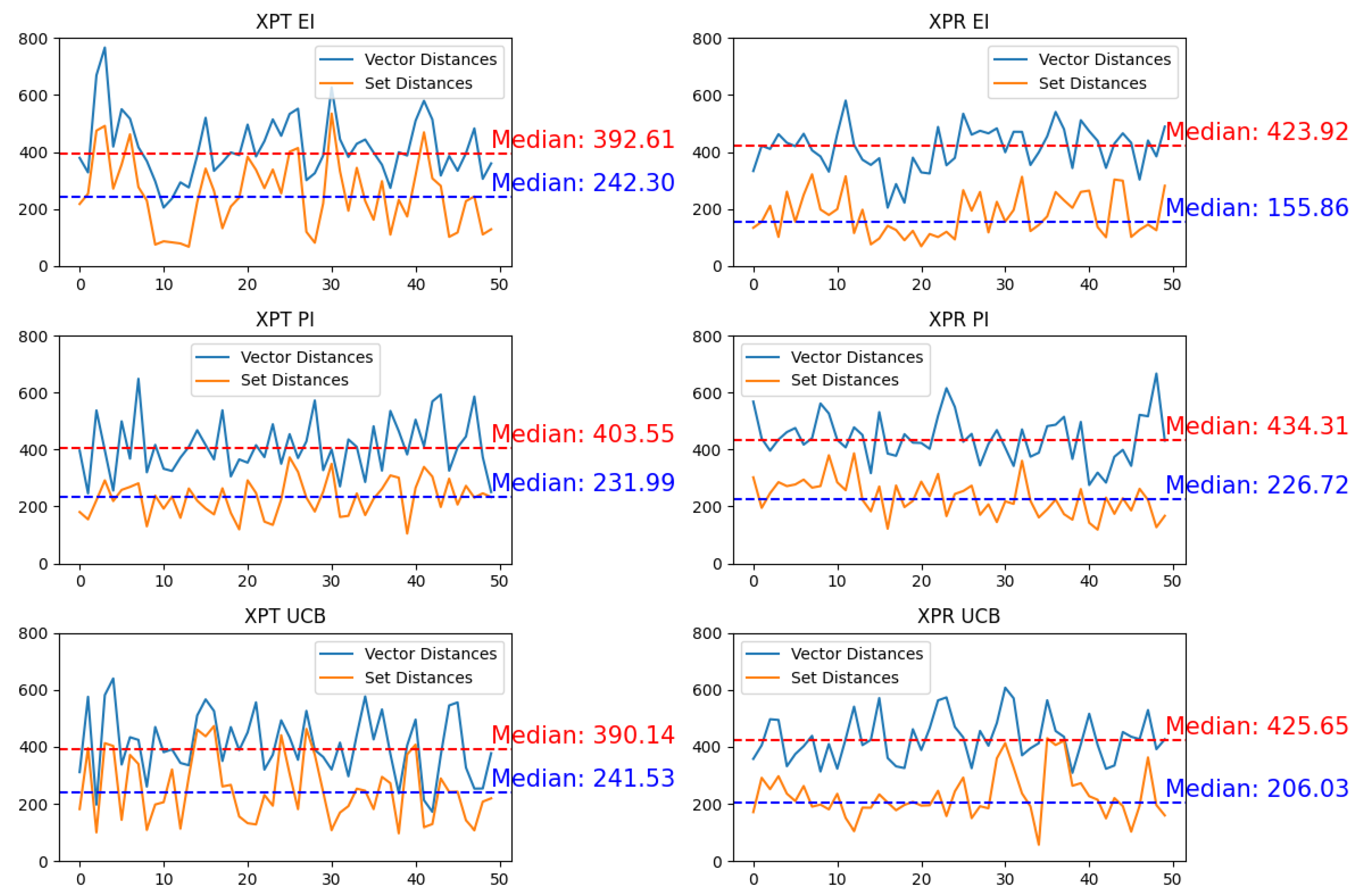
Preprints 101122 g008
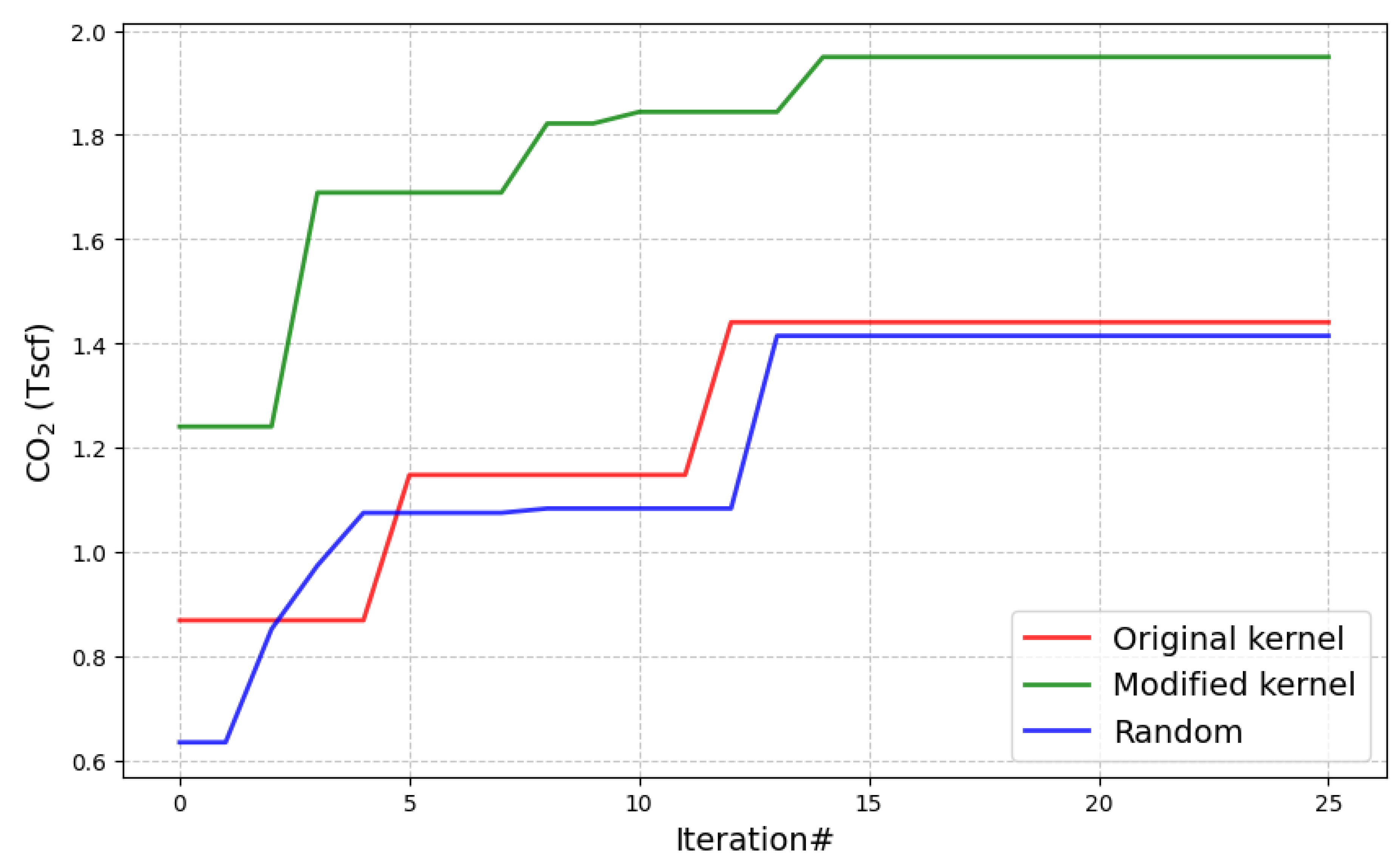
Preprints 101122 g009
Figure 9. Maximum CO2 sequestered volume achieved value vs iteration number
Figure 9. Maximum CO2 sequestered volume achieved value vs iteration number
Preprints 101122 g009
Preprints 101122 g010
Figure 10. Maximum obtained CO2 volume value vs iteration number
Figure 10. Maximum obtained CO2 volume value vs iteration number
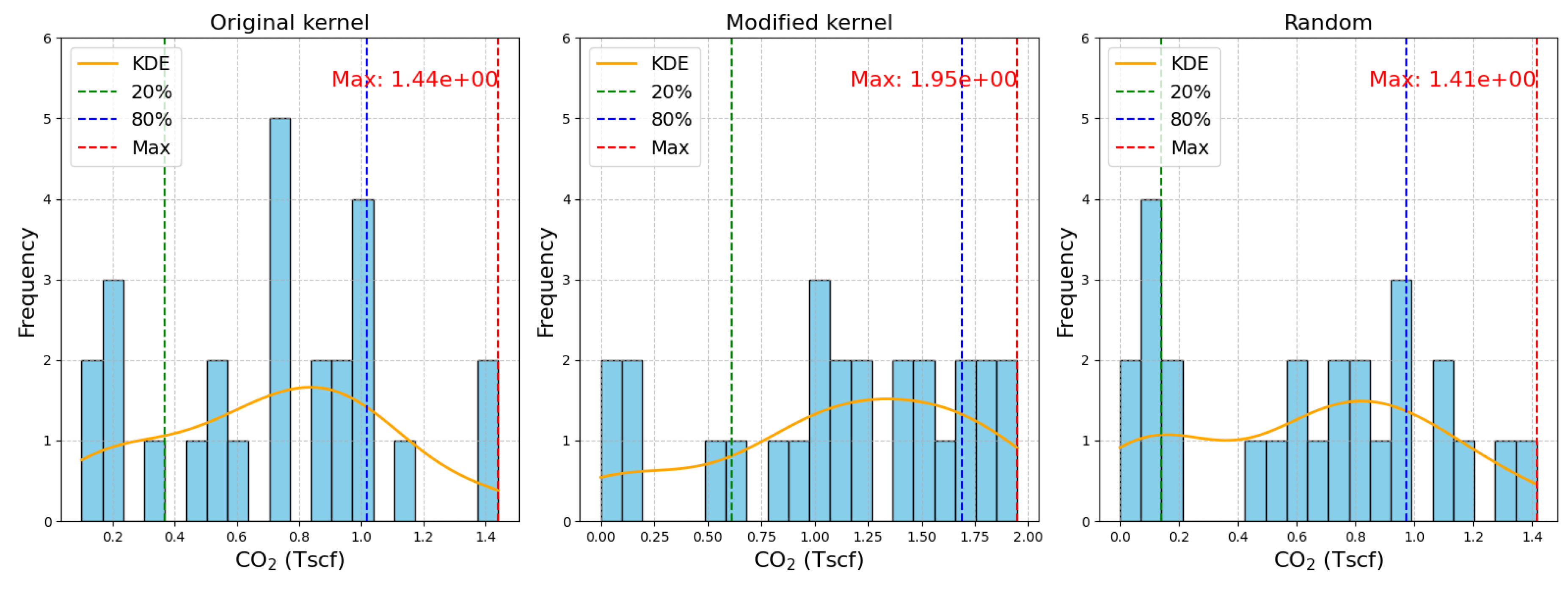
Preprints 101122 g010
Preprints 101122 g011
Figure 11. Optimal well placement achieved by the proposed algorithm
Figure 11. Optimal well placement achieved by the proposed algorithm
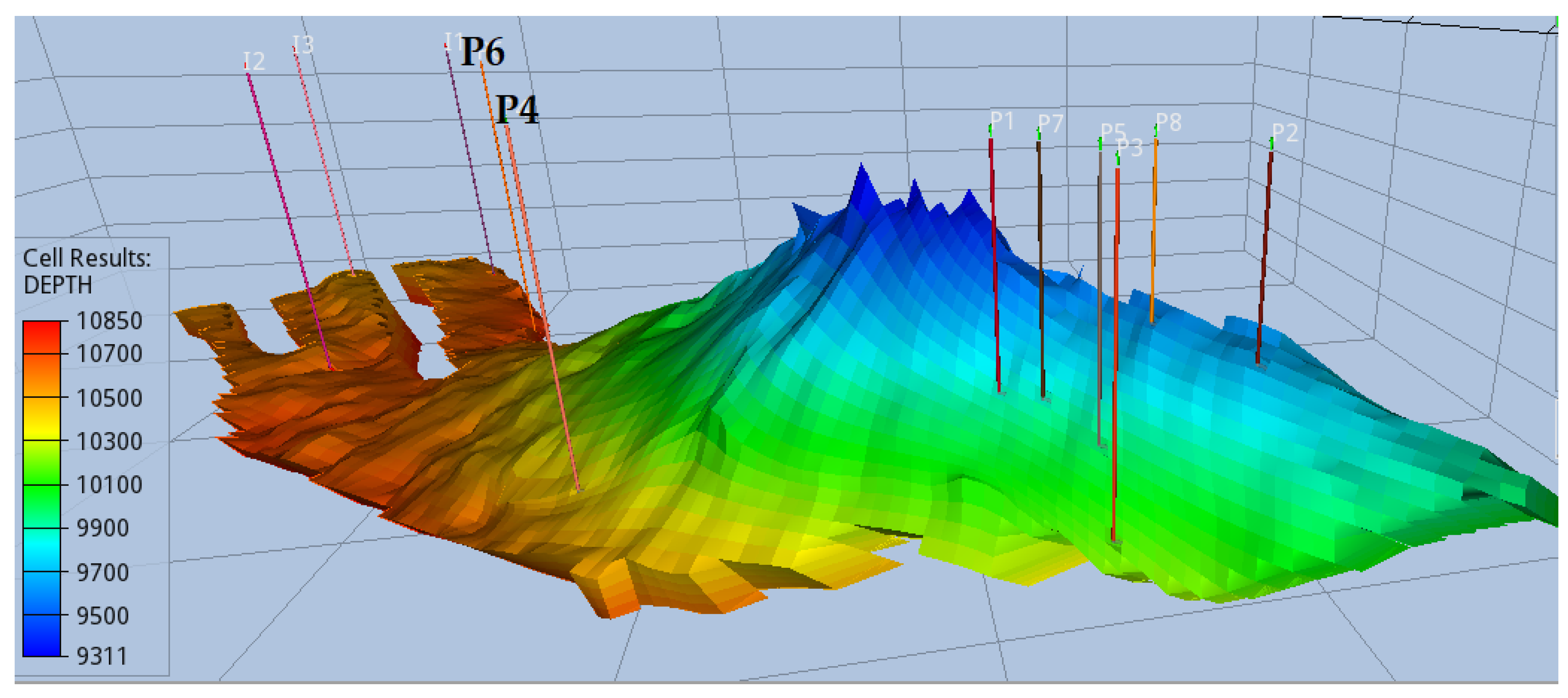
Preprints 101122 g011
Preprints 101122 g012
Figure 12. Even plume front when CO2 reaches the crest.
Figure 12. Even plume front when CO2 reaches the crest.
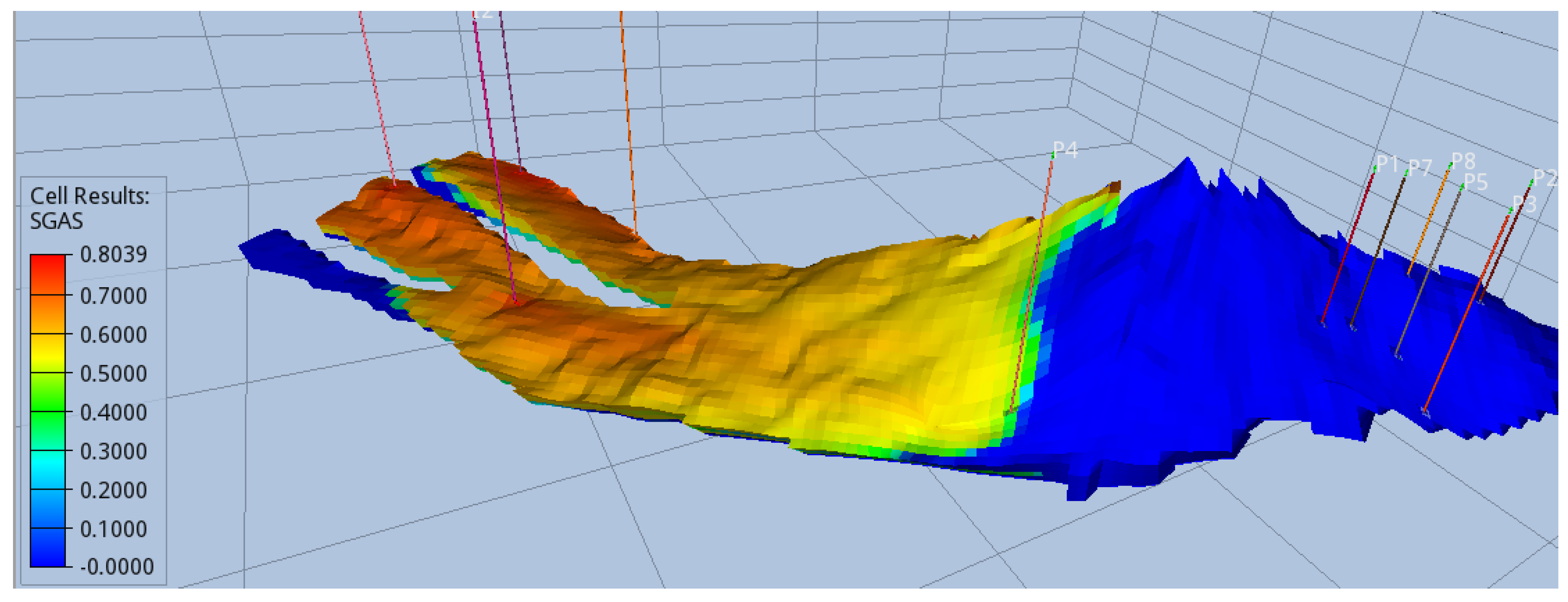
Preprints 101122 g012
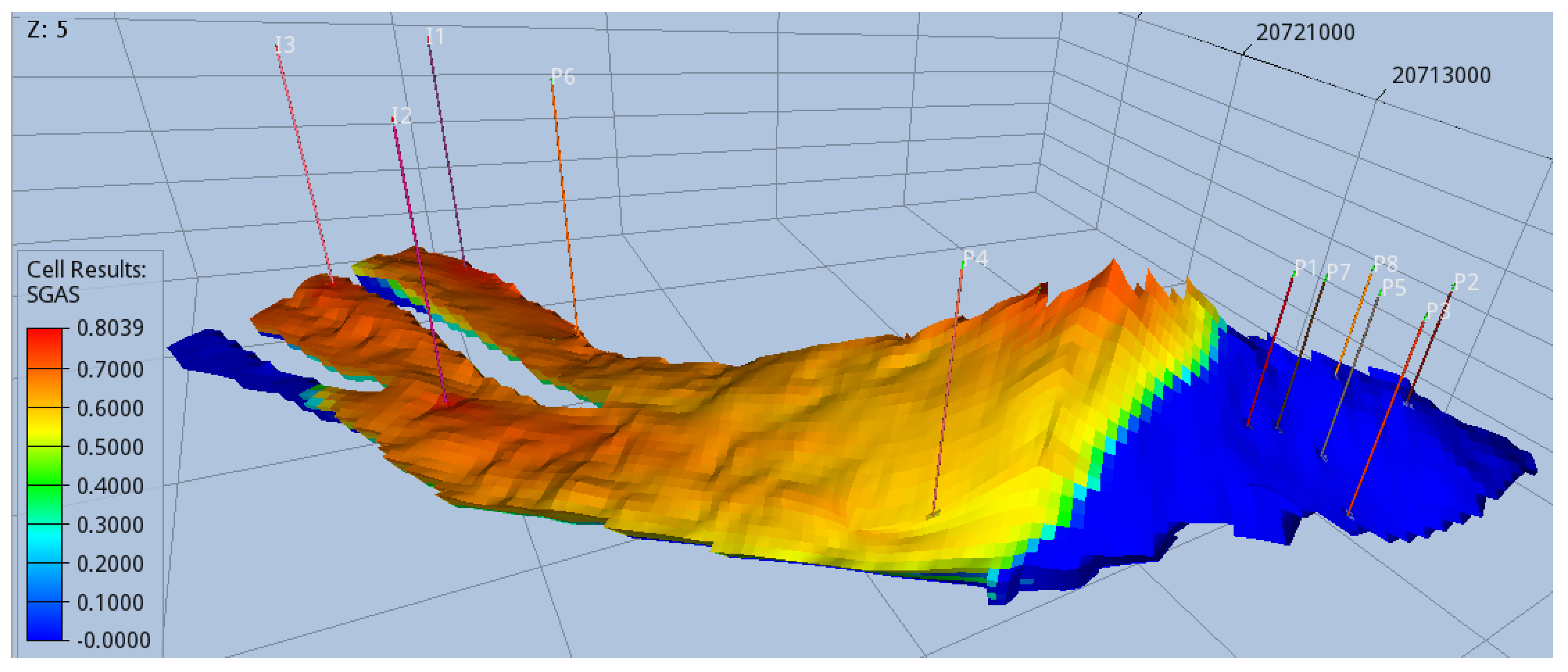
Preprints 101122 g013
Figure 13. End of simulation
Figure 13. End of simulation
Preprints 101122 g013
Table 1. Aquifer characteristics
Table 1. Aquifer characteristics
Parameter Value Units
Average pressure (P) 5 , 00 P s i
Temperature (T) 200 °F
Porosity ( ϕ ) 0.25
Average depth (D) 10 , 180 f t
Average xy permeability (k) 300 m D
Bulk volume (V) 2.4 · 10 11 s c f
Water in place 1.7 · 10 9 S T B
Table 2. Distance matrix D
Table 2. Distance matrix D
y 1 y 2 ⋯ y n
x 1 d 11 d 12 ⋯ d 1 n
x 2 d 21 d 22 ⋯ d 2 n
⋮ ⋮ ⋮ ⋱ ⋮
x n d n 1 d n 2 ⋯ d n n
Table 3. Schedule targets and constraints
Table 3. Schedule targets and constraints
Parameter Value
(Target) Injection Rate (CO2) 110 MMscf/day
(Target) Production Rate (Water) 50 Mstb/day
(Constraint) Max Production Rate (CO2) 5 MMscf/day
(Constraint) Max Bottomhole Pressure 9,000 psi
(Constraint) Min Bottomhole Pressure 3,000 psi
Duration ≈ 40 years
Theoretical maximum sequestration Volume (CO2) 1.58 Tscf
Table 4. Schedule targets and constraints
Table 4. Schedule targets and constraints
Parameter Value
(Target) Injection Rate (CO2) 170 MMscf/day
(Target) Production Rate (Water) 77 Mstb/day
(Constraint) Max Production Rate (CO2) 5 MMscf/day
(Constraint) Max Bottomhole Pressure 9,000 psi
(Constraint) Min Bottomhole Pressure 3,000 psi
Duration ≈ 40 years
Theoretical maximum sequestration Volume (CO2) 2.44 Tscf
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated