Prerpints.org logo
Preprint
Article

Judging Rainfall Intensity From Inter-tip Times: Comparing ‘Straight-Through’ and Syphon-Equipped Tipping-Bucket Rain Gauge Performance

Altmetrics

Downloads

72

Views

21

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 March 2024

Posted:

14 March 2024

You are already at the latest version

Alerts
Abstract
The inter-tip times (ITTs) of tipping-bucket rain gauges potentially provide the highest-resolution intensity data that can be acquired from this type of gauge. At an intensity of 100 mm h-1, a typical gauge with a sensitivity of 0.2 mm of rainfall would be expected to tip every 7.2 seconds. However, TBRGs are often equipped with syphons, to reduce the dynamic calibration error that results from continued (and unmeasured) inflow to a bucket as it tips. This increases the accuracy of rainfall depth recording, but the time to fill and empty the syphon can reduce the ability of a TBRG to respond to (and for the ITTs to reflect) short-term intensity fluctuations. This ability is already limited by the discretisation arising from the filling and emptying of the buckets themselves. Laboratory tests with controlled water inflow rates were performed using two high-quality TBRGs, one a 'straight-through' design and the other syphon-equipped. These confirmed that at all intensities at which the syphon operates, a regular sequence of fixed-duration ITTs (such as the 7.2 s mentioned above) does not occur. Rather, the ITTs are perturbed by the syphon cycling. The gauges were also co-located in the field, and linked to carefully synchronised event data loggers. Data collected during several rainfall events revealed differences in the ITTs, and again confirm that the ITT sequence of a syphon-equipped TBRG exhibits artefacts related to syphon operation, that are not present in the 'straight-through' data. These artefacts can result in ITT differences of many minutes, depending on the rainfall intensity, and are problematic for the use of ITTs to estimate intensity. Peaks and troughs in the intensity profile also differed between the two gauges. It is recommended that in the application of TBRGs for studies where short-term intensity data are required, 'straight-through' gauges should be used, and syphon-equipped gauges avoided.
Keywords: 
Subject: Environmental and Earth Sciences  -   Atmospheric Science and Meteorology

1. Introduction

Tipping-bucket rain gauges (TBRGs) are widely-used globally, both for routine climatological data collection, and for the provision of ground truth against which various other methods of rainfall recording, such as remotely-sensed satellite data, can be validated. It is well-known that TBRGs have several inherent limitations (Segovia-Cardozo et al. 2021, 2023 [1,2]), including the time delay arising from bucket-filling, especially in rain of low intensity, which may result in the beginning of rain being recorded later than the true commencement time. TBRGs may also fail to record the last phases of a rainfall event, if a bucket remains only partially filled. Even when seemingly high-resolution, one-minute rainfall totals are recorded, the smallest amount of rain that can be recorded in one minute is typically 0.2 mm (the sensitivity of many TBRGs). This means that rainfall rates can only be recorded in steps of 12 mm h-1 (60 min x 0.2 mm), which is rather poor resolution. Two tips in one minute would then suggest a rainfall rate of 24 mm h-1, three tips in one minute 36 mm h-1, and so on. Clearly, even one-minute TBRG data, often portrayed as being 'high-resolution' data, are incapable of approximating moment-to-moment intensity fluctuations. This situation has led to the analysis of the sequence of individual bucket tip events and the inter-tip time (ITT) between them, which can readily be logged to 1 s resolution using inexpensive event data loggers, such the Hobo event logger (https://www.onsetcomp.com/products/data-loggers/ua-003-64, accessed 5 March 2024), which record, for each tip, the Gregorian calendar date and time. Such data are regarded as providing the highest temporal resolution achievable with a TBRG (Cauteruccio et al. 2021 [3]). The potential for improved ability to capture intensity fluctuations can be seen from considering the typical values of ITT in rain of varying intensity. For a TBRG with 0.2 mm sensitivity, the ITT at 50 mm h-1 is 14.4 s, and this declines to 4.8 s at 150 mm h-1. Thus, in rain whose intensity fluctuates between 50 mm h-1 and 150 mm h-1, there may be approximately 4 - 12 tips of varying duration in each minute. The information contained in the durations of the associated ITTs is sacrificed if data are aggregated even to 1 min accumulation times and logged at that rate. Data aggregated to 5 min level (e.g. Saidi et al. 2014, [4]) during which time there could be 21 – 63 tip events, sacrifice correspondingly more resolution. Hourly data reveal little about actual rainfall intensities (Costello & Williams 1991, [5]), since they cannot reveal intensity fluctuations nor sub-hourly intermittency. The analysis of intensity from the unaggregated sequence of ITTs logged during rainfall can thus potentially unlock a much higher level of temporal resolution in intensity data. A study of Arkansas rainfall (Costello & Williams 1991, [5]) provides a useful example. Logging individual tip times for a 0.5 mm sensitivity gauge, they reported a maximum intensity of 500 mm h-1 (indicated by an ITT of < 4 s) but a maximum 1-minute intensity of only 296 mm h-1.
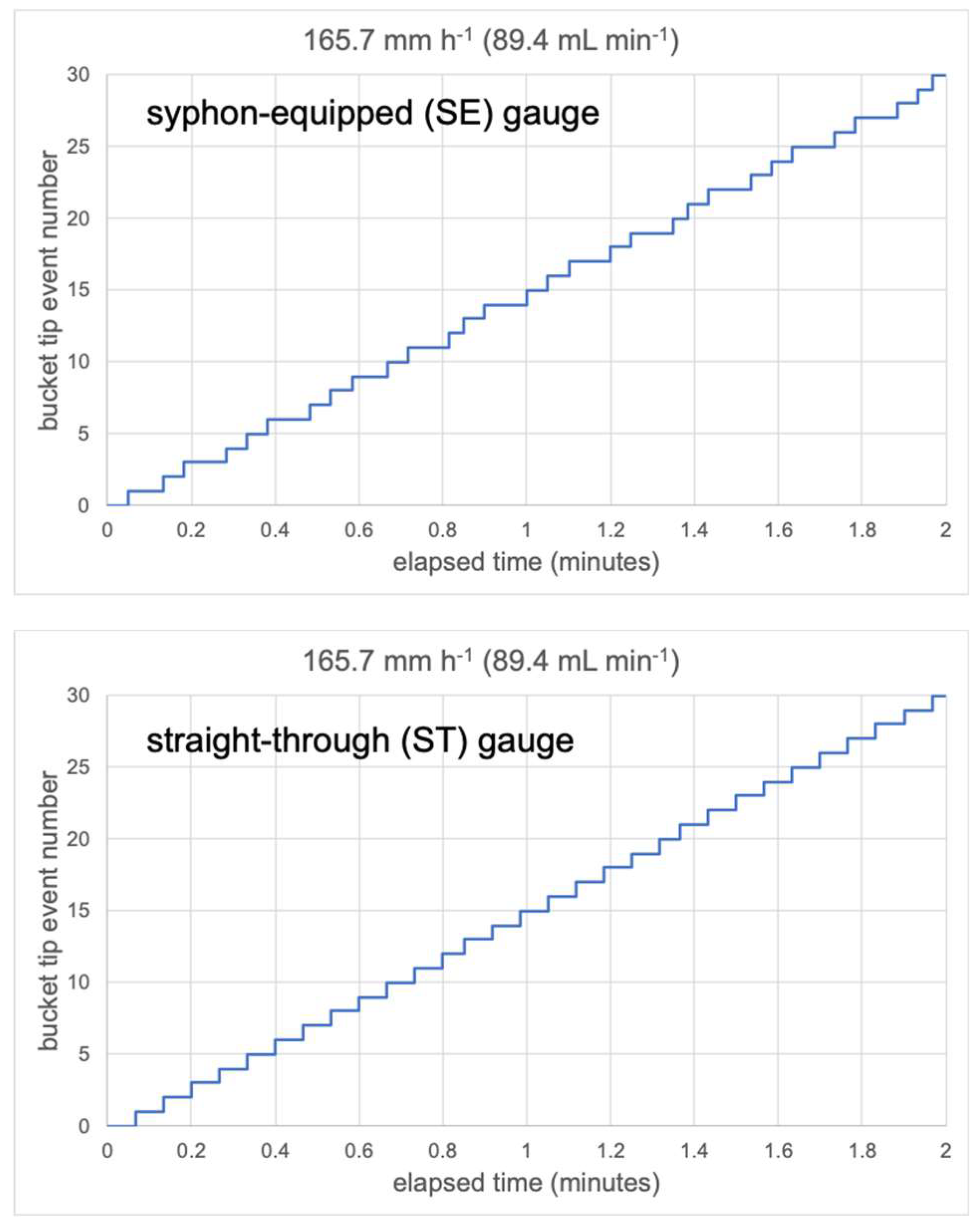
To improve the undercatch exhibited by TBRGs at high rainfall intensities (Humphrey et al. 1997 [6], Santana et al. 2015 [7], Sypka 2019 [8]), many are equipped with a small bell syphon. The purpose of the syphon is to deliver the water in rapid bursts that regulate some of the fluctuations in inflow rates to the TBRG mechanism caused by intensity variation. Nevertheless, some proportion of the water always remains unmeasured and contributes to undercatch. Syphon-equipped gauges (hereafter SE gauges) tend to record more rainfall at higher intensities than do 'straight-through' gauges (those without a syphon; hereafter ST gauges). This effect was quantified by Kimball et al. (2010 [9]) who analysed 1-minute data from several Alabama locations, and showed that there was little difference between the two types of gauge at low intensities. However, at a 1-min intensity of 240 mm h-1, the SE gauge recorded a mean intensity that was ≥ 48 mm h-1 higher than the ST gauge, for which more water went unmeasured owing to continued inflow to a bucket during tipping.
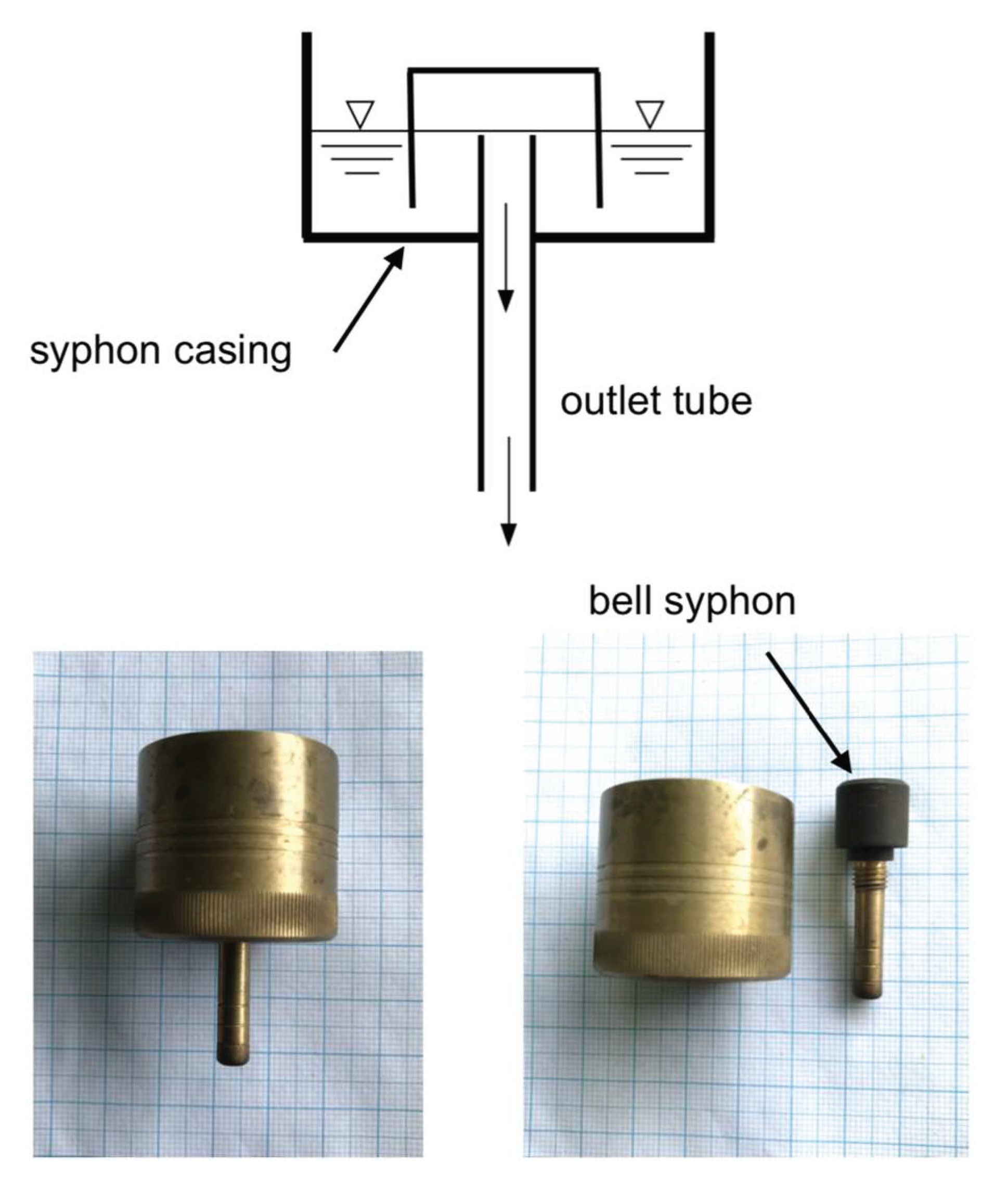
SE TBRGs introduce a further complication in the analysis of unaggregated ITTs. This is because, across a fairly wide range of rainfall intensities, syphons accumulate water draining from the gauge collecting funnel, without releasing any to the tipping-bucket mechanism. Once filled to a critical level, the syphon emptying cycle begins, discharging its stored contents rapidly into the tipping buckets. Suppose that the syphon chamber discharges a volume of 4 mL when it empties. Then, for a TBRG having a collecting funnel 203 mm in diameter exposed to rain at 1 mm h-1, the syphon will take ~ 7.4 min to fill before it passes anything to the tipping-bucket mechanism. The TBRG can record nothing until this time has elapsed. The bucket volume of this TBRG needed to trigger a tip event would nominally be 6.47 mL. Thus, the first syphon emptying would only be sufficient to fill a bucket to 62% of its capacity, and no tip event would result. A further 7.4 min for the syphon to fill a second time would be needed to trigger another syphon emptying cycle and fill the bucket. This is a total delay of almost 15 minutes before any rain could be recorded by the TBRG, even though with no syphon, the bucket would have been filled in 12 minutes. Thus, the syphon has lengthened the ITT by 25%. A further problem then emerges. Having filled the first bucket, and triggered a tip event, the syphon emptying would then deliver the excess water, i.e., 1.53 mL, into the second bucket. A third syphon emptying would add 4 mL to the existing 1.53 mL, filling the second bucket to 5.53 mL, or ~ 85.5% capacity. Again, no tip would occur, and a fourth syphon cycle, with a total bucket filling time again totalling almost 15 minutes, would be needed to trigger a tip. This would fill the bucket to tipping with an additional 0.94 mL, and the excess 3.06 mL would drain to the first bucket. The next syphon cycle would then be sufficient to cause an immediate tip, since (4 mL + 3.06 mL) = 7.06 mL, which exceeds the nominal bucket volume. Therefore, some syphon emptyings fail to trigger a bucket tip, while other emptyings do, in a repeating sequence. Then, even in rain of constant intensity (in this simple example, 1 mm h-1), the ITTs are not of constant duration, some being approximately 15 min and some being about half this (~ 7.4 min). This variability is entirely the result of the syphon operation, and does not reflect actual changes in rainfall intensity. The actual durations of short and long ITTs of course depend on the rainfall intensity and the syphon and bucket volumes. Moreover, in natural rainfall in which the intensity is not constant but rather variable from moment to moment, a complex series of ITTs results, in which some part of the variation in ITT duration is due to true intensity fluctuations, and the remainder to syphon operation. It is therefore not readily possible to derive an unambiguous measure of the rainfall intensity from logged ITT data if the TBRG is syphon-equipped. However, the magnitude of the perturbations of the ITTs in natural rainfall is not well-known and needs to be established. This is done in the present study.
It is appropriate to emphasise here two important characteristics of syphon operation. First, syphon emptying is rapid, taking approximately 2 s (Cai et al. 2020, [10]). For a typical syphon volume of 4.2 mL, the value for the TBRGs tested below, the 2 s discharge occurs at a rate equivalent to the very high intensity of 233.6 mm h-1. Therefore, while the filling time for a syphon can be long, the emptying time can be brief. Thus, in the situation where a tipping-bucket is almost full, and the syphon suddenly empties, a tip event would occur, and the excess would rapidly part-fill the next bucket, such that it would in turn tip earlier than would otherwise have been the case. Therefore, it can be understood that some ITTs are lengthened, and some shortened, by syphon operation. Second, although it seems not to have been stated explicitly previously, it is also important to bear in mind that whilst syphon emptying requires ~ 2 s, TBRG buckets typically swing and empty even more rapidly, typically taking ~ 0.5 s from initial movement to the empty rest position (Duchon et al. 2014 [11], Liao et al. 2021 [12]). Thus, a single syphon emptying can fill a first partially-full bucket, resulting in a tip, and continue to empty into a second bucket, causing a second tip, and, at high rainfall intensities, possibly even partially refilling the first bucket. This all occurs at the high equivalent rainfall intensity of > 200 mm h-1 as noted above, with much shorter ITTs than would otherwise occur in light of the actual intensity. This suggests that at high intensities, there could be multiple short ITTs followed by a longer interval as the syphon refills and in turn partially refills a bucket. Experimental data showing this effect will be presented below.
The influence of a syphon on TBRG performance has been noted in various prior studies. The pioneering study, to the best of the authors knowledge, was that of Parkin et al. (1982 [13]), at the Australian Commonwealth Scientific and Industrial Organisation (the CSIRO), who were concerned to use the best quality rainfall data in a study of cloud-seeding experiments. They showed that perturbations to ITTs can occur in SE TBRGs. Other studies include the work of Maksimović et al. (1991 [14]), who, like Parkin et al. (1982 [13]) identified primarily what they referred to as 'double tipping', in which two tips occur in close succession. Anomalous tips were also noted in SE gauges by Harremoës et al. (1995 [15]), while Overgaard et al. (1998 [16]) recommended that to minimise these effects, the syphon should have a volume of less than half that of the associated tipping buckets. No studies seem to have studied syphon effects over a wide range of rainfall intensities, nor quantified syphon-induced perturbations and their effect on estimated rainfall intensities in field data collected under the fluctuating intensities of natural rainfall.
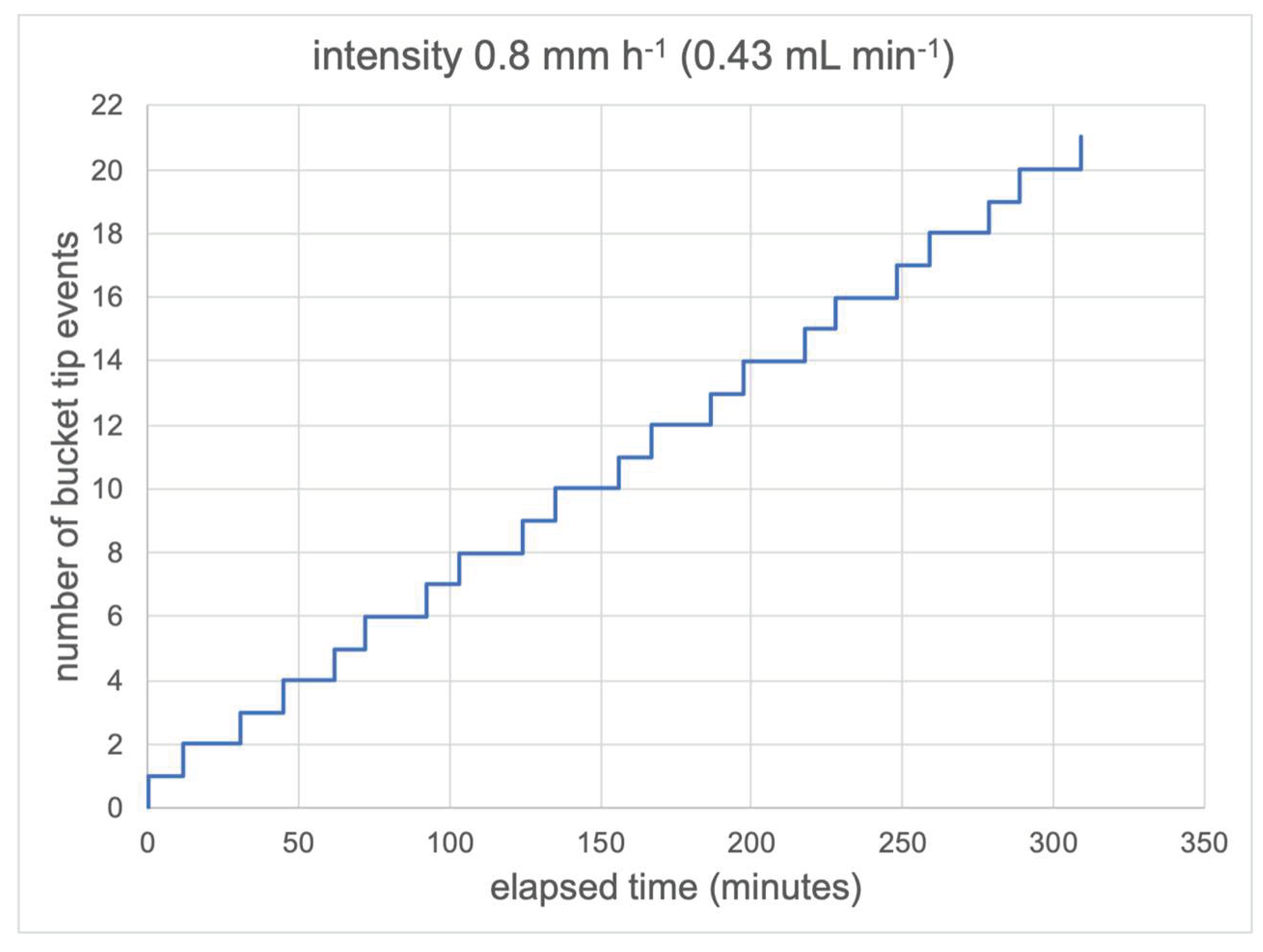
The purpose of the research reported here was to explore these phenomena further, using data collected in controlled experiments in the laboratory, as well as during natural rainfall in the field. The lab experiments were carried out in order to be able to focus on syphon behaviour under carefully controlled pumped flow rates (equivalent to constant rainfall intensities) without the complication of continuous intensity variation as occurs in natural rainfall. An inter-comparison of recordings of natural rainfall ITTs using co-located SE and ST TBRGs is then undertaken in order to characterise syphon artefacts under varying intensities. To the writer's knowledge, this has not been attempted previously.
The particular questions asked are as follows:
a) How does the presence of a syphon perturb the sequence of ITTs when the TBRG is fed with a constant, pumped water flow equivalent to rain of a constant intensity? By how much are the ITTs altered?
b) does the presence of a syphon perceptibly perturb the recorded sequence of ITTs during natural rainfall of varying intensity?
c) what artefacts in the apparent rainfall intensities derived from the individual ITTs result? (in other words, by how much are estimates of intensity perturbed by syphon operation?).
d) given that when rain begins, a syphon may be empty or may already be partially filled owing to prior rainfall, or may remain partially filled at the cessation of rainfall, just as tipping buckets can, by how much can estimates of rainfall intensity and rainfall commencement and cessation times be perturbed by these combined effects?
Methods and apparatus are described in detail below (refer to the Methods section) following a brief review of the use of unaggregated ITTs to estimate rainfall intensities, which provides some further context for the present research.

1.1. Estimating Intensity from Unaggregated ITTs

Reliable data on rainfall intensity become necessary in many fields. Notably, 'ground truth' data are necessary for the calibration and validation of newer methods for recording rainfall occurrence, such as the use of commercial microwave link beam attenuation, and similar approaches using video broadcast and other signals (Chwala et al. 2012 [17], Colli et al. 2019 [18], Adirosi et al. 2021 [19], Gianoglio et al. 2023 [20]). This has led to multiple studies focussing on the resolution in intensity that is achievable from conventional TBRGs, and on the precision with which rainfall amounts can be recorded (Yu et al. 2013 [21], Chan et al. 2015 [22], Stagnaro et al. 2016a [23], 2016b [24]). In some studies, unaggregated ITTs are used, whilst in others, one-minute rainfall rates are estimated. This is done either by counting all tips occurring in one clock minute, and allocating that amount of rain to that minute, or else by distributing a part of the rainfall into prior or subsequent minutes, in proportion to the fraction of the ITTs lying within the boundaries of a clock minute (Shedekar et al. 2009 [25], Stagnaro et al. 2016b [24], Rachmawati et al. 2022 [26]). Various kinds of post-processing of the tip event data have also been examined, such as the fitting of smoothed intensity curves using splines (Song et al. 2017 [27]). The smooth fitted curves are not ideal as they can conceal rapid intensity fluctuations, and sometimes yield negative intensities (Song et al. 2017 [27]).
One-minute data can sacrifice temporal resolution, being limited to 1440 values per day. Rain at > 12 mm h-1 all day would generate more ITTs, and rain at 40 mm h-1 for 8 h would generate almost 1600 ITTs. These figures apply to a TBRG having 0.2 mm sensitivity, and would double to almost 3200 ITTs for a gauge having 0.1 mm sensitivity. Data aggregated to 1 min level are also unable to record brief intensity bursts faithfully (Dunkerley 2019b [28]). Consequently, unaggregated ITTs have been preferred in multiple studies of rainfall temporal patterns (Dunkerley 2015 [29], 2019a [30], 2021 [31]). Deriving an estimate of intensity from each ITT is based on the presumption that during the ITT, the rainfall intensity is constant (Mandeep & Hassan 2008 [32], Muñoz et al. 2016 [33]). From this, the mean equivalent rainfall intensity (rainfall rate, R, mm h-1) during the inter-tip duration T (minutes) is given by
R = TBRGsens / (T/60) …. [1]
where TBRGsens is the bucket capacity or sensitivity of the TBRG in mm (commonly 0.2 mm).
This is unlikely to be problematic in intense rainfall, when the ITTs are measured in seconds. However, in rain of low intensity, it becomes less defensible for ITTs measured in minutes or event tens of minutes. The duration of an ITT is determined by the lapse of time between an initial tip and a subsequent tip. Thus, for instance, for a TBRG with 0.2 mm sensitivity, an ITT of 10 minutes would be interpreted as having a fixed rainfall rate of 1.2 mm h-1. A 20 min ITT would indicate a rainfall rate of 0.6 mm h-1. Evidently, ITTs of increasingly long duration can be interpreted as signifying progressively lower rainfall rates. There is no fully rigorous way to identify when a long ITT actually signifies a break in rainfall followed by a recommencement. Therefore, an arbitrary maximum ITT has to be adopted to signify 'no rain', and to demarcate one event from the following event. Widely varying values have been adopted for this purpose. For instance, Gianoglio et al. (2023 [20]) identified a rainfall event when the intensity was > 0.1 mm min-1 (6 mm h-1). Lower intensities were classed as indicating 'not raining'. It is not uncommon for considerable amounts of rain to fall at intensities below this value. However, some such 'presence / absence' or 'raining / not raining' criterion is necessary, since diving 0.2 mm by the ITT duration never yields zero intensity, and can therefore not conclusively indicate whether or not rain is actually falling. Other criteria for 'no rain' have been adopted. For instance, Dunkerley (2015 [29]) adopted 0.1 mm h-1, which is more stringent than the criterion adopted by Gianoglio et al. (2023 [20]), and which, for a TBRG with 0.2 mm sensitivity, requires 2 h with no recorded tip event. Such values seem justifiable, since they are probably less than wet-canopy evaporation rates, and are unlikely to contribute to surface runoff.
However, in many studies that have explored the use of ITTs to estimate intensity, the role of the syphon appears to have been largely neglected. Published studies of this kind commonly do not indicate whether the TBRG used was of the SE or the ST design, and the effect of the syphon may have been overlooked. The methods used in the present work to explore the impact of a syphon on the sequence of ITTs are reported in the next section.

2. Materials and Methods

The data used to explore the research questions were derived in part from controlled laboratory experiments. However, the primary data collected here were to document syphon effects in natural rainfall. To achieve this, two identical, high-quality TBRGs were co-located in the field. The syphon had been removed from one gauge, to form a ST gauge, while the second remained SE.
The laboratory tests were made with constant pumped delivery of water to both forms of TBRG, at various fixed flow rates designed to correspond to a range of rainfall intensities. From a constant inflow rate, a series of identical ITTs would be expected, except for any perturbations caused by the filling and emptying of the syphon. These tests allowed the size of this effect to be quantified. The field tests using paired, co-located gauges, allowed the influence of syphon operation on ITTs and intensities during natural rainfall, during which intensity fluctuates, to be observed.

2.1. Laboratory Tests at Constant Inflow Rates

Water was supplied to the test TBRG either by a Masterflex L/S peristaltic pump capable of delivering flow rates from 15 mm h-1 to 400 mm h-1, or, for lower rainfall intensities, by a smaller, stepper-motor driven peristaltic pump controlled by in-house circuitry and software. The use of a stepper motor permits very low flow rates to be achieved and accurately maintained. Constant flow rates equivalent of < 1 mm h-1 were delivered in this way, and could be sustained for many hours.
Pumping tests were carried out at flow rates corresponding to constant intensities of < 1 mm h-1 to > 300 mm h-1. Particular emphasis was placed on tests representing low rainfall intensities, since it is under these conditions that the ITTs become long and the assumption of constant rainfall rate during an ITT is questionable. All pump rates reported below are based on volume measurements (using calibrated laboratory measuring cylinders, or for very small amounts by weighing to 0.01 g) of the water caught in a tray mounted underneath the TBRG, and which held all water passing through the tipping buckets. Nominal manufacturers calibrations of pump flow rates were not relied upon.
Timing during experiments where this was necessary was done using a stopwatch read to 0.01 s.

2.2. Field Tests with Paired Gauges

The gauges deployed to the field test site (and used for the lab tests) were both high-quality RIMCO model 8020 devices (refer to Table 1 for details). These gauges, originally made by McVan Instruments, Melbourne, Australia (gauges of the same design are now distributed by the Observator group: https://observator.com/, accessed 5 March 2024) have gold-plated brass buckets, and were equipped with machined brass syphons. Syphon dimensions are presented in Table 1.
To establish the contrasting behaviour of ITTs, the syphon was removed from one gauge, and the outlet tube (Figure 1), which was part of the syphon, replaced with a similar length of hard PVC tubing having the same inside diameter. These tubes are needed to ensure that the water discharged from the syphon drains vertically to the required location directly above the hinge on which the buckets rotate as they tip. (It is worth noting here that whilst the tested gauges were of a common size, having a collecting funnel of 203 mm diameter (collecting area 320.5 cm2) there are much larger gauges whose performance might well be different. An example is the Italian CAE 'PMB2' gauge (https://www.cae.it/, accessed 5 March 2024) which has 0.2 mm sensitivity but a collecting funnel area of 1000 cm2, or more than three times that of gauges of the more common size).
The field site was located at about 700 m above sea level, on the Atherton Tableland, inland from the city of Innisfail (far northern Queensland, Australia). This area lies within the wet tropics of Australia, and has a mean annual rainfall of about 3000 mm. Rainfall is delivered in the form of trade-wind showers, originating in the adjacent tropical Coral Sea, or from convective storms that occur primarily in the 'build-up' months prior to the main wet season, which runs from February to July. The data analysed were collected during January and February 2024, mostly from convective showers. Descriptions of rainfall events for this area were reported previously (Dunkerley 2019c [34]).
The gauges were located about 25 cm above ground level on stable concrete slabs, and approximately 70 cm apart. Each was equipped with a Hobo event data logger (time resolution 1 s). Every one to two days, the loggers were re-launched within a few minutes of each other, via a laptop running HoboWare data logger software (available from Onset Computer Corp., https://www.onsetcomp.com/products/software/hoboware, accessed 5 March 2024). This resets the logger clocks, and was done to ensure that the loggers recorded tip events on the same timescale (i.e., to reduce the effects of any time-drift in their internal clocks).
The logged records of tip events were exported to tab-delimited files, and processed using in-house FORTRAN programs. Prior to analysis, the logged dates and times were converted from the Gregorian calendar used in the loggers to Modified Julian dates (MJDs), in which date and time are expressed in a single decimal number. The subroutines used were from the SOFA library of the International Astronomical Union (http://www.iausofa.org/, accessed 5 March 2024). The MJDs recording each successive tip event can then simply be subtracted (using double-precision arithmetic), to determine the ITT duration with high precision. Sections of the logger records were plotted as graphs showing the number of tip events (dependent variable) against MJD (independent variable), to aid the comparison of the records from the two TBRGs. From the field data, intensity-time plots were also generated.

3. Results

3.1. Lab Tests at Constant Pumped Flow Rates

These tests confirmed that there are clear artefacts in the ITT sequence that result from the operation of the syphon.
By way of example, Figure 2 shows the ITT sequence from a SE gauge for a 305 min (>5 hour) lab test at a pump flow rate of 0.43 mL min-1 (equivalent to 0.8 mm h-1). During the test, 130 mL of water was discharged, and there were 22 bucket tip events and 31 syphon emptying cycles. The average ITT was 14.7 min (minimum 9.8 min, maximum 21.1 min). However, the ITTs exhibited two distinct values: 10 had durations of ~ 10 min, and the remainder of ~ 20 min. Evidently, to fill the syphon at this rainfall intensity requires ~ 10 min, and when two syphon cycles are needed to discharge sufficient water to fill and tip a bucket, two cycles occur in succession (ITT = ~ 20 min) before the tip occurs. As Figure 2 shows, neither the ~ 10 min nor the ~ 20 min ITTs exhibited precisely constant values, but rather varied somewhat. Had the 22 tip events occurred separated by unvarying ITTs, as would be expected in view of the constant pumped inflow rate, then the average ITT would have been (305 min/21 ITTs) = ~ 14.5 min. As the results just presented show, this was not close to the duration of any of the ITTs actually recorded, which were either shorter or longer. Thus, the syphon operation has perturbed the ITT sequence, as already described in principle in the Introduction.
The mean volume delivered by the syphon during this test was 4.2 mL per emptying cycle. This is ~ 65% of the nominal bucket volume of 6.47 mL, representing 0.2 mm of rain. Given that the 22 tip events discharged the observed 130 mL of water, the mean volume per tip was 5.91 mL, which is significantly less than the nominal volume suggested by the 0.2 mm sensitivity. Reasons for this are considered in the Discussion section. However, it is appropriate to note here that this anomalously low tip volume means that at a rainfall rate of 0.8 mm h-1, the SE TBRG over-reports the rainfall depth, and hence slightly overstates the mean rainfall intensity. Had the bucket filled to the nominal capacity of 6.47 mL, only ~ 20 tips should have been recorded. A total of 22 tips suggests a rainfall volume of (22 x 6.47) = 142.3 mL, which is ~ 9.5% too high. It should also be noted here that despite the pump inflow rate being equivalent to a rainfall rate of 0.8 mm h-1, the ~ 10 min and ~ 20 min ITTs suggest, respectively, rainfall rates of 1.2 mm h-1 and 0.6 mm h-1, neither of which corresponds to the true rate. However, averaging these distinct ITTs does yield a value (0.9 mm h-1) that is close to being correct. It is important to understand that this is only so because the pump flow rate was held precisely constant for > 5 h. This would probably never occur in natural rainfall, and more widely-varying ITTs would then occur.
There is insufficient space to discuss further results from the pump tests made at other intensities. However, all tests on SE gauges showed perturbations of the ITT sequence, and at higher intensities, the regular short-long ITT sequence described above was often more complex, with multiple short ITTs between successive longer ITTs. This is well illustrated in an example from an SE gauge test at a fixed pump inflow rate corresponding to 165.7 mm h-1 (Figure 3), which is close to the intensity at which the syphon is overwhelmed and drains continually, rather than cycling. Figure 3 also shows, for comparison, the test results for a ST gauge at the same flow rate (intensity) for comparison. The ST data show a completely regular sequence of virtually constant ITTs. The SE data in contrast show a long sequence of variable ITTs, in which the pattern is one short ITT followed by one long ITT, then two short ITTs followed by one long ITT, with this cycle being repeated continuously. These ITTs indicate intensities ranging from ~ 103 mm h-1 to 360 mm h-1. The mean of the recorded ITTs (4.1 s) was close to the expected mean ITT (assuming a gauge calibration of 0.2 mm per tip), which was 4.3 s. However, the minimum and maximum ITTs were respectively 2 s and 7 s. Given the repeating pattern of ITTs recorded in this test, at least one full cycle of the repeating ITT pattern would be required to correctly estimate the mean intensity. The duration of this would include three short ITTs and two long ITTs, such that a total duration of ~ 18 - 20 s of data would be needed. The mean ITT from the ST gauge data was identical to that of the SE gauge (i.e., 4.1 s) but, owing to their relative constancy, could be closely approximated from a single ITT. Thus, the syphon has precluded estimating the intensity from ~ 4 s ITTs, and instead requires about 5 times longer in order to fully represent the perturbed series of ITTs.

3.2. Field Tests Using Two Co-Located Rain Gauges

The SE and ST gauges were each equipped with an event data logger. Given that their clocks were reset regularly, the two data loggers remained closely synchronised, and the same general temporal pattern of rainfall arrival is evident in the data logged by each gauge. Figure 4 shows a representative example of the rainfall recorded during 75 minutes of convective rainfall associated with a thunderstorm cell. The upper panel shows the SE gauge data and the lower panel the ST gauge data. Figure 4 provides an example of the kind of temporal resolution that can be derived from unaggregated ITT records. A small initial burst of rainfall reaching > 10 mm h-1 is followed by about 40 minutes of continuous rain, reaching a peak intensity of ~ 65 mm h-1.
Detailed examination of the two graphs reveals a number of differences. The SE gauge record shows an increase in intensity to ~ 6 mm h-1 just prior to the main, 65 mm h-1 peak. This is absent from the ST record. There are several ITTs having intensities < 20 mm h-1 in the SE data which are absent from the ST data. Several ITTs having intensities of ~ 8 mm h-1 are present in the SE data but absent from the ST data. More tip events are visible in various sections of the ST data (e.g. during the intensity decline after the last intensity peak running from MJD 60356.694 to 60356.7). Rain begins somewhat later, and the first period of rain is of shorter duration, in the SE data. There is an intensity peak of 40 mm h-1 in the SE data at MJD 60356.6936, which is not present in the ST data, which show only a smaller peak intensity of 31.1 mm h-1. The explanation for the presence of higher intensity peaks in the SE data is likely to be the rapid filling and tipping of a partially-filled bucket caused by the syphon emptying. Given that the syphon empties in ~ 2 s, and delivers 4.2 mL of water, the flow rate is the equivalent of a rainfall intensity of 233.6 mm h-1. This is an extreme intensity and if delivered to an almost-full bucket, could result in a tip event and most of the discharged volume passing to the next bucket.
Table 2 summarises the ITT and intensity data from the period of rain shown in Figure 4. Whilst the minimum and maximum intensities are in good agreement, the ITTs recorded by the SE gauge are considerably more variable than those of the ST gauge, and the maximum ITT is very much larger. In terms of intensities derived from the ITTs, it is apparent that the SE gauge suggests a considerably lower minimum intensity and a somewhat higher mean intensity. As Figure 4 shows, the temporal pattern of rainfall arrival recorded by the ITT sequences of the two gauges are distinct in numerous significant ways, and portray intensity variations through the 75 minutes of rainfall quite differently. In broad terms, the SE gauge data exhibit more large jumps from low intensities to high intensities than do the ST gauge data. This is especially noticeable in the burst of rain having a peak intensity of ~ 52 mm h-1 which follows the first, 65 mm h-1 intensity peak. These large jumps in intensity are here interpreted as evidence of the syphon filling and emptying. The ST data in contrast show only smaller fluctuations in intensity, and confirm that the repeated jumps in intensity seen in the SE data are artefacts, and do not reveal the true pattern of intensity fluctuations.
The median intensity recorded by the SE gauge is 13% (~ 3 mm h-1) higher than that of the ST gauge (26.7 mm h-1 vs. 23.6 mm h-1). Correspondingly, the median ITT is 13% shorter (27 s for the SE gauge vs. 30.5 s for the ST gauge). These values are only illustrative of the kinds of differences that can emerge between the two forms of gauge, and it seems reasonable to expect that differences in other rainfall types and rainfall events might well show different patterns. These differences could result for instance from variation in the actual rate of intensity change during any particular event, the duration of intensity peaks, and other event characteristics such as periods of intermittency, as well as TBRG characteristics (syphon and bucket volumes, discharge rate of the syphon, and others).

4. Discussion

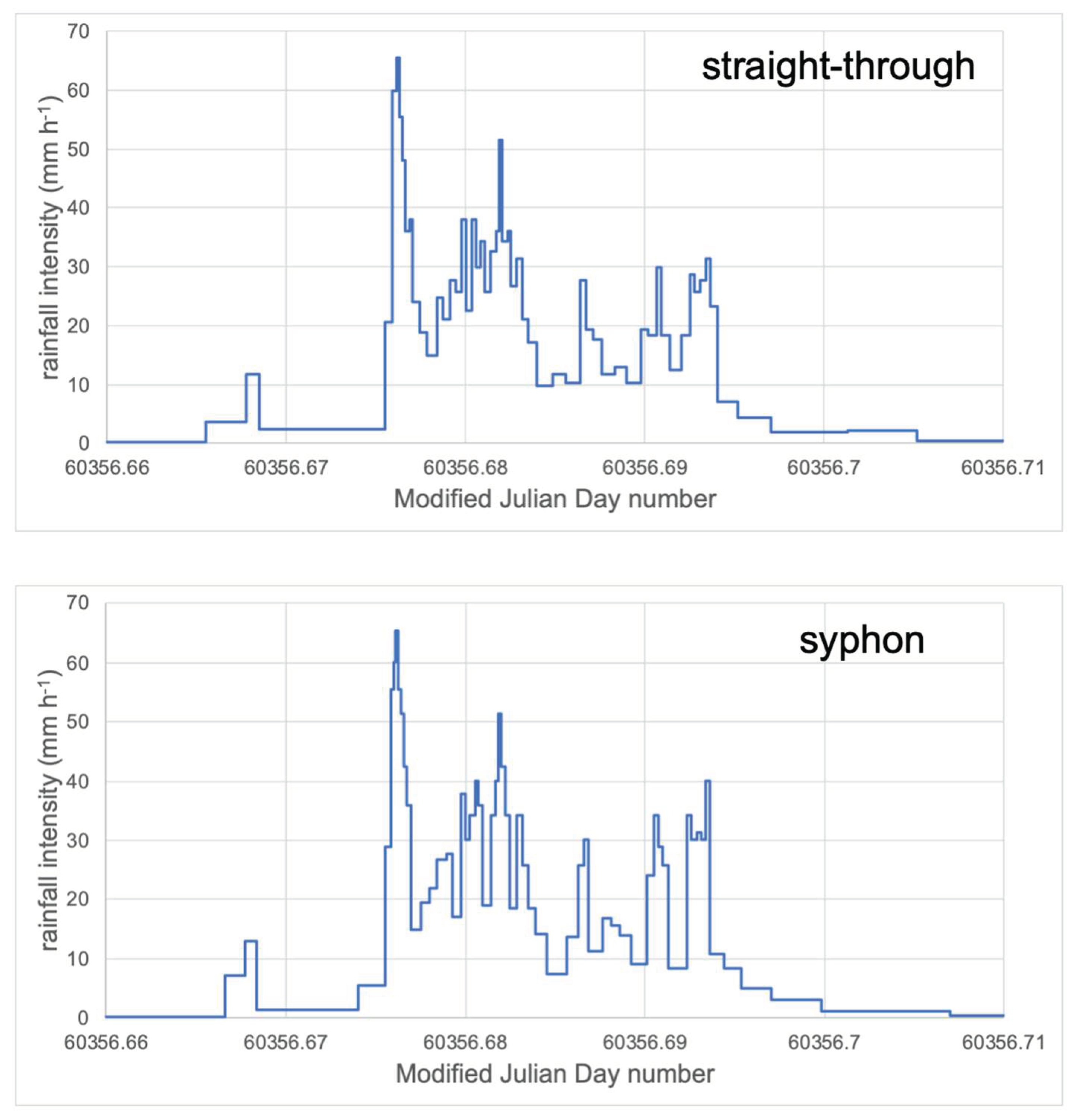
The lab tests established that even at constant inflow rate, the sequence of ITTs recorded by a SE gauge is perturbed such that some ITTs are shortened and others lengthened. This leads to intensities based on the durations of individual ITTs that are either too high or too low. Only the average ITT, analysed over several syphon cycles, corresponds to the true average intensity through that period. Thus, data from a SE gauge offer reduced temporal resolution in rainfall intensity than do ST gauges. Given that individual ITTs depart from the mean by an additional but variable amount owing to surface tension and other effects in the syphon, greater precision in the mean would require and even longer integration time, spanning more long and short ITTs - perhaps 20 minutes. The presence of the syphon therefore further degrades the resolution of rainfall intensity data that can be obtained from the sequence of ITTs. At high intensities, the syphon emptying time becomes progressively longer, as continuing inflow replaces some of the water being discharged. This is an important effect, which can result in syphon emptying, perhaps sustained over 6 - 8 seconds or more, being sufficient to fill three or more buckets, such that a series of unexpectedly short ITTs is generated.
The pump tests at constant flow rate reported here, though they are informative, are able only to indicate the kinds of syphon-induced perturbations to the series of ITTs that can arise. Rainfall intensity never remains absolutely constant in the field, but rather varies from moment-to-moment, with brief intensity peaks and possibly short or long periods of intra-event intermittency. Under such conditions, more variable sequences of ITTs will inevitably result. Interpreting the sequence of ITTs logged by a SE TBRG with a known level of accuracy will then be virtually impossible. At the start of rain, the notional volumes and timings presented earlier can become inapplicable if the syphon (and perhaps tipping bucket) are already partially filled. This is generally unknown, but seems highly likely, given the low probability that prior rain ceased precisely as the syphon emptied and a bucket tip occurred. In an environment with significant intra-event intermittency, this problem could be compounded through multiple commencements and cessations of rainfall during a day, such as the maximum of 15 separate rainfall events recorded per day at several Australian locations (Connolly et al. 1998 [35]) and up to 24 cessations of rain per day recorded in northern Australia (Dunkerley 2024 [36]). Thus, the cumulative daily raining time, from which the mean rainfall rate might be estimated, would itself become biased. In such situations, even though the rainfall depth might be well recorded by either SE or ST gauges, rain duration is likely to be less well known from SE TBRG data than from ST data.
There are additional factors beyond those considered here, that might influence syphon perturbations of the ITT sequence. The syphons are small devices, with narrow spaces through which water needs to flow, and small-diameter outlet tubes that feed water to the tipping buckets. In all of these locations, surface tension effects may arise and retard the free flow of water. For instance, during the lab experiments described earlier, a growing meniscus was often observed at the lower end of the syphon outlet tube. The syphon was only able to discharge freely when this curving meniscus was broken by the weight of water retained behind it. Effects of this kind may well vary with the condition of the metal syphon components, including corrosion or oxidation, as well as with the water composition. Given the small passages and chamber of the syphon, the viscosity of the water seems likely also to be a factor that would influence syphon behaviour. This might vary seasonally (summer vs. winter), or between diurnal and nocturnal rainfall. To the best of the writer's knowledge, these influences remain to be evaluated.

5. Conclusions

The present results confirm that across the range from very low intensities to very high intensities, SE TBRGs generate artefacts in the sequence of ITTs, arising from the filling and emptying of the syphon, and the changing relation between the volume of water discharged to the tipping-bucket and the remaining capacity in the receiving bucket. Under constant inflow, one common pattern at moderate intensities is for some ITTs to be roughly twice as long as others, even though ITTs should be constant under these conditions. At high intensities, more complex sequences of ITTs, with repeating patterns, can occur (illustrated in Figure 3 for an intensity of 165.7 mm h-1). During natural rainfall, these artefacts are not as readily identifiable because they are confounded with actual intensity fluctuations. However, as Figure 4 showed, anomalously long ITTs (and correspondingly low apparent intensities) in SE data that are not seen in ST data, and changes in the number and size of intensity fluctuations, clearly suggest the presence of these artefacts. In the example of Fig 4 and Table 2, some measures of intensity and of ITT durations differed by ~ 13%. The magnitude of the syphon artefacts however would vary among rainfall events, depending on the rapidity of intra-event intensity fluctuations, the durations of intensity peaks, and of course the key syphon and bucket volumes. This warrants further investigation in a range of rainfall climates, and where intermittency is present to varying degrees, as well as in other TBRG designs.
If a research project needs to acquire the highest measures of rainfall intensity that can be derived from a TBRG, then the conclusion from the work reported here is that SE gauges should be avoided, and preference given to ST gauges.

Funding

This research received no external funding.

Data Availability Statement

Data may be made available by the author upon reasonable request.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Segovia-Cardozo, D.A.; Rodríguez-Sinobas, L.; Díez-Herrero, A.; Zubelzu, S.; Canales-Ide, F. Understanding the Mechanical Biases of Tipping-Bucket Rain Gauges: A Semi-Analytical Calibration Approach. In Water, 2021; Vol. 13.
  2. Segovia-Cardozo, D.A.; Bernal-Basurco, C.; Rodríguez-Sinobas, L. Tipping Bucket Rain Gauges in Hydrological Research: Summary on Measurement Uncertainties, Calibration, and Error Reduction Strategies. In Sensors, 2023; Vol. 23.
  3. Cauteruccio, A., Colli, M., Stagnaro, M., Lanza, L., Vuerich, E. In-situ precipitation measurements. In Springer Handbook of Atmospheric Measurements., Foken, T., Ed. Springer Nature: Switzerland, 2021. [CrossRef]
  4. Saidi, H.; Ciampittiello, M.; Dresti, C.; Turconi, L. Extreme rainfall events: evaluation with different instruments and measurement reliability. Environmental Earth Sciences 2014, 72, 4607–4616. [Google Scholar] [CrossRef]
  5. Costello, T.A.; Williams, H.J. Short duration rainfall intensity measured using calibrated time-of-tip data from a tipping bucket raingage. Agricultural and Forest Meteorology 1991, 57, 147–155. [Google Scholar] [CrossRef]
  6. Humphrey, M.D.; Istok, J.D.; Lee, J.Y.; Hevesi, J.A.; Flint, A.L. A New Method for Automated Dynamic Calibration of Tipping-Bucket Rain Gauges. Journal of Atmospheric and Oceanic Technology 1997, 14, 1513–1519. [Google Scholar] [CrossRef]
  7. Santana, M.A.A.; Guimarães, P.L.O.; Lanza, L.G.; Vuerich, E. Metrological analysis of a gravimetric calibration system for tipping-bucket rain gauges. Meteorological Applications 2015, 22, 879–885. [Google Scholar] [CrossRef]
  8. Sypka, P. Dynamic real-time volumetric correction for tipping-bucket rain gauges. Agricultural and Forest Meteorology 2019, 271, 158–167. [Google Scholar] [CrossRef]
  9. Kimball, S.K.; Mulekar, M.S.; Cummings, S.; Stamates, J. The University of South Alabama Mesonet and Coastal Observing System: A Technical and Statistical Overview. Journal of Atmospheric and Oceanic Technology 2010, 27, 1417–1439. [Google Scholar] [CrossRef]
  10. Cai, Z.; Liu, J.; Liao, A.; Li, X.; Liao, M. Numerical and Experimental Investigation on the Function of Siphons for Tipping-Bucket Rain Gauges. Journal of Atmospheric and Oceanic Technology 2020, 37, 1189–1201. [Google Scholar] [CrossRef]
  11. Duchon, C.; Fiebrich, C.; Grimsley, D. Using High-Speed Photography to Study Undercatch in Tipping-Bucket Rain Gauges. Journal of Atmospheric and Oceanic Technology 2014, 31, 1330–1336. [Google Scholar] [CrossRef]
  12. Liao, M.; Liao, A.; Liu, J.; Cai, Z.; Liu, H.; Ma, T. A novel method and system for the fast calibration of tipping bucket rain gauges. Journal of Hydrology 2021, 597, 125782. [Google Scholar] [CrossRef]
  13. Parkin, D.A.; King, W.D.; Shaw, D.E. An Automatic Recording Raingage Network for a Cloud-Seeding Experiment. Journal of Applied Meteorology (1962-1982) 1982, 21, 227–236. [Google Scholar] [CrossRef]
  14. Maksimović, Č.; Bužek, L.; Petrović, J. Corrections of rainfall data obtained by tipping bucket rain gauge. Atmospheric Research 1991, 27, 45–53. [Google Scholar] [CrossRef]
  15. Harremoës, P.; Mikkelsen, P.S. Properties of extreme point rainfall I: Results from a rain gauge system in Denmark. Atmospheric Research 1995, 37, 277–286. [Google Scholar] [CrossRef]
  16. Overgaard, S.; El-Shaarawi, A.H.; Arnbjerg-Nielsen, K. Calibration of tipping bucket rain gauges. Water Science and Technology 1998, 37, 139–145. [Google Scholar] [CrossRef]
  17. Chwala, C.; Gmeiner, A.; Qiu, W.; Hipp, S.; Nienaber, D.; Siart, U.; Eibert, T.; Pohl, M.; Seltmann, J.; Fritz, J. , et al. Precipitation observation using microwave backhaul links in the alpine and pre-alpine region of Southern Germany. Hydrol. Earth Syst. Sci. 2012, 16, 2647–2661. [Google Scholar] [CrossRef]
  18. Colli, M.; Stagnaro, M.; Caridi, A.; Lanza, L.G.; Randazzo, A.; Pastorino, M.; Caviglia, D.D.; Delucchi, A. A Field Assessment of a Rain Estimation System Based on Satellite-to-Earth Microwave Links. IEEE Transactions on Geoscience and Remote Sensing 2019, 57, 2864–2875. [Google Scholar] [CrossRef]
  19. Adirosi, E.; Facheris, L.; Giannetti, F.; Scarfone, S.; Bacci, G.; Mazza, A.; Ortolani, A.; Baldini, L. Evaluation of Rainfall Estimation Derived From Commercial Interactive DVB Receivers Using Disdrometer, Rain Gauge, and Weather Radar. IEEE Transactions on Geoscience and Remote Sensing 2021, 59, 8978–8991. [Google Scholar] [CrossRef]
  20. Gianoglio, C.; Alyosef, A.; Colli, M.; Zani, S.; Caviglia, D.D. Rain Discrimination with Machine Learning Classifiers for Opportunistic Rain Detection System Using Satellite Micro-Wave Links. Sensors (Basel) 2023, 23. [Google Scholar] [CrossRef]
  21. Yu, C.L. , Sin, K. C., Chan, Shaoguan, Guangdon, 9-10 January 2013, Y.W. Inter-comparison of 0.1-mm resolution raingauges in the measurement of rainfall amount and rainfall intensity/. In Proceedings of 27th Guangdong - Hong Kong - Macao seminar on meteorological science and technology; p. 16.
  22. Chan, Y. , Yu, C., Tam, K. Inter-comparison of raingauges on rainfall amount and intensity measurements in a tropical environment. Journal of Geodesy and Geomatics Engineering 2015, 1, 12–25. [Google Scholar]
  23. Stagnaro, M.; Colli, M.; Lanza, L.G.; Chan, P.W. Performance of post-processing algorithms for rainfall intensity using measurements from tipping-bucket rain gauges. Atmos. Meas. Tech. 2016, 9, 5699–5706. [Google Scholar] [CrossRef]
  24. Stagnaro, M., Colli, M., Lanza, L., Chan, P.W. Assessing rainfall intensity calculation algorithms for tipping bucket rain gauges at a field test site. In Proceedings of European Geosciences Union, General Assembly, Vienna, Austria, 17-22 April 2016.
  25. S Shedekar, V.; C Brown, L.; Heckel, M.; W King, K.; R Fausey, N.; Daren Harmel, R. Measurement Errors in Tipping Bucket Rain Gauges under Different Rainfall Intensities and their implication to Hydrologic Models. Proceedings of 2009 Reno, Nevada, 2009, St. Joseph, MI., June 21 - June 24.
  26. Rachmawati, L.M.; Mardiansyah, A.; Kinanti, I.W.; Ramadhan, A.; Adiwidya, A.S.; Jalasena, A.; Chandra, I. Natural, Meteorology, And Novel – IAP Data Processing Method for Tipping Bucket Based Rain Gauge. Journal of Physics: Conference Series 2022, 2243, 012071. [Google Scholar] [CrossRef]
  27. Song, Y.; Han, D.; Rico-Ramirez, M.A. High temporal resolution rainfall rate estimation from rain gauge measurements. Journal of Hydroinformatics 2017, 19, 930–941. [Google Scholar] [CrossRef]
  28. Dunkerley, D.L. Rainfall intensity bursts and the erosion of soils: an analysis highlighting the need for high temporal resolution rainfall data for research under current and future climates. Earth Surf. Dynam. 2019, 7, 345–360. [Google Scholar] [CrossRef]
  29. Dunkerley, D. Intra-event intermittency of rainfall: an analysis of the metrics of rain and no-rain periods. Hydrological Processes 2015, 29, 3294–3305. [Google Scholar] [CrossRef]
  30. Dunkerley, D. What does I30 tell us? An assessment using high-resolution rainfall event data from two Australian locations. Catena 2019, 180, 320–332. [Google Scholar] [CrossRef]
  31. Dunkerley, D. Intermittency of rainfall at sub-daily timescales: New quantitative indices based on the number, duration, and sequencing of interruptions to rainfall. Atmospheric Research 2021, 253, 105475. [Google Scholar] [CrossRef]
  32. Mandeep, J.S.; Hassan, S.I.S. 60- to 1-Min Rainfall-Rate Conversion: Comparison of Existing Prediction Methods with Data Obtained in the Southeast Asia Region. Journal of Applied Meteorology and Climatology 2008, 47, 925–930. [Google Scholar] [CrossRef]
  33. Muñoz, P.; Celleri, R.; Feyen, J. Effect of the Resolution of Tipping-Bucket Rain Gauge and Calculation Method on Rainfall Intensities in an Andean Mountain Gradient. Water 2016, 8, 534. [Google Scholar] [CrossRef]
  34. Dunkerley, D. How does sub-hourly rainfall intermittency bias the climatology of hourly and daily rainfalls? Examples from arid and wet tropical Australia. International Journal of Climatology 2019, 39, 2412–2421. [Google Scholar] [CrossRef]
  35. Connolly, R.D.; Schirmer, J.; Dunn, P.K. A daily rainfall disaggregation model. Agricultural and Forest Meteorology 1998, 92, 105–117. [Google Scholar] [CrossRef]
  36. Dunkerley, D. Sub-daily rainfall intermittency: Is it really stochastic? A test at two Australian locations. International Journal of Climatology 2024, n/a. [Google Scholar] [CrossRef]
Preprints 101061 g001
Figure 1. Schematic of syphon (upper) showing the position of the water surface at the moment when the syphon is about to empty, and photos showing the syphon installed in the outer casing (lower left) and with the bell syphon removed (lower right).
Figure 1. Schematic of syphon (upper) showing the position of the water surface at the moment when the syphon is about to empty, and photos showing the syphon installed in the outer casing (lower left) and with the bell syphon removed (lower right).
Preprints 101061 g001
Preprints 101061 g002
Figure 2. Graph showing the pattern of tip events and ITTs for a pumped test at a fixed flow rate equivalent to 0.8 mm h-1. The ITTs are the horizontal lines, whose length shows the ITT duration. Note the sequence of short - long - short ITTs, though with some variation in the durations of each. This pumped test was run for slightly more than 5 hours, in order to generate sufficient tip events for analysis.
Figure 2. Graph showing the pattern of tip events and ITTs for a pumped test at a fixed flow rate equivalent to 0.8 mm h-1. The ITTs are the horizontal lines, whose length shows the ITT duration. Note the sequence of short - long - short ITTs, though with some variation in the durations of each. This pumped test was run for slightly more than 5 hours, in order to generate sufficient tip events for analysis.
Preprints 101061 g002
Preprints 101061 g003
Figure 3. Graph showing the pattern of tip events and ITTs for a pumped test at a fixed flow rate equivalent to 165.7 mm h-1. The ITTs are the horizontal lines, whose length shows the ITT duration. Only the first 2 minutes of data from a longer test are shown. Note the repeating sequence of ITTs in the SE data (upper panel) in which long ITTs are separated by either two or three shorter ITTs, and the marked contrast with the regular sequence of uniform ITTs in the ST data (lower panel). The pumped flow rate was the same for each test. Note that the slope of the line, proportional to the intensity, is the same for both panels. Refer to text for fuller details.
Figure 3. Graph showing the pattern of tip events and ITTs for a pumped test at a fixed flow rate equivalent to 165.7 mm h-1. The ITTs are the horizontal lines, whose length shows the ITT duration. Only the first 2 minutes of data from a longer test are shown. Note the repeating sequence of ITTs in the SE data (upper panel) in which long ITTs are separated by either two or three shorter ITTs, and the marked contrast with the regular sequence of uniform ITTs in the ST data (lower panel). The pumped flow rate was the same for each test. Note that the slope of the line, proportional to the intensity, is the same for both panels. Refer to text for fuller details.
Preprints 101061 g003
Preprints 101061 g004
Figure 4. Intensity - time plots of a 75-minute rainfall event as logged using an ST gauge (upper panel) and a SE gauge (lower panel). Horizontal lines in each graph represent the ITTs, and these become shorter during more intense rainfall. Note the evident differences between the ST and SE data in portraying intensity fluctuations during this convective rainfall event. The time axis is labelled in Modified Julian days. The increment between axis labels is 0.01 days, or approx. 15 minutes. Refer to text for a fuller description.
Figure 4. Intensity - time plots of a 75-minute rainfall event as logged using an ST gauge (upper panel) and a SE gauge (lower panel). Horizontal lines in each graph represent the ITTs, and these become shorter during more intense rainfall. Note the evident differences between the ST and SE data in portraying intensity fluctuations during this convective rainfall event. The time axis is labelled in Modified Julian days. The increment between axis labels is 0.01 days, or approx. 15 minutes. Refer to text for a fuller description.
Preprints 101061 g004
Table 1. Dimensions of the RIMCO rain gauges.
Table 1. Dimensions of the RIMCO rain gauges.
Parameter RIMCO model 8020
syphon casing
outside diameter		 31.5 mm
syphon casing inside diameter 22 mm
syphon casing height 27.5 mm
bell syphon diameter 12.5 mm
bell syphon height 11 mm
bell syphon outlet tube length 25 mm
bell syphon outlet tube outside diameter 5 mm
bell syphon outlet tube inside diameter 2.6 mm
Table 2. Statistics of the calculated ITTs and the corresponding rainfall intensities for the two co-located TBRGs. The rainfall event had a duration of 75 minutes, and delivered 28.8 mm of rain (assuming 0.2 mm per tip was applicable to each of the 144 logged tip events). The mean intensity for the whole event was 23.0 mm h-1, and the momentary peak intensity 65 mm h-1. Note the clear differences in the median ITT and median rainfall intensity between the two gauges.
Table 2. Statistics of the calculated ITTs and the corresponding rainfall intensities for the two co-located TBRGs. The rainfall event had a duration of 75 minutes, and delivered 28.8 mm of rain (assuming 0.2 mm per tip was applicable to each of the 144 logged tip events). The mean intensity for the whole event was 23.0 mm h-1, and the momentary peak intensity 65 mm h-1. Note the clear differences in the median ITT and median rainfall intensity between the two gauges.
parameter syphon-equipped (SE) gauge straight-through (ST) gauge

ITTs
(units: seconds)		 mean 59.12 59.17
std. deviation 101.46 80.72
minimum 11.0 11.0
maximum 615.0 367.0s
median 27.0 30.5

intensities
(units: mm h-1)		 mean 26.19 24.77
std. deviation 15.32 14.97
minimum 1.17 1.96
maximum 65.45 65.45
median 26.67 23.61
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated