Prerpints.org logo
Preprint
Article

Forecasting the Performance of the Energy Sector at the Saudi Stock Exchange Market by Using GBM and GFBM

Altmetrics

Downloads

104

Views

28

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

11 March 2024

Posted:

14 March 2024

You are already at the latest version

Alerts
Abstract
The future index prices are viewed as a critical issue for any trader and investor. For this craving, various models have shown up in the literature. The Geometric Brownian motion (GBM) is one of the popular models. This work examines four types of GBM as per the presence of memory or kind of volatility. These models include classical GBM with memoryless and constant volatility assumptions, SVGBM with memoryless and stochastic volatility assumption, GFBM with memory and constant volatility assumption, and SVGFBM with memory and stochastic volatility assumption. These models are utilized in an empirical study to forecast the future index price of Energy Sector in the Saudi Stock Exchange Market. The assessment was led by utilizing two error standards, mean square error (MSE) and mean absolute percentage error (MAPE). The outcomes showed that the SVGFBM occupies the highest level of accuracy according to smallest values of MSE and MAPE. While the accuracy of GBM come in the tail of the list models under study. These results have affirmed the positive affection of combining memory and stochastic volatility assumption into the GBM model, which agreed findings of numerous earlier works. Furthermore, the findings showed the GFBM models are more accurate than GBM models regardless of the type of volatility. While, under the same type of memory, the models with stochastic volatility assumption are more accurate than the corresponding models of constant volatility assumption. In general, all models considered in this work uncovered high accuracy through the value of MAPE ≤ 10%. This indicates of the ability of applying these models in a real financial environment. Through this empirical study, we can say that the Energy Sector in Saudi Arabia is predictable and stable and afterward we urge financial investors and stockholder to trade and invest in this sector.
Keywords: 
Subject: Computer Science and Mathematics  -   Probability and Statistics

1. Introduction

The Kingdom of Saudi Arabia is the largest producer and exporter of oil in the world. For this reason, Saudi Arabia recognizes the significance of diversifying its energy mix to keep long-term economic prosperity. Both domestic and foreign partners in the energy sector are playing an important role in the transformation of the Kingdom to the direction of a sustainable and renewable future. Therefore, the Energy sector is very important in the Saudi Exchange stock market. It consists of six companies with a total capital exceeding 7 trillion Saudi Riyals (SAR). ($1,86 trillion). Hence, there are a large number of investors, traders, and speculators considering this sector. Therefore, the future performance of this sector is considered a fundamental issue for all types of traders to gain profits and avoid possible losses. For this purpose, a need for a tool that can forecast future prices as precisely as possible arose. Many scholars proposed several models as a tool that employing historical data to forecast future prices such as random walk, jump diffusion, Brownian motion process, and geometric Brownian motion (GBM) models. This work investigates some of the GBM models by incorporating the assumptions of stochastic volatility and memory.

2. Geometric Brownian Motion Models

The econophysics concept of GBM explains the nature of stock price randomness and arbitrary fluctuations calculations more accurately (Kumar et al. 2024). Occasionally, GBM has been called “the standard model of finance” (Ibe, 2013), where it is employed in forecasting the price of a stock over time. GBM is the adapted version of Brownian motion (BM) process.
Definition 1.
A   Wiener   Process   or   Brownian   motion   ( BM )   is   a   stochastic   process   B t   that   satisfies the   next   conditions :
i.
B t is   a   continuous   function   of   time   with   B 0   =   0
ii.
B t has   independent   increments   ( B t   −   B s and B v   −   B u   are   independent   for   all   v > v > t > s ) .
iii.
B t   −   B s ~ N ( 0 , t − s )   for   all t > s .
According to the definition above, BM process is continuous everywhere but it is not differentiable anywhere. BM is self-similar (i.e if any part of the BM time series trajectory is like the entire trajectory). If BM touches any specific value, it will return to this value again infinitely many times.
These properties encouraged Ross in 1999 to model stock prices directly depending on BM. However, this way of modeling has faced reasonable blame because of the nature of BM that permits the price to be negative where the stock price is supposed to be a normal random variable. As a treatment of this issue, GBM has been presented as an adaptation of BM.
Model 1: Geometric Brownian Motion (GBM)
T h e   s t o c h a s t i c   p r o c e s s   X t   i s   s a i d   t o   f o l l o w   G B M   i f   i t   s a t i s f i e s   t h e   n e x t   s t o c h a s t i c   d i f f e r e n t i a l   e q u a t i o n   ( S D E ) :
d X t = μ X t d t + σ X t d B t
w h e r e   B t   i s   a   B M , μ   a n d   σ   a r e   d r i f t   a n d   v o l a t i l i t y   r e s p e c t i v e l y .   T h e   g e n e r a l   s o l u t i o n   o f   t h i s   S D E   i s   g i v e n   b y
X t = X 0 exp ⁡ μ − 1 2 σ 2 t + σ B t     w h e r e   X 0   i s   a n   i n i t i a l   v a l u e .
GBM is a non-negative variation of BM. Consequently, GBM can be employed in many financial applications such as index prices, exchange rates, option pricing, mortgage insurance, and value at risk. GBM model is valuable for modeling random price fluctuation over time and investigating the commodity’s price performance. Hence, GBM is used widely to predict future prices.
The classical GBM model assumes the independence of prices. Meanwhile, many researchers attracted attention to the existence of memory in the GBM model. For example Han etal. (2020), Rejichi and Aloui (2012), Alhagyan & Yassen (2023), Painter (1998), Alhagyan (2018), Grau-Carles (2000), Abbas and Alhagyan (2023) and Kim et al. (2020).
This implied the necessity to develop the GBM model by incorporating the properties of memory. The developed model is called Geometric Fractional Brownian Motion (GFBM). The GFBM model is obtained by replacing the classical BM -process (no memory) with a developed process called fractional Brownian motion FBM-process (with memory).
Definition 2.
 
T h e   f r a c t i o n a l   B r o w n i a n   m o t i o n   ( F B M ) , { B H ( t ) } , w i t h   H u r s t   p a r a m e t e r   H ∈ ( 0 , 1 )   i s   a   c e n t e r e d   G a u s s i a n   p r o c e s s   w h o s e   p a t h s   a r e   c o n t i n u o u s with probability 1 and its distribution is defined by the covariance structure:
E [ B H t B H s ] = 1 2 ( t 2 H + s 2 H − t − s 2 H )
The correlation between the increments of FBM ( B H t − B H s and B H v − B H u   f o r   a l l   v > v > t > s ) fluctuates conveniently with self–similarity or Hurst parameter H . Hurst parameter name referred to Harold Edwin Hurst (1880–1978) who examined the erratic rainfall and drought circumstances along the Nile River over a long period. Three types of memories appeared according to the value of   H , short memory when 0 < H < 0.5 , no memory if H = 0.5 , and long memory when 0.5 < H < 1 . Now, by replacing BM in Equation (1) with FBM, we got the GFBM model that is presented as follows.
Model 2: Geometric Fractional Brownian Motion (GFBM)
T h e   s t o c h a s t i c   p r o c e s s   X t   i s   s a i d   t o   f o l l o w   G F B M   i f   i t   s a t i s f i e s   t h e   n e x t   S D E
d X t = μ X t d t + σ X t   d B H 1 ( t )
w h e r e   B H 1 t   i s   F B M , μ   a n d   σ   a r e   d r i f t   a n d   v o l a t i l i t y   r e s p e c t i v e l y . T h e   s o l u t i o n   i s   g i v e n   b y
X ( t ) = X 0 exp ⁡ μ − 1 2 σ 2 t 2 H 1 − 1 t + σ B H 1 t w h e r e   X 0   i s   a n a r b i t r a r y   i n i t i a l   v a l u e .
The GFBM model is considered a developed version of GBM, thus they can be employed in the same financial applications. For example, option pricing (Misiran et al. 2010; 2012, Alhagyan et al. 2016 a; 2016), index prices (Alhagyan & Al-Duais 2020, Abbas & Alhagyan 2022; 2023, Xiao et al. 2015), value at risk (Alhagyan et al. 2021, Wang et al. 2017), exchange rate (Gözgör 2013, Mansour and Alhagyan 2022, Alhagyan 2022, Abbas and Alhagyan 2023), and mortgage insurance (Bardhan et al. 2006, Alhagyan et al. 2021, Chen et al. 2013).
Constant assumption of volatility ( σ ) was used in the models of GBM to simplify calculations. However, this assumption was not supported by some empirical studies like Stein (1989), Bakshi et al. (2000), and Aїt–Sahalia and Lo (1998) where they concluded that the assumption of constant volatility does not describe the real situation accurately. For this reason, there have been many efforts to deal with this issue by replacing the constant volatility ( σ ) in GBM models deterministic function of a stochastic process or volatility process σ ( Y t ) where Y t is the solution of other stochastic differential equation (SDE) that is driven by other noise stochastic volatility. For example the efforts of Scott 1987, Hull and White (1987), Alhagyan et al. (2016 a; 2016 b), Stein and Stein (1991), Heston (1993), Alhagyan and Yassen (2023), Hagan et al. (2002), Alhagyan (2022), Comte and Renault (1998), Chronopoulou and Viens (2012 a; 2012 b), Wang and Zhang (2014) and Alhagyan (2018).
The SV models are considerable in the environment of financial market because its ability to capture the effect of time–varying volatility. SV models permit of both volatility and common dependence between variables to fluctuate over. This implies that SV models have two sources of randomness. Table 1 presents some SDE equations describing the stochastic process Y t .
In the following, two models of SV under study are presented.
Model 3: GBM perturbed by FOU (SVGBM)
T h e   s t o c h a s t i c   p r o c e s s   X t   i s   s a i d   t o f o l l o w   G B M   p e r t u r b e d   b y   S V F O U   i f   i t   s a t i s f i e s t h e   n e x t   S D E :
d X t = μ X t d t + σ ( Y t ) X t d B 1 t
w h e r e   μ   i s   a   m e a n   o f   r e t u r n ,   Y t   i s   a   s t o c h a s t i c   p r o c e s s ,   B 1 t   i s   a   B M ,   a n d   σ ( Y t ) =   Y t   i s   a   d e t e r m i n i s t i c   f u n c t i o n . L e t   t h e   d y n a m i c s   o f   v o l a t i l i t y   Y t   f o l l o w   f r a c t i o n a l   O r n s t e i n –
U h l e n b e c k   ( F O U )   p r o c e s s   w h i c h   i s   t h e   s o l u t i o n   o f   t h e   f o l l o w i n g   S D E
d Y t = α ( m − Y t ) d t + β d B H 2 ( t )
w h e r e   α , β   a n d   m   a r e   m e a n   r e v e r t i n g   o f   v o l a t i l i t y ,   v o l a t i l i t y   o f   v o l a t i l i t y ,   a n d   m e a n
o f   v o l a t i l i t y , r e s p e c t i v e l y .   B H 2 ( t )   i s   a   F B M   w h i c h   i s   i n d e p e n d e n t   f r o m   B 1 t .
Model 4: GFBM perturbed by FOU (SVGFBM)
T h e   s t o c h a s t i c   p r o c e s s   X t   i s   s a i d   t o   f o l l o w   a   G F B M   p e r t u r b e d   b y   S V ( F O U )   i f   i t   s a t i s f i e s   t h e   f o l l o w i n g   S D E :
d X t = μ   X t d t + σ ( Y t ) X t d B H 1 ( t )
w h e r e   μ   i s   m e a n   o f   r e t u r n ,   Y t   i s   a   s t o c h a s t i c   p r o c e s s ,   B H 1 ( t )   i s   a   F B M   w i t h   H u r s t   i n d e x
H 1 , a n d   σ Y t = Y t   i s   a   d e t e r m i n i s t i c   f u n c t i o n .   L e t   t h e   d y n a m i c s   o f   v o l a t i l i t y   Y t   b e
d e s c r i b e d   b y   f r a c t i o n a l   O r n s t e i n – U h l e n b e c k   ( F O U ) p r o c e s s   w h i c h   i s   s o l u t i o n   o f   t h e
  f o l l o w i n g   S D E
d Y t = α ( m − Y t ) d t + β d B H 2 ( t )
w h e r e   α , β   a n d   m   a r e c o n s t   a n t p a r a m e t e r s   t h a t   r e p r e s e n t   m e a n   r e v e r t i n g   o f   v o l a t i l i t y ,
v o l a t i l i t y   o f   v o l a t i l i t y ,   a n d   m e a n   o f   v o l a t i l i t y ,   r e s p e c t i v e l y .   B H 2 ( t )   i s   a   F B M   w h i c h   i s
i n d e p e n d e n t   f r o m   B H 1 ( t ) .

3. Forecasting

This work employs the four models mentioned in the previous section to forecast future index prices of seven companies in the energy sector in Saudi Arabia depending on historical data. In this empirical study, we examine the influence of incorporating both memory and stochastic volatility into the GBM model.
We relied on two measures of error to evaluate and compare the performance of each model under study. These measures are mean square error ( M S E ) and mean absolute percentage error ( M A P E ).
M S E = ∑ i = 1 n Y i − F i 2 n   &   M A P E = ∑ i = 1 n Y i − F i Y i n
, where F i and Y i represent forecast and price actual price at day   i , respectively. While n the total of forecasting days. Lawrence (2009) recapped the judgment on any forecasting method using MAPE in the following table.
Table 2. M A P E   t o   j u d g m e n t   a c c u r a c y   o f   f o r e c a s t i n g   m e t h o d .
Table 2. M A P E   t o   j u d g m e n t   a c c u r a c y   o f   f o r e c a s t i n g   m e t h o d .
Judgment of Accuracy MAPE
Highly accurate MAPE < 10 %
Good accurate 10 % ≤ MAPE < 20 %
Reasonable 20 % ≤ MAPE < 50 %
Inaccurate MAPE ≥ 50 %

3.1. Description of Historical Data

The historical data is available online at https://www.saudiexchange.sa. The total working days are 43 days begin from 1st November 2023 to 31st December 2023. To avoid high fluctuation in data, return series is considered in logarithm (i.e., r n = l n ⁡ ( S / S n − 1 )). Figure 1 and Figure 2 show the close prices and its return series.

3.2. Forecasting and Evaluation

According to the historical data of energy sector indices, all parameters involved in the four models under study are calculated by using Mathematica 10 software and then employed to compute constant volatility and stochastic volatility. Table 3 lists all computed parameters and volatilities.
Then the forecasting of close price of the next month (Jan 2024) is conducting based on the values of the parameters in Table 3. The forecasting is computed using four models; GBM, GFBM, SVGBM, and SVGFBM. Table 4 shows the level of accuracy of each model. Meanwhile, Table 5 shows the forecasted prices in addition to the actual prices of energy indices.
That is what the discoveries showed, in light of the smaller MSE and MAPE values; SVGFBM has the first level in accuracy. This outcome was accomplished due to the presence of two sources of memory ( H 1 and H 2 ) along with stochastic volatility assumption. While GBM placed last because of the existence of one sources of randomness in addition to constant volatility assumption. The outcomes endorsed that models under memory assumption (SVGFBM and GFBM) are more appropriate in forecasting future stock costs than the models without memory (SVGBM and GBM).
As per Lawrence’s table (Table 2) all models achieved MAPE <10% which indicating that high accuracy in forecasting by these models. Moreover, one can observe that the values of MSE of SVGFBM, GFBM, and SVGBM are close together while GBM is relatively far. These outcomes run in the same direction as many experimental researches for instance Willinger et al. (1999), Rejichi and Aloui (2012), Alhagyan (2022), Painter (1998), Alhagyan and Yassen (2023), Alhagyan and Alduais (2020), and Abbas and Alhagyan (2022; 2023). Figure 3 illustrates the comparison between the actual close prices versus forecasted close prices. This Figure showed that the forecasted prices are less fluctuated than the actual prices and ensured that the forecasted prices are closer together.

4. Conclusion

Index price reflects the financial stability and level of economic growth. Therefore, forecasting the future performance of index prices is in the top tasks of stakeholders and investors. For this task, several models have been presented in literature. GBM model is one of the famous and important models. There are some models emanated from classical GBM model. This emanation depending the assumption of existence (or absence) of memory in time series financial data in addition to the assumption of volatility (constant or stochastic). To discuss the affection of these assumptions on GBM model, this work examined four models of GBM including; classical GBM (absence of memory and constant volatility), GFBM (existence of memory and constant volatility), SVGBM (absence of memory and stochastic volatility), and SVGFBM (memory and stochastic volatility). All these models stated in Section 2 of this manuscript. The examination was conducted by exploiting these models to forecast Energy Sector in the Saudi Stock Exchange Market. Two statistical criterions of error was utilized (MSE and MAPE) to evaluate the performance of each model.
The findings of this empirical examination exposed that SVGFBM achieved the smallest values of both MSE and MAPE and then the best performance. This result achieved because of the existence of two sources of randomness with memory ( d B H 1 & d B H 2 ) and the assumption of stochastic volatility. While GBM ranked last because of existence of one source of randomness without memory ( H = 0.5 ) and the assumption of constant volatility.
The results ensured that GFBM models are more accurate than GBM models for forecasting future stock prices. Furthermore, under the same assumption of memory, the models of stochastic volatility assumption are more accurate than the models of constant volatility assumption. This outcome has proved that the direct positive affection of incorporating memory and stochastic volatility together into GBM.
Moreover, values of the MSE and MAPE for SVGFBM, GFBM, and SVGBM are relatively close together while GBM was moderately far. Generally, according to the Lawrence’s table to judgment accuracy (Table 2), all models exhibited high level of performance because of the MAPE <10% which indicate that all models under study can used as a tool of forecasting future index price of Energy Sector in Saudi Arabia.
In general, the empirical results of this study agree with earlier empirical works such as Abbas & Alhagyan (2022; 2023), Mansour & Alhagyan (2022), Alhagyan & Yassen (2023), Alhagyan (2022), Willinger et al. (1999), Painter (1998), Rejichi & Aloui (2012) and Alhagyan & Alduais (2020) to name just a few. Subsequently, we are strongly recommend investors and trader to invest in the Energy Sector in Saudi Arabia because of its predictability and stability.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors extend their appreciation to Prince Sattam Bin Abdulaziz University for funding this research work through the project number (IF2/PSAU/ 2023/01/24999).

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

  1. Abbas, A., & Alhagyan, M. (2022). The effect of incorporating memory and stochastic volatility into geometric Brownian motion in forecasting the performance of Tadawul all share Index (TASI). Advances and Applications in Statistics, 74, 47-62.‏.
  2. Abbas, A., & Alhagyan, M. (2023). Forecasting Exchange Rate of Sar/Cny By Incorporating Memory and Stochastic Volatility Into GBM Model. Advances and Applications in Statistics, 86(1), 65-78.‏.
  3. Aït–Sahalia, Y., & Lo, A. W. (1998). Nonparametric estimation of state–price densities implicit in financial asset prices. The Journal of Finance, 53(2), 499- 547.
  4. Alhagyan, M. (2022). The effects of incorporating memory and stochastic volatility into GBM to forecast exchange rates of Euro. Alexandria Engineering Journal, 61(12), 9601-9608.‏.
  5. Alhagyan, M. K. M. (2018). Modeling financial environments using geometric fractional Brownian motion model with long memory stochastic volatility. Universiti Utara Malaysia.‏.
  6. Alhagyan, M., & Alduais, F. (2020). Forecasting the performance of Tadawul all share index (TASI) using geometric Brownian motion and geometric fractional Brownian motion. Adv. Appl. Stat, 62(1), 55-65.‏.
  7. Alhagyan, M., & Yassen, M. F. (2023). Incorporating stochastic volatility and long memory into geometric Brownian motion model to forecast performance of Standard and Poor’s 500 index. AIMS Mathematics, 8(8), 18581-18595.‏.
  8. Alhagyan, M., Misiran, M. & Omar, Z. (2016 a). Geometric fractional Brownian motion perturbed by fractional Ornstein-Uhlenbeck process and application on KLCI option pricing. Open Access Library Journal, 3(08), 1.‏.
  9. Alhagyan, M., Misiran, M. & Omar, Z. (2021). “On effects of stochastic volatility and long memory towards mortgage insurance models: an empirical study”, Advances and Applications in Statistics, vol. 66, no.2, pp. 165-174.
  10. Alhagyan, M., Misiran, M. & Omar, Z. (2016 b). Estimation of geometric fractional Brownian motion perturbed by stochastic volatility model. Far East Journal of Mathematical Sciences, 99(2), 221.‏.
  11. Alhagyan, M., Misiran, M., & Omar, Z. (2016 b). Estimation of geometric fractional Brownian motion perturbed by stochastic volatility model. Far East Journal of Mathematical Sciences, 99(2), 221.‏.
  12. Bakshi, G., Cao, C., & Chen, Z. (2000). Pricing and hedging long–term options. Journal of Econometrics, 94, 277-318.
  13. Bardhan, A., Karapandža, R., & Urošević, B. (2006). Valuing mortgage insurance contracts in emerging market economies. The Journal of Real Estate Finance and Economics, 32(1), 9-20.
  14. Chen, C. C., Lin, S. K., & Chen, W. S. (2013). Mortgage insurance premiums and business cycle. Tunghai University working paper.
  15. Chronopoulou, A., & Viens, F. G. (2012 a). Estimation and pricing under long– memory stochastic volatility. Annals of Finance, 8(2), 379-403.
  16. Chronopoulou, A., & Viens, F. G. (2012 b). Stochastic volatility and option pricing with long–memory in discrete and continuous time. Quantitative Finance, 12(4), 635-649.
  17. Comte, F. & Renault, E. (1998). Long memory in continuous-time stochastic volatility models. Mathematical Finance, 8(4), 291-323.
  18. Gozgor, G. (2013). The application of stochastic processes in exchange rate forecasting: Benchmark test for the EUR/USD and the USD/TRY. Economic Computation and Economic Cybernetics Studies and Research, 47 (2), 225-246.
  19. Grau–Carles, P. (2000). Empirical evidence of long–range correlations in stock returns. Physica A: Statistical Mechanics and its Applications, 287(3), 396-404.
  20. Hagan, P. S., Kumar, D., Lesniewski, A. S., & Woodward, D. E. (2002). Managing smile risk. The Best of Wilmott, 1, 249-296.
  21. Han, C., Wang, Y., & Xu, Y. (2020). Nonlinearity and efficiency dynamics of foreign exchange markets: evidence from multifractality and volatility of major exchange rates. Economic research-Ekonomska istraživanja, 33(1), 731-751.‏.
  22. Heston, S. L. (1993). A closed–form solution for options with stochastic volatility with applications to bond and currency options. Review of Financial Studies, 6(2), 327-343.
  23. Hull, J. & White,A. (1987). The pricing of options on assets with stochastic volatilities. Journal of Finance, 42, 281-300.
  24. Ibe, O. C. (2013). Markov processes for stochastic modeling. Elsevier.
  25. Kim, K. H., Kim, N. U., Ju, D. C., & Ri, J. H. (2020). Efficient hedging currency options in fractional Brownian motion model with jumps. Physica A: Statistical Mechanics and its Applications, 539, 122868.‏.
  26. Kumar, A., Jamadar, I., Goel, R., Petluri, R. C., & Feng, W. (2024). Mathematically Forecasting Stock Prices with Geometric Brownian Motion. The North Carolina Journal of Mathematics and Statistics, 10(1), 1-14.‏.
  27. Lawrence, K. D., Klimberg, R. K., & Lawrence, S. M. (2009). Fundamentals of forecasting using excel. New York: Industrial Press. Industrial Press: D., Klimberg, R. K., & Lawrence, S. M. (2009). Fundamentals of forecasting using excel. New York.
  28. Misiran, M. (2010). Modeling and pricing financial assets under long memory processes (Doctoral dissertation). Curtin University of Technology.
  29. Misiran, M., Zudi, L.U., Teo, K. L., & Grace, A. W. (2012). Estimating dynamic geometric fractional Brownian motion and its application to long–memory option pricing. Dynamic Systems and Applications, 21(1), 49–66.
  30. Painter, S. (1998). Numerical method for conditional simulation of Levy random fields. Mathematical Geology, 30(2), 163-179.
  31. Rejichi, I. Z., & Aloui, C. (2012). Hurst exponent behavior and assessment of the MENA stock markets efficiency. Research in International Business and Finance, 26(3), 353–370.
  32. Ross, S. M. (1999). An introduction to mathematical finance: option and other topics. Cambridge University Press.
  33. Scott, L. O. (1987). Option pricing when the variance changes randomly: Theory, estimation, and an application. Journal of Financial and Quantitative analysis, 22(4), 419-438.
  34. Sheldon, M. R. (1999). An introduction to mathematical finance: Options and other topics.‏.
  35. Stein, E. M. & J. Stein (1991). Stock price distributions with stochastic volatility: an analytic approach. Review of Financial Studies, 4, 727-752.
  36. Stein, J.C.(1989). Overreactions in the options market. Journal of Finance, 44, 1011- 1023.
  37. Wang, X., & Zhang, W. (2014). Parameter estimation for long-memory stochastic volatility at discrete observation. In Abstract and Applied Analysis, (2014). Hindawi Publishing Corporation.
  38. Wang, X., Xie, D., Jiang, J., Wu, X., & He, J. (2017). Value-at-Risk estimation with stochastic interest rate models for option-bond portfolios. Finance Research Letters, 21, 10-20.
  39. Willinger, W., Taqqu, M. S., & Teverovsky, V. (1999). Stock market prices and long– range dependence. Finance and Stochastics, 3(1), 1-13.
  40. Xiao, W., Zhang, W., & Zhang, X. (2015). Parameter identification for the discretely observed geometric fractional Brownian motion. Journal of Statistical Computation and Simulation, 85(2), 269-283.
Preprints 101052 g001
Figure 1. Daily energy index close price.
Figure 1. Daily energy index close price.
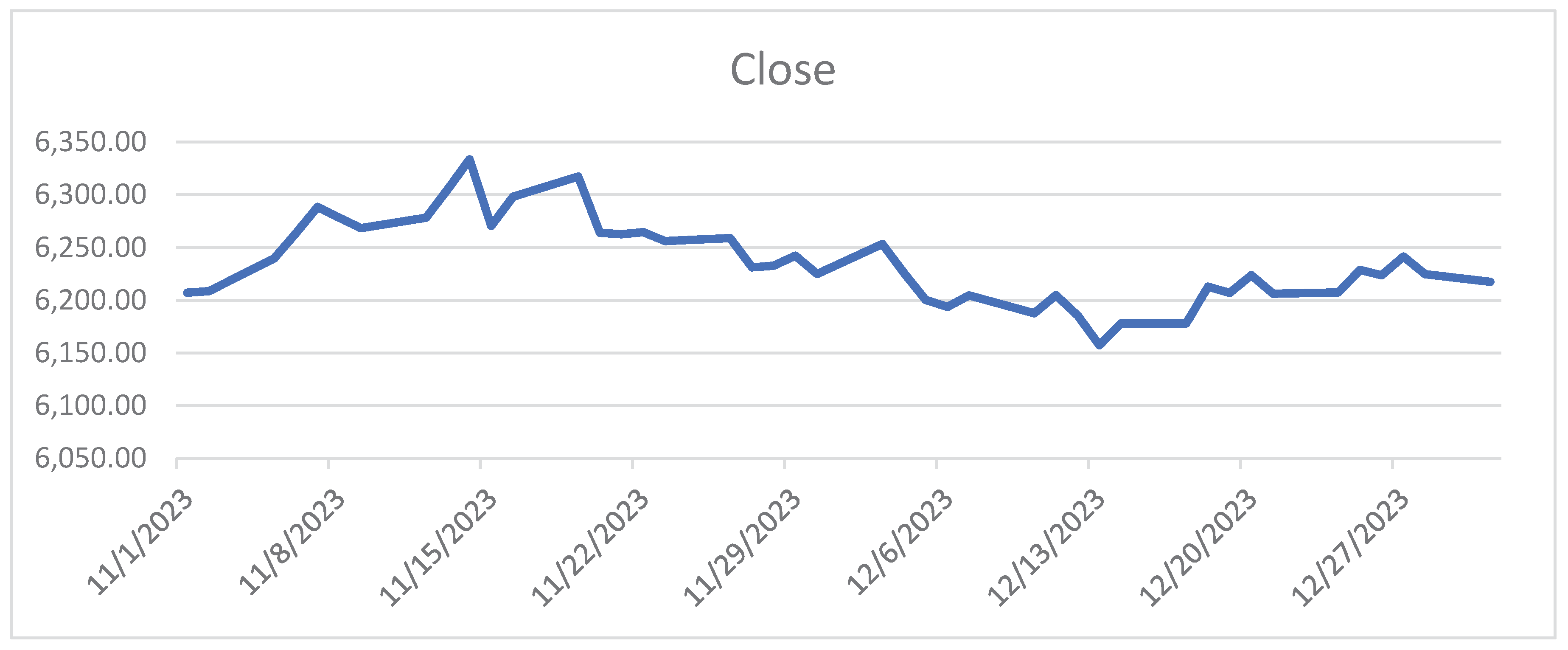
Preprints 101052 g001
Preprints 101052 g002
Figure 2. Daily returns of energy index.
Figure 2. Daily returns of energy index.
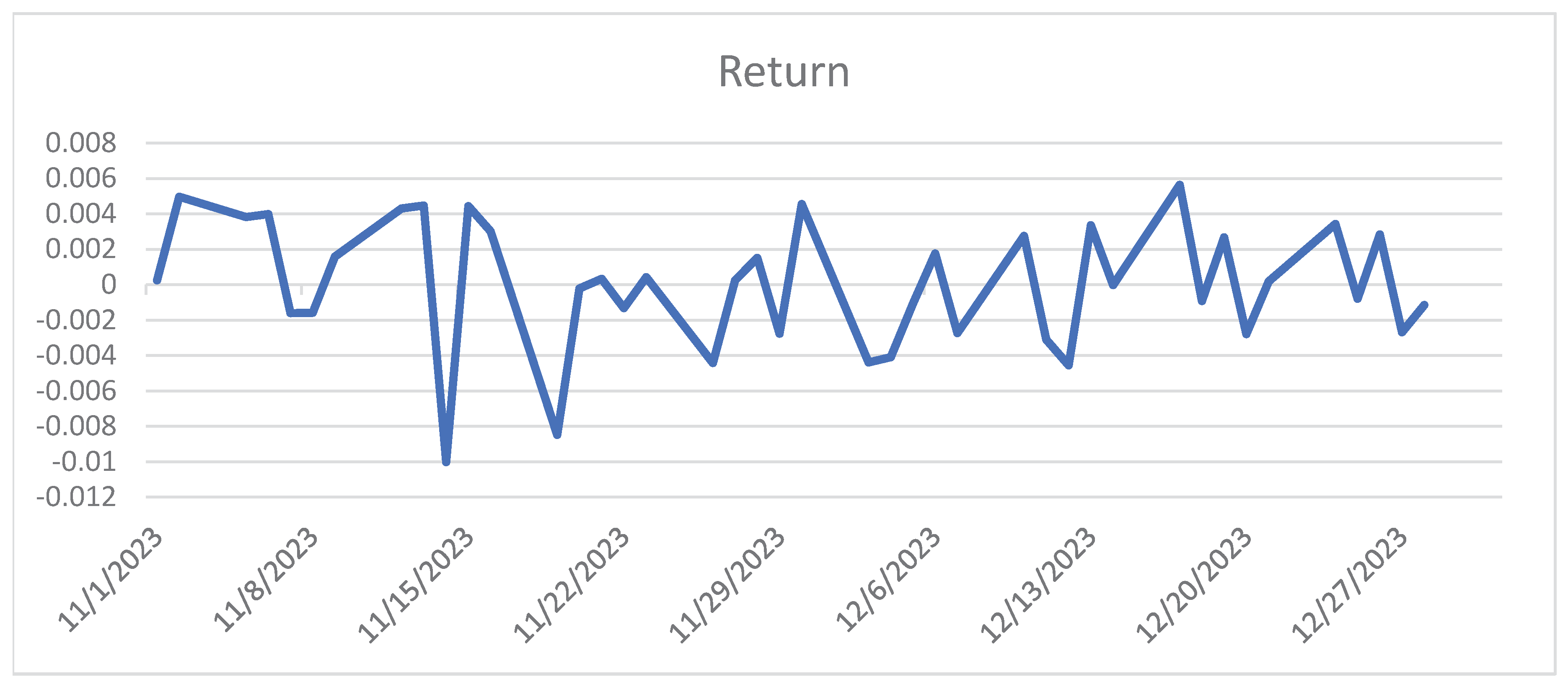
Preprints 101052 g002
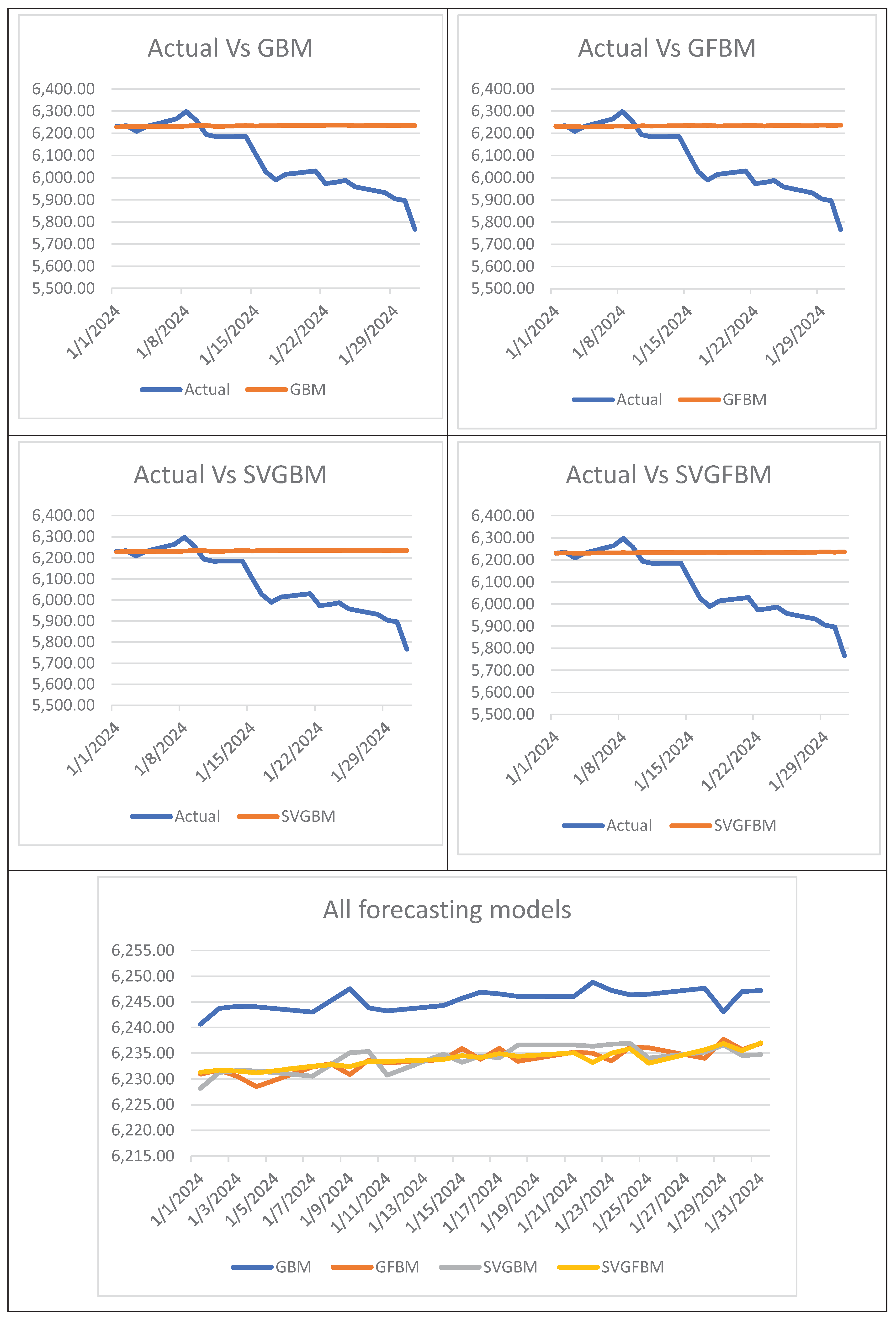
Preprints 101052 g003
Figure 3. Actual prices vs Forecast prices.
Figure 3. Actual prices vs Forecast prices.
Preprints 101052 g003
Table 1. Models of stochastic processes describing Y_t in SV models.
Table 1. Models of stochastic processes describing Y_t in SV models.
Name Model
L o g – n o r m a l   p r o c e s s d Y t = α Y t d t + β Y t d B 2 t
C o x – I n g e r s o l l – R o s s   ( C I R )   p r o c e s s d Y t = θ ω − Y t d t + ξ Y t d B 2 t
O r n s t e i n – U h l e n b e c k   ( O U )   p r o c e s s d Y t = α m − Y t d t + β d B 2 t
N o t   m e a n   r e v e r t i n g   p r o c e s s d Y t = α Y t d B 2 t
F r a c t i o n a l   O r n s t e i n – U h l e n b e c k   ( F O U )   p r o c e s s d Y t = α m − Y t d t + β d B H 2 ( t )
Table 3. P a r a m e t e r s   a n d   v o l a t i l i t i e s   v a l u e s   o f   A R A M C O .
Table 3. P a r a m e t e r s   a n d   v o l a t i l i t i e s   v a l u e s   o f   A R A M C O .
Parameter Value Parameter Value
H 1 0.3279 β 0.00002
H 2 0.2520 m 0.00001
μ 0.00004 α 4.62705
Computed Volatility
σ 0.0036
σ ( Y t ) 0.0010
Table 4. The accuracy ranking level of forecasting model based on MAPE and MSE.
Table 4. The accuracy ranking level of forecasting model based on MAPE and MSE.
Model MAPE MSE
SVGFBM 2.753% 44861
GFBM 2.758% 44921
SVGBM 2.759% 44946
GBM 2.887% 48457
Table 5. Actual and forecasted prices.
Table 5. Actual and forecasted prices.
Date Actual GBM GFBM SV GBM SV GFBM
1/1/2024 6,231.24 6,240.65 6,230.96 6,228.20 6,231.33
1/2/2024 6,234.45 6,243.74 6,231.77 6,231.27 6,231.74
1/3/2024 6,208.98 6244.15 6230.47 6,231.68 6231.56
1/4/2024 6,231.12 6244.03 6228.52 6231.59 6231.21
1/7/2024 6,264.88 6243 6232.38 6230.56 6232.46
1/8/2024 6,298.10 6245.29 6232.93 6232.84 6232.8
1/9/2024 6,258.55 6247.55 6230.89 6235.09 6232.42
1/10/2024 6,194.68 6243.82 6233.67 6235.34 6233.37
1/11/2024 6,184.72 6243.25 6233.11 6230.77 6233.4
1/14/2024 6,185.47 6244.28 6233.75 6234.82 6233.76
1/15/2024 6,104.82 6245.72 6235.91 6233.24 6234.54
1/16/2024 6,026.77 6246.9 6233.81 6234.45 6234.14
1/17/2024 5,989.73 6246.56 6235.95 6234.11 6234.92
1/18/2024 6,014.71 6246.06 6233.42 6236.59 6234.4
1/21/2024 6,030.20 6246.09 6235.19 6236.62 6235.07
1/22/2024 5,973.57 6248.83 6235.01 6236.35 6233.2
1/23/2024 5,978.97 6247.24 6233.49 6236.75 6234.97
1/24/2024 5,987.34 6246.39 6236.14 6236.91 6235.89
1/25/2024 5,958.15 6246.5 6236.04 6234.04 6233.04
1/28/2024 5,932.13 6247.66 6234.01 6235.19 6235.66
1/29/2024 5,904.70 6243.1 6237.73 6236.62 6236.87
1/30/2024 5,896.26 6247.03 6235.71 6234.57 6235.5
1/31/2024 5,766.84 6247.19 6236.92 6234.71 6237.01
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated