Prerpints.org logo
Preprint
Article

Innate and Adaptive Regulation of Cognition

Altmetrics

Downloads

119

Views

41

Comments

0

This version is not peer-reviewed

Submitted:

11 March 2024

Posted:

12 March 2024

You are already at the latest version

Alerts
Abstract
The draconian regulation required by the inherent instability of cognitive phenomena -- gene expression, immune function, cancer suppression, wound healing, animal consciousness, machine intelligence, network stabilization, institutional cognition, and their many and varied composites -- can be viewed through the lens of the asymptotic limit theorems of both information and control theories. Here, we explore the dynamics and sometimes highly punctuated failures of the regulation of cognition under increasing `noise'. The approach parallels, and indeed generalizes, the Data Rate Theorem of control theory, extending the theorem's requirement of a minimum channel capacity necessary for stabilization of an inherently unstable system. Various models are explored across different basic underlying probability distributions characteristic of the system under study, and across different hierarchical scales, finding the addition of adaptive -- learned -- regulation greatly extends the reach of innate -- e.g., AI-driven or otherwise pre-programmed -- regulation. This work points toward the construction of new statistical tools for the analysis of observational and empirical data across a wide spectrum of inherent pathologies and adversarial challenges afflicting a wide variety of cognitive processes.
Keywords: 
Subject: Biology and Life Sciences  -   Ecology, Evolution, Behavior and Systematics

1. Introduction

…[C]ognition can be seen as a multiscale web of dynamic information processing distributed across a vast array of complex cellular... and network systems, operating across the entire body, and not just in the brain.
— Ciauncia et al. [1].
As a consequence of the inherent unruliness of biological, institutional, and machine cognition – and their many composites – under real-world stress, there are surprisingly few foundational ‘basic principles’ available to the intrepid explorer of such landscapes.
The principle most often recognized is, of course, some form of Darwinian variation-and-selection underlying all path-dependent evolutionary trajectories [2].
A second is the assertion by Maturana and Varela [3] that the living state in particular is cognitive at every scale and level of organization. Machine intelligence and institutional function follow increasingly closely.
A further principle was articulated by Dretske [4] and Atlan and Cohen [5], who recognized that all cognitive process – most particularly, for Dretske, those that bear particular meaning and are semantic – must be constrained by necessary conditions imposed by the asymptotic limit theorems of information theory. The basic statement that emerges from the work of Atlan and Cohen is that cognition requires choice and choice inherently reduces uncertainty. The reduction of uncertainty implies the existence of an information source ‘dual’ to the cognitive process studied. The inference is direct, intuitive, and unambiguous.
Wallace ([6], Ch. 4) expands the Dretske/Atlan-Cohen insights by noting that, for the living state in particular, cognition must be paired with regulation, since cognition, is generally inherently unstable because it must act in the real world that imposes it’s own ‘topological information’ on most processes of cognition. Again, real-world cognition demands stabilization by imposition of control information at a rate greater than the cognitive system is burdened by extrinsic topological information. The resulting dynamics can be viewed from perspectives of both the Data Rate Theorem (DRT) of control theory [7], and the Rate Distortion Theorem (RDT) of information theory [8].
Thus gene expression must be highly regulated during early development for successful growth, and failure of regulation is a burden of aging. The immune system must be constrained from self-attack, while directed to engage in vigorous cancer identification and suppression, pathogen resistance, and routine tissue maintenance. For higher animals, the stream of consciousness must be constrained by cultural and social riverbanks to realms useful for the individual animal, the local social grouping, and the full species. Coordinated social behaviors are constrained by cultural norms. Institutions must respond to extrinsic topological information and noise from the perspective of internal ‘doctrine’ in a large sense. Machine cognition in its various forms that is faced with twisting roadway dynamics falls under much the same rubric.
We attempt a formal model, focusing on the added affordance provided by an ‘adaptive’, in addition to an ‘innate’, regulatory capacity.
First, some methodological boilerplate through which we all must pass in the address of these issues.

2. Two Approaches

A pair of very strong asymptotic limit theorems of probability theory can be invoked in the study of control system dynamics. The first is the Data Rate Theorem (DRT).

The Data Rate Theorem: Punctuated Degradation

Real-time, real-world embodied cognition is – most often – inherently unstable. Envision a vehicle driven at night on a twisting, pot-holed roadway. This requires, in addition to a competent driver, good headlights, a stable motor, and reliable, responsive, brakes and steering.
The DRT, classically taken as extending the Bode Integral Theorem, establishes the minimum rate at which externally-supplied control information must be provided for such an inherently unstable control system to remain stable. For a standard proof, see [7].
The standard analysis makes a first-order linear expansion near a nonequilibrium steady state (nss) as follows.
An n-dimensional parameter vector at time t, x t , is taken as determining the state at time t + 1 near nss according to the linear approximation
x t + 1 ≈ A x t + B u t + W t
A and B are assumed to be fixed n × n matrices. u t is the vector of control information, and W t is an n-dimensional vector usually taken as Brownian ‘white noise’.
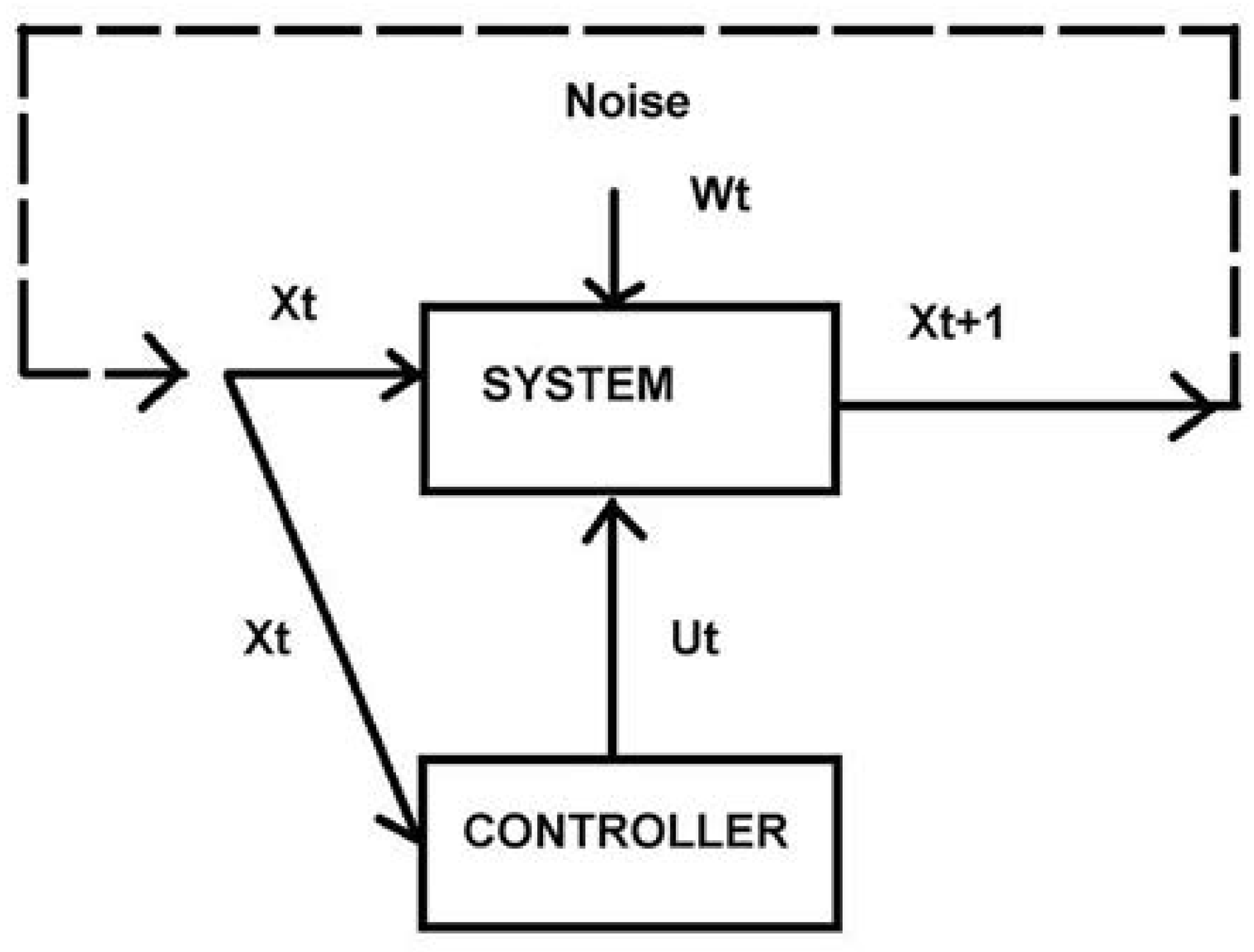
Figure 1 projects the centrality of any command-and-control structure in the presence of noise onto an irreducible minimum. This projection might include unanticipated difficulties and occurrences that are most often modeled as an undifferentiated Brownian white noise spectrum. Noise, however, can be colored, having a shaped power spectrum, requiring more complicated models.
The DRT holds that the minimum rate at which control information H must be provided for stability of the inherently unstable system
H > log [ | det [ A m ] | ] ≡ H 0
det is the determinant of the matrix A m .
Taking m ≤ n , A m is the subcomponent of A having eigenvalues ≥ 1 . The right hand side of Eq.(2) is the rate at which the system generates it’s own ‘topological information’. Again, Nair et al. [7] provide details.
If the condition of Eq.(2) is violated, stability fails. For night-driving, if the headlights go out, or steering becomes unreliable, twisting roadways – that generate their own ‘topological information’ at a rate dependent on vehicle speed – cannot be navigated at high speed.
French et al. [9], however, taking a different approach, explored the dynamics of a neural network model of the famous Yerkes-Dodson mechanism [10], interpreting that mechanism in terms of a necessary real-time data compression that eventually fails as task complexity increases. Data compression inherently involves matters central to information theory, in addition to those of control theory. And there is a formal context: the Rate Distortion Theorem [8].

The Rate Distortion Theorem: More General Patterns of Degradation

Information theory has three classic asymptotic limit theorems [8,11]:
• The Shannon Coding Theorem. This states that, for a fixed – i.e., stationary – transmission channel, a message recoded so as to be ‘typical’ with respect to the probabilities of that channel, can be transmitted without error at a channel capacity rate C characteristic of the channel. One can, vice versa, argue for a tuning theorem variant of the coding theorem in which a transmitting channel is tuned to be made typical with respect to the message being sent (Wallace et al. [12], p.83), so that, formally, the channel is, in a sense, ‘transmitted by the message’ at a dual channel capacity C * .
• The Shannon-McMillan or Source Coding Theorem. This states – for our purposes – that messages transmitted by an information source along a stationary channel can be divided into sets, a very small one congruent with a characteristic grammar and syntax, and a much larger one of vanishingly small probability that is not congruent. For stationary (in time), ergodic sources, where long-time averages are cross-sectional averages, the splitting criterion dividing the two sets is given by the classic Shannon uncertainty. For nonergodic sources, which are likely to predominate in biological and ecological circumstances, matters are more complex, requiring a ‘splitting criterion’ that must be associated with each individual high-probability message [11].
• The Rate Distortion Theorem (RDT). This addresses the question of message transmission under conditions of noise for a particular information channel. There will be, for that channel, given a particular scalar measure of average distortion, D, between what is sent and what is received, a minimum necessary channel capacity R ( D ) . In a sense, the theorem asks what is the ‘best’ channel for transmission of a message with the least possible average distortion. R ( D ) can be defined for nonergodic information sources via a limit argument based on the ergodic decomposition of a nonergodic source into a ‘sum’ of ergodic sources.
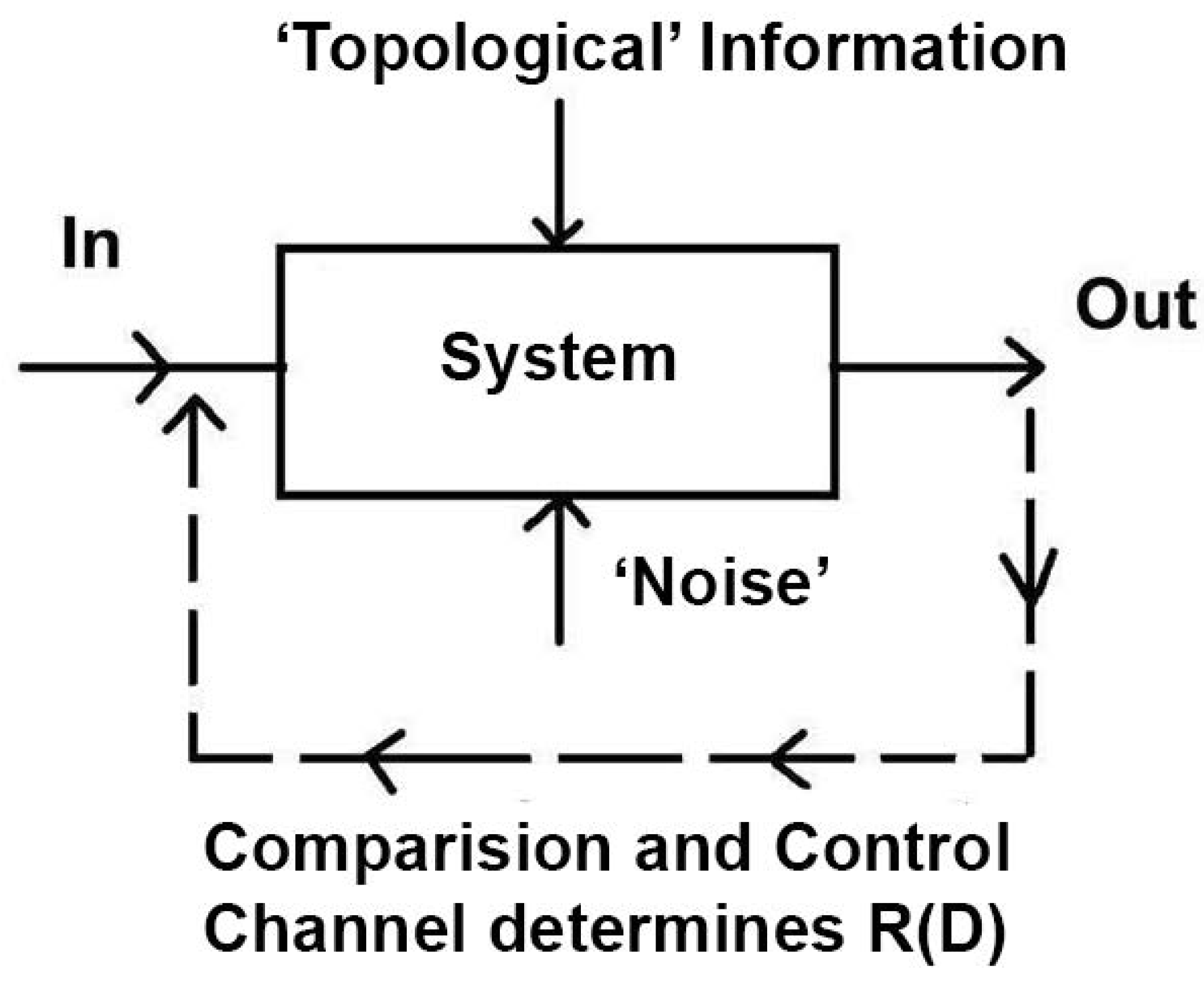
The RDT can be reconfigured in a control theory context, if we envision a system’s topological information as another form of noise, adding to the average distortion D. See Figure 2. The punctuation implied by Eq.(2) can emerge from this model if there is a critical maximum average distortion that characterizes the system. Other systems may degrade more gracefully, or, as we will show below, have even more complicated patterns of punctuation that, in effect, generalize the Data Rate Theorem.
Here, we expand perspectives on the dynamics of biocognition/bioregulation dyads across rates of arousal, across the possibly manifold set of basic underlying probability distributions that characterize such dyads at different scales, levels of organization, and indeed, across various intrinsic patterns of arousal.
In the Mathematical Appendix we show that, under modest assumptions, a form of the DRT can be derived using the RDT.

3. Scalarizing Resource Rates

The Rate Distortion Theorem asserts that, for a particular assigned scalar measure of distortion D between a sequence of signals that has been sent and the sequence that has actually been received in message transmission – measuring the difference between what was ordered and what was observed – there is a minimum necessary channel capacity R ( D ) in the classic information theory sense that is, in turn, determined by the rate at which a set of essential resources, indexed by some particular scalar measure Z, can be provided to the system ‘sending the message’ in the presence of noise and an opposing rate of topological information characteristic of the inherent instability of the control system under study.
The Rate Distortion Function (RDF) R ( D ) is always convex in the scalar distortion measure D, so that d 2 R / d D 2 ≥ 0 [8,13,14]. For a nonergodic process, where the cross-sectional mean is not the same as time-series mean, the Rate Distortion Function can be determined as an average across the RDF’s of the ergodic components of that process, and can thus be expected to remain convex in the distortion measure D.
The relations between the minimum necessary channel capacity R ( D ) and any possible essential resource rate scalar index Z are subtle.
The scalar resource rate index Z will be composed of a minimum of three interacting components. These are
• The rate at which subcomponents of the organism can communicate with each other, a channel capacity C.
• The rate at which ‘sensory’ information is provided from the embedding environment, a channel capacity H.
• The rate M at which metabolic and other free energy or materiel resources can be provided to a subsystem of a full entity, organism, institution, machine, and so on.
These rates must be compounded into an appropriate scalar measure Z ( C , H , M ) . Most simply, this might perhaps be taken as the product C × H × M , or the sum of their logs. It will, however, likely be necessary to more fully characterize Z, since C , H , and M, may interact, resulting in a three-by-three matrix Z similar to – but different from – the more usual correlation matrix.
An n-dimensional square matrix X will have scalar invariants r 1 , . . . , r n under some set of transformations as given by the characteristic equation
p ( γ ) = det [ X − γ I ] = ( − 1 ) n γ n + ( − 1 ) n − 1 r 1 γ n − 1 + ( − 1 ) n − 2 r 2 γ n − 2 − . . . − r n − 1 γ + r n
I is the n-dimensional identity matrix, det the determinant, and γ a real-valued parameter. The first invariant, r 1 , is the matrix trace, and the last, r n , the matrix determinant.
Given these scalar invariants, it will often be possible to project the full matrix down onto a single scalar index Z = Z ( r 1 , . . . , r n ) retaining, hopefully, much of the basic structure. The idea is analogous to the conduct of a principal component analysis, which does much the same thing for a correlation matrix. Wallace [15] provides an example in which two such indices are necessary. This becomes very complicated, requiring Lie Group methods.

4. The Basic Model

Feynman [16] and Bennett [17], using a powerful but elementary argument, show that information should be viewed as free energy, not as an ‘entropy’, in spite of information theory’s Shannon uncertainty taking the same mathematical form as entropy for an ergodic system. Feynman even provides an elementary ideal machine that converts information in a message into work.
Here, in first approximation, we impose the standard formalisms of statistical mechanics – given a proper definition of ‘temperature’ – for a cognitive, as opposed to a ‘simply’ physical, system. This leads to an important diversion from simple physical theory-based arguments.
We examine an ensemble of possible developmental trajectories Y j , j = 1 , 2 , . . . , each having a Rate Distortion Function-defined minimum needed channel capacity R j for a particular maximum average scalar distortion D j . Then, given some basic underlying probability model having distribution ρ ( c , x ) , where c is a parameter set, we define a pseudoprobability for a meaningful ‘message’ Y j sent into the system of Figure 2 as
P j = ρ ( c , R j / g ( Z ) ) ∑ k ρ ( c , R k / g ( Z ) ) ≡ ρ ( c , R j / g ( Z ) ) h ( g ( Z ) )
Again, Y j is a particular trajectory, and the sum is over all possible such paths of the system.
We next impose the Shannon-McMillan Source Coding Theorem so that the overall set of possible system trajectories can be divided in two. These are, first, a very large set of measure zero – vanishingly low probability – that is not consistent with the underlying grammar and syntax of some basic information source, and a much smaller consistent set [11].
R j is the RDT channel capacity that keeps the average distortion less than the limit D j for message Y j . It is important to realize that g ( Z ) is a as-yet-to-be determined temperature analog depending on the resource rate Z. ρ ( c , x ) , for physical systems, is usually taken as the Boltzmann distribution: ρ ( x ) = exp [ − x ] . We suggest that, for the cognitive phenomena studied here – from the living and institutional to the machine and composite – it will be necessary to move beyond physical system analogs, exploring the influence of a variety of different probability distributions, including those with ‘fat tails’, on the dynamics of cognition/regulation stability.
Abducting standard methodology from statistical physics [18], the denominator of Eq.(4) is to be characterized as a partition function. This allows definition of an iterated free energy-analog F
ρ ( c , F / g ( Z ) ) ≡ ∑ k ρ ( c , R k / g ( Z ) ) = h ( g ( Z ) ) g ( Z ) = R o o t O f [ h ( X ) − ρ ( c , F / X ) ]
The RootOf construct simply sets the equation equal to zero and solves for X.
RootOf, however, used in definition of a temperature-analog, immediately, and surprisingly, provides deep results. That is, g ( Z ) , as the solution of a complicated equation, can have imaginary-valued components. This directly introduces ‘Fisher-Zero’ phase transitions analogous to those found in physical systems [19,20,21].
For a continuous system, where the probability density function ρ ( c , x ) is defined on the interval 0 → ∞ ,
ρ ( c , F / g ( Z ) ) = ∫ 0 ∞ ρ ( c , R / g ( Z ) ) d R = g ( Z )
Again abducting a central and standard argument, this time from chemical physics [22], we are able to define a cognition rate for the system as a reaction rate analog
L ≡ ∑ R j > R 0 ρ ( c , R j / g ( Z ) ) ∑ k ρ ( c , R k / g ( Z ) ) = 1 g ( Z ) ∫ R 0 ∞ ρ ( c , R / g ( Z ) ) d R
Here, R 0 is the channel capacity needed to keep the average distortion below a critical value D 0 . For continuous systems, the sum is replaced by an integral.
The basic underlying probability model of Eq.(4) – via Eq.(7) – determines system dynamics, but not system structure, and cannot be associated with a particular underlying network conformation, although these are related [23,24]. That is, a set of markedly different networks may all be mapped on to any single given dynamic behavior pattern and, indeed, vice-versa, That is, the same static network may display a spectrum of behaviors [25]. We are restricting focus to dynamics rather than network topology.
Next, abducting a canonical first-order approximation from nonequilibrium thermodynamics [26], we define a ‘real’ entropy – as opposed to a ‘Shannon uncertainty’ that is basically Feynman’s [16] free energy – from the iterated free energy F by taking the standard Legendre Transform [18], so that
S ≡ − F + Z d F / d Z
The usual first-order Onsager approximation is then
∂ Z / ∂ t ≈ d S / d Z = Z d F 2 / d Z 2
The scalar diffusion coefficient has been set equal to one. Expansion of the formal Onsager perspective is discussed in the Mathematical Appendix.
It is important to note that, for multidimensional systems, there can be no Onsager reciprocal relations between components of the diffusion tensor, since information sources are not micro reversible. For example, in English the term ‘ eht ’ does not have the same probability as ‘ the ’.
The next step is to impose a burden of stochastic noise on the system. This is done in classic manner via the stochastic differential equation [27]
d Z t = Z t d 2 F / d Z 2 d t + σ Z t d B t
where the last term is simple volatility in the white noise d B t , with the scalar value σ characterizing the magnitude of the effect [28,29].
A basic assumption is that, to survive, the cognitive system of interest must have stability in the variance of Z, so that the nonequilibrium steady state condition < d Z t 2 > = 0 is maintained. Application of the Ito Chain Rule to Z t 2 based on Eq.(10) finds
< d Z t 2 > = 2 Z 2 d 2 F / d Z 2 + σ 2 Z 2 = 0 F ( Z ) = − σ 2 Z 2 4 + C 1 Z + C 2
Determination of F ( Z ) from Eq.(11), in turn, determines the temperature analog g ( Z ) via Eq.(6). We can then calculate the cognition rate from Eq.(7).

5. ‘Innate’ and ‘Adaptive’ Regulation

The next step is deceptively simple. We break the regulatory channel into two distinct components, having respective channel capacities R – innate – and α R – adaptive – that, in first approximation, combine into a single value ( 1 + a ) R . After some elementary calculus, the relations of interest become
ρ ( c , F / g ) = g 1 + a L = ∫ R 0 ( 1 + a ) / g ∞ ρ ( c , u ) d u
The first expression, based on defining F according to Eq.(11) so that the variance of Z is confined to a nonequilibrium steady state, gives g ( Z ) . The second, based on the calculation for g ( Z ) , determines the cognition rate of the combined innate/adaptive system as a function of a , σ and Z.
Examples are both surprising and contradictory.

The Boltzmann Distribution

For the Boltzmann Distribution, taking C 1 = − 1 , C 2 = 3 in the expression of F for Eq.(11),
exp [ − F / g ] = g 1 + a g = − F W n , − F 1 + a L = exp [ − R 0 ( 1 + a ) / g ]
W ( n , x ) is the Lambert W-function of order n that satisfies the relation
W ( n , x ) exp [ W ( n , x ) ] = x
It is real-valued only for n = 0 , − 1 in the range x > − exp [ − 1 ] .
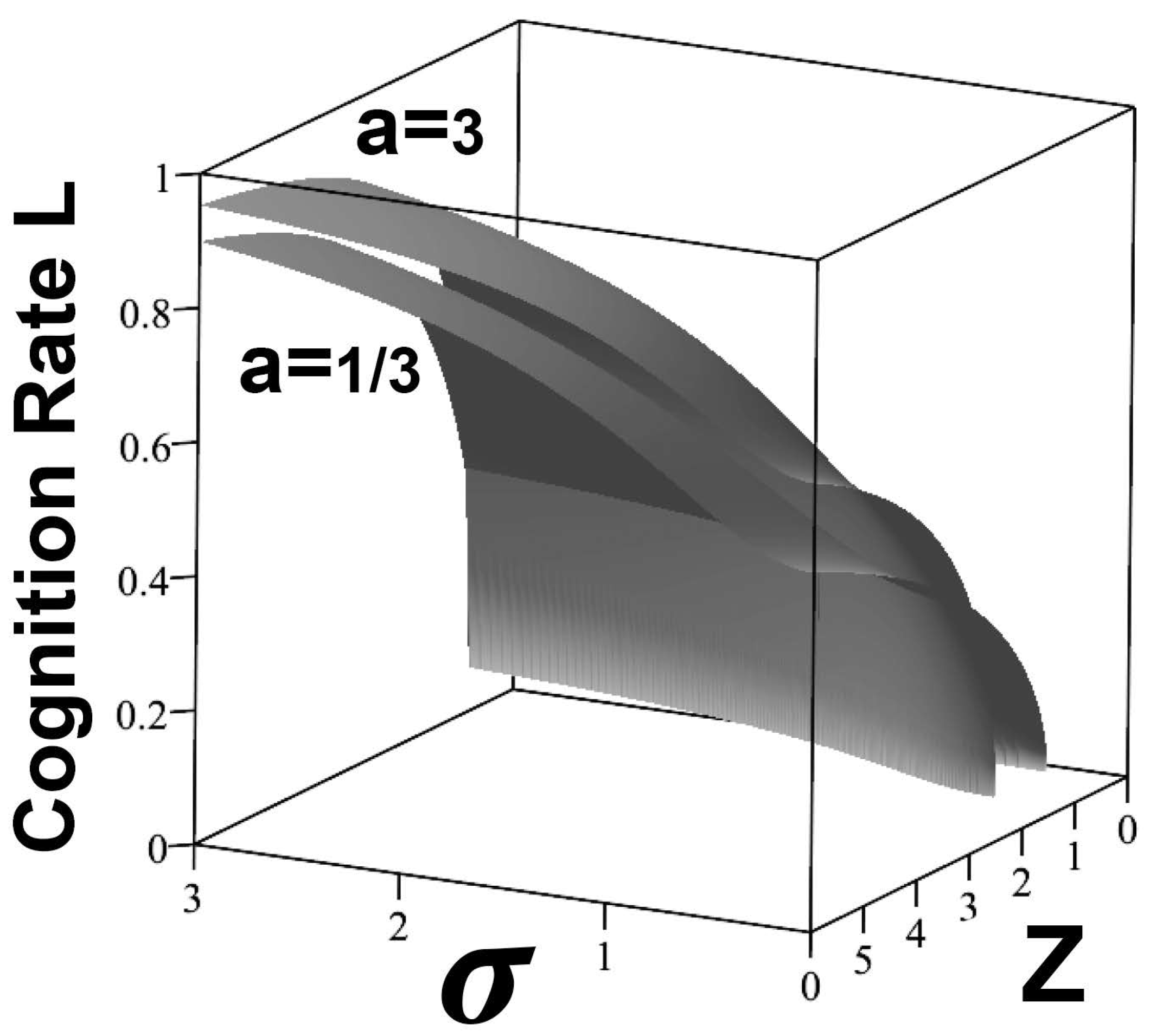
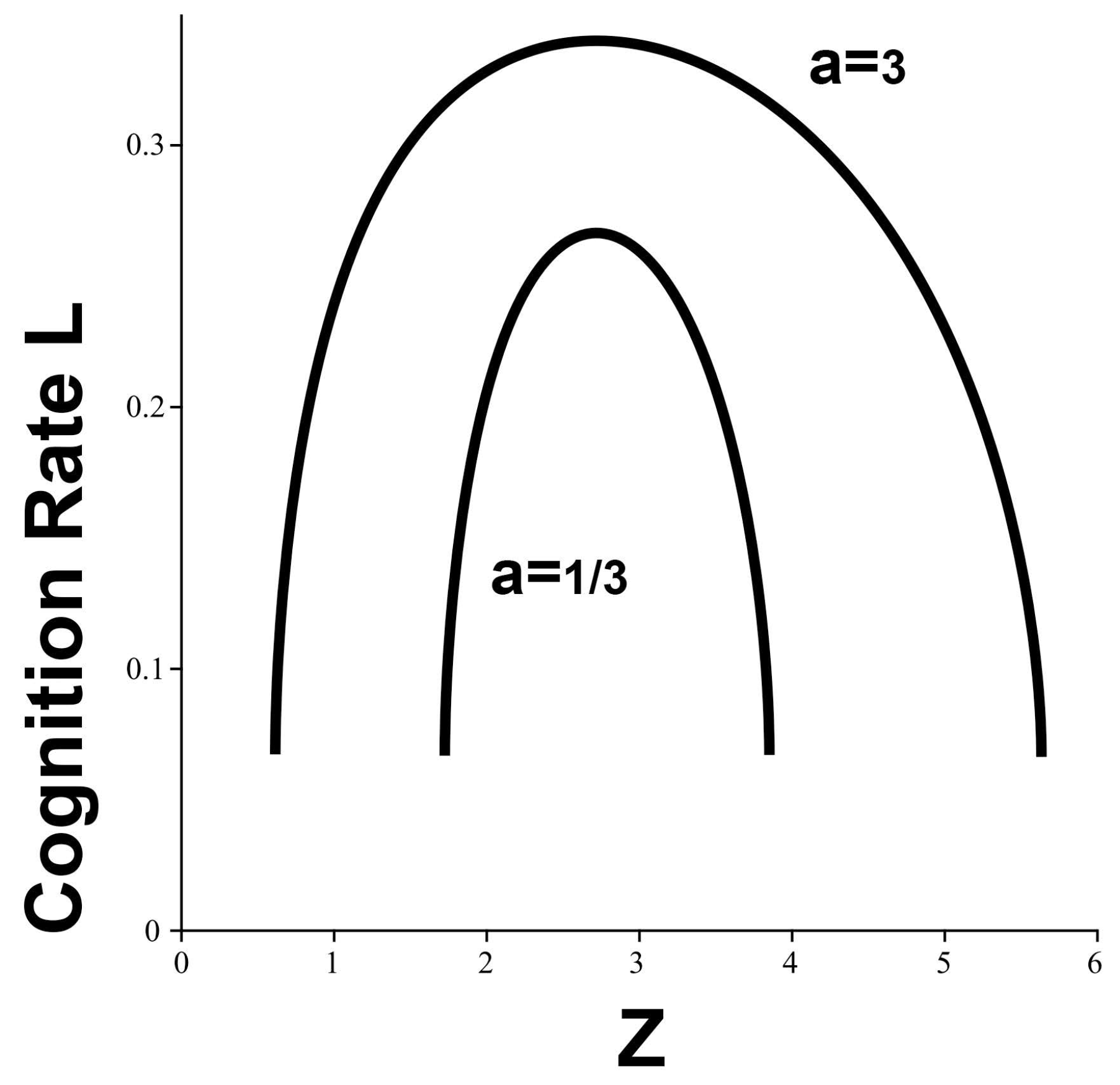
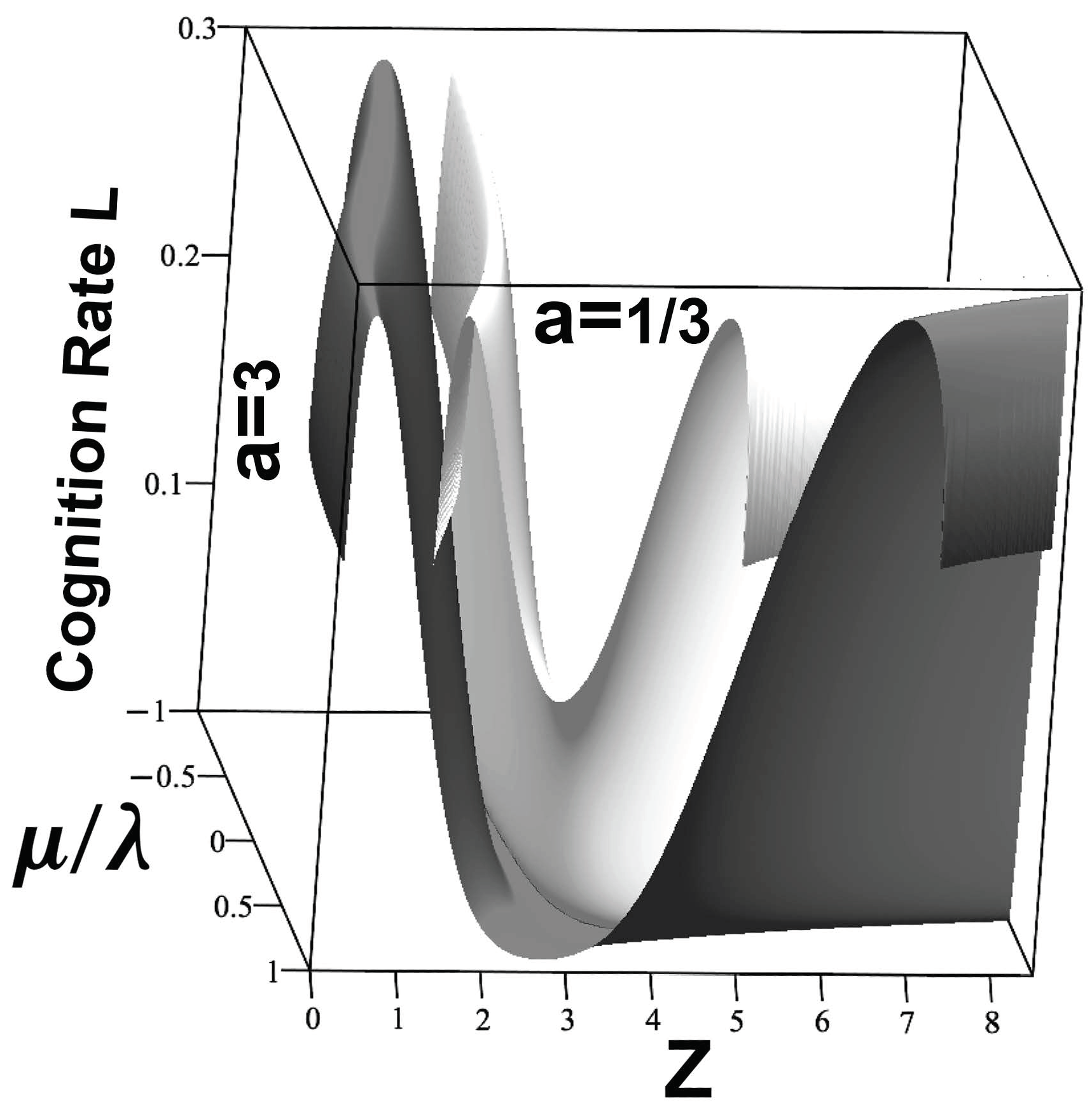
Taking a = 1 / 3 , 3 gives the cognition rates of Figure 3. Here, the essential point is not that the relations for the different values of a are similar, but that the cognition rate needed to maintain stability in variance for the resource rate Z increases relentlessly with rising noise σ at all values of Z. Cognitive systems are all rate-limited to some maximum horizontal plane across Figure 3, say L = 0.6 . 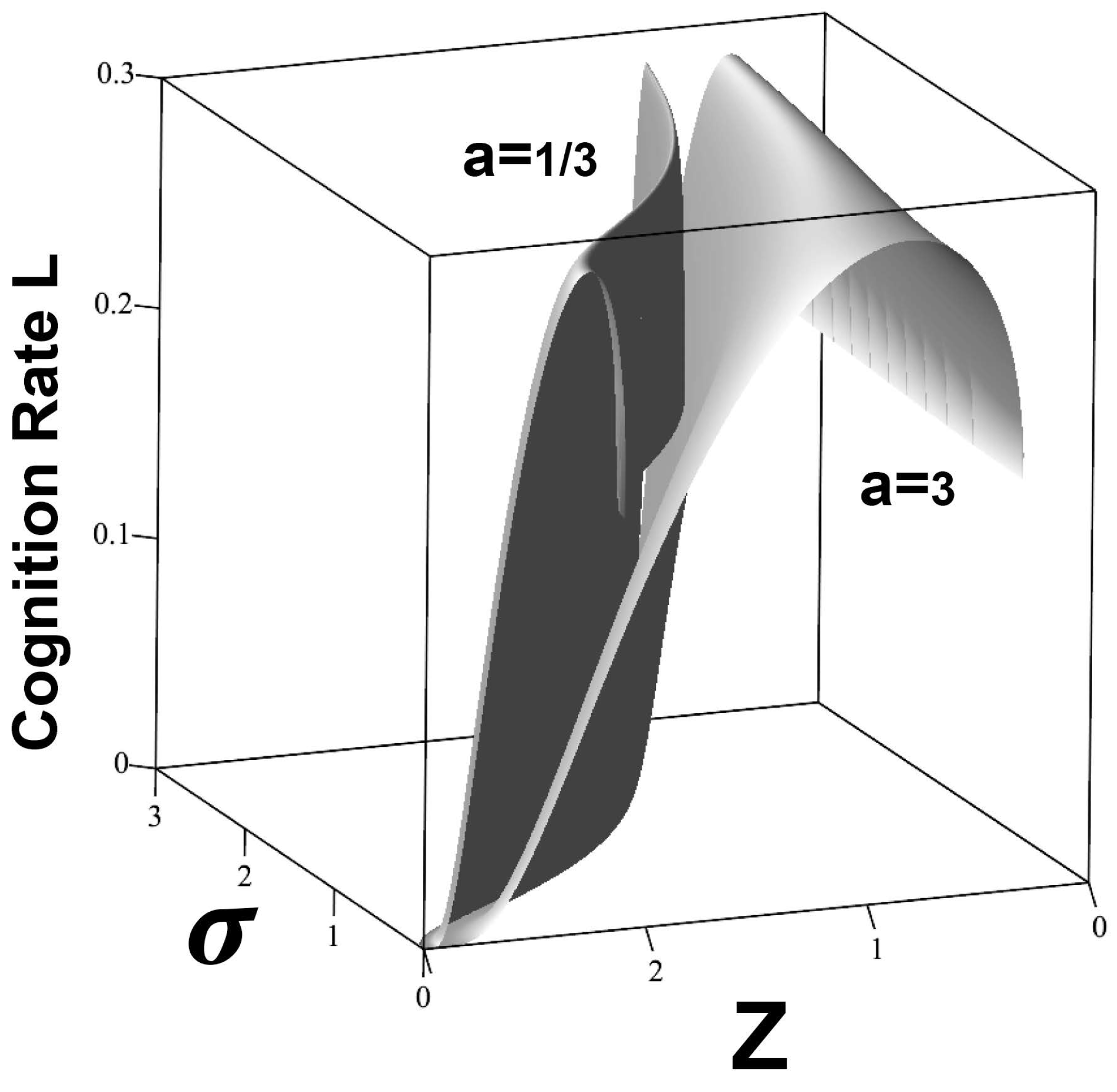Increasing the burden of noise σ much beyond 1 will violate that condition in this case. Thus, under constraints on cognition rate, sufficient ‘noise’ can literally ‘fry’ the agent, triggering instability.

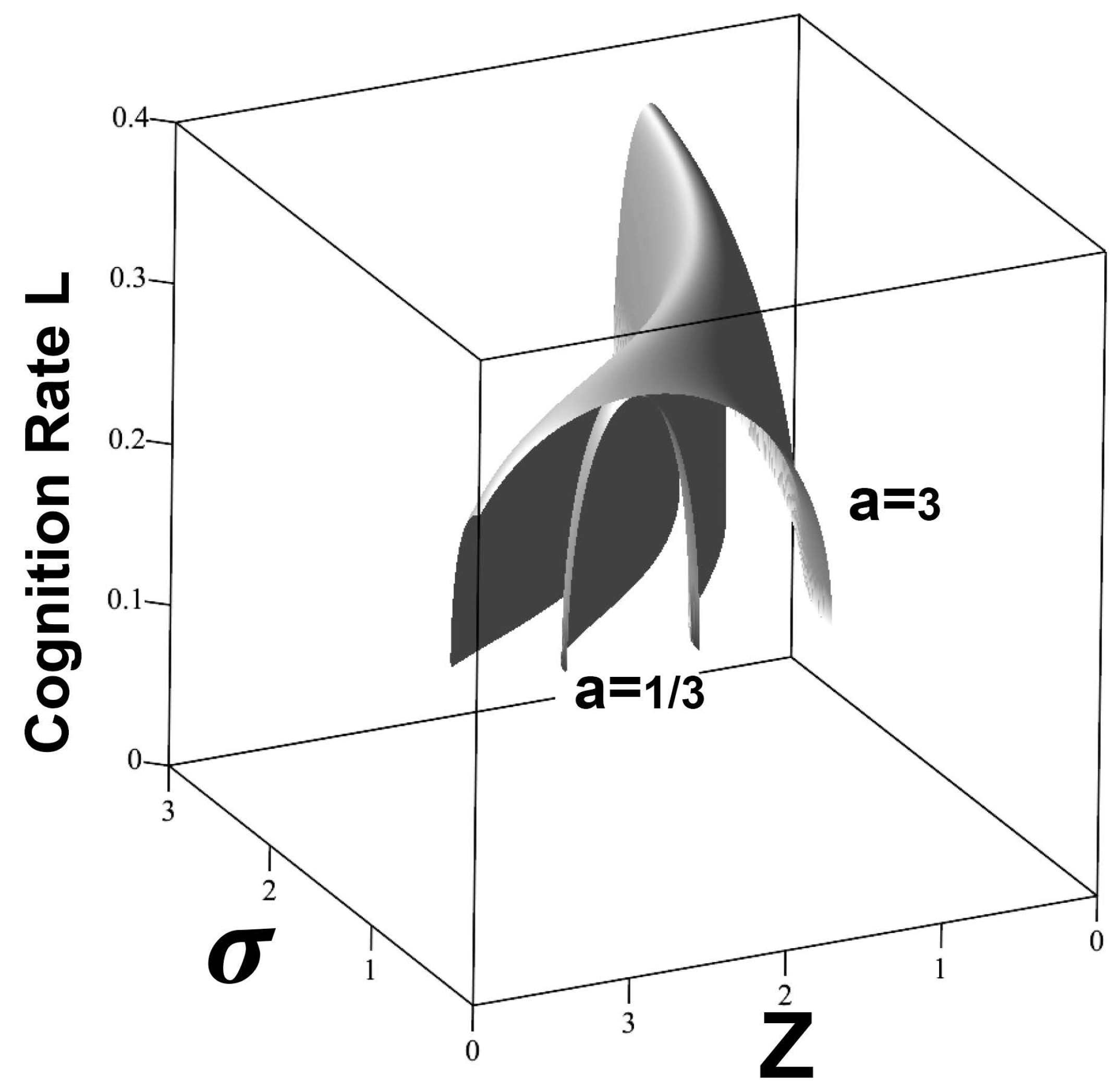
The Cauchy Distribution

The Cauchy Distribution, having undefined mean and variance, gives a different pattern. The basic relations, again taking F as above, are
2 s π F 2 g 2 + s 2 = g a + 1 g = 1 π s 1 + a + a 2 + 2 a + 1 − π 2 F 2 L = 1 − 2 π arctan R 0 ( a + 1 ) g s
Taking a = 1 / 3 , 3 , s = 1 , gives Figure 4, much different from the Boltzmann example in two important ways. Here, rising noise σ drastically narrows the agent’s ecological niche regardless of a, the relative index of adaptive regulation. It is striking, however, that for the Cauchy Distribution, a higher level of adaptive regulation greatly broadens the niche at low noise.

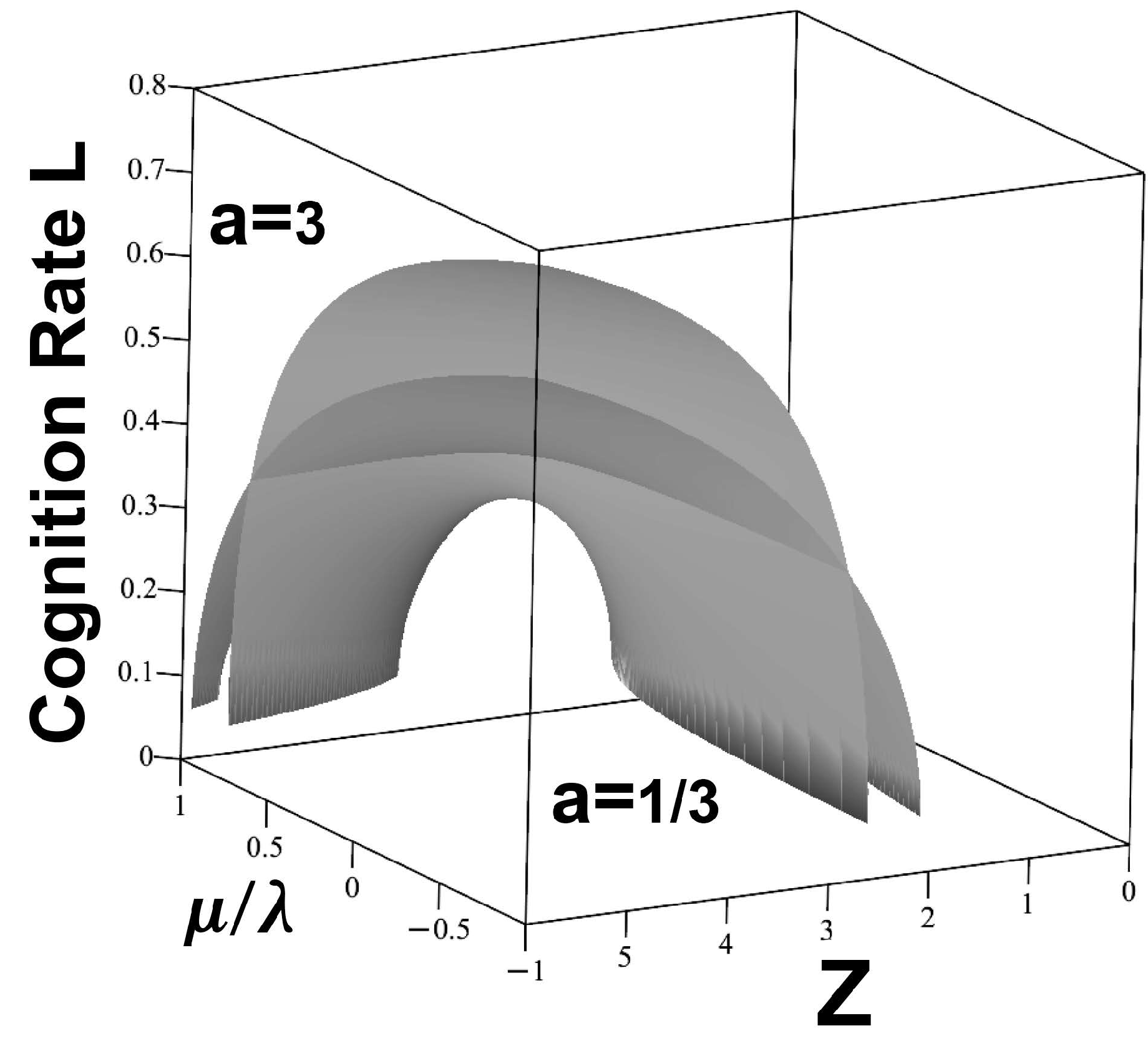
The Gamma Distribution

The full Gamma Distribution model is
F g k − 1 e − F g θ Γ k θ k = g 1 + a g = − F k θ W − F θ k Γ k 1 + a 1 k k θ L = 2 g 2 + 2 a + 2 g + 1 + a 2 e − 1 − a g 2 g 2
noting that the mean and variance are, respectively, k θ and k θ 2 . Again, W ( x ) is the zero-order Lambert W-function, and the full expression for cognition rate L is graced by a Whittaker M-function and many terms. Here, for L, we have set k = 3 , θ = 1 .
This particular model representation is shown in Figure 5, again with a = 1 / 3 , 3 , and F as above. Although, here, the two niches are not nested, again niche width collapses with increasing σ , and the width for a = 3 is much greater than for a = 1 / 3 .
Many other distributions, e.g., the lognormal, give results recognizably similar to Figure 4 and Figure 5. Here, Figure 3 - the exponential/Boltzmann distribution, seems a distinct outlier.
Matters rapidly become more complex under hierarchical structuring.

6. Hierarchy under Environmental Constraint

We next examine a networked multicomponent cognition/regulation system where subcomponents operate under the ‘Onsager’ relations of Eq.(9)
∂ Z i / ∂ t ≈ d S i / d Z i = Z i d 2 F i / d Z i
The full system has i = 1 , 2 , . . . , m cooperating linked units that must be individually supplied with resources at rates Z i under overall constraints of resources and time as ∑ i Z i = Z , ∑ i T i = T . We seek to optimize – minimize – the overall distortion under these constraints.
There are, of course, quite complicated general approaches to optimization [30], but here simple Lagrangian optimization across the sum of the distortions D i provides a sufficient formal base:
L = ∑ i D i + λ Z − ∑ i Z i + μ T − ∑ i T i ∂ L / ∂ Z = λ , ∂ L / ∂ T = μ , ∂ D i / ∂ Z i = λ , ∂ D i / ∂ T i = μ
In economic theory, the undetermined multipliers λ and μ represent ‘shadow prices’ imposed on system dynamics by environmental constraints, in a large sense [31,32].
Again, simple Lagrangian optimization is enough to outline the basic mechanism.
We are now concerned with the overall relations ∂ L / ∂ Z = λ and ∂ L / ∂ T = μ . Heuristically,
∂ Z / ∂ T = μ / λ ≡ Z d 2 F / d Z 2 F = μ λ Z ln ( Z ) − 1 + C 1 Z + C 2
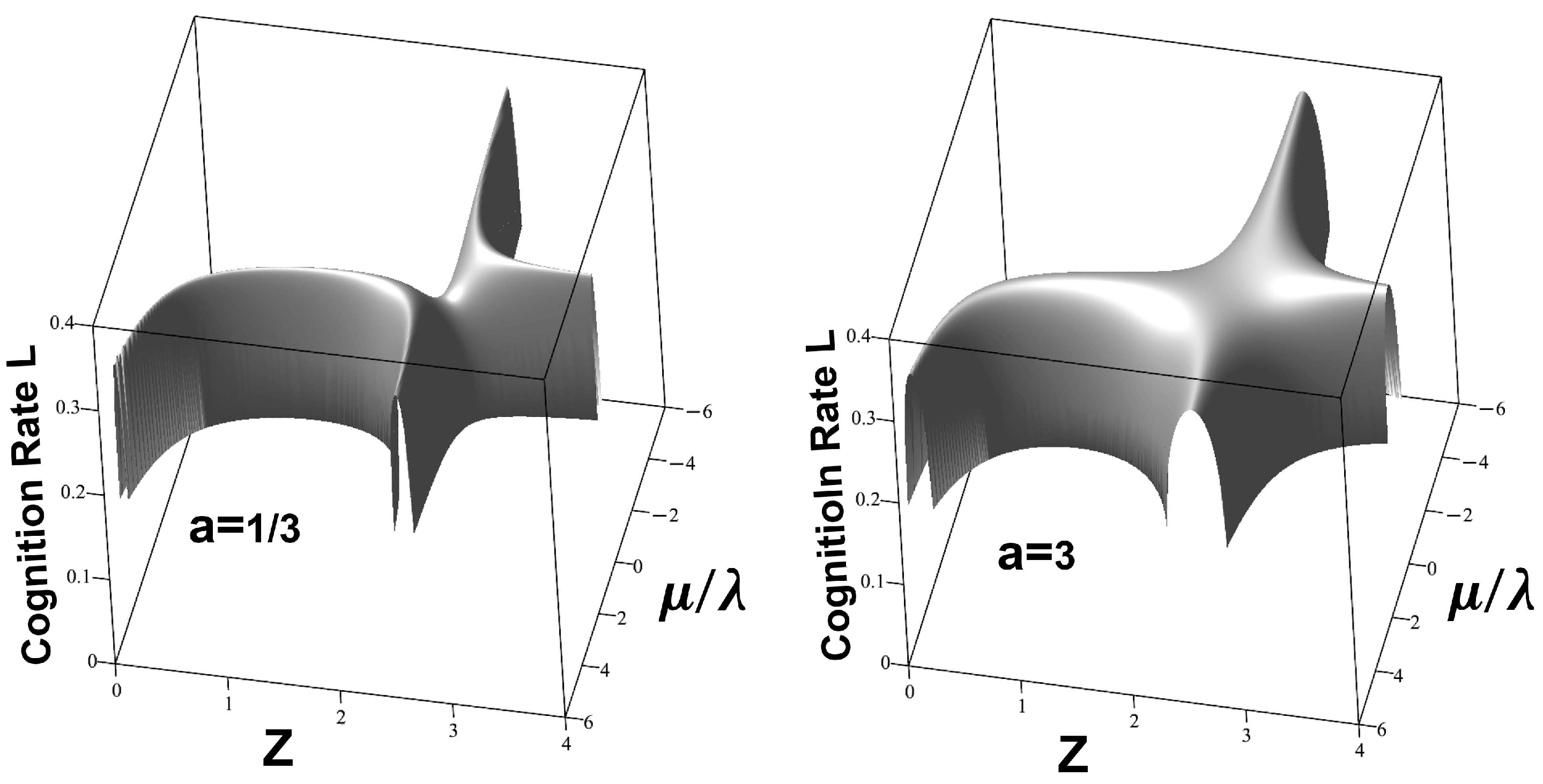
where F is a new – global – free energy construct on which there are imposed the distribution constraints of Eq.(12) in Section 5. We use the Boltzmann Distribution relations of Eq.(13), but now founded on F of Eq.(18), not on Eq.(11). Here, λ = μ = R 0 = 1 , with C 1 = − 1 , C 2 = 3 in Eq.(18). Figure 6 shows the cognition rate calculations for a = 1 / 3 , 3 .
The Boltzmann Distribution over the full hierarchical system now manifests a more-or-less standard inverted-U signal transduction Yerkes-Dodson effect [10]. Again, however, niche width increases with the degree of ‘adaptive’ regulatory capacity.
These patterns are profoundly affected by the shadow price ratio, as shown in Figure 7, where μ / λ varies between ± 1 . Again, R 0 = 1 . Certain combinations of shadow price ratio and Z constrict niche width.
The hierarchical cognition rate calculation can be carried out for the Cauchy Distribution example, again using Eq.(18). Here, s = R 0 = 1 and F is as in Figure 7, again taking a = 1 / 3 , 3 . While the cognition rate surfaces are more complicated than for the Boltzmann example, the inverted-U reappears. Again, the niche for a = 3 is broader than for a = 1 / 3 .
Similarly, the Gamma Distribution cognition rate example can be recalculated for the hierarchical model, again setting k = 3 , θ = 1 , R 0 = 1 , and taking F as in Figure 6, Figure 7 and Figure 8. This is shown in Figure 9, again with a = 1 / 3 , 3 and C 1 = − 1 , C 2 = 3 . The inverted-U signal transduction reemerges, with the higher a-value both broader and less compacted by decline in shadow price ratio.
The interested reader can explore these matters for other probability distributions. Inverted-U signal transduction – the Yerkes-Dodson effect – is ubiquitous under the hierarchical structure defined by Eq.(18).

7. Discussion

As argued elsewhere [33,34], building some recognizable form of ‘machine consciousness’ – of dubious actual utility – seems only a matter of cleverly assembling current off-the-shelf commodity electronic components. This is because higher animal consciousness, to meet 100 ms time constant requirements, is a grossly simplified version of mechanisms exapted by evolutionary process from the inevitable crosstalk between cognitive subcomponents of organisms [35,36]. Wound healing, gene expression, immune maintenance-and-response, and so on, by virtue of their extended time horizons, can entertain multiple, interacting, dynamic global workspaces. A 100 ms neural system cannot, even with a metabolic temperature-equivalent an order of magnitude higher than muscle tissue. For organic systems, high speed requires simple structures under metabolic constraints: classic tradeoff.
A fast multiple workspace cognitive process of any nature – effectively, a high speed artificial immune system – must, like the organic varieties, be heavily regulated, if only to prevent autoimmune self-attack. In addition, of course, there is the problem of simultaneous, coordinated effort in multiple targeting. These matters already confront and confound military air defense systems and, indeed, ‘ordinary’ civilian air (and other) traffic control.
We have deconstructed and parsed, in a sense, an evolutionary solution to some of these ambiguities: the innate and adaptive immunities. A high speed immune system’s innate artificial intelligence would, in this portrait, have been carefully trained on preexisting observational or experimental data. The adaptive system would, in some contrast, be expected to learn on-the-job, as it were, to continually fine-tune and update response/control mechanisms. This is likely to be a good deal harder to engineer well than a single global-workspace conscious machine. The payoff, however, would be considerable.
In addition to such venture capital matters, we have explored the more general dynamics – and sometimes highly punctuated failures – of the regulation of cognition under increasing noise of any sort. The approach parallels, and indeed generalizes, the Data Rate Theorem of control theory, extending the theorem’s requirement of a minimum channel capacity necessary for stabilization of an inherently unstable system. This work has studied various models across different basic underlying probability distributions characteristic of systems of possible interest, and across different hierarchical scales. We have explored in detail how the addition of adaptive – learned – regulation greatly extends the reach of innate – e.g., genetic, AI-driven, doctrinal, or otherwise pre-programmed – regulation.
This work, at the very least, indicates how to construct a new set of robust statistical tools for the analysis of observational and empirical data across a wide spectrum of pathologies and adversarial challenges afflicting a wide variety of important cognitive phenomena.

8. Mathematical Appendix

Deriving the DRT from the RDT

Assume control information is supplied to an inherently unstable system at a rate H. We take R ( D ) as the Rate Distortion Function from Figure 2 representing the relation between system intent and system operational effect. The scalar distortion measure D represents the disjunction between intent and impact of the regulator. Assume R t is the Rate Distortion Function at time t. We impose noise and volatility so that system dynamics are represented by the stochastic differential equation
d R t = f ( R t , t ) d t + b R t d B t
d B t is ordinary Brownian white noise, f is an appropriate function, and b is a scalar noise parameter.
H ( R t , t ) is the incoming rate of control information needed to impose control. We can then apply the standard Black-Scholes argument [37,38], expanding H in terms of R by using the Ito Chain Rule on Eq.(19). At nonequilibrium steady state, ‘it is not difficult to show’ that
H n s s ≈ κ 1 R + κ 2
for appropriate constants κ i .
For a Gaussian channel, R = 1 / 2 log [ σ 2 / D ] , and, recalling Feynman’s [16] characterization of information as a form of free energy, we can – again – define an entropy as the Legendre transform of R, here S = − R ( D ) + D d R ( D ) / d D . This leads – again – to an Onsager approximation for the dynamics of the distortion scalar D:
d D / d t ≈ μ d S / d D = μ 2 D ( t ) D ( t ) ≈ μ t
In the absence of control, D undergoes a classic diffusion to catastrophe.
This correspondence reduction to ordinary diffusion suggests an iterative approximation leading to the stochastic differential equation
d D t = [ μ 2 D t − M ( H ) ] d t + β D t d B t
where M ( H ) is an undetermined function of the rate at which control information is provided, and the last term is a volatility in Brownian noise.
The nonequilibrium steady state expectation of Eq.(22) is
D n s s = μ 2 M ( H )
Application of the Ito Chain Rule to D t 2 via Eq.(21) implies the necessary condition for stability in variance is
M ( H ) ≥ β μ
From Eqs.(20) and (23)
M ( H ) ≥ μ 2 σ 2 exp [ 2 ( H − κ 2 ) / κ 1 ] ≥ β μ
implying a necessary condition for stability in second order
H ≥ κ 1 2 log 2 β σ 2 μ + κ 2 ≡ H 0
Channels having other algebraic expressions for the RDF will nonetheless have similar results as a consequence of the inherent convexity of the RDF [8].

Expanding the Formal Perspective

Eq.(8) is only the first in a much larger class of possible ‘cognitive regression models.’ Dimensionally-consistent extensions of the Onsager approximation, albeit without cross-terms, can be expressed as
S ≡ − F ( Z ) + Z d F / d Z + ∑ n = 2 ∞ ϵ n Z n d n F / d Z n ∂ Z / ∂ t = μ d S / d Z + ∑ n = 2 ∞ μ n n − 1 d n S / d Z n
Jackson et al. [39] describe a far more general approach:
[T]he Legendre transform can be viewed as mapping the coefficients of one formal power series into the coefficients of another formal power series. Here, the term ‘formal’ does not express ‘mathematically nonrigorous’, as it often does in the physics literature. Instead, the term ‘formal power series’ is here a technical mathematical term, meaning a power series in indeterminates. Formal power series are not functions. A priori, formal power series merely obey the axioms of a ring and questions of convergence do not arise.
Determination of the ϵ and μ spectra of Eq.(27) – and possible series crossterms – express something of the usual empirical difficulties associated with all statistical models, analogous to fitting regression equations to observational or experimental data.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

The author thanks Dr. D.N. Wallace for useful discussions.

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Ciauncia, A., E. Shmeleva, M. Levin, The brain is not mental! coupling neuronal and immune cellular processing in human organisms. Frontiers in Integrative Neuroscience 2023, 17, 1057622. [CrossRef]
  2. Gould, S.J. The Structure of Evolutionary Theory, Harvard University Press, Cambridge MA. 2002. [Google Scholar]
  3. Maturana, H., F. Varela, 1980, Autopoiesis and Cognition: The Realization of the Living, Reidel, Boston.
  4. Dretske, F. The explanatory role of information. Philosophical Transactions of the Royal Society A 1994, 349, 59–70. [Google Scholar]
  5. Atlan H., I. Cohen, Immune information, self-organization, and meaning. International Immunology 1998, 10, 711–717. [CrossRef] [PubMed]
  6. Wallace, R., 2023a, Essays on the Extended Evolutionary Synthesis: Formalizations and extensions, Springer, New York.
  7. Nair, G., F. Fagnani, S. Zampieri, R. Evans, Feedback control under data rate constraints: an overview. Proceedings of the IEEE 2007, 95, 108138.
  8. Cover, T., J. Thomas, 2006, Elements of Information Theory, Second Edition, Wiley, New York.
  9. French, V., E. Anderson, G. Putman, T. Alvager, The Yerkes-Dodson law simulated with an artificial neural network. Cognitive Systems 1999, 5, 136–147.
  10. Fricchione, G. Mind body medicine: a modern bio-psychosocial model forty-five years after Engel. BioPsychoSocial Medicine 2023, 17, 12. [Google Scholar] [CrossRef] [PubMed]
  11. Khinchin, A., 1957, Mathematical Foundations of Information Theory, Dover, New York.
  12. Wallace, R., (ed.), 2022, Essays on Strategy and Public Health: The systematic reconfiguration of power relations, Springer, New York.
  13. Effros, M., P., Chou, R. Gray, Variable-rate source coding theorems for stationary nonergodic sources. IEEE Transactions on Information Theory 1994, 40, 1920–1925. [CrossRef]
  14. Shields, P., D. Neuhoff, L. Davisson, F. Ledrappier, The Distortion-Rate function for nonergodic sources. The Annals of Probability 1978, 6, 138–143.
  15. Wallace, R. How AI founders on adversarial landscapes of fog and friction. Journal of Defense Modeling and Simulation 2021. [Google Scholar] [CrossRef]
  16. Feynman, R., 2000, Lectures on computation,Westview Press, New York.
  17. Bennett, C.H. The thermodynamics of computation. International Journal of Theoretical Physics 1982, 21, 905–940. [Google Scholar] [CrossRef]
  18. Landau, L., E. Lifshitz, 2007, Statistical Physics, 3rd Ed. Part 1, Elsevier, New York.
  19. Dolan, B., W. Janke, D. Johnston, M. Stathakopoulos, Thin Fisher zeros. Journal of Physics A 2001, 34, 6211–6223.
  20. Fisher, M., 1965 Lectures in Theoretical Physics vol. 7, University of Colorado Press, Boulder.
  21. Ruelle, D., 1964, Cluster property of the correlation functions of classical gases, Reviews of Modern Physics, April, 580-584.
  22. Laidler, K., 1987, Chemical Kinetics, 3rd ed, Harper and Row, New York.
  23. Watts, D., S. Strogatz, Collective dynamics of small world networks. Nature 1998, 393, 440–442. [CrossRef] [PubMed]
  24. Barabasi, A., R. Albert, Emergence of scaling in random networks. Science 1999, 286, 509–512. [CrossRef] [PubMed]
  25. Harush, U., B. Barzel. Dynamic patterns of information flow in complex networks. Nature Communications 2017, 8, 2181. [CrossRef] [PubMed]
  26. de Groot, S., P. Mazur, 1984, Nonequilibrium Thermodynamics, Dover, New York.
  27. Protter, P., 2005, Stochastic Integration and Dierential Equations,Second Edition, Springer, New York.
  28. Derman, E., M. Miller, D. Park, 2016, The Volatility Smile, Wiley, New York.
  29. Taleb, N. N. (ed.), 2020, Statistical Consequences of Fat Tails: Real world preasymptotics, epistemology, and applications, STEM Academic Press.
  30. Nocedal, J., S. Wright, 2006, Numerical Optimization, Second Edition, Springer, New York.
  31. Jin, H., Z. Hu, X. Zhou, A convex stochastic optimization problem arising from portfolio selection. Mathematical Finance 2008, 18, 171–183. [CrossRef]
  32. Robinson, S. Shadow prices for measures of effectiveness II: General model. Operations Research 1993, 41, 536–548. [Google Scholar] [CrossRef]
  33. Wallace, R. On ‘Machine Consciousness’. Journal of Artificial Intelligence and Consciousness 2023, 10, 125–148. [Google Scholar] [CrossRef]
  34. Butlin, P., et al., 2023, Consciousness in Artificial Intelligence: Insights from the Science of Consciousness, https://arxiv.org/abs/2308.08708.
  35. Wallace, R. Consciousness, crosstalk, and the mereological fallacy: an evolutionary perspective. Physics of Life Reviews 2012, 9, 426–453. [Google Scholar] [CrossRef] [PubMed]
  36. Wallace, R., 2022, Consciousness, Cognition and Crosstalk: The evolutionary exaptation of nonergodic groupoid symmetry-breaking, Springer, New York.
  37. Black, F., M. Scholes, The pricing of options and corporate liabilities. Journal of Political Economy 1973, 81, 637–654. [CrossRef]
  38. Wallace, R., 2021, Carl von Clausewitz, the Fog-of-War, and the AI Revolution: The real world is not a game of Go, Springer, New York.
  39. Jackson, D., A. Kempf, A. Morales. A robust generalization of the Legendre transform for QFT. Journal of Physics A 2017, 50, 225201. [CrossRef]
Preprints 101107 g001
Figure 1. A control system at a nonequilibrium steady state under the Data Rate Theorem. The state of the system X, is compared with what is wanted, and a corrective control signal U then sent at an appropriate rate, under conditions of noise represented as W. The rate of transmission of the control signal must exceed the rate at which the inherently unstable system generates it’s own ‘topological information’.
Figure 1. A control system at a nonequilibrium steady state under the Data Rate Theorem. The state of the system X, is compared with what is wanted, and a corrective control signal U then sent at an appropriate rate, under conditions of noise represented as W. The rate of transmission of the control signal must exceed the rate at which the inherently unstable system generates it’s own ‘topological information’.
Preprints 101107 g001
Preprints 101107 g002
Figure 2. Reinterpretation of ‘control’ in terms of the Rate Distortion Theorem. An unstable system’s topological information is seen as added to the effects of noise to determine the minimum channel capacity R ( D ) needed to assure transmission with average distortion D. The punctuation implied by Eq.(2) can emerge from this model if there is a critical maximum average distortion that characterizes the system. Some systems may degrade more gracefully, or, by contrast, have even more complex patterns of punctuation that generalize the Data Rate Theorem.
Figure 2. Reinterpretation of ‘control’ in terms of the Rate Distortion Theorem. An unstable system’s topological information is seen as added to the effects of noise to determine the minimum channel capacity R ( D ) needed to assure transmission with average distortion D. The punctuation implied by Eq.(2) can emerge from this model if there is a critical maximum average distortion that characterizes the system. Some systems may degrade more gracefully, or, by contrast, have even more complex patterns of punctuation that generalize the Data Rate Theorem.
Preprints 101107 g002
Preprints 101107 g003
Figure 3. For a relatively low maximum possible cognition rate, under a Boltzmann Distribution sufficient noise σ can ‘fry’ the agent into variance instability.
Figure 3. For a relatively low maximum possible cognition rate, under a Boltzmann Distribution sufficient noise σ can ‘fry’ the agent into variance instability.
Preprints 101107 g003
Preprints 101107 g004
Figure 4. Here, using F as above, with C 1 = − 1 , , C 2 = 3 and s = 1 , rising ‘noise’ σ drastically narrows an agent’s ecological niche regardless of a, the relative index of adaptive regulation. It is striking, however, that for the Cauchy Distribution, a higher level of adaptive regulation greatly broadens the niche at low noise.
Figure 4. Here, using F as above, with C 1 = − 1 , , C 2 = 3 and s = 1 , rising ‘noise’ σ drastically narrows an agent’s ecological niche regardless of a, the relative index of adaptive regulation. It is striking, however, that for the Cauchy Distribution, a higher level of adaptive regulation greatly broadens the niche at low noise.
Preprints 101107 g004
Preprints 101107 g005
Figure 5. Cognition rates for the Gamma Distribution models, setting k = 3 , θ = 1 , and again taking a = 1 / 3 , 3 and F as above. Although the two niches are not nested in this example, again niche width implodes with rising σ , and the width for a = 3 is much greater than for a = 1 / 3 .
Figure 5. Cognition rates for the Gamma Distribution models, setting k = 3 , θ = 1 , and again taking a = 1 / 3 , 3 and F as above. Although the two niches are not nested in this example, again niche width implodes with rising σ , and the width for a = 3 is much greater than for a = 1 / 3 .
Preprints 101107 g005
Preprints 101107 g006
Figure 6. Hierarchical cognition rate based on the Boltzmann Distribution. Here λ = μ = R 0 = 1 for L, while C 1 = − 1 , C 2 = 3 in F . The full system now manifests a standard inverted-U signal transduction.
Figure 6. Hierarchical cognition rate based on the Boltzmann Distribution. Here λ = μ = R 0 = 1 for L, while C 1 = − 1 , C 2 = 3 in F . The full system now manifests a standard inverted-U signal transduction.
Preprints 101107 g006
Preprints 101107 g007
Figure 7. Extension of Figure 6, allowing the shadow price ratio μ / λ to vary. Again, R 0 = 1 . Certain combinations of shadow price ratio and resource rate constrict niche width.
Figure 7. Extension of Figure 6, allowing the shadow price ratio μ / λ to vary. Again, R 0 = 1 . Certain combinations of shadow price ratio and resource rate constrict niche width.
Preprints 101107 g007
Preprints 101107 g008
Figure 8. The calculation of Figure 7 can be reprised for the Cauchy Distribution, taking s = R 0 = 1 . F is as in Figure 7. While the cognition rate surfaces are more complex than for the Boltzmann example, inverted-U signal transduction reappears, with the niche for a = 3 generally broader than for a = 1 / 3 .
Figure 8. The calculation of Figure 7 can be reprised for the Cauchy Distribution, taking s = R 0 = 1 . F is as in Figure 7. While the cognition rate surfaces are more complex than for the Boltzmann example, inverted-U signal transduction reappears, with the niche for a = 3 generally broader than for a = 1 / 3 .
Preprints 101107 g008
Preprints 101107 g009
Figure 9. The Gamma Distribution model in the hierarchical case again shows the inverted-U signal transduction, with the cognition rate broadened and stabilized by the larger adaptive index a.
Figure 9. The Gamma Distribution model in the hierarchical case again shows the inverted-U signal transduction, with the cognition rate broadened and stabilized by the larger adaptive index a.
Preprints 101107 g009

Short Biography of Authors

Rodrick Wallace is a research scientist in the Division of Epidemiology at the New York State Psychiatric Institute, associated with the Columbia University Department of Psychiatry. He has an undergraduate degree in mathematics and a PhD in physics from Columbia, and completed post-doctoral training in the epidemiology of mental disorders at Rutgers. He has worked as a public interest lobbyist, conducting empirical studies of fire service deployment, and received an Investigator Award in Health Policy Research from the Robert Wood Johnson Foundation. In addition to material on public health and public policy, he has authored peer reviewed studies modeling evolutionary process and heterodox economics, as well as quantitative analyses of institutional and machine cognition. He publishes in the military science literature, and received one of the UK MoD RUSI Trench Gascoigne Essay Awards.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated