Prerpints.org logo
Preprint
Article

PointNet++ Network with Contextual Feature and Mutual Learning for Point Sets

Altmetrics

Downloads

359

Views

115

Comments

0

This version is not peer-reviewed

Submitted:

12 March 2024

Posted:

13 March 2024

You are already at the latest version

Alerts
Abstract
The research of object classification and part segmentation is a hot topic in computer vision. A considerable number of studies have been carried out about deep learning on 3D point clouds. However,it is challenging to achieve effective feature learning due to sparsity of point clouds. Recently, a variety of Transformers have been adopted to improve point cloud processing and display great potential. Nevertheless, large numbers of Transformer layers tend to incur huge computational and memory costs. PointNet++ is one of the most influential neural architectures for point cloud understanding. Although the accuracy of PointNet++ has been largely surpassed by recent networks, this does not mean that PointNet++ has no potential.Thus, this paper offer two major contributions that significantly improve PointNet++ performance. Firstly, we introduce a novel contextual feature extraction (CFE) block that significantly enhances the feature extraction capabilities of PointNet++ networks. Secondly, to further enhance feature fusion, we seamlessly integrate a mutual learning (ML) block into the network architecture. By embedding these two innovative blocks within each layer of the network, we not only enrich the network's functionality but also impart it with greater robustness and adaptability. The specific experiments were conducted on the S3DIS (6-fold cross-validation) and Modelnet40 datasets with 86.5% and 92.7% accuracy, respectively, which proved that our model is comparable or even better than most existing methods for classification and segmentation tasks.
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Vision and Graphics

1. Introduction

In recent years, the continuous evolution of 3D data acquisition techniques has fostered a significant surge in interest towards comprehending point clouds. As a result, numerous applications have surfaced, including indoor navigation [1], self-driving vehicles [2], robotics [3], hand pose estimation [4], underground mining environments [5], face recognition [6], city building reconstruction [7], multi-target recognition [8,9], and beyond.
Unlike images with their neatly organized regular pixel grids, 3D point clouds exist as sets within a continuously varying space, distinguished by sparsity, irregularity, and disorder. This poses a significant obstacle for convolutional neural network-based models, even with their notable accomplishments in computer vision. The reason lies in the inherent structural mismatch between these models and 3D point cloud data, preventing a straightforward application for processing the latter. Consequently, it becomes imperative to craft a bespoke deep neural network model that caters to the distinctive structural nuances of 3D point cloud data. In response to this challenge, numerous approaches to deep learning on 3D point clouds have surfaced.
Qi et al. were the pioneers in introducing PointNet [10], a deep learning network designed for feature learning through the utilization of multi-layer perceptrons (MLPs) and maxpooling operations. However, a limitation of PointNet is its inability to capture local features, which is a crucial capability exhibited by convolutional neural networks. PointNet++ [11] addresses this limitation by introducing a hierarchical structure that enables the extraction of local features. Nevertheless, it fails to consider the mutual learning among points, resulting in limitations to its local feature extraction capability. Such limitations may adversely affect the network's performance.
In this work, we construct the Mutual Learning(ML) block and the Contextual Feature Extraction(CFE) block for effectively extends the PointNet++ model. The intuition behind these blocks is intuitive: to enhance the network's ability to integrate local features. Specifically, PointNet++ utilizes points to represent local structural information, but overlooks the connection between these points. If we express structural information according to extract more point features and promote the further integration of feature information between centroid points, it will definitely improve the ability to integrate local features and the performance of the whole network model.
In this paper, we propose an enhanced version of PointNet++ that conbines contextual feature extraction with mutual learning among points. This network effectively extracts spatial and semantic information from points, and utilizes the ML block to enhance the integration of feature information among centroid points. The ML block uses residual connections [12], grouped vector self-attention operator, and trainable position encoding [13].Extensive experiments have demonstrated that our model is able to process raw point sets efficiently and robustly on both 3D object datasets and indoor remote-sensing datasets.
In summary, the contribution of this work is two-fold:
  • We propose an enhanced version of PointNet++ network. This approach utilizes the CFE block and the ML block to enhance the local feature integration capability of Point-Net++ and improve the overall robustness of the network.
  • The performance of the proposed approach is evaluated on public datasets, ranging from shape classification to scene semantic segmentation. The results demonstrate that the approach significantly outperforms most existing methods.

2. Related Works

With the rapid evolution of deep learning methods, various deep neural networks have emerged for the processing of point clouds and can be broadly categorized into two groups. One approach involves projecting the 3D point clouds data to a regular structure where convolutional neural networks can be effortlessly applied for representation. Alternatively, another approach involves directly consuming the point clouds.

2.1. Projecting 3D Point Clouds Data to Regular Structure

Previous approaches typically focused on projecting 3D point clouds data to a regular structure, such as collections of images or 3D voxel grids, before feeding the data into deep neural networks. Image-based networks often employ multi-view representations, utilizing a set of 2D images rendered from the point cloud at various viewpoints [14,15,16,17]. MVCNN [18] projects 3D point clouds from different perspectives to 2D images through spatial projection, and processes the 2D data using traditional convolutional neural networks. To depart from selecting a global projection viewpoint, [19] proposed projecting local neighborhoods to local tangent planes and processing them using 2D convolutions. ShapeNets [20] and VoxNet [21] transform the unordered point clouds into a regular 3D grid via voxelization and proceed with feature learning using a 3D Convolutional Neural Network. Despite achieving commendable results, these works face a dilemma: 2D convolution falls short in capturing essential 3D geometry information like normals and shape, while 3D convolution demands extensive computation on the sparse 3D mesh resulting from voxelization. Utilizing sparse structures such as octrees or hash-maps enables the handling of larger grids and improved performance [22,23]. However, these methods still rely on the subdivision of a bounding volume rather than leveraging local geometric structure.

2.2. Manipulating Point Clouds Directly

Given the reasons outlined above, state-of-the-art deep neural networks are purposefully crafted to tackle the irregularity of point clouds. These networks directly manipulate raw point cloud data, bypasses the need for conversion to intermediate regular representations, such as voxelization or 2D images. This innovative approach was pioneered by PointNet [10], which achieves permutation invariance by extracting features of individual points through vanilla MLP layer and subsequently applying a symmetric function to form global features after accumulating them. However, one limitation of this approach is that it treats each point independently, disregarding the geometric relationships among them. Consequently, local features that encode crucial spatial information may be overlooked.
To overcome these limitations, subsequent to PointNet, PointNet++ [11] introduces a neural network structure that leverages PointNet in a hierarchical fashion. This approach employs query ball grouping and farthest point sampling (FPS) to meticulously construct local neighborhoods, enabling the network to capture richer geometric relationships and spatial patterns. The emergence of PointNet and PointNet++ has led to a surge in popularity for directly processing entire point clouds in an unstructured format using deep convolutional neural networks. Jiang et al. [24] proposed a module called PointSIFT that encodes information of different orientations and is adaptive to scale of shape. This module effectively stacks and encodes data from eight key spatial orientations through a three-stage sequential convolution process. PointWeb [25] extracts contextual features from the local neighborhood and enhances point features through the utilization of the Adaptive Feature Adjustment (AFA) module.
Multiple methods center on the development of explicit convolution kernels for enhanced feature extraction at points. PCCN [26] represents convolutional kernels as MLPs. SpiderCNN [27] defines its kernel as a family of polynomial functions, with each neighbor receiving a unique weight. Spherical CNN [28] addresses the issue of 3D rotation equivariance by designing spherical convolutions. PointCNN [29] utilizes X-transformation to rearrange points into a latent and potentially canonical order, subsequently employing traditional convolutional operators for effective feature extraction.
Multiple methods focus on Graph-CNN as a key component for enhancing feature extraction and overall network performance in point cloud analysis. DGCNN [30] constructed dynamic neighborhoods using the k-nearest neighbor (k-NN) algorithm and subsequently performed edge convolution operations on these neighborhoods. ECC [31] designs dynamic edge-conditioned filters that are tailored based on edge labels, enabling flexible and adaptive feature extraction in point cloud analysis. DeepGCNs [32] delve into the construction of exceptionally deep GCNs, leveraging residuals and dilation convolution, techniques commonly employed by CNNs to enhance depth and optimize network performance.
Recently, Transformer, which has dominated the field of natural language processing, has made significant strides in computer vision, showcasing its exceptional global feature learning capabilities. Consequently, it has found applications in a diverse range of point cloud processing tasks. Point Cloud Transformer(PCT) [33] innovates by replacing the shared MLP layer of PointNet with the original Transformer block with Offset-Attention, and introduces neighbourhood information embedding to achieve state-of-the-art performance. Point Transformer [13] utilizes a hierarchical Transformer block with a vector self-attention operator to extract local features from the point cloud. To reduce the resolution, it leverages transition down modules. Subsequently, global features are derived through a global average pooling operation.
Despite their success, pure Transformer architectures such as these networks have a significant drawback: the self-attention mechanism involves numerous linear transformations, potentially leading to information redundancy and significant computational and memory costs. PointNet++ is a classically popular and widely utilized network that, despite its commendable feature extraction capability compared to PointNet, has limitations. Specifically, it primarily focuses on extracting point coordinate information without delving into additional contextual details. Furthermore, it neglects the mutual learning among neighboring points, limiting its overall representational power. Therefore, we hypothesized that the learning capabilities of PointNet++ could be significantly enhanced by leveraging a robust self-attention mechanism and refining its feature extraction capabilities.

3. Methods

In this section, we introduce two blocks: one dedicated to feature extraction and the other to mutual learning. Leveraging recent advancements in deep learning for point clouds and drawing inspiration from classical point cloud networks, our method effectively captures local feature information, leading to improved model performance. Specifically, we introduce an innovative feature extraction block within PointNet++ to capture a richer set of information. Additionally, we employ the novel ML block grounded in a grouped vector self-attention operator, that not only enhances the capa-bilities of the PointNet++ network but also mitigates some of the limitations inherent in pure Transformer architectures.
The first section provides a comprehensive explanation of the CFE block. The second section details the specific design of the ML block. Finally, the last section presents the overall architecture of the method.

3.1. Contextual Feature Extraction Block

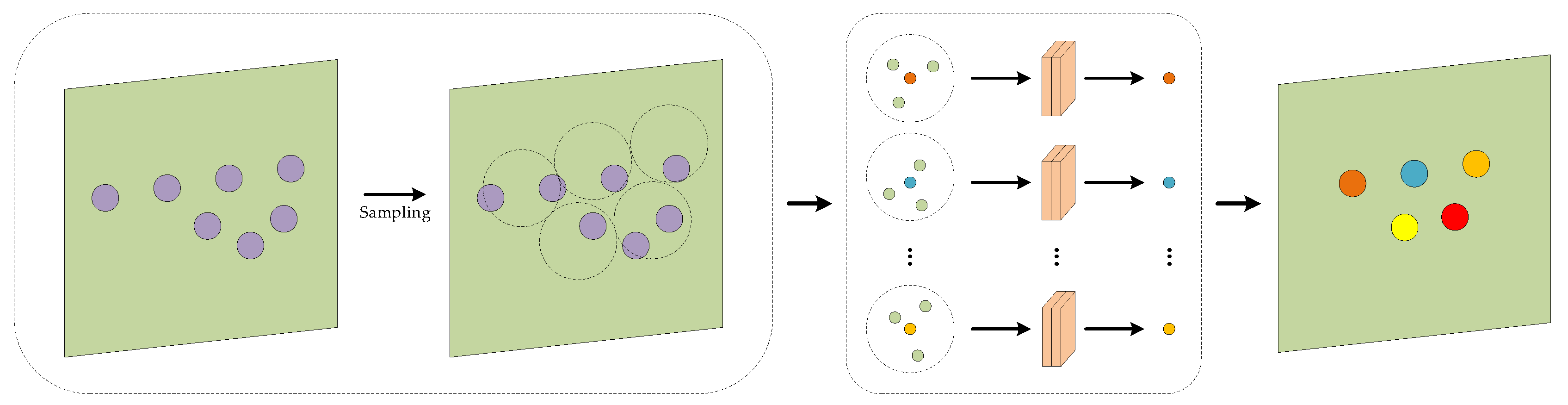
The CFE block effectively achieves local feature extraction by aggregating relevant local features onto the corresponding sampling points. The specific structure is shown in Figure 1 as an example. Given the input point cloud, we employed FPS to generate a subset of the point cloud, referred to as the sampling point set. For the neighborhood of a sampling point, we presented a context fusion method that effectively encodes and combines both coordinate and feature information. This approach has been validated as effective in previous research [34]. The proposal of this method is motivated by our suspicion that the feature extraction layer in PointNet++ is limited to basic extraction of neighborhood features, thereby failing to fully capitalize on the informational richness within the local vicinity.
For each neighbor x j within the neighborhood of a sampled point x i , two distinct contexts emerge: a spatial context P j , which characterizes geometric information, and a feature context F j , which embodies semantic information. To achieve a comprehensive representation of these contexts, we integrated both P j and F j as follows:
C j = P j ⊕ F j
where C j is the contextual representation of x j . Using these representations as a foundation, we formulate the relationship between x i and x j as follows:
∆ C i j = P i ⊕ P j ⊕   P i − P j   ⊕   C i − C j  
where ⊕ is the concatenation operation, and   P i − P j   calculates the Euclidean distance between the neighbouring and center points.
In this way, we can acquire initial local information that serves as a foundation for subsequent feature aggregation. Subsequently, we aggregate the information to form a comprehensive local information representation. Specifically, ∆ C i j is encoded using a MLP, followed by a max-pooling function to extract the novel feature. The above operations can be summarized as:
y i = max k ⁡ (   M L P   (   ∆ C i j   )   )
By doing so, we arrive at a precise feature representation of the sampled point's local neighborhood.

3.2. Mutual Learning Block

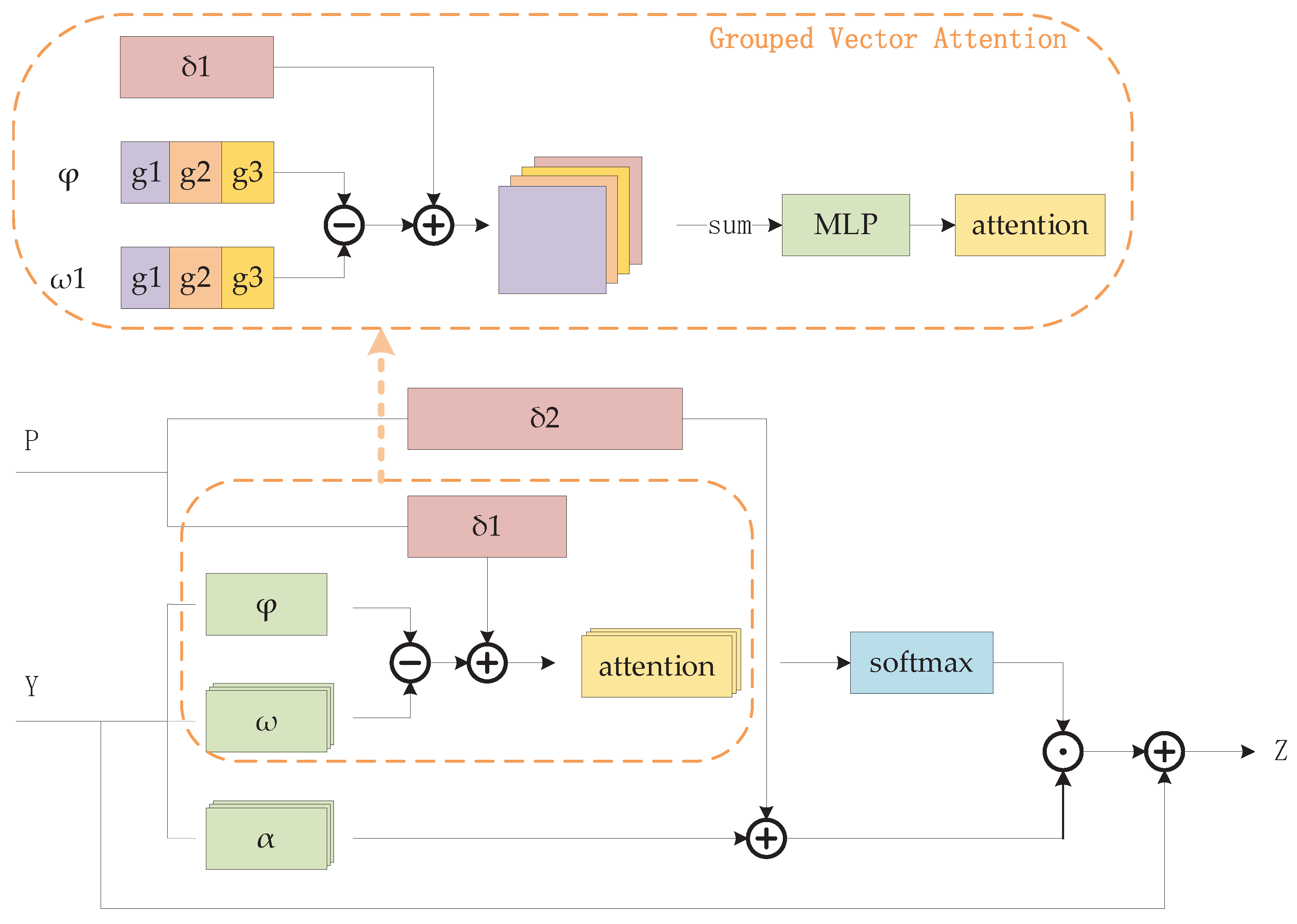
To enhance the capture of local structures and elevate network performance, we need to integrate the features of the point set more comprehensively. Consequently, we design the ML block between neighborhoods to facilitate this integration. The ML block employs a grouped attention mechanism along with a vector attention operator, incorporating a trainable positional coding.
We assume that the input point clouds of each ML block, denoted as y 1 , y 2 , ⋯ , y n , are represented by Y with dimensions B × N × C . Here, B refers to the batch size, N represents the number of point clouds per sample, and C denotes the number of channels. First, the k-NN algorithm is employed to identify k neighboring points for each point in Y, subsequently organizing them into n distinct neighborhoods. Then, the relationships within each neighborhood are thoroughly analyzed and precisely calculated.
To compute neighborhood relations, we initially elaborate on the grouping vector self-attention operator, followed by the introduction of trainable positional coding. For the neighborhood of a sampling point y i , the classical vector attention operator employing the subtraction relation can be represented as follows:
z i = ∑ j = 1 k ρ γ φ y i − ω y j + δ ⊙ α y j + δ
where z i is the output feature. φ , ω , and α are linear layers, implemented as a 1 × 1 convolution. δ is a position encoding function and ρ is a normalization function such as softmax. The mapping function γ is an MLP with two linear layers and one ReLU nonlinearity.
To achieve a lighter and more efficient version, we utilize grouped vector self-attention. We divide the φ q i and the ω q j into G groups along the channel direction, denoted as φ i 1 , φ i 2 , ⋯ , φ i G and ω j 1 , ω j 2 , ⋯ , ω j G . Equation 4 can be reformulated as follows:
z i = ∑ j = 1 k ρ γ ∑ g = 1 G φ i g − ω j g + δ 1 ⊙ α q j + δ 2
where δ 1 and δ 2 represent trainable location codes. Utilizing a grouping cumulative approach, we can effectively amplify useful information, ultimately leading to the extraction of more recognizable features.
Position encoding plays a crucial role in self-attention mechanisms, enabling the operator to adaptively capture local structural patterns within the data, as highlighted in [35]. In the vector attention mechanism, a learnable position encoding is introduced to effectively fuse local spatial information. Let P = p 1 , p 2 , ⋯ , p n represent a set of vectors encoding the coordinates of points within a neighborhood. Our 3D position coding function is defined as follows:
δ = θ p 1 − p 1 p 2 − p 1 ⋮ p n − p 1 p 1 − p 2 p 2 − p 2 ⋮ p n − p 2 ⋯ ⋯ ⋱ ⋯ p 1 − p n p 2 − p n ⋮ p n − p n
and θ is implemented as an MLP consisting of two linear layers interspersed with batch normalization and ReLU activation functions. In Eq.(5), δ 1 and δ 2 serve to transform the 3D coordinate information into the corresponding dimension, facilitating channel summation.
To improve the selectivity and adaptability of the network learning process, and to prevent network degradation, the output establishes a residual connection with the original input. The structure of the ML block is shown in Figure 2 as an example.

3.3. Overall Architecture

The overall pipeline of our network, as depicted in Fig. 3. Taking the original point cloud as input, the network can be categorized into two main parts: the front-end and the back-end. The front-end serves as the core component of the network, responsible for feature extraction. For the classification task, the front-end comprises two modules, whereas for the segmentation task, it consists of four modules. Each module within the front-end incorporates two blocks: the CFE block and the ML block, which operate on the set of points.
Preprints 101151 g003
Figure 3. The proposed network architecture is tailored for classification (c) and segmentation (s) tasks. It features a front end, which is constructed from a stack of modules that seamlessly integrate CFE blocks with ML blocks. The subsequent component, comprising the remainder of the architecture, serves as the back end.
Figure 3. The proposed network architecture is tailored for classification (c) and segmentation (s) tasks. It features a front end, which is constructed from a stack of modules that seamlessly integrate CFE blocks with ML blocks. The subsequent component, comprising the remainder of the architecture, serves as the back end.
Preprints 101151 g003
In the classification task, the sampling point set of the two modules is configured with [ N /2, N /8] points respectively, where N denotes the total number of input points. Following this, the back-end component employs an MLP layer to enhance the extracted features to 1024 dimensions. Subsequently, a global max pooling operation is applied to derive the definitive global feature representation for the target point cloud. Ultimately, global classification results are achieved through the utilization of an FC layer, which comprises three linear layers, incorporating batch normalization and ReLU activation. For the segmentation task, the sampling point set of the four modules is configured with [N, N/4, N/8, N/16] points, respectively. The back-end component consists of four FP modules (Feature Propagation Modules) and two linear layers, incorporating batch normalization and ReLU activation.

4. Experiment Result and Discussion

In this section, we meticulously evaluate the efficiency of our proposed framework across multiple benchmark datasets. Initially, we undertake a comprehensive assessment of the segmentation task model, specifically utilizing the challenging Stanford Large-Scale 3D Indoor Spaces (S3DIS) dataset [36]. Subsequently, we expand our experimental horizons to encompass the classification task on the ModelNet40 [20] dataset, conducting ablation experiments to further validate our approach.
For our specific parameter settings, we utilize the Adam optimizer as the chosen optimization method. We use the Adam optimizer with momentum and weight decay set to 0.9 and 0.0001. The initial learning rate was set to 0.01, with a cosine annealing schedule to adjust the learning rate at every epoch. It is noteworthy that all our experiments are conducted on an Intel Xeon(R) Platinum 8350C 2.6GHz CPU, equipped with a powerful NVIDIA GeForce RTX 3090 GPU.

4.1. Segmentation Results

The S3DIS [36] dataset, designed for semantic scene parsing, comprises 271 rooms spanning six areas from three distinct buildings. Each point in the scans is annotated with a semantic label from a total of 13 categories, including ceiling, floor, table, and others. Consistent with standard evaluation practices outlined in [11], we evaluate the proposed approach in two distinct modes: (a) Area 5 is exclusively reserved for testing purposes and is excluded from the training process, and (b) a thorough 6-fold cross-validation is conducted to ensure robust and reliable performance assessment.
We treat each scene as a unit sample and randomly select 4096 point clouds from each sample for training. For training, we adopt a batch size of 16 and conduct 32 epochs to ensure sufficient iterations for effective learning. Additionally, we set the number of CFE blocks and ML blocks to 4, which are key components in our architecture. Table 1 presents the segmentation results of our proposed method in comparison with other techniques. We offer a thorough evaluation by reporting the mean classwise intersection over union (mIoU) and overall accuracy (OA) to demonstrate the performance of our approach. As evident from Table 2, our method achieved a notable improvement of 5.5% in OA and 9.2% in mIoU. These experimental results clearly indicate that our network model exhibits excellent performance in the task of semantic segmentation.

4.2. Classification Results

ModelNet40, the benchmark dataset for 3D shape classification tasks, comprises a diverse collection of 12,311 CAD models, encompassing 40 distinct categories of man-made objects. For our experiments, we utilize the point cloud representation of ModelNet40, as provided by [10]. This representation involves sampling 1024 points uniformly from the mesh surface of each model, taking into account the face area, and subsequently normalizing them into a unit sphere. We adhere to the official split, employing 9843 shapes for training and reserving 2468 for testing purposes.
We establish the batch size as 24 and proceed with 200 epochs of training. Additionally, we set the number of CFE blocks and ML blocks to 2, ensuring the optimal configuration for our model. Table 2 presents the findings of the classification task, wherein our proposed method surpasses most of the current methodologies on this particular dataset. For the conducted experiments, we utilized the (x, y, z)-coordinates of 1024 points as the primary input. Specifically, our proposed method demonstrates a significant improvement in overall accuracy, surpassing ShapeNets by 8.0% and VoxNet by 6.8%. In comparison to PointNet++, our method achieves an impressive OA of 92.7% and mAcc of 90.2%, representing a notable increase of 2% and 2.6%, respectively, over the original network. To further validate the effectiveness of each block, we conducted ablation experiments. The results revealed that the CFE block contributes to a 1.1% OA improvement and a 1.7% mAcc enhancement, while the ML block enhances OA by 1.6% and mAcc by 2.3%. These outcomes firmly establish the superiority of our method and validate the effectiveness of its constituent blocks. Additionally, by learning sufficiently enriched features, our method outperforms SpiderCNN by 0.3% in OA, further confirming its competitiveness.

5. Conclusions

We introduce an enhanced version of the PointNet++ network, focusing on advancements in both feature extraction and aggregation. Leveraging the downsampled point cloud as our input, our method meticulously extracts global features by seamlessly integrating two distinct blocks. Initially, we capture the contextual features of the point cloud through the CFE block. Subsequently, we employ the ML block to further consolidate these features, harnessing the self-attention mechanism to enable sampling points to mutually learn from each other. By conducting ablation experiments within a single dataset and comparing our method with others across different datasets, we demonstrate the efficient and robust capabilities of our proposed approach in processing raw point sets, whether it be on 3D object datasets or indoor remote-sensing datasets. Specifically, our proposed method achieves a prediction accuracy of 88.4% on the S3DIS dataset and 92.7% on the ModelNet40 dataset, respectively. Furthermore, on the ModelNet40 dataset, the CFE block enhances accuracy by 1.1%, while the ML block boosts it by 1.6%. The experimental results clearly demonstrate that our proposed network outperforms other point cloud-based methods on the semantic segmentation task. This superior performance is attributed to the network's ability to efficiently learn contextual features and facilitate mutual learning among sampling points. In processing tasks involving point sets, our proposed network model has achieved comparable or superior performance compared to most existing networks.
While the method proposed in this research demonstrates promising results, it is not without limitations. One such limitation lies in the feature extraction process, as the CFE block does not fully maximize the extraction of relevant features. Additionally, the FPS method utilized in our approach could benefit from further optimization techniques that are now available. Moreover, the self-attention operator remains an underexplored area in point cloud tasks, offering ample opportunities for further exploration. In the future, we aim to delve deeper into these areas and enhance our method's performance even further.

References

  1. Zhu, Y.; Mottaghi, R.; Kolve, E.; Lim, J.J.; Gupta, A.; Fei-Fei, L.; Farhadi, A. Target-Driven Visual Navigation in Indoor Scenes Using Deep Reinforcement Learning. In Proceedings of the 2017 IEEE international conference on robotics and automation (ICRA); IEEE, 2017; pp. 3357–3364. [Google Scholar]
  2. Qi, C.R.; Liu, W.; Wu, C.; Su, H.; Guibas, L.J. Frustum Pointnets for 3d Object Detection from Rgb-d Data. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 918–927. [Google Scholar]
  3. Rusu, R.B.; Marton, Z.C.; Blodow, N.; Dolha, M.; Beetz, M. Towards 3D Point Cloud Based Object Maps for Household Environments. Robotics and Autonomous Systems 2008, 56, 927–941. [Google Scholar] [CrossRef]
  4. Li, S.; Lee, D. Point-to-Pose Voting Based Hand Pose Estimation Using Residual Permutation Equivariant Layer. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2019; pp. 11927–11936. [Google Scholar]
  5. Ren, Z.; Wang, L.; Bi, L. Robust GICP-Based 3D LiDAR SLAM for Underground Mining Environment. Sensors 2019, 19, 2915. [Google Scholar] [CrossRef] [PubMed]
  6. Mokhayeri, F.; Granger, E. A Paired Sparse Representation Model for Robust Face Recognition from a Single Sample. Pattern Recognition 2020, 100, 107129. [Google Scholar] [CrossRef]
  7. Zhang, L.; Zhang, L. Deep Learning-Based Classification and Reconstruction of Residential Scenes from Large-Scale Point Clouds. IEEE Transactions on Geoscience and Remote Sensing 2017, 56, 1887–1897. [Google Scholar] [CrossRef]
  8. Chen, M.; Tang, Y.; Zou, X.; Huang, K.; Li, L.; He, Y. High-Accuracy Multi-Camera Reconstruction Enhanced by Adaptive Point Cloud Correction Algorithm. Optics and Lasers in Engineering 2019, 122, 170–183. [Google Scholar] [CrossRef]
  9. Wu, F.; Duan, J.; Chen, S.; Ye, Y.; Ai, P.; Yang, Z. Multi-Target Recognition of Bananas and Automatic Positioning for the Inflorescence Axis Cutting Point. Frontiers in plant science 2021, 12, 705021. [Google Scholar] [CrossRef] [PubMed]
  10. Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. Pointnet: Deep Learning on Point Sets for 3d Classification and Segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2017; pp. 652–660. [Google Scholar]
  11. Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. Pointnet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space. Advances in neural information processing systems 2017, 30. [Google Scholar]
  12. He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2016; pp. 770–778. [Google Scholar]
  13. Zhao, H.; Jiang, L.; Jia, J.; Torr, P.H.; Koltun, V. Point Transformer. In Proceedings of the IEEE/CVF international conference on computer vision; 2021; pp. 16259–16268. [Google Scholar]
  14. Boulch, A.; Le Saux, B.; Audebert, N. Unstructured Point Cloud Semantic Labeling Using Deep Segmentation Networks. 3dor@ eurographics 2017, 3, 17–24. [Google Scholar]
  15. Lawin, F.J.; Danelljan, M.; Tosteberg, P.; Bhat, G.; Khan, F.S.; Felsberg, M. Deep Projective 3D Semantic Segmentation. In Proceedings of the Computer Analysis of Images and Patterns: 17th International Conference, CAIP 2017, Ystad, Sweden, August 22-24, 2017, Proceedings, Part I 17; Springer, 2017; pp. 95–107. [Google Scholar]
  16. Zhang, L.; Sun, J.; Zheng, Q. 3D Point Cloud Recognition Based on a Multi-View Convolutional Neural Network. Sensors 2018, 18, 3681. [Google Scholar] [CrossRef] [PubMed]
  17. Gao, Q.; Shen, X. ThickSeg: Efficient Semantic Segmentation of Large-Scale 3D Point Clouds Using Multi-Layer Projection. Image and Vision Computing 2021, 108, 104161. [Google Scholar] [CrossRef]
  18. Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-View Convolutional Neural Networks for 3d Shape Recognition. In Proceedings of the IEEE international conference on computer vision; 2015; pp. 945–953. [Google Scholar]
  19. Tatarchenko, M.; Park, J.; Koltun, V.; Zhou, Q.-Y. Tangent Convolutions for Dense Prediction in 3d. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 3887–3896. [Google Scholar]
  20. Wu, Z.; Song, S.; Khosla, A.; Yu, F.; Zhang, L.; Tang, X.; Xiao, J. 3d Shapenets: A Deep Representation for Volumetric Shapes. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2015; pp. 1912–1920. [Google Scholar]
  21. Maturana, D.; Scherer, S. Voxnet: A 3d Convolutional Neural Network for Real-Time Object Recognition. In Proceedings of the 2015 IEEE/RSJ international conference on intelligent robots and systems (IROS); IEEE, 2015; pp. 922–928. [Google Scholar]
  22. Graham, B.; Engelcke, M.; Van Der Maaten, L. 3d Semantic Segmentation with Submanifold Sparse Convolutional Networks. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 9224–9232. [Google Scholar]
  23. Riegler, G.; Osman Ulusoy, A.; Geiger, A. Octnet: Learning Deep 3d Representations at High Resolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2017; pp. 3577–3586. [Google Scholar]
  24. Jiang, M.; Wu, Y.; Zhao, T.; Zhao, Z.; Lu, C. Pointsift: A Sift-like Network Module for 3d Point Cloud Semantic Segmentation. arXiv 2018, arXiv:1807.00652. [Google Scholar]
  25. Zhao, H.; Jiang, L.; Fu, C.-W.; Jia, J. Pointweb: Enhancing Local Neighborhood Features for Point Cloud Processing. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2019; pp. 5565–5573. [Google Scholar]
  26. Wang, S.; Suo, S.; Ma, W.-C.; Pokrovsky, A.; Urtasun, R. Deep Parametric Continuous Convolutional Neural Networks. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 2589–2597. [Google Scholar]
  27. Xu, Y.; Fan, T.; Xu, M.; Zeng, L.; Qiao, Y. Spidercnn: Deep Learning on Point Sets with Parameterized Convolutional Filters. In Proceedings of the European conference on computer vision (ECCV); 2018; pp. 87–102. [Google Scholar]
  28. Cohen, T.S.; Geiger, M.; Köhler, J.; Welling, M. Spherical Cnns. arXiv 2018, arXiv:1801.10130. [Google Scholar]
  29. Li, Y.; Bu, R.; Sun, M.; Wu, W.; Di, X.; Chen, B. Pointcnn: Convolution on x-Transformed Points. Advances in neural information processing systems 2018, 31. [Google Scholar]
  30. Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph Cnn for Learning on Point Clouds. ACM Transactions on Graphics (tog) 2019, 38, 1–12. [Google Scholar] [CrossRef]
  31. Simonovsky, M.; Komodakis, N. Dynamic Edge-Conditioned Filters in Convolutional Neural Networks on Graphs. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2017; pp. 3693–3702. [Google Scholar]
  32. Li, G.; Muller, M.; Thabet, A.; Ghanem, B. Deepgcns: Can Gcns Go as Deep as Cnns? In Proceedings of the IEEE/CVF international conference on computer vision; 2019; pp. 9267–9276. [Google Scholar]
  33. Guo, M.-H.; Cai, J.-X.; Liu, Z.-N.; Mu, T.-J.; Martin, R.R.; Hu, S.-M. Pct: Point Cloud Transformer. Computational Visual Media 2021, 7, 187–199. [Google Scholar] [CrossRef]
  34. Qiu, S.; Anwar, S.; Barnes, N. PU-Transformer: Point Cloud Upsampling Transformer. In Proceedings of the Asian Conference on Computer Vision (ACCV), December 2022; pp. 2475–2493. [Google Scholar]
  35. Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Advances in neural information processing systems 2017, 30. [Google Scholar]
  36. Armeni, I.; Sener, O.; Zamir, A.R.; Jiang, H.; Brilakis, I.; Fischer, M.; Savarese, S. 3d Semantic Parsing of Large-Scale Indoor Spaces. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2016; pp. 1534–1543. [Google Scholar]
  37. Huang, Q.; Wang, W.; Neumann, U. Recurrent Slice Networks for 3d Segmentation of Point Clouds. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 2626–2635. [Google Scholar]
  38. Landrieu, L.; Simonovsky, M. Large-Scale Point Cloud Semantic Segmentation with Superpoint Graphs. In Proceedings of the IEEE conference on computer vision and pattern recognition; 2018; pp. 4558–4567. [Google Scholar]
  39. Yang, J.; Zhang, Q.; Ni, B.; Li, L.; Liu, J.; Zhou, M.; Tian, Q. Modeling Point Clouds with Self-Attention and Gumbel Subset Sampling. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition; 2019; pp. 3323–3332. [Google Scholar]
Preprints 101151 g001
Figure 1. The CFE block structure. From left to right, the three key steps are: sampling and grouping, contextual feature extraction, and local feature aggregation.
Figure 1. The CFE block structure. From left to right, the three key steps are: sampling and grouping, contextual feature extraction, and local feature aggregation.
Preprints 101151 g001
Preprints 101151 g002
Figure 2. The ML block structure, which adopted the grouped vector attention mechanism.
Figure 2. The ML block structure, which adopted the grouped vector attention mechanism.
Preprints 101151 g002
Table 1. Comparison of Semantic segmentation results on the S3DIS dataset, evaluated with 6-fold cross-validation.
Table 1. Comparison of Semantic segmentation results on the S3DIS dataset, evaluated with 6-fold cross-validation.
Method mIoU(%) OA(%)
PointNet [10] 47.6 78.5
RSNet [37] 56.5 -
PointNet++ [11] 54.5 81.0
DGCNN [30] 56.1 84.1
SPGraph [38] 62.1 85.5
DeepGCN [32] 60.0 85.9
ours 63.7 86.5
Table 2. Comparison of Classifification results on ModelNet40 dataset.
Table 2. Comparison of Classifification results on ModelNet40 dataset.
Method Input mAcc(%) OA(%)
3DShapeNets [20] 1024 77.3 84.7
VoxNet [21] - 83.0 85.9
MVCNN [18] - - 90.1
PointNet [10] 1024 86.2 89.2
PAT [39] 1024 - 91.7
PointCNN [29] 1024 88.1 92.2
DGCNN [30] 1024 90.2 92.2
SpiderCNN [27] 1024 - 92.4
PointNet++ [11] 1024 87.6 90.7
PointNet++(+CFE) 1024 89.3 91.8
PointNet++(+ML) 1024 89.9 92.3
ours 1024 90.2 92.7
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated