Preprint

Article

Finite Element Analysis versus Empirical Modal Analysis of a Basketball Rim and Backboard

Altmetrics

Downloads

Views

101

Comments

A peer-reviewed article of this preprint also exists.

Daniel Winarski^*

,Kip P. Nygren,Tyson Winarski

Daniel Winarski^*

,Kip P. Nygren,Tyson Winarski

This version is not peer-reviewed

Submitted:

05 March 2024

Posted:

13 March 2024

You are already at the latest version

Alerts

Abstract

The ANSYS 2024R1 student edition was used to create a finite element model of a basketball rim and backboard. This finite element model included the use of steel for the rim and its mount, a tempered glass backboard, and an aluminum frame behind the backboard. After a mesh was created, fixed support boundary conditions were applied to the four corners of the aluminum frame. The subsequently calculated mode shapes and frequencies were compared to empirical modal analysis previously done at the United States Military Academy at West Point, New York. Four mode shapes and frequencies agreed rather well between the theoretical finite element analysis and previously published empirical modal analysis, specifically where the rim was vibrating in the vertical direction, which was the direction that the accelerometer was aligned for modal analysis. However, three mode shapes missed by the empirical modal analysis were found where the vibration of the rim was confined to the horizontal plane, which was orthogonal to the orientation of our accelerometer.

Keywords:

Subject: Engineering - Mechanical Engineering

1. Introduction

This study was inspired by the work of Javorski [1], who first characterized the dynamic behavior of a ceiling-mounted basketball goal using an impact hammer and a fixed-location accelerometer, and then compared that empirical analysis to a theoretical finite element analysis. Empirical vibration measurements were taken at fourteen nodes, ten of which were on the frame supporting the basketball rim and backboard. Only four nodes were measured on the backboard, at the corners of the backboard, and none on the rim itself. Overall, 36 frequency response functions were measured, and this study concentrated mostly on structural vibrations between 2 and 10 Hz. Thus, this important study was focused more on the structural support of the backboard and rim rather than the elastic vibrations of the backboard and rim themselves.

ANSYS was chosen as our finite element package of choice for two major reasons. The first reason was that bundled education on this package was available online through Cornell University [2]. MAE-141 taught the conceptual foundations of finite element analysis, MAE-142 taught ANSYS mechanical concepts and implementation, MAE 143 taught elasticity applications, and MAE-144 taught beam and shell applications. Most importantly, the final module in this bundle, MAE-145, taught vibration applications, which was very helpful. Each of these five modules contained lecture materials, quizzes, and a comprehensive hands-on student project. The second reason was the free ANSYS 2024R1 Student Edition [3].

Another important source to get us pointed in the right direction was the basketball rim and backboard modeled in ANSYS by Tickoo [4]. Tickoo’s modeling did not use the precise dimensions as specified by the NCAA [5] or Gared [6]. However, he did get us started using DesignModeler within ANSYS for creating our geometry. We followed his lead of first creating the toroidal rim. Secondly, we followed his process of creating a new offset plane, followed by sketching a rectangle (saw icon), then extruding that rectangle from the offset plane to the toroidal rim to create the top of the mount. Finally, we followed his process of creating yet another new offset plane, followed by sketching yet another rectangle (saw icon), then extruding that rectangle from that second new plane to create the back of the mount. The use of ANSYS to study plate vibrations by Nkounhawa, et-al., [7] and Guguloth, et-al., [8] were also very helpful.

2. Materials and Methods

We first launched ANSYS Workbench 2024R1, then double-clicked on MODAL under Analysis Systems in Workbench. This caused the MODAL cell to be displayed in the project schematic window. We then right-clicked on Geometry within MODAL and selected DesignModeler Geometry from the menu. We did use English units because all of the dimensions of the basketball rim, mount, and backboard are specified in inches in the United States. Figure 1, Figure 2 and Figure 3 define how we established the geometry for the rim, its mount, the backboard, and the aluminum frame.

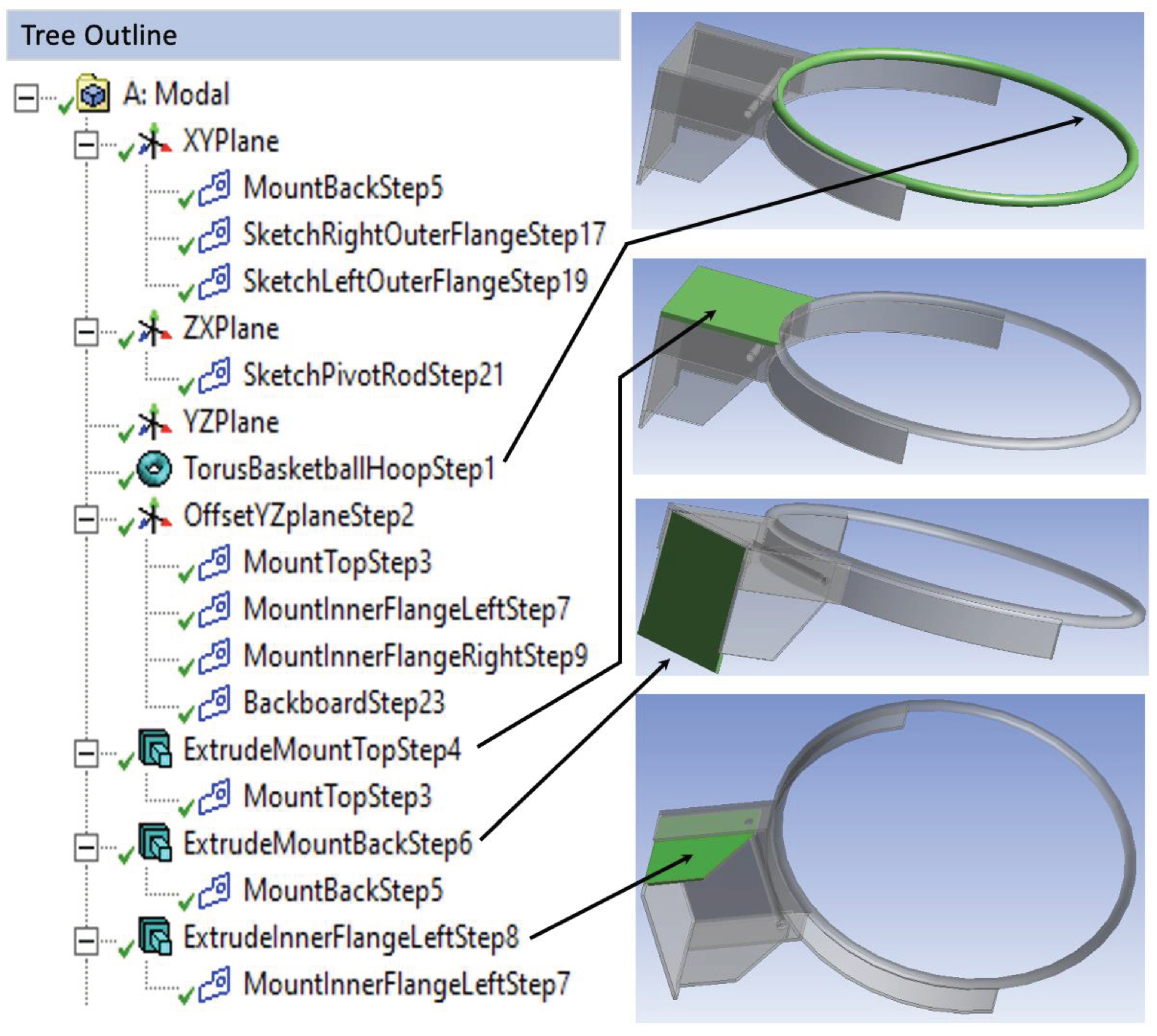
As shown in Figure 1, step 1 was to create the toroidal rim. For this, we used the toroid listed in the create-primitives section. Step 2 was used to create an offset-YZ plane, followed by sketching a rectangle (saw icon) in step 3, then extruding that rectangle from the offset-YZ plane to the toroidal rim to create the top of the mount, step 4.

Steps 2-4 began a repetitive process in Figure 1, Figure 2 and Figure 3 of sketching a geometry (typically a rectangle) and extruding that geometry, and creating a new plane when needed. For example, the rectangle used to create the back of the mount was defined in step 5, then that rectangle was extruded to create the back of the mount in step 6. Finally, in Figure 1, a rectangle was sketched in step 7 and extruded in step 8 to create the left inner mount flange.

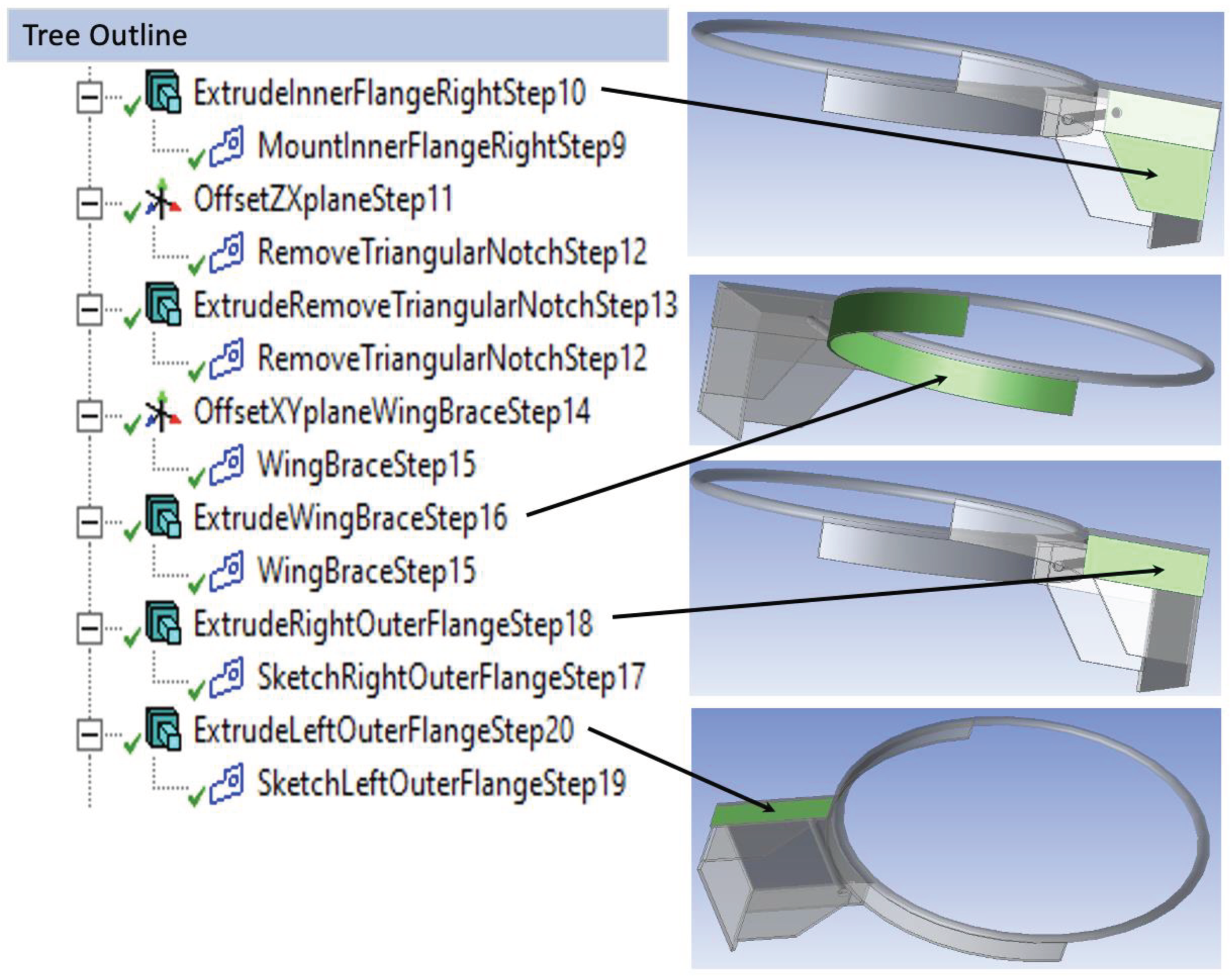
In Figure 2, a rectangle was sketched in step 9 and extruded in step 10 to create the right inner mount flange. In step 11, an offset-ZX plane was created, then a sketch of a triangular cutout was made in step 12. In step 13, this triangular cutout was extruded as a material removal, to finalize the five-sided inner flanges. In step 14, a horizontal offset-XY plane was created, then a pair of concentric semicircles were connected at their ends in sketch step 15 before being extruded in step 16 to create the wing brace which attached to the rim. This was followed by sketching a rectangle in step 17 and extruding it in step 18 for form the right outer flange. Then a matching rectangle was created in step 18 and extruded in step 19 to form the left outer flange.

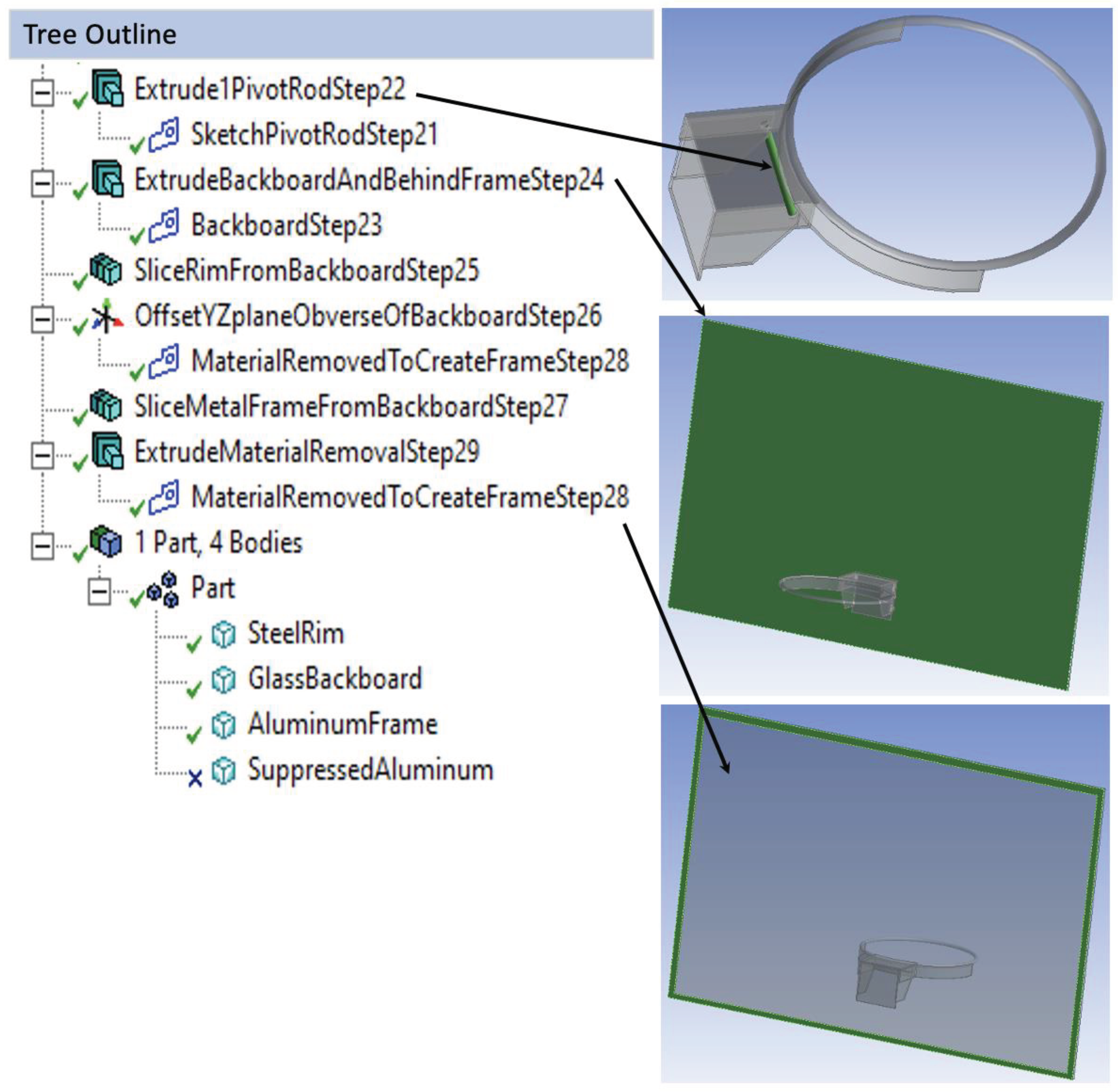
In Figure 3, a circle was sketched in step 21 and then extruded in step 22 to form the pivot rod of the break-away release mechanism. This completed the geometric definition of the rim and its mount. Next came a rectangular sketch of the backboard in step 23, and the extrusion of that backboard and its frame in step 24. Step 25 utilized the slice function to separate the rim and its mount from the backboard so that the rim and mount could be declared to be made of steel. Specifically, we used slice – select face – generate. The rim-mound subassembly was then reunited with the backboard by the use of form-new-part to create an assembly of the individual component parts, as shown in Figure 3.

When the backboard was extruded, its thickness was declared to be the thickness of the tempered glass and the thickness of the aluminum frame behind the tempered glass. In step 26, an offset-YZ plane was created so that the metal frame could be sliced from the obverse side of the backboard in step 27. This allowed the backboard to be declared to be made of tempered glass and the metal frame to be made of aluminum. At this point, the metal frame was a rectangle the same width and height of the backboard. To make the aluminum frame into a border frame, a second slightly smaller rectangle was created in step 28 and extruded as a slice in step 29, to remove unwanted aluminum. This concluded the geometry definition with one part comprising four bodies, the steel rim, the glass backboard, the aluminum border frame, and the material removed from the solid piece of aluminum to make the aluminum border frame. The material removed to create the aluminum border frame was then suppressed to take it out of the analysis; hence the “x” next to it at the bottom-left of Figure 3.

The next step was to exit Geometry and enter Model within the MODAL cell. Once in Model, the mesh seen in Figure 5 was created. All mesh parameters were set to program default.

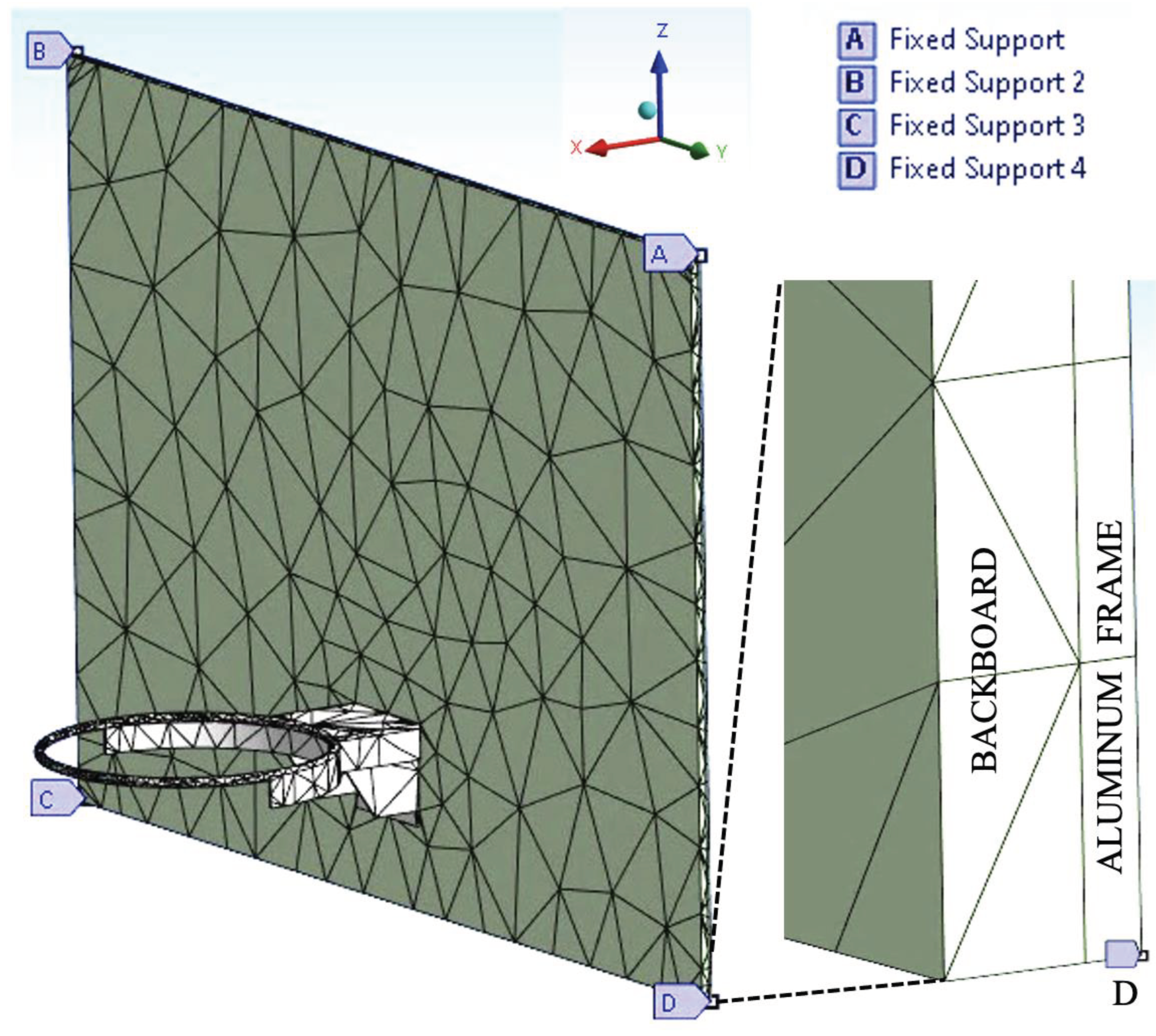
After the mesh was created, four fixed support conditions were applied, one to each of the four outer corner vertices of the aluminum frame behind the backboard, as shown in Figure 4. The zoom showing the location of fixed support “D” at an outer corner is equally applicable of fixed supports “A,” “B,” and “C.” The choice of the four fixed support conditions was based on our previously published mode shapes [9].

With the help of the “Details of Mesh” feature of ANSYS, Figure 4 was summarized in Table 1. Because elements are not shared between individual parts, the sum of the elements by individual parts equaled the total (4,618) number of elements.

At this point, the finite element model was ready for the calculation of theoretical mode shapes and frequencies, as shown in Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. Figure 5, Figure 6, Figure 7 and Figure 8 compared our previously published empirically measured frequencies [9] with the theoretical output of this ANSYS finite element analysis, as tabulated in Table 2. The bold arrows in Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 represent eigenvectors, which explain the relative motions seen in the respective figures.

Figure 5 exhibited an in-phase rocking motion of the rim and backboard, which was indicative of a lower-frequency mode.

Figure 6 and Figure 7 were interesting because the bowing of the backboard in Figure 7 was 180^o out of phase from the backboard in Figure 6.

Figure 8 was interesting because both the empirical modal analysis and the theoretical finite element analysis showed that the steel rim was flexing. As the mount and inner portion of the rim flexed upward, the outer portion of the rim flexed downward, and visa-versa. The characteristic oscillating central bulge in the backboard plate prominent in Figure 9 can also be found in [10,11,12,13].

Figure 5, Figure 6, Figure 7 and Figure 8 all showed that the basketball rim was oscillating perpendicular to the XY (horizontal) plane. As stated in [9], the fixed-location accelerometer used in the empirical modal analysis was at the outer end of the rim and pointed in the vertical Z direction, so the accelerometer would be primarily sensitive to motion perpendicular to the horizontal XY plane. Thus, it is understandable that the theoretical finite element modes shown in Figure 9, below, were missed by the empirical modal analysis because the theoretical motion of the rim in each mode in Figure 9 was entirely within the XY plane.

The missed mode at 11 Hz comprised a piston-motion of the rim and mount in the + X direction. The missed modes at 29 Hz and 49 Hz comprised the reciprocating rotational motion of the rim and mount about the Z-axis. The missed mode at 29 Hz had previously perplexed the authors’ empirical modal analysis [9] as that was a common mode of vibrations in plates [11,12,13]. But we now understand that the lack of vertical motion of the rim in Figure 9 meant that any signal from the vertically-oriented accelerometer could have easily been overlooked as noise.

3. Discussion and Conclusions

This paper gives a process of creating a geometry, mesh, and boundary conditions for a basketball rim, mount, backboard, and border frame, for the purpose of theoretical finite element analysis. Four empirical modes of vibration compared favorably with this theoretical finite element analysis.

There are many possible designs of rims, backboards, and frames which meet NCAA standards, so this study is not comprehensive across the sport of basketball. However, our efforts of finite element analysis did match four empirically measured mode shapes and frequencies of our previously published data. Also, we showed the potential need for a triaxial accelerometer for any future empirical modal analysis efforts involving basketball rims and backboards.

Author Contributions

Conceptualization, K.P.N.; methodology, D.W.; validation, K.P.N., D.W. and T.W.; formal analysis, D.W. and T.W.; investigation, D.W. and T.W.; writing—original draft preparation, D.W.; writing—review and editing, K.P.N., D.W. and T.W.; visualization, K.P.N. and D.W.; supervision, K.P.N.; project administration, K.P.N. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The archived 2024R1 Work Bench Project Zip file, *.wbpz, with all ANSYS commands used in this paper, will be freely available through MDPI.

Acknowledgments

Ms. Donna Robinson Winarski is acknowledged for her support of this research, both at the United States Military Academy at West Point, New York, and at Tucson, Arizona. Her assistance with initial editing as well as data taking was very much appreciated.

Conflicts of Interest

The authors declare no conflict of interest.

References

Javorski, M.; Čermelj, P.; Boltežar, M. Characterization of the Dynamic Behaviour of a Basketball Goal Mounted on a Ceiling. J. Mech. Eng./Stroj. Vestn. 2010, 56. Available online: https://www.sv-jme.eu/?ns_articles_pdf=/ns_articles/files/ojs3/1513/ submission/1513-1-2001-1-2-20171103.pdf&id=5958 (accessed on 9 September 2023).
Finite Element Analysis, Cornell Certificate Program. Available online: https://ecornell.cornell.edu/certificates/engineering/finite-element-analysis/ (accessed on 24 January 2024).
ANSYS 2024 R1 Student Edition: Available online: https://www.ansys.com/academic/students/ansys-student.
Tickoo, Sham. "ANSYS Workbench 2023 R2: A Tutorial Approach." (2023), pp. 5-24 to 5-37.
2023-2024 NCAA Men’s Basketball Rules Handbook, updated November 27, 2023. Manuscript Prepared By: Jeff O’Malley, Secretary-Rules Editor, NCAA Men’s Basketball Rules Committee. Edited By: Andy Supergan, Assistant Director of Playing Rules and Officiating. Available online: https://www.ncaapublications.com/productdownloads/BK24-20231127.pdf (accessed on 22 February 2024).
Model 3500 Positive Lock Breakaway Goal. Updated 21 January 2010. Gared Holdings, LLC. Available online: https://www. garedsports.com/sites/default/files/import/files/3500I%2520spec%2520-revA.pdf (accessed on 7 September 2023).
Nkounhawa, P.K.; Ndapeu, D.; Kenmeugne, B.; Beda, T. Analysis of the Behavior of a Square Plate in Free Vibration by FEM in Ansys. World J. Mech. 2020, 10, 11–25. [Google Scholar] [CrossRef]
Guguloth, G.N.; Singh, B.N.; Ranjan, V. Free vibration analysis of simply supported rectangular plates. Vibroengineering PROCEDIA 2019, 29, 270–273. [Google Scholar] [CrossRef]
Winarski, D.; Nygren, K.P.; Winarski, T. Modes of Vibration in Basketball Rims and Backboards and the Energy Rebound Testing Device. Vibration 2023, 6, 726–742. [Google Scholar] [CrossRef]
Irvine, T.; The Natural Frequency of a Rectangular Plate Point-Supported at Each Corner, Revision C. 1 August 2011. Available online: http://www.vibrationdata.com/tutorials2/plate_point_corner.pdf (accessed on 25 July 2023).
Dumond, P.; Monette, D.; Alladkani, F.; Akl, J.; Chikhaoui, I. Simplified setup for the vibration study of plates with simply-supported boundary conditions. MethodsX 2019, 6, 2106–2117. [Google Scholar] [CrossRef] [PubMed]
Anđelić, N., M. Čanađija, and Z. Car. "Determination of Natural Vibrations of Simply Supported Single Layer Graphene Sheet using Non-Local Kirchhoff Plate Theory." IN-TECH 2017 International Conference on Innovative Technologies. 2017, p.5.
Geveci, Berk, and J. D. A. Walker. "Nonlinear resonance of rectangular plates." Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 457.2009 (2001): 1215-1240. [CrossRef]

Figure 1. DesignModeler Geometry – Tree Outline 1-of-3.

Figure 2. DesignModeler Geometry – Tree Outline 2-of-3.

Figure 3. DesignModeler Geometry – Tree Outline 3-of-3.

Figure 4. Mesh and Fixed Supports At Corner Vertices Of Aluminum Frame.

Figure 5. Empirical Modal 23.62 Hz (top) versus ANSYS FEM 22.181 Hz (bottom).

Figure 6. Empirical Modal 33.08 Hz (top) versus ANSYS FEM 37.315 Hz (bottom).

Figure 7. Empirical Modal 51.45 Hz (top) versus ANSYS FEM 50.875 Hz (bottom).

Figure 8. Empirical Modal 78.14 Hz (top) versus ANSYS FEM 83.14 Hz (bottom).

Figure 9. Missed Modes Predicted by ANSYS FEM at 11, 29, and 49 Hz.

Table 1. Summary of Materials, Mesh, and Boundary Conditions.

Part	Material	Elements	Fixed Support Conditions
Rim	Structural Steel	1,979
Backboard	Tempered Glass	2,435
Frame	6061T6 Aluminum	204	4
Total		4,618	4

Table 2. Favorable Frequency Comparisons.

Figure	Empirical Modal Analysis [9]	ANSYS Finite Element Analysis
5	23.62 Hz	22.181 Hz
6	33.08 Hz	37.315 Hz
7	51.45 Hz	50.857 Hz
8	78.14 Hz	83.14 Hz

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.