Submitted:
13 March 2024
Posted:
13 March 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Literature Review
2.1. Hands Free Interaction
2.2. Point Clouds
2.2.1. Generative Adversarial Network for the Point Cloud Generation
2.3. Object Detection
3. Methodology
3.1. Proposed Solution
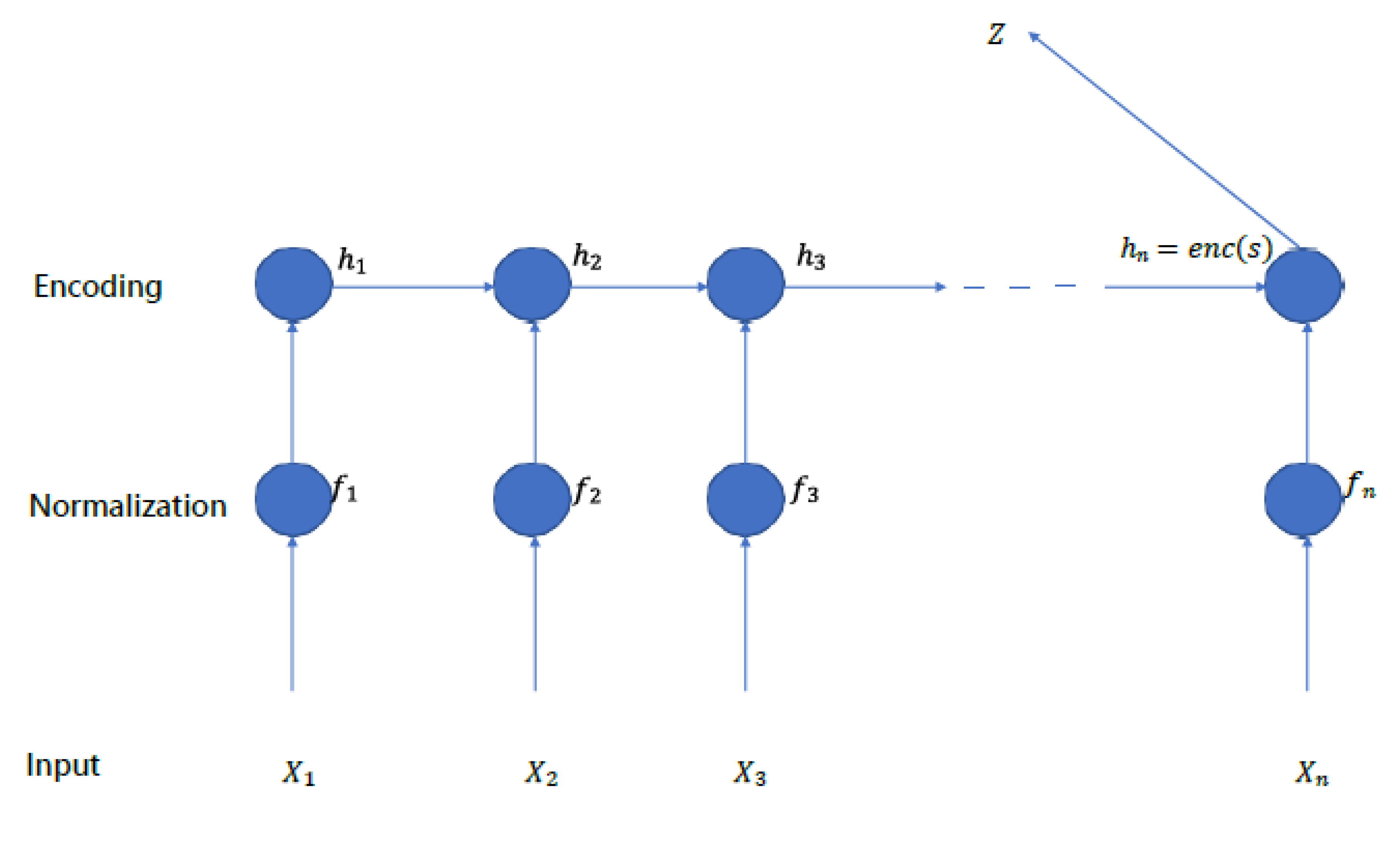
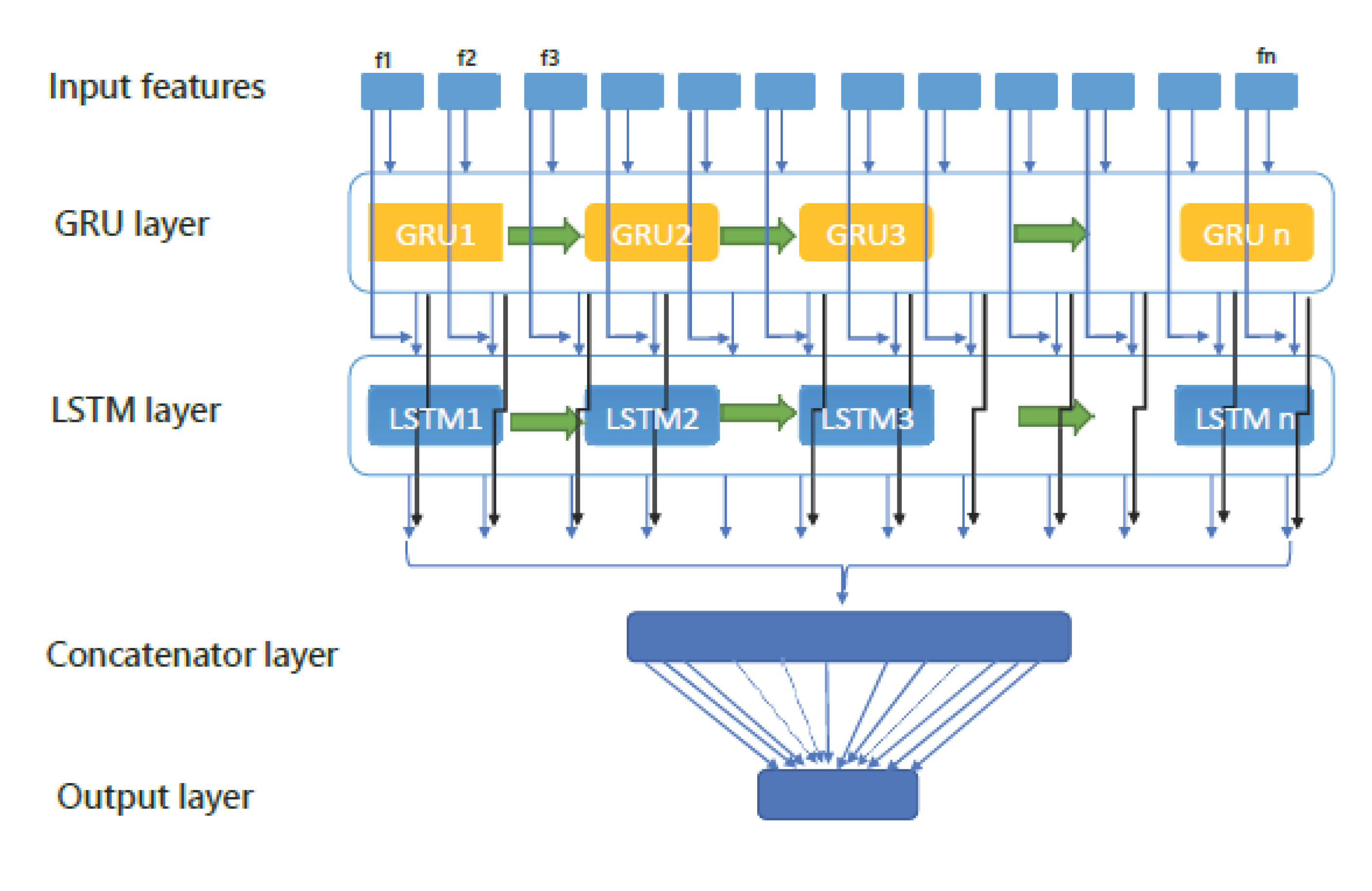
- Input layer: In this layer, each of the input features that are related to a classifi- cation are given to the GRU inputs.
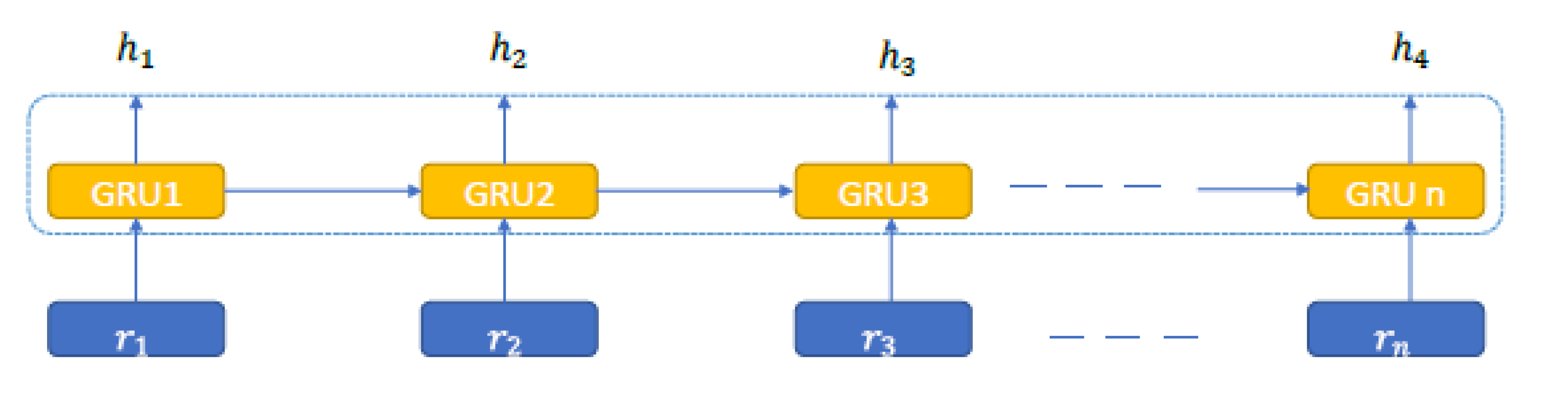
- GRU layer: The inputs of the GRU layer are vectors derived from the input layer.
- LSTM layer: The inputs of the LSTM layer are vectors derived from the GRU layer.
- Output layer: The output of the LSTM network is initially flattened.
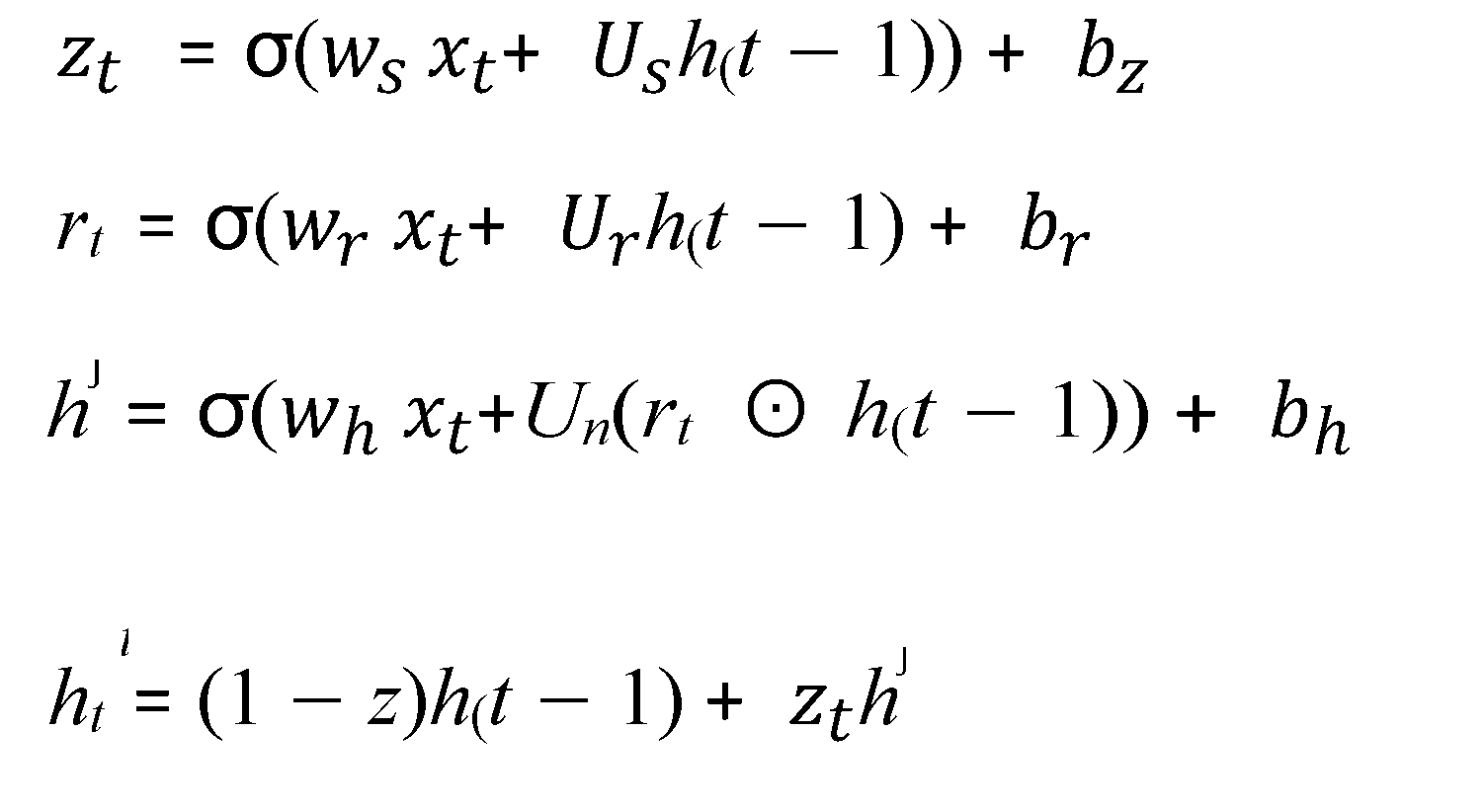
 an element-wise multi-plication.
an element-wise multi-plication.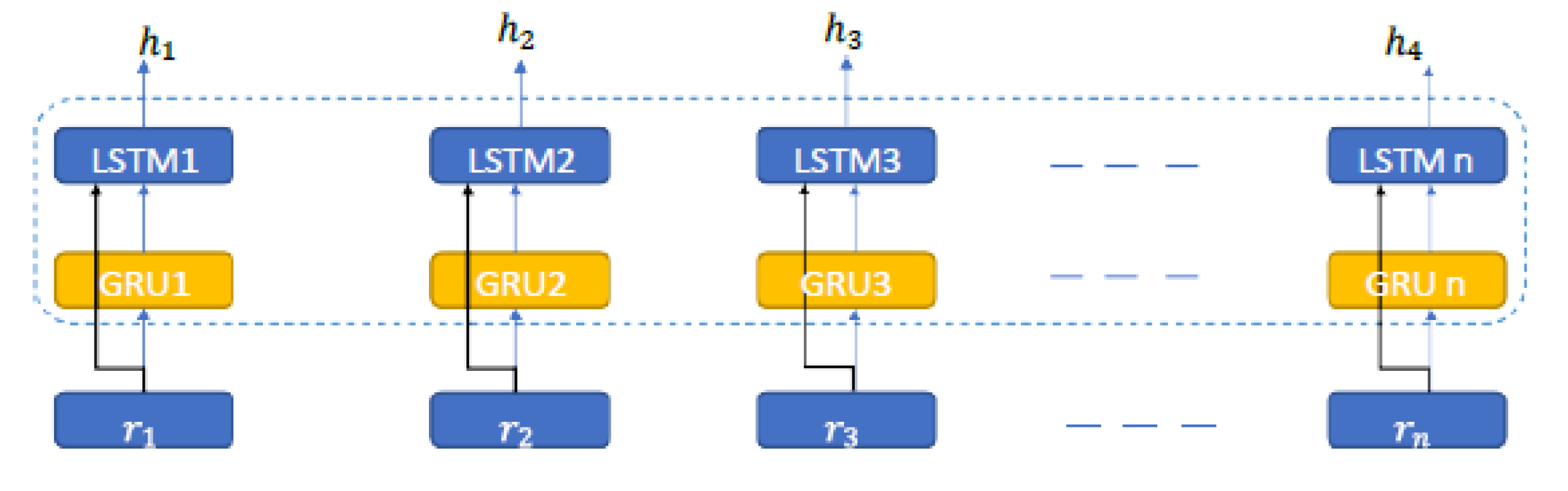
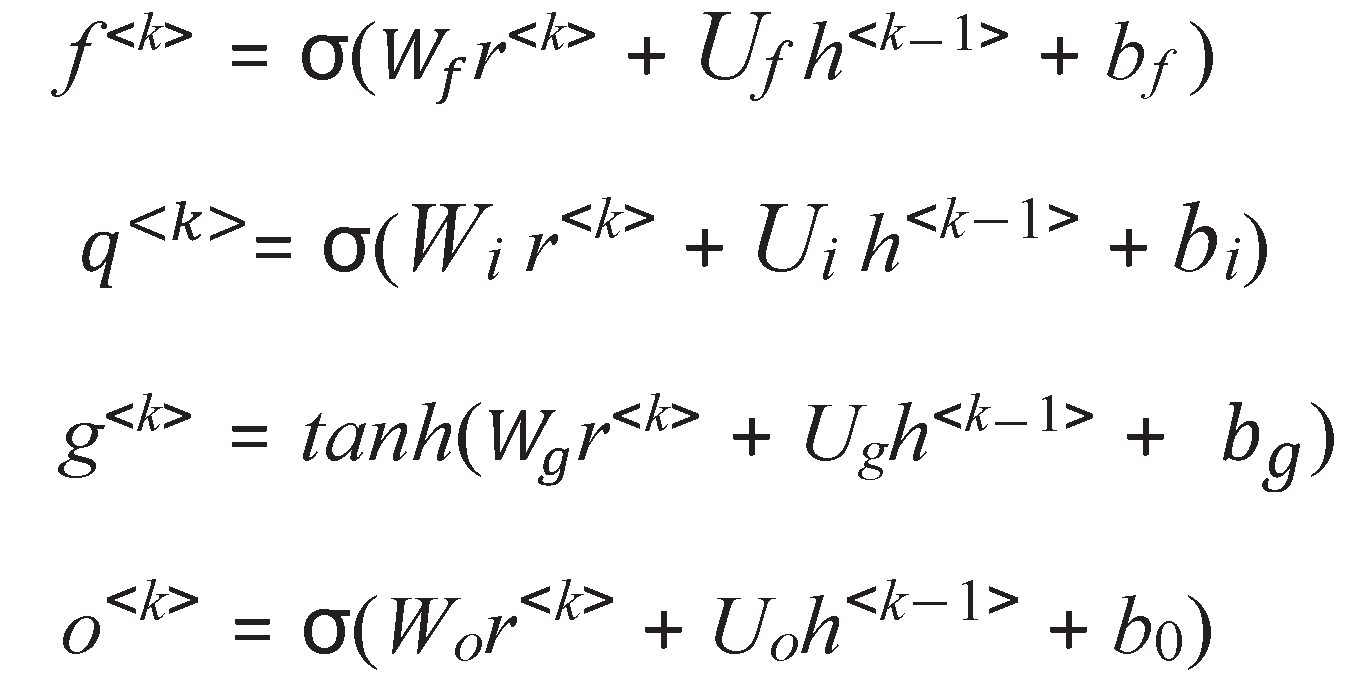
3.2. Point Cloud Data
3.3. Used Tools and Software
3.4. Preparing Point Cloud Data
- Normalization: We normalized the input because of the varying numerical scale of the input components. We use Linear Scale Transformation (Max-Min)[22]. for this purpose. We calculate the normalized value for each index of the input component according to the following equation:
- 1)
- Sliding Window: In this step, sliding windows are formed for forecasting. Figure 3 shows how this process works. For example, for predicting X11 time, all previous values from X1 to X10 are considered as input, and similarly, for predict- ing X12, previous values from X2 to X11 are considered as input. This operation is used for all data, including training and test data. The remarkable thing about this model is that time can be used for hours, days and weeks.
4. Result and Discussion
4.1. Baseline Models
- Gradient Boosting Classifier: This method is used to develop classification and regression models to optimize the model learning process, which is primarily non-linear and is more commonly known as decision or regression trees. Re- gression and classification trees, individually, are poor models, but when con- sidered as a set, their accuracy is greatly improved. Therefore, the sets are built gradually and incrementally so that each set corrects the error of the previous set mathematically in the form of the following equation [23]:

- 2.
- Support Vector Machine(SVM):The purpose of this classifier is to make a hy- pothesis or train a model that predicts the class labels of unknown data or valida- tion data samples that consist only of features. This model tries to find the largest margin between the data by creating a hyperplane. SVM kernels are generally used to map non-linear separable data into a higher-dimensional feature space sample consisting only of features[24]:
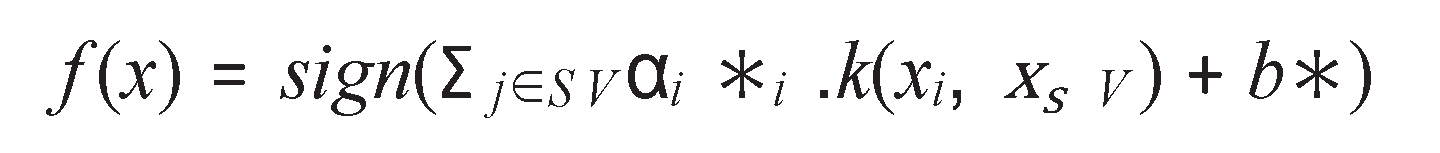
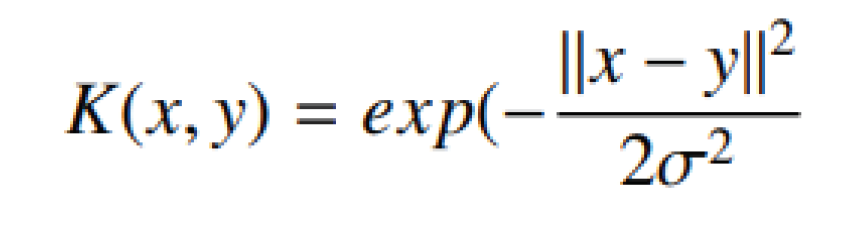
- 3.
- XGBoost : XGBoost [25] is widely used by data scientists to achieve advanced results in many machine learning challenges. The main idea of this algorithm is to present a new algorithm with dispersion awareness for scattered data, and a quantitative scheme for approximate tree learning. XGBoost has a very high predictive power, which makes it the best option for accuracy in various events because it can be used in both linear and tree models. This algorithm is approxi- mately 10 times faster than existing gradient upgrade algorithms. This algorithm includes various objective functions, regression, classification and ranking. XG- Boost works as follows: If, for example, we have a DS dataset that has m attributes and n instances of DS = (hi, <!-- MathType@Translator@5@5@MathML2 (no namespace).tdl@MathML 2.0 (no namespace)@ --><math><mrow><msub><mrow><mtext>y</mtext></mrow><mrow><mtext>i </mtext></mrow></msub></mrow></math><!-- MathType@End@5@5@ -->) : i = 1, ..., n, hi ∈ Rm, y ∈ R. pred The yi predicted output is a group tree model produced by following equations[26]:
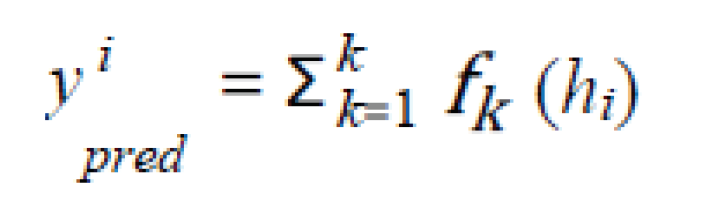
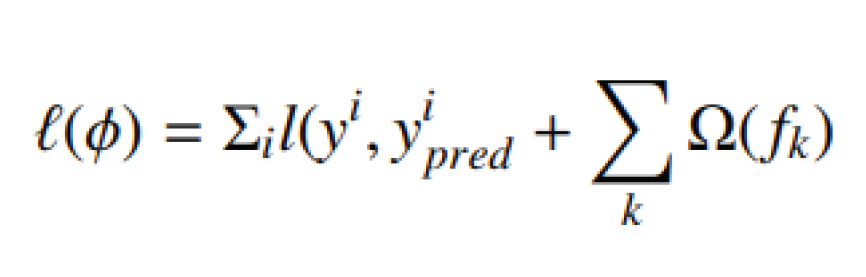
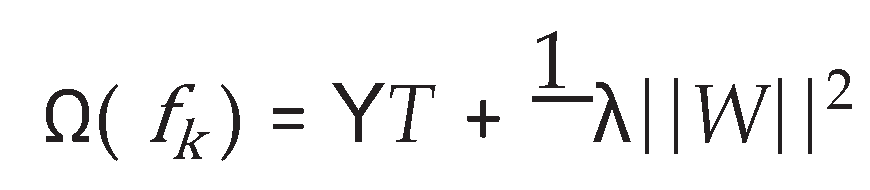
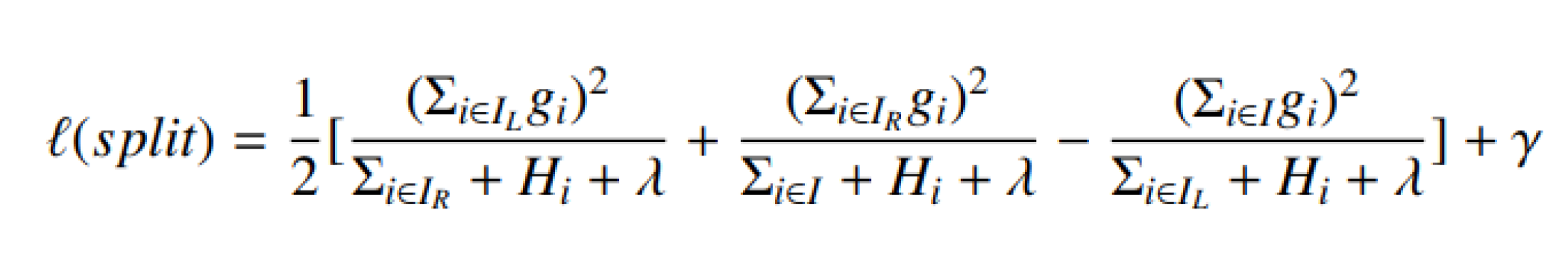
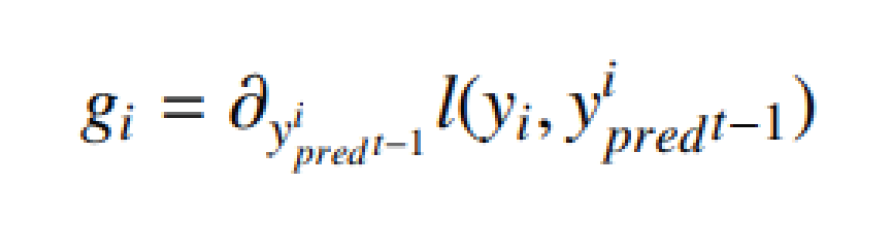
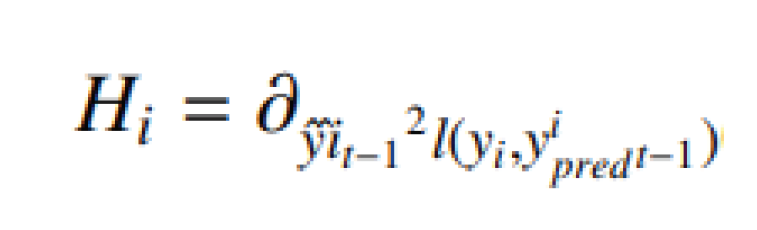
- 4.
- Random forests(RF): RF consist of a set of decision trees(DT)[27]. Mathemat- ically, let Cˆb(x) be the class prediction of the bth tree; the class obtained from the random forest Cˆr f (x) is defined as follows:
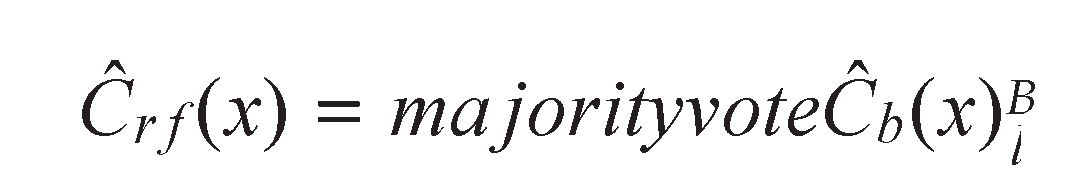
- 5.
- Decision tree(DT):DT are powerful and popular tools used for both classifi- cation and prediction tasks. A DT represents rules that can be understood by humans and used in knowledge systems such as databases. These classification systems are in the form of tree structures. One of the most important questions that arise in decision tree-based models is how to choose the best split. The data set used is assumed to be a sample representation of real data, in which case reducing the error on the training data set can reduce the error on the test data. For this purpose, an attribute should be selected for the split that causes the sep- aration of training samples of each class as much as possible, in other words, it causes the child nodes with less impurity. The following three different criteria can be used for this purpose[28,29]:
- Gini
- Entropy
| Model | Hyper parameters | ||||
|---|---|---|---|---|---|
| Gradient Boosting Classifier | n estimators=3000, learning rate=0.05, max depth=4, subsample=1.0, criterion=’friedman mse’, min samples split=2, min samples leaf=1 | ||||
| XGB Classifier | learning rate=0.1, n estimators=200, nthread=8, max depth=5, subsample=0.9, colsample bytree=0.9 | ||||
| SVM | C=1.0, kernel=’rbf’, degree=3, gamma=’scale’, coef0=0.0, shrinking=True, tol=0.0001 | ||||
| Random Forest | n estimators=100 | ||||
| Decision Tree | n estimators=100 | ||||
| LSTM | LSTM Block=100, Dropout=0.5, layers(LSTM(100),Dropout(0.5),Dense(100),Dense(8)) | ||||
| GRU | GRU Block=100, layers(GRU(200),Dense(100),Dense(8)) | ||||
| GRU+LSTM | GRU Block=100, LSTM Block=100, layers(GRU(100), LSTM(100), Dense(100) ,Dense(8)) | ||||
| Decision Tree | 0.9489 | 0.9535 | 0.9524 | 0.9529 | |
| Model | Accuracy | Precision | Recall | F1-Score |
| Gradient Boosting Classifier | 0.8775 | 0.8627 | 0.9207 | 0.8904 |
| SVM | 0.8823 | 0.9212 | 0.9178 | 0.9194 |
| XGB Classifier | 0.9183 | 0.9234 | 0.9118 | 0.9175 |
| Random Forest | 0.9345 | 0.9347 | 0.9336 | 0.9341 |
| Decision Tree | 0.9489 | 0.9535 | 0.9524 | 0.9529 |
4.2. Proposed Models
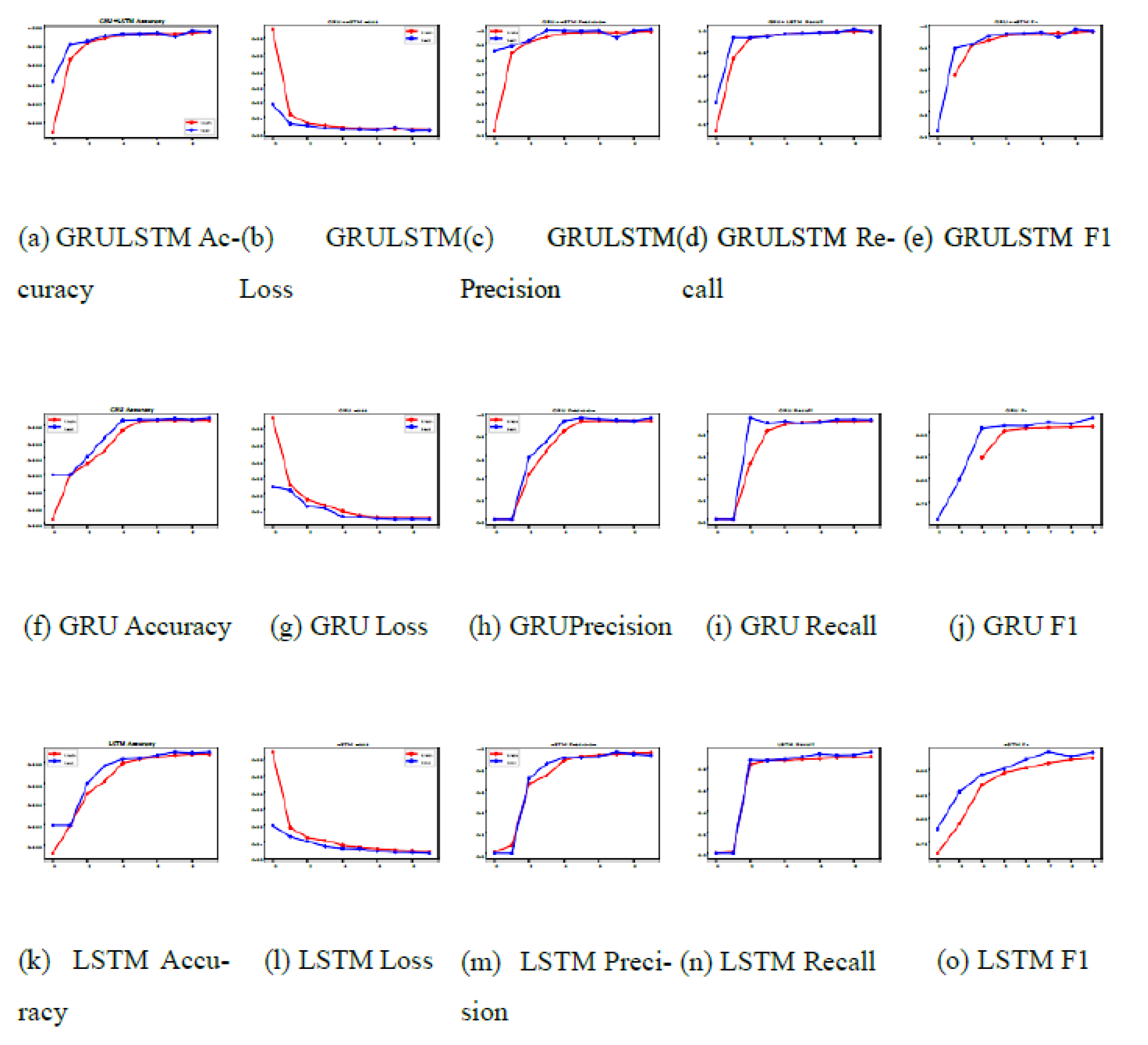
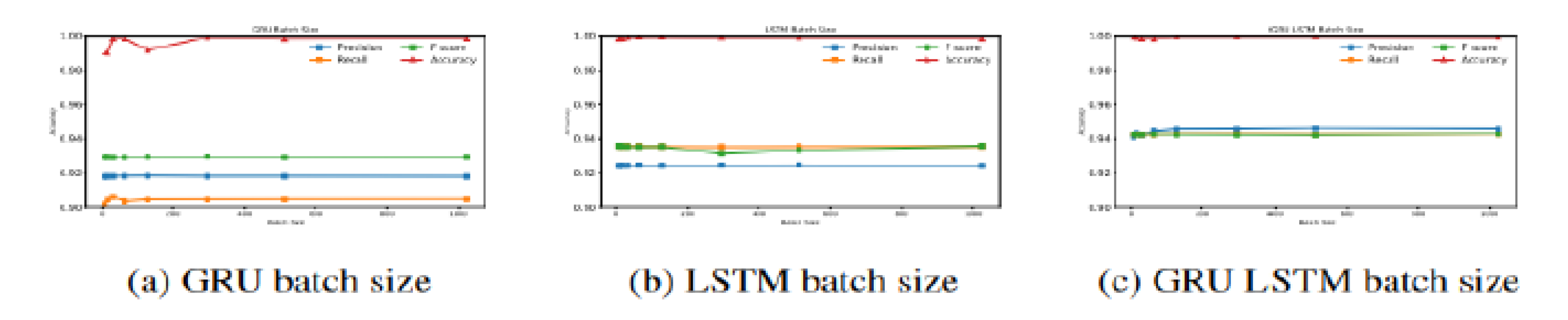
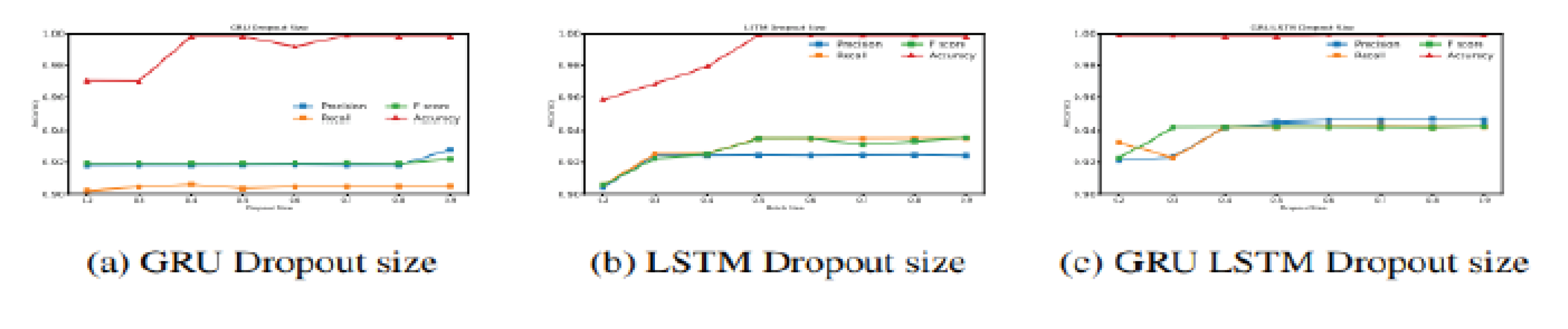
5. Conclusions
References
- Ca˘lin, Ra˘zvan-Alexandru. ”Virtual reality, augmented reality and mixed reality- trends in pedagogy.” Social Sciences and Education Research Review 2018, 5.1, 169-179.
- Subramanyam, Shishir, et al. ”User centered adaptive streaming of dynamic point clouds with low complexity tiling.” Proceedings of the 28th ACM international conference on multimedia. 2020.
- Ackerly, Brooke A., and Kristin Michelitch. ”Wikipedia and Political Science: Ad- dressing Systematic Biases with Student Initiatives.” PS: Political Science Politics 2022, 55.2, 429-433.
- Monteiro, P.; Goncalves, G.; Coelho, H.; Melo, M.; Bessa, M. Hands-free interaction in immersive virtual reality: A systematic review. IEEE Trans. Vis. Comput. Graph. 2021, 27, 2702–2713. [Google Scholar] [CrossRef] [PubMed]
- Rebol, Manuel, et al. ”Remote assistance with mixed reality for procedural tasks.” 2021 IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW). IEEE, 2021.
- Subramanyam, S.; Viola, I.; Hanjalic, A.; Cesar, P. User Centered Adaptive Streaming of Dynamic Point Clouds with Low Complexity Tiling. MM '20: The 28th ACM International Conference on Multimedia.
- Thiel, F. , et al. ”Interaction and locomotion techniques for the exploration of mas- sive 3D point clouds in VR environments.” The International Archives of the Pho- togrammetry, Remote Sensing and Spatial Information Sciences 42 (2018): 623- 630.
- Garrido, Daniel, et al. ”Point cloud interaction and manipulation in virtual reality.” 2021 5th International Conference on Artificial Intelligence and Virtual Reality (AIVR). 2021.
- binti Azizo, Adlin Shaflina, et al. ”Virtual reality 360 UTM campus tour with voice commands.” 2020 6th International Conference on Interactive Digital Me- dia (ICIDM). IEEE, 2020.
- WANG, Qianwen, et al. ”Visual analysis of discrimination in machine learn- ing.(2021).” IEEE Transactions on Visualization and Computer Graphics: 1-11.
- Zhang, Han, et al. ”Self-attention generative adversarial networks.” International conference on machine learning. PMLR, 2019.
- Achlioptas, Panos, et al. ”Learning Representations and Generative Models for 3D Point Clouds–Supplementary Material–.
- Shu, Dong Wook, Sung Woo Park, and Junseok Kwon. ”3d point cloud generative adversarial network based on tree structured graph convolutions.” Proceedings of the IEEE/CVF international conference on computer vision. 2019.
- Mo, Kaichun, et al. ”PT2PC: Learning to generate 3D point cloud shapes from part tree conditions.” Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, –28, 2020, Proceedings, Part VI 16. Springer Interna- tional Publishing, 2020. 23 August.
- Li, Y.; Baciu, G. HSGAN: Hierarchical Graph Learning for Point Cloud Generation. IEEE Trans. Image Process. 2021, 30, 4540–4554. [Google Scholar] [CrossRef] [PubMed]
- Singh, Prajwal, Kaustubh Sadekar, and Shanmuganathan Raman. ”TreeGCN- ED: encoding point cloud using a tree-structured graph network.” arXiv preprint arXiv:2110.03170 (2021). arXiv:2110.03170 (2021).
- Li, Ruihui, et al. ”SP-GAN: Sphere-guided 3D shape generation and manipula- tion.” ACM Transactions on Graphics (TOG) 40.4 (2021): 1-12.
- Yun, Kyongsik, Thomas Lu, and Edward Chow. ”Occluded object reconstruction for first responders with augmented reality glasses using conditional generative adversarial networks.” Pattern Recognition and Tracking XXIX. Vol. 10649. SPIE, 2018.
- Lan, G.; Liu, Z.; Zhang, Y.; Scargill, T.; Stojkovic, J.; Joe-Wong, C.; Gorlatova, M. Edge-assisted Collaborative Image Recognition for Mobile Augmented Reality. ACM Trans. Sens. Networks 2021, 18, 1–31. [Google Scholar] [CrossRef]
- Ma, Yan, et al. ”Background augmentation generative adversarial networks (BAGANs): Effective data generation based on GAN-augmented 3D synthesiz- ing.” Symmetry 10.12 (2018): 734.
- Du, L.; Ye, X.; Tan, X.; Johns, E.; Chen, B.; Ding, E.; Xue, X.; Feng, J. AGO-Net: Association-Guided 3D Point Cloud Object Detection Network. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 1–1. [Google Scholar] [CrossRef] [PubMed]
- Patro, S. G. O. P. A. L., and Kishore Kumar Sahu. ”Normalization: A preprocess- ing stage.” arXiv preprint arXiv:1503.06462 (2015). arXiv:1503.06462 (2015).
- Peter, Sven, et al. ”Cost efficient gradient boosting.” Advances in neural informa- tion processing systems 30 (2017).
- Jakkula, Vikramaditya. ”Tutorial on support vector machine (svm).” School of EECS, Washington State University 37.2.5 (2006): 3.
- Chen, Tianqi, et al. ”Xgboost: extreme gradient boosting.” R package version 0.4-2 1.4 (2015): 1-4.
- Osman, A.I.A.; Ahmed, A.N.; Chow, M.F.; Huang, Y.F.; El-Shafie, A. Extreme gradient boosting (Xgboost) model to predict the groundwater levels in Selangor Malaysia. Ain Shams Eng. J. 2021, 12, 1545–1556. [Google Scholar] [CrossRef]
- Kavzoglu, Taskin, Furkan Bilucan, and Alihan Teke. ”Comparison of support vector machines, random forest and decision tree methods for classification of sentinel-2A image using different band combinations.” 41st Asian Conference on Remote Sensing (ACRS 2020). Vol. 41. 2020.
- Charbuty, B.; Abdulazeez, A. Classification Based on Decision Tree Algorithm for Machine Learning. J. Appl. Sci. Technol. Trends 2021, 2, 20–28. [Google Scholar] [CrossRef]
- Gulati, Pooja, Amita Sharma, and Manish Gupta. ”Theoretical study of decision tree algorithms to identify pivotal factors for performance improvement: A re- view.” International Journal of Computer Applications 141.14 (2016): 19-25.
- Ismail Fawaz, Hassan, et al. ”Inceptiontime: Finding alexnet for time series clas- sification.” Data Mining and Knowledge Discovery 34.6 (2020): 1936-1962.
- Tanha, Jafar, et al. ”Boosting methods for multi-class imbalanced data classifica- tion: an experimental review.” Journal of Big Data 7 (2020): 1-47.
- Shifaz, A.; Pelletier, C.; Petitjean, F.; Webb, G.I. TS-CHIEF: a scalable and accurate forest algorithm for time series classification. Data Min. Knowl. Discov. 2020, 34, 742–775. [Google Scholar] [CrossRef]
- Thabtah, F.; Hammoud, S.; Kamalov, F.; Gonsalves, A. Data imbalance in classification: Experimental evaluation. Inf. Sci. 2019, 513, 429–441. [Google Scholar] [CrossRef]
| Model | Accuracy | F1 | Recall | Precision |
|---|---|---|---|---|
| GRU | 0.9989 | 0.9294 | 0.9049 | 0.9182 |
| LSTM | 0.9990 | 0.9354 | 0.9495 | 0.9240 |
| GRULSTM | 0.9991 | 0.9420 | 0.9425 | 0.9452 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





