Prerpints.org logo
Preprint
Article

Exploring Dengue Dynamics: Multi-Scale Analysis of Spatio-Temporal Trends in Ibagué, Colombia

Altmetrics

Downloads

187

Views

204

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (348.76KB )

Submitted:

12 March 2024

Posted:

13 March 2024

You are already at the latest version

Alerts
Abstract
Our study examines how dengue incidence is associated with spatial (demographic and socioeconomic) alongside temporal (environmental) factors at multiple scales. We used the incidence of dengue in Ibagué, Colombia, from 2013 to 2018, to examine the associations with climate, socioeconomic and demographic factors from the census and satellite imagery at various levels of local spatial aggregation, including Manzanas, Secciones, Sectores, and Comunas. Our findings show a significant effect of spatial variables at finer levels of aggregation, showing varying degrees of correlation with dengue incidence. Temporal variables such as temperature and precipitation displayed consistent patterns across all spatial levels, with notable variations in Relative Risk (RR). Our study employs Geographically Weighted Regression (GWR) to identify relevant socioeconomic and demographic predictors. Then, these predictors were integrated into hierarchical models implemented in Integrated Nested Laplace Approximation (INLA) at each spatial level to assess spatiotemporal interactions. We comprehensively analyzed the three distinct models developed for each level: spatial, temporal, and spatiotemporal. A comparative evaluation of the models reveals that while higher aggregation levels often yield a better overall model fit, finer levels offer more detailed insights into the localized impacts of socioeconomic and demographic variables on dengue incidence. Our results underscore the importance of considering macro and micro-level factors in epidemiological modeling and highlight the potential for targeted public health interventions based on localized risk factor analysis. Notably, the intermediate level Secciones emerged as the most informative, balancing spatial heterogeneity and case distribution density, thereby providing a robust framework for understanding the spatial determinants of dengue.
Keywords: 
Subject: Medicine and Pharmacology  -   Epidemiology and Infectious Diseases

1. Introduction

Dengue fever (DENV), a mosquito-borne viral disease [1], has become a critical public health issue globally, particularly in tropical and subtropical regions [2,3]. Ibagué, Colombia, exemplifies an urban area significantly affected by dengue, with its incidence rising notably over the past years [4]. Ibagué's rapid urbanization over the past two decades has led to densely populated, low-income neighborhoods that often lack regular access to water and adequate infrastructure. These socioeconomic conditions have been linked to higher dengue incidences and mosquito populations [5,6,7]. Additionally, the city's specific environmental characteristics, including its elevation (1,225 meters above sea level) and average temperature (24°C), create a conducive environment for Aedes mosquitoes, further exacerbating the situation [8,9,10].
Dengue transmission dynamics are complex and influenced by a myriad of factors, including urbanization, demographic changes, and environmental conditions [11,12]. Prior research has demonstrated the important role of socioeconomic and demographic variables in dengue spread [13,14]. However, a significant gap still needs to be addressed in understanding the interaction of these variables at different urban scales, namely levels of aggregation, particularly in rapidly urbanizing cities in developing countries [15].
Different approaches have been considered to identify and understand the underlying behavior of diseases in urban environments and their relationship with socioeconomic and environmental variables. For instance, in 2001, authors studied the relationship between neighboring socioeconomic effects and health outcomes, finding consistent results on the influence of neighborhood effects on health [16]. Other studies between 2000 and 2010 asserted a correlation between neighborhood distribution and health status, suggesting not only the use of distance and proximity to determine neighborhoods’ composition but also random effects regarding the neighboring structures to account for the possible connectivity between them [17,18,19,20]. The latter has been widely used in the statistical modeling of DENV using a spatially structured random effect to consider spatial correlation [21,22,23].
To assess the significance of socioeconomic and environmental variables regarding dengue incidence and relative risk (RR), authors have implemented a General Linear Model (GLM) Log-linear model to associate the socioeconomic typology with the risk of dengue infections during winter in a 250 x 250 m grid of Delhi, India [24]. They found out that the lack of constant access to tap water was a risk factor for dengue infections; also, densely populated areas did not necessarily have higher mosquito populations, mainly because of the need for available breeding sites. Finally, high DENV seropositivity was found in wealthier neighborhoods, while low mosquito exposure was explained by mobility within the city. However, this study only considered socioeconomic variables but not demographic predictors, and they ignored possible random effects regarding spatial and seasonal variability. Other authors followed a different approach, implementing a Bayesian Hierarchical Model to determine the association between the relative risk of dengue and lag response in hydrometeorological hazards at a microregion level. The results showed that droughts increase the relative risk of dengue infection in urban areas, while wet conditions increase the risk of infection in rural areas [25].
Specifically in Colombia, authors have implemented a similar methodology for DENV in the city of Cali, using a Space-Time Conditional Autoregressive Model with added autocorrelated random effects for spatial structures and time [26]. This study was conducted on a neighborhood level, where socioeconomic variables were controlled using a Principal Component Analysis (PCA) approach, and several environmental variables were included and lagged to consider the delayed effect. The results showed that lagged weather variables could help to identify when the peaks in the risk of transmission occur. Additionally, they proved that dengue infections are not exclusive to poor areas, and the risk of infection is related to spatial and temporal distribution. The proposed aggregation level of neighborhoods offers very sparse data observations with clear socioeconomic and demographic trends.
Bayesian models have shown that they can be used to assess significance and make inferences about the predictors [22,25,26,27]. The implementation usually calculates the posterior distributions via Markov Chain Monte Carlo Simulations (MCMC) or Integrated Nested Laplace Approximation (INLA). MCMC has been widely used to identify marginal distributions and inference [28,29]; however, it takes a very high computational time [30]. To solve this issue, authors proposed the INLA methodology, which uses local approximations and Laplace transformations, providing very similar results around 300 times faster.
While the importance of spatial and temporal variables in dengue transmission is recognized [31], limited research has been conducted on integrating these factors at different levels of urban spatial aggregation. This study aims to bridge this gap by leveraging detailed demographic and socioeconomic data from the census, provided by the National Administrative Department of Statistics (Departamento Administrativo Nacional de Estadística - DANE), and environmental variables derived from satellite imagery and previous studies. We seek to unravel the spatial and temporal dynamics influencing dengue incidence in Ibagué between 2013 and 2018, examining these factors across various levels of spatial aggregation - Manzanas, Secciones, Sectores, and Comunas [32]. We introduce a novel approach by employing Geographically Weighted Regression (GWR) to isolate key socio-economic and demographic predictors at varying spatial scales [33]. Additionally, the use of INLA models allows for an in-depth examination of spatio-temporal correlations and their posterior distributions [34], offering new insights into the localized dynamics of dengue transmission.
The methodological innovation of this study lies in its tripartite modeling strategy, encompassing spatial, temporal, and combined spatio-temporal models at each level of spatial aggregation. This approach allows for a comprehensive analysis of the varying impacts of different factors on dengue incidence, providing a nuanced understanding of the disease's transmission dynamics in an urban setting. Our findings will contribute significantly to public health, particularly in developing targeted dengue control strategies [35]. The study's framework also offers a valuable model for similar epidemiological investigations in other urban settings, enhancing our understanding of vector-borne diseases in global urbanization trends.

2. Materials and Methods

2.1. Study Site and Data

Ibagué is the most populated city in the department of Tolima, with an estimated population of 541,101 people for 2020 [36]. According to DANE, the city’s urban area is divided into 13 Comunas, 65 Sectores, 272 Secciones, and 5,574 Manzanas, which will be used as levels of spatial aggregation. Groups of the minimum level, Manzanas, create the rest of the levels, as can be observed in supplementary Figure S1. The demographic and socioeconomic data was obtained in all four levels from the National Geostatistical Framework (Marco Geoestadístico Nacional - MGN) and National Population and Dwelling Census (Censo Nacional de Población y Vivienda - CNPV), which were compiled in 2018 [37].
Socioeconomic predictors included variables related to strata, water access and disposal, access to gas, garbage pick-up service, and internet connection, which allows to identify lower income and utility access areas inside the city. Demographic variables divide the population according to age, gender, and educational level. Finally, environmental variables were obtained from satellite images via Google Earth Engine using MODIS1A1 for Mean Temperature [38], MODIS13Q1 for NDVI [39], CHIRPS PENTAD for Total Precipitation [40], and previous studies on the city for wet days and hot days (over 32°C) [41]. The variables and their description are shown in supplementary materials.
Data on dengue cases was obtained from the dataset provided by the local government. Out of the total 17,707 DENV recorded from 2013 to 2018, 16,183 were included according to the spatial levels of the city. The remaining cases had no readable address or were reported in the city's rural area. Figure 1 displays the evolution of the virus over the years. 2013 and 2015 showed the most extensive outbreaks, with 5,383 and 4,885 cases respectively, with another outbreak following during the first months of 2016. Notably, the number of cases in 2017 and 2018 was significantly lower, with each year reporting fewer than 1,000 cases.

2.2. Methodology

2.2.1. Variable Selection and Transformation

To demonstrate association between the variables and dengue incidence per 100,000 inhabitants, and reduce the dimensionality of spatial variables, we used GWR through the package GWModel in R [42,43]. This methodology allows the creation of different local regressions using Ordinary Least Squares (OLS) for every spatial feature, adding a weight parameter that was obtained from the distance between the geometries and a calculated bandwidth [44,45]. This analysis was performed for socioeconomic and demographic predictors on every level of aggregation. Only variables that were shown to be significant, at least in one global regression at any level of aggregation, were used as final predictors for the inference model.
We also used a Wavelet Coherence analysis to confirm an existing correlation between DENV cases and temporal variables. This was used to analyze non-stationary time series. The methodology implements a decomposition between time and frequency using a windowed Fourier transform, which allows for local time-frequency properties while adjusting for high and low-frequency structures [46]. The wavelet coherence was computed for the aggregated environmental variables in the whole city. Results are evaluated graphically using the biwavelet library in R, keeping the variables that showed high correlation and significance in the wavelet coherence analysis as the final predictors [47]. All temporal predicted were included, since they displayed high correlation with DENV cases as shown in Figure S2.
The temporal predictors were later lagged using a Distributed Lag Nonlinear model (DLNM). This methodology considers delayed effects and nonlinear relationships between dengue and environmental time-dependent variables [48]. The package dlnm was used on R [49]; obtaining, as a result, a matrix that accounts for the nonlinear exposure and a delayed effect.

2.2.2. Model fitting.

The latent marginal distribution of chosen predictors was approximated using INLA, wherein the spatio-temporal influence of these predictors was considered. This approach relies on Latent Gaussian Models (LGM), specifically, a Latent Gaussian Markov Random Field with a sparse and factorizable precision matrix. Such a structure enables numeric approximations, leading to quicker outcomes than conventional LGM techniques like Markov Chain Monte Carlo (MCMC) [34].
In this project, we specifically fitted a negative binomial model to the number of cases Y s t for each spatial unit s at a given time t , having an estimated mean of μ s t and a dispersion parameter ϕ . This model allows us to account for overdispersion in the number of cases at each scale. Our link function considers μ s t from the population p s t and the monthly incidence at the same location and time ( ρ s t ) . The model is depicted in equations (1) to (3).
Y s t | μ s t ~ N B ( μ s t , ϕ )
log ⁡ μ s t = log ⁡ p s t + l o g ⁡ ( ρ s t )
log ⁡ ρ s t = X T β + γ s t + η s t
We also included two random effects that were considered to account for unobserved variability. An unstructured random effect for seasonal autocorrelation, regarding possible relationships in time for each structure along the months, being cyclic over the six-year analysis; and a second structured random effect, that encompasses spatial autocorrelation between the neighborhoods along the years regarding interconnection, interventions, herd immunity, etc. [25] The incidence was calculated from the fixed effects X T and the two random effects: γ s t for the unstructured effect using a random walk, and η s t for the structured one using a Besag-York-Molliè model [50]. Precision priors are defined from the precision parameter P σ > 0.5 = 0.01 .
An adaptative strategy was selected as it is considered the best fit from Gaussian and simplified Laplace approximations. Finally, the hyperparameters posterior distributions were calculated with a Central Composite Design as it offers the best tradeoff between precision and computational time among the possible strategies implemented in the R library INLA [30,34,51].
Three models were adjusted per level: one containing only spatial variables (socioeconomic and demographic), a second containing only temporal variables (environmental), and a third containing both. This enabled us to distinguish between the effects of spatial and temporal covariates, while assessing whether incorporating both yielded a more informative model. Comparison was performed for the models at each level using the Deviance Information Criterion (DIC) and Widely Applicable Information Criterion (WAIC).

2.2.3. Aggregation Level Comparison

From selected best-fitting models at each level of aggregation, fitted values were obtained from the marginal posterior distributions of the selected models at each level of aggregation. These values were then compared with the observed data over the study period to determine the best fitting model at each level considering the Root Mean Squared Error (RMSE).

3. Results

3.1. Variable Selection

The Geographically Weighted Regression (GWR) analysis revealed a significant association for seven critical variables at a minimum of one spatial level over different years. These variables encompassed critical aspects of the socio-economic landscape, including population density (Density), sewage connection (Sewage), gas connection (Gas), garbage collection service (Garbage), population with higher education degrees (Higher Ed.), percentage of women (Women), and percentage of children (Children).
Figure 2 visually presents the space-time trends of these variables across diverse spatial levels. The visualization aids in understanding the spatial patterns and temporal changes exhibited by each variable, contributing to a comprehensive understanding of the intricate dynamics within the studied region. This provides a concise summary of the outcomes derived from the GWR analysis, emphasizing the spatial and temporal significance of the identified variables.

3.2. Model Fitting and Comparison

Table 1 shows the results of model selection based on DIC and WAIC by level of aggregation. It is important to note that these models can be compared within the same level but not across different levels. A significant shift in both DIC and WAIC values is evident in the temporal models as opposed to the spatial models. Notably, the spatio-temporal models, which integrate a comprehensive set of covariates encompassing socioeconomic, demographic, and transformed environmental predictors, exhibit the most favorable scores in these comparison metrics across all levels and were selected as the best model for multilevel comparison.
Figure 3 provides an insight into the spatial fixed effects of each spatiotemporal model inferred from posterior distributions, showing the variations of these effects across different levels of spatial aggregation.
At the level of Comunas, spatial variables exhibit non-significance, as indicated by the inclusion of zero within the 95% credible intervals for all variables. This lack of significance aligns with the comparable DIC and WAIC values observed for both temporal and spatiotemporal models in Table 1, implying that incorporating spatial variables at this aggregation level does not substantially enhance the model’s explanatory capacity for DENV incidence.
For the intermediate level of Sectores, certain variables such as garbage collection, higher education, and the percentage of children demonstrate significance and display inverse correlations with DENV incidence. The negative coefficients suggest that improved access to garbage collection, higher educational attainment, and a larger proportion of children are associated with reduced DENV spread, potentially highlighting the impact of enhanced public services and education on disease mitigation.
At the Secciones level, most spatial variables exhibit significance, with garbage collection and the percentage of women showing negative correlations with DENV cases. This inverse relationship suggests that areas with more efficient waste management and a higher proportion of women tend to have lower DENV prevalence. Moreover, factors such as higher population density, gas connections, education levels, and the percentage of children consistently demonstrate negative correlations with DENV cases, echoing the trends observed at the Sectores level and underscoring the influence of these variables on disease incidence.
Finally, at the granular level of Manzanas, sewage connection emerges with a unique positive correlation with DENV cases. Conversely, population density, higher education, and the percentage of children maintain inverse correlations with DENV incidence, aligning with observations made at the Secciones level. This consistency across different levels of spatial analysis suggests that certain factors consistently relate to lower disease incidence despite the finer granularity of data.
Integrating this insight into the preceding analysis highlights a consistent negative correlation between spatial variables such as higher education, population density, and the percentage of children with DENV incidence across various levels, while the association between garbage collection services and DENV cases appears less definitive, suggesting disparities in waste management service.
Complementing the spatial analysis, Figure 4 introduces lagged temporal predictors through contour plots, which offer insight into the temporal dynamics of the disease. The data underlying the cyclical influence of weather patterns on the RR associated with DENV. For instance, temperature-related metrics, such as mean temperature and the number of days exceeding 32°C, reveal a lower RR at cooler temperatures and greater lags, transitioning to a higher RR as temperatures climb and lag decreases. Conversely, precipitation indicators, such as total precipitation and number of wet days, demonstrate an inverse relationship, with higher precipitation levels correlating with a decreased RR in subsequent periods. Additionally, the NDVI exhibits variability and lacks consistency across different levels of aggregation, suggesting complex interactions between vegetation density and disease transmission that warrant further investigation.

3.3. Level Comparison

Figure 5 depicts the compared values of observed DENV cases and the fitted values from posterior distributions at each level, aggregated for the entire city.
The model's performance varies across different levels of spatial aggregation. At the Comunas level, the model achieves a high degree of correlation with the actual DENV case data, although it tends to underestimate case numbers during outbreak peaks, a trend that was particularly pronounced towards the end of 2015. In times of lower disease incidence, such as December 2017 and June 2018, the model also falls short of accurately capturing the case numbers. Despite these limitations, it performs commendably in periods of low case counts, notably, throughout most of 2017 and the early months of 2018.
Moving to the Sectores level, the model has a propensity to overestimate the incidence of DENV cases, with this trend being especially evident in January 2015 and January 2016. This tendency for overestimation continues through the endemic years of 2017 and 2018. Moreover, there is a noticeable misalignment in the timing of predicted outbreaks compared to actual data, highlighting a phase discrepancy between model predictions, and observed case trends.
Similarly, in Secciones level, there is a need for phase alignment. Still, the model demonstrates an accurate fit during epidemic periods, both in terms of case count and pattern, as seen between September 2015 and January 2016. This level also accurately captures smaller peaks during endemic periods, such as December 2016 and June 2018. However, during periods characterized by generally low DENV activity, such as the late 2017 to early 2018 timeframe, the model tends to overpredict the number of cases, indicating a challenge in accurately modeling low incidence rates.
At the most granular level of spatial aggregation, Manzanas, the model's fit shows the greatest fluctuation among all levels. While it aligns more closely with the observed data during epidemic periods, similar to Secciones, its predictive performance is significantly less accurate during endemic years, indicating a disparity in model fit across different disease prevalence periods.
The differences in model performance underscore the challenges in capturing the complex dynamics of DENV transmission, which vary temporally with epidemic and endemic cycles and spatially at different levels of urban granularity. These insights emphasize the need for models that can adjust to both the scale of analysis and the fluctuating nature of disease transmission, highlighting the intricate balance between spatial resolution and predictive accuracy in epidemiological modeling.
Table 2 rectifies the observed behavior observed in Figure 5. Lower RMSE was found for Comunas, since it provided the best overall fit; however, the level of Secciones provided a lower RMSE than Manzanas and Sectores, which might be due to the better fit exhibited during epidemic seasons.

4. Discussion

GWR analysis shows variation for spatial covariates among levels of aggregation. Socioeconomic predictors are mostly significance at the lowest level, Manzanas, while demographic predictors were also significant at intermediate levels like Secciones or Sectores. Only two predictors were significant at Comunas. GWR analysis solely identifies significant spatial variables and overlooks non-linear interaction, which is crucial for understanding the endemic-epidemic patterns of DENV. This limitation may result in models that only partially capture the disease's dynamics.
Our study shows that the spatio-temporal models, which integrate spatial and temporal variability, generally offered a better fit, and were selected for further analysis at all levels of aggregation. However, the improvement in the spatio-temporal models at levels like Comunas and Sectores was minimal, indicating that the added complexity of spatio-temporal models may only sometimes lead to significantly improved fit. This underscores the importance of careful consideration when increasing model complexity and highlights the need to balance detailed spatial-temporal dynamics with model simplicity.
The significance of spatial predictors in DENV incidence varied markedly across different levels of spatial aggregation. At the highest levels, namely Comunas and Sectores, many variables were found to be non-significant, possibly due to the homogeneity within these broader spatial categories. The lack of variability within spatial covariates at these levels leads to a limited ability to discern significant impacts on DENV cases, as observed in the narrow covariate ranges detailed in supplementary Table S1. In contrast, population density was notably significant at the more granular Secciones and Manzanas levels and inversely correlated with DENV incidence. However, This counterintuitive finding is supported by previous studies that have suggested that higher densities may not favor mosquito breeding, particularly in areas with sufficient sanitation and utility services [52,53].
Socioeconomic variables, such as sewage, gas connection, and garbage collection service, exhibit diverse correlations with DENV cases. Sewage connection is positively correlated, attributed to urban infrastructure and vector ecology (adaptation to breed in manmade environments), including improperly designed systems creating mosquito breeding sites [54,55,56,57]. Conversely, areas with higher gas connection rates tend to have lower DENV incidence, reflecting socioeconomic status. The relationship with garbage collection services varies; a positive correlation at the Secciones level and an inverse relationship at Sectores suggest complex dynamics influenced by local practices and infrastructure. [58,59].
The observed variability among socioeconomic variables underscores the intricate interplay of individual and collective dynamics, sometimes resulting in counterintuitive outcomes. Nevertheless, these variables offer valuable insights into the internal dynamics of spatial distribution, exhibiting distinct characteristics across different levels of spatial aggregation.
Demographic predictors, including higher education, percentage of children, and percentage of women, demonstrate a consistent pattern across spatial levels. Higher educational attainment in populations may lead to increased implementation of disease prevention measures, potentially reducing breeding sites and subsequent DENV cases [60,61]. The inverse correlation with the percentage of children may reflect the demographic profile of DENV cases during specific outbreaks, with adults and young adults being more frequently affected. Lastly, the percentage of women may reflect the broader demographic composition of the city and the roles women play in household management and potential exposure to mosquito breeding sites.
Variations in correlation between spatial variables and DENV incidence across different spatial aggregation levels indicate diverse roles of socioeconomic and demographic factors in disease transmission dynamics. While broader scales may obscure these factors amidst other influences, finer scales highlight their heterogeneity, allowing for a more precise understanding of their impact on DENV transmission. This underscores the complexity of disease incidence modeling and emphasizes the importance of considering scale when interpreting variable influences.
Despite consistent trends in temporal variables across all spatial aggregation levels, subtle variations in relative risk suggest differing degrees of correlation with DENV cases. Temperature and precipitation influence were relatively consistent across the city's spatial structures, resulting in similar impacts on relative risk regardless of aggregation level. Our results show an association between Mean Temperature and increased Relative Risk (RR) during high-temperature periods (zero-month lag), and elevated disease risk due to total precipitation at a three to six-month lag across Comunas, Sectores, and Secciones, which underscores the influence of weather patterns on DENV transmission in urban areas. This relationship, consistent with regional climate patterns where cooler seasons precede warmer periods by approximately four to six months [62], which is further intensified by ENSO phenomena, such as the El Niño events of 2015 and 2016. These extreme weather events, characterized by higher temperatures and drought, impact mosquito breeding and access to utilities in vulnerable areas, leading to community adjustments in water management practices and influencing DENV transmission dynamics [25,63].
Days Over 32°C exhibited a comparable trend with mean temperature, where a higher frequency of hot days at shorter lags was linked to an increased RR. The same relationship is displayed by the number of wet days and total precipitation, with increased RR at two and six-month lags, reflecting bimodal rainy seasons. Finally, NDVI showed irregular patterns, with minimal variation at broader levels like Comunas and Sectores due to its non-seasonal nature.
While the temporal patterns hold consistently across spatial aggregation levels, the changes in RR's for each covariate vary, suggesting differing strengths of correlation with DENV incidence. This variance could stem from how DENV cases are distributed across each spatial level and how spatial covariates account for the observed effects at more granular levels.
This study highlights the importance of considering temporal and spatial variables in understanding DENV transmission dynamics. While temporal variables play a significant role, spatial covariates at finer levels of aggregation are also crucial for a nuanced understanding of DENV transmission. The analysis suggests that the Comunas level model provides the best overall fit for the city, with the Secciones level model closely following. However, the Manzanas level model performs weaker due to extreme case dispersion. Despite this, intermediate aggregation levels like Secciones reveal discernible links with socioeconomic and demographic variables, aiding in understanding local patterns for targeted interventions. This underscores the importance of considering macro and micro-level factors in epidemiological modeling and intervention planning to tailor public health strategies and reduce disease prevalence effectively.
The accuracy of DENV case reporting relies on local population engagement, often hampered by underreporting due to symptom recognition without seeking formal diagnosis and the prevalence of asymptomatic cases [64]. This underreporting significantly impacts case counts' accuracy, hindering model precision [65]. Census data limitations are apparent, with only 2018 data available, assuming socio-economic and demographic variables remain unchanged over six years, neglecting potential variations. Modeling efforts focusing on endemic or epidemic periods may offer immediate insights into socio-economic and demographic influences on disease patterns but may overlook long-term effects. Detailed research at lower observational levels is needed to address data scarcity and the influence of local entomological and virological factors on disease dynamics.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org, Table S1: List of independent socioeconomic, demographic, and environmental variables for Ibagué; Figure S1: Ibagué’s spatial division, from which aggregation levels are obtained. Comunas are the biggest group, each composed of multiple manzanas as shown in the figure. Smaller groups of manzanas build secciones and sectores; Figure S2: Wavelet coherence analysis for environmental variables. Each plot shows the coherence between the environmental variables and DENV cases. High-significance (0.05) regions are plotted as bounded areas. A cone of influence is included to discard any significant regions outside it. Arrows indicate the relationship of the two series included in each plot.

Author Contributions

Conceptualization, M.S.-V., A.T., and J.O.; methodology, M.S.-V., A.T., and J.O.; software, J.O.; formal analysis, J.O.; investigation, J.O., M.S.-V., and A.T.; resources, M.S.-V.; data curation, J.O. and M.S.-V.; writing—original draft, A.T., J.O. and M.S.-V.; writing—review and editing, A.T., J.O. and M.S.-V.; visualization, J.O.; supervision, A.T. and M.S.-V. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

All data and code is available at https://github.com/jd-otero/dengue_ibague.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kurane, I. Dengue Hemorrhagic Fever with Special Emphasis on Immunopathogenesis. Comparative Immunology, Microbiology and Infectious Diseases 2007, 30, 329–340. [Google Scholar] [CrossRef]
  2. Dengue and Severe Dengue. Available online: https://www.who.int/news-room/fact-sheets/detail/dengue-and-severe-dengue (accessed on 28 October 2022).
  3. Silva, M.M.O.; Rodrigues, M.S.; Paploski, I.A.D.; Kikuti, M.; Kasper, A.M.; Cruz, J.S.; Queiroz, T.L.; Tavares, A.S.; Santana, P.M.; Araújo, J.M.G.; et al. Accuracy of Dengue Reporting by National Surveillance System, Brazil. Emerg. Infect. Dis. 2016, 22, 336–339. [Google Scholar] [CrossRef]
  4. Padilla, J.C.; Rojas, D.P.; Sáenz Gómez, R. Dengue en Colombia: epidemiología de la reemergencia a la hiperendemia; Primera edición en español.; Verlag nicht ermittelbar: Erscheinungsort nicht ermittelbar, 2012; ISBN 978-958-46-0661-7. [Google Scholar]
  5. Guha-Sapir, D.; Schimmer, B. Dengue Fever: New Paradigms for a Changing Epidemiology. Emerg Themes Epidemiol 2005, 2, 1. [Google Scholar] [CrossRef] [PubMed]
  6. Reiter, P.; Lathrop, S.; Bunning, M.; Biggerstaff, B.; Singer, D.; Tiwari, T.; Baber, L.; Amador, M.; Thirion, J.; Hayes, J.; et al. Texas Lifestyle Limits Transmission of Dengue Virus. Emerg. Infect. Dis. 2003, 9, 86–89. [Google Scholar] [CrossRef] [PubMed]
  7. Queiroz, E.R. da S.; Medronho, R. de A. Spatial Analysis of the Incidence of Dengue, Zika and Chikungunya and Socioeconomic Determinants in the City of Rio de Janeiro, Brazil. Epidemiol. Infect. 2021, 149, e188. [Google Scholar] [CrossRef]
  8. Alcaldía Municipal de Ibagué - Ibagué Vibra Available online:. Available online: https://ibague.gov.co/portal/seccion/contenido/index.php?type=3&cnt=53 (accessed on 28 October 2022).
  9. Carrasquilla, M.C.; Ortiz, M.I.; León, C.; Rondón, S.; Kulkarni, M.A.; Talbot, B.; Sander, B.; Vásquez, H.; Cordovez, J.M.; González, C.; et al. Entomological Characterization of Aedes Mosquitoes and Arbovirus Detection in Ibagué, a Colombian City with Co-Circulation of Zika, Dengue and Chikungunya Viruses. Parasites Vectors 2021, 14, 446. [Google Scholar] [CrossRef] [PubMed]
  10. Faruk, M.O.; Jannat, S.N.; Rahman, Md.S. Impact of Environmental Factors on the Spread of Dengue Fever in Sri Lanka. Int. J. Environ. Sci. Technol. 2022, 19, 10637–10648. [Google Scholar] [CrossRef]
  11. Rose, N.H.; Sylla, M.; Badolo, A.; Lutomiah, J.; Ayala, D.; Aribodor, O.B.; Ibe, N.; Akorli, J.; Otoo, S.; Mutebi, J.-P.; et al. Climate and Urbanization Drive Mosquito Preference for Humans. Current Biology 2020, 30, 3570–3579. [Google Scholar] [CrossRef]
  12. Lee, S.A.; Jarvis, C.I.; Edmunds, W.J.; Economou, T.; Lowe, R. Spatial Connectivity in Mosquito-Borne Disease Models: A Systematic Review of Methods and Assumptions. J. R. Soc. Interface. 2021, 18, 20210096. [Google Scholar] [CrossRef]
  13. Kuddus, M.A.; Tynan, E.; McBryde, E. Urbanization: A Problem for the Rich and the Poor? Public Health Rev 2020, 41, 1. [Google Scholar] [CrossRef] [PubMed]
  14. Vatanpour, N.; Malvandi, A.M.; Hedayati Talouki, H.; Gattinoni, P.; Scesi, L. Impact of Rapid Urbanization on the Surface Water’s Quality: A Long-Term Environmental and Physicochemical Investigation of Tajan River, Iran (2007–2017). Environ Sci Pollut Res 2020, 27, 8439–8450. [Google Scholar] [CrossRef]
  15. Romeo-Aznar, V.; Picinini Freitas, L.; Gonçalves Cruz, O.; King, A.A.; Pascual, M. Fine-Scale Heterogeneity in Population Density Predicts Wave Dynamics in Dengue Epidemics. Nat Commun 2022, 13, 996. [Google Scholar] [CrossRef]
  16. Pickett, K.E. Multilevel Analyses of Neighbourhood Socioeconomic Context and Health Outcomes: A Critical Review. Journal of Epidemiology & Community Health 2001, 55, 111–122. [Google Scholar] [CrossRef]
  17. Diez Roux, A.V. Investigating Neighborhood and Area Effects on Health. Am J Public Health 2001, 91, 1783–1789. [Google Scholar] [CrossRef]
  18. Waller, L.A.; Gotway, C.A. Applied Spatial Statistics for Public Health Data; Wiley series in probability and statistics; John Wiley & Sons: Hoboken, N.J, 2004; ISBN 978-0-471-38771-8. [Google Scholar]
  19. Chaix, B.; Merlo, J.; Evans, D.; Leal, C.; Havard, S. Neighbourhoods in Eco-Epidemiologic Research: Delimiting Personal Exposure Areas. A Response to Riva, Gauvin, Apparicio and Brodeur. Social Science & Medicine 2009, 69, 1306–1310. [Google Scholar] [CrossRef]
  20. Diez Roux, A.V.; Mair, C. Neighborhoods and Health: Neighborhoods and Health. Annals of the New York Academy of Sciences 2010, 1186, 125–145. [Google Scholar] [CrossRef] [PubMed]
  21. Jaya, I.G.N.M.; Folmer, H. Bayesian Spatiotemporal Mapping of Relative Dengue Disease Risk in Bandung, Indonesia. J Geogr Syst 2020, 22, 105–142. [Google Scholar] [CrossRef]
  22. Rotejanaprasert, C.; Ekapirat, N.; Areechokchai, D.; Maude, R.J. Bayesian Spatiotemporal Modeling with Sliding Windows to Correct Reporting Delays for Real-Time Dengue Surveillance in Thailand. Int J Health Geogr 2020, 19, 4. [Google Scholar] [CrossRef] [PubMed]
  23. Sani, A.; Abapihi, B.; Mukhsar, M.; Kadir, K. Relative Risk Analysis of Dengue Cases Using Convolution Extended into Spatio-Temporal Model. Journal of Applied Statistics 2015, 42, 2509–2519. [Google Scholar] [CrossRef]
  24. Telle, O.; Nikolay, B.; Kumar, V.; Benkimoun, S.; Pal, R.; Nagpal, B.; Paul, R.E. Social and Environmental Risk Factors for Dengue in Delhi City: A Retrospective Study. PLoS Negl Trop Dis 2021, 15, e0009024. [Google Scholar] [CrossRef] [PubMed]
  25. Lowe, R.; Lee, S.A.; O’Reilly, K.M.; Brady, O.J.; Bastos, L.; Carrasco-Escobar, G.; de Castro Catão, R.; Colón-González, F.J.; Barcellos, C.; Carvalho, M.S.; et al. Combined Effects of Hydrometeorological Hazards and Urbanisation on Dengue Risk in Brazil: A Spatiotemporal Modelling Study. The Lancet Planetary Health 2021, 5, e209–e219. [Google Scholar] [CrossRef]
  26. Desjardins, M.R.; Eastin, M.D.; Paul, R.; Casas, I.; Delmelle, E.M. Space–Time Conditional Autoregressive Modeling to Estimate Neighborhood-Level Risks for Dengue Fever in Cali, Colombia. The American Journal of Tropical Medicine and Hygiene 2020, 103, 2040–2053. [Google Scholar] [CrossRef]
  27. Mukhsar; Abapihi, B. ; Sani, A.; Cahyono, E.; Adam, P.; Aini Abdullah, F. Extended Convolution Model to Bayesian Spatio-Temporal for Diagnosing the DHF Endemic Locations. Journal of Interdisciplinary Mathematics 2016, 19, 233–244. [Google Scholar] [CrossRef]
  28. Krüger, F.; Lerch, S.; Thorarinsdottir, T.L.; Gneiting, T. Predictive Inference Based on Markov Chain Monte Carlo Output. 2016. [Google Scholar] [CrossRef]
  29. Speagle, J.S. A Conceptual Introduction to Markov Chain Monte Carlo Methods. 2019. [Google Scholar] [CrossRef]
  30. Martino, S. ; Havard Rue Implementing Approximate Bayesian Inference Using Integrated Nested Laplace Approximation: A Manual for the Inla Program 2009.
  31. Scott, T.W.; Morrison, A.C. Vector Dynamics and Transmission of Dengue Virus: Implications for Dengue Surveillance and Prevention Strategies. In Dengue Virus; Rothman, A.L., Ed.; Current Topics in Microbiology and Immunology; Springer Berlin Heidelberg: Berlin, Heidelberg, 2010; Volume 338, pp. 115–128. ISBN 978-3-642-02214-2. [Google Scholar]
  32. MANUAL DE USO DEL MARCO GEOESTADÍSTICO NACIONAL EN EL PROCESO ESTADÍSTICO; Departamento Administrativo Nacional de Estadística, 2018; p. 40.
  33. McMillen, D.P. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships. American Journal of Agricultural Economics 2004, 86, 554–556. [Google Scholar] [CrossRef]
  34. Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian Inference for Latent Gaussian Models by Using Integrated Nested Laplace Approximations. Journal of the Royal Statistical Society Series B: Statistical Methodology 2009, 71, 319–392. [Google Scholar] [CrossRef]
  35. Kyle, J.L.; Harris, E. Global Spread and Persistence of Dengue. Annu. Rev. Microbiol. 2008, 62, 71–92. [Google Scholar] [CrossRef] [PubMed]
  36. DANE La información del DANE en la toma de decisiones regionales: Ibagué, Colombia 2020.
  37. Departamento Administrativo Nacional de Estadística Geoportal DANE Available online:. Available online: https://geoportal.dane.gov.co/servicios/descarga-y-metadatos/descarga-mgn-marco-geoestadistico-nacional/ (accessed on 23 November 2022).
  38. Wan, Z.; Hook, S.; Hulley, G. MODIS/Terra Land Surface Temperature/Emissivity Daily L3 Global 1km SIN Grid V061 2021.
  39. Didan, K. MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V061 2021.
  40. Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—a New Environmental Record for Monitoring Extremes. Sci Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
  41. Kache, P.; Ruiz-Carrascal, D.; Lowe, R.; Stewart-Ibarra, A.M.; Seto, K.; Diuk-Wasser, M.; Santos-Vega, M. Climate Extremes Increase Dengue Risk along Socio-Economic and Elevation Gradients. Nature Climate Change. Under review.
  42. Gollini, I.; Lu, B.; Charlton, M.; Brunsdon, C.; Harris, P. GWmodel : An R Package for Exploring Spatial Heterogeneity Using Geographically Weighted Models. J. Stat. Soft. 2015, 63. [Google Scholar] [CrossRef]
  43. Lu, B.; Harris, P.; Charlton, M.; Brunsdon, C. The GWmodel R Package: Further Topics for Exploring Spatial Heterogeneity Using Geographically Weighted Models. Geo-spatial Information Science 2014, 17, 85–101. [Google Scholar] [CrossRef]
  44. Thapa, R.B.; Estoque, R.C. Geographically Weighted Regression in Geospatial Analysis. In Progress in Geospatial Analysis; Murayama, Y., Ed.; Springer Japan: Tokyo, 2012; pp. 85–96. ISBN 978-4-431-53999-5. [Google Scholar]
  45. Wheeler, D.C.; Páez, A. Geographically Weighted Regression. In Handbook of Applied Spatial Analysis; Fischer, M.M., Getis, A., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2010; pp. 461–486. ISBN 978-3-642-03646-0. [Google Scholar]
  46. Cazelles, B.; Chavez, M.; Berteaux, D.; Ménard, F.; Vik, J.O.; Jenouvrier, S.; Stenseth, N.C. Wavelet Analysis of Ecological Time Series. Oecologia 2008, 156, 287–304. [Google Scholar] [CrossRef]
  47. Gouhier, T.C.; Grinsted, A.; Simko, V. R Package Biwavelet: Conduct Univariate and Bivariate Wavelet Analyses 2021.
  48. Lowe, R.; Gasparrini, A.; Van Meerbeeck, C.J.; Lippi, C.A.; Mahon, R.; Trotman, A.R.; Rollock, L.; Hinds, A.Q.J.; Ryan, S.J.; Stewart-Ibarra, A.M. Nonlinear and Delayed Impacts of Climate on Dengue Risk in Barbados: A Modelling Study. PLoS Med 2018, 15, e1002613. [Google Scholar] [CrossRef]
  49. Gasparrini, A. Distributed Lag Linear and Non-Linear Models in R: The Package Dlnm. Journal of Statistical Software 2011, 43, 1–20. [Google Scholar] [CrossRef]
  50. Besag, J.; York, J.; Molliè, A. Bayesian Image Restoration, with Two Applications in Spatial Statistics. Ann Inst Stat Math 1991, 43, 1–20. [Google Scholar] [CrossRef]
  51. Martins, T.G.; Simpson, D.; Lindgren, F.; Rue, H. Bayesian Computing with INLA: New Features. Computational Statistics & Data Analysis 2013, 67, 68–83. [Google Scholar] [CrossRef]
  52. Schmidt, W.-P.; Suzuki, M.; Dinh Thiem, V.; White, R.G.; Tsuzuki, A.; Yoshida, L.-M.; Yanai, H.; Haque, U.; Huu Tho, L.; Anh, D.D.; et al. Population Density, Water Supply, and the Risk of Dengue Fever in Vietnam: Cohort Study and Spatial Analysis. PLoS Med 2011, 8, e1001082. [Google Scholar] [CrossRef]
  53. Romeo-Aznar, V.; Paul, R.; Telle, O.; Pascual, M. Mosquito-Borne Transmission in Urban Landscapes: The Missing Link between Vector Abundance and Human Density. Proc. R. Soc. B. 2018, 285, 20180826. [Google Scholar] [CrossRef]
  54. Rasid, H.; Mallsk, A.U. Living on the Edge of Stagnant Water: An Assessment of Environmental Impacts of Construction-Phase Drainage Congestion along Dhaka City Flood Control Embankment, Bangladesh. Environmental Management 1996, 20, 89–98. [Google Scholar] [CrossRef]
  55. Chitolina, R.F.; Anjos, F.A.; Lima, T.S.; Castro, E.A.; Costa-Ribeiro, M.C.V. Raw Sewage as Breeding Site to Aedes ( Stegomyia ) Aegypti (Diptera, Culicidae). Acta Tropica 2016, 164, 290–296. [Google Scholar] [CrossRef] [PubMed]
  56. Foster, W.A.; Walker, E.D. MOSQUITOES ( Culicidae). In Medical and Veterinary Entomology; Elsevier, 2002; pp. 203–262. ISBN 978-0-12-510451-7. [Google Scholar]
  57. Sur, D.; Von Seidlein, L.; Manna, B.; Dutta, S.; Deb, A.K.; Sarkar, B.L.; Kanungo, S.; Deen, J.L.; Ali, M.; Kim, D.R.; et al. The Malaria and Typhoid Fever Burden in the Slums of Kolkata, India: Data from a Prospective Community-Based Study. Transactions of the Royal Society of Tropical Medicine and Hygiene 2006, 100, 725–733. [Google Scholar] [CrossRef] [PubMed]
  58. Krystosik, A.; Njoroge, G.; Odhiambo, L.; Forsyth, J.E.; Mutuku, F.; LaBeaud, A.D. Solid Wastes Provide Breeding Sites, Burrows, and Food for Biological Disease Vectors, and Urban Zoonotic Reservoirs: A Call to Action for Solutions-Based Research. Front. Public Health 2020, 7, 405. [Google Scholar] [CrossRef]
  59. Klafke, F.; Barros, V.G.; Henning, E. Solid Waste Management and Aedes Aegypti Infestation Interconnections: A Regression Tree Application. Waste Manag Res 2023, 41, 1684–1696. [Google Scholar] [CrossRef] [PubMed]
  60. Naqvi, S.A.A.; Sajjad, M.; Tariq, A.; Sajjad, M.; Waseem, L.A.; Karuppannan, S.; Rehman, A.; Hassan, M.; Al-Ahmadi, S.; Hatamleh, W.A. Societal Knowledge, Attitude, and Practices towards Dengue and Associated Factors in Epidemic-Hit Areas: Geoinformation Assisted Empirical Evidence. Heliyon 2024, 10, e23151. [Google Scholar] [CrossRef]
  61. Diaz-Quijano, F.A.; Martínez-Vega, R.A.; Rodriguez-Morales, A.J.; Rojas-Calero, R.A.; Luna-González, M.L.; Díaz-Quijano, R.G. Association between the Level of Education and Knowledge, Attitudes and Practices Regarding Dengue in the Caribbean Region of Colombia. BMC Public Health 2018, 18, 143. [Google Scholar] [CrossRef] [PubMed]
  62. Urrea, V.; Ochoa, A.; Mesa, O. Seasonality of Rainfall in Colombia. Water Resour. Res. 2019, 55, 4149–4162. [Google Scholar] [CrossRef]
  63. Santoso, A.; Mcphaden, M.J.; Cai, W. The Defining Characteristics of ENSO Extremes and the Strong 2015/2016 El Niño. Reviews of Geophysics 2017, 55, 1079–1129. [Google Scholar] [CrossRef]
  64. Elsinga, J.; Lizarazo, E.F.; Vincenti, M.F.; Schmidt, M.; Velasco-Salas, Z.I.; Arias, L.; Bailey, A.; Tami, A. Health Seeking Behaviour and Treatment Intentions of Dengue and Fever: A Household Survey of Children and Adults in Venezuela. PLoS Negl Trop Dis 2015, 9, e0004237. [Google Scholar] [CrossRef]
  65. Duong, V.; Lambrechts, L.; Paul, R.E.; Ly, S.; Lay, R.S.; Long, K.C.; Huy, R.; Tarantola, A.; Scott, T.W.; Sakuntabhai, A.; et al. Asymptomatic Humans Transmit Dengue Virus to Mosquitoes. Proc. Natl. Acad. Sci. U.S.A. 2015, 112, 14688–14693. [Google Scholar] [CrossRef]
Preprints 101223 g001
Figure 1. Dengue Virus Cases from 2013 to 2018 in Ibagué. (A) Time series of aggregated cases for the whole city. (B) Kernel density estimation for georeferenced cases for each year of the studied period.
Figure 1. Dengue Virus Cases from 2013 to 2018 in Ibagué. (A) Time series of aggregated cases for the whole city. (B) Kernel density estimation for georeferenced cases for each year of the studied period.
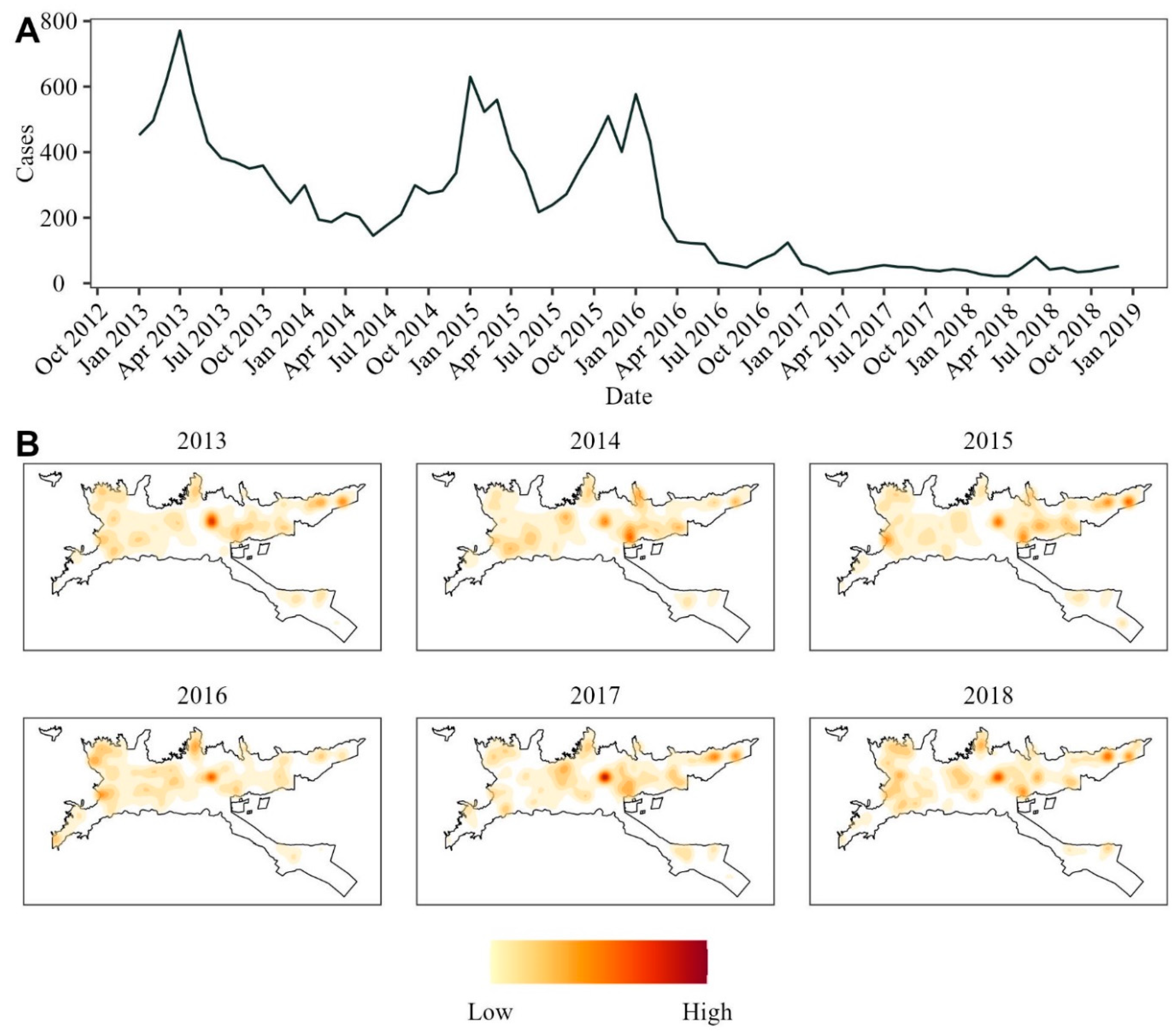
Preprints 101223 g001
Preprints 101223 g002
Figure 2. GWR significance for individual spatial features at each level. Columns represent the different levels, while rows are the significant variables. Colored areas indicate statistical significance in local regressions.
Figure 2. GWR significance for individual spatial features at each level. Columns represent the different levels, while rows are the significant variables. Colored areas indicate statistical significance in local regressions.
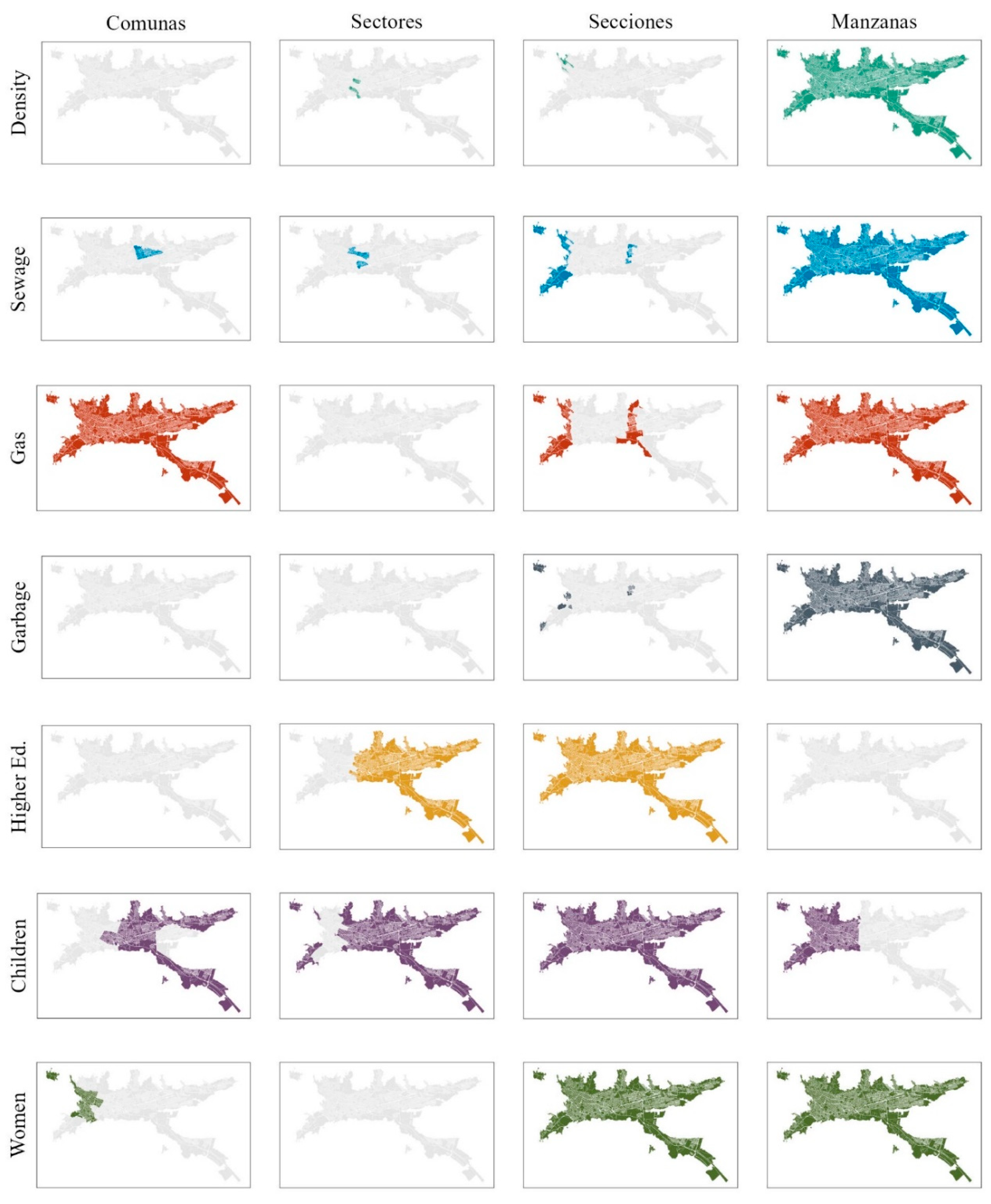
Preprints 101223 g002
Preprints 101223 g003
Figure 3. Results for spatial fixed effects in spatio-temporal fitted models. Points represent the median of the marginal posterior distributions, and the lines draw the 95% credible interval for each level.
Figure 3. Results for spatial fixed effects in spatio-temporal fitted models. Points represent the median of the marginal posterior distributions, and the lines draw the 95% credible interval for each level.
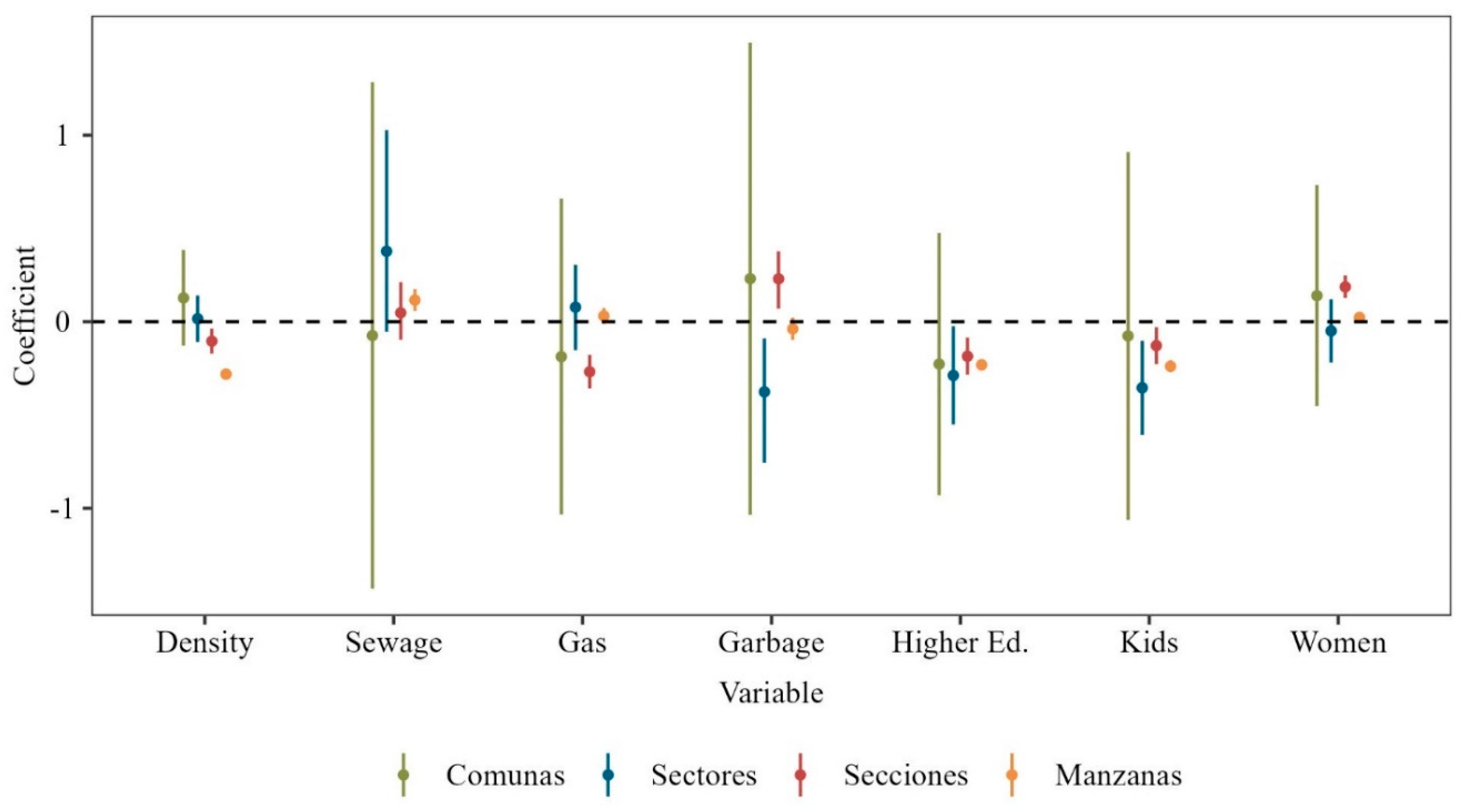
Preprints 101223 g003
Preprints 101223 g004
Figure 4. Contour plots for the results of temporal variables showing relative risk of dengue cases from exposure and different time lags. Relative risk is calculated from baseline observations for each covariate as follows: mean temperature risk is calculated relative to 22°C, Total precipitation relative to 0 mm/month, and NDVI, Wet Days and Days Over 32°C are calculated relative to 0.
Figure 4. Contour plots for the results of temporal variables showing relative risk of dengue cases from exposure and different time lags. Relative risk is calculated from baseline observations for each covariate as follows: mean temperature risk is calculated relative to 22°C, Total precipitation relative to 0 mm/month, and NDVI, Wet Days and Days Over 32°C are calculated relative to 0.
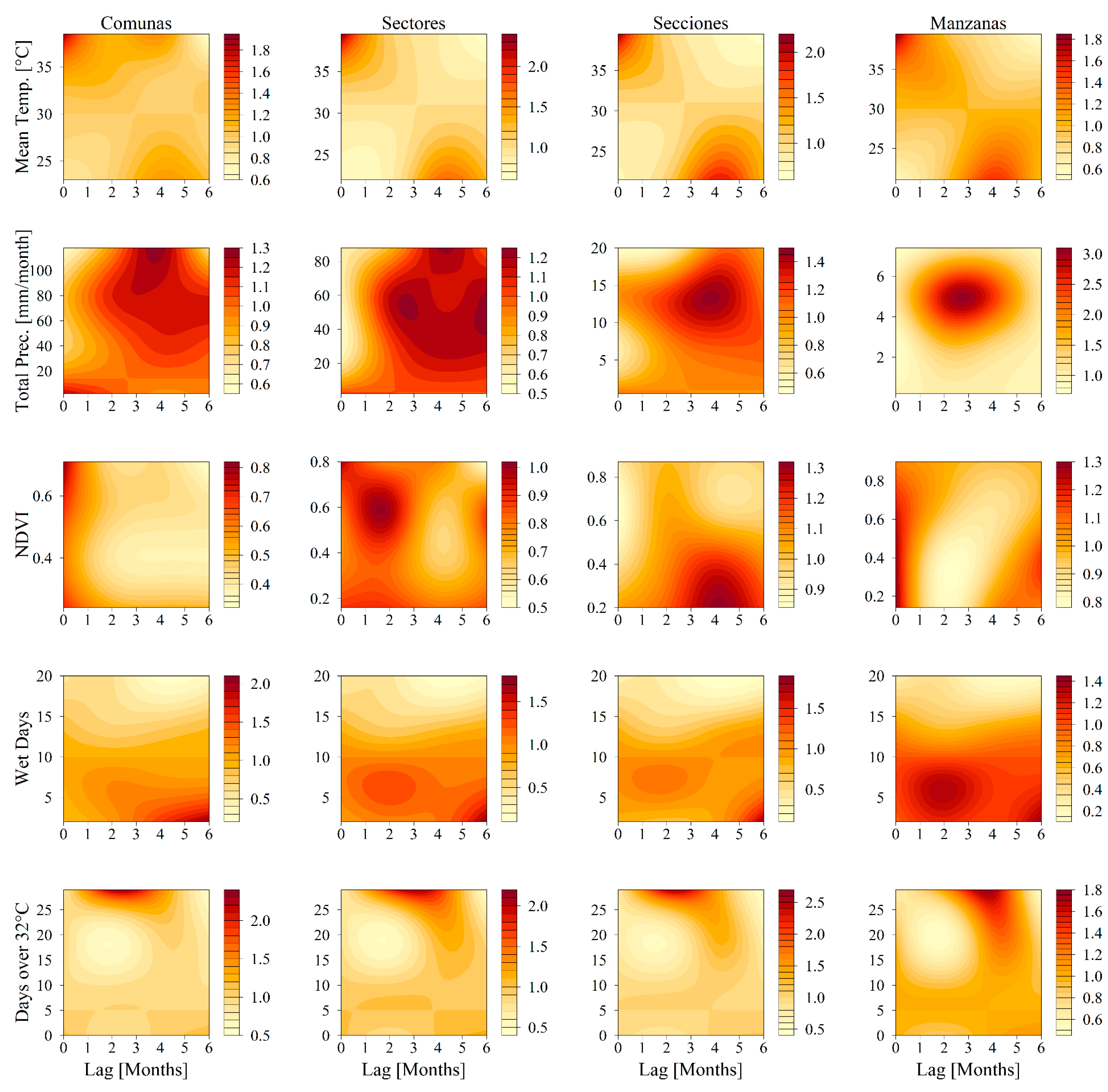
Preprints 101223 g004
Preprints 101223 g005
Figure 5. Aggregated fitted values from marginal posterior distributions, compared to observed DENV cases in the city for the studied period. Fitted values are plotted with a 95% credible interval at each level.
Figure 5. Aggregated fitted values from marginal posterior distributions, compared to observed DENV cases in the city for the studied period. Fitted values are plotted with a 95% credible interval at each level.
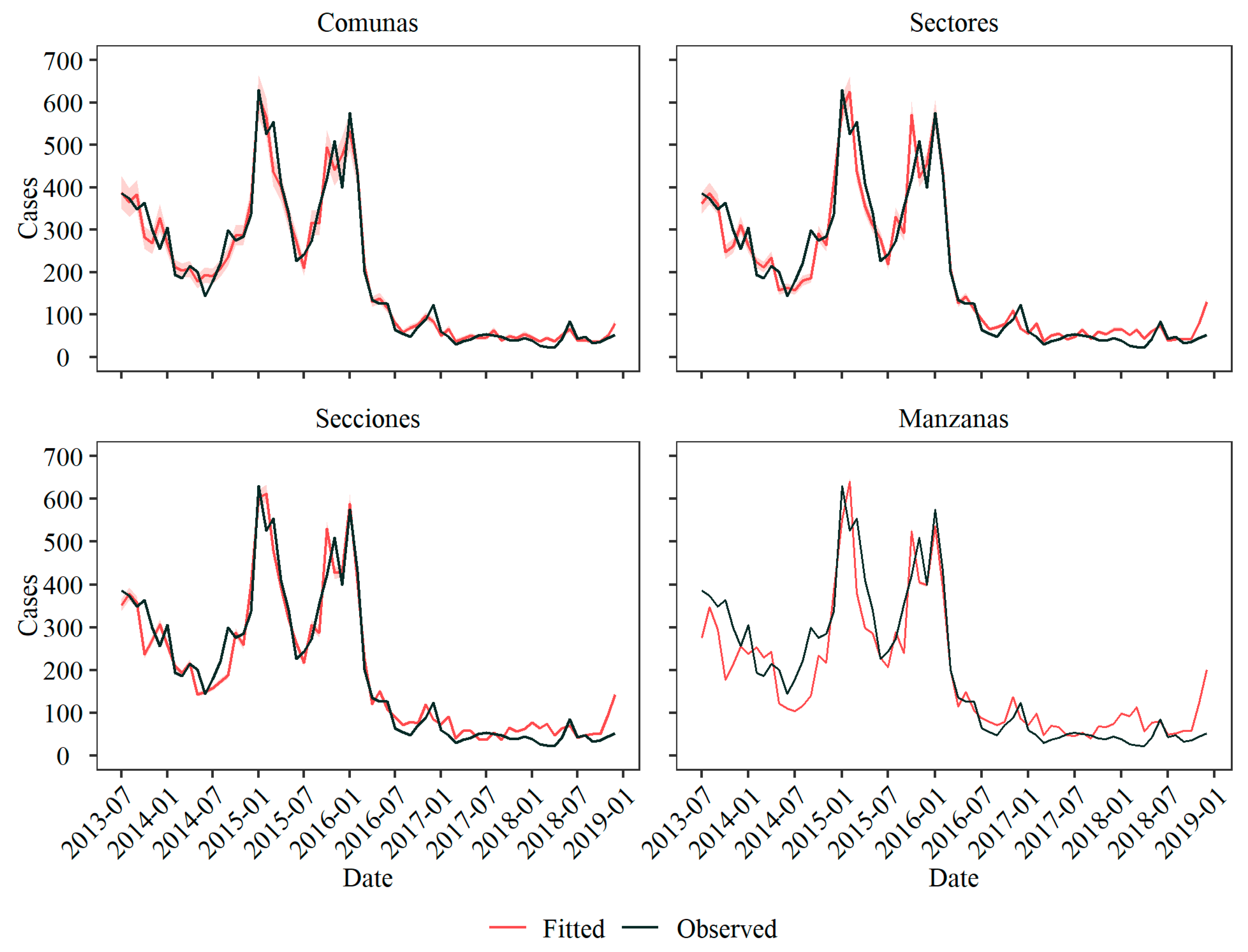
Preprints 101223 g005
Table 1. Model comparison using DIC and WAIC at each level of spatial aggregation.
Table 1. Model comparison using DIC and WAIC at each level of spatial aggregation.
Model
Level Metric Spatial Temporal Spatio-temporal
Comunas DIC 5,345 4,861 4,860
WAIC 5,358 4,863 4,863
Sectores DIC 14,646 13,874 13,871
WAIC 14,656 13,874 13,869
Secciones DIC 33,942 32,206 32,163
WAIC 33,871 32,185 32,139
Manzanas DIC 89,900 84,728 84,051
WAIC 89,845 84,667 83,988
Table 2. Root Mean Square Error (RMSE) for each level’s posterior marginals.
Table 2. Root Mean Square Error (RMSE) for each level’s posterior marginals.
Comunas Sectores Secciones Manzanas
RMSE 32.69 45.80 42.34 66.63
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated