Prerpints.org logo
Preprint
Article

The Computational Universe: EPR Paradox and Pre-Measure Reality, Actual Time in Spacetime, Free Will and the Classical Limit Problem in Quantum Loop Gravity, Causal Dynamical Triangulation and Holographic Principle

Altmetrics

Downloads

139

Views

53

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

12 March 2024

Posted:

13 March 2024

You are already at the latest version

Alerts
Abstract
The Simulation analogy presented in this work enhances the accessibility of abstract quantum theories, specifically the stochastic hydrodyanimc model (SQHM), by relating them to our daily experiences. The SQHM incorporates the influence of fluctuating gravitational background, resembling dark energy, into quantum equations. This model successfully addresses key aspects of Objective-Collapse Theories, including resolving the 'tails' problem through the definition of quantum potential length in addition to the De Broglie length, beyond which coherent Schrödinger quantum behavior and wavefunction tails cannot be maintained. The SQHM emphasizes that an external environment is unnecessary, asserting that the quantum stochastic behavior leading to wave-function collapse can be an inherent property of a system in a spacetime with fluctuating metrics. Embedded in relativistic quantum mechanics, the theory establishes a coherent link between the uncertainty principle and the constancy of light speed, aligning seamlessly with finite information transmission speed. Within a fluctuating quantum system, the SQHM derives the indeterminacy relation between energy and time, offering insights into measurement processes impossible within a finite time interval in a truly quantum global system. Experimental validation is found in confirming the Lindemann constant for solid lattice melting points and the transition from fluid to superfluid states. The SQHM's self-consistency lies in its ability to describe wavefunction collapse and the measure process. Additionally, the theory resolves the Pre-existing Reality problem by showing that large-scale systems naturally decay into decoherent states stable in time. Continuing, the paper demonstrates that the physical dynamics of SQHM can be analogized to a computer simulation employing optimization procedures for realization. This perspective elucidates the concept of time in contemporary reality and enriches our comprehension of free will. The overall framework introduces an irreversible process impacting the manifestation of macroscopic reality at the present time, asserting that the multiverse exists solely in future states, with the past comprising the formed universe after the current moment. Decoherence at the present time functions as a reduction of the multiverse to a single universe. The macroscopic reality, characterized by fractal consistency where microscopic domains with quantum properties coexist, provides insights into how our consciousness apprehends dynamic reality, the spontaneous emergence of gravity in discrete spacetime evolution, and the attainment of the classical General Relativity limit in Quantum Loop Gravity and Causal Dynamical Triangulation. The Simulation Analogy highlights a strategy focused on minimizing information processing, facilitating the universal simulation in solving its predetermined problem. From within, reality becomes the manifestation of specific physical laws emerging from the inherent structure of the simulation devised to address its particular issue. In this context, the reality simulation appears to employ an entropic optimization strategy, minimizing information loss while efficiently compressing data in line with the simulation's intended purpose.
Keywords: 
Subject: Physical Sciences  -   Mathematical Physics

1. Introduction

One of the most interesting innovating opinion of nowadays physics refers to the treatment of infinitesimals and infinities as mathematical abstractions more than real entities. This convincement has already brought important outputss as the quantum loop gravity [1,2] and the non-commutative string theories [3,4].
In this study, we aim to demonstrate that adopting this perspective can provide fresh insights into longstanding issues in physics.
On a well-founded hypothesis that spacetime is not continuous but rather discrete, we illustrate the feasibility of drawing an analogy between our universe and a computerized N-Body Simulation.
Our goal is to present a sturdy framework of reasoning, which will be subsequently utilized to attain a more profound comprehension of our reality. This framework is founded on the premise that anyone endeavoring to create a computer simulation resembling our Universe will inevitably confront the same challenges as the entity responsible for constructing the Universe itself.
The fundamental aim is that, by tackling these challenges, we may unearth insights into the reasons behind the functioning of the Universe. This is based on the notion that constructing something as extensive and intricate at higher levels of efficiency might have only one viable approach. The essence of the current undertaking is eloquently aligned with the dictum of Feynman: ‘What I cannot create, I do not understand”. Conversely, here, this principle is embraced in the affirmative: ‘What I can create, I can comprehend.”
One of the primary challenges in achieving this objective is the need for a physical theory that comprehensively describes reality, capable of portraying the N-body evolution across the entire physical scale, spanning from the microscopic quantum level to the macroscopic classical realm.
Regarding this matter, established physics falls short in providing a comprehensive and internally consistent theoretical foundation [5,6,7,8,9,10]. Numerous problematic aspects persist to this day, including the challenge posed by the probabilistic interpretation assigned to the wavefunction in quantum mechanics. Others persistent issues are the impossibility of assuming a well-defined concept of pre-existing reality before measurement and ensuring local relativistic causality.
Quantum theory, despite its well defined mathematical apparatus, remains incomplete with respect to its foundational postulates. Specifically, the measurement process is not explicated within the framework of quantum mechanics. This requires acceptance of its probabilistic foundations regardless of the validity of the principle of causality.
This conflict is famously articulated through the objection posed by the EPR paradox. The EPR paradox, as detailed in a renowned paper [5], is rooted in the incompleteness of quantum mechanics concerning the indeterminacy of the wavefunction collapse and measurement outcomes. These fundamental aspects do not find a clear placement within a comprehensive theoretical framework.
The endeavor to formulate a theory encompassing the probabilistic nature of quantum mechanics within a unified theoretical framework can be traced back to the research of Nelson [6] and has persisted over time. However, Nelson’s hypotheses ultimately fell short due to the imposition of a specific stochastic derivative with time inversion symmetry, limiting its generality. Furthermore, the outcomes of Nelson’s theory do not fully align with those of quantum mechanics concerning the incompatibility of contemporary measurements of conjugated variables, as illustrated by Von Neumann’s proof [7] of the impossibility of reproducing quantum mechanics with theories based on underlying classical probabilistic variables.
Moreover, the overarching goal of incorporating the probabilistic nature of quantum mechanics while ensuring its reversibility through “hidden variables” in local classical theories was conclusively proven to be impossible by Bell [8]. Nevertheless, Bohm’s non-local hidden variable theory [11] has arisen with some success. He endeavors to restore the determinism of quantum mechanics by introducing the concept of a pilot wave. The fundamental concept posits that, in addition to the particles themselves, there exists a “guidance” or influence from the pilot wave function that dictates the behavior of the particles. Although this pilot wave function is not directly observable, it does impact the measurement probabilities of the particles.
A more sophisticate model is based on the Feynman integral path representation [12] of quantum mechanics. Here, as shown by Kleinert [13], it is established that quantum mechanics can be conceptualized as an imaginary time stochastic process. These imaginary time quantum fluctuations differ from the more commonly known real-time fluctuations of the classical stochastic dynamics. They result in the “reversible” evolution of probability wave (wavefunction) that shows pseudo-diffusion behavior of the mass density.
The distinguishing characteristic of quantum pseudo-diffusion is the inability to define a positive diffusion coefficient. This directly stems from the reversible nature of quantum evolution, which, within a spatially distributed system, may demonstrate local entropy reduction over specific spatial domains. However, this occurs within the framework of an overall reversible deterministic evolution with a net entropy variation of zero [14].
This aspect is clarified by the Madelung quantum hydrodynamic model [15,16,17], which is perfectly equivalent to the Schrödinger description while being a specific subset of the Bohm theory [18]. In this model, quantum entanglement is introduced through the influence of the so-called quantum potential.
Recently, with the emergence of evidence pointing to dark energy manifested as a gravitational background noise (GBN), whether originating from relics or the dynamics of bodies in general relativity, the author demonstrated that the quantum hydrodynamic representation provides a means to describe self-fluctuating dynamics within a system without necessitating the introduction of an external environment [19]. The noise generated by spacetime curvature ripples can be integrated into Madelung’s quantum hydrodynamic description by utilizing the foundational assumption of relativity, permitting the consideration of the energy associated with spacetime curvature as virtual mass.
The resulting stochastic quantum hydrodynamic model (SQHM) avoids introducing divergent results that contradict established theories such as decoherence [9] and the Copenhagen foundation of quantum mechanics; instead, it enriches and complements our understanding of these theories. It indicates that in the presence of noise, quantum entanglement and coherence can be maintained on a microscopic scale much smaller than the De Broglie length and the range of action of the quantum potential. On a scale with a characteristic length much larger than the distance over which quantum entanglement operates, classical physics naturally emerges [19].
While the Bohm theory attributes the indeterminacy of the measurement process to the undeterminable pilot wave, the SQHM attributes its unpredictable probabilistic nature to the fluctuating gravitational background. Furthermore, it is possible to demonstrate a direct correspondence between the Bohm non-local hidden variable approach developed by Santilli in IsoRedShift Mechanics [20] and the SQHM. This correspondence reveals that the origin of the hidden variable is nothing but the perturbative effect of the fluctuating gravitational background on quantum mechanics [21].
The stochastic quantum hydrodynamic model (SQHM), adept at describing physics across various length scales, from the microscopic quantum to the classical macroscopic [19], offers the potential to formulate a comprehensive simulation analogy to the N-body evolution within the discrete spacetime of the Universe.
The work is organized as follows:
  • Introduction to the Stochastic Quantum Hydrodynamic Model (SQHM);
  • Quantum to classical transition and the emerging classical mechanics on large size systems;
  • The measurement process in the quantum stochastic theory: the role of the finite range of non-local quantum potential interactions;
  • Minimum measurement uncertainty in spacetime with fluctuating background and finite speed of light;
  • Minimum discrete length interval in 4D spacetime;
  • Dynamics of Wavefunction Collapse;
  • Evolution of the mass density distribution of quantum superposition of states in spacetime with GBN;
  • EPR Paradox and Pre-existing Reality from the standpoint of the SQHM;
  • The computer simulation analogy for the N-body problem;
  • How the Universe computes the next state: the unraveling of the meaning of time;
  • The Free Will;
  • The Universal “Pasta Maker” and the Actual Time in 4D spacetime;
  • Discussion and future Developments;
  • Extending Free Will;
  • Best Future States Problem Solving Emergent from the Darwinian Principle of Evolution;
  • How the coscience captures the reality dynimcs;
  • The spontaneous appearance of gravity in a discrete spacetime simulation;
  • The classical General Relativity limit problem in Quantum Loop Gravity and Causal Dynamical Triang3ulation

2. The Quantum Stochastic Hydrodynamic Model

The Madelung quantum hydrodynamic representation transforms the Schrodinger equation [15,16,17]
− i ℏ ∂ t ψ = ( ℏ 2 2 m ∂ i ∂ i − V ( q ) ) ψ
for the complex wave function ψ = | ψ | e − i S ℏ , into two equations of real variable: the conservation equation for the mass density | ψ | 2
∂ t | ψ | 2 + ∂ i ( | ψ | 2 q ˙ i ) = 0
and the motion equation for the momentum m q ˙ i = p i = ∂ i S ( q , t ) ,
q ¨ j ( t ) = − 1 m ∂ j ( V ( q ) + V q u ( n ) )
where S ( q , t ) = − ℏ 2 l n ψ ψ * and where
V q u = − ℏ 2 2 m 1 | ψ | ∂ i ∂ i | ψ |
By treating the energy content of the gravitaional background noise (GBN) as virtual mass density, the quantum potential genertes a stochastic force with correlation function shape    F ( λ ) generalizing the Madelung hydrodynamic analogy into a quantum-stochastic problem. As shown in [19] the SQHM is defined on the following assumptions:
1. The virtual mass density fluctuations genrated by the GBN are described by the wave function ψ g b n  with density | ψ g b n | 2 ;
2. The associated energy density E (of the spacetime background fluctuations) is proportional to | ψ g b n | 2 ;
3. The virtual mass m g b n is defined by the identity E = m g b n c 2 | ψ g b n | 2
4. The virtual mass is assumed to not interact with the mass of the physical system (since the gravitational interaction is sufficiently weak to be disregarded).
In this case, the wave function of the overall system ψ t o t reads
ψ t o t ≅ ψ ψ g b n
Moreover, since the energy density E of the GBN is quite small, the viryal mass density | ψ g b n | 2 is assumed to bew much smaller than the the body mass density | ψ | 2 (usually considered in lhysical problems). Therefore, considering the virtual mass m g b n much smaller than the mass of the system and assuming in equation (4) that m t o t = m g b n + m ≅ m , the overall quantum potential can be expressed as follows:
V q u ( n t o t ) = − ℏ 2 2 m t o t | ψ | − 1 | ψ g b n | − 1 ∂ i ∂ i | ψ | | ψ g b n | = = − ℏ 2 2 m ( | ψ | − 1 ∂ i ∂ i | ψ | + | ψ g b n | − 1 ∂ i ∂ i | ψ g b n | + | ψ | − 1 | ψ g b n | − 1 ∂ i | ψ g b n | ∂ i | ψ | ) .
Expression (6) allows to derive the shape G ( λ ) of the correlation function of the quantum potential fluctuations that reads [19,22]:
G ( λ ) ∝ ∫ − ∞ + ∞ e x p [ i k λ ] S ( k ) d k ∝ ∫ − ∞ + ∞ e x p [ i k λ ] e x p [ − ( k λ c 2 ) 2 ] d k ∝ π 1 / 2 λ c e x p [ − ( λ λ c ) 2 ] .
where
λ c = 2 ℏ ( m k T ) 1 / 2
is the De Broglie length. The expression (7-8) reveals that uncorrelated mass density fluctuations on increasingly shorter distances with respect to λ c are gradually suppressed by the quantum potential. This suppression enables the realization of conventional quantum mechanics, representing the zero-noise “deterministic” limit of the Stochastic Quantum Hydrodynamics Model (SQHM), for systems with a physical length much smaller than the De Broglie length λ c .
In presence of GBN, accounted as virtual mass fluctuations, the mass distribution density (MDD) becomes a stochastic function, such as | ψ | 2 → n ˜ , that we can ideally pose n ˜ = n ¯ + δ n , where δ n is the fluctuating part, and n ¯  is the regular part. All these variables are connected by the limiting condition
l i m T → 0 n ˜ = l i m T → 0 n ¯ = | ψ | 2
Furthermore, the characteristics of the Madelung quantum potential, that in the presence of stochastic noise, fluctuates, can be derived by generally posing that it is composed of the regular part V q u ( n ˜ ) ¯ (to be defined) plus the fluctuating part V s t , such as
V q u ( n ˜ ) = − ℏ 2 2 m n ˜ − 1 / 2 ∂ i ∂ i n ˜ 1 / 2 = V q u ( n ˜ ) ¯ + V s t
where the stochastic part of the quantum potential V s t  leads to the force noise
− ∂ i V s t = m ϖ ( q , t , T )
leading to the stochastic motion equation
q ¨ j ( t ) = − 1 m ∂ j ( V ( q ) + V q u ( n ˜ ) ¯ ) + ϖ ( q , t , T )
Moreover, the regular part V q u ( n ˜ ) ¯ for microscopic systems ( L λ c ≪ 1 ), without loss of generality, can be rearranged as
V q u ( n ˜ ) ¯ = − ℏ 2 2 m ( n ˜ − 1 / 2 ∂ i ∂ i n ˜ 1 / 2 ) ¯ = − ℏ 2 2 m 1 ρ 1 / 2 ∂ i ∂ i ρ 1 / 2 + Δ V ¯ = V q u ( ρ ) + Δ V ¯
Leading to the motion equation
q ¨ j ( t ) = − 1 m ∂ j ( V ( q ) + V q u ( ρ ) + Δ V ¯ ) + ϖ ( q , t , T )
where ρ ( q , t ) is the probability mass density function (PMD) associated with the stochastic process (12) [23] that, in the deterministic limit, obeys to the condition l i m T → 0 ρ ( q , t ) = l i m T → 0 n ˜ = l i m T → 0 n ¯ = | ψ | 2 .
For the sufficiently general case to be of practical interest, the correlation function of noise ϖ ( q , t , T )  can be assumed to be Gaussian with null correlation time, isotropic into the space and independent among different coordinates, taking the form
l i m T → 0 < ϖ ( q α , t ) , ϖ ( q β + λ , t + τ ) > ≅ < ϖ ( q α ) , ϖ ( q β ) > ( T )   G ( λ ) δ ( τ ) δ α β
with
l i m T → 0 < ϖ ( q α ) , ϖ ( q β ) > ( T ) = 0
Furthermore, given that for microscopic systems (i.e., L λ c ≪ 1 )
l i m T → 0 G ( λ ) ∝ 1 λ c e x p [ − ( λ λ c ) 2 ] ≅ 1 λ c ( 1 − ( λ λ c ) 2 ) ≅ 1 λ c = 1 ℏ m k T 2
It follows that
l i m T → 0 < ϖ ( q α , t ) , ϖ ( q β + λ , t + τ ) > ≈   < ϖ ( q α ) , ϖ ( q β ) > ( T ) λ c δ ( τ ) δ α β
and the motion described by equation (12) takes on the stochastic form of the Markovian process [19]
q ¨ j ( t ) = − κ q ˙ j ( t ) − 1 m ∂ ( V ( q ) + V q u ( ρ ) ) ∂ q j + κ D 1 / 2 ξ ( t )
where
D 1 / 2 = ( L λ c ) ( γ D ℏ 2 m ) 1 / 2 = γ D L 2 k T 2 ℏ
where γ D is a non-zero pure number.
In this case, ρ ( q , t ) is the probability mass density function determined by the probability transition function (PTF) P ( q , z | t , 0 ) [23] through the relation
ρ ( q , t ) = ∫ P ( q , z | t , 0 ) ρ ( z , 0 ) d 6 N z
where P ( q , z | t , 0 )  obeys to the Smolukowsky conservation equation for the Markov process (19)
P ( q , q 0 | t + τ , t 0 ) = ∫ − ∞ ∞ P ( q , z | τ , t )   P ( z , q 0 | t − t 0 , t 0 )   d 6 N z
Therefore, for the complex field
ψ = ρ 1 / 2 e − i S ℏ
the quantum-stochsatic hydrodynamic sistem of equation reads:
ρ ( q , t ) = ∫ P ( q , z | t , 0 ) ρ ( z , 0 ) d r z
m q ˙ i = p i = ∂ i S ( q , t ) ,
q ¨ j ( t ) = − κ q ˙ j ( t ) − 1 m ∂ ( V ( q ) + V q u ( ρ ) ) ∂ q j + κ D 1 / 2 ξ ( t )
V q u = − ℏ 2 2 m 1 ρ 1 / 2 ∂ i ∂ i ρ 1 / 2
Where
S ( q , t ) = − ℏ 2 l n ψ ψ *
In the context of (23-26), ψ does not denote the quantum wavefunction; rather, it represents the generalized quantum-stochastic probability wave. With the exception of some unphysical singular cases, this probability wave adheres to the limit.
l i m T → 0 ψ = ψ
It is worth noting that the SQHA equations (23-26) show that the gravitational dark energy leads to a self-fluctuating system where the noise is an intrinsic property of the spacetime dynamical geometry that does not require the presence of an environment.
The agreement between the SQHM and the well-established quantum theory outputs can be additionally validated by applying it to mesoscale systems ( L < ∼ λ c ). In this scenario, the SQHM reveals that ψ adheres to the generalized Langevin-Schrodinger equation, which, for time-independent systems, is expressed as follows
− i ℏ ∂ t | ψ | = ℏ 2 2 m ∂ i ∂ i ψ − ( V ( q ) + C o n s t + κ S − q i 1 / 2 q i 1 / 2 m κ D 1 / 2 ξ ( t ) + i Q d i s s ( q , t ) 2 | ψ | 2 ) ψ
that by using (??) can be readjusted as:
− i ℏ ∂ t | ψ | = ( ℏ 2 2 m ∂ i ∂ i − V ( q ) − κ ( ℏ 2 l n ψ ψ * + q i 1 / 2 q i 1 / 2 m D 1 / 2 ξ ( t ) ) − i Q d i s s ( q , t ) 2 | ψ | 2 ) ψ
Moreover, by introducing, close to the zero noise, the semiempirical parameter α , defined by the relation [19 and references therein]
l i m L λ c → 0 κ ≅ α 2 k T m D ,
and characterizing the ability of the system to dissipate, the realization of quantum mechanics is ensured by the condition l i m T → 0 α = 0 . On this ansatz, (29) reads as
− i ℏ ∂ t | ψ | = ℏ 2 2 m ∂ i ∂ i ψ − ( V ( q ) − α 2 k T D ( ℏ 2 m l n ψ ψ * + q i 1 / 2 q i 1 / 2 D 1 / 2 ξ ( t ) ) + i Q d i s s ( q , t ) 2 | ψ | 2 ) ψ
where Q d i s s ( q , t ) accounts for the compressibility of the mass density distribution | ψ | 2  as a consequence of dissipation [19].
In ref. [19] it is shown that for highly dissipative quantum system with l i m T → 0 α ≠ 0 equation (32) converges to the Langevin-Schrodinger equation.

2.1. Emerging Classical Mechanics on Large Size Systems

When manually nullifying the quantum potential in the equations of motion for quantum hydrodynamics (1-3), the classical equation of motion emerges [17]. However, despite the apparent validity of this claim, such an operation is not mathematically sound as it alters the essential characteristics of the quantum hydrodynamic equations. Specifically, this action leads to the elimination of stationary configurations, i.e., eigenstates, as the balancing force of the quantum potential against the Hamiltonian force [24]—which establishes their stationary mass density distribution condition—is nullified. Consequently, even a small quantum potential cannot be disregarded in conventional quantum mechanics as described by the zero-noise ‘deterministic’ quantum hydrodynamic model (2-4).”
Conversely, in the stochastic generalization, it is possible to correctly neglect the quantum potential in (19, 4.7) when its force is much smaller than the force noise ϖ such as | 1 m ∂ i V q u ( ρ ) | ≪ | ϖ ( q , t , T ) |  that by (4.7) leads to condition
| 1 m ∂ i V q u ( ρ ) | ≪ κ ( L λ c ) ( γ D ℏ 2 m ) 1 / 2 = κ ( L m k T 2 ℏ ) ( γ D ℏ 2 m ) 1 / 2 ,
and hence, in a coarse-grained description with elemental cell side Δ q , to
l i m q → Δ q | ∂ i V q u ( ρ ) | ≪ m κ ( L λ c ) ( γ D ℏ 2 m ) 1 / 2 = m κ γ D L 2 k T 2 ℏ ,
where L is the physical length of the system.
It is worth noting that, despite the noise ϖ ( q , t , T ) having a zero mean, the mean of the fluctuations in the quantum potential, denoted as V ¯ s t ( n , S ) ≅ κ S , is not null. This non-null mean contributes to the dissipative force − κ q ˙ ( t )  in equation (6.22). Consequently, the stochastic sequence of noise inputs disrupts the coherent evolution of the quantum superposition of states, causing them to converge to a stationary mass density distribution with q ˙ ( t ) = 0 . Moreover, by observing that the stochastic noise
κ ( L λ c ) ( γ D ℏ 2 m ) 1 / 2 ξ ( t )
grows with the size of the system, for macroscopic systems (i.e., L λ c → ∞ ), condition (33) is satisfied if
l i m q λ c → ∞ ( L λ c = ∞ ) | 1 m ∂ i V q u ( n ( q ) ) | < ∞ .
In order to achieve a large-scale description completely free from quantum correlations for any finite values of the physical length L  of the system, a more rigorous requirement must be imposed, such as
l i m q λ c → ∞ | 1 m ∂ i V q u ( ρ ( q ) ) | = l i m q λ c → ∞ 1 m ∂ i V q u ( ρ ( q ) ) ∂ i V q u ( ρ ( q ) ) = 0 .
Hence, recognizing that for linear systems
l i m q → ∞ V q u ( q ) ∝ q 2 ,
it readily concludes that these systems are incapable of generating the macroscopic classical phase. In general, as the Hamiltonian potential strengthens, the wave function localization increases, and the quantum potential behavior at infinity becomes more prominent.
This is demonstrable by considering the MDD
| ψ | 2 ∝ e x p [ − P k ( q ) ] ,
where P k ( q ) is a polynomial of order k, and it becomes evident that a finite range of quantum potential interaction is achieved for k < 3 2 .
Hence, linear systems, characterized by k=0k=0, exhibit an infinite range of quantum potential action.
On the other hand, for instance, for gas phases with particles that interact by the Lennard-Jones potential, whose long-distance wave function reads [25]
l i m r → ∞ | ψ | ∝ a − 1 / 2 1 r ,
the quantum potential reads
l i m r → ∞ V q u ( ρ ) ≅ l i m q → ∞ ℏ 2 2 m 1 | ψ | ∂ r ∂ r | ψ | = 1 r 2 = ℏ 2 m a | ψ | 2
leading to the quantum force
l i m r → ∞ − ∂ r V q u ( ρ ) = l i m q → ∞ ℏ 2 2 m ∂ r 1 | ψ | ∂ r ∂ r | ψ | = ℏ 2 2 m ∂ r r ∂ r ∂ r 1 r = − 2 ℏ 2 m 1 r 3 = 0 ,
that by (33, 37), can lead to large-scale classical behavior [19] in a sufficiently rarefied phase.
It is interesting to note that in (41), the quantum potential is at the basis of the hard sphere potential of the “pseudo potential Hamiltonian model” of the Gross-Pitaevskii equation [26,27], where a 4 π  is the boson-boson s-wave scattering length.
By observing that, to fulfill condition (37), we can sufficiently require that
∫ 0 ∞ r − 1 | 1 m ∂ i V q u ( ρ ( q ) ) | ( r , θ , φ ) d r   <   ∞ ∀ θ , φ ,
so that it is possible to define the quantum potential range of interaction λ q u as [19]
λ q u = λ c ∫ 0 ∞ r − 1 | ∂ i V q u ( ρ ( q ) ) | ( r , θ , φ ) d r | ∂ i V q u ( ρ ( q ) ) | ( r = λ c , θ , φ ) = λ c I q u .   I q u > 1
Relation (44) provides a measure of the physical length associated with quantum non-local interactions.
It is worth mentioning that the quantum non-local interaction extends themselves up to the distance of order of the largest length between λ q u  and λ c . Below λ c , an even feeble quantum potential emerges because of the damping of the noise, above λ c but below λ q u the quantum potential is strong enough to overcome the fluctuations. The quantum non-local effects can be extended by increasing λ c as a consequence of lowering the temperature or the mass of the bodies (see § 2.3), while λ q u grows by strengthening the Hamiltonian potential. In the latter case, for instance, larger values of λ q u can be obtained by extending the linear range of Hamiltonian interaction between particles (see § 2.2).
As a direct consequence of equation (39), when examining phenomena at intermolecular distances where the interaction is linear, the behavior exhibits quantum characteristics (e.g., X-ray diffraction). However, when observing macroscopic properties that involve the non-linear behavior of the Lennard-Jones potential—decreasing to zero at infinity, such as in the case of low-frequency acoustic waves with wavelengths much larger than the linear range of interatomic force—there is a transition to classical behavior, being the range of interaction of the quantum potential λ q u  finite (see § 5.1).

2.2. The Lindemann Constant for Quantum Lattice-to-Classical Fluid Transition

For a system of Lennard-Jones interacting particles, the quantum potential range of interaction λ q u  reads
λ q u ≅ ∫ 0 d d q + λ c 4 ∫ d ∞ 1 q 4 d q = d ( 1 + 1 3 ( λ c d ) 4 )
where d = r 0 + Δ = r 0 ( 1 + ε ) (with ε = Δ r 0 ) represents the distance up to which the interatomic force is approximately linear, and r 0 denotes the atomic equilibrium distance.
Experimental validation of the physical significance of the quantum potential length of interaction is evident during the quantum-to-classical transition in a crystalline solid at its melting point. This transition occurs as the system shifts from a quantum lattice to a fluid amorphous classical phase.
Assuming that, within the quantum lattice, the atomic wave function (around the equilibrium distance  r 0 ) extends over a distance smaller than the quantum coherence length, it can be inferred that at the melting point, its variance is equal to λ q u − r 0
Based on these assumptions, the Lindemann constant L C defined as [28]
L C = { wave   function   variance at   transition } r 0
can be expressed as L C = λ q u − r 0 r 0  and it can be theoretically calculated, as
λ q u ≈ r 0 ( ( 1 + ε ) + 1 3 ( λ c r 0 ) 3 )
that, being typically ε ≈ 0 , 05 ÷ 0 , 1 and λ c r 0 ≈ 0 , 8 , leads to
L C ≈ 0 , 217 ÷ 0 , 267 .
A more precise assessment, utilizing the potential well approximation for molecular interaction [29,30], results in λ q u ≅ 1 , 2357   r 0 , and yields a value L C = 0 , 2357  for the Lindemann constant consistent with measured values, falling within the range of 0.2 to 0.25 [28].

2.3. The Fluid-Superfluid 4He λ − Transition

Given that the De Broglie distance λ c is temperature-dependent, its impact on the fluid-superfluid transition in monomolecular liquids at extremely low temperatures, as observed in 4He, can be identified. The approach to this scenario is elaborated in reference [30], where, for the 4He -4He interaction, the potential well is assumed to be.
V ( r ) = ∞       0 < r < σ
V ( r ) = - 0 , 82   U         σ < r < σ + 2 Δ
V ( r ) = 0         σ + 2 Δ < r
In this context, U = 10 , 9   k B = 1 , 5 × 10 − 22 J represents the Lennard-Jones potential depth, σ + Δ = 3 , 7 × 10 . − 10   m denotes the mean 4He -4He inter-atomic distance where Δ = 1 , 54 × 10 . − 10   m .
Ideally, at the superfluid transition, the De Broglie length attains approximately the mean 4He -4He atomic distance. However, the induction of the superfluid 4He -4He state occurs as soon as the De Broglie length overlaps with the 4He -4He wavefunctions within the potential depth. Therefore, we observe the gradual increase of 4He superfluid concentration within the interval
σ < λ c < σ + 2 Δ .
For λ c < σ , we have, that no superfluid 4He. For λ c > ≈ σ + 2 Δ 100% of 4He is in the superfluid state. Therefore, given that
λ c = 2 ℏ ( m k T ) 1 / 2 ,
When the superfluid/normal 4He density ratio is 50%, it follows that the temperature T 50 % , for the 4He mass of m 4 H e = 6.6 × 10 . − 27 k g , is given by
T 50 % = 2 ℏ 2 m k ( 1 σ + Δ ) 2 = 1 , 92   ° K
which is in good agreement with the experimental data from reference [31], which is approximately 1 , 95   ° K .
On the other hand, since for  λ c = σ + 2 Δ all the couples of 4Hefall into the quantum state, the superfluid ratio of 100% is reached at the temperature
On the other hand, given that for λ c = σ + 2 Δ , all pairs of 4He enter the quantum state, the superfluid ratio of 100% is attained at the temperature
T 100 % ≈ 2 ℏ 2 m k ( 1 σ + 2 Δ ) 2 = 0 , 92   ° K
also consistent with the experimental data from reference [31], which is approximately 1 , 0   ° K .
Moreover, by employing the superfluid ratio of 38% at the λ -point of 4He, such that λ c = σ + 38 % ( 2 Δ ) , the transition temperature T λ is determined as follows
T λ ≈ 2 ℏ 2 m k ( 1 σ + 0 , 76 Δ ) 2 = 2 , 20   ° K
in good agreement with the measured superfluid transition temperature of 2 , 17   ° K .
As a final remark, it is worth noting that there are two ways to establish quantum macroscopic behavior. One approach involves lowering the temperature, effectively increasing the de Broglie length. The second approach is to enhance the strength of the Hamiltonian interaction among the particles within the system.
Regarding the latter, it is important to highlight that the limited strength of the Hamiltonian interaction over long distances is the key factor allowing classical behavior to manifest. When examining systems governed by a quadratic or stronger Hamiltonian potential, the range of interaction associated with the quantum potential becomes infinite, as illustrated in equation (68). Consequently, achieving a classical phase becomes unattainable, regardless of the system’s size.
In this particular scenario, we exclusively observe the complete manifestation of classical behavior on a macroscopic scale within systems featuring interactions that are sufficiently weak, weaker even than linear interactions, which are classically chaotic. In this case, the quantum potential lacks the ability to exert its nonlocal influence over extensive distances.
Therefore, classical mechanics emerges as a decoherent outcome of quantum mechanics when fluctuating spacetime background is involved.

2.4. Measurement Process and the Finite Range of Nonlocal Quantum Potential Interactions

Throughout the course of measurement, there exists the possibility of a conventional quantum interaction between the sensing component within the experimental setup and the system under examination. This interaction concludes when the measuring apparatus is relocated to a considerable distance from the system. Within the SQHM framework, this relocation is imperative and must surpass specified distances λ c  and  λ q u .
Following this relocation, the measuring apparatus takes charge of interpreting and managing the “interaction output.” This typically involves a classical, irreversible process characterized by a distinct temporal progression, culminating in the determination of the macroscopic measurement result.
Consequently, the phenomenon of decoherence assumes a pivotal role in the measurement process. Decoherence facilitates the establishment of a large-scale classical framework, ensuring authentic quantum isolation between the measuring apparatus and the system, both pre and post the measurement event.
This quantum-isolated state, both at the initial and final stages, holds paramount significance in determining the temporal duration of the measurement and in amassing statistical data through a series of independent repeated measurements.
It is crucial to underscore that, within the confines of the SQHM, merely relocating the measured system to an infinite distance before and after the measurement, as commonly practiced, falls short in guaranteeing the independence of the system and the measuring apparatus if either λ c = ∞ or  λ q = ∞ is met. Therefore, the existence of a macroscopic classical reality remains indispensable for the execution of measurement process.

2.5. Minimum Measurement Uncertainty of Quantum Systems in Fluctuating Spacetime Background

Any quantum theory aiming to elucidate the evolution of a physical system across various scales, at any order of magnitude, must inherently address the transition from quantum mechanical properties to the emergent classical behavior observed at larger magnitudes. The fundamental disparities between the two descriptions are encapsulated by the minimum uncertainty principle in quantum mechanics, signifying the inherent incompatibility of concurrently measuring conjugated variables, and the finite speed of propagation of interactions and information in local classical relativistic mechanics.
Should a system fully adhere to the “deterministic” conventions of quantum mechanics up to a distance, possibly smaller than, where its subparts lack individual identities, the independent observer, to gain information about the system, needs to maintain a separation distance bigger than both before and after the process.
Should a system fully adhere to the conventional quantum mechanics within a physical length  ℒ q , smaller than λ c , where its subparts lack individual identities, the independent observer, that wants to gain information about the system, needs to maintain a separation distance bigger than ℒ q both before and after the process.
Therefore, due to the finite speed of propagation of interactions and information, the process cannot be executed in a time frame shorter than
Δ τ min > ℒ q c ∝ λ c c ∝ 2 ℏ ( 2 m c 2 k T ) 1 / 2 .
Furthermore, considering the Gaussian noise (20) with the diffusion coefficient proportional to  k T , we find that the mean value of energy fluctuation is δ E ( T ) = k T 2  for the degree of freedom. As a result, a nonrelativistic ( m c 2 > > k T ) scalar structureless particle, with mass m, exhibits an energy variance Δ E  of
Δ E ≈ ( < ( m c 2 + δ E ( T ) ) 2 − ( m c 2 ) 2 > ) 1 / 2 ≅ ( < ( m c 2 ) 2 + 2 m c 2 δ E − ( m c 2 ) 2 > ) 1 / 2 ≅ ( 2 m c 2 < δ E > ) 1 / 2 ≅ ( m c 2 k T ) 1 / 2
from which it follows that
Δ E Δ t > Δ E Δ τ min ∝ ( m c 2 k T ) 1 / 2 λ c c ) ∝ 2 ℏ ,
It is noteworthy that the product Δ E Δ τ  remains constant, as the increase in energy variance with the square root of T  precisely offsets the corresponding decrease in the minimum acquisition time τ . This outcome holds true when establishing the uncertainty relations between the position and momentum of a particle with mass m.
If we acquire information about the spatial position of a particle with precision Δ L , we effectively exclude the space beyond this distance from the quantum non-local interaction of the particle, and consequently
ℒ q < Δ L .
the variance Δ p of its relativistic momentum ( p μ p μ ) 1 / 2 = m c due to the fluctuations reads
Δ p ≈ ( < ( m c + δ E ( T ) c ) 2 − ( m c ) 2 > ) 1 / 2 ≅ ( < ( m c ) 2 + 2 m δ E − ( m c ) 2 > ) 1 / 2 ≅ ( 2 m < δ E > ) 1 / 2 ≅ ( m k T ) 1 / 2
and the uncertainty relation reads
Δ L Δ p > ℒ q ( m k T ) 1 / 2 ∝ λ c ( m k T ) 1 / 2 ) ∝ 2 ℏ
Equating (62) to the uncertainty value, such as
Δ L Δ p > ℒ q ( 2 m k T ) 1 / 2 = ℏ 2
or
Δ E Δ t > Δ E Δ τ min = ( 2 m c 2 k T ) 1 / 2 ℒ q c = ℏ 2 ,
It follows that  ℒ q = λ c 2 2 represents the physical length below which quantum entanglement is fully effective, and it signifies the deterministic limit of the SQHM, specifically the realization of quantum mechanics.
As far as it concerns the theoretical minimum uncertainty of quantum mechanics, obtainable from the minimum indeterminacy (59, 62) in the limit of quantum mechanics ( T = 0  and  λ c → ∞ ) in the non-relativistic limit (), we have that
With regard to the minimum uncertainty of quantum mechanics, attainable from the minimum indeterminacy (59, 62) in the limit of T = 0 ( λ c → ∞ ), in the non-relativistic limit ( c → ∞ ), it follows that
Δ τ min = λ c 2 c 2 → ∞
Δ E ≅ ( m c 2 k T ) 1 / 2 = 2 ℏ c λ c → 0
ℒ q = λ c 2 2 → ∞
Δ p ≅ ( m k T ) 1 / 2 ≅ 2 ℏ λ c → 0
and therefore that
Δ E Δ t > Δ E Δ τ min = ℏ 2
Δ L Δ p > ℒ q ( m k T ) 1 / 2 = ℏ 2
That constitutes the minimum uncertainty in quantum mechanics, obtained as the deterministic limit of the SQHM.
It’s worth noting that, owing to the finite speed of light, the SQHM extends the uncertainty relations to all conjugate variables of 4D spacetime. In conventional quantum mechanics, deriving the energy-time uncertainty is not possible because the time operator is not defined.
Furthermore, it is interesting to note that in the relativistic limit of quantum mechanics ( T = 0  and  λ c → ∞ ), influenced by the finite speed of light, the minimum acquisition time of information in the quantum limit is expressed as follows
Δ τ min = ℒ q c → ∞ .
The result (71) indicates that performing a measurement in a fully deterministic quantum mechanical global system is not feasible, as its duration would be infinite.
Given that non-locality is restricted to domains with physical lengths on the order of λ c 2 2 , and information about a quantum system cannot be transmitted faster than the speed of light (violating the uncertainty principle otherwise), local realism is established within the coarse-grained macroscopic physics where domains of order of λ c 3 reduce to a point.
The paradox of “spooky action at a distance” is confined to microscopic distances (smaller than λ c 2 2 ), where quantum mechanics is described in the low-velocity limit, assuming c → ∞ and λ c → ∞ . This leads to the apparent instantaneous transmission of interaction over a distance.
It is also noteworthy that in the presence of noise, the measure indeterminacy has a relativistic correction since
leading to the minimum uncertainty in a quantum system submitted to gravitational background noise ( T > 0 )
It is also noteworthy that in the presence of noise, the measured indeterminacy undergoes a relativistic correction, as expressed by Δ E ≅ ( m c 2 k T ( 1 + k T 4 m c 2 ) ) 1 / 2 , resulting in the minimum uncertainty in a quantum system subject to gravitational background noise ( T > 0 ):
Δ E Δ t > ℏ 2 ( 1 + k T 4 m c 2 ) 1 / 2
and
Δ L Δ p > ℏ 2 ( 1 + k T 4 m c 2 ) 1 / 2
This can become significant for light particles (with m → 0 ), but in quantum mechanics, at T = 0 , the uncertainty relations remain unchanged.

2.6. Minimum Discrete Interval of Spacetime

Within the framework of the SQHM, incorporating the uncertainty on measure in fluctuating quantum system and the maximum attainable velocity of the speed of light
x · ≤ c ,
it follows that the uncertainty relations
x · ≥ Δ x · = Δ p m = ℏ 2 m Δ x ,
leads to ℏ 2 m Δ x ≤ c  and, consequently, to
Δ x > ℏ 2 m c = R c 2 .
where R c  is the Compton’s length.
Identity (76) reveals that the maximum concentration of the mass of a body is within an elemental volume with a side length equal to half of its Compton wavelength.
This result holds significant implications for black hole (BH) formation. To form a BH, all the mass must be contained within the gravitational radius  R g , giving rise to the relationship:
R g = 2 G m c 2 > Δ x 2 = r min = R c 4 ,
which further leads to the condition:
R c 4 R g = ℏ 8 m c R g = ℏ c 8 m 2 G = π m p 2 m 2 < 1
indicating that the BH mass cannot be smaller than π m p = ℏ c 8 m 2 G .
The validity of the result (76) is substantiated by the gravitational effects produced by the quantum mass distribution within spacetime [32,33]. This demonstration elucidates that when mass density is condensed into a sphere with a diameter equal to half the Compton length, it engenders a quantum potential force that precisely counters the compressive gravitational force within a black hole.
Considering the Planck mass black hole as the lightest configuration, with its mass compressed within a sphere of half the Compton wavelength, it logically follows that black holes with masses greater than m p [19] exhibit their mass compressed into a sphere of smaller diameter. Consequently, given the significance of elemental volume as the volume inside which content is uniformly distributed, the consideration of the Planck length as the smallest discrete elemental volume of spacetime is not sustainable. This would make it impossible to compress the mass of large black holes within a sphere of a diameter of half Compton’s length, consequently preventing the achievement of gravitational equilibrium [33].
This output holds significant importance, as it forms the basis for both loop quantum gravity and non-commutative string theories. The former theory relies on the postulate that there exists an absolute limitation on length measurements in quantum gravity.
While, in principle, it is correct to steer clear of the unrealizable concepts of infinite and infinitesimal, the fundamental arguments of these theories assume that to pinpoint a particle within a sphere of a Planck length radius, an energy greater than the Planck mass is required that shields whatever occurs within the Schwarzschild radius. Consequently, this represents the smallest ‘quanta’ of space and time. This assumption conflicts with the fact that any existing black holes compress their mass into a nucleus smaller than the Planck length [33].
This compression is only feasible if spacetime discretization allows elemental cells of smaller volume, thereby distinguishing between the minimum measurable distance and the minimum discrete element of distance in the spacetime lattice. In the simulation analogy, the maximum grid density is equivalent to the elemental cell of the spacetime. Additionally, the vacuum in the collapsed branched phase envisioned by pure quantum gravity cannot occupy a spacetime volume smaller than one elemental cell.
Finally, it is worth noting that the current theory leads to the assumption that the elemental discrete spacetime distance corresponds to the Compton length of the maximum possible mass, which is the energy/mass of the Universe. Consequently, we have a criterion to rationalize the mass of the Universe—why it is not higher than its value—being intricately linked to the minimum length of the discrete spacetime element. If the pre-big-bang black hole (PBBH) has been generated by a fluctuation anomaly in an elemental cell of spacetime, it could not have a mass/energy content smaller than that which the universe possesses.

2.6.1. Dynamics of Wavefunction Collapse

The Markov process (17) can be described by the Smolukowski equation for the Markov probability transition function (PTF) [23]
P ( q , q 0 | t + τ , t 0 ) = ∫ − ∞ ∞ P ( q , z | τ , t )   P ( z , q 0 | t − t 0 , t 0 )   d r z
where the PTF P ( q , z | τ , t )  is the probability that in time interval τ is transferred to point q.
The conservation of the PMD shows that the PTF displaces the PMD according to the rule [23]
ρ ( q , t ) = ∫ P ( q , z | t , 0 ) ρ ( z , 0 ) d r z
Generally, for the quantum case, Equation (79) cannot be reduced to a Fokker–Planck equation (FPE). The functional dependence of V q u ( ρ )  by ρ ( q , t ) , and by the PTF P ( q , z | t , 0 ) , produces non-Gaussian terms [19].
Nonetheless, if, at initial time, ρ ( q , t 0 ) is stationary (e.g., quantum eigenstate) and close to the long-time final stationary distribution ρ e q , it is possible to assume that the quantum potential is constant in time as a Hamilton potential following the approximation
V q u ≅ − ( ℏ 2 4 m ) ( ∂ q ∂ q ( l n ρ e q ( q ) ) + 1 2 ( ∂ q ( l n ρ e q ( q ) ) ) 2 ) .
Being the quantum potential independent by the mass density time evolution, the stationary long-time solutions ρ e q ( q ) can be approximately described by the Fokker–Planck equation
∂ t P ( q , z | t , 0 ) + ∂ i P ( q , z | t , 0 ) ⋅ υ i = 0
where
υ i = 1 m κ ∂ i ( ℏ 2 4 m ( ∂ j ∂ j l n ρ e q − 1 2 ( ∂ j l n ρ e q ) 2 ) + V ( q ) ) − D 2 ∂ i l n ρ e q
leading to the final equilibrium of the stationary quantum configuration
1 m κ ∂ i ( V ( q ) − ℏ 2 4 m ( ∂ j ∂ j ( l n ρ e q ( q ) ) + 1 2 ( ∂ j ( l n ρ e q ( q ) ) ) 2 ) ) + D 2 ∂ i ( l n ρ e q ) = 0
In ref. [19] the stationary states of a harmonic oscillator obeying (84) are shown. The results show that the quantum eigenstates are stable and maintain their shape (with a small change in their variance) when subject to fluctuations.
It is worth mentioning that in (84) ρ  and does not represent the fluctuating quantum mass density | ψ | 2  but is the probability mass density (PMD) of it.

2.6.2. Evolution of the PMD of Superposition of States Submitted to Stochastic Noise

The quantum evolution of not-stationary state superpositions (not considering fast kinetics and jumps) involves the integration of Equation (17) that reads as
q ˙ = − 1 κ m ∂ q ( V ( q ) − ℏ 2 4 m ( ∂ q ( ∂ q l n ρ ) + 1 2 ( ∂ q l n ρ ) 2 ) ) + D 1 / 2 ξ ( t )
By utilizing both the Smolukowski Equation (85) and the associated conservation Equation (80) for the PMD ρ , it is possible to integrate (85) by using its second-order discrete expansion
q k + 1 ≅ q k − 1 m κ ∂ k ( V ( q k ) + V q u ( ρ q k , t k ) ) Δ t k − 1 m κ d d t ∂ k ( V ( q k ) + V q u ( ρ q k , t k ) ) Δ t k 2 2 + D 1 / 2 Δ W k
where
q k = q ( t k )
Δ t k = t k + 1 − t k
Δ W k = W ( t k + 1 ) − W ( t k )
where Δ W k has a Gaussian zero mean and unitary variance which probability function P ( Δ W k , Δ t ) , for Δ t k = Δ t   ∀   k , reads as
l i m Δ t → 0 P ( Δ W k , Δ t ) = l i m Δ t → 0 D − 1 / 2 ( 4 π Δ t ) 1 / 2 e x p − Δ W k 2 4 Δ t = l i m Δ t → 0 D − 1 / 2 ( 4 π Δ t ) 1 / 2 e x p − 1 4 Δ t ( q k + 1 − < q k + 1 > ) 2 D = ( 4 π D Δ t ) − 1 / 2 e x p − 1 4 Δ t ( q k + 1 − q k − < q ¯ ˙ k > Δ t − < q ¯ ¨ k > 2 Δ t 2 ) 2 D
where the midpoint approximation has been introduced
q ¯ k = q k + 1 + q k 2 ,
and where
< q ¯ ˙ k > = − 1 m κ ∂ ( V ( q ¯ k ) + V q u ( ρ q ¯ k t k ) ) ∂ q ¯ k
and
< q ¯ ¨ k > = − 1 2 m κ d d t ∂ ( V ( q ¯ k ) + V q u ( ρ ( q ¯ k ) , t k ) ) ∂ q ¯ k
are the solutions of the deterministic problem
< q k + 1 > ≅ < q k > − 1 m κ ∂ k ( V ( q k ) + V q u ( ρ q k , t k ) ) Δ t k − 1 m κ d d t ∂ k ( V ( q k ) + V q u ( ρ q k , t k ) ) Δ t k 2 2 .
As shown in ref. [19], the PTF P ( q k , q k − 1 | Δ t , ( k − 1 ) Δ t ) can be achieved after successive steps of approximation and reads as
P ( q k , q k − 1 | Δ t , ( k − 1 ) Δ t ) = l i m u → ∞ P ( u ) ( q k , q k − 1 | Δ t , ( k − 1 ) Δ t ) ≅ ( 4 π D Δ t ) − 1 / 2 e Δ t 4 D [ − ( q ˙ k − 1 − < q ˙ k > ( ∞ ) + < q ˙ k − 1 > 2 ) 2 + D ( ∂ q k < q ˙ k > ( ∞ ) + ∂ q k − 1 < q ˙ k − 1 > ) ] .
and the PMD at the k -th instant reads as
ρ ( ∞ ) ( q k , k Δ t ) = ∫ − ∞ ∞ P ( ∞ ) ( q k , q k − 1 | Δ t , ( k − 1 ) Δ t )   ρ ( q k − 1 , ( k − 1 ) Δ t ) d q k − 1 .
leading to the velocity field
< q ˙ k > ( ∞ ) = − 1 m κ ∂ q k ( V ( q k ) − ℏ 2 4 m ( ∂ q ∂ q ( l n ρ ( ∞ ) ) + 1 2 ( ∂ q ( l n ρ ( ∞ ) ) ) 2 ) )
Moreover, the continuous limit of the PTF gives
P ( q , q 0 | t − t 0 , 0 ) = l i m Δ t → 0 P ( ∞ ) ( q n , q 0 | n Δ t , 0 ) = l i m Δ t → 0 ∫ − ∞ ∞ ∏ k = 1 n d q k − 1 P ( ∞ ) ( q k , q k − 1 | Δ t , ( k − 1 ) Δ t ) = ∫ q 0 q D q e [ − 1 2 D ∑ k = 1 n < q ¯ ˙ k − 1 > ( ∞ ) Δ q k ] e − Δ t 4 D [ ∑ k = 1 n ( q k − q k − 1 Δ t ) 2 − 2 D ∂ < q ¯ ˙ k − 1 > ( ∞ ) ∂ q ¯ k − 1 + < q ¯ ˙ k − 1 > ( ∞ ) 2 ] = ( e ∫ q 0 q 1 2 D < q ˙ > d q ) ∫ q 0 q D q e − 1 4 D ∫ t 0 t d t ( q ˙ 2 + < q ˙ > 2 + 2 D ∂ q < q ˙ > )
where  < q ¯ ˙ k − 1 > ( ∞ ) = 1 2 ( < q ˙ k > ( ∞ ) + < q ˙ k − 1 > ( ∞ ) ) .
The resolution of the recursive Expression (98) offers the advantage of being applicable to nonlinear systems that are challenging to handle using conventional approaches [34,35,36,37].

2.6.3. General Features of Relaxation of the Quantum Superposition of States

The classical Brownian process admits the stationary long-time solution
P ( q , q − ∞ | t − t − ∞ , t − ∞ ) = l i m t 0 → − ∞ N e 1 D ∫ q − ∞ q < q ˙ > ( q ′ ( t , t 0 ) ) d q ′ = N e 1 D ∫ q − ∞ q K ( q ′ ) d q ′
where  K ( q ) = − 1 m κ ∂ V ( q ) ∂ q , leading to solution [13]
P ( q , q 0 | t − t 0 , t 0 ) = ( e x p ∫ q 0 q 1 2 D K ( q ′ ) d q ′ ) ∫ q 0 q D q e x p − 1 4 D ∫ t 0 t d t ( q ˙ 2 + K 2 ( q ) + 2 D ∂ q K ( q ) )
As far as it concerns < q ˙ > ( ∞ ) ( q , t )  in (98,) it cannot be expressed in a closed form, unlike (99), because it is contingent on the particular relaxation path ρ ( q , t )  the system follows toward the steady state. This path is significantly influenced by the initial conditions, namely the MDD | ψ | 2 ( q , t 0 ) = ρ ( q , t 0 ) as well as < q ˙ > ( q , t 0 ) , and, consequently, by the initial time t 0 at which the quantum superposition of states is subjected to fluctuations.
In addition, from (86), we can see that q t k  depends on the exact sequence of inputs of stochastic noise, since, in classically chaotic systems, very small differences can lead to relevant divergences of the trajectories in a short time. Therefore, in principle, different stationary configurations ρ ( q , t = ∞ ) (analogues of quantum eigenstates) can be reached whenever starting from identical superposition of states. Therefore, in classically chaotic systems, Born’s rule can also be applied to the measurement of a single quantum state.
Even if L ≪ λ c ∪ λ q u , it is worth noting that, to have finite quantum lengths λ c  and λ q u (necessary to have the quantum stochastic dynamics) and the quantum decoupled (classical) environment or measuring apparatus), the nonlinearity of the overall system (system–environment) is necessary: Quantum decoherence, leading to the decay of superposition states, is significantly promoted by the widespread classical chaotic behavior observed in real systems.
On the other hand, a perfect linear universal system would maintain quantum correlations on a global scale and would never allow quantum decoupling between the system and the experimental apparatus performing the measure (see § 5). It should be noted that even the quantum decoupling of the system from the environment would be impossible, as quantum systems function as a unified whole. Merely assuming the existence of separate systems and environments subtly introduces the classical condition into the nature of the overall supersystem.
Furthermore, given that the relationship (19) (see Equations A31,A38, in ref.19]) is valid only in the leading order of approximation of q ˙ (i.e., during a slow relaxation process with small amplitude fluctuations), in instances of large fluctuations occurring on a timescale much longer than the relaxation period of ρ ( q , t ) , transitions may occur to n ˜ ( q , t )  that are not captured by (98), potentially leading from a stationary eigenstate to a general superposition of states.
In this case, relaxation will follow again toward another stationary state. The ρ ( q , t ) (96), describes the relaxation process occurring in the time interval between two large fluctuations rather than the system evolution toward a statistical mixture. Due to the extended timescales associated with these jumping processes, a system comprising a significant number of particles (or independent subsystems) undergoes a gradual relaxation towards a statistical mixture. The statistical distribution of this mixture is dictated by the temperature-dependent behavior of the diffusion coefficient.

2.7. EPR Paradox and Pre-Existing Reality

The SQHM highlights that quantum theory, despite its well-defined reversible deterministic theoretical framework, remains incomplete with respect to its foundational postulates. Specifically, the SQHM underscores that the measurement process is not explicated within the deterministic “Hamiltonian” framework of standard quantum mechanics. Instead, it manifests as a phenomenon comprehensively described within the framework of a quantum stochastic generalized approach.
The SQHM reveals that quantum mechanics represents the deterministic (zero noise) limit of a broader quantum-stochastic theory induced by spacetime gravitational background fluctuations.
From this standpoint, the zero-noise quantum mechanics defines the deterministic evolution of the “probabilistic wave” of the system. Moreover, the SQHM suggests that the term “probabilistic” is inaccurately introduced, arising from the inherent probabilistic nature of the measurement process, as the standard quantum mechanics itself cannot fully describe its output. Given the capacity of the SQHM to describe both wavefunction decay and the measurement process, thereby achieving a comprehensive quantum theory, the term “state wave” is a more appropriate substitute for the expression “probabilistic wave”. The SQHM theory reinstates the principle of determinism into quantum theory, emphasizing that it delineates the deterministic evolution of the “state wave” of the system. It elucidates the probabilistic outcomes as a consequence of the fluctuating gravitational background.
Furthermore, it is noteworthy to observe that the SQHM addresses the lingering question of preexisting reality before measurement. In contrast, the Copenhagen interpretation posits that only the measurement process allows the system to decay into a stable eigenstate, establishing a persistent reality over time. Consequently, it remains indeterminate within this framework whether a persistent reality exists prior to measurement.
About this point, the SQHM introduces a simple and natural innovation showing that the world is capable of self-decaying through macroscopic-scale decoherence, wherein only the stable macroscopic eigenstates persist. These states, being stable with respect to fluctuations, establish an enduring reality that exists prior to measurement.
Regarding the EPR paradox, the SQHM demonstrates that, in a perfect quantum deterministic (coherent) universe is not feasible to achieve the complete decoupling between the subparts of the system, namely the measuring apparatus and the measured system, and carry out the measurememnt in a finite time interval. Instead, this condition can only be realized within a large-size classical supersystem—a quantum system in a 4D spacetime with fluctuating background —where the quantum emtanglement, due to the quantum potential, extends up to a finite distance [19]. Under these circumstaance, the SQHM shows that it is possible to restore the local relativistic causality (see § 2.5).
If the Lennard-Jones interparticle potential yields a sufficiently weak force, resulting in a microscopic range of quantum non-local interaction and a large-scale classical phase, photons, as demonstrated in reference [19], maintain their quantum behavior at the macroscopic level due to their infinite quantum potential range of interaction. Consequently, they represent the optimal particles for conducting experiments aimed at demonstrating the characteristics of quantum entanglement over a distance.
In order to clearly describe the standpoint of the SQHM on this argument, we can analyze the output of two entangled photon experiments traveling in opposite directions in the state
| ψ > = 1 2 | H 1 , H 2 > + e i φ | V 1 , V 2 >
where V and H are vertical and horizontal polarizations, respectively, and ϕ is a constant phase coefficient.
Photons “one” and “two” impact polarizers P a (Alice) and P b (Bob) with polarization axes positioned at angles α  and β relative to the horizontal axis, respectively. For our purpose, we can assume ϕ = 0 .
The probability that photon “two” also passes through Bob’s polarizer is P ( α , β ) = 1 2 cos 2 ( α − β ) .
As widely held by the majority of the scientific community in quantum mechanics physics, when photon “one” passes through polarizer P a with its axes at an angle of α , the state of photon “two” instantaneously collapses to a linear polarized state at the same angle α , resulting in the combined state | α 1 , α 2 > = | α 1 > | α 2 > .
In the context of the SQHM, able to describe the kinetics of the wavefunction collapse, the collapse is not instantaneous, and following the Copenhagen quantum mechanics standpoint, it needs to assert rigorously that the state of photon “two” is not defined before its measurement at the polarizer P b .
Therefore, after photon “one” passes through polarizer P a , from the standpoint of SQHM, we have to assume that the combined state is | α 1 , S > = | α 1 > | Q P 1 , S 2 > , where the state | Q P 1 , S 2 >  represents the state of photon “two” in the interaction with the residual quantum potential field Q P 1 generated by photon “one” at polarizer P a . The spatial extension of the field | Q P 1 , S 2 >  of the photon two, in the case the photons travel in opposite direction, is the double of that one crossed by the photon one before its adsorption. In this regard, it is noteworthy that the quantum potential is not proportional to the intensity of the field. Instead, it is proportional to its second derivative. Therefore, a minor perturbation in the field with a high frequency at the tail of photon two (during the absorption of photon one) can give rise to a significant quantum potential field Q P 1 .
When the residual part of the two entangled photons | Q P 1 , S 2 >  also passes through Bob’s polarizer, it makes the transition | Q P 1 , S 2 > → | β 2 > with probability P ( α , β ) = 1 2 cos 2 ( α − β ) . The duration of the photon two adsorption (wavefunction decay and measurement) due to its spatial extension, and finite light speed, it is just the time necessary to transfer the information about the measure of photon one to the place of photon two measurement. A possible experiment is proposed in ref. [19].
Summarizing, the SQHM reveals the following key points:
  • The SQHM posits that quantum mechanics represents the deterministic limit of a broader quantum stochastic theory;
  • Classical reality emerges at the macroscopic level, persisting as a preexisting reality before measurement;
  • The measurement process is feasible in a classical macroscopic world, because we can have really quantum decoupled and independent systems, namely the system and the measuring apparatus;
  • Determinism is acknowledged within standard quantum mechanics under the condition of zero GBN;.
  • Locality is achieved at the macroscopic scale, where quantum non-local domains condense to punctual domains.
  • Determinism is recivered in quantum mechannics representing the zero-noise limit of the SQHM. The probabilistic nature of quantum measurement is introduced by the GBN.
  • The maximum light speed of the propagation of information and the local relativistic causality align with quantum uncertainty;
  • The SQHM addresses the GBN as playng the role of the hidden variable in the Bohm non-local hidden variaboe theory: The Bohm theory ascribes the indeterminacy of the measurement process to the unpredictable pilot wave, whereas the Stochastic Quantum Hydrodynamics attributes its probabilistic nature to the fluctuating gravitational background. This background is challenging to determine due to its predominantly early-generation nature during the Big Bang, characterized by the weak force of gravity without electromagnetic interaction. In the context of Santilli’s non-local hidden variable approach in IsoRedShift Mechanics, it is possible to demonstrate the direct correspondence between the non-local hidden variable and the GBN. Furthermore, it must be noted that the consequent probabilistic nature of the wavefunction decay, and measure output, is also compounded by the inherently chaotic nature of the classical law of motion and the randomness of the GBN, further contributing to the indeterminacy of measurement outcomes.

2.8. The SQHM and the Objective-Collapse Theories

The SQHM well inserts itself into the so-called Objective Collapse Theories [38,39,40,41]. In collapse theories, the Schrödinger equation is augmented with additional nonlinear and stochastic terms, referred to as spontaneous collapses, that serve to localize the wave function in space. The resulting dynamics ensures that, for microscopic isolated systems, the impact of these new terms is negligible, leading to the recovery of usual quantum properties with only minute deviations.
An inherent amplification mechanism operates to strengthen the collapse in macroscopic systems comprising numerous particles, overpowering the influence of quantum dynamics. Consequently, the wave function for these systems is consistently well-localized in space, behaving practically like a point in motion following Newton’s laws.
In this context, collapse models offer a comprehensive depiction of both microscopic and macroscopic systems, circumventing the conceptual challenges linked to measurements in quantum theory. Prominent examples of such theories include: Ghirardi–Rimini–Weber model [38], Continuous spontaneous localization model [39] and the Diósi–Penrose model [40,41].
While the SQHM aligns well with existing Objective-Collapse models, it introduces an innovative approach that effectively addresses critical aspects within this class of theories. One notable achievement is the resolution of the ‘tails’ problem by incorporating the quantum potential length of interaction, in addition to the De Broglie length. Beyond this interaction range, the quantum potential cannot maintain coherent Schrödinger quantum behavior and wavefunction tails.
The SQHM also highlights that there is no need for an external environment, demonstrating that the quantum stochastic behavior responsible for wave-function collapse can be an intrinsic property of the system in a spacetime with fluctuating metrics due to the gravitational background. Furthermore, situated within the framework of relativistic quantum mechanics, which aligns seamlessly with the finite speed of light and information transmission, the SQHM establishes a clear connection between the uncertainty principle and the invariance of light speed.
The theory also derives, within a fluctuating quantum system, the indeterminacy relation between energy and time—an aspect not expressible in conventional quantum mechanics—providing insights into measurement processes that cannot be completed within a finite time interval in a truly quantum global system. Notably, the theory finds support in the confirmation of the Lindemann constant for the melting point of solid lattices and the transition of He4 from fluid to superfluid states. Additionally, it proposes a potential explanation for the measurement of entangled photons through a Heart-Moon-Mars experiment [19].

3. Simulation Analogy: Complexity in Achieving Future States

The discrete spacetime structure that comes from the finite spedd of ligth together with the quantum uncertainty (???) allows the implementation of a discrete simulation of the universe’s evolution.
In this case, the programmer of such universal simulation has to face with the following problems:
  • One key argument revolves around the inherent challenge of any computer simulation, namely the finite nature of computer resources. The capacity to represent or store information is confined to a specific number of bits. Similarly, the availability of Floating-point Operations Per Second (FLOPS) is limited. Regardless of efforts, achieving a truly “continuous” simulated reality in the mathematical sense becomes unattainable due to these constraints. In a computer-simulated universe, the existence of infinitesimals and infinities is precluded, necessitating quantization, which involves defining discrete cells in spacetime.
  • The speed of light must be finite. Another common issue in computer-simulation arises from the inherent limitation of computing power in terms of the speed of executing calculations. Objects within the simulation cannot surpass a certain speed, as doing so would render the simulation unstable and compromise its coherence. Any propagating process cannot travel at an infinite speed, as such a scenario would require an impractical amount of computational power. Therefore, in a discretized representation, the maximum velocity for any moving object or propagating process must conform to a predefined minimum single-operation calculation time. This simulation analogy aligns with the finite speed of light (c) as a motivating factor.
  • Discretization must be dynamic The use of fixed-size discrete grids is clearly a huge dispersion of computational resource in spacetime regions where there are no bodies and there is nothing to calculate (so that we can fix there just one big cell saving computational resources). On the one hand, the need to increase the size of the simulation requires lowering the resolution; on the other hand, it is possible to achieve better resolution within smaller domains of the simulation. This dichotomy is already present to those creating vast computerized cosmological simulations [42]. This problem is attaked by varying the mass quantization grid resolution as a function of the local mass density and other parameters leading to the so-called Automatic Tree Refinement (ATR). The Adaptive Moving Mesh Method, a similar approach [43] to that of ATR would be to vary the size of the cells of the quantized mass grid locally, as a function of kinetic energy density while at the same time varying the size of the local discrete time-step, which should be kept per-cell as a 4th parameter of space, in order to better distribute the computational power where it’s needed the most. By doing so, the grid would result as distorted having different local sizes. In a 4D simulation this effect would also invole the time that be perceived as flowing differently in different parts of the simulation: faster for regions of space where there’s more local kinetic energy density, and slower where there’s less. [additional consequences are reported and discussed into the section 3.3].
In principle, there are two instruments or methods for computing the future states of a system. One involves utilizing a classical apparatus composed of conventional computer bits. Unlike Qbits, these classical bits cannot create, maintain, or utilize the superposition of their states, rendering them classical machines. On the other hand, quantum computation employs a quantum system of Qbits and utilizes the quantum law of evolution for calculations.
However, the capabilities of the classical and quantum approaches to predict the future state of a system differ. This distinction becomes evident when considering the calculation of the evolution of many-body. In the classical approach, computer bits must compute the position and interactions of each at every calculation step. This becomes increasingly challenging (and less precise) due to the chaotic nature of classical evolution. In principle, the classical N-body simulations are straightforward as they primarily entail integrating the 6N ordinary differential equations that describe particle motions. However, in practice, the sheer magnitude of particles, N, is often exceptionally large (of order of millions or ten billions like in the Millennium simulation [43]). Moreover, the computational expense becomes prohibitive due to the quadratic increase N 2 in the number of particle-particle interactions that need to be computed. Consequently, direct integration of the differential equations requires an exponential increase of calculation and data storage resources for large scale simulations.
On the other hand, quantum evolution doesn’t require defining the state of each particle at every step. It addresses the evolution of the global wave of superposition of states for all particles. Eventually, when needed or when decoherence is induced or spontaneously occurs, the classical state of each particle at a specific instant is obtained through the wavefunction decay (under this standpoint, calculated is the analogous of “measured”). This represents a form of optimization: sacrificing the knowledge of the classical state at each step, but being content with knowing the classical state of each particle at discrete time instants (just every a large number of calculation steps). This approach allows for a quicker computation of the future state of reality with a lesser use of resources. Moreover, since the length of quantum coherence λ q u is finite, the group of entangled particles undergoing to the common wavefunction decay, are of smaller finite number, further simplifying the algorithm of the simulation.
The advantage of quantum calculus over classical calculus can be metaphorically demonstrated by addressing the challenge of finding the global minimum. When using classical methods like maximum descent gradient or similar approaches, the pursuit of the global minimum—such as in the determination of prime numbers—results in an exponential increase in the calculation time as the maximum value of the prime numbers rises.
In contrast, employing the quantum method allows us to identify the global minimum in linear or, at least, polynomial time. This can be loosely conceptualized as follows: in the classical case, it’s akin to having a ball fall into each hole to find a minimum, and then the values of each individual minimum must be compared with all possible minima before determining the overall minimum. The utilization of the quantum method involves using an infinite number of balls, spanning the entire energy spectrum. Consequently, at each barrier between two minima (thanks to quantum tunneling), some of the balls can explore the next minimum almost simultaneously. This simultaneous exploration (quantum computing) significantly shortens the time needed to probe the entire set of minima, then wavefunction decay allows to measure (or detect) the outcome of the process (measure).
If we aim to create a simulation on a scale comparable to the vastness of the Universe, we must find a way to address the many-body problem. Currently, solving this problem remains an open challenge in the field of Computer Science. However, Quantum Mechanics appears to be a promising candidate for making the many-body problem manageable. This is achieved through the utilization of the Entanglement process, which encodes coherent particles and their interaction outcomes as a wavefunction. The wavefunction evolves without explicit solving and, when coherence diminishes, the wavefunction collapse leads to calculate (as well determine) the essential classical properties of the system given by the underlying physics at discrete time steps.
This sheds light on the reason why physics properties remain undefined until measured; from the standpoint of the simulation analogy it is a direct consequence of the quantum optimization algorithm, where properties are computed only when necessary. Moreover, the combination of the coherent quantum evolution with the wavefunction collapse has been proven to constitute a Turing-complete computational process, as evidenced by its application in Quantum Computing for performing computations.
An even more intriguing aspect of the possibility that reality can be virtualized as a computer simulation is the existence of an algorithm capable of solving the intractable many-body problem, challenging classical algorithms. Consequently, the entire class of problems characterized by a phenomenological representation, describable by quantum physics, can be rendered tractable through the application of quantum computing. However, it’s worth noting that very abstract mathematical problems, such as the ‘lattice problem’ [44], may still remain intractable. Currently, the most well-known successful examples of quantum computing include Shor’s algorithm [45] for prime number discovery and Grove’s algorithm [46] for inverting ‘black box functions.’
Classical computation categorizes the determination of prime numbers as an NP (non-polynomial) problem, whereas quantum computation classifies it as a P (polynomial) problem with the Shor’s Algorithm. However, not all problems considered NP in classical computation can be reduced to P problems by utilizing quantum computation. This implies that quantum computing may not be universally applicable in simplifying all problems but a certain limited class.
The possibility of acknowledging the universe many-body problem as a computer simulation requires that the NP problem of N-body is tractable. In such a scenario, it becomes theoretically feasible to utilize universe-like particle simulations for solving NP problems by embedding the problem within specific assigned particle behavior. This concept implies that the Laws of Physics are not inherently given but are rather formulated to represent the solution of specific problems
To clarify further: if various instances of universe-like particle simulations were employed to tackle distinct problems, each instance would exhibit different Laws of Physics governing the behavior of its particles. This perspective opens up the opportunity to explore the purpose of the Universe and inquire about the underlying problem it seeks to solve.
In essence, it prompts the question: What is the fundamental problem that the Universe is attempting to address?

3.1. How the Universe Computes the Next State: the Unraveling of the Meaning of Time and Free Will

At this stage, in order to analyze the universal simulation, producing the evolution with the characteristics of the SQHM in a flat space (at this stage) so that gravity is exclued except for the gravitational background noise that generates the quantum decoherence, let’s consider the local evolution, in a cell of spacetime of order of few De Broglie lengths or quantum coherence lengths λ q u [19]. After a certain characteristic time, the superposition of states, evolving following the motion equation (19), decays into one of its eigenstates and leads to a stable state that, surviving to fluctuations, constitutes a lasting over time measurable state: we can define it as reality since, for its stability, gives the same result even after repeated measurements. Moreover, given the macroscopic decoherence, the local domain in different places are quantum disentangled eachother, Therefore, their decay to the stable eigenste cannot contemporarely happen. Due to the perceived randomness of the GBN, this process can be assumed stochasticly distributrd into the space, leading to a fractal classical reality into the spacetime that in this way results locally quantum but globally classic.
Furthermore, after an interval of time much larger than the wavefunction decay one, each domain is perturbed by a large fluctuation that is able to let it to jump to a quantum superposition that re-starts to evolve following the quantum law of evolution for a while, before new wavefunction collapse, and so on.
From the standpoint of the SQHM, the universal computation method exploits the quantum evolution for a while and then by the decoherence derives the classical N-body state at certain discrete instants by the wavefunction collapse exatly as a universal quantum computer. Then it goes to the next step by computing the evolutin of the quantum entangled wavefunction evolution, saving up of classically calculating the state of the N-bodies repeatedly, deriving it only when the quantum state decays into the classical one (as in a measure).
Practically, the universe realizes a sort of computational optimization to speed up the derivation of its future state by usitilizing a Qbits-like quantum computation..

3.1.1. The Free Will

Following the pigeonhole principle, which states that any computer that is a subsystem of a larger one cannot handle the same information (thus cannot produce a greater power of calculation in terms of speed and precision) as the larger one, and considering the inevitable information loss due to compression, we can infer that a human-made computer, even utilizing a vast system of Q-bits, cannot be faster and more accurate than the universal quantum computer.
Therefore, the temporal horizon of predicting the future states, before they happen, is by force limited inside the reality. Therefore, among the many future states possible, we can infer that we can determine or choose the future output within a certain temporal horizon and that free will is limited. Moreover,since the decision of what reality state we want to realize is not connected to the preceeedings events before a certain preceding interval of time (4D disentanglement), we can also say that such decision it is not predetermined.
Nevertheless, other than the will is free but limited, from the present analysis there is an additional aspect of the concept of free will that comes out. Specifically pertaining to whether many possible states of reality exist in future scenarios, providing us with the genuine opportunity to choose which of them to attain.
In this context, within the deterministic quantum evolution framework, or even in classical scenarios, with precisely defined initial conditions in 4D spacetime, such a possibility is effectively prohibited since the future states are predetermined. Time in this context does not flow but merely serves as a “coordinate” of the 4D spacetime where reality is depicted, losing the significance it holds in the real life.
In absence of GBN, knowing the initial condition of the universe at initial instant of the big-bang and the laws of physics precisely, it is possible to predict the future of the universe.
This is because, unless you introduce noise in the simulation, the basic quantum law of physics are deterministic..
Actually, in the context of stochastic quantum evoltion, the random nature of the GBN plays an important role in shaping the future states of the universe. From the standpoint of the simulation anaòpgy the nature of GBN presents important informational aspects.
The randomness introduced by this noise renders the simulation inherently unpredictable to an internal observer. Even if the internal observer employs the identical algorithm as the simulation to forecast future states, the absence of access to the same noise source results in rapid divergence in their predictions of future states. This is due to the critical influence of each individual fluctuation on the wavefunction decay (see section ??). In other words, to the internal observer, the future would be encrypted by such noise. Furthermore, if the noise that would be used in the simulation analogy evolution would be a pseudo-random noise with enough unpredictability, only who is in possession of the seed would in fact be able to predict the future or invert the arrow of time. Even if the noise is a pseudo-random, the problem of deriving the cryptation key can practically be intractable. Therefore, in presence of GBN, the future outcome of the computation is “encrypted” by the randomness of the GBN.
Moreover, if the simulation makes use of a pseudo-random routine to generate the GBN and it appears truly-random inside the reality, it follows that the seed “encoding GBN” is kept outside the simulated reality, and is unreachable to us. In this case we are in front of an instance of a “one-time pad”, effectively equating to deletion, which is proven unbreakable. Therefore, in principle, the simulation could effectively conceal information about the key used to encrypt the GBN noise in a manner that remains unrecoverable.
From this perspective, the renowned Einstein quote, “God does not play dice with the universe,” is aptly interpreted. In this context, it implies that the programmer of the universal simulation does not engage in randomness, as everything is predetermined for him. However, from within the reality, we remain unable to ascertain the seed of the noise, and the noise manifests itself as genuinely random. Furthermore, even if from the inside reality we would be able to detect the pseudo-random nature of the GBN, featuring a high level of randomness, the challenge of deciphering the key remains insurmountable [47] and the encryption key practically irretrievable.
Thus, we would never be able to tracing back to the encryption key and completely reproduce the outcomes of the simulation even knowing the initial state and all the laws of physics perfectly since the simulated evolution depends by the form of each single fluctuation.
This universal behavior emphasizes the concept of ‘free will’ as a constrained capability, unable to access information beyond a specific temporal horizon. Furthermore, the simulation analogy delves deeper into this idea, portraying free will as a faculty originating in macroscopic classical (living) systems characterized by fractal dimensions in spacetime. Consequently, free will lacks perfect definition in our consciousness. Nonetheless, through the exercise of our free will, we can impact the forthcoming macroscopic state, albeit with a certain imprecision and ambiguity in our intentions, yet not predetermined by preceding states of reality beyond a specific interval of time.

3.2. The Universal “Pasta Maker” and the Actual Time in 4D spacetime

Working with a discrete spacetime offers advantages that are already supported by lattice gauge theory [48]. This theory demonstrates that in such a scenario, the path integral becomes finite-dimensional and can be assessed using stochastic simulation techniques, such as the Monte Carlo method.
In our scenario, the fundamental assumption is that the optimization procedure for universal computation has the capability to generate the evolution of reality. This hypothesis suggests that the universe evolves quantum mechanics in polynomial time, efficiently solving the many-body problem and transitioning it from NP to P. In this context, quantum computers, employing Q-bits with wavefunction decay that both produces and effectively computes the result, utilize a method inherent to the physical reality itself.
From a global spacetime perspective, aside from the collapses in each local domain, it is important to acknowledge a second fluctuation-induced effect. Larger fluctuations taking place over extended time intervals can induce a jumping process in the wavefunction configuration, leading to a generic superposition of states. This prompts a restart in its evolution following quantum laws. As a result, after each local wavefunction decay, a quantum resynchronization phenomenon occurs, propelling the progression towards the realization of the next local classical state of the universe.
Furthermore, with quantum synchronization, at the onset of the subsequent moment, the array of potential quantum states (in terms of superposition) encompasses multiple classical states of realization. Consequently, in the current moment, the future states form a quantum multiverse where each individual classical state is potentially attainable depending on events (such as the chain of wave-function decay processes) occurring beforehand. As the present unfolds, marked by the quantum decoherence process leading to the attainment of a classical state, the past is generated, ultimately resulting in the realization of the singular (fractal) classical reality: the Universe.
Moreover, if all possible configurations of the realizable universe exist in the future (extending past our ability to determine or foresee over a finite temporal extent), the past is comprised of fixed events (universe) that we are aware of but unable to alter.
In this context, we can metaphorically illustrate spacetime and its irreversible universal evolution as an enormous pasta maker. In this analogy, the future multiverse is represented by a blob of unshaped flour dough, inflated because it contains all possible states. This dough, extending up to the surface of the present, is then pressed into a thin pasta sheet, representing the quantum superposition decay to the classical state realizing the universe.
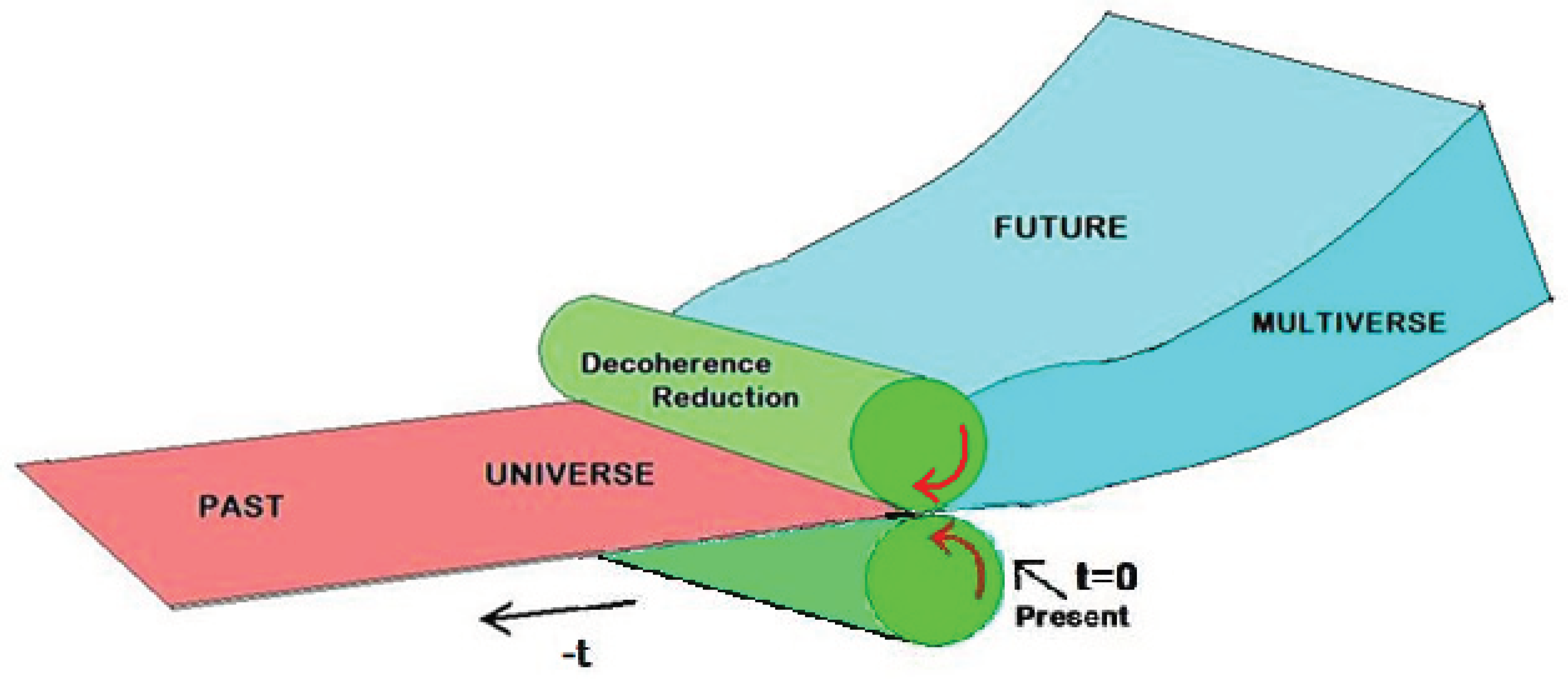
Preprints 101218 g001
Figure 1. The Universal “Pasta-Maker”.
Figure 1. The Universal “Pasta-Maker”.
Preprints 101218 g001
The 4D surface boundary between the future multiverse and the past universe marks the instant of present time. At this point, the irreversible process of decoherence occurs, entailing the computation or reduction to the present classical state. This specific moment defines the current time of reality, a concept that cannot be precisely located within the framework of relativistic spacetime.

3.3. Quantum and Gravity

Until now, we haven’t adequately discussed how gravity arises from the discrete nature of the universal ‘calculation.’ Nevertheless, it’s interesting to provide some insights into the issue because, viewed through this perspective, gravity naturally emerges as quantized.
Considering the universe as an extensive quantum computer operating on a predetermined spatiotemporal grid doesn’t yet represent the most optimized simulation. In fact, the fixed dimensions of the elemental grid haven’t been considered in the optimization of the simulation. This becomes apparent when we realize that maintaining constant elemental cell dimensions leads to a significant dispersion of computational resources in spacetime regions devoid of bodies or any need for calculation. In such regions, we could simply allocate one large cell, thereby conserving computational resources.
This perspective aligns with a numerical algorithm employed in numerical analysis known as adaptive mesh refinement (AMR). This technique dynamically adjusts the accuracy of a solution within specific sensitive or turbulent regions during the calculation of a simulation. In numerical solutions, computations often occur on predetermined, quantified grids, such as those in the Cartesian plane, forming the computational grid or ‘mesh.’ However, many issues in numerical analysis do not demand uniform precision across the entire computational grid as, for instance, used for graph plotting or computational simulation. Instead, these issues would benefit from selectively refining the grid density only in regions where enhanced precision is required.
The local adaptive mesh refinement (AMR) creates a dynamic programming environment enabling the adjustment of numerical computation precision according to the specific requirements of a computation problem, particularly in areas of multidimensional graphs that demand precision. This method allows for lower levels of precision and resolution in other regions of the multidimensional graphs. The credit for this dynamic technique of adapting computation precision to specific requirements goes to Marsha Berger, Joseph Oliger, and Phillip Colella [49,50], who developed an algorithm for dynamic gridding known as AMR. The application of AMR has subsequently proven to be widely beneficial and has been utilized in the investigation of turbulence problems in hydrodynamics, as well as the exploration of large-scale structures in astrophysics, exemplified by its use in the Bolshoi Cosmological Simulation [51]
An intriguing variation of Adaptive Mesh Refinement is the Adaptive Moving Mesh Method proposed by Huang Weizhang and Russell Robert [52]. This method employs an r-adaptive (relocation adaptive) strategy to achieve outcomes akin to those of Adaptive Mesh Refinement. Upon reflection, an r-adaptive strategy, grounded in local energy density as a parameter, bears resemblance to the workings of curved space-time in our Universe.
Conceivably, a more sophisticated cosmological simulation could leverage an advanced iteration of the Adaptive Moving Mesh Method algorithm. This iteration would involve relocating space grid cells and adjusting the local delta time for each cell. By moving cells from regions of lower energy density to those of higher energy density at the system’s speed of light and scaling the local delta time accordingly, the resultant grid would appear distorted and exhibit behavior analogous to curved space-time in General Relativity.
Furthermore, as cell relocation induces a distortion in the grid mesh, updating the grid at the speed of light, as opposed to simultaneous updating, would disperse computations across various time frames. In this scenario, gravity, time dilation, and gravitational waves would spontaneously manifest within the simulated universe, mirroring their emergence from curved space-time in our Universe.
A criterion for reducing the grid step is based on providing a more detailed description in regions with higher mass density (more particles or energy density) and a higher amplitude of induced quantum potential fluctuations that reduces the De Broglie length of quantum coherence.
This point of view finds an example in the Lagrangian approach, as outlined in ref. [53], where the computational mesh dynamically moves with the matter being simulated. This results in an increased resolution, characterized by smaller mesh cells, in regions of high density, while decreasing resolution in other areas. While this approach holds significant potential, it is not without its challenges and limitations, as highlighted in the work of Gnedin and Bertschinger [54].
The variability of the mesh introduces noticeable apparent forces, which are deemed undesirable in the method [55] due to their tendency to violate energy conservation. Consequently, countermeasures are implemented to eliminate or rectify this inconvenience.
From the standpoint of the Simulation Analogy, where a field of force naturally emerges due to lattice cell distortion caused by its density variability, this effect is not as problematic as it might initially appear. The force field resulting from this optimization process in the calculation effectively represents gravity as an ‘apparent’ force arising from lattice cell distortion. The 4D non-uniform lattice network of the universal algorithm replicates reality by depicting 3D space within curved spacetime, incorporating the influence of gravity. The universal algorithm includes rules for modulating the variable density of the computational grid to simulate the curved spacetime observed in reality.
From this perspective, gravity may arise as an apparent force resulting from the optimization process of AMR to streamline the advancement of the RS, and the emergence of gravity can be attributed to the algorithmic optimization. The theoretical framework for transitioning from the variable mesh of the computer simulation to the discrete 4D curved spacetime with gravity has the potential to provide insights into the spontaneous generation of quantized gravity.
From this line of reasoning, an intriguing observation emerges: dynamically enlarging grid cells in regions where less computational power is needed inevitably results in the creation of vast cells corresponding to empty spacetime. The constraint of limited resources makes it impossible to achieve an infinitely large grid cell, preventing the realization of completely flat space within any cell.
In the context of the quantum geometrization of spacetime [33], leading to a quintessence-like interpretation of the cosmological constant that diminishes with the universe’s expansion, the finite maximum size of the simulation cell implies that the cosmological constant can be arbitrarily small but not zero. This aligns with the implications of pure quantum gravity, which posits that a vacuum with zero cosmological constant collapses into a polymer-branched phase devoid of physical significance.
Moreover, due to the discrete nature of spacetime, the cosmological constant is also discrete, and the smallest discrete value before zero decreases as the universe expands. This raises the question: is there a minimal critical value for the cosmological constant (at a certain degree of universe inflation) below which the vacuum will collapse to the polymer-branched phase prompting an envisioning of the ultimate fate of the universe?
If achieving a zero-grid dimension is deemed impossible, the inquiry into the minimum elemental size of spacetime naturally arises. In this context, as highlighted in [19], the SQHM emphasizes the existence of a finite minimum discrete element of distance. Consequently, spacetime can be conceptualized as a lattice composed of elemental cells of discrete size, distinct from the minimum detectable distance governed by the gravitational radius of a black hole of Planck mass.
To establish the order of magnitude for the elemental size of spacetime, we can assert that the volume of such an elemental cell must not exceed the volume within which the matter of the pre-big-bang black hole collapses [33,56]. This condition ensures the presence of a quantum potential repulsive force equal to the attractive gravitational force, establishing the black hole equilibrium configuration, leading to the expression:
Δ x min = ℏ 2 m max c = ℏ 2 m u c = ℏ c 2 E u
where m u  is the mass equivalent to the total universe energy of the universe  E u ≅ 10 53 ÷ 60 j [57], leading to
Δ x min = ℏ c 2 E u ≈ 6.62 × 10 × − 34 3 × 10 8 2 × 10 53 ÷ 60 ≈ 10 − ( 78 ÷ 85 ) m
where, being c , ℏ , E u , physical constants, make also Δ x min a physical universal constant. Furthermore, for the time coordinate this requires that
Δ t min = ℏ c 2 c E u ≈ 3 × 10 − ( 87 ÷ 94 ) s

3.3.1. The Classical Limit Problem in Quantum Loop Gravity (QLG) and Causal Dynamical Triangulation (CDT)

Even if from the standpoint of the simulation analogy both QLG and CDT take support and endorsement, also a contradictory aspect emerges in the procedure to achieve the classical limit of the theories, namely the general relativity.
About this point, the SQHM asserts that achieving classical macroscopic reality requires not only imposing the condition l i m ℏ → 0 , but enforcing the double conditions
l i m m a c r o ≡ l i m d e c l i m ℏ → 0 = l i m ℏ → 0 l i m d e c
where the subscript “dec” stands for decoherence defined as
l i m d e c ψ = l i m d e c ∑ k = k min k = k max b k | ψ k | e x p [ i S ( k ) ℏ ] = b k ˜ | ψ k ˜ | e x p [ i S ( k ˜ ) ℏ ]
where k min < k ˜ < k max is one of the k max − k min  eigenstates and holding.
The SQHM demonstrates that in the so-called semiclassical limit, attained by the condition l i m ℏ → 0 , applied to the (zero-noise) quantum mechanics, the quantum entanglement between particles persists and influences interactions even at infinite distances. Thus, rather than a genuine classical limit, it portrays a large-scale quantum description. This approach implicitly supports the idea that the properties of the vacuum at a macroscopic large-scale replicate those at a small scale, which is not true due to the breaking of scale invariance symmetry by the De Broglie length.
This aspect can be analytically examined by exploring the least action principle [19,32], generalized in the Madelung hydrodynamic formulation.
In the quantum hydrodynamic approach, the quantum equation of motion for the complex wavefunction is separated into two equations involving real variables. These equations pertain to the conservation of mass density distribution and its evolution, which is described by a Hamilton-Jacobi-like equation. This evolution can be expressed through a generalized hydrodynamic Lagrangian function that adheres to a generalized stationary action condition principle.
By utilizing the quantum hydrodynamic Lagrangian, the variation of the quantum hydrodynamic action for a general quantum superposition of states (2.1.1) can be expressed as [32]
δ S = − 1 c ∫ ∭ | ψ | 2 ∑ k ( ( p ˜ ( k ) ∂ q ˙ ( k ) ν ∂ q μ ) δ q μ − ( ∂ L ˜ ( k ) ∂ | ψ k | − ∂ μ ∂ L ˜ ( k ) ∂ ∂ μ | ψ k | ) δ | ψ k | ) d Ω = δ ( Δ S Q m i x + Δ S Q ) ≠ 0
where
Δ S Q = 1 c ∫ ∭ | ψ | 2 ∑ k ( ∂ L ˜ ( k ) ∂ | ψ k | − ∂ μ ∂ L ˜ ( k ) ∂ ∂ μ | ψ k | ) δ | ψ k | d Ω
is the variation of the action generated by quantum effects and where
δ ( Δ S Q m i x ) = − 1 c ∫ ∭ | ψ | 2 ∑ k p ˜ ( k ) ∂ q ˙ ( k ) ν ∂ q μ δ | ψ k | d Ω
The expression (109) arises from the quantum mixing of superposition states, as the variation of the action solely due to eigenstates is represented by:
δ S = ∫ ∭ | ψ | 2 ( ∑ k ∂ L ˜ ( k ) ∂ x μ ( k ) ) δ x μ ( k ) d V d t = ∫ ∭ | ψ | 2 ∑ k ( ∂ L ˜ ( k ) ∂ q μ δ q μ + ∂ L ˜ ( k ) ∂ q ˙ ( k ) μ δ q ˙ ( k ) μ + ∂ L ˜ ( k ) ∂ | ψ k | δ | ψ k | + ∂ L ˜ ( k ) ∂ ∂ μ | ψ k | δ ∂ μ | ψ k | ) d V d t = 1 c ∫ ∭ | ψ | 2 ∑ k ( ( ∂ L ˜ ( k ) ∂ q μ − d d t ∂ L ˜ ( k ) ∂ q ˙ ( k ) μ ) δ q μ + ( ∂ L ˜ ( k ) ∂ | ψ k | − ∂ μ ∂ L ˜ ( k ) ∂ ∂ μ | ψ k | ) δ | ψ k | ) d Ω = δ ( Δ S Q ) ≠ 0
Moreover, given that the quantum motion equations for the k-th eigenstate (2.1.14-15) satisfies the condition
( ∂ L ˜ ( k ) ∂ q μ − d d t ∂ L ˜ ( k ) ∂ q ˙ ( k ) μ ) = 0
the variation of the action δ S for the k-th eigenstates reads
δ S = δ ( Δ S Q ( k ) ) = 1 c ∫ ∭ | ψ k | 2 ( ∂ L ˜ ( k ) ∂ | ψ k | − ∂ μ ∂ L ˜ ( k ) ∂ ∂ μ | ψ k | ) δ | ψ k | d Ω
and therefore by (??) it follows both that
l i m d e c δ S = ( Δ S Q ( k ) )
and that
l i m d e c δ ( Δ S Q m i x ) = 0
Furthermore, since in the semiclassical limit, for ℏ → 0  and consequently  V q u → 0 , we have that
∂ ( l i m ℏ → 0 L ( k ) ) ∂ | ψ k | = 0
∂ ( l i m ℏ → 0 L ( k ) ) ∂ μ | ψ k | = 0
and that
l i m ℏ → 0 δ ( Δ S Q ( k ) ) = 0
By utilizing (114, 117), it follows that
l i m ℏ → 0 l i m d e c δ S = 0
The classical least action law is recovered when the quantum hydrodynamic equations transition into their classical counterparts through the same limiting procedure.
From this perspective, it is not possible for any quantum gravity theory to achieve the classical limit of General Relativity solely by imposing l i m ℏ → 0 . This limitation arises because the classical least action, a fundamental principle of General Relativity, cannot be restored with a straightforward condition l i m ℏ → 0 .
This goes beyond a mere formal theoretical bottleneck; it is a genuine condition positing that spacetime at the macroscopic level undergoes decoherence and lacks quantum properties. This holds true, at least, in regions governed by Newtonian gravity. However, in high-gravity areas near black holes and within them, the strong gravitational interaction can give rise to macroscopic quantum entanglement over significant distances [56].
In this context, it is conceivable that quantum gravity approaches, such as QLG and CDT, might face substantial challenges in achieving the classical limit of General Relativity solely by taking the limit of a null Planck constant. Furthermore, given that the quantum uncertainty and the finite speed of light rules out the existence of a continuum limit, deeming it devoid of physical significance, CDT could encounter difficulties in attempting to derive it.

3.3.2. The Simulation Analogy and the Holographic Principle

Even if the Holographic Principle and the Simulation Analogy support the idea that reality is a phenomenon stemming from a computing process encoding it, some notable differences arise. The simulation analogy portrays the real world as if it were being orchestrated by a computational procedure subject to various optimization methods. The macroscopic classical reality, characterized by fractal patterns with short discrete time intervals in microscopic quantum domains, clearly shows that scale invariance is a broken symmetry in spacetime: The properties of the vacuum on a small scale are quite different from those on a macroscopic scale, at least in regions subjected to low gravity conditions [19], where the De Broglie length defines the absolute scale.
Conversely, the Holographic Principle, based on the insightful observation that 3-D space can be traced back to an informationally equivalent 2D formulation, that allows for the development of a theory where gravity and quantum mechanics can be described together, implicitly assumes that the properties of the vacuum at a macroscopic scale replicate those at a small scale, which is not accurate. Essentially, the holographic principle takes a similar shortcut to Quantum Loop Gravity and Causal Dynamical Triangulations, facing challenges in describing macroscopic reality and General Relativity (except possibly in cases of high gravity, like black holes, where quantum entanglement can extend over large distances [56]).
To address this gap, the theory must integrate the decoherence process, which involves leakage of information. A sort of condition of bounded information loss should be introduced to ensure a more comprehensive understanding of classical reality and make the theory less abstract, potentially paving the way for experimental confirmations.

4. Philosophical Breakthrough

The spacetime structure, governed by its laws of physical evolution that enable the modeling of reality as a computer simulation, eliminates the possibility of a continuous realization in both time and space. This applies both to quantum microscopic world and to classical objects with their dynamic behavior, encompassing living organisms and their information processing

4.1. Extending Free Will

Although we cannot predict the ultimate outcome of our decisions beyond a certain point in time, it is feasible to develop methods that enhance the likelihood of achieving our desired results in the distant future. This forms the basis of ‘best decision-making.’ It’s important to highlight that having the most accurate information about the current state extends our ability to forecast future states. Furthermore, the farther away the realization of our desired outcome is, the easier it becomes to adjust our actions to attain it. This concept can be thought of as a preventive methodology. By combining information gathering and preventive methodology, we can optimize the likelihood of achieving our objectives and, consequently, expanding our free will.
Additionally, to streamline the evaluation process of ‘what to do,’ in addition to the rational-mathematical calculations that dynamically exatly e detailed reconstruct the pathway to our final state, we can focus solely on the probability of a certain future state configuration being realized, adopting a faster evaluation (a sort of Monte Carlo approach). This allows us to potentially identify the best sequence of events to achieve our objective. States beyond the time horizon in a realistic context can be accessed through a multi-step tree pathway. A practical example of this approach is the widely recognized cardiopulmonary resuscitation procedure [58,59]. In this procedure, even though the early assurance of the patient’s rescue may not be guaranteed, it is possible to identify a sequence of actions that maximizes the probability of saving their life.
In the final scenario, free will is the ability to make the desired choice at each step, shaping the optimal path that enhances the probability of reaching the future desired reality. Considering the simulated nature of the universe, it becomes evident that utilizing powerful computers and softwares, such as those at the basis of artificial intelligence, for acquiring and handling information can significantly enhance the decision-making process. However, a comprehensive analysis and development of this argument extend beyond the scope of the current work and are deferred to future research.

4.2. Methodological Approaches, Emergent from the Darwinian Principle of Evolution, for the Best Future States Problem Solving

Considering intelligence as a function that, in certain circumstances, aids in finding the most effective way to achieve desired or useful outcomes, it’s conceivable that methods beyond slow and burdensome rational calculations exist to attain results. This concept aligns with emotional intelligence, a basic mechanism that, as demonstrated by psychology and neuroscience, initiates subsequent purposeful rational evaluation.
The simulation nature of reality demonstrates a form of intelligence (with both emotional and rational components) that has evolved through a selection process favoring the ‘winner is the best solution.’ Although this work does not delve into introducing another aspect, the physical law governing matter self-assembling [60] leading to the appearance of life, it can be asserted that two ‘methodologies of intelligence’ have emerged. The first is ‘captative intelligence’ where the subject, overcoming and/or destroying the antagonist, acquires its resources, and the second is ‘synergic intelligence’ seeking collaborative actions to share the gained resources or construct a more efficient system or structure. The latter form of natural intelligence has played a crucial role in shaping organized systems (living organism) and social structures and their behaviors. However, a detailed examination of these dynamics goes beyond the scope of this work and is left for future analysis.

4.3. Dynamical Conscience

By adhering to the quantum but macroscopically classical dynamics of the SQHM, all objects, including living organisms, within the simulation analogy undergo fresh re-calculations at each time step. This process propels them forward into the future within the reality. The compilation of previous instant states, stored and processed within an energy-information handling system, such as the brain, encapsulates the dynamics of evolution and forms the foundation of consciousness in living organisms [61,62,63].
Neuroscience conceptualizes the consciousness of the biological mind as a three-level process. Starting from the outermost level and moving inward, we have the cognitive calculation, the orientative emotional stage, and, at the most fundamental level, the discrete time acquisition routine. This routine captures the present state, compares it with the anticipated state from the previous time step, and projects the future state for the next acquisition step. The comparison between the anticipated and realized states provides input for decision-making at higher levels. Additionally, this comparison generates awareness of changes in reality and the speed of those changes, allowing for adjustments in the adaptive time scan velocity. In situations where reality is rapidly evolving with the emergence of new elements or potential dangers, the scanning time velocity is increased. This process gives rise to the perception of time dilation, where a few moments appear as a significantly prolonged period in the subject’s mind.
Considering the inherent nature of universal time progression, where optimal performance is attained through the utilization of quantum computation involving stepwise quantum evolution and wavefunction decay (output extraction), it becomes inevitable that, as a result of selective processes such as matter self-assembling and subsequent Darwinian evolution, the living system, optimized for maximum efficiency, inevitably adopts the highest-performing intelligence for a sub-universal system (the minds of living organisms) through the replication of the universal quantum computing method. This suggests that groups of interconnected neurons implement quantum computing at the microscopic level of their structure, resulting in their output and/or overall state being the outcome of multiple local wavefunction decays.
The macroscopic classical reality, characterized by fractal patterns and brief discrete time and microscopic space quantum domains, aligns with the Penrose-Hameroff theory [64] proposing that a quantum mechanical approach to consciousness can account for various aspects of human behavior, including free will. According to this theory, the brain utilizes the inherent property of quantum physical systems to exist in multiple superposed states, allowing it to explore a range of different options in the shortest possible period of time.

4.4. Intentionality of Conscience

Intentionality” is contingent upon the fundamental function of intelligence, which empowers the intelligent system to respond to environmental situations. Following calculation or emotional evaluation, when potential beneficial objectives are identified, intentionality is activated to initiate action. However, this reliance is constrained by the underlying laws of physics explicitly defined in the simulation. Essentially, the intelligent system is calibrated to adhere to the physics of the simulation. In our reality, it addresses all needs essential for development of life and organized structures, encompassing basic requirements, for instance, such as the necessity to eat, freedom of movement, association, and protection from cold and heat and many others.
This problem-solving disposition is, however, constrained by the physics of the environment. When it comes to artificial machines, they cannot develop intentionality solely through calculations because they lack integration with the world. In biological intelligence, the “hardware” is intricately linked with the physics of the environment. Not only does it manage energy and information, but there’s also an inverse influence: energy shapes and develops the hardware.
In contrast, a computational machine lacks the capacity to autonomously modify its hardware and establish criteria for its safe maintenance or enhancement. In other words, intentionality, the driving force behind the pursuit of desired solutions, cannot be developed by computational procedure executed by hardware. Intentionality serves as a safety mechanism, or navigation system, for a continually evolving intelligent system whose hardware is seamlessly integrated into its functionality and continuously updated. To achieve this, a physically self-evolving wetware is necessary.

4.5. Final Considerations

Considering that the maximum entropy tendency is not universally valid [65,66,67], but rather the most efficient energy dissipation with order and living structures formation is the emergent law [60], we are positioned to narrow down the goal, motivating the simulation, to two possibilities: the generation of life and/or the realization of an efficient intelligent system.
Furthermore, as the physical laws, along with the resulting evolution of reality, are embedded in the problem that the simulation seeks to address, intentionality and free will must be inherently manifested within the (simulated) reality to achieve the simulation’s objective

5. Conclusions

The stochastic quantum hydrodynamic model achieves a significant advancement by incorporating the influence of the fluctuating gravitational background, akin to a form of dark energy, into quantum equations. This approach offers solutions that effectively tackle crucial aspects within the realm of Objective-Collapse Theories. A notable accomplishment lies in resolving the ‘tails’ problem through the definition of the quantum potential length of interaction, supplementing the De Broglie length. Beyond the quantum interaction range, the quantum potential is unable to sustain coherent Schrödinger quantum behavior and wavefunction tails.
The SQHM additionally emphasizes that an external environment is unnecessary, illustrating that the quantum stochastic behavior leading to wave-function collapse can be an intrinsic property of the system within a spacetime characterized by fluctuating metrics. Moreover, positioned within the framework of relativistic quantum mechanics, seamlessly aligning with the finite speed of light and information transmission, the SQHM establishes a distinct connection between the uncertainty principle and the invariance of light speed
The theory further deduces, within a fluctuating quantum system, the indeterminacy relation between energy and time—an aspect not expressible in conventional quantum mechanics. This revelation offers insights into measurement processes that cannot be concluded within a finite time interval, particularly within a genuinely quantum global system. Remarkably, the theory garners experimental validation through the confirmation of the Lindemann constant concerning the melting point of solid lattices and the transition of 4He from fluid to superfluid states.
The self-consistency of the SQHM is guaranteed by its ability to depict the collapse of the wavefunction within its theoretical framework. This characteristic allows it to demonstrate the compatibility of the relativistic locality principle with the non-local property of quantum mechanics, specifically the uncertainty principle. Furthermore, by illustrating that large-scale systems naturally transition into decoherent stable states, the SQHM effectively resolves the Pre-existing Reality problem in quantum mechanics
Moving forward, the paper demonstrates that the physical dynamics of the SQHM can be analogized to a computer simulation where various optimization procedures are applied to bring it into realization. This conceptual framework leading to macroscopic reality of fractal consistency, wherein microscopic domains with quantum properties coexist, helps in elucidating the meaning of time in our contemporary reality and deepens our understanding of free will. The overarching design, introducing irreversible processes influencing the manifestation of macroscopic reality in the present moment, posits that the multiverse exists solely in future states, with the past constituted by the formed universe after the present instant. The decoherence at the present time represents a kind of multiverse reduction to a universe.
The discrete simulation analogy lays the foundation for a profound understanding of several crucial questions. It addresses inquiries about, the emergence of gravity in a discrete spacetime evolution, and the recovery of the classical General Relativity limit in Quantum Loop Gravity and Causal Dynamical Triangulation.
The Simulation Analogy reveals a strategy that minimizes the amount of information to be processed, thereby facilitating the operation of the simulated reality in attaining the solution of its predefined founding problem. From the perspective within, reality is perceived as the manifestation of simulation-specific physical laws. In the scenario under consideration, the simulation appears to employ an entropic optimization strategy, minimizing information loss while achieving maximum useful data compression and maintenance. All this in alignment with the simulation’s intended purpose.

References

  1. Ashtekar, A.; Bianchi, E. A short review of loop quantum gravity. Rep. Prog. Phys. 2021, 84, 042001. [Google Scholar] [CrossRef]
  2. Rovelli, C. Loop Quantum Gravity. Living Rev. Relativ. 1998, 1, 1–75. [Google Scholar] [CrossRef]
  3. Carroll, S.M.; Harvey, J.A.; Kostelecký, V.A.; Lane, C.D.; Okamoto, T. Noncommutative Field Theory and Lorentz Violation. Phys. Rev. Lett. 2001, 87, 141601. [Google Scholar] [CrossRef]
  4. Douglas, M.R.; Nekrasov, N.A. Noncommutative field theory. Rev. Mod. Phys. 2001, 73, 977–1029. [Google Scholar] [CrossRef]
  5. Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. B 1935, 47, 777–780. [Google Scholar] [CrossRef]
  6. Nelson, E. Derivation of the Schrödinger Equation from Newtonian Mechanics. Phys. Rev. B 1966, 150, 1079–1085. [Google Scholar] [CrossRef]
  7. Von Neumann, J. Mathematical Foundations of Quantum Mechanics; Beyer, R.T., Translator; Princeton University Press: Princeton, NJ, USA, 1955. [Google Scholar]
  8. Bell, J.S. On the Einstein Podolsky Rosen Paradox. Phys. Phys. Физика 1964, 1, 195–200. [Google Scholar] [CrossRef]
  9. Zurek, W. Decoherence and the Transition from Quantum to Classical—Revisited Los Alamos Science. 27 Number 2002. Available online: https://arxiv.org/pdf/quantph/0306072.pdf (accessed on 10 Jun 2003).
  10. Bassi, A.; Großardt, A.; Ulbricht, H. Gravitational decoherence. Class. Quantum Gravity 2016, 34, 193002. [Google Scholar] [CrossRef]
  11. Bohm, D. A Suggested Interpretation of the Quantum Theory in Terms of ‘Hidden Variables’ I and II. Physical Review 1952, 85, 166–179. [Google Scholar] [CrossRef]
  12. Feynman, R.P. Space-Time Approach to Non-Relativistic Quantum Mechanics. Rev. Mod. Phys. 1948, 20, 367–387. [Google Scholar] [CrossRef]
  13. Kleinert, H.; Pelster, A.; Putz, M. V. Variational perturbation theory for Marcov processes. Phys. Rev. E 2002, 65, 066128. [Google Scholar] [CrossRef]
  14. Mita, K. Schrödinger’s equation as a diffusion equation. Am. J. Phys. 2021, 89, 500–510. [Google Scholar] [CrossRef]
  15. Madelung, E. Quantentheorie in hydrodynamischer Form. Eur. Phys. J. A 1926, 40, 322–326. [Google Scholar] [CrossRef]
  16. Jánossy, L. Zum hydrodynamischen Modell der Quantenmechanik. Eur. Phys. J. A 1962, 169, 79–89. [Google Scholar] [CrossRef]
  17. Birula, I.B.; Cieplak, M.; Kaminski, J. Theory of Quanta; Oxford University Press: New York, NY, USA, 1992; pp. 87–115. [Google Scholar]
  18. Tsekov, R. Bohmian mechanics versus Madelung quantum hydrodynamics. arXiv 2011, arXiv:0904.0723v8. [Google Scholar]
  19. Chiarelli, P. Quantum-to-Classical Coexistence: Wavefunction Decay Kinetics, Photon Entanglement, and Q-Bits. Symmetry 2023, 15, 2210. [Google Scholar] [CrossRef]
  20. Santilli, R. M. A Quantitative Representation of Particle Entanglements via Bohm’s Hidden Variable According to Hadronic Mechanics. Progress in Physics 2002, 1, 150–159. [Google Scholar]
  21. Chiarell, P. The Stochastic Nature of Hidden Variables in Quantum Mechanics. Hadronic Joutnal 2023, 46, 315–38. [Google Scholar]
  22. Chiarelli, P. Can fluctuating quantum states acquire the classical behavior on large scale? J. Adv. Phys. 2013, 2, 139–163. [Google Scholar]
  23. Rumer, Y.B.; Ryvkin, M.S. Thermodynamics, Statistical Physics, and Kinetics; Mir Publishers: Moscow, 1980; pp. 444–459. [Google Scholar]
  24. H.
  25. Bressanini, D. An Accurate and Compact Wave Function for the 4He Dimer. EPL 2011, 96, 23001. [Google Scholar] [CrossRef]
  26. Gross, E.P. Structure of a quantized vortex in boson systems. Il Nuovo Cimento 1961, 20, 454–477. [Google Scholar] [CrossRef]
  27. Pitaevskii, P.P. Vortex lines in an Imperfect Bose Gas. Sov. Phys. JETP 1961, 13, 451–454. [Google Scholar]
  28. Rumer, Y.B.; Ryvkin, M.S. Thermodynamics, Statistical Physics, and Kinetics; Mir Publishers: Moscow, Russia, 1980; p. 260. [Google Scholar]
  29. Chiarelli, P. Quantum to Classical Transition in the Stochastic Hydrodynamic Analogy: The Explanation of the Lindemann Relation and the Analogies Between the Maximum of Density at He Lambda Point and that One at Water-Ice Phase Transition. Phys. Rev. Res. Int. 2013, 3, 348–366. [Google Scholar]
  30. Chiarelli, P. The quantum potential: The missing interaction in the density maximum of He4 at the lambda point? Am. J. Phys. Chem. 2014, 2, 122. [Google Scholar] [CrossRef]
  31. Andronikashvili, E.L. Zh. Zh. Éksp. Teor. Fiz 1946, 16, 780, 1948, 18, 424.
  32. Chiarelli, P. The Gravity of the Classical Klein-Gordon Field. Symmetry 2019, 11, 322. [Google Scholar] [CrossRef]
  33. Chiarelli, P. Quantum Geometrization of Spacetime in General Relativity; Sciencedomain International: Delhi, NCR, India, 2023; pp. 1–274. [Google Scholar]
  34. Ruggiero, P.; Zannetti, M. Quantum-classical crossover in critical dynamics. Phys. Rev. B 1983, 27, 3001–3011. [Google Scholar] [CrossRef]
  35. Ruggiero, P.; Zannetti, M. Critical Phenomena at T = 0 and Stochastic Quantization. Phys. Rev. Lett. 1981, 47, 1231. [Google Scholar] [CrossRef]
  36. Ruggiero, P.; Zannetti, M. Microscopic derivation of the stochastic process for the quantum Brownian oscillator. Phys. Rev. A 1983, 28, 987–993. [Google Scholar] [CrossRef]
  37. Ruggiero, P. ; Zannetti, M Stochastic description of the quantum thermal mixture 1982. Phys. Rev. Lett. 1982, 48, 963. [Google Scholar] [CrossRef]
  38. Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470–491. [Google Scholar] [CrossRef]
  39. Pearle, P. Combining stochastic dynamical state-vector reduction with spontaneous localization. Phys. Rev. A 1989, 39, 2277–2289. [Google Scholar] [CrossRef]
  40. Diósi, L. Models for universal reduction of macroscopic quantum fluctuations. Phys. Rev. A 1989, 40, 1165–1174. [Google Scholar] [CrossRef]
  41. Penrose, R. On Gravity's role in Quantum State Reduction. Gen. Relativ. Gravit. 1996, 28, 581–600. [Google Scholar] [CrossRef]
  42. Berger, M.J.; Oliger, J. Adaptive mesh refinement for hyperbolic partial differential equations. J. Comput. Phys. 1984, 53, 484–512. [Google Scholar] [CrossRef]
  43. Huang, W.; Russell, R.D. Adaptive Moving Mesh Method; Springer, 2010; ISBN 978-1-4419-7916-2. [Google Scholar]
  44. Micciancio, D.; Goldwasser, S. Complexity of lattice problems: a cryptographic perspective; Springer Science & Business Media, 2002; Vol. 671. [Google Scholar]
  45. Monz, T.; Nigg, D.; Martinez, E.A.; Brandl, M.F.; Schindler, P.; Rines, R.; Wang, S.X.; Chuang, I.L.; Blatt, R. Realization of a scalable Shor algorithm. Science 2016, 351, 1068–1070. [Google Scholar] [CrossRef]
  46. Long, G.L. Grover algorithm with zero theoretical failure rate. Phys. Rev. A 2001, 64, 022307. [Google Scholar] [CrossRef]
  47. Chandra, S.; Paira, S.; Alam, S.S.; Sanyal, G. A comparative survey of symmetric and asymmetric key cryptography. In Proceedings of the 2014 International Conference on Electronics, Communication and Computational Engineering (ICECCE), Hosur, India, 17–18 November 2014; pp. 83–93. [Google Scholar] [CrossRef]
  48. Makeenko, Y. Methods of contemporary gauge theory; Cambridge University Press: Cambridge, 2002; ISBN 0-521-80911-8. [Google Scholar]
  49. Berger, M.J.; Oliger, J. Adaptive mesh refinement for hyperbolic partial differential equations. J. Comput. Phys. 1984, 53, 484–512. [Google Scholar] [CrossRef]
  50. Berger, M.; Colella, P. Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 1989, 82, 64–84. [Google Scholar] [CrossRef]
  51. Klypin, A.A.; Trujillo-Gomez, S.; Primack, J. Dark Matter Halos in the Standard Cosmological Model: Results from the Bolshoi Simulation. Astrophys. J. 2011, 740, 102. [Google Scholar] [CrossRef]
  52. Huang, W.; Robert, D. R. Adaptive moving mesh methods; Springer Science & Business Media, 2010; Vol. 174. [Google Scholar]
  53. Gnedin, N.Y. Softened Lagrangian hydrodynamics for cosmology. Astrophysical Journal Supplement Series 1995, 97, 231–257. [Google Scholar] [CrossRef]
  54. Gnedin, N.Y.; Bertschinger, E. Building a cosmological hydrodynamic code: consistency condition, moving mesh gravity and slh-p3m. Astrophys. J. 1996, 470, 115. [Google Scholar] [CrossRef]
  55. Kravtsov, A.V.; Klypin, A.A.; Khokhlov, A.M. Adaptive Refinement Tree: A New High-ResolutionN-Body Code for Cosmological Simulations. Astrophys. J. Suppl. Ser. 1997, 111, 73–94. [Google Scholar] [CrossRef]
  56. Chiarelli, P. Quantum Effects in General Relativity: Investigating Repulsive Gravity of Black Holes at Large Distances. Technologies 2023, 11, 98. [Google Scholar] [CrossRef]
  57. Valev, D. ESTIMATIONS OF TOTAL MASS AND ENERGY OF THE OBSERVABLE UNIVERSE. Phys. Int. 2014, 5, 15–20. [Google Scholar] [CrossRef]
  58. DeBard, M.L. Cardiopulmonary resuscitation: Analysis of six years' experience and review of the literature. Ann. Emerg. Med. 1981, 10, 408–416. [Google Scholar] [CrossRef]
  59. Cooper, J.A.; Cooper, J.D.; Cooper, J.M. Cardiopulmonary resuscitation: history, current practice, and future direction. Circulation 2006, 114, 2839–2849. [Google Scholar] [CrossRef] [PubMed]
  60. Chiarelli, P. Far from Equilibrium Maximal Principle Leading to Matter Self-Organization. J. Adv. Chem. 2009, 5, 753–783. [Google Scholar] [CrossRef]
  61. Seth, A.K.; Suzuki, K.; Critchley, H.D. An interoceptive predictive coding model of conscious presence. Front. Psychol. 2012, 2, 18458. [Google Scholar] [CrossRef] [PubMed]
  62. Ao, Y.; Catal, Y.; Lechner, S.; Hua, J.; Northoff, G. Intrinsic neural timescales relate to the dynamics of infraslow neural waves. NeuroImage 2024, 285, 120482. [Google Scholar] [CrossRef]
  63. Craig, A.D. The sentient self. Anat. Embryol. 2010, 214, 563–577. [Google Scholar] [CrossRef] [PubMed]
  64. Hameroff, S.; Penrose, R. Consciousness in the universe. Phys. Life Rev. 2014, 11, 39–78. [Google Scholar] [CrossRef]
  65. Prigogine, I. Le domaine de validité de la thermodynamique des phénomènes irréversibles. Physica 1949, 15, 272–284. [Google Scholar] [CrossRef]
  66. Sawada, Y. A thermodynamic variational principle in nonlinear non-equilibrium phenomena. Prog. Theor. Phys. 1981, 66, 68–76. [Google Scholar] [CrossRef]
  67. Malkus, W.V.R.; Veronis, G. Finite amplitude cellular convection. J. Fluid Mech. 1958, 4, 225–260. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated