Preprint
Article
Development and Optimization of PIR and QIR Maintenance Strategies Using Monte Carlo Method
Altmetrics
Downloads
77
Views
32
Comments
0
This version is not peer-reviewed
Submitted:
13 March 2024
Posted:
14 March 2024
You are already at the latest version
Alerts
Abstract
Every firm is devoted to polishing and fine-tuning its maintenance strategy. More exactly, when we develop robust and efficient preventive and conditional maintenance approaches, our objective is to combine performance and robustness to increase maintenance decision-making. This, in turn, leads to a reduction in system failures and a subsequent drop in related expenses. This impulse drives the origin of this essay: to provide fresh criteria that allow us to improve and optimize maintenance techniques. Furthermore, our study has been realistically utilized via the deployment of condition-based maintenance (CBM) techniques, which are commonly regarded as a critical lever that allows firms to gain a competitive advantage in the context of the fourth industrial revolution.
Combining both perfect and imperfect maintenance actions into CBM strategies appears to be an effective technique to obtain high economic performance and robustness in the maintenance strategies of the companies. Following this idea, we propose and optimize in this paper a set of criteria enabling the combined assessment of the mean economic performance and the resilience of various kinds of maintenance techniques. The advantage of the proposed criterion is that it adapts to different types of maintenance strategies and provides access to a simple and relevant evaluation model. Thanks to this new criterion, we will be able to choose the better maintenance strategies that have more performance and robustness between these strategies for a system with more or less stable behavior. The Monte Carlo Method is incorporated into the comparative assessment of maintenance methods, adding a layer to the evaluation of the performance and robustness of each adaptation in decision-making.
Keywords:
Subject: Engineering - Mechanical Engineering
I. Introduction
The execution of an efficient maintenance plan is of essential relevance for firms in all industries [1]. For this reason, we resort to maintenance methods from the Condition-Based Maintenance (CBM) techniques family [2], especially a periodic inspection and replacement strategy (PIR) and a quantile-based replacement strategy (QIR).
Firstly, let’s try to state various responsibilities and advantages if organizations apply these maintenance procedures in their production system. Firstly, the maintenance method offers for huge cost reductions. By anticipating maintenance and replacement requirements, firms minimize the excessive expenses associated with unexpected failures and emergency repairs. Furthermore, it helps prolong the lifetime of equipment, therefore preventing early expenditures in new assets.Simultaneously, the adoption of these maintenance procedures seeks to guarantee the dependability of operations. Through frequent and focused treatments, the chances of serious breakdowns are considerably decreased. Unplanned downtime, frequently expensive and disruptive, is reduced, guaranteeing continuity in production or services delivered.
Based on all these factors, it can be claimed that the implementation of maintenance techniques plays a very essential role for all firms. This is why we have prepared this post focused on the creation and optimization of these maintenance procedures. Indeed, our investigation is carried out employing CBM procedures, notably the PIR and QIR strategies. First, we remind the reader of the sort of system under consideration. It is a system with a more or less steady behavior, and this sort of system experiences slow degeneration [3]. The homogenous Gamma process will be utilized to simulate its path towards failure. In these two techniques, PIR and QIR, we present a novel economic criteria that allows for the combined assessment of the performance and resilience of the PIR and QIR strategies [4,5]. In this research, the maintenance cost per renewal cycle (MCPRC) is taken as the performance criteria [6], and the robustness is of the first sort,This criteria comprises a linear combination of the asymptotic average cost per unit of time and the the standard deviation of the MCPRC of the maintenance cost rate over a certain replacement cycle. Mathematical cost models based on this criteria are created for both PIR and QIR techniques. Through these models, we review the suggested maintenance techniques to acquire a more detailed perspective of their performance when robustness is taken into consideration.
Consequently, to fulfill our aims, the ensuing portions of this work are constructed in the following manner: In Section II, we briefly cover the deterioration and failure model. Section III provides the maintenance assumptions and cost models for the PIR, and QIR techniques. Section IV dives into the reasons why the standard long-term projected maintenance cost rates are no longer acceptable for assessing maintenance plans and how the suggested criteria gives a more suited approach. Detailed comparisons between the two procedures - PIR, and QIR - utilizing the new criteria, are presented in Section V. In conclusion, we review the study and give some insights in Section VI.
II. Degradation and Failure Model
We analyze the degradation of a system by utilizing the scalar random variable 𝑋𝑡, which represents the cumulative degradation at time 𝑡 ≥ 0. In the absence of maintenance actions, the sequence { 𝑋𝑡 } 𝑡≥0 forms an increasing stochastic process. This process starts from 𝑋0 = 0, indicating the system’s initial state when it is in a new condition.
To model the evolution of the system’s degradation, we make an assumption that the degradation increment between time points 𝑡 and 𝑠 (where 𝑡 ≤ 𝑠), denoted as 𝑋𝑠 − 𝑋𝑡, is independent of the degradation levels observed before time 𝑡. This assumption implies that the future degradation increment depends solely on the current degradation level and the time interval under consideration, without any influence from the past degradation history.
To capture the stochastic nature of the degradation process, we can employ any monotonic stochastic process from the Lévy family [7]. The Lévy family encompasses a range of stochastic processes that exhibit monotonicity, allowing us to model the system’s degradation trajectory effectively. By selecting an appropriate process from this family, we can simulate the system’s degradation over time and gain insights into its future behavior.
The primary focus of this research paper is to employ the well-established homogeneous Gamma process for modeling system degradation. The homogeneous Gamma process is characterized by two key parameters: the shape parameter 𝛼 and the scale parameter 𝛽. The selection of this process is supported by a multitude of practical applications, including corrosion damage mechanisms [8], degradation of carbon-film resistors [9], SiC MOSFET threshold voltage degradation [10], fatigue crack propagation [11], and performance loss in actuators [12]. The wide range of these practical applications demonstrates the versatility and effectiveness of the homogeneous Gamma process in capturing degradation phenomena across different domains. Furthermore, the suitability of this process is endorsed by experts in the field [13], further validating its adoption for degradation modeling.
One of the major advantages of utilizing the homogeneous Gamma process lies in its mathematical tractability. The process exhibits a well-defined probability density function, enabling rigorous mathematical analyses and advancements. This mathematical tractability allows researchers to derive analytical expressions, establish meaningful performance measures, and make informed decisions based on quantitative assessments. By leveraging the mathematical properties of the Gamma distribution, researchers can gain valuable insights into the degradation process and its underlying characteristics.
In the context of the homogeneous Gamma process, the degradation increment between two time points, denoted as 𝑋𝑠 − 𝑋𝑡, follows a Gamma distribution with a specific probability density function. The shape parameter 𝛼 and the scale parameter 𝛽 determine the characteristics of this distribution. The Gamma distribution is a versatile probability distribution that can accurately represent various degradation phenomena, providing a comprehensive framework for modeling system degradation. It enables researchers to analyze degradation rates, forecast future degradation levels, and assess the reliability and remaining useful life of the system under study. Therefore, for 𝑡 ≤ 𝑠, the increase in degradation 𝑋𝑠 − 𝑋𝑡 follows a Gamma distribution with a probability density function:
and survival function:
Where and represent the complete and upper incomplete Gamma functions, respectively. The indicator function 1{⋅} is used to represent a concept that yields a value of 1 if the argument is true and 0 otherwise. It is a concise notation for indicating binary outcomes.
When modeling degradation behaviors, the pair of parameters (𝛼, 𝛽) can capture a wide range of degradation patterns, from nearly deterministic to highly erratic ones. These parameters are important in characterising the degradation process.
The average degradation rate, denoted as ‘m’, is defined as the ratio of α to β, where α represents the degradation rate and β represents the level of variability or randomness in the degradation process. A higher α relative to β implies a higher average degradation rate, indicating that the system tends to degrade more rapidly over time. Conversely, if β is smaller than α, it suggests a higher level of variability, resulting in less predictable degradation behavior.
Similarly, the variance of the degradation process, denoted as var, is quantified by the ratio . A larger α relative to indicates a higher degree of variability in the degradation process, leading to a wider dispersion of degradation values and increased uncertainty in the system’s degradation behavior.
In this context, maintenance strategies are implemented in systems with relatively stable behaviour. The parameters are set to 𝛼 = 0.5 and 𝛽 = 0.5, which corresponds to an average degradation rate (m) of 1 and a variance (var) of 2. To define failure in the context of system degradation, a threshold-type model is adopted. This model considers economic factors, such as subpar product quality or excessive consumption of raw materials, as well as safety concerns, such as a high risk of hazardous breakdowns.
According to this model, a system fails when it can no longer fulfill its intended purpose in an acceptable condition, even if it remains technically operational. Therefore, it is undesirable for the system to degrade significantly as it can impact economic and safety considerations.
We propose that the system fails when its degradation level exceeds a predetermined critical threshold L. Once the degradation level surpasses this threshold, the system is considered to have failed, regardless of its operational status. This approach recognises that a considerable amount of degradation can render the system unable to meet the necessary standards or specifications, which can have economic or safety implications.
In this scenario, 𝜏𝐿 denotes the random failure time of the system, which can be expressed as:
The density function of at time 𝑡 ≥ 0 is given by [6] :
Where is known as digamma function.
III. Maintenance Strategies and Cost Models
This section provides a comprehensive exploration of three maintenance strategies: block replacement (BR) as a representative of time-based maintenance (TBM), and the Periodic Inspection and Replacement strategy (PIR) and the quantile-based inspection and replacement strategy (QIR) as representatives of condition-based maintenance (CBM). By outlining assumptions, presenting decision criteria, and formulating the MCPRC, we aim to facilitate an in-depth understanding of these strategies and their application in real-world maintenance scenarios.
- A.
- Maintenance assumptions
In the considered system, there are two maintenance operations available: Preventive Replacement (PR) and Corrective Replacement (CR). These replacement operations are intended to swiftly restore the system to a condition equivalent to being brand new. The replacement process can involve a true physical replacement or a comprehensive repair or overhaul.
However, in practice, the costs associated with Preventive Replacement (PR) and Corrective Replacement (CR) activities may differ. Corrective Replacement (CR), which is unplanned and can potentially cause environmental damage, typically incurs higher costs compared to Preventive Replacement (PR) [15]. This is because Corrective Replacement is reactive and requires immediate action to address a failure, often involving more urgent and costly measures. On the other hand, Preventive Replacement is planned in advance, allowing for more efficient scheduling and potentially lower costs.
Furthermore, even when employing the same type of maintenance activities (PR or CR), the costs can vary depending on the degradation level of the system. Maintenance performed on a more deteriorated system is likely to be more intricate and, consequently, more costly. As the degradation level of the system increases, the associated costs for both Preventive Replacement (PR) and Corrective Replacement (CR) also increase.
Let Cp(Xt) and Cc(Xt) denote the costs of Preventive Replacement (PR) and Corrective Replacement (CR) at time t, respectively. These costs are both increasing functions of the degradation level Xt of the system. Additionally, the relationship 0 < Ci < Cp(Xt) < Cc(Xt) holds, indicating that the cost of inspection (Ci) is lower than the cost of Preventive Replacement (PR) at any given degradation level, and the cost of Preventive Replacement (PR) is lower than the cost of Corrective Replacement (CR) at the same degradation level.
Moreover, since replacement can only occur at discrete times (such as inspection times in the PIR and QIR strategies or at predetermined calendar time bloc T in the BR strategy), there is a downtime period for the system after a failure occurs. During this downtime, an additional cost is incurred from the moment of failure until the subsequent replacement time. This cost is represented by a constant cost rate Cd > 0, reflecting the expenses associated with the system being non-operational and the need to address the failure before the next replacement opportunity.
Considering these factors, maintenance decision-makers must carefully evaluate the costs and benefits associated with different maintenance strategies, taking into account the degradation level of the system, the costs of inspection and replacement, and the downtime after a failure. By optimizing these factors, they can make informed decisions to ensure the reliability, performance, and cost-effectiveness of the production system.
- B.
- Maintenance strategies
- 1)
- Periodic inspection and replacement strategy (PIR):
A basic CBM strategy is represented by the PIR strategy. This approach links planned inspections to preventative replacement (PR) and corrective replacement (CR) activities by following a set inspection interval. The decision-making process follows a well defined path: No matter how old or in good shape it is, the system is inspected on a fixed schedule. Tk = kδ refers to these inspection cases, where k is any number between 1 and 2. Decisions are made based on the degree of degradation seen XTk during the Tk examination:
- If XTk is more than L, the system is malfunctioning and needs to be fixed by replacing it with a new one at Tk.
- The system is still operational if M ≤ XTk < L, however it should be replaced before Tk since it is deemed to be too compromised.
- If XTk < M, then Tk is not affected, indicating that the system is still regarded as healthy.
Whichever form of intervention was done previously, Tk+1 = Tk + δ is the time for the next system examination.The effectiveness of this strategy depends on two factors: the PR threshold M and the inspection duration δ.
- 2)
- Quantile-based inspection and replacement strategy (QIR):
QIR evaluates the system using a quantile schedule set by the parameter α, where 0 < α < 1, in contrast to the PIR technique.
Where XT0 = X0 = 0, The conditional reliability of the system at time t is represented as R(t | ) given the system’s degradation level at the inspection time Tk, denoted by xk. The following may be done to ascertain this conditional dependability employing :
where is given by (2). The system dependability is at least equal to α over the inspection period [Tk, Tk+1], as per formula (5). Put otherwise, the quantile-based inspection method ensures that α will be the lowest dependability level over the duration of the system.
- C.
- Maintenance cost per renewal cycle
When examining the robustness of maintenance schemes like PIR and QIR, one of the most important metrics to consider is the Maintenance Cost per Renewal Cycle (MCPRC). The MCPRC provides information on the efficacy and efficiency of various tactics for controlling maintenance expenses during renewal cycles.
The interval of time between subsequent maintenance procedures, including inspections or replacements, is referred to as the renewal cycle. The system is subjected to potential repairs, maintenance, and monitoring during every renewal cycle.
The MCPRC may be computed by dividing the total maintenance cost (represented by 𝐶(𝑆)) by the cycle’s duration (expressed by 𝑆). The average cost spent per unit of time during the course of the maintenance cycle is obtained from this computation.
Decision-makers may assess each strategy’s efficiency and cost-effectiveness by comparing the MCPRC for various approaches. A lower MCPRC suggests a more resilient and financially feasible method by demonstrating how well the plan manages maintenance expenses in relation to the length of the renewal cycle, the MCPRC is defined by:
Since 𝐾 is a random variable, we attempt to assess it using the standard deviation and mean value 𝜇 = 𝐸 (𝐾).
Higher values of 𝜎 have a detrimental effect on the robustness of the maintenance strategies. In the subsequent sections, we will provide the analytical expressions for 𝜎 for both of the considered strategies.
- 1)
- Standard formulation of the MCPRC for the PIR strategy :
Assuming that the system experiences k inspection costs throughout a renewal cycle of duration 𝑆𝑘 = 𝑘Δ𝑇, and that it undergoes preventative or corrective replacement at the k-th inspection time (k = 1, 2,...). If it is still in use at the end of the cycle, there is also a preventative replacement (PR) cost. Alternatively, in the event of a failure, it covers the expenses of k inspections, corrective replacement (CR), and downtime. Therefore, the PIR strategy’s Mean Cost Per Renewal Cycle (MCPRC) may be expressed as follows:
In this case, PIR strategy’s 𝑊𝑑,PIR stands for the system downtime that occurs inside the time span [𝑆𝑘−1, 𝑆𝑘] (and hence, throughout a renewal cycle). It is expressed as:
The mean MCPRC of the PIR strategy 𝜇𝑃𝐼𝑅 = 𝐸[𝐾𝑃𝐼𝑅] is thus computed as
where and are derived from (1), (2) respectively.The associated mean of square 𝐸[(𝐾𝑃𝐼𝑅)2] is given by
Equations (1) and (4) provide the formulae for 𝑓𝛼(⋅),𝛽 and 𝑓𝜏𝐿 . By using these values to replace equation (8), we can get the formula for the standard deviation 𝜎𝑃𝐼𝑅 of the MCPRC under the PIR method.
- 2)
- Standard formulation of the MCPRC for the QIR strategy:
Similar to the derivation of the standard deviation for the PIR (Preventive Inspection and Replacement) strategy, the standard deviation of the Mean Cost Per Renewal Cycle (MCPRC) for the QIR (Quality Inspection and Replacement) strategy can be determined. Assuming preventive or corrective replacement occurs at the k-th inspection time (k = 1, 2, ...), the MCPRC for the QIR strategy over a renewal cycle is expressed as the sum of costs weighted by their respective probabilities. This includes the costs of inspections, preventive replacement (PR), corrective replacement (CR), and downtime, as well as the failure costs associated with k inspections, CR, and downtime, all multiplied by the probability of failure. Calculating the MCPRC and its standard deviation allows for the assessment of the average cost per renewal cycle and the variability in cost outcomes, providing insights into the cost-effectiveness and risk associated with the QIR strategy, the MCPRC of the QIR strategy over a renewal cycle can be expressed as:
Where the downtime of the system over a refresh cycle under the QIR strategy is given by :
Equation (5) is used in the QIR technique to iteratively calculate Tk. It is quite difficult to calculate μQIR = E[𝐾QIR] and E[(𝐾QIR)2] analytically from equation (13) because of the dynamic inspection schedule. As a result, we employ a Monte Carlo simulation technique to determine the Mean Cost Per Renewal Cycle (MCPRC) standard deviation σQIR for the QIR method.
IV. Maintenance Strategies Assessment
Scholarly publications frequently use the widely-accepted long-term expected maintenance cost rate criteria to assess the efficacy of maintenance strategies [16]. Through the use of the conventional renewal-reward theorem, this need may be explicitly expressed as previously illustrated in previous research [17]:
In this case, y is the length of a renewal cycle, and c(y) is the total amount of maintenance spent throughout this cycle. The average values of the renewal cycle and the associated maintenance cost are specifically addressed in equation (15), but the variations in maintenance costs across cycles are not taken into consideration. In essence, assessing maintenance plans for robustness and performance may need more than just depending on the long-term predicted maintenance cost rate. We suggest employing a cost criteria that combines the MCPRC’s standard deviation, 𝜎, with the long-term projected maintenance cost rate, 𝐶∞, in order to overcome this constraint. This has the following mathematical expression:
In Section III–C, the formulae for computing 𝜎 under the PIR and QIR techniques are described in detail. These methods of maintenance are used to a system that behaves in a reasonably steady manner.
Let’s look at a system where the PR cost is expressed as a quadratic function of the degradation level to show the advantages of the new criterion. This cost of PR can be stated as follows:
Here, we conduct a thorough analysis of cost models in the context of a stochastically degrading production system with the parameters a = 0.1, b = 0.1, and L = 29. We clarify the complexities of cost models, focusing on a system represented by a quadratic function of the degradation level, in which L is the critical threshold, 𝐶𝑐 denotes the CR cost, 𝑀𝑠 denotes a PR threshold, and 𝐶0 denotes a basic PR cost. The CR cost stays fixed at 𝐶c = 98, but we also set our selected inspection cost (𝐶i = 5) and system downtime cost rate (𝐶d = 34). Equation (17) defines the system degradation threshold (𝑀s = 14) and the basic PR cost (𝐶0 = 48).
This section aims to accomplish two main goals: firstly, it will identify the best configurations for the suggested criteria φ for PIR and QIR strategies; secondly, it will investigate the correlation between robustness and performance in comparison to the traditional 𝐶∞ criterion.
In order to accomplish the first goal, numerical examples are used to clarify the best φ settings for PIR and QIR techniques. A Monte Carlo simulation technique with 2500 histories is used to guarantee the convergence of the cost functions due to the intricacy of the analytical calculation. Setting the weight 𝜆 to 1.4 results in cost function shapes that, when shown in Table 1, validate the best choice variable adjustments based on the new economic criterion.
Proceeding to the second goal, several 𝜆 values (2.4, 1.4, and 0 for PIR and QIR techniques) are used to investigate the link between robustness and performance. Based on criteria (16), optimization is carried out, and the results are shown in Figure 1.
The ideal configuration of various maintenance techniques is represented by the histograms of 𝐾 and the long-term predicted maintenance cost rate, 𝐶∞, as shown in Figure 1. Table 2 presents the analysis of 𝐶∞ and standard deviations of MCPRC 𝜎. The results show that larger 𝜆 values lead to smaller standard deviations of MCPRC 𝜎, showing improved robustness. However, this implies a trade-off between resilience and performance since it comes at the expense of a higher long-run anticipated maintenance cost rate.
Table 2 sheds light on the subtle distinctions between QIR and PIR tactics. For example, the QIR approach is more efficient overall (see Table 1) even though it has larger MCPRC standard deviation values. However, it also has smaller long-run projected cost rates than the PIR method.
Ultimately, the use of this novel criteria illuminates the intrinsic conflict between robustness and performance. A issue we explore more in Section V, finding a balance between these conflicting ideas is essential for efficient planning and budget allocation in maintenance tasks.
V. Maintenance Strategies Comparisons
As mentioned earlier, the system in which the comparative study of maintenance methods is carried out has different levels of stability (m = 1, var = 2, 𝛼 = 0.5, and 𝛽 = 0.5). In this part, we conduct a thorough analysis within this system to determine the effectiveness and resilience of the QIR and BR techniques.
We provide a range of scenarios in our study, including variations in the relative weight parameter λ values and various configurations of maintenance costs. We want to identify the maintenance approach that best fits particular goals or situations by looking at how the optimum decision variables for various strategies change across these scenarios.
This analysis is essential to determine the best maintenance strategy configurations for our particular requirements, taking into account the interaction between maintenance expenses and system attributes. In the end, it helps us to make knowledgeable judgments about maintenance plans, maximizing robustness and performance in line with our goals.
- A.
- Sensitivity to the maintenance costs
This study helps us identify the major elements impacting performance and robustness objectives in a system with different degrees of stability and provides insightful information on how to pick maintenance techniques for these goals. With this information at our disposal, we may perhaps lessen any negative consequences.
For our particular system, we keep the CR cost constant at Cc = 98 and set λ to 1.4. With the following parameters: C0 = 48, Ms = 14, 𝛼 = 0.1, 𝛽 = 0.1, and L = 29, we apply the PR cost function found in equation (17). We then take into account the next two configurations for the expenses of inspection and downtime:
- Variable Inspection Cost: The downtime cost per unit of time is set at Cd = 19, and Ci fluctuates with an increment of 1 from 1 to 45.
- Variable Downtime Cost per Unit of Time: The inspection cost is fixed at Ci = 7, and Cd changes with an increment of 1 from 10 to 50.
The maintenance expenses fulfill the criteria 0 < Ci < Cp (Xt) < Cc (Xt), it should be emphasized.
- 1)
- Sensitivity to the Inspection Cost Ci:
This situation is consistent with the findings illustrated in Figure 2. The development of the two techniques’ ideal decision variables and the associated costs for these optimal choices are shown in Figure 2a. Inspection expenses have a significant impact on both the PIR and QIR techniques, and their decision factors are tightly correlated with its variations.
To be more precise, Figure 2a shows that optimum choice variables for the QIR approach (αopt) tend to be high and those for the PIR method (∆Topt) tend to be low when inspection costs are relatively low (small values of Ci). This guarantees that the deterioration condition of the system is monitored more often. In the meanwhile, in an effort to increase the system’s usable life, the optimal preventative thresholds (Mopt) for both techniques are set to high levels.
Both maintenance techniques aim to reduce the frequency of inspections when inspection costs rise, leading to modifications such as raising ∆Topt and reducing αopt. Under some conditions, most especially when Ci reaches very high levels, both techniques’ optimal preventative thresholds (Mopt) are reduced. This allows for system replacement starting on the date of the first inspection, which reduces system downtime and avoids unnecessary inspection costs.
Both the QIR and PIR techniques show a similar trend of altering decision variables in the system shown (Figure 2a), such as reducing αopt and Mopt and increasing ∆Topt when Ci increases. On the other hand, a significant difference appears in the case of low inspection costs (small values of Ci), where the QIR method sets Mopt to a large value, which tends to extend the system’s operation.
This arrangement works well for a system that has a variability rating of two, which indicates minimal variability. However, it is essential to acknowledge that the system is managed by inter-inspection intervals that are designed in accordance with an extremely high conditional reliability threshold, where αopt is almost equal to 1.
As Figure 2b illustrates, there are notable benefits to both the PIR and QIR techniques when inspection costs are modest. However, because inspection activities incur additional expenses, this benefit wanes as inspection costs rise.
Additionally, Figure 2b shows that for both techniques, the standard deviation of MCPRC σ is mostly constant as Ci varies. This suggests that changes in the cost of inspections have no effect on how strong the tactics are.
Additionally, it is noted that, while not statistically significant, the PIR strategy’s MCPRC standard deviation is somewhat higher than the QIR strategy’s. This implies that, in comparison to the QIR method, the PIR strategy’s decision framework could be a little less reliable.
The QIR method does, in fact, excel at reducing maintenance costs, which bolsters its performance advantage. Despite this, both maintenance techniques show significant resilience when compared to the standard deviation values of MCPRC (σ scale) measured for our system, since σ does not surpass 1.5.
To choose the best framework, a careful balance between the robustness and performance of maintenance procedures must be struck. As Figure 2b shows, the objective function φ is a trustworthy tool for making decisions. In terms of the objective function φ, the PIR method performs better than the QIR technique, demonstrating its superiority in striking the right balance between resilience and performance.
- 2)
- Sensitivity to the system downtime cost rate Cd:
The goal of this study is to analyze the impact of the system downtime cost rate Cd on the second cost configuration shown in Figure 3. In particular, as mentioned at the beginning of this paragraph, we just adjust the Cd while maintaining the same unit prices for every other expense.
The case study’s numerical results are presented in Figure 3. It is clear that the configuration with Cd = 19, which was examined in the second case study, corresponds with the Ci = 7 situation from the first case study.
A proportionate sensitivity of cost to this parameter explains the rather irregular growth of the preventative threshold (Mopt) for the QIR and PIR techniques in Figure 3a. This explains its supporting role, in which it acts as an extra regulator to help the strategies reach their ideal configurations.
There is a noticeable change in the way the QIR and PIR methods adapt the decision variables when Cd rises to high values, above the Cd = 34 threshold. By making this change, they guarantee more regular system monitoring in order to reduce the expenses related to system outages. As a result, the QIR strategy’s decision variable αopt quickly becomes near to 1, whereas the PIR strategy’s à Topt takes a lower value.
Regarding our system, based on the MCPRC standard deviation scale for this kind of system (Figure 3b), both approaches demonstrate high resilience, with σ not exceeding 1.5. As a result, in this case, the effect of fluctuation in Cd on the resilience of maintenance plans is significantly reduced, as seen by the comparatively constant standard deviation values for MCPRC.
Moreover, Figure 3b makes clear that in this case, the QIR strategy’s cost objective function (φ) outperforms the PIR strategy’s cost functions. This confirms that the QIR approach constantly achieves the best possible balance between performance and resilience.
- B.
- Sensitivity to the relative weight of the cost variability λ
This investigation aims to quantify how the parameter λ, representing the relative weight of cost variability, captures the financial variability and risk tolerance of decision-makers in selecting a maintenance regimen. It is crucial to quantify how λ impacts the robustness and performance of the considered maintenance strategies. For this purpose, we standardize maintenance costs to Ci = 5, Cd = 34, Cc = 98, and C0 = 48. Subsequently, we systematically vary λ from 0 to 3 with increments of 0.1, meticulously observing the trajectories of pivotal decision variables ∆Topt, αopt, and Mopt. Additionally, we scrutinize the corresponding cost metrics φopt, C∞, and σ across the two maintenance strategies under consideration: PIR and QIR. This comprehensive methodology is implemented across our system, as delineated at the outset of this section. The outcomes of this inquiry are visually presented in Figure 4a and Figure 4b.
The increase in λ suggests a conscious move away from performance and toward emphasizing the resilience of maintenance techniques. The QIR technique greatly increases the values of αopt and makes efficient use of its dynamic conditioning feature, as can be seen from the data shown in Figure 4a. Further evidence is shown in Figure 4b, which shows the opposite trends in the standard deviation of the MCPRC, σ, and the asymptotic average cost per unit of time, C∞, for the two techniques as λ varies. This confirms that performance and robustness always have to trade off. It is important to note that the QIR method regularly performs better than the PIR strategy in terms of the final goal function φopt, even if creating a maintenance strategy that incorporates both resilience and high performance may be difficult. This demonstrates how much better the QIR approach is at striking a more harmonic balance between robustness and performance.
VI. Conclusion and Perspectives
In this paper, we propose a unique method for assessing the resilience and performance of condition-based maintenance (CBM) techniques in systems that behave in a relatively steady manner. To create a new criteria, our method combines the long-term predicted maintenance cost rate (C∞), the relative weight of cost variability (λ), and the standard deviation of the MCPRC (σ). The quality-based inspection and replacement (QIR) method, which uses non-periodic inspections, and the periodic inspection and replacement (PIR) strategy are the two CBM strategies that we examine.
Our findings reveal an inverse link between robustness and performance in maintenance strategies: improving robustness tends to decrease performance, and vice versa. The numerical outcomes are consistent with previous research, suggesting that the QIR approach performs better than the PIR approach in most cases. Furthermore, our results highlight how downtime maintenance costs have a major impact on strategy robustness.
Finally, we claim that the QIR technique is more resilient than the PIR strategy, especially when it comes to efficiently handling system downtime for systems that exhibit relatively consistent behavior.
References
- K. Cheikh, E.M. Boudi,R. Rabi and H. Mokhliss, “Influence of the Relative Weight of the Performance and Robustness of Condition -Based Maintenance Strategies and Time-Based Maintenance Strategies,” Journal of Harbin Engineering University 2024, 45, pp. 93–98.
- K. Cheikh and E.M. Boudi, “Evaluating the Performance and Robustness of Condition- Based Maintenance Strategies and Time-Based Maintenance Strategies,” Journal Mechanical Engineering Research and Developments 2023, 46, 76–85.
- Huynh, K. T. Quantification de l’apport de l’information de surveillance dans la prise de d’ecision en maintenance. PhD thesis, Universit´e de Technologie de Troyes, 2011.
- Taguchi, G. , Clausing, D., et al. Robust quality. Harvard Business Review 68, 1 (1990), 65–75.
- Asmussen, S. (2003). Applied Probability and Queues, volume 51 of Applications of Mathematics - Stochastic Modelling and Applied Probability. Springer, 2nd edition.
- Chen and, J. Jin, “Cost-variability-sensitive preventive maintenance considering management risk,”IIETransactions,vol.35,no.12,pp.1091–1101,2003.
- Abdel-Hameed, M. Lévy Processes and Their Applications in Reliability and Storage, ser. SpringerBriefs in Statistics. Springer, 2014.
- American Petroleum Institute, Washington D.C., Publication API581: RiskBased Inspection - Base Resource Document, 1st Edition (May 2000).
- Bagdonavicius, V.; Nikulin, M.S. Estimation in Degradation Models with Explanatory Variables. Lifetime Data Anal. 2000, 7, 85–103. [Google Scholar] [CrossRef] [PubMed]
- Meeker W, Escobar L. Statistical methods for reliability data. New-York: John Wiley & Sons; 1998.
- Barlow R, Proschan F. Statistical Theory of Reliability and Life Testing. International Series in Decision Processes; EditionHolt. Rinehart and Winston: New York, 1975. [Google Scholar]
- Domínguez-García, A.D.; Kassakian, J.G.; Schindall, J.E.; Zinchuk, J.J. An integrated methodology for the dynamic performance and reliability evaluation of fault-tolerant systems. Reliab. Eng. Syst. Saf. 2008, 93, 1628–1649. [Google Scholar] [CrossRef]
- Boursier, J. , Desjardins, D. and Vaillant, F. (1995). The influence of the stain-rate on the stress corrosion cracking of alloy 600 in high temperature primary water. Corrosion Science 37(3), 493–508.
- Dekker, R.; Scarf, P.A. On the impact of optimisation models in maintenance decision making: the state of the art. Reliab. Eng. Syst. Saf. 1998, 60, 111–119. [Google Scholar] [CrossRef]
- Bond, L.J.; Taylor, T.T.; Doctor, S.R.; Hull, A.B.; Malik, S.N. Proactive Management of Materials Degradation for nuclear power plant systems. 2008 International Conference on Prognostics and Health Management (PHM); pp. 1–9.
- Valdez-Flores, C.; Feldman, R.M. A survey of preventive maintenance models for stochastically deteriorating single-unit systems. Nav. Res. Logist. (NRL) 1989, 36, 419–446. [Google Scholar] [CrossRef]
- Scarf, P.A. A Framework for Condition Monitoring and Condition Based Maintenance. Qual. Technol. Quant. Manag. 2007, 4, 301–312. [Google Scholar] [CrossRef]
Figure 1.
MCPRC Histogram.
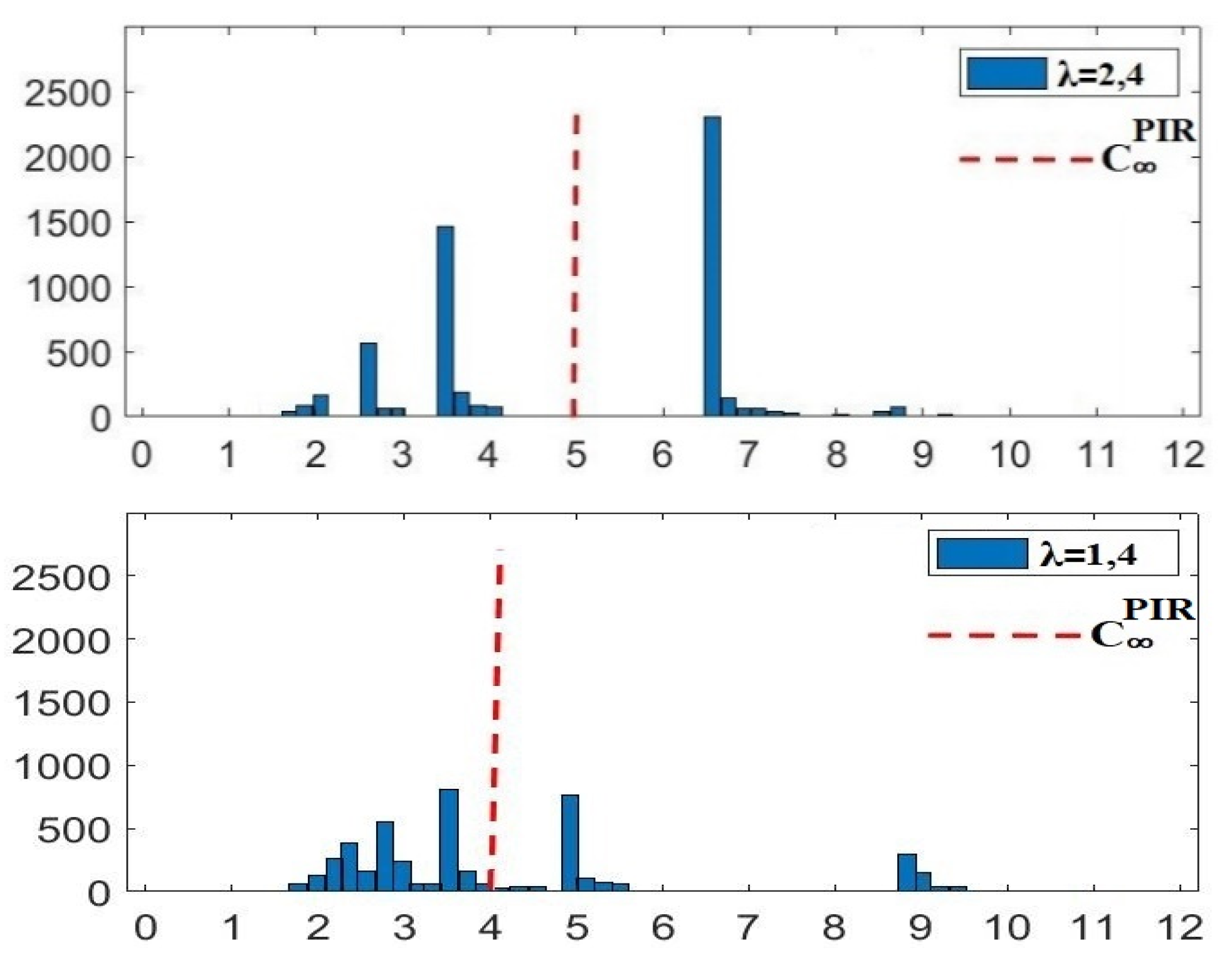
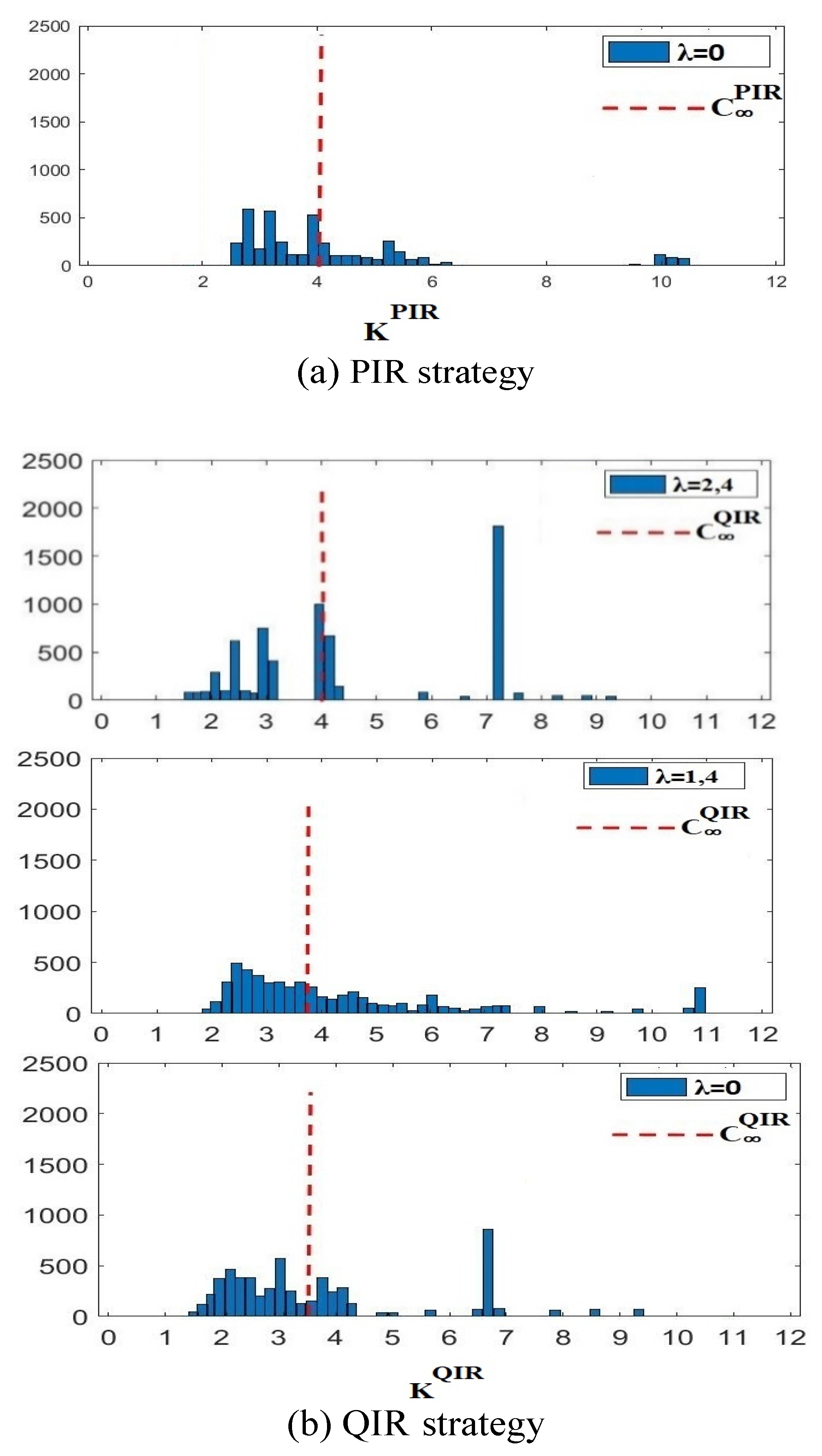
Figure 2.
Sensitivity to the inspection cost Ci.
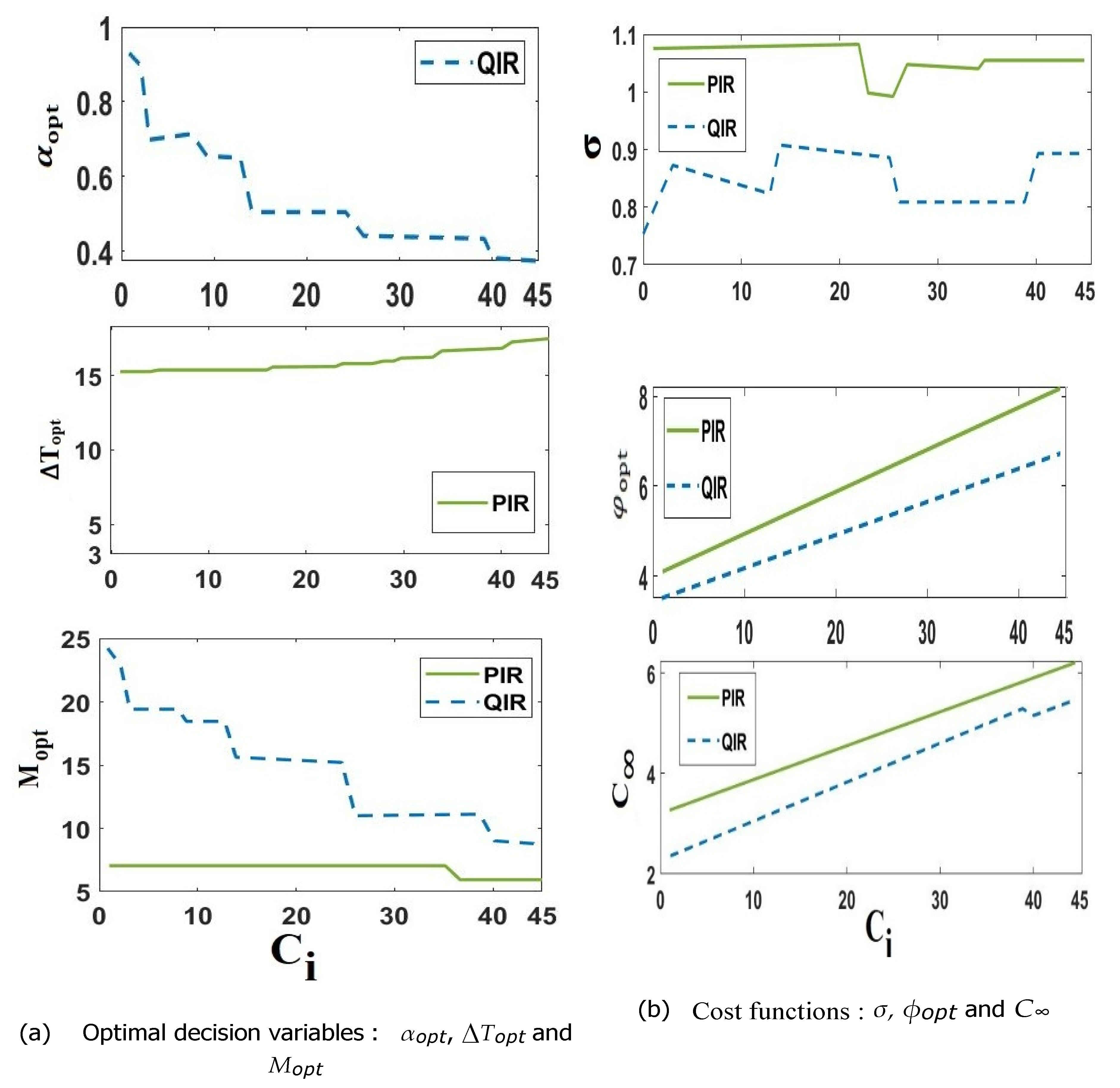
Figure 3.
Sensitivity to the system downtime cost rate Cd.
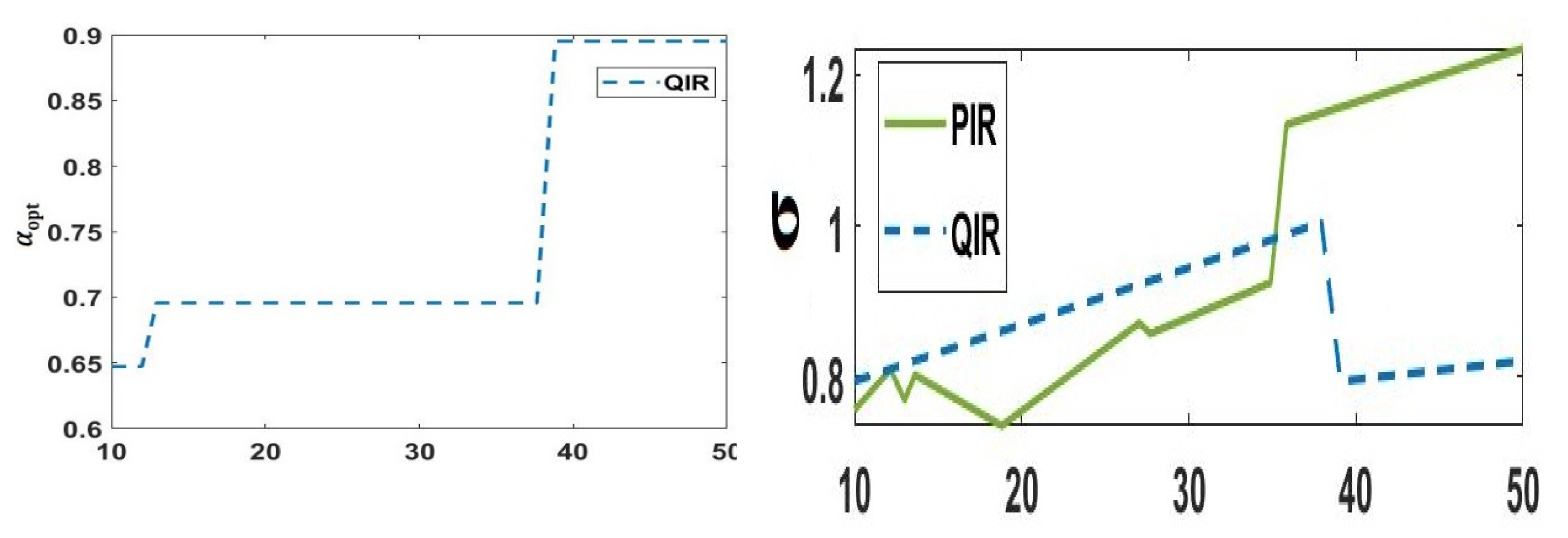
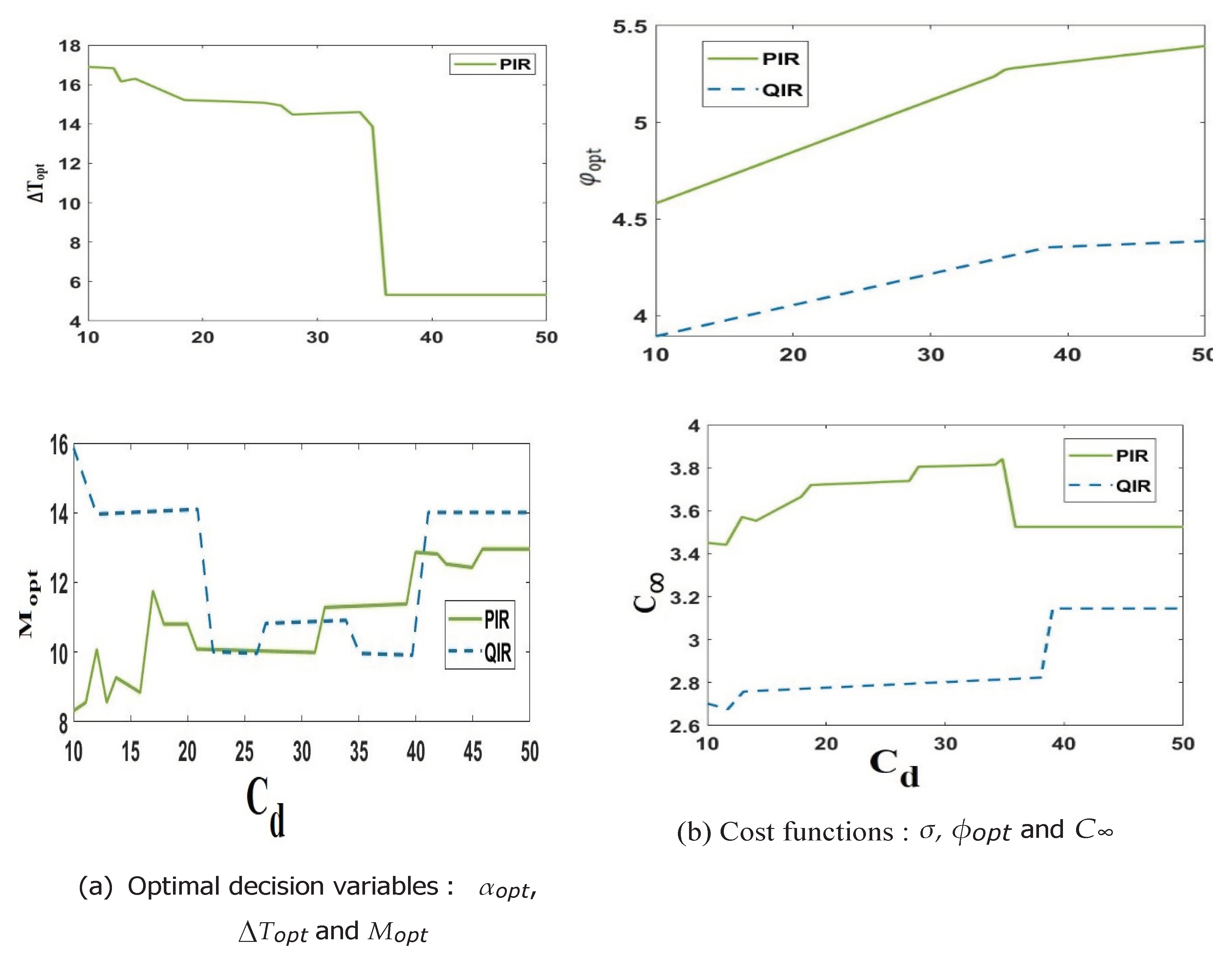
Table 1.
Optimal configurations of the PIR and QIR strategies
| .Strategies | Relative weight | Optimal decision variables | |
|---|---|---|---|
| PIR |
|
||
| QIR |
|
Table 2.
Maintenance strategies optimization of the PIR and QIR strategies.
| Strategies | Relative weight | Optimal decision variables | Long-run expected cost rate | Standard deviation of MCPRC |
|---|---|---|---|---|
| PIR |
|
|||
|
|
||||
|
|
||||
| QIR |
|
|||
|
|
||||
|
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






