Prerpints.org logo
Preprint
Article

Sustainability Assessment of Machinery Safety in a Manufacturing Organisation – Supporting Machinery Safety Decision Making with AHP and CART Methods

Altmetrics

Downloads

95

Views

32

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 March 2024

Posted:

14 March 2024

You are already at the latest version

Alerts
Abstract
Machine safety is not only a prerequisite for successful production, but also the foundation for sustainability and growth of any manufacturing organisation. The latest approaches in this rapidly developing field are the integration of effective risk management tools and strategies into occupational health and safety (OHS) systems. In this article, using a specific example from practice, we will show how using multi-criteria decision making (AHP) support Machinery Safety Decision Making (MSDM) from the point of reducing losses. Using Classification and Regression Tree Analysis (CART), we estimated the efficiency, cost-effectiveness and thus the sustainability level of the relevant safety measures. These were proposed risk reduction measures that typically raised uncertainty among managers regarding the estimation of cost-effectiveness. The advantage of application decision trees approach is possibility to identify and establish relatively homogeneous groups of undesirable events and their impact on the organisation's objectives. A comprehensive model has been developed to support management decision making in manufacturing organizations in implementing and improving safety measures in line with manufacturing sustainability goals.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Safety Related Data (SRD) are essential to maximise the effectiveness of the risk assessment process. SRDs need to be as accurate and detailed as possible at all stages of the system life cycle, however, at the design stage they are the basis for achieving the required level of Occupational Health and Safety (OHS). According to Badri et al. [1], to improve the process of Safety Decision-Making (SDM) to achieve safety level, SRDs can be considered as the most valuable assets for all safety professionals. The combination of historical and current data strengthens real-time decision making during the manufacturing process, which positively affects the performance, safety, reliability, and sustainability of industrial systems [2].
In the field of machinery safety, it is very important to identify all hazards associated with machinery by collecting accurate and relevant safety data. Accurate Machine Safety Related Data (MSRD) analysis is needed to use machine safety knowledge and to make more realistic risk assessments. However, the lack of appropriate communication between machine manufacturers and end-users further magnifies the existing problem and hinders sufficient transfer of MSRD and feedback from end-user experience [3].
Taking care of employee safety and minimising the impact of hazards when in contact with machinery is a multi-dimensional and necessary prerequisite for any sustainable production. In addition to the technical, economic, health, social, motivational, or legislative aspects, it also has a highly ethical dimension. According to Lee et al. [4], most organizations strive for sustainability by providing workplace conditions that contribute to employee health and safety. Therefore, developing a workplace safety culture is a competitive factor for sustainable companies.
Managers at all levels of management are responsible not only for their subordinates but also for managing safety within their scope of responsibility [5,6,7]. Any misconduct by a manager is usually perceived with great sensitivity by the injured person, but also by the wider community. On the other hand, all relevant measures to improve OHS require incurring considerable costs. It is often economically prohibitive to carry out all remedial measures at once. From the organisation's perspective, it should be a process that ensures the cost acceptability of fulfilling the requirements to maintain and improve the safety of machinery. However, this is no cheap proposition. Particularly in larger manufacturing operations, which contain number of machines at different levels of wear and tear (resulting from lifetime) operating within several production lines, usually on a single shop floor, the sustainability of their safety is almost always a serious economic issue.
Machinery in manufacturing creates a dynamic environment, especially with respect to the requirements of Industry 4.0 [8] where quality, accuracy and efficiency are paramount. However, this also poses specific risks for their operators, but also for other people in the vicinity of the machine. Ensuring safety in manufacturing is not only a legal requirement [9], but also a moral obligation to protect employees and sustain operations. Leveson [10] defines "safety as the absence of accidents, where an accident is defined as an event involving unplanned and unacceptable loss". Safety is also associated with low and acceptable risk [11,12,13].
Nowadays, the concept of any development is associated with the concept of sustainability. Some authors point out [14,15] that occupational health and safety (OHS) and injury and illness prevention are issues that may raise concerns in terms of sustainability. Boileau [14] highlights three areas to consider in sustainable safety: integrating safety requirements at the system design stage, incorporating OSH into strategic plans, and implementing a safety culture into the organization. According to Hogevold et al. [16] and Dyllick and Muff [17], sustainable business is business that is economically, socially and environmentally responsible, without negative impacts on all these areas. Currently, the direction of business from small to large organisations is contributing to a more sustainable future.
However, if organisations fail to procure and maintain machine safety, provide adequate Personal Protective Equipment (PPE), ensure proper training for employees, or implement a safety culture, a variety of undesirable events that threaten the sustainability of the business are likely to occur. If an undesirable event occurs due to insufficient approaches to OHS management, the manufacturing organization may incur various costs. Many of these costs can be direct and immediate, but often more significant are the so-called indirect costs [18]. Indirect costs (“hidden” or “invisible”) of an undesirable event can include negative impact on the employer's reputation, lost time due to injury investigation, cleanup of the incident site, and reduced productivity and morale among employees [19].
Bearing the initial costs of implementing and complying with a comprehensive occupational health and safety program (e.g., with the support of an ISO 45001 OHS management system [20,21]), complying with regulations, and providing employees with proper training and PPE is much more likely to save more costs than the costs associated with the occurrence of an undesirable event [21].
However, safety in manufacturing is not just about compliance, it is about promoting a safety culture, minimising risks and optimising productivity. It is a multifaceted effort that requires a holistic approach [22]. By implementing strict safety procedures, investing in appropriate machinery safety devices, and promoting a safety culture, machinery can significantly reduce the number of undesirable events in the workplace, protect employees, and ensure business continuity. Safety can be understood in a generic sense as a fundamental pillar of any manufacturing organization that adds value to the business sustainability [23].
A sustainable approach to machine operator safety in an organisation involves integration of environmental, social, and economic aspects into OHS management to not only protect the health and safety of workers, but also to ensure the long-term sustainability of the business and to minimise environmental impact. This approach requires comprehensive planning, implementation, monitoring and continuous improvement of safety procedures and systems. The perception of safety as the opposite of risk, i.e. that the lower the risk, the higher the safety and vice versa, has been challenged by several authors. Already Möller et al. [24] concluded that it is necessary to go beyond thinking in this relationship of “safety as an antonym of risk”. A different approach to risk is taken by Aven and Renn [25], who view it as uncertainty and its impact on activities. It is clear that health and safety of machine operators should be seen as part of a broader corporate sustainability strategy (Corporate Social Responsibility, CSR). This approach involves considering safety measures in the context of environmental responsibility (e.g. minimising waste and emissions, efficient use of energy, etc.) and social responsibility (e.g. ensuring fair working conditions, promoting the health and well-being of employees) [26,27].
Integrating safety objectives into the overall sustainability goals of the organisation allows better coordination and more efficient use of resources. Sustainable safety emphasizes preventive measures that focus on preventing accidents and injuries before they occur. This includes comprehensive risk identification, analysis and assessment, as well as the development and implementation of innovative technological solutions and safety systems. A preventive approach also encourages investment in the development and training of employees to be better prepared to identify and respond correctly to potential risk situations in machinery. The safety of machinery operators in an organisation is a complex area that requires a multidisciplinary approach involving engineering, ergonomics, occupational psychology and legislation.
The aim of our research was: (1) to apply risk assessment procedures based on the analysis of available data on the status of 124 devices in the manufacturing organization (Machinery safety related data MSRD); (2) to support the estimation of the cost-effectiveness of selected measures to reduce unacceptable risks using the AHP method; and (3) to use the CART technique to support the decision making process (Machinery safety decision making MSDM) to assess the effectiveness and efficiency of the proposed measures.

2. Material and Methods

2.1. Machinery Safety Analysis

The research was conducted at an organisation that is a global manufacturer of healthcare products and technologies. It focuses on the manufacture of market-leading medical devices. These devices are in the areas of advanced wound care, ostomy care, continence and critical care, and infusion devices.
A key step to ensure safety when working with machinery is to identify the potential risk scenarios associated with its operation (hazard → hazardous situation / event → harm). This process “Machinery safety related data” (MSRD) involves analysing all data on the machine's operation, including potential failures, accidents or hazardous situations that could cause an accident. After identification of the hazards, a risk assessment must be carried out, i.e. to determine the probability of occurrence of harm related to the hazardous situation ( P ) and severity of harm ( S ). These estimates are usually represented by a numerical scale corresponding to a verbal expression.
Note: To understand when data is collected by the organization's staff, probability of hazardous situation occurrence ( P ) is simplistically understood as the total probability of hazard exposure to persons during a given activity on a machine, combined with the probability of occurrence of a hazardous event, which in describing an accident scenario is related to e.g. unintentional human error or machine failure resulting in harm.
Due to the variety of machines in operation at the company, and their life cycle (some machines were more than 20 years old), a risk assessment methodology (ISO 12100 [28], see Table 1, Table 2 and Table 3) was designed by the research team and agreed by the OHS management of the organization. The specific score value for the assessed risk parameters was estimated based on the available safety information for individual machines and consultations with safety engineers, operators, and maintenance staff.
Risk ( R ) is the expressed combination of the probability of occurrence of harm related to the hazardous situation ( P ) and the severity of that harm ( S ) [28] as shown in Equation 1:
R = P * S
Based on the assessment of R according to the risk matrix, risk minimisation measures are then developed and implemented (see Table 3).
Although the organisation had previously written operational documentation in accordance with the current legislation on machinery (Directive 2006/42/EC [29]), due to the age of the machinery and the statistics of OHS accidents in the organisation, the management was not satisfied with its relevance. A new “Machinery Risk Assessment” document was prepared by experts for each machine, which included an analysis and risk assessment of the machinery based on the OHS methodology approved by the management.
An example of machinery risk analysis is selected in Table 4. Based on the results of the analyses (MSRD) from all 124 machines, a total of 5260 hazardous situations (HSs) and their resulting risks were identified. To assess the effectiveness and efficiency of the measures, the expert team, in cooperation with OHS management, focused on those risks whose value was higher than 9 and less than 20. Values R that were less than 9 and greater than 20 were not considered. Lines with a value of less than 9 represented a lower priority risk of harm from machinery, lines with a value of more than 20 represented the highest non-comparable priority, the so-called STOP-STOP category (see Table 3), meaning immediate stoppage of machine operation (a highly unacceptable risk). The result was a database containing 489 data reaching the so-called critical risks, for which it was important to prioritize their reduction or elimination by adding additional measures. From this database, 49 machines (see Table 5) with the most frequently recurring types of hazardous situations (HS) were selected by the experts. These were type-non-homogeneous, variously worn-out machines, some of which are part of different production lines. They are arranged in the production halls in such a way that their individual danger zones overlap each other. Therefore, the analysis included an assessment of the safety of the machinery in relation to both its layout and its interconnection within the production lines. Despite the heterogeneity mentioned above, these are machines that process the same material, contain similar components and their operation is also very similar. Some types of hazardous situations were often repeated, others were identical in content, just described differently.
This allowed experts to introduce a standard designation for the identified hazardous situations ( H S ). A total of 10 main H S i types ( i = 1 ,   … ,   10 ) could be obtained from the 489 HSs after standardization, which were recurrent in the machine analysis. Table 6 shows the H S i types with their number of occurrences O on the machines (see Table 6).
Possibility of avoidance of harm or impending HS is a very important parameter for risk management by appropriate measures. The expert group proposed to complement relationship (1) with the parameter P N D - Probability of non detection of HS, which consider whether the undesirable situation ( H S ) can be prevented by preventive measures or only after its occurrence (so called corrective measures). The experts proposed to extend the risk estimation with one column labelled “Probability of non-detection of HS” ( P N D ), inspired by the approach applied in Failure Modes, Effects and Criticality Analysis (FMECA) [30,31]. The scores of this column are described in Table 7, applying the Braglia [32] approach. In collaboration with the OHS organization experts, the relation for risk estimation was modified (see Equation (2)) and then applied to all 489 data, see Table 8.
Note: HS – Hazardous situations; PND - Probability of non-detection HS/E.
Table 8 contains the assessment of R M (Machine Risk) based on two parameters obtained from the performed risk analysis and the third parameter P N D which we have added based on Table 7. Specific quantification R M is given by the relation:
R M = P * S * P N D
This is a similar relationship to the one used in the FMECA method [30,31], with the only difference that the parameters mentioned above are estimated using a 5-step scale, whereas FMECA uses standard 10-step scales. The individual rows of Table 8 contain the above-mentioned main H S s obtained from the safety analyses of the individual machines. Numerical values of the parameters P , S a P N D represent the maximum of the values of similar parameters from the risk assessment analysis of the machinery for a particular combination H S . Each risk presents the possibility of loss for the organisation [19], the impact of which can be of different nature e.g. loss of customer, penalties, loss of reputation, etc.). For this reason, Table 8 has been extended with a column allowing to assign a parameter to determine the significance value of negative impacts ( E ) from the point of view of the organisation's management when a given hazardous situation occurs ( H S ) in the performance of the activity (maintenance or operation) and severity of harm.

2.2. Estimation of Expected Cost Using the AHP Method

Estimation of the expected costs ( E C ) caused by the severity of harm (e.g., direct, and indirect costs associated with injury caused by machine hazardous situation) generally cannot be estimated with sufficient precision [33]. On the other hand, the above-mentioned costs are an important indicator of the effectiveness of measures that reduce or even eliminate the assessed risks. This problem can be solved e.g. by using the Analytic Hierarchy Process (AHP) multicriteria decision-making method. In this method, it is not necessary to accurately estimate the amount of expected costs for a specific criterion. It is sufficient if we can perform a pairwise comparison of the mentioned criteria [34].
AHP belongs to multicriteria decision making methods, with the level of information about criteria preferences based on pairwise comparisons [35,36]. It is a powerful and flexible multicriteria decision making tool for complex problems where both qualitative and quantitative aspects need to be considered. It allows analysts to organize the critical aspects of a problem into a hierarchical structure similar to a family tree. By reducing complex decisions to a series of simple comparisons and rankings and then synthesizing the results, it supports come to the best decision, but also provides a clear reason for the decisions made.
Once the AHP hierarchy was defined (see Figure 1), it was possible to prioritize among the elements within each level of the hierarchy of our researched model. As mentioned above, both qualitative and quantitative criteria can be compared using informal judgments to derive priorities.
Part (a) of the Table 9 presents the pairwise comparison matrix of expected costs E C for all combinations of Hazardous situation/Effect ( H S / E ) of the analysed HS and the severity of their E described in Table 8. Using the AHP method, the calculated priorities of each combination are expressed as Expected Cost ( E C ), which form part (b) of Table 9.
These are the values obtained using the following steps [37]:
  • The calculation of the normalized comparison matrix was performed.
  • The average weights (priorities) for each element were determined.
  • Calculated maximum eigenvalue ( λ m a x ).
  • Calculated specific coherence indices ( C I ) and coherence ratio ( C R ) to verify the consistency of the comparison matrix.
The normalized matrix Table 9 part (a) was used to determine the priorities of each HS/E combination (Priority vector). Since the normalized matrix is of order 15 x 15, we used the Random Index R I = 1,59 for the calculation:
  • The priority vector for each HS/E combination (Table 9 part (b)) represents the priority or weight of the relevant element compared to the other elements;
  • The maximum eigenvalue represents the value λ m a x = 16,886 ;
  • The consistent index is equal to C I = 0,1347 ;
  • The coherence ratio is equal to C R = 0,0847 .
Given that the coherence ratio ( C R ) is lower than 0,1 , the comparison matrix can be considered sufficiently consistent by AHP standards. This means that the identified priorities can be considered reliable in the evaluation of alternatives.
In the next step of the analysis, we performed pairwise comparisons at the first level of the hierarchy to obtain value judgments. Table 10 part (a) shows the matrix A obtained from the pairwise comparison of criteria performed with the help of experts and OHS management. The comparison was performed in terms of the 5 criteria described in the previous section. The prioritization of the performance criteria was calculated similarly to the previous case. The prioritization vector (Table 10 part (b)) was determined by calculating the normalized components of the right eigenvector of the corresponding matrix.
The values in the Table 10 represent pairwise comparison weights, indicating how one criterion was evaluated against another. On the diagonal, the default values are 1 because each criterion is equally important in comparison to itself.
Similar to the first set, we proceeded as follows to calculate the priorities and consistency of this AHP matrix:
  • We filled the diagonal with units and mirrored the values in the lower half of the matrix to the upper half to make it symmetric.
  • We have normalized the matrix.
  • We calculated the average weights (priorities) for each criterion.
  • We verified the consistency of the matrix by calculating the consistency ratio ( C R ).
In the calculation described above it was calculated:
  • The maximum eigenvector is λ m a x = 5,1835 ;
  • Consistent index is equal to C I = 0,0459 ;
  • The coherence ratio is equal to C R = 0,0409 .
Coherence ratio ( C R ) is again lower than 0,1 , so the comparison matrix is considered sufficiently consistent by AHP standards. Also in this case, the identified priorities can be considered reliable in the evaluation of alternatives.
Table 10 part (b) shows the priorities for each criterion, i.e. their degree of importance, are as follows:
  • Probability of HS: P = 0,2084 ;
  • Severity of Harm: S = 0,1802 ;
  • Number of HS occurrences: O = 0,2177 ;
  • Probability of non-detection of HS: P N D = 0,0889 .
  • The most important are the expected costs: E C = 0,3048 ;
The value of the inconsistency ratio is equal to 0,04 < 0,1 , i.e. it is acceptable. We call this variant of pairwise comparison Variant A.
After evaluating the different causes of undesirable events (HS) with respect to the criteria under consideration, all the evaluations must be aggregated in a hierarchical tree. Table 12 shows the priority of the probability of occurrence H S with respect to the five criteria from a local and total perspective (i.e. criterion priority multiplied by local cause priority ( H S )). It means, in the next step we set local and then total priorities for all 5 risk management parameters. The three “quantifiable” criteria can be evaluated by normalizing the quantitative assessments. These are the risk estimation parameters P , S a P N D (see Equation (2)). The normalization is performed by using the sums of all their scores (see the last row of Table 9). For example, for the parameter P is the value of T o t a l = 49 . The local prior for the parameter P and the value of E 1 we calculated as 3 / 49 = 0,061 . We followed a similar calculation for all rows for the three risk parameters mentioned above R M . In the same way, we calculated the row values of the local priority for the parameter O . The local prior for the value of E 1 and parameter O we calculate as 41 / 489 = 0,084 . The local priority for the parameter E C is represented by the priority vector described in Table 10 part (b). In the following step, we computed the total priorities for each parameter. We used the values from the vector of priorities described in Table 11 part (b) for the calculation. E.g. for the value of E 1 a parameter P we calculated the total prior of the parameter P as the product of the local priority times the corresponding priority from the aforementioned priority vector, namely 0,061 * 0,2084 = 0,013 .
We followed a similar procedure for calculating the other values of the total priority parameter P , but also all other parameters. After calculating all 5 total priorities by multiplying them in the corresponding row, we obtain the values of the last column of Table 11 under the name “Evaluation”. As soon as the prioritization of the performance criteria is achieved by composing pairwise comparisons, the last step involves using the AHP framework to evaluate the different causes of failure. The last column of Table 11 shows the final ranking of the 15 causes/effects considered, i.e., the hazardous situations analysed and their effects ( H S / E ).
As indicated in the table above, falling objects during machine maintenance ( H S 5 ) in terms of expected costs E5 resulting from the severity of harm when this hazardous event occurs, it emerges as the most critical problem among the 15 alternatives with an overall priority score of 0,092 . This is followed by ignition of combustible material during maintenance resulting in fire E2.1 with a value of 0,091 and ignition of combustible material E2.2 resulting in explosion, similarly with a value of 0,087 during maintenance of the machine.
As can be seen, in the case of E5 the final result of this analysis, is different than the results of the previous analysis based on the risk calculation alone R M (Table 8). The most critical undesirable events are E2.2 with a corresponding value of R M = 4 * 5 * 5 = 100 and E2.1 with the value R M = 4 * 5 * 4 = 80 . These represent a high degree of probability of an undesirable event occurring that is both very serious and difficult to detect. This apparent contradiction is due to the way the table for Variant A has been constructed.

2.3. Sensitivity analysis

The solution based on the Table 10, for Variant A, reflected a possible scenario where the most important criteria are the expected costs ( E C ) and the number of undesirable event occurrences ( O ). In general, the model solutions may change in line with changes in the logic of the approach, given the focus of the analysis.
The sensitivity or robustness of the model solution to potential shifts in strategy priority creates the opportunity to analyse the sensitivity of the criteria weights to changes in the priority (relative importance) of the weights. In fact, each criterion is characterized by an important degree of sensitivity, i.e., the ranking of all causes of failure changes dramatically across the weight range [38]. Therefore, it is important to control to what extent the evaluation ratings changes may lead to more or less significant changes in the final order of priorities. Sensitivity analysis is used to examine the sensitivity of alternatives to changes in the priority of criteria immediately below the target. The proposed analysis highlights the priorities of the five criteria used in the model and how a change in the priority of one criterion affects the priorities of the others. Clearly, as the priority of one criterion increases, the priorities of the remaining criteria must decrease in proportion to their original priorities, and the global priorities of the alternatives (see Table 11) must be recalculated.
Table 12 shows the priorities for each criterion, which, in that order, are the most important:
  • The chance of failure (Probability of HS): P = 0,127 ;
  • Severity of Harm: S = 0,1802 ;
  • Number of HS occurrences: O = 0,369 ;
  • The chance of not detecting an undesirable event: P N D = 0,08 ;
  • Expected costs: E C = 0,279 .
This variant of the pairwise comparison will be named as Variant B.
In the calculation described above it was calculated:
  • The largest eigenvector is λ m a x ​ = 5,587 ;
  • The consistency index is C I = 0,072 ;
  • The consistency ratio is C R = 0,064 .
Consistency ratio ( C R ) is less than 0,1 , which is the generally accepted threshold for an acceptable level of consistency in AHP analysis. This means that the comparisons between criteria in this analysis are sufficiently consistent and the priority results can be considered as reliable.
From Table 13 we can see the priorities for each criterion, which are the most important in that order:
  • Severity of harm: S = 0,395 ;
  • The chance of failure (undesirable event): P = 0,258 ;
  • Number of HS Occurrences: O = 0,16 ;
  • Expected costs: E C = 0,109 ;
  • The chance of not detecting an undesirable event: P N D = 0,078 .
This variant of pairwise comparison will be named as Variant C.
Similarly to the previous cases, we verify the consistency of the matrix by calculation:
  • The largest eigenvector: λ m a x ​ = 5,331 ;
  • Consistency index: C I = 0,083 ;
  • Consistency ratio: C R = 0,074 .
Consistency ratio ( C R ) lower than 0,1 indicates that the comparison matrix is sufficiently consistent for the purposes of AHP analysis. This indicates that the comparisons between criteria are consistent and the results of the analysis are reliable (see Table 14).
We note that the sensitivity analysis is only relevant for the priorities of the five criteria. If we were to change the values of the only one attribute at a time, one at a time, only the "main effects" would be considered, thus the "interaction effects" of changes in two or more of the weights would be neglected. We therefore adopted an approach whereby we varied different combinations of parameters for each variant, depending on the focus of the analysis and in consultation with OHS management.
Even after different, radical changes in preferences in pairwise comparisons, some robustness can be observed for variants A, B and C. Albeit in a different order, the first four riskiest events in all variants are identical (E2.1, E2.2, E3, E5). Moreover, this (except for the E3 case) corresponds in some way to the assessment based on R M (see penultimate column of Table 8 or the last two columns of Table 14). We note that in the original evaluation based on R M only the three parameters P , S and P N D were considered. Thus, the other two parameters were not considered E C , i.e. the expected unit cost of the alternative, as well as O , i.e. the frequency of occurrence of the given alternative across all the machinery. In the third place, when assessing the parameter R M three alternatives E2.4, E4.1 and E8 were recorded immediately, but when evaluated according to the five parameters (Variants A to C) their priority was ranked at 4 and above. On the other hand, the parameter E3 was ranked R M ranked as high as 9, but when evaluated on a variant-by-variant basis, it was ranked up to rank 4. This apparent mismatch in priorities is due to a more complex view, where alternative E3, although with a low-risk number R M = 36 , has an order of magnitude higher occurrence than the other alternatives.

3. Results of the Evaluation of the Effectiveness and Efficiency of the Proposed Measures

In the previous section, we used the AHP method to determine the priority of each H S / E according to the severity of the overall impacts on the whole group of considered machinery. Thus, it was about the amount of additional costs or losses that could potentially be incurred by the organization with respect to each of the considered alternatives. In this section we focus on the performance of the individual measures that have been proposed within the framework of the aforementioned "Machinery Risk Assessment" document. This is an important element in ensuring the sustainability of machinery safety. The MSRD process involves, in addition to the assessment of the assigned risks, the proposal of more or less effective and efficient measures. Within the framework of the document referred to above, experts have defined the most appropriate types of measures M s for each H S / E .
This means that for each of the 489 identified H S specific measures have been proposed as well as estimated how these measures will reduce the resulting risk number. We will refer to this reduced risk number as R A M .
After consideration of the OHS by management and evaluation of all the proposed measures, it was found that in many cases they are repetitive and can be standardly divided into 7 basic types (see Table 15). All proposed measures represent some combination of the aforementioned measures and risk management hierarchy according to NIOSH (National Institute for Occupational Safety and Health) [39].
Two of them, i.e. M 6 a M 7 do not require any additional cost increase. These are measures that are routinely implemented in the organisation. However, they have almost always been recommended in risk analyses only because many accidents or hazardous situations have been reported where these generally legislated safety measures have not been followed. Compliance with these two measures is therefore considered to be the absolute basis for the risk management of machinery and has therefore not been taken into account in the following assessment.
Based on consultation with OHS management, we estimated the expected costs associated with implementing each machine and each of the five proposed measures. We note that the costs for each measure were estimated only as an approximation at approximately the same time, without taking into consideration possible material price fluctuation and labor changes, etc. The costs associated with the introduction of each measure were influenced not only by the specific machinery, but also by its location in the plant or its proximity to other machinery. Table 16 shows the minimum and maximum estimated unit costs. Thus, these are the CM costs budgeted for each event, the machinery as well as the type of measure proposed.
The effectiveness of the measures was assessed by the so-called index A E I (Action Effectiveness Index), whereby A E I is a metric used to assess the effectiveness of proposed or implemented corrective actions in reducing risk R M . It aimed to quantify whether the proposed actions M i reduce risk or improve detection capability H S before it could have a negative impact on the machinery operator.
Calculation of the index A E I is based on a comparison of the values of R M before and after the implementation of the measures, in our case R A M (AM – after measure). The index of effectiveness of the measures ( A E I ) can thus be calculated as a percentage change that shows how much the risk ( R M ) has been reduced as a result of the implementation of the measures. The following relation applies:
A E I = R M − R A M   R M   * 100 %
This calculation provides a quantitative indicator of measures effectiveness. If a high percentage is achieved it is clear that the measures have significantly reduced the risk. On the other hand, a low or negative percentage could indicate that the measures have not been sufficiently effective or that the risk has not changed or has even increased.
It is important to note that the specific calculation methods and values may depend on the specific practices and policies of the organization. Therefore, when calculating A E I it is always advisable to follow internal guidelines. Calculation of the index A E I was used to estimate the effectiveness of the implementation of the 5 proposed measures mentioned above ( M 1 to M 5 ). We note that for each H S / E were almost always a combination of several of the 5 measures M 1 to M 5 . Thus, the estimation of the resulting costs implied an accumulation of the mentioned values. Therefore, for M i ( M 1 to M 5 ) we defined the value C M i for each H S / E . These are the costs that potentially need to be incurred in relation to the measure M i . If any measures M i are not for a given H S i proposed, the value C M i ( i = 1 , … , 5 ) is zero. The resulting expected costs C M for each H S / E are therefore given by the relation:
C M = ∑ i = 1 5 C M i
The costs assigned to each measure as well as the values P a S described in relation (1) were used as predictor variables in the Classification and Regression Trees (CART) method. This is a method focusing on regression trees to model the relationship between the dependent variable (in our case A E I ) and several predictor variables, i.e. P , S , C M 1 to C M 5 ).

3.1. Applying the CART Method for Assessing Effectiveness of M i

This is a 7-node CART regression analysis, focusing on regression trees to model the relationship between the dependent variable ( A E I ) and the predictor variables ( S , P , C M 1 to C M 5 ). The key parameters of the CART analysis include [40]: Node Splitting, Optimal Tree, Model Validation, R_squared, RMSE (Root Mean Squared Error) and MSE (Mean Squared Error), MAD (Mean Absolute Deviation) and MAPE (Mean Absolute Percent Error), which allow alternative measures of prediction error, important for understanding model accuracy in practical terms.
Based on previous analyses related to machine risk assessment and their impacts on the organization, specified criteria for classifying subjects into the best terminal nodes were developed as predictor variables and their thresholds define the division of data and the assignment of cases to different subgroups for prediction. These criteria and the assignment to nodes were the basis for creating a model that maps the relationships between the predictor variables and the dependent variable. Minitab software was used to analyse the regression decision tree and applied to an extended database with 489 rows. As mentioned above, we considered the response index A E I and the predictor parameters P , S , a C M 1 to C M 5 characterizing the expected unit cost for one machine, one event, and the specific measure proposed.
Figure 2 is a graphical representation of the dependence between the number of terminal nodes in the network and the R-squared value. R-squared is a statistical measure that expresses the degree to which the variability of the dependent variable is explained by the independent variable. In this case, the dependent variable is the number of terminal nodes and the independent variable is R-squared. Axis X shows the number of terminal nodes in the network, with the values on the axis X range from 2 to 11. Y shows the value of R-squared and the values on the axis Y ranges from 0 to 85%. The curve in the graph shows the trend of the relationship between the number of terminal nodes and the R-squared value.
The curve has an increasing trend, indicating the number of terminal nodes increases, the R-squared value also increases. The optimal R-squared value, which is 84.08%, is also indicated in the graph. This value has been achieved with 8 terminal nodes. The graph shows the number of terminal nodes increases, the R-squared value also increases to explain the variability in the number of terminal nodes. This indicates the number of terminal nodes increases, the model becomes more accurate in predicting the number of terminal nodes. The optimal value of R-squared indicates the model is most accurate in predicting the number of terminal nodes at this point. Increasing the number of terminal nodes above 8 would lead to a decrease in the accuracy of the model. This shows there is a strong dependence between the number of terminal nodes and the R-squared value.
The overall importance of the nodes in the CART tree (see Figure 3) lies in their ability to partition the dataset into predictively homogeneous groups, allowing for more accurate predictions and a better understanding of the relationships in the data. It describes the specific data in the tree nodes and the criteria for classifying subjects into the best terminal nodes within the CART model.
Figure 4 compares the relative importance of each cost measure C M 1 to C M 5 and parameters S a P . It shows that the costs of the measures C M 4 , C M 1 a C M 2 have a large impact on the formation of the predictive model.
, S and C M 1 to C M 5 (source: own design).
The following Table 17 provides quantitative measures of model accuracy, i.e., the performance of the CART regression model on the training and test sets. The low values of RMSE, MSE, MAD and MAPE indicate good prediction accuracy of the model.
The R-squared (86.75% on the training set and 84.08% on the test set) indicates the model explains the variability of the dependent variable relatively well. Overall, these figures show the CART model can accurately predict the dependent variable with a high degree of accuracy and has low prediction errors on both the training and test sets. The following Table 18 describes the criteria for the 7 Terminal Node.
The greatest efficiency in terms of the greatest percentage of the index value A E I is represented by terminal node 4, specifically 75%, but on the other hand, this node refers to the application of measures H S / E . The path to it from the root goes through node 2 and node 4, i.e. that for each of the 4 events it is necessary to spend C M 4 (from 0 to 50 Euros) + C M 2 (from 44 to 88 Euros) + C M 1 (78 Euros). This can be interpreted as the implementation of measures M 4 : Education - training, M 2 : E- STOP and M 1 : LOTO - Safety padlock at unit costs ranging from 132 Euros to 216 Euros. This is therefore a high efficiency of the measures in relation at a relatively low cost. The problem is, as we have already mentioned, that only 4 undesirable events ( H S / E ) are affected. Another of the nodes Terminal Node 7 achieves success in reducing the criticality of the event with measures M4 and M3 at corresponding costs ranging from 1200 Euros to 1500 Euros. In a similar way, we calculated the unit cost for the proposed measures with respect to their effectiveness as measured by A E I for all 489 undesirable events ( H S / E ) considered. Thus, using the CART method, we divided the individual events H S / E into relatively homogeneous groups according to the relationship between A E I and costs C M (divided into 5 groups according to each measure; M 1 up to M 5 ) as well as parameters P a S . We note that the parameters P a S were the basis for calculating the risk number R and thus naturally influence the parameter A E I . In the following, we show how both applied methods can be used simultaneously.
In Chapter 2.3, we performed the ranking of the results of the AHP method for the 5 investigated parameters and 3 different pairwise comparison matrices (Variant A, B, C, Table 14). By comparing the aforementioned rankings, we found independently of the different variants, there are four basic types of negative effects (namely E2.1, E2.2, E3 and E5) once they occur, will imply the largest total costs (losses) related to failure. In the following, we have therefore reduced the identified 489 H S / E to 4 types of significant undesirable events mentioned. The resulting reduced database contained 188 H S / E that corresponded to any of the 4 types of undesirable events mentioned above. We then applied the CART method to this database. We again used the index as the response A E I , parameters were used as predictors P , S , C M 1 to C M 5 . The results of the regression decision tree are presented in Figure 5.
We describe the resulting model parameters as follows. The R-squared (91.04% on the training set and 84.08% on the test set) indicates the model explains the variability of the dependent variable relatively well. Overall, these figures show that the CART model is able to accurately predict the dependent variable with a high degree of accuracy and has low prediction errors on both the training and test sets. The following Table 19 describes the criteria for the 3 Terminal Node.
The final evaluation of the decision tree is presented in summary in the following Table 20. It can be concluded which undesirable events can be expected to result in the greatest cost savings, i.e. both the cost of failure (losses from undesirable events) and the cost of the measures that will most reduce the existing risk. The presented results are obtained by the AHP method for 3 different variants A, B and C of the pairwise comparisons matrices. The table shows the order of importance of the 4 events with the highest priority for all three variants. These are the 188 events selected for E2.1, E2.2, E3 and E5. Three Terminal Nodes were obtained from the CART technique applied to the set of all events of these types. Each of them represents the percentage of expected criticality reduction for each event. The table also lists the measures that are expected to result in a given criticality reduction. The unit and total costs that will be incurred by implementing the prescribed combination of measures are also included in the table.
From the table is clear the event with the highest efficiency has the designation E5 and a frequency of 51. Approximately 65% reduction in criticality for all events of this type requires the implementation of combinations of measures M1, M2 and M4 with a unit cost of 666 Euros and a total cost of 33 966 Euros. In other words, up to about 65% reduction in criticality for the 51 most serious failures, as assessed by all three variants, can be achieved with the measures M 1 , M 2 a M 4 at the lowest possible unit cost of € 666. With even lower unit costs, it is possible to implement the measures M 1 , M 2 a M 3 to reduce by 1/3 from 46 events E3. We can estimate the costs for the other events in the same way. If the management of the organisation decides to reduce all 188 most critical events, it would need to cover costs of about 192 776 Euros.

4. Discussion

The presented five-parameter machinery safety analysis appears to be an effective tool to perform a comprehensive risk assessment analysis of machinery. The proposed procedure allows obtaining a ranking of the causes and consequences of undesirable events, which include several types of information ( P - Probability of hazardous situation; P N D - Probability of non-detection of HS; S - Severity of Harm; E C - Expected cost; O - Number of HS Occurrence). The approach based on the implementation of the AHP method for multi-attribute analysis provides a framework in which the selection of the most critical undesirable events can be performed using different relevant characteristics. The AHP method helps safety analysts to work in a systematic and analytical manner, addressing each aspect of the failure in a stepwise hierarchy. The qualitative and subjective judgments of multiple individuals can be incorporated into the prioritization process. Using a series of paired evaluations, the AHP can obtain a direct (quantitative) assessment based on intangible (qualitative) criteria. Specifically, the problem is how to assign scores based on tables listing vague and unreliable verbal ratings. However, the great advantage is that if reliable quantitative judgements are available for some criteria, they can easily be included in the AHP analysis. This possibility means that our proposed procedure can replace, complement or integrate into a more comprehensive approach to safety studies.
Using the AHP method and the 5 basic parameters, we have shown a way to estimate the most critical undesirable events ( H S / E ). Risk management is based on E C and is applied to the whole group of machinery also based on the estimation of the parameter O . The result of such an approach is a procedure that allows designing an effective plan of action to minimize the expected losses due to undesirable events in an organization.
Another way to increase the effectiveness of machinery safety management is to maximise the effect of the measures taken at a cost-effective cost. For this purpose, we apply the CART technique. As a response we selected the parameter A E I , which evaluates the effectiveness of the proposed or implemented corrective actions in reducing the risk of failure. As predictors, we worked with expected unit cost for each machine (cause or effects). In the case study we conducted that it is possible to develop a model we proposed, which can predict which group of measures, at what expected unit cost, will reduce the criticality of a particular undesirable event to what extent.

5. Conclusions

Machinery safety should be a priority for the management of every operation in an organisation. As significant resources are usually required to ensure safety or reduce risks, it is appropriate to carefully consider the priority of the relevant measures as well as the expected costs of their implementation. We have shown it is possible to determine, on the basis of existing safety analyses, in a relatively simple way, those undesirable events, the fulfilment of which entails the greatest risk of an often-unexpected increase in costs (losses). Although it is almost impossible to define these costs in an exact way, we have shown that by using the AHP multicriteria decision-making method, it is possible to prioritize them using pairwise comparisons. Increasing the efficiency of machinery safety assurance can also be achieved by efficiently spending resources on individual proposed measures aimed at reducing the risk of undesirable events. Using the CART tool, we have identified how the cost of individual measures affects the degree of criticality reduction for each type of undesirable event. Overall, the CART model in this analysis provides an accurate and reliable technique for prediction, indicating its suitability for the data analysed even when expanding operations to include similar machinery.
Finally, we have shown how the combination of the AHP method and the CART technique can be used to extract and cost-estimate those measures that will most effectively reduce both the unit and total cost of failures within the operations of a manufacturing organization.

Author Contributions

Management and validation, writing and final review, H.P. and R.T.; Application of statistical, mathematical techniques, R.T.; Development of methodology, R.T.; Data collection and final review of the paper, H.P. and D.O.; Research, data collection, H.P., J.G. and D.O. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Acknowledgments

This contribution is the result of the projects implementation: APVV No. 19-0367 “Framework of the Integrated Process Safety Management Approach for the Intelligent Enterprise”.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Badri, A.; Boudreau-Trudel, B.; Souissi, A.S. Occupational health and safety in the industry 4.0 era: A cause for major concern? Saf. Sci. 2018, 109, 403–411. [Google Scholar] [CrossRef]
  2. Vogl, G.W.; Weiss, B.A.; Helu, M. A review of diagnostic and prognostic capabilities and best practices for manufacturing. J. Intell. Manuf. 2019, 30, 79–95. [Google Scholar] [CrossRef] [PubMed]
  3. Jocelyn, S.; Chinniah, Y.; Ouali, M-S. ; Yacout, S. Application of logical analysis of data to machinery related accident prevention based on scarce data. Reliab. Eng. Syst. Saf. 2017, 159, 223–236. [Google Scholar] [CrossRef]
  4. Lee, D. The Effect of Safety Management and Sustainable Activities on Sustainable Performance: Focusing on Suppliers. Sustainability 2018, 10, 4796. [Google Scholar] [CrossRef]
  5. Xue, Y.; Fan, Y.; Xie, X. Relation between senior managers’ safety leadership and safety behavior in the Chinese petrochemical industry. J. Loss Prev. Process Ind. 2020, 65, 104142. [Google Scholar] [CrossRef]
  6. Roger, I.; Flin, R.; Mearns, K.J.; Hetherington, C. Safety Leadership: A View of the Senior Managers' Role. In SPE Offshore Europe Oil and Gas Conference and Exhibition. OnePetro, Aberdeen, UK, 2009. [Google Scholar] [CrossRef]
  7. Pham, H.; Kim, S.-Y. The effects of sustainable practices and managers’ leadership competences on sustainability performance of construction firms. Sustain. Prod. Consum. 2019, 20, 1–14. [Google Scholar] [CrossRef]
  8. Anunciação, P.; Dinis, V.; Peñalver, A.; Esteves, F. Functional Safety as a critical success factor to industry 4.0. Procedia Comput. Sci. 2022, 204, 45–53. [Google Scholar] [CrossRef]
  9. Balážiková, M.; Pačaiová, H.; Tomašková, M. A Proposal for Risk Assessment of Low-Frequency Noise in the Human–Machine–Environment System. Appl. Sci. 2023, 13, 13321. [Google Scholar] [CrossRef]
  10. Leveson, N. A new accident model for engineering safer systems. Saf. Sci. 2004, 42, 237–270. [Google Scholar] [CrossRef]
  11. Manuele, F.A. On the practice of safety., 4th ed.; Wiley & Sons: Hoboken, New Jersey, 2003. [Google Scholar]
  12. Ayyub, B.M. Risk analysis in engineering and economics., 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 2003. [Google Scholar]
  13. Harms-Ringdahl, L. Safety analysis: principles and practice in occupational safety., 2nd ed.; CRC Press: London, 2001. [Google Scholar]
  14. Boileau, P.E. Sustainability and prevention in occupational health and safety. Ind Health. 2016, 54, 293–295. [Google Scholar] [CrossRef]
  15. Nawaz, W.; Linke, P.; Koҫ, M. Safety and sustainability nexus: A review and appraisal. J. Clean. Prod. 2019, 216, 74–87. [Google Scholar] [CrossRef]
  16. Hogevold, N. M.; Svensson, G.; Wagner, B.; Petzer, D. J.; Klopper, H. B.; Sosa Varela, J. C.; Padin, C.; Ferro, C. Sustainable business models: Corporate reasons, economic effects, social boundaries, environmental actions and organizational challenges in sustainable business practices. Balt. J. Manag. 2014, 9, 357–380. [Google Scholar] [CrossRef]
  17. Dyllick, T.; Muff, K. Clarifying the Meaning of Sustainable Business: Introducing a Typology From Business-as-Usual to True Business Sustainability. Organ. Environ. 2016, 29, 156–174. [Google Scholar] [CrossRef]
  18. Bayram, M.; Ünğan, M.C.; Ardıç, K. The relationships between OHS prevention costs, safety performance, employee satisfaction and accident costs. Int. J. Occup. Saf. Ergon. 2016, 23, 285–296. [Google Scholar] [CrossRef]
  19. Jallon, R.; Imbeau, D.; Marcellis-Warin, N. Development of an indirect-cost calculation model suitable for workplace use. J. Saf. Res. 2011, 42, 149–164. [Google Scholar] [CrossRef] [PubMed]
  20. Šolc, M.; Blaško, P.; Girmanová, L.; Kliment, J. The Development Trend of the Occupational Health and Safety in the Context of ISO 45001:2018. Standards 2022, 2, 294–305. [Google Scholar] [CrossRef]
  21. Kineber, A.F.; Antwi-Afari, M.F.; Elghaish, F.; Zamil, A.M.A.; Alhusban, M.; Qaralleh, T.J.O. Benefits of Implementing Occupational Health and Safety Management Systems for the Sustainable Construction Industry: A Systematic Literature Review. Sustainability 2023, 15, 12697. [Google Scholar] [CrossRef]
  22. Botti, L.; Melloni, R.; Oliva, M. Learn from the Past and Act for the Future: A Holistic and Participative Approach for Improving Occupational Health and Safety in Industry. Saf. Sci. 2022, 145, 105475. [Google Scholar] [CrossRef]
  23. Fonseca, L.; Carvalho, F. The Reporting of SDGs by Quality, Environmental, and Occupational Health and Safety-Certified Organizations. Sustainability 2019, 11, 5797. [Google Scholar] [CrossRef]
  24. Möller, N.; Hansson, S. O.; Peterson, M. Safety is more than the antonym of risk. J. Appl. Philos. 2006, 23, 419–432. [Google Scholar] [CrossRef]
  25. Aven, T.; Renn, O. On risk defined as an event where the outcome is uncertain. J. Risk Res. 2009, 12, 1–11. [Google Scholar] [CrossRef]
  26. Kóča, F.; Pačaiová, H.; Turisová, R.; Sütőová, A.; Darvaši, P. The Methodology for Assessing the Applicability of CSR into Supplier Management Systems. Sustainability 2023, 15, 13240. [Google Scholar] [CrossRef]
  27. Tsalis, T.A.; Stylianou, M.S.; Nikolaou, I.E. Evaluating the quality of corporate social responsibility reports: The case of occupational health and safety disclosures. Saf. Sci. 2018, 109, 313–323. [Google Scholar] [CrossRef]
  28. Standard ISO 12100. Safety of Machinery - General Principles for Design–Risk Assessment and Risk Reduction; ISO: Geneva, Switzerland, 2010. [Google Scholar]
  29. European Parliament and of the Council. Directive 2006/42/EC of the European Parliament and of the Council of 17 May 2006 on Machinery and Amending Directive 95/16/EC (Recast); European Parliament and of the Council: Brussels, Belgium, 2006. [Google Scholar]
  30. Dudek, E.; Kozłowski, M. The concept of risk tolerability matrix determination for aeronautical data and information chain. J. KONBiN 2017, 43, 69–94. [Google Scholar] [CrossRef]
  31. Tanasić, Z.; Kecman, B.; Janjić, G. QFD METHOD-A MODEL FOR PRODUCT IMPROVEMENT AND DEVELOPMENT. Ann. Fac. Eng. Hunedoara 2021, 19, 75–80. [Google Scholar]
  32. Braglia, M. MAFMA: Multi-attribute failure mode analysis. Int. J. Qual. Reliab. Manag. 2000, 17, 1017–1033. [Google Scholar] [CrossRef]
  33. Robinson, L.S.; Sarkies, M.; Brown, T.; O’Brien, L. Direct, indirect and intangible costs of acute hand and wrist injuries: a systematic review. Injury 2016, 47, 2614–2626. [Google Scholar] [CrossRef]
  34. Leal, J.E. AHP-express: A simplified version of the analytical hierarchy process method. MethodsX 2020, 7, 100748. [Google Scholar] [CrossRef] [PubMed]
  35. Saaty, T.L. The Analytical Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
  36. Saaty, T.L. How to make a decision: the analytic hierarchy process. Eur. J. Oper. Res. 1990, 48, 9–26. [Google Scholar] [CrossRef]
  37. Munier, N.; Hontoria, E. Uses and Limitations of the AHP Method. A Non-Mathematical and Rational Analysis. In Management for Professionals; Springer: Berlin, Germany, 2021. [Google Scholar]
  38. Min, H.; Melachrinoudis, E. The relocation of a hybrid manufacturing/distribution facility from supply chain perspectives: a case study. Omega 1999, 27, 75–85. [Google Scholar] [CrossRef]
  39. Ajslev, J.Z.N.; Møller, J.L.; Andersen, M.F.; Pirzadeh, P.; Lingard, H. The Hierarchy of Controls as an Approach to Visualize the Impact of Occupational Safety and Health Coordination. Int. J. Environ. Res. Public Health 2022, 19, 2731. [Google Scholar] [CrossRef] [PubMed]
  40. Jian, Z.; Zhaowei, W.; Changsong, Q. Study on the key quality parameter decision for multi-process by CART method. In 2010 International Conference on Computer Application and System Modeling, 2010. [Google Scholar] [CrossRef]
Preprints 101365 g001
Figure 1. Model of a three-level Hierarchical framework for machine risk management (source: own design).
Figure 1. Model of a three-level Hierarchical framework for machine risk management (source: own design).
Preprints 101365 g001
Preprints 101365 g002
Figure 2. R-squared vs Number of Terminal Nodes Plot (source: own design).
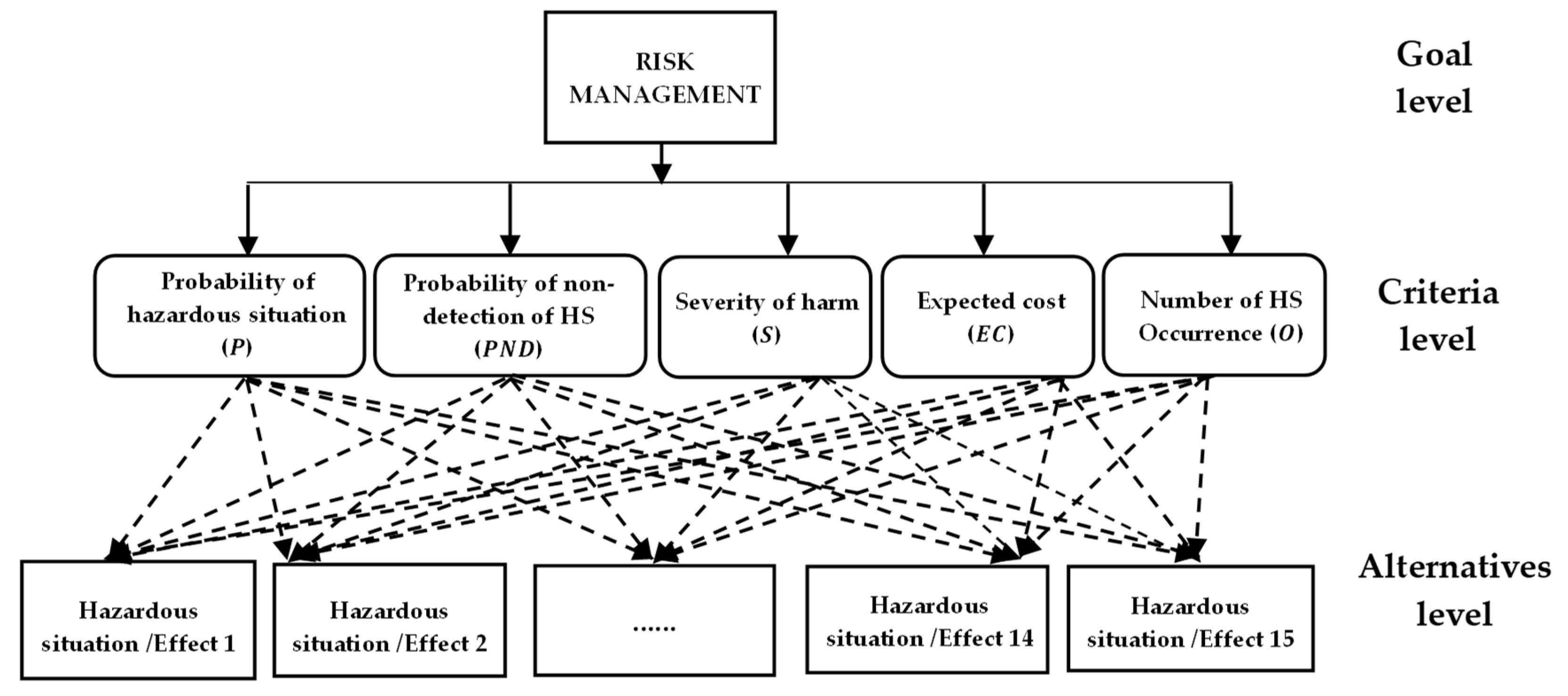
Figure 2. R-squared vs Number of Terminal Nodes Plot (source: own design).
Preprints 101365 g002
Preprints 101365 g003
Figure 3. Optimal Tree Diagram for 7 Terminal Node (source: own design).
Figure 3. Optimal Tree Diagram for 7 Terminal Node (source: own design).
Preprints 101365 g003
Preprints 101365 g004
Figure 4. Relative Variable Importance for P
Figure 4. Relative Variable Importance for P
Preprints 101365 g004
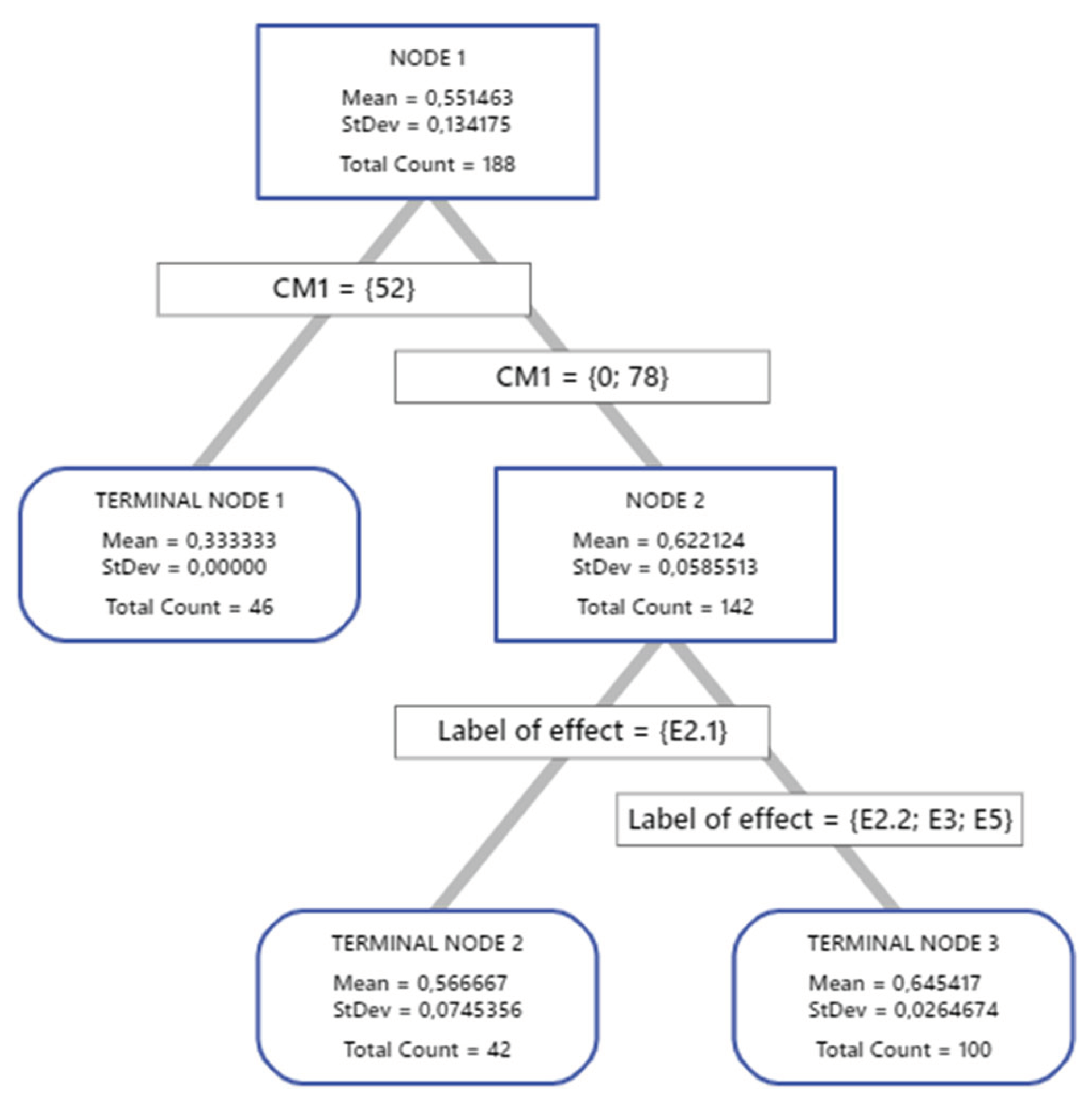
Preprints 101365 g005
Figure 5. Relative Variable Importance for 3 Terminal Node.
Figure 5. Relative Variable Importance for 3 Terminal Node.
Preprints 101365 g005
Table 1. Probability of exposure of operator to the HS scale ( P ).
Table 1. Probability of exposure of operator to the HS scale ( P ).
Verbal Evaluation Probability   of   HS   ( P ) Corresponding to the Occurrence of Once Per: Score
Very unlikely > 3 years 1
Unlikely 1 - 3 years 2
Possible 6 months to a year 3
Likely 1 month to six months 4
Very likely < 1 month 5
Table 2. Severity of harm scale ( S ).
Table 2. Severity of harm scale ( S ).
Verbal Evaluation Severity of that Harm (𝑺) Score
Negligible A near miss with little potential for injury, or an injury that does not require treatment. 1
Minor Injury requires treatment at the workplace but without incapacity for work. Examples include a scratch, minor cut,bruise, such as one requiring first aid. 2
Moderate Injury requiring medical treatment by a medical professional. An example is a more serious cut or sprain. Work can usually only be carried out after medical treatment. 3
Major Possible injury with prolonged incapacity for work. 4
Severe Serious injury with long-term incapacity for work or death. 5
Table 3. Risk Scoring Matrix
Table 3. Risk Scoring Matrix
Severity   of   harm   ( S )
R = P * S Negligible
1		 Minor
2		 Moderate
3		 Major
4		 Severe
5
Probability   of   failure   ( P ) Very unlikely
1		 1 2 3 4 5
Unlikely
2		 2 4 6 8 10
Possible
3		 3 6 9 12 15
Likely
4		 4 8 12 16 20
Very likely
5		 5 10 15 20 25
Risk assessment - Risk category
LOW
Score: 1 - 3		 Low or acceptable risk. Proceed with due care and attention, following instructions and procedures.
MEDIUM
Score: 4 - 7		 Moderate or tolerable risk. Task must be carried out according to training and in accordance with safety procedures. Any appropriate control measures must be in place before the task/activity commences.
HIGH
Score: 8 - 14		 High or undesirable risk. Management consideration and authorization is required for its tolerance. Where possible the task should be reassessed to take account of the associated risks and additional control measures put in place to reduce the risk (if feasible).
STOP
Score: 15 - 20		 Very high or unacceptable risk. This role must not be continued. Further action needs to be reviewed or implemented immediately. These measures should be reconsidered.
STOP - STOP
Score: 25		 A strongly unacceptable risk. Operation must be stopped immediately. Redesign of the machine must be considered.
Table 4. Machinery risk assessment - example.
Table 4. Machinery risk assessment - example.
Process Activity Type of Hazard Hazardous Situation (HS) Possible
Consequences		 Risk
P S R Category
Manufacturing: Cartoon maker Material handling; Shutdown and start-up Mechanical kinetic energy
(occurrence in the zone of product movement on the machine conveyor, movement of packaging machine parts)		 ejection, crushing 4 4 16 STOP
compressed air
(activity in the vicinity of compressed air pipelines)		 ejection, crushing, abrasion 3 4 12 H
Electrical electric arc
(arc flash zone)		 burn, death 3 5 15 STOP
inappropriate contact
(contact with live parts of electrical wiring)		 burn, death 2 5 10 H
Radiation hazard optical radiation
(exposure to optical radiation when checking product labelling)		 discomfort, fatigue, damage to eyes 3 4 12 H
high frequency el. magnetic radiation (activity in the zone of wireless transmission of production data). discomfort, fatigue (in the case of a pacemaker, even death) 3 4 12 H
Material and substances air pollution
(environmental pollution by dusty waste)		 over sensitization, infection 3 4 12 H
combustible materials
(combustible dust in the workplace)		 over sensitization 3 5 15 STOP
fire, explosion, 3 5 15 STOP
Table 5. Types of analysed machinery.
Table 5. Types of analysed machinery.
Machinery Number Machinery Number
APS Inline Pre-Made Pouches 7 Automatic labelling system 10
FUT Urostomy product 2 Extruder 21
Ostomy pouches 1 Material handling system 1
Cutter 2 Mixer 1
Folding machine 2 Cartoon maker 2
Table 6. Number of occurrences of standardised H S on machinery.
Table 6. Number of occurrences of standardised H S on machinery.
H S i Hazardous   situation   ( H S ) Number   of   HS   occurrences   ( O )
H S 1 air pollution 41
H S 2 combustible materials 74
H S 3 compressed air 92
H S 4 electric arc 76
H S 5 falling objects (e.g. tools and materials) 52
H S 6 high frequency electromagnetic radiation 9
H S 7 inappropriate contact 87
H S 8 instability (loose parts) 39
H S 9 kinetic energy 8
H S 10 optical radiation 15
Total sum 489
Table 7. Quantified score values P N D
Table 7. Quantified score values P N D
Identifiable by Human Senses Automatic Detection Detection after H S Occurrence (Corrective Measures) Detection before H S Occurrence (Preventive Measures) Score P N D
Yes Partially No Directly Indirectly No Yes No Yes No
o 1 1
o o 1 1
o 2 o 2
o 2 o o 2
o 3 o o 3
o 3 o o 3
o 4 o o 4
o 4 o o 4
o 4 o o 4
o 5 o o o 5
o 5 o o o 5
o 5 o o o 5
o 5 o o o 5
Table 8. Main H S and assignment of parameters to determine their effects ( E ).
Table 8. Main H S and assignment of parameters to determine their effects ( E ).
Label   of   H S   Number   of   O Process Type of hazard Description   of   H S Potential harm P S P N D R M Label   of   E
CAUSE H S 1 41 operation Material/ substance air pollution over sensitization, infection 3 4 3 36 E1 EFFECT
H S 2 15 maintenance Material/ substance combustible materials local fire 4 5 4 80 E2.1
4 explosion 4 5 5 100 E2.2
12 operation over sensitization 3 5 4 60 E2.3
43 fire, explosion 2 5 5 50 E2.4
H S 3 92 operation Mechanical compressed air ejection, crushing, abrasion 3 4 3 36 E3
H S 4 31 maintenance Electrical electric arc burn, death 3 5 5 75 E4.1
45 operation burn, death 2 5 4 40 E4.2
H S 5 52 maintenance Mechanical falling objects (e.g. tools and materials) crushing, contusion, throwing 4 4 4 64 E5
H S 6 9 operation Radiation high frequency electromagnetic radiation discomfort, fatigue (in the case of a pacemaker, even death) 3 4 5 60 E6
H S 7 32 operation Electrical inappropriate contact burn, death 2 5 3 30 E7.1
51 maintenance Mechanical impact, crushing, ejection 4 3 2 24 E7.2
H S 8 39 maintenance Mechanical instability (loose parts) impact, crushing 5 3 4 60 E8
H S 9 8 operation Mechanical kinetic energy ejection, crushing 4 4 3 48 E9
H S 10 15 operation Radiation optical radiation discomfort, fatigue, damage to eyes 3 4 5 60 E10
Total 489 x x x x x x x 823 x
Note: HS - hazardous situations; O - Number of HS occurrences; P – Probability of HS; S – Severity of the harm; PND - Probability of non-detection of HS; R_M - Risk of machinery; E – Effects.
Table 9. Pairwise combination comparison matrix E for estimating E C .
Table 9. Pairwise combination comparison matrix E for estimating E C .
E1 E2.1 E2.2 E2.3 E2.4 E3 E4.1 E4.2 E5 E6 E7.1 E7.2 E8 E9 E10 Local priority   E C
E1 X 0,2 0,2 0,2 0,2 0,25 0,33 2,00 0,25 1 1 2 0,33 0,25 5 0,027
E2.1 5 X 1 4 4 4 4 8 2 4 5 2 6 2 5 0,157
E2.2 5 1 X 4 4 4 4 8 2 4 5 2 6 2 5 0,157
E2.3 5 0,25 0,25 X 1 2 1 4 0,33 0,5 4 3 2 2 3 0,069
E2.4 5 0,25 0,25 1 X 2 1 4 0,33 0,5 4 3 2 2 3 0,069
E3 4 0,25 0,25 0,5 0,5 X 2 6 0,33 4 0,5 5 1 0,33 3 0,056
E4.1 3 0,25 0,25 1 1 0,5 X 6 0,33 4 2 0,25 1 0,33 2 0,049
E4.2 0,5 0,13 0,13 0,25 0,25 0,17 0,17 X 0,13 0,5 0,2 1 0,2 0,13 0,5 0,013
E5 4 0,5 0,5 3 3 3 3 8 X 6 3 6 3 1 4 0,115
E6 2 0,25 0,25 2 2 0,25 0,25 2 0,17 X 0,33 2 0,33 0,17 3 0,039
E7.1 2 0,2 0,2 0,25 0,25 2 0,5 5 0,33 3 X 5 1 0,33 2 0,046
E7.2 0,5 0,5 0,5 0,33 0,33 0,2 4 1 0,17 0,5 0,2 X 0,2 0,13 1 0,033
E8 3 0,17 0,17 0,5 0,5 1 1 5 0,33 3 1 5 X 0,33 4 0,049
E9 4 0,5 0,5 0,5 0,5 3 3 8 1 6 3 8 3 X 5 0,101
E10 0,2 0,2 0,2 0,33 0,33 0,33 0,5 2 0,25 0,33 0,5 1 0,25 0,2 X 0,020
(a) (b)
Table 10. Variant A – pairwise comparison of criteria at the first level of the AHP hierarchy.
Table 10. Variant A – pairwise comparison of criteria at the first level of the AHP hierarchy.
Criteria P P N D S E C O Priority
P x 3 1 1 0,50 0,2084
P N D 0,33 x 0,50 0,33 0,50 0,0889
S 1 2 x 0,50 1 0,1802
E C 1 3 2 x 2 0,3048
O 2 2 1 0,50 x 0,2177
(a) (b)
Table 11. Resulting prioritisations for all parameters examined
Table 11. Resulting prioritisations for all parameters examined
Alternative Probability of HS ( P ) 0,2084 Severity ( S ) 0,1802 Probability   of   non - detection   ( N D ) 0,0889 Expected cost ( E C ) 0,3048 Occurrence count (O) 0,2177 Evaluation
P Local   priority   P Total   priority   P S Local   priority   S Total   priority   S N D Local   priority   N D Total   priority   N D Local   priority   E C Total   priority   E C O Local   priority   O Total   priority   O
E1 3 0,061 0,013 4 0,062 0,011 3 0,051 0,005 0,027 0,008 41 0,084 0,018 0,055
E2.1 4 0,082 0,017 5 0,077 0,014 4 0,068 0,006 0,157 0,047 15 0,031 0,007 0,091
E2.2 4 0,082 0,017 5 0,077 0,014 5 0,085 0,008 0,157 0,047 4 0,008 0,002 0,087
E2.3 3 0,061 0,013 5 0,077 0,014 4 0,068 0,006 0,069 0,021 12 0,025 0,005 0,059
E2.4 2 0,041 0,009 5 0,077 0,014 5 0,085 0,008 0,069 0,021 43 0,088 0,019 0,070
E3 3 0,061 0,013 4 0,062 0,011 3 0,051 0,005 0,056 0,017 92 0,188 0,041 0,086
E4.1 3 0,061 0,013 5 0,077 0,014 5 0,085 0,008 0,049 0,015 31 0,063 0,014 0,063
E4.2 2 0,041 0,009 5 0,077 0,014 4 0,068 0,006 0,013 0,004 45 0,092 0,020 0,052
E5 4 0,082 0,017 4 0,062 0,011 4 0,068 0,006 0,115 0,035 52 0,106 0,023 0,092
E6 3 0,061 0,013 4 0,062 0,011 5 0,085 0,008 0,039 0,012 9 0,018 0,004 0,048
E7.1 2 0,041 0,009 5 0,077 0,014 3 0,051 0,005 0,046 0,014 32 0,065 0,014 0,055
E7.2 4 0,082 0,017 3 0,046 0,008 2 0,034 0,003 0,033 0,011 51 0,104 0,023 0,062
E8 5 0,102 0,021 3 0,046 0,008 4 0,068 0,006 0,049 0,015 39 0,080 0,017 0,068
E9 4 0,082 0,017 4 0,062 0,011 3 0,051 0,005 0,101 0,031 8 0,016 0,004 0,067
E10 3 0,061 0,013 4 0,062 0,011 5 0,085 0,008 0,020 0,006 15 0,031 0,007 0,044
Total 49 1 0,2084 65 1 0,1802 59 1 0,0889 1 0,3048 489 1 0,2177 1
Note :   P   -   Probability   of   HS ;   P N D   -   Probability   of   non - detection   of   H S ;   S   -   Severity   of   Harm ;   E C   -   Expected   cos t ;   O   -   Number   of   H S Occurrence.
Table 12. Variant B – pairwise comparison of criteria at the first level of the AHP hierarchy.
Table 12. Variant B – pairwise comparison of criteria at the first level of the AHP hierarchy.
Criteria P P N D S E C O Priority
P x 3 1 0,33 0,33 0,127
P N D 0,33 x 0,50 0,33 0,33 0,078
S 2 2 x 0,33 0,33 0,145
E C 3 3 3 x 0,50 0,279
O 3 3 3 2 x 0,369
(a) (b)
Note: P - Probability of HS; PND - Probability of non-detection of HS; S - Severity of harm; EC - Expected cost; O - Number of\ HS Occurrence.
Table 13. Variant C – pairwise comparison of criteria at the first level of the AHP hierarchy.
Table 13. Variant C – pairwise comparison of criteria at the first level of the AHP hierarchy.
Criteria P P N D S E C O Priority
P x 3 0,33 3 3 0,258
P N D 0,33 x 0,33 0,5 0,33 0,078
S 3 3 x 0,33 3 0,395
E C 0,33 2 0,33 x 0,50 0,109
O 0,33 3 0,33 2 x 0,16
(a) (b)
Note: P - Probability of HS; PND - Probability of non-detection of HS; S - Severity of harm; EC - Expected cost; O - Number of\ HS Occurrence.
Table 14. Comparison of the priorities set for the different risk assessment Variants.
Table 14. Comparison of the priorities set for the different risk assessment Variants.
Alternative Evaluation - Variant A Order of events Variant A Evaluation - Variant B Order of events Variant B Evaluation - Variant C Order of events Variant C Risk R M Order   of   events   by   R M
E1 0,055 11 0,059 7 0,057 11 36 9
E2.1 0,091 2 0,082 3 0,076 4 80 2
E2.2 0,087 3 0,075 4 0,079 2 100 1
E2.3 0,059 10 0,053 10 0,060 9 60 5
E2.4 0,070 5 0,075 4 0,072 6 75 3
E3 0,086 4 0,106 1 0,077 3 36 9
E4.1 0,063 8 0,063 6 0,071 7 75 3
E4.2 0,052 12 0,059 7 0,059 10 50 6
E5 0,092 1 0,096 2 0,082 1 64 4
E6 0,048 13 0,041 11 0,061 8 60 5
E7.1 0,055 11 0,057 9 0,052 12 40 8
E7.2 0,062 9 0,068 5 0,059 10 60 5
E8 0,068 6 0,068 5 0,075 5 75 3
E9 0,067 7 0,058 8 0,060 9 48 7
E10 0,044 14 0,040 12 0,061 8 60 5
Total 1 x 1 x 1 x x x
Table 15. Individual measures.
Table 15. Individual measures.
M i Measures Hierarchy of control [39]
M1 LOTO - safety padlock Isolate people from the hazard
M2 Emergency stop button (ESB) Isolate people from the hazard
M3 Guard Elimination
M4 Education - training Administration
M5 Automated ventilation system Engineering
M6 PPE (personal protective equipment) PPE (personal protective equipment)
M7 Periodic maintenance - inspections Engineering
Node: Mi – Measures (i=1,\ \ldots,\ 7); LOTO - Lockout/Tagout devices.
Table 16. Estimated unit costs for the identified measures.
Table 16. Estimated unit costs for the identified measures.
M i Measures C M
Min (Eur) Max (Eur)
M 1 LOTO - Safety padlock 25 78
M 2 E - STOP 44 88
M 3 Guard 500 1000
M 4 Education - training 50 500
M 5 Automated ventilation system 600 1000
Note: Mi – Measures; LOTO - Lockout/Tagout devices; CM – Cost of Measures; E-STOP – emergency stop button.
Table 17. Model Summary for 7 Terminal Node.
Table 17. Model Summary for 7 Terminal Node.
Statistics Training Test
R-squared 86,75% 84,08%
RMSE 0,0469 0,0514
MSE 0,0022 0,0026
MAD 0,0120 0,0137
MAPE 0,0231 0,0279
Note: RMSE - Root mean squared error; MSE - Mean squared error; MAD - Mean absolute deviation; MAPE - Mean absolute percent error.
Table 18. Criterion for 7 Terminal Node.
Table 18. Criterion for 7 Terminal Node.
Terminal Node Number of HS events I A E Criterion Total Cost
4 4 75% CM1 = {78}; CM2 = {44; 88}; CM4 = {0; 50} {122; 216}
7 70 66,43% CM3 = {1000}; CM4 = {200; 500} {1200; 1500}
6 147 59,85 P> 3.5; CM3 = {0; 500}; CM4 = {200; 500}; {200; 1000}
2 52 50,58% P > 3.5; CM2 = {0; 67}; CM4 = {0; 50} {0; 117}
3 83 50% CM1 = {0; 25; 52}; CM2 = {44; 88}; CM4 = {0; 50} {44; 190}
1 130 33,72% P <= 3.5; CM2 = {0; 67}; CM4 = {0; 50}; {0; 117}
5 3 33,33% P <= 3.5; CM3 = {0; 500}; CM4 = {200; 500} {200;1000}
Note: AEI - Action Effectiveness Index; P - Probability of hazardous situation; CM1 to CM5 - Cost of Measure.
Table 19. Model Summary for 3 Terminal Node.
Table 19. Model Summary for 3 Terminal Node.
Statistics Training Test
R-squared 91,04% 89,97%
RMSE 0,0402 0,0425
MSE 0,0016 0,0018
MAD 0,0245 0,0250
MAPE 0,0444 0,0451
Note: RMSE - Root mean squared error; MSE - Mean squared error; MAD - Mean absolute deviation; MAPE - Mean absolute percent error.
Table 20. Criterion for 3 Terminal Node.
Table 20. Criterion for 3 Terminal Node.
Terminal Node Reduction of the criticality of the event Events in the node H S / E O Priorities under Variant A Priorities under Variant B Priorities under Variant C M i (i = 1 to 5) Unit   cos ts   C M in Eur Total cost in EUR
3 64,54% 100 E2.2 3 3 4 2 M4, M5 1500 4500
E3 46 4 1 3 M1, M2, M3, M4 1366 62836
E5 51 1 2 1 M1, M2, M4 666 33966
2 56,66% 42 E2.1 42 2 3 4 M4, M5 1500 63000
1 33,33% 46 E3 46 4 1 3 M1, M2, M3 619 28474
Note: HS/E - Hazardous Situations analysed and their effects; O - Number of\ HS Occurrence; Mi – Measures; CM – Cost of Measures.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated