Prerpints.org logo
Preprint
Article

Uttarakhand State Earthquake Early Warning System: A Case Study of Himalayan Environment

Altmetrics

Downloads

123

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 March 2024

Posted:

15 March 2024

You are already at the latest version

Alerts
Abstract
High seismic activity in the Himalayas and the increasing urbanization of its surrounding areas in the northern Indian region pose significant threats to both lives and properties. To mitigate the risk of seismic events, an earthquake early warning system can be used in the region. This system would be particularly beneficial to cities and towns in the mountainous and foothill regions that are located near earthquake sources. The government and the science and engineering community have re-sponded to this call by establishing the Uttarakhand State Earthquake Early Warning System (UEEWS). The system became fully operational on August 4, 2021, after being launched by the government of Uttarakhand. The UEEWS includes 170 accelerometers in the seismogenic part of the Uttarakhand region of the Himalayas. Ground motion data is transmitted to a central server through a dedicated private telecommunication network 24 hours a day, seven days a week.The system is designed to issue warnings for moderate to high-magnitude earthquakes via a mobile application installed on users' devices and sirens installed in government-owned public buildings. The UEEWS has successfully issued alerts for light earthquakes that occurred in the instrumented region and warnings for moderate earthquakes that occurred in the vicinity of the instrumented area. This paper provides an overview of the design of the UEEWS, details of the instrumentation, adaptation of attributes and their relation to earthquake parameters, the operational flow of the system, and information about the dissemination of warnings
Keywords: 
Subject: Computer Science and Mathematics  -   Computer Networks and Communications

1. Introduction

The economic repercussions of disasters have multiplied significantly and are projected to continue rising in the coming years [1]. In 2012, climate-related financial losses accounted for 1% of the gross domestic product (GDP) of developing countries [2]. Furthermore, losses due to seismic activities are also on the rise. The Himalayan region has seen many destructive earthquakes in the past, and their recurrence in the future is predicted by many [3,4,5,6,7,8]. The occurrence of earthquakes can not be stopped but their impact on society can be minimized by applying scientific, engineering, technological and innovative approaches.
The unpredictable nature of earthquakes makes them more dangerous than other hazards. Seismologists analyzed many precursors to forecast earthquakes. Still, none could get complete confidence in all scenarios in which earthquakes occur [53]. Therefore, a new approach came into existence called the EEW system. It is one of the tools to reduce the danger of earthquakes as the information provided to the users can help in saving their lives. EEW systems have the potential to reduce casualties and fully developed systems around the world have shown their utility during past earthquakes [54,55,56]. The EEW system describes a real-time earthquake information system that can detect the onset of an earthquake, estimate the potential size of an earthquake, and issue warnings before significant ground shaking reaches at the user's site [57]. The concept of the EEW system was developed in 1868 by Dr. J.D. Cooper, who suggested arranging for a mechanical contrivance to issue earthquake alerts in the San Francisco area [58]. The EEW system focuses primarily on issuing alerts with the sufficient lead time required to take precautionary measures and shut down key facilities, but not on determining precise earthquake parameters.
The foundation of an EEW system relies on the variance in propagation speeds among various seismic waves, which occur as a result of stress released during fault rupture. The secondary waves, also known as shear waves or S-waves, inflict notable damage as they travel roughly at half the velocity of primary waves and are considerably slower than electromagnetic signals. Therefore, a system can be developed to take advantage of data transmission speed from sensors to a server for streaming the initial portion of less-destructive primary waves (P-waves) and then perform analysis and issue the warning before damaging S-waves arrive at the user’s sites. There are two types of EEW systems, namely onsite- and regional- EEW systems. Both systems take advantage of the faster speed of P-wave. In an onsite-EEW system, either a standalone sensor or sensors in a group installed in close proximity are used to analyze the initial portion of P-waves to make the decision. While in a regional EEW system, sensors are installed in a large region, and data is transmitted to the central processing server established in a control room. The server unit is an assembly of high-performance computers to perform computational operations and other transmission equipment (e.g., switch, router, etc.). The high-speed telecommunication and data transmission facility between the sensors and server in this modern era builds confidence in the success of an EEW system. The EEW algorithms work over real-time data, and decision-making modules issue the warning based on preset threshold parameters. Lead time / waring time depends on the distance of the target cities, the epicenter, and the geographical distribution of the stations around the epicenter. The analyses of these waves are done by various EEW parameters or a combination of these parameters [59]. It is preferred to establish precise threshold values ​​of EEW parameters to obtain accurate, reliable and fast results from continuously streamed waveforms. [60].
The initial EEW system, employing the front detection technique, was created for the Tohoku Shinkansen railway system in Japan in 1982 [61]. Mexico's seismic alert system in 1991 also adopted a comparable approach [62]. UrEDAS, an enhanced front detection technique, commenced operation for the Tokaido Shinkansen line in 1992, utilizing the initial three seconds of P-wave motion following P-wave detection [61]. Following the achievements of the EEW systems in Mexico and Japan, numerous other countries initiated efforts to develop EEW systems tailored to their regions. Substantial advancements have been witnessed in this field over the past three decades. EEW systems are operational in select countries and regions, such as Japan [63,64], Taiwan [65,66,67], Mexico [54,68,69], South Korea [70] issue nationwide warnings, meaning alerts are broadcast to the entire public. While some countries issue region-specific warnings, as seismic vulnerability is localized to certain areas, such as Anatolia in Turkey [71,72], Southwest Iberia [73,74,75], Southern Italy [76,77,78], Vrancea-Romania [79,80,81], China [82,83], Chili [84], Costa Rica [85,86], Switzerland [87], Nicaragua [88], Israel [89,90] and United States of America [56,91]. As the advancement of the EEW system is pivotal for reducing seismic risk, enhancing its capacity to offer more lead time is equally imperative [92]. Its usefulness towards risk reduction is based on how fast the information is provided to the users so that they have more lead time to react. This time can be gained by developing better algorithms to pick the EEW attributes and estimate the earthquake’s metadata for issuing warnings in a very short time.

1. Seismic activity in the Himalayas and the region of interest.

The Himalayas represent one of the most seismically active areas globally. The current seismic events in this region have given rise to numerous intricate tectonic clusters due to ongoing convergence over approximately the last 50 million years. After the collision era, the Indian tectonic plate steadily moves northward at an average rate of approximately 50 mm per year [9]. The collision of the continental plate boundaries (namely, Indian and Eurasian plate boundaries) resulted in the underthrusting of the Indian plate beneath the Eurasian plate [10,11]. This underthrusting caused deformation in the southward direction and created faults, folds and prominent structural features of the Himalayan orogenic belt [12]. The significant tectonic features include the Main Frontal Thrust (MFT), Main Central Thrust (MCT), Main Boundary Thrust (MBT), and the Indus-Tsangpo Suture Zone (ITSZ), respectively [13,14,15]. The ITSZ dips in the south while MCT and MBT dip in the north [16]. The MCT was active at an early age and is regarded as the oldest thrust system. In contrast, MBT exhibits an active thrust system now. The MFT is the southernmost and youngest thrust system. The movements of tectonic plates induce strain at fault plate boundaries, leading to the generation of stress [17]. Earthquakes are the consequence of the catastrophic failure of rocks and the sudden release of accumulated stress [18].
The geodynamic system in the Himalayas has produced many devastating earthquakes among many, the most recent was the April 25th, 2015, Mw 7.6 Nepal earthquake and its subsequent aftershocks which caused substantial economic loss to the Himalayan country. The government of Nepal conducted a Post Disaster Need Assessment of this earthquake, and the estimated value of the total loss from the direct and indirect impact on the Nepalese economy was close to United States of America dollars (USD) 7 Billion (i.e., equivalent to one-third of the country’s GDP in the year) [19]. The notable past earthquakes in the Himalayas are the April 4th, 1905 Kangra Valley earthquake of Ms 7.8, which was the first of several devastating earthquakes of the 20th -century. The then Punjab government estimated ~20000 casualties among her ~375000 population. The economic cost of recovering from this earthquake was estimated at ~2.9 Million (1905) rupees [20].
Similarly, the June 12th, 1897 Great Assam earthquake of Mw 8.0 was very devastating, and its tremors were felt up to the Peshawar region (now in Pakistan). The then British government surveyed post-earthquake damage and stated in the reports that the infrastructure of the eastern region was majorly devastated [21]. The August 15th, 1950 Tibet-Assam Great earthquake of Mw 8.6 had shocked the eastern Himalayan region [22] and caused 1526 casualties and extreme economic loss of ~25 Million USD at the time of the earthquake [23]. The January 15th, 1934 Bihar-Nepal earthquake of Mw 8.0 had rattled the border region, and tremors were felt over the area of ~49,20,000 square km in India, Nepal, and Tibet [24]. This earthquake caused great destruction, created numerous fractures and landslides [25], and took ~12,000 human lives [26]. In the 1990s, two strong earthquakes rattled the Garhwal region of Uttarakhand. On October 19th, 1991 Uttarkashi earthquake of Mw 6.8 and on March 28th, 1999 Chamoli earthquake of Mw 6.6 caused a lot of losses in the Uttarakhand region [27,28,29]. Sharma (2003) has worked out the return periods of moderate to great earthquakes and the conclusions were similar to other studies [30,31,32,33] expressing the higher scale of occurrence and immediate attention is required for mitigation measures [34,35,36,37,38,39]. The epicentral distance of the 2015 Nepal earthquake was ~450 km to the Uttarakhand region. If an earthquake of this magnitude scale occurs in the Uttarakhand region, as Uttarakhand has similar seismological conditions as in Nepal, it may create havoc. Therefore, a lot of efforts are being made to curtail the exposure and vulnerability in view of future earthquakes in Uttarakhand.
After the 1950 Assam earthquake, no great earthquake (Mw 8 or above) occurred in the Himalayas. Srivastava et al. (2015) analyzed Himalayan seismicity by examining seismic patterns, local tectonics, global positioning system (GPS) observations, microearthquakes, paleoseismicity, and other pertinent datasets. They identified two distinct types of seismic gaps with unique characteristics [33]. Category-1 seismic gaps are found in regions where significant earthquakes (Mw ≥ 8) have occurred historically or are anticipated in the future. Specifically, Category-1 gaps include the Kashmir seismic gap, West Himachal-Pradesh seismic gap, Uttarakhand-Dharachula seismic gap, Central Nepal-Bihar seismic gap, Arunachal seismic gap, and Shillong seismic gap. Category-2 gaps delineate those regions where significant earthquakes (Mw < 8) have taken place historically or are expected to occur in the future. These encompass the Jammu, East Himachal-Pradesh, Western Nepal, and Sikkim-Bhutan seismic gaps. The area between the 1905 Kangra earthquake and the 1934 Bihar-Nepal earthquake is known as the central seismic gap [40].
The Uttarakhand-Dharchula seismic gap is situated within the central seismic gap and has not experienced any significant or major earthquake events in the recent recorded history. This seismic gap comprises an approximately 800 km long central segment commonly referred to as the Garhwal-Kumaun Himalaya. It is purportedly characterized as an unbroken section of the Himalayan arc [31]. The GPS measurements conducted in the Himalayan regions suggest that strain is building up in this area, potentially leading to the occurrence of one or more significant earthquakes [41,42]. After a thorough examination of the intricacies involved, the utilization of constant seismicity and constant moment rate methods, along with time-dependent occurrence models, has revealed varying seismic hazard rates in the Himalayas [43,44,45,46].
The Himalayan region is experiencing swift urban expansion, rapid settlement, and significant infrastructure development [47,48,49]. The Indian Himalayan region from Kashmir in the north to Arunachal Pradesh in the east comprises around 52.8 million population as per the 2011 census [50]. With an annual growth rate of 3.30%, by the end of 2061, it will exceed 260 million [51]. In the event of a major earthquake occurring in the central seismic gap region, there could be thousands of casualties and substantial economic losses amounting to billions of USD [52]. Given the elevated seismic risk, urgent implementation of mitigation measures and disaster risk reduction strategies in this region is imperative. Following an examination of the elevated seismic risk and the scattered distribution of the most susceptible areas within the central seismic gap, an earthquake early warning (EEW) system has been developed for this region. Initially, a two-pronged approach was undertaken. This involved conducting a feasibility study followed by researching and studying the available emergent solutions. Subsequently, the decision was made to develop the first Indian regional EEW system, the UEEWS, in the Uttarakhand region. This paper outlines the developmental stages of the system, including instances of successful notifications, alerts, and warnings issued by it.

3. Structure of UEEWS

UEEWS was developed and proposed with specific needs for Uttarakhand in central Himalaya after a comprehensive study of existing EEW systems present in the world [93,94,95,96]. Due to high seismicity and the pressing need for mitigation measures, the central seismic gap region was chosen for the establishment of India’s first EEW system. The performance-cost analysis was conducted, following which the selection of sensors was finalized [93]. For this, the available strong ground motion recording sensors were scrutinized before the purchase of the sensors. The cost was a limiting factor, and additionally, a significant number of sensors were required for establishing a regional earthquake early warning system. Therefore, low-cost Micro-electromechanical Systems (MEMS)-based sensors were opted. The developed system is based on the regional early warning approach; hence a control room has been set up at the Earthquake Early Warning System Laboratory in the Centre of Excellence in Disaster Mitigation & Management (CoEDMM), Indian Institute of Technology (IIT) Roorkee.

3.1. Seismic Network

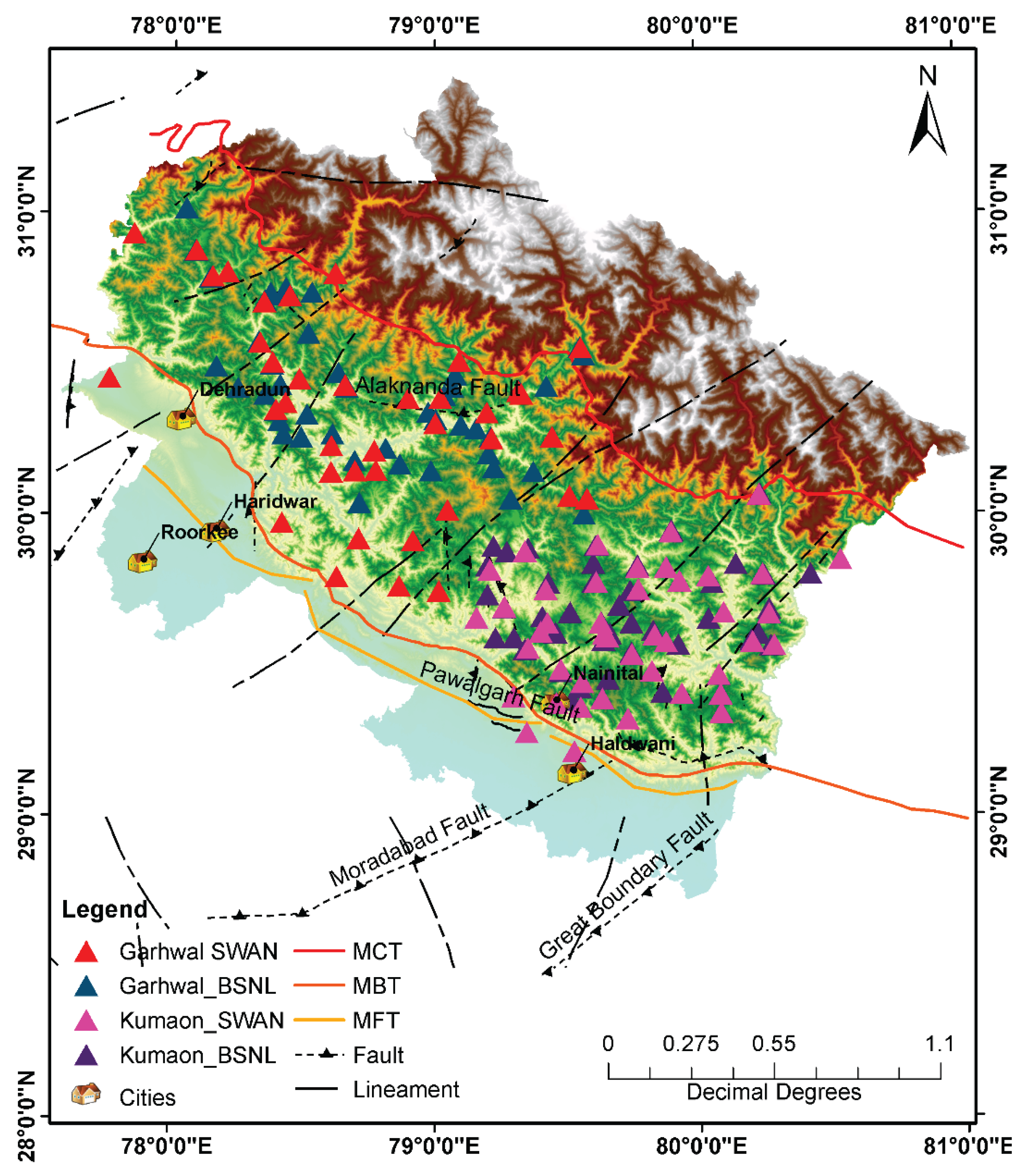
In the initial instrumentation phase, the Garhwal region in the central Himalayas, stretching from Joshimath in the East (30.5616°N, 79.5594°E) to Mori in the West (31.0183°N, 78.0409°E), was chosen. This area encompasses approximately 150 by 50 square kilometers across five districts of the Uttarakhand province, namely Uttarkashi, Tehri, Rudraprayag, Pauri, and Chamoli. As a dense network is preferred for a regional earthquake early warning system; therefore, low-cost MEMS-based sensors were selected. These sensors have a relatively lower dynamic range compared to conventional high-cost forced balance accelerometers (FBA) with larger dynamic ranges. The MEMS-based accelerometer (i.e., pAlert) fulfills the requirement of regional EEW systems and is cost-effective compared to conventional FBA. These sensors comprise tri-axial MEMS accelerometers paired with a 16-bit 80 MHz CPU, offering an output resolution of 16 bits and a dynamic range exceeding 86 dB. The required EEW parameter (the low pass filtered vertical displacement, Pd) is efficiently calculated from the data retrieved from these sensors. These sensors have undergone testing and have been successfully deployed in Taiwan's EEW system as well. [97,98].
The pAlert has the capability to transmit data to two servers via the internet by running the PALERT2EW module on the server and automatically synchronizing its time through the Network Time Protocol (NTP) server. PC-Utility software is utilized for remote access to the pAlert and for configuration purposes. The initial phase of the UEEWS was concluded as a pilot project spanning from 2014 to the middle of 2017. Figure 1 shows the location of the 84 sensors installed in the first phase. These sensors are mounted on the ground floor of government-owned offices of the Base Transceiver Station (BTS) of Bharat Sanchar Nigam Limited (BSNL) and Point of Presence (PoP) of the State Wide Area Network (SWAN) available in the Garhwal region of Uttarakhand.
In order to encompass the remaining portion of the current seismogenic source, the instrumentation was expanded to cover the Kumaun region of Uttarakhand in mid-2017. The seismic zone in this area encompasses four districts: Bageshwar, Pithoragarh, Champawat, and Nainital. This time, an enhanced version of the sensor (pAlert+) was employed. These sensors are equipped with 24-bit tri-axial MEMS accelerometers featuring an internal memory capacity of 8 GB and a dynamic range exceeding 100 dB. These sensors are mounted on the ground floor of BSNL’s BTS and SWAN’s PoP in the Kumaun region. As depicted in Figure 1, an additional 86 sensors are installed in the Kumaun region. Thus, a total of 170 sensors are deployed in this region, with an inter-station spacing ranging from about 10 to 20 km. Therefore, the network now meets both criteria of the regional EEWS: the required sensor density and the spatial coverage of the seismogenic source in Uttarakhand, enabling the detection of large earthquakes in the instrumented region.

3.2. Data Streaming

The decision to install sensors in BSNL's BTS and SWAN's PoP buildings was made due to their provision of power availability, dedicated Virtual Private Network over Broadband (VPNoBB), and security features. All sensors are mounted on the ground floor of these buildings, transmitting ground motion data to the server located in the EEW system laboratory via a dedicated private network provided by BSNL, operating continuously in real-time, 24 hours a day, 7 days a week. 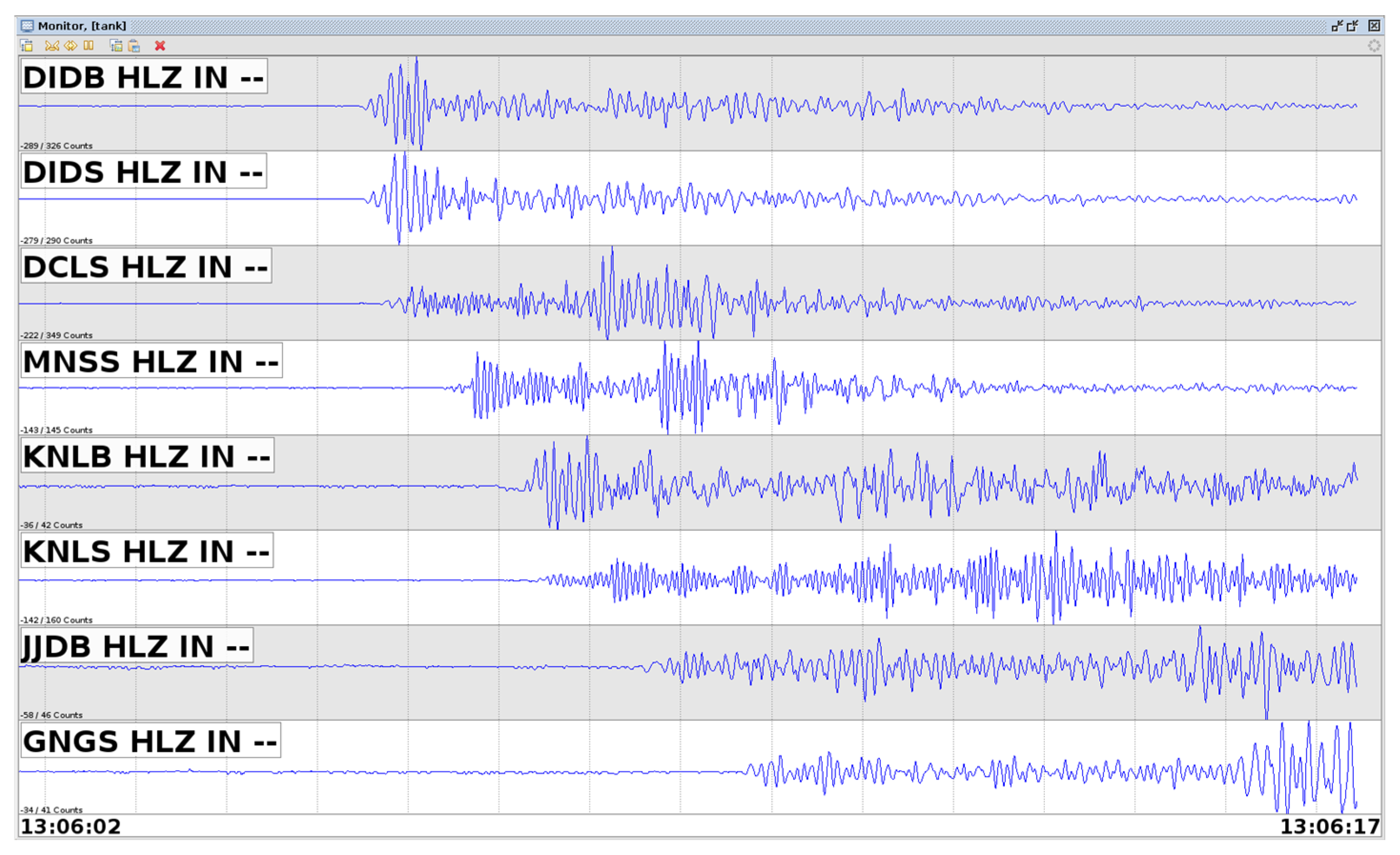Figure 2 shows the streaming data from sensors to servers in real-time on swarm software. The sensors transmit data every second via a private network, packaged into 1200-byte packets. As all sensors within the network synchronize their clocks with the UEEWS server, the NTP server adjusts the sensor’s time accordingly.

3.3. Data Processing

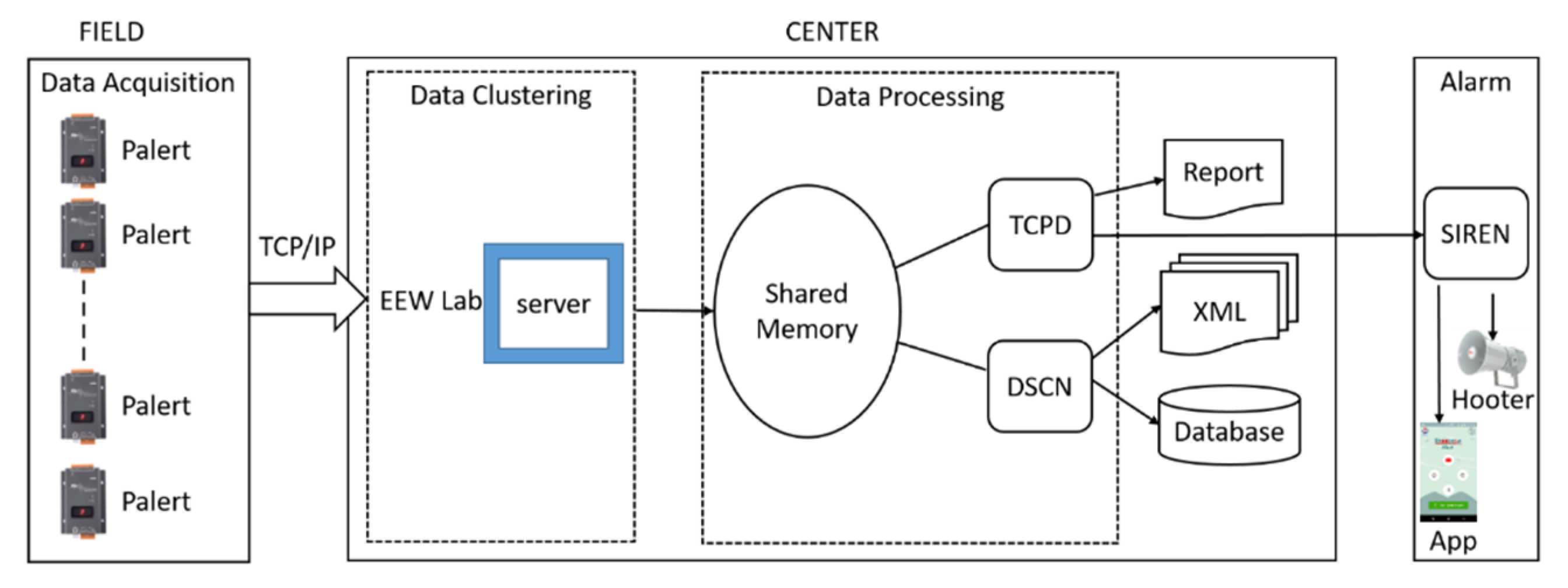
Since the UEEWS is the first system developed for a Himalayan region, therefore, efforts have been made to keep the open-source software for this so that the same may be adopted easily for other areas of the Himalayas. Earthworm, an open-source platform, is used to monitor earthquakes and volcanoes to process seismic data [99,100] and is a module-based seismic network processing platform. Since the platform is open source, modules can be customized as per the requirements. Leveraging the flexibility of Earthworm, the central server is set up with a customized module (PICK_EW) and the incorporation of new modules (such as PALERT2EW, and TCPD) tailored to our specific needs for earthquake parameter estimation. A two-pole Butterworth high pass filter with a cut-off frequency of 0.075 Hz is applied over the streamed data to remove low-frequency noises in real time. The PALERT2EW module is used to fetch the streamed data into the shared memory called WAVE_RING. The WAVE_SERVERV module is used to store and provide seismic waveforms over a period of time and is used to display streamed data. The data is fetched into standard shared memory, WAVE_RING, where real-time streamed data is available for processing and archiving. Figure 3 shows the data flow from the field to the central server. Swarm, an open-source software, displays the accelerograms of the data. It lists the streaming stations in real time and also helps in analyzing the historical data.

3.4. Event Detection

The accurate identification of the initiation of the P-phase within the continuously streaming seismic signals is the most crucial aspect of a successful EEW system. Many algorithms have been developed in the past for picking the P-phase onset in seismic signals [101,102,103,104,105,106,107,108,109,110]. The UEEWS utilizes an enhanced version of the standard short-term average (STA) and long-term average (LTA) algorithm. [66,111,112].
The PICK_EEW module is deployed to detect P-wave arrivals from the up-down channel of the continuously streaming seismic data. This module also calculates peak amplitudes of P-wave displacement (Pd), velocity (Pv), and acceleration (Pa) from a 3-second time windowed data following P-onset. It then forwards this information to another shared memory named PICK_RING. The PICK_EEW module [66] is an improved version of the PICK_EW module, which comes inherently with Earthworm. The PICK_EEW module applies the standard STA-LTA algorithm [111,112]. Since seismic sensors are positioned in various locations, there may be varying levels of noise due to natural surroundings and human activities at each installation site. Hence, the PICK_EEW module applies two more parameters Pa and Pv, to avoid false picking caused by background noises [66]. The PICK_EEW module reads a configuration file. This file contains the threshold values of the parameters to get the true picks of the P-onset. Values of these parameters are different for each station. Therefore, improvements in the configuration file are made site-by-site basis following the analysis of the collected earthquake data since 2014, the year of commencing of this project. To achieve this, the recorded data was replayed on the offline server.

3.5. Estimation of Earthquake Parameters

A module called TCPD was created in the C programming language to estimate earthquake parameters, ensuring compatibility with the Earthworm platform [97]. The TCPD module was modified as per the requirements. This module accesses the PICK_RING and conducts analysis to estimate earthquake parameters such as location, magnitude, depth and origin time. This module updates the information obtained from this ring and transfers it to another memory location known as EEW_RING.

3.5.1. Location Estimation

The earthquake hypocenter estimation involves two steps. Initially, the Geiger method, an inversion process, is utilized to determine the epicenter [113]. This method requires a P-wave velocity profile specific to the instrumented region. The half-space velocity model of the Uttarakhand region, recommended by a study conducted in this area, has been chosen [114]. In the second step, the grid search method is utilized to determine the actual depth of the earthquakes, with depths ranging from 0 to 50 km. Alternative methods, such as the back azimuth method employing principal component analysis, offer the benefit of locating long-distance earthquakes. However, they are found to be unsuitable for near-source recordings [115]. In the grid search method, theoretical travel times to each triggered station are calculated and then compared with the observed depth at each iteration. The depth of the earthquake is determined by identifying the step at which the minimum residual is encountered. Initially, at least four triggered stations are used, and the search point that yields the minimum residual is selected as the focal point. For the UEEWS, the search region is confined within a radius of 200 km from the position of the initial trigger and to a depth of 50 km, ensuring that the search area remains within the array. However, in the case of earthquakes originating from outside the instrumented area, the search region is extended beyond the instrumented area (within 200 km from the location of the first trigger).
The limit of 200 km was set after considering the area of instrumentation. The east-west and north-south expansion of instrumentation is 280 km and 130 km, respectively. Suppose an earthquake triggers in the boundary region; then its motion will spread in all directions, and as the sensors are installed up to 280 km in the east-west direction and 130 km in the north-south direction of the instrumentation, therefore the ground motion recorded by these sensors will also be used in the location estimation.
This method offers a focus location accuracy of approximately 5 km for earthquakes with epicenters within the search region. Therefore, accurate locations can be determined for earthquakes originating outside but in close proximity to the instrumented areas. This approach, which achieves accurate epicenter location with approximately 5 km precision in focal depth, while requiring fewer computations compared to classical methods, renders it well-suited for the EEW system [66].
This whole procedure is written as a function in the TCPD module which is called when at least four picks of seismic waveforms from different sensors are available. As soon as this condition is met by the TCPD module, the procedure to locate the hypocenter begins. If the estimated root mean square (RMS) of travel-time residuals obtained from the inversion process exceeds the specified threshold, the pick with the most substantial travel-time residuals is eliminated, and the inversion process is repeated. In the meantime, if a new pick is found, the procedure to find the hypocenter restarts again and updates the previously estimated hypocenter.

3.5.2. Magnitude Estimation

Once the hypocenter is determined within the TCPD module, another function is invoked to estimate the magnitude. This function utilizes a regression model to calculate the magnitude of earthquakes. The mathematical expression of the employed model is as follows:
M = A× log (Pd) + B× log(R) + C
In the equation, R represents the hypocentral distance, calculated as the square root of the sum of the squares of epicentral distance (d) and focal depth (h), denoted as R = √(d2 + h2). The coefficients in Equation (1) vary depending on the dataset of different regions and are specific to each region.
Initially, Wu and Zhao (2006) utilized this model to estimate Pd-based magnitude as follows:
MPd = 4.748+1.371×log(Pd)+1.883×log(R)
After the p-onset, 3 seconds of data is used to calculate peak displacement (Pd) and its corresponding magnitude, MPd. A form of regression relationship between Pd and MPd, given in Equation (3), was developed using the data set of Taiwan and the USA [116].
MPd = 5.067+1.281*log10 (Pd )+1.760*log10 (dis)
where MPd is Pd-based magnitude, Pd is peak displacement, and dis is the epicentral distance to the sensor’s locations.
A model has been devised to calculate magnitude based on the displacement amplitude (Pd) of the P-wave's vertical component, utilizing 70 records of 13 earthquakes that transpired in the Uttarakhand region between 2005 and 2020. The attenuation relationship of Pd with Hypocentral distance (R) and Magnitude (Mw) is given below (Equation 4).
log(Pd ) = -2.6826+0.52258×Mw - 1.2011×log(R) ±0.252
The dataset used in the development of this new model is limited and includes records of 3.6<Mw<5.5 with 15<R<100. Thus, the model is a good fit for small earthquakes (3<Mw<5). After inverting this new relationship, MPd can be estimated, and it has a 1:1 relationship with catalog magnitude (Mw).
Currently, the model established by Hsiao et al. (2011) is employed in the UEEWS for estimating Pd-based magnitude (Equation 5).
MPd = 3.905+2.198×log(Pd )+2.703×log(R)

3.5.3. Report Generation

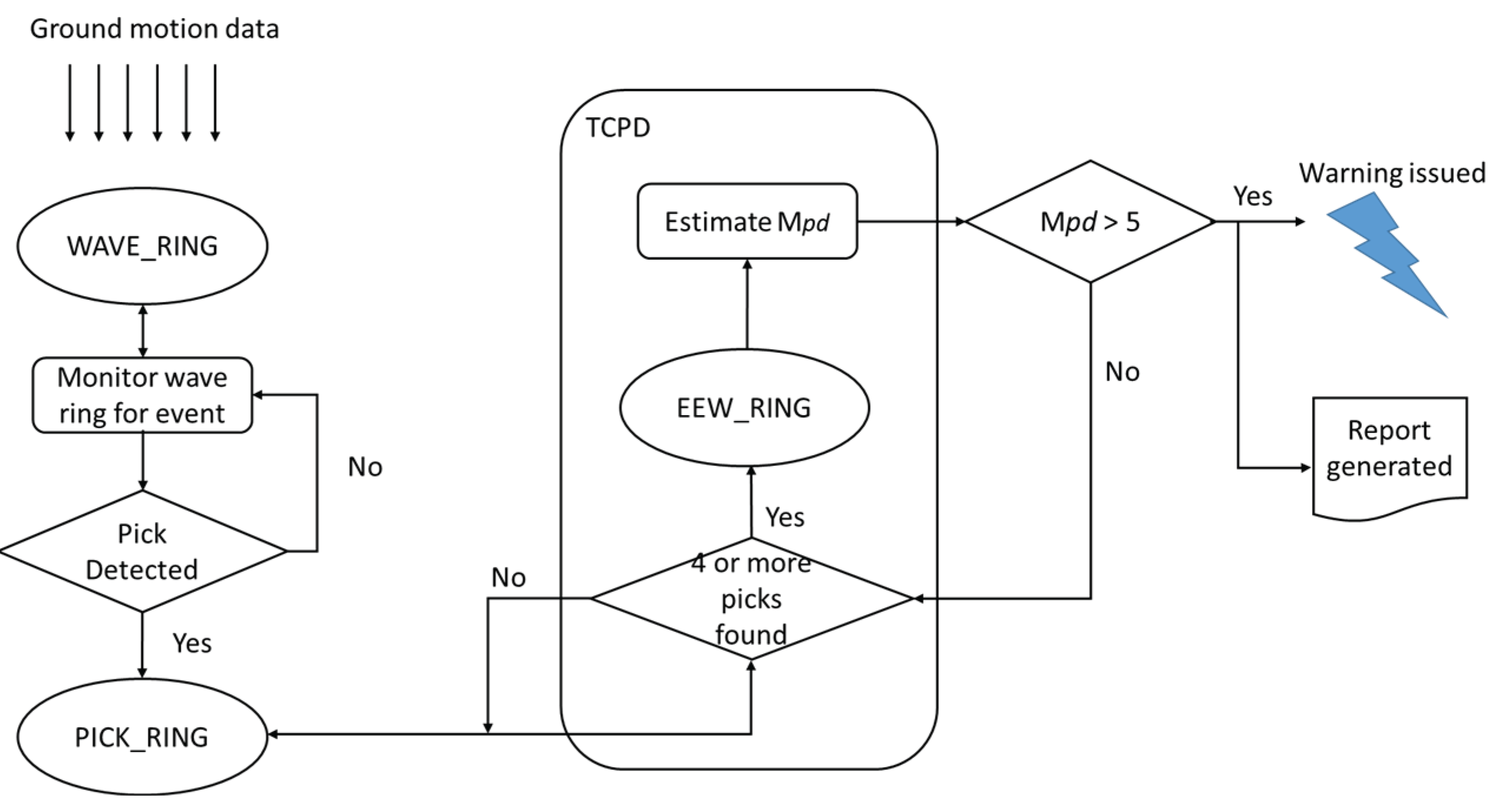
The TCPD module produces a report and saves it in a location specified by the user for archival purposes. Upon report generation, a warning is promptly issued to the public. A threshold of magnitude five has been set to issue warnings. Earthquake report is significant and consists of parameters like latitude, longitude of the epicenter, depth, origin time, list of triggered stations, P-pick arrival time, etc. Figure 4 shows a flowchart of decision-making to issue warnings. The parameters of small earthquakes generated by the UEEWS are listed in Table 1. The source parameters for the same earthquakes, as reported by the National Center for Seismology (NCS), Government of India, are also presented in Table 2 for comparison purposes.

4. Warning Modes

Warnings to the public can be disseminated through multiple channels, including application-specific sirens, television broadcasts, AM/FM radio, mobile messages, and mobile applications. In the current implementation of the UEEWS, people are alerted through two channels: sirens and mobile applications. Sirens have been strategically installed on government-owned buildings, schools, hospitals, and residential complexes, while the mobile application is available for download by the general public.

4.1. Sirens

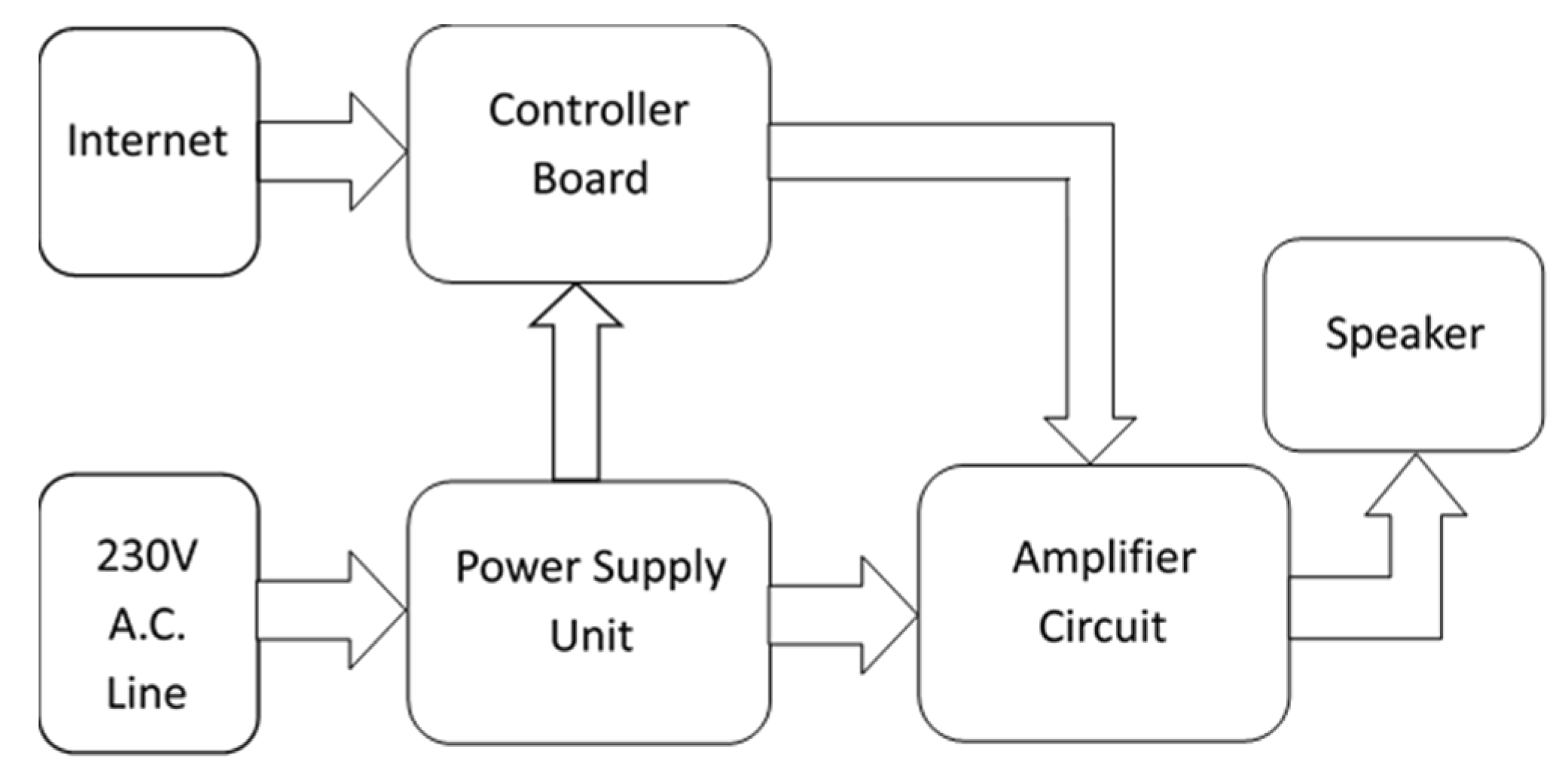
The EEW system laboratory internally produces the sirens. The design of the UEEWS siren can be categorized into four major modules [118]. The initial component is the controller board, responsible for managing the siren and storing different sounds for warning functions. The second part comprises an amplifier circuit, which amplifies the sound signal from the controller board. Next is the speaker/hooter, which transforms these electrical signals into loud sounds. Finally, there is the power supply unit, which converts 230V AC current into DC, essential for operating the controller and amplifier. Figure 5 illustrates a flowchart of these modules.
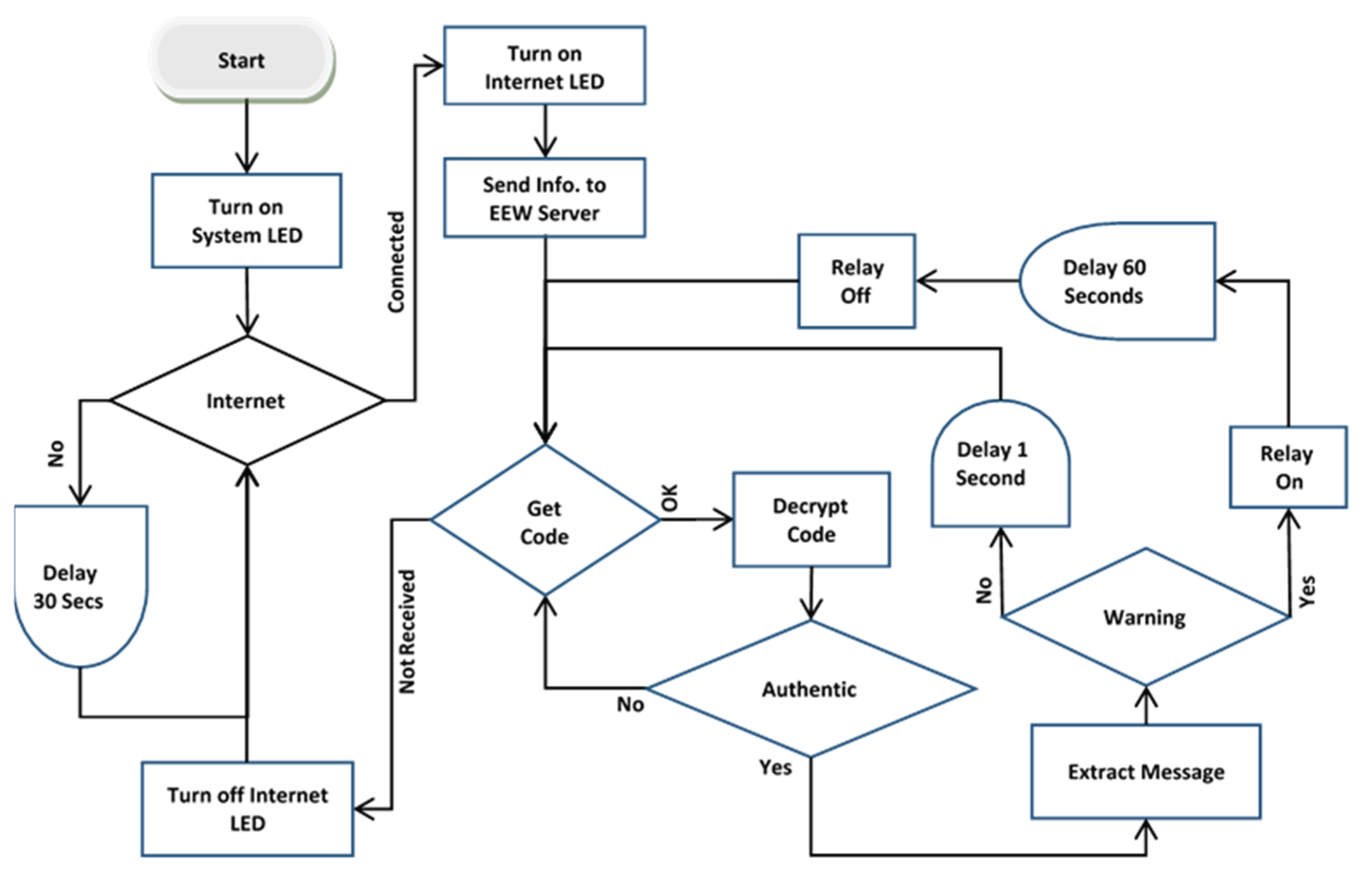
The Controller board functions as a microcomputer, such as a Raspberry Pi, linked to the internet through a LAN port. It includes general-purpose input-output (GPIO) pins for interfacing with other devices. A computer program communicates with the warning server over the internet to receive real-time warning messages and manages hooter/speaker relays via GPIO pins. Figure 6 illustrates the logic diagram detailing the operation of the computer program.
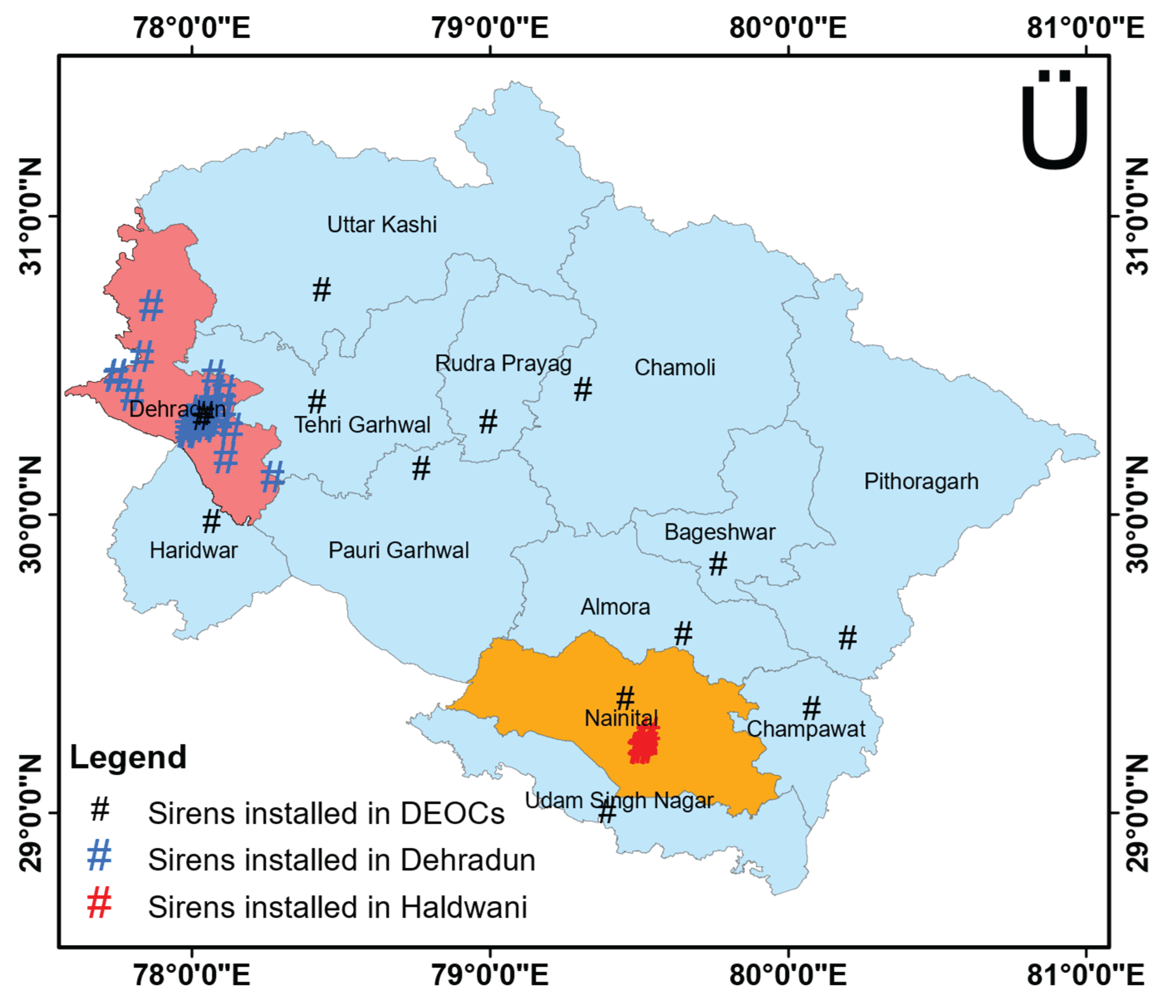
Figure 7 illustrates the placement of sirens across various locations, including the State Emergency Operation Center (SEOC) in Dehradun, the capital city of Uttarakhand, all District Emergency Operation Centers (DEOC) within the province, as well as key government buildings in the two major cities of the state, Dehradun and Haldwani.

4.2. Mobile Application

The Uttarakhand government, in collaboration with IIT Roorkee, has installed public sirens in two major cities, namely Dehradun and Haldwani, as well as at various District Emergency Operation Centers (DEOCs). However, due to the extensive area and large population, a considerable number of sirens would be necessary to cover Uttarakhand, demanding significant investment of both funds and time. This prompted us to explore alternative options to enhance the effectiveness of the developed system. In the contemporary era, Android and iOS-based smartphones are exceedingly prevalent and are owned by a significant portion of the population. Thus, it was imperative that warning messages be distributed through mobile applications. These applications should be designed to emit distinctive sounds on mobile phones, ensuring users are promptly alerted on receive of warnings. The app should also include guidance on the actions to take in the event of an earthquake and instructions on identifying safe areas within homes for taking cover during seismic activity. Additionally, the app should feature a graphical interface displaying a visual representation of the remaining time before the S-wave reaches the location of the mobile phone user.
Hence, IIT Roorkee has created a smartphone app BhuDEV (Bhukamp Disaster Early Vigilantè) for distributing earthquake early warnings, aiming to alert users to take precautions before destructive seismic waves reach their vicinity. To receive such warnings, users must install the app and provide essential details during the setup. The application includes instructional videos to assist users in taking appropriate actions during earthquakes for their safety. Presently, the app offers early warnings for damaging earthquakes originating solely in Uttarakhand.
Public warnings are issued when the server predicts an impending earthquake of magnitude five or higher, indicating potential damage. Conversely, notifications are sent out for earthquakes of lesser magnitude, below five. The application necessitates permission to send SMS alerts to registered contacts following earthquake emergencies, including the user's current location in the SOS message. Therefore, access to location sharing is required, and users are advised to grant permission for location sharing with the Uttarakhand State Disaster Management Authority (USDMA) during the app installation process. This location-sharing aids search and rescue teams in initiating operations swiftly during emergencies. The app receives warnings via the internet, requiring users to maintain an internet connection at all times. However, data usage is limited to earthquake notifications only. Additionally, the app simulates earthquake scenarios during mock exercises and provides video links for preparedness and a better understanding of earthquakes within the application.
On August 4th, 2021, the honorable Chief Minister of Uttarakhand officially launched this application for public use. The app can be downloaded either by scanning the QR code or by accessing it from the Play Store or App Store. The app icon is provided in Figure 8 for easy identification and showcases the home page of the mobile app post-installation.

5. Lead Time for the People of Uttarakhand

Lead time refers to the duration of warning time provided to users during earthquake events. It indicates the time remaining for the arrival of S-waves at the designated site, which varies depending on the distance of human settlements from the earthquake's epicenter. Settlements situated farther away receive a longer lead time compared to those nearest to the epicenter. The current system operates based on the regional Earthquake Early Warning (EEW) concept, requiring a few seconds to make decisions. These seconds encompass the time required to gather at least 3 seconds of data from a minimum of four sensors, transmit the data, process it, estimate magnitude and hypocenter, and subsequently relay the decision to the warning server for broadcasting alerts regarding the approaching secondary waves to the public.
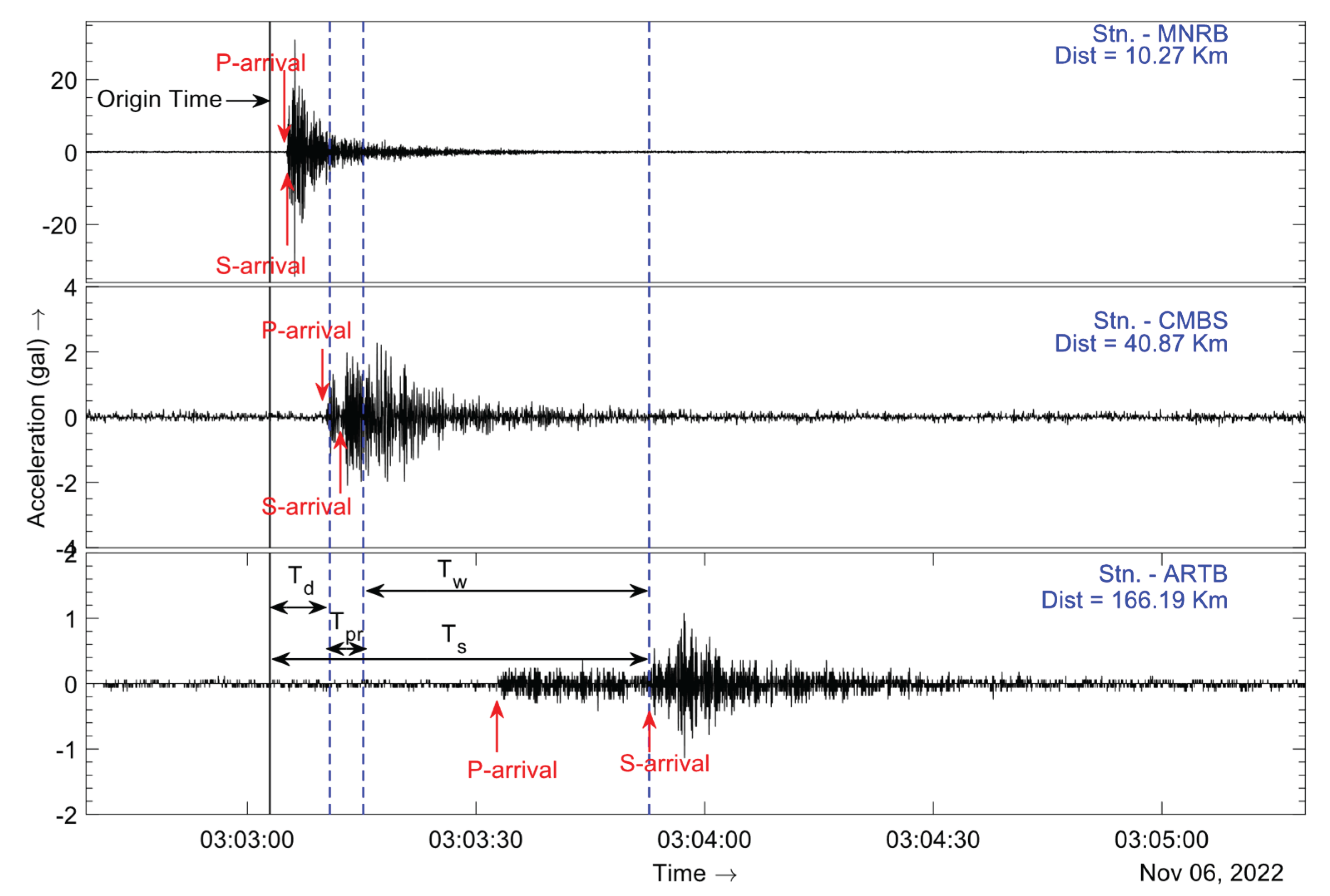
The lead time can be calculated using the formula Tw = Ts - Tr [117], where the reporting time Tr = Td + Tpr represents the time required (Td) to trigger and record an adequate length of waveforms, along with the time (Tpr) needed to process the waveforms for determining the hypocenter and magnitude. Ts denotes the travel time of the destructive S-wave, and for the advanced warning, it is essential to have Tw > 0. This condition implies that Ts must exceed (Td + Tpr). Settlements with Tw < 0 are classified as blind zones, suggesting the need for an onsite warning system. The EEW system laboratory is currently engaged in developing such a system. The lead time is elaborated with an example in detail.
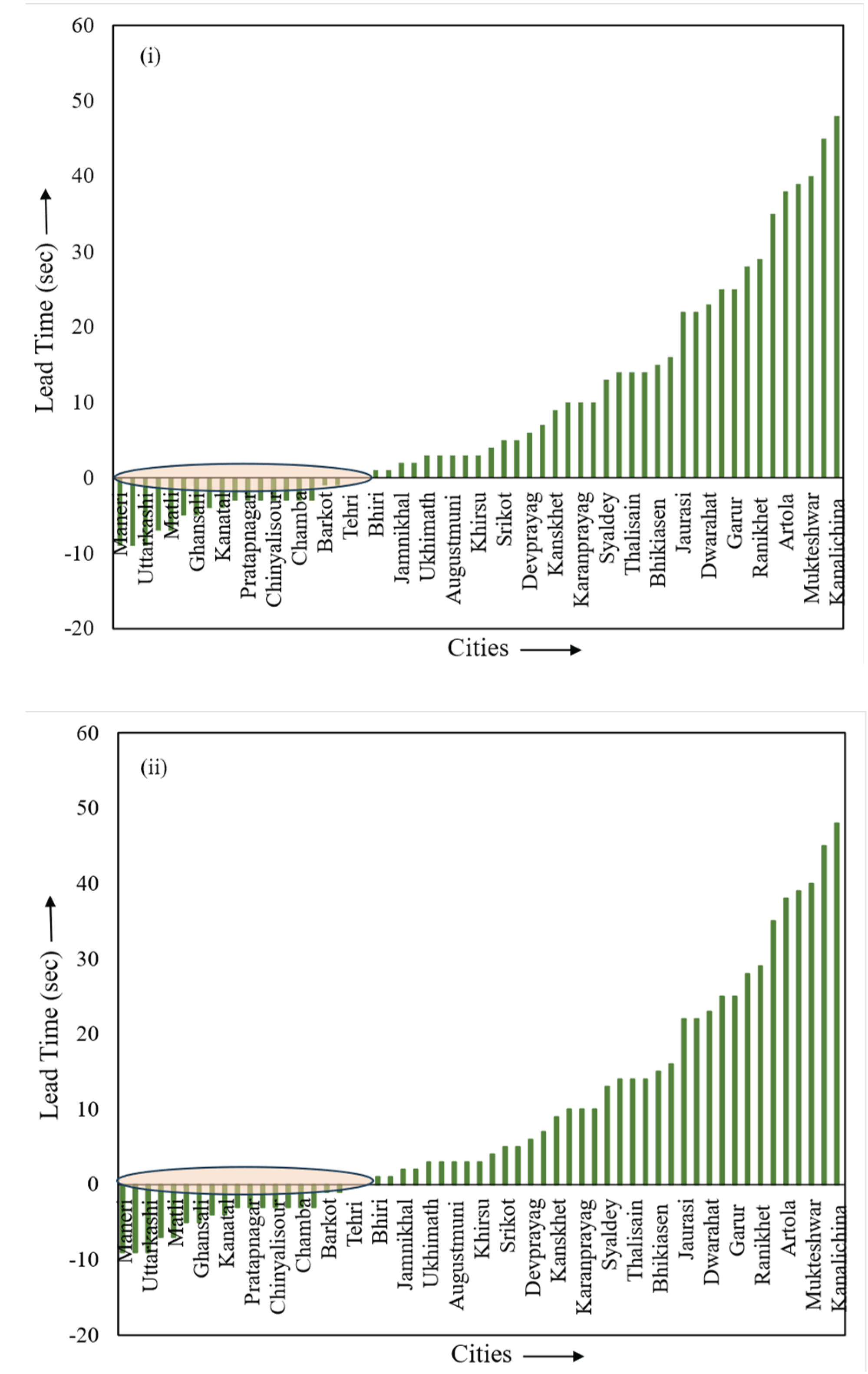
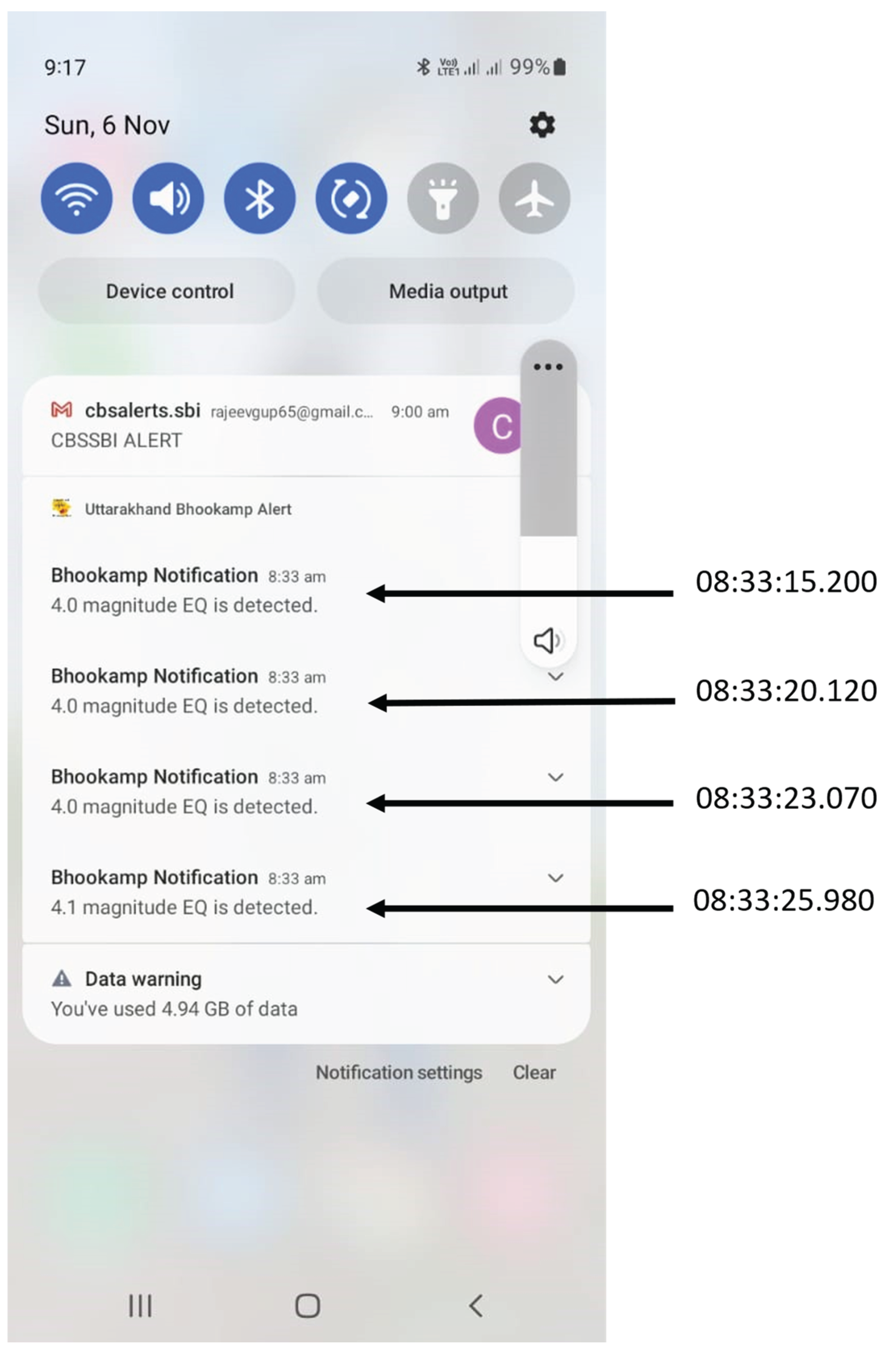
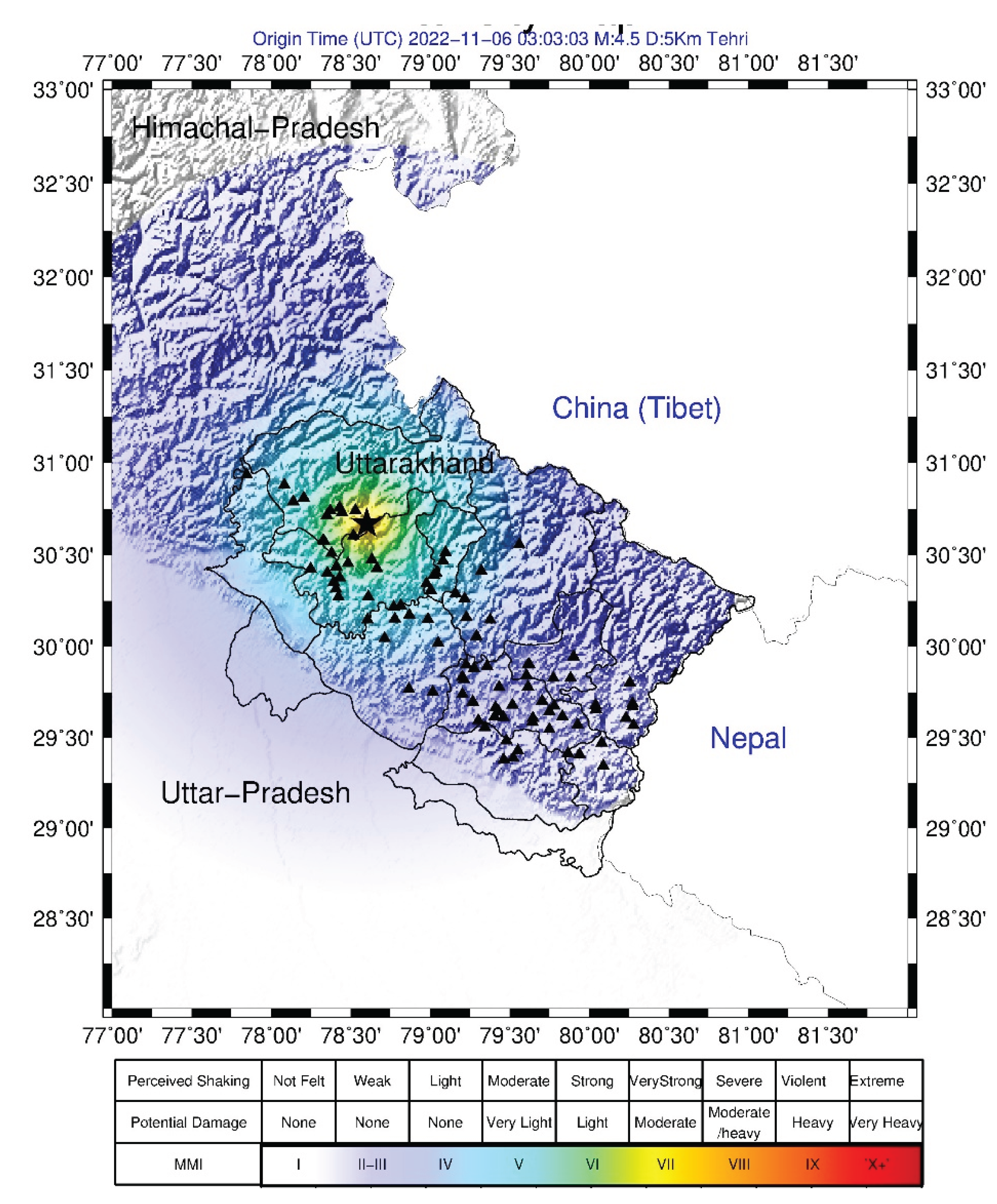
Figure 9 depicts a diagram illustrating discrete times based on data from the Tehri Garhwal earthquake on November 6th, 2022, at 03:03:03 UTC, with a magnitude of 4.5 and a depth of 5 km. The Maneri (MNRB) site was situated 10.27 km from the epicenter, the Chamba (CMBS) site was 40.87 km away, and the Artola (ARTB) site was at a distance of 166.19 km. In this earthquake event, the MNRB site detected the P-onset first, while the CMBS site registered the last P-onset during the initial report generated by the TCPD module. Consequently, the time required for triggering and recording sufficient primary wave data (Td) was 7.81 seconds from the origin time. The processing time (Tpr) to calculate the hypocenter and magnitude was 4.38 seconds. Hence, there was a lead time (Tw) of approximately 38 seconds for the ARTB site before the arrival of destructive waves, which took approximately 50 seconds (Ts) to reach this site.
The TCPD module promptly generates earthquake reports upon detecting P-Onset signals from at least four stations. It initiates the earthquake parameter estimation process and generates a report accordingly. Upon report generation, the information is relayed to a warning server, which, based on the estimated magnitude, issues either alerts or notifications. Warnings are issued for earthquakes with a magnitude exceeding 4.5, while notifications are dispatched for those below 4.5 magnitude. If the TCPD module detects another new P-Onset, it reinitiates the parameter estimation process, generates earthquake reports, and disseminates warnings/alerts to the public.
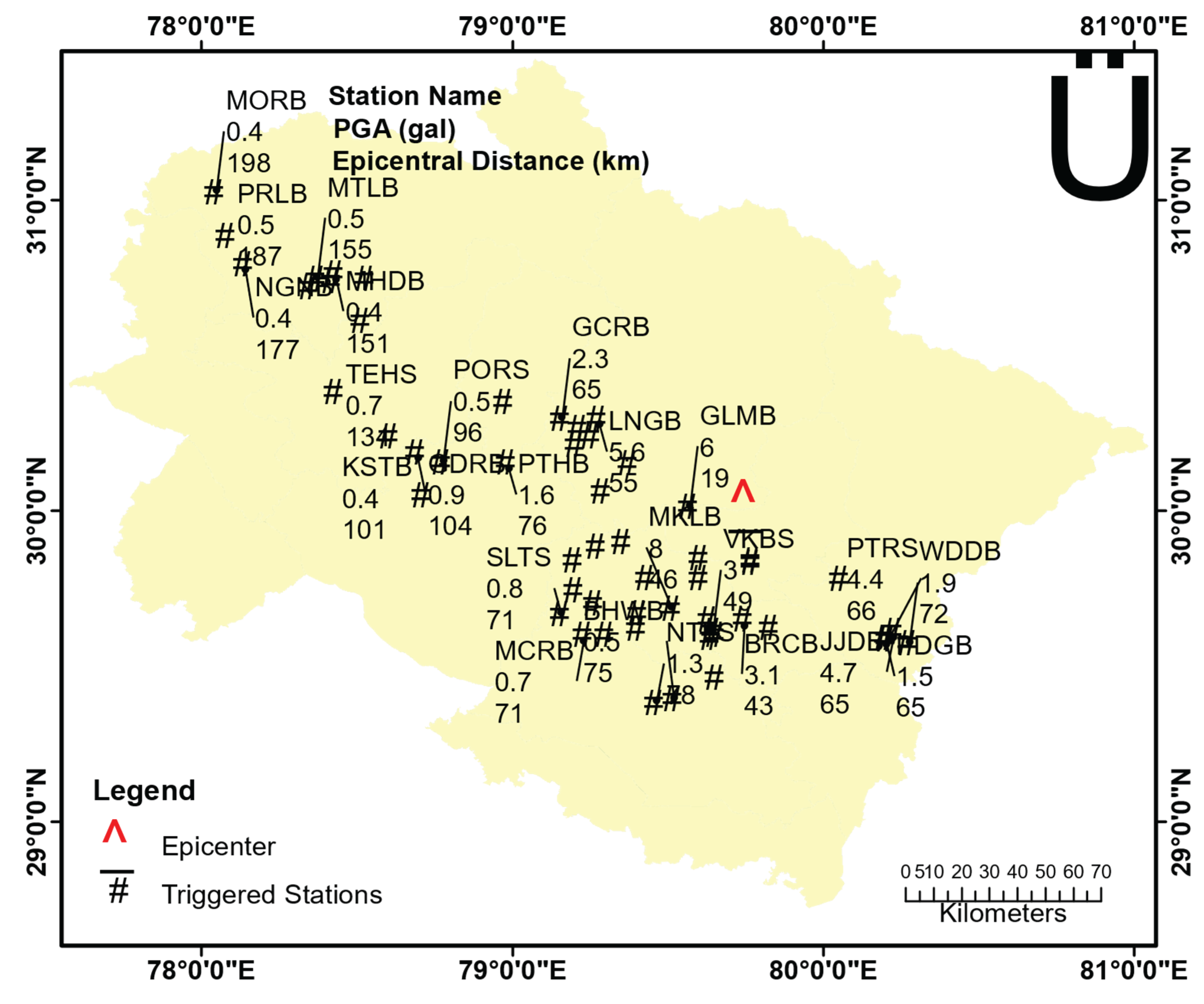
During the Tehri Garhwal earthquake on November 6th, 2022, the TCPD module generated six reports. Seismic data from this earthquake were recorded at 96 stations, and we conducted post-processing to identify P-onset and S-onset signals, estimating the time it took for the S-waves to reach these sites after notification issuance. The lead time was calculated based on the time difference between the warning issuance and the arrival of S-waves. Figure 10 illustrates the lead time for all operational stations at that time. The pink oval represents a blind zone area where no warning was available, as the EEWS requires processing time to estimate parameters and issue warnings, during which S-waves may have already passed through those locations.
Figure 11 displays a screenshot of the notifications received by a user during this earthquake. Notifications are issued to the public starting from the 3rd generated report onwards, while for the initial two reports, we wait to confirm that they are indeed generated due to earthquakes. The user's mobile time is shown in the hh:mm format without seconds. The notification timings, issued by the server, are provided in the Indian Standard Time format for precise information. The developed intensity map of this earthquake is also shown in Figure 12.

6. Performance of UEEW System

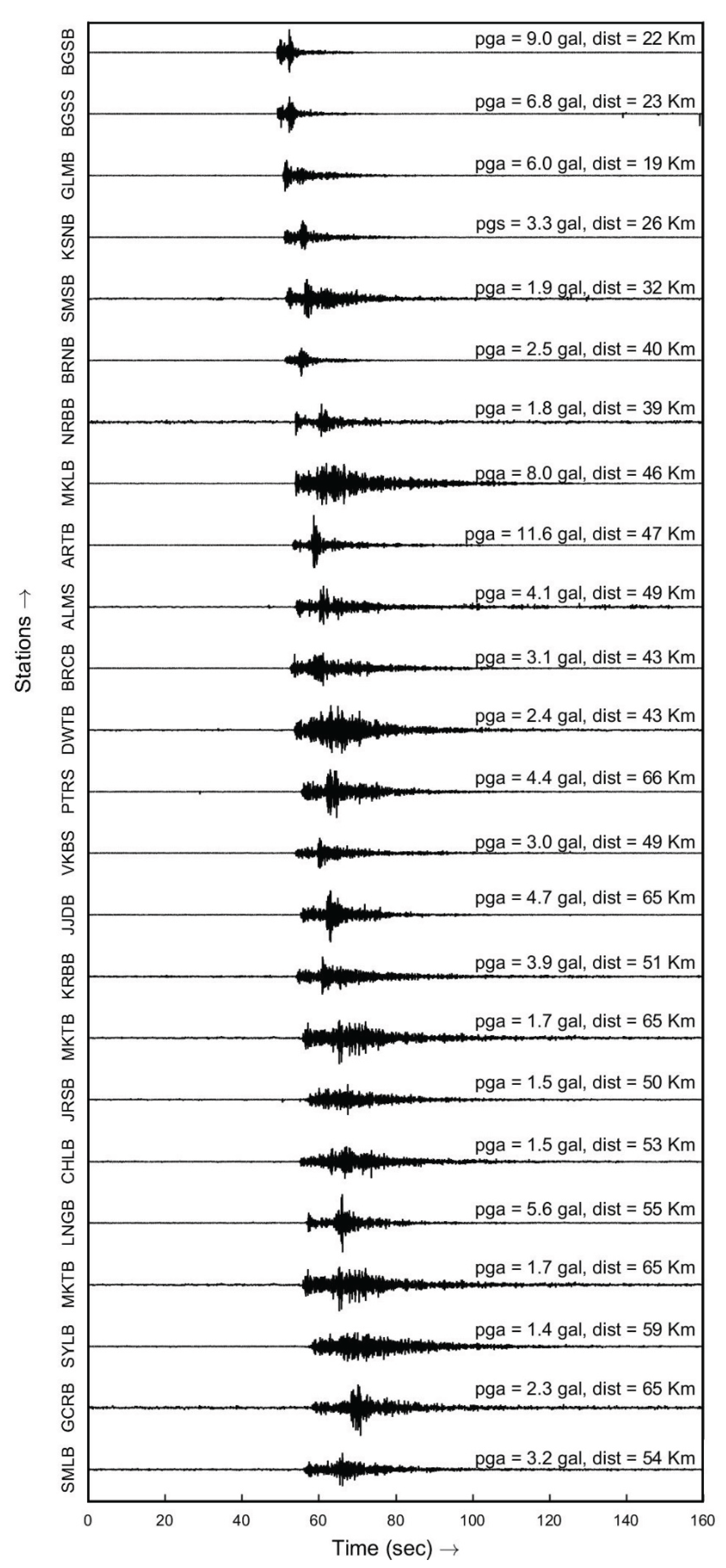
The dense instrumentation of the UEEW system ensures that any earthquake above magnitude 4.0 in the instrumented region is recorded by at least 4 stations. On February 8th, 2020, at 01:01:50 UTC, a light earthquake with a magnitude of 4.7 and a depth of 48.2 km struck the district of Pithoragarh, Uttarakhand. Figure 13 illustrates the epicenter's location and the triggered sensors, while Figure 14 depicts the vertical component accelerograms of this earthquake. An early notification was automatically sent solely to a close group of researchers since the system was not inaugurated to the public.
On September 11th, 2021, a magnitude 4.7 earthquake struck the Chamoli region. This event marked the first earthquake following the launch of the mobile app and the inauguration of the system to the public. Since it was a minor earthquake, alert messages were disseminated to the public. This incident represented the initial successful alert sent to the public.
The UEEWS has produced reports for 19 earthquakes from 2015 to the present (Table 1). Among these, 14 earthquakes were triggered in the Uttarakhand region, while 5 occurred in Nepal. In line with the UEEWS objectives, our analysis focused solely on earthquakes triggered in the Uttarakhand region. 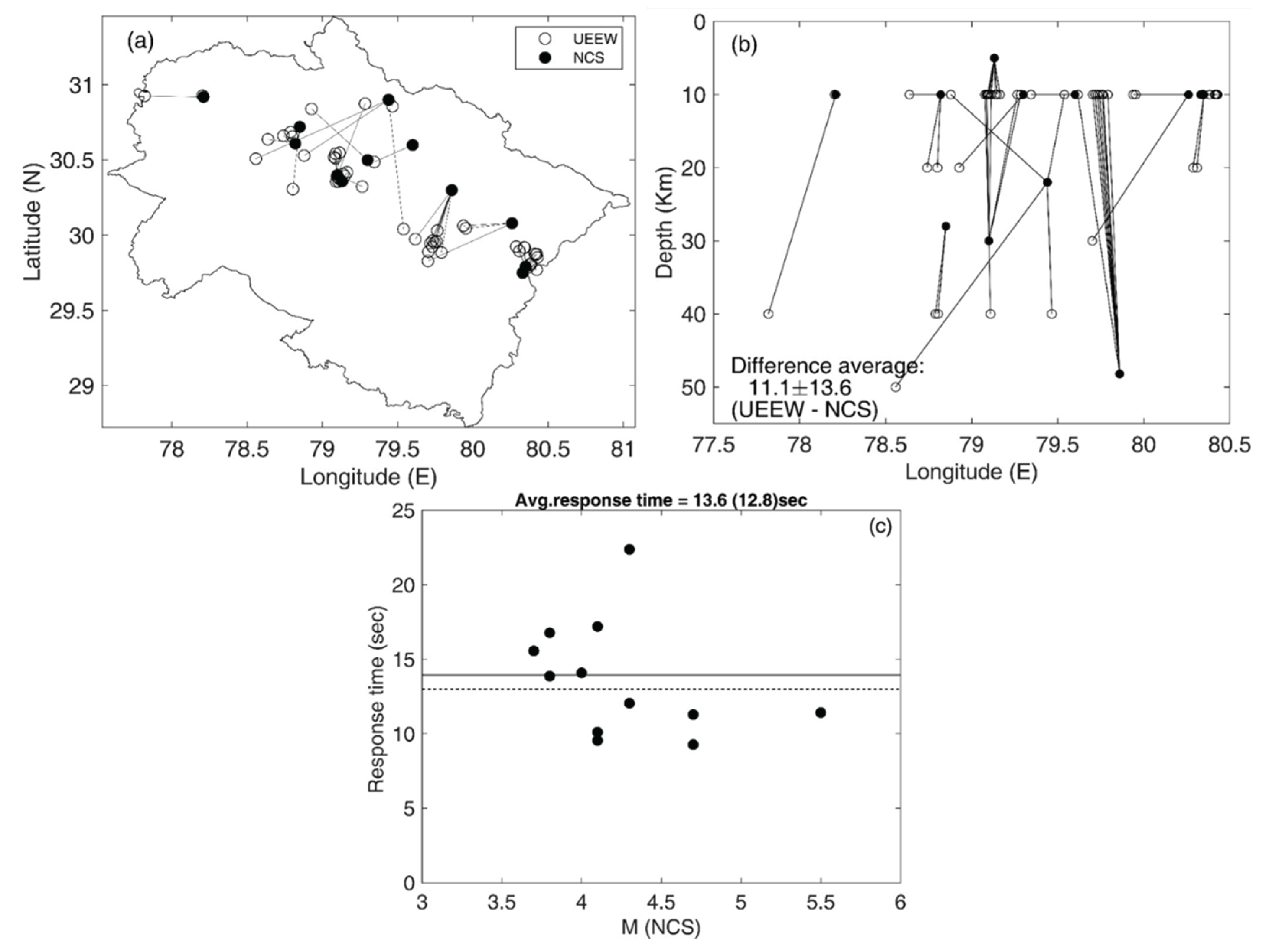The comparison of earthquake information (magnitude, location) estimated by the UEEWS and NCS is given in Table 2 and shown in Figure 15 which reveals significant variation in the epicenter and depth. The location estimation section describes the procedure to estimate the epicenter and depth. The variations in hypocenter determination between the UEEWS and NCS are influenced in part by differing velocity models and phase-picking methods. Additionally, the UEEWS employs cost-effective MEMS-based accelerometers, whereas NCS utilizes high-end state-of-the-art broadband seismographs and strong motion accelerographs. Furthermore, the UEEWS relies on the real-time analysis of the initial segment of seismic records while NCS utilizes the complete earthquake signature and provides source parameters in ~5–10 minutes after the earthquake with an average of about 8.0 minutes [119].
The average disparity in the estimated depth and epicenter between the UEEWS and NCS is 11.1 ± 13.6 km and 24.5 ± 22.6 km, respectively. The response time of the system is calculated as the duration between the origin time and the moment when the initial report is generated on the server. The average response time based on the reports generated during fourteen earthquakes (Table 1) is estimated as 13.6 ± 3.8 seconds. In one event (23/05/2021), the average response time was 22.38 seconds and after excluding this event the average response time came down to 12.8 seconds. On average, the UEEWS can provide a timely alert to locations approximately 45 km from the earthquake's hypocenter, prior to the arrival of the destructive S-waves
Magnitude estimates are derived from P-wave data, leading to significant uncertainties in magnitude determination. The estimated MPd from the UEEWS server and magnitude (Mw) from the NCS catalog are plotted in a 1:1 relationship. This discrepancy arises from the use of various regression equations (Eq. 2, 3, 4, and 5) at different points in time and their subsequent updates. 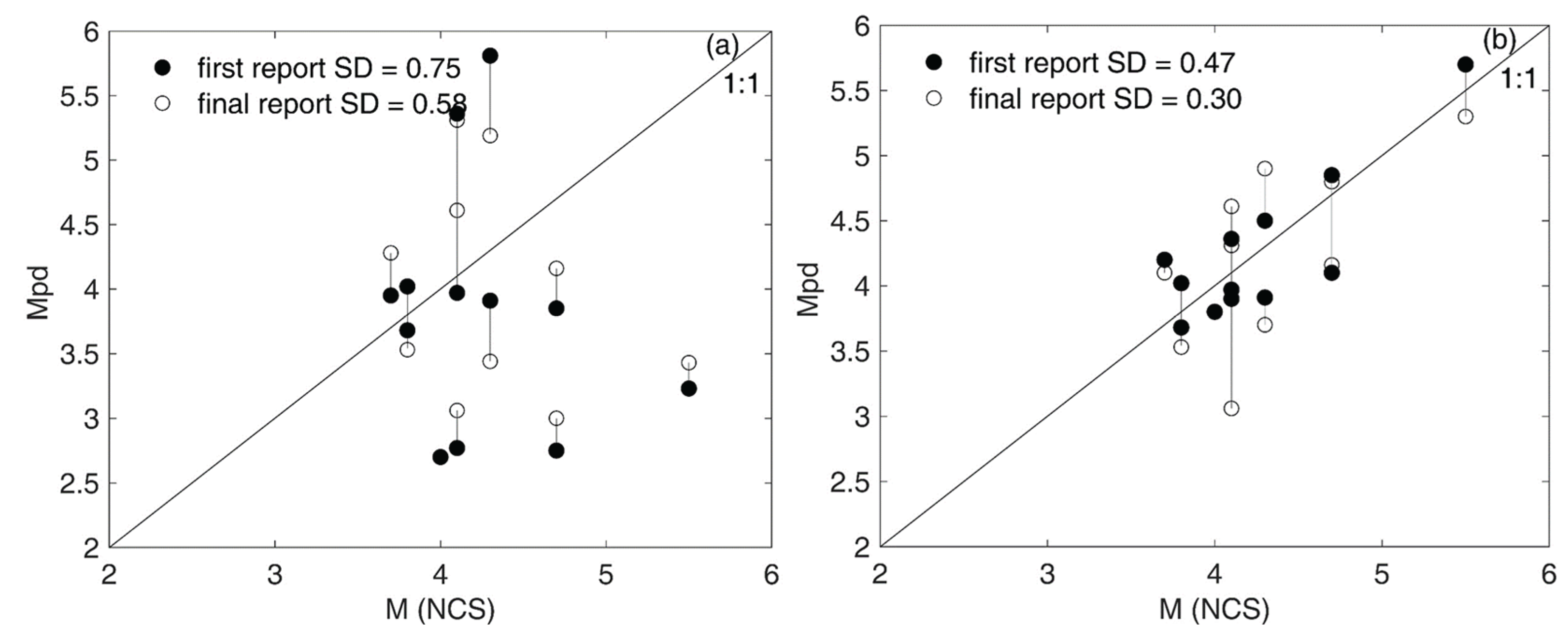In UEEWS, the magnitude estimation relies solely upon the initial portion of the P-wave following the p-onset (e.g., 3 seconds P-wave data); therefore the estimated magnitude exhibits variation compared to the magnitude based on the moment estimated by NCS (Figure 16a). The standard deviation between the estimated magnitudes of the initial and final reports from the UEEWS and the magnitudes in the NCS catalog is 0.76 and 0.58, respectively. The disparity in magnitude estimation arises from variations in location determination and the data segment utilized (NCS utilizes the complete waveform, while UEEWS employs the initial portion. The discrepancy in the determined earthquake source parameters fluctuates with the generated earthquake reports on the server and improves as more triggered sensors are identified. The earthquake records given in Table 2, underwent re-analysis on the offline server, utilizing the model outlined in Equation 5, resulting in notable enhancements in the estimated magnitudes. Consequently, the standard deviation of the first and final reports compared to the NCS catalog magnitude improved to 0.47 and 0.30, respectively (Figure 16b).

7. Way Forward

The current system relies on the VPNoBB feature provided by BSNL and the SWAN network. However, communication can be disrupted by various factors such as severe weather conditions, landslides, damage to optical fiber cables, power outages, interruptions in data streaming, etc. Hence, it might be beneficial to consider alternative options like public networks, cloud-based services, and solar power backups.
  • Currently, the warning system doesn't provide information about the intensity of the earthquake at the observer's location. This feature may be incorporated once the prediction of strong ground motion and its conversion to intensity is integrated into the algorithm.
  • At present, warnings are issued based on Peak Displacement (Pd) of the first three seconds of P-wave data after p-onset from at least four sensors. However, there are various other attributes such predominant period ( τ p i ), characteristic period ( τ c ), cumulative absolute velocity (CAV), squared velocity integral ( I V 2 ), log averaged period ( τ l o g ), root some square cumulative velocity (RSSCV), and others may be explored in the future.
  • Given the complexity of Himalayan tectonics, it is advisable to deploy denser networks with wider aperture arrays.
  • The issuance of warnings should also be vetted for their societal and management aspects.

8. Discussion and Conclusion

The EEW system laboratory effectively crafted the regional UEEWS by leveraging insights gained from other EEW systems worldwide. Following the completion of a pilot project titled 'Earthquake Early Warning System for North India' in 2017, the Uttarakhand government assumed responsibility for this initiative [93,120,121]. Instrumentation began to extend into the Kumaun region of Uttarakhand in mid-2017. Currently, 170 sensors have been deployed to encompass the entire Uttarakhand region. Internet connectivity is essential for streaming ground motion data, which can be challenging to maintain, particularly in the rugged terrain of the Himalayas. As a result, the system is under constant surveillance.
This system is currently operational, issuing warnings to the public by blowing installed sirens and sending warnings on the mobile app installed on smartphones by the users. This mobile app provides an SOS button useful for users during earthquakes. Upon pressing this button, the user's location is transmitted to the disaster management authority and two designated relatives. The mobile numbers of relatives are entered during the registration process of the mobile app. Upon receiving the location of the disaster victim, the disaster management authority initiates search and rescue operations. The developed system serves not only to issue warnings to the public but also to establish a robust ground motion database, proving invaluable for earthquake and civil engineering applications. [122]. It could be employed in analyzing seismic hazards in the region and formulating new ground-motion prediction equations [120,123,124,125]. The developed system offers lead times ranging from seconds to tens of seconds to urban areas, towns, and rural villages within the state. One significant outcome of such initiatives is the heightened public awareness regarding natural hazards, as evidenced by the significant number of downloads of the mobile app.

Data and Resources

URLs of the BhiDEV mobile application are as follows:
For Android users - https://play.google.com/store/apps/details?id=com.iitr.eews&pcampaignid=web_share
For iPhone users - https://apps.apple.com/in/app/bhudev/id1661902248

Declaration of Competing Interests

The authors acknowledge no conflicts of interest recorded and declare that they have no known competing financial interests or personal relationships that could have influenced the work reported in this paper.

Funding

This project “Earthquake Early Warning System for Uttarakhand” is being funded by USDMA, Dehradun, Government of Uttarakhand under the grant number USD-1077-DMC.

Acknowledgments

The authors are thankful to USDMA, Dehradun, Uttarakhand for providing funds to run this project and the Ministry of Earth Sciences for funding the pilot project. The discussions held with NDMA, Uttarakhand administration, and NCS officials are gratefully acknowledged. The authors are also thankful to Prof. Ashok Kumar, Prof. Ajay Gairola, Dr. Himanshu Mittal, Dr. Bhanu Pratapa Chamoli, Dr. Bhavesh Pandey, Dr. Govind Rathore for their support in establishing this system. The help provided by the Centre of Excellence in Disaster Mitigation & Management and the Department of Earthquake Engineering, IIT Roorkee, is thankfully acknowledged.

References

  1. Bahinipati, C.S.; Patnaik, U.; Viswanathan, P.K. What Causes Economic Losses from Natural Disasters in India. In Handbook of Research on Climate Change Impact on Health and Environmental Sustainability; Dinda, S., Ed.; IGI Global: 701 E. Chocolate Avenue Hershey PA, USA, 2015; ISBN 9781466688148. [Google Scholar]
  2. IPCC Summary for Policymakers. Managing the risks of extreme events and disasters to advance climate change adaptation; 2012. 2012.
  3. Narayan, J.P.; Sharma, M.L.; Kumar, A. A seismological report on the 26 January 2001 Bhuj, India Earthquake. Seismol. Res. Lett. 2002, 73, 343–355. [Google Scholar] [CrossRef]
  4. Sharma, M.L. Seismic Hazard in the Northern India Region. Seismol. Res. Lett. 2003, 74, 141–147. [Google Scholar] [CrossRef]
  5. Shanker, D.; Sharma, M.L. Estimation of Seismic Hazard Parameters for the Himalayas and its Vicinity from Complete Data Files. Pure Appl. Geophys. 1998, 152, 267–279. [Google Scholar] [CrossRef]
  6. Sharma, M.L.; Arora, M.K. Prediction of Seismicity Cycles in the Himalayas Using Artificial Neural Network. Acta Geophys. Pol. 2005, 53, 299–309. [Google Scholar]
  7. Bilham, R.; Larsont, K.; Freymueller, J. GPS measurements of present-day convergence across the Nepal Himalaya. Nature 1997, 386, 61–63. [Google Scholar] [CrossRef]
  8. Sharma, M.L.; Lindholm, C. Earthquake Hazard Assessment for Dehradun, Uttarakhand, India, Including a Characteristic Earthquake Recurrence Model for the Himalaya Frontal Fault (HFF). Pure Appl. Geophys. 2012, 169, 1601–1617. [Google Scholar] [CrossRef]
  9. Paudyal, H.; Panthi, A. Seismic Vulnerability in the Himalayan Region. Himal. Phys. 2010, 1, 14–17. [Google Scholar] [CrossRef]
  10. Gansser, A. Geology of the Himalaya; SITTER, L.U. DE, Ed.; Library of.; INTERSCIENCE PUBLISHERS, a division of John Wiley & Sons Ltd: LONDON - NEW YORK - SYDNEY, 1964; ISBN 0470290552. [Google Scholar]
  11. Bhatia, S.C.; Kumar, M.R.; Gupta, H.K. A probabilistic seismic hazard map of India and adjoining regions. Ann. di Geofis. 1999, 42, 1153–1164. [Google Scholar]
  12. Valdiya, K.S. Aspects of TECTONICS: Focus on South Central Asia; Tata McGraw-Hill Pub. Co.: New Delhi, India, 1984; ISBN 0074519727. [Google Scholar]
  13. Zhang, P.; Yang, Z.; Gupta, H.K.; Bhatia, S.C.; Shedlock, K.M. Global Seismic Hazard Assessment Program (GSHAP) in continental Asia. Ann. di Geofis. 1999, 42, 1167–1190. [Google Scholar] [CrossRef]
  14. Malik, J.N.; Nakata, T.; Philip, G.; Suresh, N.; Virdi, N.S. Active Fault and Paleoseismic Investigation: Evidence of a Historic Earthquake along Chandigarh Fault in the Frontal Himalayan Zone, NW India. Himal. Geol. 2008, 29, 109–117. [Google Scholar]
  15. Gupta, H.K.; Gahalaut, V.K. Can an earthquake of Mw~9 occur in the Himalayan region? Geol. Soc. Spec. Publ. 2015, 412, 43–53. [Google Scholar] [CrossRef]
  16. Khattri, K.M.; Tyagi, A.K. Seismicity Patterns in the Himalayan Plate Boundary and Identification of the Areas of High Seismic Potential. Tectonophysics 1983, 96, 281–297. [Google Scholar] [CrossRef]
  17. Sreejith, K.M.; Sunil, P.S.; Agrawal, R.; Saji, A.P.; Rajawat, A.S.; Ramesh, D.S. Audit of stored strain energy and extent of future earthquake rupture in central Himalaya. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
  18. Gupta, H.K.; Rao, N.P.; Rastogi, B.K.; Sarkar, D. The Deadliest Intraplate Earthquake. Science (80-. ). 2001, 291, 2101–2102. [Google Scholar] [CrossRef] [PubMed]
  19. Gauchan, D.; Joshi, B.K.; Ghimire, K. Impact of 2015 Earthquake on Economy , Agriculture and Impact of 2015 Earthquake on Economy , Agriculture and Agrobiodiversity in Nepal. In Proceedings of the Proceedings of Sharingshop on Germplasm Rescue; pp. 201719–25.
  20. Ambraseys, N.; Bilham, R. A note on the Kangra Ms = 7. 8 earthquake of 4 April 1905. Curr. Sci. 2000, 79, 45–50. [Google Scholar]
  21. Oldham, R.D. Report on the Great Earthquake of 12th June, 1897. Mem. Geol. Surv. India 1899, 29. [Google Scholar]
  22. Priyanka, R.S.; Jayangondaperumal, R.; Pandey, A.; Mishra, R.L. Primary surface rupture of the 1950 Tibet-Assam great earthquake along the eastern Himalayan front, Sci. Rep. 2017, 1–12. [Google Scholar] [CrossRef] [PubMed]
  23. USGS National Earthquake Information Center M 8.6 - 1950 Assam-Tibet Earthquake Available online: https://earthquake.usgs.gov/earthquakes/eventpage/official19500815140934_30/impact.
  24. Singh, D.D.; Gupta, H.K. Source Dynamics of two Great Earthquakes of the Indian Subcontinent: The Bihar-Nepal Earthquake of January 15, 1934 and The Quetta Earthquake of May 30, 1935. Bull. Seismol. Soc. Am. 1980, 70, 757–773. [Google Scholar] [CrossRef]
  25. Nasu, N. The Great Indian Earthquake of January 15, 1934. Bull. Earthq. Res. Inst. 1934, 13, 417–440. [Google Scholar]
  26. Gunn, A.M. Bihar, India, Earthquake. In Encyclopedia of Disasters. Environment Catastrophes and Human Tragedies. Volume 1; Greenwood Press, 88 Post Road West, CT 06881, USA, 2008; pp. 337–339 ISBN 978–0–313–34004–8.
  27. Jain, S.K.; Singh, R.P.; Gupta, V.K.; Nagar, A. Garhwal Earthquake of Oct. 20, 1991. EERI Spec. Earthq. Report, EERI Newsl. 1991, 26, 1–8. [Google Scholar]
  28. Jain, S.K.; Murty, C.V.R.; Arlekar, J.N. Chamoli (Himalaya, India) Earthquake of 29 March 1999. EERI Spec. Earthq. Report, EERI Newsl. 1999, 33. 29 March.
  29. Kamal, K.; Chabak, S.K. Chamoli aftershocks : A view from the nearest seismic observatory. Himal. Geol. 2002, 23, 63–67. [Google Scholar]
  30. Mahajan, A.K.; Thakur, V.C.; Sharma, M.L.; Chauhan, M. Probabilistic seismic hazard map of NW Himalaya and its adjoining area, India. Nat. Hazards 2010, 53, 443–457. [Google Scholar] [CrossRef]
  31. Khattri, K.N. Great Earthquakes, Seismicity Gaps and Potential for Earthquake Disaster along the Himalaya Plate Boundary. Tectonophysics 1987, 138, 79–92. [Google Scholar] [CrossRef]
  32. Srivastava, H.N. Earthquake Prediction Studies in Himalaya Critical Evaluation. Mem. Geol. Soc. India 1992, 23, 151–172. [Google Scholar]
  33. Srivastava, H.N.; Verma, M.; Bansal, B.K.; Sutar, A.K. Discriminatory characteristics of seismic gaps in Himalaya. Geomatics, Nat. Hazards Risk 2015, 6, 224–242. [Google Scholar] [CrossRef]
  34. Cuéllar, A.; Suárez, G.; Ibarrola, G.; Uribe, A.; Rodríguez, F.H.; Islas, R.; Rodríguez, G.M.; García, A.; Frontana, B. Early Warning for Geological Disasters. 2014, 71–87.
  35. Cuéllar, A.; Espinosa-Aranda, J. M. Suárez, R.; Ibarrola, G., Uribe, A., Rodríguez, F.H., Islas, R., Rodríguez, G.M., García, A., Frontana, B. The Mexican Seismic Alert System (SASMEX): Its Alert Signals, Broadcast Results and Performance during the M 7.4 Punta Maldonado Earthquake of March 20th. In Early Warning for Geological Disasters, Wenzel, F., Zschau, J., Eds.; Springer-Verlag Berlin Heidelberg: Springer Heidelberg New York Dordrecht London, 2014; ISBN 978-3-642-12232-3. [Google Scholar]
  36. Suárez, G.; Novelo, D.; Mansilla, E. Performance evaluation of the seismic alert system (SAS) in Mexico City: A seismological and a social perspective. Seismol. Res. Lett. 2009, 80, 707–716. [Google Scholar] [CrossRef]
  37. Okada, Y. Preliminary report of the 2011 off the Pacific coast of Tohoku Earthquake; 2011;
  38. Honma, F.; Ichikawa, F. Earthquake Early Warning Disaster Mitigation System for Protecting Semiconductor Plant in Japan. In Proceedings of the 14th World Conference on Earthquake Engineering; Beijing, China; 2008; pp. 1–2. [Google Scholar]
  39. Kodera, Y.; Yamada, Y.; Hirano, K.; Tamaribuchi, K.; Adachi, S.; Hayashimoto, N.; Morimoto, M.; Nakamura, M.; Hoshiba, M. The propagation of local undamped motion (PLUM) method: A simple and robust seismic wavefield estimation approach for earthquake early warning. Bull. Seismol. Soc. Am. 2018, 108, 983–1003. [Google Scholar] [CrossRef]
  40. Khattri, K.N. Seismic gaps and likelihood of occurrence of larger earthquakes in Northern India. Curr. Sci. 1993, 64, 885–888. [Google Scholar]
  41. Bilham, R.; Gaur, V.K.; Molnar, P. Himalayan Seismic Hazard. Science (80-. ). 2001, 293, 1442–1444. [Google Scholar] [CrossRef]
  42. Bilham, R. Earthquakes in India and the Himalaya: Tectonics, geodesy and history. Ann. Geophys. 2004, 47, 839–858. [Google Scholar] [CrossRef]
  43. Bajaj, S.; Sharma, M.L. Modeling Earthquake Recurrence in the Himalayan Seismic Belt Using Time-Dependent Stochastic Models : Implications for Future Seismic Hazards. Pure Appl. Geophys. 2019, 176, 5261–5278. [Google Scholar] [CrossRef]
  44. Bajaj, S.; Sharma, M.L. Time dependent probabilities for earthquake occurrence in Central Himalaya. In Proceedings of the 16th Symposium on Earthquake Engineering, 20-22 December, IIT Roorkee, India; 2018; pp. 1–10. [Google Scholar]
  45. Chaudhary, C.; Sharma, M.L. Probabilistic Models For Earthquakes With Large Return Periods In Himalaya Region. Pure Appl. Geophys. 2017, 174, 4313–4327. [Google Scholar] [CrossRef]
  46. Choudhary, C.; Sharma, M.L. Global strain rates in western to central Himalayas and their implications in seismic hazard assessment. Nat. Hazards 2018, 94, 1211–1224. [Google Scholar] [CrossRef]
  47. Gupta, H.K. Seismicity in the Vicinity of Dams on Himalayan Rivers and the Problem of Reservoir Induced Earthquakes. Journal-Geological Soc. India 1984, 25, 85–93. [Google Scholar]
  48. Gupta, H.K. Major and Great Earthquakes in the Himalayan Region: An Overview; Balassanian, S., Cisternas, A., Melkumyan, M., Eds.; Springer Science+Business Media, B.V., 2012; Vol. 12; ISBN 9788578110796.
  49. Bansal, B.K.; Verma, M. Science and Technology Based Earthquake Risk Reduction Strategies: The Indian Scenario. Acta Geophys. 2013, 61, 808–821. [Google Scholar] [CrossRef]
  50. Census of India; 2011;
  51. Apollo, M. The Population of Himalayan Regions by the Numbers: Past, Present and Future. In Contemporary Studies in Environment and Tourism; Efe, R., Öztürk, M., Eds.; Cambridge Scholars Publishing, 2017; pp. 145–159 ISBN 1-4438-7283-0.
  52. Wyss, M.; Wang, R.J.; Zschau, J.; Xia, Y. Earthquake Loss Estimates in Near Real-Time. EOS, Trans. Am. Geophys. Union 2006, 87, 477–479. [Google Scholar] [CrossRef]
  53. Mckenna, P. Why earthquakes are hard to predict. New Sci. 2011, 1–3. [Google Scholar]
  54. Espinosa-Aranda, J.M.; Cuellar, A.; Garcia, A.; Ibarrola, G.; Islas, R.; Maldonado, S.; Rodriguez, F.H. Evolution of the Mexican Seismic Alert System (SASMEX). Seismol. Res. Lett. 2009, 80, 694–706. [Google Scholar] [CrossRef]
  55. Mittal, H.; Wu, Y.M.; Sharma, M.L.; Yang, B.M.; Gupta, S. Testing the performance of earthquake early warning system in northern India. Acta Geophys. 2019, 67, 59–75. [Google Scholar] [CrossRef]
  56. Allen, R.M.; Melgar, D. Earthquake Early Warning: Advances, Scientific Challenges, and Societal Needs. Annu. Rev. Earth Planet. Sci. 2019, 47, 361–388. [Google Scholar] [CrossRef]
  57. Allen, R.M.; Brown, H.; Hellweg, M.; Khainovski, O.; Lombard, P.; Neuhauser, D. Real-time earthquake detection and hazard assessment by ElarmS across California. Geophys. Res. Lett. 2009, 36, 1–6. [Google Scholar] [CrossRef]
  58. Cooper, J.D. The San Francisco Daily Evening Bulletin. San Francisco 1868, p. 1.
  59. Bhardwaj, R.; Sharma, M.L.; Kumar, A. Multi-parameter algorithm for Earthquake Early Warning. Geomatics, Nat. Hazards Risk 2016, 7, 1242–1264. [Google Scholar] [CrossRef]
  60. Wu, Y.M.; Kanamori, H. Rapid assessment of damage potential of earthquakes in Taiwan from the Beginning of P waves. Bull. Seismol. Soc. Am. 2005, 95, 1181–1185. [Google Scholar] [CrossRef]
  61. Nakamura, Y.; Saita, J. FREQL and AcCo for a quick response to earthquakes. Earthq. Early Warn. Syst. 2007, 307–324. [Google Scholar]
  62. Aranda, J.M.E.; Jimenez, A.; Conteras, O.; Ibarrola, G.; Ortega, R. Mexico City Seismic Alert System 315–324.
  63. Hoshiba, M.; Kamigaichi, O.; Saito, M.; Tsukada, S.; Hamada, N. Earthquake early warning starts nationwide in Japan. Eos (Washington. DC). 2008, 89, 73–74. [Google Scholar] [CrossRef]
  64. Kamigaichi, O.; Saito, M.; Doi, K.; Matsumori, T.; Tsukada, S.; Takeda, K.; Shimoyama, T.; Nakamura, K.; Kiyomoto, M.; Watanabe, Y. Earthquake Early Warning in Japan: Warning the General Public and Future Prospects. Seismol. Res. Lett. 2009, 80, 717–726. [Google Scholar] [CrossRef]
  65. Hsiao, N.C.; Wu, Y.M.; Shin, T.C.; Zhao, L.; Teng, T.L. Development of earthquake early warning system in Taiwan. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
  66. Chen, D.Y.; Hsiao, N.C.; Wu, Y.M. The earthworm based earthquake alarm reporting system in Taiwan. Bull. Seismol. Soc. Am. 2015, 105, 568–579. [Google Scholar] [CrossRef]
  67. Wu, Y.M.; Liang, W.T.; Mittal, H.; Chao, W.A.; Lin, C.H.; Huang, B.S.; Lin, C.M. Performance of a low-cost earthquake early warning system (P-Alert) during the 2016 ML 6.4 Meinong (Taiwan) earthquake. Seismol. Res. Lett. 2016, 87, 1050–1059. [Google Scholar] [CrossRef]
  68. Espinosa-Aranda, J.M.; Jimenez, A.; Ibarrola, G.; Alcantar, F.; Aguilar, A.; Inostroza, M.; Maldonado, S. Results of the Mexico city early warning system. In Proceedings of the Eleventh World Conference on Earthquake Engineering; 1996; pp. 1–8. [Google Scholar]
  69. Espinosa-Aranda, J.M.; Cuéllar, A.; Ibarrola, G.; Islas, R.; García, A.; Rodríguez, F.H.; Frontana, B. The Seismic Alert System of Mexico (SASMEX) and their Alert Signals Broadcast Results. In Proceedings of the 15th World Conference on Earthquake Engineering; 2012; pp. 1–9. [Google Scholar]
  70. Sheen, D.; Park, J.; Chi, H.; Hwang, E.; Lim, I.; Seong, Y.J.; Pak, J. The First Stage of an Earthquake Early Warning System in South Korea. Seismol. Res. Lett. 2017, 88, 1491–1498. [Google Scholar] [CrossRef]
  71. Erdik, M.; Fahjan, Y.; Ozel, O.; Alcik, H.; Mert, A.; Gul, M. Istanbul earthquake rapid response and early warning system. Bull. Earthq. Eng. 2003, 1, 157–163. [Google Scholar] [CrossRef]
  72. Alcik, H.; Ozel, O.; Apaydin, N.; Erdik, M. A study on warning algorithms for Istanbul earthquake early warning system. Geophys. Res. Lett. 2009, 36, 3–5. [Google Scholar] [CrossRef]
  73. Carranza, M.; Buforn, E.; Colombelli, S.; Zollo, A. Earthquake early warning for southern Iberia : A P wave threshold-based approach. Geophys. Res. Lett. 2013, 40, 4588–4593. [Google Scholar] [CrossRef]
  74. Pazos, A.; Romeu, N.; Lozano, L.; Colom, Y.; Mesa, M.L.; Goula, X.; Jara, J.A.; Cantavella, J. V.; Zollo, A.; Hanka, W.; et al. A Regional Approach for Earthquake Early Warning in South West Iberia : A Feasibility Study. Bull. Seismol. Soc. Am. 2015, 105, 560–567. [Google Scholar] [CrossRef]
  75. Romeu Petit, N.; Colom Puyané, Y.; Jara Salvador, J.A.; Goula Suriñach, X.; Susagna Vidal, T. Development of an Earthquake early warning system based on Earthworm: Application to Southwest Iberia. Bull. Seismol. Soc. Am. 2016, 106, 1–12. [Google Scholar] [CrossRef]
  76. Zollo, A.; Iannaccone, G.; Convertito, V.; Elia, L.; Iervolino, I.; Lancieri, M.; Lomax, A.; Martino, C.; Satriano, C.; Weber, E.; et al. Earthquake EarlyWarning System in Southern Italy 2395–2421.
  77. Zollo, A.; Iannaccone, G.; Lancieri, M.; Cantore, L.; Convertito, V.; Emolo, A.; Festa, G.; Gallovič, F.; Vassallo, M.; Martino, C.; et al. Earthquake early warning system in southern Italy: Methodologies and performance evaluation. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
  78. Satriano, C.; Elia, L.; Martino, C.; Lancieri, M.; Zollo, A.; Iannaccone, G. PRESTo, the earthquake early warning system for Southern Italy: Concepts, capabilities and future perspectives. Soil Dyn. Earthq. Eng. 2011, 31, 137–153. [Google Scholar] [CrossRef]
  79. Wenzel, F.; Oncescu, M.C.; Baur, M.; Fiedrich, F.; Ionescu, C. An Early Warning System for Bucharest. Seismol. Res. Lett. 1999, 70, 161–169. [Google Scholar] [CrossRef]
  80. Böse, M.; Sokolov, V.; Wenzel, F. Shake map methodology for intermediate-depth Vrancea (Romania) earthquakes. Earthq. Spectra 2009, 25, 497–514. [Google Scholar] [CrossRef]
  81. Böse, M.; Ionescu, C.; Wenzel, F. Earthquake early warning for Bucharest, Romania: Novel and revised scaling relations. Geophys. Res. Lett. 2007, 34, 1–6. [Google Scholar] [CrossRef]
  82. Peng, H.; Wu, Z.; Wu, Y.-M.; Yu, S.; Zhang, D.; Huang, W. Developing a Prototype Earthquake Early Warning System in the Beijing Capital Region. Seismol. Res. Lett. 2011, 82, 394–403. [Google Scholar] [CrossRef]
  83. Wang, Y.; Li, S.; Song, J. Threshold - based evolutionary magnitude estimation for an earthquake early warning system in the Sichuan – Yunnan region, China. Sci. Rep. 2020, 1–12. [Google Scholar] [CrossRef] [PubMed]
  84. Crowell, B.W.; Schmidt, D.A.; Bodin, P.; Vidale, J.E.; Baker, B.; Barrientos, S.; Geng, J. G-FAST Earthquake Early Warning Potential for Great Earthquakes in Chile. Seismol. Res. Lett. 2018, 89, 542–556. [Google Scholar] [CrossRef]
  85. Brooks, B.A.; Protti, M.; Ericksen, T.; Bunn, J.; Al, B.E.T. Robust Earthquake Early Warning at a Fraction of the Cost : ASTUTI Costa Rica. AGU Adv. 2021, 2, 1–17. [Google Scholar] [CrossRef]
  86. Porras, J.; Massin, F.; Arroyo-solórzano, M.; Arroyo, I. Preliminary Results of an Earthquake Early Warning System in Costa Rica. Front. Earth Sci. 2021, 9, 1–13. [Google Scholar] [CrossRef]
  87. Massin, F.; Clinton, J.; Böse, M. Status of Earthquake Early Warning in Switzerland. Front. Earth Sci. 2021, 9, 1–20. [Google Scholar] [CrossRef]
  88. Strauch, W.; Talavera, E.; Tenorio, V.; Ramírez, J.; Argüello, G.; Herrera, M.; Acosta, A.; Morales, A. Toward an Earthquake and Tsunami Monitoring and Early Warning System for Nicaragua and Central America. Seismol. Res. Lett. 2018, 89, 399–406. [Google Scholar] [CrossRef]
  89. Nof, R.N.; Lior, I.; Kurzon, I. Earthquake Early Warning System in Israel — Towards an Operational Stage. Front. Earth Sci. 2021, 9, 1–12. [Google Scholar] [CrossRef]
  90. Nof, R.N.; Kurzon, I. TRUAA — Earthquake Early Warning System for Israel : Implementation and Current Status. Seism. Instruments 2021, 92, 325–341. [Google Scholar] [CrossRef]
  91. Cua, G.; Fischer, M.; Heaton, T.; Wiemer, S. Real-time Performance of the Virtual Seismologist Earthquake Early Warning Algorithm in Southern California. Seismol. Res. Lett. 2009, 80, 740–747. [Google Scholar] [CrossRef]
  92. Allen, R.M.; Brown, H.; Hellweg, M.; Khainovski, O.; Lombard, P.; Neuhauser, D. Real-time earthquake detection and hazard assessment by ElarmS across California. Geophys. Res. Lett. 2009, 36, 1–6. [Google Scholar] [CrossRef]
  93. Chamoli, B.P.; Kumar, A.; Chen, D.Y.; Gairola, A.; Jakka, R.S.; Pandey, B.; Kumar, P.; Rathore, G. A Prototype Earthquake Early Warning System for Northern India. J. Earthq. Eng. 2019, 25, 2455–2473. [Google Scholar] [CrossRef]
  94. Mittal, H.; Kumar, A.; Ramhmachhuani, R. Indian National Strong Motion Instrumentation Network and Site Characterization of Its Stations. Int. J. Geosci. 2012, 03, 1151–1167. [Google Scholar] [CrossRef]
  95. Dimri, V.P. Uttarakhand had early warning communication in 1894 ! Curr. Sci. 2013, 105, 152. [Google Scholar]
  96. Bhardwaj, Rakhi Analysis of Tauc (tc ) and Pd attributes for Earthquake Early Warning in India. 15th World Conf. Earthq. Eng. 2012.
  97. Wu, Y.M.; Chen, D.Y.; Lin, T.L.; Hsieh, C.Y.; Chin, T.L.; Chang, W.Y.; Li, W. Sen; Ker, S.H. A high-density seismic network for earthquake early warning in Taiwan based on low cost sensors. Seismol. Res. Lett. 2013, 84, 1048–1054. [Google Scholar] [CrossRef]
  98. Wu, Y.-M.; Lin, T.-L. A Test of Earthquake Early Warning System Using Low Cost Accelerometer in Hualien, Taiwan. Wenzel, F. J. Zschau (Eds.), Early Warn. Geol. Disasters - Sci. Methods Curr. Pract. Adv. Technol. Earth Sci. Springer Berlin Heidelberg, New York 2014, 307–331.
  99. Johnson, C.E.; Bittenbinder, A.; Bogaert, B.; Dietz, L.; Kohler, W. Earthworm: A Flexible Approach to Seismic Network Processing. IRIS Newsl. U.S. Geol. Surv. Menlo Park 1995, 14, 1–4. [Google Scholar]
  100. STI Earthworm Central Available online: http://www.earthwormcentral.org/.
  101. Saragiotis, C.D.; Hadjileontiadis, L.J.; Panas, S.M. PAI-S/K: A robust automatic seismic P phase arrival identification scheme. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1395–1404. [Google Scholar] [CrossRef]
  102. Akazawa, T. A Technique for Automatic Detection of Onset Time of P- and S-Phases in Strong Motion Records. In Proceedings of the 13 th World Conference on Earthquake Engineering; 2004; p. 786. [Google Scholar]
  103. Gentili, S.; Michelini, A. Automatic picking of P and S phases using a neural tree. J. Seismol. 2006, 10, 39–63. [Google Scholar] [CrossRef]
  104. Ait Laasri, E.H.; Akhouayri, E.S.; Agliz, D.; Atmani, A.; Hassan, E.; Laasri, A.; Akhouayri, E.S.; Agliz, D.; Atmani, A. Automatic detection and picking of P-wave arrival in locally stationary noise using cross-correlation. Digit. Signal Process. 2014, 26, 87–100. [Google Scholar] [CrossRef]
  105. Ross, Z.E.; Ben-Zion, Y. Automatic picking of direct P, S seismic phases and fault zone head waves. Geophys. J. Int. 2014, 199, 368–381. [Google Scholar] [CrossRef]
  106. Kalkan, E. An automatic P-phase Arrival-Time Picker. Bull. Seismol. Soc. Am. 2016, 106, 971–986. [Google Scholar] [CrossRef]
  107. Chi-Durán, R.; Comte, D.; Díaz, M.; Silva, J.F. Automatic detection of P- and S-wave arrival times: new strategies based on the modified fractal method and basic matching pursuit. J. Seismol. 2017, 21, 1171–1184. [Google Scholar] [CrossRef]
  108. Zhang, Y.; Chen, Q.; Liu, X.; Zhao, J.; Xu, Q.; Yang, Y.; Liu, G. Adaptive and automatic P- and S-phase pickers based on frequency spectrum variation of sliding time windows. Geophys. J. Int. 2018, 215, 2172–2182. [Google Scholar] [CrossRef]
  109. Zhu, M.; Wang, L.; Liu, X.; Zhao, J.; Peng, P. Accurate identification of microseismic P- and S-phase arrivals using the multi-step AIC algorithm. J. Appl. Geophys. 2018, 150, 284–293. [Google Scholar] [CrossRef]
  110. Ahmed, A.; Sharma, M.L.; Sharma, A. Wavelet Based Automatic Phase Picking Algorithm for 3-Component Broadband Seismological Data. J. Seismol. Earthq. Eng. 2007, 9, 15–24. [Google Scholar]
  111. Allen, R. V. Automatic earthquake recognition and timing from single traces. Bull. Seismol. Soc. Am. 1978, 68, 1521–1532. [Google Scholar] [CrossRef]
  112. Allen, R. Automatic phase pickers: Their present use and future prospects. Bull. Seismol. Soc. Am. 1982, 72, S225–242. [Google Scholar] [CrossRef]
  113. Geiger, L. Probability method for the determination of earthquake epicenters from the arrival times only. Bull. Saint Louis Univ. 1912, 8, 60–71. [Google Scholar]
  114. Kanaujia, J.; Kumar, A.; Gupta, S.C. 1D velocity structure and characteristics of contemporary local seismicity around the Tehri region, Garhwal Himalaya. Bull. Seismol. Soc. Am. 2015, 105, 1852–1869. [Google Scholar] [CrossRef]
  115. Eisermann, A.S.; Ziv, A.; Wust-Bloch, G.H. Real-Time Back Azimuth for Earthquake Early Warning. Bull. Seismol. Soc. Am. 2015, 105, 2274–2285. [Google Scholar] [CrossRef]
  116. Kuyuk, H.S.; Allen, R.M. A global approach to provide magnitude estimates for earthquake early warning alerts. Geophys. Res. Lett. 2013, 40, 6329–6333. [Google Scholar] [CrossRef]
  117. Satriano, C.; Wu, Y.M.; Zollo, A.; Kanamori, H. Earthquake early warning: Concepts, methods and physical grounds. Soil Dyn. Earthq. Eng. 2011, 31, 106–118. [Google Scholar] [CrossRef]
  118. Rathore, G.; Kumar, A.; Jakka, R.S.; Chamoli, B.P. Development of Earthquake Early Warning Siren for Regional Earthquake Early Warning System in India. In Proceedings of the 16th Symposium on Earthquake Engineering, IIT Roorkee, India; 2018; pp. 1–9. [Google Scholar]
  119. Bansal, B.K.; Pandey, A.P.; Singh, A.P.; Suresh, G.; Singh, R.K.; Gautam, J.L. National Seismological Network in India for Real-Time Earthquake Monitoring. Seismol. Res. Lett. 2021, 92, 2255–2269. [Google Scholar] [CrossRef]
  120. Kumar, P.; Chamoli, B.P.; Kumar, A.; Gairola, A. Attenuation Relationship for Peak Horizontal Acceleration of Strong Ground Motion of Uttarakhand Region of Central Himalayas. J. Earthq. Eng. 2019, 25, 2537–2554. [Google Scholar] [CrossRef]
  121. Kumar, P.; Pandey, B.; Kamal. ; Kumar, A. Site classification of seismic recording stations of Garhwal region of earthquake early warning system for Uttarakhand, India. Vietnam J. Earth Sci. 2022, 44, 369–394. [Google Scholar]
  122. Kumar, A.; Mittal, H.; Sachdeva, R. Indian Strong Motion Instrumentation Network. Seismol. Res. Lett. 2012, 83, 59–66. [Google Scholar] [CrossRef]
  123. Sharma, M.L. Attenuation Relationship for Estimation of Peak Ground Horizontal Acceleration Using Data From Strong-Motion Arrays in India. Bull. Seismol. Soc. Am. 1998, 88, 1063–1069. [Google Scholar] [CrossRef]
  124. Sharma, M.L. A New Empirical Attenuation Relationship for Peak Ground Horizontal Acceleration for Himalayan Region using Indian and Worldwide Data Set. Jour. Geophys. 2005, 26, 151–158. [Google Scholar]
  125. Sharma, M.; Douglas, J.; Bungum, H.; Kotadia, J. Ground-motion prediction equations based on data from the Himalayan and Zagros region. J. Earthq. Eng. 2009, 13, 1191–1210. [Google Scholar] [CrossRef]
Preprints 101336 g001
Figure 1. Location of the sensors installed in seismogenic areas of Uttarakhand.
Figure 1. Location of the sensors installed in seismogenic areas of Uttarakhand.
Preprints 101336 g001
Preprints 101336 g002
Figure 2. Streaming of accelerograms from sensors to the server in real-time during the event of an earthquake.
Figure 2. Streaming of accelerograms from sensors to the server in real-time during the event of an earthquake.
Preprints 101336 g002
Preprints 101336 g003
Figure 3. The data process flowchart of the UEEWS.
Figure 3. The data process flowchart of the UEEWS.
Preprints 101336 g003
Preprints 101336 g004
Figure 4. The decision-making flowchart of the UEEWS.
Figure 4. The decision-making flowchart of the UEEWS.
Preprints 101336 g004
Preprints 101336 g005
Figure 5. Flowchart depicting the modules of the UEEWS siren.
Figure 5. Flowchart depicting the modules of the UEEWS siren.
Preprints 101336 g005
Preprints 101336 g006
Figure 6. The schematic diagram for the sirens.
Figure 6. The schematic diagram for the sirens.
Preprints 101336 g006
Preprints 101336 g007
Figure 7. Placement of sirens in Uttarakhand.
Figure 7. Placement of sirens in Uttarakhand.
Preprints 101336 g007
Preprints 101336 g008
Figure 8. The icon and QR codes for the Uttarakhand Earthquake Alert App, along with the few pages of the installed and registered mobile application, are displayed.
Figure 8. The icon and QR codes for the Uttarakhand Earthquake Alert App, along with the few pages of the installed and registered mobile application, are displayed.
Preprints 101336 g008
Preprints 101336 g009
Figure 9. The diagram illustrates the data-recording time (Td), data-processing time (Tpr), event-reporting time (Tr), target-area lead time (Tw), and shear-wave travel time (Ts) during the Tehri Garhwal earthquake on November 6th, 2022.
Figure 9. The diagram illustrates the data-recording time (Td), data-processing time (Tpr), event-reporting time (Tr), target-area lead time (Tw), and shear-wave travel time (Ts) during the Tehri Garhwal earthquake on November 6th, 2022.
Preprints 101336 g009
Preprints 101336 g010aPreprints 101336 g010bPreprints 101336 g010c
Figure 10. Estimated lead time for cities during the Tehri Garhwal earthquake on November 6th, 2022.
Figure 10. Estimated lead time for cities during the Tehri Garhwal earthquake on November 6th, 2022.
Preprints 101336 g010aPreprints 101336 g010bPreprints 101336 g010c
Preprints 101336 g011
Figure 11. The screenshot of the notification received on the mobile app by a user.
Figure 11. The screenshot of the notification received on the mobile app by a user.
Preprints 101336 g011
Preprints 101336 g012
Figure 12. The developed intensity map during the Tehri Garhwal earthquake on November 6th, 2022.
Figure 12. The developed intensity map during the Tehri Garhwal earthquake on November 6th, 2022.
Preprints 101336 g012
Preprints 101336 g013
Figure 13. The illustration displays the positions of the triggered sensors along with the epicenter of the earthquake that occurred on February 8th, 2020, in Pithoragarh.
Figure 13. The illustration displays the positions of the triggered sensors along with the epicenter of the earthquake that occurred on February 8th, 2020, in Pithoragarh.
Preprints 101336 g013
Preprints 101336 g014
Figure 14. The vertical component accelerograms from various stations during the Pithoragarh earthquake on February 8th, 2020.
Figure 14. The vertical component accelerograms from various stations during the Pithoragarh earthquake on February 8th, 2020.
Preprints 101336 g014
Preprints 101336 g015
Figure 15. Comparison between earthquake information, including (a) epicenters, (b) depths, and (c) response times estimated by the UEEWS server and NCS published on its website. In (c), the response time is estimated based on the first reports. The dashed line in (c) represents the average response time of 13.1 seconds, excluding the maximum response time of one report, which was 22.38 seconds.
Figure 15. Comparison between earthquake information, including (a) epicenters, (b) depths, and (c) response times estimated by the UEEWS server and NCS published on its website. In (c), the response time is estimated based on the first reports. The dashed line in (c) represents the average response time of 13.1 seconds, excluding the maximum response time of one report, which was 22.38 seconds.
Preprints 101336 g015
Preprints 101336 g016
Figure 16. Comparison of the earthquakes’ magnitude estimated by (a) the UEEW system in real-time and NCS, and (b) re-running recorded data in offline mode and NCS. The filled circles indicate the estimated magnitude in the final report, and the open circles depict the estimated magnitude in the first report.
Figure 16. Comparison of the earthquakes’ magnitude estimated by (a) the UEEW system in real-time and NCS, and (b) re-running recorded data in offline mode and NCS. The filled circles indicate the estimated magnitude in the final report, and the open circles depict the estimated magnitude in the first report.
Preprints 101336 g016
Table 1. List of earthquakes for which the central server of the UEEWS generated reports.
Table 1. List of earthquakes for which the central server of the UEEWS generated reports.
Event
No. * 		dd/mm/yyyy
 Reporting Time (UTC) Origin
Time (UTC)		 Location
(lat, long)		 Depth
(km)		 Magnitude
(Mpd)
1 29/11/2015 02:47:51.49 02:47:37.4 30.4863,79.3448 10 2.7
2 06/12/2017 15:19:53.19 15:19:41.77 30.5194,79.0776 10 3.23
2 06/12/2017 15:19:53.29 15:19:41.35 30.5418,79.0876 10 3.25
2 06/12/2017 15:19:53.29 15:19:41.35 30.5418,79.0876 10 3.25
2 06/12/2017 15:19:56.19 15:19:41.29 30.548,79.1144 10 3.29
2 06/12/2017 15:19:57.20 15:19:45.24 30.3236,79.2647 10 2.98
2 06/12/2017 15:19:58.20 15:19:35.24 30.8739,79.2841 10 3.7
2 06/12/2017 15:19:58.20 15:19:42.07 30.5123,79.0864 10 3.22
2 06/12/2017 15:19:58.30 15:19:44.92 30.3556,79.1095 40 3.43
3 17/05/2019 19:38:49.14 19:38:32.36 30.8397,78.9278 20 3.68
4 08/02/2020 01:01:58.29 01:01:47.00 29.9462,79.7177 10 2.75
4 08/02/2020 01:02:05.68 01:01:46.67 29.9233,79.731 10 2.81
4 08/02/2020 01:02:16.65 01:01:46.62 29.9634,79.7324 10 2.75
4 08/02/2020 01:02:24.66 01:01:47.73 29.8904,79.704 10 3.26
4 08/02/2020 01:02:29.67 01:01:46.60 29.9521,79.7446 10 2.82
4 08/02/2020 01:02:38.65 01:01:46.60 29.96,79.7581 10 2.83
4 08/02/2020 01:02:48.63 01:01:48.61 29.8858,79.7914 10 3.23
4 08/02/2020 01:02:55.65 01:01:48.83 29.9737,79.6174 10 3.13
4 08/02/2020 01:03:03.37 01:01:46.90 30.0308,79.7639 10 3
5 23/05/2021 19:02:24.34 19:02:1.96 30.8563,79.4656 40 5.81
5 23/05/2021 19:02:30.16 19:02:2.21 30.5294,78.8786 10 5.04
5 23/05/2021 19:02:33.17 19:02:18.65 30.0403,79.5388 10 4.37
5 23/05/2021 19:02:35.22 19:02:12.29 30.5087,78.5582 50 5.19
6 28/06/2021 06:48:23.12 06:48:7.56 29.8284,79.7013 30 3.95
6 28/06/2021 06:48:33.25 06:48:12.27 30.0456,79.9528 10 3.97
6 28/06/2021 06:48:43.30 06:48:12.26 30.0627,79.938 10 4.28
7 11/09/2021 00:28:42.15 00:28:32.88 30.418,79.1635 10 3.85
7 11/09/2021 00:28:45.20 00:28:33.18 30.4073,79.1369 10 3.87
7 11/09/2021 00:28:50.73 00:28:33.92 30.3856,79.1033 10 3.84
7 11/09/2021 00:28:54.30 00:28:34.08 30.3915,79.0967 10 3.96
7 11/09/2021 00:28:58.80 00:28:33.81 30.372,79.1132 10 3.93
7 11/09/2021 00:29:03.55 00:28:34.11 30.3562,79.0924 10 3.86
7 11/09/2021 00:29:07.30 00:28:33.11 30.3935,79.1481 10 4.16
8 04/12/2021 20:33:00.19 20:32:46.32 30.6556,78.8006 20 4.02
8 04/12/2021 20:33:01.20 20:32:47.12 30.6612,78.7411 20 3.92
8 04/12/2021 20:33:06.63 20:32:49.33 30.6377,78.6378 10 3.53
9 29/12/2021 19:08:29.14 19:08:19.59 29.8527,80.4285 10 2.77
9 29/12/2021 19:08:30.14 19:08:19.59 29.8527,80.4285 10 2.77
9 29/12/2021 19:08:31.14 19:08:19.35 29.875,80.4245 10 2.98
9 29/12/2021 19:08:36.32 19:08:19.53 29.8694,80.4184 10 3.04
9 29/12/2021 19:08:45.13 19:08:19.47 29.8766,80.412 10 3.06
10 24/01/2022 19:39:11.18 19:38:59.13 29.9247,80.2875 20 3.91
10 24/01/2022 19:39:12.15 19:38:59.79 29.8952,80.3093 20 3.63
10 24/01/2022 19:39:17.16 19:38:59.90 29.9196,80.3407 10 3.41
10 24/01/2022 19:39:25.04 19:38:59.98 29.918,80.3445 10 3.72
10 24/01/2022 19:39:29.56 19:39:1.76 29.7706,80.424 10 3.2
10 24/01/2022 19:39:33.07 19:39:1.95 29.8117,80.3844 10 3.19
10 24/01/2022 19:39:38.07 19:39:1.74 29.802,80.3832 10 3.44
11 11/02/2022 23:34:06.22 23:33:49.02 30.6858,78.7893 40 5.36
11 11/02/2022 23:34:11.33 23:33:45.38 30.3062,78.804 40 4.61
12 09/04/2022 11:22:35.16 11:22:35.16 30.928,78.2043 10 3.97
12 09/04/2022 11:22:35.16 11:22:35.16 30.928,78.2043 10 3.97
12 09/04/2022 11:22:24.76 11:22:24.76 30.926,77.8187 40 5.31
13 11/05/2022 04:33:18.20 04:33:6.72 29.905,80.3747 10 3.81
13 11/05/2022 04:33:18.20 04:33:7.22 29.9052,80.3738 10 3.97
13 11/05/2022 04:33:18.23 04:33:6.62 29.9105,80.3847 10 3.87
13 11/05/2022 04:33:22.99 04:33:7.47 29.904,80.378 10 3.98
13 11/05/2022 04:33:26.53 04:33:6.86 29.9018,80.3744 10 3.97
14 06/11/2022 03:03:15.19 03:03:2.89 30.7034,78.5735 10 3.97
14 06/11/2022 03:03:15.20 03:03:2.91 30.7022,78.5715 10 4.06
14 06/11/2022 03:03:15.20 03:03:2.94 30.7035,78.5717 10 4.07
14 06/11/2022 03:03:20.12 03:03:2.91 30.704,78.5739 10 4.04
14 06/11/2022 03:03:23.07 03:03:4.49 30.68,78.4674 10 3.95
14 06/11/2022 03:03:25.98 03:03:3.65 30.6839,78.526 10 4.04
15 08/11/2022 20:27:55.13 20:27:37.05 29.4852,80.4608 30 4.96
15 08/11/2022 20:27:56.14 20:27:36.84 29.6299,80.5183 20 4.75
15 08/11/2022 20:27:57.14 20:27:44.87 29.5721,79.8488 10 3.74
15 08/11/2022 20:28:01.68 20:27:40.50 29.5372,80.1791 40 4.62
15 08/11/2022 20:28:04.58 20:27:46.66 29.5067,79.7675 20 3.76
15 08/11/2022 20:28:04.58 20:27:46.11 29.5403,79.8131 20 4.08
15 08/11/2022 20:28:04.58 20:27:46.59 29.5749,79.7956 20 4.2
15 08/11/2022 20:28:07.43 20:27:46.27 29.5368,79.8036 20 4.04
15 08/11/2022 20:28:10.29 20:27:46.39 29.502,79.7674 20 4.13
15 08/11/2022 20:28:15.16 20:27:53.34 29.8195,79.3817 20 3.94
15 08/11/2022 20:28:28.18 20:28:12.62 29.564,79.4362 40 5.21
15 08/11/2022 20:28:28.18 20:28:17.49 29.7588,79.2381 20 4.47
15 08/11/2022 20:28:28.18 20:28:13.56 29.6138,79.4733 10 4.48
15 08/11/2022 20:28:31.17 20:28:14.67 29.8597,79.5053 20 4.78
15 08/11/2022 20:28:33.19 20:28:14.31 29.7838,79.4785 20 5.01
16 12/11/2022 14:27:41.34 14:27:18.33 29.6791,80.5748 10 4.76
16 12/11/2022 14:27:43.14 14:27:18.63 29.7032,80.5524 10 5.07
16 12/11/2022 14:28:11.20 14:27:47.20 29.6864,80.2348 80 5.94
16 12/11/2022 14:28:12.10 14:27:57.58 29.8083,79.5232 10 4.47
16 12/11/2022 14:28:12.10 14:27:57.81 29.7662,79.414 20 4.54
16 12/11/2022 14:28:16.73 14:27:55.67 29.8034,79.6264 20 4.85
16 12/11/2022 14:28:22.18 14:27:57.43 29.7977,79.7098 10 5.31
17 24/01/2023 08:59:11.12 08:58:44.19 29.6906,81.3695 60 5.79
17 24/01/2023 08:59:12.13 08:58:30.25 29.395,82.2557 20 6.3
17 24/01/2023 08:59:12.23 08:58:53.05 29.6871,80.4168 20 4.49
17 24/01/2023 08:59:17.14 08:58:43.25 29.5046,81.1573 30 5.55
17 24/01/2023 08:59:47.46 08:59:26.27 29.6626,79.8292 10 4.66
17 24/01/2023 08:59:47.46 08:59:24.80 29.6885,79.9168 20 5.32
17 24/01/2023 08:59:49.17 08:59:29.67 29.6095,79.6486 10 4.58
18 03/10/2023 09:21:34.16 09:21:2.26 29.5995,81.9826 70 6.87
18 03/10/2023 09:21:34.19 09:21:2.26 29.5995,81.9826 70 6.87
18 03/10/2023 09:21:34.20 09:21:21.30 29.6806,80.1117 50 5.1
19 03/11/2023 18:04:01.15 18:03:47.16 29.5394,80.2398 50 5.77
19 03/11/2023 18:04:09.18 18:03:44.01 29.2213,80.7229 20 5.89
Note - Multiple times, the same serial number indicates that the UEEWS generated more than one report for that earthquake.
Table 2. Information about the earthquakes is from the National Center for Seismology (NCS), Ministry of Earth Sciences, Government of India, which determines and reports source parameters of the earthquakes in this region.
Table 2. Information about the earthquakes is from the National Center for Seismology (NCS), Ministry of Earth Sciences, Government of India, which determines and reports source parameters of the earthquakes in this region.
Event No.
 dd/mm/yyyy
 Origin time
(UTC)		 Location
(lat, long)		 Depth
(km)		 Magnitude
(Mw)		 Region
1 29/11/2015 02:47:38 30.6,79.6 10 4 Chamoli
2 06/12/2017 15:19:54 30.4,79.1 30 5.5 Rudraprayag
3 17/05/2019 19:38:44 30.5,79.3 10 3.8 Chamoli
4 08/02/2020 01:01:49 30.3,79.86 48.2 4.7 Pithoragarh
5 23/05/2021 19:01:45 30.9,79.44 22 4.3 Chamoli
6 28/06/2021 06:48:05 30.08,80.26 10 3.7 Pithoragarh
7 11/09/2021 00:28:33 30.37,79.13 5 4.7 Chamoli
8 04/12/2021 20:32:47 30.61,78.82 10 3.8 Tehri
9 29/12/2021 19:08:21 29.75,80.33 10 4.1 Pithoragarh
10 24/01/2022 19:39:00 29.79,80.35 10 4.3 Pithoragarh
11 11/02/2022 23:33:34 30.72,78.85 28 4.1 Tehri
12 09/04/2022 11:22:36 30.92,78.21 10 4.1 Uttarkashi
13 11/05/2022 04:33:09 29.73,80.34 5 4.6 Pithoragarh
14 06/11/2022 3:03:03 30.67,78.6 5 4.5 Tehri Garhwal
15 08/11/2022 20:27:24 29.24,81.06 10 5.8 Dipayal, Nepal
16 12/11/2022 14:27:06 29.28,81.2 10 5.4 Dipayal, Nepal
17 24/01/2023 8:58:31 29.41,81.68 10 5.8 Nepal
18
19		 03/10/2023
03/11/2023		 09:21:04
18:02:54		 29.39,81.23
28.84,82.19		 5
10		 6.2
6.4		 Nepal
Nepal
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated