Preprint

Article

Comparative Analysis of Estimated Small Wind Energy Using Different Probability Distributions in a Desert City in Northwestern Mexico

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

Submitted:

15 March 2024

Posted:

15 March 2024

You are already at the latest version

Alerts

Abstract

In this paper, four probability functions are compared with the purpose of establishing a methodology to improve the accuracy of the estimated wind energy in a desert city in northwestern Mexico. For the statistical modeling, 3 time series of wind speed data were used, corresponding to the years 2017, 2018, and 2019, recorded with a sonic anemometer at a sampling frequency of 10 Hz. From these, the analysis is performed with different stationarity periods (5, 30, 60, and 600 seconds). The estimation of the parameters characterizing the probability density functions was performed using different methods; the statistical models were evaluated by the coefficient of determination and the Nash-Sutcliffe efficiency coefficient, while their accuracy by the measured quadratic error, the mean square error, the mean absolute error, and the mean absolute percentage error. It was found that Weibull with the energy pattern factor method and Gamma using the method of moments were the probability density functions that best describe the statistical behavior of the wind speed and, therefore, better estimate the energy generated, so it is concluded that the proposed methodology will allow having greater confidence, both in the estimation of the wind speed and in the small wind energy available for its use.

Keywords:

Subject: Engineering - Energy and Fuel Technology

1. Introduction

The global climate emergency has caused great interest in the energy transition to try to mitigate CO2 emissions caused by the generation of energy from conventional sources. The penetration of renewable energies plays a significant role in this transition. To achieve this, it is necessary to give certainty to the estimation of energy from these sources.

During 2020 there was a reduction in global electricity demand, while in 2021 global electricity demand grew by 6%, one of the largest annual growth rates since the monetary crisis of 2010 [1]. Electricity consumption is expected to average 2.7% annual growth during the period 2022-2024 [1]. With the potential future demand, the high energy costs of conventional energy resources and their environmental impact, the interest in using alternative energy sources has increased more than before, arising the need to evaluate the technical characteristics of these sources [2]. In the case of wind energy, the estimation is made from a methodology based on medium-term average values (of the order of minutes) [3] without considering short-term variability (of the order of seconds), causing an underestimation [4].

Compared to fossil fuels, renewable energy offers some advantages, such as the relative availability of distributed renewable resources, the access and modularity of its technologies and the potential for each user to generate their own energy [5]. In this sense, Wind Energy (WE) is one of the most widely used renewable sources and has contributed to the global electricity system with an installed capacity of 840 GW until 2021 [6]. In the case of small wind, or low-power wind energy, it is beginning to contribute to the electricity system and is expected to increase the use of its technology by contributing with photovoltaic systems to distributed generation. As of the end of 2019, mini-wind power had an installed capacity of 1,295 GW worldwide [6]. Small-wind installations have their own characteristics such as: capacity to provide energy in a distributed manner, operation with moderate winds, use of small sites, integration in urban, semi-urban, industrial and agricultural environments, especially associated with the generation of energy close to the points of consumption [7].

Resource assessment is an important element in determining wind energy penetration [8,9]. To achieve this, it is imperative that the probability density function faithfully describes the statistical behavior of the wind. In a generalized way, the Weibull probability density function has been used for this purpose, but different wind regimes could be better represented by other functions. According to Chang [10] and Cheng [11], the wind speed distribution for a particular location determines the available wind energy and the performance of an energy conversion system. Therefore, determining the function that best represents the wind regime at a location will contribute to a better estimation. In this regard, several studies [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] have used different probability density functions, such as Weibull, Gamma, Raleigh, Beta, log-normal, and some combinations with them. On the other hand, Wais [12,13] mentions that the two-parameter Weibull distribution is recognized as an appropriate model and the most widely used in the wind industry, but also concludes that the two-parameter Weibull distribution is not always sufficient to specify the wind speed distribution and evaluate the available wind energy. In addition, it is observed that the three-parameter Weibull distribution can offer the advantage for some wind data analyses and fits certain data better than the typical Weibull distribution. In the literature, it is also mentioned that combined functions tend to have better statistical behavior compared to methods using a single function [17]. These combined distributions can be more efficient than single-function distributions for some wind regimes, although despite the advantages, the main drawbacks of combined distributions are their complexity and the computational time required in estimating the associated parameters [22]. In this sense, it is especially important to select the probability density function(s) appropriate to the data measured in the study area to obtain reliable energy estimation [8,10] and Cheng [11] mentions the importance of performing the analysis considering high sample frequency wind data, i.e., considering the short-term variability of the wind.

On the other hand, the probability density functions are characterized by the statistical parameters of shape and scale, these can be obtained by different numerical methods, among the most used are the Maximum Likelihood Method (ML), Method of Moments (MM) Justus Empirical Method (EJ), Lysen Empirical Method (EL), Energy Pattern Method (EP), Graphical Method (GP), Standard Deviation Method (SD) and Modified Maximum Likelihood Method (MLM) [30]. Some researchers [30,31,32,33,34,35,36,37,38,39] use the mentioned methods for comparisons. Tizgui et al. [32] have found with monthly data that EJ and MLM have better estimation for the Weibull probability density function, while Bilir et al. [19] consider the EJ method to be more accurate for annual estimation with hourly data and the Weibull probability density function.

To evaluate the wind resource, the International Standard IEC-61-400-12-1 [3] establishes the estimate of the wind potential must be made from ten-minute wind speed data, obtained by averaging every 10 minutes the wind velocity recorded with a specific sampling frequency (e.g., 1 Hz). The time of averaging or stationarity period, defined as the time interval in which the wind velocity can be considered statistically constant, plays an important role in the wind potential estimate. As the stationarity period increases, it causes a decrease in the wind variability recorded in the time series, which causes a diminish in the energy estimate. Rodriguez-Hernandez et al. [8] estimated an energy difference of 17% between stationarity periods of 1 and 10 minutes, while Arredondo et al. [4] found that the available energy density using 600 seconds (10 minutes) as the stationarity period underestimates by 1%, 8%, 10%, 13.7%, 19.4% and 22.7% concerning stationarity periods of 300, 60, 30, 5, 1 and 0.1 seconds, respectively.

Consequently, improving the current methodology for estimating wind energy considering the variability of the resource, the probability density function and the appropriate method, would help to have greater certainty of the energy that can be generated, thus contributing to the penetration of wind energy in the residential and commercial sectors. In this sense, the objective of this research focuses on determining the methodology that best estimates the energy that can be obtained from a small wind turbine. To achieve the above, this paper is structured as follows; Section 2 describes the data collection and analysis, the determination of the probability density functions, the calculations for energy estimation and the statistical tests to validate such estimates. Section 3 presents the results obtained and, finally, Section 4 presents the conclusions of the research.

2. Methodology

The data used in this study were measured during 2017, 2018 and 2019 with a Campbell Scientific CSAT3 sonic anemometer, which records the orthogonal components

u_{x}

u_{y}

and

u_{z}

, of the wind speed, so the magnitude of the wind speed is obtained with the equation.

v = \sqrt{{u_{x}}^{2} + {u_{y}}^{2} + {u_{z}}^{2}}

(1)

The anemometer has the capacity to record with sampling frequencies from 1 to 100 Hz, with measurement errors of ±8.0 cm/s and ±4.0 cm/s in the horizontal and vertical components, respectively. The instrument is located 20 meters above ground level at the UABC Engineering Institute in Mexicali B.C., geographically located at coordinates

32 ° 37^{'} 52.32 ″ N

and

115 ° 26^{'} 40.48 ″ W

. Mexicali’s climate is classified as dry desert (BW), with extreme summer (Average maximum temperature between 41°C and 43°C) and winter (Average maximum temperature between 11°C and 13°C) temperatures. The average annual temperature is between 21°C to 23°C [38]. In 2022, the population of Mexicali was 1,049,792 residents [41] and electricity consumption of 4736.29 GWh until 2016 [42]. A sampling frequency of 10 Hz was used in this study, thus obtaining 864,000 daily data equivalents to more than

3 \times 10^{8}

data per year. From the original time series, time series of average values were obtained every 5 seconds, 30 seconds, 60 seconds and 600 seconds, which would be equivalent to recording the wind with those average sampling times.

2.1. Probability Density Functions and Methods for Statistical Parameter Estimation

Four different probability density functions, Weibull, Gamma, Rayleigh and a combination of the previous three, were used to describe the statistical behavior of the data. The shape and scale parameters of each function were determined from the methods explained below.

2.1.1. Weibull Probability Density Function

The Weibull likelihood function is used to determine the characterization of the wind resource, because it reliably describes the wind behavior in different regions [27].

f (v) = \frac{α}{β} {(\frac{v}{β})}^{α - 1} e^{- {(\frac{v}{α})}^{α}}

(2)

The two parameters, the shape

(α)

and the scale

(β)

, were determined by the empirical methods of Justus, Lysen, and the energy pattern

2.1.1.1. Empirical Justus Method (EJ)

In this method the parameters

α

β

are calculated from the following expressions

α = {(\frac{σ}{\bar{v}})}^{- 1.086}

(3)

β = \frac{\bar{v}}{Γ (1 + \frac{1}{α})}

(4)

where

\bar{v}

the mean wind speed and

σ

the standard deviation, while

Γ

is the Gamma function [43].

2.1.1.2. Empirical Lysen Method (EL)

In this method, the parameter

α

is calculated by means of Equation 3, while the parameter

β

is calculated by the following expression [44]

β = \bar{v} {(0.568 + \frac{0.433}{α})}^{\frac{- 1}{α}}

(5)

2.1.1.3. Energy Pattern Factor Method ( $E_{p f}$ )

In this method it is necessary to determine the energy pattern factor

(E_{p f})

on which the shape factor depends, while for the scale factor equation 4 is used. The factor

E_{p f}

is the ratio between the total power available in the wind and the power corresponding to the cube of the average wind speed [45,46].

E_{p f} = \frac{\bar{v^{3}}}{{\bar{v}}^{3}}

(6)

α = 1 + \frac{3.69}{{(E_{p f})}^{2}}

(7)

2.1.2. Rayleigh Probability Density Function

The Rayleigh probability density function is a special form of the Weibull distribution in which the shape parameter is always equal to 2 and only the dispersion parameter (standard deviation) is used [23].

f (v) = \frac{v}{σ^{2}} e^{- \frac{v^{2}}{2 σ^{2}}}

(8)

2.1.3. Probability density function Gamma

The shape and scale parameters of the Gamma pdf are obtained using the methods of moments and maximum likelihood [47]

f (v) = \frac{{(\frac{v}{β})}^{α - 1} e^{\frac{- v}{β}}}{β^{α} Γ (α)}

(9)

2.1.3.1. Method of Moments (MM)

In the method of moments, the parameters are obtained as follows [47].

α = \frac{{\bar{v}}^{2}}{σ^{2}}

(10)

β = \frac{σ^{2}}{\bar{v}}

(11)

2.1.3.2. Maximum Likelihood Method (ML)

In this method, the parameters are obtained as follows

α = \frac{1 + \sqrt{1 + \frac{4 D}{3}}}{4 D}

(12)

β = \frac{\bar{v}}{α}

(13)

where D is given by [47]

D = l n (\bar{v}) - \frac{1}{n} \sum_{i = 1}^{n} l n (v_{i})

(14)

2.1.4. pdf Mix

The pdf Mix is developed with the objective of evaluating a function that best describes the statistical behavior of the wind in each speed interval (bin) and to determine if it causes an improvement in the estimation of wind energy. To achieve the above, the distribution is selected, with its corresponding method, that best fits in each class.

2.2. Energy Estimation with Pdf

The annual energy estimate for each year (2017, 2018 and 2019) and each time series (0.1, 5, 30, 60 and 600 seconds) is calculated using the pdfs and power curve of a wind turbine. First, the probability that the wind speed is in the i-th interval [a, b] is calculated, using the equation

p (a < v_{i} < b) = F (v) = \int_{a}^{b} f (v) d v = F (b) - F (a)

(15)

where, f(v) is the pdf used while a and b are the lower and upper bounds, respectively, of the i-th class of the velocity frequency histogram, and the function F (v) is the cumulative probability function given by eq.

F (v) = \int_{0}^{v} f (x) d x

(16)

The interval probability found represents the percentage of the time, of the complete series, in which wind speeds

v_{i}

occurred. This percentage is converted to hours

(Δ t

) by multiplying it by the total number of hours in the time series.

As a second step, the power curve of the wind turbine is used to determine the power that, according to the manufacturer, the wind turbine delivers when the wind is flowing at speed

v_{i}

. Then the two previous values are multiplied, duration times power, to obtain the energy that the ABP would be delivering when the wind is flowing at wind speed

v_{i}

. This procedure is repeated for each of the n intervals or classes. Finally, the estimation of the total energy generated per year,

E_{w}

, is obtained by summing the estimated energies in each speed interval as indicated in the equation.

E_{w} = \sum_{i = 1}^{n} P (v_{i}) Δ t

(17)

where, P

(v_{i})

is the power corresponding to the mean interval velocity.

2.2.1. Comparison betweem Estimated and Generated Energy

For the energy comparison, a small 200 W small wind turbine was used, with a start-up speed of 1 m/s, a survival speed of 50 m/s and the power curve provided by the manufacturer in the data sheet. This wind turbine is ideal for operating at a height of 20 m with wind speed starting at 1 m/s.

The generated energy is obtained from the power curve, considering the instantaneous power corresponding to each of the m values of wind speed in each series, by means of the following equation

E_{r} = \sum_{i = 1}^{m} P (v_{i}) Δ t_{e}

(18)

where,

Δ t_{e}

is the time corresponding to the stationarity period, P

(v_{i})

is the instantaneous power delivered by the wind turbine when the wind has the speed

v_{i}

Energy comparisons were performed for each measurement year and each stationarity period, to observe which pdf give us a more accurate estimation compared with the energy produced by a wind turbine. The estimation error percentage is obtained from the expression [32]

% E = \frac{E_{r} - E_{w}}{E_{r}} * 100 %

(19)

2.3. Statistical Tests

The performance of the probabilistic models obtained was evaluated based on the statistical tests described below, where

y_{i}

is the relative frequency of the observed velocity values,

\bar{y}

is the mean relative frequency, and

x_{i}

is the expected frequency calculated with the theoretical distributions.

2.3.1. Coefficient of Determination $(R^{2})$

The coefficient of determination is a measure of the relationship between a predicted probability density function and the measured data. Mathematically it is obtained as follows [48]

R^{2} = 1 - [\frac{\sum_{i = 1}^{n} {(y_{i} - x_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}]

(20)

its maximum value is 1, such that the closer it is to 1 the better its fit.

2.3.2. Chi-Square ( $X^{2}$ )

The chi-square test is determined with the association between two variables, showing the association of the observed value with the estimated value. The closer the result is to 0, the better accuracy is considered [32]

X^{2} = \sum_{i = 1}^{n} \frac{{(y_{i} - x_{i})}^{2}}{x_{i}}

(21)

2.3.3. Nash-Sutcliffe Efficiency Coefficient (NSEC)

The efficiency coefficient is another way to obtain the accuracy of a prediction model, it is performed between the values of the probability density function and the relative frequency of the measured values. Like the

R^{2}

the closer to 1 the more accurate the value is considered [49]

N S E C = 1 - \frac{\sum_{i = 1}^{n} {(x_{i} - \bar{y})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}

(22)

2.3.4. Root Means Square Error (RMSE)

Root means square error is an error that estimates the accuracy of the method by comparing the difference between the estimated values and the actual values. As the value approaches zero the method is considered more accurate [36].

R M S E = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(x_{i} - y_{i})}^{2}}

(23)

2.3.5. Mean Square Error (MSE)

Mean square error is a method that calculates the difference of the mean square error between the estimated values and the true value. Like RMSE the value that is close to zero is the certain result [36]

M S E = \frac{1}{n} \sum_{i = 1}^{n} {(x_{i} - y_{i})}^{2}

(24)

2.3.6. Mean Absolute Error (MAE)

The mean absolute error is an absolute test of the difference between two variables. It is the average of the absolute errors between the frequency of each pdf and the relative frequency of the measured data. The closer to zero is considered better result [36].

M A E = \frac{1}{n} \sum_{i = 1}^{n} | {(x_{i} - y_{i})}^{2} |

(25)

2.3.7. Mean Absolute Percentage Error (MAPE)

Mean absolute percent error is a relative measure that indicates the percentage error between the pdf and the relative frequency of the measured data. Like MAE, the MAPE value should be the lowest for best accuracy [50]

M A P E = \frac{1}{100} \sum_{i = 1}^{n} | \frac{x_{i} - y_{i}}{y_{i}} |

(26)

3. Results and Discussion

The results of the behavior of the statistical parameters, statistical tests and energy comparison are described below.

3.1. Results of Statistical Parameters

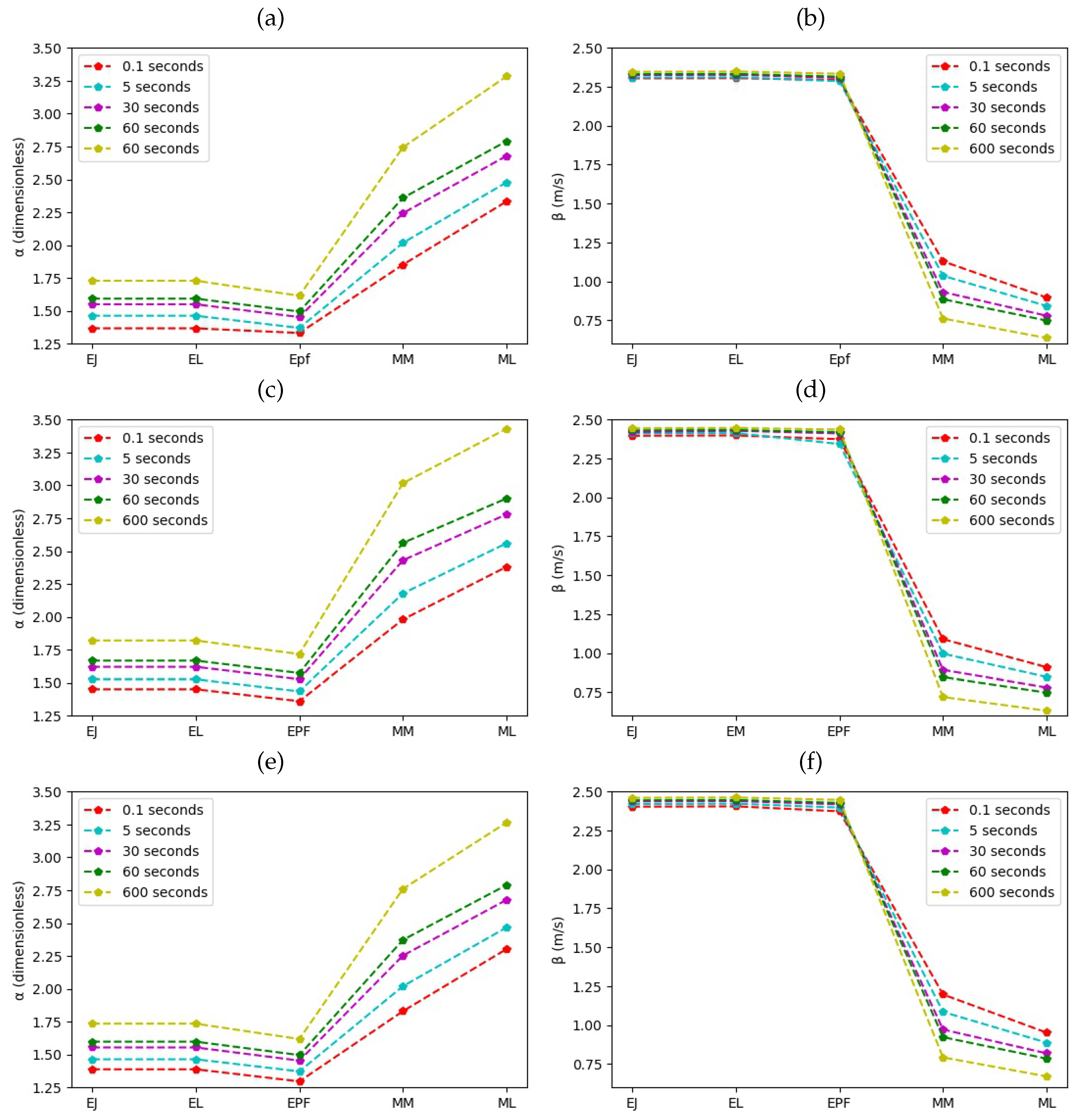
Table 1 describes the annual data of the statistical parameters in the respective periods of stationarity for each year analyzed; it can be observed that the average wind speeds are 2.09 m/s, 2.17 m/s and 2.19 m/s and that the standard deviation decreases as the period of stationarity increases due to the loss of variability.

Table 2 presents the shape

(α)

and scale

(β)

parameters defining the pdf for each year. The EJ, EL and

E_{p f}

methods were used for the Weibull pdf. For the Rayleigh pdf, the SD method was used. For the Gamma pdf, the MM and ML methods were used.

Figure 1 shows the behavior of the shape and scale parameters for the period analyzed, using each of the methods mentioned above. It can be observed that the behavior is similar for each parameter during the three years. It is also observed the importance of the variability considered in each stationarity period, as was reported in other studies [4,8], because both parameters

(α

β)

present different values in each of these periods. This will result in a different function even using the same method, additional to the analysis performed by other authors using a single function with different methods [10,27]. The consequence of this result is that the estimated energy in the different stationarity periods varies even when using the same pdf with a specific method, as shown in the following subsection.

Another aspect to note is that of the 5 methods two are very sensitive to short term variability, MM and ML, so using these methods to determine the parameters of the functions would result in a larger energy estimation error.

Figure 1. Shape and scale parameters. (a) Shape parameters for 2017. (b) Scale parameters for 2017. (c) Shape parameters for 2018. (d) Scale parameters for 2018.(e) Shape parameters for 2019. (f) Scale parameters for 2019.

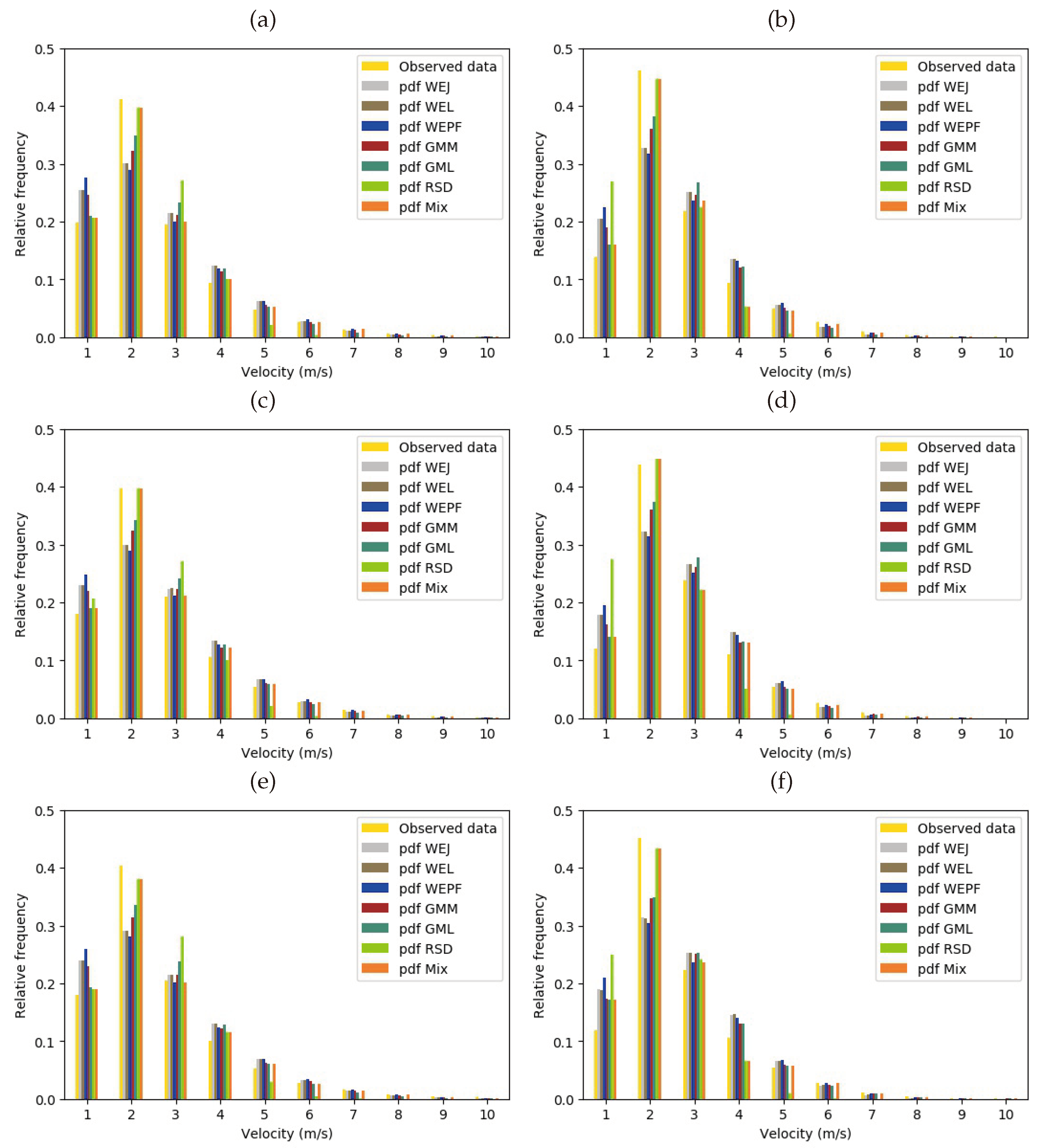
With respect to the pdf mix, the distributions that best fit the measured data were selected in its construction. For example, in general, in the first class (0-1 m/s) the value of the Gamma function method of moments was taken, in the second class (1-2 m/s) the value of the Rayleigh function, in the third class (3-4 m/s) the Weibull distribution with the energy pattern method, and for the rest of the classes, the best approximation was obtained using the Gamma function with its two methods, MM and ML.

The comparison shown in Figure 2 is presented only for the stationarity periods of 5 and 600 seconds for the three years of measurement. It can be observed that the behavior is similar in both stationarity periods, as well as in the different years of data. This behavior was also observed in the other periods.

3.2. Statistical Test Results

The results of the statistical tests were grouped by period of stationarity, indicating the method and year of the data series. In every test, the fit of each of the distributions is compared, as shown in Tables 3–7. In general, it is observed that the pdf Mix and the pdf GMM present the best fit, as indicated by the values of the different test. This result was expected because the pdf Mix is mostly composed of the pdf GMM. However, the other functions also present a good fit, with differences of the order of thousandths being observed. Because of this, the MAPE test was used to help determine with greater certainty the best fit.

Table 3 presents the results for the stationarity period at 0.1 seconds. It is shown that for each year analyzed the values of the different tests place the pdf Mix and the pdf GMM as the best fit. In the case of the rest of the functions, they present satisfactory results, but, as mentioned above, the MAPE test gives us the guideline not to select them.

Table 4 shows the results for the stationarity period of 5 seconds. Similar behavior to that presented in Table 3 is observed. The GMM and Mix functions provide the best fit.

Table 5, Table 6 and Table 7, which correspond to stationarity periods of 30, 60 and 600 seconds, respectively, present results like those observed in Table 3 and Table 4.

3.3. Estimated vs Generated Energy

Table 8 shows the amount of generated energy obtained from the power curve of the Aelos 200 W wind turbine, as well as the energy estimated by each of the pdfs with their different methods for the three years of study. It is possible to observe the decrease in the estimated energy as the stationarity period increases, because of the decrease in variability. For example, when using the Weibull pdf with the Justus method for the year 2017, differences of 1.9%, 4.3%, 5.4% and 8.26% are presented in the periods of 5, 30, 60 and 600 seconds, respectively, with respect to the period of 0.1 seconds. In the case of the Rayleigh pdf, the decrease ranges from 5.5%, 12.6%, 15.1% and 23.3%, while for the Gamma pdf in either of its two methods, energy differences of 1%, 2.2%, 3.1% and 5.6%, approximately, can be observed. In the case of the pdf Mix function, decreases of 3%, 6.2%, 6.4% and 14.9% can be observed. It is important to note that this decrease does not depend on the methods used but on the short-term loss of variability, indicated by the standard deviation values in Table 1, which results in a lower energy estimate.

Table 9 shows the percentage error between the generated energy and the estimated energy for each pdf, with its respective method, in the different periods of stationarity and for each year of study; the negative sign indicates an estimate greater than the generated energy. The table suggests that, based on percentage errors, the W

E_{p f}

pdf and the GMM pdf generally have the smallest errors, making them more suitable for energy estimation. For example, for the year 2019, the GMM pdf has a percentage error in the energy estimation of 8.53, 10.21, 12.23, 13.11 and 15.36, while the W

E_{p f}

pdf presents a percentage error of 5.95, 8.23, 10.81, 11.51, 14.43, with respect to the generated energy, for each stationarity period. In addition, the pdf Mix could be considered because it has relatively small errors, being 5.73, 9.87, 13.05, 13.97 and 18.31 with respect to the generated energy. In the case of the pdf Rayleigh, it is the distribution with the highest error, so it is not a good option for the estimation of the energy in the study area.

4. Conclusions

In this study, four probability density functions were used to estimate the energy that a small wind turbine installed for domestic use in a desert city in northwest Mexico can generate. The results indicate that the precision of the energy estimates decreases as the stationarity period increases, using the energy calculated from the wind turbine power curve as a reference. It means that, as the period of stationarity increases, the estimated energy decreases due to minimizing the short-term wind variability in the averaging process.

On the other hand, using different numerical methods to calculate shape and scale statistical parameters leads to distinct versions of the probability density function, resulting in differences in the estimated energy. It became more evident when comparing the energy estimates of various periods of stationarity, particularly when the methods of moments (MM) and maximum likelihood (ML) were used, which were found to be the most sensitive to the loss of variability.

In the statistical modeling of the wind data, it is shown that the Weibull distribution using Empirical Lysen or Empirical Justus methods was not the function that best describes the behavior of the wind in the study area. Instead, the W

E_{p f}

, GMM, and Mix pdfs are highlighted as having generally small errors and are likely better choices for energy estimation in the specified study area, showing a better fit, although the Mix function involves a more complex construction process but is still considered a viable option. Thus, when comparing the estimated energy with that calculated from the wind turbine power curve, the W

E_{p f}

, the GMM and Mix functions provided, in general, the best estimates for each period of stationarity in the three years analyzed. The WEJ, WEL and GML functions had slightly larger errors, but they were not significant. During the three years of observation, the RSD function displayed the highest percentage of error in estimating energy. This was true for every period of stationarity, indicating that it is not a suitable density function for wind energy estimates in the study area. The above highlights the importance of selecting a priori the probability density function, and the numerical method to determine the shape and scale parameters, to be used in the feasibility analysis methodology of a small wind energy project.

In this sense, the use of the Weibull probability distribution, established by the International Standard IEC61400-12-1 [3], as a probabilistic model to estimate potential energy production, can lead to unreliable evaluations and economic losses as a result of the underestimation of the resource [51]. The latter, in turn, causes a lower penetration of small wind energy in locations such as the city of Mexicali where electricity consumption is above the national average as a consequence of its intense hot season. Therefore, by increasing the reliability of energy estimates using small wind turbines, the viability of small wind energy projects will have greater certainty, promoting greater penetration of this renewable source, particularly in the residential and commercial sectors.

Author Contributions

Conceptualization, A.A.L-A. and J.A.B-P.; methodology, A.A.L-A., O.R.G-C. and J.A.B-P.; software, J.A.B-P; validation, A.A.L-A., O.R.G-C. and J.A.B-P.; formal analysis, A.A.L-A., O.R.G-C. and J.A.B-P.; investigation, A.A.L-A., O.R.G-C. and J.A.B-P.; resources, O.R.G-C., N.S–S., D.E.F-J. and J.A.B-P.; data curation, J.A.B-P., O.R.G-C., N.S–S. and A.A.L-A.; writing—original draft preparation, J.A.B-P., O.R.G-C., E.V. and A.A.L-A.; writing—review and editing, J.A.B-P., A.A.L-A.,O.R.G-C., E.V., N.S-S. and D.E.F-J.; visualization, A.A.L-A.,O.R.G-C., E.V., N.S-S. and D.E.F-J.; supervision, A.A.L-A., O.R.G-C., E.V., N.S-S. and D.E.F-J.; project administration, A.A.L-A. and O.R.G-C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are not available yet due to research work in process.

Acknowledgments

The authors are grateful to the Engineering Institute of Autonomous University of Baja California for the support given to conduct this project and to the National Council of Science and Technology (CONACYT) for the grant otorged to Juan Alberto Burgos Peñaloza.

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Samples of the compounds ... are available from the authors.

Abbreviations

The following abbreviations are used in this manuscript:

pdf	Probabilty Density Function
WE	Wind Energy
pdf W	Weibull Probability Density Function
EJ	Empirical Justus Method
EL	Empirical Lysen Method
$E_{p f}$	Energy Pattern Factor Method
$E_{w}$	Energy estimation
$E_{r}$	Actual energy
pdf R	Rayleigh Probability Density Function
pdf G	Gamma Probability Density Function
MM	Method of Moments
ML	Maximum likelihood Method
pdf Mix	Mix Probability Density Function
$R^{2}$	Coefficient of Determination
$x^{2}$	Chi-Square
NSEC	Nash-Sutcliffe Efficency Coefficent
RMSE	Root Mean Square Error
MSE	Mean Square Error
MAE	Mean Absolute Error
MAPE	Mean Absolute Percentage Error

References

International Energy Agency. Available online: https://www.iea.org/ (accessed on 22 april 2022).
Boroumandjazi, G.; Saidur, R.; Rismanchi, B.; Mekhilef, S. A review on the relation between the energy and exergy efficiency analysis and the technical characteristic of the renewable energy systems. Renewable and Sustainable Energy Reviews 2008, 16, 3131–3135. [Google Scholar] [CrossRef]
International standard IEC 61400-12-1. 2005. Available online: http://www.iec.ch/.
Arredondo, M.G. Variabilidad a corto plazo de la velocidad de viento y su efecto en la estimación del potencial eólico. Master degree. Instituto de Ingeniería UABC, Mexicali, B.C; México, 02 Octuber 2018.
Burke, M.J.; Stephens, J.C. Political power and renewable energy futures: A critical review. Energy Research and Social Science 2018, 35, 78–93. [Google Scholar] [CrossRef]
World Wind Energy Association. Available online: https://wwindea.org/ (accessed on 24 March 2022).
Aerogeneradores Enair, Minieólica eficiente y evolucionada. Available online: https://www.enair.es/ (accessed on 24 March 2022).
Rodriguez-Hernandez, O.; del Río, J.A.; Jaramillo, O.A. The importance of mean time in power resource assessment for small wind turbine applications. Energy forSustainable Development 2016, 30, 32–38. [Google Scholar] [CrossRef]
Rodriguez-Hernandez, O.; Martinez, M.; Lopez-Villalobos, C.; Garcia, H.; Campos-Amezcua, R. Techno-Economic Feasibility Study of Small Wind Turbines in the Valley of Mexico Metropolitan Area. Energies 2019, 12, 890. [Google Scholar] [CrossRef]
Chang, T.P. Estimation of wind energy potential using different probability density functions. Apleid energy 2011, 88, 1848–1856. [Google Scholar] [CrossRef]
Cheng, K.-S.; Ho, C.-Y.; Teng, J.-H. Wind Characteristics in the Taiwan Strait: A Case Study of the First Offshore Wind Farm in Taiwan. Energies 2020, 13, 6492. [Google Scholar] [CrossRef]
Wais, P. A review of Weibull functions in wind sector. Renewable and Sustainable Energy Reviews. Renewable Energy 2017, 70, 1099–1107. [Google Scholar]
Wais, P. Two and three-parameter Weibull distribution in available wind power analysis. Renewable Energy 2017, 103, 15–29. [Google Scholar] [CrossRef]
Jaramillo, O.A.; Borja, M.A. Wind speed analysis in La Ventosa, Mexico: A bimodal probability distribution case. Renewable Energy 2004, 29, 1613–1630. [Google Scholar] [CrossRef]
Shoaib, M.; Siddiqui, I.; Amir, Y.M.; Rehman, S.U. Evaluation of wind power potential in Baburband (Pakistan) using Weibull distribution function. Renewable and Sustainable Energy Reviews 2017, 70, 1343–1351. [Google Scholar] [CrossRef]
Jung, C.; Schindler, D. Global comparison of the goodness-of-fit of wind speed distributions. Energy Conversion and Management 2017, 133, 216–234. [Google Scholar] [CrossRef]
Jung, C.; Schindler, D.; Laible, J.; Buchholz, A. Introducing a system of wind speed distributions for modeling properties of wind speed regimes around the world. Renewable Energy 2017, 144, 181–192. [Google Scholar] [CrossRef]
Datta, D.; Datta, D. Comparison of Weibull Distribution and Exponentiated Weibull Distribution Based Estimation of Mean and Variance of Wind Data. International Journal of Energy, Information and Communications 2013, 4, 1–12. [Google Scholar]
Bilir, L.; Imir, M.; Devrim, Y.; Albostan, A. Seasonal and yearly wind speeddistribution and wind power density analysis based on Weibull distribution function. International Journal of Hydrogen Energy. 2015, 40, 15301–15310. [Google Scholar] [CrossRef]
Hernandez-Escobedo, Q. Wind energy assessment for small urban communities in the Baja California Peninsula, Mexico. Energies 2016, 9, 805. [Google Scholar] [CrossRef]
Dabbaghiyan, A.; Fazelpour, F.; Abnavi, M.D.; Rosen, M.A. Evaluation of wind energy potential in province of Bushehr, Iran. Renewable and Sustainable Energy Reviews 2016, 55, 455–466. [Google Scholar] [CrossRef]
Mohammadi, K.; Alavi, O.; McGowan, J.G. Use of Birnbaum-Saunders distribution for estimating wind speed and wind power probability distributions: A review. Renewable Energy 2017, 143, 109–122. [Google Scholar] [CrossRef]
Pishgar-Komleh, S.H.; Keyhani, A.; Sefeedpari, P. Wind speed and power density analysis based on Weibull and Rayleigh distributions (a case study: Firouzkooh county of Iran). Renewable and Sustainable Energy Reviews 2015, 42, 313–322. [Google Scholar] [CrossRef]
Ouarda, T.B.M.J.; Charron, C.; Shin, J.Y.; Marpu, P.R.; Al-Mandoos, A.H.; Al-Tamimi, M.H.; Ghedira, H.; Al Hosary, T.N. Probability distributions of wind speed in the UAE. Energy Conversion and Management 2015, 93, 414–434. [Google Scholar] [CrossRef]
Shu, Z.R.; Li, Q.S.; Chan, P.W. Statistical analysis of wind characteristics and wind energy potential in Hong Kong. Energy Conversion and Management 2015, 101, 644–657. [Google Scholar] [CrossRef]
Kantar, Y.M.; Usta, I.; Arik, I.; Yenilmez, I. Wind speed analysis using the Extended Generalized Lindley Distribution. Renewable Energy 2018, 118, 1024–1030. [Google Scholar] [CrossRef]
Wais, P. A review of Weibull functions in wind sector. Renewable and Sustainable Energy Reviews 2017, 70, 1099–1107. [Google Scholar] [CrossRef]
Murthy, K.S.R.; Rahi, O.P. A comprehensive review of wind resource assessment. Renewable and Sustainable Energy Reviews 2017, 72, 1320–1342. [Google Scholar] [CrossRef]
Teimourian, H.; Abubakar, M.; Yildiz, M.; Teimourian, A. A Comparative Study on Wind Energy Assessment Distribution Models: A Case Study on Weibull Distribution. Energies 2022, 15, 5684. [Google Scholar] [CrossRef]
Khan, J.K.; Uddin, Z.; Tanweer, I.S.; Ahmed, F.; Aijaz, A.; Jilani, S.U. Analysis of Wind Speed Distribution and comparison of five numerical methods for Estimating Weibull Parameters at Ormara, Pakistan. EUROPEAN ACADEMIC RESEARCH 2015, II, 14007–14015. [Google Scholar]
Carta, J.A.; Ramírez, P.; Velázquez, S. A review of wind speed probability distributions used in wind energy analysis. Case studies in the Canary Islands. Renewable and Sustainable Energy Reviews 2009, 13, 933–955. [Google Scholar] [CrossRef]
Tizgui, I.; El Guezar, F.; Bouzahir, H.; Benaid, B. Comparison of methods inestimating Weibull parameters for wind energy applications. International Journal of Energy Sector Management. International Journal of Energy Sector Management 2017, 11, 650–663. [Google Scholar] [CrossRef]
Usta, I. An innovative estimation method regarding Weibull parameters for wind energy applications. Energy 2016, 106, 301–314. [Google Scholar] [CrossRef]
Teyabeen, A.A.; Akkari, F.R.; Jwaid, A.E. Comparison of Seven Numerical Methods for Estimating Weibull Parameters for Wind Energy Applications. In Proceedings of the 2017 UKSim-AMSS 19th International Conference on Modelling and Simulation, Institute of Electrical and Electronics Engineers Inc, UK, Date of Conference (5 April 2017); pp. 173–178. [CrossRef]
Wang, J.; Hu, J.; Ma, K. Wind speed probability distribution estimation and wind energy assessment. Renewable and Sustainable Energy Reviews 2016, 60, 881–899. [Google Scholar] [CrossRef]
Aukitino, T.; Khan, M.G.M.; Ahmed, M.R. Wind energy resource assessment for Kiribati with a comparison of different methods of determining Weibull parameters. Renewable Energy 2017, 151, 641–660. [Google Scholar] [CrossRef]
Indhumathy, D.; Seshaiah, C.V.; Sukkiramathi, K. Estimation of Weibull Parameters for Wind speed calculation at Kanyakumari in India. International Journal of Innovative Research in Science 2014, 3, 8340–8345. [Google Scholar]
Bukala, J.; Damaziak, K.; Kroszczynski, K.; Krzeszowiec, M.; Malachowski, J. Investigation of parameters influencing the efficiency of small wind turbines. Journal of Wind Engineering and Industrial Aerodynamics 2015, 146, 29–38. [Google Scholar] [CrossRef]
Akgül, F.G.; Senotlu, B.; Arslan, T. An alternative distribution to Weibull for modeling the wind speed data: Inverse Weibull distribution. Energy Conversion and Management 2016, 114, 234–240. [Google Scholar] [CrossRef]
Secretaría de Protección al Ambiente de Baja California. Available online: https://www.gob.mx/cms/uploads/attachment/file /69289/12_ProAire_Mexicali.pdf (accessed on 05 December 2017).
Instituto Nacional de Estadística y Geografía. Available online: https://cuentame.inegi.org.mx/monografias/informacion /bc/poblacion/ (accessed on 04 November 2022).
Secretaría de Energía. Available online: https://www.gob.mx/sener/acciones-y-programas/estadisticas-del-sector-electrico-e-indicadores-de-cfe (accessed on 05 December 2017).
Justus, C.G.; Hargraves, W.R.; Mikhail, A.; Graber, D. Methods for estimating wind speed frequency distributions. Journal of Applied Meteorology 1978, 17, 350–353. [Google Scholar] [CrossRef]
Lysen, E.H. Introduction to wind energy, 2nd ed.; SWD Publication: The Netherlands, 1983; pp. 82–1. [Google Scholar]
Akdaǧ, S.A.; Dinler, A. A new method to estimate Weibull parameters for wind energy applications. Energy Conversion and Management 2009, 50, 1761–1766. [Google Scholar] [CrossRef]
Akdaǧ, S.A.; Guler, O. A novel energy pattern factor method for wind speed distribution parameter estimation. Energy Conversion and Management 2015, 106, 1124–1133. [Google Scholar] [CrossRef]
Wilks, D.S. Statistical methos in the atmospheric sciences, 2nd ed.; International geophysics series; Elsevier: UK, 2006; pp. 95–98. [Google Scholar]
Baseer, M.A.; Meyer, J.P.; Rehman, S.; Alam, M.M. Wind power characteristics of seven data collection sites in Jubail, Saudi Arabia using Weibull parameters. Renewable Energy 2017, 102, 35–49. [Google Scholar] [CrossRef]
Nash, Sutcliffe. Pronóstico del caudal de los ríos a través de modelos conceptuales parte I—Una discusión de principios. Revista de hidrología 1970, 10, 282–290. [Google Scholar]
Mohammadi, K.; Alavi, O.; Mostafaeipour, A.; Goudarzi, N.; Jalilvand, M.W. Assessing different parameters estimation methods of Weibull distribution to compute wind power density. Energy Conversion and Management 2016, 108, 322–335. [Google Scholar] [CrossRef]
Rodriguez-Hernandez, O.; Jaramillo, O.A.; Andaverde, J.A.; del Río, J.A. Analysis about sampling, uncertainties and selection of a reliable probabilistic model of wind speed data used on resource assessment. Renewable Energy 2013, 50, 244–252. [Google Scholar] [CrossRef]

Figure 2. Comparison of relative frequencies with the stationarity periods indicated. (a) 5 seconds for 2017. (b) 600 seconds for 2017. (c) 5 seconds for 2018. (d) 600 seconds for 2018. (e) 5 seconds for 2019. (f) 600 seconds for 2019.

Table 1. Statistical parameters for the different stationarity periods for 2017, 2018 and 2019.

	0.1 s		5 s		30 s		60 s		600 s	Year
$\bar{v}$	$σ$	$\bar{v}$	$σ$	$\bar{v}$	$σ$	$\bar{v}$	$σ$	$\bar{v}$	$σ$
2.09	1.54	2.09	1.47	2.09	1.39	2.09	1.36	2.09	1.26	2017
2.17	1.54	2.17	1.47	2.17	1.39	2.17	1.35	2.17	1.25	2018
2.19	1.62	2.19	1.54	2.19	1.46	2.19	1.42	2.19	1.31	2019

Table 2. Shape

(α)

and scale

(β)

parameters for the different stationarity periods for 2017, 2018 and 2019.

Table 2. Shape

(α)

and scale

(β)

parameters for the different stationarity periods for 2017, 2018 and 2019.

Method		0.1 s		5 s		30 s		60 s		600 s	Year
	$α$	$β$	$α$	$β$	$α$	$β$	$α$	$β$	$α$	$β$
EJ	1.367	2.304	1.463	2.309	1.550	2.325	1.593	2.331	1.729	2.346	2017
	1.451	2.396	1.526	2.411	1.620	2.420	1.667	2.431	1.820	2.444	2018
	1.388	2.403	1.464	2.420	1.554	2.437	1.598	2.444	1.735	2.460	2019
EL	1.367	2.305	1.463	2.311	1.550	2.327	1.593	2.333	1.729	2.348	2017
	1.451	2.398	1.526	2.413	1.620	2.428	1.667	2.433	1.820	2.446	2018
	1.388	2.405	1.464	2.422	1.554	2.439	1.598	2.446	1.735	2.462	2019
$E_{p f}$	1.332	2.293	1.370	2.286	1.453	2.307	1.495	2.315	1.615	2.334	2017
	1.360	2.374	1.435	2.343	1.526	2.411	1.573	2.419	1.717	2.436	2018
	1.296	2.373	1.372	2.397	1.454	2.418	1.496	2.427	1.618	2.447	2019
MM	1.851	1.129	2.017	1.036	2.243	0.932	2.359	0.886	2.744	0.762	2017
	1.980	1.090	2.178	0.997	2.430	0.893	2.562	0.847	3.016	0.720	2018
	1.830	1.197	2.020	1.085	2.253	0.972	2.372	0.923	2.760	0.793	2019
ML	2.332	0.897	2.477	0.843	2.678	0.78	2.475	0.845	3.283	0.637	2017
	2.380	0.910	2.559	0.848	2.779	0.781	2.900	0.748	3.430	0.632	2018
	2.302	0.952	2.466	0.888	2.676	0.819	2.789	0.785	3.264	0.671	2019

Table 3. Results of goodness of fit test/errors between observed and predicted data at 0.1 seconds.

Methods	$R^{2}$	NSEC	$x^{2}$	RMSE	MSE	MAE	MAPE	Year
pdf WEJ	0.92285	0.92036	0.07964	0.02710	0.00073	0.01041	66.4059	2017
	0.93750	0.93506	0.06494	0.02380	0.00057	0.00917	65.5379	2018
	0.91842	0.91580	0.08420	0.02717	0.00074	0.01022	63.6357	2019
pdf WEL	0.92282	0.92029	0.07971	0.02712	0.00073	0.01041	66.3419	2017
	0.93750	0.93497	0.06503	0.02382	0.00057	0.00918	65.4738	2018
	0.91842	0.91573	0.08427	0.02718	0.00074	0.01023	63.5873	2019
pdf W $E_{p f}$	0.89940	0.89781	0.10219	0.03070	0.00094	0.01092	55.6649	2017
	0.91837	0.91636	0.08364	0.02701	0.00073	0.00968	57.0964	2018
	0.89130	0.88978	0.11022	0.03108	0.00097	0.01138	51.6974	2019
pdf GMM	0.94768	0.94500	0.05500	0.02252	0.00051	0.00858	39.3980	2017
	0.96301	0.96080	0.03921	0.01850	0.00034	0.00693	45.7116	2018
	0.94442	0.94177	0.05823	0.02259	0.00051	0.00828	42.1631	2019
pdf GML	0.97249	0.97100	0.02899	0.01635	0.00027	0.00690	66.3538	2017
	0.97858	0.97756	0.02244	0.01399	0.00020	0.00593	63.0985	2018
	0.97109	0.96942	0.03057	0.01637	0.00027	0.00696	64.3871	2019
pdf RSD	0.95583	0.95144	0.04857	0.02117	0.00045	0.00967	82.8553	2017
	0.96865	0.96134	0.03866	0.01837	0.00034	0.00797	81.8300	2018
	0.94752	0.94329	0.05671	0.02230	0.00050	0.01070	82.2250	2019
pdf Mix	0.99521	0.99351	0.00649	0.00774	0.00001	0.00338	33.8132	2017
	0.99779	0.92036	0.00234	0.00452	0.00000	0.00199	44.7972	2018
	0.99268	0.93506	0.01049	0.00959	0.00001	0.00412	38.8530	2019

Table 4. Results of goodness of fit test/errors between observed and predicted data at 5 seconds.

Methods	$R^{2}$	NSEC	$x^{2}$	RMSE	MSE	MAE	MAPE	Year
pdf WEJ	0.92412	0.92114	0.07885	0.02767	0.00077	0.01091	66.8784	2017
	0.93596	0.93286	0.06714	0.02630	0.00069	0.01120	60.9770	2018
	0.91871	0.91540	0.08459	0.02757	0.00076	0.01054	66.9761	2019
pdf WEL	0.92408	0.92105	0.07895	0.02768	0.00077	0.01092	66.8227	2017
	0.93589	0.93274	0.06726	0.02632	0.00069	0.01120	60.9140	2018
	0.91866	0.91531	0.08469	0.02759	0.00076	0.01055	66.9149	2019
pdf W $E_{p f}$	0.90144	0.89913	0.10087	0.03129	0.00098	0.01141	56.1221	2017
	0.91746	0.91445	0.08555	0.02969	0.00088	0.01157	51.3477	2018
	0.89541	0.89281	0.10719	0.03104	0.00096	0.01113	56.4037	2019
pdf GMM	0.95177	0.94891	0.05109	0.02227	0.00050	0.00855	41.5378	2017
	0.96562	0.96299	0.03701	0.01953	0.00038	0.00806	34.7031	2018
	0.94893	0.94566	0.05434	0.02210	0.00049	0.00823	39.6690	2019
pdf GML	0.97245	0.97108	0.02892	0.01676	0.00028	0.00717	64.2016	2017
	0.97804	0.97704	0.02296	0.01538	0.00024	0.00711	54.8807	2018
	0.96951	0.96781	0.03219	0.01700	0.00029	0.00719	63.3709	2019
pdf RSD	0.97012	0.96475	0.03525	0.01850	0.00034	0.00818	81.5834	2017
	0.97664	0.96655	0.03345	0.01856	0.00034	0.00944	78.8445	2018
	0.96595	0.96090	0.03910	0.01875	0.00035	0.00889	82.1526	2019
pdf Mix	0.99849	0.99833	0.00167	0.00402	0.00016	0.00197	37.7363	2017
	0.99635	0.99602	0.00398	0.00641	0.00017	0.00268	36.1189	2018
	0.99593	0.99527	0.00473	0.00652	0.00004	0.00291	38.0726	2019

Table 5. Results of goodness of fit test/errors between observed and predicted data at 30 seconds.

Methods	$R^{2}$	NSEC	$x^{2}$	RMSE	MSE	MAE	MAPE	Year
pdf WEJ	0.92201	0.91838	0.08162	0.03017	0.00091	0.01286	64.0270	2017
	0.93539	0.93203	0.06797	0.02794	0.00078	0.01266	59.3342	2018
	0.91267	0.90812	0.09188	0.03177	0.00101	0.01381	55.4190	2019
pdf WEL	0.92193	0.91825	0.08175	0.03020	0.00091	0.01286	63.9369	2017
	0.93498	0.93141	0.06858	0.02807	0.00079	0.01268	58.9407	2018
	0.91259	0.90798	0.09202	0.03179	0.00101	0.01382	55.3578	2019
pdf W $E_{p f}$	0.90443	0.90092	0.09908	0.03325	0.00111	0.01329	54.4361	2017
	0.91966	0.91562	0.08438	0.03113	0.00097	0.01298	49.2061	2018
	0.89027	0.88594	0.114056	0.03539	0.00125	0.014216	54.5651	2019
pdf GMM	0.95480	0.95145	0.04855	0.02328	0.00165	0.00970	41.5393	2017
	0.96901	0.96634	0.03366	0.01966	0.00136	0.00868	25.9264	2018
	0.95009	0.94587	0.05413	0.02438	0.00059	0.01031	23.2579	2019
pdf GML	0.97032	0.96896	0.03104	0.01861	0.00035	0.00841	56.1773	2017
	0.97728	0.97634	0.02366	0.01648	0.00027	0.00786	47.0188	2018
	0.96593	0.96401	0.035987	0.01988	0.00040	0.009364	47.6466	2019
pdf RSD	0.97273	0.96432	0.03568	0.01995	0.00040	0.01076	80.7793	2017
	0.96792	0.95220	0.04780	0.02343	0.00071	0.01800	79.7015	2018
	0.96740	0.95942	0.04058	0.02111	0.00045	0.01182	69.4238	2019
pdf Mix	0.99724	0.99719	0.00282	0.00561	0.00031	0.00278	31.3789	2017
	0.99903	0.99696	0.00303	0.00591	0.00046	0.00401	23.2060	2018
	0.99741	0.99727	0.00273	0.00548	0.00030	0.00266	18.8184	2019

Table 6. Results of goodness of fit test/errors between observed and predicted data at 60 seconds.

Methods	$R^{2}$	NSEC	$x^{2}$	RMSE	MSE	MAE	MAPE	Year
pdf WEJ	0.90673	0.89857	0.10143	0.03782	0.00143	0.01856	48.3084	2017
	0.93364	0.92991	0.07009	0.02923	0.00085	0.01371	58.2624	2018
	0.90966	0.90465	0.09535	0.03434	0.00118	0.01578	57.4877	2019
pdf WEL	0.90656	0.89833	0.10167	0.03787	0.00143	0.01858	48.2022	2017
	0.93352	0.92974	0.07026	0.02927	0.00086	0.01568	58.1640	2018
	0.90956	0.90449	0.09551	0.03437	0.00118	0.01805	57.4260	2019
pdf W $E_{p f}$	0.89074	0.88165	0.11835	0.04085	0.00167	0.01927	30.5040	2017
	0.91972	0.91512	0.08488	0.03217	0.00103	0.01387	48.4072	2018
	0.88848	0.88326	0.11674	0.03800	0.00144	0.01618	44.7211	2019
pdf GMM	0.95192	0.94767	0.05233	0.02717	0.00074	0.01323	25.1835	2017
	0.96457	0.95895	0.04105	0.02237	0.00050	0.00100	23.4617	2018
	0.94864	0.94693	0.05307	0.02562	0.00066	0.01149	40.9010	2019
pdf GML	0.95630	0.95391	0.04609	0.02550	0.00065	0.01288	40.3172	2017
	0.97684	0.97592	0.02408	0.01713	0.00029	0.00836	43.7285	2018
	0.96708	0.96599	0.03401	0.02051	0.00042	0.01031	41.1514	2019
pdf RSD	0.96603	0.95506	0.04494	0.02517	0.00063	0.01564	75.3075	2017
	0.95533	0.93529	0.06471	0.02809	0.00079	0.01614	80.1333	2018
	0.96145	0.95148	0.04852	0.02450	0.00060	0.01447	77.8835	2019
pdf Mix	0.99654	0.99625	0.00375	0.00727	0.00005	0.00390	16.7428	2017
	0.99899	0.99554	0.00446	0.00788	0.00006	0.00428	22.2970	2018
	0.99752	0.99740	0.00260	0.00567	0.00003	0.00299	29.6507	2019

Table 7. Results of goodness of fit test/errors between observed and predicted data at 600 seconds.

Methods	$R^{2}$	NSEC	$x^{2}$	RMSE	MSE	MAE	MAPE	Year
pdf WEJ	0.88586	0.87805	0.12195	0.04604	0.00212	0.02483	55.1617	2017
	0.91137	0.90533	0.09467	0.03841	0.00148	0.02000	56.7452	2018
	0.87419	0.86513	0.13487	0.04742	0.00225	0.02535	53.4893	2019
pdf WEL	0.88583	0.87797	0.12203	0.04606	0.00212	0.02485	55.1464	2017
	0.91118	0.90507	0.09493	0.03846	0.00148	0.02002	56.6542	2018
	0.87401	0.86487	0.13513	0.04747	0.00225	0.02537	53.3943	2019
pdf W $E_{p f}$	0.86432	0.85520	0.14480	0.05017	0.00252	0.02527	44.2167	2017
	0.89855	0.89042	0.10958	0.04132	0.00171	0.02005	46.9639	2018
	0.85274	0.84197	0.15803	0.05134	0.00264	0.02541	42.8839	2019
pdf GMM	0.93902	0.93149	0.06855	0.03452	0.00119	0.01820	25.1186	2017
	0.96143	0.95665	0.04335	0.02599	0.00068	0.01319	28.4373	2018
	0.93223	0.92348	0.07652	0.03572	0.00128	0.01867	28.8496	2019
pdf GML	0.95445	0.95165	0.04835	0.02899	0.00084	0.01660	45.4149	2017
	0.96826	0.96670	0.03330	0.02278	0.00052	0.01256	38.2368	2018
	0.93372	0.92536	0.07464	0.03528	0.00124	0.01857	30.2912	2019
pdf RSD	0.91035	0.89512	0.10488	0.04270	0.00182	0.02312	77.6386	2017
	0.87896	0.84829	0.15171	0.04862	0.00236	0.02514	83.0592	2018
	0.90280	0.88828	0.11172	0.04316	0.00186	0.02489	78.4083	2019
pdf Mix	0.99323	0.99281	0.00719	0.01118	0.00013	0.00666	19.9490	2017
	0.99499	0.99430	0.00570	0.00942	0.00089	0.00552	24.4279	2018
	0.98198	0.97968	0.02033	0.01842	0.00034	0.01003	25.7630	2019

Table 8. Generated and estimated energy (kWh) results for the different stationarity periods for 2017, 2018 and 2019.

	0.1 s	5 s	30 s	60 s	600 s	Year
Aeolos 200W	227.11	227.11	227.11	227.11	227.11	2017
	177.93	177.93	177.93	177.93	177.93	2018
	267.73	267.73	267.73	267.73	267.73	2019
Method
pdf WEJ	225	220.6	215.2	212.76	206.2	2017
	175.1	171	166.5	165.2	159.8	2018
	244.7	239	233	230.2	222.8	2019
pdf WEL	225.3	220.9	215.6	213.06	206.4	2017
	175.4	171.6	167.4	165.4	160	2018
	245.1	239.3	233.4	230.5	223.1	2019
pdf W $E_{p f}$	231.4	227	220.3	218.49	211.6	2017
	179.7	176.1	171.4	169.2	163.2	2018
	251.8	245.7	238.8	236.8	229.1	2019
pdf GMM	222.7	220.2	217.8	215.7	210.2	2017
	175.9	172.9	169.1	167.51	163	2018
	244.9	240.4	235	232.62	226.6	2019
pdf GML	215.9	213.5	210.7	209.4	204.5	2017
	169.9	167.6	165.2	163.8	159.4	2018
	234.5	231.5	227.9	225.88	220.2	2019
pdf RSD	172.9	163.3	151.1	146.7	132.5	2017
	129.4	121	112	107.7	97.2	2018
	188.2	174.5	161.5	155.6	140.9	2019
pdf Mix	229.6	222.69	215.2	214.7	195.3	2017
	178	172.6	169.5	167.8	166.1	2018
	252.4	241.3	232.8	230.33	218.7	2019

Table 9. Energy estimation percentage error for the different stationarity periods for 2017, 2018 and 2019.

Methods vs Aeolos 200 W	0.1 s	5 s	30 s	60 s	600 s	Year
pdf WEJ	0.929	2.866	5.244	6.319	9.207	2017
	1.591	3.895	6.424	7.154	10.19	2018
	8.602	10.73	12.97	14.02	16.78	2019
pdf WEL	0.797	2.736	5.068	6.186	9.119	2017
	1.422	3.558	5.918	7.042	10.08	2018
	8.453	10.62	12.82	13.91	16.67	2019
pdf W $E_{p f}$	-1.889	0.048	2.999	3.796	6.829	2017
	-0.995	1.028	3.670	4.4906	8.279	2018
	5.950	8.228	10.81	11.55	14.43	2019
pdf GMM	1.942	2.162	4.099	5.024	7.446	2017
	1.141	2.827	4.963	5.856	8.391	2018
	8.527	10.21	12.23	13.11	15.36	2019
pdf GML	4.936	5.993	7.226	7.798	9.956	2017
	4.513	5.806	7.154	7.941	10.41	2018
	12.41	13.53	14.88	15.63	17.75	2019
pdf RSD	23.87	28.10	33.47	35.41	41.66	2017
	27.27	32.00	37.05	39.47	45.37	2018
	29.71	34.82	39.68	41.88	47.37	2019
pdf Mix	-1.096	1.946	5.244	5.464	14.01	2017
	-0.039	2.996	4.738	5.693	6.649	2018
	5.726	9.872	13.05	13.97	18.31	2019

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Comparative Analysis of Estimated Small Wind Energy Using Different Probability Distributions in a Desert City in Northwestern Mexico

Abstract

1. Introduction

2. Methodology

2.1. Probability Density Functions and Methods for Statistical Parameter Estimation

2.1.1. Weibull Probability Density Function

2.1.1.1. Empirical Justus Method (EJ)

2.1.1.2. Empirical Lysen Method (EL)

2.1.1.3. Energy Pattern Factor Method ( E p f )

2.1.2. Rayleigh Probability Density Function

2.1.3. Probability density function Gamma

2.1.3.1. Method of Moments (MM)

2.1.3.2. Maximum Likelihood Method (ML)

2.1.4. pdf Mix

2.2. Energy Estimation with Pdf

2.2.1. Comparison betweem Estimated and Generated Energy

2.3. Statistical Tests

2.3.1. Coefficient of Determination ( R 2 )

2.3.2. Chi-Square ( X 2 )

2.3.3. Nash-Sutcliffe Efficiency Coefficient (NSEC)

2.3.4. Root Means Square Error (RMSE)

2.3.5. Mean Square Error (MSE)

2.3.6. Mean Absolute Error (MAE)

2.3.7. Mean Absolute Percentage Error (MAPE)

3. Results and Discussion

3.1. Results of Statistical Parameters

3.2. Statistical Test Results

3.3. Estimated vs Generated Energy

4. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Sample Availability

Abbreviations

References

MDPI Initiatives

Important Links

Subscribe

2.1.1.3. Energy Pattern Factor Method ( $E_{p f}$ )

2.3.1. Coefficient of Determination $(R^{2})$

2.3.2. Chi-Square ( $X^{2}$ )