Prerpints.org logo
Preprint
Article

Acoustic properties of surfaces covered by multipole resonators

Altmetrics

Downloads

112

Views

22

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

15 March 2024

Posted:

15 March 2024

You are already at the latest version

Alerts
Abstract
Different types of resonators are used to create acoustic metameterials and metasurfaces. Recent studies focused on the use of multiple resonators of dipole, quadrupole, octupole and even hexadecapole types. This paper considers the theory of an acoustic metasurface, which is a flat surface with a periodic arrangement of multiple resonators. The sound field reflected by the metasurface is determined. If the distance between the resonators is less than a half the wavelength of the incident plane wave, the far field can be described by a reflection coefficient that depends on the angle of incidence. This allows to characterize the acoustic properties of the metasurface by a homogenized boundary condition, which is a high order tangential impedance boundary condition. The tangential impedance depending on the multiple order of the resonators is introduced. In addition, we analyze sound absorption properties of these metasurfaces, which are a critical factor in determining their performance. The paper presents a theoretical model that accounts for the multiple orders of resonators and their impact on sound absorption. The maximum absorption coefficient for a diffuse sound field, as well as the optimal value for the homogenized impedance, are calculated for arbitrary multipole orders.
Keywords: 
Subject: Physical Sciences  -   Acoustics

1. Introduction

Resonators are often used as meta-atoms to create acoustic metamaterials, which are complex structures with specific properties. At scales significantly exceeding the sound wavelength the acoustic metamaterial behaves like a continuous media described by macroscopic effective parameters [1]. In some case the effective parameters have features, which cannot be met in natural materials. For example, the acoustic metamaterial with the negative effective density or negative bulk modulus are known as well as double-negative media having both parameters simultaneously negative [2]. The elastic media with monopole resonators has the negative bulk modulus at certain frequency range [3]. The well-known example is liquid with gas bubbles, which are considered as isotropic scatterers [4]. The negative effective density can be achieved by dipole resonators [3] included into the natural media. The light dipoles in liquid provide very wide frequency range of the negative density [5]. One of the simplest double-negative acoustic material is a dispersive composite in the form of an elastic porous medium with empty spherical cavities [6]. The similar idea has been recently proposed in [7] investigating crack-like inhomogeneities or voids in a multilayer structure.
Researchers apply different types of the resonators in order to construct metamaterials and metasurfaces. The most popular type is monopole resonators like Helmholtz resonators, quarter- and half-wave resonators, folded tubes, membranes [8,9]. The resonator should be much smaller than the controlled wavelength to apply homogenization [1] for derivation of effective bulk parameters of the metamaterials or an equivalent boundary condition for the metasurfaces. An array of identical monopole resonators on a rigid backing can be described by an ordinary impedance boundary condition [10]. If the resonators’ parameters vary periodically in the array, the gradient phase metasurface is formed [11]. Such surfaces can redirect the incident sound wave in a different way with respect to the traditional low of reflection.
The resonators with higher order of multiplicity are increasingly being used as the meta-atoms. The resonator of the next order after the monopole one belongs to the dipole type. The simplest physical model of the dipole resonator is a rigid sphere on a spring [12]. Also, the dipole resonator can be implemented by a membrane in a ring oscillating at the first eigenmode [12] or a membrane embedded in a rigid baffle oscillating at the second eigenmode [13]. Two coupled Helmholtz resonators have a mode, for which they oscillate with opposite phases [14], hence two monopole resonators can form the dipole one. The meta-atom with monopole and dipole moments proposed in [15] provides more benefits for sound field control. Note that a combination of the monopole and dipole resonators named monopole-dipole resonators was suggested earlier for noise reduction in tubes [16,17]. A regular array formed by the monopole-dipole resonators can totally absorb an incident sound wave in free space [18] or in a waveguide [19]. It is important that a surface covered by the dipole resonators can not be described by the ordinary acoustic impedance. The special boundary condition in form of a tangential impedance is needed for the equivalent surface with uniform properties [20]. Alternatively, the dipole-type metasurface can be formed by a set of short beams clamped on one side [21].
Two coupled dipole resonators give a quadrupole resonator, which is used for a higher-order topological insulator [22]. A 2D lattice made of the quadrupole resonators is realized and experimentally studied in [23]. An elastic sphere has a lot of eigenmodes [24], the third one provides the quadrupole scattering of sound wave. So, the elastic sphere as well as an elastic cylinder can be assumed as the quadrupole resonator at certain frequency. Another quadrupole resonator for water is composed of a hard cylinder with an elliptical rubber coating [25]. The coupling of two quadrupole resonators allows to build an octupole resonator [26], while the coupling of two octupole resonators results in an hexadecapole resonator [27]. By repeating this process, we can create resonators of any order of multiplicity. Recent reviews [28,29,30] have shown growing interest in the development of metamaterials using higher-order topological resonators. Following this trend, this paper is dedicated to studying the homogenized acoustic properties of the metasurfaces formed by the multipole resonators.
In this study, we investigate the acoustic properties of a rigid surfaces covered by multiple resonators. In Section 2 the physical model of a multiple resonator and its characteristic are described. In section 3 the sound reflection properties of the surface with a periodic array of the resonators are considered and the homogenized boundary condition for the metasurface is introduced. Sound absorption properties of the metasurfaces are analyzed in Section 4. In Section 5 the found results are discussed.

2. Linear Multipole

A multiple sound source can be described by a set of monopole sources. If the monopoles are located on a straight line, the multiple source is linear [31]. In the same way a multiple sound scatterer can be presented as a system of the monopoles which volume velocities are not independent, but they are fitted to yield a specific scattered sound field. Let us combine the monopoles to obtain the multiple sound scatterers.

2.1. Monopole

The simplest scatterer contains only one monopole with the volume velocity q . The sound pressure field P consists of two components: the first one is the incident field p and the second one is the own field of the monopole p 0 . Due to the superposition principle, we can write P = p + p 0 . The impedance of the monopole scatterer is
Z 0 = − P q .
The motion of the monopole scatterer is excited by sound pressure. In general way the equation of motion is given by
m w ¨ + γ w ˙ + κ w = − σ P ,
where m on the mass of the monopole, κ is its stiffness, γ is the friction coefficient, w is the displacement of the moving part, σ is the surface of the moving part. The volume velocity is connected with the displacement by q = σ w ˙ . From (1) and (2) we can find the monopole impedance
Z 0 = 1 σ 2 γ − i ω m 1 − ω 0 2 ω 2 ,
where ω 0 2 = κ / m is the resonant frequency.
Note that the impedance Z 0 is defined only by own parameters of the scatterer and does not depend on radiation conditions. They are usually described by the radiation impedance, which is a ratio of the own field to the volume velocity
R 0 = p 0 q .
The volume velocity of the monopole scatterer in response to the incident field  p is found from (1) and (4)
q = − p Z 0 + R 0 .
On resonance the volume velocity is maximal. The resonance condition follows from (5)
Im Z 0 + R 0 = 0 .
The condition (6) is well-known: at resonant frequency the image of the resonator impedance compensates the image part of the radiation impedance. Commonly the frequency ω 0 differs from the resonant frequency Ω 0 found from the condition (6). Speaking further about resonators, we mean that the structure of the resonating scatterer is such that there is a certain frequency at which the conditions are met.
The equations (1-6) are enough to describe the movement of the monopole resonator and its interaction with the external sound field.

2.2. Dipole

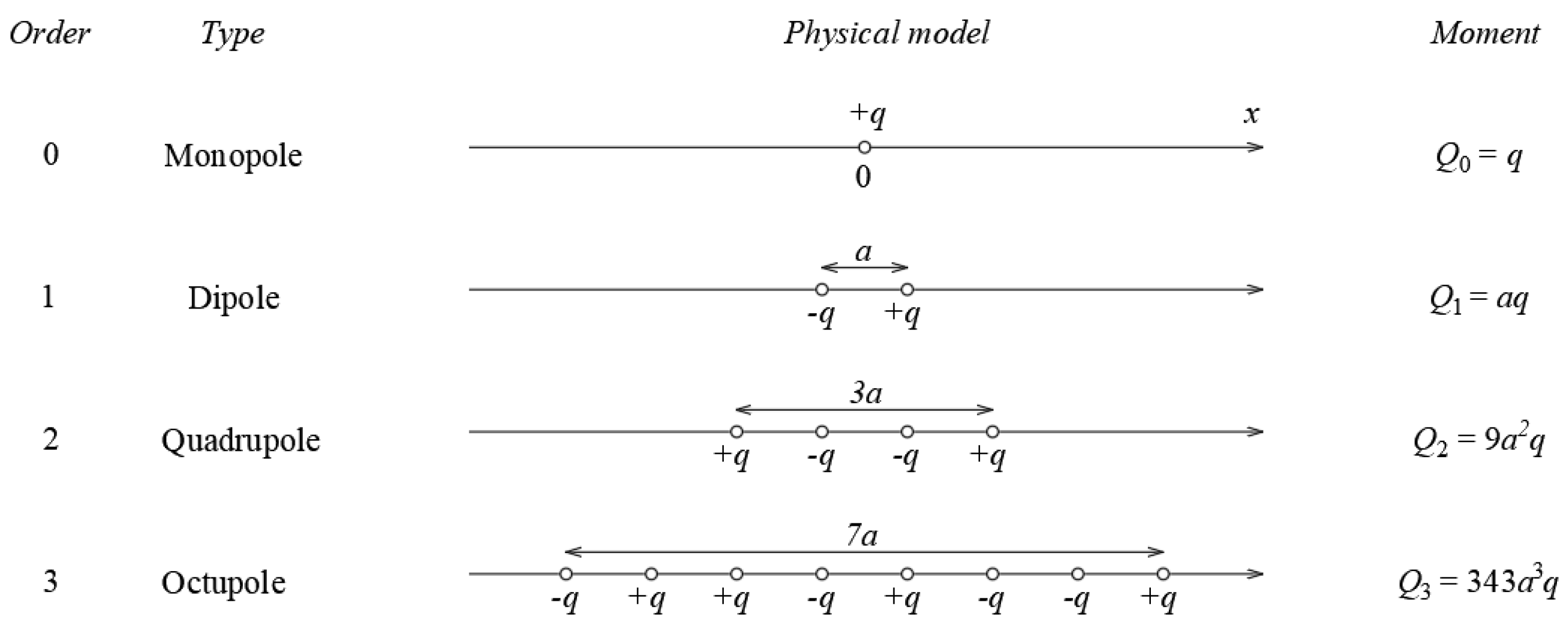
Now we apply the same formalism for the sound scatterers of higher order of multiplicity, which is indicated by N . The dipole scatterer has the order N = 1 and is assumed as a pair on the monopoles with the opposite volume velocities at a distance a as shown in Figure 1. Both monopoles are on the axis x ; the monopoles with the volume velocities + q and − q are located at the points x = a / 2 and x = − a / 2 respectively.
The sound field generated by two monopoles is p 1 and the total field is P = p + p 1 . Using (2) we obtain two equations of motion
− q Z 0 = − P x = − a 2 ,
q Z 0 = − P x = a 2 .
Subtracting (8) from (7) we can find
2 Z 0 q = P x = − a 2 − P x = a 2 .
The dipole moment is Q 1 = a q . Decomposing P near x = 0 into a Fourier series, we find the impedance of the dipole scatterer
Z 1 = − ∂ P / ∂ x x = 0 Q 1 .
Formally, the monopole and dipole impedances are connected by the ratio Z 1 = 2 Z 0 / a 2 . But the impedance Z 1 is determined by the construction of the dipole resonator and can be expressed in another way. At the same time equation (10) establishes the universal relationship between the forcing acting on the dipole by the sound field given by ∂ P / ∂ x , the moment Q 1 characterizing the movement of the resonator and the impedance   Z 1 defining the mechanical properties of the resonator.
presented as a set of the monopoles with the volume velocities + q and − q .

2.3. Quadrupole

If N = 2 we deal with a quadrupole resonator, which can be presented as an array of four monopoles (Figure 2) at a distance a from each other. The monopoles with the volume velocities + q and − q are located at the points x = − 3 a / 2 , x = 3 a / 2 and x = − a / 2 , x = a / 2 respectively. The equations of motion for four monopoles are
q Z 0 = − P x = − 3 a 2 ,   − q Z 0 = − P x = − a 2 ,   − q Z 0 = − P x = a 2 ,   q Z 0 = − P x = 3 a 2 .
The length of the quadrupole is 3 a , therefore we can introduce the quadrupole moment Q 2 = 3 a 2 q . From (11) we obtain the impedance of the quadrupole scatterer
Z 2 = − ∂ 2 P / ∂ x 2 x = 0 Q 2 .
The impedance of the monopoles and the quadrupole are related by Z 2 = 2 Z 0 / 3 a 4 .

2.4. Multipole

A linear multipole of an arbitrary order can be built in the same way. Figure 1 shows the octupole ( N = 3 ) consisting of eight monopoles. The multipole of order N is formed by 2 N monopoles. Its length is l N = 2 N − 1 a . The multipole moment is defined as Q N = l N N q , for the monopole we have N = 0 and Q 0 = q . The impedance of the multiple scatterer is
Z N = − ∂ N P / ∂ x N x = 0 Q N .
where P = p + p N is the total sound field, p N is the own field of the scatterer. Its radiation impedance is defined in ordinary way
R N = p N Q N .
The moment of the scatterer in response to the incident field  p is
Q N = − ∂ N p / ∂ x N x = 0 Z N + R N .
The condition of the resonance is
Im Z N + R N = 0 .
We assume that equation (16) is satisfied at certain frequency Ω N . So, the multiple scatterer is a resonator and below we will focus on this specific case. However, equations (13-15) remain valid for any scatterer not just those that are resonant, and can be used to describe the multiple scatterers regardless of how they are formed. The main goal is to determine the impedance Z N , which is heavily influenced by the structure of the scatterer. If the scatterer consists of a linear array of monopoles, with an impedance Z 0 , as in Figure 1, then the impedance of the entire system is Z N = C N Z 0 / a 2 N , where C N is a coefficient that depends only by the order N of the array.
It is important to note that the impedances of the multipole scatterer introduced by (13) have different dimensions depending on the order N .

3. Array of Multipoles

In this section we consider the acoustic properties of surfaces covered by a periodic array of multipole scatterers. These surfaces are named metasurfaces due to their unusual equivalent boundary condition. First of all, we find the sound field reflected by the metasuface. Next, we introduce a homogenized boundary condition used to describe the far-field behavior of the reflected sound.

3.1. Reflection Coefficient

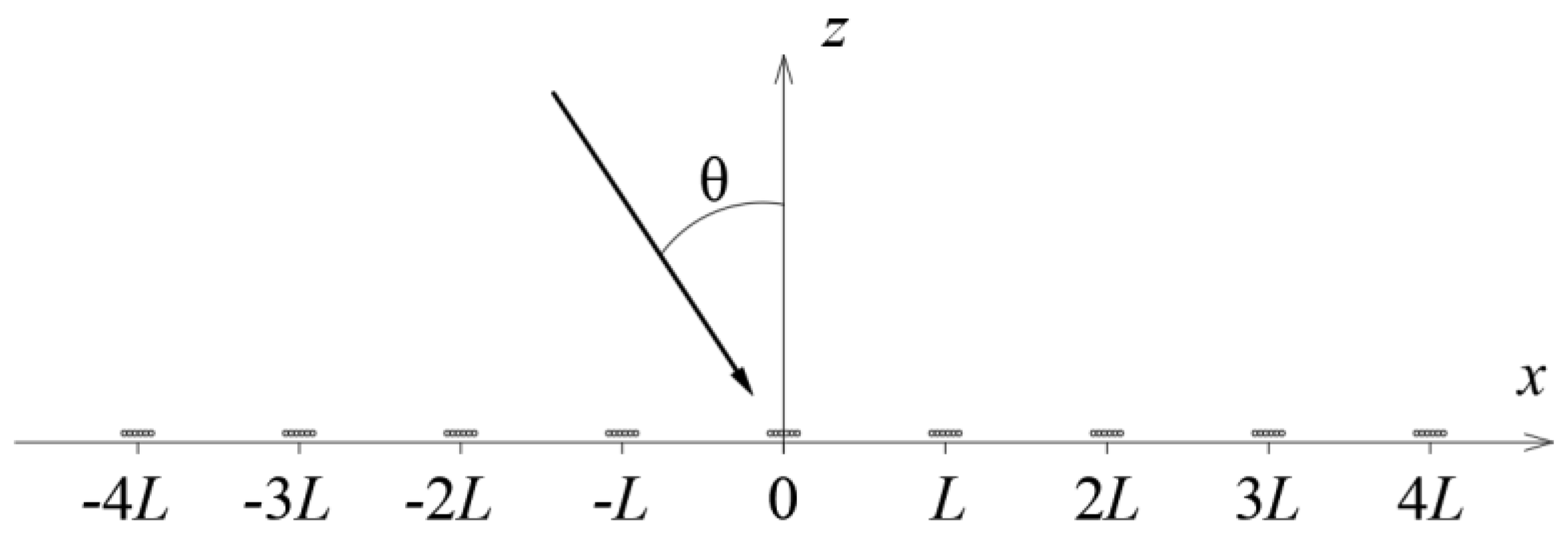
The studied metasurface is shown in Figure 2. The scatterers with the order of multiplicity N are located periodically with a distance L near a rigid surface. We consider the two-dimensional problem, so the surface coincides with the plane z = 0 and the scatterers are at points x n = n L , where n is the number of the resonator. Assuming a time-harmonic disturbance in the form of e − i ω t , where t is time, ω is an angular frequency, the sound pressure in the half space z ≥ 0 can be given as follows
P = A e i ξ 0 x − i κ 0 z + A e i ξ 0 x + i κ 0 z + p N ,
where p N is the sound field radiated by the array, A is an amplitude of the incident plane wave, ξ 0 and κ 0 are the components of the wave vector. The second term in the right part of (17) is the reflected plane wave by the rigid surface. Also, we can use an incidence angle θ , which is related with the wave vector components by the equations ξ 0 = k sin θ and κ 0 = k cos θ , where k = ω / c , c is speed of sound.
The sound field of the array formed by the monopole scatterers is found in [13] and given by
p 0 = Q 0 ω ρ L ∑ n e i ξ n x + i κ n z κ n ,
where ξ n = ξ 0 + 2 π n / L , κ n = k 2 − ξ n 2 , ρ is the density of the medium, Q 0 is the monopole moment of the scatterer placed at the point x = 0 .
The sound field produced by the array consisting of the N -pole scatterers can be found by differentiation (18) by the coordinate x [32]. For arbitrary multipoles we have
p N = Q N − 1 N N ! ∂ N p 0 ∂ x N = Q N ω ρ L − i N N ! ∑ n ξ n N e i ξ n x + i κ n z κ n ,
where Q N is the multipole moment of the scatterer placed at the point x = 0 .
Substituting (19) into (17) and then (17) into (13) we obtain the multipole moment
Q N = − 2 A i N ξ 0 N Z N + R N ,
where the radiation impedance of the multipole is introduced as follows
R N = ω ρ L N ! ∑ n ξ n 2 N κ n .
From (19) and (20) we find the sound field of the array
p N = − 2 A ω ρ L ( Z N + R N ) N ! ξ 0 N ∑ n ξ n N e i ξ n x + i κ n z κ n .
The field (22) is valid for the arbitrary period L . Further we limit this study by the period L < λ / 2 , where λ = 2 π / k is a wavelength. All waves with n ≠ 0 are nonuniform and decay along the z -axis. So, the array radiates only one plane wave e i ξ 0 x + i κ 0 z . In this case the radiation impedance can be written as
R N = R ′ N + i R ′ ′ N = ω ρ L N ! ξ 0 2 N κ 0 − i ω ρ L N ! ∑ n ≠ 0 ξ n 2 N α n ,
where α n = ξ n 2 − k 2 .
At far distances k z ≫ 1 the field (17) is P = A e i ξ 0 x − i κ 0 z + A V e i ξ 0 x + i κ 0 z , where V is the reflection coefficient of the metasurface. Using (22) we find the reflection coefficient
V = Z N + i R ″ N − R ′ N Z N + i R ″ N + R ′ N .
By means of the incidence angle θ equation (24) is transformed into
V = Z ~ N cos ⁡ θ − sin 2 N ⁡ θ Z ~ N cos ⁡ θ + sin 2 N ⁡ θ ,
where Z ~ N is a dimensionless value given by
Z ~ N = L N ! ω ρ Z N + i R ″ N .
At far distances the sound field reflected by the metasurface is simply a specular reflected plane wave. The reflection coefficient is calculated by (24) or (25). Note that for a more detailed analysis of the near field equation (22) can be used.

3.2. Equivalent Boundary Condition

Equations (17) and (22) yield the sound field in a half-space z > 0 , however at distances k z ≫ 1 it is enough to know only the reflection coefficient (24) in order to calculate the sound field. It means that it is possible to apply a uniform boundary condition for the surface z = 0 , which provides the same far field. In this sense the boundary condition is equivalent to the considered metasurface. The homogenization swaps the difficult structure for a simple model convenient to characterize the interaction of the sound fields and metasurfaces. If the periodic array shown in Figure 1 consists of the monopole scatterers, the usual impedance is the equivalent boundary condition [10]. It has a form at z = 0
Z 0 ′ = P v z ,
where v z is the normal velocity of the metasurface.
In case of the dipole scatterers [13] the equivalent boundary condition is
Z 1 ′ = − ∂ 2 P / ∂ x 2 v z .
Taking into account (27) and (28) it is possible to assume that the array of the scatterers of the order N has the following equivalent boundary condition at z = 0
Z N ′ = − 1 N v z ∂ 2 N P ∂ x 2 N .
Applying the boundary condition (29) for the plane z = 0 and using the relation i ω ρ v z = ∂ P / ∂ z , we can find the reflection coefficient of a plane wave with the incidence angle θ
V = Z N ′ cos ⁡ θ − ρ c k 2 N sin 2 N ⁡ θ Z N ′ cos ⁡ θ + ρ c k 2 N sin 2 N ⁡ θ .
Comparing (26) and (30), we can state that the reflection coefficient (25) of the rigid surface covered by the multipole scatterers and the reflection coefficient (30) with the uniform impedance (29) are the same. The relation of the impedances in (25) and (30) is as follows
Z N ′ = ρ c k 2 N Z ~ N .
Now the physical senses of the values in (31) are clear. Z ~ N   is the dimensionless impedance characterizing the metasuface formed by the array of the scatterers at certain frequency ω . Whereas, Z N ′ is the homogenized boundary condition, which does not depend directly on frequency. The impedance Z N ′ is local and can be used for metasurfaces without taking into account the structure. For N = 0 the impedance Z 0 ′ is the ordinary impedance, which is a ratio of the sound pressure to the normal velocity. For N ≥ 1 the motion of the surface is excited by a tangential forcing, therefore, the condition (29) can be called the tangential impedance [13,20].
Boundary conditions similar to (29) are widely known in electromagnetism [33,34], they belong to high order impedance boundary conditions or HOIBC. At the same time in acoustics the HOIBC are not often met.

4. Metasurface Formed by Resonators

In this section, we analyze the acoustic properties of the metasurfaces with boundary condition (29) and assume the scatterers as resonators. We are interested in case when the condition (16) is fulfilled. In other words, we consider behavior of the metasurface at resonant frequency of the scatterers. According to (16) the impedances Z ~ N and Z N ′ are real at this frequency as well as the reflection coefficient.

4.1. Reflection Coefficient

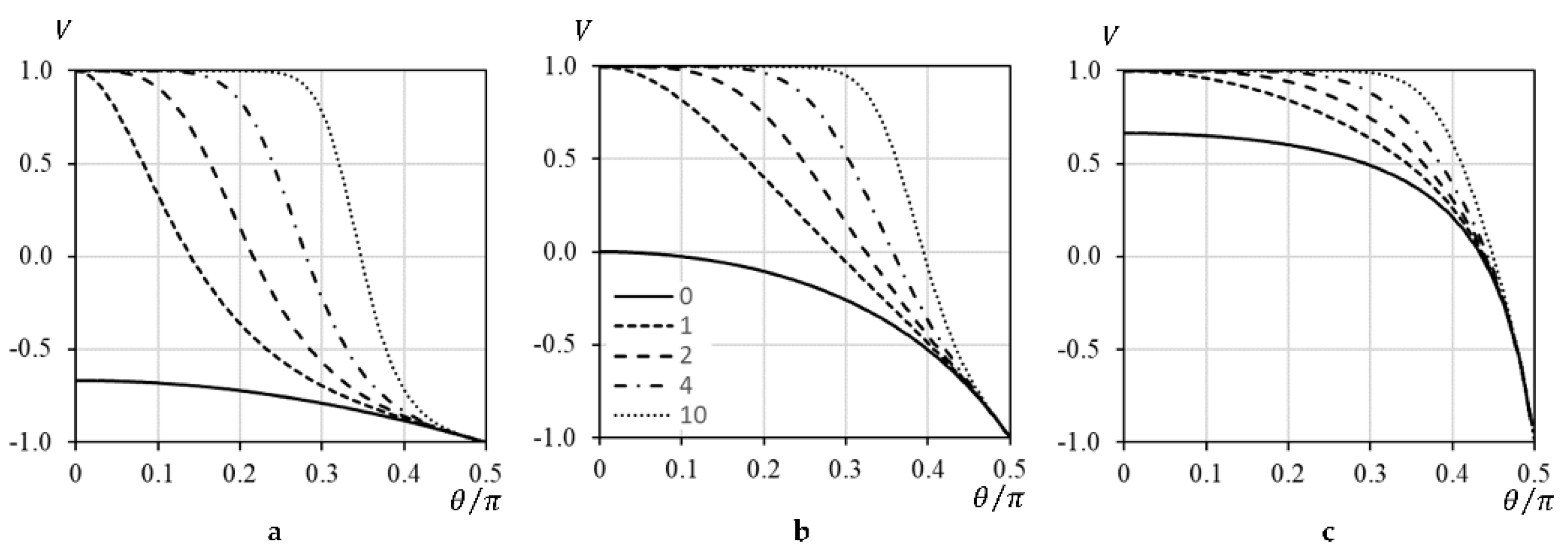
The reflection coefficient from the metasurface with the boundary condition (29) is given by (25) and (30). Figure 3 shows the dependence of the reflection coefficient V on the incidence angle θ for different values of the dimensionless impedance Z ~ N . The reflection coefficient is calculated for five orders of multiplicity.
For N ≥ 1 at normal incidence ( θ = 0 ) the reflection coefficient is 1. It means that the normally incident plane wave does not excited motion of the scatterers and the metasurface is rigid. With increase the incident angle the reflection coefficient changes from 1 to − 1 . For all values of   Z ~ N there is the incidence angle θ ′ at which V = 0 , hence the incident wave is totally absorbed by the metasurface. The angle θ ′ increases with the order N , and the range of the incidence angles at which absorption is effective ( V ≪ 1 ) decreases.
The surface with the normal impedance ( N = 0 ) absorbs the normally incident wave at any value of Z ~ N , but total absorption at the certain angle is possible only if Z ~ N ≥ 1 . This is the main difference between normal and tangential impedances.
Under the gliding incidence, when θ → π / 2 , all metasurfaces behave like a soft boundary, because the reflection coefficient V → − 1 . As one can see in Figure 3 the function V ( θ ) at θ ≈ π / 2 is the same for any order of the multiplicity N and impedance Z ~ N .

4.2. Diffuse Field Absorption

Let us consider sound absorption by the metasurfaces. The absorption coefficient of the plane wave is α = 1 − V 2 and can be found using (30). The considered metasurface can completely absorb the incident wave at a certain angle. In case of a diffuse sound field the absorption coefficient should be averaged over angle. So, the diffuse absorption coefficient is
α d = 2 π ∫ 0 π 2 α d θ .
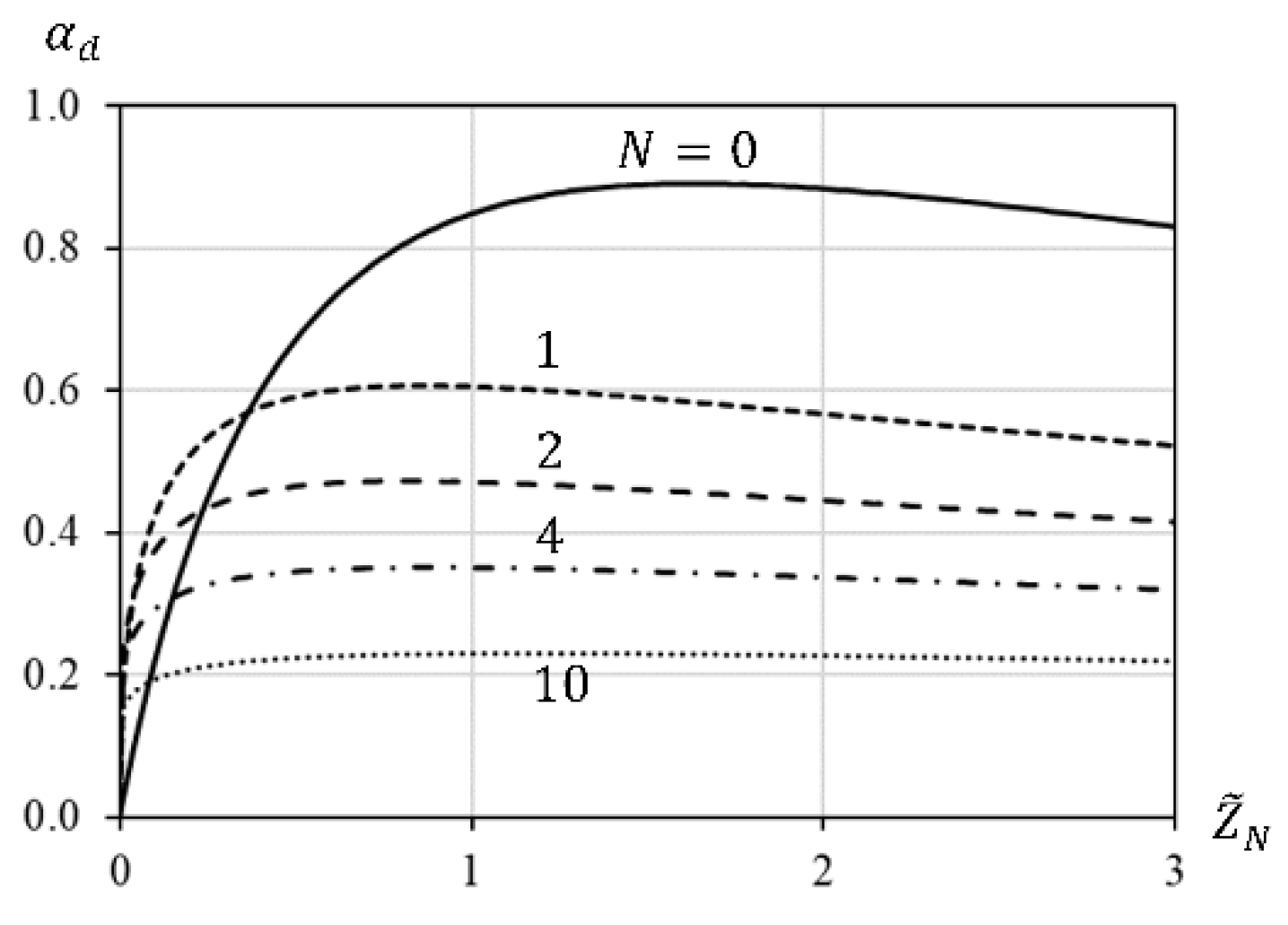
Figure 4 presents the calculation of the diffuse absorption coefficient α d for the real values of the impedance Z ~ N and different orders N . If the impedance is close to zero the absorption coefficient is about zero as well. All curves have a maximal, therefore the impedance of the metasurfaces can be optimized to provide maximal absorption. After the maximum the absorption coefficient slowly decreases with increase of Z ~ N .The maximums of the curves in Figure 4 are not sharp peaks, so, efficiency of sound absorption has values close to maximal one in a wide range of Z ~ N .
The fundamental difference of the metasurfaces formed by the scatterers of different order N is that the sound absorption decreases with the increase of the order N . For example, the absorption coefficient is only about 0.2 for N = 10 . Also, it is clear form Figure 3, where we can notice that the reflection coefficient is V ≈ 1 for the incidence angles θ < π / 4 .

4.3. Optimal Impedance

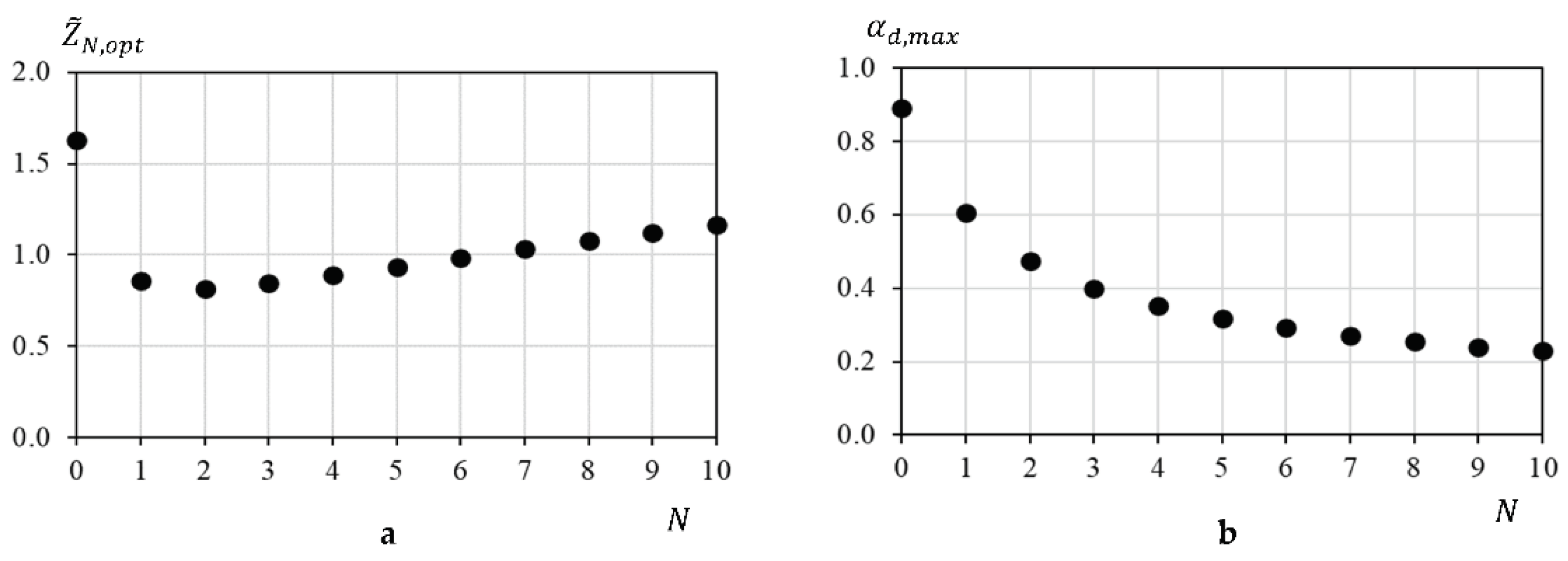
Figure 4 shows that sound absorption can be maximized. The optimal impedance is found from the equation d α d / d Z ~ N = 0 , which gives the optimal values Z ~ N , o p t for the metasurface formed by the N -pole resonators. They are shown in Figure 5a. For the monopole resonators the optimal impedance is Z ~ 0 , o p t = 1.63 , whereas for N ≥ 1 it has the values Z ~ N , o p t ≈ 1 . This simple approximation can be used for rough estimation of absorption provided by the metasurface.
The maximal absorption coefficient is α d , m a x = α d ( Z ~ N , o p t ) , which is shown in Figure 5b. The found values α d , m a x decrease with the order N . For N ≥ 2 the absorption coefficient is less than 0.5. We can state that the sound absorbing properties of the metasurfaces decrease with the order of multiplicity.

5. Discussion

The acoustic properties of a rigid surface covered with ae periodic array of linear multiple scatterers are analyzed. First of all, the sound field scattered from the surface with the scatterers is found analytically. If the distance between the scatterers is less than half of a wavelength, the scattered field is just the plane wave whose direction coincides with that of the plane wave reflecting from the rigid surface. This means that at far distances a reflection coefficient can be used to calculate the sound field and a homogenized boundary condition can be imposed on the surface. The found dependence of the reflection coefficient on the incidence angle can not be obtained using an ordinary impedance if the order of the multiple scattering is 1 or greater. In this case, a special boundary condition is required to match the exact solution, which is a tangential impedance (29) that depends on the multiple order. Due to the unusual homogenized boundary condition the surfaces with the resonators are referred to metasurfaces.
The equivalent boundary condition for a metasurface formed by the   N -pole scatterers is the ratio of a derivative of the sound pressure of the order 2 N along the metasurface to its normal velocity. This type of boundary conditions is known as a high order impedance boundary condition. The tangential impedance (29), given in a simple form, can be used to describe surfaces with complex microstructures for the study of acoustic metasurfaces.
Resonant scatterers are of particular interest. If a multipole scatterer is the resonator, there is frequency at which a sum of the image parts of its impedance and the radiation impedance is zero, and the equivalent impedance is real. This situation is analyzed and the optimal impedance as well as the maximum absorption coefficient for a diffuse sound field are found. With increase of the multiple order of the resonators the absorption efficiency decreases. It means that the metasurfaces made up of the high order multiple resonators are not effective absorbers.
The proposed high order multiple metasurfaces exhibit interesting acoustic properties that can be applied to and studied in various problems. Examples may include the attenuation of sound waves propagating in ducts or enclosed spaces, as well as the control of sound fields scattered by various obstacles.

Funding

This research received no external funding.

Data Availability Statement

Not applicable.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Auriault, J.-L.; Boutin, C., Geindreau, C. Homogenization of Coupled Phenomena in Heterogenous Media; ISTE Ltd and John Wiley & Sons, Inc.: London, UK and Hoboken, USA, 2009.
  2. Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602(R). [CrossRef]
  3. Burov, V.A.; Dmitriev, K.V.; Sergeev, S.N. Acoustic double-negative media. Acoust. Phys. 2009, 55, 298–310. [CrossRef]
  4. Foldy, L.L. Multiple scattering of waves. Phys. Rev. 1945. 67. 107-119. [CrossRef]
  5. Mironov, M. The dipole resonator and dipole waveguide insulator in dense liquid medium. Acoustics 2022, 4, 469-478. [CrossRef]
  6. Fedotovskii, V.C. A porous medium as an acoustic metamaterial with negative inertial and elastic properties. Acoust. Phys. 2018, 64, 548-554. [CrossRef]
  7. Golub, M.V.; Moroz, I.A.; Wang, Y.; Khanazaryan, A.D.; Kanishchev, K.K.; Okoneshnikova, E.A.; Shpak, A.N.; Mareev, S.A.; Zhang, C. Design and manufacturing of the multi-layered metamaterial plate with interfacial crack-like voids and experimental-theoretical study of the guided wave propagation. Acoustics 2023, 5, 122-135. [CrossRef]
  8. Ma, G., Sheng, P. Acoustic metamaterials: From local resonances to broad horizons. Sci. Adv. 2016, 2, 1501595. [CrossRef]
  9. Du, Y.; Wu, W.; Chen, W.; Lin, Y.; Ghi, Q. Control the structure to optimize the performance of sound absorption of acoustic metamaterial: A review. AIP Advances 2021, 11, 060701. [CrossRef]
  10. Schwan, L.; Umnova, O.; Boutin, C. Sound absorption and reflection from a resonant metasurface: Homogenisation model with experimental validation. Wave Motion 2017, 72, 154–172. [CrossRef]
  11. Wang, X.; Dong, R.; Li, Y.; Jing, Y. Non-local and non-Hermitian acoustic metasurfaces. Rep. Prog. Phys. 2023, 86, 116501. [CrossRef]
  12. Kanev, N.G.; Mironov, M.A. Dipole resonance scatterer of sound. Acoust. Phys. 2003, 49, 312–315. [CrossRef]
  13. Kanev, N. Resonant metasurfaces with a tangential impedance. Acoustics 2022, 4, 903-914. [CrossRef]
  14. Sabat, R.; Pennec, Y.; Lévêque, G.; Torrent, D.; Ding, C.; Djafari-Rouhani, B. Single and coupled Helmholtz resonators for low frequency sound manipulation. J. Appl. Phys. 2022, 132, 064505. [CrossRef]
  15. Melnikov, A., Chiang, Y.K., Quan, L. et al. Acoustic meta-atom with experimentally verified maximum Willis coupling. Nat Commun. 2019, 10, 3148. [CrossRef]
  16. Lapin, A.D. Monopole-dipole type resonator in a narrow pipe. Acoust. Phys. 2003, 49, 731-732. [CrossRef]
  17. Kanev, N.G.; Mironov, M.A. A Monopole–dipole resonance absorber in a narrow waveguide. Acoust. Phys. 2005, 51, 89–94. [CrossRef]
  18. Lapin, A.D.; Mironov, M.A. Sound absorption by a planar array of monopole-dipole scatterers. Acoust. Phys. 2006, 52, 425-428. [CrossRef]
  19. Lapin, A.D. Sound absorption by monopole-dipole resonators in a multimode waveguide. Acoust. Phys. 2005, 51, 362-364. [CrossRef]
  20. Kanev, N.G. Tangential impedance. Acoust. Phys. 2023, 69, 278-282. [CrossRef]
  21. Dauchez, N.; Li, K.; Nennig, B. On the use of structured poroelastic materials for noise control at low frequency. In Proceedings of Forum Acusticum, Turin, Italy, 11-15 September 2023. [CrossRef]
  22. Qi, Y.; Qiu, C.; Xiao, M.; He, H.; Ke, M.; Liu, Z. Acoustic realization of quadrupole topological insulators. Phys. Rev. Lett. 2020, 124, 206601. [CrossRef]
  23. Fan, H.; Gao, H.;, Liu, T.; An, S.; Kong, X.; Xu, G.; Zhu, J.; Qiu, C.W.; Su, Z. Reconfigurable topological modes in acoustic non-Hermitian crystals. Phys. Rev. B 2023, 107, L201108. [CrossRef]
  24. Guild, M.D.; Alu, A.; Haberman, M.R. Cancellation of acoustic scattering from an elastic sphere. J. Acoust. Soc. Am. 2011, 129, 1335-1365. [CrossRef]
  25. Liu, M.Y.; Li, P.; Du, Q.J.; Peng, P. Reflected wavefront manipulation by acoustic metasurfaces with anisotropic local resonant units. Europhys. Lett. 2019, 125, 54004. [CrossRef]
  26. Xue, H.; Ge, Y.; Sun, HX. et al. Observation of an acoustic octupole topological insulator. Nat. Commun. 2020, 11, 2442. [CrossRef]
  27. Zhang, W.; Zou, D.; Bao, J. et al. Topolectrical-circuit realization of a four-dimensional hexadecapole insulator. Phys. Rev. B 2020, 102, 100102. [CrossRef]
  28. Liu, D.; Hao, L.; Zhu, W.; Yang, X.; Yan, X.; Guan, C.; Xie, Y.; Pang, S.; Chen, Z. Recent Progress in Resonant Acoustic Metasurfaces. Materials 2023, 16, 7044. [CrossRef]
  29. Chen, Y.-F.; Chen, Z.-G.; Ge, H. et al. Various topological phases and their abnormal effects of topological acoustic metamaterials. Interdiscip. Materials 2023, 2, 179–230. [CrossRef]
  30. Zabihi, A.; Ellouzi, C.; Shen, C. Tunable, reconfigurable, and programmable acoustic metasurfaces: A review. Front. Mater. 2023, 10, 1132585. [CrossRef]
  31. Arabadzhi, V.V. Absorption of long waves by linear structures. Acoust. Phys. 2010, 56, 996-1003. [CrossRef]
  32. Landau, L.D.; Lifshitz, E.M. The classical theory of fields, 3rd ed.; Pergamon Press: Oxford, New York, Toronto, Sydney, Paris, Braunschweig, 1971.
  33. Senior, T. B. A.; Volakis, J. L. Approximate boundary conditions in electromagnetics; Inst. Elect. Eng.: London, UK, 1995.
  34. Rahmat-Samii, Y.; Daniel, J.H. Impedance boundary conditions in electromagnetics; Taylor & Francis: Boca Raton, London, New York, 1995.
Preprints 101419 g001
Figure 1. Physical models of the multiple sound scatterers with the orders N = 0,1 , 2,3
Figure 1. Physical models of the multiple sound scatterers with the orders N = 0,1 , 2,3
Preprints 101419 g001
Preprints 101419 g002
Figure 2. An array of linear multiple scatterers near a rigid surface.
Figure 2. An array of linear multiple scatterers near a rigid surface.
Preprints 101419 g002
Preprints 101419 g003
Figure 3. The reflection coefficients of the metasurface in dependence on the incidence angle for Z ~ N = 1 / 5 (a), Z ~ N = 1 (b), Z ~ N = 5 (c) and orders N = 0 ,   1 ,   2 ,   4 ,   10 .
Figure 3. The reflection coefficients of the metasurface in dependence on the incidence angle for Z ~ N = 1 / 5 (a), Z ~ N = 1 (b), Z ~ N = 5 (c) and orders N = 0 ,   1 ,   2 ,   4 ,   10 .
Preprints 101419 g003
Preprints 101419 g004
Figure 4. The diffuse absorption coefficient of the metasurfaces formed by the resonators with the orders N
Figure 4. The diffuse absorption coefficient of the metasurfaces formed by the resonators with the orders N
Preprints 101419 g004
Preprints 101419 g005
Figure 5. The optimal impedance (a) and maximum absorption coefficient (b) of the metasurface in dependence on the order N
Figure 5. The optimal impedance (a) and maximum absorption coefficient (b) of the metasurface in dependence on the order N
Preprints 101419 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated