Prerpints.org logo
Preprint
Article

Enhancing Crop Yield Predictions with PEnsemble 4: IoT and ML-Driven for Precision Agriculture

Altmetrics

Downloads

132

Views

46

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

14 March 2024

Posted:

18 March 2024

You are already at the latest version

Alerts
Abstract
This paper presents the PEnsemble 4 model, a sophisticated machine learning framework that integrates IoT-based environmental data to accurately forecast maize yield. With the projected significant growth in global maize demand over the next decade, the inherent risks posed by the crop’s dependence on weather conditions necessitate improved prediction capabilities. The PEnsemble 4 model, developed with high accuracy, incorporates comprehensive datasets encompassing soil attributes, nutrient composition, weather conditions, and UAV-captured vegetation imagery. By employing a combination of Huber and M estimates, the PEnsemble 4 model effectively analyzes temporal patterns in vegetation indices, specifically CIre and NDRE, which serve as reliable indicators of canopy density and plant height. In addition, this research significantly contributes to precision agriculture by offering an efficient and sustainable alternative to conventional farming practices through precise yield predictions. Notably, the PEnsemble 4 model enables earlier estimation, advancing the timeline for yield prediction from the conventional day 100 in the R6 stage to day 79 in the R2 stage. This improvement enhances decision-making processes in farming operations. The remarkable accuracy rate of 91% underscores the importance of adopting a multifaceted data approach that harnesses IoT-derived environmental insights. Additionally, the PEnsemble 4 model extends its benefits beyond yield prediction, facilitating the detection of water and crop stress, as well as disease monitoring in broader agricultural contexts. Ultimately, the PEnsemble 4 model establishes a new standard in maize yield prediction, revolutionizing crop management and protection through the synergistic utilization of IoT and machine learning technologies.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Maize plays a vital role in global cereal markets and its demand continues to increase, particularly for animal feed purposes. The main import destinations for maize include Mexico, the European Union, Japan, Egypt, and Vietnam. Thailand is also an importer of maize, primarily for the food industry[1]. However, one of the main challenges in maize production is productivity, as domestic supplies often do not meet demand. Several factors affect maize productivity, such as water availability, seed quality, weather conditions, pests, diseases, soil management, and fertilizer nutrient content. Plant diseases [2] such as downy mildew and common rust, as well as pests such as corn armyworm[3,4,5] can significantly affect maize yields, leading to global supply and price fluctuations. Prediction of grain yield [6] is a critical process to estimate the amount of grain that a specific crop will produce. It assists in optimizing crop production, aiding decisions related to planting, fertilization, and harvest. Various methods are employed for grain yield prediction, including statistical modeling, machine learning algorithms, and crop simulation models. Statistical models utilize historical data on crop yields and weather patterns to forecast future yields. Machine learning algorithms, on the other hand, can be trained on historical data and use multiple variables, such as weather data, soil quality, and management practices, to make predictions. Crop simulation models employ complex mathematical equations to simulate crop growth and development based on inputs such as weather data, soil properties, and crop management practices. These models enable yield predictions under different scenarios, facilitating informed decision-making for farmers and agronomists regarding crop management strategies. Accurate prediction of grain yields requires precise data collection, robust statistical and mathematical models, and expert knowledge of crop management practices. Grain yield prediction is the process of estimating the grain production of a specific crop, considering diverse factors like weather conditions, soil quality, seed variety, and management practices [7]. This information is crucial for farmers and agricultural organizations as it optimizes crop production [8] and guides decisions on planting, fertilization, and harvest. Numerous methods exist for predicting grain yield, such as statistical modeling, machine learning algorithms [9], and crop simulation models.
Statistical models utilize historical data on crop yields and weather patterns to anticipate future outcomes. Meanwhile, machine learning algorithms can be trained on historical data to make predictions based on a wide array of variables, encompassing weather data, soil quality, and management practices. On the other hand, crop simulation models employ intricate mathematical equations to simulate crop growth and development over time. By utilizing inputs like weather data, soil properties, and crop management practices, these models can forecast grain yields under various environmental and management scenarios. This valuable information aids farmers and agronomists in making well-informed decisions about crop management.
In conclusion, achieving accurate grain yield predictions necessitates the amalgamation of precise data collection, robust statistical and mathematical models, and expert knowledge of crop management practices. By leveraging these tools, the agricultural sector can enhance productivity and adapt to changing conditions, ultimately contributing to global food security.
Through extensive analysis of existing literature, it has become evident that a significant research gap exists in the domain of crop health prediction. Current studies predominantly rely on publicly available datasets and utilize deep computer vision techniques to forecast the health of diverse crops. However, these studies primarily prioritize optimizing algorithmic accuracy, often overlooking the crucial aspect of real-time applications. As a result, there is an urgent need to develop a solution that allows for the real-time monitoring and detection of factors that directly impact crop health throughout their life cycle.
In the realm of modern agriculture [10], the precise prediction of grain yield stands as a paramount concern. Accurate forecasts not only hold the key to optimizing crop production but also reducing wastage, thus ensuring the sustainability of our food systems. While various methods have been employed to address this critical need, there remains a noticeable gap in harnessing the full potential of emerging technologies.
This research embarks on a mission to fill this void by presenting a groundbreaking approach that leverages the combined power of the IoT and AI. [11,12] Our innovative system stands as a pioneering solution that stands to revolutionize the agricultural landscape.
At its core, the research aims to tackle the following core objectives:
  • Continuous Crop Monitoring: Our research seeks to create a continuous monitoring system that offers real-time insights into a multitude of environmental and crop-specific parameters. By integrating IoT devices into agricultural practices, we enable the collection of dynamic data, enabling farmers and agronomists to have an unobstructed view of their crops’ health and growth.
  • Precise Predictive Modeling: The heart of our research lies in the utilization of advanced AI models. These models are designed to analyze the IoT-derived data with precision, providing timely and accurate information about crop health and growth trajectories. This, in turn, empowers stakeholders to implement targeted interventions, thereby optimizing resource allocation and bolstering crop quality.
In essence, our research stands as a testament to the transformative potential of the synergy between IoT and AI technologies. By bridging the existing gap in crop health prediction, we endeavor to usher in an era of precision agriculture. We envision a future where farmers and agronomists can make informed decisions that not only enhance crop growth but also foster a more sustainable and productive agricultural sector.

1.1. Our Main Contribution

To the best of the authors’ knowledge, this paper presents a novel and comprehensive approach that significantly differs from existing works in predicting crop yields. While previous studies have explored various methodologies, such as statistical modeling [7], and deep learning techniques [13,14], none have integrated multi-temporal images and machine learning algorithms in the manner proposed here.
By integrating remote sensing data with machine learning techniques, our study offers a practical and innovative framework for forecasting crop yields. The incorporation of multi-temporal images allows for a holistic understanding of crop growth patterns and their response to changing environmental conditions over time, enabling more precise predictions.
By harnessing the power of various vegetation indices and employing machine learning algorithms, our research achieves remarkable accuracy in forecasting crop yields. This advancement holds significant implications for enhancing global food security and optimizing crop management practices, as it empowers farmers with valuable insights for making informed decisions.
Moreover, our study contributes to the expanding body of research on the integration of machine learning and remote sensing in agriculture, emphasizing the importance of interdisciplinary collaborations between the fields of agriculture and technology. This interdisciplinary synergy has the potential to revolutionize agricultural practices and pave the way for a more sustainable and productive future in the face of increasing challenges in the agricultural sector.
The objectives of our study can be summarized as follows:
  • To study factors impacting the life cycle of maize, including the pre-planting stage, growth stage, and post-production stage in maize fields.
  • To collect and analyze environmental factors, including evapotranspiration, rain rate, wind speed, temperature, humidity, NPK nutrients, pH.
  • To calculate 12 vegetation indices, including Chlorophyll index green (CIgr), Chlorophyll index red edge (CIre), enhanced vegetation index 2 (EVI2), green normalized difference vegetation index (GNDVI), modified Chlorophyll absorption ratio index 2 (MCARI2), modified triangular vegetation index 2 (MTVI2), normalized difference red edge (NDRE), normalized difference vegetation index (NDVI), normalized difference water index (NDWI), optimized soil-adjusted vegetation index (OSAVI), renormalized difference vegetation index (RDVI), red–green–blue vegetation index (RGBVI) with multispectral imagery from unmanned aerial vehicles (UAVs) equipped with multispectral cameras.
  • To predict the growth stage and productivity of maize using machine learning Regression techniques [15,16] including CatBoost Regression, Decision tree Regression, ElasticNet Regression, Gradient boosting Regression, Huber Regression, K-Nearest neighbors Regression (KNN), Lasso Regression, Linear Regression, M estimators, Passive aggressive Regression, Random forest (RF) Regression, Ridge Regression, Support vector Regression (SVR), XGBoost Regression algorithms.
The subsequent sections of this paper are structured as follows: In Section IV, we provide a comprehensive description of the materials and methods employed in our study, encompassing details about the study locations, climate conditions, soil characteristics, and agricultural practices. Section V elaborates on the specific approaches and techniques utilized. Moving forward, Section VI discusses the key findings of our research, highlighting both the strengths and limitations of the proposed approach while identifying potential avenues for future exploration. Finally, in Section VII, we summarize the principal conclusions of our study and outline the practical implications it holds for precision agriculture and sustainable crop management.

2. Materials and Methods

2.1. Study Area

In the study, the planting area is located in the Manorom District, Chai Nat, encompassing a total area of 88,000 m 2 as shown in Figure 1. The planting period for this area is scheduled from January to May 2023. It is divided into the three following plots, i.e., Plot 1, Plot 2, and Plot 3, with areas of 24,000 m 2 , 33,600 m 2 , and 30,400 m 2 , respectively. In total, these three plots comprised 5,337 blocks, with each block measuring 4.5×4.5 square meters. To predict grain yield, an ROI consisting of 270 blocks was selected for analysis. In the analysis, the total productivity for the three plots mentioned was considered.

2.2. Unmanned Aerial Vehicle (UAV) Data Acquisition

The DJI phantom 4 multispectral (P4M) quadcopter, equipped with six sensors, including an RGB sensor with 2.08 megapixels, Blue sensor (450 nm ± 16 nm), Green sensor (560 nm ± 16 nm), Red sensor (650 nm ± 16 nm), Red edge sensor (730 nm ± 16 nm), and Near-infrared sensor (840 nm ± 26 nm), is utilized to capture multispectral images. The flight missions of the unmanned aerial vehicle (UAV) are conducted using DJI GS Pro software, with specific settings applied: a speed of 3.2 milliseconds, a shutter interval of 2 seconds, a front overlap ratio of 75%, a side overlap ratio of 75%, and a course angle of 119 degrees at flight altitudes of 30 m and 100 m. To minimize the impact of varying sunlight angles, the UAV flights are scheduled between 10:00 am and 12:00 pm.
With our aim, we would like to address which stages are mutually correlated with the width of the seed of our approach. The observations of maize growth continue every week during the growth of the plant in a total of 17 flight missions of the total plant plan in 115 days, since the details of the flights are provided in Table 1. RGB and multispectral images are acquired for flight altitudes of 30 m and 100 m starting with day one on 11 January 2023 for the VE stage. After days 8 of maize growth, the leaf started to appear from one leaf to ten on days 56. Sufficient moisture is essential between stage V6 - V10 on days 30 to 60, and prolonged drought can lead to a potential yield decrease of up to 25%. In stage V10 to stage of tasseling (VT), which is completely visible when the plant has reached its full height and will begin to shed its pollen on days 55- 60. Nutrients and water are in high demand to meet growth needs. Insect and hail injury can reduce the number of kernels that develop. Therefore, we decide to start fertilizing the soil with precision fertilizer technology. R1 on days 65 is the silking stage, which is one of the most critical stages in determining the yield potential. Physiological maturity can be estimated by adding 50 to 55 days from the silking date. Stage R2 on days 73 of maize growth to blistering. Moisture in the soil and weather stress are critical because drought conditions can reduce the potential yield by up to 50% or 60% per day during a drought. On days 85, the kernels begin to yellow outside and contain a milky white inner fluid known as stage R3. After stage R3, many leaves change from green to yellow, indicating that the kernels begin to gain dry weight and size and have a "doughy" consistency in stage R4. Around days 100 in stage R5, known as dent stage, the kernels begin to dry out and have a dented appearance. Weather stress at this point will reduce kernel weight, but not kernel number. R6 as maturity stage on days 113, all kernels have reached maximum dry weight. The husks and many leaves are no longer green. The farmer uses between the stages R5 and R6, on days 100 - 110, to estimate the production yield. Ground control points (GCPs) are captured during all flights and used as references to create image mosaics, ensuring consistency and facilitating comparison between images captured on different dates. The resulting mosaic images have a ground sampling distance (GSD) of 0.016 m and 0.053 m for flight altitudes of 30 m and 100 m, respectively. These images undergo processing to maintain consistency across all images acquired during different stages of growth.

2.3. Image Processing

The RGB and multispectral (MS) images undergo pre-processing using DJI Terra, a photogrammetry software developed in Shenzhen, China. Red, blue, green, NIR, red edge, and RGB in each wavelength are used to process. For flight altitude 30 m, collect 3,172 ".tif" files for plot 1 in each flight and 835 ".tif" files with flight altitude 100 m for plots 1, 2, and 3. The data sets of the.tif file images to process are 53,924 with flight altitude 30 m and 14,195 with flight altitude 100 m. This software utilizes scene illumination, reference panels, and sensor specifications to automatically generate orthomosaic images in ".tif" format from both datasets. This preprocessing step is crucial for improving the radiometric quality of orthomosaic images. Additionally, surface reflectance imagery is generated from the multispectral camera and vegetation index (VI) images are created under consistent lighting conditions to facilitate better data comparisons. DSM (Digital Surface Model) data in ".tif" format is obtained from the RGB images using DJI Terra. The raw data types, orthomosaic images and DSM data are subsequently processed to extract digital traits, as depicted in Figure 2.

2.3.1. Vegetation Indices

The present study utilizes multispectral surface reflectance images to estimate grain yield by generating twelve commonly used vegetation indices (VIs) in agriculture as shown in Table 2 including Chlorophyll index green (CIgr), Chlorophyll index red edge (CIre), Enhanced vegetation index 2 (EVI2), Modified chlorophyll absorption ratio index 2 (MCRI2), Modified triangular vegetation index 2 (MTVI2), Normalized difference red edge (NDRE), Normalized difference vegetation index (NDVI), Normalized difference water index (NDWI), Optimized soil-adjusted vegetation index (OSAVI), Renormalized difference vegetation index (RDVI) and Red–Green–Blue vegetation index (RGBVI). To remove the influence of the soil surface from each VI image, a soil mask layer is created using the soil-adjusted vegetation index. The polygons defining each plot consist of 270 subplots (4.5×4.55 m per subplot) and are digitized in a shape file (*.shp) format using the open-source software quantum GIS (QGIS, version 3.28.3-Firenze). Harvested ground reference data from the same area are employed to estimate the canopy volume (CV) based on the subplot polygons. Subsequently, the plot segmentation shape files are imported into the developed algorithm. Image features such as maximum (Max), average (Mean), sum, standard deviation, 95 th percentile, 90 th percentile, and 85 th percentile (representing the highest data values extracted after removing 5%, 10%, and 15% of the data following the soil subtraction process from the VI images, respectively, referred to as 95P, 90P, and 85P) are extracted for each subplot within each VI image. These features are computed using the Python libraries NumPy and Rasterstats. During the plot segmentation creation process, these feature data are labeled and subsequently exported as a comma-separated values (CSV) file.

2.3.2. Canopy Height Model from Digital Surface Model

In this study, the authors utilize a canopy height model (CHM) [27] to estimate the height of the crops within each subplot. To accomplish this, they employ QGIS software to create a digital terrain model (DTM) that represents the topography of the field. By subtracting the digital surface model (DSM) data from the DTM, they generate the CHM using Python. To ensure accuracy, pixels with a height below a threshold of 0.05m are eliminated from the CHM image layer.
Subsequently, the CHM image layer is segmented using a plot segmentation shapefile, enabling the extraction of statistical data for each subplot. The authors then multiply the data for the crop coverage area by the corresponding CHM data to calculate the canopy volume (CV) for each subplot. This process is performed for all regions of interest (ROIs) in the study.

2.4. Optimal IoT Design and Ground Measurements

This paper emphasizes the vital role of soil properties and environmental data in understanding plant growth dynamics, encompassing factors like soil temperature, humidity, NPK nutrient levels, pH, electrical conductivity (EC), solar radiation, evapotranspiration, daily rain, rain rate, humidity, temperature, and wind speed. For comprehensive monitoring, we utilize a Vantage Pro2 weather station [28] from Davis Instruments Corporation, USA shown in Figure 3A., and the Soil Sensors Display Terminal Moisture Temperature EC PH NPK Soil Analyzer from Weihai JXCT Electronic Technology Co., Ltd., China [29] shown in Figure 3B.
In our study, we detail the circuit design for our soil health monitoring system and the network transmission process depicted in Figure 3C. The prototype system with the Smart Trap for insect monitoring illustrated in Figure 3D. Our research utilizes these IoT-based ground measurements [30] to gain insights into the interplay between soil properties, environmental variables, and plant growth dynamics. Specifically, we develop IoT devices tailored for measuring soil parameters, including pH, NPK levels, EC, moisture, and location with low-power transmission LoRaWAN technique [31].
For data collection, our IoT devices are programmed to send and retrieve data at five-minute intervals over seven days, powered by a 3.7V 3000mAh battery. Covering approximately 2 kilometers, our system ensures comprehensive data collection within the plant’s vicinity. The experimental setup features a LoRa Gravitech S767 microcontroller from CAT Telecom, Thailand, which instituting the LoRa WAN network for seamless data transmission. Simultaneously, an Arduino Nano interfaces with soil sensors via RS485 communication, incorporating location data for precision (latitude and longitude from Tiny GPS).
Expanding our focus, the research includes smart trap monitoring and insect counting using a Raspberry Pi controller and advanced object detection techniques such as YOLOv5 shown in Figure 3D. The integrated approach empowers real-time decision-making in precision agriculture, minimizing chemical usage, promoting sustainable crop protection, and optimizing crop yield and quality.
This confluence of IoT technology, soil health monitoring, and smart trap monitoring provides invaluable data insights for agriculture, enabling proactive measures and seamless precision agriculture. Research, which stands as a beacon of progress, offers practical tools for informed, data-driven decision-making in crop management, fostering a future marked by sustainable and productive farming practices.

2.5. Machine Learning Methods for Grain Yield Predictions

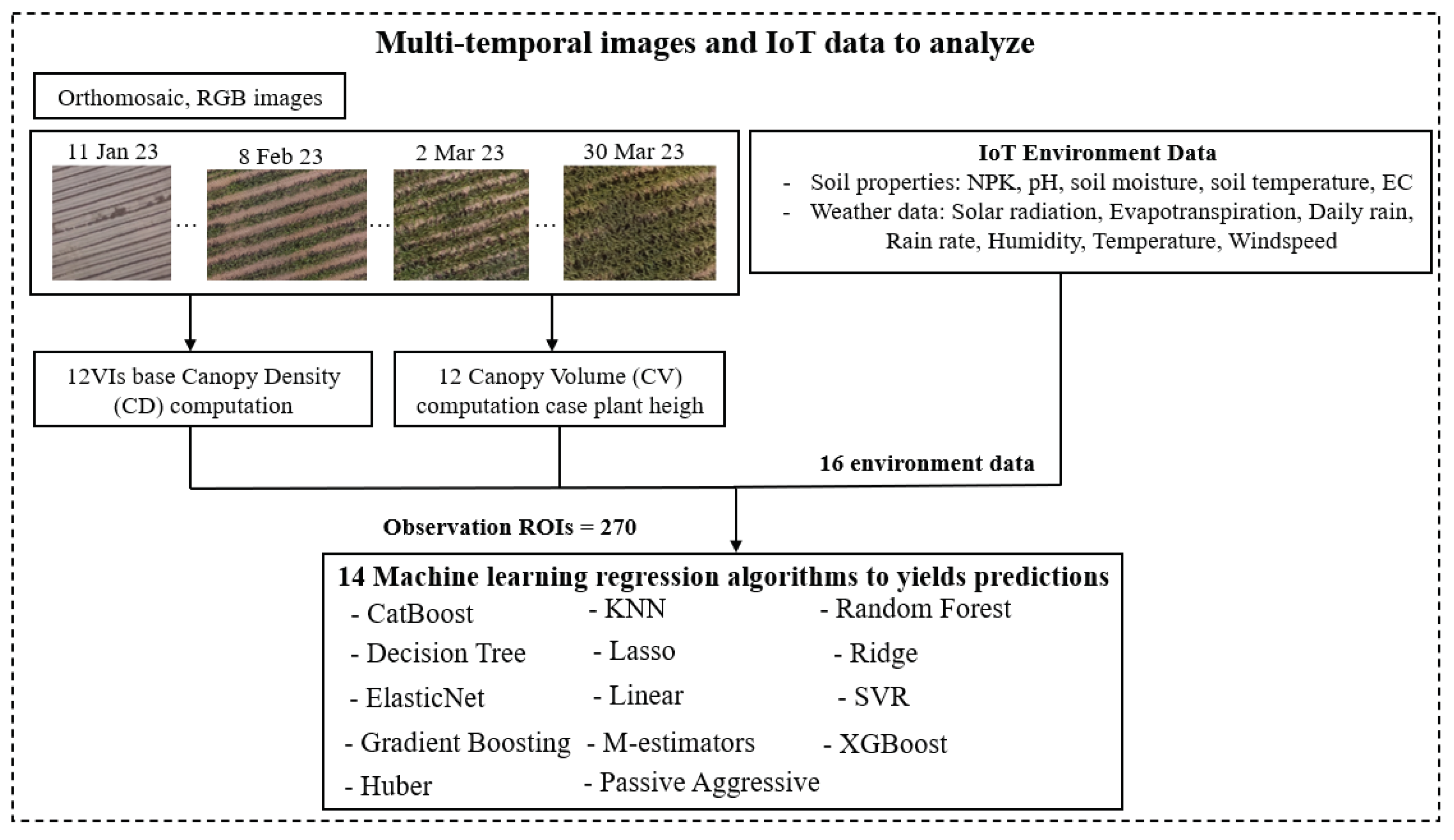
In this study, we present a comprehensive flow chart designed to predict crop yields using machine learning (ML) techniques, as depicted in Figure 4. The flow chart comprises two primary components: the first part involves the analysis of multi-temporal images, while the second part focuses on the utilization of ML algorithms for crop yield prediction.
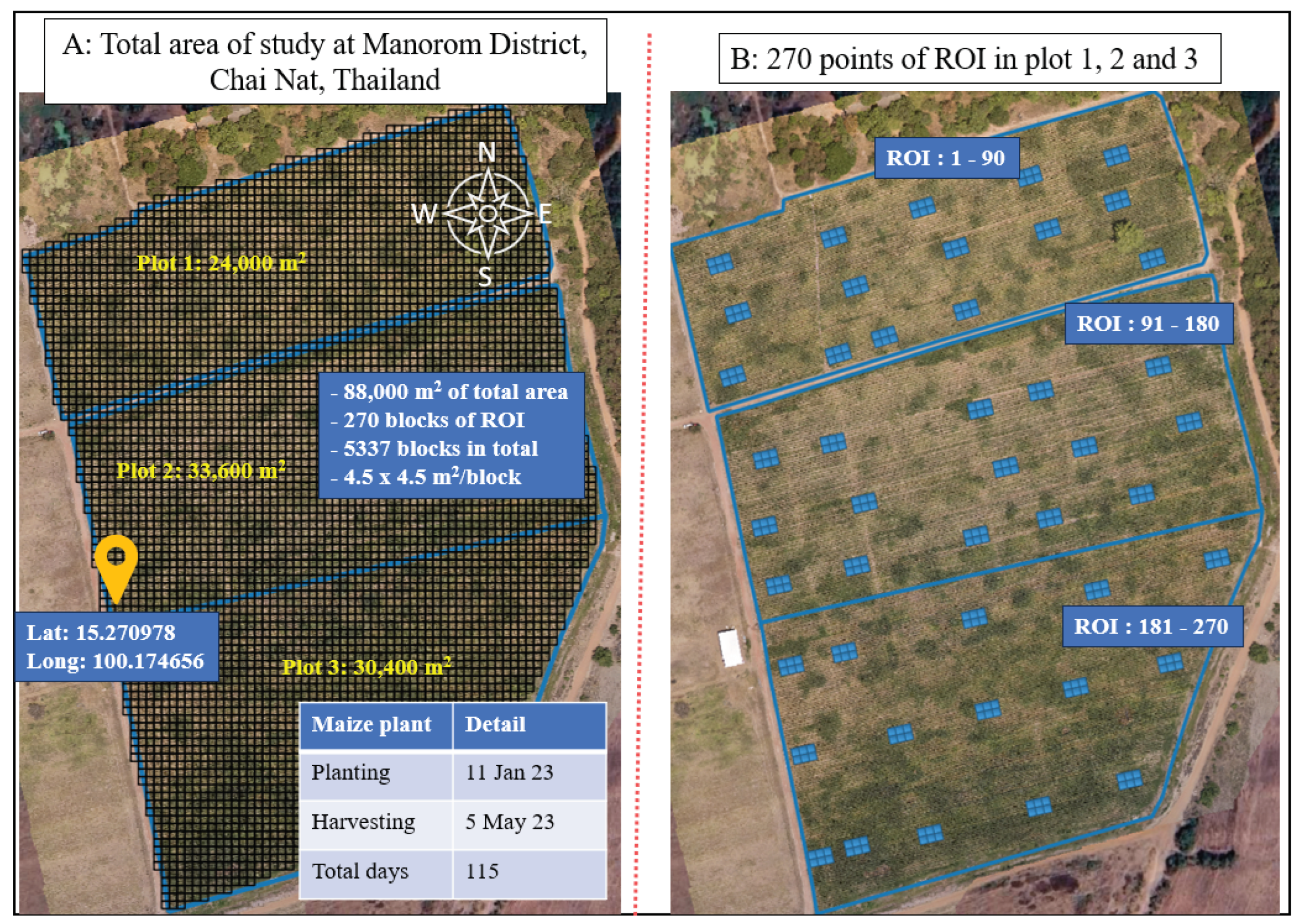
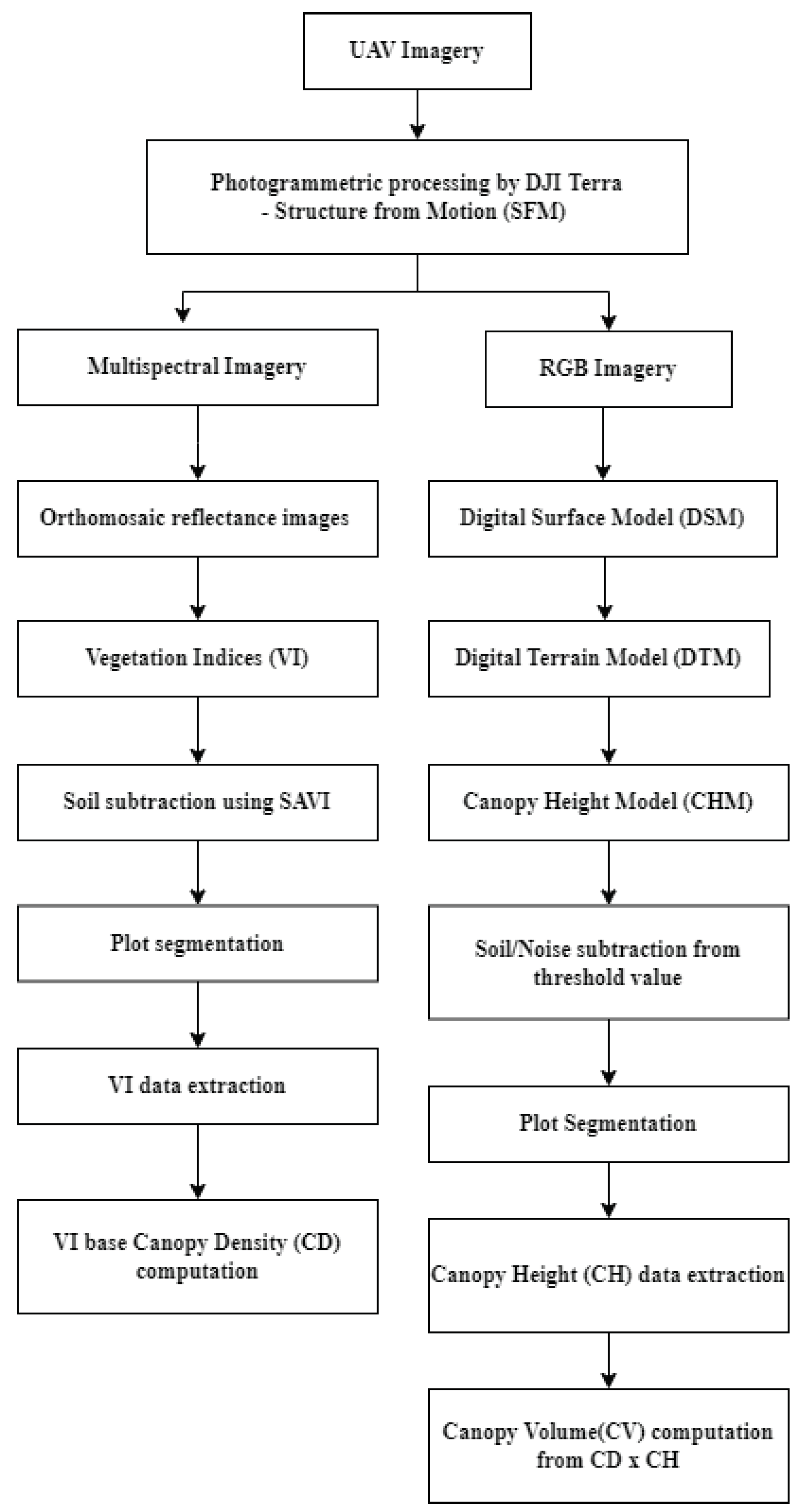
Within the first part of the diagram, multi-temporal images are subjected to thorough analysis, and various essential features are extracted. These features include vegetation indices and chlorophyll contents, among others. The imagery, spanning 17 different dates, is meticulously spliced together, incorporating precise geographic coordinates obtained through ground control points (GCPs) using standard procedures. This procedure results in the acquisition of 4,590 subsample plots (17 dates × 270 plots = 4,590) which are stitched 14,195 images from DJI Terra software as mentioned in the image processing section, each representing distinct regions of interest (ROI) within the agricultural fields. These sub-sample images of plot serve as the basis for computing VI-based canopy density, which facilitates the classification of pixels into two categories: green pixels and non-green pixels with potentially disruptive background elements, such as soil. By focusing only on green pixels, the values of twelve vegetation indices are computed for the sub-sample images. This information is then employed to establish linear relationships between chlorophyll contents, maize yields, and the vegetation indices.
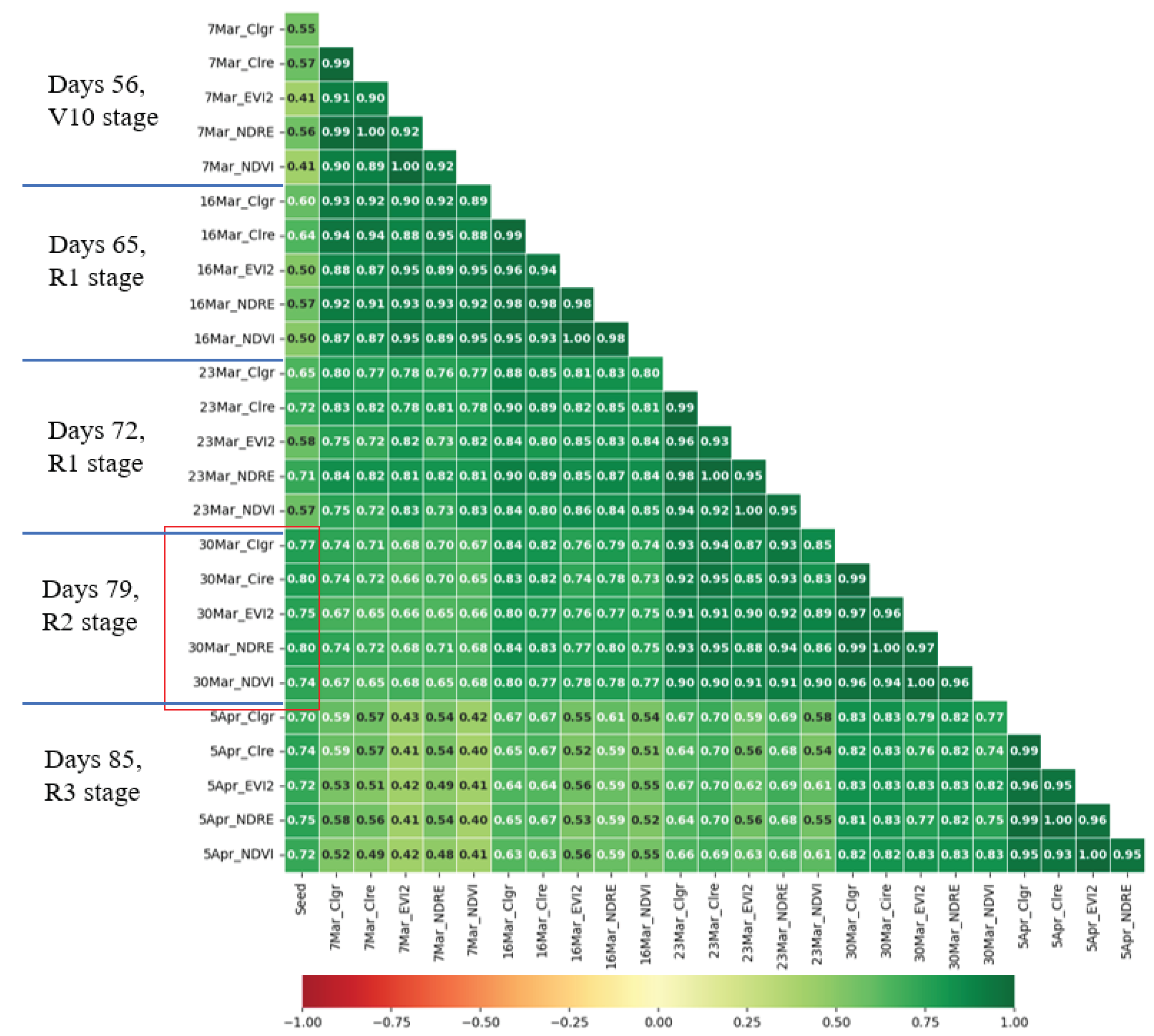
To assess the performance of the various vegetation indices during critical growth stages, we obtain the R-squared (R2) values. These R2 values serve as indicators of the predictive capabilities of the different vegetation indices. By identifying the most effective indices during important growth stages, we can gain valuable insights into growth monitoring and make more accurate yield predictions.
Overall, this flow chart offers a robust methodology for predicting crop yields by leveraging the power of machine learning and in-depth analysis of multi-temporal images. The extracted vegetation indices and their associations with chlorophyll contents and maize yields are vital in understanding the growth dynamics and making informed decisions in agricultural practices.
ML algorithms outperform and show great potential in various applications such as object detection, image classification, recognition patterns, computer vision, and other domains. In supervised learning, sample data are divided into training and testing sets to build non-linear relationships between independent and dependent variables. The effectiveness of trained models is assessed using test samples. Several machine learning algorithms such as backpropagation neural network (BP), support vector machine (SVM), random forest (RF), and extreme learning machine (ELM) can be used for supervised learning tasks such as classification and regression. XGBoost is also a gradient boosting algorithm that is used for both regression and classification tasks. LASSO is a regression method that performs feature selection using L1 regularization. A hybrid approach can use XGBoost and LASSO together for feature selection and model building. Many studies have evaluated BP, SVM, RF, ELM, LASSO, and XGBoost in remote sensing domains.
In this study, the authors utilized twelve vegetation indices (VIs) based on canopy density (CD), which were calculated from images collected over a long time series for each plot. These VIs served as independent variables, and the maize yields in each plot were used as dependent variables. Additionally, canopy volume (CV) was derived by multiplying CD with plant height. We utilized a diverse set of 14 machine learning algorithms to predict the growth stage and productivity of maize. These algorithms include CatBoost Regression, decision tree Regression, ElasticNet Regression, gradient boosting Regression, Huber Regression, K-nearest neighbors Regression (KNN), Lasso Regression, linear Regression, M estimators, passive-aggressive Regression, random forest (RF) Regression, Ridge Regression, support vector Regression (SVR), and XGBoost Regression. This investigation employed a diverse array of machine learning algorithms, each meticulously chosen for its distinct characteristics to thoroughly analyze multi-temporal satellite imagery data and forecast crop yields. Each model has the following characteristics:
Model 1 (CatBoost Regression): This algorithm was chosen for its adeptness in handling categorical features prevalent in such data. By employing ordered boosting and symmetric trees, CatBoost effectively captured temporal variations and seasonality patterns, ensuring a high level of predictive accuracy.
Model 2 (Decision Tree Regression): Selected to interpret the impact of different temporal features on crop yields, Decision Tree Regression leveraged its hierarchical structure to represent complex relationships within the data.
Model 3 (ElasticNet Regression): Addressing multicollinearity and performing feature selection simultaneously, ElasticNet Regression proved crucial for high-dimensional multi-temporal data. Its combination of L1 and L2 regularization techniques played a pivotal role in achieving these objectives.
Model 4 (Gradient Boosting Regression): Demonstrating efficacy in handling complex relationships and temporal dependencies, Gradient Boosting Regression built an ensemble of decision trees sequentially, enhancing predictive accuracy in the process.
Model 5 (Huber Regression): Chosen for its robustness in accommodating outliers prevalent in agricultural datasets, Huber Regression minimized the impact of extreme values through a parameter balancing Mean Absolute Error (MAE) and Mean Squared Error (MSE).
Model 6 (K-Nearest Neighbors Regression - KNN): Predicting grain yields based on similar multi-temporal patterns observed in the past, KNN Regression relied on the assumption that analogous temporal patterns yield similar crop yields. However, consideration of an appropriate k value and computational cost for larger datasets was warranted.
Model 7 (Lasso Regression): Serving as a feature selection technique, Lasso Regression incorporated L1 regularization to encourage some feature coefficients to be exactly zero, facilitating the identification of key temporal features.
Model 8 (Linear Regression): Providing a baseline model to understand the overall trend between crop yields and multi-temporal features, Linear Regression assumed a linear relationship, offering valuable insights into the general temporal trend of grain yield.
Model 9 (M Estimators): Chosen for their robustness in handling outliers and noise in agricultural datasets, M Estimators provided flexibility in choosing the loss function, making them suitable for data with non-Gaussian noise.
Model 10 (Passive Aggressive Regression): As an online learning algorithm, Passive Aggressive Regression adapted quickly to temporal changes in crop yield patterns, making it suitable for real-time predictions, particularly in rapidly evolving agricultural conditions.
Model 11 (Random Forest Regression - RF): Handling high-dimensional multi-temporal data, Random Forest Regression provided robust predictions by building multiple decision trees on different data subsets and averaging their predictions.
Model 12 (Ridge Regression): Beneficial when dealing with multicollinear features in multi-temporal data, Ridge Regression applied L2 regularization to stabilize the model and reduce the impact of multicollinearity.
Model 13 (Support Vector Regression - SVR): Chosen for its capability to capture non-linear relationships between multi-temporal features and crop yields, SVR mapped data into a higher-dimensional space, enabling the identification of non-linear patterns.
Model 14 (XGBoost Regression): Selected for its effectiveness in various regression tasks, XGBoost Regression constructed an ensemble of decision trees using gradient boosting and regularization techniques, offering high predictive accuracy.
Collectively, these machine learning algorithms formed a comprehensive toolkit for analyzing multi-temporal satellite imagery data and predicting crop yields, effectively addressing challenges such as handling outliers, feature selection, non-linearity, and temporal dependencies.
Selection of Best-suited Models:
The selection of the best-suited models depends on the specific characteristics of the multi-temporal imagery and the nature of the grain yield data. For instance, CatBoost Regression and Gradient Boosting Regression are well-suited to capture temporal patterns and seasonality effects. ElasticNet and Lasso Regression can be useful for feature selection when dealing with high-dimensional data. Huber Regression and M Estimators are appropriate for handling outliers in crop yield data. Given the variety of scenarios and combinations of variables explored in the study, it is crucial for researchers to carefully evaluate the performance of each algorithm using the specified evaluation metrics. This thorough evaluation process will enable them to identify the most effective models for predicting grain yield in their specific agricultural context, ultimately leading to more accurate and reliable predictions.
To evaluate the performance of these various algorithms, the authors used several metrics, including mean squared error (MSE), root mean square error (RMSE), mean absolute error (MAE), and R-squared ( R 2 ) as
M S E = 1 N ∑ i = 1 N ( y i − y ^ i ) 2 ,
R M S E = 1 N ∑ i = 1 N ( P i − M i ) 2 ,
M A E = ∑ i = 1 N | P i − M i | N ,
and
R 2 = 1 − ∑ i = 1 N ( y i − y ^ i ) 2 ∑ i = 1 N ( y i − y ¯ ) 2 ,
where N is the number of all samples, and M and P are the true values and predicted values of the yields, y i represents the actual values, y ^ i represents the predicted values, | · | represents the absolute value, and y ¯ represents the mean of the actual values, respectively. These metrics provide insights into the accuracy and predictive power of each algorithm in estimating the growth stage and productivity of maize.
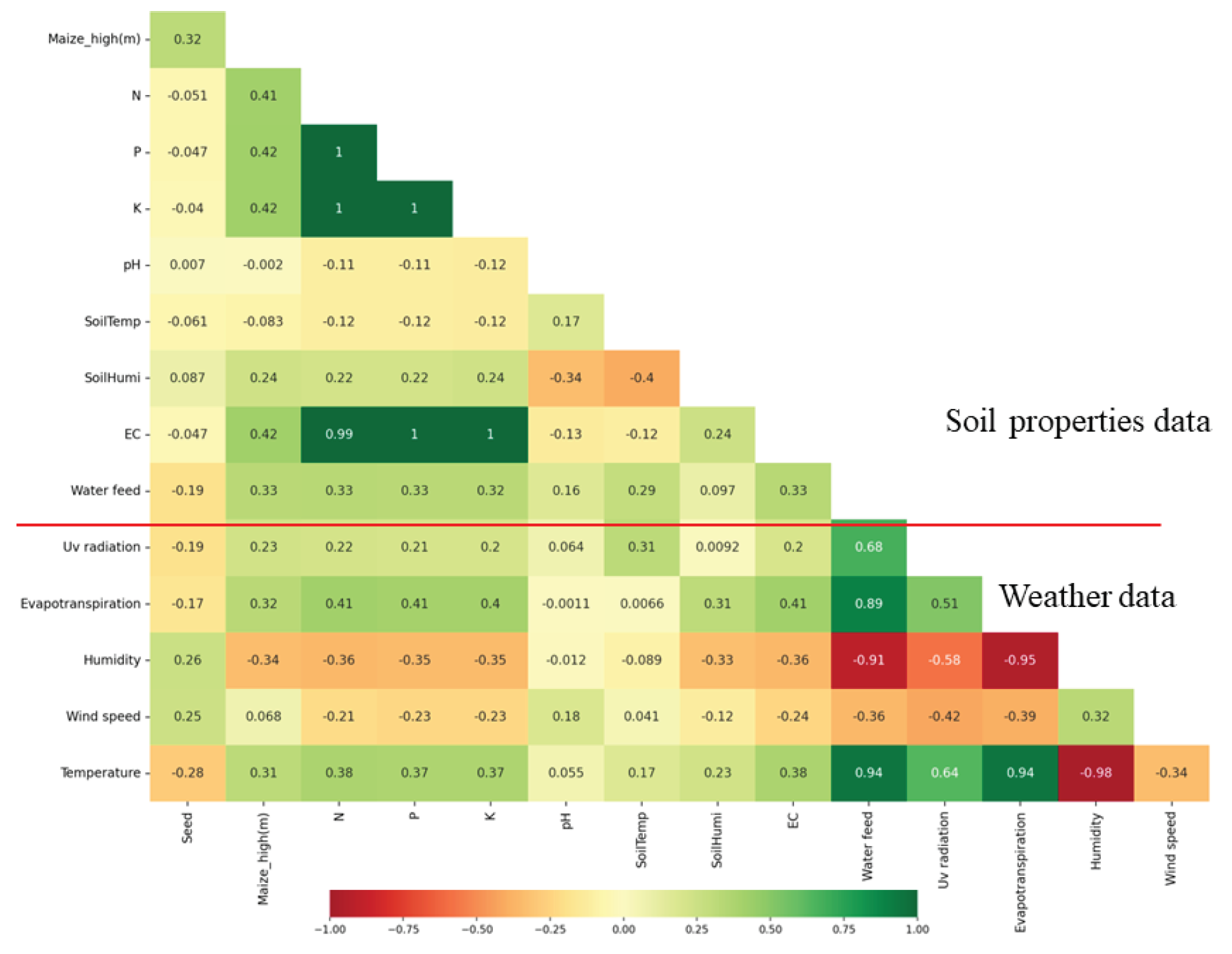
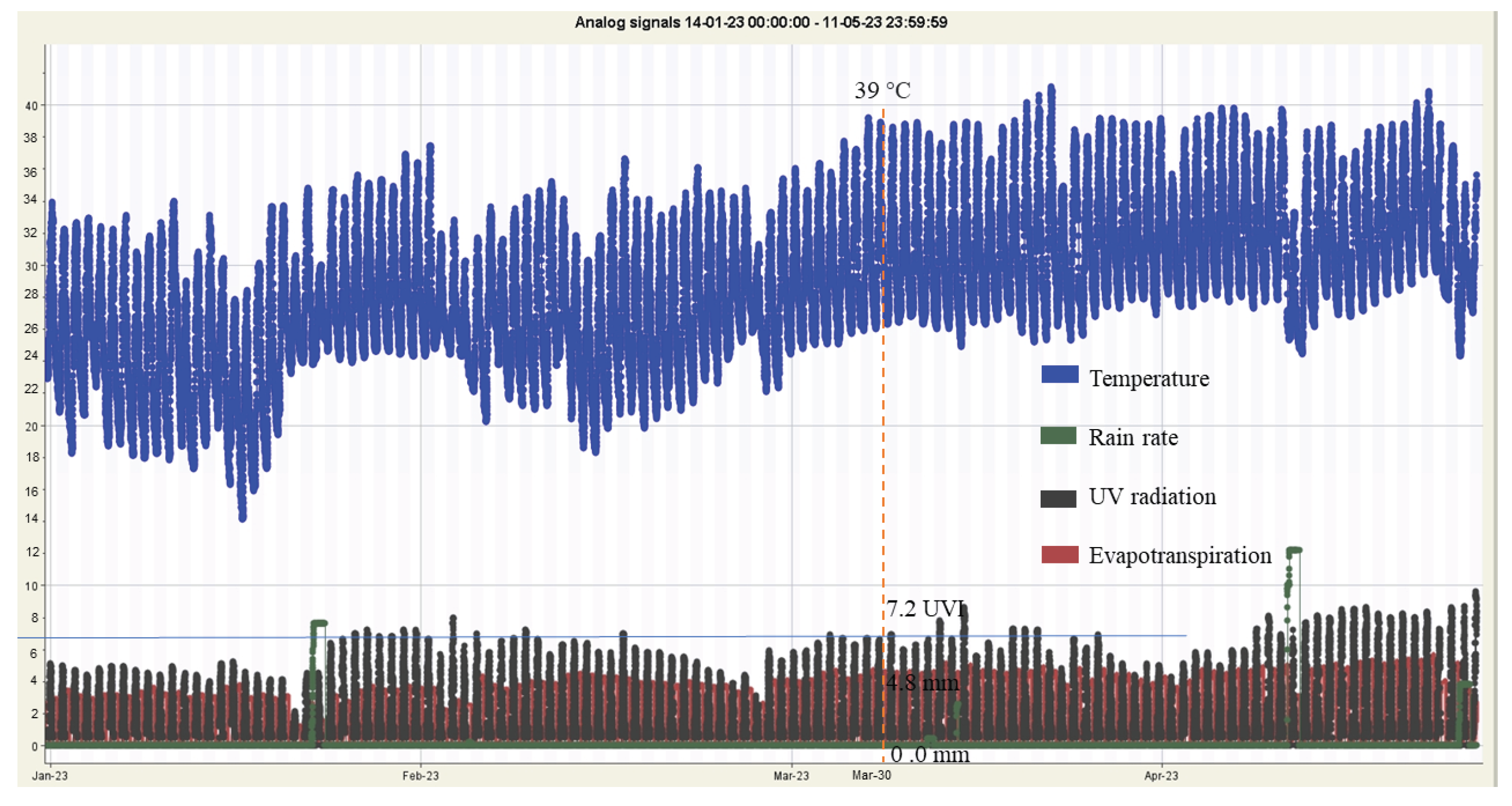
Indeed, the study encompasses a comprehensive set of forty features to feed into the machine learning models for predicting crop growth and yield. These features consist of eight factors measured from the soil, which include N, P, K, pH, soil temperature, soil humidity, EC and maize high. Additionally, there are eight parameters collected from environmental data, comprising water feed , UV radiation, evapotranspiration, daily rain, rain rate, humidity, wind speed, and temperature. Furthermore, there are twenty four feature from twelve VIs as CIgr, CIre, EVI2, GNDVI, MCARI2, MTVI2, NDRE, NDVI, NDWI, OSAVI, RDVI and RGBVI with CD and CV.
By incorporating this diverse set of forty features, the machine learning models can analyze the complex interplay between soil properties and environmental conditions that significantly influence crop health and productivity. The fusion of these factors and parameters empowers the models to make highly accurate predictions, providing valuable insights to farmers and agronomists for optimizing crop management practices, resource allocation, and decision-making in precision agriculture.
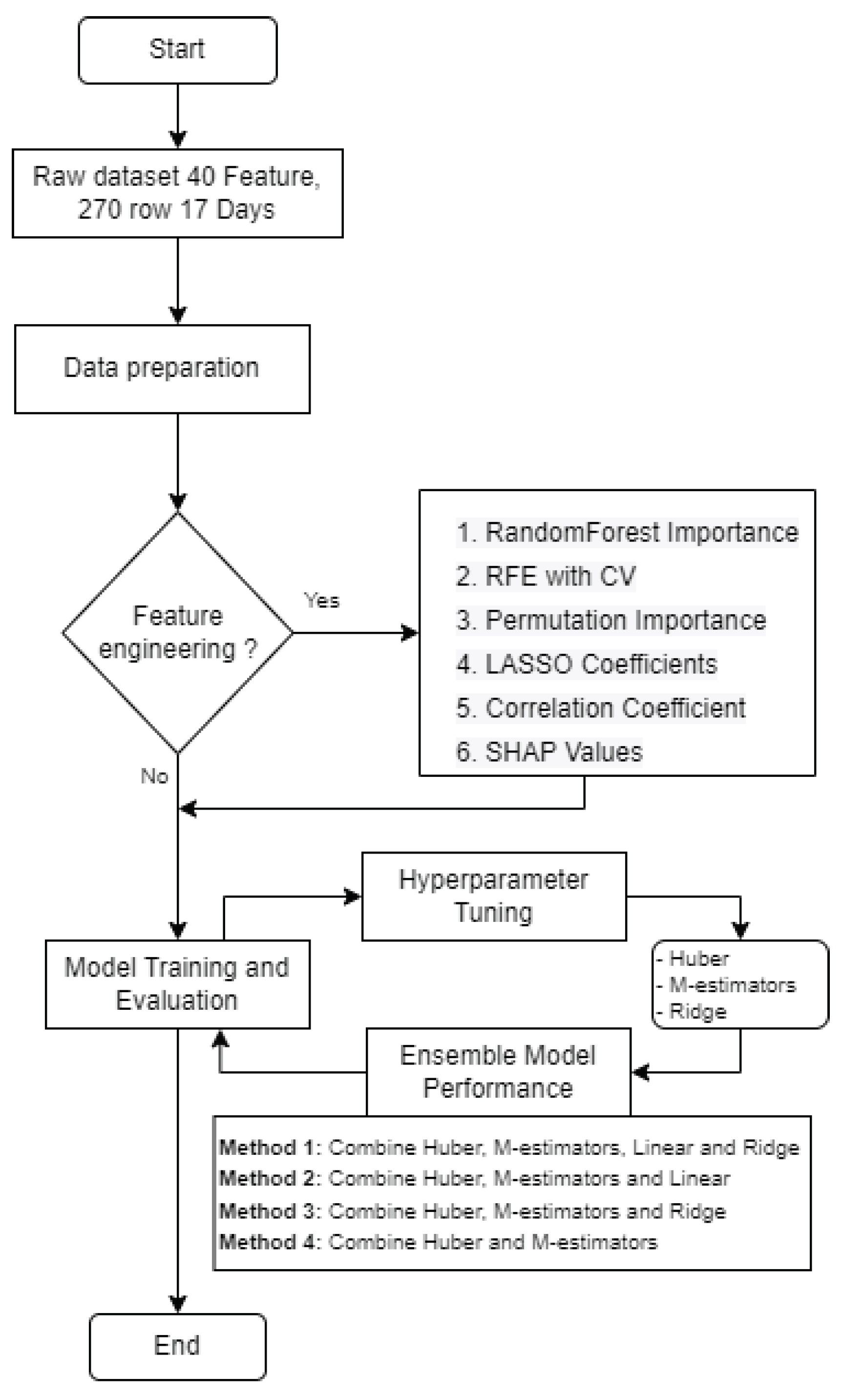
In this subsection, we introduce an ensemble machine learning model that enhances the accuracy and reliability of grain yield predictions by leveraging the strengths of multiple individual models. The ensemble approach combines the predictive power of various machine learning algorithms, optimizing their collective performance for more robust yield forecasts.
Ensemble models have gained prominence in the field of agricultural data analysis due to their ability to mitigate the limitations of individual models. By combining the outputs of multiple models, an ensemble can capture diverse patterns and relationships present in the data, leading to more accurate predictions.
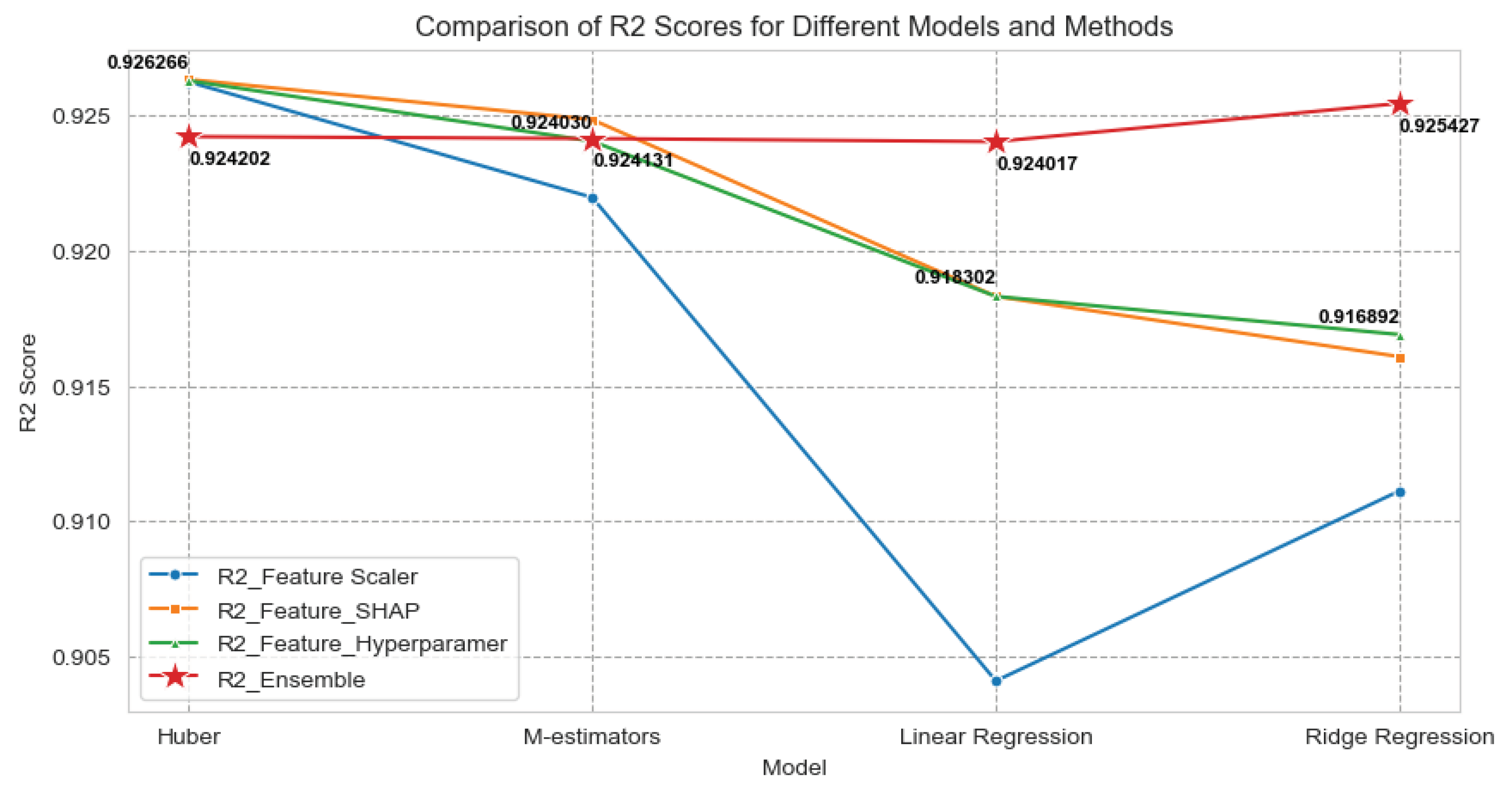
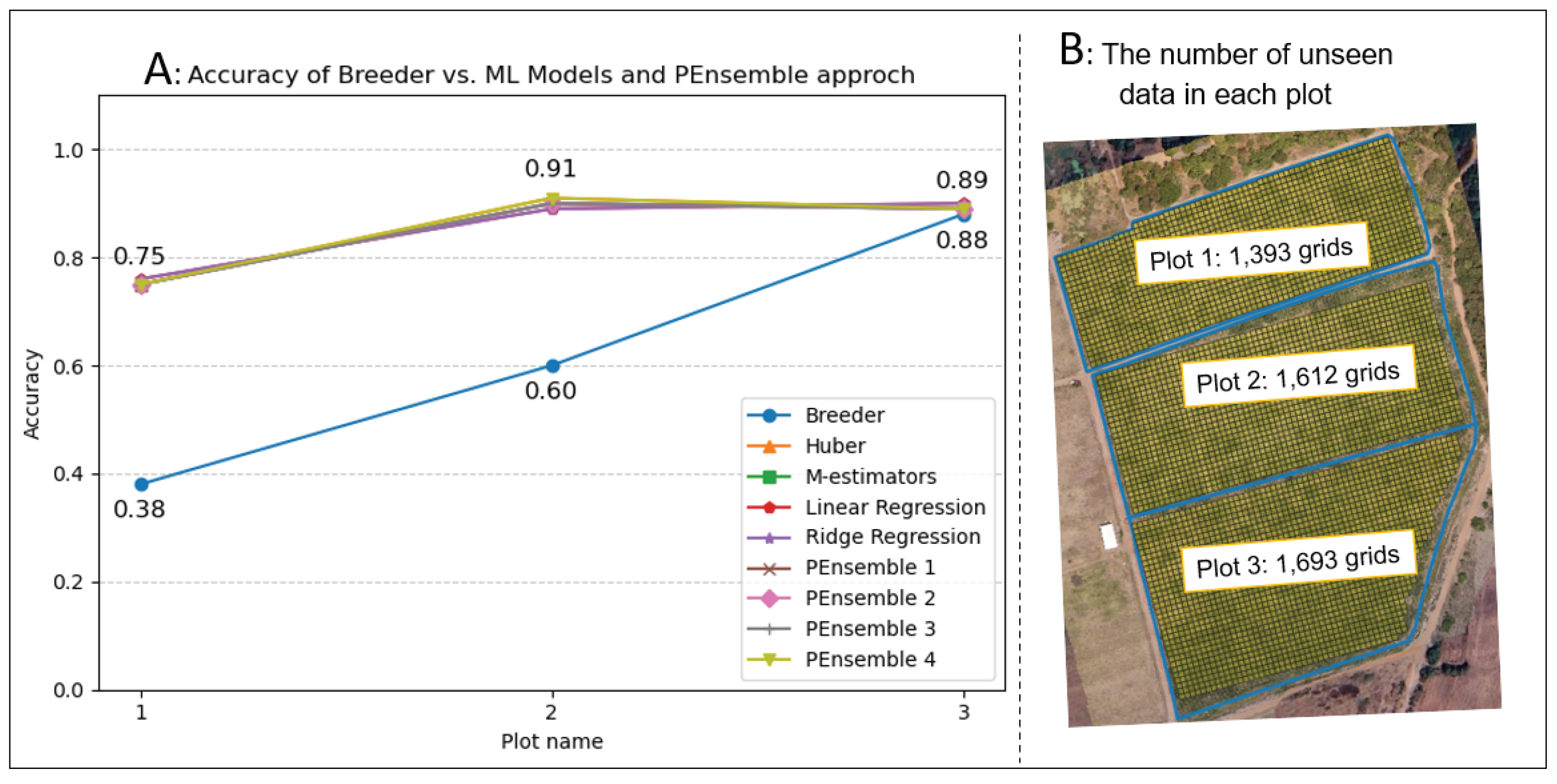
Our ensemble model comprises an arbitrary number of top-performing machine learning algorithms meticulously chosen from a pool of options, including Huber Regression, M-estimators, Linear Regression, Ridge Regression, and others. These algorithms have consistently demonstrated their effectiveness in capturing temporal variations, handling multicollinearity, and accommodating outliers within the dataset.
The ensemble model is designed to work as follows:
  • Data Preparation: To combine the data from various sources, we collect the following
    -
    Twenty four VIs with CD and CV (CIgr, CIre, EVI2, GNDVI, MCARI2, MTVI2, NDRE, NDVI, NDWI, OSAVI, RDVI and RGBVI).
    -
    Six teen environmental data following (maize high, N, P, K, pH, soil temperature, soil humidity, EC, water feed, uv radiation, evapotranspiration, daily rain, rain rate, humidity, wind speed, temperature).
    In summary, we have forty features with two hundred seventy data plots on each seventeen dates to process, with in total 137,700 records from the dataset. In addition, data cleaning, missing values handling, and null entries removal are also included.
  • Feature Engineering: Use six different feature importance techniques to extract significant features.
    -
    RandomForest importance consist of a large number of individual decision trees that operate as an ensemble. Each individual tree in the random forest outputs a class prediction, and the class with the most votes becomes the model prediction. The importance of each feature is determined by the average impurity decrease calculated from all decision trees in the forest.
    -
    Recursive feature elimination (RFE) with cross-validation is a method that fits the model multiple times and at each step, it removes the weakest feature (or features). RFE with cross-validation uses the cross-validation approach to find the optimal number of features.
    -
    Permutation Importance can be used with any model. After a model is trained, the values in a single column of the validation data are randomly shuffled. Then the model performance metric (such as accuracy or R 2 ) is re-evaluated with the shuffled data. Features that have a significant impact on performance are considered important.
    -
    LASSO Regression coefficients is a regression analysis method that performs both variable selection and regularization to enhance the prediction accuracy and interpretability of the statistical model. Features with non-zero coefficients are selected by LASSO.
    -
    Correlation coefficient to measure the linear relationship between the target and the numerical features. Features that have a higher correlation with the target variable are considered important.
    -
    Shapley additive explanations (SHAP) values is a unified measure of feature importance. It assigns each feature an importance value for a particular prediction.
  • Model Selection: We meticulously evaluate the performance of various machine learning algorithms on our grain yield prediction task. The top arbitrary number models, based on evaluation metrics such as mean squared error (MSE), root mean square error (RMSE), mean absolute error (MAE), and R-squared ( R 2 ), are chosen for ensemble construction.
  • Training: Each of the selected models is trained on our dataset, utilizing the same training, testing and validation splits with 70%, 20%, and 10%, respectively, to ensure consistency and fairness in the comparison. Fourteen different ML models are trained and evaluated the data. The models include:
    -
    CatBoost, Decision Tree, ElasticNet, Gradient Boosting, Huber, KNN, Lasso Regression, Linear Regression, M-estimators, Passive Aggressive, RF, Ridge Regression, SVR and XGBoost.
  • Ensemble Building: We create the ensemble by combining the predictions of the top arbitrary number models using weighted averaging. The weights assigned to each model are determined based on their individual performance during training. This process optimizes the ensemble’s predictive accuracy.
    The weighted ensemble prediction P Ensemble is given by
    P Ensemble = w 1 P Model 1 + w 2 P Model 2 + w 3 P Model 3 w 1 + w 2 + w 3 ,
    where w 1 , w 2 , and w 3 represent the weights assigned to each model, and P Model 1 , P Model 2 , and P Model 3 are the predictions made by each individual model.
    We fine-tune the weights (denoted as w 1 , w 2 , and w 3 ) based on the preliminary evaluation results, exploring various weight combinations to optimize the ensemble model’s performance.
  • Evaluation: The ensemble model’s performance is evaluated using the same evaluation metrics employed for individual models. We compare its results to those of individual models to gauge the improvement achieved through ensemble modeling.
  • Hyperparameter Tuning: If necessary, we fine-tune the hyperparameters of our ensemble model to further enhance its predictive capabilities. Techniques such as grid search or random search are employed for this purpose.
By incorporating the ensemble model into our grain yield prediction framework, we aim to provide more accurate and reliable forecasts, ultimately assisting farmers and agronomists in optimizing crop management practices and decision-making in precision agriculture. The fusion of multiple machine learning algorithms within the ensemble harnesses the strengths of each model, resulting in a robust tool for agricultural yield predictions.

3. Results

Through a comprehensive analysis of environmental factors and various vegetation indexes, this study aims to determine which aspects of the maize growth stage and other factors can be adjusted to predict seed weight. In the first part of the study, a total of seventeen UAV flights were conducted to collect images from a bird’s-eye view, creating a detailed map of the study area. The images’ data from each day were then computed for twenty four vegetation indexes with both CD and CV, namely CIgr_CD, CIre_CD, EVI2_CD, GNDVI_CD, MCAR2_CD, MTVI2_CD, NDRE_CD, NDVI_CD, NDWI_CD, OSAVI_CD, RDVI_CD, RGBVI_CV, CIgr_CV, CIre_CV, EVI2_CV, GNDVI_CV, MCAR2_CV, MTVI2_CV, NDRE_CV, NDVI_CV, NDWI_CV, OSAVI_CV, RDVI_CV, and RGBVI_CD.
The goal was to identify which specific days of the growth stage and vegetation indexes show high correlations with seed weight. The results are presented in Figure 5, which highlights five dates and five vegetation indexes (VIs) that display a strong correlation with seed weight. These include days 56 of stage V10, days 65, 72 stage R1, and 79 of stage R2, and days 85 of stage R3. Additionally, the VIs with the highest correlation are CIre_CD, NDRE, CIgr, EVI2, and NDVI. Notably, on day 79 of stage R2, the VI indexes CIre, NDRE, CIgr, EVI2, and NDVI demonstrate particularly high correlations of 0.80, 0.80, 0.77, 0.75, and 0.74, respectively. Forty features with two hundred seventy data plots on day 79 of stage R2 are selected to feed to ML to predict grain yield.
In this study, all ground truth data were gathered simultaneously on a singular date and time during the Unmanned Aerial Vehicle (UAV) flight missions. The collected data were bifurcated into two distinct categories: the first encompassing soil properties data, which entailed NPK nutrient levels, pH, EC, soil temperature, soil humidity, water feed per area (m3/dunam), and maize height (m); and the second comprising weather data, including ultraviolet radiation (UV), evapotranspiration, daily rain, rain rate, humidity, wind speed, and temperature. The weather-related data were consistently captured at five-minute intervals throughout the entire growing season.
Figure 6 depicts the correlation between seed weight and sixteen factors derived from the soil properties and weather data used for the analysis. Daily rain and rain rate were excluded from this correlation analysis due to their predominantly negligible values throughout the entire growing season, with most observations indicating zero or minimal rainfall. Among the various factors examined, several displayed a modest correlation with seed weight. These factors encompassed high maize height, temperature, humidity, wind speed, UV radiation, water feed, and evapotranspiration, exhibiting correlation coefficients of 0.32, 0.28, 0.26, 0.25, 0.19, 0.19, and 0.17, respectively.
To facilitate analysis, the weather data obtained on days 79, corresponding to stage R2 or March 30, 2023, during the time interval from 10.00 AM to 2.00 PM, were averaged. These weather data were collected using internet of things (IoT) sensors and included measurements of temperature (39 ∘C), rainfall (0.0 mm), UV index (7.2 UV), and evapotranspiration rate (4.8 mm). Evapotranspiration refers to the movement of water from the land surface to the atmosphere through the processes of evaporation and transpiration, as depicted in Figure 7.

3.1. Best-Suited Model Selection for Maize Grain Yield Prediction

This experiment is geared towards predicting maize grain yield by utilizing multi-temporal imagery to extract vegetation indices (VI) based on canopy density (CD) and canopy volume (CV), derived from the product of canopy density and plant height. The analysis incorporates ground truth environmental data (Env), encompassing NPK nutrient levels, pH, EC, soil temperature, soil humidity, water feed per area (m3/dunam), and maize height (m). Additionally, weather data such as ultraviolet radiation (UV), evapotranspiration, daily rain, rain rate, humidity, wind speed, and temperature are considered.
On day 79 (30 March 2023) of stage R2, we identify CIre, NDRE, CIgr, EVI2, and NDVI, determining which days of the growth stage and vegetation indices are highly correlated with the target variable and can be effectively utilized for prediction in our research.
To contribute to the understanding of our methodology, the author provides the ensemble machine learning model pipeline, as depicted in Figure 8.
The initial phase of this study involves meticulous data preparation, where the dataset undergoes thorough collection, and cleaning procedures are implemented to address missing values and eliminate null entries.
Subsequently, in the feature engineering stage, six distinct techniques are applied to extract significant features. These methods encompass selecting all 40 features (excluding the target for predicting ’Seed’), utilizing RandomForest Importance to identify features like ’Cire_CD,’ ’NDRE_CD,’ ’Cigr_CD,’ ’EVI2_CD,’ and ’NDVI_CD,’ employing Recursive Feature Elimination with Cross-Validation (RFE with CV) to highlight features such as ’Cire_CD,’ ’NDRE_CD,’ ’Cigr_CD,’ ’EVI2_CD,’ and ’NDVI_CV,’ and utilizing Permutation Importance to pinpoint features like ’Cire_CD,’ ’NDRE_CD,’ ’Cigr_CD,’ and ’EVI2_CD.’ Additionally, features are selected based on LASSO Coefficients (’Cigr_CD,’ ’Cigr_CV,’ ’SoilHumi,’ ’Wind speed’), Correlation Coefficient (’NDRE_CD,’ ’Evapotranspiration,’ ’Humidity,’ ’Temperature,’ ’EC’), and SHAP Values (’Cire_CD,’ ’NDRE_CD’).
Following feature engineering, the study progresses to model training and evaluation, employing a diverse set of fourteen machine learning models, including CatBoost, Decision tree, ElasticNet, Gradient boosting, Huber, KNN, Lasso Regression, Linear Regression, M-estimators, Passive aggressive, RF, Ridge Regression, SVR, and XGBoost.
Hyperparameter tuning is then conducted to optimize specific models, namely "Huber," "M-estimators," "Linear Regression," and "Ridge Regression." This fine-tuning process utilizes GridSearchCV to identify and implement the most effective hyperparameters for enhanced model performance.
Finally, the study explores ensemble techniques to amalgamate predictions from multiple models, thereby improving overall performance. Four distinct ensemble methods, labeled PEnsemble1, PEnsemble2, PEnsemble3, and PEnsemble4, are implemented, combining various models such as "Huber," "M-estimators," "Linear Regression," and "Ridge Regression" in different configurations to leverage the strengths of individual models and enhance predictive accuracy.
To determine the most suitable model prior to employing ensemble techniques, the authors have adopted six distinct methods of feature engineering:
  • RandomForest Importance: This method leverages the RandomForest algorithm, which constructs a multitude of decision trees during training. The importance of a feature is computed by observing how often a feature is used to split the data and how much it improves the model’s performance.
  • Recursive Feature Elimination (RFE) with Cross-Validation: RFE is a technique that works by recursively removing the least important feature and building a model on the remaining features. The process is repeated until the desired number of features is achieved. Cross-validation is integrated into this process to optimize the number of features and prevent overfitting.
  • Permutation Importance: This technique gauges the importance of a feature by evaluating the decrease in a model’s performance when the feature’s values are randomly shuffled. A significant drop in performance indicates high feature importance.
  • LASSO Regression Coefficients: LASSO is a regression analysis method that uses L1 regularization. It has the capability to shrink some regression coefficients to zero, effectively selecting more significant features while eliminating the less impactful ones.
  • Correlation Coefficient: This method calculates the linear correlation between each feature and the target variable. Features that have strong correlation coefficients are deemed important, as they have a substantial linear association with the target.
  • SHAP Values: SHAP values furnish a metric for gauging the influence of each feature on the model’s prediction. By attributing the difference between the prediction and the average prediction to each feature, SHAP provides a more intuitive comprehension of feature importance, particularly in the context of complex models.
The study employs six different feature engineering techniques to prioritize the selection of features based on their importance, ensuring the utilization of the most significant predictors in the model. Table 3 and Table 4 present the performance of various machine learning models across these distinct feature engineering methods.
Among the top-performing models, the Huber model stands out, achieving the best R 2 value of 0.926313 with features selected using SHAP Values. This combination demonstrates minimal errors with MAE 0.278809, MSE 0.516539, and RMSE 0.718707, explaining approximately 92.63% of the variance in the dependent variable. The Huber model, when paired with features selected using Correlation Coefficient, Permutation Importance, RandomForest Importance, and RFE with CV, consistently maintains R 2 values exceeding 92.63%, indicating its robust performance. The M-estimators model, coupled with features selected using SHAP Values and Permutation Importance, also showcases strong performance with an R 2 value above 92.46%.
Conversely, the top 10 worst-performing models include the Decision Tree model with features selected using All Features, Permutation Importance, and LASSO Coefficients, exhibiting R 2 values below 43%. This suggests potential overfitting to the training data or the decision tree model’s limited suitability for the dataset. The Passive Aggressive model, using the Correlation Coefficient feature selection method, and the ElasticNet model, utilizing both Correlation Coefficient and LASSO Coefficients, also present low R 2 values, indicating weaker performance. The XGBoost model with features selected using SHAP Values and the Decision Tree model with features selected using RFE with CV both have R 2 values below 65%, further suggesting challenges with these combinations.
In summary, the results highlight that the Huber model consistently demonstrates strong performance across multiple feature selection methods, indicating its suitability for this dataset and problem. Conversely, the Decision Tree model appears less suited, producing some of the lowest R 2 values, suggesting it might not be the optimal choice or may require further refinement through hyperparameter tuning or constraints to prevent overfitting. The study also underscores the effectiveness of feature selection methods such as SHAP Values, Correlation Coefficient, Permutation Importance, RandomForest Importance, and RFE with CV, particularly when combined with the Huber model.
Consequently, Huber, M-estimators, Ridge Regression, and Linear Regression are selected from six different feature importance techniques for further processing with the hyperparameter tuning technique—an essential step in the machine learning workflow. The primary objective is to search for the optimal combination of hyperparameters that yields the best model performance.
The GridSearchCV method facilitates an exhaustive search over a specified parameter grid, employing cross-validation to estimate the performance of each combination. For the Huber model, the best parameter tuning results in an achieved R 2 of 0.926266, setting the regularization strength ( α ) to 1, Huber threshold ( ϵ ) to 1.0, and the maximum number of iterations (max_iter) to 100.
For the parameters of M-estimators within the RANSACRegressor algorithm, the minimum number of samples (min_samples) is set to 0.7 of randomly available data samples for each iteration, and the stop-iterating probability (stop_probability) is set to 0.9. The obtained R 2 of 0.924029 is achieved when 70% of the samples are used to fit the model in each iteration, and the algorithm iterates until there is a 96% probability of correctly identifying the inliers.
The Linear Regression model, configured with fit_intercept=True, enhances flexibility, allowing it to better capture data patterns, resulting in an achieved R 2 of 0.918301. Fine-tuning the parameters of the Ridge Regression model involves setting the alpha to 0.615848211066026, fit_intercept to True, and selecting ’lsqr’ as the solver. The ’lsqr’ solver, representing "Least Squares QR Decomposition," proves efficient in solving the least squares problem. The Ridge Regression model yields the best R 2 score of 0.916892 when the regularization strength is 0.615848211066026, an intercept is included, and the lsqr solver computes the coefficients. A summarized overview of the hyperparameter tuning results is presented in Table 5.

3.2. Results of Ensemble Models

In this subsection, we delve into the outcomes of our top three ensemble models designed for predicting maize grain yield. These ensembles, meticulously curated by harnessing the strengths of various machine learning algorithms, underwent a comprehensive evaluation based on predefined performance metrics like MSE, RMSE, MAE, and R 2 . Our analysis provides a detailed examination of each ensemble model’s precision and effectiveness in capturing intricate connections within multi-temporal satellite imagery data, environmental variables, and maize yields. Additionally, we conduct a comparative assessment to identify the top-performing ensemble, characterized by its accuracy and reliability in predicting grain yields.
Our presentation of these findings aims to offer valuable insights into the potential of ensemble modeling for maize grain yield prediction. We believe that such insights can prove instrumental for decision-makers in agriculture and precision farming, guiding them toward more informed practices and strategies.
Following thorough feature engineering and hyperparameter tuning, our results highlight the effectiveness of the Huber, M-estimators, Ridge Regression, and Linear Regression models when paired with features ’Cire_CD’ and ’NDRE_CD’ derived from the SHAP Values technique for predicting maize grain yield. Building on these findings, we opt to utilize the VotingRegressor to create ensembles for each method, thereby enhancing the predictive capabilities of our model as follows:
  • PEnsemble 1: Using Huber, M-estimators (RANSAC), Linear Regression, and Ridge Regression, the weighted ensemble prediction is given by
    P Ensemble 1 = w 1 P Huber + w 2 P M - estimators + w 3 P Linear Regression + w 4 P Ridge Regression w 1 + w 2 + w 3 + w 4 .
  • PEnsemble 2: Using Huber, M-estimators (RANSAC), and Linear Regression, the weighted ensemble prediction is given by
    P Ensemble 2 = w 1 P Huber + w 2 P M - estimators + w 3 P Linear Regression w 1 + w 2 + w 3 .
  • PEnsemble 3: Using Huber, M-estimators (RANSAC), and Ridge Regression, the weighted ensemble prediction is given by
    P Ensemble 3 = w 1 P Huber + w 2 P M - estimators + w 3 P Ridge Regression w 1 + w 2 + w 3 .
  • PEnsemble 4: Using Huber and M-estimators (RANSAC), the weighted ensemble prediction is given by
    P Ensemble 4 = w 1 P Huber + w 2 P M - estimators w 1 + w 2 .
The results, reflecting the weights assigned to each model in the ensemble methods, are presented in Table 6.
Method 1 (PEnsemble1) employs four distinct models: Huber, M-estimators, Linear Regression, and Ridge Regression, each assigned weights of 0.5, 0.3, 0.1, and 0.1, respectively. The Huber model is granted the highest weight, emphasizing its substantial impact on ensemble prediction. This aligns with the robust nature of Huber’s Regression, particularly beneficial in datasets susceptible to outliers. The obtained R 2 score is 0.924202, signifying commendable predictive performance.
In Method 2 (PEnsemble2), three models—Huber, M-estimators, and Linear Regression—are included, with weights of 0.45, 0.35, and 0.2, respectively. Huber remains dominant, though to a lesser extent than in Method 1. The increased weight assigned to M-estimators suggests a more balanced reliance on the robustness of both Huber and M-estimators. The resulting R 2 score is 0.924131, slightly lower than Method 1 but still impressive.
Method 3 (PEnsemble3) utilizes three models—Huber, M-estimators, and Ridge Regression—with weights of 0.45, 0.35, and 0.2, respectively. Similar to Method 2 in terms of weights, it substitutes Linear Regression with Ridge Regression. Ridge Regression introduces L2 regularization, potentially preventing overfitting and enhancing generalization. However, the R 2 score is 0.924017, slightly lower than the scores obtained in the previous two methods.
Method 4 (PEnsemble4) employs only two models—Huber and M-estimators—with weights of 0.6 and 0.4, respectively. Despite its simplicity, this ensemble heavily relies on the Huber model and achieves the highest R 2 score of 0.925427 among all methods. This result suggests that, at times, using fewer models with appropriate weighting can lead to superior predictions.
In summary, the results indicate that while all ensemble methods exhibit robust performance, PEnsemble4 stands out for its superior prediction quality. The pronounced reliance on the Huber model, renowned for its resilience to outliers, is a key factor contributing to this exceptional performance. It’s important to recognize that the efficacy of ensemble methods can be contingent on the quality and characteristics of the data. Consequently, diverse datasets or varying feature sets may lead to divergent outcomes.
In summarizing the methodology employed in this study to predict maize yield using an ensemble machine learning model with IoT environmental data and UAV vegetation indices, we focused on assessing the performance of diverse models through varied approaches to feature selection, hyperparameter tuning, and ensembling. The comparative evaluation of scores for different models and methods is presented in Table 7 and Figure 9.
For feature scaling, the R 2 Feature Scaler utilized the StandardScaler to scale the training and testing datasets, standardizing them to have a mean of 0 and a standard deviation of 1. This process ensures that all features have the same scale, which is crucial for certain algorithms sensitive to feature scale.
Feature importance, evaluated through R 2 Feature SHAP, involved employing SHAP to understand the importance of features in the model. SHAP provides a unified measure of feature importance, aiding in understanding which features the model deems significant.
Hyperparameter tuning, denoted as R 2 Feature Hyperparameter, involved fine-tuning the model’s hyperparameters using GridSearchCV. This step ensures the selection of the best set of hyperparameters for the model, optimizing its performance.
In the ensembling phase, labeled R 2 Ensemble, models were combined using four different methods and weights. PEnsemble 1 combined Huber, M-estimators, Linear Regression, and Ridge Regression with weights [0.5, 0.3, 0.1, 0.1], resulting in an R 2 score of 0.924202. PEnsemble 2 combined Huber, M-estimators, and Linear Regression with weights [0.45, 0.35, 0.2], resulting in an R 2 score of 0.924131. PEnsemble 3 combined Huber, M-estimators, and Ridge Regression with weights [0.45, 0.35, 0.2], resulting in an R 2 score of 0.924017. PEnsemble 4 combined Huber and M-estimators with weights [0.6, 0.4], achieving the highest R 2 score of 0.925427.
In summary, the use of different strategies yielded diverse R 2 scores. Through ensembling, the strengths of individual models were effectively combined, potentially leading to improved and more robust predictions. Notably, the results indicate that the ensemble method, particularly Method 4 (incorporating Huber and M-estimators), achieved a slightly superior R 2 score compared to other ensemble methods and individual models. Importantly, the ensemble model demonstrated robustness in handling unseen data, enhancing its utility for predictive tasks.

4. Discussion

4.1. Validating the Model with Unseen Data

In practical terms, the conventional breeder’s approach to yield prediction involves random sampling, as illustrated for each plot in Table 8.
For Plot 1, covering an area of 24,000 m 2 and hosting 8,960 maize plants, a sampled cob contains 360 seeds. The weight of 100 seeds is 26 g, and the entire cob weighs 93.6 g. This translates to 3,846 seeds per kilogram. Moving on to Plot 2, spanning 33,600 m 2 with a slightly larger population of 9,173 maize plants, a cob from this plot carries 288 seeds. The weight measurements indicate 21 g for 100 seeds and 60.48 g for the full cob. Here, one kilogram is equivalent to 4,762 seeds. Finally, Plot 3, occupying an area of 30,400 m 2 , has the highest population among the three plots, housing 9,813 maize plants. A single cob from this plot contains 300 seeds, with the weight of 100 seeds at 19.4 g and the entire cob at 58.2 g. The actual harvested weights for plots 1, 2, and 3 are 1,314.44 kg, 236.92 kg, and 387.82 kg, respectively.
In this comparative analysis, we evaluate the performance of different approaches in predicting maize harvest yields, contrasting them with the traditional breeder’s method, as illustrated in Table 9.
The examined methods encompass a traditional breeder’s approach, five machine learning models, and four ensemble methods denoted as PEnsemble 1 through 4. To gauge accuracy, we compute the percentage errors between the actual harvest yields and predictions for three distinct plots with varying actual harvests: 1314.44 kg for Plot 1, 236.92 kg for Plot 2, and 387.82 kg for Plot 3. For Plot 1, where the actual harvest is 1314.44 kg, the traditional breeder’s method predicted a yield of 503.19 kg, resulting in a substantial 62% error. Meanwhile, the Huber model predicted 986.23 kg with a more moderate 25% error, and the M-estimators model also predicted 991.44 kg with a 25% error. The Linear Regression and Ridge Regression models forecasted 998.47 kg and 999.03 kg, respectively, both exhibiting a 24% error. Additionally, the four PEnsemble models provided predictions and errors ranging from 988.31 kg (25% error) to 990.61 kg (25% error).
Moving to Plot 2, where the actual harvest is 236.92 kg, the traditional breeder’s method predicted 332.87 kg, resulting in a substantial 40% error. Notably, models like Huber and PEnsemble 4 predicted yields around 258.2 kg to 258.75 kg, both showcasing error rates below 10%. Other models, including M-estimators, Linear Regression, Ridge Regression, and other PEnsemble models, had predictions ranging from 259.45 kg to 263.05 kg, with error rates from 10% to 11%.
For Plot 3, with an actual harvest of 387.82 kg, the traditional breeder’s method estimated a yield of 342.67 kg, resulting in a 12% error. Most of the machine learning models and the PEnsemble methods predicted yields between 345.22 kg and 348.57 kg, with errors between 10% and 11%.
In summary, this table provides an insightful overview of the accuracy of various predictive methods against actual harvest yields across different plots. While the traditional breeder’s method tends to yield higher error rates, especially in Plot 1, machine learning models and PEnsemble methods exhibit relatively lower error percentages, underscoring their potential for more accurate yield predictions.
In the context of our study, the accuracy of our model, validated with previously unseen data on the number of subgrids to coverage in each plot, is visually presented in Figure 10 B. The plots—Plot 1, Plot 2, and Plot 3—comprise 1,393 grids, 1,612 grids, and 1,693 grids, respectively. Figure 10 A illustrates the accuracy trends of various prediction models, encompassing both traditional and machine learning methodologies, across these distinct plots.
  • Breeder (Traditional Method): Our traditional approach exhibits varying accuracy levels across plots, with the lowest accuracy observed in Plot 1 and higher accuracies in Plots 2 and 3. Notably, it appears less effective for Plot 1, indicating potential limitations when predicting yields for certain scenarios.
  • Machine Learning Models (Huber, M-estimators, Linear Regression, Ridge Regression): These models consistently demonstrate a stable accuracy range of 75%-90% across all three plots. Linear Regression and Ridge Regression, in particular, closely mirror each other in terms of predictive accuracy.
  • PEnsemble Approaches: Our ensemble methods (PEnsemble 1 to 4) showcase accuracies akin to individual machine learning models. Noteworthy is PEnsemble 4, exhibiting slightly superior performance across all plots, suggesting effective amalgamation of the strengths of individual models.
In summary, the traditional "Breeder" approach exhibits varied performance across plots, notably with lower accuracy in Plot 1. Additionally, machine learning models, overall, present more consistent and higher accuracy across all plots compared to the traditional method. Particularly, PEnsemble 4 stands out marginally, underscoring its potential as an effective ensemble approach for maize yield prediction. This analysis suggests that machine learning models, especially ensemble methods, can serve as potent tools for predicting maize yields with higher accuracy than traditional methods, particularly in scenarios where the traditional approach might encounter challenges.

4.2. Implications of The Study

The outcomes of this study carry significant implications for agricultural practices, particularly in precision agriculture. The identification of specific growth stages and vegetation indices correlated with seed weight offers valuable guidance for farmers engaging in precision agriculture. By concentrating efforts such as irrigation and nutrient management during these critical periods, farmers can optimize seed yield. Additionally, the study underscores the importance of understanding the correlations between environmental factors, including weather and soil conditions, and seed weight. This knowledge empowers farmers to make informed decisions regarding irrigation, pest control, and other environmental management practices to enhance crop production.

4.3. Limitations and Challenges

However, it is crucial to acknowledge the limitations and challenges associated with this study. Data collection for environmental factors and vegetation indices introduces the possibility of errors and variability. Ensuring the accuracy and consistency of data collection methods becomes paramount to the reliability of the study’s findings. Moreover, while the study identifies correlations between factors and seed weight, it does not imply causation. Other unmeasured variables may contribute to seed weight, necessitating caution in drawing causal relationships from correlations alone.
The exclusion of certain weather factors, such as daily rain and rain rate, from the correlation analysis due to negligible values presents a limitation. These factors, though seemingly insignificant, might still influence crop yield, and their omission could impact the comprehensiveness of the analysis. Additionally, the study’s findings are specific to the study area and conditions, and generalizing these results to different regions or crops may require additional validation.
In conclusion, this study contributes valuable insights into the intricate relationships between environmental factors, vegetation indices, and maize seed weight. These insights can inform more precise decision-making in agriculture, especially in the context of precision farming. Nevertheless, it is imperative to consider the study’s limitations and potential data variability when applying these results to real-world farming scenarios. Further research and validation efforts may be necessary to establish causation and extend the applicability of these findings to broader agricultural contexts.

5. Conclusions and Possible Future Works

In summary, our study introduces an alternative method for farmers to leverage technology effectively, enhancing production, plant management, and crop protection. This approach allows for early estimation of maize grain yield on day 79 of the R2 stage, a substantial improvement over the traditional black layer stage prediction on day 100 of the R6 stage. While CIre and NDRE prove highly indicative in predicting grain yield, environmental data exert a more significant influence compared to yield data. In contrast, the integration of IoT and environmental data offers broader benefits, including the identification of water and crop stress and the monitoring of plant diseases. Notably, our PEnsemble 4 approach achieves an impressive accuracy of 91%, marking a substantial advancement in grain yield prediction compared to traditional methods.
In this investigation, we have successfully employed machine learning techniques to craft a comprehensive model for maize yield prediction. By tapping into environmental data from IoT sources and utilizing data captured by UAVs, including soil properties, nutrients, weather conditions, and vegetation indicators, our model delivers precise and data-driven crop yield predictions. This research endeavors to significantly boost agricultural productivity by providing farmers with valuable insights for informed decision-making and sustainable farming practices.
The optimal model choice depends on the characteristics of specific analysis scenarios. For capturing temporal patterns in canopy density, ensemble and tree-based models prove effective. Models integrating plant height with canopy density perform well when plant height is a crucial factor. In complex scenarios with multiple variables, robust models capable of handling high dimensionality and complexity excel. Furthermore, scenarios with engineered features benefit from models capable of feature selection and managing high-dimensional data.
In our ongoing efforts to enhance predictive capabilities, we plan to continually refine and optimize the machine learning model. Exploring advanced algorithms and employing feature engineering techniques will contribute to this optimization. Extending the data collection period to cover multiple growing seasons and diverse environmental conditions will provide insights into crop response and yield variations. Integrating satellite imagery data with UAV data will enhance coverage and resolution, enabling more robust yield predictions. Developing a real-time monitoring system using live IoT data will empower farmers with timely information for proactive interventions. Expanding the model’s scope to predict crop diseases and pest infestations will provide vital insights for effective disease management. Incorporating additional soil health indicators will enable comprehensive assessments of the long-term impacts of agricultural practices on soil quality. Lastly, we aim to explore the model’s applicability in addressing challenges posed by climate change on crop growth and yield, guiding farmers in making informed decisions to adapt their practices to changing environmental conditions.
In conclusion, this research establishes an innovative, data-driven approach to crop yield prediction, offering valuable insights for farmers to optimize agricultural practices, enhance productivity, and contribute to the sustainability of our food systems. Future endeavors will further enhance the model’s capabilities, extending its applicability to foster more resilient and efficient agricultural practices amidst evolving environmental and societal challenges.

Author Contributions

Conceptualization, N.P. and A.T.; methodology, N.P. and K.S.; software, N.P.; validation, N.P., A.T. and K.S.; formal analysis, N.P.; investigation, N.P.; resources, K.S.; writing—original draft preparation, N.P.; writing—review and editing, A.T.; visualization, N.P.; supervision, A.T.;All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The financial support of the project is funded in part by a scholarship from the National Science and Technology Development Agency. Charoen Pokphand Foods Public Company Limited (CPF) and Chainat College of Agriculture and Tecnology, Chainart, Thailand, provide the experimental area and plant management. Research and development team of K.S.P Equipment Co.,Ltd. to provide hardware and collect ground-truth data part

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. OECD.; Food.; of the United Nations, A.O. OECD-FAO Agricultural Outlook 2020-2029; OECD Publishing, 2020; p. 330. [CrossRef]
  2. Saleem, M.H.; Potgieter, J.; Arif, K.M. Plant Disease Detection and Classification by Deep Learning. Plants 2019, 8. [Google Scholar] [CrossRef]
  3. Ohlson, E.; Wilson, J.R. Maize Lethal Necrosis: Impact and Disease Management. Outlooks on Pest Management 2022, 33, 45–51. [Google Scholar] [CrossRef]
  4. Seye, D.; Silvie, P.; Brévault, T. Effect of maize seed treatment on oviposition preference, larval performance and foliar damage of the fall armyworm. Journal of Applied Entomology 2023, 147, 299–306. [Google Scholar] [CrossRef]
  5. Tao, W.; Wang, X.; Xue, J.H.; Su, W.; Zhang, M.; Yin, D.; Zhu, D.; Xie, Z.; Zhang, Y. Monitoring the Damage of Armyworm as a Pest in Summer Corn by Unmanned Aerial Vehicle Imaging. Pest Management Science 2022. [Google Scholar] [CrossRef]
  6. Liu, F.; Jiang, X.; Wu, Z. Attention Mechanism-Combined LSTM for Grain Yield Prediction in China Using Multi-Source Satellite Imagery. Sustainability 2023. [Google Scholar] [CrossRef]
  7. García-Martínez, a.M.A. Corn grain yield estimation from vegetation indices, canopy cover, plant density, and a neural network using multispectral and rgb images acquired with unmanned aerial vehicles. Agriculture (Switzerland) 2020, 10, 1–24. [Google Scholar] [CrossRef]
  8. Uysal, I. Precision Agriculture Using Soil Sensor Driven Machine Learning for Smart Strawberry Production. Sensors 2023. [Google Scholar] [CrossRef]
  9. Michaud, E.J.; Liu, L.; Tegmark, M. Precision Machine Learning. Entropy 2022. [Google Scholar] [CrossRef]
  10. Bondre, D.A.; Mahagaonkar, S. Prediction of crop yield and fertilizer recommendation using machine learning algorithms. IJEAST 2019, 04, 371–376. [Google Scholar] [CrossRef]
  11. M, S.V.; Lakshmi. ; P, S.L.; Ch, U.; G, H.V. SMART IRRIGATION SYSTEM USING IoT. Journal of emerging technologies and innovative research 2019. [Google Scholar]
  12. Singh, R.K.; Rahmani, M.H.; Weyn, M.; Berkvens, R. Joint Communication and Sensing: A Proof of Concept and Datasets for Greenhouse Monitoring Using LoRaWAN. Sensors 2022. [Google Scholar] [CrossRef]
  13. peng Zhao, J.; Kumar, A.; Banoth, B.N.; Marathi, B.; Rajalakshmi, P.; Rewald, B.; Ninomiya, S.; Guo, W. Deep-Learning-Based Multispectral Image Reconstruction from Single Natural Color RGB Image - Enhancing UAV-Based Phenotyping. Remote sensing 2022. [Google Scholar]
  14. Obasekore, H.; Fanni, M.; Ahmed, S.M.; Parque, V.; Kang, B.Y. Agricultural Robot-Centered Recognition of Early-Developmental Pest Stage Based on Deep Learning: A Case Study on Fall Armyworm (Spodoptera frugiperda). Sensors 2023. [Google Scholar] [CrossRef]
  15. Sekerogiu, B.; Ever, Y.K.; Dimililer, K.; Al-Turjman, F. Comparative Evaluation and Comprehensive Analysis of Machine Learning Models for Regression Problems. Data intelligence 2022. [Google Scholar] [CrossRef]
  16. Velichko, A.; Belyaev, M.; Wagner, M.P.; Taravat, A. Entropy Approximation by Machine Learning Regression: Application for Irregularity Evaluation of Images in Remote Sensing. Remote sensing 2022. [Google Scholar] [CrossRef]
  17. Gitelson, A.A.; Gritz †, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. Journal of Plant Physiology 2003, 160, 271–282. [Google Scholar] [CrossRef]
  18. Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sensing of Environment 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
  19. Gitelson, A.A.; Merzlyak, M.N. Remote sensing of chlorophyll concentration in higher plant leaves. Advances in Space Research 1998, 22, 689–692. [Google Scholar] [CrossRef]
  20. Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sensing of Environment 2004, 90, 337–352. [Google Scholar] [CrossRef]
  21. Gitelson, A.; Merzlyak, M.N. Quantitative estimation of chlorophyll-a using reflectance spectra: Experiments with autumn chestnut and maple leaves. Journal of Photochemistry and Photobiology B: Biology 1994, 22, 247–252. [Google Scholar] [CrossRef]
  22. Yue, J.; Tian, J.; Philpot, W.; Tian, Q.; Feng, H.; Fu, Y. VNAI-NDVI-space and polar coordinate method for assessing crop leaf chlorophyll content and fractional cover. Computers and Electronics in Agriculture 2023, 207, 107758. [Google Scholar] [CrossRef]
  23. S. K.McFEETERS. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. International Journal of Remote Sensing 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
  24. Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sensing of Environment 1996, 55, 95–107. [Google Scholar] [CrossRef]
  25. Roujean, J.L.; Breon, F.M. Estimating PAR absorbed by vegetation from bidirectional reflectance measurements. Remote Sensing of Environment 1995, 51, 375–384. [Google Scholar] [CrossRef]
  26. Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. International Journal of Applied Earth Observation and Geoinformation 2015, 39, 79–87. [Google Scholar] [CrossRef]
  27. Sangjan, W.; McGee, R.J.; Sankaran, S. Optimization of UAV-Based Imaging and Image Processing Orthomosaic and Point Cloud Approaches for Estimating Biomass in a Forage Crop. Remote Sensing 2022, 14. [Google Scholar] [CrossRef]
  28. Vantage Pro2. Available online:https://www.davisinstruments.com/pages/vantage-pro2. accessed on 13 January 2023.
  29. Soil Sensors Display Terminal Moisture Temperature EC PH NPK Soil Analyzer. Available online:https://www.jxct-iot.com/product/showproduct.php?id=196. accessed on 13 January 2023.
  30. Sangjan, W.; Pukrongta, N.; Carter, A.H.; Pumphrey, M.O.; Sankaran, S. Development of IoT-based camera system for automated in-field monitoring to support crop breeding Programs. ESS Open Archive 2022. [Google Scholar] [CrossRef]
  31. Pukrongta, N.; Kumkhet, B. The relation of LoRaWAN efficiency with energy consumption of sensor node. 2019 International Conference on Power, Energy and Innovations (ICPEI), 2019, pp. 90–93. [CrossRef]
Preprints 101380 g001
Figure 1. Area of study.
Figure 1. Area of study.
Preprints 101380 g001
Preprints 101380 g002
Figure 2. Image processing pipeline.
Figure 2. Image processing pipeline.
Preprints 101380 g002
Preprints 101380 g003
Figure 3. IoT design for ground measurements A) Vantage Pro2 weather station B) NPK Soil Analyzer C) Our design for soil health monitoring and D) Prototype of Smart trap.
Figure 3. IoT design for ground measurements A) Vantage Pro2 weather station B) NPK Soil Analyzer C) Our design for soil health monitoring and D) Prototype of Smart trap.
Preprints 101380 g003
Preprints 101380 g004
Figure 4. The flow diagram of ML methods for grain yield predictions.
Figure 4. The flow diagram of ML methods for grain yield predictions.
Preprints 101380 g004
Preprints 101380 g005
Figure 5. Five high correlation of date of growth stage and VIs with seed weight.
Figure 5. Five high correlation of date of growth stage and VIs with seed weight.
Preprints 101380 g005
Preprints 101380 g006
Figure 6. Sixteen features environment data to correlate with seed weight. Daily rain and rain rate, value are zero which does not appear in correlation chart.
Figure 6. Sixteen features environment data to correlate with seed weight. Daily rain and rain rate, value are zero which does not appear in correlation chart.
Preprints 101380 g006
Preprints 101380 g007
Figure 7. The environment data of Temperature, Rain rate, UV radiation and Evapotranspiration of the day of prediction on 30 March 2023.
Figure 7. The environment data of Temperature, Rain rate, UV radiation and Evapotranspiration of the day of prediction on 30 March 2023.
Preprints 101380 g007
Preprints 101380 g008
Figure 8. Ensemble pipeline of our purpose.
Figure 8. Ensemble pipeline of our purpose.
Preprints 101380 g008
Preprints 101380 g009
Figure 9. Comparison of R 2 Scores for Different Models and Ensemble method.
Figure 9. Comparison of R 2 Scores for Different Models and Ensemble method.
Preprints 101380 g009
Preprints 101380 g010
Figure 10. A: Accuracy of different ML model and PEnsemble approch vs Breeder and B: the number of unseen data to predict grain yield.
Figure 10. A: Accuracy of different ML model and PEnsemble approch vs Breeder and B: the number of unseen data to predict grain yield.
Preprints 101380 g010
Table 1. Images Acquisition by UAV Flights.
Table 1. Images Acquisition by UAV Flights.
No.of flight Maize growth days Date of flight Growth stage Flight altitude (m)
1 1 11-Jan-23 VE 30,100
2 8 18-Jan-23 VE 30,100
3 15 25-Jan-23 V2 30,100
4 22 1-Feb-23 V2 30,100
5 29 8-Feb-23 V4 30,100
6 36 15-Feb-23 V6 30,100
7 43 22-Feb-23 V6 30,100
8 51 2-Mar-23 V8 30,100
9 56 7-Mar-23 V10 30,100
10 65 16-Mar-23 R1 30,100
11 72 23-Mar-23 R1 30,100
12 79 30-Mar-23 R2 30,100
13 85 5-Apr-23 R3 30,100
14 92 12-Apr-23 R4 30,100
15 99 19-Apr-23 R5 30,100
16 106 26-Apr-23 R5 30,100
17 113 3-May-23 R6 30,100
Table 2. Summary of vegetation indices that were extracted in the study.
Table 2. Summary of vegetation indices that were extracted in the study.
Vegetation Formulation Reference
CIgr N I R G r e e n − 1 [17]
CIre N I R R e d E d g e − 1 [17]
EVI2 2.5 × ( N I R − R e d ) 1 + N I R + ( 2.4 × R e d ) [18]
GNDVI N I R − G r e e n N I R + G r e e n [19]
MCARI2 1.5 × [ ( 2.5 × ( N I R − R e d ) ) − ( 1.3 × ( N I R − G r e e n ) ] ( 2 × N I R + 1 ) 2 − ( 6 × N I R − 5 × R e d ) − 0.5 [20]
MTVI2 1.5 × [ ( 1.2 × ( N I R − G r e e n ) ) − ( 2.5 × ( R e d − G r e e n ) ] ( 2 × N I R + 1 ) 2 − ( 6 × N I R − 5 × R e d ) − 0.5 [20]
NDRE N I R − R e d E d g e N I R + R e d E d g e [21]
NDVI N I R − R e d N I R + R e d [22]
NDWI G r e e n − N I R G r e e n + N I R [23]
OSAVI N I R − R e d N I R + R e d + 0.16 [24]
RDVI N I R − R e d ( N I R + R e d ) [25]
RGBVI G r e e n 2 − ( B l u e × R e d ) G r e e n 2 + ( B l u e × R e d [26]
Table 3. Top 10 best performances of fourteen ML model across six distinct methods of feature engineering.
Table 3. Top 10 best performances of fourteen ML model across six distinct methods of feature engineering.
Feature Set Model MAE MSE RSME R 2
SHAP Values Huber 0.278809 0.516539 0.718707 0.926313
Correlation Coefficient Huber 0.278873 0.516555 0.718717 0.926311
Permutation Importance Huber 0.279073 0.516604 0.718752 0.926304
RandomForest Importance Huber 0.279069 0.516617 0.718760 0.926302
RFE with CV Huber 0.279063 0.516617 0.718761 0.926302
All Features Huber 0.279325 0.517176 0.719150 0.926222
SHAP Values M-estimators 0.299684 0.526963 0.725922 0.924826
Permutation Importance M-estimators 0.303802 0.528391 0.726905 0.924622
RandomForest Importance M-estimators 0.303904 0.528540 0.727007 0.924601
RFE with CV M-estimators 0.304337 0.529960 0.727983 0.924398
Table 4. Top 10 worst performances of fourteen ML model across six distinct methods of feature engineering.
Table 4. Top 10 worst performances of fourteen ML model across six distinct methods of feature engineering.
Feature Set Model MAE MSE RSME R 2
All Features Decision Tree 0.987037 4.735048 2.176017 0.324520
Permutation Importance Decision Tree 0.996296 4.731600 2.175224 0.325012
Correlation Coefficient Passive Aggressive 1.620354 4.476983 2.115888 0.361334
LASSO Coefficients Decision Tree 0.940370 4.000685 2.000171 0.429281
SHAP Values Decision Tree 0.748519 3.459833 1.860063 0.506436
SHAP Values XGBoost 0.763426 2.624211 1.619942 0.625642
Correlation Coefficient ElasticNet 1.237896 2.548584 1.596428 0.636431
LASSO Coefficients ElasticNet 1.213348 2.533981 1.591848 0.638514
RFE with CV Decision Tree 0.878889 2.498648 1.580711 0.643554
LASSO Coefficients Gradient Boosting 0.841662 2.399104 1.548904 0.657755
Table 5. Summary parameter for hyperparameter.
Table 5. Summary parameter for hyperparameter.
Model Parameter Value R 2
alpha 1
Huber epsilon 1 0.926266
max_iter 100
M-estimators min_samples 0.7 0.924029
stop probability 0.96
Linear Regression fit_intercept TRUE 0.918301
alpha 0.615848211
Ridge Regression fit_intercept TRUE 0.916892
solver lsqr
Table 6. Evaluation metrics for different ensemble methods.
Table 6. Evaluation metrics for different ensemble methods.
Method Model MAE MSE RMSE R 2
PEnsemble 1 Huber, M-estimators, Linear Regression, Ridge Regression 0.308433 0.531334 0.728926 0.924202
PEnsemble 2 Huber, M-estimators, Linear Regression 0.308890 0.531836 0.729271 0.924131
PEnsemble 3 Huber, M-estimators, Ridge Regression 0.311677 0.532635 0.729818 0.924017
PEnsemble 4 Huber, M-estimators 0.291894 0.522753 0.723016 0.925427
Table 7. Comparison of R 2 Scores for Different Models.
Table 7. Comparison of R 2 Scores for Different Models.
Model R 2 Feature Scaler R 2 Feature_SHAP R 2 Feature_Hyperparamer R 2 Ensemble
Huber 0.926222 0.926313 0.926266 0.924202
M-estimators 0.921954 0.924826 0.924030 0.924131
Linear Regression 0.904104 0.918302 0.918302 0.924017
Ridge Regression 0.911118 0.916077 0.916892 0.925427
Table 8. Collection of ground data for maize plants using the traditional approach.
Table 8. Collection of ground data for maize plants using the traditional approach.
Plot name No.of seed with one cob Weight of 100 seed (g) Weight of seed one cob (g) No.of seed one kilogram Actual harvesting (kg)
1 360 26 93.6 3,846 1,314.44
2 288 21 60.48 4,762 236.92
3 300 19.4 58.2 5,155 387.82
Table 9. A comparison of the percentage error between the actual harvest grain yield and the predictions from various approaches.
Table 9. A comparison of the percentage error between the actual harvest grain yield and the predictions from various approaches.
Actual harvesting (kg) Plot1:1314.44 %Error plot1 Plot2:236.92 %Error plot2 Plot3:387.82 %Error plot3
Breeder 503.19 0.62 332.87 0.40 342.67 0.12
Huber 986.23 0.25 258.20 0.09 345.22 0.11
M-estimators 991.44 0.25 259.58 0.10 346.97 0.11
Linear Regression 998.47 0.24 262.01 0.11 348.57 0.10
Ridge Regression 999.03 0.24 263.05 0.11 348.01 0.10
PEnsemble 1 990.30 0.25 259.48 0.10 346.36 0.11
PEnsemble 2 990.50 0.25 259.45 0.10 346.50 0.11
PEnsemble 3 990.61 0.25 259.65 0.10 346.39 0.11
PEnsemble 4 988.31 0.25 258.75 0.09 345.92 0.11
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated