1. Introduction
Over the past few decades, the development of technology, especially carbon fiber and lithium polymer batteries, has facilitated the use of drones for last mile delivery. For example, Zipline has completed over 14,000 medical supply deliveries in Rwanda since 2016 ([
1]). In 2019, Google’s Wing and Amazon received Federal Aviation Administration (FAA) approval to begin commercial delivery by drone ([
2,
3]).
In recent years, researchers have shown a growing interest in last-mile delivery that incorporates drones ([
4,
5]). The drone delivery problems can be categorized as drone-only or truck-drone tandem problems. The first uses only drones for parcel delivery, while the second uses both drones and trucks to deliver. The alternative objectives of drone delivery problems are to minimize delivery time or minimize operational cost ([
6]). Numerous variants of these problems have been suggested, such as heterogeneous drones ([
7]) or multiple trucks ([
8,
9]).
Compared with traditional truck transportation, drone delivery is faster and less affected by road systems, in addition, it can save a lot of labor and time costs ([
10]). These benefits allow logistics companies to dispatch drones for parcel delivery. On the other hand, a drone’s endurance is constrained by its battery’s capacity, which is further impacted by parcel weight, speed, and weather conditions ([
11,
12,
13]). In the literature involving drone delivery, one typical assumption is that drones fly at constant or maximum speed, regardless of their payload or speed. Thus, speed is not taken into consideration during the decision-making procedure. In fact, operating drones to fly at a fixed speed may lead to increased energy consumption, thus resulting in an energy-infeasible route or an inability to serve long-distance customers because the energy consumption of drones is severely impacted by parcel weight and speed. Therefore, it is crucial to consider the impact of payload and speed on endurance in drone routing problems.
The motivation for considering flight speeds as decision variables is the influence of drone energy consumption on flight endurance and range.
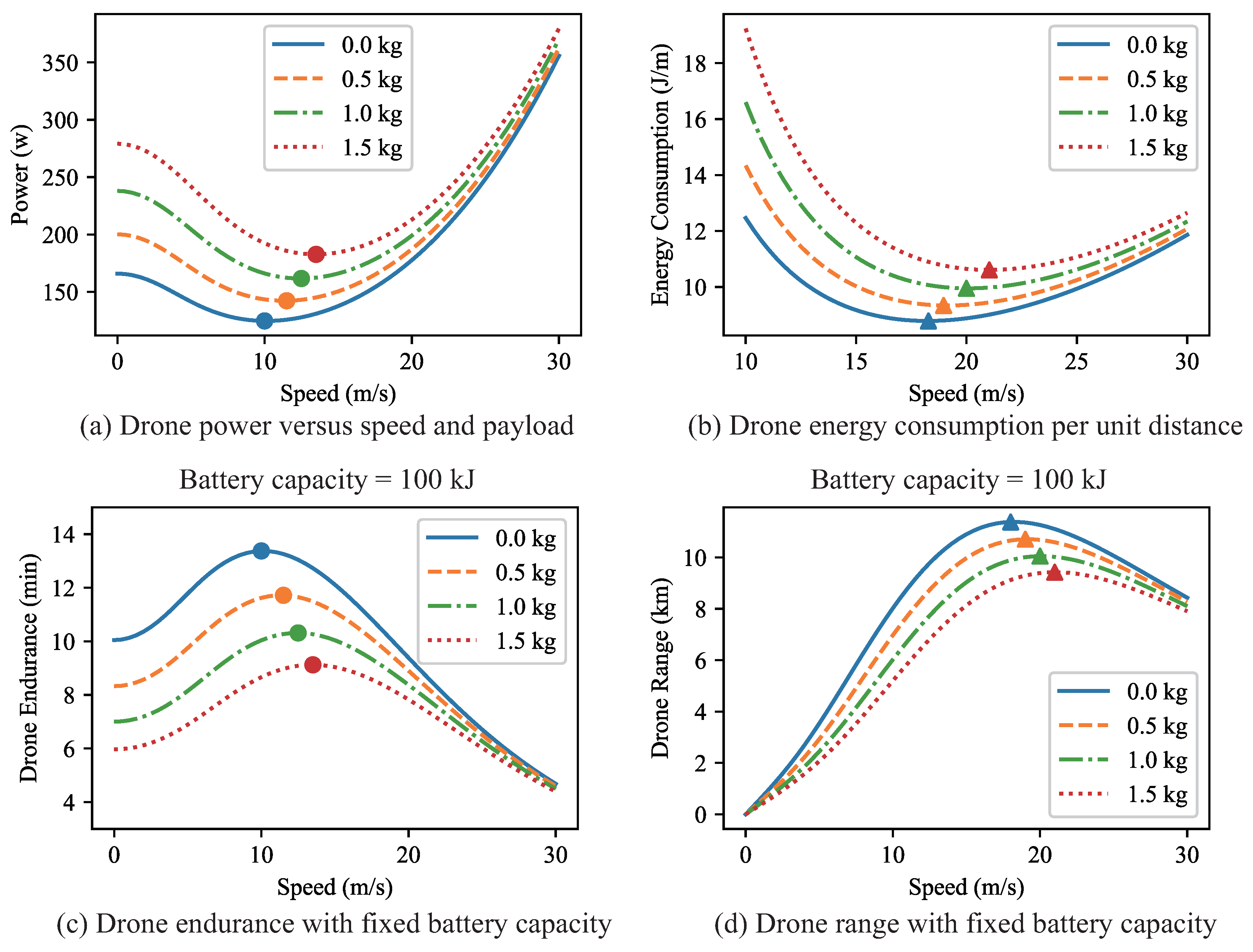
Figure 1(a) shows the power rate of drones under different payloads, using the model suggested by [
12]. The circular marks indicate optimal drone speeds that maximize the drone endurance under any onboard battery capacity, which can be seen more clearly from
Figure 1(c).
Figure 1(b) shows the drone energy consumption per unit traveling distance with varying payloads. The triangular symbols indicate optimal drone speeds that maximize the total traveling distance with fixed battery capacity, which can be observed more distinctly from
Figure 1(d). It can be seen from
Figure 1(b) that the drone energy consumption per unit distance initially decreases and subsequently rises again as the speed increases. This is because there is a balance between the flight duration and the energy consumption. Flying at lower speeds requires less power, which leads to a longer flight duration. In contrast, higher speeds result in more power being consumed, but the makespan is reduced. Therefore, the flight range notably depends on its speed, and faster flight speeds are not always optimal. Consequently, higher speeds can cause faster deliveries but with reduced range and increased energy consumption. This is essential within the scope of drone delivery systems because, in some cases, the customer is sufficiently remote from the warehouse, and flying at maximum speed can lead to a shorter range that falls short of the distance necessary to reach the customer. It may be beneficial to fly at lower speeds which can improve range and serve more customers. Moreover, speed adjustments can enhance endurance, which enables drones to serve more customers. As such, it is imperative to factor in drone speeds during deliveries when considering energy consumption.
This paper introduces the multi-trip drone routing problem with variable flight speeds (DRP-VFS), an extension of the DRP proposed by [
14]. In this problem, a fleet of homogeneous drones delivers multiple parcels to customers while minimizing energy consumption. In this case, drones can perform multiple trips and only be dispatched from and returned to the depot once per trip. While existing literature on the DRP assumes that drones fly at constant speeds in advance, the DRP-VFS considers drone speeds as decision variables when drones make deliveries.
This paper has the following contributions.
We introduce and formally define a multi-trip drone routing problem, aiming to achieve operational cost minimization, where drone speeds are considered as decision variables rather than constants.
We clearly consider drone energy consumption as a nonlinear function of both flight speed and payload rather than supposing that flight endurance and range are constants.
We proposed a three-phased method integrating variable drone speed to solve DRP-VFS, which can improve the solution in terms of computational time to a greater extent than MILP.
The rest of this paper is structured as follows. In
Section 2, we present a review of the literature.
Section 3 presents the formal description of DRP-VFS and its MILP formulation. In
Section 4, an efficient heuristic method proposed to solve large-scale instances is introduced.
Section 5 demonstrates the case study and verifies the effectiveness of the proposed method. In the end, conclusions are drawn, and future research work is discussed in
Section 6.
Figure 1.
The required power, energy consumption per unit distance, endurance, and range of a drone versus speed and payload referenced from [
15].
Figure 1.
The required power, energy consumption per unit distance, endurance, and range of a drone versus speed and payload referenced from [
15].
2. Literature Review
Over the past years, there have been increasing studies on the civil application of drones ([
4,
16]). These studies reported that operational planning for drone delivery is a well-studied problem. There already exists a lot of literature on the vehicle routing problem (VRP) involving conventional delivery vehicles and its variants ([
17,
18]). However, adapting the VRP to drones is faced with additional challenges since delivery by drones must account for extra constraints such as lower battery capacity and higher sensitivity of energy cost to payload and flight speed ([
6]).
Most drone studies have assumed either a fixed endurance or a constant speed ([
10,
19,
20,
21,
22,
23,
24]). Obviously, under this assumption, drones flying at higher speed have longer ranges. Other studies consider a constant range of UAVs. These two assumptions are equivalent when drone speeds are constant. However, both of them fail to consider the influence of payload and speed on the drone’s energy consumption, thus limiting the flexibility of drone delivery. For example, drones can extend their flight endurance by adjusting speed to serve customers further away from the depot.
Some studies have improved the fixed endurance/range model by considering drone power consumption dependent on payload while remaining unrelated to drone speed. [
25] apply the UAV power rate function proposed by [
26] and assume that the UAV maintains the maximum power during flight to calculate the load-dependent UAV speed during delivery. [
27] propose a package delivery schedule utilizing drones and consider the drone’s power rate varies linearly with its payload. [
6] propose two drone routing problems where customers are served by drones only. The authors consider the power rate function linearly dependent on payload weight and develop a simulated annealing (SA) algorithm to address the problems. The power rate function adopted in [
6] pertains solely to hovering without encompassing that of actual flight. [
14] adopt the same energy consumption as in [
6], but instead of approximating the power rate function, they develop an exact algorithm adding logical and subgradient cuts to solve a DRP with time windows. [
28] use the UAV power rate proposed by [
29] as a piecewise linear function of package weight in their DRP. [
30] also consider the influence of package weight on energy consumption using the same model as [
6]. However, different from the proposed model based on varying speeds, the studies in the above papers only consider constant drone speeds. Moreover, the proposed energy-consumption models are mainly about hovering and do not consider the energy cost of actual flight status. Other studies apply an energy consumption model related to the payload and the drone speed during forward flight. [
31] adopt an energy model by [
26], which is linearly dependent on payload and speed. [
32] also consider the energy consumption function introduced in [
11] in the multiple flying sidekicks traveling salesman problem (mFSTSP). However, the UAV speeds are fixed in these two papers, limiting the potential time and energy savings from flying at varying speeds.
Some recent studies have considered variable flight speeds in drone routing problems. For instance, [
33] considers the reciprocal of the flight speed to be approximately linear with the weight of loads. However, they consider drone speed as a function of the load, which can be regarded as a fixed parameter related to given loads rather than as a decision variable to be optimized. [
34] consider drone speeds as decision variables and use the energy model introduced by [
12]. Besides, [
35] employs the multi-rotor UAV energy consumption model developed by [
11] and considers power rate as a function of a UAV’s payload and speed. [
35] investigate the mFSTSP with variable drone speeds. These two studies treat drone speeds as decision variables and demonstrate that operating drones at varying speeds contribute to delivery cost and time reductions, respectively. Moreover, [
34] emphasizes that using fixed speeds may result in infeasibility in some instances. These two papers consider drone and truck tandem delivery, whereas our focus is solely on drone-only deliveries. As far as we know, this paper presents for the first time a DRP-VDS that considers UAV energy consumption and variable flight speeds.
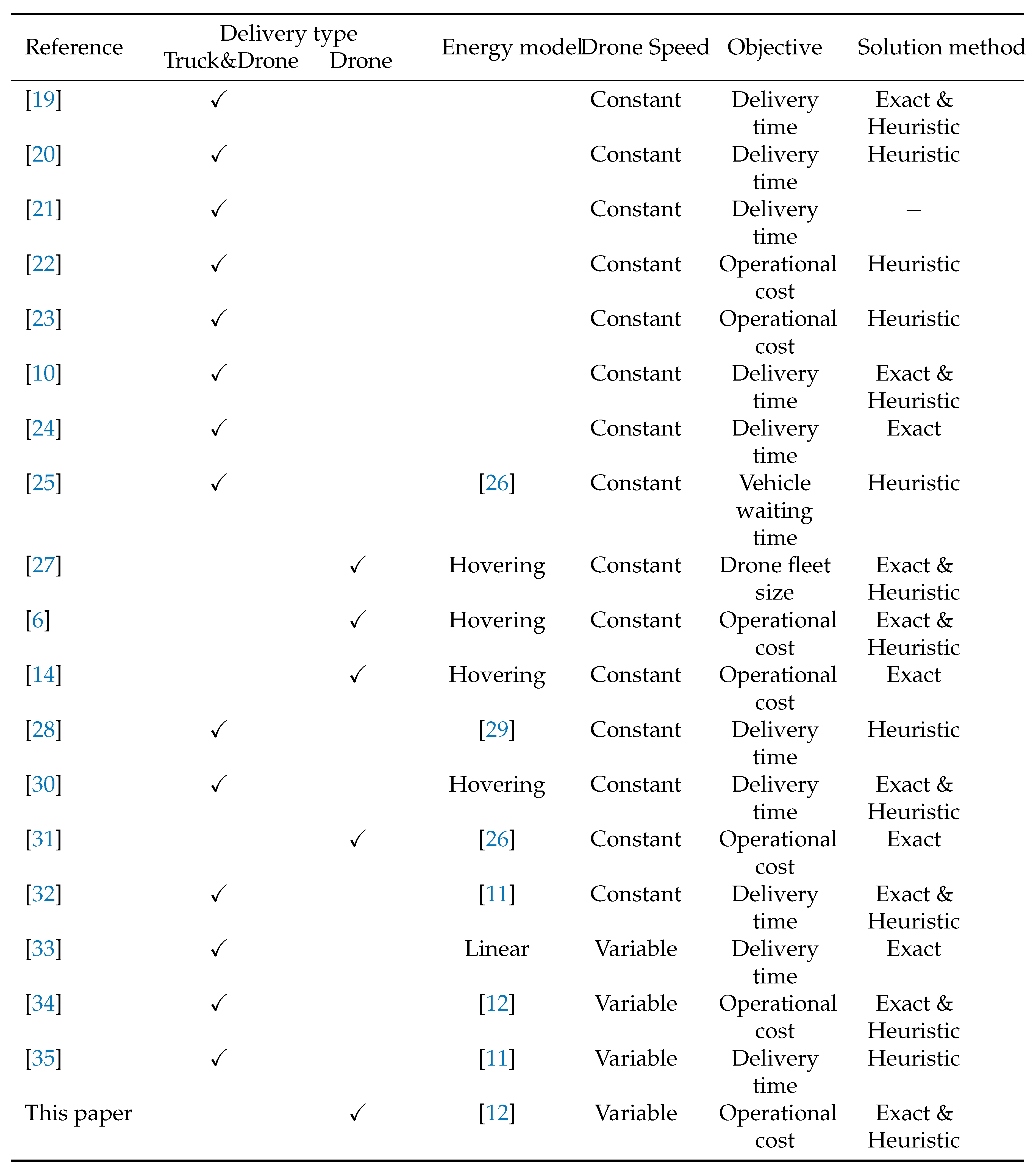
Table 1 demonstrates a summary of relevant studies on the drone delivery problem reviewed in this paper. The studies are compared using the following factors: (i) the type of delivery (truck-drone tandem or drone-only), (ii) whether the endurance of drones is fixed or evaluated by energy consumption model, (iii) the drone speed (constant or variable), (iv) the objective function used, and (v) whether the solution methods are exact or heuristic. In the literature mentioned above, it is evident that only a few papers clearly consider the energy cost model and even fewer take drone speeds into account as decision variables. Because the finite drone range is susceptible to speed and payload weight, it is essential to consider variable drone speed and payload in drone delivery systems. In this study, a DRP-VFS is proposed to consider the energy constraints and variable speed and payload of the drone delivery systems for last-mile delivery systems. Also, a three-phased heuristic method is proposed to solve large-scale scenarios. The performance of the proposed heuristic is evaluated by comparing it to the exact method.
3. Model Formulation
This section presents a formulation of the DRP-VFS, and introduces piecewise linearization to approximate the nonlinear energy consumption function.
3.1. Problem Definition
The multi-trip drone routing problem with variable flight speeds (DRP-VFS) is defined on a complete directed graph , where represents the set of all nodes with the node 0 and corresponding to the depot (distribution center) from which all drones must originate and return. The set of customers is denoted by associated with the distinct parcels. To simplify notation, we introduce to indicate the set of nodes from which a drone can depart and to describe the set of nodes that a drone may visit. Let denote the set of arcs. Additionally, we define sets and to denote the forward and backward nodes of node i, respectively.
Each customer has a positive demand and a hard time window . The drones are allowed to arrive early but need to wait until to begin serving the customer. A fleet of U homogeneous multi-rotor drones departs from the depot with a fully charged battery. Q represents the drone’s maximum payload, and we suppose that , while E is the maximum energy provided by a fully charged battery. The service time for each customer is . Every drone can implement multiple trips and serve several customers within one delivery. represents flight distance on arc , which is assumed to be symmetric. Since the drone speeds are decision variables in this paper, the flight time on arc is non-constant, as discussed later. The maximum speed limit is represented by .
We make the following assumptions:
Parcels are delivered by drones only.
There is only one depot from which drones can depart.
We neglect the time of loading parcels and swapping batteries.
Without loss of generality, we ignore the influence of weather, i.e., wind impact is not considered.
Drones can fly at a constant speed between two locations. The speed of each flight can vary.
3.2. Mathematical Model
DRP-VFS involves two sets of binary variables: if a drone flies across arc , and otherwise. if a trip ends in node i and is immediately succeeded by another trip with node j as the first customer. Additionally, there are six sets of continuous variables: is the parcel’s weight transported across the arc (kg). denotes the drone speed from node to node (m/s). is the service start time of customer (second). represents the time required to fly through arc . denotes the total energy a drone consumes when it arrives at customer i (kWh). indicates the energy consumed through arc , measured in kWh.
The constraints of route feasibility can be expressed as follows:
Constraints (1) and (2) guarantee that each customer is served only once. Constraint (3) guarantees that the number of trips leaving the depot equals the number returning to the depot.
We apply demand constraints through
Constraints (4) ensure that the demand of each customer can be satisfied, and also eliminate sub-tours. Consequently, the payload decreases to zero when the drone returns to the depot as specified by constraints (5). With constraints (6), the total weight of parcels carried by a drone in a trip must not exceed its payload capacity.
The following equations are formulated to enforce time-related constraints.
Constraints (7) require that the total of the arrival time and service time in
i and travel time across the arc
not greater than the arrival time at the customer
j (the immediate successor of
i). Constraints (8) indicate that the arrival time to customer
i falls within its designated time window
. Constraints (9) indicate the temporal relationship between successive trips executed by one drone, including the return time. Note that constraints (7) are nonlinear due to
, we will introduce a piecewise linear method to convert them into linear ones in
Section 3.3.
In this paper, we allow drones to change batteries and place parcels for new trips when they return to the depot. We adopt a 2-index formulation inspired by [
14] to formulate the multi-trip characteristics of drone delivery. Therefore, we can achieve the reusability of drones by incorporating the following constraints:
Constraints (10) and (11) establish a relationship between variables and . Constraint (12) limits the number of drones that can be used.
To evaluate the energy usage during delivery, we adopt the power rate model according to [
12].
where
is the average profile drag coefficient,
is the air density,
s is the rotor solidity,
is the angular velocity of the rotor,
is the blade tip speed,
R is the rotor radius,
D is the rotor disc area,
is the correction factor to ideal induced power,
is the induced velocity in hovering,
is the equivalent flat plate area of the drone.
w is the total weight of the drone, including the unloaded weight
of the drone and the weight
of parcels. Thus,
on the forward flight to customers, where
g is the gravitational acceleration. To simplify the above formula, define
and
as the blade profile power and induced power when hovering.
By transforming (
13), we derive an energy consumption formula denoted as
(
/
) for a drone’s travel over per unit distance at a constant speed
v, and calculated as
Thus, the energy consumption for drone on arc
, denoted as
can be expressed as
where
and
are the distance and payload on arc
. It is worth noting that (
15) is nonlinear when
and a piecewise linear method will be applied to deal with them in the next subsection.
Hence, drones’ energy constraints are written as
Constraint (16) signifies that the initial energy consumption of each trip is set to zero. Constraints (17) indicate the energy consumed across the arc . Constraint (18) guarantees the battery’s energy capacity constraint must be imposed.
The domain of the variables is shown below.
3.3. Piecewise Linearization
Piecewise linearization can approximate a nonlinear univariate function using a set of non-negative variables of special ordered sets type 2 (SOS2), where at most two adjacent variables can be positive, while the sum of all variables equals 1 ([
36]). For univariate functions like
, the piecewise linearization approximation is realized by sampling
K points
as breakpoints on the
v-axis. After that, the linear segments
are used to approximate
.
In this case, we define a set of continuous variable
for each breakpoint. The value of
on arc
is represented by
The approximation value of the reciprocal of speed
is
which can be calculated by (
26).
The SOS2 variables
need to satisfy the following constraints.
Most modern MIP solvers, such as Gurobi and CPLEX, can address specially ordered sets of types 1 and 2 automatically. Consequently, constraints (
25)–(
27) are sufficient to produce the correct computation. Consequently, the nonlinear constraints in (
7) are approximated by replacing
with
.
Similarly, we introduce a set of SOS3 variables
to linearly approximate the two-variable energy consumption function dependent on drone speed and parcel weight in (
14). Similar to the SOS2, the SOS3 variables require that at most three adjacent components be greater than 0. The difference is that the set of SOS2 variables is one-dimensional, while the set of SOS3 variables is two-dimensional. Consider again
S sampling coordinates
on the
v-axis and
T sampling coordinates
on the
m-axis. The function
is determined by each breakpoint
.
In our problem, the value of
and
on arc
are represented by
The approximation value of the energy consumption is
which can be calculated by using (
31).
The SOS3 variables
should satisfy (32) and (33).
However, unlike SOS1 and SOS2, modern MIP solvers don’t have an automatic syntax for imposing SOS3. For this reason, we utilize the triangle method proposed by [
37] to impose corresponding constraints. Consider the rectangle corresponding to intervals
and
and the two triangles generated by its diagonal
. We introduce two sets of binary variables
and
to represent the upper and lower triangles in the rectangle, respectively, with dummy values
and
at the boundaries. The additional constraints are shown as follow:
The constraint (34) requires that just one triangle be chosen from all possible triangles. Constraints (35) guarantee that the only values greater than 0 can be those corresponding to the three vertices of such a triangle. Accordingly, the nonlinear energy-related constraints in (17) are approximated by replacing with .
The objective function is minimizing the total energy consumption during delivery.
The model described above is a mixed-integer linear programming (MILP) model which can be solved efficiently by commercial MIP solvers such as Gurobi. While MILP solvers find optimal solutions, the computational time required is substantial, even for scenarios with several customers. In
Section 4, we propose a three-phased heuristic algorithm aimed at finding suboptimal solutions within computational time constraints.
4. Solution Method
The DRP-VFS extends the classical VRP and is an NP-hard problem. Owing to the NP-hardness of the DRP-VFS, a three-phased heuristic is proposed to effectively tackle practical large-scale scenarios.
The solution of DRP-VFS can be represented by , where is the number of trips. The contains a vector of customers that a drone will visit, which can be expressed as , where is the number of customers assigned to the kth trip.
4.1. Initialization
There are numerous heuristic approaches that can efficiently search for a feasible solution for the VRP, such as CW savings algorithm and sweep algorithm. In our method, we first apply an improved k-means algorithm that includes capacity and Euclidean distance as constraints to partition customers into several subsets (Algorithm ). Next, a traveling salesman problem with time windows (TSPTW) is solved within each subset to determine the customer sequence a drone serves. This algorithm is executed while satisfying the capacity, energy, and time window constraints. The number of clusters is calculated by the total demands and capacity of the drone as
The
centroids are randomly initialized in the customers’ coordinate range. The Euclidean distances between each customer and all
centroids are calculated. Sort customers by demand from largest to smallest and assign each customer to the nearest centroids. The total demands for each subset of clusters cannot exceed the drone’s capacity. The selected customer will be assigned to the next nearest centroid if the capacity constraint is not satisfied. The centroid of
kth cluster
is calculated based on its members using (
38).
The iterative procedure is repeated until the cluster is unchanged or the maximum iteration is reached.
The TSPTW is a special case of DRP-VFS since only one drone is used. Thus, we just need to remove the reusability constraints (10)-(12) and modify constraints (3) to the following.
Therefore, an initial feasible solution can be obtained quickly.
4.2. Local Search
In this section, we propose a speed optimization model to adjust the flight speed in a trip and calculate the cost of a DRP-VFS solution, and the Adaptive Large Neighborhood Search (ALNS) algorithm is used to enhance the solution quality.
4.2.1. Speed Optimization
The speed optimization problem (SOP) involves adjusting the flight speed in order to minimize energy consumption. The SOP is defined on a route
consisting of customers served by a single drone, where
and
represent the depot corresponding to 0 and
, respectively.
and
denote the flight speed and payload carried by a drone between node
and its successor. The SOP is formulated as follows:
subject to
The nonlinear energy function is linearized using SOS2 variables introduced in
Section 3.3. Since
is calculated in advance using (42), the
between node
and its successor depends only on
. We introduce
to linearly approximate the energy consumption function. Hence, the value of
and the approximate value of
can be represented by
To deal with
, the same method can be used. However, to speed up the solving process, we introduce a convexification method, i.e., replace
with an auxiliary variable
to avoid reintroducing integer variables:
Meanwhile, the following inequality should be imposed to ensure
converges to
.
It can be seen that constraint (
52) is a quadratic and convex constraint. Therefore, the SOP is modeled as a mixed-integer quadratically constrained programming (MIQCP) and can be solved by commercial solvers.
4.2.2. ALNS heuristics
In this subsection, an adaptive large neighborhood search algorithm is adopted to improve the initial solution obtained by
Section 4.1. The ALNS framework has demonstrated successful results in solving multiple variants of vehicle routing problems ([
38]). By removing selected nodes from the solution and reinserting them, we obtain a neighborhood of the given solution. The operators are dynamically chosen based on their previous performance. For this reason, each operator is given a score that increases if it enhances the current solution. A new solution is accepted if it meets the criteria specified by the local search scheme, such as simulated annealing.
In this paper, we apply two removal operators and two insertion operators to effectively destroy and repair a DRP-VFS solution. In addition, for every
iteration, the TSPTW model is solved once within each trip to adjust the customer sequence. The framework of the ALNS algorithm is presented in Algorithm .
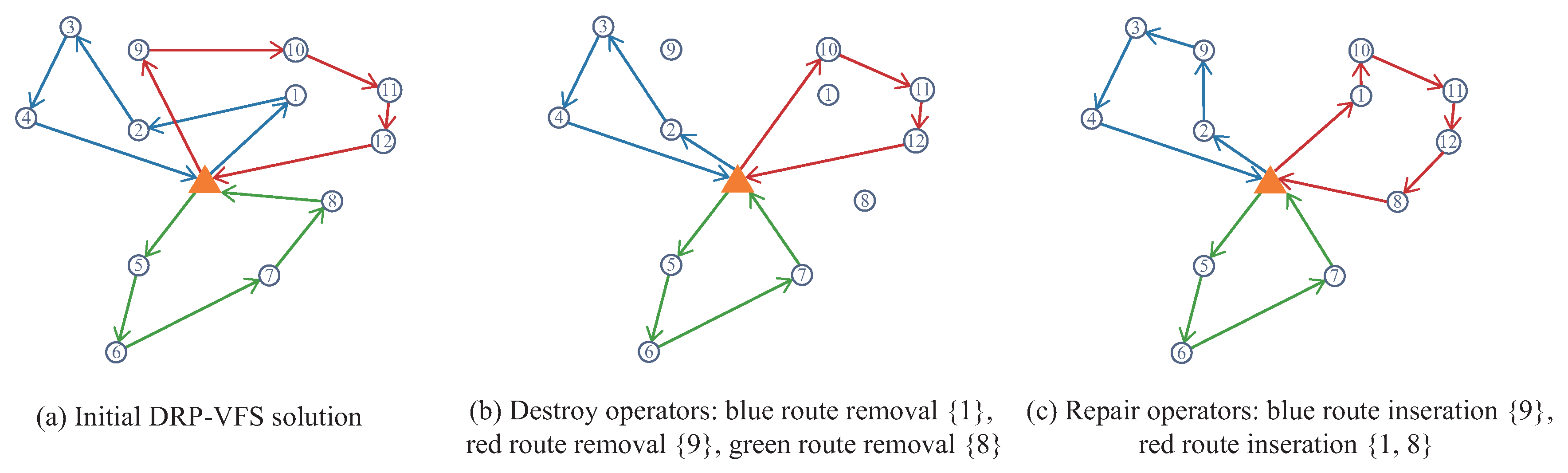
Figure 2(a)-(c) depict the initial solution, the solution after applying two destroy operators and the solution after executing two repair operators.
The destroy operators involve primarily removing several nodes from the current solution and placing them in a removal list . We present the removal operators involved in our approach as follows:
- (1)
Random removal: This operator removes several nodes at random from the current solution.
- (2)
Worst removal: This operator removes the highest-cost node from the solution, where the cost is determined by solving SOP.
The insertion operators are applied to repair a partly destroyed solution by reinserting the nodes from back into the solution. The insertion operators employed in our algorithm include:
- (1)
Greedy insertion: This operator repeatedly removes a node from and inserts it into the lowest cost position of a route.
- (2)
Regret insertion: An obvious disadvantage of greedy insertion is that it defers node insertion to later iterations where few feasible moves are available. The regret operator in our algorithm uses a 2-regret criteria. Define as the cost change incurred by inserting node i into the route where the cost is jth cheapest. The 2-regret criteria inserts the node i based on , where and are the best and second-best insertion of node i. We iterate the procedure until no more nodes in can be inserted.
We describe the adaptive weight adjustment process below. The operators are chosen by the roulette-wheel method. In the beginning, all operators are equally likely. They are updated as during program execution, where is the probability of operator i at the tth iteration, is the parameter of roulette wheel, denotes the score of operator i and indicates times it was selected in the previous iterations. The score reflects the performance of each operator. When a new best solution is found, the related operators’ scores are increased by . If the new solution outperforms the current one, the score is increased by . If the new solution falls short of the current one but meets the acceptance criteria, the score is increased by .
Our ALNS algorithm applies the simulated annealing as an acceptance criterion. We calculate the probability in line to determine whether to update the current solution and decrease the initial temperature T according to , where is a constant indicating the cooling rate. The algorithm produces the best solution that has been found after iterations.
4.3. Assignment
In this section, we describe a list schedule algorithm to minimize the number of drones. The delivery time, denoted by
h, is the latest allowable departure time from the depot, whereas the arrival time, denoted by
l, indicates when the drone reaches the depot upon finishing the delivery. The two times are calculated by using (
53).
where
and
are the starts of service time at the first and last nodes in a route,
and
is the distance and speed at the first and last flights in a route, and
is the service time of the last node.
We allocate routes to U drones using the list scheduling algorithm (Algorithm ). First, sort routes by delivery time in ascending order. A binary heap is used to get the route with minimum arrival time quickly. Next, traverse the routes; if the delivery time of is greater or equal to the arrival time of the heap top route, then is appended to this route. Otherwise, a new drone should be added. The time complexity is . In conclusion, our heuristic method finds a near-optimal solution for DRP-VFS.
5. Results and Discussion
In this section, numerical experiments have been carried out to verify the computational efficiency of the proposed heuristic method for the DRP-VFS. Firstly, the computational performance of the ALNS algorithm is revealed by comparing its solution quality and CPU time to those of the exact method with small-scale scenarios in
Section 5.2. Secondly, the performance of ALNS implementation in large-scale instances is demonstrated in
Section 5.3. Finally, we compare the solutions generated by fixed-speed and variable-speed in
Section 5.4. It is demonstrated that the energy consumption of variable-speed solutions decreases notably compared to that of fixed-speed solutions. All computational work was conducted on the computer configuration with an Intel i7 CPU and 16 GB RAM. The heuristic algorithm was coded in Python 3.7 and Gurobi 9.5.0 was used to solve the mathematical models.
5.1. Parameter Settings
We use two sets of benchmark instances introduced by [
14], named
and
. The
is created based on [
39] and [
6], which contains 10-50 customers. The
is an extension of Solomon’s instance, which contains 10-100 customers. We use
to validate the effectiveness of MILP and ALNS implementation and energy savings with variable flight speeds. We use
to validate the efficiency of ALNS implementation on large-scale instances. We execute the MILP implementation once for each instance. We execute the ALNS algorithm 10 times for each instance and calculate the average objective value and computational time. The parameter settings of drones and the ALNS algorithm are shown in
Table 2 and
Table 3. For
instances, the battery energy capacity is set to
kWh; For
instances, we set
kWh.
5.2. Performance Comparison between MILP and ALNS Implementations
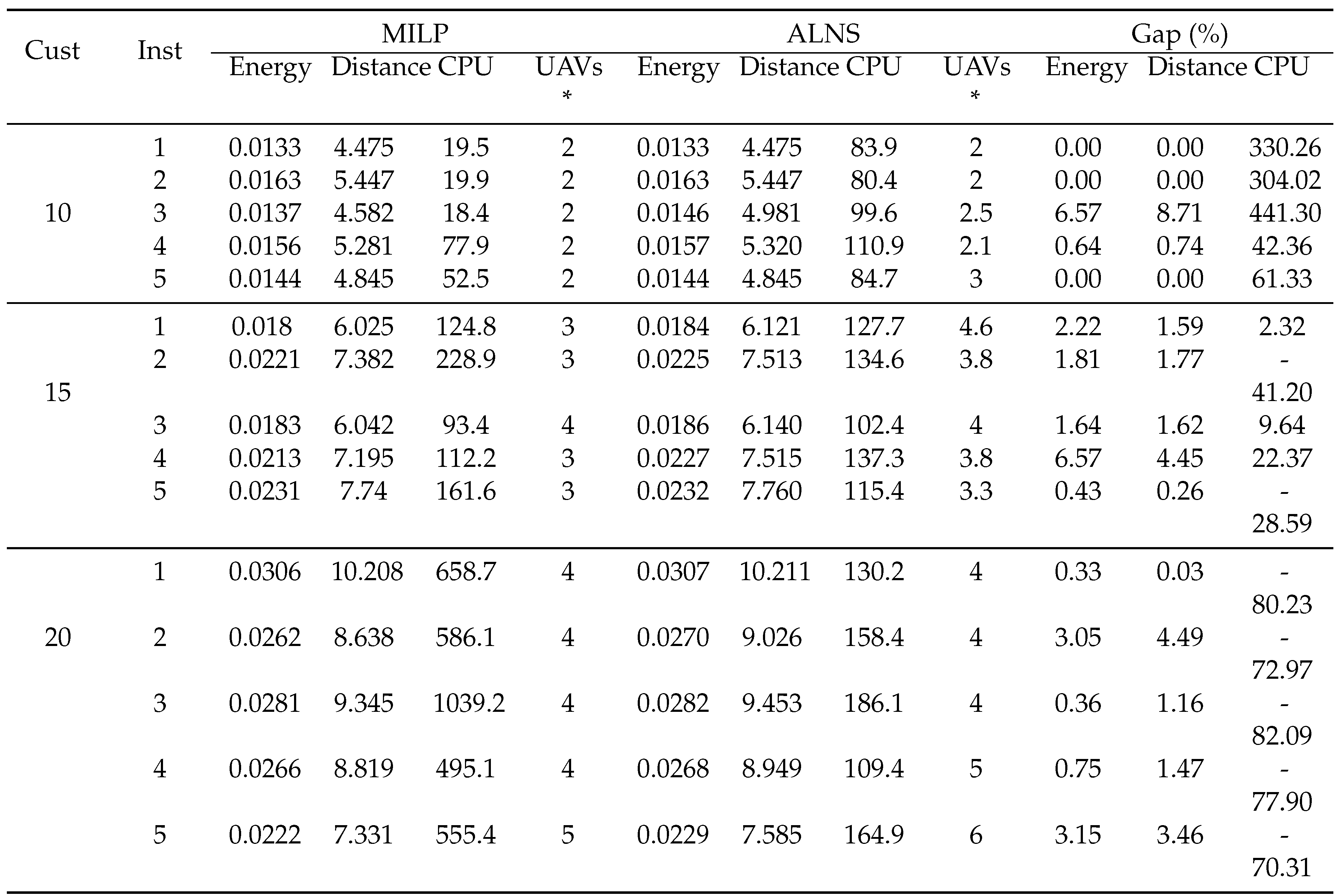
In this section, we compare the performance of the MILP implementation with the ALNS implementation to demonstrate that the ALNS algorithm is effective in finding near-optimal solutions to small DRP-VFS instances. The results of MILP and ALNS are presented in
Table 4. CPU is the computational time taken to solve the problem. The last three columns in
Table 4 are the percentage differences of ALNS versus MILP in terms of energy consumption, total flight distance, and computational time. The reason why ALNS needs more drones than MILP is that the time window is not fully utilized when calculating the delivery time and arrival time using (
53). For example, when appending
to
, the delivery time of
is possible to postpone backward while satisfying the time window constraint. Nevertheless, ALNS does not take this scenario into account due to the challenges associated with its implementation.
We can observe that the CPU time of MILP grows exponentially with the number of customers. For instance, the average CPU time increases from
to
, up by
when solving the 20-customer problem compared to the 15-customer problem. The average CPU time of the ALNS increases from
to
, a growth of
. Moreover, for the first two instances with 10 customers, ALNS finds the optimal solution. It can be obviously found from
Table 4 that the difference in energy consumption and travel distance between ALNS and MILP is less than 10 , which reveals that ALNS is capable of finding near-optimal solutions in small scenarios.
5.3. Performance of ALNS on Large-Scale Instances
Additionally, the ALNS algorithm is used to solve large-scale instances.
Table 5 indicates the results of
instances with 100 customers. Trips is the number of trips that drones would execute. The ALNS algorithm can find feasible solutions for large instances within a limited time. However, due to its high spatial complexity, the MILP model can’t be solved. As shown in
Table 5, the average computational time is
, indicating the high computational efficiency of the proposed heuristic algorithm.
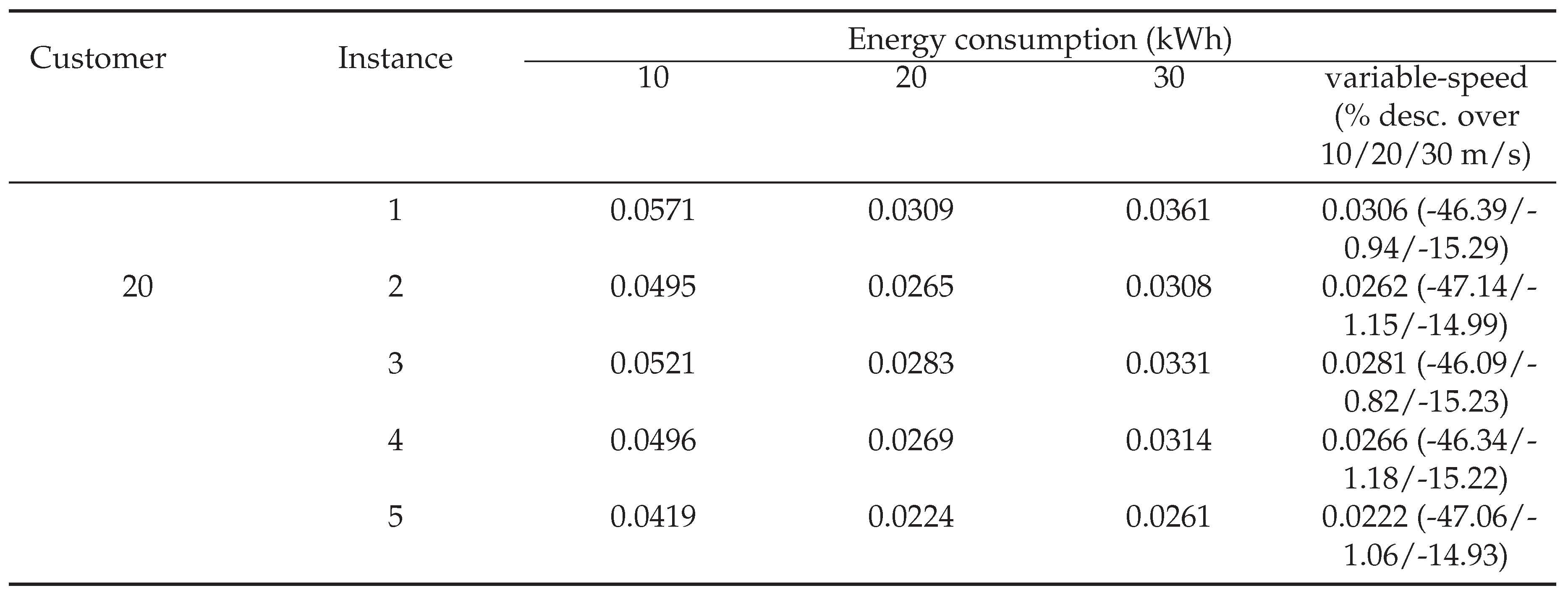
5.4. Comparison between Variable-Speed and Fixed-Speed
This section provides the energy saving achievable by enabling drones to fly at variable speeds. The MILP implementation is run with varying speeds and three fixed speeds (10/20/30
/
) to generate solutions for the DRP-VFS.
Table 6 shows that the average total energy consumption can be reduced by up to
against the 10
/
case,
against the 20
/
case and
against the 30
/
case. The drone speeds in variable speed cases are all located at maximum-range speed since this is the most energy-efficient speed for drones. The results in
Table 6 demonstrate that variable flight speeds result in lower energy consumption than fixed speeds in most instances. Reducing energy consumption could enable the utilization of smaller-capacity batteries, resulting in weight savings and possibly extending the flight range.
6. Conclusion and Future Work
This paper extends the multi-trip DRP with time windows to incorporate variable flight speeds. We proposed a MILP formulation for DRP-VFS that minimizes total cost while considering the energy consumption model, flight speed, payload weight, and drone reuse. To tackle practical instances, we proposed a three-phased ALNS heuristic algorithm. Numerical results indicate that optimizing drone speeds is an important consideration for drone delivery. Variable-speed resulted in about 46 and 15 improvements in total energy consumption compared to fixed-speed 10 / and 30 / cases, respectively. Numerical experiments also revealed that the three-phased heuristic performed well in both solution quality and CPU times in small and large DRP-VFS instances.
There are multiple opportunities for further research in this scope. For instance, exact solution methods can be explored to address the nonlinear energy function. To extend the flight range of drones, multiple depots or recharging stations might be investigated. More destruction and repair operations can be applied to improve solution quality. Additionally, the problem could be raised by considering heterogeneous drones or collaborative delivery of drones and trucks.
Author Contributions
Conceptualization, Shaofeng Lu; Investigation, Minling Feng; Methodology, Kunpeng Wu; Project administration, Shaofeng Lu and Zenghao Lu; Resources, Zenghao Lu; Software, Kunpeng Wu, Shaofeng Lu and Minling Feng; Supervision, Shaofeng Lu; Writing – original draft, Kunpeng Wu; Writing – review & editing, Shaofeng Lu.
Funding
This research was funded by the National Science Foundation of Guangdong Province, China under Grant 2023A1515012949; in part by the 2022 Fundamental and Applied Fundamental Research Project of Guangzhou Municipal Basic Research Program under Grant 202201010716.
Acknowledgments
In this section you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).
References
- Zipline. Drones to the rescue: Zipline’s blood deliveries save lives in Rwanda. 2018. Available online: http://ruralreporters.com/drones-to-the-rescue-ziplines-blood-deliveries-save-lives-in-rwanda/.
- Wing. Google’s Wing Gets First-Ever FAA Approval For Commercial Delivery Via Drone. 2019. Available online: https://interdrone.com/news/googles-wing-gets-first-ever-faa-approval-for-commercial-delivery-via-drone.
- Amazon. Amazon receives U.S. regulatory approval to start drone delivery trials. 2019. Available online: https://www.reuters.com/article/us-amazon-prime-air-idUSKBN25R2NG.
- Viloria, D.R.; Solano-Charris, E.L.; Muñoz-Villamizar, A.; Montoya-Torres, J.R. Unmanned aerial vehicles/drones in vehicle routing problems: a literature review. Int. Trans. Oper. Res. 2020, 28, 1626–1657. [Google Scholar] [CrossRef]
- Moshref-Javadi, M.; Winkenbach, M. Applications and Research avenues for drone-based models in logistics: A classification and review. Expert Systems with Applications 2021, 177, 114854–10. [Google Scholar] [CrossRef]
- Dorling, K.; Heinrichs, J.; Messier, G.G.; Magierowski, S. Vehicle Routing Problems for Drone Delivery. IEEE Transactions on Systems, Man, and Cybernetics: Systems 2017, 47, 70–85. [Google Scholar] [CrossRef]
- Kang, M.; Lee, C. An Exact Algorithm for Heterogeneous Drone-Truck Routing Problem. Transp. Sci. 2021, 55, 1088–1112. [Google Scholar] [CrossRef]
- Wang, Z.; Sheu, J.B. Vehicle routing problem with drones. Transportation Research Part B: Methodological 2019, 122, 350–364. [Google Scholar] [CrossRef]
- Ermagun, A.; Tajik, N. Multiple-Drones-Multiple-Trucks Routing Problem for Disruption Assessment. Transportation Research Record 2022, 2677, 725–740. [Google Scholar] [CrossRef]
- Agatz, N.; Bouman, P.; Schmidt, M. Optimization Approaches for the Traveling Salesman Problem with Drone. Transportation Science 2018, 52, 965–981. [Google Scholar] [CrossRef]
- Liu, Z.; Sengupta, R.; Kurzhanskiy, A. A power consumption model for multi-rotor small unmanned aircraft systems. 2017 International Conference on Unmanned Aircraft Systems (ICUAS), 2017, pp. 310–315. [CrossRef]
- Zeng, Y.; Xu, J.; Zhang, R. Energy Minimization for Wireless Communication With Rotary-Wing UAV. IEEE Transactions on Wireless Communications 2019, 18, 2329–2345. [Google Scholar] [CrossRef]
- Gao, N.; Zeng, Y.; Wang, J.; Wu, D.; Zhang, C.; Song, Q.; Qian, J.; Jin, S. Energy model for UAV communications: Experimental validation and model generalization. China Communications 2021, 18, 253–264. [Google Scholar] [CrossRef]
- Cheng, C.; Adulyasak, Y.; Rousseau, L.m. Drone routing with energy function : Formulation and exact algorithm. Transportation Research Part B 2020, 139, 364–387. [Google Scholar] [CrossRef]
- Tamke, F.; Buscher, U. The vehicle routing problem with drones and drone speed selection. Computers & Operations Research 2023, 152, 106112. [Google Scholar] [CrossRef]
- Otto, A.; Agatz, N.; Campbell, J.; Golden, B.; Pesch, E. Optimization approaches for civil applications of unmanned aerial vehicles (UAVs) or aerial drones: A survey. Networks 2018, 72, 411–458. [Google Scholar] [CrossRef]
- Küçükoglu, I.; Dewil, R.; Cattrysse, D. The electric vehicle routing problem and its variations: A literature review. Comput. Ind. Eng. 2021, 161, 107650. [Google Scholar] [CrossRef]
- Moghdani, R.; Salimifard, K.; Demir, E.; Benyettou, A. The green vehicle routing problem: A systematic literature review. Journal of Cleaner Production 2021. [Google Scholar] [CrossRef]
- Murray, C.C.; Chu, A.G. The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery. Transportation Research Part C: Emerging Technologies 2015, 54, 86–109. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, Z.; Shi, J. A Two-Echelon Cooperated Routing Problem for a Ground Vehicle and Its Carried Unmanned Aerial Vehicle. Sensors 2017, 17. [Google Scholar] [CrossRef]
- Wang, X.; Poikonen, S.; Golden, B. The vehicle routing problem with drones: several worst-case results. Optimization Letters 2017, 11, 679–697. [Google Scholar] [CrossRef]
- Ha, Q.M.; Deville, Y.; Pham, Q.D.; Hà, M.H. On the min-cost Traveling Salesman Problem with Drone. Transportation Research Part C: Emerging Technologies 2018, 86, 597–621. [Google Scholar] [CrossRef]
- Boysen, N.; Briskorn, D.; Fedtke, S.; Schwerdfeger, S. Drone delivery from trucks: Drone scheduling for given truck routes. Networks 2018, 72, 506–527. [Google Scholar] [CrossRef]
- Poikonen, S.; Golden, B.; Wasil, E.A. A Branch-and-Bound Approach to the Traveling Salesman Problem with a Drone. INFORMS J. on Computing 2019, 31, 335–346. [Google Scholar] [CrossRef]
- Deng, X.; Guan, M.; Ma, Y.; Yang, X.; Xiang, T. Vehicle-Assisted UAV Delivery Scheme Considering Energy Consumption for Instant Delivery. Sensors 2022, 22. [Google Scholar] [CrossRef] [PubMed]
- D’Andrea, R. Guest Editorial Can Drones Deliver? IEEE Transactions on Automation Science and Engineering 2014, 11, 647–648. [Google Scholar] [CrossRef]
- Torabbeigi, M.; Lim, G.J.; Kim, S.J. Drone Delivery Scheduling Optimization Considering Payload-induced Battery Consumption Rates. Journal of Intelligent & Robotic Systems 2020, 97, 471–487. [Google Scholar] [CrossRef]
- Poikonen, S.; Golden, B. Multi-visit drone routing problem. Computers and Operations Research 2020, 113, 104802. [Google Scholar] [CrossRef]
- Stolaroff, J.K.; Samaras, C.; Mitchell, A.S.; Ceperley, D.; Neill, E.R.O.; Lubers, A. Energy use and life cycle greenhouse gas emissions of drones for commercial package delivery. Nature Communications 2018, pp. 1–13. [CrossRef]
- Jeong, H.Y.; Song, B.D.; Lee, S. Truck-drone hybrid delivery routing: Payload-energy dependency and No-Fly zones. International Journal of Production Economics 2019, 214, 220–233. [Google Scholar] [CrossRef]
- Choi, Y.; Schonfeld, P.M. Optimization of Multi-package Drone Deliveries Considering Battery Capacity. Transportation Research Board 96th Annual Meeting 2017, p. 16.
- Murray, C.C.; Raj, R. The multiple flying sidekicks traveling salesman problem: Parcel delivery with multiple drones. Transportation Research Part C: Emerging Technologies 2020, 110, 368–398. [Google Scholar] [CrossRef]
- Nishira, M.; Ito, S.; Nishikawa, H.; Kong, X.; Tomiyama, H. An ILP-based Approach to Delivery Drone Routing under Load-dependent Flight Speed. 2022 International Conference on Electronics, Information, and Communication (ICEIC), 2022, pp. 1–4. [CrossRef]
- Dukkanci, O.; Kara, B.Y.; Bektaş, T. Minimizing energy and cost in range-limited drone deliveries with speed optimization. Transportation Research Part C: Emerging Technologies 2021, 125, 1–33. [Google Scholar] [CrossRef]
- Raj, R.; Murray, C. The multiple flying sidekicks traveling salesman problem with variable drone speeds. Transportation Research Part C: Emerging Technologies 2020, 120, 102813. [Google Scholar] [CrossRef]
- Beale, E.; Tomlin, J. Special facilities in a general mathematical programming system for nonconvex problems using ordered sets of variables. Operational Research 1969, 69, 447–454. [Google Scholar]
- D’Ambrosio, C.; Lodi, A.; Martello, S. Piecewise linear approximation of functions of two variables in MILP models. Operations Research Letters 2010, 38, 39–46. [Google Scholar] [CrossRef]
- Pisinger, D.; Ropke, S. A general heuristic for vehicle routing problems. Computers & Operations Research 2007, 34, 2403–2435. [Google Scholar] [CrossRef]
- Solomon, M.M. Algorithms for the Vehicle Routing and Scheduling Problems with Time Window Constraints. Oper. Res. 1987, 35, 254–265. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).