A Machine Learning-Assisted Classification Algorithm for the Detection of Archaeological Proxies (Cropmarks) Based on Reflectance Signatures

Preprint

Article

A Machine Learning-Assisted Classification Algorithm for the Detection of Archaeological Proxies (Cropmarks) Based on Reflectance Signatures

Altmetrics

Downloads

116

Views

103

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

17 March 2024

Posted:

19 March 2024

You are already at the latest version

Alerts

Abstract

Detection of subsurface archaeological remains using a range of remote sensing methods, poses several challenges until today. Recent studies regarding the detection of archaeological proxies like those of cropmarks highlight the complexity of the phenomenon. In this work we present three different methods, and associated indices, for identifying stressed reflectance signatures indicating buried archaeological remains, based on a dataset of measured ground spectroradiometric reflectance. Several spectral profiles between the visible and near infrared part of the spectrum, were taken over a controlled environment in Cyprus during the 2011-2012 and are re-used in this study. The first two (spectral) methods are based on a suitable analysis of the spectral signatures in (1) the visible part of the spectrum, and in particular in the neighborhood of 570 nm, and (2) the red edge-near infrared part of the spectrum, in the neighborhood of 730 nm. Machine learning (decision trees) allows for the deduction of suitable wavelengths to focus on, in order to formulate the proposed indices and the associated classification criteria (decision boundaries) that can enhance the detection probability of stressed vegetation. Noise in the signal is taken into account by simulating reflectance signatures perturbed by white noise. Applying decision tree classification on the ensemble of simulations and basic statistical analysis we refine the formulation of the indices and criteria for the noisy signatures. The success rate of the proposed methods is over 90%. The third method rests on the estimation of vegetation/canopy reflectance parameters through inversion of the physical-based PROSAIL reflectance model and the associated classification through machine learning methods. The obtained results provide further insights into the formation of stress vegetation that occurred due to the presence of shallow buried archaeological remains, which are well aligned with physical-based models and existing empirical knowledge. To the best of the authors' knowledge, this is the first study demonstrating the usefulness of radiative transfer models such as PROSAIL for understanding the formation of cropmarks. Similar studies can support future research directions towards the development of regional remote sensing methods and algorithms if systematic observations are adequately dispersed in space and time.

Keywords:

Subject: Environmental and Earth Sciences - Remote Sensing

1. Introduction

Remote sensing techniques have been long practiced in archaeological research [1,2,3,4]. Several studies have been focused on the detection of archaeological proxies, i.e., detection of areas with potential subsurface archaeological remains [5,6,7,8,9]. One of the most widely used methods for this is the detection of the so-called cropmarks [10,11,12]. Cropmarks, either stressed or positive, are usually created in areas where vegetation (crops) overlays near-surface archaeological remains. Buried archaeological features might retain soil moisture with a different percentage of moisture compared to non-archaeological areas and therefore impact the growth and phenological cycle of the cultivated crops on top of the surface [13,14,15,16,17].

Detection of archaeological proxies has been studied in different environments and contexts, using optical satellite imagery with the support of other means and remote sensors. For instance, in [18,19,20,21,22,23,24,25] different remote sensors have been proposed to detect archaeological proxies, based on integrated signals from optical and radar sensors. Spaceborne, airborne, low-altitude and ground sensors providing satellite imageries, aerial photographs and lidar data, as well as ground spectroradiometric and geophysical prospection approaches have been implemented towards the enhancement of the signal anomaly, and anomalies detection, which in their turn are linked to potential (archaeological) subsurface targets. Further related studies focusing on cropmarks can be found in [26,27].

Nevertheless, the detection success of the cropmarks using earth observation satellite imagery might varied, from time to time as well from the selected area. This remark is well familiar to experts in the field, as they recognized that the formation of the cropmarks is influenced by different factors such as the soil properties, soil conditions, climatic variables, cultivation practices and of course the same archaeological remains themselves [13,14,15]. This research gap, i.e., that local remote sensing outcomes and methods that fit only in the local landscape level has overshadowed all relevant research in the field, prohibiting research field progress.

Hence, it is important to better understand the physical mechanisms that enable the formation of cropmarks as well as to further study ways for developing robust supervised classifications methods on not so well-studied archaeological landscapes. This will allow the scientific community to establish regional remote sensing methods that can enhance the presence of cropmarks in different environments and therefore increase the success rate of these methods.

To do so, simulation experiments and tests in controlled fields are essential to isolate the different factors, minimize potential noise and errors, and therefore provide through systematic phenological observations the necessary dataset for further statistical evaluation. In this study, we recall the experiment took place in Alambra test field in Cyprus during the period 2011-2012, as part of the PhD thesis of the first author [28]. This dataset is ideal for the needs of this study as it was based on ground calibrated spectral signatures, minimizing thus potential noise (e.g. atmospheric impact) and errors, taken during a complete phenological cycle of the barley crops.

2. Materials and Methods

Ground spectral signatures were systematically collected over a test field developed near Alampra village in Cyprus. Details for this test field as well as more results on the processing of the ground spectral signatures can be found in [28] and [29]. As mentioned in [29] a 5 × 5 m square was constructed to replicate "tombs" 25 cm below the surface. Maintaining the soil's natural stratigraphy—that is, placing the original ground surface at the top—was a primary priority when constructing the controlled field. At that time, the entire region was cultivated with barley crops and Global Navigation Satellite Systems (GNSS) was used to locate the "tombs."

Several ground spectroradiometric measurements were made in each campaign, both across the "archaeological" area and the non-archaeological area. A handheld GER 1500 spectroradiometer that has been calibrated was utilized for this purpose. With 512 distinct channels and a range of around 1.5 nm, this device can record electromagnetic radiation from the visible to near infrared spectrum (400–1,050 nm). Additionally, all of the observations made over the crops were calibrated and the incoming sun radiation was measured using a Lambertian spectralon panel. The instrument's field of view (FOV) was adjusted to 4 degrees (≈0.02 m² from 1.2 m above the ground.) The reference measurement at the spectralon Lambertian surface panel was used to determine the incoming radiance at first, whereas the subsequent measurements were followed.

Figure 1. (a) Photo from the construction of the controlled archaeological environment located at the Alampra village. (b) The area was then cultivated with barley crops. (c) Photo of the barley crop during its full growth. The linear cropmarks formed in the area above the archaeological environment is shown with an arrow (source [29]).

3. Results

The above-mentioned ground spectroradiometric datasets were further elaborated in the Python programming language [30]. The different processing steps and their results are illustrated in the following subsections.

3.1. Analysis of the Dataset and Data Transformation

Multi-temporal ground spectroradiometric campaigns have been carried out over the simulated test field between October 2011 until April 2012. In particular, there are 16 days of observation, with a varying number of measurements in each day. The number of A and H reflectance observations ρ in dates where measurements are given in the following Table 1. Label A refers to the measurements taken over the simulated “archaeological” subsurface target and Label H refers to the measurements taken over healthy vegetation (crops)

Our analysis of this dataset proceeds as follows. Consider the measured A reflectance curves of a single day of observation, e.g. 11022012, for shown in Figure 2a. The spectral profile of these curves is characteristic as the one we see in health vegetation: low reflectance values in the visible part of the spectrum, i.e., approximately between 450-630 nm, with a small increase in the green part of the spectrum around 560 nm, and a sudden increase in the near infrared part after 700nm. Between the 630 and the 700nm is the so-called red edge part of the spectrum. Observing these curves, we can see that there is a certain degree of similarity between them, indicating a nearly similar and a difference in scale (i.e., absolute reflectance values).

Therefore, the next step could be to isolate this pattern of the curves. Therefore, we transform (shift and rescale) each curve by linearly mapping the reflectance so that its range becomes [0, 1], i.e. its minimum and maximum are mapped into 0 and 1 respectively based on Equation 1:

{\bar{ρ}}_{i} (λ) = \frac{ρ_{i} (λ) - \min (ρ_{i})}{\max (ρ_{i}) - \min (ρ_{i})}

(1)

The index i runs over the number of observed curves. The transformed reflectance curves

{\bar{ρ}}_{i} (λ)

for the given date are shown in Figure 2b.

The effect of this transformation is clear: The relative significance of the differences in pattern, e.g. between the visible spectrum and the red edge, as shown in Figure 2b is much more pronounced than before (Figure 2a). In contrast the differences in absolute reflectance values observed in the near infrared part of the spectrum are not further visible. Our further analysis will be based on the transformed reflectance curves (Figure 2b).

Let us now plot the (transformed) reflectance curves against each other, which we may call reflectance-against-reflectance plots. In Figure 3, for a given day of observation (17032012) the A and H reflectance curves are plotted against each other, in all distinct combinations of A and H in the following manner: in Figure 3a all H measured curves of the day are plotted against a single H curve which serves as the horizontal axis. Similarly, for the other two figures (all A against a single H in Figure 3b and all H against a single H curve in 3c.).

One observes a specific pattern in the A against H graph in Figure 3b, i.e. A curve values are depressed relative to the H curve values at the same wavelength. The patterns shown in Figure 3, are characteristic of any given between day in the January-February-March (JFM) period and for any A and H curve is used to serve as the horizontal axis as shown in Figure 3. The period JFM was selected from the overall observation timeframe as this is the period (phenological cycle) where the crops start to grow in the area, and therefore we can observe the spectral signature pattern shown on Figure 2a.

On the other hand, if the same analysis is in any observation date in other phenological periods the result is qualitatively different, as can be seen in Figure 4 for the date 31102011. During that period the crops have just been seeded and therefore the spectral signatures correspond to those of soil targets rather than crops. Therefore, one realizes that one should focus on the JFM period, which is consistent with the growth stage of barley. The JFM period contains a dataset of 107 observations (reflectance signatures) to work with.

We may momentarily pause to generalize what we have done so far, thinking in terms of an unknown dataset of similar spread through the months of the year. Let us pretend that the given dataset (spectral signature) is unknown, and in any specific measurement day pick any reflectance curve and set all the others against it. Then do that for all curves of the day (we refer always to the transformed ones). In Figure 5 we show the results of doing that for a date in the JFM period, we have chosen 04032012, for two reflectance curves we called X_1 (unknown #1) and X_2 (unknown #2). It is clear that unknown #1 must be A while unknown #2 must be H. Indeed, Figure 5a indicates a stressed pattern (below the diagonal line 1:1) while in contrast in Figure 5b a healthy crop profile (near and above the diagonal line 1:1)

In the reflectance-against-reflectance type of plot, as in the case of Figures 3 to 5, it is not clear which part of the spectrum they mainly visualize. In Figure 6 we plot an A reflectance curve against an H in any specific date in the JFM period (here we have chosen 04032012). Restricting suitably the range, it is clarified that the main phenomena refer to the red edge part of the spectrum. Anticipating a discussion that will be the subject of subsection 3.6 we may observe that the resulting trend, which can be fitted with near perfection with very simple functions, suggests that quite specific physical phenomena are at work here producing this result.

3.2. Definition of a (Single-Wavelength) Classifying Index within the Visible Spectrum

The previous discussion suggests that in a dataset of (transformed) reflectance curves, the A reflectance curves have in general smaller ordinates than the H reflectance curves, at least in a part of the spectrum. In order to make such observations general and quantitative, we may form ratios of the reflectance curves using Equation 2:

ρ {- ratio}_{i, j} (λ) = \frac{{\bar{ρ}}_{i} (λ)}{{\bar{ρ}}_{j} (λ)}

(2)

That is, for the i-th reflectance curve we obtain N ρ-ratio curves (where N is the size of the original dataset), or more precisely, N-1 non-trivial ones. We may now observe that if the i-th curve is an A reflectance, then its ρ-ratio curves will lie lower that the ρ-ratio curves of an i′-th curve which is H reflectance. This statement can be made specific, by averaging the ρ-ratio curves corresponding to any specific observed reflectance (Equation 3):

mean ρ {- ratio}_{i} (λ) = \frac{1}{N - 1} \sum_{j \neq i} ρ {- ratio}_{i} (λ) = \frac{1}{N - 1} \sum_{j \neq i} \frac{{\bar{ρ}}_{i} (λ)}{{\bar{ρ}}_{j} (λ)}

(3)

That is, for every wavelength λ, we average ρ-ratios of any reflectance curve relatively to any other reflectance curve in the dataset (referring always to the transformed ones). Given our discussion above, the guess is that there might be a critical value of the mean ρ-ratio, serving as a decision boundary, separating the A from the H reflectance curves (with an acceptably high success rate).

A technical detail that should be taken care of, is that the denominator of ratios of normalized reflectances may be zero for certain wavelengths in the visible spectrum (see Figure 2b). This can be done by introducing a small cutoff, that is, we shall clip all values below that cutoff and set them equal to it. That cutoff should only serve as a facilitator of calculations, that is, its value should not affect the final results if it is small enough. Indeed, it turns out that any cutoff value below 5×10^–5 produces the same results.

The mean ρ-ratios for all observed reflectance curves and for all wavelengths are shown in Figure 7. One may then discover by mere inspection that in the vicinity of the peak of the original reflectance curves in the visible spectrum, i.e. near 560 nm, there is very clear separation between the A and H mean ρ-ratios. We should emphasize again that this fact survives for all small values of the cutoff, which primarily affect these curves near the blue and red edges.

At first, we may proceed empirically. The most promising region is the one around the peak of the reflectance within the visible region (~550 nm). By inspection one finds that the mean ρ-ratio at (a round) 570 nm is the most suitable variable to define a decision boundary between the A and H observations. Therefore, we shall define the following index (Equation 4):

{Index}_{570} = mean ρ - ratio (570 nm)

(4)

In Figure 8, we plot this index for all observations. We find that there is indeed a distinctive decision boundary between A and H observations at the value Index₅₇₀ = 1.2 (at one decimal point).

To be more precise, if we identify an observation as A if its Index₅₇₀ is greater than 1.2, then the standard classification scores of this method show no failure (Table 2).

We may note at this point that score values such as those observed in Table 2, usually imply excessive overfitting. But it is hard to argue for such an interpretation given that the results were obtained with a single degree of freedom. Then, another interpretation might be that the dataset is -in some way- too biased. Indeed, the dataset does not have the complications and deficiencies of satellite imagery, neither it is spread across many different test cases. Simulating a certain level of noise in the measured reflectance signatures adds some realism into the quality of the data, and its effects can be quantified. This is indeed done below. Moreover, we shall be able to argue that the classification methods discussed here can be directly interpreted in terms of the physical properties of the canopy, thereby adding a certain amount of generality/universality to our results.

3.3. Machine Learning Methods: Analysis with Logistic Regression and Decision Tree Classifiers

Although the 570 nm wavelength and the value 1.2 for the Index was found in an empirical fashion by inspecting the patterns in Figure 7, we would like to obtain the decision boundary and the associated wavelength(s) in a systematic way, as well to know why that worked given the hundreds of degrees of freedom present in the mean ρ-ratio curve. More importantly, given that real (i.e., satellite observations) data will have a more complex structure than our dataset, it is necessary to look at and understand alternative ways to identify the A observations.

To simplify our analysis, we group the wavelengths between the 400 nm – 900 nm (covering the visible to near infrared part of the spectrum), into bands of 10 nm averaging the values of mean ρ-ratio in every band. We use the central points of the bands, i.e. 405, 415,…,895, as the name of the corresponding feature (variable), reducing the number of the features to 50. We first calculate the 50 × 50 correlation matrix of the features, which is visualized in Figure 9.

We observe that the correlation matrix is nearly block-diagonal, forming two blocks in the visible/red-edge and the near infrared part of the spectrum. Especially the latter, forms a block of strongly correlated features. We observe that the wavelengths in the neighborhood of 550 nm are weekly correlated with other wavelengths, except for the wavelengths at the outer part of the red edge. This may be regarded as an explanation why the Index defined above can carry so much information alone. The wavelengths in the neighborhood of the 680 nm, as well as of 480 nm, are negatively correlated with the near infrared. In fact, 680 nm wavelengths are quite strongly correlated with a large part of the visible spectrum. Overall, these strong correlations imply that the effective degrees of freedom are much less the number of features.

Let us first model the classification of the curves into A and H through the logistic regression classifiers available in the Python language libraries [31]. Logistic regression involves all degrees of freedom (features) simultaneously finding the relative weight (importance) of them in obtaining the answer. Although the empirical analysis of the problem suggests that regression is not the most suitable method to consider, it is interesting to see how it performs and obtain the pattern regarding the importance of features.

After reshuffling, we split the available datasets of 107 observations into 85 observations (80%) for the training set and 22 (20%) for the validation set. The obtained model performance is given again by Table 2, i.e. perfect scores. It should be noted though that the 10 nm bands appear to be the coarser resolution producing the best results: with bands of 20 nm scores get lowered to 96%. The importance of every feature (wavelength), that is, the coefficients of the fitted logistic regression model is shown in Figure 10.

In this method, the classification is described quite differently than the single wavelength Index₅₇₀. Wavelengths around 660 nm have the greatest relative (positive) importance, while wavelengths around 480 and 680 nm do contribute significantly but counterbalancing (by having the opposite sign) the contributions of the majority of the features (appearing in the blocks of the correlation matrix). Also, the wavelengths in the upper block contribute significantly and rather equally.

Decision tree classifiers are more pertinent to the problem at hand, as the method finds decision boundaries examining sequentially its features [31]. Indeed, constructing again a training and validation set, and using gini impurity as a measure of the quality of the splits, we find that for a simple depth equal to 1 (one node) we find a decision boundary a single dominant feature at 571 nm i.e., the only wavenumber with a non-zero weight and equal to 1 (Figure 11), and a decision boundary (threshold) 1.191 shown in Figure 12, where our decision tree is visualized. This is in accordance with our expectations from the analysis that led to the Index₅₇₀ and the associated decision boundary. The decision tree classification allowed us to validate and refine that analysis, as well as to deduce these results in a systematic way, i.e. through algorithm instead of inspection.

Upon checking the fitted model on the validation set we find again the perfect scores given in Table 2.

3.4. Simulating the Effects of Noise: Statistics of the Classifying Index₅₇₀

At this point, it is necessary to incorporate in our analysis the presence of noise which is always part of real (e.g., satellite imagery) observations. We shall simulate adding white (i.e., uncorrelated) noise, drawn from a normal distribution N(μ,σ) with mean value μ equal to the value ρ of the (original) reflectance signature curve (at any given wavelength λ) and standard deviation σ=CV*ρ, where CV is the coefficient of variance, that will be fixed at 5%. That is (Equation 5),

ρ_{simulated} ~ N (ρ, CV * ρ)

(5)

This way, an ensemble of simulations of the dataset may be generated and the previous analyses may be applied for each element (dataset) of the ensemble. In particular, two important analyses may be applied: (1) To investigate the performance of Index₅₇₀ with decision boundary 1.2, that is, determine the statistics of the classification scores, and (2) to investigate the statistics of the decision boundary as that it is determined by a decision tree.

First, we would like to visualize how the mean ρ-curves of the ensemble of A and H observations look like. These curves are shown in Figure 13 for 100 simulations of the dataset with noise.

Once the ensemble of mean ρ-curves for the A and H observations has been constructed it is straightforward to apply classification methods and evaluate the statistics of the success rate. First, we do that for the Index₅₇₀ and deduce the score statistics for the associated classification criterion proposed in this work, i.e. that a reflectance signature is A if its Index₅₇₀<1.2.

The results shown in Table 3, indicate that the classification based on the Index₅₇₀ performs very well even in the presence of noise, roughly, we obtain success rate 97%±2%. Hence, it might turn out to be an effective tool in actual applications.

Our second task is to study these simulations through the decision tree method in order to obtain the statistics of the dominant wavenumber and thresholds. In this case, both the chosen wavelength and the decision boundary will be discovered by the method itself and hence they will vary. The obtained results will allow us to refine the definition of the Index when dealing with noisy dataset. As mentioned earlier, the decision tree classification has a greater affinity to the Index method proposed in this work and can naturally be regarded as a validation as well as refinement of the latter.

Indeed, in the case of the simulations ensemble, a tree depth equal to 2 was needed in some of the realizations, that is, at most two wavenumbers had a non-zero weight. It should be mentioned that the classification scores on the validation set remain essentially the same from depth 1 to depth 2, hence we shall proceed with depth 2. As the decision boundary is, in general, a multidimensional boundary surface in the feature space, we quote here the thresholds at which the tree splits data for the dominant wavelength. For more stable statistical results, we use an ensemble of 5000 simulations. The statistics of the classification scores are given in Table 4, together with the dominant wavelength (with importance ~0.95 or higher) and the associated threshold. Classification scores come as high as 98%.

The distribution of the dominant wavelength (frequency of appearance) is presented in Figure 14. On top of every bar is shown the mean value of the threshold for that wavelength. 568 nm is the most frequently arising wavelength of the distribution, but there are other values with significant rates of appearance. Table 5 shows certain important percentiles of the distribution. We see that between the 5^th and 95^th percentile there are many wavelengths which arise with significant probability.

Inspection of the threshold values in Figure 14 shows that the threshold values increase with the wavelength in this part of the spectrum. This is shown more concretely in Figure 15, where one may see a very distinct trend in (roughly) the 5 – 95^th percentile interval of the wavelength distribution. Outside this interval the events in every wavelength are too few, hence the (plotted) mean value of the threshold fluctuates a lot even in 5000 simulations.

The simple (monotonic) trend shown in Figure 15 facilitates the definition of a classification index for the noisy data and the choice of the decision boundary to form a classification criterion. We may define the index as the average of mean ρ-ratios over the interval containing the representative wavelengths, 555 – 572 nm. We formalize that in Equation 6:

{Index}_{570} = mean ρ - ratio (555 - 572 nm) < 1.17

(6)

Then, choosing the decision boundary from the thresholds of the smaller wavelengths (smaller thresholds) we will have great precisions (few false positives) but relatively low recall (low success rate in the identification of positives). If on the other hand, we choose the decision boundary from the thresholds of the larger wavelengths (larger thresholds) and particularly the value 1.17 corresponding to the 95^th percentile of the wavelength distribution, a nice balance between the magnitudes of the classification scores is attained. The very good performance of this criterion is given in Table 6.

3.5. The Red Edge

Our analysis in section 2 suggests that classification in the red edge part of the spectrum could be done, with a high degree of success, by mere visual inspection, at least in the given dataset. We would like to systematize this analysis and hence to quantify its performance for this observation. We shall do that by using decision tree classification.

Indeed, applying this method to the mean ρ-ratio curves for 680 – 760 nm, we find that there is a dominant wavelength (with importance 0.91) at 731 nm. In Figure 16 is given a visualization of this decision tree. We see that depth 3 is required in the case of the red edge. The threshold of the dominant value comes at 1.065. The obtained model returns classification scores 1.0 in the validation set. This information is summarized in Table 7.

Next, we investigate the effects of noise applying the same analysis in its element of the ensemble of simulated reflectance signatures. The mean values of the classification scores on the validation set attain a peak for tree depth 3, hence we stop there and in what follows we quote these results. For more stable statistical results we use again an ensemble of 5000 simulations. The statistics of the performance of decision tree model are shown in Table 8. Classification scores turn out to be 91%. Overall, one may conclude that using indices in the red edge regime of the spectrum is expected to be less effective than within the visible spectrum.

The distribution of the dominant wavelength (whose importance is always greater than 0.79) is shown in the histogram of Figure 17. One top of every bar of the histogram is shown the mean value of the threshold for that wavelength. The wavelength distribution has a mean ± standard deviation at 728 ± 5 nm. The interval 728 – 731 nm can be regarded as representative. Certain percentiles of the distribution are given in Table 9.

Thresholds are plotted against the corresponding wavelength in Figure 18. There is again a strong trend, as we also saw in the visible spectrum analysis, only this time is decreasing. As before, the trend is less clear outside the 5 – 95^th percentile interval due to fewer events there. The simplicity (monotonicity) of the relationship allows us to easily deal with the tradeoff between precision and recall in the way we define a classification index and choose the decision boundary, as it also occurred in the case of the visible spectrum. Defining the index by the wavelengths of the representative interval and choosing the decision boundary from the thresholds of the larger wavelengths (smaller thresholds), we will have great precisions relatively low recall. Alternatively, choosing the decision boundary from the thresholds of the smaller wavelengths (larger thresholds), and specifically, the value 1.10 corresponding to the 5^th percentile of the wavelength distribution, we manage again to have a nice balance between the classification scores.

Indeed, we define form the classification criterion as follows.

{Index}_{730} = mean ρ - ratio (728 - 731 nm) < 1.10

(7)

The performance of the criterion in equation 7 is given in Table 10. As expected, this method of classification performs less well than the visible spectrum one, the analogous scores shown in Table 6.

3.6. Interpretation and Classification on Physically-Based Modelling (PROSAIL)

The high correlation between degrees of freedom (wavelengths) we have seen in Figure 9 means that the actual degrees of freedom are actually far fewer than the hundreds of reflectance values in a reflectance signature. PROSAIL model produces reflectance signatures from about a dozen physical parameters modelling the leaves optical properties and the canopy reflectance properties [32,33]. PROSAIL belongs to a class of radiative transfer models and allows for a physically based retrieval of the plant properties [34,35,36].

In this section we present a preliminary work in relating the physical properties of vegetation and canopy with the A and H classification. We shall use plausible values and ranges for the PROSAIL input parameters based on the literature [33; 35] given in Table 11.

Four variables will be let to vary: Cab, Car, LAI, and lidfa. Inversion is done using the PROSAIL module [37] and standard optimizers of Python libraries. The statistics of fitting them across the dataset of 107 observations is given in Table 12:

Scatterplots of the estimated parameters are given in Figure 19, for some of the possible pairs of parameters. As it will be further understood shortly, the leaf chlorophyll content Cab is the most important and robust parameter, in the sense of being less sensitive to different choices of parameters to estimated and their assumed bounds (that experimentation cannot be shown here).

A linear relationship between the Car and Cab parameters known in the literature, see e.g. [38], is verified here, although it was not adopted. The highly important leaf area index (LAI) parameter is estimated to have relatively large values which is consistent with the growth stage of the plant [35]. The average leaf angle is estimated to be above 40 degrees for all observations and in fact above 55 degrees for the A observations. The leaf angle proved to be crucial for good fitting of the reflectance signatures. These observations are consistent with the literature [38].

Inspection of these scatterplots suggests that it is quite meaningful to construct decision boundaries for and A and H classification, that is, construct the boundary surface in the four-dimensional parameters space. Hence, we next turn to decision trees to provide us with information of that kind.

The four-feature (physical parameters) dataset estimated from the PROSAIL inversion is labeled by A and H, is split randomly with an 80-20 proportionality into training and validation set. Table 13 shows one of the classification scores (accuracy) on the validation set of the decision tree models built for different depths of the tree. This analysis is necessary to avoid overfitting and hence avoid drawing non-generalizable conclusions from the decision boundary. We see that the scores decrease beyond depth 1, that is, beyond the first split on the dominant variable which is always the Cab parameter. As we proceed deeper the scores do not always change, but the relative importance of the parameters does change (not quoted here). The importance of Cab is larger than 78% in all cases. These result means that the construction of a non-trivial boundary surface requires (1) a larger dataset and/or (2) more detailed work on the physical parameter constraints (e.g. regarding season or interdependence) that lies beyond the scope of the present work.

Hence, physically- based classification is expressed in terms of a one-dimensional decision boundary for the parameter the chlorophyll content Cab. That boundary (threshold value for the split) is found to be 28 at two significant figures (Figure 20): the chlorophyll content of an observed signature is predicted lower than 28 then the observation is classified as H, otherwise as A.

We formalize this statement by introducing a physical index which is equal to the chlorophyll content in the usual units (μg cm^-2). Then an observation is classified as A if

{Index}_{p h y s} = C_{a b} > 28

(8)

Let us then run this criterion directly over the dataset of the estimated values of the Cab parameter. Table 14 summarizes the scores found. This index is not as effective as Index₅₇₀, but it does have a high enough success rate.

Having understood the importance of the Cab parameter, we are in a position to trace the origin of the nearly mathematically perfect pattern observed in the (rescaled) reflectance-against-reflectance curves, deduced from the observed reflectance signatures in e.g. Figures 5 or 6. To this end, we plot a (rescaled) reflectance-against-reflectance curve as they come out from PROSAIL keeping all parameters the same, except Cab for which the larger value is put on the y-axis, shown in Figure 21. The result is the pattern we have noticed in the observed curves in Figure 5 and Figure 6.

4. Conclusions

This study introduces and analyzes classification indices and criteria (two spectral and one physical index) of the spectral signatures taken during a complete phenological cycle over crops, in a controlled environment. This environment was constructed to simulate cultivate areas with shallow buried archaeological remains. The results obtained here provide some interesting insights regarding the optimum wavelength for detection of cropmarks.

The main findings of this work can be summarized as follows.

Classification is greatly facilitated by normalizing (rescaling) the calibrated reflectance signatures to the unit interval.
Reflectance-to-reflectance plots between pairs of rescaled signatures offer a visual means to identify (with great but not absolute success) the stressed signatures in the red-edge part of the spectrum.
Two very effective spectral indices (Index₅₇₀ and Index₇₃₀) can be defined in a small band of wavelengths around the 570 and 730 nm, respectively, by dividing the rescaled reflectance of its observation with that of any other observation in the dataset and averaging the result per wavelength and per band. The classification criteria for stresses signatures correspond to the indices being less than 1.2 and 1.1 respectively. The indices operate independently, and the visible spectrum index is more effective than the red edge one.
The indices and criteria are found algorithmically by decision tree classification methods.
The effect of noise in the observed signatures is taken into account by simulating noise-affected signatures. By deducing and analyzing distributions of the dominant wavelength (Index) and classification thresholds by decision tree methods, we are able to formulate the previously defined indices and criteria for noisy signatures. The proposed methods shown to be robust with classification scores to be always greater than 90%.
An index based on the physical properties of the leaf and canopy (Index_phys) is introduced by analyzing the estimated parameters of the PROSAIL model obtained from the observed signatures by inversion. We find that the leaf chlorophyll content Cab is the dominant classification parameter. For the specific (barley) crop under study we find that stressed signatures tend to have Cab greater than 28 μg cm^-2 (with over 90% success rate).

It should be noted that the spectral indices are expected to be more robust than the physically based one, as the former indices are dimensionless and the associated criteria quantify the tendency of the stressed crop signatures to be smaller than the healthy crop signatures.

The absence of the near infrared part of the spectrum in the above mentioned indices (excluding the red-edge related index provided in eq. 7), which is usually used for the detection of cropmarks e.g. through the use of the Normalised Difference Vegetation Index – NDVI, should be linked directly to the proposed methodology and overall analysis carried out here, i.e., by normalizing the reflectance curves the obvious absolute differences between the spectral signatures observed in the near infrared part of the spectrum (see Figure 2a) are now minimized (see Figure 2b).

It is important to highlight that the findings from the analysis of the cropmarks using physically based models such as those of PROSAIL can be considered quite novel. To the best of the authors’ knowledge this is the first study ever that attempts to model stressed vegetation due to the presence of buried archaeological remains with physical properties and modelling. The overall results are quite interesting as the model depicts the most significant parameters that affect the formation of cropmarks in the specific area, and especially the Cab. One may argue that the soil associated parameters are less significant as the area compared between H and A measurements was in a very close proximity. Even though these findings can be considered as peculiar, i.e., for the specific soil context, similar studies in other environments might reveal potential comparisons.

The overall indices proposed in this study are targeted for hyperspectral data. Nevertheless, it should be noted that such hyperspectral data beyond ground spectroradiometers used in the study, are quite rare with lower spatial resolution. In contrast there is a plethora of multispectral satellite, aerial and low-altitude sensors that are widely used for archaeological purposes. Therefore, future directions can be to downscale the results moving from hyperspectral to multispectral bands, which might have a more practical meaning for studying archaeological areas.

Author Contributions

Conceptualization, A.A. and Ε.G.; methodology, A.A. and Ε.G.; data curation, A.A. and Ε.G.; writing—original draft preparation, A.A. and Ε.G.; writing—review and editing, A.A. and Ε.G.; visualization, A.A. and Ε.G.. All authors have read and agreed to the published version of the manuscript.

Funding

This project has received funding from the European Union’s Horizon Europe Framework Programme (HORIZON-WIDERA-2021-ACCESS-03, Twinning Call) under the grant agreement no. 101079377 and the UKRI under project number 10050486.

Data Availability Statement

No new data was created during this study.

Conflicts of Interest

The authors declare no conflict of interest. Views and opinions expressed are, however, those of the authors only and do not necessarily reflect those of the European Union or the UKRI. Neither the European Union nor the UKRI can be held responsible for them.

References

Luo, L.; Wang, X.; Guo, H.; Lasaponara, R.; Zong, X.; Masini, N.; Wang, G.; Shi, P.; Khatteli, H.; Chen, F.; et al. Airborne and spaceborne remote sensing for archaeological and cultural heritage applications: A review of the century (1907–2017). Remote Sens. Environ. 2019, 232, 111280. [Google Scholar] [CrossRef]
Agapiou, A.; Lysandrou, V. Remote sensing archaeology: Tracking and mapping evolution in European scientific literature from 1999 to 2015. J. Archaeol. Sci. 2015, 4, 192–200. [Google Scholar] [CrossRef]
Opitz, R.; Herrmann, J. Recent Trends and Long-standing Problems in Archaeological Remote Sensing. J. Comput. Appl. Archaeol. 2018, 1, 19–41. [Google Scholar] [CrossRef]
Noviello, M.; Ciminale, M.; De Pasquale, V. Combined Application of Pansharpening and Enhancement Methods to Improve Archaeological Cropmark Visibility and Identification in QuickBird Imagery: Two Case Studies from Apulia, Southern Italy. J. Archaeol. Sci. 2013, 40, 3604–3613. [Google Scholar] [CrossRef]
Brivio, P.A.; Pepe, M.; Tomasoni, R. Multispectral and multiscale remote sensing data for archaeological prospecting in an alpine alluvial plain. J. Cult. Herit. 2000, 1, 155–164. [Google Scholar] [CrossRef]
Lasaponara, R.; Masini, N. Detection of archaeological crop marks by using satellite Quick Bird multispectral imagery. J. Archaeol. Sci. 2007, 34, 214–221. [Google Scholar] [CrossRef]
Rajani, M.B.; Rajawat, A.S. Potential of satellite-based sensors for studying distribution of archaeological sites along palaeochannels: Harappan sites a case study. J. Archaeol. Sci. 2011, 38, 2010–2016. [Google Scholar] [CrossRef]
Lasaponara, R.; Masini, N. Beyond modern landscape features: New insights in the archaeological area of Tiwanaku in Bolivia from satellite data. Int. J. Appl. Earth Obs. Geoinform. 2014, 26, 464–471. [Google Scholar] [CrossRef]
Orengo, H.; Petrie, C. Large-Scale, Multi-Temporal Remote Sensing of Palaeo-River Networks: A Case Study from Northwest India and its Implications for the Indus Civilisation. Remote Sens. 2017, 9, 735. [Google Scholar] [CrossRef]
Agapiou, A.; Alexakis, D.D.; Sarris, A.; Hadjimitsis, D.G. Evaluating the Potentials of Sentinel-2 for Archaeological Perspective. Remote Sens. 2014, 6, 2176–2194. [Google Scholar] [CrossRef]
Šošić Klindžić, R.; Šiljeg, B.; Kalafatić, H. Multiscale and Multitemporal Remote Sensing for Neolithic Settlement Detection and Protection—The Case of Gorjani, Croatia. Remote Sens. 2024, 16, 736. [Google Scholar] [CrossRef]
Verhoeven, G.J. Near-Infrared Aerial Crop Mark Archaeology: From Its Historical Use to Current Digital Implementations. J. Archaeol. Method Theory 2012, 19, 132–160. [Google Scholar] [CrossRef]
Czajlik, Z.; Árvai, M.; Mészáros, J.; Nagy, B.; Rupnik, L.; Pásztor, L. Cropmarks in aerial archaeology: New Lessons from an Old Story. Remote Sensing, 2021, 13(6), p.1126. [CrossRef]
Agapiou, A.; Hadjimitsis, D.G.; Sarris, A.; Georgopoulos, A.; Alexakis, D.D. Optimum temporal and spectral window for monitoring crop marks over archaeological remains in the Mediterranean region. J. Archaeol. Sci., 2013, 40(3), pp.1479-1492. [CrossRef]
Ruciński, D.; Rączkowski, W.; Niedzielko, J. A Polish perspective on optical satellite data and methods for archaeological sites prospection. In Third International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2015), 2015, 9535, pp. 258-265. SPIE.
Bini, M.; Isola, I.; Zanchetta, G.; Ribolini, A.; Ciampalini, A.; Baneschi, I.; Mele, D.; D’Agata, A.L. Identification of leveled archeological mounds (Höyük) in the alluvial plain of the Ceyhan River (Southern Turkey) by satellite remote-sensing analyses. Remote Sensing, 2018, 10(2), p.241. [CrossRef]
Schneidhofer, P.; Tonning, C.; Cannell, R.J.; Nau, E.; Hinterleitner, A.; Verhoeven, G.J.; Gustavsen, L.; Paasche, K.; Neubauer, W.; Gansum, T. The influence of environmental factors on the quality of GPR data: the Borre Monitoring Project. Remote Sensing, 2022, 14(14), 3289. [CrossRef]
Cozzolino, M.; Longo, F.; Pizzano, N.; Rizzo, M.L.; Voza, O.; Amato, V. A Multidisciplinary Approach to the Study of the Temple of Athena in Poseidonia-Paestum (Southern Italy): New Geomorphological, Geophysical and Archaeological Data. Geosciences, 2019,9(8), 324. [CrossRef]
Kalayci, T.; Simon, F.X.; Sarris, A. A manifold approach for the investigation of Early and Middle Neolithic settlements in Thessaly, Greece. Geosciences, 2017, 7(3), p.79. [CrossRef]
Campana, S. Emptyscapes: filling an ‘empty’Mediterranean landscape at Rusellae, Italy. Antiquity, 2017, 91(359), 1223-1240.
Saey, T.; Van Meirvenne, M.; De Smedt, P.; Neubauer, W.; Trinks, I.; Verhoeven, G.; Seren, S. Integrating multi-receiver electromagnetic induction measurements into the interpretation of the soil landscape around the school of gladiators at Carnuntum. European Journal of Soil Science, 2013, 64(5), pp.716-727. [CrossRef]
Masini, N.; Capozzoli, L.; Chen, P.; Chen, F.; Romano, G.; Lu, P.; Tang, P.; Sileo, M.; Ge, Q.; Lasaponara, R. Towards an operational use of geophysics for archaeology in Henan (China): Methodological approach and results in Kaifeng. Remote Sensing, 2017, 9(8), p.809. [CrossRef]
Donati, J.C.; Sarris, A.; Papadopoulos, N.; Kalaycı, T.; Simon, F.X.; Manataki, M.; Moffat, I.; Cuenca-García, C. A regional approach to ancient urban studies in Greece through multi-settlement geophysical survey. Journal of Field Archaeology, 2017, 42(5), 450-467. [CrossRef]
Doneus, M.; Briese, C. Airborne Laser Scanning in forested areas–potential and limitations of an archaeological prospection technique. Remote sensing for archaeological heritage management, 2011, 3, pp.59-76.
Sarris, A.; Papadopoulos, N.; Agapiou, A.; Salvi, M.C.; Hadjimitsis, D.G.; Parkinson, W.A.; Yerkes, R.W.; Gyucha, A.; Duffy, P.R. Integration of geophysical surveys, ground hyperspectral measurements, aerial and satellite imagery for archaeological prospection of prehistoric sites: the case study of Vésztő-Mágor Tell, Hungary. Journal of Archaeological Science, 2013, 40(3), pp.1454-1470. [CrossRef]
Cowley, D.C.. Creating the cropmark archaeological record in East Lothian, southeast Scotland. Prehistory without Borders: Prehistoric Archaeology of the Tyne-Forth Region. Oxford: Oxbow, 2016, pp.59-70.
Agapiou, A.; Hadjimitsis, D.G.; Sarris, A.; Georgopoulos, A.; Alexakis, D.D. Optimum temporal and spectral window for monitoring crop marks over archaeological remains in the Mediterranean region. Journal of Archaeological Science, 2013, 40(3), 1479-1492. [CrossRef]
Agapiou, A. Development of a novel methodology for the detection of buried archaeological remains using remote sensing techniques, PhD thesis, Cyprus University of Technology, 2013, https://hdl.handle.net/20.500.14279/877.
Agapiou, A.; Hadjimitsis, D.G.; Alexakis, D.D. Evaluation of Broadband and Narrowband Vegetation Indices for the Identification of Archaeological Crop Marks. Remote Sens. 2012, 4, 3892–3919. [Google Scholar] [CrossRef]
Python programming language, https://www.python.org/ (accessed 14^th of March 2024).
Géron, A. Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow. O'Reilly Media, 2022, Inc.
Féret, J. B.; Gitelson, A. A.; Noble, S. D.; Jacquemoud, S. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sensing of Environment, 2017, 193, 204-215. [CrossRef]
erger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the PROSAIL model capabilities for future hyperspectral model environments: A review study. Remote Sensing, 2018, 10(1), 85. [CrossRef]
Duan, S. B.; Li, Z. L.; Wu, H.; Tang, B. H.; Ma, L.; Zhao, E.; Li, C. Inversion of the PROSAIL model to estimate leaf area index of maize, potato, and sunflower fields from unmanned aerial vehicle hyperspectral data. International Journal of Applied Earth Observation and Geoinformation, 2014, 26, 12-20. [CrossRef]
Li, Z.; Jin, X.; Yang, G.; Drummond, J.; Yang, H.; Clark, B.; Zhao, C. Remote sensing of leaf and canopy nitrogen status in winter wheat (Triticum aestivum L.) based on N-PROSAIL model. Remote Sensing, 2018, 10(9), 1463. [CrossRef]
Berger, K.; Verrelst, J.; Féret, J. B.; Wang, Z.; Wocher, M.; Strathmann, M.; Hank, T. Crop nitrogen monitoring: Recent progress and principal developments in the context of imaging spectroscopy missions. Remote Sensing of Environment, 2020, 242, 111758. [CrossRef]
Sinha, S. K.; Padalia, H.; Dasgupta, A.; Verrelst, J.; Rivera, J. P. Estimation of leaf area index using PROSAIL based LUT inversion, MLRA-GPR and empirical models: Case study of tropical deciduous forest plantation, North India. International Journal of Applied Earth Observation and Geoinformation, 2020, 86, 102027. [CrossRef]
Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Fitted PROSAIL parameterization of leaf inclinations, water content and brown pigment content for winter wheat and maize canopies. Remote Sensing, 2019, 11(10), 1150. [CrossRef]

Figure 2. Measured and transformed A reflectance curves for a given day. (a) Spectral signatures are captured from the spectroradiometer and (b) transformed reflectance curves based on equation 1.

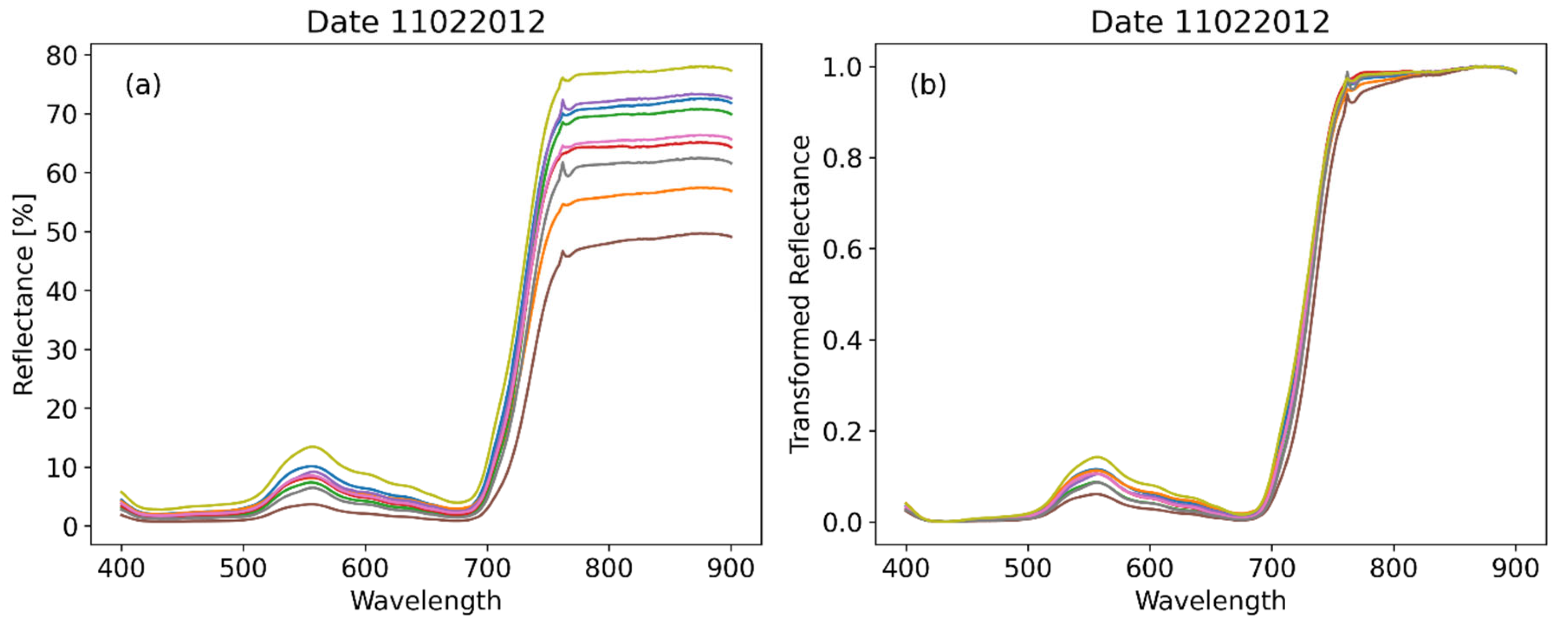
Figure 3. Reflectance-against-reflectance curves (all combinations) from a date in JFM period.

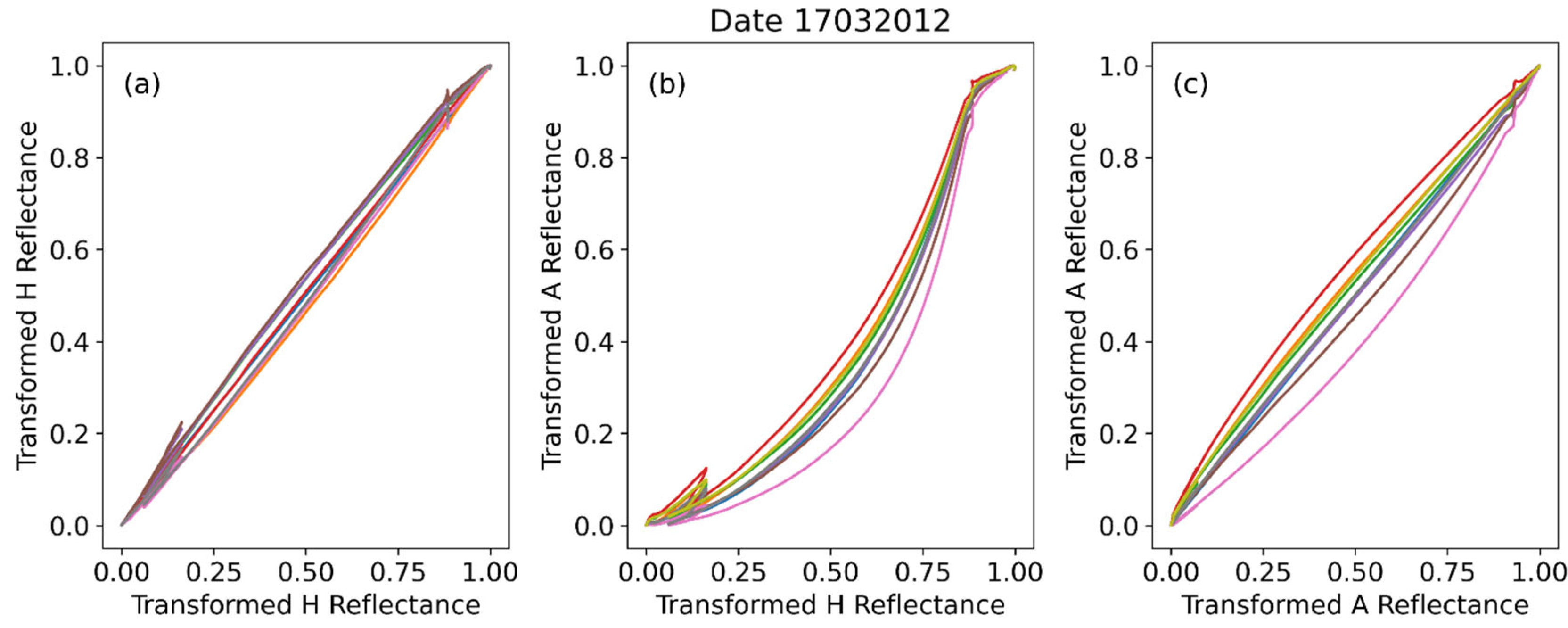
Figure 4. Reflectance-against-reflectance curves (all combinations) from a date outside the JFM period.

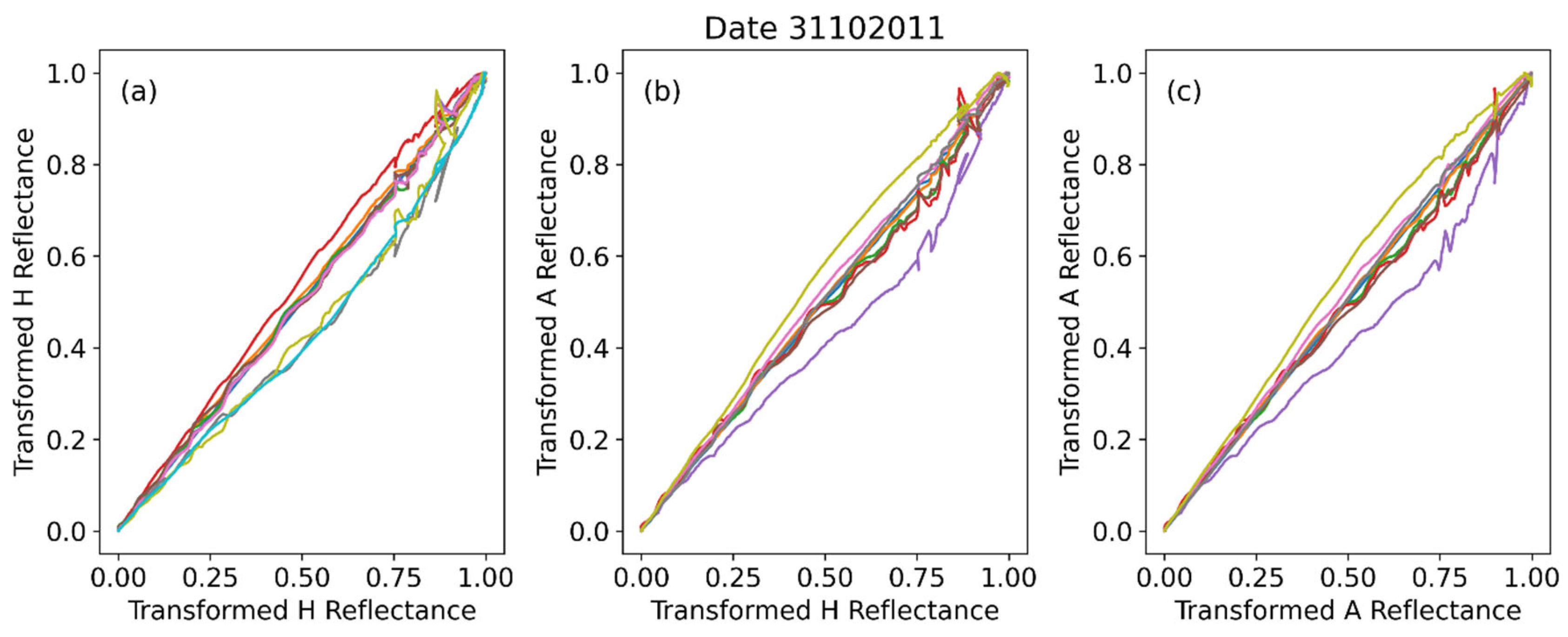
Figure 5. Analysis of an ‘unknown’ dataset by inspection. The observations X_1 and X_2 can be identified as A and H respectively based on their pattern.

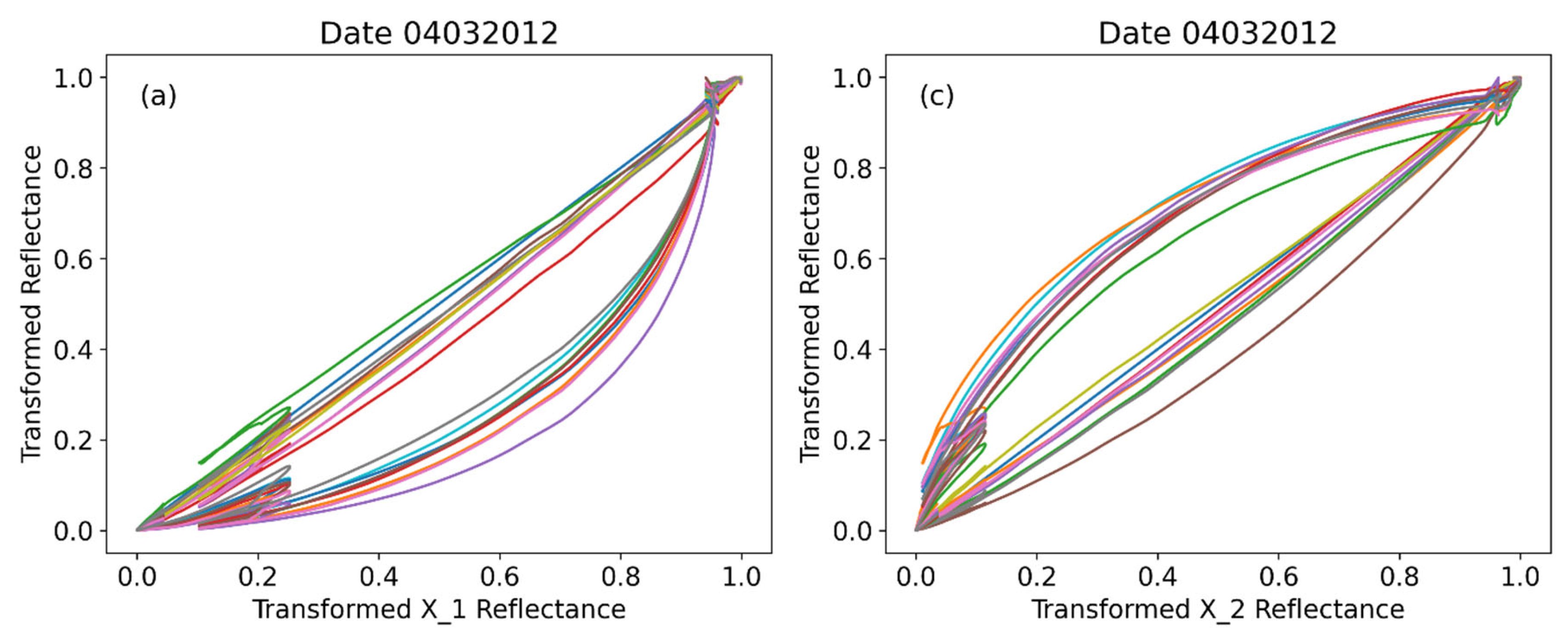
Figure 6. Reflectance-against-reflectance curves emphasize the red edge part of the spectrum.

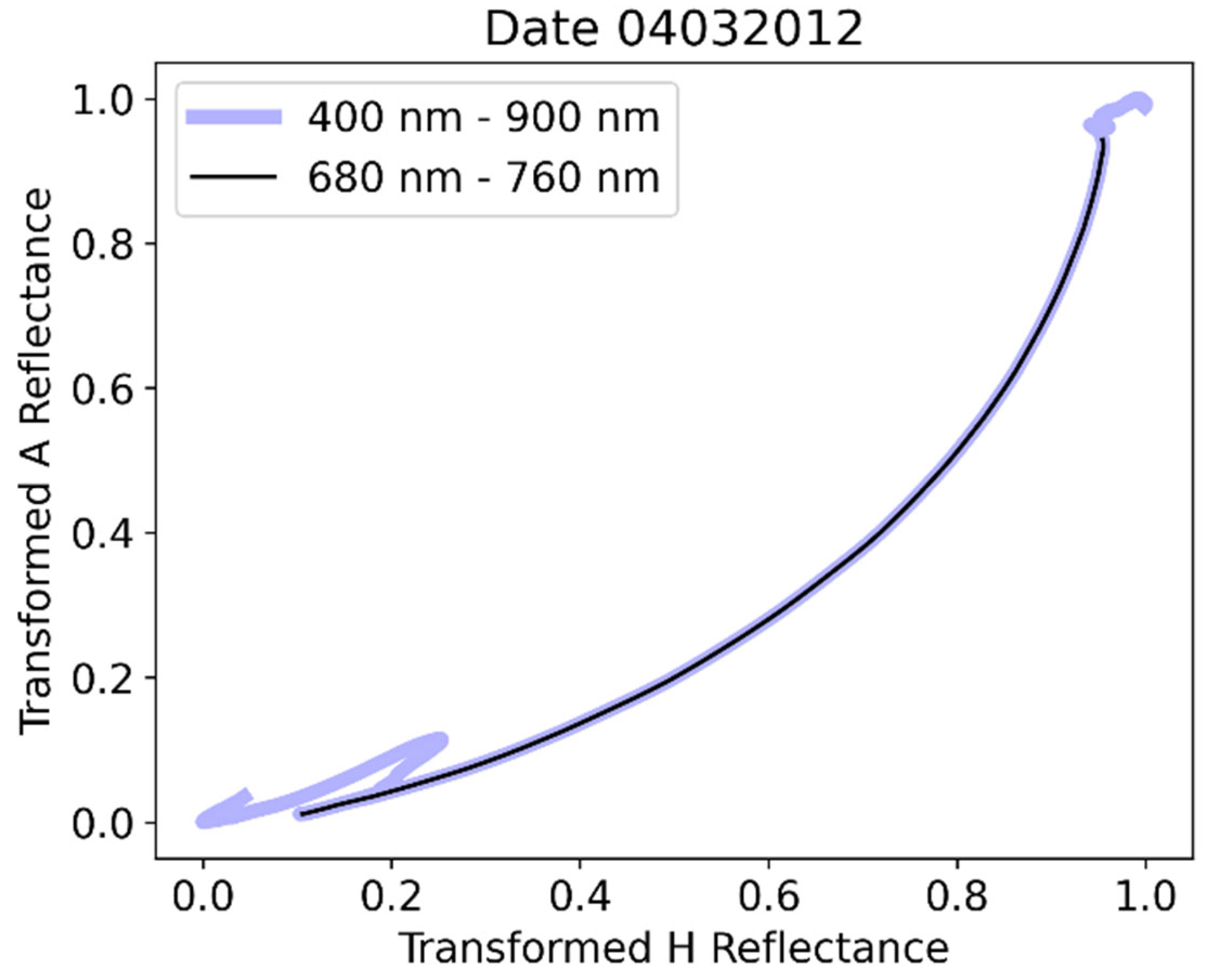
Figure 7. Mean ρ-ratio curves associated with each observed reflectance curve.

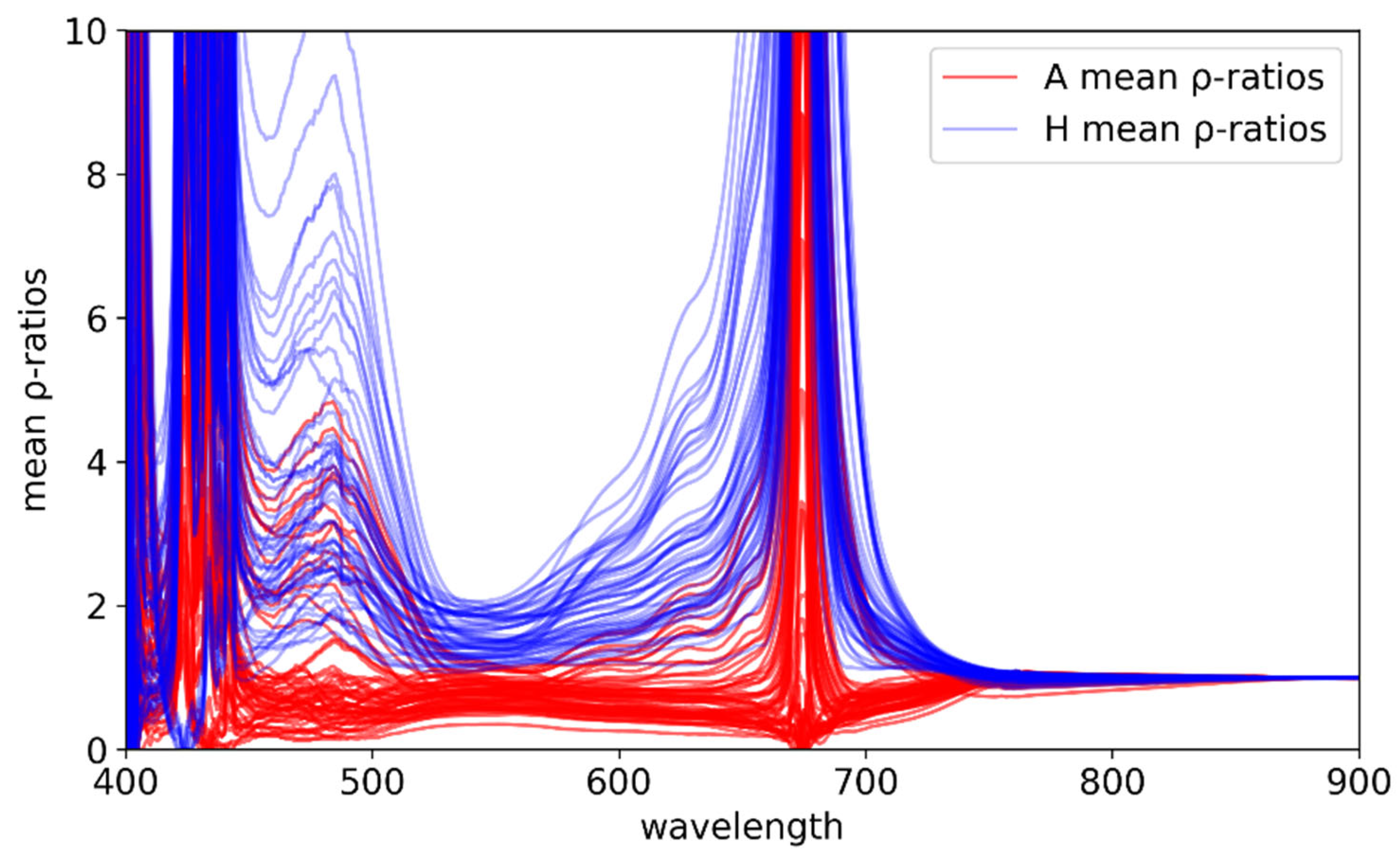
Figure 8. Index₅₇₀ for all A and H observations and the decision boundary at 1.2.

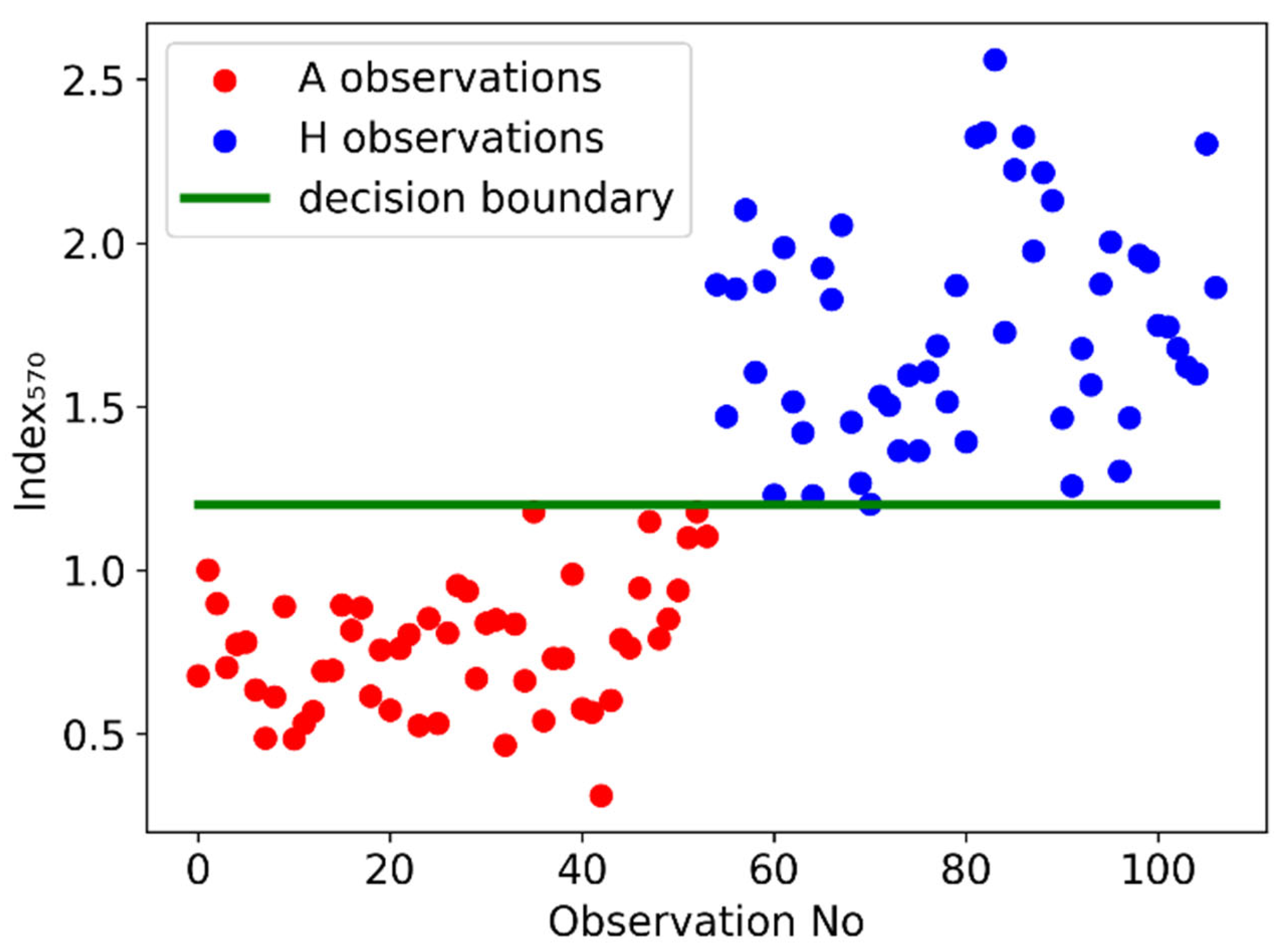
Figure 9. Correlation matrix of the mean ρ-curves averaged over 10 nm.

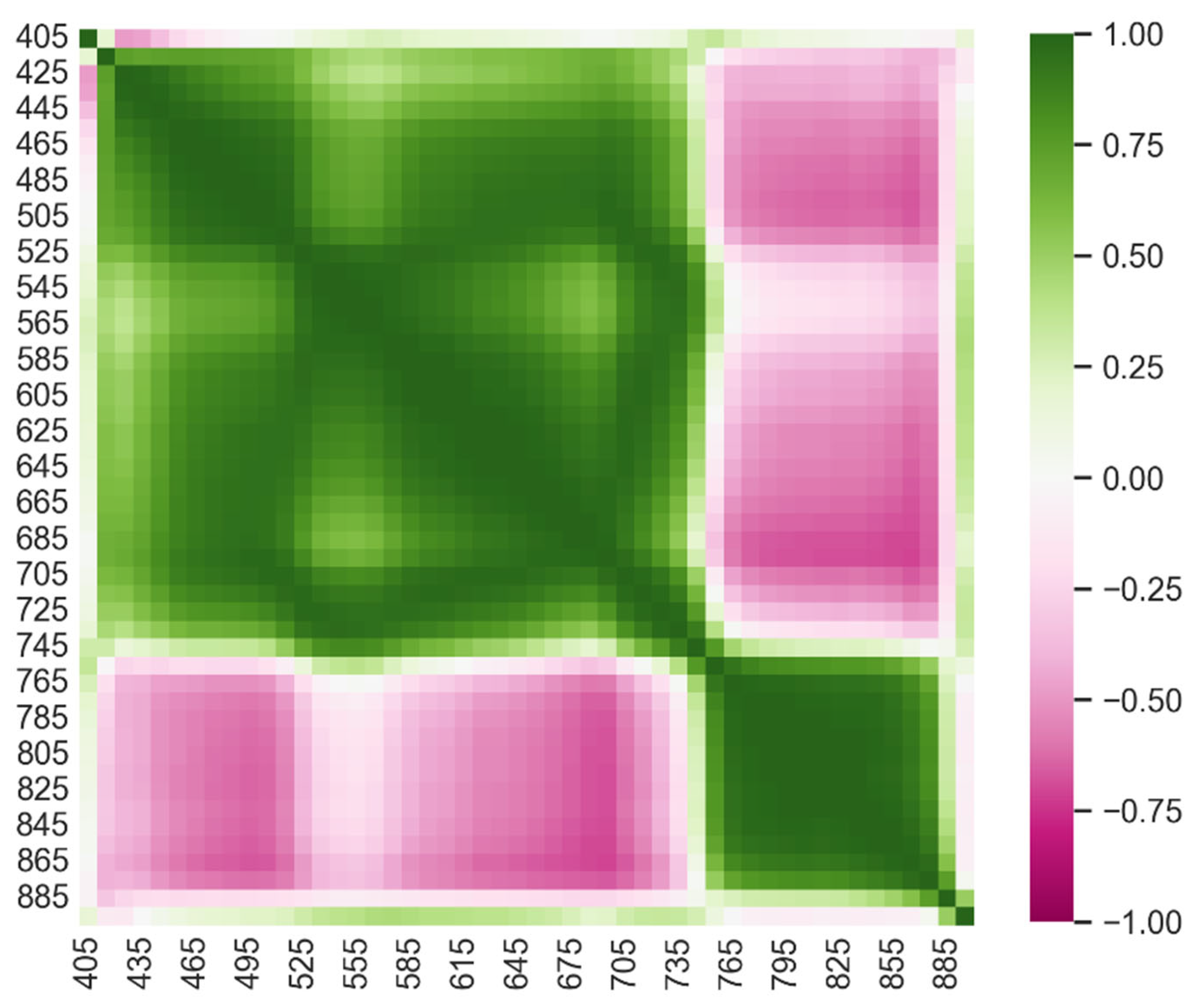
Figure 10. Feature importance for the logistic regression model. Positive values are given in orange, while negative in cyan.

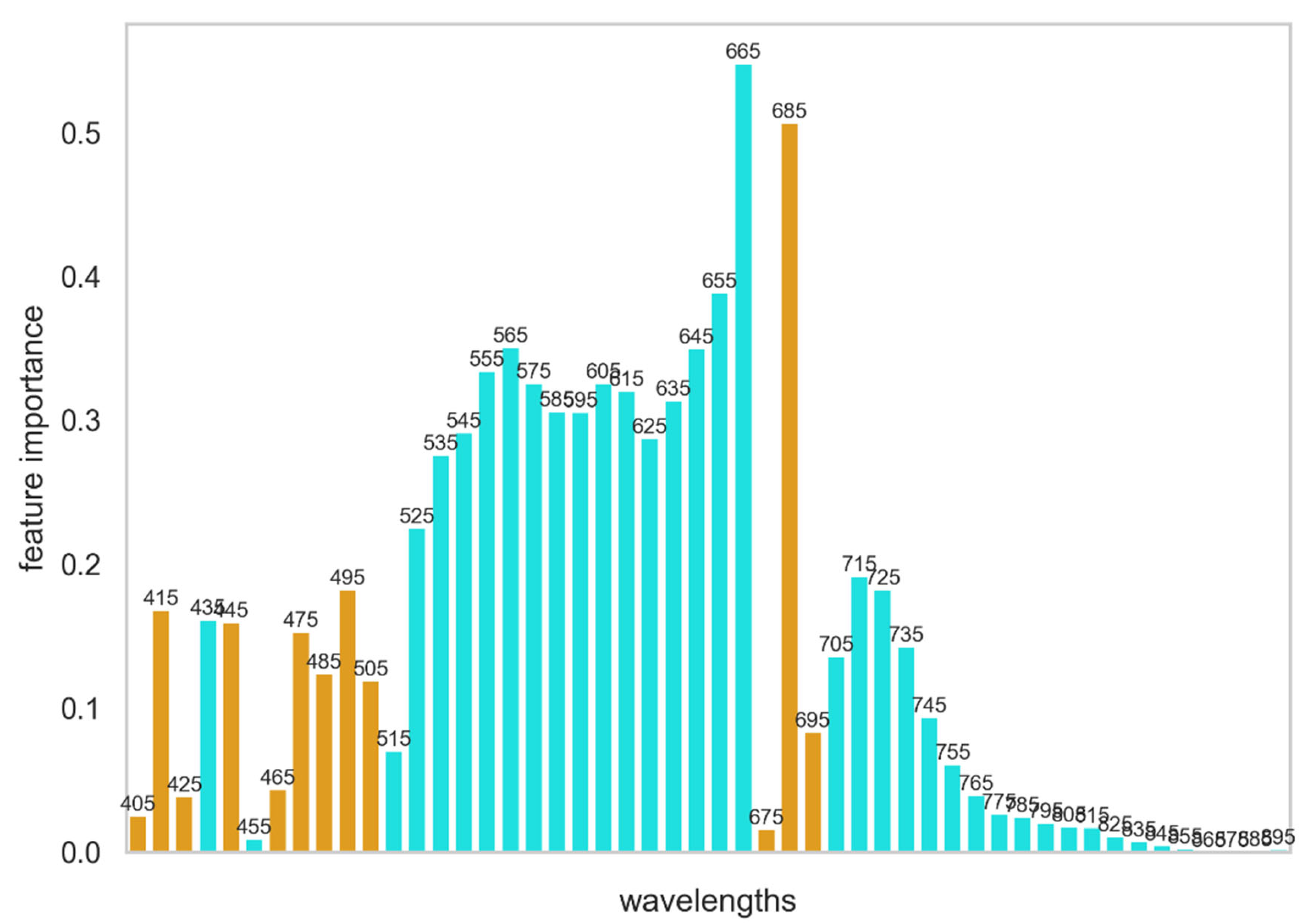
Figure 11. Feature importance for the decision tree model. A single feature dominates.

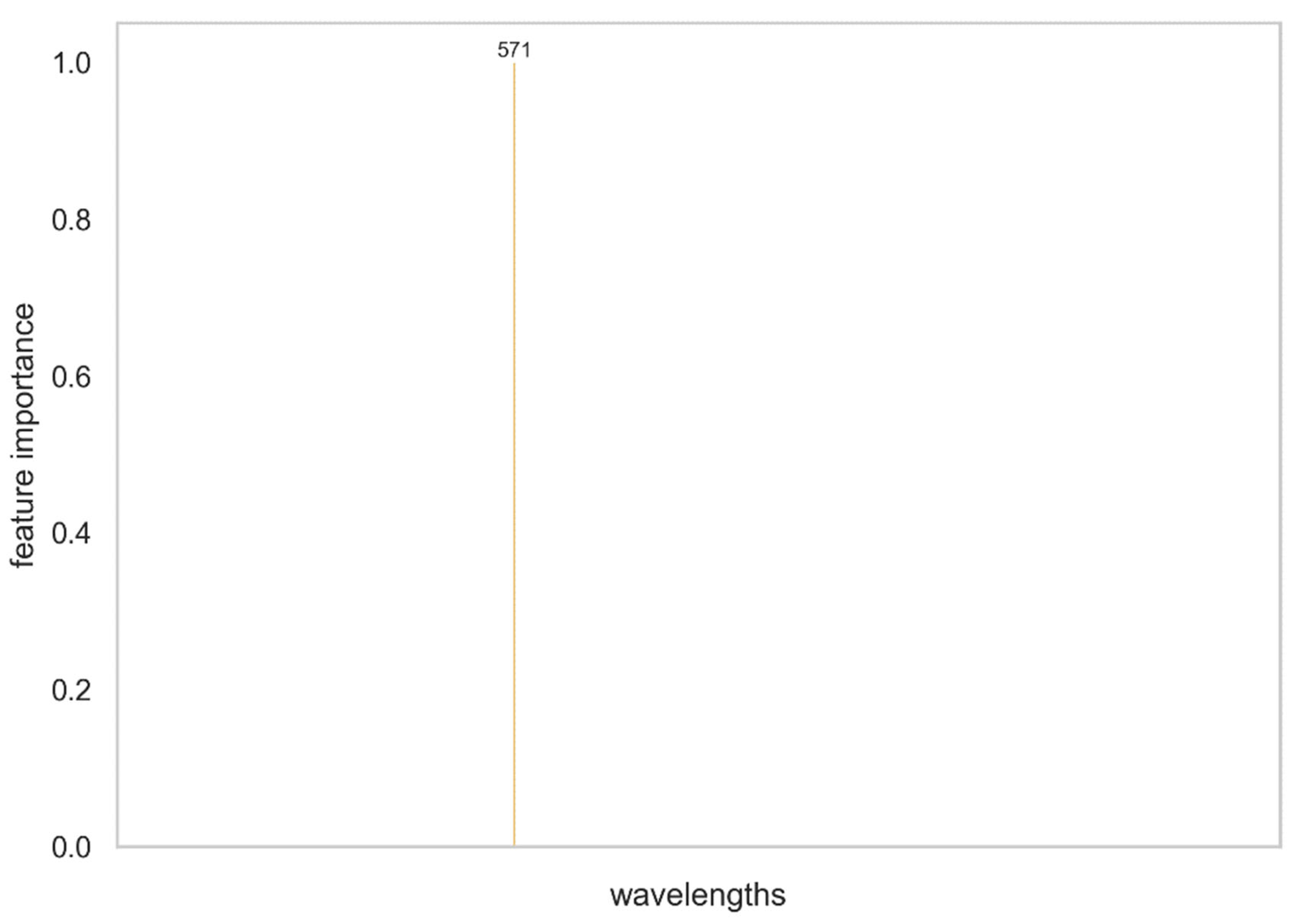
Figure 12. Visualization of the decision tree.

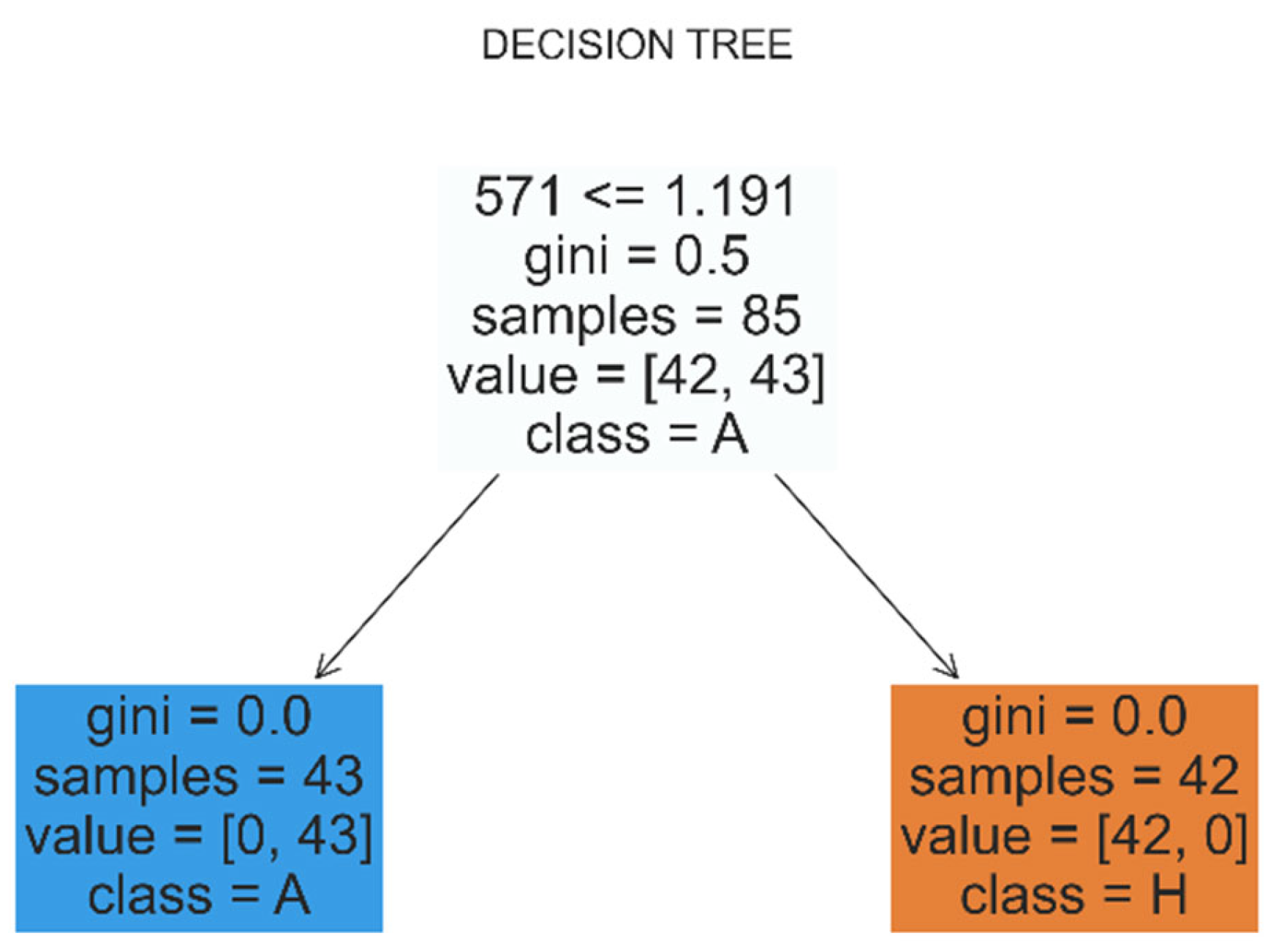
Figure 13. Mean ρ-curves of an ensemble of simulated observations, totally 100×107 curves.

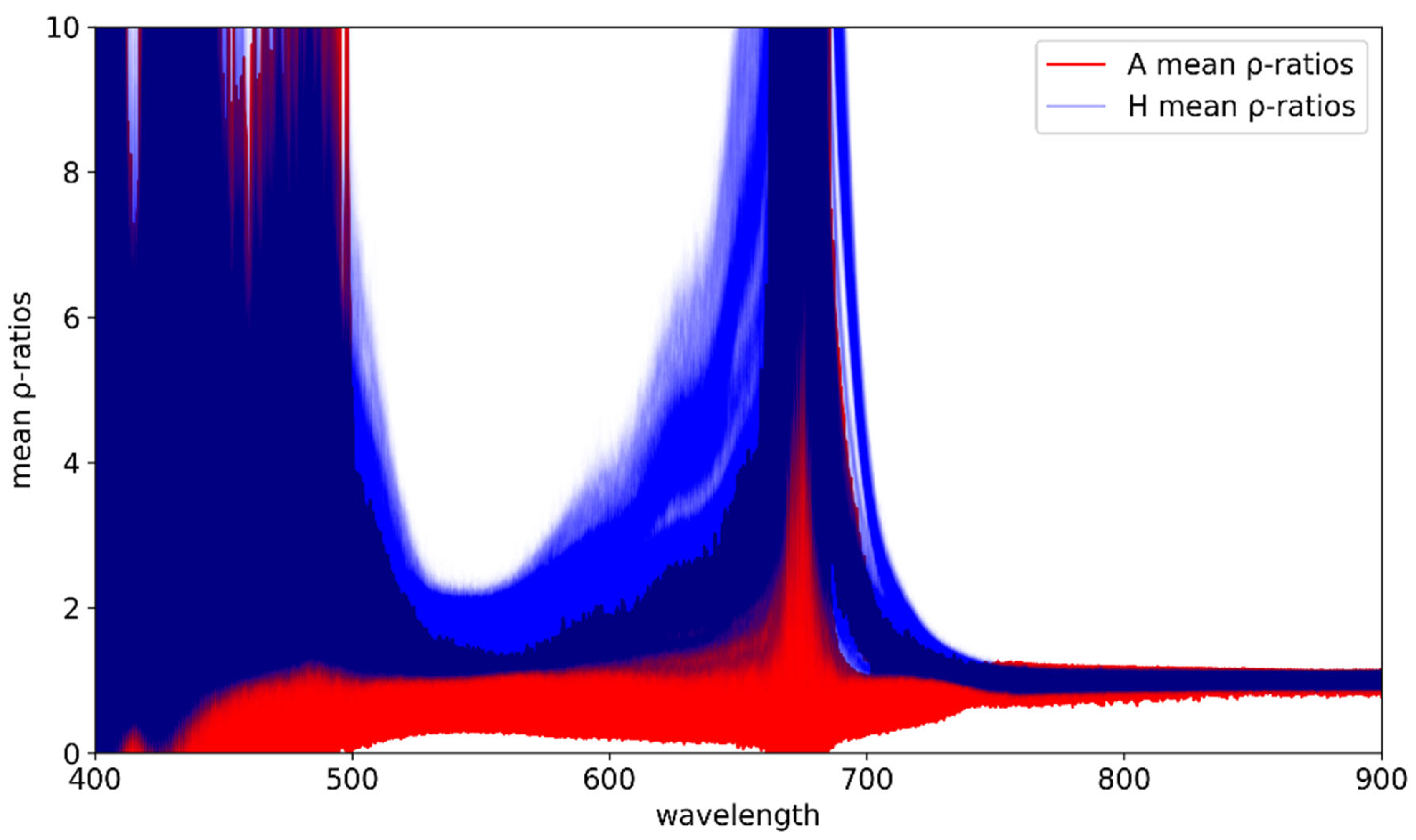
Figure 14. Histogram of the dominant wavelength values for the 5000 simulations. On top of every bar is shown the mean value of the threshold for that wavelength.

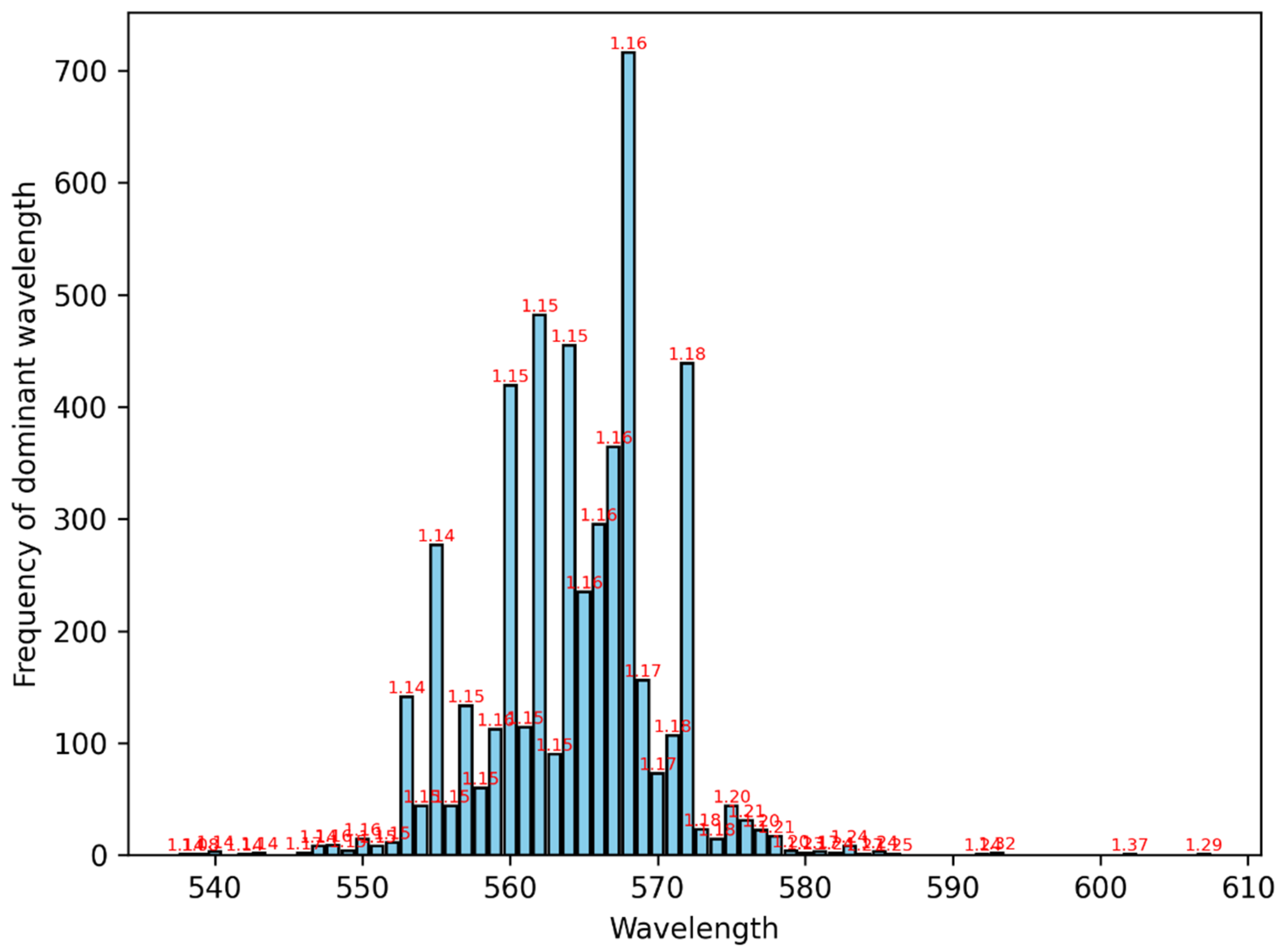
Figure 15. The average threshold as a function of the corresponding dominant wavelength value for the visible part of the spectrum.

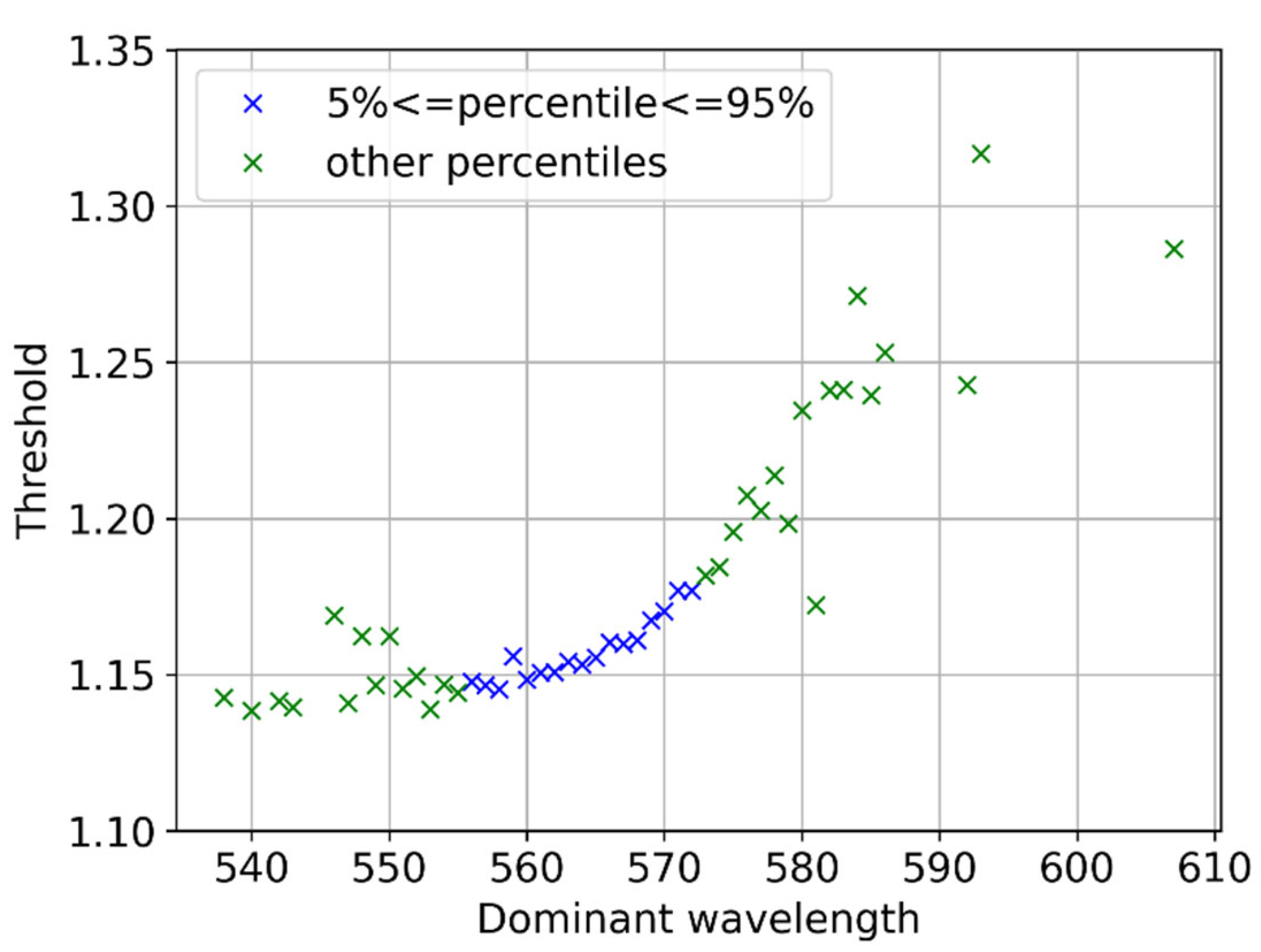
Figure 16. Visualization of the decision tree classification in the red edge.

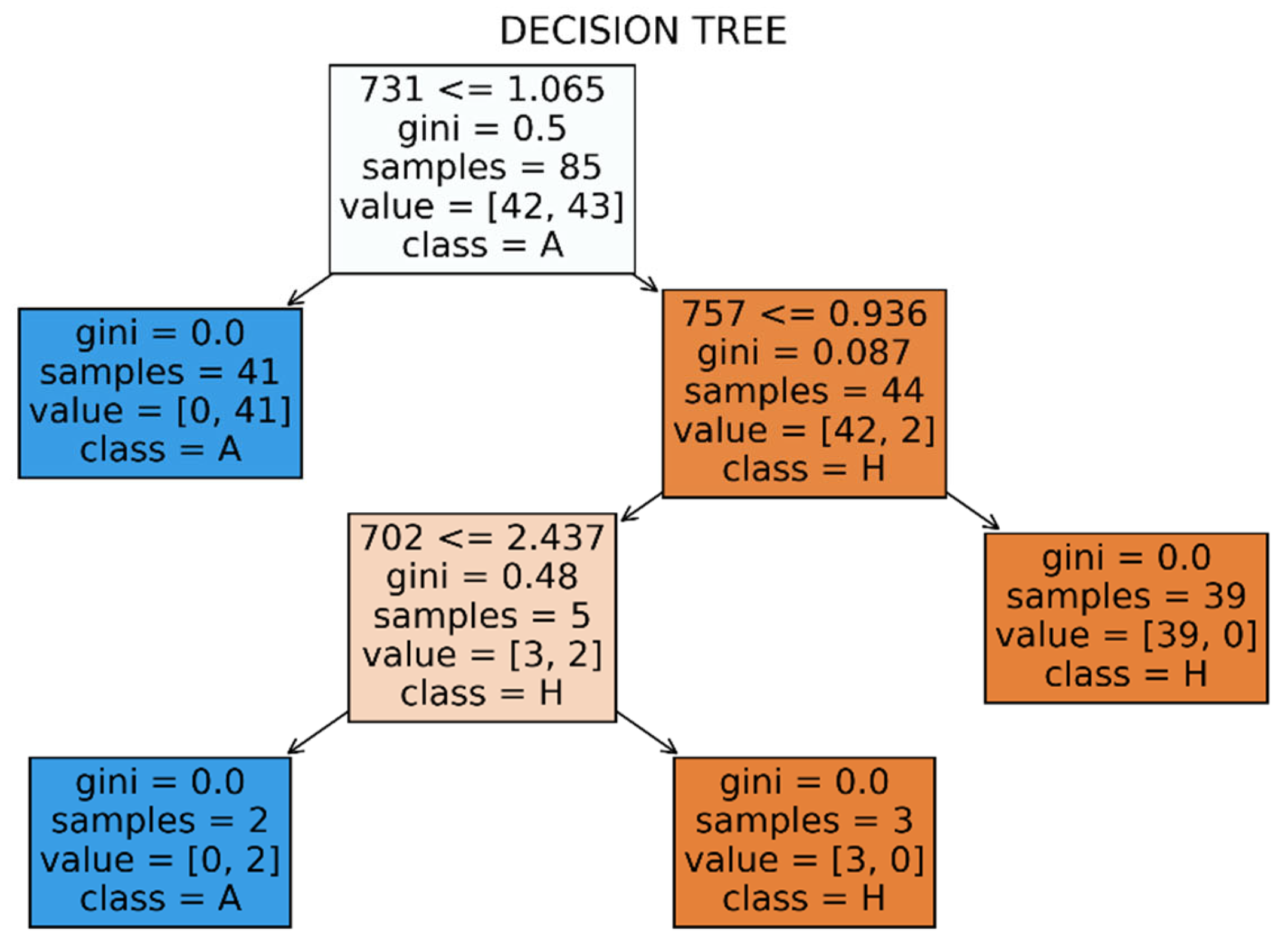
Figure 17. Histogram of the dominant wavelengths’ values for the 5000 simulations from the red edge. On top of every bar, it is shown the mean value of the threshold for that wavelength.

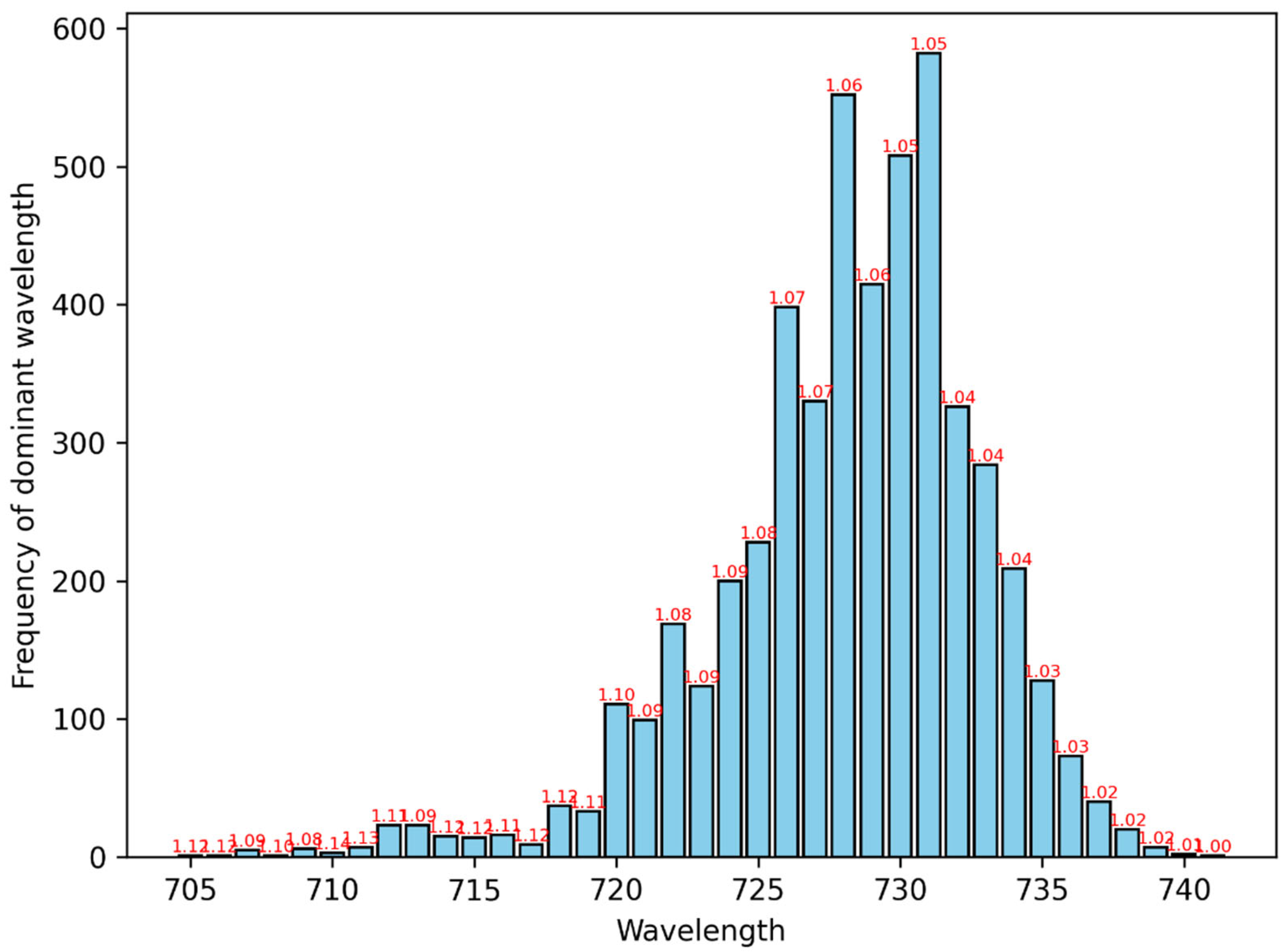
Figure 18. The trend of the average threshold against the corresponding dominant wavelength value for the red edge part of the spectrum.

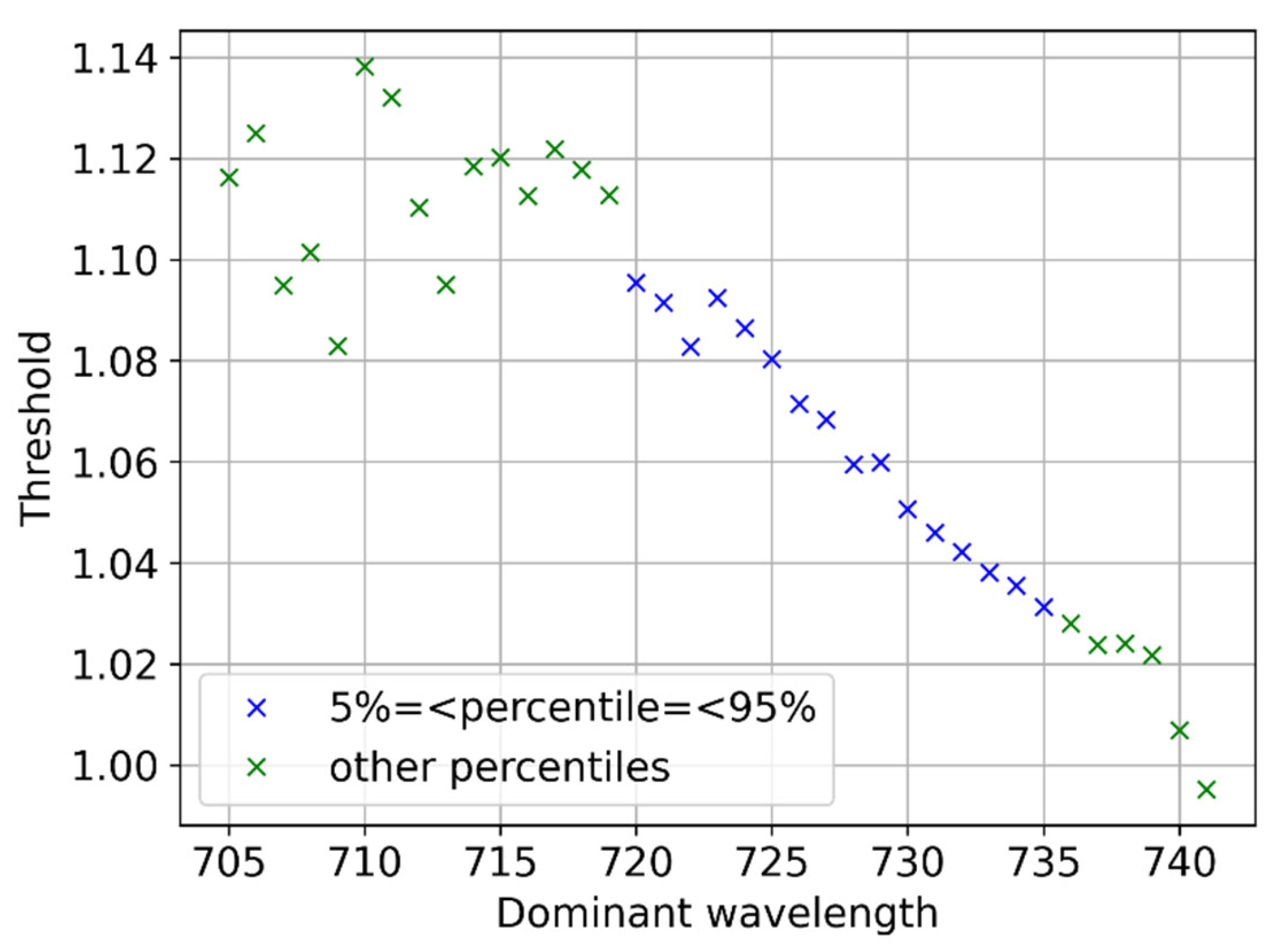
Figure 19. Scatter plot of the estimated parameters with some of the possible combinations of two.

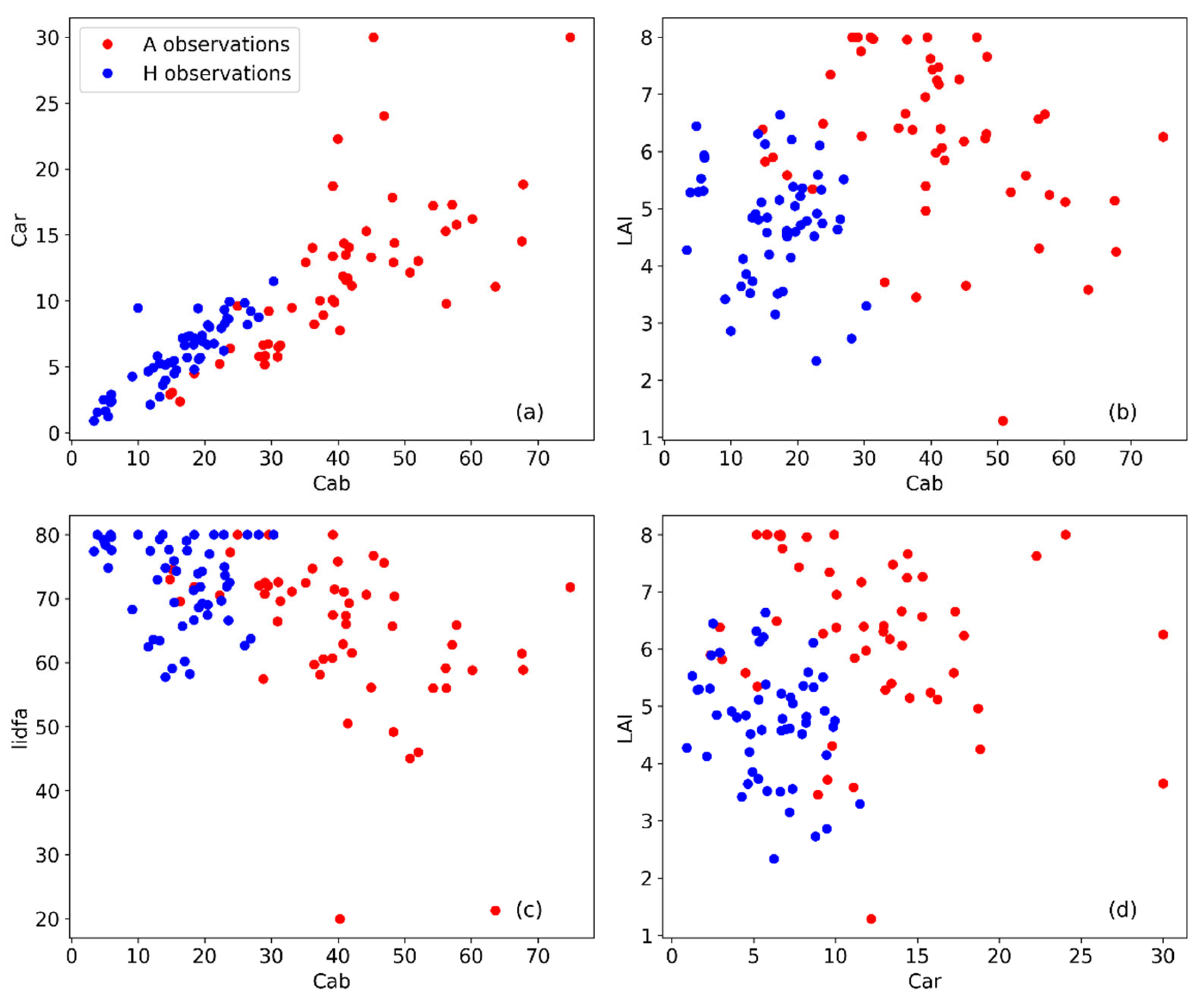
Figure 20. Depth 1 decision tree for the physical-parameter classification.

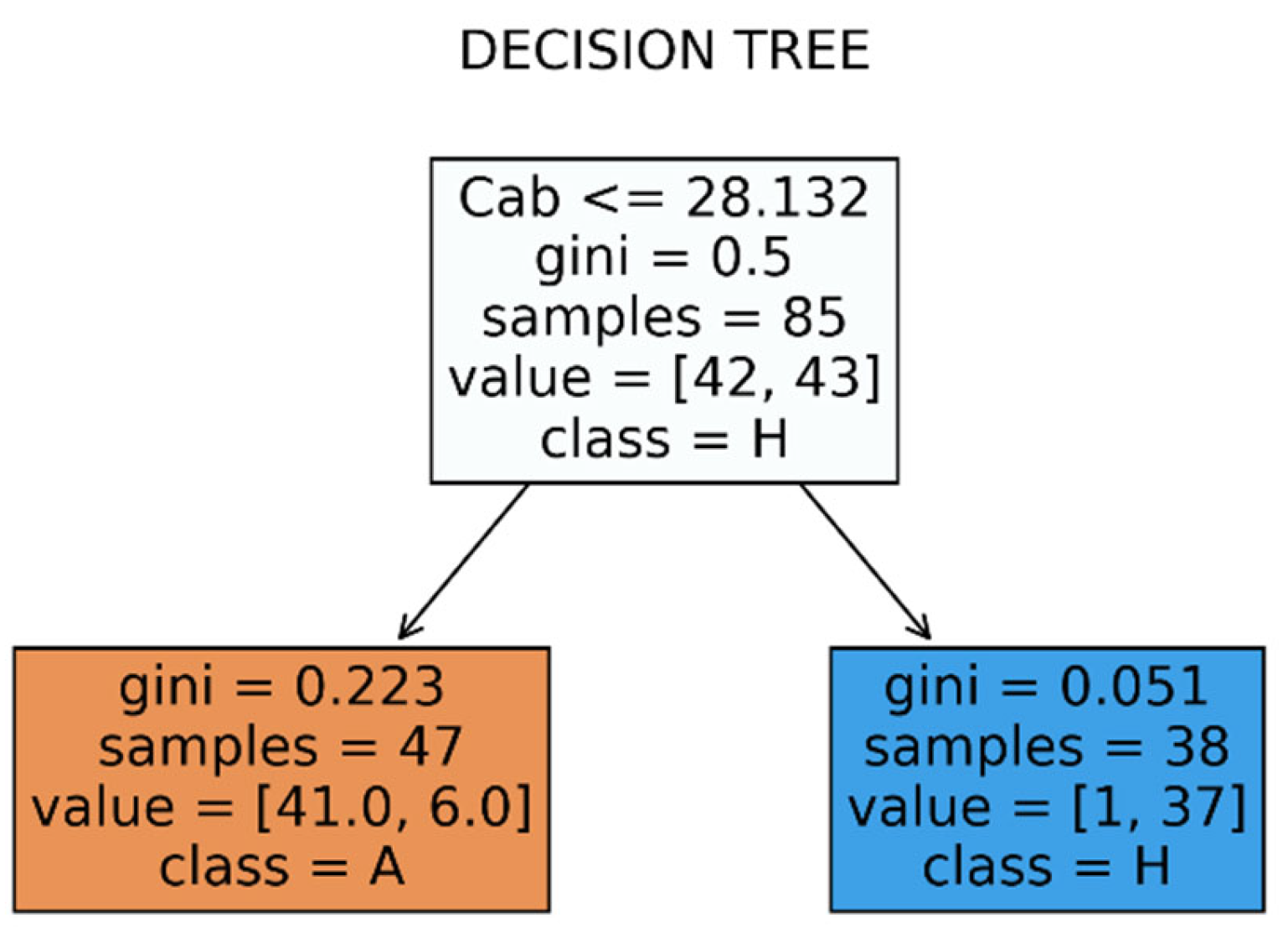
Figure 21. PROSAIL reflectance-against-reflectance curves for different Cab.

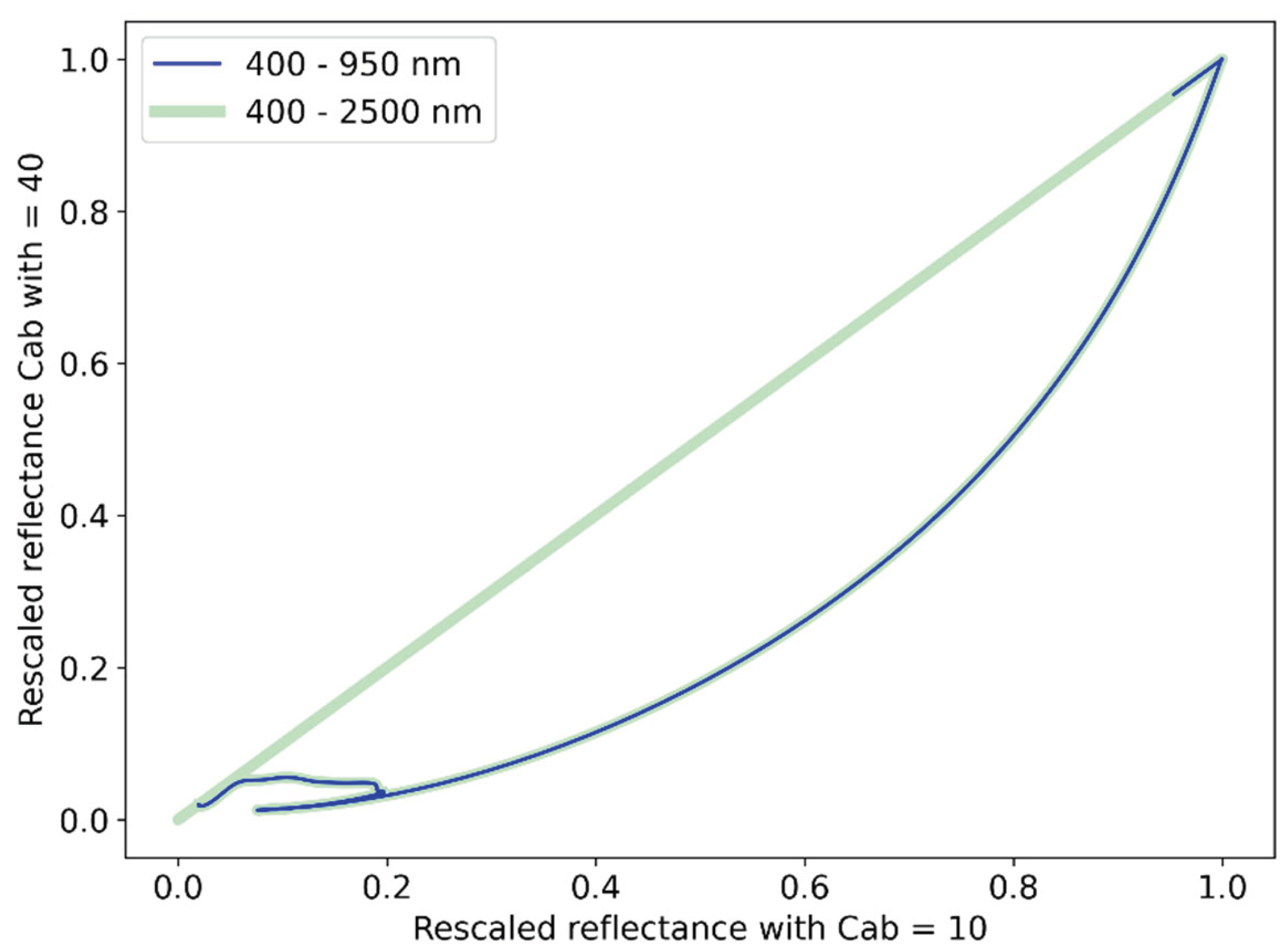
Table 1. Observations per day.

Date	# of A obs	# of H obs	Date	# of A obs	# of H obs
17102011	19	19	20122011	9	9
26102011	18	18	03012012	9	9
31102011	9	9	11022012	9	9
09112011	9	9	21022012	9	9
16112011	5	5	04032012	9	9
23112011	9	9	17032012	9	9
28112011	9	9	29032012	9	9
13122011	9	9	17042012	9	9

Table 2. Classification scores for Index₅₇₀ decision boundary at 1.2.

Accuracy	Precision	Recall	F₁ Score
1.0	1.0	1.0	1.0

Table 3. Statistics of classification scores for the Index₅₇₀<1.2 criterion.

Scores	Mean Value	Standard Deviation
accuracy	0.970	0.014
precision	0.968	0.020
recall	0.974	0.019
F1 score	0.971	0.014

Table 4. Statistics of classification parameters for the decision tree method.

Parameter	Mean Value	Standard Deviation
accuracy	0.975	0.025
precision	0.977	0.023
recall	0.975	0.025
F1 score	0.975	0.025
Dominant wavelength	564	6

Table 5. Percentiles of the dominant wavelength distribution.

Percentile	5	25	50	75	95
Wavelength	555	560	565	568	572

Table 6. Statistics of classification parameters for the Index570<1.17 criterion over the ensemble.

Score	Mean Value	Standard Deviation
accuracy	0.988	0.009
precision	0.988	0.012
recall	0.988	0.013
F1 score	0.988	0.009

Table 7. Classification parameters for red edge using decision trees.

Parameter	Mean Value
accuracy	1.0
precision	1.0
recall	1.0
F1 score	1.0
dominant wavelength	731
threshold	1.065

Table 8. Statistics of classification parameters for the decision tree method.

Parameter	Mean Value	Standard Deviation
accuracy	0.913	0.049
precision	0.917	0.048
recall	0.913	0.049
F1 score	0.913	0.049
dominant wavelength	728	5

Table 9. Percentiles of the dominant wavelength distribution.

Percentile	5	25	50	75	95
Wavelength	720	726	729	731	735

Table 10. Statistics of classification parameters for the Index730<1.1 criterion over the ensemble.

Score	Mean Value	Standard Deviation
accuracy	0.927	0.016
precision	0.924	0.025
recall	0.933	0.018
F1 score	0.928	0.015

Table 11. The values and the ranges of the PROSAIL input parameters used in this study. Parameters with (*) are fitted within the quoted bounds.

Parameter	Value
Leaf structure index, N [-]	1.5
Leaf chlorophyll content, Cab* [μg cm^-2]	0 - 100
Leaf carotenoid content, Car* [μg cm^-2]	0 - 30
Leaf dry matter content, Cm [g cm^-2]	0.002
Equivalent water thickness, Cw [cm]	0.02
Brown pigment content, Cbrown [-]	0
Leaf anthocyanin content, Cant [μg cm^-2]	0
Leaf area index, LAI* [m² m^-2]	0.5 - 8
Average leaf angle, lidfa* [deg]	20 - 80
Hot-spot size parameter, hspot [m m^-1]	0.1
Soil reflectance, psoil [-]
Sun zenith angle [deg]	0
View zenith angle [deg]	0
Relative azimuth angle [deg]	0

Table 12. Statistics of fitting the PROSAIL parameters across the dataset of observations.

Parameter	Mean value	Standard Deviation
RMSE	0.0098	0.0031
R²	0.996	0.004

Table 13. Statistics of accuracy on the validation set for different tree depths.

	Decision Tree Depth
Score	depth 1	depth 2	depth 3	depth 4
accuracy	0.955	0.909	0.909	0.909

Table 14. Classification scores for Index_phys with decision boundary at 28.1.

Accuracy	Precision	Recall	F₁ Score
0.915	0.959	0.870	0.913

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

A Machine Learning-Assisted Classification Algorithm for the Detection of Archaeological Proxies (Cropmarks) Based on Reflectance Signatures

Abstract

1. Introduction

2. Materials and Methods

3. Results

3.1. Analysis of the Dataset and Data Transformation

3.2. Definition of a (Single-Wavelength) Classifying Index within the Visible Spectrum

3.3. Machine Learning Methods: Analysis with Logistic Regression and Decision Tree Classifiers

3.4. Simulating the Effects of Noise: Statistics of the Classifying Index570

3.5. The Red Edge

3.6. Interpretation and Classification on Physically-Based Modelling (PROSAIL)

4. Conclusions

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe

3.4. Simulating the Effects of Noise: Statistics of the Classifying Index₅₇₀