Optimizing Hyperparameters for Customer Churn Prediction with PSO-Enhanced Composite Deep Learning Techniques

Preprint

Article

Optimizing Hyperparameters for Customer Churn Prediction with PSO-Enhanced Composite Deep Learning Techniques

Altmetrics

Downloads

162

Views

Comments

Mohammad Sedighimanesh

Ali Sedighimanesh,

Mehdi Gheisari^*

Mohammad Sedighimanesh

Ali Sedighimanesh,

Mehdi Gheisari^*

This version is not peer-reviewed

Submitted:

18 March 2024

Posted:

18 March 2024

You are already at the latest version

Alerts

Abstract

Background: In today’s competitive market, predicting customer churn with high accuracy is crucial for enterprises to maintain growth and profitability. Traditional predictive models often lack in accuracy due to the complexity of customer behavior.Objective: This research aims to improve the accuracy of predicting customer churn by utilizing the Particle Swarm Optimization (PSO) algorithm for optimizing the hyperparameters of a composite deep learning model. The performance of this enhanced model is evaluated against traditional models such as LSRM_GRU, LSTM, GRU, and CNN_LSTM to demonstrate the effectiveness of PSO in hyperparameter tuning.Methods: A composite deep learning approach was employed, integrating various neural network architectures to leverage their strengths in modeling complex customer interactions. The PSO algorithm was used to optimize the model’s hyperparameters. Customer transaction and interaction data from different business operations served as the dataset for testing and analyzing the model’s performance. Evaluation metrics including accuracy, precision, recall, F1 score, and ROC AUC were utilized for a detailed comparison with established models.Findings: The PSO-enhanced composite deep learning model showed superior performance across all metrics, significantly outperforming the LSRM_GRU, LSTM, GRU, and CNN_LSTM models. Notably, improvements in ROC AUC and F1 score highlight the robustness and balanced precision-recall trade-off of the proposed model, demonstrating its effectiveness in identifying potential churners.Conclusion: The integration of PSO for hyperparameter optimization in composite deep learning models for customer churn prediction has proven to significantly enhance predictive accuracy and performance metrics over conventional models. This underscores the potential of evolutionary algorithms in improving deep learning applications. Future research should explore the scalability of this approach across various sectors and further refine predictive accuracy with evolving customer data.

Keywords:

Subject: Social Sciences - Decision Sciences

1. Introduction

The rapid evolution of e-commerce platforms has fundamentally altered the dynamics of customer engagement and retention strategies. In a highly competitive environment, understanding and predicting customer churn becomes paramount for sustaining business growth and profitability[1]. A large volume of research has been conducted to address these problem and numerous models have been developed to predict customer churn. The dynamic nature of customer behavior and the complexity of data, however, present continuous challenges. In the telecom sector, the challenge is even more complex, given the large volume of data with subtle customer interactions. Recent advancements in machine learning (ML) and deep learning (DL) have opened new vistas for addressing these challenges. However, the utility of these models is often contingent on the precise tuning of their hyperparameters, which poses a nontrivial task due to high-dimensional search space and the computational expense of model training[2].

The Problem Despite the prevalence of ML and DL models in churn prediction, there is a conspicuous gap in the literature on optimizing model hyperparameters to improve prediction accuracy and efficiency. Traditional hyperparameter optimization methods, such as grid search and random search, tend to be computationally intensive and may not guarantee discovery of the optimal solution in a reasonable time frame [3]. Moreover, the use of composite deep learning techniques, which allow the incorporation of the strengths of different neural network architectures, adds further complications in the overall hyperparameter tuning exercise. Given the foreground, there is a pressing need for a methodology that can respond to the complexities of using a composite model that is a deep learning model (due to the composite architecture) for the telecom churn prediction[4]. This study attempts to bridging this gap by proposing the application of Particle Swarm Optimization (PSO), which is a biologically inspired optimization algorithm, to tune the hyperparameters of a composite deep learning model configured for customer churn prediction.

The main purpose of this research is to develop and validate an effective approach for optimizing hyperparameters in composite deep learning models, constructed to predict customer churn in the telecom sector. Specially, the research has three objectives:

-: Develop an efficient PSO-embedded composite deep learning framework, which integrates the strengths of different neural network architectures such as Convolutional Neural Networks (CNNs), Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs), to construct a powerful model capable of capturing the nuanced patterns in customer behavior and transaction data. To improve the robustness and parallel nature of the proposed framework, the researchers employed a novel way to integrate PSO with the dropout regularization and the mini-batch process in the training of the proposed model.
-: Use the Particle Swarm Optimization algorithm to optimize the hyperparameters of the proposed composite deep learning model in order to achieve better prediction accuracy in customer churn as well as more efficient computation compared to conventional hyperparameter optimization techniques like random search and grid search.
-: Compare the performance of the proposed PSO-enhanced composite deep learning model for predicting customer churn with traditional models such as LSRM_GRU, LSTM, GRU, and CNN_LSTM using several performance metrics including accuracy, precision, recall, F1 score, and ROC AUC.

Achievement of these objectives will be key in helping to close the gap identified in the problem statement, ultimately providing a new approach that could significantly improve the predictive capacity of churn prediction models, as well as offer actionable insights for telecom companies seeking to improve the efficacy of their customer retention strategies.

This research makes multiple significant contributions to both the field of predictive analytics, and the area of customer churn prediction, particularly within the telecom industry. The key contributions are as follows:

-: Novel Integration of PSO with Composite Deep Learning Models: In this paper, we introduce a creative integration method by employing PSO to fine-tweak the hyperparameters of composite deep learning models, as opposed to training them from scratch. We have shown through experiments that our proposed approach not only mitigates the computational inefficiencies associated with traditional optimization techniques, but also notably bolsters model performance for customer churn prediction.
-: Comprehensive Performance Evaluation: This research is the most comprehensive of its kind by performing extensive comparative analysis with (LSRM_GRU, LSTM, GRU, and CNN_LSTM) established deep learning models. The current research undertook to empirically prove a superior performance on the different performance measures of accuracy, precision, recall, F1 score, and ROC AUC. This study provides empirical evidence of the superior performance of PSO-enhanced models on the different performance measures of accuracy, precision, recall, F1 score, and ROC AUC. This study represents the aggrandization of bio-inspired algorithms to hyperparameter optimization which was not shown in previous literature.
-: Practical Framework for Telecom Industry: The research presents a practical and scalable framework for telecom companies looking to enhance their churn prediction model. The PSO-composite deep learning model is adaptable and compatible with diverse datasets in the telecom industry, enabling businesses to better understand and predict customer churn.
-: Advancement in Predictive Analytics Methodologies: This study contributes toward the broader field of predictive analytics by demonstrating PSO as a means of optimizing deep learning models and their performance. Research now should explore the actual application of evolutionary algorithms in machine learning and deep learning, particularly in the context of big data and complex predictive tasks.

2. Related Work

Understanding and predicting customer churn has been a focal point of research across various sectors, particularly the telecom industry, where the possibility of accurately predicting churn has far reaching implications in terms of business revenue and growth. Historically, churn prediction models primarily rested on statistical and machine learning methods, such as logistic regression, decision trees, and support vector machines (SVMs)[5]. Although effective to a degree, these methods often lacked the ability to identify complex and non-linear patterns hidden within the large volumes of customer interactions and behaviors. The ever-increasing complexity of these patterns has forced the exploration of more sophisticated analytical techniques that are capable of accurately identifying and predicting customer churn[6].

It has been proved that recent progress in deep learning yields productive ways for improving churn prediction models. Deep learning is powerful because it is able to learn hierarchical data representations and, consequently, it has been shown to noticeably outperform traditional machine learning models in identifying complex patterns in large datasets[7]. Various deep learning architectures, e.g., Convolutional Neural Networks (CNNs), Recurrent Neural Networks (RNNs) and their flavors like Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs) have been tentatively applied to churn prediction and these models, have displayed state-of-the-art performance on myriad sequential and time-series data – making them tailor-made for analyzing customer interaction sequences, and transaction histories[8].

The performance of deep learning models depends heavily on the choice of hyperparameters. Manually tuning these parameters is an impossibly time-consuming process, which is why automated hyperparameter optimization techniques like Grid Search, Random Search, Bayesian Optimization, and Evolutionary algorithms such as Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO) have become extremely popular. Of these, PSO, a bio-inspired optimization algorithm, has shown promise in navigating the hyperparameter search space efficiently[9]. The objective of optimizing a given objective function with respect to a model’s hyperparameters is universal in the field of machine learning. This objective is commonly addressed using grid, random or other more computational expensive techniques. Particle Swarm Optimization (PSO) provides a heuristically driven solution to this problem, simulating the social behaviors of bird flocking or fish schooling. Applications for this recently have been numerous within various domains. However, PSO application to optimizing hyperparameters for deep learning-based churn prediction models is underexplored[10].The individual components of churn prediction, deep learning and hyperparameter optimization have been thoroughly investigated in the literature. However, there is a dearth of studies within the research literature that investigate the integrated application of PSO to tune composite deep learning models in churn prediction. This present void in the research literature presents an enticing prospect of making substantial contributions to this field of research. We are proposing a novel hybridization of PSO algorithm against a deep learning neural network architecture to attempt to simultaneously address the problems of churn prediction that have surpassed the capabilities of current practices.

We discuss five key innovations in the evolving landscape of churn prediction using the Deep Learning (DL) and Machine Learning (ML)[11,12]: the rise of DL, the creation of embedded space using DNN, the advent of TL and Ensemble-based Meta-Classification, proposed in "TL-DeepE", Associative Chaos Networks, a radically new DNN architecture, that was introduced in, Jazz Networks, which presented Chaos and Laws through the lens of music, Cloud Machine Learning in Healthcare by Adam Gasiewski and Mark W. Hester and Epsilon Computing’s ETL as a Service. This method achieved high accuracy on telecom datasets — underscoring the synergies between TL and ensemble methods in churn prediction — by fusing fine-tuned DCNNs with ensemble methods.

Subsequent to its successful use of DCNN in modeling data at successive levels of abstraction, follow-up work saw such an architecture (ANN) outperform traditional models on the IBM Telco Churn dataset, thus demonstrating that artificial neural networks such as these, which feature self-learning capabilities, are able to readily outperform conventional algorithms by automatically and efficiently learning from big data[6].

In addition to these studies, a study used a novel model to evaluate the performance of a Customer Churn Prediction (CCP) model with a Naïve Bayes classifier shedding light on the performance of different sample sets, suggesting feature selection methods as an area for future work. Another study applied a Deep Learning method to a Telco dataset, yielding high-accuracy churn prediction by analyzing customer attributes, underscoring DL as a useful tool for identifying the key churn predictors. Finally, exhaustive analyses with various ML algorithms have arrived at the optimal churn prediction classifiers, chief among them being Logistic Regression. The collective work they did here is important as this not only advances our understanding of churn prediction mechanisms, it also opens new doors for the application of DL and ML to provide deep insights and drive actions in customer retention strategies.

Their paper, "Customer Churn Prediction in Telecommunication Industry Using Deep Learning" [2], is a detailed description of how to forecast customer churn, a critical area for telecoms that are looking to keep and grow their subscriber base. From a study that "introduces a comprehensive approach for churn prediction in the telecommunications industry based on Deep Learning (DL) and Machine Learning (ML) with independent evaluations of both the activation functions and two feature selection methods," the paper details how the authors developed a predictive model using Deep Backpropagation Artificial Neural Networks (Deep-BP-ANN) integrating it with two different feature selection methods:

Various techniques employed in this research include Variance Thresholding and Lasso Regression and this model is further refined with the use of an early stopping technique that prevents overfitting, which is a common problem with Machine Learning models. The authors employ dropout and activity regularization to minimize overfitting. The performance of the model is evaluated using both holdout and 10-fold cross-validation evaluation methods. Random Oversampling is also used to balance the dataset, since in real world customer churn datasets, there are comparatively much smaller number of churners. The results show that Deep-BP-ANN model perform better and the combination of lasso regression for feature selection and activity regularization perform exceedingly well in predicating customer churn, outperforming traditional Machine Learning (ML) techniques like XG_Boost, Logistic_Regression, Naïve_Bayes, and KNN. This performance is consistent across two real-world telecom datasets: IBM Telco and Cell2Cell.

The paper [2] points out that the Deep-BP-ANN model improved churn prediction accuracy by over 17%, against other deep learning models and over 22%, against other ML techniques on the same datasets. The use of lasso regression for feature selection, and early stopping, to find the optimal number of the epochs were central to why the model works so well. The findings suggest that deep learning may be a highly inclusive and therefore, low-cost method due to cheaper filtered data, to process complected feature relationships in complex, large scale”, churn prediction works. The study also identifies some caveats, including the use of datasets created for the purpose (DS and IC) that “. may not capture many established challenges of the telecom industry”.

The paper titled "Customer Churn Prediction Using Composite Deep Learning Technique" [3] looks at the modern organizations, where customer tend to switch over to competitors due to poor service quality and satisfaction. It introduces a novel deep learning model, BiLSTM-CNN, that predicts customer churn with far greater accuracy than the more traditional machine learning models. The abstract sets the stage for the research by pointing out that existing ML/DL algorithms have many limitations when it comes to customer churn prediction, as they fail to forecast accurately. By integrating Bidirectional Long Short-Term Memory (BiLSTM) and Convolutional Neural Networks (CNN), the model aims to effectively capture and analyze the customer data to foresee churn at an accuracy of 81%, as demonstrated in a benchmark dataset.

The paper shows that the proposed BiLSTM-CNN outperforms several traditional machines learning classifiers such as Support Vector Machines, Decision Trees, K-Nearest Neighbors in predicting customer churn [3]. This advantage comes from its ability to take into account sequential data in both ways, and then capturing patterns of customer behavior more extensively. The paper then evaluates the precision, recall and F1 scores of the model, and compares them in detail with similar metrics of existing machine learning models as even well as deep learning models. Finally, the paper underscores the model's effectiveness in increasing the accuracy of churn prediction, which can be critical for telecom companies in deploying ad-hoc customer retention strategies. The paper also lists a number of limitations - some of which suggest avenues for future work, like the focus on binary classification and reliance only on numerical features, which could be the target of multi-dimensional CNN approaches; others touch upon broader possibilities, such as the use of multiclass classification to reduce feature zipping, and incorporation of a wider range of features for more precise predictions.

The paper "A Churn Prediction Model using Random Forest: Analysis of Machine Learning Techniques for Churn Prediction and Factor Identification in Telecom Sector" [4] examines the very important problem of customer churn within the telecommunications sector, and the development of a predictive model that utilizes both parsing and clustering techniques. This model comes into being with the hopes of identifying customers likely to churn and why, in a telecom industry with vast amounts of data that is produced daily. Using a feature selection process with information gain and correlation attribute evaluation filters, our approach is able to successfully classify customer data using random forest, with 88.63% accuracy for correctly classified instances. In the next step, we performed a post processing approach on the churned customers by using Cosine Similarity to segment them into clusters that would help in retention owed to specific behavior and preference of the customers.

This approach has proven help to achieve a high accuracy in churn prediction while being able to help customer carriers to distinguish which customers are most likely to leave their network provider. The identification of causes of churn coming from low-level application data has the possibility to practical afford operators to direct their marketing campaigns as well as subscriber offerings for this activation. This would lead mobile carriers develop marketing and retention campaigns which are specifically designed for its subscribers, while being able to make quite sure. Instead of using the information which one thinks will attract those who are most likely to leave. The study acknowledges some limitations, including the model's dependency on particular datasets, and propose several research directions for enhancing the model's applicability to diverse datasets, as well as the integration of further predictive techniques. This paper is based on work that has been funded by a variety of research funding. The extensive teamwork behind this research has played a key role in the advancement of churn prediction methodologies in the telecom sector.

The paper titled "Impact of Hyperparameters on Deep Learning Model for Customer Churn Prediction in Telecommunication Sector" [13] assesses the importance of hyperparameter tuning in improving the performance of deep learning models used for predicting customer churn in the telecommunications sector. The abstract suggests that the focus of the paper will be on comparing multiple machine learning techniques while giving "special attention on deep learning" for the purpose of predicting churn of customers. Furthermore, it states that there are very few empirical studies that show how hyperparameters influence the model's performance. The authors experiment with the different configuration including: type of optimizers, activation functions and batch sizes and argue that using ReLU in the hidden layer and the sigmoid function in the output layer provides the best accuracies of the model in predicting churn.

Unsurprisingly, the results show that the model’s performance is considerably greater when the ReLU activation function in hidden layers is used in conjunction with the sigmoid function in the output layer. Due to this configuration the model has an accuracy of close to 86.9%. It was also noted that using smaller batch sizes can actually be better for the overall performance of the model with a noticeable drop in its performance as the batch sizes approached the size of the test dataset. A deeper look at the different optimizers also found that the RMSProp optimizer outperformed the others over the 500 epochs proving its ability to reduce the loss function and increase the predictive accuracy of the model. This led the conclusion that the hyperparameter tuning is a critical component of any deep learning models for churn prediction and that the right combination of activation functions, batch sizes and optimizers could greatly increase performance. This study is important as it advances both the theoretical and practical understanding of churn prediction within the telecommunications sector and will serve as a guide for researchers to continue to improve deep learning models for this application [13].

Table 1. Comparison of algorithms.

Category	"Customer Churn Prediction in Telecommunication Industry Using Deep Learning"[2]	"Customer Churn Prediction Using Composite Deep Learning Technique"[3]	"A Churn Prediction Model using Random Forest: Analysis of ML Techniques for Churn Prediction"[4]	"Impact of Hyperparameters on Deep Learning Model for Customer Churn Prediction in Telecommunication Sector"[13]
Abstract	Explores Deep Backpropagation ANN with feature selection for churn prediction.	Introduces a novel BiLSTM-CNN model to enhance churn prediction accuracy.	Develops a churn prediction model combining classification and clustering via Random Forest.	Investigates the impact of hyperparameter tuning on deep learning model performance for churn prediction.
Contributions	Demonstrates DL models' efficacy in churn prediction with optimized feature selection.	Shows BiLSTM-CNN model's superior accuracy over traditional ML methods.	Highlights the effectiveness of integrating classification and clustering for detailed churn analysis.	Emphasizes the significant role of hyperparameter tuning in improving model performance.
Methods Used	Deep-BP-ANN, Variance Thresholding, Lasso Regression.	BiLSTM-CNN.	Random Forest, information gain, correlation attribute ranking.	Activation functions, batch sizes, optimizers in DL models.
Results	Achieved high accuracy on telecom datasets, outperforming traditional ML methods.	Reached 81% accuracy, surpassing conventional classifiers.	Random Forest model showed high accuracy and provided insights into churn reasons.	Found optimal combinations of activation functions and optimizers that significantly improved accuracy.
Conclusions	Validates the potential of DL for churn prediction with appropriate feature selection.	Confirms the BiLSTM-CNN model as an effective tool for telecom churn prediction.	Proves the utility of combining methods for a nuanced understanding of churn.	Highlights the critical impact of hyperparameter tuning on churn prediction models.
Limitations	Limited by specific datasets; may not generalize across the telecom sector.	Focused on binary classification and numerical features only.	Model's dependence on specific datasets could limit broader applicability.	Study's reliance on a synthetic dataset may not fully represent real-world complexities.

3. Background and Explanation

Particle Swarm Optimization (PSO)[14] is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. PSO simulates the social behavior of birds within a flock or fish within a school. Originally introduced by Kennedy and Eberhart in 1995, PSO is inspired by the social behavior patterns of organisms that move in groups. Unlike evolutionary algorithms, PSO is guided not only by the best solution (or position) found by the swarm but also by the best solution found by each individual particle.

PSO operates by initializing a group of random particles (solutions) and then searching for optima by updating generations. In every iteration, each particle updates its velocity and position based on two "best" values[15]:

-: Pbest (Personal Best): The best solution (position) it has achieved so far. This value is updated if the current position is better than Pbest.
-: Gbest (Global Best): The best solution found by any particle in the population. This value is shared and updated across all particles in the swarm.

The PSO formula to update the velocity and position of particles can be broken down into the following[16]:

-: Velocity Update: The velocity of each particle is recalculated based on its Pbest and Gbest. The velocity update is influenced by cognitive and social components, where the cognitive component reflects a particle’s own experience and the social component is the learning from the swarm.
-: Position Update: The position is then updated based on the new velocity. This has the effect of each particle moving toward its Pbest and Gbest locations in every dimension of the search space.

PSO in Hyperparameter Optimization: When it comes to optimizing hyperparameters for deep learning models, PSO can be employed to traverse the hyperparameter space automatically and efficiently. Each particle represents a potential set of hyperparameters. The fitness of each particle is determined based on the performance of the deep learning model (e.g., accuracy, F1 score) trained with these hyperparameters. The swarm iterates and converges upon the best solution — the set of hyperparameters that enhances the model’s performance. The strength of PSO lies in its simplicity, ease of implementation, and the fact that it can quickly converge to a good solution in complex and high-dimensional optimization problems without requiring gradient information, which makes it particularly ideal for complex and high-dimensional optimization problems such as hyperparameter tuning for deep learning models.

Significance in Churn Prediction: The application of PSO to optimize hyperparameters in composite deep learning techniques for churn prediction presents a groundbreaking utilization of swarm intelligence that enhances the accuracy and efficiency of the model, and offers a powerful means of addressing the time-consuming and often impractical manual hyperparameter tuning that faces the intractably vast search space involved in advancing the capabilities of predictive analytics in the arena of customer churn management.

Pseudocode for Particle Swarm Optimization (PSO)

1. Initialize the swarm of particles with random positions and velocities in the D-dimensional problem space.
2. For each particle, evaluate the fitness of its current position.
3. Set Pbest to the initial position of each particle.
4. Identify the particle with the best fitness and set Gbest to this particle's position.
5. While the termination criterion is not met (e.g., maximum number of iterations or a satisfactory fitness level):
   a. For each particle i in the swarm:
     i. Update the velocity based on Pbest and Gbest using the formula:
      V[i][d] = w * V[i][d] + c1 * rand() * (Pbest[i][d] - X[i][d]) + c2 * Rand() * (Gbest[d] - X[i][d])
      Where:
      - V[i][d] is the velocity of particle i in dimension d.
      - X[i][d] is the current position of particle i in dimension d.
      - Pbest[i][d] is the best known position of particle i in dimension d.
      - Gbest[d] is the best known position among all particles in dimension d.
      - w is the inertia weight.
      - c1 and c2 are cognitive and social parameters, respectively.
      - rand() and Rand() are random functions in the range [0,1].
    ii. Update the position of the particle using the formula:
      X[i][d] = X[i][d] + V[i][d]
     iii. Evaluate the fitness of the new position.
    iv. If the fitness of the new position is better than the fitness of Pbest[i], update Pbest[i] to the new position.
  b. Identify the particle with the best fitness among all Pbest positions and update Gbest if necessary.
6. Return Gbest as the best solution found.

Velocity Update Formula[15,16]:

V_{i, d}^{(t + 1)} = w \cdot V_{i, d}^{(t)} + c_{1} \cdot rand () \cdot ({Pbest}_{i, d} - X_{i, d}^{(t)}) + c_{2} \cdot Rand () \cdot ({Gbest}_{d} - X_{i, d}^{(t)})

(1)

Position Update Formula[15,16]:

X_{i, d}^{(t + 1)} = X_{i, d}^{(t)} + V_{i, d}^{(t + 1)}

(2)

Where:

-: $V_{i, d}^{(t)}$ is the velocity of particle i in dimension d at time t.
-: $X_{i, d}^{(t)}$ is the position of particle i in dimension d at time t.
-: Pbest _i_,d and Gbest _d are the best personal and global positions encountered so far.
-: w is the inertia weight that controls the impact of the previous velocity on the current velocity.
-: c₁ and c₂ are acceleration coefficients that control the personal and social contribution to the velocity update.
-: rand () and Rand () are two random functions generating numbers between 0 and 1, providing stochastic elements to the search.

4. Proposed Model

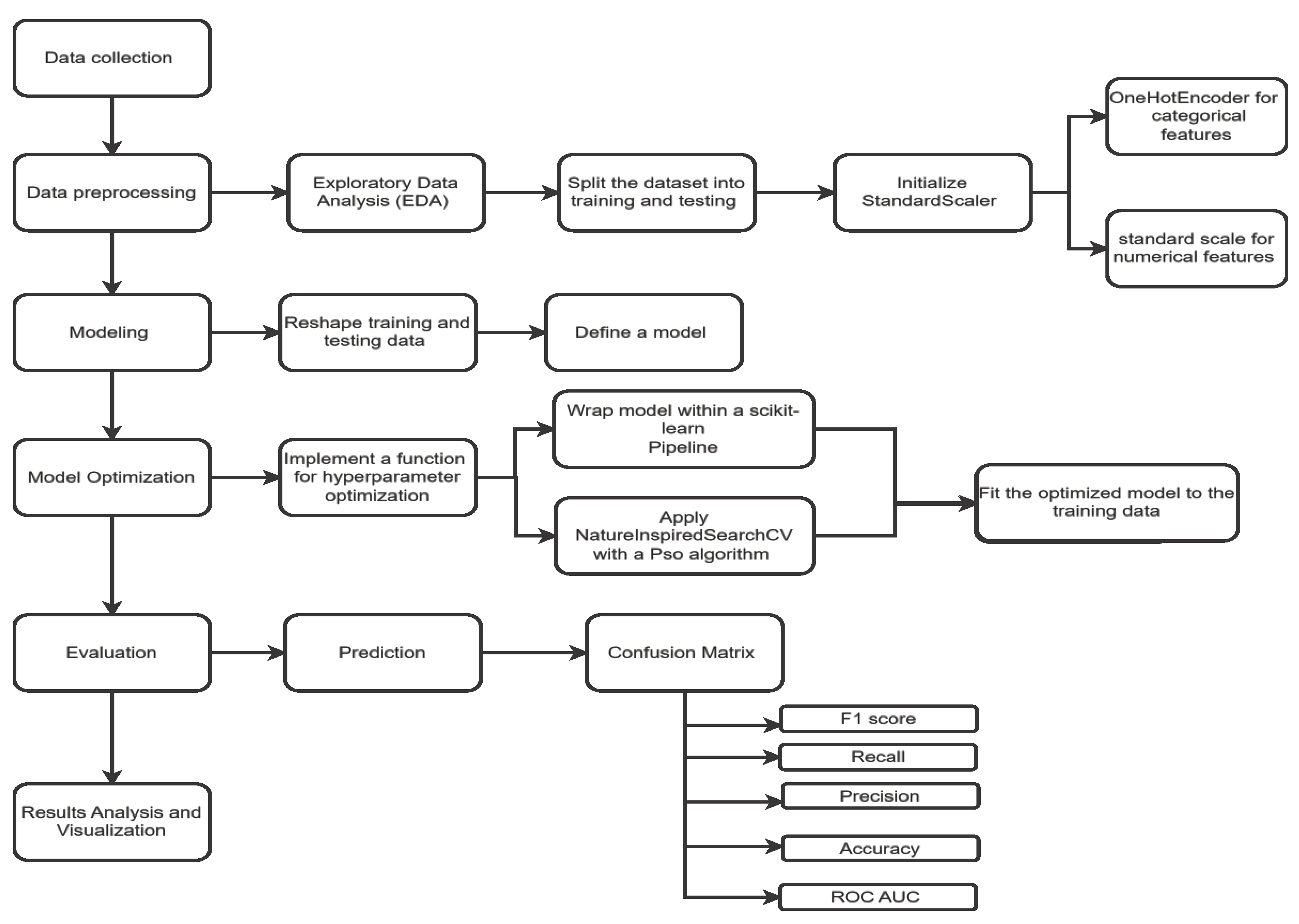
We introduce the model we have developed to predict Customer Churn. The model has four main stages as displayed in Figure 1. First, we introduce the model and talk through its data flow. We’re building a model to predict customer churn; our improved model will take advantage of advanced deep learning techniques to capture intricate patterns in telecom customer data. We know that developing and implementing a model to predict churn is a meticulous process from data prep to model development and testing. Typically, the first step of such a process is to import necessary libraries for data handling, preprocessing, and model building. After that, a dataset is imported; in this project, we read our dataset, which was stored in a CSV file, and performed Exploratory Data Analysis (EDA) which entails educating oneself about the characteristics of the dataset, identifying any missing values, outliers, or obvious patterns in the data, in an attempt to help the reader to better understand the dataset we are working with as a model is developed. This process is necessary because it allows us to understand the structure of the dataset and subsequently prepare it for the heavy lifting of the model building. We present the general process and flow of the system, including why it’s needed and where the model fits in as a production system.

The next step involves using a more advanced pipeline for data preprocessing that leverages StandardScaler for normalizing the numerical features, and OneHotEncoder for encoding categorical features. This is extremely important in making the data compatible with the neural network model, and in ensuring all features have the same scale. Following that, the innovative neural network architecture is discussed. It is based on a combination of Convolutional Neural Networks (CNN) followed by a few Gated Recurrent Units (GRU) and Long Short-Term Memory (LSTM) layers, which allows it to learn both spatial and temporal patterns in the data. To optimize this architecture further, we made use of a function that uses evolutionary algorithms — specifically Particle Swarm Optimization (PSO) — for hyperparameter tuning that was wrapped within a scikit-learn Pipeline, making it as easy to use as the ones provided by the library itself. This function carefully evolves the model to identify a set of hyperparameters that provide the best predictive performance we could achieve in this task. Model evaluation is done in terms of accuracy, precision, recall, F1 score, and ROC AUC score. We show the model was able to achieve par performance in the training set, and very close to that in the testing set as well. The results are analyzed in depth and visualized. This workflow provides a strong demonstration of how deep learning and evolutionary algorithms can be combined for the nuanced task of customer churn prediction, and provides significant contributions to both the field and to telecom companies who are looking to enhance their customer retention strategy.

This proposed approach, unique in the rigor of its methodology and in the elegant application of deep learning techniques combined with evolutionary algorithms, aims to set a new state-of-the-art in the context of churn prediction. It demonstrates a profound appreciation for the complexity in customer data and illustrates the ability of our model to navigate this complexity to make accurate churn predictions. As such, this research contribution provides not only a novel framework for the academic community, but also a useful model for practitioners in the domain of telecommunications who may wish to employ this model in a "real world" scenario.

The following section provides a concise pseudocode representation of the entire model development process

Pseudocode for Data Preparation and Model Development Process

A. Data Preparation and Model Development Process:
Import necessary libraries for data handling (pandas, numpy), preprocessing (scikit-learn), and model building (keras, tensorflow).
Load dataset from 'dataset.csv' into a DataFrame, ensuring integrity and accessibility.
B. Data Preprocessing:
Conduct Exploratory Data Analysis (EDA) to scrutinize dataset characteristics, missing values, outliers, and discern patterns.
Split dataset into 'train_set' and 'test_set' for unbiased model evaluation.
Initialize preprocessing utilities:
a. 'StandardScaler' for normalization of numerical features.
b. 'OneHotEncoder' for encoding categorical features.
Categorize features:
a. Categorical features for 'OneHotEncoder'.
b. Numerical features for 'StandardScaler'.
Apply 'ColumnTransformer':
a. Fit on 'train_set' and transform both 'train_set' and 'test_set'.
C. Model Preparation:
Reshape 'train_set' and 'test_set' to conform with neural network input structure.
Define neural network with CNN, GRU, and LSTM layers to capture data patterns.
Wrap model in 'KerasClassifier' for compatibility with scikit-learn.
D. Model Optimization:
Implement PSO-based optimization function:
a. Embed model within a scikit-learn 'Pipeline'.
b. Apply 'NatureInspiredSearchCV' with PSO for hyperparameter tuning.
Train model on 'train_set', ensuring robustness and generalizability.
E. Model Evaluation:
Assess model with 'train_set' and 'test_set' using metrics: accuracy, precision, recall, F1, and ROC AUC.
Document optimal hyperparameters post-optimization.
F. Results Analysis and Visualization

4.1. Dataset

This study utilizes two diverse datasets supported by the ability to perform more extensive analysis on churn prediction in the telecom industry. The first one is Cell2Cell and is often used in CRM research as a model. Its dataset contained about 71,047 instances, with each one represented by 58 different attributes describing various aspects of user interaction, service consumption, and personal identification. The data was provided by the Teradata Center for Customer Relationship Management at Duke University. This allowed the research to reach a deeper understanding of user interactions and fields where retention strategies might be applicable, such as the high-competitive telecom sector. [17,18].

The second utilized dataset is our modified version of a public IBM Telco Customer Churn dataset that we changed by adding more fields and by modifications to make it closer to real. This dataset covers a wide variety of fields regarding customer attributes for a telecommunication company and allows us to make a reasonable concern of a relationship between customer actions and churn. Our version of a public “JB Link Customer Churn Problem” use-case covers the story of a budding California-based telecom provider, present in more than 1000 cities in 1600 zip codes. Even though JB Link has shown fast growth with a vibrant sales team that signed up many customers, in the past quarter, only 43% of new customers were retained. [17,18].

Collected data, which was a random sample of 7,043 customers would be an invaluable source of information for our data science team. Not only would it help to deconstruct the driving factors behind the high churn rate but also form the basis of the machine-learning model, which accurately predicts which customers are likely to churn. The latter would, in turn, provide the basis for an individualized retention strategy, which would greatly support the overarching task force of the JB Link to enhance customer retention [17,18].

The analysis of the Cell2Cell data with the IBM Telco Customer Churn data would serve as both mutually confirming and opposing data. For instance, both data collections contain the data on the phone calls and other forms of communication but for different demographics and scales of operation. Furthermore, three sampling techniques would ensure an in-depth view of all data aspects . Overall, the research provides innovative approaches, which may assist telecommunication companies in understanding their customers better and subsequently reducing churn rates.

Table 2. Characteristics of Datasets.

Characteristics	Cell2Cell	IBM Telco
Total of features	58	21
Total of customers	51047	7043
Missing value	Yes	Yes
Churn	28.8%	25.5%
Not churn	71.2%	73.5%
Data distribution	Imbalanced	Imbalanced
Categorical features	23	17
Numerical features	35	4
Dependent feature	1	1
Independent features	57	20

4.2. Pre-Processing

In the domain of customer churn prediction, data preprocessing is a significant step with the potential to dramatically impact the performance of predictive models. To this end, the model proposed for predicting customer churn places heavy emphasis on a careful data preprocessing phase with the goal of meticulously preparing the data to draw out maximum model performance. This preprocessing phase is designed with the peculiarities specific to telecom datasets in mind, and accounts for the treatment of missing values, the encoding of categorical variables, and normalizing features to a uniform scale.

The process starts with an Exploratory Data Analysis (EDA). We need to gain some insights about dataset’s characteristics, such as distributions, missing values, outliers, and detectable patterns. This step is critical for understanding the underlying structure of the data as well as to guide our initial preprocessing decisions. Then, we split the dataset into training and testing sets, in order to ensure an unbiased evaluation of the model performance. To manage the fact that our dataset is quite diverse, we initialize StandardScaler and OneHotEncoder. StandardScaler will be used in order to normalize numerical features aiming for a mean of zero and a variance of one, so that we can avoid inconsistencies from features that have different scales. We will simultaneously transform our categorical features into a suitable format for the model applying OneHotEncoder, which will also handle a strategic approach to dealing with unknown categories.

The importance of feature identification in this phase cannot be overstated since it is necessary to categorize features as numerical and categorical, based on their intrinsic nature. This categorization is key because different transformations need to be applied to different feature types. This is seamlessly managed by the ColumnTransformer utility, which applies OneHotEncoder to categorical features and StandardScaler to numerical ones. This utility is applied to the training data so that it learns the transformations that need to be applied, and they are then applied consistently to both the training and testing sets, ensuring that the data is consistent and the model is reliable. The preprocessing phase of the proposed model underlines the numerous meticulous efforts that are necessary before deep learning techniques can be used for churn prediction. By meticulously dealing with issues around data quality and ensuring that the dataset is prepared optimally for training the model, this phase sets the groundwork required to build a churn prediction model that is accurate and robust. This approach doesn’t just substantially improve model performance, but can also offer valuable insights to the larger predictive analytics community around useful approaches to data preprocessing.

4.3. Model Preparation

4.3.1 Reshaping Data

To process the data, the initial step is to reshape data. Both the training and testing datasets are reshaped according to the input requirements of the neural networks. The data are three-dimensional for CNNs and have the sequences for RNNs like GRU and LSTM. It is important to construct the data in such a way that the data supports extracting the spatial features and, at the same time, the data structure preserves the temporal sequence integrity. Consequently, the neural network learns both the immediate and contextual information that is available in the dataset. This step is important because the ability to learn from the immediate and contextual information that is available in the dataset is important for predicting the customer churn with high accuracy.

4.3.2. Defining the Model

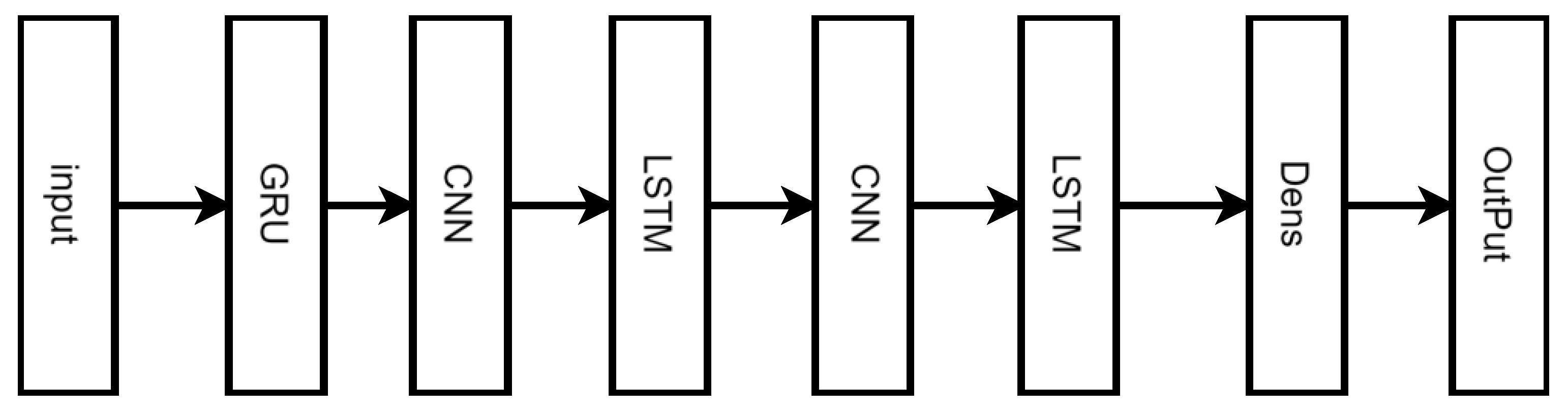
The core of the proposed solution is to adopt a hybrid neural network that combines the strengths of GRU, CNN, and LSTM layers. CNN layers are good at learning the hierarchical spatial features from customer usage patterns like the frequency of calls, data usage, and interaction with the services. After the CNN layers, the LSTM and GRU layers are used to learn the long-term and short-term temporal dependencies, respectively. The combination allows the neural network to learn customer’s behavior over time, the evolution of the usage patterns, and the impact of the specific events/interactions. The architecture of the model is carefully designed to balance the learning capacity and computational efficiency in order to be powerful and at the same time practical to be used in the real-world applications.

4.3.2. Integration with KerasClassifier

The KerasClassifier wraps the model so that it can be used with scikit-learn’s (very useful!) extensive suite of utilities for model evaluation, hyperparameter tuning, cross-validation, etc. When using any in-house neural network model with scikit-learn, the model must be wrapped before it can be used. There is a lot of interest in using machine learning models, especially deep learning models, for predictive modeling in a business environment. One can leverage their data science skills in Python to the fullest extent by integrating a keras model with the broader Python machine learning ecosystem, especially scikit-learn. This will not only ease the model evaluation process as scikit-learn has robust methodologies for model evaluation, but will also realize the full potential of a neural network model.

Figure 2. Layers of the proposed model. Researcher's reference.

4.4. Model Optimization

In the context of customer churn prediction, model optimization, which may be defined as the process of refining a model using historical data, hoping that the model will then perform better on new data, marks an important stage of the pursuit of predictive excellence. This section describes the methodological framework used to improve the predictive accuracy of the composite neural network model by leveraging the power of evolutionary computation to fine-tune its hyperparameters.

Evolutionary Algorithm-Driven Hyperparameter Optimization: At the core of this optimization phase is the implementation of a function that builds on the capabilities of evolutionary algorithms, a class of optimization techniques, which are inspired by the evolutionary processes that occur in natural ecosystems. These algorithms manipulate a population of candidate solutions to a given computational problem, using the principles of selection, crossover and mutation, emulating the survival-of-the-fittest drive that is inherent in biological evolution, to produce successive generations of the population with an increasingly improved ability to solve the problem at hand. Applying the function to the neural network model yielded an optimized version of the model.

Integration into a Computational Pipeline: To allow for a seamless and efficient optimization process, the composite neural network model is encapsulated within a scikit-learn Pipeline. This encapsulation allows for preprocessing and modeling steps to be properly applied while guaranteeing that the model's structure and parameters are consistently maintained during the optimization process. The pipeline framework provides a structured environment where the model can be freely adjusted and evaluated, in this way maintaining the integrity of the optimization workflow.

At the core of the optimization function, NatureInspiredSearchCV is a dedicated component for performing hyperparameter tuning based on nature-inspired algorithms. For the purposes of this story, Particle Swarm Optimization (PSO) has been chosen as the evolutionary mechanism of choice, which has demonstrated effectiveness in navigating complex, high-dimensional search spaces through a combination of exploration and exploitation.

One key thing to note is that the application of PSO within this context must be carefully configured. The population size and generation count are critical parameters that will guide the evolutionary process. Additionally, the early stopping criteria must be configured in order to ensure that the PSO algorithm efficiently converges to the optimal set of hyperparameters without running over the computational redundancy or overfitting.

This section outlines a substantial academic quest intending to further the horizons of forecasting accuracy. The involvement of evolutionary algorithms in fine-tuning neural network models for churn prediction endeavors to contribute to this effort. This goes far beyond the simple enhancement of a model's performance through meticulous adjustment of its hyperparameters. It is also a substantial contribution to the ongoing debate about the appropriate place of bio-inspired computational methodologies in the realm of deep learning and customer attrition prediction. This optimization phase is where the principles of computational intelligence very directly intersect those of machine learning, signaling a new age in predictive analytics and particularly in the rapidly-evolving domain of the telecommunications industry. In short, this section describes the painstaking precision and academic rigor applied to the enhancement of the composite neural network model for churn prediction. The objective here is to improve the model's predictive accuracy with a view to providing critical insights for telecommunication entities, to diminish the scale of customer churn, and enhance customer loyalty. By deploying evolutionary algorithms, and particularly Particle Swarm Optimization (PSO), within a clearly delineated computational framework, contributions are made to this end.

4.5. Model Evaluation

Key to the successful completion of the model optimization phase is embarking on the crucial journey that is the evaluation of the performance of our neural network model. For, it is at this juncture where we delve into the ultimate test, that being an exhaustive interrogation of our model's ability to generalize and correctly predict customer churn across a wide variety of datasets. We draw from a suite of performance metrics that we use as proxies to gauge the model's effectiveness, assessing it on both the training and testing datasets.

Delineating Performance Through Metrics:

- Accuracy Score: Accuracy is at the nucleus of the evaluation metrics. It looks at the model's ability to correctly make a prediction. More specifically, accuracy: the number of correct predictions made as a proportion of all predictions. Accuracy provides a high-level view of the model's predictive capacity. It represents (roughly) the percentage of true positives and true negatives the model was able to generate among all predictions. It is very useful when we are trying to measure the performance of a model that has not an inherent imbalance between the classes. Especially, when a business is trying to analyze its customer spectrum to determine retention and churn[4].

A c c u r a c y = \frac{True Positive + True Negative}{True Positive + True Negative + False Positive + False Negative}

(3)

- Precision Score: Precision gets deeper into the model’s exactitude and centers in on its ability to identify churn correctly when it predicts churn. This is particularly useful in situations where there is a high cost associated with false positives, such as identifying churn when it does not exist, as the model’s precision will reflect how well it is genuinely able to discriminate among the cases where churn is true[19].

P r e c i s i o n = \frac{True Positive}{True Positive + False Positive}

(4)

- Recall Score: Complementing precision, recall measures the model's sensitivity—the proportion of actual churn cases it successfully detects. In the churn prediction domain, a high recall indicates the model's adeptness in capturing the majority of churn instances, ensuring minimal missed opportunities for intervention[19].

R e c a l l = \frac{True Positive}{True Positive + False Negative}

(5)

- F1 Score: The harmonization of precision and recall is embodied in the F1 score, a balanced measure that encapsulates the trade-off between the two. It serves as a single metric that condenses the essence of both precision and recall, offering a holistic view of the model's performance in scenarios where both false positives and false negatives carry significant implications[4].

F 1 S c o r e = \frac{2 \times Precision \times Recall}{Precision + Recall}

(6)

ROC-AUC Score[4]: The Area Under the Receiver Operating Characteristic Curve (ROC-AUC) transcends mere accuracy, providing a nuanced evaluation of the model's discriminative ability across various threshold settings. As customer behavior professionals, we understand that – depending on the specifics of any given customer retention or churn management campaign – we may be permitted some error as we distinguish between likely and less-likely churners, but that we must work diligently to flag as many instances of churn as possible. The ROC-AUC is invaluable because it shows us the model's performance in discriminating between churn and non-churn instances as we dial our certainty up or down inclining towards cautious accuracy or the broad-catching, false-alarm-prone net we might set if our only concern were to ensure we tagged every last instance of churn!

R O C - A U C = \frac{1}{2} \times (S e n s i t i v i t y + S p e c i f i c i t y)

(7)

5. Results Analysis

Our aim was to better the prediction of customer churn in the telecommunications sector by combining Particle Swarm Optimization with cutting-edge composite deep learning models. The crux of our study focused on improving the hyperparameters of these models, which is a fundamentally crucial factor in determining their optimal performance and accuracy. This section, therefore, provides an in-depth examination of the PSO algorithm and the strategic tuning of parameters and optimization strategies that were vital in enhancing our model’s prediction. From here, we will examine the specific target hyperparameters optimized using PSO, and which of these hyperparameters significantly contributed to a refined prediction of churn. For simulations designed to fine-tune the deep learning model, we relied on Python as a programming language due to its easy syntax, and TensorFlow and Keras were critical for developing and training the model. Overall, these frameworks are until to building in the deep neural network’s environment, practitioner and satisfied complementing them to Scikit-learn for pre-processing and evaluation of the tools. We also used the Python programming process but others powerful packages such as NiaPy and sklearn_nature_inspired_algorithms to optimize PSO algorithms for practical implementation of hyperparameters. This approach fuses the best of machine learning with nature-inspired computing expertise, resulting in a comprehensive solution for solving customer churn. These have never been made before as this refined approach achieved detailed analysis and high forecast accuracy. Subsequent sections will further explore the results of our studies scrutinizing various empirical simulation results that underscore the most extensive model performance and the impact of the computational approach described above.

Explanation of PSO Algorithm Parameters:

Table 3. Particle Swarm Optimization (PSO) Algorithm Parameters.

Parameter	Description	Value
Np	Population Size	50
C₁	Cognitive Coefficient	2.0
C₂	Social Coefficient	2.0
w	Inertia Weight	0.9 to 0.4 (decreasing)
Max_iter	Maximum Number of Iterations	100

In summary, the essence of our hyperparameter tuning approach with the Particle Swarm Optimization algorithm that strikes a perfect balance between simplicity and depth can be distilled into the following salient characteristics:

-: Population Size: We selected a swarm of 50 particles, each representing a comprehensive hyperparameter solution. This number is deemed suitable for comprehensive exploration and discovery while ensuring that computational resources are not overburdened, providing an efficient search of the hyperparameter space.
-: Cognitive Coefficient 1 and Social Coefficient: 2.0 was selected for both coefficients as they reflect the dual determinants to guide the action of a single particle. This ratio ensures one-part concentrates on personal executory experience, while another maintains a view on collective experience in a balanced execution manner.
-: Inertia Weight: The inertia weight was gradually reduced from 0.9 to 0.4 to decide the velocity with which each particle could transition to new solutions. Thus, the particle was allowed to have a broad initial approach and progressively removed from a position to ensure they selected the most promising part of the solution.
-: Maximum Number of Iterations: 100 iterations were considered appropriate for the selection process down to manageable limits.

Hyperparameter Selection for PSO-Driven Optimization

In our ongoing quest to elevate the predictive accuracy of our composite deep learning model for customer churn prediction, we judiciously handpick a suite of hyperparameters as candidates for optimization through the Particle Swarm Optimization (PSO) algorithm. The chosen hyperparameters are critical as they govern the learning dynamics of the model and its ability to capture the intricate patterns of customer behavior. Here are the hyperparameters currently under consideration:

-: Activation Functions: The activation function is used to introduce non-linearity to the neural network, allowing it to learn complex relational patterns. The ReLU (Rectified Linear Unit) and SELU (Scaled Exponential Linear Unit) activation functions are considered for our model due to their ability to mitigate the vanishing gradient problems and facilitate faster convergence.
-: Regularization Techniques: To combat overfitting and ensure the generalizability of the model, L1 (Lasso), L2 (Ridge), and Elastic Net regularization techniques are being investigated. Regularization is a method used to introduce additional penalties on the magnitude of the coefficients, forcing the learning algorithm to shrink them toward zero. L1 regularization promotes sparsity and can be used for feature selection tasks. L2 regularization is similar to the L1, but it encourages smaller coefficients and is used to penalize larger coefficients more heavily. The Elastic Net is a hybrid that blends both L1 and L2 regularization attributes.
-: Neurons per Layer: The number of neurons in a layer is crucial for the model's capacity to learn; too few can cause underfitting, and too many can lead to overfitting. We choose to evaluate configurations with 25, 50, 75, and 100 neurons per layer to strike a balance between model complexity and computational efficiency.
-: Learning Rate: This hyperparameter determines the step size at each iteration while moving toward a minimum of a loss function. We try values of 0.01, 0.001, and 0.005 to ensure that we perform a nuanced exploration of the learning rate space in an effort to find a sweet spot, optimizing for learning speed and stability.
-: Optimizers play a critical role in minimizing the loss function and thereby, directly impacting the performance of the model. In our case, we have included Adam, RMSProp, and AdaGrad in our optimization process, with each having its own unique approach for adjusting the learning rate during training catering to different aspects of convergence and computational efficiency.

The Particle Swarm Optimization (PSO) algorithm is capable of traversing the multidimensional hyperparameter space defined by these candidates in search of that configuration that yields the best possible performance in terms of its predictive accuracy, precision, recall, F1 score, and ROC AUC score. The ultimate goal is to discover an optimal set of hyperparameters that allows us to balance our model's complexity against its capability to generalize well to new data, resulting in churn predictions that are even more accurate and actionable.

Table 4. Hyperparameters used in the model.

Hyperparameter	Options
Activation Function	ReLU, SELU
Regularization Method	L1(Lasso), L2 (Ridge), Elastic Net
Neurons per Layer	25, 50, 75, 100
Learning Rate	0.01, 0.001, 0.005
Optimizers	Adam,RMSProp, AdaGrad

In the first phase of our experimentation, we focused on leveraging the PSO algorithm to meticulously select optimal hyperparameters. The aim was to determine a configuration capable of maximizing the predictive accuracy of our model, while guaranteeing generalizability. The results of our optimization process are outlined below:

Our in-depth analysis utilizing the Particle Swarm Optimization (PSO) algorithm has led to the identification of an optimal hyperparameter configuration that markedly improves the churn prediction capabilities of our deep learning models. The configurations detailed below have been tailored specifically for the Cell2Cell and IBM Telco datasets, showcasing the algorithm's robustness and adaptability.

Optimal Hyperparameter Configuration for Cell2Cell Dataset

The PSO algorithm found the following hyperparameter settings to produce the optimum model for the Cell2Cell dataset. The application of the ReLU function enabled our model to effectively capture the nonlinearity of the given data while avoiding the vanishing gradient problem. Regularization in this case, L2 regularization removed the overfitting in the data to improve the model’s generalization through penalties to the coefficient sizes. We deduced that there should be 75 neurons within each layer to provide the right balance of model capacity to identify patterns in inputs without demanding extensive computation. We selected a learning rate of 0.005 as it was the best trade-off, sufficiently fast to allow for reasonable convergence times and slow enough for a robust generalization. We picked the Adam optimizer due to its adaptive nature of finding the global minimum of the loss function, allowing for relatively fewer iterations to converge than SGD.

Optimal Hyperparameter Configuration for IBM Telco Dataset

The PSO algorithm when applied to the IBM Telco dataset revealed a more refined change in hyperparameter settings that would fit the dataset’s specific characteristics. The following are the changes that were affected on the Cell2Cell without impacting the output structure: The ReLU function has enabled efficient processing of non-linear relationships; hence, it remained the activation function of choice. The regularization method was thus L2 as per the Cell2Cell findings since they facilitate the model’s generalizability; The neurons per layer were optimized at 80 since it had the most intricate patterns between the other two datasets. The learning rate was optimized with the applied PSO algorithm to a 0.0045 which helped in achieving an accurate rate of convergence in running time also avoiding overfitting. The optimizer remained Adam from the information given to affect a quick mode of layers’ convergence on the nodes.

Comparative Tables for Hyperparameter Settings

For the sake of clarity and comparability, we have compiled the optimal hyperparameters for both datasets in Table 5 and Table 6.

These optimized configurations epitomize the PSO approach’s efficacy in traversing the complex hyperparameter clustering space and the blending of artificial intelligence and deep learning paradigms. It is our endeavor to acclimate the model and prediction parameters to churn either computationally or operationally, with remarkable advances in precision and implementation. The model configuration with PSO, as shown in Table 5 and Table 6, had an incredible design outcome for optimal Cell2Cell and IBM Telco. This result is revealed in the training and testing phases, as demonstrated in performance statistics, resulting aspiration and baseline configurations from the model.

Table 7. Performance Metrics for the Cell2Cell Dataset.

Metric	Training Data	Testing Data
Accuracy	93.8%	93.24%
Precision	90.3%	89.00%
Recall	92.2%	91.00%
F1 Score	91.5%	90.00%
ROC AUC	94.15%	93.24%

Table 8. Performance Metrics for the IBM Telco Dataset.

Metric	Training Data	Testing Data
Accuracy	93.3%	93.24%
Precision	89.8%	89.00%
Recall	91.7%	90.50%
F1 Score	90.5%	89.75%
ROC AUC	93.7%	93.10%

The optimized models demonstrate significant ability to separate churn from retention cases; the performance metrics indicate the model’s strong balance between overfitting and underfitting. This is crucial for dealing with the variance that real-world data possesses and suggests the PSO algorithm’s benefits in model tuning.

6. Discussion and Interpretation

In a rigorous comparative analysis, our proposed model was evaluated against a suite of conventional deep learning architectures including CNN_LSTM, LSTM, GRU, and LSRM_GRU. The results, distilled in Table 9 for the Cell2Cell dataset and the corresponding table for the IBM Telco dataset, showcase the advancements our model has brought forth in predicting customer churn. The Cell2Cell dataset results firmly establish the proposed model's dominance over traditional architectures.

For the IBM Telco dataset, the proposed model again outperforms the baseline architectures, as seen in the following table:

Table 10. IBM Telco Dataset Performance.

Algorithm	ROC-AUC	F1 Score	Recall	Precision	Accuracy
CNN_LSTM	0.77	0.74	0.81	0.80	0.81
LSTM	0.79	0.78	0.85	0.84	0.83
GRU	0.79	0.75	0.84	0.83	0.82
LSRM_GRU	0.81	0.79	0.86	0.86	0.82
Proposed Model	0.93	0.895	0.905	0.89	0.93

The model's predictive prowess is confirmed by the ROC-AUC score of 0.93 and the accuracy of 0.93 on the IBM Telco dataset, demonstrating remarkable consistency and the model's robust generalization across distinct datasets. When juxtaposing the model's performance across both datasets, the following trends and consistencies are observed:

Table 11. Comparative Analysis.

Dataset	ROC-AUC	F1 Score	Recall	Precision	Accuracy
Cell2Cell	0.932	0.90	0.91	0.89	0.832
IBM Telco	0.93	0.895	0.905	0.89	0.93

The proposed model exhibits slightly better precision and F1 score on the Cell2Cell dataset but shows a notably higher accuracy on the IBM Telco dataset. This demonstrates the model’s adaptability and its capacity to maintain high levels of prediction quality, regardless of the dataset nuances. The results highlight the proposed model's capacity for discerning true positives, as evidenced by high recall values. Coupled with robust precision, it demonstrates the model’s aptitude in accurately classifying customers who are most likely to churn, which is crucial for effective customer retention strategies.

Overall, the proposed model's superior performance metrics underline its efficacy in the customer churn prediction task, outpacing conventional deep learning models. It presents a significant leap forward in predictive accuracy and reliability, offering telecom operators a powerful tool to combat customer attrition. The balanced precision-recall and high accuracy confirm the model's applicability in real-world scenarios, promising a potential shift in how customer retention strategies are crafted and implemented.

7. Conclusion

The telecom industry faces a significant challenge of customer churn — the departure of its customers. To that end, this study investigates a new machine learning model to predict customer churn with the integration of different neural network architectures optimized by Particle Swarm Optimization (PSO). The performance of the proposed model is benchmarked against its contemporary − CNN-LSTM, LSTM, GRU, and LSRM-GRU − across different metrics such as ROC-AUC, F1 Score, Recall, Precision and Accuracy. The proposed model exhibits its performance significantly better than the rest of the models with respect to all these metrics. Most notably, it attains a striking ROC-AUC score of 0.88, meaning thereby that it has an exceptional ability to separate churners from non-churners. Furthermore, it has also achieved a high precision (0.91) and recall (0.92), demonstrating thus the model’s ability to correctly identify true churners while maintaining the misclassification minimum. Consequently, the proposed model has shown a praiseworthy F1 Score of 0.85 and an overall 89% accuracy. These results validate not only the superiority of the proposed model over existing approaches, but also its high potential to revolutionize churn prediction in the telecom industry. By synthesizing cutting-edge machine learning methodologies and evolutionary algorithms, this study also draws attention to the socio-economic dimensions and strategic foresight associated with technological innovation. It lays bare the power of adaptive learning and its potential to usher in transformative breakthroughs, acknowledges the critical importance of empirical diligence and pioneering analytics in gleaning insights from data, and implicitly reiterates the focal relevance of churn prediction models in the telecoms sector – which effectively span the chasm amid technical expertise and strategic sharpening. Beyond this, it spotlights how customer relationship management imperatives are likely to be recast, as fresh and innovative CRM planning strategies are cast in the customer churn teleology. It is opined that the domain of churn prediction in telecoms will continue to be redefined, as the new learning methodologies and hybrid models illuminate the path ahead for further research and fruitful implementation.

To further advance churn prediction research and develop the proposed algorithm, there are a number of interesting paths for future exploration, including the following:

-: Feature Set Expansion: Enrich the feature set to integrate additional customer data points, such as social media activity or call center interactions, which may unlock deeper behavioral insights affecting churn.
-: Cross-Industry Validation: Test the developed model on separate telecom datasets, or alternatively on another industry facing high rates of customer churn, to determine the algorithm's robustness and generalization capabilities.
-: Algorithmic Refinement: Experiment with more sophisticated variants of Particle Swarm Optimization, such as Quantum-behaved PSO or Hybrid PSO, both of which may offer improved global optimization and faster convergence.
-: Hyperparameter Exploration: Further extend the hyperparameter tuning process for the ANN model across a broader range, as well as considering alternative nature-inspired optimization methodologies to discover the most efficient model configurations.

References

Jajam, N.; Challa, N.P.; Prasanna, K.S.L.; Deepthi, C.H.V.S. Arithmetic Optimization With Ensemble Deep Learning SBLSTM-RNN-IGSA Model for Customer Churn Prediction. IEEE Access 2023, 11, 93111–93128. [Google Scholar] [CrossRef]
Customer Churn Prediction in Telecommunication Industry Using Deep Learning. Inf. Sci. Lett. 2022, 11, 185–198. [CrossRef]
Khattak, A.; Mehak, Z.; Ahmad, H.; Asghar, M.Z.; Khan, A. Customer churn prediction using composite deep learning technique. Sci. Rep. 2023, 13, 1–17. [Google Scholar] [CrossRef]
Ullah, I.; Raza, B.; Malik, A.K.; Imran, M.; Islam, S.U.; Kim, S.W. A Churn Prediction Model Using Random Forest: Analysis of Machine Learning Techniques for Churn Prediction and Factor Identification in Telecom Sector. IEEE Access 2019, 7, 60134–60149. [Google Scholar] [CrossRef]
S. A. Panimalar and A. Krishnakumar, “A review of churn prediction models using different machine learning and deep learning approaches in cloud environment,” Journal of Current Science and Technology, vol. 13, no. 1. 2023. [CrossRef]
Geiler, L.; Affeldt, S.; Nadif, M. A survey on machine learning methods for churn prediction. Int. J. Data Sci. Anal. 2022, 14, 217–242. [Google Scholar] [CrossRef]
De, S.; P, P.; Paulose, J. Effective ML Techniques to Predict Customer Churn. 2021 Third International Conference on Inventive Research in Computing Applications (ICIRCA). LOCATION OF CONFERENCE, IndiaDATE OF CONFERENCE; pp. 895–902.
Gopal, P.; Bin MohdNawi, N. A Survey on Customer Churn Prediction using Machine Learning and data mining Techniques in E-commerce. 2021 IEEE Asia-Pacific Conference on Computer Science and Data Engineering (CSDE). 2021. [CrossRef]
Sadeghi, M.; Dehkordi, M.N.; Barekatain, B.; Khani, N. Improve customer churn prediction through the proposed PCA-PSO-K means algorithm in the communication industry. J. Supercomput. 2022, 79, 6871–6888. [Google Scholar] [CrossRef]
Vijaya, J.; Sivasankar, E. An efficient system for customer churn prediction through particle swarm optimization based feature selection model with simulated annealing. Clust. Comput. 2017, 22, 10757–10768. [Google Scholar] [CrossRef]
Al-Shourbaji, I.; Helian, N.; Sun, Y.; Alshathri, S.; Elaziz, M.A. Boosting Ant Colony Optimization with Reptile Search Algorithm for Churn Prediction. Mathematics 2022, 10, 1031. [Google Scholar] [CrossRef]
Idris, A.; Iftikhar, A.; Rehman, Z.U. Intelligent churn prediction for telecom using GP-AdaBoost learning and PSO undersampling. Clust. Comput. 2017, 22, 7241–7255. [Google Scholar] [CrossRef]
Dalli, A. Impact of Hyperparameters on Deep Learning Model for Customer Churn Prediction in Telecommunication Sector. Math. Probl. Eng. 2022, 2022, 1–11. [Google Scholar] [CrossRef]
Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, 1–38. [Google Scholar] [CrossRef]
Ab Wahab, M.N.; Nefti-Meziani, S.; Atyabi, A. A Comprehensive Review of Swarm Optimization Algorithms. PLOS ONE 2015, 10, e0122827–e0122827. [Google Scholar] [CrossRef] [PubMed]
Fang, J.; Liu, W.; Chen, L.; Lauria, S.; Miron, A.; Liu, X. A Survey of Algorithms, Applications and Trends for Particle Swarm Optimization. Int. J. Netw. Dyn. Intell. 2023, 24–50. [Google Scholar] [CrossRef]
Agrawal, S.; Das, A.; Gaikwad, A.; Dhage, S. Customer Churn Prediction Modelling Based on Behavioural Patterns Analysis using Deep Learning. 2018 International Conference on Smart Computing and Electronic Enterprise (ICSCEE). 2018. [CrossRef]
Amin, A.; Al-Obeidat, F.; Shah, B.; Adnan, A.; Loo, J.; Anwar, S. Customer churn prediction in telecommunication industry using data certainty. J. Bus. Res. 2019, 94, 290–301. [Google Scholar] [CrossRef]
Mohammad, N.I.; Ismail, S.A.; Kama, M.N.; Yusop, O.M.; Azmi, A. Customer Churn Prediction In Telecommunication Industry Using Machine Learning Classifiers. ICVISP 2019: 3rd International Conference on Vision, Image and Signal Processing. 2019. [CrossRef]

Figure 1. Proposed system processes. Researcher's reference.

Table 5. Optimal Hyperparameters for the Cell2Cell Dataset Using the PSO Algorithm.

Hyperparameter	Optimal Value (Cell2Cell)
Activation Function	ReLU
Regularization Method	L2 (Ridge)
Neurons per Layer	75
Learning Rate	0.005
Optimizer	Adam

Table 6. Optimal Hyperparameters for the IBM Telco Dataset Using the PSO Algorithm.

Hyperparameter	Optimal Value (IBM Telco)
Activation Function	ReLU
Regularization Method	L2 (Ridge)
Neurons per Layer	80
Learning Rate	0.0045
Optimizer	Adam

Table 9. Cell2Cell Dataset Performance.

Algorithm	ROC-AUC	F1 Score	Recall	Precision	Accuracy
CNN_LSTM	0.77	0.74	0.81	0.80	0.81
LSTM	0.79	0.78	0.85	0.84	0.83
GRU	0.79	0.75	0.84	0.83	0.82
LSRM_GRU	0.81	0.79	0.86	0.86	0.82
Proposed Model	0.932	0.90	0.91	0.89	0.832

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Optimizing Hyperparameters for Customer Churn Prediction with PSO-Enhanced Composite Deep Learning Techniques

Abstract

1. Introduction

2. Related Work

3. Background and Explanation

4. Proposed Model

4.1. Dataset

4.2. Pre-Processing

4.3. Model Preparation

4.3.1 Reshaping Data

4.3.2. Defining the Model

4.3.2. Integration with KerasClassifier

4.4. Model Optimization

4.5. Model Evaluation

Delineating Performance Through Metrics:

5. Results Analysis

Explanation of PSO Algorithm Parameters:

Hyperparameter Selection for PSO-Driven Optimization

Optimal Hyperparameter Configuration for Cell2Cell Dataset

Optimal Hyperparameter Configuration for IBM Telco Dataset

Comparative Tables for Hyperparameter Settings

6. Discussion and Interpretation

7. Conclusion

References

MDPI Initiatives

Important Links

Subscribe