Preprint
Article
Prediction of Ground Reaction Forces and Moments and Joint Torques during Level Walking through Optical Motion Capture using a Multibody Dynamics Model and Foot Deformations without Optimization Techniques
Altmetrics
Downloads
163
Views
62
Comments
0
A peer-reviewed article of this preprint also exists.
supplementary.zip (820.00KB )
This version is not peer-reviewed
Submitted:
19 March 2024
Posted:
19 March 2024
You are already at the latest version
Alerts
Abstract
Predicting ground reaction forces (GRFs) and ground reaction moments (GRMs) through a biomechanical model-based approach offers advantages for biomechanical analysis, particularly in situations where the application of a statistical model is limited by insufficient training data. However, the current prediction method is unsuitable for clinical applications due to its long computational time. The present study developed a new optical motion capture (OMC)-based method to predict GRFs, GRMs, and joint torques. The proposed approach performed the estimation process by distributing external forces, as determined by the equation of motion, between the left and right feet based on foot deformations, thereby predicting the GRFs and GRMs without relying on machine learning or optimization techniques. We investigated the prediction accuracy during walking by comparing a conventional analysis using a force plate with the OMC results. The comparison revealed excellent or strong correlations between the prediction and measurement for all GRFs, GRMs, and lower limb joint torques. The proposed method, which provides practical estimation with low computational cost, facilitates efficient biomechanical analysis and rapid feedback of analysis results, thereby increasing its applicability for kinetics estimation in clinical settings.
Keywords:
Subject: Engineering - Bioengineering
1. Introduction
In the fields of rehabilitation and sports, analyzing ground reaction forces (GRFs) and ground reaction moments (GRMs) offers advantages in assessing the risk of musculoskeletal disorders and evaluating physical performance [1,2]. To address the challenges associated with the complexity of recording GRFs and GRMs, previous studies have developed simplified measurement techniques that do not require a force plate. One such technique involves wearable systems for recording GRFs and GRMs, such as pressure insoles or instrumented force shoes [3]. These systems offer advantages in recording GRFs and GRMs with fewer limitations on measurement location. However, concerns remain regarding their low durability and the impact of the weight and height of the wearable instruments on the motion of participants.
Another technique for measuring GRFs involves a prediction approach using kinematic data recorded by optical motion capture (OMC) or inertial measurement units (IMUs) [3,4]. This technique includes two approaches: the statistical model-based method and the biomechanical model-based method. The statistical model-based approach enables the prediction of GRFs and GRMs with high accuracy, relying on statistical algorithms such as machine learning [5,6,7,8,9,10]. However, this method has a disadvantage in its application to situations where obtaining sufficient training data is challenging, thus limiting the range of movements that can be analyzed.
The biomechanical model-based approach enables the estimation of GRFs and GRMs using multibody dynamics calculations [3,4]. Although this method has the potential to be applied in various movements, it faces limitations in making accurate predictions during the double-support phase due to the closed-loop structure between humans and the ground. To address this challenge, several studies have proposed computational techniques within the biomechanical model-based approach. While artificial neural networks and smooth transition assumptions have been employed as accurate estimation methods [11,12], they lack applicability due to the need for training data and gait assumptions. In contrast, some studies have proposed computational techniques that incorporate a contact model in which the contact state between the foot and the ground is represented by a mathematical model, such as a spring-damper model [13,14]. Since this method calculates GRFs and GRMs from the measured contact state between the foot and the ground, it does not require any training data or gait assumptions, making it applicable to activities other than walking [15,16].
Previously, we developed the contact model-based approach for predicting GRFs, GRMs, and joint torques [17]. This method employs multibody dynamics calculations based on kinematic data for GRF prediction without requiring training data or making gait assumptions, thus providing advantages in terms of versatility and applicability. However, our study faced a limitation of significant computational cost due to the optimization technique to tune the parameters necessary for estimating GRFs and GRMs. Similarly, other studies using the contact model-based approach also rely on optimization processes to tune parameters such as the coefficients of the spring-damper model [13,14,15,16]. While alternative methods exist for estimating GRFs and GRMs using different computational techniques [18,19], these methods also incorporate optimization techniques for GRF prediction. Therefore, a prediction method focused on reducing computational time could significantly contribute to the clinical applications of GRF estimation, such as improving the efficiency of the biomechanical analysis and rapidly presenting analysis results to medical staff and patients.
This study developed a new prediction method for GRFs, GRMs, and joint torques with low computational cost by focusing on deformations of the foot alignment. Previous studies have reported that the foot arch and soft tissues contribute to foot deformations under load, reaching magnitudes of millimeters or centimeters under the load of the human body mass [20,21]. Based on this fact, we hypothesized that the load condition of the foot can be predicted from foot deformations recorded using OMC. Furthermore, if the load condition can be estimated from foot deformations, GRFs and GRMs during the double support phase can be predicted without optimization techniques by distributing external forces calculated by the biomechanical model according to the load condition. Therefore, this study developed a new OMC-based prediction method for GRFs, GRMs, and joint torques using a hybrid approach of a multibody dynamics model and foot deformations and evaluated the estimation accuracy and its advantages for biomechanical analysis.
2. Materials and Methods
2.1. Participants
This study volunteered eighteen participants (10 males, 8 females; mean age: 23.3 ± 2.5 years; mean height: 1.67 ± 0.10 m; mean weight: 55.2 ± 7.46 kg) with no history of musculoskeletal disorders. Approval for the study was obtained from the Ethics Committee of Tokyo Metropolitan University. Prior to the experiment, all participants received both verbal and written explanations regarding the study’s content, and they provided written informed consent.
2.2. Conditions
As the initial step in developing the prediction method, this study evaluated the accuracy of estimation during level walking with bare feet, a fundamental human motion. The experiment included three walking speeds: normal, fast, and slow. The normal speed was adjusted to each participant’s preferred walking pace, while the fast and slow speeds were approximately +20 % and -20 % of the normal walking speed, respectively. Before the experiment, participants were familiarized with each walking speed.
2.3. Measurements
The three-dimensional coordinates, denoted as x for the anterior-posterior axis, y for the vertical axis, and z for the latero-medial axis, of markers attached to the whole body were measured using an OMC system (OptiTrack Flex3; Natural Point Inc., USA). A total of 49 reflective markers were placed on various body locations based on the marker set of the gait 2392 musculoskeletal model in OpenSim [22]. The marker data were digitally filtered (low-pass filter, Butterworth fourth-order type, -3 dB at 6 Hz) and were sampled at 100 Hz.
To validate the OMC results, the GRF and GRM were measured using a force plate (TF-4060-D; Tec Gihan Co. Ltd., Japan). The force data were digitally filtered (low-pass filter, Butterworth fourth-order type, -3 dB at 18 Hz) and were sampled at 1,000 Hz.
2.4. Data Analysis
2.4.1. Kinematics
At the beginning of the prediction procedure, the kinematics of each joint, segment, and contact point were computed based on the three-dimensional coordinates of markers recorded by the OMC system. The joint and segment kinematics were calculated using the gait 2392 musculoskeletal model in OpenSim [22]. This model consists of 12 segments, including the torso, pelvis, femurs, tibias, taluses, calcanei, and toes. The model has 23 degrees of freedom (DOFs). The hip and back joints have three DOFs expressed in Euler angles with the sequence Z (flexion-extension) X (abduction-adduction) Y (rotation). The knee, ankle, subtalar, and metatarsophalangeal joints each have one DOF in flexion-extension or dorsiflexion-plantarflexion. The pelvis has six DOFs for global coordinates, which include three translational DOFs and three rotational DOFs expressed in Euler angles with the sequence Z (flexion-extension) X (abduction-adduction) Y (rotation). The inverse kinematics using the model in OpenSim computed the joint kinematics vector , which includes the joint angles of all joints, and the segment kinematics vectors , , and , which include the translational position of the center of mass (COM) of all segments.
To compute GRFs and GRMs based on foot deformations, a total of 20 contact points (10 per foot) were positioned on the calcaneus and toe segments, as shown in Figure 1. The horizontal locations of the contact points were derived from the marker positions based on the marker set of the gait 2392 musculoskeletal model. The vertical locations of the contact points were set to have an offset of 30 mm toward the ground during static standing, using the OMC data of the static standing calibration with weight on the heel side. Subsequently, the contact point computation yielded translational positions of the contact points on the foot, represented by , , and .
2.4.2. Ground Reaction Forces and Moments
Before computing GRFs and GRMs, the total external forces acting on the human body were calculated using the translational equations of motion. The external forces , , and were expressed as follows:
where , , and represent the anterior, vertical, and lateral position of the COM of the sth segment, which are components of , , and , respectively; is the mass of the sth segment; and is gravitational acceleration.
Because the external forces, calculated from the equation of motion, represent the total forces applied to the human body, it is necessary to allocate these forces to each foot to calculate the GRFs and GRMs. The present study determined the amount of sinkage to the ground at the ith contact point position based on the contact point positions, and the total external force was distributed to each contact point based on the ratio of to the overall sinkage. The vertical GRF , frontal GRM , and sagittal GRM applied to one foot were computed as follows:
where , , and represent the anterior, vertical, and lateral position of the ith contact point, which are components of , , and , respectively, and and are the critical position and velocity of the contact point, respectively, which were set to = 0 and = 0.05, as determined empirically. In this study, the ground height was set to = 0. The origin of the horizontal directions and was positioned at the ankle joint, as measured by OMC (the midpoint of the markers of the lateral and medial malleolus).
During the single support phase, the anterior GRF and lateral GRF applied to one foot were determined using the horizontal external forces calculated from the equation of motion, as follows:
During the double support phase, the anterior and lateral GRFs were calculated using a different method compared to the single support phase. Previous studies have reported that the GRF vector intersects a point located above the COM of the system, referred to as the virtual pivot point (VPP), in a dynamic system such as a human in motion [23]. Accordingly, the present study computed the horizontal GRF based on the assumption that the GRF vector intersects the VPP of the human body. First, three-dimensional positions of the center of pressure (COP) of the GRF, which is the starting point of the GRF vector, are calculated by the vertical GRF and the GRM around the horizontal axis, as follows:
where the vertical position of the COP was set to the ground height, that is, = 0. Then, if the GRF vector is assumed to intersect the VPP, the GRF can be expressed as a vector connecting the COP and the VPP multiplied by a real number. Consequently, the anterior GRF and lateral GRF during the double support phase are calculated using the real number , as follows:
where , , and represent the anterior, vertical, and lateral positions of the VPP of the entire body, respectively. The VPP position was defined as 37.5 mm upward along the axis direction represented in the trunk segment coordinate system from the COM of the whole body, after a previous experimental study [23]. The whole-body COM was determined from the segment kinematics vectors , , and . Subsequently, the transverse GRM was computed using the horizontal GRFs and the COP of the GRF, as follows:
2.4.3. Joint Torques
Joint torques were determined through inverse dynamics analysis using the estimated GRFs and GRMs. The joint torque vector was computed as follows:
where represents the inertia matrix and is a vector consisting of Coriolis, centrifugal, gravitational, and external forces. The inverse dynamics analysis was conducted with the gait 2392 musculoskeletal model in OpenSim [22], which is the same model used in the inverse kinematics analysis.
2.5. Accuracy and Sensitivity Analysis
To evaluate the prediction accuracy, the predicted GRFs and GRMs were compared with the force plate data. The predicted joint torques were compared with an inverse dynamics solution using the gait 2392 musculoskeletal model in OpenSim with the input measurement data [22]. The agreement between the prediction and measurement was evaluated using Pearson’s correlation coefficient (), which was classified as follows: for weak, for moderate, for strong, and for excellent correlation [24]. In addition, we computed the root mean square error () and relative (), which normalized the by the average peak-to-peak amplitude for the two solutions [12]. All statistical analyses were performed using MATLAB 9.9 (MathWorks, Inc., USA).
In the proposed method, which relies on foot deformation, the measurement error of the contact point may have a significant impact on the estimation accuracy. Therefore, a sensitivity analysis was conducted to investigate the influence of the measurement error of the contact point on prediction accuracy. To simulate data with measurement errors, white noise was added to all contact point positions , , and using the rand function in MATLAB. This study compared the RMSE and rRMSE of the GRFs and GRMs under three conditions with maximum white noise amplitudes of 1, 10, and 100 mm.
3. Results
The GRF and GRM curves throughout a gait cycle during normal-speed walking are shown in Figure 2, and the joint torque curves throughout a gait cycle during normal-speed walking are shown in Figure 3, respectively. At all three experimental walking speeds, excellent or strong correlations were observed for all GRFs, GRMs, and joint torques. The results of the statistical analysis for each speed are summarized in Table S1. The time series data for each speed are included in Dataset S1.
The RMSEs and rRMSEs of the GRFs and GRMs with white noise in contact point position data during normal-speed walking are presented in Table 1.
The computational time from OMC data input to GRFs and GRMs output was approximately 4 sec for one trial (CPU: Intel Core i7-10700 with 4.0 GHz of average speed; memory: 32 GB; software: MATLAB 9.9 and OpenSim 4.1; OS: Windows 11 Home).
4. Discussion
The present study observed excellent or strong correlations between the estimation and experimental data for all GRFs, GRMs, and joint torques. The proposed method also demonstrated estimation accuracy comparable to that of previous studies, as shown in Table 2 and Table 3 [11,12,15]. Thus, the proposed approach, which does not rely on optimization techniques, succeeds in achieving these estimation accuracies for GRFs, GRMs, and joint torques at a low computational cost of a few seconds. In previous studies that employed optimization techniques for prediction, the computational time was relatively long because the parameters for computing the estimated values had to be determined through exploratory calculations [17]. Although the computational time depends on various factors, it is assumed that optimization approaches requiring exploratory calculations involve a computational cost at least on the order of several minutes. Therefore, the proposed method offers advantages over conventional methods, such as rapid feedback of the analysis results, thereby contributing to the clinical application of these kinetic factor estimation methods.
Another feature of the proposed method is its potential applicability as a GRF estimation technique for various activities. In previous studies, the smooth transition assumption approach has been applied to GRF estimation only during walking [12,25]. Although the artificial neural network approach can be extended to GRF estimation for activities other than walking [26], its applicability might be constrained in situations where sufficient training data cannot be obtained. In contrast, because the present method operates independently of statistical models or walking assumptions, it has the potential to be applied to GRF estimation across a wide range of activities, such as sports, daily activities, and orthopedic or prosthetic conditions.
Here, we provide a detailed description of the prediction accuracy of the proposed method. All GRFs exhibited excellent or strong correlations between the predictions and measurements. Nevertheless, the RMSEs and rRMSEs of the GRFs were comparatively low compared to those reported in previous studies, as shown in Table 2 [11,12,15]. Although previous studies estimated GRFs during the single support phase using an approach relying on the equation of motion as used in our study, GRFs during the double support phase were calculated using complex computational techniques, such as a statistical model, walking assumptions, and optimization [11,12,13,14,15,16,17,18,19]. In contrast, our proposed estimation method calculated GRFs using only the external force derived from the equation of motion and the amount of sinkage at the contact point. Consequently, the prediction results of this study were more susceptible to the influence of measurement errors compared to conventional approaches. Hence, the simplicity of the computational method employed in this study had a detrimental impact by producing a lower prediction accuracy for the GRFs.
All GRMs exhibited excellent or strong correlations between the predictions and measurements. Additionally, the RMSEs and rRMSEs of the GRMs were relatively high compared to those reported in previous studies, as shown in Table 2 [11,12,15]. Previous studies estimated the GRMs using the equation of motion and some computational techniques, similar to their GRF prediction [11,12,13,14,15,16,17,18,19]. However, the estimated GRMs based on the rotational equation of motion could include modeling errors related to the mass, moment of inertia, and COM of each body segment. These errors potentially degrade the estimation accuracy compared to the GRF prediction based on the translational equation of motion, which only incorporates modeling errors of the mass of each body segment. On the contrary, the proposed estimation method computed the GRMs using the estimated GRFs and the position of the contact point, thereby eliminating the modeling errors associated with the moment of inertia and COM of each body segment from the GRM prediction. Consequently, the accuracy of GRM estimation for the entire gait cycle was improved compared to previous studies.
Joint torques exhibited excellent or strong correlations between the predictions and measurements. The present study also observed good estimation accuracy for joint torques through the inverse dynamics calculation using the estimated GRFs and GRMs obtained by the proposed method. Comparison of the estimation accuracies with those reported in previous studies (Table 3) shows that the proposed method provided estimation accuracies comparable to those of the estimation method based on the smooth transition assumption [12]. In addition, a previous study has reported that the optimization approach provides joint torque prediction accuracy levels similar to those of the smooth transition assumption [15]. Therefore, while the proposed method does not achieve an estimation accuracy comparable to the artificial neural network approach, which provides superior estimation accuracy compared to other methods, the present study demonstrates a practical accuracy of the proposed approach comparable to that of the smooth transition assumption and the optimization approach.
The sensitivity analysis presented in Table 1 confirms that the estimation accuracies of GRFs and GRMs tend to deteriorate as the amplitude of the white noise increases. While the GRF prediction was not significantly affected by white noise up to 10 mm, the GRM prediction showed a deterioration in accuracy at 10 mm of white noise. In the proposed prediction method, noise in the contact point positions influences the distribution of the external force computed by the equation of motion, but not for the magnitude of the external force. Therefore, the noise in the contact point positions has less impact on the GRFs, which are calculated as the sum of the forces acting on the contact points of each foot. In contrast, the distribution of the external force at each contact point has a significant effect on the COP, leading to a deterioration in estimation accuracy for the GRMs. Based on the results of the sensitivity analysis, it is expected that the estimation accuracy of GRMs will decline if the proposed method is applied to IMU-based prediction, which has fewer limitations for measurement locations and lower measurement accuracy than that of the OMC-based approach. Nevertheless, the present method has the potential for application in IMU-based methods with practical accuracy because the estimation accuracy with white noise at 10 mm was not greatly different from the estimation accuracy in some previous studies, as shown in Table 2 [12,15].
Several limitations of this study are noted. Although the present study developed the GRF estimation method to address the location limitations of force plates, the proposed method can only be applied in situations where an OMC system can be installed. While the location limitations of the present method can potentially be relieved by employing IMUs instead of an OMC system, a critical challenge remains in determining the position of the foot contact points when using IMUs, as IMUs cannot directly measure three-dimensional coordinates.
The present study conducted the experiment with participants in bare feet to accurately capture foot deformations. Consequently, this study cannot ensure prediction accuracy under conditions other than bare feet, such as when shoes are worn. To extend the applicability of the method to various motions in the future, the accuracy of this method should be confirmed under conditions other than bare feet.
This study estimated GRFs and GRMs for movement on level ground by assuming the critical position shown in Eq. (4) to be constant. While the prediction accuracy needs confirmation, the proposed method may be applicable beyond level ground to situations where the critical position can be formulated, such as when the ground has a constant slope. However, it is challenging to apply this method to a rough walking surface with irregularities in the ground.
The estimation accuracy in this study was confirmed only for healthy young adults walking at three different speeds. Although the proposed method is expected to be applicable to various activities other than walking, further accuracy verification is necessary to apply the proposed method to those activities.
5. Conclusion
The proposed OMC-based method successfully estimated GRFs, GRMs, and joint torques with practical estimation accuracy while maintaining low computational costs. This achievement can be attributed to the reduction of biomechanical modeling errors in GRF prediction, which was realized through the foot deformation approach. The proposed method, characterized by its low computational time without optimization techniques, is expected to enable clinical applications of GRF estimation. Furthermore, the proposed method has the potential for application to GRF estimation for various activities, as it operates independently of walking assumptions or training data. It is also applicable to IMU-based approaches, as it performs predictions under the influence of 10 mm of white noise.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.: Table S1 (manuscript_table.docx) and Dataset S1 (manuscript_dataset.csv).
Author Contributions
Conceptualization, K.H.; methodology, N.H.; software, N.H.; validation, N.H.; formal analysis, N.H.; investigation, N.H.; resources, K.H. and N.H.; data curation, N.H.; writing—original draft preparation, N.H.; writing—review and editing, K.H.; visualization, N.H.; supervision, K.H.; project administration, K.H.; funding acquisition, K.H. and N.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JST SPRING grant number JPMJSP2156.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Ethics Committee of Tokyo Metropolitan University (protocol code H4-80 and approved on March 24, 2022).
Informed Consent Statement
Informed consent was obtained from all participants involved in the study. Written informed consent was also obtained from the participants to publish this paper.
Data Availability Statement
The data presented in this study are available as Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadpoor, A.A.; Nikooyan, A.A. The relationship between lower-extremity stress fractures and the ground reaction force: A systematic review. Clin. Biomech. 2011, 26, 23–28. [CrossRef]
- You, X.; Xu, Y.; Liang, M.; Baker, J.S.; Gu, Y. The relationship between ground reaction forces, foot positions and type of clubs used in golf: A systematic review and meta-analysis. Appl. Sci. 2023, 13, 7209. [CrossRef]
- Shahabpoor, E.; Pavic, A. Measurement of walking ground reactions in real-life environments: A systematic review of techniques and technologies. Sensors 2017, 17, 2085. [CrossRef]
- Ancillao, A.; Tedesco, S.; Barton, J.; O’Flynn, B. Indirect measurement of ground reaction forces and moments by means of wearable inertial sensors: A systematic review. Sensors 2018, 18, 2564. [CrossRef]
- Johnson, W.R.; Mian, A.; Donnelly, C.J.; Lloyd, D.; Alderson, J. Predicting athlete ground reaction forces and moments from motion capture. Med Biol Eng Comput 2018, 56, 1781–1792. [CrossRef]
- Mundt, M.; Koeppe, A.; David, S.; Bamer, F.; Potthast, W.; Markert, B. Prediction of ground reaction force and joint moments based on optical motion capture data during gait. Med Eng Phys 2020, 86, 29–34. [CrossRef]
- Karatsidis, A.; Bellusci, G.; Schepers, H.M.; de Zee, M.; Andersen, M.S.; Veltink, P.H. Estimation of ground reaction forces and moments during gait using only inertial motion capture. Sensors 2017, 17, 75. [CrossRef]
- Lam, S.K.; Vujaklija, I. Joint torque prediction via hybrid neuromusculoskeletal modelling during gait using statistical ground reaction estimates: An exploratory study. Sensors 2021, 21, 6597. [CrossRef]
- Zhang, L.; Soselia, D.; Wang, R.; Gutierrez-Farewik, E.M. Lower-limb joint torque prediction using LSTM neural networks and transfer learning. IEEE Trans. Neural Syst. Rehabilitation Eng. 2022, 30, 600–609. [CrossRef]
- Mundt, M.; Thomsen, W.; Witter, T.; Koeppe, A.; David, S.; Bamer, F.; Potthast, W.; Markert, B. Prediction of lower limb joint angles and moments during gait using artificial neural networks. Med Biol Eng Comput 2020, 58, 211–225. [CrossRef]
- Oh, S.E.; Choi, A.; Mun, J.H. Prediction of ground reaction forces during gait based on kinematics and a neural network model. J Biomech 2013, 46, 2372–2380. [CrossRef]
- Ren, L.; Jones, R.K.; Howard, D. Whole body inverse dynamics over a complete gait cycle based only on measured kinematics. J Biomech 2008, 41, 2750–2759. [CrossRef]
- Dorschky, E.; Nitschke, M.; Seifer, A.K.; van den Bogert, A.J.; Eskofier, B.M. Estimation of gait kinematics and kinetics from inertial sensor data using optimal control of musculoskeletal models. J Biomech 2019, 95, 109278. [CrossRef]
- Karatsidis, A.; Jung, M.; Schepers, H.M.; Bellusci, G.; de Zee, M.; Veltink, P.H.; Andersen, M.S. Musculoskeletal model-based inverse dynamics analysis under ambulatory conditions using inertial motion capture. Med Eng Phys 2019, 65, 68–77. [CrossRef]
- Fluit, R.; Andersen, M.S.; Kolk, S.; Verdonschot, N.; Koopman, H.F.J.M. Prediction of ground reaction forces and moments during various activities of daily living. J Biomech 2014, 47, 2321–2329. [CrossRef]
- Skals, S.; Jung, M.K.; Damsgaard, M.; Andersen, M.S. Prediction of ground reaction forces and moments during sports-related movements. Multibody Syst Dyn 2017, 39, 175–195. [CrossRef]
- Haraguchi, N.; Hase, K. Prediction of ground reaction forces and moments and joint kinematics and kinetics by inertial measurement units using 3D forward dynamics model. J. Biomech. Sci. Eng. 2023, Advance online publication, 23-00130. [CrossRef]
- Xiang, Y.; Arora, J.S.; Rahmatalla, S.; Abdel-Malek, K. Optimization-based dynamic human walking prediction: One step formulation. Int. J. Numer. Meth. Engng 2009, 79, 667–695. [CrossRef]
- Audu, M.L.; Kirsch, R.F.; Triolo, R.J. Experimental verification of a computational technique for determining ground reactions in human bipedal stance. J Biomech 2007, 40, 1115–1124. [CrossRef]
- Kouchi, M.; Kimura, M.; Mochimaru, M. Deformation of foot cross-section shapes during walking. Gait Posture 2009, 30, 482–486. [CrossRef]
- Xiong, S.; Goonetilleke, R.S.; Zhao, J.; Li, W.; Witana, C.P. Foot deformations under different load-bearing conditions and their relationships to stature and body weight. Anthropol. Sci. 2009, 117, 77–88. [CrossRef]
- Delp, S.L.; Anderson, F.C.; Arnold, A.S.; Loan, P.; Habib, A.; John, C.T.; Guendelman, E.; Thelen, D.G. OpenSim: Open-source software to create and analysis dynamics simulations of movement, IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [CrossRef]
- Maus, H.M.; Lipfert, S.W.; Gross, M.; Rummel, J.; Seyfarth, A. Upright human gait did not provide a major mechanical challenge for our ancestors. Nat. Commun 2010, 1, 70. [CrossRef]
- Taylor, R. Interpretation of the correlation coefficient: A basic review. J Diagn Med Sonogr 1990, 6, 35–39. [CrossRef]
- Villeger, D.; Costes, A.; Watier, B.; Moretto, P. An algorithm to decompose ground reaction forces and moments from a single force platform in walkng gait. Med Eng Phys 2014, 36, 1530–1535. [CrossRef]
- Choi, A.; Lee, J.M.; Mun, J.H. Ground reaction forces predicted by using artificial neural network during asymmetric movements. Int. J. Precis. Eng. Manuf. 2013, 14, 475–483. [CrossRef]
Figure 1.
Locations of the contact points. The cross marks represent the contact points, and the circle symbols represent the reflective markers used in the optical motion capture. A total of 20 contact points, 10 per foot, were placed in the calcaneus and toe segments. The horizontal locations of the contact points were derived from the marker positions based on the marker set of the musculoskeletal model employed in this study, and the vertical locations of the contact points were set to have an offset of 30 mm toward the ground during static standing. Unit: mm.
Figure 1.
Locations of the contact points. The cross marks represent the contact points, and the circle symbols represent the reflective markers used in the optical motion capture. A total of 20 contact points, 10 per foot, were placed in the calcaneus and toe segments. The horizontal locations of the contact points were derived from the marker positions based on the marker set of the musculoskeletal model employed in this study, and the vertical locations of the contact points were set to have an offset of 30 mm toward the ground during static standing. Unit: mm.
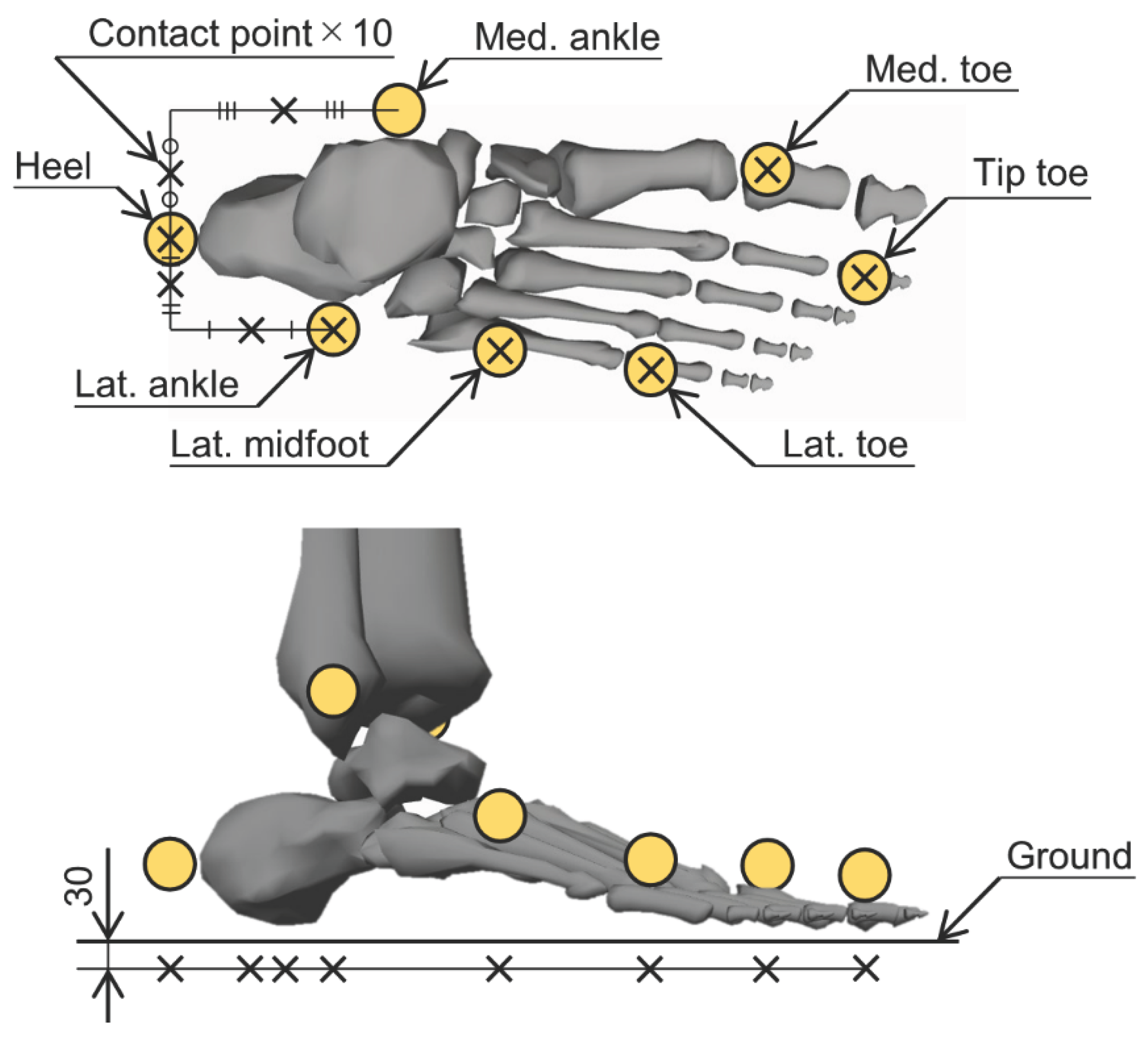
Figure 2.
Ground reaction forces (GRFs) in the (a) antero-posterior axis with the anterior direction as positive, (b) latero-medial axis with the lateral direction as positive, and (c) vertical axis with the upward direction as positive, and ground reaction moments (GRMs) in the (d) frontal plane around the anterior axis, (e) sagittal plane around the lateral axis, and (f) transverse plane around the vertical upward axis during normal-speed walking. The solid and dashed curves represent the average and standard deviation of the predictions, respectively, while the gray shading represents the average and standard deviation of the measurements. The upper right text of each graph shows Pearson’s correlation coefficient (), the root mean square error (), and the relative (). The magnitudes of the curves are normalized to the body mass of participants.
Figure 2.
Ground reaction forces (GRFs) in the (a) antero-posterior axis with the anterior direction as positive, (b) latero-medial axis with the lateral direction as positive, and (c) vertical axis with the upward direction as positive, and ground reaction moments (GRMs) in the (d) frontal plane around the anterior axis, (e) sagittal plane around the lateral axis, and (f) transverse plane around the vertical upward axis during normal-speed walking. The solid and dashed curves represent the average and standard deviation of the predictions, respectively, while the gray shading represents the average and standard deviation of the measurements. The upper right text of each graph shows Pearson’s correlation coefficient (), the root mean square error (), and the relative (). The magnitudes of the curves are normalized to the body mass of participants.
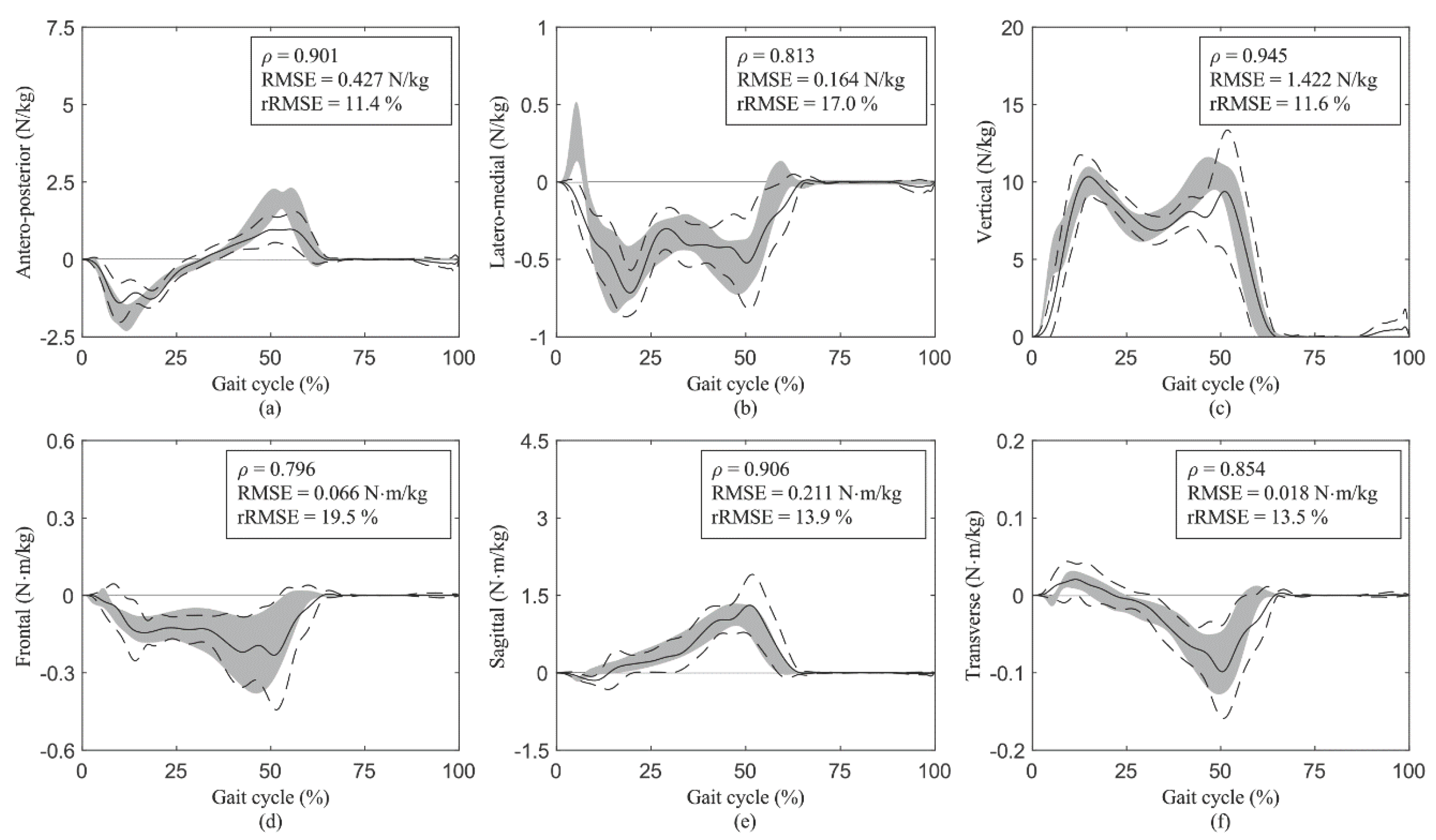
Figure 3.
Joint torques of the (a) hip abduction, (b) hip flexion, (c) hip external rotation, (d) knee abduction, (e) knee flexion, (f) knee external rotation, (g) ankle eversion, (h) ankle dorsiflexion, and (i) ankle external rotation during normal-speed walking. The solid and dashed curves represent the average and standard deviation of the predictions, respectively, while the gray shading represents the average and standard deviation of the measurements. The upper right text of each graph shows Pearson’s correlation coefficient (), the root mean square error (), and the relative (). The magnitudes of the curves are normalized to the body mass of participants.
Figure 3.
Joint torques of the (a) hip abduction, (b) hip flexion, (c) hip external rotation, (d) knee abduction, (e) knee flexion, (f) knee external rotation, (g) ankle eversion, (h) ankle dorsiflexion, and (i) ankle external rotation during normal-speed walking. The solid and dashed curves represent the average and standard deviation of the predictions, respectively, while the gray shading represents the average and standard deviation of the measurements. The upper right text of each graph shows Pearson’s correlation coefficient (), the root mean square error (), and the relative (). The magnitudes of the curves are normalized to the body mass of participants.

Table 1.
Root mean square errors (RMSEs) and relative RMSEs (rRMSEs) of ground reaction forces (GRFs) and moments (GRMs) with three levels of white noise in the contact point position data during normal-speed walking. The average and standard deviation (SD) for all participants are displayed, with magnitudes normalized to the body mass of participants.
Table 1.
Root mean square errors (RMSEs) and relative RMSEs (rRMSEs) of ground reaction forces (GRFs) and moments (GRMs) with three levels of white noise in the contact point position data during normal-speed walking. The average and standard deviation (SD) for all participants are displayed, with magnitudes normalized to the body mass of participants.
| Noise level | ±1 mm | ±10 mm | ±100 mm | |||||
| RMSE (SD) (N/kg or Nm/kg) |
rRMSE (SD) (%) |
RMSE (SD) (N/kg or Nm/kg) |
rRMSE (SD) (%) |
RMSE (SD) (N/kg or Nm/kg) |
rRMSE (SD) (%) |
|||
| Anterior GRF | 0.426 (0.134) | 11.4 (3.9) | 0.432 (0.138) | 11.6 (4.1) | 0.739 (0.098) | 24.1 (2.1) | ||
| Lateral GRF | 0.165 (0.029) | 17.1 (3.6) | 0.178 (0.029) | 18.3 (4.3) | 0.213 (0.045) | 22.7 (3.5) | ||
| Vertical GRF | 1.414 (0.678) | 11.5 (5.4) | 1.384 (0.680) | 11.2 (5.4) | 3.587 (0.397) | 31.6 (4.1) | ||
| Frontal GRM | 0.068 (0.029) | 19.7 (7.4) | 0.105 (0.036) | 27.3 (10.8) | 0.397 (0.085) | 46.6 (9.3) | ||
| Sagittal GRM | 0.213 (0.080) | 14.0 (7.8) | 0.245 (0.075) | 15.6 (7.2) | 0.420 (0.105) | 25.8 (6.2) | ||
| Transverse GRM | 0.019 (0.007) | 13.7 (5.5) | 0.026 (0.009) | 16.9 (6.3) | 0.036 (0.009) | 19.5 (4.0) | ||
Table 2.
Comparison of root mean square errors (RMSEs) and relative RMSEs (rRMSEs) in ground reaction forces (GRFs) and moments (GRMs) during normal-speed walking with results of previous studies [11,12,15]. The average and standard deviation (SD) for all participants N are displayed, with magnitudes normalized to the body mass of participants.
Table 2.
Comparison of root mean square errors (RMSEs) and relative RMSEs (rRMSEs) in ground reaction forces (GRFs) and moments (GRMs) during normal-speed walking with results of previous studies [11,12,15]. The average and standard deviation (SD) for all participants N are displayed, with magnitudes normalized to the body mass of participants.
| Method | Artificial neural network [11] |
Smooth transition assumption [12] |
Optimization approach [15] |
Foot deformation approach (this study) |
|||||||
| Participants | N = 5 | N = 3 | N = 9 | N = 18 | |||||||
| RMSE (SD) (N/kg or Nm/kg) | rRMSE (SD) (%) |
RMSE (SD) (N/kg or Nm/kg) | rRMSE (SD) (%) |
RMSE (SD) (N/kg or Nm/kg) | rRMSE (SD) (%) |
RMSE (SD) (N/kg or Nm/kg) | rRMSE (SD) (%) |
||||
| Anterior GRF | 0.154 (0.057) | 7.3 (0.8) | 0.473 (0.068) | 10.9 (0.8) | 0.38 (0.07) | 9.3 (2.0) | 0.427 (0.135) | 11.4 (3.9) | |||
| Lateral GRF | 0.040 (0.022) | 10.9 (1.8) | 0.191 (0.034) | 20.0 (2.7) | 0.17 (0.04) | 14.9 (3.4) | 0.164 (0.029) | 17.0 (3.6) | |||
| Vertical GRF | 0.649 (0.182) | 5.8 (1.0) | 0.710 (0.190) | 5.6 (1.5) | 0.74 (0.13) | 6.6 (1.1) | 1.422 (0.678) | 11.6 (5.4) | |||
| Frontal GRM | 0.052 (0.029) | 22.8 (4.9) | 0.148 (0.013) | 32.5 (4.3) | 0.11 (0.02) | 22.9 (5.9) | 0.066 (0.028) | 19.5 (7.1) | |||
| Sagittal GRM | 0.081 (0.045) | 9.9 (1.9) | 0.199 (0.106) | 12.2 (4.8) | 0.18 (0.05) | 12.4 (3.5) | 0.211 (0.080) | 13.9 (7.9) | |||
| Transverse GRM | 0.032 (0.018) | 25.5 (4.5) | 0.039 (0.015) | 26.2 (9.4) | 0.22 (0.06) | 40.6 (11.3) | 0.018 (0.007) | 13.5 (5.4) | |||
Table 3.
Comparison of root mean square errors (RMSEs) and relative RMSEs (rRMSEs) in joint torques during normal-speed walking with results of previous studies [11,12]. The average and standard deviation (SD) for all participants N are displayed, with magnitudes normalized to the body mass of participants.
Table 3.
Comparison of root mean square errors (RMSEs) and relative RMSEs (rRMSEs) in joint torques during normal-speed walking with results of previous studies [11,12]. The average and standard deviation (SD) for all participants N are displayed, with magnitudes normalized to the body mass of participants.
| Method | Artificial neural network [11] |
Smooth transition assumption [12] |
Foot deformation approach (this study) |
|||||
| Participants | N = 5 | N = 3 | N = 18 | |||||
| RMSE (SD) (Nm/kg) |
rRMSE (SD) (%) |
RMSE (SD) (Nm/kg) |
rRMSE (SD) (%) |
RMSE (SD) (Nm/kg) |
rRMSE (SD) (%) |
|||
| Hip abduction | 0.052 (0.006) | 5.1 (0.9) | 0.106 (0.008) | 9.9 (0.9) | 0.168 (0.046) | 14.5 (3.4) | ||
| Hip flexion | 0.056 (0.041) | 9.7 (2.0) | 0.469 (0.067) | 20.9 (2.1) | 0.307 (0.095) | 15.0 (2.5) | ||
| Hip rotation | 0.029 (0.040) | 12.0 (1.0) | 0.051 (0.006) | 15.0 (1.2) | 0.032 (0.007) | 11.3 (2.6) | ||
| Knee abduction | 0.033 (0.019) | 6.4 (1.6) | 0.100 (0.017) | 15.3 (2.8) | 0.054 (0.023) | 16.3 (6.4) | ||
| Knee flexion | 0.020 (0.007) | 8.1 (1.8) | 0.307 (0.056) | 18.7 (2.9) | 0.187 (0.053) | 18.3 (3.7) | ||
| Knee rotation | 0.043 (0.036) | 13.8 (2.7) | 0.042 (0.012) | 25.4 (5.1) | 0.040 (0.016) | 18.4 (7.0) | ||
| Ankle eversion | 0.053 (0.028) | 22.7 (5.0) | 0.134 (0.012) | 35.8 (4.6) | 0.039 (0.016) | 22.1 (7.2) | ||
| Ankle dorsiflexion | 0.091 (0.052) | 10.5 (4.8) | 0.190 (0.112) | 9.7 (4.8) | 0.186 (0.096) | 10.8 (8.5) | ||
| Ankle rotation | 0.033 (0.022) | 25.0 (4.4) | 0.039 (0.015) | 26.1 (9.3) | 0.053 (0.024) | 17.9 (6.9) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






