Prerpints.org logo
Preprint
Article

New Insight into Electric Force in Metal and the Quadratic Electrical Resistivity Law of Metals at Low Temperatures

Altmetrics

Downloads

86

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 March 2024

Posted:

19 March 2024

You are already at the latest version

Alerts
Abstract
: Considering that Einstein's relation between the diffusion coefficient and the drift mobility of the free randomly moving charge carriers in homogeneous materials including metals is always valid, it is shown that the effective electric force acting on free electrons in metal depends on the ratio between the kinetic free electron energy at the Fermi surface to the classical particle energy 3kT/2. The electrical resistivity of elemental metals dependence on very low temperatures has the quadratic term, which has been explained by electron-electron scattering. In this paper, it is shown that the quadratic term of the electrical resistivity at low temperatures is caused by scattering of the free RM electrons by electronic defects due to linear effective free electron scattering cross-section dependence on temperature, but not by electron-electron scattering.
Keywords: 
Subject: Physical Sciences  -   Condensed Matter Physics

1. Introduction

An investigation of the electron transport in  metals began over a hundred years ago when the free electrons were postulated  by Drude [1] to explain the conductivity of  metals. At the same time, the properties of the electrons in metals have been  analyzed by using the classical statistical methods of the gases. It was assumed  that the density of the free electrons is equal to the density of atoms, and  the mean free path of the electrons can be determined from comparison with an  experiment. The Drude theory failed to explain why the electron in a pure metal  can freely travel over a hundred atomic distances without being scattered.  Later a mental imagination that all metal valence electrons become delocalized  and are shared by all atoms in the solid forming a “sea” of negative charge [2,3], and are no longer associated with a given  atom [4]. The nuclei with their core electrons  form ions, which are immersed in this sea of valence electrons. Such ungrounded  imagination about free electron transport in metals has continued for nearly  the last century.
Usually, metal atoms are arranged in regular  three-dimensional periodic lattices. Hard spheres of metal atoms are packed in  such crystal structures: face-centered cubic (FCC), body-centered cubic (BCC),  hexagonal close-packed (HCP), orthorhombic (ORC), and tetragonal (TET). The dependences  of the metal atoms to various lattice structures and their distribution on the  periodic table are presented in Figure 1 [5,6].
As can be seen from Figure 1, almost all metal atom packing density is close to the ideal  close-packing value of 0.73, and it does not depend on the lattice structure,  only for Ga, Rb, Cs, and Sn the packing density is smaller than the ideal close  packing density value.
The interaction of the valence electrons with the  ion cores produces the main contribution to the binding energy and lowering of  the energy of the valence electrons in metal compared with that of the free  atom causes the metallic binding [7–9]. The  total number of bonds in metal is considerably large, and not all valence  electron bonds have the same binding energy.
Some difficulties in the explanation of the  electron transport in metals by classical statistics have been understood by  quantum mechanics: the Pauli exclusion principle and Fermi-Dirac statistics. According  to quantum mechanics the free electrons as the Bloch waves can freely move in  the ideal periodic lattice of the metal without any scattering by lattice ions [3,7–10]. The scattering of the free electrons can  be only in spots where there are distortions of the periodicity of the  potential energy of the ideal lattice structure.
The electrons in an ideal periodicity crystal are  arranged in energy bands (allowed zones) separated by forbidden regions in  energy (energy gaps). Each primitive cell exactly contributes only one  independent value of the wave vector k to each energy band [10–12]. The valence electrons occupy the lowest  energy levels in the conduction band below the Fermi level energy, and their  distribution on energy E is described by Fermi distribution function f(E).  Though the valence electron wave functions overlap with that of neighbor atoms [6–8], they remain associated with native ion cores.  Only valence electrons, which have energies close to the Fermi level energy due  to lattice atom vibrations can be released, and can randomly move in metal [13,14]. The effective density neff  of the free randomly moving (RM) electrons in metals and other materials has  been defined in [15] as
n e f f = ∫ 0 ∞ g E f E 1 − f E d E  
where g E  is the density of states (DOS) in the conduction  band. It let to show that the effective density neff of the  free RM electrons in metals can be described as n e f f = g E F k T , where g E F = g ( E )  at E=EF. It also lets us  show that the Einstein′s relation between the diffusion coefficient D and the drift mobility μ drift  of the free RM charge carriers D / μ drift = k T / q  is valid in all cases with one type of charge  carriers. In [16], there is at the first time  presented the probability density function of the free RM electron distribution  on energy: p E = f E 1 − f E / k T , which meets all requirements of the probability  theory [17,18].
Though the value of the neff  reaches only a few per cents of the total density n of the valence  electrons of metals at room temperature, the total density of the valence  electrons n has been traditionally used for description of the  electrical conductivity σ in  metals and superconductors in the normal state by σ = q 2 n / τ m * where q, τ, and m * are, respectively, the electron charge, the average electron relaxation time, and its effective mass. From a comparison of the Drude and Sommerfeld conductivity formulae, it has been stated that there is only a difference in the definition of the relaxation time of the free electrons [10]. The Drude conductivity formula can be used for descriptions of the conductivity of weakly doped semiconductors, but it is completely not applicable to describe the conductivity of metals and other materials with degenerate electron gas.
The resistivity of metals linear increase with a temperature above Debye's temperature was usually explained by charge carriers scattering due to lattice atom vibrations: due to an increase of the electron scattering cross-section [6,9–12,19–22]. As shown in [13,14], the electron scattering cross-section at a temperature above the Debye temperature does not depend on temperature, and the lattice vibrations play another role: they produce the free RM electrons, and at the same time they produce the electronic defects (weakly screened ions, which lost valence electrons). The effective density of the electronic defects N e f f = n e f f . The rest part N – Neff of atoms which have the valence electrons with energy lower than the Fermi level energy does not have sufficient thermal vibration energy to excite their valence electrons. As it is pointed in [13], the rest part n – neff of the valence electrons, which energy is lower by a few kT than Fermi level energy, due to the Pauli exclusion principle and Fermi-Dirac statistics can not change their energy, and they cannot scatter the free RM electrons.

2. Effective Drift Velocity of the Free RM Electrons, and Effective Electric Force Acting to Free Electrons in Metals

The current density j in homogeneous material is described as
j x = σ E x = q n e f f v x d r i f t = q n e f f μ drift E x ,
where σ is the conductivity of the material, Ex is the external applied electric field strength in the x-direction, neff is the effective density of the free randomly moving electron density, vx drift is their drift velocity in the electric field, and μ drift is the free electron drift mobility.
Considering that Einstein's relation between the diffusion coefficient D and the drift mobility μ drift is valid for free RM electrons in metal, one can express the drift mobility of the free RM electrons in the following way:
μ drift = q D k T = q < v 2 > < τ > 3 k T = q < τ > m * < E > ( 3 / 2 ) k T = q < τ > m * α ε ,
where the parameter
αε=<E>/ [ (3/2) kT] shows how many times the average free RM electron kinetic energy exceeds the average classical particle energy (3/2) kT. Therefore, the drift velocity of the free RM electron can be described as
v x d r i f t = < τ > m * α ε q E x = < τ > m * F x e f f ,
where Fxeff is the effective electric force acting on the free RM electron in the material. In the case of semiconductors with non-degenerate electron gas, α ε = 1 , and
F x e f f = q E x ,
i. e., the effective electric force is described by the usual relation. Though the average drift velocity contribution to the direct current in materials without degenerate electron gas with and without accounting the electron distribution on energy gives the same result, the electrons with higher velocities give relatively higher contribution to the total current. In the case of metals, the effective electric force acting on the free RM electron is equal to
F x e f f = α ε q E x = E F ( 3 / 2 ) k T q E x .
Impulse of force I acting on the free electrons during their scattering by electronic defects
I = F e f f Δ t = α ε q E d e f   Δ t ,
where Δ t is the acting time, Edef is the electric field strength produced by electronic defect. On the other hand, F e f f = Δ p / t = ħ Δ k / Δ t (here p is the momentum, and k is the wave vector of the electron. If the average energy of the free electron during scattering change is about 1.64kT [14], the wave vector due to parameter αε experiences a very large exchange of the direction.
Thus, the free electron motion in material must be described by such general equation:
m d v d r i f t d t = q α ε E − m v d r i f t < τ > ,
which is valid for homogeneous materials at any degree of degeneration of electron gas. In stationary state dvdrift/dt=0, and vdrift is described by Eq. (4).
Similar, the free electron motion in electric and magnetic fields can be described as
m d v d r i f t d t = q ( α ε E + v B ) − m v d r i f t < τ > ,
where B is the magnetic flux density. For static electric and magnetic fields, this equation can be presented as
q α ε E + v B = m v d r i f t < τ > .
The solution of this equation for the Hall coefficient RH gives the well-known result [14]:
R H σ 0 = q < τ > m * r H = μ H ,
where σ 0 is the material conductivity at B=0, r H is the Hall factor, and μ H is the Hall mobility. So, in the general case μ d r i f t = μ H α ε / r H , for non-degenerate electron gas μ d r i f t = μ H / r H , and for metals and materials with highly degenerate electron gas μ d r i f t = μ H α ε , and can many times exceed the Hall mobility.
The fact that the free electron mean path is a hundred times larger than the atomic distance, especially at low temperatures, where the mean free path is over tens millimeters, which shows that the displacement of atoms from their equilibrium positions due to thermal vibrations weakly distorts the potential periodicity in the lattice. The free RM electrons are scattered only at electronic defects with absorption and emission of phonons, usually, a single phonon takes place, because multiple-phonon process contribution is scarcely probable. It is related to the fact that at thermal equilibrium conditions, the lattice atom vibration energy is small. On the other hand, the electron energy distribution is limited by the Pauli exclusion principle and the Fermi-Dirac statistics. The statement that in a perfect crystal below the Debye temperature, the scattering angle becomes smaller and smaller and that it causes the resistivity T 5-law at low temperatures, is ungrounded. As it follows from Eq. (7), the free electron wave vector during scattering at electronic defect change Δ k is very remarkable due to multiplier αε, and after each collision with the electronic defect, the free electron wave vector is completely randomized.

3. The Study of the Electrical Resistivity Law AT 2 of Metals at very Low Temperatures

The idea that electron-electron scattering contributes to electrical and thermal resistivities of metals was proposed by Landau and Pomeranchuk [23], but about 20 years the resistivity dependence ρ e e T = A e e T 2 has not been observed in simple metal. On the base of the conservation of the quasi-momentum and energy of free electrons, it has been proposed that the electron-electron scattering rate changes as T2, and as a consequence it must give the law T2 of the electrical resistivity at very low temperatures. According to [9], the electron-electron scattering rate τ e e − 1 ε can be described as
1 τ e e = A 0 1 ħ ( k T ) 2 E F ,
where A0 is the non-dimensional quantity. On the base of this relation, it is believed that relaxation time changes as 1/T2, and that it can take part only at very low temperatures in very pure metals. From it also follows that temperature dependence of resistivity ρ ( T ) for a three-dimensional metal due to electron-electron scattering can be described as ρ T = A T 2 .
A detailed analysis of the electron-electron scattering and its contribution to the electrical resistivity for conducting materials is presented in [24]. The problem of electron-electron scattering in metals also have been solved by using the Boltzmann kinetic equation [25] Recently [26], it has been shown that Eq. (12) is correct with A0 = Nimp/4π2, where Nimp is the number of impurities (or scattering centers) in a given sample. The effects of electron-electron scattering in metals also have been investigated theoretically in both a simple tight-binding model and in a transition metal tungsten by calculating the electron scattering rate at the Fermi surface [27].
Considering that the contribution of the term A T 2 to resistivity at very low temperatures is very small, it was needed the extremely precise measurement technique, better than p.p.m. relative accuracy in the measurement of the low-temperature electrical resistivity, which appeared only a half-century ago [24,28,29,30]. High-resolution measurements of the electrical resistivity of simple metals at low temperatures have yielded new data that were in contradiction to the generally accepted theories. It has been found that the electrical resistivity does not follow the expected A T 5 law for any metal at very low temperatures.
A detailed analysis of the electrical resistivity of the alkali metals at low temperatures is presented in [24,31,32]. It is shown that for potassium at low temperatures, the phonon drag can play an important role leading to an exponential decrease with temperature [33,34]. It has been believed that the experimental parameter Aexp would be the same for all samples of the same metal, but the values Aexp are different about ten times. For lithium, it has been expected that values Aexp would be similar to K, but the observed values are more than an order larger [24,35,36].
The electrical resistivity of noble metals at low temperatures has been investigated by many authors [37,38,39,40]. It has been shown that the electrical resistivity of copper and silver at low temperatures has approximate T 4 behavior, and the term T 2 appears only below 2 K [37]. From the measurement of the electrical resistivity of high-quality copper whiskers taking account of the surface scattering at different magnetic fields, it has been estimated the parameter A for the electrical resistivity of bulk copper [38]. Temperature dependence of the scattering rate in copper also has been investigated by radio frequency size effect to extract the contribution of electron-electron collisions [39]. The observed T 4 behavior for the low-temperature electrical resistivity of Ag is related to the simultaneous presence of both electron-phonon and electron-electron scattering [40]. To observe the term T 2 in noble metals it is needed very low temperatures and very pure metals.
Aluminum is a simple polyvalent metal, which electron-electron scattering has been intensively investigated [41,42,43,44]. In [41], it has been presented that the electrical resistivity of aluminum at low temperatures has the term AT 2. The surface scattering contribution for electrical resistivity of high-purity aluminum samples in the thickness range from 0.1 μm to 7 mm has been investigated in [42]. It is shown that surface scattering of the conduction electrons affects the temperature dependence of the resistivity for samples less than 0.5 mm in thickness. The electrical resistivity term AT 2is attributed to electron-electron scattering, and it is shown that coefficient A practically does not depend on the residual resistivity value [43]. The influence of the electron-phonon interaction on electron-electron scattering is described within the framework of the Landau Fermi-liquid theory, and electron-electron scattering contribution to the low-temperature resistivity of aluminum can be enhanced by a factor of ~20 due to electron-phonon interaction [44].
Due to that transition group metals differ from simple metals, which have partially filled d- and s-band electrons it has been believed that for transition metals the major contribution to resistivity ρ e e ( T ) should be caused by highly mobile s-electrons being scattered by the “heavy” d-electrons, i. e. the so-called sd-scattering. It is observed that coefficient A for transition metals is often one or two orders of magnitude larger than for simple metals. Quadratic temperature dependence for ρ e x p ( T ) for many transition metals has been demonstrated at low temperatures [45,46,47,48,49,50], but interpretations are different. In [45], it is shown that there is some correlation between coefficient Aexp and the electronic heat capacity parameter γ. The electron-electron scattering in tungsten has been investigated by using radio-frequency size-effect for electron scattering rate estimation [46]. The term AT 2 has been found over the temperature range 1.5–5 K for molybdenum, it was concluded that the quadratic term in the temperature dependence of the scattering rate in molybdenum is due to the electron-electron scattering [47]. The electrical resistivity of a single crystal of vanadium at low temperatures has been analyzed in terms of electron-impurity, electron-electron, and electron-phonon scatterings [48]. They have obtained the term AT 2 with coefficient A≈(1.6 – 0.2)⋅10-11 Ωcm/K2. The effects of electron-electron scattering in vanadium have been investigated theoretically, and the calculated scattering rates agree with experimental measurement results [49]. The electron-electron scattering in high-purity single crystals of molybdenum has been measured at low temperatures [50], it is shown that when approaching an ideal metallic crystal structure, there have been observed the deviations from the Ohm’s law.
The traditional explanation [10] for the large magnitude of Aexp due to sd-scattering in transition metals is based on the prepositions that the effective mass of the d-electron is very high, implying that its velocity vd is very low compared with the velocity vs of the s-electron. These arguments are very questionable because the drift mobility and drift velocity of metals (see Eqs. (2) and (3)) do not depend on the electron mass. All electrons at the Fermi surface have the same Fermi level energy and are randomly moving with the same Fermi velocity. Often in many cases there is confused the large density of states at the Fermi surface with the effective mass of electrons.
There we want to point attention to the fact that conservation of the quasi-momentum and energy of free electrons due to electron-electron scattering do not produce energy losses, and consequently, this process is elastic and has no affect on material resistivity. It is confirmed by the thermal noise relation with the material resistivity [51], and by the fluctuation-dissipation theorem [52,53]. Therefore, almost for all elemental metals the electrical resistivity at low temperatures has the term AT 2, but its explanation by electron-electron scattering is doubtful.
In [13,14], it has been shown that the lattice atom vibrations produce not only the effective density of free randomly moving electrons n e f f = g E F k T (here g E F is the density of states at the Fermi level energy), but also the same density of electronic defects (not completely screened ions) is produced N e f f = n e f f . In Figure 2, there are demonstrated the electronic defect dependence on temperature for aluminum, and for transition group metal tungsten. As can be seen, the effective density of the electronic defects even at temperature 1 K is higher than 1018 cm-3, and these electronic defects cannot be, in principle, decreased as it can be done with the residual defects.
As it is shown in [13,14], the resistivity of the elemental metals dependence on temperature can be described as
ρ T = ρ 0 + ρ ( T 0 ) ( T / T 0 ) η p h ( T / Θ ) ,
where Θ is the Debye temperature, η p h ( T / Θ ) is the phonon mediation factor accounting the free RM electron scattering by electronic defects:
η p h ( T / Θ ) = ( T / Θ ) 4 ∫ 0 Θ / T 4 x 5 d x ( e x − 1 ) ( 1 − e − x ) ,
The resistivity ρ T 0 at T=T0 is described as
ρ T 0 = 1 q 2 g E F D = 3 q 2 g E F l F v F = 3 σ e f f 0 k T 0 q 2 v F
here we used l F = 1 / ( σ e f f 0 N e f f ) = 1 / [ σ e f f 0 g E F k T 0 ] , where σ e f f 0 is the effective scattering cross-section estimated at temperature T0. The value of the temperature T0 must be taken from the linear resistivity dependence range on temperature. Then the effective scattering cross-section is estimated as
σ e f f ( T ) = σ e f f 0 η p h ( T / Θ ) .
For further study of the resistivity dependence on temperature, we shall investigate the elemental metals from various sites of the periodic tables: the alkali group metal Li, the noble metal Cu, the second group IIB metal Zn, the third group IIIA metal Al, and the transition group metals Mo and W. The resistivity dependences on temperature for these metals are presented in Figure 3: dots are the experimental results, and the solid lines are calculated by Eq. (13). As can be seen, the resistivity ρ(T) of metals has three clearly expressed parts: i) at low-temperature so-named residual resistivity caused by impurity and structural imperfections of metal, ii) so-named phonon-assisted part with ρ ~ T 5, which at higher temperatures crosses to iii) the linear resistivity dependence on temperature.
Even though the entire description of the resistivity of metals by Eq. (13) is sufficiently good, at temperatures below 20 K there is a small inadequacy for metals Al, Zn, Mo, and W. Considering the earlier presented experimental results of the electrical resistivity term AT 2, we shall see further, what causes such electrical resistivity dependence on very low temperatures.
Considering the so-named law ρ=AT 2 at low temperatures, we shall carefully investigate the resistivity dependence on low temperatures on the sample of Al. For this aim, we shall find what characteristics cause such resistivity ( ρ T − ρ 0 ) dependence on temperature. In Figure 4 there are presented the resistivity ρ T and ρ T − ρ 0 dependences on low temperatures for aluminum.
As can be seen, the resistivity ( ρ T − ρ 0 ) without residual resistivity ρ 0 has a well-expressed dependence on temperature term AT 2, where proportionality coefficient A≈6.5 fΩm K-2. Accounting that the resistivity of metals is described as ρ = ( 1 / σ ) = 1 / [ q 2 g E F D ] , where D is the diffusion coefficient of free RM charge carriers. The diffusion coefficient of free RM charge carrier dependence on temperature is shown in Figure 5a. As can be seen, the diffusion coefficient at very low temperatures changes as T -2, and then crosses to the proportionality T -5 as the temperature is over 20 K.
The mean free path of charge carriers has been estimated as l = 3 D / v F , and l c o r r = 3 D c o r r / v F , which are presented in Figure 5b. As can be seen, the mean free path l c o r r at very low temperatures changes as T -2, and exceeds several centimeters. It seems that precise resistivity measurements should be done with a very large sample that the transverse dimensions which should greatly exceed the mean path of the charge carriers in order to vanish the charge carrier scattering from the sample boundaries.
The relaxation time of charge carriers has been evaluated as τ = l / v F and τ c o r r = l c o r r / v F , which are presented in Figure 6a. It is believed, that the relaxation time τ c o r r changes with temperature as T -2 at low temperatures. Now let's estimate the effective scattering cross-section of free RM electrons by electronic defects:
σ e f f = 1 l c o r r N e f f = 1 l c o r r g E F k T ,
where Neff is the electronic defect density. The effective scattering cross-section dependence on temperature is presented in Figure 6b. As can be seen, the effective scattering cross-section at very low temperatures is proportional to temperature T, and at higher temperatures coincides with σ e f f 0 η p h ( T / Θ ) , and is proportional to T 4. It seems that the resistivity term AT 2 at low temperatures, the solution key is related to the linear effective scattering cross-section dependence on temperature.
In Figure 7, there are presented the heat capacity dependence on temperature for conductors (Pt and W), and pure Si, which at low temperatures is an insulator. The heat capacity of the insulator is described by the Debye′s model, for which the heat capacity at low temperatures increases as T 3 , or the thermal energy (quantity of heat) increases as T 4 . In the case of metals, the heat capacity at low temperatures changes slower, approximately linearly, and thermal energy changes as T 2. As can be seen, to increase the metal of the one mole mass from 1 K to 5 K, it is needed a larger amount of heat, then it is needed for the insulator. This difference is related to the free electrons random moving, and due to their scattering by electronic defects. In equilibrium, the thermal energies between free electrons and lattice atoms are changing by the interaction of free electrons with the electronic defects.
Earlier for estimation of the phonon mediation factor η p h ( T / Θ ) (Eq. 14) has been accounted only for the lattice thermal energy based on the Debye model. Additional thermal energy for conductors is caused by free randomly moving charge carriers, which are scattered by electronic defects. It gives a correction to phonon mediation factor η p h ( T / Θ ) :
η ( T ) = ( T / Θ ) 4 ∫ 0 Θ / T 4 x 5 d x ( e x − 1 ) ( 1 − e − x ) + Δ η p h ( T )
where the correction factor
Δ η p h ( T ) = Δ E p h 1 E e 1
is equal to the ratio between the ratio of the thermal (phonon) energy increase Δ Eph1 of the metal atom caused by free RM electron interaction with electronic defects and the average free RM electron energy Ee1=1.64kT at low temperatures. The variation of the thermal energy of the metal atom due to interaction with free randomly moving electrons can be estimated as
Δ E p h 1 = [ ( π 2 / 6 ) g ( E F ) ( k T ) 2 / N A ] ,
where NA is the Avogadro constant. The Eq. (20) can be rewritten as
Δ E p h 1 = ( 1 / 2 ) γ T 2 / N A ,
where γ is the electronic heat capacity parameter. Then the correction factor can be described in the following form:
Δ η p h ( T ) = γ T 2 2 E e 1 N A = γ T 2 3.28 k T N A = γ T 3.28 R .
where R=kNA=8.31 J/ (mol K) is the universal gas constant.
Therefore, the corrected phonon mediation factor can be presented as
η ( T ) = γ T 3.28 R + ( T / Θ ) 4 ∫ 0 Θ / T 4 x 5 d x ( e x − 1 ) ( 1 − e − x ) ,
and the resistivity can be described as
ρ T = ρ 0 + ( ρ T 0 ) ( T / T 0 ) η ( T ) ,
and
ρ T − ρ 0 = ( ρ T 0 ) η ( T / T 0 ) ( T ) ,
Now let us describe the elemental metals from different columns of the periodic table Al, W, Mo, Zn, Li, and Cu resistivity dependences on a very wide temperature range accounting the obtained correction factor. In Figure 8a, there are presented resistivity and corrected phonon mediation factor dependences on temperature for aluminum, and in Figure 8b for wolfram. In Figure 8, the small black dots are the experimental dots of the resistivity [54], and the solid by the black line calculated by Eq. (24); the red dots are experimental data of ( ρ T − ρ ) 0 , the red solid line is calculated by Eq. (25), the corrected phonon mediation factor η ( T ) is calculated by Eq. (23), the dash line proportional to T − 4 is estimated by Eq. (14) the phonon mediation factor without correction. From the comparison of the resistivity ( ρ T curves in Figure 2 and Figure 8a, it is seen that Eq. (24) very well describes the experimental results below 25 K temperature. As can be seen from Figure 8a, at low temperatures the resistivity ( ρ T − ρ ) 0 A T 2 , where A≈6 fΩm/K2.
The similar results to aluminum shown in Figure 8a, in Figure 8b there are presented the investigation results for wolfram. Though the wolfram has a two times larger number of valence electrons than aluminum, the DOS g(EF) of wolfram is about 1.3 times smaller than that of aluminum. The residual resistivity of a given sample of wolfram is about ten times smaller than that of aluminum. The difference between resistances ρ T and ( ρ T − ρ ) 0 at low temperatures for aluminum begins at T<20 K, while for wolfram at T<8 K, and the coefficient A≈8 fΩm/K2. The phonon mediation factor η(T) dependences on temperature are almost the same for both metals.
In Figure 9a, there are presented resistivity and corrected phonon mediation factor dependences on temperature for molybdenum, and in Figure 9b for zinc. The Debye′s temperature obtained from resistivity dependence on temperature for Mo and Al is the same 410 K, and corrected phonon mediation factors are close one to other, while the residual resistivity of a given sample of molybdenum is about 10 times larger than that of aluminum. The resistivity ( ρ T − ρ 0 ) proportionality to T 2 for molybdenum is obtained at T<10 K. The characteristics of the two-valent zinc (Figure 9b) differ from those of molybdenum (Figure 9a). It is related to the Debye′s temperature of zinc 177 K, which is over two times smaller than that of Mo 410 K shifts the resistivity characteristic to the lower temperatures. Besides, the DOS g(EF) of zinc is about two times smaller than that of molybdenum. As a consequence, the phonon mediation factor linear part begins at a lower temperature, which causes the resistivity ( ρ T − ρ ) 0 proportionality to T 2 would be observed only at T<4 K.
In Figure 10, there are presented the resistivity and the corrected phonon mediation factor dependences on temperature for copper and lithium. Considering that the presented sample of the copper resistivity data has sufficiently high residual resistivity, there was not capable to observe the T 2 dependence on temperature (Figure 10a). As it is seen from this Figure, the resistivity ( ρ T − ρ 0 ) changes at low temperatures approximately as T4, the similar behavior has been observed for other noble metals by [37,40]. On the other hand, the linear part of the corrected phonon mediation factor begins only below 4 K, from this follows that the resistivity law AT 2 can be obtained at resistivity values smaller than 10 fΩm. Maybe, it explains that the resistivity law AT 2 for noble metals is difficult to obtain. In Figure 10b, there are presented the resistivity and corrected phonon mediation factor dependences for lithium. As can be seen, the linear part of the corrected phonon mediation factor begins below 7 K, the square resistivity dependence on temperature is observed at a temperature below 7 K, and the proportionality coefficient A is approximately equal to 20 fΩm/K2.
As can be seen, the resistivity ( ρ T − ρ 0 ) proportionality to T 2 at low temperatures are observed for alkali, noble, simple polyvalent or transition group metals, and temperatures at which it takes place depend on both the Debye temperature, and on the DOS at the Fermi surface of metals.
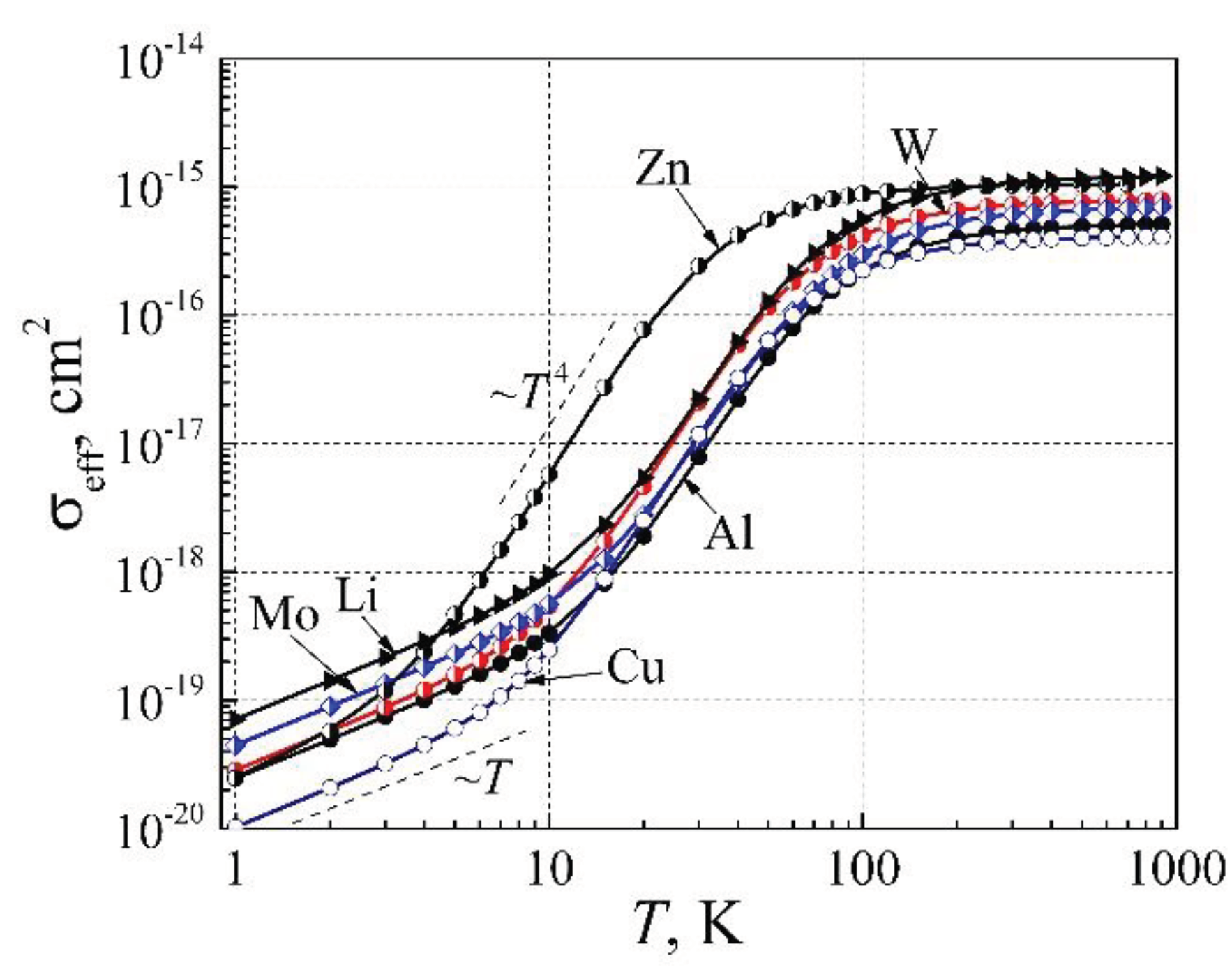
In Figure 11, there are presented the effective electron scattering cross-section dependences on temperature for the analyzed metals Al, Cu, Li, Mo, W, and Zn. As can be seen, the effective free electron scattering cross-section dependences on temperature have three characteristic parts: (i) the linear ~T at T < 10 K; (ii) proportional to T 4 in the transition temperature range below the Debye′s temperature; and (iii) the constant at T > 200 K. The constant part of the effective free electron scattering cross-section shows that earlier explanations that free electron scattering cross-section at room and higher temperature increases proportional to temperature T due to lattice atom vibrations [7,8,9,10,11,19,20,21,22] are unfounded. The linear η(T) increase at very low temperatures is caused by the linear heat capacity increase with temperature, which causes the quadratic resistivity of elemental metals dependence on temperature. Therefore, it shows that the earlier explanation of metal resistivity by electron-electron scattering at very low temperatures is not acceptable.
From free RM electron effective scattering cross-section dependence on temperature follows such resistivity of elemental metals dependence on temperature characteristic parts: (i) the quadratic term AT 2at T<10 K (by eliminating the residual resistivity), (ii) the term ~ T 5 in the transition temperature range below the Debye′s temperature, and (iii) the linear term ~T at T>200 K. The whole resistivity (including the residual resistivity) temperature dependence is described by Eq. (24) accounting the corrected phonon mediation factor (Eq. (23)), i.e. the elemental metal resistivity in the overall temperature range can be explained by free randomly electron scattering by electronic defects accounting the phonon mediation factor.

4. Conclusion

Accounting that the Einstein relation between the diffusion coefficient and the drift mobility of the free randomly moving electrons in a metal is always valid, the effective electric force in metals is enhanced by a factor α ε = E F / k T . Free RM electrons are scattered only by electronic defects (weakly screened ions, which lost the valence electrons), the electron wave vector during a collision with electronic defect changes very remarkably, and after each collision, electron wave vector direction is completely random. The electrical resistivity of almost all elemental metals at very low temperatures has the term AT 2, which has been explained on the base of the Landau and Pomeranchuk Fermi liquid model by electron-electron scattering. In this work, it is shown that the electrical resistivity term AT 2 at very low temperatures is caused by free RM electron scattering by electronic defects, i.e. it is related to the linear effective scattering cross-section dependence on temperature due to free RM electrons scattering by electronic defects. The value of the parameter A depends on both the DOS at the Fermi surface and the Debye temperature. It is shown that the effective scattering cross-section of the free RM electrons by electronic defects dependence on temperature has three characteristic parts: (i) constant at T>200 K, (ii) proportional to T4 in the transition range below the Debye temperature, and (iii) the linear ~T at very low temperatures.

Author Contributions

VP is the author of this manuscript, wrote the text, performed calculations, and prepared all Figures.

Funding

The research received no external funding.

Data Availability Statement

Data are provided in the Figures of the article. All data generated and analyzed during this study are included in the presented manuscript and are available from the author upon reasonable request.

Conflict of Interest

The author declares no conflict of interest.

References

  1. Drude, P. Zur Elektronentheorie der Metale. Ann. Phys. 1900, 306, 441–624. [Google Scholar] [CrossRef]
  2. Kaxiras, E. Atomic and Electronic Structure of Solids; Cambridge University Press (Online): Cambridge, UK, 2014. [Google Scholar]
  3. Sander, L.M. Advanced Condencedmoving Matter Physics; Cambridge University Press (Online): Cambridge, UK, 2014. [Google Scholar]
  4. Blakemore, J. S. Solid State Physics; Cambridge University Press, Cambridge, UK 1985.
  5. Lide, D.E. (Ed.) Handbook of Chemistry and Physics, 84th ed.; CRC Press LLC: Boca Raton, FL, USA, 2004. [Google Scholar]
  6. Grigoryev, L.S. , Meilikhov, E.Z. (Eds.) Handbook of the Physical Quantities; Energoatomizdat: Moscow, Russia, 1991. [Google Scholar]
  7. Mizutani, U. Introduction to the Electron Theory of Metals; Cambridge University Press (Online): Cambridge, UK, 2014. [Google Scholar]
  8. Dugdale, J.S. The Electrical Properties of Disordered Metals; Cambridge University Press (Online): Cambridge, UK, 1985. [Google Scholar]
  9. Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Harcourt College Publ.: New York, NY, USA, 1976. [Google Scholar]
  10. Ziman, J.M. The Theory of Transport Phenomena in Solids; Oxford University Press: Oxford,, UK, 2001. [Google Scholar]
  11. Kittel, C. Introduction to Solid State Physics; John Wiley and Sons, Inc.: New York, NY, USA, 1976. [Google Scholar]
  12. Blokhintsev, D.L. Quantum Mechanics; Reidel Publ. Comp,: Dordrecht, The Netherlands, 1964. [Google Scholar]
  13. Palenskis, V.; Žitkevičius, E. Summary of new insight into electron transport in metals. Crystals 2021, 11, 622. [Google Scholar] [CrossRef]
  14. Palenskis, V.; Jonkus, V. Study of the free randomly moving electron transport peculiarities in metals. Metals 2023, 13, 1551. [Google Scholar] [CrossRef]
  15. Palenskis, V. Drift mobility, diffusion coefficient of randomly moving charge carriers in metals and other materials with degenerate electron gas. World J. Cond. Matt. Phys. 2013, 3, 73–81. [Google Scholar]
  16. Palenskis, V. The effective density of randomly moving electrons and related characteristics of materials with degenerate electron gas. AIP Adv. 2014, 4, 047119. [Google Scholar] [CrossRef]
  17. Stirzaker, D.R. Elementary Probability; Cambridge University Press (Online): Cambridge, UK, 2014. [Google Scholar]
  18. Grimmet, G.R.; Stirzaker, D.R. Probability and Random Processes; Cambridge University Press (Online): Cambridge, UK, 2020. [Google Scholar]
  19. Abrikosov, A.A. Fundamentals of the Theory of Metals; North-Holland Publication: Amsterdam, The Netherlands, 1988. [Google Scholar]
  20. Lundstrom, M. Fundamentals of Carrier Transport; Cambridge University Press (Online): Cambridge, UK, 2014. [Google Scholar]
  21. Rossiter, P.L. The Electrical Resistivity of Metals and Alloys; Cambridge University Press (Online): Cambridge, UK, 2014. [Google Scholar]
  22. Schulze, G.E.R. Metallphysik; Akademie-Verlage: Berlin, Germany, 1967. [Google Scholar]
  23. Landau, L.D.; Pomeranchuk, I.Ya. On properties at very low energies. Zh. Eksp. Teor. Phys. 1937, 7, 379. [Google Scholar]
  24. Kaveh, M. : Wiser, N. Electron-electron scattering in conducting materials. Adv. Phys. 1984, 33, 257–372. [Google Scholar] [CrossRef]
  25. Schulz, W.W.; Allen, P.A. Transport in metals with electron-electron scattering. Phys. Rev. B, 1995, 52, 7994. [Google Scholar] [CrossRef]
  26. Arulsamy, A.D. Low-temperature small-angle electron-electron scattering rate in Fermi metals, Zeitschrift für Naturforschung A, 2024, 79, 83–99.
  27. Potter, C.; Morgan, G.J. Electron-electron scattering effects in metals. J.Phys. F: Met. Phys. 1979, 9, 493. [Google Scholar] [CrossRef]
  28. Van Kampen, H.; Neyenhuisen, H.W.; Ribot, J.H.J.M. Semiautomatic bridge for high-precision dc resistance measurements on pure metals at low temperatures. Rev. Sci. Instrum. 1979, 50, 161–164. [Google Scholar] [CrossRef]
  29. Zwart, J.W.; Pratt, W.P.; Schroeder, P.A.; Caplic, A.D. High-precision measurements of the resistivity of strained dilute copper-silver alloys below 1 K. J. Phys.: Met. Phys. 1983, 13, 2595–2602. [Google Scholar] [CrossRef]
  30. Barnard, B.R.; Caplin, A.D. A simple high-resolution cryogenic resistance bridge using a SQUID null detector. J. Phys. E: Sci. Instrum. 1978, 11, 1117. [Google Scholar] [CrossRef]
  31. Kaveh, M.; Wiser, N. General theory of the electrical resistivity of the alkali metals at low temperatures. Phys. Rev. B 1974, 9, 4042. [Google Scholar] [CrossRef]
  32. MacDonald, A.H.; Taylor, R.; Geldart, D. J. W. , Umklapp electron-electron scattering and the low-temperature electrical resistivity of the alkali metals. Phys. Rev. B 1981, 23, 2718. [Google Scholar] [CrossRef]
  33. Kaveh, M.; Wiser, N. Electrical resistivity of potassium at low temperatures. Phys. Rev. B 1974, 9, 4053. [Google Scholar] [CrossRef]
  34. Van Kampen, H.; Ribot, J.H.J.M.; Wyder, P. The electrical resistivity of potassium at low temperatures. J. Phys.: Met. Phys. 2000, 11, 597. [Google Scholar] [CrossRef]
  35. Awasthi, O.N.; Pundhir, V.K. Electron-electron interactions and the electrical resistivity of lithium at low temperatures. Pramana J. Phys. 2007, 68, 67–74. [Google Scholar] [CrossRef]
  36. Sinvani, M.; Greenfield, A.; Danino, M.; Kaveh, M.; Wiser, N. ,Anomalous electron-electron scattering contribution to the electrical resistivity of lithium. J Phys. F: Met. Phys. 1981, 11, L73. [Google Scholar]
  37. Sathish, S.; Awasthi, O.N. Electron-electron scattering and low-temperature electrical resistivity in copper and silver. Phys. Lett. A 1984, 100, 215–217. [Google Scholar] [CrossRef]
  38. Thummes, G.; Kötzler, J. Magnetic-field-enhanced electron-electron scattering in the resistivity of copper. Phys. Rev. B 1985, 31, 2535. [Google Scholar] [CrossRef] [PubMed]
  39. Gasparov, V.A.; Harutunian, m.H. To the question on electron-electron scattering in metals. Solid State Commun. 1976, 19, 189–192. [Google Scholar] [CrossRef]
  40. Bergmann, A.; Kaveh, M.; Wiser, N. Explanation of the anomalous T 4 behaviour of the low-temperature electrical resistivity of silver. J. Phys. F: Met. Phys. 1980, 10, L71. [Google Scholar] [CrossRef]
  41. Kaveh, M.; Wiser, N. Evidence for the electron-electron scattering contribution to the electrical resistivity of aluminum. Phys. Lett. A 1975, 51, 89–90. [Google Scholar] [CrossRef]
  42. Sambles, J.R.; Elsom, K.C.; Sharp-Dent, G. The effect of sample thickness on the resistivity of aluminum. J. Phys. F: Met. Phys 1981, 11 1075.
  43. Ribot, J.H.J.M.; Bass, J.; Van Kampen, H.; Wyder, P. Further evidence for electron-electron scattering in aluminum. J. Phys. F: Met. Phys. 1981, 9, L117. [Google Scholar] [CrossRef]
  44. MacDonald, A.H. Electron-phonon enhancement of electron-electron scattering in Al. Phys. Rev. Lett. 1980, 44, 489. [Google Scholar] [CrossRef]
  45. Volkenshtein, N.V.; Novolselov, V.A.; Startsev, V.E. Role of interelectron collisions in the electric resistance of transition metals. Sov. Phys. JETP 1971, 33, 58–587. [Google Scholar]
  46. Van der Mass, J.; Huguenin, R.; Gasparov, V.A. Electron-electron scattering in tungsten. J. Phys. F: Met. Phys. 1985, 15, L271. [Google Scholar] [CrossRef]
  47. Gasparov, V.A.; Voloshin, I.F.; Fisher, L.M. On electron-electron scattering in molybdenum. Solid State. Commun. 1979, 29, 43–46. [Google Scholar]
  48. Gautron, G.J.; Zablocki, J.E.; Hsiang, T.Y.; Weinstock, H.; Schmidt, F.A. Electron-electron scattering in vanadium. J. Low Temp. Phys. 1982, 49, 185–191. [Google Scholar] [CrossRef]
  49. Potter, C.; Morgan, G.J. Electron-electron scattering effects in metals. J. Phys. F: Met. Phys. 1979, 9, 493. [Google Scholar] [CrossRef]
  50. Elefant, D. Limits of Ohm’s law in ultra-pure metals with almost ideal crystal lattices. J. Appl. Phys. 2023, 134, 205102. [Google Scholar] [CrossRef]
  51. Nyquist, H. Thermal agitation of electric charge in conductors. Phys. Rev. 1928, 32, 110–113. [Google Scholar] [CrossRef]
  52. Kubo, R. Statistical-mechanical theory of irreversible processes. I. General theory and simple applications to magnetic and conduction problems. J. Phys. Soc. Jap. 1957, 12, 570–586. [Google Scholar] [CrossRef]
  53. Kubo, R.A. General expression for the conductivity tensor. J. Phys. (Canada) 1956, 34, 1274–1277. [Google Scholar] [CrossRef]
  54. Lide, D.R. (Ed.) Handbook of Chemistry and Physics, 84th ed.; CRC Press LLC: Boca Raton, FL, USA, 2004. [Google Scholar]
Preprints 101611 g001
Figure 1. Packing density of various elemental metal distribution on the periodic table. Here lattices: BCC – body-centered cubic; HCP – hexagonal close-packed; FCC – face-centered cubic; ORC – orthorhombic; TET – tetragonal. The dashed line (0.73) corresponds to the ideal close-packed lattice.
Figure 1. Packing density of various elemental metal distribution on the periodic table. Here lattices: BCC – body-centered cubic; HCP – hexagonal close-packed; FCC – face-centered cubic; ORC – orthorhombic; TET – tetragonal. The dashed line (0.73) corresponds to the ideal close-packed lattice.
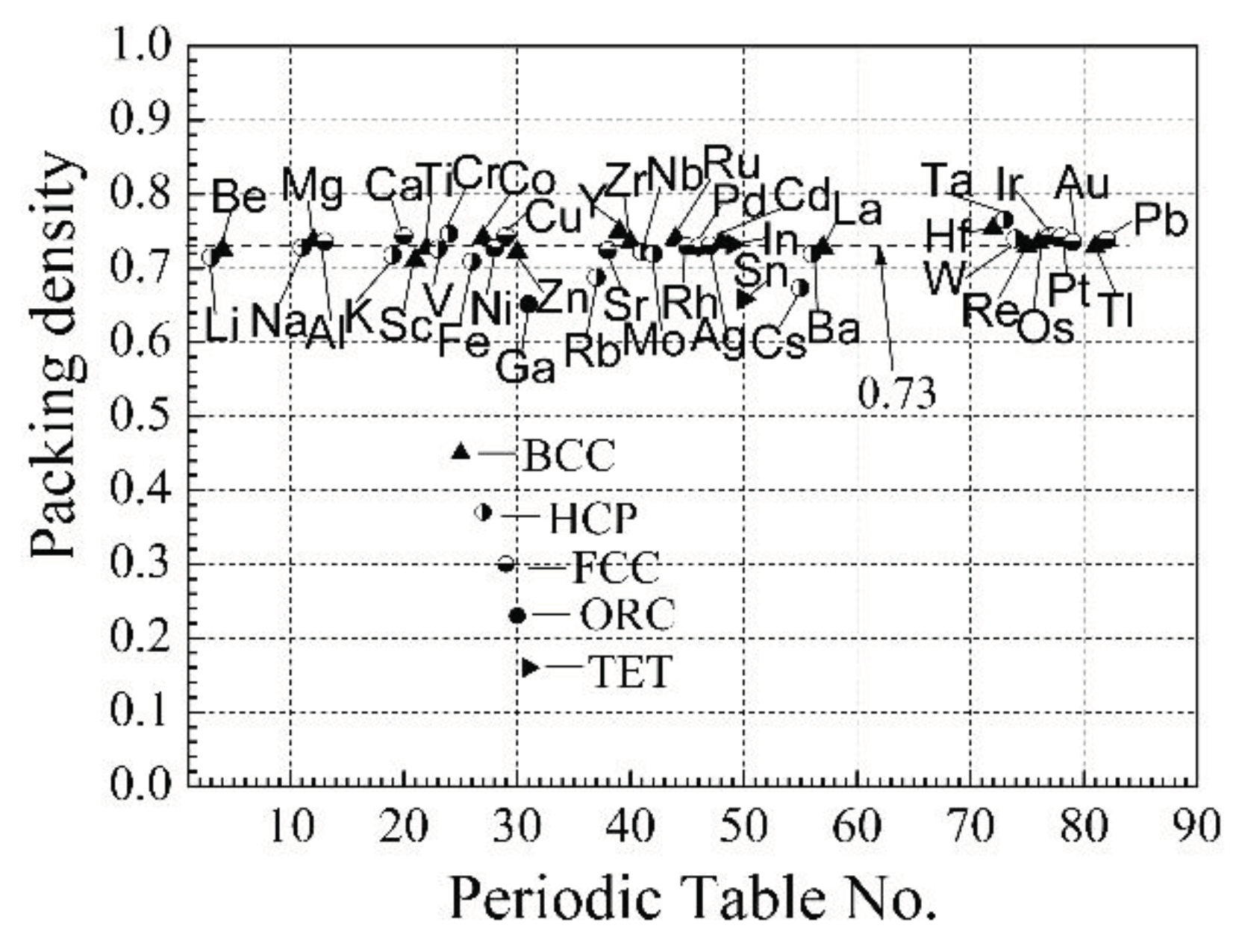
Preprints 101611 g001
Preprints 101611 g002
Figure 2. The electronic defect density Neff (left scale), and free RM electron density neff (right scale) dependences on the temperature for metals Al and W.
Figure 2. The electronic defect density Neff (left scale), and free RM electron density neff (right scale) dependences on the temperature for metals Al and W.
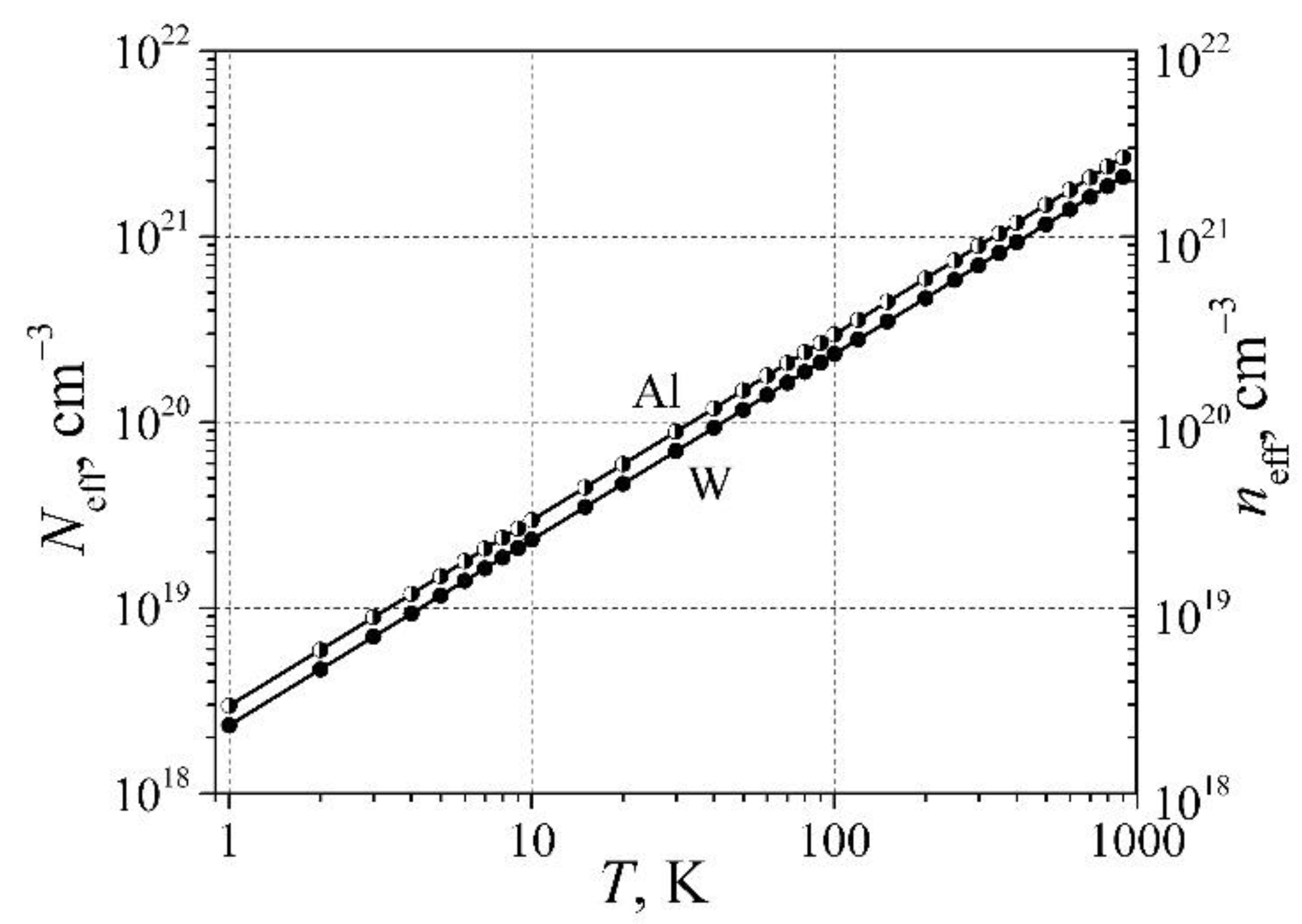
Preprints 101611 g002
Preprints 101611 g003
Figure 3. Resistivity dependence on temperature of elemental metals Al, Cu, Li, Mo, W, and Zn. Dots are experimental data from Handbook [54], and solid lines are calculated by Eq. (13); the number near the chemical symbol is the Debye′s temperature of this metal used for calculations.
Figure 3. Resistivity dependence on temperature of elemental metals Al, Cu, Li, Mo, W, and Zn. Dots are experimental data from Handbook [54], and solid lines are calculated by Eq. (13); the number near the chemical symbol is the Debye′s temperature of this metal used for calculations.
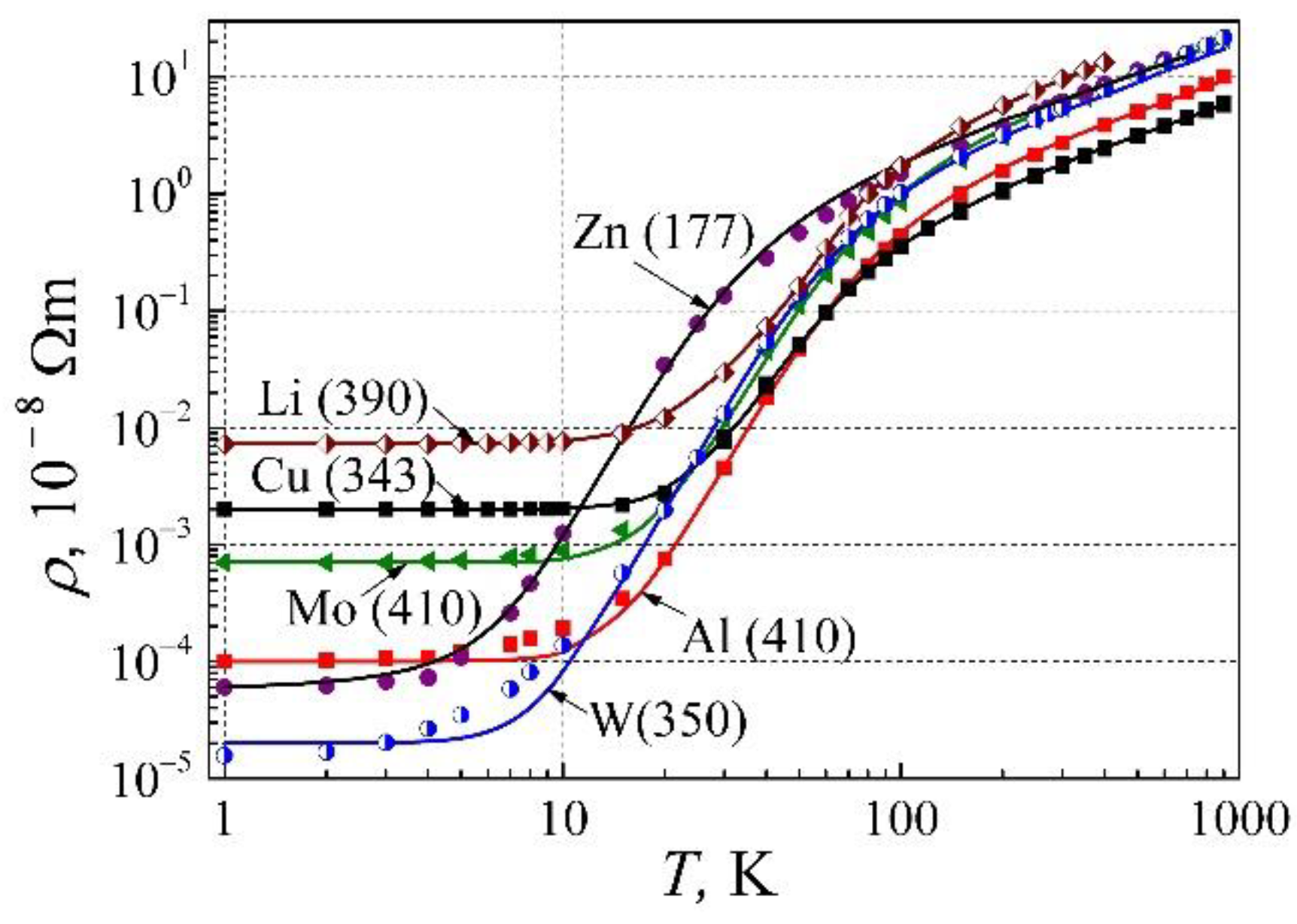
Preprints 101611 g003
Preprints 101611 g004
Figure 4. The aluminum electrical resistivity dependence on temperature at low temperatures.
Figure 4. The aluminum electrical resistivity dependence on temperature at low temperatures.
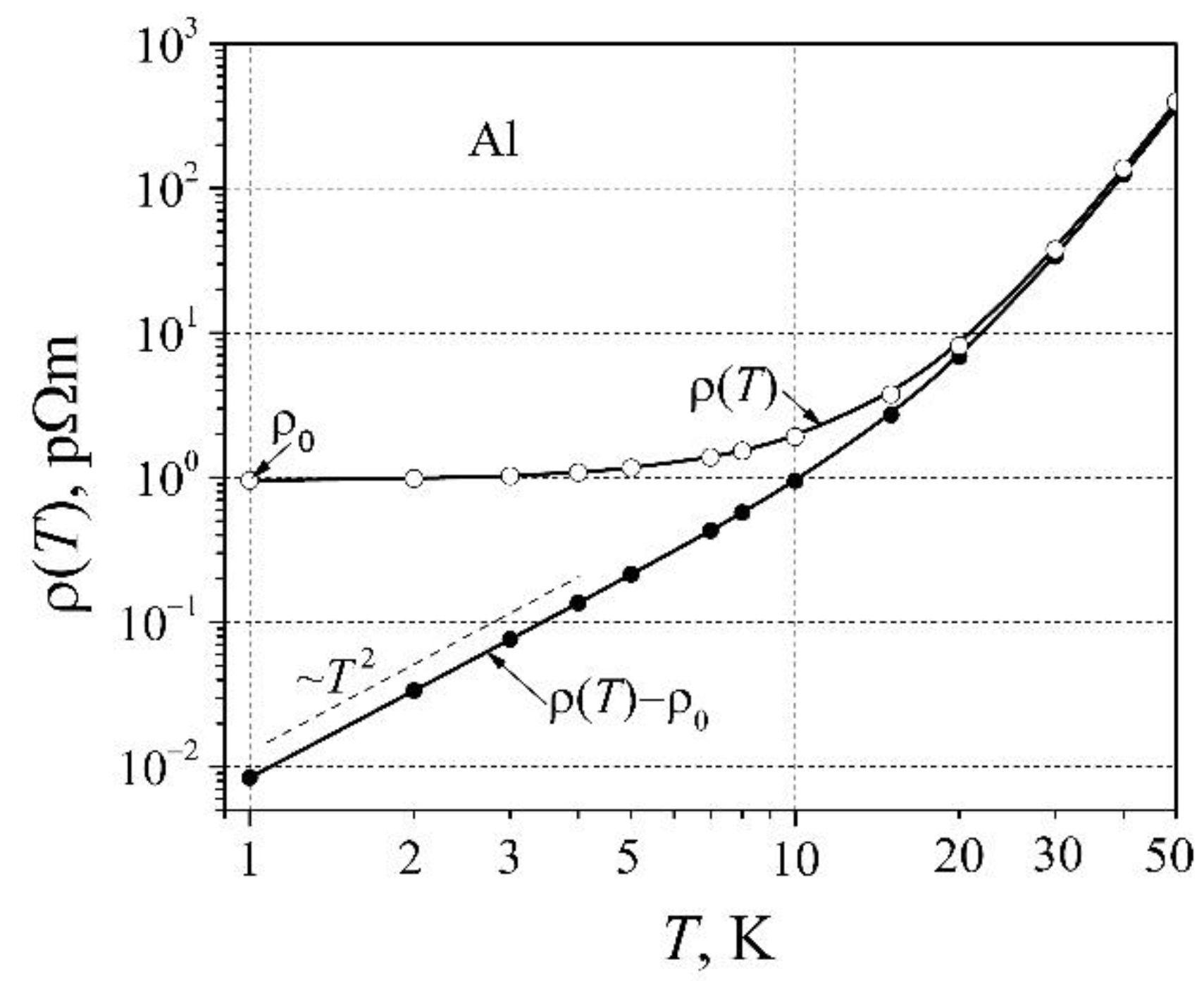
Preprints 101611 g004
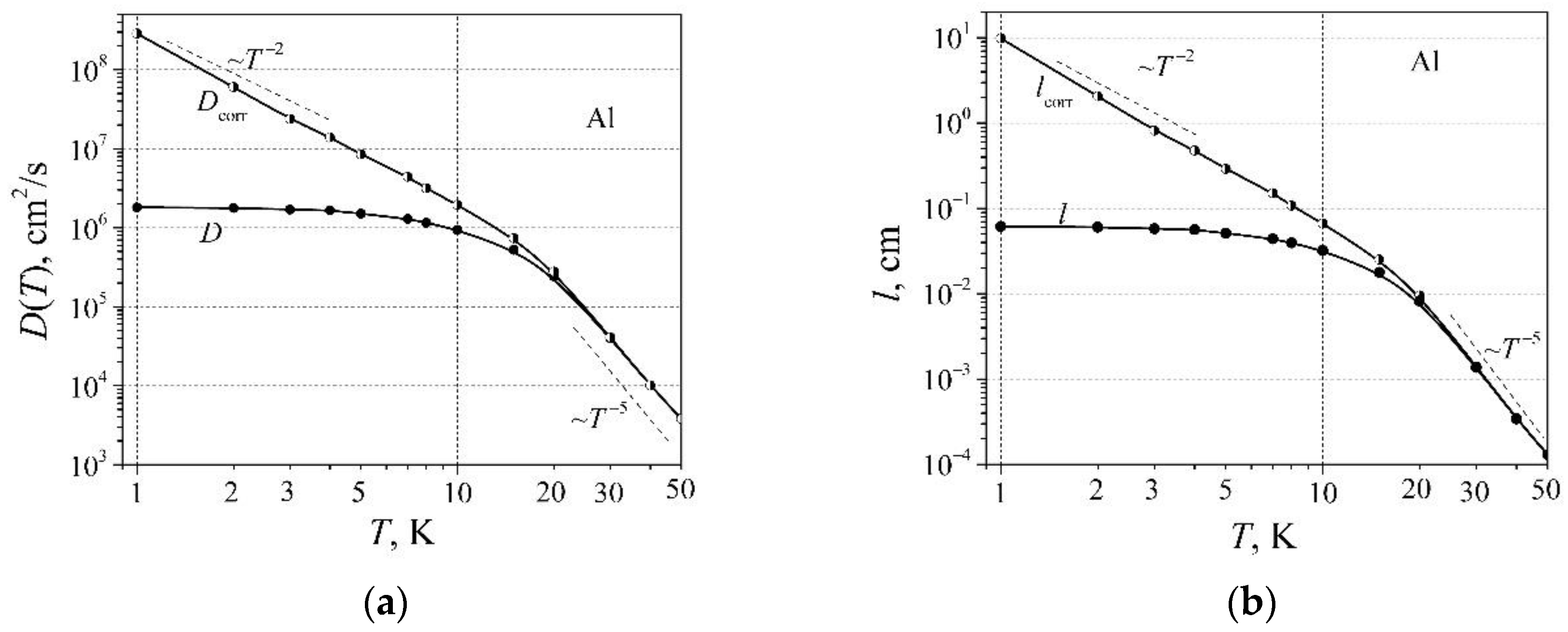
Preprints 101611 g005
Figure 5. Diffusion coefficient (a) and mean free path (b) of free RM charge carrier dependence at low temperatures for Al. D = 1 / [ ρ T q 2 g E F ] ,   D c o r r = 1 / [ ( ρ T − ρ 0 ) q 2 g E F ] , and l = 3 D / v F ,   l c o r r = 3 D c o r r / v F .
Figure 5. Diffusion coefficient (a) and mean free path (b) of free RM charge carrier dependence at low temperatures for Al. D = 1 / [ ρ T q 2 g E F ] ,   D c o r r = 1 / [ ( ρ T − ρ 0 ) q 2 g E F ] , and l = 3 D / v F ,   l c o r r = 3 D c o r r / v F .
Preprints 101611 g005
Preprints 101611 g006
Figure 6. The relaxation time (a) and the effective scattering cross-section (b) dependences on the temperature at low temperatures for aluminum (the σ e f f is described by Eq. (17), and η p h ( T / Θ ) by Eq. (16)).
Figure 6. The relaxation time (a) and the effective scattering cross-section (b) dependences on the temperature at low temperatures for aluminum (the σ e f f is described by Eq. (17), and η p h ( T / Θ ) by Eq. (16)).
Preprints 101611 g006
Preprints 101611 g007
Figure 7. Heat capacity dependence on temperature for conductors (Pt and W), and silicon.
Figure 7. Heat capacity dependence on temperature for conductors (Pt and W), and silicon.
Preprints 101611 g007
Preprints 101611 g008
Figure 8. Resistivity (left scale), and corrected phonon mediation factor η(T) (right scale) dependences on temperature for aluminum (a), and for wolfram (b).
Figure 8. Resistivity (left scale), and corrected phonon mediation factor η(T) (right scale) dependences on temperature for aluminum (a), and for wolfram (b).
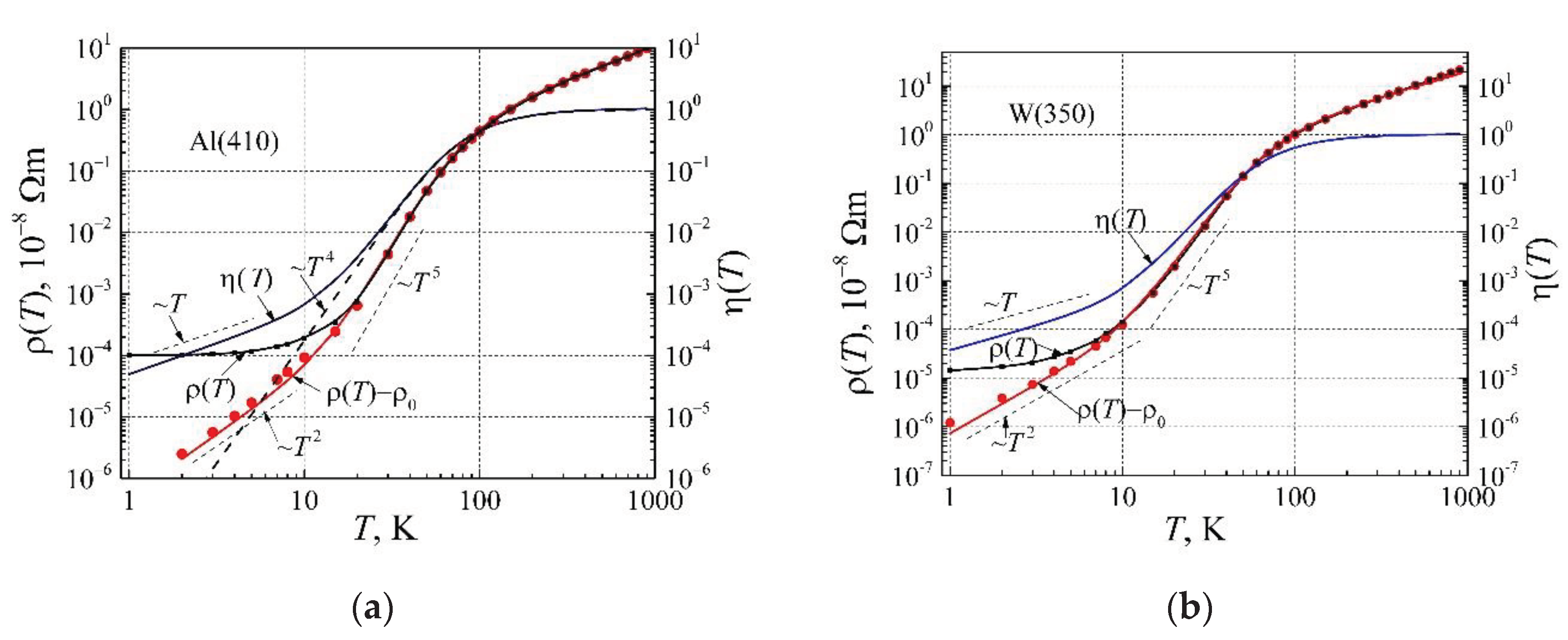
Preprints 101611 g008
Preprints 101611 g009
Figure 9. Resistivity (left scale), and corrected phonon mediation factor (right scale) dependences on temperature for molybdenum (a), and for zinc (b).
Figure 9. Resistivity (left scale), and corrected phonon mediation factor (right scale) dependences on temperature for molybdenum (a), and for zinc (b).
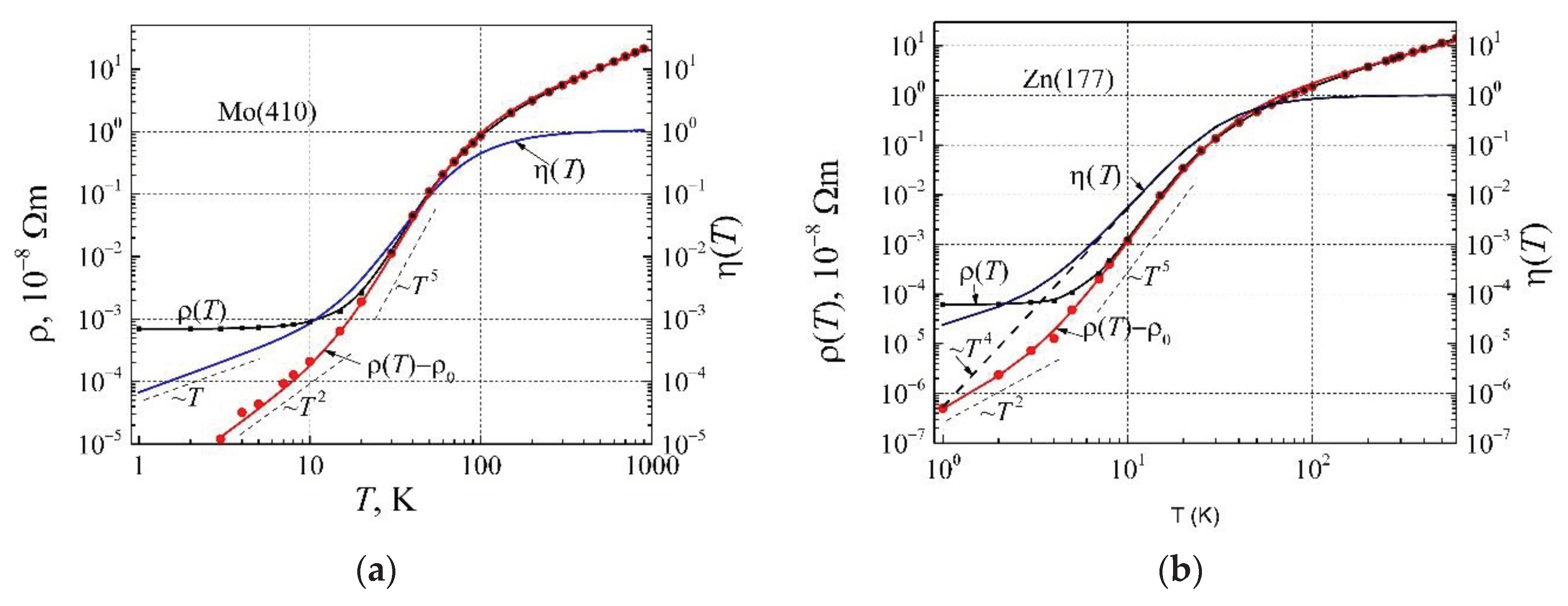
Preprints 101611 g009
Preprints 101611 g010
Figure 10. The resistivity (left scale) and corrected phonon mediation factor (right scale) dependences on the temperature for copper (a), and lithium (b).
Figure 10. The resistivity (left scale) and corrected phonon mediation factor (right scale) dependences on the temperature for copper (a), and lithium (b).
Preprints 101611 g010
Preprints 101611 g011
Figure 11. The effective free RM electron scattering cross-section dependences on temperature for metals Al, Cu, Li, Mo, W, and Zn.
Figure 11. The effective free RM electron scattering cross-section dependences on temperature for metals Al, Cu, Li, Mo, W, and Zn.
Preprints 101611 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated