Comprehensive Empirical Modeling of Shear Strength Prediction in Reinforced Concrete Deep Beams

Preprint

Article

Comprehensive Empirical Modeling of Shear Strength Prediction in Reinforced Concrete Deep Beams

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

18 March 2024

Posted:

21 March 2024

You are already at the latest version

Alerts

Abstract

This paper presents a thorough investigation into the shear strength capacity of reinforced concrete deep beams, with a focus on improving predictive accuracy beyond existing code provisions. Analyzing 198 deep beams from 15 investigations, the study considers parameters such as concrete compressive strength (fc’), shear span to effective depth ratio (av/d), and reinforcement ratios (ρs, ρv, ρh ). Introducing a novel predictive model (Equation 7), the study rigorously evaluates it using nonlinear regression analysis and statistical metrics (MAE, RMSE, R2). The proposed model demonstrates a significant reduction in the coefficient of variation (COV) to 27.08%, surpassing existing codes' limitations. Comparative analyses highlight the model's robustness, revealing improved convergence of data points and minimal sensitivity to variations in key parameters. The findings suggest that the proposed model offers enhanced predictive accuracy across diverse scenarios, making it a valuable tool for structural engineers. This research contributes to advancing the understanding of shear strength in reinforced concrete deep beams, offering a reliable and versatile predictive model with implications for refining design methodologies and enhancing the safety and efficiency of structural systems.

Keywords:

Subject: Engineering - Civil Engineering

1. Introduction

A deep beam, conventionally defined by a span-to-depth ratio (h/L) of ≤ 4 or with a shear span smaller than twice the depth, is primarily governed by shear strength rather than flexure, given sufficient longitudinal reinforcement utilization, as depicted in Figure 1(b) [1]. Additionally, deep beams with a span ratio (h/L ≤ 2.5) are classified as such and find extensive applications in constructions like squat walls, foundation pile caps, and deep foundations, as illustrated in Figure 1(c) [2].

Numerous studies have explored the structural behavior of reinforced concrete (RC) deep beams, employing experimental, analytical, and numerical approaches. Eyad et al. (2018) [3], investigated a simply supported deep beam subjected to a uniform distributed load, providing a comprehensive analysis of cracking effects and ultimate shear strength.

Albidah (2023) [4], conducted tests on six metakaolin-fly ash-based geopolymer concrete beams, considering parameters such as steel fiber content and shear reinforcement percentage. The study demonstrated a significant enhancement in shear strength by 16.7% and 31.6% with the addition of steel fibers at rates of 0.35% and 0.70%, respectively. Eyad et al.[5], explored the impact of confining the strut region through the use of struts reinforcement, while Eyad et al. [6], proposed an empirical formula for the strut efficiency factor (B_s) in RC deep beams, derived from a comprehensive analytical study based on the strut and tie model. Other researchers have numerically investigated main parameters influencing the behavior and shear capacity of RC deep beams [7,8].

Despite numerous experimental and numerical investigations into reinforced concrete deep beams, which have considered factors such as concrete compressive strength, (a_v/d) ratio, and reinforcement directions in relation to shear capacity, the current ACI 318R-5 [1] code and BS 8110 [9] codes still do not incorporate these factors comprehensively. The formulas that provided in these codes are primarily limited to the concrete compressive strength, web width (b_w) and depth (d) factors only as presented in equations 1, 2 and 3, respectively. Due to this fact, the current study found that the predictive accuracy of ACI 318R-5 code [1] and BS 8110 code [9] is restricted, with coefficients of variation (CV) for shear capacity prediction. This study offers a thorough examination of deep beams, taking into account pivotal factors that influence the concrete compressive strength (f_c'), shear span-to-depth ratio (a_v/d), web width (b_w), ratios of longitudinal (P_s), vertical (P_v), and horizontal (P_h) reinforcement, depth (d), yield strength of vertical stirrups (f_yv), and the concrete area (web width × depth (b_w×d)). The assessment relies on an extensive dataset comprising 198 deep beams sourced from 15 investigations [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. These studies were chosen for their detailed information on test conditions and material properties, thus forming a robust database conducive to scrutinizing code provisions and affirming the proposed predictive model.

Introducing a novel model for predicting the shear strength of reinforced concrete deep beams generated from the analysis of 198 experimental simply supported RC deep beams subjected to concentrated and uniform loads. The proposed model demonstrates a remarkable improvement in accuracy, outperforming the predictions of both ACI 318R-5 and BS 8110 by a remarkable percentage. This significant enhancement can be credited to the model's comprehensive consideration of (10) various factors influencing the shear strength of reinforced concrete deep beams, unlike the restrictive focus solely on concrete compressive strength found in the ACI and BS standards.

2. Methodology

To achieve the research objective, twelve (12) empirical equations were developed to theoretically predict the shear strength of reinforced concrete deep beams. A total of 198 experimental simply supported RC deep beams subjected to concentrated and uniform loads have been used to establish the empirical factors. The effects of several parameters (Table 1) were considered, such as the concrete compressive strength (fc'), shear span-to-depth ratio (a_v/d), web width (b_w), ratios of longitudinal (P_s), vertical (P_v), and horizontal (P_h) reinforcement, depth (d), yield strength of vertical stirrups (f_yv), and the concrete area (web width × depth (b_w×d)). The conducted results from the experimental tests were used to verify the developed empirical formula.

To develop the empirical equations, various input data from the selected parameters, as well as the results from experimental simply supported RC deep beams were exported manually into Microsoft Excel software. The study suggests writing program using the ‘Microsoft Visual Basic’ (MVB) in Microsoft Excel software to calculate relevant results/values required to establish twelve (12) empirical equations. In addition, the MVB was used to compute the relevant results based on codes methods formulas in order to be compared with the developed empirical formula.

To improve the readability and clarity, this study suggests organizing the methodology in three separate phases, existing experimental investigations, codes methods for determining RC deep beam shear strength, and an examination of the statistical properties of the dataset.

2.1. Existing Experimental Investigations

The dataset of the current study, generated from 15 literature references [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], consists of 198 simply supported RC deep beam subjected to shear testing. The main variables that imported from these tests including concrete compressive strength (f_c'), shear span-to-depth ratio (a_v/d), web width (b_w), ratios of longitudinal (P_s), vertical (P_v), and horizontal (P_h) reinforcement, depth (d), yield strength of vertical stirrups (f_yv), and the concrete area (web width × depth (b_w×d)), as presented in Table 1. The study found that, the resulting range of ultimate shear forces (V_u) varied from 77.8 kN to 6294 kN, providing a comprehensive dataset for assessing the shear behavior of RC deep beams. This study reviewed the literature to selects all these key variables which considered influential in shear failure. By assembling this diverse dataset, this research facilitates a comprehensive exploration of how these variables impact the shear capacity of deep beams. This approach affords deep understanding of the relationship between these variables and the ultimate shear strength, thereby enhancing the ability to develop new empirical equation to predict and interpret accurate shear failure. Figure 2 shows the typical design, geometry, and failure pattern characterized by a shear diagonal fracture in a representative deep beam, all the variable that considered in this study were pointed in the figure as well.

2.2. Codes Procedure, for Calculating the Resistance of RC Beams

When determining the shear strength of RC deep beams, different design codes provide unique methods for assessment. The upcoming sections detail the approaches outlined by two standards, ACI 318 R 15 [1] and BS 8110 [9], explaining the formulas for computing the nominal shear strength. These methods are available, in assisting engineers to design RC beams safely against shear force. The equations of both codes were offers limited variables form the factors that affected on the nominal shear strength of the deep beams such as: shear span-to-depth ratio (a_v/d), ratios of longitudinal (P_s), vertical (P_v), and horizontal (P_h) reinforcement, yield strength of vertical stirrups (f_yv), and the concrete area (web width × depth (b_w×d)).

ACI 318 R-15 [1]

The ACI 318R-15 code delves into the details of shear strength (V_{n ACI}) determination, limited to a few factors such as concrete compressive strength (f’_c), web width (b_w), and depth (d) as presented in Equation (1).

V_{n ACI} = \frac{5}{6} \sqrt{{f'}_{c}} b_{w} d

(1)

BS 8110 [9]

BS 8110 code is a very popular analytical method for calculating the nominal shear strength in RC deep beams. the formulas of this code were presented through Equations (2) and (3), involves considerations of shear stress limits based on the concrete compressive strength (f’_c), web width (b_w), and depth (d), highlighting safety and efficiency in FC deep beams structural design.

v_{n BS} ≤ \{\begin{matrix} 0.8 \sqrt{f_{cu}} \\ o r \\ 5 N / {mm}^{2} \end{matrix}

(2)

V_{n BS} = v_{n BS} b_{w} d

(3)

2.3. Statistical Properties of Dataset

The study suggests presenting very simple equation for predicting the nominal shear strength (V_n). The suggested equation of calculating the nominal shear strength of the deep beams can be divided into two terms, concrete shear strength (V_c) and shear reinforcement strength (V_s) as presented in equation (4):

V_{n} = V_{c} + V_{s}

(4)

It was suggested to analyze the effect of each term (V_c and V_s) in separate sections, to provide a clear understanding of how this study suggests developing the new empirical equation encompassing various factors affecting the shear strength of RC deep beams, including the concrete compressive strength (f’_c), shear span-to-depth ratio (a_v/d), web width (b_w), ratios of longitudinal (P_s), vertical (P_v), and horizontal (P_h) reinforcement, depth (d), yield strength of vertical stirrups (f_yv), and the concrete area (web width × depth (b_w×d)).

Concrete Shear Strength Term (Vc)

The concrete shear strength (V_c) term is formulated in eight equations (Equations 5-8 and Equations 11-14), each tailored to specific conditions. These equations will be divided into three different stages, each stage carrying the effect of different variables.

The first stage comprises four equations (Equation 5 to Equation 8), which are related to concrete compressive strength (f’c) and longitudinal reinforcing percentage (p_s) variables, a phenomenon known as dowel action.

A * f ʻ c^{B} {* p}_{s}^{C}

(5)

A * (f ʻ c^{B} + p_{s}^{C})

(6)

A * (f ʻ c^{B} + C {* p}_{s}^{C})

(7)

A * f ʻ c^{B} {* K}^{C}

(8)

The value of the uncracked compression zone depth (K) is introduced as an essential parameter in this term, it can be calculated based on multiplying the longitudinal reinforcing percentage (p_s) by the ratio of the modulus of elasticity of longitudinal reinforcement (E_s) to the modulus of elasticity of concrete (E_c) as presented in equation (9) and equation (10).

K = \sqrt{p_{s}^{C} n^{2} + 2 p_{s}^{C} n} - p_{s}^{C} n

(9)

n = \frac{E_{s}}{E_{c}}

(10)

Derived from deep beam geometry, the second stage comprises three equations (Equation 11, 12 and 13) which are related to the shear span to effective depth ratio (a_v/d) variable.

(a_{v} / d)^{F}

(11)

\frac{D}{E + (a_{v} / d)^{F}}

(12)

D + \frac{E}{(a_{v} / d)^{F}}

(13)

Accounting for the size effect of diagonal shear strength in deep beams, the third stage comprises one Equation (Equation 14) which related to the effective depth (d) variable.

{(\frac{G}{d})}^{H}

(14)

Shear Reinforcement Strength Term (V_s)

The shear reinforcement strength (V_s) term is expressed in four equations (Equation 15 to Equation 17), each customized for specific conditions. These equations will be segmented into two different stages, with each stage reflecting the influence of distinct variables.

The first stage comprises two equations (Equation 15 and Equation 16) related to the transverse vertical shear reinforcement (p_v) which can be presented as following.

k_{v} * p_{v} * f_{yv}

(15)

k_{v} = (\frac{1 + (\frac{a_{v}}{d})}{6})

(16)

The second stage comprises two equations as well (Equation 17 and Equation 18) but these equations were related to the transverse horizontal shear reinforcement (p_h), which can be represented as following:

k_{h} * p_{v} * f_{yv}

(16)

k_{h} = (\frac{5 - (\frac{a_{v}}{d})}{6})

(17)

The coefficients (k_v) and (k_h) are determined based on the ratio (a_v/d) instead of clear span to effective depth ratio (l_n/d), reflecting the influence of shear reinforcement on the deep beam. The sum of k_v and k_h is constrained to unity (k_v+k_h=1) emphasizing the proportionality of vertical and horizontal shear reinforcement. Figure 3 shows the variation of the coefficient (k_v and k_h) with respect to (a_v/d).

When the ratio (a_v/d) is low, the angle (θ) between vertical reinforcement and the failure line (diagonal shear crack) is minimal. In such cases, horizontal reinforcement proves more effective in resisting tension stresses (those that cannot be borne by the concrete) compared to vertical reinforcement, (k_v > k_h), as the ratio (a_v/d) increases, the significance of vertical reinforcement in resisting tension stresses becomes more pronounced. When ((a_v/d) = 2), both types of reinforcement exhibit equal effectiveness, with (k_v = k_h = 0.5).

3. The Proposed Empirical Equations

This study suggests presenting 12 different combinations to develop the empirical equation for estimating the nominal shear strength (V_n) of RC deep beams, as presented in Table 2. Then, collinear regression analysis served as the cornerstone for determining the coefficients (A-H) in the proposed empirical equations. This intricate process involved the utilization of Microsoft Excel Software which replaced the test results for the nominal shear strength of the selected 198 deep beams (V_n) in these calculations. The main objective of this study was to increase the accurate and find reliable estimation of the nominal shear strength through the proposed equations. So, the study suggests adopting the error values and calculate it to assess the precision and efficacy of each suggested term in each developed equation. Three key statistical metrics were employed to verify the developed equations, mean absolute error (MAE), root mean square error (RMSE), and the coefficient of multiple determinations (R²).

MAE represents the average absolute discrepancy between expected and observed values in the verification model. It is a collinear score that weighs each variable similarly. RMSE represent the root mean square error, which it is a squared and averaged measure of the difference between expected and observed values. MAE and RMSE work in tandem to diagnose erroneous variations in predicted values, with individual mistakes in a sample always being equal to or greater than RMSE. The coefficient of multiple determinations (R²) gauges how much variability the regression model can account for. A value of (R² = 1) suggests that the regression models accurately describe the data, while (R² = 0) indicates otherwise. As the optimum empirical equations, the recommended models are chosen based on having the lowest MAE and RMSE values and the highest (R²) value, aligning with the desired precision and reliability. These coefficients were calculated using Equations 19, 20 and 21 respectively.

MAE = \frac{1}{N} \sum_{i = 1}^{N} |x_{i} - y_{i}|

(19)

RMSE = \sqrt{\frac{\sum_{i = 1}^{N} {(x_{i} - y_{i})}^{2}}{N}}

(20)

R^{2} = 1 - \frac{SSE}{SST} = 1 - \frac{\sum_{i = 1}^{N} {(x_{i} - y_{i})}^{2}}{\sum_{i = 1}^{N} {(x_{i} - \bar{x})}^{2}}

(21)

Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8, showed the relationship between the effect of the main parameters on the shear resistance prediction and the value of V_exp/V_n .

Despite variations in f’_c between 16.08 and 47.6 MPa as presented in Figure 4, the proposed method (proposal 7) exhibits minimal change, contrasting with other methods (ACI and BS) that yield significantly uneconomic strength predictions with increasing f’_c).

Figure 5 shows little change in prediction for the proposed method with (a_v/d) ranging from 0.19 to 2.5. Conversely, other methods experience a decline in the ratio of (V_exp/V_n) with the highest values of (a_v/d).

Figure 6, Figure 7 and Figure 8 highlight the substantial influence of (p_vfyv), (p_sfy), and (p_hfyv) on the proposed method, varying between 0.053 and 10.29 MPa, 0.405 to 14.11 MPa, and 0 to 5.56 MPa, respectively. This influence surpasses that of other methods.

Following a meticulous regression analysis, the proposed Equation (22) is selected as the forecast model for the nominal shear strength of deep beams (V_{n Prop}) (proposal 7 in Table 2). This decision is grounded in its exceptional performance, boasting the lowest MAE and highest RMSE values, coupled with an (R²) value that closely approaches unity. The study suggests presenting the redemption factors that adopted in the proposed equation in a tabular form (Table 3) for clear understanding.

V_{n, Prop .} = 0.004 ({f_{c}^{'}}^{0.17} + {0.65 p}_{s}) {(\frac{a_{v}}{d})}^{- 0.3} {(\frac{1}{d})}^{0.17}) b_{w} d + ((\frac{1 + (\frac{a_{v}}{d})}{6}) p_{v} + {(\frac{5 - (\frac{a_{v}}{d})}{6}) p}_{h}) * 10^{- 6} f_{y v} b_{w} d

(22)

4. Evaluation of the Developed Empirical Equation

As a result, this study assesses the performance of nominal shear strength predictions of RC deep beams by comparing the proposed method with existing approaches, through a comprehensive evaluation of existing experimental results.

In the comparison shown in Figure 9, the proposed empirical equation demonstrates a strong correlation between experimental and theoretical results. The data points of the proposed equation are more convergent compared to other methods, indicating its superior predictive accuracy.

Mean value (Mean) Equation (23): Represents the average of ratios of experimental (V_exp) to predicted shear strength values (V_n) for all deep beams. Where, (N) is the total number of deep beams, equal to 198 in this study.

Mean = \sum_{i = 1}^{N} (V_{\exp} / V_{n})_{i} / N

(23)

Standard deviation (S.D.) Equation (24): Measures the dispersion of values of (V_exp/V_n), Avg representing the average of the V_exp/V_n.

S . D . = \sqrt{\frac{\sum_{i = 1}^{N} {((V_{e x p} / V_{n})_{i} - A v g .)}^{2}}{N}}

(24)

Coefficient of variation (CV %) Equation (25): Indicates the relative variability of values of (V_exp/V_n), Avg representing the average of the V_exp/V_n.

CV (%) = \frac{S . D .}{Avg .} x 100

(25)

Maximum value (Max.): Represents the maximum shear strength ratio.

Minimum value (Min.): Represents the minimum shear strength ratio.

Range value (Range) Equation (26): Indicates the spread between the maximum and minimum values.

Range = Max . / Min .

(26)

The detailed comparison involves examining the ratio of the shear resistance of tested beam (V_exp) to the calculated nominal shear resistance based on different methods of prediction (V_n), denoted as (V_exp/V_n). This evaluation is detailed in Appendix A, and Table 3 presents the outcomes for all 198 tested beams using different prediction methods. The last column in Table 3 illustrates the results of the proposed method (Equation 7). Notably, the coefficient of variation (CV %) values range between 29.03% and 29.53% for ACI and BS methods. However, by incorporating the effects of vertical and horizontal reinforcement ratios, the proposed method significantly improves CV% to a value of 27.08%.

Table 4. Comparative Analysis of Shear Strength Ratios.

Details	ACI Method [1]	BS 8110 Method [9]	Proposed method
Equation	(1)	(3)	(7)
Mean	1.15	1.10	1.15
Standard deviation	0.34	0.32	0.31
CV %	29.53	29.03	27.08
Max. ratio	2.49	2.25	2.23
Min. ratio	0.43	0.45	0.44
Range (max/min)	5.55	4.97	5.11
Number of tested beams that V_exp ˂ V_n	70	80	65

5. Discussion

The findings of this study underscore the significance of considering multiple factors such as: concrete compressive strength (f’_c), shear span-to-depth ratio (a_v/d), web width (b_w), ratios of longitudinal (P_s), vertical (P_v), and horizontal (P_h) reinforcement, depth (d), yield strength of vertical stirrups (f_yv), and the concrete area (web width × depth (b_w×d)). By analyzing a comprehensive dataset consists of 198 experimental simply supported RC deep beams, this study proposes a novel empirical equation for predicting the nominal shear strength of RC deep beams, outperforming the existing codes such as ACI and BS.

Twelve different sets of empirical equations were developed to create a new empirical equation to estimate the nominal shear strength (V_n) of RC deep beams. Hence, collinear regression analysis served as the cornerstone for determining the coefficients (A-H) in the proposed empirical equations.

The coefficient of multiple determinations (R²) was used to make a comprehensive comparison between the results of the proposed variables. The results of R² showed a difference in the range from 0.001 to 0.4, which is considered less than 0.5, but the study suggested specifying the coefficients (A-H) and applying them to the proposed components of the equation. Then, the coefficient (R²) was calculated for the results of the proposed empirical equation, and it was equal to 0.94, which is considered a truly acceptable value, especially when compared to the value of R² for ACI and BS, which was equal to 0.8 and 0.7, respectively.

The study presented a detailed comparison between the current empirical equation and the ACI and BS codes equations to evaluate the ratio of the nominal shear strength of the experimental beam to the calculated nominal shear strength (V_exp/V_n). Based on the comparison results, the study found that the proposed equation outperformed the equations of the ACI and BS codes in all details, such as: Mean, Standard deviation CV%, Max. ratio, Min. ratio and Range(max/min).

The findings of this study bring positive improvements for code development and structure design. By using the proposed empirical equation, the structural designers can improve the effectiveness of structural designs by obtaining higher accuracy in predictions the nominal shear strength for the RC deep beams. As presented earlier, code committees may think about including the examined factors that effect on the shear behavior into the existing standards, like ACI 318R-15 and BS 8110.

6. Conclusions

This study suggests investigating the effect of various parameters on the shear strength capacity of RC deep beams, including the concrete's compressive strength (f’_c), shear span-to-depth ratio (a_v/d), web width (b_w), ratios of longitudinal (P_s), vertical (P_v), and horizontal (P_h) reinforcement, depth (d), vertical stirrups' yield strength (f_yv), and the concrete area (web width × depth (b_w×d)). This inquiry goes beyond what can be done with current codes, such BS 8110 and ACI 318R-5, which have a large coefficient of variation (CV) when it comes to forecasting shear capacity.

Through a comprehensive evaluation of 198 deep beams, imported from an extensive dataset around 15 investigations, this research proposes a novel predictive empirical equation for shear strength. The proposed equation (22), take into account all the mentioned key parameters and it is rigorously assessed through collinear regression analysis and statistical metrics, MAE, RMSE and R².

The results proved that the proposed empirical equation was significantly enhanced the prediction accuracy compared to the ACI and BS codes achieving a CV, SD, Max. ratio, Min ratio equal to 27.08%, 31.10%, 2.23% and 0.44% respectively, and the range was equal to 5.11. Both vertical and horizontal reinforcement ratios was considered in the proposed empirical equation and it leads for this improvement. The suggested empirical equation outperforms Aci and BS codes in a wide range of cases and exhibits robustness to changes in f'_c and a_v/d.

Furthermore, the comparative study highlights how were the accuracy of the suggested model, with better data point convergence and little susceptibility to changes in important parameters. This present that the suggested model has a higher degree of predictability for shear strength, which makes it a useful tool for structural engineers and practitioners.

This study advances the knowledge of shear strength in the simply supported RC deep beams by providing a more precise and adaptable predictive empirical equation that takes into account the complexities of real-world applications. The results of this study have significance for improving design techniques and raising the security and effectiveness of deep beam structural systems.

Author Contributions

Conceptualization: Eyad. K. Sayhood, Nisreen S. Mohammed, Salam J. Hilo.; Data curation: Eyad. K. Sayhood, Nisreen S. Mohammed, Salam J. Hilo and Salih S. Salih.; Formal analysis: Eyad. K. Sayhood and Salam J. Hilo.; Funding acquisition: Eyad. K. Sayhood, Nisreen S. Mohammed, Salam J. Hilo and Salih S. Salih.; Investigation: Eyad. K. Sayhood, Nisreen S. Mohammed, Salam J. Hilo and Salih S. Salih.; Methodology: Eyad. K. Sayhood, Nisreen S. Mohammed, Salam J. Hilo and Salih S. Salih. ;Project administration: Eyad. K. Sayhood, Nisreen S. Mohammed.; Validation: Eyad. K. Sayhood, Nisreen S. Mohammed, Salam J. Hilo and Salih S. Salih.; Resources: Eyad. K. Sayhood and Salam J. Hilo.; Software: Nisreen S. Mohammed, Salam J. Hilo and Salih S. Salih.; Supervision: Eyad. K. Sayhood, Nisreen S. Mohammed.; Visualization: Eyad. K. Sayhood, Nisreen S. Mohammed, Salam J. Hilo and Salih S. Salih.; Writing—original draft: Eyad. K. Sayhood, Nisreen S. Mohammed, Salam J. Hilo and Salih S. Salih .; Writing—review and editing: Eyad. K. Sayhood, Nisreen S. Mohammed, Salam J. Hilo and Salih S. Salih.

Funding

This research received no external funding.

Data Availability Statement

The data are presented in the article.

Acknowledgments

The authors highly acknowledge their institutes and universities for their support in preparing and completing this research.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A

Comparison of the ratio (V_exp/V_n) for all 198 beams with codes

Ref. No.	Beam No.	$V_{E x p .} (k N)$	$V_{n A C I} (k N)$	$V_{E x p .} / V_{n A C I}$	$V_{n B S} (k N)$	$V_{E x p .}$ $/ V_{n B S}$	$V_{n, P R O P .} (k N)$	$V_{E x p .}$ $/ V_{n, P R O P .}$
[19]	1	2530	2627.04	0.96306	2623.4	0.96440	1964	1.28819
	2	2922	2648.78	1.10315	2623.4	1.11382	1971	1.48250
	3	2019	2280.33	0.88540	2417.48	0.83517	1865	1.08257
	4	2348	2338.28	1.00416	2478.91	0.94719	1877	1.25093
	5	2224	2078.59	1.06996	2203.6	1.00926	1916	1.16075
	6	2121	2142	0.99020	2270.82	0.93402	1925	1.10182
	7	2824	2354.58	1.19936	2496.19	1.13132	1956	1.44376
	8	2655	2410.74	1.10132	2555.73	1.03884	1964	1.35183
	9	1783	2027.37	0.87946	2149.3	0.82957	1833	0.97272
	10	1490	2032.08	0.73324	2154.29	0.69164	1834	0.81243
	11	1463	2467.56	0.59289	2615.97	0.55926	1897	0.77122
	12	2522	2499.51	1.00900	2623.4	0.96135	1901	1.32667
	13	2170	2321.87	0.93459	2461.51	0.88157	1877	1.15610
	14	2295	2321.87	0.98843	2461.51	0.93235	1888	1.21557
	15	1832	2564.44	0.71439	2623.4	0.69833	1959	0.93517
	16	1214	2569.65	0.47244	2623.4	0.46276	1862	0.65199
	17	2095	2085.47	1.00457	2210.9	0.94758	1900	1.10263
	18	2081	2085.47	0.99786	2210.9	0.94125	1842	1.12975
	19	3763	2326.49	1.61746	2466.41	1.52570	2121	1.77416
	20	3687	2360.82	1.56175	2502.8	1.47315	2184	1.68819
	21	1325	2474.46	0.53547	2623.28	0.50509	1744	0.75975
	22	2295	2539.12	0.90386	2627.85	0.87334	1810	1.26796
	23	3393	4563.6	0.74349	4696.6	0.72244	3148	1.07783
	24	3745	4563.6	0.82062	4696.6	0.79739	3244	1.15444
	25	2268	4599.41	0.49311	4698.34	0.48272	2902	0.78153
	26	5440	4594.16	1.18411	4692.98	1.15918	3563	1.52680
	27	1463	1183.85	1.23580	1255.05	1.16569	1088	1.34467
	28	1543	1190.44	1.29616	1262.04	1.22262	1061	1.45429
	29	716	1244.22	0.57546	1319.05	0.54281	983	0.72838
	30	2633	1252.06	2.10293	1327.37	1.98362	1214	2.16886
	31	5017	4116.49	1.21876	4364.07	1.14961	3781	1.32690
	32	4136	3521.41	1.17453	3733.19	1.10790	3694	1.11965
	33	6294	4116.49	1.52897	4364.07	1.44223	4200	1.49857
	34	4901	3401.89	1.44067	3606.48	1.35894	3598	1.36215
	35	4875	4500.61	1.08319	4646.14	1.04926	3833	1.27185
[10]	36	369.35	259.958	1.42081	275.592	1.34021	364.4	1.01358
	37	467.25	277.967	1.68095	294.685	1.58559	383.5	1.21838
	38	493.95	280.903	1.75844	297.797	1.65868	421	1.17328
	39	407.15	289.763	1.40511	307.19	1.32540	386	1.05479
	40	416.05	290.266	1.43334	307.723	1.35203	430	0.96756
	41	445	288.247	1.54381	305.583	1.45623	383	1.16188
	42	389.35	280.176	1.38966	297.026	1.31083	392.1	0.99299
	43	262.55	147.103	1.78480	155.95	1.68355	228.2	1.15053
	44	333.75	157.294	2.12182	166.754	2.00145	170.9	1.95290
	45	378.25	158.955	2.37960	168.515	2.24461	288.6	1.31064
	46	302.6	158.68	1.90698	168.223	1.79880	234.1	1.29261
	47	300.35	158.955	1.88953	168.515	1.78233	286.7	1.04761
	48	295.9	157.85	1.87456	167.343	1.76822	231.7	1.27708
	49	289.25	148.48	1.94807	157.41	1.83756	255	1.13431
[12]	50	449.7	355.34	1.26555	363.141	1.23836	283.4	1.58680
	51	465.2	355.34	1.30917	363.141	1.28105	283.4	1.64150
	52	434.1	299.234	1.45070	305.803	1.41954	243.6	1.78202
	53	452.1	299.234	1.51086	305.803	1.47840	243.6	1.85591
	54	443	241.934	1.83108	247.245	1.79175	217.3	2.03866
	55	419.1	241.934	1.73229	247.245	1.69508	217.3	1.92867
[22]	56	161	111.669	1.44176	118.385	1.35997	156.7	1.02744
	57	148	109.559	1.35087	116.148	1.27424	157.7	0.93849
	58	141	107.097	1.31656	113.538	1.24187	158.6	0.88903
	59	170.5	117.205	1.45472	124.254	1.37219	161.2	1.05769
	60	184	118.619	1.55118	125.753	1.46319	163.1	1.12814
	61	174.5	120.294	1.45061	127.528	1.36833	168.6	1.03499
	62	170.5	114.907	1.48381	121.817	1.39964	168.7	1.01067
	63	171.5	116.348	1.47403	123.346	1.39040	170.7	1.00469
	64	161.5	112.857	1.43101	119.645	1.34983	171.4	0.94224
	65	161	110.77	1.45346	117.432	1.37101	183.4	0.87786
	66	172.5	113.152	1.52450	119.957	1.43802	185.5	0.92992
	67	178.5	117.773	1.51563	124.856	1.42965	188.3	0.94796
	68	168	115.196	1.45838	122.125	1.37564	189.2	0.88795
	69	147	121.397	1.21090	128.698	1.14221	146.3	1.00478
	70	143.5	115.774	1.23948	122.737	1.16917	146.5	0.97952
	71	140	117.773	1.18873	124.856	1.12129	148.5	0.94276
	72	153	114.033	1.34172	120.891	1.26560	149.3	1.02478
	73	128.5	112.561	1.14160	119.331	1.07684	149.3	0.86068
	74	131	112.561	1.16381	119.331	1.09779	150.8	0.86870
	75	126	108.027	1.16638	114.524	1.10021	151.3	0.83278
	76	150	120.57	1.24409	127.822	1.17351	154.2	0.97276
	77	145	114.907	1.26189	121.817	1.19031	154.5	0.93851
	78	130.5	106.472	1.22567	112.876	1.15614	153.7	0.84906
	79	158.5	115.485	1.37247	122.431	1.29461	159.7	0.99249
	80	158	112.561	1.40368	119.331	1.32405	160.5	0.98442
	81	155	113.152	1.36984	119.957	1.29213	162.2	0.95561
	82	166	117.205	1.41632	124.254	1.33597	164.7	1.00789
	83	153.5	106.472	1.44169	112.876	1.35990	136.5	1.12454
	84	118.5	113.152	1.04726	119.957	0.98785	131.7	0.89977
	85	123	120.847	1.01782	128.115	0.96007	134.8	0.91246
	86	131	123.034	1.06475	130.434	1.00434	136.8	0.95760
	87	122	120.57	1.01186	127.822	0.95445	137.9	0.88470
	88	124	115.196	1.07643	122.125	1.01535	135.7	0.91378
	89	103.5	113.152	0.91470	119.957	0.86281	136.8	0.75658
	90	115	113.446	1.01370	120.269	0.95619	136.8	0.84064
	91	124.5	116.635	1.06743	123.649	1.00688	139.1	0.89504
	92	124	117.773	1.05287	124.856	0.99314	140.9	0.88006
	93	140.5	118.337	1.18729	125.455	1.11992	143.3	0.98046
	94	124.5	106.785	1.16589	113.207	1.09976	142.3	0.87491
	95	127.5	110.468	1.15418	117.112	1.08870	144.7	0.88113
	96	137	112.561	1.21712	119.331	1.14807	146.8	0.93324
	97	146.5	114.325	1.28143	121.201	1.20874	148.3	0.98786
	98	128.5	111.37	1.15381	118.068	1.08836	145.3	0.88438
	99	152	113.152	1.34333	119.957	1.26712	151.1	1.00596
	100	152.5	111.07	1.37301	117.75	1.29512	152.3	1.00131
	101	159.5	118.9	1.34146	126.05	1.26537	149.3	1.06832
	102	87	103.551	0.84017	109.779	0.79250	122.1	0.71253
[20]	103	754	822.787	0.91640	872.272	0.86441	576.3	1.30835
	104	350.3	572.572	0.61180	536.524	0.65291	339.3	1.03242
	105	206	480.714	0.42853	456.045	0.45171	262.3	0.78536
[23]	106	874.2	575.944	1.51786	610.583	1.43175	663.1	1.31835
	107	650.9	589.867	1.10347	618.963	1.05160	594.9	1.09413
	108	437.4	572.598	0.76389	607.036	0.72055	542.9	0.80567
	109	1175	834.823	1.40748	874.713	1.34330	893.7	1.31476
	110	952.3	877.025	1.08583	874.713	1.08870	801.1	1.18874
	111	804.4	866.789	0.92802	875.326	0.91897	732.1	1.09876
	112	1636.3	1151.22	1.42136	1092.14	1.49825	1094	1.49570
	113	1244	1155.41	1.07667	1090.82	1.14043	969.2	1.28353
[24]	114	1615.5	1908.61	0.84643	1924.72	0.83934	1448	1.11568
[24]	115	1592.9	1897.8	0.83934	1924.72	0.82760	1446	1.10159
[26]	116	2563.7	2410.19	1.06369	2447.87	1.04732	2155	1.18965
[17]	117	284.8	263.28	1.08174	279.114	1.02037	270.2	1.05403
	118	377.6	263.28	1.43421	279.114	1.35285	275.5	1.37060
	119	358.1	263.28	1.36015	279.114	1.28299	281.8	1.27076
	120	228.7	263.28	0.86866	279.114	0.81938	242	0.94504
	121	255.7	263.28	0.97121	279.114	0.91611	242	1.05661
	122	208.7	263.28	0.79269	279.114	0.74772	242	0.86240
[20]	123	276.9	466.875	0.59309	437.482	0.63294	267.9	1.03359
[20]	124	455.8	461.146	0.98841	437.482	1.04187	301	1.51429
[13]	125	350.8	305.71	1.14749	324.096	1.08240	269.3	1.30264
	126	305.8	321.653	0.95071	335.448	0.91162	234	1.30684
	127	257.8	298.99	0.86224	316.972	0.81332	203.8	1.26497
	128	156.1	179.872	0.86784	190.69	0.81861	153.9	1.01429
	129	140.4	196.011	0.71629	207.799	0.67565	138.4	1.01445
	130	123.6	184.235	0.67088	195.316	0.63282	124.8	0.99038
[25]	131	606.7	392.608	1.54531	413.845	1.46601	364.9	1.66265
[25]	132	351.8	383.198	0.91806	406.245	0.86598	298.9	1.17698
[21]	133	116.75	186.528	0.62591	197.746	0.59040	249.9	0.46719
	134	114.53	191.167	0.59911	202.664	0.56512	251.5	0.45539
	135	105.65	192.993	0.54743	204.601	0.51637	256.2	0.41237
	136	166.8	191.952	0.86897	203.497	0.81967	219.3	0.76060
	137	177.93	188.856	0.94215	200.214	0.88870	219.5	0.81062
	138	205.75	193.788	1.06173	205.442	1.00150	234.4	0.87777
[16]	139	239.2	197.718	1.20980	209.609	1.14117	221.2	1.08137
	140	208.1	166.239	1.25181	176.237	1.18080	184.9	1.12547
	141	172.5	133.883	1.28844	141.935	1.21535	149.1	1.15694
	142	127.16	101.956	1.24720	108.087	1.17646	114	1.11544
	143	77.8	65.0963	1.19515	69.0114	1.12735	78.68	0.98882
[20]	144	348	570.945	0.60952	535	0.65047	331.1	1.05104
[17]	145	284.1	263.698	1.07737	279.557	1.01625	268.8	1.05692
	146	377	263.698	1.42967	279.557	1.34856	273.3	1.37944
	147	357.5	263.698	1.35572	279.557	1.27881	278.6	1.28320
[11]	148	1357	1137.29	1.19319	1205.69	1.12550	845.3	1.60535
	149	1134	1032.33	1.09849	1094.42	1.03617	774.2	1.46474
	150	1286	1077.28	1.19375	1142.07	1.12603	830.4	1.54865
[18]	151	251	216.932	1.15704	229.979	1.09140	267.8	0.93727
	152	237	216.932	1.09251	229.979	1.03053	267.8	0.88499
	153	456	266.817	1.70904	281.25	1.62133	276.2	1.65098
	154	426	266.817	1.59660	281.25	1.51467	276.2	1.54236
[16]	155	239	212.613	1.12411	225.4	1.06034	291.1	0.82102
	156	224	187.532	1.19446	198.81	1.12670	243.6	0.91954
	157	190	137.056	1.38629	145.299	1.30765	192.2	0.98855
	158	164	100.022	1.63964	106.037	1.54663	144.7	1.13338
	159	90	63.7259	1.41230	67.5585	1.33218	97.9	0.91931
	160	249	200.919	1.23931	213.003	1.16900	228.3	1.09067
	161	224	163.066	1.37368	172.873	1.29575	188	1.19149
	162	216	132.787	1.62667	140.774	1.53437	152.4	1.41732
	163	140	103.727	1.34970	109.966	1.27312	117.3	1.19352
	164	100	61.3316	1.63048	65.0202	1.53798	79.54	1.25723
[14]	165	222.5	327.225	0.67996	346.906	0.64138	356.2	0.62465
	166	209.1	320.505	0.65241	339.781	0.61540	355.1	0.58885
	167	222.5	319.144	0.69718	338.339	0.65762	354.9	0.62694
	168	244.7	328.553	0.74478	348.313	0.70253	356.4	0.68659
	169	278.8	319.144	0.87359	338.339	0.82403	372.9	0.74765
	170	256.6	332.504	0.77172	352.501	0.72794	375.2	0.68390
	171	284.8	321.184	0.88672	340.501	0.83641	373.3	0.76293
	172	268.1	318.462	0.84186	337.615	0.79410	372.8	0.71915
	173	241.5	327.225	0.73802	346.906	0.69615	374.3	0.64520
	174	301.1	317.778	0.94752	336.89	0.89376	372.7	0.80789
	175	322.2	338.343	0.95229	358.692	0.89826	376.1	0.85669
	176	334.9	329.215	1.01727	349.014	0.95956	374.6	0.89402
	177	379.3	428.076	0.88606	395.85	0.95819	389.8	0.97306
	178	277.7	333.81	0.83191	353.886	0.78472	330.7	0.83973
	179	311.1	338.343	0.91948	358.692	0.86732	331.5	0.93846
	180	245.9	323.21	0.76081	342.649	0.71764	328.7	0.74810
	181	285.9	355.286	0.80470	376.654	0.75905	334.4	0.85496
	182	290	320.505	0.90482	339.781	0.85349	349.9	0.82881
	183	301.1	329.875	0.91277	349.715	0.86099	351.6	0.85637
	184	323.7	323.883	0.99943	343.362	0.94274	350.5	0.92354
	185	288.2	342.816	0.84068	363.434	0.79299	353.9	0.81435
	186	309.3	326.56	0.94715	346.2	0.89341	390.8	0.79145
	187	423.8	443.556	0.95546	395.85	1.07061	409.8	1.03416
	188	434.9	441.096	0.98595	395.85	1.09865	409.4	1.06229
	189	428.6	455.18	0.94161	395.85	1.08273	411.5	1.04156
	190	301.1	337.699	0.89162	358.009	0.84104	335.4	0.89773
	191	356.7	337.054	1.05829	357.325	0.99825	335.3	1.06382
	192	256.6	326.56	0.78577	346.2	0.74119	333.2	0.77011
	193	290	323.21	0.89725	342.649	0.84635	341.8	0.84845
	194	312.2	335.76	0.92983	355.954	0.87708	344.3	0.90677
	195	334.4	328.553	1.01780	348.313	0.96006	342.9	0.97521
	196	334.9	326.56	1.02554	346.2	0.96736	342.5	0.97781
	197	394.9	350.351	1.12716	371.423	1.06321	423.9	0.93159
	198	312.2	317.092	0.98457	336.163	0.92872	378.3	0.82527

References

Committee, A. Building code requirements for structural concrete (ACI 318-05) and commentary (ACI 318R-05). 2005.
Almasabha, G.; Murad, Y.; Alghossoon, A.; Saleh, E.; Tarawneh, A. Sustainability of Using Steel Fibers in Reinforced Concrete Deep Beams without Stirrups. Sustainability 2023, 15, 4721. [Google Scholar] [CrossRef]
Sayhood, E.K.; Resheq, A.S.; Habeeb, A.J. Shear strength of concrete deep beam subjected to uniformly distributed load. Engineering and Technology Journal 2018, 36, 125–135. [Google Scholar] [CrossRef]
Albidah, A.S. Shear behviour of metakaolin-fly ash based geopolymer concrete deep beams. Engineering Structures 2023, 275, 115271. [Google Scholar] [CrossRef]
Sayhood, E.K.; Abdullah, K.N.; Kazem, S.J. Strut Confinement of Simply Supports Deep Beam Using Strut Reinforcement. Engineering and Technology Journal 2020, 38, 605–613. [Google Scholar] [CrossRef]
Mohammed, E.K.S.a.N.S. EFFECT FACTORS OF STRUT STRENGTH FOR REINFORCEMENT DEEP BEAMS. ARPN Journal of Engineering and Applied Sciences 2019, 14, 2843–2856. [Google Scholar]
Arabzadeh, A.; Hizaji, R. A simple approach to predict the shear capacity and failure mode of fix-ended reinforced concrete deep beams based on experimental study. International Journal of Engineering 2019, 32, 474–483. [Google Scholar]
Rahimi, S.B.; Jalali, A.; Mirhoseini, S.M.; Zeighami, E. Experimental Comparison of Different Types of FRP Wrapping in Repairing of RC Deep Beams with Circular Openings. International Journal of Engineering 2021, 34, 1961–1973. [Google Scholar]
Standard, B. Structural use of concrete, Part 1, Code of practice for design and construction. BS 8110: Part 1.
Rashid, M.A.; Kabir, A. Behaviour of reinforced concrete deep beam under uniform loading. Journal of Civil Engineering, The Institution Of Engineers, Bangladesh, Vol CE 1996, 24. [Google Scholar]
Aguilar, G.; Matamoros, A.B.; Parra-Montesinos, G.; Ramírez, J.A.; Wight, J.K. Experimental evaluation of design procedures for shear strength of deep reinfoced concrete beams. 2002.
Ahmad, S.; Shah, A.; ZAMANI, K.N.; Salimullah, K. Design and evaluation of the shear strength of deep beams by strut and tie model (STM). 2011.
Ashour, A. Shear capacity of reinforced concrete deep beams. Journal of Structural Engineering 2000, 126, 1045–1052. [Google Scholar] [CrossRef]
Clark, A.P. Diagonal tension in reinforced concrete beams. In Proceedings of the Journal Proceedings; 1951; pp. 145–156. [Google Scholar]
Birrcher, D.B. Design of reinforced concrete deep beams for strength and serviceability; The University of Texas at Austin: 2009.
Kong, F.-K.; Robins, P.J.; Cole, D.F. Web reinforcement effects on deep beams. In Proceedings of the Journal Proceedings; 1970; pp. 1010–1018. [Google Scholar]
Oh, J.-K.; Shin, S.-W. Shear strength of reinforced high-strength concrete deep beams. Structural Journal 2001, 98, 164–173. [Google Scholar]
Quintero-Febres, C.G.; Parra-Montesinos, G.; Wight, J.K. Strength of struts in deep concrete members designed using strut-and-tie method. ACI Materials Journal 2006, 103, 577. [Google Scholar]
Tuchscherer, R.G. Strut-and-tie modeling of reinforced concrete deep beams: Experiments and design provisions; The University of Texas at Austin: 2008.
Rogowsky, D.M.; MacGregor, J.G.; Ong, S.Y. Tests of reinforced concrete deep beams. 1983.
Sazzad, M.M.; Ali, M.; Nizamud-Ooulah, S. Study of behaviour of reinforced concrete deep beam under two points loading and the effect of shear reinforcement. In Proceedings of the 27th Conference on Our World in Concrete and Structures; 2002; pp. 29–30. [Google Scholar]
Smith, K.; Vantsiotis, A. Shear strength of deep beams. In Proceedings of the Journal Proceedings; 1982; pp. 201–213. [Google Scholar]
Tan, K.; Lu, H. Shear behavior of large reinforced concrete deep beams and code comparisons. Structural Journal 1999, 96, 836–846. [Google Scholar]
Uribe, C.; Alcocer, S. Behavior of Deep Beams Designed with Strut-and-Tie Models. Centro Nacional de Prevención de Disastres 2001.
Yang, K.-H.; Chung, H.-S.; Ashour, A.F. Influence of inclined web reinforcement on reinforced concrete deep beams with web openings. 2007.
Williams, C.S.; Deschenes, D.J. A PRAGMATIC APPROACH TO STRUT-AND-TIE MODELING.

Figure 1. Deep beams application in reinforced concrete structures.

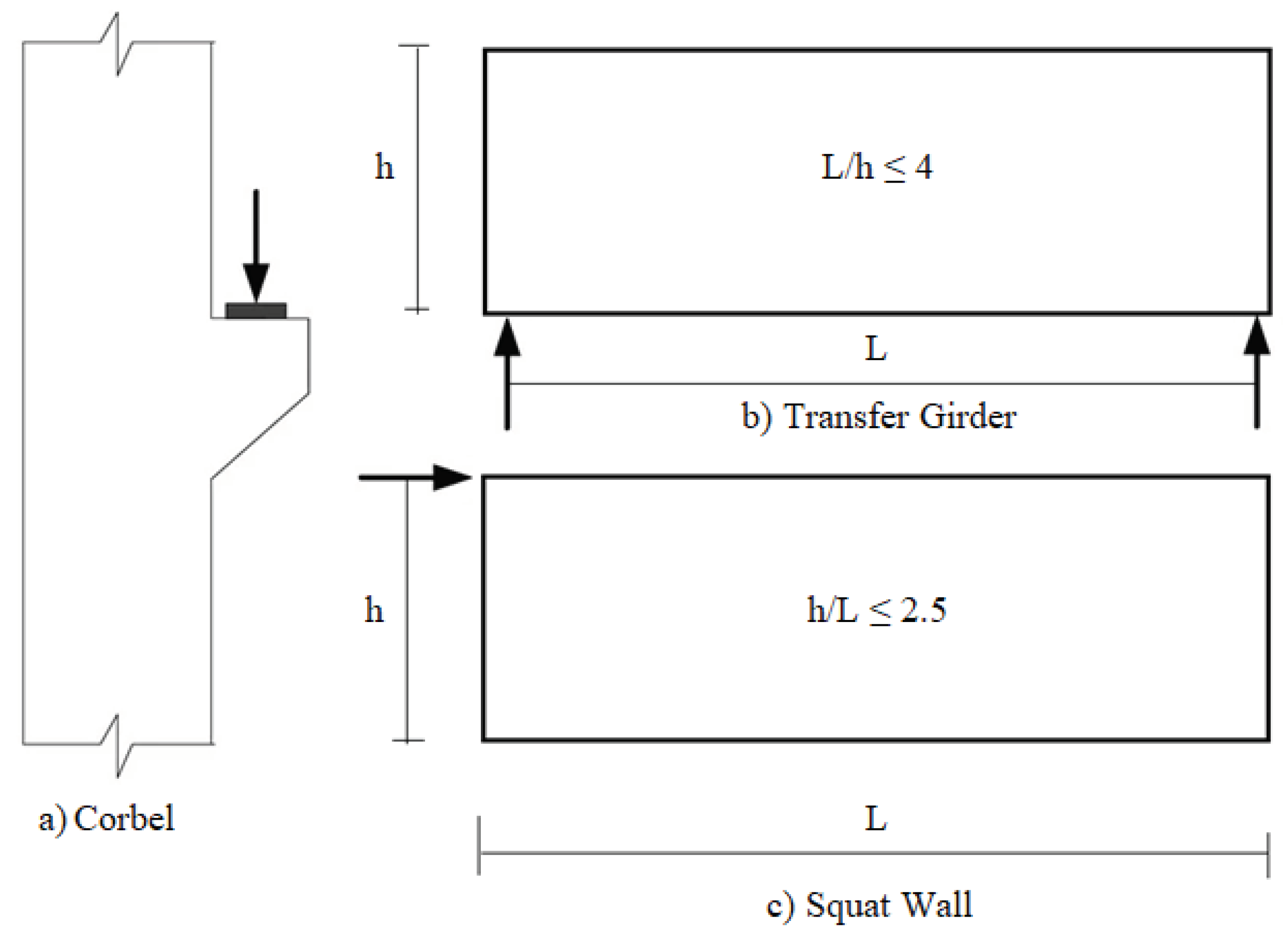
Figure 2. Simply supported RC deep beam showing the typical design, geometry, and failure pattern.

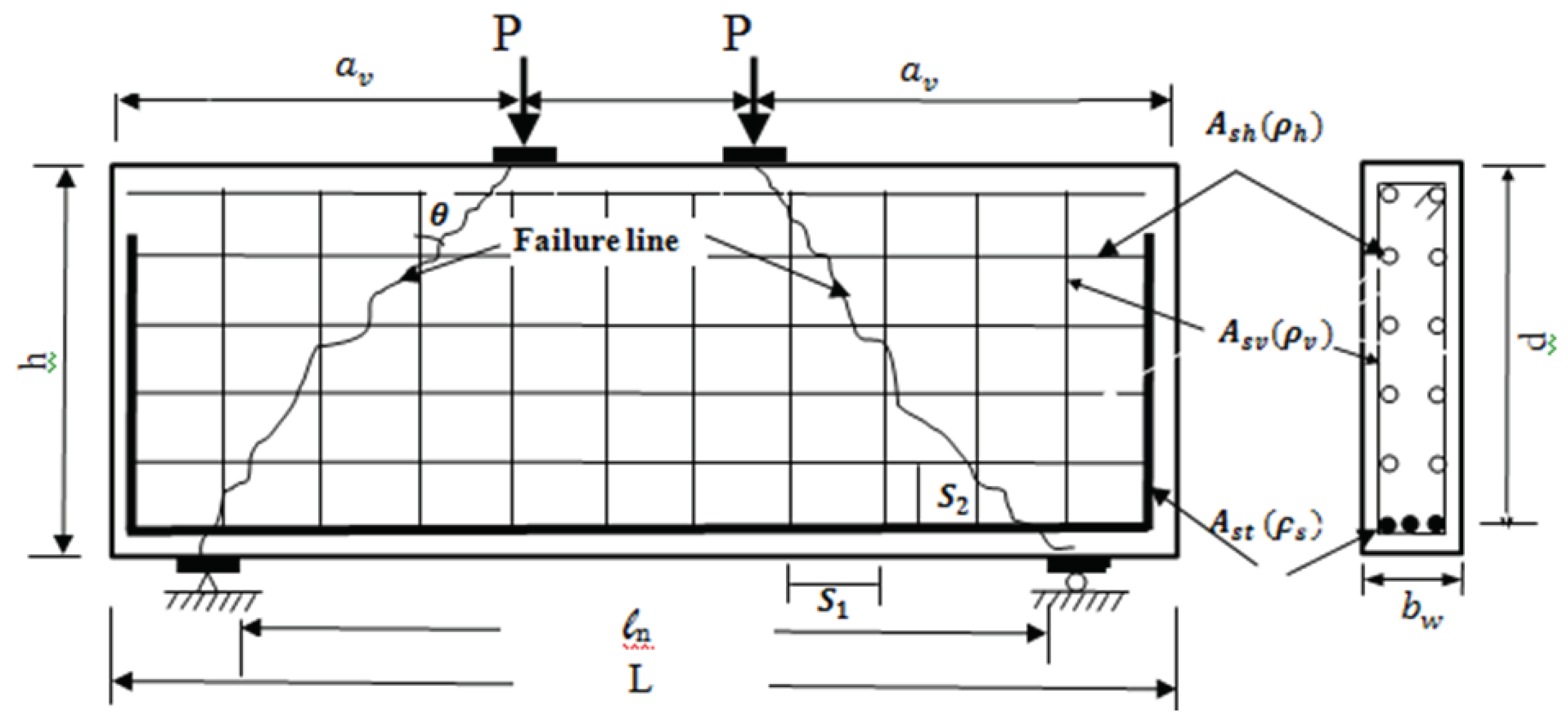
Figure 3. Coefficient of effectiveness for vertical and horizontal transverse shear reinforcement.

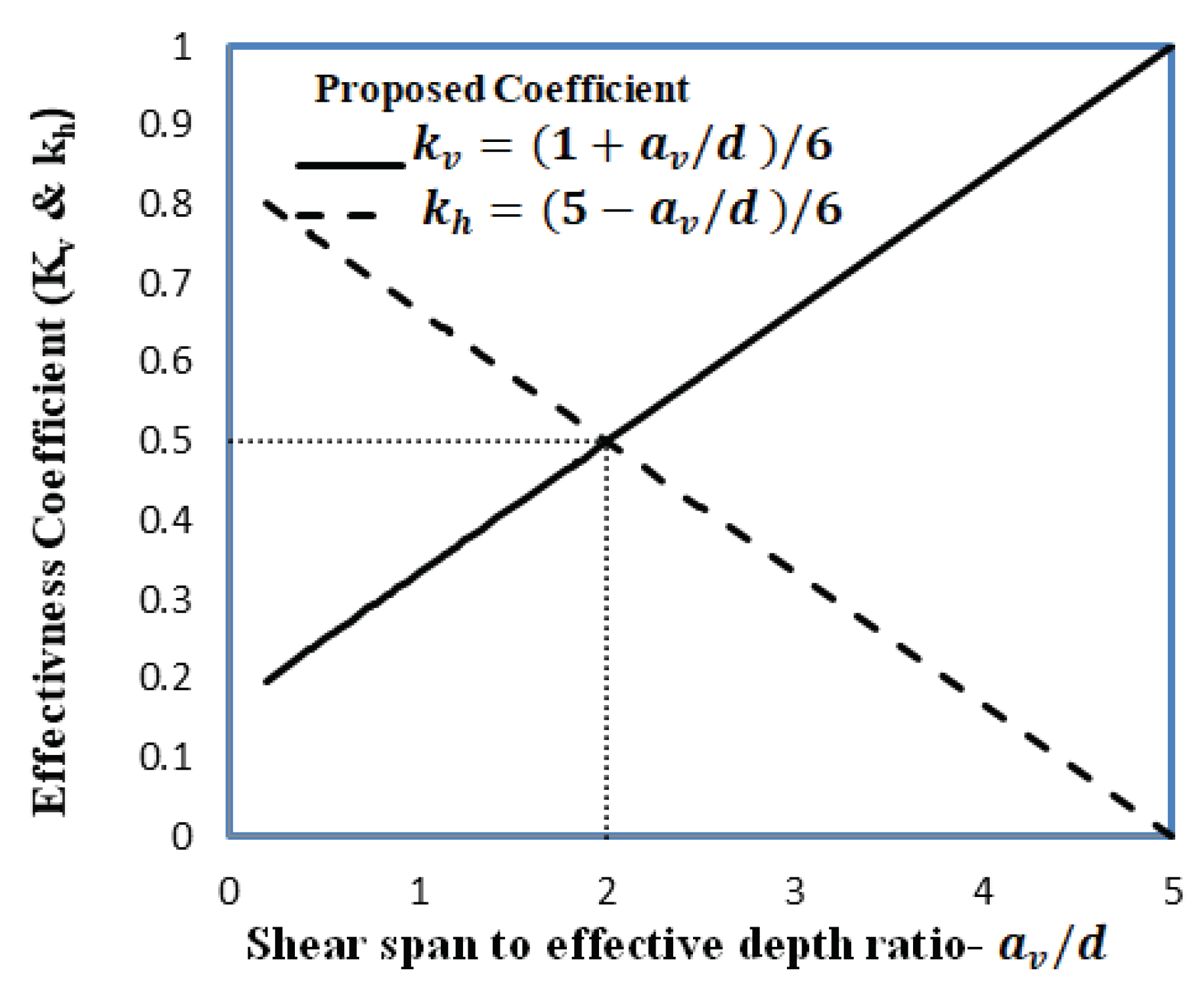
Figure 4. Effect of

f_{c}^{'}

(MPa) on the ratio of (V_exp/V_n) for the ACI, BS and proposed methods.

Figure 4. Effect of

f_{c}^{'}

(MPa) on the ratio of (V_exp/V_n) for the ACI, BS and proposed methods.

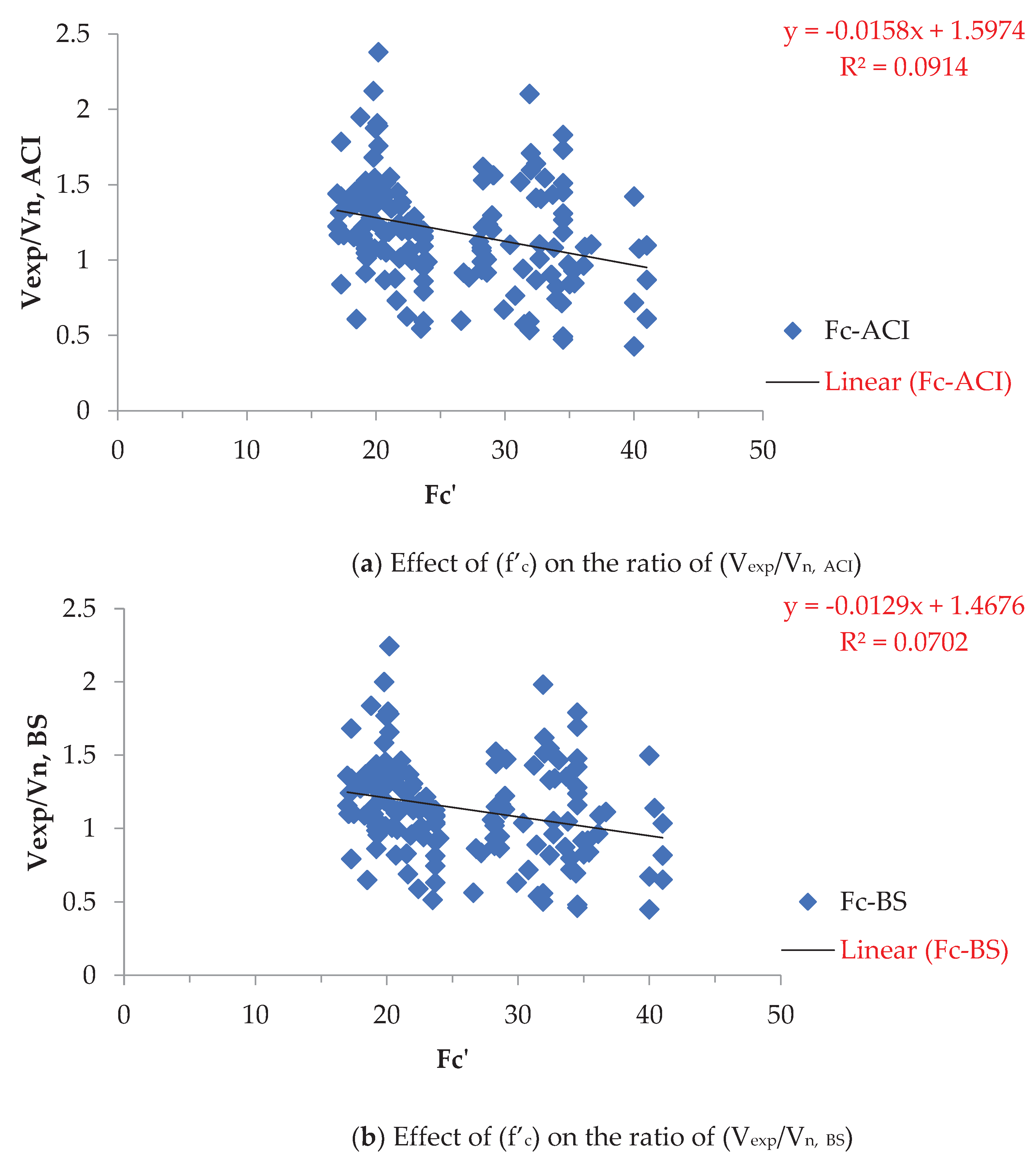
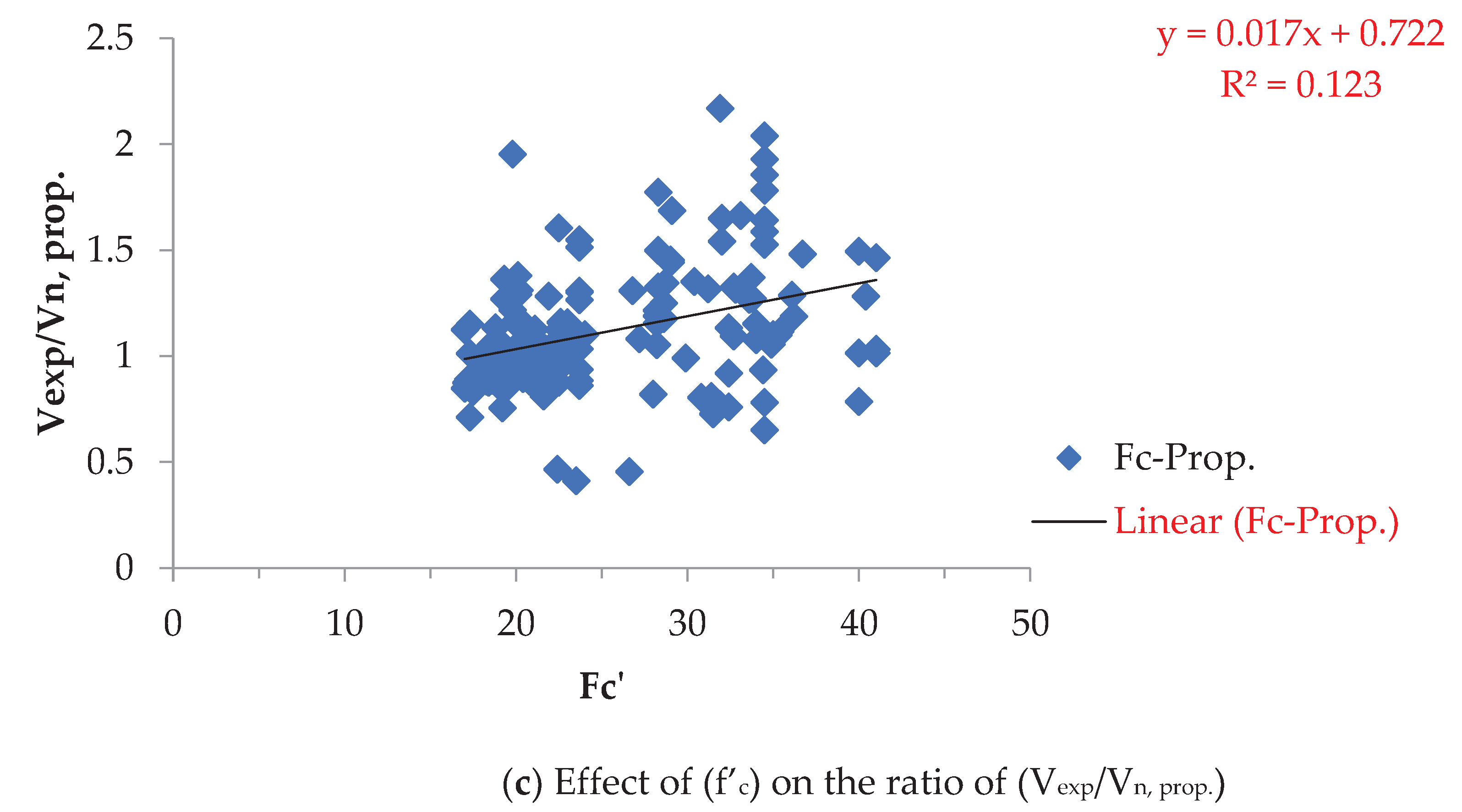
Figure 5. Effect of a_v/d on the ratio of (V_exp/V_n).

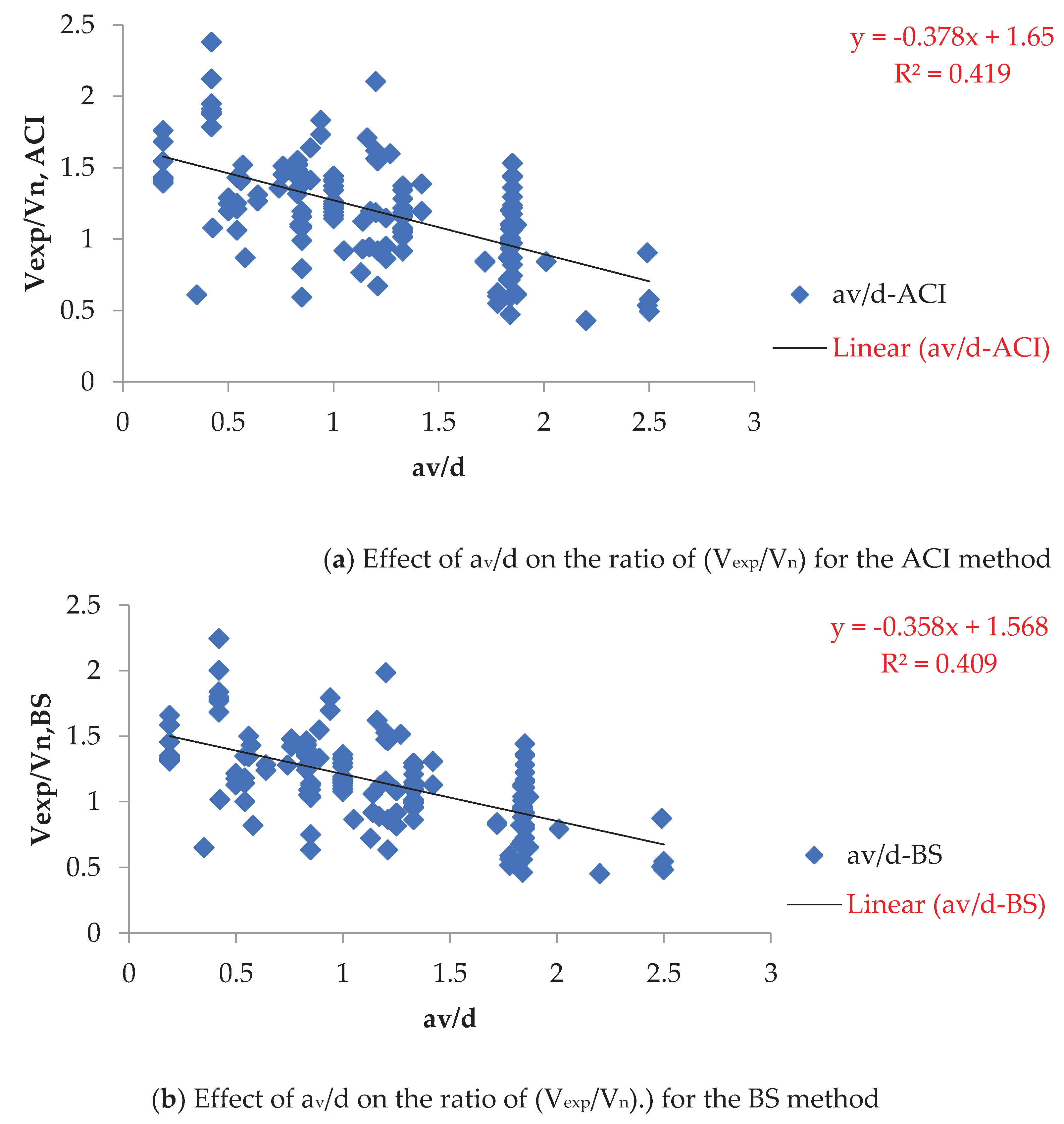
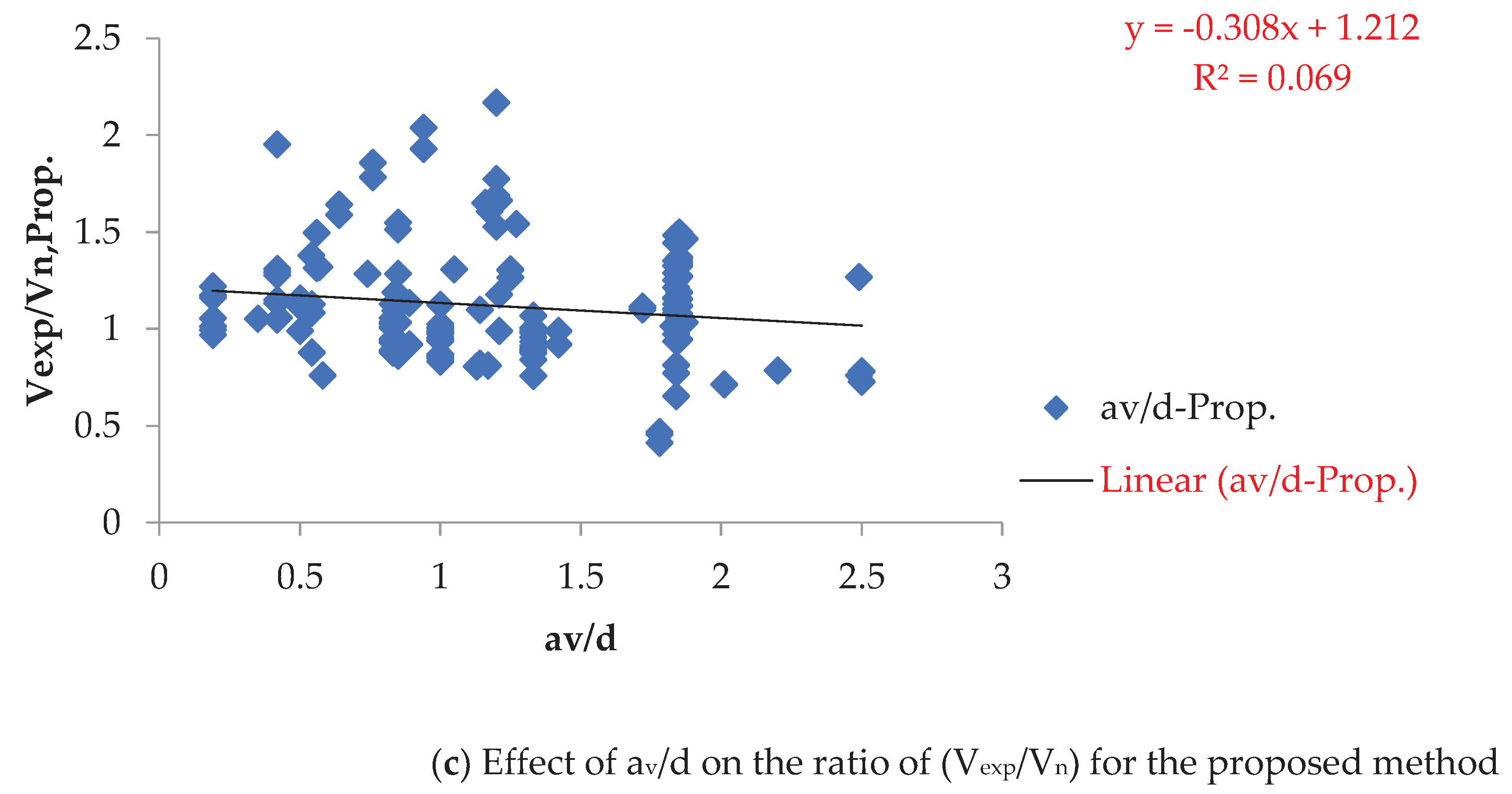
Figure 6. Effect of p_vf_yv (MPa) on the ratio of (V_exp/V_n).

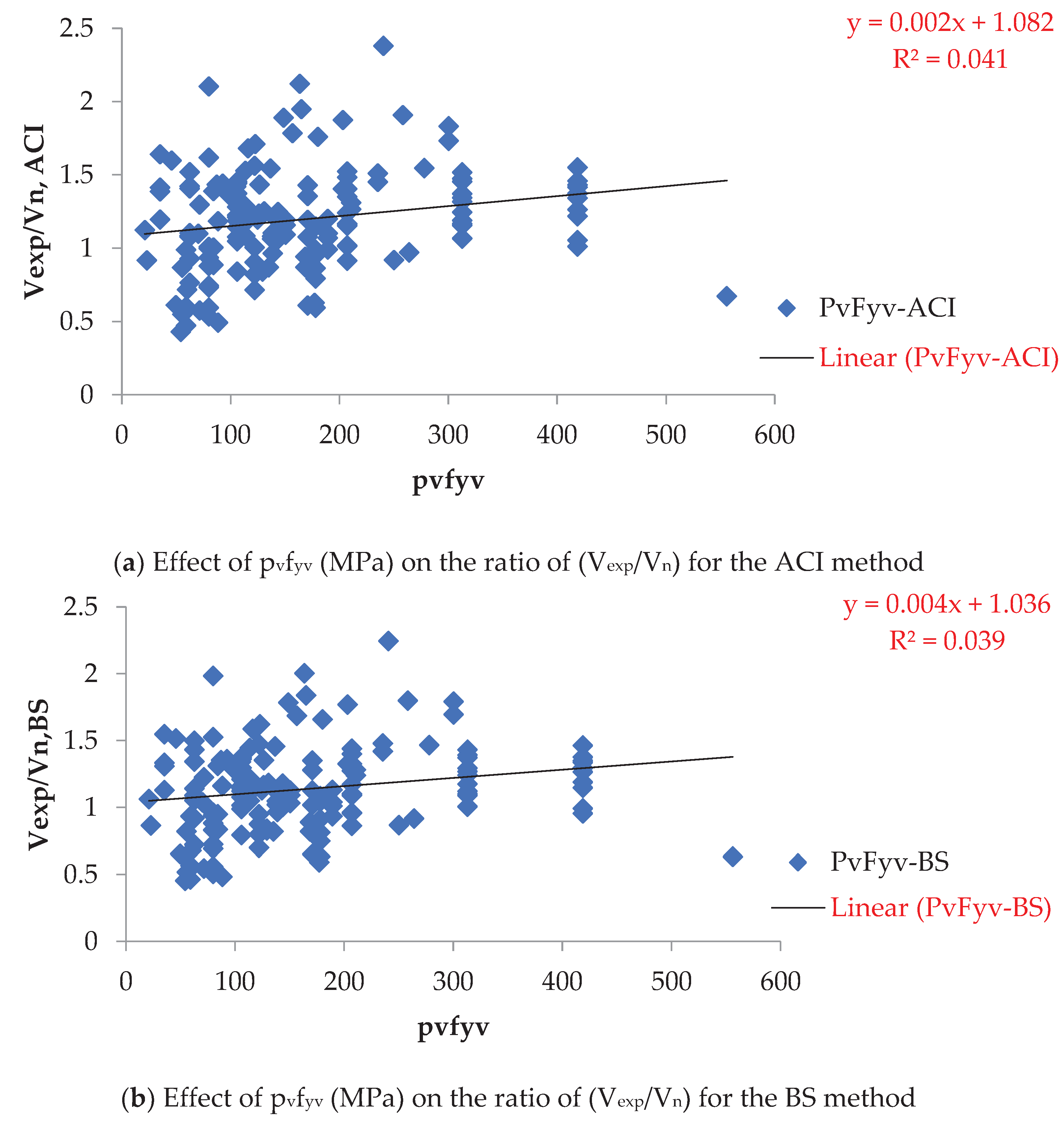
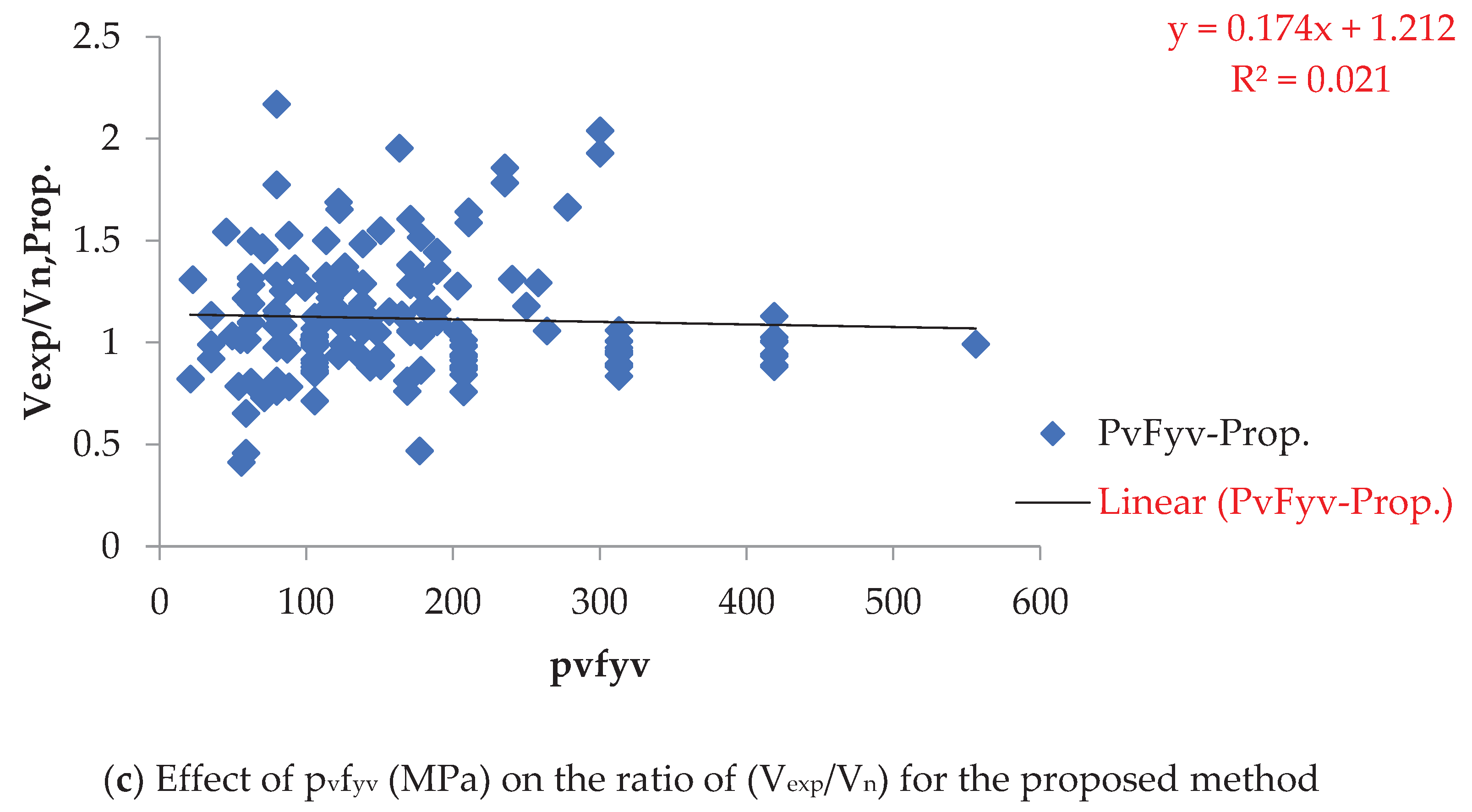
Figure 7. Effect of p_sf_y on the ratio of (V_exp/V_n).

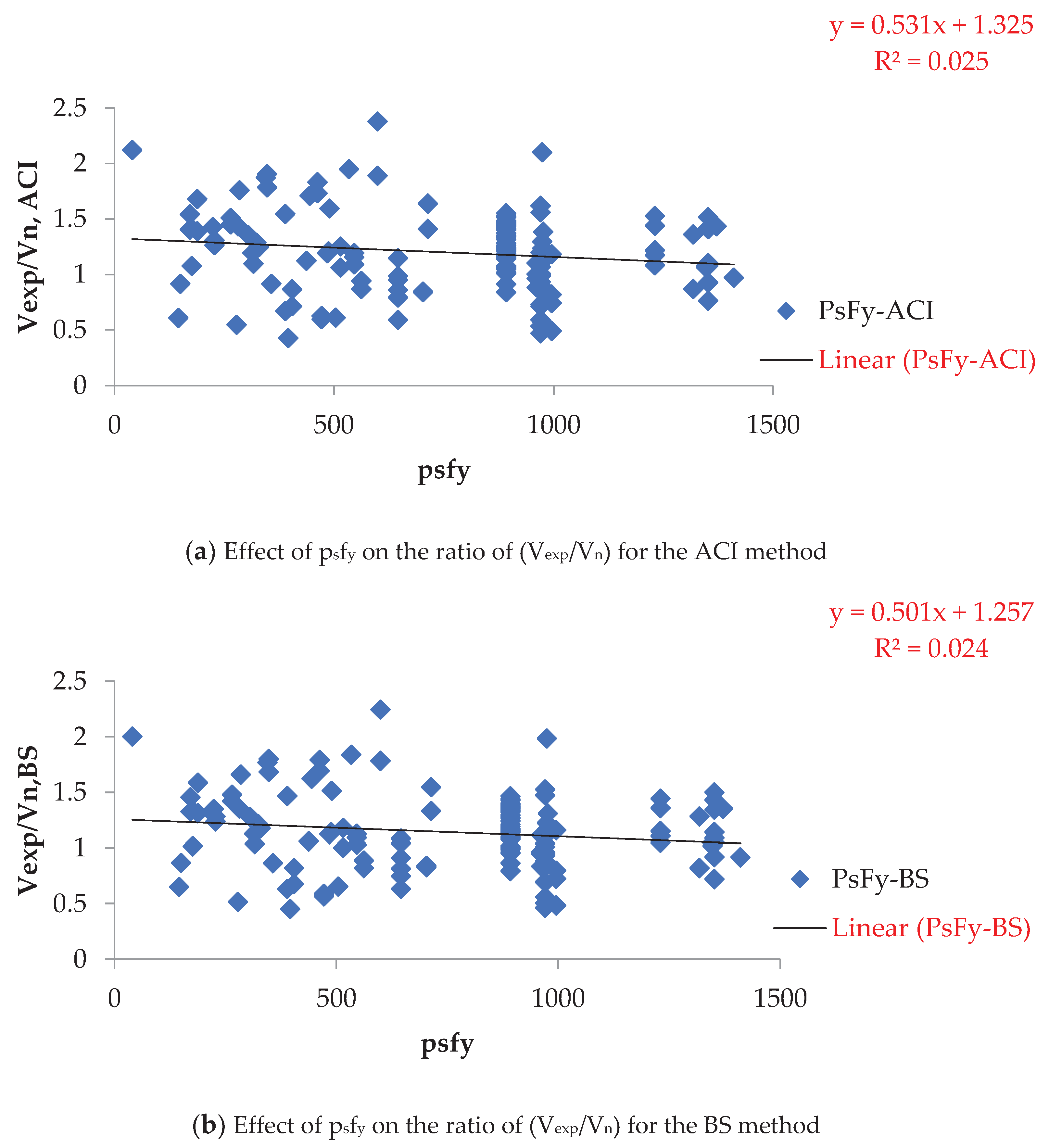
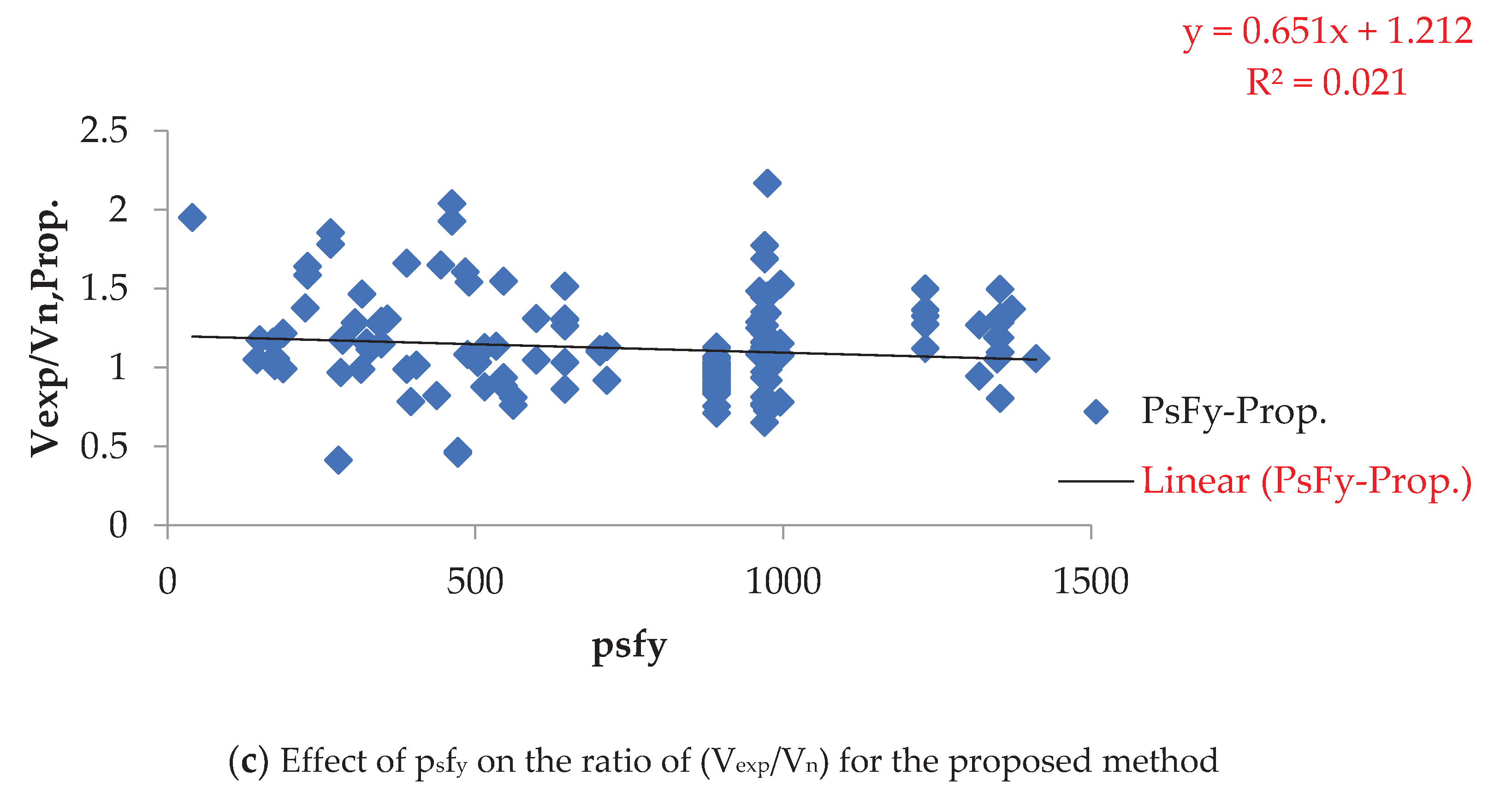
Figure 8. Effect of p_hf_yv on the ratio of (V_exp/V_n).

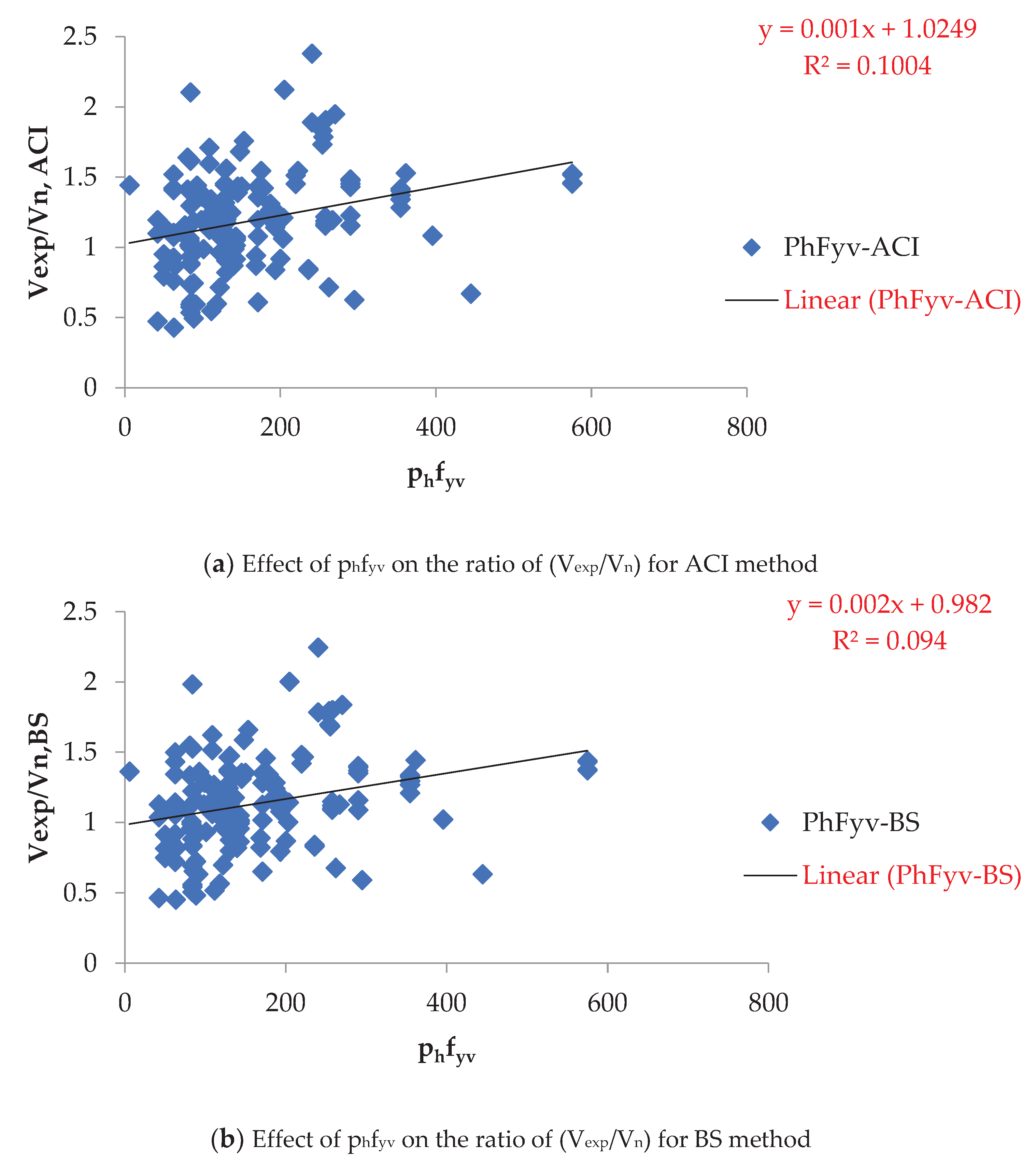
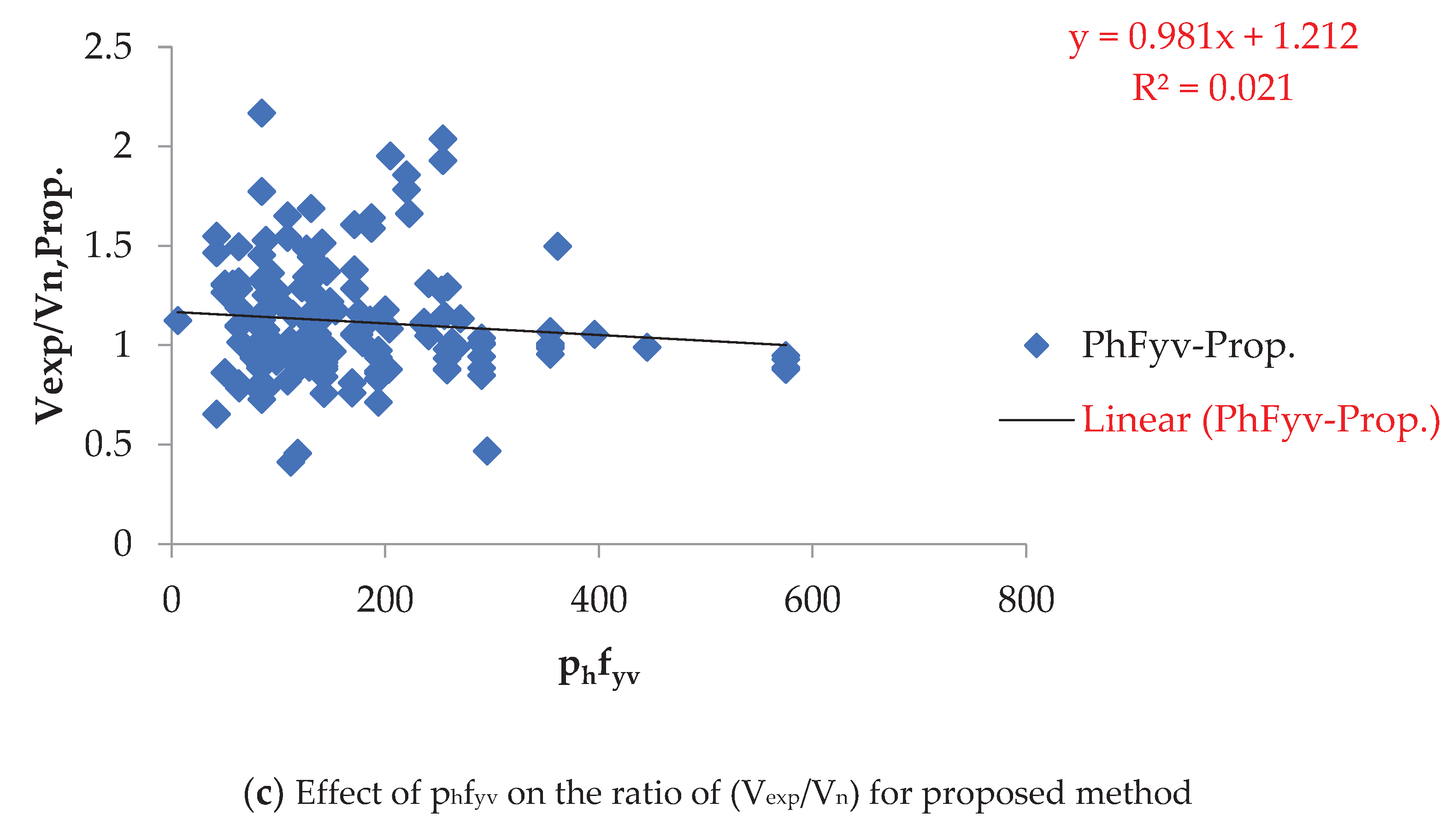
Figure 9. Comparison between experimental V_exp and predicted V_n shear strength for existing and proposed equations.

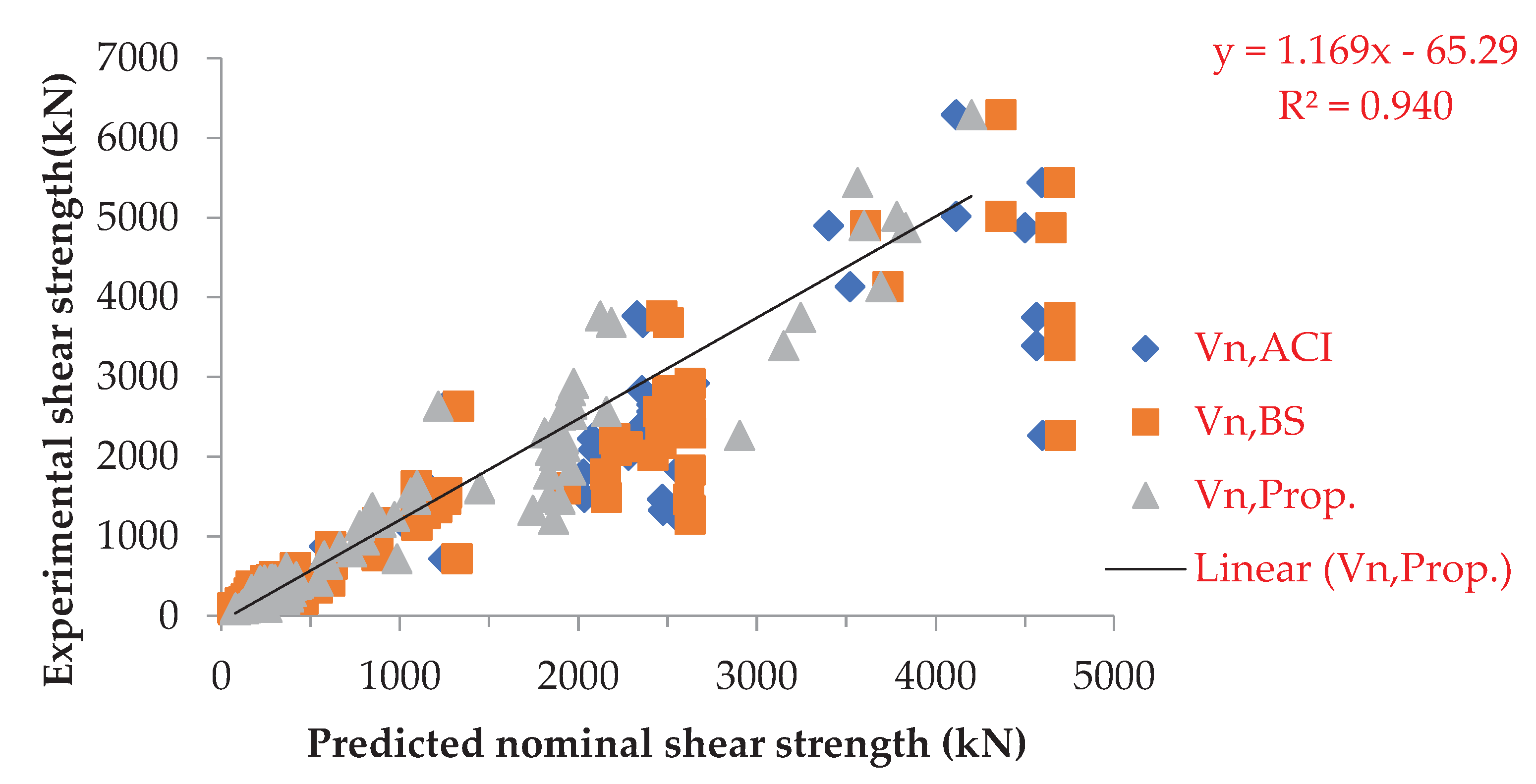
Table 1. The range data of the selected variables.

No.	Variable	Unit	Range
1	f’_c	MPa	16.08 -47.6
2	a_v/d	----	0.19-2.5
3	b_w	mm	76-914.4
4	p_s	----	0.176-3.1%
5	p_v	---	0.13-2.45%
6	p_h	-----	0-1%
7	d	mm	215.9-1752
8	f_yv	MPa	230-590
9	b_w×d	mm²	16416-939667.7
10	Vu	kN	77.8 -6294

Table 2. Empirical Equations for Estimating the nominal Shear Strength (V_n) RC Deep Beam.

Proposal No.	Combination of Equations	Proposed Empirical Equations
1	5×11×14+(15+17)	$A * {f ʻ c}^{B} * {p_{s}}^{C} * (\frac{a_{v}}{d})^{F} * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
2	5×12×14+(15+17)	$A * {f ʻ c}^{B} * {p_{s}}^{C} * (\frac{D}{E + (a_{v} / d)^{F}}) * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
3	5×13×14+(15+17)	$A * {f ʻ c}^{B} * {p_{s}}^{C} * (D + E / (a_{v} / {d)}^{F}) * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
4	6×11×14+(15+17)	$A * ({f ʻ c}^{B} + {p_{s}}^{C}) * (\frac{a_{v}}{d})^{F} * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
5	6×12×14+(15+17)	$A * ({f ʻ c}^{B} + {p_{s}}^{C}) * (\frac{D}{E + (a_{v} / d)^{F}}) * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
6	6×13×14+(15+17)	$A * ({f ʻ c}^{B} + {p_{s}}^{C}) * (D + \frac{E}{(a_{v} / d)^{F}}) * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
7	7×11×14+(15+17)	$A * ({f ʻ c}^{B} + C {* p}_{s}) * (\frac{a_{v}}{d})^{F} * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
8	7×12×14+(15+17)	$A * ({f ʻ c}^{B} + C {* p}_{s}) * (\frac{D}{E + a_{v} / d)^{F}}) * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
9	7×13×14+(15+17)	$A * ({f ʻ c}^{B} + C * p_{s}) * (D + \frac{E}{(a_{v} / d)^{F}}) * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
10	8×11×14+(15+17)	$A * {f ʻ c}^{B} * K^{C} * (\frac{a_{v}}{d})^{F} * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
11	8×12×14+(15+17)	$A * {f ʻ c}^{B} * K^{C} * (\frac{D}{E + (a_{v} / d)^{F}}) * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p_{h}) * f_{yv} * (b_{w} d)$
12	8×13×14+(15+17)	$A * {f ʻ c}^{B} * K^{C} * (D + \frac{E}{(a_{v} / d)^{F}}) * (\frac{G}{d})^{H} * (b_{w} d) + (k_{v} p_{v} + k_{h} p) * f_{yv} * (b_{w} d)$

Table 3. Values of the Coefficients (A-C and F-H) that used in the Selected Empirical Equation.

Coefficients	A	B	C	F	G	H
Values	0.004	0.17	0.65	-0.3	1	0.17

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Comprehensive Empirical Modeling of Shear Strength Prediction in Reinforced Concrete Deep Beams

Abstract

1. Introduction

2. Methodology

2.1. Existing Experimental Investigations

2.2. Codes Procedure, for Calculating the Resistance of RC Beams

2.3. Statistical Properties of Dataset

3. The Proposed Empirical Equations

4. Evaluation of the Developed Empirical Equation

5. Discussion

6. Conclusions

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

Appendix A

References

MDPI Initiatives

Important Links

Subscribe