Prerpints.org logo
Preprint
Article

Robust Combined Adaptive Passivity-Based Control for Induction Motors

Altmetrics

Downloads

85

Views

29

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

18 March 2024

Posted:

22 March 2024

You are already at the latest version

Alerts
Abstract
The need for industrial and commercial machinery to maintain high torque while accurately following a variable angular speed is increasing. To meet this demand, induction motors (IMs) are commonly used with variable speed drives (VSDs) that employ a field-oriented control (FOC) scheme. Over the last thirty years, IMs have been replacing independent connection direct current motors due to their cost-effectiveness, reduced maintenance needs, and increased efficiency. However, IMs and VSDs exhibit nonlinear behavior, uncertainties, and disturbances. This paper proposes a robust combined adaptive passivity-based control (CAPBC) for this class of nonlinear systems that applies to angular rotor speed and stator current regulation inside an FOC scheme for IMs´ VSDs. It uses general Lyapunov-based design energy functions and adaptive laws with σ-modification to assure robustness after combining control and monitoring variables. Lyapunov’s second method and Barbalat Lemma prove that the control and identification error tends to be zero over time. Moreover, comparative experimental results with standard Proportional Integer controller (PIC) and direct APBC, show the proposed CAPBC effectiveness and robustness under normal and changing conditions
Keywords: 
Subject: Engineering  -   Control and Systems Engineering

1. Introduction

Since the late 1800s, machines used in industry and commerce have relied on direct current (DC) motors with DC variable speed drives (VSDs) based on Thyristor rectifiers for high starting torque and variable speed accuracy. However, these DC motors tend to spark and are susceptible to threading, grooving, and flashover, as noted in [1]. As a result, induction motors (IMs), particularly the squirrel cage type, have gradually replaced them over the past three decades. IMs are more cost-effective and efficient and require less maintenance, as stated in [2]. Consequently, the sales of IMs have increased by 85%, accounting for 60% of the total electricity consumption in the industrial sector [2].
However, due to their nonlinear characteristics, alternating current (AC) VSDs are more complex than DC VSDs [2]. They require IGBT-based inverters to regulate the stator voltage and frequency. AC VSDs may use three control schemes: scalar control [3], direct torque control (DTC) [4,5], and field-oriented control (FOC) [6,7]. Nevertheless, the indirect FOC (IFOC) scheme [7] delivers higher output torque, higher stationary speed accuracy, and fast and non-oscillatory transient behavior. It performs more closely to DC’s VSDs for the machinery under study in this manuscript.
The IFOC method simplifies the mathematical model of an IM by choosing a specific electrical angular slip. This simplification allows for the independent control of the electromagnetic torque and the rotor magnetic flux [8]. The basic IFOC relies on knowledge of the rotor time constant ( τ r ) and uses proportional integral controllers (PICs). These PICs assume constant angular rotor speed operation and neglect disturbances such as load torque and the inverter model uncertainty to deal with simple linear dynamical systems (LDSs) [9]. Adjusting them also requires information on all the motor-load parameters, which can be obtained from diverse methods [10], such as offline algorithms [11,12], offline tests [13,14], and self-commissioning tests [15,16].
As an alternative, robust adaptive controllers ensure robustness under parameter variations without relying on their explicit knowledge [17,18,19]. There are three approaches to adaptive control - direct (D), indirect (I), and combined (C) [19]. The direct method is the most widely used. It has been applied to various applications such as self-piloted crafts [20,21,22], robotics [23,24,25], power systems [26,27], including induction motors [28,29,30]. However, the combined method proposed in the work [31] aims to improve the transient performance beyond the direct and indirect dynamic methods. Therefore, this manuscript uses the combined method.
In particular, [31] introduced the C approach for the model reference adaptive control (MRAC) technique applied scalar LDS. Later, [32] applied CMRAC to pH control for a chemical reactor, outperforming a PID controller and DMRAC. The method was then extended to single-input and single-output (SISO) LDS by controlling longitudinal airplane movement [33]. These studies consider unknown plant parameters with the known sign of the input parameter b, referred to as the Known Control Direction (KCD). The KCD assumes that the input parameter equals its unknown modulus multiplied by its known sign. This is valid for SISO plants and MIMO systems with a diagonal input matrix B where B = | B | s i g n ( B ) , such as IMs.
On the other hand, [34,35] propose a CMRAC for MIMO LDS. However, they assume a known input matrix B, substantially simplifying the adaptive control problem. Meanwhile, [36] considered an adaptive control law with a known input matrix substituted by its estimate. Lastly, [37,38] neglected the estimation error and considered an unknown input matrix to control uncrewed underwater and air vehicles, respectively. Hence, this manuscript uses the ideas originally proposed by CMRAC [31,32,33] to extend the D adaptive-passivity-based control (APBC) technique [30], which is ensure faster results than MRAC for the IFOC scheme.
As a contribution, this paper proposes a new control technique called CAPBC for a broader class of MIMO nonlinear linear dynamical systems (NLDS). The proposed technique can handle systems with unknown time-varying parameters and bounded external disturbance, including the case of IMs. The CAPBC takes into account the closed-loop estimation error, which was first introduced by Duarte et al. [31], and uses time-varying gains (TVGs) [39]. To ensure robustness, the CAPBC incorporates a MIMO sigma-modification [17,18,19]. The proposed technique was applied to the outer and inner controllers of an IFOC scheme for IMs and tested in a laboratory. The contributions of this proposal are detailed as follows:
1.
Proposing a novel CAPBC. The paper proposes a novel CAPBC technique that extends the existing DAPBC scheme from [30]. Compared to previous works [31,32,33], the CAPBC can handle a wider range of MIMO NLDS with bounded external disturbance and unmodeled dynamic. In contrast to [34,35,36,38], the proposal considers the estimation error originally proposed by [31,32,33].
2.
Implementing a SISO CAPBC angular speed control. The proposed technique is applied to the outer loop of an IFOC for IMs, where it controls the angular speed. Implementing the CAPBC is more complex than the DAPBC from [30] but improves performance by incorporating online parameters adaptive estimation. The controller does not require knowledge of the motor load mechanical parameters, unlike the PIC.
3.
Implementing a MIMO CAPBC d-q axis current control. The proposed technique is also applied to the inner loop of an IFOC for IMs, where it controls the stator current vector components. In contrast to previous works [34,35,36,38], the CAPBC can handle systems with an utterly unknown B with a known control direction - UCD, which is the case for IMs.
4.
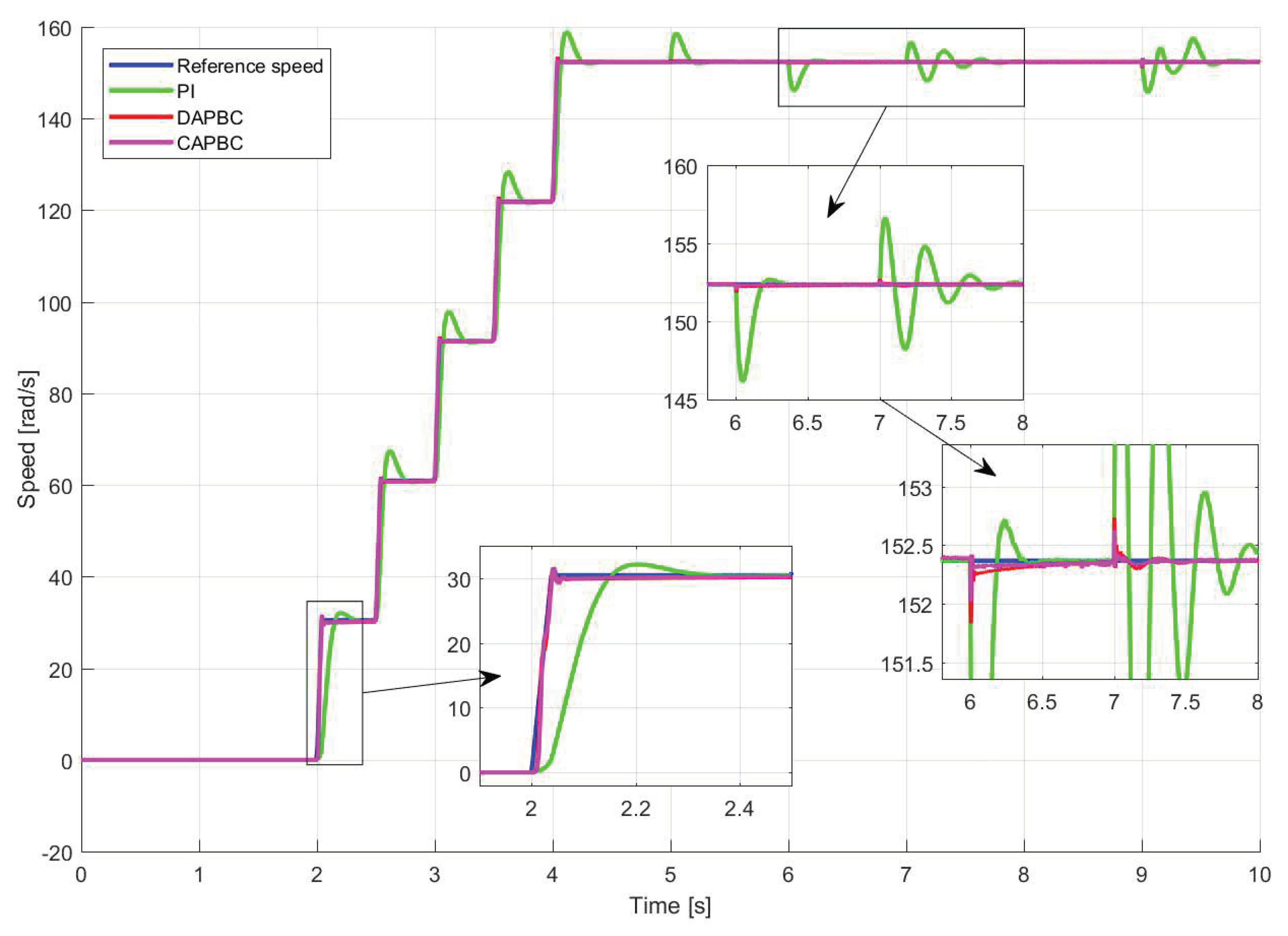
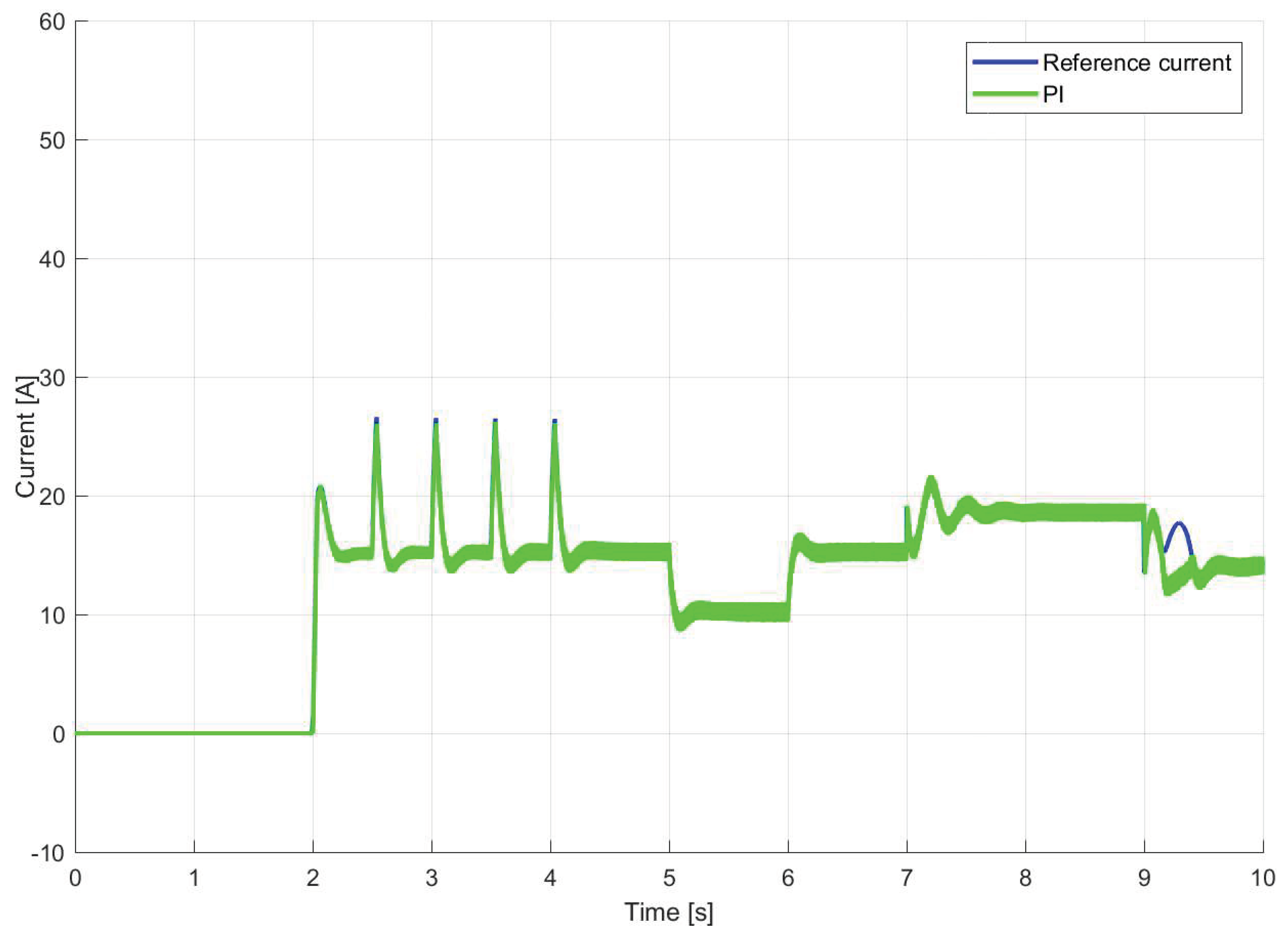
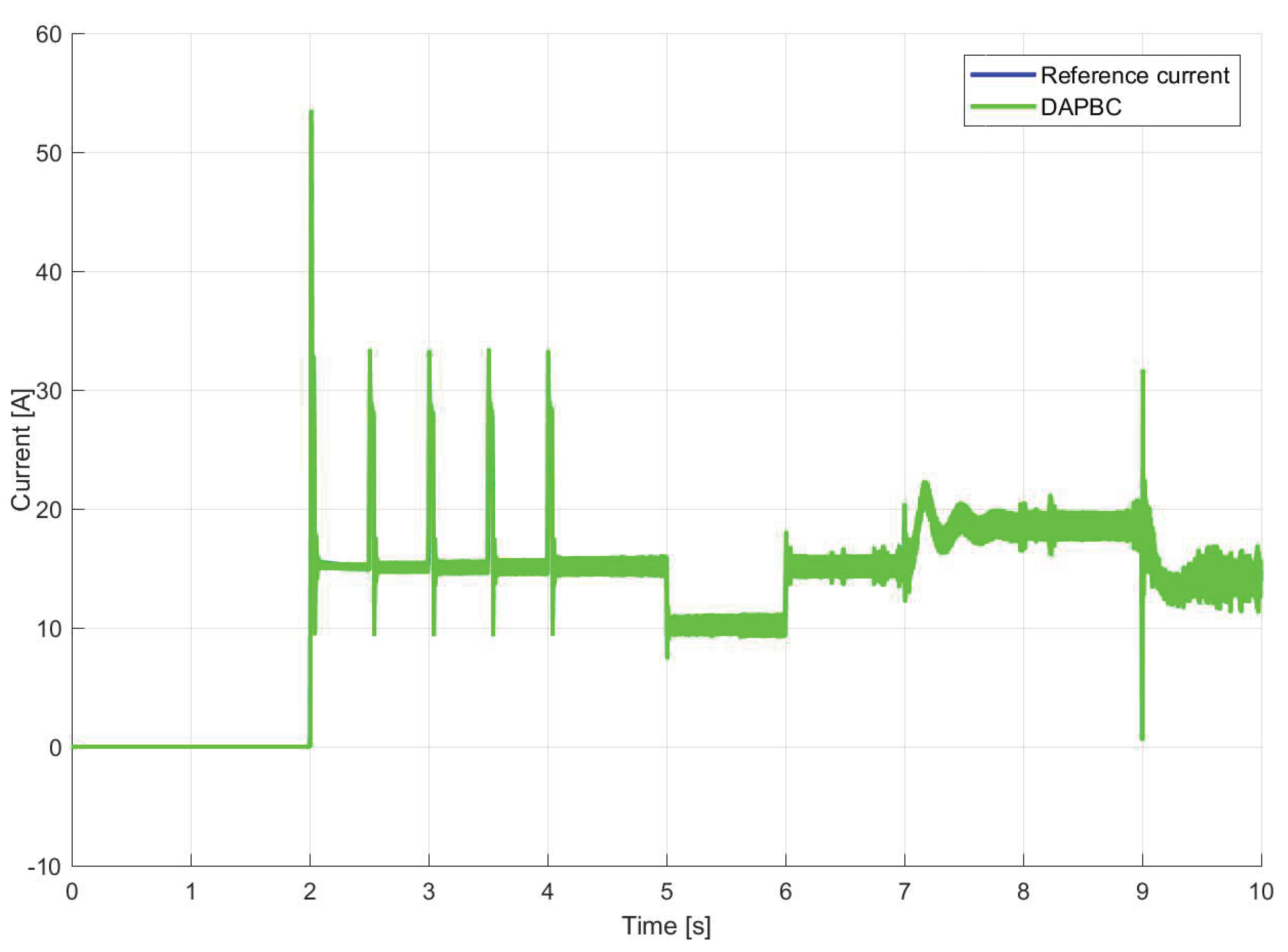
Presenting comparative experimental results. The paper presents experimental results that compare the proposed CAPBC, DAPBC, and PIC techniques in an IFOC scheme for IMs. These tests include more changes than the ones considered in previous studies [28,29,30]. Specifically, the tests consider changes in angular speed reference, parameters that affect field orientation, and load torque. The results demonstrate that the proposed technique is effective and outperforms DAPBC and PIC techniques.
This paper has five sections. The first section is the introduction. Section 2 explains the IM dynamical model and the IFOC control scheme for IMs. This section also provides detailed information on the PIC adjustments and CMRAC basis. Section 3 proposes the CAPBC method for a specific type of nonlinear system that includes IMs. In addition, the authors provide theoretical proof of the proposed method. Section 4 depicts comparative experimental results with PIC and DAPBC, showing the effectiveness and robustness of CMRAC. This section also includes a discussion of the results. Lastly, Section 5 concludes the findings of the paper.

2. Preliminaries

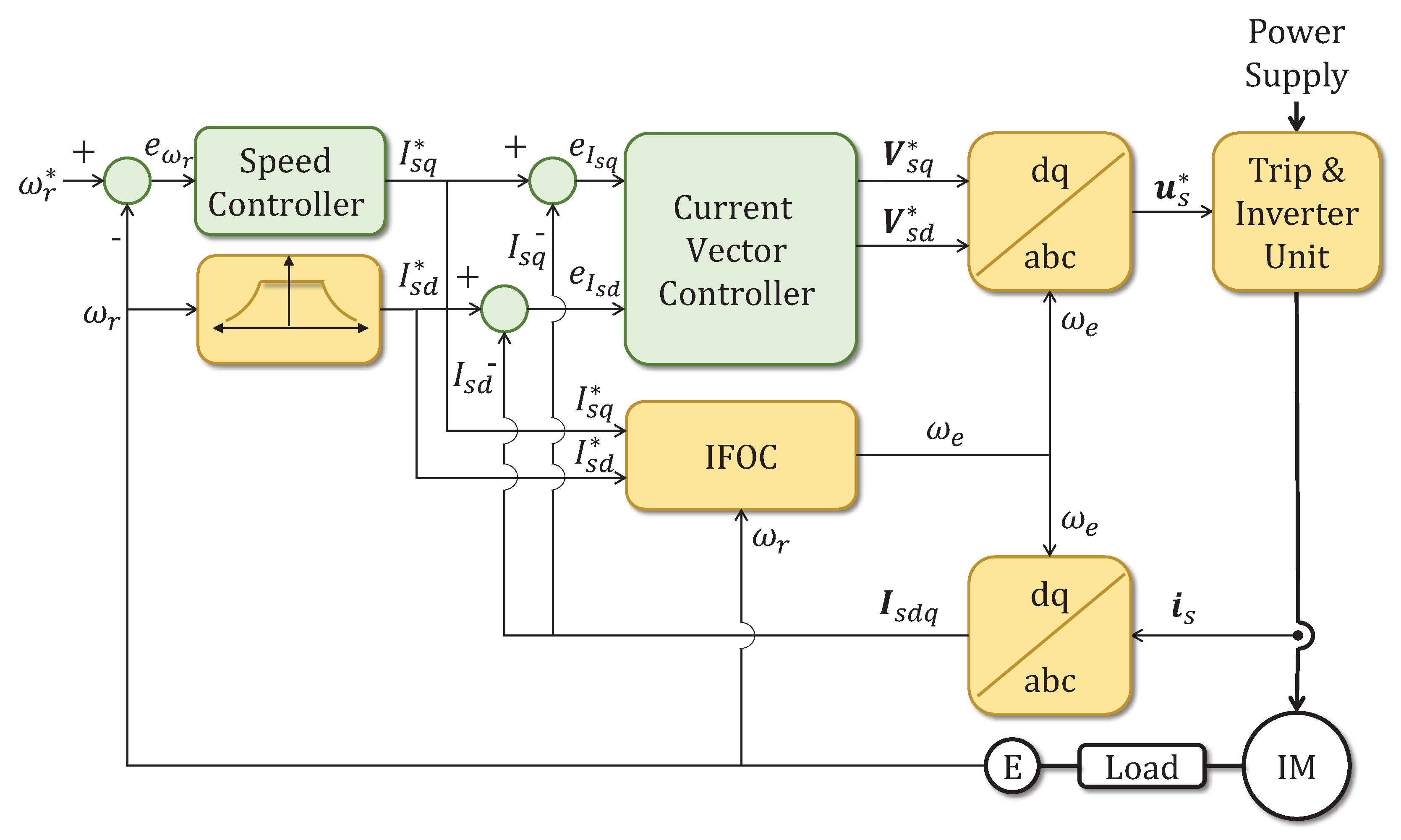
2.1. d-q IM Dynamic Model and IFOC Diagram

The IM model considers a two-pole machine whose results can be expanded for more poles. It is assumed that the rotor and stator windings are distributed symmetrically, the signals are sinusoidal (neglecting the harmonic effects), hysteresis, iron losses, and saturation are negligible. The machine operates within the linear zone, and all motor parameters are constant and referred to the stator. Moreover, a quadrature-phase machine with a smooth air gap is considered [40] (Section 2.1.5). Kirchhoff laws for the stator and rotor circuit are applied [40], and the Park transformation [41] is used to shift the electrical equations to a rotating synchronous reference frame. The vectors are then split into real and imaginary parts, and the IM d-q model used by the FOC scheme is obtained. This is combined with the motion equation obtained from the second Newton law for rotational motion, resulting in:
I ˙ s d = − R s ′ σ L s I s d + ω e I s q + R r L m σ L s L r 2 Ψ r d − L m σ L s L r p 2 ω r Ψ r q + 1 σ L s V s d , I ˙ s q = − R s ′ σ L s I s q − ω e I s d + R r L m σ L s L r 2 Ψ r q + L m σ L s L r p 2 ω r Ψ r d + 1 σ L s V s q , Ψ ˙ r d = − R r L r Ψ r d + ω e − p 2 ω r Ψ r q + R r L m L r I s d , Ψ ˙ r q = − R r L r Ψ r q − ω e − p 2 ω r Ψ r d + R r L m L r I s q , ω r ˙ = − D J ω r − 1 J ( T e − T l ) , with T e = 3 2 p 2 L m L r Ψ r d I s q − Ψ r q I s d
Here, the variables are the amplitude of the sinusoidal signals at the motor terminals expressed as the direct and quadrature stator current amplitudes I s d , I s q , the direct and quadrature stator voltage amplitudes V s d , V s q , and the direct and quadrature rotor flux amplitudes Ψ r d and Ψ r q . ω r is the rotor angular speed at the shaft, ω e is the angular electrical frequency or speed of the synchronous reference frame, T e is the electromagnetic motor output torque and T l is the load torque. The parameters R s , R r are the stator and rotor resistances of a phase winding, p are the poles number, J is the motor-load inertia, and D is the viscous coefficient, L s , L r and L m are the stator, rotor, and magnetizing inductances respectively, σ = 1 − L m 2 L r L s is the dispersion coefficient and R s ′ = R s + L m 2 R r L r 2 is the stator transient resistance.
Remark 1: The coupling between electromagnetic torque, stator current, and rotor flux can be observed in equation (1). As a solution, the IFOC is then achieved for the IM d-q model (1) after imposing the following electrical angular frequency (please see details in Appendix 6) and operating with a fixed I s d *
ω e = p 2 ω r + α 1 τ ^ r I s q * I s d * .
Here, τ ^ r is the estimated rotor time constant given by τ ^ r = L r R r ^ and α = 1 . As a result, the quadrature component of the rotor flux tends to zero Ψ r q → 0 , Thus Ψ r d → L m I s d and the electromagnetic torque T e → K T e I s q , with a constant K T e = 3 2 p 2 L m 2 L r I s d . Therefore, the following simplified IM d-q model is obtained:
I ˙ s d = − R s ′ σ L s I s d + ω e I s q + R r L m 2 σ L s L r 2 I s d + 1 σ L s V s d , I ˙ s q = − R s ′ σ L s I s q + − ω e I s d + L m 2 σ L s L r p 2 ω r I s d + 1 σ L s V s q , ω r ˙ = − D J ω r − K T e I s q + 1 J T c .
Then I s d is fixed and controlled to achieve constant rotor flux control and I s q is used to control the electromagnetic torque the load demands at different rotor speeds. This way torque and flux can be controlled independently, similar to DC machines, which is the aim of the IFOC (3). Figure 1 depicts the IFOC block diagram.
Remark 2: The simplified d-q model (3) has the nonlinear terms ω e I s d , ω e I s q , and ω r I s d . Moreover, the load torque term T l is often considered as a disturbance.
The following section describes the adjustment of the basic PIC considered for rotor angular speed and stator current vector of the IFOC for IMs. This controller assumes the operation at a fixed angular rotor speed. Thus, ω e and ω r are constant, and model (3) behaves as an LDS. Furthermore, the outer loop PIC neglects the T l disturbance and expects robustness in front of its variations.

2.2. PIC adjustment

Appendix 7 describes the PIC adjustment theory in detail. As a summary, the inner current controllers’ parameters are computed as follows:
V s q * = K p i e I s q + K i i ∫ e I s q d τ and V s d * = K p i e I s d + K i i ∫ e I s d d τ where K p i = R s ′ τ i ω n i 2 K c H i and K p i = R s ′ ( τ i 2 ξ i ω n i − 1 K c H i .
Here, V s q * and V s d * are the direct and quadrature stator voltage references, K p i and K i i are the PICs inner proportional and integer parameters, e I s q and e I s d are the direct and quadrature stator current errors, τ i is the electrical time-constant, K c is the inverter gain, and H i is the current sensor gain.
As design criteria, a root locus method is often applied. The inner damping coefficient value ξ i is chosen between 0 . 5 and 0 . 8 , with the most common value for this application considering ξ i = 2 2 ≈ 0 . 707 . The inner natural frequency equals ω n i = 2 . 3 τ i [42], which in this AC drive case should be higher than the switching frequency of the inverter´s IGBTs having a value between 1.7 kHz and 16 kHz for output powers between 1500 kW and under 37 kW, respectively [43].
Moreover, the outer angular speed controllers’ parameters are computed as follows:
I s q * = K p o e ω r + K i o ∫ e ω r d τ K T e − 1 where K i o = H i D τ o ω n o 2 H o and K p o = H i D ( 2 ξ o ω n o τ o − 1 ) H o ,
where I s q * is the quadrature stator current set point, K p o and K i o are the PICs outer proportional and integer parameters, e ω r is the rotor angular speed error, τ o is the mechanical time-constant, H o is the speed sensor gain. Here, the squared outer natural frequency is ω n o 2 = ( K i o H o ) / ( H i D τ o ) , which is used to obtain the fixed-gain parameter K i o of the controller after considering ω n o = ω n i 15 [42,44]. The term depending on the outer natural frequency ω n o and the outer damping coefficient ξ o is 2 ξ o ω n o = ( H i D + K p o H o ) / ( H i D τ o ) , and it is used to compute the fixed-gain parameter K p o of the controller.
Remark 3: Please observe that PIC adjustment depends on the knowledge of the plant parameter values. Here, the resistances vary with the motor temperature, for instance. Therefore, using an adaptive controller would assure robustness regarding parameter variations.
The following section describes the CMRAC basis that this manuscript considers when proposing CAPBC.

2.3. CMRAC basis to be expanded for APBC

The CMRAC applies to scalar LDS dynamical systems, with relative degree 1 of the following form:
y ˙ ( t ) = a y ( t ) + b u ( t ) .
Here, the plant parameters a, and b, ∈ R are constant and unknown, with known s i g n ( b ) . The variable y r ( t ) ∈ R is the reference model output and y ^ ( t ) ∈ R is the identification model output. The bounded reference trajectory is y * ( t ) ∈ R . Furthermore, e c = ( y r ( t ) − y ( t ) ) ∈ R and e i ( t ) = ( y ^ − y ( t ) ) ∈ R are the control and identification errors. The adaptive parameters for control is θ ^ c ( t ) and for identification θ ^ i ( t ) . The designer chooses the model parameters b r , k c ∈ R + and k i ∈ R , and ω c , ω i ∈ R 2 are the control and identification vector information. Finally, the ideal controller parameters θ 1 , θ 2 ∈ R fulfill the condition:
− ( a + k c ) + b θ 1 = 0 and − b r + b θ 2 = 0 .
Figure 1 shows the CMRAC control diagram for LDS dynamical systems.
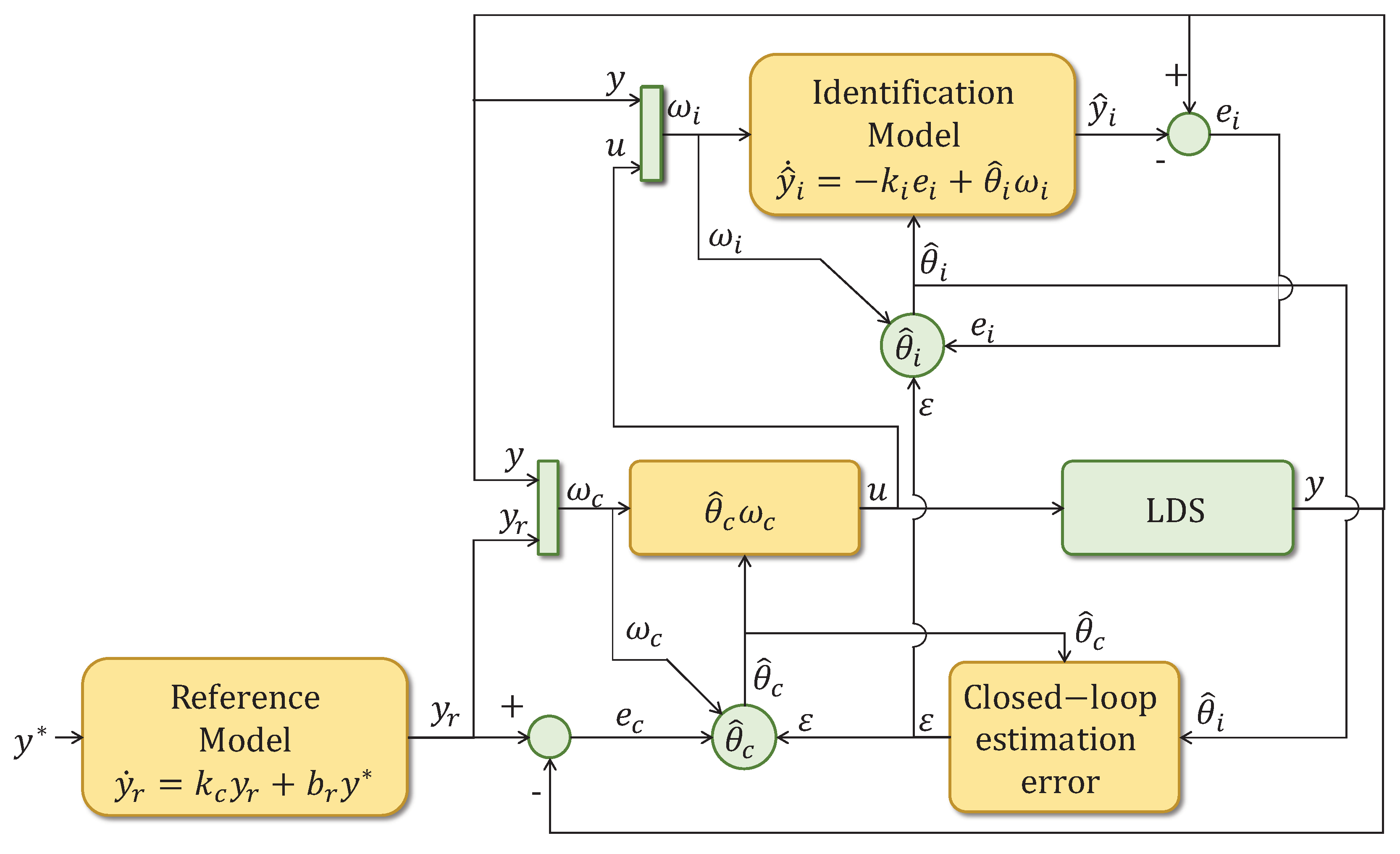
Preprints 101620 g002
Figure 2. CMRAC diagram.
Figure 2. CMRAC diagram.
Preprints 101620 g002
The CMRAC has associated the following equations [31]:
y ˙ r ( t ) = − k c y r ( t ) + b r y * ( t ) , Reference model
y ^ ˙ ( t ) = − k i e i + θ ^ i ω i , Identification model
u ( t ) = θ ^ c ω c , Control law
θ ˙ 1 ( t ) = s i g n ( b ) e c ( t ) y ( t ) + ε 1 ( t ) , θ ˙ 2 ( t ) = s i g n ( b ) e c ( t ) y r ( t ) + ε 2 ( t ) , Control adaptive law
ε 1 ( t ) = − ( a ^ + k c ) + b ^ ( t ) θ 1 ( t ) , ε 2 ( t ) = − b r + b ^ ( t ) θ 2 ( t ) , Closed - loop estimation error
a ^ ˙ ( t ) = − e i ( t ) y ( t ) − ε 1 ( t ) , b ^ ˙ ( t ) = − e i ( t ) u ( t ) − ε 1 ( t ) θ 1 ( t ) − ε 2 ( t ) θ 2 ( t ) . Identification adaptive law
Once applied this CMRAC to system (6) and assumed b = | b | s i g n ( b ) , the obtained closed-loop autonomous system ensures that e c ( t ) , e i ( t ) , ε 1 ( t ) and ε 2 ( t ) tends asymptotically to zero.
Remark 4: The C approach improves the D and I approaches after considering the closed-loop estimation error. However, it does not apply to NDSL with disturbances and unmodeled dynamics.
Based on the previous background and as a solution to the described issues, the following section proposes a robust CAPBC for MIMO NLDS.

3. Proposed CAPBC

Figure 2 shows the proposed CAPBC diagram.
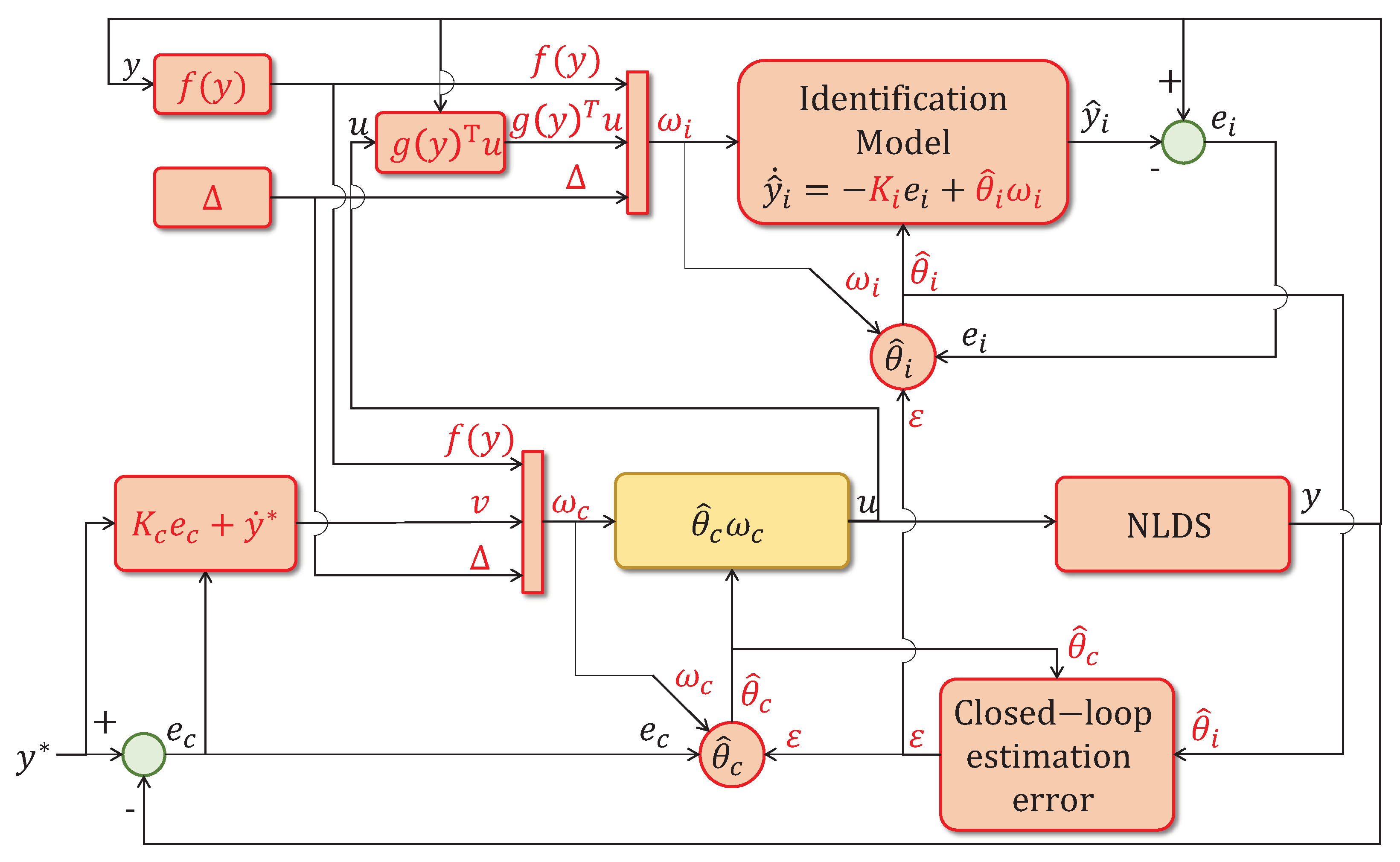
Preprints 101620 g003
Figure 3. Proposed CAPBC diagram for MIMO NLDS, remarking the differences in red.
Figure 3. Proposed CAPBC diagram for MIMO NLDS, remarking the differences in red.
Preprints 101620 g003
It applies to MIMO dynamical systems of the form:
y ˙ ( t ) = A T f ( y ) + B T g ( y ) T u + δ T Δ + ζ .
Here, the output y ( t ) ∈ R n and the input u ( t ) ∈ R n are accessible. The functions g ( y ) ∈ R n x n , and f ( y ) ∈ R m are known, like the disturbance portion Δ ∈ R n . The unmodeled dynamics ζ ∈ R n is unknown, as well as the plant parameters A T ∈ R n x m , B T , δ T ∈ R n x n .
The following theorem details the proposed CAPBC for the class of MIMO NLDS (14):
Theorem 1: The following CAPBC assures the output y ( t ) ∈ R n of NLDS (14) tracks the reference y * ( t ) ∈ R n while observe it via y ^ ( t ) ∈ R n :
y ^ ˙ ( t ) = − K i ▿ V e i ( t ) T + θ ^ i T ω i , Identification model
u ( t ) = g ( y ) − 1 θ ^ c T ω c , Control law
θ ^ ˙ c T = S T ▿ V e c ω c T − S T ε T Γ ε − 1 + σ c θ ^ c T Γ c , Control adaptive law
ε = ε 1 ε 2 ε 3 = B ^ T θ ^ 1 T + A ^ T B ^ T θ ^ 2 T − I n B ^ T θ ^ 3 T + δ ^ T , Closed - loop estimation error
θ ^ ˙ i T = ω i T ▿ V e i − ε T Γ ε − 1 ( P 1 T + θ ^ c P 2 T ) + σ i θ ^ i T Γ i , Identification adaptive law
Here, ▿ V e c ∈ R 1 x n and ▿ V e i ∈ R 1 x m are the gradients of the design Lyapunov-type energy functions V e c and V e i . The control and identification errors are e c ( t ) = y * ( t ) − y ( t ) and e i ( t ) = y ( t ) − y ^ ( t ) , with e c ( t ) , e i ( t ) ∈ R n . The adaptive controller and identification parameters are θ ^ c T and θ ^ i T ( t ) ∈ R n x ( 2 n + m ) , depending on the control and identification adaptive law modifications σ c and σ i ∈ R n x n , which are positive-definite. The information vectors for control and identification are ω c and ω i ∈ R ( 2 n + m ) x 1 , where ω c T = f ( y ) T ( K c e c + y ˙ * ) T Δ T T and ω i T = f ( y ) T ( g ( y ) T u ) T Δ T T . The auxiliary known parameters P 1 = I m 0 0 0 0 n 0 0 0 I n and P 2 = 0 m I n 0 n , where I m and I n are identity matrix of order m and n, respectively. Moreover, 0 n and 0 m are null matrix of order n and m, respectively. The estimated plant parameter θ ^ i T = A ^ T B ^ T δ ^ T (19), finds A ^ ∈ R n x m and B ^ , and δ ^ ∈ R n x n . The estimated controller parameter θ ^ c T = θ ^ 1 T θ ^ 2 T θ ^ 3 T (17), computes θ ^ 1 ∈ R n x m and θ ^ 2 , and θ ^ 3 ∈ R n x n . Later, these results allow implementing the closed-loop estimation error (18).
The designer adjusts the control and identification gains Γ c , Γ i and Γ ε ∈ R ( 2 n + m ) x ( 2 n + m ) , where Γ c = Γ ε = μ c 1 + ω c n T ω c n , Γ i = μ i 1 + ω i n T ω i n , where ω c n and ω i n are the vectors containing the upper operational range of each element of ω c and ω i . Also, it adjusts the forgetting factors μ c ∈ R + , and μ i ∈ R + [45] - (Section 4.3.6) & (Remark 4.3.7). Furthermore, designer adjusts controller parameters K c , and K i ∈ R n x n . The ideal control and identification parameters are θ c T and θ i T ∈ R n x ( 2 n + m ) , which are defined as follows:
θ i T = A T B T δ T
B T θ 1 T + A T = 0 , B T θ 2 T − I n = 0 and B T θ 3 T + δ T = 0 .
The error of the parameters are Φ c T , and Φ i T ∈ R n x ( 2 n + m ) given by ϕ c T = θ c T − θ ^ c T , and ϕ i T = θ i T − θ ^ i T .
Appendix 8 describes the CAPBC stability proof. ⋄
The following section discusses the comparative experimental results that were obtained.

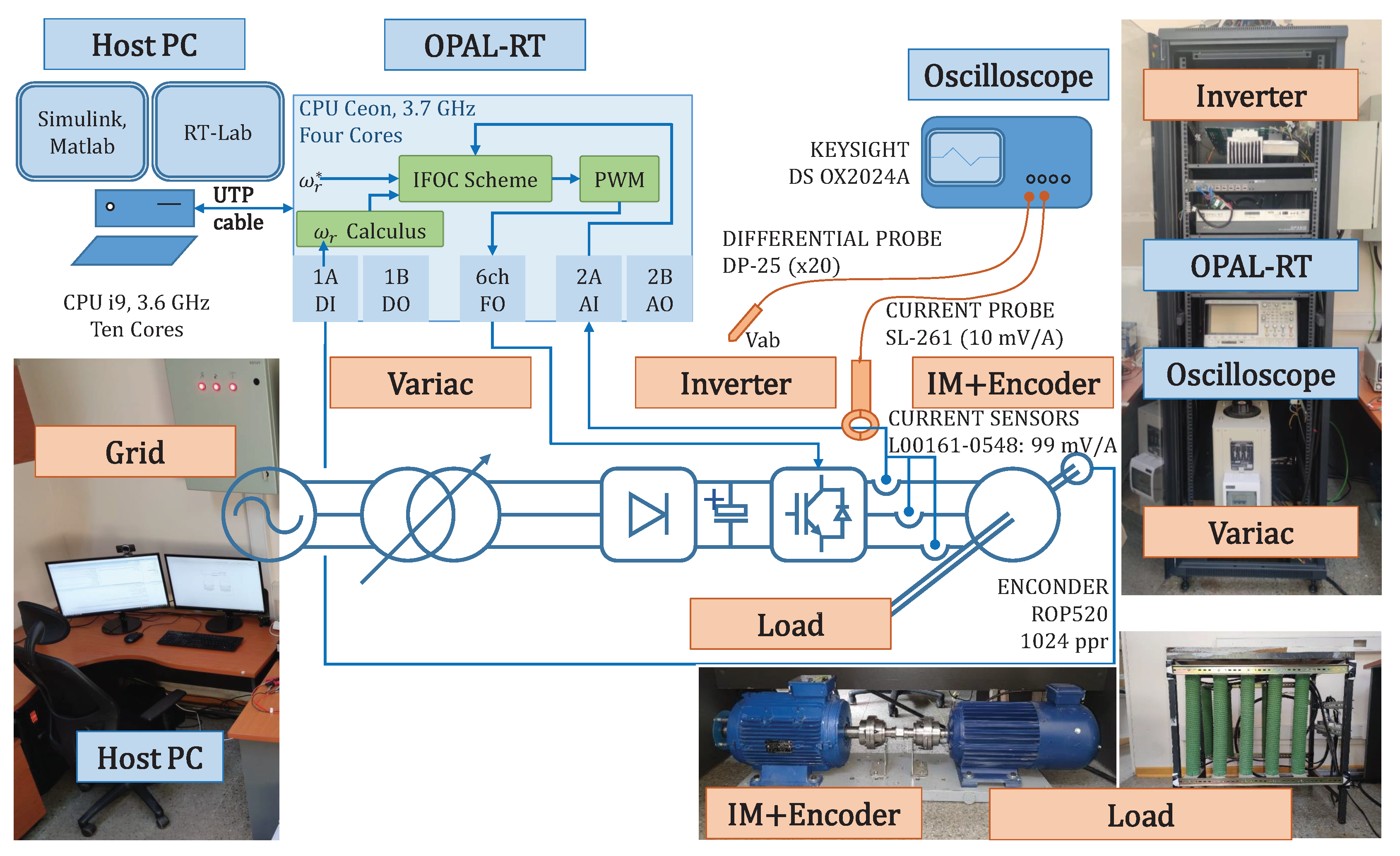
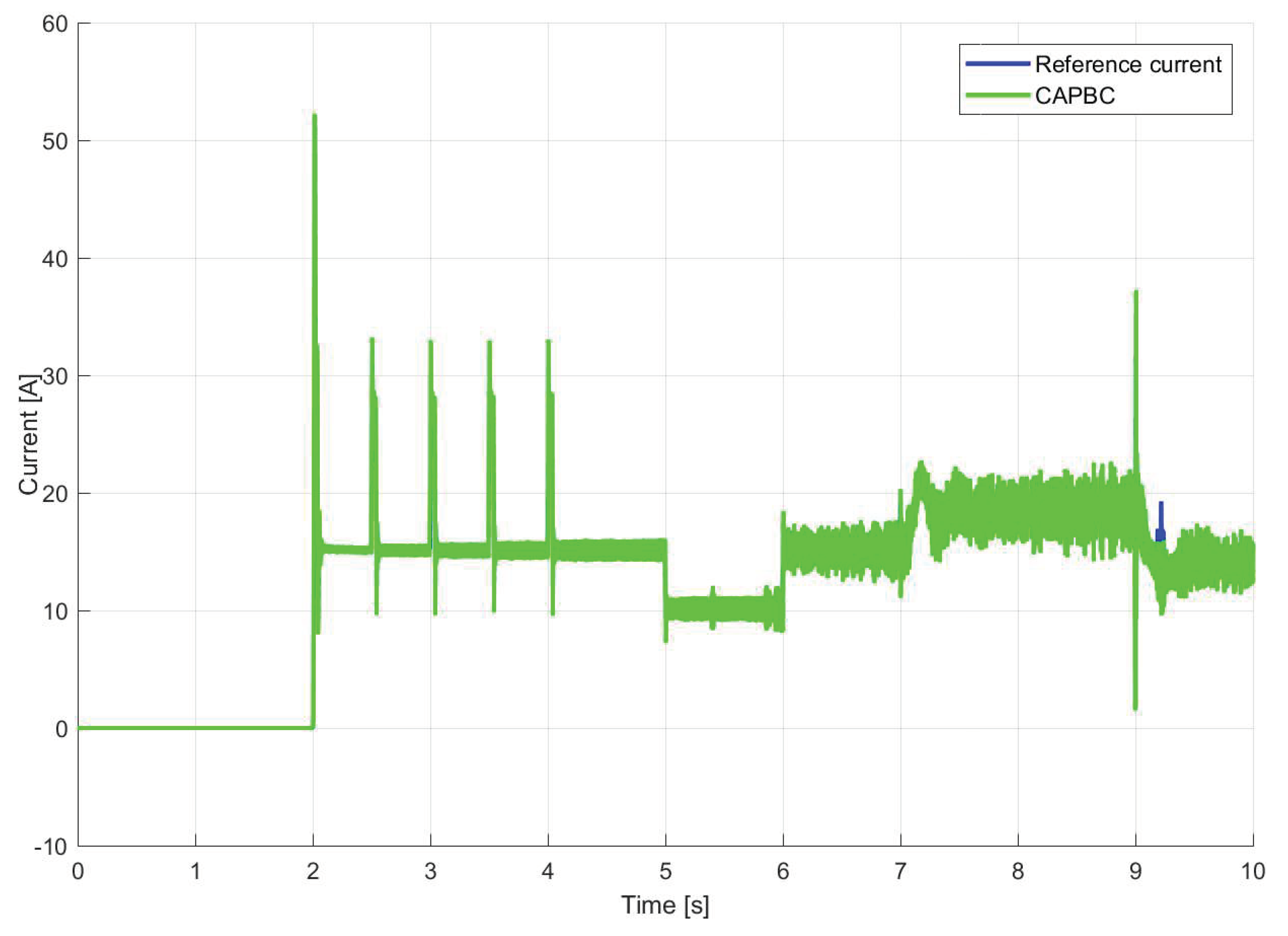
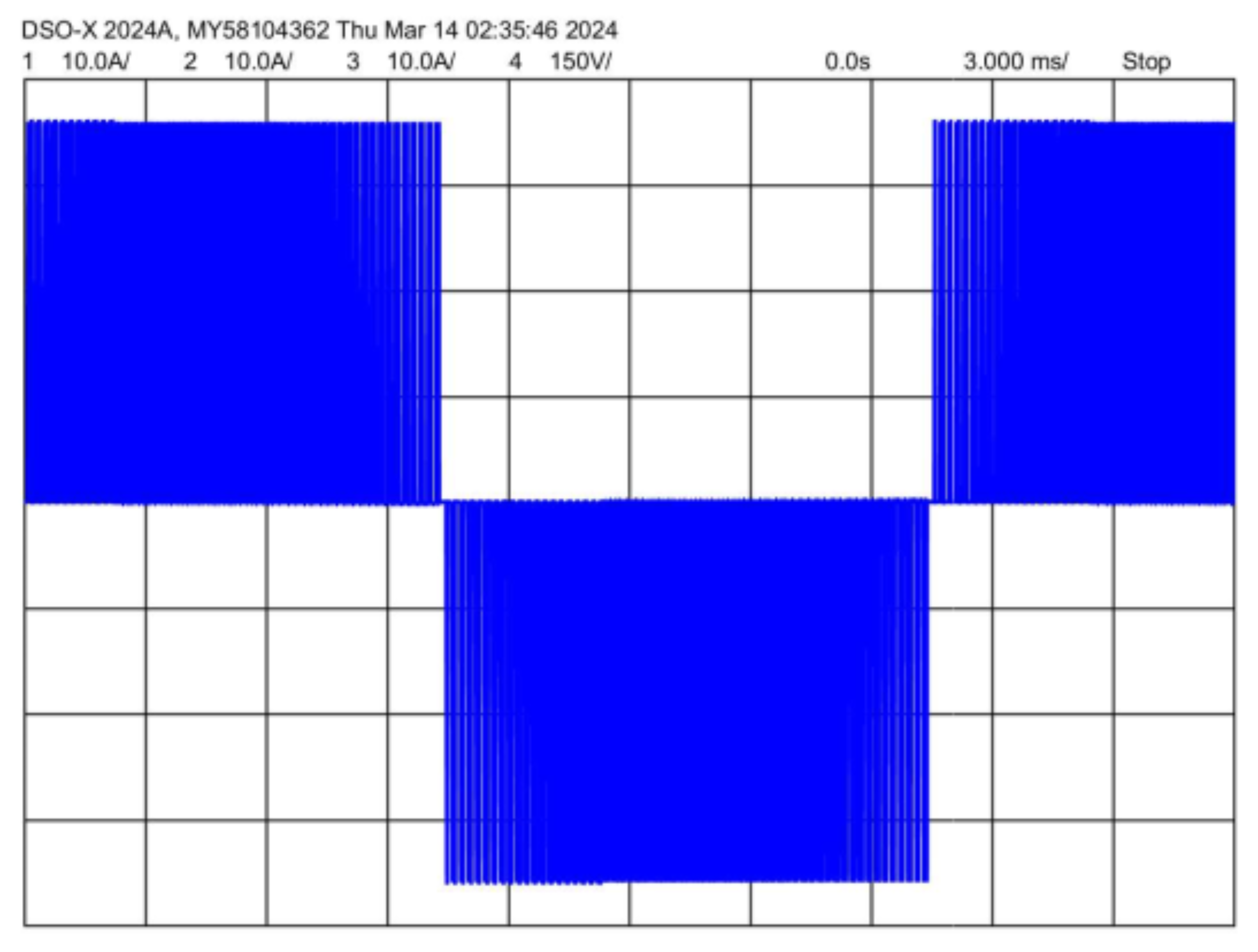
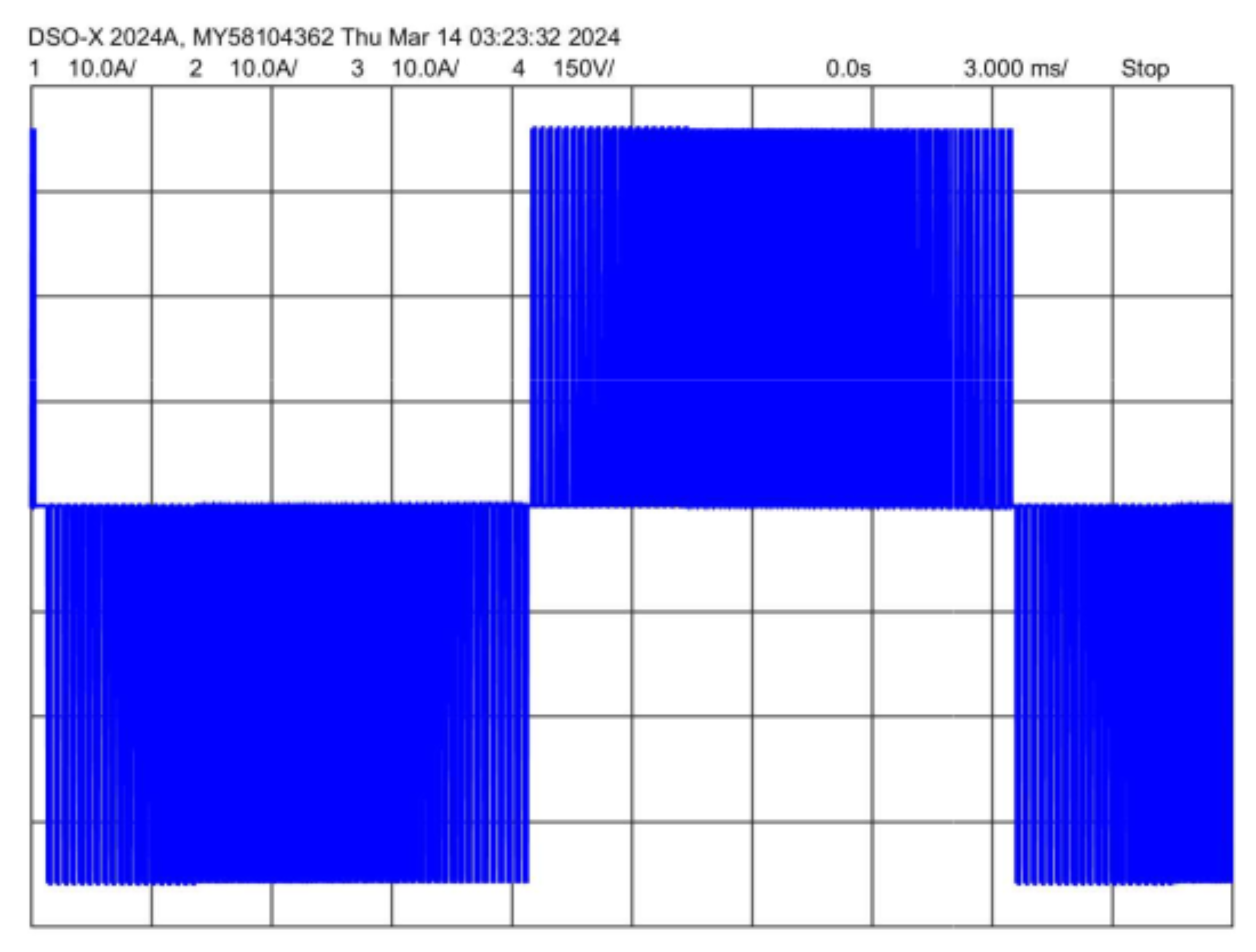
4. Experimental Results

Figure 4 shows the pictures of the test bench used to validate the proposal, joined with its control diagram.
It has a real-time simulator controller OPAL-RT 4510 v2 that inherently uses a bipolar pulse width modulation (PWM), switching at 8 kHz. It commands a two-level voltage source inverter that feeds an IM-load assembly, sending the trip pulses via fiber optic (FO) cables. Simulink version 10.4 of Matlab R2021b (9.11.0.1769968) for Win64 running on a Host PC allows building the IFOC scheme of Figure 1 using PIC, DAPMC, and the proposed CAPBC and downloading them to the control platform using the software RT-LAB v2020.2.2.82. The motor data plate has 7 , 500 k W , 380 V , 50 H z , 1455 r p m , f p = 0 . 85 , two pair of poles p = 2 . A rotor time constant of τ r = 0 . 221 was used to implement FOC (2.1), which is taken from previous measurements [16, Tables IV, Motor II].
Into the IFOC scheme, the following controllers were programmed:
1.
PIC (4) and (5). These controllers were adjusted as described in the Section 2.2 and using the motor-load parameter values from [16](Tables III, IM 2). that followed the IEEE standard 112A, including DC injection, locked rotor, and free load [13](Section 5.9).
2.
DNAPBC [30](Theorem 1) It uses a SISO controller I s q * = θ ^ o c ω o c and a MIMO controller V s q * V s d * = θ ^ i c ω i c both as in [30](Equation (4)). The motor-load parameter does not need to be known to adjust DNAPBC.
3.
Proposed CAPBC from Theorem 1. It also uses a SISO controller I s q * = θ ^ o c ω o c and a MIMO controller V s q * V s d * = θ ^ i c ω i c both as in (10).
The same 10-second duration test applies to the PIC, DAPBC, and proposed CAPBC strategies. It considers the IM starts with a 66 % torque load, and applying a step speed command of 25 rad/s, 60 rad/s, 85 rad/s, 120, and 152 . 36 rad/s, at times 2 s, 2 . 5 s, 3 s, 3 . 5 s, and 4 s, respectively. Later, the load decreases to 40 % at 5 s and increases again to 66 % at 6 s. Finally, the field disorientation is considered adjusting the value of α from IFOC (2.1) to α = 0 . 8 at 7 . 5 s and increases again to α = 1 . 1 at 9 s, simulating step changes for the rotor time constant.
Figure 5 exhibits the controller’s comparative rotor angular speed response. It can be seen that adaptive controllers are more robust against different variations, including load torque and IFOC-impacting parameter variations. All controllers track the reference speed. However, adaptive controllers exhibit lower maximum overshoot (MO) and fester response than PIC in all scenarios. Here, the proposed CAPBC have the lowest MO and the fastest response. The effectiveness of the proposed CAPBC is superior for the different step changes in the reference speed occurring every 2 . 5 seconds until the 4 seconds, as well as for the torque and IFOC variations.
Figure 6, Figure 7 and Figure 8 show the consumed and reference q-axis current torque-producing for the PIC, DPABC, and CAPBC, respectively.
Finally, Figure 9, Figure 10 and Figure 11 show the oscilloscope line voltage a-b around 6.5 seconds for the PIC, DPABC, and CAPBC, respectively.
It can be seen in Figure 6, Figure 7, and Figure 8 that the faster speed responses of adaptive controllers are achieved with a higher reference and consumed q-axis current torque-producing, as expected. Moreover, the line voltages have the typical PWM wayform with the 50 H z frequency corresponding to the nominal rotor angular speed, as can be seen in Figure 9, Figure 10, and Figure 11.

5. Conclusions

This paper introduced a novel CAPBC tailored for a class of nonlinear systems encompassing the IMs under an IFOC scheme, including perturbances and unmodeled dynamics. It expands the DAPBC technique [30] based on the combined approach previously proposed for MRAC [31,32,33]. The theoretical underpinnings of the proposed CAPBC are detailed in Theorem 1, and the stability proof is exhibited in Appendix 8.
Later, the proposal implemented a SISO CAPBC angular speed control for the outer loop of an IFOC for IMs in cascade with the inner loop MIMO CAPBC d-q axis current control. The paper presents comparative experimental results between the proposed CAPBC, the DAPBC, and PIC techniques in an IFOC scheme for an IM of 7,5 kW. These tests included changes in the rotor angular speed reference, parameters that affect field orientation, and load torque. The results demonstrate that the proposed technique is effective and outperforms DAPBC and PIC techniques. It shows a faster rotor angular speed response than PIC and DPABC and the lowest MO.
Unlike traditional PICs, the CAPBC does not need knowledge of the motor-load parameters. Like its DPBC counterpart, the proposed CAPBC’s adjustment relies solely on IM nameplate information.

Author Contributions

Conceptualization, methodology, writing—original draft preparation, and visualization, J.C.T.-T.; investigation, formal analysis, supervision, project administration, data curation, and resources and funding acquisition, J.C.T.-T., A.R., and N.A.-C.; validation, software, and writing—review and editing; A.R. and N.A.-C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by ANID Chile, grant IT23I0117; FONDECYT Chile, grant 1220168; This work was funded by the National Agency for Research and Development (ANID) / Scholarship Program / DOCTORADO BECAS CHILE/2023 - 21230599

Conflicts of Interest

The authors declare no conflict of interest.

6. IFOC Method Basis

Basic IFOC method [46] imposes an electrical angular frequency equal to:
ω e = p 2 ω r + L ^ m τ ^ r I s q Ψ ^ r d .
Here, substituting (22) into Equations (1)c and (1)d, the rotor flux dynamical equations from (1) takes the form
Ψ ˙ r d = − 1 τ r Ψ r d + L ^ m τ ^ r I s q Ψ ^ r q Ψ r q + L m τ r I s d , Ψ ˙ r q = − 1 τ r Ψ r q + L m τ r 1 − τ r L ^ m L m τ ^ r Ψ r d Ψ ^ r d I s q .
Then, if the term τ r L ^ m L m τ ^ r Ψ r d Ψ ^ r d = 1 in this last equation with accurate estimations, the dynamical equation of the quadrature rotor flux component Ψ r y have an exponential behavior tending to zero over time Ψ r q → 0 , reaching over the 99% of this final value after five times the rotor-time constant τ r [9]. Later Ψ r d → L m I s d and the electromagnetic torque T e → 3 2 p 2 L m 2 L r I s d I s q , obtaining the simplified d − q model (3).
However, using equation (22) to achieve IFOC needs a flux estimator to obtain Ψ ^ r d , which is the reason why it is not used in this paper. Therefore, the alternative and more practical method, using the electrical angular frequency (Section 2.1) is performed in this paper [40]( Section 4.1.2.2.1), [47].
The authors haven’t found explicit proof of this method in the literature. Thus, we describe it herein. After considering the definition of the rotor time constant τ r = L r R r and substituting (2.1) into equations (1)c and (1)d, the rotor flux dynamical equations from (1) takes the form
Ψ ˙ r d Ψ ˙ r q = A Ψ r d Ψ r q + L m I s d I s q , whit A = − 1 − τ r τ ^ r I s q * I s d * τ r τ ^ r I s q * I s d * − 1 .
After applying the Laplace transform [47] to this last equation, considering constant I s d I s q T and the initial condition Ψ s d ( 0 ) Ψ s q ( 0 ) T , we obtain
Ψ r d Ψ r q = ( τ r s − A ) − 1 L m s − 1 I s d I s q + ( τ r s − A ) − 1 Ψ r d ( 0 ) Ψ r q ( 0 ) .
Applying the final value theorem [47], where lim t → ∞ f ( t ) = lim s → 0 s F ( s ) , we have lim t → ∞ Ψ s d ( t ) Ψ s q ( t ) T = L m A − 1 I s d I s q T . As a result Ψ r d Ψ r q → L m 1 − τ r τ ^ r I s q * I s d * τ r τ ^ r I s q * I s d * 1 I s d I s q . Then, Ψ r d Ψ r q → L m 1 + ( τ r I s q * τ ^ r I s d * ) 2 I s d 1 + τ r I s q * I s q τ ^ r I s d * I s d I s q 1 − τ r I s q * I s d τ ^ r I s d * I s q . Here, if τ r I s q * I s d τ ^ r I s d * I s q = 1 we get Ψ r d Ψ r q → L m I s d 0 achieving field orientation. This could be obtained under the presence of accurate parameters estimation, similar to the basic IFOC method, thus τ r τ ^ r = 1 ; and even if I s d ≠ I s d * and I s q ≠ I s q * , but I s q * I s d * I s d I s q = 1 , which is a valid case not considered in [47].

7. PIC Adjustment

The adjustment of the PI controllers starts from the simplified IM d-q model (3) and the IFOC block diagram of Figure 1. These are re-expressed as the transfer function block diagram [44] of Figure 12 in Laplace domain; after considering all the motor-load parameters and the operating point constant and known.
Preprints 101620 g0a1
Figure 12. Transfer function block diagram of Basic IFOC for IM.
Figure 12. Transfer function block diagram of Basic IFOC for IM.
Preprints 101620 g0a1
Inner loop is first adjusted after neglecting the nonlinear terms σ L s ω e I s q + R r L m 2 L r 2 I s d and
− σ L s ω e I s d + L m 2 L r ω r I s d . Moreover, it considers the closed-loop transfer functions property of F T = G 1 + G H with H = H i and G = K c ( K p i + K i i s ) ( 1 / R s ′ τ i s + 1 ) [44], obtaining the transfer function shown in Figure 12, of the form F T i = ω n 2 K p i ( s + a ) / K i i H i s 2 + 2 ξ i ω n i s + ω n i 2 . Here, the squared inner natural frequency ω n i 2 = K c K i i H i R s ′ τ i is used to obtain the fixed-gain parameter K i i of the controller. The term depending on the inner natural frequency ω n i and the inner damping coefficient ξ i is 2 ξ i ω n i = R s ′ + K c K p i H i R s ′ τ i ; and it is used to compute the fixed-gain parameter K p i of the controller. The inner PICs adjustment results in Equation (4).
Later, it is assumed that the inner loop is stabilized. Therefore, applying the final value theorem [47], where lim t → ∞ f ( t ) = lim s → 0 s F ( s ) , we have that F T i → H i − 1 and the block diagram of Figure 12 becomes
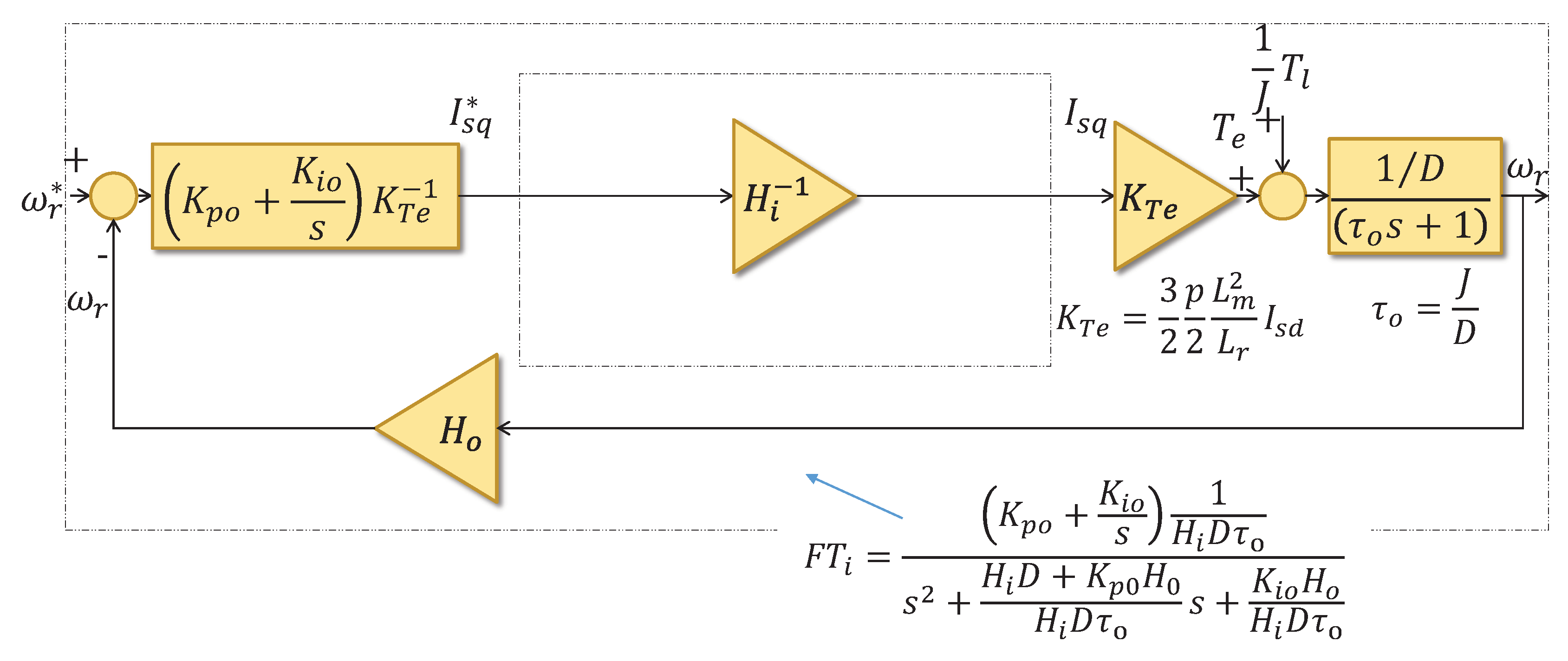
Preprints 101620 g0a2
Figure 13. Transfer function block diagram of Basic IFOC for IM once stabilized the inner loop.
Figure 13. Transfer function block diagram of Basic IFOC for IM once stabilized the inner loop.
Preprints 101620 g0a2
In a similar way than the inner loop, after considering the load torque term 1 J T c as a disturbance that is neglected, and considering the closed-loop transfer functions property, the transfer function F T o = ω n 2 K p o ( s + a ) / K i o H i s 2 + 2 ξ o ω n o s + ω n o 2 is obtained [42,44]. Here, the squared outer natural frequency is ω n o 2 = K i o H 0 H i B τ o , and is used to obtain the fixed-gain parameter K i o of the controller. The term 2 ξ o ω n o = H i B + K p o H o H i B τ o , depending on the outer natural frequency and the outer damping coefficient, is used to compute the fixed-gain parameter K p o of the controller. Finally, the outer PIC is adjusted as in Equation (5).

8. CAPBC Stability Proof

Obtaining the Errors Dynamical Equations
Subtracting equations (14) minus (15) and regrouping terms the following identification error is obtained:
e ˙ i = − K i e i + Φ i T ω i + ζ ,
It considers the previously given definitions of e i = y − y ^ , θ i , ω i . Moreover, the identification parameter error Φ i T ∈ R n x ( 2 n + m ) is defined as Φ i = θ i − θ i ^ .
Multiplying both sides of the model plant (14) by − 1 . Adding and subtracting the term K c e c + y ˙ * , regrouping and considering previously definitions of e c = y * − y , θ c , ω c the control error is:
e ˙ c = − K c e c + B T ϕ c T ω c − ζ ,
where Φ c T ∈ R n x ( 2 n + m ) .
In contrast to D and I approaches, the C technique considers B ^ T θ ^ 1 T + A ^ T ≠ 0 , B ^ T θ ^ 2 T − I n ≠ 0 and B ^ T θ ^ 3 T + δ ^ T ≠ 0 obtaining the closed-loop estimation error (18).
Subtracting in (18) minus (21) (since (21) is equals to zero doesn’t change the equation), to the right side, respectively, and regrouping terms we obtain:
ε 1 ε 2 ε 3 = − ( B T − B ^ T ) θ ^ 1 T − ( A T − A ^ T ) − B T ( θ 1 T − θ ^ 1 T ) − ( B T − B ^ T ) θ ^ 2 T − B T ( θ 2 T − θ ^ 2 T ) − ( B T − B ^ T ) θ ^ 3 T − ( δ T − δ ^ T ) − B T ( θ 3 T − θ ^ 3 T ) = − Φ B T θ ^ 1 T − Φ A T − B T Φ 1 T − Φ B T θ ^ 2 T − B T Φ 2 T − Φ B T θ ^ 3 T − Φ δ T − B T Φ 3 T .
This result equals:
ε = − Φ i T P 1 − Φ i T P 2 θ T − B T Φ c T .
Finally, as Φ i = θ i − θ ^ i and Φ c = θ c − θ ^ c , and the identification and control ideal parameters θ i and θ c are constant, we have that Φ ˙ i = − θ ^ ˙ i and Φ ˙ c = − θ ^ ˙ c . Therefore, from (17) and (19) we have:
ϕ c ˙ T = − S T ▿ V e c ω c T − S T ε T Γ ε − 1 + σ c θ ^ c T Γ c ,
ϕ i ˙ T = − ω i T ▿ V e i − ε T Γ ε − 1 ( P 1 T + θ ^ c P 2 T ) + σ i θ i T Γ i .
Stability Proof of the Errors Dynamical Equations
The system composed by the errors dynamical equations (26), (27), (29), and (30), has an associated Lyapunov function, which is positive and depends on the design energy function V e .
V ( e c , Φ c , e i , Φ i ) = V e c + 1 2 T r a c e ( | B | Φ c T Γ c − 1 Φ c ) + V e i + 1 2 T r a c e ( Φ i T Γ i − 1 Φ i ) .
The first time derivative of (31) gives:
V ˙ ( e c , Φ c , e i , Φ i ) = ▿ V e c T e ˙ c + T r a c e ( | B | Φ ˙ c T Γ c − 1 Φ c ) + ▿ V e i T e ˙ i + T r a c e ( Φ ˙ i T Γ i − 1 Φ i ) .
Substituting (26) and (27) into (32), we obtain:
1 − 1 V ˙ ( e c , Φ c , e i , Φ i ) = ▿ V e c T ( − K c e c + B T ϕ c T ω c − ζ ) + Trace ( | B | Φ ˙ c T Γ c − 1 Φ c )
+ ▿ V e i T ( − K i e i + Φ i T ω i + ζ ) + Trace ( Φ ˙ i T Γ i − 1 Φ i )
Regrouping terms, it gives:
1 − 1 V ˙ ( e c , Φ c , e i , Φ i ) = − ▿ V e c T K c e c + ▿ V e c T B T ϕ c T ω c − ▿ V e c T ζ + Trace ( | B | Φ ˙ c T Γ c − 1 Φ c )
− ▿ V e i T K i e i + ▿ V e i T Φ i T ω i + ▿ V e i T ζ + Trace ( Φ ˙ i T Γ i − 1 Φ i )
Substituting (29) and (30) into the last equation, it gives:
V ˙ ( e c , Φ c , e i , Φ i ) = − ▿ V e c T K c e c − ▿ V e i T K i e i + ▿ V e c T B T ϕ c T ω c + ▿ V e i T Φ i T ω i − ▿ V e c T ζ + ▿ V e i T ζ − T r a c e | B | S T ▿ V e c ω c T − | B | S T ε T Γ ε + | B | σ c θ ^ c T Γ c Γ c − 1 Φ c − T r a c e ω i T ▿ V e i − ε T Γ ε − 1 ( P 1 T + θ ^ c P 2 T ) + σ i θ ^ i T Γ i Γ i − 1 Φ i
Now, considering | B | S T = B , Γ c Γ c − 1 = 1 and Γ i Γ i − 1 = 1 , and regrouping terms, it follows
V ˙ ( e c , Φ c , e i , Φ i ) = − ▿ V e c T K c e c − ▿ V e i T K i e i + ▿ V e c T B T ϕ c T ω c + ▿ V e i T Φ i T ω i − ▿ V e c T ζ + ▿ V e i T ζ − Trace B ▿ V e c ω c T Φ c − B ε T Γ ε − 1 Φ c + | B | σ c θ c T Φ c − Trace ω i T ▿ V e i Φ i − ε T Γ ε − 1 ( P 1 T Φ i + θ ^ c P 2 T Φ i ) + σ i θ ^ i T Φ i
Moreover, the authors consider the two vectors’ property, where a T b = T r a c e ( a b T ) , to write the terms ▿ V e c T B T ϕ c T ω c and ▿ V e i T Φ i T ω i into the trace as follows
V ˙ ( e c , Φ c , e i , Φ i ) = − ▿ V e c T K c e c − ▿ V e i T K i e i − Trace − B ▿ V e c ω c T Φ c + B ▿ V e c ω c T Φ c − B ε T Γ ε − 1 Φ c + | B | σ c θ c T Φ c + ζ T ▿ V e c − Trace − ω i T ▿ V e i Φ i + ω i T ▿ V e i Φ i − ε T Γ ε − 1 ( P 1 T Φ i + θ ^ c P 2 T Φ i ) + σ i θ ^ i T Φ i − ζ T ▿ V e i
Simplifying the last equation, after canceling identical terms with opposite signs and regrouping the terms with ε T Γ ε − 1 conveniently to obtain equation (28), it gives
V ˙ ( e c , Φ c , e i , Φ i ) = − ▿ V e c T K c e c − ▿ V e i T K i e i − Trace ε T Γ ε − 1 ε − Trace | B | σ c θ c T Φ c − Trace ζ T ▿ V e c − Trace σ i θ ^ i T Φ i + Trace ζ T ▿ V e i
In this scenario, we assume that all parameters involved, K c , K i , | B | , σ c , σ i , and Γ ε , are strictly positive. Additionally, we know that the parameters characterizing the plant, along with their first derivatives with respect to time, remain within certain bounds.
However, upon inspection of Equation (33), it becomes evident that while the first terms indicate negativity, the signs of the subsequent four terms are not immediately discernible. To address this ambiguity, we aim to reformulate Equation (33) using modulus and norm properties, as demonstrated in [27].
Using properties of the Frobenius norm and the Cauchy–Schwarz inequality where T r a c e ( A B C ) ≤ | | A | | F | | B | | F | | C | | F . The terms become − T r a c e | B | σ c θ ^ c T Φ c ≤ | | | B | σ c | | F | | θ ^ c T | | F | | Φ c | | F , − T r a c e σ i θ ^ i T Φ i ) ≤ | | σ i | | F | | θ ^ i T | | F | | Φ i | | F , Trace ζ T ▿ V e c ≤ | | ζ T | | F | | ▿ V e c | | F and Trace ζ T ▿ V e i ≤ | | ζ T | | F | | ▿ V e i | | F . Using the property 2 a b ≤ a 2 + b 2 , we have − T r a c e | B | σ c θ ^ c T Φ c ≤ 1 2 | | | B | σ c | | F | | θ ^ c T | | F 2 + | | Φ c | | F 2 , − T r a c e σ i θ ^ i T Φ i ) ≤ 1 2 | | σ i | | F | | θ ^ i T | | F 2 + | | Φ i | | F 2 , Trace ζ T ▿ V e c ≤ 1 2 | | ζ T | | F 2 + | | ▿ V e c | | F 2 and Trace ζ T ▿ V e i ≤ 1 2 | | ζ T | | F 2 | | ▿ V e i | | F 2 .
As a result, equation (33) becomes:
V ˙ ( e c , Φ c , e i , Φ i ) ≤ − ▿ V e c T K c e c − ▿ V e i T K i e i − T r a c e ( ε T Γ ε − 1 ε ) − 1 2 | | | B | σ c | | F | | θ ^ c T | | F 2 + | | Φ c | | F 2 − 1 2 | | ζ T | | F 2 + | | ▿ V e c | | F 2 − 1 2 | | σ i | | F | | θ ^ i T | | F 2 + | | Φ i | | F 2 + 1 2 | | ζ T | | F 2 + | | ▿ V e i | | F 2
which equals a hyperelliptical paraboloid of parameter r:
V ˙ ( e c , Φ c , e i , Φ i ) = − ▿ V e c T K c e c − ▿ V e i T K i e i − T r a c e ( ε T Γ ε − 1 ε ) + r 2 − 1 2 | | | B | σ c | | F | | θ ^ c T | | F 2 + | | Φ c | | F 2 − 1 2 | | ζ T | | F 2 + | | ▿ V e c | | F 2 − 1 2 | | σ i | | F | | θ ^ i T | | F 2 + | | Φ i | | F 2 + 1 2 | | ζ T | | F 2 + | | ▿ V e i | | F 2
Therefore, V ˙ ≤ 0 only outside the region Ω , which is the following instability hyper elliptical paraboloid that is compact, closed, and includes the origin:
Ω = 1 2 | | | B | σ c | | F | | θ ^ c T | | F 2 + | | Φ c | | F 2 + 1 2 | | ζ T | | F 2 + | | ▿ V e c | | F 2 1 2 | | σ i | | F | | θ ^ i T | | F 2 + | | Φ i | | F 2 − 1 2 | | ζ T | | F 2 + | | ▿ V e i | | F 2 ≤ r 2
Hence, using Lyapunov’s second method, it can be concluded that the variables of the closed-loop dynamical Equations (27), (26), (29) and (30) are bounded outside Ω . In case the errors take small enough values that result in V ˙ ≤ 0 (inside the instability compact and closed region Ω , including the origin); these will be pushed back to a stable boundary. In practice, the values of σ c , σ i , Γ c , Γ i and Γ ε are chosen so the permanent errors are smaller as possible, as can be seen in the following section.
Thus, e c ( t ) , e i ( t ) , Φ c ( t ) , and Φ i ( t ) are bounded outside Ω , i.e., e c ( t ) , e i ( t ) , Φ c ( t ) , and Φ i ( t ) ∈ L ∞ outside Ω . Since e c = y * − y and e i = y − y ^ are bounded, it implies that y, y ^ and are bounded as y * is a bounded reference. As Φ c ( t ) and Φ i ( t ) are bounded, and we have bounded plant parameters, then the adaptive parameters θ c and θ i are bounded, since θ ^ i = θ i − Φ i and θ ^ c = θ c − Φ c . Having all these bounded signals outside Ω , and that V, e c ( t ) , e i ( t ) , Φ c ( t ) and Φ i ( t ) ∈ L ∞ , from (27), (26), (29) and (30), we have that e ˙ c ( t ) , e ˙ i ( t ) , Φ ˙ c ( t ) and Φ ˙ i ( t ) ∈ L ∞
Integrating both sides of V ˙ ( e c , Φ c , e i , Φ i ) in the interval ( 0 , ∞ ) , it gives
V ( ∞ ) − V ( 0 ) = ∫ 0 ∞ ( − ∇ V e c T K c e c − ∇ V e i T K i e i − Trace ( ε T Γ ε − 1 ε ) + r 2 − 1 2 ∥ B σ c ∥ F ∥ θ ^ c T ∥ F 2 + ∥ Φ c ∥ F 2 − 1 2 ∥ ζ T ∥ F 2 + ∥ ∇ V e c ∥ F 2 − 1 2 ∥ σ i ∥ F ∥ θ ^ i T ∥ F 2 + ∥ Φ i ∥ F 2 + 1 2 ∥ ζ T ∥ F 2 + ∥ ∇ V e i ∥ F 2 ) d τ
as V is bounded outside Ω , from the right-hand side of this last equation; we have e c ( t ) and e i ( t ) ∈ L 2 outside Ω .
Furthermore, as e c ( t ) , e ˙ c ( t ) ∈ L ∞ and e c ( t ) ∈ L 2 , and e i ( t ) , e ˙ i ( t ) ∈ L ∞ and e i ( t ) ∈ L 2 , all outside Ω , using Barbalat´s Lemma [19](Section 4.5.2) we have that e c ( t ) and e i ( t ) , both tend asymptotically to zero outside Ω . Hence y ( t ) → y * and y ^ ( t ) → y ( t ) outside Ω C . We do not ensure parameter convergence. This concludes the proof. ⋄

References

  1. Ivanov-Smolenskij, A.; Kuznecov, B. Electrical machines: Vol. 1; Number v. 3, Mir, 1983.
  2. Hannan, M.; Ali, J.A.; Mohamed, A.; Hussain, A. Optimization techniques to enhance the performance of induction motor drives: A review. Renewable and Sustainable Energy Reviews 2018, 81, 1611–1626. [CrossRef]
  3. Travieso-Torres, J.C.; Contreras-Jara, C.; Diaz, M.; Aguila-Camacho, N.; Duarte-Mermoud, M.A. New Adaptive Starting Scalar Control Scheme for Induction Motor Variable Speed Drives. IEEE Transactions on Energy Conversion 2021, 37, 729–736. [CrossRef]
  4. Depenbrock, M. Direkte selbstregelung (DSR) für hochdynamische drehfeldantriebe mit stromrichterspeisung. etz-Archiv 1985, 7, 211–218.
  5. Vas, P. Sensorless vector and direct torque control. (No Title) 1998.
  6. Hasse, K. Zur Dynamic Drehzahlgeregelter Antriebe mit stromaschinen, techn, Hoschsch. Darmstadt. PhD thesis, Dissertation, 1969.
  7. Blaschke, F. The principle of field orientation as applied to the new transvector closed-loop control system for rotating-field machine. Siemens review 1772, 34, 217–220.
  8. Desoer, C.; Lin, C.A. Tracking and disturbance rejection of MIMO nonlinear systems with PI controller. IEEE Transactions on Automatic Control 1985, 30, 861–867. [CrossRef]
  9. Ogata, K. Ingeniería de control moderna; Pearson Educación, 2003.
  10. Sengamalai, U.; Anbazhagan, G.; Thamizh Thentral, T.; Vishnuram, P.; Khurshaid, T.; Kamel, S. Three phase induction motor drive: a systematic review on dynamic modeling, parameter estimation, and control schemes. Energies 2022, 15, 8260. [CrossRef]
  11. Amaral, G.F.V.; Baccarini, J.M.R.; Coelho, F.C.R.; Rabelo, L.M. A high precision method for induction machine parameters estimation from manufacturer data. IEEE Transactions on Energy Conversion 2020, 36, 1226–1233. [CrossRef]
  12. Perin, M.; Pereira, L.A.; Silveira, G.B.; Haffner, S. Estimation of the parameters for multi-cage models of induction motors using manufacturer data and PSO. Electrical Engineering 2023, pp. 1–19. [CrossRef]
  13. Engineers, E.; Board, I. IEEE Standard Test Procedure for Polyphase Induction Motors and Generators. IEEE Standards Boards Std 112-2017 (Revision of IEEE Std 112-2004) 2018, pp. 1–115. [CrossRef]
  14. Yoo, J.; Lee, J.H.; Sul, S.K. FEA-Assisted Experimental Parameter Map Identification of Induction Motor for Wide-Range Field-Oriented Control. IEEE Transactions on Power Electronics 2023. [CrossRef]
  15. Véliz-Tejo, A.; Travieso-Torres, J.C.; Peters, A.A.; Mora, A.; Leiva-Silva, F. Normalized-Model Reference System for Parameter Estimation of Induction Motors. Energies 2022, 15, 4542. [CrossRef]
  16. Travieso-Torres, J.C.; Lee, S.S.; Veliz-Tejo, A.; Leiva-Silva, F.; Ricaldi-Morales, A. Self-Commissioning Parameter Estimation Algorithm for Loaded Induction Motors. IEEE Transactions on Industrial Electronics 2024, pp. 1–11. [CrossRef]
  17. Ioannou, P.A.; Sun, J. Robust adaptive control; Vol. 1, PTR Prentice-Hall Upper Saddle River, NJ, 1996.
  18. Åström, K.J.; Wittenmark, B. Adaptive control; Courier Corporation, 2008.
  19. Narendra, K.; Annaswamy, A. Stable Adaptive Systems; Dover Books on Electrical Engineering, Dover Publications, 2012.
  20. Tiwari, M.; Prazenica, R.; Henderson, T. Direct adaptive control of spacecraft near asteroids. Acta Astronautica 2023, 202, 197–213. [CrossRef]
  21. Artuc, M.B.; Bayezit, I. Robust adaptive quadrotor position tracking control for uncertain and fault conditions. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering 2023, 237, 3172–3184. [CrossRef]
  22. Wang, Y.; Shen, C.; Huang, J.; Chen, H. Model-free adaptive control for unmanned surface vessels: a literature review. Systems Science & Control Engineering 2024, 12, 2316170. [CrossRef]
  23. Liu, Z.; Zhao, Y.; Zhang, O.; Chen, W.; Wang, J.; Gao, Y.; Liu, J. A Novel Faster Fixed-Time Adaptive Control for Robotic Systems With Input Saturation. IEEE Transactions on Industrial Electronics 2023.
  24. Burghi, T.; Iossaqui, J.; Camino, J. A general update rule for Lyapunov-based adaptive control of mobile robots with wheel slip. International Journal of Adaptive Control and Signal Processing.
  25. Mirzaee, M.; Kazemi, R. Direct adaptive fractional-order non-singular terminal sliding mode control strategy using extreme learning machine for position control of 5-DOF upper-limb exoskeleton robot systems. Transactions of the Institute of Measurement and Control 2024, p. 01423312231225605. [CrossRef]
  26. Abubakr, H.; Vasquez, J.C.; Mohamed, T.H.; Guerrero, J.M. The concept of direct adaptive control for improving voltage and frequency regulation loops in several power system applications. International Journal of Electrical Power & Energy Systems 2022, 140, 108068. [CrossRef]
  27. Travieso-Torres, J.C.; Ricaldi-Morales, A.; Véliz-Tejo, A.; Leiva-Silva, F. Robust Cascade MRAC for a Hybrid Grid-Connected Renewable Energy System. Processes 2023, 11, 1774. [CrossRef]
  28. Karami-Mollaee, A.; Barambones, O. Higher Order Sliding Mode Control of MIMO Induction Motors: A New Adaptive Approach. Mathematics 2023, 11, 4558. [CrossRef]
  29. Çavuş, B.; Aktaş, M. A New Adaptive Terminal Sliding Mode Speed Control in Flux Weakening Region for DTC Controlled Induction Motor Drive. IEEE Transactions on Power Electronics 2023.
  30. Travieso-Torres, J.C.; Duarte-Mermoud, M.A.; Díaz, M.; Contreras-Jara, C.; Hernández, F. Closed-Loop Adaptive High-Starting Torque Scalar Control Scheme for induction Motor Variable Speed Drives. Energies 2022, 15, 3489. [CrossRef]
  31. Duarte, M.A.; Narendra, K.S. Combined direct and indirect approach to adaptive control. IEEE Transactions on Automatic Control 1989, 34, 1071–1075. [CrossRef]
  32. Duarte-Mermoud, M.A.; Rojo, F.A.; Pérez, R. Experimental evaluation of combined model reference adaptive controller in a pH regulation process. International Journal of Adaptive Control and Signal Processing 2002, 16, 85–106. [CrossRef]
  33. Duarte-Mermoud, M.A.; Rioseco, J.S.; González, R.I. Control of longitudinal movement of a plane using combined model reference adaptive control. Aircraft Engineering and Aerospace Technology 2005. [CrossRef]
  34. Lavretsky, E. Combined/composite model reference adaptive control. IEEE Transactions on Automatic Control 2009, 54, 2692–2697. [CrossRef]
  35. Xie, J.; Yan, H.; Li, S.; Yang, D. Almost output regulation model reference adaptive control for switched systems: combined adaptive strategy. International Journal of Systems Science 2020, 51, 556–569. [CrossRef]
  36. Roy, S.B.; Bhasin, S.; Kar, I.N. Combined MRAC for unknown MIMO LTI systems with parameter convergence. IEEE Transactions on Automatic Control 2017, 63, 283–290. [CrossRef]
  37. Makavita, C.D.; Nguyen, H.D.; Ranmuthugala, D.; Jayasinghe, S.G. Composite model reference adaptive control for an unmanned underwater vehicle. Underwater Technology 2015, 33, 81–93. [CrossRef]
  38. Abdul Ghaffar, A.F.; Richardson, T.; Greatwood, C. A combined model reference adaptive control law for multirotor UAVs. IET Control Theory & Applications 2021, 15, 1474–1487. [CrossRef]
  39. Narendra, K.; Khalifa, I.; Annaswamy, A. Error models for stable hybrid adaptive systems. IEEE transactions on automatic control 1985, 30, 339–347. [CrossRef]
  40. Vas, P. Electrical machines and drives: a space-vector theory approach; Vol. 1, Clarendon press Oxford, 1992.
  41. Park, R.H. Two-reaction theory of synchronous machines generalized method of analysis-part I. Transactions of the American Institute of Electrical Engineers 1929, 48, 716–727. [CrossRef]
  42. Bishop, R.C.D.R.H. Modern control systems; 2011.
  43. Siemens. SIMOVERT MASTERDRIVES Vector Control 2003/2004. Catalog DA 65.10.
  44. Schiff, J.L. The Laplace transform: theory and applications; Springer Science & Business Media, 1999.
  45. Travieso-Torres, J.C.; Contreras, C.; Hernández, F.; Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Orchard, M.E. Adaptive passivity-based control extended for unknown control direction. ISA transactions 2022, 122, 398–408. [CrossRef]
  46. Feraga, C.E.; Sedraoui, M.; Bachir Bouiadjra, R. Enhanced Indirect Field-Oriented Control of Single-Phase Induction Motor Drive Using H∞ Current Controller. Arabian Journal for Science and Engineering 2019, 44, 7187–7202. [CrossRef]
  47. Cao, P.; Zhang, X.; Yang, S. A unified-model-based analysis of MRAS for online rotor time constant estimation in an induction motor drive. IEEE Transactions on Industrial Electronics 2017, 64, 4361–4371. [CrossRef]
Preprints 101620 g001
Figure 1. IFOC diagram for IMs.
Figure 1. IFOC diagram for IMs.
Preprints 101620 g001
Preprints 101620 g004
Figure 4. Test bench pictures and control diagram.
Figure 4. Test bench pictures and control diagram.
Preprints 101620 g004
Preprints 101620 g005
Figure 5. Comparative rotor angular speed.
Figure 5. Comparative rotor angular speed.
Preprints 101620 g005
Preprints 101620 g006
Figure 6. Consumed and reference q-axis current torque-producing for PIC.
Figure 6. Consumed and reference q-axis current torque-producing for PIC.
Preprints 101620 g006
Preprints 101620 g007
Figure 7. Consumed and reference q-axis current torque-producing for DAPBC.
Figure 7. Consumed and reference q-axis current torque-producing for DAPBC.
Preprints 101620 g007
Preprints 101620 g008
Figure 8. Consumed and reference q-axis current torque-producing for the proposed CAPBC
Figure 8. Consumed and reference q-axis current torque-producing for the proposed CAPBC
Preprints 101620 g008
Preprints 101620 g009
Figure 9. Line voltage a-b around second 6.5 for PIC.
Figure 9. Line voltage a-b around second 6.5 for PIC.
Preprints 101620 g009
Preprints 101620 g010
Figure 10. Line voltage a-b around second 6.5 for DAPBC.
Figure 10. Line voltage a-b around second 6.5 for DAPBC.
Preprints 101620 g010
Preprints 101620 g011
Figure 11. Line voltage a-b around second 6.5 for the proposed CAPBC
Figure 11. Line voltage a-b around second 6.5 for the proposed CAPBC
Preprints 101620 g011
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated