Preprint
Article
Stochastic Compartment Model With Mortality and Its Application to Epidemic Spreading in Complex Networks
Altmetrics
Downloads
74
Views
25
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
18 March 2024
Posted:
22 March 2024
You are already at the latest version
Alerts
Abstract
We study epidemic spreading in complex networks by a multiple random walker approach. Each walker
performs an independent simple Markovian random walk on a complex undirected (ergodic) random
graph where we focus on Barabási-Albert (BA), Erdös-Rényi (ER) and Watts-Strogatz (WS) types. Both,
walkers and nodes can be either susceptible (S) or infected and infectious (I) representing their states of
health. Susceptible nodes may be infected by visits of infected walkers, and susceptible walkers may be
infected by visiting infected nodes. No direct transmission of the disease among walkers (or among nodes)
is possible. This model mimics a large class of diseases such as Dengue and Malaria with transmission
of the disease via vectors (mosquitos). Infected walkers may die during the time span of their infection
introducing an additional compartment D of dead walkers. Infected nodes never die and always recover
from their infection after a random finite time. This assumption is based on the observation that infectious
vectors (mosquitos) are not ill and do not die from the infection. The infectious time spans of nodes and
walkers, and the survival times of infected walkers, are represented by independent random variables.
We derive stochastic evolution equations for the mean-field compartmental populations with mortality of
walkers and delayed transitions among the compartments. From linear stability analysis, we derive the
basic reproduction numbers R M , R 0 with and without mortality, respectively, and prove that R M < R 0 .
For R M , R 0 > 1 the healthy state is unstable whereas for zero mortality a stable endemic equilibrium
exists (independent of the initial conditions) which we obtained explicitly. We observe that the solutions
of the random walk simulations in the considered networks agree well with the mean-field solutions for
strongly connected graph topologies, whereas less well for weakly connected structures and for diseases
with high mortality. Our model has applications beyond epidemic dynamics, for instance in the kinetics of chemical reactions, the propagation of contaminants, wood fires, among many others.
Keywords:
Subject: Physical Sciences - Other
1. Introduction
Sudden or recurrent emergence of epidemics has been an everlasting thread to humanity. Highly infectious and fatal diseases such as pestilence, typhus, cholera, and leprosy were among the main causes of death in medieval times in Europe and until 20th century a major scourge of humanity [1]. This permanent challenge has naturally driven interest in protective measures and predictive models.
The systematic mathematical study of epidemic spreading began only a century ago with the seminal work of Kermack and McKendrick [2]. They were the first to introduce what we call nowadays a “compartment model”. In their so called SIR-model the individuals are categorized in compartments susceptible - S, infected - I, recovered (immune) - R characterizing their states of their health. Whereas standard SIR type models are able to capture main features of a certain class of infectious diseases such as mumps, measles and rubella, they fail to describe persistent oscillatory behaviors and spontaneous outbursts which are observed in many epidemics.
A large amount of work still is devoted to compartmental models [3,4] where an impressive field has emerged [5,6] and the interest was again considerably enhanced by the context of COVID-19 pandemics [7]. Beside purely macroscopic models, the study of epidemic dynamics in complex networks has attracted considerable attention [9,10,11]. In these works the importance of the graph topology for spreading phenomena has been highlighted. In particular, Pastor-Satorras and Vespignani showed that for a wide range of scale free networks no critical threshold for epidemic spreading exists [10]. The topological features crucial for epidemic spreading include the small world property (short average network distances1) and a high clustering coefficient measuring the existence of redundant paths between pairs of nodes [25,27].
Further interesting directions are represented by combinations of network science and stochastic compartmental models [16,17,28,29,31]. Such models include Markovian and non-Markovian approaches [23,30,35,36,37] where non-Markovianity is introduced by non-exponentially distributed sojourn times in the compartments [33,34]. In these works explicit formulae for the endemic equilibrium in terms of mean compartmental sojourn times and the basic reproduction number are derived and numerically validated in random walk simulations. A further non-Markovian model appeared recently [12] where non-Markovianity comes into play by introducing an "age of infection" allowing individuals to recover when their infection period exceeds a certain threshold, generalizing the initial idea of Kermack and McKendrick.
Other recent works emphasize the importance of spatial heterogeneity effects of infection patterns in epidemic spreading phenomena [38] and the role of local clusters to generate periodic epidemic outbursts [39] and see [40] for a review of these effects. A cluster model to explain periodic behavior was introduced a long time ago [41]. The role of the complex interplay of retardation (delayed compartmental transitions) and fluctuations for oscillatory behavior has been investigated in one of our recent works [35].
The aim of the present paper is to study the spreading of a certain class of diseases in a population of individuals (random walkers) moving on complex graphs aiming to mimic human mobility patterns in complex environments such as cities, street, and transportation networks. Essential elements in our model are the account for the mortality of infected individuals (random walkers) and an indirect transmission pathway via vectors (detailed below).
The present paper is organized as follows. In Section 2 we establish a stochastic mean field model for the evolution of the compartmental populations. The special case of zero mortality is considered in Section 3 where we obtain an explicit formula for the endemic equilibrium (stationary constant compartmental populations for infinite time). In this way we identify a crucial parameter controlling the stability of the healthy state having the interpretation of the basic reproduction number (Section 4) where the healthy state is stable for and unstable for . A detailed proof of the stability of the endemic state for is provided in Appendix A.2. In Section 5 we analyze stability of the healthy state with mortality and derive the basic reproduction number and prove that , i.e., mortality reduces the basic reproduction number. In Section 6 we test robustness of our mean field model under "complex real world conditions" by implementing its assumptions into multiple random random walkers simulations on Barabási-Albert (BA), Erdös-Rényi (ER) and Watts-Strogatz (WS) type graphs ([16,17,24] and Appendix A.3). These graph types have different complexity and connectivity features with impact on the spreading.
2. Compartmental Model with Mortality
The goal of this section is to develop a mean field model for a certain class of diseases with indirect infection transmission via vectors which includes Dengue, Malaria (transmission by mosquitos) or Pestilence (transmission by fleas) and others [8,9]. To that end we consider a population of Z random walkers navigating independently on a connected (ergodic) graph. Each walker performs independent steps from one to another connected node on the network (specified subsequently). We assume that walkers and nodes are in one of the compartments, S (susceptible) and I (infected). In addition, walkers can be in compartment D (dead) whereas nodes never die.
Let () be the number of walkers (nodes) in compartments S and I, and the non-decreasing number of walkers (in compartment D) died from the disease up to time t. We consider walkers (Z independent of time) and a constant number of nodes . We assume at instant the first spontaneous occurrence of the disease of a few infected walkers or nodes (and no dead walkers ). We introduce the compartmental fractions , , for the walkers (normalized with respect to Z) with , and , with . To limit the complexity of our model we do not consider the demographic evolution, i.e., there are no natural birth and dead processes. We denote with the infection rates (rates of transitions S → I) of walkers and nodes, respectively. We assume the following simple bi-linear forms
with constant rate parameters (independent of time). indicates the infection rate of walkers where its dependence of is telling us that susceptible walkers can be infected only by (visiting) infected nodes. stands for the infection rate of nodes depending on indicating that susceptible nodes can only be infected by (visits of) infected walkers. There are no direct transmissions among walkers and among nodes. Infections of walkers (nodes) take place with specific transmission probabilities in a contact of a node and a walker which are captured by (yet not identical with) the transmission rate constants .
The infection time spans without mortality (waiting times in compartment I) of walkers and nodes are assumed to be independent random variables drawn from specific distributions specified hereafter. As only admitted dead process we assume that infected walkers may die within the time span of their infection. To capture this kind of mortality caused by the disease, we introduce a further independent random variable which indicates the life span of an infected walker. Both the infection and life time spans are counted from the time instant of the infection. A walker survives the disease if and dies from it for . With these assumptions, we give first a stochastic formulation of the evolution equations
where indicates the (non-negative) mortality rate of walkers. We indicate with average over the contained (set of independent) random variables outlined hereafter and in Appendix A.1. stands for the Heaviside function (A2), and for the Dirac’s -distribution. An epidemic always starts from “natural” initial conditions , (globally healthy state) where at the first infections occur spontaneously and can be “generated” by adding the source terms to the infection rates of walkers and nodes, respectively. Equivalently, we introduce initial conditions () with consisting typically of a few infected walkers and/or nodes in a large susceptible population without dead walkers .
The interpretation of system (2) is as follows. The instantaneous infection rate governs the transitions S → I of walkers (due to visits of infected nodes). The term describes the rate of walkers recovering at time t and infected at , i.e., their infection time span has elapsed and they survived as (indicated by ). Then captures the rate of walkers infected at dying at at time t during the infection time span (indicated by for ).
Remark I
The infection time span of a walker (sojourn time in compartment I) is , i.e., if (where the walker survives the disease), and is if the walker dies within the infectious time span (). is the walker’s infection time span without mortality (retrieved for ). The probability of persistence of a walker’s infection at time t, given the infection starts at time 0 is (see (7)). Note that only if , i.e., when the walker is in compartment I. As a crucial element of our model, we will analyze the statistics of the walker’s infection time span .
The initially infected walkers and nodes are as well subjected to the transition pathways, i.e., walkers either recover (alive) with rate or they die with rate , and nodes always recover with rate . For these terms are evanescent thus the initial conditions do not affect large time limits (endemic state for zero mortality). The importance of these terms can be seen by setting (no infections). Without these terms the initially infected walkers and nodes would stay infected forever, inconsistent with our assumptions.
The rate equations for the nodes can be interpreted in the same way as interplay of instantaneous infections and delayed recovery without mortality. We emphasize that the evolution equations of the nodes and walkers are non-linearly coupled by the implicit dependencies of the infection rates (1). In order to derive an explicit representation of system (2), we need to have a closer look on the averaging procedures and the involved distributions related to the independent random variables drawn from specific probability density functions (PDFs) which we define by
with their respective PDFs (kernels) which are normalized . Then recall the averaging rule for (suitable) functions of the random variable T which we use throughout the paper
see also Appendix A.1. An important case is . Then by applying (4) we introduce the persistence probabilities of walker’s (node’s) infection (without mortality)
and the probability of walker’s survival up to time t (given )
The persistence probabilities fulfill the initial condition corresponding to the normalization of the waiting time PDFs and are vanishing at infinity . To evaluate the averages in (2) we will use the following quantities:
In these averages we make use of the independence of the waiting times , and of causality of and the kernels (i.e., for ). Of utmost importance are the "defective" PDFs (DPDFs) of death and recovery. "Defective" means that are no proper PDFs since they are not normalized to one, but rather to , respectively. Consult [13] for a recent account of defective distributions and related stochastic processes. They have the following interpretation. is the probability of transition I → D within of an infected walker (infected at ). is the probability of transition I → S within of a walker infected at . Therefore,
is non-negative (as are , ) and is a proper well-normalized PDF of all exits of walkers from compartment I (i.e., I → S + I → D). Without mortality () this PDF retrieves .
The quantities introduced in (7) have the following interpretation. is the probability that a walker infected at instant 0 is at time t in compartment S (i.e., recovered prior or up to time t). is the probability that a walker infected at instant 0 is at time t in compartment D (i.e., died prior and up to time t). Important are the infinite time limits: has the interpretation of the overall probability that an infected walker survives the infection, and is the overall probability for an infected walker to die from the disease. We refer also to as "overall mortality". It must not be confused with the infinite time limit of dead walkers fraction which is different from as we will see in details subsequently. A small value may cause a high value of for instance for short infectious periods where walkers may be repeatedly infected.
In most cases not all infected walkers die from their disease (in an infinite observation time), hence (as is defective). represents the limit of a fatal disease, and a disease without mortality. (as is defective) is the complementary probability with .
With these remarks, system (2) reads
The PDF (8) that a walker leaves compartment I (either by recovery or by death) allows to rewrite the second equation of (9) as
Worthy of closer consideration is the mortality rate of the infected walkers (representing the total mortality – entry rate into the D compartment)
where clearly . Integrating this relation yields the fraction of dead walkers
An interesting quantity is the cumulative recovery rate of walkers (integrated entry rates of walkers into the S compartment, see first equation in (2))
The quantity records all recovery events of walkers up to time t, where individual walkers may suffer repeated infections and recoveries. We observe that (see (7))
Relation (12) records all dead events of walkers up to time t. Since each walker may die only once, it follows indeed that . Contrarily, the quantity is not restricted to this interval as walkers may be repeatedly infected and recovered but due to mortality eventually only a finite number of times (, see (18)). Mortality renders the chain of infection and recovery events transient (due to the defective feature of ). To shed more light on the behavior of consider for a moment zero mortality () and : We then have (shown in Section 3) thus coming along with an infinite chain of recurrent infection and recovery events (as turns into the proper non-defective PDF ).
Using (7) we can rewrite (2) in equivalent integral form
and with (redundant) Equation (12) for the fraction of dead walkers. (15) is a self-consistent system since the infection rates are implicit functions of susceptible and infected population fractions , (see (1)). Explore now the infinite time limit of (15) where it is convenient to consider the Laplace transformed equations. We introduce the Laplace transform (LT, denoted with a hat) of a function as
where denotes the (suitably chosen) Laplace variable. In order to retrieve infinite time limits we use the asymptotic feature
Observing that the LT of is and where (see (7)), we arrive at
where . In the same way one obtains
Since is non-zero, the asymptotic values depend on the initial condition and the infection (rate) history. This is not any more true for zero mortality () and considered in Section 3. We define the overall probability that a walker dies ( survives) the disease
consistent with our previous interpretation of , and the ratio
The quantities (19) and (20) depend only on the stochastic features of and . They are independent of the infection rates and initial conditions and therefore of the topological properties of the network. In addition, they also do not depend on the stochastic features of the node’s infection time span .
Markovian (memoryless) case
Generally the system (9) contains the history of the process (memory) which makes the process non-Markovian. The only exception is when all waiting times are exponentially distributed, namely , , (, ). Then (9) takes with (15) the memoryless form
Putting the left-hand sides to zero yields the stationary state
Let us check whether this result is consistent with (17). To this end, we integrate the second equation in (21) knowing that leading to
thus . Plugging this relation into (22) and accounting for recovers indeed the representation of expression (17).
A few more words on waiting time distributions
In our simulations we assume that the time spans are independent random variables drawn from specific Gamma distributions. The advantage to use Gamma distributions is that they may realize a large variety of shapes, see Figure 1 for a few examples. To generate Gamma distributed random numbers we employ the PYTHON random number generator (library numpy.random). Recall the Gamma distribution
where is the so called `shape parameter’ and the rate parameter (often is used the term ’scale parameter’ ) and stands for the Gamma function. We also will subsequently use the LT of the Gamma PDF
The Gamma PDF has finite mean and for the Gamma-PDF is weakly singular at and recovers exponential PDFs. For the Gamma PDF is completely monotonic (CM) (see Appendix, (A9) for a definition). For the range the Gamma-PDF has a maximum at and becomes narrower the larger (while keeping its mean fixed), especially we can generate sharp waiting times using the feature
We also will use subsequently the persistence probability of the Gamma distribution (see right frame of Figure 1)
where indicates the upper incomplete Gamma function with . (27) fulfills necessarily the initial condition and is vanishing at infinity .
3. Endemic Equilibrium for Zero Mortality
Here we consider the large time asymptotics of the compartment populations without mortality () where the self-consistent system (15) reads
The endemic state emerging in the large time asymptotics does not depend on the initial conditions as . For what follows it is convenient to consider the LTs of (28) which read
where are the LTs of the persistence distributions, and reflecting constant populations of walkers and nodes. In order to determine the endemic equilibrium, we assume that the mean infection time spans for the nodes and walkers exist
thus the admissible range of the Laplace variable is (if chosen real). Now using (16) we obtain the endemic equilibrium from where the initial conditions are wiped out at infinity as . Assuming that the infection rates are constant in the endemic equilibrium we have , () and arrive at
thus
One can see that the globally healthy state is also a solution of this equation. Beside that, only solutions correspond to an endemic equilibrium. One gets
for the endemic equilibrium which is independent of the initial conditions . It depends only on the phenomenological rate constants and the mean infection time spans . We point out that the endemic equilibrium (33) has exchange symmetry between walkers and nodes reflecting this feature in the system (2) of evolution equations without mortality. The endemic values are within , i.e., existing only if . We interpret as the basic reproduction number (average number of new infections at – nodes or walkers – due to one infected node or walker at ). That this is really the appropriate interpretation can be seen by the following somewhat rough consideration of the infection rates at . Assume we have initially one single infected node and no infected walkers . The expected number of walkers infected by this first infected node during its infectious period is
The number of nodes getting infected by these infected walkers during their infectious time is
Hence is the average number of infected nodes caused by the first infected node (with zero initially infected walkers). Due to the exchange symmetry (nodes ↔ walkers) of the infection rates, this argumentation remains true when we start with one infected walker and no infected nodes.
We infer that the globally healthy state is unstable for where the endemic equilibrium (33) is a unique stable fixed point and attractor for all initial conditions . We will confirm this in the next section by a linear stability analysis of the globally healthy state. The stability of the endemic state is demonstrated in the next section with Appendix A.2.
Remarkable is the limit (while are kept constant) where all walkers become infected but not all nodes and vice versa. We plot the endemic state in Figure 2 versus where positive values for occur only for which correspond to endemic states. Next we perform a linear stability analysis of the endemic and healthy state where we will indeed identify as crucial control parameter.
4. Stability Analysis of Endemic and Healthy State without Mortality
Here we are interested in the condition of spreading for zero mortality, or equivalently in the condition for which the globally healthy state (endemic state) is unstable (stable). To check stability of the endemic fixed point , we set
where are `small’ constant amplitudes. This ansatz accounts for the constant populations of nodes and walkers. Then we have for the infection rates up to linear orders in the amplitudes
Plugging these relations in our evolution equations (2) without mortality, omitting two redundant equations leads to the system
where we have used and the cases of -distributed are contained for . We point out that in ansatz (35) we relax causality i.e., we admit for thus
The solvability of this matrix equation requires the determinant to vanish leading to a transcendental characteristic equation for
Generally, a fixed point is unstable if solutions with positive real part of exist. Consider this first for the globally healthy state for which Equation (38) reads
where we notice that are the LTs of the persistence probabilities of the infection time spans. Consider this equation for and take into account (30) we arrive at
We observe that for . On the other hand, we have for that and hence
One can hence infer from complete monotony of and therefore of (see Appendix A.2, Equation (A9) for a precise definition), that () thus has one single positive zero only if , i.e., for which therefore is the condition of instability of the healthy state (spreading of the disease). Conversely, for the healthy state turns into a stable fixed point where there is no spreading of the disease. In particular, the healthy state is always unstable () if at least one of mean infection time spans . This is true for fat-tailed kernels scaling as () for . We consider such a distribution briefly in subsequent section. We plot function versus for different for Gamma-distributed in Figure 3.
Now we consider the stability of the endemic state with where from (38) this function reads
with
On the other hand, (as ) and from monotony of follows that there is no positive solution of for . We plot in Figure 4 for different values of and Gamma distributed . In Appendix A.2 we complete the analytical proof that for .
5. Stability Analysis of the Healthy State with Mortality
An important question is, how mortality does modify the instability of the healthy state and the basic reproduction number. To shed light on this question we perform a linear stability analysis of the healthy state where we set
with and . Plugging this ansatz for into three independent equation of (2), say the first, third and fourth one, and performing the averages (relaxing causality as previously) we arrive at
Putting the determinant of the matrix to zero yields the condition
where the LTs of the DPDFs defined in (7) come into play. We are interested under which conditions there is a positive solution (instability of healthy state) of (46). Since and with we see that is solution of (46). Recall from (7) that is the (properly normalized) PDF (8). Condition (46) then reads
where is the LT of the persistence probability of the walker’s infection, i.e., the probability that (see Remark I). For zero mortality we have , ( and ) retrieving condition (39). The mean sojourn time in compartment I with mortality yields
where we arrive at
Relation (48) shows that (equality only for zero mortality). On the other hand we have , so there is a positive solution of only if
where is the basic reproduction number modified by mortality with (equality only for zero mortality). To visualize the effect of mortality on the instability of the healthy state we plot for a few values of in Figure 5. Increasing mortality turns an unstable healthy state into a stable one.
In the random walk simulations we deal with Gamma distributed where the persistence probabilities are then normalized incomplete Gamma functions (27). To explore the effect of mortality for such cases, we determine by numerical integration of (48) as a function of the mortality rate parameter and plot the result in Figure 6 where one can see that is monotonous decreasing with mortality rate . We also include a case of a fat-tailed (Mittag-Leffler) distributed which we discuss hereafter. The parameters in Figure 6 are such that the zero mortality case occurs with as the upper bound. The essential feature is that decays monotonically with increasing mortality rate parameter approaching zero for . Diseases with high mortality stabilize the healthy state even for .
Consider briefly the case where is exponentially distributed (i.e., in the Gamma distribution of ) with . Then we have thus
The zero mortality case is recovered for with . For Gamma distributed this yields
where , are the parameters of the respective Gamma distributions of the infection times of nodes and walkers. The Markovian case where all waiting times are exponentially distributed is covered for and yields
containing the zero mortality case for .
Fat-tailed distributed :
Finally, an interesting case emerges if follows a fat-tailed distribution, i.e., for t large () and , . Let us have a look, how mortality is affecting this situation. Fat tailed distributions describe diseases where the infectious periods are very long and the healthy state without mortality is extremely unstable (). Infected walkers can infect many nodes during their long infection time spans. An important case of this class is constituted by the Mittag-Leffler (ML) distribution where indicates the Mittag-Leffler function, see [14,15] and references therein for representations and connections with fractional calculus. The ML function recovers the exponential for (). Assuming exponential mortality one obtains with (51)
containing the LT of the ML persistence probability distribution . The essential feature here is that is weakly singular at with a monotonously decreasing scaling law, where the healthy state becomes stable for mortality parameters larger as . We depict this case in Figure 6 for (violet curve).
6. Random Walk Simulations
The remainder of our paper is devoted to test the mean field model under "real world conditions" which we mimic by random walkers navigating independently on an undirected connected (ergodic) graph. In our simulations we focused on Barabási-Albert (BA), Erdös-Rényi (ER) and Watts-Strogatz (WS) graphs [29,42,43] (see Appendix A.3 for a brief recap) and implemented the compartments and transmission pathway for walkers and nodes outlined in Section 2. A susceptible walker gets infected with probability by visiting an infected node, and a susceptible node gets infected with probability at a visit of an infectious walker. We assume that the infection probabilities are constant for all nodes and walkers, respectively. They are related yet not identical with the macroscopic rate constants . A critical issue is whether the simple bi-linear forms for the mean field infection rates (1) still capture well the complexity of the spreading in such "real world" networks. One goal of the subsequent case study is to explore this question.
We characterize the network topology by nodes with the adjacency matrix where if the pair of nodes is connected by an edge, and if the pair is disconnected. Further, we assume to avoid self-connections of nodes. We confine us to undirected networks where the edges have no direction and the adjacency matrix is symmetric. The degree of a node i counts the number of neighbor nodes (edges) of this node. Each walker performs simultaneous independent random steps at discrete time instants from one to another connected node. The steps from a node i to one of the neighbor nodes are chosen with probability , following for all walkers the same transition matrix
which is normalized . This is a common way to connect the network topology with simple Markovian random walks [24,42]. In the simulations the departure nodes at of the walkers are randomly chosen. The path of each walker is independent and not affected by contacts with other walkers or by transition events from one to another compartment.
Case study and discussion
In order to compare the epidemic dynamics of the mean field model and random walk simulations we integrate the stochastic evolution Eqs. (2) numerically as follows. We average the increments of the compartmental fractions in a generalized Monte-Carlo sense converging towards the convolutions of the right hand side of (9) where we use the Monte-Carlo convergence feature
for random variables T drawn from PDFs . We perform this average for any time increment with respect to all involved independent random time spans (see Appendix A.1) and integrate the averaged compartmental increments in a fourth order Runge-Kutta scheme (RK4). We use in the random walk simulations and the Monte-Carlo (mean field) integration exactly the same (Gamma distributed) random values (PYTHON seeds) for the . The values of the infection rate parameters used in the mean field integration are determined from Equation (32) by plugging in the large time asymptotic values of the random walk simulation with identical parameters (without mortality). The compartmental fractions in the random walk simulations are determined by simply counting the compartmental populations at each time increment of walker’s steps. The so determined rate parameters plugged into the mean field integration depend in a complex manner on the infection probabilities and topology of the network. In this way this information is also contained in the basic reproduction numbers with and without mortality.
We explore the spreading in random graphs of different complexity such as represented in Figure 7. The BA graph is small world with power law distributed degree (Appendix A.3) which means that there are many nodes having a few connections, and a few (hub) nodes with a huge number of connections. The average distance between nodes becomes small, as it is sufficient that almost every node is only a few links away from a hub node. The ER graph is small world due to a broad degree distribution. The WS graph with the choice of connectivity parameter in Figure 7 has long average distances and is large world. Intuitively, one infers that a small world structure is favorable for spreading processes, a feature which was already demonstrated in the literature [9,10]. In our simulations spreading in network architectures with increased connectivity comes along with increased values of and , respectively.
We identify the starting time instant () of the evolution in the mean field model with the time instant of the first infection of a walker in the random walk simulations. In all cases we start with a small number of randomly chosen initially infected nodes () and no infected or dead walkers. To reduce the numbers of parameters and to concentrate on topological effects we have put in all simulations the transmission probabilities . We refer to [46] for the PYTHON codes2 and animated simulation videos related to the present study. In order to visualize a typical spreading process, we depict in Figure 8 a few snapshots in a Watt-Strogatz graph with rather high overall mortality probability of . In this case a single infection wave emerges where a large part of walkers gets repeatedly infected increasing their probability to die. This leads to a very high fraction of eventually dead walkers and small fraction of surviving walkers corresponding to the stationary state (17) which is taken as soon as the disease gets extinct . Figure 8 shows that first the infection gains large parts of the network consistent to the large value of observed in this case. After the first wave the disease gets extinct by the high mortality of the walkers. A disease with a similar high mortality characteristics is for instance Pestilence. The process of Figure 8 is visualized in an animated video. Figure 9 and Figure 10 show the evolution in WS graphs with identical parameters and Gamma distributions of as in Figure 8 but with different mortality rate parameter and a much smaller overall mortality . The different network connectivity leads to different values of and mean field solutions in Figure 9 and Figure 10. In addition, the networks of Figure 9 and Figure 10 have different connectivity features. The graph of Figure 9 is small world (highly connected) whereas the WS graph in Figure 10 is weakly connected and large world. One observes in Figure 9 that the infection numbers exhibit strong and immediate increases followed by attenuated oscillations around the endemic equilibrium (for zero mortality) with high values and . The basic reproduction numbers with mortality are in both graphs only slightly smaller as . This is due to a rather small overall mortality of . This effect can also be seen in the small overlap of the Gamma distributions of and in the histogram. Recall that a small value of does not necessarily mean small as this quantity depends also on the infection rates and network topology (see (17)) and is sensitive to repeated infections. repeated infections may indeed play an important role here as is rather small.
In Figure 10 the infections of the random walk simulations are increasing slower (red curves) compared to Figure 9. The structure with higher connectivity Figure 9 shows excellent quantitative agreement of random walk and mean field solutions for the walkers and nodes capturing well the attenuated oscillations, especially for zero mortality. In the network with smaller connectivity of Figure 10 the increase of the infections is delayed compared to the mean field. On the other hand, for non-zero mortality the mean field and random walk dynamics for the walkers diverge slightly with time. We infer that mortality may deviate the infection rates from (1).
The comparison of the spreading in Figure 9 and Figure 10 shows clearly the role of the connectivity: The mean field model captures better the spreading in networks with higher connectivity (short average distances between nodes) and with low mortality. The following cases give further evidence for these observations.
Next we explore the spreading on an ER graph in Figure 11. The agreement of random walk simulations and mean field model is impressive where this holds for both with and without mortality. One can see by the degree distribution in Figure 7 that for these connectivity parameters the graph is well connected and small world giving strong evidence that the mean field approach is here well capturing the spreading dynamics.
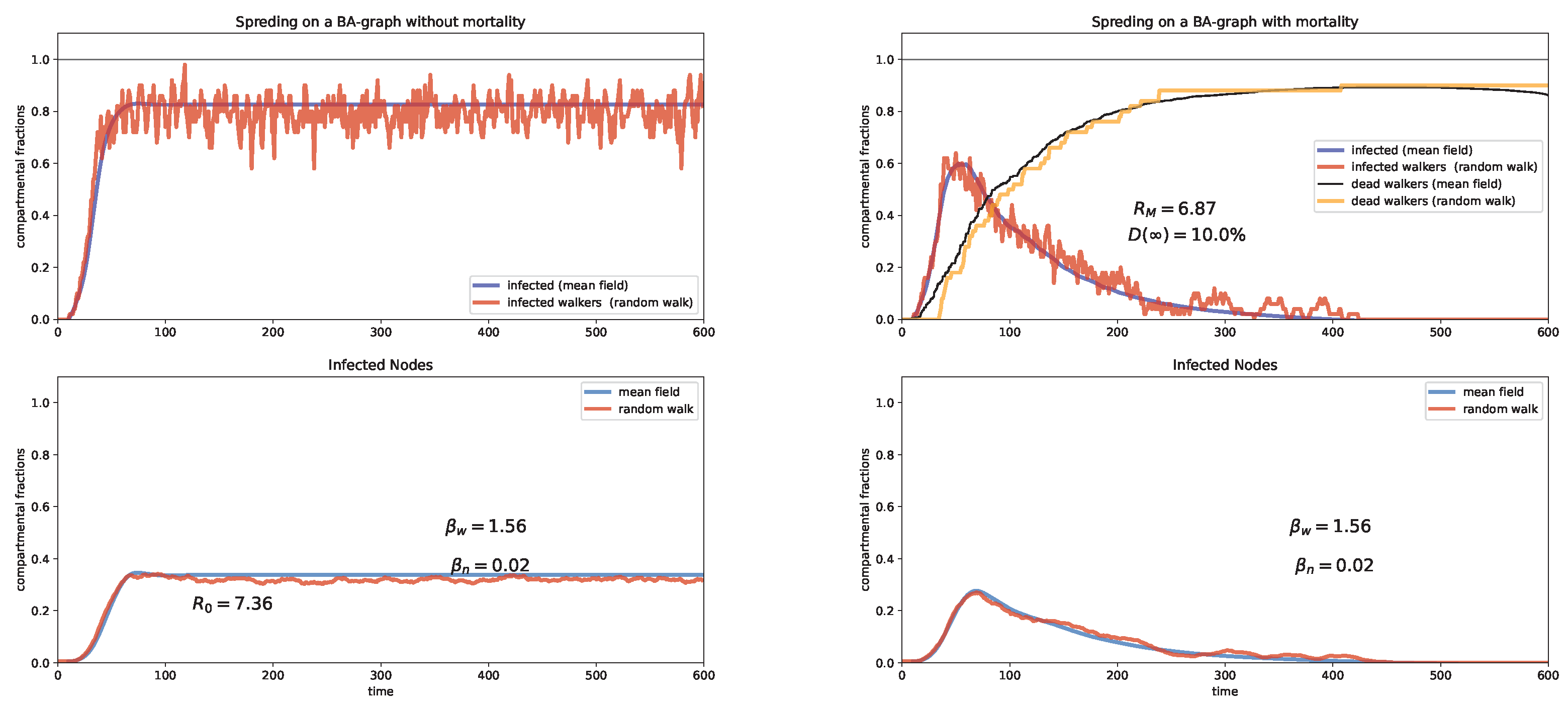
Finally we explore in Figure 12 the dynamics on a BA network. In the right frame we have high overall mortality of probability for a walker to die from an infection. In this example the disease is starting to spread as where only a single infection wave emerges which is extinct by the high mortality. Recall that that is only telling us that the healthy state is unstable, i.e., that the disease is starting to spread. It does not contain the information whether the spreading is persistent or whether the disease is eventually extinct. To explore the role of topological features such as average distances between nodes we perform the same simulation experiment with identical parameters and less () nodes, i.e., higher density of walkers (Figure 13).
The accordance of mean field model and random walk simulation is also in Figure 13 indeed excellent. We explain this by the fact that the BA network is a strongly connected structure with pronounced small world property. The higher density of walkers lead to increased and compared to Figure 12. There is also only a single infection wave occurring with a higher maximum value compared to Figure 12. In both cases (Figure 12 and Figure 13, right frames) the infection waves are extinct by the high mortality of walkers where stationary states (17) with of dead walkers are taken. When we switch off mortality (left frames), stable endemic states emerge more rapidly in Figure 13 (case with higher density of walkers).
Further simulation experiments (not shown here) reveal that the mean field model and random walk simulations exhibit excellent accordance when we further increase the attachment parameters m or the density of walkers with otherwise identical parameters. For higher mortality the agreement becomes less well and diverges with increasing observation time. This observation suggests that mortality modifies the infection rates in the network for larger observation times. We leave this issue for future research.
Our overall finding from this case study is that the mean field approach (with infection rates (1)) is particularly well suited to mimic spreading in strongly connected environments with pronounced small world feature, but is less well for higher mortality.
7. Conclusions
We studied epidemic spreading in complex graphs where we focused on transmission pathway via vectors mimicking the spreading of a certain class of diseases such as Dengue, Malaria or Pestilence and others. We developed a stochastic compartment model for the walkers and nodes with mortality for the walkers. For zero mortality we obtained the endemic equilibrium in explicit form (Equations (33)). Stability analysis of the endemic and healthy states reveal the crucial control parameter for spreading, the basic reproduction number. We obtained the basic reproduction numbers and with and without mortality, respectively, where we proved that , (relations (50) with (48)). For the healthy state is an unstable fixed point where the endemic equilibrium exists for zero mortality as a unique stable fixed point independent of the initial conditions. The basic reproduction numbers depend on the means of the compartmental sojourn times in compartment I of the nodes and walkers and on the topology of the network captured by the mean field rate constants .
Our model has applications beyond epidemic dynamics, for instance in chemical reaction models [45]. An interesting question to explore in a follow-up project is whether our class of compartment models with indirect transmission pathways may exhibit (for zero mortality) persistent oscillations (Hopf instabilities) (See our brief discussion at the end of Appendix A.2.). An open problem also remains how large world network topology may be included into such a mean field model, modifying the infection rates. Further promising directions include an account for immune and incubation compartments, effects of mitigation measures, vaccination among many others.
Acknowledgments
T.G. gratefully acknowledges to have been hosted at the Institut Jean le Rond d’Alembert in the framework of an internship (stage M1 Physique ) for the development of the PYTHON simulation codes and participation in the present study.
Appendix A
Appendix A.1. Some Basic Notions
Here we recall briefly some basic notions used in the paper. The infection rates are a causal functions
where indicates the Heaviside step function defined by
with and in or definition . Its derivative yields the Dirac -distribution . We use throughout the paper mutually independent strictly positive random variables The random variables are assumed to follow their specific PDFs
where the PDFs are causal functions as a consequence of the positiveness of the . Then applies the averaging rule
for suitable functions f. For using independence of the this yields
Important cases emerge by applying (A4) to exponentials
In this relation the LTs of the PDFs come into play
where reflects the normalization of PDFs (A3). A further observation is
where ★ stands for convolution of the causal PDFs.
Appendix A.2. Proof of Stability of the Endemic Equilibrium
Here we develop the rest of the proof stability of the endemic equilibrium, i.e., we show that the function (42) is strictly positive for with . First, we observe that with and . For our convenience, we introduce the functions
which the LTs of the normalized and which are by virtue of Bernstein’s theorem [44] completely monotonic (CM) with respect to , i.e.,
inheriting this feature from the exponential (). Therefore,
(as ) exists thus is monotonously decreasing with with . Further we observe in Eqs. (33) that , thus
Then reads
Now we observe that thus a lower bound function is generated by replacing in the second line. Now it is sufficient to prove that . We hence get for this lower bound function
and with and it follows that concluding the proof of stability of the endemic equilibrium.
A few remarks on the possibility of oscillatory (Hopf) instabilities of the endemic equilibrium
Let us briefly explore whether an oscillatory (Hopf) instability of the endemic equilibrium is possible. To that end we write as
where and is a non-negative CM function (see Figure 4) with maximum value . Then the following two cases may occur.
- Case (i); ():
Then can be represented as LT of a non-negative function and consider now with thus the real part of can be written as
with and clearly . Therefore,
Hence in the range of case (i) there is no oscillatory (Hopf) instability of the endemic state possible3.
- Case (ii); :
Here we have two pertinent ranges of . The first is the range (a) (i.e., ) and the second one (b) is . Clearly in the range (a) (A14) remains true and strictly positive. Hence for no Hopf instability is possible.
This changes in the range (b) since thus may become negative. Therefore, for a Hopf instability of the endemic state becomes possible. However, the possibility that is only necessary but not sufficient for a Hopf instability. One also needs simultaneously that the imaginary part is vanishing for the same . In the simulations performed for this paper, we did not observe persistent oscillations. We leave the exploration of this issue for future research in a follow-up project.
Appendix A.3. A Very Brief Recap of Random Graphs
Here we recall briefly some essential features of the three classes of random graphs, which we use in the random walk simulations. For an extended outline, consult e.g., [18]. The three classes of random graph models depicted herafter are motivated by the observation that complex random network structures are encountered ubiquitously and crucially determine human and animal mobility patterns including epidemic propagation.
- (i)
- Erdös and Rényi (ER) graph
The ER graph is one of the most basic variants of a random graph, which was introduced in 1959 by Erdös and Rényi [20]. We use is the so-called variant of random ER graph model (which is actually due to Gilbert [22]) which is generated as follows [16,25]. Given are N labeled nodes. Any pair of nodes is connected independently by an edge with uniform probability p. The probability that a node has connections is given by a binomial distribution
where denotes the average degree. For (while is kept constant) the degree distribution converges to a Poisson distribution representing the infinite graph limit of the ER -model. Therefore, is rapidly decaying with degree k, so the number of nodes with a high number of connections is very small. In order to obtain in the -model a connected graph, it is necessary that is above the percolation limit [20,24].
- (ii)
- Watts-Strogatz (WS) network
The WS graph model [21,25,26] starts with a ring of N nodes where each node is connected symmetrically with a number to left and right neighbor nodes by an edge such that each node has connections. In the second step, each of the connections of node i is replaced with probability p by a randomly chosen connection uniformly among other nodes avoiding self-connections and link duplication, so that each connection is chosen only once. There are two noteworthy limits for a WS graph. For (no rewiring of links) we have a regular ring with constant degree for all nodes. In the limit an ER graph is emerging with probability for a link. The WS graph has the small-world property (short average distances between pairs of nodes) and a high tendency to develop clusters of nodes [26].
- (iii)
- Barabási-Albert (BA) graph
The BA graph is generated by a preferential attachment mechanism for newly added nodes [16,17,18,19]. One starts with nodes and adds new nodes. Any newly added node is connected with existing nodes (m is referred to as the attachment parameter) where most likely with nodes of high degrees. In this way nodes with high degree receive further links. This leads to an asymptotically scale-free network with a power law degree-distribution
As the decrease in this power law is relatively slow, there might exist quite a few nodes with many links (hub nodes) and many nodes with few links. BA graphs are believed to mimic a large class of real-world networks including the world wide web, citation-, social-, and metabolic networks.
Realizations of these three types of random graph types used in our multiple random walkers simulations are shown in Figure 7.
References
- Rhodes, P.; Bryant, J.H. Public Health. Encycl. Br. 2024. Available online: https://www.britannica.com/topic/public-health.
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. Roy. Soc. A 1927, 115, 700–721. [Google Scholar]
- Liu, W.M.; Levin, H.W.H.H.W.S.A. Dynamical behavior of epidemiological models with non-linear incidence rate. J. Math. Biol. 1987, 25, 359–380. [Google Scholar] [CrossRef]
- Li, M.Y.; Graef, J.R.; Wang, L.; Karsai, J. Global dynamics of a SEIR model with varying total population size. Math. Biosci. 1999, 160, 191–213. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Infectious Diseases in Humans; Oxford University Press: Oxford, 1992. [Google Scholar]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer, 2015. [Google Scholar]
- Harris, J.E. Population-Based Model of the Fraction of Incidental COVID-19 Hospitalizations during the Omicron BA.1 Wave in the United States. COVID 2023, 3, 728–743. [Google Scholar] [CrossRef]
- Whitehead, S.S.; Blaney, J.E.; Durbin, A.P.; Murphy, B.R. Prospects for a dengue virus vaccine. Nat Rev Microbiol 2017, 5, 518–528. [Google Scholar] [CrossRef] [PubMed]
- Pastor-Satorras, R.; Castellano, C.; Mieghem, P.V.; Vespignani, A. Epidemic processes in complex networks. Rev. Mod. Phys. 2015, 87, 925–979. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic dynamics and endemic states in complex networks. Phys. Rev. E 2001, 63, 066117. [Google Scholar] [CrossRef]
- Shudo, Y.O.Y.A. Microscopic Numerical Simulations of Epidemic Models on Networks. Mathematics 2021, 9, 932. [Google Scholar]
- Basnarkov, L.; Tomovski, I.; Sandev, T.; Kocarev, L. on-Markovian SIR epidemic spreading model of COVID-19. Chaos, Solitons and Fractals 2022, 160, 112286. [Google Scholar] [CrossRef]
- d’Onofrio, G.; Michelitsch, T.M.; Polito, F.; Riascos, A.P. On discrete-time arrival processes and related random motions. arXiv 2024, arXiv:2403.06821. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion : A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Mainardi, F.; Gorenflo, R.; Scalas, E. A fractional generalization of the Poisson processes. Vietnam J. Math. 2004, 32, 53–64. [Google Scholar]
- Barabási, A.-L. Network Science; Cambridge University Press: Cambridge, 2016. [Google Scholar]
- Barabási, A.-L.; Albert, R. Emergence of Scaling in Random Networks. Science 1999, 286, 509. [Google Scholar] [CrossRef] [PubMed]
- Barabási; Albert, R. ; Jeong, H. Mean-field theory for scale-free random networks. Physica A 1999, 272, 173–187. [Google Scholar] [CrossRef]
- Jeong, H.; Tombor, B.; Albert, R.; Oltvai, Z.N.; Barabási, A.L. The large-scale organization of metabolic networks. Nature 2000, 407, 651–4. [Google Scholar] [CrossRef]
- Erdös, P.; Rényi, A. On Random Graphs I. Publ. Math. 1959, 6, 290–297. [Google Scholar] [CrossRef]
- Erdös, P.; Rényi, P. On the evolution of random graphs. Publ. Math. Inst. Hung. Acad. Sci 1960, 5, 17. [Google Scholar]
- Gilbert, E.N. Random Graphs. Annals Math. Sci. 1959, 30, 1141–1144. [Google Scholar] [CrossRef]
- Ross, S.M. Stochastic Processes; John Wiley & Sons: New York, 1996. [Google Scholar]
- Newman, M.E.J. Networks: An Introduction; Oxford University Press: Oxford, 2010. [Google Scholar]
- Newman, M.E.J.; Watts, D.J.; Strogatz, S.H. Random graph models of social networks. PNAS 2002, 99, 2566–2572. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef]
- Eraso-Hernandez, L.K.; Riascos, A.P.; Michelitsch, T.M.; Wang-Michelitsch, J. Evolution of transport under cumulative damage in metro systems. Int. J. Mod. Phys. C 2023, 2450037. [Google Scholar] [CrossRef]
- Barrat, A.; Barthélemy, M.; Vespignani, A. Epidemic spreading in population networks. In Dynamic Processes on Complex Networks; Cambridge University Press, 2008; pp. 180–215. [Google Scholar] [CrossRef]
- Riascos, A.P.; Sanders, D.P. Mean encounter times for multiple random walkers on networks. Phys. Rev. E 2021, 103, 042312. [Google Scholar] [CrossRef] [PubMed]
- Bestehorn, M.; Riascos, A.P.; Michelitsch, T.M.; Collet, B.A. A Markovian random walk model of epidemic spreading. Continuum Mech. Thermodyn. 2021, 33, 1207–1221. [Google Scholar] [CrossRef] [PubMed]
- Michelitsch, T.M.; Riascos, A.P.; Collet, B.A.; Nowakowski, A.F.; Nicolleau, F.C.G.A. Fractional Dynamics on Networks and Lattices; ISTE/Wiley: London, 2019. [Google Scholar]
- Riascos, A.P.; Mateos, J.L. Long-range navigation on complex networks using Lévy random walks. Phys. Rev. E 2012, 86, 056110. [Google Scholar] [CrossRef] [PubMed]
- Bestehorn, M.; Michelitsch, T.M.; Collet, B.A.; Riascos, A.P.; Nowakowski, A.A.F. Simple model of epidemic dynamics with memory effects. Phys. Rev. E 2022, 105, 024205. [Google Scholar] [CrossRef] [PubMed]
- Granger, T.; Michelitsch, T.M.; Bestehorn, M.; Riascos, A.P.; Collet, B.A. Four-compartment epidemic model with retarded transition rates. Phys. Rev. E 2023, 107, 044207. [Google Scholar] [CrossRef]
- Bestehorn, M.; Michelitsch, T.M. Oscillating Behavior of a Compartmental Model with Retarded Noisy Dynamic Infection Rate. Int. J. Bifurcation Chaos 2023, 33, 2350056. [Google Scholar] [CrossRef]
- van Kampen, N.G. Stochastic processes in chemistry and physics; North Holland: Amsterdam, 1981. [Google Scholar]
- Mieghem, P.V. Exact Markovian SIR and SIS epidemics on networks and an upper bound for the epidemic threshold. arXiv 2014, arXiv:1402.1731. [Google Scholar]
- Zhu, Y.; Shen, R.; Dong, H.; Wang, W. Spatial heterogeneity and infection patterns on epidemic transmission disclosed by a combined contact-dependent dynamics and compartmental model. PLoS ONE 2023, 18, e0286558. [Google Scholar] [CrossRef]
- Gostiaux, L.; Bos, W.J.T.; Bertoglio, J.-P. Periodic epidemic outbursts explained by local saturation of clusters. Phys. Rev. E 2023, 107, L012201. [Google Scholar] [CrossRef]
- Peyrard, M. What can we learn from the dynamics of the Covid-19 epidemic? arXiv 2023, arXiv:2308.14090. [Google Scholar] [CrossRef] [PubMed]
- Soper, H.E. The interpretation of periodicity in disease prevalence. J. Royal Statistical Society 1929, 92, 34–61. [Google Scholar] [CrossRef]
- Noh, J.-D.; Rieger, H. Random walks on complex networks. Phys. Rev. Lett. 2004, 92. [Google Scholar] [CrossRef] [PubMed]
- Michelitsch, T.; Riascos, A.P.; Collet, B.A.; Nowakowski, A.; Nicolleau, F. Fractional Dynamics on Networks and Lattices; ISTE-Wiley: London, 2019. [Google Scholar]
- Schilling, R.; Song, R.; Vondraček, Z. Bernstein functions. In Theory and Applications, Studies in Mathematics, 37; de Gruyter: Berlin, 2010. [Google Scholar]
- Simon, C.M. The SIR dynamic model of infectious disease transmission and its analogy with chemical kinetics. PeerJ Physical Chemistry 2020. [Google Scholar] [CrossRef]
- Supplementary materials: PYTHON codes (© Téo Granger 2023) and animated films. Available online: https://sites.google.com/view/scirs-model-supplementaries/accueil.
| 1 | The network `distance’ of two nodes is the number of edges of the shortest path connecting them. |
| 2 | Free to download and non-commercial use. |
| 3 | A similar consideration of function of (39) shows as well that the healthy state for does not exhibit an oscillatory instability. |
Figure 1.
Left frame: Gamma distribution for four different cases: Weakly singular (at ) [, ], exponential [, ], broad [, ], and narrow [, ]. Right frame: Their Persistence (survival) probability distributions of Equation (27) where the same color code is used.
Figure 1.
Left frame: Gamma distribution for four different cases: Weakly singular (at ) [, ], exponential [, ], broad [, ], and narrow [, ]. Right frame: Their Persistence (survival) probability distributions of Equation (27) where the same color code is used.
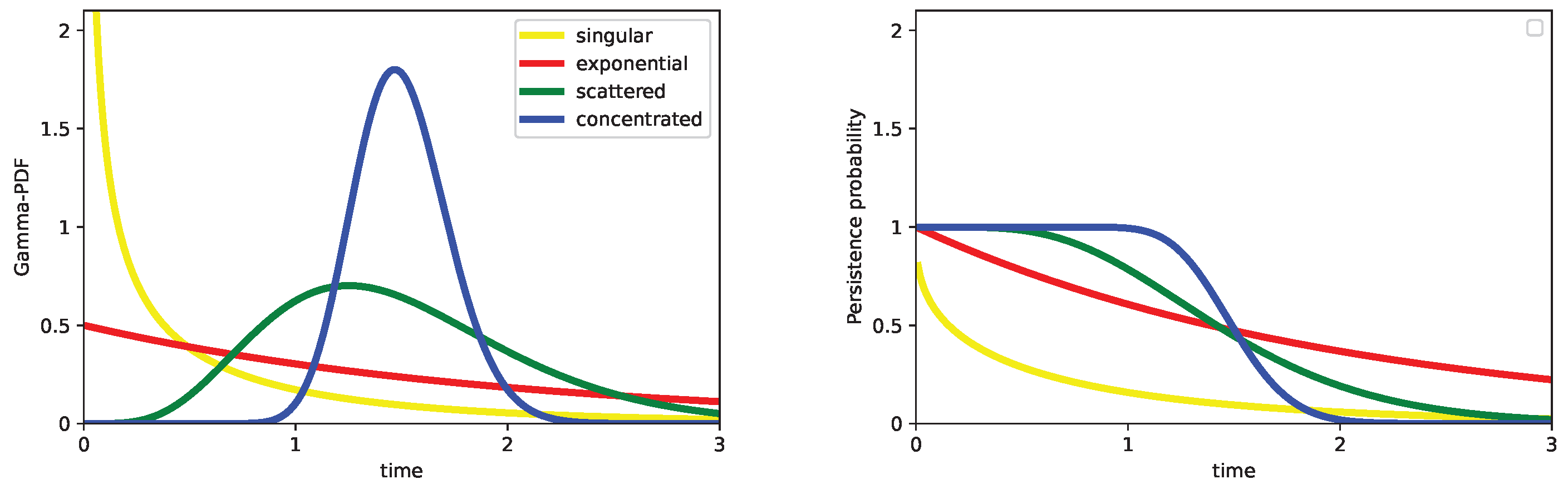
Figure 2.
Endemic states of infected walkers/nodes versus for various values of parameter r which has to be read () for the walker’s (node’s) endemic states.
Figure 2.
Endemic states of infected walkers/nodes versus for various values of parameter r which has to be read () for the walker’s (node’s) endemic states.
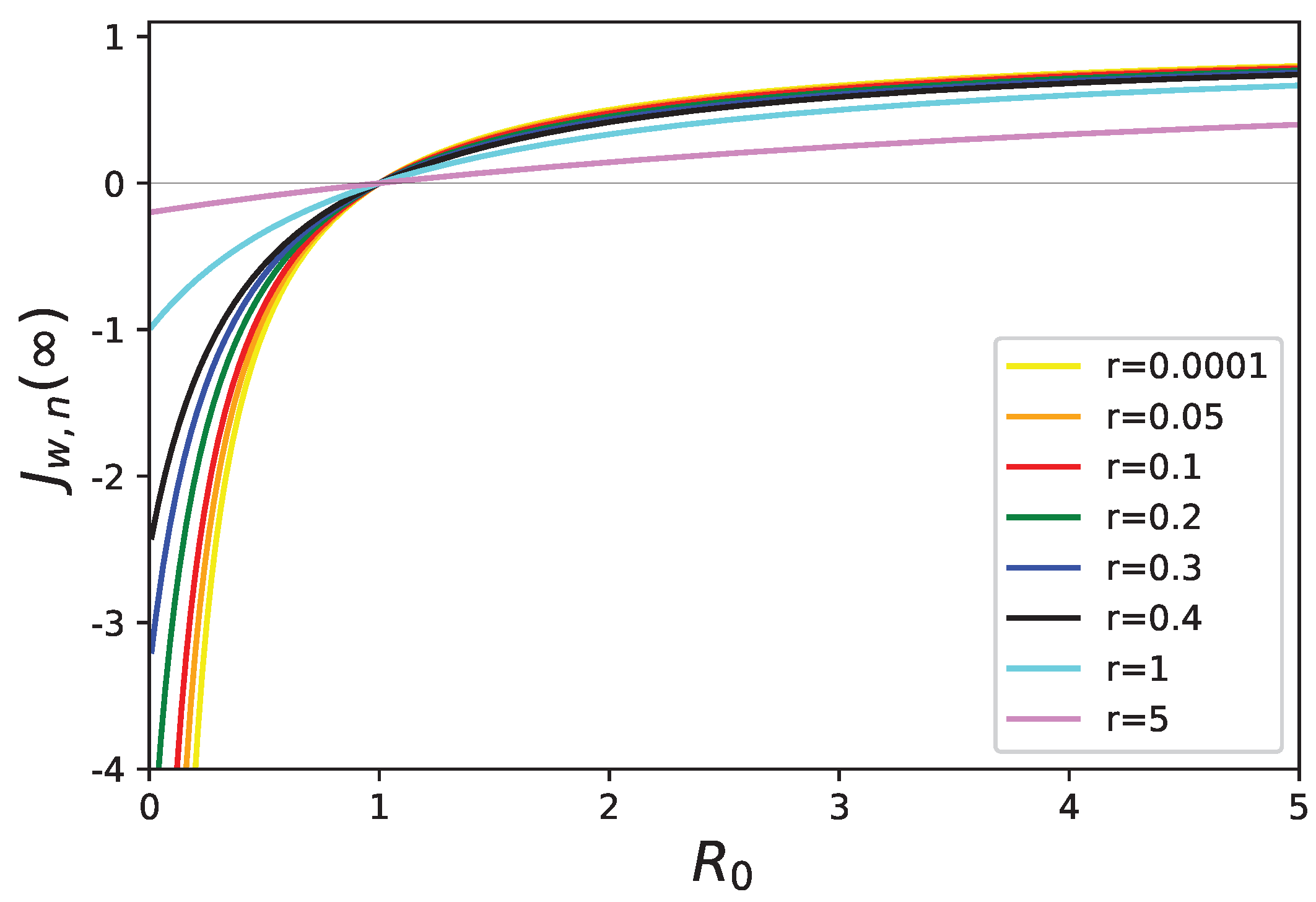
Figure 3.
of (39) for a some Gamma distributed . Positive zeros of exist only for (instability of globally healthy state).
Figure 3.
of (39) for a some Gamma distributed . Positive zeros of exist only for (instability of globally healthy state).
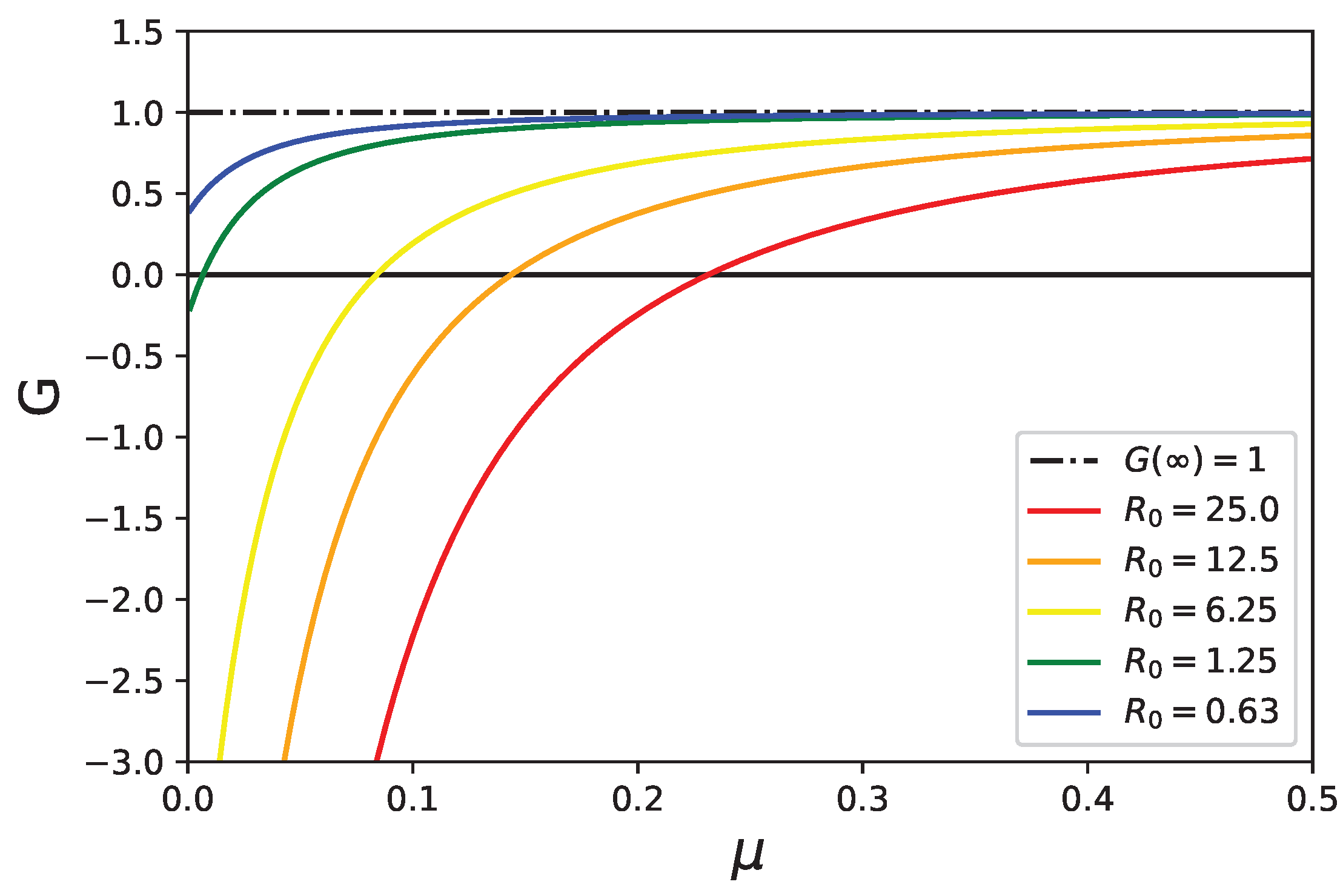
Figure 4.
of (42) for different values of where for (stability of the endemic state).
Figure 4.
of (42) for different values of where for (stability of the endemic state).
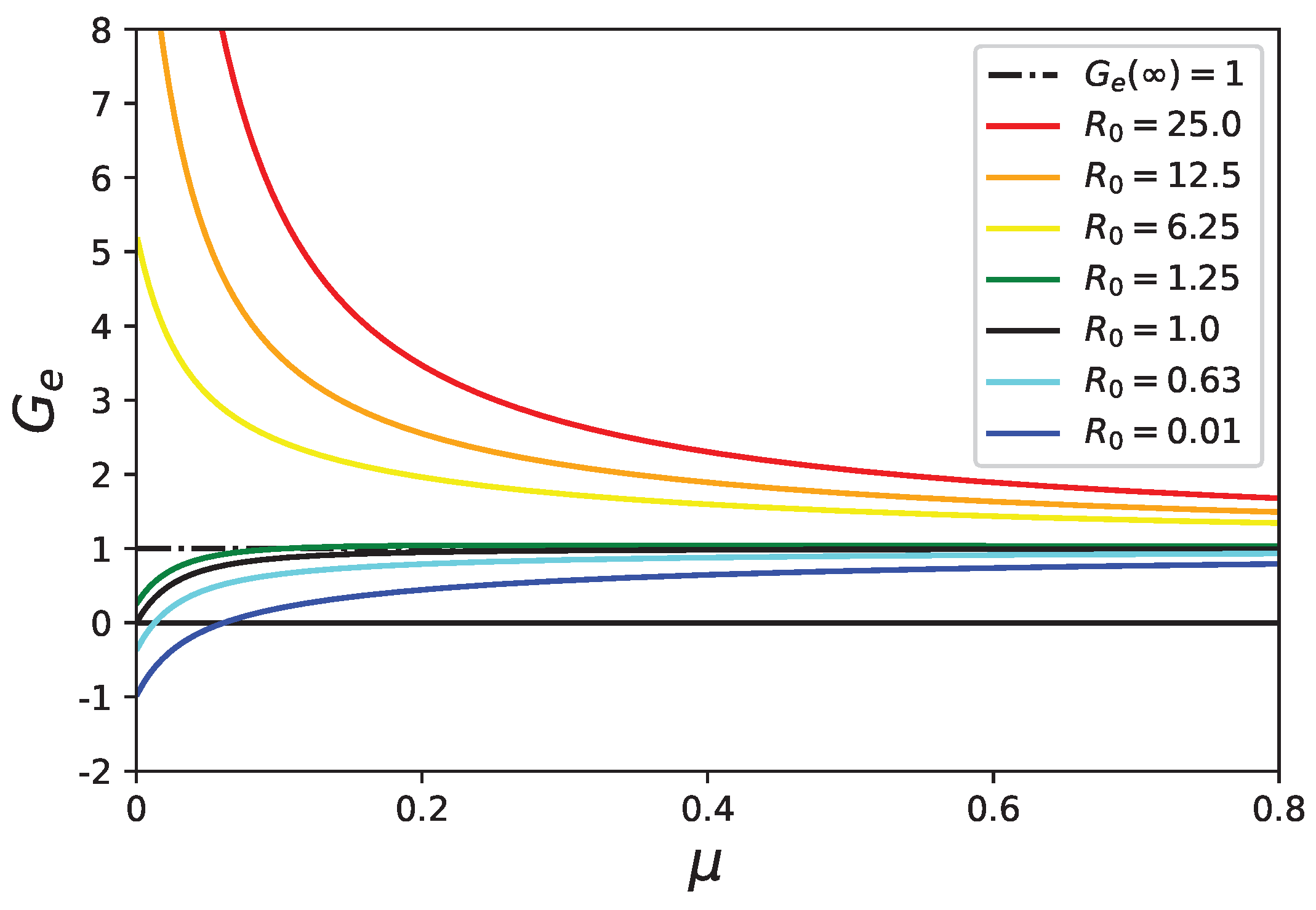
Figure 5.
We depict function of Equation (47) for a few values of for exponentially distributed . The basic reproduction number is monotonously decreasing with increasing mortality parameter (see Figure 6). The parameters are , , , , with where here .
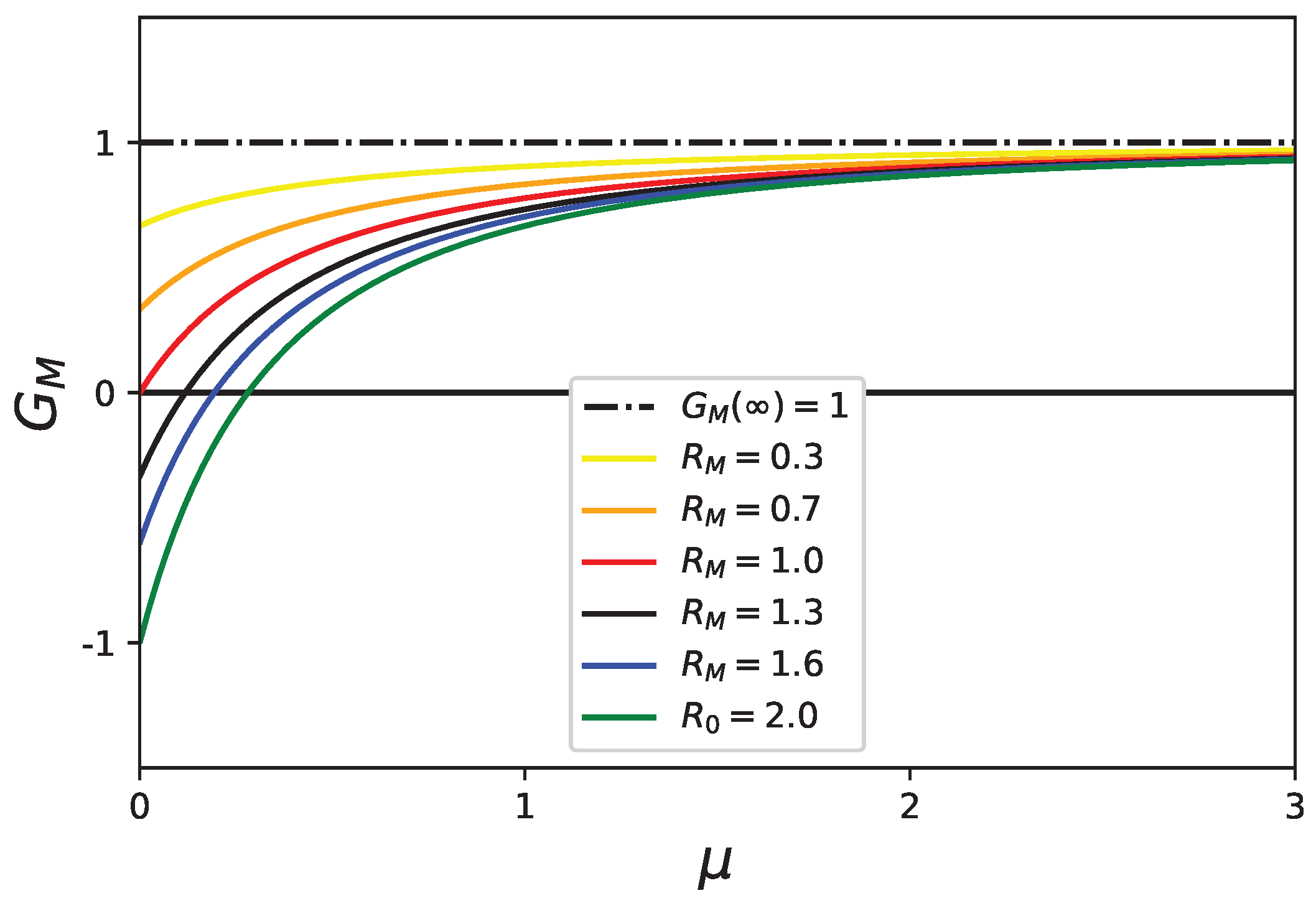
Figure 6.
Basic reproduction number of Equation (50) versus mortality rate parameter for Gamma distributed for various where we have set , () and , for the Markovian case which is recovered by Equation (53).
Figure 7.
Barabási-Albert, Erdös-Renyi and Watts-Strogatz types with 300 nodes and connectivity parameters used in some of the simulations. The WS graph for connectivity parameter lacks the small world property resembling a complex real world structure. The ER network has a broad degree distribution and the small world property. The BA graph is for asymptotically scale-free with a power law degree distribution and the small world feature where a large number of nodes have small degrees and a few (hub) nodes with very large degrees. Almost all nodes are only a few links away from hub nodes.
Figure 7.
Barabási-Albert, Erdös-Renyi and Watts-Strogatz types with 300 nodes and connectivity parameters used in some of the simulations. The WS graph for connectivity parameter lacks the small world property resembling a complex real world structure. The ER network has a broad degree distribution and the small world property. The BA graph is for asymptotically scale-free with a power law degree distribution and the small world feature where a large number of nodes have small degrees and a few (hub) nodes with very large degrees. Almost all nodes are only a few links away from hub nodes.
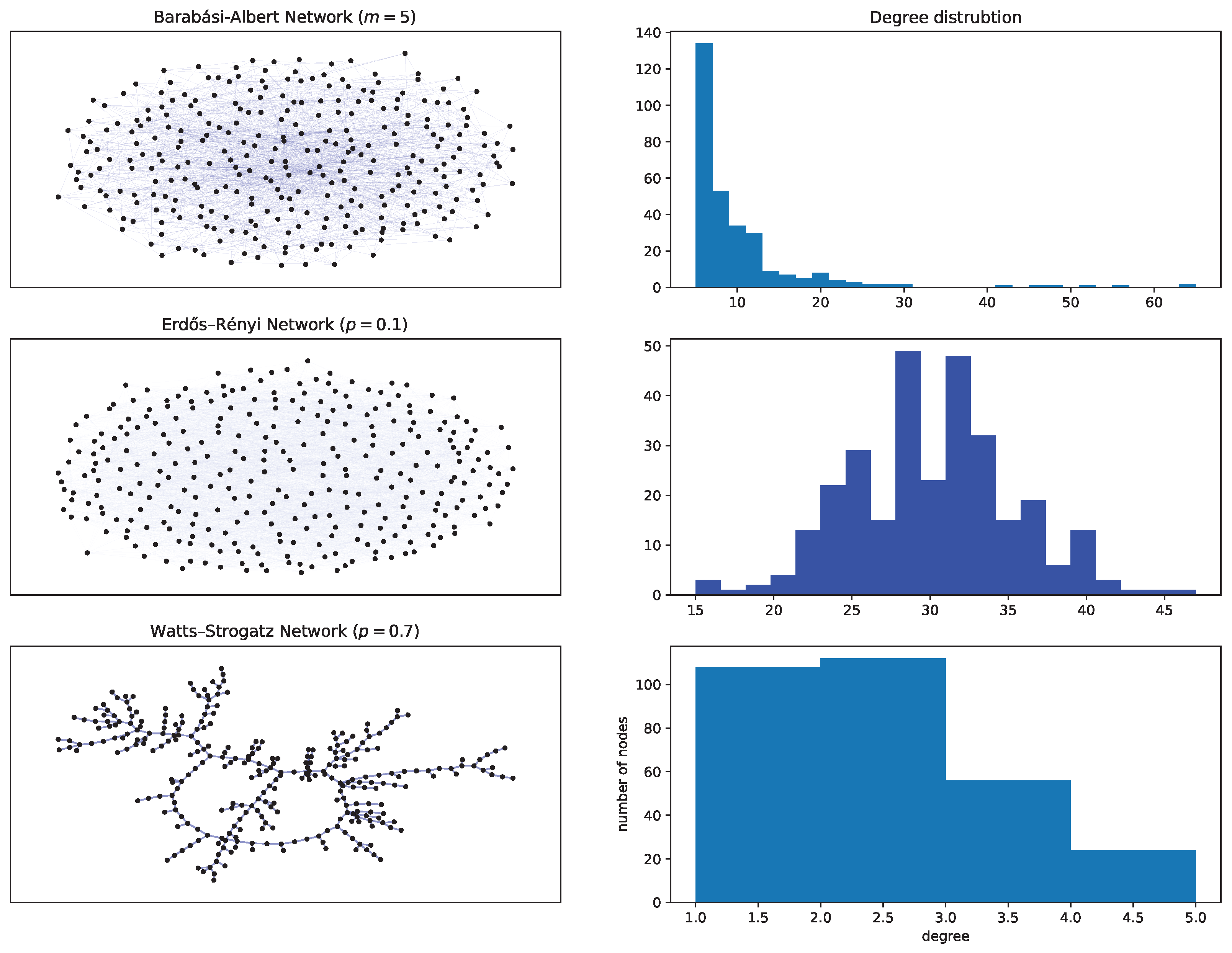
Figure 8.
Snapshots of spreading in a WS graph ( walkers, nodes, connectivity parameter ) and mortality parameter with . The remaining parameters are the same as in Figure 10. One observes and with only about 20 surviving walkers after extinction of the disease. S walkers are in cyan color, I walkers red, D walkers invisible and nodes without walkers are represented in black. Consult here an animated video of this process.
Figure 8.
Snapshots of spreading in a WS graph ( walkers, nodes, connectivity parameter ) and mortality parameter with . The remaining parameters are the same as in Figure 10. One observes and with only about 20 surviving walkers after extinction of the disease. S walkers are in cyan color, I walkers red, D walkers invisible and nodes without walkers are represented in black. Consult here an animated video of this process.
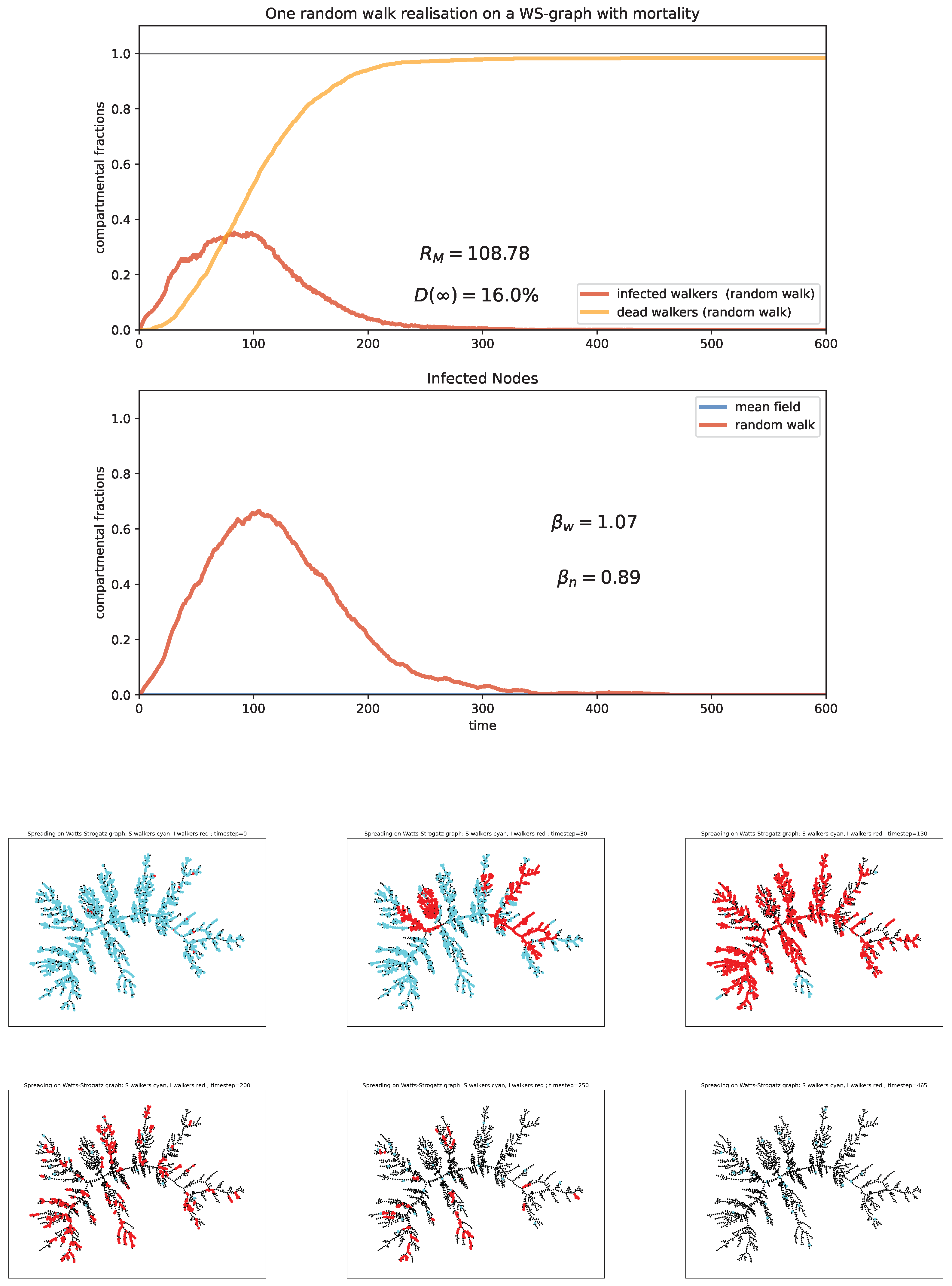
Figure 9.
The plots show the evolution on WS graph with walkers for connectivity parameter and rewiring probability () without mortality (left frame) and with mortality (right frame). are Gamma distributed with the parameters , , , , and , , see histogram. and is determined by numerical integration of (7).
Figure 9.
The plots show the evolution on WS graph with walkers for connectivity parameter and rewiring probability () without mortality (left frame) and with mortality (right frame). are Gamma distributed with the parameters , , , , and , , see histogram. and is determined by numerical integration of (7).
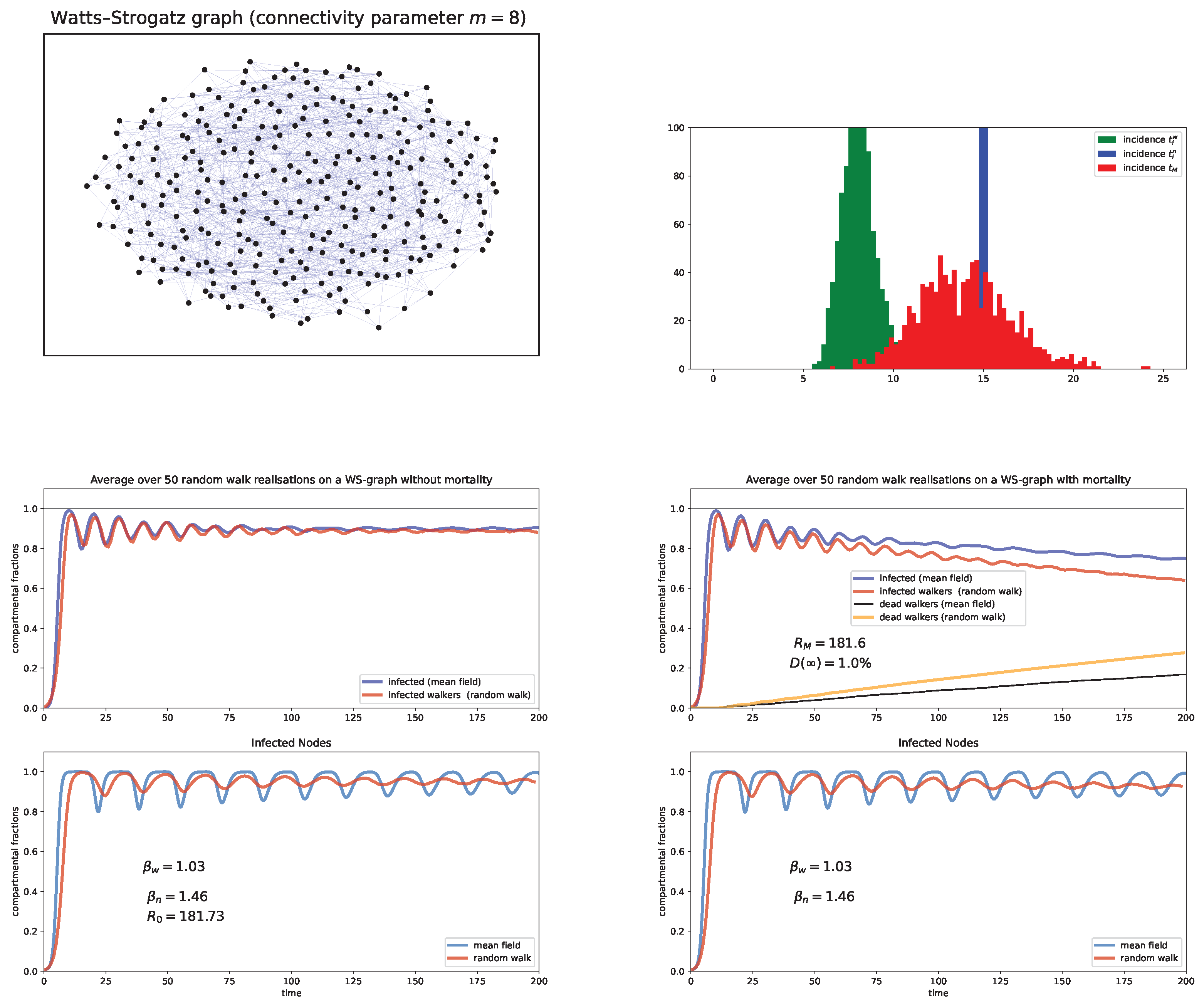
Figure 10.
Evolution on WS graph with walkers and nodes for the same parameters as in Figure 9 but with reduced connectivity parameter . The upper frame shows a snapshot () of the spreading in one random walk realization (susceptible walkers green, susceptible nodes black, infected nodes red).
Figure 10.
Evolution on WS graph with walkers and nodes for the same parameters as in Figure 9 but with reduced connectivity parameter . The upper frame shows a snapshot () of the spreading in one random walk realization (susceptible walkers green, susceptible nodes black, infected nodes red).
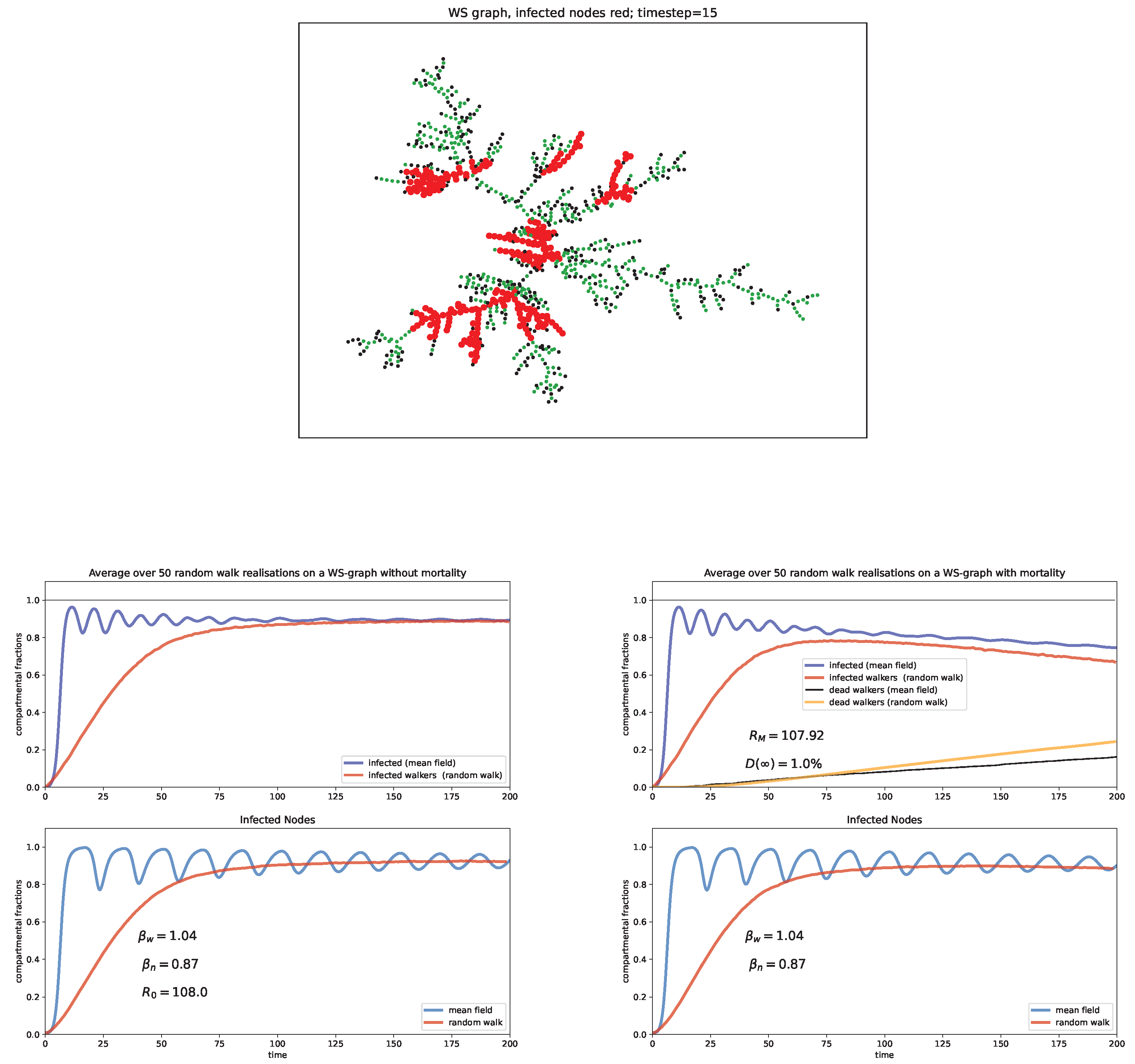
Figure 11.
Evolution on ER graph () with walkers and small rewiring probability (above the percolation limit to ensure a connected structure). The parameters are , , , , , . The left upper frame shows a snapshot of the evolution (same color code as in Figure 10).
Figure 11.
Evolution on ER graph () with walkers and small rewiring probability (above the percolation limit to ensure a connected structure). The parameters are , , , , , . The left upper frame shows a snapshot of the evolution (same color code as in Figure 10).
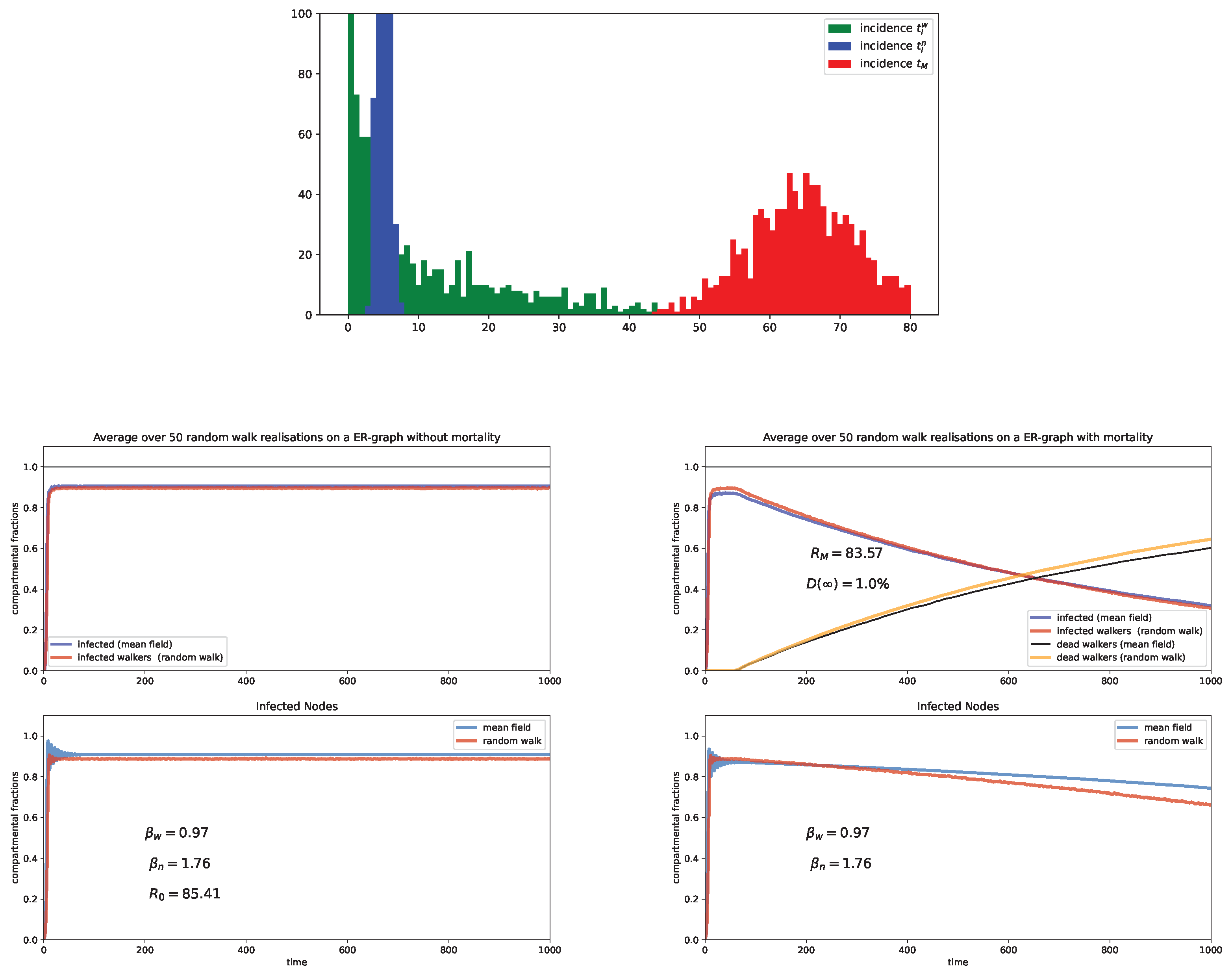
Figure 12.
Evolution on BA graph with walkers and nodes () with parameters , , , (sharp ), , . The basic reproduction number is here only slightly smaller than without mortality. The left upper frame shows a snapshot of the evolution (same color code as in Figure 11).
Figure 12.
Evolution on BA graph with walkers and nodes () with parameters , , , (sharp ), , . The basic reproduction number is here only slightly smaller than without mortality. The left upper frame shows a snapshot of the evolution (same color code as in Figure 11).
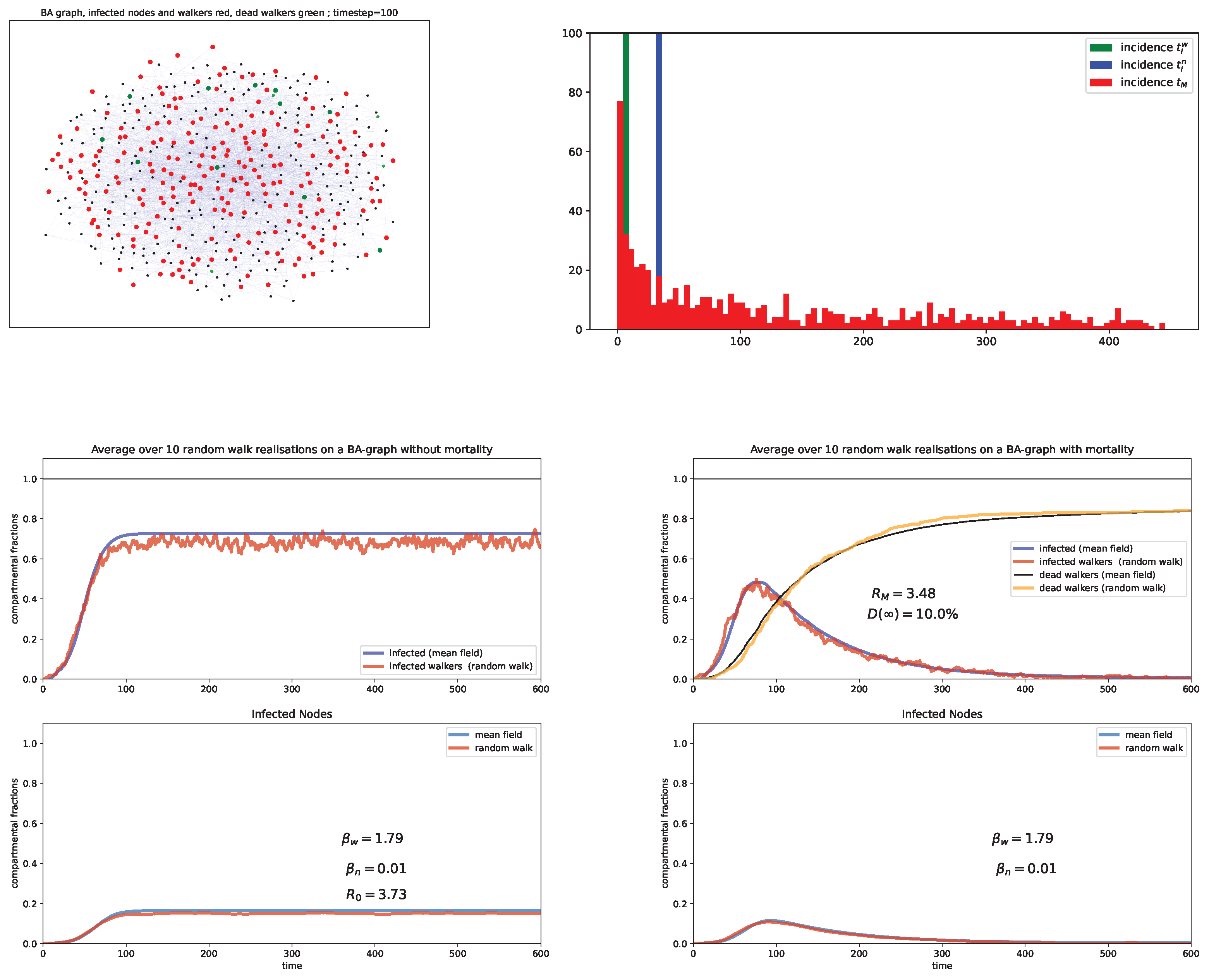
Figure 13.
Evolution with the same parameters and number of walkers () as in Figure 12 but less nodes () for one random walk realization. We interpret the increase of and due to more frequent passages of susceptible walkers on infected nodes (higher infection rates).
Figure 13.
Evolution with the same parameters and number of walkers () as in Figure 12 but less nodes () for one random walk realization. We interpret the increase of and due to more frequent passages of susceptible walkers on infected nodes (higher infection rates).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





