Preprint
Article
TEOS-10 Equations for the Lifted Condensation Level (LCL) and Climatic Feedback of Marine Clouds
Altmetrics
Downloads
105
Views
84
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
19 March 2024
Posted:
20 March 2024
You are already at the latest version
Alerts
Abstract
At an energy flux imbalance of about 1 W m–2, the ocean is storing 90 % of the heat accumulating by global warming. However, neither the causes nor the responsible geophysical processes are sufficiently well understood. More detailed investigations of the different phenomena contributing to the oceanic energy balance are warranted. Here, the role of low-level marine clouds in the air-sea interaction is analysed. TEOS-10, the International Thermodynamic Equation of State of Seawater – 2010, is exploited for a rigorous thermodynamic description of the climatic trend of the Lifted Condensation Level (LCL) of the marine troposphere. Rising Sea-Surface Temperature (SST) at constant Relative Humidity (RH) is elevating marine clouds, cooling the cloud base and reducing the downward thermal radiation. This LCL feedback effect is negative and counteracting ocean warming. At the current global SST of about 292 K, the net radiative heat flux from the ocean surface to the LCL cloud base is estimated to 24 W m–2. Per degree of SST increase, this net flux is expected to be enhanced by almost 0.5 W m–2. The climatic LCL feedback effect is relevant for the ocean’s energy balance and may thermodynamically rigorously be modelled in terms of TEOS-10 equations. LCL height may serve as a remotely measured, sensitive estimate for sea surface relative fugacity, or conventional relative humidity.
Keywords:
Subject: Physical Sciences - Thermodynamics
1. Introduction
In typical global balance models, the energy exchange at the ocean-atmosphere interface includes quantitative estimates of five major contributions, namely, solar downward irradiation (≈ 165 W m-2), thermal upward radiation from the sea surface (≈ – 400 W m-2), thermal downward radiation from clouds and greenhouse gases (≈ 343 W m-2), latent heat of evaporated water (≈ – 95 W m-2), and sensible heat exchange (≈ – 12 W m-2) by molecular conduction across the interface (Budyko 1963; Josey et al. 2013; Macdonald and Baringer 2013; Rapp 2014). The figures given in brackets are respective rough estimates for the enthalpy fluxes per ocean surface area, which result in a net imbalance of about 1 W m-2 that is warming up the ocean, an amount 25 times as large as the world’s total energy consumption by humans in 2022 (You 2024). Similarly, the long-term global energy balance at the top of the atmosphere also amounts to about 1 W m-2 (Meehl et al. 2011). This way, to the globally accumulated energy of the warming climate, the ocean contributes about 89 % (von Schuckmann et al. 2023) or 90 % (Abraham et al. 2013; Cheng et al. 2024) while the atmosphere takes only a minor share of just 1 %. With the advent of the Thermodynamic Equation of State of Seawater – 2010 (TEOS-10) as the current comprehensive international geophysical thermodynamic standard, previous methods for estimating the ocean heat content (Abraham et al. 2013) could be replaced by more accurate modern formulas (McDougall 2003; McDougall et al. 2021), see Section 3.
Each of the energy fluxes mentioned above may, to some extent, be responsible for the observed ocean warming. However, identifying the causes and processes of the enhanced ocean heat imbalance is scientifically challenging. The magnitude of the air-sea flux imbalance is well below the typical uncertainty threshold of at least 10 W m-2 of climate models (Josey et al. 2013). “The drivers of a larger [Earth energy imbalance] EEI in the 2000s than in the long-term period since 1971 are still unclear, and several mechanisms are discussed in literature. For example, Loeb et al. (2021) argue for a decreased reflection of energy back into space by clouds (including aerosol cloud interactions) and sea ice and increases in well-mixed greenhouse gases (GHG) and water vapor to account for this increase in EEI. Kramer et al. (2021) refer to a combination of rising concentrations of well-mixed GHG and recent reductions in aerosol emissions to be accounting for the increase, and Liu et al. (2020) address changes in surface heat flux together with planetary heat redistribution and changes in ocean heat storage. Future studies are needed to further explain the drivers of this change, together with its implications for changes in the Earth system” (von Schuckmann et al. 2023).
Figure 1.
Scattered subtropical marine cumulus clouds developing above a uniform lifted condensation level (LCL). Photo taken at Las Brujas, Cuba, in February 2014.
Figure 1.
Scattered subtropical marine cumulus clouds developing above a uniform lifted condensation level (LCL). Photo taken at Las Brujas, Cuba, in February 2014.

“Low-altitude clouds with cloud top temperatures close to the ground environment generally lead to a weak greenhouse effect. In addition, the radiative cooling at the cloud top and the warming at the cloud base may enlarge the vertical temperature gradient and consequently intensify the turbulence” (Yang et al. 2021: p. 1). However, in some climate models “the low cloud response to [sea-surface temperature] SST change may be too weak” (Loeb et al. 2022: p. 14). As a contributor to the marine heat balance, low-level clouds affect the upwelling thermal radiation by the surface area fraction they cover, as well as by their altitude and the related cloud-base temperature driving their downward longwave radiation. As a function of the surface temperature and relative humidity (RH), an adiabatically ascending air parcel reaches its dew-point at the so-called lifted condensation level (LCL). In this article, equations for the LCL are derived from the international standard TEOS-10, the Thermodynamic Equation of Seawater – 2010 (IOC et al. 2008). As a longwave radiation feedback effect, deviations of the downward black-body radiation of those clouds can this way be estimated from observed trends related to global warming of the ocean surface.
In Section 2 of this paper, selected details of ocean warming are briefly reviewed and discussed in relation to other climatic trends, such as cloudiness reduction, SST increase, or apparently constant marine RH and wind speeds. Section 3 provides a short introduction into the thermodynamic framework of TEOS-10. In Section 4, TEOS-10 equations are formulated for the LCL pressure and temperature as functions of surface pressure, temperature and relative humidity. Rigorous results from those international standard equations may serve as reference values for other estimates. In addition to selected numerical results obtained from an iteration scheme, analytical approximations are suggested for the almost saturated marine troposphere as well as for the tutorial case of simple crude Gibbs function, as explicitly defined in Appendix C. Section 5 investigates the climatic sensitivity of the LCL temperature on the SST at constant RH, with selected numerical solutions of TEOS-10 equations and approximate formulas for crude Gibbs functions. Section 6 concludes the paper with a discussion of the climatological context and derived solutions. Appendix A introduces the Jacobi method for a convenient manipulation of partial derivatives used in TEOS-10. Appendix B calculates from TEOS-10 an equation for the adiabatic lapse rate of the dew point, as required in Section 4. Appendix D mathematically explains Lambert’s W function that is frequently encountered in atmospheric balance equations. Finally, Appendix E provides a list of symbols used in this paper.
2. Ocean Warming and Cloudiness
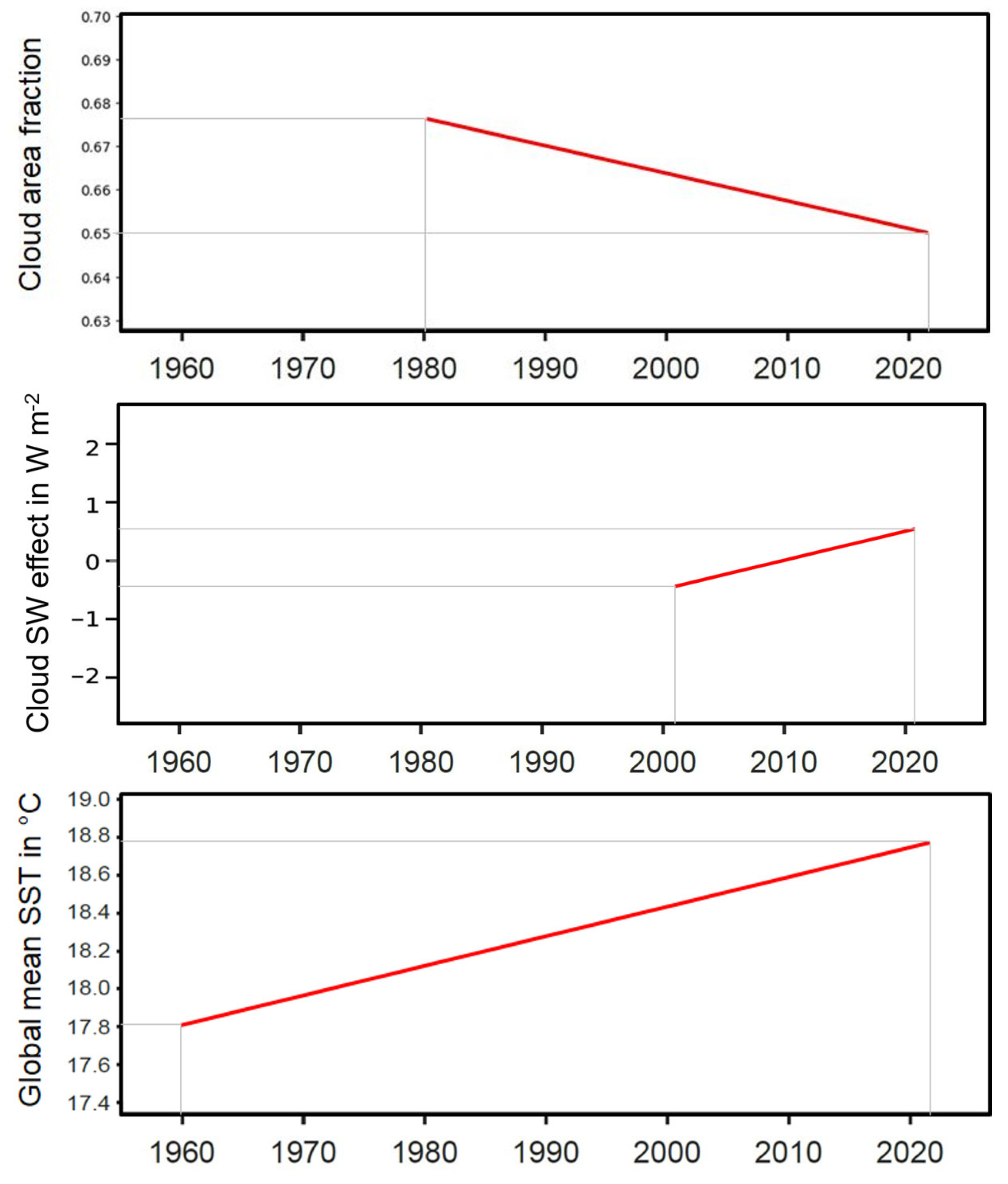
Through the last 70 years, the global mean sea surface temperature (SST) has increased from about 17.8 °C in 1955 to about 18.8 °C in 2023 (Cheng et al. 2024), see Figure 5 below, with an estimated linear trend of
Here, is the number of the calendar year. Accordingly, depending on the dataset used for the analysis, the heat content of the upper 2000 m of the world ocean is currently increasing at a rate of either about 0.9 W m-2 or 1.3 W m-2 per ocean surface area (You 2024). These values are consistent with the total Earth energy imbalance exceeding 1 W m-2 (Loeb et al. 2022) and the fact that the ocean alone stores 90 % of the globally accumulated heat (Cheng et al. 2024).
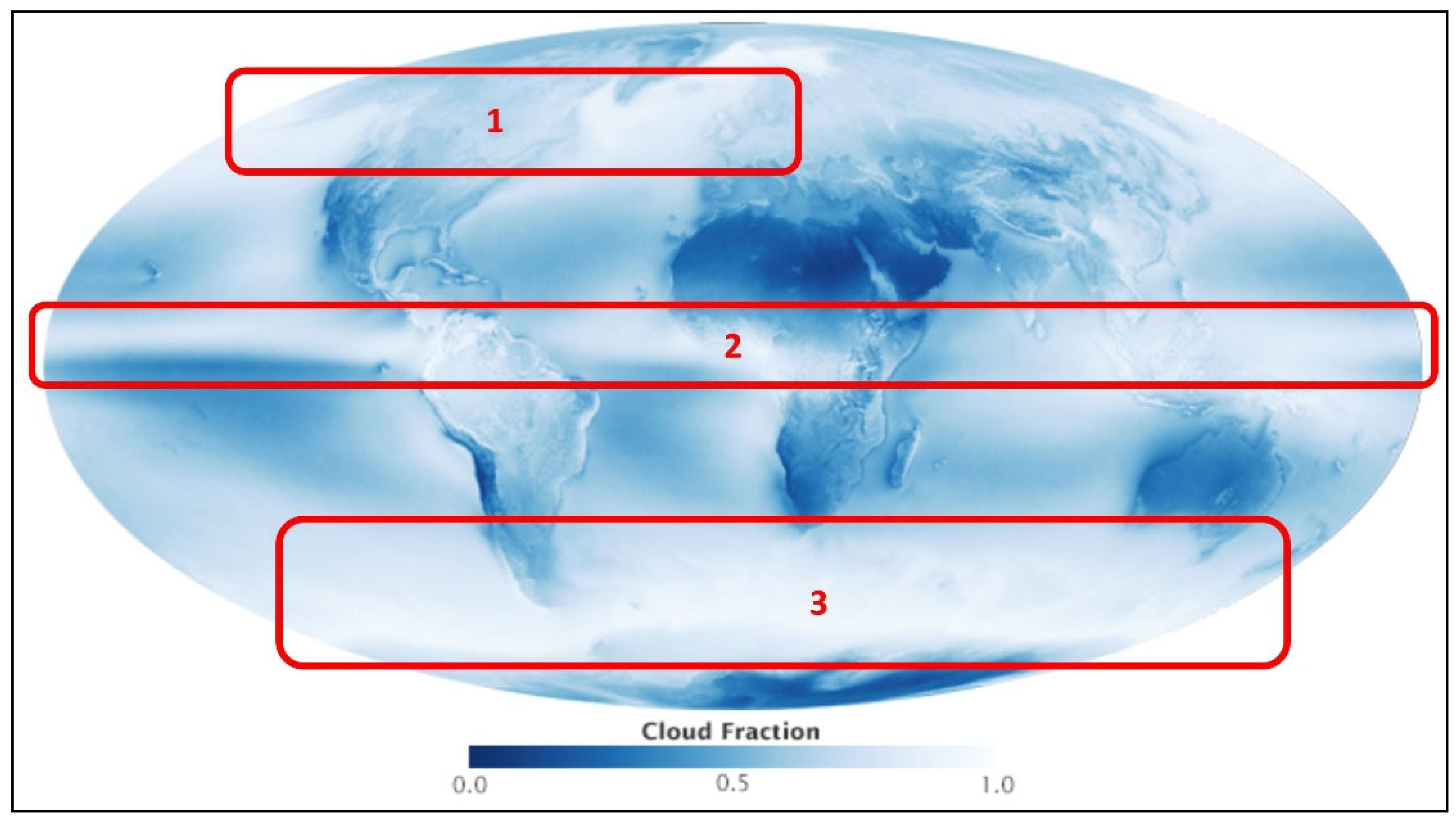
Recent ocean warming is strongest along the global west-wind belts, Figure 2, and is spatially correlated with regions of high mean cloud coverage, Figure 3.
On the input side of the ocean’s energy imbalance, the systematic global reduction of cloudiness is estimated by the linear trend (Foster et al. 2023),
Here, is defined by the fraction of the surface area covered by clouds. Evidently, this trend is negatively correlated with the tropospheric increase of temperature and specific humidity. Consistent with reduced cloudiness, between 1998 and 2017 Earth’s albedo declined by 0.5 W m-2 (Goode et al. 2021; Feistel and Hellmuth 2021).
Decreased cloudiness has increased the mean solar irradiation, , passing through clear-sky regions,
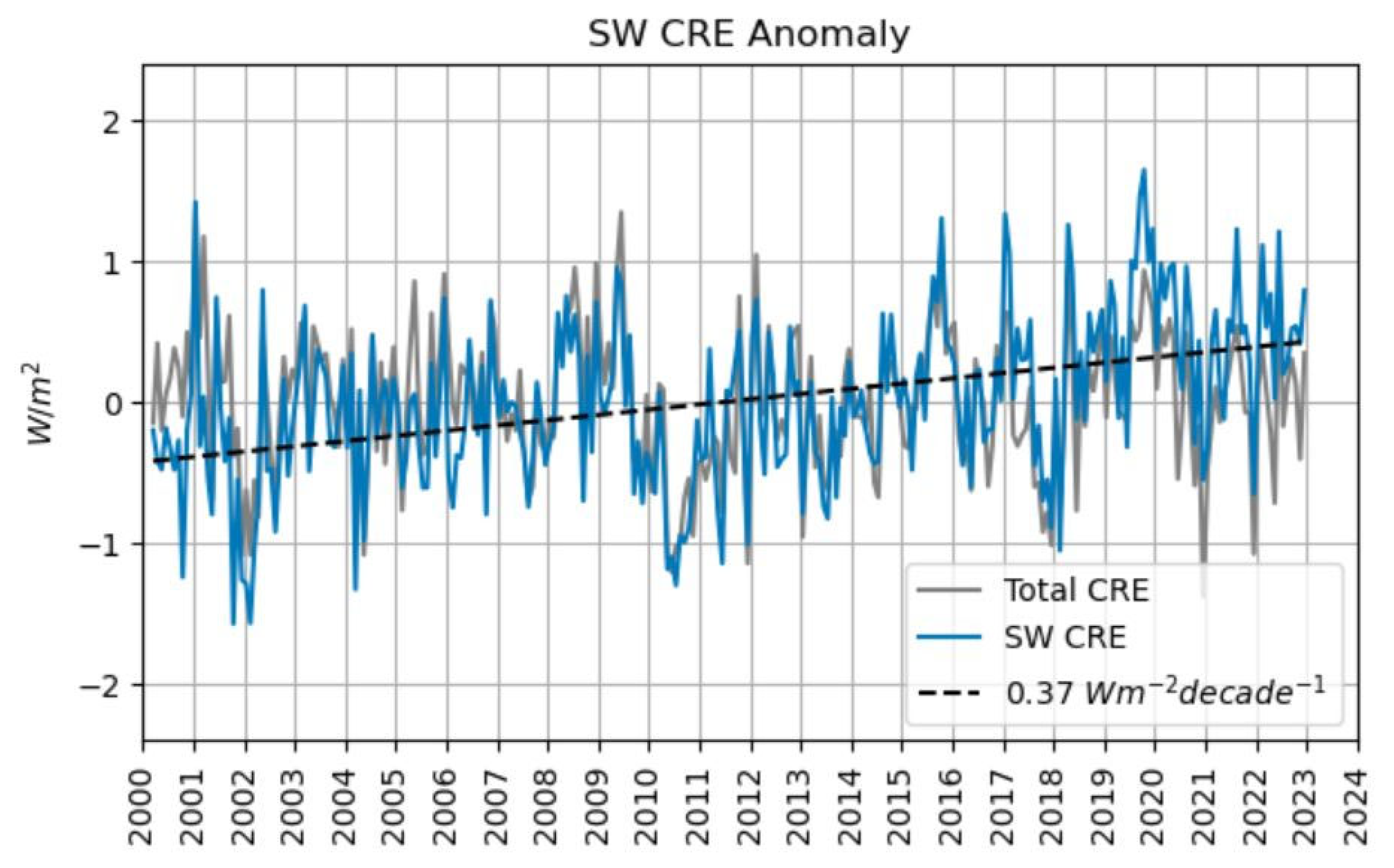
by about 0.74 W m-2 in the past 20 years (Phillips and Foster 2023), see Figure 4 below. This phenomenon is known as the warming “shortwave cloud radiative effect” (SW CRE). Possibly, this value may explain the observed ocean warming if the ocean’s heat loss remains sufficiently below the SW CRE heat gain.
Figure 2.
Observed upper 2000 m ocean heat content trend (i.e., energy difference divided by observation period) from 1958 to 2022 (WMO 2024). Image reproduction permitted by WMO Copyright. Image modified here by indicating regions 1, 2 and 3 of strongest cloudiness, see Figure 3.
Figure 2.
Observed upper 2000 m ocean heat content trend (i.e., energy difference divided by observation period) from 1958 to 2022 (WMO 2024). Image reproduction permitted by WMO Copyright. Image modified here by indicating regions 1, 2 and 3 of strongest cloudiness, see Figure 3.
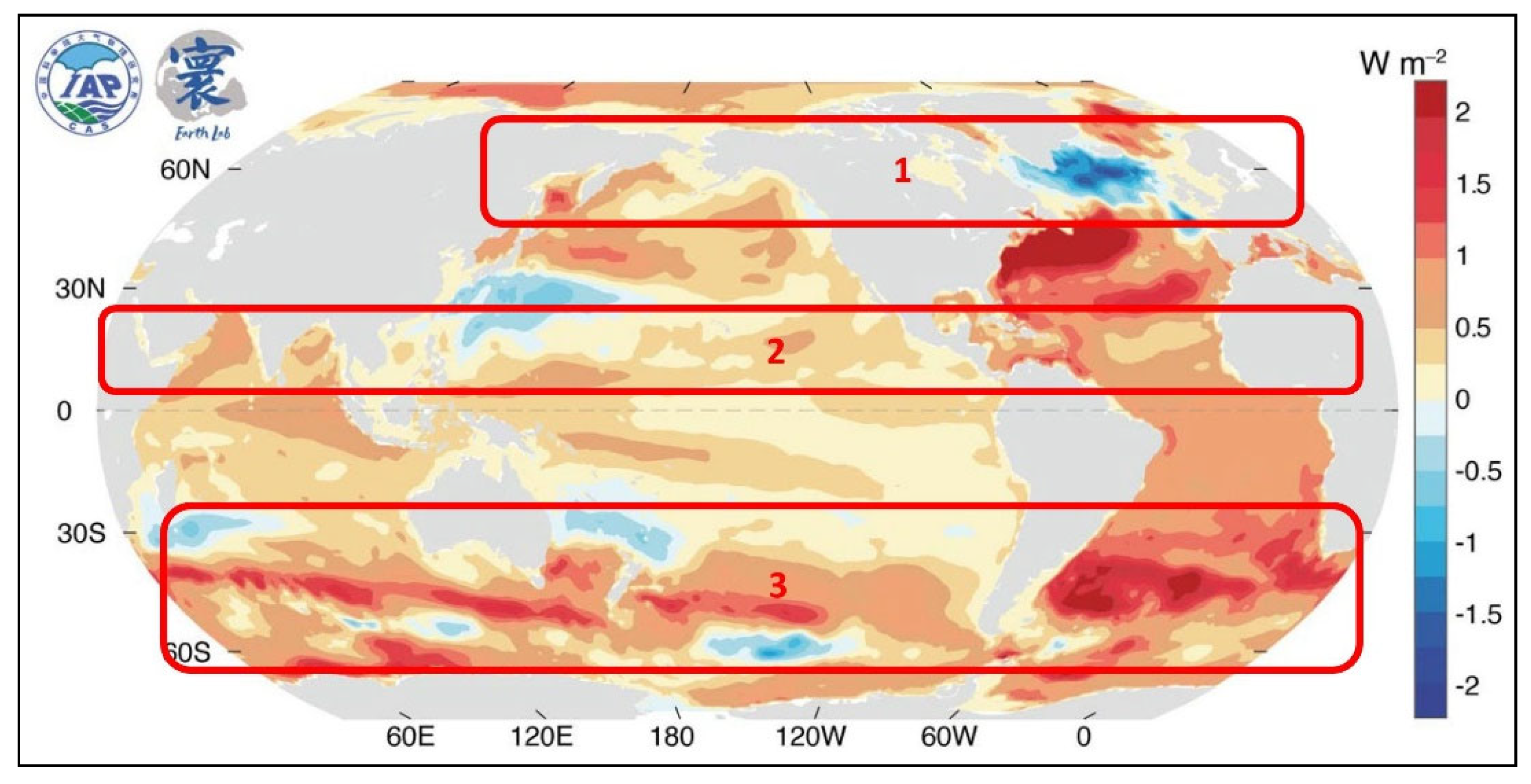
Figure 3.
Global distribution of cloudiness July 2002 - April 2015. NASA Earth Observatory image by Jesse Allen and Kevin Ward, using data provided by the MODIS Atmosphere Science Team, NASA Goddard Space Flight Center. https://earthobservatory.nasa.gov/images/85843/cloudy-earth . Image reproduction permitted by NASA Copyright. Image modified here by adding a legend and indicating regions 1, 2 and 3 of strongest cloudiness for comparison with Figure 2.
Figure 3.
Global distribution of cloudiness July 2002 - April 2015. NASA Earth Observatory image by Jesse Allen and Kevin Ward, using data provided by the MODIS Atmosphere Science Team, NASA Goddard Space Flight Center. https://earthobservatory.nasa.gov/images/85843/cloudy-earth . Image reproduction permitted by NASA Copyright. Image modified here by adding a legend and indicating regions 1, 2 and 3 of strongest cloudiness for comparison with Figure 2.
On the output side of the ocean’s energy imbalance, the sensible heat exchange of roughly 10 W m-2 between ocean and atmosphere is relatively small and does not exceed the uncertainty of flux estimates (Josey et al. 2013). The ocean’s heat capacity exceeds that of the atmosphere by a factor of 1000, so that 1 % of added ocean’s heat content corresponds to an atmospheric temperature increase 10 times as large as that of the ocean. Sensible heat flux may be decreasing due to the faster rise of tropospheric temperatures compared to those of the sea. Estimates for such a trend are not available, though, and the quantitative contribution of sensible heat flow to ocean warming remains a pending problem.
Figure 4.
The shortwave cloud radiative effect (SW CRE, blue curve) on solar irradiation has an increasing annual trend of 0.037 W m-2 (dashed line). However, in the total cloud radiative effect (CRE, grey curve) this warming is almost completely cancelled against the cooling effect of reduced cloudiness on the ocean’s thermal radiation. Figure kindly provided by Coda Phillips (priv. comm. 10 Feb 2024). Note that this figure is slightly corrected in comparison to the original publication (Phillips and Foster 2023).
Figure 4.
The shortwave cloud radiative effect (SW CRE, blue curve) on solar irradiation has an increasing annual trend of 0.037 W m-2 (dashed line). However, in the total cloud radiative effect (CRE, grey curve) this warming is almost completely cancelled against the cooling effect of reduced cloudiness on the ocean’s thermal radiation. Figure kindly provided by Coda Phillips (priv. comm. 10 Feb 2024). Note that this figure is slightly corrected in comparison to the original publication (Phillips and Foster 2023).
On the output side of the ocean’s energy imbalance, the problem of ocean warming is closely related to a suspected change of the strength of the hydrological cycle. Cheng et al. (2024: p. 6) argue that the observed increase in salinity contrast in the upper 2000 m “is generally consistent with many atmosphere-based estimates and strengthens the evidence that the global water cycle has been amplified with global warming”. On the other hand, Held and Soden (2006: p. 5687-5689) had already emphasised that “it is important that the global-mean precipitation or evaporation, commonly referred to as the strength of the hydrological cycle, does not scale with Clausius–Clapeyron. … We can, alternatively, speak of the mean residence time of water vapor in the troposphere as increasing with increasing temperature”. In contrast to some model predictions (Weller et al. 2022), there is no evidence yet that mean global marine evaporation has intensified which in that case would have cooled the ocean in contrast to the observed warming in reality (Feistel and Hellmuth 2021, 2023; Blunden et al. 2023).
Quantitatively, corresponding to about 1200 mm of annual evaporation, the latent heat exchange of roughly 100 W m-2 between ocean and atmosphere is the dominating way of oceanic heat loss and atmospheric energy supply (Randall 2012; Rapp 2014; Feistel and Hellmuth 2021). According to the Dalton equation, the evaporation flux depends mainly on the RH and the wind speed (Stewart 2008; Feistel and Hellmuth 2023, 2024). Trends in marine surface RH are weak and are, if at all, well below measurement uncertainty (Lovell-Smith et al. 2016; Dunn et al. 2023; Willett et al. 2023). “There is a tendency for the RH of the air to remain approximately constant as the climate changes” (Randall 2012: p. 147). Similarly, there is no significant trend in marine wind speeds (Azorin-Molina et al. 2023), so that relevant trends in global mean marine evaporation rates are neither expected nor observed (Held and Soden 2006). However, the high sensitivity of latent heat flux with respect to RH may be estimated to about 5 W m-2 per %rh (Feistel and Hellmuth 2021), so that a small increase by 0.2 %rh may already suffice to explain the oceanic warming rate. Such a minor change of RH, however, could be disguised by the much larger observation uncertainty of 1 – 5 %rh (Lovell-Smith et al. 2016). “Relative humidity over oceans remained highly uncertain” (Willett et al. 2023: p. S49). Therefore, the relevance of latent heat with respect to ocean warming remains unclear.
Figure 5.
Correlated, approximate linear long-term trends of observed global mean cloudiness (top, Foster et al. 2023), of solar irradiation (from Figure 4) and of global mean oceanic sea surface temperature (bottom, Chen et al. 2024).
Figure 5.
Correlated, approximate linear long-term trends of observed global mean cloudiness (top, Foster et al. 2023), of solar irradiation (from Figure 4) and of global mean oceanic sea surface temperature (bottom, Chen et al. 2024).
On the output side of the ocean’s energy imbalance, the thermal radiation of the sea surface may easily be estimated from the Stefan-Boltzmann law of black-body radiation. Only a small fraction of this radiation may pass the troposphere in the so-called atmospheric window at about 8-11 µm wavelength, see Figure 6; most energy is blocked by the infrared opacity of clouds and greenhouse gases which send back down to the ocean long-wave radiation, according to their particular altitudes and temperatures. This “longwave cloud radiative effect” (LW CRE) of reduced cloudiness is cooling the ocean by letting more thermal radiation pass to space and emitting less downward radiation, Figure 7. It is estimated (Phillips and Foster 2023) that this cooling LW CRE almost completely cancels out the warming SW CRE of cloudiness, so that, following that analysis, ocean warming may be attributed to decreasing cloudiness only to a minor extent.
Figure 6.
Spectral distribution of radiative opacity between 70 % and 85 % of the troposphere. This figure was prepared by Robert A. Rohde for the Global Warming Art project. Reproduction permitted by Creative-Commons Copyright, https://de.m.wikipedia.org/wiki/Datei:Atmospheric_Transmission.png.
Figure 6.
Spectral distribution of radiative opacity between 70 % and 85 % of the troposphere. This figure was prepared by Robert A. Rohde for the Global Warming Art project. Reproduction permitted by Creative-Commons Copyright, https://de.m.wikipedia.org/wiki/Datei:Atmospheric_Transmission.png.
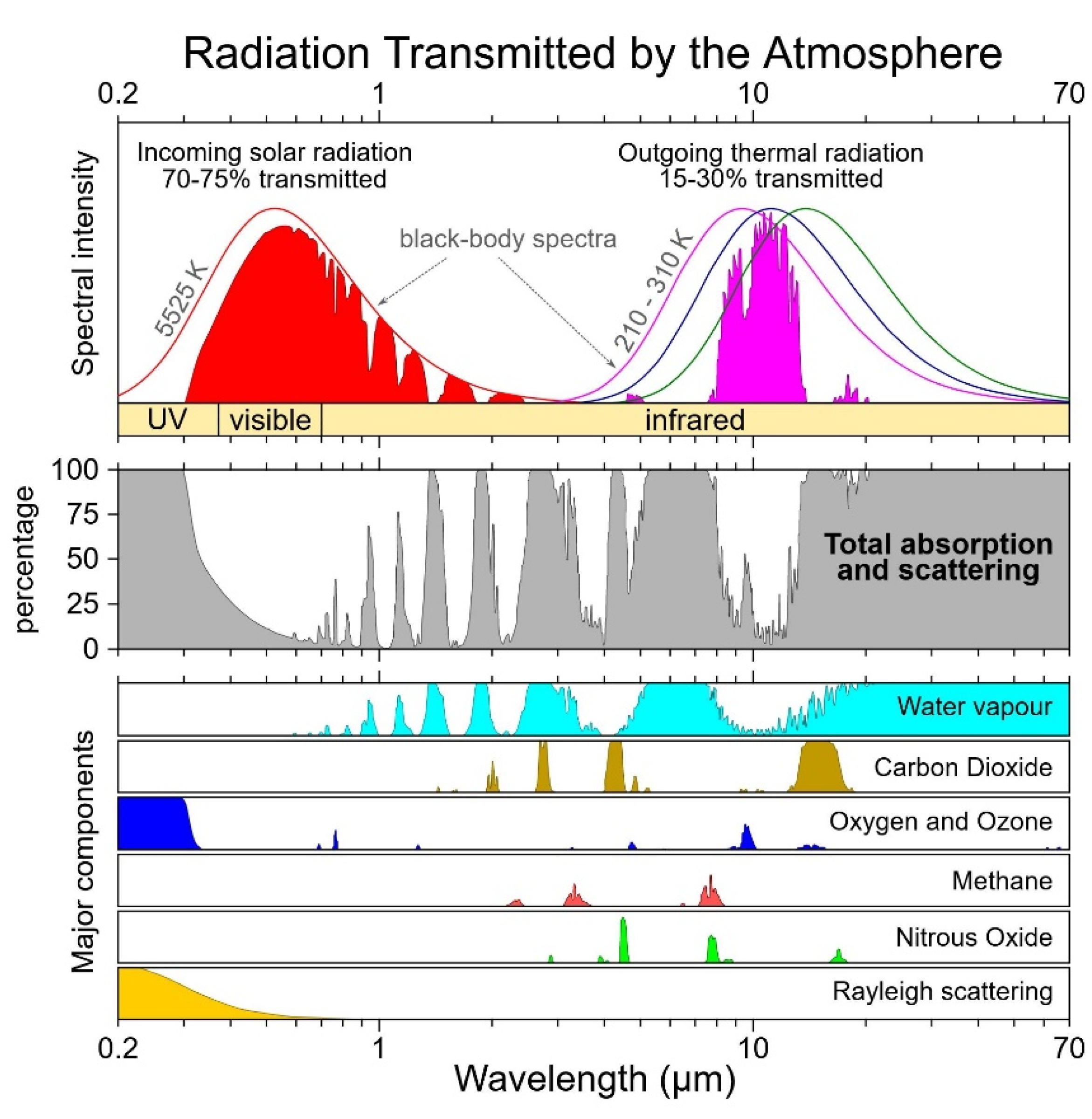
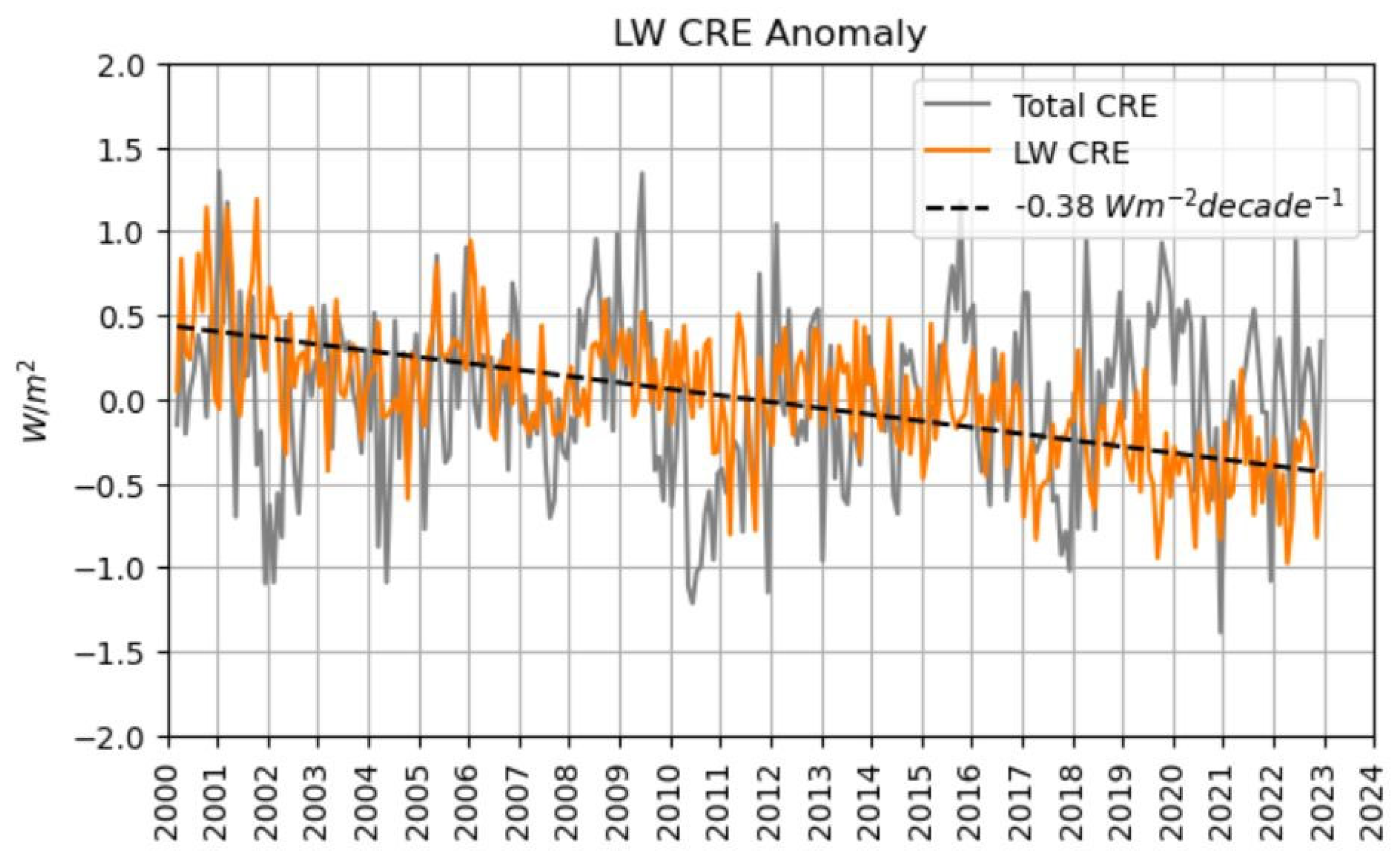
Figure 7.
The longwave cloud radiative effect (LW CRE, orange curve) on thermal surface radiation has a decreasing annual trend of –0.038 W m-2 (dashed line). However, in the total cloud radiative effect (CRE, grey curve) this cooling is almost completely cancelled against the warming effect of reduced cloudiness on solar irradiation. Figure kindly provided by Coda Phillips (priv. comm. 10 Feb 2024). Note that this figure is slightly corrected in comparison to the original publication (Phillips and Foster 2023).
Figure 7.
The longwave cloud radiative effect (LW CRE, orange curve) on thermal surface radiation has a decreasing annual trend of –0.038 W m-2 (dashed line). However, in the total cloud radiative effect (CRE, grey curve) this cooling is almost completely cancelled against the warming effect of reduced cloudiness on solar irradiation. Figure kindly provided by Coda Phillips (priv. comm. 10 Feb 2024). Note that this figure is slightly corrected in comparison to the original publication (Phillips and Foster 2023).
In addition to merely the lateral area covered by clouds, the mutual energy balance between SW and LW CRE is influenced also by other processes.
- (i)
- By contrast to the SW CRE, the LW CRE depends strongly on the concentration of greenhouse gases present in the cloudless sky. If the clear sky absorbs infrared radiation to a similar extent as the clouds do, the greenhouse effect will not decrease significantly by the substitution of a cloud fraction by a cloudless fraction. The increasing concentration of water vapour in the marine troposphere (Willett et al. 2023) results in a stronger absorption of longwave radiation (Goody and Robinson 1951; Goody 1952; Rothmann et al. 2004; Zhong and Haigh 2013; Feistel and Hellmuth 2021). The vertically distributed opacity of the clear-sky troposphere results in an effective radiating height of roughly 5000 m at 500 hPa, where the temperature is around 255 K (Colman and Soden 2021). According to Figure 5, the infrared opacity of the troposphere is between 70 % and 85 %. A rule-of-thumb estimate (Feistel and Hellmuth 2021) for the tropical marine infrared absorption coefficient of 71 % is consistent with that range. These values are relatively close to the opacity of clouds. “The clear-sky infrared absorption/emission is very important, so ideally the assumed value for the clear sky is calculated using a radiative transfer model … driven by reanalysis fields. Cloud radiative effect [as shown in Figure 7] is the difference between the all-sky observed and this modeled cloudless atmosphere” (Coda Phillips, priv. comm.).
- (ii)
- The SW CRE is relevant at day time only, while the LW CRE is acting all day and night. It is unclear weather the reported reduction of global cloudiness is different between day and night (Turbet et al. 2021) and may have distinct impacts on SW and LW CRE in that case.
- (iii)
- Cloudiness is most pronounced in the tropics and the west-wind bands (Figure 3). Moreover, the SW CRE is most relevant at low latitudes, while the LW CRE is acting all over the globe. It is unclear how the reported reduction of global cloudiness is correlated with latitude and may have different impacts on SW and LW CRE.
- (iv)
- Through the LCL, the increasing ocean SST has an effect on the altitude of cloud formation which is changing the cloud base temperature and, in turn, its downward thermal radiation. This feedback effect is analysed thermodynamically in Section 4 and Section 5 of this paper. In addition, low-level cumulus cloud formation is highly correlated with the diurnal cycle of solar irradiation, with latitude and with land-ocean distribution.
- (v)
- Through the LCL, a so far unnoticed minor increase of ocean surface RH may have an effect on the altitude of cloud formation which is changing the cloud base temperature and, in turn, its downward thermal radiation in opposite direction compared to the SST trend. This negative feedback effect is briefly quantified thermodynamically in Section 4.2.
3. TEOS-10 Equations of State
The world ocean is a vast and dynamically changing storage of heat, however, the theoretical description of its heat transport and conversion processes is thermodynamically challenging (McDougall 2003; Abraham et al. 2013; McDougall et al. 2013, 2021, 2023; Graham and McDougall 2013; Tailleux and Dubos 2024). For example, the former 1980 Equation of State of Seawater (EOS-80) did not provide any equations for the calculation of seawater entropy or enthalpy (Unesco 1981; Fofonoff and Millard 1983). In order to meet the growing demands of climate research and to support numerical circulation models of the ocean, starting in 2005 an improved comprehensive standard description of seawater thermodynamics had been developed by the SCOR/IAPSO Working Group 127 in cooperation with the International Association for the Properties of Water and Steam (Pawlowicz et al. 2012).
Proper axiomatic systems of mathematical statements possess the internal properties of independence, consistency and completeness. In contrast to any earlier collections of empirical seawater property equations, the International Thermodynamic Equation of Seawater – 2010 (TEOS-10) is designed in such an axiomatic manner and offers a comprehensive description of thermodynamic properties of water in its geophysical mixtures, phases and mutual equilibria. Thermodynamics has a reputation of being mathematically difficult. For beginners, though, an encouraging anecdote quoted by Fink (2009: p.1) is Arnold Sommerfeld’s experience with the use of the thermodynamic formalism: “Thermodynamics is a funny subject. The first time you go through it, you don’t understand it at all. The second time you go through it, you think you understand it, except for one or two points. The third time you go through it, you know you don’t understand it, but by that time you are so used to that subject, it doesn’t bother you anymore.” Appendix A provides a brief tutorial introduction into the mathematics used throughout TEOS-10. However, extensive software libraries are available from the web (www.teos-10.org), as outlined in the digital supplement of Wright et al. (2010), which conveniently provide direct access to numerical properties without detailed expertise to be required regarding sometimes demanding algorithms behind (Feistel et al. 2010a; Wright et al. 2010).
More than 150 years ago, in 1873, Willard Gibbs had discovered that a single mathematical function is sufficient to describe all thermodynamic properties of a given substance in its equilibrium state. Such functions are known as “thermodynamic potentials”. At its very core, TEOS-10 is mathematically defined (IOC et al. 2010) in terms of empirical correlation equations for just three thermodynamic potentials, namely,
- (i)
- the specific Gibbs energy of seawater, , as a function of absolute salinity, , absolute temperature, , and absolute pressure, , (Wagner and Pruß 2002; Millero et al. 2008; Feistel 2008),
- (ii)
- the specific Gibbs energy of ambient hexagonal ice Ih, , as a function of temperature and pressure (Feistel and Wagner 2005, 2006), and
- (iii)
- the specific Helmholtz energy of humid air, , as a function of the dry-air mass fraction, , and the mass density of humid air, (Lemmon et al. 2000; Feistel et al. 2010b). From these potential functions, all thermodynamic properties of seawater, ice and humid air, as well as their mutual equilibria, can be derived mathematically in a perfectly consistent way by analytical or numerical means (IAPWS AN6-16 2016; Feistel 2018).
“Helmholtz energy” is sometimes also known as “free energy”, and “Gibbs energy “ as “free enthalpy” in the literature. In TEOS-10, temperature is expressed on the 1990 International Temperature Scale (ITS-90, Preston-Thomas 1990). In the vicinity of the triple point of water, ITS-90 deviates only insignificantly from the current Thermodynamic Temperature Scale (BIPM 2019) and will remain in practical use for the foreseeable future (Harvey et al. 2023). The isotopic composition of water is assumed to be that of Vienna Standard Mean Ocean Water (VSMOW, IAPWS G5-01 2016). Salinity of IAPSO Standard Seawater is defined by the Reference-Composition Salinity Scale (Millero et al. 2008) as the mass fraction of dissolved salt in seawater. The dry-air mass fraction of humid air is related to the specific humidity , the mixing ratio and the water-vapour mole fraction by
Here, and , respectively, are the molar masses of water and of dry air (IAPWS G08-10 2010). The freely adjustable constants for the absolute energies and entropies of water, sea salt and dry air are consistently defined at reference states chosen to be the triple point of water and the standard ocean state (Wagner and Pruß 2002; Feistel et al. 2008, 2010a,b; Feistel 2018).
The Gibbs function of freshwater, , equals the Gibbs function of liquid water derived from the specific Helmholtz energy,, of fluid water (Wagner and Pruß 2002) evaluated at high densities of liquid water,
where the pressure is given by
The specific entropy of seawater, , is available from the Gibbs function by
and the specific enthalpy of seawater, , by
This way, the ocean heat content, , is estimated from the integral (McDougall et al. 2021),
carried out over the ocean’s volume with its local in-situ properties . By definition (Feistel et al. 2008; IOC et al. 2010; Feistel 2018), the TEOS-10 enthalpy of the standard-ocean reference state is . The local in-situ density is available from the relation
Formula (9) describes a fictitious process by which each mass element, , in the volume is isentropically lifted to the surface pressure,, where it transfers all its excess enthalpy, , via sensible heat flux to an external measurement device. Subsequently, the same amount of heat is reversibly conducted back, after which the parcel returns to its original spatial position. Then, is the total amount of heat reversibly removed from the ocean across its surface by this process.
The approach of eq. (9) is therefore consistent with the fact that thermodynamically, heat is an exchange quantity rather than a state quantity, so that, rigorously spoken, any kind of stored “heat content” does not unambiguously exist but only an amount of heat which is exchanged between a given system and its surrounding (Landau and Lifschitz 1966: §13). According to Clausius (1876) and Gibbs (1873),
is the proper thermodynamic expression for heat exchange at constant pressure and constant amounts of water and salt. Here, is the parcel’s changing surface temperature during the fictitious heat transfer process, and is its isobaric heat capacity.
The Helmholtz function of dry air, , equals (up to modified reference-state conditions) the equation of state of Lemmon et al. (2000),
The Helmholtz function of pure water vapour, , equals the specific Helmholtz energy,, of fluid water (Wagner and Pruß 2002) evaluated at low densities of water vapour
For the following calculations of condensation levels, the specific entropy of humid air, , is available from the related Gibbs function
by
Note that derived from (14) for atmospheric applications, a simplified analytical low-pressure formulation for the Gibbs function is available from Appendix B of Feistel and Hellmuth (2023).
The specific enthalpy of humid air is computed from the Gibbs function as
For the computation of phase equilibria such as dew- or frost-points, TEOS-10 provides the chemical potentials of water in the different phases or mixtures.
The chemical potential of water vapour, , in humid air is available from the Gibbs function by
or equivalently from the enthalpy by, see eq. (A26),
The chemical potential of liquid water equals its specific Gibbs energy,
and, similarly, the chemical potential of ice is,
The dry-air mass fraction, , of humid air saturated with respect to liquid water is defined by the equilibrium condition
and with respect to ice by
To make the use of TEOS-10 equations more convenient, the numerical solutions of eqs. (21) and (22) for either , , or , together with numerous other properties (Feistel et al. 2010a; Wright et al. 2010), are implemented in the freely available from the open source code, sea-ice-air (SIA) library of TEOS-10, accessible at www.teos-10.org.
After the official adoption of TEOS-10, the IAPSO/SCOR/IAPWS Joint Committee on the Properties of Seawater (JCS) continued to address pending climate-related problems (Feistel et al. 2016) that could have not yet or only insufficiently been addressed by TEOS-10. Among those is the ambiguity and mutual inconsistency of different definitions of RH in practical use, such as between meteorology and climatology (Lovell-Smith et al. 2016). With respect to deviations from water phase equilibria such as saturation properties, the real-gas equivalent of conventional RH is the relative fugacity (RF) (Feistel et al. 2010b: eq. (10.10) therein, Feistel and Lovell-Smith 2017),
Here, is the specific gas constant of water, and is the universal molar gas constant. As a function of , the chemical potential at saturation, , may be expressed by means of either eq. (21) or (22). Note that eq. (23) is valid only for temperatures below the boiling point of water at the given pressure (Feistel and Lovell-Smith 2017), a condition which is naturally fulfilled under ambient geophysical conditions.
In ideal-gas approximation, RF is identical with conventional RH in terms of water-vapour partial pressures. For air close to saturation, such as the marine surface layer with about 80 %rh, the Clausius-Clapeyron formula is an excellent approximation of TEOS-10 values for RF, even if refraining from the perfect-gas assumption (Feistel et al. 2022). RF appears naturally in expressions for the Onsager driving force of non-equilibrium fluxes, such as evaporation from the ocean surface (Feistel and Hellmuth 2023, 2024). For the numerical computation of RF, a source code extension to the SIA library is available from Feistel et al. (2022).
Mathematical transformation between different thermodynamic quantities and partial derivatives with respect to alternative independent variables, such as frequently exploited in TEOS-10 to derive the desired functional dependencies, may conveniently and error-free be executed by means of the formal Jacobi method developed by Norman Shaw (1935), as briefly described in Appendix A.
4. Isentropically Lifted Condensation Level (LCL)
“Synoptic weather observations from ships throughout the World Ocean have been analyzed to produce a climatology of total cloud cover and the amounts of nine cloud types. … Among the cloud types, the most widespread and consistent relationship is found for the extensive marine stratus and stratocumulus clouds” (Eastman et al. 2011: p. 5914). Subtropical marine clouds show a pronounced “transition between unbroken sheets of stratocumulus and fields of scattered cumulus“ (Sandu et al. 2010). The cumulus cloud base is typically observed below 500 m height, as shown in Figure 1. For the climatic feedback effect of marine clouds, the lifted condensation level (LCL) is a key parameter that describes the pressure (or altitude) at which an isentropically ascending parcel reaches its dew- or frost-point, starting from given values of temperature and RH, such as at the sea surface. A typical empirical equation for the LCL height, , is
where , and , respectively, are the initial values of the parcel’s height, in-situ and dew-point temperature. Commonly, the latter is related to the saturation vapour pressure and the RH by the Clausius-Clapeyron formula. Previous estimates for the coefficient range widely between and (Romps 2017), with an optimum of suggested by Lawrence (2005). Also, nonlinear mathematical expressions, more complicated than eq. (24), had been suggested in the literature, derived from varying approximate thermodynamic relations for humid air, liquid water and ice. Often, such relations are chosen according to the authors’ personal preferences and are scarcely supported by internationally agreed standard formulations. In Section 4.2 below, for typical values of the marine troposphere, selected highly accurate TEOS-10 results for range between 125 and 129 .
Humid air at the sea surface has a typical climatological RH of about 80 %rh, a value that may vary seasonally or regionally between 70 %rh and 90 %rh, but appears likely to be only very weakly affected by global warming, if at all (Thomas and Stamnes 1999; Liou 2002; Dai 2006; Randall 2012; Rapp 2014; Blunden 2023). Assuming that an air parcel starts ascending at constant specific humidity, , from the sea surface at the air pressure, , and the sea surface temperature, , the value of the initial air fraction can be computed in implicit form from the sea surface relative fugacity, , using eq. (23), by
Here, surface values of independent variables are indicated by the subscript 0 which may be dropped at constant for simplicity. Similarly, the subscript LCL is used for those properties at the lifted condensation state. Associated function values such as or are without state-dependent subscript as long as there is no risk of confusion.
The tropospheric entropy, assumed to remain constant during the uplift, can be expressed by eq. (15),
At the LCL, the entropy value,
needs to be the same as at the surface, eq. (26), and may be eliminated from the mathematical problem by equating eq. (26) with (27),
The LCL pressure, , is approached when at fixed values of the temperature has dropped to the dew-point, , eq. (21), that means,
The chemical potential of water vapour in humid air, , may be expressed by the related Gibbs function, eq. (17),
If the initial value of RH is given, rather than the initial specific humidity, , then eq. (25) may be added to the system in the form of
Eqs. (28), (30) and (31) constitute a closed system of three nonlinear implicit equations for the three unknowns as functions of the given input values . These thermodynamic relations are the exact conditions for the LCL properties with the only minor approximation that the dissolution of air in liquid water, influencing the saturation state, is neglected. This system may be solved iteratively using the TEOS-10 functions implemented in the SIA library, see Appendix B, or it may be exploited analytically after introducing quantitatively reasonable approximations.
4.1. Numerical Iterative Solution
The system of equations, (28) and (30), for the calculation of from , and of eq. (31) for the determination of from the given surface values of and the relative fugacity, can be solved iteratively, with highest accuracy currently available. Expanding eq. (31) into a power series up to linear terms in the increment, , of a starting estimate, ,
leads to the solution for the improvement, , of iteration step ,
Practically, this Newton-Cotes iteration may start from almost dry air, such as .
In a similar manner, the other increments follow from eqs. (28) and (30), in matrix notation,
By Cramer’s rule, the solution is
and
The coefficients of this system are
All derivatives required here are numerically available from the TEOS-10 SIA library (Wright et al. 2010).
Table 1 reports selected LCL states computed from TEOS-10, iteratively solving eqs. (34), (35), (36) at and . Results rounded to 6 digits. The climatic warming trend moves LCL to higher altitudes () where the temperature difference between ocean () and cloud base () gets larger and consequently, the downward radiative heat flux becomes reduced as compared to (fictitious) lower clouds. This cooling effect is a negative, stabilising feedback of the cloud cover, slowing down ocean warming. The observed shrinking cloudiness, in turn, likely renders this cooling influence of clouds globally smaller.
4.2. Linear Analytical Approximation
If the initial temperature, , is only slightly higher than the dew point, , such as typically at the ocean surface, the LCL pressure may be estimated from TEOS-10 equations linearised in the small differences and . Doing this, the relative fugacity may be very accurately expressed by the Clausius-Clapeyron equation for the dew point (Feistel and Hellmuth 2022: eq. 14 therein),
Here, is the specific evaporation enthalpy of liquid water at equilibrium with (saturated) humid air. Its value is available from the thermodynamically rigorous relations (Feistel et al. 2010b; Feistel and Hellmuth 2022: eqs. C.5 and C.6 therein),
which is equivalent to
Here, and , respectively, are the specific entropies of humid air and liquid water.
Eq. (43) represents the initial linear term of a truncated Taylor series with respect to powers of , regardless of whether ideal-gas assumptions have been applied or not.
A similar series expansion of the Gibbs function of liquid water in eq. (30) with respect to and gives
The expansion coefficients are the specific entropy, , and the specific volume, , of liquid water at ,
A similar expansion about can be carried out for the Gibbs function of humid air,
Subtracting eq. (31) from (30) results in
which may by expressed in terms of the linear offsets (47), (48), as
Up to small terms linear in the subsaturation, , at the surface, the coefficient of equals the specific evaporation entropy, eq. (44),
and the term in front of equals approximately the specific evaporation volume (Feistel et al. 2010b),
Still in linear approximation with respect to the LCL pressure and temperature offset, eq. (50) then reads
During adiabatic uplift, temperature and pressure change are mutually related by the moist lapse rate, eq. (A18),
Similar to eq. (24), the final formula (53) for the LCL pressure is therefore, making also use of eq. (43),
Here, the lapse rate of the dew-point is negative, see Appendix B, eq. (B5),
The hydrostatic balance equation (height , gravity constant ),
can be integrated along an isentropic vertical profile, due to the thermodynamic relation,
to give
This enthalpy difference may be used to estimate the coefficient of the LCL height, eq. (24), from the LCL pressure, through
Rigorous numerical TEOS-10 results for and from eqs. (59) and (60) at selected typical marine conditions, obtained through iteratively solving eqs. (34), (35), (36) are reported in Table 2 and Table 3.
A linear approximation based on the LCL pressure, eq. (55), is
In Table 3, in addition to the calculated LCL coefficients, also the climatic feedback to possible RH trends is reported as the thermal radiation flux, , downward from the cloud base, which tends to warm the ocean if RH is rising.
If in eq. (52) the specific volume of humid air is much larger that the remaining terms of the evaporation volume, , the simplified LCL coefficient given by eq. (61) is, expressing the lapse rate by eq. (A18), , in terms of the thermal expansion coefficient, , and the specific isobaric heat capacity, , of humid air, by virtue of eq. (56) and ,
In ideal-gas approximation, , this becomes
Here, is the evaporation entropy of liquid water, eq. (51).
Analytical low-pressure approximations for the TEOS-10 Gibbs functions of liquid water and humid air are provided by Feistel and Hellmuth (2023: Appendix A therein) and in extremely simplified, crude form in Appendix C of this paper, as successfully used in the following section.
4.3. Clausius-Clapeyron Expansion
In the context of global warming, the Clausius-Clapeyron equation for the saturated vapour pressure of water has become a widely exploited and sufficiently accurate approximation for estimating the increasing humidity of the troposphere. Here, an expression for the LCL is derived with a similar accuracy from the TEOS-10 equations.
Eqs. (28), (30) and (31) constitute a closed system of three nonlinear implicit equations for the three unknowns as functions of the given input values . These relations may be formulated in terms of “crude” approximations, taking all heat capacities as constant, liquids as incompressible, and gases as perfect gases. Related crude Gibbs functions, and , are indicated here by tildes and are provided in Appendix C.
Using those Gibbs functions, the conservation of entropy during adiabatic ascent, eq. (28),
takes the form of the conventional adiabatic equation of state,
Here, and , respectively, are the heat capacity and the specific gas constant of humid air.
The saturation of air at the LCL, eq. (30), expresses equation chemical potentials of water in the gas and the liquid phase,
In crude approximation, this condition reads
Here, and , respectively, are temperature and pressure at the triple point of water, and is the density of liquid water. They appear in this context because that triple point is used as the reference state at which the arbitrary constants and have been adjusted to the phase equilibrium properties of fluid water, computed from TEOS-10, see Appendix C.
Finally, the relative fugacity (or RH) at the surface is specified by eq. (31) in terms of crude Gibbs functions
Inserting the crude equations given in Appendix C, results in
From the latter equation, the vapour mole fraction at the surface, , is obtained from the relative fugacity, ,
From , the dry-air mass fraction is available through eq. (4).
Subtracting eq. (67) from (69) and inserting entropy conservation (65) as
the saturation equation (68) can be written in the form
Here, the abbreviation
is introduced. The commonly used Clausius-Clapeyron equation for the saturation vapour pressure makes use of the fact that far from the critical point of water, the liquid density is much higher than the vapour density. This may be quantified by saying that the dimensionless parameter
is a small number. Of the perturbation expansion
applied to eq. (72), the leading term may be regarded as Clausius-Clapeyron approximation,
Eq. (76) may be rearranged into the form
with the abbreviations,
The solution of the nonlinear equation (77) is
Here, the function is the well-defined Lambert W function, see Appendix D, which is one of the two solutions of the equation
Because is negative, such as at , solutions for the lower branch, , must be chosen here,
Eventually, by means of eq. (71), the Clausius-Clapeyron approximation for the LCL pressure is
In fact, these “crude” Clausius-Clapeyron approximations (80) and (83) agree already quite well with the rigorous iterative TEOS-10 results of eq. (34), see Table 4.
5. Marine Climatic LCL Feedback
Refraining from the complexity of spectrally resolved greenhouse-gas attenuation as shown in Figure 6 and from proper 3D radiation propagation models (Pelkowski 2012, 2014; Zhong and Haigh 2013), low-level marine clouds as well as the ocean surface may approximately be described as planar black bodies, mutually interacting according to the Stefan-Boltzmann law of thermal radiation, Figure 8.
Denoting the Stefan-Boltzmann constant by , the net radiative heat loss, , of the cloud-covered ocean is in a 1D model,
Its sensitivity with respect to ocean warming is
assuming that the marine surface RH remains unaffected by the SST change. For the LCL values listed in Table 1, the upward and downward radiative fluxes, and , respectively, as well as estimated sensitivities, eq. (85), are calculated in Table 5.
The mathematical dependence of on is complicated, even in the case of crude approximations, eq. (80). In this section, a rigorous theoretical expression for this dependence is derived systematically from the TEOS-10 approach. As an aside, note that this longwave radiative interaction is an irreversible process with an entropy production rate of (Planck 1906; Kabelac 1994; Feistel 2011)
Latest assessments (Blunden et al. 2023) have shown that at the ocean surface, current climate change is characterised by an increase of SST along with constant surface RH, or similarly, in the TEOS-10 formalism, with constant relative fugacity, . As a dimensionless quantity, a suitable thermodynamic expression describing a related climatic trend of the LCL greenhouse effect is the sensitivity of the cloud base temperature, , with respect to an increase of the surface temperature, ,
This LCL temperature sensitivity controls the sensitivity of the ocean-cloud heat flux balance, eq. (85), with respect to rising SST. A rigorous formula for this sensitivity may be derived from the set of LCL equations, which describe entropy conservation during uplift, eq. (28),
air saturation at the cloud base, eq. (30),
and the given relative humidity at the sea surface, eq. (31),
During the climatic increase of the SST, , at constant RH,, and surface pressure,, these equations remain always fulfilled, for ,
so that other properties, namely, , may vary along with . Taking the partial derivatives of the functions , and with respect to , while considering the dependence of on , a set of three equations is obtained for their three unknown sensitivities with respect to ocean warming,
These derivatives are mutually related by eqs. (91),
In matrix notation, this is
By Cramer’s rule, the solution of this system for the LCL sensitivity is straight forward,
The coefficients of this system of linear equations are:
All partial derivatives required here, eq. (96) through eq. (104), are explicitly numerically available from the TEOS-10 SIA library. Reported in Table 1, the LCL sensitivities computed from eq. (94) are the rigorous figures close to the previous estimates of Section 4. A value of means that is rising slower than , so that the net radiation balance between sea surface and cloud base is distorted in favour of the upward heat flux, reducing the ocean’s warming rate.
The cloud base is cooling along with global SST warming, see Figure 5, and the net upward radiative heat flux of about 24 W m–2 is intensifying by 0.45 W m–2 per each °C of SST, as a negative feedback to the warming ocean by currently about 1 W m–2 (You 2024). This feedback does not provide a possible explanation for the warming, on the opposite, it tightens the problem. While the LCL feedback is not dominating the sea-air energy transfer, it is anyway large enough to not remain ignored. The effect is about 100 times as large as the rate of atmospheric warming.
For tutorial reasons or first estimates, the coefficients of eq. (94) may be expressed in crude approximation of the Gibbs functions, Appendix C. These are:
With either the TEOS-10 SIA library functions, or even with the simplified equations of Appendix C, the calculation of the LCL sensitivity, eq. (95) is straight forward but does likely require to be carried out numerically.
6. Discussion
Climate research relies on observation and causal prediction models. Causality itself cannot be observed but is the most reliable prediction tool (Hume 1967; Russell 1919; Feistel 2023a, b). The comparison of predicted phenomena with future observations serves as a validity criterion for causal models (Hertz 1894; Stips et al. 2016). In 2023, the global ocean heat content (OHC) has increased by , a value 25 times as large as the world’s total human energy consumption (You 2024), and even at least 100 times exceeding the atmospheric heat gain (von Schuckmann et al. 2023). This currently observed excessive OHC increment (Cheng et al. 2023) at a rate of 1.3 W m–2 remains largely unexplained so far (Loeb et al. 2021; Blunden et al. 2023), and raises questions regarding correctness, completeness and internal consistency of climate models.
The dominating input-output processes of the ocean heat balance include solar shortwave and tropospheric longwave irradiation, thermal radiation from the ocean surface, latent heat exchange by phase transitions including water vapour and ice, and sensible heat exchange with the atmosphere and lithosphere. The input and output processes each amount to a total of about 500 W m–2, and the observed imbalance arises from a small mutual mismatch by just 0.2 % between those. Evidently, to reasonably explain a small difference of 1 W m–2 between two big numbers of about 500 W m–2, each of those must be known to within an uncertainty below 1 W m–2. A key question is how this small amount may selectively be attributed to the various individual physical contributions involved. Unfortunately, at the ocean-atmosphere interface, current climate models exhibit uncertainties larger than 10 W m–2 and cannot reliably resolve the requisite heat flux differences.
TEOS-10, the Thermodynamic Equation of Seawater – 2010, provides the most accurate and mutually consistent equations currently available for the thermodynamic properties of seawater, humid air and ice. It was adopted as an international geophysical standard by IOC/UNESCO in 2009 and by IUGG in 2011 to support climate research.
Current numerical climate models tend to underestimate ocean warming (). They typically implement Dalton equations to estimate evaporation rates (Stewart 2008) in a historic form which forces increasing evaporation as a consequence of rising temperature and, in turn, of the vapour pressure of seawater. Quantitatively underpinned by TEOS-10, irreversible thermodynamics, however, suggests constant marine relative humidity (RH) as the driving force of evaporation, rather than increasing vapour pressure (Feistel and Hellmuth 2023, 2024). A putative tiny increase of global mean RH, even below instrumental resolution, may suffice to explain the rate of ocean warming; this renders latent heat a preferred candidate to be responsible for the observed OHC imbalance (Feistel and Hellmuth 2021).
A second candidate possibly contributing to the OHC increase is the radiation balance, strongly affected by clouds and greenhouse gases. Global cloudiness has systematically been decreasing in the past decades, this way enhancing oceanic shortwave irradiation by decreasing shadowed areas. At the same time, the downward longwave irradiation from those clouds is also decreasing with an estimated result that these two effects almost completely cancel one another (Phillips and Foster 2023). However, global warming does not only reduce cloudiness, the trend of higher sea-surface temperature (SST) also elevates marine clouds by an increasing lifted condensation level (LCL), in turn cooling the cloud base and reducing their downward thermal radiation. In order to include such a cooling effect in the OHC balance investigations, in this paper the sensitivity of LCL and of the related ocean-cloud radiation balance is analysed with the TEOS-10 thermodynamic formalism. Rigorous equations are derived for estimating LCL effects in numerical climate models.
The 2023 global mean SST is about 292 K. At this temperature, the upward thermal radiation flux from the sea surface is 412 W m–2 (Table 5) while the downward flux from the LCL cloud base is 388 W m–2. Under LCL cloud cover, the remaining net upward radiation of 24 W m–2 will grow by 0.45 W m–2 per one degree of further ocean warming. This LCL feedback effect is relevant in comparison to the 2023 OHC gain of 1.3 W m–2 and may not be ignored in balance investigations. As a negative, cooling feedback this LCL effect does not help to explain observed ocean warming, rather, it enlarges the problematic heating rate to be explained by other contributing effects of the OHC balance, such as a putative uncertain minor climatic change of evaporation.
However, atmospheric RH can be observed to within an uncertainty in the range 1 %rh - 5 %rh (Lovell-Smith et al. 2016). An increase of ocean surface RH by 1 %rh is estimated to reduce the latent heat flux of evaporation by about 5 W m–2 (Feistel 2015; Feistel and Hellmuth 2021, 2023), thus warming up the ocean by this rate. In addition, a 1 %rh increase may lower the LCL by about 25 m, in turn intensifying the thermal downward radiation flux from the cloud bottom by more than 1 W m–2 (see Table 3). LCL height may serve as a remotely measured, sensitive estimate for sea surface relative fugacity or conventional RH. It appears a plausible working hypothesis that the excessive ocean warming of 2023 by 1.3 W m–2 may be caused to a large extent by slightly rising ocean surface RH not exceeding the uncertainty of observation.
Author Contributions
R.F.: Manuscript idea and draft, elaboration of the theory; O.H.: independent verification of the theory and calculus, discussion and revision. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
All data used are published in the cited literature, such as in open-access IAPWS and TEOS-10 documents.
Acknowledgments
Authors are grateful to Jessica Blunden and Coda Phillips for clarifying details of the published “State of the Climate in 2022”. This work contributes to the tasks of the IAPSO/SCOR/IAPWS Joint Committee on the Properties of Seawater (JCS).
Conflicts of Interest
The authors declare no conflict of interest.
7. Appendix A: The Jacobi Method
Consider mathematical functions, , depending on independent variables, . The matrix, , consisting of the pairwise partial derivatives,, as its elements, is regarded as the Jacobian matrix of this set of functions. The determinant, , of this matrix is commonly referred to as the functional determinant, or the Jacobian (Bronstein and Semendjajew 1979; Kaplan 1984; Gradshteyn and Ryshik 2000). It is convenient to write in the form
For , the Jacobian equals the partial derivative,
Determinants of higher dimensions can be evaluated from their Laplace expansion with respect to their minors of dimension . For , the Jacobian can be reduced to two Jacobians of dimension 1,
For , the Laplace expansion takes the form of a linear combination of three Jacobians of dimension 2,
in which the two-dimensional Jacobians are subsequently evaluated according to (A3).
Jacobians possess some helpful and convenient properties which simplify their formal manipulations. To bring the variables in a desired sequence, following from the general properties of determinants, swapping of any pair of variables inverts the sign of the Jacobian, such as
and similarly,
For , this means
As special cases for , the backward sequence of variables inverts the sign,
while the rotation of variables preserves the sign,
If one (or more) of the functions is an identity, say, , the Jacobian reduces by one (or more) dimension, due to the Laplace expansion,
In particular, the identical Jacobian equals unity,
In higher dimensions, the product rule of functional determinants is a generalisation of the chain rule for usual derivatives. If a set of functions depends on the variables , which in turn depend on the variables , then the relation between their Jacobians is (Bronstein and Semendjajew 1979),
In particular, if the functions are chosen to be , then for the inverse functions there follows from (A12) the rule,
The Jacobi method developed by Shaw (1935) is the mathematically most elegant way of transforming the various partial derivatives of different potential functions into each other, exploiting the convenient formal calculus of functional determinants (Margenau and Murphy 1943, Landau and Lifschitz 1966).
Thermodynamic partial derivatives are commonly written in such a way that all variables are indicated which are kept constant when a particular derivative is carried out.
As a first example for applying the Jacobi method, the adiabatic lapse rate of humid air is defined as the change of a parcel’s temperature with pressure while its entropy and specific humidity remain fixed, i.e.,
By the Jacobi method, making use of the property (A10), the constant variables may be included in the Jacobian so that this derivative is written as
If, say, the Gibbs function, , of humid air is given, it may be desired to express the lapse rate in terms of that thermodynamic potential (similar rules apply to any other available such potential). To achieve this, the Jacobian (A15) may be transformed to the associated set of independent variables of this special case, , making use of the “chain rule” (A12) and rearranging the quantities in the numerators by (A8), (A9) in a sequence similar to those of the denominators,
Now, using (A10) again, the new Jacobians can be collapsed back to usual partial derivatives
Entropy is the negative temperature derivative, eq. (26), of the Gibbs function, so that the final result of this formal procedure is the lapse rate formula
Here, , and are, respectively, the thermal expansion coefficient, the specific volume and the specific isobaric heat capacity of humid air, available from the related TEOS-10 Gibbs function.
Alternatively, if enthalpy is available as a thermodynamic potential, such as from the TEOS-10 SIA library, similar manipulations lead to the simple expression
Let a second example be the chemical potential of water in humid air, eq. (17),
which is responsible for equilibria between humid air and condensed water phases, such as at saturation conditions. If adiabatic processes are studied, it is helpful to replace the Gibbs function, , by the enthalpy, ,
To achieve this, a transformation of the relative chemical potential,
to the new set of variables is required, using (A16) and (A3),
Now the derivatives of may be replaced by those of , using eq. (A21) so that the plain terms disappear,
Next, can be expressed by enthalpy, , to let several terms cancel out,
Together with (A21), in terms of enthalpy and entropy, the final formula for the chemical potential of water in humid air is,
8. Appendix B: Adiabatic Lapse Rate of the Dew-Point Temperature
The adiabatic lapse rate of the in-situ temperature of a humid air parcel is given by eq. (A19),
The related lapse rate of the dew-point is
At given composition, , and pressure, , the parcel’s dew-point does not depend on its in-situ temperature, . The dew-point is implicitly defined by the equilibrium condition for the chemical potential of water in humid air and in liquid water,
Taken at constant , the pressure derivative of this equation is
Up to a minus sign, the factor in front of is the evaporation entropy, eq. (44),
and the r.h.s. of (B4) equals the excess volume of evaporation at equilibrium, eq. (52),
The final formula for the lapse rate of the dew-point is
Due to the negative sign of this lapse rate, upon falling pressure of an ascending parcel, the dew-point is rising, opposite to the in-situ temperature.
9. Appendix C: Crude Gibbs Function Approximations
For practical rule-of-thumb estimates as well as for tutorial purposes, it is often sufficient to employ crude approximations for the thermodynamic properties of liquid water and humid air. In this sense, gases may be considered as perfect gases with constant heat capacities, and liquids as being incompressible, also with constant heat capacities. For liquid water, water vapour, dry air and humid air, respectively, such “crude” Gibbs functions , , and are provided here along with their 1st and 2nd partial derivatives. The tilde indicates such crudely approximated functions and variables. Those Gibbs functions may be defined by (see Feistel et al. 2010b; Appendix H therein),
Here, , and are the constant specific isobaric heat capacities of liquid water, water vapour and dry air, respectively. The constant density of liquid water is , and and are temperature and pressure, respectively, at an arbitrary reference state, here chosen to be the triple point of water.
Absolute energy and absolute entropy of any given substance cannot be measured and are irrelevant in empirical thermodynamics; they may only be determined from theoretical models (Planck 1906; Feistel 2019). In TEOS-10, these coefficients are carefully specified by practically useful reference-state conditions (Feistel et al. 2008, Feistel 2018). Here, and are such coefficients that will be adjusted below to the liquid-vapour equilibrium at the triple point, , as well as to the related evaporation enthalpy. Related coefficients of water vapour and of dry air are put to zero here for simplicity of the formulas, but without affecting any measurable properties. Note that such crude approximations of thermodynamic potentials need to be used with care; for example, does not permit a reasonable computation of sound speed, in contrast to the original TEOS-10 Gibbs function.
In Table 6, the 1st and 2nd partial derivatives of the crude Gibbs functions are reported for completeness and convenience. For quantitative estimates, the crude Gibbs functions may be adjusted to the properties of real substances at a suitably selected state. Here, for water the TEOS-10 triple-point properties at and are used, rounded to 6 digits (Wagner and Pruß 2002; Feistel et al. 2008, 2010b):
Evidently, away from the triple point, the crude properties will deviate from those of TEOS-10.
The enthalpies of liquid water, , and of water vapour, ,
differ by the latent heat of evaporation at the triple point,
The TEOS-10 value of the evaporation enthalpy of liquid water at the triple point is (Feistel et al. 2008)
For the liquid-vapour equilibrium at the triple point, defined by equal chemical potentials,
the adjustable constants take the values
Note that the latter figure is numerically crucial for the mutual consistency between the Gibbs functions of water but the value itself has no physical relevance and cannot be measured.
Up to 6 digits of the latest value, being exact by definition, the molar gas constant is (BIPM 2019)
and the specific gas constants are for water,
and for dry air,
It should be noted that these crude Gibbs functions are not consistent with the TEOS-10 reference-state conditions (Feistel et al. 2008; Feistel 2018). Consequently, attempts to compute phase-transition properties from combining proper TEOS-10 functions with these crude equations are strongly discouraged and will give unreasonable results.
10. Appendix D: Lambert’s W Function
The solution of the nonlinear equation
is mathematically well studied and is known as “Lambert’s W function” (Corless et al. 1996; Kalugin et al. 2012; Loczi 2022).
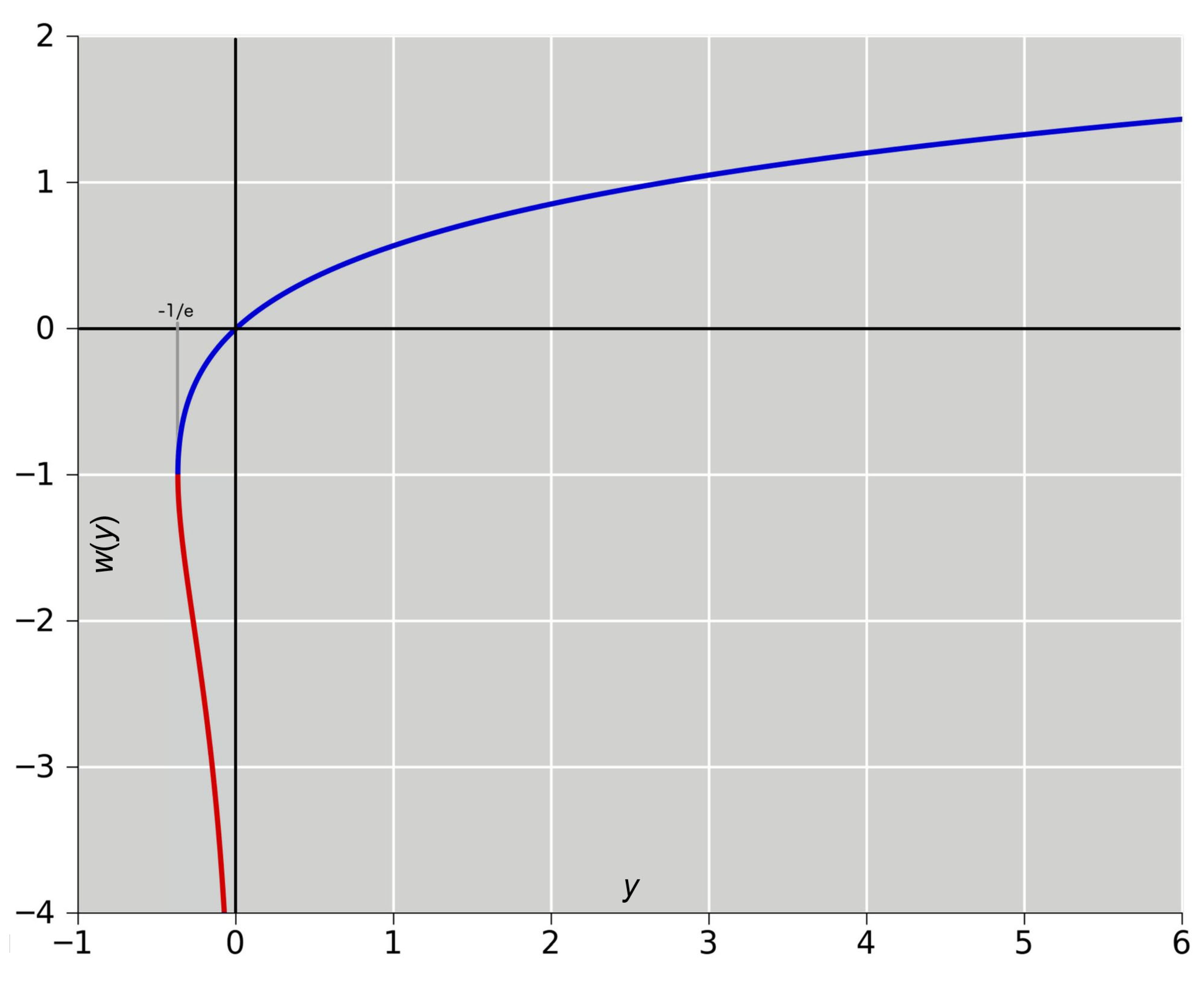
For, the function has real values. Special values areV
The value of is regarded as the mathematical “Omega constant”.
For arguments , is a unique function. For , has two branches, see Figure 9. The upper “principal” branch has values , the lower branch has values .
Numerically, the function can be computed by Newton-Cotes iteration of eq. (D1) or by various approximation expressions found in mathematical textbooks. For the principal branch, a simple formula is the series expansion
Figure 9.
Plot of Lambert’s W function. The blue upper curve is the principal branch. Public domain graphics from https://de.wikipedia.org/wiki/Lambertsche_W-Funktion, modified.
Figure 9.
Plot of Lambert’s W function. The blue upper curve is the principal branch. Public domain graphics from https://de.wikipedia.org/wiki/Lambertsche_W-Funktion, modified.
11. Appendix E: List of Symbols and Abbreviations
| Symbol | Remark | Basic Unit |
| Dry-air mass fraction in humid air | ||
| … | Matrix of coefficients | |
| … | Matrix of coefficients, crude approximation | |
| Dry-air mass fraction of saturated humid air | ||
| Abbreviation, | 1 | |
| … | Vector of coefficients | |
| Cloudiness: cloud-covered surface fraction | m-2 / m-2 | |
| Specific isobaric heat capacity of humid air | ||
| Specific isobaric heat capacity of seawater | ||
| Crude specific isobaric heat capacity of dry air, | ||
| Crude specific isobaric heat capacity of humid air | ||
| Crude specific isobaric heat capacity of water vapour, | ||
| Crude specific isobaric heat capacity of liquid water, | ||
| CRE | Cloud radiative effect | W m-2 |
| Euler number, | ||
| Abbreviation, | 1 | |
| EEI | Earth energy imbalance | |
| Specific Helmholtz energy of dry air | ||
| Specific Helmholtz energy of humid air | ||
| Specific Helmholtz energy of fluid water | ||
| Specific Gibbs energy of humid air | ||
| Crude specific Gibbs energy of humid air | ||
| Gravitational acceleration, | ||
| GHG | Greenhouse gas | |
| Specific Gibbs energy of ambient hexagonal ice | ||
| Specific Gibbs energy of seawater | ||
| Specific Gibbs energy of liquid water | ||
| Crude specific Gibbs energy of liquid water | ||
| Adjustable constant, | ||
| Adjustable constant, | ||
| Specific enthalpy of humid air | ||
| Specific enthalpy of seawater | ||
| Specific enthalpy of the standard-ocean reference state | ||
| IAPSO | International Association for the Physical Sciences of the Oceans | |
| IAPWS | International Association for the Properties of Water and Steam | |
| ITS-90 | 1990 International Temperature Scale | |
| JCS | Joint Committee on the Properties of Seawater | |
| Ocean-cloud radiative exchange flux | W m-2 | |
| Upward thermal radiation flux | W m-2 | |
| Downward thermal radiation flux | W m-2 | |
| LCL | Lifted condensation level | m |
| Specific evaporation enthalpy of liquid water | ||
| Crude specific evaporation enthalpy of liquid water, | ||
| LW CRE | longwave cloud radiative effect | W m-2 |
| molar mass of dry air, | ||
| molar mass of water, | ||
| OHC | Ocean heat content | J |
| Pressure | Pa | |
| Entropy production per surface area | ||
| Sea surface air pressure | Pa | |
| Lifted condensation level pressure | Pa | |
| Triple-point pressure of water, | Pa | |
| Specific humidity | ||
| Abbreviation, | 1 | |
| Mixing ratio | ||
| Molar gas constant, | ||
| Specific gas constant of dry air, | ||
| Specific gas constant of humid air, | ||
| RF | Relative fugacity | %rh |
| RH | Relative humidity | %rh |
| Specific gas constant of water, | ||
| Seawater salinity | ||
| SCOR | Scientific Committee on Oceanic Research | |
| SST | Sea surface temperature | K, °C |
| SW CRE | Shortwave cloud radiative effect | W m-2 |
| Celsius temperature | °C | |
| Absolute temperature, ITS-90 | K | |
| Sea surface temperature | K | |
| Dew-point temperature | K | |
| Lifted condensation level temperature | K | |
| Triple point temperature of water, | K | |
| TEOS-10 | Thermodynamic Equation of Seawater - 2010 | |
| Specific volume of humid air | ||
| VSMOW | Vienna Standard Mean Ocean Water | |
| Specific volume of liquid water | ||
| Lambert’s W function | 1 | |
| water-vapour mole fraction | ||
| Calendar year number (Common Era) | ||
| Vertical coordinate | m | |
| Lifted condensation level height | m | |
| Humidity sensitivity | ||
| Thermal expansion coefficient of humid air | ||
| LCL temperature sensitivity | 1 | |
| Adiabatic lapse rate of humid air | ||
| Adiabatic lapse rate of the humid-air dew-point | ||
| LCL pressure sensitivity | ||
| LCL height coefficient | ||
| Increment of dry-air mass fraction | ||
| Solar irradiation increase | W m-2 | |
| Ocean-cloud exchange flux increase | W m-2 | |
| Pressure increase | Pa | |
| LCL pressure increase | Pa | |
| Temperature increase | K | |
| SST increase | K | |
| LCL temperature increase | K | |
| Specific evaporation volume of liquid water | ||
| Specific evaporation entropy of liquid water | ||
| Clausius-Clapeyron expansion parameter | 1 | |
| Specific entropy | ||
| Specific entropy of humid air | ||
| Specific entropy of seawater | ||
| Specific entropy of liquid water | ||
| chemical potential of water vapour in humid air | ||
| chemical potential of ambient hexagonal ice | ||
| chemical potential of liquid water | ||
| Mass density | ||
| Mass density of seawater | ||
| Crude mass density of liquid water, | ||
| Stefan-Boltzmann constant, | ||
| Relative fugacity |
References
- Abraham, J.P., Baringer, M., Bindoff, N.L., Boyer, S.T., Cheng, L.J., Church, J.A., Conroy, J.L., Domingues, C.M., Fasullo, J.T., Gilson, J., Goni, G., Good, S.A., Gorman, J.M., Gouretski, V., Ishii, M., Johnson, G.C., Kizu, S., Lyman, J.M., Macdonald, A.M., Minkowycz, W.J., Moffitt, S.E., Palmer, M.D., Piola, A.R., Reseghetti, F., Schuckmann, K., Trenberth, K.E., Velicogna, I., Willis, J.K. (2013): A Review of Global Ocean Temperature Observations: Implications for Ocean Heat Content Estimates and Climate Change. Reviews of Geophysics 51, 450-483. [CrossRef]
- Azorin-Molina, C., Dunn, R.J.H., Ricciardulli, L., Mears, C.A., Nicolas, J.P., McVicar, T.R., Zeng, Z., Bosilovich, M.G. (2023): Land and Ocean Surface Winds. In: Blunden, J., Boyer, T., Bartow-Gillies, E. (eds.): State of the Climate in 2022. Bull. Amer. Meteor. Soc. 104, S72–S74, . [CrossRef]
- BIPM (2019): The International System of Units (SI). 9th edition of the SI Brochure. https://www.bipm.org/en/publications/si-brochure/ (accessed on 15 March 2023).
- Blunden, J., Boyer, T., Bartow-Gillies, E. (eds. 2023): State of the Climate in 2022. Bull. Amer. Meteor. Soc. 104, Si–S501. [CrossRef]
- Bronstein, I.N., Semendjajew, K.A. (1979): Taschenbuch der Mathematik. Nauka, Moscow, and Teubner, Leipzig.
- Budyko, M.I. (1963): Der Wärmehaushalt der Erdoberfläche. Fachliche Mitteilungen der Inspektion Geophysikalischer Beratungsdienst der Bundeswehr im Luftwaffenamt, Vol. 100, 3–282.
- Cheng, L., Abraham, J., Trenberth, K.E., Boyer, T., Mann, M.E., Zhu, J., Wang, F., Yu, F., Locarnini, R., Fasullo, J., Zheng, F., Li, Y., Zhang, B., Wan, L., Chen, X., Wang, D., Feng, L., Song, X., Liu, Y., Reseghetti, F., Simoncelli, S., Gouretski, V., Chen, G., Mishonov, A., Reagan, J., Von Schuckmann, K., Pan, Y., Tan, Z., Zhu, Y., Wei, W., Li, G., Ren, Q., Cao, L., Lu, Y. (2024): New record ocean temperatures and related climate indicators in 2023. Advances in Atmospheric Sciences, . [CrossRef]
- Clausius, R. (1876): Die mechanische Wärmetheorie. Friedrich Vieweg und Sohn, Braunschweig, Germany.
- Colman, R., Soden, B.L. (2021): Water vapor and lapse rate feedbacks in the climate system. Rev. Mod. Phys. 93, 045002. [CrossRef]
- Corless, R.M., Gonnet, G.H., Hare, D.E.G., Jeffrey, D.J., Knuth, D.E. (1996): On the Lambert W Function. Advances in Computational Mathematics 5, 329–359. [CrossRef]
- Dai, A. (2006): Recent Climatology, Variability, and Trends in Global Surface Humidity. J. Clim. 19, 3589–3606. [CrossRef]
- Dunn, R.J.H., Miller, J.B., Willett, K.M., Gobron, N. (eds. 2023): Global Climate. In: Blunden, J., Boyer, T., Bartow-Gillies, E. (eds.): State of the Climate in 2022. Bull. Amer. Meteor. Soc. 104, S20-S26. [CrossRef]
- Eastman, R., Warren, S.G., Hahn, C.J. (2011): Variations in Cloud Cover and Cloud Types over the Ocean from Surface Observations, 1954–2008. J. Climate 24, 5914-5934. [CrossRef]
- Feistel, R. (2008): A Gibbs function for seawater thermodynamics for –6 to 80 °C and salinity up to 120 g kg–1. Deep-Sea Res. Pt. I 55, 1639–1671. [CrossRef]
- Feistel, R. (2011): Entropy Flux and Entropy Production of Stationary Black-Body Radiation. J. Non-Equilib. Thermodyn. 36, 131–139. [CrossRef]
- Feistel, R. (2015): Salinity and relative humidity: climatological relevance and metrological needs, Acta IMEKO 4, 57–61, . [CrossRef]
- Feistel, R. (2018): Thermodynamic properties of seawater, ice and humid air: TEOS-10, before and beyond. Ocean Sci. 14, 471–502. [CrossRef]
- Feistel, R. (2019): Distinguishing between Clausius, Boltzmann and Pauling Entropies of Frozen Non-Equilibrium States. Entropy 21, 799. [CrossRef]
- Feistel, R. (2023a): On the Evolution of Symbols and Prediction Models. Biosemiotics 16, 311–371. [CrossRef]
- Feistel, R. (2023b): Self-Organisation of Prediction Models. Entropy 25, 1596. [CrossRef]
- Feistel, R., Hellmuth, O. (2021): Relative Humidity: A Control Valve of the Steam Engine Climate. Journal of Human, Earth, and Future 2, 140-182. [CrossRef]
- Feistel, R., Hellmuth, O. (2023): Thermodynamics of Evaporation from the Ocean Surface. Atmosphere 14, 560. [CrossRef]
- Feistel, R., Hellmuth, O. (2024): Irreversible Thermodynamics of Seawater Evaporation. J. Mar. Sci. Eng. 12, 166. [CrossRef]
- Feistel, R., Hellmuth, O., Lovell-Smith, J.W. (2022): Defining relative humidity in terms of water activity: III. Relations to dew-point and frost-point temperatures. Metrologia 59, 045013. [CrossRef]
- Feistel, R., Lovell-Smith, J.W. (2017): Defining relative humidity in terms of water activity. Part 1: definition. Metrologia 54, 566–576, . [CrossRef]
- Feistel, R., Wagner, W. (2005): High-pressure thermodynamic Gibbs functions of ice and sea ice. J. Mar. Res. 63, 95–139, . [CrossRef]
- Feistel, R., Wagner, W. (2006): A new equation of state for H2O ice Ih. J. Phys. Chem. Ref. Data 35, 1021–1047. [CrossRef]
- Feistel, R., Wielgosz, R., Bell, S.A., Camões, M.F., Cooper, J.R., Dexter, P., Dickson, A.G., Fisicaro, P., Harvey, A.H., Heinonen, M., Hellmuth, O., Kretzschmar, H.-J., Lovell-Smith, J.W., McDougall, T.J., Pawlowicz, R., Ridout, R., Seitz, S., Spitzer, P., Stoica, D., Wolf, H. (2016): Metrological challenges for measurements of key climatological observables: Oceanic salinity and pH, and atmospheric humidity. Part 1: overview. Metrologia 53, R1–R11, . [CrossRef]
- Feistel, R., Wright, D.G., Jackett, D.R., Miyagawa, K., Reissmann, J.H., Wagner, W., Overhoff, U., Guder, C., Feistel, A. Marion, G.M. (2010a): Numerical implementation and oceanographic application of the thermodynamic potentials of liquid water, water vapour, ice, seawater and humid air – Part 1: Background and equations. Ocean Science 6, 633–677. [CrossRef]
- Feistel, R., Wright, D.G., Kretzschmar, H.-J., Hagen, E., Herrmann, S., Span, R. (2010b): Thermodynamic Properties of Sea Air. Ocean Science 6, 91-141. [CrossRef]
- Feistel, R., Wright, D.G., Miyagawa, K., Harvey, A.H., Hruby, J., Jackett, D.R., McDougall, T.J., Wagner, W. (2008): Mutually consistent thermodynamic potentials for fluid water, ice and seawater: a new standard for oceanography. Ocean Sci. 4, 275–291, . [CrossRef]
- Fink, J.K. (2009): Chapter 1: Mathematics of Thermodynamics. In: Physical Chemistry in Depth. Springer, Berlin, Heidelberg. [CrossRef]
- Fofonoff, N.P., Millard, R.C. (1983): Algorithms for the computation of fundamental properties of seawater, Unesco Technical Papers in Marine Science 44, Paris. [CrossRef]
- Gibbs, J.W. (1873): Graphical methods in the thermodynamics of fluids. Transactions of the Connecticut Academy of Arts and Science 2, 309–342. https://www3.nd.edu/~powers/ame.20231/gibbs1873a.pdf.
- Goode, P.R., Pallé, E., Shoumko, A., Shoumko, S., Montañes-Rodriguez, P., Koonin, S.E. (2021): Earth's albedo 1998–2017 as measured from earthshine. Geophysical Research Letters 48, e2021GL094888. [CrossRef]
- Goody, R.M. (1952): A statistical model for water-vapour absorption. Quarterly Journal of the Royal Meteorological Society 78, 165-169. [CrossRef]
- Goody, R.M., Robinson, G.D. (1951): Radiation in the troposphere and lower stratosphere. Reviews of Modern Meteorology 77, 151-187. [CrossRef]
- Gradshteyn, I.S., Ryzhik, I.M. (2000): Tables of Integrals, Series, and Products. Academic Press, San Diego, CA.
- Graham, F.S., McDougall, T.J. (2013): Quantifying the Nonconservative Production of Conservative Temperature, Potential Temperature, and Entropy, J. Phys. Oceanogr. 43, 838–862. [CrossRef]
- Harvey, A.H., Hrubý, J., Meier, K. (2023): Improved and Always Improving: Reference Formulations for Thermophysical Properties of Water. J. Phys. Chem. Ref. Data 52, 011501. [CrossRef]
- Held, I.M., Soden, B.J. (2006): Robust Responses of the Hydrological Cycle to Global Warming. J. Climate 19, 5686-5699. [CrossRef]
- Hertz, H. (1894): Die Prinzipien der Mechanik. Johann Ambrosius Barth, Leipzig. Photocopy reprint (1963): Wissenschaftliche Buchgesellschaft, Darmstadt.
- Hume, D. (1967): Eine Untersuchung über den menschlichen Verstand. Ditzingen, Reclam.
- IAPWS AN6-16 (2016): Advisory Note No. 6: Relationship between Various IAPWS Documents and the International Thermodynamic Equation of Seawater—2010 (TEOS-10). The International Association for the Properties of Water and Steam: Dresden, Germany. http://www.iapws.org.
- IAPWS G08-10 (2010): Guideline on an Equation of State for Humid Air in Contact with Seawater and Ice, Consistent with the IAPWS Formulation 2008 for the Thermodynamic Properties of Seawater. The International Association for the Properties of Water and Steam: Niagara Falls, Canada. http://www.iapws.org.
- IAPWS G5-01 (2016): Guideline on the Use of Fundamental Physical Constants and Basic Constants of Water. The International Association for the Properties of Water and Steam: Dresden, Germany. http://www.iapws.org.
- IOC, SCOR, IAPSO (2010): The International Thermodynamic Equation of Seawater-2010: Calculation and Use of Thermodynamic Properties. Intergovernmental Oceanographic Commission, Manuals and Guides No. 56, UNESCO (English), Paris. http://www.TEOS-10.org.
- Josey, S.A., Gulev, S., Yu, L. (2013): Exchanges through the ocean surface. In: Siedler, G., Griffies, S.M., Gould, J., Church, J.A. (Eds.): Ocean Circulation and Climate. A 21st Century Perspective. Elsevier, Amsterdam, The Netherlands, pp. 115–140. [CrossRef]
- Kabelac, S. (1994): Thermodynamik der Strahlung. Vieweg, Braunschweig & Wiesbaden.
- Kalugin, G.A., Jeffrey, D.J., Corless, R.M., Borwein, P.B. (2012): Stieltjes and other integral representations for functions of Lambert W. Integral Transforms and Special Functions 23, 581-593, . [CrossRef]
- Kaplan, W. (1984): Advanced Calculus. Addison-Wesley, Reading, MA.
- Landau, L.D., Lifschitz, E.M. (1966. Statistische Physik. Akademie-Verlag, Berlin.
- Lawrence, M.G. (2005): The relationship between relative humidity and the dewpoint temperature in moist air: A simple conversion and applications. Bull. Amer. Meteor. Soc. 86, 225–233. [CrossRef]
- Lemmon, E.W., Jacobsen, R.T., Penoncello, S.G., Friend, D.G. (2000): Thermodynamic Properties of Air and Mixtures of Nitrogen, Argon and Oxygen From 60 to 2000K at Pressures to 2000MPa. J. Phys. Chem. Ref. Data 29, 331–362. [CrossRef]
- Liou, K.N. (2002): An Introduction to Atmospheric Radiation, 2nd ed. In: International Geophysics Series Vol. 84. Academic Press, New York, NY, USA. https://www.sciencedirect.com/bookseries/international-geophysics/vol/84/suppl/C.
- Loczi, L. (2022): Guaranteed- and high-precision evaluation of the Lambert W function. Applied Mathematics and Computation 433, 127406. [CrossRef]
- Loeb, N.G., Johnson, G.C., Thorsen, T.J., Lyman, J.M., Rose, F.G., Kato, S. (2021): Satellite and Ocean Data Reveal Marked Increase in Earth’s Heating Rate. Geophys. Res. Lett. 48, e2021GL093047. [CrossRef]
- Loeb, N.G., Mayer, M., Kato, S., Fasullo, J.T., Zuo, H., Senan, R., Lyman, J.M., Johnson, G.C., Balmaseda, M. (2022): Evaluating twenty-year trends in Earth's energy flows from observations and reanalyses. J. Geophys. Res. Atmos. 127, e2022JD036686. [CrossRef]
- Lovell-Smith, J.W., Feistel, R., Harvey, A.H., Hellmuth, O., Bell, S.A., Heinonen, M., Cooper, J.R. (2016): Metrological challenges for measurements of key climatological observables. Part 4: atmospheric relative humidity. Metrologia, 53, R40–R59. [CrossRef]
- Macdonald, A.M., Baringer, M.O. (2013): Ocean Heat Transport. In: Siedler, G., Griffies, S.M., Gould, J., Church, J.A. (eds.): Ocean Circulation and Climate. A 21st Century Perspective. Elsevier, Amsterdam, The Netherlands, pp. 115–140. [CrossRef]
- Margenau, H., Murphy, G.M. (1943): The Mathematics of Physics and Chemistry. D. van Nostrand Company, Inc., New York.
- McDougall, T.J. (2003): Potential enthalpy: A conservative oceanic variable for evaluating heat content and heat fluxes. J. Phys. Oceanogr. 33, 945–963. [CrossRef]
- McDougall, T.J., Barker, P.M., Feistel, R., Roquet, F. (2023): A thermodynamic potential of seawater in terms of Absolute Salinity, Conservative Temperature, and in situ pressure. Ocean Sci. 19, 1719–1741. [CrossRef]
- McDougall, T.J., Barker, P.M., Holmes, R.M., Pawlowicz, R., Griffies, S.M., Durack, P.J. (2021): The interpretation of temperature and salinity variables in numerical ocean model output and the calculation of heat fluxes and heat content. Geoscientific Model Development 14, 6445–6466. [CrossRef]
- McDougall, T.J., Feistel, R., Pawlowicz, R. (2013): Thermodynamics of Seawater. In: Siedler, G., Griffies, S.M., Gould, J., Church, J.A. (eds): Ocean Circulation and Climate, A 21st Century Perspective. Elsevier, Amsterdam, The Netherlands, pp. 141–158. [CrossRef]
- Meehl, G., Arblaster, J., Fasullo, J., Hu, A., Trenbert, K.E. (2011): Model-based evidence of deep-ocean heat uptake during surface-temperature hiatus periods. Nature Climate Change 1, 360–364. [CrossRef]
- Millero, F.J., Feistel, R., Wright, D.G., McDougall, T.J. (2008): The composition of Standard Seawater and the definition of the Reference-Composition Salinity Scale. Deep-Sea Res. Pt. I, 55, 50–72, . [CrossRef]
- Pawlowicz, R., McDougall, T.J., Feistel, R., Tailleux, R. (2012): An historical perspective on the development of the Thermodynamic Equation of Seawater – 2010. Ocean Sci., 8, 161–174. [CrossRef]
- Pelkowski, J. (2012): Of entropy production by radiative processes in a conceptual climate model. Meteorologische Zeitschrift 21, 439–457. [CrossRef]
- Pelkowski, J. (2014): On the Clausius-Duhem Inequality and Maximum Entropy Production in a Simple Radiating System. Entropy 16, 2291–2308. [CrossRef]
- Phillips, C., Foster, M.J. (2023): Cloudiness. In: Blunden, J., Boyer, T., Bartow-Gillies, E. (eds.): State of the Climate in 2022. Bull. Amer. Meteor. Soc., 104 (9), S60–S61, . [CrossRef]
- Planck, M. (1906): Vorlesungen über die Theorie der Wärmestrahlung. Johann Ambrosius Barth, Leipzig.
- Preston-Thomas, H. (1990): The International Temperature Scale of 1990 (ITS-90). Metrologia 27, 3–10. [CrossRef]
- Randall, D.A. (2012): Atmosphere, Clouds, and Climate. Princeton University Press, Princeton, NJ, USA.
- Rapp, D. (2014): Assessing Climate Change in Temperatures, Solar Radiation, and Heat Balance. Springer, Cham, Switzerland.
- Romps, D.M. (2017): Exact Expression for the Lifting Condensation Level. Journal of the Atmospheric Sciences 74, 3891–3900. [CrossRef]
- Rothman, L.S., Jacquemart, D., Barbe, A., Chris Benner, D., Birk, M., Brown, L.R., Carleer, M.R., Chackerian, C., Chance, K., Coudert, L.H., Dana, V., Devi, V.M., Flaud, J.-M., Gamache, R.R., Goldman, A., Hartmann, J.-M., Jucks, K.W., Maki, A.G., Mandin, J.-Y., Massie, S.T., Orphal, J., Perrin, A., Rinsland, C.P., Smith, M.A.H., Tennyson, J., Tolchenov, R.N., Toth, R.A., Vander Auwera, J., Varanasi, P., Wagner. G. (2005): The HITRAN 2004 molecular spectroscopic database. Journal of Quantitative Spectroscopy and Radiative Transfer 96, 139-204. [CrossRef]
- Russell, B. (1919): Mysticism and Logic and Other Essays. Chapter IX: On the Notion of Cause. Longmans, Green and Co., London, p. 180–208. https://en.wikisource.org/wiki/Mysticism_and_Logic_and_Other_Essays.
- Sandu, I., Stevens, B., Pincus, R. (2010): On the transitions in marine boundary layer cloudiness. Atmos. Chem. Phys. 10, 2377–2391. [CrossRef]
- Schneider, M. (1996): Leonardo da Vinci – Das Wasserbuch. Schirmer/Model, München Paris London.
- Shaw, A.N. (1935): The Derivation of Thermodynamical Relations for a Simple System. Philosophical Transactions of the Royal Society of London A 234, 299-328. [CrossRef]
- Stewart, R.H. (2008): Introduction to Physical Oceanography. Texas A & M University: College Station, TX, USA, . [CrossRef]
- Stips, A., Macias, D., Coughlan, C., Garcia-Gorriz, E., Liang, X.S. (2016): On the causal structure between CO2 and global temperature. Scientific Reports 6, 21691. [CrossRef]
- Tailleux, R., Dubos, T. (2024): A simple and transparent method for improving the energetics and thermodynamics of seawater approximations: Static energy asymptotics (SEA). Ocean Modelling 188, 102339. [CrossRef]
- Thomas, G.E., Stamnes, K. (1999): Radiative Transfer in the Atmosphere and Ocean. Cambridge University Press, Cambridge, UK.
- Turbet, M., Bolmont, E., Chaverot, G., Ehrenreich, D., Leconte, J., Marcq, E. (2021): Day–night cloud asymmetry prevents early oceans on Venus but not on Earth. Nature 598, 276–280. [CrossRef]
- Unesco (1981): Background papers and supporting data on the International Equation of State of Sea water 1980. Unesco Technical Paper Marine Science 38, UNESCO, Paris. https://unesdoc.unesco.org/ark:/48223/pf0000047363.
- Von Schuckmann, K., Minère, A., Gues, F., Cuesta-Valero, F.J., Kirchengast, G., Adusumilli, S., Straneo, F., Ablain, M., Allan, R.P., Barker, P. et al. (2023): Heat stored in the Earth system 1960–2020: Where does the energy go? Earth Syst. Sci. Data 15, 1675–1709. [CrossRef]
- Wagner, W., Pruß, A. (2002): The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data 31, 387–535. [CrossRef]
- Weller, R.A., Lukas, R., Potemra, J., Plueddemann, A.J., Fairall, C., Bigorre, S. (2022): Ocean Reference Stations: Long-Term, Open-Ocean Observations of Surface Meteorology and Air–Sea Fluxes Are Essential Benchmarks. Cover. Bull. Am. Meteorol. Soc. 103, E1968–E1990. [CrossRef]
- Willett, K.M., Simmons, A.J., Bosilovich, M., Lavers, D.A. (2023): Surface Humidity. In: Blunden, J., Boyer, T., Bartow-Gillies, E. (eds.): State of the Climate in 2022. Bull. Amer. Meteor. Soc., 104 (9), S49-S52, . [CrossRef]
- WMO (2024): Provisional State of the Global Climate 2023. World Meteorological Organization, Geneva. https://wmo.int/publication-series/provisional-state-of-global-climate-2023.
- Wright, D.G., Feistel, R., Reissmann, J.H., Miyagawa, K., Jackett, D.R., Wagner, W., Overhoff, U., Guder, C., Feistel, A., Marion, G.M. (2010): Numerical implementation and oceanographic application of the thermodynamic potentials of liquid water, water vapour, ice, seawater and humid air – Part 2: The library routines. Ocean Sci. 6, 695–718, . [CrossRef]
- Yang, X., Ge, J., Hu, X., Wang, M., Han, Z. (2021): Cloud-Top Height Comparison from Multi-Satellite Sensors and Ground-Based Cloud Radar over SACOL Site. Remote Sens. 13, 2715. [CrossRef]
- You, X. (2024): Oceans break heat records five years in a row. The heat stored in the world’s oceans increased by the greatest margin ever in 2023. Nature 625, 434-435, . [CrossRef]
- Zhong, W., Haigh, J.D. (2013): The greenhouse effect and carbon dioxide. Weather 68, 100-105. [CrossRef]
| 1 | Schneider (1996): p. 79 |
Figure 8.
Radiative heat exchange between ocean surface and low-level cloud base, both modelled as plane black bodies in the longwave spectrum.
Figure 8.
Radiative heat exchange between ocean surface and low-level cloud base, both modelled as plane black bodies in the longwave spectrum.
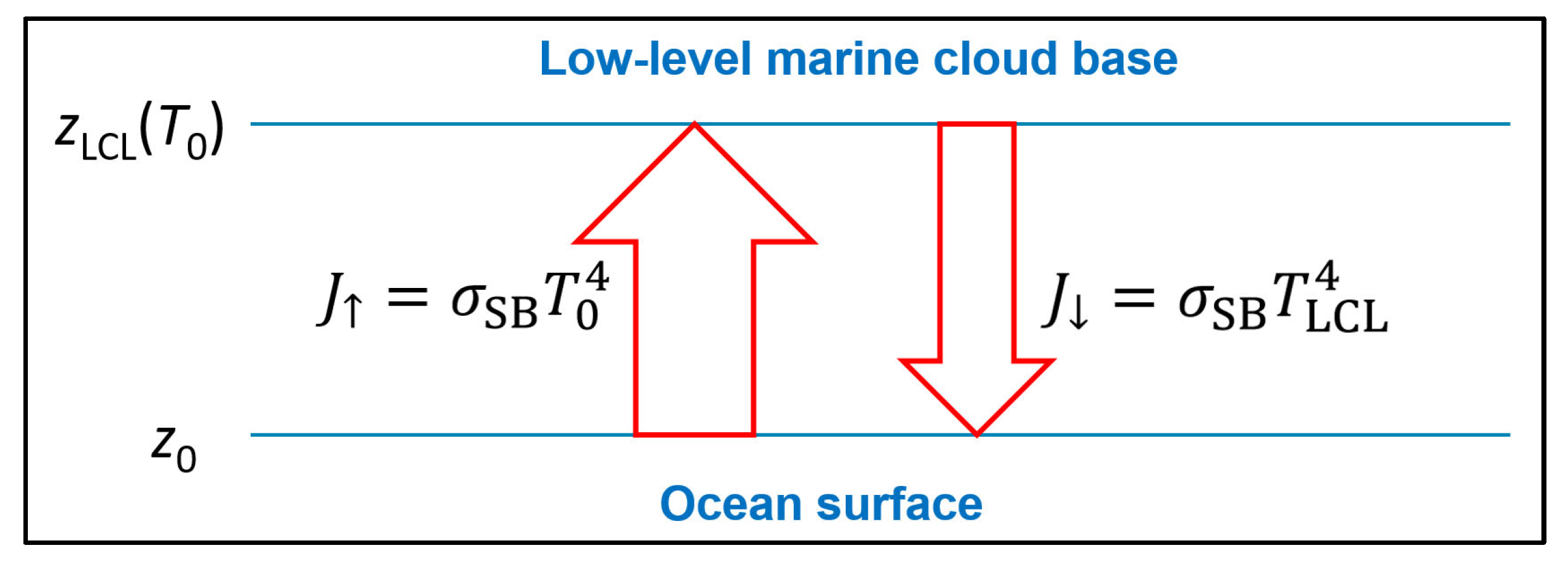
Table 1.
At constant surface RH of 80 %rh and pressure of 1013.25 hPa, as functions of the surface temperature and the surface dew-point temperature , reported in the columns are dry-air mass fraction , LCL pressure , sensitivity of LCL pressure with respect to SST increase, LCL temperature and the sensitivity of that temperature with respect to increasing SST. The values result from iteratively solving TEOS-10 eqs. (34), (35), (36). Differences , and are obtained from lower minus upper row of the related values, so that their signs reflect the climatic warming trend. Climatic sensitivities α, γ and of , and , respectively, are defined in eqs. (87), (92) and computed from eq. (94), see Section 5. All values calculated with full TEOS-10 accuracy and rounded only upon printing. The row printed in bold approximates the current global mean SST (Figure 5).
Table 1.
At constant surface RH of 80 %rh and pressure of 1013.25 hPa, as functions of the surface temperature and the surface dew-point temperature , reported in the columns are dry-air mass fraction , LCL pressure , sensitivity of LCL pressure with respect to SST increase, LCL temperature and the sensitivity of that temperature with respect to increasing SST. The values result from iteratively solving TEOS-10 eqs. (34), (35), (36). Differences , and are obtained from lower minus upper row of the related values, so that their signs reflect the climatic warming trend. Climatic sensitivities α, γ and of , and , respectively, are defined in eqs. (87), (92) and computed from eq. (94), see Section 5. All values calculated with full TEOS-10 accuracy and rounded only upon printing. The row printed in bold approximates the current global mean SST (Figure 5).
|
K |
K |
% |
α % K–1 |
hPa |
γ hPa K–1 |
K |
K K–1 |
||
| 286 | 282.633 | 99.2655 | –0.0483 | 963.093 | –0.2757 | –0.2742 | 281.883 | 0.9632 | 0.9634 |
| 288 | 284.580 | 99.1631 | –0.0542 | 962.542 | –0.2773 | 283.810 | 0.9629 | ||
| 290 | 286.526 | 99.0482 | –0.0608 | 961.984 | –0.2823 | –0.2806 | 285.735 | 0.9621 | 0.9624 |
| 292 | 288.471 | 98.9196 | –0.0680 | 961.419 | –0.2841 | 287.659 | 0.9619 | ||
| 294 | 290.416 | 98.7758 | –0.0759 | 960.847 | –0.2897 | –0.2878 | 289.583 | 0.9611 | 0.9614 |
| 296 | 292.361 | 98.6154 | –0.0846 | 960.268 | –0.2917 | 291.505 | 0.9608 | ||
| 298 | 294.305 | 98.4368 | –0.0942 | 959.680 | –0.2981 | –0.2959 | 293.426 | 0.9600 | 0.9603 |
| 300 | 296.248 | 98.2381 | –0.1047 | 959.084 | –0.3004 | 295.346 | 0.9597 |
Table 2.
Iteratively solving the rigorous eqs. (34), (35), (36) TEOS-10 values of LCL height, , computed from eq. (59), and LCL coefficient, from eq. (60) at surface pressure 1013.25 hPa and marine relative fugacity for selected SST values, . The row printed in bold approximates current global mean SST.
Table 2.
Iteratively solving the rigorous eqs. (34), (35), (36) TEOS-10 values of LCL height, , computed from eq. (59), and LCL coefficient, from eq. (60) at surface pressure 1013.25 hPa and marine relative fugacity for selected SST values, . The row printed in bold approximates current global mean SST.
|
K |
%rh |
K |
% |
m |
m K–1 |
| 286 | 80 | 282.633 | 99.2655 | 423.468 | 125.778 |
| 288 | 80 | 284.580 | 99.1631 | 431.481 | 126.157 |
| 290 | 80 | 286.526 | 99.0482 | 439.660 | 126.553 |
| 292 | 80 | 288.471 | 98.9196 | 448.017 | 126.967 |
| 294 | 80 | 290.416 | 98.7758 | 456.561 | 127.403 |
| 296 | 80 | 292.361 | 98.6154 | 465.305 | 127.862 |
| 298 | 80 | 294.305 | 98.4368 | 474.263 | 128.345 |
| 300 | 80 | 296.248 | 98.2381 | 483.449 | 128.857 |
Table 3.
Iteratively solving the rigorous eqs. (34), (35), (36) TEOS-10 values of LCL height, , computed from eq. (59), and LCL coefficient, from eq. (60) at surface pressure 1013.25 hPa and SST of for selected relative fugacities . The row printed in bold approximates current global mean SST. Note the significant sensitivity of the LCL height on RH, affecting the LCL temperature, , as well as the related downward thermal radiation flux, .
Table 3.
Iteratively solving the rigorous eqs. (34), (35), (36) TEOS-10 values of LCL height, , computed from eq. (59), and LCL coefficient, from eq. (60) at surface pressure 1013.25 hPa and SST of for selected relative fugacities . The row printed in bold approximates current global mean SST. Note the significant sensitivity of the LCL height on RH, affecting the LCL temperature, , as well as the related downward thermal radiation flux, .
|
K |
%rh |
K |
% |
m |
m K–1 |
K |
W m–2 |
| 292 | 74 | 287.262 | 99.0012 | 600.040 | 126.632 | 286.182 | 380.348 |
| 292 | 76 | 287.674 | 98.9740 | 548.289 | 126.745 | 286.685 | 383.030 |
| 292 | 78 | 288.077 | 98.9468 | 497.632 | 126.857 | 287.177 | 385.668 |
| 292 | 80 | 288.471 | 98.9196 | 448.017 | 126.967 | 287.659 | 388.263 |
| 292 | 82 | 288.857 | 98.8923 | 399.396 | 127.076 | 288.131 | 390.818 |
| 292 | 84 | 289.235 | 98.8650 | 351.724 | 127.184 | 288.594 | 393.334 |
| 292 | 86 | 289.604 | 98.8378 | 304.959 | 127.291 | 289.048 | 395.812 |
| 292 | 88 | 289.966 | 98.8105 | 259.061 | 127.396 | 289.493 | 398.255 |
Table 4.
Comparison of LCL temperatures and pressures of the rigorous TEOS-10 solutions of eq. (34) with the Clausius-Clapeyron approximations, eqs. (80) and (83).
Table 4.
Comparison of LCL temperatures and pressures of the rigorous TEOS-10 solutions of eq. (34) with the Clausius-Clapeyron approximations, eqs. (80) and (83).
|
K |
K |
K |
hPa |
hPa |
| 286 | 281.883 | 281.883 | 963.093 | 963.066 |
| 288 | 283.810 | 283.810 | 962.542 | 962.525 |
| 290 | 285.735 | 285.735 | 961.984 | 961.972 |
| 292 | 287.659 | 287.658 | 961.419 | 961.395 |
| 294 | 289.583 | 289.584 | 960.847 | 960.858 |
| 296 | 291.505 | 291.506 | 960.268 | 960.276 |
| 298 | 293.426 | 293.428 | 959.680 | 959.712 |
| 300 | 295.346 | 295.348 | 959.084 | 959.118 |
Table 5.
At given surface RH of and pressure, , as functions of the SST, , the columns report upward thermal radiation flux , LCL temperature , downward thermal radiation flux , upward net flux , and the estimated sensitivity of the net flux with respect to increasing SST. The row printed in bold approximates the current global mean SST (Figure 5).
Table 5.
At given surface RH of and pressure, , as functions of the SST, , the columns report upward thermal radiation flux , LCL temperature , downward thermal radiation flux , upward net flux , and the estimated sensitivity of the net flux with respect to increasing SST. The row printed in bold approximates the current global mean SST (Figure 5).
|
K |
W m–2 |
K |
W m–2 |
W m–2 |
|
| 286 | 379.381 | 281.883 | 358.006 | 21.375 | 0.419 |
| 288 | 390.105 | 283.810 | 367.893 | 22.213 | |
| 290 | 401.055 | 285.735 | 377.977 | 23.078 | 0.447 |
| 292 | 412.233 | 287.659 | 388.263 | 23.971 | |
| 294 | 423.644 | 289.583 | 398.751 | 24.893 | 0.476 |
| 296 | 435.290 | 291.505 | 409.444 | 25.846 | |
| 298 | 447.174 | 293.426 | 420.345 | 26.829 | 0.508 |
| 300 | 459.300 | 295.346 | 431.455 | 27.845 |
Table 6.
Analytical 1st and 2nd partial derivatives of the crude Gibbs functions (C1) - (C4). Note that , and . The water-vapour mole fraction is defined by eq. (4), .
Table 6.
Analytical 1st and 2nd partial derivatives of the crude Gibbs functions (C1) - (C4). Note that , and . The water-vapour mole fraction is defined by eq. (4), .
| 0 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | ||||
| 0 | ||||
| 0 | 0 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated






