Prerpints.org logo
Preprint
Article

Impact of Copolymer Architecture on Demicellization and Cargo Release via Head-to-Tail Depolymerization of Hydrophobic Moieties

Altmetrics

Downloads

83

Views

20

Comments

0

A peer-reviewed article of this preprint also exists.

supplementary.docx (736.73KB )

Submitted:

19 March 2024

Posted:

20 March 2024

You are already at the latest version

Alerts
Abstract
Motivated by experimental success in designing linear amphiphilic copolymers with selective demicellization capabilities through head-to-tail depolymerization triggered by specific stimuli, we advanced the design paradigm by increasing the number of triggering groups on the copolymer chain through architectural modifications. Utilizing molecular dynamics simulations, we explored the demicellization and cargo release dynamics of linear and miktoarm copolymers, featuring one, two and three hydrophobic block or branches, each capable for head-to-tail depolymerization. Our findings revealed that, under stoichiometric trigger molecule concentrations, miktoarms with three branches exhibited consistently faster depolymerization rates than those with two branches and linear copolymers. Conversely, at constant trigger molecule concentrations, the depolymerization rates of copolymers exhibited more complex behavior influenced by two opposing factors: the excess of trigger molecules, which increased with a decrease in the number of hydrophobic branches or blocks, and simultaneous head-to-tail depolymerization, which intensified with an increasing number of branches. Our study elucidates the intricate interplay between copolymer architecture, trigger molecule concentrations, and depolymerization dynamics, providing valuable insights for the rational design of amphiphilic copolymers with tunable demicellization and cargo release properties.
Keywords: 
Subject: Chemistry and Materials Science  -   Theoretical Chemistry

1. Introduction

Hydrophobic drugs and nucleic acid vectors used in therapeutics face significant challenges, including low stability, in vivo degradation, and difficulties in reaching the target site [1]. Consequently, a robust delivery system is essential to transport these agents safely and efficiently. In recent years, polymeric micelles have emerged as highly effective cargo carriers, owing to their biocompatibility, facile preparation, tunable size and shape, prolonged stability in blood circulation, and enhanced in vivo retention at the target site [2,3,4,5,6]. Typically, polymeric micelles consist of pre-synthesized diblock copolymer chains, comprising a hydrophilic and a hydrophobic block, or a mixture of double hydrophilic diblock copolymers with neutral and oppositely charged blocks, that become hydrophobic upon complexation [7,8]. The hydrophobic segments form the micelle core, while the hydrophilic ones create the surrounding corona. These micelles are derived from dilute polymer concentrations exceeding the critical micelle concentration (CMC). Recently, innovative assembly models (PISA and PIESA) have allowed micellization at high monomer concentrations, combining diblock copolymer synthesis and micellization in a single process [9,10]. The coassembly of cargo molecules with copolymer chains results in the encapsulation of hydrophobic cargo within the micelle core due to the hydrophobic interactions with the solvent.
Smart polymeric micelles, responsive to the microenvironment of the target site, can be designed by incorporating stimuli-responsive switches either assembled into micelles or covalently grafted onto copolymer chains. These switches, responsive to pH, light, heat, redox reactions, and enzymes, facilitate efficient drug delivery [11,12,13]. However, challenges may arise in achieving complete cargo release due to the incomplete dissociation of the micelle. Polymeric micelle carriers with degradable copolymer chains have gained attention for offering controlled yet complete release of cargo molecules and preventing the accumulation of micelles at the target point [14,15,16].
In a noteworthy study Kim et. al. designed amphiphiles based on poly(benzyl-ether) capable of selective demicellization through head-to-tail depolymerization triggered by hydrophobic fluolid molecules [17]. A labile end-capping unit attached to the end of hydrophobic block is buried inside the core of the micelle, preventing detachment of the labile units and rendering the demicellization signal specific. Fluolid molecules trigger the detachment of the end-capping unit in the hydrophobic block, after which the entire chain spontaneously and continuously depolymerizes in a head-to-tail manner without the need for additional stimuli. Loading doxorubicin inside the micelles led to their molecular-level degradation, resulting in controlled and complete release of the cargo molecules.
The depolymerization-induced disassembly mechanism has primarily been explored for amphiphiles with a linear chain architecture carrying one labile end cap unit. The design of amphiphiles with a different architecture, bearing more labile end cap units, can further enhance the control of depolymerization and the cargo release, which is useful for biological and environmental applications. Due to the lack of such studies, we conducted coarse-grained molecular dynamics simulations of micelles formed by a) Linear AB diblock copolymer with one hydrophilic (A type) and one hydrophobic (B type) block, featuring one end cap unit. b) Miktoarm star copolymer A(B)2 with one hydrophilic and two hydrophobic branches, equipped with two end cap units. c) Miktoarm star copolymer A(B)3 with three hydrophobic branches and three end cap units. We calculated the mass distributions of micelles formed by different copolymers before and after cargo loading, the kinetics of the head-to-tail depolymerization of hydrophobic moieties and the kinetics of cargo release triggered by hydrophobic small molecules.

2. Model

2.1. Coarse-Grained Molecular Dynamics Simulation Details

Amphiphilic AB linear diblock copolymers, miktoarm star copolymers, and cargo molecules are modeled as bead-spring chains comprising Lennard-Jones beads with a diameter σ. In all simulations, the copolymer chains collectively consist of 30 A-type hydrophilic and 30 B-type hydrophobic beads. In linear AB diblock copolymers, denoted as A30B30, the hydrophilic and hydrophobic beads are distributed in one block each. In miktoarm star copolymers with 3 and 4 branches, denoted as A30(B15)2 and A30(B10)3, the 30 hydrophobic beads are distributed in 2 or 3 branches, respectively. The free end bead of the hydrophobic block or branch is designated as an end cap unit. The cargo molecules are linear chains containing 3 C-type hydrophobic beads, denoted as C3. The trigger molecule consists of a single T-type hydrophobic bead with a diameter σ. All copolymer chains, including those with linear and star architecture, as well as cargo and trigger molecules are illustrated in Figure 1.
In the current study, simulations were contacted for mixtures comprising a) A30B30 with C3 b) A30(B15)2 with C3 and c) A30(B10)3 with C3, collectively containing 1000 copolymer chains and 2000 or 4000 cargo molecules. In all cases, the total concentration of beads (including copolymer and cargo beads) was maintained at [Φ]=0.12 where most micelles are formed.
Excluded volume, bead-bead interactions were considered to mimic the macroscopic solvent conditions. These interactions were calculated using a truncated Lennard-Jones potential [8,18]:
U L J r i j = 4 ε σ r i j 12 − σ r i j 6 − σ r c i j 12 + σ r c i j 6 ,   r i j ≤ r c i j 0 , r i j > r c i j  
where ε is the well-depth and rcij is the cutoff radius. Different beads were connected with finitely extensible nonlinear elastic bonds (FENE). The FENE potential is expressed as [8]
U B o n d r i j = − 0.5 k R 0 2 l n 1 − r i j R 0 2 ,   r i j ≤ R 0 ∞ , r i j > R 0  
where rij is the distance between beads i and j  ,   k = 25 ε / σ 2 and R0 is the maximum extension of the bond [19] ( R 0 = 1.5 σ ) . The solvent molecules are implicitly considered.
Molecular dynamics simulations with a Langevin thermostat were conducted in a cubic box with periodic boundary conditions, using the open-source massive parallel simulator LAMMPS [20]. The reduced temperature of the simulation T* was set to T*=kBT/ε=1.8 (ε=1) corresponding to bad solvents conditions [8]. Different cutoff distances and epsilon parameters in the Lennard-Jones potential were employed to describe the interactions between copolymer units. The B-B, B-C, and C-C interactions were considered attractive. Specifically, the B-B interactions consistently corresponded to T*=1.8 while the B-C and C-C interactions were even more attractive, corresponding to lower temperatures (T*=1.8, 1.4 and T*=1.8, 1.6, 1.5 and 1.4 respectively) with a cutoff distance rcij of 2.5σ (εBB=1, εij= T*/1.8, for i, j≠B). Conversely, the A-A, A-B, and A-C interactions were considered repulsive with cutoff distance rcij of 21/6σ. In the latter case, the Lennard Jones potential is shifted by ε. For simplicity, all types of beads were assumed to have the same mass (m= mi =1) and diameter (σ=1).
Following the Stillinger criterion [21] two moieties were considered to reside to the same micelle if the distance between any two nonbonded hydrophobic beads, belonging to different chains, were found to be within 1.5σ.
We performed 2 million timesteps with an integration step t = 0.006 τ ( τ = m σ 2 ε ) , setting all cutoff radii equal to rcij=21/6σ to eliminate any bias introduced from the initial conformation. Subsequently, the system was allowed to equilibrate for 30 million timesteps. The simulation was then extended to 300 to 600 million timesteps. The duration of the simulation was evaluated by calculating the tracer autocorrelation function [7]:
C t = N t 0 + t N ( t 0 ) − N ( t 0 ) 2 N 2 t 0 − N ( t 0 ) 2   ,
where N(t) is the number of molecules in the micelle in which the copolymer resides at time t. We considered all copolymers as tracers, with each time step serving as the time origin t0. The characteristic relaxation time trelax is defined as the time required for C(t) to reach the value [7,8] of 1/e = 0.37. Each simulation was conducted for a minimum of 10trelax to ensure 10 independent conformations. The properties of interest were calculated as averages from 4000 snapshots using the block average method with ten blocks.

2.2. Depolymerization and Cluster Analysis

The stochastic depolymerization of the hydrophobic monomers of amphiphilic copolymers as depicted in Figure 2, utilized the “bond /react” functionality of LAMMPS. This feature allows the breaking of bonds between beads based on distance-dependent probabilistic criteria. Topology changes are specified in pre- and post-reaction molecule templates. Two distinct depolymerization steps were undertaken: (a) the breaking of bonds between the hydrophobic end cap and B-type beads, triggered by the presence of T-type molecule within Rcutoff = 1σ from the end cap bead, with a predetermined reaction probability (RP) (Figure 2a). (b) The spontaneous propagation of depolymerization of hydrophobic beads with a predetermined RP occurring without any external stimuli (Figure 2b).
We utilized graph clustering analysis to analyze the simulation data. Initially, we identified micelles employing the data clustering algorithm DBSCAN implemented in the Python library Sklearn [22], with a maximum allowable neighborhood radius of 1.5σ. For a point (bead) to be classified as a core point, a minimum of two points (including the point itself) must be within the neighborhood. A precomputed neighbor sparse array was utilized as input for the DBSCAN algorithm. To construct this array, the KDTree neighbor data structure from the Python library SciPy [23] was employed, specifically the Sparse Distance Matrix algorithm with a maximum distance of 1.5σ between two points. It’s worth noting that the distance matrix algorithm disregards points with a distance greater than the maximum distance parameter. The KDTree neighbor data structure takes periodic boundary conditions into account, ensuring that the clustering analysis includes the periodic images.
For the identification of polymer chains, we employed the Python NetworkX library [24]. In this context, beads were represented as nodes, and bonds were represented as edges. From the graph created by this library, we extracted the polymer chains using the “Connected/Components” algorithm. This algorithm generates connected components from a graph, corresponding to bead spring chains in our case. Subsequently, the polymer chains were assigned to micelles based on the previous steps. To compute properties such as the radius of gyration of the micelles (core, corona, and total) and the shape anisotropy parameter κ2, we utilized the outbox coordinates. To achieve this, micelles that split due to the periodic conditions (inbox coordinates) were identified and consolidated using the data clustering algorithm DBSCAN, KDTree neighbor data structure, and Sparse Distance Matrix algorithm without periodic conditions.

3. Results and Discussion

3.1. Micellization and Cargo Encapsulation

The micellization of amphiphilic linear A30B30, miktoarm star A30(B15)2, and A30(B10)3 copolymers was studied prior to cargo encapsulation at T*=1.8 and [Φ]=0.12. We calculated the aggregate mass distribution, the gyration radius, and the shape anisotropy of micelles. In Figure 3, the mass distribution of the aggregates is depicted. Peak values corresponding to the preferential aggregation number Np are higher for linear copolymers and decrease as the number of arms in miktoarm copolymers increases, aligning with previous simulation results [25]. This behavior can be attributed to varying interfacial energy per chain required from these copolymers during the aggregation process [26]. In the case of linear copolymers, the long hydrophobic arm may extend far from the connection point with the hydrophilic block, reducing the interface with the solvent and, consequently, the enthalpic interactions [27]. Additionally, the extension of the large hydrophobic block increases the interface exposed to other copolymers’ hydrophobic arms, enhancing the probability of interaction reducing the free energy. For miktoarm copolymers with two or three shorter arms, many beads are confined near the connection point with the hydrophilic arm. This leads to a larger interface with the solvent molecules, resulting in greater interfacial energy and a smaller aggregate. Furthermore, the concentration of beads near the star center hinders their interaction with other hydrophobic units, further reducing free energy.
The encapsulation of cargo molecules was examined for different interaction parameters between hydrophobic C-C and B-C beads. Simulations of mixtures containing 1000 copolymer chains with 2000 or 4000 cargo molecules C3 were contacted at [Φ]=0.12, and the results are presented in Table S1. For linear A30B30 copolymers, an increase in the strength of attractions between C-C beads from T*C-C =1.8 to 1.4 had minimal effect on the percentage of encapsulated cargo molecules (41% to 43%). In contrast, a similar increase in the strength of attractions between B-C beads (T*B-B=1.8 and T* B-C = T*C-C=1.4) dramatically increased the percentage of encapsulated molecules to 83%, aligning with previous findings [28]. The copolymer architecture did not influence the encapsulation of cargo molecules, as the driving force for this process is the hydrophobicity between B and C beads. In a mixture of A30B30 with 4000 C3 molecules and attractive interactions corresponding to T*B-B=1.8 and T*B-C = T*C-C=1.4, the percentage of encapsulated cargo molecules remained constant at 82%. Free cargo molecules were in dynamic equilibrium with the encapsulated ones. The loading capacity [17] (LC) of the micelle, defined as the w/w percentage of the cargo accommodated in the loaded micelle carrier for the two different cargo concentrations, was found to be 7.6% and 14.1%, respectively. Encapsulation of hydrophobic molecules in the micelle core altered the hydrophilic/hydrophobic balance, triggering the association of free copolymer chains into the micelles and resulting in a higher aggregation number for all copolymer architectures (Figure 3 and Table S2). The Np of loaded micelles with LC=7.6% increased by approximately 16%, 30%, and 35% for the linear A30B30, miktoarm star A30(B15)2, and A30(B10)3 copolymer mixtures, respectively. This higher increase in Np in miktoarm copolymers reflects the more efficient packing of B and C beads in the micelle core, facilitating the decrease in free energy. The autocorrelation function indicates that the micelles of A30B30 copolymers with LC=14.1% were kinetically frozen even after 600 million timesteps and were not further studied.
The mean squared radius of gyration <Rg2>, serves as a measure expressing the size of both ‘empty’ and loaded micelles. The calculation of <Rg2> focused solely on copolymer beads to maintain consistent molecular weight in micelles sharing the same aggregation number N. In the case of preferential micelles, <Rg2> was observed to be higher in loaded micelles by approximately 9%, 16%, and 16% for A30B30, A30(B15)2, and A30(B10)3 copolymers, respectively. This elevation can be attributed to the increased Np of loaded micelles, with the disparity in Np becoming more pronounced in miktoarm star copolymers. Figure 4 illustrates the results for <Rg2> for both types of micelles with the same Np. For A30B30 copolymers, the <Rg2> is marginally higher in loaded micelles, a consequence of cargo molecules enlarging the micelle core and leading to a slight increase in <Rg2>. A similar trend is observed in micelles formed by A30(B15)2, and A30(B10)3 copolymers up to N=40 and 27, respectively. However, for higher N values the <Rg2> of ‘empty’ micelles surpasses that of loaded ones. The anisotropy shape parameter [27,29] κ2 values, depicted in Figure 5 reveal that ‘empty’ micelles exhibit an elongated shape in contrast to the more spherical shape loaded micelles. This distinction arises from the improved packing of hydrophobic content in the micelle core, leading to higher <Rg2> values for ‘empty’ micelles compared to the loaded ones. Notably, A30B30 copolymers form very spherical micelles in both ‘empty’ and loaded states, while the differences in κ2 values for A30(B15)2, and A30(B10)3 copolymers increase with the number of hydrophobic arms.

3.2. Kinetics of Depolymerization

The depolymerization and the subsequent degradation of loaded micelles were carried out using two distinct concentrations of hydrophobic trigger molecules. The first concentration aligns with the stoichiometry of the total end cap beads in A30B30, A30(B15)2, and A30(B10)3 copolymer solutions, accounting for 1000, 2000 and 3000 T-type molecules, respectively. The second concentration is maintained at a constant level, with 4000 T-type molecules applied to all copolymer solutions. These trigger molecules were randomly inserted into the simulation box, representing the final snapshot of the trajectory of copolymer comicellization involving cargo C3 molecules. This configuration served as the initial state for the depolymerization process. The introduction of trigger molecules led to an adjustment in overall solution concentration, reaching up to [Φ]=12.6. The attractive interactions between T-T, B-T, and T-C beads consistently corresponded to T*=1.8 while the T-A interactions were considered repulsive.
When T-type molecules infiltrate the hydrophobic core of the micelle, they can initiate the rapture of bonds between the hydrophobic end cap and B-type beads if the distance of T-type molecule is within Rcutoff = 1σ from the end cap bead, governed by a predetermined reaction probability, RPT. Subsequently, spontaneous head-to-tail depolymerization of hydrophobic B-type beads may occur, guided by a predetermined reaction probability, RPB, and this process takes place without any external stimuli. Simulations were conducted to explore scenarios where the end cap bond-breaking occurs more easily, equivalently, or more difficultly than the B-B bond (with RPB values of 10-3, 10-4 and RPT values of 10-2, 10-3 and 10-4).
The results depicting the fraction of end cap bonds broken with RPT=10-4 and RPB=10-3, are showcased in Figure 6 for both stoichiometric and constant concentrations of trigger molecules. Notably, the depolymerization of end cap beads in A30(B10)3 copolymers at a stoichiometric concentration of trigger molecules surpasses the rates observed in A30(B15)2 and A30B30 copolymers. This heightened efficacy is attributed to the doubled and tripled presence of T-type molecules in A30(B10)3 mixtures compared to their counterparts in A30(B15)2 and A30B30 mixtures, thereby increasing the probability of infiltration into the hydrophobic core. Furthermore, the elongated sphere scheme (depicted in Figure 5) of A30(B10)3 micelles contribute to a larger core surface exposed to the solvent compared to other copolymers. This structural characteristic facilitates the penetration of trigger molecules, contributing to the observed faster depolymerization in A30(B10)3 copolymers. Conversely, contrasting trends are noted in the depolymerization process under constant T-type molecules concentration (Figure 6b). The excess of trigger molecules is fourfold, twofold and 1.5 times higher than the stoichiometric case for A30B30, A30(B15)2 and A30(B10)3 mixtures, respectively, leading to a quicker penetration of trigger molecules and depolymerization of linear copolymers followed by miktoarm star copolymers. Various factors, including micelle corrosion, also influence the penetration of trigger molecules into the micelle core and subsequently the breaking of the end cap bonds with B-type beads. Higher values of RPT simply reduce the time for the completion of end cap removal without affecting the order of copolymer depolymerization in both stoichiometric and constant concentration cases (Figure S1). Similarly, an increase by x times in the T-type molecule concentrations in all copolymer mixtures results in faster end cap removal without altering the order of copolymer depolymerization (Figure S2).
The results of the depolymerization of hydrophobic beads, including both end cap and B-type beads, are presented in Figure 7 under constant and stoichiometric concentrations of trigger molecules. When the breaking of the end cap bond with the B-type bead is more challenging than the bond between B-type beads (RPT=10-4, RPB=10-3), the rate of depolymerization for hydrophobic beads is governed by the slower step. Consequently, the depolymerization trends among copolymer architectures align with those observed in the end cap bond break. Specifically, A30B30 exhibits faster depolymerization, followed by A30(B15)2 and A30(B10)3 mixtures (Figure 7a) for the same reasons outlined earlier. However, at RPT=10-2 and RPB=10-3, where the breakage of the bond between B-type beads becomes the slower reaction step, the branching architecture significantly influences the depolymerization process. The head-to-tail depolymerization of B-type beads occurs simultaneously in all branches resulting in faster depolymerization in A30(B10)3 with three branches, followed by A30(B15)2 and A30B30 with two and one branches respectively. Notably, when 65% of the total bonds of hydrophobic beads are broken, the depolymerization rate of A30(B15)2 copolymers surpasses that of A30(B10)3 copolymers (Figure 7b). This is attributed to the higher excess of trigger molecules in A30(B15)2 mixtures, facilitating the faster removal of end cap beads from the hydrophobic branch. Similarly, the depolymerization rate of A30B30 copolymers exceeds that of A30(B10)3 and A30(B15)2 copolymers when the fraction of total bonds breakage reaches 0.85 and 0.95 respectively. Beyond these values, the order of depolymerization rates reverts to the pattern observed at RPT=10-4 and RPB=10-3. In actuality, the reversal in the depolymerization order occurs in the case of RPT=10-4 and RPB=10-3, but the crossovers between the depolymerization rates are confined to a narrow range, specifically between 0.03 and 0.06. When RPT=RPB=10-3, the depolymerization rate of hydrophobic beads for different architectures is determined by two opposite factors: the excess of trigger molecules, which increases as the number of hydrophobic branches or blocks decreases, and the simultaneous head-to-tail depolymerization of beads, which intensifies with an increasing number of branches. As depicted in Figure 7c, the crossover of depolymerization curves occurs within the range of 0.20 to 0.55. Beyond this fraction, A30B30 exhibits faster depolymerization, followed by A30(B15)2 and A30(B10)3 mixtures.
In the case of depolymerization of hydrophobic beads under stoichiometric concentration of T-type molecules with the end cap beads (Figure 8), the rate of depolymerization is consistently faster in A30(B10)3 followed by A30(B15)2 and A30B30 mixtures. This can be attributed to the same factors explained earlier in the context of end cap depolymerization, coupled with the higher number of branches that are potentially subject to simultaneous head-to-tail depolymerization of B-type beads.

3.3. Demicellization

The depolymerization of hydrophobic moieties in a head-to-tail fashion results in copolymer chains that are either shorter or lack hydrophobic block or branches. The reduction in hydrophobic content within the copolymer corresponds to an increase in the critical micelle concentration. Consequently, these chains migrate into the solution, triggering the gradual demicellization of the mixtures. Figure 9, Figure 10 and Figure 11 and S3–S8 present the results regarding the micelle mass distribution at various fractions of bond breakage between hydrophobic beads (approximately 0, 0.15, 0.30, 0.45, 0.60, and 0.75) for stochiometric and constant concentrations of trigger molecules. Micelle mass distributions were computed from a single snapshot, and their normalization is based on the total micelle content at the specific snapshot. Copolymer chains devoid of B-type beads lose the ability to participate in micelles and are excluded from the count as single chains in the micelle distribution. Across all figures, it is evident that the aggregation number of micelles (N) progressively decreases with simulation time. This decline signifies the gradual loss of copolymer chains from micelles without micelle breaking.
In the case of A30B30 copolymers with stoichiometric mixtures of trigger molecules and the end cap beads (RPT=10-4 and RPB=10-3), Figure 9 illustrates that all chains leaving the micelles consist solely of A-type beads. This is attributed to the faster depolymerization of B-type beads in the B-type block of a copolymer chain due to the higher RPB compared to RPT. Conversely, in the case of single miktoarm copolymers, the chains exiting the micelles are composed of B-type moieties, characterized by a reduced content of B-type beads (Figure 10 and Figure 11). At a bond break fraction of 0.68, the aggregation number of A30B30 copolymer micelles remains substantial. However, in A30(B15)2 and even more so in A30(B10)3 copolymers, the aggregation numbers diminish at similar bond break fraction.
The same trends are observed in the micelles mass distribution for mixtures with a constant concentration of trigger molecules (Figures S3–S5). However, at the same bond break fraction, the aggregation numbers are noticeable smaller. When reaction probabilities for both reactions are equal (RPT=RPB=10-3), micelles and single corroded copolymer chain are in equilibrium, but the aggregation number of micelles is smaller compared to the case with RPT=10-4 and RPB=10-3 at the same constant concentration. Increasing the reaction probability of end cap bonds (RPT=10-2 and RPB=10-3) leads to even smaller aggregation numbers for micelles of all architectures. Nonetheless, A30B30 micelles consistently exhibit higher aggregation numbers than the A30(B15)2 and A30(B10)3 for the same bond break fraction (Figures S6–S8).

3.4. Kinetics of Cargo Release

In this section, the mobility of cargo molecules was investigated through the calculation of their mean squared displacement (MSD) as a function of time. The study utilized 90 cargo molecules residing within a micelle formed by A30B30 copolymers with N=50 for mixtures with RPT=10-4 and RPB=10-3, maintaining a constant concentration of trigger molecules. Results for MSD were averaged across the cargo tracers and are depicted in Figure 12. The exponent α corresponding to the scaling behavior of time was determined to be unity, suggesting normal diffusion in the release of cargo molecules. Notably, even before demicellization occurred in the tracer micelle, a substantial exchange of cargo molecules with different micelles and the solution was observed. Approximately, 18% of tracer molecules left the tracer micelle, while others were inserted, maintaining the number of encapsulation cargo molecules nearly constant. As the micelles underwent depolymerization and corrosion, the number of encapsulated cargo molecules decreased, while the number of molecules released into solution increased. The fraction ratio of released cargo molecules to the initially encapsulated ones in all micelles in the mixture is illustrated as a function of time in Figure 13 and Figure 9S. The observed noise in the curves is a result of released cargo molecules or others from the solution being inserted into other micelles. In general, the cargo release rates mirror the depolymerization rates of copolymers. Specifically, at a constant concentration of trigger molecules and RPT=10-4, RPB=10-3, the release of cargo molecules is faster in linear A30B30 followed by A30(B15)2 and A30(B10)3 miktoarm copolymers. Conversely, for stoichiometric concentration of trigger molecules with the end cap beads, the release of cargo molecules is faster in A30(B10)3 followed by A30(B15)2 and linear A30B30 copolymers. This trend aligns with the decreasing hydrophobic content of B-type beads in micelles due to depolymerization and demicellization allowing fewer hydrophobic cargo molecules to be accommodated. However, the fraction of cargo molecules released to the solution is not directly proportional to the fraction of depolymerized B-type beads. For a 0.60 degradation of hydrophobic beads, the fraction of cargo release is approximately 0.34, 0.39 and 0.43 for A30B30, A30(B15)2 and A30(B10)3, respectively at both stoichiometric and constant concentrations of trigger molecules with RPT=10-4 and RPB=10-3. This is attributed to the existence of micelles with higher N in A30B30 than in the miktoarm copolymer mixtures, allowing them to accommodate a larger number of cargo molecules (Figure 9, Figure 10 and Figure 11).
To quantitatively analyze the release of cargo molecules, the non-linear Korsmeyer-Peppas equation was employed [30,31]:
Μ t Μ ∞ = k t n
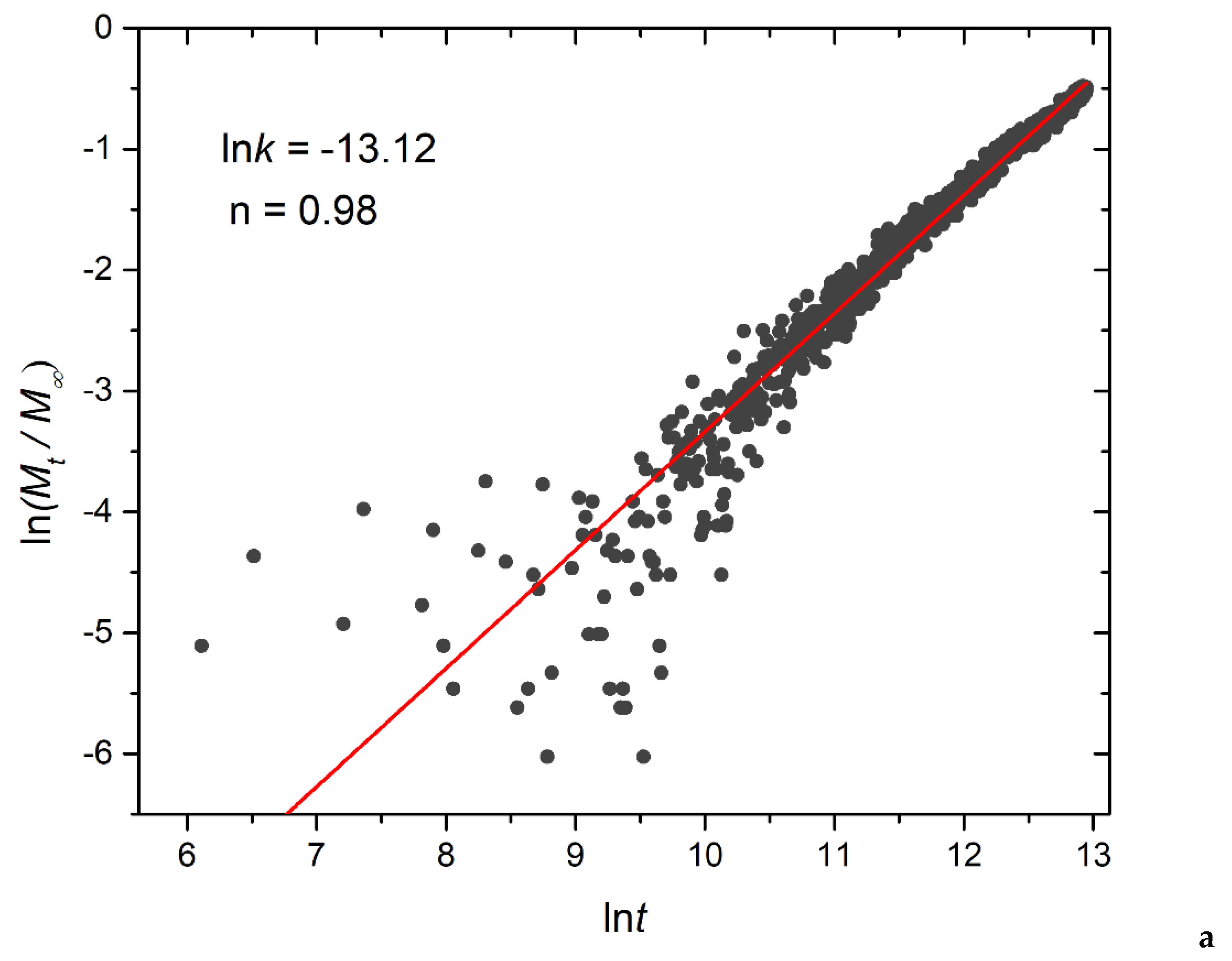
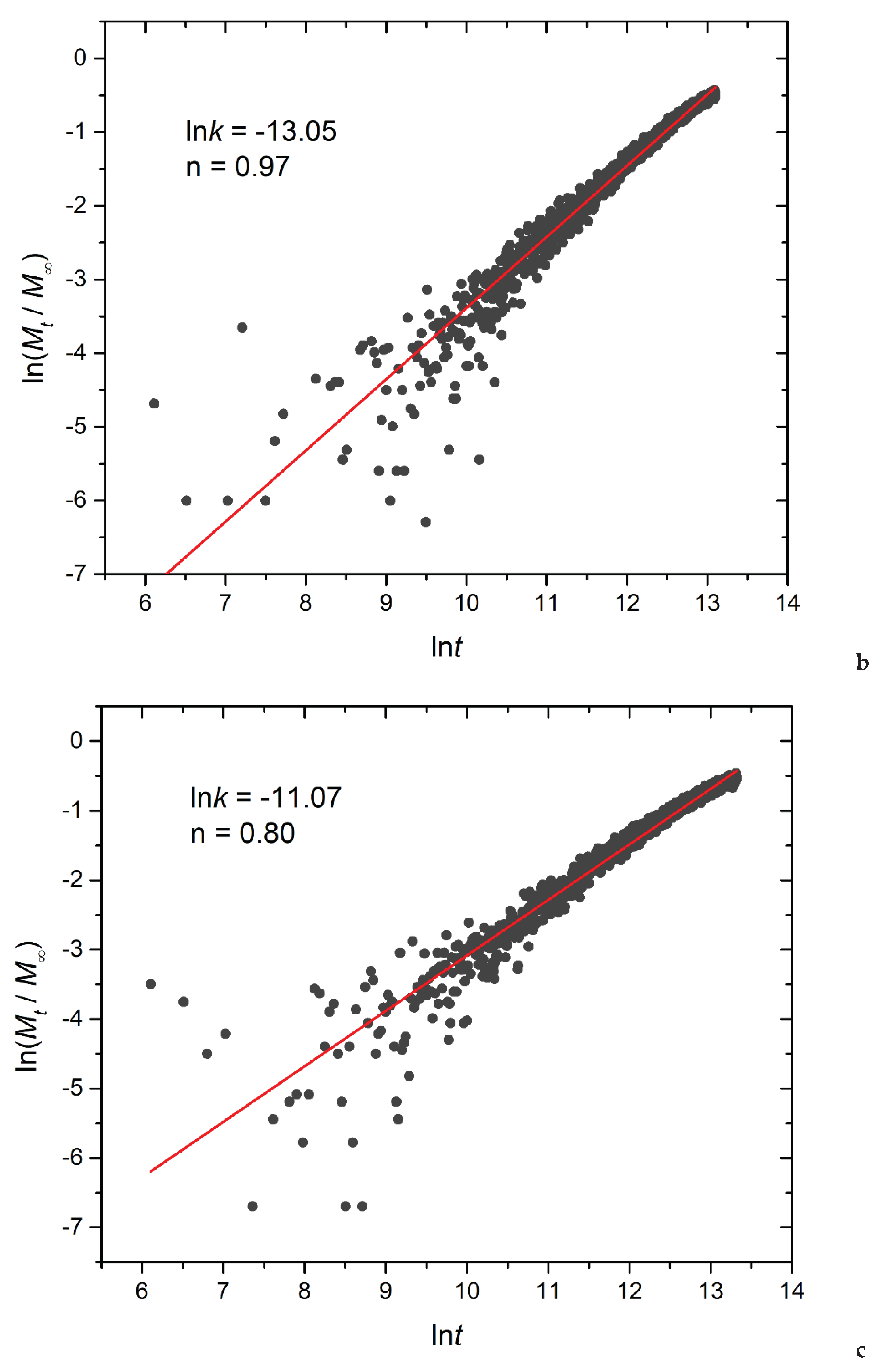
In this equation, Mt/Μ∞ signifies the fraction of released cargo molecules, t denotes the release time, k is the kinetic constant (with dimensions of τ-1), and n is the diffusional exponent for cargo release (dimensionless). The kinetic constant k primarily conveys information about the drug formulation’s characteristics, particularly those related to micelles, whereas n is related to the drug release mechanism. For 0.45<n<1 the release is non-Fickian, and both diffusion and micelle relaxation-corrosion contribute to the release mechanism [31] The analysis focused on the initial 60% of the release curve. Logarithmic plots for constant and stoichiometric trigger molecule concentrations (RPT=10-4 and RPB=10-3) are presented in Figure 14 and Figure S10, respectively. Notably, for constant trigger molecule concentration, n values exhibit a decreasing trend from 0.98 to 0.97 to 0.80 as the number of hydrophobic blocks or branches increases, whereas the constant k values manifest the opposite trend. For stoichiometric mixtures, the variation of n is non-monotonic, with values ranging from 0.77 for A30B30, 0.85 for A30(B15)2, to 0.70 for A30(B10)3, respectively, and similarly for k. Consequently, our findings strongly suggest that the release of cargo from degradable micelles follows a non-Fickian pattern, where both diffusion and corrosion mechanisms contribute to the release process. This observation aligns with the consistent n values obtained in a previous study involving the cationic drug release from four arm starblock copolymers where the release behavior was dominated by chain relaxation-erosion induced by ion exchange that was dependent on pH [32].

4. Conclusions

To elucidate the impact of copolymer architecture on demicellization and cargo release through head-to-tail depolymerization triggered by specific stimuli, we conducted comprehensive molecular dynamics simulations. The depolymerization reaction involved two distinct steps: (a) the rapture of bonds between the hydrophobic end cap and B-type beads, initiated by the presence of T-type molecules with a predefined reaction probability (RPT); (b) depolymerization in the absence of external stimuli, with reaction probability (RPB). Our investigation focused on linear A30B30 and miktoarm star A30(B15)2 and A30(B10)3 copolymers, featuring one, two and three hydrophobic arms (and end caps) respectively. We explored these copolymers under constant and stoichiometric concentrations of trigger molecules relative to end cap beads, examining a range of RPT and RPB values. Our findings revealed that the preferential aggregation number of micelles (Np) was higher for linear copolymers and decreased as the number of arms in miktoarm copolymers increased. Interestingly, copolymer architecture did not impact the loading capacity of micelles (LC). However, for LC=7.6%, loaded micelles exhibited an increase of approximately 16%, 30%, and 35% in Np, and a 9%, 16%, and 16% rise in the radius of gyration for the A30B30, A30(B15)2, and A30(B10)3 copolymers respectively. The rate of depolymerization of hydrophobic beads under stoichiometric T-type molecules concentration was consistently faster in A30(B10)3 followed by A30(B15)2 and A30B30 mixtures. For constant trigger molecule concentrations, the depolymerization rate depended on two opposite factors: the excess of trigger molecules, which increased as the number of hydrophobic branches or blocks decreased, and simultaneous head-to-tail depolymerization, which intensified with an increasing number of branches. Initially, at low break fractions, A30B30 exhibited faster depolymerization, followed by A30(B15)2 and A30(B10)3 mixtures. For higher break fractions, the order is reversed, depending on RPT and RPB values. Generally, cargo release rates mirrored copolymer depolymerization rates. However, the fraction of cargo molecules released was not directly proportional to the fraction of depolymerized B-type beads. For a 0.60 degradation of hydrophobic beads, the fraction of cargo release was approximately 0.34, 0.39 and 0.43 for A30B30, A30(B15)2 and A30(B10)3, respectively, at both stoichiometric and constant trigger molecule concentrations with RPT=10-4 and RPB=10-3. Utilizing the non-linear Korsmeyer-Peppas equation, our results strongly suggest that the release of cargo molecules from degradable micelles follows a non-Fickian pattern, where both diffusion and corrosion mechanisms contribute to the release process. These insights may inform the design of copolymers chains with more triggering groups, proving valuable in the development of delivery vehicles for bio and environmental applications.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org.

Acknowledgments

This work was supported (a) by computational time granted from the Greek Research & Technology Network (GRNET) in the National HPC facility ARIS under project ID pr014023– PISSA_Depolymerization. (b) by project “Dioni: Computing Infrastructure for Big-Data Processing and Analysis” (MIS No. 5047222) co-funded by European Union (ERDF) and Greece through Operational Program “Competitiveness, Entrepreneurship and Innovation”, NSRF 2014-2020.

References

  1. Kulkarni, J.A.; Witzigmann, D.; Thomson, S.B.; Chen, S.; Leavitt, B.R.; Cullis, P.R.; van der Meel, R. The Current Landscape of Nucleic Acid Therapeutics. Nature Nanotechnology. 2021. [CrossRef] [PubMed]
  2. Sinani, G.; Durgun, M.E.; Cevher, E.; Özsoy, Y. Polymeric-Micelle-Based Delivery Systems for Nucleic Acids. Pharmaceutics. 2023. [CrossRef] [PubMed]
  3. Tanbour, R. , M Martins, A., G Pitt, W. and A Husseini, G. Drug Delivery Systems Based on Polymeric Micelles and Ultrasound: A Review. Curr Pharm Des 2016, 22. [Google Scholar] [CrossRef] [PubMed]
  4. Negut, I.; Bita, B. Polymeric Micellar Systems—A Special Emphasis on “Smart” Drug Delivery. Pharmaceutics. 2023. [CrossRef] [PubMed]
  5. Li, Z.; Liu, M.; Ke, L.; Wang, L.J.; Wu, C.; Li, C.; Li, Z.; Wu, Y.L. Flexible Polymeric Nanosized Micelles for Ophthalmic Drug Delivery: Research Progress in the Last Three Years. Nanoscale Advances. 2021. [CrossRef] [PubMed]
  6. Sun, C.; Lu, J.; Wang, J.; Hao, P.; Li, C.; Qi, L.; Yang, L.; He, B.; Zhong, Z.; Hao, N. Redox-Sensitive Polymeric Micelles with Aggregation-Induced Emission for Bioimaging and Delivery of Anticancer Drugs. J Nanobiotechnology 2021, 19. [Google Scholar] [CrossRef]
  7. Gioldasis, C.; Gergidis, L.N.; Vlahos, C. Micellization through Complexation of Oppositely Charged Diblock Copolymers: Effects of Composition, Polymer Architecture, Salt of Different Valency, and Thermoresponsive Block. Journal of Polymer Science 2021, 59, 191–204. [Google Scholar] [CrossRef]
  8. Suek, N.W.; Lamm, M.H. Computer Simulation of Architectural and Molecular Weight Effects on the Assembly of Amphiphilic Linear-Dendritic Block Copolymers in Solution. Langmuir 2008, 24, 3030–3036. [Google Scholar] [CrossRef]
  9. Ding, Y.; Zhao, Q.; Wang, L.; Huang, L.; Liu, Q.; Lu, X.; Cai, Y. Polymerization-Induced Self-Assembly Promoted by Liquid-Liquid Phase Separation. ACS Macro Lett 2019, 8. [Google Scholar] [CrossRef]
  10. György, C.; Armes, S.P. Recent Advances in Polymerization-Induced Self-Assembly (PISA) Syntheses in Non-Polar Media. Angewandte Chemie - International Edition. 2023. [CrossRef]
  11. Kim, J.H.; Li, Y.; Kim, M.S.; Kang, S.W.; Jeong, J.H.; Lee, D.S. Synthesis and Evaluation of Biotin-Conjugated PH-Responsive Polymeric Micelles as Drug Carriers. Int J Pharm 2012, 427. [Google Scholar] [CrossRef]
  12. Yadav, S.; Ramesh, K.; Reddy, O.S.; Karthika, V.; Kumar, P.; Jo, S.H.; Yoo, S.I. I.; Park, S.H.; Lim, K.T. Redox-Responsive Comparison of Diselenide and Disulfide Core-Cross-Linked Micelles for Drug Delivery Application. Pharmaceutics 2023, 15. [Google Scholar] [CrossRef]
  13. Alvarez-Lorenzo, C.; Bromberg, L.; Concheiro, A. Light-Sensitive Intelligent Drug Delivery Systems. Photochemistry and Photobiology. 2009. [CrossRef] [PubMed]
  14. Park, J.; Jo, S.; Lee, Y.M.; Saravanakumar, G.; Lee, J.; Park, D.; Kim, W.J. Enzyme-Triggered Disassembly of Polymeric Micelles by Controlled Depolymerization via Cascade Cyclization for Anticancer Drug Delivery. ACS Appl Mater Interfaces 2021, 13. [Google Scholar] [CrossRef] [PubMed]
  15. Sirianni, Q.E. A.; Liang, X.; Such, G.K.; Gillies, E.R. Polyglyoxylamides with a PH-Mediated Solubility and Depolymerization Switch. Macromolecules 2021, 54. [Google Scholar] [CrossRef]
  16. Liu, G.; Wang, X.; Hu, J.; Zhang, G.; Liu, S. Self-Immolative Polymersomes for High-Efficiency Triggered Release and Programmed Enzymatic Reactions. J Am Chem Soc 2014, 136. [Google Scholar] [CrossRef] [PubMed]
  17. Kim, J.W.; Kim, H.J.; Park, J.; Chae, J.A.; Song, H.W.; Choi, E.; Kim, H. Self-Immolative and Amphiphilic Poly(Benzyl Ether)-Based Copolymers: Synthesis and Triggered Demicellization via Head-to-Tail Depolymerization. Macromolecules 2022, 55. [Google Scholar] [CrossRef]
  18. Miliou, K.; Gergidis, L.N.; Vlahos, C. Polyelectrolyte Micelles in Salt-Free Solutions: Micelle Size and Electrostatic Potential. J Polym Sci B Polym Phys 2018, 56, 924–934. [Google Scholar] [CrossRef]
  19. Murat, M.; Grest, G.S. Molecular Dynamics Study of Dendrimer Molecules in Solvents of Varying Quality. Macromolecules 1996, 29, 1278–1285. [Google Scholar] [CrossRef]
  20. Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J Comput Phys 1995, 117, 1–19. [Google Scholar] [CrossRef]
  21. Stillinger, F.H. Rigorous Basis of the Frenkel-Band Theory of Association Equilibrium. J Chem Phys 1963, 38. [Google Scholar] [CrossRef]
  22. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. Journal of Machine Learning Research 2011, 12. [Google Scholar]
  23. Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat Methods 2020, 17. [Google Scholar] [CrossRef] [PubMed]
  24. Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function Using NetworkX. In 7th Python in Science Conference (SciPy 2008); 2008.
  25. Cheng, L.; Cao, D. Effect of Tail Architecture on Self-Assembly of Amphiphiles for Polymeric Micelles. Langmuir 2009, 25, 2749–2756. [Google Scholar] [CrossRef] [PubMed]
  26. Nagarajan, R. Molecular Theory for Mixed Micelles. Langmuir 1985, 1. [Google Scholar] [CrossRef]
  27. Georgiadis, C.; Moultos, O.; Gergidis, L.N.; Vlahos, C. Brownian Dynamics Simulations on the Self-Assembly Behavior of AB Hybrid Dendritic-Star Copolymers. Langmuir 2011, 27, 835–842. [Google Scholar] [CrossRef] [PubMed]
  28. Hwang, D.; Ramsey, J.D.; Kabanov, A.V. Polymeric Micelles for the Delivery of Poorly Soluble Drugs: From Nanoformulation to Clinical Approval. Advanced Drug Delivery Reviews. 2020. [CrossRef]
  29. Theodorou, D.N.; Suter, U.W. Shape of Unperturbed Linear Polymers: Polypropylene. Macromolecules 1985, 18, 1206–1214. [Google Scholar] [CrossRef]
  30. Peppas, N.A.; Sahlin, J.J. A Simple Equation for the Description of Solute Release. III. Coupling of Diffusion and Relaxation. Int J Pharm 1989, 57. [Google Scholar] [CrossRef]
  31. Ritger, P.L.; Peppas, N.A. A Simple Equation for Description of Solute Release II. Fickian and Anomalous Release from Swellable Devices. Journal of Controlled Release 1987, 5. [Google Scholar] [CrossRef]
  32. He, E.; Yue, C.Y.; Tam, K.C. Binding and Release Studies of a Cationic Drug from a Star-Shaped Four-Arm Poly(Ethylene Oxide)-b-Poly(Methacrylic Acid). J Pharm Sci 2010, 99, 782–793. [Google Scholar] [CrossRef]
Preprints 101746 g001
Figure 1. Cartoon representation of (a) linear diblock copolymer A6B6 (b) miktoarm star copolymer A6(B3)2 (c) miktoarm star copolymer A6(B2)3 with one, two and three end cap beads (orange). T-type trigger (purple) and cargo (green) C2 molecules are also presented.
Figure 1. Cartoon representation of (a) linear diblock copolymer A6B6 (b) miktoarm star copolymer A6(B3)2 (c) miktoarm star copolymer A6(B2)3 with one, two and three end cap beads (orange). T-type trigger (purple) and cargo (green) C2 molecules are also presented.
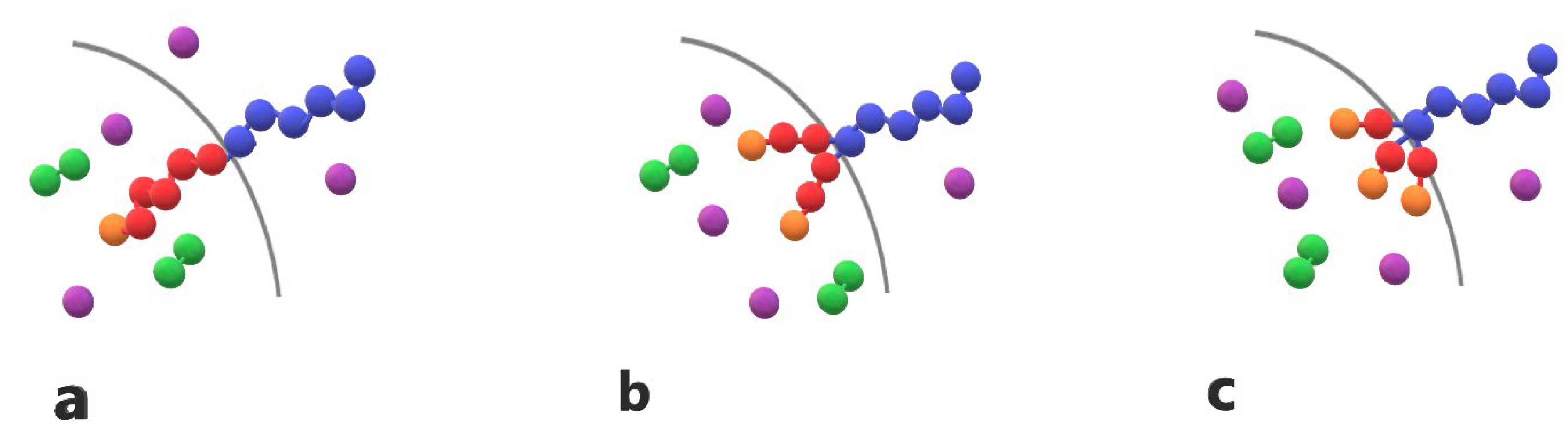
Preprints 101746 g001
Preprints 101746 g002
Figure 2. Cartoon representation of depolymerization algorithm (a) the breaking of bond between end cap (orange) and B-type bead (red) triggered by T-type molecule (purple) (b) the head-to-tail breaking of bond between two B-type beads (red) without stimuli.
Figure 2. Cartoon representation of depolymerization algorithm (a) the breaking of bond between end cap (orange) and B-type bead (red) triggered by T-type molecule (purple) (b) the head-to-tail breaking of bond between two B-type beads (red) without stimuli.
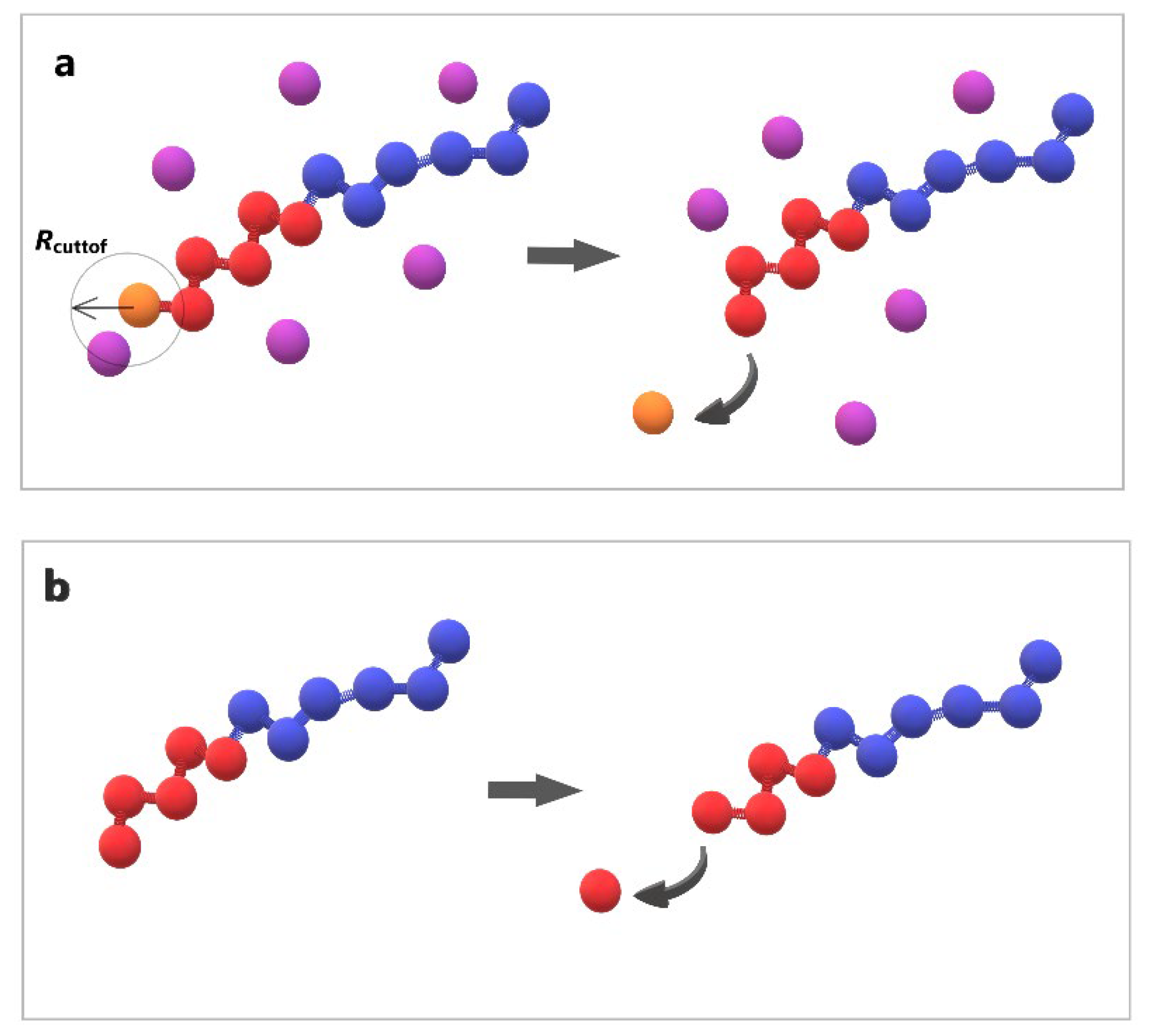
Preprints 101746 g002
Preprints 101746 g003
Figure 3. Mass distribution of micelles as a function of the aggregation number N formed by (a) A30B30, (b) A30(B15)2, and (c) A30(B10)3 copolymers. ibid for mixtures: (d) A30B30 + C3, (e) A30(B15)2 + C3 and (f) A30(B10)3 + C3. In all simulations, [Φ]=0.12.
Figure 3. Mass distribution of micelles as a function of the aggregation number N formed by (a) A30B30, (b) A30(B15)2, and (c) A30(B10)3 copolymers. ibid for mixtures: (d) A30B30 + C3, (e) A30(B15)2 + C3 and (f) A30(B10)3 + C3. In all simulations, [Φ]=0.12.
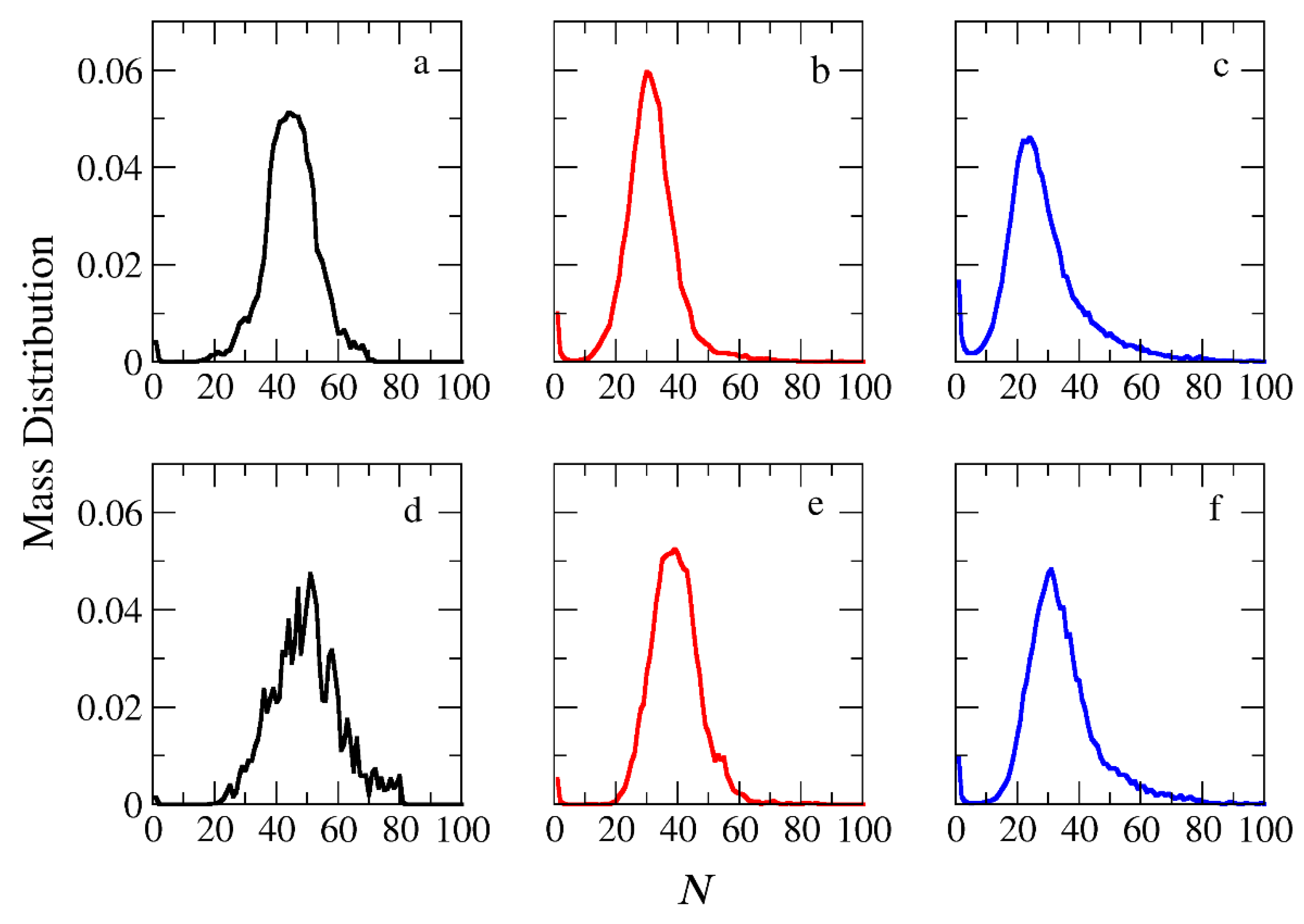
Preprints 101746 g003
Preprints 101746 g004
Figure 4. The mean squared radius of gyration a) for ‘empty’ micelles formed by A30B30, A30(B15)2, and A30(B10)3 copolymers and b) for micelles formed by mixtures with 2000 C3 cargo molecules, plotted against N. Standard deviation is indicated by the error bars.
Figure 4. The mean squared radius of gyration a) for ‘empty’ micelles formed by A30B30, A30(B15)2, and A30(B10)3 copolymers and b) for micelles formed by mixtures with 2000 C3 cargo molecules, plotted against N. Standard deviation is indicated by the error bars.
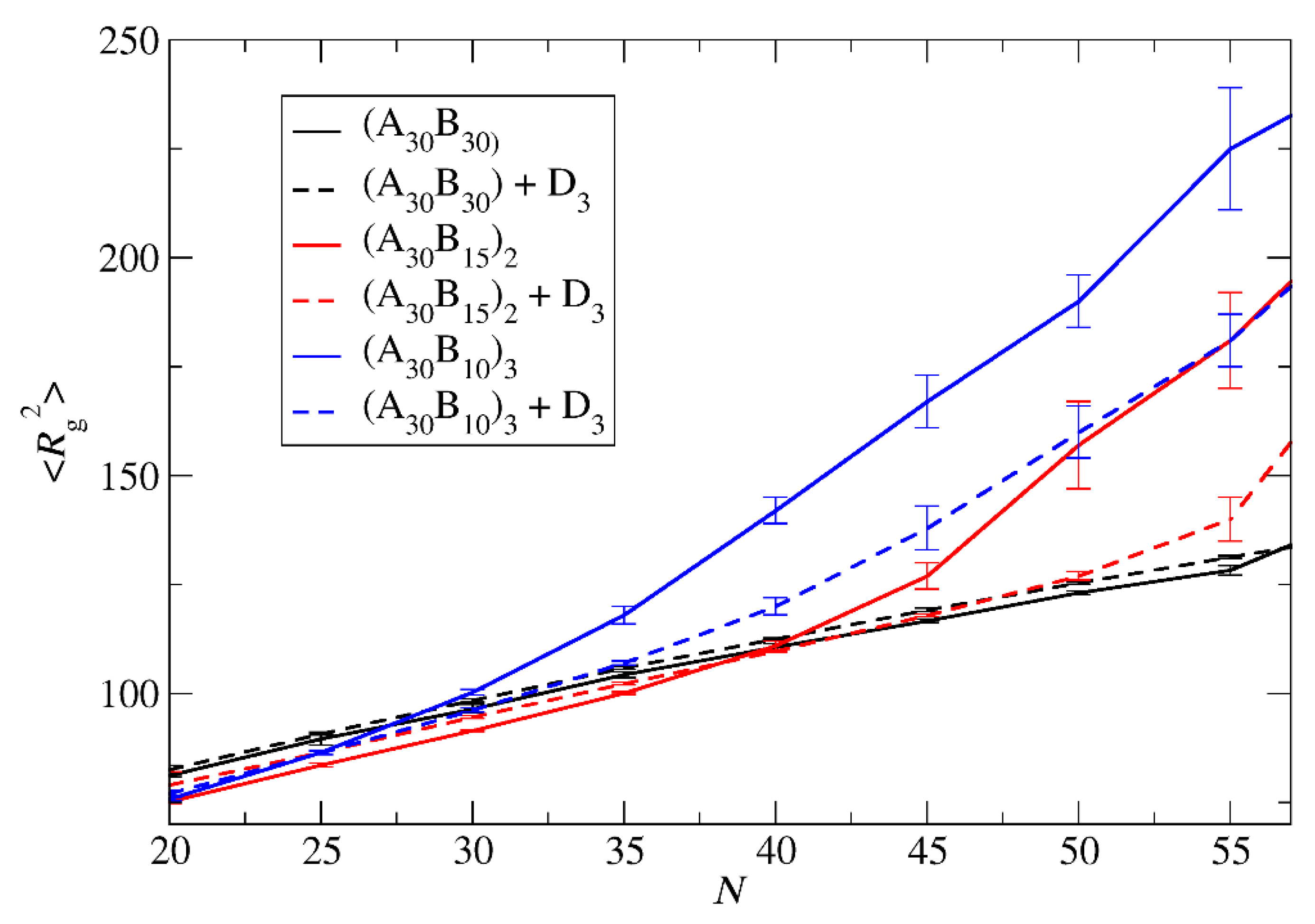
Preprints 101746 g004
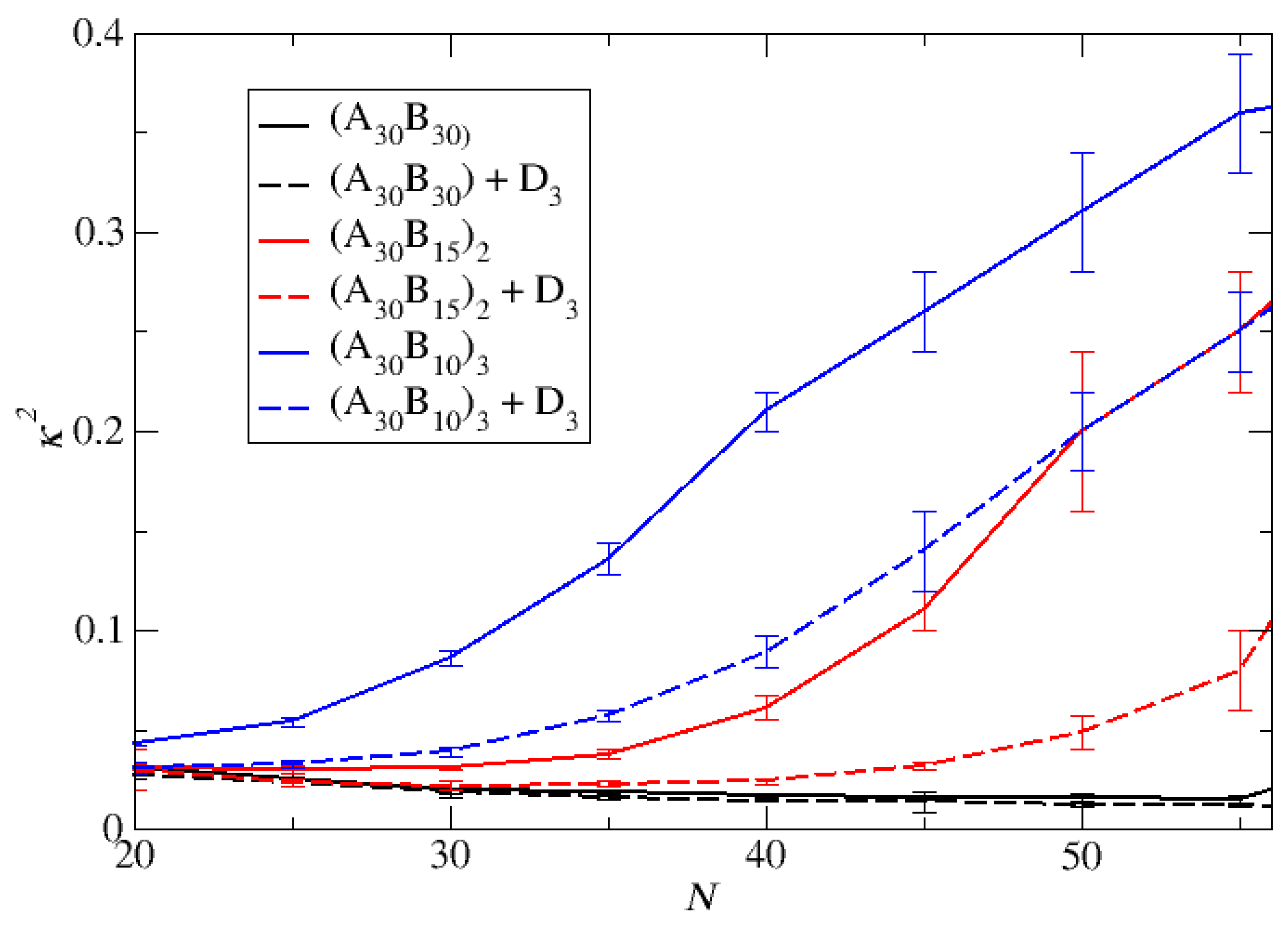
Preprints 101746 g005
Figure 5. The mean shape anisotropy parameter κ2 a) for ‘empty’ micelles formed by A30B30, A30(B15)2, and A30(B10)3 copolymers and b) for micelles formed by mixtures with 2000 C3 cargo molecules, plotted against N. Standard deviation is indicated by the error bars.
Figure 5. The mean shape anisotropy parameter κ2 a) for ‘empty’ micelles formed by A30B30, A30(B15)2, and A30(B10)3 copolymers and b) for micelles formed by mixtures with 2000 C3 cargo molecules, plotted against N. Standard deviation is indicated by the error bars.
Preprints 101746 g005
Preprints 101746 g006
Figure 6. Depolymerization fraction of end cap beads of A30B30, A30(B15)2, and A30(B10)3 copolymers as a function of time for a) stoichiometric trigger molecules concentration, b) constant trigger molecules concentration. RPT=10-4, RPB=10-3. [ec]0 is the initial end cap beads concentration, [ec]t is the end cap concentration.
Figure 6. Depolymerization fraction of end cap beads of A30B30, A30(B15)2, and A30(B10)3 copolymers as a function of time for a) stoichiometric trigger molecules concentration, b) constant trigger molecules concentration. RPT=10-4, RPB=10-3. [ec]0 is the initial end cap beads concentration, [ec]t is the end cap concentration.
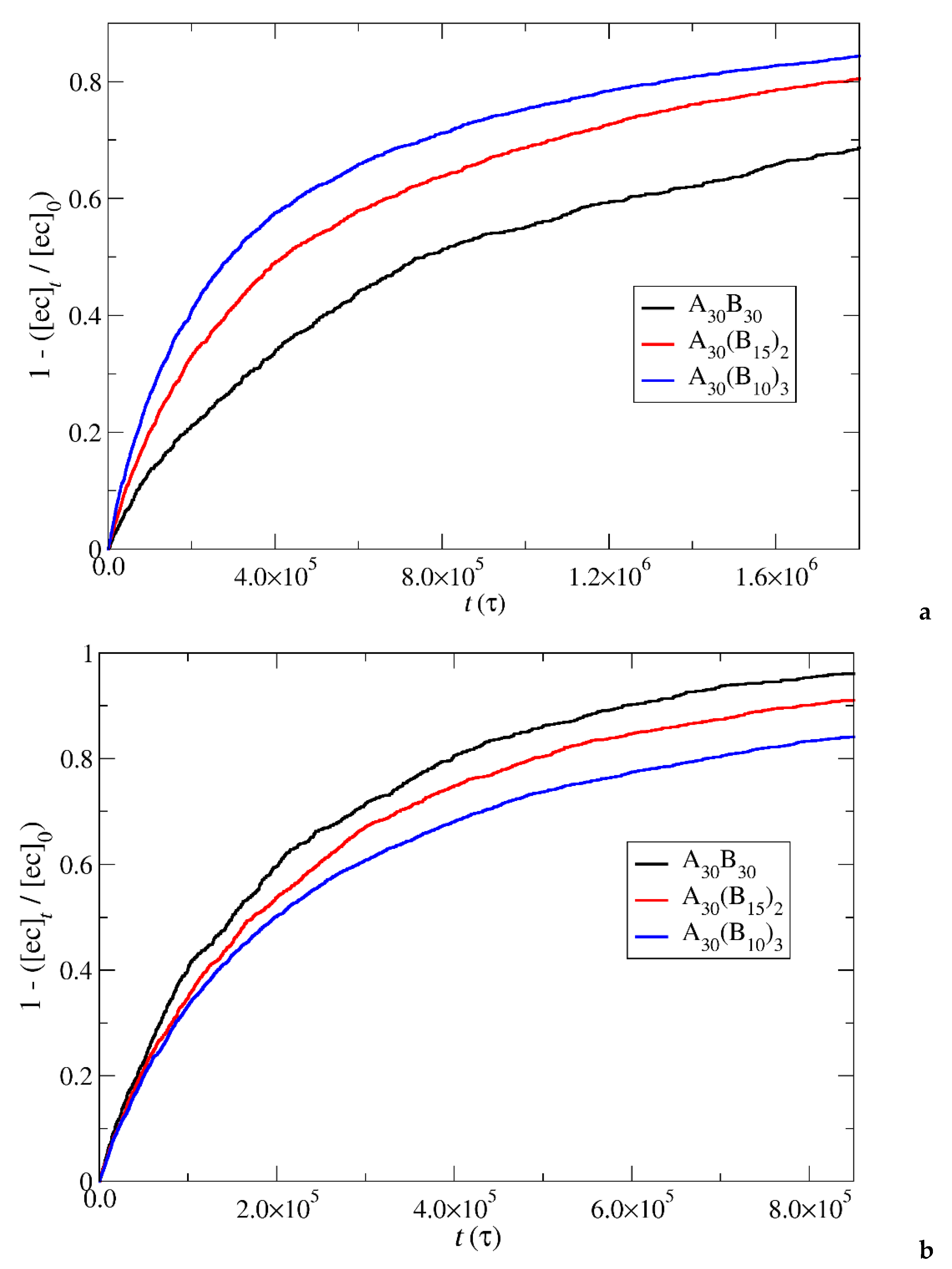
Preprints 101746 g006
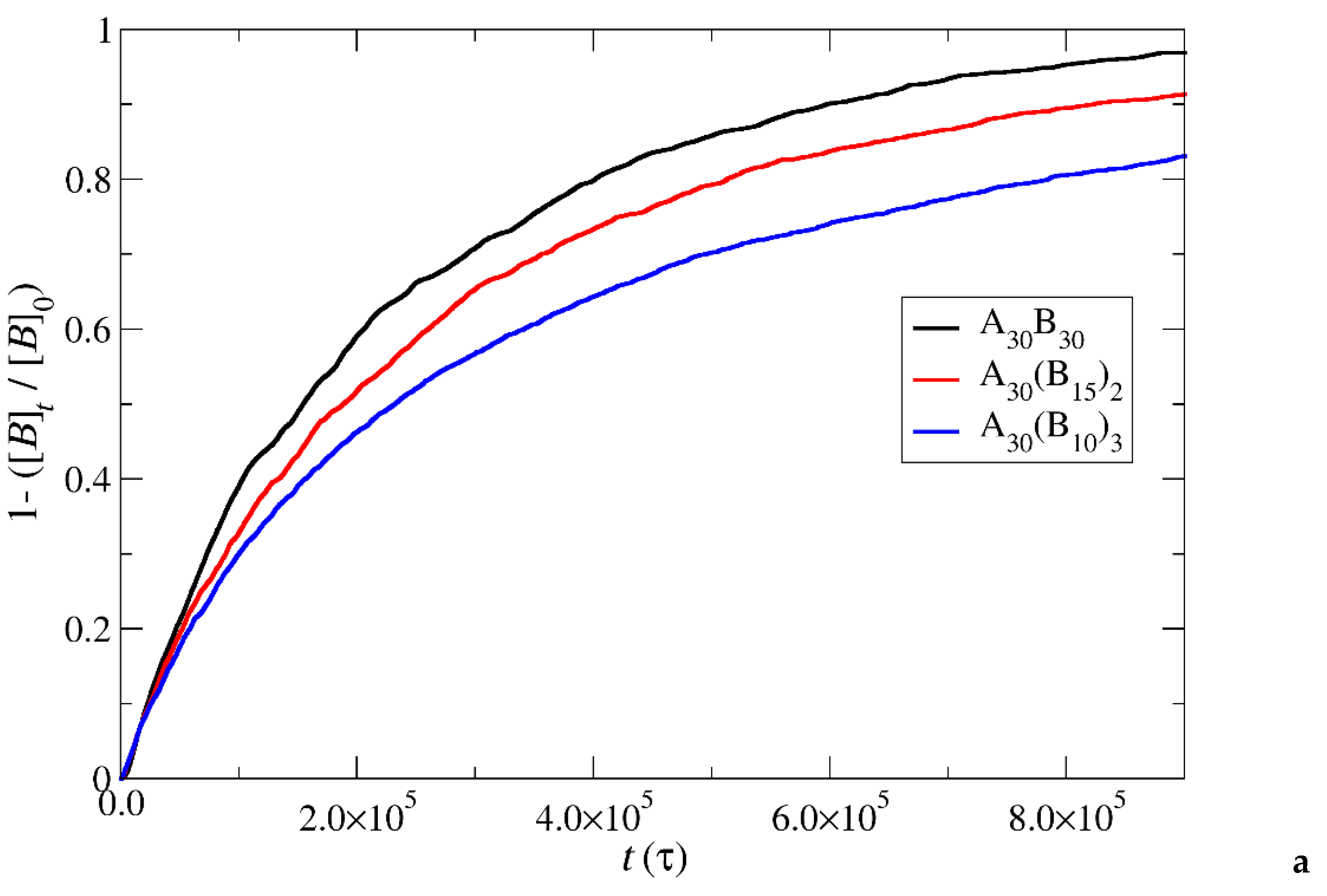
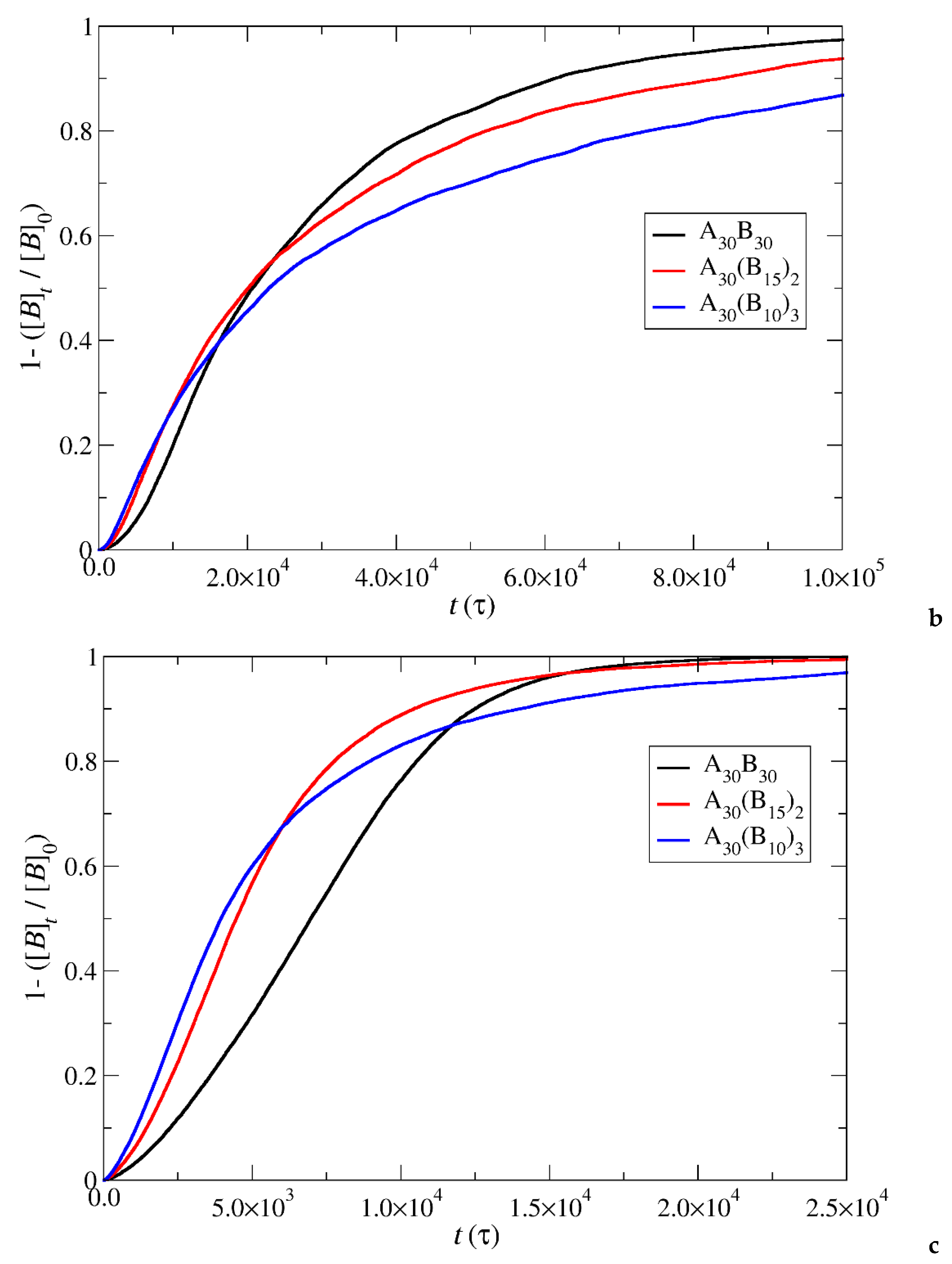
Preprints 101746 g007aPreprints 101746 g007b
Figure 7. Depolymerization fraction of all hydrophobic beads of A30B30, A30(B15)2, and A30(B10)3 copolymers plotted against time for constant trigger molecule concentration: a) RPT=10-4, RPB=10-3, b) RPT=10-2, RPB=10-3 and c) RPT=10-3, RPB=10-3. [B]0 is the initial hydrophobic beads concentration, [B]t is the hydrophobic beads concentration.
Figure 7. Depolymerization fraction of all hydrophobic beads of A30B30, A30(B15)2, and A30(B10)3 copolymers plotted against time for constant trigger molecule concentration: a) RPT=10-4, RPB=10-3, b) RPT=10-2, RPB=10-3 and c) RPT=10-3, RPB=10-3. [B]0 is the initial hydrophobic beads concentration, [B]t is the hydrophobic beads concentration.
Preprints 101746 g007aPreprints 101746 g007b
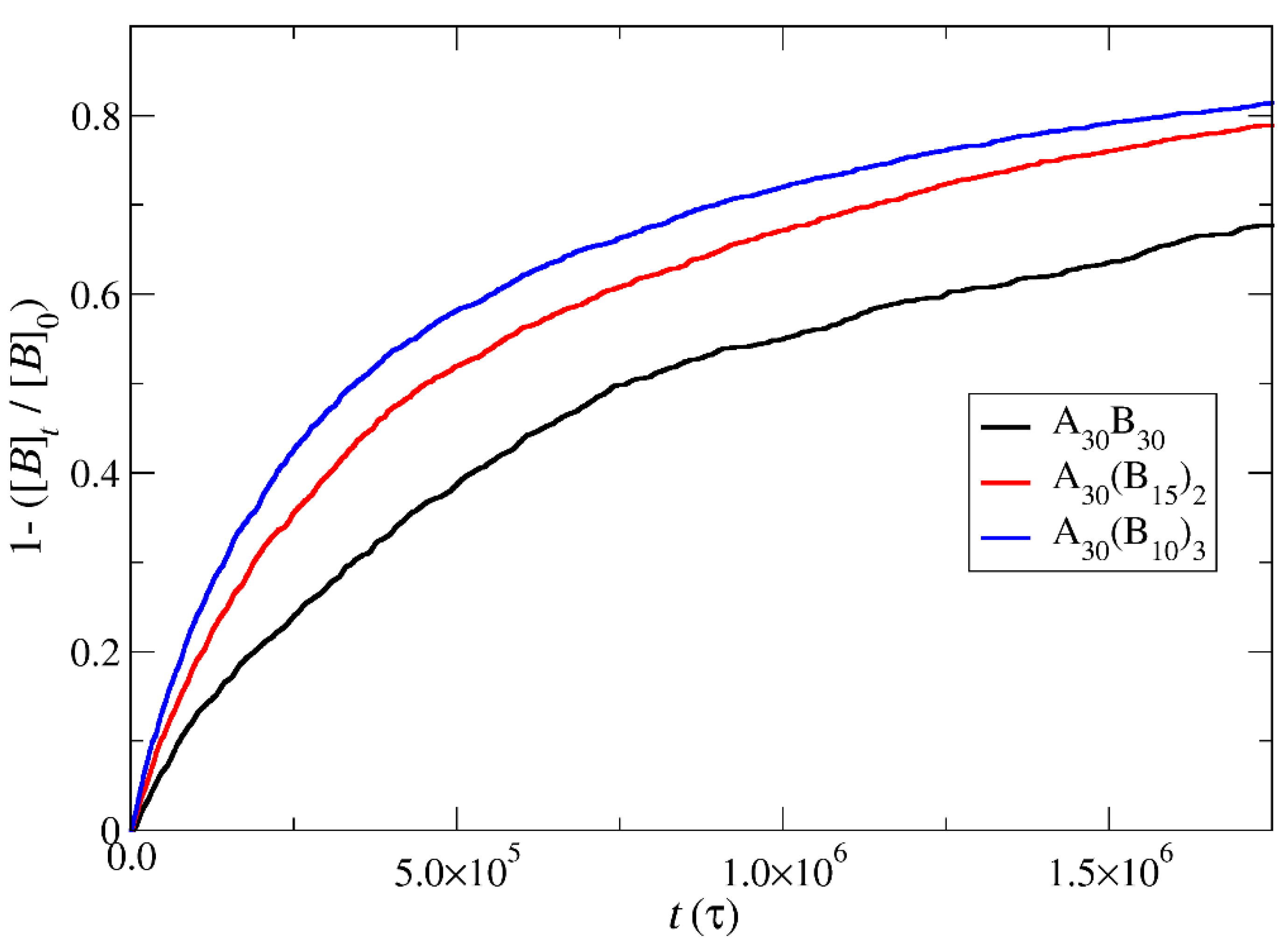
Preprints 101746 g008
Figure 8. Depolymerization fraction of all hydrophobic beads of A30B30, A30(B15)2, and A30(B10)3 copolymers plotted against time for stoichiometric trigger molecules concentration. RPT=10-4, RPB=10-3. [B]0 is the initial hydrophobic beads concentration, [B]t is the hydrophobic beads concentration.
Figure 8. Depolymerization fraction of all hydrophobic beads of A30B30, A30(B15)2, and A30(B10)3 copolymers plotted against time for stoichiometric trigger molecules concentration. RPT=10-4, RPB=10-3. [B]0 is the initial hydrophobic beads concentration, [B]t is the hydrophobic beads concentration.
Preprints 101746 g008
Preprints 101746 g009
Figure 9. Mass distribution of micelles formed by linear A30B30 copolymers across various time points and depolymerization fractions of all hydrophobic beads: a) t=0, 0, b) t=135000τ, 0.15, c) t=360000τ, 0.31, d) t=630000τ, 0.45, e) t= 1260000τ, 0.60, f) t= 1800000τ, 0.68. The trigger molecule concentration is maintained stoichiometric to end cap beads in all cases. RPT=10-4 and RPB=10-3.
Figure 9. Mass distribution of micelles formed by linear A30B30 copolymers across various time points and depolymerization fractions of all hydrophobic beads: a) t=0, 0, b) t=135000τ, 0.15, c) t=360000τ, 0.31, d) t=630000τ, 0.45, e) t= 1260000τ, 0.60, f) t= 1800000τ, 0.68. The trigger molecule concentration is maintained stoichiometric to end cap beads in all cases. RPT=10-4 and RPB=10-3.
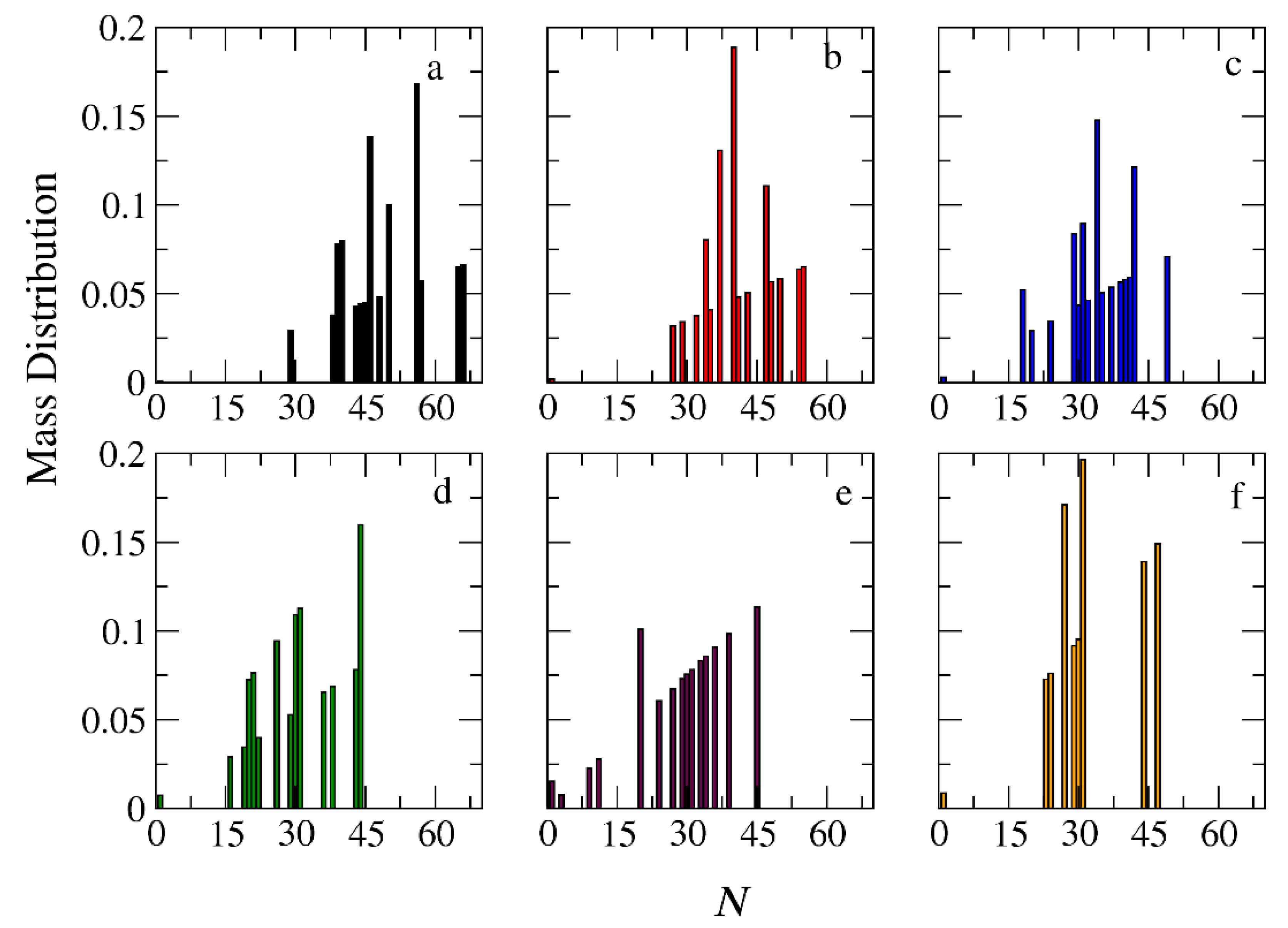
Preprints 101746 g009
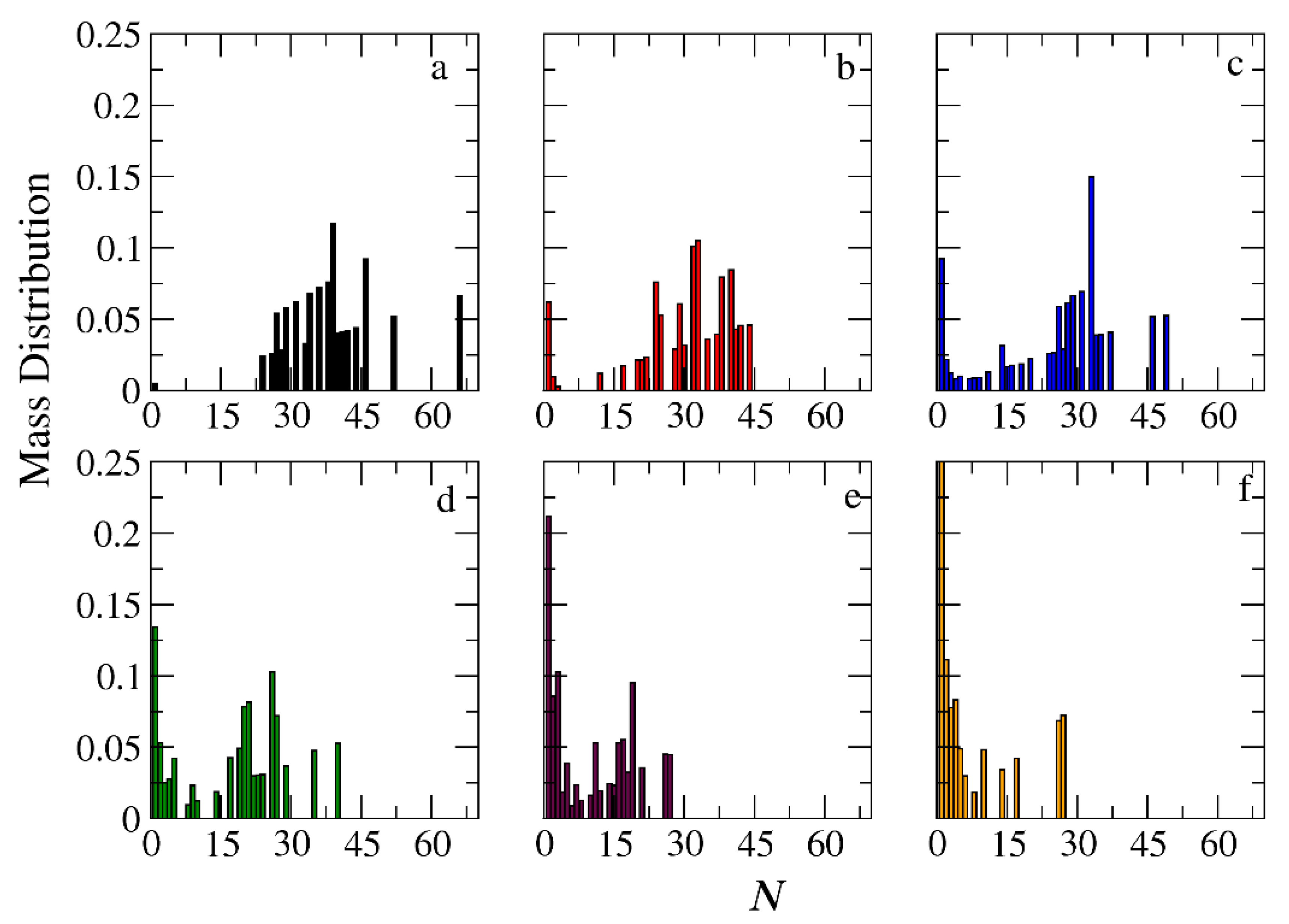
Preprints 101746 g010
Figure 10. Mass distribution of micelles formed by miktoarm A30(B15)2 copolymers across various time points and depolymerization fractions of all hydrophobic beads: a) t=0, 0, b) t=90000τ, 0.17, c) t=180000τ, 0.29, d) t=360000τ, 0.44, e) t= 720000τ, 0.60, f) t= 1440000τ, 0.75. The trigger molecule concentration is maintained stoichiometric to end cap beads in all cases. RPT=10-4 and RPB=10-3.
Figure 10. Mass distribution of micelles formed by miktoarm A30(B15)2 copolymers across various time points and depolymerization fractions of all hydrophobic beads: a) t=0, 0, b) t=90000τ, 0.17, c) t=180000τ, 0.29, d) t=360000τ, 0.44, e) t= 720000τ, 0.60, f) t= 1440000τ, 0.75. The trigger molecule concentration is maintained stoichiometric to end cap beads in all cases. RPT=10-4 and RPB=10-3.
Preprints 101746 g010
Preprints 101746 g011
Figure 11. Mass distribution of micelles formed by miktoarm A30(B10)3 copolymers across various time points and depolymerization fractions of all hydrophobic beads: a) t=0, 0, b) t=45000τ, 0.13, c) t=135000τ, 0.29, d) t=270000τ, 0.44, e) t= 540000τ, 0.59, f) t= 1170000τ, 0.75. The trigger molecule concentration is maintained stoichiometric to end cap beads in all cases. RPT=10-4 and RPB=10-3.
Figure 11. Mass distribution of micelles formed by miktoarm A30(B10)3 copolymers across various time points and depolymerization fractions of all hydrophobic beads: a) t=0, 0, b) t=45000τ, 0.13, c) t=135000τ, 0.29, d) t=270000τ, 0.44, e) t= 540000τ, 0.59, f) t= 1170000τ, 0.75. The trigger molecule concentration is maintained stoichiometric to end cap beads in all cases. RPT=10-4 and RPB=10-3.
Preprints 101746 g011
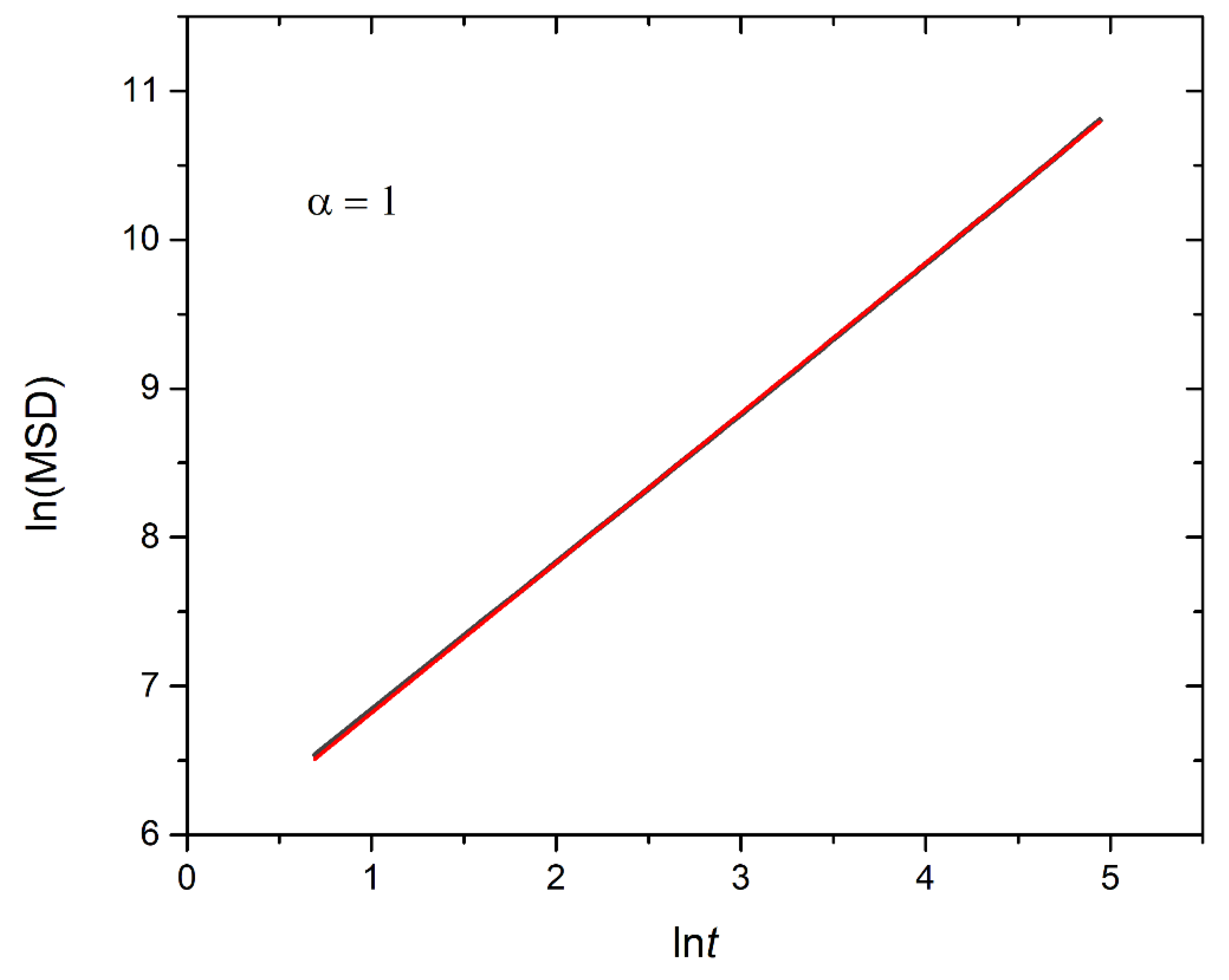
Preprints 101746 g012
Figure 12. Logarithmic plot illustrating the mean squared displacement calculated from 90 cargo molecules within an A30B30 micelle with N=50, against time for stoichiometric trigger molecule concentration with end cap beads and RPT=10-4 and RPB=10-3. The exponent α corresponds to the scaling behavior of t.
Figure 12. Logarithmic plot illustrating the mean squared displacement calculated from 90 cargo molecules within an A30B30 micelle with N=50, against time for stoichiometric trigger molecule concentration with end cap beads and RPT=10-4 and RPB=10-3. The exponent α corresponds to the scaling behavior of t.
Preprints 101746 g012
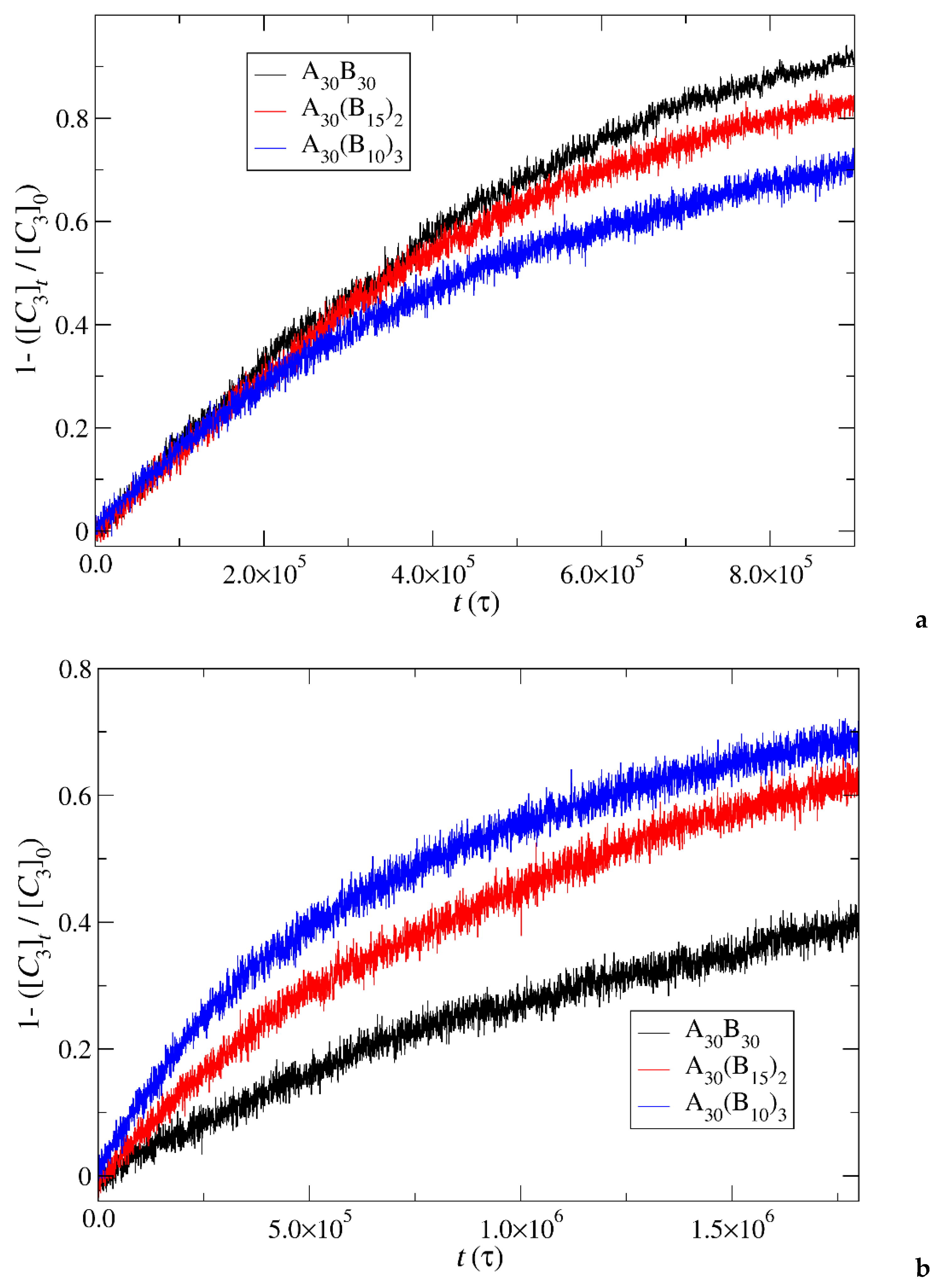
Preprints 101746 g013
Figure 13. Cargo molecules release fraction from A30B30, A30(B15)2, and A30(B10)3 copolymer mixtures plotted against time for a) constant trigger molecule concentration, and b) stoichiometric trigger molecule concentration with end cap beads. RPT=10-4 and RPB=10-3. [C3]0 is the initial cargo molecules concentration, [C3]t is the cargo molecules concentration.
Figure 13. Cargo molecules release fraction from A30B30, A30(B15)2, and A30(B10)3 copolymer mixtures plotted against time for a) constant trigger molecule concentration, and b) stoichiometric trigger molecule concentration with end cap beads. RPT=10-4 and RPB=10-3. [C3]0 is the initial cargo molecules concentration, [C3]t is the cargo molecules concentration.
Preprints 101746 g013
Preprints 101746 g014aPreprints 101746 g014b
Figure 14. Logarithmic plot depicting the fraction of released cargo molecules against time for a) linear A30B30, b) miktoarm A30(B15)2, and c) miktoarm A30(B10)3 copolymers. Fitting lines, k and n correspond to the Korsmeyer-Peppas equation. Trigger molecule concentration is maintained constant in all cases. RPT=10-4 and RPB=10-3.
Figure 14. Logarithmic plot depicting the fraction of released cargo molecules against time for a) linear A30B30, b) miktoarm A30(B15)2, and c) miktoarm A30(B10)3 copolymers. Fitting lines, k and n correspond to the Korsmeyer-Peppas equation. Trigger molecule concentration is maintained constant in all cases. RPT=10-4 and RPB=10-3.
Preprints 101746 g014aPreprints 101746 g014b
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated