Preprint
Article
The κ-Model under Test of the Sparc Database
Altmetrics
Downloads
82
Views
21
Comments
0
A peer-reviewed article of this preprint also exists.
This version is not peer-reviewed
Submitted:
16 March 2024
Posted:
21 March 2024
You are already at the latest version
Alerts
Abstract
Our main goal is here to make a comparative analysis between the well-known MOND theory and a more recent model called κ-model. An additional connection, between the κ-model and two other novel MOND-type theories: Newtonian Fractional-Dimension Gravity (NFDG) and Refracted Gravity (RG), is likewise presented. All these models are built to overtake the DM paradigm, or at least to strongly reduce the dark matter content. Whereas they rely on different formalisms, however, all four seem to suggest that the universal parameter, a0, appearing in MOND theory could intrinsically be correlated to either the sole baryonic mean mass density (RG and κ-model) and/or to the dimension of the object under consideration (NFDG and κ-model). We could then confer to the parameter a0 a more flexible status of multiscale parameter, as required to explain the dynamics together in galaxies and in galaxy clusters. Eventually, the conformal gravity theory (CFT) also seems to have some remote link with the κ-model, even though the first one is an extension of general relativity, and the second one is Newtonian in essence. The κ-model has been tested on a small sample of spiral galaxies and in galaxy clusters. Now we test this model on a large sample of galaxies issued from the SPARC database.
Keywords:
Subject: Physical Sciences - Astronomy and Astrophysics
1. Introduction
As it is well known, all the studies conducted on galaxies and galaxy clusters, lead to the seemingly firm conclusion that a significant portion of the mass in the Universe seems to be hidden from the view of the observers. This invisible (non-baryonic) matter is called dark matter (DM). It is true that DM is the more simple and economic hypothesis. However, the major problem with this paradigm is that the dark matter/baryonic (DM/B) mass ratio is incredibly huge, of the order of 6. It is not simply an addition of a small quantity of missing matter to a dominant form of visible (baryonic) matter. This is even the opposite, and the baryonic component eventually appears negligible in the Universe. This situation seems to be surprising and even rather unconfortable, the visible sector being explained by an undefined invisible sector about which we know nothing. De facto the explanation of the flatness of the rotation spiral galaxy curves with DM is fully indirect. A very pertinent parallel can be drawn with the phlogistic theory, a dominant theory in nascent chemistry during the 18th century. The phlogistic hypothesis was based on the existence of an illusive "substance" (the phlogiston) with indeterminate properties and thus without real physical support. The theory of phlogiston was finally disproved by the French chemist Antoine-Laurent Lavoisier through a series of experiments in the late eighteenth century. Is it the fate that awaits DM? At the present time the existence of DM is inferred only through gravitational effects. A direct proof is missing from both an observational and an experimental point of view.
The MACHOs (Massive Compact Halo Objects), possibly detected through gravitational microlensing in the Galactic halo, have been ruled out as a dark matter candidate [1]. Another interesting interrogation is that if DM particles are really existing, these particles can very possibly decay. Strangely enough, X-ray space telescopes like Chandra, XMM-Newton, and Fermi have not observed any excess of DM decay [2]. Eventually a major trouble for DM is the tantamount difficulties observing the DM particles in the laboratory. Large classes of candidates have been suggested following highly speculative theoretical models, such as Hidden-Sector Dark Matter particles, completely neutral under Standard Model forces, but interacting through a new force; or still Ultra-Light Dark Matter particles with predicted masses from 10-22 eV to about a keV, and that can be produced during inflation or phase transitions in the very early Universe [3]. However the existing dark matter experimental programs are now more reasonably focused on weakly-interacting massive particles (WIMPs) [4–6]. Unfortunately the conclusions of all these very costly studies are always negative. All direct detections have come up empty. The persisting non-detection in space and in the laboratory of DM in spite of very intense efforts is rather discouraging. A simple, but very frustating, conclusion would be that if DM interacts uniquely gravitationally with baryonic matter and definitely not through one of the other known three forces (the strong, weak or electromagnetic forces), we might never detect it. Another possibility is that DM interacts with itself and with baryonic matter but via an unknown (fifth) force. In spite of all of that, DM remains the leading explanation for the dynamics of galaxies, very likely for its high flexibility adaptable to various situations (galaxies, galaxy clusters and cosmology). This view can unfortunately persist for a very long time because the DM paradigm seems to be unfalsifiable. Yet a good question put by McGaugh [7] is however: Is it a missing mass problem or rather an acceleration-velocity discrepancy when observing the galaxies? Indeed the mass is an indirect data contrarily to the acceleration which can be directly measured. Di Paolo and coauthors [8] have remarked that there exists a mysterious link between DM and the baryonic component. In fact this link is easily explained if DM is a property of the baryonic mass itself.
Alternatively a lot of authors have tried to circumvent the trouble by exploring other paths than DM. Without DM it is true that the Newtonian theory of gravity, and even its basic relativistic version, i.e. the general relativity, seem to fail on galactic scales. The first model that has been developed in this sense is the Modified Newtonian Dynamics or MOND [9–11]. Remarkably the basic idea of this model is thus as simple and economic as DM concerning the theoretical background. The initial aim was to explain the flatness of the rotation velocity curves of the spiral galaxies uniquely with help of the observed baryonic matter. In MOND the second law of Newton () is modified in the very low regime of acceleration , being a universal constant. MOND replaces the acceleration a by . Assuming then a test particle surrounding an attractive mass M, with a circular orbit of radius r and with , we have or For the velocity we directly obtain . This leads to the flatness of the observed rotation curves of spiral galaxies but, much more, results in the Tully-Fisher law in a very natural manner [12].
Furthermore, MOND is sustained by the empirical Renzo’s rule. The empirical Renzo’s rule highlights the correspondence between detailed features observed in the observational rotational curves of spiral galaxies and the same features seen in their Newtonian counterparts [13]. This statement, that the observational rotation profiles seem to be a magnification of the Newtonian counterparts, appears quite natural when baryonic matter dominates the mass, but not if DM is the dominant form of matter. Another strong support for MOND, as seen above, is the direct deduction, within a calculation that takes just a few lines, of the Tully-Fisher relation. These two facts are difficult to explain within the DM paradigm, except in an ad hoc manner. Eventually MOND has predicted, well in advance, the profile of the rotation curves in the case of low surface brightness galaxies (LSB), once again a feat not possible for DM [13]. However, the MOND phenomenology fails to explain the dynamics of galaxy clusters. A natural remedy has been found by adopting a multiscale approach [14]1. In any way as for gravitational lensing and cosmology, the classic modified-(gravity+inertia) MOND in its initial form [9] is not applicable. Various relativistic versions of MOND (RMOND) have been proposed making clear predictions regarding gravitational lensing and cosmology. The latest in date is that of Skordis and Złośnik [15]. The latter version of RMOND reproduces the galactic and lensing phenomenology and also the key cosmological observables2.
Another well known modified-gravity theory is the covariant scalar-vector-tensor modified-gravity (MOG) built by J. Moffat [17]. MOG is based on a pseudo-Riemannian metric, a spin 1 vector field, a corresponding second-rank skew field , and eventually three dynamical scalar fields G (the gravitational constant), and . The heavy price to be paid is the addition of extra vector and scalar fields to the gravity field. On the other hand in MOG the gravitational constant G is assumed to vary with space and time. Moreover the introduction of new fields means that new particles are surreptitiously hypothesized. We are not far from DM with its elusive particles, even though MOG is much more subtle than DM because the particles in MOG are virtual, and may not be directly observable in the laboratory. MOG has been largely applied with some success to spiral galaxy curves, to galaxy clusters, to gravitational lensing and eventually to cosmology [18]. RMOND and MOG are the two main models built to get rid of DM fairly efficiently. These two models are the only models that have been extensively studied and involved in concrete comparisons with the observational data. Unfortunately with the relativistic extension of MOND, or with its main concurrent MOG, one moves away from the beautiful simplicity of the Newtonian mechanics and even of general relativity. Let us note that RMOND and MOG appear very much alike. Thus the major pitfall of RMOND and MOG is the introduction of other subsidiary extra scalar and vector fields that have not been tested in the laboratory.
A broad number of other models also exist, but they have been more sporadically applied to real situations. Conformal gravity theories (CFT), which are compelling alternatives to general relativity theory, have been claimed to explain the observed flat rotation profiles of spiral galaxies, without invoking DM or other exotic modifications of gravity [19,20]. Nevertheless the extension of this type of models to the field of cosmology appears to be questionable. Thus it seems that the Weyl CFT3 cannot accurately describe the stated lensing observations without again considering dark matter [21]. Eventually another very different way is to conceive gravity, not as a conventional interaction, but rather as an emergent property [22]. In this case, gravity is seen as an entropic force, i.e. closely related to thermodynamics. Testing this hypothesis in the galaxy world is underway.
Are there other options to get rid of DM ? We can answer this question in the affirmative. Very recently and quasi-simultaneously, a lot of new models have been proposed by following original, even though speculative, ways [23–27]. These models sound similar, even though they use a different formalism. The aim is then to satisfy a principle of parsimony in the introduced concepts. It is indeed about three different strategies, but which share a number of common features. All these ideas are new and still need deep understanding.
One very aesthetic strategy is to assume that spacetime is multifractal in nature. This property is revealed in the most prominent quantum gravity theories in a natural manner [28]. This concept of fractional-dimension space applied to Newtonian gravity has been suggested as an alternative to DM [23,29–32]. In the latter work a connection has been established between the Newtonian Fractional-Dimension Gravity (NFDG) with MOND. The MOND acceleration constant can be related to a natural scale length in NFDG, i.e., , for any astrophysical structure of mass M, and the deep-MOND regime appears in regions of space where the dimension is reduced to .
A second strategy is Refracted Gravity [33,34]. Refracted Gravity mimics dark matter by introducing a gravitational equivalent to a permittivity, seen as a monotonic function of the local mean volumetric mass density. This function is parametrized by three coefficients which are free as in the case of DM, but which are expected to be universal, contrarily to DM where the parameters are free and, additionally different for each galaxy. Once again even if this second strategy apparently relies on a very different formalism than NFDG, both share strong links with MOND.
We turn now to the third strategy, i.e. the -model. The aim of the -model is to reflect on how the mean volumetric mass density (estimated at a very large scale), surrounding a given observer, can modify his view of the Universe.
In the framework of this model [16,25–27] it is hypothesized that it is the perception of the observer, modified by his environment (the local mean volumetric mass density, calculated at a very large scale around him), that creates the observed anomalies and also his proper experience of gravity (with today the need to call for a hypothetical dark matter in order to explain these anomalies). This idea is speculative, but it strongly resembles the models for which we have given an overview above [23,24]. However one point of difference is that the effects described in the -model are only apparent, depending on the observer (excepting the spectroscopic velocities whose measurement is universal, see [16] par. 2 eq. 10). It is almost as if we are looking at any object through a perfect, even though fictive, optical device (such as an aberration-free flat superlens4, but without being aware of the presence of this device (which obviously does not exist). Clearly, the object has not changed but both its apparent size and velocity can now appear magnified from the point of view of a distant observer. Admittedly both the inertia and the gravity seem to be modified in the -model, but it is a pseudo-modified-gravity, it is not of the same nature that a real modified-gravity as introduced, for instance in MOG or RMOND. Moreover, in the -model the gravitational constant (and the speed of light), locally measured by any observer, are invariant. The gravitational constant, the speed of light and all physical constants are universal in the -model. To make variable a constant in physics, in our case G here, could require to make variable other constants (for instance the speed of light) with, may be, unpredictable consequences. Furthermore no new field or exotic particles, undetected in the laboratory, are assumed in the -model. We think that it is a very important point that obeys a principle of parsimony. Eventually even though the -model is Newtonian in essence, its great advantage is that it can be naturally made relativistic. A first draft of what might be a relativistic version of the -model is presented in the reference [25]. However in a galaxy the velocities v of stars and gas are low compared to the speed of light c (the ratio ), and the nonrelativistic approximation is sufficient, especially in the outskirts of galaxies where gravity is weak. The same arguments also apply to MOND. For MOND a notable relativistic version has however been proposed [15]. Nevertheless the elegant simplicity of the initial version of MOND has unfortunately disappeared in the operation. At the Newtonian level the -effect is mimicked by an apparent local scaling transformation applied in an Euclidean space [16,26]. In a Riemannian structure of space a local scaling transformation could be applied exactly in the same manner. Eventually let us note that the multiscale approach already suggested in [14] is directly included in the -model, which assumes that the larger the characteristic dimension (the scale) of a system, the weaker the local mean volumetric mass density and the stronger the magnification [16].
In order to avoid any misunderstanding, three velocities are defined in the -model: the Newtonian velocities, , which are directly calculable from the mean surface mass density profiles, but which are virtual and not measurable, the radial velocities, which are given by (observationally the universal spectroscopic velocities, ) and the tangential velocities which are given by (observationally the proper motions). Following a more mathematical approach within the formalism of bundles, the Newtonian velocities are "located" in the base (not reachable) and both the measurable radial and tangent velocities are "located" in a sheet, attached to a given observer in the bundle situated "above" the base [16]. The latter mathematical considerations will be shortly developed in an up-coming paper. We are only concerned here with the observational aspect.
The synoptic table below summarizes the applicability domains of the different models discussed in this paper :
| Model | Main features |
| MOND | Very low acceleration |
| κ-model | Very low mean mass density Geometry of the matter distribution (bulge, disk) Compactness (stars, gas) |
| NFDG | Variable dimension of the matter distribution, between (sphere) and (disk) |
| RG | Very low mean mass density Geometry of the matter distribution (bulge, disk) |
2. Calculation Details
In the SPARC catalogue [35] each galaxy is usually identified by three independent main components for the densities : the bulge labeled b in the following, the stellar disk labeled d.st and the gaseous disk labeled d.g. This hierarchy is also preserved in the κ-model where both the geometry and the relative values taken by the mean densities (compact masses for the stellar component, or diffuse masses for the gaseous component) are now playing a new role by their implication in a magnification factor at a very large scale. A similar idea appears in the NFDG theory, but it is the dimension of the matter distribution that plays a major role. Let us note that the so-called κ-effect (a retranscription of the DM-like effect), said in a practical way, is a "huge-volume-effect" and it only occurs at a very large scale; it is inexistent at the solar system level (a bit like the quantum effects are fully imperceptible at the macroscopic level). In the framework of the κ-model, the relationship associating the corresponding (fictive) Newtonian velocities to the measured spectroscopic velocity is [16,26,27]
where each peculiar velocity is weighted by a -ratio. The origin of the -ratios results from the need to take into account explicitly both the matter distribution dimension (bulge or disk) and the compactness of this matter (stars or gas). In the -model all these coefficients are directly linked to the mean volumetric mass densities by a simple and universal relationship (ln denotes the natural logarithm)
with the necessary condition . The indexes "1,2" run on all the mentioned indexes. The relation (2) is called universal in the sense that this relation is valid whatever the type of galaxies, and also for galaxy clusters [16,26]. In MOND the analog of is not a logarithmic function of the density, but a rational function of the distance [9–11] (but both are sensibly equivalent in the case of an exponential distribution of matter). In relation (1) the indexes , , , and respectively designate the reference value for the density, the maximum value M of the total density, t, (stellar bulge, , + stellar disk, , + gaseous disk, ) estimated at the center of the galaxy, and the maximum value M of each of the independent components, also estimated at the center of the galaxy. The non-indexed coefficient is the local one (there where resides the observer who feels the gravitational field). For practical purposes concerning the disk components, the density can be expressed as a function of the observable surface mass density (indirectly obtained from the brightness measurement), i.e. with the thickness , the latter quantity being here assumed to be constant throughout a galaxy disk. Apparently, the thickness of the disks seems to play a role in the -model, very similarly to what is assumed in the model, even though in the model it is the dimension of the mass distribution that intervenes instead of the thickness [23,30]. A variable thickness along a galactic radius in the -model could have a close connection with the variable dimension D in the model. However it isn’t as simple as it appears, and we return to this issue in the following. The magnification coefficients of the active mass composing both the stellar and gaseous components are expressed separately, resp. and but are still calculated with the same universal relationship (2). When the mean surface mass density is larger than , a saturation effect appears for , and then in all the cases we put this factor invariably equal to , as provided by the relation (2). However, in a few rare situations, especially for galaxies with a big bulge, and in order to adequately fit the observational profiles in the inner regions, we should adjust the factor to a value between 0.45 and 1. An explanation to this statement is that, in fact, the relation (2) is valid for a thin disk, but not for a 3D bulge. At this level a clear reference to the NFDG model where the dimension plays a major role can be noticed. Another explanation is that the bulge of a spiral galaxy is a very complex system where the stellar orbits are randomly oriented. Then we know that a severe velocity dispersion, larger than a few kpc from the center, can strongly affect the extraction of the pure rotation velocity (see for instance the reference [36] for the Milky Way). The part of the cylindrical rotational support in the inner regions of a spiral galaxy is generally difficult to estimate when the bulge is dominant.
A fundamental question is: how many free parameters are used in the -model ? We know that in physics, the fewer parameters, the better the model. Yet by consulting relation (1), we see immediately that four parameters (the -ratios) appear. Following the parsimony principle it is not a "good" model. In fact, once the density in the bulge, in the stellar and gaseous disks is provided, the -ratios, which are directly issued from observational data, are automatically determined, there is no longer free parameters and the -model eventually becomes parameter-free (the only parameters being, as usually, the observables, i.e. the surface brightness, the inclination and the distance, even though unfortunately not very well known in some cases). This is in strong contrast with DM where two or three free external, and arbitrarily chosen, parameters are introduced to just obtain the expected results. However given that the -ratios are dependent on the densities, the parameters in the -model can now vary from one object to another, and this confers some flexibility to the model with no violation of the parsimony principle. For instance, the -model has been applied with success to the physics of galaxy clusters [16]. The mean mass density in a galaxy cluster is lower by three orders of magnitude compared to the mean mass density in a galaxy. The -model is then naturally a multiscale model (or density-dependent scale model), like the one proposed in [14] for the application of MOND to galaxy clusters. The difference is that in the -model the scaling is not imposed, but appears in essence, taking its origin in the hierarchy of the mean mass densities. By contrast, MOND [9–11] with just one universal parameter or even the Refracted Gravity [33,34] with three universal parameters seems to be too rigid. On the other hand, the -model can naturally be made relativistic [25], making possible its extension to cosmology, especially to the analysis of the fluctuation density in the CMB. In this case it is the density anisotropies to mean density ratio which intervene in the relationship (2). The latter very important topic will be examined in a next paper.
Now, if we want to compare the -model and MOND, we must define a reference point for the mean mass density . Unfortunately, this quantity is only indirectly known by the ratio (surface mass density, , over the disk thickness, in a spiral galaxy such as the Milky Way). The link between the acceleration parameter of MOND and the reference surface density is
Let us note that this value is relatively close to the galactic surface mass density estimated in the solar region () (in comparison with the high range of surface densities seen in a disk galaxy, varying from in the inner regions, from the center, to in the outskirts, from the centre). Taking into account the fact that the range of mean mass densities is very extended in the Universe, this appears indeed very odd if we see the parameter as a cosmological parameter; because in this case we must assume that our situation in the Universe is privileged. In reality, the -model easily explains this rather strange coincidence. We chose this reference taking into account our position in the galaxy, but which has nothing special. Another observer, located elsewhere, will take his own reference. The relation (1), giving a universal result in the framework of the -model, his measurements would lead exactly to the same results for the spectroscopic velocities as ours, even though with his proper local reference for the mean mass density.
Figure 1 displays a panel of velocity profiles for MOND and the -model, in the schematic situation of a disk of matter where the mean surface mass density varies exponentially (the thickness is assumed to be constant following the radius r). The comparison between MOND and the -model shows that the logarithmic relation (2) is a very good choice. In MOND the function plays a very similar role (see eqs. (7) and (8) of the reference [13]), even though in MOND is not a logarithmic function, but a simple rational function. We can note that the -effect (or MOND-effect) plays a decreasing role, when going from low mass surface density (LSB galaxies) toward high mass surface density (HSB galaxies), as confirmed by the observations. This finding, naturally explained with MOND or the -model, remains unexplained in DM. A difference between MOND and the -model is however perceptible for the schematic representation of a so-called super spiral [37]. For a high surface density (, see for instance the reference [38]) the -model curve is located more than above the MOND profile for the terminal velocity (Figure 1d).
In the more concrete cases, the situation is obviously different from the previous trial examples with a simple exponential disk. In reality, we encounter in the SPARC catalog a number of situations where it is not possible to fit the mean surface mass density of both thin stellar, , and gaseous, , disks by just adopting a simple exponential fit. In these situations, we had to add to the exponential component one, or sometimes two, decentered gaussian components. The velocity curve is then deduced from the self-evident, more general formula (still assuming an axisymmetric disk) valid for one component (stars or gas)
As a first step the operational method consists to fit the Newtonian velocities available from the SPARC catalog, for the distributions of stars and gas, taken individually, and for each galaxy. In simple terms we fit the dashed-red (stars) and dashed-green (gas) curves of Figure A. In this case the relationship (4) is applied with (this is the usual Newtonian level). Secondly, the same relationship (4) is again used, but incorporating this time the coefficient that depends on the volumetric mass density (eq. 2). This second step automatically provides the corresponding -model curves. The great benefit of the method is that all parameters are internal to the theory, and supported by the sole observational data, essentially the baryonic mass density. There is no arbitrary parameter such as the ad hoc DM/B ratio in DM.
Eventually, when a bulge is present, a de Vaucouleurs formula [39] is used to fit the surface mass density of the bulge. Two other parameters, intervening in the -model, are still the thickness (scale height) of the stellar (thick) disk, , and that of the gaseous (thin) disk, . For all the galaxies under study (SPARC catalog), these parameters have been taken to be equal to the reference values estimated for the Milky Way in the vicinity of the Sun, respectively and . Given that the galaxies are diversely oriented with any inclination angle, these parameters are difficult to estimate and certainly variable along a galactic radius. Our analysis of the SPARC galaxies seems to indicate a neat trend where the thickness decreases when going from the core regions to the outskirts in the flattened galaxies.
Globally, for a mean orientation of the thickness along the line of view is increased by a factor of In this case the rotation profiles provided by the model have to be magnified by a few percent. In fact, the logarithmic function flattens the density ratios in relation (2) and the influence of the variation of the thickness has a strongly reduced, even though not negligible, impact on the corresponding -ratios (of the order of for a thickness variation of a factor 2. For orientations larger than the magnification can obviously be much larger than ). Let us note that in other models where the density is assumed to play a role, for instance in [24,30], the conclusions should be very similar when applied to a large sample of galaxies, such as the SPARC database. The thickness of various types of spiral galaxies has been estimated by different methods [40–42]. For irregular dwarf galaxies, the situation appears relatively confusing, but the latter category can exhibit quasi-round galaxies with a high mean thickness [40]. The measurement of the thickness seems to give values of the order of or to within a multiplicative in the range 0.25 (in the outer regions) to 4 (in the inner regions toward the bulge if existing), compared to the reference values, independent of the size of the galaxy (with a few exceptions for the very small galaxies, where smaller values for the thickness are favored). Thus, a positive point is that an estimate of the thickness can be reached in the framework of the -model. However in Figure A, for all the galaxies and for the sake of homogeneity, the thickness has been taken as invariable throughout the stellar and gaseous disks. The corresponding values are indicated in each individual figure. Taking into account a variable thickness would make it possible to obtain better profiles. A work that remains to be done.
Additionally, let us specify that the observations rather provide non-monotonous galactic rotation profiles. Nevertheless it is illusory to try to perfectly fit the rotational curves with their delicate patterns of bumps and wiggles. Very likely, these patterns are caused by the presence of spiral arms or portions of rings, a variable thickness or inclination, not taken into account by assuming smoothed axisymmetric and monotonous density profiles. Even DM with two or even three external parameters cannot make that5. One of the better DM methods, built on the Einasto profiles with three ad hoc parameters in the fits, is discussed in reference [45]. We can see that the fine details cannot be adequately fitted (see, for instance, NGC6015, NGC 7793, NGC3726, IC4202, NGC0289, UGC06787, etc). In any case a lot of physical parameters are very poorly known: the inclination of the galaxy (moreover, very likely variable along the galactic radius), the mass-to-light ratio, the thickness along the line of sight, the distance, etc. We must add that the observational profiles can substantially differ in some cases from one author to another, sometimes by more than . We can compare two different catalogs, for instance, that of Sofue [46] versus SPARC [35], when the rotation curve for the same galaxy is presented (see especially NGC 2903 where a discrepancy of can be notified). Even for the Milky Way, in the vicinity of the Sun, divergences also exist [47]. Let us note that the DM paradigm could, however, be made in agreement with any inclination by adequately adjusting the DM/B rate! A contrario both MOND and the -model apparently fail if the inclination is not accurately estimated [26]. An example where the inclination factor can sometimes play an important role in the determination of the rotation velocity profiles is given in [48]. In the latter paper it is shown that the inclination can vary by following the authors, eventually favoring a model rather than another one. Eventually, we can say that, unfortunately, the determination of the inclination is not the sole trouble. Additionally the gas and the stars in a galaxy, following their types, do not rotate in the same manner, the velocities are not circular, the galaxy disks are not symmetric, etc. The multiple consequences on the observational profiles are difficult to estimate. This is why various observational techniques can lead to different profiles for the same galaxy.
In spite of these difficulties, and in order to make a valuable comparative analysis between different theoretical models, the idea is to use a same set of extended data. For instance, the SPARC catalog seems in this case necessary. This catalog gathers a large, and homogeneous, sample of rotation profiles. A very good point of the SPARC database is that it represents a uniform estimate of the surface densities of galaxies, starting from Spitzer near-infrared data [35]. Then our procedure as to starting from mean fits of the Newtonian curves, and then mean fits for the observed rotational curves can be deduced. In some cases, the DM fits seem to be much more impressive [44,45], but a major drawback for a physical model is that the DM technique of fitting is not at all predictive. Then, starting from any Newtonian curve (even false), we can build any "good" predicted profiles, obviously by adding the "good" rate of DM. Admittedly, MOND and -model profiles are generally of lesser quality, but in most cases, both of them produce a good trend for the fits compared to the observational rotation curves. Let us specify again that the latter ones, empaired by various biases, are also not perfect either.
3. Results
3.1. MOND versus -Model
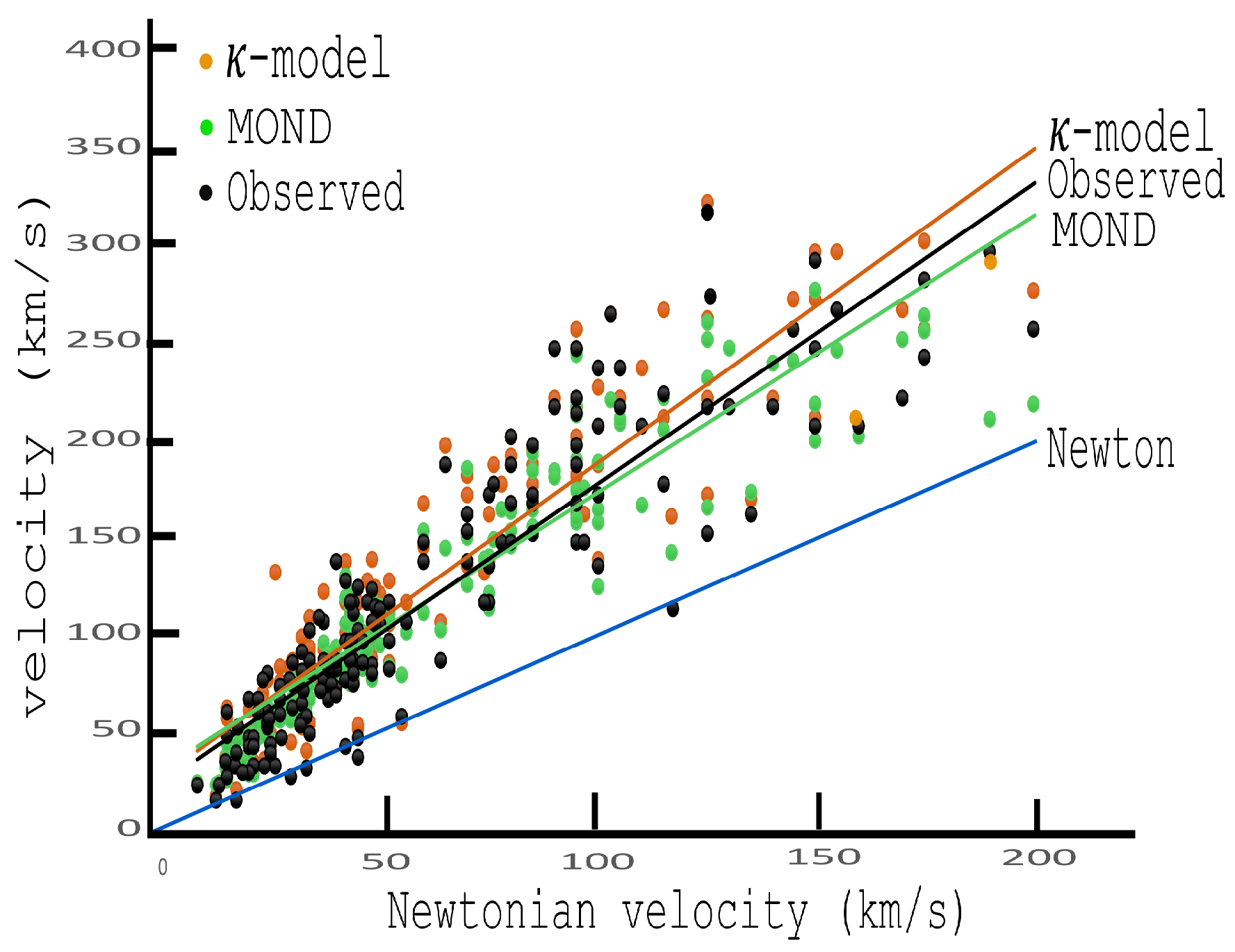
The results of the calculations for the individual galaxies in the SPARC catalog are collected in Figure A in the Appendix. The galaxies have been classified in alphabetical order to facilitate the research. For the disks, it is assumed that the thickness is constant along a radius of the galaxy. In most cases, the thickness has been taken to be equal to the corresponding reference values taken at the Sun position in the Milky Way, for both the stellar, let , and gaseous disk, let . In view of the results, a first general remark is that the -model is clearly as predictive as MOND6. For both models, the results statistically deviate by less than as for the prediction of the terminal velocities (Figure 2).
Examining the individual cases, by browsing Figure A, we can see that the -model leads to predictions similar to the MOND phenomenology, even though in some cases, the profiles are not quite identical. Moreover, a comparison with the observational profiles shows that the predicted curves for both MOND and the -model don’t perfectly match the observations7. Reporting to Figure A we see that the theoretical curves predicted by MOND or the -model can be indifferently located slightly above or below the observational curves. However, there are remedies for this. First, in the outer regions, the predicted curve is quite often located above the observational one. In MOND the bias can then be corrected by EFE (External Field Effect) [52]. Likewise, this bias could be corrected by a diminushing thickness of the disks (at constant surface density ) in the -model. A contrario, there exist a number of cases where the predicted curve is located below the observational one, especially in the innermost regions of galaxies (for instance, in the more striking cases: F563-V2, F568-1, F568-V1, F571-8, F579-V1, F583-1, NGC 2915, NGC 3992, NGC 5907, NGC 5985, NGC 6674, UGC 00128, UGC 00731, UGC 02259, UGC 6446, UGC 06667, UGC 07399, UGC 7490, and UGC 8286). It is interesting to note that the magnitude of this bias is very similar in both MOND and in the -model for a given galaxy. Very possibly, a modification of the inclination in MOND (and also in the -model) could partially remove the discrepancy in the inner regions for these galaxies. As demonstrated in [48] the modification of the inclination can substantially modify the profile of the rotation curve. However this effect appears rather systematic throughout figure A in the inner regions. In other words, the measurement of the inclination would be systematically biased in the inner of spiral galaxies and, strangely enough, always in the same direction. This hypothesis is hardly acceptable. The fact that the MOND curve is located below the observational one results from the fact that the acceleration a is equal to or larger than the critical value in the inner regions. In this case, we are in a domain where the Newtonian regime is still supposed to be valid. To save MOND, we can then assume that the parameter is larger in the inner region, but then this parameter is no longer universal. Another solution is that the baryonic mass-to-light ratios are largely underestimated (by a factor 2) in the inner regions of the quoted galaxies. Eventually, a more credible explanation is to imagine that some non-exotic form of DM exists in the innermost regions of galaxies. We could invoke, for instance, a neutrino species with mass (but in acceptable quantity with ). A very similar idea has been assumed for the inner regions of galaxy clusters [53]. This hypothesis appears admittedly reasonable; however, the -model can propose another natural solution. In the -model, the leading role is not held by a fixed parameter, i.e. the acceleration , but by the mean volumetric mass density. This hypothesis makes the -model more flexible than MOND. Figure A displays the results under the reductive hypothesis of a constant thickness throughout the galactic disks. However an increase in disk thickness (at constant mean mass surface density) in the inner regions of spiral galaxies could help to lessen the discrepancy. An interesting conclusion is that the -model could hence help to obtain an estimation of the mean thickness, a parameter difficult to derive from the observations. In any case in the cases mentioned above, even if the -model gives imperfect fits in the innermost regions of these galaxies, we can see that the terminal velocities are correctly predicted. A simple response to these statements is that the empirical relationship (2) is very well adapted to a thin disk, but far less applicable to a thick disk or a 3D bulge. For the galaxies listed just above, where a discrepancy exists between the -model (or equivalently MOND) and the observational data, a comparison with DM profiles with two or three (ad hoc) parameters (as in reference [44]) appears very interesting. Examining the cases displayed in Figure 6.10 of [44], we can see that the underlined discrepancy also persists in some of the cases, even though slightly lessened (see, for instance, the rotation profiles for F568-1, F579-V1, NGC 2915, NGC 5907 and NGC 6674). F571-8 is a pathological example where MOND, the -model and DM yet provide very similar profiles, but paradoxically enough far from the observational one in the outer regions. The three theoretical profiles, even though very similar, are located below the observational profile in the outer regions. In any way, we know that trying to predict the rotation velocity curves with a better statistical precision than (and even, in some pathological cases, the incertitude can rise to ) appears unwarranted, considering the dispersion in the observational data coming from various sources. That matter aside, in the framework of the -model, at least we have a fairly good estimation of the terminal velocities (Figure 2 and see also Figure A for the individual cases), a conclusion that cannot be reached by the ad hoc DM methodology. Obviously, the flexibility of the -model by taking into account a variable thickness in the stellar and gaseous disks would allow to fix the residual discrepancy between the theoretical curves and the observational ones. In the same vein, this statement is rather attractive because it implies that the model could predict the variation of the thickness in spiral galaxies along a radius. This data is indeed difficult to obtain by sole observation.
3.2. Newtonian Fractional-Dimension Gravity
Newtonian Fractional-Dimension Gravity (NFDG) is an extension of the laws of Newtonian gravitation to lower dimensional spaces, including those with non-integer, "fractional" dimension (for a general introduction see [23]). NFDG is based on a generalization of the gravitational Gauss’s law, replacing standard space integration over with an appropriate Hausdorff measure over the space, which was related to Weyl’s fractional integrals. As for MOND or -model, the goal of NFDG is to describe galactic dynamics without using the controversial DM component. A quick review of NFDG is presented in the reference [30]. NFDG was introduced heuristically by extending Gauss’s law for gravitation to a lower dimensional space-time , where can be a non-integer space dimension. A scale length, , is needed to ensure the dimensional correctness of all expressions for . Let us note that NFDG does not imply a change in the tri-dimensionality of space in galaxies, but rather the local Hausdorff dimension is associated to the matter distribution (bulge or disk). In this sense there is an analogy with the -model, where the ratios (eq. 1) are assumed to be dependent on both the dimension of the matter distribution (bulge or disk), and also the compactness of matter (stars or gas).
In [29] Varieschi discusses in depth the case of NGC 6503. For NFDG with a dimension , the theoretical curve is slightly above the observational one and is remarkably flat (see Figure 6 of [29]). However, assuming that NGC 6503 behaves as a fractal medium, with a variable fractional dimension, NFDG can produce a curve with a perfect superimposition with the observational one. Reporting now to Figure A for this galaxy we can see that both the MOND and -model curves are slightly below the observational curve in the inner regions and slightly above in the outskirts. In the -model framework, the statement of variable fractional dimension could be re-interpreted as a variable thickness of the disk. In the case of NGC 6503 for instance, an increase in the thickness in the inner regions (thick disk) and, concomitantly, a decrease in the thickness in the outer regions (thin disk), could also lead to an improved profile, such as in NFDG theory. In [30] the same author applies his analysis to other rotationally supported galaxies : NGC 7814 and NGC 3741, for which very good NFDG fits are supplied. If we consider these galaxies, MOND and the -model provide a fairly good value for the terminal velocity. However, a same bias is perceptible for the inner velocities (the predicted curve is below the observational one). This bias is not present on the NFDG profiles, which perfectly fit the corresponding observational curves, even with their humps and wiggles. However this perfect fit results from the fact that the NFDG theory imposes on the fractional dimension to vary in "an appropriate manner" along a galactic radius, in order to obtain a "good" profile. Nevertheless, the positive point of this procedure is that NFDG can thus be predictive for variable dimension. Once again, the -model can correct the mentioned bias by invoking a variable thickness. In the framework of this model, a volume-effect, i.e. the influence of the mean volumetric mass density surrounding a given observer, and estimated at a very large scale, is playing a similar role to that of the dimension in NFDG. Yet Varieschi underlines that the variable dimension D should be interpreted as the dimension of the matter distribution of the galactic structure and definitely not at all as the local space dimension that an observer would measure at a specific galactic location. In any event, the link between a variable dimension in NFDG theory and a variable thickness in the -model could be more subtle, and should be reconsidered in more depth. Furthemore, examining relation (1), we can see that the coefficients for the bulge and the stellar and gaseous disks are different. For the bulge and the disk, the dimensions are admittedly different, but what about for the stellar versus gas components ? All these questions deserve further examination.
It will be very interesting for comparison with the -model that the NFDG theory be applied to a larger sample of galaxies, for instance, the totality of the galaxies of the SPARC database. A particular attention must then be paid to the following cases : F563-V2, F568-1, F568-V1, F571-8, F579-V1, F583-1, NGC 2915, NGC 3992, NGC 5907, NGC 5985, NGC 6674, UGC 00128, UGC 00731, UGC 02259, UGC 6446, UGC 06667, UGC 07399, UGC 7490, and UGC 8286, for which both MOND and -model substantially differ from the observational profiles in the innermost regions, while however providing fairly good estimates in the outskirts of these galaxies (the terminal velocities).
3.3. Refracted Gravity
Along with the NFDG model, another new classical gravity modified theory is the so-called Refracted Gravity (RG) [24,33,34]. RG can be reformulated as a scalar-tensor theory [34]. RG mimics DM with a gravitational permittivity (a kind of variable gravitational "constant" G), and that boosts the gravitational field in low-density environments. In RG the link between the volumetric mass density and the gravitational permittivity is expressed by using the relationship
where , Q and are three free parameters. The formula (6) is an arbitrary monotonic function of the volumetric mass density with the asymptotic limits for and for . This formula is the equivalent in RG of the relation (2) in the -model. This permittivity also shares a very strong analogy with the function in MOND [13], or still the function in the -model [16,26]. However is supported by three universal parameters, instead of just one, for instance as in MOND (). Thus RG seems, at first sight, to be less economic than MOND, but its great interest is that it is now a multiscale version of MOND. In this sense, the objective of RG is very similar to that proposed by the -model; but with an essential difference : the -model model uses exclusively internal parameters (i.e. the mean volumetric mass densities of the bulge, stellar and gaseous disk components) and no free external parameters. Then, by contrast in RG the three arbitrary parameters still need to be obtained through a long statistical analysis of the observational data [24]. RG has been applied to both flattened galaxies [24] and a small number of elliptical galaxies [33]. The results presented in [24] rely on setting the three free parameters for each individual galaxy. However, the authors show that the variations of these parameters from galaxy to galaxy can, in principle, be ascribed to statistical fluctuations. Then the authors adopt an approximate procedure to estimate a single series of parameters that may properly describe the kinematics of the entire sample of galaxies, They eventually conclude that the gravitational permittivity is indeed a universal function. Unfortunately, a direct, and yet fruitful, comparison between RG and the -model is difficult because the galaxies under consideration are not issued from the same catalog. However, a close examination of the results displayed in [24] leads to the firm conclusion that the fits of the rotation profiles are of similar quality to those produced by MOND and the -model.
3.4. Conformal Gravity
Eventually, a comparison with conformal gravity can also be proven worthwhile. In the Conformal Gravity (CFT) [20] two universal parameters are introduced, setting apart the usual observational data, i.e. the luminosity and the ratio, the distance, and the inclination, common to any model. The first parameter () is related to the local geometry, while the second parameter () describes the global geometry due to all the other galaxies in the Universe. These two parameters are statistically derived from the observational rotation curves of a chosen sample of 104 galaxies (this sample is limited to the galaxies whose mass density is fittable by a simple exponential thin disk). By comparison, we recall that in the -model the coefficients are calculated from the mean mass density profiles attached to each galaxy. However, it is very difficult to decide which model is the best. Statistically, MOND, the -model and CFT provide equivalent results as for the proximity of the theoretical curves to the observational ones. We can examine the fit through the individual cases presented in [20]. For NGC 1003, NGC 3972, NGC 5585, and UGC 7089, MOND and -model fit is better than the CFT fit. For NGC 2903, UGC 5005,and UGC 5999 the fits are equivalent, For NGC 4100 the CFT fit is better than the MOND and -model fits, etc. Some cases are favorable to MOND or to the -model while in other cases the CFT is better. At the present time, this situation is very embarrassing because each author can validly support his own model against that of others through a judicious choice of the data. It is for that reason that the models have to be compared on a very large sample of galaxies such as the SPARC database, and not on a very small sample of a few galaxies.
4. Conclusion
This paper is a discussion on the capacity of a number of MOND-type models [16,23,24] and a CFT-based model [20], which have been recently proposed, to understand the dynamics of a large variety of flattened galaxies. Admittedly, these models do not provide very perfect fits (except may be NFDG that possesses a flexible dimension associated to the mass distribution), but, nonetheless, they produce fairly predictive mean rotational curves. It is nonetheless true that DM can indeed lead to better fits with two or still three [44, 45] parameters, but unfortunately, these parameters are freely adjusted to each galaxy. This implies that by starting from any Newtonian profile, even one strongly empaired by various biases, we can derive a "very good" fit for any given observational rotation profile8. MOND and the -model are at least falsifiable and upgradable, while DM definitively not. For a physicist, the choice is quickly made. With no confirmation by experimental methods, DM unfortunately has very limited scientific significance. Obviously this conclusion would drastically change if, one day, we discover the signature of DM in the laboratory. We can always expect it over the next few years. Even though obviously the -model is not a definitive solution, at least it shows that the baryonic mean mass density could play an unexpected role in the determination of the galactic rotational velocities and that both are strongly correlated. If this model is on the right track, then the rotational velocities alone could allow us to directly determine the baryonic mean mass density (and not indirectly from the brightness measurements) and vice versa in a self-consistent manner. In this case, the delicate step, i.e. brightness mean mass density would be short-circuited. After an analysis of spiral galaxies and galaxy clusters, the work is far from finished. The -model has to be still applied to the elliptical galaxies, to the globular clusters, to the formation and stability of primordial galaxies, and eventually to CMB/cosmology. Let us also note the very captivating open debate concerning the wide binary stars ([54] versus [55]). The -model obviously predicts a very weak -effect in the immediate vicinity of the Sun, i.e. the motion of the wide binaries is predicted to be quasi-keplerian in this region. Much work remains to be done. It would be interesting to concomitantly perform the same studies, on the same collection of galaxies, with other models, such as the Newtonian Fractional-Dimension Gravity [29–32], the Refracted Gravity [33,34] and also the CFT model [20].
Appendices
A. Section Rotation Curve fits Results
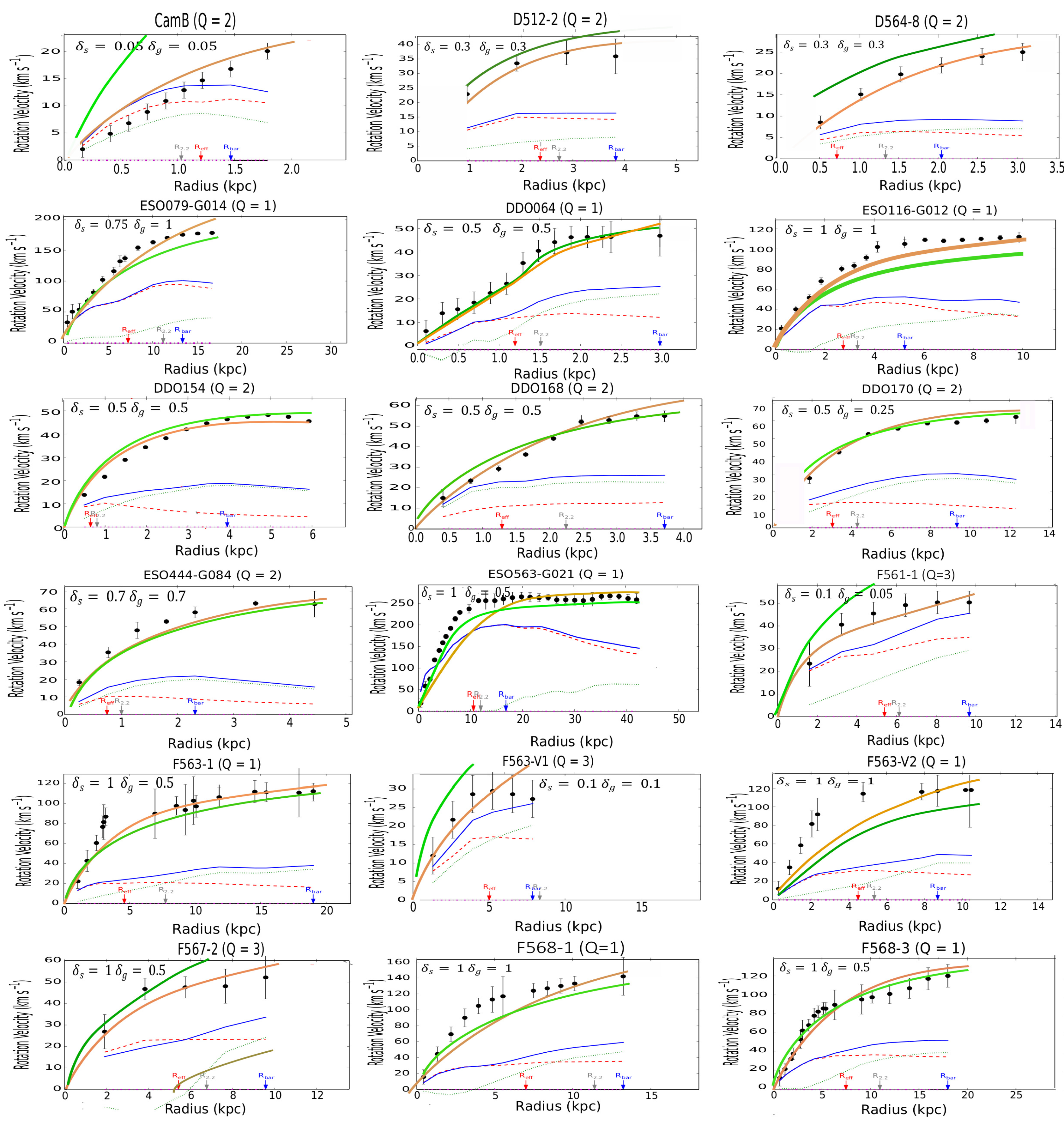
Figure A Rotation curves of the SPARC galaxies. The green line is predicted by MOND, the amber line is predicted by the -model, the red dashed line represents the stars, the green dotted line represents the gas, the blue line represents the sum of all baryonic components (stars + gas). The observed velocities are shown as a series of filled black circles.
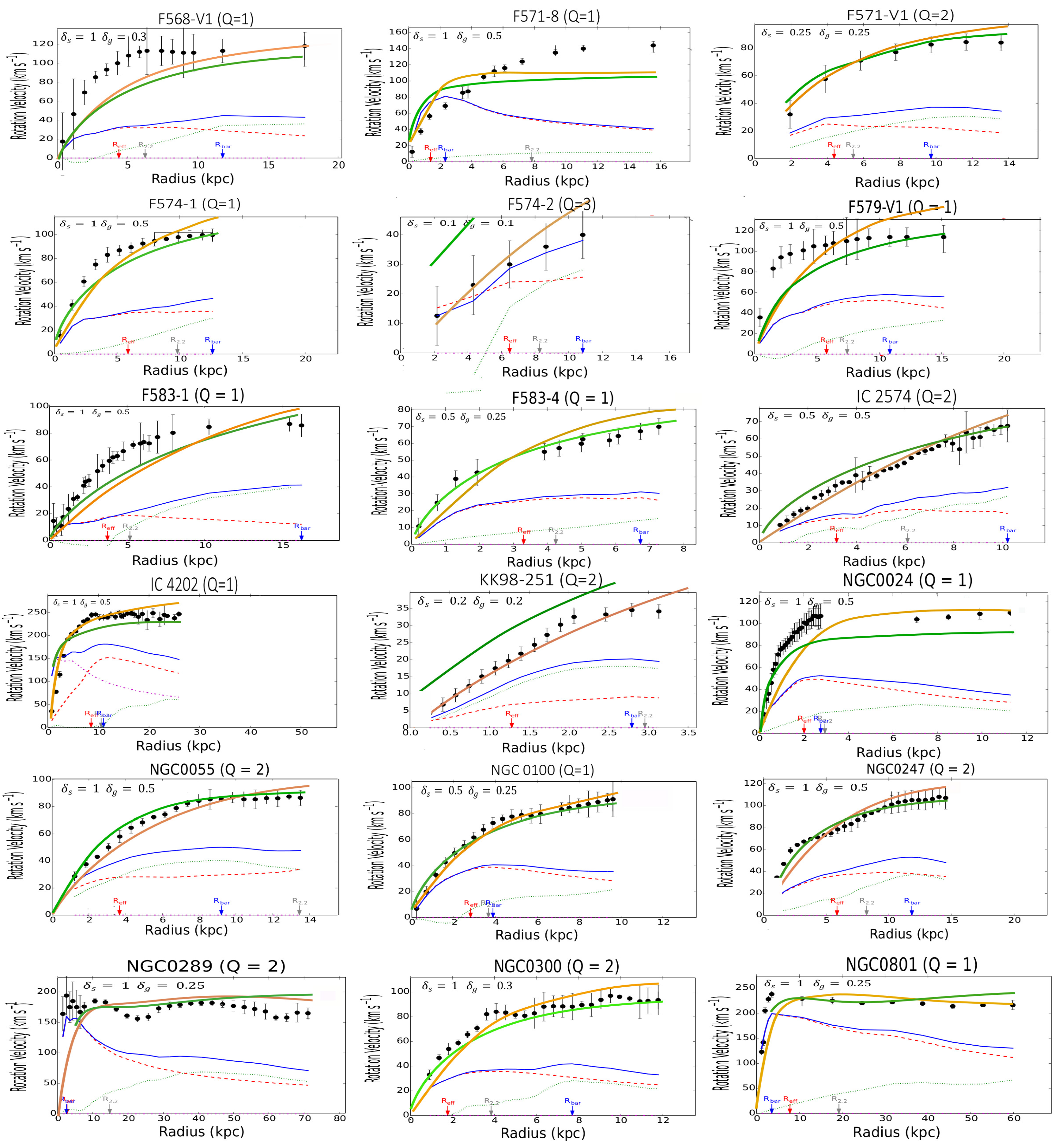
Figure A : Continued rotation profiles
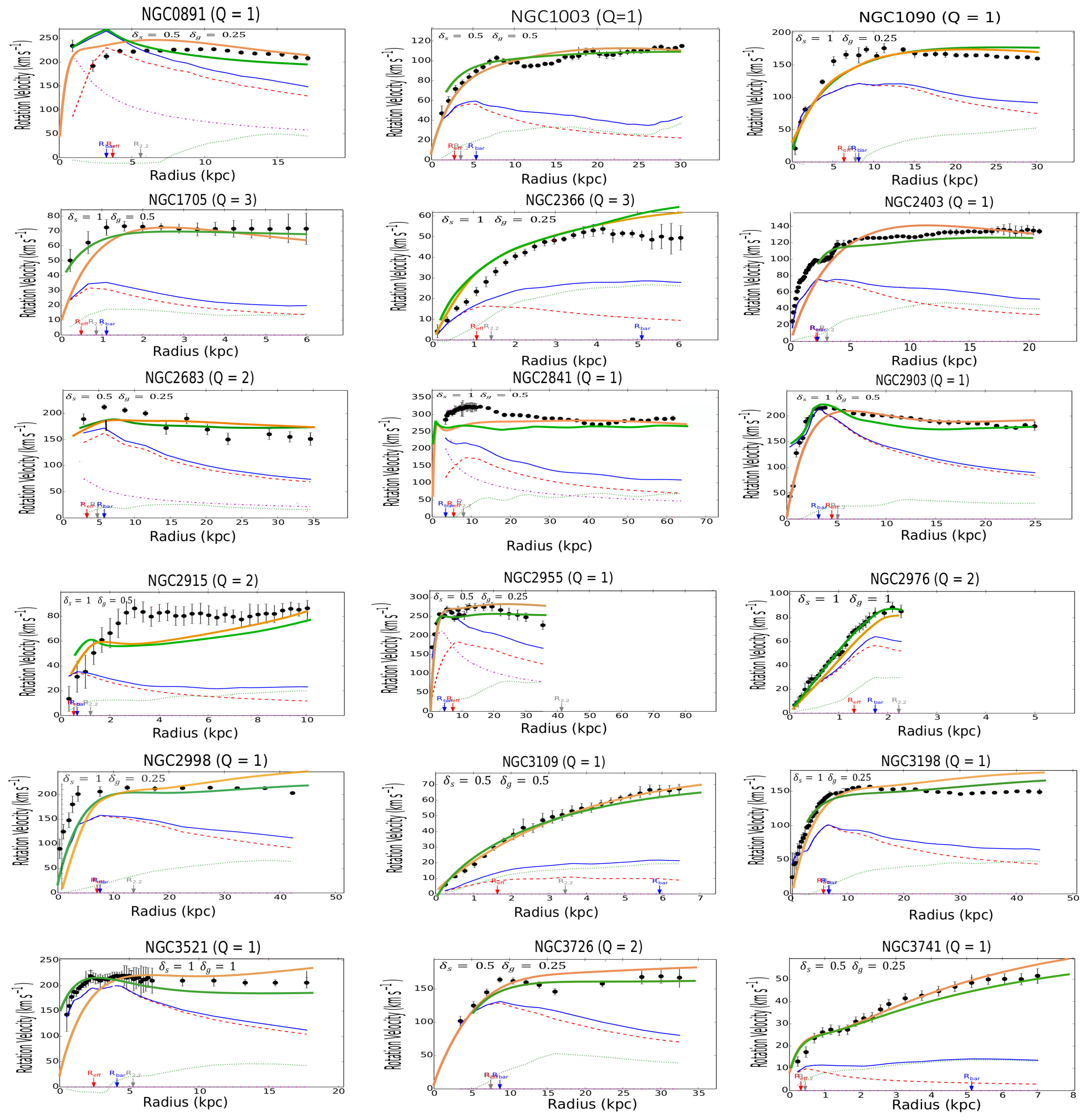
Figure A : Continued rotation profiles
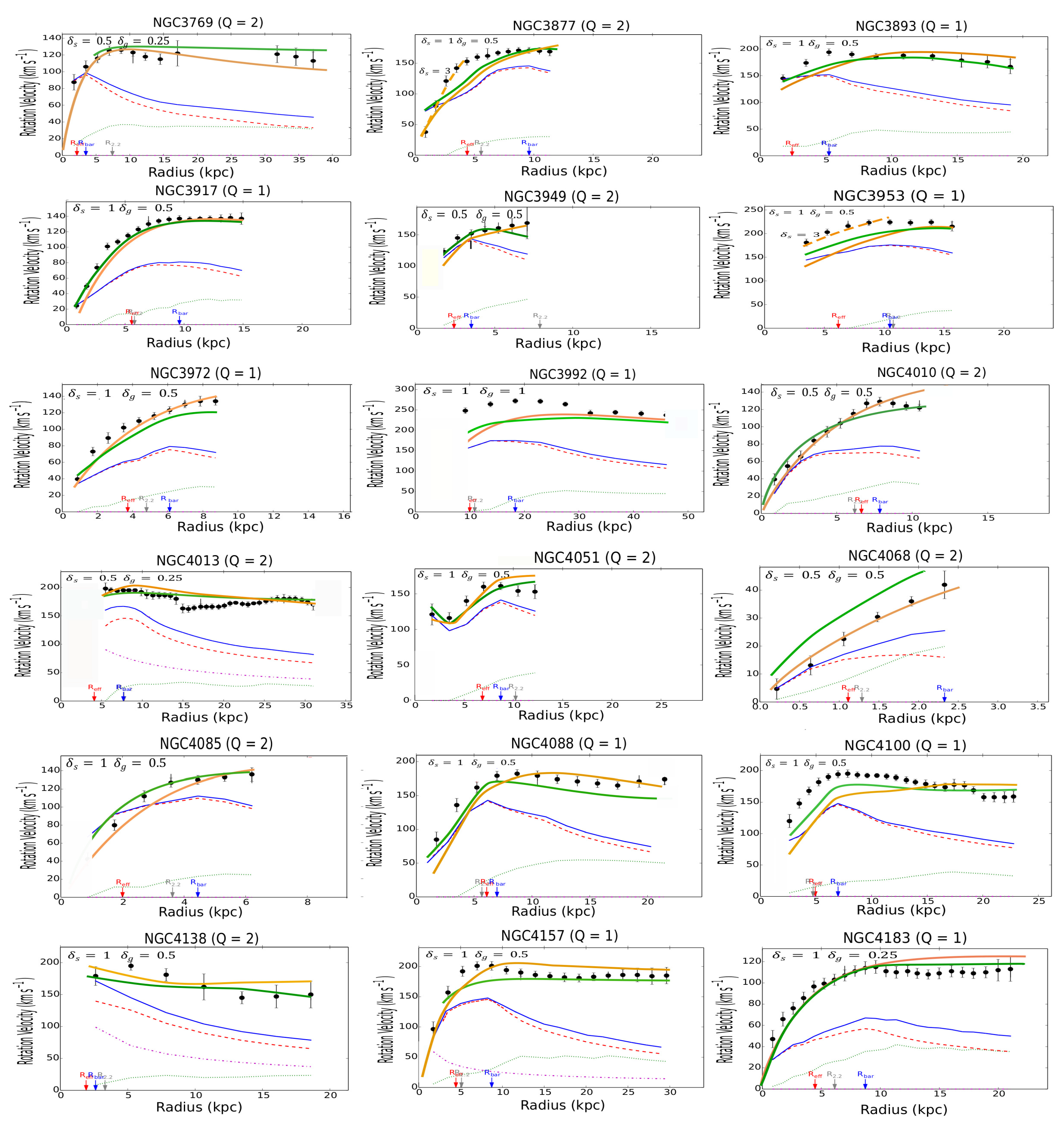
Figure A : Continued rotation profiles
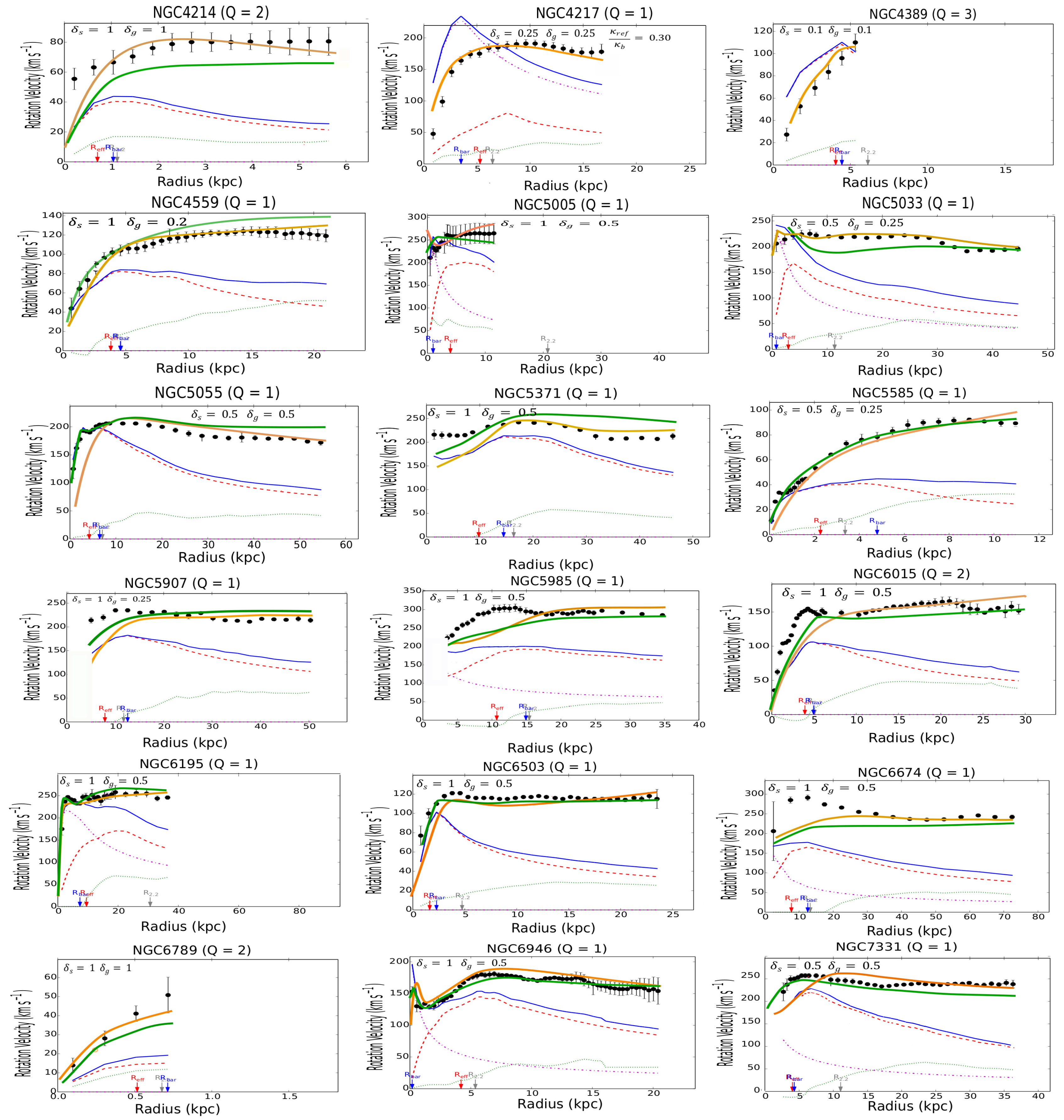
Figure A : Continued rotation profiles
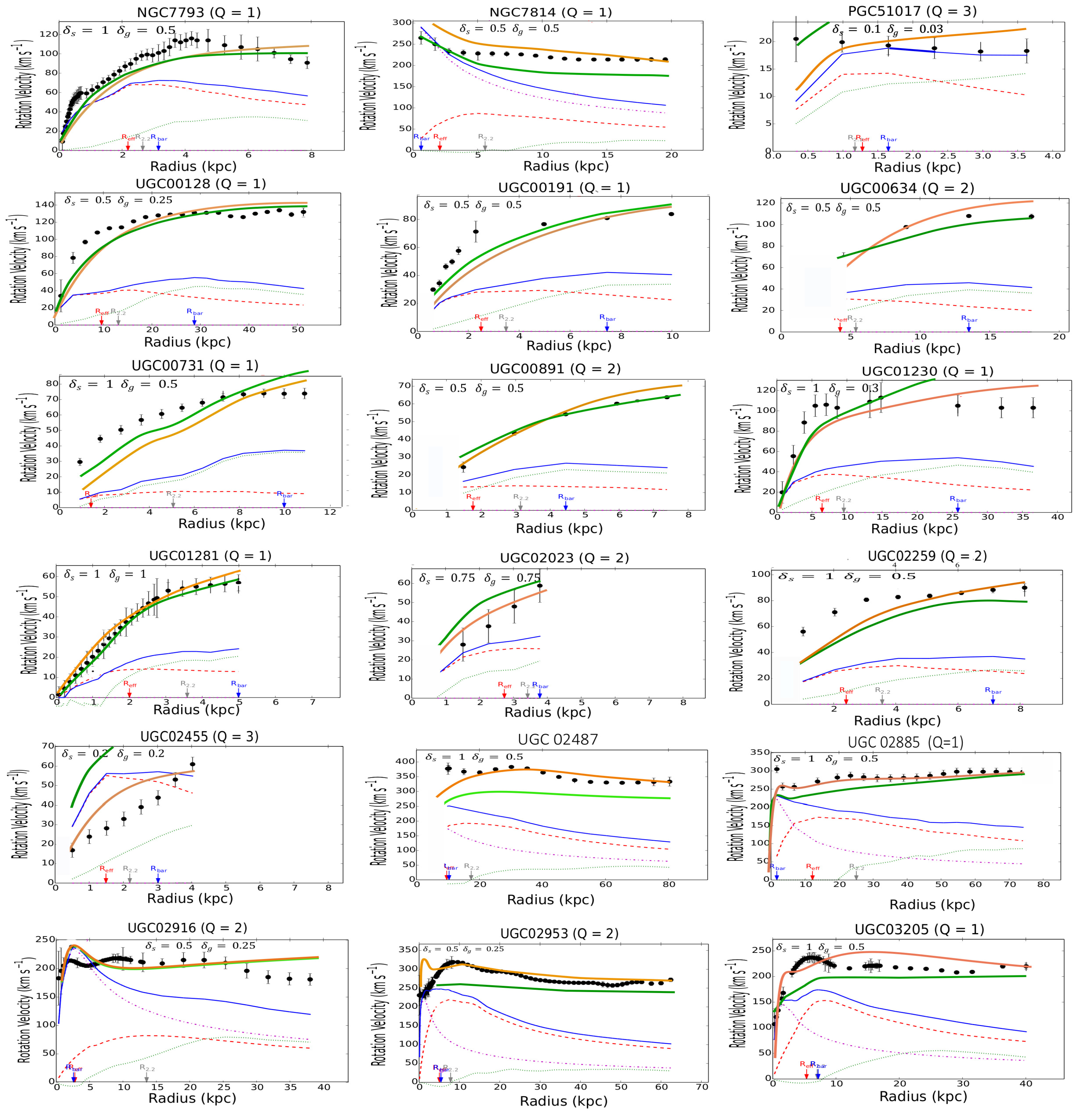
Figure A : Continued rotation profiles
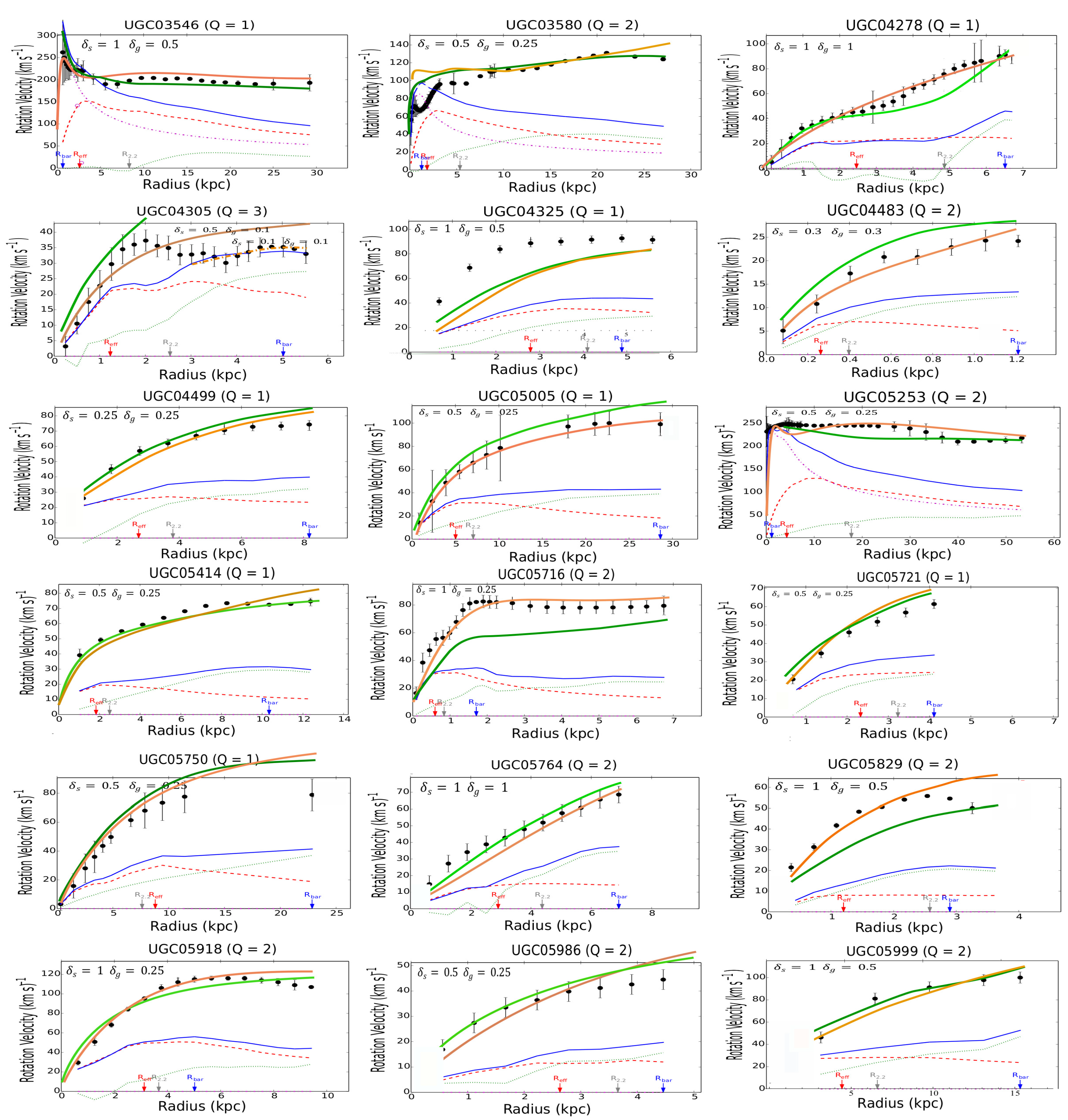
Figure A : Continued rotation profiles
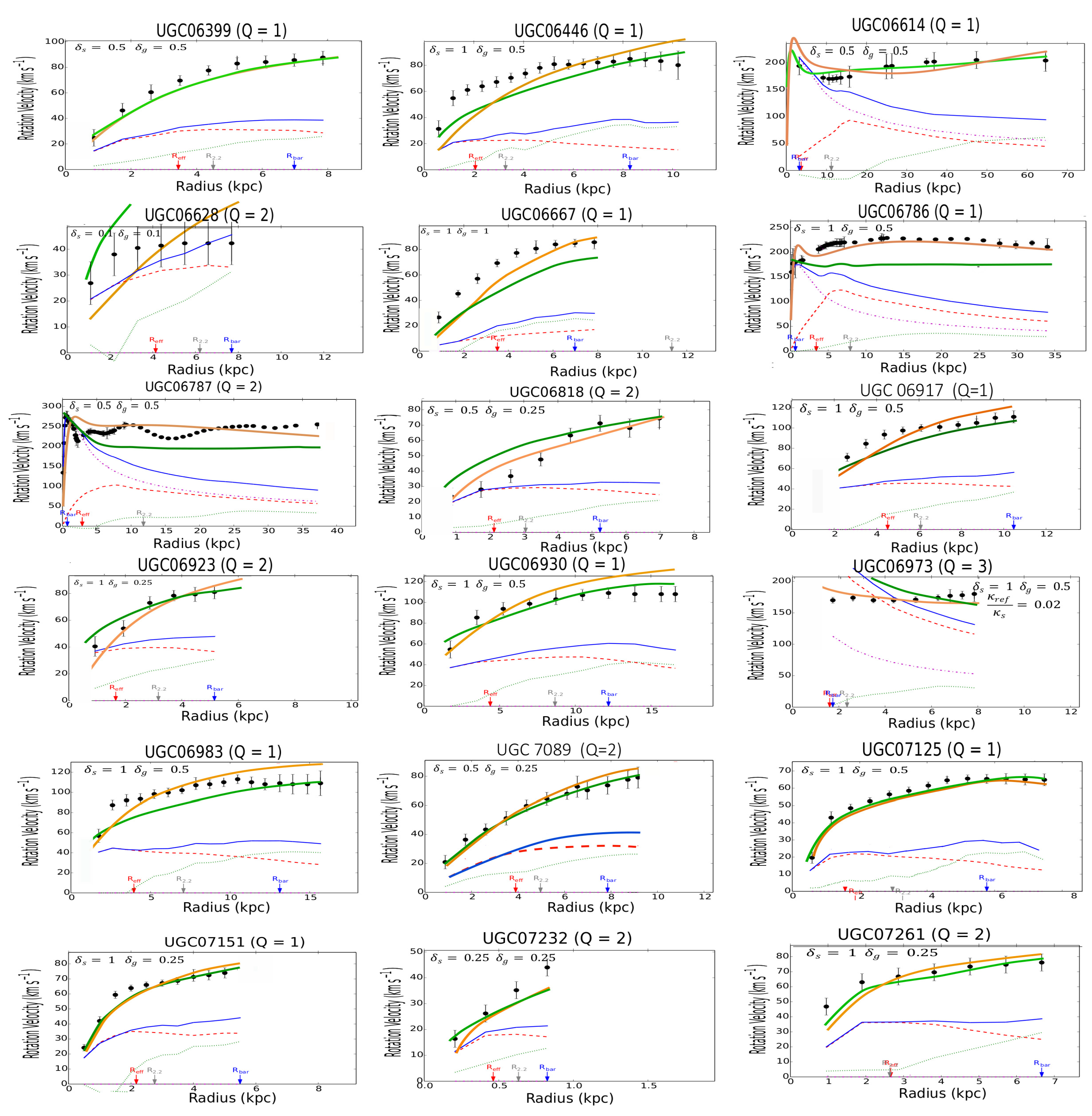
Figure A : Continued rotation profiles
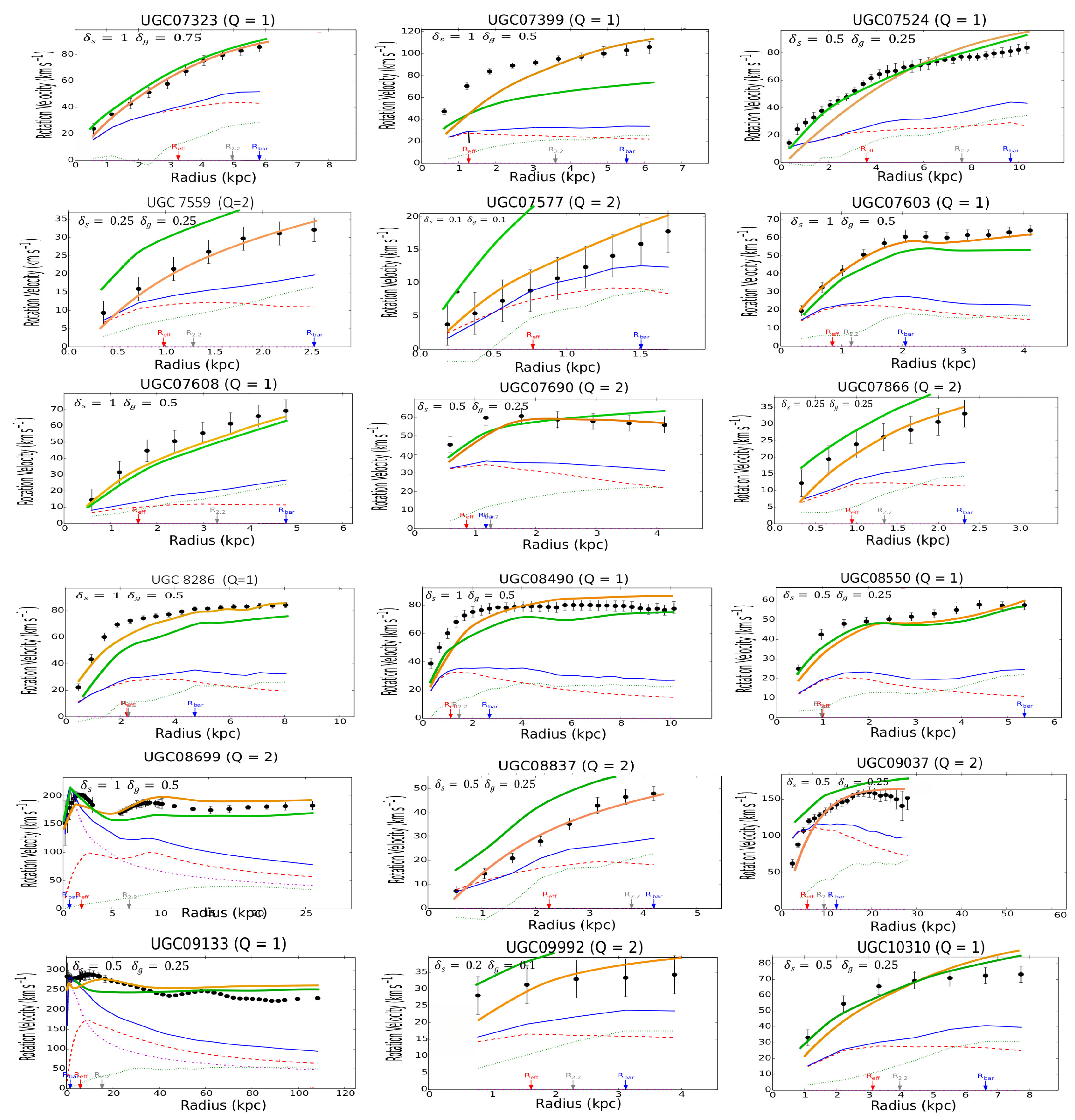
Figure A : Continued rotation profiles
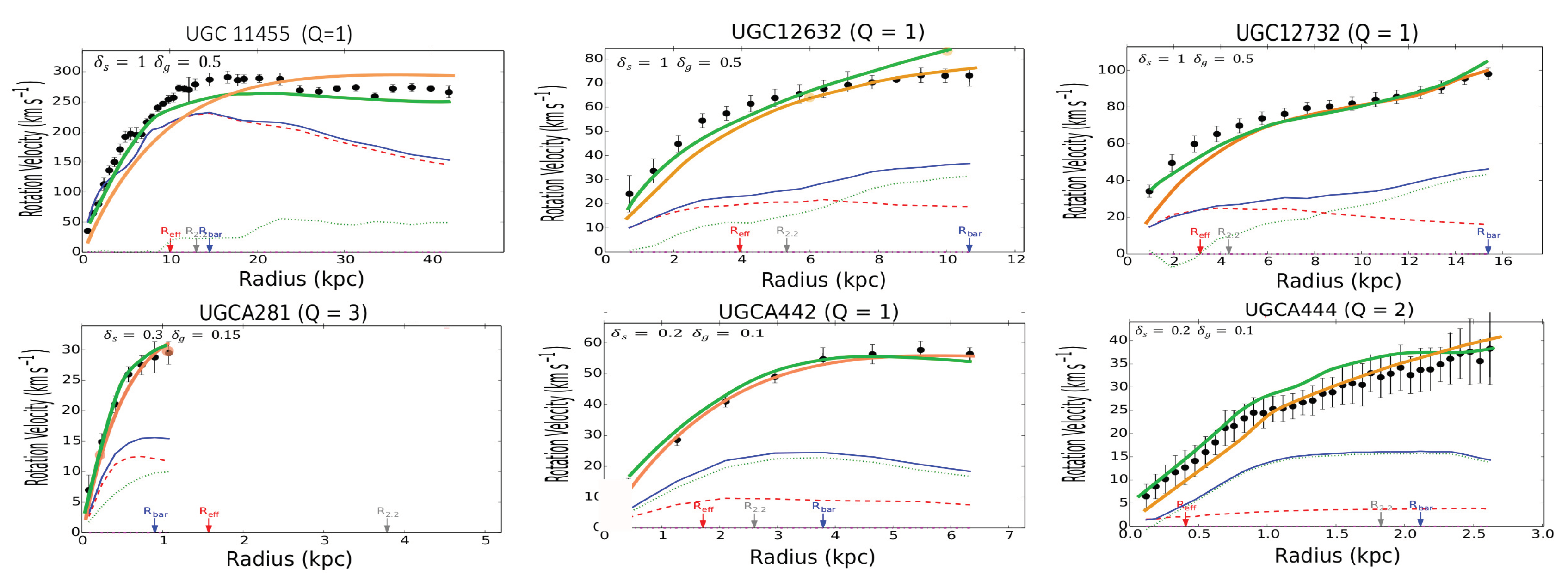
Figure A : Continued rotation profiles
Data Availability Statement
The author confirms that the data supporting the findings of this study are available within the article and the reference list.
Acknowledgments
The author sincerely thanks the three referees whose suggestions and corrections improved this paper.
Conflicts of Interest
The author declares no conflict of interest.
References
- Mirhosseini A. and Moniez M., A&A, 2018, 618, L4.
- Ackermann M., et al., Phys. Rev. Lett., 2015, 115, 231301.
- Battaglieri M. et al, 2017, arXiv:1707.04591 [hep-ph].
- Amaudruz P A et al., (DEAP Collaboration) Astropart. Phys., 2019, 108, 1.
- Amaudruz P A et al., (DEAP Collaboration) Nucl. Instrum. Methods Phys.Res. A, 2019, 922, 373.
- Arnquist I. et al (Damic-M Collaboration), Physical Review Letters, 2023, 130, 171003.
- McGaugh S., Can. J. Phys., 2015, 93, 250.
- Di Paolo C. Salucci P. and Erkurt A., MNRAS, 2019, 490, 5451.
- Milgrom M., Astrophysical Journal, 1983, 270, 365.
- Milgrom M., Can. J. Phys., 2015, 93(2), 107.
- Milgrom M., Studies in History and Philosophy of Modern Physics, 2020, 7,170.
- McGaugh S., Astrophys. J., 2005, 632, 859.
- Famey B. and Mc Gaugh S., Living Rev. Relativity, 2012, 15, 10.
- Hodson A.O. and Zhao H., A&A, 2017, 598, A127.
- Skordis C, and Złośnik T., Phys. Rev. Lett., 2021, 127, 161302.
- Pascoli G., Can. J. Phys., 2023, 101, 11.
- Moffat, J.W., JCAP, 2006, 2006, 004.
- Rouhani S., and S. Rahvar S., MNRAS, 2024, 427, 2831.
- Mannheim P.D., Prog.Part.Nucl.Phys. 2006, 56, 340.
- Li Q., and Modesto L., Grav. Cosmol., 2020, 26, 99.
- Ghosh S., Bhattacharya M., Sherpa1 Y., and Bhadra A., JCAP, 2023, 07, 008.
- Verlinde E., SciPost Phys., 2017, 2, 016.
- Varieschi G., Found Phys., 2020, 50, 1608.
- Cesare V., Diaferio A., Matsakos T., and Angus, G. 2020, A&A, 637, A70.
- Pascoli, G., and Pernas, L., 2020, hal.archives-ouvertes.fr/hal-02530737.
- Pascoli G., Astrophys. Space Sc., 2022, 367, 62.
- Pascoli G., arXiv:2307.01555 [astro-ph.CO]. arXiv:2307.01555 [astro-ph.
- Calcagni G., JCAP, 2013, 12, 041.
- Varieschi G., Eur. Phys. J. Plus, 2021, 136, 183.
- Varieschi G., 2021, MNRAS. 503 2, 1915.
- Varieschi G., Eur. Phys. J. Plus, 2022, 137, 1217.
- Varieschi G., Universe, 2023, 9(6), 246.
- Cesare V., Diaferio A., and Matsakos T., 2022, A&A, 657, A133.
- Cesare V., Universe, 2023, 9, 56.
- Lelli F., McGaugh S.S., and Schombert J.M., Astron. J., 2016, 152,157.
- Valenti, E., Zoccali, M., Mucciarelli, A., Gonzalez, O.A., Surot1, F., Minniti, D., Rejkuba1, M., Pasquini, L., Fiorentino, G., Bono, G., Rich, R.M., and Soto, M., A&A, 2018, 616, A83.
- Ogle P. M., Jarrett T., Lanz L., Cluver M., Alatalo K., Appleton P.N. and Mazzarella J. M., ApJ. Letters, 2019, 884.
- Lisenfeld, U., Ogle, P.M., Appleton, P.N., Jarrett, T.H., and Moncada-Cuadri, B.M., 2023, A&A, 673, A87.
- de Vaucouleurs, G. 1958, ApJ, 128, 465.
- Yoachim P. and Dalcanton J..J, AJ, 2006, 131, 226.
- Johnson M.C., Hunter D.A., Kamphuis P., and Wang J. MNRAS, 2017, 465, L49.
- Li X., Shi Y., Zhang Z.Y., Chen J., Yu X., Wang J., Gu Q., and Li S., MNRAS, 2022, 516, 4220.
- Merritt, D., Graham, A. W., Moore, B., Diemand, J. and Terzić, B., AJ, 2006, 132, 6, 2685.
- Li P., Thesis, Case Reserve Western University, 2020.
- Ghari A., Famaey B., Laporte C., and Haghi H., A&A, 2019, 623, A123.
- Sofue Y. 2015 PASJ, 68, 2. 2015; 68.
- Mc Gaugh S.S., ApJ, 2019, 885, 87.
- Mancera Piña P.E., Fraternali F., Oosterloo T., Adams E.A.K., Oman K.A., and Leisman L., MNRAS, 2022, 512, 3230.
- Mc Gaugh S., Studies in History and Philosophy of Science, 2021, 88 suppl C, 220. [CrossRef]
- Loizeau N. and Farrar G.R., ApJ Letters, 2021, 920, L10.
- Randriamampandry T.H and Carignan C., MNRAS, 2014, 439, 2132.
- Haghi H., Bazkiaei A.E., Zonoozi A.H., and Kroupa P., MNRAS, 2017, 469, 3909.
- Nieuwenhuizen T. M., 2017, Fortschr. Phys., 65, 201600050.
- Hernandez X., Verteletskyi V., Nasser L., and Aguayo-Ortiz A., arXiv:2309.10995v2.
- Banik I., Pittordis C., Sutherland W., Famaey B., Ibata R., Mieske S., and Zhao H., arXiv:2311.03436v1.
| 1 | In the context of MOND, a multiscale approach adapts the parameter to the size of the system studied. However, in this case the parameter is no longer universal. |
| 2 | How the -model performs with lensing is presented in the reference [16]. |
| 3 | The Weyl CFT is built by replacing the Einstein-Hilbert Lagrangian density, proportional to the Ricci curvature scalar, by a quadratic contraction of the conformal Weyl tensor. |
| 4 | A superlens is a flat, lightweight option that can replace bulky traditional lenses and other components in optical systems. It is a lens that goes beyond the diffraction limit. |
| 5 | A list of DM methods with two or three ad hoc parameters is presented in the references [43,44]. |
| 6 | The MOND profiles have been obtained with the formula
|
| 7 | We can remark that whereas some authors affirm that the MOND fits are fairly good [47,49], on the other hand, other authors, who rather seem to defend the DM paradigm, conclude that the MOND fits are bad in a large percentage of analyzed individual cases [50,51]. It is true that MOND gives fairly acceptable fits in a large number of cases and is less good in other cases. This situation can easily be explained if we admit that the mass-to-light ratios, the inclinations, and the distances are poorly known. We can then postulate that MOND systematically provides "perfect" fits and can then predict the inclinations and distances. A contrario DM fits are apparently better but, ironically enough, even if we choose a bad inclination or an erroneous distance. |
| 8 | Once again in the framework of the -model starting from the Newtonian curves, we generate a predictive profile for the observational one in an univocal manner. The baryonic mean mass density alone is the conductor of the situation. |
Figure 1.
Schematic galaxy velocity curves fitted with a simple exponential surface mass density profile of uniform thickness (in the approximation of the thin disk). MOND is the green line, and the -model is the amber line. The dashed red line is the Newtonian curve (baryons). The reference value for the surface density is .
Figure 1.
Schematic galaxy velocity curves fitted with a simple exponential surface mass density profile of uniform thickness (in the approximation of the thin disk). MOND is the green line, and the -model is the amber line. The dashed red line is the Newtonian curve (baryons). The reference value for the surface density is .
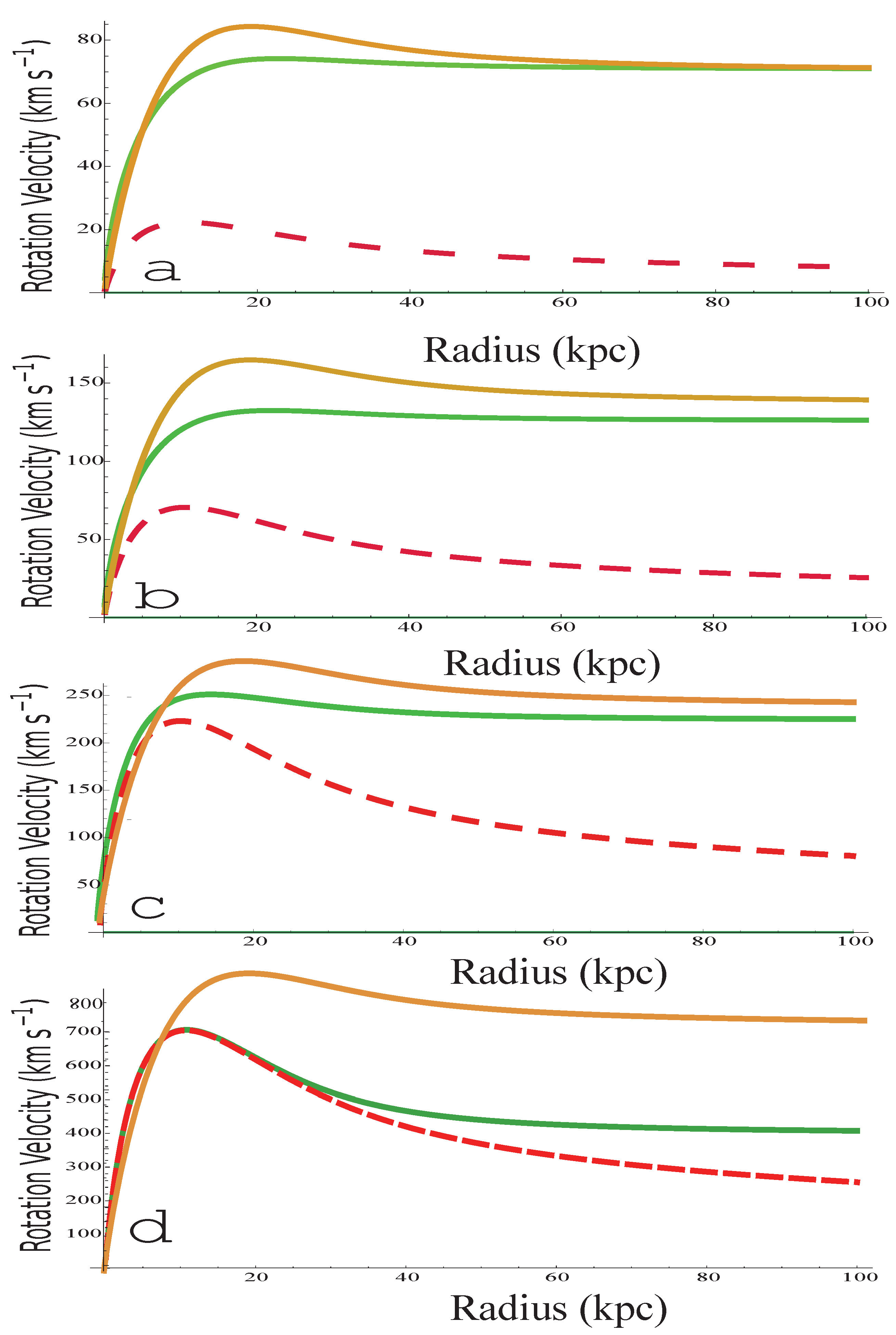
Figure 2.
The terminal velocities for the sample of galaxies (SPARC data base). MOND is in green, the -model is in amber, and the observed velocities, provided by the SPARC database, are represented in black. Linear regression lines are also represented.
Figure 2.
The terminal velocities for the sample of galaxies (SPARC data base). MOND is in green, the -model is in amber, and the observed velocities, provided by the SPARC database, are represented in black. Linear regression lines are also represented.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated





