The Circular Fluid Heating – Transient Entropy Generation

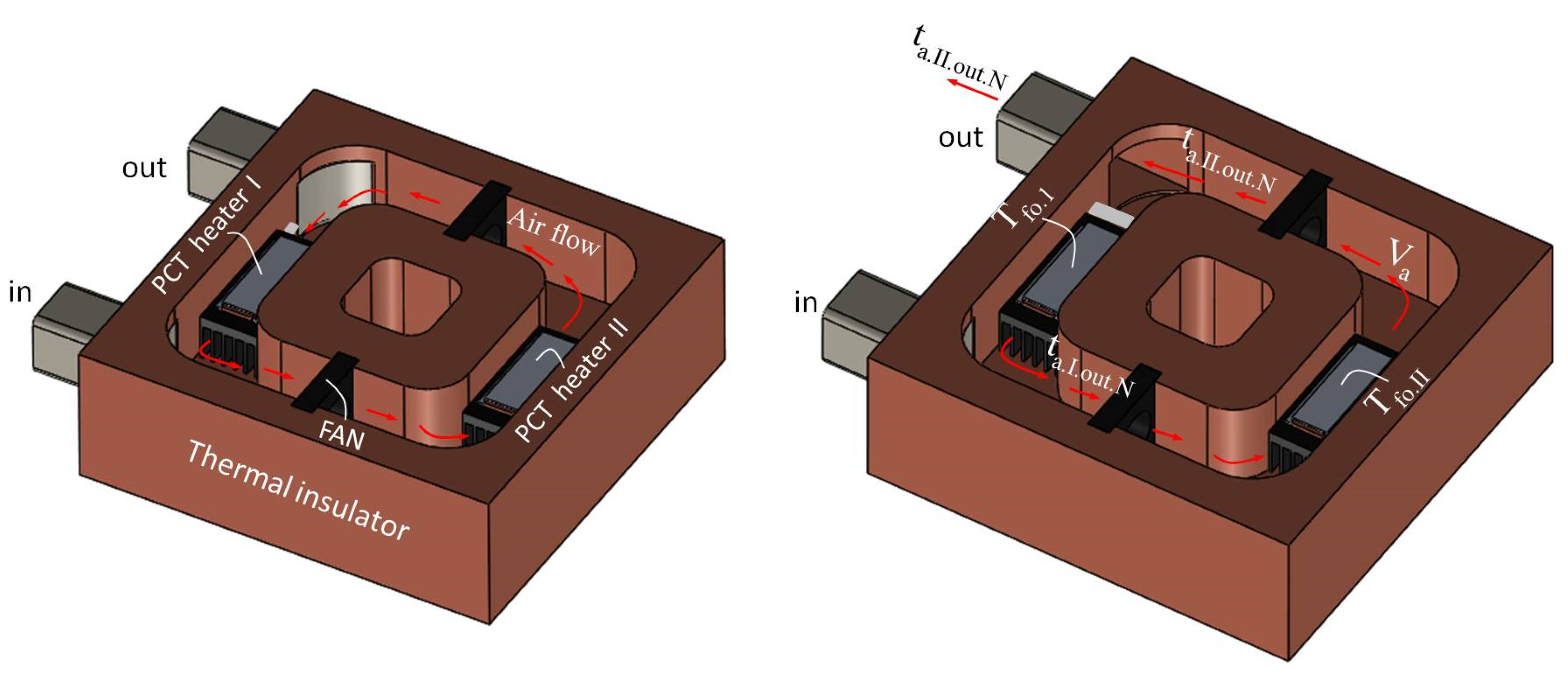
1. Introduction

Convective fluid heating is carried out inside the channels of various shapes and dimensions so that the heat directly or indirectly passes from the heater to the fluid. The convective surface is often finned so that the total heat transfer taken by the fluid is increased. In addition to increasing heat exchange, a larger and more compact convective surface causes a pressure drop of the fluid. Thus, the maximization of heat transfer by using finned heating channels is accompanied by an increase in hydraulic fluid losses. In various process heating systems, the source is an electric heater that is integrated on the finned surface. In most cases, a constant heat flux is established between the convective surface of the heater and the fluid, while the temperature of its surface is variable. Furthermore, heaters of various shapes and sizes were placed within the channel, which convectively heated the fluid. Circular fluid flow within a closed loop and thermal interaction of the fluid with the heat source and heat receiver is a very common case in various process applications. A large number of researchers have analyzed and examined the forced cooling and heating of fluids within closed loops. Research is usually focused on the heat exchange between the heat source and the heat sink. Experimental testing of the natural heating of different fluids within a closed loop was carried out by several researchers, Ma, Lei et al. [1], Archana et al. [2], Sharma et al. [3], and Zixu Hu et al. [4]. Closed channels for fluid transfer between heat source and sink can be found in various technical systems and devices, examples are engine cooling, geothermal heating and solar panels. Heat transfer within a closed loop with thermoelectric generators, compact heat sink and working fluid was analyzed by several researchers, Songkran and Paisarn [5], Siddique et al. [6]. Many researchers analyzed the effects of various convective elements within the different tubes, on heating efficiency, (Chang et al. [7]; Chyu [8]; Hsiao et al. [9], Wang et al.[10]. Alic [11,12] studied the combination of profiled heating elements of different powers inline placed inside the channel and their influence on total irreversibility. Minimizing the entransy dissipation of different cross-sections of rube tube heat exchanger is investigated by Wei et al. [13]. Wu and Liang [14] analyze the entransy dissipation extrememum even with established radiative heat transfer. In this analysis, an analytical model of thermal and hydraulic entropy due to fluid flow through heating elements is implemented. Based on previous analyzes and research, the idea was initiated that the fluid is heated multiple times before the fluid exits the heating channel. In most process cases, the fluid passes through the convective heating surfaces, heats up and leaves the heating device. In order to achieve the required temperature of the fluid, the electric power of the heating sources is increased or its flow is reduced. Both of the mentioned procedures cannot always be applied within process systems. Therefore, in the conducted analysis included in this paper, the fluid (air) is heated multiple times within the channel with two installed finned heating sources. The closed circular channel inside the thermal insulation case is connected to the inlet and outlet pipelines with installed valves. Air flow inside the channel is provided by an axial fan. After reaching the required temperature, the outlet channel is opened and the hot air leaves the housing, while the process of heating the incoming air continues.

2. Methodology

2.1. Analytical Approach

Two finned heating surfaces with straight longitudinal fins are located inside the profiled housing made of thermal insulation material. The heating of the finned surfaces is established by electric PTC heaters, which ensures a constant temperature at the bottom of the fins, Figure 1. In the conducted analytical approach, it is considered that the temperature of the heat sources is constant during the heating time. The circular flow of air through the heating fins is provided by an axial fan. During the air heating process, the inlet and outlet channels of the housing are closed, while the air flows circularly through both heaters, Figure 1a. The air temperature at the exit from the first PTC heater A represents the temperature entering the PTC heater A and the heating process is continuously repeated. After the circular air heating through both heaters, its temperature reaches the required temperature, and then the outlet channel opens, Figure 1b. After the exit of the hot air from the housing, the outlet channel is closed and the process is repeated with the entry of unheated air through the inlet channel. The heat balance covered by this analysis implies a forced circular convective heating of the air within the housing channel. The convective surface of both finned surfaces consists of the fins and the interfin surface.

For case A, the temperatures of both PTC heaters are the same (t_fo.I = t_fo.II = t_fo), the heat balance is established within the sections of both heating finned sources and the fluid (air), Eq(1). It is assumed that the current mean air temperature inside the entire enclosure is constant and increases during time. The final air temperature is equal to the required temperature during the heating process. The established methodology gives the possibility that both finned heaters have different dimensions and characteristics. For the analyzed case A, the transient air temperature is obtained from the balance,

$${\rho }_a{c}_a{V}_a\frac{d{t}_{a.A}}{d\tau }={\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)\left(t_{fo}-t_{a.A}\right)+{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)\left(t_{fo}-t_{a.A}\right)$$

(1)

and after separating the variables

$$\frac{d{t}_{a.A}}{t_{fo}-t_{a.A}}=\left[\frac{{\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)+{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)}{{\rho }_a{V}_a{c}_a}\right]d\tau$$

(2)

by introducing the same average air temperatures

$${t_{a1}=t}_{a1.I}=\frac{t_{a1.I.in}+t_{a1.I.out}}{2}=\left|\begin{array}{c}{t}_{a1.I.in}=t_{a1.II.out}\\ t_{a1.II.out}=t_{a1.I.in}\end{array}\right|=\frac{t_{a1.II.in}+t_{a1.II.out}}{2}=t_{a1.II}$$

(3)

and after integrating equation (2), the transient temperature of the air inside the profiled heated housing is

$$t_{a.A}\left(\tau \right)=t_{fo}-\left(t_{fo}-t_{a.o}\right)exp\left[\frac{{-\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)-{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)}{{\rho }_a{V}_a{c}_a}\tau \right]$$

(4)

where V_a is the volumetric air flow through the channel, t_a.o is the initial air temperature, t_fo is the temperature of the inter-finned surface and the bottom of the fin, while α_I and α_II are the convective heat transfer coefficients in the finned heating sources. The temperature t_fo is kept constant by using a PCT heater installed at the bottom of the finned surface, Figure 1. For case B, the temperatures of the PTC heaters (t_fo.I, t_fo.II) are different, the transient change in air temperature is obtained from the balance,

$${\rho }_a{c}_a{V}_a\frac{d{t}_{a.B}}{d\tau }=\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)\left(t_{fo.I}-t_{a.B}\right)+\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)\left(t_{fo.II}-t_{a.B}\right)$$

(5)

and after the separation of variables and integration, the transient air temperature is obtained, Eq(6).

$$\begin{gathered} t_{a.B}\left(\tau \right)=\left[t_{a.o}-\frac{{\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)\mathrm{}{t}_{fo.I}+{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)t_{fo.II}}{{\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)+{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)}\right] \\ exp\left\{-\frac{\left[{\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)+{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)\right]}{{\rho }_a{V}_a{c}_a}\tau \right\} \\ +\frac{{\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)\mathrm{}{t}_{fo.I}+{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)t_{fo.II}}{{\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)+{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)} \end{gathered}$$

(6)

In the previous equations, the conductive coefficient of heat transfer within the channel calculated according to expression (7).

The convective heat transfer coefficient for the case of fluid flow between two vertical parallel walls (longitudinal fins), according to Teertstra et al. [15], is

$$\alpha =\frac{{\lambda }_a}{\delta }{\left[{\left(\frac{{PrRe}_{\delta }^{*}}{2}\right)}^{-3}+{\left(0.664{Pr}^{\frac{1}{3}}\sqrt{{Re}_{\delta }^{*}}·\sqrt{1+\frac{3.65}{\sqrt{{Re}_{\delta }^{*}}}}\right)}^{-3}\right]}^{-\frac{1}{3}}$$

(7)

where modified Reynolds number is

$${Re}_{\delta }^{*}={Re}_{\delta }\left(\frac{\delta }{L}\right)=\frac{w_a\delta }{{\nu }_a}\left(\frac{\delta }{L}\right)=\frac{w_a}{{L\nu }_a}{\delta }^2.$$

(8)

$${Re}_{D_h}=\frac{w_{ch}}{{\nu }_a}{D}_h=w_{a.o}\left(1+\frac{{\delta }_f}{\delta }\right)\frac{1}{{\nu }_a}\frac{{4A}_{ch}}{P_{ch}}=w_{a.o}\frac{\left(\delta +{\delta }_f\right)}{\left(\delta +h\right)}\frac{2h}{{\nu }_a}$$

(9)

where δ_f is the fin thickness, Re_Dh channel Reynolds number, D_h hydraulic diameter of the channels, w_ch fluid velocity inside the channel, w_a.o the velocity of the fluid immediately before entering the channel, δ fin spacing. The mean temperature of the fin at its height h was obtained according to the boundary conditions; a) the temperature at the bottom of the fin has a constant value t_fo , b) the top of the fin is thermally insulated, so it can be represented by the expression,

$$t_f=\frac{1}{h}\underset{0}{\overset{h}{\int }}{t}_f\left(y\right)dy=\frac{1}{h}\underset{0}{\overset{h}{\int }}\left\{t_a+\left(t_{fo}-t_a\right)\frac{cosh\left[{\left(\frac{\alpha P}{A_f{\lambda }_f}\right)}^{0.5}\left(h-y\right)\right]}{cosh\left[{\left(\frac{\alpha P}{A_f{\lambda }_f}\right)}^{0.5}h\right]}\right\}dy{=t}_a+\left(t_{fo}-t_a\right)\frac{tanh\left[mh\right]}{mh}$$

(10)

where m=(αP/λ_fA_f)^0.5 fin parameter, P fin perimeter, A_f the cross-sectional area of the fin, and λ_f is the conductive heat transfer coefficient of the fin. The characteristic dimensions of the channels, finned surfaces and the process characteristics of the analyzed circular air heating are shown in Table 1.

During the circular heating of air inside a closed channel with finned PTC heating sources, at constant temperatures, there is a continuous increase in its temperature. In the conducted analysis, the avearge temperature of the fin along its length L is used. As a result of the heat exchange between the finned heating sources and the air that flows within the housing channel, transient thermal irreversibilities or thermal entropy occur.

For the analyzed cases A and B, the transient thermal entropy of air in the process of circular heating can be represented by expressions (11) and (12), respectively.

$$S_{gen.a.A}\left(\tau \right)=\frac{d}{d\tau }\left[{\rho }_a{V_{a}c}_{a}ln{T}_{a.A}\left(\tau \right)\right]=\frac{\left[{\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)+{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)\right]}{T_{a.A}\left(\tau \right)}\left(T_{fo}-T_{a.o}\right)exp\left[\frac{{-\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)-{\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)}{{\rho }_a{V}_a{c}_a}\tau \right]$$

(11)

$$S_{gen.a.B}\left(\tau \right)=\frac{d}{d\tau }\left[{\rho }_a{V_{a}c}_{a}ln{T}_{a.B}\left(\tau \right)\right]=\left|\begin{array}{c}where\\ \begin{array}{c}{C}_1={\alpha }_I\left(A_{fo.I}+{\eta }_{f.I}{A}_{f.I}\right)\\ C_2={\alpha }_{II}\left(A_{fo.II}+{\eta }_{f.II}{A}_{f.II}\right)\end{array}\end{array}\right|=-\frac{\left\{T_{a.o}\left(C_1+C_2\right)-\left[T_{fo.I}{C}_1+T_{fo.II}{C}_2\right]\right\}}{T_{a.B}\left(\tau \right)}exp\left[-\frac{\left(C_1+C_2\right)}{{\rho }_a{V}_a{c}_a}\tau \right]$$

(12)

The transient thermal entropy of the heating PTC source includes the thermal irreversibility of its finned and non-finned surface inside the housing. The temperature of the fins is adopted as the average value (T_f.avr ), while the temperature of the surface between the fins is constant (T_fo ). For case A, the thermal entropy of the heat source has the form,

$$\begin{gathered} S_{gen.hs.A}\left(\tau \right)=-\frac{Q_{fins.A}}{T_{f.avr}}-\frac{Q_{no.fins.A}}{T_{fo}} \\ =-\frac{{\alpha }_I{A}_{f.I}\left(T_{f.I.avr}-T_{a.A}\right)}{T_{a.A}+\left(T_{fo}-T_{a.A}\right){\eta }_{f.I.avr}}-{\alpha }_{II}{A}_{fo.II}\left(1-\frac{T_{a.A}}{T_{fo}}\right) \\ -\frac{{\alpha }_I{A}_{f.II}\left(T_{f.II.avr}-T_{a.A}\right)}{T_{a.A}+\left(T_{fo}-T_{a.A}\right){\eta }_{f.II.avr}}-{\alpha }_I{A}_{fo.II}\left(1-\frac{T_{a.A}}{T_{fo}}\right) \end{gathered}$$

(13)

while for case B

$$\begin{gathered} S_{gen.hs.B}\left(\tau \right)=-\frac{Q_{fins.I}}{T_{f.avr.I}}-\frac{Q_{no.fins.I}}{T_{fo.I}}-\frac{Q_{fins.II}}{T_{f.avr.II}}-\frac{Q_{no.fins.II}}{T_{fo.II}} \\ =-\frac{{\alpha }_I{A}_{f.I}\left(T_{f.I.avr}-T_{a.A}\right)}{T_{a.A}+\left(T_{fo}-T_{a.A}\right){\eta }_{f.I.avr}}-{\alpha }_{II}{A}_{fo.II}\left(1-\frac{T_{a.A}}{T_{fo}}\right) \\ -\frac{{\alpha }_I{A}_{f.II}\left(T_{f.II.avr}-T_{a.A}\right)}{T_{a.A}+\left(T_{fo}-T_{a.A}\right){\eta }_{f.II.avr}}-{\alpha }_I{A}_{fo.II}\left(1-\frac{T_{a.A}}{T_{fo}}\right). \end{gathered}$$

(14)

2.2. Experimental Approach

In order to verify the results obtained on the basis of analytical modeling, a test module was created that fully corresponds to the model that was previously analytically modeled. Two PCT heaters are located inside the thermal insulation housing, located in a channel of square cross-section, Figure 2. Measurement of inlet air temperature and the temperature of the first heater was measured using an Omegaetee temperature humidity meter, HH314. The air temperature inside the housing of one heater were measured using a precision 0.01 degree thermometer Lutron TM-917. Air flow was measured with a Lutron YK-2005AH hot wire anemometer. The geometrical characteristics of the housing, the finned surface and the power of the heater are shown in Table 1. Experimental determination of the air thermal entropy is carried out indirectly based on the results of measuring its temperature. Air temperature is measured directly and is approximated by a polynomial function which is differentiated by time. A finned heating surface with longitudinal heating fins and an installed PTC heater is shown in Figure 2. The thermogram of the described heating system is shown in the same figure. To conduct the experimental test, two heating assemblies (finned surface and heater) of different temperatures and power were used.

During the test time, the volumetric air flow is constant. The thermal entropy of the heating sources was determined in the same way, so that the total thermal entropy of the analyzed heating system is shown by equation (15).

$$\begin{gathered} S_{gen}\left(\tau \right)=\frac{d}{d\tau }\left[{\rho }_a{V_{a}c}_{a}ln{T}_{a.A}\left(\tau \right)\right]-\frac{d}{d\tau }\left[m_{hs}{c}_{hs}ln{T}_{hs.A}\left(\tau \right)\right]-\frac{d}{d\tau }\left[m_{hs}{c}_{hs}ln{T}_{hs.B}\left(\tau \right)\right] \\ =\left|\begin{array}{c}{T}_{a.A}\left(\tau \right)=A{\tau }^2+B\tau +C\\ A,B,C\to const.\\ \begin{array}{c}{T}_{hs.A}\left(\tau \right)=D{\tau }^2+E\tau +F\\ D,E,F\to const.\\ T_{hs.B}\left(\tau \right)=G{\tau }^2+H+I\\ G,H,I\to const.\\ V_a=const.\end{array}\end{array}\right|={\rho }_a{V_{a}c}_a\frac{2A\tau +B}{A{\tau }^2+B\tau +C}-{m_{hs}c}_{hs}\left[\frac{2D\tau +E}{D{\tau }^2+E\tau +F}+\frac{2G\tau +H}{G{\tau }^2+H\tau +I}\right] \end{gathered}$$

(15)

3. Results and Discussion

The analysis carried out included the convective air heating inside a closed channel in a heat-insulating casing with a total length of 1.3m. Two PTC heaters are placed inside the channel on a longitudinal finned surface with a total length of 0.1m. The volumetric air flow and the length of its heating are variable and limited to 0.00006 m³s^-1 and 60s, respectively. Constant temperatures of heating sources of 423K and 473K are ensured by using PTC heaters. The initial air temperature inside the housing is 293K. In both examined cases, A and B, two identical finned surfaces were used with the geometric parameters shown in Table 1. In case A, both heaters have the same temperature of 423K, so the change in air temperature is shown in Figure 3a. Furthermore, in the same figure, Figure 3b, the change in air temperature at a constant temperature of both heating sources of 473K is shown. A rapid increase in air temperature occurs with an increase in air flow and heating time. The maximum air heating time is 60s. In Figure 3b, the temperature of one heating source is 423K while the temperature of the other is 473K, while the flow rate and heating time are varied.

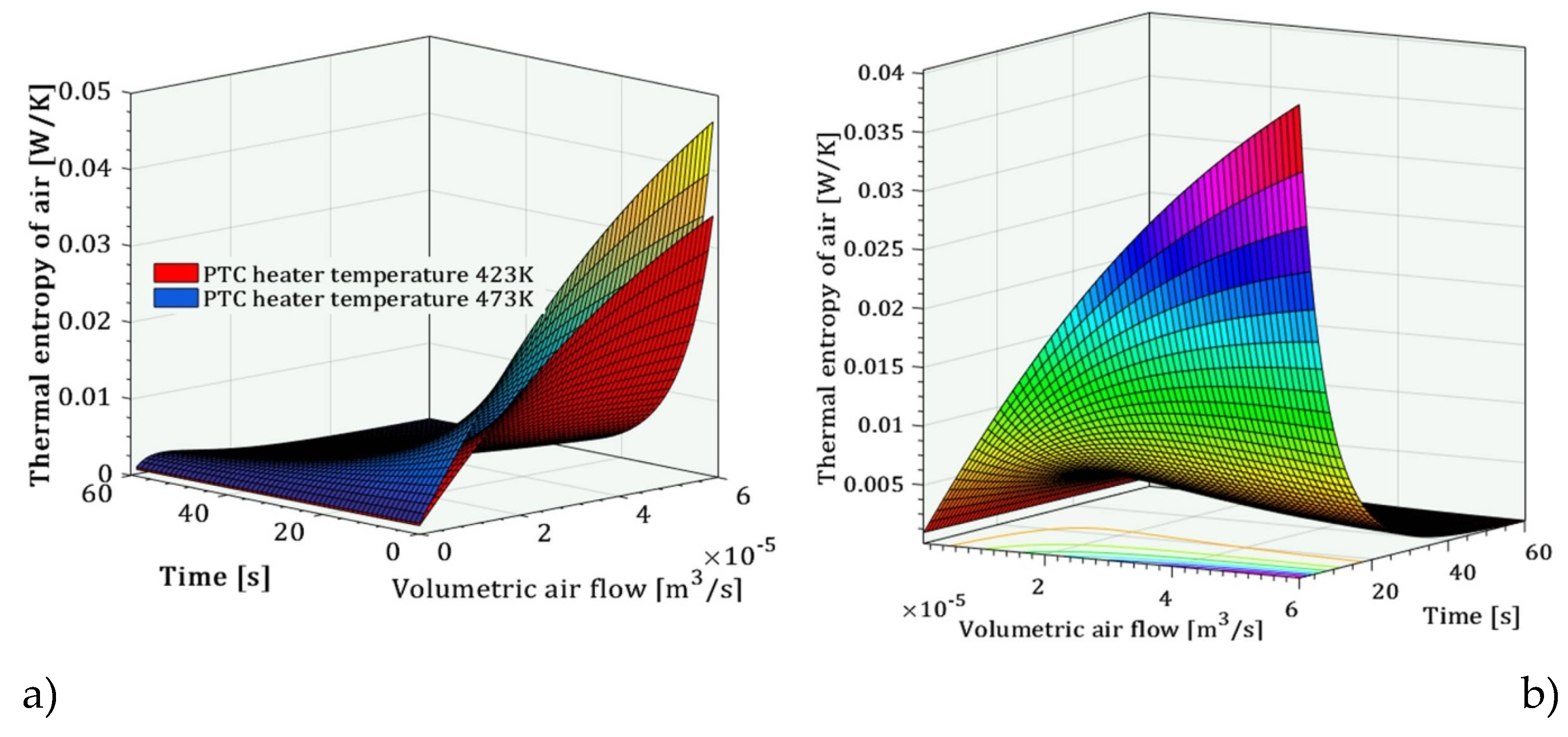
Thermal entropy of the air during circular flow in a closed channel is shown in Figure 4. The hydraulic entropy was not included in this analysis. The rapid increase in the thermal entropy of the air is caused by the increase in the temperature of the heating sources, from 423K to 473K. In Figure 4a, the temperatures of the heating sources are the different and constant, while Figure 4b shown constant temperature of both heating sources of 473K.

The thermal entropy of the heating source has a negative value and increases in absolute value with the increase of volumetric air flow, Figure 5. In Figure 5a, the temperatures of the heating sources are the different and constant, while Figure 5b shown constant temperature of both heating sources of 473K.

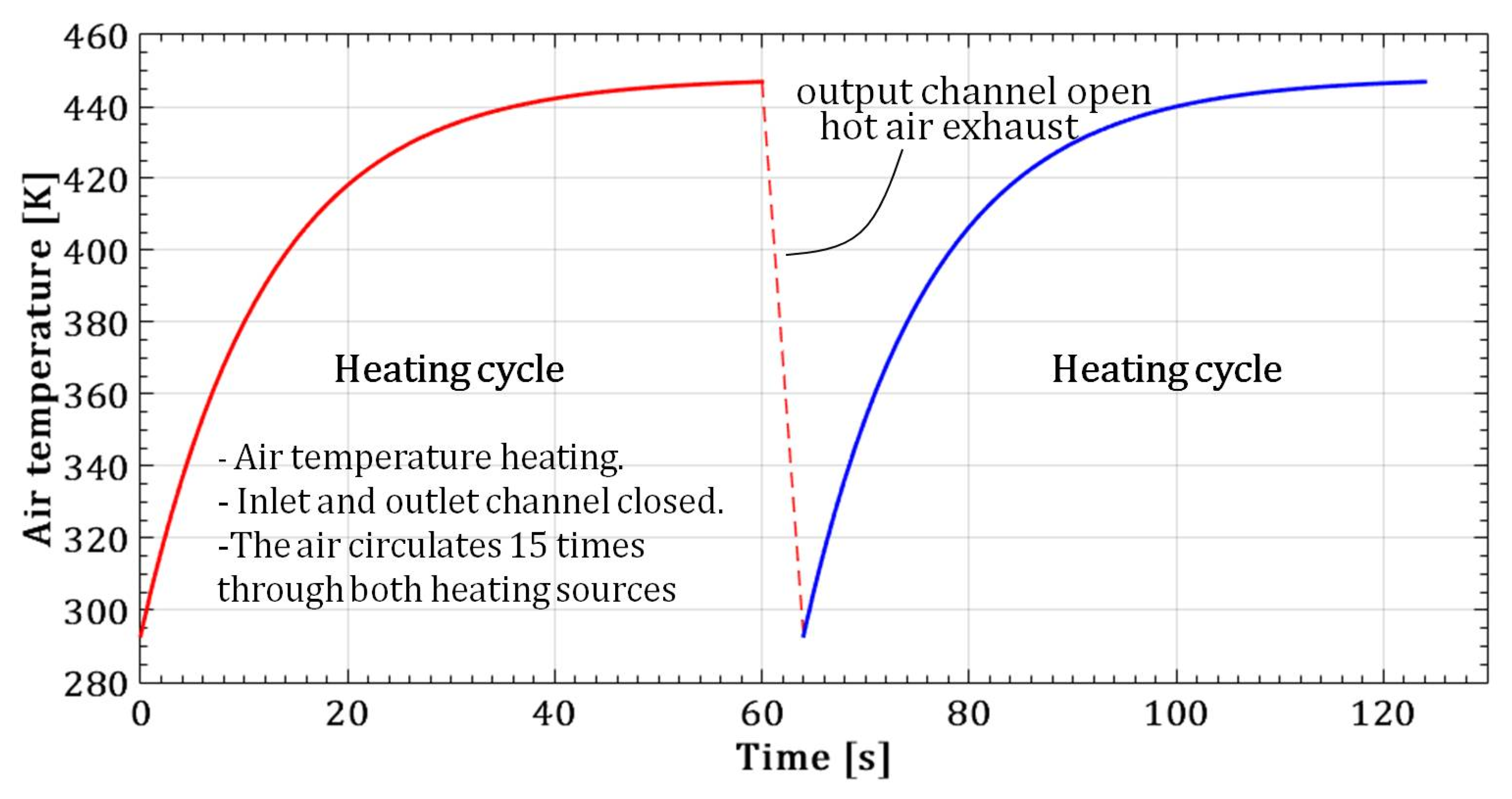
According to the established circular process of air heating inside the profiled closed channel, its required final temperature depends on several factors. At a constant temperatures of two heating sources of 423K and 473K and air flow rate of 0.00005 m³s^-1, during 60s of heating, the increase in air temperature is shown in Figure 6. Since the total length of both heating sources is 0.2m while the length of the closed channel is 1m, the air flows cyclically 15 times through each heating source in the course of 60s. After reaching a temperature of about 450K, the outlet channel opens and the hot air leaves the housing. The process of heating the air that entered the housing continues after the outlet valve is closed, Figure 1 and Figure 6.

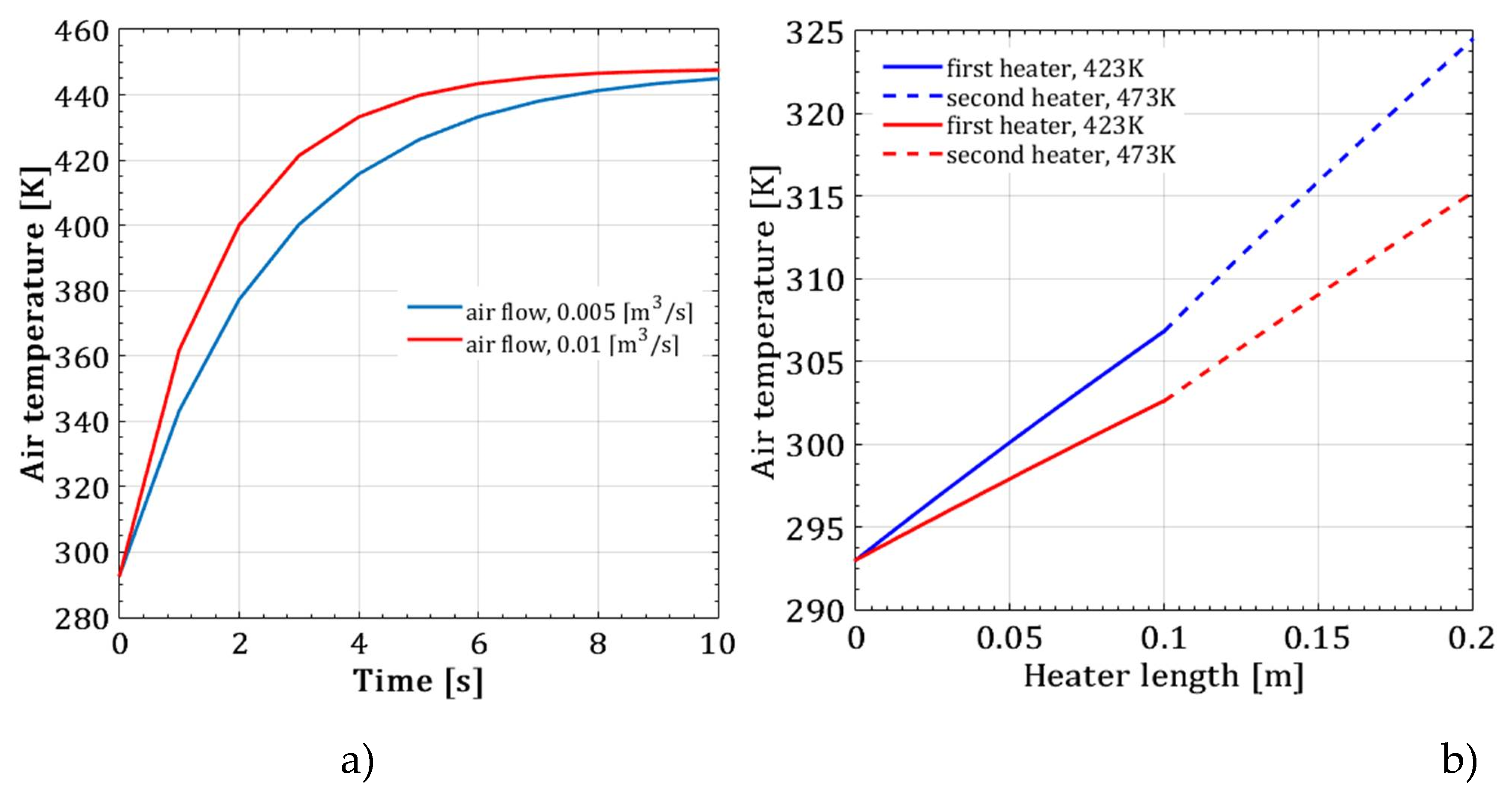
If the air volumetric flow through the channel increases several times, at values of 0.005 m³s^-1 and 0.01m³s^-1, the required air temperature of 450K is achieved in time up to 10s, Figure 7a. A higher air volumetric flow ensures a increased air velocity and a shorter time to reach its required temperature during its circular heating. Under the same process conditions, in case the air is heated in an open channel during a single passage of air, the exit temperature of the air is many times lower, Figure 7b. Compared to the previous case, the air outlet temperature decreases due to the shorter heating time inside both channels with a total length of 0.2m. At a lower flow rate of 0.005 m³s^-1, the outlet air temperature is about 325K, which is about 120K lower compared to air circular heating at the same flow rate, Figure 7a.

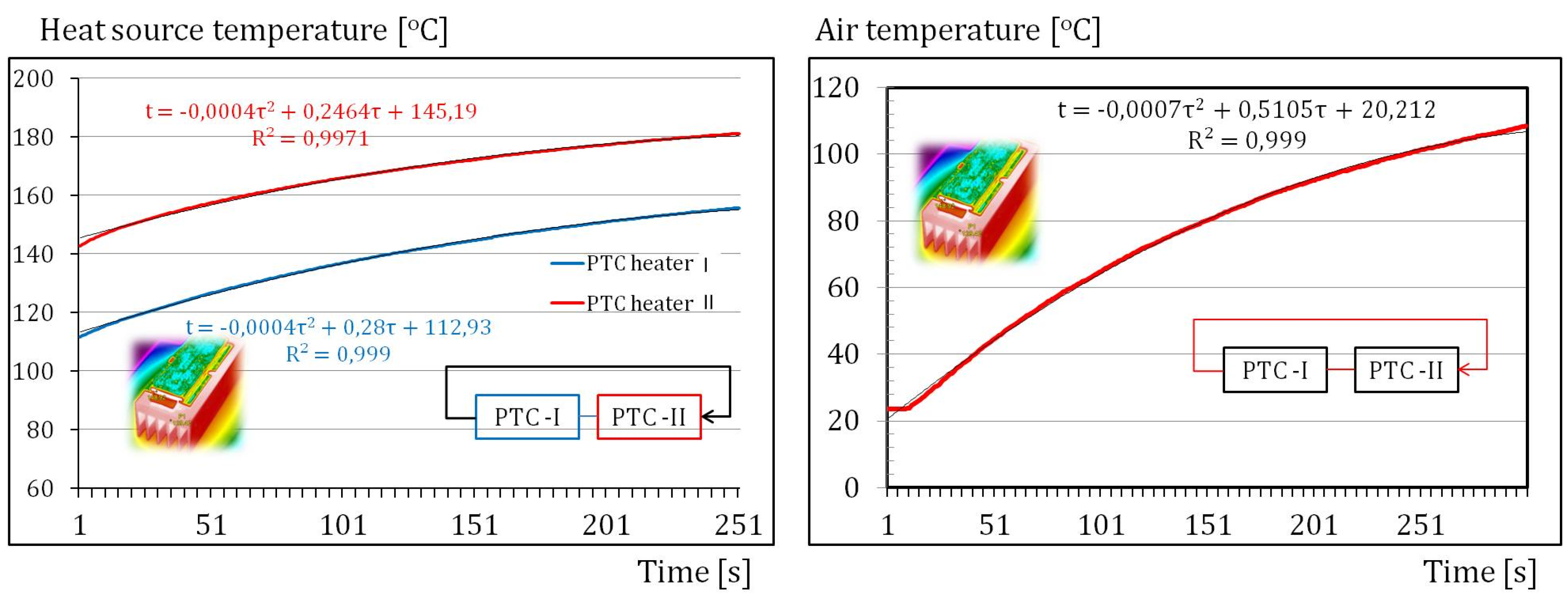
In the conducted experimental testing, two PTC electric heaters were used, which are placed inside a closed channel, with characteristic dimensions shown in Table 1. The channel housing is thermally insulated from the ambient. The axial fan established a circular flow of air with a constant volumetric flow rate of 0.005 m³s^-1 and an initial temperature of 20^oC. Within the closed channel designed in this work, the air is continuously heated, which causes increased temperatures of both heaters in the analyzed time interval of 300s, Figure 8a. The temperature of the heaters A and B, as well as the air temperature, shown in the Figure 8, after 50s from the start of heating. The temperatures of both heaters and the air temperature were approximated by polynomial functions, which, according to equations (15) and (16), were used to determine the thermal entropy.

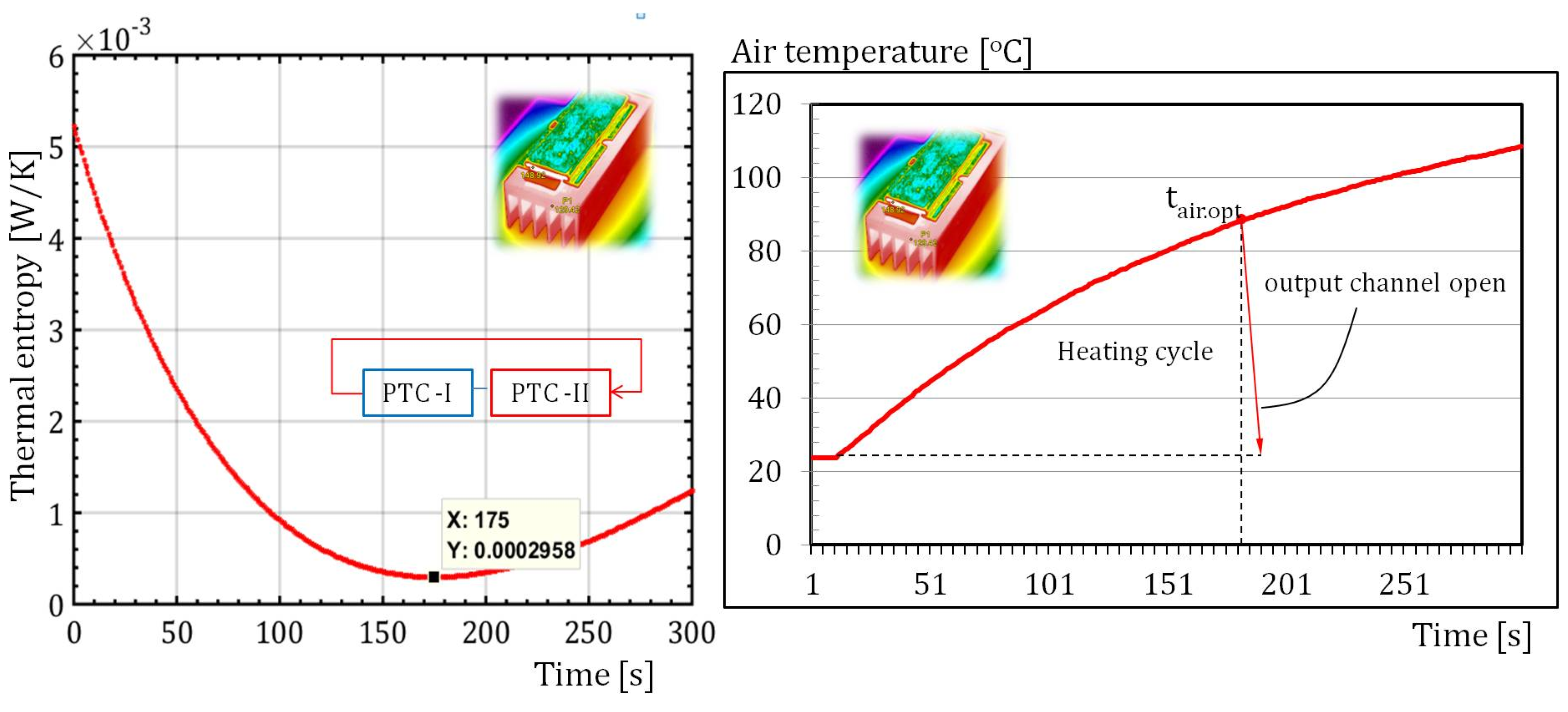
The total transient thermal entropy of the air and both heating sources during the circular heating process at a constant air volumetric flow rate of 0.005 m³s^-1 is shown in Figure 9. During the air heating process, the minimum thermal entropy occurs 175s after the start of heating. From the aspect of the minimum thermal entropy as an optimization criterion, the optimal term for releasing the fluid from the closed case is 175s after the start of heating, Figure 9b. In this case, the periodic exit of the hot air from the circular channel is valid if the air and the housing cool down to the initial temperature of 20^oC. Since the internal temperature of the housing will rise during the air heating time, the channel opening period will be shorter than 175s.

The established methodology of transient thermal entropy enables its indirect minimization and finding the optimal opening time of the casing output channel. By reducing the geometrical and process limitations, it is possible to establish a general optimization criterion based on the minimal transient thermal entropy.

4. Conclusions

Two electrical PTC heaters by various temperatures and placed inside a closed circular channel. An axial fan provides a circular air flow within the channel, whereby the air is heated. The housing of the channel is made of thermal insulation material, which prevents the loss of heat to the ambijent. PTC heaters heat the bottom of the finned surface, which consists of six longitudinal fins. The air circulates inside the channel and after a limited time reaches the required temperature. Then the hot air leaves the housing, while the ambient air enters the same housing and the heating process continues. In the described manner, heat exchange due to heating generates thermal irreversibilities, while its flow through narrow longitudinal channels will cause hydraulic irreversibilities. In the implemented methodology and established limitations, the hydraulically generated air entropy due to friction and local losses was not taken into consideration. In the context of the conducted analysis, the following results were reached:

-

Transient thermally generated air entropy during circular heating increases rapidly with the increase of heating time and volumetric air flow inside the channel. Also, a higher temperature of the heating source generates an increase in thermal entropy.

-

The minimum of transient entropy also implies the optimal time of channel opening and exit of heated air.

-

The air temperature during the circular heating rises rapidly, and according to the required temperature, the hot air leaves the housing.

The establishment of the methodology included in this work provides a reliable basis for optimizing the geometric and process parameters of the analyzed heating system. By removing the defined limitations, the methodology developed in this paper will have a more general application.