Preprint
Article
Application of the Discrete Wavelet Transform to Damage Detection in a Guy Cable of Guyed Antenna Mast
This is a preprint, it has not been peer-reviewed.
Submitted:
20 March 2024
Posted:
21 March 2024
You are already at the latest version
Abstract
The paper delves into the critical issue of damage detection within the guy cable of a truss steel mast, a pivotal component in structural integrity. It introduces a model wherein damage manifests as a localized cross-section reduction in a single element of the cable. Employing Discrete Wavelet Transform (DWT), a pioneering methodology, the study scrutinizes the behavior of the affected elements through static structural analyses. Signal decomposition via the Mallat pyramid algorithm facilitates comprehensive examination. Static displacements at the connection point between the cable and the truss mast serve as the measured variables. Through systematic investigation, the paper evaluates the impact of damage size and location, external loading force, and cable tension force on the efficacy of the proposed approach. Utilizing data derived from Finite Element Method (FEM) computations for wavelet analysis the authors substantiate the findings with numerical examples, thus offering valuable insights into damage detection strategies for structural health monitoring and engineering applications.
Keywords:
-
1. Introduction
Early detection, localization and estimation of structural damage is nowadays one of the most important engineering problems that has focused much attention over the last years. When a defect occurs in the structural element, it can seriously disrupt its functioning. There are different non-destructive techniques which enable the identification of defective part of a structure, most of them base on the analysis of the structural response signals. Different approaches and many advanced methods have been developed, e.g. radiography [1], ultrasonic [2], acoustic emission [3], magnetic field [4], and eddy current [5] methods. Damage identification method which combines empirical mode decomposition (EMD) and Autoregressive Integrated Moving Average (ARIMA) models was presented in [6]. Thermal testing [7] or making use of RGB-D camera [8] also proved to be an effective method in structural health monitoring. A great potential is assigned to soft methods, mainly evolutionary algorithms [9] and artificial neural networks [10].
Different types of structural response, namely eigenfrequencies, displacements, angles of rotation, velocities or accelerations can be useful to assess the reliability of the structure. The method which enables to extract the desired detailed information from a numerous data representing the global response of a defective structure is called Wavelet Transform (WT). In the paper it is applied in its discrete form (DWT). An indicator of the damage presence and location in this type of analysis are strong disturbances of the transformed signal. Previous studies of the authors [11,12,13] proved that, in the class of considered problems, the most effective appeared to be the Daubechies wavelet [14]. Similar study has been carried out for damage detection in beams [15] and mining machines [16]. The comparison between the efficiency of Haar, Daubechies and Coiflet wavelet in damage detection was discussed in [17]. Wavelet functions proved to be highly useful in many applications as well, including their implementation to the theory of homogenization [18].
Steel masts are the lightweight structures, which behaviour has been discussed in many papers, e.g. the dynamic analysis was presented in [19] and analysis taking into account the geometric and physical non-linearity of the guys in [20]. In the present work, the authors took up the topic of analyzing a mast with guy cables, taking into account their weakening, the location of which is made possible by the use of the Discrete Wavelet Transform in the analysis of the structure’s response signal.
2. Theoretical foundations
2.1. Discrete Wavelet Transform (DWT)
At the beginning of theoretical considerations, let there be a given function , which is continuous and belong to the field of . This function may be called the wavelet function (mother function) and must satisfy the condition of admissibility [17]. The mother function may be real- or complex-valued. The real-valued wavelets will be applied in the considered cases. For signal decomposition the set of wavelets (wavelet family) is needed. This set of functions is obtained by translating and scaling the function ψ, what can be written by means of the relation:
where t is a time or space coordinate, a and b are the scale and translation parameters respectively. The parameters a and b take real values and additionally . The element expresses the scale factor which ensures the constant wavelet energy regardless of the scale, i.e. .
In the present analysis, Discrete Wavelet Transform (DWT) plays the leading role. The wavelet family can be obtained by substitution and in Equation (2.1). This yields the relation:
in which k and j are scale and translation parameters, respectively.
The Discrete Wavelet Transformation (DWT) of the signal (e.g. the response function of the structure) is expressed by the equation:
The scalar product of the response function and the wavelet function allows to find the set of wavelet coefficients .
In identifying of singularities of the tested signals the vanishing moments of the wavelet function play a significant role. A wavelet has k vanishing moments if the subsequent relation is fulfilled:
The wavelet of order n has vanishing moments and is orthogonal to polynomials up to .
In the case of above mentioned Daubechies wavelets which are of order from 2 to 20, always even numbers, a number of vanishing moments equal to half of the order, e.g. for Daubechies 4 there are 2 vanishing moments. Vanishing moments restrict the capability of wavelets to represent polynomial behavior or information in a signal, meaning that, e.g. Daubechies 6 encodes constant, linear and quadratic signal components.
For 1-D DWT analysis, decomposition of the discrete signal is carried out according to the Mallat pyramid algorithm [21] which can be generally presented in the simple form:
where each component in signal representation is coupled with a specific range of frequency and provides information at the scale level . The discrete parameter describes the level of a multi-resolution analysis (MRA), expresses the smooth signal representation, is the detail of the transformed signal at the scale level and corresponds to the most detailed representation of the transformed signal. The function must be approximated by discrete values to fulfill the dyadic requirements of DWT.
2.2. Finite Element Method
The Finite Element Method (FEM) has been applied to the numerical, geometrically non-linear analysis of the antenna guyed mast. The finite element describing the behaviour of the lattice part of the entire mast is shown in Figure 1. It is a typical two-node element with six degrees of freedom per node. The general description of the guy (cable) element is shown in Figure 2.
The displacement formulation of the FEM carries a typical matrix notation:
where is the global structural stiffness matrix, is the global structural displacement vector and is the external loading vector.
The global stiffness matrix is composed of three matrices:
where the first one , is the classic linear stiffness matrix of the whole structure, the second one is the first non-linear stiffness matrix, commonly called geometric matrix, whose terms depend on the value of the axial force and only on structural geometry (and at the level of a finite element on its geometry) and finally, the last one is the strongly non-linear stiffness matrix that depends simultaneously on the geometry of the structure and displacements. These matrices can be derived in an uncomplicated way by writing the expression for the potential energy and postulating the equilibrium condition by its stationarity. An comprehensive description of non-linear stiffness matrices for a simple flat two-node element is given by Rakowski and Kacprzyk [22] and similar procedures have been introduced here.
Cable non-linearity affects the calculation model and analysis by the initial geometry of the cable and, as a consequence, its finite element mesh, the initial tension of the cable, and finally linear and nonlinear behaviors of the element [23].
3. Numerical Examples
The numerical analysis was performed for the antenna guyed mast described in paper [24] and shown in Figure 3. The mast, 204 m high, is designed as a steel spatial truss with a triangular cross-section. The width of the truss side is 2.7 m. The edge bars are made of round tubes with a diameter of 193.7 mm and a wall thickness of 10 mm, while diagonals are made of round tubes with a diameter of 88.9 mm and a wall thickness of 5 mm. The mast has three levels of fastening guy lines in height of 67.18, 126.58 and 176.08 m. The parameters for the guy lines are as for steel rope with a diameter of 36 mm, T1x61-Z-II-g (7.66 cm2) structure, made of wire with a strength of 1570 MPa and nominal strength breaking force 1195 kN. The assumed values of the initial tension of the guy cables at the individual attachment levels are, respectively: 40, 70, and 100 kN. As signals for the wavelet analysis, the displacements (utot) of the node in which the guy cable is connected to the mast truss were assumed. The values of these displacements were calculated numerically using the Finite Element Method, taking into account the non-linear theory.
The problem of mechanics (statics) of a three-dimensional truss structure with guy wires was solved using the Finite Element Method (FEM) in the commercial SCIA Engineer program [25], appropriate to structural systems containing elements that require geometrically nonlinear analysis. The discrete structure response signal thus obtained was subjected to a Discrete Wavelet Transformation, which was carried out using the Mathcad package.
3.1. Case 1 – Variable Loading Force
In this model, the defect is modeled as 50% reduction of the cross-section within the length of 10 cm, is located in the middle of the guy cable fastened at the highest level (with a tension force of 100 kN). Moving concentrated vertical force P = 100 kN was applied in 64 nodes with equal time intervals. The number of measurements N = 64. The nodal points where the concentrated force is applied are located along the damaged cable structural element. The response signal has been analyzed and transformed using DWT procedures. The Daubechies 12 wavelet has been applied to the preliminary analysis. Performed analysis precisely indicate, by the clear peak in the transformation window (detail 1 – D1), the damage position, which is shown in Figure 4.
In the next calculations the weakening of the cross-section is introduced, as in the previous example (50 % reduction of the cross-section within the length of 10 cm and located in the middle of the guy cable which is fastened at the highest level). The tension force is 100 kN. The external loading force takes the following values: 25 kN, 50 kN, 100 kN and 150 kN.
The DWT procedures have been carried out using Daubechies 8 wavelet family in all examples considered. The moving external vertical force was applied in the same way as in the previous example. The calculation results are shown in Figure 5 and Figure 6 for 25 and 50 kN, respectively. The presence of a defect was identified by a clear perturbation of the transformed signal.
Worth noting is that the shape of the decomposed with Daubechies 8 data is independent of the value of the external loading forces. The only change was observed in the range of wavelet coefficients which increased proportionally to the external loading force value. The results has been compiled in Table 1.
The above observation is true if the value of external loading forces is sufficiently high, i.e. above 20 kN. Although, in the case of decomposition of a displacement structural response signal induced by the force of 5 kN with Daubechies 8 wavelet, the defect was correctly located, the disturbances occurring to the right and left hand side of the peaks indicating the defect in the transformation window already disrupt the unambiguity of the results (see Figure 7).
Finally, the external loading force value was reduced to 1kN. In this case the proposed method turned out to be ineffective for detecting damage, see Figure 8. Even for increased wavelet order there are no disturbances in the transformed signal which is visible in Figure 9. Further attempts to decompose the signal with higher order Daubechies wavelets, i.e. 10, 12, 14 did not bring satisfactory results, even though the intensity of defect was significant, i.e. 50% reduction on cross-section area in one FEM element. The higher details, namely detail 2, 3 and 4 of Daubechies 6 wavelet, were also considered; however, the damage was not detected.
3.2. Case 2 – Variable Damage Size
In the following examples the manner of introducing damage is identical to the previous ones. The damage intensity has been decreased to 25 % reduction of the cross-section within the length of 10 cm (the reduced cross-sectional area is located over a length of 10 cm, symmetrical to the entire length of the cable), the location is in the middle of the guy cable fastened at the highest level (with a tension force of 100 kN). The external loading force takes the value 5 kN. The number of mesurements is the same as in the previous model (N = 64).
The DWT procedures have been carried out using subsequently Daubechies 8, 6 and 4 wavelet. The moving external vertical force was applied at 64 points (nodes) of the cable. The calculation results are shown in Figure 10, Figure 11 and Figure 12.
The analyses presented in Figure 10 and Figure 11 clearly indicate the presence and location of the defect, whereas the signal decomposition depicted in Figure 12 gives no information about the damage existence. This implies that the signal has constant, linear and quadratic components, because to reveal its singularity the wavelet with three vanishing moments, i.e. Daubechies 6, was necessary.
An attempt has been made to assess the impact of the successive reduction the damage intensity and external loading force on the effectiveness of the proposed method. In the subsequent analyses, 10% area of the cross-section reduction is assumed. The external loading force takes the value 5 kN.
The DWT procedure has been carried out while using Daubechies 6 wavelet. The external force was applied at 64 points (nodes) of the guy cable. The results are presented in Figure 13, where evident disturbance of the transformed signal is an indicator of the defect presence and location can be observed.
3.3. Case 3 – Variable Tension Force
Subsequently, the effect of increasing the cable tension force on the efficiency of damage detection while applying DWT was examined. In the analyses, 25% area of the cross-section reduction is assumed, the external loading force applied at 64 points (nodes) of the guy cable takes the value 5 kN. In the first step, the tension of the guy cable has been increased from 100 kN to 150 kN.
The signal transformation using Daubechies 6 wavelet for tension force 150 kN is presented in Figure 14. The high peak clearly indicates the presence and position of the defect.
In the second step, the tension of the guy cable has been increased to 200 kN. The DWT of the obtained response signal, neither with Daubechies 6 (see Figure 15) nor Daubechies 8 wavelet (see Figure 16), did not indicate the existence of the damage.
An increase in the tensile strength of the mast cable made it impossible to detect the defective area. Therefore, increasing the stiffness of the entire system, resulting in a decrease in the value of total displacements of selected measurement point (see Figure 17 a,b), makes the proposed method less effective for detecting damage.
3.4. Case 4 – Variable Location of Damage
In order to additionally verify the calculations, two examples were considered in which the cable damage is introduced asymmetrically in relation to its length. First, let the weakening of the cable cross-section be introduced in 1/4 of its length, counting from its fixing in the foundation. The loading force of 5 kN is applied identically as in the previous examples, and the cable cross-sectional area has been reduced by 25%. The weakening of the cable cross-section takes place over a distance of 10 cm. The measuring point is placed at the end of the cable, where the guy is connected with the mast. The number of measurements is the same as in previous examples (N = 64). The results of DWT for Daubechies 6 family of wavelets are presented in Figure 18, where observable disturbance of the transformed signal is an indicator of the defect presence.
In the second approach, an asymmetrical weakening of the cross-section was introduced at a distance of 1/4 from the point of connection of the cable with the mast. The results of DWT are presented in Figure 19, where observable disturbance of the transformed signal is similar to the previous one.
4. Concluding Remarks
Application of 1-D Discrete Wavelet Transform (DWT) to recognition of structural response signal discontinuity in the analysis of a guy cable of the guyed antenna mast was discussed in the paper, which is a novel approach in examining the flaccid elements. The advantages and limitations of the proposed method have been described.
Measured response signal has been assumed as the static total deflection given at the selected point for 64 positions of the moving force. Parametric analyses of the impact of the damage size (reduction of the cross-sectional area of the bar) and the value of the external load on the effectiveness of the structure damage location were carried out. The Daubechies wavelet was used in the analyses. In the class of considered signals, it was shown that a minimum wavelet order of 6 is necessary for the correct location of the defect. The position of defects was correctly identified by the evident disturbances and high peaks of the transformed data. It has also been proven that increasing the cable tension force adversely affects the effectiveness of damage detection with the proposed method. The displacement calculations were made without random environmental influences, such as wind or temperature. These interactions can significantly affect the results, thus taking them into account is an interesting direction for the development of further research.
Summary in Polish
Zastosowanie dyskretnej transformacji falkowej do wykrywania uszkodzeń w odciągu masztu antenowego
Słowa kluczowe: stalowy maszt kratownicowy, odciągi linowe, metoda elementów skończonych, wykrywanie uszkodzeń, dyskretna transformata falkowa
Streszczenie: W artykule przedstawiono problem wykrywania uszkodzeń w odciągach stalowego kratowego masztu antenowego. Uszkodzenie w jednym odciągu jest modelowane jako miejscowa redukcja pola przekroju jednego elementu. Analizy statycznych odpowiedzi strukturalnych przeprowadzane są z wykorzystaniem dyskretnej transformaty falkowej (ang.: Discrete Wavelet Transform – DWT), które to podejście jest nowatorskim do badania elementów wiotkich. Zastosowano dekompozycję sygnału odpowiedzi konstrukcji (elementu konstrukcji) zgodnie z algorytmem Mallata. Mierzone zmienne to statyczne przemieszczenia punktu, w którym kabel łączy się z masztem kratownicy. Uszkodzenie kabla zostało wprowadzone jako miejscowe zmniejszenie pola poprzecznego jego przekroju. Zbadano wpływ wielkości uszkodzenia, wartości siły wzbudzenia oraz siły naciągu odciągu na skuteczność proponowanego podejścia. Dane do analizy falkowej uzyskano z wyników obliczeń metody elementów skończonych (MES) dla geometrycznie nieliniowego sformułowania zadania. Zaprezentowano przykłady numeryczne, które wykazały skuteczność zaprezentowanej metody wykrywania uszkodzeń.
Funding
Financial support by Institute of Structural Analysis grant 0411/SBAD/0008 is kindly acknowledged.
References
- T. Kersting, N. Schönartz, L. Oesterlein, A. Liessem, “High end inspection by filmless radiography on LSAW large diameter pipes”, Nondestructive Testing and Evaluation International, vol. 43, no. 3, pp. 206-209, 2010. [CrossRef]
- R. Drelich, M. Rosiak, M. Pakula, “Application of non-contact ultrasonic method in air to study fiber-cement corrugated boards”, Bulletin of the Polish Academy of Sciences: Technical Sciences, vol. 69, no. 2, p. 136740, 2021. [CrossRef]
- R. Skłodowski, M. Drdácký, M. Skłodowski, “Identifying subsurface detachment defects by acoustic tracing”, Nondestructive Testing and Evaluation International, vol. 56, pp. 56-64, 2013. [CrossRef]
- X. Wang, J. Tang, “Structural damage detection using a magnetic impedance approach with circuitry integration”, Smart Materials and Structures, vol. 20, no. 3, p. 035022, 2008. [CrossRef]
- T. Chen, G.Y. Tian, A. Sophian, P.W. Que, “Feature extraction and selection for defect classification of pulsed eddy current NDT”, Nondestructive Testing and Evaluation International, vol. 41, no. 6, pp. 467-476, 2008. 2008. [CrossRef]
- W. Lu, J. Dong, Y. Pan, G. Li, J. Guo, “Damage identification of bridge structure model based on empirical mode decomposition algorithm and Autoregressive Integrated Moving Average procedure”, Archives of Civil Engineering, vol. 48, no 4, pp. 653-667, 2022. [CrossRef]
- K. Ziopaja, Z. Pozorski, A. Garstecki, “Damage detection using thermal experiments and wavelet transformation”, Inverse Problems in Science and Engineering, vol. 19, no, 1, pp. 127-153, 2011. [CrossRef]
- B. Wójcik, M. Żarski, “The measurements of surface defect area with an RGB-D camera for a BIM-backed bridge inspection”, Bulletin of the Polish Academy of Sciences: Technical Sciences, vol. 69, no. 3, p. 137123, 2021. [CrossRef]
- T. Burczyński, W. Kuś, A. Długosz, P. Orantek, “Optimization and defect identification using distributed evolutionary algorithms”, Engineering Applications of Artificial Intelligence, vol. 17, pp. 337-344, 2004. [CrossRef]
- M. Skowron, Application of deep learning neural networks for the diagnosis of electrical damage to the induction motor using the axial flux, Bulletin of the Polish Academy of Sciences: Technical Sciences, vol. 68, no. 5, pp. 1031-1038, 2020. [CrossRef]
- Knitter-Piątkowska, M. Guminiak, M. Przychodzki, “Application of Discrete Wavelet Transformation to defect detection in truss structures with rigidly connected bars”, Engineering Transactions, vol. 64, no. 2, pp. 157-170, 2016.
- Knitter-Piątkowska, O. Kawa, M. Guminiak, “Damage localization in truss girders by an application of the discrete wavelet transform”, Bulletin of Polish Academy of Sciences, vol. 71, no. 1, 2023. [CrossRef]
- Knitter-Piątkowska, A. Dobrzycki, “Application of Wavelet Transform to damage identification in the steel structure elements”, Applied Sciences, vol. 10, no. 22, p. 8198, 2020. [CrossRef]
- Daubechies, Ten lectures on wavelets. Philadelphia: Society for Industrial and Applied Mathematics, 1992.
- R. Nigam, S. Singh, “Crack detection in a beam using wavelet transform and photographic measurements, Structures”, vol. 25, pp. 436-447, 2020. [CrossRef]
- R. Zimroz, “Application of wavelet analysis in the diagnosis of damage to local drive systems of mining machines”, Diagnostyka, vol. 1, no. 49, pp. 113-122, 2009 (in Polish).
- M. Hanteh, O. Rezaifar, M. Gholhaki, “Selecting the appropriate wavelet function in the damage detection of precast full panel building based on experimental results and wavelet analysis”, Journal of Civil Structural Health Monitoring, vol. 11, pp. 1013-1036, 2021. [CrossRef]
- M. Kamiński, “Wavelet-based Finite Elastodynamic Analysis of Composite Beams”, Proceedings of the Fifth World Congress on Computational Mechanics, July 7–2, 2002, Vienna, Austria, Eds.: H.A. Mang, F.G. Rammerstorfer, J. Eberhardsteiner, 2002. 7 July.
- Bredow, M. Kamiński, “Dynamic analysis of steel mast under some environmental uncertainties”, Lightweight Structures in Civil Engineering, Contemporary Problems, Eds.: J. Szafran, M. Kamiński. Łódź University of Technology Press: pp. 171-180, 2021.
- M. Matuszkiewicz, R. Pigoń, “Parametric analysis of mast guys within the elastic and inelastic range”, vol. 48, no. 1, pp. 169-187, 2022. [CrossRef]
- S.G. Mallat, A wavelet tour of signal processing. Academic Press, San Diego, 1999.
- Rakowski G., Kacprzyk Z., Finite Element Method in structural mechanics, Publishing House of Warsaw University of Technology, 2005 (in Polish).
- E. Coarita, L. Flores, “Nonlinear analysis of Structures Cable-Truss”, International Journal of Engineering and Technology, vol. 7, no. 3, pp. 160-169, 2015. [CrossRef]
- M. Matuszkiewicz, “Calculation of guyed lattice masts according to PN-EN 1993-3-1”, Inżynieria i Budownictwo, vol. 4, pp. 194-199, 2010 (in Polish).
- Scia Engineer help [Online], Available https://help.scia.net/22.0/en/#analysis/nonlinear_analysis/cables/ advanced_cable_analysis.htm [Accessed: 3. Dec. 2022].
Figure 1.
The two-node finite element used for description of the antenna mast [22].
Figure 1.
The two-node finite element used for description of the antenna mast [22].
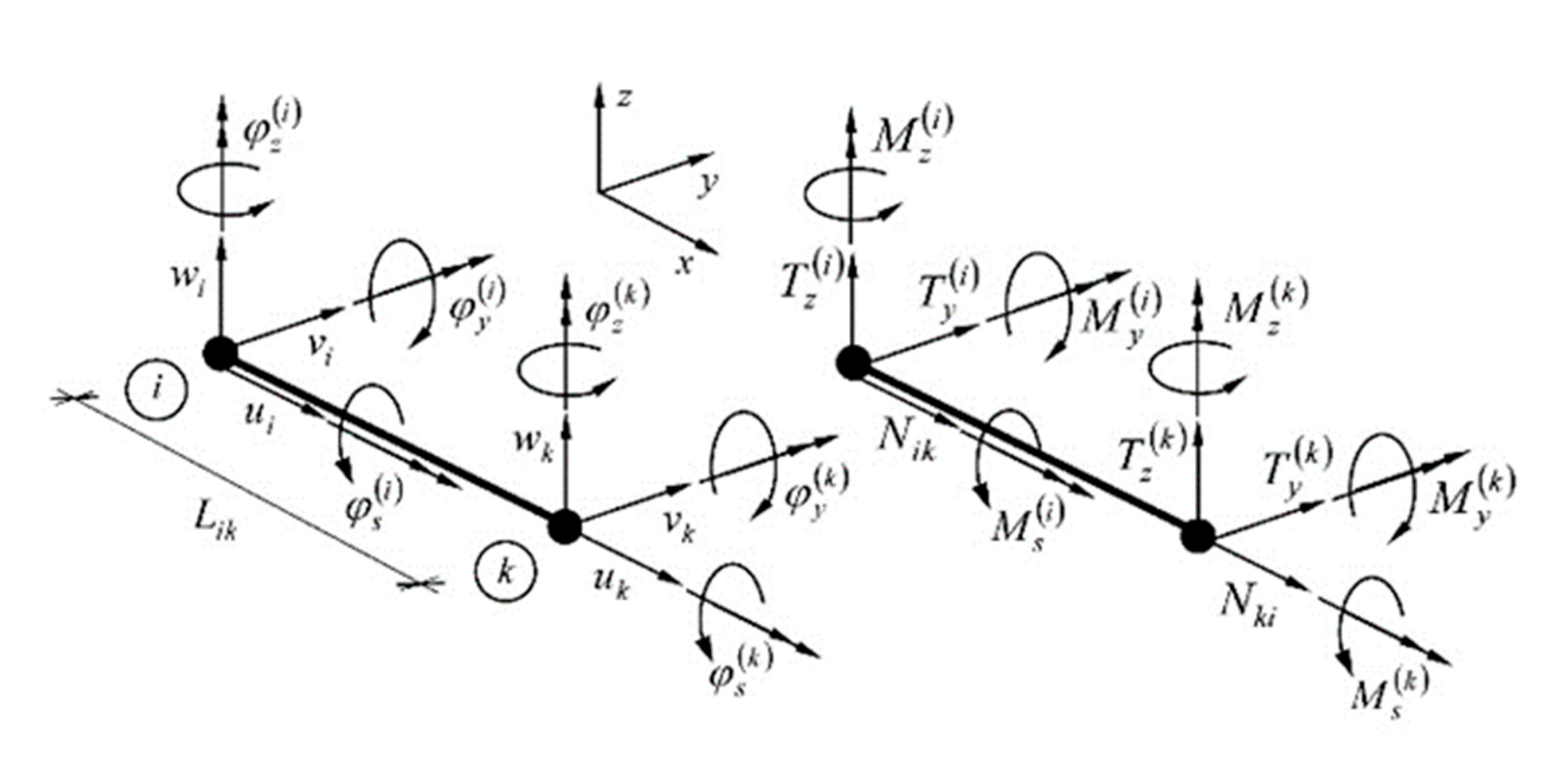
Figure 2.
The two-node finite element used for description of the guy (cable) [23].
Figure 2.
The two-node finite element used for description of the guy (cable) [23].
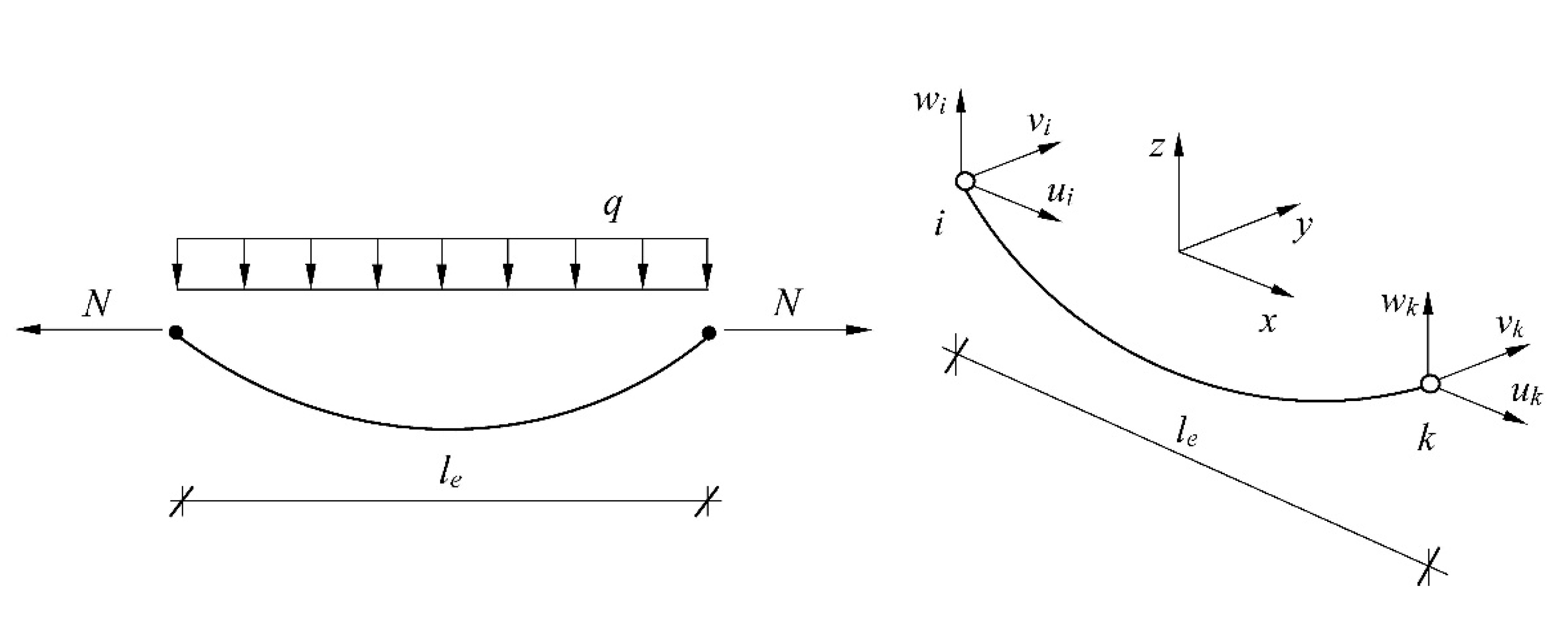
Figure 3.
Analyzed truss steel guyed mast: (a) location of damage and measurement point; (b) view from the top; (c) cross-sections of the bars.
Figure 3.
Analyzed truss steel guyed mast: (a) location of damage and measurement point; (b) view from the top; (c) cross-sections of the bars.
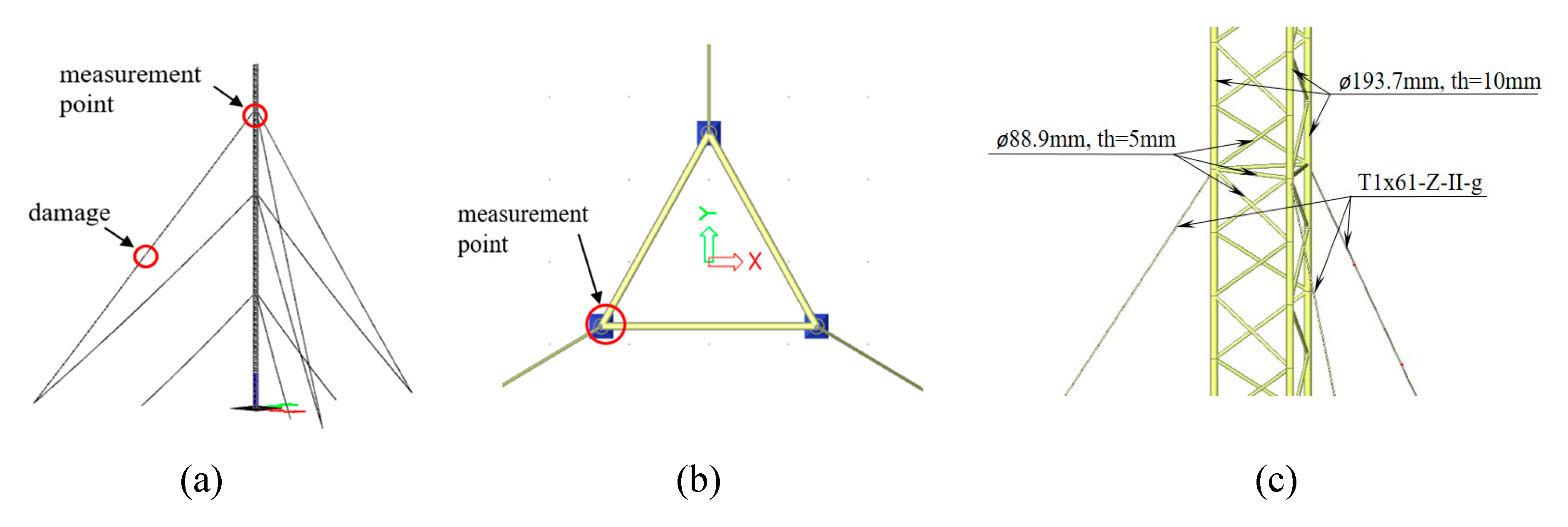
Figure 4.
1-D DWT of utot, Daubechies 12 (D1), external load: 100 kN, damage: 50% reduction of cross section.
Figure 4.
1-D DWT of utot, Daubechies 12 (D1), external load: 100 kN, damage: 50% reduction of cross section.
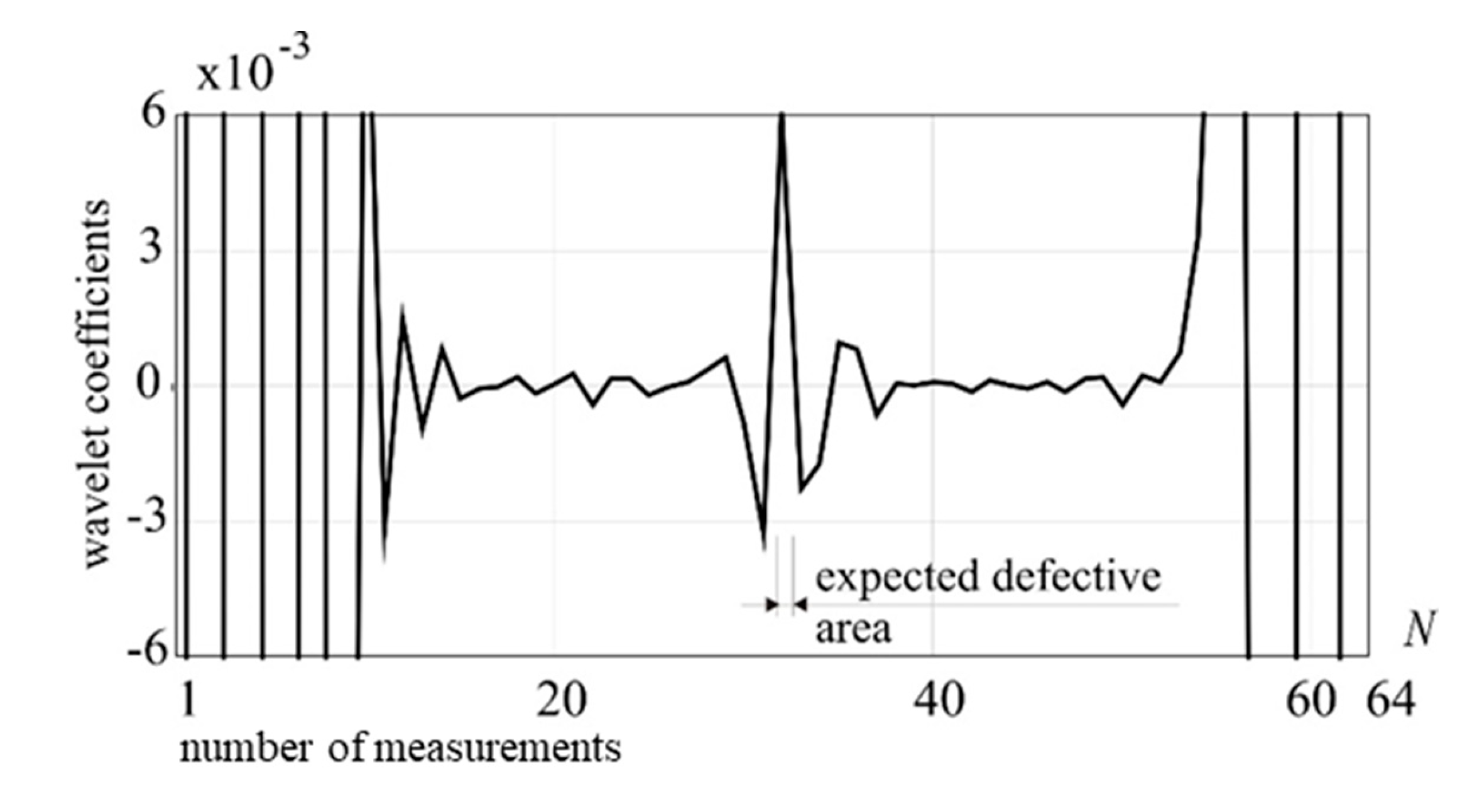
Figure 5.
1-D DWT of utot, Daubechies 8 (D1), external load: 25 kN, damage: 50% reduction of cross section.
Figure 5.
1-D DWT of utot, Daubechies 8 (D1), external load: 25 kN, damage: 50% reduction of cross section.
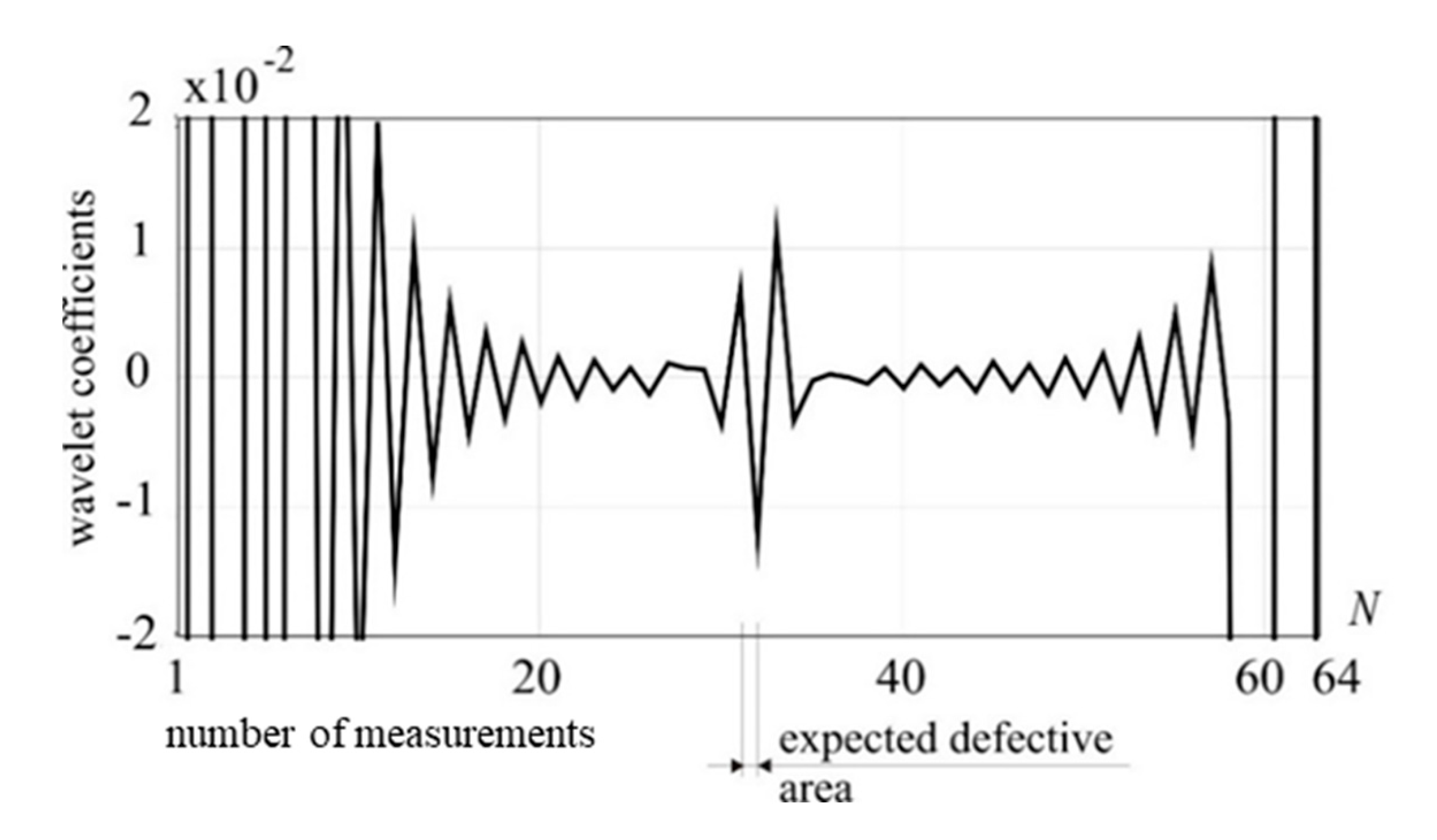
Figure 6.
1-D DWT of utot, Daubechies 8 (D1), external load: 50 kN, damage: 50% reduction of cross section.
Figure 6.
1-D DWT of utot, Daubechies 8 (D1), external load: 50 kN, damage: 50% reduction of cross section.
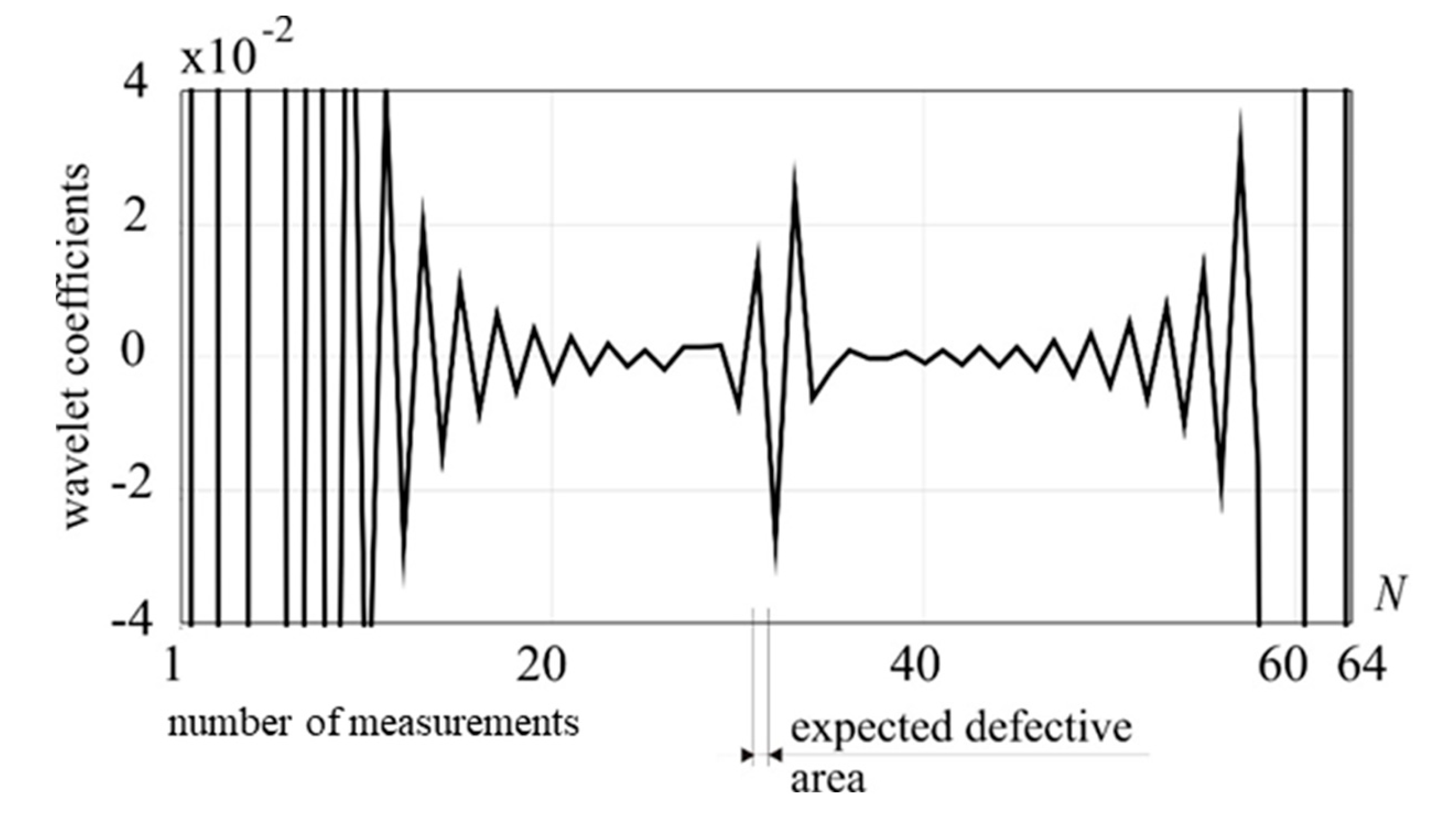
Figure 7.
1-D DWT of utot, Daubechies 8 (D1), external load: 5 kN, damage: 50% reduction of cross section.
Figure 7.
1-D DWT of utot, Daubechies 8 (D1), external load: 5 kN, damage: 50% reduction of cross section.
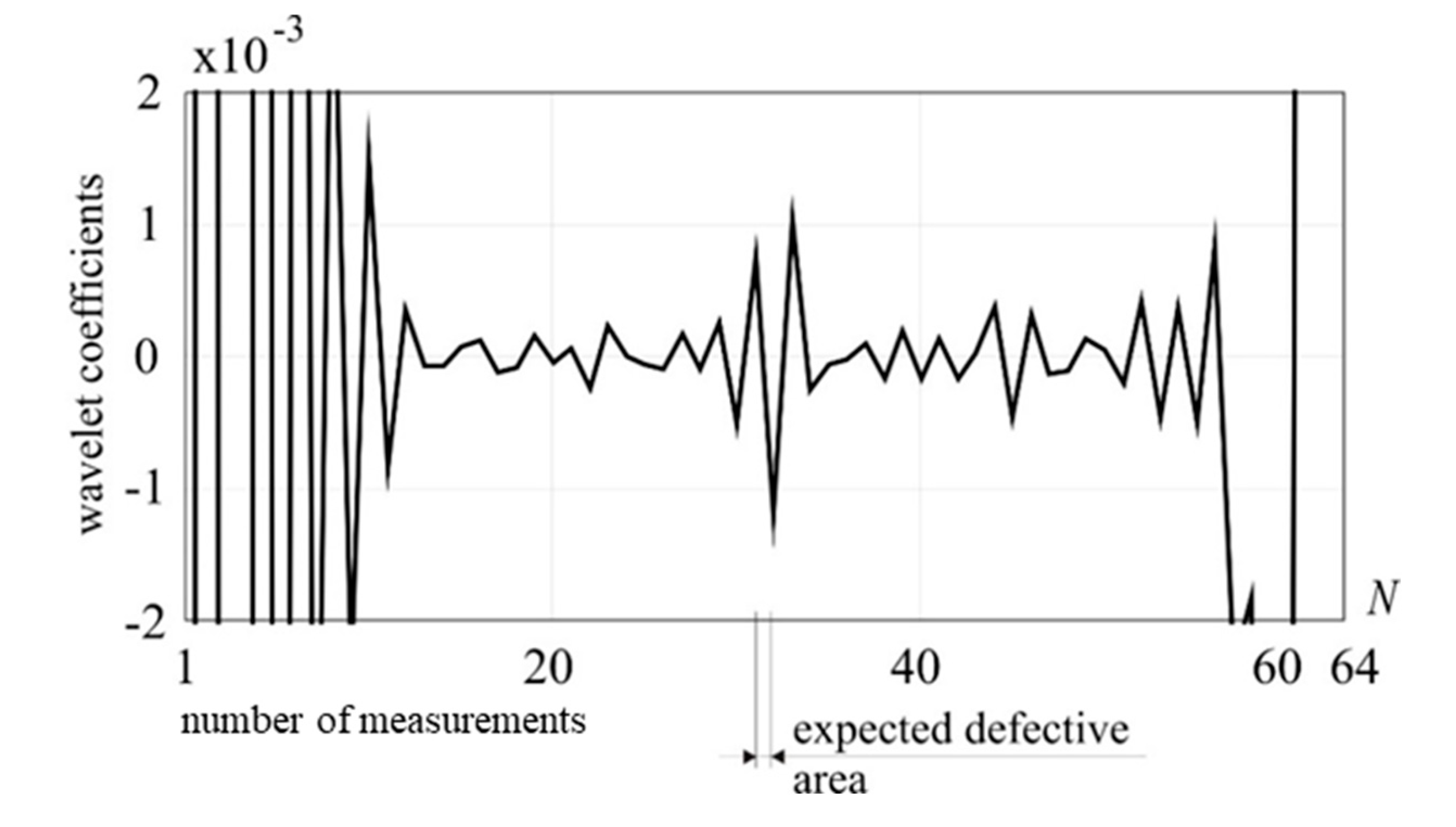
Figure 8.
1-D DWT of utot, Daubechies 6 (D1), external load: 1 kN, damage: 50% reduction of cross section.
Figure 8.
1-D DWT of utot, Daubechies 6 (D1), external load: 1 kN, damage: 50% reduction of cross section.
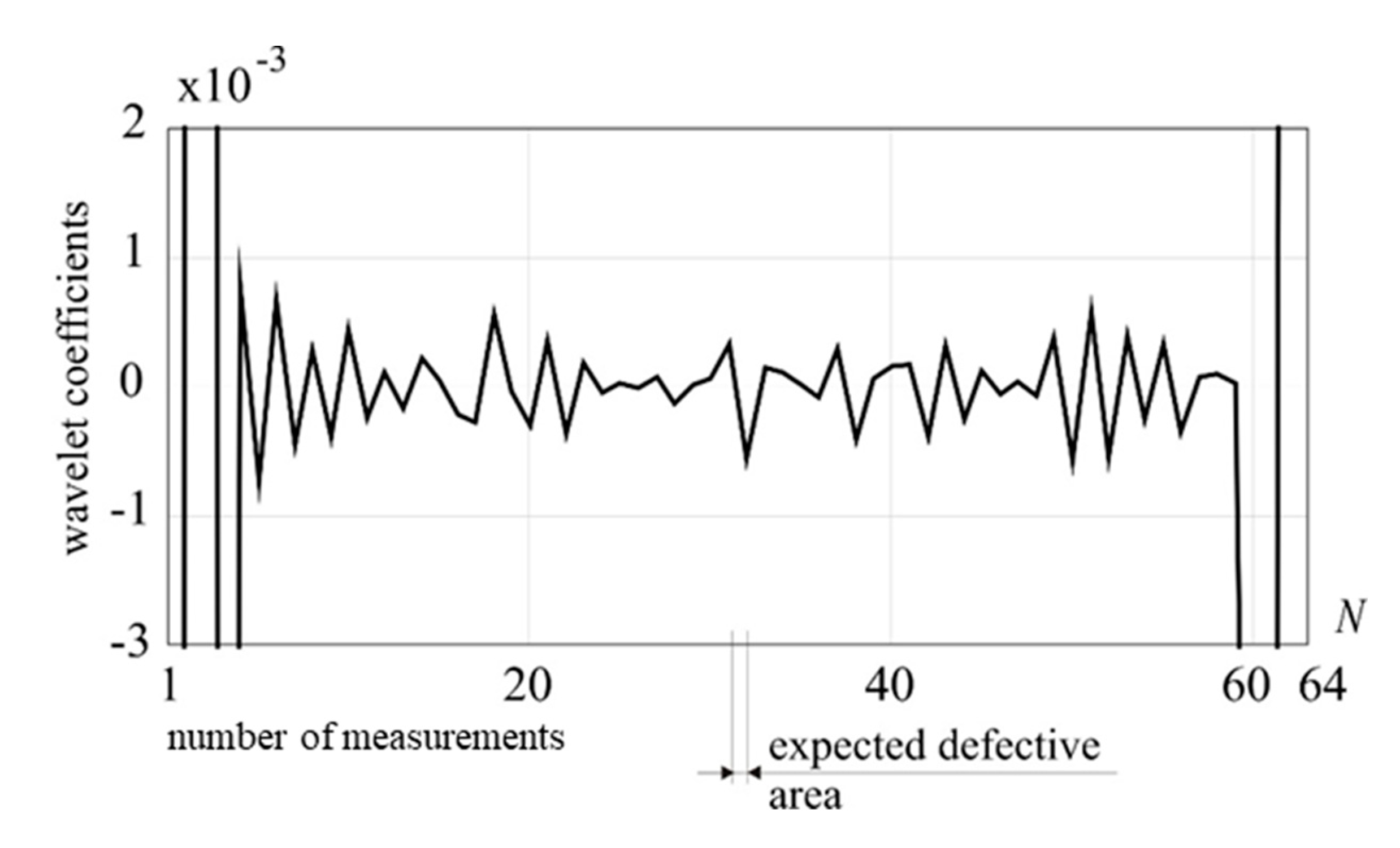
Figure 9.
1-D DWT of utot, Daubechies 8 (D1), external load: 1 kN, damage: 50% reduction of cross section.
Figure 9.
1-D DWT of utot, Daubechies 8 (D1), external load: 1 kN, damage: 50% reduction of cross section.
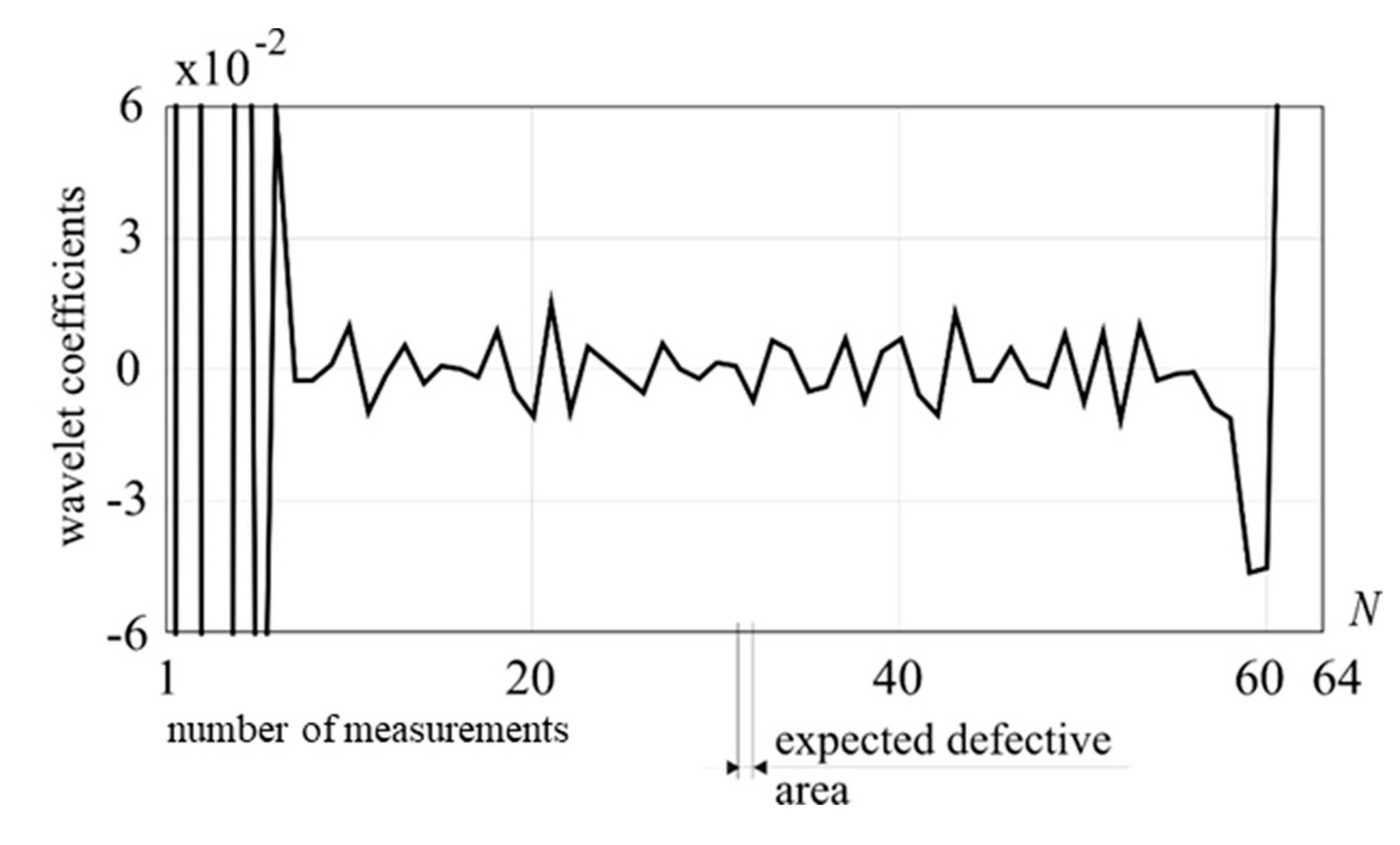
Figure 10.
1-D DWT of utot, Daubechies 8 (D1), external load: 5 kN, damage: 25% reduction of cross section.
Figure 10.
1-D DWT of utot, Daubechies 8 (D1), external load: 5 kN, damage: 25% reduction of cross section.
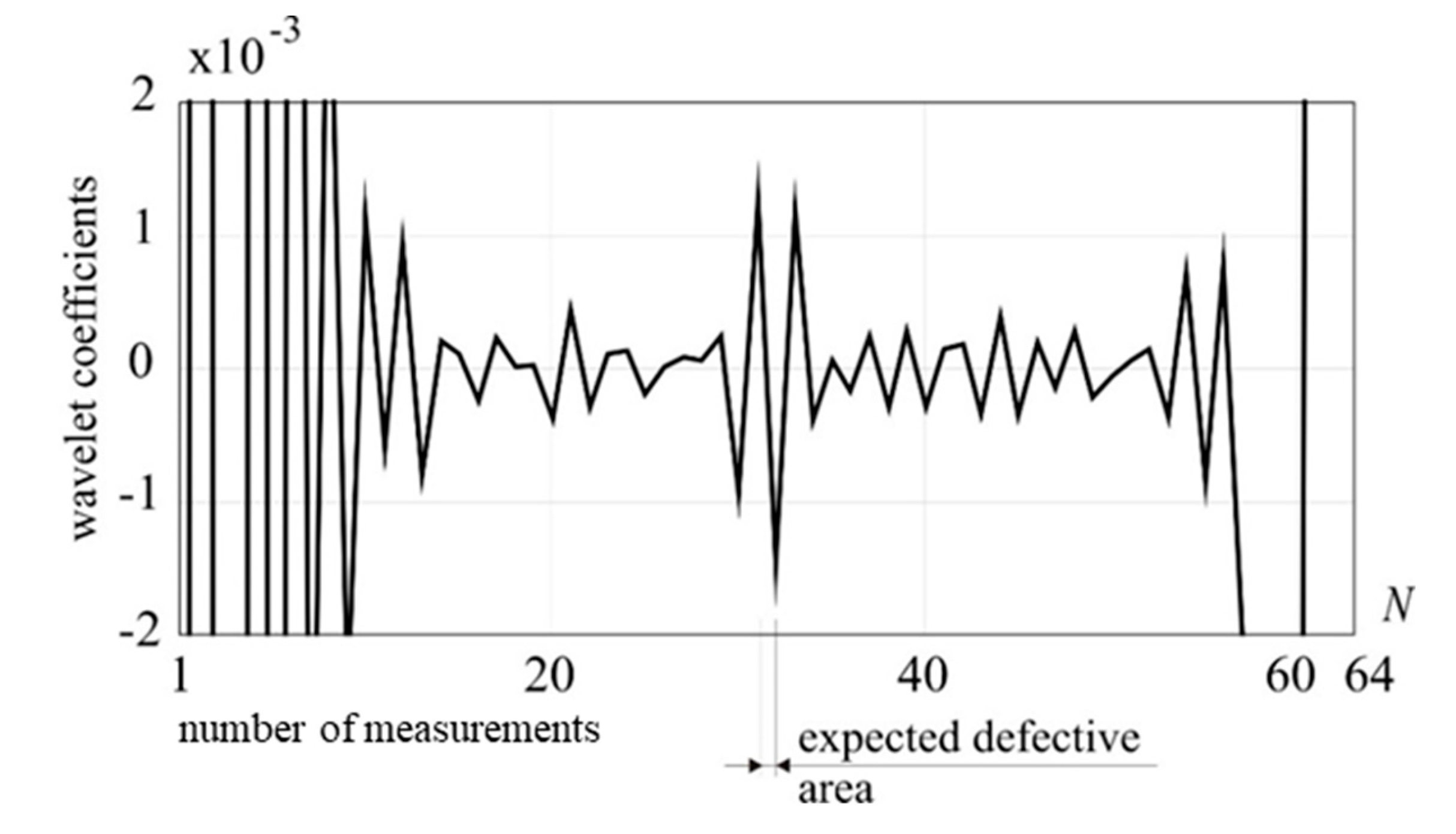
Figure 11.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 25% reduction of cross section.
Figure 11.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 25% reduction of cross section.
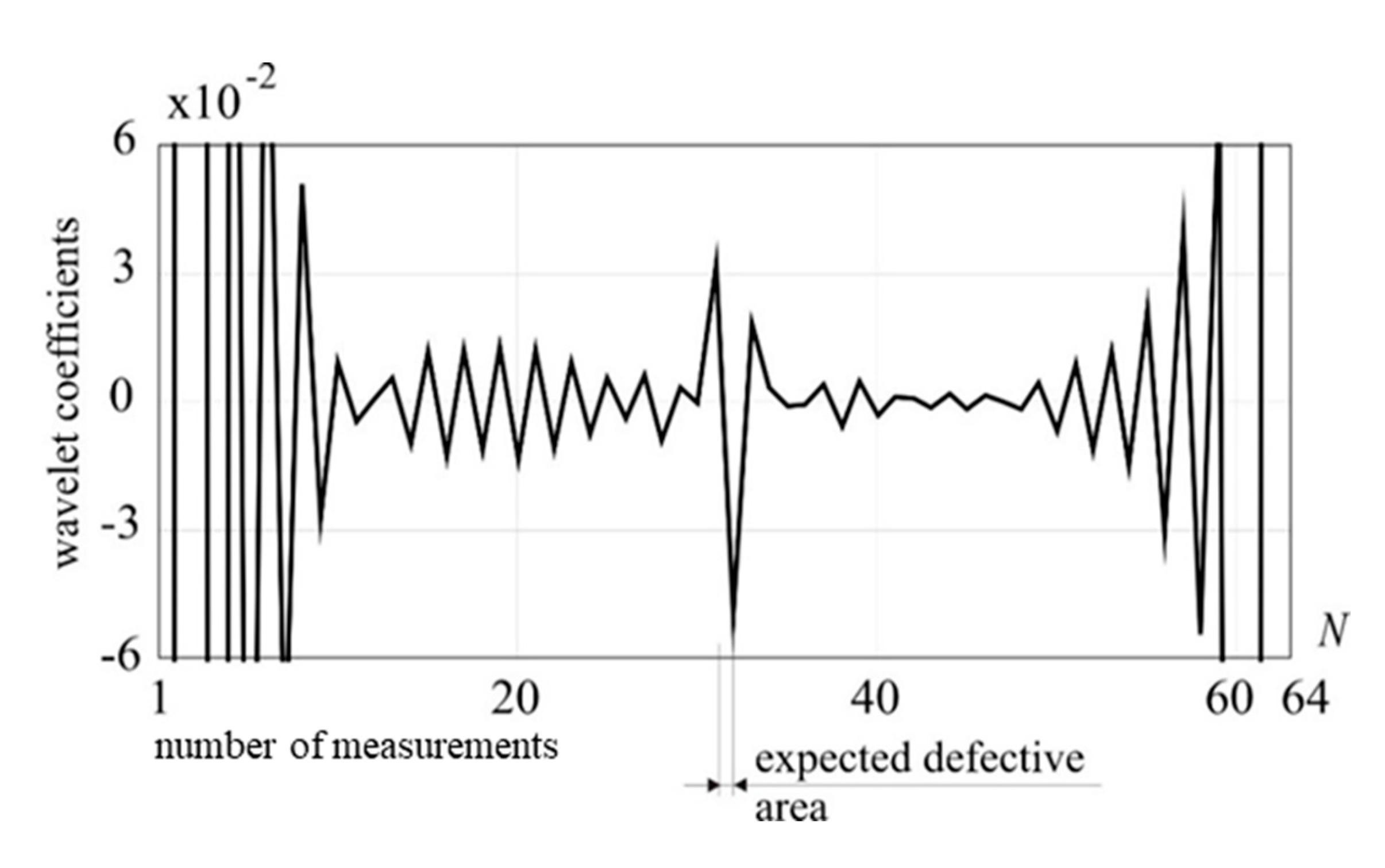
Figure 12.
1-D DWT of utot, Daubechies 4 (D1), external load: 5 kN, damage: 25% reduction of cross section.
Figure 12.
1-D DWT of utot, Daubechies 4 (D1), external load: 5 kN, damage: 25% reduction of cross section.

Figure 13.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 10% reduction of cross section.
Figure 13.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 10% reduction of cross section.
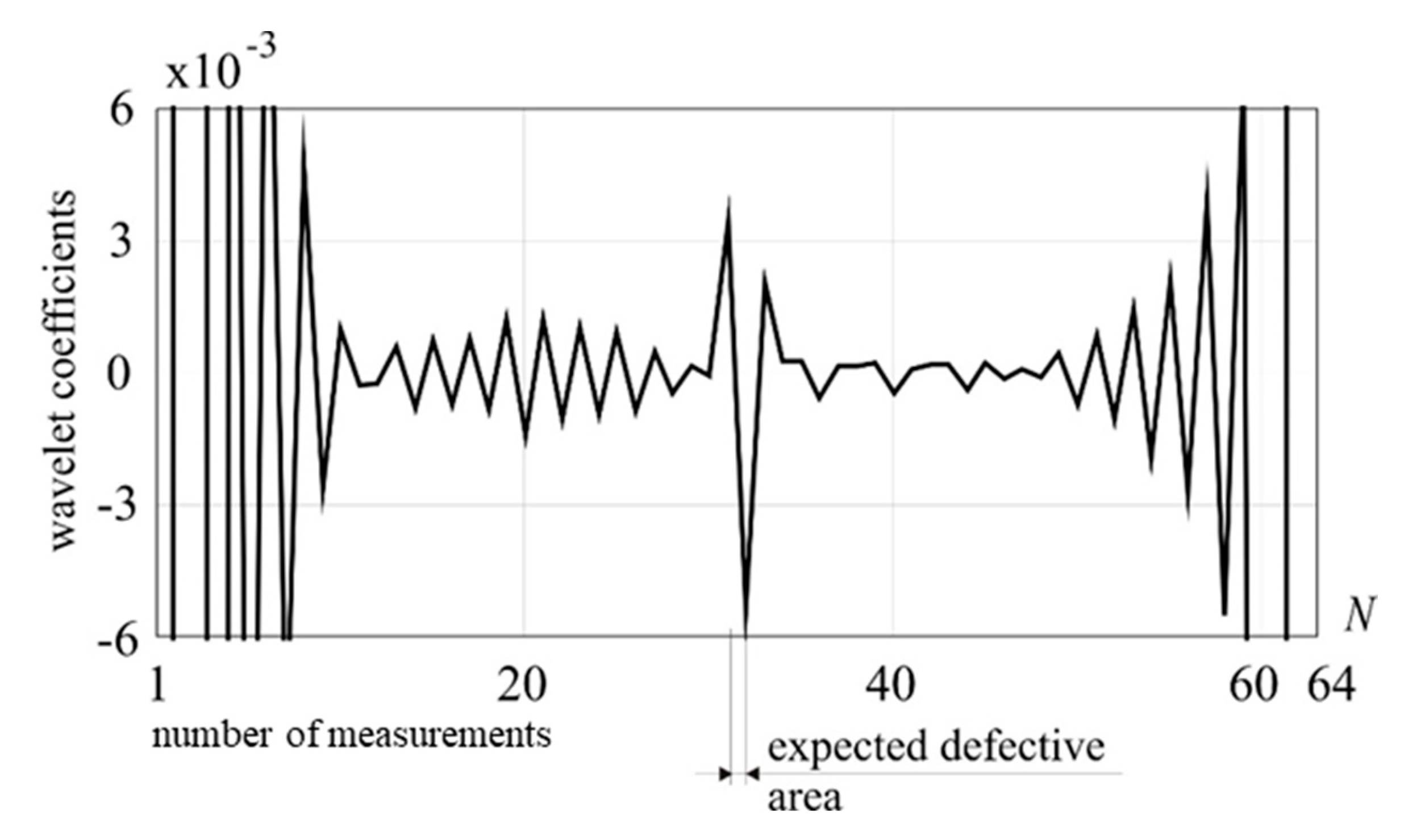
Figure 14.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 25% reduction of cross section, tension force in a guy cable: 150 kN.
Figure 14.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 25% reduction of cross section, tension force in a guy cable: 150 kN.
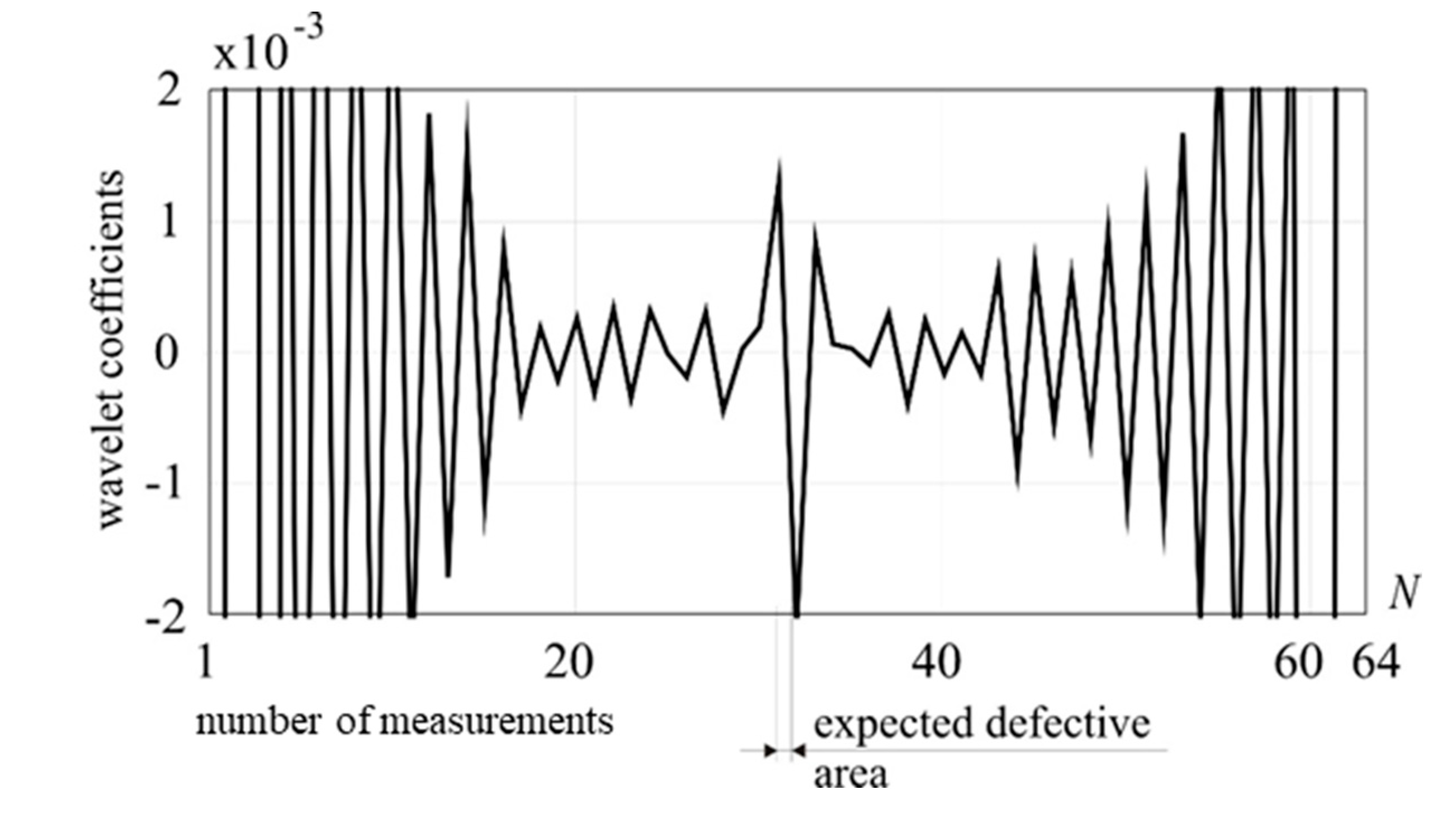
Figure 15.
1-D DWT of the total displacements, Daubechies 6 (detail 1), external load: 5 kN, damage: 25% reduction of cross section, tension force in a guy cable: 200 kN.
Figure 15.
1-D DWT of the total displacements, Daubechies 6 (detail 1), external load: 5 kN, damage: 25% reduction of cross section, tension force in a guy cable: 200 kN.
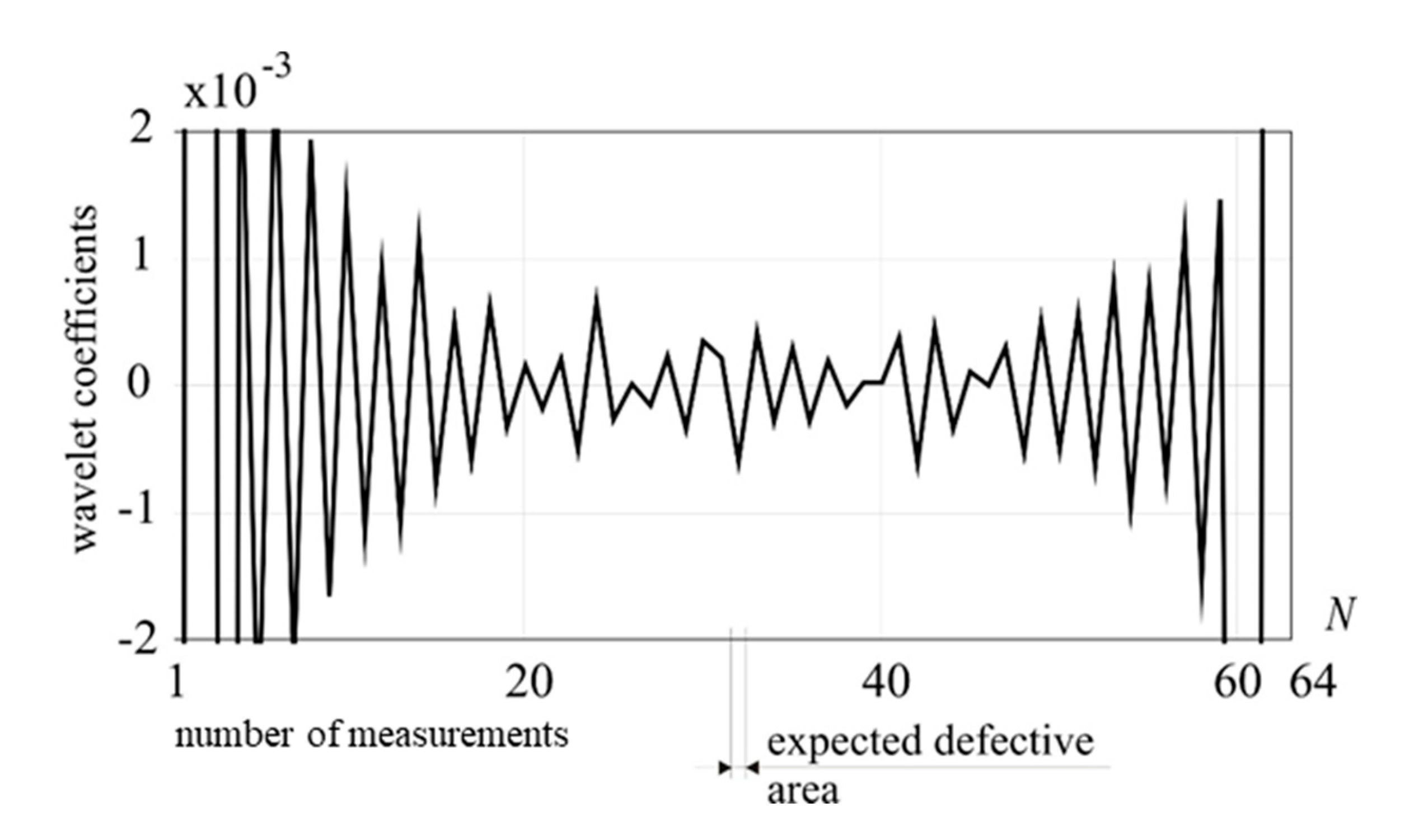
Figure 16.
1-D DWT of the total displacements, Daubechies 8 (detail 1), external load: 5 kN, damage: 25% reduction of cross section, tension force in a guy cable: 200 kN.
Figure 16.
1-D DWT of the total displacements, Daubechies 8 (detail 1), external load: 5 kN, damage: 25% reduction of cross section, tension force in a guy cable: 200 kN.
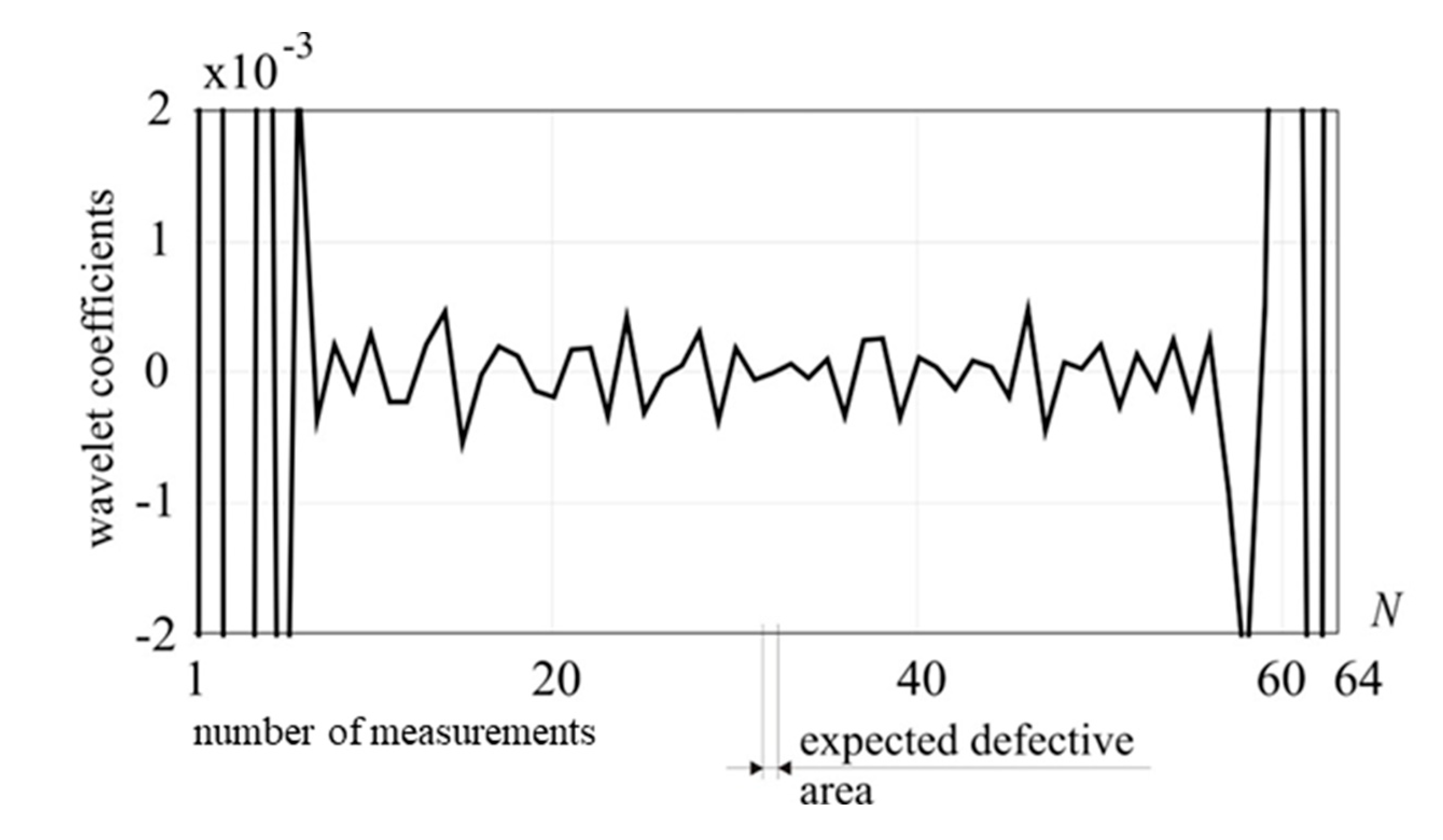
Figure 17.
Total displacements of the measurement point, damage 25% reduction of cross-section: (a) tension force in a guy cable 150 kN; (b) tension force in a guy cable 200 kN.
Figure 17.
Total displacements of the measurement point, damage 25% reduction of cross-section: (a) tension force in a guy cable 150 kN; (b) tension force in a guy cable 200 kN.
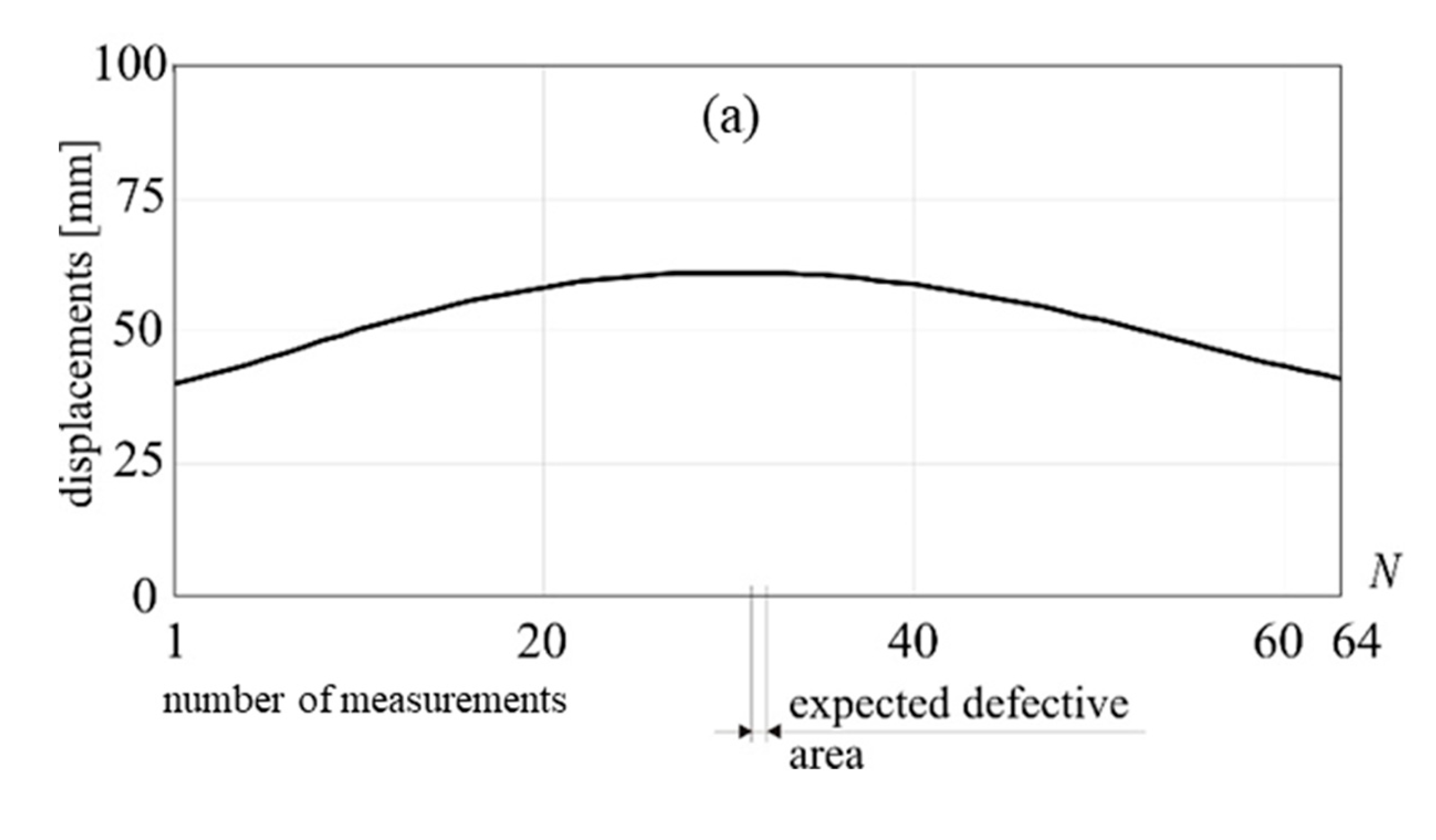
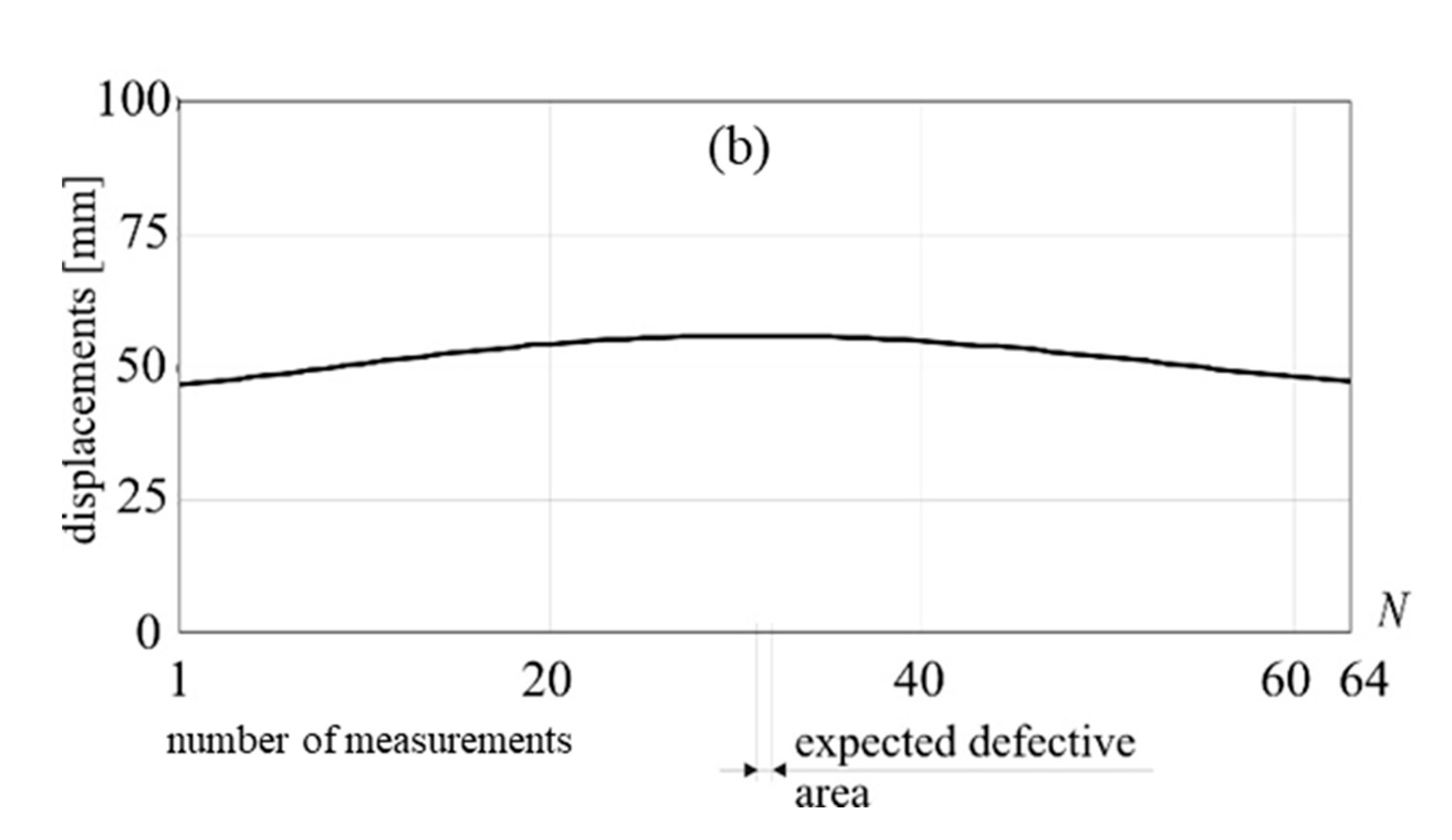
Figure 18.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 25% reduction of cross-section in a lower part of the guy cable.
Figure 18.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 25% reduction of cross-section in a lower part of the guy cable.
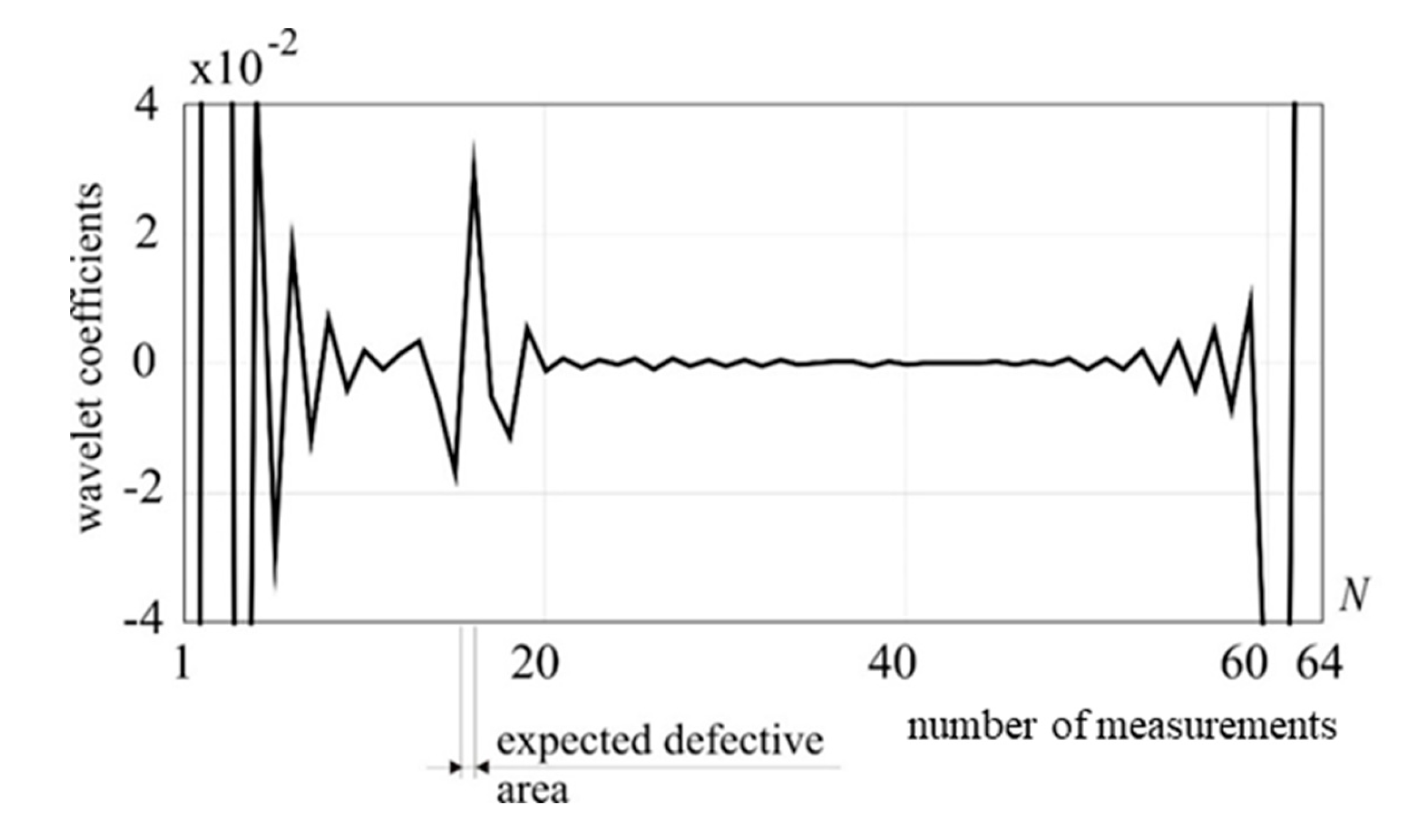
Figure 19.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 25% reduction of cross-section in an upper part of the guy cable.
Figure 19.
1-D DWT of utot, Daubechies 6 (D1), external load: 5 kN, damage: 25% reduction of cross-section in an upper part of the guy cable.
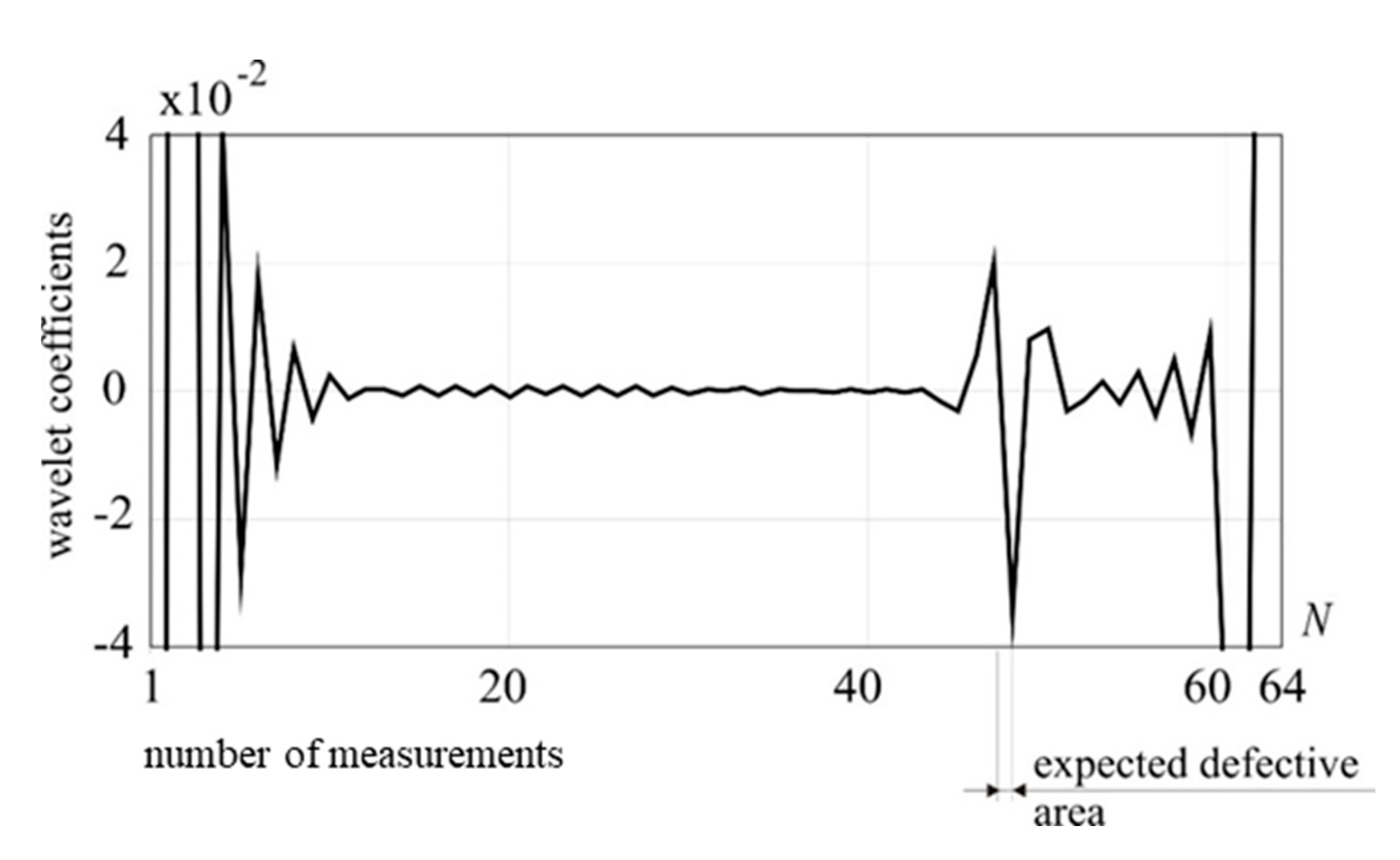
Table 1.
Change in wavelet coefficients’ range with respect to the external loading force value.
| External loading force [kN] | Wavelets coefficients’ range [–] |
| 25 | <–0.02 to 0.02> |
| 50 | <–0.04 to 0.04> |
| 100 | <–0.08 to 0.08> |
| 150 | <–0.12 to 0.12> |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
MDPI Initiatives
Important Links
© 2024 MDPI (Basel, Switzerland) unless otherwise stated








