Prerpints.org logo
Preprint
Article

Economic Cycles and the Thermodynamic Uncertainty Relations

Altmetrics

Downloads

80

Views

22

Comments

0

This version is not peer-reviewed

Submitted:

18 March 2024

Posted:

22 March 2024

You are already at the latest version

Alerts
Abstract
In the century and a half since Maxwell first conjured his “finite being” which Lord Kelvin subsequently dubbed a “daemon”, researchers have explored the connections between non-equilibrium thermodynamics, entropy, and information theory. In recent years various Thermodynamic Uncertainty Relations (TURs) have been derived to inform upon the relationship between the entropy production and the precision possible in thermodynamic machines and processes. In this paper the recently derived TURs are applied to the hypothetical thermodynamic economy as described by Parker [1]. The TURs define the lower bound on the total entropy production of the economy. Changes in this entropy production rate has consequences on the stability of the economic system and plays a central role in the business cycle. This new perspective has important implications for policy makers, researchers, and other economic actors.
Keywords: 
Subject: Business, Economics and Management  -   Economics

1. Introduction

Researchers have explored the connections between economics and thermodynamics and have produced numerous models detailing these connections. These models in various forms have been studied over the years by several authors. Researchers such as Chen [2] have attempted to describe the physical foundations of economic activity in terms of thermodynamics. Kümmel [3] related thermodynamic energy conversion and entropy production to natural, technological, and social evolution. Other researchers such as Baumgarter [4] focused on the thermodynamics of waste from economic activities, while Grisolia et al. [5] introduced a new bioeconomic indicator based on the exergy analysis of dissipation and irreversibility.
In recent years many new thermodynamic theories have been developed. These include the derivations of the thermodynamic uncertainty relations (TURs). Researchers have used these new tools to study a wide variety of classical, quantum, chemical, mechanical, and biological systems. In this paper TURs will be used to provide another perspective on the behavior of interest rates over the business cycle.

2. Materials and Methods

2.1. The Thermodynamic Economy

The thermodynamic economy modeled in this paper is an open nonequilibrium system that exchanges matter, energy, and information with the external environment. Our economy is not a single monolithic structure but is composed of many interlinked subsystems. The various parts of the open economy have different proportions of the matter and energy needed as inputs. For example, stock markets have very little direct matter exchanges with the outside environment. Instead, energy (and the information embedded within it) drive the market. Construction companies on the other hand have a larger relative proportion matter to energy as required inputs. However, both systems have information as an input which is mostly embedded in the energy inputs.
Figure 1 presents a depiction of the fundamental parts of the thermodynamic economy. These structures include the external environment from which the economy receives matter, energy, and information. The decentralized thermodynamic economy is composed of several interacting parts as seen in Figure 1. In reality the many interacting parts and processes complete their steps at different times and in parallel. This simplified hypothesized economy highlights the components central to the analysis while remaining consistent with the rules of thermodynamics.
A wide range of information is sampled from the environment at various timescales in a process represented by filters. This new information from the outside environment is stored in the economy’s memory. The processor takes the information and uses it to compute the next state of the economy. The economy is reorganized in the next step to the state previously computed, and waste heat is expelled into the surrounding environment. The final step following from the Landauer’s Principle is the erasure of the memory to prepare for the arrival new information from the environment. Landauer [6] computed the theoretical minimum energy required to erase one bit as E ≥ k b T l n 2 . This erasure leads to the irreversible loss of information as the entropy outside of the economy is increased and the net entropic accounting is balanced.

2.2. The Thermodynamic Economy

The entropic yield curve was derived in Parker [7] and provides a relationship between an economy’s ability to process information and interest rates. The thermodynamic interpretation of the entropic yield curve was presented in Parker [1,7]. Specifically, it was demonstrated that the entropic yield curve also represents the amount of entropy generated at each timescale:
r = 1 − e − C 1 1 − R C l n t   t − e − C 1 1 − R C l n σ t = T o t a l   E n t r o p y   ( P a r k e r   [ 7 ] )

2.3. Landauer’s Principle and the Thermodynamic Economy

In this paper’s model the economy is represented as large, decentralized information processing computer. This hypothetical computer gets information inputs from the economy and uses these inputs to compute the next state of the economy. In other words, information is being used to organize the real structure of the economy. This model can be viewed as an example of Maxwell’s famous demon who decreases the entropy of a system of interest using only information. By the Second Law of Thermodynamics this entropy decrease must be accompanied by an entropy increase elsewhere of at least the same magnitude.
The hypothetical economic computer determines the future state of the economy using the inputs and its internal programming. After this calculation the economy’s computational system must erase the no longer needed data filling its finite computer memory. Landauer [6] computed the theoretical minimum energy required to erase one bit as E ≥ k b T l n 2 . This erasure leads to the irreversible loss of information as the entropy outside of the economy is increased and the net entropic accounting is balanced.
While modern computers operate at orders of magnitude above the Landauer energy minimum, they are still bound by another consequence of the theory. For a given level of technology there is a maximum rate at which heat can be dissipated as information is erased. This means there exists a maximum computation rate. Exceeding this rate leads to incomplete erasures, calculation mistakes, and even damage to the computational system. The less efficient the economy’s information processing capability, the lower its currency’s purchasing power and the higher its inflation rate.
r = 1 − e − C 1 1 − R C l n t   t − e − C 1 1 − R C l n σ t
Rearranging the entropic yield curve equation, the total entropy equals the entropy of the true system minus the entropy caused by the irreversible erasure of information and the errors in the computation. The first two terms to the right of the equality represent the information used in the computations and then erased and the final term represents the errors in those computations, respectively.
r = l n t   t − e − C 1 1 − R C l n t   t − e − C 1 1 − R C l n σ t
r = l n t   t − p l n t   t − p l n σ t
Parker [7] used Landauer’s Principle and the entropic yield curve to explain the ending of the business cycle. Specifically, it was found that at the shortest timescales the economy exceeds the Shannon [8] and Landauer limits. In the next sections the entropic yield curve is used to model the evolution yield curve from the perspective of the thermodynamic uncertainty relations.

2.4. Thermodynamic Economy and the Multiscale Entropic Yield Curve

Using the entropic yield curve, Parker [1] examines the business cycle from the perspective of the multiscale entropic lifecycle (MSELC) of the yield curve. Specifically, the structure and evolution of the yield curve is described as a process dominated by the shortest end of the yield curve. Late in the business cycle the total volume of data in the shorter timescales exceeds the economic system’s channel capacity or the Landauer’s limit as seen in Parker [1].
Figure 2 displays the typical sequence of yield curve shapes seen throughout the business cycle. The entropic yield curve easily generates these shapes as described in Parker [1,7]. Most of the movement in the curve occurs in the shorter end of the maturity axis.
At the end of the business cycles the yield curve takes the shape shown below in Figure 3. This shape implies that at the lowest end of the time to maturity axis entropy production falls below that of the longer times to maturity Parker [1,7,10]. It is notable that this terminal shape seen at the end of all business cycles is not described elsewhere in the literature. This may be due to the lack of traditional explanations for this specific shape and its importance from standard economic theory).

2.5. Thermodynamic Uncertainty Relations

Barato and Seifert [9] derived the original Thermodynamic Uncertainty Relation (TUR) in 2015 as seen below. Many other forms and generalizations of the TUR have been developed. All derivations share the central unifying principle that there is a thermodynamic cost to the precision of thermodynamic machines and processes. Specifically, the precision or variance of a variable of interest J (produced by the thermodynamic machine) defines the minimum amount of entropy needed to maintain that precision.
σ ≥ 2 J 2 V a r J
This relationship implies that as entropy production decreases, the variance of interest rates will increase.
σ ↓   → V a r J ↑
In Parker [1] it was demonstrated that at the shortest timescales entropy production falls near the end of the business cycle. This fall in entropy production is predicted to be accompanied by an increase in the variance of the interest rates at those shortest timescales. This implies that early in the business cycle interest rates will have relatively similar variances. Near the end of the cycle the shorter timescale rates should increase in variance relative to the longer timescales. In the following section this relationship is empirically studied over three business cycles.

3. Results

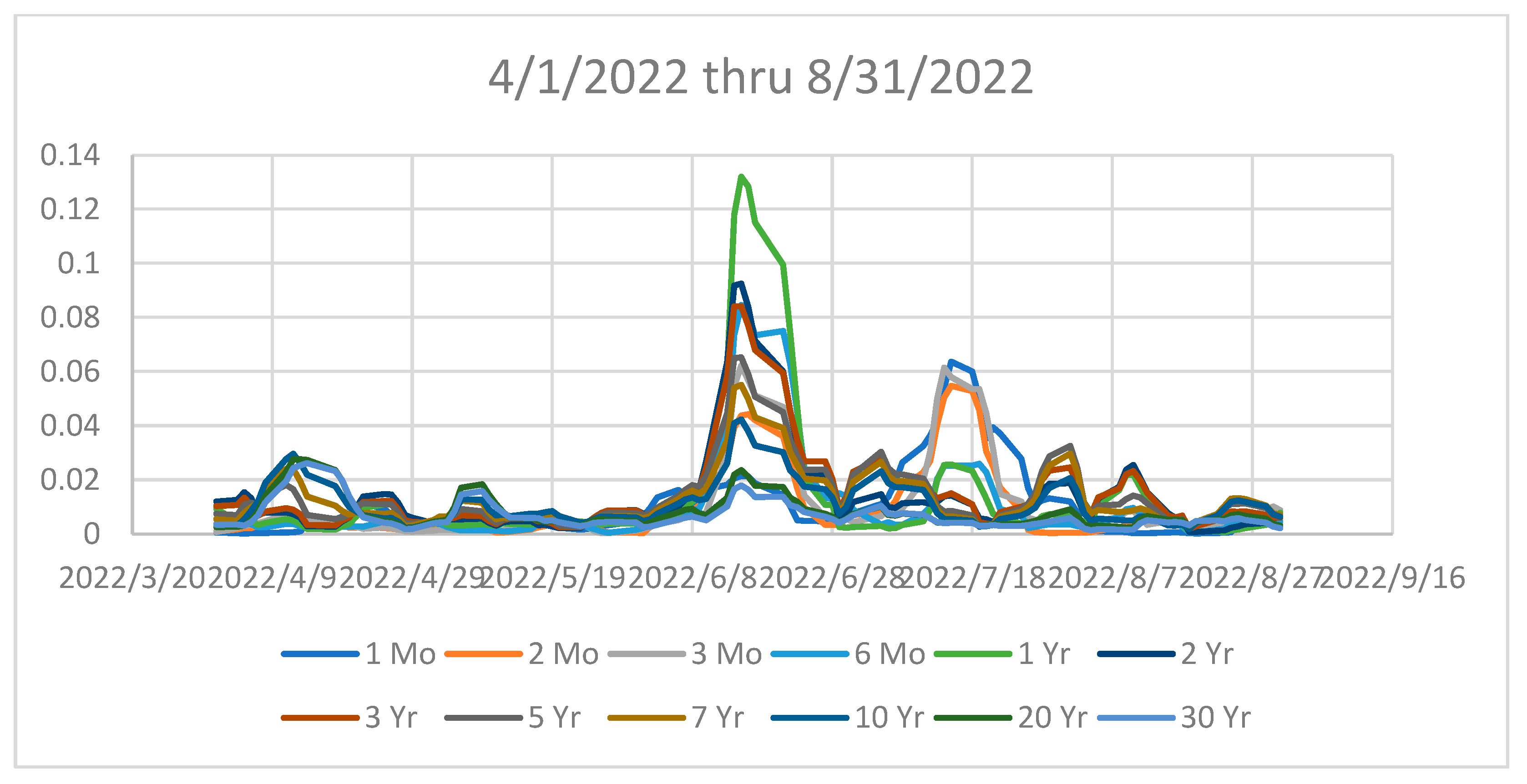
In this section the variance of the United States yield curve at all available terms to maturity is studied over three business cycles. The starting dates of equity bear markets is used to define the end of the cycle. These three periods had bear market starts in 2007, 2020, and 2022 respectively. Figure 4 displays the variances of the complete yield curve over the entire sample period for perspective. Figure 5, Figure 6 and Figure 7 provide a more detailed view of the curves around the time of the bear market starts in 2007, 2020, and 2022 respectively.
All three sample periods have large variance spikes in the relatively shorter times to maturity curves. This behavior is consistent with the predictions from the TUR perspective. The notable exceptions are the 1-month and 2-month yield curves as seen in Figure x in 2022 which does not exhibit the same relatively large spikes as seen in the 1-year, 2-year, 3-month, and 6-month yield curves (Note: the spikes seen are still relatively focused on the shorter end of the curve). This may be due to the historic anti-inflationary intervention in the bond market by the Federal Reserve beginning in 2022.

4. Discussion

As has been shown the recent derivations of the TURs have important implications for the stability and growth of the economy. The TURs state that the precision (or stability of the economic system or subsets of that system) defines the lower bound on the total entropy production of the economy. This relationship implied a divergence in the variances of short term versus long term rates. Specifically, it was found that the variance of short-term rates increases dramatically in comparison to long term rates consistent with the effect predicted by the TURs. Potential directions for future study include studying the impact of the TURs on other economic and financial variables and processes of interest such as price stability, inflation, and the volatility surface.

Supplementary Materials

The historical yield curve rates used in this paper can be downloaded at www.treasury.gov and other background material is available at www.entropicfinance.com.

Author Contributions

N/A

Funding

This research received no external funding.

Data Availability Statement

We encourage all authors of articles published in MDPI journals to share their research data. In this section, please provide details regarding where data supporting reported results can be found, including links to publicly archived datasets analyzed or generated during the study. Where no new data were created, or where data is unavailable due to privacy or ethical restrictions, a statement is still required. Suggested Data Availability Statements are available in section “MDPI Research Data Policies” at https://www.mdpi.com/ethics.

Acknowledgments

In this section, you can acknowledge any support given which is not covered by the author contribution or funding sections. This may include administrative and technical support, or donations in kind (e.g., materials used for experiments).

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. Parker, E. The Signal, Entropic Finance, and the Digital Economy: New Perspectives at the Intersection of Information Theory, Entropy, and Finance, 2nd ed.; KDP Publishing: United States, 2024; pp. 140–160. [Google Scholar]
  2. Chen, J. (2005). The Physical Foundation of Economics: An Analytical Thermodynamic Theory. [CrossRef]
  3. Kümmel, R. The Second Law of Economics: Energy, Entropy, and the Origins of Wealth; Springer: Berlin, 2011; ISBN 978-1-441-99364-9. [Google Scholar]
  4. Baumgärtner, S. (2002). `Thermodynamics of waste generation´. [CrossRef]
  5. Grisolia, G.; Fino, D.; Lucia, U. (2020). Thermodynamic optimization of the biofuel production based on mutualism. Energy Reports. 6. 1561-1571. [CrossRef]
  6. Landauer, R. “Irreversibility and Heat Generation in the Computational Process,” IBM Journal of Research and Development, Vol. 5, No. 3, 1961, pp. 183-191. [CrossRef]
  7. Parker, E. The Entropic Linkage between Equity and Bond Market Dynamics. Entropy 2017, 19, 292. [Google Scholar] [CrossRef]
  8. Shannon, C.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Chicago, IL, USA, 1949. [Google Scholar]
  9. Barato, A.C.; Seifert, U. Thermodynamic uncertainty relation for biomolecular processes. Physical review letters 2015, 114, 158101. [Google Scholar] [CrossRef] [PubMed]
  10. Parker, E. (2019). Entropy, the Information Processing Cycle, and the Forecasting of Bull and Bear Market Peaks and Troughs. International Journal of Productivity Management and Assessment Technologies (IJPMAT), 7. [CrossRef]
Preprints 101644 g001
Figure 1.
Figure 1.
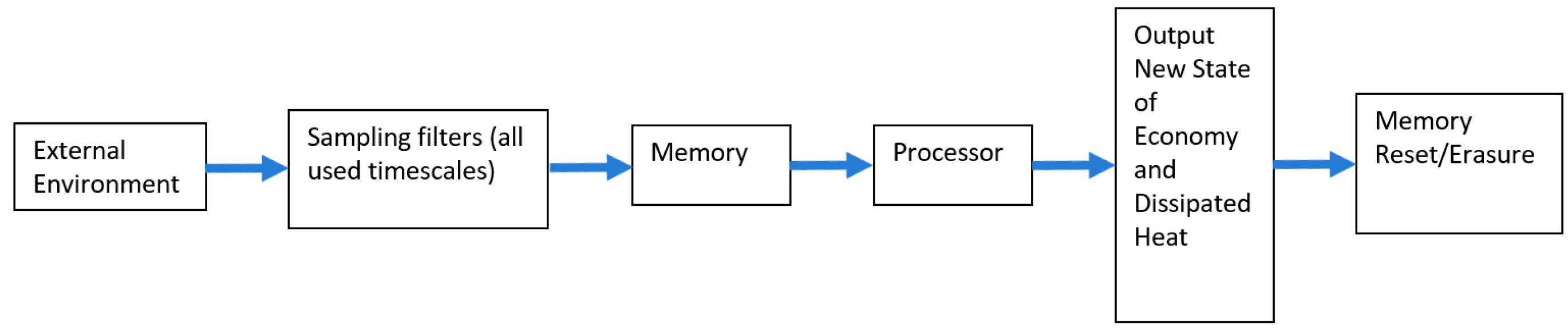
Preprints 101644 g001
Preprints 101644 g002
Figure 2.
Figure 2.
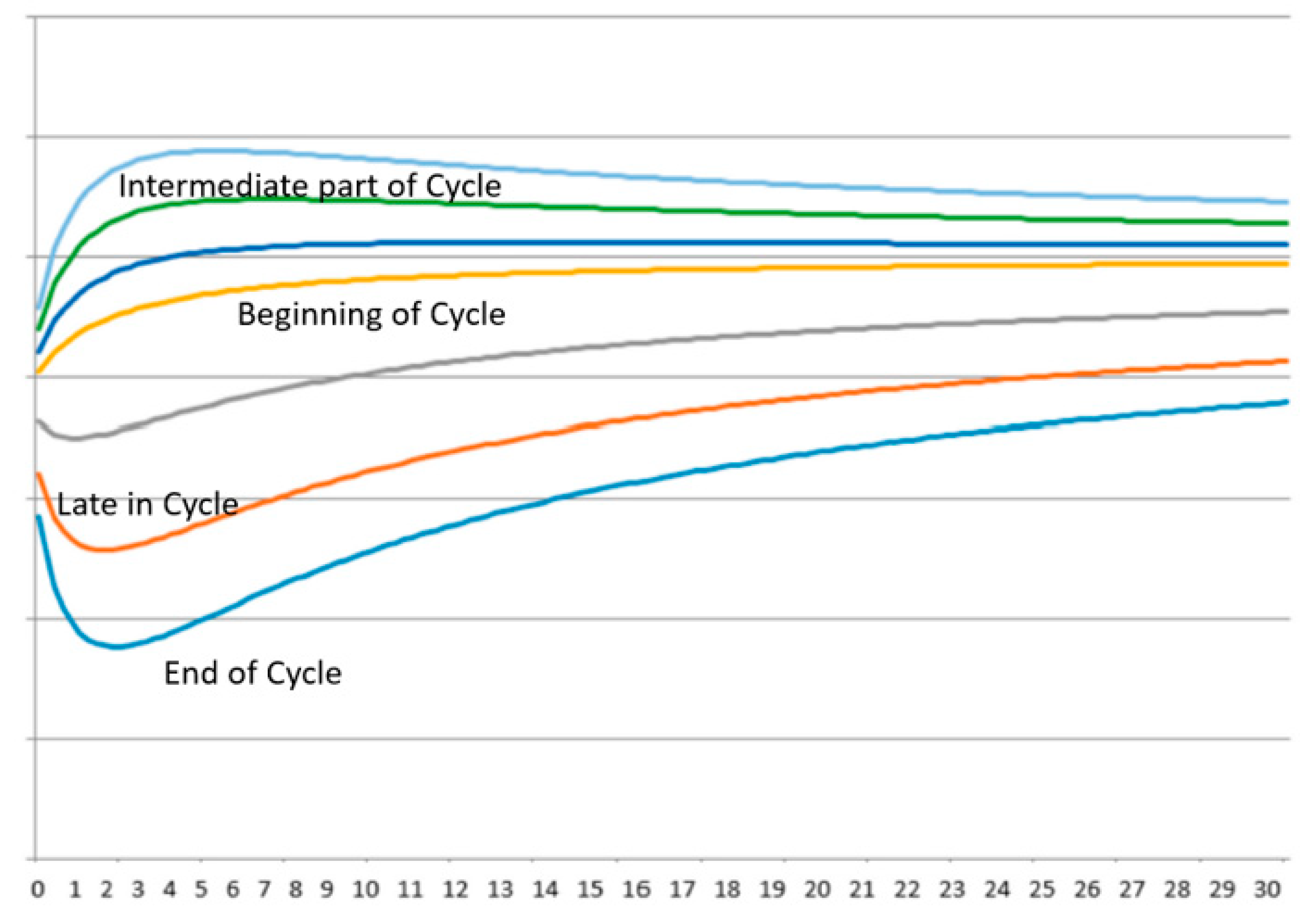
Preprints 101644 g002
Preprints 101644 g003
Figure 3.
Figure 3.
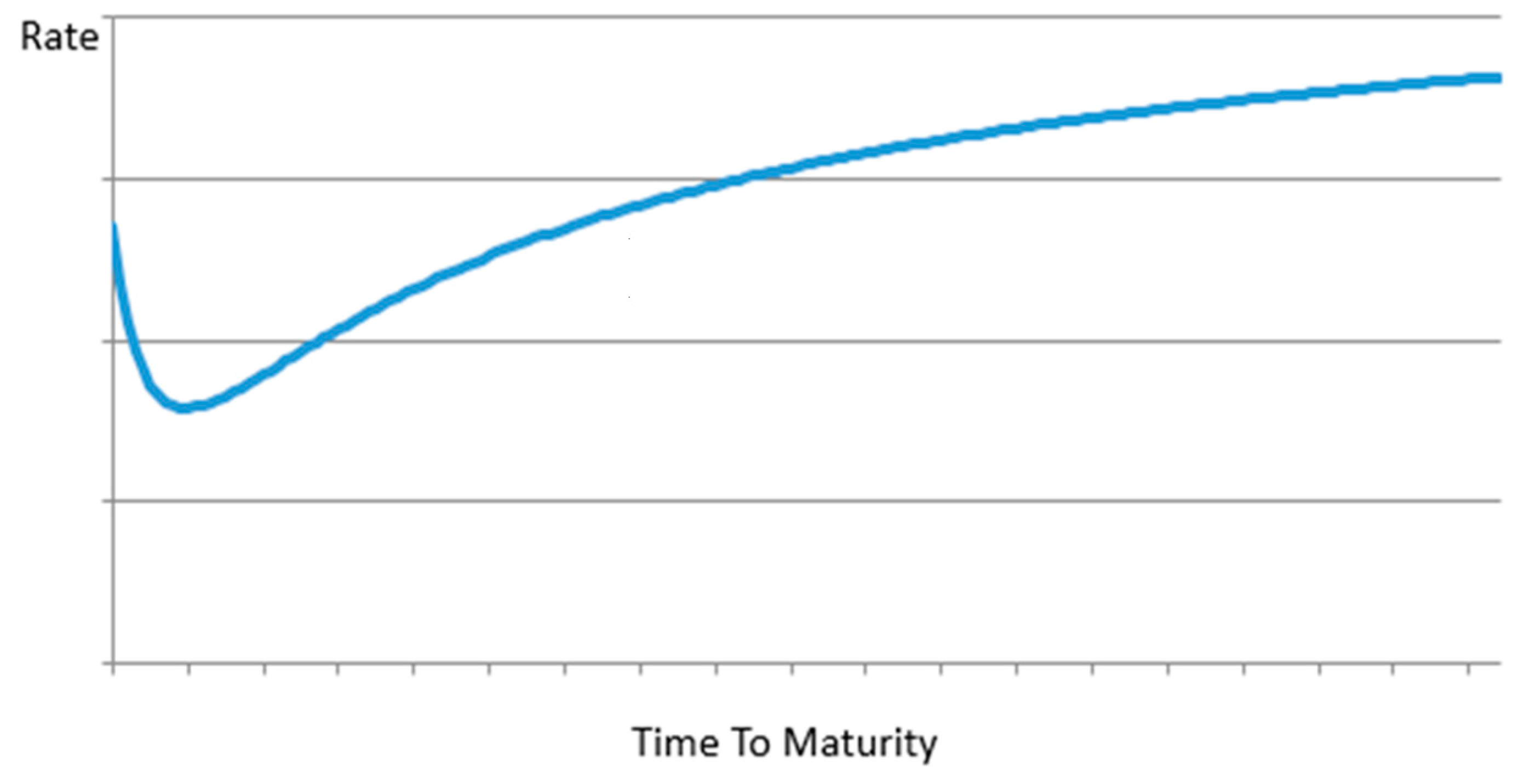
Preprints 101644 g003
Preprints 101644 g004
Figure 4. Variance of the Yield Curve over the Entire Sample Period (2007-2022).
Figure 4. Variance of the Yield Curve over the Entire Sample Period (2007-2022).
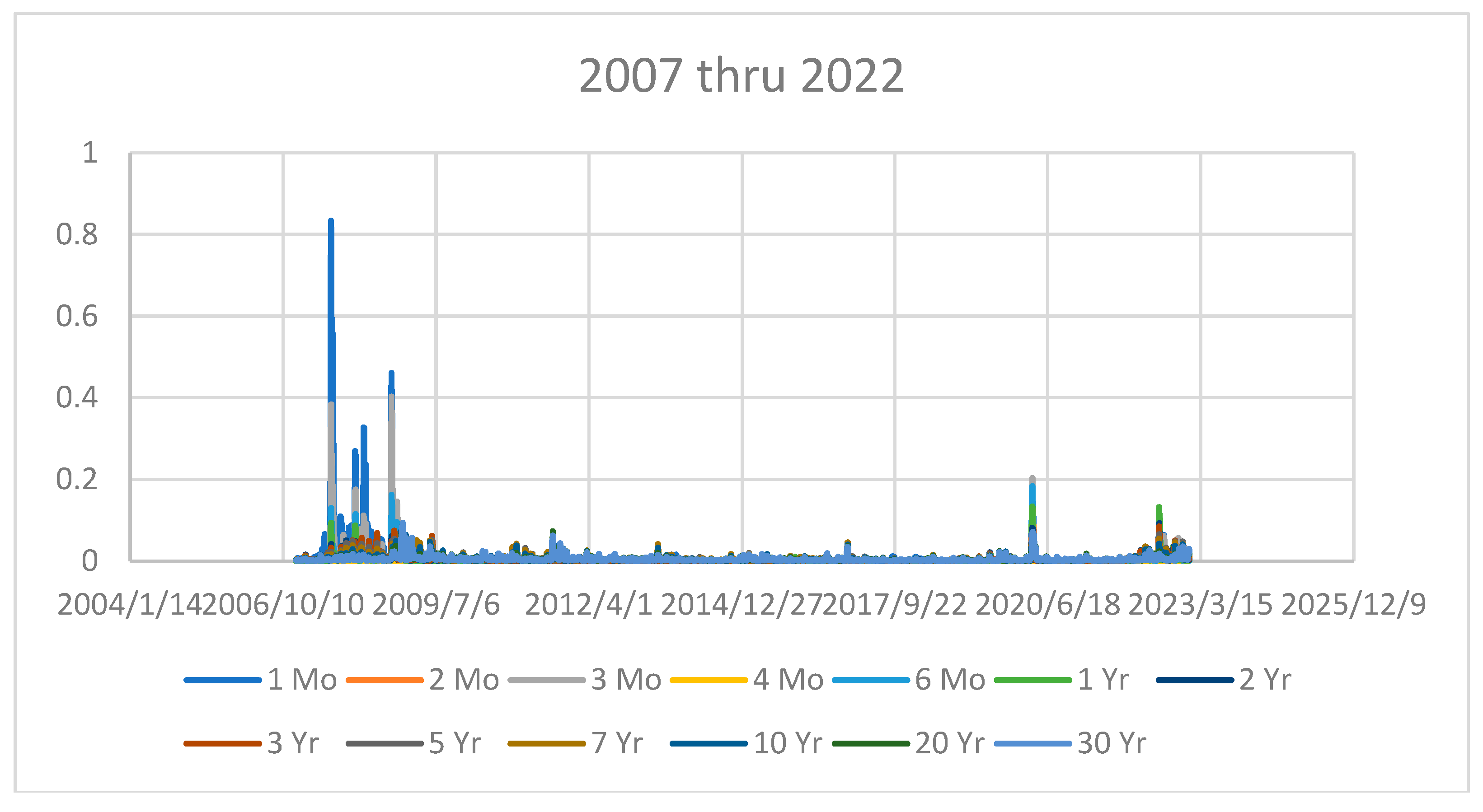
Preprints 101644 g004
Preprints 101644 g005
Figure 5. Yield Curve Variances: Spike of the 1 month, 3 month, and 6 month yield curve variances (2007).
Figure 5. Yield Curve Variances: Spike of the 1 month, 3 month, and 6 month yield curve variances (2007).
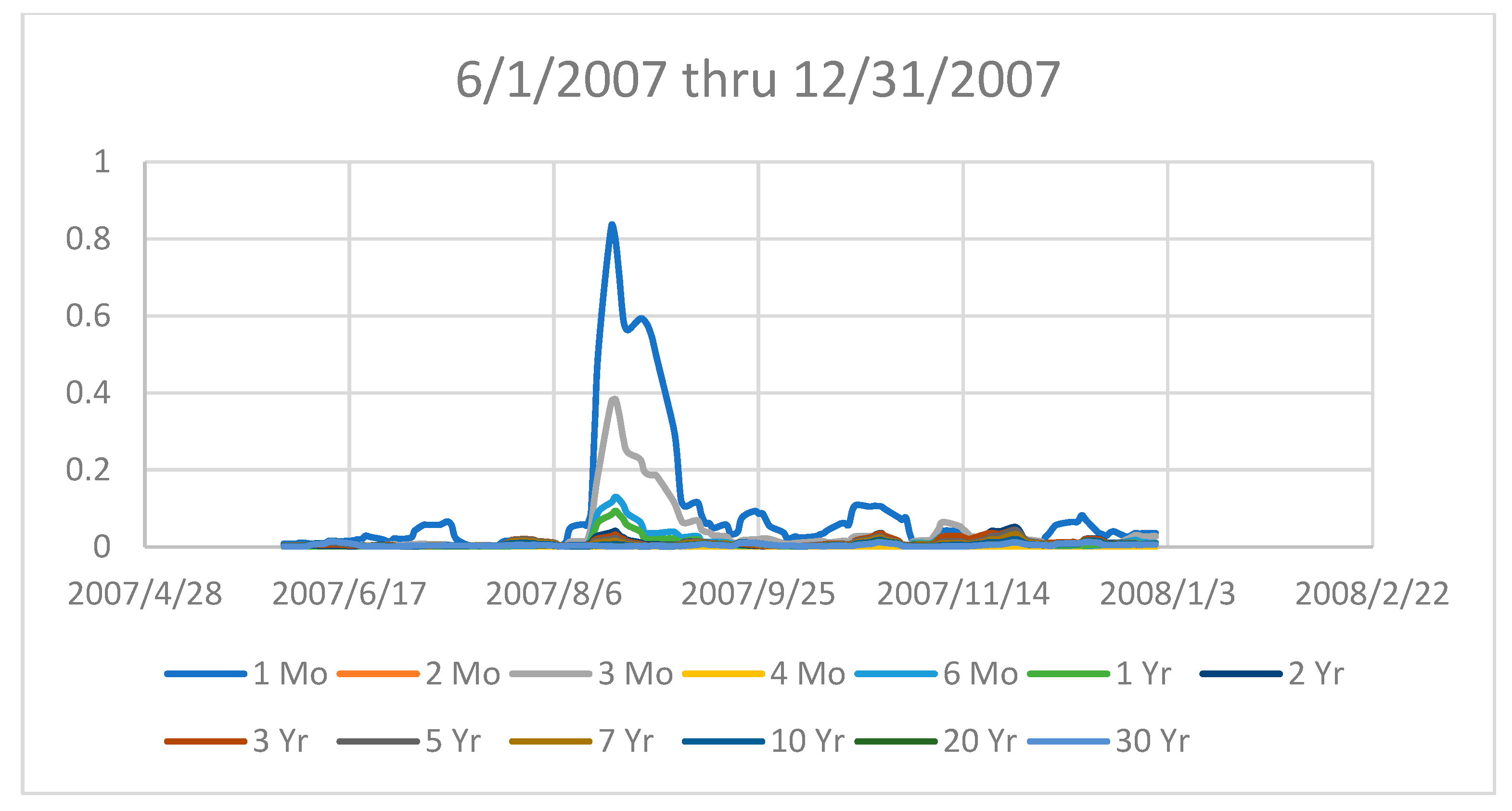
Preprints 101644 g005
Preprints 101644 g006
Figure 6. Yield Curve Variances: Spike of the 1 month, 2, month, 3 month, and 6 month yield curve variances (2020).
Figure 6. Yield Curve Variances: Spike of the 1 month, 2, month, 3 month, and 6 month yield curve variances (2020).
Preprints 101644 g006
Preprints 101644 g007
Figure 7. Yield Curve Variances: Spike of the 1 year, 2 year, month, 3 month, and 6 month yield curve variances (2022).
Figure 7. Yield Curve Variances: Spike of the 1 year, 2 year, month, 3 month, and 6 month yield curve variances (2022).
Preprints 101644 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated