Prerpints.org logo
Preprint
Article

Algebraic Nexus of Fibonacci Forms and 2-Simplex Topology in Multicellular Morphogenesis

Altmetrics

Downloads

151

Views

64

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

19 March 2024

Posted:

22 March 2024

You are already at the latest version

Alerts
Abstract
Background: Fibonacci patterns and tubular forms both arose early in the phylogeny of multicellular organisms. Tubular forms offer the advantage of a regulated internal milieu, and Fibonacci forms may offer packing efficiencies. The underlying mechanisms behind the cellular genesis of Fibonacci and tubular forms remain unknown.
Keywords: 
Subject: Biology and Life Sciences  -   Cell and Developmental Biology

1. Introduction

The Golden Ratio ( 1 + 5 ) / 2 ≈ 1.618 was recognized at least as early as 500 BCE by Phidias, after whom the symbol Φ remains named [1]. Naturalists over the centuries have commented on its presence in plants, mollusks, and vertebrates, it has been depicted in the arts, and it has been the subject of teleological conjecture [2,3,4]. Multicellular organisms evolved from unicellular organisms in the Precambrian period 580 million years ago, and appear to have done so on more than one occasion [5]. Fibonacci forms are found among these organisms [6], and are found among primitive plants such as algae [7]. Nevertheless, the molecular or cellular mechanisms for its presence in multicellular organisms remain unknown. It plays a role in plant phyllotaxis and perhaps in cellular packing, but a broader adaptive value, if any, remains unknown [8,9,10,11]. We investigate Golden Ratio mathematics and its implications regarding the ontogeny of multicellular organisms.
The Golden Ratio is real-valued while cell population counts are whole-numbered. The Fibonacci numbers are the particular whole numbers that obey the recurrence relation F n + 1 = F n + F n − 1 , with F 0 = 1 and F 1 = 1 , giving the sequence 1 , 1 , 2 , 3 , . . . . Binet’s formula offers a way to connect the Golden Ratio to the Fibonacci numbers,
F n = 1 5 Φ n − ( − 1 / Φ ) n = 1 5 ( 1 + 5 ) 2 n − ( 1 − 5 ) 2 n .
Like the Golden Ratio, forms of the Fibonacci numbers appear in ancient culture [12,13].
In this paper, we shift the Fibonacci index by one, with f n = F n + 1 . With f 1 = 1 and f 2 = 2 , this gives the sequence ( 1 , 2 , 3 , 5 , 8 , . . . ) . Under this convention, if we start with one cell and assume the cell population grows as the Fibonacci numbers, then f n gives the population cell count at the n t h generation. Furthermore, this convention offers a combinatorial interpretation of f n , giving the number of ways that the number n can be composed as sums of 1 and 2 [14]. This is seen in Section 7.
Single-celled and multicellular organisms both perform replication. Some single-celled organisms exhibit adhesion. For example, the bacterium Streptococcus pneumonia may adhere into pairs and chains, and Staphylococcus aureus may adhere into clusters. We hypothesize that multicellular organisms differ from single-celled organisms by having replication and adhesion be mutually regulated phenomena. An example in multicellular organisms is contact inhibition, where the adhesion between two cells yields the coordinated replication of only one of them [15]. The inter-regulation of adhesion and replication enables more extensive structures having cellular specialization amidst topological variations.

1.1. Replication

A cell in a multicellular organism has a cell cycle divided broadly into two intervals, interphase and mitosis, as shown in Figure 1. Interphase includes the time interval where a cell makes its specialized contribution to an organism and is where it makes preparatory changes so that it may divide. The proportions of time spent in interphase and mitosis vary greatly, but generally, a cell spends much more time in interphase.
The first phase in interphase is G 1 (G as in gap). In G 1 a cell increases its supply of proteins, organelles (such as mitochondria, which catalyze the conversion of oxygen into energy), and it grows in size. It may transition to and from a non-growing phase G 0 .
Chromosomal DNA is replicated in the S interval of interphase. After DNA replication, each chromosome has a pair with an identical DNA sequence. G 2 is a growth phase after DNA replication.
Mitosis (M) is a brief interval of the cell cycle where the cell divides into two. It consists of prophase where the chromosomes become dense, metaphase where the chromosome pairs line up on the equatorial plane, anaphase where the chromosome pairs detach into sister chromatids, telophase where the sister chromatids move apart and form separate nuclei, and abscission where the membranes cleave to form 2 progeny cells.
Cytokinesis is the interval of mitosis between anaphase and telophase when the sister chromatids segregate. They are pulled apart by mitotic spindles composed of tubulin. Cytokinesis provides the proper distribution of genetic material and cytoplasm between the two progeny cells. It involves the formation of a contractile ring, composed of actin and myosin filaments, at the equatorial plane of the dividing cell. The contractile ring is oriented perpendicular to the spindles. The contractile ring contracts, leading to the formation of a cleavage furrow and eventually to abscission, the detachment of the two progeny cells. The relationships between the contractile ring and the spindle at abscission can encode polarities in the mitotic progeny [16,17,18,19,20].

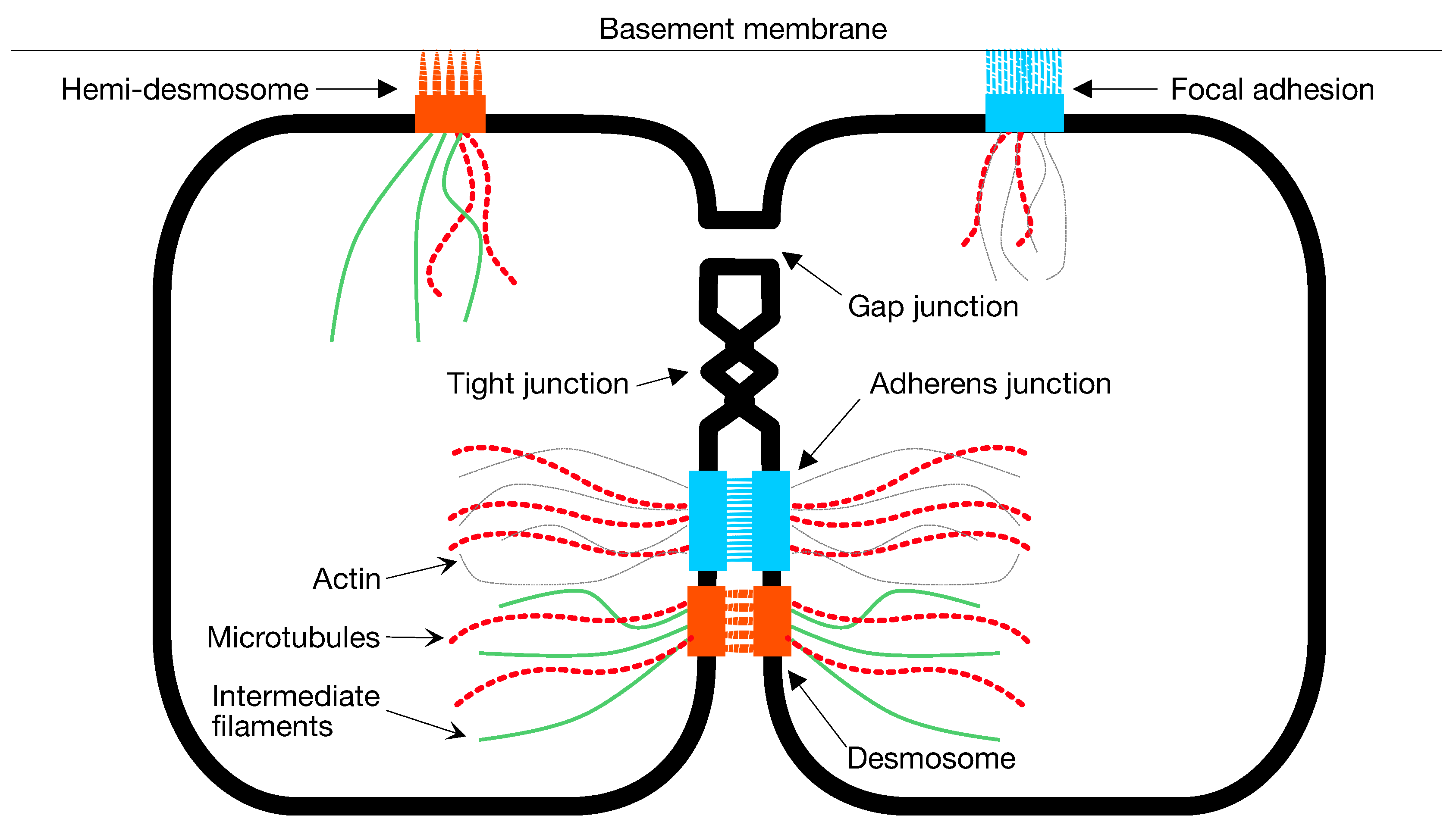
1.2. Adhesion

Adhesion is a persistent cell-to-cell connection with binding molecules that maintain physical proximity between the adhered cells. It may occur by direct cell-cell contact or be mediated by an intervening extracellular matrix. It may offer modes of communication or coordination between the cells.
There are broadly five types of molecular cell-cell adhesion by direct contact, illustrated in Figure 2. A cell’s intracellular content is separated from the extracellular content by a bilipid membrane. With two of the adhesion types, gap junctions and tight junctions, lipid cell membranes between adjacent cells are intermingled. These adhesion types allow for the exchange of molecules between intracellular spaces. For the other three adhesion types, adherens junctions, desmosomes, and focal adhesions (having tunneling nanotubes) the adhesion is mediated by a multi-subunit protein structure that spans the extra to the intracellular space [21]. The binding to the outer surface cell junctions generally induces metabolic changes within the cell. There is evidence that adhered cells can coordinate their cell cycles [22,23,24]. Furthermore, the tunneling nanotubes of focal adhesions enable intercellular exchange of DNA and RNA [21].
On the internal cell surface, the adhesion protein complex commonly binds to elements of the cytoskeleton. There are broadly three types of cytoskeleton protein. These are actin filaments, microtubules, and intermediate filaments such as vimentin [25]. Of these, actin filaments and microtubules are capable of active contraction. They play roles in modifying cell shape and in cell migration. The cytoskeleton binds the inner surface of cell adhesion sites to intracellular organelles, including the cell nucleus. In mitosis, microtubules bind to chromosome pairs and pull them apart as a cell replicates. The cytoskeleton offers intracellular binding between the inner surface of cell adhesion sites [26].
The five types of cell-cell adhesions have differences in their properties, but the property they have in common is that they physically bind adjacent cells together and may offer signaling channels. This is the property of cell adhesion that we focus on, and we use adhesion as an umbrella term, but we do not treat the five cell-cell adhesion types separately. The extracellular matrix may offer indirect forms of cell to cell communication between cells not sharing a membrane to membrane adhesion. For example, molecules of the extracellular matrix may be anisotropic, and this anisotropy may be reflected intracellularly in the cellular cytoskeleton [27,28,29].

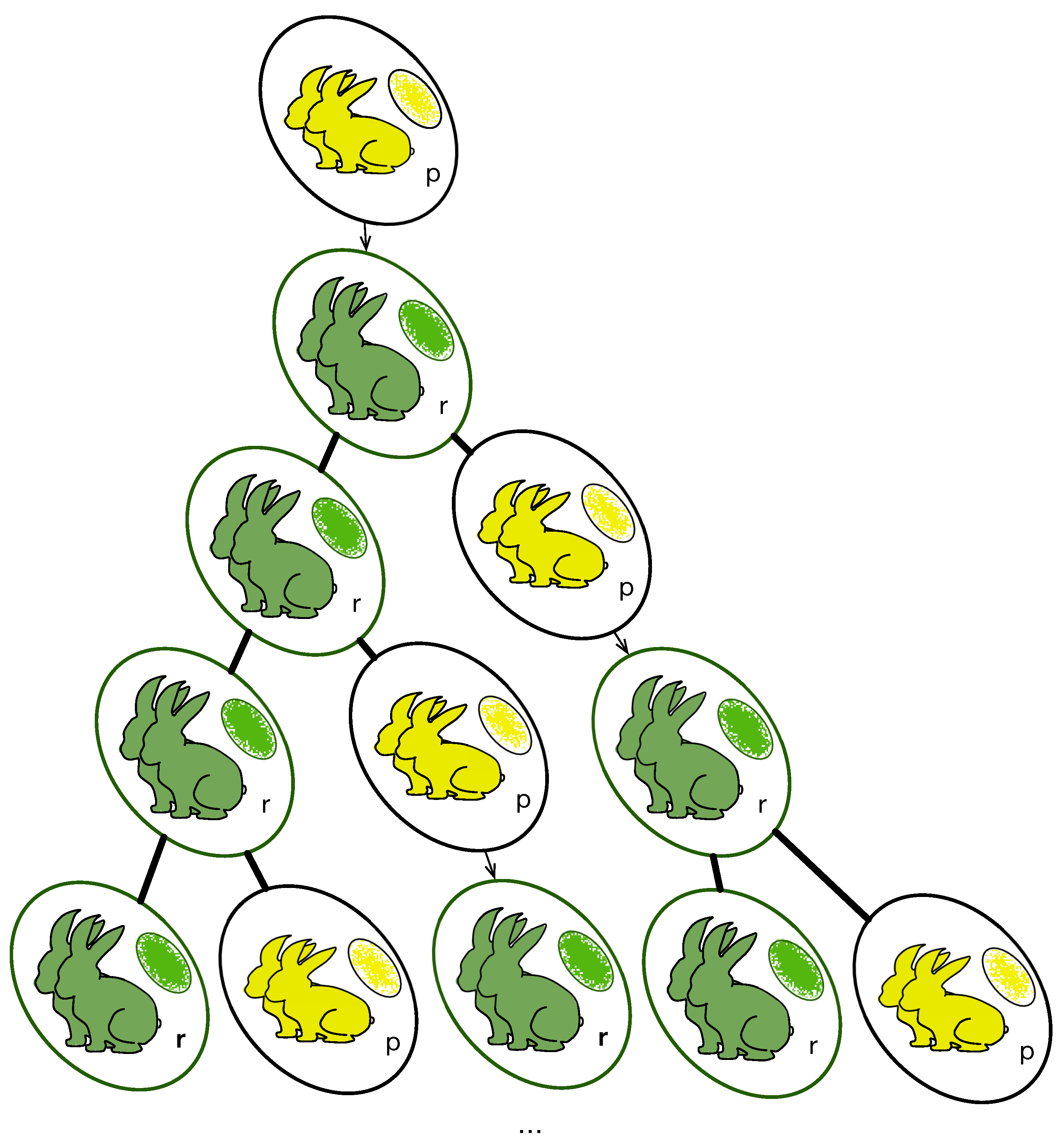
2. Cellular Adhesion and Replication Patterns that May Produce Fibonacci Population Counts

We identify patterns of cellular replication and adhesion that may produce Fibonacci population cell counts. For each of these, we ask what are candidates for the underlying molecular apparatus. Then we examine the properties of these cellular and molecular options for adaptive advantage.
When we consider candidate molecular mechanisms behind Fibonacci cell kinetics, as per the central dogma of molecular biology [30], we assume that mitotic progeny share identical DNA sequences. Meiosis, not under consideration here, is a different type of cellular replication where by design the ultimate meiotic progeny have different chromosomes.

2.1. Differential Mitosis Timing between Progeny

Fibonacci (Leonardo Pisano) described a rabbit reproduction model based on two rabbit progeny having a different interval between birth and reproduction (Figure 3) [13]. The rabbit population grows as the Fibonacci numbers. We adapt this model to cell kinetics, substituting the replication unit of a rabbit pair with a cell in a multicellular organism. In this pattern, cells are assigned at birth to one of two cell cycle timing classes, r (replicate) and p (pause). Aside from cell cycle timing, the cells are of the same phenotype.
Analogous to Fibonacci’s rabbit reproduction model, at each generation we model an r cell to replicate to another r cell plus a p cell. An r cell proceeds to mitosis while the p pauses for one generation then matures into an r cell that divides,
r ↦ r + p p ↦ r
We subscript to indicate the number of r and p cells at generation n,
r n + 1 = r n + p n p n + 1 = r n .
We express this in matrix notation as
r n + 1 p n + 1 = 1 1 1 0 r n p n
where we recognize the Fibonacci Q matrix [31]
Q = 1 1 1 0 .
The Q matrix can be used to generate the n t h Fibonacci number
f n f n − 1 f n − 1 f n − 2 = Q n .
Furthermore, Golden Ratios appear in Q’s eigenvalues ( Φ and − 1 / Φ ) [32]. Having Golden Ratio eigenvalues signifies that this model of divergent cell cycle timing can produce Φ generational sizes based on cells of two types of replication timing [33,34].
This has similarities to the mathematics of L-systems as pioneered by Lindenmayer [35,36,37], and bears to work on cellular automata [36,38,39,40].

2.1.1. Epigenomic Divergence

Epigenomics is the study of heritable changes in gene expression that do not rely on the primary DNA sequence [41]. Epigenomic phenomena participate in the regulation of cell metabolism, growth, and mitosis [42]. A differential mitosis timing between progeny could be accounted for if progeny were to diverge in their molecular epigenomics [43]. For example, there is an enzymatic apparatus that attaches methyl groups to cytosine of DNA prior to replication in the S interval of interphase (Figure 1) [44]. This apparatus appears to have arisen early among eukaryotic cells, which are the foundation of multicellular organisms [45]. The methylated cytosine is not copied when a double strand of DNA is copied into two double strands in preparation for mitosis. Just one of the two progeny carries a particular cytosine methylation [46]. Insofar as this influences mitosis timing, it might account for differential mitosis timing between progeny.
Histone methylation is another candidate mechanism for differential epigenomics [47,48]. The histone proteins help organize DNA strands into compact structures that can be contained in a cell nucleus. Histone methylation can influence the expression of genes in the associated DNA. Copies of histones are passed to mitotic progeny. This poses another opportunity for differential mitosis behavior between mitotic progeny.
There can be polarities in the mitotic progeny that derive from the relationship between the involuting spindle and the plane of the contractile ring at abscission [16,17,18,19,20].

2.2. Contact Inhibition

In the model above, Fibonacci cell counts are generated by differential mitosis timing between progeny based on properties that are inhibited at cell birth. There is evidence though that cell cycle and mitosis timing can be coordinated by cell contact [15]. We ask if there is a formalism to generate Fibonacci cell counts where cells that adhere coordinate to restrain mitosis in one of the two cells whereas cells without contact (adhesion) mitose.
In one such pattern, adhered cell pairs coordinate their cell cycles so that only one undergoes mitosis. A single cell replicates to yield two cells
Preprints 101778 i001
whereas with an adhered cell pair, but one undergoes mitosis, producing three cells
Preprints 101778 i002
This is contact inhibition [15].
Proposition 1.
There is an additive and recursive Fibonacci growth pattern based on contact inhibition. For illustration, we employ the language of biological cells.
Proof. 
We demonstrate the existence of such an algorithm where upon replication single cells go from count 1 to count 2 and cells pairs go from count 2 to count 3. The double arrow ⇒ denotes a replication step. We start with count 1.
f 1 ⇒ f 2
The 2 cells of f 2 coordinate to replicate into 3 cells. One cell comprising f 2 takes no replicative action. The other produces a copy of itself to give net
f 2 ⇒ f 3 .
We proceed by induction for any n ≥ 3 . We start by rearranging
f n = f n − 1 + f n − 2 = ( f n − 2 + f n − 3 ) + f n − 2
to give f n − 2 pairs as
f n = ( f n − 2 + f n − 2 ) + f n − 3
In the replication step, each pair coordinates to produce one more cell, ( f n − 2 + f n − 2 ) → 3 f n − 2 and each unpaired cell produces two, f n − 3 → 2 f n − 3 . This gives upon replication
f n ⇒ 3 f n − 2 + 2 f n − 3 ( replication step ) = f n − 2 + 2 ( f n − 2 + f n − 3 ) = f n − 2 + 2 f n − 1 = ( f n − 2 + f n − 1 ) + f n − 1 = f n + f n − 1 = f n + 1 .
□
A given cell population may deviate from precise Fibonacci cell counts if for example in Equation 4 some of the cells enumerated by the f n − 3 term form coordinated pairs, in which case they might form the epicenter of a new Fibonacci pattern, or if some cells in the f n − 2 terms do not. A biological interpretation may be of variations in the local availability of cells to induce contact inhibition.
We introduce some terminology. In an adhered cell pair that undergoes replication, we term one cell the partner cell and the other the mitosis cell. There are two polarities that can be named. The orientation of the two cells relative to each other may be termed the pair polarity. With a mitosis cell, there is a mitosis polarity. It is given by the axis of sister chromatid separation. This corresponds to the axis from the centrosome at one pole of the cell to the centrosome at the other pole. The mitosis polarity is perpendicular to the plane defined by the contractile ring.
When two cells adhere, there may be a preference as to which the partner cell and which is the mitosis cell. Furthermore, these preferences may have a relation to some directionality in the pair and mitosis polarities. Such a preference may be encoded intracellularly or in a difference in relationship between a cell cytoskeleton and the extracellular matrix.

2.3. Cooperative Mitosis and Adhesion

In the above model of contact inhibition, when a pair of cells adhere there is no preference as to which undergoes mitosis. However, recognizing the presence of epigenomic and polarity differences between mitotic progeny, there may be a biological circumstance where when two cells adhere, there is a molecular distinction between them that makes one in particular more apt to undergo mitosis. The biomolecular mechanisms behind such a distinction may transpire intracellularly or extracellularly, perhaps depending on polarities between a cell cytoskeleton and the extracellular matrix [49]. Let us assume that there are two cell types, a and b, that are similar in every way other than having a different preference to undergo mitosis when they adhere.
Proposition 2.
There is an additive and recursive Fibonacci growth pattern based on contact inhibition between cell types a and b. We denote this cell type by a left superscript. Replication from 2 cells to 3 is based on a pairing of an a cell with a b cell, ( a + b ) ⇒ 2 a + b . An unpaired a cell replicates into an a cell and a b cell, a ⇒ a + b .
Proof. 
Proceeding as above, and starting with n,
f n = f a n − 1 + f b n − 2 = ( f a n − 2 + f b n − 2 ) + f a n − 3 f n ⇒ ( 2 f a n − 2 + f b n − 2 ) + ( f a n − 3 + f b n − 3 ) ( replication step ) = ( 2 f a n − 2 + f a n − 3 ) + f b n − 2 + f b n − 3 ) = f a n − 2 + f a n − 1 + f b n − 1 = f a n + f b n − 1 = f n + 1 .
□
A replication behavior that depends on and produces oriented adhesion between two cell types generates opportunities for emergent tissue patterns [49]. For example, using a half arrow head ⇀ to denote an oriented adhesion between cells, we find that a number of tissue patterns may arise over three generations,
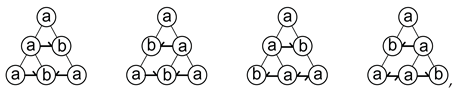
Preprints 101778 i003
as indicated by the local orientations of cell types a and b.
A replication pattern based on cooperation between adhered cell pairs may approximate local Fibonacci growth for small n but it may not necessarily generate global Fibonacci patterns for large n.

3. Candidate Molecular Mechanisms

An assignment at adhesion to mitose or not is consistent with laboratory evidence that the five categories of cell adhesion (Figure 2) participate in gene and cell cycle regulation [50,51,52,53,54,55]. If these adhesion categories are able, in particular, to establish semaphore cell cycle coordination so that one of a pair undergoes mitosis, then Fibonacci population counts might be observed. If the paired cells are identical and the adhesion communication are symmetric, then it may be equal odds as to which cell of the adhered pair undergoes mitosis.
The molecular data are consistent with mutually reinforcing roles for mitosis and adhesion [15]. This might be the case if there is polarity among mitotic progeny that influences the mitosis semaphore at adhesion. The polarity-dependent mitotic behavior could span generations. A candidate molecular mechanism might be a cytoskeletal polarity that is linked across the cell membrane to polarities of extracellular adhesion and the extracellular matrix [27,28,29,56,57]. For example, the midbody, which forms along the cleavage line at telophase and can be asymmetrically inherited by a progeny [58], is involved in cell proliferation [59], and has attachment to cell surface adhesion structures [54].
There are other opportunities for stereochemical variations between mitotic progeny with extracellular linkage. When chromosomes condense in the cell nucleus in prophase, mitotic spindles form between centrosomes at opposite poles of the cell and attach to the kinetochores of the chromosomes (Figure 1). The spindles consist of microtubules which are motoric protein structures. They have a left chiral orientation as they link centrosome to centrosome at opposite cell poles. They attach to the kinetochores of chromosomes. Their chirality causes them to apply torque to chromosomes when they contract [60]. The helical spindle attachment to chromosomal kinetochores opens opportunities for stereoisomeric distinction upon chromosomal separation [61] Figure 1). This opens an opportunity for enantiomeric chromosomal differences after metaphase that remain coordinated with extracellular adhesion patterns.

4. Simplicial Steps by Replication and Adhesion

The sheer accumulation of mass by replication and adhesion may not be the most efficient way for a multicellular organism to gain an adaptive edge. There may be instead advantages from qualitative changes in shape. We ask how replication and adhesion, founded in molecular and cell biology, can enable the topological transformation of organism shape.
A topological transformation of bioontology interest is the adoption of a tubular form. It enables a primitive organism to maintain a regulated internal environment with openings for exchanging nutrients and waste products with the external environment [49]. A hollow morphology that hosts a separated internal environment arises in some of the earliest multicellular organisms in the Precambrian period 580 million years ago, such as those from the phylum Cnidaria [62,63]. Fibonacci forms are found among these tubular plants and animals [6,7].
Another topological form of biological interest is the torus. It is a surface of revolution of a circle about a coplanar axis, reminiscent of a “donut" [64]. An internal torus form may offer a circulatory system. It may require a mechanical pump to impel cyclical fluid motion corresponding to a heart. There exist algorithms to construct three-dimensional objects such as a torus from 2-simplex meshes [65]. A biological topic for investigation is whether there exist cellular and molecular mechanisms that might act like such algorithms to produce a torus. A torus provides greater control of the internal environment than a tube since the torus shape does not include a mouth-like opening. Instead, it relies on diffusion for chemical exchange with the environment. Among vertebrates, the circulatory system exchanges oxygen and carbon dioxide with the external environment by diffusion in the lungs.
We focus on the adoption by organisms of simple topological forms, the simplices. A topological k-simplex is a generalization of a directed multigraph having k vertices and a directed edge connecting every vertex pair, a face connecting every vertex triplet, and so on. A simplex reflects the most complex topological form representable by the fewest points. For a biological interpretation, we view cells as vertices and adhesions as edges, and we ask whether these roles might enable simplicial topological transformation. The study of simplices might offer insight into the genesis of complex biological forms from simpler ones by cellular replication and adhesion programs. A 0-simplex is a point, a 1-simplex is two points with an edge between them, a 2-simplex is a triangle having an outer boundary and a flat inner region, and so on.
In topology, there is an equivalence termed a homotopy between shapes that can be transformed into each other. If they can be continuously and invertibly transformed into each other, they are termed a homeomorphism. For example, the boundary of a 2-simplex is the maximally continuously contracted form of a circle, and a circle is a continuously contracted form of a tube. Transitively, the boundary of a 2-simplex is the maximally contracted form of a tube. We ask if there is an algebraic way to replicate the vertices of a n-simplex to produce an n + 1 -simplex. If so, we ask if there exists a cellular and molecular apparatus for executing this algebraic procedure to produce a biological 2-simplex. If so, we further ask if there is a cellular and molecular apparatus for extending a biological 2-simplex toward a circle of enlarging cellular diameter. A desired property of the cellular and molecular apparatus is that it enables a self-similar automaton program where individual cells act similarly in response to similar stimuli.
We define a simplex in terms of the barycentric coordinate system.
Definition 1
(n-Simplex). Given n + 1 points v 0 , v 1 , . . . , v n in R n that are affinely independent, the n-simplex is the set of all points C n
C n = { λ 0 v 0 + λ 1 v 1 + . . . + λ n v n ∣ ∑ i = 0 n λ i = 1   and   all   λ i ≥ 0 } .
The affine dependence criterion assures that the simplex properties are preserved by an affine transform, which can include a linear scaling, a rotation, or a translation.
Definition 2
(Vertex Replication). In an n-simplex with points C n , the replication of the k t h point is given by a process:
  • Increase the space dimensions from R n to R n + 1 .
  • This increases the vector length of every point. Let w 0 , w 1 , . . . , w n be the first n + 1 points. Let each w i be a copy of v i with a 0 placed in the last position.
  • Let w n + 1 be a copy of the point to be replicated, v k , with a 1 placed in the last position.
Here is an example progression from a 0-simplex to a 1-simplex to a 2-simplex by two vertex replications.
Preprints 101778 i019
We find that a vertex replication in an n-simplex yields an n + 1 -simplex.
Theorem 1
(Simplex Growth by Vertex Replication). A vertex replication in an n-simplex produces an n + 1 -simplex. The new simplex is given by the set of points
C n + 1 = { λ 0 v 0 + λ 1 v 1 + . . . + λ n + 1 v n + 1 ∣ ∑ i = 0 n + 1 λ i = 1 a n d a l l λ i ≥ 0 } .
Proof. 
By assumption, prior to replication, the points v 0 , v 1 , . . . , v n in R n are affinely independent. It suffices to show that the produced points w 0 , w 1 , . . . , w n + 1 in R n + 1 are affinely independent. This holds because the point produced by replication, w n + 1 , differs from all other points by having a 1 in its last vector position, whereas the n + 1 other points have a 0 in that position. Therefore w n + 1 is affinely independent of all other points, which by assumption are affinely independent. □
In the contact inhibition model of Fibonacci cell count growth, an adhered cell pair assigns one to be a partner cell and the other a mitosis cell. Upon telophase, the mitosis cell forms a contractile ring. At cytokinesis, the contractile ring becomes the plane of abscission (Figure 1). We hypothesize that if the pair polarity is perpendicular to the mitosis polarity, then upon abscission the polarity of the progeny cells will be perpendicular to the preceding pair polarity. This perpendicularity is equivalent to affine independence of the progeny adhesion direction to the preceding pair polarity. In addition, if the mitosis polarity of the mitosing cell relative to the partner cell is such that their adhesion spans the contractile ring, then both progeny cells will inherit adhesion to the partner cell, in addition to retaining adhesion to each other, as shown in the first three steps here
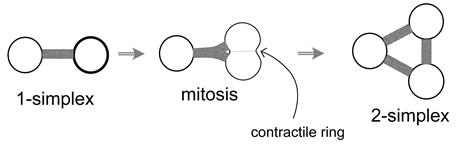
Preprints 101778 i004
According to the simplex growth by vertex replication theorem, if the mitosis polarity is perpendicular to the pair polarity and if parental adhesions are inherited, then the original single cell produces a 2-simplex at the third generation.
The capacity for a mitosing cell to split and share adhesions among progeny cells to a partner cell as in Equation 6 implies particular properties of cell membranes and their embedded adhesion molecules. Rather than be an infinitesimally thin vertex between nodes as in graph theory, this implies an adhesion to be a bundle with a certain thickness that can be split. This appears to be consistent with the fluid mosaic biochemical theory where "cell membranes are viewed as two-dimensional solutions of oriented globular proteins and lipids" [66]. Under this interpretation, the adhesion on the left hand side of Equation 6 is formed by an arrangement of oriented proteins shared by segments of the liquid membranes of the two partner cells on the left. If the liquid zone of the dividing cell spans the plane of abscission, then both progeny cells inherit an adhered liquid zone on their cell membrane. If the two progeny cells retain adhesion by oriented proteins between them as their liquid membrane zones split across the plan of abscission, the resulting three cells will have the triangular shape of a 2-simplex. These phenomena are consistent with the view of a cell membrane as a dynamic structure [67].
For mitoses starting with the fourth generation, the partner cell’s adhesion does not span the contractile ring or the plane of abscission. The restriction of the adhesion to one side of the plane of abscission allows the 2-simplex to grow as a circle shape with every cell having a similar automaton program. The ensuing steps are not simplex progression because the orientations of the replication progeny are no longer affinely independent. After the 2-simplex the structure takes the form of a graph. An automaton program of self-similar replication and adhesion may be postulated for growth from a circle to a tube.
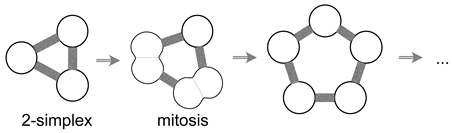
Preprints 101778 i005
If the polarity of mitosis in the 1-simplex relative to the partner cell is such that adhesion does not span the contractile ring, then a 2-simplex will not form, as illustrated here.
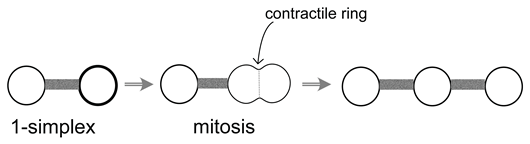
Preprints 101778 i006
A tubular morphology opens an opportunity for cellular specialization [49]. A two-layered cellular boundary that segregates an internal environment appears in some of the earliest multicellular organisms, such as those from the phylum Cnidaria [49,62,63,68]. The outer layer is termed the epidermis, and the inner layer the gastrodermis [63].
In vertebrates, tubular structures appear as the aero-digestive tract, the urinary tract, or endocrine/glandular secretion tracts—the hole in the 2-simplex functions as a mouth for nutrient entry into a regulated internal environment. There are internal structures that do not have a “mouth,” such as the circulatory system, the lymphatic system, and the cerebrospinal fluid system. These do not contract to a 2-simplex.
With classical power of two replication, two cells mitose simultaneously in the transition from the second to the third generation. The topological shape of the four-cell adhered product depends on each cell’s relation to the other’s contractile ring and abscission plane. If the mitotic polarity of each dividing cell is perpendicular to that of the other cell, and if each progeny retains adhesion to its sibling and inherits the adhesion of its parent, then the four-cell unit should take the shape of a tetrahedron. This shape is akin to a 3-simplex, which is the simplest contraction of a sphere. It has an internal environment without an opening to exchange nutrients and waste products with the external environment. If neither cell’s adhesions span the other’s contractile ring, then the four-cell result should take the shape of a row, as in Equation 8.

5. A Visual Representation for Algebraic Topology of Replication and Adhesion

While Fibonacci replication with adhesion across three generations to produce a 2-simplex offers the most direct path for an organism to form an internal environment, we wish to identify other paths toward hollow organs. For example, we may explore the more general ontogenic circumstance where asynchronously stem cells migrate into a vicinity, individually replicate, and then aggregate into cellular assemblies possibly having topological holes.
We offer a visual representation for symbolizing algebraically the replication and adhesion status of cellular aggregations, while depicting visually the opportunities for topological transformations. Plural adhesion slots per cell may be depicted. An arrow symbol gives the adhesion direction. The arrowhead is the = symbol, and adhesions on the left-hand side match to the right-hand side. Branches on either side of the arrowhead are interpreted as addition, +.
We select the arrowhead as the = symbol because the molecular apparatus of cellular adhesion and the extracellular matrix both appear to be anisotropic [27,69,70]. While this implies that cell adhesion slots are anisotropic, this assumption is unnecessary. The visual representation could be adjusted accordingly, such as by using double-headed arrows.
In the following examples, we treat cells as replicating in Fibonacci patterns, but this restriction is unnecessary with this visual representation. Let us assume that a progenitor cell replicates in generations with cell counts given by the Fibonacci numbers ( 1 , 2 , 3 , 5 , 8 , . . . ) . We assume that the two progeny cells of a replication adhere to each other. We refer to these as the horizontal cell adhesion slot for the convenience of representation on the printed page. We further assume that the individual cells in an aggregation may adhere to cells in another aggregation. We refer to these as the vertical cell adhesion slots for presentation on the printed page. We provide an over and under arrow notation to track adhesions between cells of different aggregations.
An example is Figure 4 having cell aggregations of sizes f 2 , f 3 , and f 4 . In Figure 4, the cells have only one vertical receptor. Therefore the assembly of Figure 4 cannot anneal with other Fibonacci-sized cell aggregations into larger structures.
The function of the horizontal and vertical cell adhesion slots may be served by the same molecular pattern, but we segregate their visual representation above and below the cell count symbol because they serve different roles. The precise positions on a cell surface are not the focus of analysis. Instead, we are interested in the qualitative topological properties and are less interested in this analysis of morphological forms that can be deformed continuously into each other as topological homotopies.
In this notation, for example, we might represent f 1 + f 2 = f 3 . These three assemblies may adhere across the = sign. We introduce an over/under arrow notation to indicate the top or bottom inter-aggregation adhesion sites. The arrowhead may be read as the equal = sign. For the top vertical slots we may have for example
Preprints 101778 i007
This may represent the biological process whereby the top inter-aggregation cell adhesion slots of cell aggregations of sizes f 1 and f 2 adhere to and occupy the top adhesion slots of a cell aggregation of size f 3 . The vertical slots have sizes given by the Fibonacci number. This notation is specific to this application and is unrelated to the Fibonacci number of a graph [71]. This triplet is the simplest Fibonacci adhesion event involving cell aggregations of different sizes.
We exclude from consideration reflexive arrangements such as
Preprints 101778 i008
and
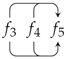
Preprints 101778 i009
that interrupt the chaining.
With this restriction, the presence of two vertical slots implies a potential for infinite chaining. For example, a set of Fibonacci-sized cell aggregations f 1 , f 2 , f 3 , f 4 , f 5 , f 6 , . . . produced by kinetically tuned mitosis might assemble by overlapping triplet adhesion into a scaffold as
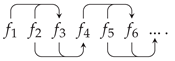
Preprints 101778 i010
Such a structure may display a self-similar scaffold across the scales of size. Such a bio-fractal form may offer the biological efficiency of reuse of the same cell-to-cell adhesion molecules to maintain structural integrity across spatial scales. The same molecular apparatus that adheres one cell to another may adhere a lobule to a lobule, up to a limb to a trunk.
The Fibonacci numbers bring a rich set of combinatorial identities [72]. These combinatorial identities may be visually encoded to depict adhesion patterns between cells and cellular aggregations. For example, some Fibonacci identities produce a larger Fibonacci number from a collection of smaller ones. An example is
3 f 1 + f 2 + f 3 + . . . + f n = f n + 2 .
If this represented a collection of Fibonacci-sized aggregations that adhered as
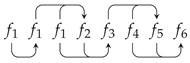
Preprints 101778 i011
then as per the identity the assembly would have f 8 cells. Accordingly, it may be contracted to the equivalent of a 0-simplex
f 8 .
When Fibonacci-sized cellular aggregations combine, the resulting cell count is given by the theory of Fibonacci compositions [73].

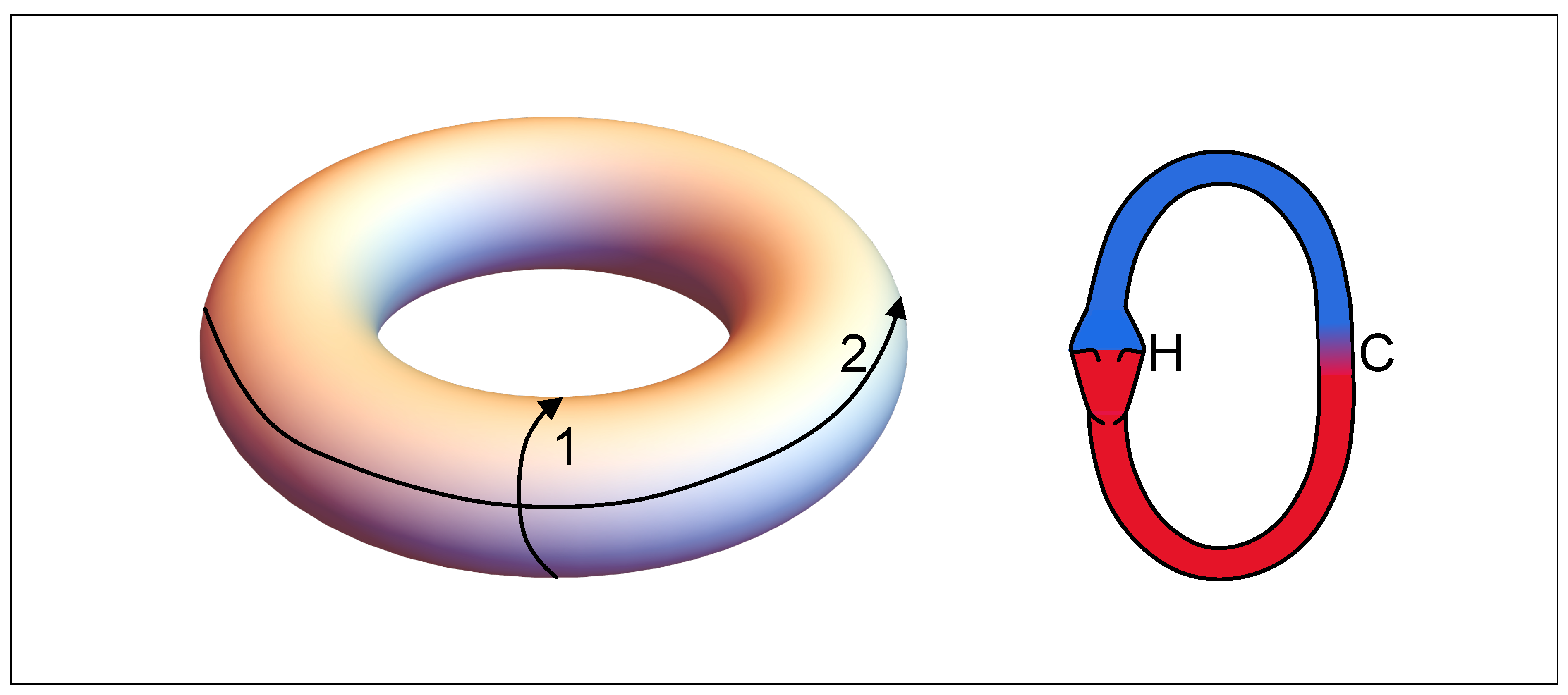
6. Non-Simplicial Topological Transformation

Topological transformations may occur by the closure of discontinuities. Cellular aggregates that do not undergo topological transformations such as into a 2-simplex per Equation 6 may nonetheless combine and and close discontinuities by adhesion. Two cellular aggregates may meet and adhere at two separate locations to achieve jointly a topological transformation. Alternately, a single cellular aggregate may fold so that formerly remote parts close by adhesion. The visual notation for representing adhesion among cellular aggregations allows us to explore circumstances where there may be topological transformations from adhesive closure of discontinuities.
When a collection of cellular aggregations finds an adhesion arrangement where all adhesion slots are occupied, we term this state full adhesion engagement. We assume that cells tend toward a fully engaged adhesion arrangement. We observe that an open scaffold such as in Equation 10 based on concatenated triplets cannot have full adhesion engagement because each terminus has one or more unoccupied adhesion slots.
However, if the two ends have unengaged vertical slots of equal size, then the structure can fold and bind into full engagement. An example is the palindrome
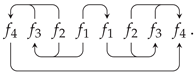
Preprints 101778 i012
A palindrome is not the only closed form with full engagement. In Additional File 1 we prove a set of conditions where a fully engaged ring can be made from random triplets of Fibonacci aggregations. With that proof in hand, we generate random numbers that conform to the terms of the proof to guarantee that the result will be a fully engaged scaffold ring (for example, see Figure 6).

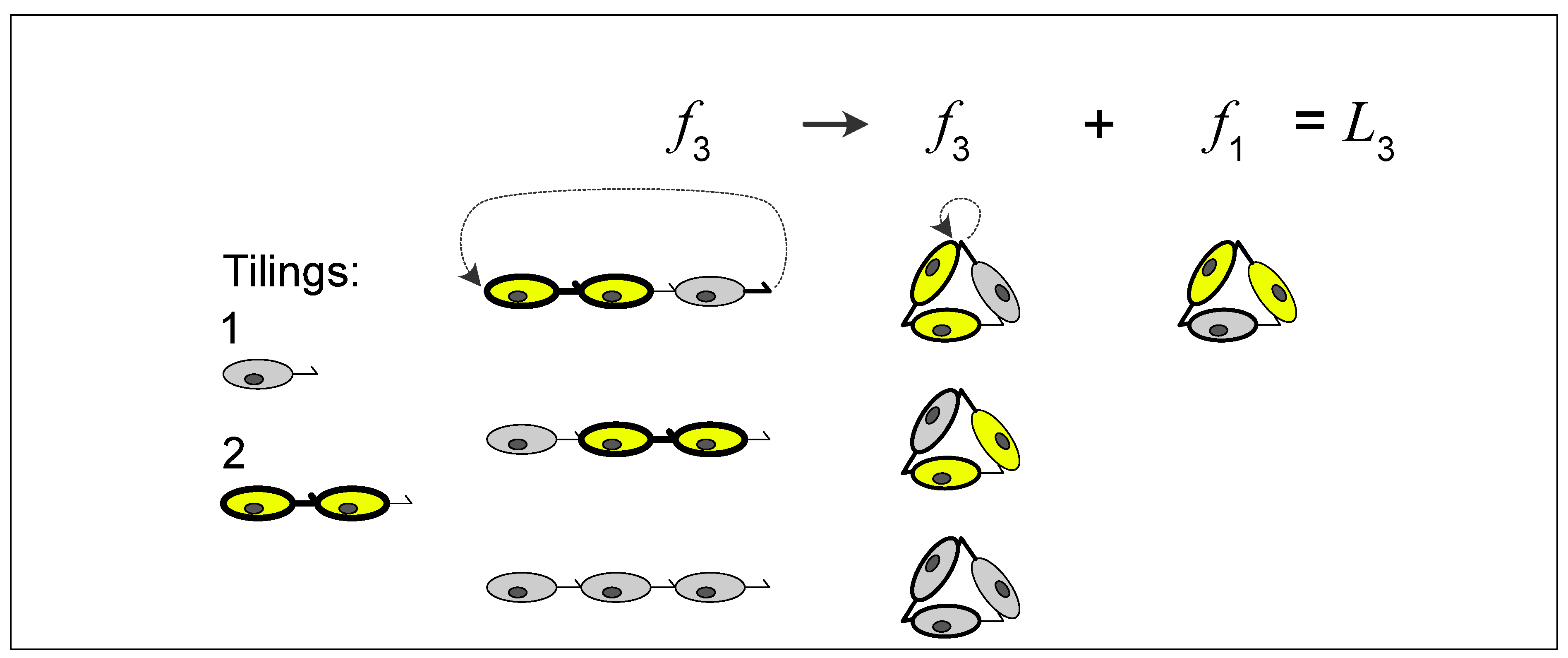
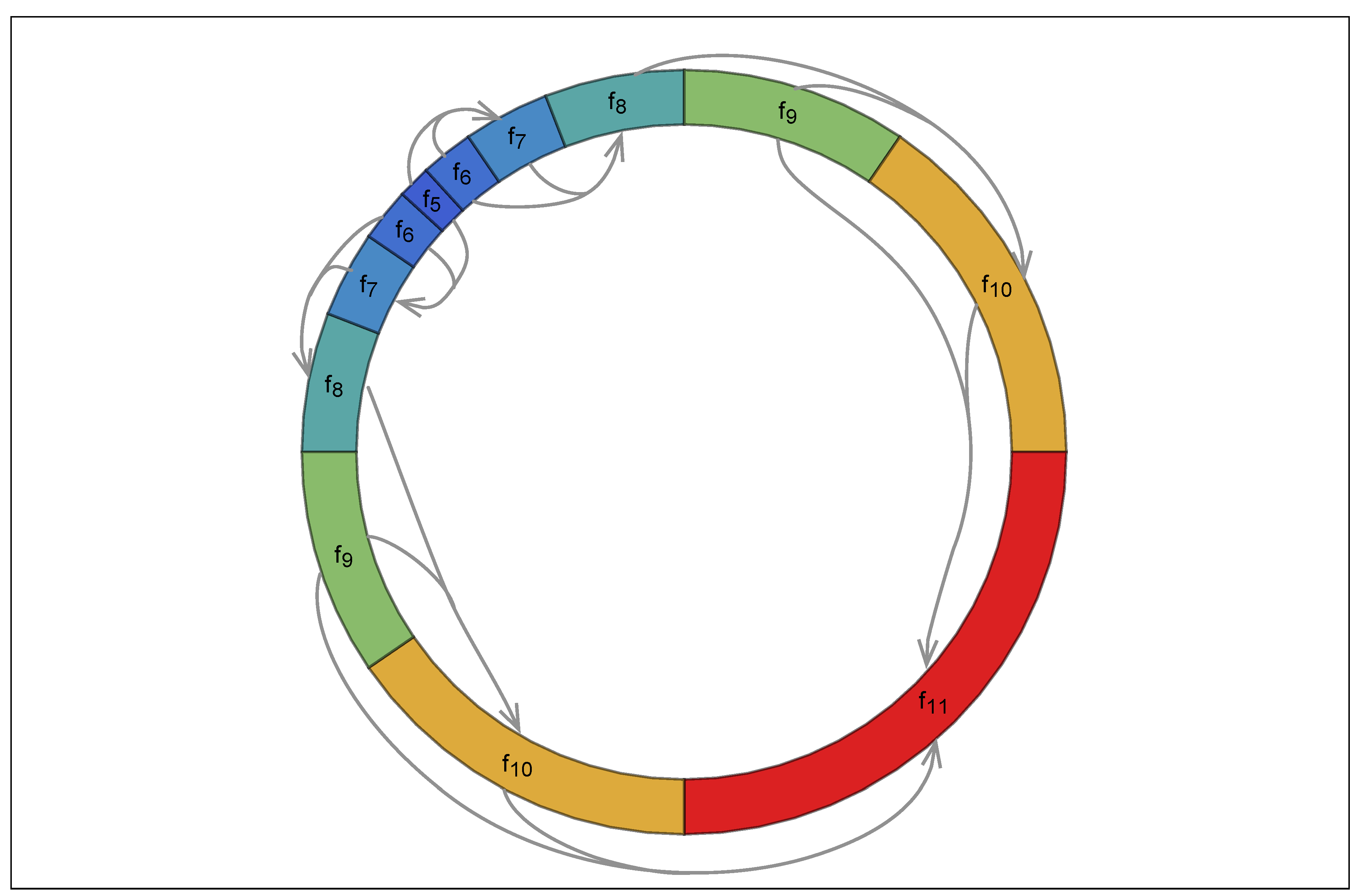
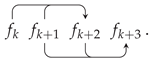
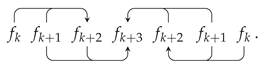
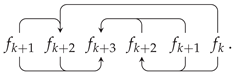
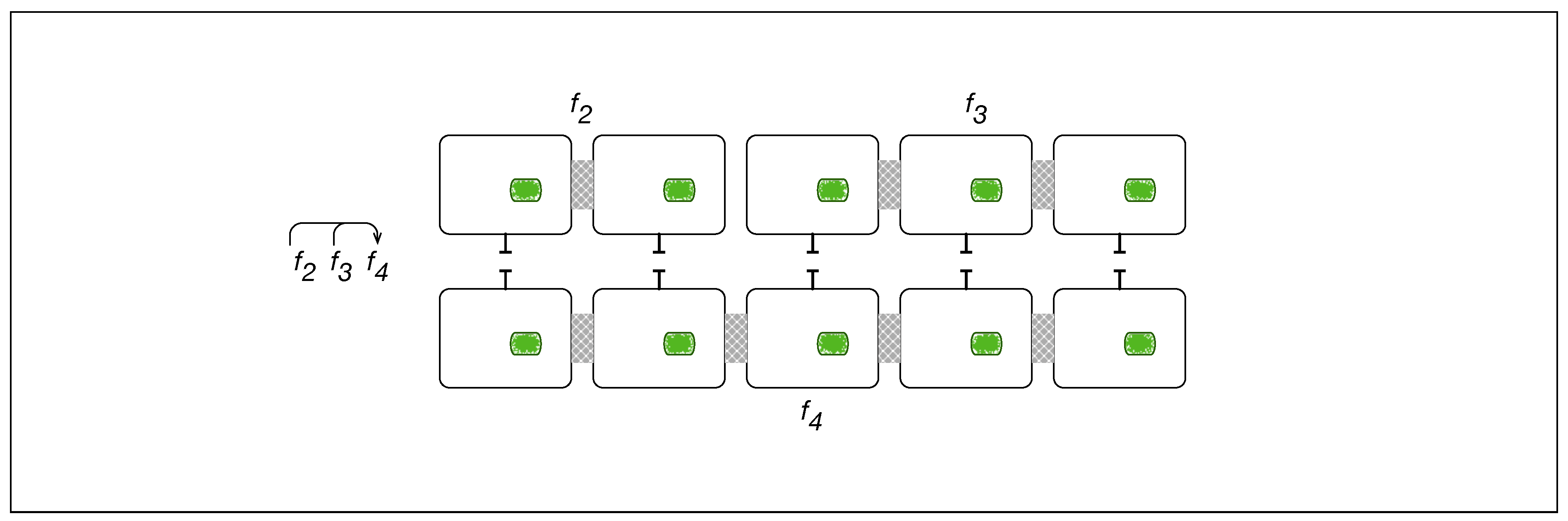
7. Combinatorial Properties of Circular Forms

If several ring shapes of the same diameter were to stack up above and below the plane of the page and each cell were to have a further pair of unoccupied inter-aggregation adhesion slots oriented in the third dimension perpendicular to the plane of the page, then the rings could anneal into a tubular structure. We use the Fibonacci numbers to count the number of cells in a cellular aggregation, but the Fibonacci numbers offer a different combinatorial interpretation. For an open form of length n cell diameters, the Fibonacci number f n carries the combinatorial interpretation of counting the number of ways to fill those n cell diameters with single cells and cell pairs. For a ring with circumference n cell diameters, that count is given by the Lucas number L n [72,74, p. 17]. For a given number of cell diameters, the Lucas numbers are larger than the Fibonacci numbers, as per the identity
L n = f n + f n − 2
recalling that in our convention F n + 1 = f n . This combinatorial relation is illustrated for a cellular 2-simplex in Figure 5. As with the Fibonacci numbers, the ratio between adjacent Lucas numbers tends toward the Golden Ratio. Since the Lucas number is larger than the Fibonacci number for the same number of cells, a ring shape as a template offers a larger number of ways for single cells and pair cells to anneal to it than an open shape.
Preprints 101778 g005
Figure 5. Cellular adhesion interpretation of the tilings heuristic for Fibonacci and Lucas numbers. There is a tiling of 1 cell (gray) and one of two cells (yellow). The number of tilings for a linear cell arrangement of length n is given by the n t h Fibonacci number f n = F n − 1 . The number of tilings for a closed arrangement is given by the n t h Lucas number L n where L n = f n + f n − 2 .
Figure 5. Cellular adhesion interpretation of the tilings heuristic for Fibonacci and Lucas numbers. There is a tiling of 1 cell (gray) and one of two cells (yellow). The number of tilings for a linear cell arrangement of length n is given by the n t h Fibonacci number f n = F n − 1 . The number of tilings for a closed arrangement is given by the n t h Lucas number L n where L n = f n + f n − 2 .
Preprints 101778 g005
Preprints 101778 g006
Figure 6. A Scaffold Ring. All inter and intra-aggregation adhesion slots are occupied. The arrows depict the inter-aggregation adhesion slot bindings.
Figure 6. A Scaffold Ring. All inter and intra-aggregation adhesion slots are occupied. The arrows depict the inter-aggregation adhesion slot bindings.
Preprints 101778 g006
A circular assembly of cells appears to have greater entropy under a combinatorial Lucas tiling argument than an open assembly. This is further illustrated in Appendix A. If the same combinatorial forces act perpendicularly on the same cells, then a torus might have greater entropy than a tube. Indeed, the topological square of a circle S 1 is a torus S 1 ⊗ S 1 . The shape resembles a circulatory system where pumped blood flows in circles. An idealized circulatory system with a two-chambered heart such as in gnathostome fish (Infraphylum Gnathostomata [75]) is illustrated in Figure 7.

8. Molecular Enablement of Simplicial Topological Steps

A multicellular organism is apt to gain adaptive advantage not so much from sheer adhered mass but by assuming topological forms not available to a unicellular organism. These topological forms can open survival strategies, such as a tubular form for hosting a regulated internal environment and providing a scaffold for cellular specialization. Under the terms of simplex topology, there is no simpler path by replication and adhesion for a multicellular organism to adopt a shape that is homotopic to a circle and a tube. An underlying molecular mechanism might be contact inhibition by adhered cells with particular polarities. Upon mitosis by one cell pair member, there is action across a fluid mosaic membrane to yield a cellular triplet in a 2-simplex form. The identification of a laboratory model of tube formation might offer an experimental testbed for these predictions. An alternate to such an analytic experimental strategy might be a synthetic strategy where notions such as these aid in a laboratory assembly of de novo tubular cellular forms [76].
This pathway depends on a contact inhibition model of replication. A pair of cells adhere to one another. By agreement, one undergoes mitosis, and the other does not. Under selected circumstances, this approximates Fibonacci growth patterns (Prop 1 ). The progression to three adhered cells comprising a 2-simplex depends on the adhered cells having a pair polarity perpendicular to a mitosis polarity and on the progeny cells inheriting the adhesions of the parent cell (Equation 6). The “transition from individual replicators,” taken to be a common element among several major evolutionary steps [77,78,79], is favored in this analysis insofar as contact inhibition may favor replication and adhesion molecular patterns that can enable simplicial topological steps. A potentially advantageous example in multicellular organisms may be the adoption of tubular forms that can enable the maintenance of a comparatively stable internal milieu.

Author Contributions

Conceptualization, W.E.B.H., H.A.L., K.K., Z.W., E.L., J.A., T.B.K. and L.T.; methodology, W.E.B.H., H.L.A. and L.T.; formal analysis, W.E.B.H., H.A.L. and L.T.; resources, W.E.B.H.; writing—original draft preparation, W.E.B.H.; writing—review and editing, W.E.B.H., H.A.L., E.L. and L.T.; visualization, W.E.B.H.; supervision, W.E.B.H. and L.T.; project administration, W.E.B.H. and L.T. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

Enrique Bojorquez critiqued the manuscript.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A. Random Ring Patterns

To nourish our intuition we wish to generate a family of random scaffold rings having full adhesion engagement. To start, we offer some definitions and provide a theorem showing that as scaffold ring as defined here has full adhesion engagement.
Definition A1.
A Fibonacci triplet is a set of three aggregations of sequential Fibonacci size that have inter-aggregation receptor bindings to each other. A relative up triplet has increasing Fibonacci numbers such that a relative up triplet to f k − 1 is
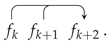
Preprints 101778 i013
and a relative down triplet is
Preprints 101778 i014
It does not matter in this definition whether the inter-aggregation bindings are top or bottom.
Definition A2.
A triplet scaffold is a structure that is composed of concatenated Fibonacci triplets where all slots are engaged and the sumands and sums are contiguous.
We observe that in such a structure, a given triplet has six vertical adhesion slots. Two serve as sumands to bind the concatenated triplet to the right. One serves as a sum to bind to two sumands from the triple to the left. These overlapping Fibonacci relations bind the triplets one to the next in the scaffold. Three slots are internal to the triplet. Two of those are summands for a sum in a third slot.
Definition A3.
A scaffold ring is a triplet scaffold where the ends have folded to meet and adhere. An example is
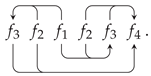
Preprints 101778 i015
Start with an arbitrary Fibonacci number, f k , append to it an equal number of relative up and down triplets in arbitrary order, and adhere the slots.
Theorem A1.
Such a ring has full adhesion engagement.
Proof. 
Start with an arbitrary initial Fibonacci number f k . Append a relative up triplet. The rightmost aggregation is of size f k + 3 because appending a triplet adds 3 to the rightmost Fibonacci index.
Preprints 101778 i016
Append a relative down triplet. This subtracts 3 from the rightmost index.
Preprints 101778 i017
There are 5 internal Fibonacci-sized aggregations. These have 10 adhesion slots available. There are 6 sumand and 4 sum slots occupied, so the internal aggregations have full engagement. The aggregations on the left and right ends each have f k occupied and f k unoccupied slots. If the structure folds, the f k -sized slots on each end will adhere because they are o the same size. Between the two triplets we can insert an equal number of relative up and down triplets in random order and there will still be adhesion closure because each end will have f k unoccupied vertical adhesion slots.
In the paragraph above, we start with a relative up triplet and end with a relative down triplet. We find however that the same argument holds whether we start or end with an up or down triplet so long as the number of them is equal. We also find that the order of the relative up and down triplets does not matter. □
Lemma A1.
In a fully engaged ring, duplicating a Fibonacci-sized aggregation number or replacing a duplicate with a single produces a longer or shorter ring that still has full engagement.
This is because inserting a duplicate number only flips the vertical polarity of the ensuing receptor orientation. This lemma is nonsensical in the case of a palindromic ring where its successive application would cause the removal of all aggregations. Hybrid forms with an inner loop and open ends are algebraically possible but not treated here.
Removing the duplicate f k from Equation A1 produces
Preprints 101778 i018
This is a triplet scaffold where the adhesions are fully engaged.
With this proof and lemma we program a computer to generate some random scaffold rings with full engagement. We randomly generate a set up relative up and down triplets, randomly insert and remove duplicates, and graph some results in Figure A1 to portray a range of allowed woven rings.
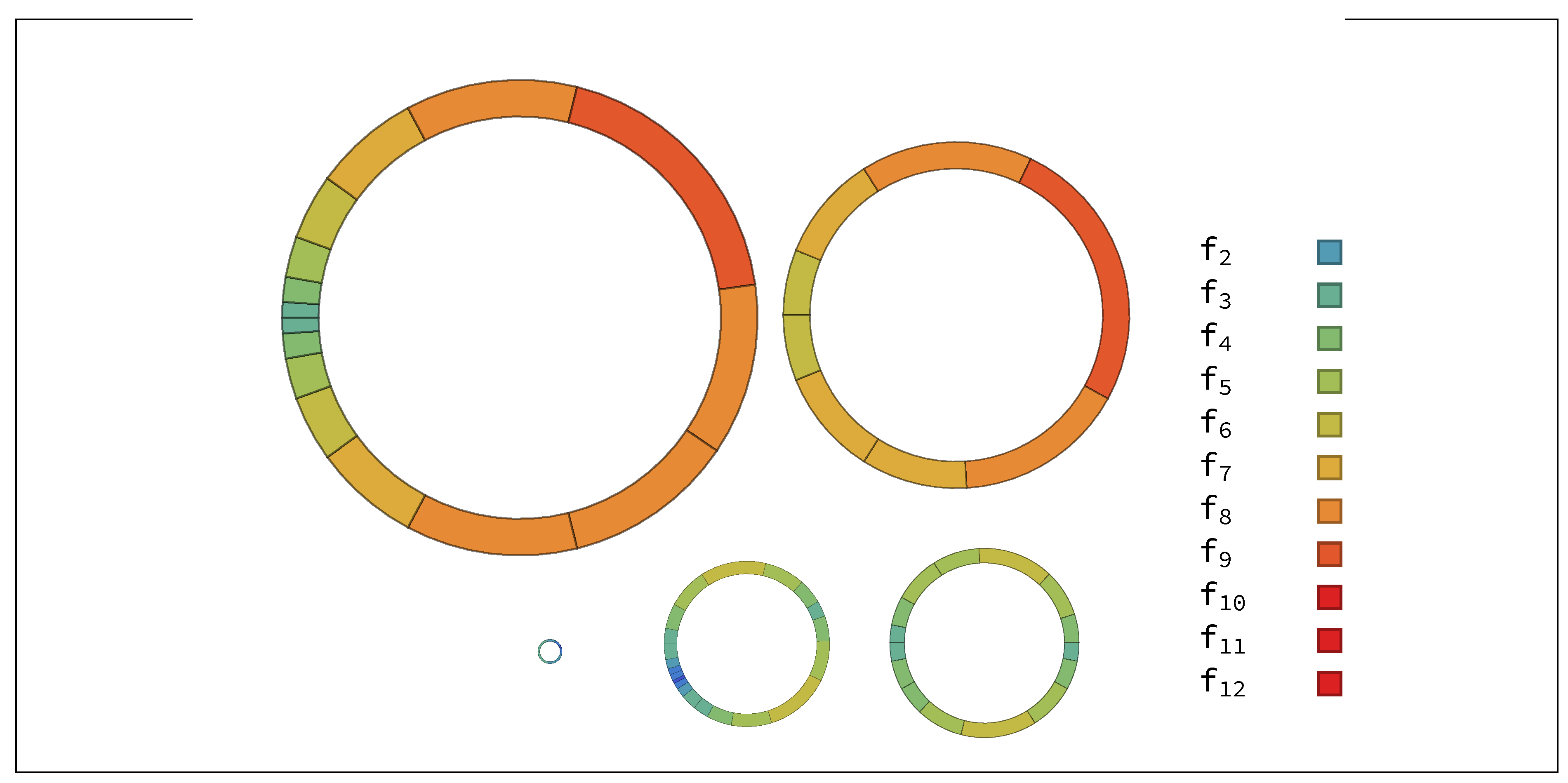
Preprints 101778 g0a1
Figure A1. Some Random Woven Rings. The legend gives the Fibonacci color code scheme. Cell binding relationships are not depicted.
Figure A1. Some Random Woven Rings. The legend gives the Fibonacci color code scheme. Cell binding relationships are not depicted.
Preprints 101778 g0a1

References

  1. Meisner, G.B. The Golden Ratio; Race Point Publishing: New York, 2018. [Google Scholar]
  2. Livio, M. The Golden Ratio; Broadway Books: New York, 2008; p. 304. [Google Scholar]
  3. de Campos, D.; Malysz, T.; Bonatto-Costa, J.A.; Pereira Jotz, G.; Pinto de Oliveira Junior, L.; Oxley da Rocha, A. Michelangelo, the Last Judgment fresco, Saint Bartholomew and the Golden Ratio. Clin Anat 2015. [Google Scholar] [CrossRef]
  4. Iosa, M.; Morone, G.; Paolucci, S. Phi in physiology, psychology and biomechanics: The golden ratio between myth and science. 2018. [Google Scholar] [CrossRef]
  5. Sebé-Pedrós, A.; Degnan, B.; Ruiz-Trillo, I. The origin of Metazoa: a unicellular perspective. Nature Reviews Genetics 2017, 18, 498–512. [Google Scholar] [CrossRef]
  6. Wille, J.J. Occurrence of Fibonacci numbers in development and structure of animal forms: Phylogenetic observations and epigenetic significance. NS 2012, 04, 216–232. [Google Scholar] [CrossRef]
  7. Peaucelle, A.; Couder, Y. Fibonacci spirals in a brown alga [Sargassum muticum (Yendo) Fensholt] and in a land plant [Arabidopsis thaliana (L.) Heynh.]: a case of morphogenetic convergence. Acta Societatis Botanicorum Poloniae 2016, 85. [Google Scholar] [CrossRef]
  8. Steurer, W.; Deloudi, S. Cluster packing from a higher dimensional perspective. Struct Chem 2011, 23, 1115–1120. [Google Scholar] [CrossRef]
  9. Malygin, A.G. Morphodynamics of phyllotaxis. International Journal of Developmental Biology 2006, 50, 277–287. [Google Scholar] [CrossRef]
  10. Mughal, A.; Weaire, D. Phyllotaxis, disk packing, and Fibonacci numbers. Physical Review E 2017, 95, 22401. [Google Scholar] [CrossRef] [PubMed]
  11. Bozdag, G.O.; Zamani-Dahaj, S.A.; Kahn, P.C.; Day, T.C.; Tong, K.; Balwani, A.H.; Dyer, E.L.; Yunker, P.J.; Ratcliff, W.C. De novo evolution of macroscopic multicellularity. bioRxiv 2021. [Google Scholar] [CrossRef] [PubMed]
  12. Singh, P. The so-called fibonacci numbers in ancient and medieval India. Historia Mathematica 1985, 12, 229–244. [Google Scholar] [CrossRef]
  13. Sigler, L. Fibonacci’s Liber Abaci: A Translation into Modern English of Leonardo Pisano’s Book of Calculation; Springer Science and Business Media: New York, 2003. [Google Scholar]
  14. Benjamin, A.T.; Plott, S.S. A combinatorial approach to fibonomial coefficients. Fibonacci Quarterly 2008, 46-47, 7–9. [Google Scholar]
  15. Schnyder, S.; Molina, J.; Yamamoto, R. Control of cell colony growth by contact inhibition. Sci Rep 2020, 10, 6713. [Google Scholar] [CrossRef] [PubMed]
  16. Lujan, P.; Rubio, T.; Varsano, G.; Köhn, M. Keep it on the edge: The post-mitotic midbody as a polarity signal unit. Commun Integr Biol 2017, 10, e1338990. [Google Scholar] [CrossRef]
  17. Juanes, M.; Piatti, S. The final cut: cell polarity meets cytokinesis at the bud neck in S. cerevisiae. Cell Mol Life Sci 2016, 73, 3115–3136. [Google Scholar] [CrossRef]
  18. Johnson, A.; McCollum, D.; Gould, K. Polar opposites: Fine-tuning cytokinesis through SIN asymmetry. Cytoskeleton (Hoboken) 2012, 69, 686–699. [Google Scholar] [CrossRef] [PubMed]
  19. Fleming, E.; Zajac, M.; Moschenross, D.; Montrose, D.; Rosenberg, D.; Cowan, A.; Tirnauer, J. Planar spindle orientation and asymmetric cytokinesis in the mouse small intestine. J Histochem Cytochem 2007, 55, 1173–1180. [Google Scholar] [CrossRef] [PubMed]
  20. Caydasi, A.; Lohel, M.; Grünert, G.; Dittrich, P.; Pereira, G.; Ibrahim, B. A dynamical model of the spindle position checkpoint. Mol Syst Biol 2012, 8, 582. [Google Scholar] [CrossRef] [PubMed]
  21. Driscoll, J.; Gondaliya, P.; Patel, T. Tunneling Nanotube-Mediated Communication: A Mechanism of Intercellular Nucleic Acid Transfer. Int J Mol Sci 2022, 23, 5487. [Google Scholar] [CrossRef] [PubMed]
  22. Gilberto, S.; Peter, M. Dynamic ubiquitin signaling in cell cycle regulation. The Journal of cell biology 2017, 216, 2259–2271. [Google Scholar] [CrossRef]
  23. Ogura, Y.; Sasakura, Y. Emerging mechanisms regulating mitotic synchrony during animal embryogenesis. Development, growth & differentiation 2017, 59, 565–579. [Google Scholar]
  24. Üretmen Kagıalı, Z.C.; Şentürk, A.; Özkan Küçük, N.E.; Qureshi, M.H.; Özlü, N. Proteomics in Cell Division. Proteomics 2017, 17, 1600100. [Google Scholar] [CrossRef] [PubMed]
  25. Tang, D.; Gerlach, B. The roles and regulation of the actin cytoskeleton, intermediate filaments and microtubules in smooth muscle cell migration. Respir Res 2017, 18, 54. [Google Scholar] [CrossRef] [PubMed]
  26. Rizzelli, F.; Malabarba, M.; Sigismund, S.; Mapelli, M. The crosstalk between microtubules, actin and membranes shapes cell division. Open Biol 2020, 10, 190314. [Google Scholar] [CrossRef] [PubMed]
  27. Dyson, R.J.; Green, J.E.F.; Whiteley, J.P.; Byrne, H.M. An investigation of the influence of extracellular matrix anisotropy and cell-matrix interactions on tissue architecture. Journal of Mathematical Biology 2016, 72, 1775–1809. [Google Scholar] [CrossRef] [PubMed]
  28. Motealleh, A.; Hermes, H.; Jose, J.; Kehr, N.S. Chirality-dependent cell adhesion and enrichment in Janus nanocomposite hydrogels. Nanomedicine: Nanotechnology, Biology, and Medicine 2018, 14, 247–256. [Google Scholar] [CrossRef] [PubMed]
  29. Walma, D.A.; Yamada, K.M. The extracellular matrix in development. Development 2020, 147. [Google Scholar] [CrossRef]
  30. Ostrander, E.A. Central Dogma of Molecular Biology, 2022.
  31. Gould, H.W. A history of the Fibonacci Q-matrix and a higher-dimensional problem. Fibonacci Quarterly 1981, 19, 250–257. [Google Scholar]
  32. Silvester, J.R. Fibonacci Properties by Matrix Methods. The Mathematical Gazette 1979, 63, 188–191. [Google Scholar] [CrossRef]
  33. Spears, C.; Bicknell-johnson, M.; Yan, J.J. Fibonacci phyllotaxis by asymmetric cell division : Zeckendorf and Wythoff trees. Congressus Numerantium 2016, 201, 257–257. [Google Scholar]
  34. Butler, W.; Kinane, T. Ring shape Golden Ratio multicellular structures are algebraically afforded by asymmetric mitosis and one to one cell adhesion. bioRxiv 2018. [Google Scholar]
  35. Lindenmayer, A. Mathematical models for cellular interactions in development I. Filaments with one-sided inputs. Journal of theoretical biology 1968, 18, 280–299. [Google Scholar] [CrossRef]
  36. Lindenmayer, A. Developmental algorithms for multicellular organisms: A survey of L-systems. Journal of Theoretical Biology 1975, 54, 3–22. [Google Scholar] [CrossRef]
  37. Kelly-Sacks, C. The biological and mathematical basis of L systems. PhD thesis, Rochester Institute of Technology, 1981.
  38. Owens, N.; Stepney, S. Investigations of Game of Life cellular automata rules on Penrose Tilings: lifetime and ash statistics. Automata 2008, 1–35. [Google Scholar]
  39. Giavitto, J.L.; Michel, O. Modeling the topological organization of cellular processes. BioSystems 2003, 70, 149–163. [Google Scholar] [CrossRef] [PubMed]
  40. Nehaniv, C.L.; Rhodes, J.L. The evolution and understanding of hierarchical complexity in biology from an algebraic perspective. Artificial Life 2000, 6, 45–67. [Google Scholar] [CrossRef] [PubMed]
  41. Kim, J.; Samaranayake, M.; Pradhan, S. Epigenetic mechanisms in mammals. Cell Mol Life Sci 2009, 66, 596–612. [Google Scholar] [CrossRef] [PubMed]
  42. Holliday, R. Epigenetics: a historical overview. Epigenetics 2006. [Google Scholar] [CrossRef]
  43. Fuentealba, L.; Eivers, E.; Geissert, D.; Taelman, V.; De Robertis, E. Asymmetric mitosis: Unequal segregation of proteins destined for degradation. Proc Natl Acad Sci U S A 2008, 105, 7732–7737. [Google Scholar] [CrossRef] [PubMed]
  44. Charlton, J.; Downing, T.; Smith, Z.; Gu, H.; Clement, K.; Pop, R.; Akopian, V.; Klages, S.; Santos, D.; Tsankov, A.; Timmermann, B.; Ziller, M.; Kiskinis, E.; Gnirke, A.; Meissner, A. Global delay in nascent strand DNA methylation. Nat Struct Mol Biol 2018, 25, 327–332. [Google Scholar] [CrossRef] [PubMed]
  45. Zemach, A.; McDaniel, I.E.; Silva, P.; Zilberman, D. Genome-wide evolutionary analysis of eukaryotic DNA methylation. Science 2010, 328, 916–919. [Google Scholar] [CrossRef]
  46. Brero, A.; Leonhardt, H.; Cardoso, M.C. Replication and Translation of Epigenetic Information. In DNA Methylation: Basic Mechanisms; 2006. [Google Scholar]
  47. Podobinska, M.; Szablowska-Gadomska, I.; Augustyniak, J.; Sandvig, I.; Sandvig, A.; Buzanska, L. Epigenetic Modulation of Stem Cells in Neurodevelopment: The Role of Methylation and Acetylation. Frontiers in cellular neuroscience 2017. [Google Scholar] [CrossRef]
  48. Laugesen, A.; Helin, K. Chromatin repressive complexes in stem cells, development, and cancer. Cell stem cell 2014. [Google Scholar] [CrossRef] [PubMed]
  49. Dickinson, D.J.; Nelson, W.J.; Weis, W.I. An epithelial tissue in Dictyostelium challenges the traditional origin of metazoan multicellularity. BioEssays 2012, 34, 833–840. [Google Scholar] [CrossRef]
  50. Yin, T.; Green, K. Regulation of desmosome assembly and adhesion. Semin Cell Dev Biol 2004, 15, 665–677. [Google Scholar] [CrossRef] [PubMed]
  51. Díaz-Coránguez, M.; Liu, X.; Antonetti, D. Tight Junctions in Cell Proliferation. Int J Mol Sci 2019, 20, E5972. [Google Scholar] [CrossRef] [PubMed]
  52. Balda, M.; Matter, K. Tight junctions and the regulation of gene expression. Biochim Biophys Acta 2009, 1788, 761–767. [Google Scholar] [CrossRef] [PubMed]
  53. Le Bras, S.; Le Borgne, R. Epithelial cell division - multiplying without losing touch. J Cell Sci 2014, 127, 5127–5137. [Google Scholar] [CrossRef]
  54. Hatte, G.; Prigent, C.; Tassan, J. Adherens junctions are involved in polarized contractile ring formation in dividing epithelial cells of Xenopus laevis embryos. Exp Cell Res 2021, 402, 112525. [Google Scholar] [CrossRef]
  55. Leithe, E. Regulation of connexins by the ubiquitin system: Implications for intercellular communication and cancer. Biochim Biophys Acta 2016, 1865, 133–146. [Google Scholar] [CrossRef]
  56. Herszterg, S.; Pinheiro, D.; Bellaïche, Y. A multicellular view of cytokinesis in epithelial tissue. Trends Cell Biol 2014, 24, 285–293. [Google Scholar] [CrossRef]
  57. Dong, L.; Gong, J.; Wang, Y.; He, J.; You, D.; Zhou, Y.; Li, Q.; Liu, Y.; Cheng, K.; Qian, J.; Weng, W.; Wang, H.; Yu, M. Chiral geometry regulates stem cell fate and activity. Biomaterials 2019, 222, 119456. [Google Scholar] [CrossRef]
  58. Farmer, T.; Prekeris. New signaling kid on the block: the role of the postmitotic midbody in polarity, stemness, and proliferation. Mol Biol Cell 2022, 33. [Google Scholar] [CrossRef] [PubMed]
  59. Peterman, E.; Prekeris, R. The postmitotic midbody: Regulating polarity, stemness, and proliferation. J Cell Biol 2019, 218, 3903–3911. [Google Scholar] [CrossRef] [PubMed]
  60. Novak, M.; Polak, B.; Simunić, J.; Boban, Z.; Kuzmić, B.; Thomae, A.W.; Tolić, I.M.; Pavin, N. The mitotic spindle is chiral due to torques within microtubule bundles. Nature Communications 2018, 9. [Google Scholar] [CrossRef] [PubMed]
  61. Satir, P. Chirality of the cytoskeleton in the origins of cellular asymmetry. Philosophical transactions of the Royal Society of London. Series B, Biological sciences 2016, 371, 20150408. [Google Scholar] [CrossRef]
  62. Schuchert, P. Phylogenetic analysis of the Cnidaria. Journal of Zoological Systematics and Evolutionary Research 2009, 31, 161–173. [Google Scholar] [CrossRef]
  63. Berzins, I.K.; Yanong, R.P.E.; LaDouceur, E.E.; Peters, E.C. Cnidaria. In Invertebrate Histology; LaDouceur, E.E., Ed.; Wiley, 2021; pp. 55–86. [Google Scholar]
  64. Weisstein, E.W. Torus. From MathWorld—A Wolfram Web Resource. Accessed 4 Oct 2022.
  65. Basic three-dimensional objects constructed with simplex meshes, Vol. (ICEEE). 1st International Conference on Electrical and Electronics Engineering, 2004., New York, 2004. IEEE.
  66. Nicolson, S.J.S.; L., G. The Fluid Mosaic Model of the Structure of Cell Membranes. Science, New Series, 175, No. 4023, 720–731.
  67. Fletcher, A. The cell membrane and receptors. Anaesthesia & Intensive Care Medicine 2007, 8, 443–446. [Google Scholar]
  68. Parfrey, L.W.; Lahr, D.J.G. Multicellularity arose several times in the evolution of eukaryotes (Response to DOI 10.1002/bies.201100187). BioEssays 2013, 35, 339–347. [Google Scholar] [CrossRef]
  69. Meng, W.; Takeichi, M. Adherens junction: molecular architecture and regulation. Cold Spring Harb Perspect Biol 2009, 1, a002899. [Google Scholar] [CrossRef]
  70. Matsuzawa, K.; Himoto, T.; Mochizuki, Y.; Ikenouchi, J. alpha-Catenin Controls the Anisotropy of Force Distribution at Cell-Cell Junctions during Collective Cell Migration. Cell Rep 2018, 23, 3447–3456. [Google Scholar] [CrossRef]
  71. Knopfmacher, A.; Tichy, R.F.; Wagner, S.; Ziegler, V. Graphs, partitions and Fibonacci numbers. Discrete Applied Mathematics 2007, 155, 1175–1187. [Google Scholar] [CrossRef]
  72. Benjamin, A.; Quinn, J. Proofs that Really Count; The Mathematical Association of America: Washington, D.C, 2009. [Google Scholar]
  73. Gessel, I.M.; Li, J. Compositions and Fibonacci Identities. arXivJournal of Integer Sequences 2013, arXiv:1303.136616. [Google Scholar]
  74. Koken, F.; Bozkurt, D. On Lucas numbers by the matrix method. Hacettepe Journal of Mathematics and Statistics 2010. [Google Scholar]
  75. Stephenson, A.; Adams, J.W.; Vaccarezza, M. The vertebrate heart: an evolutionary perspective. Journal of anatomy 2017, 231, 787–797. [Google Scholar] [CrossRef] [PubMed]
  76. Schwille, P. Jump-starting life? Fundamental aspects of synthetic biology. J Cell Biol 2015, 210, 687–690. [Google Scholar] [CrossRef] [PubMed]
  77. Szathmáry, E.; Smith, J.M. The major evolutionary transitions. Nature 1995, 374, 227–232. [Google Scholar] [CrossRef] [PubMed]
  78. Grosberg, R.K.; Strathmann, R.R. The Evolution of Multicellularity: A Minor Major Transition? Annual Review of Ecology, Evolution, and Systematics 2007, 38, 621–654. [Google Scholar] [CrossRef]
  79. Fisher, R.M.; Cornwallis, C.K.; West, S.A. Group formation, relatedness, and the evolution of multicellularity. Current Biology 2013, 23, 1120–1125. [Google Scholar] [CrossRef]
Preprints 101778 g001
Figure 1. Cell cycle. Mitosis (M) occurs a small fraction of the interval. The stages of mitosis are expanded. Some examples of potential differential epigenomics are shown. A methyl group (M) can be attached to a cytosine of a DNA strand prior to DNA replication. After replication, only one chromosome copy retains the methyl group. Where spindles are helical, they can form enantiomeric relationships with chromosomal kinetochores upon chromosomal separation. A midbody positions itself along the contractile ring, then may be inherited asymmetrically by one progeny cell upon abscission.
Figure 1. Cell cycle. Mitosis (M) occurs a small fraction of the interval. The stages of mitosis are expanded. Some examples of potential differential epigenomics are shown. A methyl group (M) can be attached to a cytosine of a DNA strand prior to DNA replication. After replication, only one chromosome copy retains the methyl group. Where spindles are helical, they can form enantiomeric relationships with chromosomal kinetochores upon chromosomal separation. A midbody positions itself along the contractile ring, then may be inherited asymmetrically by one progeny cell upon abscission.
Preprints 101778 g001
Preprints 101778 g002
Figure 2. Adhesion types. The basement membrane is a form of extracellular matrix binding.
Figure 2. Adhesion types. The basement membrane is a form of extracellular matrix binding.
Preprints 101778 g002
Preprints 101778 g003
Figure 3. Fibonacci population growth in rabbits and cells with progeny having different lag after each reproduction. The thin horizontal lines represent adhesions.
Figure 3. Fibonacci population growth in rabbits and cells with progeny having different lag after each reproduction. The thin horizontal lines represent adhesions.
Preprints 101778 g003
Preprints 101778 g004
Figure 4. Single Combinatorial Engagement Between Three Fibonacci-Sized Cell Aggregations. Cell aggregations of sizes f 2 , f 3 , and f 4 assemble by one-to-one cell adhesion slots. Without dual adhesion by each cell there is no chaining.
Figure 4. Single Combinatorial Engagement Between Three Fibonacci-Sized Cell Aggregations. Cell aggregations of sizes f 2 , f 3 , and f 4 assemble by one-to-one cell adhesion slots. Without dual adhesion by each cell there is no chaining.
Preprints 101778 g004
Preprints 101778 g007
Figure 7. The topological square of a circular cellular aggregation (1) is a torus (2). This shares topological features with a primitive circulatory system shown here having an idealized two-chambered heart (H), an arterial component (red), a venous component (blue), and a capillary bed (C).
Figure 7. The topological square of a circular cellular aggregation (1) is a torus (2). This shares topological features with a primitive circulatory system shown here having an idealized two-chambered heart (H), an arterial component (red), a venous component (blue), and a capillary bed (C).
Preprints 101778 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated