Prerpints.org logo
Preprint
Article

Experimental Verification of Geometric Changes Caused by the Release of Residual Stresses for Large-Scale Welded Frames

This version is not peer-reviewed.

Submitted:

20 March 2024

Posted:

26 March 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
This paper presents geometric analyses of welded frames after free relaxing and vibratory stress relief (VSR). Respected frames were tested components of a prototype packaging machine. Two types of relaxation were carried out to remove stresses introduced as a result of welding process. One of the frame was subjected to free relaxing, while the other one to accelerated vibration relaxing. Detection of the frame geometry changes was performed using a photogrammetric system. In addition, an evaluation of the geometry change was conducted for fifteen variants of steel frame support. A comparative analysis of the geometric deviations of the frames after free and vibratory stress relief confirmed the assumption that the frame after vibration stress relief better reproduces the nominal dimensions. Nevertheless, it should be emphasized that after vibratory stress relief the frame is not subject to further deformation, which is a desirable effect. In the case of free relaxing, the frame undergoes dimensional changes in a random manner. In summary, carrying out accelerated vibratory stress relief allows control of spontaneous dimensional changes in the designed frame of a packaging machine resulting from spontaneous relaxation of stresses arising from the welding process. The shortening of the relaxation process of the welded frame is also an unquestionable advantage.
Keywords: 
Subject: 
Engineering  -   Mechanical Engineering

1. Introduction

Residual stresses occur in metal structures during many technological processes. They can arise as a result of body force or surface stress, under the action of temperature, or are as result of phase changes occurring in the material [1,2]. The phenomenon of residual stresses is undesirable because it negatively affects the dimensional stability of the structure, causing it to deform over a long period of time as a result of the spontaneous removal of these stresses, and it also increases susceptibility to cracking and stress corrosion cracking [3,4]. The authors of the paper [5] presented the thesis that residual stresses do not always limit the functionality of the material. Wang et al. described in the paper [5] that the peening process aims to improve the fatigue properties of the material by introducing residual compressive stress at the surface of the specimen.
One of the technological processes affecting residual stresses in steel structures is welding. This is a process during which a welded component is subjected to complex thermal processes, which leads to structural changes. The ultimate effect of this process is the formation of stresses, the distributions of which vary greatly, both in direction and value. This, in turn, is the cause of geometric deformations [2].
One way to reduce over time the stresses present in a component after the welding process until they are completely removed is relaxation [2]. Several relaxation methods can be distinguished: annealing relaxation [6,7], ultrasonic relaxation [8], rolling [9], explosive method [10] and vibratory stress relief [11,12]. The authors of the paper [13] also presented a hybrid method that combines the advantages of the thermal-vibration stress relief (TVSR).
The method of residual stress relaxation by vibratory stress relief (VSR) is irreplaceable in many cases due to its short time. Vibratory stress relief (VSR) consists of accelerated seasoning of machine and structural components by subjecting them to mainly resonant vibrations. By forcing various forms of resonant vibration throughout the volume of the vibrated component, there is a significant reduction in peak internal (weld) stresses [14].
As highlighted in the article [15] applied vibratory loading to reduce residual stress levels in mechanical components can be a potential alternative to some thermal annealing processes. As highlighted by the author of [15], the use of the vibratory stress relief (VSR) process has been limited in use due to a poor understanding of the process. The paper [16] presents various variants of vibratory stress relief (VSR) annealing. The authors of the paper [17,18] listed advantages, disadvantages and applicability in various industrial conditions of VSR variants such as Resonant VSR, Sub-Harmonic VSR and Modal Sub-Resonant VSR. An applied use of vibratory stress relief for the relaxation of welded bridge structural components was presented by [19], while the authors of the paper [20] used VSR for the relaxation of residual stresses after the rolling process, as an alternative to the much more time-consuming temperature method.
In another application example, the vibratory stress relief (VSR) procedure was used to reduce welding induced residual stresses in the rails of a magnetic levitation transport system (MAGLEV) [21]. Authors of the paper [22] showed that the fatigue life of thermally relaxed samples de-creased by 43%, while samples subjected to vibration showed an increase of 17% to 30%.
Stress relaxation techniques should be performed immediately after the technological process, as otherwise free relaxation may occur, i.e. the stresses will be removed spontaneously. However, it should be borne in mind that the relaxation process, whether free or forced, causes deformation of the component, and these deformations can negatively affect the functionality of the finished product.
Therefore, an important issue during the stress-removal process is the dimensional and shape control of relaxed objects. The propagation of geometric deformations during and after the vibratory stress relief process is currently not described in detail in the literature. Knowledge of the described relationships is important in determining the direction and value of geometric deformation, which clearly affects the final functionality of the product.
Measuring methods, due to the contact of the measuring instrument with the tested object, can be divided into contact and non-contact [23,24]. Contact methods include traditional measurements with CMMs, where the measurement is realized by the point of con-tact between the tip of the measuring head (usually spherical) and the surface to be measured [25]. This method has certain limitations related to the size and shape of the object under test. The second group of measurement methods are non-contact methods in which there is no contact between the measuring instrument and the object being measured [26,27]. This allows for accurate measurements of objects with complex shapes, both small and large size [28,29,30,31], as well as those made of flexible materials such as sponges, foams or plastics [32,33] or made by additive technologies [34,35,36] also for metal elements manufactured by Wire Arc Additive Manufacturing [37]. For such large components as the welded frame under study, the use of a photogrammetric method is preferred as well as reasonable.
3D scanning technology is increasingly used in industry to control dimensions of objects with different spatial configurations. The wide application and development prospects of 3D scanning technology are presented in the article [38]. Quality requirements for manufactured products have enforced the use of a method to analyze them in terms of shape and dimensions. Robotized measuring systems using optical scanners, in addition to a large number of measuring points and the lack of need for physical contact with the part being measured, also provide speed and repeatability of measurements [39]. There is a growing potential of using this technology also for smaller scales [40]. Thus, the use of 3D scanning technology is becoming an integral condition for ensuring that manufactured products have the required quality and for eliminating errors in the process of production preparation and execution.
The main objective of research presented in this article was to evaluate dimensional changes of welded frames subjected to spontaneous, free relaxation (frame No. 1) and rapid relaxation using vibratory stress relief method (frame No. 2). The study also made it possible to assess the quality of frame assembly using welded joints from the perspective of dimensional and shape accuracy. Research components are frames of a prototype packaging machine designed and built by PROTiM.
In addition, an effect of the number and arrangement of support points on the welded frame geometric deformation was analyzed. Due to its dimensions, only a selected part of the frame, which is the basis of the test stand, was adopted for analysis. The frame intended for testing in the following part of the work was named frame No. 3. During the measurement process, temperature changes were recorded at selected points of tested objects.

2. Materials and Methods

2.1. Process of Vibratory Stress Relief of Welded Frames

Vibratory stress relief consisted of subjecting mechanical structure, in this case the welded frame, to forced vibration. The forcing was carried out at resonant frequencies corresponding to different forms (modes) of natural vibration of the frame. As a result of the forced vibration of mechanical structure residual stresses are relaxed, which should prevent further deformation and/or cracking of the frame once it is installed in the target machine during its service life.
Figure 1 shows the vibratory stress relief kit used in the study. It consisted of a control and monitoring unit from Wibropol and a WC2020 eccentric vibrator mounted on the frame being relaxed. The place of attachment of the vibrator is crucial. It should ensure that the structure can be stimulated to vibrate with multiple modes. Thus, the vibrator should be attached preferably in places where the nodal points of individual vibration forms are not located. The adopted method of attaching the vibrator (its orientation) with respect to the frame made it possible to effectively excite the structure to vibration in the vertical Z and horizontal Y directions (Figure 1).
Information on the RMS values of vibration accelerations from two accelerometers mounted vertically and horizontally on the frame was acquired from the control panel. The vibration transducers were mounted near the vibrator in the y-z plane, the plane of excitation of the frame to vibration. The diagram (Figure 2) shows the course of sequential vibratory stress relief process. The course marked in red corresponds to vibration accelerations recorded in the vertical z-direction, in blue to vibrations in the y-direction. Values of the vertical axis of the graph express voltage [V] proportional to the RMS values of vibration accelerations recorded by accelerometers. On the horizontal axis time is presented in seconds. Table 1 lists parameters of sequentially conducted vibratory stress relief . Meanwhile, the dependence of the centrifugal force generated in the vibration stress relief process on the frequency of the eccentric vibrator shaft is provided in Figure 3.

2.2. Analysis of Geometric Features Using Spatial Photogrammetry

To measure geometric features of the steel frames a laser scanner from Creaform was used, working with VXelements software. It is a fast and accurate scanner that can be used on production lines for automatic or manual 3D inspection of parts. The scanner can find many applications, such as product quality control, evaluation of 3D models' compatibility to the nominal model, and enables reverse engineering, 3D scanning to CAD, CAD modeling or finite element analysis. Analysis of the scans obtained was carried out using GOM Inspect software. Prior to taking measurements with a 3D scanner, reference points were attached to the frame. These points were placed randomly with the assumption that the scanner would "see" at least four in each shot (Figure 4).
The presented tests of welded frames (frame No. 1 and frame No. 2) were carried out at the headquarters of PROTiM. Tests on the impact of the location of support points (frame No. 3) were carried out in the research laboratory located at the Department of Metrology and Measurement Systems of the Poznan University of Technology.
As a result of the measurements, the measurement data obtained in the form of a point cloud were subjected to further processing and optimization. Point clouds corresponding to the measurement data were polygonized. It consists in building a model in the form of a triangle grid, with vertices located at individual points in the collection. This generated files in STL format and created 3D models of the measured objects. The scanning of each object produces many individual scans, which must be automatically combined using an intelligent algorithm based on surface matching and on the combination of reference points to obtain the most complete model possible. An example of a measurement point cloud of a scanned welded frame is shown in Figure 5.
Next steps of the measurement and data analysis procedure of the obtained point cloud are presented below in the form of a graphic diagram (Figure 6).
Presented tasks related to the determination of geometric characteristics were carried out for different states of the frame:
  • Scanning of a welded steel frame (frame No. 1) - measurement immediately after welding.
  • Scanning of a welded steel frame (frame No. 1) - measurement after free relaxation.
  • Scanning of a welded steel frame (frame No. 2) - measurement before vibratory stress relief (measurement immediately after welding).
  • Scanning of a welded steel frame (frame No. 2) - measurement after vibratory stress relief .
  • Measurement of temperature distribution at the characteristic points of the tested frames during the measurement.
The comparison of elements is presented in the form of a colorful map, where deviations at the inspection points are represented by a color scale. One of the criteria for properly measuring of welded structure geometry is proper location of their support points.
In this case, where analyzed structure is the base of packaging machine, the length of profiles required proper placement of support points so as not to affect the deflection of them. Defined the same as support points of final machine. In order to verify assumptions, an analysis of a welded steel frame with different support points was carried out - 15 variants (frame No. 3). The study was conducted for a welded frame made of the same profiles as a vibration relaxed frame that is a section of the original final frame.
Figure 7 shows the schematics of designed frame for analysis of the effect of support points distribution on result of the measurement, along with the marked support points.

3. Results and Discussion

3.1. Analyses of the Obtained Results

Analysis of geometric features of welded frames after free relaxation and after vibratory stress relief included:
  • Comparison of the geometry of frame 1 immediately after welding with the CAD model.
  • Comparison of the geometry of frame 1 after free relaxation with the CAD model.
  • Comparison of the geometry of frame 1 immediately after welding and after free relaxation.
  • Comparison of the geometry of frame 2 immediately after welding with the CAD model.
  • Comparison of the geometry of frame 2 after vibratory stress relief with CAD model.
  • Comparison of the geometry of frame 2 immediately after welding and after vibratory stress relief .
The following analyses were conducted for each comparison:
7.
Frame matching according to the best-fit method:
  • colorful deviation map with indication of max/min deviation in each area;
  • Y-axis inspection sections with indication of max/min deviation values in individual areas;
  • cross-section in the Z-axis - the front plane of the frame with indication of max/min deviations in individual areas.
8.
Frame matching according to the 3-2-1 method (plane - straight - point):
  • colorful deviation map with indication of max/min deviation in individual areas;
  • Y-axis inspection sections with indication of max/min deviation in individual areas;
  • cross-section in the Z-axis - the front plane of the frame with indication of max/min deviations in individual areas.
9.
Measurement of the frame face flatness.

3.2. Comparison of the Geometry of Frame 1 Immediately after Welding with the CAD Model

The geometry analysis was carried out in two alignments. The first is based on aligning the mesh representing measured element with a nominal spatial model in the form of a CAD model, according to the best-fit (based on least-squares method). In this comparison, digital representation of the real element is aligned with the CAD model in such a way that the sum of deviations squares between corresponding points tends to 0. On the basis of this alignment the colorful map of deviations is presented. Distribution of values shows how complex the nature of the deformation is between the real and the nominal element. The spread of obtained values reaches nearly 4.7 mm, while the flatness of the upper frame surface is 3.35 mm. Figure 8a shows an example of a colorful deviation map for the comparison of the geometry of frame 1 immediately after welding with the CAD model.
Analyzing cross sections parallel to the Y axis, it can be seen that the displacement of mounting posts is -0.88 mm for the former, and -0.64 mm for the latter. The frontal section shows in 2D the nature of frame No. 1 deformation.
The entire analysis was repeated using the second concept of alignment - the 3-2-1 method. In this method, the alignment of the CAD model and the measured mesh representing real element was done using geometric elements receiving successive degrees of freedom of the element (plane - 3 degrees of freedom, line - 2, point - 1). Here both values and distribution of deviations take on a different character. The spread of deviation is 5.6 mm, nearly 1 mm more than in the case of the first concept. The diagonal beam in both cases shows convexity, and mounting posts are offset in the negative direction, while averaging the fit (best-fit) this offset has a larger absolute value. In both alignments, the largest value of deviation at the face occurs at the same place - that is, at the longest edge of the frame. Analyzing the beam that forms the longest edge of the frame and the other, located on the opposite side of the element, one can see a protrusion on both sides of the element. For the 3-2-1 alignment, this is a deviation of flatness of lateral surface is 1.46 mm on one side and 1.53 mm on the other. For the best-fit method, it is 1.36 mm and 1.28 mm, respectively. The front cross-section in the 3-2-1 alignment shows that the largest deviations occur in the axis perpendicular to the longest edge of the frame, and this is the issue to focus on.

3.3. Comparison of Frame 1 Geometry after Free Relaxation with CAD Model

The next analysis shows the comparison of frame 1 after free relaxation to the nominal CAD model. The analysis methodology presented in the previous section is retained. For the best-fit alignment, the colorful deviation map shows two characteristic areas on the face of the frame where deviations have the largest values. These values show the propagation of frame deformation due to stress relaxation. The sections also show further displacement of the mounting posts and are -1.35 mm and -0.72 mm, respectively. Noteworthy is the issue of deviation of the longest beam location, which is +1.84 mm, showing an increase in convexity in this area. Figure 8b shows a colorful deviation map for the comparison of the geometry of frame 1 after free relaxation with the CAD.
Using 3-2-1 alignment, it can be seen that the flatness of the front surface is 2.92 mm. In the central part of the frame, a concavity of up to - 1.43 mm is observed, while a deviation of + 2.37 mm is observed at the point of the highest surface elevation. The mounting posts for this method of aligning are in the correct place, but the offset of the beams parallel to the longest edge of the frame reaches + 2 mm, which can seriously disrupt the assembly process of the final structure.

3.4. Comparison of the Geometry of Frame 1 Immediately after Welding and after Free Relaxation

The ambiguity of the results obtained, as well as some difficulties in correctly interpreting the changes in deviations when comparing the measured frame with the CAD model both immediately after welding and after free relaxation, led to another analysis, which consisted of comparing two frame scans with each other. Figure 9 illustrates a colorful deviation map exemplifying the comparison of frame 1 geometry immediately after welding and following a period of free relaxation (best-fit alignment).
The starting element, taken as a nominal one, was established as the frame scan obtained immediately after welding. A scan of the same frame after free relaxation was then aligned to it and the results compared. According to the assumptions, the analysis was carried out in two coordinate systems (using two alignment) - best-fit and the 3-2-1 method. Analyzing results of the comparison according to the best-fit method, one can see deviation values of up to 1.5 mm, which shows the order of magnitude of deformation with such a large frame resulting from the release of residual welding stresses. Some reciprocal torsion between the components can be seen here, as shown by deviations on the longest beam of the frame. On the opposite beam, on the other hand, concavity is observed, that is, as a result of relaxation, the central part of this beam has deformed in the positive direction less than in the node area of the structure, where the deviation values are 4-5 times higher.
Using 3-2-1 alignment, a similar trend of concavity is noticed, but with different proportions. Here the change in deviation on the central part of the beam and on nodes is 2-3 times. With this method of aligning, the torsion of the system is significantly reduced and amounts to 0.2 mm, which, for a welded element of such large dimensions, does not seem to be significant. What is significant, however, are values of displacement of the position of mounting posts, which are +0.45 mm and +0.84 mm. The frontal section shows a displacement of the beams reaching +1.32 mm, which suggests that special attention should be focused on this particular area when assembling subsequent elements of the device.

3.5. Comparison of Frame 2 Geometry Immediately after Welding with CAD Model

According to the geometric specifications, a second sample, called "frame 2", was prepared. It was subjected to an analogous analysis as frame 1. In the first step, frame 2 was compared immediately after welding with the nominal model - the CAD model, according to two strategies: best-fit (Figure 10a) and 3-2-1 (Figure 10b).
Figure 10 presents a colorful deviation map as an illustration of comparison between geometry of frame 2 right after welding and the corresponding CAD model. Based on the best-fit alignment, a colorful map of deviations was presented, from which it can be observed that - as in the case of frame 1 - there are two crucial points on the front surface, where the deviations take the largest values. In contrast, there is a concavity in the central part of the frame. The flatness deviation of the front surface is 3.35 mm. The position of the mounting posts shows no deviations greater than 0.5 mm. On the frontal cross-section, it can be seen that the longest beam of the frame shows convexity - the spread of deviation values from the nominal is 2.58 mm. In contrast, the opposite beam of the structure is offset by 0.72.
Based on the 3-2-1 alignment (Figure 10b), the front surface deviations indicate a spread of 0.5 mm greater than that of the best-fit alignment, i.e. 3.9 mm. The location of the point with the largest deviation of the frame face coincides with that obtained by the previous method, and similarly the location of the concavity at the top of the frame. The longest beam on the side surface has a characteristic convexity that is 1.32 mm, which in the next stage of the analysis has a decisive influence on the design of the datum system and the torsion of the component model relative to CAD. The mounting posts are offset by about 2.5 mm in this setup. The center beam of the frame parallel to the longest beam is offset by nearly 3 mm. During further analysis and subsequent assembly, this suggests that these are the aspects to focus on.

3.6. Comparison of Frame 2 Geometry after Vibratory Stress Relief with CAD Model

After vibratory stress relief , the frame was scanned again, and result was compared with the CAD model. The colorful deviation map determined from the best-fit (Figure 11a) shows that locations of the extreme deviation are situated in the same places as before relaxation. However, their values have changed. On the front surface, the spread of values is 3.67 mm, an increase of nearly 0.3 mm. The position of the mounting posts also changed by about 0.3 mm. The longest frame beam on the side surface has a characteristic convexity that is 1.32 mm, which has a decisive impact on the design of the datum system in the next stage of the analysis. The flatness of the front surface is 3.23 mm.
In the 3-2-1 alignment (Figure 11b), the axis of the system runs along the longest beam of the frame, the aforementioned convexity determines the twist of the model measured against the CAD. This results in a deepening of the tendencies noted during the analysis of frame 2 scanned immediately after welding. The mounting posts are shifted by 3.95 mm and 2.94 mm, respectively, and the middle beam parallel to the longest one is shifted by 3.49 mm, which are definitely higher values than those obtained directly after welding.

3.7. Comparison of Frame 2 Geometry Immediately after Welding and After Vibratory Stress Relief

Comparing frame 2 scanned directly after welding and after vibratory stress relief , aligning was performed according to the best-fit and 3-2-1 strategies. Figure 12 shows an example of a colorful deviation map for the comparison of frame 1 geometry immediately after welding and after vibratory stress relief .
The frame directly after welding was established as the reference. In the best-fit alignment, a slight range of deviations can be seen on the front surface. In all other parts of the frame, the spread is 1.47 mm. The convexity of the side surface of the longest frame beam increased by 0.92 mm. On the opposite parallel beam, there was a nonlinear deformation consisting of a bidirectional displacement of one node by -0.48 mm in one direction and -0.58 mm in the other direction. The mounting pillars also shifted after stress release by about 0.5 mm. On the basis of the best-fit alignment, a very complex manner of the element deformation due to stress release is visible. On the longest beam, a "rippling" of the lateral surface is visible, where deviations successively increase - decrease - increase - decrease. The extreme longitudinal beam is displaced in the positive direction by 0.63 mm, while the central beam is displaced in the opposite direction by -0.69 mm, which increases their mutual distance by 1.32 mm. The frontal cross-section shows how in about halfway through the frame there is a shift of the frame in the negative direction by an average of 0.6 mm.
The 3-2-1 alignment also shows a slight change in flatness on the face. Determining the axis of the fit along the longest edge, where the so-called waviness was noted earlier, resulting in the consequent displacement of the remaining beams relative to the layout. The mounting pillars are shifted by 1.28 mm and 0.46 mm, which are significantly higher values than those obtained from previous analyses. Similarly, the deformation of the frame in the extreme area of the longest beam is 50% higher than the corresponding area on the comparison of frames after free relaxation, suggesting that the process of free relaxation should be carried out longer to release all accumulated stresses and finish the deformation of the frame.

3.8. Analysis of Geometric Features of Welded Frame (Frame 3) for Different Support Methods

The geometry analysis, as for frames 1 and 2, was performed in two coordinate systems. The first is based on aligning the mesh of measured element with a nominal spatial model in the form of a CAD model, according to the best-fit method, while the second is based on aligning according to the 3-2-1 method based on substitute geometric elements. Both approaches present colorful maps of deviations based on alignment with the CAD model, as well as cross-sections in 3 axes showing deformation of the component.
To evaluate the impact of the support point location strategy, a key aspect is the analysis of cross-sections in the X and Y axes, as well as the flatness of the frame face. Table 2 shows for each support variant and both alignment strategies extreme values of deviations (max, min), range and flatness of the front surface.
The nature of the distribution of deviations for the front surface does not generally change using different support strategies. Location of extreme deviations are constant, i.e. the minimum value is located in central part of the central crossbeam, while the maximum value is at one of the beam's corners - the one located at the beginning of the coordinate system. Only in the case of strategy 14, i.e. four-point support distributed at the corners of the frame, did a change in this trend. Then the level of the beam in Y-axis of the system was aligned in best-fit, and for the 3-2-1 method the deviation difference in this axis is 0.05 mm.
In each considered cases, convexity on the diagonal beam and concavity of the beams parallel to the X-axis in the center of the frame are observed. No support method reversed this trend, even concentrating supports in the central part of the frame (variants 10, 12, 13) did not cause significant deformation of the frame.
For best-fit alignment, the spread of maximum deviations is 0.15 mm, for minimum deviations it is 0.09 mm, while for total spread it is 0.15 mm. For 3-2-1 alignment, the spread of maximum deviations is 0.05 mm, for minimum deviations 0.07 mm while for total spread 0.09 mm.
Comparing the values of boundary deviations and range for the tested spacing strategies of supports, it can be observed that, depending on the aligning used, the absolute values of boundary deviations are symmetrically distributed. Larger spreads were obtained for the best-fit method. Although the difference in the spreads does not exceed 0.1 mm for any strategy, as shown in the table 2.

4. Conclusions

This paper presents geometric analyses of welded frames made of 120x80x8 welded hollow profiles (ISO102010). These frames were a research component of a prototype packaging machine. Analyzed objects were submitted to two types of stress relaxation, carried out to remove the stresses created during the welding process. One of the frames was subjected to free relaxation, while the other was subjected to accelerated vibratory stress relief . Geometric dimensions of tested frames were measured using a photogrammetric system. In addition, an analysis of the effect of support points on the dimension and shape deformation of the welded frame was carried out. During all measurements, the temperature of the measured object was controlled. The range of temperature values did not exceed ±1°C, so there was no need to carry out corrections related to temperature errors. The reference temperature was 20°C.
The geometry analyses presented in this paper were performed in two coordinate systems. The first was based on aligning mesh of the measured element with a nominal spatial model in the form of a CAD model, according to the best-fit, or least-squares, method. In this comparison, the digital representation of the real element is matched with the CAD model in such way that the sum of squares of deviations between corresponding points tends to 0.
The second aligning concept used in the analysis of scanned frames was the 3-2-1 (plane-line-point) method. In this method, the CAD model and the measured mesh representing real element were aligned using substitute geometric elements receiving successive degrees of freedom of the element (plane - three degrees of freedom, line - two degrees of freedom, point - one degree of freedom).
In the two adopted alignment, both values and distribution of deviations take on a different character. The ambiguity of obtained results, as well as some difficulties in correct interpreting of changes in deviations when comparing the measured frame with the CAD model for both immediately after welding and after free relaxation, led to another analysis, which consisted of comparing the two frame scans with each other. The starting element, taken as a reference, was established as the frame scan obtained immediately after welding. A scan of the same frame after free relaxation was then applied to it. Similarly, a comparative analysis was carried out for a set of measurements of a frame subjected to vibratory stress relief (nominal element - frame scan immediately after welding). According to the assumptions, the analysis was carried out in two coordinate systems (using two aligning methods).
Comparative analysis of geometric deviations of frames after free relaxation and vibratory stress relief led to the assumption that dimensions of the frame subjected to vibratory stress relief deviate to a greater extent from the nominal dimensions is confirmed. Nevertheless, it should be emphasized that after vibratory stress relief the frame is not subject to further deformation, which is a desirable effect. In the case of free relaxation, the frame undergoes dimensional changes in a random manner.
In summary, conducting accelerated vibratory stress relief allows to control spontaneous changes in dimensions of the designed frame (No.1) of the packaging machine resulting from spontaneous relaxation of stresses arising from the welding process. The shortening of the relaxation process for the welded frame is also an unquestionable advantage in comparison to free relaxation.
In addition, as part of the metrological analysis, an evaluation of geometry change was carried out for fifteen variants of steel frame support. The considered frame was made of the same hollow profiles as the frame constituting the test object for the implementation of vibratory stress relief. As in the earlier case, the analyses were carried out in two coordinate systems.
To assess the influence of the support point placement strategy, a key aspect was the analysis of cross-sections in the X and Y axes, as well as the flatness of the frame face.
The analyses carried out allow us to conclude that the nature of deviations distribution for the front surface essentially does not change with different support strategies. This demonstrates the appropriate selection of structural elements to ensure the stiffness of the sleeping frame of the designed device. The location of the extreme deviations is constant, i.e. the minimum value is located in the central part of the central crossbeam, while the maximum value, in one of the corners of the beam - the one located at the beginning of the coordinate system.

Author Contributions

Conceptualization, M.J., and R.B.; methodology, M.J., L.M.-P., B.G., R.B., and B.J.; validation, M.J., L.M.-P., B.G., and R.B.; formal analysis, M.W. and R.K.; investigation, M.J., L.M.-P., B.G., R.B., and B.J.; resources, M.J.; writing—original draft preparation, M.J.; writing—review and editing, M.J., M.W. and R.K.; visualization, M.J., L.M.-P. and B.J.; supervision, M.W. R.B., and C.J; project administration, M.J., F.R. and C.J; funding acquisition, F.R. and C.J. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by The National Centre for Research and Development, grant number: POIR.01.01.01-00-0538/19; A modular system of packing products into collective cardboard packaging – PROTiM Sp. z o. o. Poznan, Poland and this research was funded by the grant no. .

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The authors would also like to acknowledge PROTiM for fabricating the samples and WIBROPOL for realization vibratory stress relief.

Conflicts of Interest

The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

  1. Chen, S.; Gao, H.; Zhang, Y.; Wu, Q.; Gao, Z.; Zhou, X. Review on residual stresses in metal additive manufacturing: formation mechanisms, parameter dependencies, prediction and control approaches. Journal of Materials Research and Technology 2022, 17, 2950–2974. [CrossRef]
  2. Masubuchi, K. Residual Stresses and Distortion in Weldments: A Review of the Present State-of-the-Art. Residual Stress and Stress Relaxation 1986, 49–59.
  3. Jing, S.; Zhang, Y.; Ke, S. The numerical simulation for effect of vibratory stress relief on titanium alloy Ti-6Al-4V fatigue life. In: Theory, Methodology, Tools and Applications for Modeling and Simulation of Complex Systems. Zhang L., Song X., Wu Y., AsiaSim 2016, SCS AutumnSim 2016. Communications in Computer and Information Science, Singapore: Springer; 2016. volume 645. pp. 530–539.
  4. Romano, S.; Brückner-Foit, A.; Brando, A.; Gumpinger, J.; Ghidini, T.; Beretta, S. Fatigue properties of AlSi10Mg obtained by additive manufacturing: defect-based modelling and prediction of fatigue strength. Engineering Fracture Mechanics 2018, 187,165–189. [CrossRef]
  5. Wang, C.; Jiang, C.; Fei, C.; Zhao, Y.; Zhu, K.; Chai, Z. Effect of shot peening on the residual stresses and microstructure of tungsten cemented carbide. Materials & Design 2016, 95, 159–164. [CrossRef]
  6. Dong, P.; Song, S.; Zhang, K.; Analysis of residual stress relief mechanisms in post-weld heat treatment. International Journal of Pressure Vessels and Piping 2014, 122, 6–14. [CrossRef]
  7. Jang, J.; Son, D.; Lee, Y-H; Choi, Y.; Kwon, D.; Assessing welding residual stress in A335 P12 steel welds before and after stress-relaxation annealing through instrumented indentation technique. Scripta Materialia 2003, 48(6), 743–748. [CrossRef]
  8. Shalvandi, M.; Hojjat, Y.; Abdullah, A.; Asadi, H. Influence of ultrasonic stress relief on stainless steel 316 specimens: A comparison with thermal stress relief. Materials & Design 2013, 46, 713–723. [CrossRef]
  9. Cozzolino, L.D.; Coules ,H.E.; Colegrove, P.A.; Wen, S. Investigation of post-weld rolling methods to reduce residual stress and distortion. Journal of Materials Processing Technology 2017, 247, 243–256. [CrossRef]
  10. Kai-Xin, L.; Jin-Xiang, Z.; Kai, Z.; Xiao-Jie, L.; Kai, Z. Mechanism of Explosive Technique on Relieving Welding Residual Stresses. Chinese Physics Letters 2005, 22(3), 744–746. [CrossRef]
  11. Lin, Q.; Chen, J.; Chen, H. Possibility of Inducing Compressive Residual Stresses in Welded Joints of SS400 Steels. Journal of Materials Science & Technology 2001, 17(6), 661–663.
  12. McGoldrick, R.T.; Saunders, H.E. Some experiments in stress relieving castings and welded structures by vibration. Journal of the American Society of Naval Engineers 1943, 55(4), 589–609. [CrossRef]
  13. Chen, S.-G.; Zhang, Y.-D.; Wu, Q.; Gao, H.-J.; Yan, D.-Y. Residual Stress Relief for 2219 Aluminum Alloy Weldments: A Comparative Study on Three Stress Relief Methods. Metals 2019, 9, 419. [CrossRef]
  14. Dawson, R.; Moffat, D.G. Vibratory Stress Relief: A Fundamental Study of Its Effectiveness. Journal of Engineering Materials and Technology 1980. 102(2), 169–176. [CrossRef]
  15. Hassan, A.H. Fundamentals of Vibratory Stress Relief. Asian Journal of Applied Sciences 2014, 7(5), 317–324. [CrossRef]
  16. Patil M.S., Wayakole R. R., Sarode K. D. Vibratory residual stress relief in manufacturing-a review. International Journal of Engineering Sciences & Research Technology 2017, 6(5), 609–613. [CrossRef]
  17. Raza Baqar, S.A.; Jain, Y.R.; Khanna, P. Vibratory Stress Relief Techniques: A Review of Present Trends and Future Prospects. International Journal of Emerging Technology and Advanced Engineering 2014, 4(11), 141–144.
  18. Shaikh, S.N. Vibratory Residual Stress Relieving- A Review. Journal of Mechanical & Civil Engineering 2016, 3, 1–4.
  19. Jurčius ,A.; Valiulis, A.V.; Černašėjus, O. Influence of Vibratory Stress Relief on Residual Stresses in Bridge Structural Members Weldments. The Baltic Journal of Road and Bridge Engineering 2011, 6(4), 243–248. [CrossRef]
  20. Walker, C.A.; Waddell, A.J.; Johnston, D.J. Vibratory Stress Relief - An Investigation of the Underlying Processes. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 1995, 209(1), 51–58. [CrossRef]
  21. Rao, D.; Chen, L. Vibratory Stress Relief in manufacturing the Rails of Maglev system. Journal of Manufacturing science and Engineering 2004, 126(2), 388–391. [CrossRef]
  22. Munsi, A.S.M.Y.; Waddell, A.J.; Walker, C.A. The influence of vibratory stress relief on the fatigue life of welds: A comparison with thermal stress relief. Strain. An International Journal for Experimental Mechanics 2001, 37(4), 141–149. [CrossRef]
  23. Krolczyk, J.; Pihan, G.; Legutko, S. Application of optical scanning system to determine the machining allowances. MATEC Web of Conferences 2017, 112, 01002. [CrossRef]
  24. Swojak, N.; Wieczorowski, M.; Jakubowicz, M. Assessment of selected metrological properties of laser triangulation sensors, Measurement 2021, 176, 109190. [CrossRef]
  25. Hocken, R.J.; Pereira, P.H. Coordinate Measuring Machines and Systems, 2nd ed., CRC Press: Boca Raton, USA, 2011.
  26. Harding, K., Handbook of Optical Dimensional Metrology, CRP Press: Boca Raton, USA, 2013.
  27. Luhmann, T.; Robson, S.; Kyle, S.; Harley, I. Close Range Photogrammetry: Principles, Techniques and Applications, Whittles Publishing: Dunbeath, Scotland, 2006.
  28. Rękas, A.; Kaczmarek, T.; Wieczorowski, M.; Gapiński, B.; Jakubowicz, M.; Grochalski, K.; Kucharski, D.; Marciniak-Podsadna, L. Analysis of Tool Geometry for the Stamping Process of Large-Size Car Body Components Using a 3D Optical Measurement System. Materials 2021, 14, 7608. [CrossRef]
  29. Kiraci, E.; Attridge, A.; Williams, M.A. The Use of Laser Scanning Technology to Improve the Design Process. Applied Mechanics and Materials 2011, 110–116, pp. 4118–4122. [CrossRef]
  30. Kuş, A. Implementation of 3D Optical Scanning Technology for Automotive Applications. Sensors 2009, 9(3), 1967–1979. [CrossRef]
  31. Liu, T.; Burner, A.W.; Jones, T.W.; Barrows, D.A. Photogrammetric techniques for aerospace applications. Progress in Aerospace Sciences 2012, 54, 1–58. [CrossRef]
  32. Gahleitner, R.; Niel, K.S.; Frank, S. Optical measurement system for characterizing plastic surfaces. Proc. SPIE 6813, Image Processing: Machine Vision Applications 2008. [CrossRef]
  33. Wieczorowski, M.; Gapiński, B.; Grzelka, M.; Szostak, M.; Szymański, M. The use of photogrammetry in improving quality of workpieces after an injection molding process. Polymers 2018, 63(2), 134–144. [CrossRef]
  34. Catalucci, S.; Senin, N.; Sims-Waterhouse, D.; Ziegelmeier, S.; Piano, S.; Leach, R. Measurement of complex freeform additively manufactured parts by structured light and photogrammetry. Measurement 2020, 164, 108081. [CrossRef]
  35. Kroma, A.; Mendak, M.; Jakubowicz, M.; Gapiński, B.; Popielarski, P. Non-Contact Multiscale Analysis of a DPP 3D-Printed Injection Die for Investment Casting. Materials 2021, 14, 6758. [CrossRef]
  36. Haleem, A.; Javaid, M.; Goyal, A.; Khanam, T. Redesign of Car Body by Reverse Engineering Technique using Steinbichler 3D Scanner and Projet 3D Printer. Journal of Industrial Integration and Management 2022, 7(2), 171–182. [CrossRef]
  37. Wieczorowski, M.; Yago, I.P.; Alejandro, P.D.; Gapiński, B.; Budzik, G.; Diering, M. Comparison of Measurements Realized on Computed Tomograph and Optical Scanners for Elements Manufactured by Wire Arc Additive Manufacturing. In Lecture Notes in Mechanical Engineering 2022, 127-141. [CrossRef]
  38. Javaid, M.; Haleem, A.; Singh, R.P.; Suman, R. Industrial perspectives of 3D scanning: Features, roles and it's analytical applications. Sensors International 2021, 2, 100114. [CrossRef]
  39. Wang, J.; Tao, B.; Gong, Z.; Yu, S.; Yin, Z. A Mobile Robotic Measurement System for Large-scale Complex Components Based on Optical Scanning and Visual Tracking. Robotics and Computer-Integrated Manufacturing 2021, 67, 102010. [CrossRef]
  40. Gapiński, B.; Wieczorowski, M.; Marciniak-Podsadna, L.; Swojak, N.; Mendak, M.; Kucharski, D.; Szelewski, M.; Krawczyk, A. Use of White Light and Laser 3D Scanners for Measurement of Mesoscale Surface Asperities. In Lecture Notes in Mechanical Engineering 2019, 239-256. [CrossRef]
Preprints 101825 g001
Figure 1. Vibratory stress relief instrumentation kit: control and monitoring unit (a); eccentric vibrator mounted on frame and vibration acceleration transducers monitoring vibration process (b).
Figure 1. Vibratory stress relief instrumentation kit: control and monitoring unit (a); eccentric vibrator mounted on frame and vibration acceleration transducers monitoring vibration process (b).
Preprints 101825 g001
Preprints 101825 g002
Figure 2. Course of sequential vibratory stress relief of the frame.
Figure 2. Course of sequential vibratory stress relief of the frame.
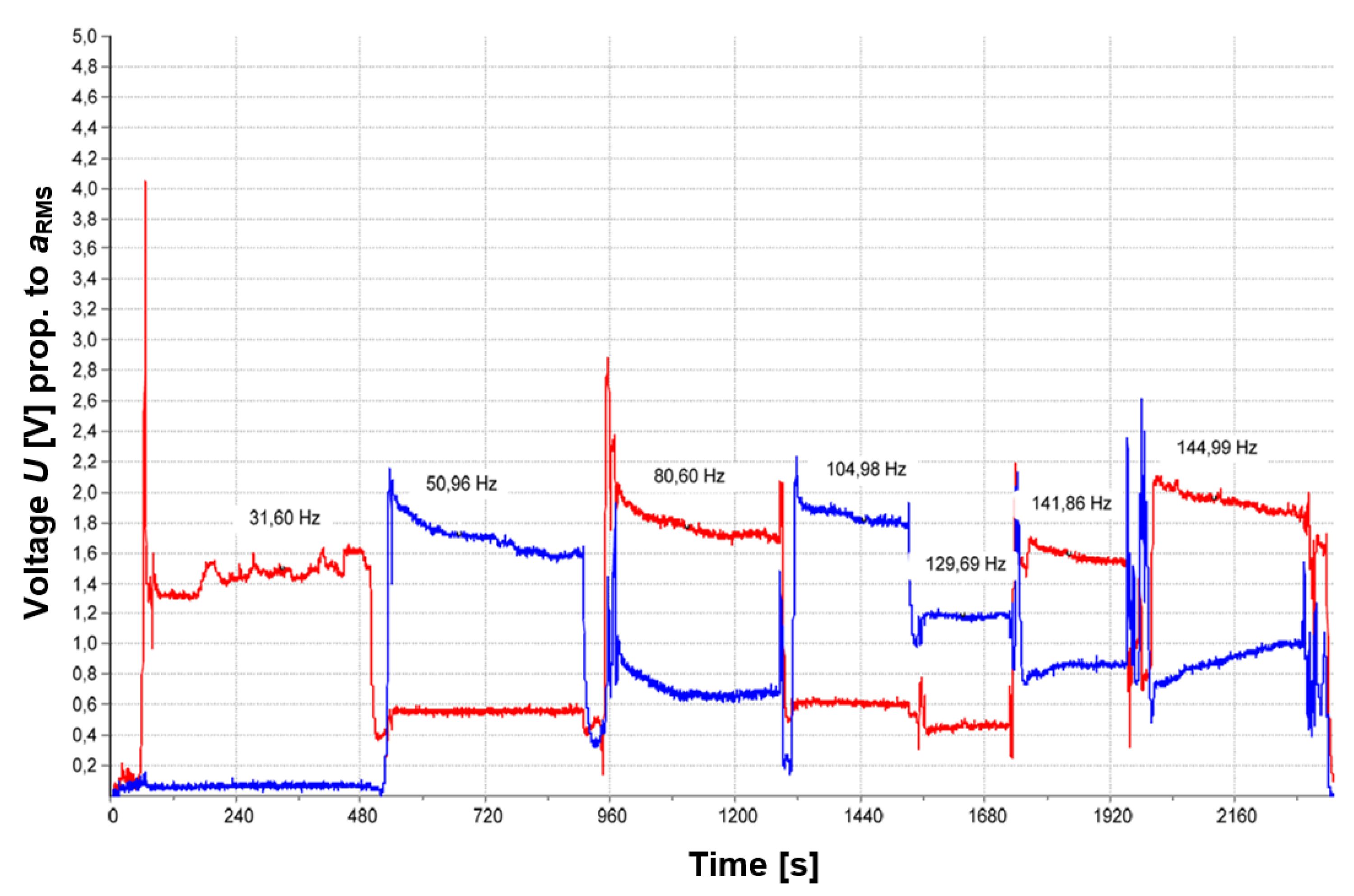
Preprints 101825 g002
Preprints 101825 g003
Figure 3. Dependence of the centrifugal force generated by an eccentric vibrator on its rotational frequency.
Figure 3. Dependence of the centrifugal force generated by an eccentric vibrator on its rotational frequency.
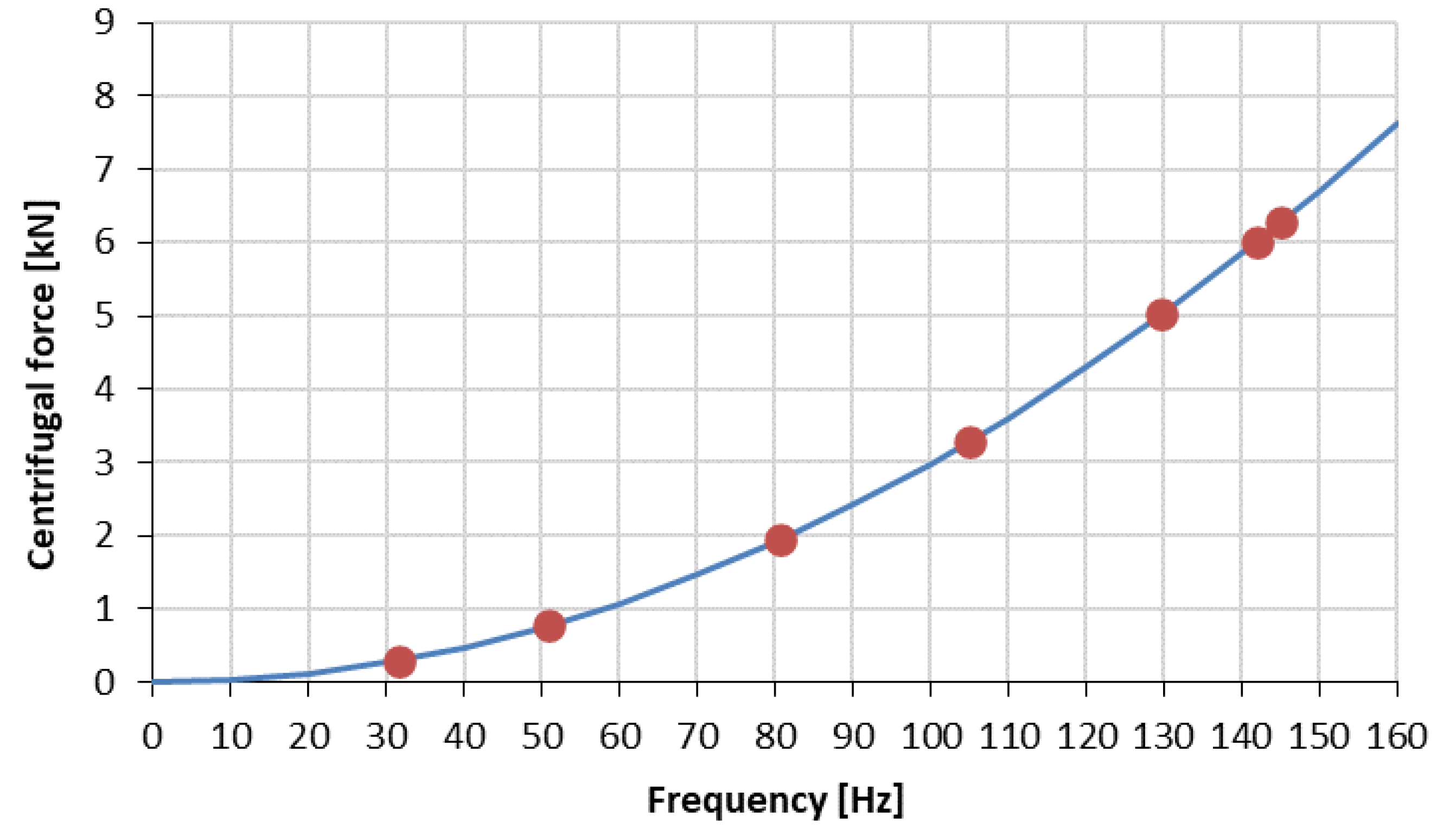
Preprints 101825 g003
Preprints 101825 g004
Figure 4. Example of the location of reference points on the tested frame No. 1.
Figure 4. Example of the location of reference points on the tested frame No. 1.
Preprints 101825 g004
Preprints 101825 g005
Figure 5. Example of a point cloud (VXelements 6.2 software).
Figure 5. Example of a point cloud (VXelements 6.2 software).
Preprints 101825 g005
Preprints 101825 g006
Figure 6. Stages of analysis of the obtained measurement results.
Figure 6. Stages of analysis of the obtained measurement results.
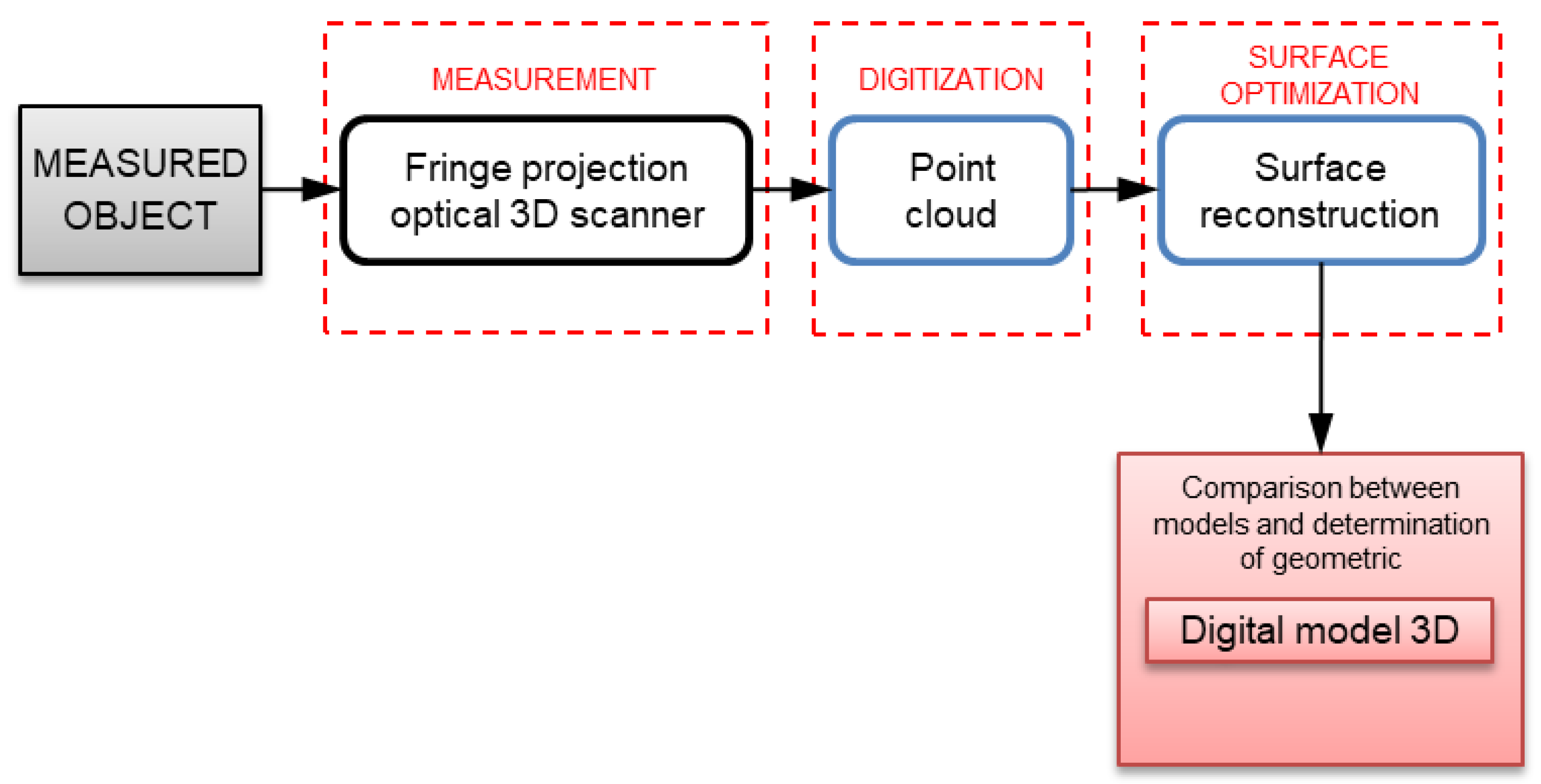
Preprints 101825 g006
Preprints 101825 g007
Figure 7. Example of the location of reference points on the tested frame No. 3.
Figure 7. Example of the location of reference points on the tested frame No. 3.
Preprints 101825 g007
Preprints 101825 g008
Figure 8. Example of comparison geometry of frame 1 immediately after welding (a) and after free relaxation (b) with the CAD model.
Figure 8. Example of comparison geometry of frame 1 immediately after welding (a) and after free relaxation (b) with the CAD model.
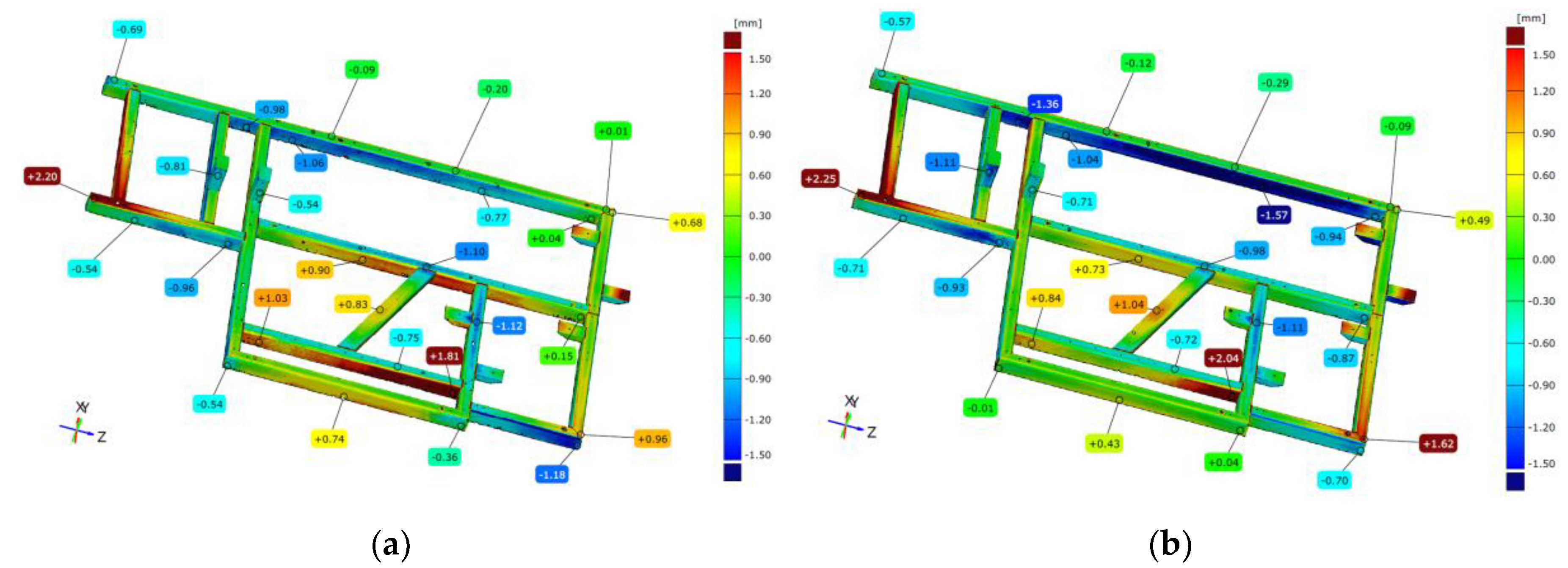
Preprints 101825 g008
Preprints 101825 g009
Figure 9. Example of comparison the geometry of frame 1 immediately after welding and after free relaxation (best-fit alignment).
Figure 9. Example of comparison the geometry of frame 1 immediately after welding and after free relaxation (best-fit alignment).
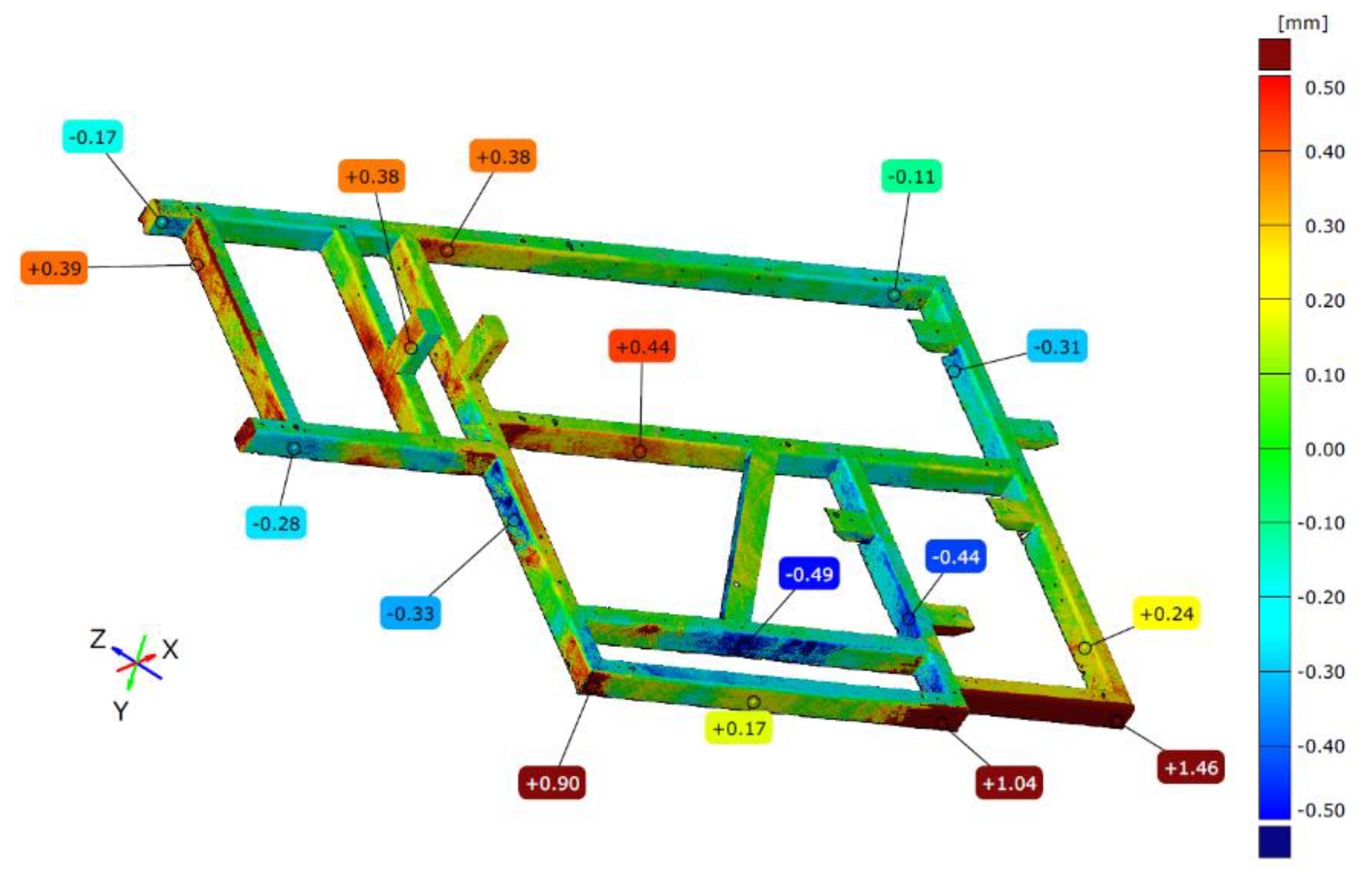
Preprints 101825 g009
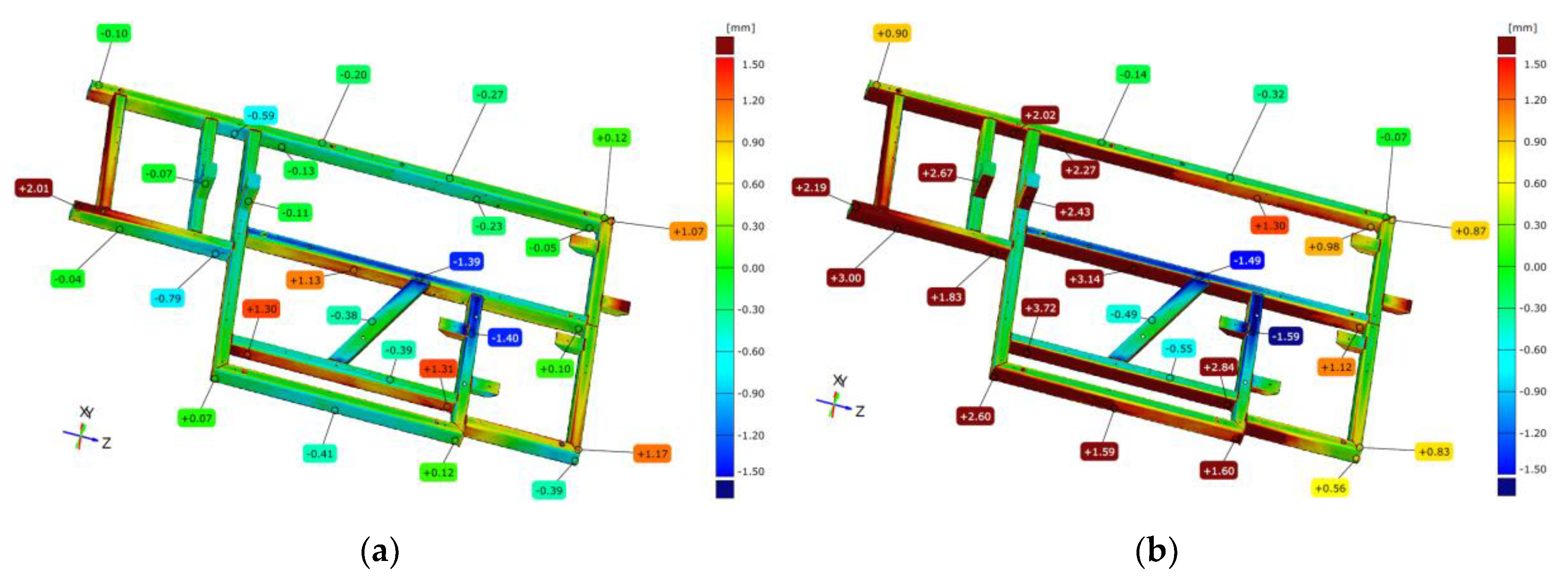
Preprints 101825 g010
Figure 10. Example of comparison of the geometry of frame 2 immediately after welding with the CAD model according to two strategies of alignment: best-fit (a) and 3-2-1 (b).
Figure 10. Example of comparison of the geometry of frame 2 immediately after welding with the CAD model according to two strategies of alignment: best-fit (a) and 3-2-1 (b).
Preprints 101825 g010
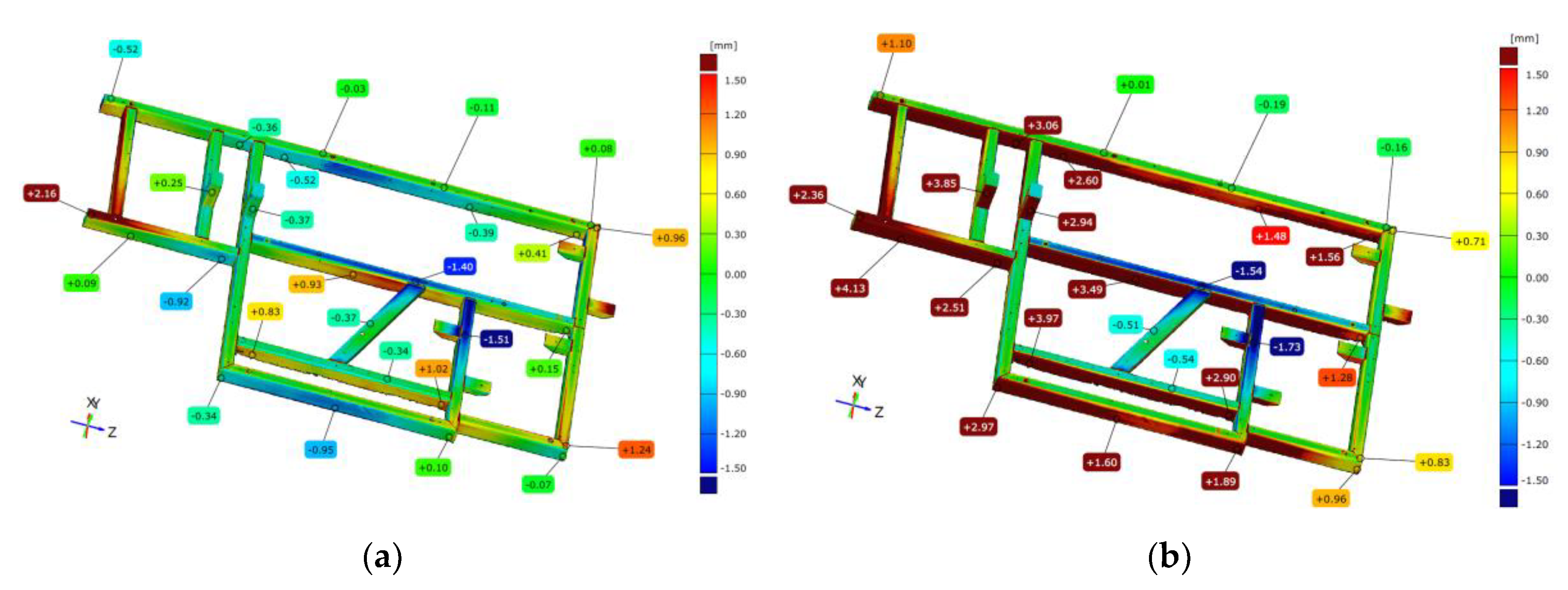
Preprints 101825 g011
Figure 11. Example of comparison of frame 2 geometry immediately after vibratory stress relief with the CAD model according to two strategies: best-fit (a) and 3-2-1 (b).
Figure 11. Example of comparison of frame 2 geometry immediately after vibratory stress relief with the CAD model according to two strategies: best-fit (a) and 3-2-1 (b).
Preprints 101825 g011
Preprints 101825 g012
Figure 12. Illustration depicting the contrast between geometry of frame 1 right after welding and its state following a period of vibratory stress relief (best-fit alignment).
Figure 12. Illustration depicting the contrast between geometry of frame 1 right after welding and its state following a period of vibratory stress relief (best-fit alignment).
Preprints 101825 g012
Table 1. Summary of parameters of sequential vibratory stress relief.
Table 1. Summary of parameters of sequential vibratory stress relief.
Sequence Rotational speed [rpm] Frequency [Hz] Time [min] Centrifugal force [kN] Direction
of response
1 1896.0 31.60 7.0 0.29803 z
2 3057.6 50.96 6.5 0.77507 y
3 4836.0 80.60 6.0 1.93888 z
4 6298.8 104.98 4.0 3.28923 y
5 7781.4 129.69 3.5 5.01989 y
6 8511.6 141.86 4.0 6.00622 z
7 8699.4 144.99 5.5 6.27419 z
Table 2. Summary of max, min, range and flatness deviation values for the frame No. 3.
Table 2. Summary of max, min, range and flatness deviation values for the frame No. 3.
Option Alignment Max [mm] Min [mm] Range [mm] Flatness [mm]
1 Best-fit 0.31 -0.21 0.52 1.19
3-2-1 0.05 -0.41 0.46
2 Best-fit 0.23 -0.26 0.49 1.18
3-2-1 0.02 -.044 0.46
3 Best-fit 0.30 -0.22 0.52 1.04
3-2-1 0.03 -0.40 0.43
4 Best-fit 0.30 -0.21 0.51 1.44
3-2-1 0.04 -0.43 0.47
5 Best-fit 0.30 -0.20 0.50 1.18
3-2-1 0.05 -0.40 0.45
6 Best-fit 0.27 -0.19 0.46 1.11
3-2-1 0.03 -0.37 0.40
7 Best-fit 0.30 -0.22 0.52 1.15
3-2-1 0.06 -0.39 0.45
8 Best-fit 0.31 -0.20 0.51 1.25
3-2-1 0.07 -0.40 0.47
9 Best-fit 0.30 -0.24 0.54 1.47
3-2-1 0.04 -0.44 0.48
10 Best-fit 0.31 -0.24 0.55 1.41
3-2-1 0.06 -0.39 0.45
11 Best-fit 0.35 -0.20 0.55 1.14
3-2-1 0.06 -0.43 0.49
12 Best-fit 0.33 -0.19 0.52 1.32
3-2-1 0.07 -0.37 0.44
13 Best-fit 0.31 -0.18 0.49 1.47
3-2-1 0.02 -0.40 0.42
14 Best-fit 0.20 -0.20 0.40 1.22
3-2-1 0.06 -0.42 0.48
15 Best-fit 0.31 -0.17 0.48 1.24
3-2-1 0.03 -0.37 0.40
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated