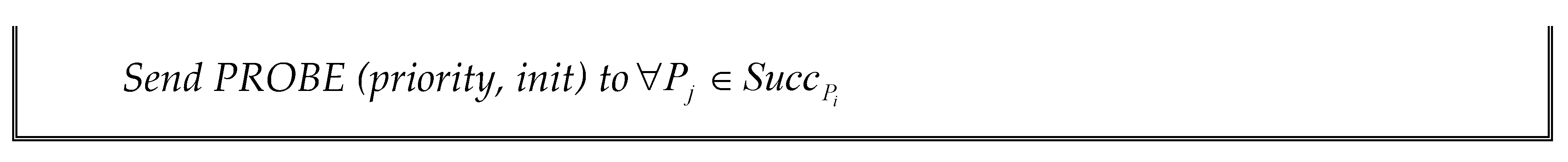An Improved Deadlock Detection and Resolution Algorithm for Distributed Computing Systems

Preprint

Article

An Improved Deadlock Detection and Resolution Algorithm for Distributed Computing Systems

Altmetrics

Downloads

253

Views

184

Comments

Tarek Helmy^*

This version is not peer-reviewed

Submitted:

21 March 2024

Posted:

26 March 2024

You are already at the latest version

Alerts

Abstract

Deadlock is a real problem that can cause expensive, time-dependent hang-ups or failures in distributed computing systems. Some studies have been conducted with deadlock detection and resolution in generalized request computing models, most of these studies are based on the diffusing computation scheme, where forward and backward propagated probe and reply messages respectively are diffused between dependent processes. The replies carry the dependency information between processes for the initiator. Using this dependency information initiator can detect and resolve the deadlock cycle. It has been proven in the literature that a deadlock cycle length distribution is skewed with a large majority of cycles (90%) having length two. Based on this fact an improved algorithm is proposed for handling deadlock detection in distributed computing systems under the distributed request model where each process has several requests at a time. The improved algorithm depends mainly on message propagation and timeout policy. Probe and reply messages are propagated between the initiator and its successors only to detect deadlock cycles between them. Global timeout policy is used to detect potential deadlock cycles with large length distribution. The proposed algorithm can handle concurrent executions. Simulation experiments are performed to see the effectiveness of the improved algorithm. It is found that the improved algorithm compares favorably with other existing algorithms and it shows better results for several performance metrics especially in reducing deadlock latency and execution time.

Keywords:

Subject: Computer Science and Mathematics - Computer Science

1. Introduction

The distributed computing system consists of a set of sites connected by a network, each site has its controller and maintains some of the resources of the system. Processes with a globally unique identifier run over a distributed system. A process makes resource requests to its local controller. If the desired resource is at a remote site, then the process sends a request message to that site. Before granting the requested resource, the sender process is blocked and said to be dependent on the process that holds the desired resource. The distributed computing system offers many advantages over a single-site system, such as data and program sharing, higher system throughput, higher system availability, load sharing, and incremental expandability [5,6,7]. Distributed computing systems are vital to many real-time applications that require guaranteed response time and continued operation in the face of system crashes. Extensive research has been carried out on distributed computing systems. Research issues include scheduling algorithms, deadlock detection, deadlock prevention, concurrency control protocols, and resource scheduling algorithms [5,6,7,8,9,10,11]. This paper is concerned with deadlock detection and resolution in distributed computing systems. A deadlock situation can arise if and only if the following four conditions hold simultaneously in a computing system.

Mutual exclusion: when a process accesses a resource, it is granted exclusive use of that resource in a non-sharable mode.
Hold and wait: a process is holding at least one resource and is waiting for one or more additional resources that are currently being held by other processes.
No preemption: a process cannot preempt or take away the resources held by another process.
Circular wait: there exists a set [P0, P1, P2, …, P n] of waiting processes such that P0 is waiting for a resource which is held by P1, P1 is waiting for a resource which is held by P2, …, Pn-1 is waiting for a resource which is held by Pn, and Pn is waiting for a resource which is held by P0.

There are three ways to deal with deadlocks; namely deadlock prevention, deadlock avoidance, and deadlock detection. Deadlock prevention is considered impractical except for systems, which have a predefined structure, where all the resources required by a process are predetermined. This constraint is not compatible with distributed computing systems. Also, deadlock avoidance is not practical in distributed computing systems because any attempt to avoid deadlock is inefficient [5,7,12]. Many researchers have tried to deal with the simpler problem of just detecting deadlocks. When a deadlock is detected in a system, it is resolved by aborting one or more processes. But when a process is aborted because it has contributed to a deadlock, the system first must be restored to the state it had before the process began.

A detection scheme is evaluated by two criteria. First, if a deadlock exists, it must be detected in a finite amount of time. Second, the scheme must not find a deadlock that is not there. A well-known approach for deadlock detection in distributed computing systems is the Wait-For Graph (WFG). WFG is a graph used to model the state of process-resource interconnections. Using WFG to detect deadlocks in distributed computing systems is inefficient because it leads to detecting false deadlocks due to incomplete or delayed information. Deadlock handling in distributed computing systems can be performed in a centralized, hierarchical, or distributed manner.

The rest of this paper is organized as follows. Section 2 addresses existing algorithms that deal with detecting deadlock cycles of skewed length distribution. Section 3 introduces the distributed computing system model as well as the new proposed deadlock detection and resolution algorithm. Section 4 presents and discusses the simulation model used for performance analysis. Section 5 presents the results of the performance evaluation. Finally, Section 6 concludes the paper and highlights future work.

2. Related Work

The deadlock problem has been extensively studied in distributed operating systems [1,2,3,4,5]. Many algorithms for centralized and distributed deadlock detection, prevention, and avoidance have been proposed in the literature [6,7,9,12,13,14]. This section surveys the research work performed in the area of distributed deadlock detection for detecting skewed deadlock cycles. Several algorithms and their ability to detect deadlock are discussed. Deadlock detection for distributed computing systems can be distributed, centralized, or hierarchical. In a distributed computing model, information must be passed between sites to detect deadlock because no single site has all the information about all processes and resources of the system. In centralized deadlock detection algorithms, systems require that all the information represented by the graph be kept at the acting controller, which is responsible for running the deadlock detection and resolution algorithms. Hierarchical deadlock schemes are based on providing several levels of hierarchy, namely, local, regional, and global. The hierarchy should be established so that deadlocks can be detected by a site as close to the sites involved in the deadlock as possible.

The main disadvantage of centralized and hierarchical detection schemes is that additional overhead is incurred due to the detection of cycles in the graph, abortion, and restart of processes upon detection of deadlocks. The distributed detection strategies may have additional overhead due to the intensive message transfers. The selection of the process to be aborted adds to the complexity of the scheme and the possibility of detecting false deadlocks. The performance of deadlock detection algorithms in distributed computing systems depends on three factors: the number of messages exchanged, the ability to detect a deadlock, and the ability to avoid detecting false deadlocks. While algorithm correctness requires that a deadlock detection algorithm detects deadlocks when they occur and does not detect false deadlocks, the number of exchange messages measures the amount of algorithm overhead to detect a deadlock. Therefore, the three criteria above are useful in determining the correctness and measuring the efficiency of a deadlock detection algorithm.

Soojung [1] proposed a centralized detection and resolution algorithm for distributed deadlocks in the generalized model. Her algorithm is based on diffusing computation techniques. She proposed two different algorithms one for single execution and the other for concurrent execution. Soojung reduces the number of propagation messages by assuming that replies to propagation are carried directly to the initiator of the algorithm. Her algorithm executes the probing phase by the initiator on the Wait-For-Graph (WFG). The initiator of the deadlock algorithm receives replies from leaf nodes only. A single execution of her suggested algorithm performs faster than the best other algorithms. It uses

2 e

messages and

d + 2

time units

e

and

d

refers to the number of edges and the diameter of the WFG involved in the algorithm execution. The proposed concurrent execution algorithm shows better results in several performance metrics such as deadlock latency, algorithm execution time, and message length.

Badal proposed a three-level algorithm [3] extended from the Obermarch algorithm. Badal assumes that most of the deadlock cycles have only a length of two and the larger a deadlock cycle is the less frequently it occurs. This fact makes his algorithm more efficient in detecting shorter global deadlocks. The basic premise of his proposed algorithm is to detect deadlock cycles with the least possible delay and number of inter-site messages.

Gray, Homan, Obermarck, and Korth [4] show in their study that deadlock cycles of length two occur more frequently than cycles of length three, cycles of length three occur more frequently than cycles of length four, and so on.

Roberto Baldoni and Sivlio Salza [2] show that the distribution of the deadlock cycle length tends to be always very skewed, with most cycles being of length two (about 90% in typical situations). According to this remark, they also propose a new hybrid approach that consists of directly detecting all the potential global deadlocks of length two and detecting the remaining ones through a global timeout. Their proposed algorithm, which they called hybrid deadlock detection (HDD), is considerably simpler and more suited for a distributed implementation.

In this paper, an improved deadlock detection algorithm is proposed. This algorithm is mainly based on the previous fact that most deadlock cycles have a length of two. The proposed algorithm not only detects deadlock cycles of length two but also can detect deadlock cycles with length distribution of more than two. The proposed algorithm deals with both local and global deadlock at a time in distributed systems. To detect local deadlocks, we use a technique based on setting a local wait timer for every local process. According to this wait timer, the local controller controls the process of local deadlock detection using the local WFG approach. To deal with global deadlocks, after a certain timeout threshold value, the initiator starts to propagate probe messages to its successors. Based on the dependency information carried by reply messages, the initiator builds a partial WFG to detect and resolve all deadlocks of length two or more. All the remaining deadlocks that cannot be detected due to their large cycle distribution are detected through a global timeout policy.

3. Proposed Deadlock Detection Algorithm

In the proposed algorithm a partial WFG will be used for detecting deadlock cycles between the initiator process and its successors and any other deadlock cycles that could exist between successors themselves. A cycle in the WFG represents a deadlock. If all items in the circular wait belong to the same site, then a local deadlock is detected. If items belong to different sites, then global deadlock is detected.

3.1. The Idea behind the Proposed Deadlock Detection Algorithm

The length of most global deadlock cycles is much skewed, with a large majority of cycles having length two. This fact has been approved by many researchers [1,2,3,4]. Soojung proposed an efficient centralized deadlock detection algorithm. She didn’t explicitly mention this fact but her simulation results show that average algorithm execution time ranges between 60-70 time units, she used an AND-OR model in her study. She assumed in her model that message transmission between two sites needs 20 time units. Victim abortion requires an extra 20-time unit. Since her algorithm is centralized, based on her results deadlock between two global nodes needs at least 60 time units. Since the average algorithm execution time is less than 70, this means that most of the deadlock cycles detected by her algorithm consist of two global processes. Based on this observation, we propose in this paper a new method. The new method uses the following strategy: detecting all global deadlocks that exist between two processes, detecting some deadlock cycles that are involved between three or more processes by analyzing processes dependencies that exist in backward report messages, using a global timeout to detect any other global deadlock corresponding to a cycle of length more than two, and detecting all local deadlocks at each site by its local process manager using waiting time policy with local WFG approach. This method for deadlock detection has several advantages over the other existing ones, which include:

Local and global deadlock detection: local deadlocks have their effect on global transaction management; this approach combines both local and global deadlock detection. Also, it can detect several deadlock cycles per single instance execution.
Latency: all deadlocks either local or global are detected within a short time.
Simplicity: building a WFG to detect global deadlocks within two global transactions in two different sites is simpler than building a complete WFG and more suitable for distributed implementation, which will reduce the total number of exchanged messages used to detect global deadlocks. Also, using a global timeout to detect other existing global deadlocks of length more than two chooses the threshold value of global timeout $t_{g}$ is a less critical problem.

3.2. Proposed Algorithm Implementation

In the improved algorithm, we assume that the global process manager communicates by exchanging messages over reliable links. Also, we assume that the identifications for global processes are unique. Each global process manager at each site maintains complete information on successor sets for all its local processes. Process successors set (

S U C C (P_{i})

) is the set of global processes that hold resources requested by the process

P_{i}

. This set is built dynamically. The successor is removed from the set as soon as

P_{i}

grants the resource that is held by that successor.

3.3. Global Process Manager Action

The distributed model we consider in this paper consists of

N

sites. At each site

S_{i}

there is a local and global process manager, a local process manager is responsible for handling local processes and detecting local deadlocks. The global process manager is responsible for handling global deadlocks. These

N

sites are connected via a computer network. Each process performs a sequence of read-and-write operations on a set of resources located at each site. In this model, we will consider that resources are accessed for writing by the processes. Local processes access items from a single site and are directly managed by the local process manager, while global processes access resources on multiple sites, and are managed by the global process manager. In this model, we consider the AND model (each process has several requests at a time).

A global process

P_{g}

at the site

S_{i}

is submitted to the global process manager, who will become its coordinator. A timer is started, and if the timeout value reaches the global timeout threshold value

t_{g}

before the process is committed, then the process is aborted due to the expected global deadlock of length more than two. When

P_{g}

requests a resource on a different site

S_{j}

, the global process manager at the site

S_{i}

, which is the coordinator of the process,

P_{g}

sends a request message to the site

S_{j}

where the required resource is located. The global process manager at the site

S_{j}

receives this request message and sends a reply message after checking the status of the resource. A reply message is a response from a site

S_{j}

to a site

S_{i}

telling whether the resource requested by the site

S_{i}

is granted or is locked by another process. If the reply message is of type lock, this means that a process locks the resource

P_{g}

, and the process

P_{g}

may proceed. If the reply message is of type wait, this means that the requested resource is locked by another active process

P_{k}

. The wait-reply message carries the identifier of the resource holder

P_{k}

. As process

P_{g}

gets the wait reply message it adds process

P_{k}

to its successor set

S U C C (P_{g})

. When the global process manager at the site

S_{i}

receives the wait-reply message, a local timeout

t_{l}

for the process

P_{g}

at the site

S_{i}

is set, if this timeout expires before a lock message is received, then the procedure to detect a global deadlock is started.

3.4. Detection Deadlock Cycles of Length Two

After the local timeout value expires before a lock messages are received. The initiator process starts sending probe messages to its successor processes. These probe messages represent the initiation phase for deadlock detection, by receiving these probe messages from successors. The successor starts responding to the received message by sending a report message. Information carried out by the report message depends on the status of the probed process. If the probed process is active, the report message will carry no useful information other than that this process is active. But if the probed process is blocked, probed by some other process initiator or the successor process itself initiates another instance of the algorithm, then information sent by the probed process depends on the priority of the recent initiator. If the recent initiator has a higher priority than the previous initiator then the probed process sends its successor set to the recent initiator, otherwise if the recent initiator has a lower priority than the previous initiator, the report message will state that the probed node is active. Active report message in case of low initiator priority is sent to the grantee avoiding unnecessary victim selection and keeping system consistency. One of the most common problems of distributed deadlock detection algorithms is synchronization. To guarantee synchronization, our proposed algorithm prevents processes from being involved in more than one algorithm instance. This prevention can be achieved by:

Ignoring any abort messages that could be received from low-priority initiators. Process judge on the priority of abort message according to the priority of probed messages it received from other initiators by holding a variable $c u r_{p r i}$ this variable is updated only if the process receives a probe message from an initiator with higher priority than what it is stored in $c u r_{p r i}$ variable.
Priority distribution is based on two things, time of initiation and process identifier. The old process has a higher priority than recent ones.
Responding to the probed messages from low-priority initiators always implies that the probed process is active because the probed node assumes that the high initiator will resolve the deadlock cycle the probed process is involved in.
Initiators with low priority will terminate the execution of their initiated algorithms upon receiving a probe message from high high-priority initiator. Terminating algorithm execution is done by ignoring all report messages that will be received from their successors.
The initiation phase ends with receiving all report messages from initiator successors.
Any process that receives a probe message must send a report message as a reply to it, the content of this report message depends on process status, initiator priority, and process priority.
In case of sending a probe message to a process that is selected as a victim and killed by some other initiator. Then it’s the responsibility of the global process manager of that process to send the abort message indicating to the initiator that this process has been aborted before.

By receiving all report messages initiator starts the detection phase. In the detection phase, it is possible to detect deadlock cycles of length two or more. Deadlock cycles of length two could occur between the initiator and one of its successors or between two successors directly. The initiator detects this deadlock cycle by checking the contents of the successor’s successor sets. Using this proposed algorithm, the initiator can detect deadlock cycles that could have more than two processes by constructing a global WFG based on the information it receives from the report messages. These extra deadlock cycles could be of length three, four, or more depending on the number of initiator successors and the number of inactive report messages that carry successors of the initiator successors. After detecting all possible deadlock cycles, the initiator starts the victim selection phase. In the victim selection phase, the initiator tries to select the optimum number of victims. The victim selection procedure is out of our study. The performance of the proposed algorithm will be evaluated by simulating the proposed algorithm. Figure 1 shows the formal description of the improved algorithm executed in the process

P_{i}

4. Discussion

In this section, we present the simulation model used for the distributed system and present the results of the proposed approach for deadlock detection. In this simulation model, the distributed computing system is represented as

N

sites. Each site runs several processes. These sites are identical and connected via a computer network. This computer network topology is a fully connected network. Each site manages the same number of resources

M

, and has the same process workload. At each site, there are two types of processes, global and local processes. The number of resources per process is generated randomly. The proposed algorithm uses an AND model, where processes request a set of resources and these resources are either local resources or global ones. The process is sustained until all requested resources are acquired then starts processing. The processing time depends on several acquired resources. Several processes

P

are kept constant during simulation time, and these processes are distributed evenly among all nodes. A new process is generated if any process is committed, and aborted processes are restarted after some random time

t_{r e s}

. The number of global transactions exceeds the number of local transactions, and the probability of generating local process is

p_{l}

, where

p_{l} < = 0.1

. The execution of the process is done as follows:

The process requests its resources in parallel, by submitting each request to the corresponding site.
Each lock is a write lock. For the simplicity of the simulated model, no replication for resources is assumed.
A transmission time $t_{c o m m}$ is needed to send a request message to the other site, and a processing time $t_{p r o c}$ for processing the acquired item. The transmission time $t_{c o m m}$ is dependent on network topology. For fully connected network $t_{c o m m}$ will be equal for all messages.
The local processes have similar structures, but request resources from their sites, and spend all processing time on their sites. For simplicity, we assume that the requesting and acquiring time for local resources is negligible.
If the requested resource is granted by some other process, then the requested site sends a wait-reply message to the requestor indicating the identifier of the process that holds the requested resource, the needed time for the wait-reply message is $t_{c o m m}$ and the process identifier is added to the requestor successor set.
A requestor that cannot grant all requested resources will initiate a deadlock detection algorithm after some timeout value $t_{l}$ .
Initiation deadlock algorithm implies sending probe messages for all requestor’s successors. Each successor sends back a report message to the initiator. Report message carries process status and its successor set if it exists.
After receiving all report messages, the initiator starts executing the deadlock algorithm to detect deadlock cycles by constructing a partial WFG based on the received information. Detecting cycles exhibits $t_{d l m s g}$ time units.
If either a local or global deadlock is detected, one of the deadlocked processes is aborted and all locked resources by that process are released, and the aborted process is restarted after a time $t_{r e s}$ . If the waiting time for any process exceeds the global timeout value $t_{g}$ then this process is assumed deadlocked and it aborts itself.

Table 1 provides a summary of the system parameters that are used in our simulation. These parameters’ values are adopted in [1] study for evaluating the efficiency of Soojung’s proposed algorithm for deadlock detection in a generalized model.

t_{p r o c}

t_{c o m m}

t_{d l m s g}

t_{l}

t_{g}

t_{p r e}

t_{r e s}

R

N

P

5. Performance Evaluation Metrics

The number of submitted processes

P

has been used as a running parameter in some experiments to represent the workload intensity. Two values were considered to represent different intensities; for lightly loaded systems

P = 25

, and heavy workloads. The same other parameter values were used for all the sites in all the experiments. As for the performance metrics we considered four main indices:

Percentage of the real and global timeout deadlock cycles detected by the proposed algorithm to the total number of deadlock cycles
Average deadlock latency; where deadlock latency is considered as the elapsed time from the instance of initiating the algorithm till the time of aborting the deadlocked process involved in the deadlock cycle. In the case of global time-out deadlocks, time latency is considered as the global timeout threshold value $t_{g}$ .
Throughput is the expected number of committed transactions to the total number of transactions submitted to the system.
Average number of deadlock detection messages

5.1. Algorithm Correctness

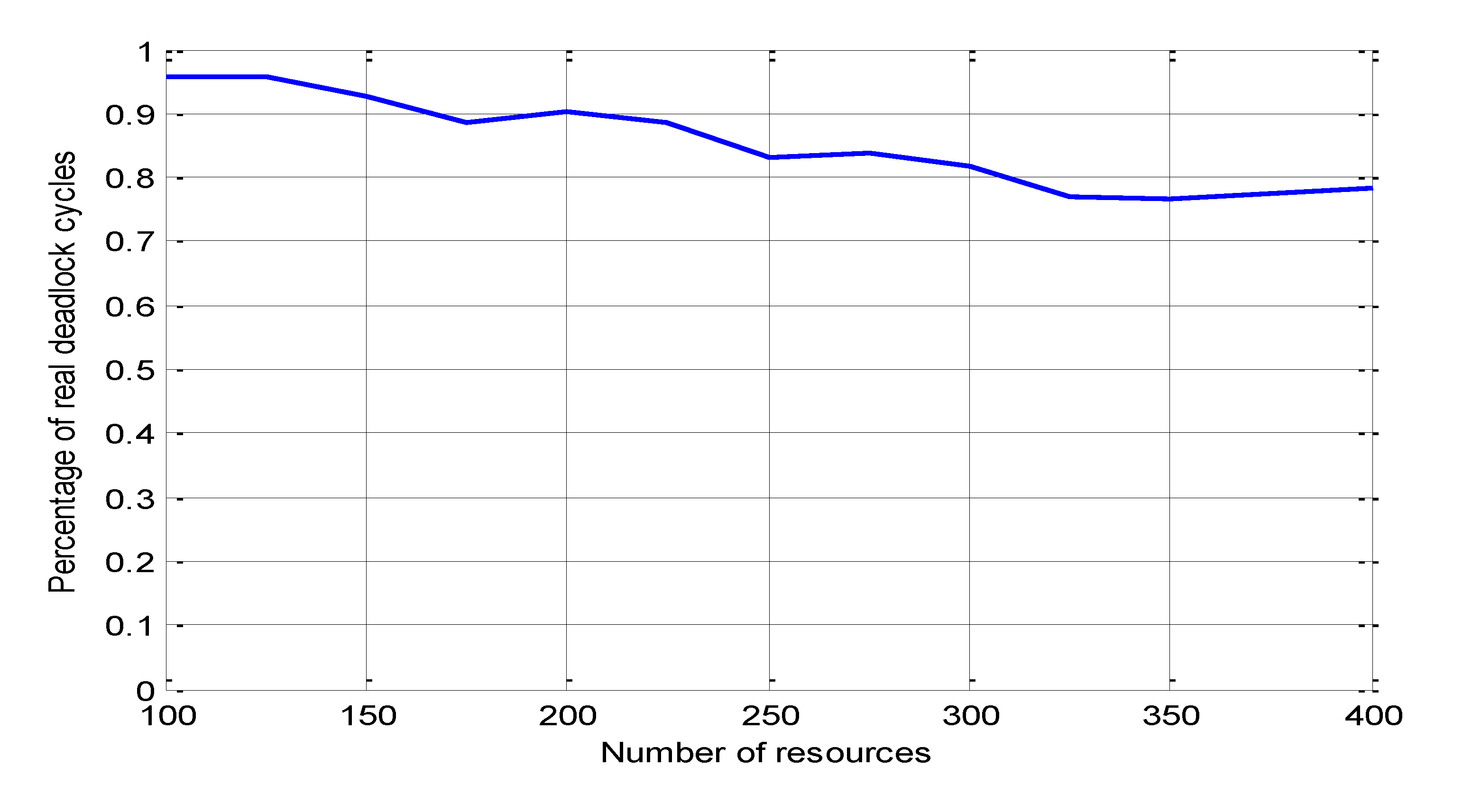
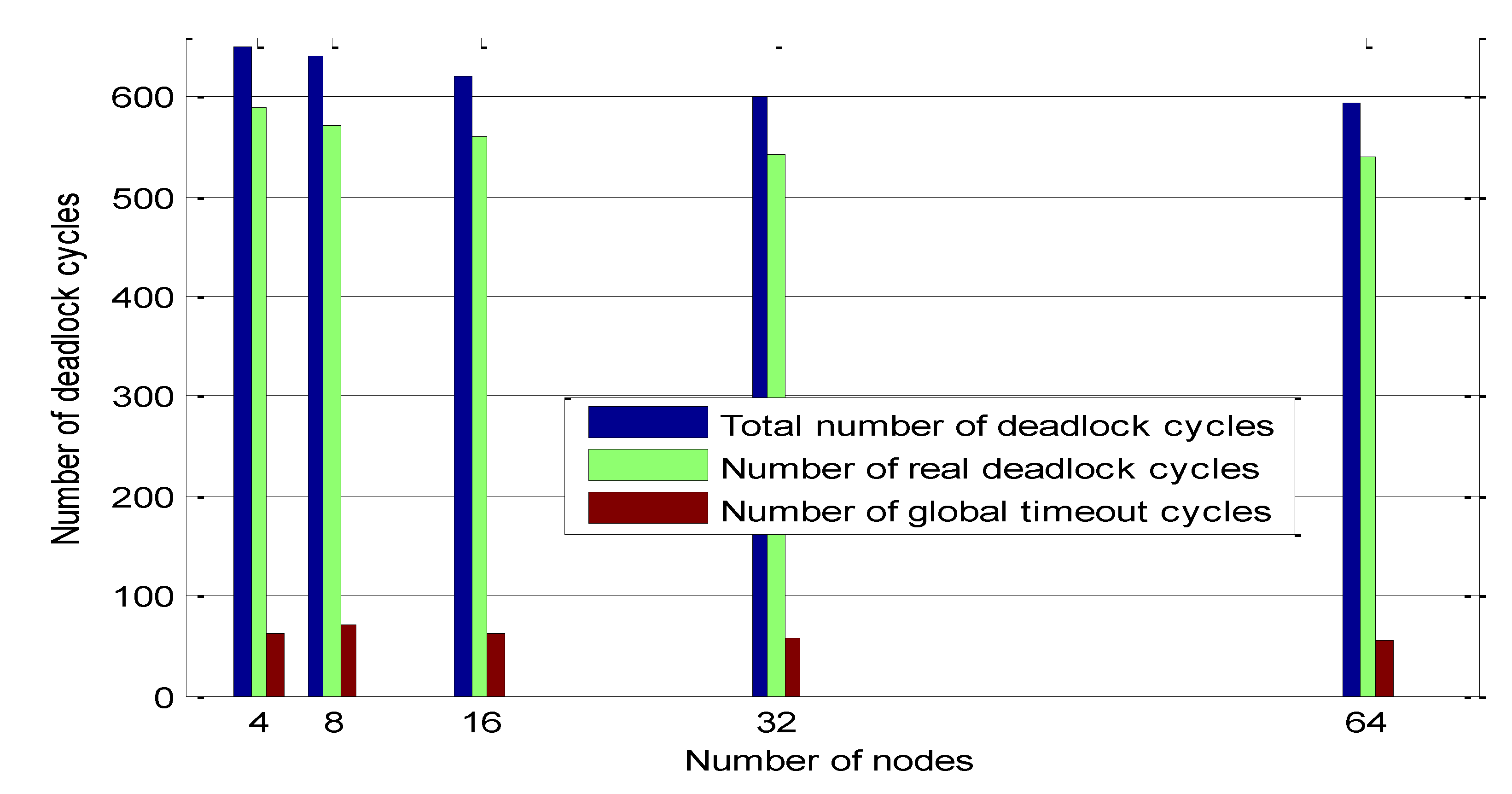
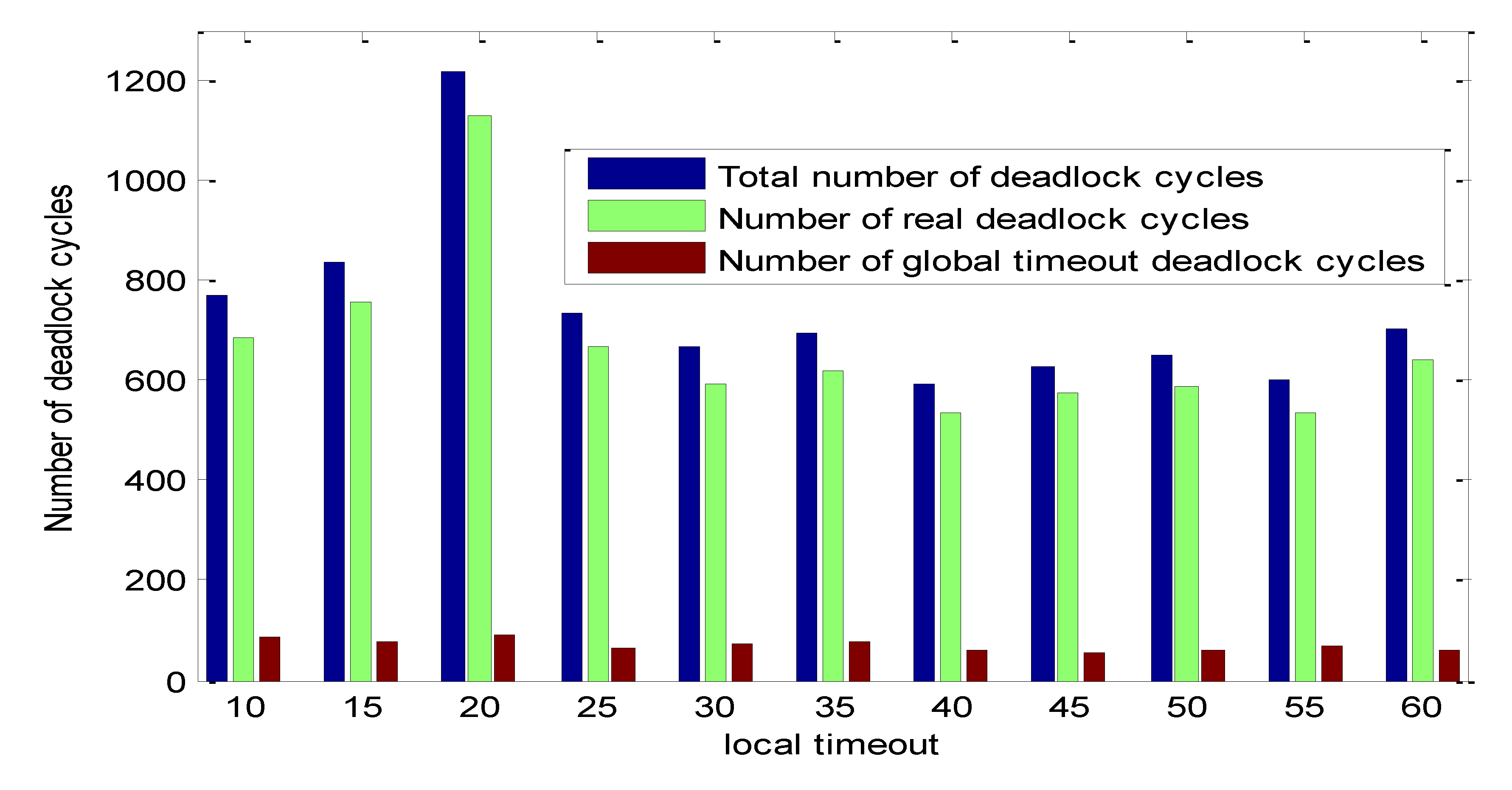
Figure 2, Figure 3 and Figure 4 show the number of real deadlocks to the total number of detected potential global deadlocks. Figure 3 shows the percentage of real deadlock detected by the proposed algorithm for different numbers of resources. Figure 4 and Figure 5 show that the number of real deadlocks is more than 87% of total deadlocks for different numbers of nodes and algorithm initiation timeout. These three figures justify the claim that this algorithm is based on.

5.2. Throughput

Figure 5 shows the throughput as a function of the workload intensity

P

. The throughput is defined as the number of committed transactions to the total number of transactions submitted to the system. The number of sites in this figure is four and the global timeout value is

t_{g} = 200

. From this figure, for a light workload, the possibility of deadlock is too low due to a large number of available resources, and the probability of requesting the same resources by the different processes is too low, therefore the throughput will be too high and it could reach 100%. But with an increasing number of nodes possibility of requesting the same resources is increased too, therefore the number of deadlocks starts increasing which yields a decrease throughout, for a large number of processes throughput reaches about 50%. Further increases in several processes will degrade the throughput, therefore, there should be a limitation on the number of processes for a certain number of resources.

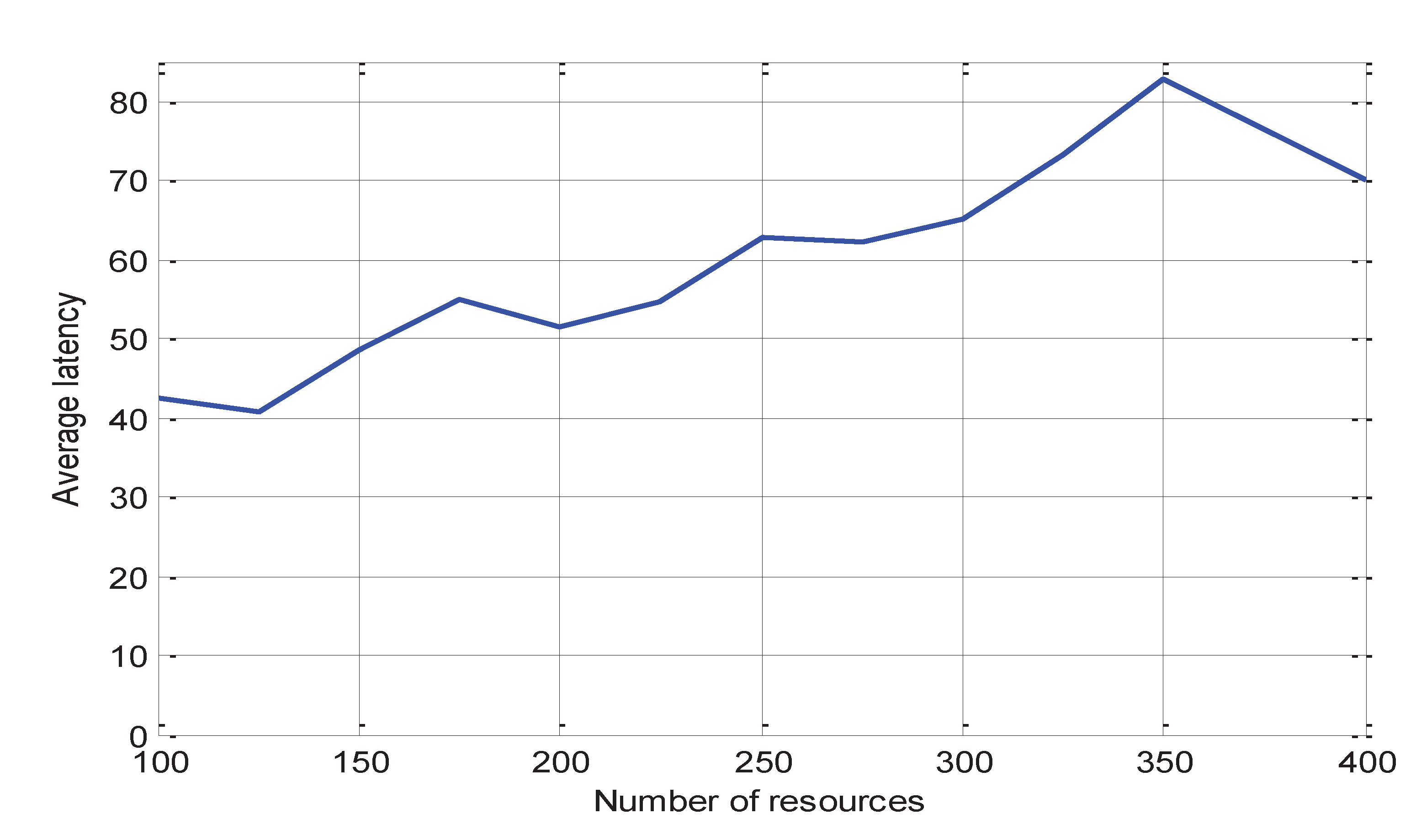
5.3. Average Latency

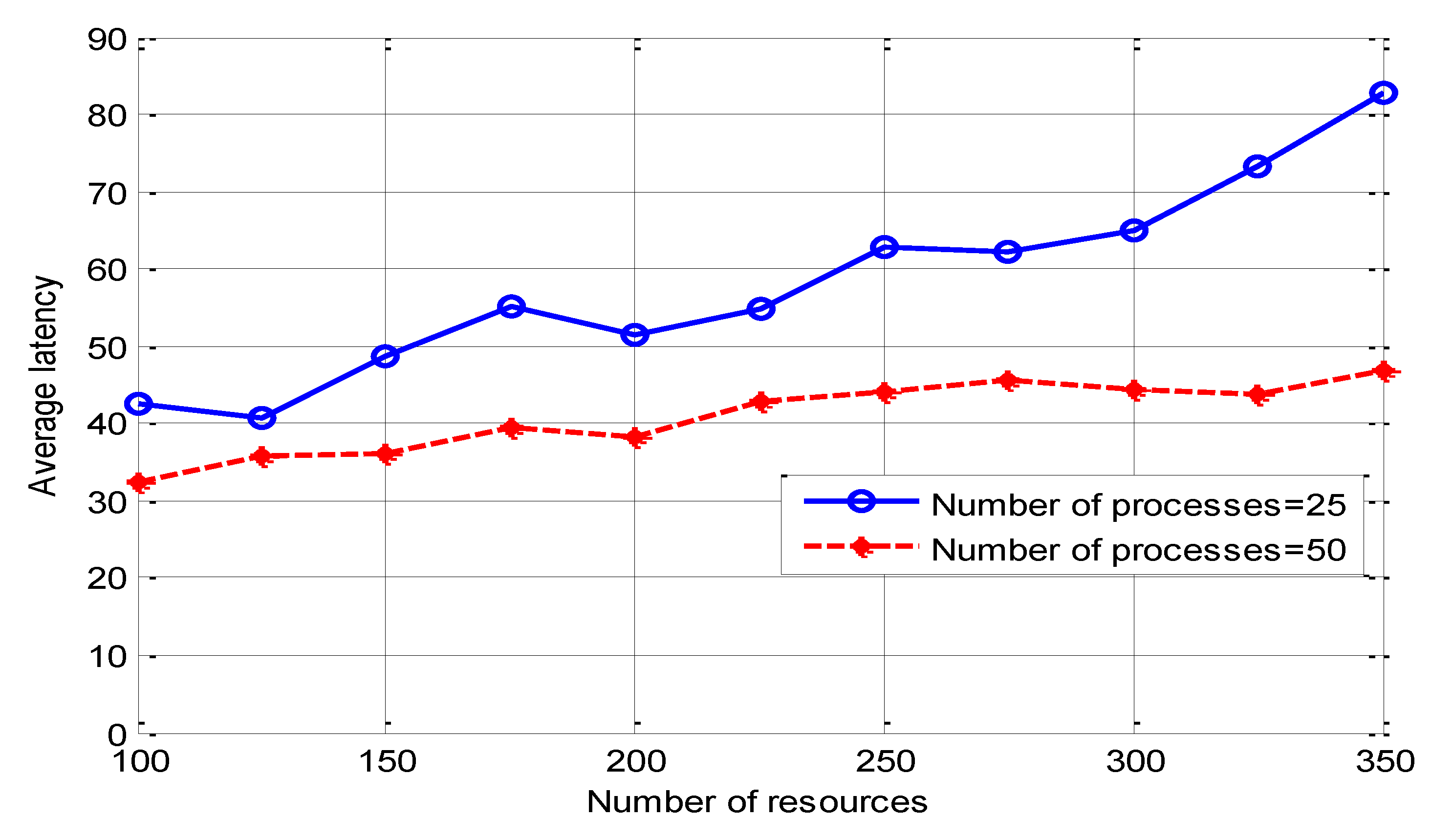
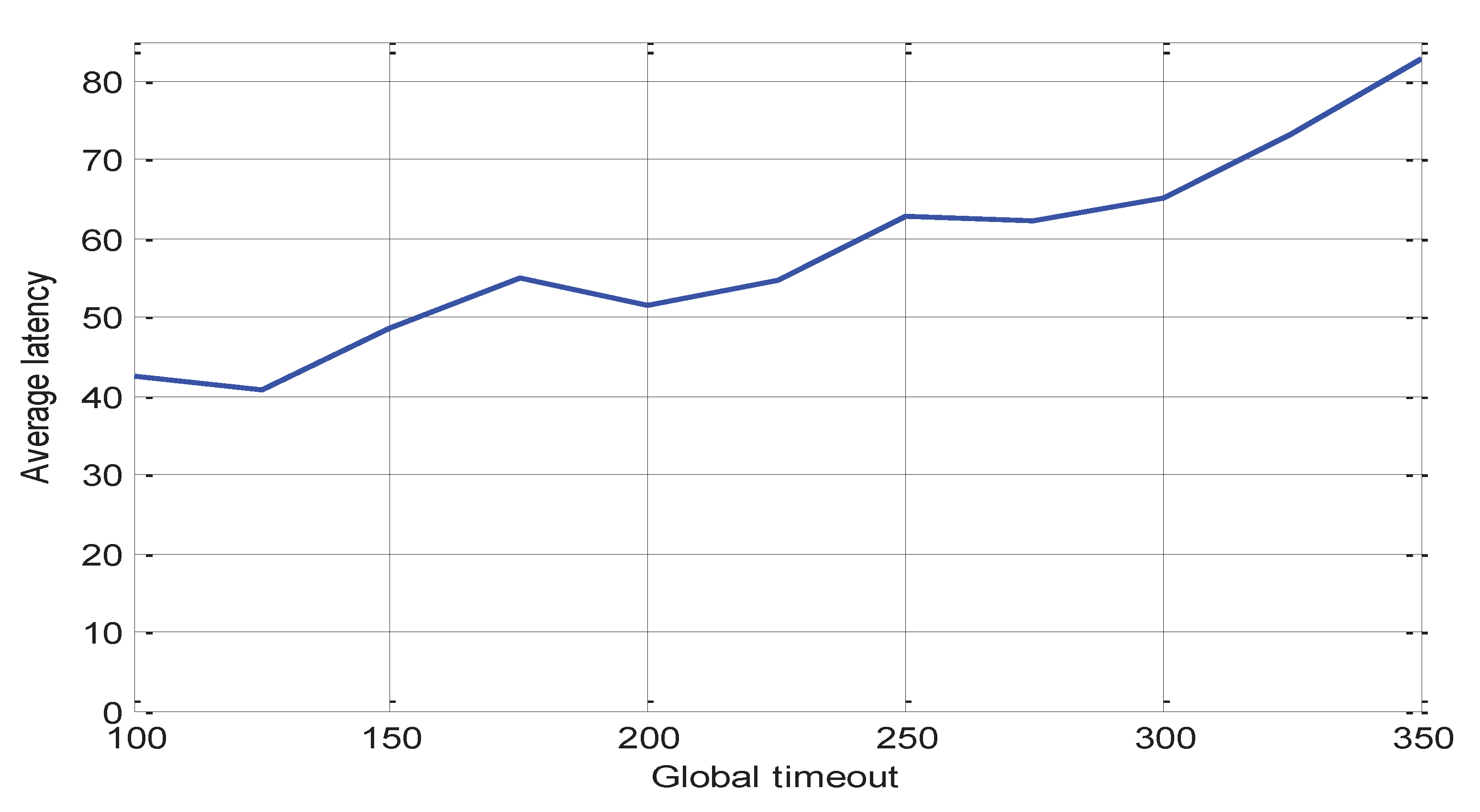
Figure 6 shows the mean deadlock latency versus number of resources. This figure shows that deadlock latency increases with an increasing number of resources. This increase in deadlock latency is because with the increasing number of resources for the low number of processes the number of deadlocks detected by the proposed algorithm will start decreasing; this decrease in the number of detected deadlock cycles will increase the number of potential deadlocks detected by global time out method. The latency for deadlocks detected by the global timeout method is larger than the latency for deadlocks detected by the proposed algorithm; therefore, average latency will start increasing due to an increase in the number of deadlocks detected by the global timeout method. To reduce this latency global timeout must be changed dynamically according to system parameters, number of resources, and number of processes. For a large number of resources and a low number of processes global timeout value must be minimized. For the low number of resources and large number of processes global timeout value will be increased to allow the proposed algorithm to detect all deadlocks before detected by the global timeout method. The effect of the number of processes and global timeout value in average latency can be deduced from Figure 7 and Figure 8 respectively.

5.4. Average Number of Deadlock Detection Messages

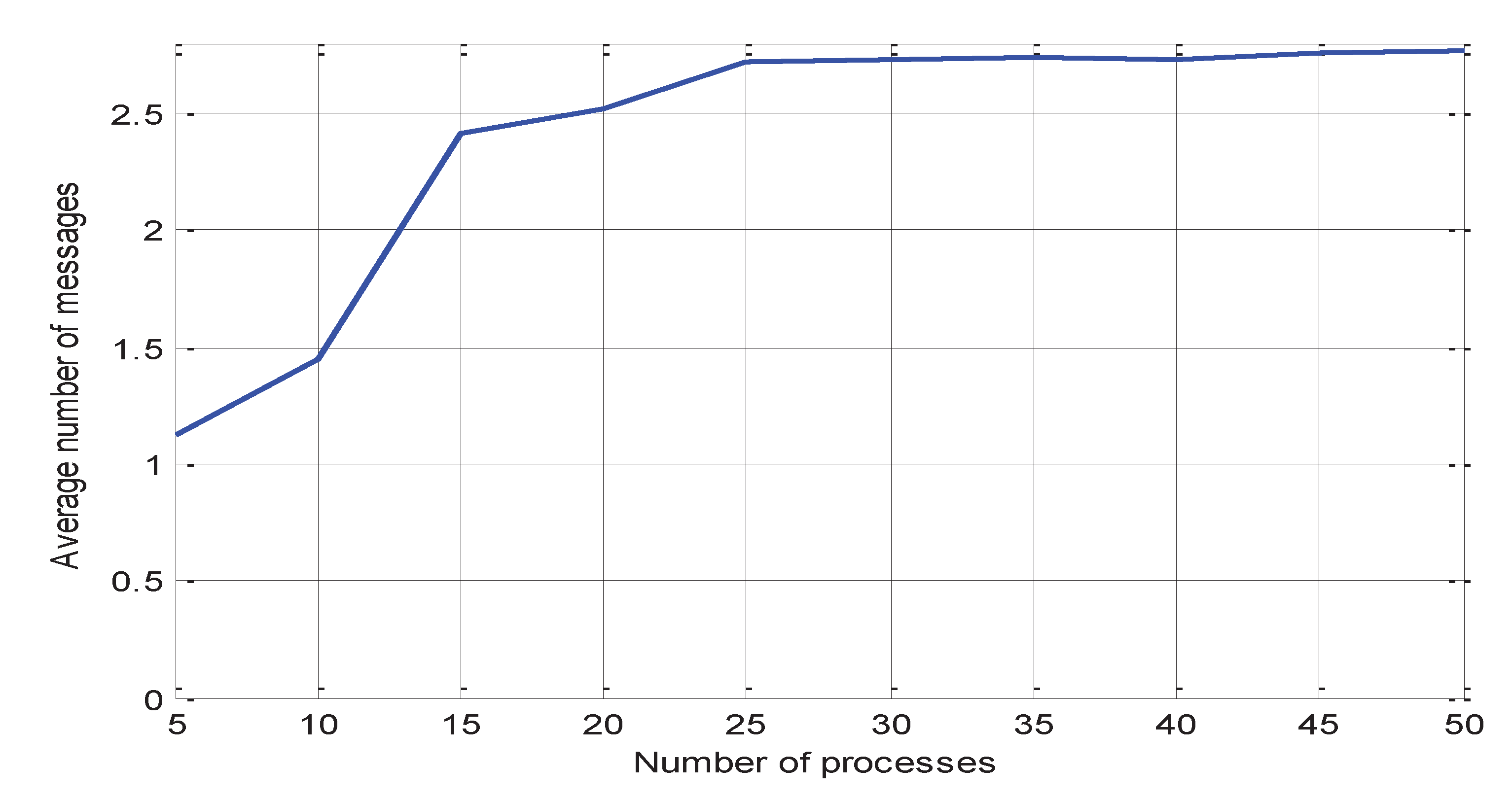
The improved algorithm reduced the number of messages needed to detect the deadlock, these messages include: sending probe messages to successors and receiving report messages from successors. The number of these messages depends mainly on the number of successors. But number of successors per request is a randomly generated number between 1 and 7. Therefore, the average number of successors is 3.5 and the number of needed messages is 8, these eight messages include seven probes and report messages and an additional message for aborting the victim. But the proposed algorithm can detect more than one deadlock cycle in each instance execution then the mean number of needed messages will be less than eight. Figure 9 shows this fact. From Figure 9 we find that the mean number of messages is less than three. This result justifies that the proposed algorithm can detect multiple cycles per instance initiation. The extra deadlock cycles detected by the algorithm will need only one message to abort the selected victim. Deadlocks detected by the global timeout method need no further messages because the victim in this case is the process itself. Figure 9 shows that for the low number of processes number of detections, and messages is low compared with the high number of processes. This low number of messages is because with the low number of processes most deadlock cycles are local ones. The local process controller could detect these local deadlocks without the need to send any probing message.

6. Conclusions and Future Work

This paper focuses on the resolution of generalized deadlocks in the AND model. Recent studies have shown that most deadlock cycles exist between two nodes, for this reason, we proposed an improvement algorithm that concentrates on detecting such minimal cycles. The proposed algorithm gathers information required for deadlock detection from a minimal number of processes and it can detect more than one deadlock cycle per instance initiation using the dependency information included in the feedback report messages. Global timeout policy is used for detecting potential global deadlock cycles that have large length distribution. This method is very suitable for a distributed computing implementation due to the limited number of messages needed to trace cycles of length two, the selection of global timeout value is less critical than it is in the global timeout approach, and most of the potential deadlocks detected in the system are real deadlocks, and the proposed algorithm reduces the deadlock average latency. The proposed improvements show better results in deadlock latency than the existing distributed algorithms and are slightly more efficient than the current best algorithm regarding message length. However, the improved algorithm outperforms other algorithms with promising performance metrics. We are going to scale up the simulation models to thoroughly evaluate their performance.

Acknowledgments

The author would like to thank the King Fahd University of Petroleum and Minerals for providing the support and facilities to perform this research work.

Conflicts of Interest

Declare conflicts of interest or state “The authors declare no conflicts of interest.” Authors must identify and declare any personal circumstances or interests that may be perceived as inappropriately influencing the representation or interpretation of reported research results. Any role of the funders in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results must be declared in this section. If there is no role, please state “The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results”.

References

Soojung Lee, “Fast, Centralized Detection and Resolution of Distributed Deadlocks in the Generalized Model.”, “IEEE Trans on Software Engineering”, Vol. 30, no. 9, pp. 561-573. September 2004.
Roberto Baldoni and Sivlio Salza, “Deadlock Detection in Multidatabase Systems: A Performance Analysis”, “Distributed System Engineering” vol. 4, pp. 244-252, 1997.
D. Z. Badal, “The distributed deadlock detection algorithm.”, “ACM Trans. Computer Systems”, Vol. no. 4, pp. 320–337, November 1986.
Gray, J., Homan, P., Obermarck, R., Korth, H.: A Straw Man Analysis of Probability of Waiting and Deadlock. IBM Research Report RJ 3066, San Jose, 1981.
Jinho Ahn, “Adaptive Sender-based Message Logging and Checkpointing Protocol for Large-Scale Distributed Systems” January 2022, Journal of Korean Institute of Information Technology 20(1):41-48. [CrossRef]
Houssem Mansouri, Al-Sakib Khan Pathan, “A Communication-Induced Checkpointing Algorithm for Consistent-Transaction in Distributed Database Systems”, Security in Computing and Communications (pp.21-32), 2021. [CrossRef]
Masoomeh Ghodrati, Ali Harounabadi, “Provide a New Mapping for Deadlock Detection and Resolution Modeling of Distributed Database to Colored Petri Net”, June 2014, International Journal of Computer Applications 95(5):1-7. [CrossRef]
Hisao Kameda, Jie Li, Chonggun Kim, Yongbing Zhang, “Optimal Load Balancing in Distributed Computer Systems, 2012.
Shigang Chen, Yibei Ling, “Stochastic Analysis of Distributed Deadlock Scheduling.”, PODC’05, July 17-20, 2005 Las Vegas, Nevada, USA.
M. van Steen and A.S. Tanenbaum, Distributed Systems, 3rd ed., distributed-systems.net, 2020.
Maarten van Steen, Andrew S. Tanenbaum, “A brief introduction to distributed systems”, 2016, https://d-nb.info/1113645695/34.
David Ola, “Deadlock Detection and Resolution in Distributed Database System”, 2015.
Marwan H. Hassan, Saad Darwish, Saleh M. Elkaffas, “An Efficient Deadlock Handling Model Based on Neutrosophic Logic: Case Study on Real-Time Healthcare Database Systems”, January 2022, IEEE Access 10(6):1-1. [CrossRef]
Wei Lu, Stephen Yong, Liqiang Wang, Weiwei Xing, “A Novel Concurrent Generalized Deadlock Detection Algorithm in Distributed Systems” November 2015. [CrossRef]

Figure 1. Formal description of the proposed algorithm.

Figure 2. The percentage of real deadlock cycles detected by the proposed the versus number of resources.

Figure 3. Number of real and global timeout deadlock cycles detected by the proposed algorithm versus number of nodes.

Figure 4. Number of real and global timeout deadlocks detected by the proposed algorithm versus local timeout.

Figure 5. Throughput versus number of processes, number of resources =200, global timeout value=200, and number of nodes=4.

Figure 6. Average latency versus the number of resources where the number of processes=25.

Figure 7. Average latency versus the number of resources.

Figure 8. Average latency versus global timeout value where the number of processes is 25.

Figure 9. The average number of deadlock detection messages versus the number of resources for the number of processes=25.

Table 1. System Parameters used by the simulation.

Parameter	Mean Value	Description
$t_{p r o c}$	30	Processing time for each acquired resource
$t_{c o m m}$	20	communication time of a message
$t_{d l m s g}$	1.5	Time to execute the routine corresponding to a deadlock detection message
$t_{l}$	20-60	Timeout threshold for initiating the algorithm
$t_{g}$	100-200	Global timeout value
$t_{p r e}$	100	Execution time of a process before making a resource request.
$t_{r e s}$	Random	Restart time for the aborted process.
$R$	100-350	Total number of resources
$N$	4-64	Total number of nodes
$P$	25-50	Total number of processes

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

An Improved Deadlock Detection and Resolution Algorithm for Distributed Computing Systems

Abstract

1. Introduction

2. Related Work

3. Proposed Deadlock Detection Algorithm

3.1. The Idea behind the Proposed Deadlock Detection Algorithm

3.2. Proposed Algorithm Implementation

3.3. Global Process Manager Action

3.4. Detection Deadlock Cycles of Length Two

4. Discussion

5. Performance Evaluation Metrics

5.1. Algorithm Correctness

5.2. Throughput

5.3. Average Latency

5.4. Average Number of Deadlock Detection Messages

6. Conclusions and Future Work

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe